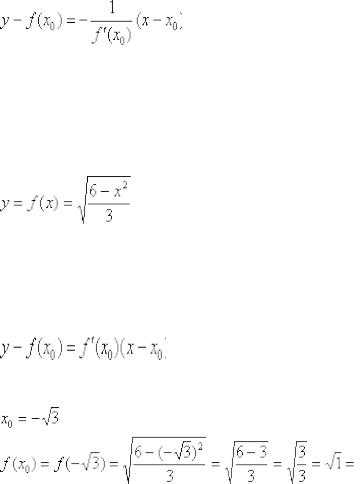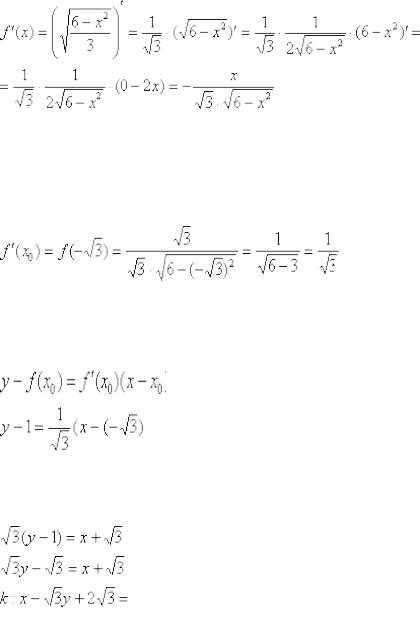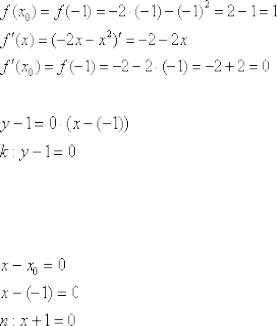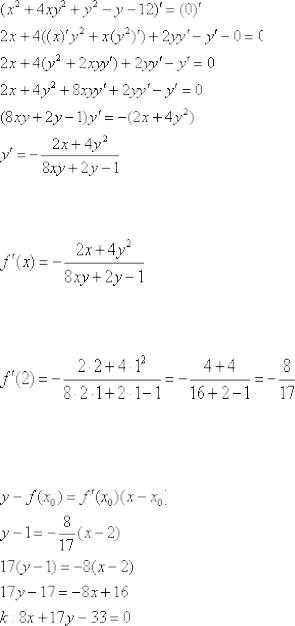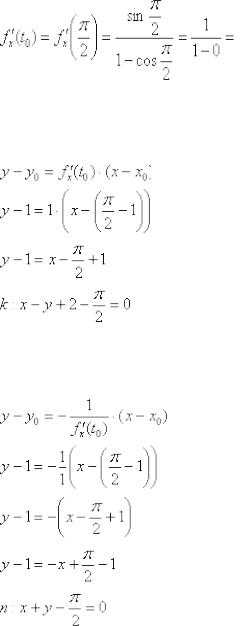правила, примеры, вычитание и сложение с разными знаками
Данная статья посвящена числам с разными знаками. Мы будем разбирать материал и пытаться выполнять вычитание между этими числами. В параграфе мы познакомимся с основными понятиями и правилами, которые пригодятся во время решения упражнений и задач. Также в статье представлены подробно разобранные примеры, которые помогут лучше понять материал.
Yandex.RTB R-A-339285-1Как правильно выполнять вычитание
Для того, чтобы лучше понять процесс вычитания, следует начать с основных определений.
Определение 1Если вычесть из числа a число b, то это можно преобразовать как сложение числа a и -b, где b и −b – числа с противоположными знаками.
Если выразить данное правило буквами, то оно выглядит так a−b=a+(−b), где a и b – любые действительные числа.
Данное правило вычитания чисел с разными знаками работает для действительных, рациональных и целых чисел. Его можно доказать на основании свойств действий с действительными числами. Благодаря им мы может представить числа как несколько равенства (a+(−b))+b=a+((−b)+b)=a+0=a. Так как сложение и вычитание тесно связаны, то равным также будет выражение a−b=a+(−b). Это значит, что рассматриваемое правило вычитания также верно.
Данное правило, которое применяется для вычитания чисел с разными знаками, позволяет работать как с положительными, так и с отрицательными числами. Также можно производить процесс вычитания из отрицательного числа из положительного, которое переходит в сложение.
Для того, чтобы закрепить полученную информацию, мы рассмотрим типичные примеры и на практике рассмотрим правило вычитания для чисел с разными знаками.
Примеры упражнений на вычитание
Закрепим материал, рассмотрев типичные примеры.
Пример 1Необходимо выполнить вычитание 4 из −16.
Для того, чтобы выполнить вычитание, следует взять число, противоположное вычитаемому 4, есть −4. Согласно рассмотренному выше правилу вычитания (−16) −4=(−16) +(−4). Далее мы должны сложить получившиеся отрицательные числа. Получаем: (−16) +(−4) =−(16+4) =−
zaochnik.com
правило, примеры, как складывать числа с разными знаками
В этом материале мы расскажем, как правильно выполнять сложение отрицательного и положительного числа. Сначала мы приведем основное правило такого сложения, а потом покажем, как оно применяется при решении задач.
Yandex.RTB R-A-339285-1Основное правило сложения положительных и отрицательных чисел
Мы уже говорили ранее, что положительное число можно рассматривать как доход, а отрицательное – как убыток. Чтобы узнать величину дохода и расхода, надо смотреть на модули этих чисел. Если в итоге окажется, что наши расходы превышают доходы, то после их взаимного учета мы останемся должны, а если наоборот, то мы останемся в плюсе. Если же расходы равны доходам, то у нас будет нулевой остаток.
Используя приведенные выше рассуждения, можно вывести основное правило сложения чисел с разными знаками.
Определение 1Для сложения положительного числа с отрицательным необходимо найти их модули и выполнить сравнение. Если значения окажутся равны, то мы имеем два слагаемых, которые являются противоположными числами, и их сумма будет нулевой. Если же они не равны, то нам надо учесть, что результат будет иметь тот же знак, что и большее число.
Таким образом, сложение в данном случае сводится к вычитанию из большего числа меньшего. Итог этого действия может быть разным: мы можем получить как положительное, так и отрицательное число. Нулевой результат тоже возможен.
Это правило распространяется на целые, рациональные и действительные числа.
Задачи на сложение положительного числа с отрицательным
Разберем, как применять на практике правило, озвученное выше. Возьмем для начала простой пример.
Пример 1Вычислите сумму 2+(-5).
Решение
Выполним последовательно шаги, которые мы изучили до этого. Найдем для начала модули исходных чисел, которые будут равны 2 и 5. Больший модуль – 5, поэтому запоминаем минус. Далее вычитаем из большего модуля меньший и получаем: 5−2=3.
Ответ: (−5)+2=−3.
Если в ус
zaochnik.com
Вычитание чисел с разными знаками
В курсе арифметики установлено, что вычитание есть действие, обратное сложению, при помощи которого по данной сумме и по одному слагаемому находят другое слагаемое.
Пользуясь этим определением, мы должны разобрать, как надо выполнять вычитание относительных чисел.
Пусть надо из (+8) вычесть (–3), т. е. пусть надо
Первое данное число выражает данную сумму, второе – данное слагаемое, а над найти другое слагаемое (для него оставлено место после знака равенства), т. е. надо решить вопрос: какое число надо сложить с (–3), чтобы в сумме получилось (+8)? Этот вопрос запишем в такой форме:
(?) + (–3) = +8.
Но сразу этот вопрос решить трудно, а поэтому сначала решим более простой, вспомогательный вопрос: какое число надо сложить с (–3), чтобы в сумме получился нуль ?, т. е.
(?) + (–3) = 0.
На этот вопрос ответ ясен: надо взять для неизвестного слагаемого число, имеющее ту же абсолютную величину, как и данное слагаемое, но обратный знак, – в данном случае надо для неизвестного слагаемого взять число +3. Теперь перейдем к решению главного вопроса: мы взяли для неизвестного слагаемого число + 3 и в сумме получился нуль, но нам надо получить в сумме число +8, поэтому надо чтобы и в другое слагаемое вошло это же число +8. Следовательно, неизвестное слагаемое должно состоять: 1) из +3, чтобы в сумме получился нуль и 2) из +8, чтобы эту сумму «нуль» довести до требуемой +8. Поэтому на месте неизвестного слагаемого пишем + 3 + 8:
(+ 8) – (– 3) = + 3 + 8 = + 11.
Последнее (= + 11) написано на том основании, что числа + 3 и + 8 надо соединить в одно или сложить.
Вот еще примеры:
(– 7) – (+ 5) = – 5 – 7 = – 12.
Искомое слагаемое должно состоять: 1) из –5, чтобы в сумме получился нуль и 2) из –7, чтобы дополнить этот нуль до требуемой суммы, до –7. Сложив числа –5 и –7, получим –12.
(– 3) – (– 8) = + 8 – 3 = + 5.
Искомое слагаемое должно состоять: 1) из +8, чтобы в сумме получился нуль и 2) из –3, чтобы дополнить этот нуль до требуемой суммы, до –3. Сложив числа +8 и –3, получим +5.
(+7) – (+9) = –9 + 7 = –2.
Искомое слагаемое должно состоять: 1) из –9, чтобы в сумме получился нуль и 2) +7, чтобы дополнить этот нуль до требуемой суммы, до +7; сложив числа –9 и +7, получим –2.
Из этих примеров видим, что вычитание в алгебре состоит лишь в умении раскрывать скобки: надо второе число (данное слагаемое или вычитаемое) написать с обратным знаком, а первое число (данную сумму или уменьшаемое) написать с тем же знаком. После того, как это сделано, т. е., когда скобки раскрыты, дело сводится к сложению, так как написаны числа рядом с их знаками, напр., в последнем примере: – 9 + 7.
Так как сумма не изменяется от перестановки слагаемых, то можно числа, полученные в разобранных примерах после раскрытия скобок, переставить, чтобы порядок был согласен с порядком данных чисел:
(+ 8) – (– 3) = + 8 + 3; (– 7) – (+ 5) = – 7 – 5;
– 3 – (– 8) = – 3 + 8; (+ 7) – (+ 9) = + 7 – 9.
Итак,
чтобы раскрыть скобки при вычитании, надо первое число (уменьшаемое) написать без изменения и приписать к нему второе число (вычитаемое) с обратным знаком.
Заметим еще, что при обозначении вычитания первое число пишется часто без скобок, а если оно положительное, то, как уже известно, знак + можно впереди не писать.
Например,
– 3 – (– 5) = – 3 + 5 = + 2; 1 – (– 6) = 1 + 6 = 7;
3 – (+ 3) = 3 – 3 = 0.
14. Примеры на сложение и вычитание. Пусть требуется вычислить:
1 – {3 + [5 – (3 – 5 – 6)]}.
Мы станем руководствоваться следующим порядком: если внутри какой-либо пары скобок нет других скобок и нет действия, то эти скобки можно раскрыть; если же внутри этих скобок есть действие (сложение), то надо сначала его выполнить. В нашем примере такой порядок: сначала выполним сложение чисел, написанных внутри маленьких скобок, потом надо эти скобки раскрыт, выполнить сложение внутри квадратных скобок, раскрыть квадратные скобки, выполнить сложение внутри витых скобок, раскрыть эти скобки и, наконец, сложить полученные числа:
1 – {3 + [5 – (3 – 5 – 6)]} = 1 – {3 + [5 – (– 8)]} = 1 – {3 + [5 + 8]} =
= 1 – {3 + [+13]} = 1 – {3 + 13} = 1 – {+ 16} = 1 – 16 = – 15.
Конечно, при навыке можно сразу выполнять несколько действий и, следовательно, укоротить вычисление.
Еще пример:
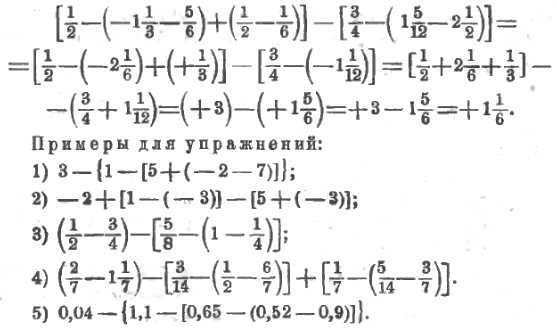
Пусть еще требуется вычислить выражение:
a – {(b – c) – [d + (e + f)]} при a = – 3; b = 1; c = 4; d = – 5; e = – 7; f = 2.
Выполним вычисления по действиям:
1) b – c = + 1 – (+ 4) = 1 – 4 = – 3;
2) e + f = (– 7) + (+ 2) = – 7 + 2 = – 5;
3) d + (– 5) = – 5 + (– 5) = – 5 – 5 = – 10;
4) (– 3) – (– 10) = – 3 + 10 = + 7;
5) – 3 – (+ 7) = – 3 – 7 = – 10.
Примеры для упражнений:
Если взять число нуль и прибавлять к нему по +1, то получим ряд постепенно увеличивающихся целых чисел:
0, +1, +2, +3, +4, +5, …..
Этот ряд совпадает (см. конец п. 10) с натуральным рядом чисел, т. е. с
0, 1, 2, 3, 4, 5 …..
Если мы, взяв число нуль, вычтем из него (+1), затем еще раз вычтем (+1) и т. д., то, согласно с тем, как мы это понимали в арифметике по отношению к натуральному ряду чисел, мы теперь признаем, что и здесь станем получать все уменьшающиеся целые числа:
1) 0 – (+ 1) = – 1; 2) (– 1) – (+ 1) = – 1 – 1 = – 2;
3) (– 2) – (+ 1) = – 3 и т. д.
Получим, идя от нуля налево, ряд уменьшающихся относительных чисел:
….., – 5, – 4, – 3, – 2, – 1, 0.
Соединяя этот ряд с предыдущим, получим полный ряд относительных чисел:
….., – 6, – 5, – 4, – 3, – 2, – 1, 0, +1, +2, +3, +4, +5, +6 …..
Этот ряд и вправо и влево идет без конца.
Всякое число в этом ряду больше другого, которое стоит левее и меньше любого, стоящего правее его. Так +1 > –3; 0 > –6; –5 < 0; –3 < +2 и т. д.
В промежутках между целыми числами этого ряда можно вставить бесконечно много дробных чисел.
maths-public.ru
Действия с числами, имеющими разные знаки. 6-й класс
Разделы: Математика
Тип урока: игра “Математический поезд”
Цели:
– систематизация знаний по данной теме;
– повторение правил сложения и вычитания чисел с одинаковыми и разными знаками;
– повторение правил умножения и деления сложения и вычитания чисел с одинаковыми
и разными знаками;
– повторение алгоритма решения уравнения;
– умение применять их при решении различных задач.
Оборудование:
– цветные жетоны;
– интерактивный комплекс.
– жетоны;
– карточки;
– схема маршрута.
“Математический поезд” состоит из 3-х вагонов: мягкого, купейного, плацкартного.
Условия игры.
1. Кассовый зал.
В кассовом зале каждый ученик получает посадочный талон с заданиями и 6
жетонов.
Решив все задачи, ученик обращается за получением билета.
Если ученик не может решить какое-либо задание, то он обращается в справочное
бюро. В зависимости от содержания справки определяется “плата”.
2. Справочное бюро.
Проверка правильности решения задачи и указание ошибки проводится бесплатно;
За наводящий вопрос, помогающий найти путь решения, платится 1 жетон;
За подсказку пути решения – 2 жетона;
За решение – 3 жетона.
3. Получения билета.
В мягкий вагон – при правильном решении всех заданий и предъявлении в кассу
более 3-х жетонов;
В купейный вагон – при решении всех заданий и предъявлении в кассу 3-х жетонов;
В плацкартный вагон – при решении всех заданий и предъявлении в кассу 1 или 2-х
жетонов.
План урока.
Кассовый зал.
I. Разминка.
Прочитать правила сложения и вычитания чисел с одинаковыми и разными знаками.
| Устно -6 – 3,5 2,8 – 1,2 8,1 + 1,9 1 – 0,25 0,6 – 1,6 |
Письменно 12,3 – 43, -33,3 + 14,8 -16,7 – 19,14 1,324 – 5,18 -36,6 + 13,4 |
При сложении двух чисел отрицательны
Надо модули сложить их обязательно.
И поставить минус перед суммой,
Только минус, обязательно подумай!
При сложении с разными знаками чисел
Надо меньший из большего модуля вычесть
И поставить того знак числа в результате,
Модуль больше которого, знай математик!
(Н. Зайцева).
Прочитать правила умножения чисел с одинаковыми и разными знаками.
| Устно 6*0,8 -4*0,7 -6,2*(-1) -0,52*100 52*0,01 |
Письменно 0,4*(-5,2) -25,3*0,1 -0,14*(-20) -4*3,5 24*15 |
Прочитать правила деления чисел с одинаковыми и разными знаками.
| Устно 4:0,4 2,4: (-12) -2,5:(-5) -3: 0,01 -0,2:0,1 |
Письменно 0,2: (-4) -56: (-0,7) -2,6: 13 763: 0,1 -0,15: 0,01 |
Не на шутку в самом деле,
Если Оля, Таня, Зина…
Умножают или делят
Два числа со знаком минус,
Получают, спора нет,
Положительный ответ.
Даже сказочный Емеля,
Чтобы спорились дела,
Умножает или делит
Разных знаков два числа.
Получает, не секрет,
Отрицательный ответ.
(Н. Зайцева).
Проверка письменных заданий проводится на интерактивной доске.
II. Выдаются посадочные талоны и жетоны.
Письменно в тетрадях.
а) раскрыть скобки
а – (с + х + у – в)
а + (-х – у + в + с)
б) привести подобные слагаемые
8х + 12а – 2х – 6а
-7х – (-4х – 3а) + 6а
7*(-2х + 3) – 4*(3х + 2)
III. После проверки выдаются “посадочные билеты”:
– желтый – в мягкий вагон;
– зеленый – в купейный вагон;
– красный – в плацкартный вагон
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Математический поезд отправляется от станции “Школьная” и следует до станции “Решай-ка”. (Звучит бодрая музыка.)
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Наш поезд прибывает на станцию “Решай-ка”. Вас встречает кандидат математических наук “Уравнение”.
“Уравнение” – “Здравствуйте, дорогие друзья. Очень радо встрече с
вами. Ответьте, пожалуйста, на мои следующие вопросы:
– что называется уравнением?
– что называется корнем уравнения?
– что значит решить уравнение?
– какие уравнения называются равносильными?
– назвать алгоритм решения уравнения”.
Самостоятельная работа по вариантам.
| 1-й в. -27х + 220 = – 5х |
2-й в. 7х = -310 + 3а |
Проверка – на интерактивной доске.
“Уравнение”: “Дорогие друзья! Вы все знаете об уравнении и умеете решать уравнения. Поэтому можете продолжить свое путешествие дальше”.
За правильное решение учащиеся получают карточку.
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Математический поезд отправляется от станции “Школьная”.
(Звучит музыка.)
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Наш поезд прибывает на станцию “Весенняя”. Здесь вас встречает
Задача: (решаем на доске).
Из одной скворечни одновременно в противоположные стороны вылетели 2 скворца. Скорость одного из них на 25 км\ч. больше скорости другого. Через 0,3 часа расстояние между ними стало 37,5 км. Найдите скорость каждого скворца.
Решение.
Пусть х км\ч. скорость первого скворца, тогда (х + 25) км\ч. – скорость
второго скворца, (х + х + 25)*0,3 = 0,6х + 7,5 км. Расстояние между ними.
Уравнение: 0,6х + 7,5 = 37,5
0,6х = 30
х = 50
50 + 25 = 75(км\ч.) скорость второго скворца.
Ответ. 50км\ч., 75км\ч.
Дано уравнение: 3х – 20 = х + 20.
Составьте по нему задачу и решите ее.
За правильное решение учащиеся получают карточку.
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Математический поезд отправляется от станции “Весенняя”.
(Звучит музыка.)
Голос диктора: “Внимание! Внимание! Прослушайте объявление! Наш поезд прибывает на станцию “Угадай-ка”. Здесь вас встречает Емеля.
Проверьте, верно ли решены уравнения:
(Решают самостоятельно за партой, затем – на доске.)
3х + 8= -17
3х = -17 + 8
3х = 9
Х = 3
Ответ. 3.
14х – 19 = 4х – 10
14х – 4х = -10 + 19
10х = 9
Х = 10:9
Х =1 1\9
Ответ. 1 1\9
3х – 6 = 2х
xn--i1abbnckbmcl9fb.xn--p1ai
Как решать примеры с минусами 🚩 примеры на плюс решить 🚩 Математика
Автор КакПросто!
Еще в начальной школе учат, как складывать и вычитать числа. Для того чтобы научиться это делать, необходимо выучить таблицу сложения и основанную на ней таблицу вычитания. Получается, первоклашка сможет из семнадцати вычесть девять или решить любой подобный пример. Однако завести в тупик его сможет пример обратного характера: как вычесть из девяти семнадцать. Примеры с отрицательными числами даются по школьной программе много позже, когда человек созревает до абстрактного мышления.

Статьи по теме:
Инструкция
Математических действий существует четыре вида: сложение, вычитание, умножение и деление. Поэтому примеров с минусами будет четыре типа. Отрицательные числа внутри примера выделяются скобками для того, чтобы не перепутать математическое действие. Например, 6-(-7), 5+(-9), -4*(-3) или 34:(-17). Сложение. Данное действие может иметь вид:1) 3+(-6)=3-6=-3. Замена действия: сначала раскрываются скобки, знак «+» меняется на противоположный, далее из большего (по модулю) числа «6» отнимается меньшее — «3», после чего ответу присваивается знак большего, то есть «-«.2) -3+6=3. Этот пример можно записать по-другому («6-3») или решать по принципу «из большего отнимать меньшее и присваивать ответу знак большего».
3) -3+(-6)=-3-6=-9. При раскрытии скобок происходит замена действия сложения на вычитание, затем суммируются модули чисел и результату ставиться знак «минус».
Вычитание.1) 8-(-5)=8+5=13. Раскрываются скобки, знак действия меняется на противоположный, получается пример на сложение.
2) -9-3=-12. Элементы примера складываются и ответ получает общий знак «-«.
3) -10-(-5)=-10+5=-5. При раскрытии скобок снова меняется знак на «+», далее из большего числа отнимается меньшее и у ответа — знак большего числа.
Умножение и деление.При выполнении умножения или деления знак не влияет на само действие. При произведении или делении чисел с разными знаками ответу присваивается знак «минус», если числа с одинаковыми знаками — у результата всегда знак «плюс».1)-4*9=-36; -6:2=-3.
2)6*(-5)=-30; 45:(-5)=-9.
3)-7*(-8)=56; -44:(-11)=4.
Арифметические действия с отрицательными числами человеку приходится выполнять довольно часто. Самый распространенный случай связан с измерениями уличной температуры. Например, вам нужно узнать, на сколько градусов температура поднялась или опустилась по сравнению с предыдущим днем. Со сложением и вычитанием отрицательных чисел сталкиваются и те, у кого возникает необходимость определить соотношение высот, если исследуемый объект находится ниже уровня моря.

Вам понадобится
- — лист бумаги;
- — карандаш;
- — линейка.
Инструкция
Вспомните, что такое модуль числа. При сложении и вычитании отрицательных чисел удобнее действовать именно с модулями, то есть с абсолютными значениями чисел. Для положительного числа и нуля модулем будет само это число, для отрицательного — только его значение, без всякого знака. Модуль принято обозначать двумя вертикальными полосками, справа и слева от числа. Например, модулем числа -6 является ?¦6¦. ?Рассмотрите, какие числа вам нужно сложить. Отрицательное число можно сложить с положительным либо же с другим отрицательным. Способы действия при этом, равно как и результаты, будут различными. При сложении двух отрицательных чисел сложите их модули и поставьте перед результатом общий знак. То есть(-10)+(-18)=(-28). ?Сложение двух отрицательных чисел ничем, кроме знака, не отличается от аналогичного действия с положительными числами. Поэтому выражение можно преобразовать. Убрав скобки, вы получите пример в виде -10-18. Знак можно вынести за скобку — тогда выражение записывается как -(10+18)=-28.?Несколько иначе обстоит дело, если одно из чисел положительное, а другое — отрицательное. В этом случае вычтите меньший модуль из большего. То есть в примере (-10)+18 необходимо отнять 10 от 18. Получается 8. Поскольку положительное число в этом случае имеет больший модуль, то и перед результатом ставится плюс или вообще ничего не пишется.
?Рассмотрите другой вариант действия с этими же модулями. Например, если положительным будет 10, то есть число с меньшим модулем. В этом случае пример выглядит как 10+(-18). Вычтите меньший модуль из большего. Получается 8, но, поскольку большее абсолютное значение у отрицательного числа, то перед результатом ставится минус.
?Действием, обратным сложению, является вычитание. При вычитании отрицательных чисел знак вычитаемого меняется на противоположный. Если из -18 вычесть -10, то пример можно преобразовать так: (-18)-(-10)=-18+10=-8. Вычитание чисел с разными знаками аналогично сложению двух отрицательных чисел. То есть (-18)-(+10)=-18-10=-28.
Полезный совет
При умножении и делении двух отрицательных чисел минус сокращается, а при этих действиях с одним положительным и одним отрицательным числом — остается.При большем количестве слагаемых сложите все положительные числа, затем все отрицательные и проведите действие точно так же, как и с двумя.
Для того чтобы лучше понять, что происходит с отрицательными числами, когда вы их складываете, сделайте числовую линейку. Это просто горизонтальная прямая. Поставьте метку «0». Вправо откладывайте равные отрезки, приняв их за положительные числа. Например, 1 будет располагаться на расстоянии 1 см от нуля. Отрицательные числа отложите влево. Отложите не числовой прямой 10 единиц влево. Получится число (-10). Чтобы прибавить к нему (-18), отложите влево 18 единиц. Чтобы отнять это число, отложите его от (-10) вправо.
www.kakprosto.ru
Сложение чисел с разными знаками
Разделы: Математика
Технологическая карта
| Класс (профиль класса) | 6 (общеобразовательный) |
| Продолжительность урока (занятия) | 45 мин |
| Тип урока (форма урока) | Открытие новых знаний |
| Цели (результаты) урока: Предметные (Пр) (ученик научится…, ученик получит возможность научиться…) Регулятивные (Р) Познавательные (П) Коммуникативные (К) Личностные (Л) |
Регулятивные:
Познавательные:
Коммуникативные:
Личностные:
|
| Автор учебника (УМК) | Математика. 6 класс: учеб. для общеобразоват. учреждений / С.М. Никольский и др. – 12-е изд., – М.: Просвещение, 2014 |
| Необходимое оборудование, материалы и другие условия для качественного проведения урока (занятия) | Компьютер, интерактивная доска |
| Указание приложений к уроку (презентации, дидактические материалы, раздаточный материал) | Презентация, раздаточный материал |
| Использованная литература, источники информации (с указанием активных ссылок) | Математика. 6 класс: учеб. для общеобразоват. учреждений /С.М. Никольский и др. – 12-е изд., – М.: Просвещение, 2014 |
Ход урока
| Деятельность учителя (краткое описание этапов урока) | Деятельность учащихся (перечень УУД, предметных результатов) | |||||||||||||||||||||||||||||||||
| Организационный момент Вступительное слово учителя: Здравствуйте ребята. Я рада видеть вас на уроке. Мы продолжаем с вами работать над положительными и отрицательными числами. Сегодня нам с вами предстоит вывести новое правило, ведь “Лучший способ изучить что-либо — это открыть самому.” (Дьёрдь Пойа). Но для этого необходим определенный багаж знаний. Ребята, чтобы нам легко работалось на уроке, давайте дадим себе установку. Повторяйте за мной: (текст на мультимедийной доске)
| Приветствуют учителя, проверяют свою
готовность к уроку. Уважительное отношение к учителю и одноклассникам | |||||||||||||||||||||||||||||||||
| 1. Мотивация (самоопределение) к учебной деятельности. | ||||||||||||||||||||||||||||||||||
| Цель этапа: включение учащихся в
учебную деятельность, создать условия для
возникновения внутренней готовности включения в
деятельность Организация учебного процесса Сейчас я вам буду говорить правила, а вы слушайте внимательно. Если я скажу правило верно, то вы поднимаете зеленую карточку, если же ошибусь – красную. Игра “Молчанка” (использование сигнальных карточек)
|
Повторить те знания, которые нам понадобятся на уроке. Коммуникативные: Уметь оформлять свои мысли в устной форме. Познавательные: Уметь ориентироваться в своей системе знаний. | |||||||||||||||||||||||||||||||||
| 2. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии. | ||||||||||||||||||||||||||||||||||
| 1. Разбейте числа, которые вы видите на
слайде на группы. 2. А что вы уже умеете делать с положительными и отрицательными числами. 3. Даны числа:
а) Укажите среди данных чисел — положительные. б) Укажите среди данных чисел — отрицательные. в) назовите модуль каждого числа; г) назовите в каждой строчке число, модуль которого больше; 4. Вычислить, подтвер | ||||||||||||||||||||||||||||||||||
xn--i1abbnckbmcl9fb.xn--p1ai
«Правила действий с числами с разными знаками» теоретический зачет
Iвариант
1.Модулем числа называют _____________________________________________________
2. Два числа называются противоположными _____________________________________________________
3.При сравнении двух отрицательных чисел, больше то ___________________________________________________
4. При сравнении нуля и отрицательного числа, больше _____________________________________________________
5. Чтобы сложить два отрицательных числа надо:
1.__________________________________________________
2. _________________________________________________
6.Чтобы сложить положительное и отрицательное число надо:
1.___________________________________________________________________________________________________
2.___________________________________________________________________________________________________
7. Чтобы из одного числа вычесть другое надо
_____________________________________________________
II вариант
1.Сумма противоположных чисел равна__________________
2. Числа, расположенные слева от начала отсчета, называются _____________________________________________________
3. При сравнении положительного и отрицательного числа , больше _________________________________________________
4. При сравнении двух отрицательных чисел, больше то _____________________________________________________
5. Чтобы из одного числа вычесть другое надо
_____________________________________________________
6.Чтобы сложить положительное и отрицательное число надо:
1.________________________________________________________________________________________________________
2.________________________________________________________________________________________________________
7. Чтобы сложить два отрицательных числа надо:
1.__________________________________________________
2. ________________________________________________
infourok.ru






















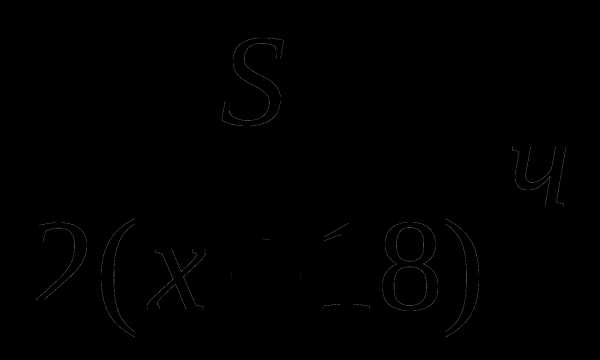
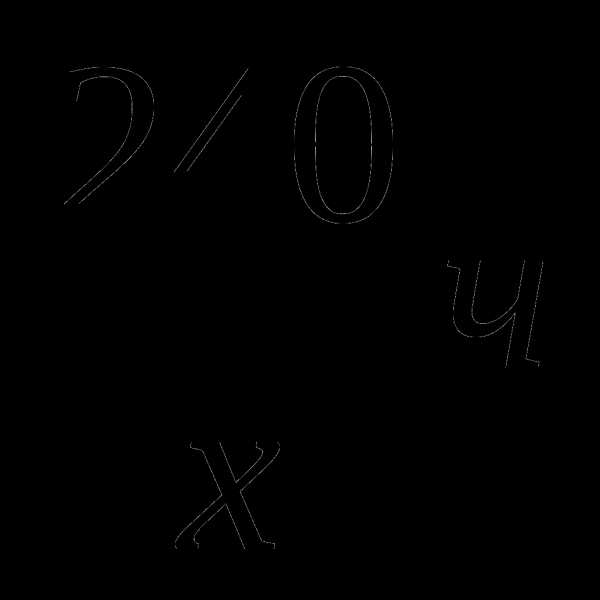
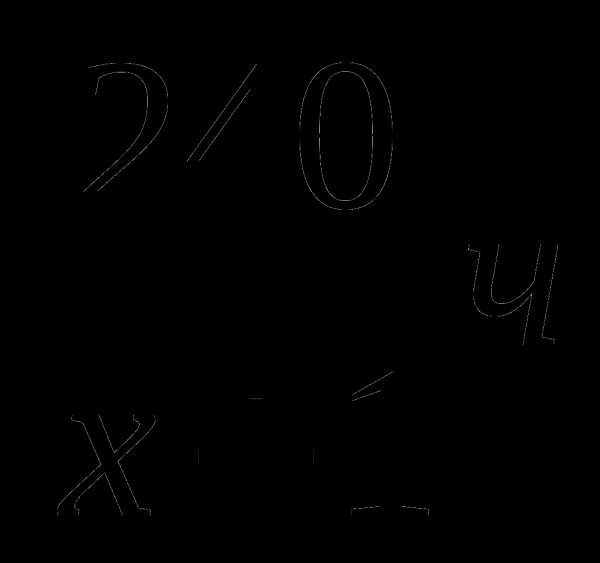
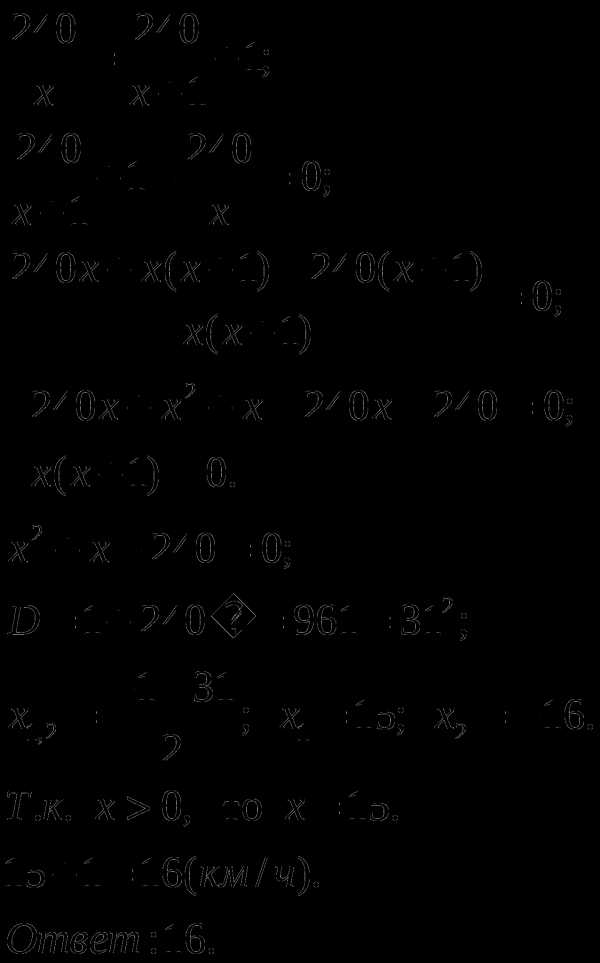
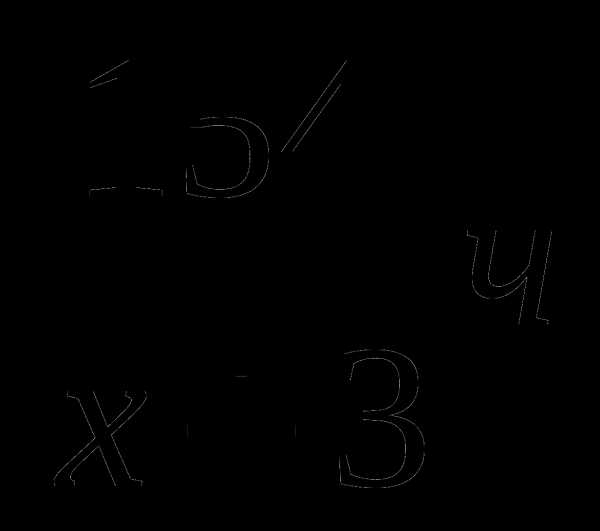
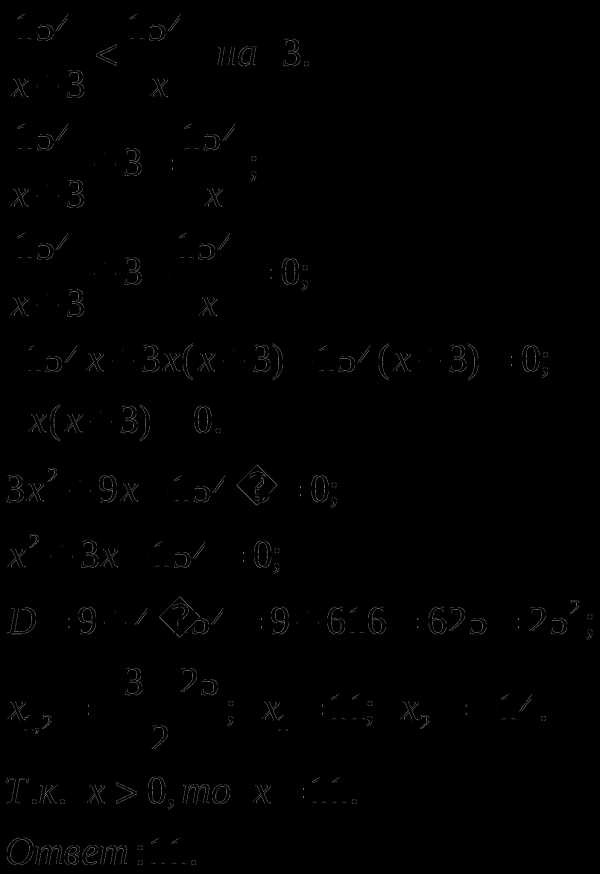
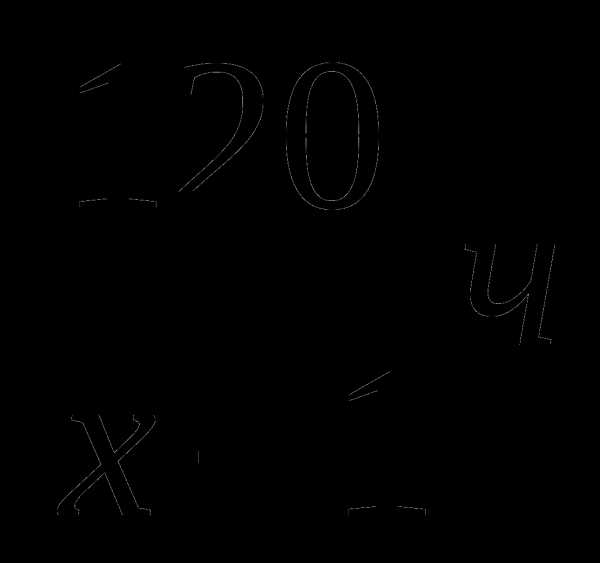
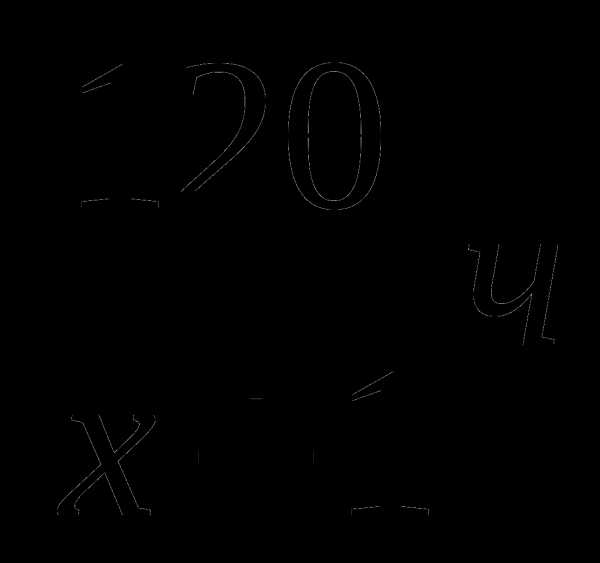
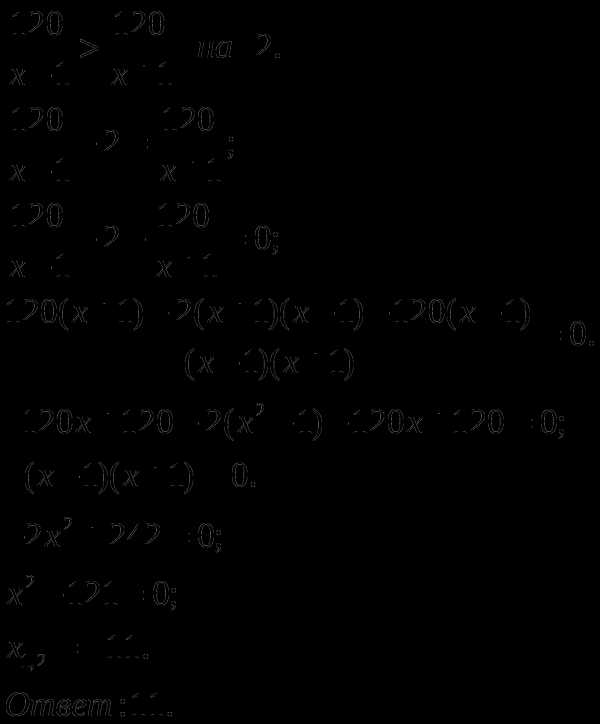
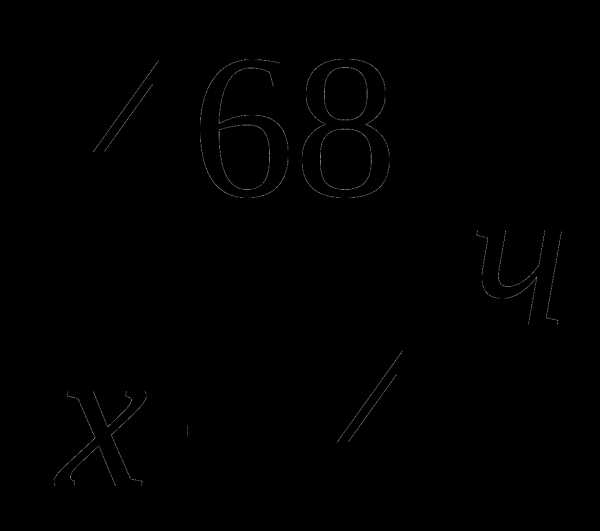
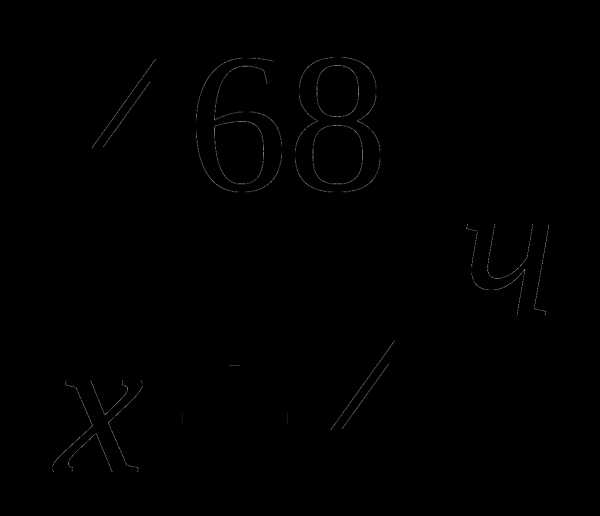
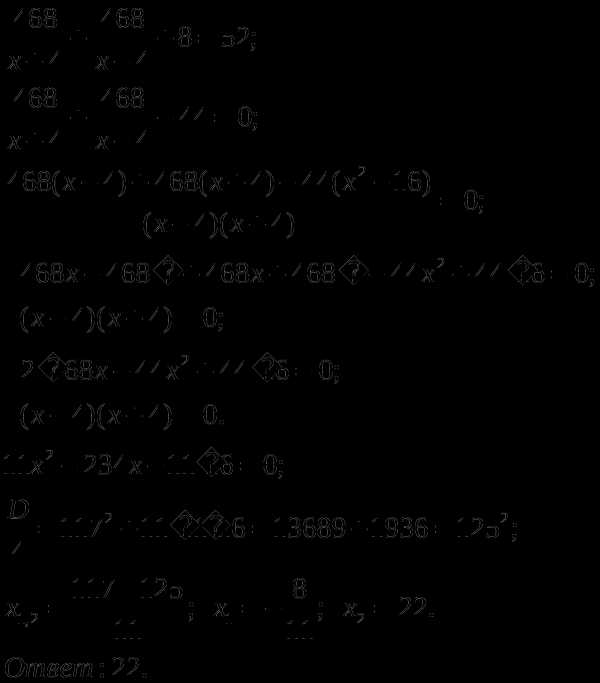
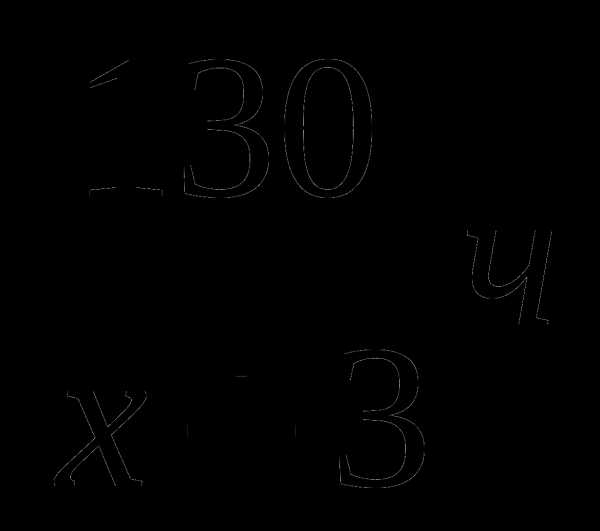
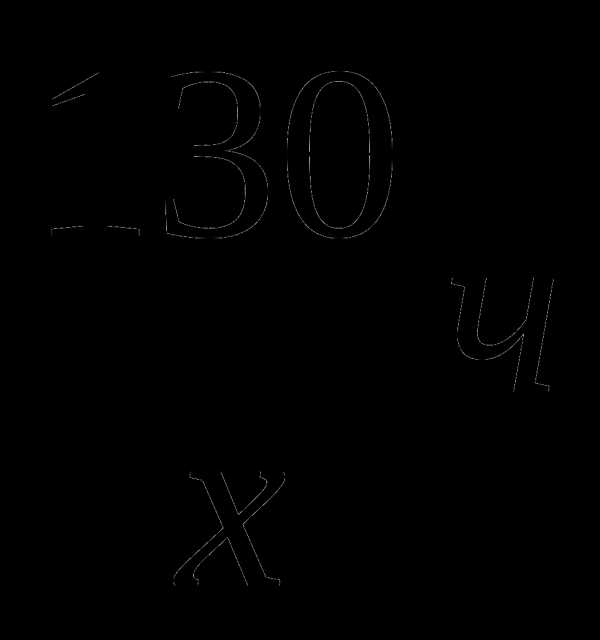
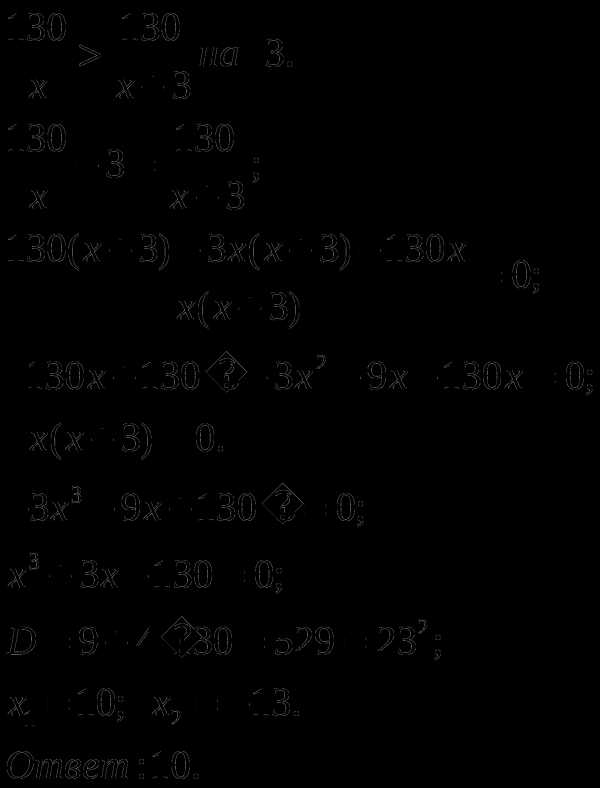
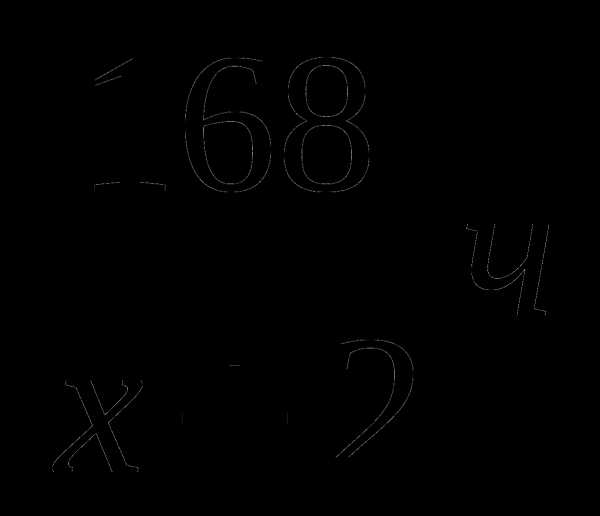
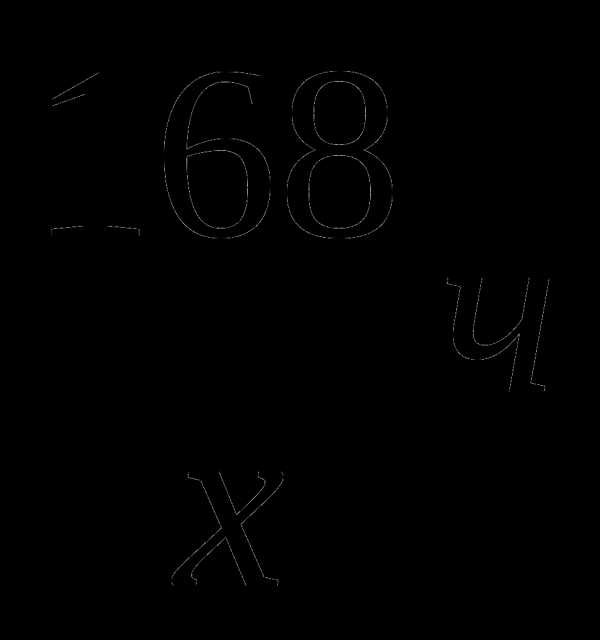
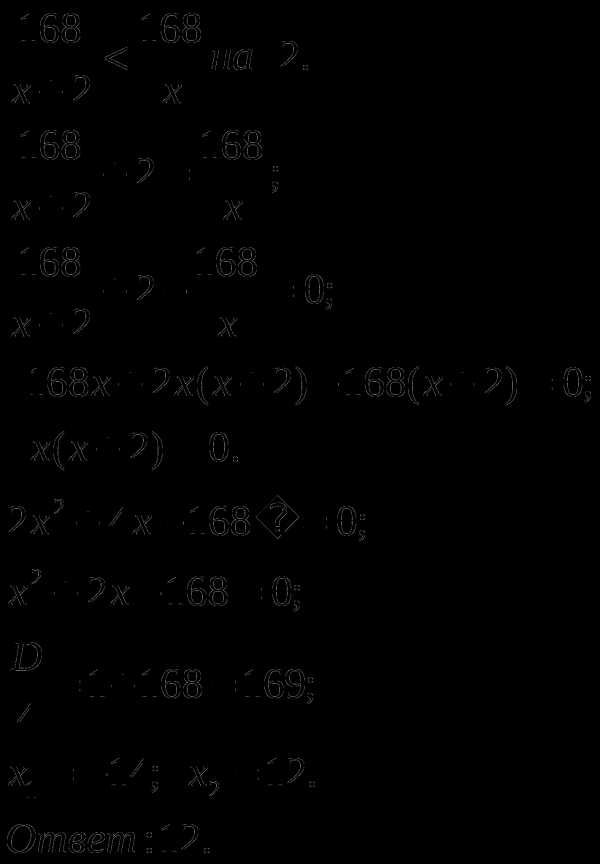
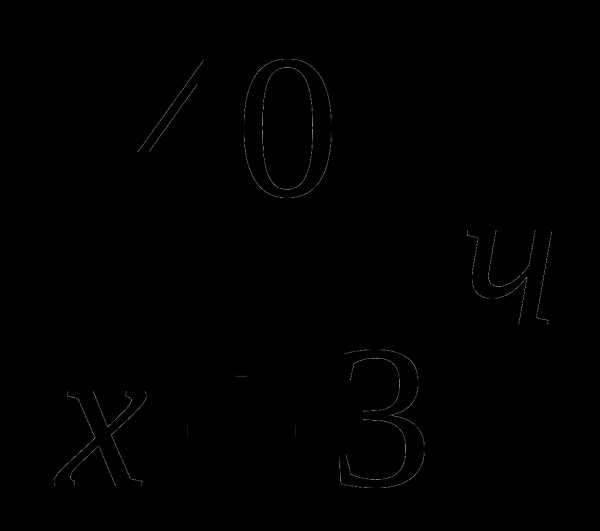
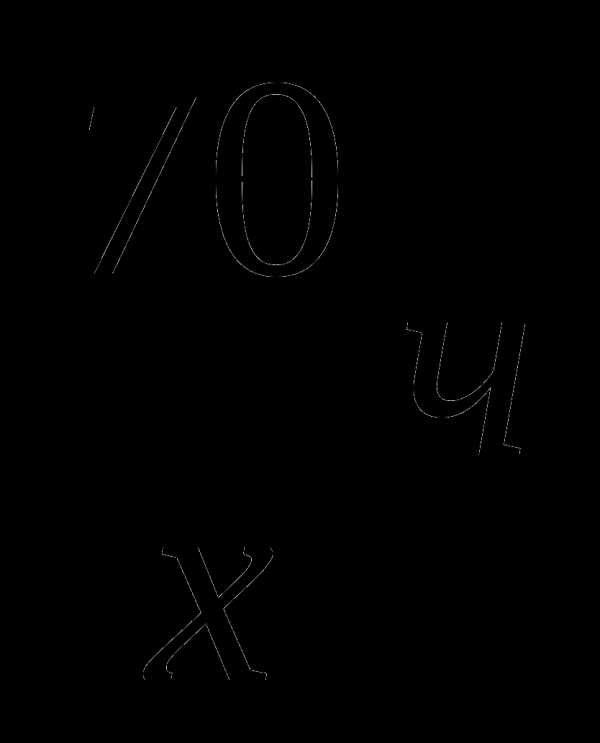
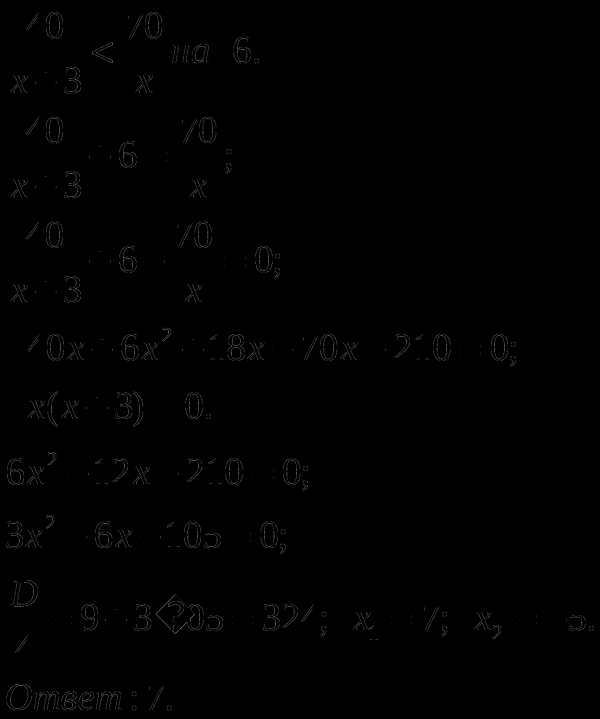
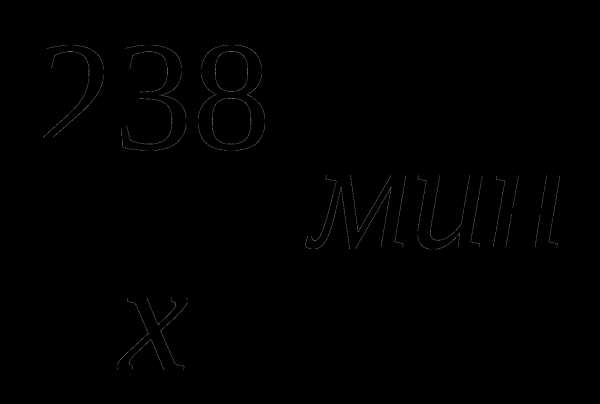
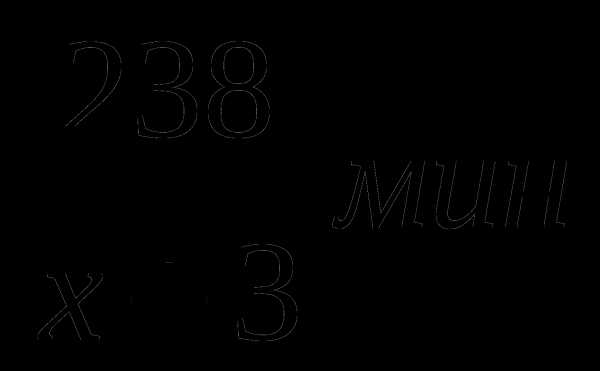






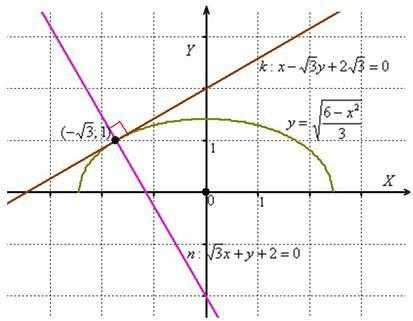
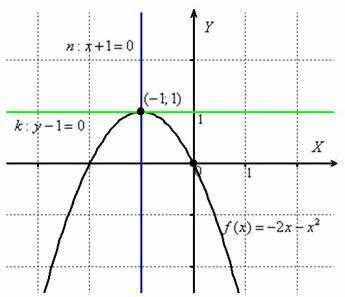
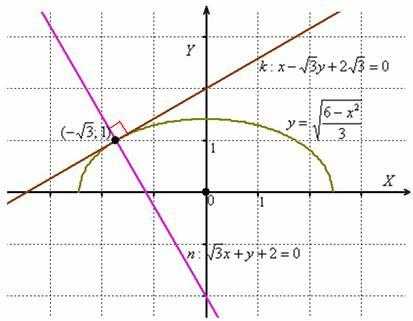 Забавно,
но фактически получилась и полная
проверка, поскольку чертёж выполнен
достаточно точно =) Кстати, функциязадаёт
верхнюю дугуэллипса.
Забавно,
но фактически получилась и полная
проверка, поскольку чертёж выполнен
достаточно точно =) Кстати, функциязадаёт
верхнюю дугуэллипса.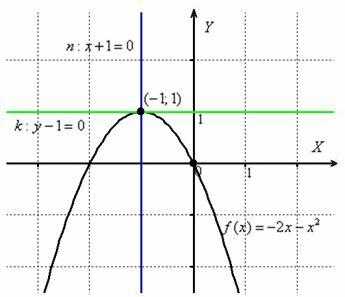
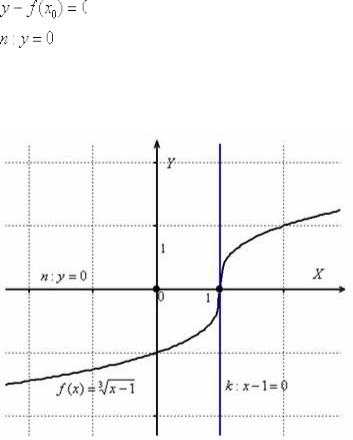
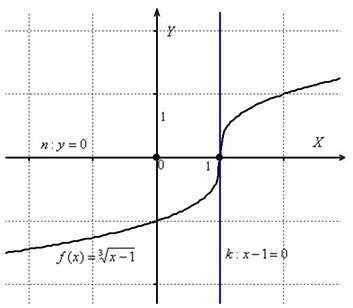 Ответ:
Ответ:  Таким
образом: Уравнение
нормали составим по формуле
: Ответ:
Таким
образом: Уравнение
нормали составим по формуле
: Ответ: