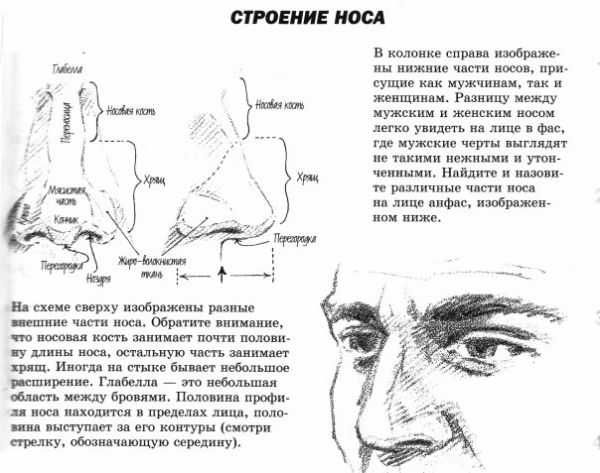
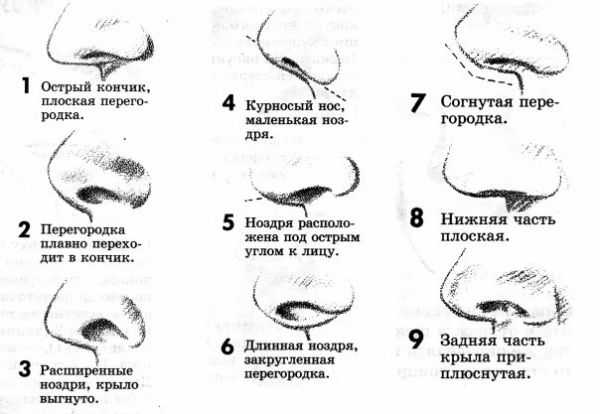
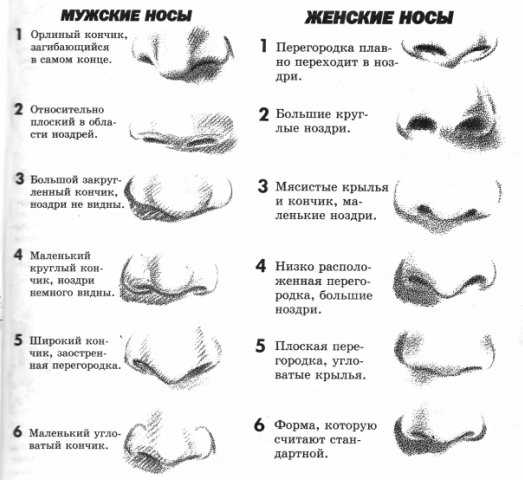
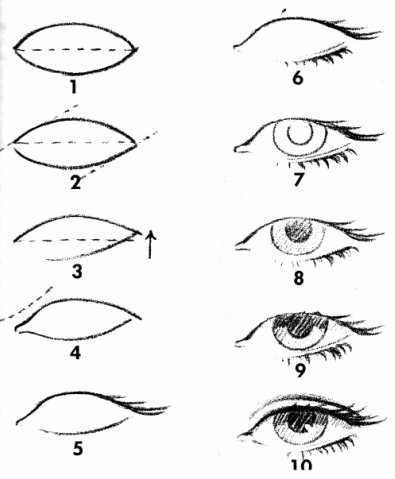
Задачи на определение среднегодовой стоимости основных производственных фондов предприятия
Задача №1. Определите
среднегодовую стоимость основных производственных фондов фирмы, если
известны стоимость основных производственных фондов принадлежащих предприятию
на начала года, сумма выбывшего из-за изношенности оборудования в начале марта
и сумма оборудования которое предприятие закупило и установило в конце сентября
этого года.
Таблица 1.1
Вариант Стоимость
ОФ: | 5 |
на начало
года, в млн. де | 280 |
введенных,
в млн. де | 38 |
выбывших, в
млн. де | 54 |
Решение.
ФСГ — среднегодовая стоимость основных фондов;
ФНГ=280
млн. де — стоимость основных фондов на начало периода;
Фвв=38
млн. де, Фвыб=54 млн. де — стоимость
вводимых и выбывающих (выводимых) основных фондов;
m1=3 — число полных месяцев работы введенных основных
фондов с момента введения до конца текущего года, месяцы;
m2=10— число полных месяцев бездействия
выбывших основных фондов с момента выведения до конца текущего года, месяцы;
Ответ:
Задача №2. Известны стоимость
основных производственных фондов фирмы на 1 января отчетного года, а также то,
что в начале II квартала было приобретено новое оборудование, а в конце IV
квартала ликвидировано изношенное оборудование. Определите среднегодовую
стоимость основных производственных фондов на 1 января следующего года,
используя данные из таблицы приведенной ниже.
Таблица 2.1
Вариант Стоимость
ОФ: | 5 |
на начало
года, в тыс. де | 705 |
введенных,
в тыс. де | 210 |
выбывших, в
тыс. де | 208 |
Решение.
ФСГ — среднегодовая стоимость основных фондов, де;
ФНГ=705
тыс. де — стоимость основных фондов на начало и конец периода, де;
Фвв=210
тыс. де, Фвыб=208 тыс. де — стоимость
вводимых и выбывающих (выводимых) основных фондов, де;
m1=9 — число полных месяцев работы введенных основных
фондов с момента введения до конца текущего года, месяцы;
m2=0— число полных месяцев бездействия
выбывших основных фондов с момента выведения до конца текущего года, месяцы;
Ответ:
Задача №3. В течение года установлено некоторое количество
нового оборудования, причем часть его введено в действие 1 апреля 2003 г., а
остальное — с 30 июля 2003 г. Из оборудования принадлежащего предприятию 1
сентября 2003 г. выбыло 12% в виду высокой степени их износа. Определите
среднегодовую стоимость основных производственных фондов, используя данные из
нижеприведенной таблицы.
Таблица 3.1
Вариант Параметры | 5 |
Стоимость
ОФ на 1 января 2003г, в млн. де | 6 |
Количество
единиц оборудования введенных: с 1 апреля
2003г, в шт. с 30 июля
2003г, в шт. | 3 7 |
Стоимость
единицы введенного оборудования, в тыс. де | 180 |
Количество
оборудования принадлежащих предприятию на 01.01.2003г, в шт. | 150 |
Стоимость
единицы выбывающего оборудования, в тыс. де | 210 |
Решение
ФСГ — среднегодовая стоимость основных фондов, де;
ФНГ=2,4
млн. де — стоимость основных фондов на начало и конец периода, де;
Фвв, Фвыб — стоимость вводимых и выбывающих (выводимых) основных
фондов, де;
m1 — число полных месяцев работы введенных основных
фондов с момента введения до конца текущего года, месяцы;
m2 — число полных месяцев бездействия выбывших основных
фондов с момента выведения до конца текущего года, месяцы;
Фвв с 1 апр.=325 тыс. де; m1=9;
Фвв с 30 июля=325 тыс.де; m1’=5.
Количество оборудования на 30 июля = 380+5+5=390 шт.
Количество выбывшего оборудования на 1 сентября = 47
шт.; m2=4.
Фвыб=47·105=4,935 млн. де.
Ответ:
Задача №4. Определите среднегодовую стоимость основных
производственных фондов согласно данным из таблицы 4.1. Причем известно, что
стоимость транспортных услуг составила 12% от стоимости приобретенных основных
фондов, а монтажа – 9%.
Таблица 4.1
Вариант Параметры | 4 |
Стоимость
ОФ на начало текущего года, в тыс. де | 400 |
Стоимость
ОФ, приобретенных: в конце сумма, в тыс. де | сентября 28 |
Стоимость
ОФ, выбывших: с сумма, в тыс. де | 01.11 28 |
Решение
ФСГ — среднегодовая стоимость основных фондов, де;
ФНГ = 400 тыс. де. — стоимость основных фондов на начало и конец
периода, де;
Фвв, Фвыб=28 тыс.де. — стоимость вводимых и выбывающих
(выводимых) основных фондов, де;
m1 = 3 — число полных месяцев работы введенных основных
фондов с момента введения до конца текущего года, месяцы;
m2 =2 — число полных месяцев бездействия выбывших
основных фондов с момента выведения до конца текущего года, месяцы;
Ответ:
Задача
№5. Определите
среднегодовую стоимость ОФ в плановом году, исходя из ниже следующих данных по
базисному и плановому годам:
Таблица 5.1
vunivere.ru
Задачи по теме: «Основные фонды»
Поиск Лекций
Тема 3: «Основные фонды предприятия»
Цель работы: приобретение практических навыков учета и оценки основных производственных фондов автотранспортного предприятия.
Определить:
1 стоимость основных фондов на начало года;
2 стоимость фондов, поступивших в течение года;
3 стоимость фондов, выбывших в течение года;
4 среднегодовую стоимость основных фондов;
5 структуру основных фондов;
6 амортизационные отчисления;
7 показатели, характеризующие техническое состояние основных фондов;
8 показатели эффективности использования основных фондов;
9 зависимость изменения показателя фондоотдачи от стоимости основных фондов.
Предложить мероприятия, повышающие эффективность использования основных фондов.
Исходные данные представлены в таблице 1
Таблица 1
Исходные данные для работы по теме «Основные фонды»
Продолжение таблицы 1
Продолжение таблицы 1
Продолжение таблицы 1
Задачи по теме: «Основные фонды»
1. Определить среднегодовую стоимость основных производственных фондов автотранспортного предприятии, если их стоимость на начало года была равна 4500 тыс.грн. Движение основных фондов в течение года характеризуется следующими данными: по состоянию на март месяц поступило основных фондов на сумму 120 тыс.грн., выбыло 80 тыс. грн.; на сентябрь поступило 240 тыс. грн., выбытия не было; на ноябрь поступило 30 тыс.грн., выбыло 10 тыс.грн.
РЕШЕНИЕ:
Среднегодовая стоимость основных фондов рассчитывается по формуле:
, грн.
2. Определить коэффициенты износа и годности основных производственных фондов, если стоимость основных фондов на начало года составляет 8600 тыс.грн., износ основных производственных фондов – 1200 тыс.грн.
РЕШЕНИЕ:
Физическое состояниеОПФ выражается при помощи показателей
износа и годности:
Коэффициент износа различных видов или групп основных фондов:
;
Коэффициент годности:
,
3. Определить коэффициенты обновления и выбытия основных производственных фондов, если первоначальная стоимость основных производственных фондов на начало года – 6700 тыс.грн.; поступление фондов в течении года – 890 тыс. грн.; выбытие за год – 700 тыс. грн.
РЕШЕНИЕ:
Для характеристики темпов воспроизводства ОПФ, изменения их физического и технического уровня используют показателидвижения основных фондов:коэффициенты обновления и выбытия основных фондов.Коэффициент обновления основных фондов, характеризует долю новых основных фондов в их общем объеме и исчисляется как отношение стоимости введенных в действие новых основных фондов за год к полной балансовой стоимости основных фондов на конец года:
,
Коэффициент выбытия основных фондов, характеризует долю выбывших основных фондов в течении года в общей их стоимости. Он исчисляется как отношение полной стоимости выбывших основных фондов к полной балансовой стоимости основных фондов на начало года:
4. Определить потребную среднегодовую стоимость основных производственных фондов при планируемом объеме доходов – 9500 тыс. грн. и планируемой фондоемкости продукции 0, 495.
РЕШЕНИЕ:
Фондоемкость продукции — величина, обратная фондоотдаче. Она
показывает долю стоимости основных фондов, приходящуюся на
каждый рубль выпускаемой продукции. Если фондоотдача должна
иметь тенденцию к увеличению, то фондоемкостъ – к снижению:
, откуда
5. Определить изменение показателя фондоотдачи основных производственных фондов в планируемом году по сравнению с отчетным, если в отчетном году среднегодовая стоимость основных производственных фондов – 5400 тыс.грн., доходы 10200 тыс.грн.; в планируемом году доходы намечено увеличить на 6,7 % по сравнению с отчетным, а стоимость производственных фондов на 3,5%.
РЕШЕНИЕ:
Для расчета величины фондоотдачи (ФО) используется формула:
.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Задачи по оборотным средствам с решением
Задачи по определению нормативов и показателей эффективности использования оборотных средств с решением
Задача № 1 Определить эффективность использования оборотных средств, если:
— годовой объем реализации продукции – 1250 тыс. грн.,
— себестоимость реализованной продукции- 1075 тыс. грн.,
— среднегодовой остаток оборотных средств – 150 тыс. грн.
Решение задачи:
1250 тыс. грн
Коэффициент оборачиваемости оборотных средств = ———————— = 8,3
150 тыс. грн
Ответ задачи: коэффициент оборачиваемости показывает, что каждая гривна оборотных средств осуществляет за год 8,3 оборота.
360 дней
Продолжительность 1 оборота, дни = ————— = 43,4 дней
8,3
Вывод: 1 оборот оборотных средств осуществляется за 43,4 дня.
150 тыс. грн
Коэффициент загрузки = ——————- = 0,12
1250 тыс. грн
Вывод: коэффициент загрузки показывает, что на каждую гривну реализованной продукции приходится 0,12 грн оборотных средств.
175 тыс. грн
Коэффициент эффективности использования оборотных средств = ——————- = 1,17
150 тыс. грн
при этом: Прибыль, тыс. грн = 1 250 тыс. грн — 1 075 тыс. грн = 175 тыс. грн
Вывод задачи по оборачиваемости: коэффициент эффективности использования оборотных средств показывает, что предприятие получает 1,17 грн прибыли в расчете на 1 грн. оборотных средств.
Задача № 2 по оборотным средствам
Предприятие в отчетном квартале реализовало продукции на 100 тыс. грн при среднем остатке оборотных средств – 25 тыс. грн.
Определить ускорение оборачиваемости оборотных средств в днях и сумму их высвобождения из оборота за счет изменения коэффициента оборачиваемости в плановом квартале, если объем реализованной продукции планируется увеличить на 25 %, а средний остаток оборотных средств не изменится.
Решение задачи по оборотным средствам:
100 тыс. грн
1. Коэффициент оборачиваемости в отчетном квартале = ———————- = 4
25 тыс. грн
90 дней
2. Продолжительность 1 оборота в отчетном квартале, дни = ————— = 22,5 дней
4
100 тыс. грн × (100% + 25%)
3. Объем реализации в плановом квартале, тыс. грн = —————————————— = 125 тыс. грн.
100 %
125 тыс. грн
4. Коэффициент оборачиваемости в плановом квартале = ——————— = 5
25 тыс. грн
90 дней
5. Продолжительность 1 оборота в плановом квартале, дни = ————— = 18 дней
5
6. Ускорение оборачиваемости оборотных средств, дней = (18 дней – 22,5 дня) = — 4,5 дня
125 тыс. грн
7. Сумма высвободившихся из оборота оборотных средств, тыс. грн = ——————— × (22,5 дня – 18 дней)= 6,25 тыс. грн
90 дней
Вывод задачи: за счет сокращения продолжительности 1 оборота на 4,5 дня из оборота планируется высвободить 6,25 тыс. грн оборотных средств.
Задача № 3 по нормативу оборотных средств
Выпуск продукции за год — 100 тыс. шт., себестоимость единицы продукции – 16 грн. Продолжительность производственного цикла изготовления единицы продукции – 7 дней, коэффициент нарастания затрат в незавершенном производстве равен 1.
Определить норматив оборотных средств в незавершенном производстве.
Решение задачи:
100 000 шт ×16 грн
1. Среднесуточный выпуск продукции, грн = —————————- = 4 444,44 грн.
360 дней
2. Норматив оборотных средств в незавершенном производстве, грн = 4 444,44 грн × 7 дней × 1 = 31 111,08 грн.
Вывод: для осуществления бесперебойного процесса производства минимальная сумма оборотных средств в незавершенном производстве должна составлять 31111,08 грн.
Задача № 4
Определить норматив оборотных средств, вложенных в производственные запасы, если:
|
производственные запасы
|
текущий запас,
дни
|
подготовительный запас,
дни
|
транспортный запас, дни
|
страховой запас,
дни
|
затраты сырья и материалов в 4 квартале,
тыс. грн
|
|
основные материалы
|
20
|
1
|
4
|
10
|
900
|
|
вспомогат. материалы
|
40
|
—
|
4
|
20
|
400
|
|
топливо
|
30
|
—
|
5
|
15
|
700
|
Решение задачи по нормативу оборотных средств:
1. Норма запаса оборотных средств, дни:
- по основным материалам, дни = 20 дней + 1 день + 4 дня + 10 дней = 35 дней,
- по вспомогательным материалам, дни = 40 дней + 4 дня + 20 дней = 64 дня,
- по топливу, дни = 30 дней + 5 дней + 15 дней = 50 дней.
(900 тыс. грн × 35 дней) + (400 тыс. грн × 64 дня) + (700 тыс. грн × 50 дней)
2. Средняя норма запаса, дни = —————————————————————————————————— = 46 дней
900 тыс. грн + 400 тыс. грн + 700 тыс. грн
900 тыс. грн + 400 тыс. грн + 700 тыс. грн
3. Дневная потре6ность в материальных ресурсах, тыс. грн = ———————————————————— = 22,2 тыс. грн.
90 дней
4. Норматив оборотных средств в производственных запасах, тыс. грн. = 22,2 тыс. грн × 46 дней = 1021,2 тыс. грн
Вывод задачи: для осуществления бесперебойного процесса производства минимальная сумма производственных запасов должна составлять 1021,2 тыс. грн.
zadachi-ru.com.ua
Задачи на применение формулы расчета амортизации задача 1
МЕЖДУНАРОДНЫЙ
БАНКОВСКИЙ ИНСТИТУТ
INTERNATIONAL BANKING INSTITUTE
Раздел
1. Общие основы экономического развития
Тема
1.5. Деньги и капитал
Практическая
работа 2
Целью данного
практикума является углубление
понимания сущности денег и капитала,
структуры капитала и его износа. Задачами практикума
является: Во-первых,
закрепление формулы подсчета основного
и оборотного капитала; Во-вторых,
приобретение навыков использования
формул расчета амортизации; В-третьих,
закрепление формул расчета времени
и числа оборотов основного, оборотного
и всего авансированного капитала; В-четвертых,
освоение формул определения потерь
от морального износа первого и второго
вида.
|
Оглавление
Задачи
на применение формулы расчета амортизации
ЗАДАЧА
1
Постановка
задачи: На
предприятии установлено оборудование
стоимостью 200 тыс. ден. ед., срок службы
которого 10 лет. Производственные здания
стоимостью 5000 тыс. ден. ед. утрачивают
свою стоимость за 50 лет. В производственном
процессе участвуют приборы, на приобретение
которых затрачено 80 тыс. ден. ед., и
инструменты на сумму 15 тыс. ден. ед. (срок
службы соответственно 4 и 3 года).
Определите годовую амортизацию основного
капитала.
Технология
решения задачи: Годовая
величина амортизационных отчислений
основного капитала состоит из суммы
амортизационных отчислений по каждому
элементу, которые определяются путем
деления балансовой стоимости на срок
службы. Следовательно, амортизация
оборудования составит: 200 : 10 = 20 тыс. ден.
ед.; амортизация производственных зданий
: 5000 : 50 = 100 тыс. ден. ед.; амортизация
приборов: 80 : 4 = 20 тыс. ден. ед. и амортизация
инструментов: 15 : 3 = 5 тыс. ден.ед. Вся
сумма годовой амортизации: 20 + 100 + 20 + 5 =
145 тыс. ден.ед.
Ответ: 145
тыс. ден. ед.
ЗАДАЧА
2
Постановка
задачи: Определите
амортизацию основного капитала к началу
4 года, исходя из следующих данных:
стоимость зданий и сооружений 160 млн.
ден.ед., машин и оборудования – 90 млн.
ден. ед., плановый срок их эксплуатации
соответственно 40 и 10 лет. В дороги и
линии электропередач предприятие
вложило 450 млн. ден.ед., срок их эксплуатации
20 лет. Используется технология, стоимость
которой 1 млн. ден. ед., срок возврата 10
лет.
Технология
решения задачи: Сначала
определяются годовые амортизационные
отчисления по отдельным элементам
основного капитала: амортизация зданий
и сооружений равна 160 : 40 = 4 млн. ден. ед.,
машин и оборудования 90 : 10 = 9 млн. ден.
ед., дорог и линий электропередач 450 : 20
= 22,5 млн. ден.ед., технологии 1: 10 = 0,1 млн.
ден. ед. Затем подсчитывается сумма
амортизации за год:
4+
9 + 22,5 + 0,1= 35,6 млн. ден. ед. К началу четвертого
года будет накоплено 35,6 * 3 = 106,8 млн. ден.
ед.
Ответ
: 106,8
млн. ден. ед.
ЗАДАЧА
3
Постановка
задачи: Первоначальная
стоимость производственных зданий и
сооружений – 100 тыс. ден. ед., машин и
оборудования – 200 тыс. ден.ед., транспортных
средств – 10 тыс. ден. ед. Определите
величину накопленных амортизационных
отчислений за шесть лет, если норма
амортизации зданий и сооружений
составляет 2,5% , машин и оборудования –
8 %, транспортных средств – 12 % в год.
Технология
решения задачи: сначала
рассчитываются амортизационные
отчисления по элементам основного
капитала путем умножения стоимости
элемента на годовую норму амортизации:
по производственным зданиям и сооружениям
100 * 2,5 % : 100 % = 2,5 тыс. ден. ед., по машинам
и оборудованию 200* 0,08 = 16 тыс. ден. ед., по
транспортным средствам 10 * 0,12 = 1,2 тыс.
ден. ед. Затем все складывается и
получается годовая амортизация: 2,5
+16+1,2 = 19,7 тыс. ден. ед. Умножить сумму на
6 лет, получается сумма накопленных за
это время амортизационных отчислений:
19,7 * 6 = 118,2 тыс. ден. ед.
Ответ
: 118,2
тыс. ден. ед.
ЗАДАЧА
4
Постановка
задачи: Стоимость
станка составляет 500 у. е., срок его службы
– 10 лет. Определите величину амортизационных
отчислений, поступивших в амортизационный
фонд за 5 лет при линейном методе
начисления амортизации. Что произойдет
с этой суммой, если на предприятии
используется метод удвоения амортизации.
Технология
решения задачи: величина
амортизационных отчислений за год при
линейном методе равна: 500:10=50 у. е.,
следовательно, за 5 лет в амортизационный
фонд поступит 50*5=250 у. е. При использовании
метода ускоренной амортизации норма
амортизации удваивается: 100 % : 10 лет * 2
= 20 %. Амортизационные отчисления составят
за год: 500*20 %:100 % = 100 у. е., за пять лет:
100*5=500 у. е.
Ответ: при
линейном методе 250 у. е., при ускоренной
амортизации вернется вся стоимость
станка.
Задачи
на расчет основного и оборотного капитала
ЗАДАЧА
5
Постановка
задачи: Стоимость
заводских зданий предприятия составила
50 млн. ден. ед., механизмов 34 млн. ден.
ед., на сырье в год потрачено 75 млн. ден.
ед., на топливо и электроэнергию 16 млн.
ден. ед. На заработную плату уходит
ежемесячно 25 млн. ден. ед. Определите
стоимость основного и оборотного
капитала.
Технология
решения задачи:
В стоимость основного капитала включается
стоимость производственных зданий и
механизмов: 50+34=84 млн. ден. ед. Оборотный
капитал состоит из стоимости сырья,
топлива и электроэнергии, заработной
платы, при этом надо подсчитать все это
за год: 75 + 16 + 25*12 = 391 млн. ден. ед.
Ответ: Основной
капитал равен 84 млн. ден. ед., оборотный
капитал – 391 млн. ден. ед.
ЗАДАЧА
6
Постановка
задачи: Авансирован
капитал: на производственные здания –
2 млн. долл., сооружений – 1,6 млн. долл.,
оборудование – 0,4 млн. долл., на закупку
сырья – 0,5 млн. долл., материалов – 0,2
млн. долл., топлива – 0,45 млн. долл., на
наём рабочей силы – 0,3 млн. долл. Определите
основной, оборотный и весь авансированный
капитал.
Технология
решения задачи: Основной
капитал включает в себя стоимость
зданий, сооружений и оборудования:
2+1,6+0,4= 4 млн. долл., оборотный капитал
состоит из стоимости сырья, материалов,
топлива и наем рабочей силы: 0,5+0,2+0,45+0,3=
1,45 млн. долл. Весь капитал равен: 4+1,45=
5,45 млн. долл.
Ответ: основной
капитал – 4 млн. долл, оборотный – 1,45
млн. долл., авансированный капитал –
5,45 млн. долл.
Задачи
на расчет времени и числа оборотов
основного, оборотного и всего
авансированного капитала
ЗАДАЧА
7
Постановка
задачи: Основной
капитал – 130 тыс. ден. ед., оборотный –
40 тыс. ден. ед., в том числе заработная
плата – 15 тыс. ден. ед. За год основной
капитал совершает 1/10 оборота, оборотный
– 4 оборота. Определите время одного
оборота всего капитала.
Технология
решения задачи: Сначала
определяется число оборотов, совершаемое
авансированным капиталом в течение
года. Для этого рассчитывается объем
оборота основного капитала (путем
умножения его стоимости на количество
оборота в год: 130 * 1/10 = 13 тыс. ден. ед.) и
оборотного капитала: 40 * 4 = 160 тыс. ден.
ед. Таким образом за год оборачивается
13 + 160 = 173 тыс. ден. ед. Надо найти число
оборотов в год, для этого обернувшийся
капитал делится на стоимость авансированного
капитала: 173 : 170 = 1,03. Теперь можно найти
время оборота капитала: 365 дней : 1,03 =
354,3 дней. Таким образом, за год возвращается
весь вложенный капитал.
Ответ: Время
оборота капитала составляет 354,3 дней.
ЗАДАЧА
8
Постановка
задачи: стоимость
зданий 2000 у. е., машин – 1000, оборудования
– 400 у. е., инструментов – 100. Амортизация
зданий происходит за 50 лет, машин за 10
лет, оборудования – за 5, а инструментов
за 2 года. Найти время оборота основного
капитала.
Технология
решения задачи: сначала
находится величина годовых амортизационных
отчислений по элементам основного
капитала: зданий составит 2000 : 50 = 40 у.
е.; машин: 1000:10= 100 у. е.; оборудования
400:5=80 у. е.; инструментов 100:2=50 у. е., затем
сумма годовой амортизации составит
40+100+80+50= 270 у. е. Потом подсчитывается
авансированный основной капитал:
2000+1000+400+100= 3500 у. е. Теперь можно подсчитать
время оборота основного капитала:
3500:270=13 лет.
Ответ: 13
лет.
ЗАДАЧА
9
Постановка
задачи: Производственный
цикл на предприятии длится 3 месяца. Для
его обеспечения требуется 300 у. е. на
покупку сырья и материалов, 100 у. е. на
топливо и 100 у. е. на электроэнергию.
Заработная плата, выплачиваемая
ежемесячно, составляет 20 у. е.
Определите
величину оборотного капитала и числа
его оборотов в течение года.
Технология
решения задачи: Подсчитайте
величину оборотного капитала:
300+100+100+20*3=560 у. е. Оборот оборотного
капитала в год составит: 560*(12месяцев:3месяца)=
2240 у. е. Число оборотов в течение года
составит: 2240:560= 4 оборота.
Ответ: 4
оборота в год.
ЗАДАЧА
10
Постановка
задачи: Оборотный
капитал предприятия равен 1000 у. е., в том
числе заработная плата 600 у. е. В течение
года капитал, вложенный в трудовой
фактор, оборачивается шесть раз, в сырье
и материалы – пять раз. Определите время
оборота оборотного капитала.
Технология
решения задачи: Капитал,
вложенный в сырье и материалы составляет:
1000 – 600 = 400 у. е. За год обернётся: 600*6 +
400*5 = 5600 у. е. За год оборотный капитал
совершит: 5600:1000=5,6 оборота. Время одного
оборота составит: 365 : 5,6 = 65 дней.
Ответ: 65
дней.
ЗАДАЧА
11
Постановка
задачи: Оборотный
капитал предприятия равен 2000 у. е., в том
числе заработная плата 1400 у. е. В течение
года капитал, вложенный в трудовой
фактор, оборачивается четыре раза, в
сырье и материалы – пять раз. Определите
величину основного капитала, если его
полный износ происходит за 10 лет, а
продолжительность оборота всего капитала
составляет 2 года.
Технология
решения задачи: Капитал,
вложенный в сырье и материалы составляет:
2000 – 1400 = 600 у. е. За год обернётся: 1400*4 +
600*5 = 8600 у. е. За год вернется 1/10 часть
основного капитала. Отношение обернувшегося
за год капитала к стоимости авансированного
капитала равно числу оборотов капитала
в год:
Решив
уравнение получаем основной капитал
равен 19000 у. е.
Ответ: 19000
у. е.
ЗАДАЧА
12
Постановка
задачи: Авансирован
капитал: на производственные здания –
1 млн. долл., сооружения – 0,6 млн. долл.,
оборудование – 0,4 млн. долл., на закупку
сырья – 0,2 млн. долл., материалов – 0,05
млн. долл., топлива – 0,15 млн. долл., на
наём рабочей силы – 0,1 млн. долл. Время
полного оборота основного капитала –10
лет. Заработная плата выплачивается 2
раза в месяц. Сырье, материалы, топливо
покупаются 1 раз в два месяца. Определите
количество оборотов в год, совершаемых
авансированным капиталом.
Технология
решения задачи: Основной
капитал составляет: 1+0,6+0,4=2 млн. долл.,
за год возвращается 1/10 его часть –
2:10=0,2 млн. долл. Оборотный капитал равен:
0,2+0,15+0,05+0,1= 0,5 млн. долл. За год обернется
4,8 млн. долл. (0,2*6 + 0,05*6 +0,15*6 + 0,1*12*2). Количество
оборотов, совершаемых авансированным
капиталом, в течение года: (0,2+4,8): (2+0,5)= 2
оборота.
Ответ: 2
оборота в год.
ЗАДАЧА
13
Постановка
задачи: Активы
компании составили 4650 млн. ден. ед., а
сумма продаж – 7050 млн. ден. ед. Сколько
оборотов совершил капитал за год?
Технология
решения задачи: Количество
оборотов подсчитывается путем деления
суммы продаж на активы компании: 7050 :
4650 = 1,5 оборотов.
Ответ: 1,5
оборота в год.
ЗАДАЧА
14
Постановка
задачи: Активы
фирмы равны 4000 у. е. За год капитал
совершил 3 оборота. Определите годовой
оборот капитала и время его оборота.
Технология
решения задачи: Годовой
оборот определяется путём перемножения
активов (капитала) фирмы на количество
оборотов: 4000*3=12000 у. е. Время оборота
можно узнать, поделив 12 месяцев на
количество оборотов в год. В данной
задаче время оборота равно 4 месяцам.
Ответ: годовой
оборот –12000 у. е., время оборота – 4
месяца.
Задачи
на определение морального износа первого
и второго вида
ЗАДАЧА
15
Постановка
задачи: Стоимость
машины, установленной на предприятии
200 тыс. ден. ед., срок её службы 10 лет.
Через 3 года, вследствие роста
производительности труда в производстве
подобных машин, рыночная стоимость их
снизилась на 20%. Определите величину
морального износа первого вида.
Технология
решения задачи: Современная
рыночная стоимость подобных машин
составляет: 200 – 0,2*200 = 160 тыс. ден. ед.
Годовая амортизация в первые три года
составляла: 200:10=20 тыс. ден. ед. За три
года перенесено: 20*3=60 тыс. ден. ед. В связи
с изменением рыночной стоимости годовая
амортизация будет равна 160:10=16 тыс. ден.
ед. За оставшиеся 7 лет будет перенесено:
16*7=112 тыс. ден. ед. Всего предприятие
вернет 60+112 = 172 тыс. ден. ед. Моральный
износ составит 200 – 172 = 28 тыс. ден. ед.
Ответ: 28
тыс. ден. ед.
ЗАДАЧА
16
Постановка
задачи: Станок,
установленный на предприятии, позволяет
выпускать 1000 ед. продукции за месяц. На
рынке появился новый станок,
производительность которого 4000 штуки
в месяц. Определите моральный износ
второго вида.
Технология
решения задачи: Моральный
износ второго вида определяется по
формуле:
Подставив
в формулу значения получим:
(4000–1000):4000*100 %=75 %
Ответ: 75
%.
ЗАДАЧА
17
Постановка
задачи: Стоимость
станка составляет 1000 у. е., срок его
службы – 10 лет. Через четыре года на
рынке стоимость таких станков составила
800 у. е. Определите потери предприятия
от морального износа при линейном методе
начисления амортизации и при использовании
метода удвоения амортизации.
Технология
решения задачи: величина
амортизационных отчислений за год при
линейном методе равна: 1000 : 10 = 100 у. е.,
следовательно, за 4 года в амортизационный
фонд поступит
100
* 4 = 400 у. е. Амортизация за последующие
годы составит 800 : 10 * 6 = 480 у. е. Всего
вернется 400 + 480 = 880 у. е. Потери от морального
износа равны 1000 – 880 =120 у. е.
При
использовании метода ускоренной
амортизации норма амортизации удваивается:
100% : 10 лет * 2 = 20%. Амортизационные отчисления
составят за год: 1000 * 20% : 100% = 200 у. е., за
четыре года 200 * 5 = 800 у. е. В пятый год: 800
* 0,2 = 160 у. е. За пять лет вернется 960 у. е.
Потери составят 40 у. е. (при условии, что
предприятие этот станок не будет больше
использовать).
Ответ: 120
при линейном методе, 40 – при ускоренной
амортизации.
ЗАДАЧА
18
Постановка
задачи: Стоимость
станка – 12000 у. е., срок его службы – 15
лет. Определите остаточную стоимость
станка через 6 лет эксплуатации.
Технология
решения задачи: Остаточная
стоимость представляет собой разность
между первоначальной стоимостью станка
и накопленной амортизацией: 12000 –
(12000:15*6)=7200 у. е.
Ответ: 7200
у. е.
ЗАДАЧА
19
Постановка
задачи: За
400 тыс у. е. предприниматель купил 100
станков. Средний срок их службы – 10 лет.
Через 6 лет стоимость подобных станков
понизилась на 25 %. Определите величину
физического и морального износа каждого
станка, а также его остаточную стоимость
на начало 7 года использования с учетом
морального износа.
Технология
решения задачи: Первоначальная
стоимость станка составляла: 400:100=4 тыс.
у. е. Через шесть лет она стала:
(400-0,25*400):100=3
тыс. у. е. Физический износ составляет:
4:10*6=2,4 тыс. у. е. Остаточная стоимость
равна: 4 – 2,4 = 1,6 тыс. у. е. В новой оценке
остаточная стоимость станка будет
равна: 3 – 3:10*6 = 1,2 тыс. у. е. Отсюда моральный
износ составляет: 1,6-1,2=0,4 тыс. у. е.
Ответ: физический
износ равен 2,4 тыс. у. е., моральный износ
– 0,4 тыс. у. е., остаточная стоимость с
учетом морального износа – 1,2 тыс. у. е.
ЗАДАЧА
20
Постановка
задачи: Две
фирмы купили одинаковые механизмы,
стоимость которых 500 у. е., срок службы
10 лет. Через 7 лет эти механизмы стали
дешевле на 40 %. Сравните сумму потерь от
морального износа у двух фирм, при
условии, что вторая фирма купила механизмы
на 2 года раньше.
Технология
решения задачи: Моральный
износ у первой фирмы составит:
(500-500:10*7) — (500 – 0,4*500):10*3= 60 у. е. Моральный
износ у второй фирмы равен: (500-500:10*9) –
(500-0,4*500):10*1= 20 у. е.
Ответ: потери
второй фирмы на 40 у. е. меньше.
ЗАДАЧА
21
Постановка
задачи: Фирма
установила 50 станков, стоимостью по
20000 у. е., срок службы 10 лет, но через 8 лет
они морально устарели. Стоимость новых
станков, появившихся на рынке, осталась
без изменения, а производительность
повысилась в 2 раза. Определите сумму
потерь от морального износа.
Технология
решения задачи: Амортизация,
приходящаяся на 1 единицу продукции,
входит в издержки производства, чем
больше производится товаров, тем меньше
издержки. Моральный износ второго вила
можно определить, сопоставив издержки
на старых и новых станках:
Чтобы
получить сумму потерь, надо остаточную
стоимость умножить на процент морального
износа : 50*20000:10*2 *50 % :100 % = 50000 у. е.
Ответ: потери
равны 50000 у. е.
gigabaza.ru


 Таблиця інтегралів
Таблиця інтегралів .
7.
.
7. 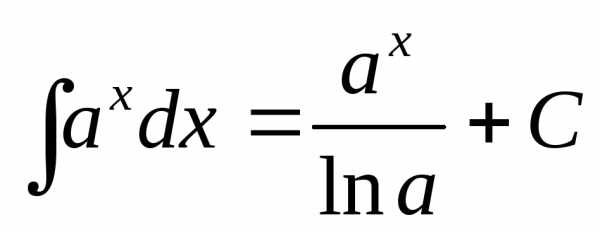 .
.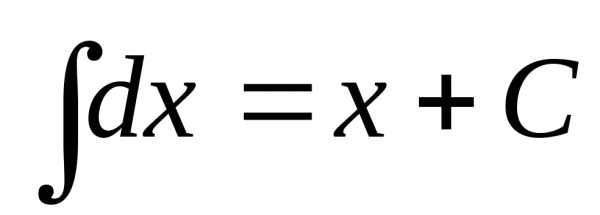 .
8.
.
.
8.
. .
10.
.
.
10.
.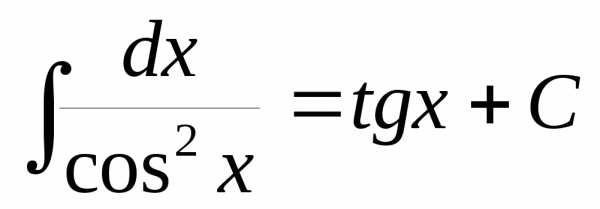 .
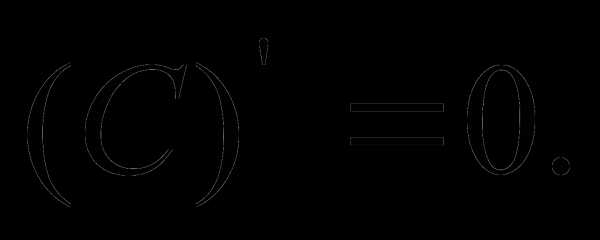
. має
первісну на проміжку(a,b), то на цьому проміжку має первісну і
функція
має
первісну на проміжку(a,b), то на цьому проміжку має первісну і
функція 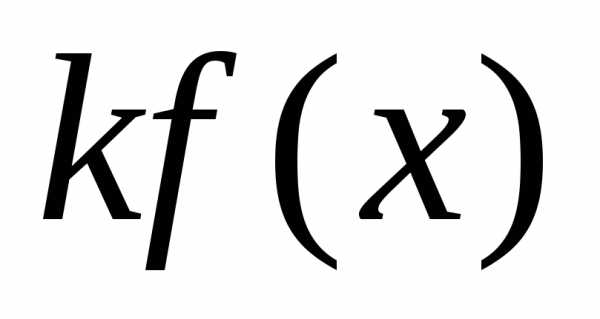 і
справедлива рівність:
і
справедлива рівність: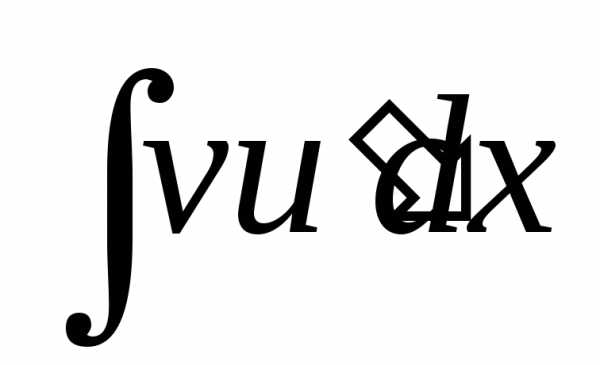 .
.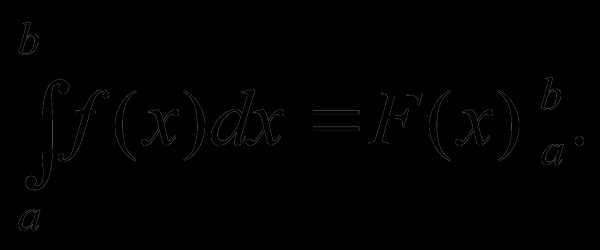
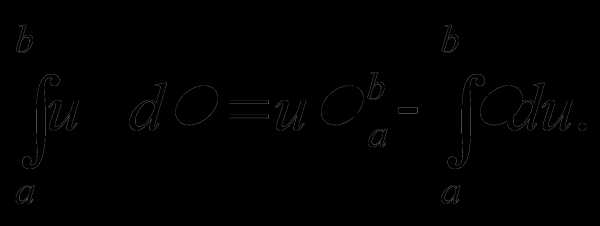

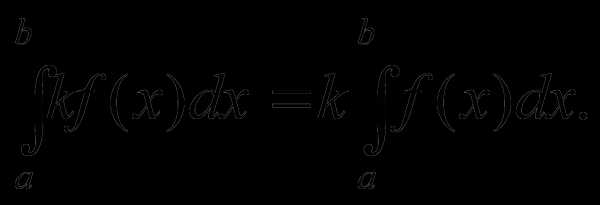

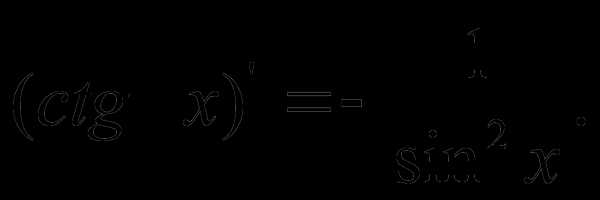

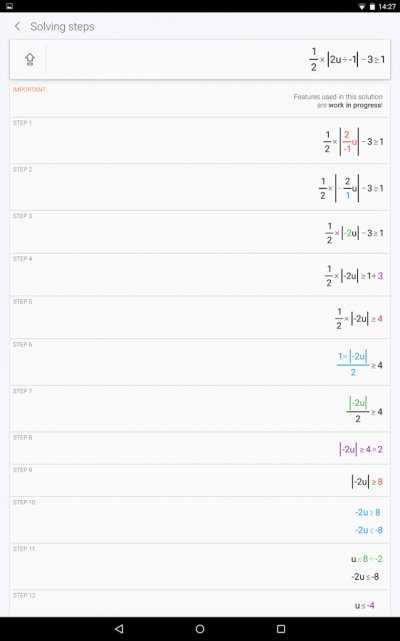
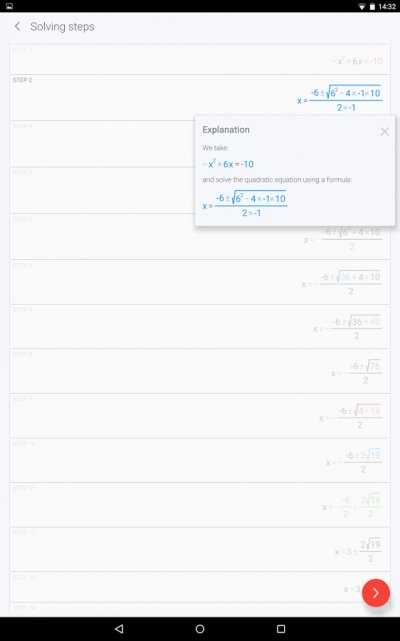

 admin on 28.02.2014 — 19:29 en Обзор программ для iOS
admin on 28.02.2014 — 19:29 en Обзор программ для iOS


 (она называется также частной производной
первого порядка). Тогда эта производная,
сама являясь функцией тех же переменных,
может иметь в некоторой точке
(она называется также частной производной
первого порядка). Тогда эта производная,
сама являясь функцией тех же переменных,
может иметь в некоторой точке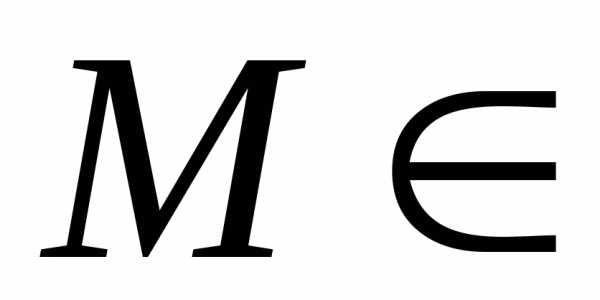 Dчастные производные
по той же
Dчастные производные
по той же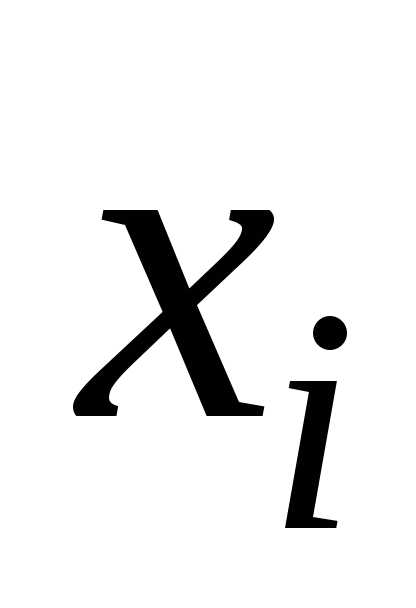 или по любой другой переменной
или по любой другой переменной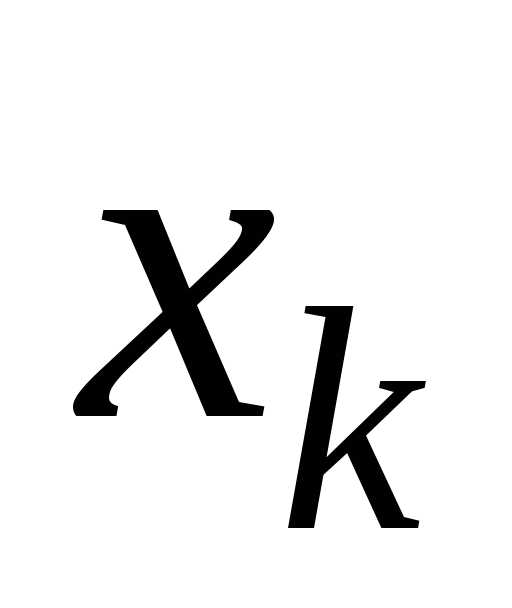 .
Для исходной функцииэти производные будут ужепроизводными
второго порядка (иливторыми частными производными). Производнаявторого
порядка функции по аргументам
.
Для исходной функцииэти производные будут ужепроизводными
второго порядка (иливторыми частными производными). Производнаявторого
порядка функции по аргументам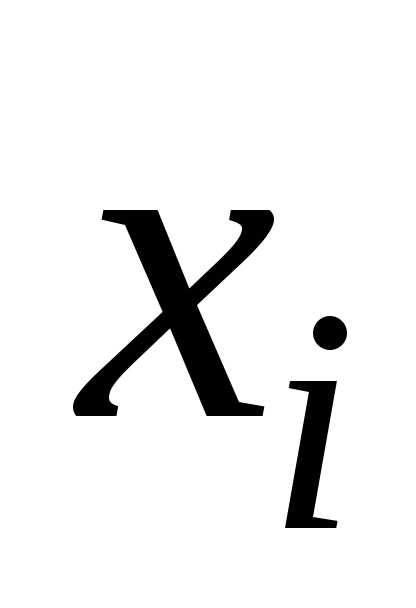 и
и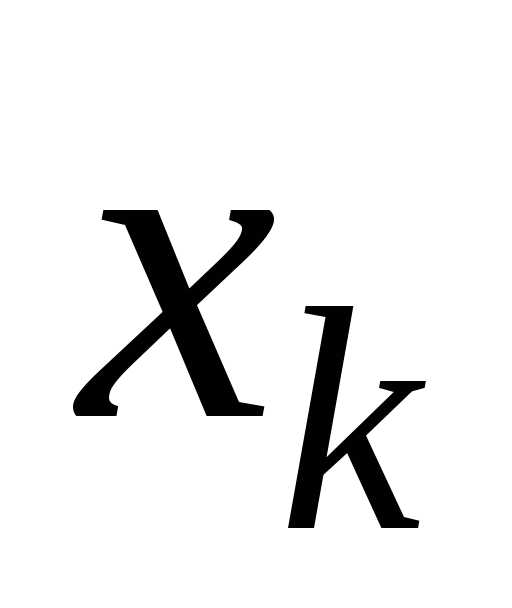 в точке
в точке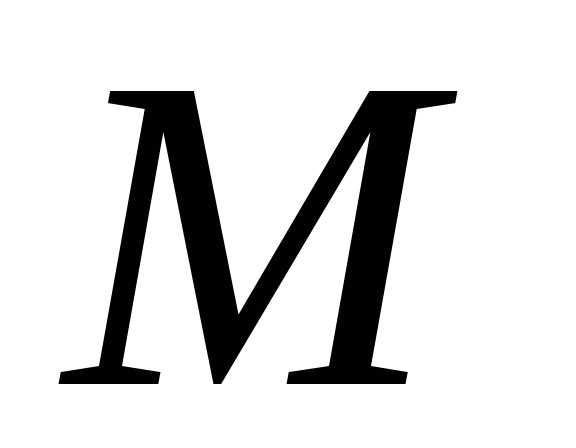 обозначается одним из следующих
символов:
обозначается одним из следующих
символов: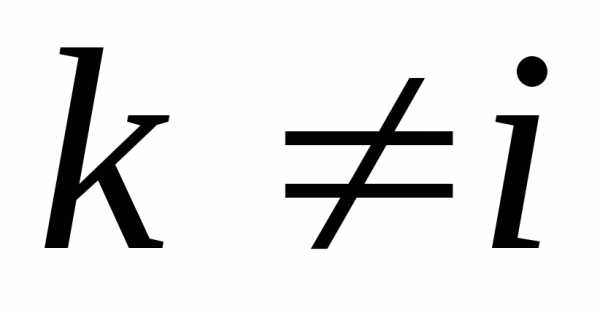 ,
точастная
производная второго порядка называется смешанной.
Если
,
точастная
производная второго порядка называется смешанной.
Если 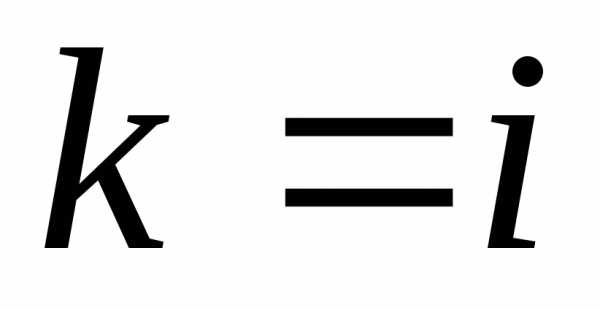 ,
то частная производная второго порядка
обозначается
,
то частная производная второго порядка
обозначается Dсмешанные частные
производные
Dсмешанные частные
производные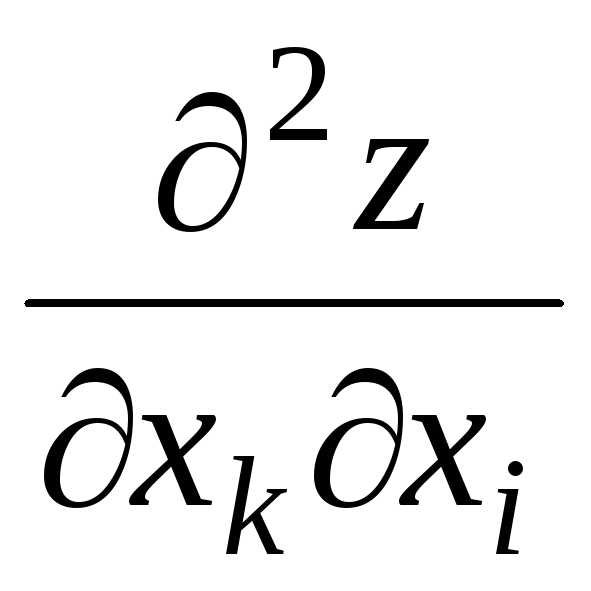 и
и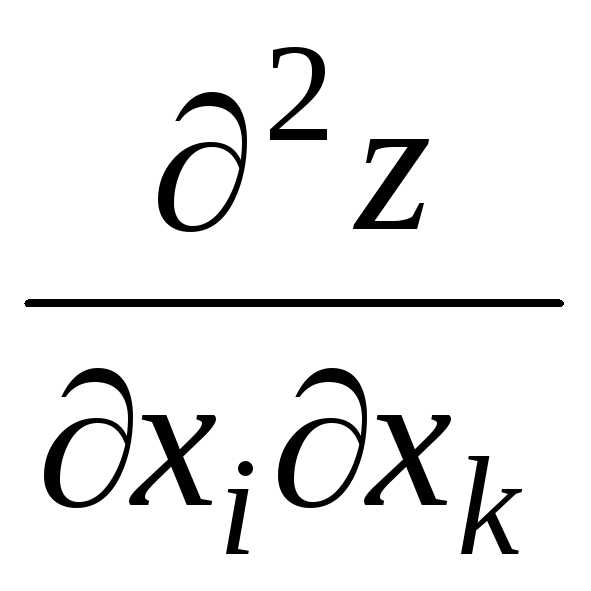 непрерывны, то они равны между собой в
этой точке, т.е.
непрерывны, то они равны между собой в
этой точке, т.е.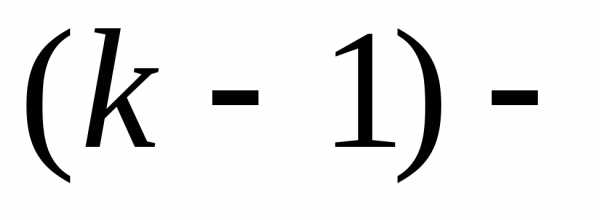 го
порядка включительно инепрерывные
в Dсмешанные
производные
го
порядка включительно инепрерывные
в Dсмешанные
производные  го
порядка, то значение любой
го
порядка, то значение любой 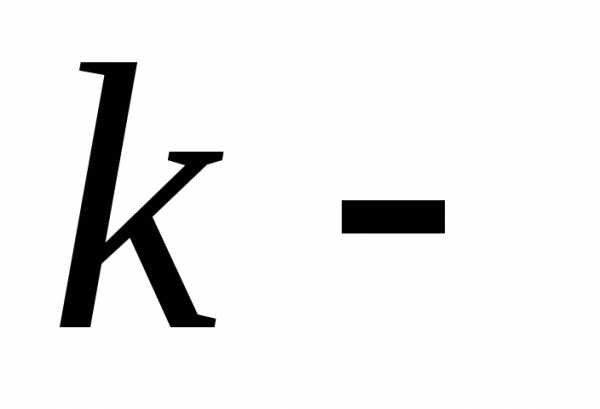 той
смешанной производной не зависит от
того порядка, в котором производятся
последовательные дифференцирования.
той
смешанной производной не зависит от
того порядка, в котором производятся
последовательные дифференцирования.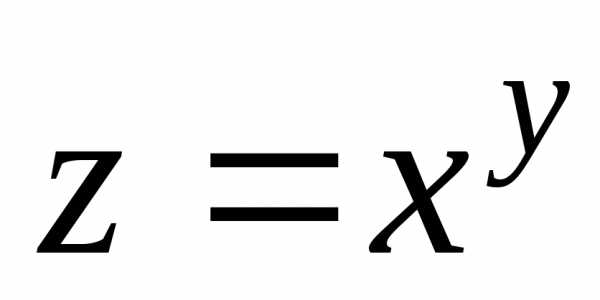 .
.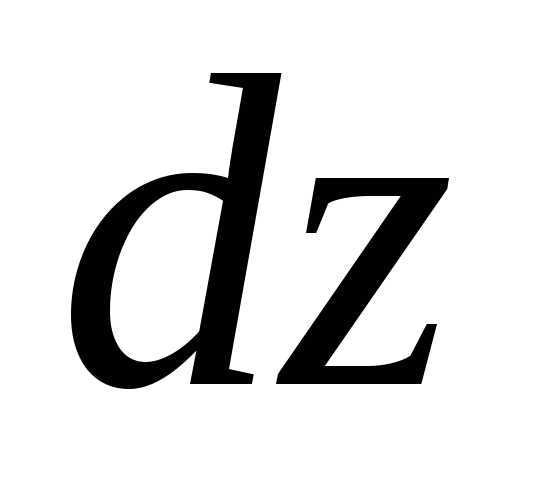 :
: ,
то в этом случае функция
,
то в этом случае функция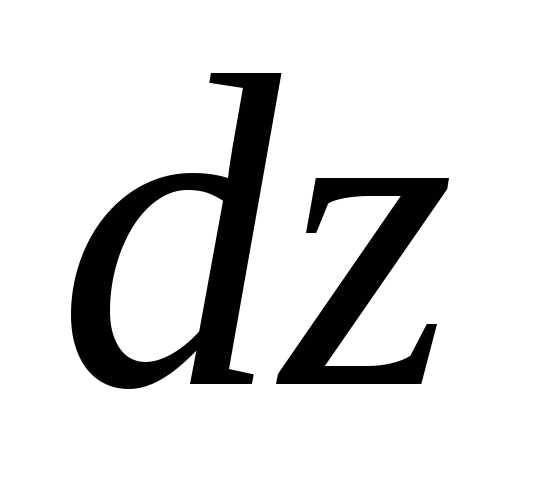 будет иметь непрерывные частные
производные первого порядка, и можно
будет говорить о дифференциале от этого
дифференциала:
будет иметь непрерывные частные
производные первого порядка, и можно
будет говорить о дифференциале от этого
дифференциала: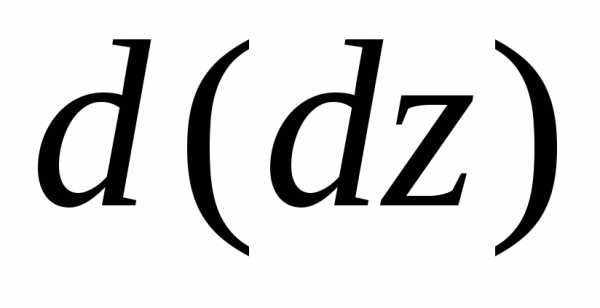 ,
который называетсядифференциалом
второго порядка (или вторым
дифференциалом)
функции
и обозначается.
,
который называетсядифференциалом
второго порядка (или вторым
дифференциалом)
функции
и обозначается. .
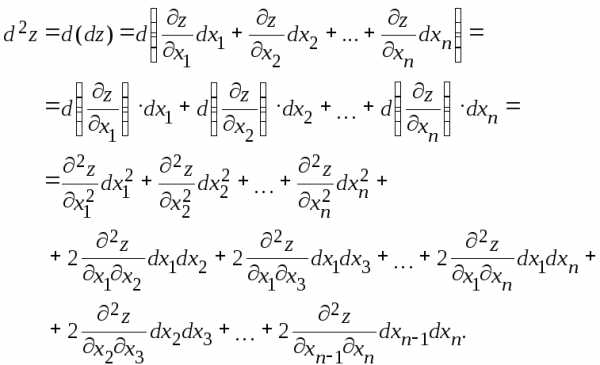
(7)
.
(7)
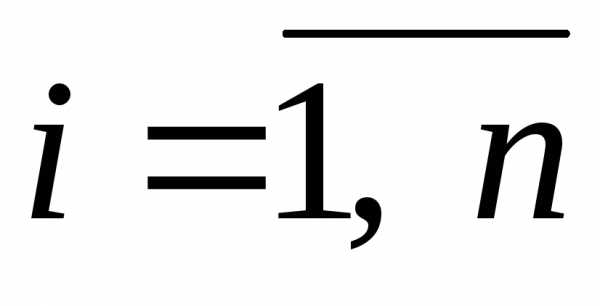 .
.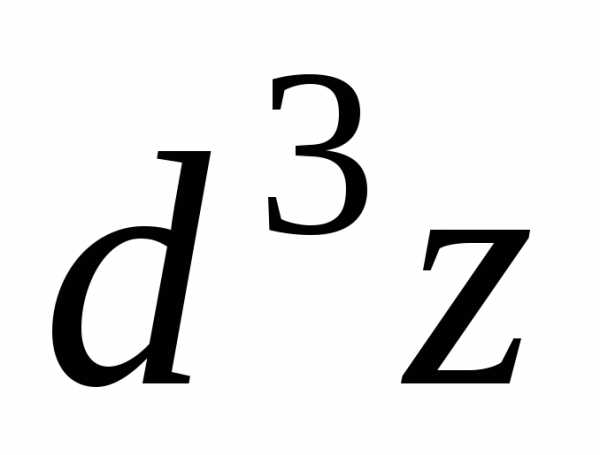 ,четвертого
,четвертого 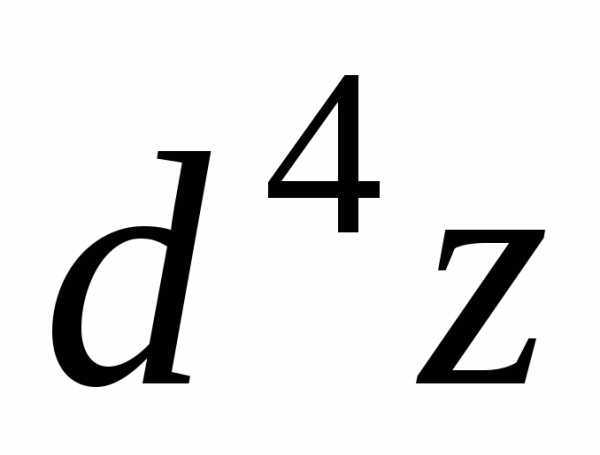 и т.д.порядков. Если определен
дифференциал
и т.д.порядков. Если определен
дифференциал 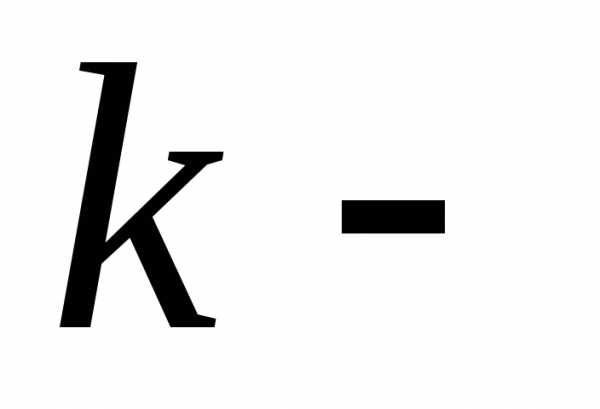 го
порядка
го
порядка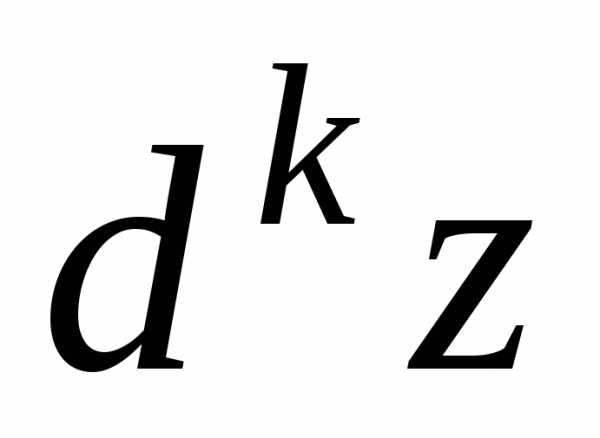 ,
то дифференциал
,
то дифференциал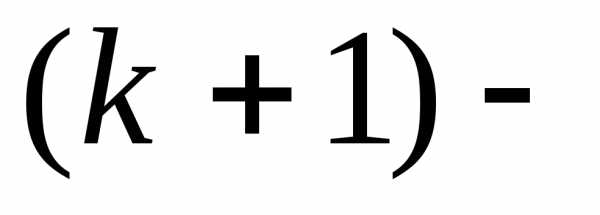 го
порядка определяется как полный
дифференциал от дифференциала
го
порядка определяется как полный
дифференциал от дифференциала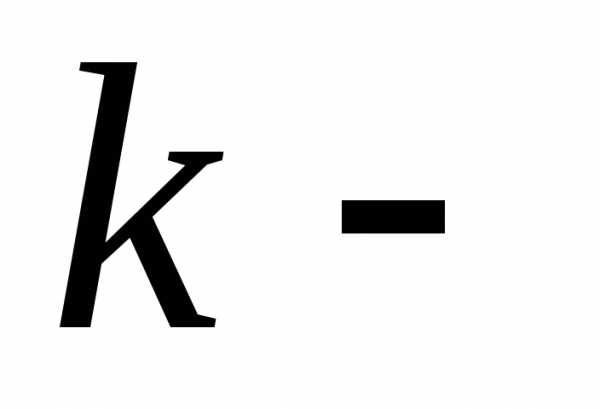 го
порядка:
го
порядка: ,
т.е.
,
т.е. дописывается в числителе каждой дроби
при
дописывается в числителе каждой дроби
при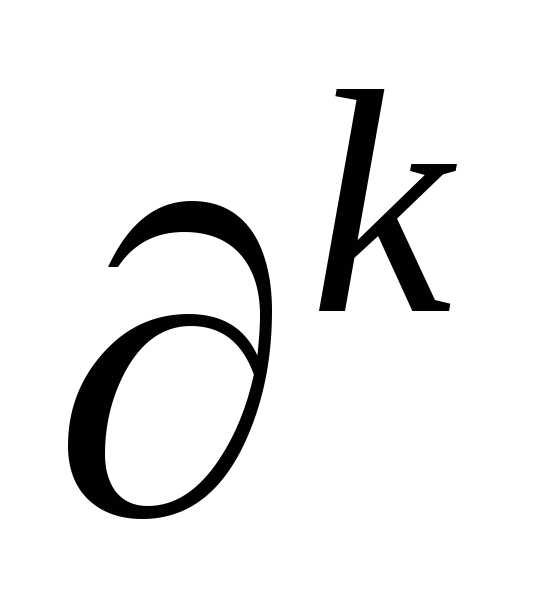 ,
а после этого всем символам возвращается
их значение производных и дифференциалов.
,
а после этого всем символам возвращается
их значение производных и дифференциалов.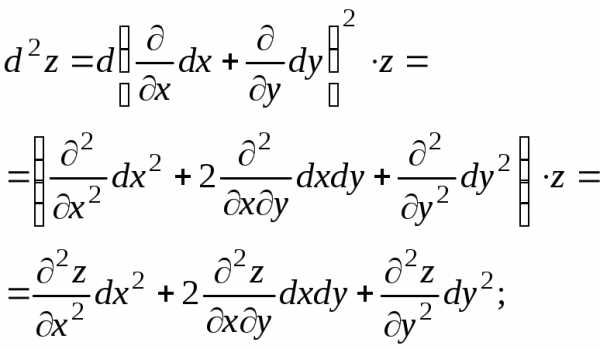

 ,
, 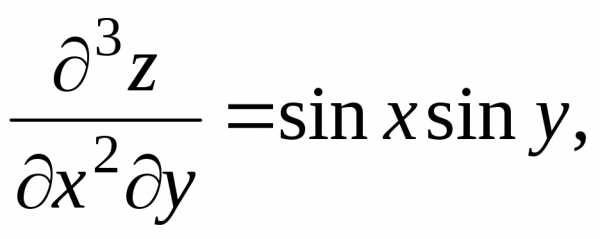
 ,
.
,
. ,
начиная со второй, равны нулю, то здесь
легко сразу воспользоваться формулами
(3) и (4):
,
начиная со второй, равны нулю, то здесь
легко сразу воспользоваться формулами
(3) и (4):
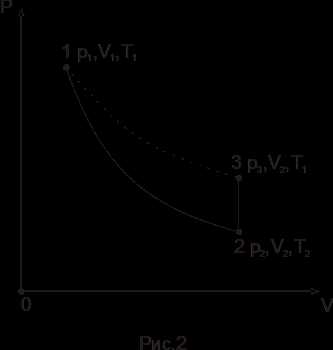
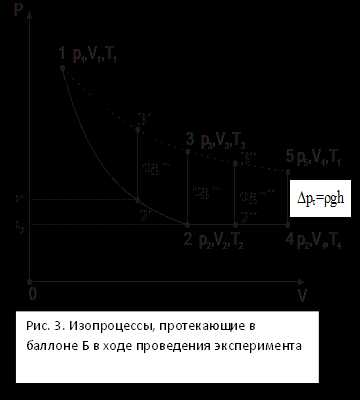 Величина H в выражении (18) получена в предположении, что краны К1 и К2 закрываются в момент окончания адиабатического процесса 1-2 (рис. 2).
Величина H в выражении (18) получена в предположении, что краны К1 и К2 закрываются в момент окончания адиабатического процесса 1-2 (рис. 2). Ln(Hτ)=ln(H)-aτ, (19)
Ln(Hτ)=ln(H)-aτ, (19)














 Нажмите на картинку, чтобы скачать эту тетрадку с заданиями для детей бесплатно.
Нажмите на картинку, чтобы скачать эту тетрадку с заданиями для детей бесплатно. Примеры страниц тетради с аппликациями для детей от 1 года до 3 лет.
Примеры страниц тетради с аппликациями для детей от 1 года до 3 лет.
 Аппликации для детей от 4 до 7 лет. Нажмите на картинку, чтобы скачать эту книгу.
Аппликации для детей от 4 до 7 лет. Нажмите на картинку, чтобы скачать эту книгу.



















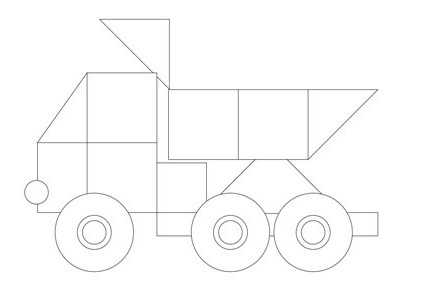
 Самосвал:
Самосвал:  Паровоз:
Паровоз:  Кораблик в море:
Кораблик в море:  Петушок:
Петушок:  Гусеница:
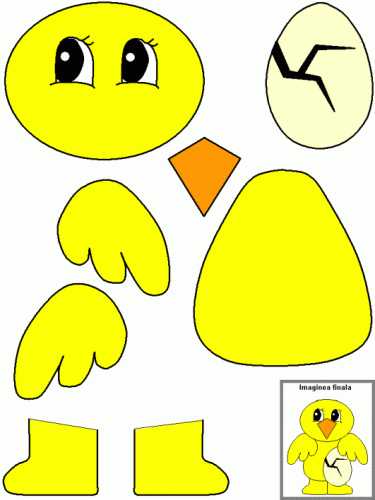
Гусеница: Лиса и колобок:
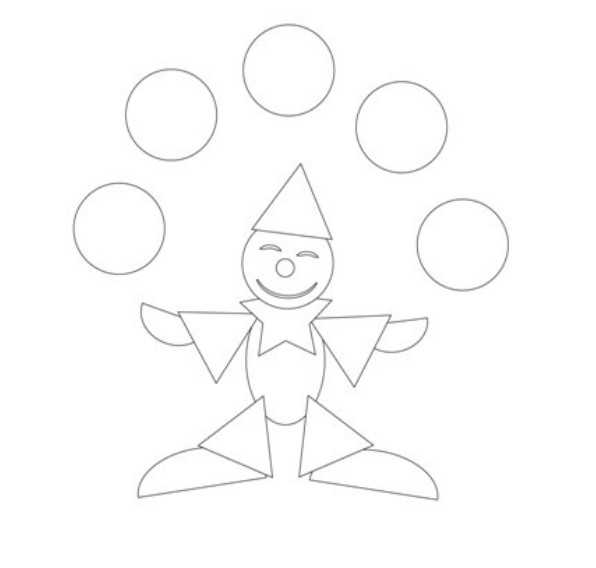
Лиса и колобок:  Клоун с шариками:
Клоун с шариками:  Бесплатные картинки для распечатки (ромб, квадрат, пятиугольник, круг, овал, треугольник, полукруг, прямоугольник, звёздочка):
Бесплатные картинки для распечатки (ромб, квадрат, пятиугольник, круг, овал, треугольник, полукруг, прямоугольник, звёздочка): 



 Предлагаем вам рассмотреть интересные сюжеты для создания аппликации. Кошечка:
Предлагаем вам рассмотреть интересные сюжеты для создания аппликации. Кошечка:  Белка:
Белка:  Лошадка из геометрических фигур:
Лошадка из геометрических фигур: 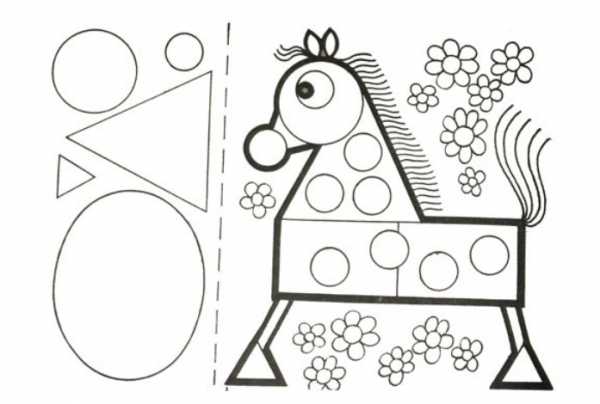 Лисичка:
Лисичка:  Серый волк:
Серый волк:  Божья коровка:
Божья коровка:  Слон:
Слон:  Мальчик и девочка:
Мальчик и девочка:  В лесу:
В лесу:  Ёлочка, дом, снеговик, холодильник, зайчик:
Ёлочка, дом, снеговик, холодильник, зайчик:  Ракеты и роботы из космоса:
Ракеты и роботы из космоса:  Курочка и цыплёнок:
Курочка и цыплёнок:  Раскраски с готовыми шаблонами для детей:
Раскраски с готовыми шаблонами для детей: 



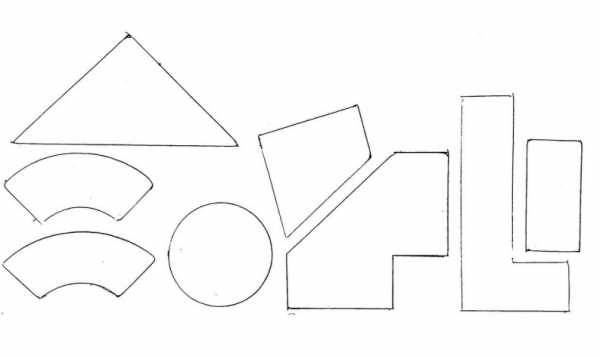
 Придумывать сюжеты для аппликации можно самостоятельно, рисуя фигурки. Космический корабль и жучок:
Придумывать сюжеты для аппликации можно самостоятельно, рисуя фигурки. Космический корабль и жучок:  Приготавливаем цветную бумагу, ножницы, клей ПВА, резак и гофрированный картон. Распечатываем для детей:
Приготавливаем цветную бумагу, ножницы, клей ПВА, резак и гофрированный картон. Распечатываем для детей: 
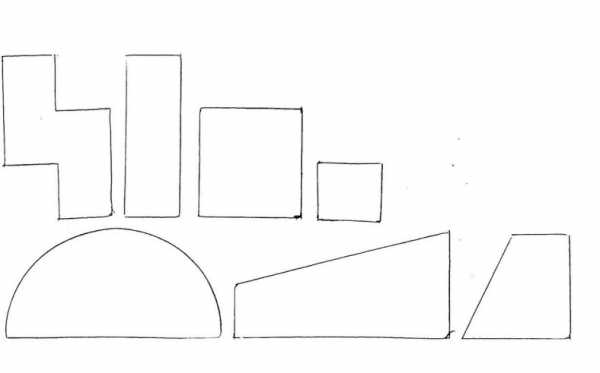
 Приклеиваем на картон:
Приклеиваем на картон: 
 Ждём, пока подсохнет, и начинаем делать своими руками самые оригинальные картинки:
Ждём, пока подсохнет, и начинаем делать своими руками самые оригинальные картинки: 

 Здесь используются заготовки с заданиями, где ребёнок должен сам дорисовать по точкам фигуры, затем раскрасить и вырезать:
Здесь используются заготовки с заданиями, где ребёнок должен сам дорисовать по точкам фигуры, затем раскрасить и вырезать: