Тест — Мегаэнциклопедия Кирилла и Мефодия — статья
Тест (англ. test) — проба, испытание, исследование. В физиологии и медицине тесты используются для изучения физиологических процессов организма (секреторных, моторных), а также для определения функционального состояния отдельных органов, тканей и организма в целом (возбудимости мышц, нервов, дыхательной функции легких). В вычислительной технике тестом называют специально подобранную задачу, предназначенную для проверки правильности функционирования компьютера, а также компьютерных программ. Некоторые тесты одновременно являются диагностическими программами. Особенно большое значение тесты приобрели в психологии и педагогике, где стали стандартизированной процедурой психологического измерения для определения выраженности у индивида психофизиологических и личностных характеристик, а также для количественной оценки знаний, умений и навыков испытуемого.
Впервые тесты в педагогике были использованы в 1864 году Дж. Фишером в Великобритании для проверки знаний учащихся. Теоретические основы тестирования разработал британский психолог Ф. Гальтон (1883). Термин «тест» ввел американский психолог Дж. Кеттел (1890). Предложенная им серия из пятидесяти тестов представляла собой программу определения примитивных психофизиологических характеристик, базирующихся на наиболее разработанных в то время психологических экспериментах. Дж. Кеттел проводил измерения силы правой и левой рук посредством динамометра, скорости реакции на звук.Французский психолог А. Бине применил принципы тестологических исследований к высшим психическим функциям человека: в его серию тестов (1891) вошли задания на испытание памяти, типа представления, внимания, эстетических и этических чувств. Первый стандартизированный педагогический тест был составлен американским психологом Э. Торнодайком. Развитие тестирования способствовало проникновению в психологию и педагогику математических методов. Американский психолог К. Спирмен разработал основные методы корреляционного анализа для стандартизации тестов.Тесты составлялись по единой схеме: определение целей тестирования, составление тестов в черновом виде, апробация тестов на репрезентативной выборке испытуемых и исправление недостатков, разработка шкалы измерений (на основе качественных соображений и статистической обработки результатов) и правил интерпретации результатов. Качество тестов определялось по таким характеристикам, как надежность, валидность (соответствие полученных результатов цели тестирования), дифференцирующая сила заданий.
В зависимости от того, представлен ли в тесте речевой компонент, тесты подразделяются на вербальные и невербальные. Например, тест на словарный запас будет классифицирован как вербальный, а тест, требующий определенных действий в качестве ответа, будет отнесен к невербальным. Групповые и индивидуальные тесты различаются тем, что при групповом тестировании исследуется группа испытуемых. Тесты достижений и личностные тесты различаются на основе того, какие из свойств личности подвергаются тестированию. К тестам достижений относятся тесты успеваемости, тесты творческих возможностей, тесты способностей, сенсорно-моторные тесты и тесты интеллекта. Личностные тесты — это тесты на установки, характерологические тесты, интересы, темперамент и мотивационные тесты. Проективные тесты отличаются отсутствием жестких рамок, их выполнение подразумевает использование фантазии, воображения, позволяет человеку раскрыть свою индивидуальность, неповторимость своего внутреннего мира. Это тесты, служащие для определения личностных особенностей при помощи фиксации реакций на неопределенные и многозначные ситуации. В качестве неопределенной ситуации могут выступать сюжетные картинки, которые надо проинтерпретировать (например, тест ТАТ, в котором испытуемому предлагается составить рассказ к серии картинок с неясным сюжетом, при этом анализ составленных рассказов позволяет выявить установки, ценности, ролевые конфликты и ориентации испытуемого), незаконченные предложения (тест Розенцвейга), чернильные пятна (тест Роршаха). Проективные тесты в результате дают проекции на неопределенные ситуации устойчивых особенностей индивида.Опросники — это разновидность тестов, при использовании которых испытуемому предъявляется ряд вопросов в письменном виде. Более формализованный вариант опросников — тест-опросники — содержат вопросы с закрытым набором ответов. Опросники, в которых вопросы обращены к знанию испытуемого о себе в наиболее прямой форме, принято называть анкетами. Традиционно считается, что анкеты — социологическая методика, а тест-опросники — психологическая. Получили распространение также критериально-ориентированные тесты, позволяющие оценивать испытуемого по отношению к заранее заданной норме, не сравнивая со среднестатистическими данными.
Нормой в тестологии называют среднестатистические данные, полученные в результате предварительного тестирования группы лиц. Переносить интерпретацию полученных результатов можно только на те группы испытуемых, которые по своим основным социокультурным и демографическим признакам аналогичны базовой. Разработка теста предполагает его статистическую проверку по критериям валидности теста, надежности теста, однородности теста, дифференцирующей силы теста, его достоверности и прогностичности.Валидностью теста (англ. validate — объявлять действительным, подтверждать) называют один из основных критериев оценки результатов теста. Понятие «валидности» отражает действительную способность теста измерять ту психологическую характеристику, для диагностики которой он предназначен. Валидность теста представляет собой не только критерий качества теста, но и показатель меры соответствия теста цели тестирования. Мерой валидности выступает коэффициент корреляции результатов теста с другими показателями.
Надежность теста характеризует его устойчивость по отношению к погрешностям измерения, возможность получения одинаковых результатов у испытуемых в различных случаях. Надежность теста определяют путем повторного тестирования через некоторые промежутки времени (от недели до года) одним и тем же тестом. Если корреляция между результатами первичного и повторного тестирования будет высокой, тест определяется как достаточно надежный.
Однородность теста подразумевает согласованность частей теста, включающего много тестовых заданий, направленных на измерение одного свойства. Дифференцирующая сила теста показывает, насколько задание выявляет различия между испытуемыми. Достоверность теста характеризует степень защищенности его результатов от сознательных или бессознательных искажений, вносимых непосредственно испытуемым. Достоверность теста измеряется путем сравнения результатов по обычной инструкции и по инструкции на фальсификацию, а также с помощью специальной шкалы лжи — специализированного теста-опросника, с помощью которого измеряется тенденция испытуемого к выбору социально одобряемых вариантов ответов. Шкалу лжи также называют шкалой социальной желательности. Прогностичность теста характеризует вероятность соответствия результатов тестирования результатам последующей деятельности.
megabook.ru
ТЕСТ это что такое ТЕСТ: определение — Философия.НЭС
ТЕСТ
англ.-проба, испытание, исследование): в психодиагностике или в учебном процессе это своего рода испытание, кратковременное стандартизированное задание, позволяющее измерить уровень формализуемых знаний, а также степень развития тех или иных психологических свойств личности, ее способностей к определенной деятельности, общению с другими людьми и т.д.
Оцените определение:
Источник: «Евразийская мудрость от а до Я», толковый словарь
ТЕСТ
испытание, цель которого — определение уровня функции (интеллекта, творческих способностей) или степени ее развитости (у молодых). Тесты могут определять не только уровень умственного развития (тесты на сбор головоломок, восстановление фигур на основе отдельных элементов и т.д.)-, но также формы характера (тест Роршаха, при котором показывают чернильное пятно и спрашивают субъекта, что оно ему напоминает). Использование тестов широко используется при приеме в армию; оно является обязательным в случае смены профессии, широко применяется в системе школьной и профессиональной ориентации. См. Разделение труда, Ум, Профессиональная ориентация, Селекция.
Оцените определение:
Источник: Философский словарь
ТЕСТ
(англ. test — проба, испытание, исследование) — 1) В психологии и педагогике: стандартизированные задания, по результатам выполнения крых судят о психофизиол. и личностных характеристиках, а также знаниях, умениях и навыках испытуемого. Нек-рые социол. вопросники и анкеты также имеют вид Т. 2) В физиологии и медицине: пробные воздействия на организм с целью изучения разл. физиол. процессов в нем, а также для определения функционального состояния отд. органов, тканей и организма в целом. 3) В технике: комплекс измерений и пробных запусков аппаратуры с целью проверки правильности ее функционирования. В вычислит. технике — контрольная задача для проверки правильности работы ЭВМ. 4) В распознавании образов: мн-во функционально взаимозависимых признаков, характеризующих образ (класс). Б.Н.Махутов
Оцените определение:
Источник: История и философия науки. Энциклопедический словарь
ТЕСТ
англ. test — проба, испытание, исследование) в психологии, стандартизированные задания, результат выполнения к-рых позволяет измерять нек-рые психофизиологич. и личностные характеристики, а также знания, умения и навыки испытуемого.
Т. начали применяться в 1864 Дж. Фишером в Великобритании для проверки знаний учащихся. Теоретич. основы тестирования были разработаны англ. психологом Ф. Гальтоном (1883). Термин «Т.» впервые ввел амер. психолог Дж. Кеттел (1890). Франц. психолог А. Бине применил принцип тестологич. исследований к высшим психич. функциям человека: в его серию Т. (1891) вошли задания на испытание памяти, типа представления, внимания, эстетич. и этич. чувства и т. д. Нем. психолог В. Штерн ввел коэффициент интеллектуальности (1911).
В нач. 20 в. начинают разграничиваться психологич. и педагогич. направления в разработке Т. Первый стандартизированный педагогич. Т. был составлен амер. психологом Э. Торндайком. Развитие тестирования было одной из причин, обусловивших проникновение в психологию и педагогику математич. методов. Статистич. методы К. Спирмена (в частности, применение факторного анализа) сыграли
terme.ru
|
|
Главная >>> Из истории тестов Сегодня тесты активно используются в образовательном процессе. А задумывались ли вы над тем когда же появился первый тест? Как оказалось, история возникновения и использования тестирования как диагностического метода уходит в глубь веков. Есть сведения, что уже с III тысячелетия до н.э. в странах Древнего Востока использовались системы конкурсных испытаний интеллектуального характера, предназначенные для отбора персонала на правительственные должности. Однако всё вышеперечисленное нельзя назвать тестами в современном понимании этого термина. Широкое развитие применение тестов в образовательном процессе
получило за рубежом. В школьной практике тесты начали применяться
Ф.Галтоном в 1892 году. В 1894 году впервые в школах появились тесты
успешности (для проверки знаний, умений и навыков учащихся п 1. Период поисков (1900—1915). На этом этапе происходило осознание и первоначальное внедрение тестов памяти, внимания, восприятия и других, предложенных французским психологом А. Бинэ. Разрабатываются и проверяются тесты интеллекта, позволяющие определять коэффициент умственного развития. 2. Последующие 15 лет — годы «шума» в развитии школьного тестирования, приведшие к окончательному осмыслению его роли и места, возможностей и ограничений. Были разработаны и внедрены тесты О. Стоуна по арифметике, Б. Зекингема для проверки правописания, Э. Торндайка по диагностике большинства школьных предметов. Т. Келли разработал способ измерения интересов и наклонностей обучаемых (при изучении алгебры), а Ч. Спирмен предложил общие основы использования корреляционного анализа для стандартизации тестов. 3. С 1931 г. начинается современный этап развития школьного тестирования. Поиски специалистов направляются на повышение объективности тестов, создание непрерывной (сквозной) системы школьной тестовой диагностики, подчиненной единой идее и общим принципах, созданию новых, более совершенных средств предъявления и обработки тестов, накопления и использования диагностической информации. Педагогика, развившаяся в России в начале века, безоговорочно приняла тестовую основу объективного школьного контроля. Первые научные труды по теории тестов появилась в начале ХХ века, на стыке психологии, социологии, педагогики и других так называемых поведенческих наук. Педагогическая тестология — это прикладная методическая теория научной педагогики. Ключевыми понятиями тестологии, как одной из методических теорий, являются измерение, тест, содержание и форма заданий, надежность и валидность результатов измерения. Кроме того, в тестологии используются такие понятия статистической науки, как выборочная и генеральная совокупность, средние показатели, вариация, корреляция, регрессия и др. Распространение психолого-педагогической диагностики в России связано с возникновением в 20-е годы XX века новой науки – педологии, которую Л.С. Выготский определял как науку о целостном развитии ребенка. Проблемой разработки тестов вплотную занимались видные российские ученые: М.С. Бернштейн, П.П. Блонский, А.П. Болтунов, С.Г. Геллерштейн, Г.И. Залкинд, И.Н. Шпильрейн, А.М. Шуберт и др. Однако, начиная с 30-х годов наука о тестах стала называться буржуазной, все её цели считались «реакционными». После известного постановления ЦК ВКП(б) «О педологических извращениях в системе Наркомпроса» (1936) были ликвидированы не только интеллектуальные, но и безобидные тесты успеваемости. Попытки возродить их в 70-х годах ни к чему не привели. В этой области наша наука и практика значительно отстали от зарубежной. Однако, в последние годы мы наблюдаем активное внедрение тестов в образовательный процесс. И не смотря на недостатки, которые имеют место при использовании такой формы контроля и оценки знаний, тестирование занимает довольно прочную позицию.
Главная >>> Из истории тестов |
www.testobr.narod.ru
Управление персоналом, образование, личное развитие. Тесты. Внимание. Память. IQ-тесты. Effecton Studio. Эффектон
Истоки экспериментальной психологии
Эксперимент в психологии стал решающим фактором в преобразовании психологических знаний, он выделил психологию из философии и превратил ее в самостоятельную науку. Различные виды исследования психики при помощи экспериментальных методов это и есть экспериментальная психология.
С конца 19 века ученые вплотную занялись изучением элементарных психических функций — сенсорных систем человека. Вначале это были первые робкие шаги, которые подвели фундамент под здание экспериментальной психологии, отделив ее от философии и физиологии.
Особенно следует заметен Вильгельм Вундт (1832-1920), немецкий психолог, физиолог, философ и языковед. Он создал первую в мире психологическую лабораторию (международный центр). Из этой лаборатории, получившей впоследствии статус института, вышло целое поколение специалистов по экспериментальной психологии.
В первых своих работах В. Вундт выдвинул план разработки физиологической психологии как особой науки, использующей метод лабораторного эксперимента для расчленения сознания на элементы и выяснения закономерной связи между ними.
Предметом психологии Вундт считал непосредственный опыт — доступные самонаблюдению явления или факты сознания; однако высшие психические процессы (речь, мышление, воля), он считал недоступными эксперименту, и предложил изучать их культурно-историческим методом.
Вначале главным объектом экспериментальной психологии считались внутренние психические процессы нормального взрослого человека, анализируемые с помощью специально организованного самонаблюдения (интроспекции), а затем эксперименты проводились над животными (К. Ллойд-Морган, Э. Ли Торндайк), исследовались душевнобольные, дети.
Экспериментальная психология начинает исследовать не только общие закономерности психических процессов, но и индивидуальные изменения чувствительности, времени реакции, памяти, ассоциаций и т.д. (Ф. Гальтон, Д. Кеттел).
Гальтон разработал приёмы диагностики способностей, которые положили начало тестированию, методы статистической обработки результатов исследований (в частности, метод исчисления корреляций между переменными), массовое анкетирование.
Кеттел рассматривал личность как совокупность некоторого числа эмпирически (при помощи тестов) установленных и более или менее автономных психологических характеристик.
Предпосылкой возникновения дифференциальной психологии, изучающей индивидуальные различия между людьми и группами, на рубеже 19 и 20 веков явилось введение в психологию эксперимента, а также генетических и математических методов.
В настоящее время методы экспериментальной психологии широко применяются в различных областях человеческой деятельности. Прогресс человеческого познания уже немыслим без методик экспериментальной психологии, тестирования, математической и статистической обработки результатов исследований. Успехи экспериментальной психологии основаны на использовании методов различных наук: физиологии, биологии, психологии, математики.
Тест, тестирование
Тест (англ. test — проба, испытание, исследование) экспериментальный метод в психологии и педагогике, стандартизированные задания, позволяющие измерить психофизиологические и личностные характеристики, а также знания, умения и навыки испытуемого.
Тесты начали применяться в 1864 году Дж. Фишером в Великобритании для проверки знаний учащихся. Теоретические основы тестирования были разработаны английским психологом Ф. Гальтоном в 1883 году: применение серии одинаковых испытаний к большому числу индивидов, статистической обработке результатов, выделение эталонов оценки.
Термин «тест» впервые ввёл американский психолог Дж. Кеттел в 1890 году. Предложенная им серия из 50 тестов фактически представляла программу определения примитивных психофизиологических характеристик: базирующихся на наиболее разработанных в то время психологических экспериментах (например, измерение силы правой и левой рук посредством динамометра, скорости реакции на звук, и т.д.)
Французский психолог А. Бине применил принципы тестологических исследований к высшим психическим функциям человека: в его серию тестов (1891) вошли задания на испытание памяти, типа представления, внимания, эстетические и этические чувства и т.д.
Первый стандартизированный педагогический тест был составлен американским психологом Э. Торнодайком. Развитие тестирования было одной из причин, обусловивших проникновение в психологию и педагогику математических методов.
Американский психолог К. Спирмен разработал основные методы корреляционного анализа для стандартизации тестов и объективного измерения тестологических исследований. Статистические методы Спирмена — применение факторного анализа — сыграли большую роль в дальнейшем развитии тестирования.
Значительное распространение тестирование получило в психотехнике для профессионального отбора. Интенсивное развитие психотехники приходится на время 1-й мировой войны 1914-1918 года, когда первоочередными стали вопросы профессионального отбора для нужд армии и военного производства. В связи с этим широкое применение в психотехнике имеет метод тестов.
Наибольшее развитие тестологического исследования получили в США (например, за время 2-й мировой войны с 1939 по 45 год при мобилизации в армию было тестировано около 20 миллионов человек). В России составление и применение тестов относится к 20-м годам прошлого века, в 1926 году была опубликована первая серия тестов для школ.
С конца прошлого века эксперимент стал применяться и в исследовании высших умственных процессов (суждения, умозаключения, мышления), хотя раньше неоднократно высказывалось убеждение, что эксперимент может применяться только к элементарным психическим процессам.
Для чего нужны психологические тесты? Чтобы выяснить, что испытуемый может, а какие задачи пока решить не в состоянии. Для этого в тест вводится определенное содержание в отношении тех знаний и умений, которые будут изучаться.
Составление тестов строится по единой схеме: определение целей тестирования, составление тестов в черновом виде, апробация тестов на репрезентативной выборке испытуемых и исправление недостатков, разработка шкалы измерений (на основе качественных соображений и статистической обработки результатов) и правил интерпретации результатов.
Качество тестов определяется по таким характеристикам, как надёжность, валидность (соответствие полученных результатов цели тестирования), дифференцирующая сила заданий и др.
Валидность теста — это его психометрическая характеристика, действительная способность теста измерять ту психологическую характеристику, для диагностики которой он заявлен и указывает на степень соответствия получаемой информации диагностируемому психическому свойству.
Количественно валидность теста может выражаться через корреляции результатов, полученных с его помощью, с другими показателями, например, с успешностью выполнения соответствующей деятельности. Совокупность характеристик валидности теста, полученных экспериментально-статистическим способом — валидность эмпирическая.
Практическое использование тестирования связано главным образом с диагностированием личностных характеристик человека, выражаемых через количественные показатели.
Виды тестов
Различают тесты вербальные и невербальные, это зависит от того, представлен или нет в тесте речевой компонент. Так, тест на словарный запас — вербальный, невербальный — тест, требующий определенных действий в качестве ответа.
Групповые и индивидуальные тесты отличаются тем, что при групповом тестировании исследуется группа испытуемых.
Тесты достижений и личностные тесты различаются на основе того, какие из свойств личности подвергаются тестированию.
Тесты достижений — это тесты успеваемости, тесты творческих возможностей, тесты способностей, сенсорно-моторные тесты и, конечно, тесты интеллекта.
Личностные тесты — это тесты на установки, характерологические тесты, интересы, темперамент и мотивационные тесты. Однако понятно, что это деление довольно схематично, возможны некоторые отклонения.
Объективные тесты включают в себя большинство тестов достижений и психофизиологических тестов. Это отличается от субъективных тестов, при выполнении которых испытуемый может не предполагать о действительной цели исследования.
Проективные тесты в результате дают ответ, который не может быть расценен как «правильный» или «не правильный», а должен быть дан свободный ответ, т.е. должен быть такой способ построения тестового задания, при котором испытуемый должен получить ответ «из головы», а не выбирать его из заданного списка.
Простые и сложные тесты различаются тем, что последние состоят из нескольких самостоятельных подтестов, по каждому из которых должен быть получен ответ, при этом высчитывается общая оценка. В случае соединения нескольких единичных тестов образуется тестовая батарея или пакет тестов.
Опросники также могут быть отнесены к тестам, если они удовлетворяют требованиям, предъявляемым к данному методу сбора психологической или социологической информации.
В настоящее время получили распространение критериально-ориентированные тесты, позволяющие оценивать испытуемого по отношению к заранее заданной норме, не сравнивая со среднестатистическими данными.
Результаты тестирования
Норма в тестологии — это среднестатистические данные, полученные в результате предварительного тестирования определенной группы лиц. Переносить интерпретацию полученных результатов можно только на те группы испытуемых, которые по своим основным социокультурным и демографическим признакам аналогичны базовой.
Для повышения надежности результатов необходимо увеличить базовые выборки, т.е. повысить репрезентативность, ввести поправочные коэффициенты с учетом характеристик выборки, ввести невербальный способ предъявления материала.
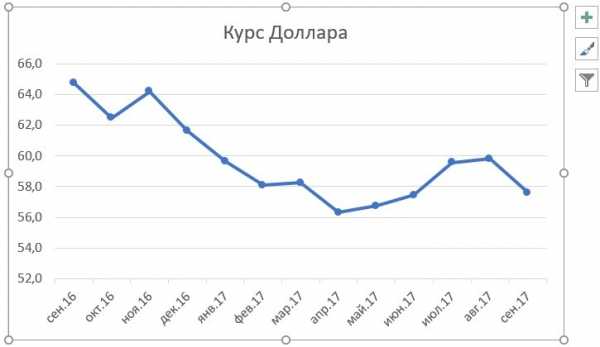
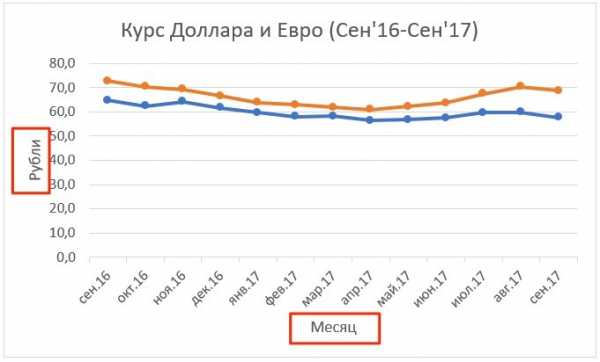
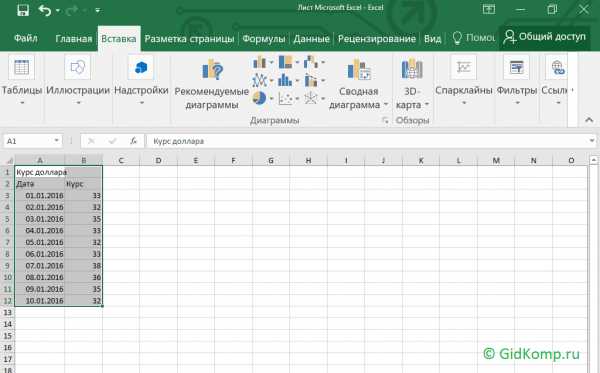
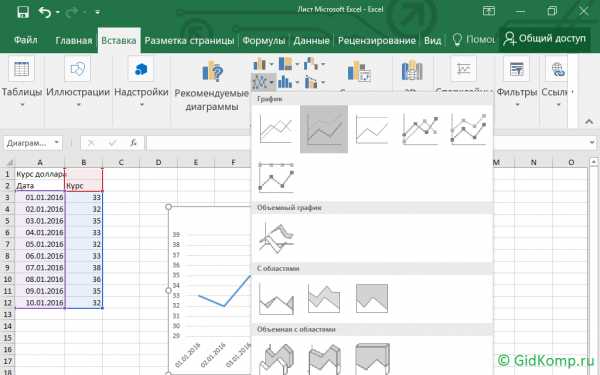
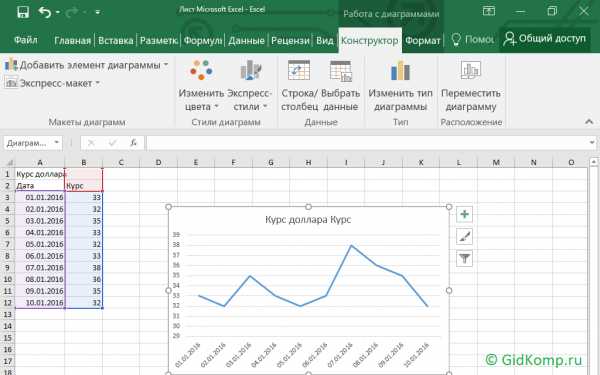
Для наглядности результаты тестирования могут быть представлены в виде графического изображения по каждому подтесту тестовым профилем.
Эксклюзивный материал сайта «www.effecton.ru — психологические тесты и коррекционные программы». Заимствование текста и/или связанных материалов возможно только при наличии прямой и хорошо различимой ссылки на оригинал. Все права защищены.
www.effecton.ru
ТЕСТЫ это что такое ТЕСТЫ: определение — Социология.НЭС
Тесты
задания, которые исследователь предлагает информантам (см. информант) (списки слов, которые надо прочитать перед микрофоном, или связный текст, также читаемый информантом вслух; письменные задания на восстановление пропущенных фрагментов текста; ответы на устные вопросы исследователя, задаваемые в определенном временном режиме).
Оцените определение:
Источник: Краткий толковый словарь социолингвистических терминов
ТЕСТ (В СОЦИОЛИНГВИСТИКЕ)
Один из методов сбора социолингвистических данных, используемый чаще всего для обследования речевых навыков билингва, состоящий в том, что информанту предлагаются устные и письменные задания, представляющие собой: 1) связные тексты; 2) списки слов; 3) задание ответить на вопросы; 4) задание на восстановление пропущенных мест в тексте и т.п.
Оцените определение:
Источник: Термины и понятия лингвистики. Общее языкознание. Социолингвистика. Словарь-справочник
ТЕСТ
от англ. test — проба, испытание, исследование) — 1. Стандартизированные задания, рез-т выполнения к-рых позволяет измерять нек-рые психофизические и личностные характеристики, а также знания, умения, навыки испытуемого. 2. Вопросник, распространяемый как материал, используемый для конкретных социологич. исследований. 3. В вычислительной технике — задача с известным решением, предназначенная для проверки правильности работы цифровой вычислительной машины.
Оцените определение:
Источник: Российская социологическая энциклопедия
ТЕСТ
от англ. test — проба, испытание, исследование) — англ. test; нем. Test. 1. Стандартизированные задания, результат выполнения к-рых позволяет измерять нек-рые психофизические и личностные характеристики, а также знания, умения, навыки испытуемого. 2. Вопросник, распространяемый как материал, используемый для конкретных социологических исследований. 3. В вычислительной технике — задача с известным решением, предназначенная для проверки правильности работы цифровой вычислительной машины.
Оцените определение:
Источник: Большой словарь по социологии, проект www.rusword.com.ua
Тест
от англ. test – испытание; проверка) метод измерения и оценки отдельных свойств индивида, плохо поддающихся прямому наблюдению, сист
voluntary.ru
Контрольный тест по социологии (вариант 1) » СтудИзба
Тесты / Социология41 179
0
Вопросы написаны с порядковым номером подчёркнутым шрифтом. Варианты ответов даны со знаком минус («—«) перед ним, а правильные ответы выделены жирным шрифтом со знаком плюс («+«) перед ним.1. Термин «социология» был предложен
— И.Кантом
+ О.Контом
— Э.Дюркгеймом
— М.Вебером
2. Вместо термина «социология» некоторое время использовался термин
— социальная философия
— обществоведение
+ социальная физика
Кстати если Вы хотите получить достойные знания по английскому языку (к примеру для поступления в ВУЗ), то рекомендуем посетить сайт https://marcuseducate.com/services/language-courses/, где без труда можно найти всё, что необходимо в области изучения иностранных диалектов. Английский язык позволяет не только работать в качестве переводчика, а сильно расширяет круг лиц, с которыми можно работать в любой области.
3. Социально-исторической предпосылкой возникновения социологии является
— формирование правового государства
— углубление расслоения общества
— повышение уровня образования населения
+ становление рыночной экономики
4. Опытно-рациональный тип познания отличается от философского
— упорядоченностью
— доказательностью
+ неаксиологичностью
— мировоззренческой направленностью
5. О.Конт назвал метафизической такую стадию развития человеческого мышления, для которой характерны
— вера в сверхъестественное
— опора на факты
— сочетание эмпирии и теории
+ поиск всеобщих сущностей
6. Принцип верификации означает
— независимость знания от ценностной позиции ученого
+ эмпирическую проверку истинности научных утверждений
— непосредственное доказательство научных выводов
— общезначимость научных выводов
7. Принцип общезначимости означает
+ повторяемость, воспроизводимость проведенного исследования
— значимость культурных ценностей для представителей другой культуры
— возможность заимствования одной культурой результатов исследования, проведенного в рамках другой культуры
— значимость результатов исследования одной науки для других наук
8. Ведущую роль в социологическом исследовании играет
— факт
— эмпирия
+ теория
— гипотеза
9. Фундаментальное исследование
— обязательно носит теоретический характер
+ направлено на выявление важнейших социальных связей и тенденций
— имеет междисциплинарный характер, учитывает достижения других наук
— не проверяется эмпирическим путем
10. Социология в отличие от истории
— опирается на факты
— устанавливает причинно-следственные связи
— стремится к индивидуализации
+ стремится к генерализации
11. К числу генерализирующих наук об обществе относится
— психология
+ экономика
— история
— теология
12. Э.Дюркгейм считал, что социология должна изучать
— конечные причины социальных явлений
— обыденные представления людей об обществе
+ социальные факты
— общество в целом
13. «Всякий объект познания, который сам по себе непроницаем для ума», Э.Дюркгейм назвал
— фактом
+ вещью
— теорией
— чувством
14. Предпонятием Э.Дюркгейм назвал понятие
— возникшее на ранних стадиях развития науки
+ сформировавшееся в обыденном сознании
— возникшее в рамках других наук
— сформулированное философией
15. Э.Дюркгейм считал, что изучение социальных фактов следует начинать с
— их индивидуальных проявлений
— выяснения их сущности
+ внешних, очевидных признаков
— образования научных понятий
16. М.Вебер полагал, что оценочные суждения на страницах научного журнала
— вообще не должны присутствовать
— допустимы при условии их критики
— допустимы, если они приближают нас к истине
+ допустимы при условии четкого отделения оценок от научных фактов
17. С точки зрения М.Вебера, создание «общезначимых последних идеалов» является задачей
— социологии
— любой эмпирической науки
+ философии
— психологии
18. Вопрос: «Какое воззрение вероятно сложится у определенных лиц в конкретных условиях…на проблему любого типа?» является
+ научным
— оценочным
— одновременно и научным, и оценочным
19. Утверждение М. Вебера о том, что в сфере социологии «проблемы складываются в результате отнесения реальностей к ценностям» означает, что
социология изучает такую реальность, которая по своей природе является ценностной
— социология не свободна от оценочных суждений
— результаты социологических исследований зависят от тех ценностей, которых придерживается исследователь
20. С точки зрения М.Вебера, понимание является категорией
— философской
— психологической
— исторической
+ социологической
21. Вебер считал, что социологические понятия в отличие от исторических обладают большей
+ однозначностью
— содержательностью
— реалистичностью
— конкретностью
22. Вебер утверждал, что идеальный тип является для социологии
+ средством познания
— целью исследования
— исследовательской гипотезой
23. С точки зрения А.Щюца, путаница в понимании соотношения методов естественных и общественных наук связана с тем, что
+ научная логика длительное время была связана с логикой естественных наук
— обществоведы слишком увлеклись философией
— общественные науки длительное время не имели общей теории
— обществоведы не могут использовать лабораторные эксперименты
24. А.Щюц понимал под термином «социальная реальность»
— все то, что происходит в обществе
+ повседневное взаимодействие людей
— все то, что не является природой
— субъективный мир человека
25. С точки зрения А.Щюца, для того, чтобы понять поступки другого человека, достаточно обладать
— научным знанием социальной реальности
— научным знанием внутреннего мира индивида
+ обыденным знанием повседневной жизни
26. А.Щюца выдвигал следующее требование к научным конструкциям. Они должны
— быть отражением системы ценностей ученого
— совпадать с конструкциями обыденного сознания
+ соответствовать конструкциям обыденного сознания
— представлять практический интерес для ученого
27. Теория Э.Дюркгейма объясняет самоубийство как результат
— недовольства собой и своей жизнью
— отклонения от социальных норм
+ социальной изоляции индивидов
— переживаний по поводу своего одиночества
— резких социальных трансформаций
28. Впервые разграничение понятий «общество» и «государство» происходит в:
— эпоху Научной революции 17 в.
— в античной философии
— в трудах О.Конта
+ в эпоху Просвещения
29. О.Конт выделял следующие стадии в развитии мышления:
+ теологическую, метафизическую, позитивную
— теологическую, биологическую, психологическую
— мифологическую, онтологическую, гносеологическую
— мифологическую, абстрактную, конкретную
30. Переход от умозрительной модели научного знания к опытно-рационалистической первыми совершили
— социальные науки
+ естественные науки
— философские науки
— исторические науки
31. Одной из предпосылок возникновения социологии явилось:
— возникновение государства
— возникновение неравенства
— появление первых университетов
+ формирование гражданского общества
32. Представителями структурно-функционального направления в социологии являются:
— М.Вебер, Г.Зиммель
— У.Томас, Р.Парк
+ Т.Парсонс, Р.Мертон
— Г.Гарфинкель, Э.Гидденс
33. С точки зрения П.Монсона парк символизирует
— социальные институты
— социальные действия
+ социальную структуру
— социальные группы
34. Феномен «топтания по клумбам» символизирует у П.Монсона
+ отклоняющееся поведение
— социальные изменения
— социальное давление
35. Поведение посетителей парка характеризует, по мнению П.Монсона, направление, называемое
— позитивизм
+ структурализм
— экзистенциализм
— неомарксизм
36. Экзистенциализм (по П.Монсону) рассматривает общество как
— самостоятельную реальность
+ как результат поступков отдельных индивидов
— заранее установленный порядок
37. Согласно З.Бауману, социология изучает
— общество в целом
+ сети социальных связей
— действия отдельных индивидов
38. Социология, в отличие от здравого смысла (согласно З.Бауману):
+ подчиняется правилам ответственных высказываний
— сужает «размеры поля», на котором собирается исследовательский материал
— объясняет социальные ситуации как результат чьих-то преднамеренных действий Рейтинг статьи:
| Поделитесь ссылкой пожалуйста: | |
Похожие статьи
Контрольный тест по социологии (вариант 2) Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.
studizba.com
Тест с ответами по переводоведению 2 курс
~1. Переводческие организации FIT и AIIC являются:
+а) международными организациями
-б) региональными организациями
-в) национальными организациями
-г) американскими организациями
~2. Первым российским ВУЗом, обучающим переводу, стал:
-а) РГГУ
-б) МГУ
+в) Московский педагогический институт им. Мориса Тореза
-г) ЛГУ
~3. Появление лингвистической теории перевода связано:
-а) с деятельностью советских переводчиков во время II Мировой войны
+б) с развитием общей лингвистики и увеличением количества переводов во всем мире
-в) с Нюренбергским процессом после II Мировой войны
-г) с научными исследованиями Л.С. Бархударова
~4. Пользующиеся переводом идентифицируют его с оригиналом функционально, структурно и семантически. Какая идентификация является самой важной?
-а) функциональная идентификация
-б) структурная идентификация
-в) функциональная и структурная идентификация
+г) семантическая идентификация
~5. Перевод с точки зрения лингвистической теории это:
+а) процесс преобразования речевого произведения на одном языке в текст на другом языке, а также результат этого процесса
-б) процесс преобразования речевого произведения на одном языке в текст на другом языке
-в) результат процесса, т.е. сам переведенный текст
-г) текст, перекодированный знаками другой семиотической системы
~6. К какой отрасли лингвистики относится теория перевода?
-а) микролингвистика и теоретическая лингвистика
+б) макролингвистика и прикладная лингвистика
-в) макролингвистика и теоретическая лингвистика
-г) прагматика
~7. Проблемами перевода с одного данного языка на другой данный язык занимается:
-а) общая теория перевода
+б) частная теория перевода
-в) процессуальная транслятология
-г) специальная теория перевода
~8. Проблемами перевода текстов разных типов и жанров занимается:
-а) история перевода
-б) частная теория перевода
-в) общая теория перевода
+г) специальная теория перевода
~9. Самый популярный искусственно созданный язык называется:
-а) паскаль
-б) банту
-в) лингво
+г) эсперанто
~10. “h3O – вода” – это пример:
-а) внутриязыкового перевода
-б) межъязыкового перевода
+в) межсемиотического перевода
-г) научного перевода
~11. Основной единицей перевода выступает:
-а) морфема
-б) слово
+в) единица любого уровня языка
-г) предложение
~12. “Birds of a feather flock together – Рыбак рыбака видит издалека”. В этом примере единицей перевода выступает:
-а) слово
+б) предложение
-в) текст
-г) словосочетание
~13. “teenager – тинэйджер”. В этом примере единицей перевода выступает:
-а) слово
-б) морфема
+в) фонема
-г) графема
~14. В зависимости от формы речи различают два основных вида перевода:
+а) письменный и устный
-б) последовательный и синхронный
-в) художественный и информативный
-г) буквальный и свободный
~15. Теории принципиальной непереводимости придерживались такие ученые как:
+а) В. Гумбольдт, Э. Сепир, Б. Уорф
-б) Декарт, Лейбниц
-в) Л.С. Бархударов, Я.И. Рецкер, В.Н. Комиссаров
-г) Аристотель, Цицерон, Тайтлер
~16. Теория языковых универсалий Н. Хомского является подтверждением
+а) абсолютной переводимости языков
-б) принципиальной непереводимости языков
-в) относительной переводимости языков
-г) структурных различий языков
~17. В отношении какой исторической концепции эквивалентности применяется термин “рабский перевод”
-а) концепция эстетического соответствия
+б) концепция формального соответствия
-в) концепция динамического соответствия Ю. Найды
-г) теория “скопоса”
~18. Какая концепция переводческой эквивалентности утверждает, что перевод является эквивалентным только в том случае, если реакция реципиента ПТ в целом совпадает с реакцией реципиента ИТ
-а) концепция эстетического соответствия
-б) концепция формального соответствия
+в) концепция динамического соответствия Ю. Найды
-г) концепция нормативно-содержательного соответствия
~19. Автором теории “скопоса” является/являются:
-а) Ю. Найда
-б) В.Н. Комиссаров
-в) В. Коллер
+г) К. Райс и Х. Фермеер
~20. Какой уровень переводческой эквивалентности характеризуется наибольшей степенью семантической близости между ИТ и ПТ?
-а) уровень цели коммуникации
-б) уровень идентификации ситуации
+в) уровень семантики слов
-г) уровень способа описания ситуации
~21. Какой уровень переводческой эквивалентности характеризуется наименьшей степенью семантической близости между ИТ и ПТ?
+а) уровень цели коммуникации
-б) уровень идентификации ситуации
-в) уровень семантики слов
-г) уровень синтаксических значений
~22. В каких типах текстов минимальной единицей перевода может выступать целый текст?
-а) юридические документы
-б) научные тексты
+в) поэзия, рекламный слоган, общественные указатели
-г) речи политиков
~23. “З хама не зробиш пана – Can the leopard change his spots?”. На каком уровне эквивалентности выполнен данный перевод?
+а) на уровне цели коммуникации
-б) на уровне идентификации ситуации
-в) на уровне способа описания ситуации
-г) на уровне синтаксических значений
~24. Степень семантической близости между ИТ и ПТ называется:
-a) принципиальной переводимостью
+б) переводческой эквивалентностью
-в) адекватным переводом
-г) семантической идентификацией ИТ и ПТ
~25. “I saw him at the theatre. – Я видел его в театре”. На каком уровне эквивалентности выполнен данный перевод?
-а) на уровне цели коммуникации
-б) на уровне идентификации ситуации
-в) на уровне синтаксических значений
+г) на уровне семантики слов
~26. Translatese – это:
-а) искусственно созданный язык
+б) перевод, в котором нарушаются нормы ПЯ, особенно стилистическая норма
-в) адекватный перевод
-г) переводческое соответствие
~27. “piece – часть, обломок, штука, пьеса, образец”. Какое переводческое соответствие иллюстрирует приведенный пример:
+а) множественное
-б) единичное
-в) окказиональное
-г) лексическое
~28. Какой из нижеприведенных примеров иллюстрирует единичное переводческое соответствие:
+а) House of Commons – Палата общин
-б) landslide victory – победа на выборах подавляющим большинством голосов
-в) piece – часть, обломок, штука, пьеса, образец
-г) Do in Rome as the Romans do – В Риме поступай так, как римляне
~29. Ситуативный контекст – это:
-а) языковое окружение, в котором употребляется та или иная единица языка в тексте
+б) обстановка, время и место, к которому относится данное высказывание
-в) условия, в которых проходит процесс перевода
-г) особенности синтаксической структуры, в которой употребляется данная языковая единица
~30. Регулярные переводческие соответствия встречаются:
-а) только на уровне слов
-б) только на уровне морфем
-в) только на уровне фонем
+г) на всех уровнях языковой системы
~31. Единичное переводческое соответствие между единицами ИЯ и ПЯ означает:
-а) соответствие 1 : много
+б) соответствие 1 : 1
-в) соответствие 1 : часть
-г) соответствие 1 : 0
~32. Назовите две основные тенденции в истории перевода.
+а) буквальный и свободный перевод
-б) письменный и устный перевод
-в) перевод религиозных текстов и перевод торговых документов
-г) художественный и технический перевод
~33. “He has friendly attitude towards all. – Он ко всем относится по-дружески”. Какой тип переводческого соответствия применяется в данном примере?
-а) множественное
-б) единичное
-в) регулярное
+г) окказиональное
~34. “He graduated from New Haven in 1915. – Он окончил Йельский университет в 1915 году”. Какой тип переводческого соответствия применяется в данном примере?
-а) множественное
-б) единичное
-в) регулярное
+г) окказиональное соответствие или контекстуальная замена
~35. При переводе Библии и других религиозных текстов в древности применялась концепция:
-а) эстетического соответствия
+б) формального соответствия
-в) адекватного перевода
-г) динамической эквивалентности
~36. Какая из перечисленных ниже стратегий перевода является неверной?
+а) Всегда следует переводить отдельные слова, а не все высказывание.
-б) Понимание ИТ всегда должно предшествовать переводу и быть обязательным условием перевода.
-в) Следует переводить значение ИТ, избегая слепого копирования формы оригинала.
-г) Перевод должен полностью соответствовать нормам и правилам ПЯ.
~37. В какую историческую эпоху к переводу предъявлялось требование улучшать оригинал, так чтобы он соответствовал некоему эстетическому идеалу?
-а) Античность
+б) Классицизм
-в) Возрождение
-г) Средние века
~38. Переводческое соответствие 1:0 по В. Коллеру означает, что:
-а) в ИЯ отсутствует данный эквивалент
+б) в ПЯ отсутствует данный эквивалент
-в) эквивалент в ПЯ является неполным
-г) в ПЯ существует несколько эквивалентов данной единице ИЯ
~39. При переводе имен собственных, терминов, географических названий, названий дней недели обычно применяются:
-а) контекстуальные замены
-б) окказионализмы
+в) единичные соответствия
-г) множественные соответствия
~40. Передача графической формы слова ИЯ при помощи другой графической системы ПЯ называется:
-а) буквальный перевод
-б) транскрипция
-в) вольный перевод
+г) транслитерация
~
testdoc.ru

 о
отдельным учебным дисциплинам – первыми стали применяться тесты для
проверки правописания). Американец В.А. Макколл разделил тесты на
педагогические (Educational Test) и психологические (Intelligence
Test) Макколл обосновал цель использования педагогических тестов –
объединение в группы учащихся, усваивающих равный по объёму материал
с одинаковой скоростью. Однако основоположником педагогических
измерений считается американский психолог Э. Торндайк (1874—1949).
Ему приписывают разработку первого педагогического теста. В
1904 году вышла его книга «Введение в теорию психологии и социальных
измерений». Признанный
авторитет в области педагогического тестирования Э. Торндайк выделяет три этапа внедрения тестирования в практику
американской школы:
о
отдельным учебным дисциплинам – первыми стали применяться тесты для
проверки правописания). Американец В.А. Макколл разделил тесты на
педагогические (Educational Test) и психологические (Intelligence
Test) Макколл обосновал цель использования педагогических тестов –
объединение в группы учащихся, усваивающих равный по объёму материал
с одинаковой скоростью. Однако основоположником педагогических
измерений считается американский психолог Э. Торндайк (1874—1949).
Ему приписывают разработку первого педагогического теста. В
1904 году вышла его книга «Введение в теорию психологии и социальных
измерений». Признанный
авторитет в области педагогического тестирования Э. Торндайк выделяет три этапа внедрения тестирования в практику
американской школы:
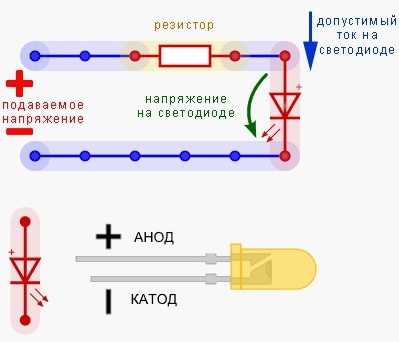
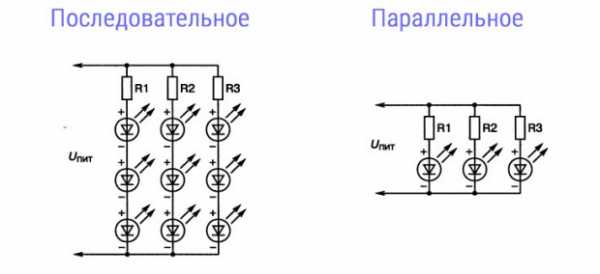
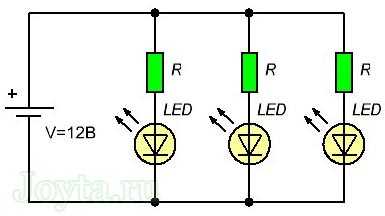
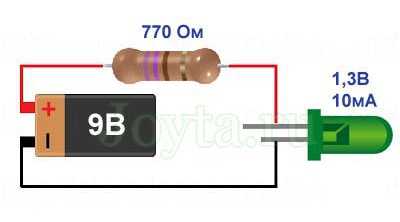
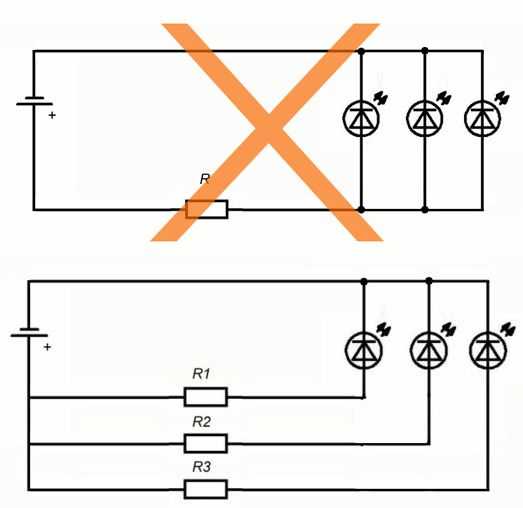
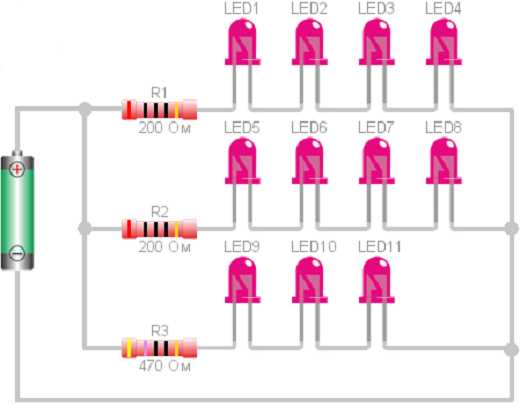
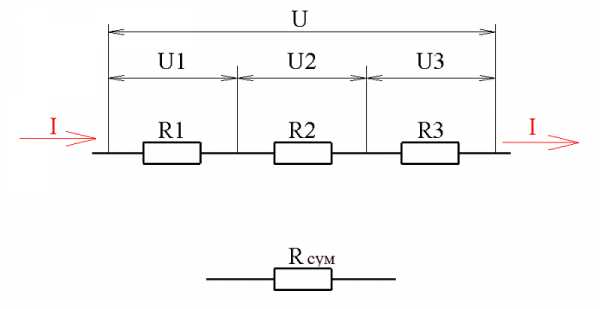 Последовательное соединение резисторов
Последовательное соединение резисторов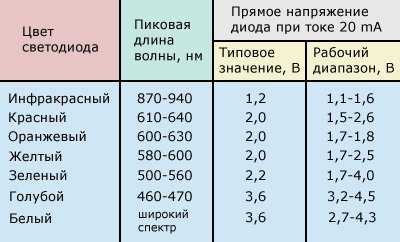
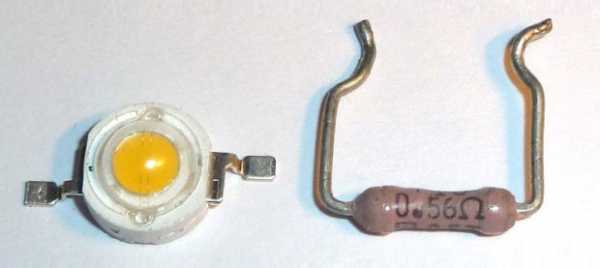

 Отличие характеристик кристаллов для дешевых ЛЕД
Отличие характеристик кристаллов для дешевых ЛЕД

 Китайские светодиодные лампы кукурузы
Китайские светодиодные лампы кукурузы Автомобильные лампы на самых слабых лед 0,1W
Автомобильные лампы на самых слабых лед 0,1W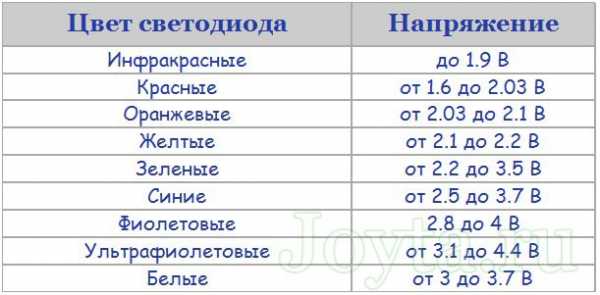



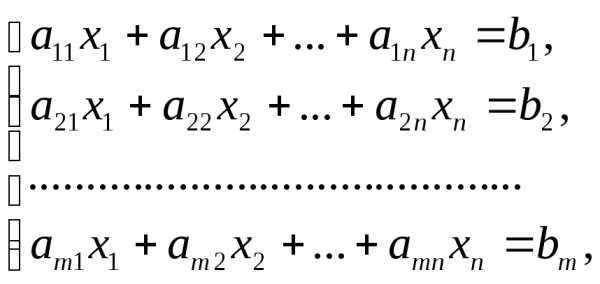
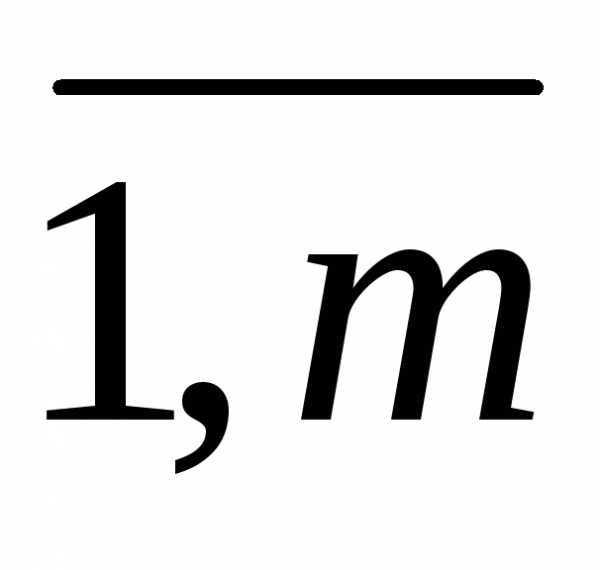 ,j=
,j=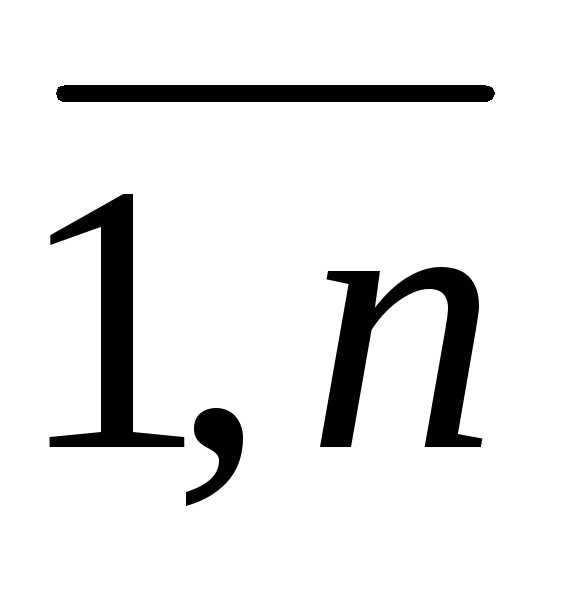 называются коэффициентами системы, числа bi – свободными членами. Подлежат нахождению числа хп.
называются коэффициентами системы, числа bi – свободными членами. Подлежат нахождению числа хп.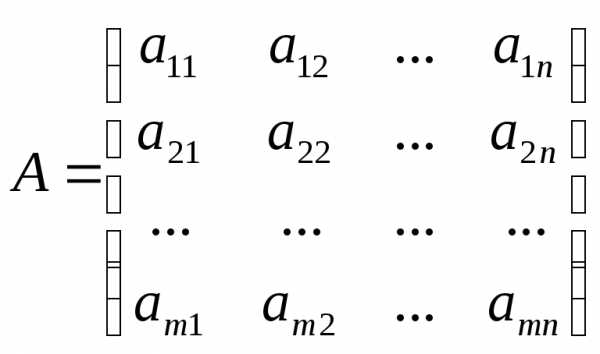 ,
,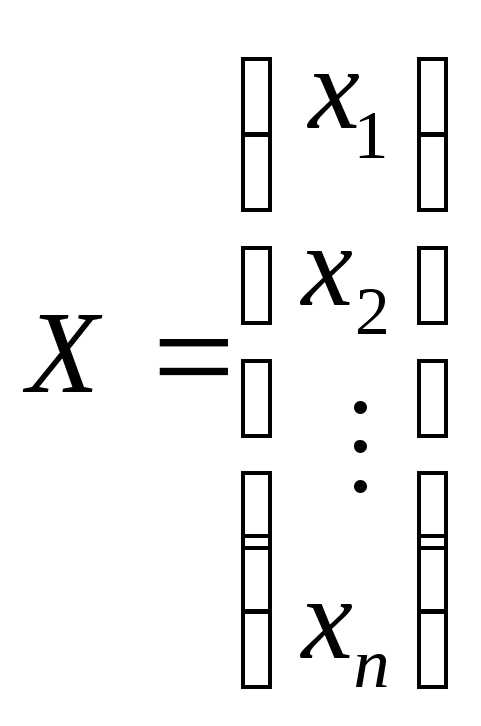 –вектор-столбец
из неизвестных хj,
–вектор-столбец
из неизвестных хj, 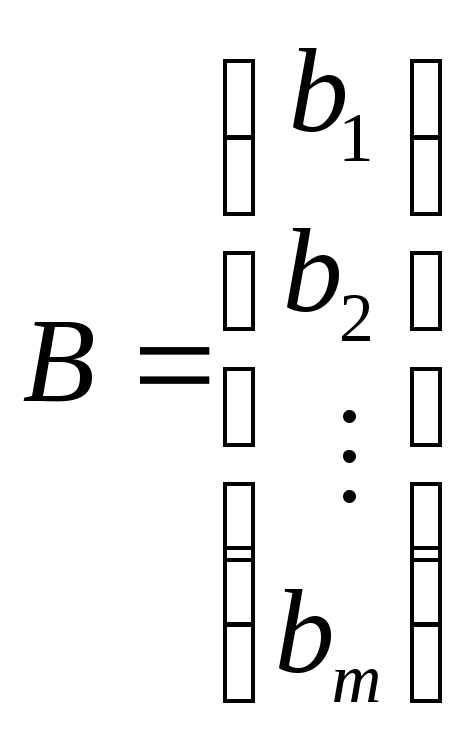 – вектор-столбец из свободных членовbi.
– вектор-столбец из свободных членовbi. системы, дополненная столбцом свободных
членов
системы, дополненная столбцом свободных
членов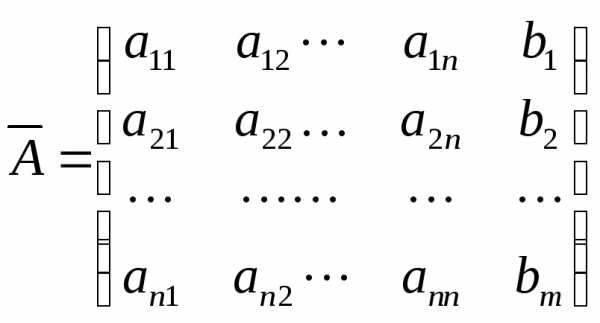 .
.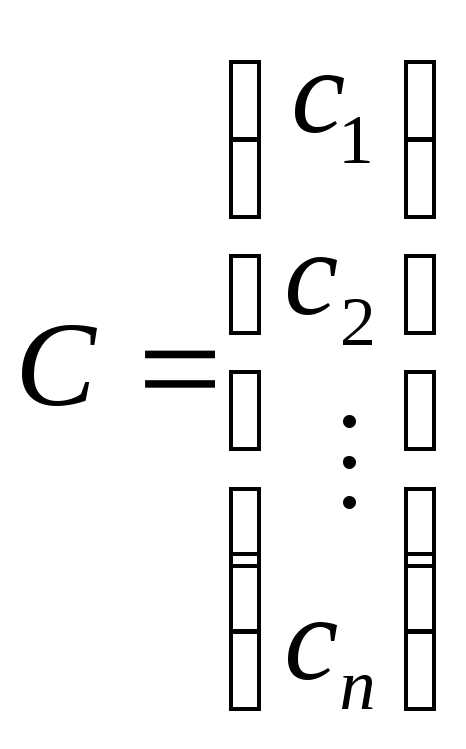 .
.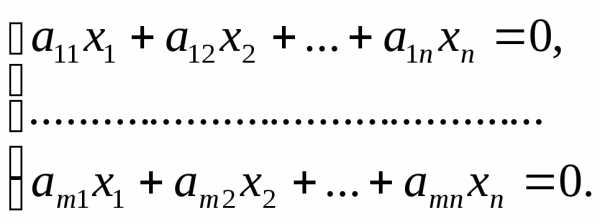
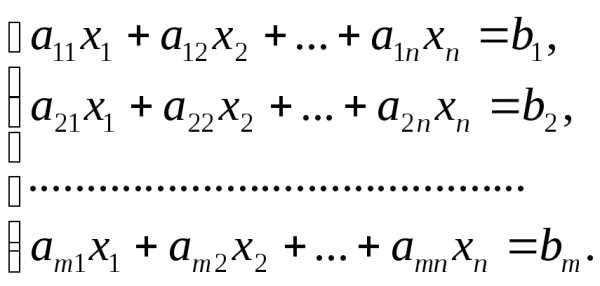
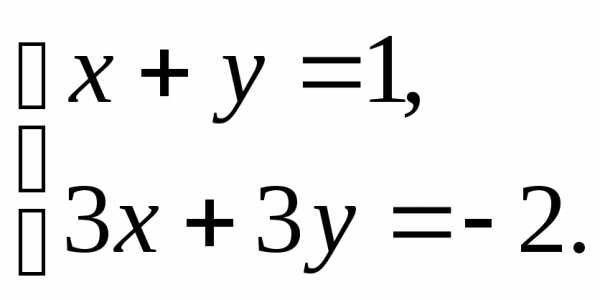
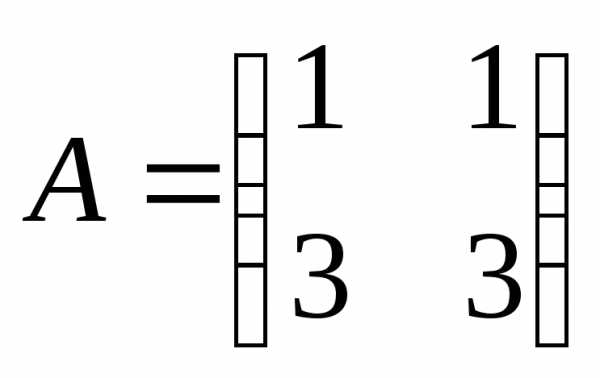 ,r(A)=1;
,r(A)=1; 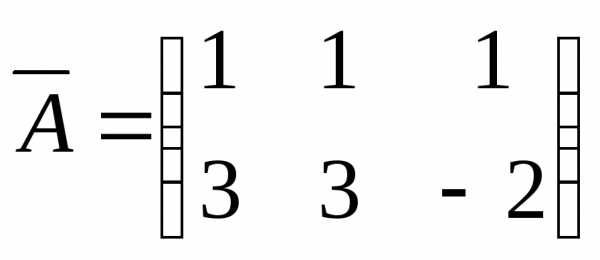 , r(
, r( )=2,
)=2, 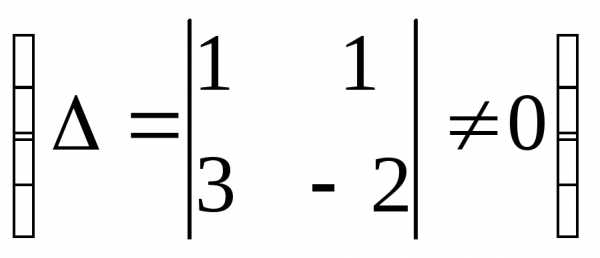 .
. ),
следовательно, система несовместна.
),
следовательно, система несовместна.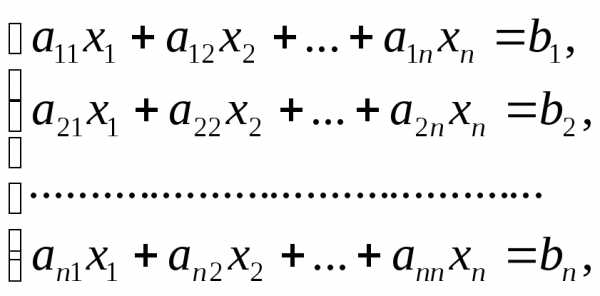
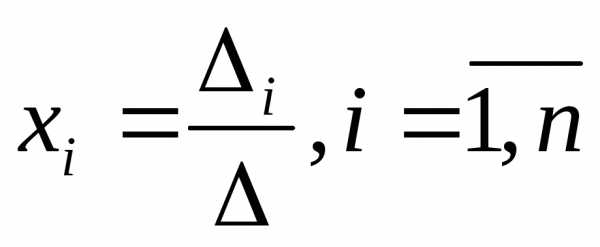 ,
где ∆ – определитель основной матрицы
системы, а ∆i – определитель, полученный из определителя
∆ путем замены i-го
столбца коэффициентов столбцом из
свободных членов.
,
где ∆ – определитель основной матрицы
системы, а ∆i – определитель, полученный из определителя
∆ путем замены i-го
столбца коэффициентов столбцом из
свободных членов.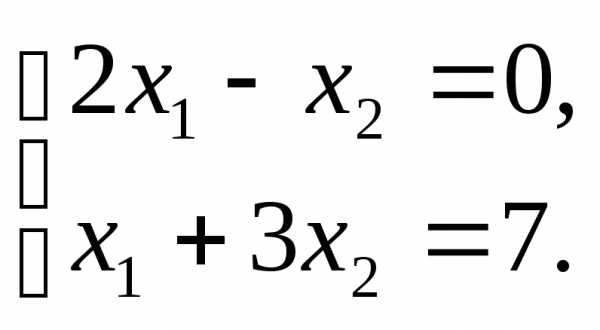
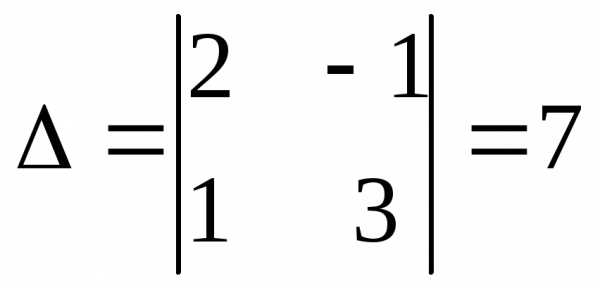 ,
70,
,
70, 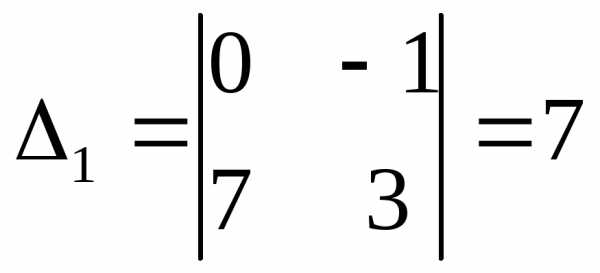 ,
,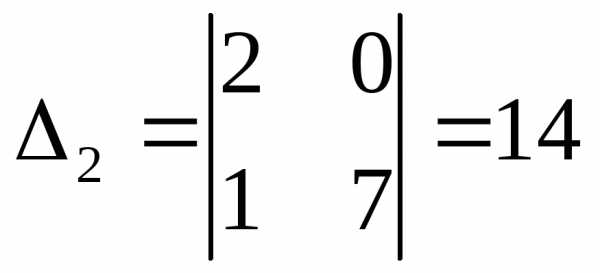 .
Значит,х1=
.
Значит,х1=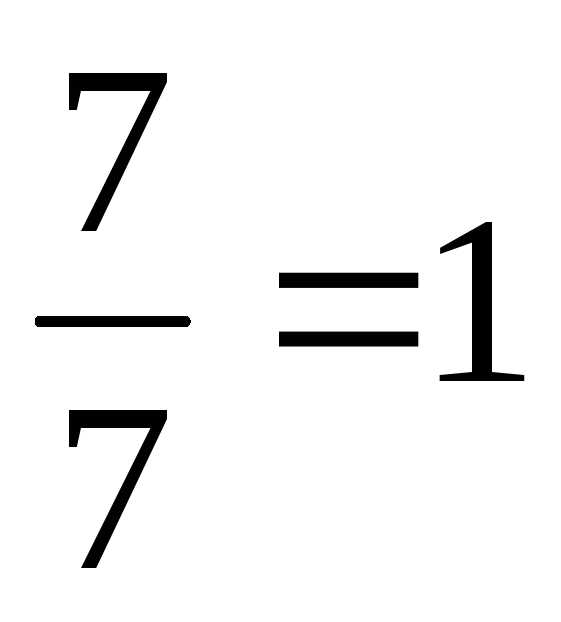 ,
х2=
,
х2=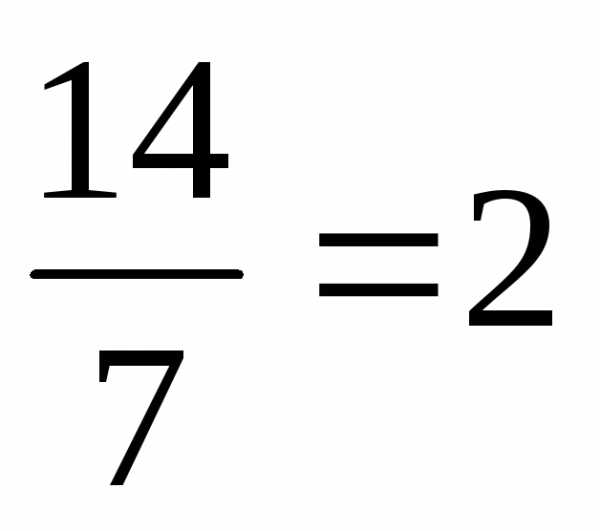 .
.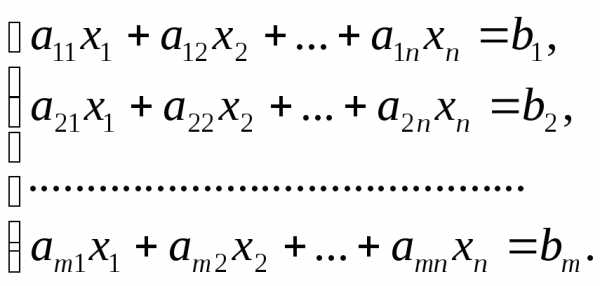
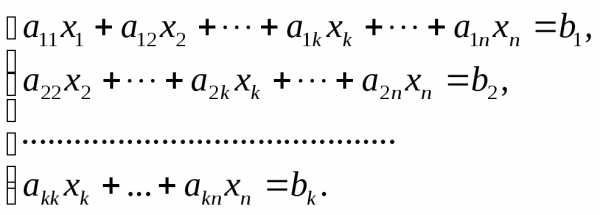
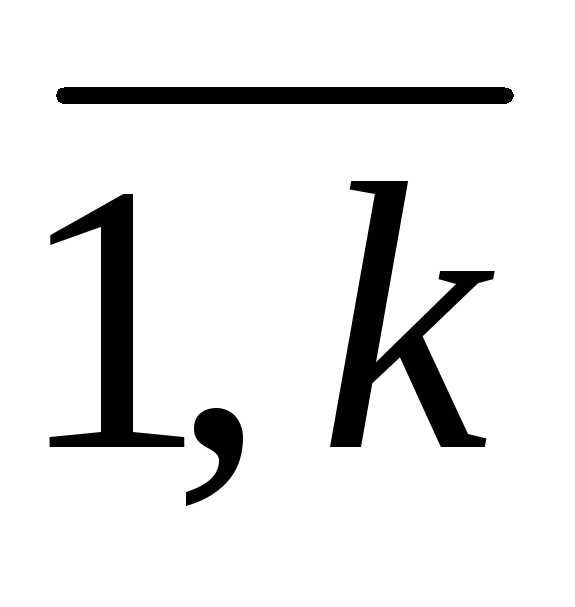 . Коэффициенты аii называются главными элементами системы.
. Коэффициенты аii называются главными элементами системы.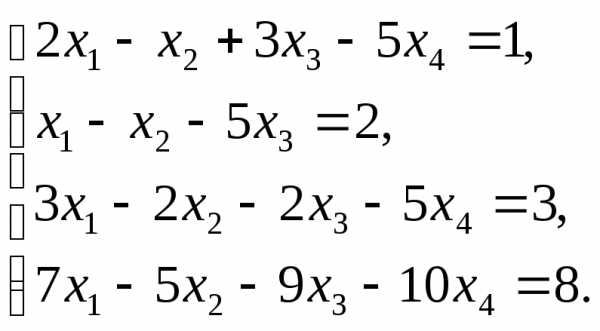
 ~
~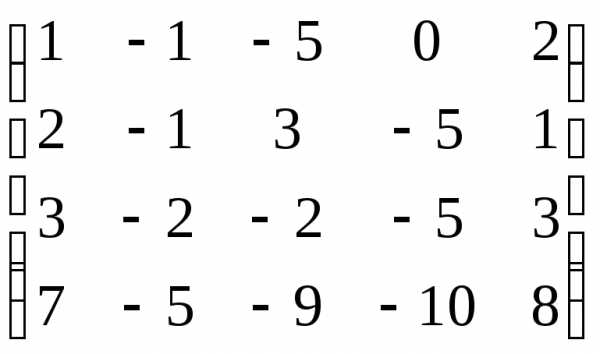 ~
~ ~
~
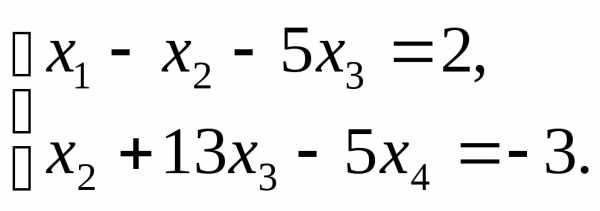
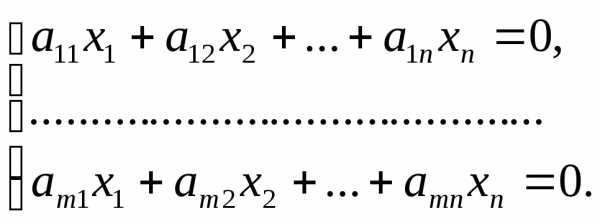
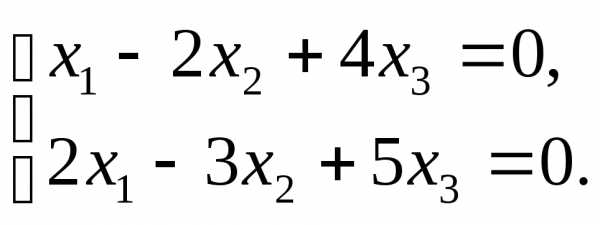
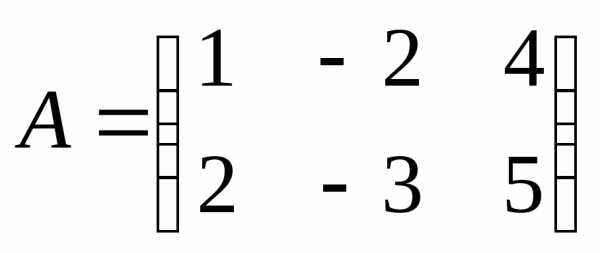 ,r(A)=2
,r(A)=2 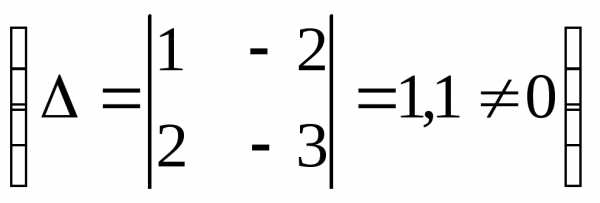 , п=3. Так как r<n, то система
имеет бесконечное множество решений.
, п=3. Так как r<n, то система
имеет бесконечное множество решений.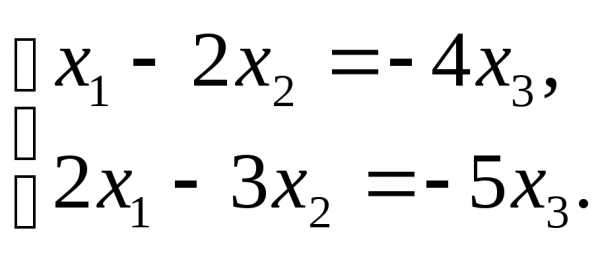
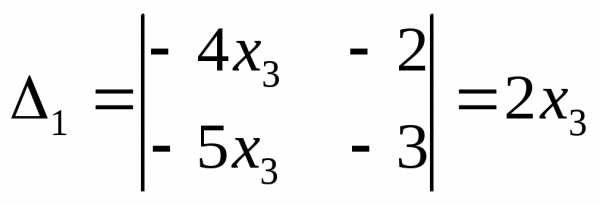 ,
, 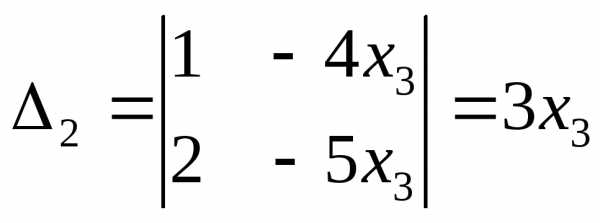 .
Стало быть,х1=
.
Стало быть,х1=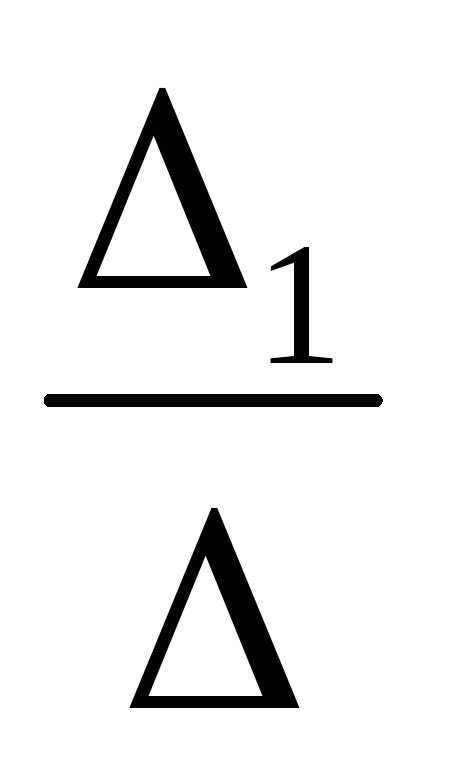 =2х3,
х2=
=2х3,
х2=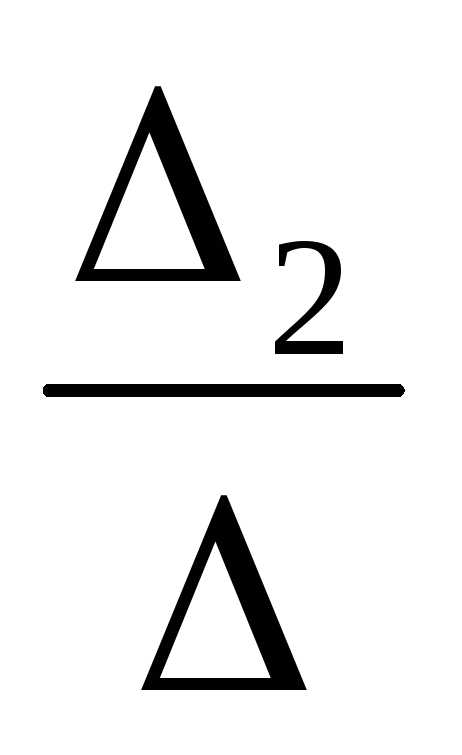 =3х3 – общее решение.
=3х3 – общее решение.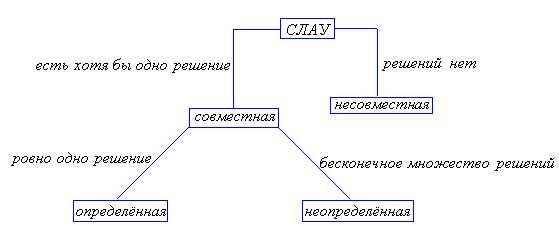
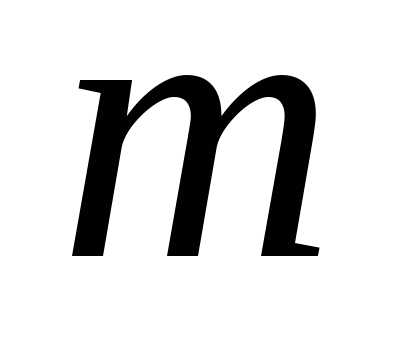 линейных уравненийс
линейных уравненийс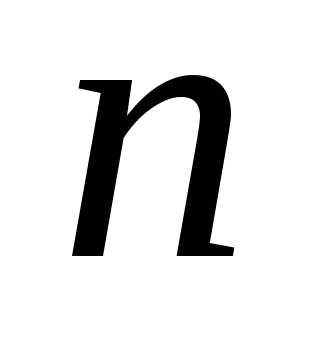 неизвестными
неизвестными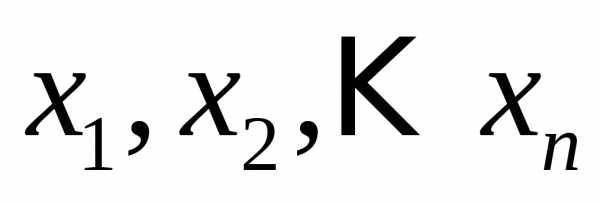 (линейной системой)
называется система вида
(линейной системой)
называется система вида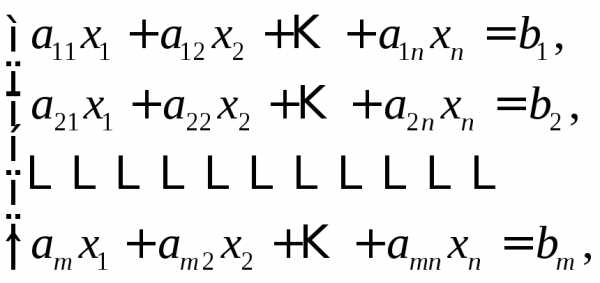 (7)
(7)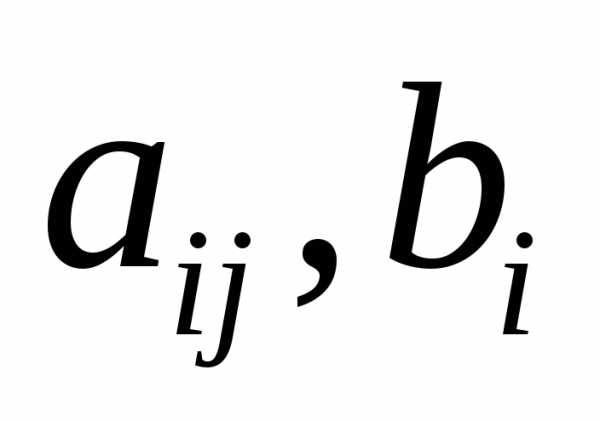 − заданные числа. Числаназываютсякоэффициентамисистемы, а числа
− заданные числа. Числаназываютсякоэффициентамисистемы, а числа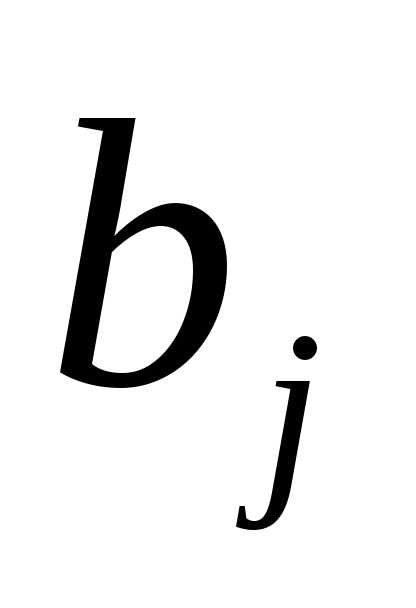 —свободными
членами.
—свободными
членами. (8)
(8)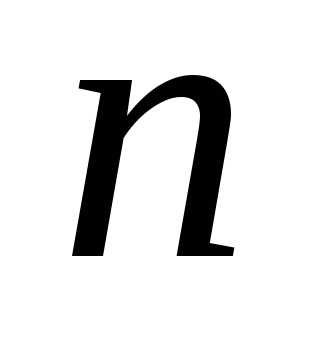 чисел:
чисел: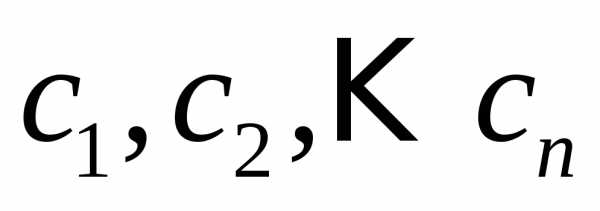 ,
(9)
,
(9)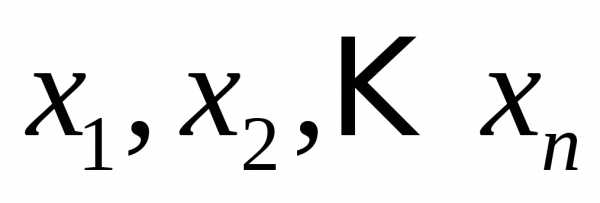 каждое уравнение системы обращается
в тождество.
каждое уравнение системы обращается
в тождество.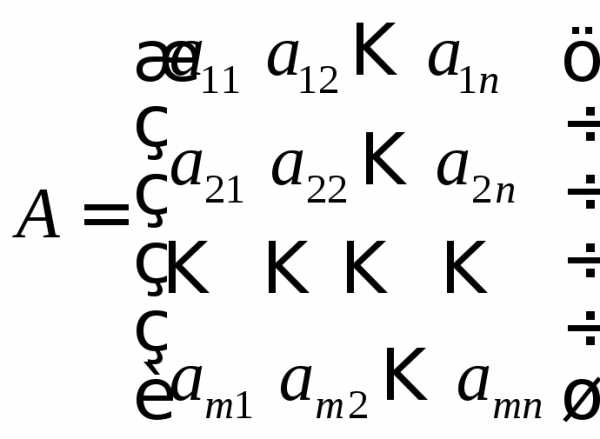 – матрица коэффициентов при неизвестных,
– матрица коэффициентов при неизвестных,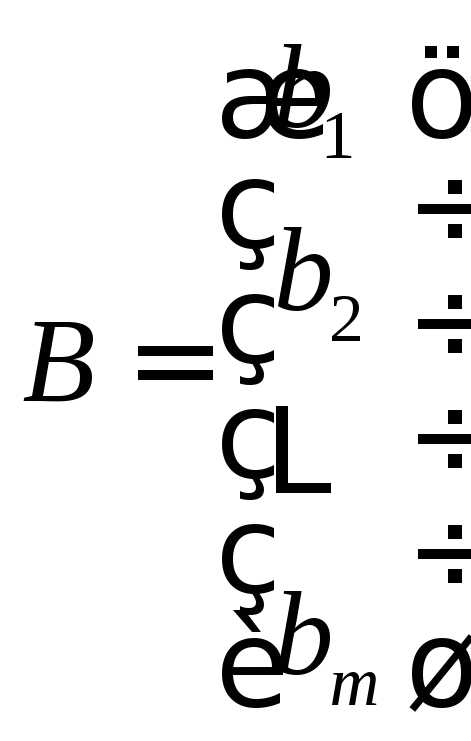 — матрица-столбец свободных членов,
— матрица-столбец свободных членов,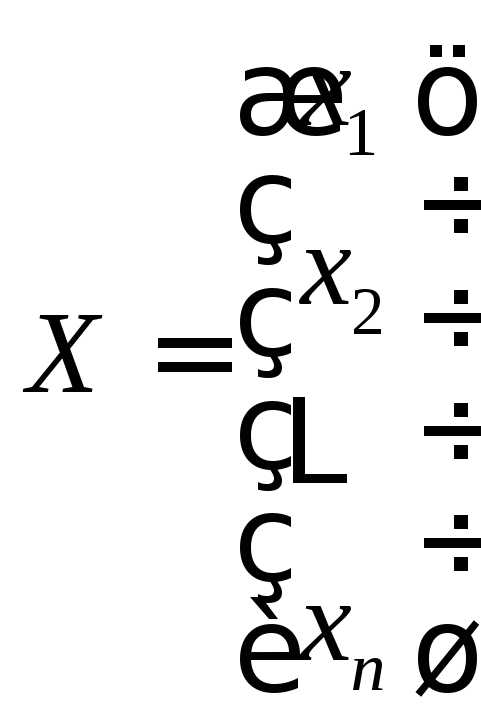 — матрица-столбец неизвестных.
— матрица-столбец неизвестных.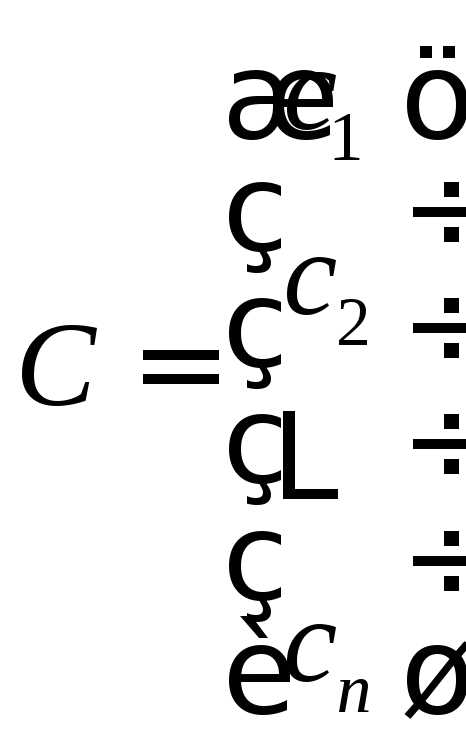 .
.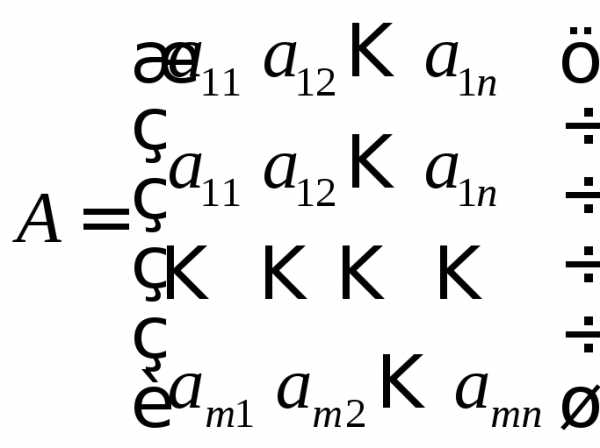

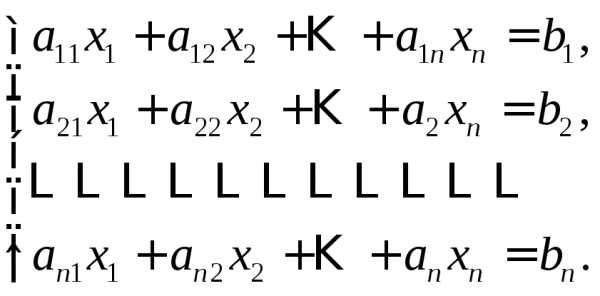 (10)
(10)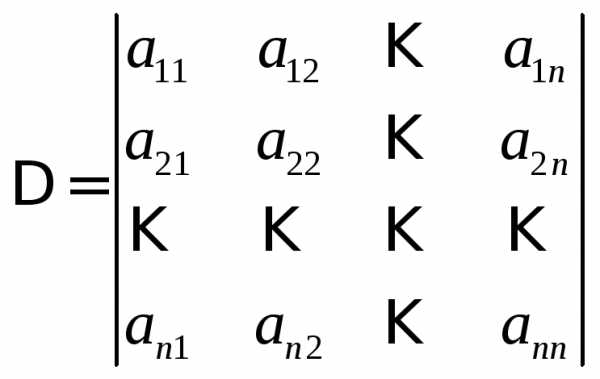 ,
(11)
,
(11)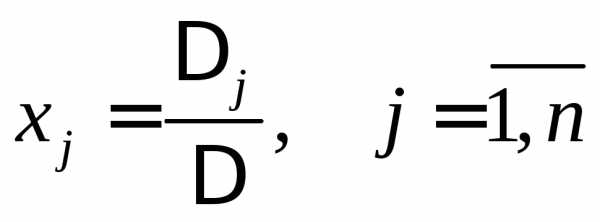 ,
где
,
где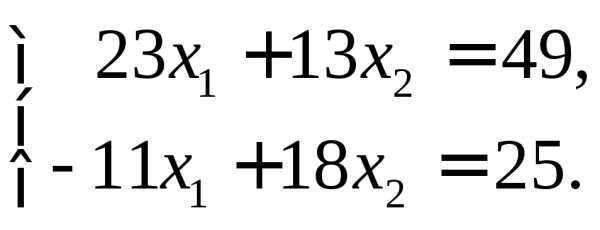
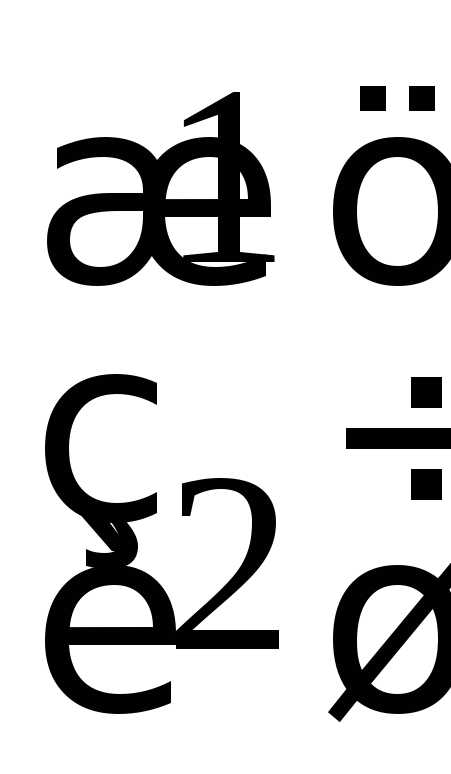 .◄
.◄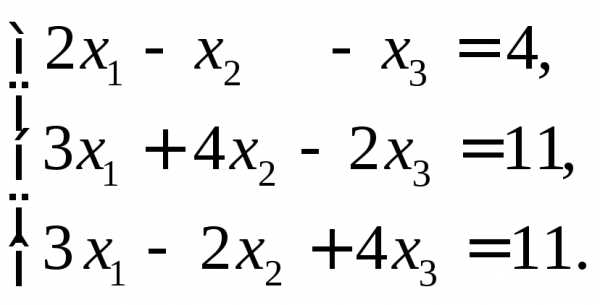 2)
2)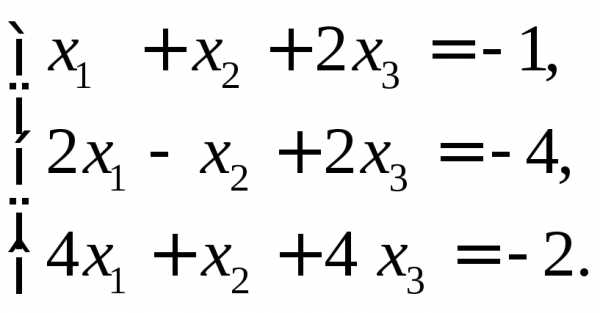 3)
3)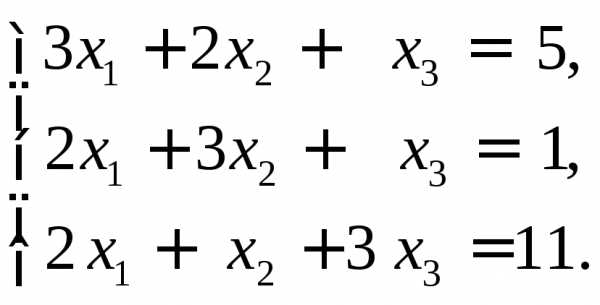
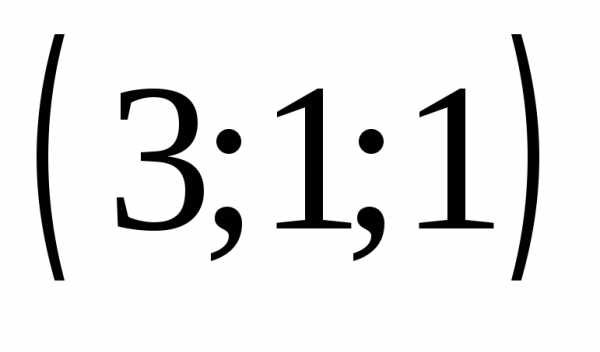 ,
2)
,
2)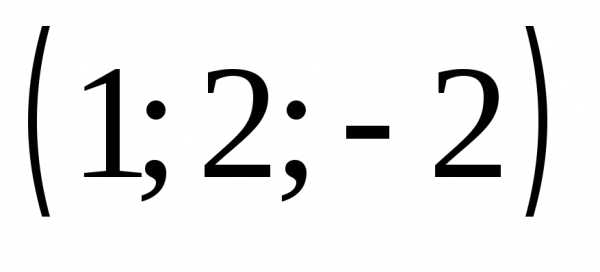 ,
3)
,
3)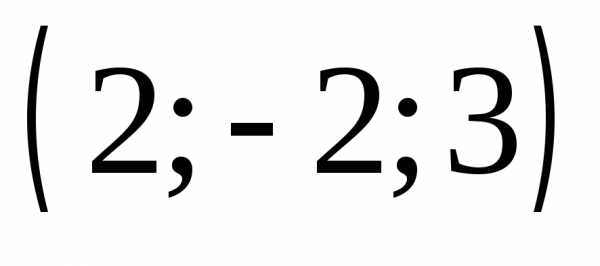 .
.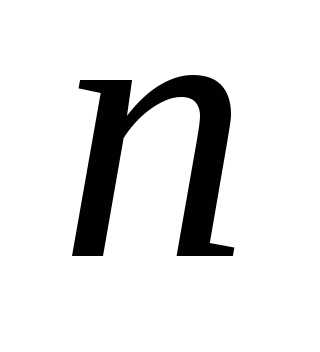 уравнений с
уравнений с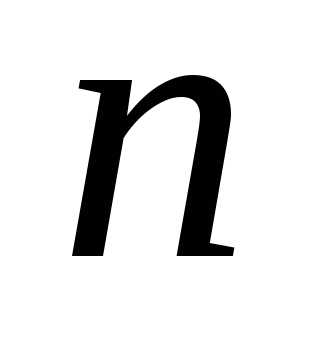 неизвестными (10) в матричной форме
имеет вид (5)
неизвестными (10) в матричной форме
имеет вид (5)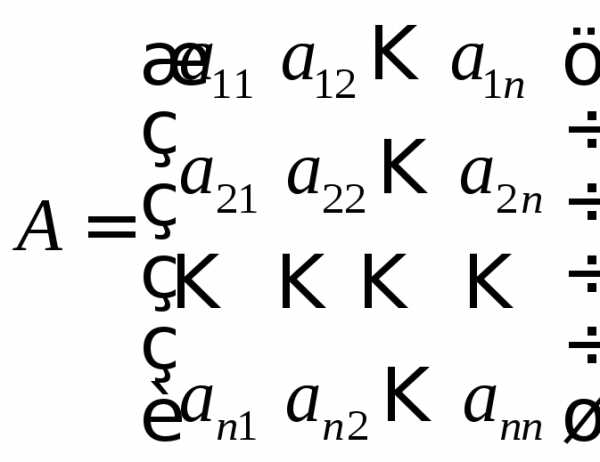 ,
,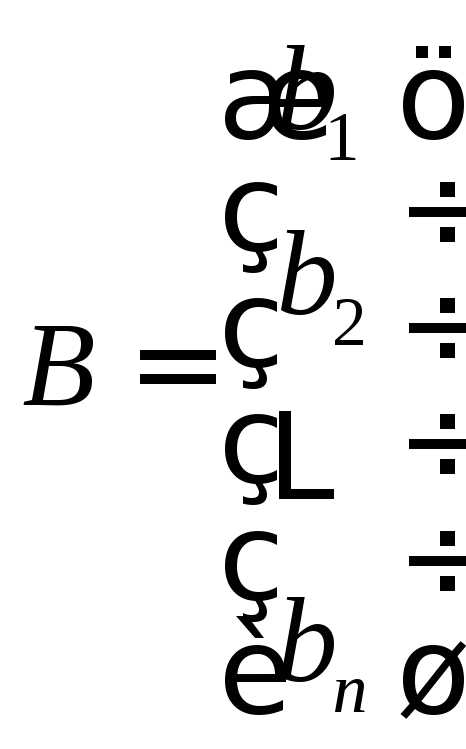 ,
,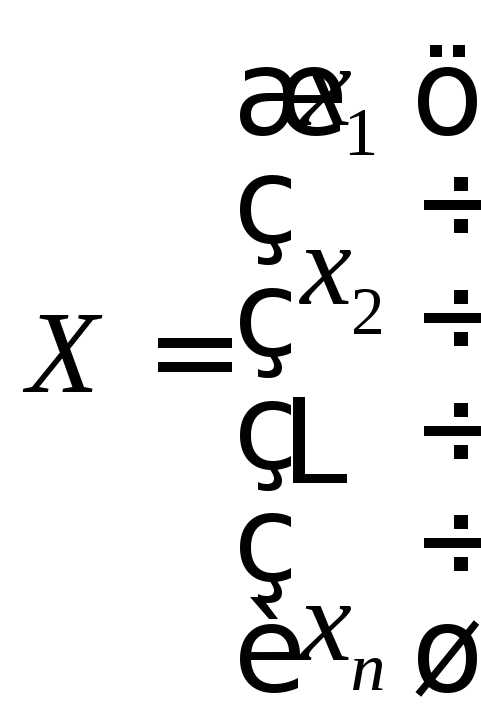 .
. невырожденная, то система имеет
единственное решение, которое вычисляется
по формуле.
невырожденная, то система имеет
единственное решение, которое вычисляется
по формуле.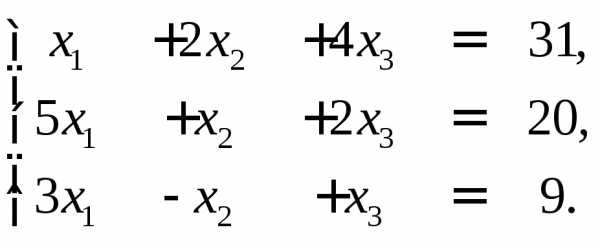
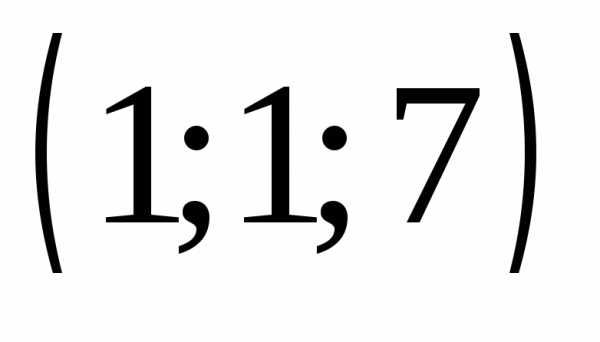 .
◄
.
◄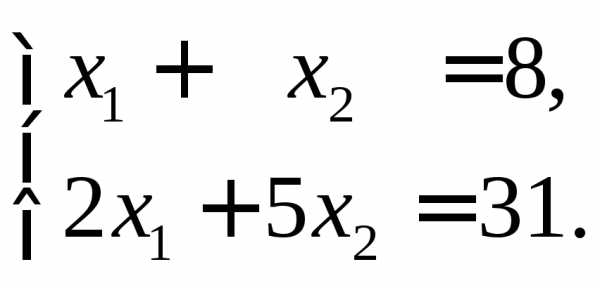 б)
б)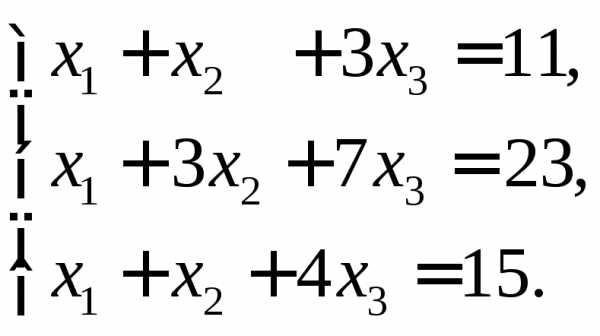 в)
в)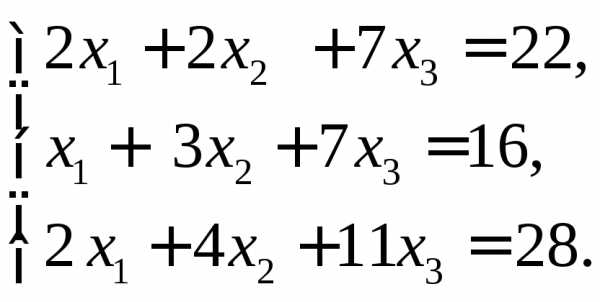
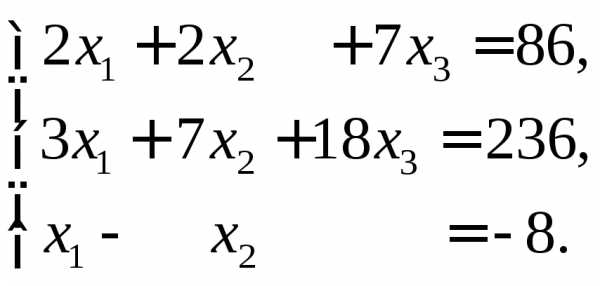 Ответы:а)
Ответы:а)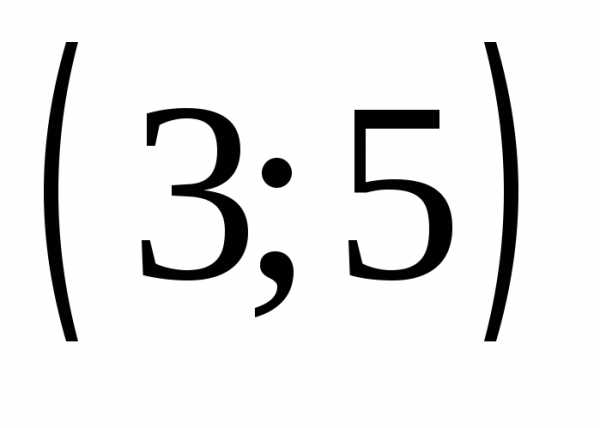 ;
б)
;
б)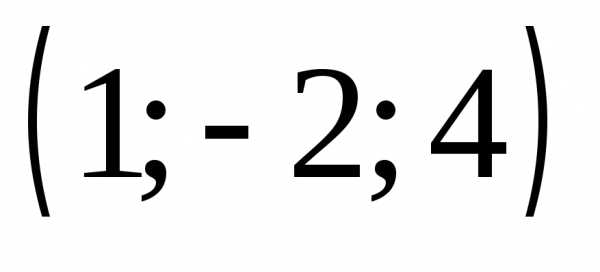 ;
в)
;
в)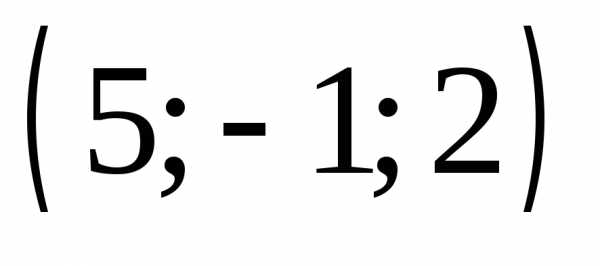 г)
г)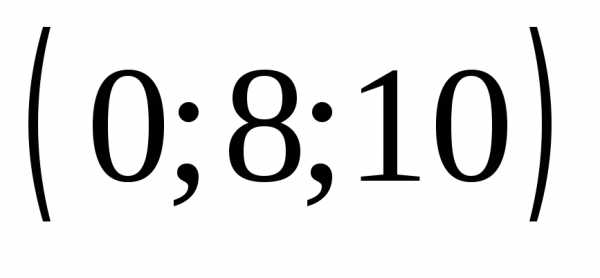 .
.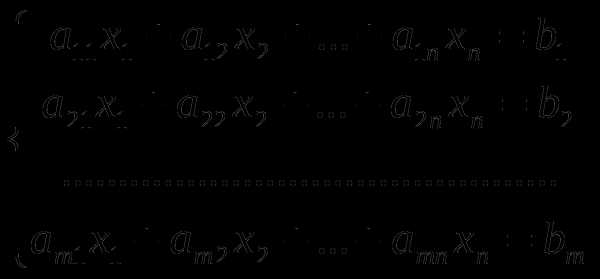

 05:05 — время глобальных перемен в вашей жизни. Главное — сохраняйте спокойствие и уверенность в себе, не сомневайтесь в своих решениях.
05:05 — время глобальных перемен в вашей жизни. Главное — сохраняйте спокойствие и уверенность в себе, не сомневайтесь в своих решениях.
 Дорин Верче — автор концепции ангельской нумерологии
Дорин Верче — автор концепции ангельской нумерологии Три тройки означают, что на вашу жизнь оказывают мощное влияние Высшие Силы
Три тройки означают, что на вашу жизнь оказывают мощное влияние Высшие Силы Три семёрки предвещают успех во всём
Три семёрки предвещают успех во всём Самый известный способ выявления посланий от ангелов — время от времени поглядывать на часы
Самый известный способ выявления посланий от ангелов — время от времени поглядывать на часы Комбинации с единицей и семёркой означают, что вы скоро достигнете своей цели
Комбинации с единицей и семёркой означают, что вы скоро достигнете своей цели Сочетание тройки и семёрки — это знак, что вы движетесь в правильном направлении
Сочетание тройки и семёрки — это знак, что вы движетесь в правильном направлении Нули и семёрки, стоящие вместе, символизируют, что Высшие Силы вас поддерживают
Нули и семёрки, стоящие вместе, символизируют, что Высшие Силы вас поддерживают