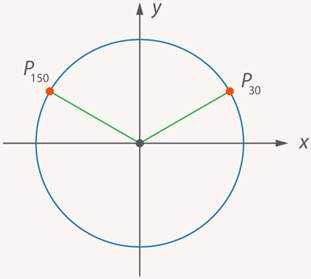
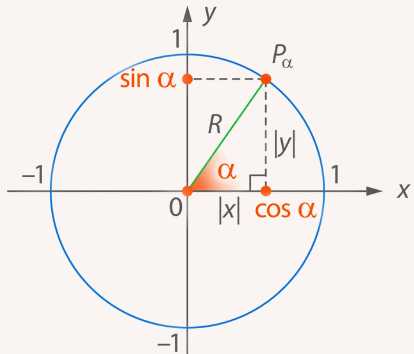
Определение вероятности. Достоверные и невозможные события
Когда футбольный судья подбрасывает монетку в начале матча, чтобы определить, какая команда будет выбирать мяч, а какая – ворота, мы считаем это справедливым. Действительно, выпадет орел или решка. В таком случае вероятность равна .
Рассмотрим другую ситуацию. Судья будет подбрасывать вместо монетки игральный кубик. Если выпадет четное число, то выбирает команда , а если нечетное, то команда . Будет ли это справедливым? Да, вероятность тоже будет , так как четных и нечетных чисел на кубике одинаковое количество. Почему мы считаем вероятность в этих случаях одинаковой? И что такое вероятность?
Мы часто оцениваем вероятность того или иного события. Например, вызовет учитель к доске или нет. Пойдёт ли днём дождь, если пасмурно с утра? В результате нашего анализа мы принимаем различные решения: например, готовиться к уроку на завтра или не брать с собой зонт. Такие решения обычно принимаются на основании наблюдений (жизненного опыта). Например, наблюдения подсказывают нам, что учитель обычно не вызывает ученика два урока подряд. Поэтому если сегодня меня вызвали к доске, то вероятность этого же события на следующем уроке я буду оценивать как низкую. Но это не гарантирует, что меня действительно не вызовут повторно.
А, например, вероятность вызова к доске на уроках математики и биологии мы никак не связываем. То, что мы отвечали на математике, не гарантирует, что нас не спросят на биологии. Как мы уже знаем, такие события называют независимыми.
Итак, мы можем выделить два важных понятия: опыт и его результат (событие). Например, если мы подбрасываем монету, то опыт «бросили монету, посмотрели – что сверху». В этом опыте возможны события (их принято обозначать буквами): А = «выпал герб» и В = «выпала решка».

Изучение опытов с непредсказуемыми заранее последствиями (типа игры в монету) показало: между опытом и событием, которое может в нём произойти, существует некая связь, её называют вероятностью события и характеризуют числом, которое проявляется только при многократном повторении опыта. Например, если мы подбрасываем монетку, то вероятность того, что выпадет герб равна . Однако это не гарантирует нам, что ровно в из подбрасываний мы увидим герб. Это лишь значит, что если мы будем очень много раз подбрасывать монету, то количество раз, когда выпал герб и когда выпала решка, будет приблизительно одинаковым.
То есть если мы проводим опыт раз и наше событие в нем происходит раз, то вероятность – это предел отношения при . Это определение означает, что если мы будем много раз проводить один и тот же эксперимент, то отношение количества благоприятных событий к общему количеству проведенных опытов будет стремиться к какому-то числу. Например, при игре правильной монетой приблизительно в половине бросков выпадал герб (многовековая практика игроков) и стали говорить «вероятность выпадения герба равна ».
В условиях задач о вероятностях нам часто говорят неявно. Например, в задаче: «В ящике лежат шары, одинаковые по форме и на ощупь, один из них отмечен. Наудачу вынимают один шар. Какова вероятность вынуть отмеченный шар?» – вероятности некоторых событий указаны условиями «одинаковые по форме и на ощупь» и «наудачу вынимают о
interneturok.ru
События, виды событий —
Опыт, эксперимент, наблюдение явления или некоторого процесса называется испытанием. Примеры испытаний: бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесённой на каждую из шести граней цифры от одного до шести), реализация некоторого физического, механического или технологического процесса и т.д. При бросании монеты исходами (событиями) являются выпадение герба или выпадение цифры, а при бросании игральной кости — выпадение какой либо цифры на верхней грани кости. Испытания сопровождаются их исходами (событиями).
Событие — это качественный и (или) количественный результат испытания (исход), осуществляемого при определённой совокупности условий. Для обозначения событий используются большие буквы латинского алфавита: А, В, С и т.д.
Различают следующие типы событий: случайные события, совместные или несовместные события, достоверные или невозможные события, зависимые или независимые события, равновозможные события, элементарные (простые, неразложимые) события, событие или совокупность событий (исходов), благоприятствующих какому-либо другому событию.
Случайное событие – это результат испытания (или величина), который нельзя заранее спрогнозировать, т.е. нельзя сказать, произойдёт это событие или не произойдёт, или, если событие произойдёт, то неизвестно, какое значение примет результат этого события.
Случайные события – первичные, неопределяемые (в строгом смысле) понятия в теории вероятностей, аналогичные понятиям точки и прямой – в геометрии.
Например, пусть игральная кость с пронумерованными гранями от 1 до 6 подбрасывается два раза. В этом опыте можно рассматривать следующие события: событие А – оба раза выпадет число 1; событие В – хотя бы один раз выпадет число 3; событие С – сумма выпавших чисел равна 8 и т.д.
Событие, которое обязательно наступит (никогда не произойдёт) в данном опыте, называется достоверным (невозможным). Достоверное событие обозначают символом Ω, а невозможное – Æ. Например, в опыте, состоящем в подбрасывании кости один раз – событие А – выпадение одного из чисел 1,2,3,4,5,6 – есть достоверное, а событие В – выпадение числа 7 – невозможное.
Два случайных события называются несовместными, если наступление одного из них исключает наступление другого в одном и том же испытании. (Таким образом, несовместные события не могут наступать одновременно). В противном случае, т.е. если наступление одного события не исключает наступление другого события в одном и том же испытании, то эти события называются совместными. Например, если событие А – появление числа 2 при одном бросании кости, а событие В – появление чётного числа в этом же бросании, то события А и В совместные, а событие С – появление числа 2 при одном бросании кости и событие D – появление числа 3 в этом бросании – события несовместные.
События А1, А2, … , Аn называются попарно несовместными, если любые два из них являются несовместными.
События называются равновозможными, если ни одно из них не является более возможным по сравнению с другими событиями.
События называются независимыми (зависимыми), если числовая характеристика возможности наступления одного события не зависит (зависит) от числовых характеристик наступления других событий (указанные числовые характеристики некоторых событий А, В, С, … называются вероятностями этих событий).
Определение. Совокупность попарно несовместных событий образуют полную группу событий для данного испытания, если в результате каждого испытания происходит одно и только одно из них.
Примеры полных групп событий: а) выпадение герба {Г} и выпадение цифры {Ц} при одном бросании монеты; б) попадание в цель и промах при одном выстреле по мишени; в) выпадение цифр «1», «2», «3», «4», «5», «6» при одном бросании кости.
Определение. События ω1, ω2, … , ωn, образующие полную группу попарно несовместных и равновозможных событий, называются элементарными событиями.
Элементарными событиями являются выпадение цифр «1», … ,«6» при бросании кости. Эти события несовместны, равновозможны и образуют полную группу (предполагается, что кость является однородной и центрированной).
Множество всех элементарных событий называется пространством элементарных событий и обозначается Ω. Например, в результате бросания кости выпадение цифры i = 1, 2, 3, 4, 5, 6 образует пространство Ω = {1, 2, 3, 4, 5, 6}.
Элементарные события, составляющие пространство Ω, обозначаются ω1, ω2, …, ω6.
Замечание. Кроме случайных событий в теории вероятностей вводятся в рассмотрение случайные величины. Случайная величина – это переменная, которая в результате испытания в зависимости от случая принимает одно из возможных значений. Случайные величины в данном пособии рассматриваются более подробно в главе 3.
einsteins.ru
экзам.тервер
1)комплекс условий,Достоверное невозможное и случайное событие.
Достоверное событие — в теории вероятности называется событие , которое в результате опыта или наблюдения непременно должно произойти.
Для достоверного события
Т.е. вероятность события равна единице.
Но, не всякое событие, вероятность которого равна 1, является достоверным
Невозмо́жным собы́тием в теории вероятности называется событие , которое в результате опытапроизойти не может.
Очевидно, что вероятность невозможного события равна нулю.
Однако, не всякое событие, вероятность которого равна нулю, является невозможным событием. Пример: событие, состоящее в том, что нормальнораспределенная случайная величина примет некоторое конкретное значение. Для любой непрерывной случайной величины верно утверждение: вероятность того, что случайная величина примет определенное, наперед заданое значение равна нулю. Другой пример события с нулевой вероятностью: эксперимент состоит в том, что монета подбрасывается бесконечное число раз. Событие «Монета бесконечное число раз упадет цифрой вверх» имеет нулевую вероятность, но оно может произойти.
Если оговорена некоторая допустимая погрешность (например, 10^(-50) ), то событие, вероятность которого не больше значения этой погрешности, называют практически невозможным.
Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.
2) Пространство элементарных событий
Пространство элементарных событий — множество всех взаимно или попарно исключающих друг друга исходов случайного эксперимента, которые вместе образуют полную группу событий.
Элемент этого множества называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его элементов конечно или счётно. Любое пространство элементарных событий не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами (нельзя произносить случайными событиями) являются точки того или иного числового арифметического или координатного пространства, то пространство называетсянепрерывным (континуум). Пространство элементарных событий вместе с алгеброй событий ивероятностью образует тройку , которая называется вероятностным пространством.
3)События.Операции над событиями
Событие-любой набор элементарных исходов или, иными словами, произвольное подмножиство пространства элементарных исходов, называют событием.
Операции над событиями.1)Пересечением(произведением) двух событий А и В называют событие С тогда, когда одновременно происходят оба события А и В. С=АВ 2)События А и В называются несовместными или, непересикающимися если их пересечения являются невозможным событием т.е. АΩВ=ø 3) Обьединением, суммой двух событий А и В называют событие С происходящее только тогда когда происходят хотябы одно из событий А или Вт.е. событие С, состоящее из тех элементарных исходов которые принадлежат хотя бы одному из подмножеств А или В. С=АUВ 4) Разностью 2х событий А и В называют событие С происходящее тогда и только тогда когда происходит событие А но не происходит событие В т.е. событие С состоящее из тех элементарных исходов, которое принадлежит А но не пренадлежит В. С=А\В 5)Дополнением события А(А) Называт событие происходящее тогда когда не происходит событие А. Событие А называют противоположным событию А. А=Ω\А.
4)Алгебра событий
Суммой событий А и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В. Пример 1. Испытание: стрельба двух стрелков (каждый делает по одному выстрелу). Событие А — попадает в мишень первый стрелок, событие В — попадает в мишень второй стрелок. Суммой событий А и В является событие С = А + В — попадает в мишень по крайней мере один стрелок. Аналогично, суммой конечного числа событий называется событие , состоящее в наступлении хотя бы одного из событий .
Из определения суммы событий непосредственно следует, что
А + В = В + А. Справедливо также и сочетательное свойство. Однако
А + А = А (а не 2А, как в алгебре). Произведением событий А и В называется событие С = А В, состоящее в том, что в результате испытания произошли и событие А, и событие В. Аналогично, произведением конечного числа событий называется событие , состоящее в том, что в результате испытания произошли все указанные события. В Примере 1 произведением событий А и В является событие С = А В, состоящее в попадании в мишень двумя стрелками.
Из определения произведения событий непосредственно следует, что
АВ = ВА.
5) Аксиометрическое опред.вероятностей свойства вероятности.
Вероятностью называется числовая функция, определенная на поле событий S и обладающая следующими свойствами: Аксиома 1. Для любого события A прин. S Р(А)>=0. Аксиома 2. Вероятность достоверного события равна единице Р (омега)=1. Аксиома 3. Вероятность объединения двух несовместных событий равна сумме вероятностей этих событий: А прин. S, В прин. S, А*В=0, Р(А+В)=Р(А)+Р(В). Док-во: Событие А является подмножеством омега, так как А={wi1,…,wim},то, согласно конечной схеме, Р(А)=сумме по l от 1 до m рil, 0<=pil<=1, l=1,…,m, поэтому Р(А)>=0, т.е. условие аксиомы 1 выполняется. Условие аксиомы 2 выполняется, поскольку омега={w1,…,wn}и на основании того, что Р(А)=сумме по l от 1 до m рil, то Р(омега)=сумма по i от 1 до n pi=1. Условие аксиомы 3 также выполняется, так как оно представляет собой содержание теоремы сложения для конечной схемы. Итак, конечная схема является примером объекта, для которого выполняется система аксиом теории вероятностей. Основные свойства вероятности. Пусть задано пространство элементарных событий Е , а вероятности Р определены на событиях из Е . Тогда:
6) Теорема сложения произвольных событий. Вероятность суммы двух произвольных событий равна разности суммы и произведения вероятностей этих событий:
P(A + B) = P(A) + P(B) — P(AB).
Следствие. Вероятность суммы произвольных событий никогда не превосходит суммы вероятностей этих событий:
P(A1 + A2 +…+ An) ≤ P(A1) + P(A2) +…+P(An).
7)Элементы комбинаторики:правило суммы произведения и размещения
Правило суммы. Если некоторый объект можно выбрать способами, а другой объект можно выбрать способами, то выбор «либо , либо » можно осуществить способами.
Правило произведения. Если объект можно выбрать способами, а после каждого такого выбора другой объект можно выбрать (независимо от выбора объекта способами, то пары объектов и можно выбрать способами.
Размещениями из элементов поназываются такие выборки, которые, имея поэлементов, выбранных из числа данныхэлементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.
Число размещений из элементов пообозначимИспользуя основное правило комбинаторики, получаем
Если , то- число таких размещений, которые отличаются только порядком расположения элементов. Такие размещения называютсяперестановками. Их число находится по формуле
Выборки из элементов, взятых из данных, отличающихся только составом элементов, называютсясочетаниями из элементов по. Числотаких сочетаний находится
9)Класическое опред.вероятности
вероятность есть число, характеризующее степень возможности появления события.
ОПРЕДЕЛЕНИЕ (классическое определение вероятности). Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.
Итак, вероятность события А определяется формулой:
(1)
где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания.
10) геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.) Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω:
11) Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Таким образом, относительная частота события А определяется формулой
W (А) = m / n,
где m — число появлений события, n — общее число испытаний.
если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах, относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Статистическая вероятность. При статистическом определении в качестве вероятности события принимают его относительную частоту.
где m — число испытаний, в которых событие A наступило, n — общее число произведённых испытаний.
12) Условная вероятность — вероятность одного события при условии, что другое событие уже произошло
Теорема умножения. Вероятность совмещения событий А и В равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие осуществилось, т. е.
Доказательство. Докажем справедливость соотношения (4), опираясь на классическое определение вероятности. Пусть возможные исходы Е1, Е2, …, ЕN данного опыта образуют полную группу равновероятных попарно несовместных событий, из которых событию A благоприятствуют M исходов, и пусть из этих M исходов L исходов благоприятствуют событию B. Очевидно, что совмещению событий A и B благоприятствуют L из N возможных результатов испытания. Это дает
; ;
13)Независимые события.События в совокупн. Попарная независимость
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:
РA (В) = Р (В). (*)
Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми.
Несколько событий называют попарно независимыми, если каждые два из них независимы. Например, события А, В, С попарно независимы, если независимы события А и В, А и С, В и С.
Несколько событий называют независимыми в совокупности (или простонезависимыми), если независимы каждые два из них и независимы каждое событие и все возможные произведения остальных. Например, если события A1, A2, А3, независимы в совокупности, то независимы события A1 и А2, А1 и А3, А2 и A3; А1 и A2A3, A2 и A1A3, А3 и A1A2.
14) Вероятность появления хотя бы одного из событий А1 , А2 , …, Аn , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
Р (A) = 1 — q1q2 … qn.(*)
Доказательство
Ч а с т н ы й с л у ч а й. Если события А1 , А2 , …, Аn имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий
P (A) = l — qn. (**)
15)Формула полн.вероятности
Формула Бейеса
16)Формула Бернули
в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях)
появлений события в независимых испытаниях
Число k0 (наступления события в независимых испытаниях, в каждом из которых вероятность появления события равна р) называют наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях k0 раз, превышает (или, по крайней мере, не меньше) вероятности остальных возможных исходов испытаний.
Наивероятнейшее число k0 определяют из двойного неравенства
np-q≤k0≤np+p,
причем:
а) если число nр-q — дробное, то существует одно наивероят нейшее чиcло k0;
б) если число nр-q — целое, то существует два наивероятнейших числа, а именно: k0 и k0+1;
в) если число nр—целое, то наивероятнейшее число k0 = nр
17)
Локальная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < р < 1), событие наступит ровно k раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)
Для определения значений φ(x) можно воспользоваться специальной таблицей.
Интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее k1 раз и не более k2 раз, приближенно равна
P(k1;k2)=Φ(x») — Φ(x’)
Здесь
—функция Лапласа
Значения функции Лапласа находят по специальной таблице.
19) ) Предельная теорема Пуассона
Если итак, что,, то
при любом постоянном .
Доказательство.
Положив , представим вероятностьв виде
.
Отсюда при получим утверждение теоремы.
20) Случайной величиной называется величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно.
Случайные величины можно разделить на две категории.
Определение. Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество (множество, элементы которого могут быть занумерованы).
Это множество может быть как конечным, так и бесконечным.
Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать и бесконечное, хотя и счетное количество значений.
Определение. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.
Очевидно, что число возможных значений непрерывной случайной величины бесконечно.
Для задания случайной величины недостаточно просто указать ее значение, необходимо также указать вероятность этого значения.
21) Закон распределения дискретной случайной величины
Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины.
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.
Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
22)
23) МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: M(X) = x1 p1+ x2 p2+…+ xn pn. Реально на основе данных выборки мы не можем вычислить M(X). Однако эту характеристику можно оценить. В качествеоценки можно использовать среднее арифметическое, то есть M(X) ≈X. Чем больше объём выборки (число наблюдений), тем точнее эта оценка. Математическое ожидание обладает следующими свойствами: 1. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C. 2. Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X). 3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M(X+Y+Z) = M(X)+M(Y)+M(Z). 4. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M(XYZ) = M(X)M(Y)M(Z). Все эти свойства имеют большое практическое значение.
24)Свойства мат.ожидания. Теорема. Математическое ожидание М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.
1) Математическое ожидание постоянной величины равно самой постоянной.
2) Постоянный множитель можно выносить за знак математического ожидания.
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
Это свойство справедливо для произвольного числа случайных величин.
4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.
25) ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D ( X ) = M ( X — M ( X )) 2. Для вычислений удобнее пользоваться формулой : D ( X ) = M ( X 2 ) — ( M ( X )) 2. Дисперсия обладает следующими свойствами. 1. Дисперсия постоянной величины С равна нулю : D ( C ) = 0. 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат : D ( CX ) = C 2D ( X ). 3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин: D ( X+Y+Z ) = D ( X )+D ( Y )+D ( Z ). 4. Дисперсия суммы постоянной величины и случайной — равна дисперсии случайной величины: D ( C+X ) = D ( X ).
26) 1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
2. Взвешенная дисперсия (для вариационного ряда):
где n — частота (повторяемость фактора Х)
27) 1) Дисперсия постоянной величины равна нулю.
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
Справедливость этого равенства вытекает из свойства 2.
Теорема. Дисперсия числа появления события А в п независимых испытаний, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и не появления события в каждом испытании.
28) Среднее квадратич.отклонение случ.величины
Определение. Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии.
Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.
29) Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид
,
где — биномиальные коэффициенты, — неотрицательное целое число.
30) Биномиальное распределение — дискретное распределение вероятностей случайной величины принимающей целочисленные значения с вероятностями:
Данное распределение характеризуется двумя параметрами: целым числом называемым числом испытаний, и вещественным числом называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из независимых испытаний, в каждом из которых может произойти «успех» с вероятностью то случайная величина, равная числу успехов во всей серии, имеет указанное распределение. Эта величина также может быть представлена в виде суммы независимых слагаемых, имеющихраспределение Бернулли.
studfiles.net
1.Случайное событие. Испытание. События достоверные и невозможные, совеместные и несовместные, полная группа событий, противоположные события.
СС – явление, которое при одних и тех же условиях иногда происходит, иногда не происходит.
Испытание (опыт, эксперимент)– осуществление этих определенных условий.
Каждое испытание приводит к заранее точно не предсказуемому результату, т.е. его результат нельзя точно предсказать. И тем не менее СС является результатом испытания.
Достоверное событие (Ω), событие, которое обязательно происходит в результате испытания, вероятность достоверного события равна единице:Р(Ω)=1; невозможное событие (знак пустого множества), не происходит ни при каком исходе случайного эксперимента, вероятность невозможного события равна нулю.
Выпадение снега в НСК 30 ноября является случайным событием. Ежедневный восход Солнца можно считать достоверным событием. Выпадение снега в Африке можно рассматривать как невозможное событие.
События А и В назыв. совместными, если они могут произойти оба в результате одного опыта. В противном события называются несовместными.
Предположим, проводится подбрасывание монеты. В результате этого эксперимента обязательно произойдет одно из следующих событий:
А: монета упадет орлом;
В: монета упадет решкой;
С: монета упадет на ребро;
Т.е. система {А;В;С}является полной группой событий.
Противоположными называются два единственно возможных события, образующих полную группу. Если одно из событий, являющихся противоположными, обозначить через А, то противоположное событие обозначают через .
2.Пространство элементар. Соб. Определение сс. Операции над соб. Основные отношения меж соб.
Элементарным (ω) называется СС, которое не разделяется на другие, более мелкие события. Пространством элементарных событий (Ω) называется множество всех элементарных событий, связанных с данным испытанием.
1.При однократном подбрасывании монеты возможны два элементарных события: ω1=Г, ω2 = Ц, которые образуют пространство элементар. соб. Ω = {Г, Ц}.
2.Двукратное подбрасывание монеты: пространство элементарных событий определяется комбинацией элементарных событий при первом и втором подбрасывании, то есть Ω = {ГГ, ГЦ, ЦГ, ЦЦ}.
В результате каждой операции над соб. получают новое событие.
Суммой (объединением) 2х событий А и В называется третье событие С, заключающееся в том, что произойдет хотя бы одно из них, то есть произойдет: 1) или только А, 2) или только В, 3) или оба вместе. Смысл суммы: событие А + В состоит из всех элементар. Соб., принадлежащих событию А или В.
Произведением (пересечением) двух событий А и В называется третье событие С, состоящее в совместном наступлении событий А и В. Обозначение произведения событий: АВ = С. Смысл произведения заключается в том, что событие АВ состоит из элементарных событий, принадлежащих одновременно событию А и В.
Св-ва операций:
1.Переместительное. А+В=В+А и АВ=ВА.
2.Сочетательное А+В+С=(А+В)+С=А+(В+С)
АВС = (АВ)С=А(ВС)
3.Распределительное А(В+С)=АВ+АС
Отношение меж. Соб:
1.Отношение включения (А влечет за собой В). А явл. подмножеством В. Если происходит А, то и происходит В, но не наоборот.
2.Отношение несовместимости, т.е. соб А иВ вместе произойти не могут.
3. Отношение равносильности, т.е. соб А = соб В
СС – явление, которое при одних и тех же условиях иногда происходит, иногда не происходит.
studfiles.net
01. Понятие события. Виды и взаимосвязь событий
Понятие события. Виды и взаимосвязь событий.
Событием называется всякий факт, который может произойти или не произойти в результате опыта.
При этом тот или иной результат опыта может быть получен с различной степенью возможности. Т.е. в некоторых случаях можно сказать, что одно событие произойдет практически наверняка, другое практически никогда.
В отношении друг друга события также имеют особенности, т.е. в одном случае событие А может произойти совместно с событием В, в другом – нет.
События называются несовместными, если появление одного из них исключает появление других.
Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте).
Полной группой событий называется совокупность всех возможных результатов опыта.
Достоверным событием называется событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта.
Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.
События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.
В приведенном выше примере появление красного и зеленого шаров – равновозможные события, если в коробке находится одинаковое количество красных и зеленых шаров.
Если же в коробке красных шаров больше, чем зеленых, то появление зеленого шара – событие менее вероятное, чем появление красного.
События, которые могут произойти в результате опыта, можно подразделить на три вида:
а) достоверное событие – событие, которое всегда происходит при проведении опыта;
б) невозможное событие – событие, которое в результате опыта произойти не может;
в) случайное событие – событие, которое может либо произойти, либо не произойти.
Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий, соответственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий.
Пример 1. Два стрелка делают по одному выстрелу по мишени. Если событие А – попадание первого стрелка, а событие В – второго, то сумма А+В – это хотя бы одно попадание при двух выстрелах.
Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события.
Пример 2. В примере 1 ( два выстрела по мишени) событием АВ будет попадание обоих
стрелков.
Разностью А\B событий А и В называется событие, состоящее в том, что
А произошло, а В – нет.
Пример 3. Вернемся к примеру 1, где А\ В – попадание первого стрелка при промахе второго.
studfiles.net
Достоверные, невозможные, случайные события. Урок математики в 5 классе
Урок математики в 5 классе
«Достоверные, невозможные, случайные события»
Миргородова Татьяна Геннадьевна
учитель математики МОУ «СОШ №1»
г. Курск
Цели урока:
— познакомить учащихся с понятиями события, достоверные, невозможные, случайные события;
— развитие умения анализировать, вычислительных навыков , навыков самоконтроля;
— воспитание математической культуры.
Ход урока.
1. Организационный этап.
Сообщение темы урока, формулировка цели урока.
2. Актуализация знаний учащихся.
Математический диктант (слайды 2-3).
Выполните действия
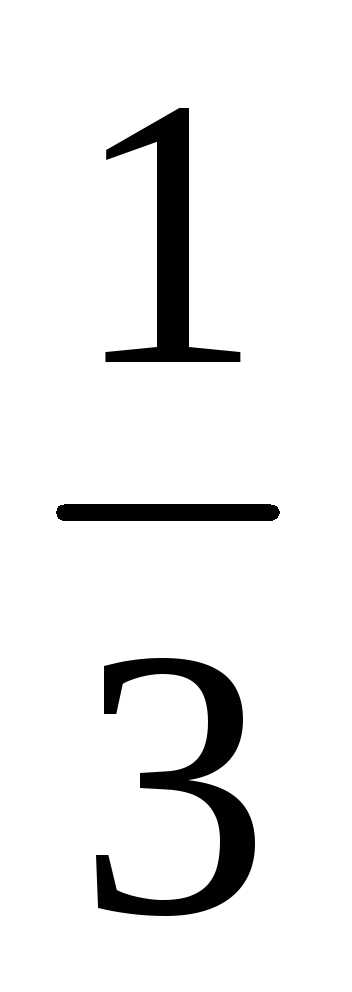
1) 1 : 2
2) 9 + 3,6
3) 2,08 : 0,4
4) 3,2 · 0,5
5) 5,2 + 4,34
6) 4 : 0,5
7) 4,7 — 2,62
8) 2,5 · 3
До того как мы откроем ключ и проверим правильность выполнения теста, давайте предположим, правильно ли вы выполнили вычисления. Высказывайте свои предположения. Например, я предполагаю, что, вероятнее всего, большинство учащихся с работой справились. А что думаете вы? (ответы детей)
Во многих наших предложениях прозвучали слова: “вероятно, наверно, может быть”. Мы попробовали предугадать результат выполнения теста. Но всё-таки давайте теперь проверим.
1) 0,5
2) 12,6
3) 5,2
4)1,6
5) 9,54
6) 8
7) 2,08
8) 7,5
Дети проверяют правильность выполнения задания по ключу, отмечают количество верных ответов.
Итак, мы имели возможность установить достоверность наших предположений. Чей прогноз оказался верным?
3. Новый материал (слайды 4 — 6)
В обычной жизни мы часто говорим: «Вероятно, сегодня будет дождь. Вероятнее всего, за контрольную работу получу 3. и т. п. ». В математике вероятность измеряется числом. Каким образом это можно сделать изучает такой раздел математики, как теория вероятностей. Сегодня мы должны познакомиться с первоначальными понятиями этого раздела науки.
На ваших столах лежат игральные кубики, подбросьте их, назовите выпавший результат. Полученный результат будем называть событием.
Интересно угадать наступление того или иного события. Сделаем предсказания:
выпадет 1,2,3,4,5 или 6.
выпадет 7.
выпадет 1.
Произойдут эти события или нет?
Давайте попробуем определить (слайды 7- 19):
Событие называется достоверным, если…
Событие называется невозможным, если…
Событие называется случайным, если…
Пример 1 (слайды 20-24) .
Вы открыли книгу на любой странице и прочитали первое попавшееся существительное. Оказалось
— в написании выбранного слова есть гласная буква;
— в написании выбранного слова есть буква «о»;
— в написании выбранного слова нет гласных букв;
-в написании выбранного слова есть мягкий знак;
— слово начинается с «ъ».
Пример 2 (слайды 25-29).
В коробке 3 красных, 3 желтых,
3 зеленых шара. Вытаскиваем, не глядя, один за другим шары. Какие из следующих событий невозможные, достоверные, случайные:
А: все вытянутые шары одного цвета;
В: все вытянутые шары разного цвета;
С: среди вытянутых есть шары разного цвета;
D: среди вытянутых есть шары всех трех цветов.
4. Формирование умений и навыков
Охарактеризуйте события, о которых идёт речь в приведённых ниже заданиях, как достоверные, невозможные, случайные.
Задача 1 (слайды 30-41)
Какие из перечисленных ниже событий случайные,
достоверные, невозможные:
а) черепаха научится говорить;
б) вода в чайнике, стоящем на плите, закипит;
в) день рождения одного из ваших знакомых – 30 февраля;
г) вы выиграете, участвуя в лотереи;
д) вы не выиграете, участвуя в беспроигрышной лотерее;
е) вы проиграете партию в шахматы;
ж) вы завтра встретите инопланетянина;
з) на следующей неделе испортится погода;
и) вы нажали на звонок, а он не звонит;
к) сегодня – четверг;
л) после четверга будет пятница;
м) после пятницы будет четверг.
Задача 2 (слайд 42)
Придумайте по три
примера достоверных, невозможных и случайных событий.
Задача 3 (слайды 43-50)
В коробке лежат 2 красных, 1 желтый и 4 зеленых шара. Из коробки наугад вынимают три шара. Какие из следующих событий невозможные, случайные, достоверные:
А: будут вытянуты три зеленых шара;
В: будут вытянуты три красных шара;
С: будут вытянуты шары трех цветов;
D: будут вытянуты шары одного цвета;
E: среди вытянутых шаров есть синий;
F: среди вытянутых шары трех цветов;
G: среди вытянутых есть два желтых шара.
Задача 4 (слайды 51-54)
Саша сравнивают свои дни рождения. Какие из следующих событий невозможные, случайные, достоверные:
а) их дни рождения не совпадают;
б) их дни рождения совпадают;
в)Маша родилась 29 февраля, а Саша 30 февраля;
г)дни рождения обоих приходятся на праздники – Новый год ( 1 января) и День независимости России ( 12 июня)
Задача 5 (слайды 55-56)
В коробке лежат черные и белые шары. Из нее наугад вытягивают один шар. Используя выражения «более вероятно», «менее вероятно», «равновероятные события», сравните возможность наступления случайных событий А и В, где
А: вытянутый шар будет белым;
В: вытянутый шар будет черным.
1 2 3 4 5
5. Итог урока
5.1 Учащиеся повторяют определения случайных, достоверных, невозможных событий.
5.2 Учащиеся выполняют тест и кодируют ответ. Затем учащимся сообщается код правильного ответа (слайды 57-63)
5.3 Учитель выставляет отметки за урок.
6. Домашнее задание.
п. 53, стр. 248 Математика 5 И.И. Зубарева, А.Г. Мордкович
№ 962, № 965
infourok.ru
Классификация случайных событий.
Стр 1 из 2Следующая ⇒
Основы теории вероятностей.
Теория вероятностей – это раздел математики, который изучает закономерности в массовых случайных событиях.
Событие – это факт, который может произойти или не произойти в результате проведения опыта или испытания.
Выделяют три вида событий:
а) достоверные
б) невозможные
с) случайные
Достоверное событие – это событие, которое обязательно произойдёт в результате данного опыта.( например: при бросании кубика выпадет 1≤целое число≤6).
Невозможное событие – это событие, которое никогда не произойдет в условиях данного опыта. .( например: при бросании кубика выпадет число≥7, например 10).
Случайное событие – это событие, которое может произойти или не произойти в результате данного опыта. ( например: бросили кубик один раз – выпадение числа 3 – случайное событие).
События обозначаются первыми заглавными буквами латинского алфавита: А, В, С, D,.
События называются массовыми, если они происходят одновременно в достаточно большом числе испытаний или многократно повторяются .( например: много людей бросают кубики или один человек бросает кубик много раз).
Классификация случайных событий.
Равновозможные события – это события такие, что ни одно из них не является более возможным, чем другие ( например: кубику всё равно на какую грань упасть).
Совместные события – это события, которые могут произойти одновременно в результате данного опыта. ( например: бросаем 2 кубика — выпадение числа 1 и выпадение числа 3 – совместные события).
Несовместные события – это равновозможные события такие, что появление одного из них исключает появление остальных.( например: бросаем 1 кубик – выпадение цифры 3 исключает выпадение остальных цифр).
Несколько случайных событий: образуют полную группу событий, если каждое из них может произойти в результате данного опыта. ( например: выпадение чисел 1,2,3,4,5,6 –полная группа событий для бросания одного кубика).
Противоположные события – это равновозможные несовместные события, образующие полную группу событий. Появление события исключает появление события . ( например: орёл или решка, попадание в мишень или промах).
Несмотря на то, что события случайные, при большом числе опытов они подчиняются закономерностям, которые изучает теория вероятностей.
Вероятность случайного события.
Вероятность случайного события (обозначается Р(А)) –это число, которое говорит нам о степени возможности наступления события .
Существуют два определения вероятности: классическое и статистическое, каждое из них имеет свои достоинства и недостатки.
Классическое определение вероятности.
Вероятность события – это отношение числа исходов, благоприятствующих данному событию (m), к общему числу всех несовместных и равновозможных исходов данного опыта (n).
Если А – случайное событие, то
Если А – достоверное событие, то
Если А – невозможное событие, то
Пример: при бросании кубика возможно 6 исходов
Событие А: выпадет четное число. Число исходов, благоприятствующих событию А, m=3.
Достоинства: можно вычислить вероятность не производя испытания.
Недостатки: 1) не всегда известно число исходов опыта,
2) часто невозможно представить результат испытаний в виде равновозможных и несовместных событий.
Поэтому на практике часто пользуются статистическим определением вероятности.
Статистическое определение вероятности.
Пусть А – случайное событие, опыт проводился n раз, в результате опыта событие А произошло m раз, тогда m— частота наступления события А, а величина называется относительной частотой события А.
Для разных n , могут заметно отличаться, но если проводим длинную серию опытов, т.е. , то к некоторому пределу.
Статистической вероятностью события А называется предел, к которому стремится его относительная частота , при неограниченном увеличении числа испытаний.
Пример: среди 1000 новорожденных 517 мальчиков. Найти относительную частоту рождения мальчиков. , тем не менее, известно, что
Так как вероятность – это число следовательно, с этими числами можно производить арифметические действия.
Формула полной вероятности.
Иногда событие А может произойти только совместно с одним из нескольких других событий, их принято называть гипотезами и обозначать Тогда полная вероятность события А вычисляется по формуле:
Пример: Н₃
Н₁ Н₂ СобытиеА:попадёмв домик.

Формулы Байеса.
До проведения опыта мы имели вероятности гипотез
(В примере ).
После проведенияопыта:
Пусть событие А произошло (т.е. попали в домик), вероятности гипотез изменились. Для того, чтобы вычислить вероятности гипотез, при условии, что произошло событие А используют формулы Байеса:
Пример
Случайная величина.
Случайная величина – это переменная, которая принимает свои значения в зависимости от случайных обстоятельств.
.Дискретная случайнаявеличина (точечная) принимает отдельные числовые значения (число студентов в аудитории, кубик: 1,2,3,4,5,6)
Непрерывная случайная величина принимает любые значения из некоторого интервала( масса тела, рост студентов).
Случайные величины обозначают заглавными последними буквами латинского алфавита:X,Y,Z…,а их возможные значения прописными буквами:
Любое правило, которое устанавливает связь между возможными значениями случайной величины и вероятностями, с которыми она эти значения принимает, называется законом распределения случайной величины.
Закон распределения случайной величины можно задавать в виде:
1).Таблицы
2). Графика
3) Функции распределения.
Функция распределения.
| 1). F(x) неубывающая: F(x2)≥F(x1) если x2≥x1 2).F(-∞)=0; F(+∞)=1 |
4). Функция плотности распределения f(x): (только для непрерывной случайной величины).
Найдём предел:
Обозначим: . это функция плотности распределения.
То есть функция распределения F(x) является первообразной для функции плотности распределения f(x).
| Площадь под кривой |
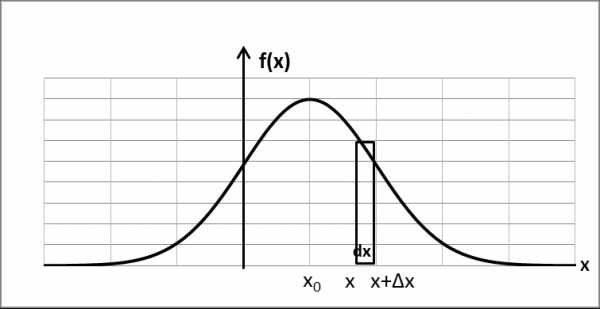
1). f(x) неотрицательная функция (f(x)≥0).
2). Вероятность попадания в элементарный интервал dx=(x+Δx)-x равна f(x)dx=dP.
3).Вероятность попадания случайной величины в интервал [a,b]:
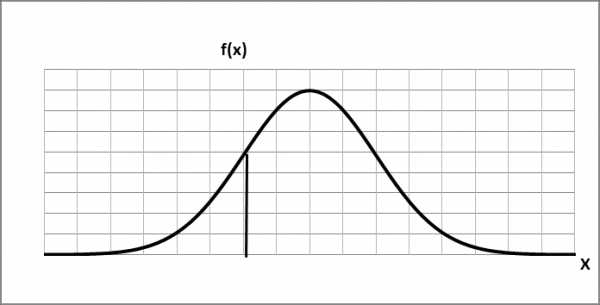
4). Условие нормировки: площадь под кривой равна единице.
Формула полной вероятности.
Формулы Байеса.
Основы теории вероятностей.
Теория вероятностей – это раздел математики, который изучает закономерности в массовых случайных событиях.
Событие – это факт, который может произойти или не произойти в результате проведения опыта или испытания.
Выделяют три вида событий:
а) достоверные
б) невозможные
с) случайные
Достоверное событие – это событие, которое обязательно произойдёт в результате данного опыта.( например: при бросании кубика выпадет 1≤целое число≤6).
Невозможное событие – это событие, которое никогда не произойдет в условиях данного опыта. .( например: при бросании кубика выпадет число≥7, например 10).
Случайное событие – это событие, которое может произойти или не произойти в результате данного опыта. ( например: бросили кубик один раз – выпадение числа 3 – случайное событие).
События обозначаются первыми заглавными буквами латинского алфавита: А, В, С, D,.
События называются массовыми, если они происходят одновременно в достаточно большом числе испытаний или многократно повторяются .( например: много людей бросают кубики или один человек бросает кубик много раз).
Классификация случайных событий.
Равновозможные события – это события такие, что ни одно из них не является более возможным, чем другие ( например: кубику всё равно на какую грань упасть).
Совместные события – это события, которые могут произойти одновременно в результате данного опыта. ( например: бросаем 2 кубика — выпадение числа 1 и выпадение числа 3 – совместные события).
Несовместные события – это равновозможные события такие, что появление одного из них исключает появление остальных.( например: бросаем 1 кубик – выпадение цифры 3 исключает выпадение остальных цифр).
Несколько случайных событий: образуют полную группу событий, если каждое из них может произойти в результате данного опыта. ( например: выпадение чисел 1,2,3,4,5,6 –полная группа событий для бросания одного кубика).
Противоположные события – это равновозможные несовместные события, образующие полную группу событий. Появление события исключает появление события . ( например: орёл или решка, попадание в мишень или промах).
Несмотря на то, что события случайные, при большом числе опытов они подчиняются закономерностям, которые изучает теория вероятностей.
Рекомендуемые страницы:
lektsia.com






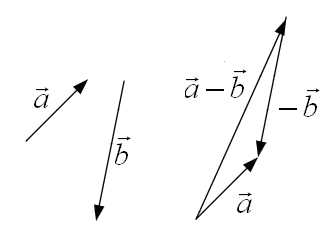
 двух векторов
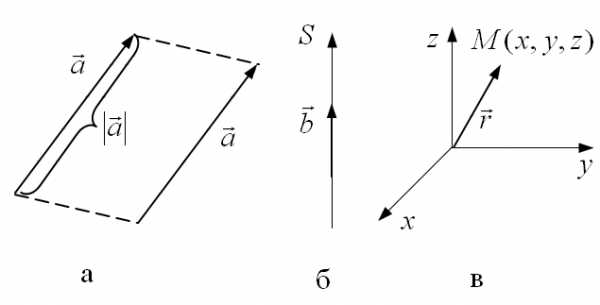
двух векторов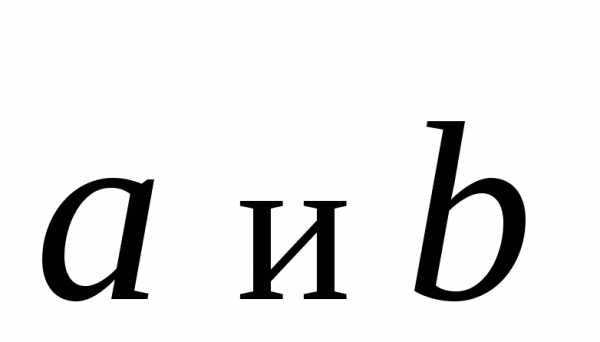 называется
вектор, идущий из начала вектора
называется
вектор, идущий из начала вектора в конец вектора
в конец вектора при условии, что начало
при условии, что начало приложено к концу вектора
приложено к концу вектора .
. существует такой
существует такой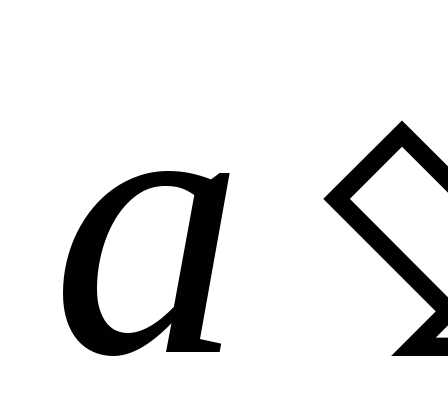 что.
что.
 где
где —
противоположный вектор вектору
—
противоположный вектор вектору .
. называется вектор
называется вектор ,
коллинеарный
,
коллинеарный ,
имеющий длину
,
имеющий длину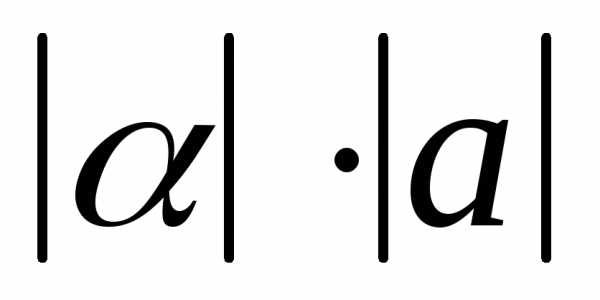 и имеющий направление, совпадающее с
и имеющий направление, совпадающее с еслии
противоположное, если.
еслии
противоположное, если. растягивается враз.
растягивается враз. коллинеарен
вектору
коллинеарен
вектору ,
то существует такое вещественное число,
что
,
то существует такое вещественное число,
что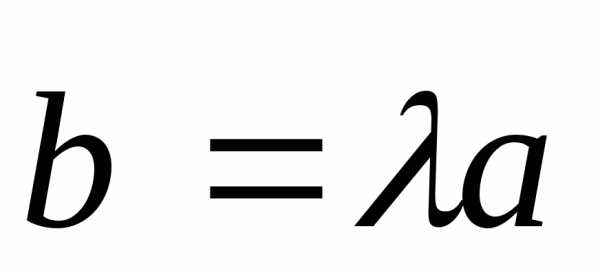 .
. и
и .
В силу коллинеарности они окажутся на
одной прямой. Т. е.
.
В силу коллинеарности они окажутся на
одной прямой. Т. е. .
Т.е. что длины их равны, направления
совпадают, коллинеарны.
.
Т.е. что длины их равны, направления
совпадают, коллинеарны. и
коллинеарности
и
коллинеарности и
и ,
равенство длин непосредственно из
определения произведения и (*). Наконец,
опять из определения произведения
следует, что если,
направления совпадают, и если,
то
,
равенство длин непосредственно из
определения произведения и (*). Наконец,
опять из определения произведения
следует, что если,
направления совпадают, и если,
то и
и —
противоположно направлены.
—
противоположно направлены. —
вещественные числа.
—
вещественные числа.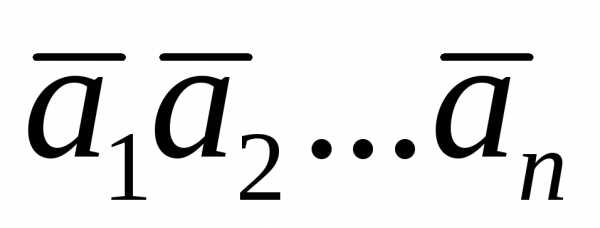 называются линейно зависимыми, если
существуют такие, хотя бы одно из которых отлично от
нуля, что имеет место равенство:
называются линейно зависимыми, если
существуют такие, хотя бы одно из которых отлично от
нуля, что имеет место равенство: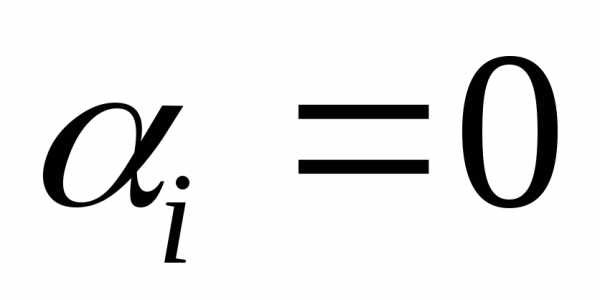 ,
то такие векторыназываются линейно независимыми.
,
то такие векторыназываются линейно независимыми.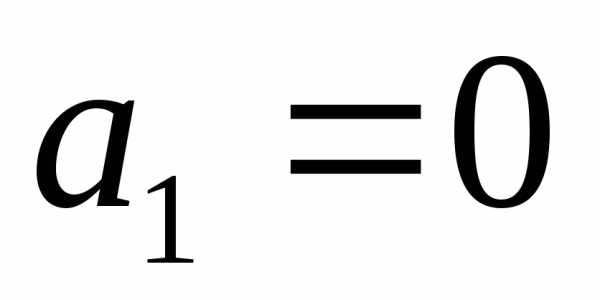 .
Тогда выполняется равенство:
.
Тогда выполняется равенство: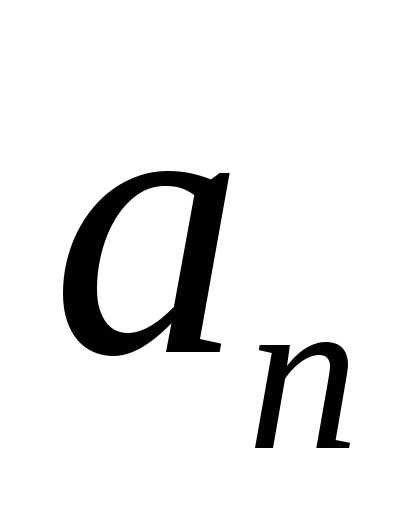 какие
либо (п-1)
линейно зависимы, то и все п являются линейно зависимы.
какие
либо (п-1)
линейно зависимы, то и все п являются линейно зависимы.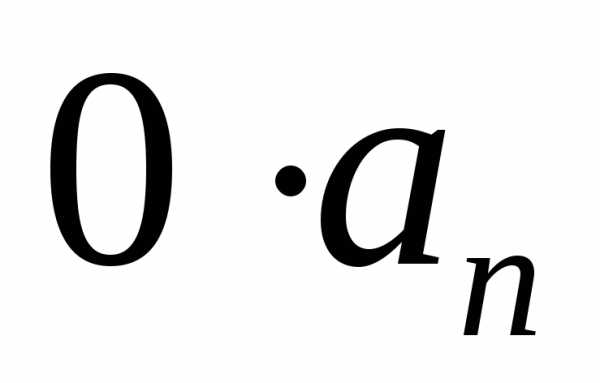 и получим,
и получим, и
и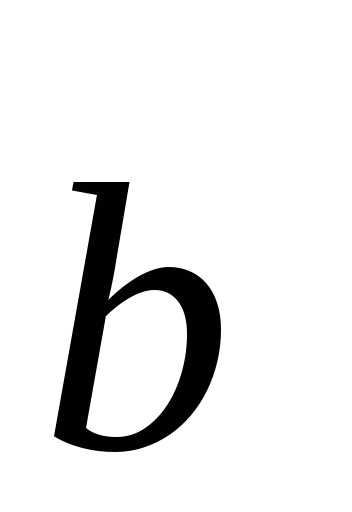 линейно зависимы. Т.е.
линейно зависимы. Т.е.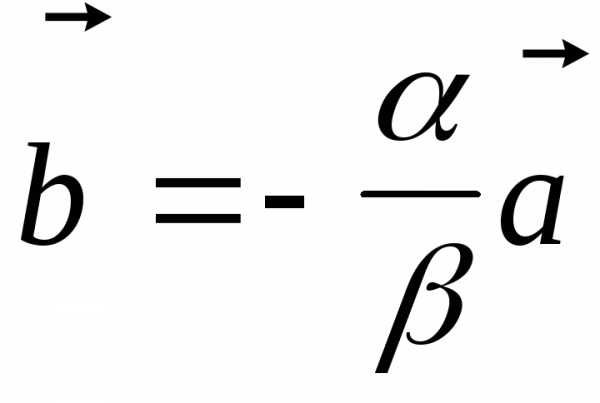 или
или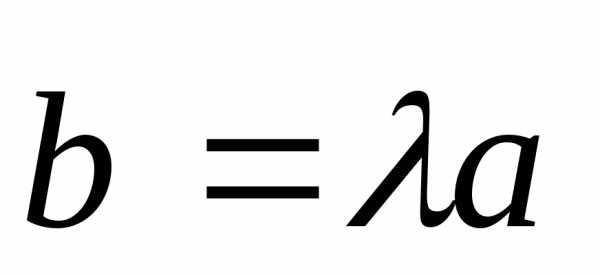 .
По определению произведения
.
По определению произведения и
и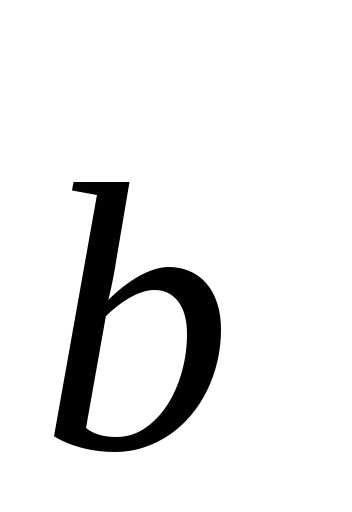 коллинеарны.
коллинеарны. и
и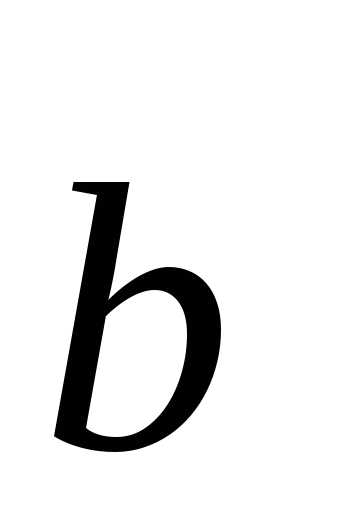 коллинеарны.
Если
коллинеарны.
Если или
или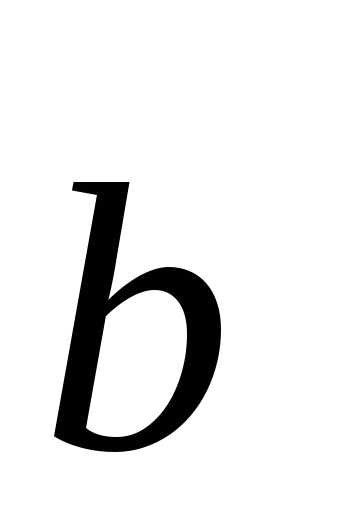 равно
нулю, то они линейно зависимы в силу
теоремы 2. Если
равно
нулю, то они линейно зависимы в силу
теоремы 2. Если и
и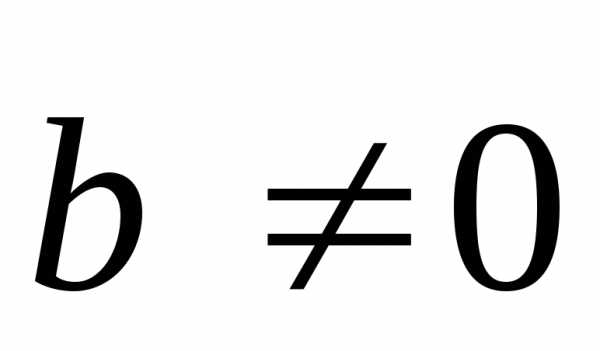 то в силу теоремы 1 имеем:
то в силу теоремы 1 имеем: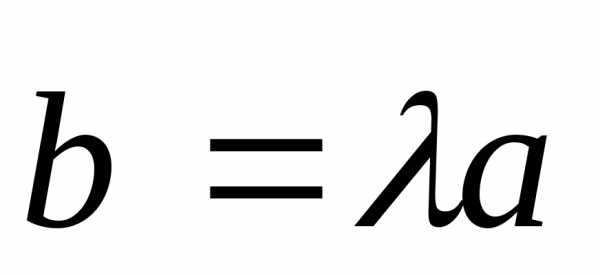 ,
или
.
,
или
. и
и .
. и
и неколлинеарны, то они линейно независимы.
неколлинеарны, то они линейно независимы.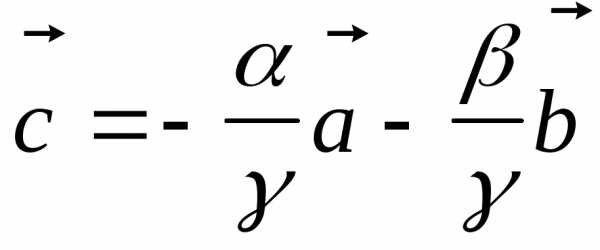 ,
или
,
или компланарны. Исключим случай, когда
пара векторов коллинеарна и когда
какой-либо вектор равен 0. Эти случаи
тривиальны. Рассмотрим случай, когда
все неколлинеарны.
компланарны. Исключим случай, когда
пара векторов коллинеарна и когда
какой-либо вектор равен 0. Эти случаи
тривиальны. Рассмотрим случай, когда
все неколлинеарны.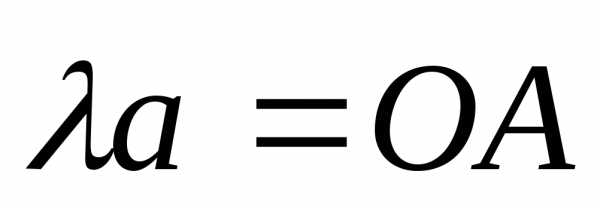

 и
и неколлинеарны,
то для любого
неколлинеарны,
то для любого ,
лежащего в одной плоскости с векторами
,
лежащего в одной плоскости с векторами и
и найдутся
такиеи,
что выполнится равенство:
найдутся
такиеи,
что выполнится равенство: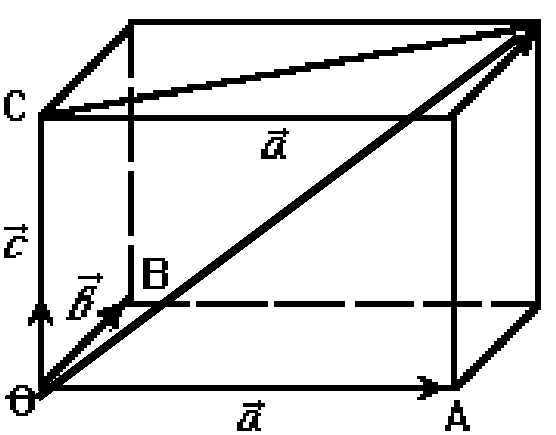
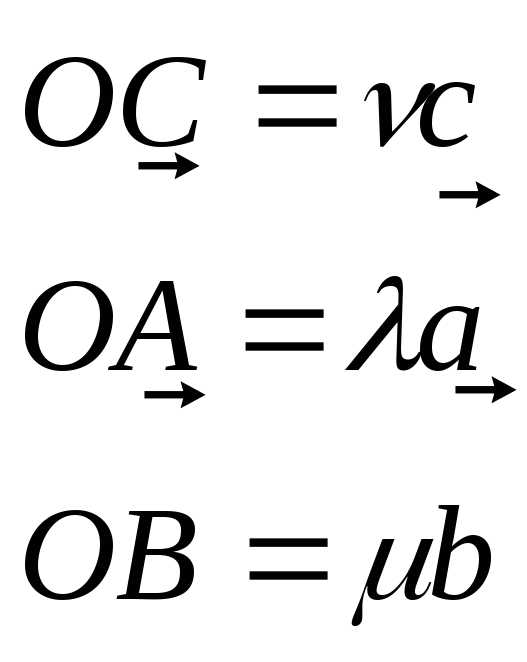
 равенилиили.
равенилиили. ,
какие-либо некомпланарные, т.е. линейно
независимые векторы, то для любого
вектора
,
какие-либо некомпланарные, т.е. линейно
независимые векторы, то для любого
вектора можно найти такие числа,
что
можно найти такие числа,
что и
и образуют
в пространстве базис, если любой вектор
образуют
в пространстве базис, если любой вектор может
быть представлен в виде линейной
комбинации векторов
может
быть представлен в виде линейной
комбинации векторов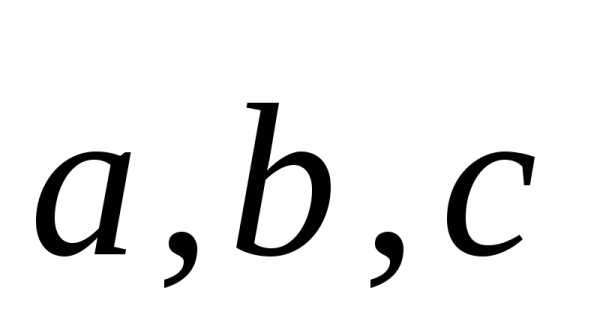
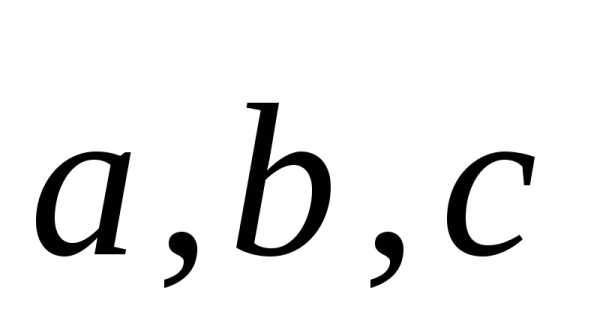 ,
а числа-координатами
вектора
,
а числа-координатами
вектора относительно
базиса
относительно
базиса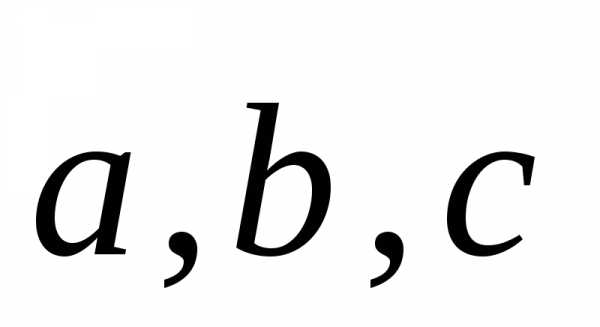 .
Причём можно доказать, что разложение
.
Причём можно доказать, что разложение по
базису
по
базису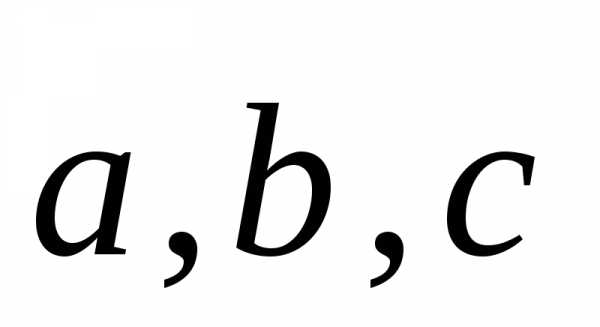 может быть единственным образом
осуществлено.
может быть единственным образом
осуществлено.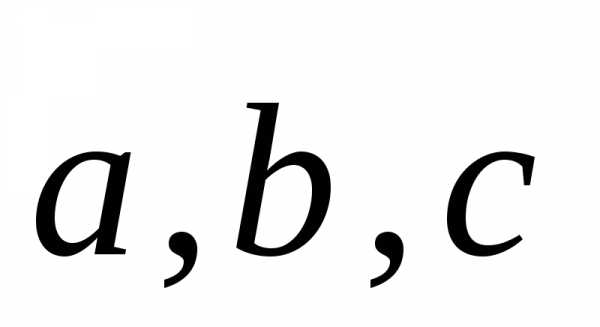 и некоторой точки О, называемой началом
координат.
и некоторой точки О, называемой началом
координат.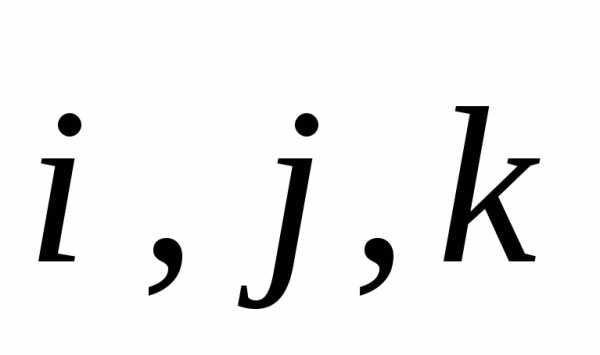 .
Для каждого вектора
.
Для каждого вектора найдётся
и при том единственная тройка чисел,
такая, что
найдётся
и при том единственная тройка чисел,
такая, что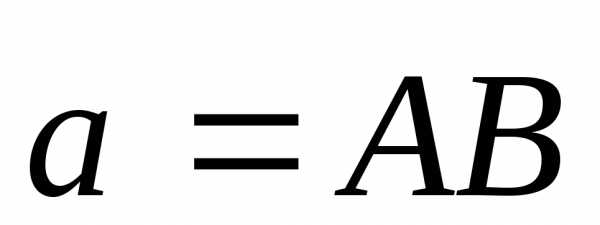 .
Опустим перпендикуляры из точек А и В
на осьv.
Основания перпендикуляров обозначим
и.
.
Опустим перпендикуляры из точек А и В
на осьv.
Основания перпендикуляров обозначим
и.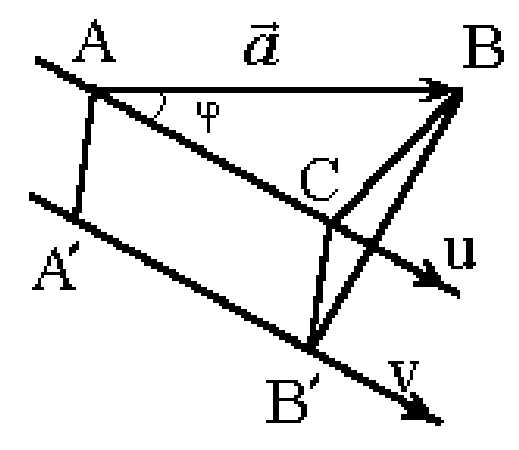
 на
осьv назовём величину направленного отрезка
на
осьv назовём величину направленного отрезка  осиv.
осиv. к осиv назовём угол
между направлением вектора
к осиv назовём угол
между направлением вектора и направлением осиv.
Из рассмотрения треугольника АВС
следует, что
.
и направлением осиv.
Из рассмотрения треугольника АВС
следует, что
. являются
проекции векторана
оси соответственно ортам:
являются
проекции векторана
оси соответственно ортам: -ось
Ох,
-ось
Ох,  -ось
Oy ,
-ось
Oy , —
ось Oz.
—
ось Oz. .
.

















 0 , и противоположно ему, если λ Пример. «
0 , и противоположно ему, если λ Пример. «
 0 λ = 3 Длина вектора увеличивается в λ раз, и направление остаётся прежним. «
0 λ = 3 Длина вектора увеличивается в λ раз, и направление остаётся прежним. «












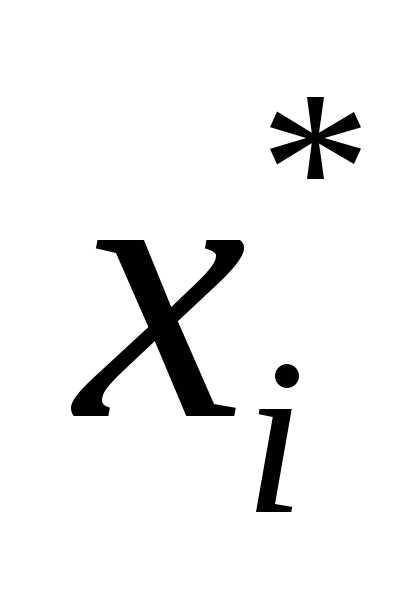 ,
то к ограничениям задачи добавляется
новое ограничение, обладающее следующими
свойствами:
,
то к ограничениям задачи добавляется
новое ограничение, обладающее следующими
свойствами: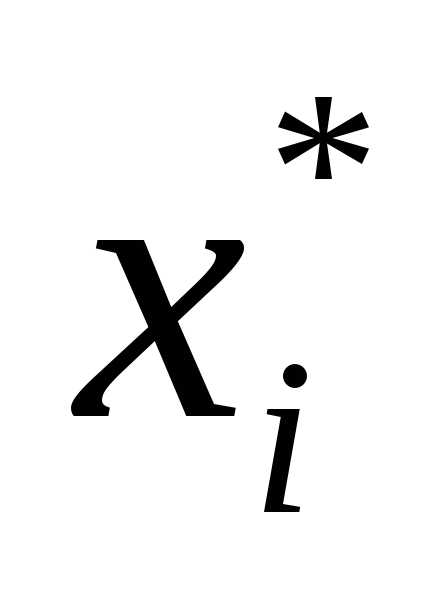 с
наибольшей дробной частью (если таких переменных несколько, то
выбираем любую).
с
наибольшей дробной частью (если таких переменных несколько, то
выбираем любую). такое, что разность между ним иа есть
[a]
– целая часть числа).
такое, что разность между ним иа есть
[a]
– целая часть числа).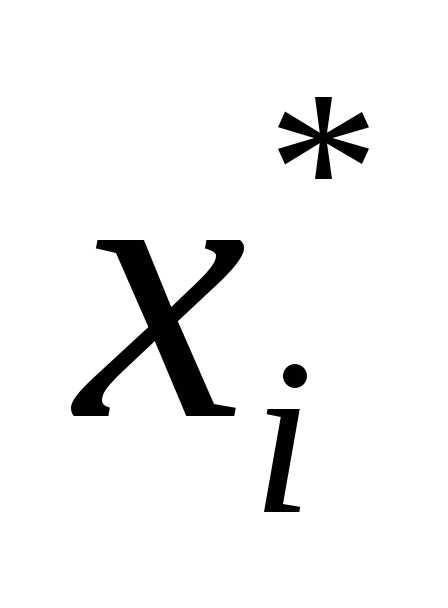 с
наибольшей дробной частью находим дробную часть
с
наибольшей дробной частью находим дробную часть 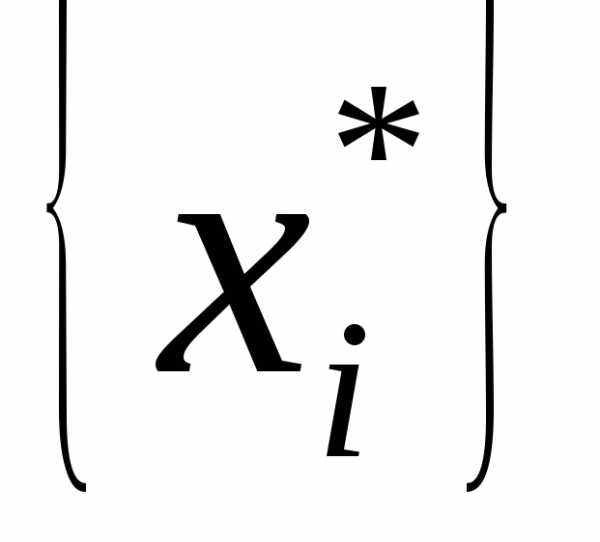 этой переменной и дробные части всех
коэффициентов при переменныхi — й строки системы ограничений
(производящей
строкой).
этой переменной и дробные части всех
коэффициентов при переменныхi — й строки системы ограничений
(производящей
строкой).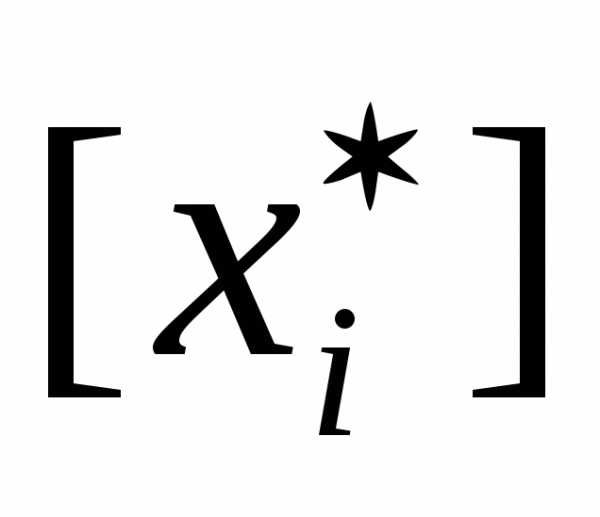 и
и целые
части чисел
целые
части чисел  и
и  .
Величины дробных частей
.
Величины дробных частей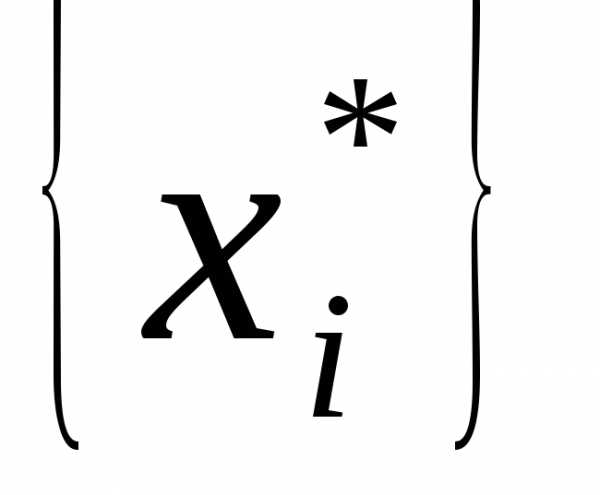 и
и ()
определяются следующим образом
()
определяются следующим образом
 или
или 
 <1,
то заменяя в правой части
<1,
то заменяя в правой части  ,
получим строгое неравенство
,
получим строгое неравенство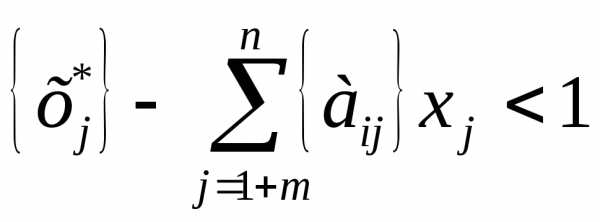

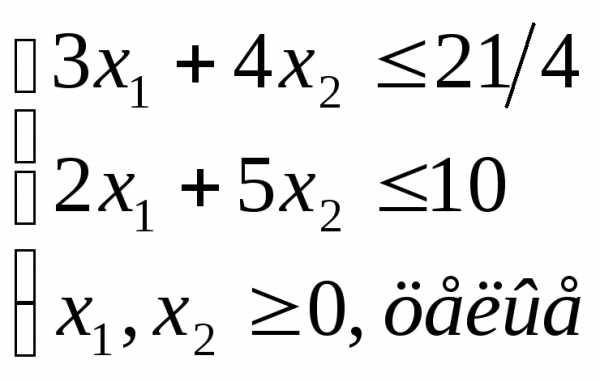
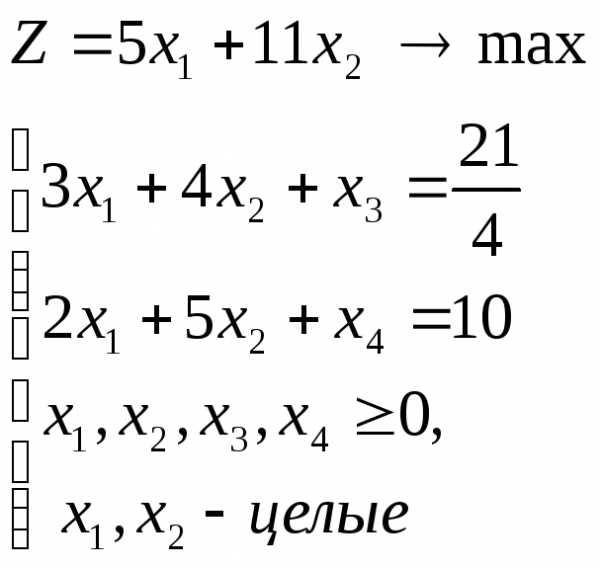
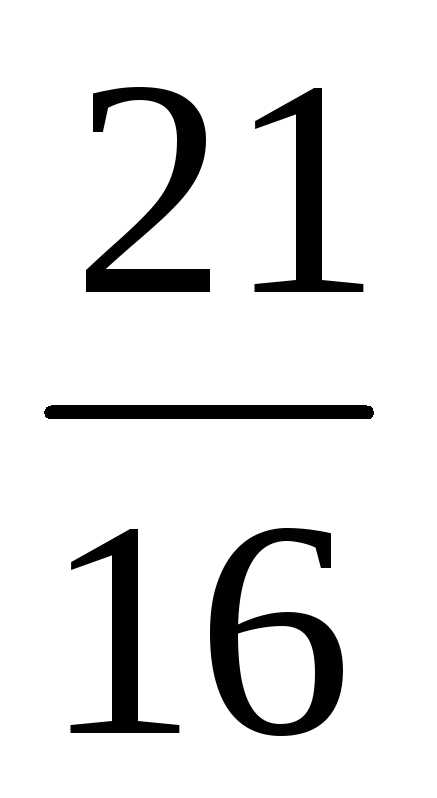
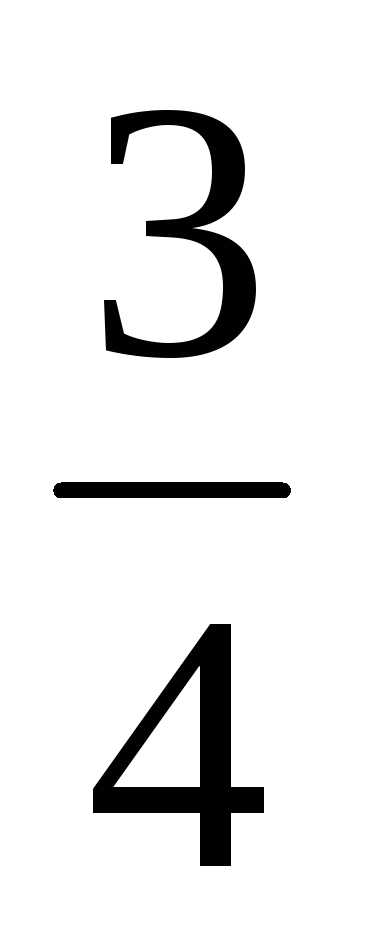

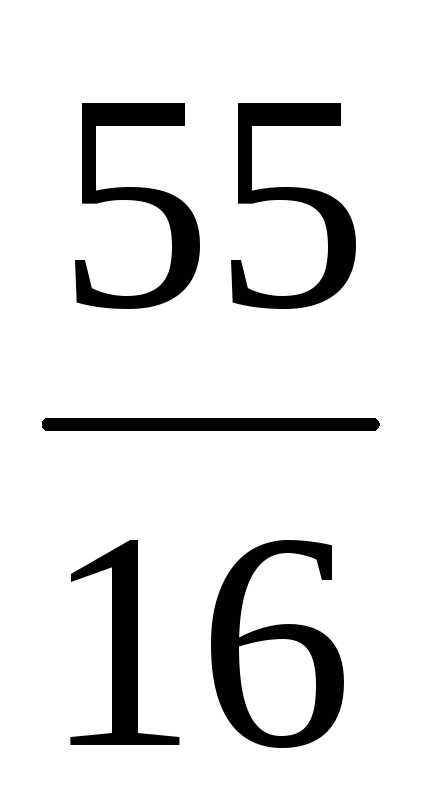
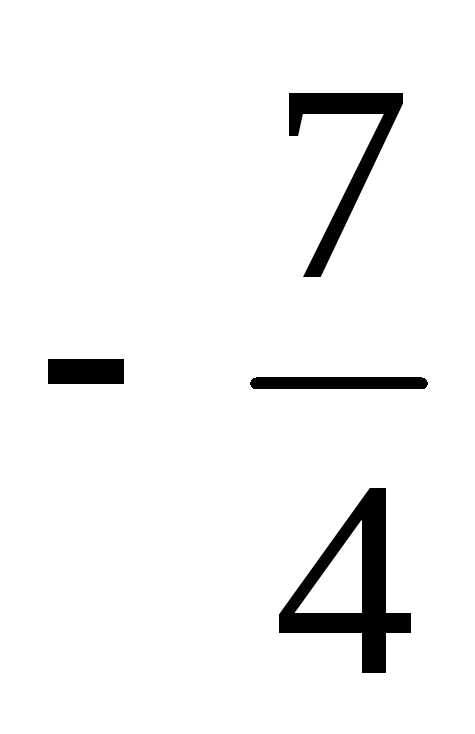
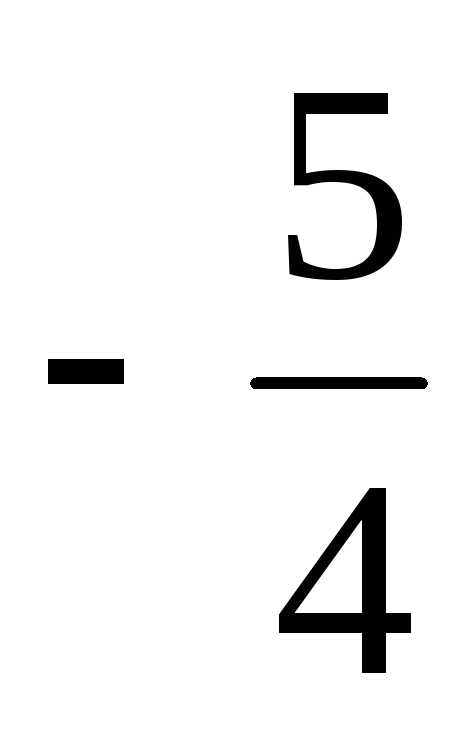

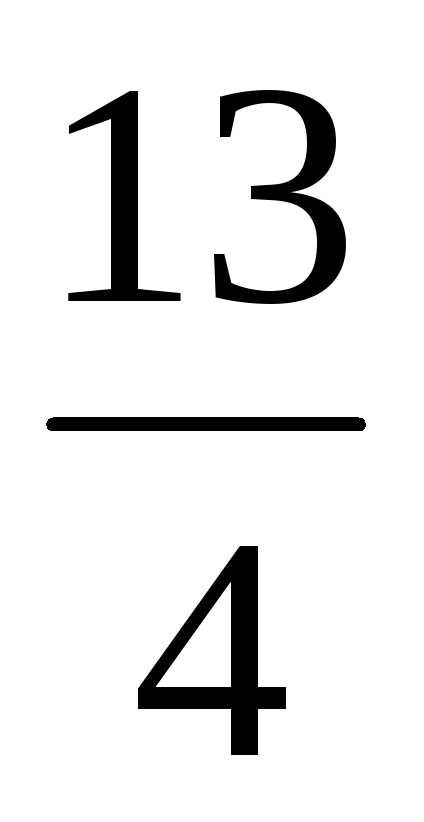
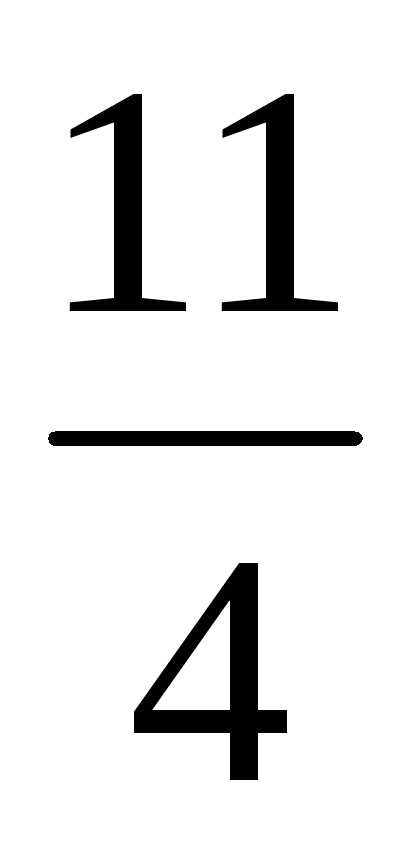
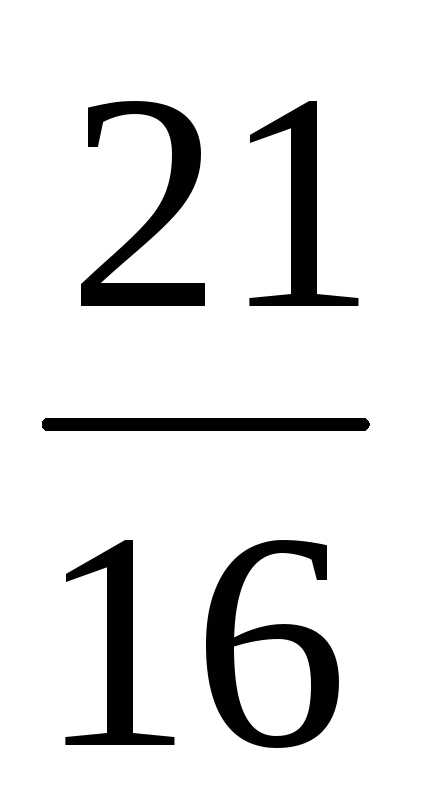
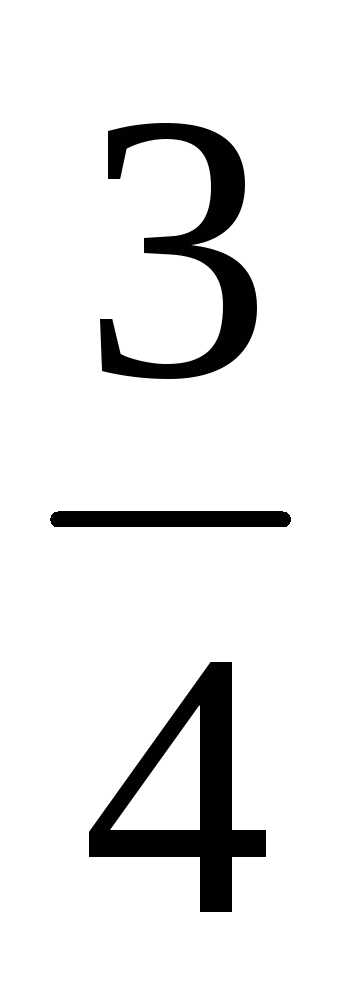
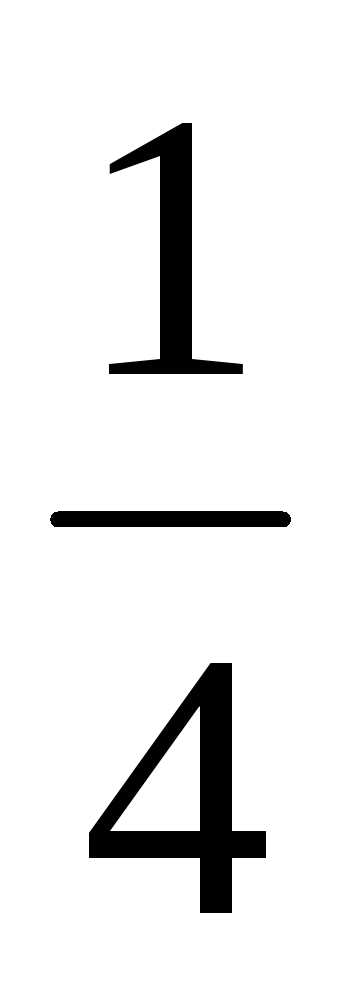

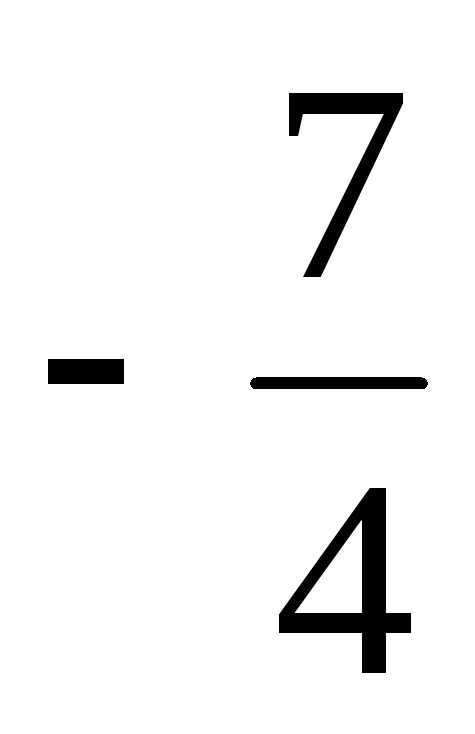
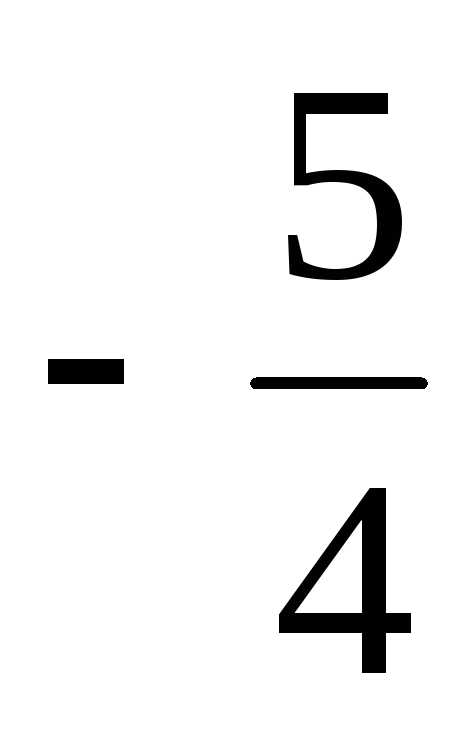
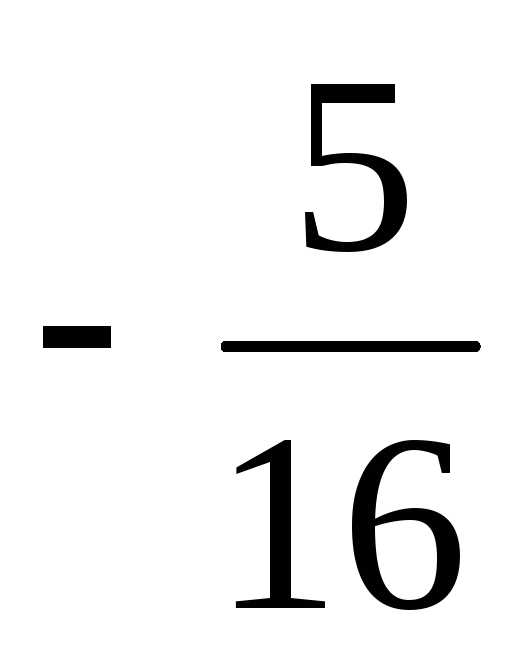
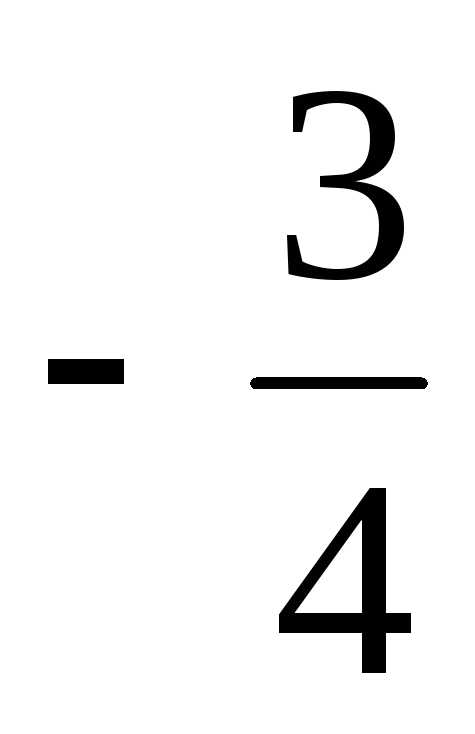
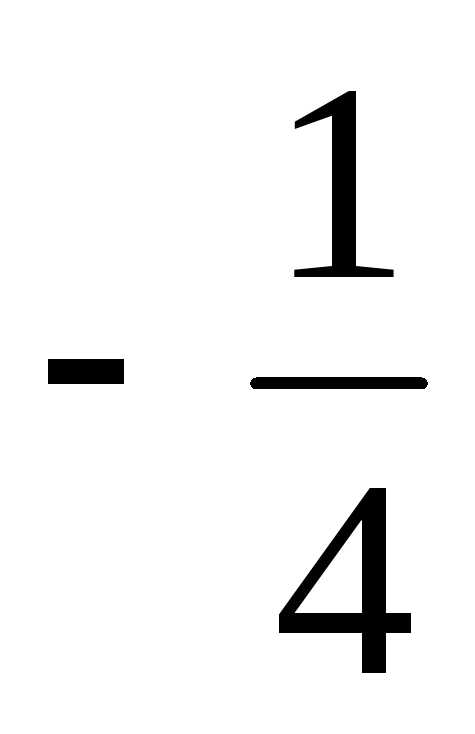


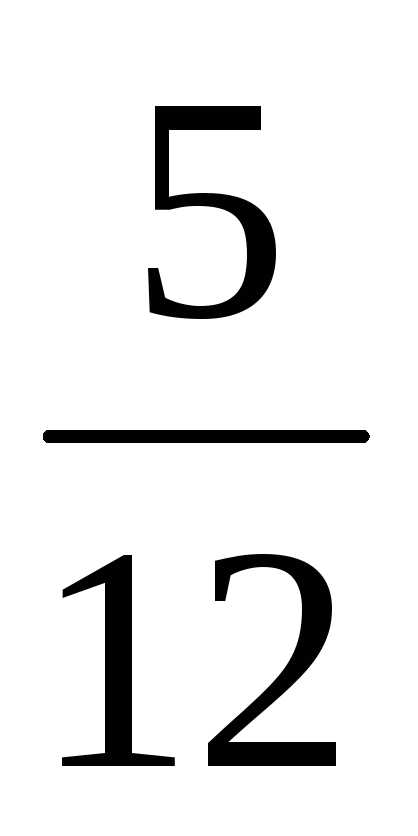
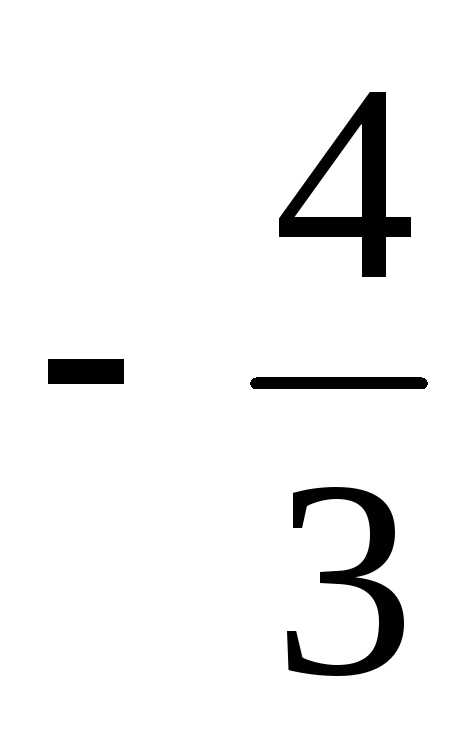
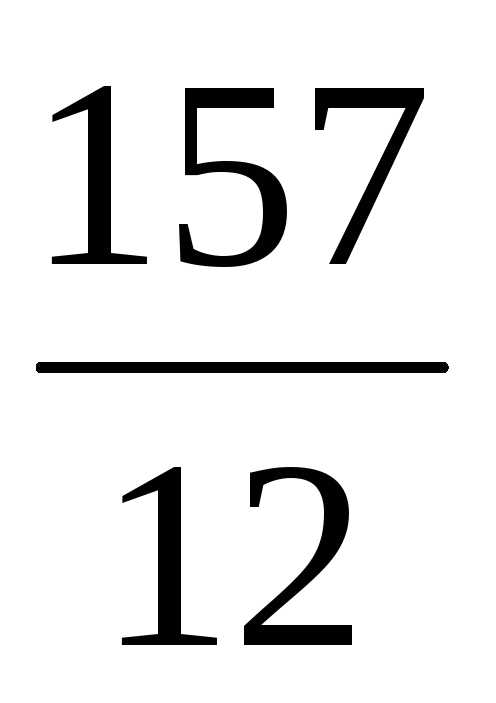

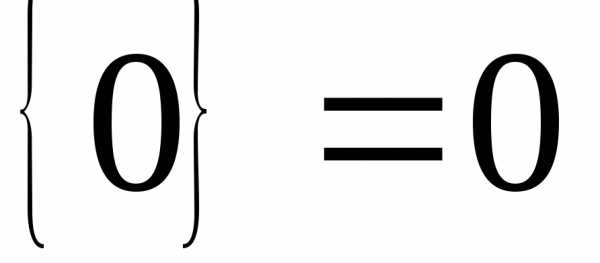


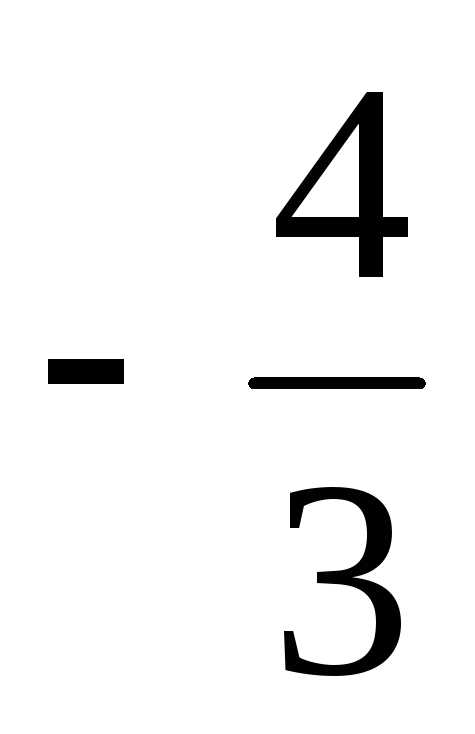
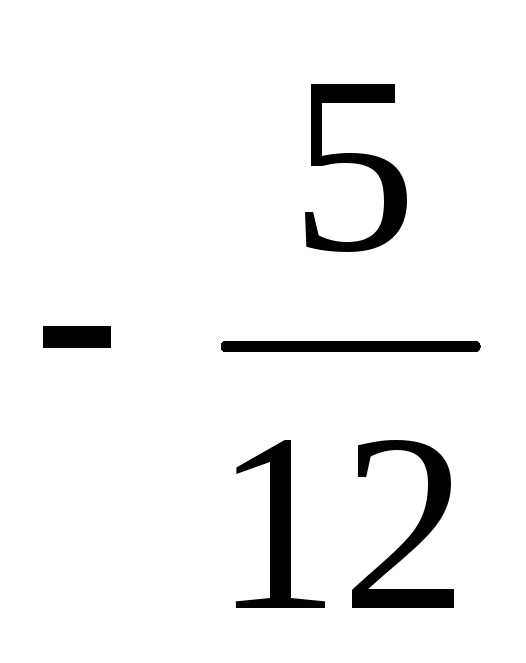
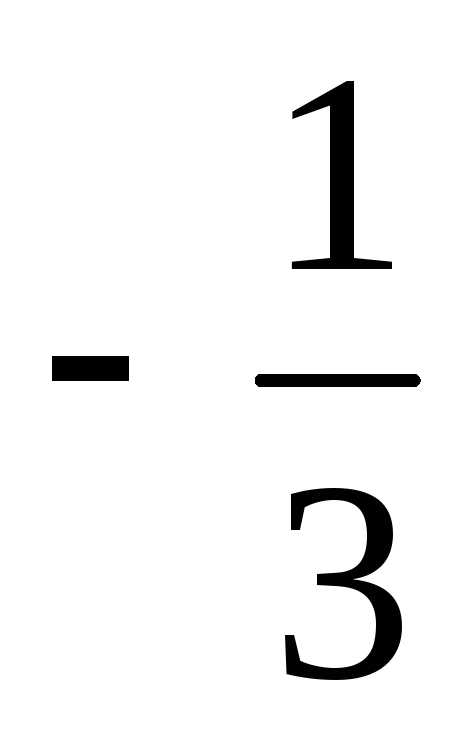

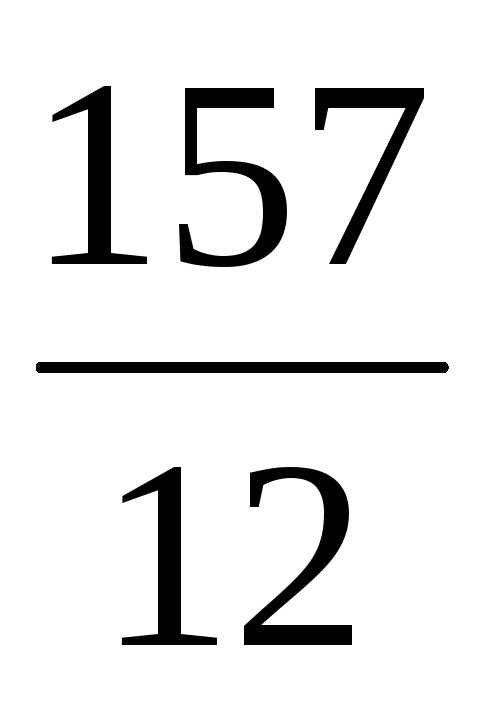
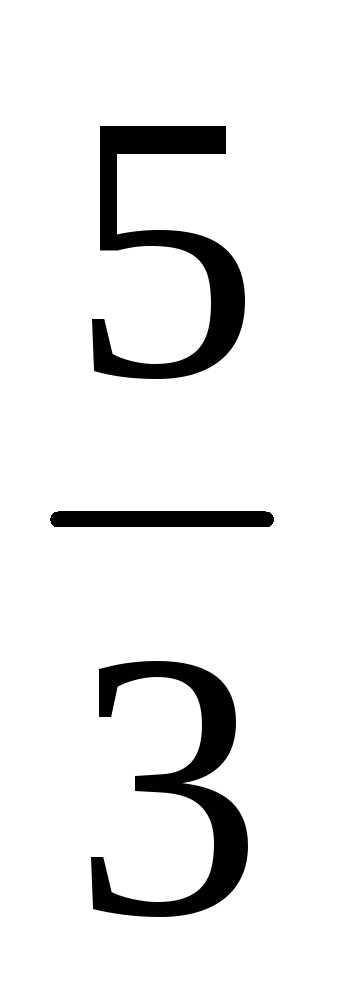
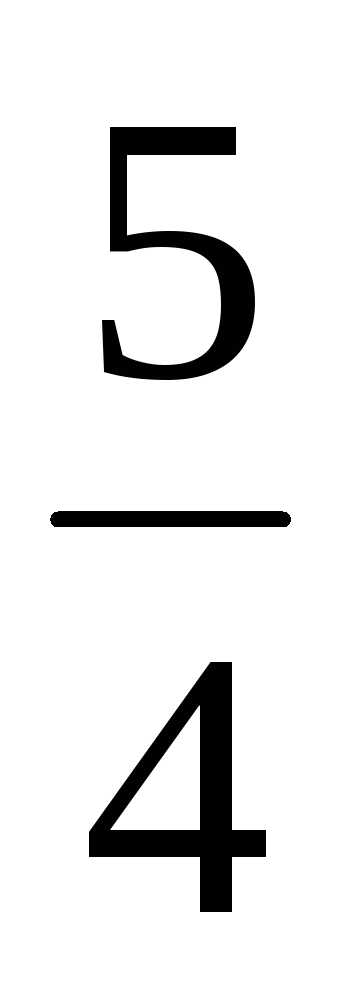
 и целыми коэффициентами в соответствующей
строке системы ограничений
и целыми коэффициентами в соответствующей
строке системы ограничений ,
то данная задача не имеет целочисленного
решения.
,
то данная задача не имеет целочисленного
решения.

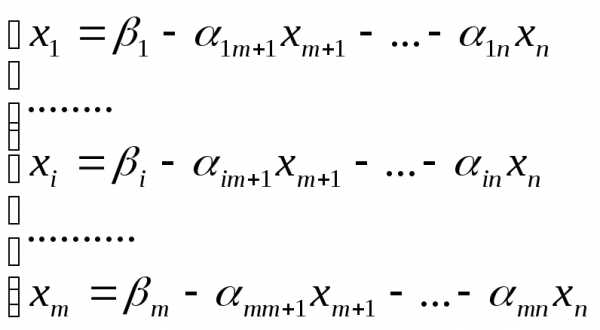

 — дробная часть числа.
— дробная часть числа.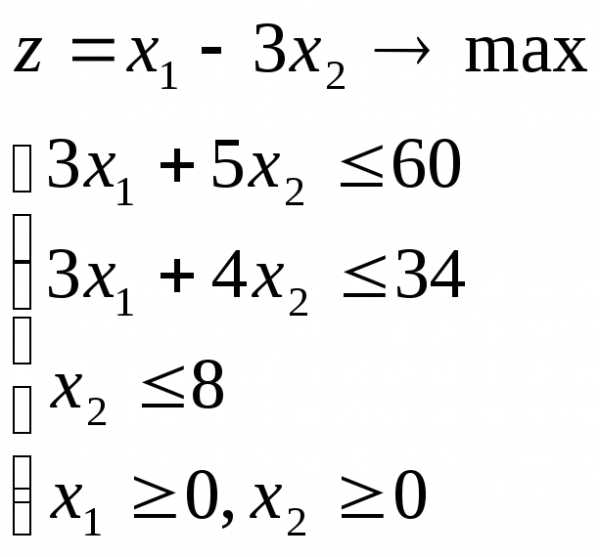
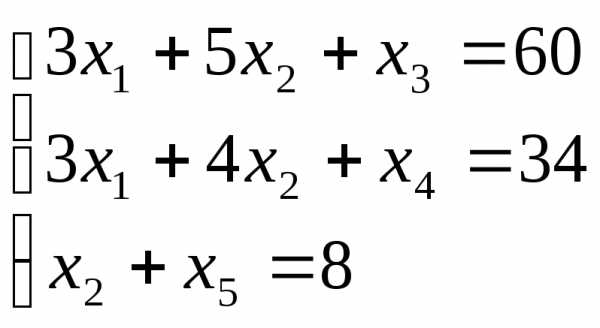
 ;
;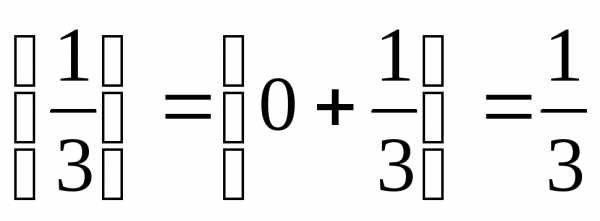 ;
;
 —
доля финансирования проекта “НТВ-Плюс”,
—
доля финансирования проекта “НТВ-Плюс”,
 —
доля финансирования проекта Europe
On
Line,
—
доля финансирования проекта Europe
On
Line,
 —
доля финансирования проекта Astra
Network,
—
доля финансирования проекта Astra
Network,
 —
доля финансирования проекта Satpro,
—
доля финансирования проекта Satpro,
 —
доля финансирования проекта Network
Service.
—
доля финансирования проекта Network
Service. (2)
(2)
 =
=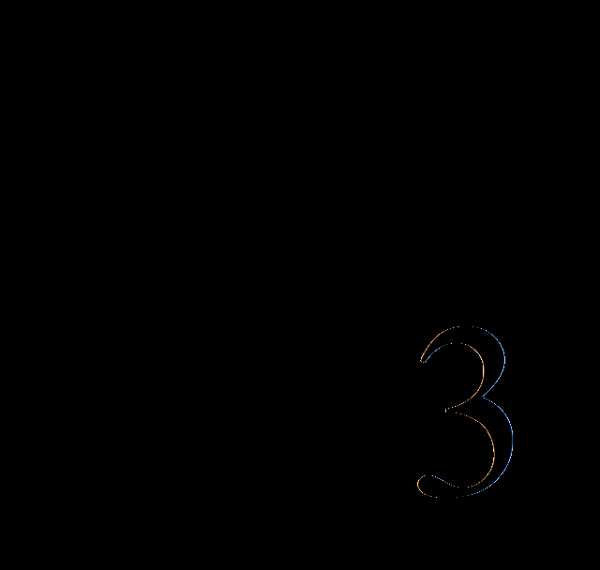 с наибольшей дробной частью:
,
,
.
Для переменной
с наибольшей дробной частью:
,
,
.
Для переменной
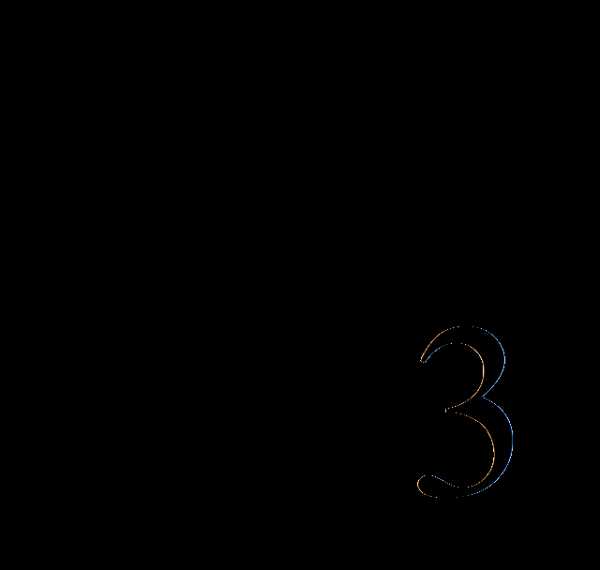 составляется уравнение.
составляется уравнение.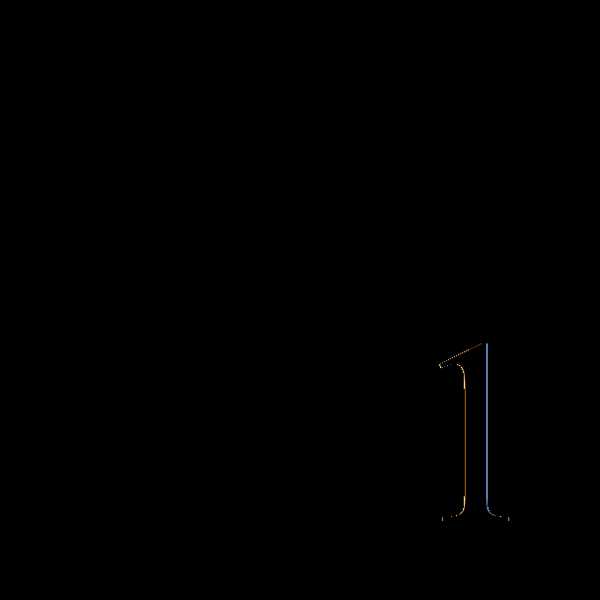 =
= =
= =
=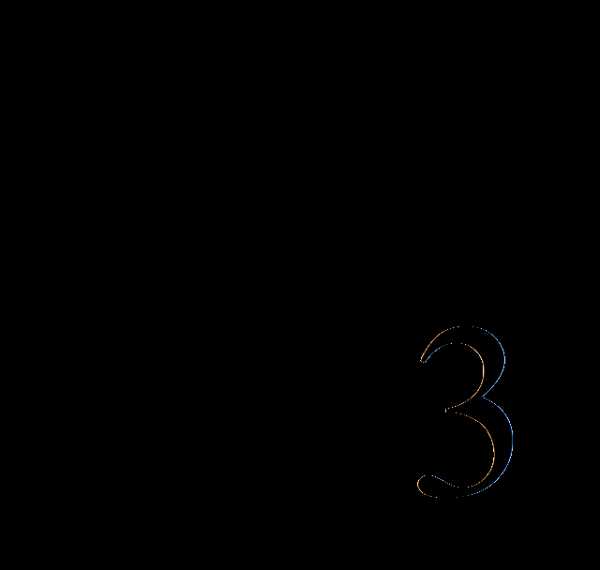 =
= =
= =
= =
= =
= =
= =
=
 =
= =
= =
= =
= =
= =
=