Инструкция: офисные калькуляторы
Электронный калькулятор предназначен для бухгалтерских и бытовых расчетов. Работа с калькулятором отличается простотой и не требует специального обучения.
ОПЕРАЦИОННЫЕ КЛАВИШИ
[ON] – включение
[OFF] – выключение. Если в течение 8–11 мин. не нажималась ни одна клавиша, калькулятор автоматически отключается.
[+][-][x][¸] – арифметические операции
[CE/C] – сброс последнего набранного числа/сброс
[AC] – общий сброс
[M+] – занесение числа в память с плюсом
[M-] – занесение числа в память с минусом
[MRC] – извлечение из памяти. После второго нажатия память обнуляется. В некоторых моделях данные функции разделены (клавиши [MR][MC])
[MII+][MII-][MIIRC] – работа со второй ячейкой памяти
[MU] – операция «Повышение цены» (может не работать)
[GT] – автоматическое суммирование операций
[%] – вычисление процентов
[√] – извлечение квадратного корня
[♪] – звуковое подтверждение нажатия клавиш вкл./выкл.
[+/-] – перемена знака
[→] – стирание последней введенной цифры
A 0 2 3 F – переключатель положения знака
<=====║> в десятичной дроби
0,2,3 – число знаков после запятой, А – режим расчета денежных единиц, F – фиксированная запятая
UP 5/4 CUT
<=║=> — переключатель режима округления
|
ИНСТРУКЦИЯ ПО ПРИМЕНЕНИЮ КАЛЬКУЛЯТОРА |
|
|
Вычисление квадратного корня = 7 3 6 + 1 3 = √ 7 Вычисление процентов 30 ´ 5 % = 1.5 3 0 ´ 5 % 1.5 Последовательные вычисления [(6 + 4) ´ 2 — 8]/5 = 2.4 6 + 4 ´ 2 — 8 / 5 = 2.4 Исправление ввода 5 + 3 = 8 5 + 4 С СЕ 3 = 8 Вычисление степени 24 = 16 2 ´ = = = 16 |
Вычисления с константами 4 ´ 3 =12, 4 ´ 5 = 20 4 ´ 3 = 12 4 ´ 5 = 20 6 / 2 = 3, 8 / 2 = 4 6 / 2 = 3 8 / 2 = 4 Вычисления с памятью (5´0.25)+(6´0.75)-(2´0.15)=5.45 5 ´ . 2 5 M+ 1.25M 6 ´ . 7 5 M+ 4.5M 2 ´ . 1 5 M+ 0.3M MRC 5.45M MRC 5.45 |
|
Питание от батареи G10*2 |
Автоматическое отключение |
Примечание. В данной модели калькулятора возможно отсутствие, объединение или дополнение некоторых операционных клавиш.
Страна-производитель: Китай
Продавец: «Первый Оптовый» (купить калькуляторы оптом можно именно у нас)
Питание калькулятора – от источника питания 1.5 в типа G13.
Рабочая температура от 0 до +40оС
Средний срок эксплуатации – 5 лет.
Гарантия — 1 месяц. Гарантия не распространяется на элементы питания.
Калькулятор не подлежит гарантийному ремонту, возврату или замене при отсутствии упаковки; при наличии механических повреждений.
1okey.ru
Использование обычного и инженерного калькулятора
ОС Windowsне просто обеспечивает работоспособность компьютера, но и предоставляет несколько простейших стандартных программ, удобных для быстрого выполнения несложных операций.
Обычный калькулятор
Для того, чтобы быстро что–то подсчитать, используют программу Калькулятор, которая вызывается так:Пуск – Программы – Стандартные – Калькулятор.Для частого использования калькулятора можно создать значок ярлыка программы наРабочем столе. Удобно пользоваться мышью, но можно нажимать и клавиши, используя дополнительную цифровую клавиатуру, где имеются все операционные клавиши. Для ввода с цифровой части клавиатуры необходимо нажать клавишуNum Lock.
Арифметические расчеты. Программа Калькулятор как и большинство настольных калькуляторов, позволяет выполнять цепочки последовательных арифметических действий. Например: 2+3*5+7/2
В этом режиме Калькулятор имеет «арифметическую» логику, то есть при расчете сложных арифметических выражений не соблюдается принятый в математике порядок действий. Выражение вычисляется слева направо, как оно записано. В нашем примере мы как бы реально вычисляем {[(2+3)*5]+7}/2=16 вместо 2+(3*5)+(7/2).
Если бы нам нужно было вычислить это выражение «по правилам», то необходимо использовать «память» нашего Калькулятора. Кнопки с красными обозначениями в левой части панели предназначены для операций с памятью.
Теперь выполнить нужную операцию несложно. Щелкните на кнопках «2», «MS» (занесли в память первое число), «3», «*» «5», «=», «М+» (вычислили произведение 3*5 и прибавили его к числу, хранящемуся в памяти), «7» «/» «2» «=» «М+» (получили окончательный результат), «MR» (вывели его на индикатор). Результат – 20,5.
Обратите также внимание на то, что когда в памяти хранится число, в окошечке над кнопками, предназначенными для работы с памятью, появляется буква М.
Кнопки с темно-синими обозначениями в правой части панели служат для выполнения некоторых специальных операций.
sqrt (Square Root) – эта кнопка позволяет извлечь квадратный корень из числа, установленного на панели индикатора.
%. Эта кнопка позволяет производить вычисление процентов. Например: чтобы ответить на вопрос «сколько будет 20 % от числа 6», щелкните на кнопках «6» «*» (обязательно умножение!) «2» «0» «%». На индикаторе появится ответ 1,2.
Темно-коричневые кнопки непосредственно под индикатором служат для редактирования вводимых чисел:
Backspace – отмена последней введенной цифры. Например, щелкните на кнопках «2» «3» «Backspace» «4». На индикаторе появится будет число 24.
CEClear Entry— удаление последнего введенного числа целиком. Например, наберите «2» «4» «+» «1» «6» «СЕ», «2» «4» «=». На индикаторе будет 48.
С Clear — полностью очищает калькулятор (кроме памяти) и готовит его к началу нового вычисления.
Инженерный калькулятор.
Инженерный калькулятор выполняет сложные инженерные и научные расчеты. Он способен вычислять большое количество разнообразных функций: тригонометрических, гиперболических, степенных, показательных, логарифмических и простейших статистических функций. Для вызова инженерного калькулятора в строке меню выберите пункт Вид – Инженерный.
В инженерном режиме калькулятор имеет «алгебраическую» логику, то есть при расчете сложных арифметических выражений соблюдается принятый порядок действий – в первую очередь выполняется умножение и деление, и только потом — сложение и вычитание. В нашем примере 2+3*7/2 будет вычислено как 2+(3*5)+(7/2)=20,5.
Кнопки с фиолетовыми обозначениями слева от кнопок для работы с памятью дают возможность выполнения математических вычислений.
Флажок «Inv» превращает функции в «обратные», например, вместо вычисления синуса будет вычисляться арксинус, вместо возведения числа Х в степеньYбудет извлекаться корень степениYиз числа Х и т.п.
Флажок «Нур» — действует только для тригонометрических функций – он превращает их в гиперболические.
Для статистических расчетов служат кнопки с синими обозначениями на левой панели Калькулятора. С их помощью можно ввести серию чисел и определить их среднее значение, сумму квадратов и стандартное отклонение (смешанное и несмешанное) для этой серии.
Кнопка | Клавиша | Функция |
Sta | Ctrl + s | Открывает окно «Статистика» и активизирует кнопки Ave,Sum,sиDat. |
Dat | Ins | Вводит число из поля ввода в окно «Статистика». Кнопка доступна после нажатия кнопки Sta. |
Ave | Ctrl + a | Вычисляет среднее арифметическое серии чисел из окна «Статистика». Для вычисления среднего квадратов используйте Inv+Ave |
Sum | Ctrl + t | Вычисляет сумму чисел в серии, отображаемых в окне «Статистика». Для вычисления суммы квадратов используйте Inv+Sum |
S | Ctrl + d | Вычисляет среднеквадратичное стандартное отклонение (несмещенное – число степеней свободы n-1) чисел из окна «Статистика». Для вычисления смещенного стандартного отклонения (число степеней свободы –n) используйтеInv+s |
В качестве примера выполним статистическую обработку серии чисел: 1,3,5,7.
Набираем в Калькуляторечисло «1»;
Открываем окно СтатистикакнопкойSta;
Отправляем его в окно Статистика кнопкой Dat;
Набираем «5»;
Отправляем Dat;
Набираем Dat;
Отправляем Dat.
Теперь вся серия чисел введена и можно приступать к ее статистической обработке. Щелкнув на кнопке Ave, получите среднее значение серии 4. Щелкнув на кнопке Sum, получите сумму чисел серии 16.
В окне «Статистика» есть еще четыре кнопки, функции которых описаны в следующей таблице:
Кнопка | Функция |
LOAD | Возвращает число в поле ввода калькулятора |
RET | Возвращает число в окно калькулятора |
CD | Удаляет выделенное число из окна «Статистика» |
CAD | Удаляет все числа из окна «Статистика» |
Рассмотрим еще один пример проведения статистических расчетов. Выполните следующие действия:
Выберите опцию Инженерный в меню калькулятора Вид;
Введите первое число 12,56;
Нажмите кнопку Sta. На экране появится окно «Статистика»;
Нажмите кнопку Dat;
Введите второе число 12,89 и нажмите кнопку Dat;
Введите третье число 12,33 и нажмите кнопку Dat;
Нажмите кнопку Sta, вы перейдете в окно «Статистика» и можете просмотреть введенные числа. Если числа не помещаются на экране, появляются полосы прокрутки для их просмотра.
Нажмите кнопку Ret для перехода в окно калькулятора;
Нажмите кнопку Ave для вычисления среднего значения. Результат – 12,593333.
Нажмите кнопку Sum для вычисления среднего значения. Результат – 37,78.
Нажмите кнопку s для вычисления несмещенного стандартного отклонения. Результат – 0,28148.
Типы данных. Кнопки с красными обозначениями на правом краю калькулятора предназначены для работы с целыми числами в различных системах счисления.
Программа позволяет работать с двоичными (Bin), восьмеричными (Oct), десятеричными (Dec) и шестнадцатеричными (Hex) числами, переводить числа из одной системы в другую, а также выполнять логические и другие целочисленные операции над числами. В следующей таблице приводятся названия флажков и клавиш для перехода к этим системам:
Название флажка | Клавиша | Система счисления | Пример представления числа 8184 |
Hex | F5 | Шестнадцатеричная | 1FF8 |
Dec | F6 | Десятичная | 8184 |
Oct | F7 | Восьмеричная | 17770 |
Bin | F8 | Двоичная | 1111111111000 |
Получение справки
Чтобы разобраться с любой кнопкой (любым элементом панели) или любой функцией программы Калькулятор, щелкните на этом элементе правой кнопкой мыши. Перед вами появится всплывающая подсказка «Что это такое?». Щелкните на ней левой кнопкой и получите ясную и понятную справку.
Задания
1. Способы загрузки программы Калькулятор (укажите не менее двух).
2. Вычислить на обычном калькуляторе:
а) 17*12/-145
б) 14,5/186+164
в) 122-17*14
г) [3,5+4,56*7,56/(12+365)]-125,24/0,05
Вычислить на инженерном калькуляторе:
а) sina*cosb*sinc, где а=1,675, b=2,842 и с=654,56
б) Даны числа: 3,56; 6,85; 4,21; 5,78; 4,87; 6,24. Определить их сумму, среднее арифметическое и стандартное среднеквадратичное отклонение.
Вопросы для самопроверки:
1. Назначение кнопок калькулятора MC, MR, MS,M+
2. Как извлекают квадратный корень от заданного числа?
3. Как найти заданный процент числа, набранного на индикаторе?
Чем отличаются кнопки СЕ и С?
Назначение кнопок Backspase?
Как превратить обычный калькулятор в инженерный?
Назначение кнопок с флажками «Inv» и «Hyp»?
Как использовать кнопки Ave, Dat, Sta, Sum, s ?
Назначение кнопок Hex, Oct, Bin, Dec?
Как перевести число из десятичной системы в двоичную, восьмеричную?
studfiles.net
Калькулятор. Скрытые функции, о которых знают только японские бухгалтера.: mil_yume

Пару дней назад я задала вопрос: какой калькулятор (какой фирмы) лучше всего выбрать бухгалтеру? Сама я на это обратила внимание только по наводке японского сенсея по бухучету. Так бы и прожила всю жизнь в неведении, если б не он… И что самое интересное, потом я прошлась подглядела, чем пользуется народ у нас в отделе — и точно! У всех калькуляторы этой фирмы! Не знаю, осознанные это были покупки или нет, но факт остается фактом: у нас бухгалтера тоже поклонники марки…
Шарп!
Казалось бы, какая разница… Считают они все одинаково, модели у всех фирм тоже разные, так что можно подобрать любой на свой вкус и цвет. А нет, кажется так только на первый взгляд! Для второго же надо прочитать инструкцию. К КАЛЬКУЛЯТОРУ, да! XD Вот, где можно познать бездну своего невежества.
Итак, что мне рассказал сенсей. Во-первых, самыми любимыми у японских бухов считаются две марки калькуляторов: Шарп и Касио. У обеих есть свои почитатели 🙂 Причем к Шарпу относится сразу несколько других производителей, таких как: Кэнон, Ситизен, Аврора, Джентос, Адессо. Касио же сам по себе. Во-вторых, сенсей настоятельно советовал Шарп.
Так в чем разница-то?
В скрытых умениях! Ну, то есть они открыты для всех, кто читает инструкцию, ага 🙂
1. Для начала рассмотрим простое действие: деление на одно и то же число.
Касио
| Последовательность нажатия кнопок | Ответ | Пояснение | |
| 5[÷][÷] | K | 5. | Запомнили деление на 5 |
| 100[=] | K | 20. | Ответ на действие 100÷5 |
| 200[=] | K | 40. | Ответ на действие 200÷5 |
| 400[=] | K | 80. | Ответ на действие 400÷5 |
Шарп
| Последовательность нажатия кнопок | Ответ | Пояснение |
| 100[÷]5[=] | 20. | Ответ на действие 100÷5. Плюс по умолчанию запоминается деление на 5. |
| 200[=] | 40. | Ответ на действие 200÷5 |
| 400[=] | 80. | Ответ на действие 400÷5 |
Уже догадались, в чем разница?
ЗЫ: Оба калькулятора запоминают деление на 5 (ну, или на сколько вы задали), но! Если вы вы хотите делить одно и то же число на кучу разных (100/2, 100/3, 100/4 и т.п.), то такое не умеет ни один из представленных! Придется каждый раз все вбивать самому старым дедовским способом.
2. Тогда идем дальше. Как высчитать проценты от одного и того же числа подряд.
| Последовательность нажатия кнопок Касио | Последовательность нажатия кнопок Шарп | Ответ | Пояснение |
| 5[×][×] | 5[×] | 5. | Запомнили «5×» |
| 100[%] | 5. | Ответ на действие 5% от 100 | |
| 200[%] | 10. | Ответ на действие 5% от 200 | |
| 400[%] | 20. | Ответ на действие 5% от 400 | |
3. Прибавлять проценты к одному и тому же числу.
| Последовательность нажатия кнопок Касио | Последовательность нажатия кнопок Шарп | Ответ | Пояснение |
| 300[×][×] | 300[+] | 300. | Запомнили «300+» |
| 105[%] | 5[%] | 315. | Ответ на действие 300+5% |
| 108[%] | 8[%] | 324. | Ответ на действие 300+8% |
| 110[%] | 10[%] | 330. | Ответ на действие 300+10% |
4. Умножать на одно и то же число подряд.
| Последовательность нажатия кнопок Касио | Последовательность нажатия кнопок Шарп | Ответ | Пояснение | |
| 5[×][×][=] | 5[×][=] | 25. | Ответ на действие 52 . Одновременно запомнили «5×». | |
| [=] | 125. | Ответ на действие 53 | ||
| [=] | 625. | Ответ на действие 54 | ||
В примере выше вычисляются степени, но принцип в том, что калькулятор автоматом запоминает действие «умножить на 5»! То есть можно еще просто разные числа умножать на пять.
| Последовательность нажатия кнопок Касио | Последовательность нажатия кнопок Шарп | Ответ | Пояснение | |
| 5[×][×]2[=] | 5[×]2[=] | 10. | Ответ на действие 5×2. Одновременно запомнили «5×». | |
| 3[=] | 15. | Ответ на действие 5×3 | ||
| 4[=] | 20. | Ответ на действие 5×4 | ||
Ну, как вам? Знали про такое? А там еще куча разных функций!
А самое главное-то: почему Шарп?! Догадались?
Можете смеяться, но в Японии эти скрытые функции действительно важны. Потому что бухгалтера сдают государственный экзамен, где время ограничено, а элементарных одинаковых рассчетов выше крыши. Тут-то они и начинают учиться пользоваться калькулятором вслепую левой рукой (правой надо быстро ответы записывать)! И старательно ищут, как сократить количество действий. Тут-то Шарп и выделяется — в вычислениях нужно нажимать на 1-2 кнопки меньше, чем в Касио! Так-то.
В России мы от всего этого освобождены. Хорошо ли, плохо ли… Но замарачиваться с калькулятором просто нет необходимости. У кого есть — те покупают математический, чтоб целые формулы целиком вводить.
А вот интересно бы вам было узнать про другие, более сложные, функции обычного калькулятора? 🙂
ПОДПИСАТЬСЯ
mil-yume.livejournal.com
7 полезных клавиш калькулятора увеличивающие скорость расчета в 2 раза! (ч.1) | Компания «Секретория»
7 полезных клавиш калькулятора увеличивающие скорость расчета в 2 раза! (ч.1)
Октябрь 26, 2016
 | А теперь внимательно посмотрите на свой настольный калькулятор. Возможно, вы до сих пор не раскрыли весь его потенциал! В нашем цикле статей мы подробно расскажем о всех возможностях вашего калькулятора, о которых вы даже не догадывались! |
| Расчет налогов | [+TAX] [-TAX] [RATE] |
Функция, позволяющая автоматически вычислять цену товара с учетом налога или без учета налога (например цена товара с НДС или без НДС). Используется в моделях калькуляторов: |  |
| Как это работает? | [+TAX] [-TAX] [RATE] |
1-й шаг Ввести число процентов в память калькулятора. Для этого нажать последовательно 18 [RATE] [+TAX] Введенное значение налога будет использоваться в дальнейшем при вычислениях и не сотрется, пока вы не замените его на новое. Чтобы посмотреть записанное число процентов, нажмите [RATE] [-TAX]. |  Калькулятор CITIZEN настольный CDC-80VRD BP, 8 разр., двойное питание. |
2-й шаг [+TAX] Если вы имеете цену без НДС, и хотите узнать цену с НДС. Введите цену товара без налога — [100], нажмите[+TAX] и цена с НДС будет указана на дисплее => [118] Нажмите[+TAX] ещё раз чтобы увидеть суму НДС: [18]
3-й шаг [-TAX] Если вы имеете цену с НДС, и хотите узнать цену без НДС. lВведите цену товара с налогом — [147,50] и нажмите [-TAX] — цена без НДС будет указана на дисплее => [125] lНажмите кнопку [-TAX] чтобы узнать сумму НДС – [22,50] |  Калькулятор CITIZEN настольный SDC-760N, 16 разр., двойное питание. |
| Переключатель запятой | |
| – F – плавающая запятая — отсутствие фиксации запятой (выключение режима округления). Если вам не нужно округлять числа всегда ставьте переключатель в положение F.
– 0– 2– 3– 4–определяют, сколько знаков после запятой будет показывать индикатор.
– A – ADD–mode — режим «Автоматической запятой«. Этот режим удобен для тех, кто постоянно работает с деньгами, вводя целые и сотые доли единиц (рубли/копейки, доллары/центы и т. п.). В этом режиме при сложении и вычитании не нужно вводить десятичную точку. Она вводится автоматически. |
Продолжение следует…..
sekretoria.com
Как выключить калькулятор без кнопки Off и другой сабж
Казалось бы, что может быть проще, чем выключить калькулятор? Нажал кнопку выключения (обозначается «OFF»), и он выключился. Очевидная вещь.
Но каково же будет удивление бухгалтера, школьника или другого пользователя новенького калькулятора, когда после нажатия на кнопку включения (ведь логично же предположить, что если она включает калькулятор, то должна и выключать) устройство продолжит работать?
Да, такие модели есть, и их не мало.
В основном это калькуляторы с солнечной батареей.
К «не выключаемым» счетным машинкам можно отнести такие модели популярных производителей, как:
- Optima 75510,
- Citizen SDC-805BN,
- CITIZEN-SDC-888T (888TII, 888X и т.п.),
- КК 402.

Первое, что стоит сделать при обнаружении такого бага/фичи – не паниковать.
Если солнечная батарея реально работающая (а не заплатка для отвода глаз, которая ни к чему даже не подключается, как на китайских подделках), то повода для беспокойства нет. Калькулятор будет работать даже без встроенной аккумуляторной батареи.
Даже если устройство не оснащается солнечной панелью, или она по факту является муляжом, переживать тоже не стоит.
Жидкокристаллический дисплей может работать во включенном состоянии годами на одной батарее, достаточно вспомнить наручные часы Montana.
- Первый вариант – просто отложить калькулятор в сторону и подождать. Он отключится автоматически через заданное производителем время при бездействии (от 2 до 10 минут в зависимости от модели и торговой марки).
- Второй вариант – попробовать отключить «дефектный» калькулятор одной из следующих комбинаций:
- Одновременно нажатые цифры «2» и «3», плюс кнопка «ON»,
- То же самое, но с цифрами «5» и «6», или «8» и «9»,
- Клавиши с операторами деления («/») и умножения («*»), плюс кнопка «ON».
Что, если указанные «комбо» не сработают?
- Можно попытаться вместо кнопки «ON» нажать клавишу «AC», или «C/CE»,
- Одновременно нажать максимальное количество цифр на клавиатуре устройства и «ON» (не сработает – меняем «ON» на «AC» или «C/CE»),
- Дважды/трижды нажать на кнопку включения,
- Все-таки подождать автовыключения, а для ускорения процесса можно дополнительно накрыть солнечную панель светонепроницаемым материалом.
Самые пытливые могут внимательно прочитать шильдик калькулятора (наклейка производителя с номером модели и технической информацией на обратной стороне корпуса прибора) в поисках надписи «reset 2 + 3 + ON» или аналогичной.
Владельцы устройств Citizen CT-500 будут удивлены комбинации выключения:
- Кнопка деления – 1 нажатие,
- Умножение – 1 раз,
- Вычисление процентов («%») – 1 раз,
- Кнопка «Check» — 1 раз,
- «Correct» — 2 раза.
Таких «комбо» даже в Mortal Combat не найти.
Что делать, если на калькуляторе не работает кнопка
Как и в любых других устройствах, в калькуляторах движущиеся механические части (кнопки) – самое слабое звено.
Через некоторое время кнопка может запасть(залипнуть) или перестать реагировать на нажатия (исправно нажимается, но ввод не происходит).
Что делать?
В первом случае наиболее вероятная неисправность – износ силиконовых или резиновых прокладок в кнопках, выполняющих роль пружины. В случае ее порчи восстановление невозможно.
Если кнопки были залиты чем-то сладким (не стоит пить кофе или чай за рабочим столом), можно разобрать устройство и протереть все элементы ватными дисками, смоченными в спирте, и после высыхания собрать обратно. Может помочь.
Если же пружина работает исправно, но сигнал не передается, возможно, стерлось токопроводящее покрытие на кнопке (оно замыкает контакты при нажатии).
Самый простой и быстрый выход из ситуации – приклеить на кнопку поверх старого покрытия небольшой кусочек алюминиевой фольги (можно взять из любой шоколадки) при помощи суперклея (на основе цианокрилата). Кнопка будет работать еще лучше, чем раньше.
Интересные факты об ошибках и «глюках» калькуляторов, приколы и т.д.
Ищите еще какие-либо фишки калькуляторов? Первое, что приходит в голову — попробуйте набрать число 0,7734 и перевернуть дисплей вверх ногами. Получится приветствие «hELLO».

Владельцы инженерных устройств смогут набрать целый текст:
1f y0u c4n r34d 7h25, u r34lly n33d 2 g37 a l1f3 (;
Этого мало?
Потренируйте устный счет, наберите комбинацию 6/2*(1+3). Что получилось – 9? Не у всех. Некоторые модели могут дать ответ 1. Кто прав? Разберет математика.
Еще один интересный глюк/фича с инженерными калькуляторами – возведение в степень отрицательного числа. Многие пользователи могут получить в результате тоже отрицательное число (например, -2˄2=-4). Почаще ставьте скобки для расстановки приоритетов операций.
Вы уверены в результате вычислений своего счетного инструмента? Тогда проведите вычисления ниже.
arcsin (arccos (arctan (tan (cos (sin (9) ) ) ) ) )
По идее, должно получиться ровно 9. Однако не у всех так.
Вот что получили другие пользователи:
 Какое значение выдал ваш кнопочный калькулятор
Какое значение выдал ваш кнопочный калькуляторНе всегда стоит доверять сложные вычисления простому устройству, погрешности и бинарный математический аппарат накладывают ряд ограничений.
neknopka.ru
Обозначение новых кнопок калькулятора — Информатика
Лабораторная работа 3.
Знакомство с операционной системой Windows 8 и её стандартными приложениями
Порядок выполнения работы:
1. Ознакомьтесь с основными возможностями и стандартными приложениями ОС Windows 8.
2. Выполните практические задания.
3. Оформите отчёт в электронном виде и сдайте преподавателю.
Методические рекомендации:
Основной системной программой для ПК является операционная система. На самом деле это комплекс программ, объединенных для одной задачи: управлять работой компьютера. ОС позволяет запускать программы, управлять запросами, выделять память под задачи, непосредственно считывать данные или записывать их и так далее.
В настоящее время имеется несколько распространенных операционных систем компании Microsoft. К ним относятся системы Windows ХР, Windows Vista, Windows 7 и Windows 8, 10. Прежние системы были довольно похожи друг на друга.
Система Windows 8 имеет некоторые отличия, так как она предназначена для работы в том числе на планшетных компьютерах.
Официально Windows 8 была выпущена осенью 2012 года. Конечно, данная система визуально выгодно отличается от предыдущих. Созданы графические эффекты выполнения режимов, появился начальный экран, дизайн рабочего стола и окон стал лучше.
Еще одно отличие от предыдущих версий Windows в том, что каждая следующая операционная система в своем составе имеет большее количество драйверов. То есть, установив новое устройство, система с большей вероятностью найдет сама для него драйвер. Так, например, в эту систему добавлена возможность поддержки USB 3.0, которая будет работать, если на компьютере поддерживается данный стандарт. Кроме того, встроен пакет Microsoft Framework 4, что позволяет установить многие бесплатные программы, не устанавливая этот дополнительный пакет. Все это относится к достоинствам.
К недостаткам нужно отнести, что Windows 8 требует больше оперативной памяти для своих задач, чем предыдущих Windows.
Задание 1. Знакомство с интерфейсом ОС Windows 8
Windows 8 можно работать в одном из режимов: Начальный экран и Рабочий стол:
Начальный экран
При включении компьютера отображается Начальный экран, который позволяет запускать приложения (далее Приложения), щелкая по живым иконкам-значкам.
Значки можно перемещать с места на место, захватив их левой кнопкой мыши. На начальном экране отображаются не все приложения и программы. Чтобы посмотреть полный список программ, нужно щелкнуть правой кнопкой мыши по любому месту Начального экрана и выбрать в появившемся нижнем меню значок Все приложения, который располагается справа.
Приложения разделены на группы. Среди них есть также и системные утилиты, например, Панель управления:
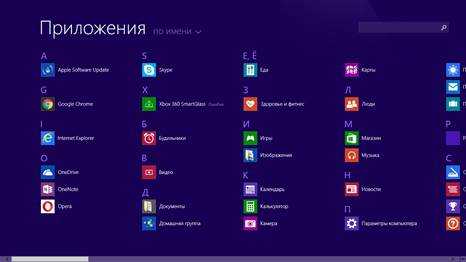
Перемещаться по экрану можно вращением колесика мыши или передвижением курсора мыши к краю экрана.
Рабочий стол
Предоставляет функции, аналогичные тем, которые предоставлял рабочий стол более ранних версий Windows:
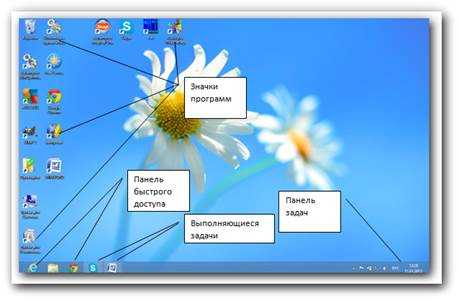
Оба режима экрана позволяют вызывать чудо-кнопки и просматривать последние открытые приложения. Для просмотра последнего открытого приложения наведите указатель мыши на верхний левый угол. Выпадет значок-миниатюра экрана приложения, щелкнув по которому, можно открыть окно этого приложения:

Если после наведения указателя на верхний левый угол провести мышью немного вниз, выпадет меню всех запущенных на данный момент приложений. Снизу списка — переход на начальный экран, так как вызов осуществлялся из Рабочего стола:

Если те же манипуляции проводить из Начального экрана, то будут сначала показаны приложения, запущенные в режиме Рабочего стола, потом, ниже приложения, запущенные из Начального экрана.
Чудо-кнопки в Windows 8
Так называемые чудо-кнопки — это новый тип меню. Оно соединяет в себе меню «Пуск» и панель управления Windows 8.
Активировать панель чудо-кнопок можно наведением курсора мыши на верхний или нижний правый угол экрана:

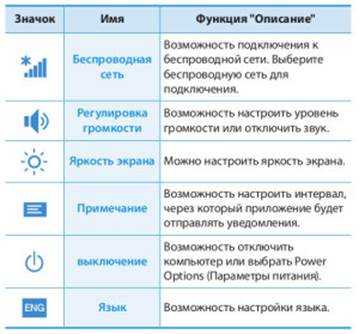
Панель имеет пять кнопок, каждая из которых отвечает за определенные действия. По центру расположена кнопка «Пуск», позволяющая запустить Начальный экран Windows 8. Документация, содержащая информацию о том, как работать в Windows 8 пользователям, предлагает следующее описание этих кнопок.
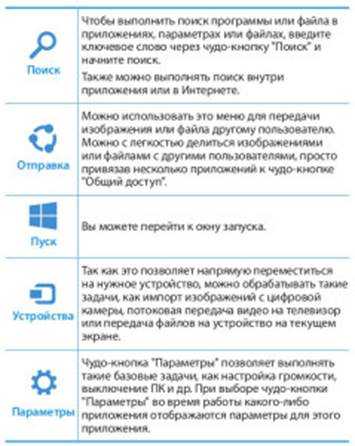
Как выключить компьютер с Windows 8 и осуществить некоторые настройки
Для выключения или перезагрузки компьютера вызовите меню чудо-кнопки и найдите кнопку Параметры:
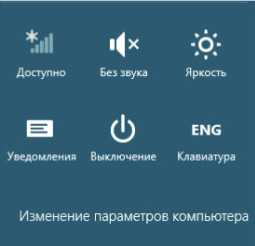
Кроме кнопки выключения на этой вкладке можно осуществить другие настройки: звук, яркость, беспроводная сеть и др.:
Задание 2. Работа со стандартными приложениями в Windows 8
Приложения (программы) могут быть запущены как в режиме рабочего стола, так и в режиме Начального экрана. Режим рабочего стола содержит окна, снабженные кнопками свернуть, развернуть и закрыть. Аналогично предыдущим версиям Windows.
Для запуска приложения из режима Начального экрана щелкните левой кнопкой мыши по его значку на экране «Пуск».
Для того, чтобы закрыть запущенное приложение, наведите курсор мыши на верхний край экрана примерно посередине так, чтобы он принял форму руки.
Теперь нажмите левую кнопку мыши и, не отпуская ее, проведите мышкой вниз. Миниатюра приложения переместится вниз и закроется:
Сворачивать приложение не требуется. Нужно просто запустить новое приложение через чудо-кнопку Пуск, наведя курсор на нижний левый угол экрана.
Так же, как и в режиме рабочего стола, можно посмотреть список уже запущенных приложений, наведя курсор на верхний левый угол экрана и проведя немного вниз.
Одновременный запуск двух приложений в Windows 8
1. Запустите приложения на Начальном экране.
2. Наведите курсор мыши на верхний край экрана.
3. Нажав и удерживая кнопку мыши, переместите курсор влево или вправо (не вниз, как для закрывания приложения), чтобы разделить экран для отображения нескольких приложений.
4. Переместите Screen Split Bar (Разделительная полоса экрана), чтобы изменить соотношение разделения экрана. Поддерживаются разделения экрана 3:7 или 7:3.
Вот как это выглядит (запущен просмотр изображений слева и видео плеер справа):

Чтобы перейти к обычному режиму, щелкните левой кнопкой мыши по трем точкам разделительной полосы и, не отпуская кнопки, переместите полосу по направлению к краю экрана.
Добавление или удаление приложения на Начальном экране
Запустите просмотр всех приложений, установленных на компьютере (см. выше). Для добавления приложения из полного списка на Начальный экран, щелкните правой кнопкой мыши на нужном приложении.
Снизу на экране появится меню, содержащее значок кнопки «Закрепить на начальном экране» или перечеркнутой кнопки «Открепить от начального экрана».
Как видно из скриншота, приложения, доступные для запуска в режиме рабочего стола имеют дополнительные пункты контекстного меню.
Знакомство с горячими клавишами ОС Windows 8
Наличие клавиатуры позволяет использовать не только мышь для управления задачами операционной системы. Windows 8 имеет свою систему горячих клавиш, использование которых позволит значительно ускорить работу.
Таблица ниже содержит список комбинаций кнопок для вызова той или иной команды:
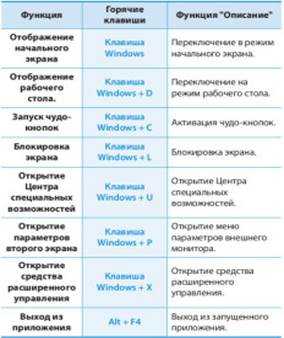
Изучите основы и узнайте о новых возможностях Windows 8.
Нажмите на клавиатуре клавиши Windows и F1 одновременно. Появится окно справки следующего вида (все скриншоты можно полноразмерно посмотреть, щелкнув по ним левой кнопкой мыши. Откроются в новой вкладке).
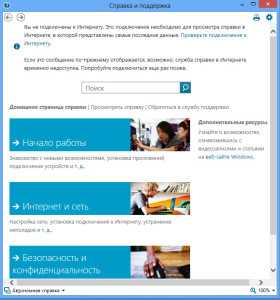
При наличии подключения к Интернету можно получить доступ к последним обновления интерактивной справки.
Также вызвать справку можно, наведя курсор мыши на верхний или нижний правый угол экрана, и выбрав Чудо-кнопки > Параметры > Справка.
| Начало работы | Можно просмотреть базовые инструкции по использованию компьютера, не исключая новых функций для ОС Windows. |
| Интернет и Сеть | После подключения к сети можно ознакомиться с разделом справки, необходимым для использования Интернета. |
| Безопасность, защита личных данных и учетной записи | Можно ознакомиться с приведенными в справке сведениями, необходимыми для защиты компьютера и личных данных. |
Задание 3. Работа с приложением Paint
Активируйте перечень стандартных приложений ОС Windows 8:
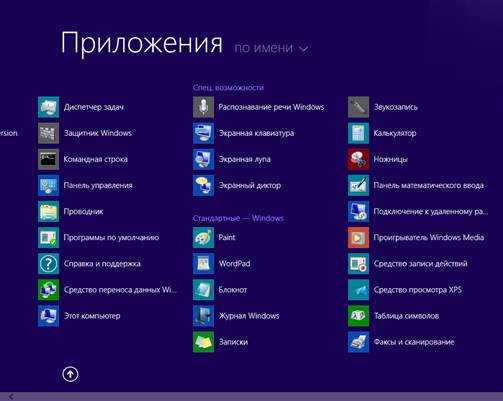
Запустите графический редактор Paint. Создайте, например, изображение книги:
Для этого:
1. Нарисовать обложку 1 (правую): Прямоугольник, Выделить, Изменить размер, Наклон по вертикали — 30 градусов.
2. Нарисовать обложку 2 (левую): Выделение (обложка 1), Правка, Копировать, Правка, Вставить, Отразить слева направо, Заливка (светло-серая), соединить с обложкой 1.
3. Нарисовать внутренний лист: Правка, Вставить, Заливка (голубая), разместить поверх обложки 1:
4. Исправить угловые соединения: Масштаб, Карандаш.
5. Закрасить торец: Заливка (синяя).
6. Нарисовать заголовок: Надпись, задать шрифт и размер букв, написать слово «Книга», выделить слово (Выделение), Рисунок, Наклон по вертикали — 30 градусов, переместить на внутренний лист.
7. Организация тени: сделать копию обложки 1, вдоль края серый Распылитель, выделить книгу (Выделение) и надвинуть на тень.
8. Сохранить рисунок в свою папку под именем: Книга.bmp.
Задание 4. Работа с приложением WordPad
Запустите текстовый редактор WordPad. Наберите с клавиатуры следующий текст:
Книга — лучший и самый надёжный друг человека на все времена.Книга никогда не предаст. Книга всегда скажет правду и покажет верный путь к истине. Конечно для этого надо уметь читать и между строк, уметь видеть истинные ценности в вещах и оценивать события с разных точек зрения.
Отформатируйте текст.
Используя буфер обмена Windows, вставьте в документ созданный ранее рисунок Книга.bmp(без связи и со связью).
Сохраните полученные файлы под именами Текст_без связи.txt и Текст_со связью.txt.
Внесите изменения в файл Книга.bmp,сохраните результат.
Откройте файлы под именами Текст_без связи.txt и Текст_со связью.txt, сделайте соответствующий вывод.
Задание 5. Работа с приложением Калькулятор.
Калькулятор — это стандартное приложение операционных систем Microsoft Windows, имитирующее работу обычного калькулятора. В это приложение не вносились изменения, начиная с операционной системы Microsoft Windows 95. В Windows 7 он сильно преобразился внешне и был добавлен новый функционал. Несмотря на то, что в нем можно выполнять простые операции, которые были доступны ранее, такие как: сложение, вычитание, умножение и деление, теперь предусмотрены возможности для выполнения простых действий, связанных с программированием, инженерных и статистических вычислений.
Как и раньше, его кнопки можно нажимать как при помощи мыши так и вводя символы с клавиатуры, доступен ввод цифр и действий с цифровой клавиатуры, когда нажата клавиша Num Lock. Также, для получения результата, можно вставлять математические выражения из буфера обмена. На следующем скриншоте отображен обычный вид калькулятора Windows 7.
Для того, чтобы открыть калькулятор нужно сделать следующее:
1. Нажмите на кнопку «Пуск» для открытия меню, Откройте «Все программы», далее откройте папку «Стандартные» и из списка стандартных программ выберите «Калькулятор»;
2. Нажмите на кнопку «Пуск» для открытия меню, в поле поиска введите Калькулятор или calc.exe и откройте приложение из найденных результатов.
Выбор требуемого режима
Существуют четыре режима калькулятора:
· обычный,
· инженерный,
· программист
· статистика.
В обычном режиме помимо вышеперечисленных возможностей также представлены функции квадратного корня, процентов, обратного значения. Для выбора режима калькулятора используется меню «Вид».
При переключении режимов все текущие вычисления удаляются, но остаются журнал вычислений и числа, сохраненные с помощью клавиш памяти. Для каждого режима (кроме статистического) ведется своя история вычислений. Рассмотрим подробно каждый из режимов калькулятора Microsoft Windows 7.
Инженерный режим
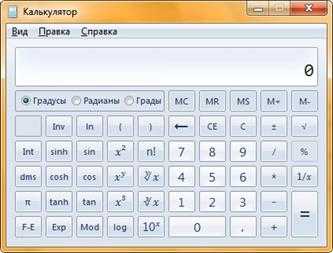 В дополнение к опциям обычного режима, в инженерном режиме доступны тригонометрические и гиперболические функции, натуральные и десятичные логарифмы, возведение в степень, обратные функции (извлечение корня для возведения в степень) доступны при нажатии на кнопку «Inv», вычисление факториалов, перевод долей градуса в минуты и секунды. На следующем скриншоте можно увидеть инженерный режим калькулятора.
В дополнение к опциям обычного режима, в инженерном режиме доступны тригонометрические и гиперболические функции, натуральные и десятичные логарифмы, возведение в степень, обратные функции (извлечение корня для возведения в степень) доступны при нажатии на кнопку «Inv», вычисление факториалов, перевод долей градуса в минуты и секунды. На следующем скриншоте можно увидеть инженерный режим калькулятора.
Для того, чтобы выбрать инженерный режим необходимо в меню «Вид» выбрать пункт «Инженерный».
Советы по использованию инженерного режима:
1. Чтобы воспользоваться обратными функциями, нажмите клавишу Inv.
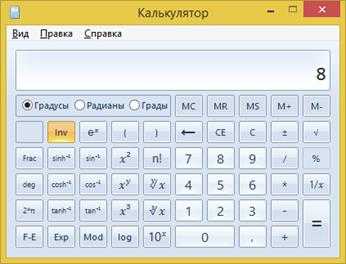
2. В инженерном режиме точность калькулятора составляет 32 значащие цифры.
3. При выполнении вычислений в инженерном режиме в калькуляторе учитывается приоритет операций.
Режим программиста
В режиме программиста доступны побитовые операции: AND, OR, NOT, XOR (перед вычислением дробная часть отбрасывается), переключатель разрядности обрабатываемых данных (8, 4, 2, 1 байт), также можно переводить числа и выполнять операции в следующих системах счисления:
· двоичная (Bin),
· восьмеричная (Oct),
· десятичная (Dec),
· шестнадцатеричная (Hex).
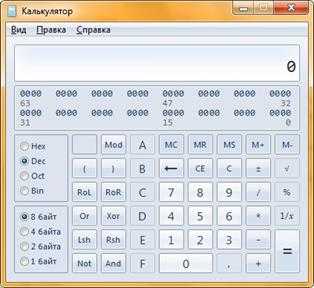
Для того, чтобы выбрать режим программиста необходимо в меню «Вид» выбрать пункт «Программист».
Советы по использованию режима программиста:
1. В режиме программиста точность калькулятора достигает 64 разрядов в зависимости от выбранного размера слова.
2. При выполнении вычислений в режиме программиста в калькуляторе учитывается приоритет операций.
3. В режиме программиста используются только целые числа. Десятичные части отбрасываются.
Режим статистики
В режиме статистики можно вводить данные для вычисления статистики, а затем выполнять вычисления. При вводе данных соответствующая информация отображается в области журнала, а в области вычислений отображается количество введенных значений.
Для того, чтобы выбрать режим статистических вычислений необходимо в меню «Вид» выбрать пункт «Статистика».
Советы по использованию режима Статистика:
1. Введите первое значение и нажмите кнопку Add (Добавить), чтобы добавить данные в набор данных.
Обозначение новых кнопок калькулятора
— Среднее значение
— Среднеквадратичное значение
— Сумма значений
— Сумма квадратов значений
— Среднеквадратичное отклонение
— Заполнение среднеквадратичного отклонения
student2.ru
Для чего нужна кнопка «MU» на калькуляторе?
Mark Up — то есть название происходит от цены «с наценкой».<br><br>Часто у этой же кнопки есть и обратная функция — Mark Down.<br><br>Пошаговые действия с этой кнопкой различны в разных калькуляторах, но идея в том, что, зная цену с наценкой (продажную цену), Вы при помощи этой кнопки сможете узнать наценку. Иногда — наоборот, то есть зная наценку, сможете узнать продажную цену.<br><br>Пример 1. Закупочная цена товара 106 р, наценка 12,5%. Надо узнать продажную цену.<br>Нажимаем на калькуляторе:<br>106 MU 12.5 %<br>Получаем:<br>121.1429<br>Такова неокругленная продажная цена.<br><br>Пример 2. Закупочная цена 100 р, продажная 120 р.<br>Нажимаем на калькуляторе:<br>120 -100 MU<br>Получаем:<br>16.6667<br>Это значит, что наценка составляет 16,6667%.
это кнопка самоуничтожения
значит фирменный — ManchesterUnited
Если 120-100 MU, то получается 20%, а не 16,6667% <img src=»//otvet.imgsmail.ru/download/184622065_7430eca9f5e89330e19d3f8730511d92_800.jpg» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/184622065_7430eca9f5e89330e19d3f8730511d92_120x120.jpg» data-big=»1″>
<a rel=»nofollow» href=»https://mcgrp.ru/files/viewer/165819/10″ target=»_blank»>https://mcgrp.ru/files/viewer/165819/10</a>
Можно решать вот такие уравнения: Х — 25% = 90 (на калькуляторе: 90 MU 25 %) или 120 — Х% = 90 (на калькуляторе: 120 — 90 MU) Используется при расчете возможных скидок для установления розничных цен.
touch.otvet.mail.ru






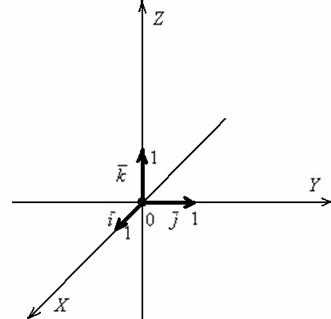
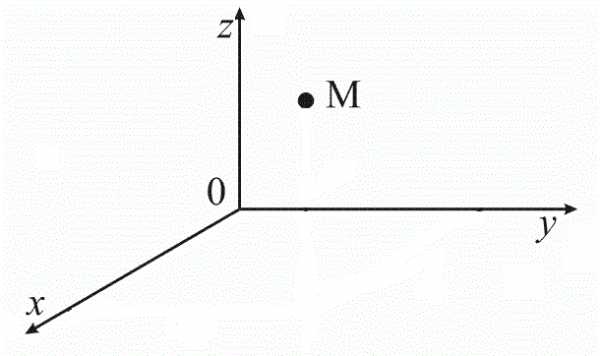
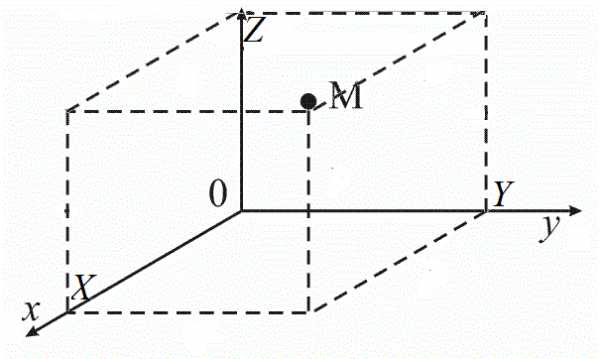
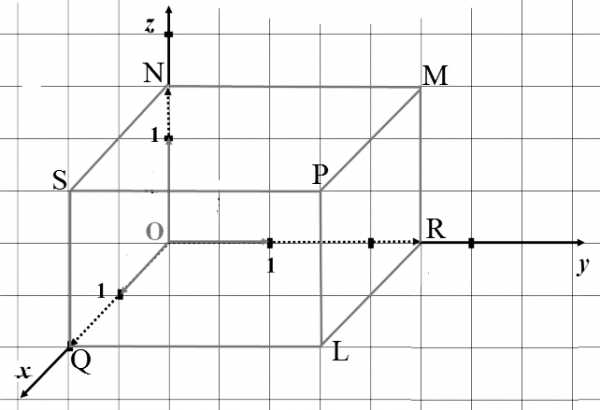
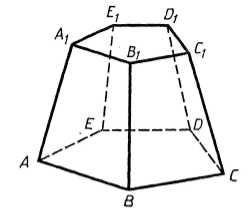


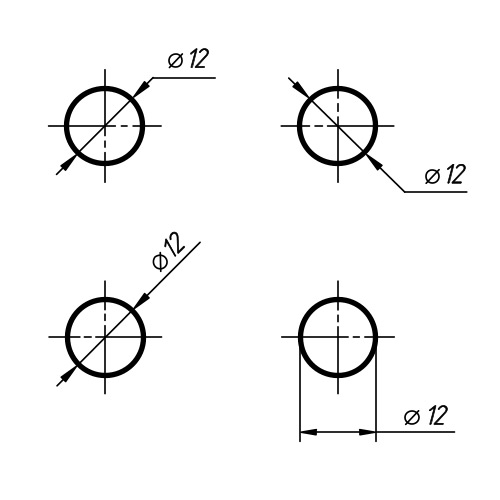
 Стандартами предусмотрены различные условные обозначения, которые позволяют производить запись геометрических и технологических параметров изображенного объекта: знаки радиуса, толщины, угла, допуска и припуска обработки. К ним же относится и диаметр, которым определяются размеры отверстий и тел вращения. Хорда, соединяющая две точки на окружности (шаре) и проходящая через ее (его) центр, и называется диаметром. Как же он обозначается на чертежах? Знак диаметра представляет собой окружность, перечеркнутую линией, наклоненной под 45о к вертикали по направлению движения часовой стрелки. В некоторых случаях используется латинская литера D, которая допускается к применению наравне с основным символом.
Стандартами предусмотрены различные условные обозначения, которые позволяют производить запись геометрических и технологических параметров изображенного объекта: знаки радиуса, толщины, угла, допуска и припуска обработки. К ним же относится и диаметр, которым определяются размеры отверстий и тел вращения. Хорда, соединяющая две точки на окружности (шаре) и проходящая через ее (его) центр, и называется диаметром. Как же он обозначается на чертежах? Знак диаметра представляет собой окружность, перечеркнутую линией, наклоненной под 45о к вертикали по направлению движения часовой стрелки. В некоторых случаях используется латинская литера D, которая допускается к применению наравне с основным символом.




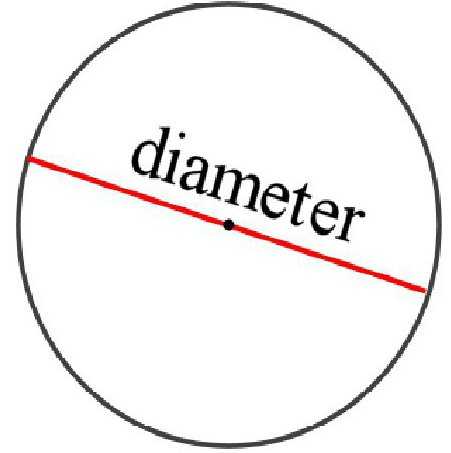


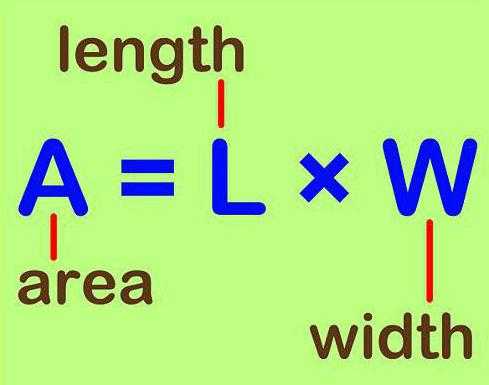 Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь – это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).
Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь – это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).
 Геометрический рисунок создающий визуальный ритм. Рисунок создан в онлайн-редакторе oboivdom.by
Геометрический рисунок создающий визуальный ритм. Рисунок создан в онлайн-редакторе oboivdom.by Крупный геометрический рисунок с эффектом 3D, без активного визуального ритма. Рисунок создан в онлайн-редакторе oboivdom.by
Крупный геометрический рисунок с эффектом 3D, без активного визуального ритма. Рисунок создан в онлайн-редакторе oboivdom.by Геометрический рисунок с визуальными эффектами, формы ромба и треугольника. Рисунок создан в онлайн-редакторе oboivdom.by
Геометрический рисунок с визуальными эффектами, формы ромба и треугольника. Рисунок создан в онлайн-редакторе oboivdom.by Геометрический рисунок со смешанными визуальными формами. Рисунок создан в онлайн-редакторе oboivdom.by
Геометрический рисунок со смешанными визуальными формами. Рисунок создан в онлайн-редакторе oboivdom.by Абстрактный рисунок с нечеткими геометрическими формами, создаёт вид колючей фактуры. Рисунок создан в онлайн-редакторе oboivdom.by
Абстрактный рисунок с нечеткими геометрическими формами, создаёт вид колючей фактуры. Рисунок создан в онлайн-редакторе oboivdom.by

 Обои с геометрическим рисунком. Интернет-магазин: www.oboivdom.by
Обои с геометрическим рисунком. Интернет-магазин: www.oboivdom.by Обои с геометрическим рисунком. Интернет-магазин: www.oboivdom.by
Обои с геометрическим рисунком. Интернет-магазин: www.oboivdom.by
 Обои гусиная лапка. Интернет-магазин: www.oboivdom.by
Обои гусиная лапка. Интернет-магазин: www.oboivdom.by Обои шевроны они же ёлочка. Интернет-магазин: www.oboivdom.by
Обои шевроны они же ёлочка. Интернет-магазин: www.oboivdom.by






























 \
\































































































 Они могут располагаться горизонтально или рисоваться под любым углом. Приветствуются всевозможные фигуры: треугольники, квадраты, ромбы и многоугольники любых форм, наносимые на поверхности ногтя хаотично или в определенном порядке. Любопытно смотрятся также геометрические иероглифы или фигурки людей, животных, птиц, прорисованные тонкими прямыми линиями.
Они могут располагаться горизонтально или рисоваться под любым углом. Приветствуются всевозможные фигуры: треугольники, квадраты, ромбы и многоугольники любых форм, наносимые на поверхности ногтя хаотично или в определенном порядке. Любопытно смотрятся также геометрические иероглифы или фигурки людей, животных, птиц, прорисованные тонкими прямыми линиями.
 Точки можно легко превратить в капли. Схема рисования такова: на точки большего размера ставят маленькие точки другого цвета. В результате получаются капельки, из которых можно создавать всевозможные композиции. Такой маникюр смотрится гармонично. Точки легко могут превратиться даже сюжетные картины на ногтях. Хорошо получаются фигурки животных, цветы, листья, облака. Отлично смотрятся точечные кружева. Можно поиграть цветом, создавая радужные переходы, или сделать акцент на размерах точек – всё зависит от вашей фантазии.
Точки можно легко превратить в капли. Схема рисования такова: на точки большего размера ставят маленькие точки другого цвета. В результате получаются капельки, из которых можно создавать всевозможные композиции. Такой маникюр смотрится гармонично. Точки легко могут превратиться даже сюжетные картины на ногтях. Хорошо получаются фигурки животных, цветы, листья, облака. Отлично смотрятся точечные кружева. Можно поиграть цветом, создавая радужные переходы, или сделать акцент на размерах точек – всё зависит от вашей фантазии.
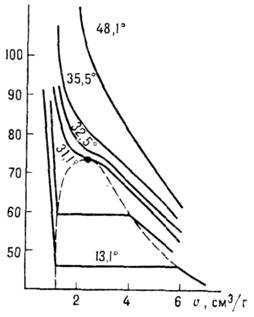

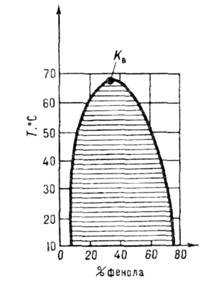
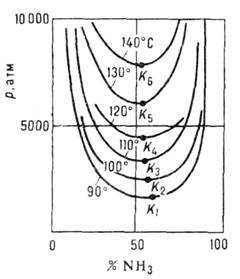
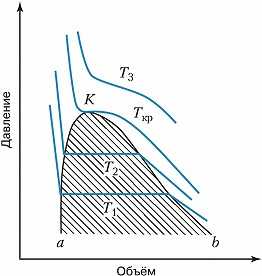
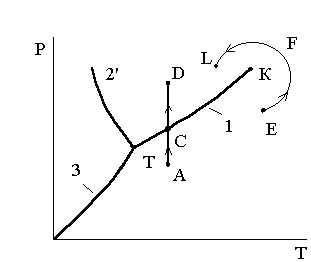

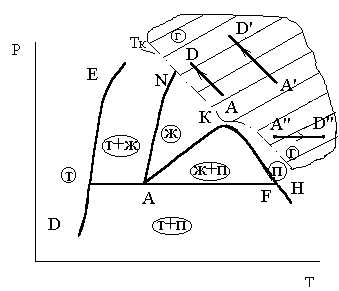
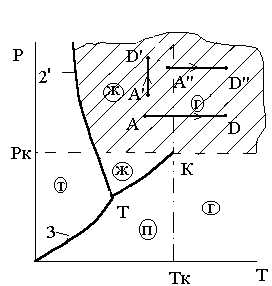
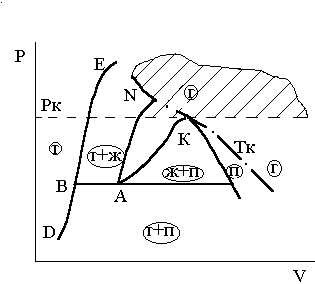


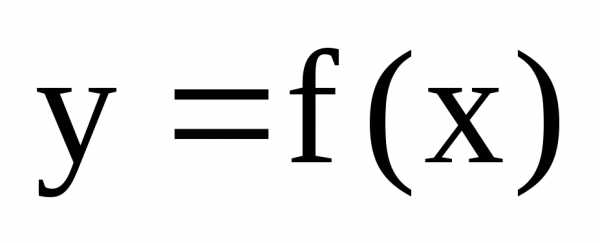 в точке
в точке равна нулю или не существует, то эта
точка – подозрительная на экстремум
(критическая точка).
равна нулю или не существует, то эта
точка – подозрительная на экстремум
(критическая точка).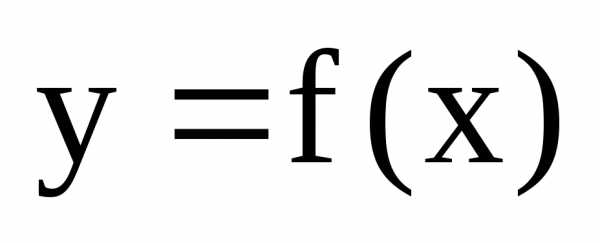 ,
дифференцируема в некоторой окрестности
точки
,
дифференцируема в некоторой окрестности
точки и при переходе через нее производная
меняет свой знак, то
и при переходе через нее производная
меняет свой знак, то — точка экстремума.
— точка экстремума. во всех точках (a;b)
имеет положительную (отрицательную)
вторую производную, то график функции
на этом интервале выпуклый вниз (вверх).
во всех точках (a;b)
имеет положительную (отрицательную)
вторую производную, то график функции
на этом интервале выпуклый вниз (вверх). называетсявыпуклым
вниз на
интервале (a;b),
если он расположен выше любой касательной
на этом интервале, выпуклым
вверх,
если он расположен ниже.
называетсявыпуклым
вниз на
интервале (a;b),
если он расположен выше любой касательной
на этом интервале, выпуклым
вверх,
если он расположен ниже. являетсявертикальной асимптотой графика функции
являетсявертикальной асимптотой графика функции  ,
если
,
если ,
или,
или
,
или,
или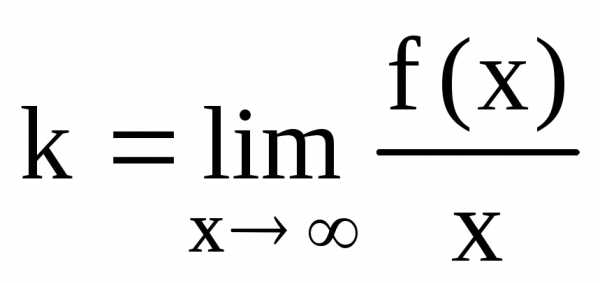 ,.
,. ),
),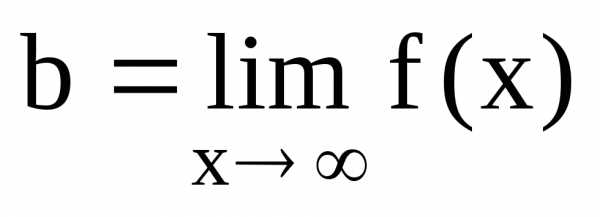
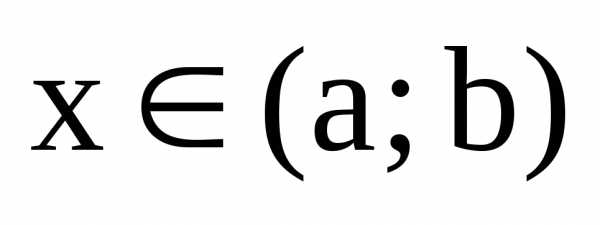 выполняется равенство(или)
выполняется равенство(или)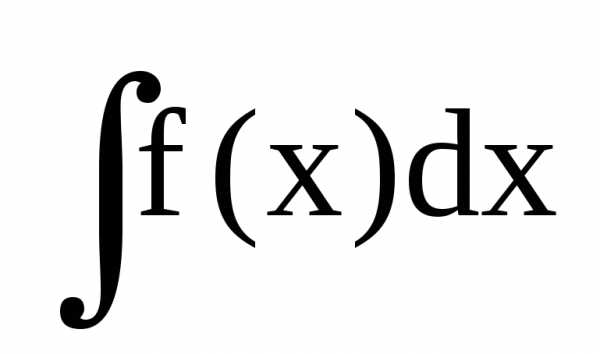
 —
знак неопределенного интеграла.
—
знак неопределенного интеграла. — произвольная функция, имеющая постоянную
производную
— произвольная функция, имеющая постоянную
производную