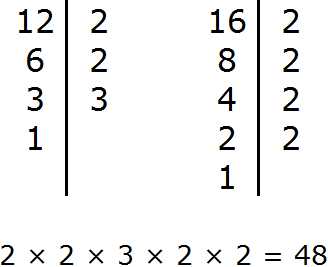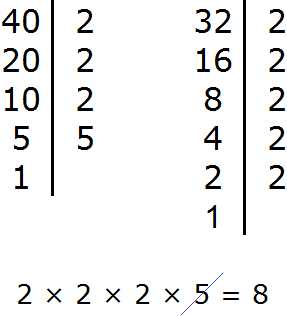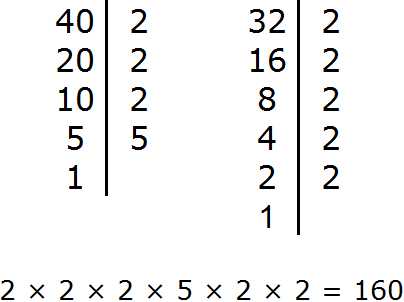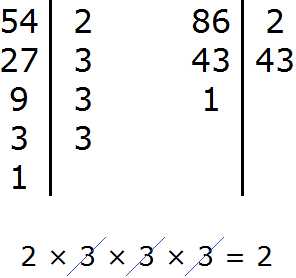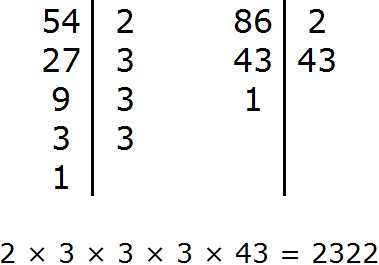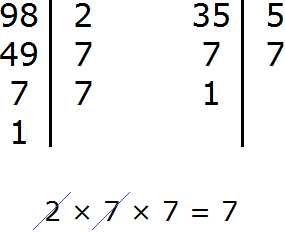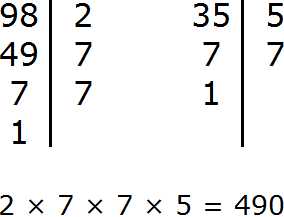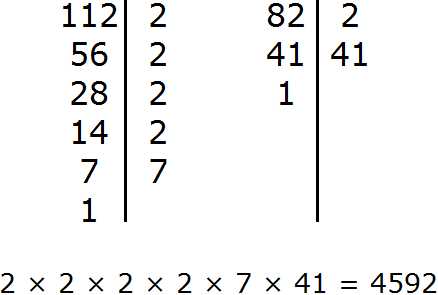Натуральный логарифм — это… Что такое Натуральный логарифм?
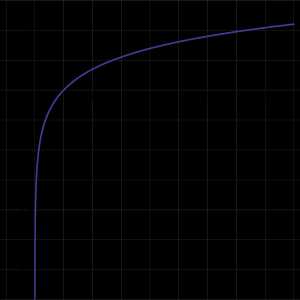График функции натурального логарифма. Функция медленно приближается к положительной бесконечности при увеличении x и быстро приближается к отрицательной бесконечности, когда x стремится к 0 («медленно» и «быстро» по сравнению с любой степенной функцией от x).Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), loge(x) или иногда просто log(x), если основание e подразумевается.[1]
Натуральный логарифм числа x (записывается как ln(x)) — это показатель степени, в которую нужно возвести число e, чтобы получить x. Например, ln(7,389…) равен 2, потому что e2=7,389…. Натуральный логарифм самого числа e (ln(e)) равен 1, потому что e1 = e, а натуральный логарифм 1 (ln(1)) равен 0, поскольку e0 = 1.
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.
Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:
Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:
Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:
Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.
История
Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia, опубликованной в 1668 году[2], хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов.[3] Ранее его называли гиперболическим логарифмом,[4] поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.
Конвенции об обозначениях
Русская (и советская в целом) система
Натуральный логарифм принято обозначать через «ln(x)», логарифм по основанию 10 — через «lg(x)», а прочие основания принято указывать явно при символе «log».
Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x)» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.
Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln2 ln3 4x5 = [ln([ln(4x5)]3)]2.
Англо-американская система
Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x)», либо «ln(x)» , а для обозначения логарифма по основанию 10 — «log10(x)».
Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x)» (или изредка «loge(x)»), когда они имеют в виду натуральный логарифм, а запись «log(x)» у них означает log10(x).
В теоретической информатике, теории информации и криптографии «log(x)» обычно означает логарифм по основанию 2 «log2(x)» (хотя часто вместо этого пишется просто lg(x)).
Техника
В наиболее часто используемых языках программирования и пакетах прикладных программ, включая C, C++, SAS, MATLAB, Фортран и BASIC функция «log» или «LOG» относится к натуральному логарифму.
В ручных калькуляторах натуральный логарифм обозначается ln, тогда как log служит для обозначения логарифма по основанию 10.
Происхождение термина натуральный логарифм
Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей.[5] Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60.[6][7][8]
loge является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:[9]
Если основание b равно e, то производная равна просто 1/x, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.
Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.[10]
Определение
ln(a) определяется как площадь под кривой f(x) = 1/x от 1 до a.Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. е. как интеграл:
Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:
Это можно продемонстрировать, допуская следующим образом:
Число e может быть определено как единственное действительное число a такое, что ln(a) = 1.
Или же, если показательная функция была определена раньше с использованием бесконечных рядов, натуральный логарифм может быть определён как обратная к ней функция, т. е. ln — это функция, такая что . Так как диапазон значений экспоненциальной функции от реальных аргументов есть все положительные вещественные числа, а экспоненциальная функция строго возрастает, то это хорошо определённая функция для всех положительных x.
Свойства
- (комплексный логарифм)
Производная, ряд Тейлора
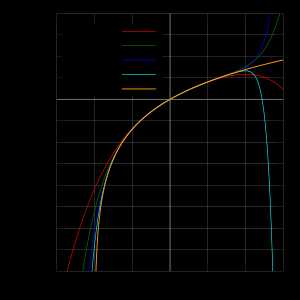Полиномы Тейлор дают точную аппроксимацию для только в диапазоне -1 x ≤ 1. Заметим, что для x > 1 полиномы Тейлора более высокой степени дают аппроксимацию хуже.Производная натурального логарифма равна
На основании этого можно выполнить разложение в ряд Тейлора около 0, называемого иногда рядом Меркатора:
Справа дано изображение и некоторых её полиномов Тейлора около 0. Эти аппроксимации сходятся к функции только в области -1 < x ≤ 1, а за её пределами полиномы Тейлора высших степеней дают аппроксимацию менее точную.
Подставляя x-1 для x, получим альтернативную форму для ln(x), а именно:
- [11]
С помощью преобразования Эйлера ряда Меркатор можно получить следующее выражение, которое справедливо для любого х больше 1 по абсолютной величине:
Этот ряд похож на формулу Бэйли—Боруэйна—Плаффа.
Также заметим, что — это её собственная инверная функция, поэтому для получения натурального логарифма определенного числа y нужно просто для x присвоить значение .
Натуральный логарифм в интегрировании
Натуральный логарифм даёт простую интегральную функцию вида g(x) = f ‘(x)/f(x): первообразная функции g(x) имеет вид ln(|f(x)|). Это подтверждается цепным правилом и следующим фактом:
В другом виде:
и
Ниже дан пример для g(x) = tan(x):
Пусть f(x) = cos(x) и f’(x)= — sin(x):
где C — произвольная константа.
Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:
- при условии, что y = (x−1)/(x+1) и x > 0.
Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:
Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.
Высокая точность
Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула:[12][13]
где M обозначает арифметико-геометрическое среднее 1 и 4/s, и
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)
Вычислительная сложность
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.
Непрерывные дроби
Хотя для представления логарифма отсутствуют простые непрерывные дроби, но можно использовать несколько обобщённых непрерывных дробей, в том числе:
Комплексные логарифмы
Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида ex для любого произвольного комплексного числа x, при этом используется бесконечный ряд с комплексным x. Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x, для которого ex = 0, и оказывается, что e2πi = 1 = e0. Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то ez = ez+2nπi для всех комплексных z и целых n.
Логарифм не может быть определён на всей комплексной плоскости, и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi. Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi, и т.д., и хотя i4 = 1, 4 log i может быть определена как 2πi, или 10πi или −6 πi, и так далее.
- Функции натурального логарифма на комплексной плоскости (главная ветвь)
Суперпозиция трёх предыдущих графиков
См. также
Примечания
- ↑ Mathematics for physical chemistry. — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5, Extract of page 9
- ↑ J J O’Connor and E F Robertson The number e. The MacTutor History of Mathematics archive (сентябрь 2001). Архивировано из первоисточника 12 февраля 2012.
- ↑ Cajori Florian A History of Mathematics, 5th ed. — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024
- ↑ Flashman, Martin Estimating Integrals using Polynomials. Архивировано из первоисточника 12 февраля 2012.
- ↑ Boyers Carl A History of Mathematics. — John Wiley & Sons, 1968.
- ↑ Harris, John (1987). «Australian Aboriginal and Islander mathematics» (PDF). Australian Aboriginal Studies 2: 29–37.
- ↑ Large, J.J. (1902). «The vigesimal system of enumeration». Journal of the Polynesian Society 11 (4): 260–261.
- ↑ Cajori first=Florian (1922). «Sexagesimal fractions among the Babylonians». American Mathematical Monthly 29 (1): 8–10. DOI:10.2307/2972914.
- ↑ Larson Ron Calculus: An Applied Approach. — 8th. — Cengage Learning, 2007. — P. 331. — ISBN 0-618-95825-8
- ↑ Ballew, Pat Math Words, and Some Other Words, of Interest. Архивировано из первоисточника 12 февраля 2012.
- ↑ «Logarithmic Expansions» at Math3.org
- ↑ (1982) «Practically fast multiple-precision evaluation of log(x)». Journal of Information Processing 5 (4): 247–250. Проверено 30 March 2011.
- ↑ (1999) «Fast computations of the exponential function» 1564: 302–312. DOI:10.1007/3-540-49116-3_28.
Ссылки
dic.academic.ru
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы логарифмов и основные формулы. Десятичные и натуральные логарифмы. Степени, корни. / / Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).
| ||||||||||||||||||||||||||||||
dpva.ru
Производная натурального логарифма — ln x
Вывод формул производных натурального логарифма и логарифма по основанию a
Производная натурального логарифма от x равна единице, деленной на x:
(1) ( ln x )′ = .
Производная логарифма по основанию a равна единице, деленной на переменную x, умноженную на натуральный логарифм от a:
(2) ( loga x)′ = .
Далее мы приводим вывод этих формул.
Доказательство
Пусть есть некоторое положительное число, не равное единице. Рассмотрим функцию, зависящую от переменной x, которая является логарифмом по основанию :
.
Эта функция определена при . Найдем ее производную по переменной x. По определению, производная является следующим пределом:
(3) .
Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам нужно знать следующие факты:
А) Свойства логарифма. Нам понадобятся следующие формулы:
(4) ;
(5) ;
(6) ;
Б) Непрерывность логарифма и свойство пределов для непрерывной функции:
(7) .
Здесь – некоторая функция, у которой существует предел и этот предел положителен.
В) Значение второго замечательного предела:
(8) .
Применяем эти факты к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим свойства (4) и (5).
.
Далее сделаем подстановку . При , . Тогда
.
Воспользуемся свойством (7) и вторым замечательным пределом (8):
.
И, наконец, применим свойство (6):
.
Логарифм по основанию e называется натуральным логарифмом. Он обозначается так:
.
Тогда ;
.
Тем самым мы получили формулу (2) производной логарифма.
Производная натурального логарифма
Еще раз выпишем формулу производной логарифма по основанию a:
.
Эта формула имеет наиболее простой вид для натурального логарифма, для которого , . Тогда
(1) .
Из-за такой простоты, натуральный логарифм очень широко используется в математическом анализе и в других разделах математики, связанных с дифференциальным исчислением. Логарифмические функции с другими основаниями можно выразить через натуральный логарифм, используя свойство (6):
.
Производную логарифма по основанию можно найти из формулы (1), если вынести постоянную за знак дифференцирования:
.
Другие способы доказательство производной логарифма
Здесь мы предполагаем, что нам известна формула производной экспоненты:
(9) .
Тогда мы можем вывести формулу производной натурального логарифма, учитывая, что логарифм является обратной функцией к экспоненте.
Докажем формулу производной натурального логарифма, применив формулу производной обратной функции:
.
В нашем случае . Обратной функцией к натуральному логарифму является экспонента:
.
Ее производная определяется по формуле (9). Переменные можно обозначить любой буквой. В формуле (9), заменим переменную x на y:
.
Поскольку , то
.
Тогда
.
Формула доказана.
Теперь докажем формулу производной натурального логарифма с помощью правила дифференцирования сложной функции. Поскольку функции и являются обратными друг к другу, то
.
Дифференцируем это уравнение по переменной x:
(10) .
Производная от икса равна единице:
.
Применяем правило дифференцирования сложной функции:
.
Здесь . Подставим в (10):
.
Отсюда
.
Пример
Найти производные от ln 2x, ln 3x и ln nx.
Решение
Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = ln nx. Затем подставим n = 2 и n = 3. И, тем самым, получим формулы для производных от ln 2x и ln 3x.
Итак, ищем производную от функции
y = ln nx.
Представим эту функцию как сложную функцию, состоящую из двух функций:
1) Функции , зависящей от переменной : ;
2) Функции , зависящей от переменной : .
Тогда исходная функция составлена из функций и :
.
Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем формулу производной сложной функции.
.
Здесь мы подставили .
Итак, мы нашли:
(11) .
Мы видим, что производная не зависит от n. Этот результат вполне естественен, если преобразовать исходную функцию, применяя формулу логарифма от произведения:
.
– это постоянная. Ее производная равна нулю. Тогда по правилу дифференцирования суммы имеем:
.
Ответ
; ; .
См. также
Все примеры вычисления производных с решениями > > >
Производная логарифма модуля x
Найдем производную от еще одной очень важной функции – натурального логарифма от модуля x:
(12) .
Рассмотрим случай . Тогда и функция имеет вид:
.
Ее производная определяется по формуле (1):
.
Теперь рассмотрим случай . Тогда и функция имеет вид:
,
где .
Но производную этой функции мы также нашли в приведенном выше примере. Она не зависит от n и равна
.
Тогда
.
Объединяем эти два случая в одну формулу:
.
Соответственно, для логарифма по основанию a, имеем:
.
Производные высших порядков натурального логарифма
Рассмотрим функцию
.
Мы нашли ее производную первого порядка:
(13) .
Найдем производную второго порядка:
.
Найдем производную третьего порядка:
.
Найдем производную четвертого порядка:
.
Можно заметить, что производная n-го порядка имеет вид:
(14) .
Докажем это методом математической индукции.
Доказательство
Подставим в формулу (14) значение n = 1:
.
Поскольку , то при n = 1, формула (14) справедлива.
Предположим, что формула (14) выполняется при n = k. Докажем, что из этого следует, что формула справедлива при n = k + 1.
Действительно, при n = k имеем:
.
Дифференцируем по переменной x:
.
Итак, мы получили:
.
Эта формула совпадает с формулой (14) при n = k + 1. Таким образом, из предположения, что формула (14) справедлива при n = k следует, что формула (14) справедлива при n = k + 1.
Поэтому формула (14), для производной n-го порядка, справедлива для любых n.
Производные высших порядков логарифма по основанию a
Чтобы найти производную n-го порядка от логарифма по основанию a, нужно выразить его через натуральный логарифм:
.
Применяя формулу (14), находим n-ю производную:
.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Какое основание у имеет логарифм log?
Чаще всего имеется в виду натуральный логарифм. Особенно если публикация математическая, и тем более переводная. На Западе математики именно так натуральный (а другие не имеют для них отличительного значения) логарифм и обозначают. Но верно также и то, что очень часто основание непринципиально. Поскольку логарифм числа прямо пропорционален натуральному логарифму этого числа: log_a (x) = log_e(x) / log_e (a) =C log x, C — константа. Непринципиально основание и в приведенном Вами примере «Следующий алгоритм имеет сложность O(кв. корень (p)*log(p))». Действительно, если вдруг логарифм и придется домножать на какую-то константу в связи с изменением основания, то O большому на это наплевать, оно такую операцию игнорирует, функции имеют одинаковый порядок роста. Итого: Ваше утверждение, будучи верным для одного основания логарифма, останется верным и для всех остальных. Когда очень надо по каким-то причинам подчеркнуть основание, обычно его пишут явно или оговаривают заранее. Дополнительно и подробно можно почитать еще <a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/Натуральный_логарифм#.D0.9A.D0.BE.D0.BD.D0.B2.D0.B5.D0.BD.D1.86.D0.B8.D0.B8_.D0.BE.D0.B1_.D0.BE.D0.B1.D0.BE.D0.B7.D0.BD.D0.B0.D1.87.D0.B5.D0.BD.D0.B8.D1.8F.D1.85″ target=»_blank» >здесь</a>.
Это уж у автора публикации в Интернете спросить надо! Интернет потому и именуют нередко «информационной помойкой», что в нем очень много совершенно безграмотной писанины. И приведенный вами пример — яркая тому иллюстрация.
Логарифмом данного числа по данному основанию называется показатель степени, в которую надо возвести это основание, чтобы получить данное число. Вместо того, чтобы писать: „логарифм числа 16 по основанию 4″ пишут сокращенно так: log4 16,
В сложности алгоритма основание у логарифмов не указывают. На практике обычно его принимают за 10
touch.otvet.mail.ru
Натуральный логарифм — Википедия (с комментариями)
Первое упоминание натурального логарифма сделал Николас Меркатор в работе Logarithmotechnia, опубликованной в 1668 году[2], хотя учитель математики Джон Спайделл ещё в 1619 году составил таблицу натуральных логарифмов.[3] Ранее его называли гиперболическим логарифмом,[4] поскольку он соответствует площади под гиперболой. Иногда его называют логарифмом Непера, хотя первоначальный смысл этого термина был несколько другой.
Соглашение об обозначениях
Обозначение «ln(x)» всегда относится к натуральному логарифму. Обозначения «lg(x)» и «log(x)» зависят от контекста и традиций, описываемых ниже.
Русская и европейская система
Натуральный логарифм принято обозначать через «ln(x)», логарифм по основанию 10 — через «lg(x)», а прочие основания принято указывать явно при символе «log».
Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x)» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.
Скобки вокруг аргумента логарифмов (если это не приводит к ошибочному чтению формулы) обычно опускают, а при возведении логарифма в степень показатель приписывают непосредственно к знаку логарифма: ln2 ln3 4x5 = [ln([ln(4x5)]3)]2.
Англо-американская система
Обозначение натурального логарифма, как <math>\ln(x)</math>, где <math>x</math> является аргументом, ввёл американский математик Ирвинг Стрингхем в 1893 году[5].
Математики, статистики и часть инженеров обычно используют для обозначения натурального логарифма либо «log(x)», либо «ln(x)», а для обозначения логарифма по основанию 10 — «log10(x)».
Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x)» (или изредка «loge(x)»), когда они имеют в виду натуральный логарифм, а запись «log(x)» у них означает log10(x).
В теоретической информатике, теории информации и криптографии «log(x)» обычно означает логарифм по основанию 2 «log2(x)» (хотя часто вместо этого пишется просто lg(x)).
Техника
В наиболее часто используемых языках программирования и пакетах прикладных программ, включая C, C++, SAS, MATLAB, Фортран и BASIC функция «log» или «LOG» относится к натуральному логарифму.
В ручных калькуляторах натуральный логарифм обозначается ln, тогда как log служит для обозначения логарифма по основанию 10.
Происхождение термина
Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей.[6] Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60.[7][8][9]
loge является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции:[10]
- <math>\frac{d}{dx}\log_b(x) = \frac{d}{dx} \left( \frac{1}{\ln(b)} \ln{x} \right) = \frac{1}{\ln(b)} \frac{d}{dx} \ln{x} = \frac{1}{x\ln(b)} </math>
Если основание b равно e, то производная равна просто 1/x, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.
Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николас Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление.[11]
Определение
Формально ln(a) может быть определён как площадь, заключённая под кривой графика 1/x на участке от 1 до a, т. е. как интеграл:
- <math>\ln(a)=\int_1^a \frac{1}{x}\,dx.</math>
Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:
- <math>\ln(ab)=\ln(a)+\ln(b)</math>
Это можно продемонстрировать, допуская <math>t=\tfrac xa</math> следующим образом:
- <math>
\ln (ab) = \int_1^{ab} \frac{1}{x} \; dx = \int_1^a \frac{1}{x} \; dx \; + \int_a^{ab} \frac{1}{x} \; dx =\int_1^{a} \frac{1}{x} \; dx \; + \int_1^{b} \frac{1}{t} \; dt = \ln (a) + \ln (b) </math>
Число e может быть определено как единственное действительное число a такое, что ln(a) = 1.
Или же, если показательная функция была определена раньше с использованием бесконечных рядов, натуральный логарифм может быть определён как обратная к ней функция, т. е. ln — это функция, такая что <math>e^{\ln(x)} = x</math>. Так как диапазон значений экспоненциальной функции от реальных аргументов есть все положительные вещественные числа, а экспоненциальная функция строго возрастает, то это хорошо определённая функция для всех положительных x.
Свойства
- <math>\ln(-1) = i \pi \quad</math> — комплексный логарифм
- <math>\ln(x) < \ln(y) \quad{\rm for}\quad 0 < x < y\;</math>
- <math>\frac{h}{1+h} \leq \ln(1+h) \leq h \quad{\rm for}\quad h > -1\;</math>
- <math>\lim_{x \to 0} \frac{\ln(1+x)}{x} = 1.</math>
Производная и разложение в ряд Тейлора
Используя то, что производная натурального логарифма равна
- <math>\frac{d}{dx} \ln(x) = \frac{1}{x},</math>
можно выполнить разложение <math>\ln(1+x)</math> в ряд Тейлора около x = 0, называемое иногда рядом Меркатора:
- <math>\ln(1+x)=\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} x^n = x — \frac{x^2}{2} + \frac{x^3}{3} — \dots \quad{\rm for}\quad \left|x\right| \leq 1\quad</math>
- <math>{\rm unless}\quad x = -1</math>
Ограничение этого бесконечного ряда i-м членом порождает многочлены Тейлора i-го порядка, содержащие степени не выше i-й. На рисунке справа приведены графики функции <math>\ln (1+x)</math> и некоторых многочленов Тейлора около x = 0. Аппроксимации сходятся к функции только в области сходимости −1 < x ≤ 1, а за её пределами быстро отклоняются от точной функции, причем многочлены высших степеней дают бо́льшую ошибку.
Подставляя x−1 вместо x, получаем альтернативную форму для ln(x), а именно:
- <math>\ln(x)=\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} (x-1) ^ n</math>
- <math>\ln(x)= (x — 1) — \frac{(x-1) ^ 2}{2} + \frac{(x-1)^3}{3} — \frac{(x-1)^4}{4} + \dots</math>
- <math>{\rm for}\quad \left|x-1\right| \leq 1\quad {\rm unless}\quad x = 0.</math>[12]
С помощью преобразования Эйлера из ряда Тейлора можно получить следующее выражение, справедливое для любого |x| > 1:
- <math>\ln{x \over {x-1}} = \sum_{n=1}^\infty {1 \over {n x^n}} = {1 \over x}+ {1 \over {2x^2}} + {1 \over {3x^3}} + \dots</math>
Этот ряд похож на формулу Бэйли—Боруэйна—Плаффа.
Также заметим, что <math> x \over {x-1} </math> — это её собственная инверсная функция, поэтому для получения натурального логарифма определенного числа y нужно просто для x присвоить значение <math> y \over {y-1} </math>.
Натуральный логарифм в интегрировании
Натуральный логарифм даёт простую интегральную функцию вида g(x) = f ‘(x)/f(x): первообразная функции g(x) имеет вид ln(|f(x)|). Это подтверждается цепным правилом и следующим фактом:
- <math>\ {d \over dx}\left( \ln \left| x \right| \right) = {1 \over x}.</math>
В другом виде:
- <math>\int { 1 \over x} dx = \ln|x| + C</math>
и
- <math>\int { \frac{f'(x)}{f(x)}\, dx} = \ln |f(x)| + C.</math>
Ниже дан пример для g(x) = tan(x):
- <math>\int \tan (x) \,dx = \int {\sin (x) \over \cos (x)} \,dx</math>
- <math>\int \tan (x) \,dx = \int {-{d \over dx} \cos (x) \over {\cos (x)}} \,dx.</math>
Пусть f(x) = cos(x) и f’(x)= — sin(x):
- <math>\int \tan (x) \,dx = -\ln{\left| \cos (x) \right|} + C</math>
- <math>\int \tan (x) \,dx = \ln{\left| \sec (x) \right|} + C</math>
где C — произвольная константа.
Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:
- <math>\int \ln (x) \,dx = x \ln (x) — x + C.</math>
Численное значение
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:
- <math>\ln(1+x)= x \,\left( \frac{1}{1} — x\,\left(\frac{1}{2} — x \,\left(\frac{1}{3} — x \,\left(\frac{1}{4} — x \,\left(\frac{1}{5}- \dots \right)\right)\right)\right)\right) \quad{\rm for}\quad \left|x\right|<1.</math>
Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:
<math>\ln(x) = \ln\left(\frac{1+y}{1-y}\right)</math> <math>= 2\,y\, \left( \frac{1}{1} + \frac{1}{3} y^{2} + \frac{1}{5} y^{4} + \frac{1}{7} y^{6} + \frac{1}{9} y^{8} + \dots \right) </math> <math>= 2\,y\, \left( \frac{1}{1} + y^{2} \, \left( \frac{1}{3} + y^{2} \, \left( \frac{1}{5} + y^{2} \, \left( \frac{1}{7} + y^{2} \, \left( \frac{1}{9} + \dots \right) \right) \right)\right) \right) </math>
- при условии, что y = (x−1)/(x+1) и x > 0.
Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:
<math>\ln(123{,}456)</math> <math>= \ln(1{,}23456 \times 10^2)</math> <math>= \ln(1{,}23456) + \ln(10^2)</math> <math>= \ln(1{,}23456) + 2 \times \ln(10)</math> <math>\approx \ln(1{,}23456) + 2 \times 2{,}3025851</math>
Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.
Высокая точность
Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.
Альтернативой для очень высокой точности расчёта является формула:[13][14]
- <math>\ln x \approx \frac{\pi}{2 M(1,4/s)} — m \ln 2</math>
где M обозначает арифметико-геометрическое среднее 1 и 4/s, и
- <math>s = x \,2^m > 2^{p/2},</math>
m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)
Вычислительная сложность
Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.
Непрерывные дроби
Хотя для представления логарифма отсутствуют простые непрерывные дроби, но можно использовать несколько обобщённых непрерывных дробей, в том числе:
- <math>
\log(1+x)=\frac{x^1}{1}-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\frac{x^5}{5}-\dots= \cfrac{x}{1-0x+\cfrac{1^2x}{2-1x+\cfrac{2^2x}{3-2x+\cfrac{3^2x}{4-3x+\cfrac{4^2x}{5-4x+\ddots}}}}} </math>
- <math>
\log \left( 1+\frac{2x}{y} \right) = \cfrac{2x} {y+\cfrac{x} {1+\cfrac{x} {3y+\cfrac{2x} {1+\cfrac{2x} {5y+\cfrac{3x} {1+\ddots}}}}}} = \cfrac{2x} {y+x-\cfrac{(1x)^2} {3(y+x)-\cfrac{(2x)^2} {5(y+x)-\cfrac{(3x)^2} {7(y+x)-\ddots}}}} </math>
Комплексные логарифмы
Экспоненциальная функция может быть расширена до функции, которая даёт комплексное число вида ex для любого произвольного комплексного числа x, при этом используется бесконечный ряд с комплексным x. Эта показательная функция может быть инвертирована с образованием комплексного логарифма, который будет обладать большей частью свойств обычных логарифмов. Есть, однако, две трудности: не существует x, для которого ex = 0, и оказывается, что e2πi = 1 = e0. Поскольку свойство мультипликативности действительно для комплексной экспоненциальной функции, то ez = ez+2nπi для всех комплексных z и целых n.
Логарифм не может быть определён на всей комплексной плоскости, и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi. Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi, и т.д., и хотя i4 = 1, 4 log i может быть определена как 2πi, или 10πi или −6 πi, и так далее.
- Функции натурального логарифма на комплексной плоскости (главная ветвь)
NaturalLogarithmAll.png
Суперпозиция трёх предыдущих графиков
См. также
Напишите отзыв о статье «Натуральный логарифм»
Примечания
- ↑ [books.google.com/books?id=nGoSv5tmATsC Mathematics for physical chemistry]. — 3rd. — Academic Press, 2005. — P. 9. — ISBN 0-125-08347-5., [books.google.com/books?id=nGoSv5tmATsC&pg=PA9 Extract of page 9]
- ↑ J J O’Connor and E F Robertson. [www-history.mcs.st-and.ac.uk/HistTopics/e.html The number e]. The MacTutor History of Mathematics archive (сентябрь 2001). [www.webcitation.org/65NiCJyO4 Архивировано из первоисточника 12 февраля 2012].
- ↑ Cajori Florian. [books.google.com/?id=mGJRjIC9fZgC&dq=%22Cajori%22+%22A+History+of+Mathematics%22+ A History of Mathematics, 5th ed]. — AMS Bookstore, 1991. — P. 152. — ISBN 0821821024.
- ↑ Flashman, Martin. [www.humboldt.edu/~mef2/Presentations/Estimations.html Estimating Integrals using Polynomials]. [www.webcitation.org/65NiCr1s9 Архивировано из первоисточника 12 февраля 2012].
- ↑ Charles Smith, Irving Stringham, Elementary algebra for the use of schools and colleges 2nd ed, (The Macmillan Company, New York, 1904)
- ↑ Boyers Carl. A History of Mathematics. — John Wiley & Sons, 1968.
- ↑ Harris, John (1987). «[www1.aiatsis.gov.au/exhibitions/e_access/serial/m0005975_v_a.pdf Australian Aboriginal and Islander mathematics]» (PDF). Australian Aboriginal Studies 2: 29–37.
- ↑ Large, J.J. (1902). «[www.jps.auckland.ac.nz/document/?wid=636 The vigesimal system of enumeration]». Journal of the Polynesian Society 11 (4): 260–261.
- ↑ Cajori first=Florian (1922). «Sexagesimal fractions among the Babylonians». American Mathematical Monthly 29 (1): 8–10. DOI:10.2307/2972914.
- ↑ Larson Ron. [books.google.com/books?id=rbDG7V0OV34C Calculus: An Applied Approach]. — 8th. — Cengage Learning, 2007. — P. 331. — ISBN 0-618-95825-8.
- ↑ Ballew, Pat [www.pballew.net/arithme1.html#ln Math Words, and Some Other Words, of Interest]. [www.webcitation.org/65NiDLLaT Архивировано из первоисточника 12 февраля 2012].
- ↑ [www.math3.org/math/expansion/log.htm «Logarithmic Expansions» at Math3.org]
- ↑ (1982) «[ci.nii.ac.jp/naid/110002673332 Practically fast multiple-precision evaluation of log(x)]». Journal of Information Processing 5 (4): 247–250. Проверено 30 March 2011.
- ↑ (1999) «Fast computations of the exponential function» 1564: 302–312. DOI:10.1007/3-540-49116-3_28.
Ссылки
- «[yasno.tv/articles/11-math/7-razbiraemsya-s-naturalnim-logarifmom Разбираемся с натуральным логарифмом]» — перевод статьи [betterexplained.com/articles/demystifying-the-natural-logarithm-ln/ Demystifying the Natural Logarithm (ln) | BetterExplained] (англ.)
Отрывок, характеризующий Натуральный логарифм
Мавра Кузминишна отперла калитку. И на двор вошел лет восемнадцати круглолицый офицер, типом лица похожий на Ростовых.– Уехали, батюшка. Вчерашнего числа в вечерни изволили уехать, – ласково сказала Мавра Кузмипишна.
Молодой офицер, стоя в калитке, как бы в нерешительности войти или не войти ему, пощелкал языком.
– Ах, какая досада!.. – проговорил он. – Мне бы вчера… Ах, как жалко!..
Мавра Кузминишна между тем внимательно и сочувственно разглядывала знакомые ей черты ростовской породы в лице молодого человека, и изорванную шинель, и стоптанные сапоги, которые были на нем.
– Вам зачем же графа надо было? – спросила она.
– Да уж… что делать! – с досадой проговорил офицер и взялся за калитку, как бы намереваясь уйти. Он опять остановился в нерешительности.
– Видите ли? – вдруг сказал он. – Я родственник графу, и он всегда очень добр был ко мне. Так вот, видите ли (он с доброй и веселой улыбкой посмотрел на свой плащ и сапоги), и обносился, и денег ничего нет; так я хотел попросить графа…
Мавра Кузминишна не дала договорить ему.
– Вы минуточку бы повременили, батюшка. Одною минуточку, – сказала она. И как только офицер отпустил руку от калитки, Мавра Кузминишна повернулась и быстрым старушечьим шагом пошла на задний двор к своему флигелю.
В то время как Мавра Кузминишна бегала к себе, офицер, опустив голову и глядя на свои прорванные сапоги, слегка улыбаясь, прохаживался по двору. «Как жалко, что я не застал дядюшку. А славная старушка! Куда она побежала? И как бы мне узнать, какими улицами мне ближе догнать полк, который теперь должен подходить к Рогожской?» – думал в это время молодой офицер. Мавра Кузминишна с испуганным и вместе решительным лицом, неся в руках свернутый клетчатый платочек, вышла из за угла. Не доходя несколько шагов, она, развернув платок, вынула из него белую двадцатипятирублевую ассигнацию и поспешно отдала ее офицеру.
– Были бы их сиятельства дома, известно бы, они бы, точно, по родственному, а вот может… теперича… – Мавра Кузминишна заробела и смешалась. Но офицер, не отказываясь и не торопясь, взял бумажку и поблагодарил Мавру Кузминишну. – Как бы граф дома были, – извиняясь, все говорила Мавра Кузминишна. – Христос с вами, батюшка! Спаси вас бог, – говорила Мавра Кузминишна, кланяясь и провожая его. Офицер, как бы смеясь над собою, улыбаясь и покачивая головой, почти рысью побежал по пустым улицам догонять свой полк к Яузскому мосту.
А Мавра Кузминишна еще долго с мокрыми глазами стояла перед затворенной калиткой, задумчиво покачивая головой и чувствуя неожиданный прилив материнской нежности и жалости к неизвестному ей офицерику.
В недостроенном доме на Варварке, внизу которого был питейный дом, слышались пьяные крики и песни. На лавках у столов в небольшой грязной комнате сидело человек десять фабричных. Все они, пьяные, потные, с мутными глазами, напруживаясь и широко разевая рты, пели какую то песню. Они пели врозь, с трудом, с усилием, очевидно, не для того, что им хотелось петь, но для того только, чтобы доказать, что они пьяны и гуляют. Один из них, высокий белокурый малый в чистой синей чуйке, стоял над ними. Лицо его с тонким прямым носом было бы красиво, ежели бы не тонкие, поджатые, беспрестанно двигающиеся губы и мутные и нахмуренные, неподвижные глаза. Он стоял над теми, которые пели, и, видимо воображая себе что то, торжественно и угловато размахивал над их головами засученной по локоть белой рукой, грязные пальцы которой он неестественно старался растопыривать. Рукав его чуйки беспрестанно спускался, и малый старательно левой рукой опять засучивал его, как будто что то было особенно важное в том, чтобы эта белая жилистая махавшая рука была непременно голая. В середине песни в сенях и на крыльце послышались крики драки и удары. Высокий малый махнул рукой.
– Шабаш! – крикнул он повелительно. – Драка, ребята! – И он, не переставая засучивать рукав, вышел на крыльцо.
Фабричные пошли за ним. Фабричные, пившие в кабаке в это утро под предводительством высокого малого, принесли целовальнику кожи с фабрики, и за это им было дано вино. Кузнецы из соседних кузень, услыхав гульбу в кабаке и полагая, что кабак разбит, силой хотели ворваться в него. На крыльце завязалась драка.
Целовальник в дверях дрался с кузнецом, и в то время как выходили фабричные, кузнец оторвался от целовальника и упал лицом на мостовую.
Другой кузнец рвался в дверь, грудью наваливаясь на целовальника.
Малый с засученным рукавом на ходу еще ударил в лицо рвавшегося в дверь кузнеца и дико закричал:
– Ребята! наших бьют!
В это время первый кузнец поднялся с земли и, расцарапывая кровь на разбитом лице, закричал плачущим голосом:
– Караул! Убили!.. Человека убили! Братцы!..
– Ой, батюшки, убили до смерти, убили человека! – завизжала баба, вышедшая из соседних ворот. Толпа народа собралась около окровавленного кузнеца.
– Мало ты народ то грабил, рубахи снимал, – сказал чей то голос, обращаясь к целовальнику, – что ж ты человека убил? Разбойник!
Высокий малый, стоя на крыльце, мутными глазами водил то на целовальника, то на кузнецов, как бы соображая, с кем теперь следует драться.
– Душегуб! – вдруг крикнул он на целовальника. – Вяжи его, ребята!
– Как же, связал одного такого то! – крикнул целовальник, отмахнувшись от набросившихся на него людей, и, сорвав с себя шапку, он бросил ее на землю. Как будто действие это имело какое то таинственно угрожающее значение, фабричные, обступившие целовальника, остановились в нерешительности.
– Порядок то я, брат, знаю очень прекрасно. Я до частного дойду. Ты думаешь, не дойду? Разбойничать то нонче никому не велят! – прокричал целовальник, поднимая шапку.
– И пойдем, ишь ты! И пойдем… ишь ты! – повторяли друг за другом целовальник и высокий малый, и оба вместе двинулись вперед по улице. Окровавленный кузнец шел рядом с ними. Фабричные и посторонний народ с говором и криком шли за ними.
У угла Маросейки, против большого с запертыми ставнями дома, на котором была вывеска сапожного мастера, стояли с унылыми лицами человек двадцать сапожников, худых, истомленных людей в халатах и оборванных чуйках.
– Он народ разочти как следует! – говорил худой мастеровой с жидкой бородйой и нахмуренными бровями. – А что ж, он нашу кровь сосал – да и квит. Он нас водил, водил – всю неделю. А теперь довел до последнего конца, а сам уехал.
Увидав народ и окровавленного человека, говоривший мастеровой замолчал, и все сапожники с поспешным любопытством присоединились к двигавшейся толпе.
– Куда идет народ то?
– Известно куда, к начальству идет.
– Что ж, али взаправду наша не взяла сила?
– А ты думал как! Гляди ко, что народ говорит.
Слышались вопросы и ответы. Целовальник, воспользовавшись увеличением толпы, отстал от народа и вернулся к своему кабаку.
Высокий малый, не замечая исчезновения своего врага целовальника, размахивая оголенной рукой, не переставал говорить, обращая тем на себя общее внимание. На него то преимущественно жался народ, предполагая от него получить разрешение занимавших всех вопросов.
– Он покажи порядок, закон покажи, на то начальство поставлено! Так ли я говорю, православные? – говорил высокий малый, чуть заметно улыбаясь.
– Он думает, и начальства нет? Разве без начальства можно? А то грабить то мало ли их.
– Что пустое говорить! – отзывалось в толпе. – Как же, так и бросят Москву то! Тебе на смех сказали, а ты и поверил. Мало ли войсков наших идет. Так его и пустили! На то начальство. Вон послушай, что народ то бает, – говорили, указывая на высокого малого.
У стены Китай города другая небольшая кучка людей окружала человека в фризовой шинели, держащего в руках бумагу.
– Указ, указ читают! Указ читают! – послышалось в толпе, и народ хлынул к чтецу.
Человек в фризовой шинели читал афишку от 31 го августа. Когда толпа окружила его, он как бы смутился, но на требование высокого малого, протеснившегося до него, он с легким дрожанием в голосе начал читать афишку сначала.
«Я завтра рано еду к светлейшему князю, – читал он (светлеющему! – торжественно, улыбаясь ртом и хмуря брови, повторил высокий малый), – чтобы с ним переговорить, действовать и помогать войскам истреблять злодеев; станем и мы из них дух… – продолжал чтец и остановился („Видал?“ – победоносно прокричал малый. – Он тебе всю дистанцию развяжет…»)… – искоренять и этих гостей к черту отправлять; я приеду назад к обеду, и примемся за дело, сделаем, доделаем и злодеев отделаем».
Последние слова были прочтены чтецом в совершенном молчании. Высокий малый грустно опустил голову. Очевидно было, что никто не понял этих последних слов. В особенности слова: «я приеду завтра к обеду», видимо, даже огорчили и чтеца и слушателей. Понимание народа было настроено на высокий лад, а это было слишком просто и ненужно понятно; это было то самое, что каждый из них мог бы сказать и что поэтому не мог говорить указ, исходящий от высшей власти.
Все стояли в унылом молчании. Высокий малый водил губами и пошатывался.
– У него спросить бы!.. Это сам и есть?.. Как же, успросил!.. А то что ж… Он укажет… – вдруг послышалось в задних рядах толпы, и общее внимание обратилось на выезжавшие на площадь дрожки полицеймейстера, сопутствуемого двумя конными драгунами.
Полицеймейстер, ездивший в это утро по приказанию графа сжигать барки и, по случаю этого поручения, выручивший большую сумму денег, находившуюся у него в эту минуту в кармане, увидав двинувшуюся к нему толпу людей, приказал кучеру остановиться.
– Что за народ? – крикнул он на людей, разрозненно и робко приближавшихся к дрожкам. – Что за народ? Я вас спрашиваю? – повторил полицеймейстер, не получавший ответа.
– Они, ваше благородие, – сказал приказный во фризовой шинели, – они, ваше высокородие, по объявлению сиятельнейшего графа, не щадя живота, желали послужить, а не то чтобы бунт какой, как сказано от сиятельнейшего графа…
– Граф не уехал, он здесь, и об вас распоряжение будет, – сказал полицеймейстер. – Пошел! – сказал он кучеру. Толпа остановилась, скучиваясь около тех, которые слышали то, что сказало начальство, и глядя на отъезжающие дрожки.
Полицеймейстер в это время испуганно оглянулся, что то сказал кучеру, и лошади его поехали быстрее.
– Обман, ребята! Веди к самому! – крикнул голос высокого малого. – Не пущай, ребята! Пущай отчет подаст! Держи! – закричали голоса, и народ бегом бросился за дрожками.
Толпа за полицеймейстером с шумным говором направилась на Лубянку.
– Что ж, господа да купцы повыехали, а мы за то и пропадаем? Что ж, мы собаки, что ль! – слышалось чаще в толпе.
Вечером 1 го сентября, после своего свидания с Кутузовым, граф Растопчин, огорченный и оскорбленный тем, что его не пригласили на военный совет, что Кутузов не обращал никакого внимания на его предложение принять участие в защите столицы, и удивленный новым открывшимся ему в лагере взглядом, при котором вопрос о спокойствии столицы и о патриотическом ее настроении оказывался не только второстепенным, но совершенно ненужным и ничтожным, – огорченный, оскорбленный и удивленный всем этим, граф Растопчин вернулся в Москву. Поужинав, граф, не раздеваясь, прилег на канапе и в первом часу был разбужен курьером, который привез ему письмо от Кутузова. В письме говорилось, что так как войска отступают на Рязанскую дорогу за Москву, то не угодно ли графу выслать полицейских чиновников, для проведения войск через город. Известие это не было новостью для Растопчина. Не только со вчерашнего свиданья с Кутузовым на Поклонной горе, но и с самого Бородинского сражения, когда все приезжавшие в Москву генералы в один голос говорили, что нельзя дать еще сражения, и когда с разрешения графа каждую ночь уже вывозили казенное имущество и жители до половины повыехали, – граф Растопчин знал, что Москва будет оставлена; но тем не менее известие это, сообщенное в форме простой записки с приказанием от Кутузова и полученное ночью, во время первого сна, удивило и раздражило графа.
Впоследствии, объясняя свою деятельность за это время, граф Растопчин в своих записках несколько раз писал, что у него тогда было две важные цели: De maintenir la tranquillite a Moscou et d’en faire partir les habitants. [Сохранить спокойствие в Москве и выпроводить из нее жителей.] Если допустить эту двоякую цель, всякое действие Растопчина оказывается безукоризненным. Для чего не вывезена московская святыня, оружие, патроны, порох, запасы хлеба, для чего тысячи жителей обмануты тем, что Москву не сдадут, и разорены? – Для того, чтобы соблюсти спокойствие в столице, отвечает объяснение графа Растопчина. Для чего вывозились кипы ненужных бумаг из присутственных мест и шар Леппиха и другие предметы? – Для того, чтобы оставить город пустым, отвечает объяснение графа Растопчина. Стоит только допустить, что что нибудь угрожало народному спокойствию, и всякое действие становится оправданным.
Все ужасы террора основывались только на заботе о народном спокойствии.
На чем же основывался страх графа Растопчина о народном спокойствии в Москве в 1812 году? Какая причина была предполагать в городе склонность к возмущению? Жители уезжали, войска, отступая, наполняли Москву. Почему должен был вследствие этого бунтовать народ?
Не только в Москве, но во всей России при вступлении неприятеля не произошло ничего похожего на возмущение. 1 го, 2 го сентября более десяти тысяч людей оставалось в Москве, и, кроме толпы, собравшейся на дворе главнокомандующего и привлеченной им самим, – ничего не было. Очевидно, что еще менее надо было ожидать волнения в народе, ежели бы после Бородинского сражения, когда оставление Москвы стало очевидно, или, по крайней мере, вероятно, – ежели бы тогда вместо того, чтобы волновать народ раздачей оружия и афишами, Растопчин принял меры к вывозу всей святыни, пороху, зарядов и денег и прямо объявил бы народу, что город оставляется.
Растопчин, пылкий, сангвинический человек, всегда вращавшийся в высших кругах администрации, хотя в с патриотическим чувством, не имел ни малейшего понятия о том народе, которым он думал управлять. С самого начала вступления неприятеля в Смоленск Растопчин в воображении своем составил для себя роль руководителя народного чувства – сердца России. Ему не только казалось (как это кажется каждому администратору), что он управлял внешними действиями жителей Москвы, но ему казалось, что он руководил их настроением посредством своих воззваний и афиш, писанных тем ёрническим языком, который в своей среде презирает народ и которого он не понимает, когда слышит его сверху. Красивая роль руководителя народного чувства так понравилась Растопчину, он так сжился с нею, что необходимость выйти из этой роли, необходимость оставления Москвы без всякого героического эффекта застала его врасплох, и он вдруг потерял из под ног почву, на которой стоял, в решительно не знал, что ему делать. Он хотя и знал, но не верил всею душою до последней минуты в оставление Москвы и ничего не делал с этой целью. Жители выезжали против его желания. Ежели вывозили присутственные места, то только по требованию чиновников, с которыми неохотно соглашался граф. Сам же он был занят только тою ролью, которую он для себя сделал. Как это часто бывает с людьми, одаренными пылким воображением, он знал уже давно, что Москву оставят, но знал только по рассуждению, но всей душой не верил в это, не перенесся воображением в это новое положение.
Вся деятельность его, старательная и энергическая (насколько она была полезна и отражалась на народ – это другой вопрос), вся деятельность его была направлена только на то, чтобы возбудить в жителях то чувство, которое он сам испытывал, – патриотическую ненависть к французам и уверенность в себе.
wiki-org.ru
Адрес для вставки QR-кода числа 212, размер 500×500:
Вас считают недобрым человеком, но вы уверены, что это совсем наоборот. Вы всего лишь пытаетесь донести до мира правду и свой взгляд на справедливость, а не стремитесь насолить ближнему своему.
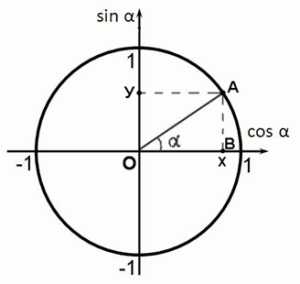
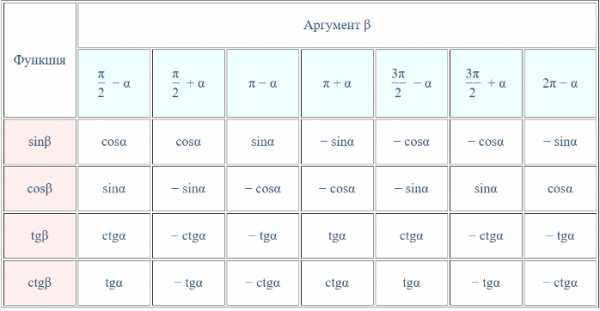
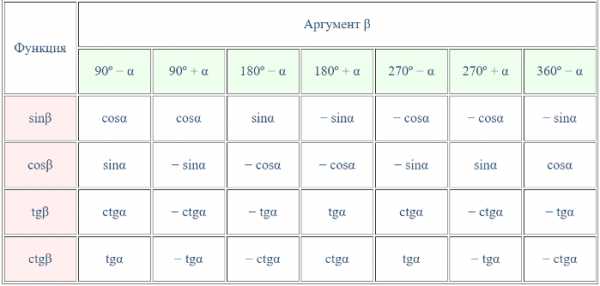
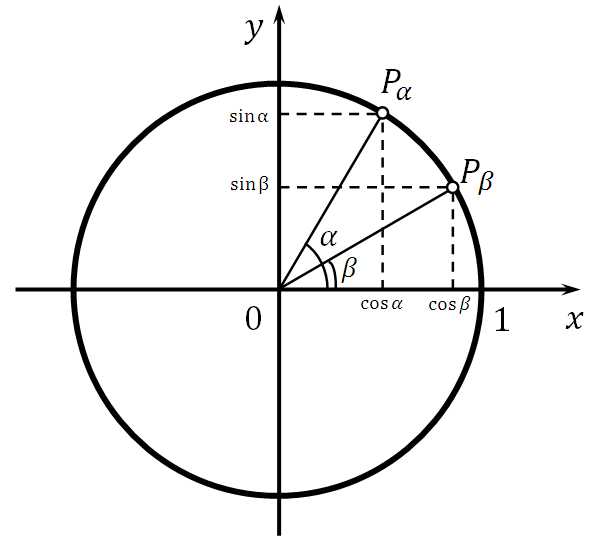
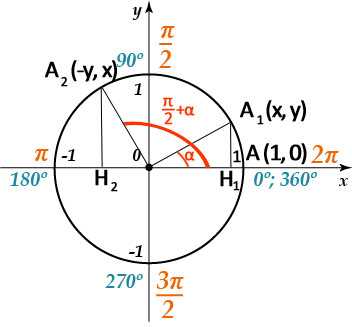угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac {\pi}2 + \alpha` в точку `А_2(-у,х)`. Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.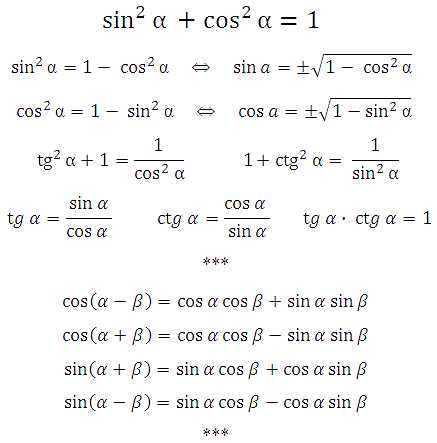
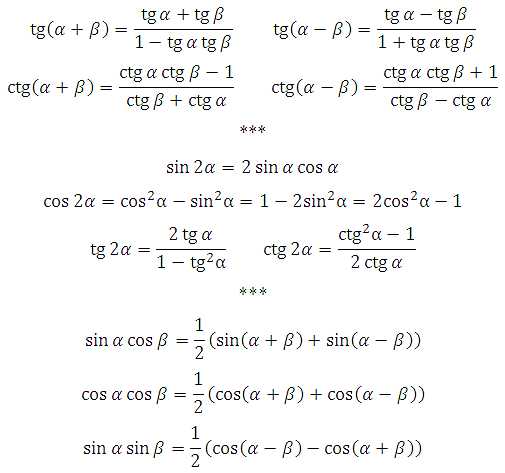
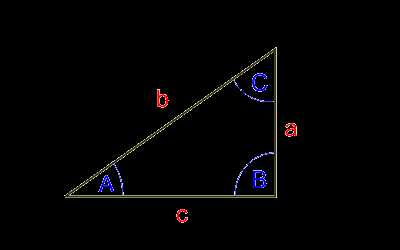Буквами A, B, C обозначены углы, буквами a, b, c — стороны,
противолежащие углам A, B, C соответственно. Угол B = 90° (прямой).
Тогда тригонометрические функции определяются следующим образом: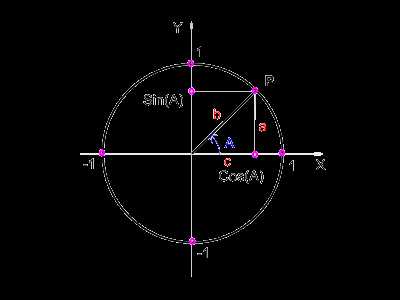
Лунтик
Маша и медведь
