Коэффициент жизненности Покровского:
Коэффициент миграции:
Коэффициент интенсивности миграционного оборота:
Коэффициент эффективности миграции:
Коэффициент общего прироста населения:
Определяем перспективную численность населения через три года:
12.6. Таблицы смертности и средней продолжительности жизни
Для анализа перспективной численности населения и средней продолжительности жизни используют таблицы смертности.
Таблица смертности представляет собой систему связанных друг с другом показателей, зависящих от уровня смертности, отнесенных к различным возрастам (табл. 12.1). На основе таблицы смертности рассчитывают среднюю ожидаемую продолжительность предстоящей жизни для отдельных возрастных групп.
Таблица 12.1
Макет таблицы смертности
Воз- раст, лет | Число доживаю-щих до возрас- та х лет | Вероят- ность до- жить до возраста (x+1) лет | Вероят-ность смерти в тече- ние года | Число живу- щих в возрас- те х лет | Предсто- ящее число чел.-лет жизни | Средняя продол-житель-ность жизни | Коэф-фициент дожития (пере- движки) |
х |
Начальными данными всех остальных показателей таблицы смертности является вероятность смерти в течение года для лиц, достигших возраста х лет. Таблица смертности строится для одного поколения, т.е. для родившихся в одном году. Численность поколения условно принимается равной 10000 или 100000 человек.
Для расчета частных показателей перспективной численности населения (например, по отдельным возрастным группам) дополнительно к общим показателям привлекаются данные о численности и возрастной структуре населения на начало планируемого периода, данные о коэффициентах дожития, рассчитанных на основе таблиц смертности (дожития), данные о возрастных коэффициентах рождаемости для женщин в возрасте 15‑49 лет и др.
Для перспективных расчетов численности населения и численности отдельных возрастных групп применяется метод передвижки по возрастам. Данный метод заключается в том, что зарегистрированная по переписи определенная численность людей каждого возраста х лет умножается на соответствующий коэффициент дожития , в результате чего определяется численность населения возраста (х+1) лет.
Коэффициент дожития или коэффициент передвижки определяется путем сравнения числа живущих в двух смежных возрастных группах (х) и (х+1) лет:
Число живущих в возрасте х лет рассчитывается по формуле:
Рассмотрим на условном примере методику расчета таблицы смертности.
Пример. Имеются данные о возрастных коэффициентах смертности:
Условное поколение принимаем в 10000 человек. Предстоящее число человеко-лет для данного поколения 660000.
На основе возрастных коэффициентов смертности можно определить:
= 0,024, = 0,004,= 0,003 и т.д.
= 1 – = 0,976;= 1 –= 0,996;= 1 –= 0,997 и т.д.
Определив вероятность дожития до возраста х (), рассчитаем число доживающих до возрастах ():
= 10000 по условию;
= ·= 10000 · 0,976 = 9760;
= ·= 9760 · 0,996 = 9721;
= ·= 9721 · 0,997 = 9692 и т.д.
Число живущих в возрасте х лет () представляет собой среднюю величину из числа доживающих до возраста х и до возраста х+1, следовательно:
Определим число предстоящих человеко-лет жизни для разных возрастов:
= 660000 по условию;
= = 660000 – 9880 = 650120;
= –= 650120 – 9740,5 = 640379,5;
= – = 640379,5 – 9706,5 = 630673 и т.д.
Средняя продолжительность предстоящей жизни населения определяется как Тх /lх. Следовательно:
Полученные данные можно представить в виде следующей таблицы смертности (табл. 12.2).
Таблица 12.2
х | |||||||
0 1 2 3 — | 10000 9760 9721 9692 — | 0,976 0,996 0,997 — — | 0,024 0,004 0,003 — — | 9880 9740,5 9706,5 — — | 660000 650120 640379,5 630773 — | 66 66,6 65,9 65,1 — | 0,99 0,99 — — — |
Контрольные вопросы
Дайте определение населения.
Перечислите основные задачи статистики населения.
Какие методы статистики используются при изучении населения?
Как определяется постоянное население?
Охарактеризуйте способы исчисления средней численности населения.
Перечислите показатели естественного движения населения.
Каким образом определяются коэффициенты брачности и разводимости?
Дайте определение механического движения населения.
Как определяются коэффициенты прибытия и выбытия?
На основе каких данных определяется общий прирост населения?
По какой формуле вычисляется перспективная численность населения?
Для чего используется таблица смертности и средней продолжительности жизни?
Задачи и упражнения
Задача 1
Имеются следующие показатели по сельскому району за год:
численность населения на начало года: 12836 чел.;
численность населения на конец года: 13154 чел.;
число родившихся: 834 чел.;
число умерших: 789 чел.
На основе этих данных определите коэффициенты:
рождаемости;
смертности;
естественного прироста населения;
жизненности Покровского.
Задача 2
Имеются следующие данные по области:
численность населения на начало года: 3296 тыс. чел.;
число родившихся: 1345 чел.;
число умерших: 1413 чел.;
прибыло на постоянное жительство: 756 чел.;
убыло в другие регионы: 872 чел.
На основе имеющейся информации определите:
среднегодовую численность населения;
коэффициент естественного прироста населения;
коэффициент прибытия;
коэффициент выбытия;
коэффициент миграции;
коэффициент интенсивности миграционного оборота;
коэффициент эффективности миграции;
коэффициент общего прироста населения;
перспективную численность населения через четыре года.
Задача 3
В 2008 г. население города в среднем составляло 64500 чел. В течение года родилось 612 чел., умерло 674 чел. В составе населения женщины в возрасте 15-49 лет составляли 32%.
Определить:
общий коэффициент рождаемости;
общий коэффициент смертности;
специальный коэффициент рождаемости;
коэффициент естественного прироста населения;
коэффициент жизненности.
Задача 4
Число живущих в возрасте 35 лет – 9346 человек. Число доживающих до 35 лет – 9416 человек. Определите число умирающих в возрасте 35 лет.
Задача 5
По имеющимся данным заполнить таблицу смертности:
х | |||||||
0 1 2 3 4 | 100000 — — — — | 0,981 — — — — | — 0,003 — — — | — — 97132 — — | — — — 6416452 — | — — — — — | — — — — 0,9987 |
studfiles.net
Коэффициент жизненности Покровского:
Коэффициент миграции:
Коэффициент интенсивности миграционного оборота:
Коэффициент эффективности миграции:
Коэффициент общего прироста населения:
Определяем перспективную численность населения через три года:
12.6. Таблицы смертности и средней продолжительности жизни
Для анализа перспективной численности населения и средней продолжительности жизни используют таблицы смертности.
Таблица смертности представляет собой систему связанных друг с другом показателей, зависящих от уровня смертности, отнесенных к различным возрастам (табл. 12.1). На основе таблицы смертности рассчитывают среднюю ожидаемую продолжительность предстоящей жизни для отдельных возрастных групп.
Таблица 12.1
Макет таблицы смертности
Воз- раст, лет | Число доживаю-щих до возрас- та х лет | Вероят- ность до- жить до возраста (x+1) лет | Вероят-ность смерти в тече- ние года | Число живу- щих в возрас- те х лет | Предсто- ящее число чел.-лет жизни | Средняя продол-житель-ность жизни | Коэф-фициент дожития (пере- движки) |
х |
Начальными данными всех остальных показателей таблицы смертности является вероятность смерти в течение года для лиц, достигших возраста х лет. Таблица смертности строится для одного поколения, т.е. для родившихся в одном году. Численность поколения условно принимается равной 10000 или 100000 человек.
Для расчета частных показателей перспективной численности населения (например, по отдельным возрастным группам) дополнительно к общим показателям привлекаются данные о численности и возрастной структуре населения на начало планируемого периода, данные о коэффициентах дожития, рассчитанных на основе таблиц смертности (дожития), данные о возрастных коэффициентах рождаемости для женщин в возрасте 15‑49 лет и др.
Для перспективных расчетов численности населения и численности отдельных возрастных групп применяется метод передвижки по возрастам. Данный метод заключается в том, что зарегистрированная по переписи определенная численность людей каждого возраста х лет умножается на соответствующий коэффициент дожития , в результате чего определяется численность населения возраста (х+1) лет.
Коэффициент дожития или коэффициент передвижки определяется путем сравнения числа живущих в двух смежных возрастных группах (х) и (х+1) лет:
Число живущих в возрасте х лет рассчитывается по формуле:
Рассмотрим на условном примере методику расчета таблицы смертности.
Пример. Имеются данные о возрастных коэффициентах смертности:
Условное поколение принимаем в 10000 человек. Предстоящее число человеко-лет для данного поколения 660000.
На основе возрастных коэффициентов смертности можно определить:
= 0,024, = 0,004,= 0,003 и т.д.
= 1 – = 0,976;= 1 –= 0,996;= 1 –= 0,997 и т.д.
Определив вероятность дожития до возраста х (), рассчитаем число доживающих до возрастах ():
= 10000 по условию;
= ·= 10000 · 0,976 = 9760;
= ·= 9760 · 0,996 = 9721;
= ·= 9721 · 0,997 = 9692 и т.д.
Число живущих в возрасте х лет () представляет собой среднюю величину из числа доживающих до возраста х и до возраста х+1, следовательно:
Определим число предстоящих человеко-лет жизни для разных возрастов:
= 660000 по условию;
= = 660000 – 9880 = 650120;
= –= 650120 – 9740,5 = 640379,5;
= – = 640379,5 – 9706,5 = 630673 и т.д.
Средняя продолжительность предстоящей жизни населения определяется как Тх /lх. Следовательно:
Полученные данные можно представить в виде следующей таблицы смертности (табл. 12.2).
Таблица 12.2
х | |||||||
0 1 2 3 — | 10000 9760 9721 9692 — | 0,976 0,996 0,997 — — | 0,024 0,004 0,003 — — | 9880 9740,5 9706,5 — — | 660000 650120 640379,5 630773 — | 66 66,6 65,9 65,1 — | 0,99 0,99 — — — |
Контрольные вопросы
Дайте определение населения.
Перечислите основные задачи статистики населения.
Какие методы статистики используются при изучении населения?
Как определяется постоянное население?
Охарактеризуйте способы исчисления средней численности населения.
Перечислите показатели естественного движения населения.
Каким образом определяются коэффициенты брачности и разводимости?
Дайте определение механического движения населения.
Как определяются коэффициенты прибытия и выбытия?
На основе каких данных определяется общий прирост населения?
По какой формуле вычисляется перспективная численность населения?
Для чего используется таблица смертности и средней продолжительности жизни?
Задачи и упражнения
Задача 1
Имеются следующие показатели по сельскому району за год:
численность населения на начало года: 12836 чел.;
численность населения на конец года: 13154 чел.;
число родившихся: 834 чел.;
число умерших: 789 чел.
На основе этих данных определите коэффициенты:
рождаемости;
смертности;
естественного прироста населения;
жизненности Покровского.
Задача 2
Имеются следующие данные по области:
численность населения на начало года: 3296 тыс. чел.;
число родившихся: 1345 чел.;
число умерших: 1413 чел.;
прибыло на постоянное жительство: 756 чел.;
убыло в другие регионы: 872 чел.
На основе имеющейся информации определите:
среднегодовую численность населения;
коэффициент естественного прироста населения;
коэффициент прибытия;
коэффициент выбытия;
коэффициент миграции;
коэффициент интенсивности миграционного оборота;
коэффициент эффективности миграции;
коэффициент общего прироста населения;
перспективную численность населения через четыре года.
Задача 3
В 2008 г. население города в среднем составляло 64500 чел. В течение года родилось 612 чел., умерло 674 чел. В составе населения женщины в возрасте 15-49 лет составляли 32%.
Определить:
общий коэффициент рождаемости;
общий коэффициент смертности;
специальный коэффициент рождаемости;
коэффициент естественного прироста населения;
коэффициент жизненности.
Задача 4
Число живущих в возрасте 35 лет – 9346 человек. Число доживающих до 35 лет – 9416 человек. Определите число умирающих в возрасте 35 лет.
Задача 5
По имеющимся данным заполнить таблицу смертности:
х | |||||||
0 1 2 3 4 | 100000 — — — — | 0,981 — — — — | — 0,003 — — — | — — 97132 — — | — — — 6416452 — | — — — — — | — — — — 0,9987 |
studfiles.net
12.3. Естественное движение населения
Основными показателями, характеризующими естественное движение населения, являются показатели рождаемости, смертности, естественного прироста, плодовитости, жизненности, брачности и разводимости.
Показатели естественного движения обычно исчисляются за год в расчете на 1000 человек, в промилле (‰).
Формулы расчета показателей естественного движения населения.
Коэффициент рождаемости:
где N – число родившихся;
среднегодовая численность населения.
Коэффициент смертности:
где M – число умерших.
Коэффициент естественного прироста населения:
или
Коэффициент плодовитости:
где – среднегодовая численность женщин в возрасте от 15 до
49 лет.
Коэффициент детской смертности:
где – число детей, умерших до 1 года.
Показатель жизненности Покровского:
Большое значение имеет группировка населения по семейному состоянию. Для этих целей определяют коэффициенты брачности и разводимости.
Коэффициент брачности:
где количество заключенных браков за год.
Коэффициент разводимости:
где количество расторгнутых браков за год.
12.4. Механическое движение населения
Численность населения как в целом по стране, так и по отдельным ее регионам меняется не только в результате его естественного движения, но и в результате механического движения.
Механическое движение населения – это изменение численности населения за счет миграции, т.е. перемещения отдельных лиц как внутри страны, так и за ее пределы.
В зависимости от географического направления различают миграцию внутреннюю и внешнюю.
Внутренняя миграция – перемещение населения внутри страны.
Внешняя миграция — перемещение населения из одной страны в другую.
Также выделяют маятниковую миграцию, т.е. перемещение населения из одного места в другое (обычно из сельской местности в город или наоборот) на кратковременной основе.
Основные показатели механического движения населения:
Коэффициент прибытия:
где П – число прибывших на данную территорию.
Коэффициент выбытия:
где В – число выбывших с данной территории.
Коэффициент миграции:
Коэффициент интенсивности миграционного оборота:
Коэффициент эффективности миграции:
На основе данных о естественном и миграционном приросте населения рассчитывают абсолютные и относительные показатели общего прироста населения.
Общий прирост населения:
S = += N – М + П – В ,
где = N – М — естественный прирост населения;
= П – В — миграционный прирост или сальдо миграции.
Коэффициент общего прироста населения:
12.5. Расчет перспективной численности населения
Одной из задач статистики населения является определение перспективной численности населения. Перспективная численность населения рассчитывается на основе данных о естественном и механическом приросте населения за определенный период и предположении о сохранении выявленной закономерности на прогнозируемый период. Применение данного метода прогноза не отличается особой точностью и применяется лишь тогда, когда показатели рождаемости, смертности и миграции за предыдущие годы достаточно стабильны.
Перспективная численность населения на определенную дату рассчитывается по формуле:
где перспективная численность населения черезn лет;
численность населения на начало периода;
число лет;
коэффициент общего прироста населения.
Рассмотрим на примере расчет показателей естественного и механического движения населения.
Пример. Имеются следующие данные по городу за год:
численность населения на начало года, чел. (): 487520;
среднегодовая численность женщин в возрасте 15–49 лет, чел. (: 138400.
число родившихся, чел. (N): 6540;
число умерших, чел. (М): 5743;
прибыло на постоянное жительство, чел. (П): 3540;
убыло в другие населенные пункты, чел. (В): 2911.
На основе этих данных определить показатели естественного и механического движения населения, а также перспективную численность населения через три года.
Решение.
Определяем численность населения города на конец года:
Рассчитываем среднюю численность населения:
Определяем коэффициент рождаемости:
Вычислим коэффициент смертности:
Коэффициент естественного прироста населения:
или
Коэффициент плодовитости:
studfiles.net
Задача №7. Расчёт коэффициентов естественного и механического движения населения
Численность населения региона характеризуется следующими данными, тыс. чел.:
1. На начало года:
фактически проживало 1504,6
в том числе временно 7,3
временно отсутствовало 4,8
2. В течение года:
родилось 7,8
в том числе постоянного населения 7,6
умерло 10,2
в том числе постоянного населения 10,1
прибыло на постоянное место жительства 35,6
выбыло постоянного населения на постоянное место жительства в другие населённые пункты 18,6
Определите:
1) численность наличного населения на конец года;
2) численность постоянного населения на начало и конец года;
3) для постоянного населения коэффициенты:
– рождаемости, смертности, естественного прироста;
– жизненности, оборота населения, экономичности воспроизводства;
– миграции, интенсивности миграционного оборота; эффективности миграции, общего прироста населения.
Решение:
1) Численность наличного населения на конец года найдём по балансовой схеме:
ННК = ННН + N – M + прибыло на постоянное место жительство +
+ вернулось из числа временно отсутствующих –
– выбыло постоянного населения на постоянное жительство в другие населённые пункты
где
ННКи ННН – численность наличного населения на конец и начало года,
N и M – число родившихся и умерших у наличного населения в течение года.
ННК = 1504,6 + 7,8 – 10,2 + 35,6 – 18,6 = 1519,2 тыс. чел..
2) Численность постоянного населения на начало года найдём по формуле:
ПНН = ННН – ВПН + ВОН,
где
ПНН, ННН, ВПН, ВОН– численность постоянного, наличного, временно проживающего и временно отсутствующего населения на начало года.
ПНН = 1504,6 – 7,3 + 4,8 = 1502,1 тыс. чел.
на конец года:
ПНК = ПНН + N – M + П – В,
где
N и M – число родившихся и умерших у постоянного населения в течение года;
П и В – число постоянного населения прибывшего и выбывшего на постоянное жительство в течение года.
ПНК = 1502,1 + 7,6 – 10,1 + 35,6 – 18,6 = 1516,6 тыс. чел.
3) Для расчёта коэффициентов естественного и механического прироста необходимо найти среднюю численность постоянного населения.
Имея данные о численности постоянного населения на начало и конец года, среднюю численность определим по формуле средней арифметической простой:
Коэффициент рождаемости рассчитывается по формуле:
Коэффициент смертности рассчитывается по формуле:
Коэффициент естественного прироста можно определить по формуле:
На каждую тысячу человек постоянного населения в течение года родилось 5 детей, умерло примерно 7 человек, естественная убыль составила приблизительно 2 человека.
Определим коэффициент жизненности (показатель Покровского), представляющий собой отношение числа родившихся к числу умерших (за год) по формуле:
Коэффициент оборота населения рассчитывается по формуле:
Число родившихся и умерших на 1000 человек населения в среднем за год равно 11,73.
Коэффициент экономичности воспроизводства показывает удельный вес естественного прироста в общем обороте населения.
Коэффициент экономичности воспроизводства населения равен:
Следовательно, в регионе доля естественной убыли в общем обороте населения составляет 14%.
Рассчитаем показатели механического движения (миграции) населения.
Механическое движение (миграция) населения – это прибытие в данный населённый пункт и выбытие из него.
Коэффициент прибытия определяется по формуле:
На каждую 1000 человек постоянного населения в среднем за год прибыло приблизительно 23 человека.
Коэффициент выбытия определяется по формуле:
Число выбывших на каждую 1000 человек населения в среднем за год составило примерно 12 человек.
Коэффициент миграции (механического прироста) рассчитаем двумя способами:
или
Приток населения на данную территорию составил 11 человек на каждую 1000 человек постоянного населения.
Коэффициент интенсивности миграционного оборота рассчитывается по формуле:
или
Коэффициент эффективности миграции рассчитывается по формуле:
Прибавив к коэффициенту естественного прироста коэффициент миграции, получим коэффициент общего прироста населения
что означает прирост на каждую 1000 человек.
ecson.ru
Презентация на тему: Коэффициент жизненности Покровского
К |
|
| N | , или КЖ | КР | |
Ж |
| КСМ | ||||
M | ||||||
|
|
|
Если КЖ>1, то наблюдается превышение родившихся над умершими.
Если КЖ<0,5, то ситуация характеризуется как «демографическая зима».
Коэффициент естественного оборота населения
КОБ N M1000
S
Показывает число родившихся и умерших на 1000 человек населения за год.
Коэффициент эффективности воспроизводства населения
КЭФ.ВОСПРN M 100
N M
Показывает долю естественного прироста в общем обороте населения.
•Коэффициент брачности
КБР БS 1000
•Коэффициент разводимости
КРАЗSР 1000
•Коэффициент соотношения браков и
разводов Б
КБР/ РАЗР 100
Ожидаемая
продолжительность жизни при рождении
число лет, которое в среднем предстояло бы прожить человеку из поколения родившихся при условии, что на протяжении всей жизни этого поколения половозрастная смертность останется на уровне того года, для которого исчислен показатель.
Брутто-коэффициентвоспроизводства населения
49
КБРУТТОКПЛdДЕВ
15
где КПЛ – коэффициент фертильности (женщин в возрасте от 15 до 49 лет) при отсутствии смертности женщин;
dДЕВ – доля девочек, рожденных живыми.
Нетто-коэффициентвоспроизводства населения
49
КНЕТТОКПЛdДЕВ/ Р15
где dДЕВ/Р – доля девочек, рожденных живыми и доживших до возраста матери, в котором она ее родила.
Коэффициент младенческой смертности
|
|
| M0 |
|
|
|
К |
|
|
| M1 | 1000 | |
|
| |||||
МСМ |
|
|
| |||
|
| N0 |
|
| ||
|
|
|
| N1 |
|
где М0(М1) – число умерших детей в возрасте до одного года в предыдущем (текущем) году;
N0(N1) – число родившихся детей в предыдущем (текущем) году.
studfiles.net
Задача №5. Расчёт показателей воспроизводства населения
Численность населения в городе на 01.01.2001 г. составляла 693 540 человек.
В течение года
родилось 9 650 тыс. человек.,
а умерло 7 520 человек.
Сальдо миграции за этот период равнялось нулю.
Определите:
1) численность населения на конец года;
2) среднегодовую численность населения;
3) абсолютный естественный прирост населения за год;
4) коэффициент естественного прироста,
5) коэффициент общей рождаемости,
6) коэффициент общей смертности,
7) коэффициент жизненности населения.
Решение:
1) Численность населения на конец года рассчитывается по формуле:
SК = SН + Δест. + Δмех. = SН + (N – M) + (П – В)
SК – численность населения на конец года,
SН – численность населения на начало года,
Δест. – сальдо естественного прироста,
Δмех. — сальдо миграции (механического прироста),
N – число родившихся,
M – число умерших,
П – число прибывших,
В – число выбывших.
SК = 693 540 + (9 650 – 7 520) + 0 = 695 670
2) Так как имеются данные о численности населения на начало и конец года, среднегодовая численность населения определяется по формуле средней арифметической простой:
3) Абсолютный естественный прирост населения за год равен:
Δест. = N – M = 9 650 – 7 520 = 2 130
4) Коэффициент естественного прироста определяется по формуле:
5) Коэффициент общей рождаемости рассчитывается по формуле:
6) Коэффициент общей смертности рассчитывается по формуле:
Коэффициент естественного прироста можно определить также по формуле:
На каждую тысячу человек в течение года родилось 14 детей, умерло 11 человек, естественный прирост составил 3 человека.
7) Определим коэффициент жизненности по формуле:
ecson.ru
Задача №24. Расчёт численности населения, абсолютных и относительных показателей
По региону известны следующие данные за 2002 г.:
Коэффициент общего прироста населения, ‰– 6;
Коэффициент естественного прироста населения, ‰– 4;
Коэффициент жизненности – 1,5;
Среднегодовая численность населения – 580 тыс. чел.;
Среднегодовой абсолютный прирост численности населения за предыдущие годы – 3,2 тыс. чел.
Определите:
1. численность населения на начало и конец 2002 г.;
2. абсолютный естественный и миграционный прирост численности населения;
3. коэффициент миграционного прироста;
4. число родившихся,
5. число умерших;
6. ожидаемую численность населения региона на 01.01.2012 г.
Решение:
Коэффициент общего прироста населения рассчитывается по формуле:
Кобщ = КN – M + КП – В
где
КN – M – коэффициент естественного прироста,
КП – В – коэффициент миграции (механического прироста)
Отсюда коэффициент миграционного прироста равен:
КП – В = Кобщ – КN – M = 6 – 4 = 2‰.
Коэффициент жизненности (показатель Покровского), представляет собой отношение числа родившихся N к числу умерших (за год) M и рассчитывается по формуле:
Отсюда
N = M × 1,5.
Коэффициент естественного прироста можно рассчитать по формуле:
По условию задания
КN – M = 4‰,
Тогда
Отсюда число умерших равно:
М = 4 640 чел.
Тогда число родившихся:
N = M × 1,5 = 6 960 чел.
Теперь определим абсолютный естественный прирост численности населения:
Δест. = N – M = 6 960 – 4 640 = 2 320 чел.
Распишем формулу расчёта коэффициента миграции:
Отсюда абсолютный миграционный прирост численности населения равен:
Найдём численность населения на начало и конец 2002 г.
Распишем формулу для расчёта среднегодовой численности населения:
Отсюда
SН + SК = 1 160 000
SК = 1 160 000 – SН
Численность населения на конец года можно также рассчитать по формуле:
SК = SН + Δест. + Δмигр.
SК – численность населения на конец года,
SН – численность населения на начало года,
Δест. – сальдо естественного прироста,
Δмех. – сальдо миграции (механического прироста).
SК = SН + 2 320 + 1 160
Решим уравнение:
1 160 000 – SН = SН + 2 320 + 1 160
SН = 578 260 чел.
Следовательно,
SК = 1 160 000 – 578 260 = 581 740 чел.
Численность населения на начало и конец 2002 г. равны соответственно 578 260 чел. и 581 740 чел.
Найдём ожидаемую численность населения региона на 01.01.2012 г.
Предполагая, что средний абсолютный прирост будет неизменным на будущий период можно определить перспективную численность населения по формуле:
St – перспективная численность населения через t лет,
– среднегодовой абсолютный прирост численности населения за предыдущие годы.
ecson.ru


 .
.


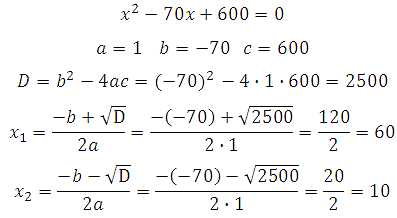
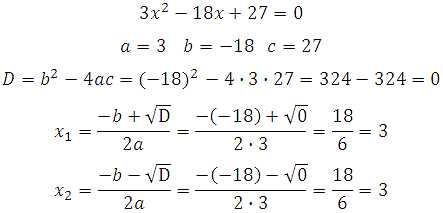
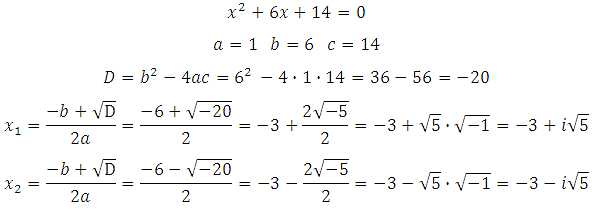
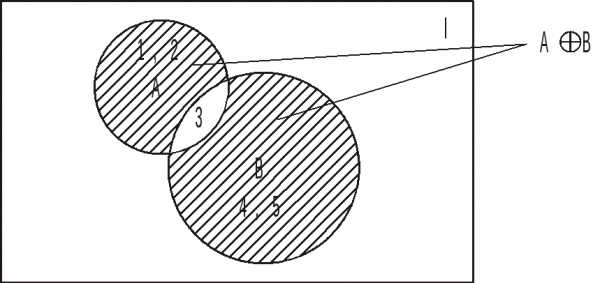
 ,
содержащее элементы универсума I, не
включенные во множество А:
,
содержащее элементы универсума I, не
включенные во множество А: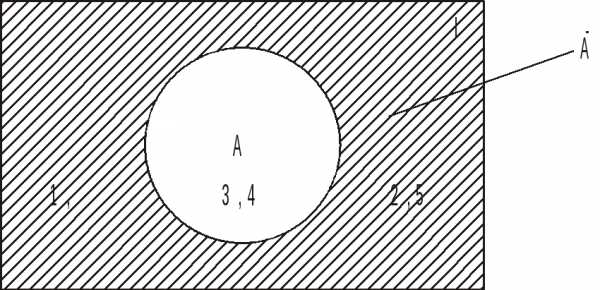
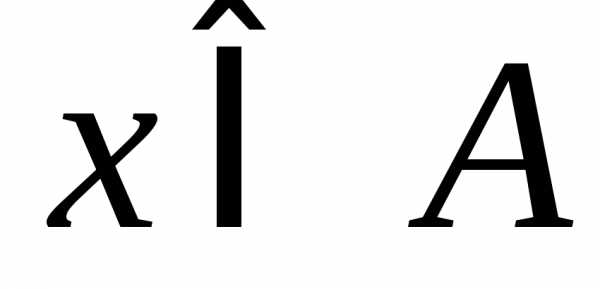 означает, что элементx принадлежит множеству A.
означает, что элементx принадлежит множеству A.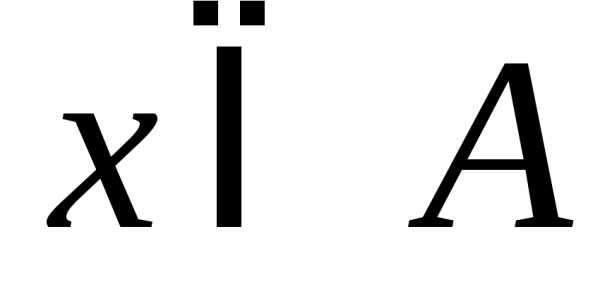 .
.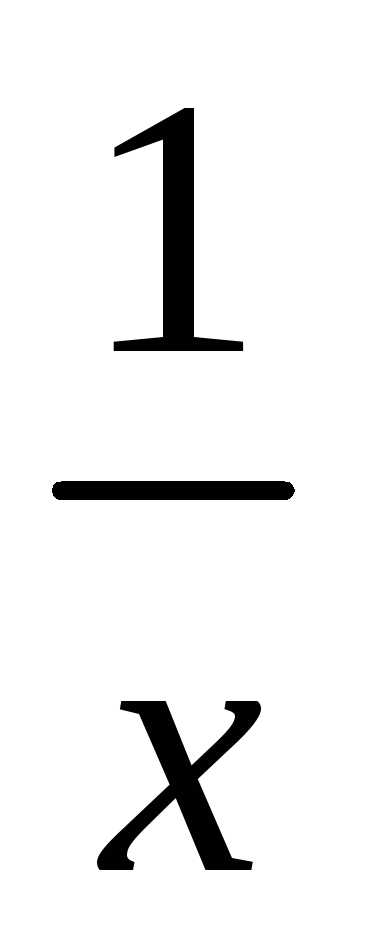 и (1x)
принадлежат X;
и (1x)
принадлежат X;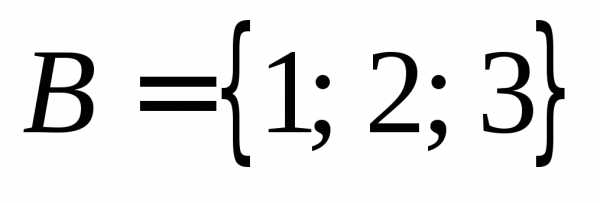 и.
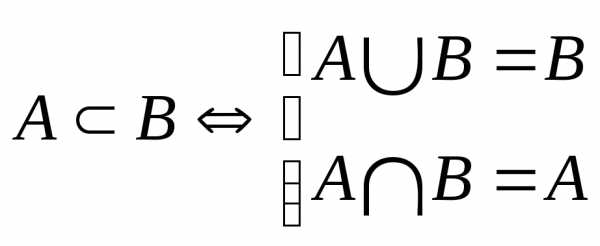
ТогдаBA.
и.
ТогдаBA.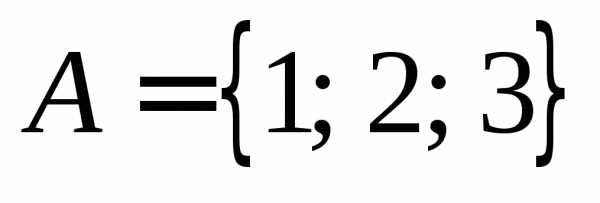 .
. )
–это
множество элементов универсума, которые
не принадлежат А, т.е.
)
–это
множество элементов универсума, которые
не принадлежат А, т.е. 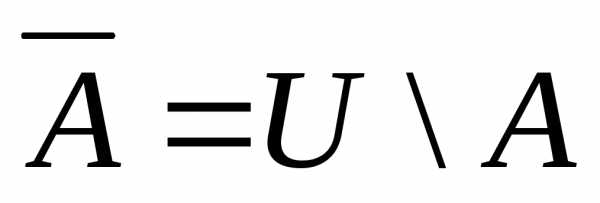 .
.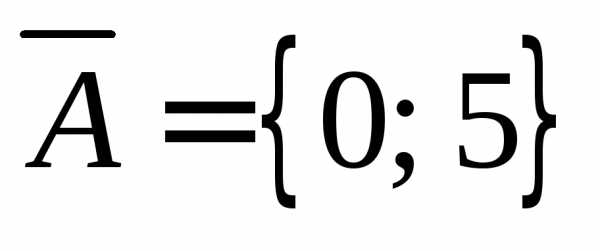 .
.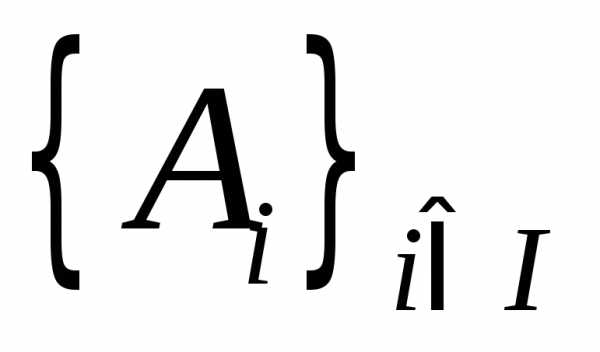 ,
где.
Тогда
,
где.
Тогда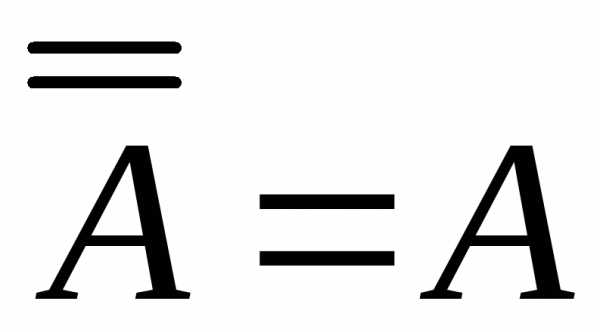
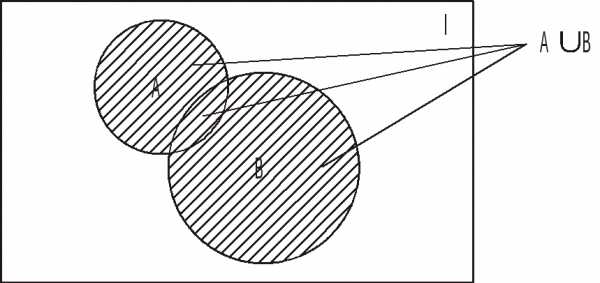
 =U
=U =
=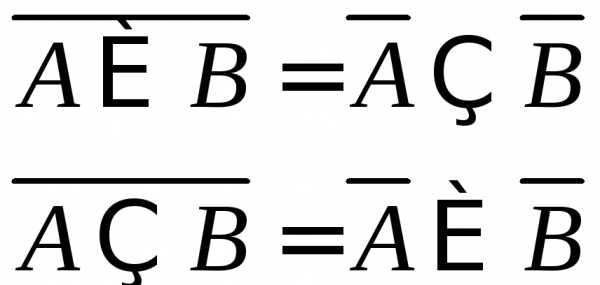
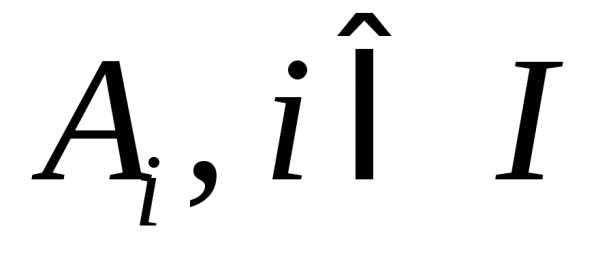 ,
гдеI – некоторое множество индексов, если
каждый элемент A принадлежит хотя бы одному из Ai.
,
гдеI – некоторое множество индексов, если
каждый элемент A принадлежит хотя бы одному из Ai.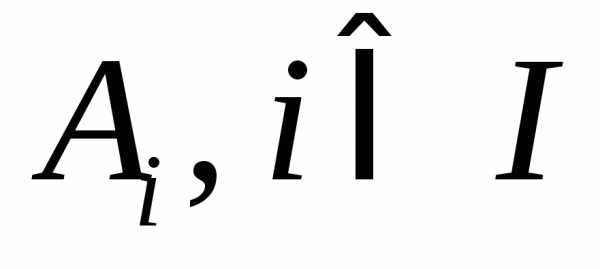 ,
гдеI – некоторое множество индексов.
,
гдеI – некоторое множество индексов.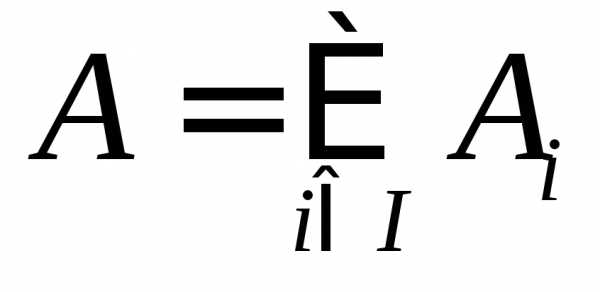 ,
т.е.aA тогда и только тогда, когда aAi для некоторого iI.
,
т.е.aA тогда и только тогда, когда aAi для некоторого iI.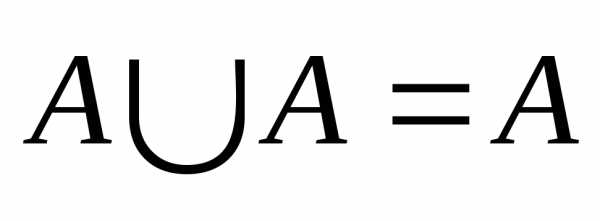
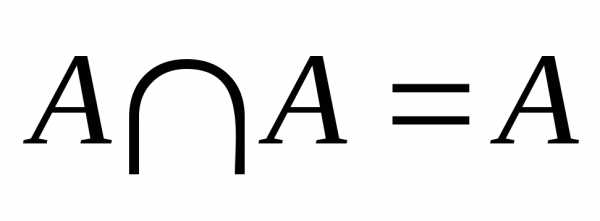

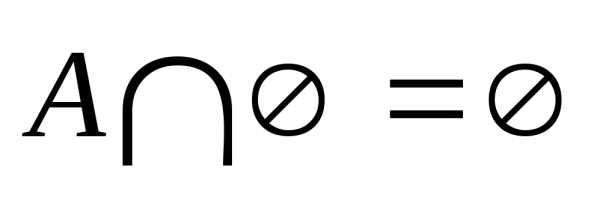
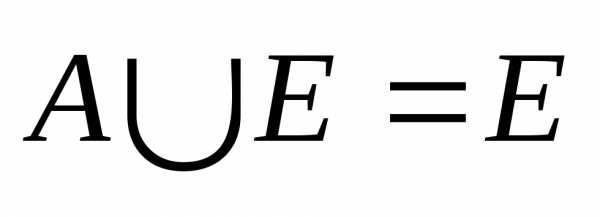
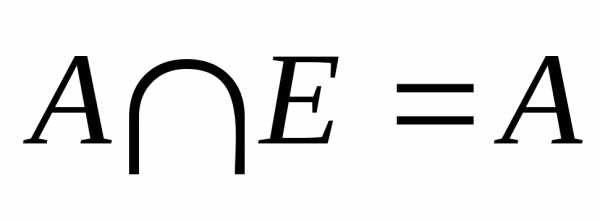
 »
на «
»
на « »
и «» на «», то получится снова одно из свойств 1
— 18. Таким образом, каждой теореме,
доказанной на основании формул 1-18,
соответствует двойственная теорема.
Свойства 6 — 18 доказывается методом
встречных включений. В качестве примера
докажем свойство 12.
»
и «» на «», то получится снова одно из свойств 1
— 18. Таким образом, каждой теореме,
доказанной на основании формул 1-18,
соответствует двойственная теорема.
Свойства 6 — 18 доказывается методом
встречных включений. В качестве примера
докажем свойство 12.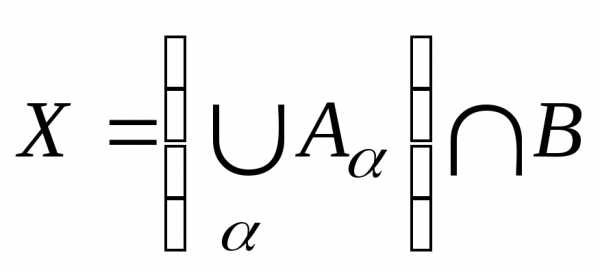 ,
,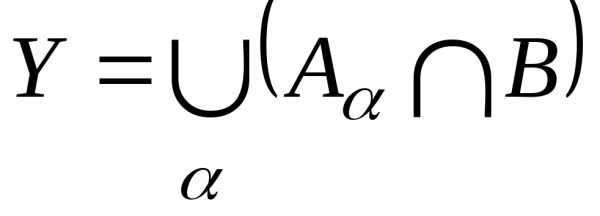 .
.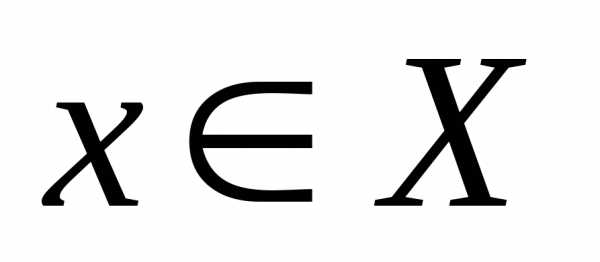 .
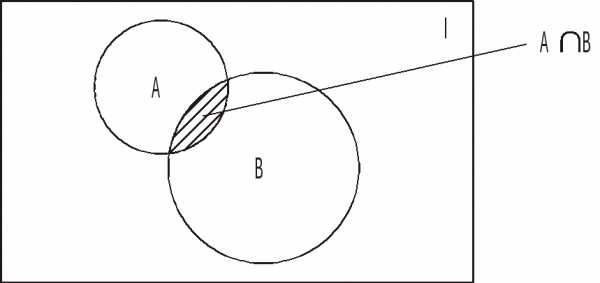
Покажем, что
.
Покажем, что .
.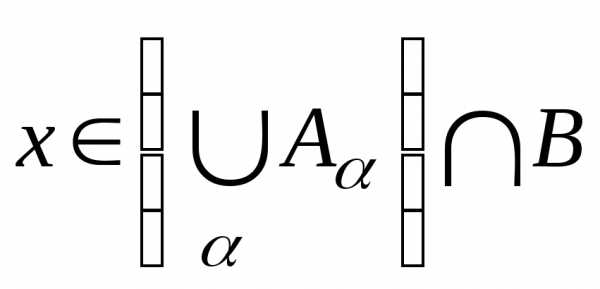 (хотя
бы одному из множеств
(хотя
бы одному из множеств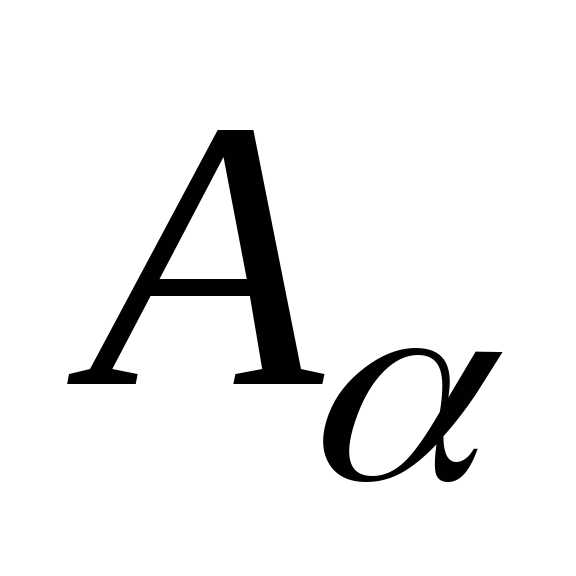 )
)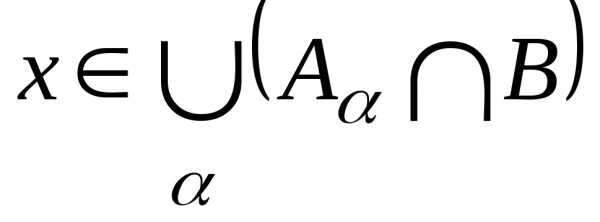
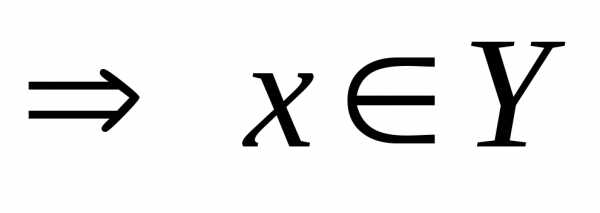 .
.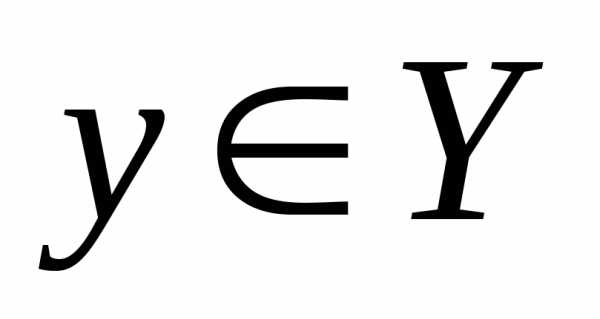 .
Покажем, что
.
Покажем, что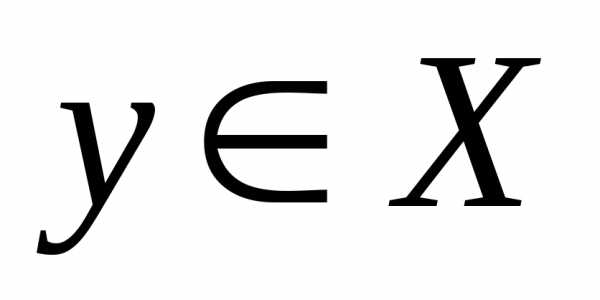 .
.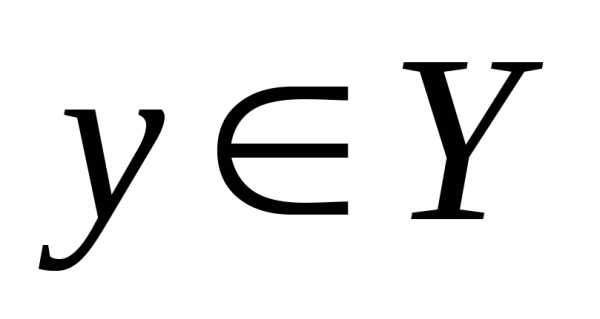
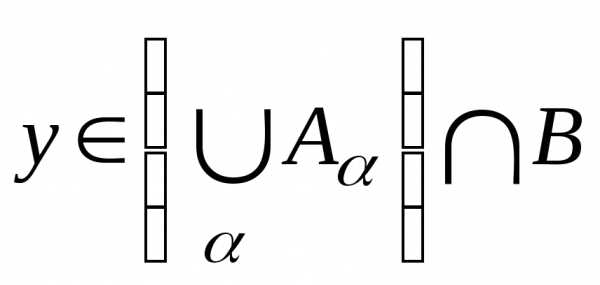 .
.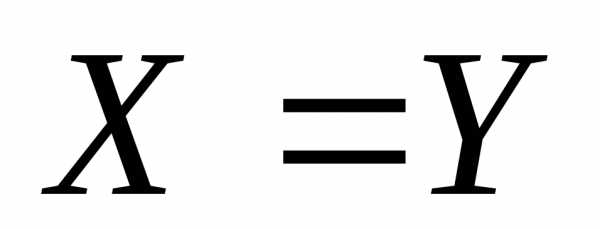 .
.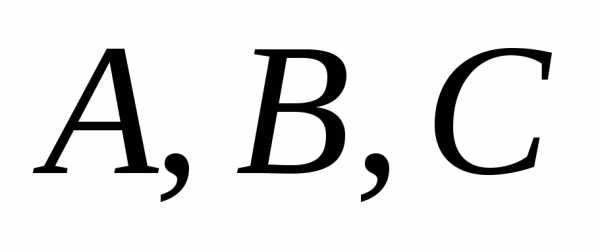 — произвольные множества. Тогда
— произвольные множества. Тогда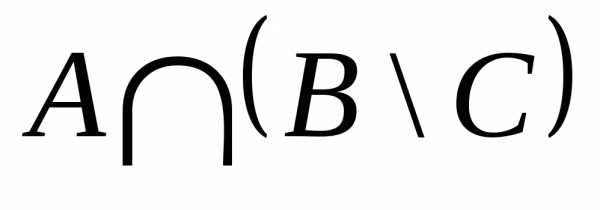 =.
=. .
. .
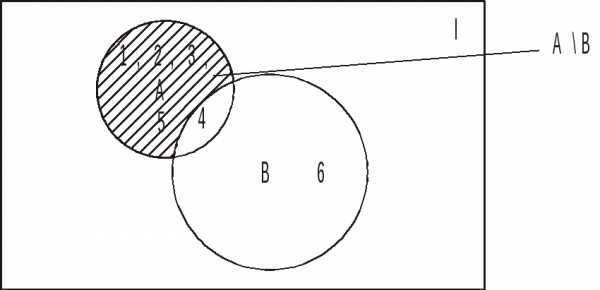
Множество
.
Множество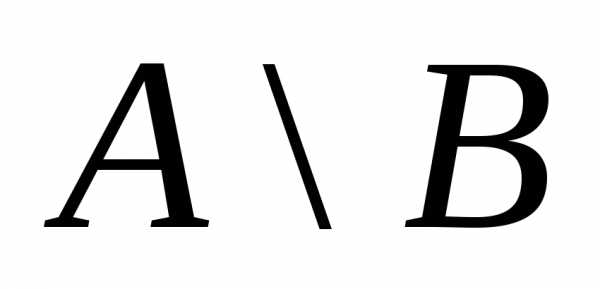 состоит из элементов множестваА,
не принадлежащих множествуВ.
Объединяя это множество со множествомВ, получим множествоА.
состоит из элементов множестваА,
не принадлежащих множествуВ.
Объединяя это множество со множествомВ, получим множествоА.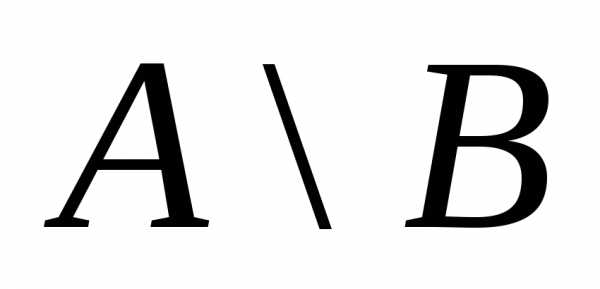 получим множество, отличное отА.
получим множество, отличное отА. ;
;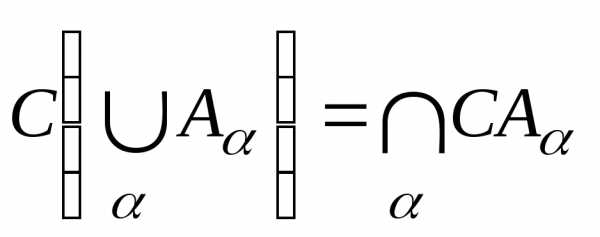 ;
;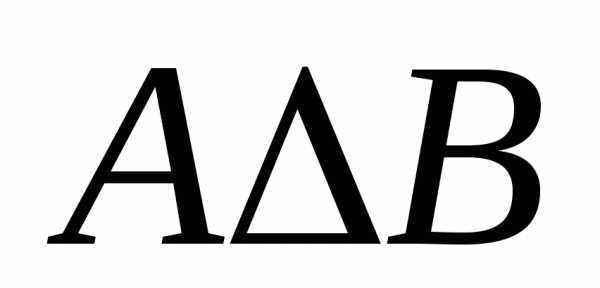 .
Легко видеть, что
.
Легко видеть, что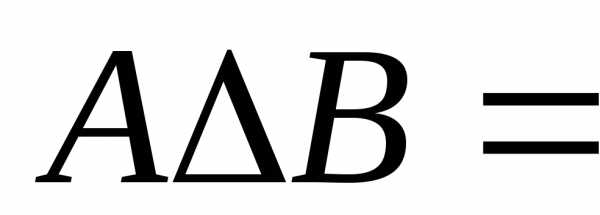 .
. относит один и только один элемент
относит один и только один элемент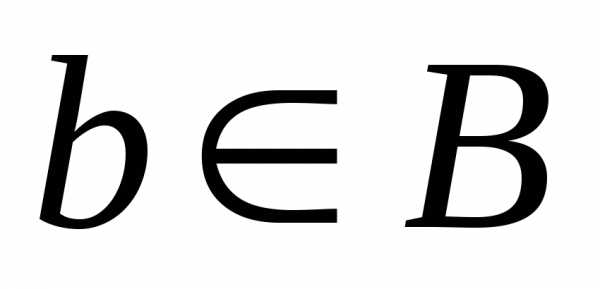 ,
который обозначается
,
который обозначается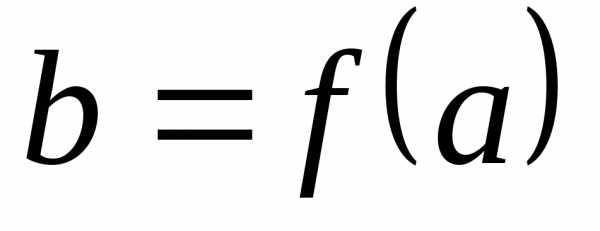 и называетсязначением
отображения f или образом элемента а
при отображении f.МножествоАназываетсяобластью
определения отображения.
и называетсязначением
отображения f или образом элемента а
при отображении f.МножествоАназываетсяобластью
определения отображения.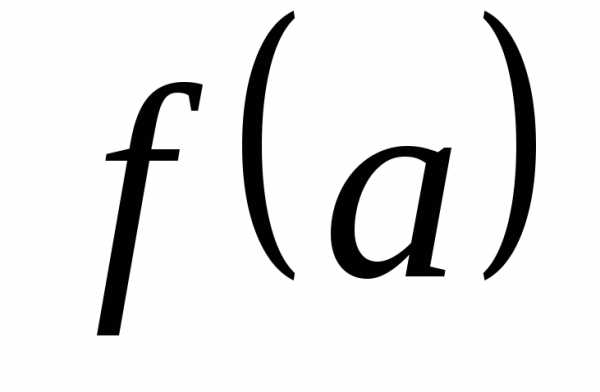 ,
гдеапробегает всё множествоD.
,
гдеапробегает всё множествоD.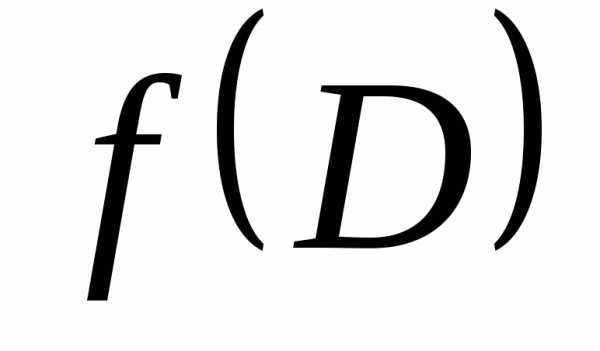 .
Таким образом,
.
Таким образом,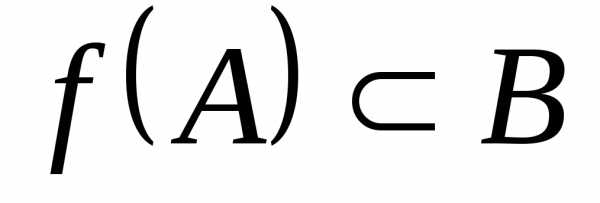 называетсямножеством
значений отображения f.
называетсямножеством
значений отображения f. ,
что
,
что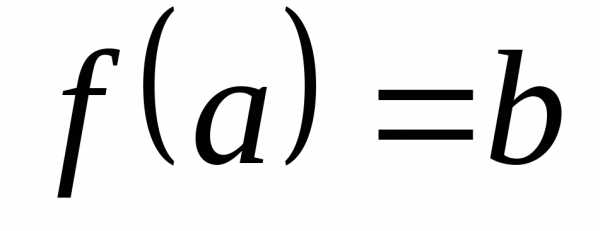 .
.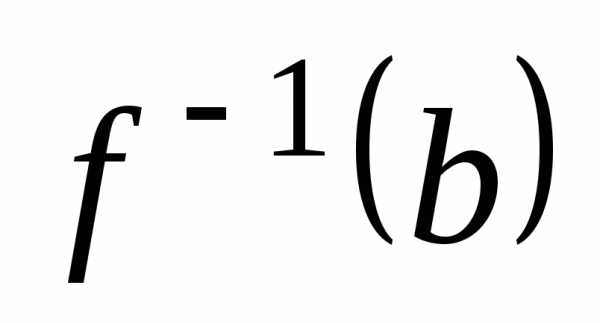 .
Таким образом,
.
Таким образом,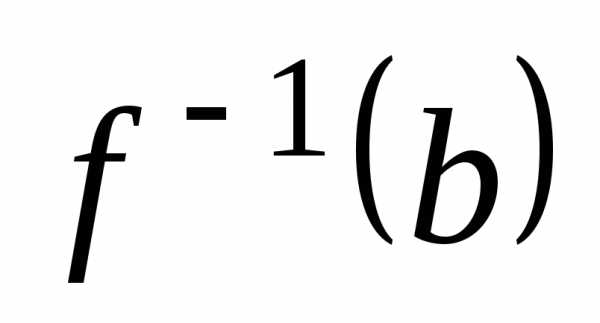 =.
=. и
и справедливы следующие соотношения:
справедливы следующие соотношения: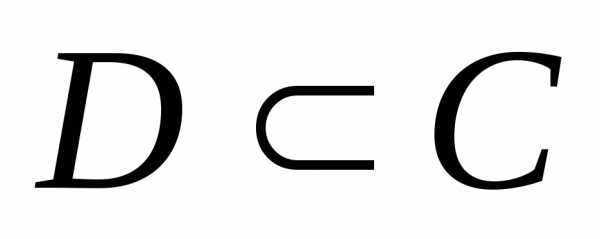 ,
то.
,
то. и
и :
: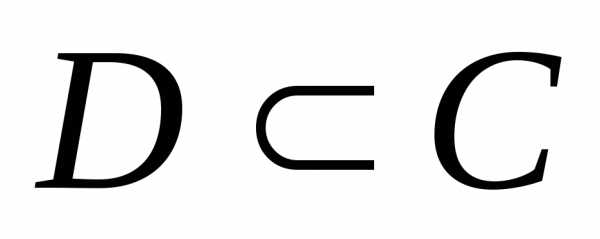 ,
то.
,
то.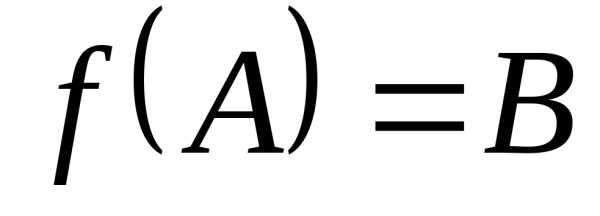 ,
то есть если
,
то есть если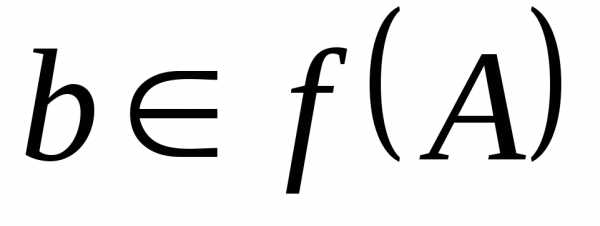 его полный прообраз
его полный прообраз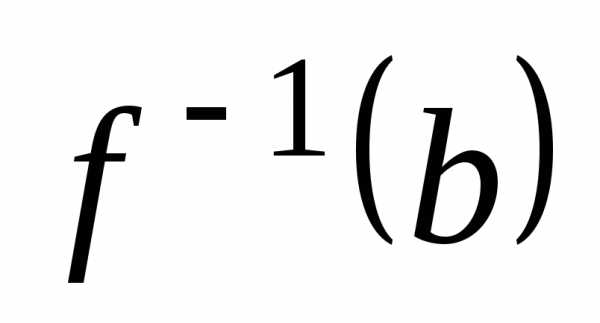 состоит ровно из одного элемента, или
если для любого элемента
состоит ровно из одного элемента, или
если для любого элемента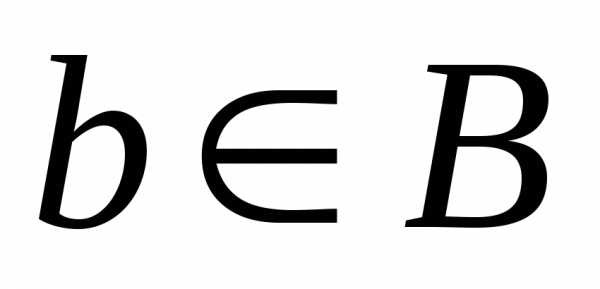 его полный прообраз состоит не более
чем из одного элемента.
его полный прообраз состоит не более
чем из одного элемента. соответствуют различные элементы
соответствуют различные элементы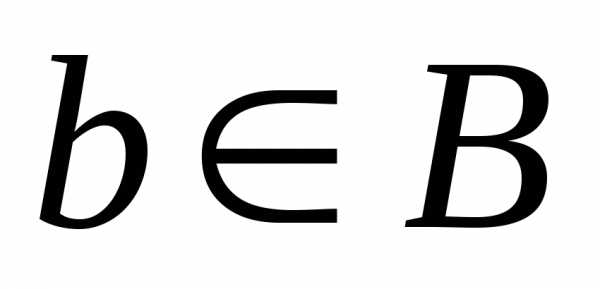 ,
то есть
,
то есть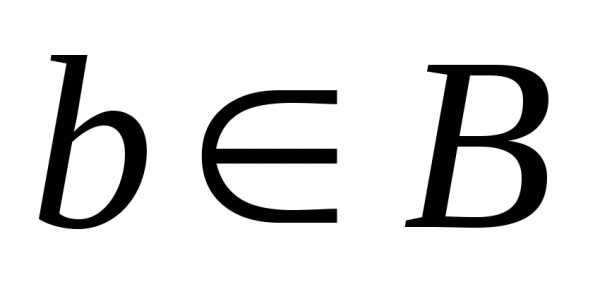 его прообраз
его прообраз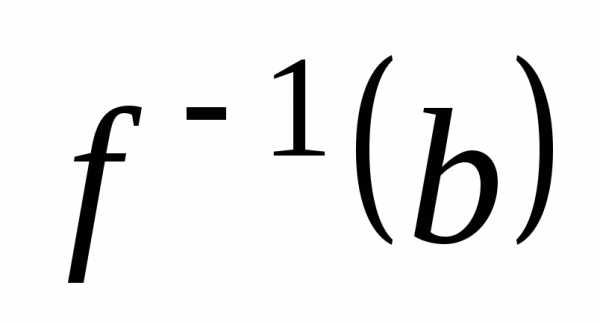 состоит ровно из одного элемента
состоит ровно из одного элемента ,
или если оно одновременно является
инъективным и сюрьективным.
,
или если оно одновременно является
инъективным и сюрьективным.


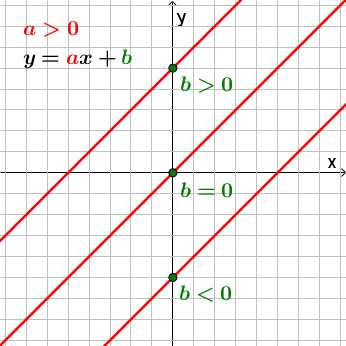
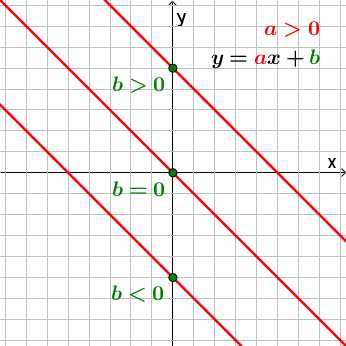
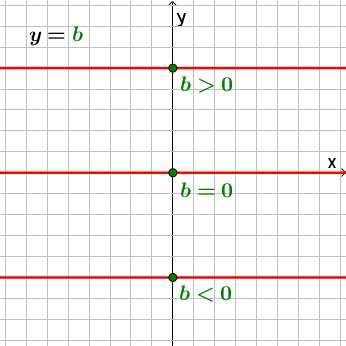
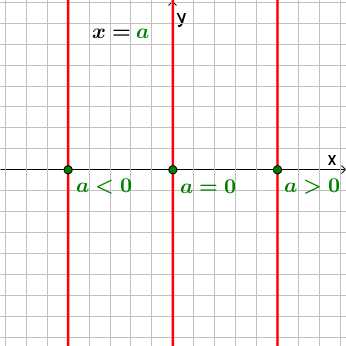
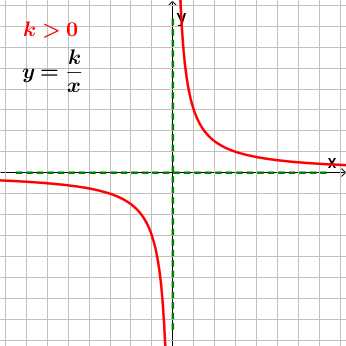
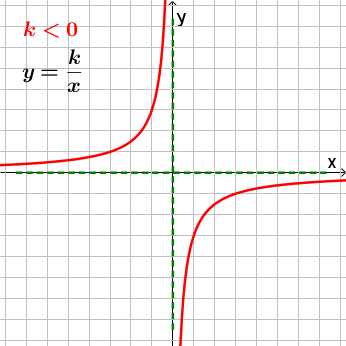
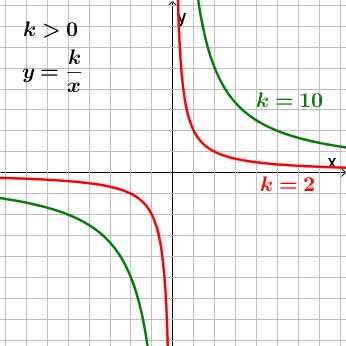
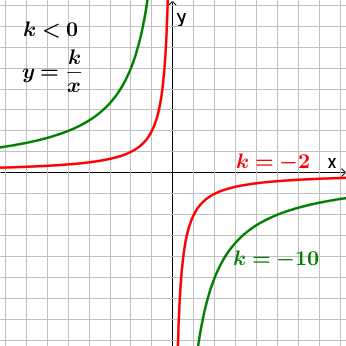
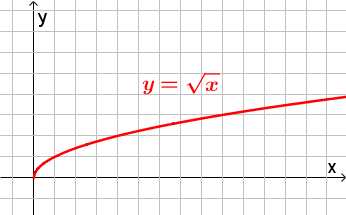
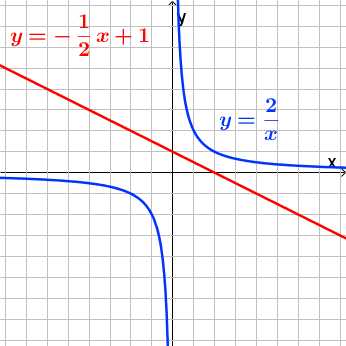


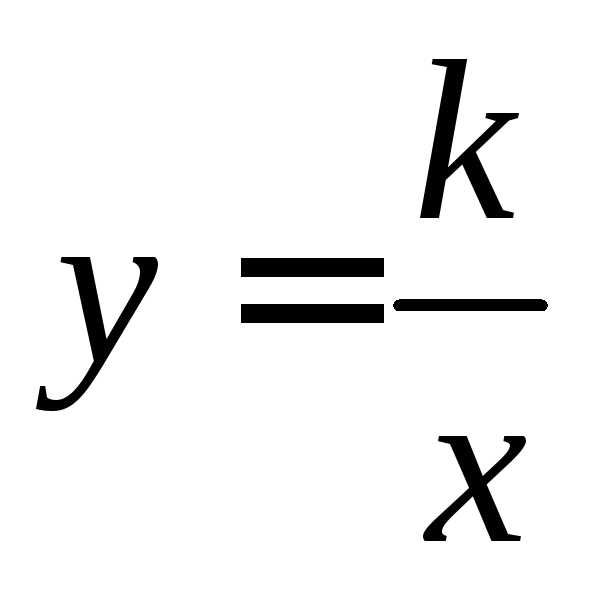 ,
где
,
где ,
,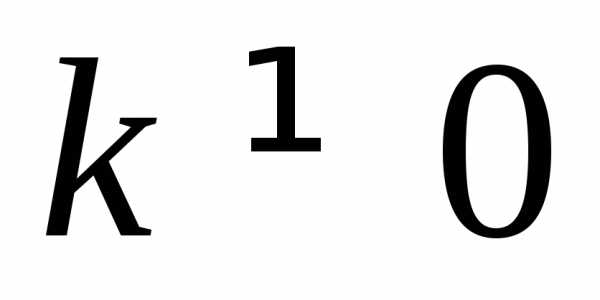 называетсяобратной
пропорциональностью.
называетсяобратной
пропорциональностью.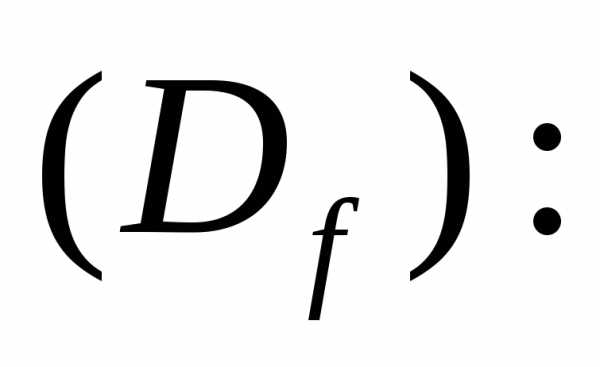
 однозначно вычисляется,
при
однозначно вычисляется,
при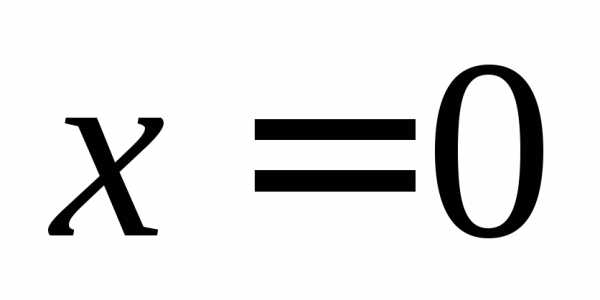 это выражение не определено(почему?),
значит
это выражение не определено(почему?),
значит
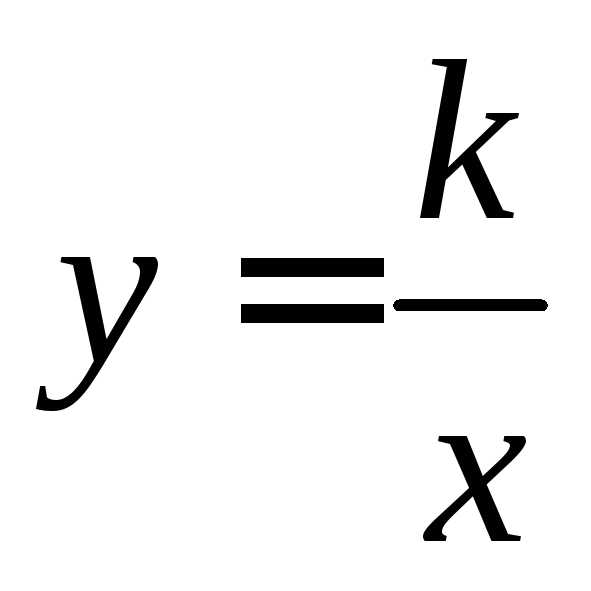 при всех значенияхимеет единственный корень, равный
при всех значенияхимеет единственный корень, равный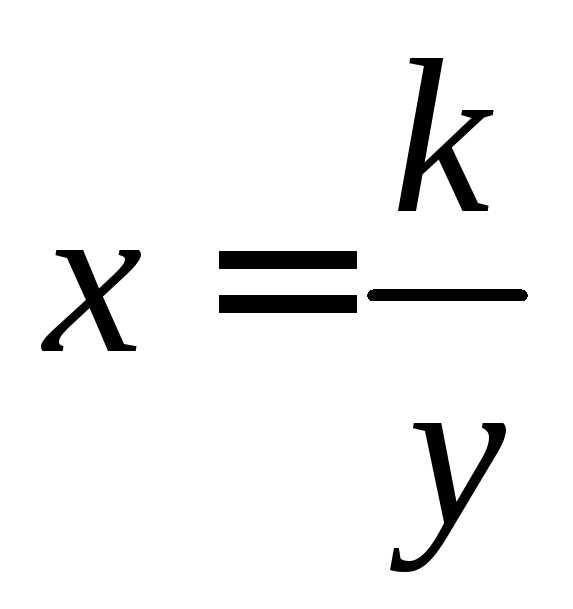
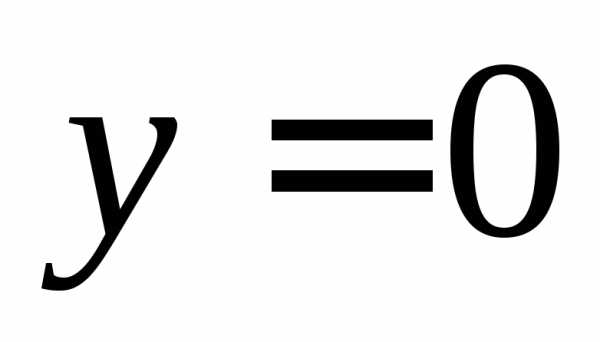 ,
то уравнение корней не имеет, значит
,
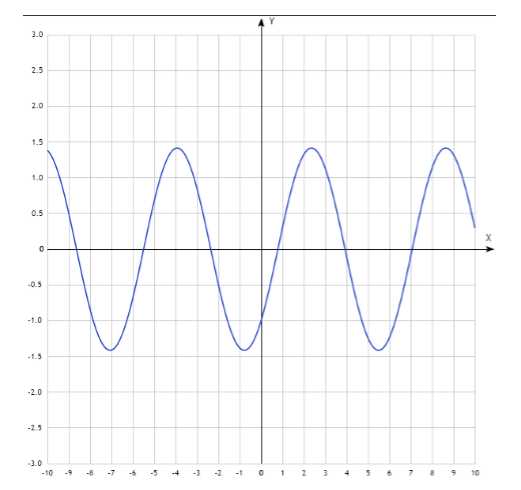
то уравнение корней не имеет, значит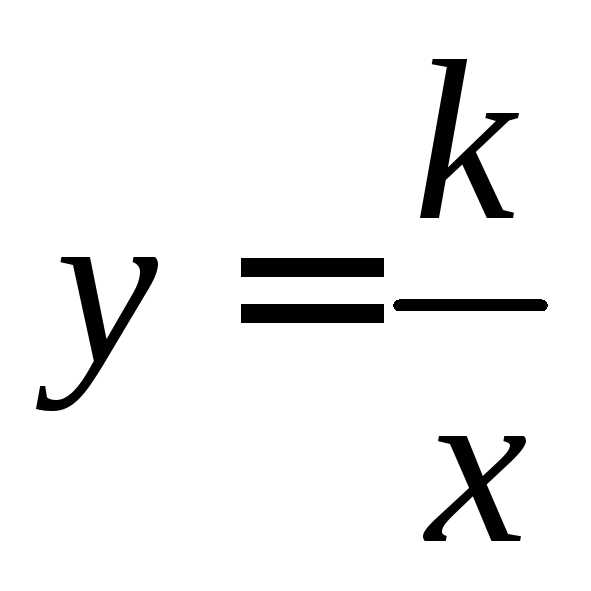 не является периодической.
не является периодической.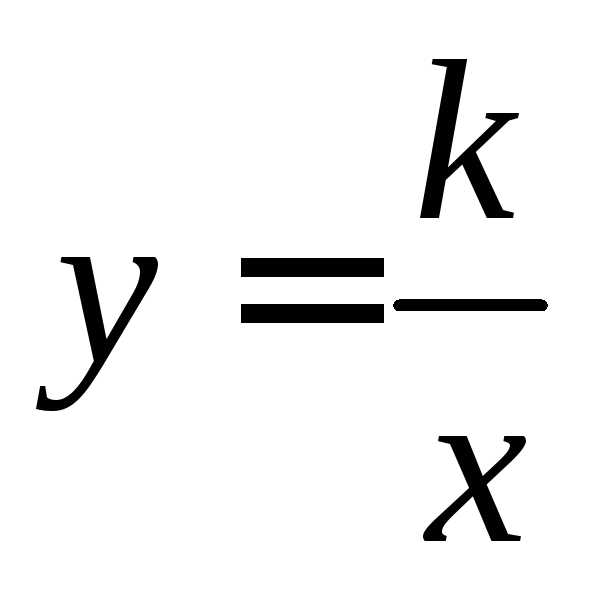 является периодической с периодом
является периодической с периодом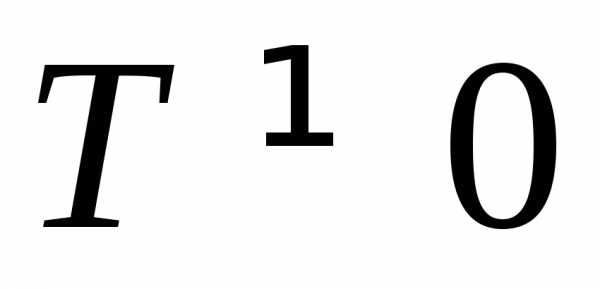 .
Это значит, что.
.
Это значит, что.
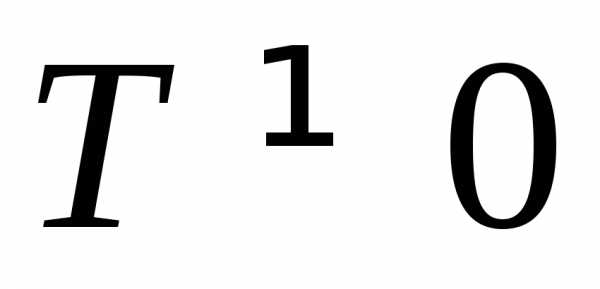 не верно, и функция обратная
пропорциональность не является
периодической.
не верно, и функция обратная
пропорциональность не является
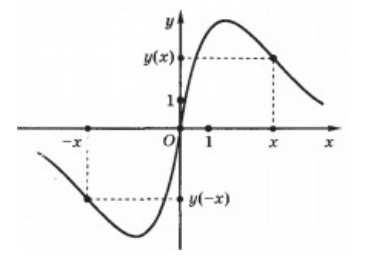
периодической.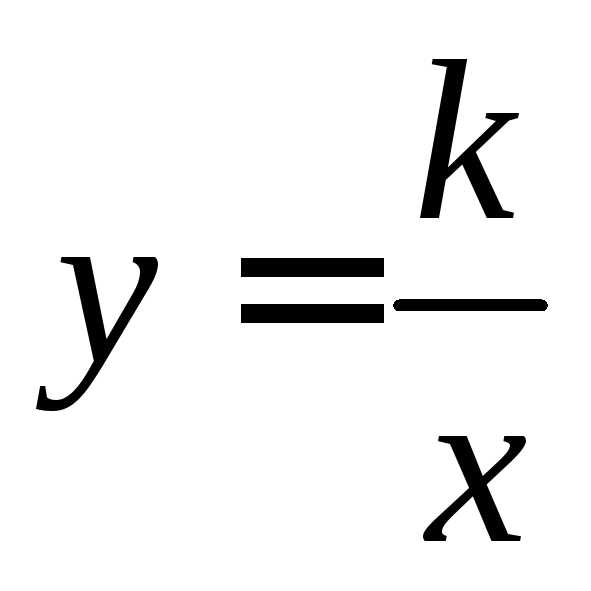 нечётная, т.к. область определения
является симметричной относительно
нуля и
нечётная, т.к. область определения
является симметричной относительно
нуля и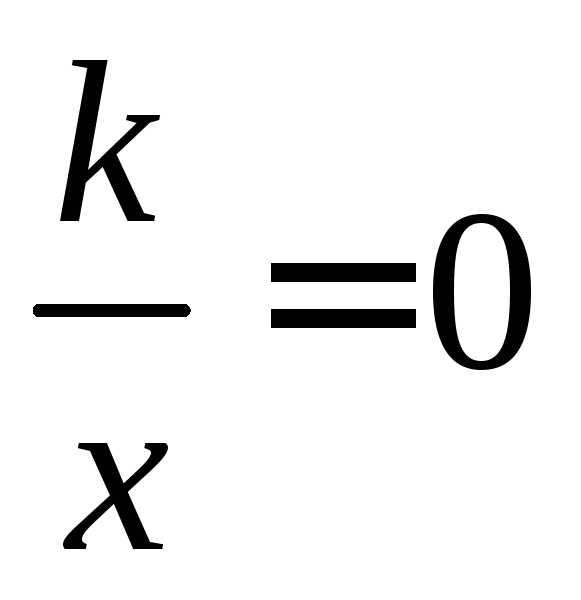 не имеет корней, то график функции
не имеет корней, то график функции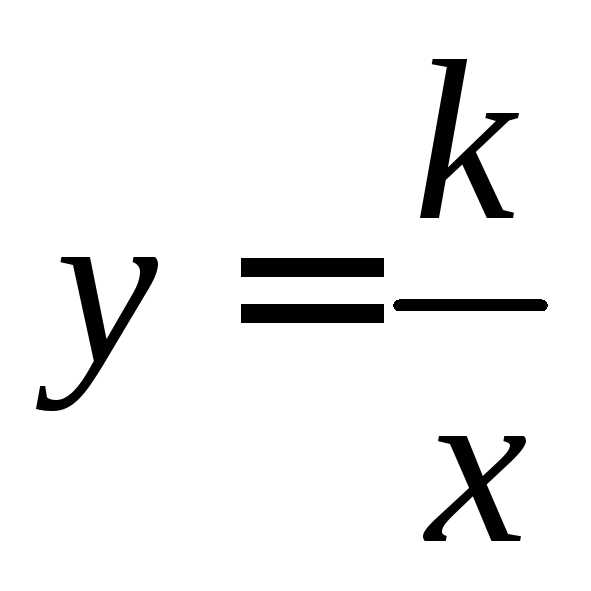 не имеет точек пересечения с осью
абсцисс.
не имеет точек пересечения с осью
абсцисс.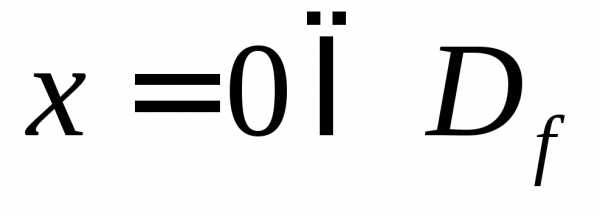 ,
то график функции точек пересечения с
осью ординат не имеет.
,
то график функции точек пересечения с
осью ординат не имеет.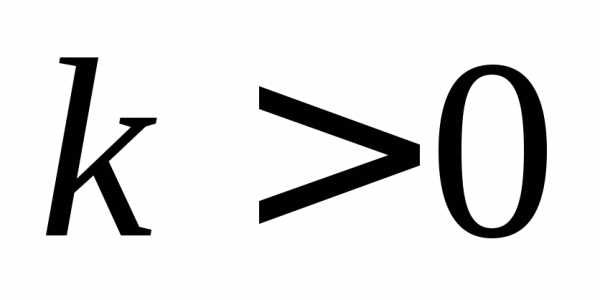 то функция убывает при
то функция убывает при и при
и при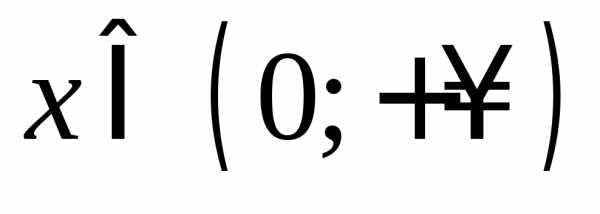
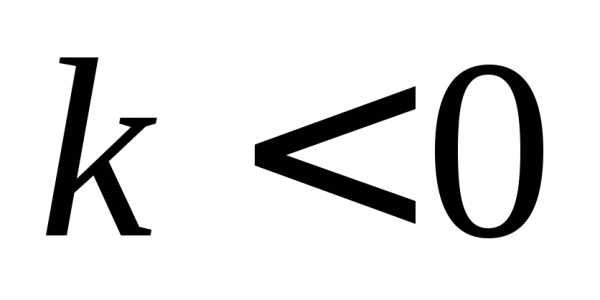 ,
то функция возрастает при
,
то функция возрастает при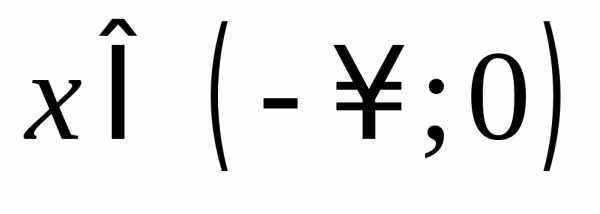 и при
и при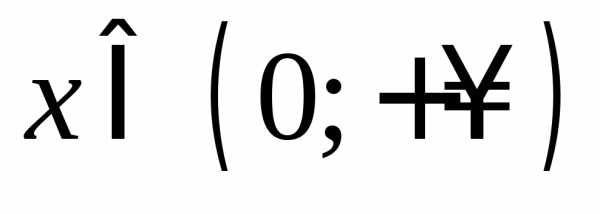
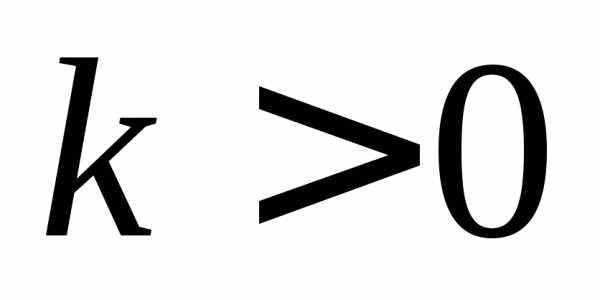 ,
тогда возьмем произвольные,
пусть для определенности
,
тогда возьмем произвольные,
пусть для определенности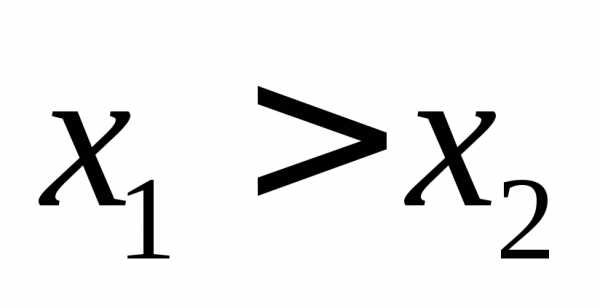 ,
тогда,
то есть,
значит функция убывает при
,
тогда,
то есть,
значит функция убывает при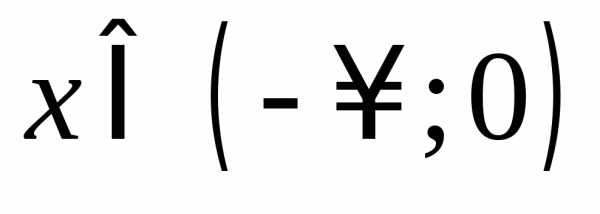 .
.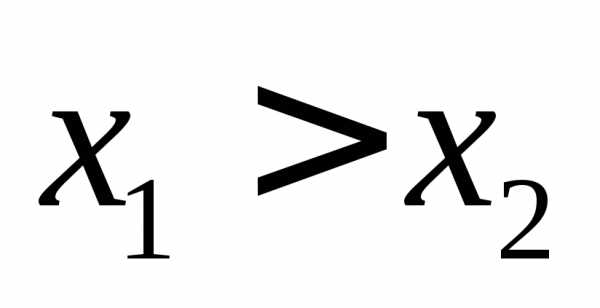 ,
,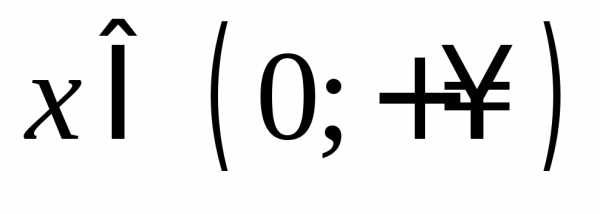 .
.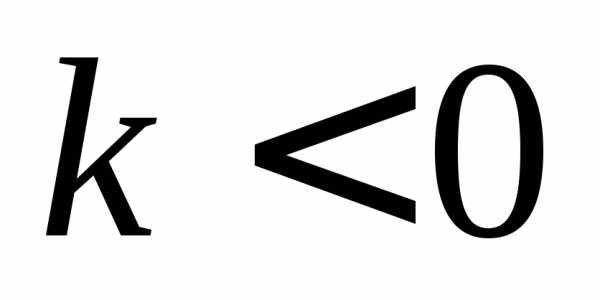 :
возьмем произвольные,
пусть для определенности
:
возьмем произвольные,
пусть для определенности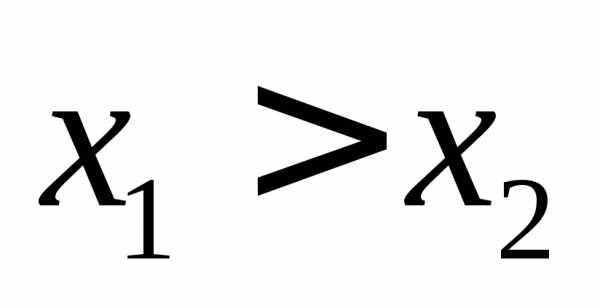 ,
тогда,
то есть,
значит функция возрастает при
,
тогда,
то есть,
значит функция возрастает при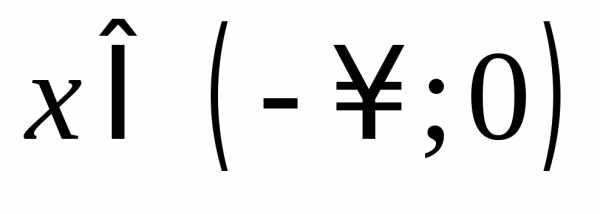 .
.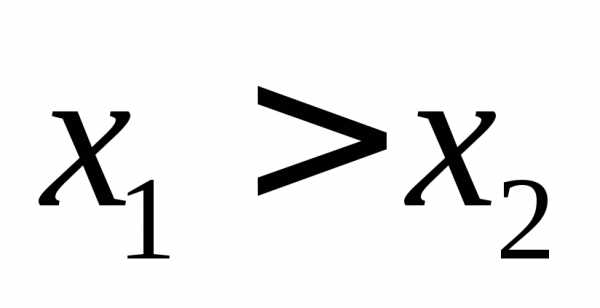 ,
тогда,
то есть,
значит функция возрастает при
,
тогда,
то есть,
значит функция возрастает при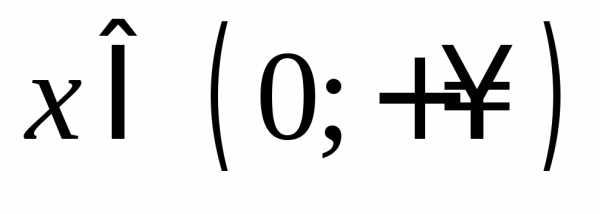 .
.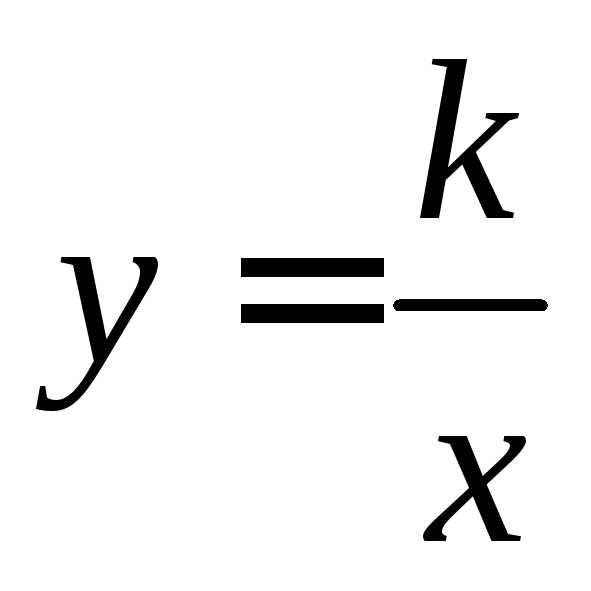 не является монотонной на всей своей
области определения !!!!!!!
не является монотонной на всей своей
области определения !!!!!!!
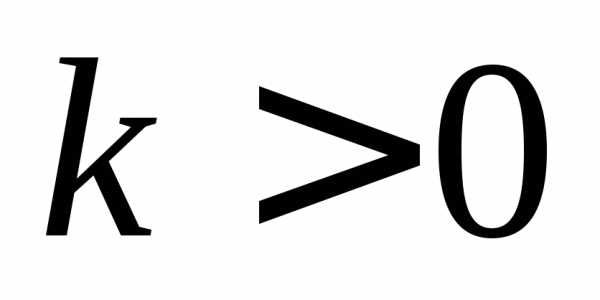 ,
то
,
то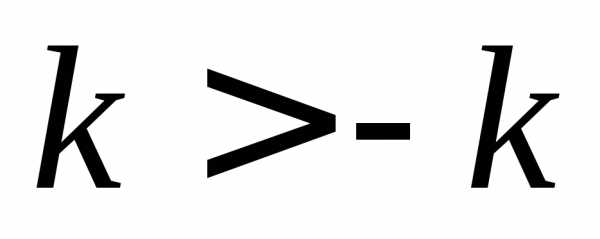 ,
что не верно, т.к. при
,
что не верно, т.к. при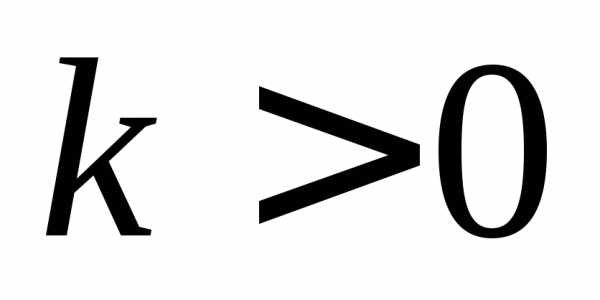 функция является убывающей и по
определению большему значению аргумента
соответствует меньшее значение функции.
функция является убывающей и по
определению большему значению аргумента
соответствует меньшее значение функции.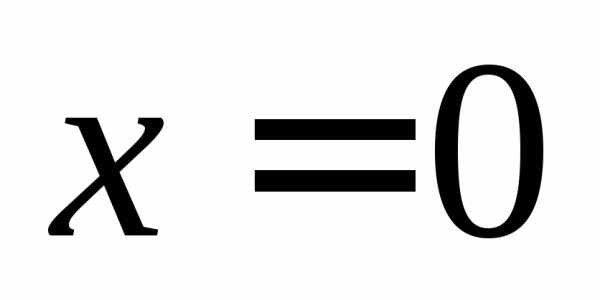 и горизонтальную
и горизонтальную .
.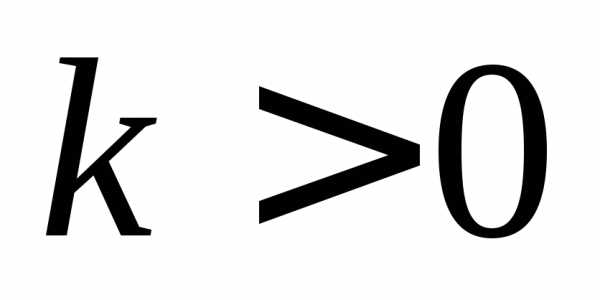 ;
и во второй и четвертой, если
;
и во второй и четвертой, если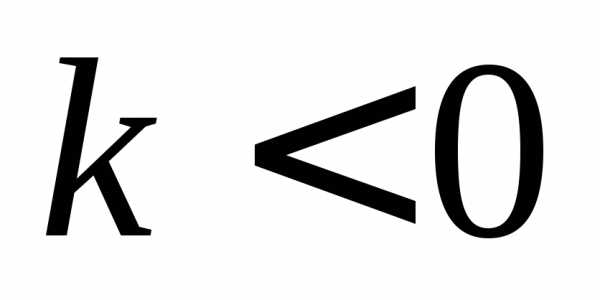 .
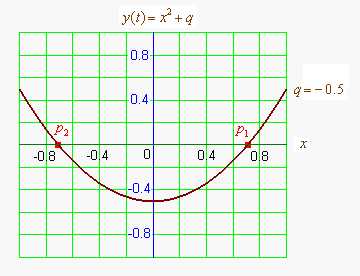
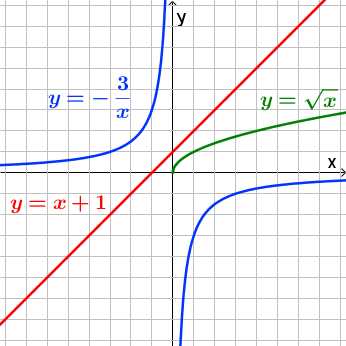
(рис.2).
.
(рис.2).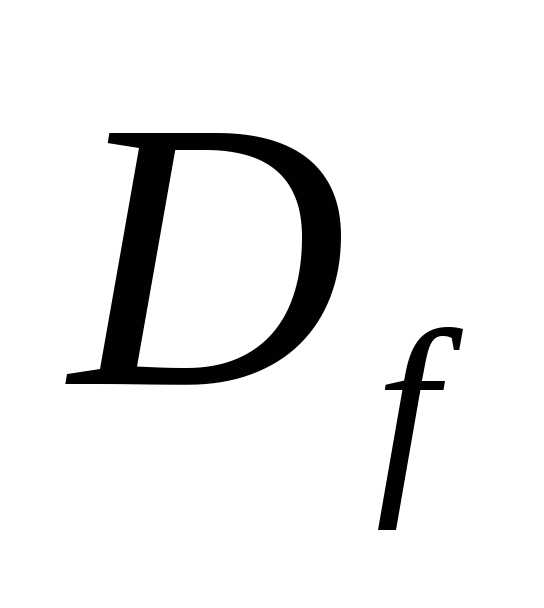 .
.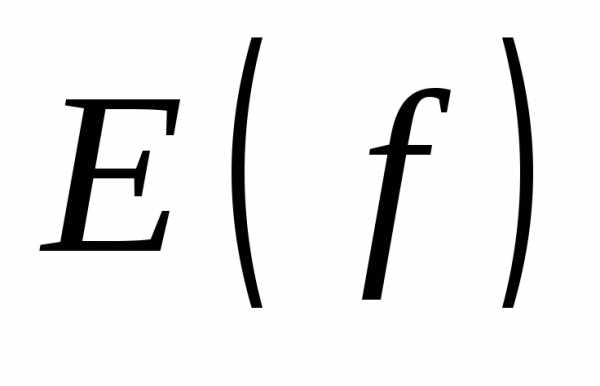
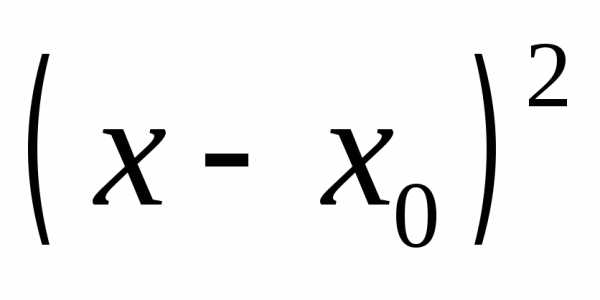 может принимать любые неотрицательные
значения в зависимости отx.
Поэтому, при
может принимать любые неотрицательные
значения в зависимости отx.
Поэтому, при 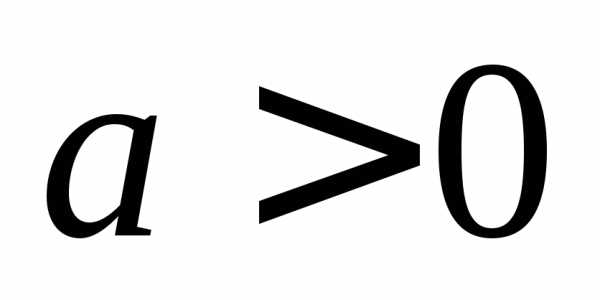 ,
а при
,
а при
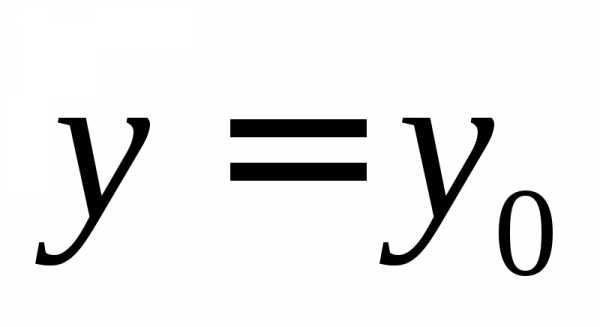 она
она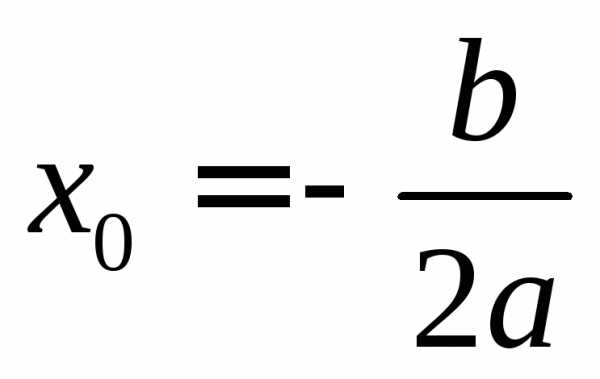 .
.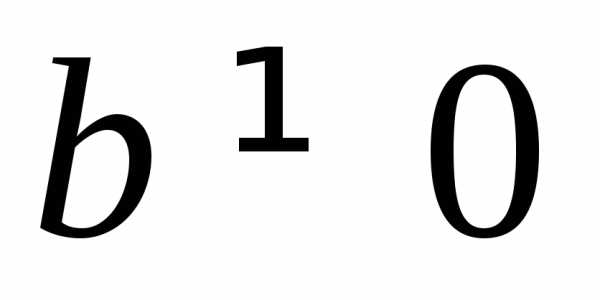 ,
то функция является функцией общего
вида (не является ни четной, ни нечетной),
т.к.,
то естьи
,
то функция является функцией общего
вида (не является ни четной, ни нечетной),
т.к.,
то естьи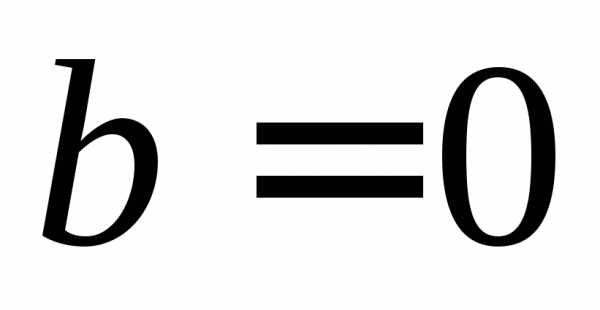 ,
то функция имеет вид
,
то функция имеет вид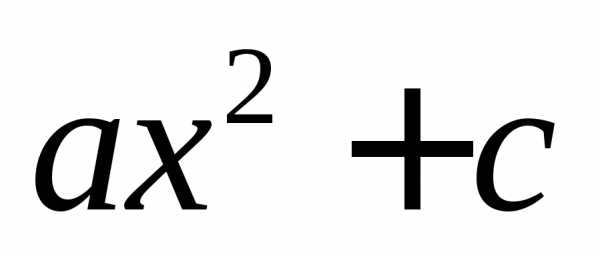 и,
значит функция четная.
и,
значит функция четная.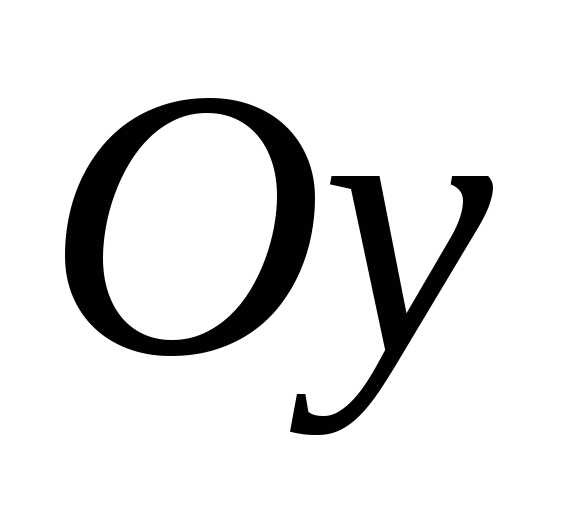 :
: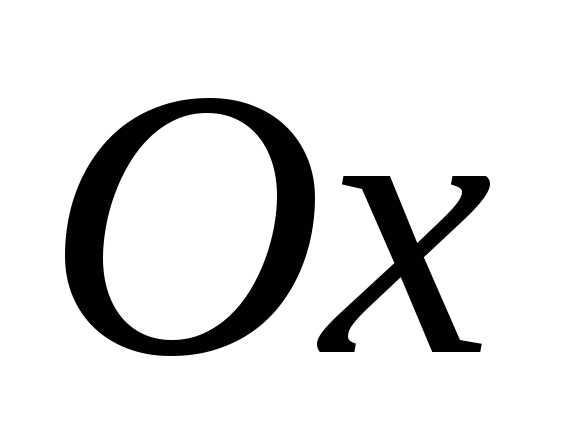 :,
корни этого уравнения существуют, если,
в противном случае точек пересечения
с осью абсцисс нет.
:,
корни этого уравнения существуют, если,
в противном случае точек пересечения
с осью абсцисс нет.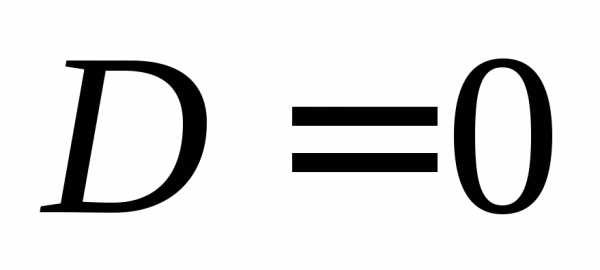 ,
то точка пересечения одна и имеет
координаты
,
то точка пересечения одна и имеет
координаты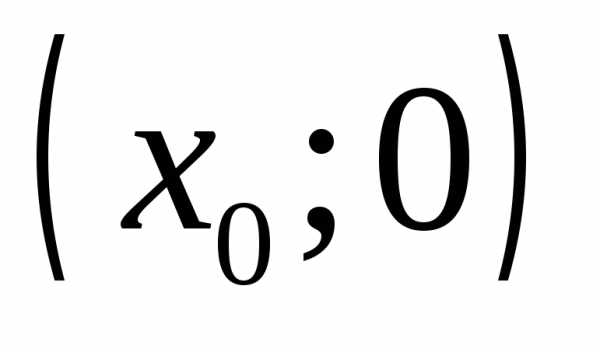
 ,
то квадратное уравнение имеет два корня,
которые вычисляются по формулам:
,
то квадратное уравнение имеет два корня,
которые вычисляются по формулам: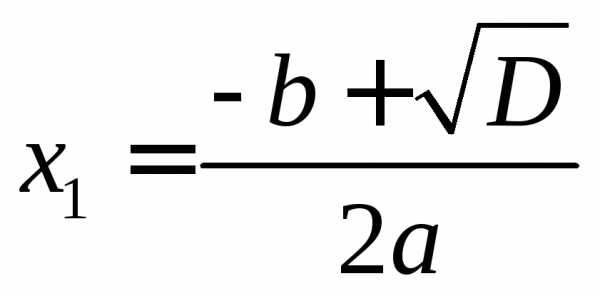 ,
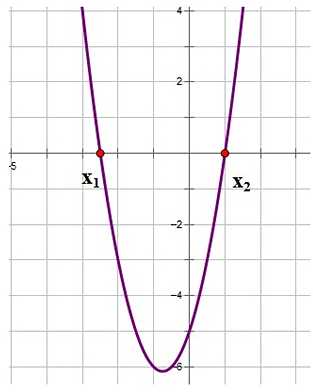
,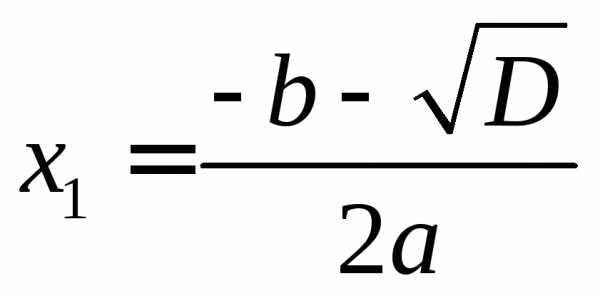
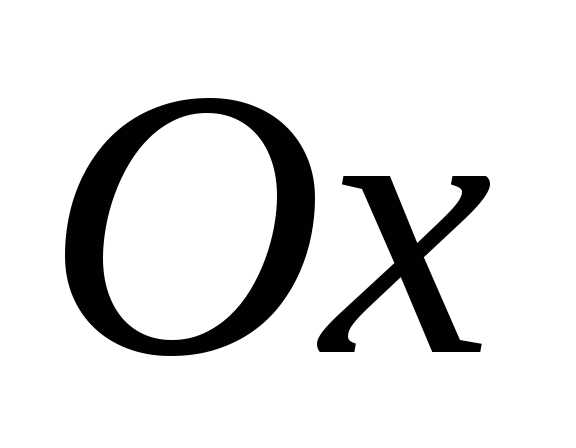 две, и они имеют координаты
две, и они имеют координаты и
и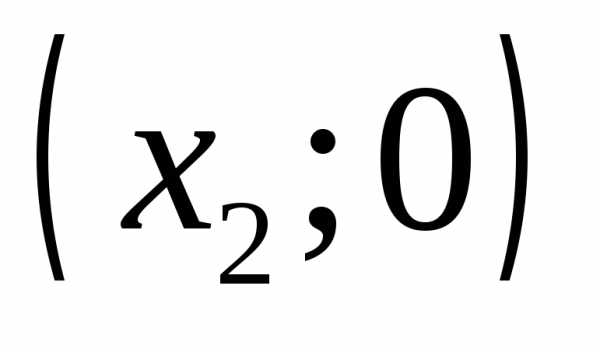
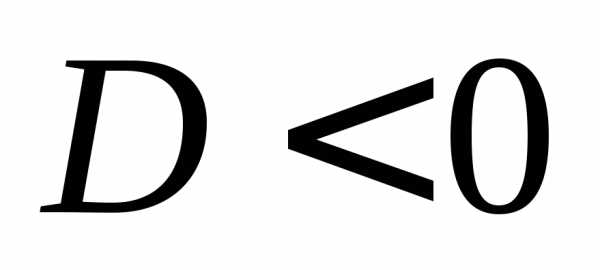 :,
то выражение вида
:,
то выражение вида для всех
для всех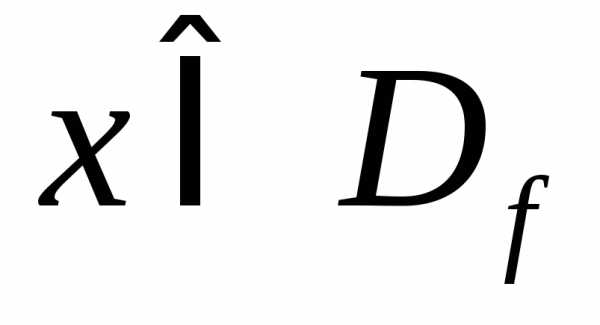 .
Значит,,.
.
Значит,,.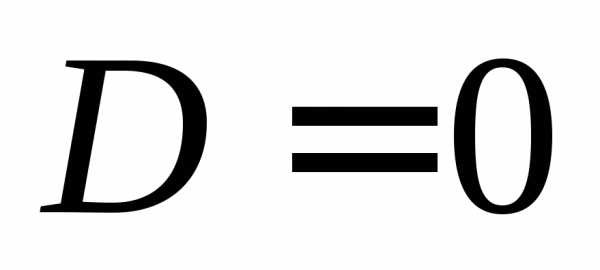 :
,
тогда,
:
,
тогда, :
,
где
:
,
где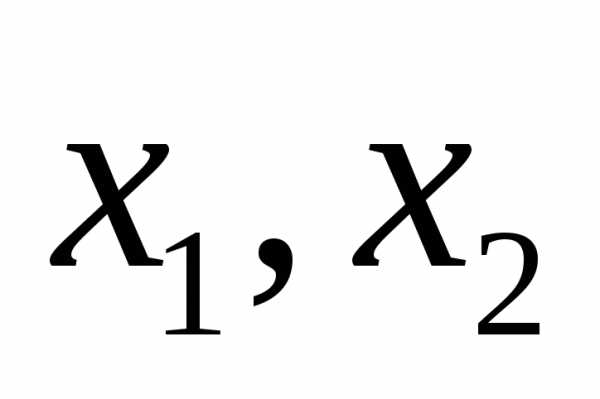 — корни уравнения.
— корни уравнения.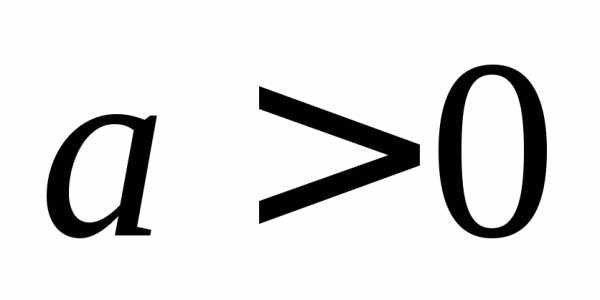 на данных промежутках квадратичная
функция будет принимать положительные
значения, а при
на данных промежутках квадратичная
функция будет принимать положительные
значения, а при — отрицательные.
— отрицательные.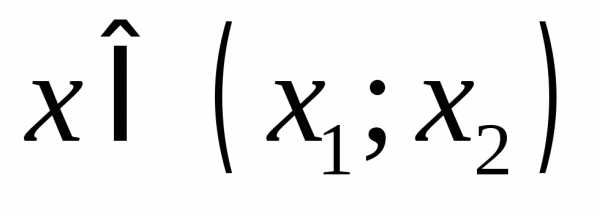 ,
то наоборот, знаки выражений в скобках
будут разными и, следовательно, из
произведение будет отрицательным.
,
то наоборот, знаки выражений в скобках
будут разными и, следовательно, из
произведение будет отрицательным.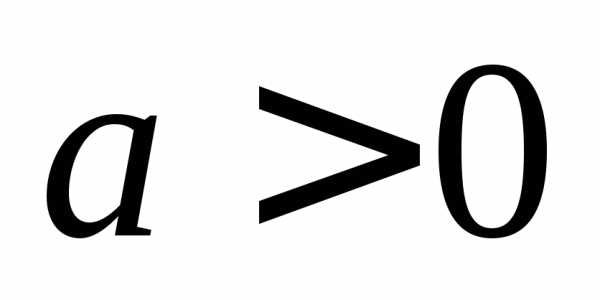 на данном промежутке функция принимает
отрицательные значения, а при
на данном промежутке функция принимает
отрицательные значения, а при — положительные.
— положительные.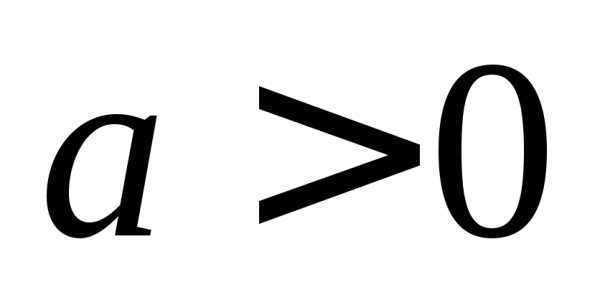 ,
то функция является возрастающей при
,
то функция является возрастающей при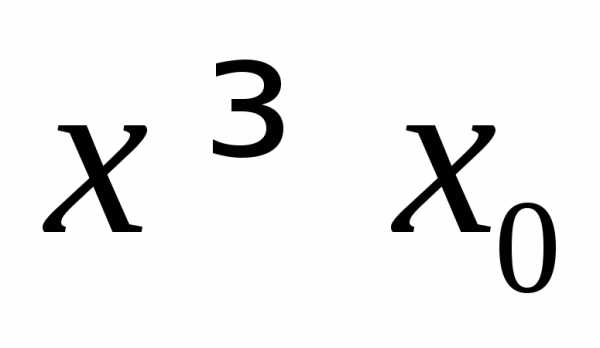 и убывающей при
и убывающей при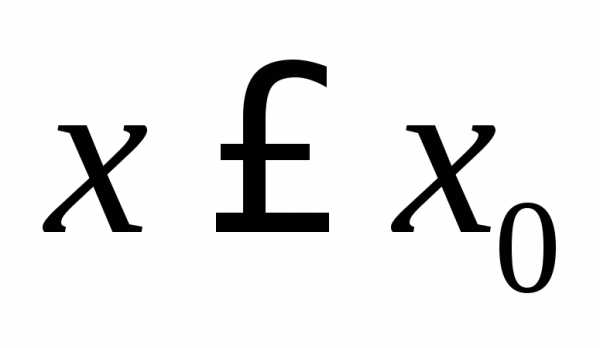
 ,
то функция является возрастающей при
,
то функция является возрастающей при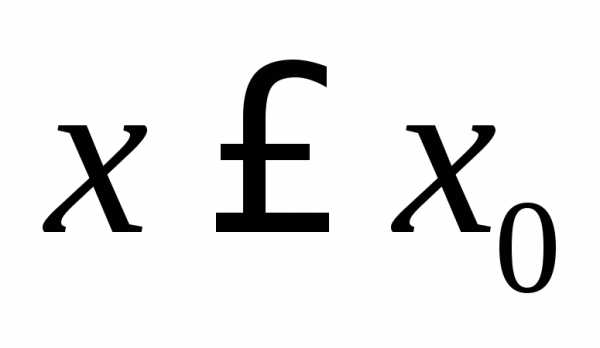 и убывающей при
и убывающей при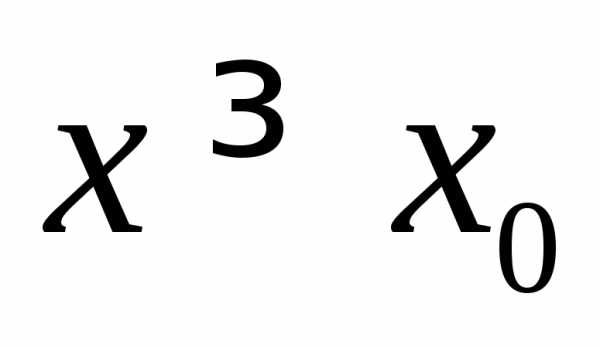
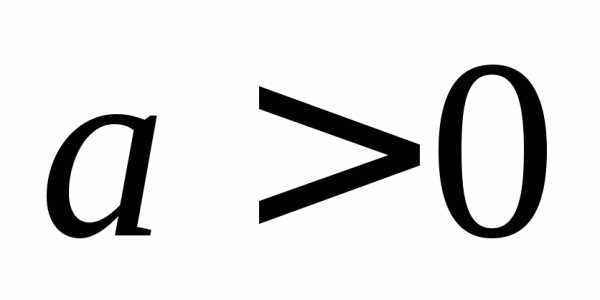 .
.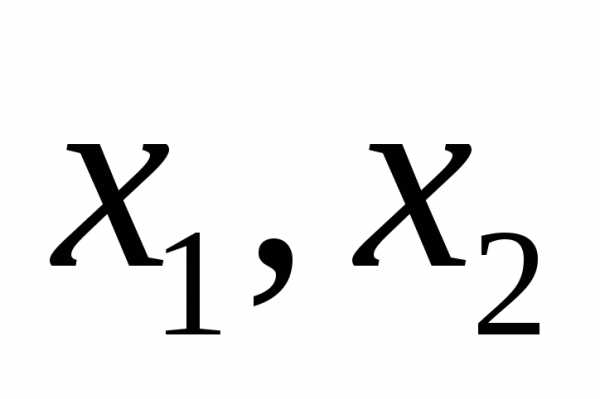 ,
таких, что
,
таких, что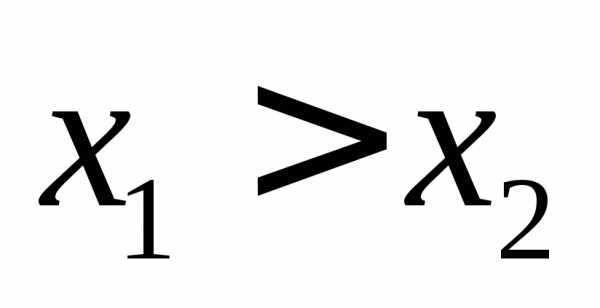
 .
Тогда все три сомножителя в полученном
выражении положительны. Это означает,
что,
т.е.,
значит, если
.
Тогда все три сомножителя в полученном
выражении положительны. Это означает,
что,
т.е.,
значит, если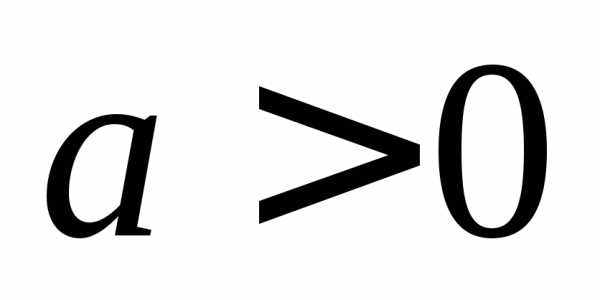 ,
то функция является возрастающей при
,
то функция является возрастающей при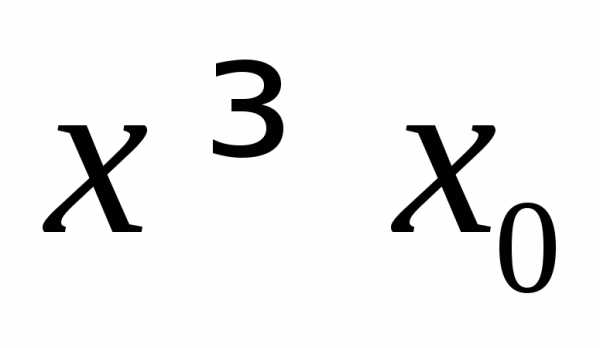 .
.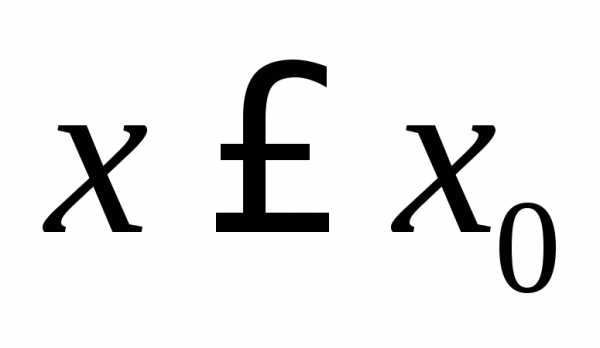 .
. рассматривается аналогично(рассмотрите
его самостоятельно).
рассматривается аналогично(рассмотрите
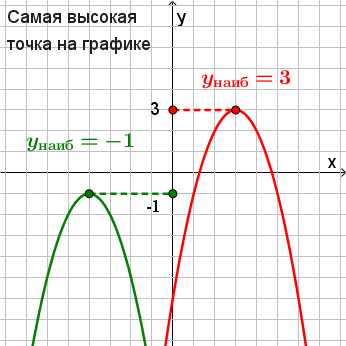
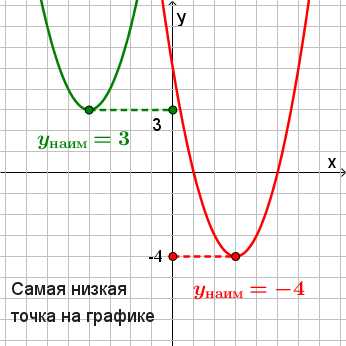
его самостоятельно).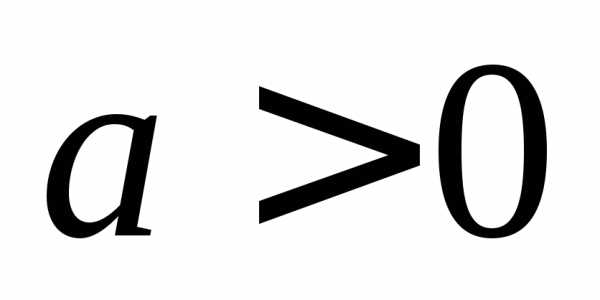 функция возрастает на
функция возрастает на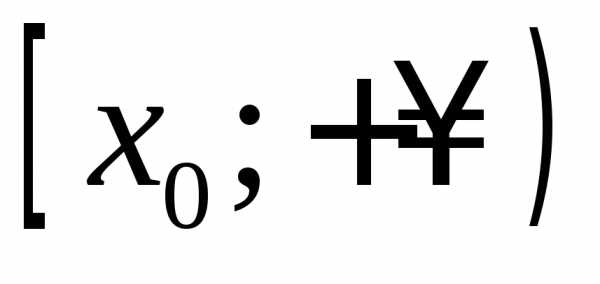 и убывает на
и убывает на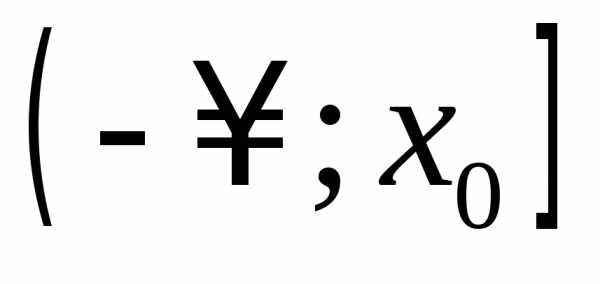 ,
то при
,
то при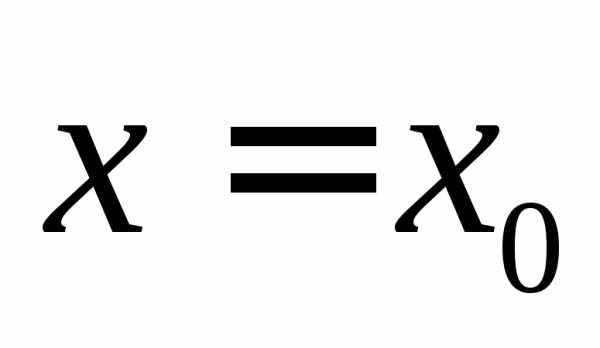 функция принимает наименьшее значение,
и оно равно
функция принимает наименьшее значение,
и оно равно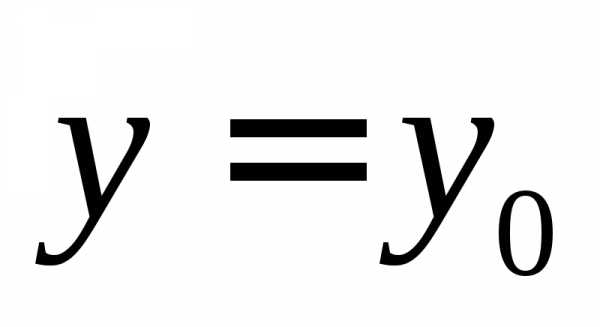 .
. функция возрастает на
функция возрастает на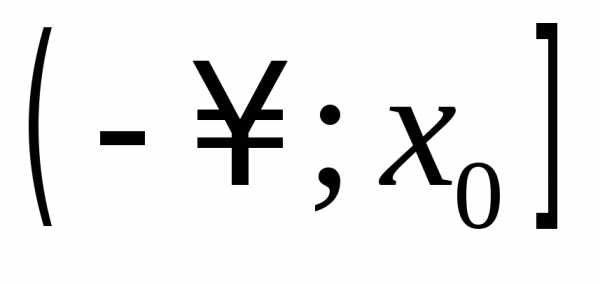 и убывает на
и убывает на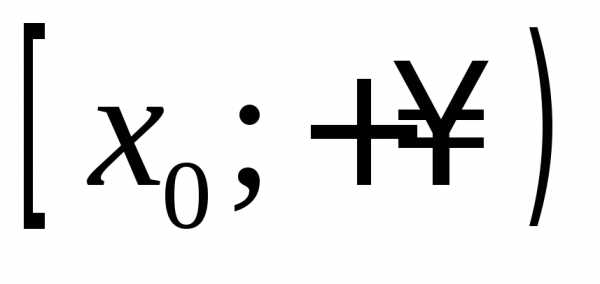 ,
поэтому при
,
поэтому при функция принимает наибольшее значение
и оно равно
функция принимает наибольшее значение
и оно равно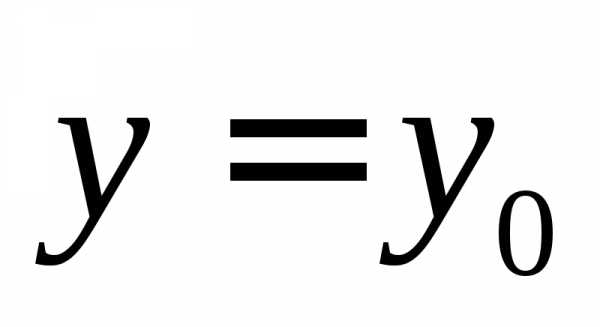 .
.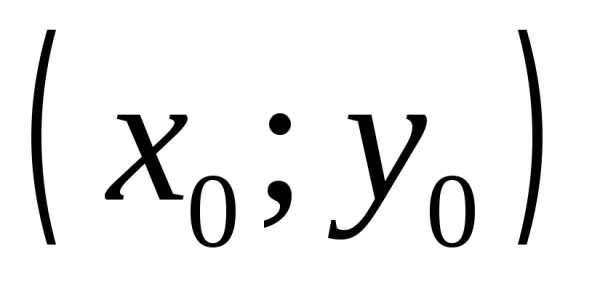 называетсявершиной
параболы.
называетсявершиной
параболы.