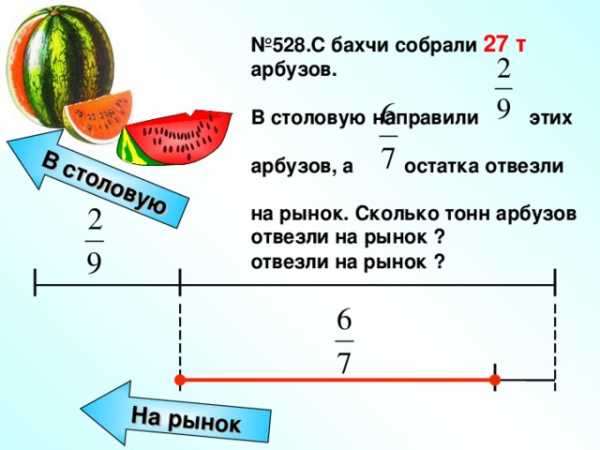
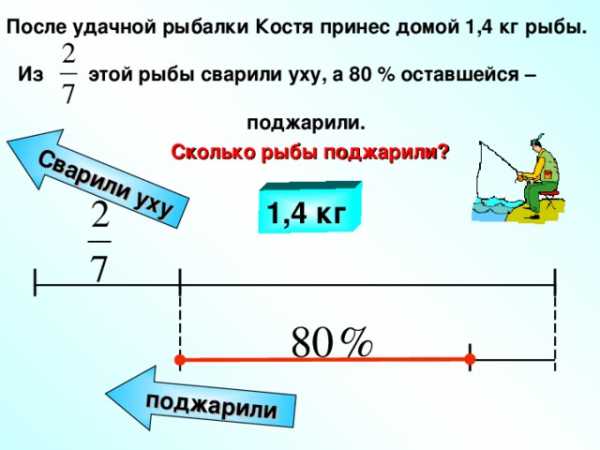
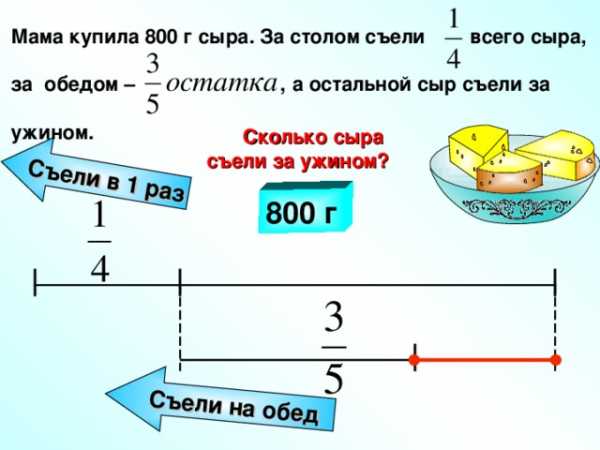
1 делить на 0 ?
неопределённость, хотя если заметил что когда делишь число на другое чесло меньше единицы, но больше нуля — то оно увеличивается, причём чем больше к нулю, тем сильнее оно увеличивается, поэтому я думаю, что сделали допущение, что всё таки существуют такие маленькие величины, на которые можно делить, но которые очень близки к нулю, деление которыми очень сильно увеличивают число
на ноль делить нельзя)
Бесконечность. Или иногда говорят, что результат «стремится к бесконечности». А бесконечность — это то, что никогда не достигается. И выполнять с ней никаких действий нельзя (в том числе умножать на 0)
НА 0 делить НЕЛЬЗЯ!!!!
Существует теория обратного числа относительно 1 то-есть обратное число 2 это 1/2(одна вторая) обратное 3 это 1/3(одна третья) , это правило работает в обе стороны то-есть обратное число 1/2(одной второй) это 2 и т. д. тут есть некая закономерность чем больше число тем меньше число ему обратное то-есть чем дальше число на числовой прямой тем ближе к нулю обратное ему число например берем 2 обатное ему-1/2(одна вторая) теперь берем 4 обратное ему 1/4(одна четвертая) 1/4 ближе к нулю чем 1/2, а 4 дальше на числовой прямой чем 2 . А теперь берём 0(ноль) — он меньше любого числа то-есть обратное ему число (1/0) БОЛЬШЕ ЛЮБОГО ПОЛОЖИТЕЛЬНОГО ЧИСЛА, а это и есть ∞(бесконечность).
1 поделить на 0 равно бесканечно
1 делить на ноль нельзя
те, кто говорят, что делить на ноль — нельзя, руководствуются лишь школьными знаниями, а следуя из них — глупо говорить так, лишь потому, что им это в голову вбивали с первого класса.
На сколько я помню, до делится не сам ноль, а переменная стремящаяся к нему, т. е. число максимально стремящееся к нулю, но не являющееся им: 0,1 0,01 0,001 и сколько угодно нулей перед единицей. Так как числовой ряд не имеет ограничений, то и результат деления будет стремиться к бесконечности и являться ею
Чем ближе делитель к нолю, тем больше число приближается к бесконечности. Тут работают уже не вычисления, а простая логика. Но так как числа тоже бесконечные, то 0 это ничего. По сути, получится не бесконечность, а ничего. Делишь на 0 — опустошаешь бытие.
1/0=бесконечность, так как 1/бесконечность=0, а 1 является одним из вариантов неопределённости бесконечность/0
Чем больше делитель тем меньше будет результат, но чем менше делитель тем больше будет результат! Если мы поделим на самое маленькое положительное число, то есть 0, то мы получим самое большое положительное число. Так как ряд натуральных чисел бесконечный, то мы не можем вычислить это число, по этому что бы не заморачиваться мы говорим что нельзя делить на 0.
Будет бесконечность. В математике не принято делить на ноль, потому что всегда ответ бекоченность и смысл решать выражение не имеет смысла, из-за этого может быть бесконечное число ответов, а это не допустимо. Поэтому деление на ноль разрешено только в пределах и там этот ответ и будет как раз бесконечность, поскольку там это значение допустимо, в отличие от других выражений и функций
Говоря проще если палку колбасы поделить на 0.1 часть то в результате получеться 10 таких кусков, а если ее поделить на 0 ю часть, то ответ предполагает бесконечное число кусков, потому что ничем можно делить бесконечно
ответ существует, уважаемые, не забывайте о применении комплексных чисел, где квадрат «мнимой единицы» равен -1, значит и существует такое число, которое получается при делении на 0, отличное от бесконечности и, скорее всего, иррациональное.
Бесконечность будет
touch.otvet.mail.ru
2 делить на 0 — Суолько будет 1 разделить на 0 ? — 22 ответа
2 разделить на 0
В разделе Естественные науки на вопрос Суолько будет 1 разделить на 0 ? заданный автором Европейский лучший ответ это Прав Lynx! Делить на ноль можно, но результат стремиться к бесконечности!
Ответ от 22 ответа[гуру]Привет! Вот подборка тем с ответами на Ваш вопрос: Суолько будет 1 разделить на 0 ?
Ответ от распространить[гуру]
Делить на ноль нельзя
Ответ от Настюша[гуру]
на ноль делить нельзя
Ответ от Afrikapilot[гуру]
на 0 не делят!!!!
Ответ от Приспособляемость[гуру]
0 будет
Ответ от Ольгунка Сухинина[активный]
0 или с другой стороны ма-ки нельзя делить….
Ответ от Виталий Жариков[новичек]
на калькуляторе будет Е
Ответ от Maria Ivanova[гуру]
на ноль делить нельзя
Ответ от Оксана Пестерева[гуру]
Смотря на какой ноль, по законом алгебры то данное действие не возможно выполнить
по законам высшей матиматике, то ответ будет стремиться к бесконечности
Ответ от Sellistar[активный]
на ноль делить нельзя… не понимаю к чему этот вопрос
Ответ от саша сапог[новичек]
Вообще, по идее, получится одна бесконечность. Если 2 разделить на 0, то — две бесконечности.. . Но это не доказано :(.
Ответ от Александр Максимов[гуру]
Нисколько
Ответ от Коля Пашков[активный]
0 будет
Ответ от Nerukoguhc[эксперт]
Делить-то можно, но получится… неопределенность:
Вспомним график функции y = 1/x: там ветки двух гипербол подходят на бесконечно малое расстояние к оси y симметрично по оси x. В случае деления на 0
мы не имеем права утверждать, что частное равно бесконечности, ведь с равным успехом мы скажем, что это минус бесконечность. А это понятия, так сказать, диаметрально противоположные. Неопределённость.
А вот делить на числа, стремящиеся к нулю, можно: получится число, стремящееся к бесконечности.
Ответ от Ёвятослав Лошкарев[активный]
0 не является натуральным числом
Ответ от Правообладатель[гуру]
Как Вы справедливо заметили -«на нуль делить нельзя» — это ответ на уровне школьного курса алгебры. А что же вы хотели? Все помнят эту фразу из школьных учебников. Теория пределов в школе не изучается уже давно.
«Если отождествить 1 как всю материю, а 0 как всю пустоту, то в пустоте материя распространяется бесконечно. » — ваша интерпретация никуда не годится, так как непонятно почему деление вы отождествляете с распространением.
Предел отношения 1/0 определен: он равен бесконечности. Неопределенности в математическом анализе: нуль делить на нуль, нуль делить на бесконечность и т. д. А вот школьники не знают что такое предел и поэтому просто исключают из своей математики это, в принципе, не нужное им действие: деление на нуль.
Нуль не является натуральным числом по определению. В теории чисел натуральные числа — числа, употребляемые для счета. Если Вы будете считать количество купюр, к примеру, то начнете явно не с нуля.
Задавая подобные вопросы (спорные хотя бы потому, что математика этого дела не до конца разработана) , оставляйте, пожалуйста, возможности для комментариев. Вдруг еще чего-нибудь вспомним из высшей и не очень высокой математики.
Ответ от Мат анализ![активный]
Это не ноль!!!! Если бесконечно малое то 1/0 = бесконечность, если ноль, то мимо!
Ответ от Мишган Копылов[новичек]
Чем меньше число, на которое делят, тем больше число получается в результате, отсюда логично. что при делении на 0 ответом станет бесконечность, что в математике вполне допустимо
Ответ от Александр Ашлапов[новичек]
0 остаток 1, а, а?!
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
Деление на ноль на Википедии
Посмотрите статью на википедии про Деление на ноль
Ответить на вопрос:
22oa.ru
Деление на ноль — Lurkmore
| « | Это уникальный случай умножения нуля на бесконечность, представленный на целом машинописном листе. | » |
| — Татьяныч | ||
| « | Деление на ноль это как секс. Всем можно, а школьникам нет. | » |
| — Анонимус | ||
| « | Hmmm… no, no… that’s wrong… that’s not right, either… a divide by zero error here… hmmm… you don’t seem to have the intelligence necessary to grasp higher mathematics. | » |
| — Проконсул Грегори из Fallout 2, проверяя результаты испытания ГГ | ||
| « | — Этой ночью, Люся, мы с тобой будем делать то, чего делать нельзя!.. — На ноль делить, что ли? | » |
| — Анекдот | ||
| « | На ноль делить нельзя. Потому что так сказал калькулятор. | » |
| — Анекдот | ||
| « | Можно сдохнуть, пытаясь делить разные числа на ноль. | » |
| — Кровосток | ||
| « | Делю на ноль. Дорого | » |
| — Анекдот | ||
Деление на ноль ÷0 (Дивайд бай зиро) — невозможное математическое действие.
[править] Деление на ноль как мем
| « | Эта грустная история о прекрасной восточной девушке Наноль, которая любит двоих прекрасных и мужественных юношей и не может выбрать. Юноши тоже любят ее. Казалось бы, в нынешние-то времена, зажить бы им простой и дружной семьей. Но трагедия в том, что Наноль делить нельзя. | » |
| — Смехуёчки | ||
| « | Я спускаюсь один в глубину ночных кварталов. Сам себе господин, нас таких осталось мало. Я забыл свою роль, я начальник всей Вселенной. Мне неведома боль, я делил все на ноль. | » |
| — группа «Технология» | ||
Физически (или физиологически) пребывать в процессе деления на ноль вполне можно. Стой себе и дели, никто же законодательно не запрещал. Проблема обычно заключается в том, чтобы получить из этого процесса хоть какой-то обоснованный наукой результат (или создать потом Вселенную заново). Проще говоря, делить на ноль можно, разделить — нельзя.
И даже в этом вашем ХоНеДеление на ноль давно стало одним из классических образцов математического юмора, поскольку в среде математиков считается, что попытка представить получающуюся в итоге актуальную бесконечность (неотъемлемая часть успешного деления на ноль, в противоположность потенциальной бесконечности из теории пределов) ведёт к сумасшествию совершившего это. И нуля-то самого никто никогда не видел (даже математики), «а тут такоє»… Алсо, в обществе прикладных математиков пожелание «делись оно всё на ноль» является аналогом широко известного рецепта «ебись оно всё конём». Поскольку численность математик-кунов в среде компьютерщиков и истинных хакеров составляет лишь чуть менее, чем 42%, этот мем проник и туда, а с возникновением форчана обогатился представлением о том, что удачное деление на ноль неотвратимо вызывает не только безумие самого экспериментатора, но и создание сингулярной аномалии бесконечной массы в точке пространства, где было произведено удачное деление. Со всеми вытекающими последствиями.
Среди менее продвинутых товарищей деление на ноль упоминается в том же смысле, что и умножение на него же. Хуже того, в очень многих статьях этого сайта можно найти это словосочетание именно в ошибочном смысле, противоположном истинному. Это ещё один аргумент в пользу ввода матан-капчи. Или против неё.
[править] Деление на ноль в математике
| ACHTUNG! Опасно для моска! Министерство здравоохранения Луркмора предупреждает: вдумчивое чтение нижеследующего текста способно нанести непоправимый ущерб рассудку. Вас предупреждали. |
[править] Классическая теория групп и полей (XIX век)
Поле действительных чисел, помимо всего прочего, как и любое другое поле, является аддитивной группой, и ноль — нейтральный элемент этой группы. Множество ненулевых действительных чисел, снабжённое операцией умножения, является мультипликативной группой. Поэтому запиливая ноль в эту группу, мы превращаем её во что-то группой не являющееся, ибо понадобилось бы как минимум запилить туда обратный нулю элемент, который, очевидно, не может быть действительным числом, а если запилить НЁХ как обратку, то ещё больше проблем будет, так как остальные элементы действительные, и понадобилось бы прописать, как они взаимодействуют с обраткой, и даже если всё цивильно получится, то полученное множество уже не будет даже изоморфно привычному множеству действительных чисел и вообще не будет кольцом. Такие дела.
[править] Алгебра (на пальцах)
Запишем деление единицы на ноль:
a = 1/0
Отсюда:
a • 0 = 1
Нужно найти такое a, которое при умножении на ноль дает единицу. Таких чисел просто нет. Так как произведение равно нулю, когда один из множителей равен нулю, получаем:
0 = 1
Но ноль не равен единице, поэтому запись 0 = 1 неверна, а запись a = 1/0 не имеет смысла (решений) при любом a. А если разделить ноль на ноль? Запишем:
a = 0/0
a • 0 = 0
Уравнение имеет смысл при любых значениях a, так как умножая 0 на a получаем:
0 = 0
Продвинутые математики говорят, что деление нуля на ноль — полная неопределенность. Продвинутые же статистики этим пользуются, поскольку в математическом моделировании(при получении допустим процентного соотношения из суммы) делить на ноль не только можно, но и нужно.
1/0=8(к сожалению вы забыли о бесконечности!!!). Причём БЕЗ знака(т.е и + и — одновременно) поскольку вот ноль — это как раз то место, где график деления (гипербола)»перескакивает» через весь набор значений «из минуса в плюс». А значит результат деления на 0 равен всем значениям одновременно. Именно осознание истинной трансцендентности этого явления и срывает пытающимся это сделать крышу.
а теперь вставьте соответствующий знак!!!
[править] Делить на бесконечно малую
Делить на бесконечно малую функцию можно, при этом получается бесконечно большая функция. То есть за результат деления на такой «ноль» можно принять предел. Засада в том, что этот предел может не существовать (получатся бесконечности разных знаков при стремлении к нулю с разных сторон, либо вообще какая-нибудь хуйня), и для каждой такой функции он свой. В общем, не ноль, а где-то рядом.
Например, 1/x стремится к +∞ при x→+0 и -∞ при x→-0. Однако, если по условиям задачи мы стремимся к нулю определенным образом (и предел существует), «деление» вполне дает результат. Например, время, за которое мы пройдем расстояние в 100 километров со скоростью v, равно 100/v. При устремлении v к +0 время, за которое мы пройдем вперёд сотню километров стоя, будет +∞.
[править] Нестандартный анализ
Для тех, кому на ноль делить все-таки очень уж хочется, в нестандартном анализе придумали гипердействительные числа; так, например, существуют нестандартные числа не равные нулю, но меньшие всех стандартных действительных чисел по модулю. При этом, на ноль делить все равно нельзя. Школьные знания здесь не помогут.
[править] Теория функций комплексной переменной
В расширенной комплексной плоскости делить на ноль можно. Это связано с тем, что в ней бесконечность — не предельно-недостижимое значение, а вполне конкретная точка, соответствующая точке (0, 0, 1) в стереографической проекции. Правда, при этом подобное множество внезапно перестает быть полем, но это мало кого волнует.
[править] Точка зрения прикладной алгебры
Деление — это не атомарная операция, а макрос — взятие обратного по умножению от делителя и умножение на делимое. Например, обратный двойке по умножению — это 2−1, 3/2 = 2−1 ∙ 3 и т. д. Операция взятия обратного по умножению определена для всех чисел, кроме нуля (говорят — нуля по сложению). Деление на ноль на самом деле не запрещено, эта операция просто не определена, как перемножение паровоза на самовар. Так-то.
[править] Точка зрения статистики
В прикладной статистике (и матмоделировании методом нейронных сетей) есть две таких забавных функции как слияние и разлияние. Первая делает сумму, выплёвывая процентное соотношение компонентов этой суммы. Второй делает «разброс» суммы по полученному процентному соотношению. Как известно, сумма может оказаться равной нулю. А чтобы получить соотношения делить надо именно на неё. Именно по этой причине в матстате на ноль делить можно. Но только ноль (с процентным соотношением равным однёрке на количество параметров). Либо на сумму модулей вместо математической суммы(чтобы был не ноль), что приводит к первоначальному варианту если мы сливаем сумму нулей.
[править] Алгебра, она такая алгебра…
Отсутствие обратного элемента для нуля это ещё полбеды. В целых числах тоже нет обратного, скажем, к 42, но это не мешает найти его в рациональных (1/42). Главная проблема здесь в том, что ноль является делителем нуля, а значит на него нельзя сокращать: из тождества «0 ∙ x = 0 ∙ y» ни разу не следует, что «x = y». Причём, если в хороших числовых системах такие корчи происходят только с нулём, то уже в седенионах или ещё проще функциях на отрезке корчи случаются на каждом шагу: вы ничего не можете сказать о функциях, для которых f(x) ∙ g(x) = 0.
[править] Мнение Wolfram|Alpha
Если ввести в Вольфрам 1/0, то получим ~∞, а если 0/0 — INDETERMINATE.
На запрос x=(0/0=1)*1 он отвечает… x=0 (он воспринимает сабж как логическое выражение по типу языка С и таки да: 0/0 не равно единице, что он и возвращает нулем…булевым)
[править] Делители нуля
Делители нуля — довольно банальные объекты у целой серии алгебр гиперкомплексных чисел, но чтоб не растекаться мыслью по континууму всевозможных алгебр, рассмотрю алгебру паракомплексных чисел, как простейшую содержащую делители нуля. Строится алгебра паракомпексных чисел подобно алгебре комплексных чисел, но в качестве мнимой единицы выбирается неравная +1 или 1 величина с квадратом равным +1. В этой алгебре справедливо: (1+i)*(1-i)=1+i-i-i^2=0… то есть 0 — это произведение правого и левого делителей нуля. Эти делители нуля к сожалению непозволят делить на нуль произвольное число, но хотябы сами на него делятся, к примеру (1+i)/0=C/(1-i), где С — произвольное конечное неравное 0 действительное число. А вот сделать что-то толковое с обратным делителем нуля неполучится, пока он не будет помножен на делитель нуля соответствующего типа в последующих вычислениях.
[править] Деление на ноль в программировании
В программировании числа целого типа (попытаться) поделить на ноль в принципе можно, но получается какая-то хуита: процессор x86 при попытке выполнить операцию целочисленного деления на ноль формирует особый случай (исключение) с номером 0, вектор которого также находится по адресу 0. Другими словами, процессор славное действие деления на ноль до конца не доводит, а перескакивает в другое место, обычно сообщая юзеру о внезапном просирании всех полимеров. На самом деле, самый влобный алгоритм деления беззнаковых целых двоичных чисел реализуется как серия сдвигов и вычитаний (соответствуя в сути своей банальному делению в столбик) и при этом выдаётся любопытный результат — в качестве результата деления X / 0 получается самое большое представимое в разрядности вычислений число — то есть все биты которого заполнены единицами (то есть число как можно большее, при повышении разрядности стремящееся к бесконечности), а в качестве остатка возвращается само делимое X. Этот результат забавным образом самосогласован, ибо если проверять результат деления с остатком через умножение, то получается совершенно справедливое: 111..111 * 0 + X = X. Так-то!
Зато числа с плавающей запятой делить на ноль можно невозбранно. При аффинном представлении бесконечностей получается плюс бесконечность (+INF) или минус бесконечность (-INF) — зависит от знака делимого числа. При проективном представлении — беззнаковая бесконечность (INF) в любом случае. Самое интересное происходит при делении на ноль самого ноля: результатом будет специально зарезервированное для подобных ситуаций (вроде извлечения квадратного корня из отрицательного числа или умножения нуля на бесконечность) значение «Не Число» (NaN, Not a Number).
Альзо, в одной книжке по процессорам Intel сказано, что NaN и Inf — вполне обычные числа. Если не обращать внимания на исключения, то с ними можно производить операции: NaN + p = NaN, NaN*p = NaN и т. д. и т. п., однако 1NaN = 1 и NaN0 = 1, так как 1 в степени чего угодно и что угодно в степени 0 будет 1.
В КофеСкрипте при делении числа на ноль возвращается «Infinity».
Также, в лаконичном языке программирования J сабж даёт бесконечность, обозначаемую как «_». Адепты данного языка ехидно заявляют, что ошибка при делении на ноль возникает исключительно в головах быдлокодеров, пытающихся освоить мозголомный синтаксис J.
[править] Деление на ноль в образной логике
Если попытаться с помощью образной логики изобразить такой математический процесс как деление, то получится раздача неких предметов неким субъектам. Например: 10 делим на 2 = мать раздаёт 10 яблок двум своим детям поровну, и у каждого в руках оказывается по 5 штук. Поэтому с точки зрения образной логики «деление на ноль» это «отсутствие деления». Скажем, 10 : 0 это 10 яблок, которые никто никому не раздаёт. Деление же ноля на ноль это «пустая корзина, в ней нет ни одного яблока, вот потому их никто никому не раздаёт».
Осталось только объяснить, почему «10 ∙ 0» равно нулю, а не отсутствию умножения. Добавим правило «от перестановки мест множителей итог не меняется» и получим «ноль, повторённый десять раз», а он равен нулю.
Если 10 яблок раздать 0 человек(не дать никому), то это можно сделать(не дать никому) сколь угодное число раз, поэтому результат будет, как при использовании пределов, бесконечность. Аналогично можно представить, что мы можем 10 раз взять 0(ничего), либо 0(ни разу) (не)взять по 10, итог один(sic!) — 0.
Алсо, если считать на палочках (как в детском саду считали), то в такой арифметике будут не все операции деления и нельзя будет вычесть из меньшего числа большее — поскольку нет дробных палочек и отрицательных палочек тоже нет.
- В рассказе Леонида Каганова «Гамлет на дне» главный герой под воздействием сектантов ушёл в подземелье и делил на ноль долгое время, пока не появился чудо-спасатель.
- «Two Divided By Zero» — песня из дебютного альбома расово британского синтипоп-дуэта Pet Shop Boys ([1]). Примечателен факт, что металлический голос, произносящий во время песни одну и ту же фразу «two divided by…», принадлежит электронному «говорящему» калькулятору, который вокалист группы, Нил Теннант, решил подарить своему отцу[1]
- ВИА «Кровосток» в тексте, простите, песни «Сдохнуть» как бы предупреждает: «можно сдохнуть пытаясь делить разные числа на ноль».
- У группы gastel?o есть песня «:0». Текст песни подтверждает [2], что его придумавший явно изящно поделил…
- Деление на ноль — это еще ничего. Для умножения на ноль уже придумали водородные и атомные бомбы типа Fat Boy.
- На испытаниях Су-24 регулярно случался отказ аппаратуры бомбометания. Причем происходило это только в том случае, если на цель заходил летчик-испытатель Ильюшин. Причина оказалось тоже не сложной. Только он заходил на цель с точностью, превышавшей машинную точность. Получался «машинный нуль», после чего шел сбой из-за попытки деления на ноль.
- В интернетах гуляет байка об аналогичном случае: мотороловцы клеили истребитель для Израиля, и он над Мертвым морем (высота над уровнем моря — нулевая или отрицательная) пытался делать сабж и самовыпиливался
- При выводе на орбиту одной космической кастрюли, созданной в лабораториях NASA, системы телеметрии в какой-то момент внезапно начали заполнять экраны мониторов сообщениями «Ошибка деления на ноль». В результате персонал был слегка обеспокоен, потому как все выглядело так, что спутник придется слить. Однако разработчик соответствующей подсистемы храбро заявил: «Я понимаю, что происходит. Это сейчас пройдет. Беру всю ответственность на себя». Самая мякотка тут в том, что этим самым разработчиком был один из Summer Student, подрабатывавший в NASA во время летних каникул. Правда, история закончилась обычным пиндосским хэппи-эндом, и в дальнейшем подобных проблем не возникало.
- Алсо, существует одноименный фантастический рассказ за авторством Теда Чана. Текст повествует об учёном-математике, который тронулся умом, внезапно обнаружив полную несостоятельность любимой науки. Мораль проста — гиковство в любой форме до добра не доводит. Такие дела.
- Алсо, у пейссателя есть книжка, где одна зверушка с IQ > 9000 способна буквально войти в кому, пытаясь в уме произвести операцию деления на ноль.
- В эпичной игре «Ядерный Титбит» свою роль в развязке сюжета сыграл суперробот, по всемогуществу сравнимый с Богом. «Когда его включили он начал смеяться. И не перестает до сих пор… Он может вообще все, но его волнует один единственный вопрос: Что будет, если единицу разделить на ноль». Для устранения бага требовались внеземные технологии и человеческий мозг, так как только люди могут держать иррациональность в голове, не сходя с ума.
- Алсо, у этого вашего Алистера Кроули есть
Каждое число равно бесконечности: в них нет различия |
- А еще это умеет делать калькулятор андроида (пруфлинк для скачивания) — при делении любого числа на ноль он выдает бесконечность. (При делении ноля на ноль он честно пишет «Ошибка». Проверено на 2.3.3 — NaN)
- А в HL2 есть оружие, делящее на ноль всех (в цитадели гравиган меняет цвет и боевые параметры). И AR2 тоже делит, шариком.
- В винрарном квесте «The Longest Journey» можно в прямом и переносном смысле поделить на ноль темного колдуна при помощи калькулятора.
- В махо-сейнен манге Mahou Senki Lyrical Nanoha Force у одного из главных героев есть магическое устройство Devider и заклинание Divide by Zero.
- При попытке деления на ноль встроенным калькулятором телефона Sony Ericsson и Nokia всплывает окошко, которое гласит «деление на ноль запрещено». Видимо, сони с нокой решили не мучать себе моск, да и другим тоже. Motorola ZN5 с английским языком при делении на 0 пишет E. Что означает Error — Ошибка — с расово-верного пиндосского языка.
- Встроенный калькулятор Windows 7 знает, что деление на ноль невозможно. Теперь и ты это знаешь. Однако, 0/0 сделать пытается, как всегда, безрезультатно.
- Встроенный калькулятор Mac OS X при делении на ноль, так и пишет: «деление на ноль». Но в последней версии, OS X Lion — «Не число».
- В расово математическом Emacs Calc при делении на ноль получаются интересные числа вида «2/0», которые при определенном умении можно даже превратить во что-то вроде «3 (2/0 + 1)». Однако попытка умножить, например, 5 на 1/0 все же заканчивается ошибкой «Division by zero».
- Первые олдскульные советские программируемые калькуляторы типа МК-52 были способны выполнять операцию деления на ноль, после чего их цифровой дисплей становился способным показывать некоторые буквенные символы, что активно использовалось продвинутыми юзерами таких калькуляторов для создания различных надписей на экране с целью их показывания друг другу и для написания экранных сообщений псевдоигровых программ в рамках возможностей данного вида калькуляторов.
- У братьев Стругацких в «Понедельнике…» делением ноля на ноль (причём с помощью настольных арифмометров) занимается целый отдел Абсолютного Знания. Что характерно, кстати, на настольном арифмометре поделить на ноль чисто технически возможно — просто после этого каретка уходила до предела вправо и там задумчиво останавливалась. Ну вроде как сейчас на калькуляторе MA ERROR пишется. Получалось, стало быть, что сотрудники отдела АЗ просто хуи на работе пинали, а не занимались антинаучной хуйнёй. Поэтому в более поздних изданиях «Понедельника…» они уже умножали ноль на бесконечность — вот этот подвиг повторить что на арифмометре, что на калькуляторе уже затруднительно будет, нес па?
- Один из первых процессоров серии Pentium при выполнении операции «деление на ноль» просто напросто зависал; приходилось перезагружать компьютер чудо-кнопкой Reset. Запрос деления на ноль мог возникать в случае коряво написанных программ или же мог быть вызван искуственно посредством Windows-калькулятора. Ошибка была исправлена в следующей модели пня.
- Олимпиады и ногомячные чемпионаты являются вовсе не попыткой создания благоприятной распильной среды, а результатом деления на ноль бюджета этой страны.
- У попсовой группы ВиаГра есть песня «Но я играю эту роль…». Так вот, анонимус однажды IRL слышал, как незнакомая красивая тян исполняла пародию на эту песню, и один из рефренов этой пародии звучал так: «Но я играю эту роль, Делю трёхзначные на ноль, В науке я неутомима. Мне теорема по плечу, Но я бессмертья не хочу, Вези в дурдом меня, любимый!» (Другие рефрены были еще более доставляющими: «…курю табак, пью алкоголь, И мне становится голимо…», «…я из ружья стреляю в моль, Но почему-то чаще мимо…»).
- Формально такими операциями, как деление и умножение на ноль (обычно алиенов, мутантов, роботов и прочей подобной пиздобратии), занимаются герои 95% быдло-фантастических книжонок и YOBA-игр. Пипл хавает и просит добавки.
- У американской панк-рок группы The Offspring есть песня Dividing By Zero.
- Тема деления на ноль чуть боле чем полностью раскрыта в аниме Cardcaptor Sakura Movie 2: The Sealed Card. Этой способностью владела 53 карта клоу и от этого досталось всем и каждому. Результат — на ноль поделен практически весь пригород Токио Томоеда и все его жители. Правда потом все по воле самой карты вернулось обратно.
- На Хабре таки поделили на ноль, и не один раз, и даже выжили!
[править] Помножить на ноль
Гепа грозит наказанием| « | Это тебе не поможет. А не лечи меня, доктор, — Это тебя не спасет. Хотя всё еще, может быть, Кто-то меня и умножит, Только не здесь и не сейчас, И только не тот, Который точно как я, Только наоборот. | » |
| — Веня Д’ркин, помноженный на ноль раком | ||
Менее известный мем. Имеется в виду то, что если число на ноль умножить, то получится ноль (то есть ничего). Пример с этого вашего плейграунда: «Извините, а как можно в Готике воскрешать героев, а то кореш-манчкин всех неписей на ноль помножил?»
Суть мема была представлена широкой публике в первой серии винрарного советского мультфильма «За задней партой», на 3:41.
« | |
| Devix: | почему нельзя делить на ноль? Умножать же можно. причем тоже ноль получается. |
| vampir_infernal: | почему нельзя? можно. только результат такого деления — бесконечность |
| Devix: | а почему не ноль? |
| vampir_infernal: | ну вот гляди. 2*0 — это два взять ноль раз, будет ноль. А 2/0 — это «сколько раз ноль умещается в двойке», бесконечность |
| Devix: | если 2/0=х, то значит 2=х*0 и… бля… 2=0. А если 2=0, значит 2/0=0! числитель пропадает в никуда? |
| vampir_infernal: | ну вот чтобы такой х**ней не страдать, математики приняли негласное соглашение, что на ноль делить нельзя |
» | |
| — 400734 | |
« | |
| ^_^: | Чего б ты щас хотел? |
| alias: | честно? |
| ^_^: | Честно. |
| alias: | делить на ноль |
» | |
| — 403615 | |
« | |
| 1: | Ниндзя — куче всех. Они умеют ходить по воде, делить на ноль и угадывать шаффл в АйПоде. |
» | |
| — 392048 | |
| 1 | 3 | yes | Показать | Скрыть |
|
- ↑ оригинальную цитату на английском искать в буклете диска «Please. Further Listening 1984—1986»
| Деление на ноль — часть точного мира чисел | |
|---|---|
lurkmore.to
Подскажите если 0 📝 умножить на 2 в 3 степени что будет
Нольсложение с нулём, вычитание нуля, умножение на ноль, деление на ноль, степень и ноль, факториал нуля, правописание слова ноль.согласно общепринятому определению, ноль — это число, отделяющее положительные числа от отрицательных на числовой прямой. ноль — это самое проблематичное место в , которое не подчиняется логике, а все действия с нулём основаны не на логике, а на общепринятых определениях.
первый пример проблематичности нуля — это натуральные числа. в школах ноль не является натуральным числом, в других школах ноль является натуральным числом. поскольку понятие «натуральные числа» — это искусственное отделение некоторых чисел от всех остальных чисел по определённым признакам, то доказательства натуральности или не натуральности нуля быть не может. ноль считается нейтральным элементом по отношению операций сложения и вычитания.
ноль считается целым, беззнаковым числом. также ноль считается чётным числом, поскольку при делении нуля на 2 получается целое число ноль.
ноль является первой цифрой во всех стандартных системах счисления. в позиционных системах счисления, к которым принадлежит привычная нам десятичная система счисления, цифрой ноль обозначают отсутствие значения данного разряда при записи числа. индейцы майя использовали ноль в принятой у них двенадцатиричной системе счисления за тысячу лет до индийских . с нулевого дня в календаре майя начинался каждый месяц. интересно, что тем же самым знаком ноль майя обозначали и бесконечность — вторую проблему современной .
слово «ноль» в арабском языке звучит как «сыфр». от арабского слова ноль (сыфр) произошло слово «цифра».
как правильно пишется — ноль или нуль? слова ноль и нуль в значении, но различаются употреблением. как правило, ноль употребляется в обиходной речи и в ряде устойчивых сочетаний, нуль — в терминологии, в научной речи. правильными будут оба варианта написания этого слова. например: деление на ноль. ноль целых. ноль внимания. ноль без палочки. абсолютный нуль. ноль целых пять десятых.
в грамматике производные слова от слов ноль и нуль пишутся так: нолевой или нулевой, нолик или нулик, ноля или нуля, нулевой или реже встречающееся нолевой, ноль-ноль. например: ниже нуля. равно нулю. свести к нулю. нулевой мередиан. нулевой пробег. в двенадцать ноль-ноль.
в действиях с нулем на сегодняшний день определены следующие результаты:
сложение — если к любому числу прибавить ноль, число останется неизменным; если к нулю прибавить любое число результатом сложения будет то же самое любое число:
a + 0 = a
0 + a = a
вычитание — если из любого числа вычесть ноль, число останется неизменным; если из нуля вычесть любое число в результате получится то же самое любое число с противоположным знаком:
a — 0 = a
0 — a = -a
умножение — если любое число умножить на ноль, результатом будет ноль; если ноль умножить на любое число в результате получится ноль:
a х 0 = 0
0 х a = 0
деление — деление на ноль запрещено, поскольку результат не существует; общепринятый взгляд на проблему деления на ноль изложен в работе александра сергеева «почему нельзя делить на ноль? »; для любознательных написана другая статья, в которой рассматривается возможность деления на ноль:
a : 0 = делить на ноль запрещено, при этом а не равно нулю
ноль разделить на ноль — выражение не имеет смысла, так как не может быть определено:
0 : 0 = выражение не имеет смысла
ноль разделить на число — если ноль разделить на число в результате всегда будет ноль, не зависимо от того, какое число находится в знаменателе (исключением из этого правила является число ноль, смотри выше):
0 : a = 0, при этом а не равно нулю
ноль в степени — ноль в любой степени равен нулю:
0a = 0, при этом а не равно нулю
возведение в степень — любое число в степени ноль равняется единице (число в степени 0):
a0 = 1, при этом а не равно нулю
ноль в степени ноль — выражение не имеет смысла, так как не может быть определено (ноль в нулевой степени, 0 в степени 0):
00 = выражение не имеет смысла
извлечение корня — корень любой степени из нуля равен нулю:
01/a = 0, при этом а не равно нулю
факториал — факториал нуля, или ноль факториал, равняется единице:
0! = 1
распределение цифр — при подсчете распределения цифр ноль считается незначащей цифрой. изменение подхода в правилах подсчета распределения цифр, когда ноль считается значащей цифрой позволит получать более точные результаты распределения цифр во всех стандартных системах счисления, в том числе в двоичной системе счисления.
кому интересен вопрос возникновения нуля, предлагаю прочесть статью « нуля» дж. дж. о’коннора и е. ф. робертсона в переводе и. ю. осмоловского.
app.yznay.com
Почему на ноль делить нельзя? | Обучение
Каких только вопросов не задают наши детки!.. А вот вопрос «Почему на ноль делить нельзя?» не задают. Почему? Потому что еще в школе учительница сказала, что НЕЛЬЗЯ. Нельзя, значит, нельзя! Много позже, уже в институтах, мы узнали, что делить оказывается все-таки можно, и получится в результате — бесконечность. Но, признайтесь, наш ум принял этот факт как некое допущение, условность, мы ведь с детства помним — нельзя. А, собственно, почему все-таки?
Для начала давайте разберемся, откуда появляется бесконечность, к понятию которой на первых курсах университета мы отнеслись с некоторой долей недоверия. Все удивительно просто: если какое-нибудь число делить на все меньшее и меньшее, то будет получаться все большее и большее значение. Чем меньше будет делитель, тем больше станет частное. Так появляется бесконечность.
Но физики и математики не любят бесконечности, потому условно принято, что на ноль делить нельзя. Получается, что допущением является невозможность делить на ноль.
Обратимся к азам математики. В арифметике существует четыре действия — сложение, вычитание, умножение и деление. Но равноправия у них нет. Математики считают основными действиями только два из них: сложение и умножение, остальные — обратные действия, следствия основных.
Рассмотрим понятие «вычитание». Для решения примера «5 — 3 = …» надо из пяти предметов убрать три, оставшееся при этом количество и будет ответом на наш пример. Но, учитывая, что основным действием считается сложение, давайте несколько изменим наш пример, записав его в виде сложения: «х + 3 = 5». То есть к какому числу надо прибавить три, чтобы получилось пять?
Так же дела обстоят с делением. Выражение «8: 4 = …» вытекает из выражения «4 • x = 8». Сколько раз по четыре надо взять, чтобы получилось восемь?
И вот он, ответ! Если 5: 0 — это вариант записи 0 • x = 5, то получается, надо найти такое число, которое при умножении на 0 даст 5. Сколько раз по нулю надо взять, чтобы получилось что-то большее, чем ничего?! Но при умножении на 0 всегда получается 0, этот факт лежит в самом определении нуля! Числа, которое при умножении на 0 дает что-то отличное от ноля, не существует. Получается, задача не имеет решения, а выражение 5: 0 не имеет смысла. Чтобы уменьшить количество бессмысленных задач, было принято, что на ноль делить нельзя.
Самые дотошные читатели непременно спросят: а как же с делением нуля на ноль?
Давайте разберемся. Получается, уравнение 0 • x = 0 имеет решение? Или бесконечное число решений? «Х» может быть равен и единице, и двум, и миллиону. Так, при х=0, получается 0 • 0 = 0, тогда 0: 0=0? А при х=1, 0 • 1 =0, значит, 0: 0 = 1?! Или 0: 0 = 1000000?!
Выходит, мы не можем найти решения выражения «0: 0», значит, и у этого выражения нет решения. Получается, ноль на ноль тоже делить нельзя.
Вот к таким интересным умозаключениям можно прийти, задумавшись над известным с начальных классов фактом: на ноль делить нельзя.
Заинтересовало? Дочитали до конца? Значит, именно из-за таких как вы и появился следующий жизненный анекдот.
— Почему нельзя делить на ноль? Умножать же можно, причем тоже ноль получается.
— Почему нельзя? Можно, только результат такого деления — бесконечность
— А почему не ноль?
— Ну вот, смотри: 2*0 — это два взять ноль раз, будет ноль. А 2/0 — это «сколько раз ноль умещается в двойке», бесконечность.
— Если 2/0=х, то значит 2=х*0, то есть 2=0. А если 2=0, значит 2/0=0!
— Ну вот, чтобы такой ерундой не заниматься, математики и приняли негласное соглашение: на ноль делить нельзя!
shkolazhizni.ru
Как делить обыкновенную дробь на обыкновенную дробь: 1 разделить на 2
Деление обыкновенной дроби на обыкновенную дробь
Известно, что деление является действием, обратным умножению (смотрите связь деления с умножением). То есть, деление предполагает нахождение неизвестного множителя, когда известно произведение и другой множитель. Этот же смысл деления сохраняется и при делении обыкновенных дробей.
Пусть нам нужно разделить обыкновенную дробь a/b на обыкновенную дробь c/d. Иными словами, нам нужно определить такое число, умножение которого на делитель c/d даст делимое a/b. Это число равно произведению (d/c – число, обратное числу c/d). Действительно, свойства умножения позволяют нам записать следующие равенства , из которых следует, что есть частное от деления a/b на c/d.
Обобщив всю приведенную информацию, получаем правило деления обыкновенных дробей: чтобы разделить обыкновенную дробь a/b на дробь c/d нужно делимое умножить на число, обратное делителю.
С помощью букв озвученное правило умножения обыкновенных дробей записывается так: .
Итак, правило деления обыкновенных дробей сводит деление к умножению. Таким образом, чтобы успешно выполнять деление дробей по этому правилу, надо уметь выполнять умножение обыкновенных дробей.
Рассмотрим примеры деления обыкновенных дробей.
Пример.
Выполните деление дроби 9/7 на дробь 5/3.
Решение.
Числом, обратным делителю 5/3, является дробь 3/5 (смотрите нахождение числа, обратного данному числу). Тогда по правилу деления обыкновенных дробей получаем .
Ответ:
Отметим, что не следует забывать про сокращение дробей и про выделение целой части из неправильной дроби.
Пример.
Проведите деление дробей .
Решение.
Перейдем от деления дробей к умножению: . Сейчас самое время провести сокращение дроби: . Осталось выделитель целую часть из неправильной дроби: . На этом деление обыкновенных дробей закончено.
Ответ:
1 Как разделить число на дробь
Запишите свой пример на черновик, чтобы у вас была возможность делать заметки и помарки. Помните, что целое число записывается между клеток, прямо на их пересечении, а дробные числа – каждая в своей клетке.
- В данном способе вам нужно перевернуть дробь вверх ногами, то есть, знаменатель записать в числитель, а числитель – в знаменатель.
- Знак деления нужно поменять на умножение.
- Теперь вам осталось выполнить умножение по уже изученным правилам: числитель умножается на целое число, а знаменатель не трогаете.
Конечно, в результате такого действия у вас получится очень большое число в числителе. В таком состоянии оставлять дробь нельзя – учитель попросту не примет этот ответ. Сократите дробь, разделив числитель на знаменатель. Целое число, которое получится в результате, запишите слева от дроби посередине клеток, а остаток и будет новым числителем. Знаменатель остается неизменным.
Этот алгоритм довольно прост, даже для ребенка. Выполнив его пять-шесть раз, малыш запомнит порядок действия и сможет применять его к любым дробям.
2 Как разделить число на десятичную дробь
Бывают дроби другого вида – десятичные. Деление на них происходит по совсем другому алгоритму. Если вы столкнулись с таким примером, то придерживайтесь инструкции:
- Для начала, превратите оба числа в десятичные дроби. Сделать это просто: делитель у вас и так представлен в виде дроби, а делимое натуральное число вы отделяете запятой, получая десятичную дробь. То есть, если делимое было числом 5, вы получаете дробь 5,0. Отделять число нужно на столько цифр, сколько стоит после запятой и делителя.
- После этого, обе десятичные дроби вы должны сделать натуральными числами. Сперва, вам покажется это немного запутанным, но это самый быстрый способ деления, который будет занимать у вас секунды, после нескольких тренировок. Дробь 5,0 станет числом 50, дробь 6,23 будет 623.
- Выполните деление. Если числа получились большие, либо деление будет происходить с остатком, выполните его в столбик. Так вы наглядно увидите все действия данного примера. Вам не нужно специально ставить запятую, так как она сама появится в процессе деления в столбик.
Данный вид деления изначально кажется слишком запутанным, так как вам нужно превратить делимое и делитель в дробь, а потом снова в натуральные числа. Но после недолгой тренировки, вы сразу станете видеть те числа, которые нужно просто разделить друг на друга.
Помните, что умение правильно делить дроби и целые числа на них могут ни раз пригодиться в жизни, поэтому, знать эти правила и простые принципы ребенку нужно идеально, чтобы в более старших классах они не стали камнем преткновения, из-за которого ребенок не может решать более сложные задачи.
Читайте также:
- Как решать дроби
Мы делили апельсин. Много нас, а он один Эта долька для ежа, эта долька для…
- Сколько будет детей
5 простых способов узнать, сколько у вас будет детейВсем нам интересно заглянуть в свое будущее…
le-protestant.ru
Бесконечность делить на ноль
Методы решения пределов. Неопределённости.Порядок роста функции. Метод замены
На уроках Пределы. Примеры решений, Замечательные пределы мы рассмотрели азы темы, и данная статья продолжает наше погружение в мир пределов. Помимо закрепления материала, будет много новой информации о методах решения пределов, и, конечно же, примеры, примеры, примеры со всеми техническими тонкостями решений. Качественная проработка урока позволит выйти на уверенный средний уровень даже полному чайнику.
Что необходимо знать и уметь на данный момент?
– Вы должны ПОНИМАТЬ, что такое предел функции. Не выучить, не зазубрить, а именно понять хотя бы на общем, интуитивном уровне. Поэтому, если пределы сродни китайской грамоте, пожалуйста, начните с базового урока Пределы. Примеры решений, а также загляните в справку Графики и свойства элементарных функций, где я проиллюстрировал геометрический смысл понятия.
– Необходимо уметь использовать основные методы решения пределов и справляться с наиболее распространёнными заданиями. Очень хорошо, если кроме примеров моих первых двух уроков, вы порешали (или попытались порешать) что-нибудь дополнительно.
Есть? Едем дальше. Начнём с пары вопросов, которые вызвали недопонимание у некоторых посетителей сайта. За 2 года в отзывах и личной переписке мне удалось выяснить те моменты, которые недостаточно подробно рассмотрены в ранних статьях. И сейчас самое время акцентировать на них внимание.
Первый вопрос затрагивает саму сущность предела. В черновой версии урока я даже процитировал Винни-Пуха: «Куда идём мы с Пятачком, большой-большой секрет». Но потом убрал… нехорошо как-то… выходит все, кто этого не понял – медведи с опилками в голове.
«Чему равен предел ?» (пример условный)
Действительно, чему?
Здесь не указано, куда стремится «икс», и такая запись не имеет смысла:
Предел функции не летает где-то по воздуху на воздушном шаре, он может существовать (или не существовать) только в определённой точке (в частности, в точке или ). Например:
Заодно вспоминаем примитивный, но важный приём – чтобы вычислить предел, сначала нужно попытаться подставить значение «икс» в функцию. В случае с бесконечностью очевидно, что:
Иными словами, если , то функция неограниченно возрастает.
А вот следующего предела не существует:
Значение не входит в область определения функции (под корнем получается «минус»).
рАвно не существует и такого предела:
Тут «икс» стремится к «минус бесконечности», и под корнем нарисуется бесконечно большое отрицательное число.
Итак, в природе не существует «просто предела». Предел может существовать (или не существовать) лишь в определённой точке, в частности, в точке «плюс бесконечность» или «минус бесконечность».
В процессе оформления практических примеров постарайтесь придерживаться следующей рекомендации: не допускайте неполной записи вроде , это одна из самых скверных оплошностей. Презумпция виновности студента утверждает, что он либо совсем не в теме, либо откуда-то впопыхах списал пример.
Второй вопрос касается путаницы с неопределённостями, которые возникают в ходе решения более сложных пределов. Систематизируем информацию:
Что в пределах функций ЯВЛЯЕТСЯ неопределённостью
и НЕ ЯВЛЯЕТСЯ неопределённостью
Прежде всего, перед решением любого предела, обязательно выполняем подстановку «икса» в функцию – неопределённости может и не быть! Однако сладостей много вредно, и на первых двух уроках мы сталкивались со следующими неопределённостями:
Кроме указанных видов, существует довольно распространённая неопределённость («бесконечность минус бесконечность»), которую мы подробно разберём в этой статье, и совсем редко встречаются неопределённости .
Для того чтобы устранить неопределённость, как вы знаете, необходимо использовать некоторые правила и методы решения пределов.
Теперь о том, ЧТО НЕ ЯВЛЯЕТСЯ неопределённостью.
Неопределённостью не является:
– Любая определённость =)
– Бесконечно малое число, делённое на ненулевую константу: . Сюда же можно отнести бесконечно малое число, делённое на бесконечно большое число:
– Ненулевая константа, делённая на бесконечно малое число, например: .
– Начинающие изучать математический анализ, часто пытаются устранить мифическую неопределённость . Но все попытки тщетны, поскольку это определённость:
представим «бесконечность делить на ноль» в виде произведения: , и, согласно предыдущему пункту: . Приведу живой пример:
Примечание: на практике значок часто записывают без «плюса»: , но, строго говоря, это две разные вещи. Для простоты я буду считать второе обозначение «плюс бесконечностью» и иногда в целях бОльшей чёткости изложения ставить знак «плюс».
– Число, не равное единице, в бесконечно большой степени не является неопределённостью. Например: . В частности: .
– Разность двух функций, каждая из которых стремится к нулю, например: . Таким образом, неопределённости «ноль минус ноль» тоже не существует – это определённость.
Многие из перечисленных неопределённостей и определённостей уже встречались и ещё неоднократно встретятся на практике.
До нового 2013 года остаются считанные дни, и в качестве подарка я принёс увесистый ящик с петардами:
Порядок роста функции
В данном параграфе будут разобраны пределы с многочленами, многочленами под корнем, когда или . Материал вам уже частично знаком, и настала пора разобраться в нём как следует. Давайте научимся находить решение в считанные секунды!
Вычислим следующий предел:
На базовом уроке Пределы. Примеры решений я рекомендовал рассуждать не совсем корректным способом: сначала «икс» равно 10, потом, 100, затем 1000, миллион и т.д. до бесконечности. В чём изъян такого подхода? Построим данную последовательность:
Исходя из полученных результатов, складывается стойкое впечатление, что предел стремится к «минус бесконечности», но на поверку впечатление кардинально ошибочно:
В этой связи необходимо знать теорию матана, а именно, некоторые выкладки о порядке роста функции.
Применительно к нашему примеру можно сказать, что слагаемое обладает более высоким порядком роста, чем сумма . Иными словами, при достаточно больших значениях «икс» слагаемое «перетянет» на «плюс бесконечность» всё остальное:
При небольших значениях «икс» – да, сладкая парочка перетягивает канат в сторону «минус бесконечности», что и привело нас к неверному первоначальному выводу. Но уже при получается гигантское положительное число .
Если сильно уменьшить первое слагаемое, то от этого ничего не изменится: , будет лишь отсрочен тот момент, когда бравая дробь «вытянет» весь предел на «плюс бесконечность». Не поможет и «усиление противовеса»:
.
Нулей можете приписать, сколько хотите (без шуток). Удивительная наука математический анализ – способна низвести любого монстра до мелочи пузатой.
Таким образом, кубическая функция имеет более высокий порядок роста, чем:
– квадратичная функция;
– линейная функция;
– функция-константа;
– сумма квадратичной функции, линейной функции и константы (в любых комбинациях).
На простейшем примере поясню геометрический смысл вышесказанного. Представьте графики линейной , квадратичной и кубической функций (см. методичку Графики и свойства функций). Легко заметить, что при увеличении значений «икс», кубическая парабола взмывает вверх гораздо быстрее и круче, чем парабола и, тем более, прямая.
Аналогичное правило можно сформулировать для любой степени:
Степенная функция данной степени растёт быстрее, чем любая степенная функция более низкой степени. И быстрее, чем сумма любого количества степенных функций более низкой степени.
Найдём предел
Значение данного предела зависит только от слагаемого . Всё остальное МЫСЛЕННО отбрасываем: , и теперь ясно как день, что предел стремится к «минус бесконечности»:
То есть, слагаемое более высокого порядка роста, чем всё остальное.
У «хвоста» могут быть сколь угодно большие константы, другие знаки, но результат от этого НЕ ИЗМЕНИТСЯ.
Сравнение бесконечно больших функций
На первом уроке мы вычислили три предела с неопределённостью :
В перечисленных примерах используется стандартный приём деления числителя и знаменателя на «икс» в старшей степени и всё расписывается подробно. Но правильный ответ легко выяснить ещё до решения!
В первом примере в числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые:
.
В таких случаях говорят, что функции числителя и знаменателя обладают одинаковым порядком роста. Или короче – числитель и знаменатель одного порядка роста. Действительно, в данном пределе и вверху, и внизу находятся квадратичные функции. Мир, равенство, братство.
Во втором примере аналогично – в числителе и знаменателе МЫСЛЕННО уберём всех малышей:
Здесь знаменатель более высокого порядка, чем числитель. Функция-многочлен 4-й степени растёт быстрее кубической функции и «перетягивает» предел на ноль.
И, наконец, в пределе карлики тоже идут лесом:
А в этом примере всё наоборот – числитель более высокого порядка, чем знаменатель. Квадратичная функция растёт быстрее линейной и «перетягивает» предел на «плюс бесконечность».
Сделаем краткую теоретическую выжимку. Рассмотрим две произвольные функции , которые определены на бесконечности.
1) Если , где – ненулевая константа, то функции имеют одинаковый порядок роста. Если , то функции называют эквивалентными на бесконечности.
2) Если , то функция более высокого порядка роста, чем .
3) Если , то функция более высокого порядка роста, чем .
! Примечание: при суть выкладок не меняется.
Подчеркиваю ещё раз, что данные факты относятся к произвольным функциям, определённым на бесконечности, а не только к многочленам. Но у нас ещё непаханое поле полиномов, поэтому, продолжаем работать с ними… да вы не грустите, для разнообразия я добавлю корней =)
Пример 1
Найти предел
В наличии неопределённость и приём решения уже знаком – нужно разделить числитель и знаменатель на «икс» в старшей степени.
Старшая степень числителя равна двум. Знаменатель…. Как определить старшую степень, если многочлен под корнем? МЫСЛЕННО отбрасываем все слагаемые, кроме самого старшего: . Константу тоже отбрасываем и выясняем старшую степень знаменателя: . Она тоже равна двум. Таким образом, числитель и знаменатель одного порядка роста, а значит, предел равен конечному числу, отличному от нуля.
Почему бы сразу не узнать ответ? В числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые: . Таким образом, наши функции не только одного порядка роста, но ещё и эквивалентны на бесконечности.
Оформляем решение:
Разделим числитель и знаменатель на
В действительности пару шагов можно пропустить, просто я подробно расписал, как в знаменателе под корень вносится .
Пример 2
Найти предел
Это пример для самостоятельного решения. Постарайтесь провести рассуждения по образцу первого примера. Также заметьте, что здесь неопределённость , что необходимо отразить в решении. Примерный образец чистового оформления примера в конце урока.
Во избежание недочёта, всегда анализируйте, какая неопределённость получается в пределах рассматриваемого вида. Помимо неопределённости может встретиться неопределённость либо . Во всех четырёх случаях числитель и знаменатель необходимо разделить на «икс» в старшей степени.
Пример 3
Найти предел
Слишком трудный предел? Лёгкий испуг от хлопушки. Главное, грамотно управиться с радикалами.
Проведём предварительный анализ:
Сначала выясним старшую степень числителя. Там сумма двух корней. Под корнем отбросим младшее слагаемое: и уберём константу: . Под корнем отбросим все младшие слагаемые: .
, значит, старшая степень числителя: .
Разбираемся с нижним этажом. Под корнем отбрасываем константу: . У многочлена старшая степень равна двум.
, значит, старшая степень знаменателя: .
Кстати, заметьте, что корень более высокого порядка роста, чем , поэтому весь знаменатель будет стремиться к «плюс бесконечности».
Сравниваем старшие степени: , следовательно, числитель более высокого порядка роста, чем знаменатель, и сразу можно сказать, что предел будет равен бесконечности.
Оформляем решение, я распишу его максимально подробно:
Разделим числитель и знаменатель на «икс» в старшей степени: :
Действия в числителе прозрачны, закомментирую знаменатель. У дроби «разнокалиберные» корни, и квадратный корень необходимо «подогнать» под кубический корень . Составим и решим уравнение: . Таким образом: .
Ну и на всякий случай напоминаю формулу , по которой выполняется деление:
Другие члены знаменателя:
Правила действий с корнями можно найти на странице Математические формулы и таблицы в методичке Горячие формулы школьного курса математики. Также на действиях с радикалами я подробно останавливался при нахождении производных.
Пример 4
Найти предел
Это более простой пример для самостоятельного решения. В предложенном примере снова неопределённость ( более высокого порядка роста, чем корень ).
Если «икс» стремится к «минус бесконечности»
Призрак «минус бесконечности» уже давно витал в этой статье. Рассмотрим пределы с многочленами, в которых . Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.
Рассмотрим 4 фишки, которые потребуются для решения практических заданий:
1) Вычислим предел
Значение предела зависит только от слагаемого , поскольку оно обладает самым высоким порядком роста. Если , то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени, в данном случае – в четвёртой, равно «плюс бесконечности»: . Константа («двойка») положительна, поэтому:
2) Вычислим предел
Здесь старшая степень опять чётная, поэтому: . Но перед расположился «минус» (отрицательная константа –1), следовательно:
3) Вычислим предел
Значение предела зависит только от . Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное число в НЕЧЁТНОЙ степени равно «минус бесконечности», в данном случае: .
Константа («четвёрка») положительна, значит:
4) Вычислим предел
Первый парень на деревне снова обладает нечётной степенью, кроме того, за пазухой отрицательная константа, а значит: Таким образом:
.
Пример 5
Найти предел
Используя вышеизложенные пункты, приходим к выводу, что здесь неопределённость . Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:
Решение тривиально:
Разделим числитель и знаменатель на
Пример 6
Найти предел
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
А сейчас, пожалуй, самый тонкий из случаев:
Пример 7
Найти предел
Рассматривая старшие слагаемые, приходим к выводу, что здесь неопределённость . Числитель более высокого порядка роста, чем знаменатель, поэтому сразу можно сказать, что предел равен бесконечности. Но какой бесконечности, «плюс» или «минус»? Приём тот же – в числителе и знаменателе избавимся от мелочи:
Решаем:
Разделим числитель и знаменатель на
Почему ?
Проанализируем бесконечно малые слагаемые знаменателя:
Если , то слагаемые с чётными степенями будут стремиться к бесконечно малым положительным числам (обозначаются через ), а слагаемые с нечётными степенями будут стремиться к бесконечно малым отрицательным числам (обозначаются через ).
Теперь зададимся вопросом, какое из этих четырёх слагаемых будет стремиться к нулю (неважно с каким знаком) медленнее всего? Вспомним наивный приём: сначала «икс» равно –10, потом –100, затем –1000 и т.д. Медленнее всего к нулю будет приближаться слагаемое . Образно говоря, это самый «жирный» ноль, который «поглощает» все остальные нули. По этой причине на завершающем этапе и появилась запись .
Следует отметить, что знаки бесконечно малых слагаемых числителя нас не интересуют, поскольку там нарисовалась осязаемая добротная единичка. Поэтому в числителе я поставил «просто нули». К слову, знаки при нулях не имеют значения и во всех примерах, где в пределе получается конечное число (Примеры №№5,6).
Без измен, на то он и математический анализ, чтобы анализировать =)
Впрочем, о бесконечно малых функциях позже, а то вы нажмёте маленький крестик справа вверху =)
Пример 8
Найти предел
Это пример для самостоятельного решения.
Рекомендую хорошо осмыслить информацию первой части урока, и по возможности сделать перерыв.
Неопределённость «бесконечность минус бесконечность»
Популярная неопределённость устраняется тремя распространёнными способами:
– приведением выражения под знаком предела к общему знаменателю;
– умножением/делением на сопряжённое выражение;
– преобразованием логарифмов.
Рассмотрим первый случай, о котором я ещё не рассказывал:
Пример 9
Вычислить предел
В данном пределе имеет место неопределённость , и общий алгоритм решения незамысловат: необходимо привести выражение к общему знаменателю, а затем попытаться что-нибудь сократить:
(1) Раскладываем знаменатели на множители: в первом знаменателе выносим «икс» за скобки, во втором знаменателе используем формулу разности кубов . Данный шаг можно было пропустить, но этим пришлось бы заниматься потом, и, на мой взгляд, разложение на множители удобнее провести сразу же.
(2) Приводим выражение к общему знаменателю.
(3) Приводим подобные слагаемые в числителе. Неопределённость трансформировалась в неопределённость , которая стандартно раскрывается разложением числителя и знаменателя на множители.
(4) Знаменатель уже разложен на множители. Раскладываем на множители числитель, в данном случае использована формула .
(5) Сокращаем числитель и знаменатель на , устраняя неопределённость.
Как видите, новизны-то особой и нет.
Аналогичное задание для самостоятельного решения:
Пример 10
Вычислить предел
Решение и ответ в конце урока
Второй вид пределов с неопределённостью представляет собой разность, в которой присутствуют два или один корень:
Пример 11
Вычислить предел
Каноничный образец. Метод решения подробно разобран на уроке Пределы. Примеры решений. Необходимо умножить и разделить на сопряженное выражение, чтобы потом воспользоваться формулой
Умножим и разделим на сопряженное выражение:
Неопределённость превратилась в неопределённость . Узнаёте? Такие семечки мы грызли в первом разделе данного урока.
Числитель и знаменатель одного порядка роста, а значит, предел равен конечному числу. Разделим числитель и знаменатель на :
Не редкость, когда в разности всего один корень, но это не меняет алгоритма решения:
Пример 12
Вычислить предел
Пример 13
Вычислить предел
Это пара коротких примеров для самостоятельного решения.
Следует отметить, что пределы рассмотренного типа не обязаны равняться конечному числу, вполне может получиться и бесконечность, причём, как «плюс», так и «минус». Кстати, в примере №13 можно посмотреть на порядок роста членов, чтобы сразу выяснить ответ 😉
Иногда на практике встречаются пределы-«обманки», в которых неопределённости «бесконечность минус бесконечность» нет вообще, вот простейший пример:
Таким образом, будьте предельно внимательны: перед решением предела необходимо убедиться, что неопределённость действительно есть!
В заключительной части статьи вернёмся к незаслуженно забытым замечательным пределам, где рассмотрим, в том числе, третий тип пределов с неопределённостью .
Метод замены переменной в пределе
Весьма ходовой приём решения. Метод замены переменной применяют чаще всего для того, чтобы свести решение к первому замечательному пределу, намного реже – к другому замечательному пределу. Рассмотрим пару типовых образцов:
Пример 14
Найти предел
Решаем:
В пределе находится арктангенс, от которого хорошо бы избавиться. Логично и очень удобно превратить «арк» в одну единственную букву. Проведём замену переменной: .
Теперь в пределе нужно выразить всё остальное через «тэ».
Во-первых, выясним, куда будет стремиться новая переменная «тэ»:
Если , то , иными словами, новоиспеченная переменная тоже будет стремиться к нулю:
Осталось в знаменателе выразить «икс» через «тэ». Для этого на обе части равенства «навешиваем» тангенсы:
В правой части две взаимно обратные функции уничтожаются:
, откуда:
Взмахи волшебной палочки закончены, остальное просто:
Используемые формулы и приёмы решения завершающего этапа очень подробно разобраны в первой части урока Замечательные пределы.
Пример 15
Найти предел
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
Ещё пара занятных примеров на тему замены переменной:
Пример 16
Найти предел
При подстановке единицы в предел получается неопределённость . Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле . Действительно, зачем нам тангенс?
Заметьте, что , поэтому . Если не совсем понятно, посмотрите значения синуса в тригонометрической таблице. Таким образом, мы сразу избавляемся от множителя , кроме того, получаем более привычную неопределённость 0:0. Хорошо бы ещё и предел у нас стремился к нулю.
Проведем замену:
Если , то
Под косинусом у нас находится «икс», который тоже необходимо выразить через «тэ».
Из замены выражаем: .
Завершаем решение:
(1) Проводим подстановку
(2) Раскрываем скобки под косинусом.
(3) Используем формулу приведения , формулы приведения также можно найти в тригонометрических таблицах.
(4) Чтобы организовать первый замечательный предел , искусственно домножаем числитель на и обратное число .
Задание для самостоятельного решения:
Пример 17
Найти предел
Полное решение и ответ в конце урока.
Это были несложные задачи в своём классе, на практике всё бывает хуже, и, помимо формул приведения, приходится использовать самые разные тригонометрические формулы, а также прочие ухищрения. В статье Сложные пределы я разобрал пару настоящих примеров =)
В канун праздника окончательно проясним ситуацию ещё с одной распространённой неопределённостью:
Устранение неопределённости «единица в степени бесконечность»
Данную неопределённость «обслуживает» второй замечательный предел, и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-й замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёт только о неопределённости и никакой другой.
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить все примеры урока Замечательные пределы, которые относятся ко 2-му замечательному пределу. Например, вычислим предел :
В данном случае , и по формуле :
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-й замечательный предел.
Всё это хорошо, правильно, но сейчас в кадре более любопытные кадры:
Пример 18
Вычислить предел
На первом шаге, не устану повторять, подставляем значение «икс» в выражение под знаком предела. А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость
Используем формулу
Чтобы не таскать за собой букву «е» и не мельчить, показатель удобнее вычислить отдельно:
В данном случае:
Таким образом:
С точки зрения техники вычислений всё рутинно: сначала приводим первое слагаемое к общему знаменателю, затем выносим константы и проводим сокращения, избавляясь от неопределённости 0:0.
В результате:
Готово.
Обещанный подарок с разностью логарифмов и неопределённостью :
Пример 19
Вычислить предел
Сначала полное решение, потом комменты:
(1)-(2) На первых двух шагах используем формулы . У сложных производных мы «разваливаем» логарифмы, а здесь, наоборот – их нужно «собрать».
(3) Значок предела перемещаем под логарифм. Это можно сделать, поскольку данный логарифм непрерывен на «минус бесконечности». Кроме того, предел же относится к «начинке» логарифма.
(4)-(5) Стандартным приёмом, рассмотренным на базовом уроке про замечательные пределы, преобразуем неопределённость к виду .
(6) Используем формулу .
(7) Экспоненциальная и логарифмическая функция – взаимно обратные функции, поэтому и «е» и логарифм можно убрать. Действительно, согласно свойству логарифма: . Минус перед дробью вносим в знаменатель:
(8) Без комментариев =)
Рассмотренный тип предела не такой редкий, примеров 30-40 у себя нашёл.
Пример 20
Вычислить предел
Это пример для самостоятельного решения. Помимо использования формулы, можно представить предел в виде и заменой свести решение к случаю .
В заключение рассмотрим пределы-«фальшивки».
Вернёмся к неопределённости . Данную неопределённость далеко не всегда можно свести к неопределённости и воспользоваться 2-м замечательным пределом либо формулой-следствием. Преобразование осуществимо в том случае, если числитель и знаменатель основания степени – эквивалентные бесконечно большие функции. На пример: .
Отвлечёмся от показателя и вычислим предел основания:
В пределе получена единица, значит, числитель и знаменатель не просто одного порядка роста, а ещё и эквивалентны. На уроке Замечательные пределы. Примеры решений мы без проблем свели данный пример к неопределённости и получили ответ.
Аналогичных пределов можно придумать очень много:
и т.д.
Дроби данных примеров объединяет вышеуказанная особенность: . В других случаях при неопределённости 2-й замечательный предел не применим.
Пример 21
Найти пределы
Как ни старайся, а неопределённость не удастся преобразовать в неопределённость
Здесь числители и знаменатели оснований одного порядка роста, но не эквиваленты: .
Таким образом, 2-й замечательный предел и, тем более формулу, ПРИМЕНИТЬ НЕЛЬЗЯ.
! Примечание: не путайте с Примером №18, в котором числитель и знаменатель основания не эквивалентны. Там готовая неопределённость , здесь же речь идёт о неопределённости .
Метод решения пределов-«подделок» прост и знакОм: нужно числитель и знаменатель основания разделить на «икс» в старшей степени (невзирая на показатель):
Если числитель и знаменатель основания разного порядка роста, то приём решения точно такой же:
Пример 22
Найти пределы
Это короткие примеры для самостоятельного изучения
Иногда неопределённости может не быть вообще:
Подобные фокусы особенно любимы составителями сборника Кузнецова. Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!
Завершая тотальное разоблачение пределов, я хочу поздравить всех посетителей сайта с новым 2013 годом! С подарком я успел, и постинг данной статьи осуществлен 31 декабря 2012 года. Вы спросите, а как же моя личная подготовка к празднику? Давно готов =) На протяжении многих лет я занимаюсь стратегическим планированием – чтобы не толкаться в очередях до и не пересекаться с краснокожими после =)
Берегите печень!
Решения и ответы:
Пример 2
Старшая степень числителя: 2; старшая степень знаменателя: 3.
Разделим числитель и знаменатель на :
Пример 4
Разделим числитель и знаменатель на :
Примечание: самым последним действием умножили числитель и знаменатель на , чтобы избавиться от иррациональности в знаменателе.
Пример 6
Разделим числитель и знаменатель на :
Пример 8
Разделим числитель и знаменатель на :
Примечание: слагаемое стремится к нулю медленнее, чем , поэтому является «главным» нулём знаменателя.
Пример 10
Пример 12
Умножим и разделим на сопряженное выражение:
Пример 13
Умножим и разделим на сопряженное выражение:
Разделим числитель и знаменатель на :
Пример 15
Проведём замену:
Если , то .
Пример 17
Проведём замену:
Если , то .
Далее используем формулу приведения , тригонометрическую формулу и первый замечательный предел:
Пример 20
Используем формулу
Пример 22
Примечание: бесконечно малая функция стремится к нулю медленнее, чем , поэтому «более большой» ноль знаменателя играет определяющую роль:
Емелин Александр
t-31.ru




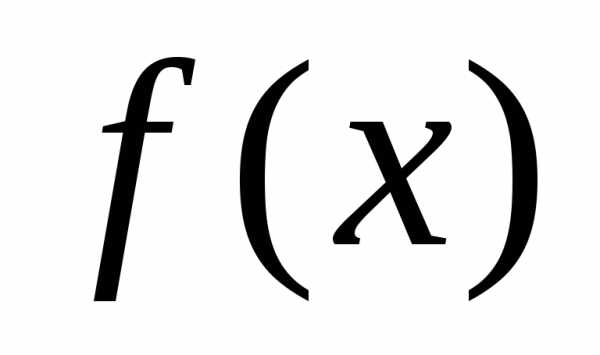 ,
определенная и бесконечно дифференцируемая
в окрестности точки
,
определенная и бесконечно дифференцируемая
в окрестности точки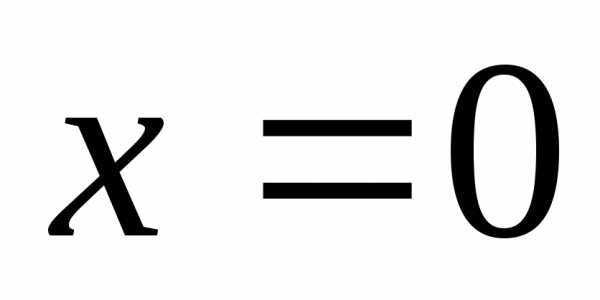 ,
может быть представлена в виде суммы
степенного ряда или, другими словами,
может быть разложена в степенной ряд
,
может быть представлена в виде суммы
степенного ряда или, другими словами,
может быть разложена в степенной ряд .
Найдем производные функции
.
Найдем производные функции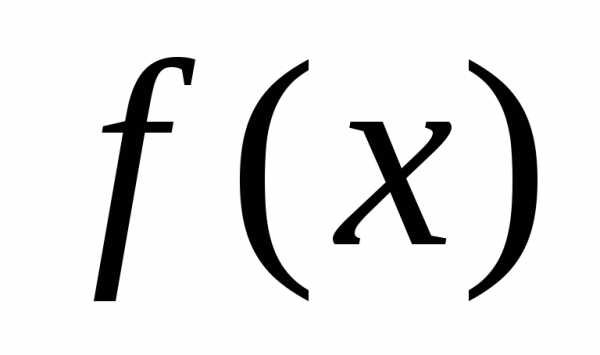 ,
почленно дифференцируя ряд
,
почленно дифференцируя ряд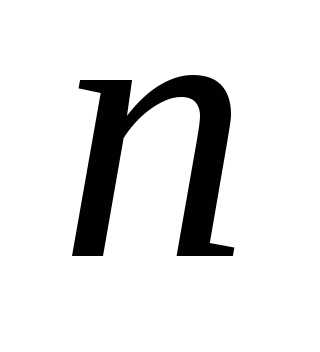 раз:
раз: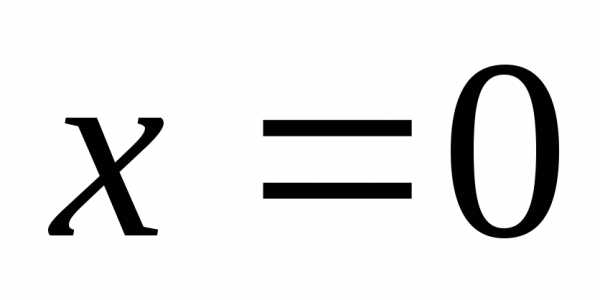 ,
получим
,
получим ,,,,
…,,
откуда
,,,,
…,,
откуда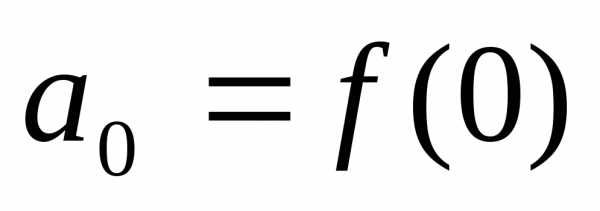 ,,
,,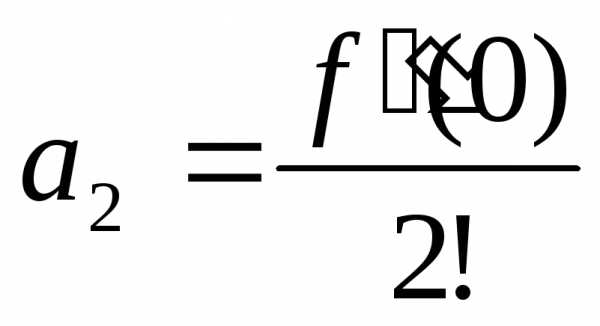 ,
,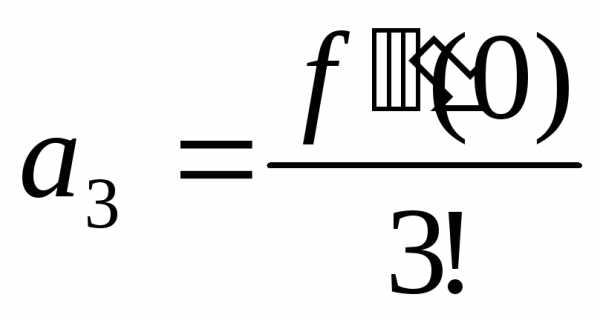 ,…,
,…,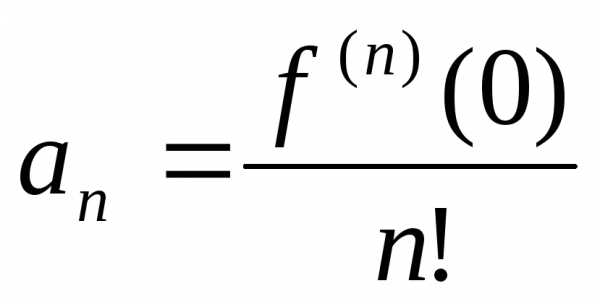 ,…
,… ,
является расходящимся или сходящимся
не к функции
,
является расходящимся или сходящимся
не к функции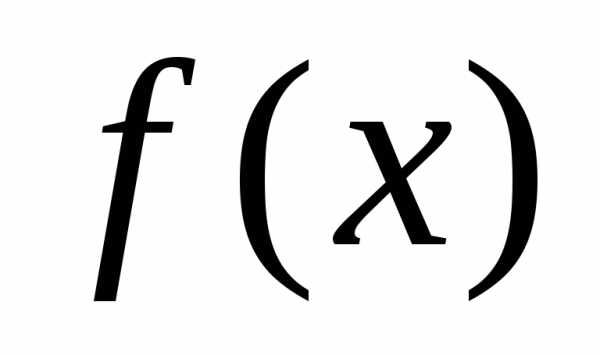 .
.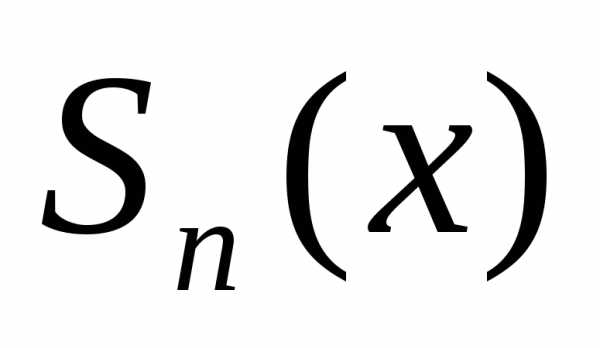 –
– 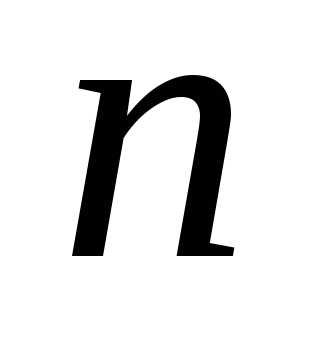 —я
частичная сумма ряда,
—я
частичная сумма ряда,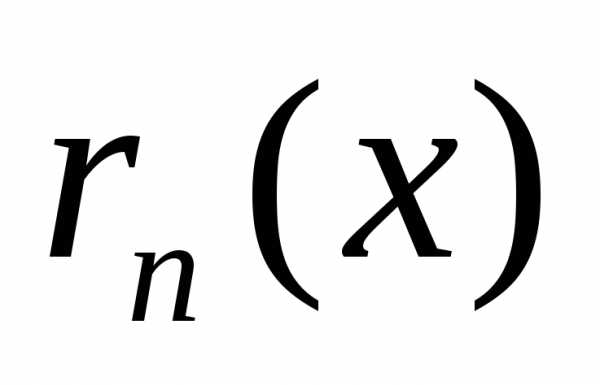 –
–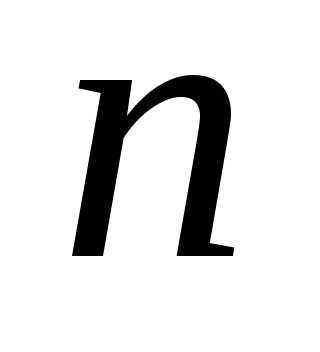 —й
остатокряда, то можно сформулировать
следующую теорему:
—й
остатокряда, то можно сформулировать
следующую теорему: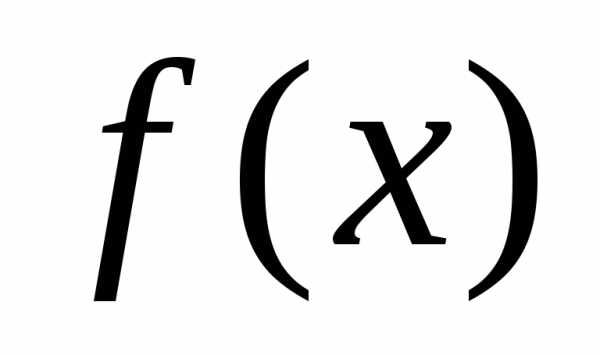 ,
необходимо и достаточно, чтобы приостаток ряда стремился к нулю, т.е.
,
необходимо и достаточно, чтобы приостаток ряда стремился к нулю, т.е. для всех значенийиз интервала сходимости ряда.
для всех значенийиз интервала сходимости ряда.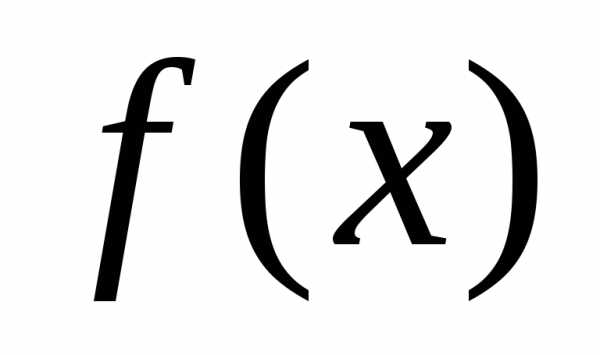 разложима в ряд Маклорена, то это
разложение единственное.
разложима в ряд Маклорена, то это
разложение единственное.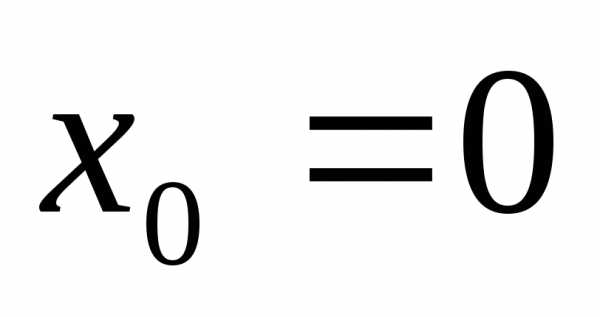
 – остаточный член формулы Тейлора,
который можно записатьв форме Лагранжа:
– остаточный член формулы Тейлора,
который можно записатьв форме Лагранжа: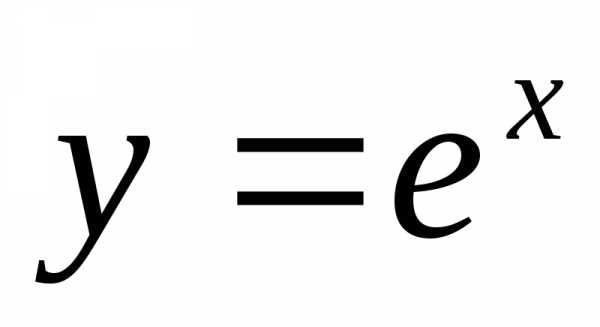
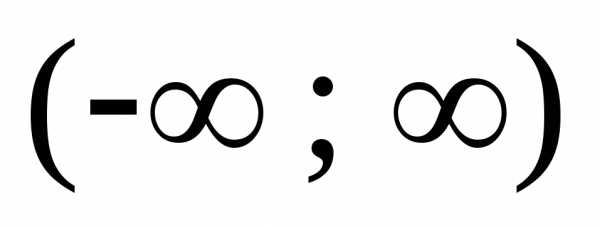 .
.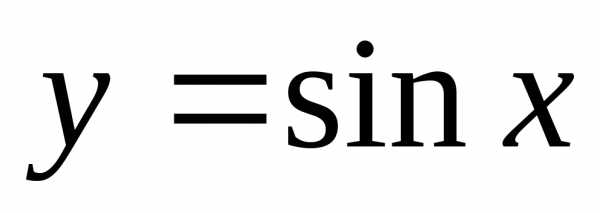
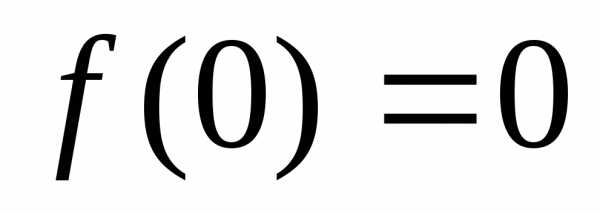 ,
,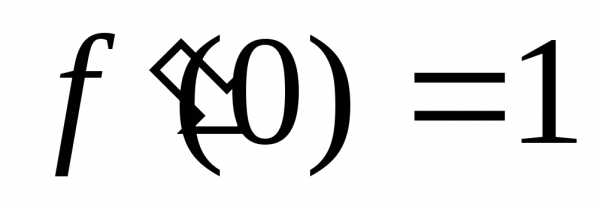 ,,,и т.д.
,,,и т.д. .
.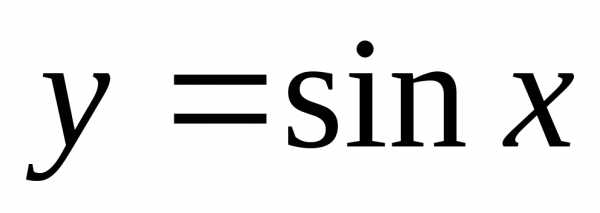 ,
получим:
,
получим: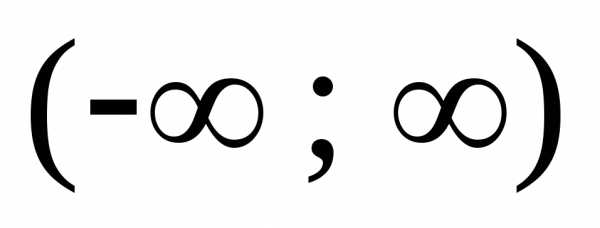 .
. – любое действительное число.
– любое действительное число.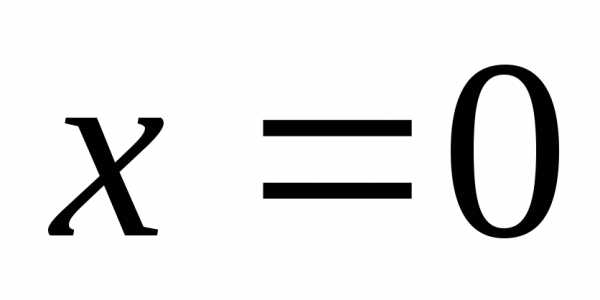 :
: ,,,
,,, .
На концах интервала при
.
На концах интервала при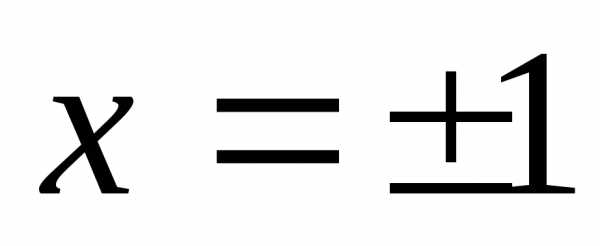 сходимость ряда зависит от конкретных
значений
сходимость ряда зависит от конкретных
значений .
. – целое положительное число, то
биномиальный ряд представляет формулубинома Ньютона, так как присомножительравен нулю, следовательно,
– целое положительное число, то
биномиальный ряд представляет формулубинома Ньютона, так как присомножительравен нулю, следовательно,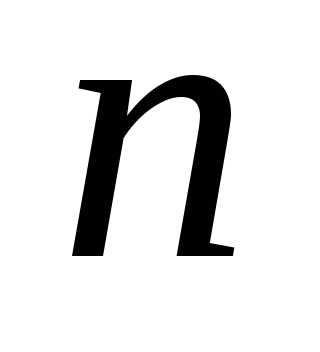 -й член ряда и все последующие равны
нулю, т.е. ряд обрывается, и вместо
бесконечного разложения получается
конечная сумма.
-й член ряда и все последующие равны
нулю, т.е. ряд обрывается, и вместо
бесконечного разложения получается
конечная сумма.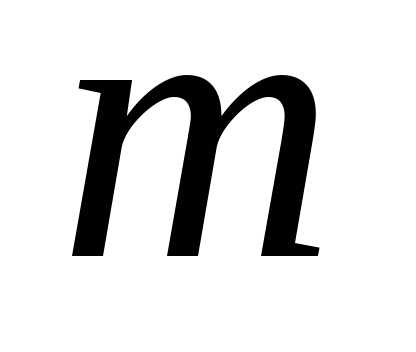 .
.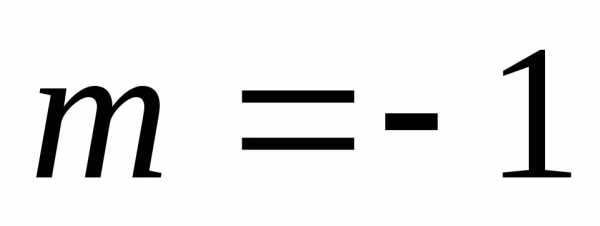 :
: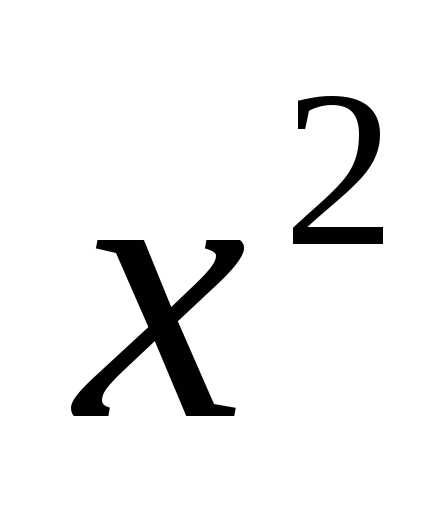 вместо
вместо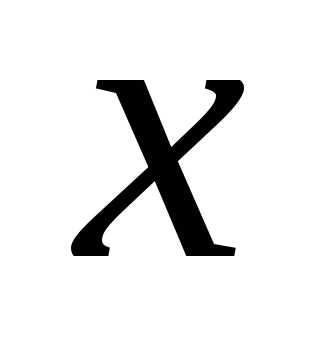 ,
получим:
,
получим: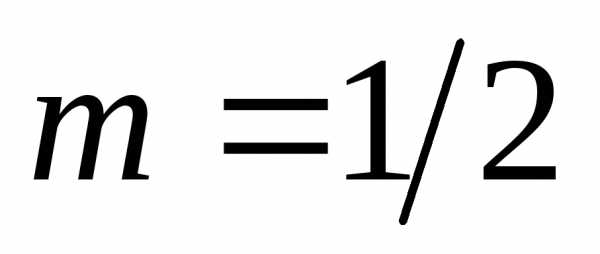 :
: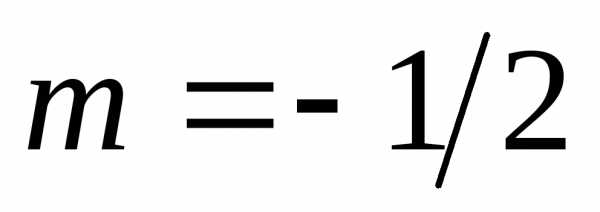 :
: ,
где
,
где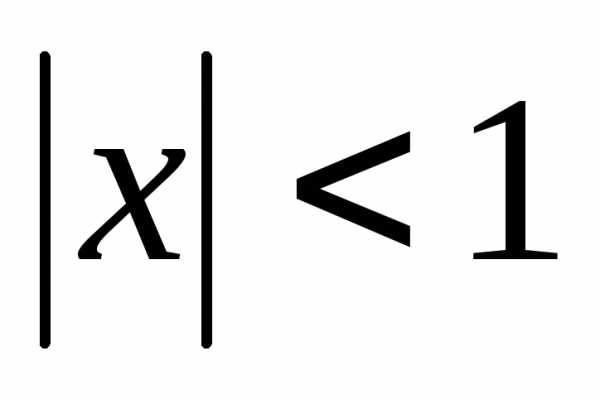 ,
с учетом того, что,
получим
,
с учетом того, что,
получим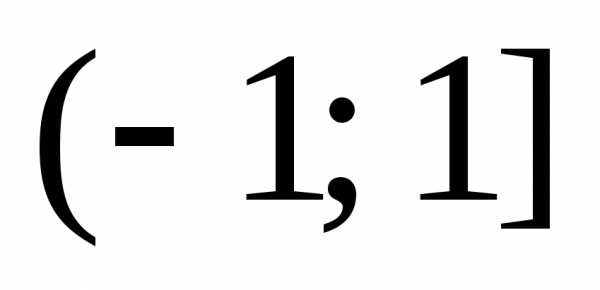 .
.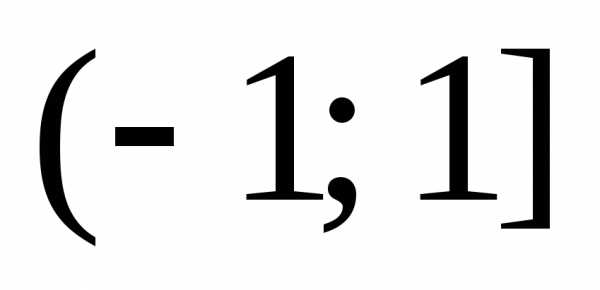 .
.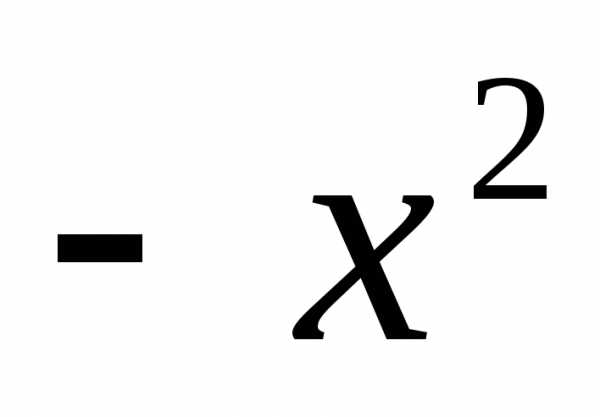 вместо
вместо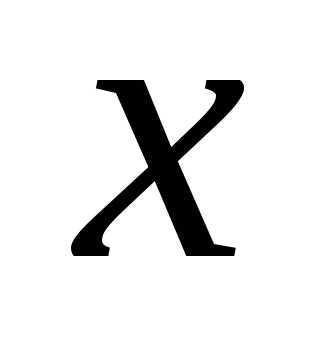 :
: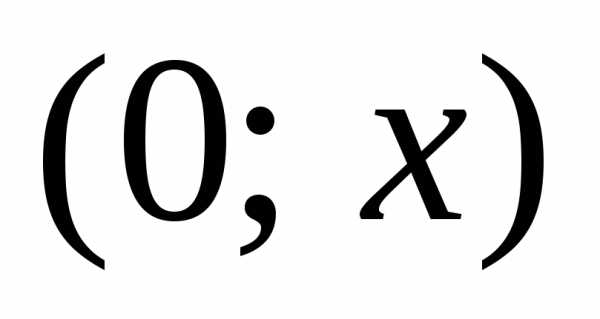 ,
где
,
где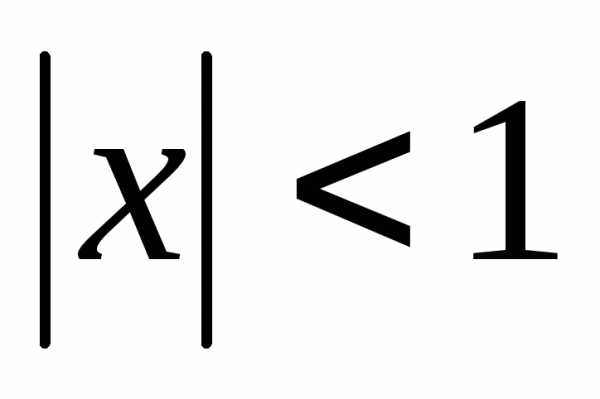 ,
получаем:
,
получаем: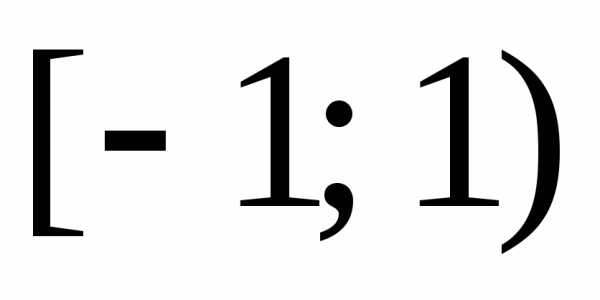
 ,
заменяя в разложении (4)
,
заменяя в разложении (4)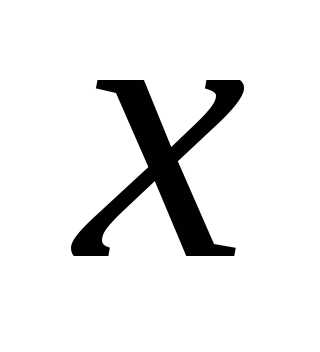 на
на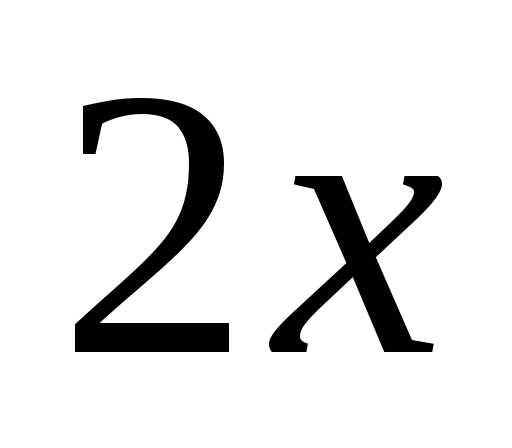 :
: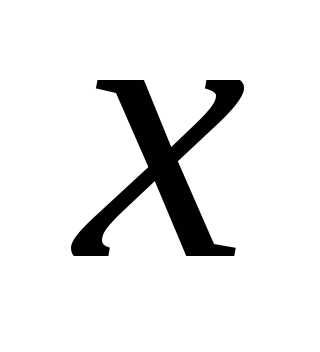 .
.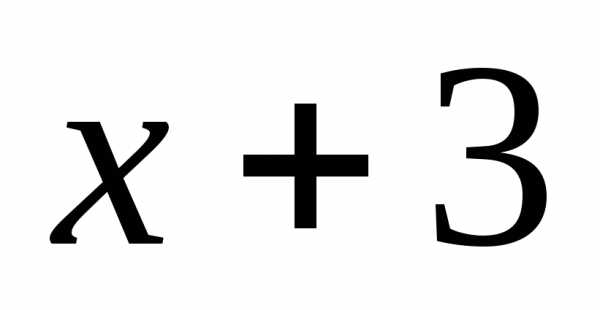 функцию
функцию
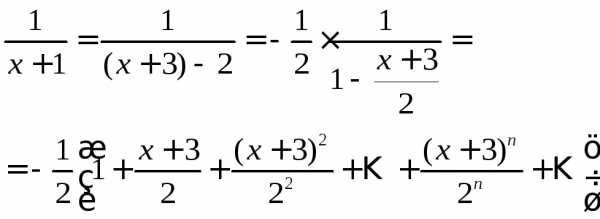
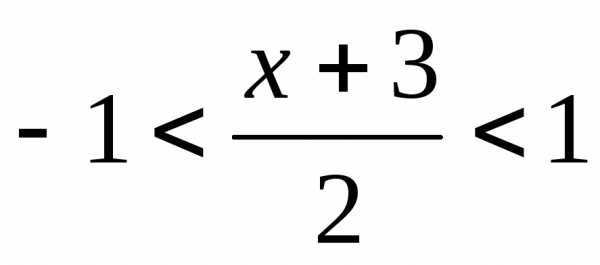 .
Отсюда получаемили.
.
Отсюда получаемили.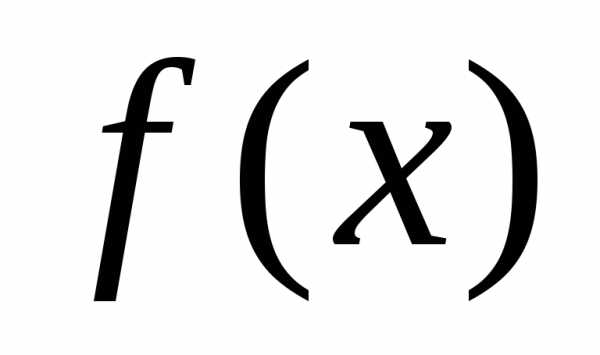 ,
имеющая на некотором отрезке производные
всех порядков, тогда она разлагается
на этом отрезке в ряд вида
,
имеющая на некотором отрезке производные
всех порядков, тогда она разлагается
на этом отрезке в ряд вида —
заданное число.
—
заданное число. имеет производные любого порядка. Однако
этот ряд будет сходиться к породившей
ее функции только при тех значениях
имеет производные любого порядка. Однако
этот ряд будет сходиться к породившей
ее функции только при тех значениях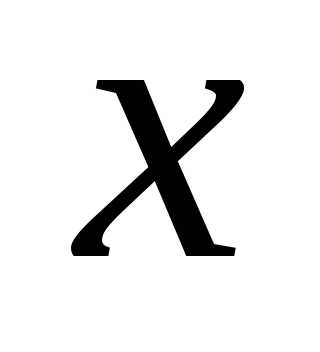 ,
при которых остаток ряда стремиться к
нулю:
,
при которых остаток ряда стремиться к
нулю: заключено между
заключено между и
и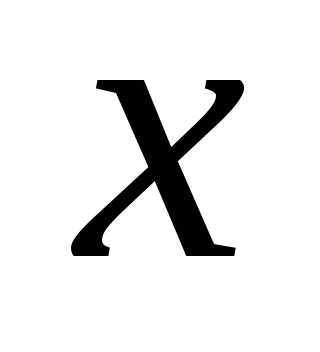 .
.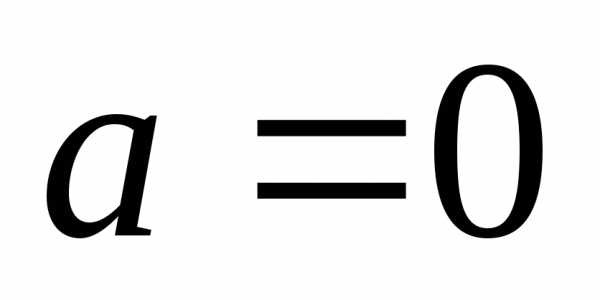 ,
то получаем частный случай ряда Тейлора,
который называетсярядом Маклорена:
,
то получаем частный случай ряда Тейлора,
который называетсярядом Маклорена: 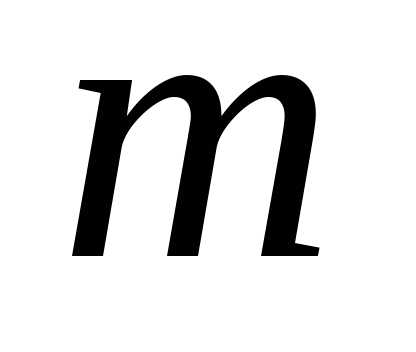 из
него получается бином Ньютона.
из
него получается бином Ньютона.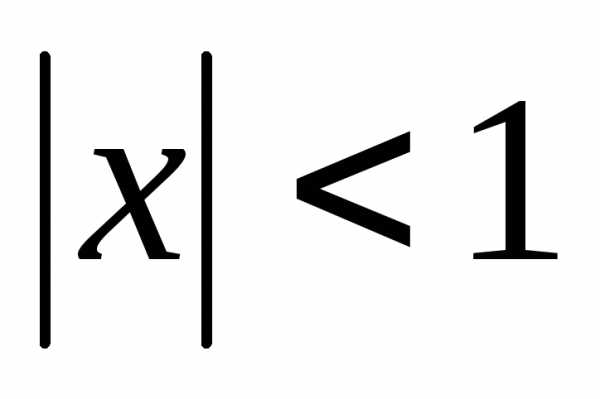 .
.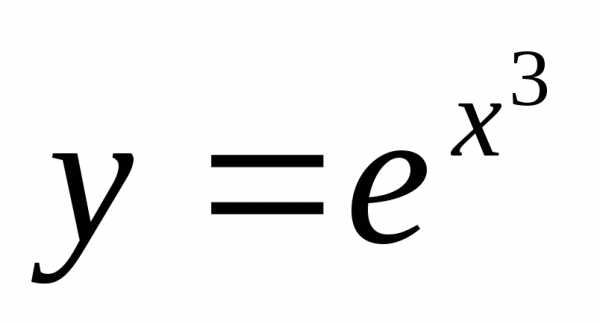 .
. :
: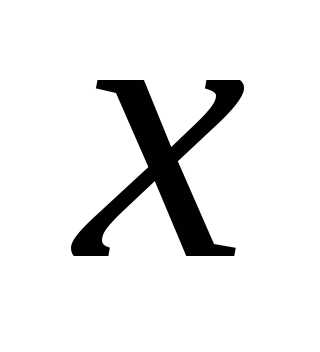 на
на :
: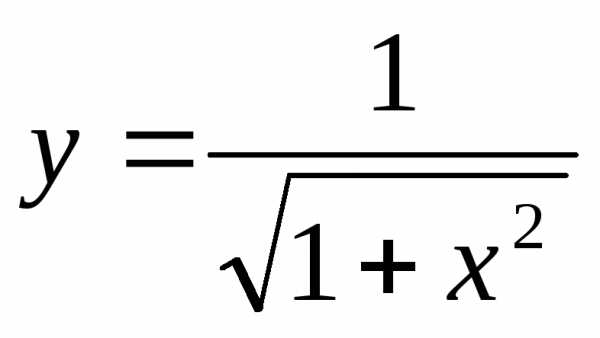 .
.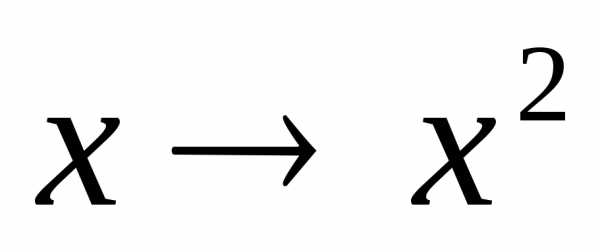 :
: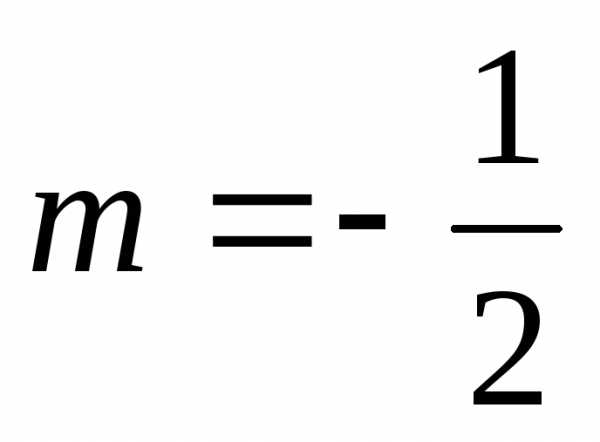 ,
подставим это значение в предыдущую
формулу:
,
подставим это значение в предыдущую
формулу: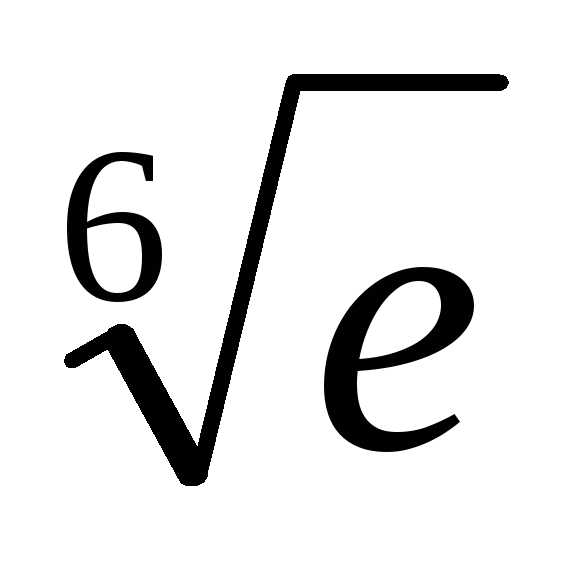 приближенно с точностью 0,0001.
приближенно с точностью 0,0001.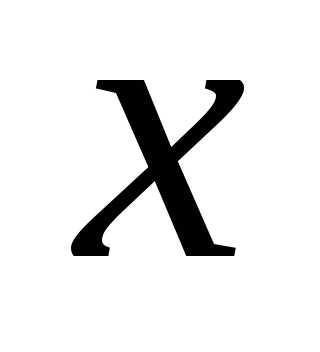 имеет место формула:
имеет место формула: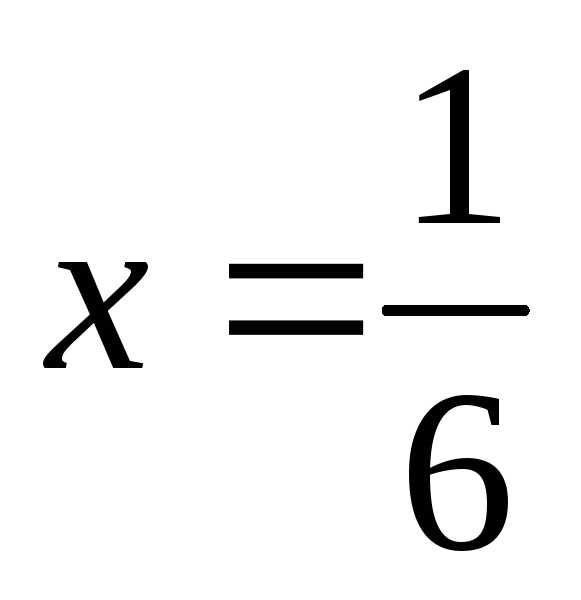 получим
получим .
.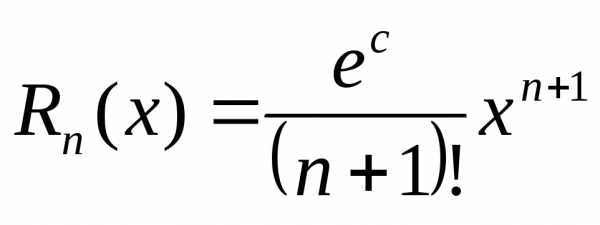 ,
, лежит между
лежит между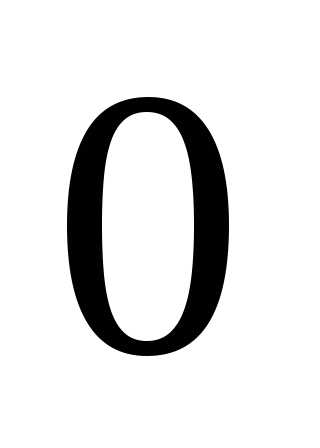 и
и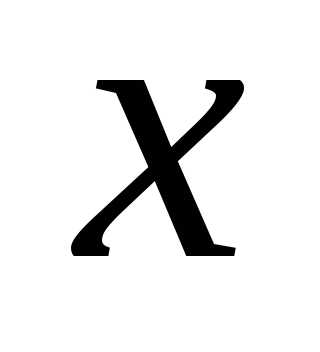 .
.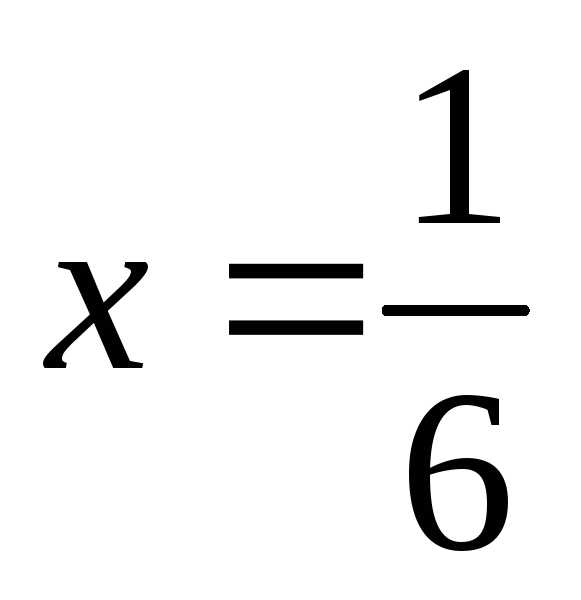 имеем
имеем .
.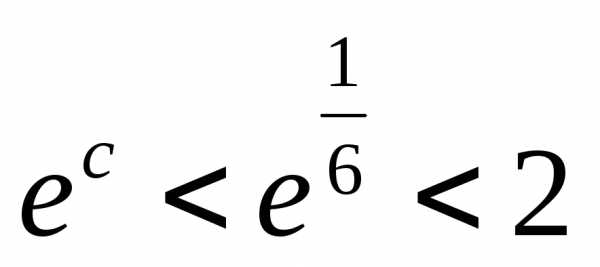 ,
получим
,
получим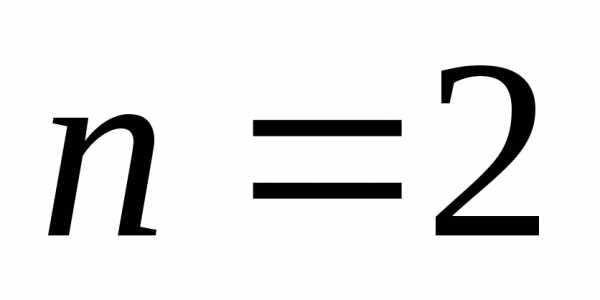
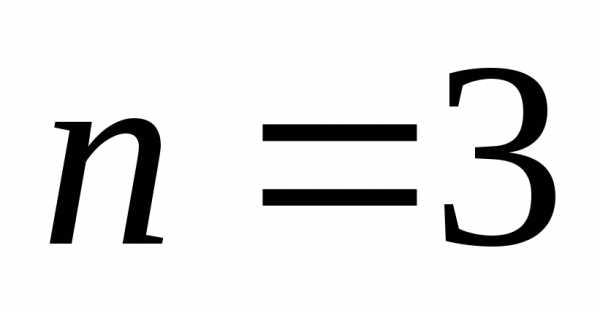
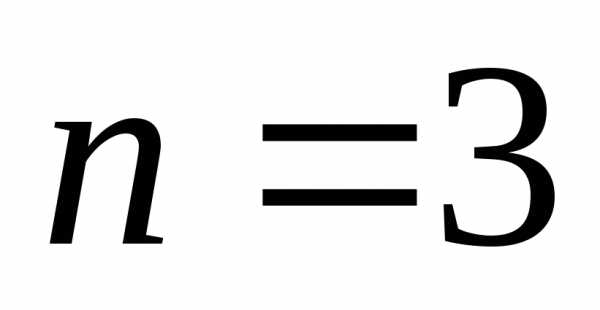 (или
более):
(или
более):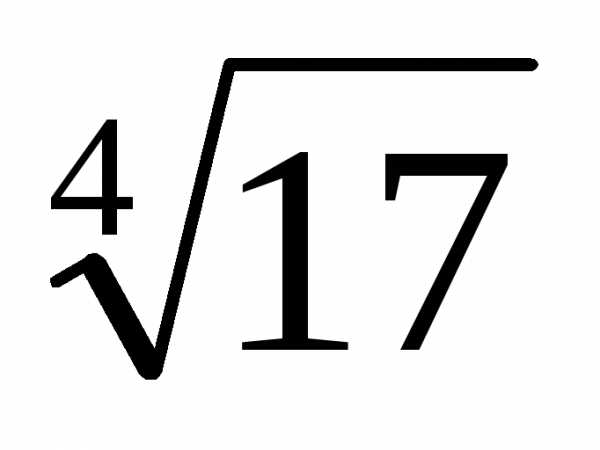 приближенно с точностью 0,0001.
приближенно с точностью 0,0001.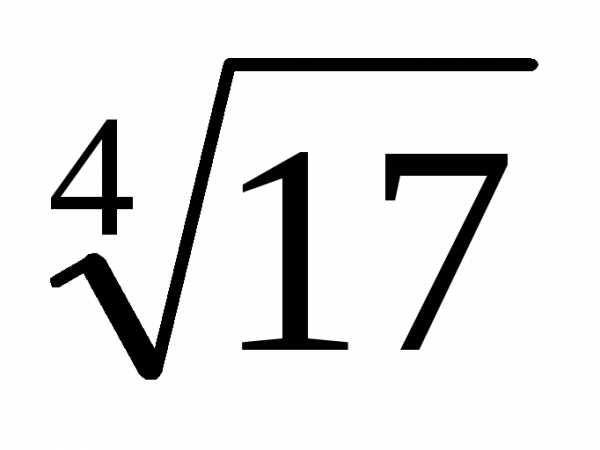 будем использовать биномиальный ряд,
который сходится только при
будем использовать биномиальный ряд,
который сходится только при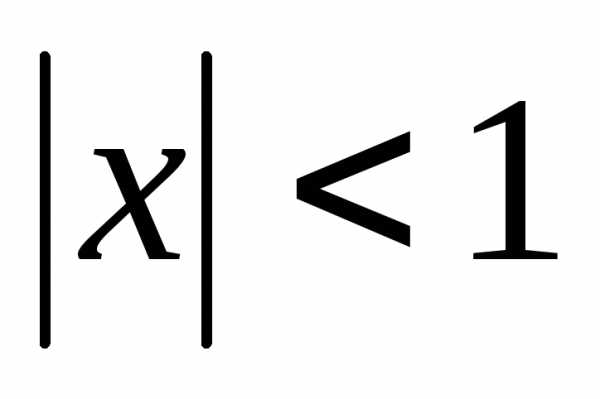 ,
поэтому сначала преобразуем данный
корень:
,
поэтому сначала преобразуем данный
корень: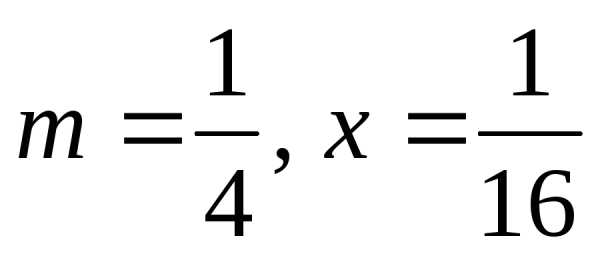 :
: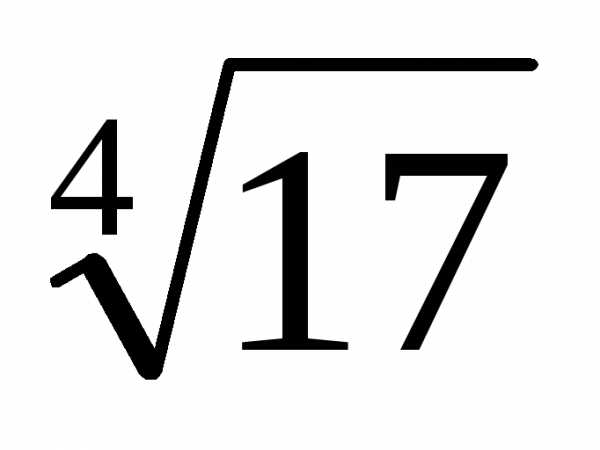 с
точностью 0,0001, вычислим последовательно
несколько первых членов ряда:
с
точностью 0,0001, вычислим последовательно
несколько первых членов ряда: :
:
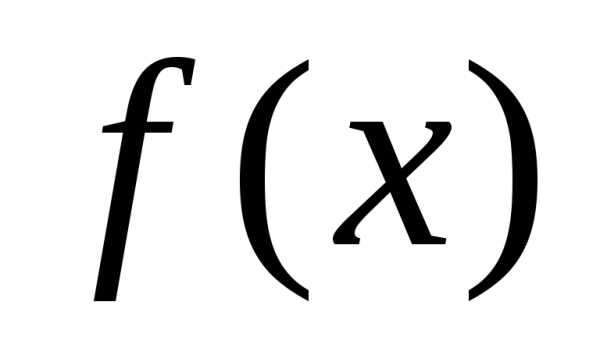 ,
первообразная которой не вычисляется
в элементарных функциях. Следовательно,
формулу Ньютона-Лейбница применить не
удается. Если
,
первообразная которой не вычисляется
в элементарных функциях. Следовательно,
формулу Ньютона-Лейбница применить не
удается. Если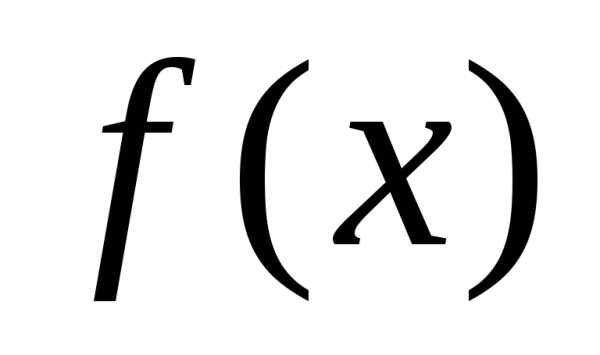 разложима в степенной ряд на отрезке
разложима в степенной ряд на отрезке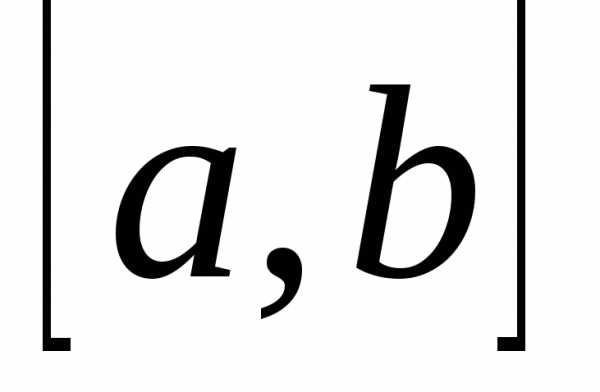 ,
принадлежащем области сходимости ряда,
то интеграл может быть вычислен
приближенно. Иногда приближенного
вычисления бывает достаточно и при
наличии первообразной функции. Для
решения такой задачи используются
ряды Тейлора. Рассмотрим примеры.
,
принадлежащем области сходимости ряда,
то интеграл может быть вычислен
приближенно. Иногда приближенного
вычисления бывает достаточно и при
наличии первообразной функции. Для
решения такой задачи используются
ряды Тейлора. Рассмотрим примеры.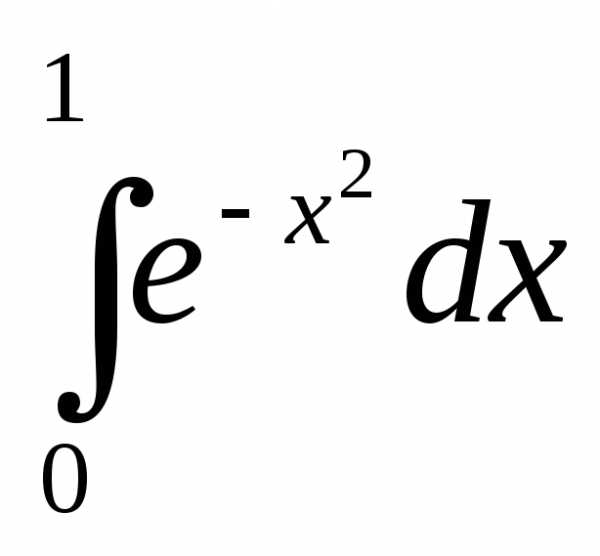 с точностью 0,01.
с точностью 0,01.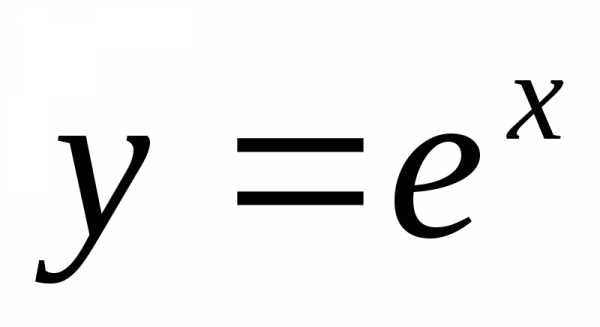 сделаем
замену
сделаем
замену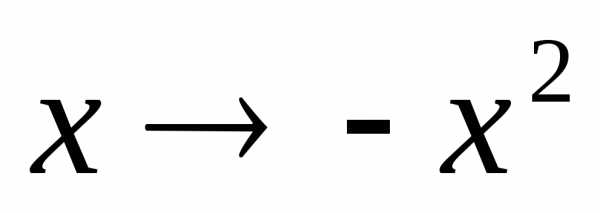 :
: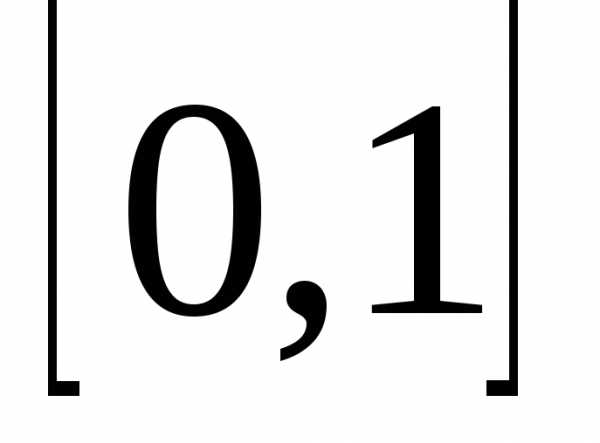 :
: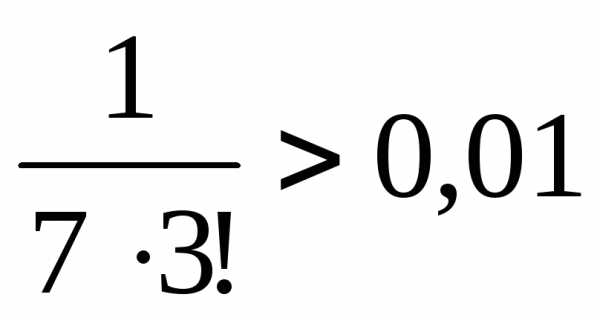 ,
,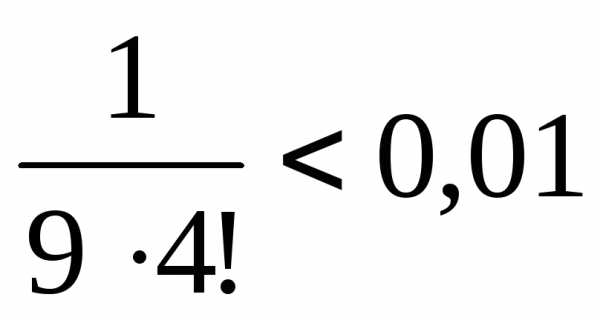 .
. 024=0,743.
024=0,743.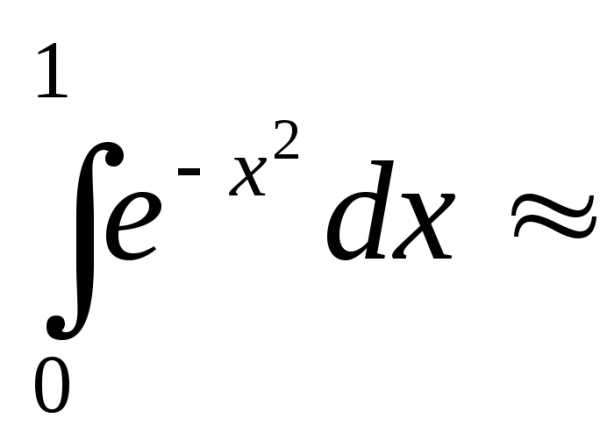 0,743.
0,743. с точностью 0,001.
с точностью 0,001.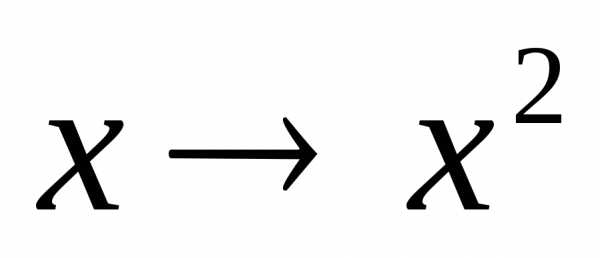 :
: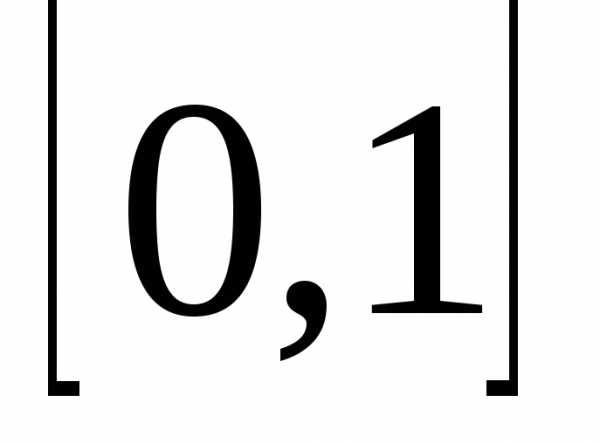 :
: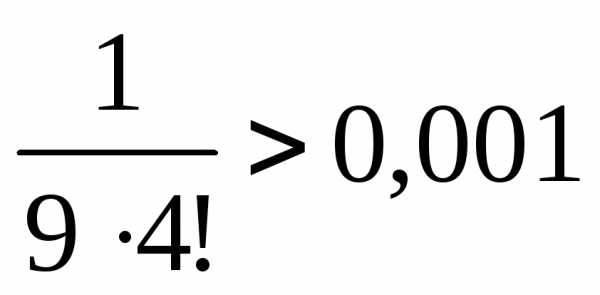 ,
,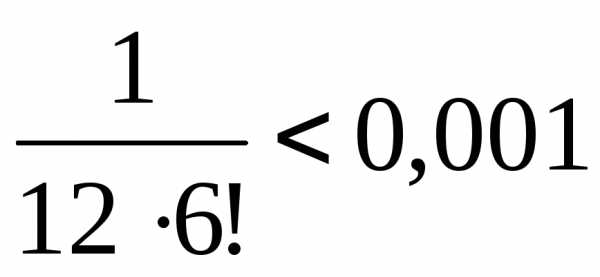 .
. .
.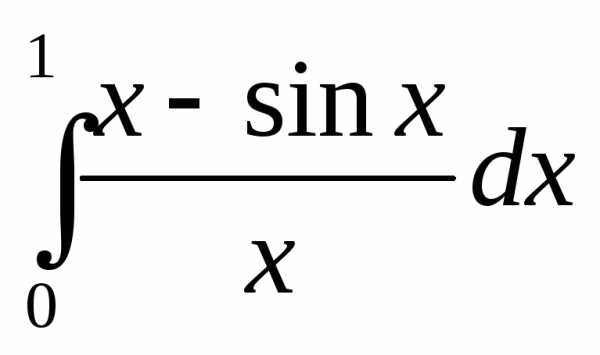 с точностью 0,001.
с точностью 0,001.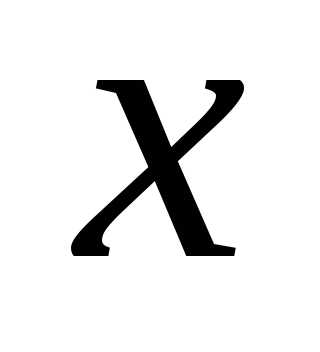 :
: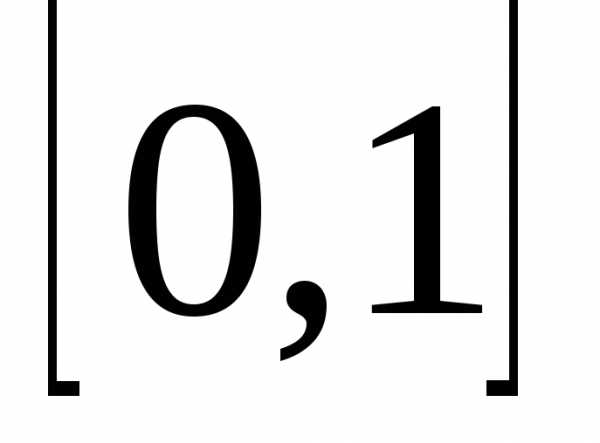 .
.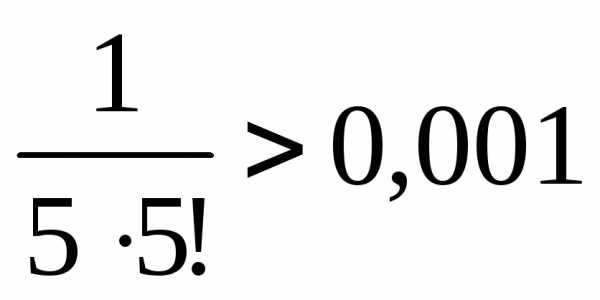 ,
, .
.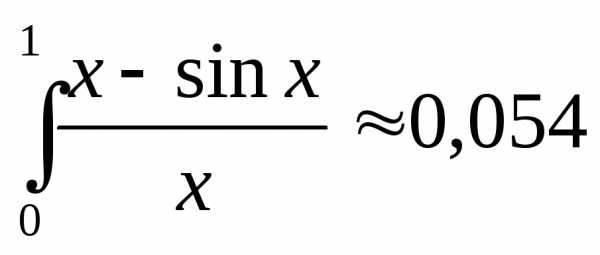 .
.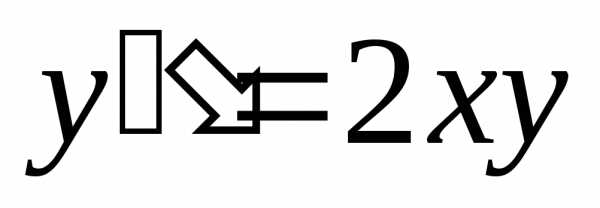 ,
удовлетворяющего начальным условиям
,
удовлетворяющего начальным условиям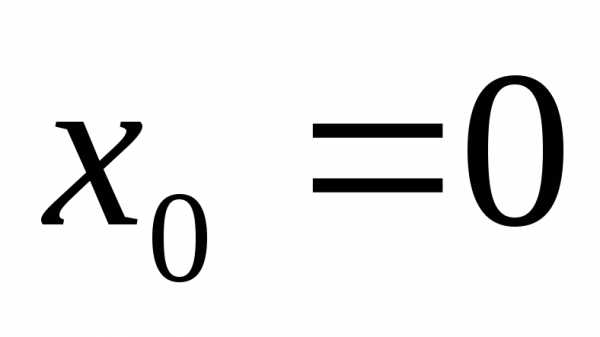 .
Для того, чтобы найти приближенное
значение функции
.
Для того, чтобы найти приближенное
значение функции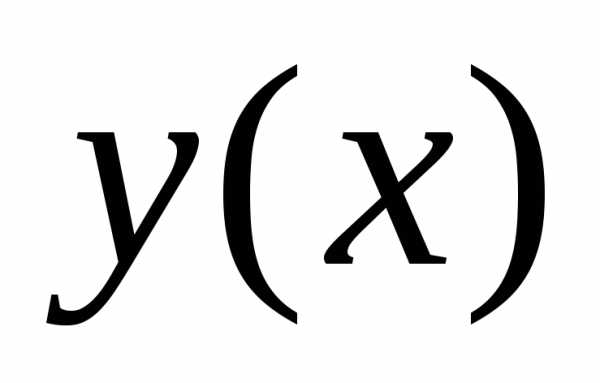 ,
нам необходимо знать значения ее второй,
третьей и четвертой производных в точке
,
нам необходимо знать значения ее второй,
третьей и четвертой производных в точке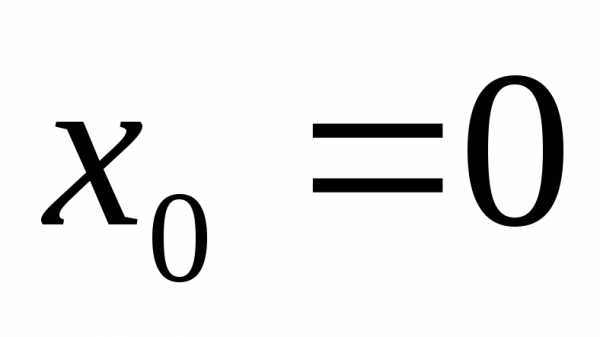 .
Значения самой функции и первой
производной в нуле даны по условию.
.
Значения самой функции и первой
производной в нуле даны по условию.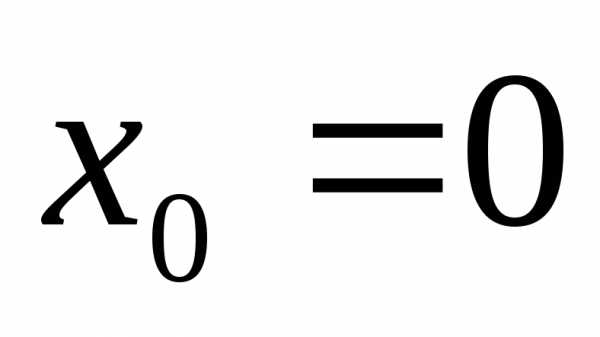 найдем из дифференциального уравнения,
подставив начальные условия:
найдем из дифференциального уравнения,
подставив начальные условия: —
это функция, а
—
это функция, а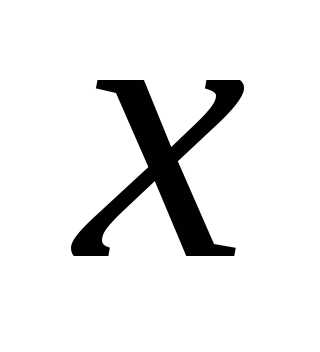 —
независимая переменная:
—
независимая переменная: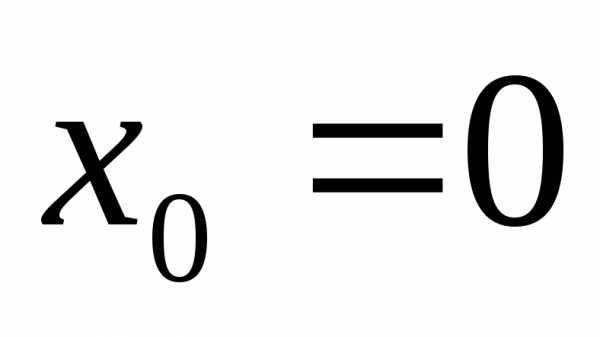 :
: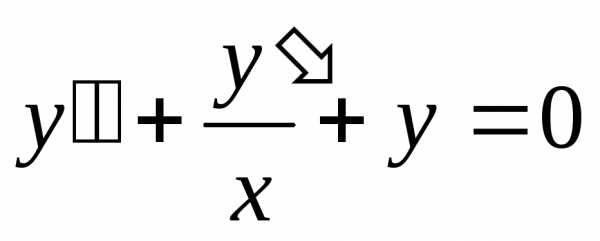 ,
удовлетворяющего начальным условиям
,
удовлетворяющего начальным условиям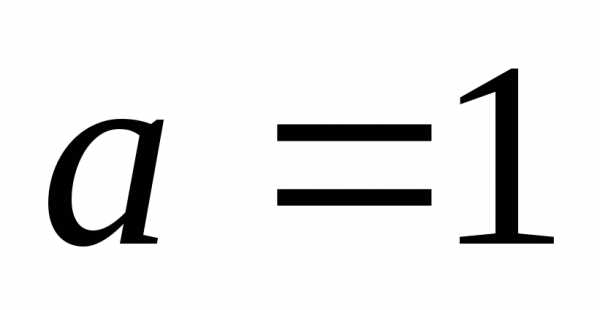 найдем
из дифференциального уравнения:
найдем
из дифференциального уравнения: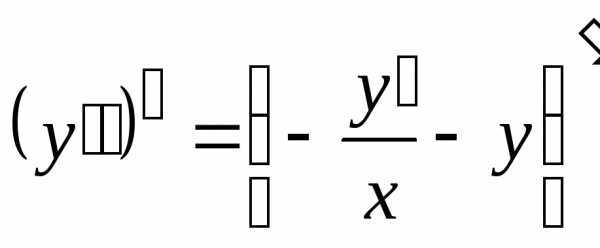 или
или 22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)
22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)
 22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)
22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)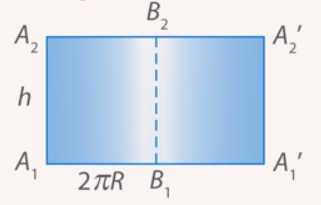
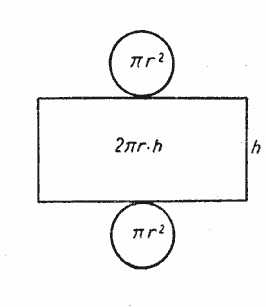
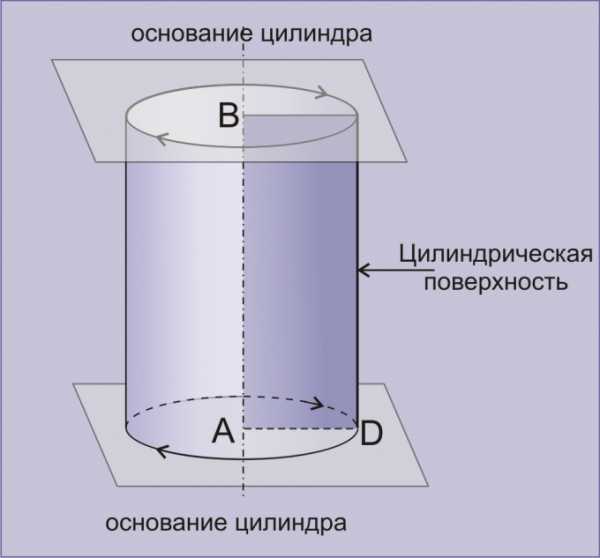
 Теперь определим площадь основания. Площадь круга, как нам тоже известно из школьной геометрии, определяется по формуле:
Теперь определим площадь основания. Площадь круга, как нам тоже известно из школьной геометрии, определяется по формуле: Стороны прямоугольника, которые пересекаются с окружностью, помечаем карандашом или маркером и соединяем прямой линией. В нашем случае это вершины треугольника В и С. Этот отрезок и есть диаметр нашей окружности. Радиус окружности равен половине ее диаметра. Делим отрезок ВС на две части. Центром окружности является точка О. Отрезки ОВ и ОС равны и являются радиусом основания данного цилиндра. Теперь подставляем полученные значения в формулу:
Стороны прямоугольника, которые пересекаются с окружностью, помечаем карандашом или маркером и соединяем прямой линией. В нашем случае это вершины треугольника В и С. Этот отрезок и есть диаметр нашей окружности. Радиус окружности равен половине ее диаметра. Делим отрезок ВС на две части. Центром окружности является точка О. Отрезки ОВ и ОС равны и являются радиусом основания данного цилиндра. Теперь подставляем полученные значения в формулу: