Учебно-методический материал (математика, 1 класс) на тему: логические задачи по математике
Логические задачи на уроках математики
Пояснительная записка
«Интеллектуализация» образования становится приоритетным направлением в педагогике и процессе формирования общелогических умений – одна из важнейших задач начального обучения. Умение мыслить логически, выполнять умозаключения без наглядной опоры, составлять суждения по определенным правилам – необходимое условие успешного усвоения учебного материала. Систематическое использование на уроках математики специальных заданий, направленных на развитие логического мышления, расширяет математический кругозор младших школьников, более уверенно ориентироваться в простейших закономерностях окружающей действительности, активнее использовать математические знания в повседневной жизни.
Основная направленность пособия ориентировано на развитие компетенций в области математики младших школьников с учетом психолого– физиологических особенностей их развития.
Пособие содержит разнообразные виды заданий: задачи – шутки, логические задачи, логические упражнения, «волшебные» квадраты, задачи с геометрическим содержанием.
Задания можно использовать на каждом уроке математики в качестве дополнительного материала, во внеклассной работе, для самостоятельных занятий.
Данное пособие предназначено для учителей начальных классов.
Логические задачи.
1. Поезд состоит из 12 вагонов. Марат сел в 6 по счёту вагон с головы поезда, а Андрей сел в 6 вагон по счёту с хвоста поезда. В одном ли вагоне ехали Марат и Андрей?
2. У трёх девочек по 2 цветных шара: у Оли синий и красный, у Кати зелёный и красный, у Ланы жёлтый и синий. Сколько различных по цвету шаров у детей?
3. Карина гуляла и видела у реки 4 уток, 2 гусей, жука, 4 бабочки и соседскую собаку. Сколько птиц видела Карина?
4. Лестница состоит из 9 ступенек. На какую ступеньку надо встать, чтобы быть на середине лестницы?
5. Мама дала сыновьям по 8 конфет. Вечером у старшего осталось 3 конфеты, а у младшего — 1 конфета. Кто съел больше?
6. Арбуз и дыня вместе весят 5 кг, а два арбуза и дыня весят 8 кг. Сколько весит один арбуз и одна дыня?
7.Два третьеклассника шли в школу во вторую смену. Они встретили трёх первоклассников – учеников первой смены. Сколько всего учеников шли в школу?
8.У брата и сестры было орехов поровну. Брат отдал сестре 3 ореха. На сколько орехов стало больше у сестры, чем у брата.
9.Руслан старше Андрея. Кирилл моложе Саши, но старше Руслана. Кто из них самый старший и самый младший?
10.Во дворе гуляли собаки и куры. Всего 10 лап. Сколько могло быть кур и сколько собак. Сколько вариантов ответа?
11.Колю угостили конфетами. Половину конфет он съел, а оставшиеся 5 конфет отнёс брату. Сколько конфет дали Коле?
12. Маме нужно засадить саженцами помидоров ряд длиной 3 м. Расстояние между саженцами 30 см. Сколько саженцев помидоров надо заготовить для посадки?
13. Толя, Шурик и Антон были на рыбалке. Каждый из них поймал разное количество рыб. Толя и Шурик вместе поймали 6 рыб, а Антон и Толя – 4 рыбы. Сколько рыб поймал каждый из мальчиков?
14. На уроке физкультуры дети выстроились в одну шеренгу с интервалом 1 м. Шеренга растянулась на 20 м. Сколько детей было на уроке?
15. Из красных и жёлтых тюльпанов Ира хочет составить букет так, чтобы в нём было 3 цветка. Сколько разных букетов может составить Ира?
16.Арбуз весит 3 кг и ещё половину арбуза. Сколько весит арбуз?
17. Масса бидона с молоком составляет 34 кг, а масса бидона, наполненного наполовину, равна 18 кг. Какова масса пустого бидона?
18. Как взвесить 4 кг сахара, если имеются гири 3 кг и 5 кг?
19. На одной чаше весов находится 5 одинаковых яблок и 3 одинаковые груши, на другой чаше – 4 яблока и 4 груши. Что легче: яблоко или груша?
20. Мама закупила продукты: 1 кг соли, 2 кг гречки, 3 кг риса, 4 кг сахара, 5 кг моркови, 6 кг лука, 7 кг картофеля. Как разложить продукты в два пакета, чтобы их масса была одинаковая.
21. На день рождения Винни-Пуху подарили бочонок с мёдом массой 7 кг. Когда Винни-Пух съел половину мёда, то бочонок с оставшимся мёдом стал весить 4 кг. Какова масса пустого бочонка?
22.Рыбак поймал 29 рыб. Из них карасей на 3 больше, чем щук. Сколько карасей и сколько щук поймал рыбак?
23. Через 7 лет Данил будет вдвое старше, чем сейчас. Сколько лет Данилу сейчас? Сколько лет будет через 7 лет?
24. Магазин при 12-часовом рабочем дне работает с 8 часов до 21 часа. Закрывают ли магазин на обеденный перерыв?
25. Аскар дал младшему брату половину своих яблок и ещё одно яблоко, и у него не осталось ни одного яблока. Сколько яблок было у Аскара?
26. Длина спички 5 см. Как из 13 спичек сложить метр?
27. Сара провела у бабушки понедельник, вторник, среду и четверг, а её младшая сестра в ту же неделю – среду, четверг, пятницу и субботу. Сколько всего дней гостили девочки у бабушки?
28. В автобусе ехало7 человек. На первой остановке вышло 3 пассажира, а село 12. На следующей — вышли 9 человек, зашли 5. Далее – вышли 7, зашли 8. Сколько было остановок?
29. В магазин привезли 6 мешков сахара по 50 кг, 8 мешков муки по 25 кг, 4 мешка риса по 10 кг, 2 мешка пшена по 12 кг. Сколько мешков с продуктами привезли?
30. Автобус с Кушмуруна до Костаная едет 2 часа 10 минут, а обратно – 130 минут. Объясни, почему?
31. Сколько различных трёхзначных чисел можно записать тремя различными цифрами?
23. Через 7 лет Данил будет вдвое старше, чем сейчас. Сколько лет Данилу сейчас? Сколько лет будет через 7 лет?
24. Магазин при 12-часовом рабочем дне работает с 8 часов до 21 часа. Закрывают ли магазин на обеденный перерыв?
25. Аскар дал младшему брату половину своих яблок и ещё одно яблоко, и у него не осталось ни одного яблока. Сколько яблок было у Аскара?
26. Длина спички 5 см. Как из 13 спичек сложить метр?
27. Сара провела у бабушки понедельник, вторник, среду и четверг, а её младшая сестра в ту же неделю – среду, четверг, пятницу и субботу. Сколько всего дней гостили девочки у бабушки?
28. В автобусе ехало7 человек. На первой остановке вышло 3 пассажира, а село 12. На следующей — вышли 9 человек, зашли 5. Далее – вышли 7, зашли 8. Сколько было остановок?
29. В магазин привезли 6 мешков сахара по 50 кг, 8 мешков муки по 25 кг, 4 мешка риса по 10 кг, 2 мешка пшена по 12 кг. Сколько мешков с продуктами привезли?
30. Автобус с Кушмуруна до Костаная едет 2 часа 10 минут, а обратно – 130 минут. Объясни, почему?
31. Сколько различных трёхзначных чисел можно записать тремя различными цифрами?
32. Две соседки измеряли длину своих дачных участков. Первая, измеряя длину, поставила 7 колышков через каждые 2 метра, вторая поставила 13 колышков через каждый метр. У кого участок длиннее?
33. Как, пользуясь банками в 3 л и 5 л, из крана набрать 1 л воды?
34. На сколько больше наименьшее двузначное число, чем наибольшее однозначное?
35. Как разложить 15 карандашей в 5 коробок так, чтобы во всех коробках было разное количество карандашей?
36. В 3 часа стенные часы отбивают три удара за 6 секунд. За сколько секунд эти часы отобьют шесть ударов в 6 часов?
37. Поставьте двух мальчиков так, чтобы Вова стоял сзади Нияза, а Нияз — сзади Вовы.
38. Моей сестре сегодня исполнилось 6 лет. Когда она родилась, мне было 3 года 6 месяцев. Сколько лет мне теперь?
39. Врач дал больному 3 таблетки и велел принимать их через каждые полчаса. Больной строго выполнил указания врача. На сколько времени хватило таблеток?
40. Белочка насушила на зиму 5 целых яблок, 10 половинок и 8 четвертинок. Сколько всего яблок у белочки?
41. Если один петух закукарекает, то человек проснётся. Сколько петухов должны закукарекать, чтобы проснулись три человека?
42. Брату и сестре вместе 10 лет. Сколько лет им будет вместе через пять лет?
43. Дамир принёс в класс 3 чистые тетради в линейку, Ваня – 6 тетрадей в клетку, а Серёжа забыл принести тетради. Ребята разделили все тетради поровну, каждый из них получил по одной тетради в линейку и по две тетради в клетку. На следующий день Серёжа принёс ребятам 45 тенге за тетради. Как должны разделить деньги между собой Дамир и Ваня, если цена тетрадей в клетку и в линейку одинаковая?
44. Вы зашли в тёмную комнату, где есть свеча, газовая плита, керосиновая лампа. Что вы зажжёте в первую очередь?
45. К празднику ученики должны украсить площадь прямоугольной формы 12 флажками так, чтобы было со всех сторон по 4 флажка. Как это сделать?
46. Как наполнить ведро три раза подряд, ни разу не опусташая?
47. В семье несколько детей. Один ребёнок говорит, что у него есть один брат и две сестры. Другой ребенок говорит, что у него одна сестра и два брата. Сколько детей в семье, девочек и мальчиков?
48.По улице шли два отца и два сына, да дедушка с внуком. Сколько всего человек шло по улице?
49. У тебя монеты по 20 тенге. У продавца только монеты по 50 тенге. Как расплатиться за булку хлеба ценой 50 тенге.
50. Бабушке и внуку вместе 65 лет. Бабушке столько лет, сколько месяцев внуку. Сколько лет бабушке и сколько внуку?
Ответы:
1. Марат и Андрей ехали в разных вагонах.
2. 4 разных цвета.
3. 6 птиц
4. На 5 ступеньку.
5. Младший сын.
6. Арбуз 3 кг, дыня 2 кг
7. 2 ученика.
8. На 6 орехов.
9. Старший – Саша, младший – Андрей.
10. 1 собака и 3 курицы или 2 собаки и 1 курица.
11. 10 конфет.
12. 11 саженцев.
13. Толя – 1 рыбу, Шурик – 5 рыб, Антон – 3 рыбы.
14. 21 ученик.
15. 4 букета.
16. 6 кг
17. 2 кг
18.
19. Масса яблока и груши одинакова.
20. По 14 кг в каждый пакет (несколько вариантов)
21. 1 кг
22. 16 карасей и 13 щук.
23. Сейчас 7 лет, будет 14.
24. Перерыв 1 час.
25. 2 яблока.
26. Сложить слово «метр».
27. 6 дней.
28. 3 остановки.
29. 20 мешков.
30. 2 ч 10 мин = 130 мин
31. 6 чисел.
32. Участки одинаковы.
33.
34. На 1
35. 1,2,3,4,5 карандашей.
36. 15 сек.
37. Спиной друг к другу.
38. 9 лет 6 месяцев.
39. На 1 час.
40. 12 яблок.
41. Один петух.
42. 20 лет.
43. 45 тенге Ване.
44. Спички.
45. По углам флажки и по 2 флажка с каждой стороны.
46. Первый раз наполнить камнями, второй – песком, третий – водой.
47. 4 детей: 2 мальчика и 2 девочки.
48. 3 человека.
49. 5 монет по 20 тенге, сдача – 50 тенге.
50. 60 лет бабушке, 5 лет внуку.
Задачи на логику. 1 класс А
- Бабушка связала Нине две пары носков. Сколько носков связала бабушка Нине?
- По двору ходят куры. У всех кур Петя насчитал 6 ног. Сколько кур?
- У Толи 2 пары варежек. Сколько варежек на левую руку?
- Какое число самое маленькое?
- В семье четверо детей: сестёр столько же, сколько братьев и сестёр. Сколько сестёр?
- Из бочки взяли 2 раза по 2 полных ведра воды. Сколько вёдер воды взяли?
- В корзине сидят котята. У всех котят 3 пары ушек. Сколько котят в корзине?
- На горке катались 6 ребят. Двое ушли обедать, но после обеда вернулись на горку. Сколько ребят стало на горке?
- У паука 4 пары ног. Сколько всего ног у паука?
- У Юры 3 кубика, а у Серёжи 2 кубика. На столе стоит коробка, в которой умещается 4 кубика. Смогут ли мальчики уложить в эту коробку все свои кубики?
- У жука 3 пары ног. Сколько всего ног у жука?
- На кусте утром было 8 бутонов. К середине дня все бутоны распустились и стали красивыми розами. Сколько бутонов осталось на этом кусте нераскрытыми?
- В пакете лежат красные и жёлтые яблоки. Из пакета взяли 4 красных и 5 жёлтых яблок, и пакет опустел. Сколько яблок было в пакете?
- Дима выиграл у Алёши 2 партии в шахматы, а Алёша выиграл 3 партии. Сколько партий сыграли мальчики?
- Каждый из троих взрослых ведёт за руку двоих детей. Сколько детей идут со всеми взрослыми?
- Сколько целых батонов можно хлеба можно составить из шести половинок?
- По дороге один за другим идут 5 детей. За каждым мальчиком, кроме последнего, идёт девочка. Сколько девочек идут по дороге?
- Я придумала два числа. Когда я их сложила, то получила 6. Когда же из одного вычла другое, то снова получила 6. Что же это за числа?
- В коробке 8 пирожных. Сколько пирожных надо взять из коробки, чтобы в ней осталось 5 пирожных?
- Катя задумала число, прибавила к нему 5 и получила 15. Какое число задумала Катя?
- В семье двое детей. Саша – брат Жени, но Женя Саше не брат. Может ли так быть? Кто Женя?
- На яблоне было 10 яблок, Садовник разрешил детям сорвать с яблони по 1 яблоку. На яблоне осталось 6 яблок. Сколько было детей?
- Поезд состоит из 10 вагонов. Петя сел в пятый вагон от начала поезда, а Федя – в пятый вагон от конца. В одном ли вагоне они едут?
- Плитка шоколада состоит из 6 квадратных долек. Сколько разломов нужно сделать, чтобы разломить эту плитку на отдельные дольки?
- Пётр сын Сергея, а Сергей – сын Фёдора. Кем приходится Пётр Фёдору?
- В саду яблонь на 3 больше, чем груш. Яблонь 7. Сколько груш?
- Из книги выпало несколько листов. На первой выпавшей странице стоит номер 5, а на последней номер 10. Сколько листов выпало из книги?
- У Зины на 4 открытки меньше, чем у Гали. У Зины 6 открыток. Сколько открыток у Гали?
- Меня зовут Иваном Сергеевичем, а моего деда (отца моего отца) – Петром Николаевичем. Запишите имя и отчество моего отца.
- Красный шнур на 1м длиннее зелёного и на 2м длиннее синего. Длина зелёного шнура 5м. Найди длину зелёного шнура.
- На вешалке висят головные уборы; шляп на 1 больше, чем беретов. Шляп 8. Сколько шапок и сколько беретов?
- Уменьшаемое больше вычитаемого на 2. Чему равна разность?
- Угадайте, сколько лет моему дедушке, если через 15 лет мы будем отмечать его семидесятилетие.
- Разность двух чисел равна вычитаемому. Придумайте такие числа и запишите пример.
- Разность двух чисел равна 0. Придумайте и запишите пример.
- Бабушка положила в тарелку 12 груш. После того как внуки взяли с тарелки по 1 груше, осталось 8 груш. Сколько у бабушки внуков?
- На уроке математики Ольга Петровна попросила Гошу назвать все числа, меньше 7, а Витю – все числа, которые больше 3 и меньше 9. Какие одинаковые числа назвали мальчики?
Ответы А - 4 носка
- 3 куры
- 2 варежки
- Число 0, т. к.
- 2 сестры
- 2+2=4 ведра
- 3 котёнка
- 6 ребят
- 8 ног
- Нет
- 6 ног
- 0
- 4+5=9 яблок
- 1+1+1=3 или 1+2=3
- 2+2+2=6 детей
- 3
- 2
- 6 и 0
- 3 пирожных
- Число 10
- Сестра
- четверо детей
- Нет
- 5
- Внуком
- 4 груши
- 3 листа
- 10 открыток
- Сергей Петрович
- 5+1=6, 6-2=4м
- 8-1=7, 7-1=6 Ответ: 7 шапок и 6 беретов
- 2
- 70-15=55(лет)
- 6-3=3, 14-7=7 и т.д.
- Например: 8-8=0
- 12-8=4 внука
- 4, 5, 6.
| Ответы А - 4 носка
- 3 куры
- 2 варежки
- Число 0, т. к.
- 2 сестры
- 2+2=4 ведра
- 3 котёнка
- 6 ребят
- 8 ног
- Нет
- 6 ног
- 0
- 4+5=9 яблок
- 1+1+1=3 или 1+2=3
- 2+2+2=6 детей
- 3
- 2
- 6 и 0
- 3 пирожных
- Число 10
- Сестра
- четверо детей
- Нет
- 5
- Внуком
- 4 груши
- 3 листа
- 10 открыток
- Сергей Петрович
- 5+1=6, 6-2=4м
31. 8-1=7, 7-1=6 Ответ: 7 шапок и 6 беретов - 2
- 70-15=55(лет)
- 6-3=3, 14-7=7 и т.д.
- Например: 8-8=0
- 12-8=4 внука
- 4, 5, 6.
| Ответы А - 4 носка
- 3 куры
- 2 варежки
- Число 0, т. к.
- 2 сестры
- 2+2=4 ведра
- 3 котёнка
- 6 ребят
- 8 ног
- Нет
- 6 ног
- 0
- 4+5=9 яблок
- 1+1+1=3 или 1+2=3
- 2+2+2=6 детей
- 3
- 2
- 6 и 0
- 3 пирожных
- Число 10
- Сестра
- четверо детей
- Нет
- 5
- Внуком
- 4 груши
- 3 листа
- 10 открыток
- Сергей Петрович
- 5+1=6, 6-2=4м
- 8-1=7, 7-1=6 Ответ: 7 шапок и 6 беретов
- 2
- 70-15=55(лет)
- 6-3=3, 14-7=7 и т.д.
- Например: 8-8=0
- 12-8=4 внука
- 4, 5, 6.
|
Б
1.Мама купила детям 3 пары варежек. Сколько всего левых варежек и сколько правых варежек?
2. В парке было 7 скамеек. 3скамейки заменили новыми. Сколько скамеек стало в парке?
3.В квартире 2 комнаты. Из одной комнаты сделали две. Сколько комнат стало в квартире?
4. Юра попросил в библиотеке журналы «Нафаня» со второго по шестой номер. Сколько журналов выдал ему библиотекарь?
5. В квартире 4 комнаты. Две комнаты соединили вместе и сделали из них одну большую комнату. Сколько комнат стало в квартире?
6. У всех цыплят, которые сидели в корзине, Юля насчитала 10 ног. Сколько цыплят было в корзине?
7. Таня сказала, что у неё кукол больше 4 и меньше 7. Сколько кукол могло быть у Тани?
8. Коля старше Серёжи, а Серёжа старше Миши. Запиши имя мальчика, который моложе всех.
9. На подоконнике лежали 8 зелёных помидоров. Через 3 дня они покраснели. Сколько зелёных помидоров осталось?
10. Кролики сидят в клетке так, что видны их уши. Вова насчитал 5 пар ушей. Сколько кроликов в клетке?
11. Кузнец подковал двух лошадей. Сколько подков ему потребовалось?
12. Алёшу угостили конфетами. Он решил дать своей сестрёнке 4 конфеты, а себе взять 3. Сколько конфет дали Алёше?
13. У Маши и Вани по 9 леденцов. Маша съела 4 леденца, и Ваня сделал тоже самое. Сколько леденцов осталось у Вани?
14. Нина задумала число. Это число она сначала прибавила к 7, а потом отняла его от 7. Ответ оказался одним и тем же – 7. Какое число задумала Нина?
15. Роме подарили столько значков сколько у него уже было. Рома пересчитал все значки, их оказалось 8. Сколько значков было у Ромы сначала?
16. Чтобы рассадить 7 детей в комнате, не хватает 2 стульев. Сколько стульев в комнате?
17. У паука 4 пары ног, а у жука 3 пары ног. На сколько ног больше у паука, чем у жука?
18. В коробке 6 ячеек. В каждой ячейке умещается только одна ёлочная игрушка. Можно ли в эту коробку положить 4 шарика и 3 шишки?
19. Сестра старше брата на 1 год. На сколько лет сестра будет старше брата через 5 лет?
20. Может ли сумма двух чисел быть равной слагаемому?
21. Может ли разность двух чисел быть равной уменьшаемому?
22. Запиши число меньшее 20, в котором число десятков на 4 меньше числа единиц.
23. На каждую страницу альбома я наклеил 4 переводных картинки. Сколько страниц заняли 8 картинок?
24. Сумма двух чисел равна 8, а их разность 4. Угадайте, какие это числа?
25. Меня зовут Нина Александровна, а моего дедушку(отца моего отца) – Иван Николаевич. Как зовут моего отца?
26. На левой чашке весов стоят пакет с мукой и гиря в 1 кг. На правой чашке весов гиря в 3 кг. Весы в равновесии. Найдите массу пакеты с мукой.
27. в обувном отделе универмага висит указатель: «Обувь 37 – 42 размеров». Можно ли в этом отделе купить обувь 39 размера?
28.Какие двузначные числа можно записать, используя цифры 5 и 6?
29.Сахар-песок продают расфасованным в пакеты по 1 кг, 2кг, 3кг. Мама выбила в кассе чек на покупку 7 кг сахара. Продавщица дала ей 3 пакета с сахаром. Сколько сахара было в каждом из пакетов? Рассмотри возможные случаи.
30. Сравни числа *2 и 95 Сделай запись с помощью одного из знаков .
31. Юля и Марина нашли в лесу поровну грибов. У Юли 4 гриба оказались червивыми, и по дороге домой она их выбросила. А Марина нашла ещё 5 грибов. На сколько грибов у Марины стало больше, чем у Юли?
32. В ящике стола лежат деньги. На эти деньги можно купить 2 одинаковых по цене стула или одно кресло. Что дороже кресло или стул?
33.На верхней полке книг столько же, сколько на нижней. На верхнюю полку поставили 3 книги, а с нижней 3 книги сняли. На какой полке стало больше книг и на сколько?
34. В коробке 12 красных и зелёных шаров. Из коробки взяли 3 красных и 4 зелёных шара. После этого в коробке зелёных шаров не осталось. Сколько красных шаров осталось в коробке?35. В корзине на 5 яблок больше, чем в пакете. Из корзины взяли 7 яблок. Где осталось яблок больше: в корзине или в пакете, и на сколько?
36. К трём замкам волшебник сделал 3 ключа: медный, серебряный и золотой. К каждому замку подходит только один ключ. Медный ключ не подходит к ни к первому, ни ко второму замку. Серебряный ключ не подходит ко второму замку. К какому замку подходит каждый из ключей?
37. У Пети на 4 конфеты меньше, чем у Серёжи. Мама дала Пете ещё 5 конфет. У кого конфет больше и на сколько?
38. Зелёная лента на 3 м длиннее красной. От зелёной ленты отрезали 5 м, а от красной 2м. Сравните длины оставшихся кусков лент.
39. У Юры денег ровно столько, чтобы купить 4 вафли или 2 конфеты. Сможет ли он на свои деньги купить 1 конфету и 4 вафли?
40. Запишите 6 чисел по такому правилу: первое 1, второе 2, а каждое следующее равно сумме двух предыдущих.
41. Оля может купить на свои деньги 4 карандаша и 3 тетради. Хватит ли у неё денег, чтобы купить 3 карандаша или 3 тетради?42. Каждой из трёх внучек дедушка разрешил сорвать с четырёх кустов по одной розе. Сколько роз сорвали все внучки?43. Запишите 5 чисел по такому правилу: первое 18, второе 10, а каждое следующее равно разности двух предыдущих.
44. Половину числа яблок, лежащих на тарелке, взяли для компота. Сколько яблок осталось на тарелке, если компот сварили из 6 яблок?
45. Купили пакет кефира. Половину всего кефира, который был в пакете, выпили Маша и Даша. В пакете осталось 2 стакана кефира. Сколько стаканов кефира было в пакете?
46. Дыня тяжелее арбуза и легче тыквы. Что самое тяжелое?
47. На столе лежат овощи: репок на 1 меньше, чем огурцов, а огурцов на 1 меньше, чем помидоров. На сколько репок меньше, чем помидоров?
48. Красная лента короче синей ленты и длиннее зелёной. Какая лента самая короткая?
49. Дима на 1 год старше Серёжи, а Серёжа на 1 год старше Ромы. На сколько лет Дима старше Ромы?
50. За каждую минуту в ванну из крана наливается 10 л воды. За то же время через неплотно прикрытое пробкой отверстие в дне ванны 2 л воды выливается. Увеличивается или уменьшается количество воды в ванне и на сколько литров каждую минуту?
51. Петя взял 3кубика и поставил их один на один так, что получилась «башня». Красный кубик оказался ниже синего, а синий ниже зелёного. Какой кубик Петя поставил выше всех?
52. Из трёх кубиков построили башню. Жёлтый кубик поставили выше синего и ниже красного. Какой кубик оказался выше всех?
53. Торт разрезали на 4 одинаковые части, а потом каждую часть разрезали на 2 одинаковые части. На сколько человек хватит торта, если каждому положить на блюдце один кусок?
54. В коробке лежат пряники и вафли: пряников на 2 меньше, чем вафель. Сколько вафель, если пряников 6?
55. Митя на 2 года старше Гены. Мите 10 лет. Сколько лет Гене?
56. Сумма двух чисел 9. Сумма больше первого слагаемого на 5.Чему равно второе слагаемое?
57. На катке катались на коньках 6 девочек и 2 мальчика. Вскоре троих детей позвали обедать, и они ушли домой. Осталась ли на катке хоть одна девочка?
58. Купили банку виноградного сока. Четверым детям налили из банки по полному стакану сока. После этого в банке осталось ровно столько, сколько выпили дети. Сколько стаканов сока было в банке?
60. Дыня на 3 кг легче арбуза. От дыни отрезали кусок массой 1 кг, а от арбуза –
кусок массой 3 кг. Чего осталось больше: дыни или арбуза, и на сколько килограммов?
Ответы Б - 3, 3
- 7
- 3
- 5
- 3
- 5
- 5 или 6
- Миша
- 8-8=0
- 5
- 4+4=8
- 4+3=7
- 9-4=5
- 0
- 4
- 7-2=5 стульев
- 8-6=2 или 4-3=1 одна пара – это две ноги
- 4+3=7 6
- на 1 год
- Да. Если одно из слагаемых равно нулю. Например: 5+0=5
- Да. Когда вычитаемое равно 0.
7-0=7 - 15
- 2
- 6 и 2
- Александр Иванович
- 3-1=2(кг)
- Да
- 55, 56, 65, 66
- 1) 3кг,3кг, 1кг; 2) 2кг, 2кг, и 3кг
- *2
- 4+5=9
- Кресло
- 3+3=6(к) > верхней полке
- 1 способ: 12-4=8, 8-3=5.
2 способ: 3+4=7. 12-7=5 - В пакете на 2 яблока >.
- Медный ключ от 3 замка, серебряный – от 1, золотой – от 2 замка.
- У Пети на 1
- Длины равны
- Нет.
- 1, 2, 3, 5, 8, 13.
- Да.
- 4+4+4=12 роз
- 18, 10, 8, 2, 6.
- 6
- 4
- Тыква
- На 2.
- Зелёная лента
- На 2 года
- 10-2=8(л.) увеличивается
- Зелёный кубик
- Красный
- На 8 человек
- 6+2=8
- 10-2=8(лет)
- 5
- 57
- Да.
- 4+4=8 стаканов
- Арбуза на 1 кг >.
| Ответы Б - 3, 3
- 7
- 3
- 5
- 3
- 5
- 5 или 6
- Миша
- 8-8=0
- 5
- 4+4=8
- 4+3=7
- 9-4=5
- 0
- 4
- 7-2=5 стульев
- 8-6=2 или 4-3=1 одна пара – это две ноги
- 4+3=7 6
- на 1 год
- Да. Если одно из слагаемых равно нулю. Например: 5+0=5
- Да. Когда вычитаемое равно 0.
7-0=7 - 15
- 2
- 6 и 2
- Александр Иванович
- 3-1=2(кг)
- Да
- 55, 56, 65, 66
- 1) 3кг,3кг, 1кг; 2) 2кг, 2кг, и 3кг
- *2
- 4+5=9
- Кресло
- 3+3=6(к) > верхней полке
- 1 способ: 12-4=8, 8-3=5.
2 способ: 3+4=7. 12-7=5 - В пакете на 2 яблока >.
- Медный ключ от 3 замка, серебряный – от 1, золотой – от 2 замка.
- У Пети на 1
- Длины равны
- Нет.
- 1, 2, 3, 5, 8, 13.
- Да.
- 4+4+4=12 роз
- 18, 10, 8, 2, 6.
- 6
- 4
- Тыква
- На 2.
- Зелёная лента
- На 2 года
- 10-2=8(л.) увеличивается
- Зелёный кубик
- Красный
- На 8 человек
- 6+2=8
- 10-2=8(лет)
- 5
- 57
- Да.
- 4+4=8 стаканов
- Арбуза на 1 кг >.
| Ответы Б - 3, 3
- 7
- 3
- 5
- 3
- 5
- 5 или 6
- Миша
- 8-8=0
- 5
- 4+4=8
- 4+3=7
- 9-4=5
- 0
- 4
- 7-2=5 стульев
- 8-6=2 или 4-3=1 одна пара – это две ноги
- 4+3=7 6
- на 1 год
- Да. Если одно из слагаемых равно нулю. Например: 5+0=5
- Да. Когда вычитаемое равно 0.
7-0=7 - 15
- 2
- 6 и 2
- Александр Иванович
- 3
|
nsportal.ru
Как научить ребенка решать любые задачи: логические, математические, олимпиадные
Мы знаем, что абсолютное большинство взрослых захотят решить предложенную задачу с помощью уравнения. Неплохой способ, но зачастую обыкновенные логические рассуждения помогают найти ответ быстрее, без ручки и бумаги, просто в уме.
Рекомендуем ознакомиться с несколькими популярными методами, описанными на примерах в материале «Как решать логические задачи»:
- метод последовательных рассуждений;
- «с конца»;
- с помощью таблиц истинности;
- метод блок-схем.
Нестандартные методы
Среди популярных, нестандартных — целенаправленный поиск «ключа» («ключей») и метод «игры в создателя» (т.е. моделирования различных вариантов принципов, использованных для создания задачи). А если подсказки, шаблоны решения отсутствуют, применяется самый сложный метод – поиска метода.
Для быстрого и правильного решения различных логических головоломок и задач на смекалку ребенку необходимо:
- знать виды логических задач;
- владеть возможными методами решения задач;
- уметь классифицировать задачу и выбирать самый простой и «красивый» способ ее решения.
Алгоритм решения задач на логику и смекалку
Основные шесть этапов, которые последовательно должен пройти ученик, решая логическую задачу:
- Ознакомление с условиями задачи.
- Понимание содержания задачи, анализ условий, моделирование.
- Поиск метода решения.
- Применение метода решения, поиск правильного ответа.
- Проверка правильности решения и оформление ответа.
- Анализ проведенного решения.
- Отработка и закрепление навыков решения аналогичных задач.
1. Внимательно прочитайте условие задачи, лучше несколько раз. Четко уясните вопрос или проблему, которую нужно разрешить. Чаще всего ошибки в решении появляются от невнимательности. Особенно это касается задач с подвохом.
2. Кратко запишите условия задачи, по возможности, опишите задачу схематически (в виде рисунка, схемы, графика, дерева, чертежа и т.д.). Наглядное представление задачи не только способствует более быстрому уяснению содержания задачи, но и поможет выявить новые связи между элементами задачи или увидеть скрытые свойства объектов. Выделите существенные и несущественные условия задачи и попробуйте упростить задачу, абстрагироваться от действительности, мысленно смоделировать описанную в задаче ситуацию.
3. Попытайтесь определить тип задачи и соответственно подобрать метод решения, который обычно применяется для решения этого вида заданий. Например, для решения задач на определение истинности или ложности высказывания удобно использовать таблицу. Для решения задач с большим количеством взаимосвязанных условий лучше использовать метод графов и т.д.
4. Используя выбранный метод, решите задачу.
5. Проверьте ваш вариант ответа. В случае письменного решения задачи надлежащим образом запишите правильный ответ.
6. Анализ проведенного решения представляет собой обсуждение всего хода мыслительных действий в процесс решения логической задачи. Это завершающий и необходимый этап решения любой задачи, не только логической. Он включает:
- поиск альтернативного, более рационального, красивого способа решения;
- анализ всего процесса, моментов, которые вызвали затруднения;
- выделение важных признаков данного типа задач;
- составление алгоритма их решения;
- систематизация полученных знаний.
Школьнику полезно записывать свои решения, алгоритмы и рассуждения в отдельную тетрадь, например, специально для занятий на ЛогикЛайк. Таким образом он будет «пропускать через моторику» свои рассуждения и всегда сможет вернуться к своим наработкам.
7. Чтобы закрепить свое умение решать головоломки определенного типа, необходимо не откладывая решить еще ряд подобных, однотипных задач с постепенным усложнением набора условий.
В учебной программе образовательной платформы LogicLike логические задачи распределены по 15 тематическим разделам. Каждая категория содержит задания разного уровня сложности.
logiclike.com
Логические задачи в школьном курсе математики
Ончукова Любовь Викторовна,старший преподаватель кафедры математического анализа и методики обучения математикеФГБОУ ВПО «Вятскийгосударственный гуманитарный университет», г. Киров
[email protected]Логические задачи в школьном курсе математики
Аннотация.Статья посвящена вопросам обучения школьников 5–7хклассов решению логических задач. Дается краткое описание пяти авторских учебных пособий по математической логике для школьников; более подробно анализируются методы решения логических задач; приводятся примеры таких задач и их решения.Ключевые слова:математическая логика, развивающее обучение, творческий подход, игровая ситуация.
Современные подходы к обучению требуют, чтобы на первое место в образовательном процессе выходило развитие личности школьника, его мышления и творческих способностей. На страницах журнала «Концепт» уже не раз авторы останавливались на вопросах совершенствования обучения математике с этих позиций, в том числе средствами математических задач с логическим содержанием [1, 2]. Наш опыт преподавания математических дисциплин студентам физикоматематических специальностей ВятГГУ и ученикам средних школ г. Кирова показывает, что добиваются хороших результатов,успешно поступают в высшие учебные заведения,легче проходят адаптационный период на младших курсах вузов,в дальнейшем учатся в нихте выпускники школ, кто в среднем звене овладел умениями: а) самостоятельно мыслить, б) творчески подходить к выполнению любого задания, в) искать различные варианты его решения, г)отбирать среди них наиболее оптимальный.Ни одна учебная дисциплина, кроме логики, не учит этому специально.При изучении даже самого элементарного курса логики школьники учатся думать и рассуждать, отстаивать в споре свою точку зрения, делать правильные выводы. Поэтому нами был разработан курс логики для учащихся 5–7хклассов для обеспечения образовательного процесса вучреждениидополнительного образования «Открытыйлицей» ВятГГУ. Программы лицея скоординированы с учебными программами школ и нацелены накачественную подготовку к поступлению и обучению в высших учебных заведениях. Курс логики в 5–7хклассах прошёл апробацию в школах №№ 3, 8, 36, 48, 49, 53, 70 города Кирова. 1. Определение логики как учебного предмета.Приступая к занятиям с учащимися 5х классов,прежде всего потребовалось сформулировать само понятие логики. С. И. Ожегов в «Словаре русского языка»даёт определение логики как науки о законах мышления и его формах [3, с.301]. Нам представляется более уместным привести здесь определение проф. ВятГГУ М.И.Ненашева, читавшего курс логики учащимся Вятской гуманитарной гимназии, которое сформулировано в его учебном пособии «Введение в логику»: «Логика–это наука о формах мышления, на которых основаны рассуждения, позволяющие получать истинное знание об окружающем мире» [4, c.3]. Это определение ближе к пониманию цели изучения курса, в основе которого лежит умение правильно рассуждать. Поэтому для школьников 5–7хклассов мы даём следующее определение: логика –это наука, изучающая такие человеческие рассуждения, которые позволяют получать истинное знание об окружающем мире.Логикой называют также ход рассуждений, умение делать правильные выводы. Такая формулировка близка к идеям, выдвинутым в предисловии к учебнику математики 5го класса под ред. Н.Я. Виленкина: «…основа хорошего понимания математики –умение считать, умение думать, рассуждать, находить удачные пути решения задач»[5, c.3].С этимсозвучна мысль, приведённая в учебнике математики 6го класса И.И. Зубаревой, А.Г.Мордковича: «Думать придётся самостоятельно. Учиться этому нужно уже сейчас.…Ученик не просто заучивает то или иное теоретическое положение, а, выполнив упражнения в определённой последовательности, получает возможность самостоятельно сформулировать правило, определение нового понятия или даже ввести новый термин» [6, с.3].В соответствии с определением логики как учебногопредмета нами определяется и понятие логической задачи. 2. Определение логической задачи.
К логическим задачам отнесём такие, при решении которых главное, определяющее –это отыскание связи между фактами, сопоставление их, построение цепочки рассуждений для достижения цели. ПрофессорЕ. С. Канин, неставя цель определить понятие «логическая задача», относит к ним такие задачи, которые на первый взгляд не являются математическими, но в то же время требуют для своего решения формулирования суждений (высказываний), построения умозаключений и их цепочек. Поскольку при решении логических задач строятся умозаключения, то при этом приходится применять иобщие методы решения математических задач, такие как метод выведения, метод исчерпывающих проб, метод сведения к противоречию и др. [7, c.17–18].Иногда приходится слышать, что любая математическая задача, не являющаяся чисто вычислительной, есть логическая задача, так как требует анализа данных, построения цепочки рассуждений, вывода, оценки его правильности. Но среди логических задач встречается множество таких, которые, на первый взгляд, не несут чисто математического содержания. Поэтому к логическим задачам отнесём такие, при решении которыхиспользуются законы логики, например, закон двойного отрицания, закон противоречия (не может быть сразу А и не А), закон исключённого третьего (или А или не А, третьего быть не может).3.Содержание и структура курса «Элементы логики» в 5–7хклассах.При построении курса логики были выделены два основных направления. Первое направление непосредственно связано с изучением основных логических операций отрицания, конъюнкции, дизъюнкции, строгой дизъюнкции, импликации, эквиваленции и их свойств с последующимприменением к решению логических задач. Содержание соответствующих разделов вошло в теоретическую часть курса. Второе направление связано с построением школьного курса математики и ориентировано на решение нестандартных задач доступными для школьников методами. Содержание этих разделов составило практическую часть курса. При создании учебного пособия автор в основном ориентировался на построение курса математики, изложенное в учебниках Н. Я. Виленкина. Таким образом,можно предложить следующее построение курса логики для учащихся 5–7хклассов.1)Теоретическая часть:изучение логических операций и их свойств с последующим применением к решению нестандартных задач.Цель:повышение культуры мышления учащихся путём развития логической составляющей школьного курса математики.Эта часть курса логики для учащихся 5–7хклассов нашла отражение в наших авторскихучебных пособиях[9–11].2)Практическая часть:решение нестандартных задач, связанных с программой школьного курса математики.Цель:совершенствование умений и навыков решения задач школьного курса доступными для учащихся 5–6хклассов методами.Эта часть курса логики для учащихся 5–7хклассов получила воплощение в еще в двухучебных пособиях[12,13]. Ниже представлена более подробная схема построения курса логики для каждого класса. 5й класс.Теоретическая часть: логические операции.Введение. Чтоизучаетлогика?1. Отрицание высказываний. Понятие отрицания.2.Решение задач с помощью отрицания.3.Свойства отрицания.4.Отрицание отрицания. Поиск противоречия.В этой части происходит знакомство учащихся с простейшими логическими задачами, которые можно решить с помощью операции отрицания, поэтапно исключая все лишние, «ненужные» случаи. При решении используются таблицы,схемы, рисунки, облегчающие понимание задачи. При этом школьники постепенно учатся сами составлять таблицы и схемы, соответствующие условию задачи.5.Утверждения, одинаковые по смыслу.Эквивалентные высказывания.Цель данной части –научиться заменять одно высказывание другим, имеющим тот же смысл, но более кратким и понятным пятиклассникам.6.Логическое следствие. Рассуждения и умозаключения.При изучении данного раздела школьники не только учатся строить цепочки умозаключений, восстанавливать пропущенные звенья в рассуждениях, но и решают задачи, в которых часть условий ложна. В процессе обучения они начинают самостоятельно находить ложные утверждения, отмечать противоречия в ходе рассуждений и в заключений, исключая при этом неверные ответы.5й класс.Практическая часть: решение линейных уравнений, неравенств и их систем нестандартными методами.
1.Решение задач с конца.2.Геометрические методы решения логических задач.3.Решение логических задач с помощью уравнений и неравенств.4.Задачи с несколькими неизвестными.Эта часть в основном посвящена пропедевтике изучения действий с дробями, методов решения уравнений, неравенств и систем уравнений. В доступной для учащихся форме излагаются принципы решения задач соответствующего содержания.6й класс. Теоретическая часть: логические операции.1. Логические операции и признаки делимости. Свойства импликации.2. Конъюнкция высказываний.3. Дизъюнкция высказываний.4. Отрицание конъюнкции.5. Отрицание дизъюнкции.В данной части учащиеся продолжают знакомство со свойствами операции импликации, а также их применением к изучению делимости чисел. Кроме того, при изучении свойств конъюнкции и дизъюнкции происходит и углубление знаний о свойствах эквиваленции, что позволяет использовать полученные знания при решении более сложных логических задач, часть условий в которых ложна.6й класс. Практическая часть: применение свойств делимости чисел при решении задач.1.Наименьшее общее кратное и наибольший общий делитель.2.Деление на части и расчёты.3.Решение логических задач с помощью уравнений и неравенств.4.Задачи с несколькими неизвестными.В представленной части рассматриваются нестандартные задачи, связанные с делимостью чисел, рассматриваются нестандартные методы решения задач с несколькими неизвестными.7й класс. Теоретическая часть: логические операции.1. Строгая дизъюнкция ( или А, или В).2. Свойства строгой дизъюнкции.3.Умозаключение в логике высказываний. Модусы.4.Модусы и решение задач.
На этом этапе учащиеся кроме новой для них операции строгой дизъюнкции и её применения для решения логических задач, имеют все возможности взглянуть на изученный в 5–6хклассах материал с новой точки зрения, обобщить и проанализировать полученные ранее знания. Понятие модуса позволяет записывать условие задачи вбуквенной форме и правильно определять, какие логические связки применялись при её составлении. Определение характера модуса, его достоверности или вероятностности позволяет сделать верное заключение. Умение правильно составить и применить модусы к решению логических задач определяет степень усвоения материала всего курса.4. Методы решения логических задач.В предлагаемой статье мы рассмотрим задачи, связанные со свойствами логической операции отрицания, рассматриваемыми в курсе логики в 5мклассе. 1.Некоторые логические задачи решаются без применения какихлибо специальных методов. При их решении достаточно проявить сообразительность, установить верный порядок рассуждений, сделать правильные выводы из условий задачи. Такие задачи встречаются по всему тексту каждой книги, оформлены в виде тестов или представлены в разделе «И» –игра.
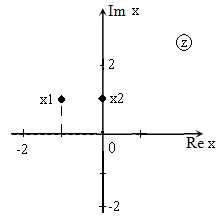
Задача 1. На острове живут два племени –аборигены и пришельцы. Аборигены всегда говорят правду, пришельцы всегда лгут. Путешественник нанял жителя острова в проводники. По дороге они встретили другого островитянина. Путешественник попросил проводника узнать, к какому племени принадлежит этот человек. Проводник вернулся и сообщил, что человек назвался аборигеном.Кем был проводник –пришельцем или аборигеном?Решение. Аборигены всегда говорят правду. На вопрос «Кто вы?» абориген ответит: «Абориген». Пришельцы всегда лгут. Поэтому на тот же вопрос пришелец тоже ответит «Абориген». Проводник, вернувшись к путешественнику, сказал правду, следовательно, он абориген.
2.Ещё одна группа задач связана с построением отрицания высказывания. Сотрицаниями высказываний мы сталкиваемся не только при решении задач, но и в реальной жизни. Поэтому важно научиться правильно формулировать отрицание заданного высказывания. Под высказыванием мы понимаем предложение, про которое можно сказать истинно оно или ложно. На первом этапе изучения свойств операции отрицания при построении отрицания какоголибо утверждения школьниками использовались слова нет,неверно,не,неявляется. Поэтому построение отрицания происходит в два приёма: сначала к предложению школьники добавляют слова «Неверно, что…», а затем стараются переформулировать его в более краткой форме. При этом обязательно внимание пятиклассников обращается на возможные логические ошибки.
Задача 2. Постройте отрицания высказываний с помощью слов «Неверно, что…», а затем запишите их в более простой форме.1) Сестра всегда старше брата.2) 25 меньше, чем 25.3) Ни одна рыба не кусается.4) У всех людей длинные волосы.5) Все пятиклассники круглые отличники.6) Саша не принёс на урок ни линейки, ни карандаша.7) У бабушки на даче есть то ли куры, то ли кролики.Решение. На первом этапе отрицания высказываний выглядят следующим образом.1) Неверно,чтосестра всегда старше брата.2) Неверно,что25 меньше, чем 25.3) Не верно, что ни одна рыба не кусается.4) Не верно, что у всех людей длинные волосы.5) Не верно, что все пятиклассники круглые отличники.6) Не верно, что Саша не принёс на урок ни линейки, ни карандаша.7) Неверно,чтоу бабушки на даче есть то ли куры, то ли кролики.
Далее ученики, проанализировав смысл полученных высказываний, должны составить следующие предложения.1) Сестра невсегда старше брата.2) 25 неменьше, чем 25.3) Естьрыбы, которые кусаются.4) Неу всех людей длинные волосы.5) Невсепятиклассники круглые отличники.6) Саша принёс на урок линейку иликарандаш.7) У бабушки на даче нетни кур, ни кроликов.
Возможные логические ошибки, на которые следует обращать внимание учеников.1) Сестра всегда младшебрата.2)25 больше, чем 25.3) Всерыбы кусаются.4) У всех людей короткиеволосы.5) Нетпятиклассников, которые являются круглыми отличниками.6) Саша принёс на урок илинейку, икарандаш.7) У бабушки на даче неткур или кроликов.Полезно каждое высказывание занести в таблицу, которая раздаётся школьникам заранее. Они заполняют её самостоятельно, что позволяет им сравнить полученные результаты.
Первоначальная формулировка отрицанияОтрицание высказыванияВозможные логические ошибки1.Неверно,чтосестра всегда старше брата.2.Неверно,что25 меньше, чем 25.3.Не верно, что ни одна рыба не кусается.4.Не верно, что у всех людей длинные волосы.5.Не верно, что все пятиклассники круглые отличники.6.Не верно, что Саша не принёс на урок ни линейки, ни карандаша.7.Неверно,чтоу бабушки на даче есть то ли куры, то ли кролики.1.Сестра невсегда старше брата.2. 25 неменьше, чем 25.3.Естьрыбы, которые кусаются.4.Неу всех людей длинные волосы.5.Невсепятиклассники круглые отличники.6.Саша принёс на урок линейку иликарандаш.7.У бабушки на даче нетни кур, ни кроликов.1.Сестра всегда младшебрата.2.25 больше, чем 25.3.Всерыбы кусаются.4.У всех людей короткиеволосы.5.Нетпятиклассников, которые являются круглыми отличниками.6.Саша принёс на урок илинейку, икарандаш.7.У бабушки на даче неткур или кроликов.3.Задачи раздела «Операция отрицания» решаются как простым рассуждением, так и с помощью таблиц. Мы не рассматриваем построение таблицы в качестве метода решения, а предлагаемучащимся в качестве удобного средства его оформления. При этом таблицы могут быть различных видов. В результате решения большого количества задач ученики сами начинают конструировать таблицы различных форм в соответствии с условием задачи, предлагая различные варианты.
Задача 3. В одной школе учатся три друга: Сергей, Коля и Максим. Их фамилии Петров, Семёнов и Иванов. Сергей учится в 5 классе, мама Коли инженер. Иванов учится в 6 классе, его мама бухгалтер. Сергей и Семёнов болеют за разные футбольные клубы.
Решение. Выпишем условия задачи в следующем порядке.1) Сергей учится в 5 классе.2) Иванов учится в 6 классе.3) Мама Коли инженер.4) Мама Иванова бухгалтер.5) Сергей и Семёнов болеют за различные футбольные клубы.Будем рассуждать и одновременнозаполнять таблицу. Известно, что Сергей учится в 5м классе, а Иванов –в 6м. Значит, Сергей и Иванов –два разных мальчика. В первой клетке третьей строки таблицы ставим знак «–». Ещё известно, что мама Коли инженер, а мама Иванова бухгалтер. Это значит, что Коля и Иванов –мальчики из разных семей. Но тогда фамилия Коли не Иванов. Во второй клетке третьей строки таблицы ставим «–». Получается, что Ивановым может быть только Максим. Сергей может быть или Петровым или Семёновым. Но в условии5 сказано, что Сергей и Семёнов болеют за разные футбольные клубы. Значит, Сергей не Семёнов. В первой клетке второй строки ставим «–». Получается, что Семёновым может быть только Коля. Тогда фамилия Сергея –Петров.
Далее рассматриваются задачи, в которых надо учесть порядок расположения элементов. Их также легко решить с помощью таблиц, сопровождаемых схематичными рисунками. Ниже приведены две такие задачи.
Задача 4.В кругу сидят четыре котёнка: Барсик, Дымок, Васька и Тимофей. Их цвета: белый, сер
e-koncept.ru
Логические задачи в математике — HintFox
Логика — это анализ суждений и использования в аргументации. Этот анализ может проводиться на очень абстрактном уровне (формальная логика) или сосредоточиваться на практическом искусстве правильного объяснения (прикладная логика). Достоверные доказательства имеют две основные формы: дедуктивную и индуктивную. Логика развивалась независимо и была приведена к некоторой степени систематизации в Китае (с 5 по 3 в. до н. э. ) и Индии (с 5 в. до н. э. по 16-17в. н. э. ). Логика происходит из Греции. Аристотель в 4 в. до н. э. разработал первую систему логики субъекта. Свой расцвет логика переживает в 14 веке. Современная логика начала развиваться с работ математика Г. В. Лейбница. Большие успехи были сделаны в 19 в. в развитии символической логики, что привело к слиянию логики и математики — формальному анализу. Современная формальная логика-это изучение форм суждения и умозаключения.
Роль логики в формировании логической культуры человека.
Из понятия логика вытекает понятие логическая культура. С общей культурой всего общества неразрывно связана культура отдельного человека. Это средства, способы и результаты той или иной его материальной или духовной деятельности, предполагающей определенные связи и отношения с другими людьми. Сюда входят культура труда, досуга и общения, политическая культура, правовая и нравственная культура (или культура поведения), эстетическая культура и т. д.
В каком отношении к этим элементам находится логическая культура? Ее не следует рассматривать как еще один из элементов такого ряда. Она буквально пронизывает каждый из этих элементов, входя в них неотъемлемой составной частью. Аналогично тому, как никакая культура невозможна без языка, так невозможна никакая материальная или духовная деятельность людей без мышления. Отсюда — особое значение логической культуры в жизни каждого культурного человека.
Что же такое логическая культура? Это культура мышления, проявляющаяся в культуре письменной и устной речи. Она включает: а) определенную совокупность знаний о средствах мыслительной деятельности, ее формах и законах; б) умение использовать эти знания в практике мышления — оперировать понятиями, правильно производить те или иные логические операции с ними, строить умозаключения, доказывать и опровергать; в) навыки анализа мыслей — как своих собственных, так и чужих, с тем чтобы вырабатывать наиболее рациональные способы рассуждения, предотвращать логические ошибки, а если они допущены, находить и устранять их.
Разумеется, выработка логической культуры — дело долгое и трудное. И значение логики здесь, несомненно, велико. Говоря об этом значении, важно избегать двух крайностей: как переоценки логики, так и ее недооценки. С одной стороны, нельзя полагать, будто логика учит нас мыслить. Это было бы большим преувеличением. Логика не учит нас мыслить так же, как физиология не учит переваривать пищу. Мышление — такой же объективный процесс, как и пищеварение. Само использование логики предполагает наличие двух необходимых условий: во-первых, определенной способности к мышлению, а во-вторых, известной суммы знаний. Люди мыслили, и мыслили более или менее правильно, задолго до появления логики. Она сама возникла лишь как обобщение практики мышления, и притом правильного мышления. Еще знаменитый оратор древности Демосфен полагал, что мы от природы, до науки умеем излагать, как было дело, и доказывать то, что нам нужно, и опровергать. И в настоящее время многие люди, не зная логики, мыслят и рассуждают довольно правильно.
Означает ли это, что без нее можно обойтись? Нет. Это было бы другой крайностью: игнорированием или преуменьшением ее значения, недооценкой. На самом деле без логики трудно обходиться, если мы хотим, чтобы наша мысль протекала правильно не только в простых, обыденных, но и в сложных, теоретических рассуждениях. Изучение логики открывает возможность надежно контролировать мышление со стороны его формы, структуры, строения, проверять его правильность, предупреждать логические ошибки или обнаруживать и исправлять их. В этом отношении она сродни грамматике, освоение которой позволяет производить лингвистический анализ письменной или устной речи, предупреждать грамматические ошибки или быстро находить их и исправлять.
Значение логики обусловлено тем, что логические ошибки допускаются весьма часто — гораздо чаще, чем думают некоторые, полагая, будто культура мышления является прирожденным качеством каждого человека. Нет, как и всякой культурой, ею нужно упорно овладевать. Ее главное значение для нас состоит в том, что она усиливает наши мыслительные способности и делает мышление более рациональным, подобно тому как знание физиологии помогает нам правильно, рационально питаться.
III Моё увлечение логическими рядами.
В нашей школе преподавание ведется по программе «Школа 2100». Авторами учебника математики, по которому я занимаюсь, являются Г. В. Дорофеев и Л. Г. Петерсон.
Этот учебник очень интересный, насыщенный. В нем есть задания для работы в классе и для работы дома, есть для повторения, но больше всего мне нравится выполнять задания под буквой «С», где главное – это смекалка. Именно здесь я нахожу логические ряды, логические задачи.
С 1 по 5 классы мне нравилось решать логические задачи, особенно логические ряды. В задании «продолжение ряда» предлагается установить закономерность числового ряда и продолжить его. Индуктивное умозаключение испытуемого состоит в том, чтобы перейти от частного к общему, исследуя отдельные группы числового ряда, можно установить его закономерность в целом.
Данные задания позволяют исследовать индуктивное мышление, способность оперировать с числами, определяют наличие у ученика математических способностей.
Логические ряды: 1)15, 16, 18, 21, 25 2) 4, 7, 13, 22, 34 3) 101, 1002, 100034) 4, 9, 6, 18, 8, 275) 0, 36, 72, 1086) 5, 6, 8, 11, 15, 207) 15, 14, 16, 13, 17, 12
Иногда я сама придумывала закономерность и составляла логические ряды. Например:
1) 1,9,3,1,5,13,. (Закономерность: +8, -6, +8, -6,. Ответ: 7,15, 9, 17,. )
2) 6,7,12,14,18,21,24,28,. (Закономерность: По-порядку и по очереди перечисляются числа, кратные 6 и 7. Ответ: 30, 35, 36, 42,. )
3) 50,25,23,69,72,18,14,. (Закономерность — :2, -2, ×3, +3, :4, -4, ×5, +5,. Ответ: 70, 75)
4) 50,49,46,48,43,36,40,. (Закономерность: -2 нечетных, + 1 четное число по порядку. Ответ: 31, 20 26)
5) 1000,998,995,990,983,972,959,942,942,923,900,. (Закономерность: по очереди вычитание простых чисел. Ответ: 869, 832,. )
В таких заданиях я часто стараюсь применять те понятия, которые мы изучаем на уроках, которые ученики часто забывают. Например: кратные числа, нечетные и четные числа, простые числа.
Именно эти задания помогают мне развивать мой логико-математический интеллект. Ведь логико-математический интеллект определяет способность исследовать и классифицировать категории и предметы, выявлять отношения между символами (числами) и понятиями путем манипулирования ими. А еще мне стало интересно, как относятся к решению задач на продолжение логических рядов в моем 5 классе. Мною была составлена анкета, на вопросы которой отвечали мои одноклассники. Таким образом, я для себя выяснила следующее:
1. В начальной школе решали подобные задачи 100%
2. Любят решать такие задачи:
Да – 38%, нет – 22%, не очень – 38%
3. Получается самостоятельно продолжать ряды:
Да – 8%, не всегда – 69%, иногда – 23%
4. Часто сами пробуют решать подобные задачи:
Всегда, когда увижу – 16%, часто – 22%, решают, но не часто – 46%, нет – 16%
5. Пробовали сами составлять подобные ряды:
Да – 54%, нет – 23%, иногда – 23%
6. По мнению моих одноклассников, такие логические ряды помогают им: развивать логическое мышление, развивают ум, внимательность, интуицию, бдительность, помогут в обучении в дальнейшем.
IV Как логика помогает в жизни.
Как же логика поможет мне в жизни? На этот вопрос есть много ответов, и первый из них – это при сдаче экзаменов. Ведь нам уже известно, что экзамены в форме ЕГЭ – это тестирование, где из четырех вариантов ответов нужно выбрать правильный. Так вот именно логическое мышление позволяет отбросить те варианты ответов, которые не могут быть верными, а из оставшихся выбрать правильный. И те ученики, которые не могу логически отбросить ненужное, которые не развивали свое логическое мышление с детства, потратят намного больше времени на выполнение задания, а может быть и вообще не выполнят его.
Логика в той или иной степени была нужна человеку всегда. Но особенно необходима она в современную эпоху. Чем выше уровень развития общества, тем большие требования предъявляются к самому человеку, уровню его собственного развития, его общей и специальной культуре. В наше время очень важно каждому человеку, который стремится чего-либо достичь, уметь принимать правильные решения, четко и быстро ориентироваться в происходящем, делать необходимые выводы. Эти требования сейчас предъявляются к каждому образованному человеку. Соответственно этому усиливается роль и значение логики как науки о мышлении.
В этих условиях особую значимость приобретает такая фундаментальная наука, как логика. В силу своей предельной общности и абстрактности она имеет отношение буквально ко всему: науке, технике, развитию общества, так как законы и правила мышления, на которых они основываются, едины. Любой логик может выдать богатейшую информацию о правильном мышлении, но не способен помочь тем, кто не учится мыслить самостоятельно.
www.hintfox.com
Логические задачи / math5school.ru
Немного теории
Часто знакомство с олимпиадной математикой начинается с логических задач. Сюда относятся, прежде всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам. При этом часть утверждений условия задачи может выступать с различной истинностной оценкой (быть истинной или ложной). К классу логических задач относятся также задачи на переливания и взвешивания.
В логических задачах нет «серьёзной» математики – нет ни сложных числовых выражений, ни функций, ни соотношений в треугольнике, ни векторов, но есть лжецы и мудрецы, фальшивые монеты и необычные шахматные фигуры, разноцветные фишки и сказочные герои. В то же время дух математики в таких задачах чувствуется весьма ярко. Половина решения логической задачи (а иногда и гораздо больше половины) состоит в том, чтобы как следует разобраться в условии, распутать все связи между участвующими объектами.
Существуют несколько различных способов решения логических задач. Вот некоторые из них:
Способ рассуждений – самый простой способ. Этим способом решаются самые простые логические задачи. Его идея состоит в том, что мы проводим рассуждения, используя последовательно все условия задачи, и приходим к выводу, который и будет являться ответом задачи.
Способ таблиц – распространённый прием, который используется при решении текстовых логических задач, заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи или ее ответ, но в значительной степени помогают делать правильные логические выводы в ходе решения задачи.
Способ «с конца» – довольно часто применим в задачах с предугадываемым ответом, и состоит в анализе ответа или конечной стадии некоторого процесса, описанного в задаче.
Способ блок-схем – подходит, например, к решению задач «на переливание». Суть этого метода состоит в следующем. Сначала выделяются операции, которые позволяют нам точно отмерять жидкость. Эти операции называются командами. Затем устанавливается последовательность выполнения выделенных команд. Эта последовательность оформляется в виде схемы. Подобные схемы называются блок-схемами. Составленная блок-схема является программой, выполнение которой может привести нас к решению поставленной задачи. Для этого достаточно отмечать, какие количества жидкости удается получить при работе составленной программы. При этом обычно заполняют отдельную таблицу, в которую заносят количество жидкости в каждом из имеющихся сосудов.
Задачи с решениями
1. На ступеньках дома сидят рядышком мальчик и девочка.
– Я мальчик, – говорит ребёнок с чёрными волосами.
– А я девочка, – говорит ребёнок с рыжими волосами.
Если по крайней мере один из детей говорит неправду, то кто из них мальчик, а кто девочка?
Решение
Для двух произвольных высказываний существуют четыре возможные комбинации типа «истина – ложь», а именно:
И – И, И – Л, Л – И, Л – Л.
Первая из них исключается, поскольку в условии оговаривается, что по крайней мере одно из высказываний является ложным. Вторая и третья комбинации также исключается, потому что если один ребёнок врал, то и другой не мог говорить правду, иначе мы бы имели дело с двумя мальчиками или с двумя девочками, что противоречит условию. Следовательно, оба говорили неправду.
Итак, у мальчика рыжие волосы, а у девочки чёрные.
2. В одной урне лежат два белых шара, в другой – два чёрных, в третьей – один белый шар и один чёрный. На каждой урне висела табличка, указывающая её состав: ББ, ЧЧ, БЧ. Но какой-то шутник перевесил все таблички так, что теперь каждая из них указывает состав урны неправильно. Разрешается вынуть шар из любой урны, не заглядывая в неё. Какое наименьшее число извлечений потребуется, чтобы определить состав всех урн? (Вы осведомлены о проделке шутника. После каждого извлечения шар опускается обратно.)
Решение
Достаточно извлечь один шар из урны с табличкой БЧ. Если он окажется белым, то в этой урне белые шары, а чёрные шары должны быть в урне с табличкой ББ, ведь не могут же они быть в урне с табличкой ЧЧ. В урне ЧЧ находятся шары разного цвета.
Если же вынут чёрный шар, то в урне с табличкой БЧ чёрные шары, в урне ЧЧ – белые, а в ББ – разного цвета.
3. Абрахам, хилый старик, подрядился выкопать канаву за 2 доллара. Он нанял Бенджамина, здоровенного парня, чтобы тот ему помог. Деньги они должны были поделить в соответствии с «копательными» способностями каждого. Абрахам копает так же быстро, как Бенджамин выбрасывает грунт, а Бенджамин копает в четыре раза быстрее, чем Абрахам выбрасывает грунт.
Каким образом они должны поделить деньги? Разумеется, соотношение сил старика и молодого человека как при копке, так и при выбрасывании грунта мы принимаем одинаковым.
Решение
Пусть, например, Бенджамин (Б) может выкопать канаву за время t, и выбросить грунт за время 2t. Тогда Абрахам (А) выкапывает канаву за время 2t часа и выбрасывает весь грунт за 4t. Следовательно, при рытье канавы их силы относятся как t к 2t, а при выбрасывании грунта – как 2t к 4t (отношение сил остаётся неизменным). При этом А может выкопать канаву за то же время, за которое Б может выбросить весь грунт (время 2t), а Б может выкопать канаву за четвёртую часть того времени, которое А тратит на выбрасывание грунта.
Следовательно, Абрахаму причитается треть всей суммы, а Бенджамину – две трети.
4. Андерсон покинул отель в Сан-Ремо в 9 часов и находился в пути целый час, когда Бакстер вышел вслед за ним по тому же пути. Собака Бакстера выскочила одновременно со своим хозяином и бегала всё время между ним и Андерсоном до тех пор, пока Бакстер не догнал Андерсона. Скорость Андерсона составляет 2 км/ч, Бакстера – 4км/ч и собаки – 10 км/ч. Сколько километров пробежала собака к моменту, когда Бакстер догнал Андерсона?
Решение
Вполне очевидно, что Бакстер догонит Андерсона через один час, поскольку к этому времени они пройдут по 4 километра в одном направлении. Так как скорость собаки составляет 10 км/ч, то за этот час она пробежит 10 километров.
Ответ: 10 км.
5. Можно ли расставить по окружности 20 красных и несколько синих фишек так, чтобы в каждой точке, диаметрально противоположной красной фишке, стояла синяя и никакие две синие фишки не стояли рядом?
Решение
Из условия следует, что красные и синие фишки должны чередоваться (на окружности), значит, всего их 40. Фишки по окружности размещаются равномерно в том смысле, что две диаметрально противоположные фишки делят множество оставшихся 38 фишек на две части по 19 фишек, расположенные в одной и другой полуокружностях относительно двух данных фишек. Это так, потому что согласно условию, каждая фишка имеет диаметрально противоположную. Диаметрально противоположные фишки имеют разный цвет, поэтому 19 фишек, расположенные в одной из полуокружностей должны чередоваться по цвету и начинаться и заканчиваться фишками разного цвета, что невозможно при нечётном 19. Следовательно, указанная в задаче расстановка фишек не возможна.
Ответ: нельзя.
6. Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. В процессе расследования каждый из них сделал по два заявления.
Браун: «Я не делал этого. Джонс не делал этого.»
Джонс: «Браун не делал этого. Смит сделал это.»
Смит: «Я не делал этого. Браун сделал это.»
Было установлено далее, что один из них дважды солгал, другой дважды сказал правду, третий – раз солгал, раз сказал правду. Кто совершил преступление?
Решение
Если вор – Смит, то и Браун, и Джонс оба сказали правду. Если вор – Джонс, то и Браун, и Смит одновременно сказали и правду, и ложь. Итак, Браун – преступник. Джонс оба раза солгал, Смит оба раза сказал правду, Браун один раз солгал, второй раз сказал правду.
7. «Суперкоролева» – это шахматный ферзь, который может ходить еще и как конь. Надо разместить четырех суперкоролев на доске 5 на 5 таким образом, чтобы ни одна из них не могла атаковать другую. Если вам это удастся, то попробуйте 10 суперкоролев разместить на доске 10 на 10 так, чтобы ни одна не имела возможности напасть на другую. Обе задачи имеют единственное решение, если не учитывать повороты доски и ее зеркальные отражения.
Решение
Оба решения показаны на следующем рисунке.
8. У автомобиля новые шины. Шина на заднем колесе выдерживает пробег 16000 км, а на переднем – 24000 км. Какой максимальный пробег можно осуществить на этих калёсах?
Решение
Будем считать, что скорость роста износа колеса является постоянной и не зависит от того насколько оно давно служит.
Очевидно, что задние колёса изнашиваются в 1,5 раза быстрее передних. Значит, когда задние колёса износятся на 60%, то передние – только на 40%. Это произойдёт после пробега
0,6 · 16000 = 0,4 · 24000 = 9600 (км).
В этот момент и следует сменить колёса. Оставшийся 40%-й ресурс задних колёс, поставленных спереди, и 60%-й ресурс передних колёс, поставленных сзади, очевидно, исчерпается одновременно, и произойдёт это ещё через 9600 км. Таким образом максимальный пробег составляет 2·9600 = 19200 км.
Замечание. Это лишь одно из множества возможных решений этой задачи. Попробуйте найти своё.
Ответ: 19200 км.
9. Переаттестация Совета Мудрецов происходит так: король выстраивает их в колонну по одному и надевает каждому колпак белого или чёрного цвета. Все мудрецы видят, какого цвета колпак каждого впереди стоящего мудреца, а цвет своего и всех стоящих сзади не видят. Раз в минуту один из мудрецов должен выкрикнуть один из двух цветов (каждый мудрец выкрикивает цвет один раз). После окончания этого процесса король казнит каждого мудреца, выкрикнувшего цвет, отличный от цвета его колпака. Накануне переаттестации все сто членов Совета Мудрецов договорились и придумали, как минимизировать число казнённых. Скольким из них гарантированно удастся избежать казни?
Решение
Ясно, что мудрец, стоящий в колонне последним, может спастись только случайно, ведь его колпака не видит никто из мудрецов. Но он может спасти всех остальных, сообщив им чётность числа белых колпаков, надетых на них (по договоренности он скажет «белый», если это число нечетно, и «чёрный» в противном случае). Теперь мудрецы должны вычислять и называть цвета своих колпаков по порядку от предпоследнего к первому: сначала предпоследний, видя колпаки впереди стоящих и зная чётность числа белых колпаков (среди колпаков впереди стоящих и своего), легко определит цвет своего колпака и назовет его; затем мудрец, стоящий перед ним, зная цвета всех тех же колпаков, кроме своего (передние он видит, а про задний только что услышал), по чётности может определить цвет своего колпака и назвать его. Остается продолжать описанную процедуру до тех пор, пока первый мудрец не определит цвет своего колпака.
Ответ: всем, кроме, быть может, одного.
10. В тюрьму поместили 100 узников. Надзиратель сказал им: «Я дам вам вечер поговорить друг с другом, а потом рассажу по отдельным камерам, и общаться вы больше не сможете. Иногда я буду одного из вас отводить в комнату, в которой есть лампа (вначале она выключена). Уходя из комнаты, вы можете оставить лампу как включенной, так и выключенной. Если в какой-то момент кто-то из вас скажет мне, что вы все уже побывали в комнате, и будет прав, то я всех вас выпущу на свободу. А если неправ — скормлю всех крокодилам. И не волнуйтесь, что кого-нибудь забудут — если будете молчать, то все побываете в комнате, и ни для кого никакое посещение комнаты не станет последним.»
Придумайте стратегию, гарантирующую узникам освобождение.
Решение
Узники выбирают одного определённого человека (будем называть его «счётчиком»), который будет считать узников по такой системе: если, приходя в комнату, он обнаруживает, что свет включён, то он прибавляет к уже посчитанному числу узников единицу и выключает свет, если же свет не горит, то он, ничего не меняя, возвращается обратно в свою камеру. Каждый из оставшихся узников действует по такому правилу: если, приходя в комнату, он обнаруживает, что свет не горит, и он до этого ни разу не включал свет, то он его включает. В остальных случаях он ничего не меняет. Когда число посчитанных узников становится равным 99, «счётчик» говорит, что все узники уже побывали в комнате.
Действительно, каждый узник, кроме «счётчика», включит свет в комнате не более одного раза. Когда «счётчик» насчитает 99, он может быть уверен, что все остальные узники уже побывали в комнате хотя бы раз, кроме того он сам уже побывал в комнате. Получается, что к этому моменту все узники заведомо побывали в комнате хоть раз.
Остаётся доказать, что каждый из 99 узников включит свет. Предположим, что это не так – свет будет включён менее 99 раз. Тогда, начиная с некоторого дня n, свет включаться не будет. Так как никакой заход в комнату не будет для счётчика последним, он побывает в комнате после этого дня (например, на m-й день, m > n). Если свет при этом горел, он его выключит. Значит, начиная с (m+1)-го дня свет будет всё время выключен. Рассмотрим узника, который свет ещё ни разу не зажигал. Так как и для него никакой заход в комнату не последний, он побывает в комнате после m-го дня. Но тогда он должен включить свет – противоречие.
Задачи без решений
1. Каково наибольшее число утверждений из приводимых ниже, которые одновременно могут быть истинными:
а) Джо ловкач,
б) Джо не везет,
в) Джо везет, но он не ловкач,
г) если Джо ловкач, то ему не везет,
д) Джо является ловкачом тогда и только тогда, если ему везет,
е) либо Джо ловкач, либо ему везет, но не то и другое одновременно.
2. Мать разделила между своими сыновьями груши. Первому она дала половину всех груш и ещё половину груши, второму – половину остатка и ещё половину груши и, наконец, третьему – половину нового остатка и ещё половину груши. Ни одной груши при этом не нужно было разрезать. Сколько груш получил каждый сын, если мать раздала все груши?
3. В гостиницу приехал путешественник. Денег он не имел, а обладал лишь серебряной цепочкой, состоящей из семи звеньев. За каждый день пребывания в гостинице он расплачивался одним звеном цепочки, при этом хозяин предупредил, что согласен взять не более одного распиленного звена.
Подскажите, как путешественнику распилить цепочку, чтобы прожить в гостинице семь дней и ежедневно расплачиваться с хозяином.
4. Имеется 10 мешков монет. В девяти мешках монеты настоящие, весят по 10 г, а в одном мешке все монеты фальшивые, весят по 11 г. Одним взвешиванием определить, в каком мешке фальшивые монеты. (Взвешивание осуществляется на весах способных показать точный вес.)
5. Переаттестация Совета Мудрецов происходит так: король выстраивает их в колонну по одному и надевает каждому колпак белого, синего или красного цветов. Все мудрецы видят цвета всех колпаков впереди стоящих мудрецов, а цвет своего и всех стоящих сзади не видят. Раз в минуту один из мудрецов должен выкрикнуть один из трех цветов (каждый мудрец выкрикивает цвет один раз). После окончания этого процесса король казнит каждого мудреца, выкрикнувшего цвет, отличный от цвета его колпака.
Накануне переаттестации все сто членов Совета Мудрецов договорились и придумали, как минимизировать число казненных. Скольким из них гарантированно удастся избежать казни?
math4school.ru
Iteach
Материал из ИнтеВики — обучающей площадкой для проведения тренингов программы Intel
Текущие событияПроектная деятельность в информационной образовательной среде 21 века/Нижний Новгород НГПУ январь 2014 года
Учебный Курс «Проектная деятельность в информационно-образовательной среде ХХI века», Ижевск, ноябрь 2013 г.
Основной курс программы Intel Обучение для будущего Новокузнецк октябрь-декабрь 2013
Основной курс программы Intel Обучение для будущего Ростовская область октябрь 2013
Проектная деятельность в информационной образовательной среде 21 века/НИРО/Курс для тьюторов/23 сентября — 20 октября 2013 года
Дистанционный курс ТЕО (Омская обл, осень 2013) преподаватель — Маркер Надежда Юрьевна
Семинар Созвездия Веб 2.0/Екатеринбург сентябрь 2013 преподаватель — Ирина Нургалеева
Обучение тьюторов, группа TEO РК, май-июнь 2013 преподаватель — Ольга Урсова
Очно-дистанционный курс программы Intel Обучение для будущего НИРО Нижний Новгород март-май 2013
Очно-дистанционный курс программы Intel Обучение для будущего НИРО Нижний Новгород февраль-апрель 2013
Курс «Информационно-коммуникационные технологии как средство реализации ФГОС» Екатеринбург — Арамиль март 2013
Тренинг по основному курсу программы «Обучение для будущего», ВГПУ, 1 курс магистратуры, исторический факультет — 6 февраля — 20 мая 2013г. — преподаватель — Ирина Суслова
Курс «Информационные технологии в практике работы учителя» 04.01.13 — 02.02.2013 — преподаватель — Анна Кологерманская
Курс для руководителей ИКТ: стратегия развития образовательного учреждения (Омский МР, декабрь 2012) — преподаватель —Любовь Мальцева
Курсы Проектная деятельность в информационной образовательной среде 21 века, Балаковская площадка, декабрь 2012 — преподаватель — Светлана Морозова
Тренинг Информационно-коммуникационные технологии в управлении воспитательным процессом,Тюкалинск,декабрь 2012 — преподаватель — Наталья Ильяш
Тренинг по основному курсу программы «Обучение для будущего»,октябрь 2012, ЯНАО г.Ноябрьск — преподаватель — Елена Ремизова
В рамках он-лайн конференции «Новая школа: мой маршрут» проводится сетевое мероприятие Проектный инкубатор-2012
Архив событий |
| |
|
|---|
- Окружающий мир – мир сложных систем (информатика, 11 класс, автор Круподерова К.Р.)
- Информационная цивилизация (информатика, 11 класс, автор Кошелев В. Г.)
- Математика для будущих банкиров (алгебра, 9 класс, автор Склемина Г. А.)
- Волшебная сила музыки (музыка, биология и др., 5-8 классы, автор Красноперова Т. В.)
- Полуостров сокровищ (окружающий мир, краеведение, 4 класс, автор Тимохина Е.Г.)
- Удивительное рядом (окружающий мир, краеведение, русский язык, 2-4 классы, автор Тимохина Е.Г.)
|
Нам уже… |
|---|
|
|
|
|
|
wiki.iteach.ru













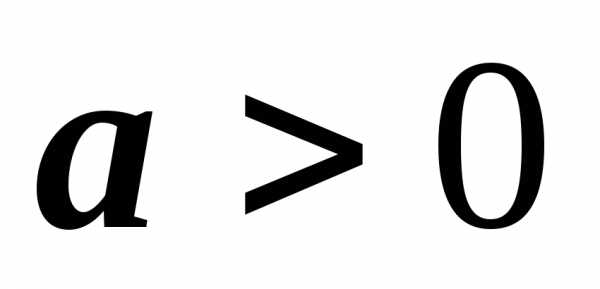 ,
,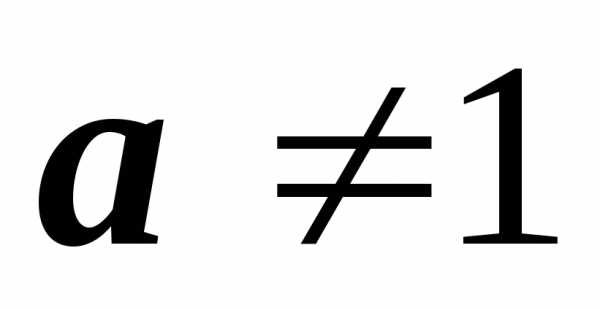 ,
,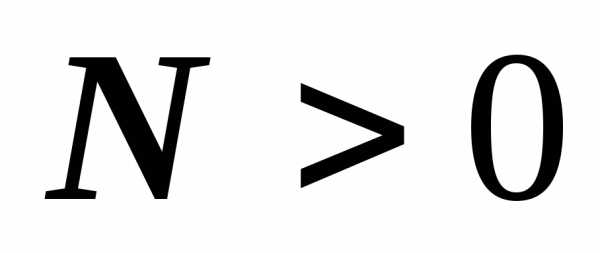

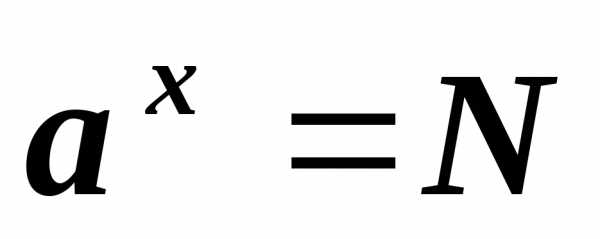 ,
т.е. — это равенство является основным
логарифмическим тождеством.
,
т.е. — это равенство является основным
логарифмическим тождеством.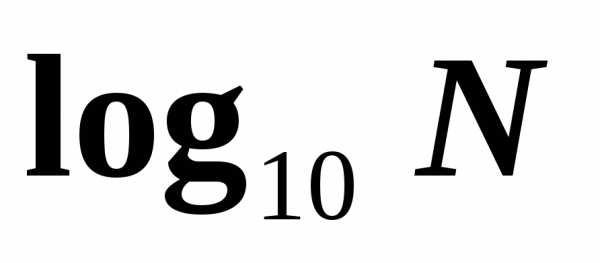 пишут
пишут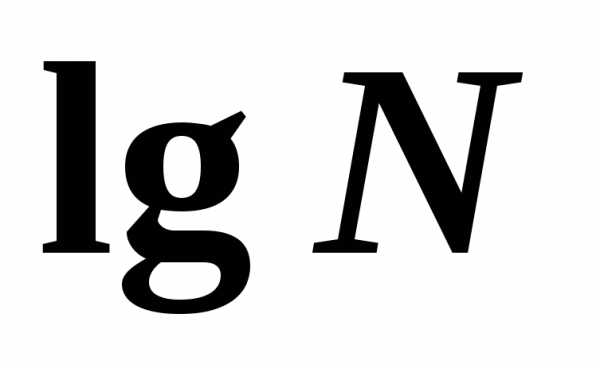 .
.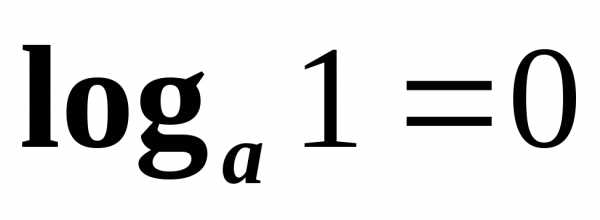
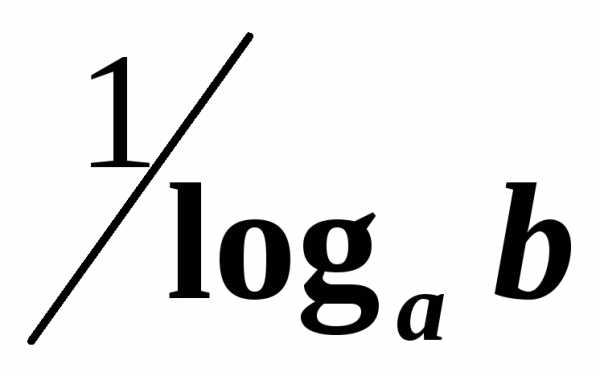 называется модулем перехода от логарифмов
при основанииa к логарифмам при основанииb.
называется модулем перехода от логарифмов
при основанииa к логарифмам при основанииb.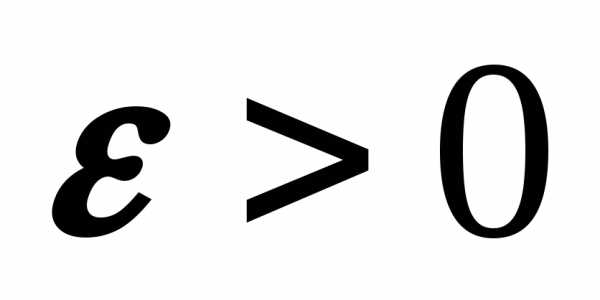 ,
найдется такое число
,
найдется такое число  ,
что как только
,
что как только 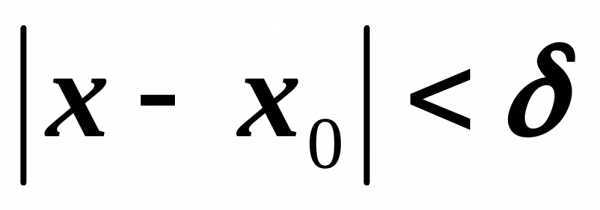 ,
то
,
то 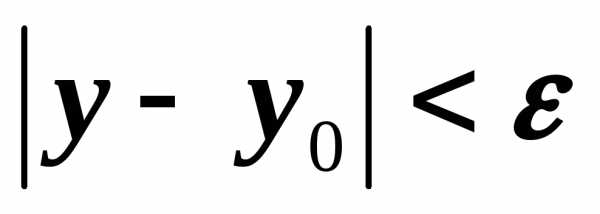 .
.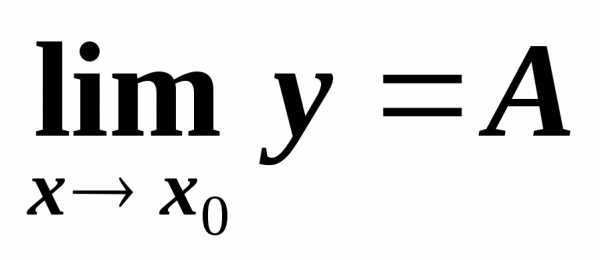
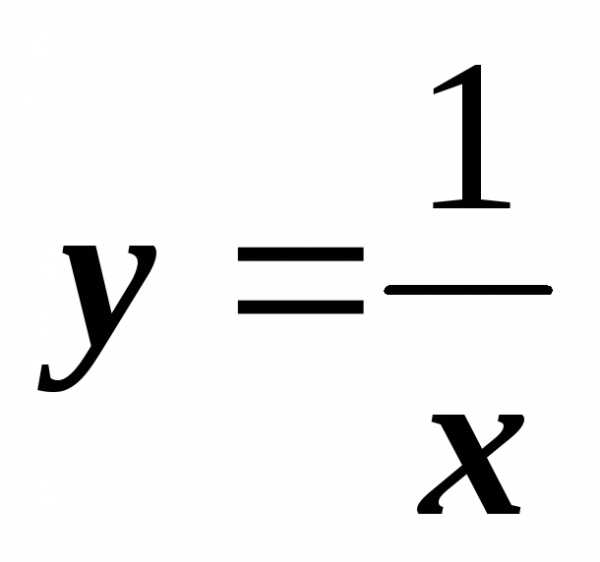 .
.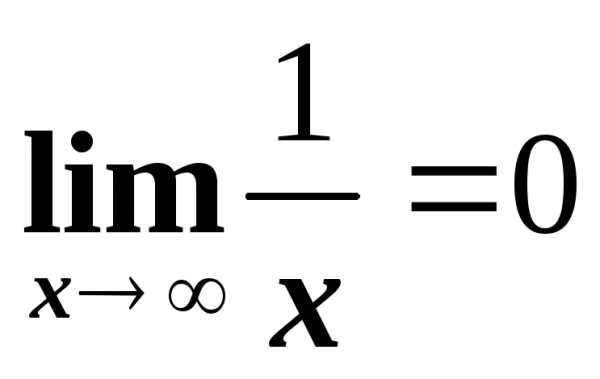
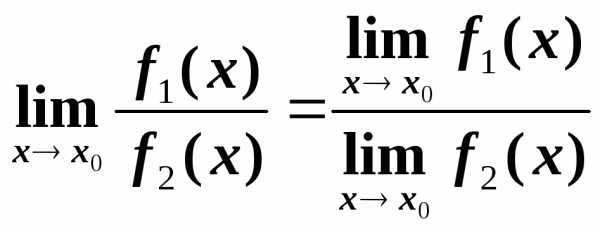
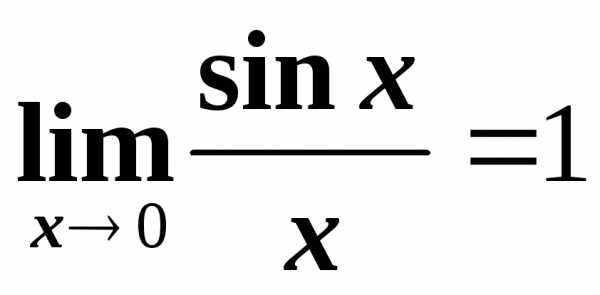 ,
, 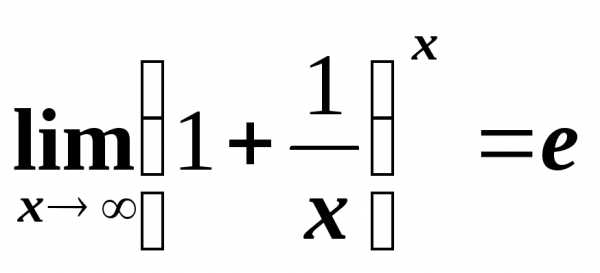 ,
где
,
где или
или 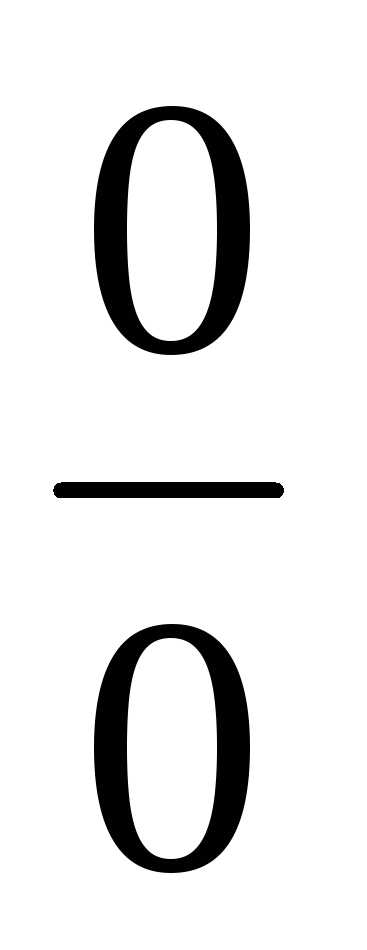 .
.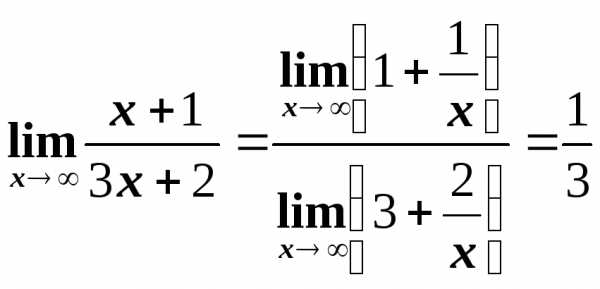 .
.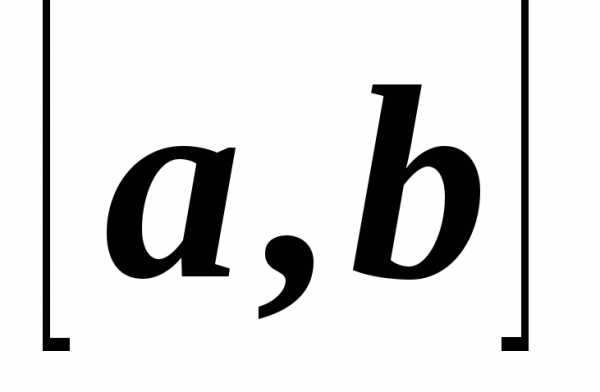 .
. получил некоторое приращение
получил некоторое приращение 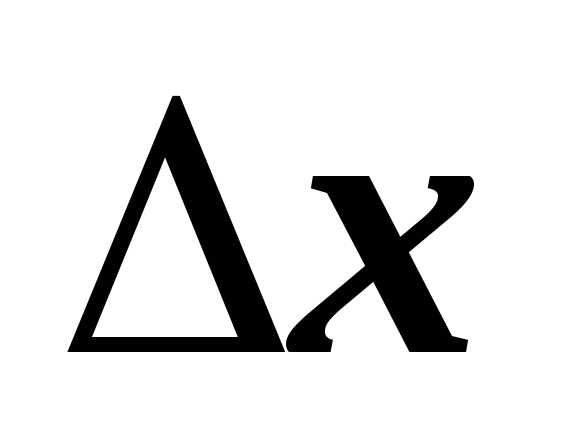 .
Тогда и функция получит приращение
.
Тогда и функция получит приращение  .
. соответствует значение функции
.
соответствует значение функции
.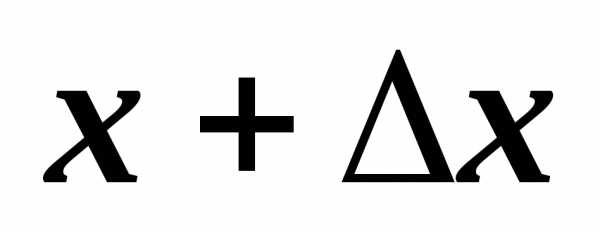 соответствует значение функции
.
соответствует значение функции
.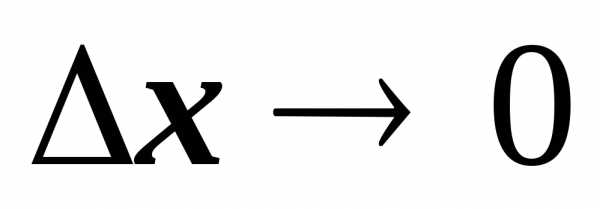 .
Если этот предел существует, то он
называется производной данной функции.
.
Если этот предел существует, то он
называется производной данной функции.

 по
аргументу
по
аргументу  называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента произвольным
образом стремится к нулю.
называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента произвольным
образом стремится к нулю.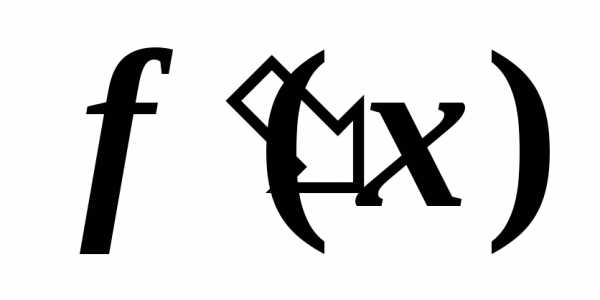 ;
;  ;
; 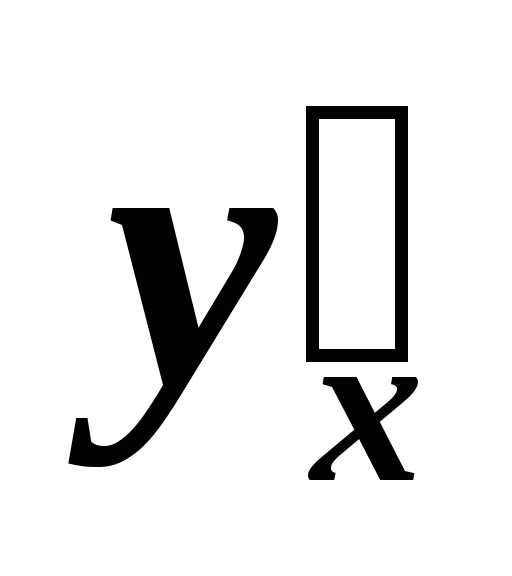 ;
; 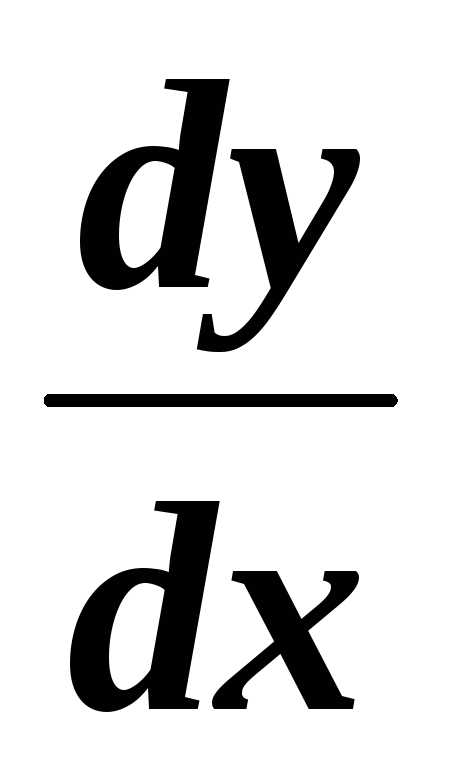 .
.
 движущаяся
точка
движущаяся
точка 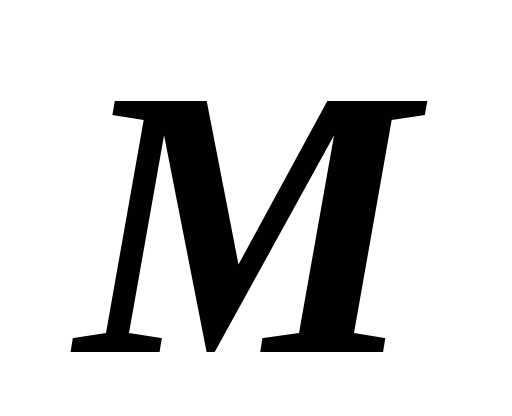 находилась на расстоянии
находилась на расстоянии  от начального положения
от начального положения 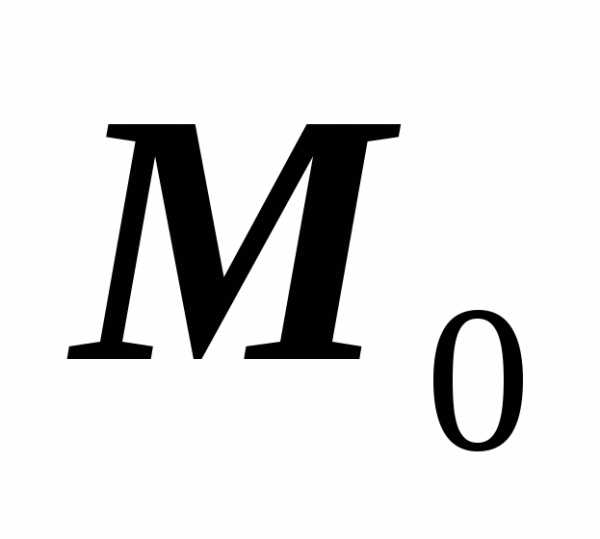 .
.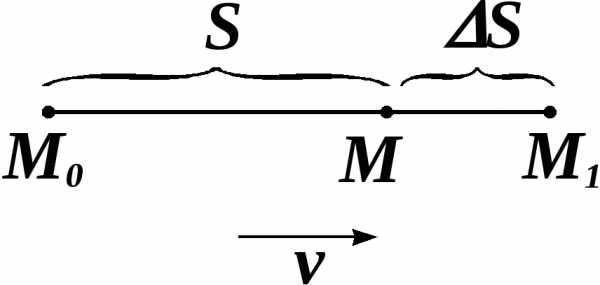
 она переместилась на расстояние
она переместилась на расстояние  .
Отношение
.
Отношение 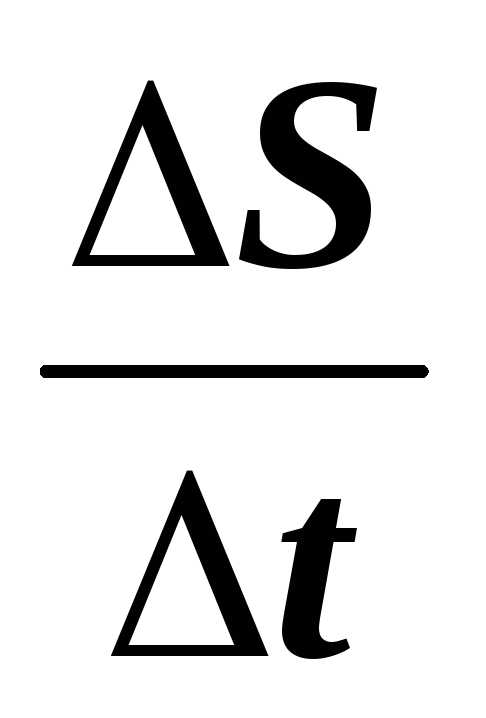 =
=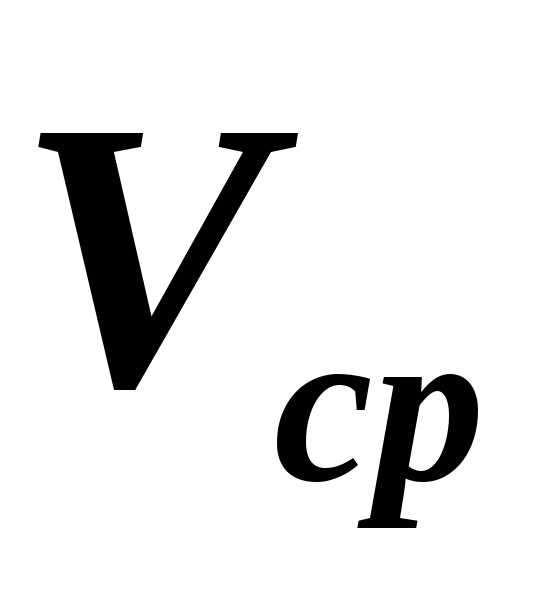 — средняя скорость материальной точки
— средняя скорость материальной точки 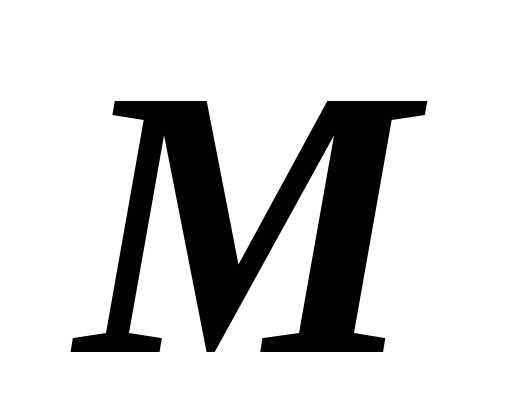 .
Найдем предел этого отношения, учитывая
что
.
Найдем предел этого отношения, учитывая
что 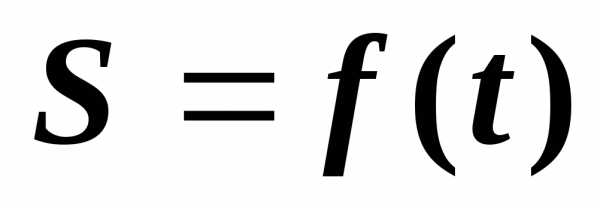 .
.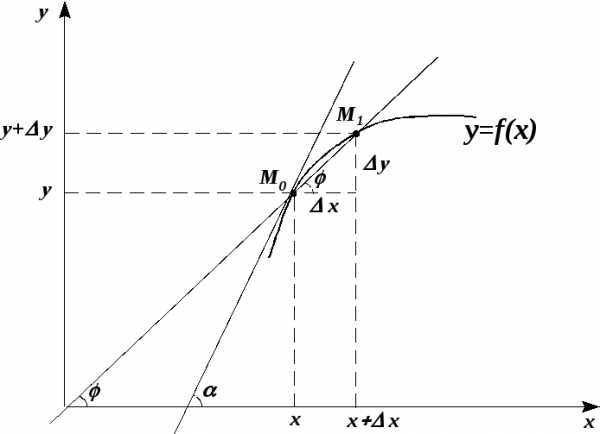
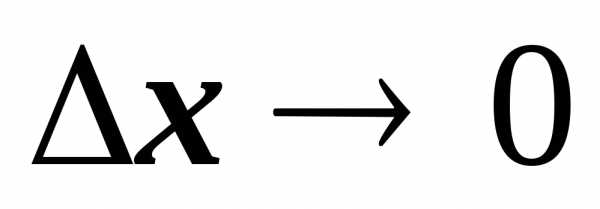 ,
то точка
,
то точка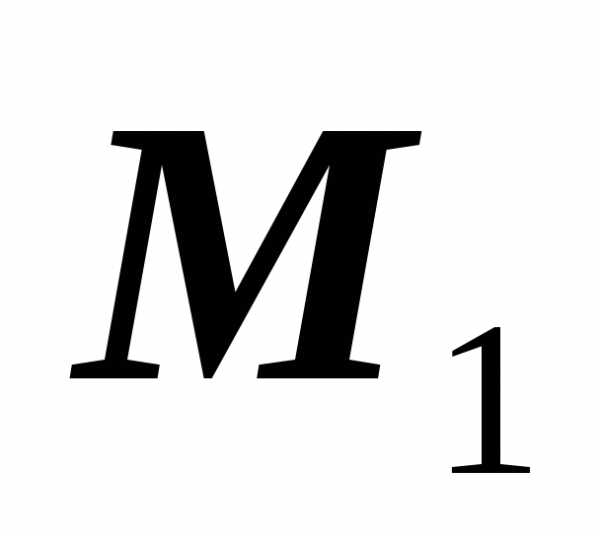 ,
будет перемещаться по кривой, приближаясь
к точке
,
будет перемещаться по кривой, приближаясь
к точке 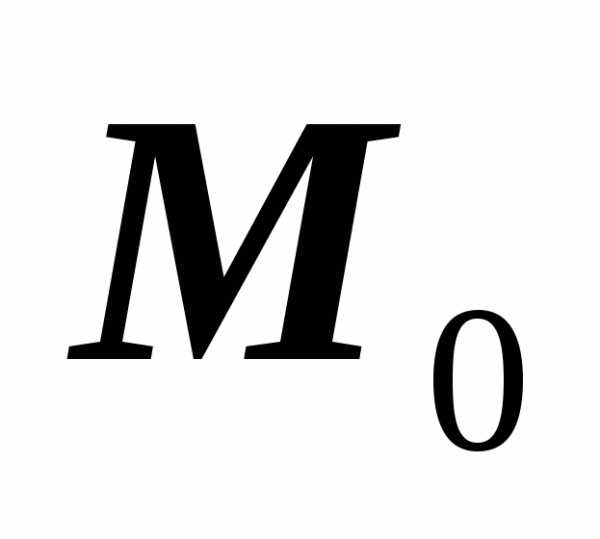 .
. численно равняется тангенсу угла
образованного касательной в данной
точке с положительным направлением оси
численно равняется тангенсу угла
образованного касательной в данной
точке с положительным направлением оси 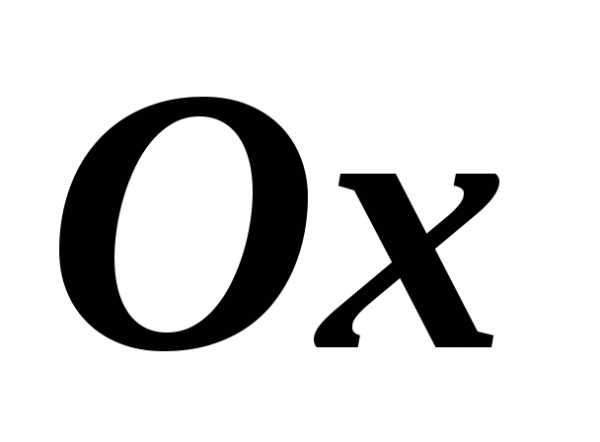 .
.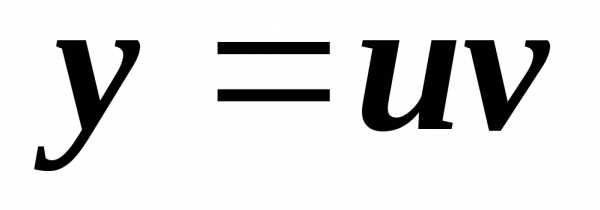
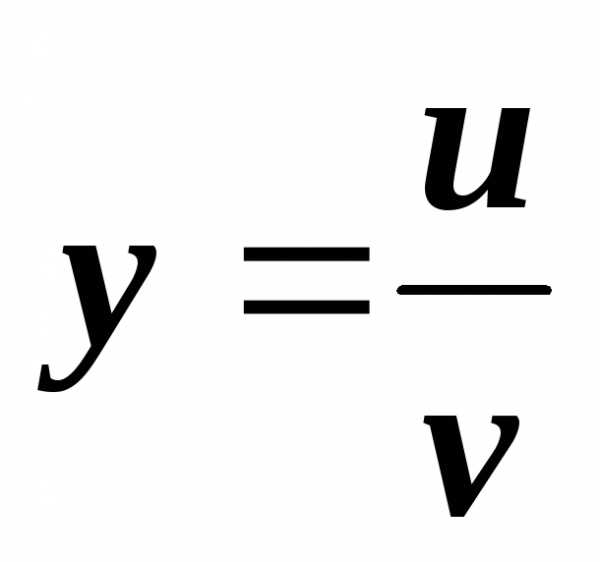
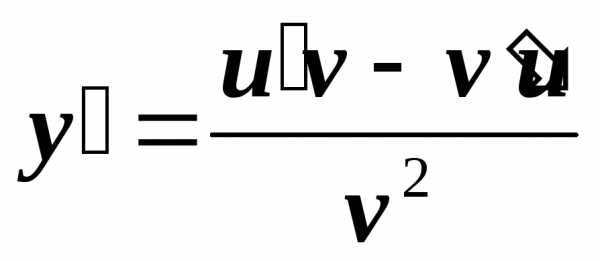
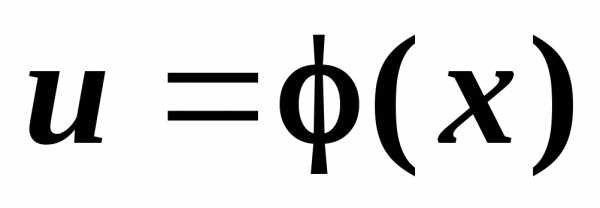 ,
где переменная
,
где переменная является промежуточным аргументом,
тогда
является промежуточным аргументом,
тогда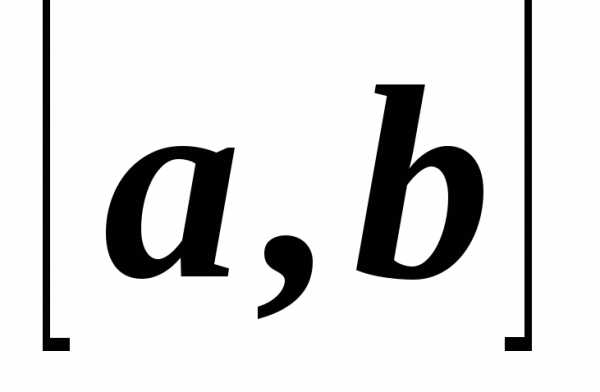 и пустьу этой функции есть производная
и пустьу этой функции есть производная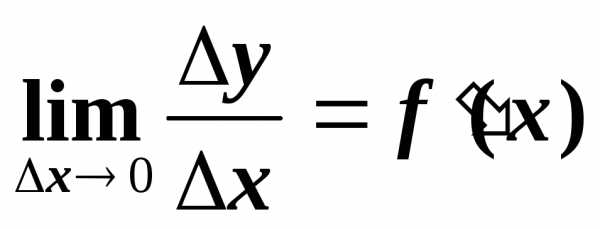 ,
,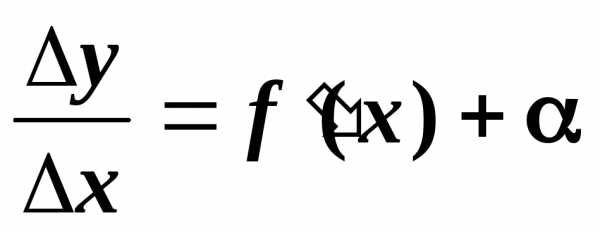 (1),
(1), — бесконечно малая величина,
— бесконечно малая величина,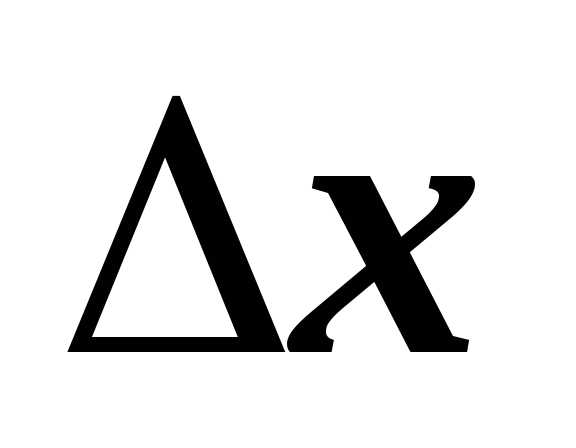 имеем:
имеем: —
б.м.в. высшего порядка.
—
б.м.в. высшего порядка.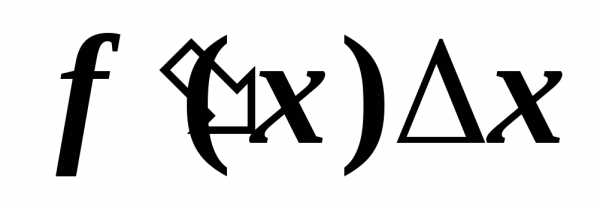 называется дифференциалом функции
называется дифференциалом функции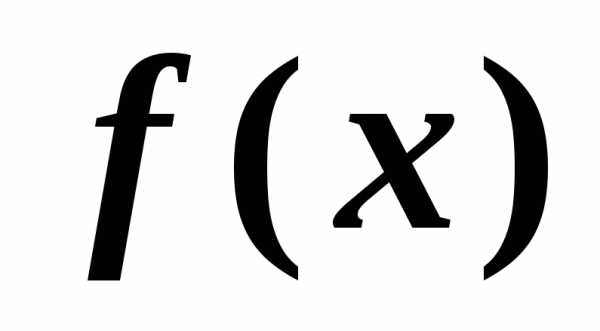 и обозначается
и обозначается
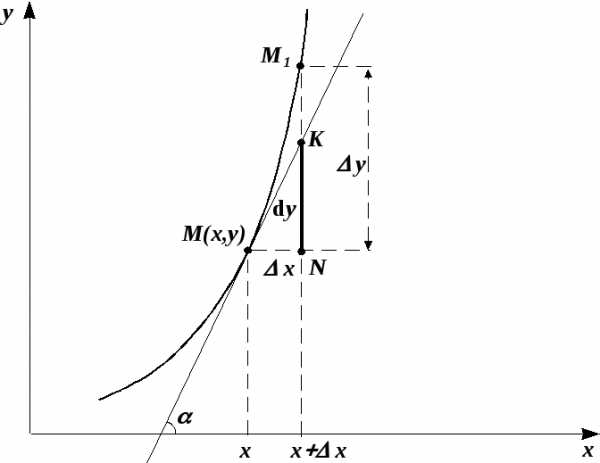
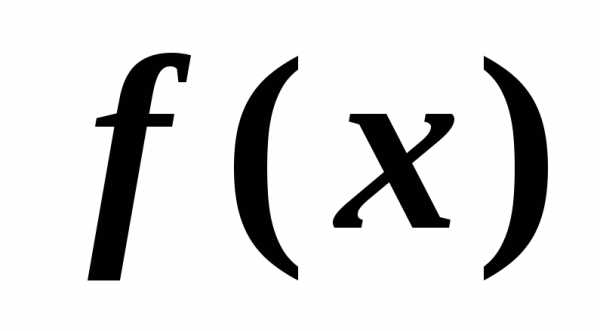 равен приращению ординаты касательной
в данной точке.
равен приращению ординаты касательной
в данной точке.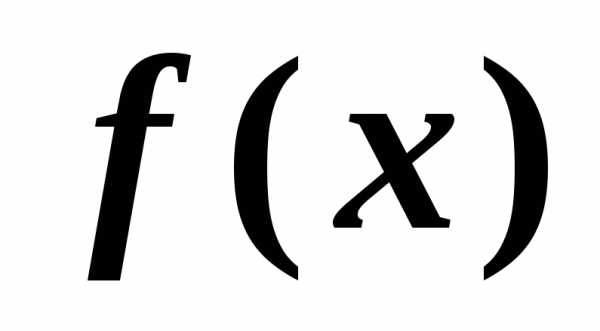 называется производная (n-1)-го
порядка и записывается:
называется производная (n-1)-го
порядка и записывается: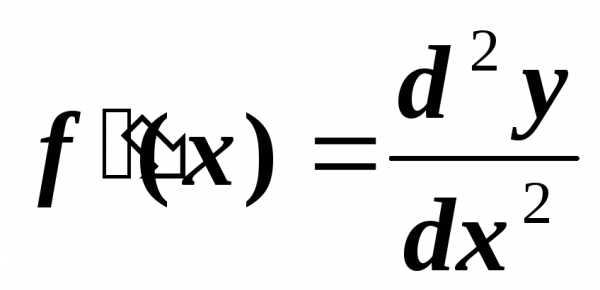
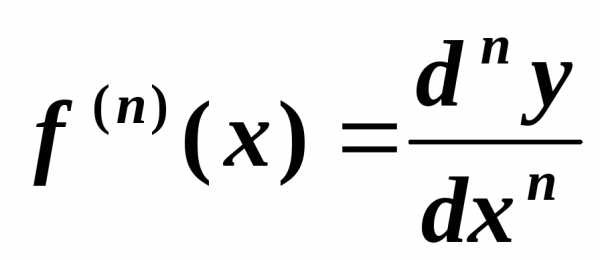 .
. ,
,
