Детские книги о математике Владимира Лёвшина
Владимир Лёвшин родился до революции, в 1904-м году.. человеком он был разносторонним, 40 лет преподавал математику в ВУЗах, увлекался и музыкой, и живописью, писал эстрадные пьесы, стихи.. однажды писатель Львовский натолкнул его на мысль писать детские математические книги, и в возрасте 60-ти лет Лёвшин написал свою первую книгу о цифрах и числах «Три дня в Карликании».. а потом одна за другой появились другие приключенческие книги о математике и физике..можно сказать, благодаря этим книгам я стала математиком.. наткнулась я на них в детстве в школьной библиотеке, перечитала все, что нашла, и залюбила математику.. а потом пошло-поехало — математические олимпиады, приглашение в математический интернат, занятия с профессором математики, математический факультет, диплом математика.. вот так детские книжки могут определить судьбу))
книги Лёвшина не были особо известными в советское время.. я всегда про них вспоминала и жалела, что о них мало кто знает..
и вот наконец-то их начали переиздавать!
кроме книг Лёвшина в детстве я зачитывалась альманахами «Эврика», в которых в популярной форме, понятной даже детям, рассказывали о научных гипотезах и открытиях.. издавались они раз в год.. вот некоторые из этих альманахов онлайн..
Эврика-72
Эврика-83/84
Эврика-90
издавались и отдельные книги этой серии.. здесь их можно скачать..
такие книги должны читать дети — умные, мотивирующие, пробуждающие интерес к знаниям, написанные образованными людьми..
(вот почему меня злит бездарная писанина недалекой домохозяйки про гарри поттера, которой пичкают детей..)
de-de-de.livejournal.com
Хорошие книги по математике | Математика, которая мне нравится
14 Декабрь 2012, 0:02
Об этой книге я уже упоминала здесь, однако более подробно ничего о ней не писала. На то была причина: найти “Элементарную алгебру’’ было довольно сложно. Издана в последний раз она была достаточно давно (у меня, например, имеется издание 1962 г.), а в электронном виде ее тое найти не удавалось. Сейчас ситуация изменилась, но об этом чуть позже. Сначала о самом учебнике.
“Элементарная алгебра’’ С.И. Туманова не зря называется пособием для самообразования. В предисловии к ней написано, что автор ставил цель, “чтобы по этому курсу можно было изучить предмет без помощи преподавателя и притом не формально, а с достаточно ясным пониманием сущности алгебры, ее связи с другими науками и ее значения для практики’’. Думаю, хороша и такая цель: “чтобы чтение курса пробуждало у учащегося интерес к алгебре и потребность к размышлениям над ее содержанием’’. На мой взгляд, эти цели достигнуты. Читать полностью ‘С.И. Туманов “Элементарная алгебра’’’ »
8 Апрель 2011, 0:05
Не секрет, что одним из разделов математики, который вызывает у школьников наибольшие затруднения и непонимание, является теория чисел. Самые начала этой теории изучают в пятом классе общеобразовательной школы, однако они очень быстро покидают головы школяров, поскольку продолжения не следует, а задачи на эту тему встречаются практически исключительно на олимпиадах. Да и сама такая олимпиада, где нужно иметь хотя бы немного знаний о целых числах, должна быть, видимо, уже хотя бы областной, а не городской и уж тем более не школьной (если где-то таковые еще остались). Читать полностью ‘И.М. Виноградов “Основы теории чисел”’ »
25 Март 2011, 0:05
Об этой книге предложил написать Владимир в комментариях здесь. Действительно, книга очень хорошая и полезная. Полностью же называется она вот так: “Волшебный двурог или правдивая история небывалых приключений нашего отважного друга Ильи Алексеевича Камова в неведомой стране, где правят: Догадка, Усидчивость, Находчивость, Терпение, Остроумие и Трудолюбие, и которая в то же время есть пресветлое царство веселого, но совершенно таинственного существа, чье имя очень похоже на название этой удивительной книжки, которую нужно читать, не торопясь’’. Первый раз книга была издана в 1949 году, последнее, третье издание – 2006 год. Так что это классика, которую читало и любит уже не одно поколение наших математиков. Читать полностью ‘Сергей Бобров “Волшебный двурог’’’ »
11 Март 2011, 9:23
Еще одна замечательная книга Наума Яковлевича Виленкина, которую тоже можно назвать классической и которая уже выдержала несколько изданий. Написана она хорошо, интересно и понятно. Рассказывается в этой книге о теории множеств Георга Кантора – достаточно сложной для понимания, но красивой и мощной теории, во многом изменившей математику. Кстати сказать, создана теория множеств была в 70-х годах XIX века. Читать полностью ‘Виленкин Н.Я. “Рассказы о множествах”’ »
4 Март 2011, 10:32
Я уже писала здесь, что хороших учебников по математике практически нет. То же относится и к другой математической литературе. Там же упоминалась и эта книга, как хорошая. Сейчас немного подробнее.
Комбинаторика нужна, причем нужна она и тем, кто планирует изучать математику дальше (так, она является основой для изучения теории вероятности), она нужна и тем, кто хочет в дальнейшем заниматься программированием (в частности, пригодится при изучении конечных автоматов). Встречаются комбинаторные задачки и в других науках, на школьном уровне – в химии, а дальше – везде, где применяется теория вероятности. Еще комбинаторика полезна для интеллектуального развития. Другие задачи, другие способы их решения. Читать полностью ‘Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. “Комбинаторика’’’ »
15 Февраль 2011, 0:10
В свое время я уже упоминала задачник по алгебре и анализу М.И. Башмакова, Б.М. Беккера, В.М. Гольхового и Ю.И. Ионина здесь. Повторюсь, лучшего задачника я не видела. Самое, на мой взгляд, полезное и правильное в нем – это то, что “упражнения с использованием одного и того же приема, как правило, не дублируются”, как написано в аннотации. Это не сборник однотипных упражнений, которые позволяют научиться решать только и именно такие задачи, нет. По этой книжке можно действительно учиться. Она помогает связать отдельные темы в общую целостную картину, осмыслить различные понятия школьного курса. Чуть не забыла . К ЕГЭ эта книжка великолепно подготовит тоже, но не натаскиванием, а осмыслением и пониманием . Читать полностью ‘Лучший школьный задачник (ИМХО)’ »
hijos.ru
Топ-лист книг по занимательной математике
После статьи о проблемах школьной математики получил несколько писем. Автор одного из них спрашивал совета о хороших книгах, способных пробудить и поддержать интерес к этой науке у школьников.
Я ответил. А потом подумал, что пусть этот ответ лежит и на всеобщем обозрении — вдруг да кому окажется полезным.
Итак, вот хорошая начальная подборка. Предполагаемая аудитория — школьники всех классов с отданием некоторого предпочтения более младшим. Всё это переиздавалось в последние годы и легко доступно, стоит только поискать.
Е.Игнатьев. «В царстве смекалки».
Классика русскоязычной популярной литературы, которой уже более ста лет. Сборник интересных старинных задач по арифметике и основам алгебры. Также содержит загадки, задачи на разрезание и складывание, забавы и головоломки «визуального» характера. Вполне может быть рекомендована даже и для занятий с дошкольниками.
В начале ХХ века книга выходила тремя томами. В наши дни переиздавали первый том (хотя в некоторых изданиях он расширен отдельными разделами из второго и третьего). Электронная версия всех трёх томов доступна на сайте издательства МЦНМО — правда, в старинной орфографии.
Я.Перельман. «Занимательная арифметика».
Тоже классика. Серьёзный уклон сделан на историю математики: способы записи чисел и действий с ними, старинные учебники и традиции преподавания. Определённое внимание уделено устному счёту. Немало задач. Целевая аудитория — все классы школы: в книге столько интересного, что любой найдёт здесь чего-нибудь любопытное для себя.
У Перельмана есть ещё две замечательные книги по математике: «Занимательная алгебра» и «Занимательная геометрия», но они рассчитаны на школьников постарше. Всё можно взять на том же сайте МЦНМО.
Р.Смаллиан. «Как же называется эта книга?».
Основное содержание — каверзные логические задачи и этюды (автор был великим мастером по части их изобретения!). Однако есть тут и занимательные истории из жизни известных учёных, а в конце книги Смаллиан просто и доступно рассказывает о весьма серьёзных понятиях из теории множеств и формальных систем. Для школьников всех возрастов.
У того же автора есть не менее замечательная книга «Алиса в стране смекалки» — но, к сожалению, на русском языке найти её весьма непросто (давно не переиздавали). Легальных электронных версий, увы, нету: ещё не истёк срок действия авторских прав.
М.Гарднер. «Нескучная математика».
Ну, имя Мартина Гарднера в особых представлениях не нуждается. Автор несколько десятилетий вёл математическую колонку в журнале «Scientific American» (на русском выходил его перевод под названием «В мире науки»), и весь богатый накопленный материал периодически издавал. Любую книгу Гарднера можно смело рекомендовать любой аудитории — от первоклассника до взрослого — и эта книга не исключение.
Я выбрал «Нескучную математику» потому, что она в большей степени, чем другие книги Гарднера, ориентирована на детей. Однако любую книгу с этим именем на обложке можно брать, не задумываясь — не прогадаете. Легальных электронных версий нету.
С.Бобров. «Волшебный двурог».
Абсолютно уникальная книга, совершенно обязательная к наличию в библиотеке любого энтузиаста математики! Охват материала широчайший (вплоть до теории графов и неевклидовой геометрии), а стиль изложения великолепен. Фактически, это почти художественное произведение. Целевая аудитория — школьники примерно от 10–11 лет.
Электронная версия есть на сайте МЦНМО. Перу Боброва принадлежит ещё одна, не менее замечательная книга «Архимедово лето» — но она, увы, много лет не переиздавалась и давно стала библиографической редкостью…
Г.Гамов, М.Стерн. «Занимательные задачи».
Великолепная подборка отлично беллетризованных задач с подробнейшими разборами решений. Тематика весьма разнообразна: здесь и логика, и вероятности, и неожиданные упрощения казавшихся сложными расчётов и много чего ещё. Целевая аудитория книги — средний школьный возраст, учащиеся в возрасте где-то от 11–12 лет.
Книга в оригинале называется «Puzzle-Math»; её более ранние переводы могут носить название «Занимательная математика». Легальных электронных версий нету. Рекомендую также обратить внимание на книгу Г.Гамова «Мистер Томпкинс в стране чудес» — суть примерно то же самое, но по физике.
Л.Кэрролл. «Логическая игра».
Да-да, тот самый Льюис Кэрролл. О содержании книги вполне красноречиво говорит авторский эпиграф: «Логика, своенравная и непокорная, отныне укрощена». Классическая аристотелева логика с человеческим лицом и в отличном изложении. Вполне подойдёт для школьников с 10 лет… хм, вообще-то, этой книгой до сих пор пользуются как учебным пособием во многих вузах! 😉
Может также встречаться в сборниках Кэрролла под названием «История с узелками». Есть и электронная версия, за которую опять же спасибо издательству МЦНМО.
michaelbalandin.wordpress.com
книги по математике для детей — Вытворяндия
Как ни крути, а математика окружает нас везде. Мы можем ограждать своих детей от нее, ждать школьного времени, когда все объяснят и разложат по полочкам. Но когда ребенок в первый раз с удивлением глядит на свою ладошку вложенную в вашу руку, он начинает осваивать «больше-меньше». Мне кажется, что именно в такие моменты начинается математика. И, наверное, те, кто сохранил это детское удивление от первых встреч, стали писать книги по математике для детей, которые раскрывают для ребят необычный мир Царицы наук.
«Кубарик и Томатик или Весёлая математика»
Предположим, что каждый ребенок в своем развитии проходит все стадии взросления человечества. Тогда становится понятно, почему самые древние люди не знали чисел. Видимо, они, как и маленькие дети примерно трех лет, только начинали разбираться в том, что такое один — много — мало, больше — меньше, длиннее — короче, выше — ниже. Открывать это раз за разом непросто, поэтому пройти по математическому пути ребенку будет гораздо веселее вместе с Кубариком и Томатиком. Книгу «Кубарик и Томатик или Весёлая математика» сорок лет назад написали Людмила Левинова и Генрих Сапгир. Это не просто история о дружбе маленького человечка и лошадки Кубарика, но и настоящее учебное пособие, благодаря которому ребенок от трёх лет сам с удовольствием отвечает на вопросы из жизни любимых героев, учится пересказывать, а заодно и разбирается в самых первых математических понятиях.

«Веселый считарь»
Мне кажется, что именно Андрей Усачев по праву может считаться одним из лучших поэтов подходящих для первого знакомства малышей с математикой. Надевая рифмы на цифры он заставляет их быть веселыми, забавными, а главное легко отыскиваемыми в окружающем мире. Вот и его «Веселый считарь» может стать верным помощником в дружбе ребенка от трех лет с цифрами. Усачев помогает детям, для которые еще не понимают абстрактности цифр, соотнести их с окружающими предметами: так, у жука всегда шесть лапок, радуга имеет семь цветов и многое другое. В книге Веселые и добрые иллюстрации, легкие рифмы и интересные сюжеты его стихов обязательно станут поводом для многократного их перечитывания. А еще в книге есть профессор Ау, который с радостью поможет родителям сделать знакомство ребенка с цифрами, сложением и вычитанием занимательным, интересным и понятным. Думаю, что книга станет хорошим помощником детям в изучении математики на многие годы.

«Веселая геометрия для самых маленьких»
Еще одним стихотворным помощником родителям в освоении с детьми математических, точнее геометрических, понятий, конечно, станет книга Александра Тимофеевского «Веселая геометрия для самых маленьких» .

На страницах книги стихи с четкими и легкими рифмами, читая которые так и представляешь ребенка, болтающего ногами, идут в одной связке с иллюстрациями Леонида Шмелькова. Каждая страница знакомит ребенка не только со стихотворением, но и с какой-либо фигурой, которая оживает в образах котов, воздушных шаров, забавных человечков. С этой книгой можно играть, поворачивая в разные стороны, делать какие-то измерения и даже ставить опыты. А еще узнавать, что в маминой юбке прячется цилиндр, а голова похожа на цилиндр, что такое далеко и близко, тонкий и толстый. Прочитав это издание, начинаешь сомневаться, что для книги объем — это главное, ведь в ней очень много полезной информации, поданной в удобной для детей форме.

«Может, Нуль не виноват?»
Что ни говорите, а Ирина Токмакова — мастер писать сказки. Под ее пером оживают и буквы, и цифры. И вот Аля, которая только что победила злобного Кляксича в букваре уже попадает в кажущийся скучным учебник математики, а там перед ней разворачивается настоящий детектив, где главные подозреваемые — цифры. Обо всем этом Ирина Токмакова рассказывает в своей книге «Может, Нуль не виноват?». Чего только не умеют делать цифры в ее книге: петь, драться, пить чай и даже собирать грибы. Детективная история так захватывает взрослых и малышей, что совершенно незаметно решаются задачи на сложение, сравнение величин и многие другие. Но самое главное ребенок от шести лет незаметно для себя открывает волшебный, удивительный и очень интересный мир математики.

«Путешествие в Цифроград»
Если уж попадаешь в страну математики, то уходить из нее, порою, совсем не хочется. Именно так произошло с девочкой Аней, которую придумала Татьяна Шорыгина. Пятилетнюю девочку ждут немало приключений в четырех книгах «Путешествие в Цифроград». Сюжет книг построен на поиске в окружающем Аню мире цифр, с которыми она постепенно знакомится. В первой книге она научилась считать до пяти, во второй разобралась с цифрами до десяти, в третьей — усвоила счет в пределах двадцати, а в четвертой части познакомилась с компьютером. Татьяна Шорыгина не навязчиво рассказывает детям, где они могут найти ту или иную цифру, например, ствол у дерева всегда один, а вот сигналов светофора — три. К каждой главе вы найдете массу заданий, стихов, загадок, но не стоит торопиться все это выдавать ребенку за один раз. Лучше выбирать пару заданий, а к остальным возвращаться в удобное время. Иначе вместо положительного отношения к цифрам у ребенка может появится недоверие к книгам по математике для детей. Книга издана на газетной бумаге, что значительно снизило ее стоимость, но от этого пострадали иллюстрации. Впрочем, язык книги живой и обязательно понравится детям.

«Три дня в Карликании»
Когда я увидела в книге Татьяны Шорыгиной карту города Цифрограда, то сразу поняла, о какой книге обязательно стоит рассказать. Конечно, это любимая многими выросшими детьми книга Владимира Лёвшина «Три дня в Карликании» . Книга и моего детства, которая абсолютно точно пробудила интерес к царице наук.

Если вашему ребенку уже исполнилось шесть лет, то можно предпринять путешествие в эту страну. История Карликании невероятно увлекательна, но на страницах книги юный читатель встретится с незнакомыми понятиями, которые могут заслонить собой сюжет. Наблюдайте за ребенком, возможно лучше отложить книгу до того момента, как ребенок будет готов встретиться с ними. И тогда через год — два он сможет полноценно погрузиться в увлекательное приключение: побродить по столице математического государства — Альджебре, увидеть развалины древних цивилизаций, узнать о характере разных чисел и их историях. С жителями Карликании ребенок обязательно подружится рано или поздно, поэтому искренне считаю ее, а также другие произведения Лёвшина «must have» на книжной полке.

Мукул Патель «Веселая математика»
Как вы думаете, а далеко ли ноль от единицы? Вопрос кажется странным лишь до того момента пока вы с ребенком от пяти лет не заглянете в книгу Мукул Патель «Веселая математика» , из которой можно узнать, например, про бесконечный путь от ноля до единицы через необычайное множество дробей. Да и вообще, откуда взялся этот самый ноль? Эта книга рассказывает о математике уже не с позиции сказки, а оглядываясь на ее прошлое и настоящее, которое вполне по силам юным исследователям. Смело пропускайте сложные для вас задания, уже одних размышлений о рождении математики, бесконечности, компьютерных числах, дробях достаточно, чтобы ребенок, оглядываясь вокруг, видел множество математических задач.

Математику называют Царицей наук, но часто случается, что школьная программа создает у подрастающего поколения впечатление, что «Её величество» — скучный предмет, где все время нужно что-то считать и только… Надеюсь, что несколько книг по математике для детей из этой подборки на вашей книжной книжной полке помогут открыть ребенку удивительный мир и подружиться с этой сложной, но чрезвычайно увлекательной наукой.
Оля Брусянина
Вам также может быть интересно::
vytvoryandia.ru










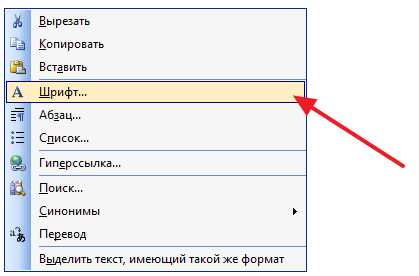
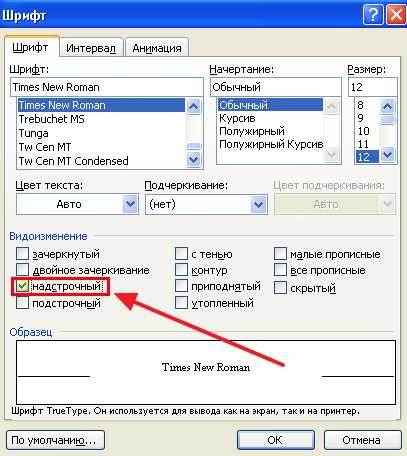
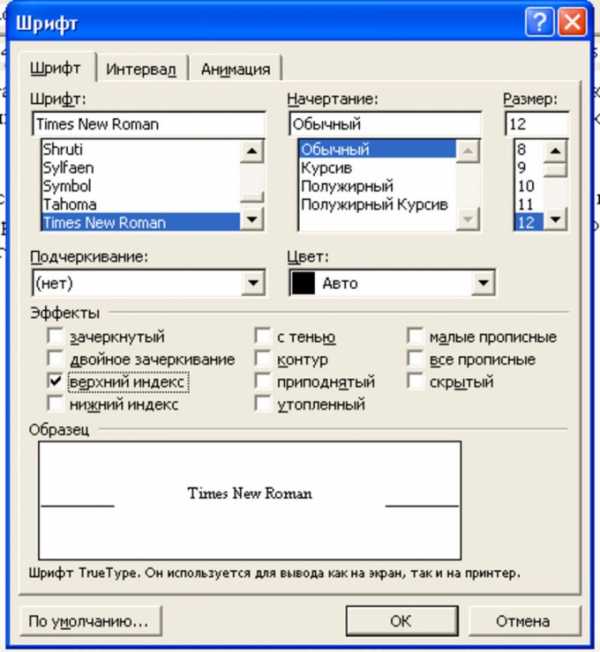 Если в документе требуется ввести не степень, а индекс числа, наберите число в цифровом виде. Затем в главном меню выбирайте «Формат» и «Шрифт». В диалоговом окне оставайтесь во вкладке «Шрифт». В группе «Эффекты» отметьте галочкой опцию «Нижний индекс» и подтвердите выбор, нажав ОК. Введите нужную цифру, затем вернитесь в диалоговое окно и снимите отметку. Подтвердите решение, нажав ОК.
Если в документе требуется ввести не степень, а индекс числа, наберите число в цифровом виде. Затем в главном меню выбирайте «Формат» и «Шрифт». В диалоговом окне оставайтесь во вкладке «Шрифт». В группе «Эффекты» отметьте галочкой опцию «Нижний индекс» и подтвердите выбор, нажав ОК. Введите нужную цифру, затем вернитесь в диалоговое окно и снимите отметку. Подтвердите решение, нажав ОК.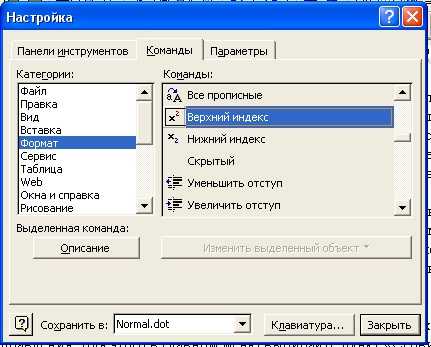


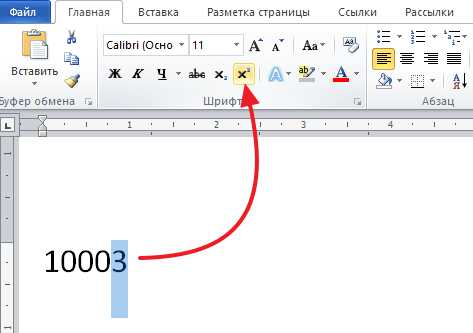
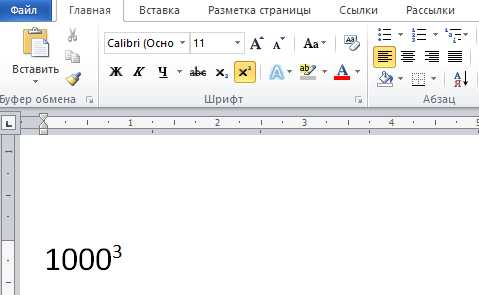












 Прежде чем вы сорветесь со стартовой площадки и побежите покорять определенные изначально 6 км дистанции, необходимо помнить о некоторых подготовительных моментах, а также общей технике выполнения таких физических упражнений.
Прежде чем вы сорветесь со стартовой площадки и побежите покорять определенные изначально 6 км дистанции, необходимо помнить о некоторых подготовительных моментах, а также общей технике выполнения таких физических упражнений.


