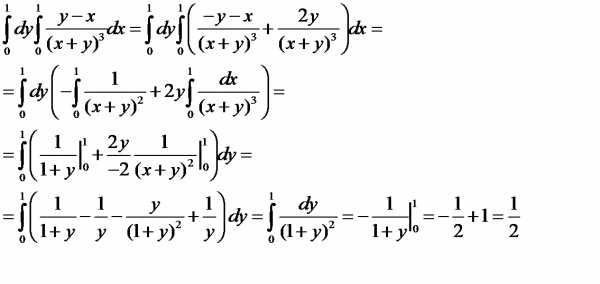Транспонирование матрицы
Транспонирование матрицы
Над матрицами определена еще одна операция, называемая транспонированием.
Определение 14.5Пусть— матрица размеров. Тогда транспонированной матрицейназывается такая матрицаразмеров, что,,.
Транспонированная матрица обозначаетсяили. Операция транспонирования заключается в том, что строки и столбцы в исходной матрице меняются ролями. В транспонированной матрице первым столбцом служит первая строка исходной матрицы, вторым столбцом — вторая строка исходной матрицы и т.д. Например,
Читатель легко проверит, что
где — число.
Предложение 14.5Если произведение определено, то
(14.8) |
Доказательство. Пусть— матрица размеров,— матрица размеров. Тогдаимеет размеры,— размеры. Число столбцов всовпадает с числом строк в, поэтому произведениенаопределено. Размеры этого произведения. Матрицаимеет размеры, поэтому— матрица размеров. Итак, матрицы в правой и левой части равенства (14.8) существуют и имеют одинаковые размеры.
Пусть ,,,,. Нам нужно показать, что,,.
По определению транспонирования . По определению умножения матриц
(14.9) |
С другой стороны,
Поэтому
Сравнивая полученный результат с (14.9), получаем.
studfiles.net
Транспонирование матрицы
Транспонированием матриц называется замена строк матрицы на её столбцы с сохранением порядка. Тогда транспонированная матрица:
Например:
Справедливы следующие свойства операции транспонирования:
При транспонировании квадратных матриц элементы, находящиеся на главной диагонали, не меняют своих позиций.
Задача. Вычислить матрицу:
Решение. Используя определение транспонированной матрицы и операцию произведения матриц, получим:
Найдем матрицу С2, используя операцию возведения в степень:
Найдем матрицу D, используя операцию сложения матриц:
Отсюда:
Работу с матричной функцией ТРАНСП в MS Excel следует выполнять в следующем порядке:
- Задать исходную матрицу.
- Отметить место для матрицы-результата.
- Обратиться к мастеру функций, найти функцию ТРАНСП и выполнить постановку задачи.
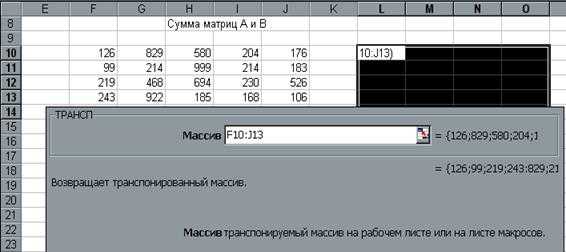
Завершить выполнение работы одновременным нажатием клавиш Shift/Ctrl/Enter
Смотри также по теме:
helpstat.ru
Транспонированная матрица — Википедия. Что такое Транспонированная матрица
Материал из Википедии — свободной энциклопедииТранспонированная матрица — матрица AT{\displaystyle A^{T}}, полученная из исходной матрицы A{\displaystyle A} заменой строк на столбцы.
Формально, транспонированная матрица для матрицы A{\displaystyle A} размеров m×n{\displaystyle m\times n} — матрица AT{\displaystyle A^{T}} размеров n×m{\displaystyle n\times m}, определённая как AijT=Aji{\displaystyle A_{ij}^{T}=A_{ji}}.
Например,
- [1234]T=[1324]{\displaystyle {\begin{bmatrix}1&2\\3&4\end{bmatrix}}^{\mathrm {T} }\!\!\;\!=\,{\begin{bmatrix}1&3\\2&4\end{bmatrix}}} и [123456]T=[135246]{\displaystyle {\begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix}}^{\mathrm {T} }\!\!\;\!=\,{\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix}}\;}
То есть для получения транспонированной матрицы из исходной нужно каждую строчку исходной матрицы записать в виде столбца в том же порядке.
Свойства транспонированных матриц
- (AT)T=A{\displaystyle (A^{T})^{T}=A}
- Дважды транспонированная матрица А равна исходной матрице А.
- (A+B)T=AT+BT{\displaystyle (A+B)^{T}=A^{T}+B^{T}}
- Транспонированная сумма матриц равна сумме транспонированных матриц.
- (AB)T=BTAT{\displaystyle (AB)^{T}=B^{T}A^{T}}
- Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.
- (λA)T=λAT{\displaystyle (\lambda A)^{T}=\lambda A^{T}}
- При транспонировании можно выносить скаляр.
- detA=detAT{\displaystyle \det A=\det A^{T}}
- Определитель транспонированной матрицы равен определителю исходной матрицы.
Связанные определения
Симметричная матрица (симметрическая матрица) — матрица, удовлетворяющая соотношению ST=S{\displaystyle S^{T}=S}.
Для того чтобы матрица S{\displaystyle S} была симметричной, необходимо и достаточно, чтобы:
Антисимметричная (кососимметричная) матрица (антисимметрическая, кососимметрическая) — матрица, удовлетворяющая соотношению AT=−A{\displaystyle A^{T}=-A}.
Для того чтобы матрица A{\displaystyle A} была антисимметричной, необходимо и достаточно, чтобы:
- матрица A{\displaystyle A} была квадратной;
- элементы, симметричные относительно главной диагонали, были равны по модулю и противоположны по знаку, то есть Aij=−Aji{\displaystyle A_{ij}=-A_{ji}}.
Отсюда следует, что элементы главной диагонали антисимметричной матрицы равняются нулю: Aii=0{\displaystyle A_{ii}=0}.
Для любой квадратной матрицы M{\displaystyle M} имеется представление M=S+A{\displaystyle M=S+A},
где S=M+MT2{\displaystyle S={\frac {M+M^{T}}{2}}} — симметричная часть, A=M−MT2{\displaystyle A={\frac {M-M^{T}}{2}}} — антисимметричная часть.
См. также
wiki.sc
Транспонирование матриц — Мегаобучалка
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.
1. Действия над матрицами.
Матрицей называется прямоугольная таблица элементов, например
Размерность матрицы обозначают , где — число строк, а — число столбцов матрицы. Например, размерность матрицы А — , матрицы В — ,
матрицы — . В общем случае элемент матрицы обозначают , где — номер строки, а — номер столбца матрицы, на пересечении которых находится этот элемент. Например, для матрицы А , для матрицы В .
Определим действия над матрицами.
Умножение матрицы на число и сложение покажем на примерах.
Умножение матрицы на число.
Пример.
или
Сложение (вычитание) матриц.
Пример.
3.Умножение матриц.
Если матрица А имеет размерность , а матрица В имеет размерность , то их можно умножать. В результате получается матрица , размерность которой будет . Например, размерности , В размерности , то будет размерности .
Пример.
Первую строку А умножаем на первый столбец В: .
Первую строку А умножаем на второй столбец В: .
Вторую строку А умножаем на первый столбец В: .
Вторую строку А умножаем на второй столбец В: .
Пример.
Пример.
Транспонирование матриц.
Чтобы транспонировать матрицу, надо строки матрицы записать в столбцы.
Пример.
Если , то транспонированная матрица
Если , то
Задание 1.Найти
Решение.
- Определители квадратных матриц.
Для квадратных матриц вводится число, которое называется определителем.
Для матриц второго порядка ( размерность ) определитель задается формулой:
Например, для матрицы ее определитель
Пример.Вычислить определители матриц.
Для квадратных матриц третьего порядка (размерность ) существует правило «треугольника»: на рисунке пунктирная линия означает – умножить числа, через которые проходит пунктирная линия. Первые три числа надо сложить, следующие три числа надо вычитать.
Пример. Вычислить определитель.
Чтобы дать общее определение определителя, надо ввести понятие минора и алгебраического дополнения.
Минором элемента матрицы называется определитель, полученный вычеркиванием — той строки и — того столбца.
Пример. Найдем некоторые миноры матрицы А.
Алгебраическим дополнением элемента называется число .
Значит, если сумма индексов и четная, то и ничем не отличаются. Если же сумма индексов и нечетная, то и отличаются только знаком.
Для предыдущего примера .
Определителем матрицыназывается сумма произведений элементов некоторой строки
( столбца) на их алгебраические дополнения. Рассмотрим это определение на матрице третьего порядка.
Первая запись называется разложением определителя по первой строке, вторая — разложение по второму столбцу, последняя – разложение по третьей строке. Всего таких разложений можно записать шесть раз.
Пример. Вычислить определитель по правилу «треугольника» и разложив его по первой строке, затем по третьему столбцу, затем по второй строке.
Разложим определитель по первой строке:
Разложим определитель по третьему столбцу:
Разложим определитель по второй строке:
Заметим, что чем больше нулей, тем проще вычисления. Например, раскладывая по первому столбцу, получим
Среди свойств определителей есть свойство, позволяющее получать нули, а именно:
Если к элементам некоторой строки (столбца) прибавить элементы другой строки (столбца), умноженные на ненулевое число, то определитель не изменится.
.
Возьмем этот же определитель и получим нули, например, в первой строке.
=
Определители более высоких порядков вычисляются таким же образом.
Задание 2.Вычислить определитель четвертого порядка:
1) разложив по любой строке или любому столбцу
2) получив предварительно нули
Получим дополнительный ноль, например, во втором столбце. Для этого элементы второй строки умножим на -1 и прибавим к четвертой строке:
- Решение систем линейных алгебраических уравнений методом Крамера.
Покажем решение системы линейных алгебраических уравнений методом Крамера.
Задание 2. Решить систему уравнений.
Надо вычислить четыре определителя. Первый называется основным и состоит из коэффициентов при неизвестных:
Заметим, что если , систему методом Крамера решить нельзя.
Три остальных определителя обозначаются , , и получаются заменой соответствующего столбца на столбец правых частей.
Находим . Для этого первый столбец в основном определителе меняем на столбец правых частей:
Находим . Для этого второй столбец в основном определителе меняем на столбец правых частей:
Находим . Для этого третий столбец в основном определителе меняем на столбец правых частей:
Решение системы находим по формулам Крамера: , ,
, ,
Таким образом решение системы , ,
Сделаем проверку, для этого найденное решение подставим во все уравнения системы.
- Решение систем линейных алгебраических уравнений матричным методом.
Если у квадратной матрицы определитель не равен нулю, существует обратная матрица , такая что . Матрица называется единичной и имеет вид
Обратная матрица находится по формуле:
Пример. Найти обратную матрицу к матрице
Сначала вычисляем определитель.
Находим алгебраические дополнения:
Записываем обратную матрицу:
Чтобы проверить вычисления, надо убедиться, что .
Пусть дана система линейных уравнений:
Обозначим
Тогда система уравнений может быть записана в матричной форме как , а отсюда . Полученная формула называется матричным способом решения системы.
Задание 3.Решить систему матричным способом.
Надо выписать матрицу системы, найти к ней обратную и затем умножить на столбец правых частей.
Обратная матрица у нас уже найдена в предыдущем примере, значит можно находить решение:
Ответ:
- Решение систем линейных алгебраических уравнений методом Гаусса.
Метод Крамера и матричный метод применяется только для квадратных систем (число уравнений равно числу неизвестных), причем определитель должен быть не равен нулю. Если число уравнений не равно числу неизвестных, или определитель системы равен нулю, применяется метод Гаусса. Метод Гаусса можно применять для решения любых систем.
Мы рассмотрим решение системы четвертого порядка. Если применять метод Крамера, придется находить пять определителей четвертого порядка. Если решиться обращать матрицу четвертого порядка, то придется находить 16 определителей третьего порядка.
Метод Гаусса состоит в приведении матрицы системы к треугольной или трапециевидной форме.
Пример. Решить систему третьего порядка методом Гаусса.
Выписываем матрицу системы, в которую включаем и правые части:

Матрица приведена к треугольной форме (столбец правых частей не считается). По матрице восстановим систему:
Из последнего уравнения находим . Подставим во второе уравнение:
. Найденные и подставим в первое уравнение:
Ответ:
Задание 5.Решить систему уравнений методом Гаусса.

По полученной матрице восстанавливаем систему:
Находим решение:
Ответ:
megaobuchalka.ru
Как выглядит транспонированная матрица? Ее свойства и определение
В высшей математике изучается такое понятие, как транспонированная матрица. Следует заметить: многим кажется, что это довольно сложная тема, которую невозможно освоить. Однако это не так. Для того чтобы понимать, как именно осуществляется настолько легкая операция, необходимо лишь немного ознакомиться с основным понятием — матрицей. Тему сможет понять любой студент, если уделит время на ее изучение.
Что же такое матрица?
Матрицы в математике довольно распространены. Следует заметить, что они также встречаются в информатике. Благодаря им и с их помощью легко программировать и создавать программное обеспечение.
Что же такое матрица? Это таблица, в которую помещены элементы. Она обязательно имеет прямоугольный вид. Если говорить простейшим языком, то матрица является таблицей чисел. Обозначается она при помощи каких-либо заглавных латинских букв. Она может быть прямоугольной или квадратной. Есть также отдельно строки и столбцы, которые названы векторами. Такие матрицы получают лишь одну линию чисел. Для того чтобы понять, какой размер имеет таблица, необходимо обратить внимание на количество строк и столбцов. Первое обозначаются буквой m, а второе — n.
Следует обязательно понимать, что такое диагональ матрицы. Есть побочная и главная. Второй является та полоса чисел, которая идет слева направо от первого к последнему элементу. В таком случае побочной будет линия справа налево.
С матрицами можно делать практически все простейшие арифметические действия, то есть складывать, вычитать, умножать между собой и отдельно на число. Также их можно транспонировать.

Процесс транспонирования
Транспонированная матрица — это матрица, в которой строки и столбцы поменяны местами. Делается это максимально легко. Обозначается как А с верхним индексом Т (AT). В принципе, следует сказать, что в высшей математике это одна из самых простых операций над матрицами. Размер таблицы сохраняется. Такую матрицу называют транспонированной.
Свойства транспонированных матриц
Для того чтобы правильно делать процесс транспонирования, необходимо понимать, какие свойства этой операции существуют.
- Обязательно существует исходная матрица к любой транспонированной таблице. Их определители должны быть равны между собой.
- Если имеется скалярная единица, то при совершении данной операции ее можно вынести.
- При двойном транспонировании матрицы она будет равна первоначальной.
- Если сравнить две сложенные таблицы с поменянными столбцами и строками, с суммой элементов, над которыми была произведена данная операция, то они будут одинаковы.
- Последнее свойство заключается в том, что если транспонировать умноженные между собой таблицы, то значение должно быть равно результатам, полученным в ходе умножения между собой транспонированных матриц в обратном порядке.
Для чего транспонировать?
Матрица в математике необходима для того, чтобы решать с ней определенные задачи. В некоторых из них требуется вычислить обратную таблицу. Для этого следует найти определитель. Далее рассчитываются элементы будущей матрицы, затем они транспонируются. Осталось найти лишь непосредственно обратную таблицу. Можно сказать, что в таких задачах требуется найти Х, и сделать это довольно легко при помощи базовых знаний теории уравнений.
Итоги
В данной статье было рассмотрено, что представляет собой транспонированная матрица. Эта тема пригодится будущим инженерам, которым нужно уметь правильно рассчитывать сложные конструкции. Иногда матрицу не так уж и просто решить, придется поломать голову. Однако в курсе студенческой математики данная операция осуществляется максимально легко и без каких-либо усилий.
fb.ru
Транспонирование матриц — Мегаобучалка
Транспонированием матрицы называется замена строк матрицы на ее столбцы с сохранением их порядка (или, что то же самое, замена столбцов матрицы на ее строки). Пусть дана исходная матрица А:
Тогда, согласно определению, транспонированная матрица А’ имеет вид
Сокращенная форма записи операции транспонирования матрицы:
Пример 3. Пусть даны матрицы А и В:
Тогда соответствующие транспонированные матрицы имеют вид
Нетрудно заметить две закономерности операции транспонирования матриц.
1. Дважды транспонированная матрица равна исходной матрице:
2. При транспонировании квадратных матриц элементы, находящиеся на главной диагонали, не меняют своих позиций, т.е. главная диагональ квадратной матрицы не меняется при транспонировании.
Умножение матриц
1. Умножение матриц — это специфическая операция, составляющая основу алгебры матриц. Строки и столбцы матриц можно рассматривать как векторы-строки и векторы-столбцы соответствующих размерностей: иными словами, любую матрицу можно интерпретировать как совокупность векторов-строк или векторов-столбцов.
Пусть даны матрица А размером т х п и матрица В размером п х k. Будем рассматривать матрицу А как совокупность т векторов-строк i размерности п каждый, а матрицу В — как совокупность k векторов-столбцов j, каждый из которых содержит по п координат:
Векторы-строки матрицы А и векторы-столбцы матрицы В показаны в записи этих матриц (13.3). Длина строки матрицы А равна высоте столбца матрицы В, и потому скалярное произведение этих векторов имеет смысл.
Определение 3. Произведением матриц А и В называется матрица С, элементы которой cij равны скалярным произведениям векторов-строк i матрицы А на векторы-столбцы jматрицы В:
Произведение матриц А и В — матрица С — имеет размер т х k, поскольку длина п векторов-строк и векторов-столбцов исчезает при суммировании произведений координат этих векторов в их скалярных произведениях, как показано в формулах (13.4). Таким образом, для вычисления элементов первой строки матрицы С необходимо последовательно получить скалярные произведения первой строки матрицы А на все столбцы матрицы В; вторая строка матрицы С получается как скалярные произведения второй вектор-строки матрицы А на все векторы-столбцы матрицы В и так далее. Для удобства запоминания размера произведения матриц нужно перемножить отношения размеров матриц-сомножителей: , т.е. размер матрицы С равен произведению оставшихся в отношении чисел: т х k.
В операции умножения матриц есть характерная особенность: произведение матриц А и В имеет смысл, если число столбцов в А равно числу строк в В. Тогда если А и В — прямоугольные матрицы, то произведение В и А уже не будет иметь смысла, так как в скалярных произведениях, формирующих элементы соответствующей матрицы, должны участвовать векторы с одинаковым числом координат.
Если матрицы А и В квадратные размером n х n, то имеет смысл как произведение матриц АВ, так и произведение матриц BA, причем размер этих матриц такой же, как и у исходных сомножителей. При этом в общем случае перемножения матриц правило перестановочности не соблюдается, т.е. АВ ≠ ВА.
Рассмотрим примеры на умножение матриц.
Решение. Поскольку число столбцов матрицы А равно числу строк матрицы В, то произведение матриц АВ имеет смысл. По формулам (13.4) получаем в произведении матрицу размером 3 х 2:
Произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А.
Решение. Здесь мы найдем произведения данных матриц АВ и ВА:
Как видно из результата, матрица произведения зависит от порядка расположения матриц в произведении. В обоих случаях произведения матриц имеют тот же размер, что и у исходных сомножителей: 2 х 2.
Решение. В данном случае матрица В представляет собой вектор-столбец, т.е. матрицу, у которой три строки и один столбец. Вообще, векторы — это частные случаи матриц: вектор-строка длины п представляет собой матрицу с одной строкой и п столбцами, а вектор-столбец высоты n — матрицу с n строками и одним столбцом. Размеры данных матриц соответственно 2 х 3 и 3 х 1, так что произведение этих матриц определено. Имеем
В произведении получена матрица размером 2 х 1 или вектор-столбец высоты 2.
Решение. Путем последовательного умножения матриц находим
2. Свойства произведения матриц. Пусть А, В и С — матрицы соответствующих размеров (чтобы произведения матриц были определены), а α — действительное число. Тогда следующие свойства произведения матриц имеют место:
1) (АВ)С = А(ВС),
2) (А + В)С = AC + ВС,
3) А(В + С) = АВ + АС,
4) α(АВ) = (αА)В = А(αВ).
В п. 1 этого раздела введено понятие единичной матрицы Е. Нетрудно убедиться, что в алгебре матриц она играет роль единицы, т.е. можно отметить еще два свойства, связанные с умножением на эту матрицу слева и справа в случае квадратных матриц:
5) АЕ = А,
6) ЕА = А.
Иными словами, произведение любой матрицы на единичную матрицу, если оно имеет смысл, не меняет исходную матрицу.
Обратная матрица
Ранг матрицы
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки (столбцы).
Для прямоугольной матрицы максимальный ранг r = min (m, n). Для квадратной матрицы размером п х n ее максимальный ранг не может превышать п: r ≤ п.
megaobuchalka.ru
Транспонирование матрицы — это… Что такое Транспонирование матрицы?
- Транспонирование матрицы
Wikimedia Foundation. 2010.
- Транспонирование
- Транспорт (скульптурные композиции, Тольятти)
Смотреть что такое «Транспонирование матрицы» в других словарях:
Произведение матрицы на число — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Примеры программ на языке Python — Содержание 1 Примеры программ на языке программирования Python. 1.1 … Википедия
Квадратная матрица — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Перемножение матриц — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Произведение матриц — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Разница матриц — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Векторное произведение — в трёхмерном пространстве. Векторное произведение это псевдовектор, перпендикулярный плоскости, построенной по двум … Википедия
Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
Векторное умножение — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства … Википедия
dal.academic.ru









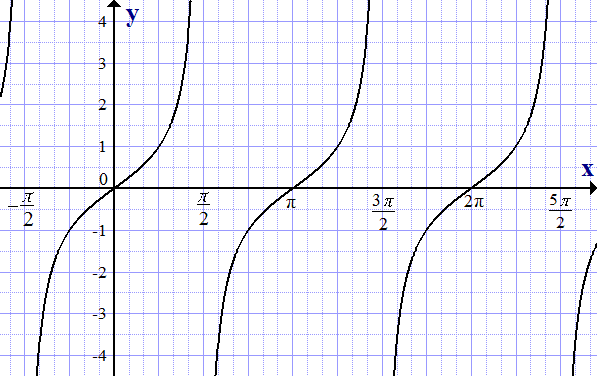
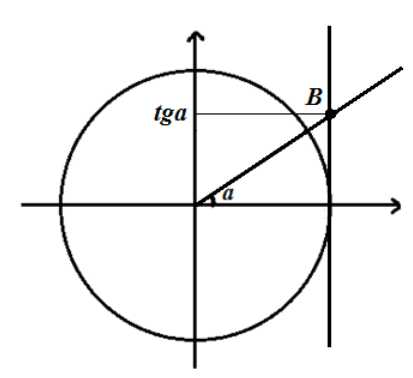
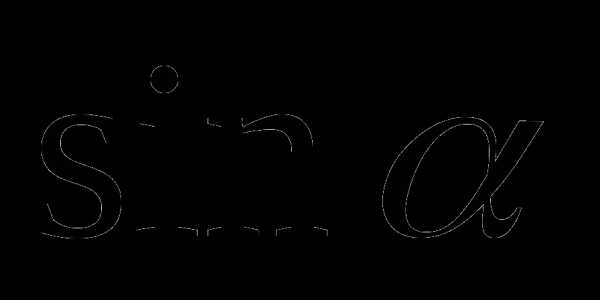 ,
, 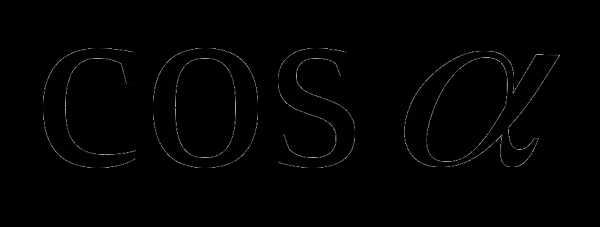 ,
, 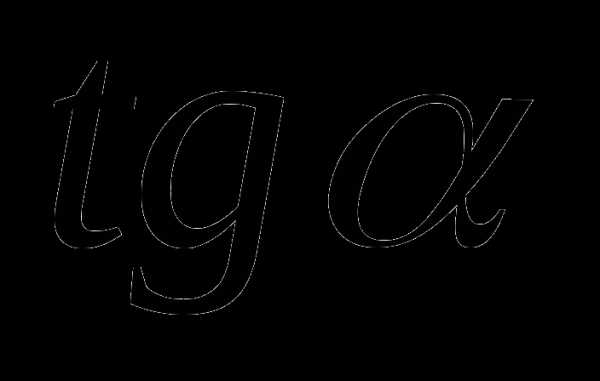 и
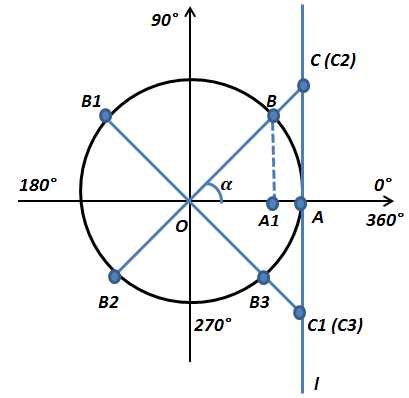
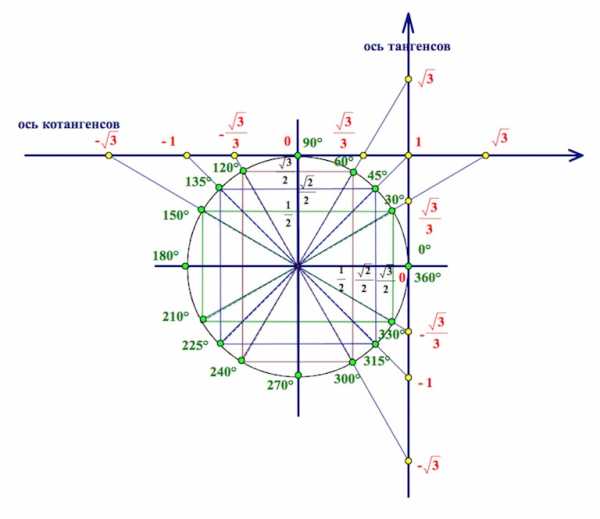
и 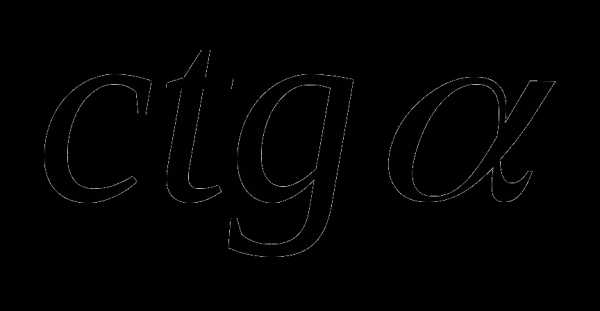 любого угла иногда удобно использовать следующие свойства:
любого угла иногда удобно использовать следующие свойства: точка
точка 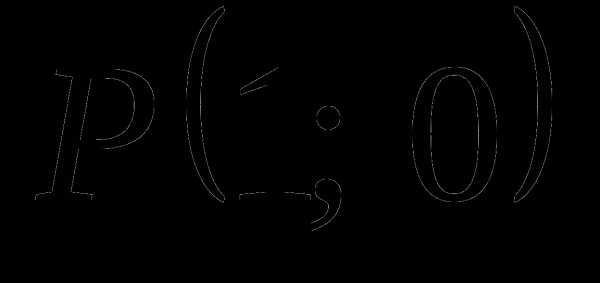 переходит в точку
переходит в точку 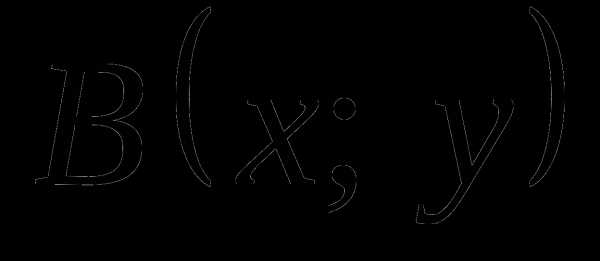 .
.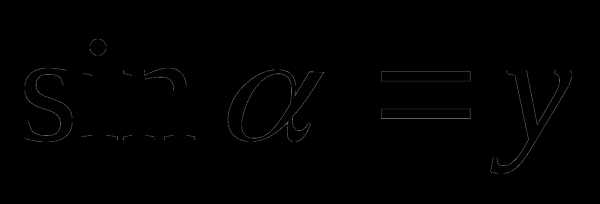 .
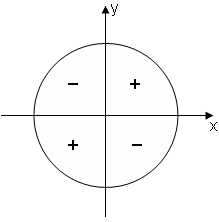
. 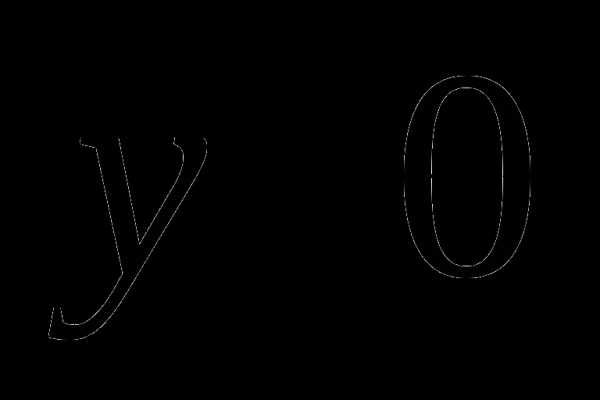 в I и II четвертях,
в I и II четвертях, 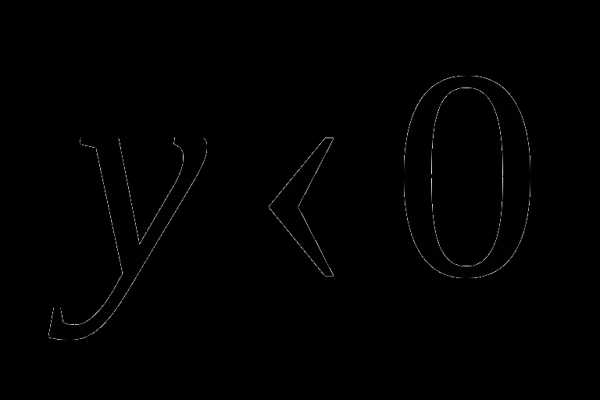 в III и IV четвертях. Значит
в III и IV четвертях. Значит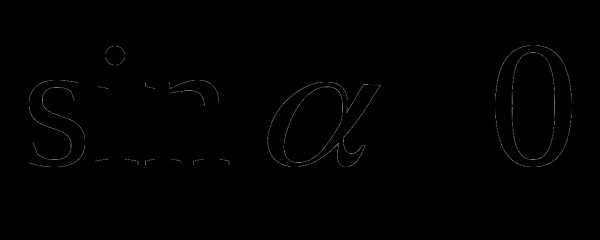 , если точка
, если точка  окажется в I или II четвертях
окажется в I или II четвертях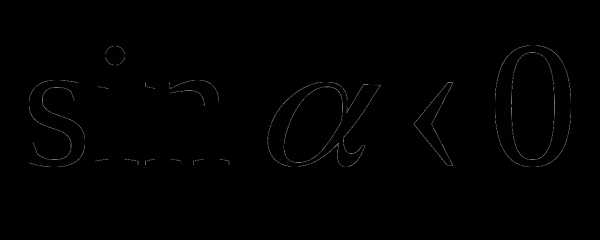 , если точка
, если точка 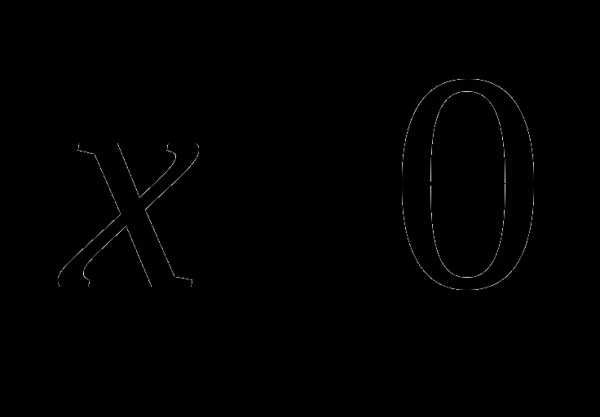 в I и IV четвертях,
в I и IV четвертях, 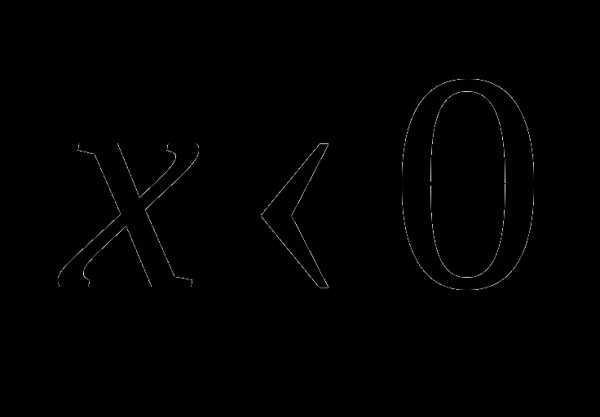 во II и III четвертях. Значит
во II и III четвертях. Значит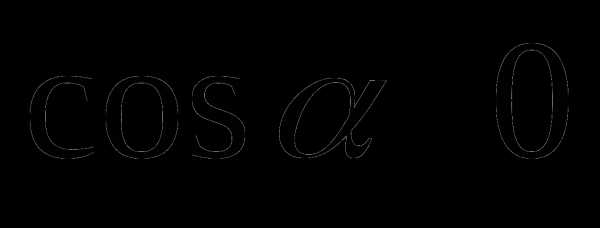 , если точка
, если точка 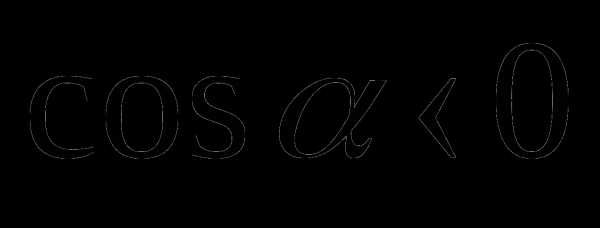 , если точка
, если точка 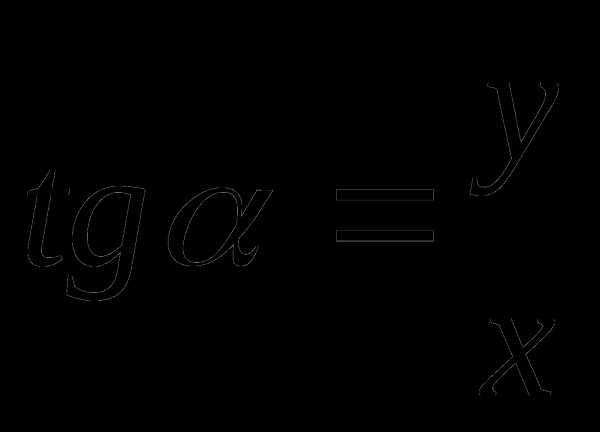 ,
, 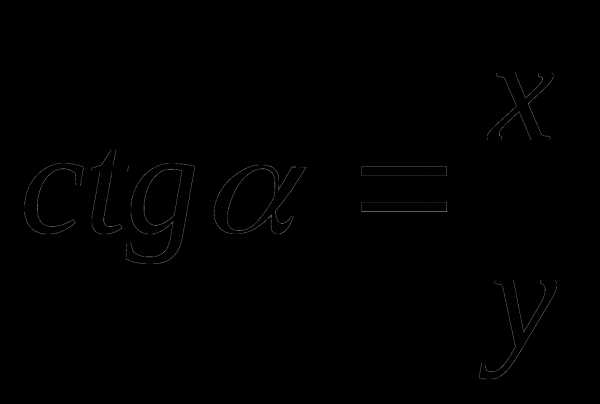 .
. 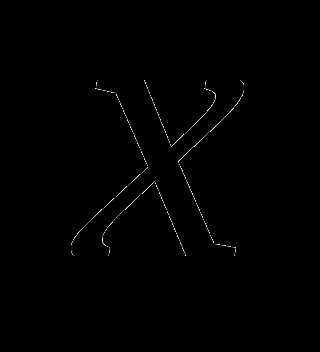 и
и  имеют одинаковые знаки в I и III четвертях и разные во II и IV четвертях. Значит
имеют одинаковые знаки в I и III четвертях и разные во II и IV четвертях. Значит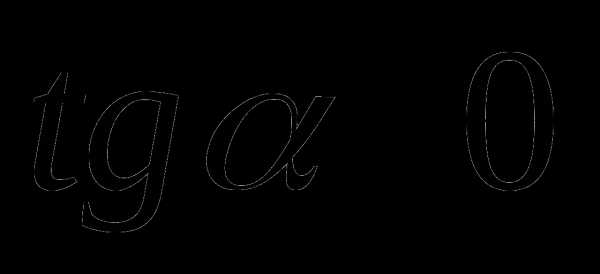 и
и 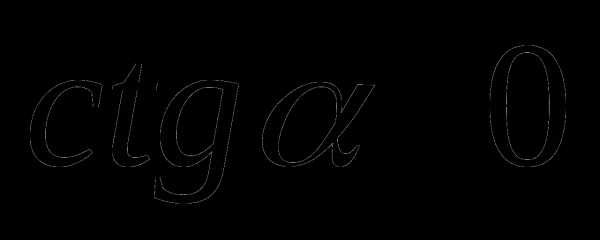 , если точка
, если точка 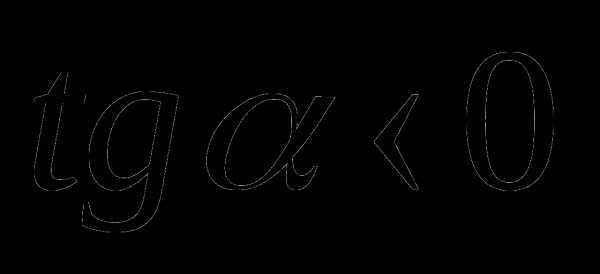 и
и 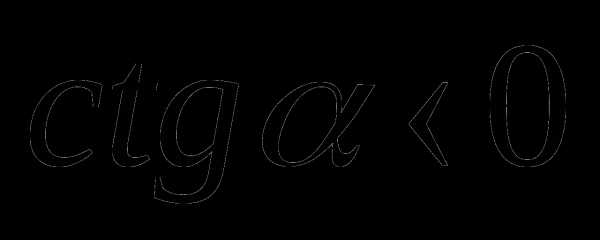 , если точка
, если точка 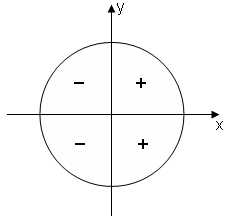
 ; б)
; б) 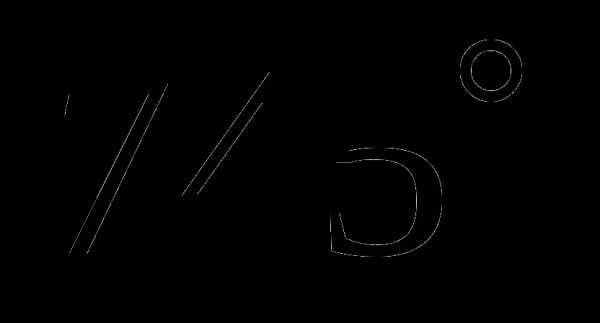 ; в)
; в) 
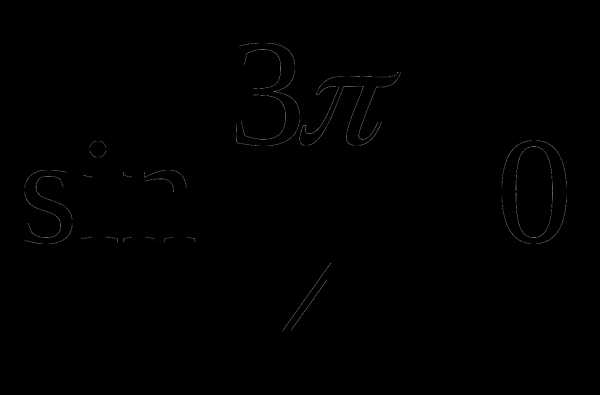 ,
,  ,
, 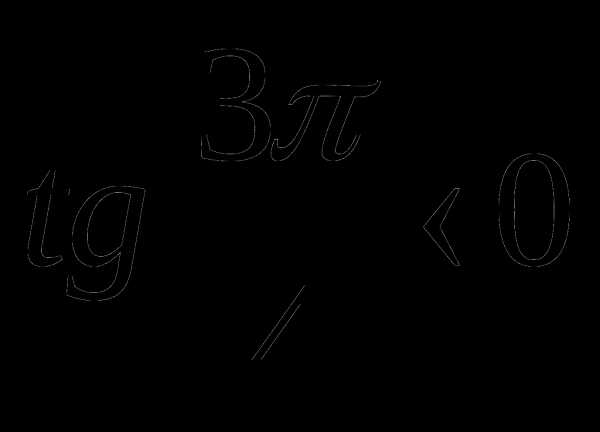 .
. на угол
на угол  , то при повороте точки
, то при повороте точки  получается точка III четверти. Поэтому
получается точка III четверти. Поэтому  ,
,  ,
,  .
. .
. единичной окружности получены поворотом точки
единичной окружности получены поворотом точки  — равнобедренный ()
— равнобедренный () — биссектриса
— биссектриса  , тогда отрезок
, тогда отрезок  — медиана и высота
— медиана и высота 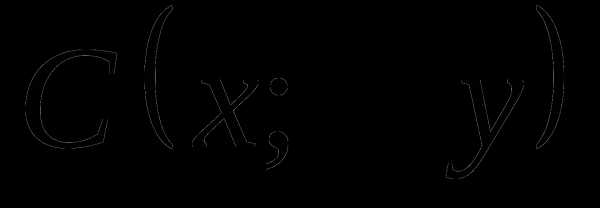 , отсюда
, отсюда равен
равен 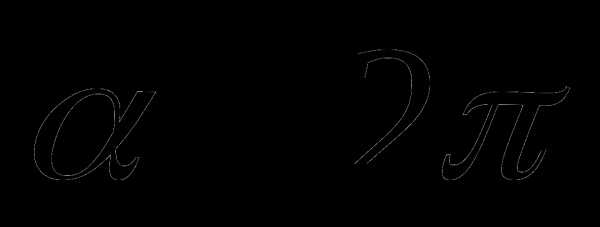 ,
,  ,
,  ,
, 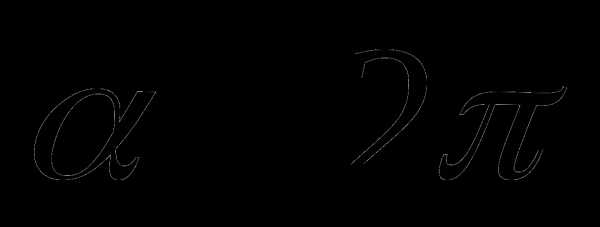 ,
,  ,
,  и т.д. точка придет из
и т.д. точка придет из  в
в  ,
, 2)
2) 
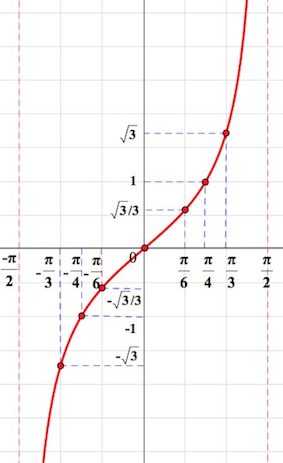
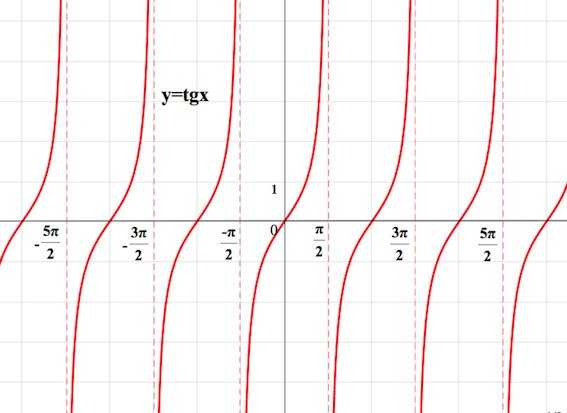
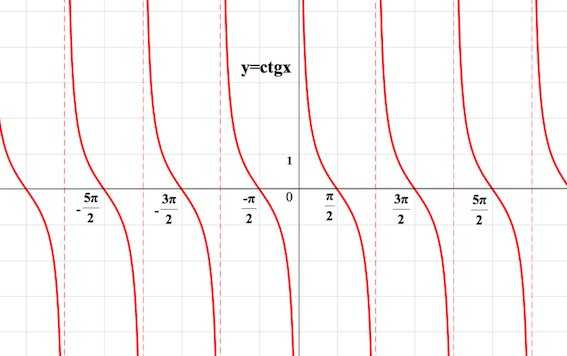



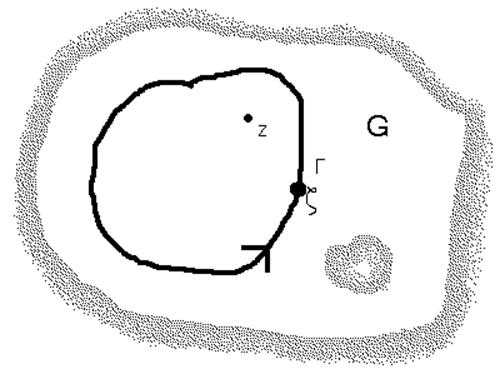
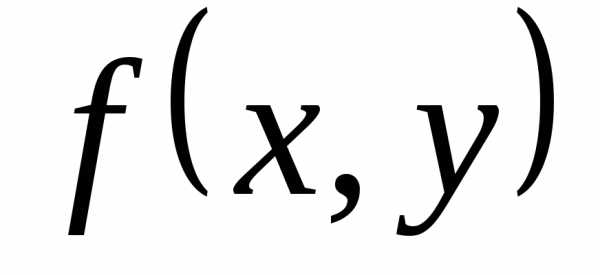 непрерывна в области
непрерывна в области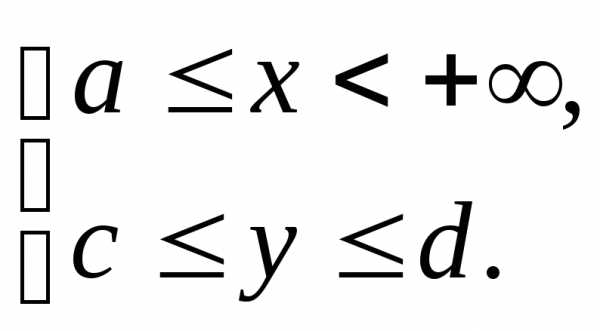
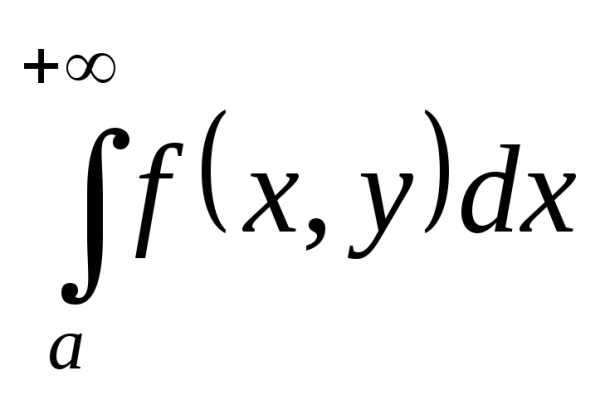 сходится равномерно
относительно у на
сходится равномерно
относительно у на 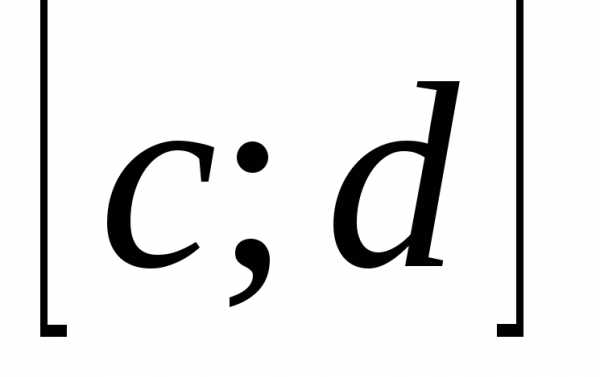 .
.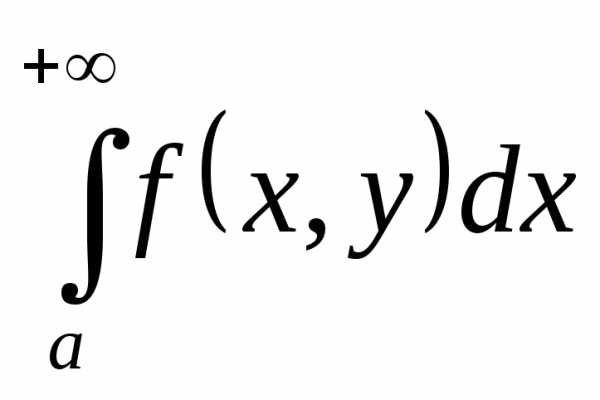 сходится равномерно относительноу на
сходится равномерно относительноу на 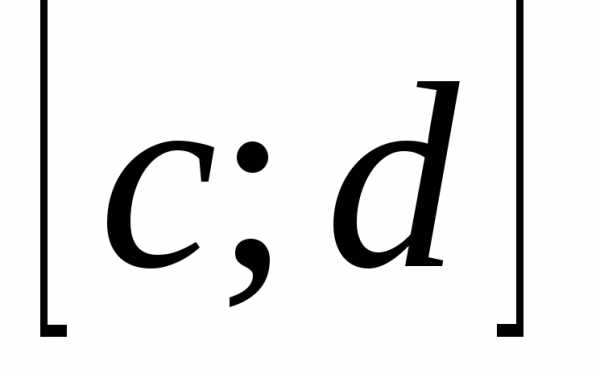 , поэтому для выбранного e
> 0 найдется число М>0, зависящее только
от e,
такое, что как только возьмем число А>M,
то сразу для всех
, поэтому для выбранного e
> 0 найдется число М>0, зависящее только
от e,
такое, что как только возьмем число А>M,
то сразу для всех 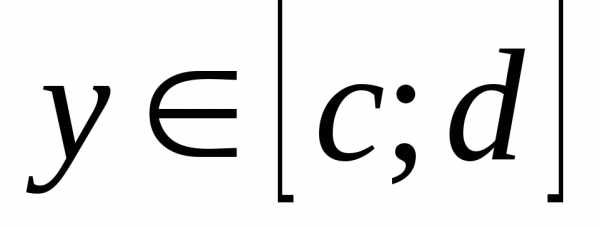 будет выполняться неравенство
будет выполняться неравенство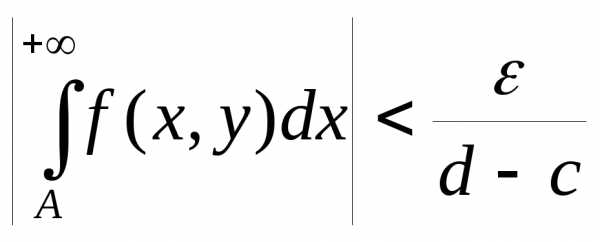 .
.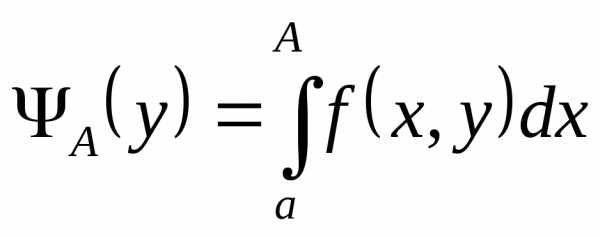 ,
сразу для всех
,
сразу для всех 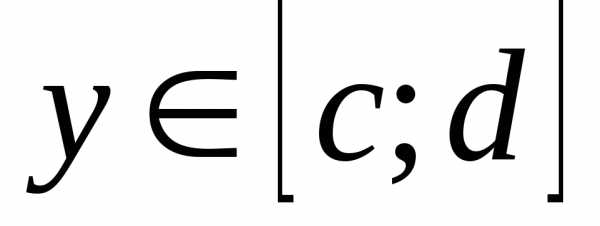 неравенство можно записать в виде
неравенство можно записать в виде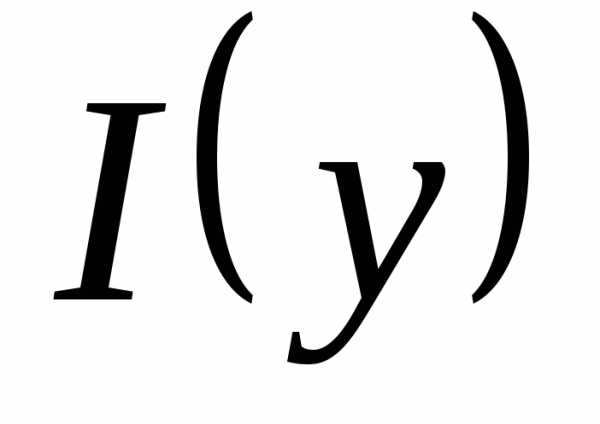 и
и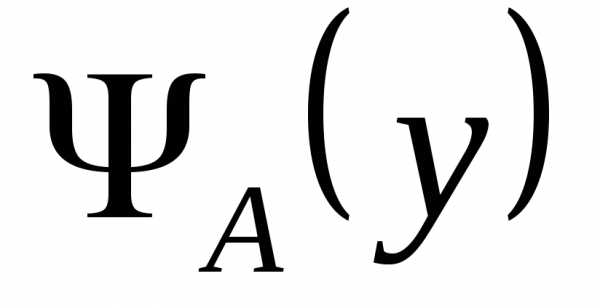 непрерывны на отрезке
непрерывны на отрезке 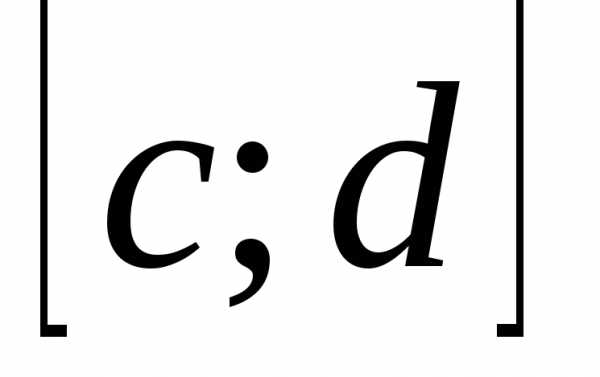 , то они и интегрируемы на нем. В силу
свойств интегралов
, то они и интегрируемы на нем. В силу
свойств интегралов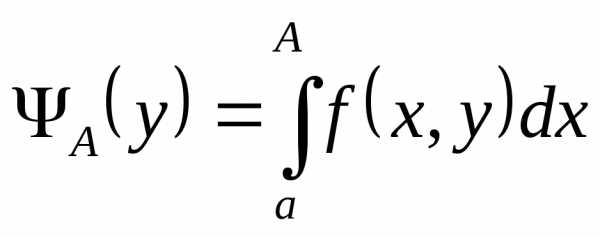 — собственный интеграл, зависящий от
параметрау. По теореме
об интегрировании по параметру
собственного интеграла можем записать
— собственный интеграл, зависящий от
параметрау. По теореме
об интегрировании по параметру
собственного интеграла можем записать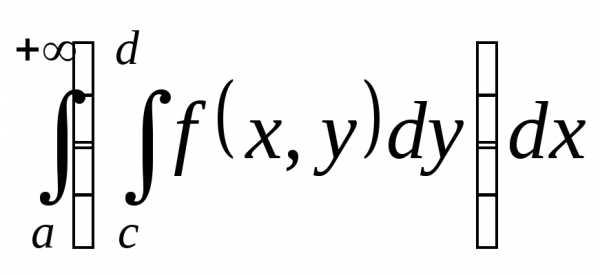
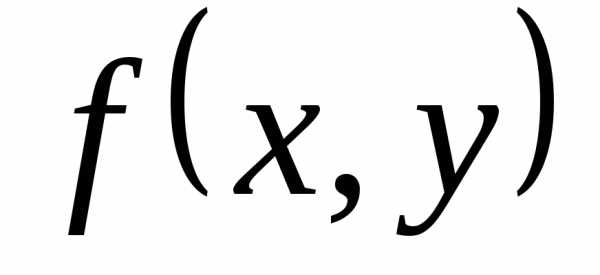 непрерывна в области
непрерывна в области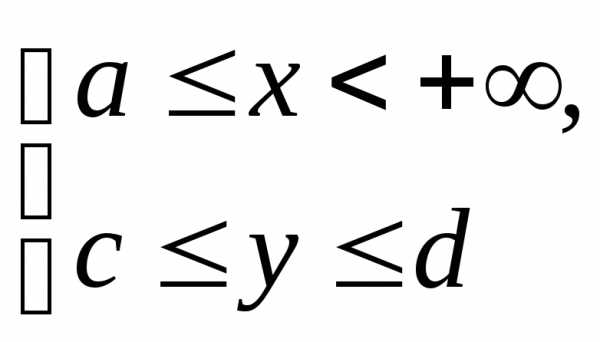 и имеет в ней непрерывную частную
производную
и имеет в ней непрерывную частную
производную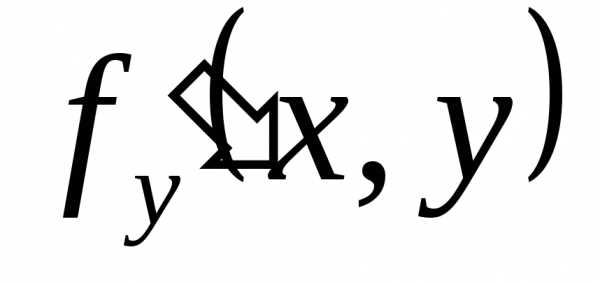 ;
;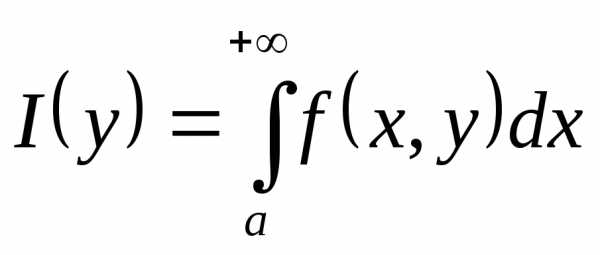 сходится при
каждом
сходится при
каждом 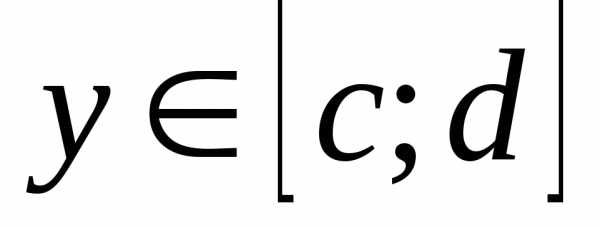 ;
;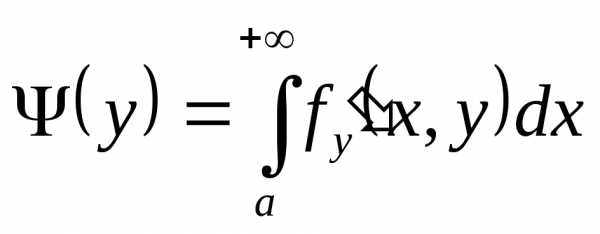 сходится равномерно
относительно у на
сходится равномерно
относительно у на 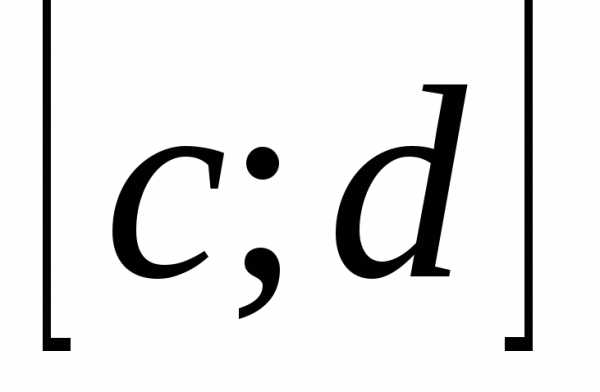 ;
;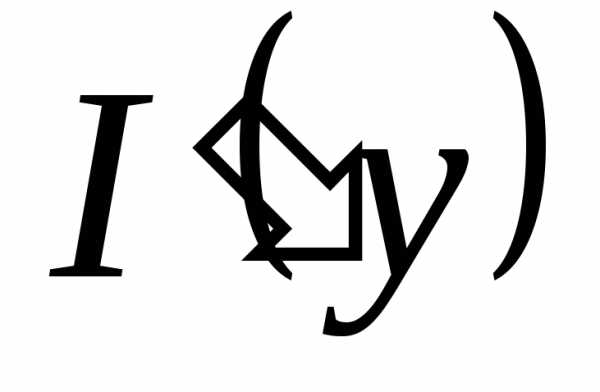 существует при
каждом
существует при
каждом 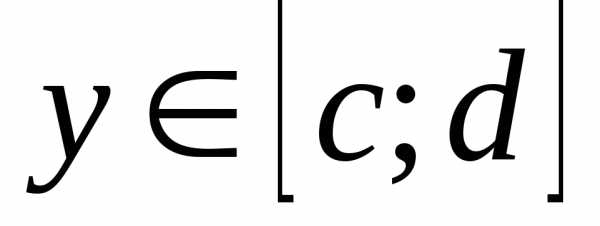 ;
;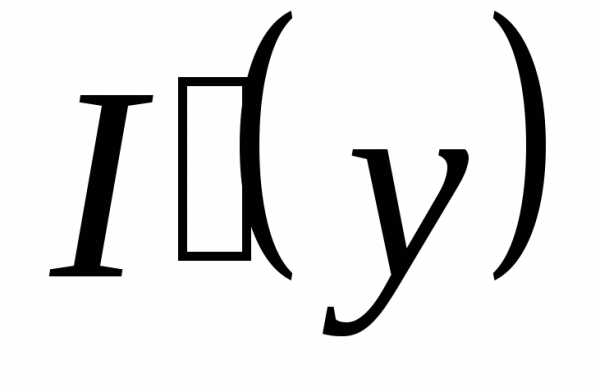 непрерывна на
непрерывна на 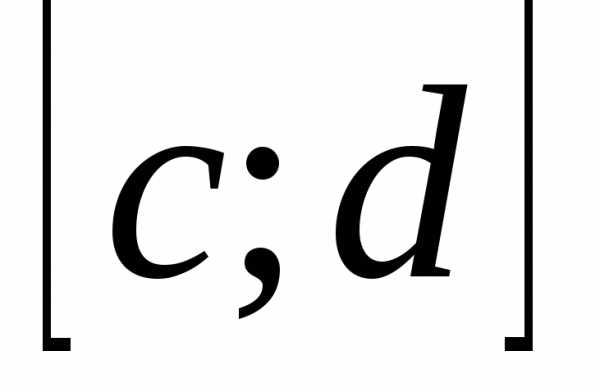 .
.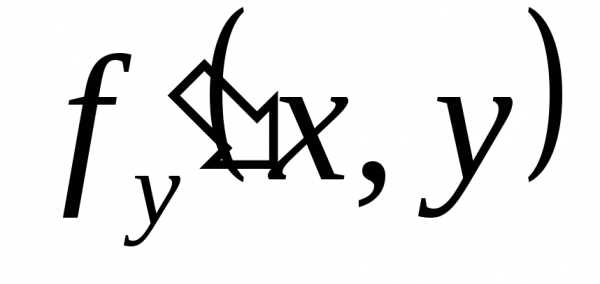 непрерывна в области
непрерывна в области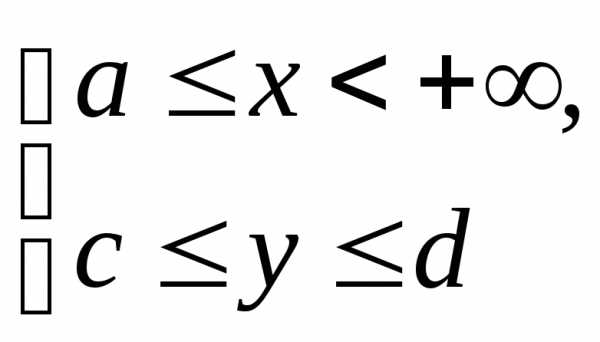 и
и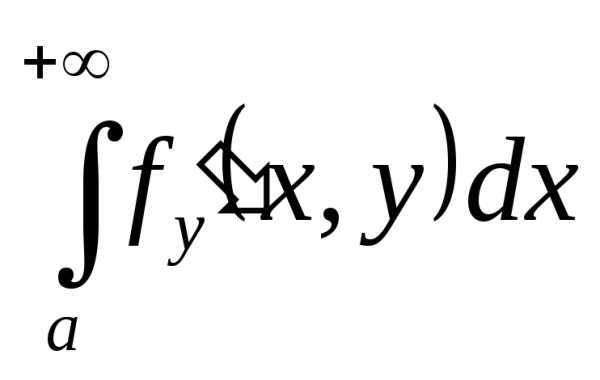 сходится равномерно относительноу на
сходится равномерно относительноу на 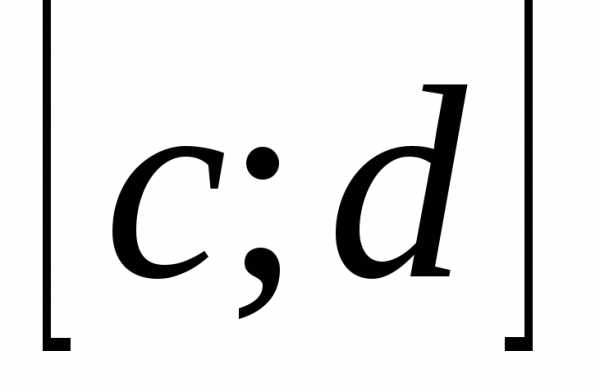 то по теореме из §2 и
то по теореме из §2 и 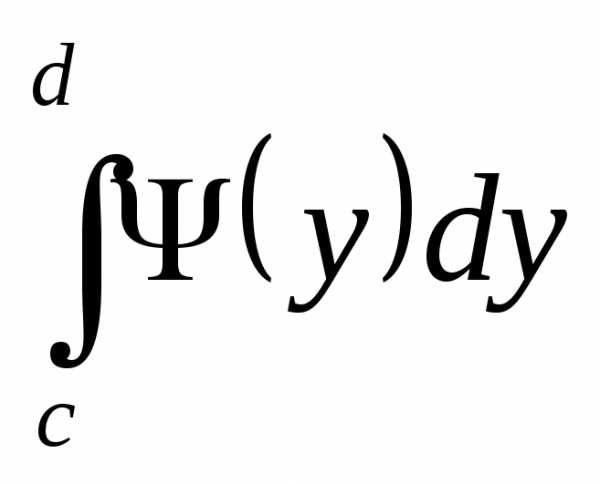 существует. В частности существует
интеграл
существует. В частности существует
интеграл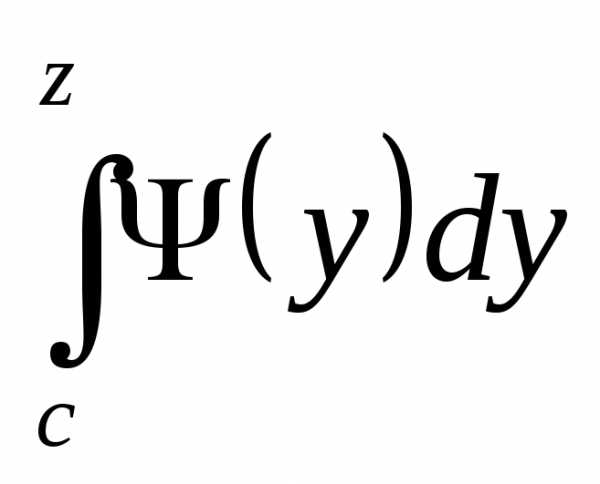 для любого
для любого ,
удовлетворяющего условиюПо теореме из §3 имеем
,
удовлетворяющего условиюПо теореме из §3 имеем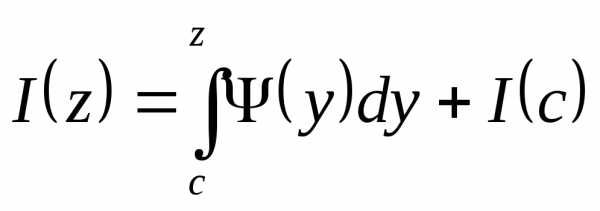
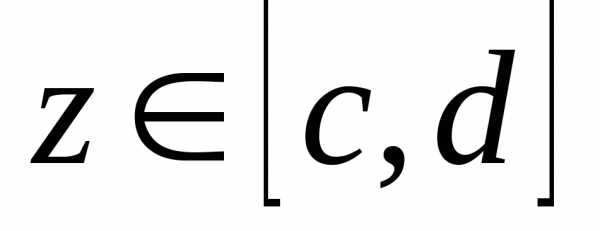 .
Таким образом доказано
.
Таким образом доказано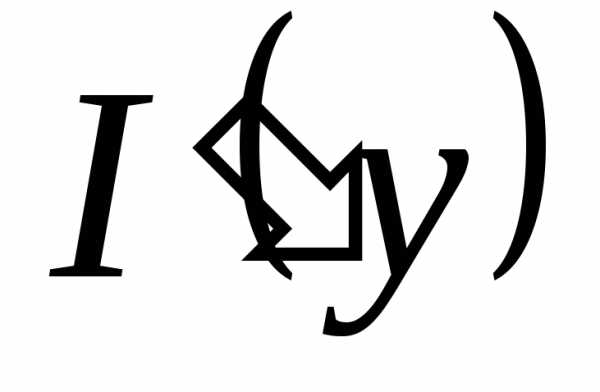 существует при
каждом
существует при
каждом 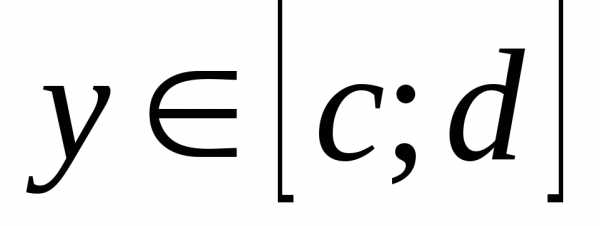 ;
;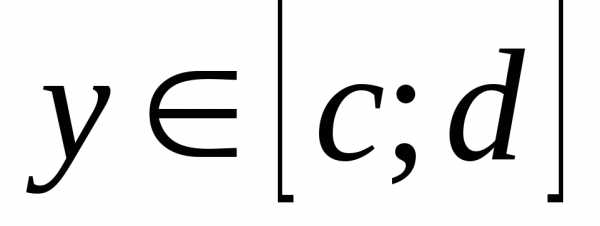 ;
;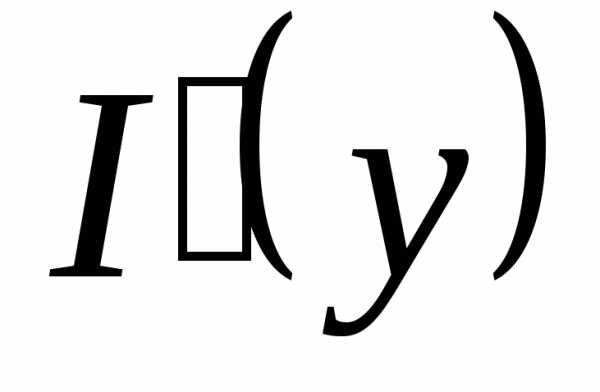 непрерывна на
непрерывна на 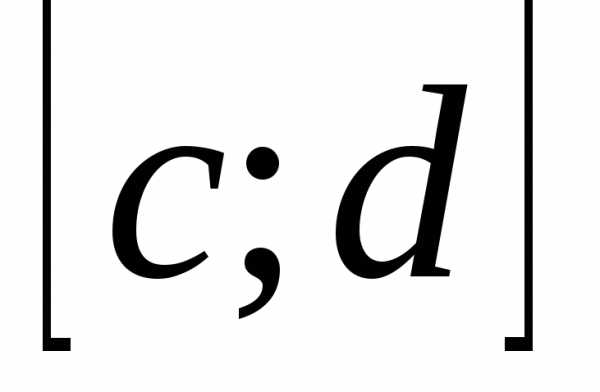 т.к.
т.к. 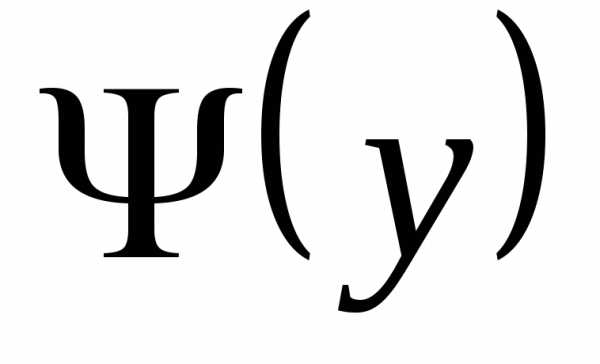 непрерывна на
непрерывна на 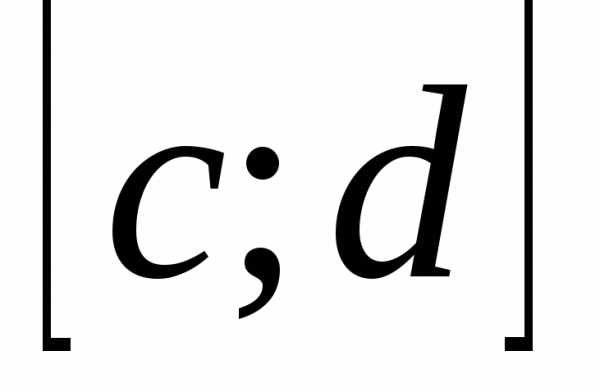 .
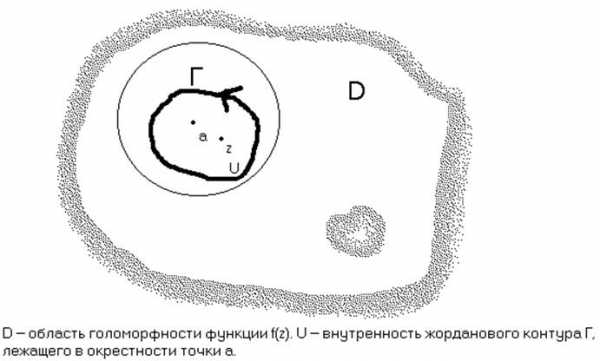
.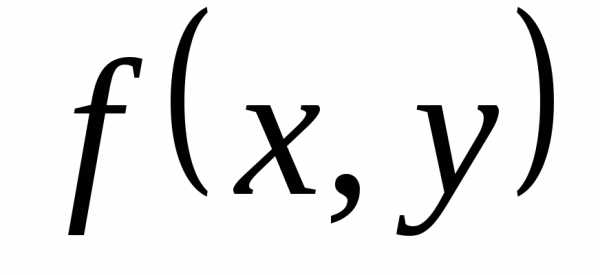 непрерывна в области
непрерывна в области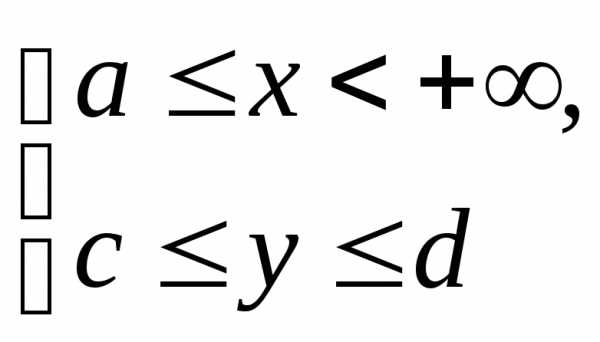
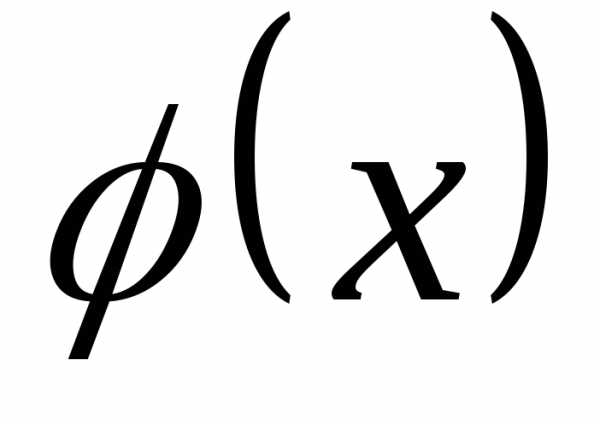 определена и непрерывна на
определена и непрерывна на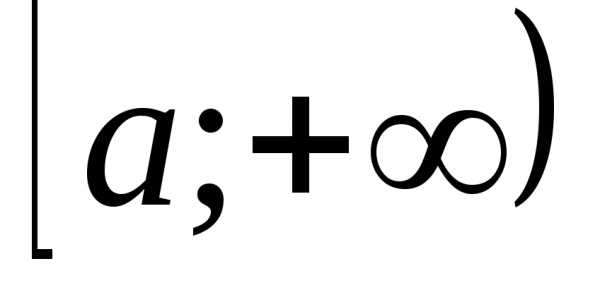 ;
;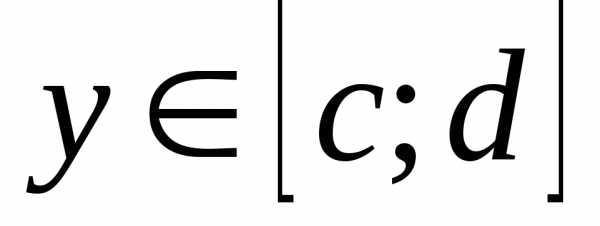 и
.
и
.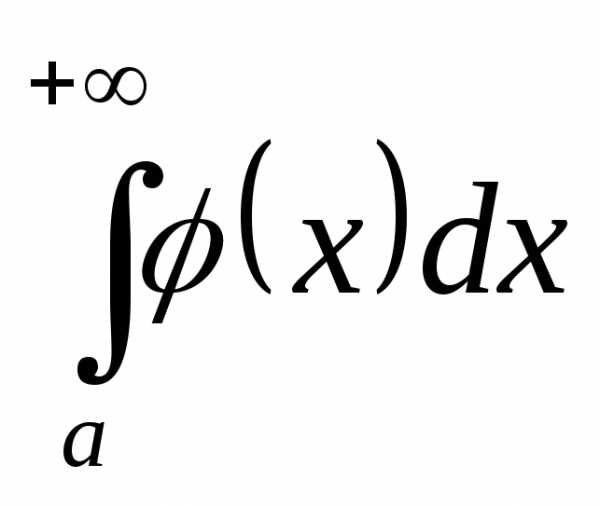 сходится, то несобственный интеграл
сходится, то несобственный интеграл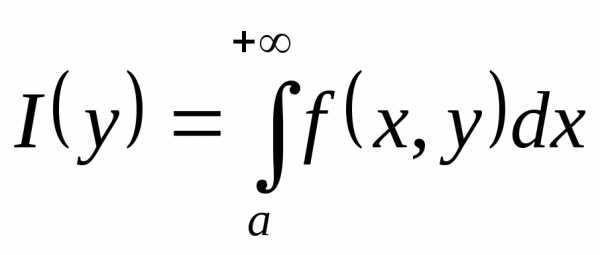 сходится равномерно относительноу на
сходится равномерно относительноу на  .
.

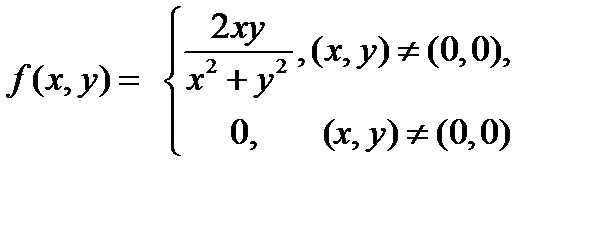 Недостаточно, чтобы f(x,y) была непрерывной по каждой из переменных. Например, функция
Недостаточно, чтобы f(x,y) была непрерывной по каждой из переменных. Например, функция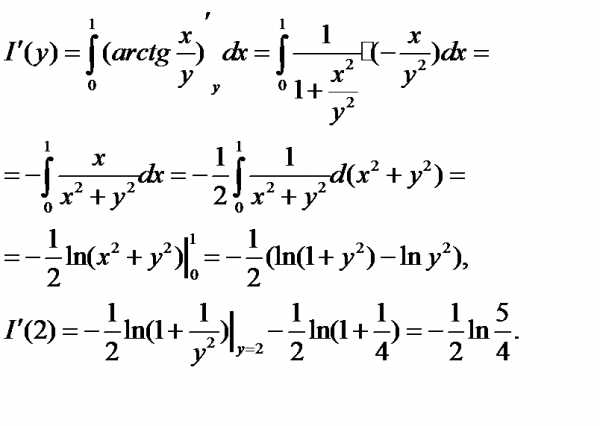 Решение. Можно, вычислив интеграл, найти явное выражение для функции I(y), а затем продифференцировать. Проще, однако, применить теорему 4:
Решение. Можно, вычислив интеграл, найти явное выражение для функции I(y), а затем продифференцировать. Проще, однако, применить теорему 4: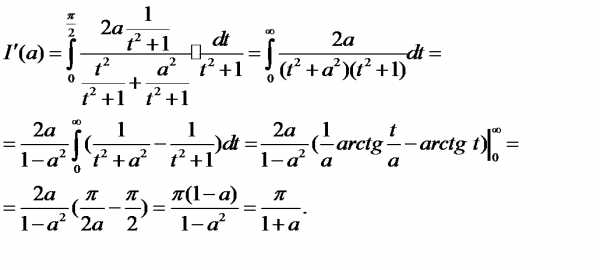
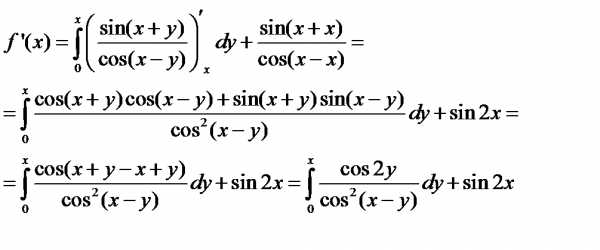 Решение. Здесь требуется дифференцировать интеграл по параметру x. Действуем по формуле теоремы 5:
Решение. Здесь требуется дифференцировать интеграл по параметру x. Действуем по формуле теоремы 5: