Рекомендации по решению нетрадиционных задач на расчет электрических цепей постоянного тока
Разделы: Физика
Введение
Решение задач — неотъемлемая часть обучения физике, поскольку в процессе решения задач происходит формирование и обогащение физических понятий, развивается физическое мышление учащихся и совершенствуется их навыки применения знаний на практике.
В ходе решения задач могут быть поставлены и успешно реализованы следующие дидактические цели:
- Выдвижение проблемы и создание проблемной ситуации;
- Обобщение новых сведений;
- Формирование практических умений и навыков;
- Проверка глубины и прочности знаний;
- Закрепление, обобщение и повторение материала;
- Реализация принципа политехнизма;
- Развитие творческих способностей учащихся.
Наряду с этим при решении задач у школьников воспитываются трудолюбие, пытливость ума, смекалка, самостоятельность в суждениях, интерес к учению, воля и характер, упорство в достижении поставленной цели. Для реализации перечисленных целей особенно удобно использовать нетрадиционные задачи.
§1. Задачи по расчету электрических цепей постоянного тока
По школьной программе на рассмотрение данной темы очень мало отводится времени, поэтому учащиеся более или менее успешно овладевают методами решения задач данного типа. Но часто такие типы задач встречаются олимпиадных заданиях, но базируются они на школьном курсе.
К таким, нестандартным задачам по расчету электрических цепей постоянного тока можно отнести задачи, схемы которых:
1) содержат большое число элементов – резисторов или конденсаторов;
2) симметричны;
3) состоят из сложных смешанных соединений элементов.
В общем случае всякую цепь можно рассчитать, используя законы Кирхгофа. Однако эти законы не входят в школьную программу. К тому же, правильно решить систему из большого числа уравнений со многими неизвестными под силу не многим учащимся и этот путь не является лучшим способом тратить время. Поэтому нужно уметь пользоваться методами, позволяющими быстро найти сопротивления и емкости контуров.
§2. Метод эквивалентных схем
Метод эквивалентных схем заключается в том, что исходную схему надо представить в виде последовательных участков, на каждом из которых соединение элементов схемы либо последовательно, либо параллельно. Для такого представления схему необходимо упростить. Под упрощением схемы будем понимать соединение или разъединение каких-либо узлов схемы, удаление или добавление резисторов, конденсаторов, добиваясь того, чтобы новая схема из последовательно и параллельно соединенных элементов была эквивалентна исходной.
Эквивалентная схема – это такая схема, что при подаче одинаковых напряжений на исходную и преобразованную схемы, ток в обеих цепях будет одинаков на соответствующих участках. В этом случае все расчеты производятся с преобразованной схемой.
Чтобы начертить эквивалентную схему для цепи со сложным смешанным соединением резисторов можно воспользоваться несколькими приемами. Мы ограничимся рассмотрением в подробностях лишь одного из них – способа эквипотенциальных узлов.
Этот способ заключается в том, что в симметричных схемах отыскиваются точки с равными потенциалами. Эти узлы соединяются между собой, причем, если между этими точками был включен какой-то участок схемы, то его отбрасывают, так как из-за равенства потенциалов на концах ток по нему не течет и этот участок никак не влияет на общее сопротивление схемы.
Таким образом, замена нескольких узлов равных потенциалов приводит к более простой эквивалентной схеме. Но иногда бывает целесообразнее обратная замена одного узла
несколькими узлами с равными потенциалами, что не нарушает электрических условий в остальной части.
Рассмотрим примеры решения задач эти методом.
З а д а ч а №1
Рассчитать сопротивление между точками А и В данного участка цепи. Все резисторы одинаковы и их сопротивления равны r.
Решение:
В силу симметричности ветвей цепи точки С И Д являются эквипотенциальными. Поэтому резистор между ними мы можем исключить. Эквипотенциальные точки С и Д соединяем в один узел. Получаем очень простую эквивалентную схему:
Сопротивление которой равно:
RАВ=Rac+Rcd=r*r/r*r+r*r/r+r=r.
З а д а ч а № 2
Решение:
В точках F и F` потенциалы равны, значит сопротивление между ними можно отбросить. Эквивалентная схема выглядит так:
Сопротивления участков DNB;F`C`D`; D`, N`, B`; FCD равны между собой и равны R1:
1/R1=1/2r+1/r=3/2r
R1=2/3*r
С учетом этого получается новая эквивалентная схема:
Ее сопротивление и сопротивление исходной цепи RАВ равно:
1/RАВ=1/r+R1+R1+1/r+R1+R1=6/7r
RАВ=(7/6)*r.
З а д а ч а № 3.
Решение:
Точки С и Д имеют равные потенциалы. Исключением сопротивление между ними. Получаем эквивалентную схему:
Искомое сопротивление RАВ равно:
1/RАВ=1/2r+1/2r+1/r=2/r
RАВ=r/2.
З а д а ч а № 4.
Решение:
Как видно из схемы узлы 1,2,3 имеют равные потенциалы. Соединим их в узел 1. Узлы 4,5,6 имеют тоже равные потенциалы- соединим их в узел 2. Получим такую эквивалентную схему:
Сопротивление на участке А-1, R 1-равно сопротивлению на участке 2-В,R3 и равно:
R1=R3=r/3
Сопротивление на участке 1-2 равно: R2=r/6.
Теперь получается эквивалентная схема:
Общее сопротивление RАВ равно:
RАВ= R1+ R2+ R3=(5/6)*r.
З а д а ч а № 5.
Решение:
Точки C и F-эквивалентные. Соединим их в один узел. Тогда эквивалентная схема будет иметь следующий вид:
Сопротивление на участке АС:
Rас=r/2
Сопротивление на участке FN:
RFN =
Сопротивление на участке DB:
RDB =r/2
Получается эквивалентная схема:
Искомое общее сопротивление равно:
RAB= r.
Задача №6
Решение:
Заменим общий узел О тремя узлами с равными потенциалами О, О1 , О2. Получим эквивалентную систему:
Сопротивление на участке ABCD:
R1=(3/2)*r
Сопротивление на участке A`B`C`D`:
R2= (8/3)*r
Сопротивление на участке ACВ
R3 = 2r.
Получаем эквивалентную схему:
Искомое общее сопротивление цепи RAB равно:
RAB= (8/10)*r.
Задача №7.
Решение:
“Разделим” узел О на два эквипотенциальных угла О1 и О2. Теперь схему можно представить, как параллельные соединение двух одинаковых цепей. Поэтому достаточно подробно рассмотреть одну из них:
Сопротивление этой схемы R1 равно:
R1 = 3r
Тогда сопротивление всей цепи будет равно:
RAB = (3/2)*r
З а д а ч а №8
Решение:
Узлы 1 и 2 – эквипотенциальные, поэтому соединим их в один узел I. Узлы 3 и 4 также эквипотенциальные – соединимих в другой узел II. Эквивалентная схема имеет вид:
Сопротивление на участке A- I равно сопротивлению на участке B- II и равно:
RI =
Сопротивление участка I-5-6- II равно:
RII = 2r
Cопротивление участка I- II равно:
RIII =
Получаем окончательную эквивалентную схему:
Искомое общее сопротивление цепи RAB=(7/12)*r.
З а д а ч а №9
В ветви ОС заменим сопротивление на два параллельно соединенных сопротивления по 2r. Теперь узел С можно разделить на 2 эквипотенциальных узла С1 и С2. Эквивалентная схема в этом случае выглядит так:
Сопротивление на участках ОСIB и DCIIB одинаковы и равны, как легко подсчитать 2r. Опять чертим соответствующую эквивалентную схему:
Сопротивление на участке AOB равно сопротивлению на участке ADB и равно (7/4)*r. Таким образом получаем окончательную эквивалентную схему из трех параллельно соединенных сопротивлений:
Ее общее сопротивление равно RAB= (7/15)*r
З а д а ч а № 10
Точки СОD имеют равные потенциалы – соединим их в один узел ОI .Эквивалентная схема изображена на рисунке :
Сопротивление на участке А ОI равно . На участке ОIВ сопротивление равно .Получаем совсем простую эквивалентную схему:
ЕЕ сопротивление равно искомому общему сопротивлению
RAB=(5/6)*r
Задачи № 11 и № 12 решаются несколько иным способом, чем предыдущие. В задаче №11 для ее решения используется особое свойство бесконечных цепей, а в задаче № 12 применяется способ упрощения цепи.
Задача № 11
Решение
Выделим в этой цепи бесконечно повторяющееся звено, оно состоит в данном случае из трех первых сопротивлений. Если мы отбросим это звено, то полное сопротивление бесконечной цепи R не измениться от этого , так как получится точно такая же бесконечная цепь. Так же ничего не измениться, если мы выделенное звено подключим обратно к бесконечному сопротивлению R, но при этом следует обратить внимание , что часть звена и бесконечная цепь сопротивлением R соединены параллельно. Таким образом получаем эквивалентную схему :
Получается уравнения
RAB=2ч +
RAB = R
Решая систему этих уравнений, получаем:
R=ч (1+ ).
§3. Обучение решению задач по расчету электрических цепей способом эквипотенциальных узлов
Задача – это проблема, для разрешения которой ученику потребуются логические рассуждения и выводы. Строящиеся на основе законов и методов физики. Таким образом, с помощью задач происходит активизация целенаправленного мышления учащихся.
В то же время. Теоретические знания можно считать усвоенными только тогда, когда они удачно применяются на практике. Задачи по физике описывают часто встречающиеся в жизни и на производстве проблемы, которые могут быть решены с помощью законов физики и, если ученик успешно решает задачи, то можно сказать, что он хорошо знает физику.
Для того, чтобы ученики успешно решали задачи, недостаточно иметь набор методов и способов решения задач, необходимо еще специально учить школьников применению этих способов.
Рассмотрим план решения задач по расчету электрических цепей постоянного тока методом эквипотенциальных узлов.
- Чтение условия.
- Краткая запись условия.
- Перевод в единицы СИ.
- Анализ схемы:
- установить, является ли схема симметричной;
- установить точки равного потенциала;
- выбрать, что целесообразнее сделать – соединить точки равных потенциалов или же, наоборот, разделить одну точку на несколько точек равных потенциалов;
- начертить эквивалентную схему;
- найти участки только с последовательным или только с параллельным соединением и рассчитать общее сопротивление на каждом участке по законам последовательного и параллельного соединения;
- начертить эквивалентную схему, заменяя участки соответствующими им расчетными сопротивлениями;
- пункты 5 и 6 повторять до тех пор, пока не останется одно сопротивление, величина которого и будет решением задачи.
- Анализ реальности ответа.
Подробнее об анализе схемы
а) установить, является ли схема симметричной.
Определение. Схема симметрична, если одна ее половина является зеркальным отражением другой. Причем симметрия должна быть не только геометрической, но должны быть симметричны и численные значения сопротивлений или конденсаторов.
Примеры:
1)
Схема симметричная, так как ветви АСВ и АДВ симметричны геометрически и отношение сопротивления на одном участке АС:АД=1:1 такое же, как и на другом участке СД:ДВ=1:1.
2)
Схема симметричная, так как отношение сопротивлений на участке АС:АД=1:1 такое же, как и на другом участке СВ:ДВ=3:3=1:1
3)
Схема не симметрична, так как отношения сопротивлений численно
не симметричны -1:2 и 1:1.
б) установить точки равных потенциалов.
Пример:
Из соображений симметрии делаем вывод, что в симметричных точках потенциалы равны. В данном случае симметричными точками являются точки С и Д. Таким образом, точки С и Д – эквипотенциальные точки.
в) выбрать, что целесообразно сделать – соединить точки равных потенциалов или же, наоборот, разделить одну точку на несколько точек равных потенциалов.
Мы видим в этом примере, что между точками равных потенциалов С и Д включено сопротивление, по которому ток не будет течь. Следовательно, мы можем отбросить это сопротивление, а точки С и Д соединить в один узел.
г) начертить эквивалентную схему.
Чертим эквивалентную схему. При этом получаем схему с соединенными в одну точку точками С и Д.
д) найти участки только с последовательным или только с параллельным соединением и рассчитать общее сопротивление на каждом таком участке по законам последовательного и параллельного соединения.
Из полученной эквивалентной схемы видно, что на участке АС мы имеем два параллельно соединенных резистора. Их общее сопротивление находится по закону параллельного соединения:
1/ Rобщ=1/R1+1/R2+1/R3+…
Таким образом 1/RAC=1/r+1/r=2/r,откуда RAC= r/2.
На участке СВ картина аналогичная:
1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.
е)начертить эквивалентную схему, заменяя участки соответствующими им расчетными сопротивлениями.
Чертим эквивалентную схему подставляя в нее рассчитанные сопротивления участков RAC и RCB:
ж)пункты д) и е) повторять до тех пор, пока останется одно сопротивление, величина которого и будет решением задачи.
Повторяем пункт д): на участке АВ имеем два последовательно соединенных сопротивления. Их общее сопротивление находим по закону последовательного соединения:
Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.
Повторяем пункт е): чертим эквивалентную схему:
Мы получили схему с одним сопротивлением, величина которого равна сопротивлению исходной схемы. Таким образом, мы получили ответ RAB = r.
Далее, для проверки усвоения данного материала можно учащимся предложить задания для самостоятельной работы, взятые из дидактического материала. (см. приложение)
Литература
- Балаш. В.А. задачи по физике и методы их решения. - М: Просвещение,1983.
- Лукашик В.И. Физическая олимпиада.- М: Просвещение, 2007
- Усова А.В., Бобров А.А. Формирование учебных умений и навыков учащихся на уроках физики.- М: Просвещение,1988
- Хацет А. Методы расчета эквивалентных схем //Квант.
- Чертов А. Г. Задачник по физике. – М.: Высшая школа,1983
- Зиятдинов Ш.Г., Соловьянюк С.Г. (методические рекомендации) г. Бирск,1994г
- Марон А.Е., Марон Е.А. Физика. Дидактические материалы. Москва, “Дрофа”, 2004г
24.03.2012
urok.1sept.ru
Упрощение сложной электрической цепи. — КиберПедия
Курсовая работа
По дисциплине: «Теоретические основы электротехники».
Тема: «Линейные электрические цепи постоянного тока. Расчёт линейной электрической цепи синусоидального тока с сосредоточенными параметрами при установившемся режиме».
Вариант 8
Выполнил:
студент 212 группы
Рыбаков Владимир Сергеевич
Проверил:
ст. преподаватель кафедры ТТЭМ
Чукита Виталий Исакович
Тирасполь, 2017
Содержание
Задание № 1. 2
1.Упрощение сложной электрической цепи. 3
2. Расчет преобразованной электрической цепи. 4
2.1 Метод наложения действий э. д. с. 4
2.2 Метод эквивалентного генератора. 6
3. Определение токов и их направлений. Построение потенциальной диаграммы. 8
4. Определение коэффициентов четырёхполюсника. 9
Задание №2. 15
Часть № 1. 16
1. Определение показаний приборов. 16
2. Построение векторных диаграмм.. 17
3. Мгновенные значения напряжений и токов. 18
4. Баланс активной и реактивной мощности. 19
5. Резонанс напряжений. 19
6. Резонанс токов. 20
Часть № 2. 21
1. Определение комплексов токов в ветвях и комплексы напряжений для всех ветвей цепи 21
2. Векторная диаграмма напряжений и токов. 22
3. Мгновенные значения напряжений и токов. 23
4. Комплексы мощностей всех ветвей. 23
5. Показания ваттметров в 3-ей и 4-ой ветвях. 23
Вывод. 24
Список литературы.. 25
Задание № 1
Расчет линейной электрической цепи постоянного тока
Вариант № 10
Исходные данные:
E1=10 В
E12=5 В
R1=R2=R3=R12=R23=R31=30 Ом
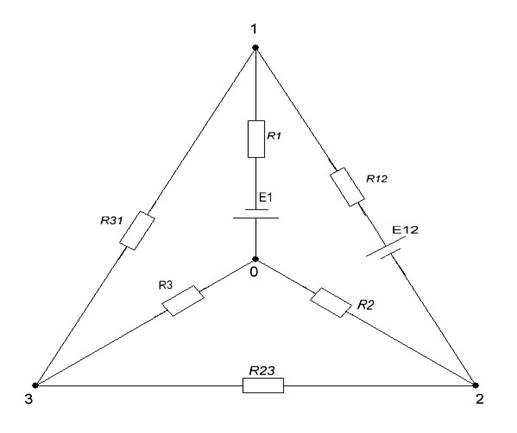
1. Упростить сложную электрическую цепь (рис. 1), используя метод преобразования треугольника и звезды. Определить токи во всех ветвях сложной цепи (рис.1), используя следующие методы:
· Метод преобразования треугольника и звезды.
2. Преобразованную электрическую цепь рассчитать:
· Методом наложения действий э. д. с.
· Методом эквивалентного генератора (определить ток в ветви без э. д. с.).
3. Определить токи, направление токов и построить потенциальную диаграмму для одного из контуров схемы с двумя э. д. с.
4. Определить коэффициенты четырёхполюсника, считая входными и выходными зажимами зажимы, к которым подключены ветви с э. д. с, и параметры Т-образной и П-образной эквивалентных схем замещения этого четырёхполюсника.
Упрощение сложной электрической цепи.
Для упрощения сложной электрической цепи (рис. 1), необходимо выбрать контур, содержащий пассивные элементы. Используем метод преобразования треугольника в звезду (рис. 2).
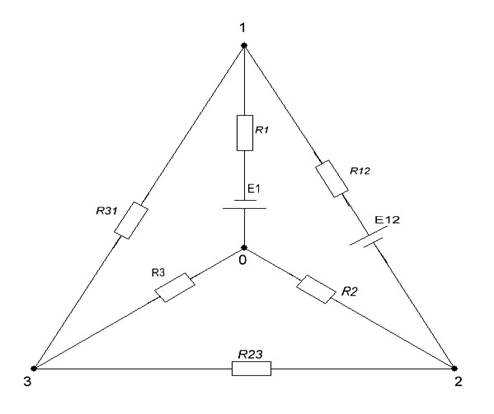
В результате цепь принимает вид (рис.3):
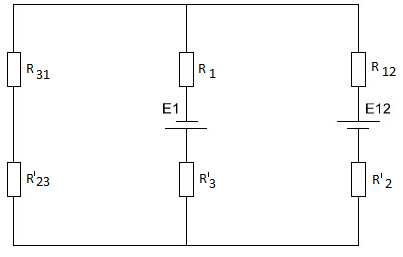
Найдем новые сопротивления преобразованной цепи. Т.к. по условию все исходные сопротивления одинаковы, то и новые сопротивления будут равны:
Расчет преобразованной электрической цепи.
Часть 1
1. Определить показания всех приборов, указанных на схеме.
2. Построить векторные диаграммы токов и напряжений.
3. Написать мгновенные значения токов и напряжений.
4. Составить баланс активной и реактивной мощности.
5. Определить для данной цепи индуктивность , при которой будет иметь место резонанс напряжений.
6. Определить емкость , при которой в ветвях 3-4 наблюдается резонанс токов.
7. Построить график изменения мощности и энергий, как функции времени , для ветвей 3-4, соответствующие резонансу токов.
Часть 2
1. Определить комплексы токов в ветвях и комплексы напряжений для всех ветвей цепи (рис. 14).
2. Построить в комплексной плоскости векторную диаграмму напряжений и токов.
3. Написать выражения мгновенных значений, найденных выше напряжений и токов.
4. Определить комплексы мощностей всех ветвей.
5. Определить показания ваттметров, измеряющих мощности в 3-ей и 4-ой ветвях.
Часть № 1
Резонанс напряжений.
Резонанс напряжений возникает в цепи с последовательным соединением индуктивного и емкостного элемента.
|
Резонанс токов.
|
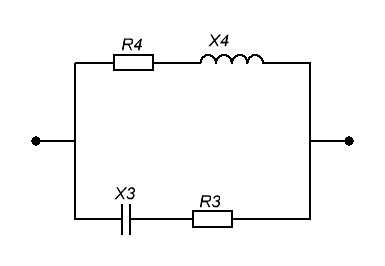
Часть № 2.
ВЫВОД
В курсовой работе рассмотрены методы расчёта линейных электрических цепей постоянного тока, определения параметров четырёхполюсника различных схем и их свойства. Так же был произведён расчет электрической цепи синусоидального тока сосредоточенными параметрами при установившемся режиме.
Список литературы:
1. Методические указания к курсовой работе по расчёту линейных электрических цепей постоянного тока. В.М. Ишимов, В.И. Чукита, г. Тирасполь 2013 г.
2. Теоретические основы электротехники В. Г. Мацевитый, г. Харьков 1970
3. Теоретические основы электротехники. Евдокимов А.М. 1982г.
Курсовая работа
По дисциплине: «Теоретические основы электротехники».
Тема: «Линейные электрические цепи постоянного тока. Расчёт линейной электрической цепи синусоидального тока с сосредоточенными параметрами при установившемся режиме».
Вариант 8
Выполнил:
студент 212 группы
Рыбаков Владимир Сергеевич
Проверил:
ст. преподаватель кафедры ТТЭМ
Чукита Виталий Исакович
Тирасполь, 2017
Содержание
Задание № 1. 2
1.Упрощение сложной электрической цепи. 3
2. Расчет преобразованной электрической цепи. 4
2.1 Метод наложения действий э. д. с. 4
2.2 Метод эквивалентного генератора. 6
3. Определение токов и их направлений. Построение потенциальной диаграммы. 8
4. Определение коэффициентов четырёхполюсника. 9
Задание №2. 15
Часть № 1. 16
1. Определение показаний приборов. 16
2. Построение векторных диаграмм.. 17
3. Мгновенные значения напряжений и токов. 18
4. Баланс активной и реактивной мощности. 19
5. Резонанс напряжений. 19
6. Резонанс токов. 20
Часть № 2. 21
1. Определение комплексов токов в ветвях и комплексы напряжений для всех ветвей цепи 21
2. Векторная диаграмма напряжений и токов. 22
3. Мгновенные значения напряжений и токов. 23
4. Комплексы мощностей всех ветвей. 23
5. Показания ваттметров в 3-ей и 4-ой ветвях. 23
Вывод. 24
Список литературы.. 25
Задание № 1
Расчет линейной электрической цепи постоянного тока
Вариант № 10
Исходные данные:
E1=10 В
E12=5 В
R1=R2=R3=R12=R23=R31=30 Ом

1. Упростить сложную электрическую цепь (рис. 1), используя метод преобразования треугольника и звезды. Определить токи во всех ветвях сложной цепи (рис.1), используя следующие методы:
· Метод преобразования треугольника и звезды.
2. Преобразованную электрическую цепь рассчитать:
· Методом наложения действий э. д. с.
· Методом эквивалентного генератора (определить ток в ветви без э. д. с.).
3. Определить токи, направление токов и построить потенциальную диаграмму для одного из контуров схемы с двумя э. д. с.
4. Определить коэффициенты четырёхполюсника, считая входными и выходными зажимами зажимы, к которым подключены ветви с э. д. с, и параметры Т-образной и П-образной эквивалентных схем замещения этого четырёхполюсника.
Упрощение сложной электрической цепи.
Для упрощения сложной электрической цепи (рис. 1), необходимо выбрать контур, содержащий пассивные элементы. Используем метод преобразования треугольника в звезду (рис. 2).

В результате цепь принимает вид (рис.3):

Найдем новые сопротивления преобразованной цепи. Т.к. по условию все исходные сопротивления одинаковы, то и новые сопротивления будут равны:
cyberpedia.su
Kvant. Преобразование эл. цепей — PhysBook
Зильберман А.Р. Преобразование электрических цепей //Квант. — 2002. — № 3. — С. 30-31,34.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В этой статье рассказывается о методе, позволяющем упрощать сложные задачи по расчету электрических цепей.
Что мы понимаем под «преобразованием цепи»? Предположим, что у нас есть сложная схема из резисторов, имеющая множество выводов и подключенная к источникам. Заменим эту схему другой, но с тем же числом выводов, причем так, чтобы сопротивления между двумя любыми выводами у новой схемы были такими же, как у старой. Ясно, что источники «ничего не узнают» об этой замене и токи, потребляемые схемой, останутся прежними. Но найти эти токи, возможно, окажется проще.
Итак, если мы хотим подсчитать токи в сложной схеме, ее можно заменить более простой эквивалентной схемой. При этом токи внутри заменяемой части меняются. Поэтому так поступать можно только с той частью схемы, которая нас непосредственно не интересует.
С подобными заменами вы, конечно же, встречались. Пусть, например, в схеме два сопротивления[1]r1 и r2 включены последовательно. Их мы можем заменить одним, равным по величине сумме r1 + r2. Если же два сопротивления включены параллельно, то их также можно заменить одним, величина которого равна \(~\frac{r_1 r_2}{r_1 + r_2}\) . Это — простейшие примеры преобразования цепей. Мы же остановимся на более сложных схемах.
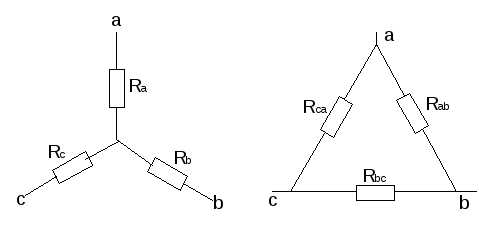
Посмотрим, как преобразуются друг в друга схемы, имеющие по три вывода, — «звезда» и «треугольник» (рис.1).
Рис. 1
Немного непривычные обозначения на рисунке 1,б очень удобны — индексы показывают, между какими точками включено сопротивление. Например, сопротивление R13 включено между точками 1 и 3 и т.д.
Если мы хотим заменить одну из этих схем другой, нужно получить такие соотношения между r и R, чтобы сопротивления между любыми точками были для обеих схем одинаковы.
В схеме «звезда» (см. рис. 1, а) сопротивление между точками 1 и 2 равно r1 + r2, а в схеме «треугольник» оно равно \(~\frac{R_{12} (R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}\) . Следовательно, для того чтобы со- противления между точками 1 и 2 были одинаковы для обеих схем, необходимо, чтобы
\(~r_1 + r_2 = \frac{R_{12} (R_{13} + R_{23})}{R_{12} + R_{13} + R_{23}}\) . (1)Аналогично, для точек 2 и 3
\(~r_2 + r_3 = \frac{R_{23} (R_{13} + R_{12})}{R_{12} + R_{13} + R_{23}}\) , (2)и для точек 1 и 3:
\(~r_1 + r_3 = \frac{R_{13} (R_{12} + R_{23})}{R_{12} + R_{13} + R_{23}}\) . (3)Система уравнений (1) — (3) легко решается. Сложим все уравнения и поделим обе части на 2:
\(~r_1 + r_2 + r_3 = \frac{R_{12} R_{13} + R_{12} R_{23} + R_{13} R_{23}}{R_{12} + R_{13} + R_{23}}\) .Вычтя теперь из этого уравнения уравнение (2), получим
\(~r_1 = \frac{R_{12} R_{13}}{R_{12} + R_{13} + R_{23}}\) .Аналогично,
\(~r_2 = \frac{R_{12} R_{23}}{R_{12} + R_{13} + R_{23}}\) ,и
\(~r_3 = \frac{R_{13} R_{23}}{R_{12} + R_{13} + R_{23}}\) .Эти результаты легко запомнить — знаменатель всюду один и тот же, а в числителе справа дважды встречается тот же индекс, что и слева\[~r_1 \to R_{12} R_{13}, r_2 \to R_{12} R_{23}, r_3 \to R_{13} R_{23}\] .
Немного сложнее получить формулы для обратного преобразования:
\(~R_{12} = \frac{r_1 r_2 + r_1 r_3 + r_2 r_3}{r_3}\) , \(~R_{13} = \frac{r_1 r_2 + r_1 r_3 + r_2 r_3}{r_2}\) , \(~R_{23} = \frac{r_1 r_2 + r_1 r_3 + r_2 r_3}{r_1}\) ,но их также легко запомнить — числитель всюду один и тот же, а в знаменателе стоит как раз тот индекс, которого недостает слева.
Пользуясь формулами, которые мы только что получили, можно производить замену одной схемы другой. Например, «звезду» с сопротивлениями 1 Ом можно заменить «треугольником» с сопротивлениями 3 Ом (рис.2).
Рис. 2
Решим теперь такую задачу: найдем сопротивление между точками A и B в схеме на рисунке 3.
Рис. 3
Это обычная схема «мостика», но в нашей задаче «мостик» неуравновешен. Такие задачи приходится решать при помощи правил Кирхгофа. В школьной программе их нет, да и вычисления с помощью этих правил очень громоздкие — в нашем случае получилась бы система пяти уравнений с пятью неизвестными. Мы поступим проще: заменим «треугольник» ACD «звездой», как показано на рисунке 4.
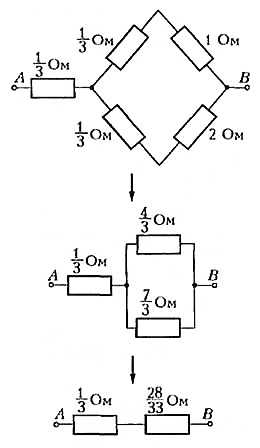
Рис. 4
Теперь ясно, что сопротивление между точками A и B будет равно
\(~R_{AB} = \frac 13 + \frac{28}{33} = \frac{13}{11}\) Ом.Мы заменяли «треугольник» ACD «звездой», но можно было решать задачу иначе — заменяя «звезду» ADB «треугольником» (проделайте зто самостоятельно).
Пусть теперь к точкам A и B подключена батарея с пренебрежимо малым внутренним сопротивлением и ЭДС ε = 1 В. Нужно найти ток через участок СВ. Понятно, что преобразовать схему надо так, чтобы не затронуть интересующее нас сопротивление СВ. Подойдет то преобразование, которое мы делали раньше (см. рис.4). Используя, что \(~R_{AB} = \frac{13}{11}\) Ом , получим
\(~I = \frac{\varepsilon}{R_{AB}} = \frac{11}{13}\) А.После разветвления токи в верхней и в нижней ветвях поделятся в отношении, обратном сопротивлениям ветвей:
\(~\frac{I_1}{I_2} = \frac 74\) .Отсюда находим
\(~I_1 = \frac{7}{13}\) А.Немного сложнее было бы найти ток, идущий через участок CD. Для этого пришлось бы еще найти ток через участок АС, а затем вычесть из него найденный уже ток через участок СВ.
Можно еще немного усложнить задачу — учесть внутреннее сопротивление батареи r. Тогда полный ток равен
\(~I = \frac{\varepsilon}{r + R_{AB}}\) ,а остальные токи находятся так же, как и раньше.
Рис. 5
Рассмотрим более интересную задачу, найдем, при каком соотношении между величинами r и R сопротивление между точками А и В в схеме, показанной на рисунке 5, максимально в крайнем положении движка потенциометра.
Рис. 6
Сначала преобразуем схему, заменив «треугольник» ACD «звездой» (рис.6). Очевидно, что сопротивление r не влияет на соотношение сопротивлений в остальной цепи. Займемся поэтому оставшейся частью схемы. Тут включены параллельно два сопротивления: 5r + R1 и 7r + R2, где R1 и R2 — сопротивления верхней и нижней частей потенциометра соответственно. При этом сумма сопротивлений 5r + R1, и 7r + R2 остается постоянной. Посмотрим, какими они должны быть, чтобы полное сопротивление было максимальным. Обозначим
\(~5r + R_1 = r_1\) и \(~7r + R_2 = r_2\).Тогда общее сопротивление включенных параллельно частей схемы равно
\(~r_0 = \frac{r_1 r_2}{r_1 + r_2}\) .Если учесть, что
\(~r_1 + r_2 = \operatorname{const} = c\) ,то
\(~r_0 = \frac{r_1 (c — r_1)}{c}\) .Это выражение максимально, когда максимален числитель. Но \(~y = cr_1 — r^2_1\) — это уравнение параболы, ветви которой пересекают ось абсцисс в точках 0 и с. Поэтому числитель дроби наибольший при \(~r_1 = \frac c2\). Так как r1 + r2 = с, то это означает, что сопротивление между точками А и В максимально, если r1 = r2, т.е.
\(~5r + R_1 = 7r + R_2\), или \(~R_1 — R_2 = 2r\).Ясно, что это возможно лишь в том случае, если сопротивление всего потенциометра R = R1 + R2 не меньше чем 2r. В противном же случае максимум сопротивления между точками A и B достигается, когда движок потенциометра находится в крайнем положении.
Итак, ответ: R ≤ 2r.
Метод, о котором мы рассказали, очень удобен для последовательного преобразования сложной схемы к простому виду. Он позволяет рассчитать практически любую сложную цепь, состоящую из сопротивлений. Однако его можно применять и к цепям, содержащим не только сопротивления. Обратим внимание на то, что мы вообще не говорили нигде о физических процессах в цепи, а пользовались только формальным выражением для закона Ома: U = rI. Из него следует, что при последовательном соединении сопротивлений их величины складываются, а при параллельном — складываются величины, обратные сопротивлениям. Понятно, что если какие-нибудь другие физические величины связаны законом, аналогичным закону Ома, то все наши выводы справедливы и для них.
Рис. 7
В качестве примера рассмотрим цепь с конденсатором (рис.7). Мы знаем, что заряд конденсатора Q связан с его емкостью C и напряжением на нем U соотношением
\(~Q = CU\), или \(~U = \frac 1C Q\).Сравним последнее выражение с выражением для закона Ома U = rI. Видно, что законы похожи, только вместо тока стоит заряд, а вместо сопротивления-величина, обратная емкости. Это означает, что для того чтобы найти, скажем, заряды на конденсаторах, можно поступить так: вместо цепи, содержащей конденсаторы, нарисовать цепь, содержащую сопротивления, причем конденсатор емкостью C(Ф) заменить сопротивлением \(~r = \frac 1C\) (Ом). После того как мы рассчитаем токи в цепи из сопротивлений, можно сразу записать, каковы заряды на конденсаторах: если по сопротивлению течет ток I = х (А), то на соответствующем конденсаторе будет заряд Q = х (Кл). ЭДС батарей при таком преобразовании цепи остаются без изменения. Но, разумеется, в цепи с конденсаторами внутренние сопротивления батарей не влияют на результат. Поэтому, преобразуя цепь, нам придется лишить батареи их внутренних сопротивлений.
Пусть, например, нужно найти заряд на конденсаторе емкостью 10 мкФ в схеме, изображенной на рисунке 8. Конденсатору емкостью С = 2 мкФ = 2·10-6 Ф соответствует сопротивление r = 5·105 Ом = 500 кОм. Далее расчет проводится уже достаточно просто (проделайте это самостоятельно).
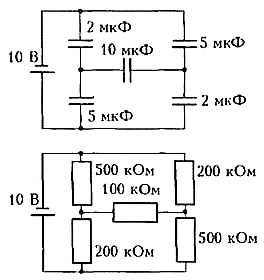
Рис. 8
Таким образом, метод преобразования цепей, как мы видим, пригоден и для схем из конденсаторов.
Примечания
- ↑ Здесь и далее более правильно говорить «два резистора с сопротивлениями r1 и r2» (Прим. ред.)
www.physbook.ru
2.5. Методы преобразования электрических цепей
Некоторые методы преобразования электрических цепей, были рассмотрены ранее. Например, последовательно соединенные n резистивных элементов ветви электрической цепи (рис. 2.79), заменяются одним эквивалентным сопротивлением:
и 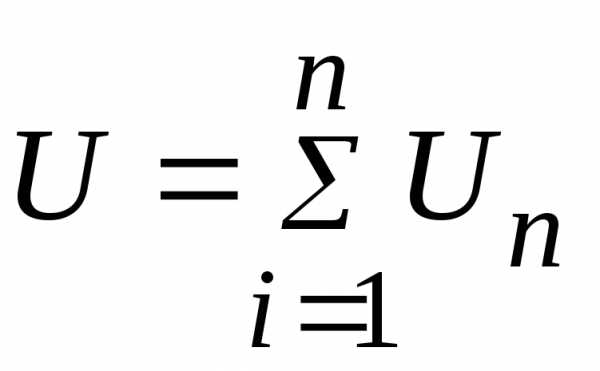 .
.
Рисунок 2.79 – Последовательное соединение резистивных элементов
Последовательно соединенные n источников ЭДС ветви электрической цепи (рис. 2.80), заменяются одним эквивалентным ЭДС, равным алгебраической сумме ЭДС источников входящих в соединение:
.
Рисунок 2.80 – Последовательное соединение ЭДС
Параллельно соединенные n резистивных элементов электрической цепи, представленной на рисунке 2.81, заменяются одним эквивалентным сопротивлением.
Для данного преобразования справедливы следующее соотношение:
.
Рисунок 2.81 – Параллельное соединение резистивных элементов
Параллельно соединенные n источников тока электрической цепи (рис. 2.82), заменяются одним эквивалентным источником тока, равным алгебраической сумме токов источников тока, входящих в соединение:
.
Рисунок 2.82 – Параллельное соединение источников тока
Вышеуказанные преобразования дают возможность рассчитывать разветвленные электрические цепи цепочного вида с одним источником питания.
2.5.1. Расчет разветвленных цепей цепочного типа
В основе метода расчета подобных цепей используются методы преобразования последовательно и параллельно соединенных элементов, а также закон Ома.
Пример 2.22. Рассмотрим расчет разветвленной цепи цепочного типа на примере электрической цепи, изображенной на рисунке 2.83, с параметрами: E=200 B, r1 = 8 Ом, r2/= 5 Ом, r2//= 15 Ом, r3 =8 Ом, r4 = 10 Ом, r5 = 20 Ом, r6 = 30 Ом. Требуется определить токи во всех ветвях электрической цепи, проверить найденные значения токов, составив баланс мощностей.
Рисунок 2.83 – Расчетная схема электрической цепи
1. Определяем входное сопротивление всей цепи.
1.1.
На первом этапе последовательно
соединенные сопротивления 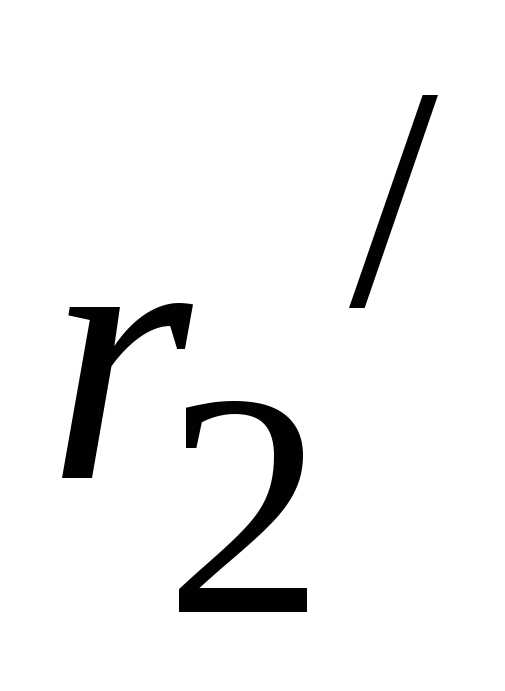 и
и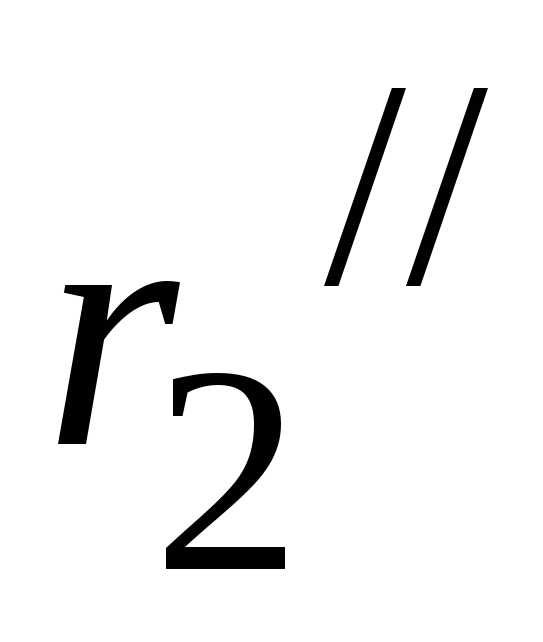 заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением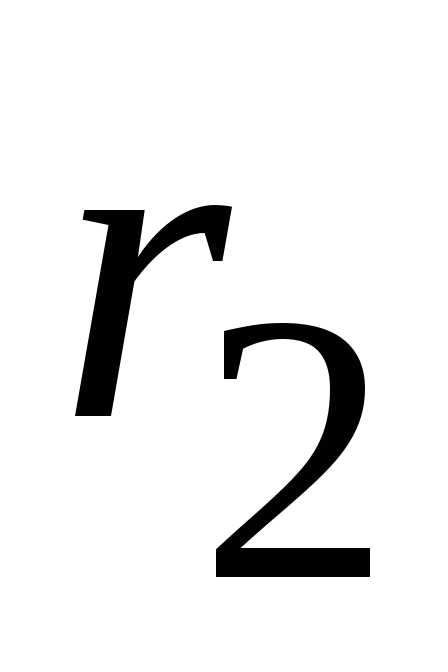 ,
а также параллельно соединенные
,
а также параллельно соединенные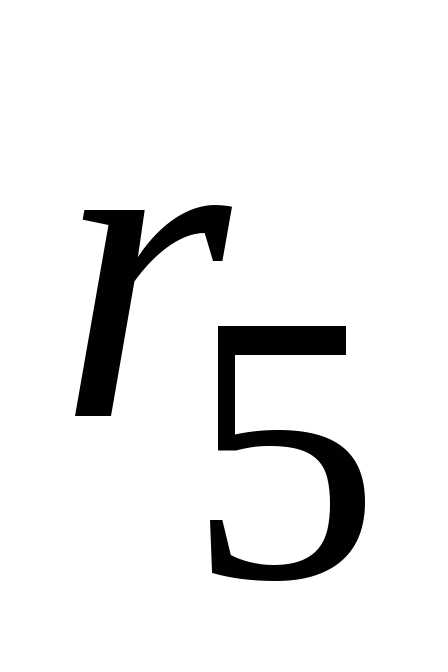 и
и заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением :
:
Ом, Ом.
В результате схема имеет вид, представленный на рисунке 2.84.
Рисунок 2.84 – Преобразованная электрическая цепь
Последовательно соединенные сопротивления
 ,
,  и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  :
:
Ом.
В результате схема имеет вид, представленный на рисунке 2.85.
Рисунок 2.85 – Преобразованная электрическая цепь
Параллельно соединенные сопротивления
 и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  :
:
Ом.
В результате схема имеет вид, представленный на рисунке 2.86.
Рисунок 2.86 – Преобразованная электрическая цепь
Определяем входное сопротивление всей цепи:
Ом.
Определяем токи в ветвях. С этой целью используем закон Ома.
2.1.
Ток 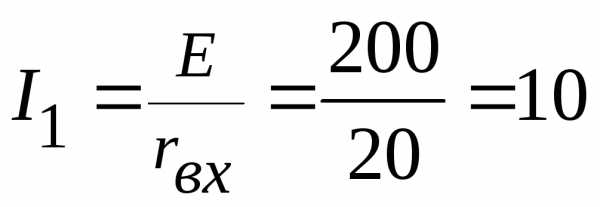 А.
А.
2.2.
Определяем токи 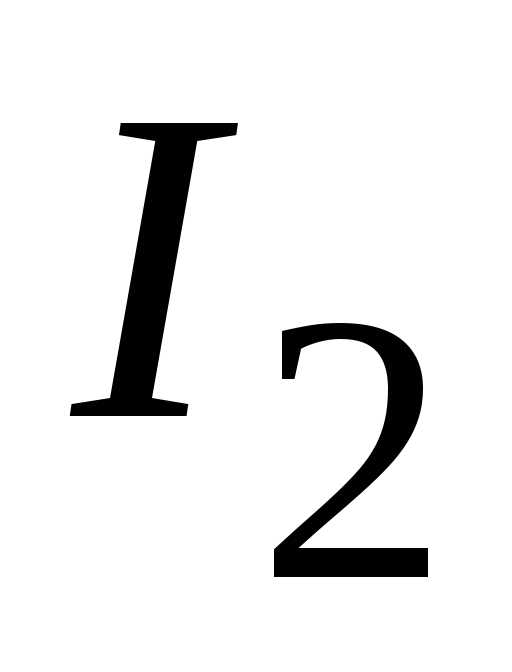 ,
,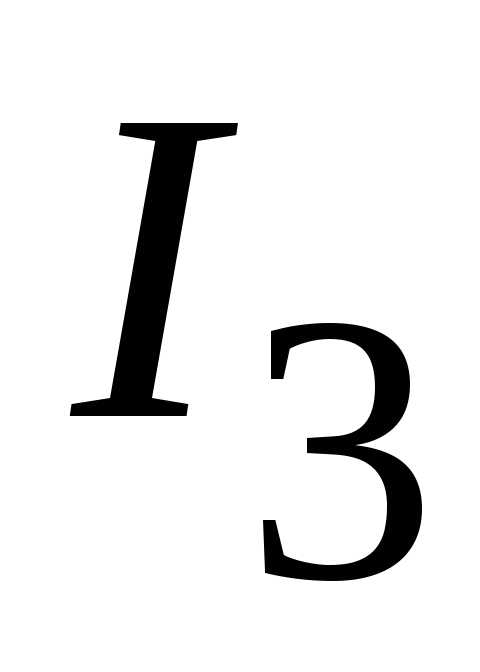 и
и 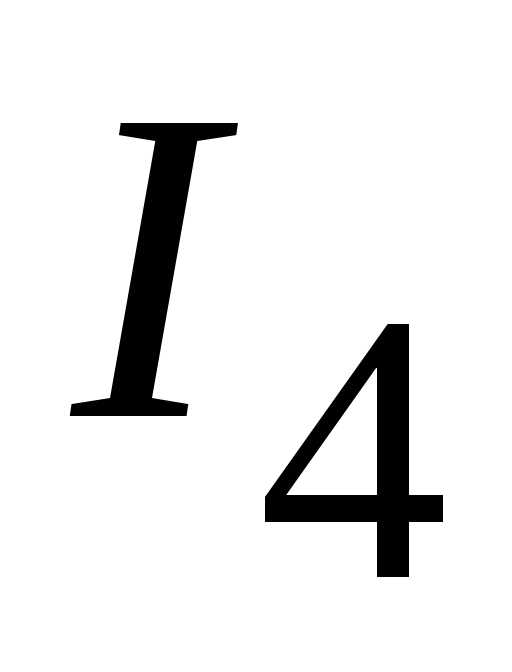 .
Для их определения необходимо
предварительно определить напряжение
.
Для их определения необходимо
предварительно определить напряжение (рис.
2.85).
(рис.
2.85).
2.2.1. Из схемы, приведенной на рисунке 2.86, следует
В, или
В.
2.2.2. Тогда токи в ветвях:
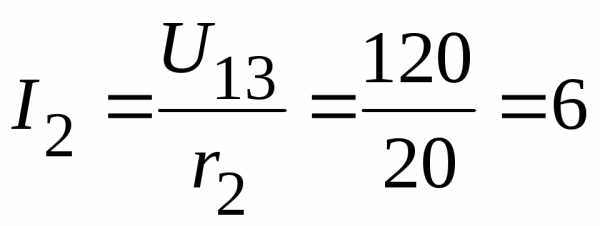 А;
А;
А, или
А.
2.3.
Определяем токи 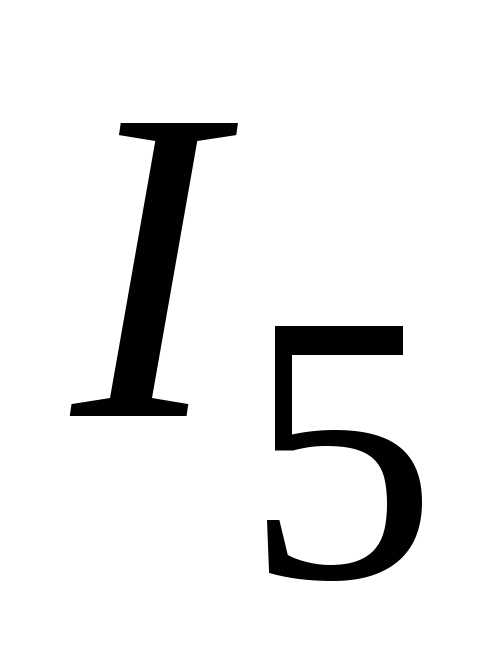 и
и 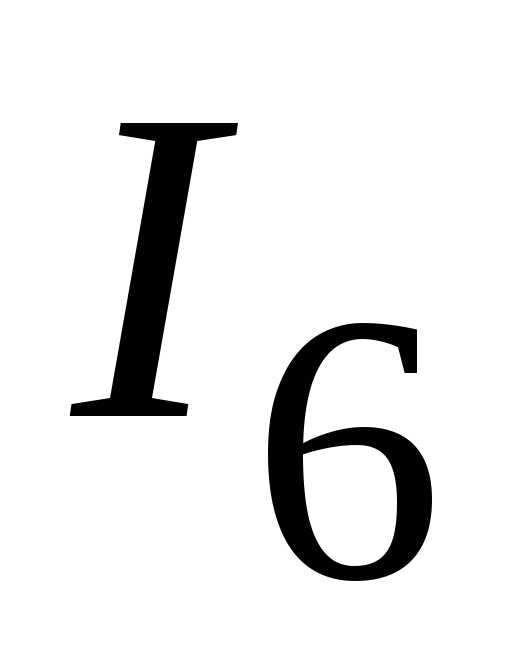 .
Для их определения необходимо
предварительно определить напряжение
.
Для их определения необходимо
предварительно определить напряжение (
рис. 2.83).
(
рис. 2.83).
2.3.1. Из схемы, приведенной на рисунке 2.84, следует
В, или
В.
2.3.2. Тогда токи в ветвях:
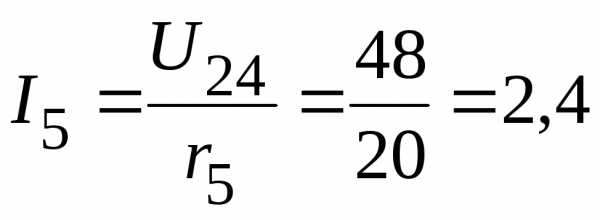 А;
А;
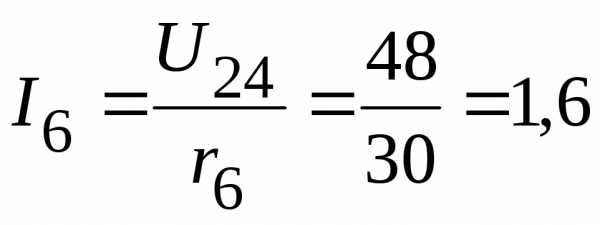 А,
или
А,
или
А.
3. Проверяем решение, составив баланс мощностей.
3.1. Мощность, генерируемая источником питания:
Вт.
3.2. Мощность, потребляемая приемниками:
Вт,
Вт,
Вт,
Вт,
Вт,
Вт.
Суммарная мощность, потребляемая приемниками:
Вт.
3.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислении и непревышает 0,5%.
Пример 2.23. Рассмотрим расчет разветвленной цепи цепочного типа на примере электрической цепи, изображенной на рисунке 2.87, с параметрами: E=21 B, r1 =100 Ом, r2=200 Ом, r3 =50 Ом, r4 =150 Ом, r5 =75 Ом, r6 =300 Ом. Требуется определить токи во всех ветвях электрической цепи, проверить найденные значения токов, составив баланс мощностей.
Рисунок 2.87 – Расчетная схема электрической цепи
1. Определяем входное сопротивление всей цепи.
1.1.
На первом этапе параллельно соединенные
сопротивления 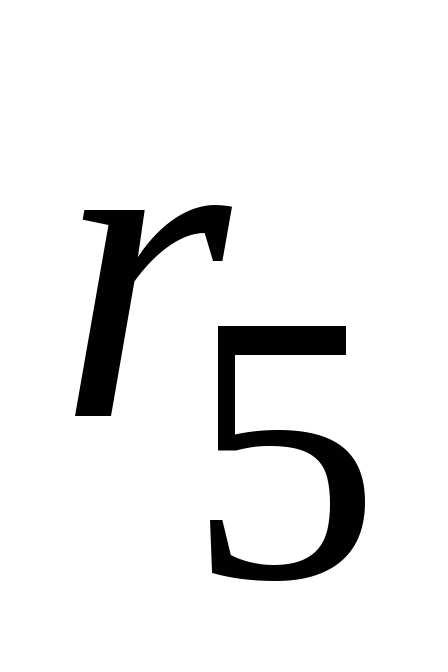 и
и заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением ,
а также параллельно соединенные
,
а также параллельно соединенные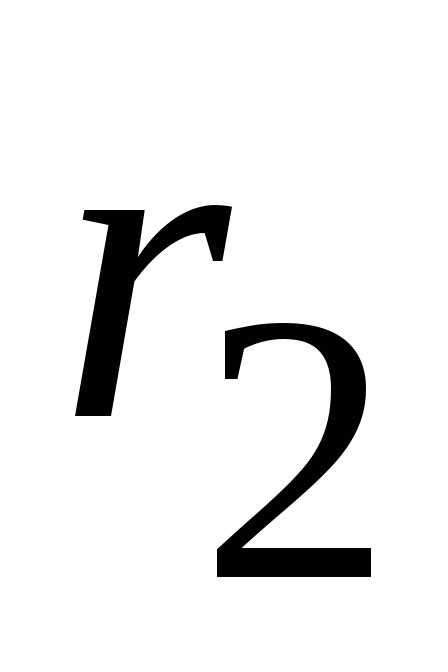 и
и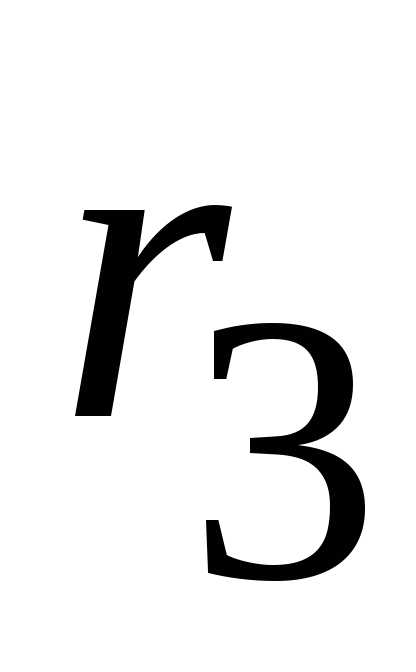 заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением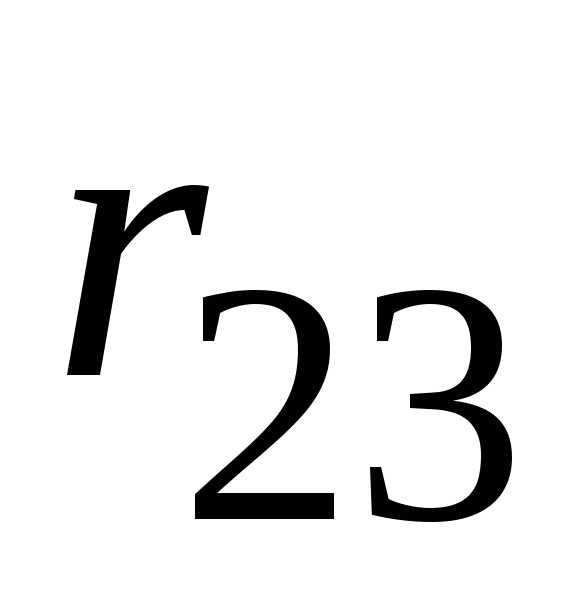 :
:
Ом, Ом.
В результате схема имеет вид, представленный на рисунке 2.88.
Рисунок 2.88 – Преобразованная электрическая цепь
Последовательно соединенные сопротивления
 и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  :
:
Ом.
В результате схема имеет вид, представленный на рисунке 2.89.
Рисунок 2.89 – Преобразованная электрическая цепь
Параллельно соединенные сопротивления
 и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  :
:
Ом.
В результате схема имеет вид, представленный на рисунке 2.90.
Рисунок 2.90 – Преобразованная электрическая цепь
Определяем входное сопротивление всей цепи:
Ом.
Определяем токи в ветвях. С этой целью используем закон Ома.
2.1. Ток мА.
2.2.
Определяем токи 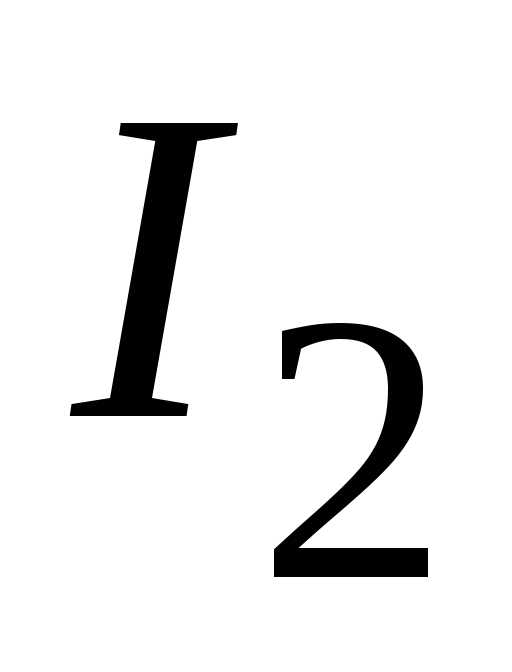 ,
,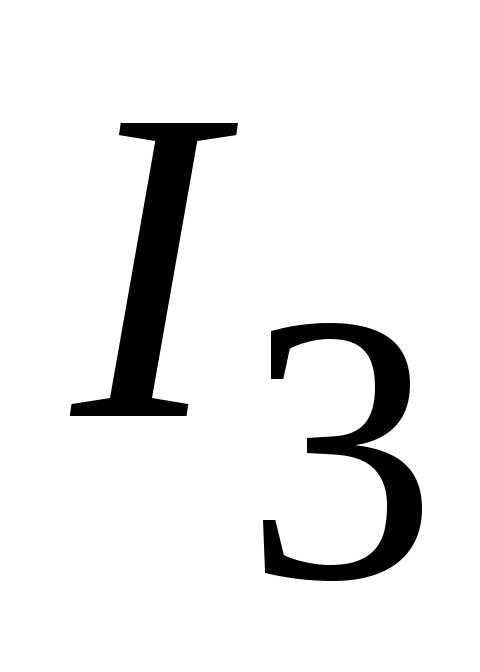 и
и 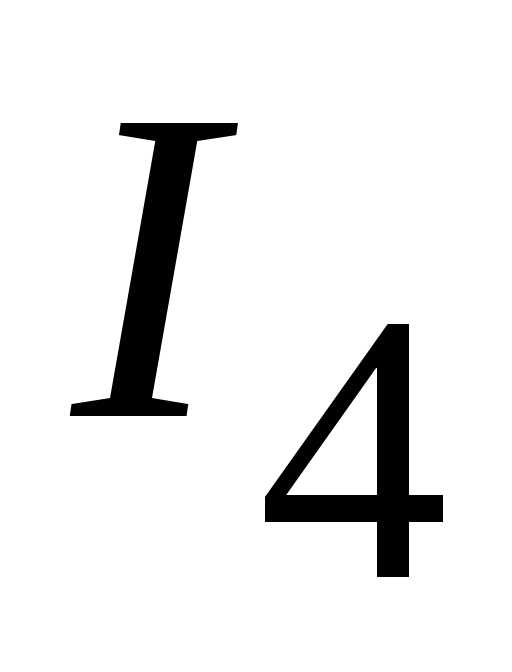 .
Для их определения необходимо
предварительно определить напряжение
.
Для их определения необходимо
предварительно определить напряжение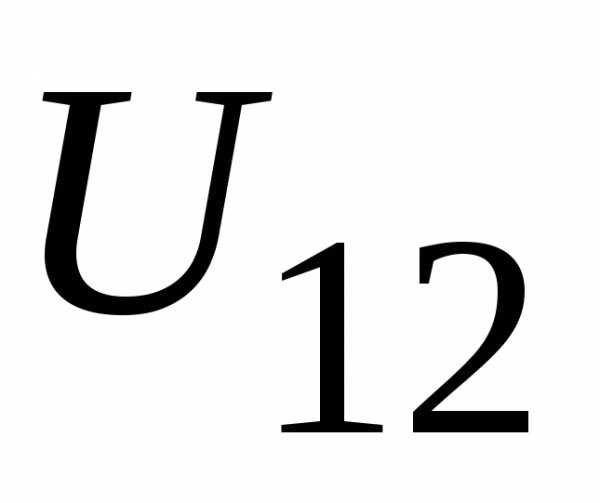 .
.
2.2.1. Из схемы, приведенной на рисунке 2.90, следует
В, или
В.
2.2.2. Тогда токи в ветвях:
мА;
мА,
мА, или
мА.
2.3.
Определяем токи 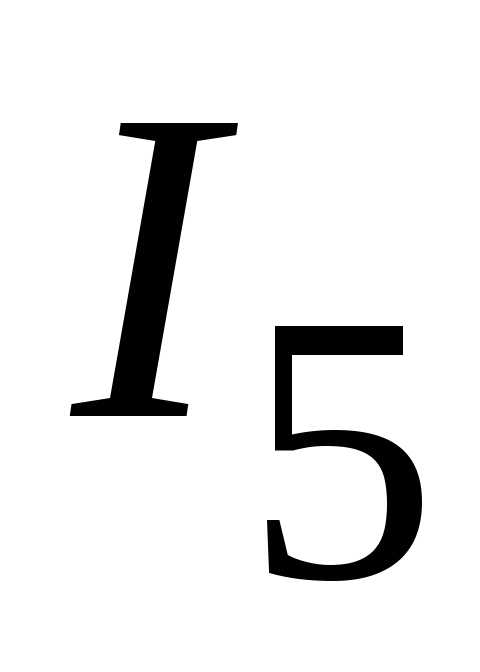 и
и 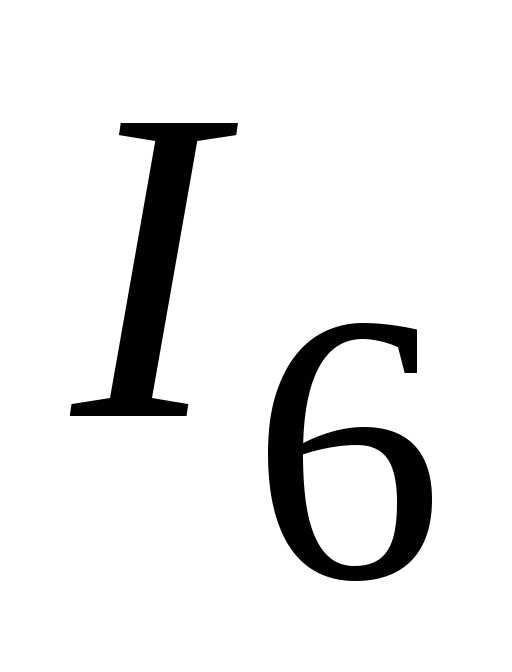 .
Для их определения необходимо
предварительно определить напряжение
.
Для их определения необходимо
предварительно определить напряжение (рис. 2.87).
(рис. 2.87).
2.3.1. Из схемы, приведенной на рисунке 2.88, следует
В, или
В.
2.3.2. Тогда токи в ветвях:
мА;
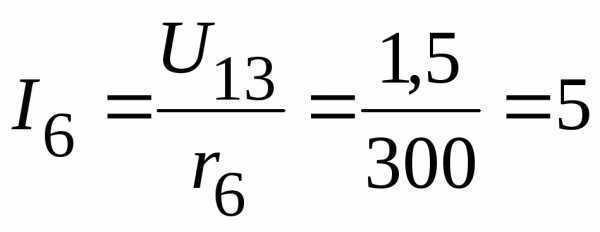 мА,
или
мА,
или
мА.
3. Проверяем решение, составив баланс мощностей.
3.1. Мощность, генерируемая источником питания:
Вт.
3.2. Мощность, потребляемая приемниками:
Вт,
Вт,
Вт,
Вт,
Вт,
Вт.
Суммарная мощность, потребляемая приемниками:
Вт.
3.3. Из сравнения генерируемой мощности источником и потребляемой мощности приемниками, следует, что погрешность вычислении и непревышает 0,5%.
studfiles.net
Электрическая цепь с последовательным соединением элементов
Рис. 1.4 | Рис. 1.5 |
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U = U1 + U2 + U3 или IRэкв = IR1 + IR2 + IR3,
откуда следует
Rэкв = R1 + R2 + R3.
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).
Рис. 1.6
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I1 + I2 + I3, т.е.
откуда следует, что
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
(1.7)
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
gэкв = g1 + g2 + g3.
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
U = IRэкв = I1R1 = I2R2 = I3R3.
Отсюда следует, что
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
Рис. 1.7
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
Рис. 1.8
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
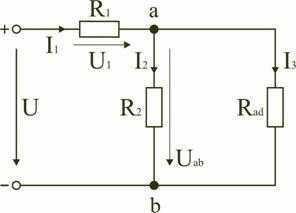
Рис. 1.9
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
.
Рис. 1.10 | Рис. 1.11 |
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
ЛИНЕЙНЫЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.
Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока
Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим.
Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной ЭДС. Простейшим генератором синусоидальной ЭДС может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω (рис. 2.1, б).

Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции ЭДС е. Нагрузку подключают к генератору с помощью щеток 1, прижимающихся к двум контактным кольцам 2, которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В, размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля vн:
e = Blvн (2.1)
где В и l — постоянные величины, a vн — переменная, зависящая от угла α. Выразив скорость vн через линейную скорость катушки v, получим
e = Blv·sinα (2.2)
В выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α.
Если угол α = π/2, то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. Em = Blv. Поэтому выражение (2.2) можно записать в виде
e = Emsinα (2.3)
Так как α есть угол поворота за время t, то, выразив его через угловую скорость ω, можно записать α = ωt, a формулу (2.3) переписать в виде
e = Emsinωt (2.4)
где е — мгновенное значение э. д. с. в катушке; α = ωt — фаза, характеризующая значение э. д. с. в данный момент времени.
Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е, напряжений и и токов i справедливы законы постоянного тока.
Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе — время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рис. 2.2 построены графики мгновенных значений э. д. с. е и е’.
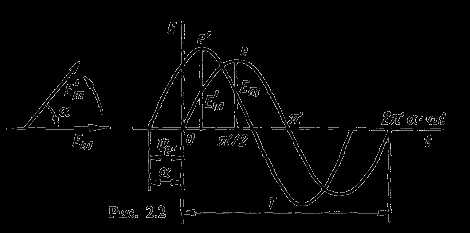
Если число пар полюсов магнитов p ≠ 1, то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,
f = Pn / 60
Из рис. 2.2 видно, что ωТ = 2π, откуда
ω = 2π / T = 2πf (2.5)
Величину ω, пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.
Графически изображенные на рис. 2.2 э. д. с. е и е’ можно описать выражениями
e = Emsinωt; e’ = E’msin(ωt + ψe’).
Здесь ωt и ωt + ψe’ — фазы, характеризующие значения э. д. с. e и e’ в заданный момент времени; ψe’ — начальная фаза, определяющая значение э. д. с. е’ при t = 0. Для э. д. с. е начальная фаза равна нулю (ψe = 0). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ (рис. 2.2) откладывают влево от начала координат (в сторону отрицательных значений ωt), а отрицательную фазу — вправо.
Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.
Разность углов φ, равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α. Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ (рис. 2.3).

Когда для синусоидальных величин разность фаз равна ±π, то они противоположны по фазе, если же разность фаз равна ±π/2, то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.
Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:
u = Umsin(ωt + ψu); i = Imsin(ωt + ψi), (2.6)
причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψu — ψi.
Уравнения (2.6) можно записать иначе:
u = Umsin(ωt + ψi + φ); i = Imsin(ωt + ψu — φ),
поскольку ψu = ψi + φ и ψi = ψu — φ.
Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ).
Формы представления синусоидальных электрических величин.
Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.
1). Аналитическая форма представления
I = Im·sin(ω·t + ψi), u = Um·sin(ω·t + ψu), e = Em·sin(ω·t + ψe),
где I, u, e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;
Im, Um, Em – амплитуды синусоидального тока, напряжения, ЭДС;
(ω·t + ψ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;
ψi, ψu, ψe – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение.
Графики мгновенных значений тока и напряжения показаны на рис. 2.3
Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψu > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψi < 0. Алгебраическая величина, равная разности начальных фаз двух синусоид, называется сдвигом фаз φ. Сдвиг фаз между напряжением и током
φ = ψu – ψi = ψu – ( — ψi) = ψu + ψi.
Применение аналитической формы для расчёта цепей является громоздкой и неудобной.
На практике приходится иметь дело не с мгновенными значениями синусоидальных величин, а с действующими. Все расчёты проводят для действующих значений, в паспортных данных различных электротехнических устройств указаны действующие значения (тока, напряжения), большинство электроизмерительных приборов показывают действующие значения. Действующий ток является эквивалентом постоянного тока, который за одно и то же время выделяет в резисторе такое же количество тепла, как и переменный ток. Действующее значение связано с амплитудным простым соотношением
2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf. Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.
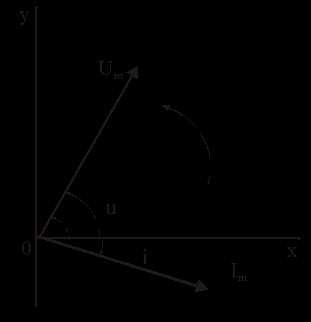 Рис.
2.4
Рис.
2.4
Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4
3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.
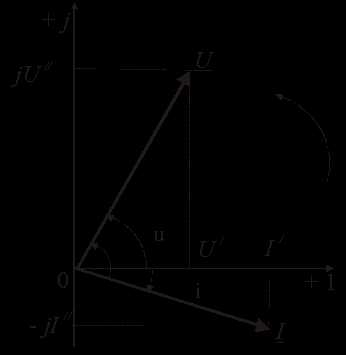 Рис.
2.5
Рис.
2.5
Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис.2.5 Ось абсцисс называют осью действительных чисел и обозначают +1, ось ординат называют осью мнимых чисел и обозначают +j. (В некоторых учебниках ось действительных чисел обозначают Re, а ось мнимых – Im). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах:
а). Алгебраической
U = U’+ jU«
I = I’ – jI«,
где U‘, U«, I‘, I» – проекции векторов на оси действительных и мнимых чисел.
б). Показательной
где U, I – модули (длины) векторов; е – основание натурального логарифма; поворотные множители, т. к. умножение на них соответствует повороту векторов относительно положительного направления действительной оси на угол, равный начальной фазе.
в). Тригонометрической
U = U·(cosψu + jsinψu)
I = I·(cosψi – jsinψi).
При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера
еj·ψ = cosψ + jsinψ.
Неразветвлённые электрические цепи
studfiles.net
Методы расчета электрических цепей
Постановка задачи: в известной схеме цепи с заданными параметрами необходимо рассчитать токи, напряжения, мощности на отдельных участках. Для этого можно использовать следующие методы:
преобразования цепи;
непосредственного применения законов Кирхгофа;
контурных токов;
узловых потенциалов;
наложения;
эквивалентного генератора.
Будем рассматривать первых два метода.
Метод преобразования цепи. Суть метода: если несколько последовательно или (и) параллельно включенных сопротивлений заменить одним, то распределение токов в электрической цепи не изменится.
а) Последовательное соединение резисторов. Сопротивления включены таким образом, что начало следующего сопротивления подключается к концу предыдущего (рис. 6).
Ток во всех последовательно соединенных элементах одинаков.
Заменим
все последовательно соединенные
резисторы одним эквивалентным (рис. 7.).
(рис. 7.).
По IIзакону Кирхгофа:
;
;
т.е. при последовательном соединении резисторов эквивалентное сопротивление участка цепи равно сумме всех последовательно включенных сопротивлений.
б) Параллельное соединение резисторов. При этом соединении соединяются вместе одноименные зажимы резисторов (рис. 8).
Все элементы присоединяются к одной паре узлов. Поэтому ко всем элементам приложено одно и тоже напряжениеU.
По Iзакону Кирхгофа:.
По
закону Ома 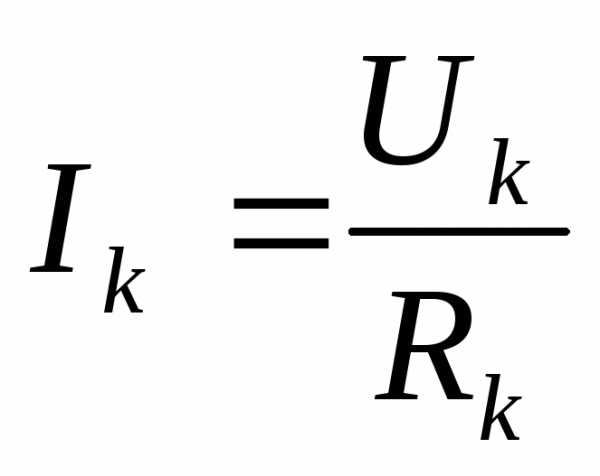 .
Тогда.
.
Тогда.
Для
эквивалентной схемы (см рис. 7): 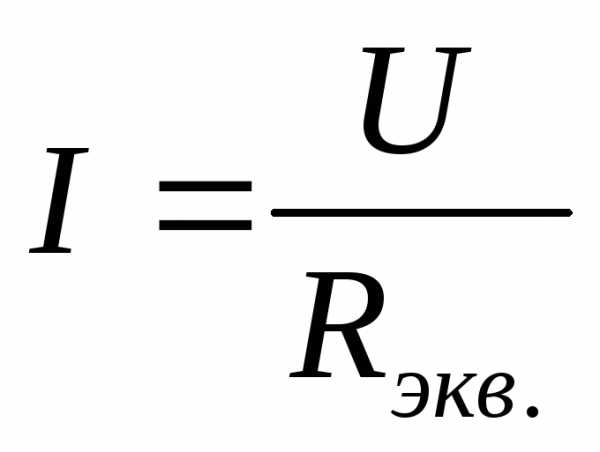 ;
.
;
.
Величина 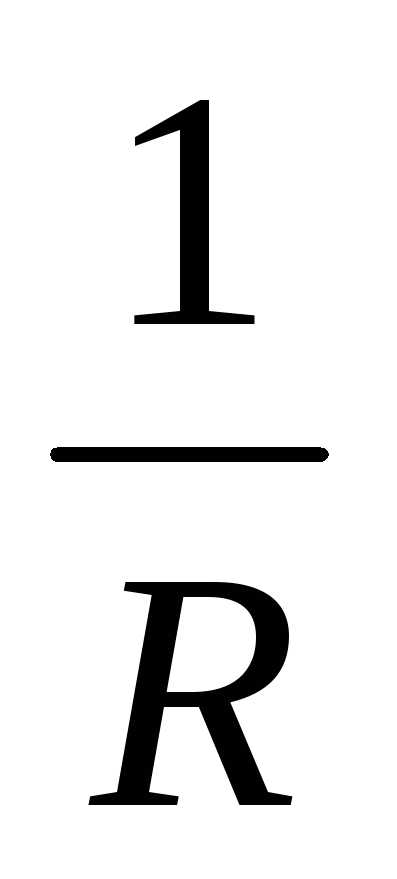 ,
обратная сопротивлению, называется
проводимостьюG.
,
обратная сопротивлению, называется
проводимостьюG.
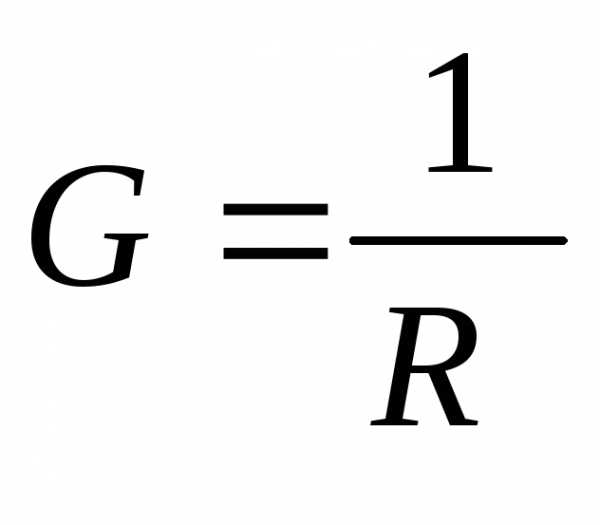 ;
;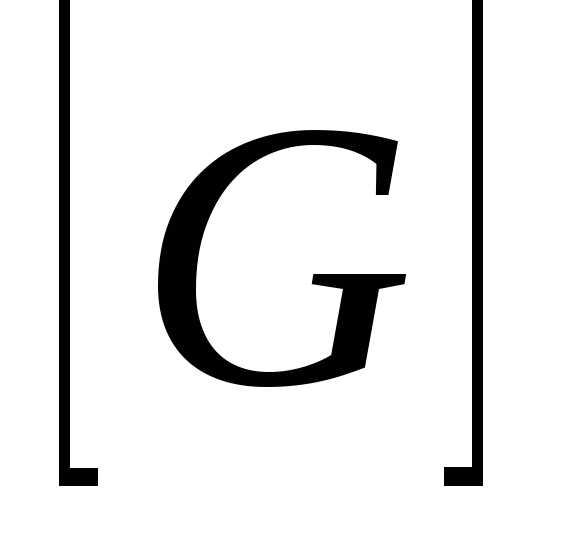 =
Сименс (См).
=
Сименс (См).
Частный случай: параллельно соединены два резистора (рис. 9).
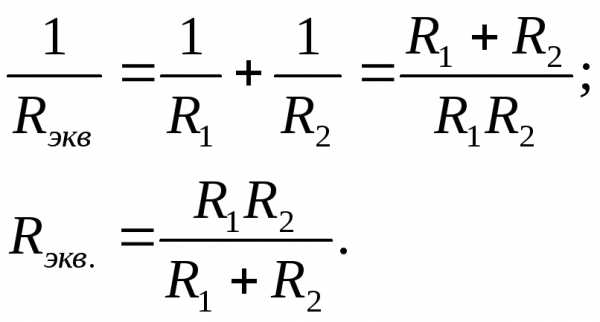


в) Взаимное преобразование звезды (рис.10а) и треугольник сопротивлений (рис. 10б).
— преобразование звезды сопротивлений в треугольник:
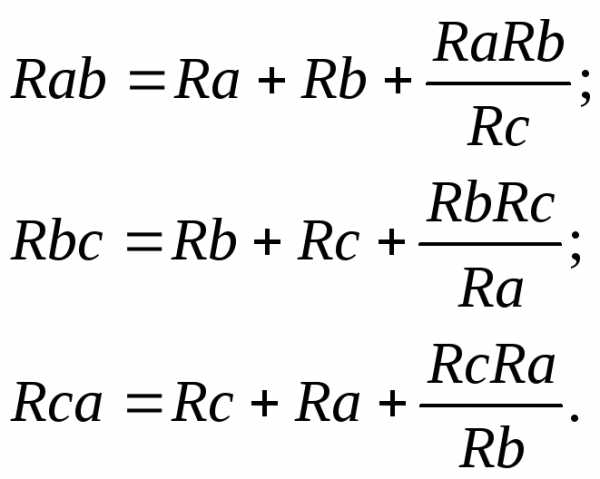
— преобразование «треугольника» сопротивлений в «звезду»:
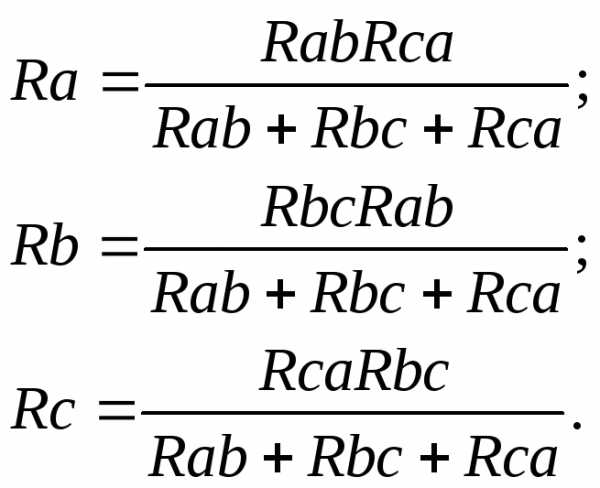
Метод непосредственного применения законов Кирхгофа. Порядок расчета:
Определить число ветвей (т.е. токов) и узлов в схеме.
Произвольно выбрать условно-положительные направления токов. Общее число уравнений должно быть равно числу неизвестных токов.
Определить, сколько уравнений должно быть составлено по Iзакону Кирхгофа, а сколько — поIIзакону Кирхгофа.
Составить уравнения для
 узлов
поIзакону Кирхгофа и
длянезависимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.
узлов
поIзакону Кирхгофа и
длянезависимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.Решить система уравнений относительно токов. Если в результате ток получился отрицательным, то его действительное направление противоположно выбранному.
Проверить правильность решения задачи, составив уравнение баланса мощности и смоделировав электрическую цепь средствами моделирующего пакета ElectronicsWorkbench.
Примечание: если есть возможность, то перед составлением системы уравнений по законам Кирхгофа, следует преобразовать «треугольник» сопротивлений в соответствующую «звезду».
Пример расчет электрических цепей постоянного тока
Расчет будем выполнять с применением законов Кирхгофа, предварительно преобразовав треугольник сопротивлений в звезду.
П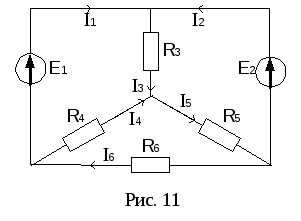 ример.
Определить токи в цепи рис. 11, еслиE1=160
В,E2=100 В,R3=100 Ом,R4=100 Ом,R5=150 Ом,R6=40
Ом.
ример.
Определить токи в цепи рис. 11, еслиE1=160
В,E2=100 В,R3=100 Ом,R4=100 Ом,R5=150 Ом,R6=40
Ом.
Преобразуем треугольник сопротивлений R4 R5 R6в звезду сопротивленийR45 R56 R64, предварительно указав условные положительные направления токов в цепи (рис. 12).
Ом;
Ом;
Ом.
а) | б) |
Рис. 12 | |
После преобразования электрическая цепь примет вид рис. 13 (в непреобразованной части электрической цепи направления токов не изменятся).
В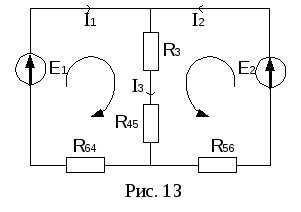 полученной электрической цепи 2 узла,
3 ветви, 2 независимых контура, следовательно,
в цепи протекает три тока (по количеству
ветвей) и необходимо составить систему
трех уравнений, из которых поIзакону Кирхгофа – одно уравнение (на 1
меньше, чем узлов в схеме электрической
цепи) и два уравнения – поIIзакону Кирхгофа:
полученной электрической цепи 2 узла,
3 ветви, 2 независимых контура, следовательно,
в цепи протекает три тока (по количеству
ветвей) и необходимо составить систему
трех уравнений, из которых поIзакону Кирхгофа – одно уравнение (на 1
меньше, чем узлов в схеме электрической
цепи) и два уравнения – поIIзакону Кирхгофа:
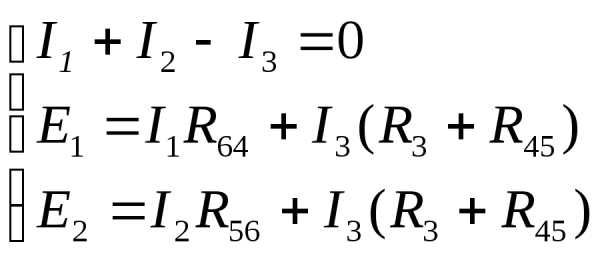
Подставим в полученную систему уравнений известные значения ЭДС и сопротивлений:
Решая систему уравнений любым способом, определяем токи схемы электрической цепи рис. 13:
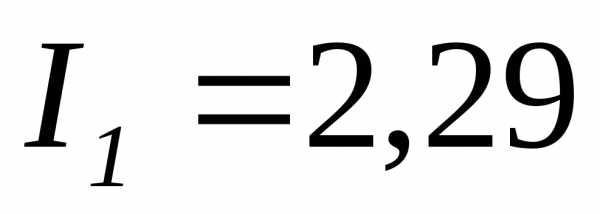 А;А;
А;А;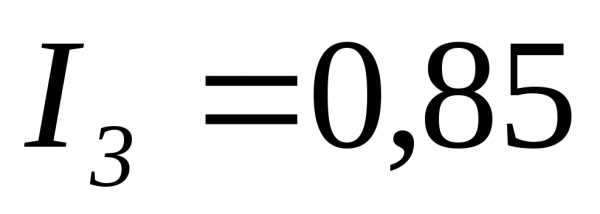 А.
А.
Переходим к исходной схеме (см. рис. 11). По IIзакону Кирхгофа:
;
А.
По Iзакону Кирхгофа:
;
А;
;
А.
Т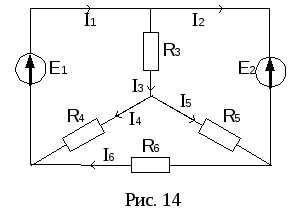 оки
оки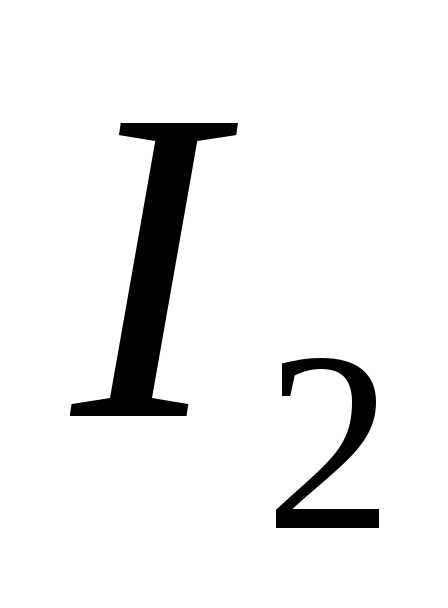 и
и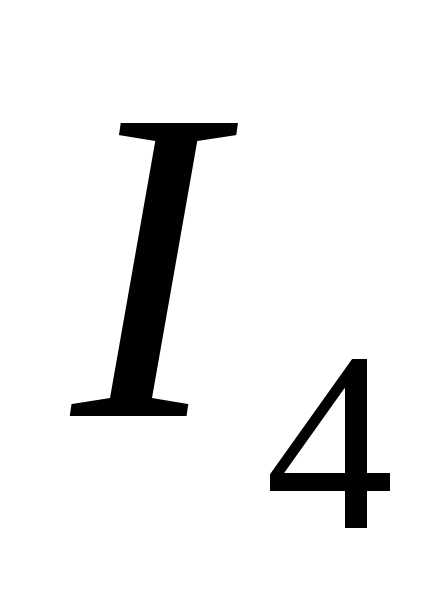 получились отрицательными, следовательно,
их действительное направление
противоположно выбранному нами (рис.
14).
получились отрицательными, следовательно,
их действительное направление
противоположно выбранному нами (рис.
14).
Правильность решения проверяем, составив уравнение баланса мощности. Мощность источников (учтем, что ЭДС источника E2направленно встречно токуI2, протекающему через него):
Вт.
Мощность потребителей:
Погрешность вычислений в пределах допустимого (меньше 5%).
Смоделируем электрическую цепь рис. 11 средствами моделирующего пакета ElectronicsWorkbench(рис. 15):
Р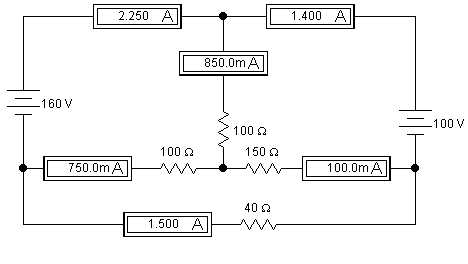 ис.
15
ис.
15
При сравнении расчетных результатов и результатов моделирования, можно увидеть, что они отличаются (различия не превышают 5%), т.к. измерительные приборы имеют внутренние сопротивления, которые моделирующая система учитывает
studfiles.net
Задача 1.1. Линейные электрические цепи постоянного тока
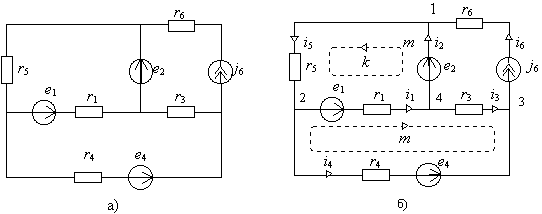
Для электрической схемы, соответствующей номеру варианта и изображенной на рис., выполнить следующее:
- Упростить схему, заменив последовательно и параллельно соединенные резисторы четвертой и шестой ветвей эквивалентными. Дальнейший расчет (п. 2-10) вести для упрощенной схемы.
- Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.
- Определить токи во всех ветвях схемы методом контурных токов.
- Определить токи во всех ветвях схемы методом узловых потенциалов.
- Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить между собой.
- Составить баланс мощностей в исходной схеме (схеме с источником тока), вычислив суммарную мощность источников и суммарную мощность нагрузок (сопротивлений).
- Определить ток I1 в заданной по условию схеме с источником тока, используя метод эквивалентного генератора.
- Начертить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
9. (Выполняется по указанию кафедры.) В заданной схеме, см. п. 1 задачи, закоротить все источники ЭДС, разомкнуть сопротивление, шунтирующее источник тока, заземлить один узел схемы и один из узлов принять за сток.
Начертить сигнальный граф, используя уравнения, составленные для получения схемы по методу узловых потенциалов, обозначить передачи ветвей как akm: индекс k соответствует узлу, к которому направлена стрелка на ветви, а индекс m – узлу, из которого ветвь исходит. Рекомендуется узлы схемы a, b, c, d заменить на 1, 2, 3, 4 соответственно. Требуется по формуле Мезона определить передачу от истока (источник тока) к стоку. В табл. указано, какой узел схемы заземлить и какой принять за сток.
10. (Выполняется по указанию кафедры.) Для исходной схемы своего варианта, см. п. 1 задачи, составить систему уравнений по методу контурных токов для нечетных вариантов и по методу узловых потенциалов для четных вариантов. При составлении уравнений по методу контурных токов использовать топологические матрицы [Kг], [Rв], матрицы [Eв], [Jв], [Ikk] и уравнение:
[Kг][Rв][Kг]T[Ikk]=[Kг]{[Eв]-[Rв][Jв]}
При составлении уравнений по методу узловых потенциалов использовать матрицы [A], [gв], [Eв], [Jв], [φ] и уравнение:
[A][gв][A]T[φ]=[A]{[Jв]-[gв][Eв]}
Download (PDF, 795KB)
Максим Декабрь 19th, 2012
Posted In: Задача, Линейные электрические цепи постоянного тока, Пример решения, ТОЭ, ТОЭ, Л.А.Бессонов, И.Г.Демидова, М.Е.Заруди
www.zachet.ru

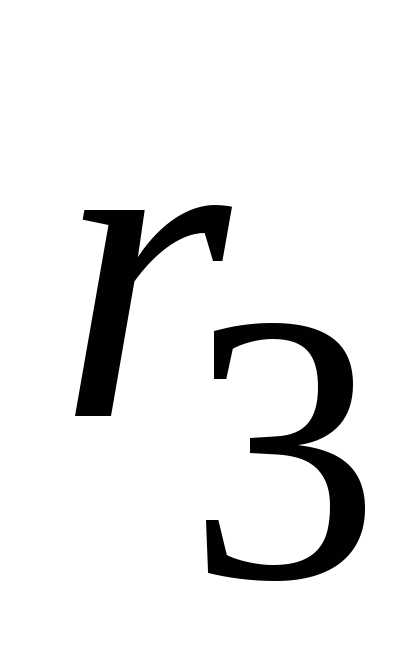 ,
,  и
и 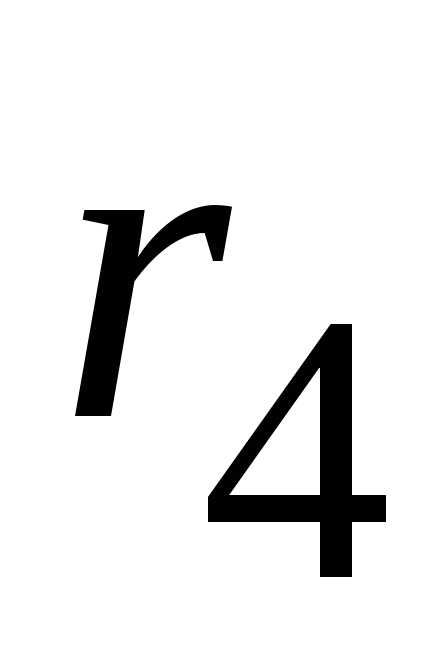 заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением 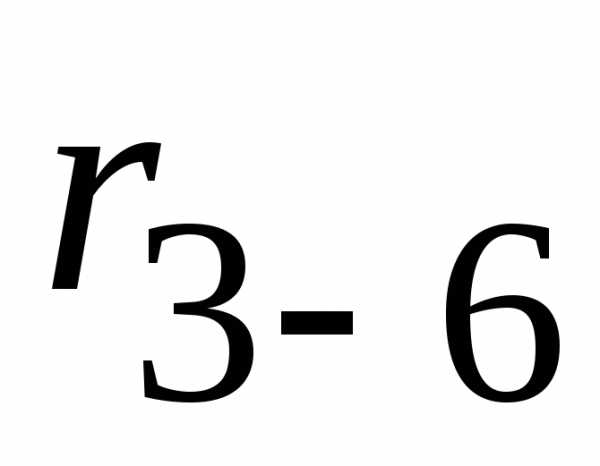 :
: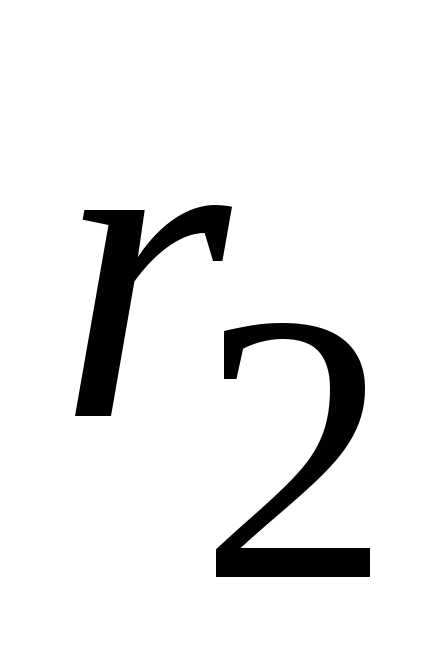 и
и 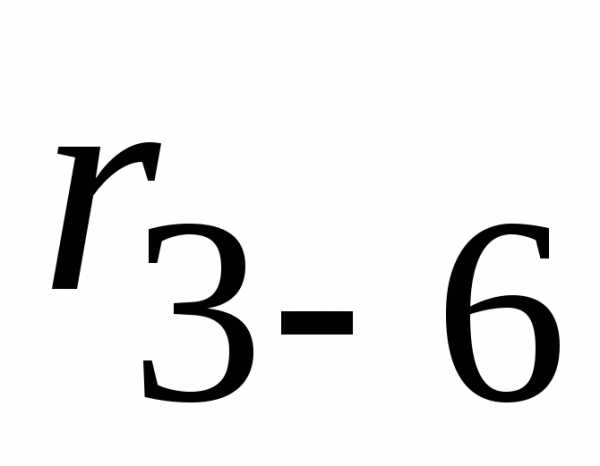 заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением 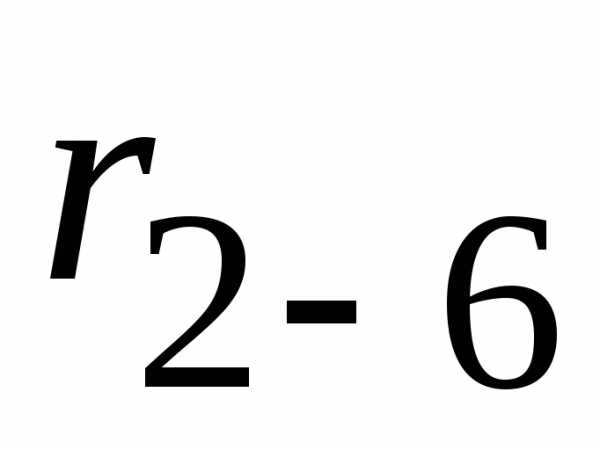 :
: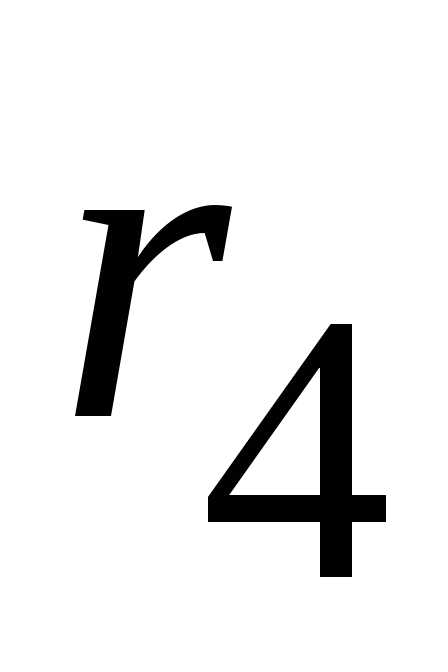 и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением  :
: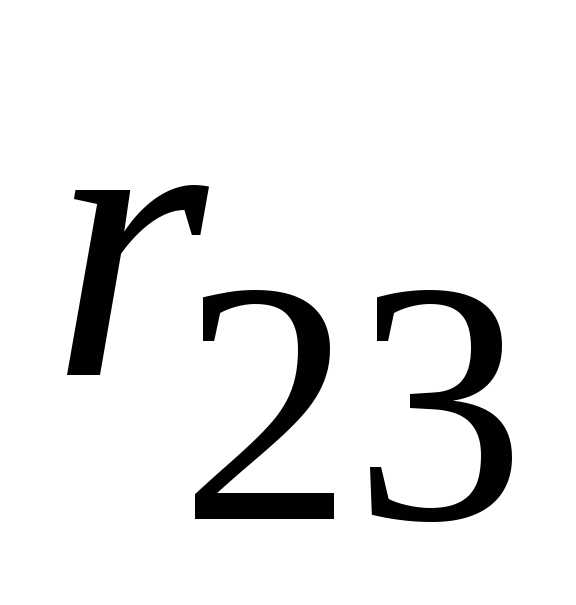 и
и  заменяем эквивалентным сопротивлением
заменяем эквивалентным сопротивлением 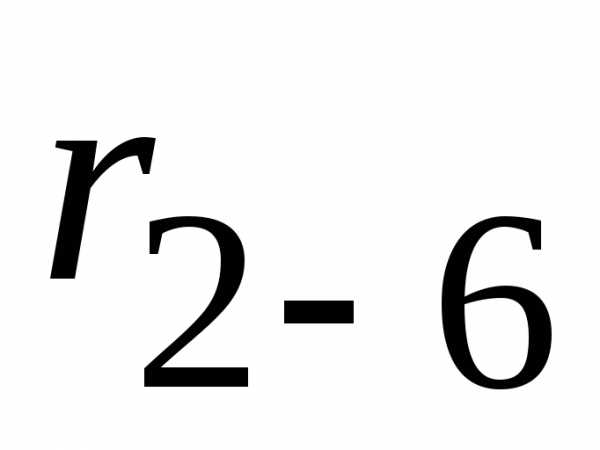 :
: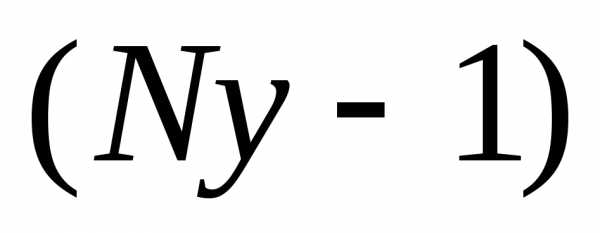 узлов
поIзакону Кирхгофа и
длянезависимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.
узлов
поIзакону Кирхгофа и
длянезависимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.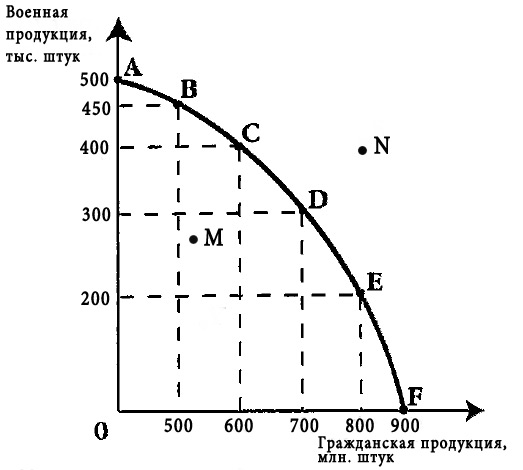


 Кривая производственных возможностей
Кривая производственных возможностей An example PPF with illustrative points marked
An example PPF with illustrative points marked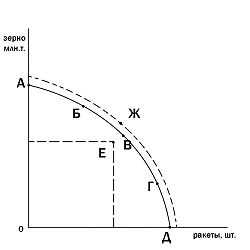 Кривая производственных возможностей
Кривая производственных возможностей An example PPF with illustrative points marked
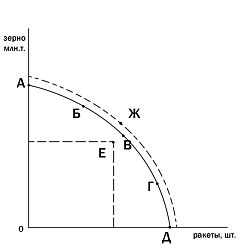
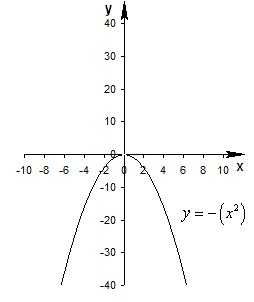
An example PPF with illustrative points marked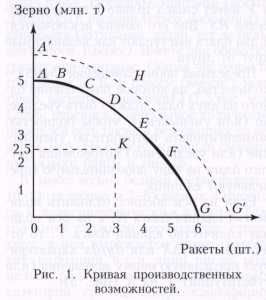 КРИВАЯ ПРОИЗВОДСТВЕННЫХ ВОЗМОЖНОСТЕЙ, показывает альтернативные варианты при полном использовании ресурсов. Производственные возможности – возможности общества по производству экономических благ при полном и эффективном использовании всех имеющихся ресурсов при данном уровне развития технологии. Именно потенциальный (возможный) выпуск продукции характеризует кривую производственных возможностей. Например, допустим, что в обществе производятся лишь два блага: зерно и ракеты. Если общество использует свои ресурсы для производства только зерна, то оно производит его 5 миллионов тонн; если же только для производства ракет, то их производится 6 штук. При одновременном производстве обоих благ возможны следующие сочетания (рис. 1). Из таблицы видно, что всякое увеличение производства ракет (с 0 до 6 штук) снижает производство зерна (с 5 миллионов тонн до 0 тонн), и наоборот. Линия ABCDEFG является кривой производственных возможностей. Все точки, расположенные внутри фигуры OAG, означают неполное использование ресурсов, например точка К (одновременное производство 2,5 миллионов тонн зерна и трёх ракет). И наоборот, любая производственная программа, характеризуемая точками за пределами фигуры OAG, не будет обеспечена наличными ресурсами (например, точка Н). Кривая производственных возможностей обычно имеет выпуклую форму (вогнута к началу координат). Это означает, что, изменяя структуру производства, например, в пользу ракет, в большей мере будут использоваться в производстве ракет сравнительно малоэффективные для этого ресурсы. Поэтому каждая дополнительная ракета требует всё большего сокращения производства зерна (и наоборот). Производство первой ракеты вызвало сокращение производства зерна на 0,2 миллиона тонн, второй – на 0,3 миллиона, третьей – на 0,6 миллиона тонн и т.д. Этот пример наглядно иллюстрирует убывающей предельной производительности закон. Кривая производственных возможностей исторична, она отражает достигнутый уровень развития технологии и степень использования имеющихся ресурсов. Если увеличиваются ресурсы или улучшается технология, площадь фигуры OAG растёт, кривая ABCDEFG сдвигается вверх и вправо.
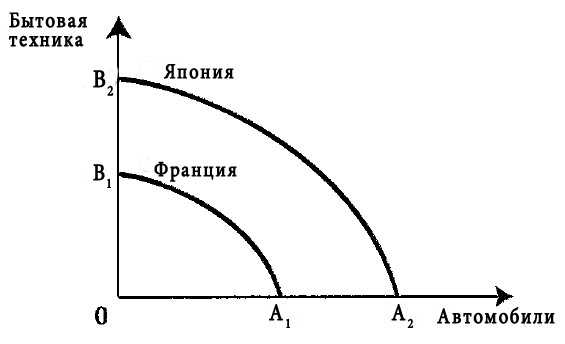
КРИВАЯ ПРОИЗВОДСТВЕННЫХ ВОЗМОЖНОСТЕЙ, показывает альтернативные варианты при полном использовании ресурсов. Производственные возможности – возможности общества по производству экономических благ при полном и эффективном использовании всех имеющихся ресурсов при данном уровне развития технологии. Именно потенциальный (возможный) выпуск продукции характеризует кривую производственных возможностей. Например, допустим, что в обществе производятся лишь два блага: зерно и ракеты. Если общество использует свои ресурсы для производства только зерна, то оно производит его 5 миллионов тонн; если же только для производства ракет, то их производится 6 штук. При одновременном производстве обоих благ возможны следующие сочетания (рис. 1). Из таблицы видно, что всякое увеличение производства ракет (с 0 до 6 штук) снижает производство зерна (с 5 миллионов тонн до 0 тонн), и наоборот. Линия ABCDEFG является кривой производственных возможностей. Все точки, расположенные внутри фигуры OAG, означают неполное использование ресурсов, например точка К (одновременное производство 2,5 миллионов тонн зерна и трёх ракет). И наоборот, любая производственная программа, характеризуемая точками за пределами фигуры OAG, не будет обеспечена наличными ресурсами (например, точка Н). Кривая производственных возможностей обычно имеет выпуклую форму (вогнута к началу координат). Это означает, что, изменяя структуру производства, например, в пользу ракет, в большей мере будут использоваться в производстве ракет сравнительно малоэффективные для этого ресурсы. Поэтому каждая дополнительная ракета требует всё большего сокращения производства зерна (и наоборот). Производство первой ракеты вызвало сокращение производства зерна на 0,2 миллиона тонн, второй – на 0,3 миллиона, третьей – на 0,6 миллиона тонн и т.д. Этот пример наглядно иллюстрирует убывающей предельной производительности закон. Кривая производственных возможностей исторична, она отражает достигнутый уровень развития технологии и степень использования имеющихся ресурсов. Если увеличиваются ресурсы или улучшается технология, площадь фигуры OAG растёт, кривая ABCDEFG сдвигается вверх и вправо. Если процесс происходит равномерно, то кривая АС симметрично смещается до положения А’G’ (рис. 1). Если происходит одностороннее увеличение эффективности технологии производства одного из благ, то сдвиг носит асимметричный характер (рис. 2). При одностороннем расширении производства зерна кривая AG смещается до положения A1G, при увеличении производства ракет – до положения AG1. Кривая производственных возможностей может быть использована для характеристики структурных сдвигов между промышленностью и сельским хозяйством, общественными и частными благами, текущим и будущим потреблением (потребительскими и инвестиционными товарами и услугами) и т.д.
Если процесс происходит равномерно, то кривая АС симметрично смещается до положения А’G’ (рис. 1). Если происходит одностороннее увеличение эффективности технологии производства одного из благ, то сдвиг носит асимметричный характер (рис. 2). При одностороннем расширении производства зерна кривая AG смещается до положения A1G, при увеличении производства ракет – до положения AG1. Кривая производственных возможностей может быть использована для характеристики структурных сдвигов между промышленностью и сельским хозяйством, общественными и частными благами, текущим и будущим потреблением (потребительскими и инвестиционными товарами и услугами) и т.д.




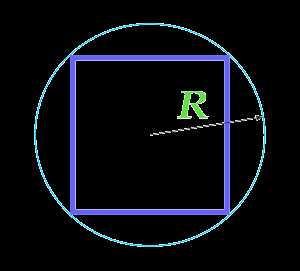




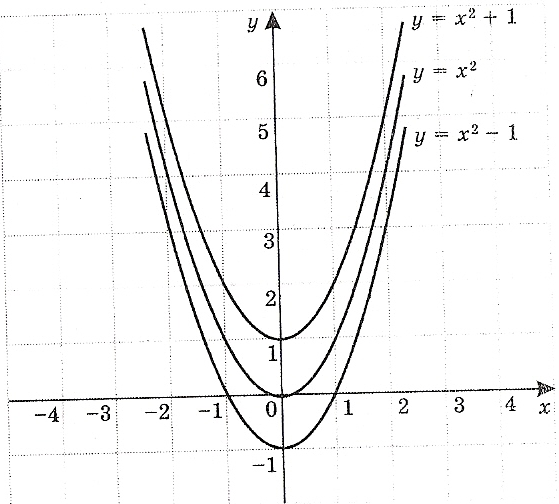
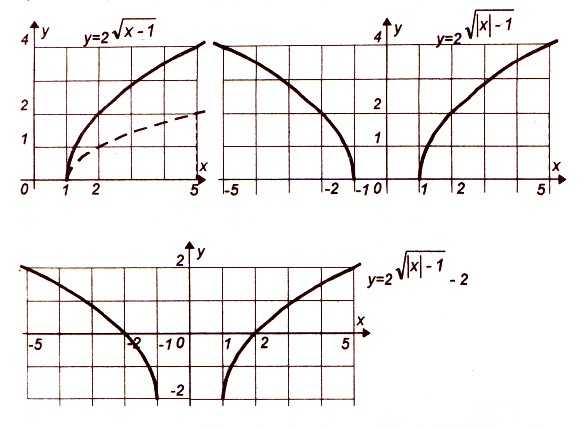
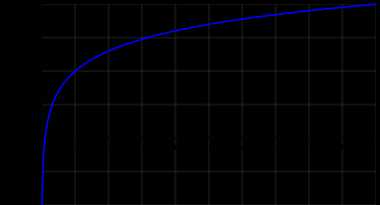 График десятичного логарифма
График десятичного логарифма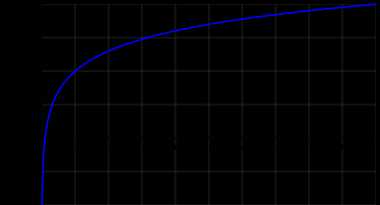 График десятичного логарифма
График десятичного логарифма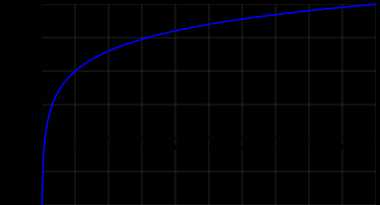 График десятичного логарифма
График десятичного логарифма
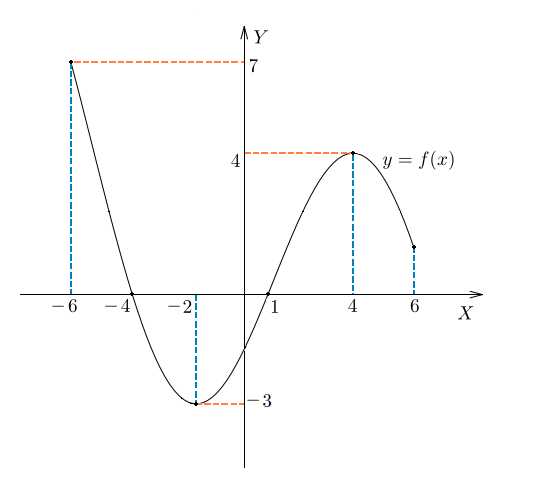
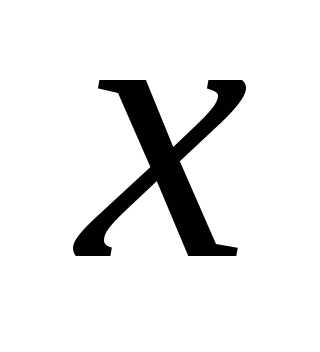 ,
при которых выражение
,
при которых выражение не теряет смысла и приобретает
действительные значения
не теряет смысла и приобретает
действительные значения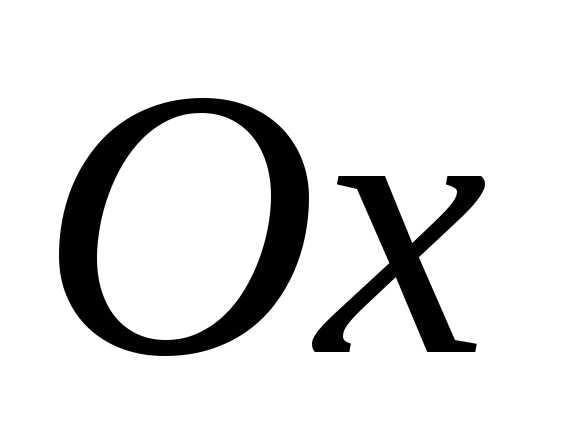 )
)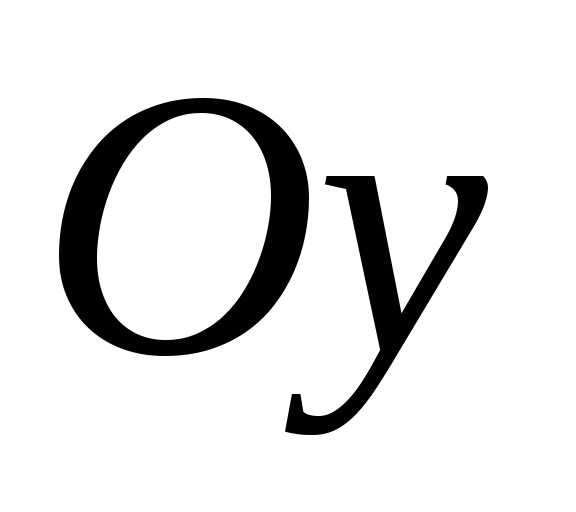 )
)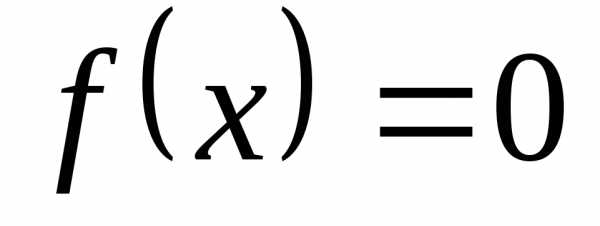
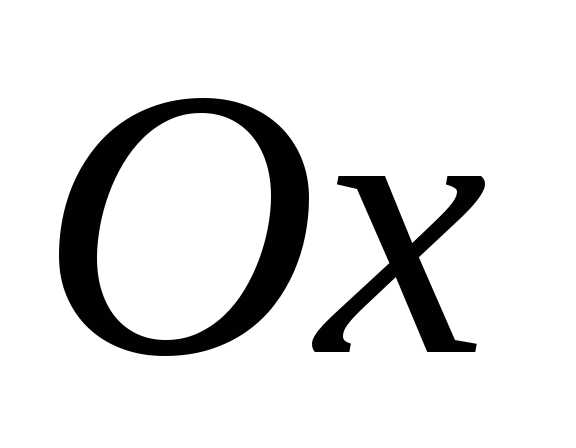 .
.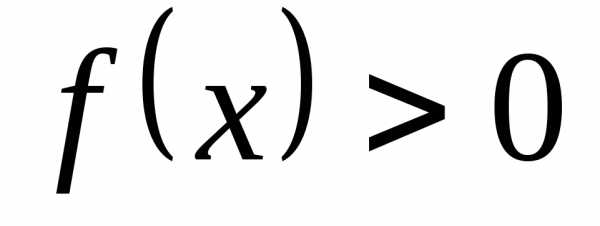 и
и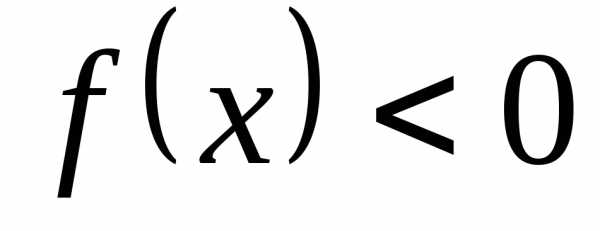
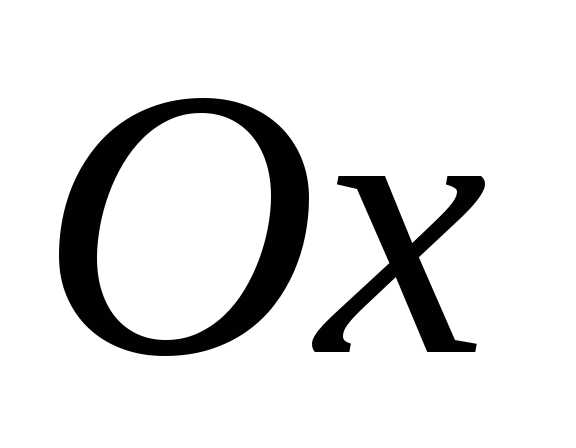 ,
которые соответствуют точкам графика
функции, расположенных выше(ниже) оси
,
которые соответствуют точкам графика
функции, расположенных выше(ниже) оси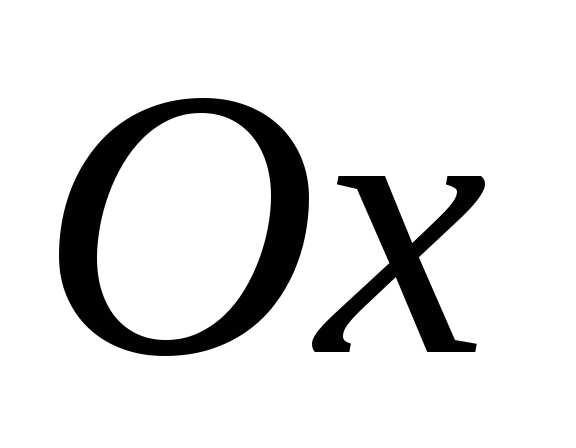
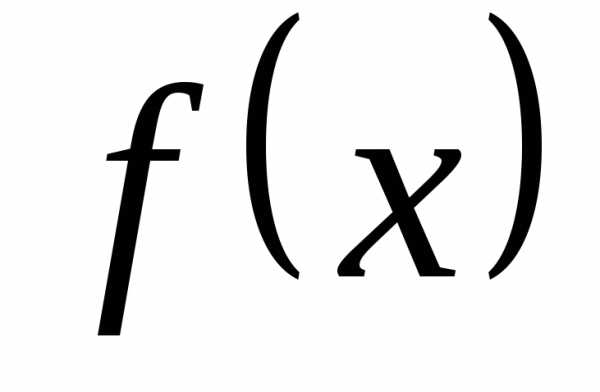 называется возрастающей на множестве
называется возрастающей на множестве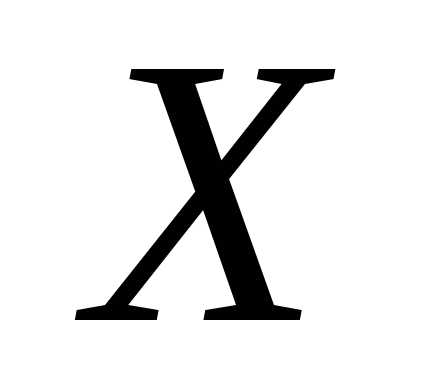 ,
если для любых точек
,
если для любых точек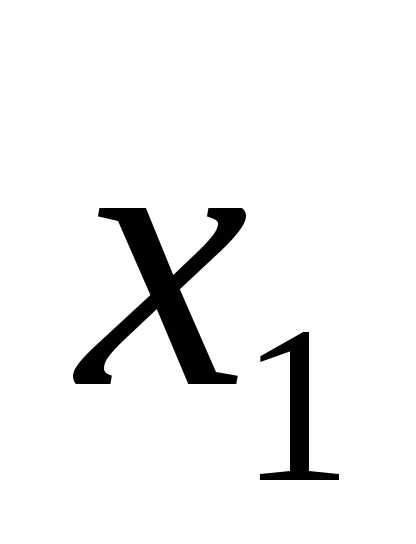 и
и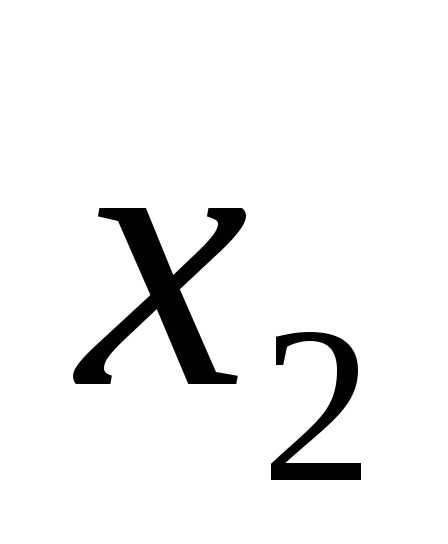 этого множества – таких, что
этого множества – таких, что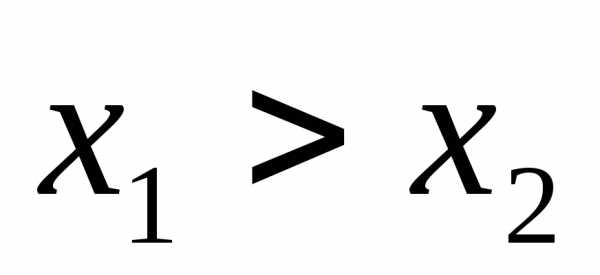 ,
-;
,
-;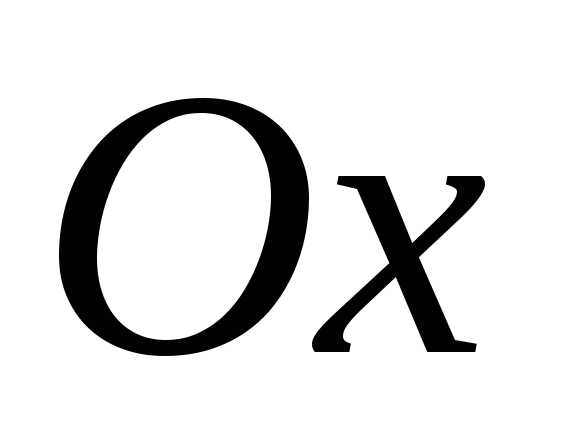 ,
где график «идет вверх» (вниз)
,
где график «идет вверх» (вниз)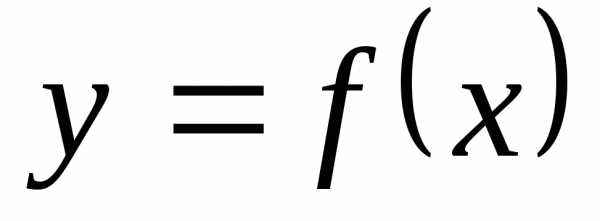 симметрична
относительно нуля и, то функция четная,
симметрична
относительно нуля и, то функция четная,

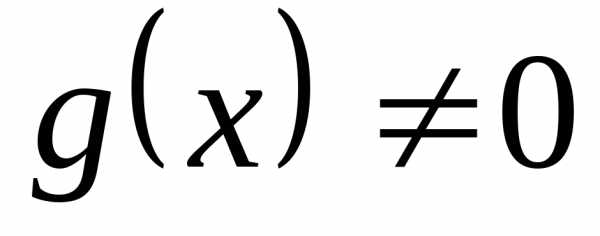
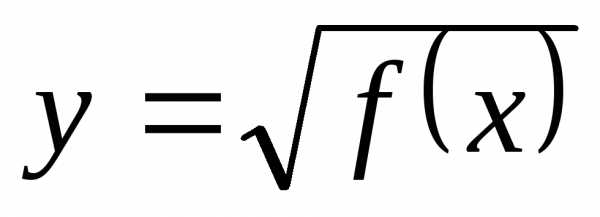
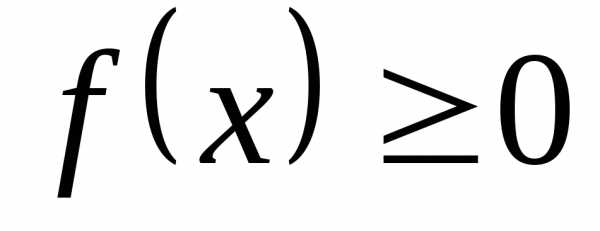
 , где первая
координата
, где первая
координата 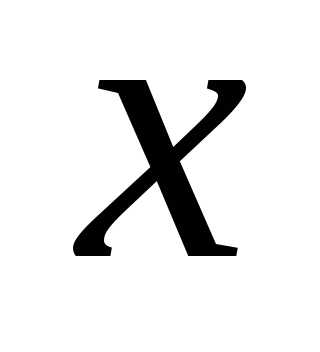 «пробегает» всю область определения
функцииf, а другая–
соответственное значение функции в
точке х.
«пробегает» всю область определения
функцииf, а другая–
соответственное значение функции в
точке х.
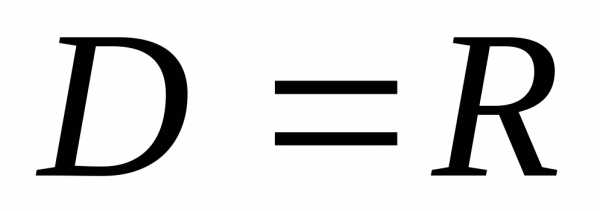 ,
, 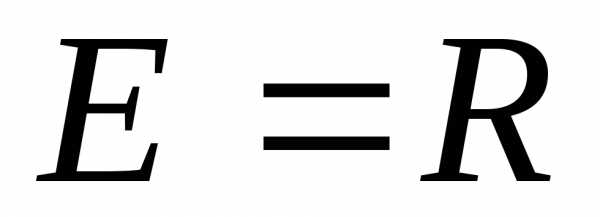
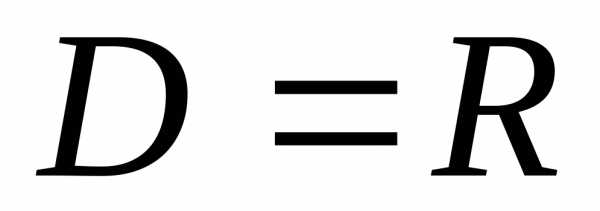
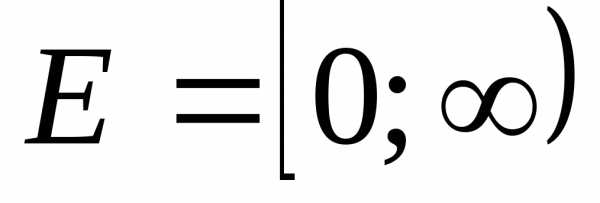


 ,
, 
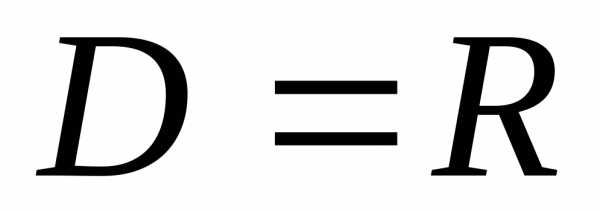 ,
, 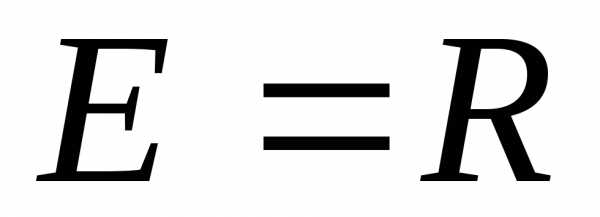
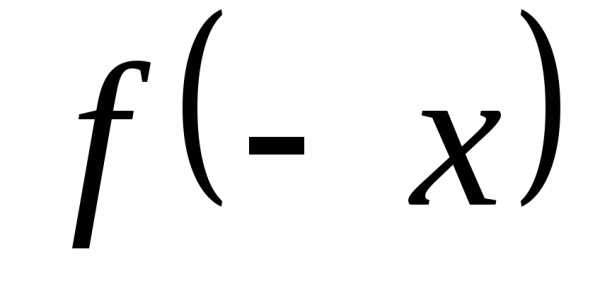 :
: — симметрична относительно нуля;
— симметрична относительно нуля;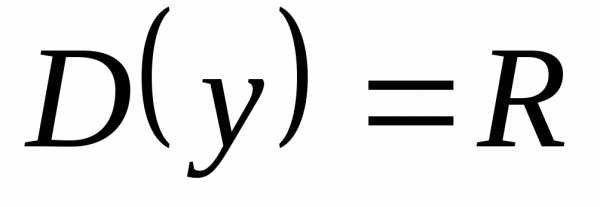 — симметрична относительно нуля;
— симметрична относительно нуля;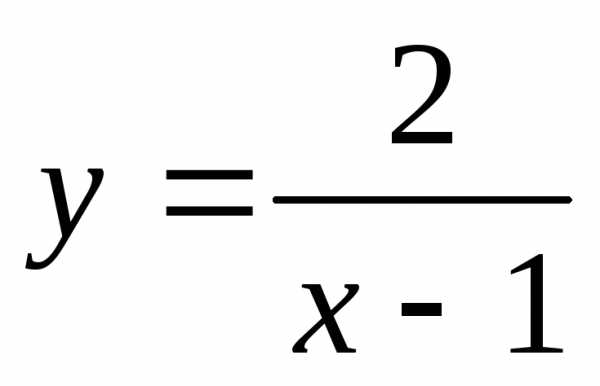 ина четность и нечетность.
ина четность и нечетность.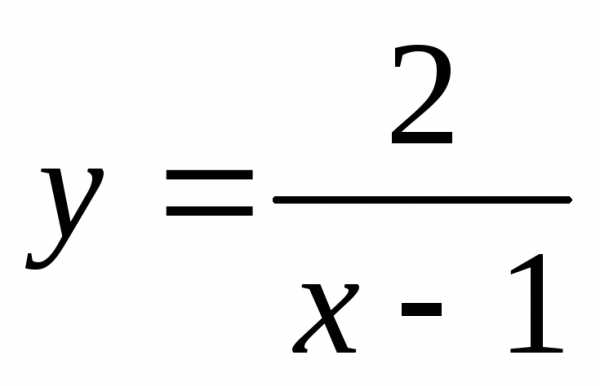 ,не симметрична относительно нуля, значит
функция ни четная, ни нечетная.
,не симметрична относительно нуля, значит
функция ни четная, ни нечетная.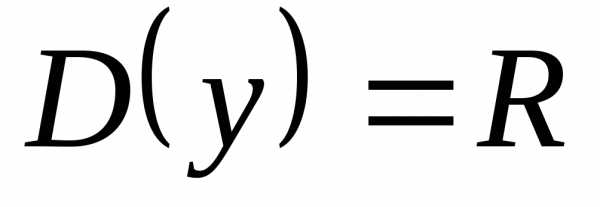 ,,,,
,,,,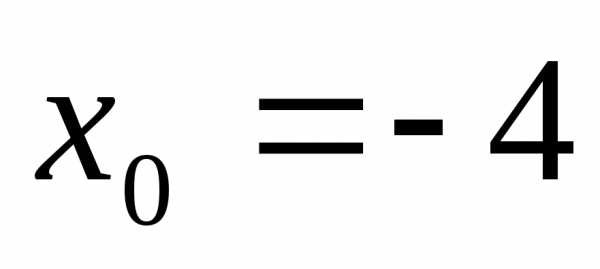 ;
2)
;
2)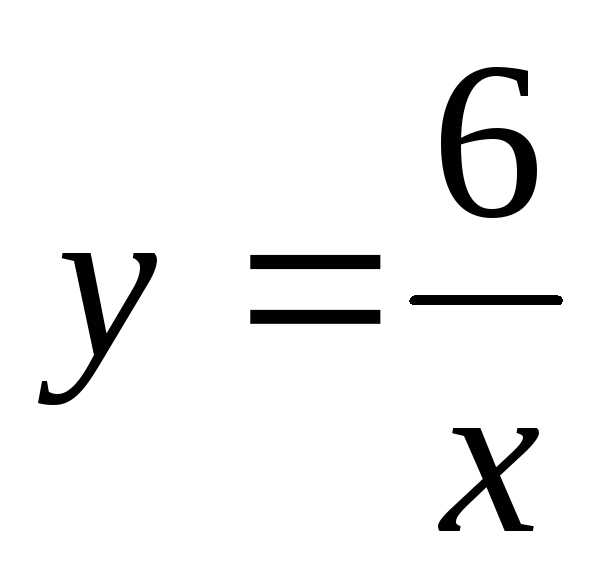 ,
, ;
3),
;
3),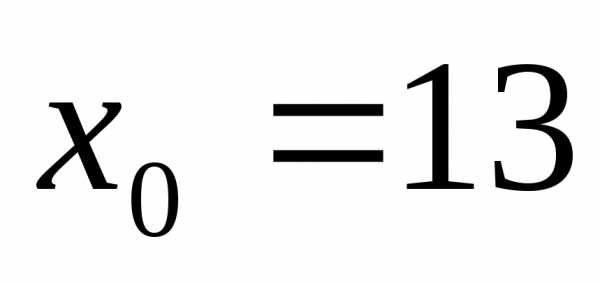 .
.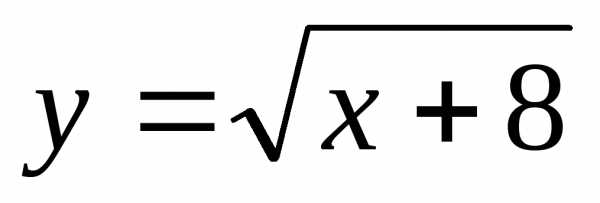 ;
2)
;
2)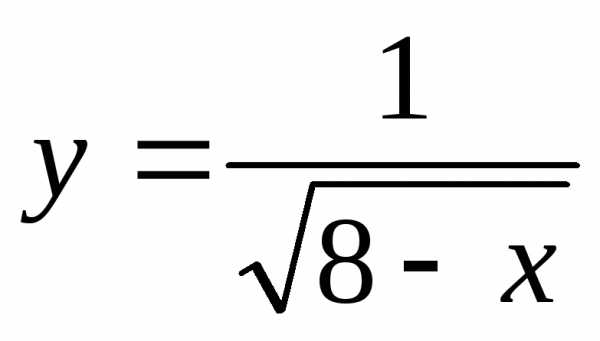 ;
3);
4)
;
3);
4)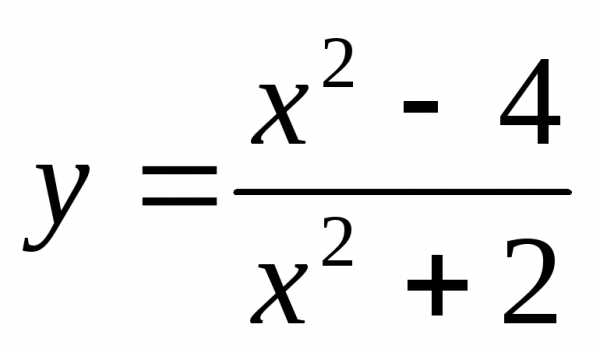 ;
5)
;
5)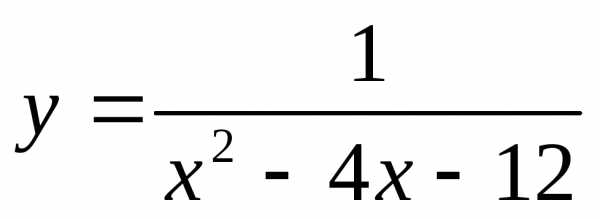 ;
;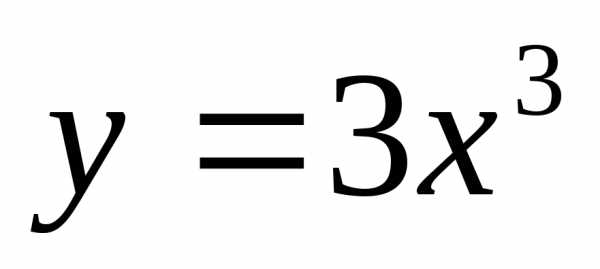 ;
;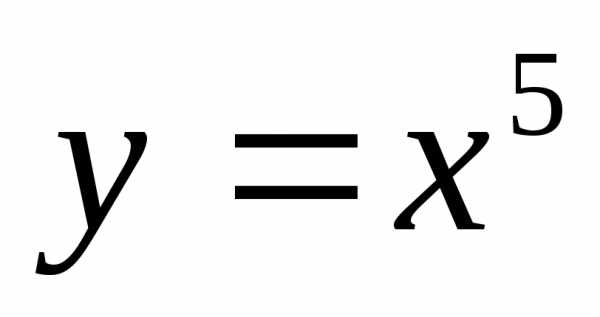 ;
2)
;
2)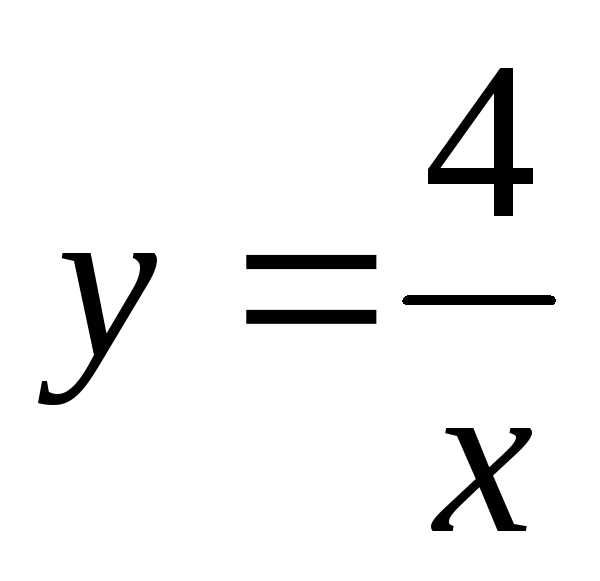 ;
3)
;
3)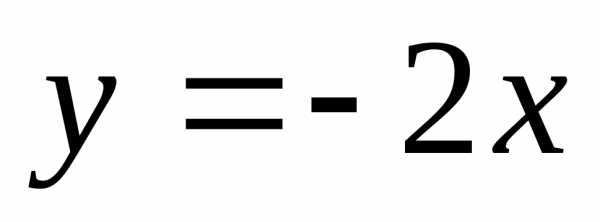 ;
4)
;
4)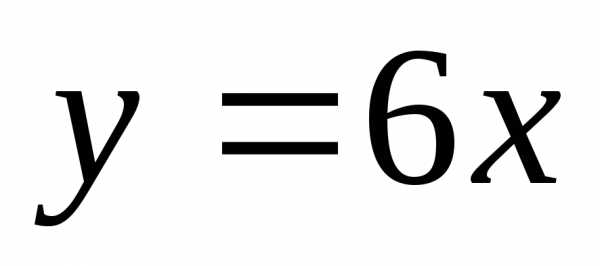 .
.
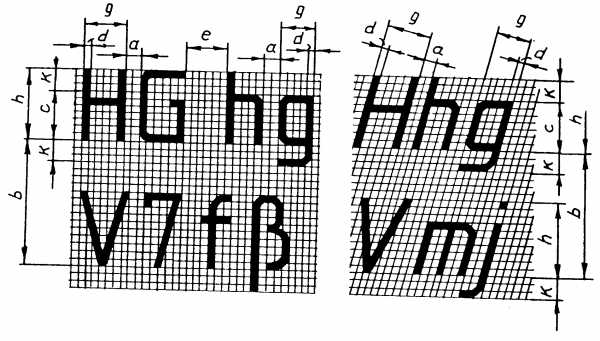 ис.
1.9. Вспомогательная сетка и параметры
шрифтов
ис.
1.9. Вспомогательная сетка и параметры
шрифтов ис.
1.10. Арабские и римские цифры
ис.
1.10. Арабские и римские цифры



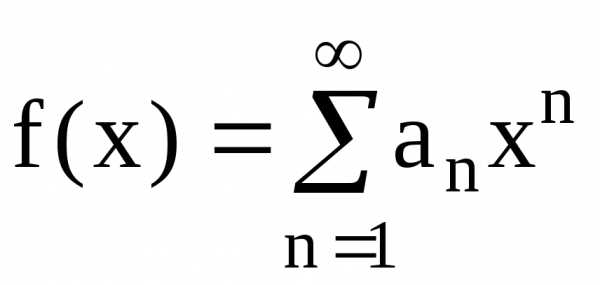 (1) и нужно вычислить ее приближенное
значение при некотором х, то достаточно
взять сумму нескольких ее первых членов
f(x)»Sn(x).
Сколько первых членов нужно взять, чтобы
обеспечить точность вычисления, на этот
вопрос дает ответ оценка остатка ряда
|rn(x)|.
(1) и нужно вычислить ее приближенное
значение при некотором х, то достаточно
взять сумму нескольких ее первых членов
f(x)»Sn(x).
Сколько первых членов нужно взять, чтобы
обеспечить точность вычисления, на этот
вопрос дает ответ оценка остатка ряда
|rn(x)|.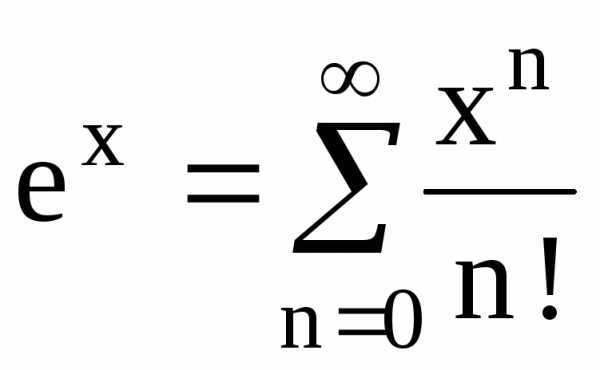 ,
то при x=1
имеем: Оценим |rn|.
,
то при x=1
имеем: Оценим |rn|.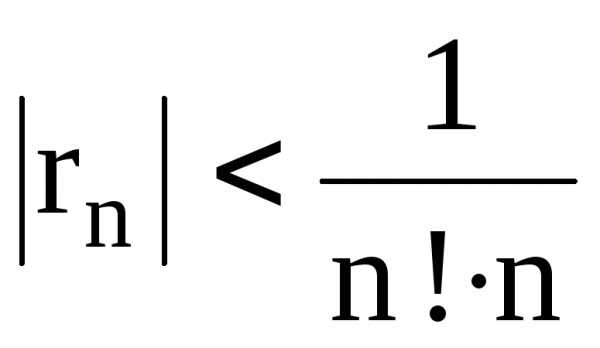 .
Должно быть
.
Должно быть 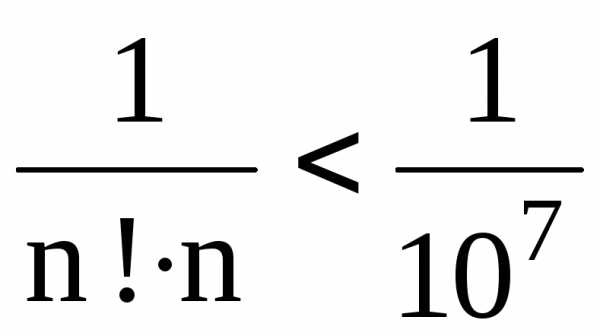 ;
видно, что при n=10 это уже есть. Поэтому
достаточно взять 11 первых членов:
;
видно, что при n=10 это уже есть. Поэтому
достаточно взять 11 первых членов: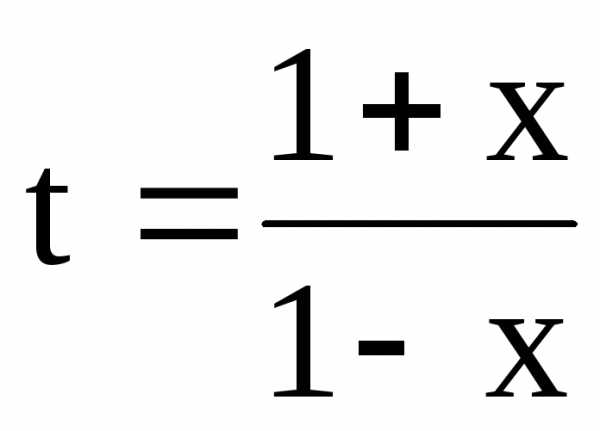 при хÎ(-1;1):
t-t×x=1+x,
при хÎ(-1;1):
t-t×x=1+x, 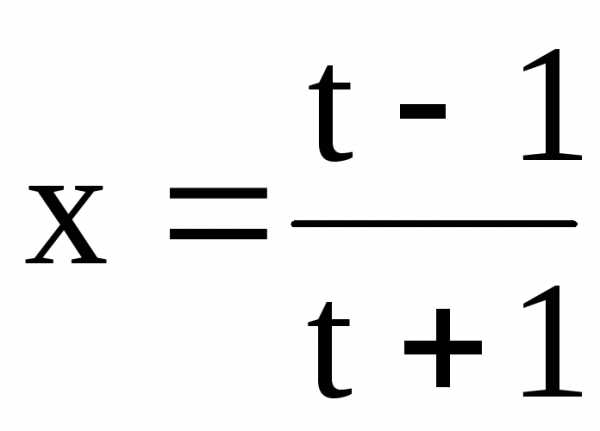 ,
потому можно вычислять:
,
потому можно вычислять: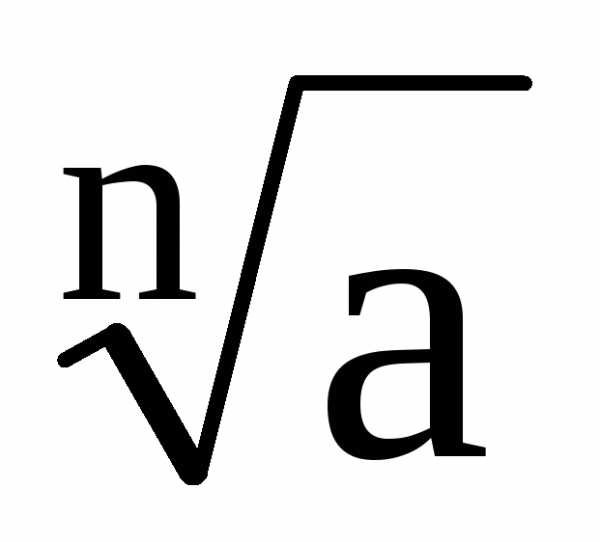 .
Допустим известно некоторое приближенное
значение этого корня
.
Допустим известно некоторое приближенное
значение этого корня 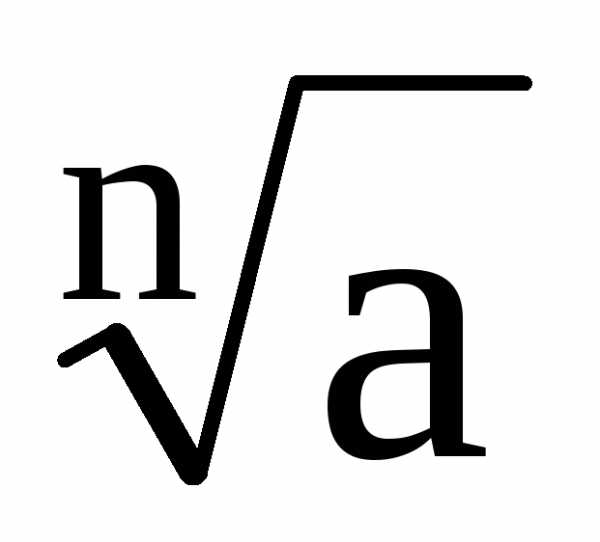 »b,
тогда a»bn,
»b,
тогда a»bn, 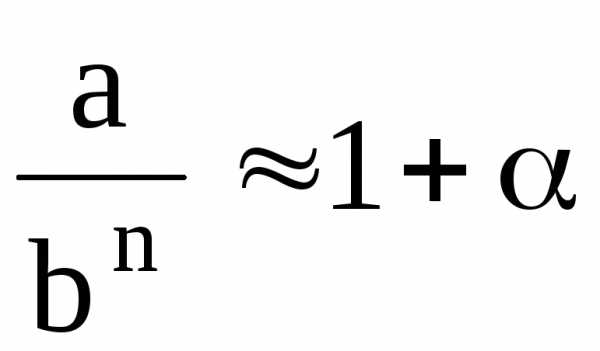 ,
где a-небольшая
величина: ½a½<1.
Тогда
,
где a-небольшая
величина: ½a½<1.
Тогда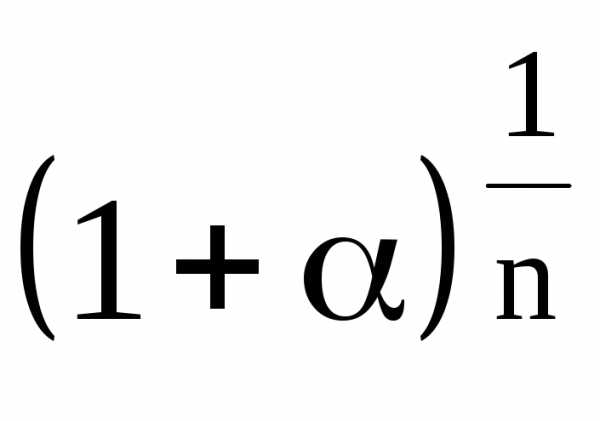 в биномиальный ряд, получим
в биномиальный ряд, получим 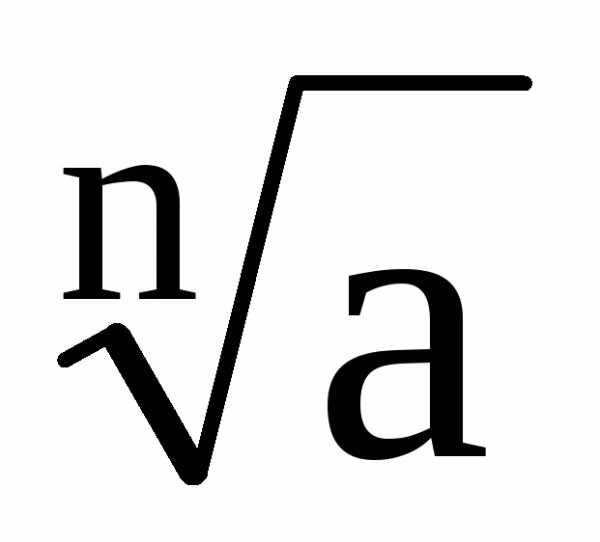 с любой точностью.
с любой точностью.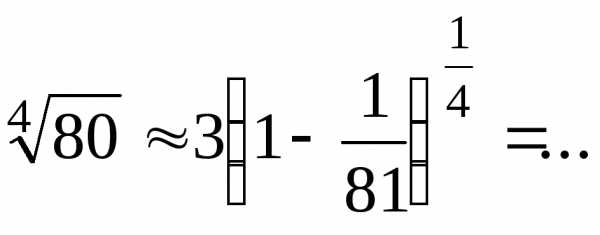
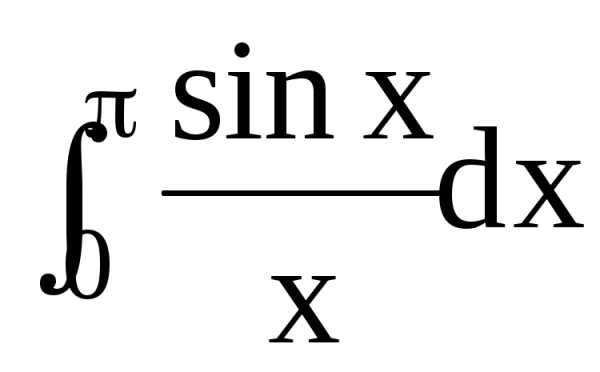 . Тогда
.
=
. Тогда
.
=