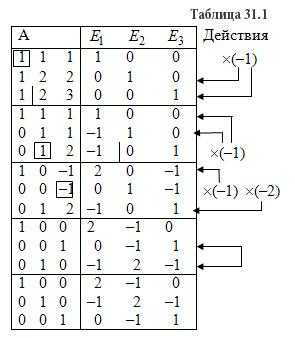
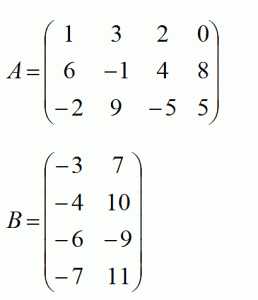Тесты по уголовному процессу с ответами
Тесты по Уголовному процессу (УПП, УП) с ответами
Правильный вариант ответа отмечен знаком +
1. Адвокат в уголовном процессе участвует в качестве:
+ защитника;
— специалиста;
— свидетеля.
2. Источниками уголовно-процессуального права являются:
+ оба ответа верные;
— Всеобщая декларация прав человека;
— Международный пакт о гражданских и политических правах.
3. Окончанием и специфическим признаком стадии уголовного процесса является:
+ вынесение уполномоченным лицом итогового процессуального решения;
— направление уголовного дела в следующую инстанцию;
— законодательное закрепление.
4. Уголовный процесс является:
+ поэтапной, основанной на законе деятельностью органов предварительного расследования, прокуратуры и суда по возбуждению, расследованию и рассмотрению уголовных дел;
— совокупностью стадий судебного производства по уголовным делам;
— процедурой возбуждения уголовных дел следователями и дознавателями и направления его в суд.
5. Источники уголовного процесса являются:
+ внешним закреплением уголовно-процессуальных норм;
— направлением действия уголовно-процессуальных норм;
— основными идеями, на которых базируется уголовный процесс.
6. Особенностью уголовного процесса является:
+ норма уголовного процесса касается не всех его субъектов, а только тех, к которым она относится;
— государство не обеспечивает исполнение уголовно-процессуальных норм силой своего принуждения;
— уголовно-процессуальные нормы устанавливаются самими субъектами уголовного процесса.
7. Специфическим принципом уголовного процесса является:
+ обеспечение права на защиту обвиняемому и подозреваемому;
— состязательности сторон;
— самостоятельность судей.
8. Принципы уголовного процесса:
+ действуют на всех его стадиях;
— действуют избирательно на отдельных субъектов;
— носят рекомендательный характер для правоприменителей.
9. Мерой пресечения в уголовном процессе является:
+ подписка о невыезде и надлежащем поведении;
— привод;
— обязательство о явке.
тест 10. Классификация доказательств в уголовном процессе по предмету доказывания:
+ прямые и косвенные;
— первоначальные и производные;
— вещественные доказательства и документы;
11. Участником уголовного процесса со стороны защиты является:
+ Гражданский ответчик;
— Гражданский истец;
— Потерпевший.
12. Преюдиция в уголовном процессе:
+ это уже установленные вступившим в силу приговором обстоятельства, которые по текущему делу признаются без дополнительной проверки;
— автоматически определяет виновность лиц, ранее не участвовавших в деле;
— применяется по усмотрению суда.
13. Особый порядок судебного разбирательства в уголовном процессе:
+ не требует исследования доказательств;
— применяется по ходатайству обвиняемого в любом случае;
— не требует согласия потерпевшего.
14. Вещественные доказательства в уголовном процессе:
+ признаются таковыми соответствующим постановлением после их осмотра;
— всегда хранятся при уголовном деле;
— не могут храниться в материалах уголовного дела.
15. Предварительное слушание в уголовном процессе:
+ проводится, если имеются основания для выделения уголовного дела;
— не может быть назначено судьей по своей инициативе;
— заканчивается в виде решения судьи, выраженного в соответствующем акте.
16. Доказывание в уголовном процессе:
+ включает сбор, оценку и проверку доказательств;
— осуществляется только органами предварительного расследования;
— происходит исключительно на стадии рассмотрения дела судом.
17. Доказательством в уголовном процессе не является:
+ предмет, обнаруженный на месте происшествия, но не осмотренный в установленном законом порядке;
— протокол проверки показаний на месте, проведенной без участия понятых;
— показания свидетеля с указанием источника осведомленности.
18. Свойство доказательств в уголовном процессе, которое заключается в законности источника их происхождения, называется:
+ допустимостью;
— достаточностью;
— относимостью.
19. Недопустимые доказательства в уголовном процессе:
+ не ложатся в основу обвинения;
— обладают юридической силой ниже, чем полученные в соответствие с законом;
— могут использоваться как косвенные доказательства.
тест_20. Предмет доказывания в уголовном процессе:
+ включает обстоятельства и условия, которые способствовали совершению преступления;
— ограничен обстоятельствами, образующими состав преступления;
— не распространяется на обстоятельства, которые способны привести к освобождению от наказания.
21. Основными субъектами доказывания в уголовном процессе являются:
+ следователь, дознаватель, прокурор, судья;
— подозреваемый, обвиняемый, защитник;
— эксперт, специалист, свидетель.
22. Процессуальные сроки в уголовном процессе:
+ восстанавливаются, если были пропущены по уважительной причине;
— могут исчисляться только сутками и месяцами;
— продлеваются по усмотрению следователя или суда.
23. Право на реабилитацию в уголовном процессе:
+ возникает при вынесении оправдательного приговора;
— не включает восстановление пенсионных прав;
— не гарантируется на уровне федерального законодательства.
24. Показания свидетеля как источник доказательств в уголовном процессе:
+ не могут быть получены до возбуждения уголовного дела;
— фиксируются протоколом допроса свидетеля;
— могут содержать сведения о личности подозреваемого или обвиняемого.
25. Мера процессуального принуждения в уголовном процессе, которая заключается в принудительном доставлении лица в органы предварительного расследования или в суд, называется:
+ приводом;
— обязательством о явке;
— задержанием.
26. Оценка доказательств в уголовном процессе:
+ подразумевает их анализ и установление значимости;
— производится любым субъектом доказывания;
— предшествует их проверке.
27. Гражданский истец в уголовном процессе:
+ выступает на стороне обвинения;
— не может быть юридическим лицом;
— вправе требовать лишь компенсации имущественного вреда.
28. Потерпевший в уголовном процессе:
+ признается таковым сразу после возбуждения уголовного дела;
— должен быть допрошен в течение 3-х суток после возбуждения уголовного дела;
— не может участвовать в прениях в суде.
29. Пределы доказывания в уголовном процессе – это:
+ те границы, за которыми осуществлять доказывание бессмысленно и нерационально;
— категория, определяющая полноту собранных доказательств;
— требования осуществления доказательственного процесса надлежащим субъектом.
тест-30. Субъектом уголовного процесса, содействующим расследованию, является:
+ переводчик;
— прокурор;
— судья.
31. Прокурор в уголовном процессе не вправе:
+ давать письменные указания следователю о направлении хода расследования;
— по мотивированному запросу знакомиться с уголовным делом до направления его для утверждения обвинительного заключения или акта;
— изымать уголовное дело у дознавателя для передачи в производство следователю.
32. Понятие доказательств в уголовном процессе:
+ Это любые сведения, которыми следователь, дознаватель, прокурор или судья определяет наличие и отсутствие обстоятельств, подлежащих доказыванию или имеющих значение для уголовного дела;
— Это любые сведения, данные подозреваемым, обвиняемым, потерпевшим или свидетелем в ходе допроса по уголовному делу и зафиксированные протоколом;
— Это любые предметы и документы, которые несут на себе следы преступления или имеют значение для установления истины по делу.
33. Собирание доказательств в уголовном процессе не может осуществлять:
+ переводчик;
— защитник;
— судья.
34. Свидетель в уголовном процессе:
+ вправе приносить жалобы на действия начальника органа дознания;
— всегда является очевидцем преступления;
— не может подвергаться приводу.
35. Защитник в уголовном процессе участвует в обязательном порядке, если:
+ подозреваемый – несовершеннолетний;
— преступление связано с незаконным оборотом наркотиков;
— так решил в своем постановлении следователь, дознаватель или судья.
36. Обвиняемый в уголовном процессе на стадии рассмотрения дела в суде именуется:
+ подсудимым;
— подследственным;
— осужденным.
37. Специалист в уголовном процессе может привлекаться для:
+ оба ответа верные;
— правильного изъятия определенных предметов;
— формулировки вопросов для судебной экспертизы.
38. На какой срок может быть задержан подозреваемый в уголовном процессе в порядке ст. 91 УПК РФ?
+ 48 часов;
— 24 часа;
— 10 суток.
39. Следственным действием в уголовном процессе не является:
+ отобрание подписки о невыезде и надлежащем поведении;
— выемка;
— очная ставка.
тест№ 40. Функция уголовного процесса, заключающаяся в полном либо частичном опровержении вины подследственного – это функция:
+ защиты;
— надзора;
— правосудия.
41. Судья в случае признания лица гражданским ответчиком в уголовном процессе выносит:
+ определение;
— постановление;
— приказ.
42. Куда подаются жалобы и представления в надзорном производстве в уголовном процессе?
+ В Верховный Суда РФ;
— В Конституционный Суд РФ;
— В Генпрокуратуру РФ.
43. В кассационном производстве в уголовном процессе производится:
+ пересмотр судебных решений, которые уже вступили в законную силу;
— обжалование судебных решений, не вступивших в законную силу;
— пересмотр судебных решений, если открылись новые обстоятельства.
44. Нравственные начала в уголовном процессе выражены в:
+ принципе уважения чести и достоинства личности;
— принципе законности;
— принципе свободы оценки доказательств.
45. Гражданский иск в уголовном процессе:
+ является требованием возместить имущественный вред, который причинен преступлением;
— сопряжен с уплатой госпошлины гражданским истцом;
— в защиту прав несовершеннолетнего подается только его законным представителем.
46. В порядке апелляции в уголовном процессе пересматриваются:
+ решения суда первой инстанции, которые в законную силу еще не вступили;
— решения суда второй инстанции, вступившие в законную силу;
— законность и достаточность доказательственной базы по уголовному делу, собранная на этапе предварительного расследования.
47. Ходатайство в уголовном процессе должно быть рассмотрено в течение:
+ незамедлительно после его подачи, если невозможно – в течение 3 суток;
— 5 суток;
— 10 суток.
48. Тип уголовного процесса, характерный для раннефеодального государства:
+ обвинительный;
— инквизиционный;
— состязательный.
49. Для какой формы уголовного процесса характерно равноправие сторон?
+ Состязательного;
— Розыскного;
— Обвинительного.
тест*50. Эксперт в уголовном процессе имеет право:
+ знакомиться с теми материалами уголовного дела, которые имеют значение для результатов экспертизы;
— собирать материалы для экспертизы самостоятельно;
— уклоняться от посещения судебного заседания, если его вызывают.
51. Какие стороны в уголовном процессе являются основными?
+ Обвинения и защиты;
— Истец и ответчик;
— Диспозиция и санкция.
52. Система принципов уголовного процесса обусловлена их:
+ взаимосвязью и взаимодействием;
— закреплением в законодательстве;
— обязательностью для всех субъектов.
53. Установление истины в уголовном процессе является:
+ целью доказывания;
— методом доказывания;
— принципом доказывания.
54. Следователь в уголовном процессе имеет право:
+ по своему усмотрению организовывать предварительное следствие и направлять ход расследования;
— самостоятельно передавать уголовные дела по подследственности;
— не уведомлять прокурора о задержании подозреваемого в порядке ст. 91 УПК РФ.
55. Подсудность гражданского иска в уголовном процессе определяется в соответствие с:
+ подсудностью самого уголовного дела;
— требованиями норм ГК РФ;
— принципом разумных сроков расследования и территориальным удобством рассмотрения дела.
56. Назначение судебной экспертизы в уголовном процессе:
+ может производиться на стадии доследственной проверки;
— возможно лишь в рамках возбужденного уголовного дела;
— производится исключительно при уведомлении заинтересованных лиц.
57. Значение доказательств в уголовном процессе:
+ они призваны установить истину по уголовному делу и лечь в основу обвинения;
— они позволяют установить обстоятельства, смягчающие и отягчающие наказание;
— они являются главным показателем следственной работы.
58. Система уголовного процесса является:
+ упорядоченной совокупностью его стадий;
— комплексом уголовно-процессуальных норм;
— набором прав и обязанностей каждого из его субъектов.
59. Проведение особого порядка судебного разбирательства в уголовном процессе возможно по уголовным делам о преступлениях, максимальное наказание за которые составляет:
+ не более 10 лет лишения свободы;
— не более 12 лет лишения свободы;
— не более 7 лет лишения свободы.
тест) 60. Цель уголовного процесса состоит в:
+ оба ответа верные;
— защите прав лиц, потерпевших от преступления;
— защите лица от незаконного и необоснованного привлечения к уголовной ответственности.
61. Кому для ознакомления не может быть передано заключение эксперта в уголовном процессе?
+ специалисту;
— представителю потерпевшего;
— свидетелю.
62. Суд в уголовном процессе полномочен:
+ прекратить уголовное дело;
— возбудить уголовное дело;
— избирать меру пресечения в виде подписки о невыезде и надлежащем поведении на стадии предварительного расследования.
63. Состязательность в уголовном процессе предусматривает, что:
+ стороны перед судом равны;
— суд выступает на стороне обвинения;
— функцию и обвинения, и защиты может выполнять одно и то же лицо либо орган.
64. В течение какого времени после провозглашения вручаются копии приговора в уголовном процессе?
+ 5 суток;
— 3 суток;
— незамедлительно.
65. Судебной стадией уголовного процесса не является:
+ допрос подозреваемого;
— апелляция;
— судебное следствие.
66. Протокол допроса в уголовном процессе подписывается допрашиваемым:
+ на каждой странице;
— на последней странице;
— только в местах показаний.
67. Прения в уголовном процессе включают:
+ речь защитника и государственного обвинителя;
— исследование доказательств;
— предоставление последнего слова подсудимому.
68. Какой метод не характерен для науки уголовного процесса?
+ Поощрения;
— Исторического анализа;
— Формально-юридический.
69. Кто первым допрашивает подсудимого в уголовном процессе?
+ Защитник;
— Прокурор;
— Судья.
70_тест. Максимальный срок проведения одной стационарной судебно-психиатрической экспертиза в уголовном процессе составляет с учетом всех продлений:
+ 90 дней;
— 60 дней;
— 30 дней.
71. Как соотносятся в уголовно-правовом значении понятия уголовного процесса и уголовного судопроизводства?
+ Они тождественны;
— Понятие уголовного процесса шире, чем уголовного судопроизводства;
— Понятие уголовного судопроизводства охватывает понятие уголовного процесса.
72. Что не является досудебной стадией уголовного процесса?
+ Предварительное слушание;
— Предварительное следствие;
— Дознание в сокращенной форме.
73. Уголовное право и процесс:
+ являются самостоятельными отраслями российского права;
— оба относятся к материальному праву;
— являются двумя составляющими одной отрасли.
74. Представитель в уголовном процессе:
+ наделяется теми же правами, что и представляемое им лицо;
— может являться только адвокатом;
— исключает участие в процессе представляемого им лица.
75. Формой предварительного расследование в уголовном процессе не является:
+ проверка по сообщениям о преступлении;
— предварительное следствие;
— дознание.
76. Специфическим признаком уголовного процесса является:
+ его обусловленность совершенным преступлением;
— его осуществление специально уполномоченными органами и должностными лицами;
— его осуществление в строгой законодательной регламентации.
77. Сокращенная форма дознания в уголовном процессе осуществляет в срок до:
+ 15 суток;
— 10 суток;
— 7 суток.
78. Жалоба в уголовном процессе рассматривается прокурором в течение:
+ 3 суток;
— 5 суток;
— 7 суток.
79. Презумпция в уголовном процессе, означающая предположение о том, что всякий гражданин знаком с действующим законодательством, — это:
+ презумпция знания уголовного закона;
— презумпция невиновности;
— презумпция отсутствия общественной опасности лица, если сроки давности по совершенному им преступления истекли.
80*тест. Понятие принципов уголовного процесса:
+ Это основные идеи, на которых строится деятельность участников уголовного процесса на всех его стадиях;
— Это средства, с помощью которых уполномоченные органы и должностные лица выполняют свои уголовно-процессуальные обязанности;
— Это идеальный результат деятельности субъектов уголовного процесса, основанный на выполнении требований закона.
81. При каком формальном условии показания в уголовном процессе признаются доказательством?
+ При их фиксации в соответствующем протоколе;
— При их фиксации с помощью технических средств;
— При их получении исключительно следователем или дознавателем.
82. Обвинение в уголовном процессе предъявляется:
+ после вынесения постановления о привлечении в качестве обвиняемого в течение 3 суток;
— в день вынесения постановления о привлечении в качестве обвиняемого;
— без предварительного извещения обвиняемого.
83. Сколько раз в год лицо вправе принимать участие в качестве присяжного заседателя в уголовном процессе?
+ 1 раз;
— 3 раза;
— Законом это не определено.
84. Судебное заседание в уголовном процессе назначается с предварительным извещением сторон о его дате и месте проведения не менее, чем за:
+ 5 суток;
— 10 суток;
— 14 суток.
85. По общему правилу максимальный срок предварительного следствия в уголовном процессе составляет:
+ 2 месяца;
— 6 месяцев;
— 1 месяц.
86. Гарантии уголовного процесса – это:
+ средства, которыми обеспечиваются права участников уголовного судопроизводства;
— условия, при которых уголовный процесс выполняет свои задачи;
— основные черты, которые отличают уголовный процесс от иных видов деятельности.
87. Предмет уголовно-процессуального права составляют:
+ уголовно-процессуальные отношения, возникающие между их субъектами;
— уголовные дела и материалы доследственной проверки сообщений о преступлениях;
— права и обязанности участников уголовного процесса.
88. Понятие уголовно-процессуального права как отрасли права:
+ Это определенная система норм, регулирующих общественные отношения между участниками уголовного процесса на различных его стадиях;
— Это совокупность взглядов и идей на уголовно-процессуальные отношения, их проблемы и правоприменительную деятельность в этой области;
— Это деятельность органов следствия, дознания, прокуратуры и суда по возбуждению, расследованию и рассмотрению уголовных дел.
89. Возбуждение дел частного обвинения не иначе как по заявлению потерпевшего – реализация метода уголовно-процессуального права:
+ диспозитивного;
— императивного;
— сравнительного.
тест» 90. Конституция РФ как источник уголовно-процессуального права:
+ содержит основные принципы уголовного процесса;
— не может противоречить УПК РФ;
— перечисляет содержание правового статуса каждой из сторон уголовного процесса.
91. Основным источником уголовно-процессуального права является:
+ Уголовно-процессуальный кодекс РФ;
— Уголовный кодекс РФ;
— Уголовно-исполнительный кодекс РФ.
92. Институты уголовно-процессуального права – это совокупность норм, регулирующих:
+ однородные общественные отношения;
— общественные отношения, складывающиеся между конкретными субъектами уголовного процесса;
— весь комплекс общественных отношений, возникающих на конкретной стадии уголовного процесса.
93. К международным источникам уголовно-процессуального права не относится:
+ уголовно-процессуальное законодательство других стран;
— общепринятые принципы международного права;
— международные договоры и соглашения.
94. Санкции в уголовно-процессуальном праве, которые указывают на несколько видов мер, применяемых к участнику уголовного процесса, не исполняющему своих обязанностей, называется:
+ альтернативной;
— абсолютно определенной;
— относительно определенной.
95. Основные понятия уголовно-процессуального права:
+ предварительное следствие, сообщение о преступлении, обвиняемый;
— адвокат, состязательность сторон, апелляционное производство;
— законность, права и свободы гражданина, прокуратура.
96. Объект уголовно-процессуального права как науки составляют:
+ уголовно-процессуальные нормы;
— уголовно-процессуальные гарантии;
— уголовно-процессуальные отношения.
testua.ru
тесты по процессу с ОТВЕТАМИ
по
уголовному процессу для компьютерного
экзамена (3-й курс очное обучение)
I:1
S:
Уголовный процесс является:
-:
Материальным правом
-:
Прикладным правом
+:
Процессуальным правом
-:
Нематериальным правом
I:2
S:Источниками
уголовно-процессуального права является
-:
УК РФ
-:
Указы и распоряжения Президента
-:
Постановления и распоряжения Глав
субъекта РФ
+:
УПК РФ
I:3
S:В
каком законодательном акте закреплены
основополагающие принципы и положения
судоустройства и судопроизводства в
РФ
-:
УПК РФ
-:
УК РФ
+:
Конституция РФ
-:
ГПК РФ
I:4
S:Действие
УПК РФ касается
-:
Только пространства
-:
Только времени
-:
Только лиц
+:Только
пространства, времени и лиц
I:5
S:Уголовное
судопроизводство имеет своим назначением
-:
Защиту интересов государства
-:
Защиту интересов участников уголовного
процесса
-:
Защиту интересов суда
+:
Защиту прав и законных интересов лиц
и организаций, потерпевших от преступлений
I:6
S:Уголовное
судопроизводство осуществляется в
-:
Одномесячный срок
-:
Трехмесячный срок
-:
Семимесячный срок
+:
Разумный срок
I:7
S:Для
уголовного судопроизводства наиболее
важно
-:
Уголовное преследование и назначение
виновным справедливого показания
-:
Отказ от уголовного преследования
невиновных, освобождение их от наказания
-:
Реабилитация каждого, кто необоснованно
подвергся уголовному преследованию
+:
И первое, и второе, и третье отвечает
назначению уголовного судопроизводства
I:8
S:Уголовное
преследование осуществляется
+:
Следователем, дознавателем, прокурором
-:
Судом;
-:
Органами полиции
-:
Органами внутренних дел
I:9
S:Уголовный
процесс состоит из стадий
-:
Двух
-:
Трех
-:
Пяти
+:
Девяти
I:10
S:Стадия
уголовного процесса завершается
-:
Окончанием дознания
-:
Началом предварительного следствия
-:
Постановлением приговора
+:
Принятием итогового процессуального
решения
I:11
S:В
качестве стадии уголовного процесса
выступает
-:
Первичная проверка материалов
+:
Предварительное расследование
-:
Предъявление обвинения
-:
Ознакомление обвиняемого с материалом
уголовного дела
I:12
S:Уголовный
процесс начинается со стадии
-:
Получения сообщения о преступлении
-:
Рассмотрение заявления о преступлении
+:
Возбуждения уголовного дела
-:
Принятия уголовного дела к производству
I:13
S:На
какой стадии уголовного процесса
решается вопрос о назначении судебного
заседания
-:
На стадии возбуждения уголовного дела
-:
На стадии предварительного расследования
+:
На стадии подготовки к судебному
заседанию
-:
На стадии судебного разбирательства
I:14
S:Уголовный
процесс Росси является
-:
Обвинительным
-:
Состязательным
-:
Судебно-следственным
+:
Смешанным
I:15
S:Принципы
уголовного процесса отличаются от
общих условий производства в отдельных
стадиях
-:
Принадлежностью к правовым нормам
-:
Тем, что закреплены в законе
+:
Действием на всех или нескольких стадиях
уголовного процесса
-:
Декларативным характером
I:16
S:В
соответствии с принципом законности
-:
Никакие доказательства не имеют заранее
установленной силы
-:
Правосудие по уголовному делу в РФ
осуществляется только судом
-:
Обвинительный приговор не может быть
основан на предположениях
+:
Нарушение следователем норм УПК влечет
за собой признание недопустимыми
полученных таким путем доказательств
I:17
S:В
соответствии с принципом осуществления
правосудия только судом
+:
Никто не может быть признан виновным
в совершении преступления и подвергнут
уголовному наказанию не иначе как по
приговору суда
-:
Никто не может быть задержан по подозрению
в совершении преступления или взят
под стражу при отсутствии законных
оснований
-:
Никто не может быть подвергнут пыткам
-:
Суд создает необходимые условия для
исполнения сторонами их процессуальных
обязанностей и осуществления
предоставленных им прав
I:18
S:В
чем проявляется принцип осуществления
правосудия только судом
-:
В обязанности суда возбудить уголовное
дело при обнаружении признаков
преступления
-:
В обязанности суда прекратить уголовное
дело при отказе прокурора от обвинения
-:
В признании лица невиновным при
прекращении уголовного дела по
реабилитирующему основанию
+:
В признании лица виновным только по
приговору суда
I:19
S:Принцип
уважения чести и достоинства личности
запрещает
-:
Производство личного обыска подозреваемого
+:
Осуществление действий, унижающих
честь участника уголовного судопроизводства
-:
Контроль и запись телефонных переговоров
без судебного решения
-:
Наложение ареста на имущество обвиняемого
I:20
S:Принцип
неприкосновенности личности
предусматривает, что
+:
Содержание под стражей до судебного
решения допускается на срок не более
48 часов
-:
Арест, заключение под стражу и содержание
под стражей допускается только в
отношении особо опасных преступников
-:
В отношении несовершеннолетних не
может быть избрана мера пресечения,
связанная с лишением свободы
-:
Лица женского пола не могут быть
подвергнуты личному обыску
I:21
S:
В соответствии с принципом охраны прав
и свобод человека и гражданина в
уголовном судопроизводстве
-:
Дознаватель, следователь, прокурор и
суд обязаны предупредить всех
допрашиваемых свидетелей, что их
показания могут использоваться в
качестве доказательств в ходе дальнейшего
производства по уголовному делу
-:
Действия и решения должностных лиц,
ущемляющие права участников
судопроизводства, могут быть обжалованы
в порядке, установленном УПК
+:
Участникам уголовного судопроизводства
должны быть разъяснены их права и
обеспечена возможность осуществления
этих прав
-:
Допрашиваемые лица должны быть
предупреждены об уголовной ответственности
за дачу ложных показаний
I:22
S:
Из презумпции невиновности следует
-:
Обязанность доказывания возлагается
на обвиняемого
+:
Недоказанная виновность означает
доказанную невиновность
-:
Обвиняемый по делам частного обвинения
обязан доказать свою невиновность
-:
Обвиняемый, содержащийся под стражей,
не может избирать и быть избранным в
представительные органы государственной
власти
I:23
S:В
каком случае обязанность доказывания
невиновности может быть возложена на
обвиняемого
-:
По делам частного обвинения
-:
Если сам обвиняемый ходатайствует об
этом
-:
Если обвиняемый имеет защитника
+:
На обвиняемого не может быть возложена
эта обязанность
I:24
S:Презумпция
невиновности означает, что
-:
Неустранимые сомнения в невиновности
обвиняемого могут быть положены в
основу обвинительного приговора
-:
Оправдательный приговор не может быть
основан на предположениях
+:
Помимо бремени доказывания обвинения
сторона обвинения несет и бремя
опровержения доводов, приводимых в
защиту подозреваемого или обвиняемого
-:
Дознаватель, следователь, прокурор
обязаны доказать виновность подозреваемого,
обвиняемого
I:25
S:Какое
из утверждений является неправильным
+:
Принцип уголовного процесса обязательно
закреплен в законе
-:Публичность
уголовного процесса обуславливает
проведение открытого судебного
разбирательства
-:
Принцип законности обращен к любому
участнику уголовного процесса
-:
Презумпция невиновности предполагает
толкование неустранимых сомнений в
виновности в пользу обвиняемого
I:26
S:Из
принципа состязательности уголовного
судопроизводства следует, что
-:
Стороны обвинения и защиты равноправны
на всех стадиях процесса
+:
Суд создает необходимые условия для
исполнения сторонами их процессуальных
обязанностей и осуществления
предоставленных им прав
-:
На стадии предварительного расследования
защитник вправе самостоятельно
производить отдельные следственные
действия
-:
Защитник опровергает доводы обвинения
I:27
S:
Право обвиняемого на защиту не включает
в себя
-:
Право пользоваться помощью защитника
или отказаться от нее
-:
Право знать, в чем именно он обвиняется
-:
Право представлять доказательства по
делу
+:
Право не являться по вызовам следствия
I:28
S:
При оценке доказательств судом,
присяжными заседателями, прокурором,
следователем, дознавателем
-:
Главную роль играет наличие формальных
доказательств
-:
Должны отдать предпочтение показаниям
потерпевших от преступлений
-:
С недоверием отнестись к показаниям
обвиняемого
+:
Они должны руководствоваться законом
и совестью
I:29
S:
Судопроизводство в военных судах РФ
ведется
-:
На языке, которым владеет председательствующий
на судебном заседании
-:
на русском языке или языке национальной
республики
+:
только на русском языке
-:
на языке большинства населения данной
личности
I:30
S:
Какие из нижеследующих утверждений
правильны
-:
в Верховном Суде республики, входящей
в РФ, уголовное судопроизводство ведется
только на государственном языке этой
республики
+:
В Верховном Суде РФ производство по
уголовным делам ведется только на
русском языке
-:
В районном суде судопроизводство
ведется на языке, которым владеет
подсудимый
-:
Уголовное судопроизводство во всех
судах ведется только на русском языке
I:31
S:
Какое утверждение является правильным
-:
Судопроизводство в РФ ведется
исключительно на русском языке
-:
Разбирательство дел в судах во всех
случаях открытое
-:
Защитник обязан принять все предусмотренные
законом меры для всестороннего, полного
и объективного исследования обстоятельств
дела
+:
Принцип уголовного процесса – это
правовая норма
I:32
S:
Вид уголовного преследования определяется
-:
Субъектом совершенного преступления
-:
Волеизъявлением потерпевшего
-:
Объектом преступления
+:
Характером и тяжестью совершенного
преступления
I:33
S:
Уголовные дела частно-публичного
обвинения
-:
Могут быть в общем случае прекращены
в связи с примирением потерпевшего с
обвиняемым
+:Могут
быть прекращены судом, следователем и
дознавателем в связи с примирением
потерпевшего с обвиняемым, если речь
идет о преступлении небольшой или
средней тяжести
-:
Могут быть прекращены только по согласию
прокурора
-:
Прекращению в связи с примирением
потерпевшего с обвиняемым не подлежат
I:34
S:
Примирения по делам частного обвинения
допускается
-:
До начала судебного заседания
-:
До начала судебных прений
+:
До удаления суда в совещательную комнату
для постановления приговора
-:
До оглашения приговора
I:35
S:
Ночное время – это промежуток времени
-:
От заката до восхода солнца
-:
с 22 до 6 часов по московскому времени
+:
с 22 до 6 часов по местному времени
-:
с 23 до 7 часов по местному времени
I:36
S:
Какие из перечисленных составов суда
возможны в суде первой инстанции
+:
Судья федерального суда общей юрисдикции
и коллегия из двенадцати присяжных
заседаний
-:
Коллегия из одного судьи и двух народных
заседателей
-:
Коллегия из двух судей федерального
суда – по делам о тяжких преступлениях
-:
Коллегия из пяти судей федерального
суда – по делам особо тяжкого преступления
I:37
S:
Какой состав суда рассматривает
уголовные дела в апелляционном порядке
+:
Судья районного суда единолично; судьи
республиканского, краевого, областного,
городского, окружного судов;
-:
Специальные судьи
-:
Присяжные заседатели
-:
Мировые судьи
I:38
S:
Какой состав суда рассматривает
уголовные дела в Кассационном порядке
+:
Коллегией из трех судей федерального
суда общей юрисдикции
-:
Председателем вышестоящего суда
-:
Коллегией присяжных заседателей
-:
Судьей федерального суда общей
юрисдикции, имеющий большой опыт работы
I:39
S:Какой
состав суда рассматривает уголовные
дела в порядке надзора
-:
Президиумом Верховного суд республик,
краев, областей
-:
Коллегия судей из пяти человек
-:
Судьями Верховного суда России
+:
Большинством членов Президиума
Верховного суда РФ
I:40
S:Какие
из перечисленных субъектов уголовного
процесса являются участниками со
стороны обвинения
-:
Мировой судья
-:
Судья федерального суда общей юрисдикции
+:
Следователь
-:
Переводчик
I:41
S:Какие
их перечисленных субъектов уголовного
процесса являются участниками со
стороны защиты
-:
Потерпевший
-:
Гражданский истец
+:
Гражданский ответчик
-:
Специалист
I:42
S:Какие
из утверждений являются неправильными
-:В
качестве прокурора в уголовном процессе
может выступить заместитель районного
прокурора
+:Прокурор
осуществляет надзор за постановлением
приговора судом
-:Компетенция
прокурора различается в зависимости
от стадий процесса
-:Прокурор
поддерживает в суде государственное
обвинение
I:43
S:
В ходе досудебного производства в
полномочия прокурора входит
-:Продление
срока предварительного следствия
-:Приостановление
или прекращение уголовного дела
-:Дача
санкции на задержание подозреваемого
+:Направление
уголовного дела в суд
I:44
S:В
ходе судебного производства по уголовному
делу публичного обвинения
+:Участие
прокурора строго обязательно
-:Участие
прокурора обязательно, если того требует
суд
-:Участие
прокурора обязательно, если того требует
сторона защиты
-:Государственным
обвинителем может быть должностное
лицо прокуратуры
I:45
S:Если
с указанием руководителя следственного
органа о квалификации преступления и
объема обвинения следователь не
согласен, то
-:Он
обязан исполнить указание, а потом
обжаловать его прокурору
-:Он
вправе передать дело другому следователю
+:
Он вправе не исполнять указание,
обжаловав его руководителю вышестоящего
следственного органа
-:
Он может обжаловать указание в суд
I:46
S:В
ходе производства по уголовному делу
следователь уполномочен:
-:
передавать уголовное дело прокурору
для направления по подследственности
+:
возбуждать уголовное дело в порядке,
установленном УПК
-:
самостоятельно принимать решения о
производстве всех следственных и иных
процессуальных действий
-:
не принимать уголовные дела к своему
производству, если считает это
нецелесообразным
I:47
S:
Несогласие следователя с какими
указаниями руководителя следственного
органа приостанавливает их исполнение
+:
о прекращении уголовного дела
-:
о назначении судебной экспертизы
-:
о допросе свидетелей
-:
о производстве освидетельствования
потерпевшего
I:48
S:
Каковы возможные решения вышестоящего
руководителя следственного органа в
случае, когда исполнение указаний
руководителя следственного органа
приостановлено в связи с несогласием
следователя
-:
Прямое указание следователю подчиниться
данным ему указаниям, невзирая на его
несогласие
-:
возбуждение перед судом ходатайства
об отводе следователя
+:
отмена указаний нижестоящего руководителя
следственного органа
-:
указание прокурору рассмотреть вопрос
по существу
I:49
S:
Какие из утверждений являются
неправильными
-:
руководитель следственного органа
вправе передавать дело от одного
следователя другому
-:
руководитель следственного органа
вправе давать следователю указания о
квалификации преступления и объеме
обвинения
+:
указания руководителя следственного
органа необязательны для следователя
-:
руководитель следственного органа
вправе лично производить предварительное
следствие
I:50
S:
Если следователь не согласен с указанием
руководителя следственного органа о
квалификации преступления или объеме
обвинения, то
-:
он обязан исполнить указание, а потом
обжаловать его прокурору
-:
он вправе передать дело другому
следователю
+:
он вправе не исполнять указание при
обжаловании его руководителю вышестоящего
следственного органа
-:
он может обжаловать указание лишь
самому руководителю следственного
органа
I:51
S:
Может ли руководитель следственного
органа отменить постановление следователя
-:
ни в коем случае
-:
да, в любом случае
+:
да, если это постановление незаконное
или необоснованное
-:
да, если об этом будет указание прокурора
I:52
S:
В полномочия руководителя следственного
органа не входит
-:
поручение производства предварительного
следствия следователю
+:
отмена незаконных или необоснованных
постановлений прокурора
-:
передача уголовного дела другому
следователю
-:
изменение состава следственной группы
I:53
S:
Какие из этих организаций не могут быть
отнесены к органам дознания
-:
органы внутренних дел РФ
-:
органы Федеральной службы судебных
приставов
+:
частные охранные предприятия
-:
органы государственной противопожарной
службы
I:54
S:
Какое из утверждений является правильным
-:
дознаватель – это начальник органа
дознания
-:
дознаватель – это начальник подразделения
дознания
+:
полномочия органов дознания различаются
в зависимости от вида дознания
-:
дознаватель обладает процессуальной
самостоятельностью
I:55
S:
Дознаватель вправе самостоятельно
принять решение
-:
о предъявлении подозреваемому обвинения
-:
о производстве обыска
+:
о производстве осмотра места происшествия
-:
о привлечении лица в качестве обвиняемого
I:56
S:
При несогласие дознавателя с указаниями
прокурора или начальника подразделения
дознания исполнение этих указаний
-:
приостанавливается, если это указания
о прекращении уголовного дела или
направлении его в суд
-:
приостанавливается, если это указания
начальника подразделения дознания,
обжалованные прокурору
-:
приостанавливается лишь по решению
суда
+:
не приостанавливается
I:57
S:
Потерпевшим может быть признано
-:
лицо, которому известны какие-либо
обстоятельства, имеющие значение для
расследования уголовного дела
-:лицо,
ошибочно оштрафованное за безбилетный
проезд в городском автобусе
+:
лицо, которому преступлением причинен
моральный вред
-:
представитель обвиняемого, оправданного
судом
I:58
S:
В комплекс прав потерпевшего входит
-:
право знакомиться в ходе предварительного
расследования со всеми материалами
уголовного дела
+:
право заявлять ходатайство и отводы
-:
право получать копии постановлений и
назначении экспертиз
-:
право участвовать в судебном
разбирательстве по вопросу об
условно-досрочном освобождении
осужденного
I:59
S:
В комплекс прав потерпевшего не входит
-:
право не свидетельствовать против
своих близких родственников
-:
право знать о наличии в деле обвиняемого
и предъявленном ему обвинении
-:
собирать доказательства
+:
право иметь более чем одного законного
представителя
I:60
S:
При неявке потерпевшего по вызову без
уважительных причин он может быть
подвергнут
-:
отстранению от должности
-:
задержанию
+:
приводу
-:
домашнему аресту
I:61
S:
Не является обязанностью потерпевшего
-:
давать правдивые показания
-:
подвергаться освидетельствованию
+:
не отлучаться с места жительства без
соответствующего разрешения
-:
соблюдать порядок в зале судебного
заседания
I:62
S:
Гражданским истцом может быть признано
-:
только физическое лицо
-:
только юридическое лицо
-:
только гражданское лицо
+:
как физическое, так и юридическое лицо
I:63
S:
Гражданский иск может быть предъявлен
-:
до окончания предварительного
расследования
+:
до окончания судебного следствия в
суде первой инстанции
-:
до окончания судебных прений
-:
до удаления суда в совещательную комнату
для постановления приговора
I:64
S:
Какое из утверждений является правильным
-:
гражданский истец всегда признается
потерпевшим по делу
-:
гражданский истец признается потерпевшим,
лишь, когда он является физическим
лицом
+:
потерпевший может быть одновременно
гражданским истцом
-:
гражданский истец имеет право на
возмещение только имущественного вреда
I:65
S:
В комплекс прав гражданского истца не
входит
+:
право иметь более чем одного представителя
-:
право заявлять ходатайства и отводы
-:
право собирать доказательства
-:
право представлять доказательства
I:66
S:
Представителями потерпевшего или
гражданского истца могут быть
-:
только профессиональные адвокаты
-:
только защитники
-:
только супруги
+:
при производстве у мирового судьи –
также один из близких родственников,
либо иное лицо, о допуске которого они
ходатайствуют
I:67
S:
Не является обязанностью подозреваемого
и обвиняемого
+:
являться по вызову
-:
не продолжать преступную деятельность
-:
давать показания по делу
-:
подвергаться освидетельствованию
I:68
S:
Подозреваемым является лицо
-:
в отношении, которого вынесено
постановление о привлечении в качестве
подозреваемого
-:
застигнутое на месте преступления
-:
задержанное постовым милиционером
+:
задержанное в соответствии со ст.91-92
УПК
I:69
S:
В комплекс прав подозреваемого не
входит право
-:
знать, в чем он подозревается
-:
отказаться от дачи объяснений и показаний
+:
собирать доказательства
-:
заявлять ходатайства и отводы
I:70
S:
Для признания лица обвиняемым необходимо
-:
постановление обвинительного приговора
-:
отмена оправдательного приговора
-:
задержание по подозрению в совершении
преступления
+:
вынесение обвинительного акта
I:71
S:
Обвиняемым признается лицо, в отношении
которого
-:
возбуждено уголовное дело
-:
произведено задержание
-:
поступило сообщение о совершении им
преступления
+:
вынесено постановление о привлечении
в качестве обвиняемого
I:72
S:
В комплекс прав обвиняемого не входит
право
studfiles.net
Онлайн-тесты на oltest.ru: Уголовно-процессуальное право
Онлайн-тестыТестыЮриспруденция, государство и правоУголовно-процессуальное правовопросы
1. Адвокат допускается к участию в уголовном деле в качестве защитника по предъявлению:
•
удостоверения адвоката и ордера2. В исключительных случаях мера пресечения может быть избрана в отношении:
• подозреваемого
3. В качестве гражданского ответчика могут быть привлечены:
• физические или юридические лица
4. В качестве законных представителей несовершеннолетнего обвиняемого могут быть допущены:
• его опекуны или попечители
5. В отношении подозреваемого мера пресечения может быть избрана на срок:
• не более 10 суток
6. В порядке надзора уголовные дела вправе рассматривать:
• президиум суда
7. В процессе доказывания совокупность полученных по делу доказательств, включающая полноту и надежность, именуется ______ доказательств.
• достаточностью
8. В соответствии с УПК РФ решение о контроле и записи телефонных и иных переговоров вправе принимать:
•
только суд9. В соответствии с УПК РФ решение о производстве выемки предметов и документов, содержащих информацию о вкладах и счетах в банках и иных кредитных организациях, вправе принимать:
• суд
10. В срок содержания под стражей не засчитывается время:
• наблюдения командования воинской части
11. В уголовном процессе для содействия в обнаружении, закреплении и изъятии предметов и документов, применении технических средств в исследовании материалов уголовного дела привлекается:
• специалист
12. В уголовном процессе не может быть понятым:
• несовершеннолетний
13. В уголовном процессе по обстоятельствам дела в качестве свидетеля не может быть допрошен:
• защитник подозреваемого
14. В уголовном судопроизводстве вещественными доказательствами могут быть признаны:
• предметы, на которые были направлены преступные действия
15. В уголовном судопроизводстве допрос эксперта проводится:
• после получения его заключения
oltest.ru
Тест с ответами: «Уголовный процесс»
1. Письменные акты, в которых дознаватель и следователь фиксируют установленные на основе непосредственного восприятия сведения, имеющие значение для правильного разрешения дела:
а) протоколы следственных действий +
б) обвинительные акты
в) протоколы судебных заседаний
2. Вынесения постановления о приостановлении расследования не требуется:
а) да
б) нет +
в) да, в редких случаях
3. Передача лица, осужденного к лишению свободы, для отбывания наказания в государстве, гражданином которого оно является, осуществляется на основании решения:
а) следователя
б) прокурора
в) суда +
4. Действие по извлечению трупа из места захоронения по постановлению следователя называется:
а) эксгумация +
б) преюдиция
в) экстрадиция
5. Действиями присяжных заседателей руководит:
а) председатель присяжных заседателей
б) старший присяжный заседатель
в) старшина присяжных заседателей +
6. Гражданский иск – юридический факт, из которого истец выдвигает свои требования и с началом которых закон связывает возникновение правоотношений между истцом и ответчиком:
а) да
б) нет +
в) в редких случаях
7. Судья, не согласный с приговором, имеет право изложить в письменном виде свое такое мнение:
а) частное
б) категорическое
в) особое +
8. Указ Екатерины II от 1765 г. устанавливал нижний порог уголовной ответственности с:
а) 10 лет +
б) 15 лет
в) 20 лет
9. Решение о признании лица в качестве потерпевшего принимается:
а) после прений сторон
б) до возбуждения уголовного дела
в) после возбуждения уголовного дела +
10. Суд вправе принять решение об удалении несовершеннолетнего подсудимого из зала судебного заседания на время исследования обстоятельств, которые могут оказать на него отрицательное воздействие, только по:
а) ходатайству родственников
б) собственной инициативе и ходатайству стороны защиты +
в) ходатайству стороны обвинения
11. Правила УПК РФ не распространяются на лиц, нуждающихся в лечении от наркомании:
а) верно +
б) неверно
в) иногда
12. Правильны ли утверждения:
1. Уголовно-процессуальными полномочиями прокурора наделены только прокуроры районов
2. Только следователь вправе возбудить уголовное дело
а) только 1
б) только 2
в) оба правильны
г) нет правильного ответа
13. Лицо, подавшее заявление в суд по уголовному делу частного обвинения и поддерживающее обвинение в суде:
а) частный обвинитель +
б) государственный обвинитель
в) потерпевший
14. Производство по уголовным делам о преступлениях, совершенных иностранными гражданами или лицами без гражданства на территории Российской Федерации, ведется в соответствии с правилами:
а) Римского статута международного уголовного суда
б) Венской конвенции о праве международных договоров
в) Уголовно-процессуального кодекса РФ +
15. Результаты произведенных экспертом исследований оформляются … эксперта:
а) заключением +
б) протоколом
в) актом
16. Кратковременное (на срок не более 48 часов) ограничение свободы лица, подозреваемого в совершении преступления:
а) ограничение свободы
б) задержание +
в) домашний арест
17. Лицо признается гражданским истцом:
а) ходатайством обвиняемого
б) приговором суда
в) постановлением судьи, следователя, дознавателя +
18. Показания обвиняемого допускаются в качестве доказательств:
а) нет
б) да +
в) в редких случаях
19. Если лицо, находящееся под стражей, переданное другому государству, не будет принято в течение … суток со дня, установленного для передачи, то оно может быть освобождено из-под стражи:
а) 25
б) 30
в) 15 +
20. Рассмотрение уголовного дела в отношении несовершеннолетних возможно в закрытом судебном заседании:
а) нет
б) да +
в) зависит от тяжести преступления
21. В американском процессе нет опознания как следственного действия:
а) да +
б) нет
в) в разных Штатах по – разному
22. Вновь открывшиеся и новые обстоятельства не могут быть установлены:
а) постановлением прокурора о прекращении уголовного дела за истечением срока давности
б) постановлением дознавателя о возбуждении уголовного дела +
в) приговором, определением или постановлением суда
23. Решение о невиновности или виновности подсудимого и назначении ему наказания либо об освобождении его от наказания, вынесенное судом первой или апелляционной инстанции:
а) обвинительный акт
б) обвинительное заключение
в) приговор +
24. Производство в кассационной инстанции возбуждается на основе кассационных:
а) ходатайств
б) жалоб +
в) определений
25. Производство в кассационной инстанции возбуждается на основе кассационных:
а) ходатайств
б) определений
в) представлений +
26. Существенные особенности по делам несовершеннолетних имеет предмет доказывания:
а) нет
б) да +
в) иногда
27. При наличии у осужденного имущества или жилища, остающихся без присмотра, суд может вынести:
а) определение +
б) акт
в) заключение
28. При наличии у осужденного имущества или жилища, остающихся без присмотра, суд может вынести:
а) заключение
б) акт
в) постановление +
29. Надзорные жалоба или представление рассматриваются судом надзорной инстанции в течение:
а) 30 суток со дня их поступления +
б) 15 суток со дня их поступления
в) 20 суток со дня их поступления
30. Применение особого порядка судебного разбирательства всегда влечет оправдание подсудимого:
а) да
б) нет +
в) в редких случаях
liketest.ru
Уголовный процесс. Тест 10 — ДЕКАН ТЕСТ
1. В какой срок стороны должны быть уведомлены о вызове на предварительное слушание
не менее чем за 3 суток со дня проведения предварительного слушания
не менее чем за 5 суток со дня проведения предварительного слушания
не менее чем за 7 суток со дня проведения предварительного слушания
не менее чем за 10 суток со дня проведения предварительного слушания
2. В соответствии с принципом законности
Никакие доказательства не имеют заранее установленной силы
Правосудие по уголовному делу в РФ осуществляется только судом
Обвинительный приговор не может быть основан на предположениях
Нарушение следователем норм УПК влечет за собой признание недопустимыми полученных таким путем доказательств
3. Действие УПК РФ касается
Только пространства
Только времени
Только лиц
Только пространства, времени и лиц
4. Заявление о преступлении может быть сделано
только в письменном виде
в устном или письменном виде
в устном виде в присутствии понятых
в электронном виде
5. Источниками уголовно-процессуального права является
УК РФ
Указы и распоряжения Президента
Постановления и распоряжения Глав субъекта РФ
УПК РФ
6. Каким должен быть первоначальный состав коллегии присяжных заседателей в начале рассмотрения уголовного дела по существу
20 присяжных заседателей
12 присяжных заседателей
12 основных и не менее 2 запасных присяжных заседателей
12 основных и 2 запасных присяжных заседателей
7. Может ли оправдательный приговор суда первой инстанции быть изменен судом апелляционной инстанции по жалобе оправданного
да, в общем случае
да, в части мотивов оправдания
да, если жалоба согласована с защитником
да, в части касающейся основания оправдания
8. Может ли приговор суда первой инстанции, не обжалованный сторонами в апелляционном порядке, быть позже обжалован
да, только потерпевшим
да, только осужденным
да, в кассационном порядке
да, в надзорном порядке
9. Может ли приговор суда первой инстанции быть изменен в суде апелляционной инстанции в сторону ухудшения положения осужденного
да, в общем случае
да, по прямому указанию председателя суда
да, по требованию общественности
да, не иначе как по представлению прокурора либо жалобе потерпевшего, частного обвинителя, их законных представителей и (или) представителей
10. Одно и то же лицо может участвовать в течение года в судебных заседаниях в качестве присяжных заседателей
не более 1 раза
не более 2 раз
не более 3 раз
не более 5 раз
11. Первым в судебных прениях выступает
потерпевший
обвинитель
подсудимый
защитник
12. Решение следователя о приостановлении предварительного следствия
требует санкции прокурора или руководителя следственного органа
не может быть принято при возражении потерпевшего
утверждается судом
принимается самостоятельно и утверждения не требует
13. Стадия уголовного процесса завершается
Окончанием дознания
Началом предварительного следствия
Постановлением приговора
Принятием итогового процессуального решения
14. Уголовное преследование осуществляется
Следователем, дознавателем, прокурором
Судом
Органами полиции
Органами внутренних дел
15. Уголовное судопроизводство имеет своим назначением
Защиту интересов государства
Защиту интересов участников уголовного процесса
Защиту интересов суда
Защиту прав и законных интересов лиц и организаций, потерпевших от преступлений
dekane.ru
Уголовно-процессуальное право. Тест для самопроверки
1. Преюдиция – это …
факты, не нуждающиеся в доказывании, пока они обоснованно не оспариваются одной из сторон
обстоятельства, вступившие в законную силу приговором, не вызывающие сомнений у суда
сведения, сообщенные официальным органам на запрос по уголовному делу
любые доказанные по уголовному делу обстоятельства, не нуждающиеся в дополнительной проверке
2. Свидетель не может быть допрошен о(об)…
фактах и обстоятельствах, входящих в предмет доказывания
личности подозреваемого, обвиняемого
своих взаимоотношениях с подозреваемым, обвиняемым
отношении к следователю
3. В качестве источника доказательств могут быть допущены протоколы …
допроса свидетелей, потерпевших, подозреваемых, обвиняемых
следственных и судебных действий
ознакомления с материалами уголовного дела
о принятии залога
4. Процессуальные издержки взыскиваются с …
обвиняемых и подозреваемых
обвиняемых и осужденных
подозреваемых, обвиняемых и осужденных
осужденных
5. Процессуальная доброкачественность доказательства – это … доказательства.
содержание
допустимость
признак
относимость
6. Гражданский иск может быть предъявлен …
в надзорной инстанции
до возбуждения уголовного дела
после возбуждения уголовного дела и до окончания судебного следствия при разбирательстве данного уголовного дела в суде первой инстанции
после предъявления обвинения на предварительном следствии
7. Реабилитация
нахождение подозреваемого или обвиняемого в момент совершения преступления в другом месте
неустановленная причастность либо установленная непричастность лица к совершению преступления
порядок восстановления прав и свобод лица, незаконно или необоснованно подвергнутого уголовному преследованию, и возмещения причиненного ему вреда
8. К органам дознания относятся …
прокуратура
органы лесного надзора
органы внутренних дел РФ
адвокатура
органы ФСБ
органы по надзору за техническим состоянием автомобилей
органы исполнительной власти, наделенные в соответствии с федеральным законом полномочиями по осуществлению оперативно-розыскной деятельности
9. Проверка доказательства – это …
сопоставление одних доказательств, имеющихся в уголовном деле, другим
соответствие полученных доказательств предъявляемым требованиям
процессуальное собирание сведений о фактах, имеющих отношение к делу
закрепление обнаруженных сведений в предусмотренной законом форме
10. Заключение эксперта – это представленные в письменном виде …
суждение по вопросам, поставленном перед экспертом лицом, осуществляющим производство по уголовному делу или сторонами
суждение по вопросам, поставленном перед экспертом сторонами
содержание исследования и выводы по вопросам, поставленными перед экспертом сторонами
содержание исследования и выводы по вопросам, поставленными перед экспертом лицом, ведущем производство по уголовному делу, или сторонами
11. Заключение под стражу в качестве меры пресечения применяется за совершение …
тяжких и особо тяжких преступлений
тяжких преступлений, за которые предусмотрено наказание в виде лишения свободы на срок свыше 5 лет, при невозможности применения более мягкой меры пресечения
преступлений, за которые предусмотрено наказание в виде лишения свободы на срок свыше 2 лет, при невозможности применения более мягкой меры пресечения
12. Относимость – это …
получение доказательств из надлежащего источника
фиксация доказательства в установленной законом процессуальной форме
характеристика доказательства, обосновывающая процессуальное решение
соответствие доказательства обстоятельствам, имеющим отношение к делу
13. Уголовное преследование осуществляет …
государственный обвинитель по уголовным делам частного, публичного и частно-публичного обвинения
прокурор от имени государства по уголовным делам публичного и частно-публичного обвинения
прокурор от имени государства, по уголовным делам частного, публичного и частно-публичного обвинения
прокурор от имени государства, а также следователь и дознаватель по уголовным делам публичного и частно-публичного обвинения
14. Хранение оружия, изъятого по уголовному делу, допускается в …
камере хранения вещественных доказательств
специально оборудованном сейфе, находящемся в оружейной комнате
индивидуальном сейфе следователя при условии его опечатывания, и сдачи помещения под охрану
оружейной комнате, с прикреплением соответствующих пояснительных надписей
15. Вердикт – это …
решение о виновности или невиновности подсудимого, вынесенное коллегией присяжных заседателей
вывод о наличии или об отсутствии в действиях лица, в отношении которого применяется особый порядок производства по уголовному делу, признаков преступления
любое решение, за исключением приговора, вынесенное судьей единолично
решение о невиновности или виновности подсудимого и назначении ему наказания либо об освобождении его от наказания, вынесенное судом первой или апелляционной инстанции
16. Подозреваемым является лицо, …
к которому применена мера пресечения до предъявления обвинения
подозреваемое в совершении преступления
в отношении которого вынесен обвинительный акт
17. Жилищем признается …
индивидуальный жилой дом с входящими в него жилыми помещениями
индивидуальный жилой дом с входящими в него жилыми и нежилыми помещениями, жилое помещение независимо от формы собственности, входящее в жилищный фонд и используемое для постоянного или временного проживания, а равно иное помещение или строение, не входящее в жилищный фонд, но используемое для временного проживания
жилое помещение независимо от формы собственности, входящее в жилищный фонд и используемое для постоянного или временного проживания
индивидуальный жилой дом с входящими в него жилыми и нежилыми помещениями, жилое помещение независимо от формы собственности, входящее в жилищный фонд и используемое для постоянного или временного проживания, а равно иное помещение или строение, используемое для временного проживания
18. Вещественные доказательства – предметы …
переданные следователю свидетелем, потерпевшим, подозреваемым, обвиняемым
изъятые с места преступления
обнаруженные на месте преступления
служившие орудием преступления или сохранившие на себе следы преступления
19. Допустимость – это …
характеристика доказательства, обосновывающая процессуальное решение
соответствие доказательства реальным обстоятельствам дела
законность получения доказательств
получение доказательств надлежащим субъектом доказывания
20. Ходатайство подлежит рассмотрению …
непосредственно после его поступления
в течение 3 суток со дня его заявления
непосредственно после его поступления, а в случае невозможности такого рассмотрения не позднее 5 суток со дня его заявления
непосредственно после его поступления, а в случае невозможности такого рассмотрения не позднее 3 суток со дня его заявления
21. Досудебное соглашение о сотрудничестве – это …
прекращение уголовного преследования в связи с деятельным раскаянием
заявление о преступлении, явка с повинной, рапорт об обнаружении преступления
соглашение между сторонами обвинения и защиты, в котором указанные стороны согласовывают условия ответственности подозреваемого или обвиняемого в зависимости от его действий после возбуждения уголовного дела или предъявления обвинения
разрешение руководителя следственного органа на производство следователем или разрешение прокурора на производство дознавателем соответствующих следственных и иных процессуальных действий и на принятие ими процессуальных решений
22. Заключение специалиста – представленное (ые) в письменном виде …
содержание исследования и выводы по вопросам, поставленными перед специалистом сторонами
суждение по вопросам, поставленным перед специалистом сторонами
суждение по вопросам, поставленным перед специалистом лицом, осуществляющим производство по уголовному делу или сторонами
содержание исследования и выводы по вопросам, поставленным перед специалистом лицом, осуществляющим производство по уголовному делу или сторонами
23. Понятыми быть не вправе …
иностранные граждане
сотрудники милиции
несовершеннолетние
лица без гражданства
24. Не подлежит доказыванию по уголовному делу
характер, размер вреда, причиненного преступлением
обстоятельства, смягчающие, отягчающие наказание
событие преступления
обстоятельства, характеризующие личность свидетеля
25. Свидетельский иммунитет не распространяется на …
защитника подозреваемого, обвиняемого – об обстоятельствах, ставших известными в связи с участием в производстве по делу
судью – об обстоятельствах, ставших известными в связи с участием в производстве по делу
лиц, которые в силу физических либо психических недостатков не могут правильно воспринимать обстоятельства дела
священнослужителя – об обстоятельствах, ставших известными в ходе исповеди
26. К субъектам, имеющим право на сбор доказательств, не относится …
дознаватель
защитник подозреваемого, обвиняемого
прокурор
следователь
27. Уголовное дело подлежит прекращению …
в связи с деятельным раскаянием
когда обвиняемый не возражает против прекращения уголовного преследования в предусмотренных законом случаях
вследствие акта об амнистии
по истечение сроков давности уголовного преследования
28. Хранение денежных средств и материальных ценностей, изъятых по уголовному делу, допускается …
в банке или иной кредитной организации
в хранилище, исключающем несанкционированный доступ посторонних лиц
в индивидуальном сейфе следователя при условии его опечатывания
при уголовном деле
29. В качестве доказательств допускаются …
показания свидетеля, который не может указать источник своей осведомленности
показания обвиняемого, не подтвержденные в суде
заключение эксперта и показания специалиста
30. В ходе досудебного производства суд правомочен принимать решение о производстве …
выемки заложенной или сданной на хранение в ломбард вещи
обыска и выемки в жилище, об избрании меры пресечения виде заключения под стражу, залога
обыска и выемки, об избрании меры пресечения виде заключения под стражу
обыска в жилище и об избрании меры пресечения виде заключения под стражу, домашнего ареста, залога
обыска и выемки в жилище, об избрании меры пресечения виде заключения под стражу, домашнего ареста, залога
31. Достаточность – это …
законность получения доказательств
соответствие доказательства обстоятельствам, имеющим отношение к делу
соответствие доказательства реальным обстоятельствам дела
совокупность доказательств, необходимая для правильного разрешения дела
32. Фиксация доказательств – это …
процесс обнаружения доказательств, их фотосъемка и упаковка
изъятие доказательств в соответствии с нормами УПК РФ
обнаружение и последующее отображение доказательства в протоколе следственного действия в соответствии с нормами УПК РФ
отражение доказательств в протоколе следственного действия
33. В качестве свидетелей не подлежит допросу …
священнослужитель — об обстоятельствах, ставших ему известными из исповеди
следователь — об обстоятельствах, ставших ему известными
понятой — об обстоятельствах, ставших ему известными
специалист — об обстоятельствах, ставших ему известными
34. Не является источником доказательств …
протокол следственных и судебных действий
разрешение судьи на проведение отдельных следственных действий
заключение и показание специалиста
35. Назначение уголовного судопроизводства имеет целью защиту прав и законных интересов …
лиц и организаций, потерпевших от преступлений; защиту личности от незаконного и необоснованного обвинения, осуждение, ограничения её прав и свобод
государства, личности от незаконного и необоснованного обвинения, осуждение, ограничения её прав и свобод, защиту прав и законных интересов лиц и организаций, потерпевших от преступлений
лиц и организаций, потерпевших от преступлений, а также защиту личности от незаконного и необоснованного обвинения
36. В ходе досудебного производства по уголовному делу прокурор уполномочен …
давать дознавателю письменные указания о направлении расследования и о проведении оперативно-розыскных мероприятий
утверждать постановление дознавателя о прекращении производства по уголовному делу
изымать любое уголовное дело у дознавателя и передавать его следователю Следственного комитета при прокуратуре РФ с обязательным указанием оснований такой передачи
поддерживать государственное обвинение
37. Достоверность – это …
совокупность доказательств, образующих логическую цепочку
получение доказательств надлежащим субъектом доказывания
соответствие доказательства реальным обстоятельствам дела
получение доказательств в соответствии с УПК РФ
38. О задержании подозреваемого уведомляется близкие родственники в течение … часов
12
39. Решение о признании гражданским истцом оформляется …
приговором суда
определением суда
постановлением прокурора
постановлением следователя
40. Доказательства в зависимости от источника бывают …
личные и вещные
первоначальные и производные
показания подозреваемого, обвиняемого
прямые и косвенные
обвинительные и оправдательные
41. Хранение изъятых по уголовному делу наркотических средств и психотропных веществ допускается …
в индивидуальном сейфе следователя при условии его опечатывания
в камере хранения вещественных доказательств
в специально оборудованном хранилище
при уголовном деле
42. Близкие родственники:
лица, состоящие в свойстве с потерпевшим, свидетелем, а также лица, жизнь, здоровье и благополучие которых дороги потерпевшему, свидетелю в силу сложившихся личных отношений
лица состоящие в родстве
супруг, супруга, родители, дети, усыновители, усыновленные, родные братья и родные сестры, дедушка, бабушка, внуки
43. Данные об обстоятельствах, входящих в предмет доказывания – это …
процессуальная доброкачественность доказательства
содержание доказательства
связь доказательства с обстоятельствами, подлежащими доказыванию по делу
предмет доказывания
44. Частный обвинитель – это …
генеральный прокурор Российской Федерации и подчиненные ему прокуроры, их заместители и иные должностные лица органов прокуратуры, участвующие в уголовном судопроизводстве и наделенные соответствующими полномочиями федеральным законом о прокуратуре
представитель по уголовным делам частного обвинения
потерпевший или его законный представитель и представитель по уголовным делам частного обвинения
45. Участник судопроизводства, не имеющий право признать доказательство недопустимым
суд
орган дознания
дознаватель
прокурор
nn.dekane.ru
Уголовный процесс: тесты oh-lain
Уголовный процесс: тесты oh-lain
www.kalinovsky-k.narod.ru
| Главная |
Публикации |
Студентам |
Библиотека |
Ссылки |
Законы |
Гостевая |
Почта |
Тесты по уголовному процессу в режиме on-lain
В данный момент предлагается программа тестирования в экспериментальном режиме.
Тест по теме № 1 «Уголовный процесс: общие положения» (24 вопроса)
Тест по досудебному производству (9 вопросов)
Теперь есть 1000 тестов, работающих
в режиме обучения, с возможностью воспользоваться текстом УПК и лекций. На вашем
компьютере прямо сейчас!
См. также тесты в виде контрольной работы и в
виде книги.
Техническая поддержка тестирования в сети:
ELLS http://goldvoron.boom.ru
Новости МАСП
Для просмотра этой RSS ленты требуется поддержка Java Script
RSS импорт: www.rss-script.ru
|
|
|
|
kalinovsky-k.narod.ru

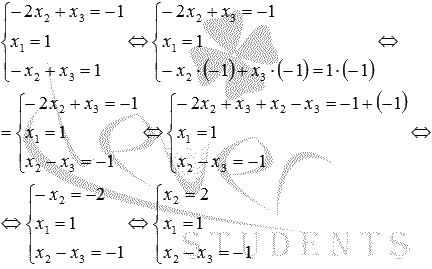


















 раздражительными, но с выполненным заданием. Но есть и второй вариант. Наши сотрудники возьмут на себя это тяжкое бремя науки, решат задачи любой сложности в то время, как Вы со спокойной душой будете заниматься своими личными делами. В назначенный строк Вы получите желаемый результат. Но мы предупреждаем Вас о том, что не несём ответственности за решение задач только в том случае, если изначально в условии были ошибки. К сожалению, так бывает. Если эта беда приключиться именно с Вами, то Вы смело можете рассчитывать на поддержку нашей команды, и мы решаем задачи по эконометрике в режиме онлайн. Мы обязательно предоставим комментарии к задачам, что бы Ваш непосредственный руководитель понял, в чём заключается загвоздка.
раздражительными, но с выполненным заданием. Но есть и второй вариант. Наши сотрудники возьмут на себя это тяжкое бремя науки, решат задачи любой сложности в то время, как Вы со спокойной душой будете заниматься своими личными делами. В назначенный строк Вы получите желаемый результат. Но мы предупреждаем Вас о том, что не несём ответственности за решение задач только в том случае, если изначально в условии были ошибки. К сожалению, так бывает. Если эта беда приключиться именно с Вами, то Вы смело можете рассчитывать на поддержку нашей команды, и мы решаем задачи по эконометрике в режиме онлайн. Мы обязательно предоставим комментарии к задачам, что бы Ваш непосредственный руководитель понял, в чём заключается загвоздка.

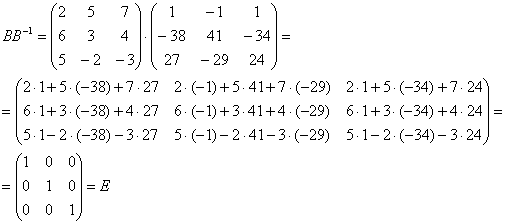
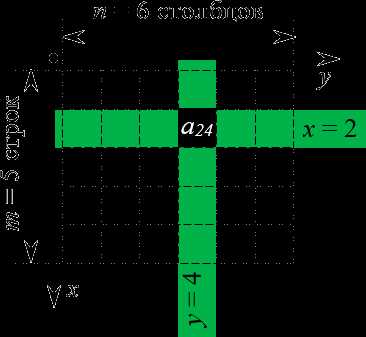 Определение индексов для клеток матрицы
Определение индексов для клеток матрицы