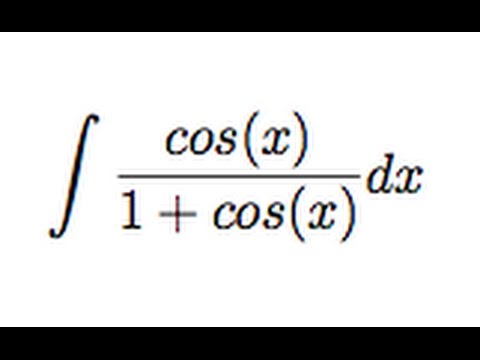ТЕСТЫ С ОТВЕТАМИ ПО ДИСЦИПЛИНЕ «ИНВЕСТИЦИОННЫЙ МЕНЕДЖМЕНТ»
Выберите один правильный ответ:
1 Инвестиции по объектам вложения средств классифицируются:
а) прямые и косвенные;
б) реальные и финансовые;
в) прямые и реальные;
г) частные, государственные, иностранные и совместные.
2 Увеличение удельного веса сбережений в общем объеме доходов:
а) не влияет на объем инвестиций;
б) приводит к росту объема инвестиций;
в) приводит к снижению объема инвестиций.
3 Эффект мультипликатора состоит:
а) в превышении темпов роста доходов над темпами роста объема чистых инвестиций;
б) в превышении темпов роста доходов над темпами роста объема валовых инвестиций;
в) в превышении темпов роста чистых инвестиций над темпами роста доходов.
4 Будущая стоимость денег:
а) сумма инвестированных в настоящий момент средств, в которую они превратятся через определенный период времени с учетом определенной ставки процента;
б) сумма средств, полученных в результате реализации инвестиционного проекта;
в) стоимость денег через определенное время.
5 Действительная стоимость денег:
а) стоимость средств в данный момент времени;
б) сумма будущих денежных поступлений, приведенных с учетом определенной ставки процента к настоящему периоду;
в) сумма средств, которую необходимо вложить в инвестиционный проект сегодня.
6 Аннуитет:
а) отдельные виды денежных потоков, осуществляемые последовательно через равные промежутки времени и в равных размерах;
б) арендная плата;
в) вид банковского кредита;
г) способ учета изменения стоимости денег во времени.
7 Номинальная стоимость денег:
а) стоимость денег с учетом инфляции;
б) показатель, характеризующий обесценение денег в процессе инфляции.
в) стоимость денег без учета инфляции
8 Темп инфляции:
а) показатель обратный индекса инфляции;
б) показатель, характеризующий прирост среднего уровня цен в рассматриваемом периоде;
в) показатель, используемый при формировании реальной ставки процента.
9 Инвестиционный риск:
а) риск, связанный с вложением средств в реальные инвестиционные проекты;
б) вероятность возникновения непредвиденных финансовых расходов в ситуации неопределенности условий инвестиционной деятельности;
в) снижение прибыли, доходов, потери капитала и др .;
г) вероятность снижения инвестиционной активности.
10 Абсолютный размер финансовых убытков это:
а) размер финансовых затрат, уменьшен на сумму убытка;
б) отношение суммы ущерба в избранное базового показателя;
в) сумма ущерба, причиненного инвестору в условиях неблагоприятных обстоятельств.
11 Ликвидность инвестиций это:
а) способность инвестора вовремя погашать долги;
б) потенциальная способность инвестиций в короткое время и без существенных финансовых потерь трансформироваться в денежные средства;
в) способность инвестиций в реинвестирования.
12 Назовите собственные источники формирования инвестиционных ресурсов компании:
а) кредиты банков и других кредитных структур;
б) эмиссия облигаций компании;
в) инвестиционный лизинг;
г) чистая прибыль; амортизационные отчисления;
д) эмиссия акций компании.
13 Назовите показатели оценки эффективности реальных инвестиций:
а) приведение к настоящей стоимости инвестированного капитала;
б) период окупаемости; индекс доходности; чистая приведенная стоимость;
в) коэффициент самофинансирования;
г) объем инвестированных средств.
14 Наиболее надежными инвестиционными инструментами являются:
а) простые акции;
б) привилегированные акции;
в) государственные облигации;
г) корпоративные облигации;
д) сберегательные сертификаты;
е) инвестиционные сертификаты.
15 Портфель ценных бумаг по сравнению с портфелем реальных инвестиционных проектов имеет:
а) более высокий уровень риска и более низкий уровень доходности;
б) более высокую ликвидность и управляемость;
в) более высокую инфляционную защищенность.
16 Продуктовые инновации это:
а) применение новых материалов, новых полуфабрикатов и комплектующих и получение принципиально новых продуктов;
б) инновации в пищевой промышленности;
в) инновации в добывающей промышленности.
17 Процессные инновации означают:
а) новые методы организации производства, новые технологии;
б) создание новых видов продукции;
в) принципиальные изменения в социальной сфере;
г) изменения в институциональной сфере.
18 Инвестиционные проекты по целям их освоения подразделяются на:
а) тактические и стратегические;
б) краткосрочные и долгосрочные;
в) государственные и частные.
19 Объектом управления инвестиционного менеджмента выступают:
а) инвестиции предприятия и его инвестиционная деятельность;
б) инвестиционная деятельность частных инвесторов;
в) организационная структура отдельных предприятий;
г) инвестиционная деятельность иностранных инвесторов.
20. Точка безубыточности:
а) параметр, характеризующий порог рентабельности;
б) показывает, при каком объеме продаж продукта будет достигнута самоокупаемость хозяйственной деятельности объекта инвестирования на стадии его эксплуатации;
в) характеризует уровень текущих затрат к объему продаж;
г) показывает уровень чистого дохода.
21 Акция:
а) срочный ценная бумага, свидетельствующая о долевом участии в уставном фонде акционерного общества;
б) ценная бумага без установленного срока обращения, которая удостоверяет долевое участие в уставном фонде акционерного общества, подтверждающая членство в акционерном обществе и право на участие в управлении им, дает право его владельцу на получение части прибыли в виде дивиденда, а также на участие в распределении имущества при ликвидации акционерного общества;
в) целевой бумага, свидетельствующая о долевом участии в уставном фонде акционерного общества, дает право ее владельцу на получение прибыли в виде дивиденда.
22 Акции по характеру обязанностей эмитенту классифицируются:
а) именные, на предъявителя;
б) срочные, бессрочные;
в) простые, привилегированные;
г) процентные, беспроцентные;
д) украинских и зарубежных эмитентов.
23 Облигация:
а) ценная бумага, свидетельствующая о внесении ее владельцем денежных средств и подтверждает обязанность эмитента возместить ему номинальную стоимость этой ценной бумаги без выплаты процентов;
б) ценная бумага, свидетельствующая о внесении ее владельцем денежных средств и подтверждает обязанность эмитента возместить ему номинальную стоимость этой ценной бумаги с выплатой фиксированного процента;
в) ценная бумага, свидетельствующая о внесении ее владельцем денежных средств и подтверждает обязанность эмитента возместить ему номинальную стоимость этой ценной бумаги с выплатой процентов в зависимости от финансового результата деятельности компании.
24. Облигации по особенностям регистрации и обращения классифицируются:
а) государственных и негосударственных компаний;
б) именные, на предъявителя;
в) процентные, целевые;
г) краткосрочные, срочные, долгосрочные;
д) срочные; бессрочные.
25 Сберегательные сертификаты:
а) ценные бумаги, свидетельствующие о депонировании средств юридических и физических лиц;
б) письменное свидетельство банка о депонировании средств, подтверждающий право вкладчика на получение по истечении срока депозита и процентов по нему;
в) письменное свидетельство банка о депонировании средств физическим лицом, подтверждающий право вкладчика на получение по истечении срока депозита и процентов по нему.
26 Сберегательные сертификаты по условиям размещения средств классифицируются:
а) краткосрочные, срочные, долгосрочные;
б) срочные, до востребования;
в) процентные, беспроцентные;
г) именные, на предъявителя;
д) украинских и зарубежных эмитентов.
27 Диверсификация инвестиционного портфеля:
а) представляет собой уменьшение числа составляющих инвестиционного портфеля с целью снижения инвестиционных рисков;
б) представляет собой расширение или изменение числа составляющих инвестиционного портфеля с целью снижения инвестиционных рисков;
в) это инвестиционная стратегия, направленная на повышение ликвидности инвестиционного портфеля.
28 Под инвестиционной стратегией компании следует понимать:
а) деятельность путем формирования инвестиционного портфеля компании;
б) реализации отдельных инвестиционных программ и проектов;
в) формирование системы долгосрочных целей инвестиционной деятельности и выбор наиболее эффективных путей их достижения;
г) набор правил для принятия решений, которыми организация руководствуется в ходе осуществления инвестиционных проектов.
29 Главной целью формирования инвестиционного портфеля компании являются:
а) обеспечение высоких темпов прироста капитала и повышения ликвидности инвестиционного портфеля;
б) увеличение темпов прироста дохода и минимизация риска;
в) обеспечение реализации инвестиционной стратегии компании путем подбора наиболее эффективных и безопасных объектов инвестирования.
30 Чистые инвестиции это:
а) сумма валовых инвестиций, уменьшенная на сумму амортизационных отчислений в определенном периоде;
б) общий объем инвестированных средств;
в) сумма валовых инвестиций, уменьшенная на сумму материальных затрат в определенном периоде.
Правильные ответы на тесты по дисциплине «Инвестиционный менеджмент»
Номер теста | Номер правильного ответа и решения |
1. | Б |
2. | Б |
3. | А |
4. | А |
5. | Б |
6. | А |
7. | В |
8. | Б |
9. | Б |
10. | В |
11. | Б |
12. | Г |
13. | Б |
14. | В |
15. | Б |
16. | А |
17. | А |
18. | А |
19. | А |
20. | Б |
21. | Б |
22. | В |
23. | Б |
24. | Б |
25. | Б |
26. | Б |
27. | Б |
28. | В |
29. | В |
30. | А |
refdocx.ru
Понятие и структура инвестиционной стратегии предприятия
Термин «стратегия” греческого происхождения, означает «искусство генерала”. Под стратегическим планированием понимаются действия и решения руководства организации,которые охватывают выбор и привлечение возможных источников финансирования инвестиционных проектов для достижения поставленных целей.
Под инвестиционной стратегией следует понимать формирование системы долгосрочных целей инвестиционной деятельности и выбор наиболее эффективных путей их достижения.
Инвестиционную стратегию можно представить как генеральный план действий в сфере инвестиционной деятельности предприятия, который определяет приоритеты ее направлений и форм, характер формирования инвестиционных ресурсов и последовательность этапов реализации долгосрочных инвестиционных целей, обеспечивают прогнозируемый общий развитие предприятия. Сочетание в инвестиционной стратегии системы целей и путей их достижения определяет пределы возможной инвестиционной активности предприятия по направлениям и формам его инвестиционной деятельности на перспективу.
Инвестиционную стратегию предприятия можно охарактеризовать также как систему формализованных критериев, по которым он оценивает и реализует свои инвестиционные возможности, моделирует свою перспективную инвестиционную позицию и обеспечивает ее достижения.
Следовательно, подытоживая вышесказанное, можно отметить, что инвестиционная стратегия представляет собой систему, охватывающую развитие инвестиционной деятельности предприятия.
Следует отметить, что процесс стратегического управления инвестиционной деятельностью компании, получаем свою дальнейшую конкретизацию в процессе тактического управления этой деятельностью путем формирования инвестиционного портфеля компании. В отличие от инвестиционной,стратегия формирования инвестиционного портфеля является среднесрочным управленческим процессом, который осуществляется в рамках стратегических решений и текущих финансовых возможностей компании. В свою очередь,процесс тактического управления инвестиционной деятельностью получаем свое детальное завершения в оперативном управлении реализацией отдельных инвестиционных программ и проектов.
Таким образом, разработка инвестиционной стратегии является только первым этапом процесса управления инвестиционной деятельностью. При разработке инвестиционной стратегии следует учитывать основные цели функционирования предприятия и его планы на будущее.
Необходимо отметить, что инвестиционная стратегия состоит из совокупности нескольких взаимосвязанных подсистем таких как:
-институциональная
-экономическая
-нормативно-правовая
-информационно-аналитическая.
Институциональная подсистема является основой для формирования инвестиционной стратегии и представляет собой совокупность следующих основных частей:
- виды инвестиций
- родники финансирования
- инвестиционный портфель
- риски.
Ее важность для формирования инвестиционной стратегии предприятия следует также из того, что предприятие в рамках каждого компонента этой подсистемы может разрабатывать свои локальные стратегии, а именно: стратегию реализации, стратегию финансирования инвестиционных проектов и др.
Нормативно-правовая подсистема инвестиционной стратегии состоит из следующих основных частей:
- законодательные и нормативно-правовые акты государства, образующие юридическую основу и формируют фискальная среда, в рамках которых предприятие формирует инвестиционную стратегию и осуществляет инвестиционный процесс;
- отраслевые нормативные акты, которые формируют конкурентную среду;
- учетная политика предприятия, внутренние регулирующие документы, обеспечивающие единый инвестиционный процесс в рамках подразделений предприятий.
Экономическая подсистема — это совокупность экономических составляющих инвестиционной стратегии, к которым относятся:
1. система экономических показателей для оценки эффективности инвестиционной деятельности предприятия;
2. процесс управления;
3. процесс финансирования инвестиционного процесса.
Информационно-аналитическая подсистема инвестиционной стратегии представляет собой систему обработки информации, которая состоит из следующих составляющих:
· сбор и сортировка информации;
· сохранение информации;
· поиск;
· анализ информации.
Система обработки информации является базисом оперативного информационного обмена в рамках инвестиционной стратегии предприятия, позволяет оперативно реагировать на изменения в юридическом и фискальном среде , прогнозировать экономические перспективы рынков и планировать изменения в рамках институциональной подсистемы и корректировать основные составляющие экономической подсистемы инвестиционной стратегии.
Таким образом, инвестиционная стратегия-единственная высоко интегрированная система состоит из различных подсистем, неразрывно связанных между собой для достижения миссии предприятия.
www.kak-chto.info
Тесты с ответами по дисциплине инвестиционный менеджмент
Выберите один правильный ответ:
1 Инвестиции по объектам вложения средств классифицируются:
А) прямые и косвенные;
Б) реальные и финансовые;
В) прямые и реальные;
Г) частные, государственные, иностранные и совместные.
2 Увеличение удельного веса сбережений в общем объеме доходов:
А) не влияет на объем инвестиций;
Б) приводит к росту объема инвестиций;
В) приводит к снижению объема инвестиций.
3 Эффект мультипликатора состоит:
А) в превышении темпов роста доходов над темпами роста объема чистых инвестиций;
Б) в превышении темпов роста доходов над темпами роста объема валовых инвестиций;
В) в превышении темпов роста чистых инвестиций над темпами роста доходов.
4 Будущая стоимость денег:
А) сумма инвестированных в настоящий момент средств, в которую они превратятся через определенный период времени с учетом определенной ставки процента;
Б) сумма средств, полученных в результате реализации инвестиционного проекта;
В) стоимость денег через определенное время.
5 Действительная стоимость денег:
А) стоимость средств в данный момент времени;
Б) сумма будущих денежных поступлений, приведенных с учетом определенной ставки процента к настоящему периоду;
В) сумма средств, которую необходимо вложить в инвестиционный проект сегодня.
6 Аннуитет:
А) отдельные виды денежных потоков, осуществляемые последовательно через равные промежутки времени и в равных размерах;
Б) арендная плата;
В) вид банковского кредита;
Г) способ учета изменения стоимости денег во времени.
7 Номинальная стоимость денег:
А) стоимость денег с учетом инфляции;
Б) показатель, характеризующий обесценение денег в процессе инфляции.
В) стоимость денег без учета инфляции
8 Темп инфляции:
А) показатель обратный индекса инфляции;
Б) показатель, характеризующий прирост среднего уровня цен в рассматриваемом периоде;
В) показатель, используемый при формировании реальной ставки процента.
9 Инвестиционный риск:
А) риск, связанный с вложением средств в реальные инвестиционные проекты;
Б) вероятность возникновения непредвиденных финансовых расходов в ситуации неопределенности условий инвестиционной деятельности;
В) снижение прибыли, доходов, потери капитала и др.;
Г) вероятность снижения инвестиционной активности.
10 Абсолютный размер финансовых убытков это:
А) размер финансовых затрат, уменьшен на сумму убытка;
likedoc.top
Под инвестиционной стратегией компании следует понимать — GameCollector
Комментарии пользователей
Forex обучение и инвестиции онлайн Стратегии
18.01.2018 — 09:27
Скоро ожидайте обновления на канале всего контента видео роликов темы(реальная поддержка и сопротивление, обновление хая и лоу рынка, торговля по профилю объема, откаты и тесты, обсуждения брокеров и терминалов, правила рискменеджмента и манименеджмента, как не сливать депозит, манипуляции маркетмейкеров против толпы, и с помощью каких алгоритмов вас разводит брокер в мт4 и прочих терминалах и многое другое. А самое главное как правильно определять цель в рынке.
семен слепаков
19.01.2018 — 15:10
не понятно как вам то брокеры позволяют выводить такие суммы? или вы сам и есть тот самый брокер?
Юрий Купро
21.01.2018 — 13:13
Я если честно то платил бы налоги,для родины всё таки!Похер что чиновники гондурасы просто за то что на этой земле родился!
семен слепаков
23.01.2018 — 12:05
вот про это бы видео показали, было бы поучительно.
Forex обучение и инвестиции онлайн Стратегии
26.01.2018 — 05:30
я вообще не вижу никаких препятствий в выводе средств. Будешь много рубить бабла так ты будешь у брокера востребован а не уволен. Вопрос в другом как тебе даст твой банк забрать такое бабло без налогов уплаты? и как на все посмотрит РосФинМониторинг
ARTANIS SV
20.01.2018 — 17:16
А вот за это видео вам Спасибо) Просто, понятно) Спасибо) Делайте такие ролики)
ARTANIS SV
23.01.2018 — 12:28
Подписка
SILKE kirsch
22.01.2018 — 02:42
Спасибо
Наталья Колбина
24.01.2018 — 21:22
Ты классный.Я много интересного узнаю. Не знала про брокеров
Сергей Корниенко
26.01.2018 — 11:41
Спасиба.
Сергей Корниенко
28.01.2018 — 17:23
Где можна такой индикатор скачать.
Forex обучение и инвестиции онлайн Стратегии
30.01.2018 — 01:52
Скажи ок гугл и он тебе в помощь найдет граальный индюк для торговли против толпы
Ирина Власова
30.01.2018 — 02:18
Неужели инвестиционные брокеры Финам, БКС — это тоже развод? С Форексом понятно, а на БИРЖУ они трейдеров тоже не выводят! И в случае слива деньги трейдеров забирают себе?
Forex обучение и инвестиции онлайн Стратегии
31.01.2018 — 06:17
все так да
Владимир Авдеев
01.02.2018 — 17:06
не совсем понятно для продажи или для покупки накапливаются объмы?
Forex обучение и инвестиции онлайн Стратегии
04.02.2018 — 06:11
скайп тот же не могу знать почему ты не можешь
Владимир Авдеев
06.02.2018 — 23:46
Роман, не могу добавить или найти вас по Скайпу.Через gazman905 не получается.
Forex обучение и инвестиции онлайн Стратегии
08.02.2018 — 10:36
а смысл зачем тебе знать куда они накапливаются что ты из этого сделаешь какой вывод
Krasnodar FX
04.02.2018 — 10:14
С каким брокером работать лучше?
Forex обучение и инвестиции онлайн Стратегии
05.02.2018 — 10:27
для этого тебе придется посмотреть еще раз наверное видосы мои
юрий подбережный
06.02.2018 — 01:17
Спасибо!
dilson swiden
09.02.2018 — 01:08
sposibo za poznavatelniy video
Зарабаток без вложений в интернете
11.02.2018 — 15:00
Очень много я узнал с ваших видео что наглядна говорит о том, что я знал о рынки все говно,спасибо большое за ваши поеснения!
павел селин
13.02.2018 — 12:40
смотрю ваше видео. сейчас не торгую в москве на заработках чтоб опять торговать. Много узнал из ваших видео.Спасибо вам огромное.
Ксана Химич
15.02.2018 — 06:34
Смотрю ваше видео недавно, огромное за них спасибо, вся информация пришла вовремя!
павел селин
16.02.2018 — 14:22
что будет то будет буду торговать до последних штанов
павел селин
18.02.2018 — 12:38
а я ни хрена не понимаю. дебил наверно. уже год сливаю семья по меру идет и не получается. наверно деьил
Happy Cat
20.02.2018 — 15:31
Если реал сливаете так уверенно, конечно это плохо. Для кого тогда автор такие видео делает. Думаю, не для профи. Хотя, кто знает, может и для них, тоже. И речь не о том дебил или не дебил, скорее всего опыта и подготовки очень мало.
Николай Шалашный
20.02.2018 — 15:56
А на каком тайм фрейме торговать?5мин,15мин,30мин.
Forex обучение и инвестиции онлайн Стратегии
21.02.2018 — 19:40
ну а когда сделка открыта можно ставить 4 часа меньше шума и развода
Forex обучение и инвестиции онлайн Стратегии
23.02.2018 — 12:51
анализ начинать делать с дневки и постепенно смотреть меньшие таймфреймы. На часовиках защищенные зоны в боковиках видно, на 5и минутках подтверждения и на минутках
Владимир Киселёв
23.02.2018 — 00:31
как индикатор называется?
AKAK ATAK
24.02.2018 — 15:35
И как же сделать. что бы профиль рынка отображался в MT?
Forex обучение и инвестиции онлайн Стратегии
26.02.2018 — 10:59
профиль рынка это называется
Алексей Теплов
25.02.2018 — 02:39
супер
asc-lada.ru
Тест по инвестиционному менеджменту с ответами
1. Главная цель инвестиционной деятельности:
1.максимизация прибыли
2.обеспечение финансового равновесия
+ 3. максимизация благосостояния собственников предприятия
2. За счет чего обеспечивается минимизация уровня инвестиционного риска
+ 1. путем диверсификации инвестиционного проекта
2.путем использования средств
3.путем нарушения финансового равновесия
3. По формам свойства с позиции инвестиционного менеджмента предприятия разделяют на:
+ 1. государственные, частные
2.акционерные общества и общества с ограниченной ответственностью
3.кооперативы
4. Не относится к классификации по признаку морального состояния на рынке:
1.предприятия — естественные монополисты
2.предприятия, осуществляющие свою деятельность в конкурентной среде
+ 3. предприятия, что находятся в состоянии жизненного цикла «юность»
5. По направлению основной деятельности инвесторов разделяют на:
+ 1. индивидуальных и институциональных
2.отечественных и иностранных
3.стратегических и портфельных
6. Согласно менталитету инвестиционного поведения инвесторы являются :
1.инвесторы не рискуют
2.инвесторы, ориентирующиеся на внешнеэкономический эффект
+ 3. консерваторами
7. По целям инвестирования инвесторов подразделяют на:
1.индивидуальных и институциональных
+ 2. стратегических и портфельных
3.зарубежных и отечественных
8. По принадлежности к резидентам инвесторов разделяют на:
1.индивидуальных и институциональных
+ 2. отечественных и зарубежных
3.стратегических и портфельных
9. По использованию в процессе форм оценки стоимости денег во времени виды процентных ставок:
+ 1. ставка наращивания и дисконтирования
2.базовая и договорная
3.периодическая и эффективная
10. К основным функциям инвестиционного менеджмента не относят:
1.разработку инвестиционной стратегии предприятий
2.осуществление планирования инвестиционной деятельности
+ 3. управления формированиями инвестиционных ресурсов
11. С учетом организационного поведения инвестиционный анализ разделяют на:
1.полный и тематический
+ 2. фундаментальный
3.внутренний и внешний
12. Инвестиционное планирование — это:
1.система основных принципов по которым осуществляется инвестиционная деятельность
+ 2. процесс разработки системы планов и плановых показателей в отношении обеспечения предприятий инвестиционными ресурсами
3.процесс проверки исполнения и обеспечения реализации управленческих решений
13. Среди представленных понятий на относятся к видам контроллинга:
1.стратегический
2.текущий
+ 3. гибкий
4.оперативный
14. Коэффициент абсолютной ликвидности:
+ 1. отношение наиболее ликвидных активов к
2.краткосрочных обязательств
3.отношение собственных средств к сумме баланса
4.отношение ликвидных активов к краткосрочным обязательствам
15. Инвестиционная привлекательность определяется:
+ 1. экономическим паспортом
2.форме №5
3.балансом
16. К коэффициентов оценки оборачиваемости инвестиционного капитала не относят:
1.коэффициент оборачиваемости всего капитала, используемого в процессе реального инвестирования
2.коэффициент оборачиваемости собственного капитала используется в процессе реального инвестирования
+ 3. коэффициент автономии
17. К коэффициентов оценки оборачиваемости операционных активов не относят:
1.коэффициент оборачиваемости всех операционных активов, используемых в определенном периоде
2.коэффициент оборачиваемости оборотных активов предприятия
+ 3. коэффициент рентабельности капитала
18. К коэффициентам оценки финансовой устойчивости предприятия не относят:
1.коэффициент автономии
2.коэффициент финансирования
+ 3. коэффициент абсолютной платежеспособности
19. К коэффициентов оценки ликвидности не относят:
1.коэффициент абсолютной платежеспособности
2.коэффициент промежуточной платежеспособности
+ 3. коэффициент маневренности
20. Коэффициент текущей платежеспособности показывает:
+ 1. в какой степени вся задолженность по краткосрочным финансовым обязательствам может быть ликвидирована за счет всех текущих активов
2.в какой степени все текущие финансовые обязательства могут быть выполнены за счет высоколиквидных активов
3.в какой степени все текущие финансовые обязательства выполнены имеющимися средствами платежей на определенную дату
21. Коэффициент маневренности собственного и долгосрочного занимаемого капитала показывает:
+ 1. какую долю занимает собственный и долгосрочный заемный капитал, инвестируемый в оборотные активы
2.в какой степени общий объем активов, используемых сформирован за счет собственного и долгосрочного занимаемого капитала
3.долю краткосрочного занимаемого капитала в зависимой его сумме
22. Коэффициент оборачиваемости привлеченного финансового кредита в анализируемом периоде определяется как:
+ 1. отношение общего объема реализованной продукции к средней сумме привлеченного финансового кредита
2.отношение общего объема реализованной продукции к средней сумме привлеченного товарного кредита
3.отношение средней суммы всего капитала к односуточному объему реализованной продукции
23. Период оборота собственного капитала используется в процессе реального инвестирования определяется как:
+ 1. отношение средней суммы собственного капитала (задействованного в формировании операционных активов) к односуточному объему реализации продукции
2.отношение средней суммы привлеченного капитала (задействованного в формировании операционных активов) к односуточному объему реализованной продукции
3.отношение общего объема реализации продукции к средней сумме привлеченного товарного кредита
24. Коэффициент финансирования определяется как:
+ 1. отношение суммы привлеченного предприятием занимаемого капитала к сумме собственного капитала предприятия
2.отношение суммы собственного капитала к общей сумме капитала предприятия
3.отношение общего объема реализованной продукции к средней стоимости всех активов, используемых
25. Коэффициент рентабельности капитала, используемого в процессе реального инвестирования определяется как:
+ 1. отношение прироста чистой прибыли с суммы капитала что инвестировался в активы предприятия к общей сумме капитала, что инвестировался в новые операционные активы
2.отношение общего объема реализованной продукции к средней стоимости всех активов, используемых на предприятии
3.отношение общего объема реализованной продукции к средней стоимости оборотных активов
26. Коэффициент маневренности собственного и долгосрочного занимаемого капитала определяется как:
+ 1. отношение суммы собственного и долгосрочного занимаемого капитала направляется на финансирование оборотных активов к сумме собственного занимаемого капитала
2.отношение суммы всех оборотных активов к сумме всех краткосрочных финансовых обязательств
3.отношение общего объема реализованной продукции к средней стоимости активов предприятия
27. Период оборота собственного капитала используется в процессе реального инвестирования определяется как:
+ 1. отношение средней суммы собственного капитала, задействованного в формировании операционных активов к односуточному объему реализованной продукции
2.отношение средней суммы привлеченного занимаемого капитала к односуточному объему реализованной продукции
3.отношение общего объема реализованной продукции к средней сумме привлеченного финансового кредита
28. Процент — это:
+ 1. сумма дохода от предоставления капитала в долг
2.сумма дохода, начисляемого к основной сумме капитала в каждом интервале
3.поток суммы доходов. что начисляется в каждом периоде и не уплачивается
29. Простой процесс — это:
+ 1. сумма дохода, начисляемого к основной сумме капитала и согласно которой дальнейшие расчеты платежей не осуществляются
2.поток денежных средств по инвестиционной деятельности, который имеет ограниченный период начисления процентов
3.период времени в течение которого осуществляется процесс дисконтирования стоимости денежных средств
30. Сложный процент — это:
+ 1. сумма дохода, начисляемого в каждом интервале, которая не выплачивается, присоединяет к основной сумме капитала
2.поток денежных средств по инвестиционной деятельности, период начисления процентов по которому не ограничен
3.общий период времени в течение которого осуществляется процесс дисконтирования стоимости денежных средств
93. Ставка процента — это:
1.(ВЕРНАЯ) удельный показатель согласно которой в установленные сроки выплачивается сумма процента в расчете на единицу капитала
2.сумма дохода, начисляемого в каждом интервале, которая не выплачивается поток денежных средств в период начисления
94. Ставка процента -это:
1.(ВЕРНАЯ) удельный показатель согласно которой в установленные сроки выплачивается сумма процента в расчете на единицу капитала
2.сумма дохода, начисляемого в каждом интервале, которая не выплачивается поток денежных средств, период начисления процентов по которому не ограничен
95. Аннуитет — это:
1.(ВЕРНАЯ) длительный инвестиционный поток платежей, характеризующийся одинаковым уровнем процентных ставок на протяжении всего периода
2.сумма дохода, начисляемого в каждом интервале, которая не выплачивается показатель согласно которого в установленный срок уплачивается сумма процента в расчете на единицу капитала
96. Будущая стоимость денег — это:
1.(ПРАВИЛЬНАЯ) сумма инвестированных в настоящий момент денежных средств, в которую они превратятся через определенный период времени с учетом определенной ставки процента
2.сумма будущих денежных средств, которые с помощью определенной ставки процента приведенная к данному периоду времени
3.процесс приведения будущей стоимости денег к их стоимости в настоящее время путем исключения суммы дисконта
97. Стоимость денег в настоящее время — это:
1.(ПРАВИЛЬНАЯ) сумма будущих денежных средств, приведенных с учетом ставки процента к настоящему периоду времени
2.сумма инвестированных в настоящий момент денежных средств, в которую они превратятся через определенный период времени с учетом определенной ставки процента
3.процесс приведения будущей стоимости денег к их стоимости в настоящее время путем исключения суммы дисконта
98. Компаудинг — это:
1.(ВЕРНАЯ) наращение стоимости
2.дисконтирование стоимости
3.аннуитет
testdoc.ru
Инвестиционная стратегия
2. Цикл реального
инвестиционного проекта 12
3. Функции
инвестиционного менеджмента фирмы 16
Заключение 20
Список
используемой литературы 21
Введение
Понятие «инвестиция» от латинского investire –
облачать.
С
течением времени слово инвестиция пополнилось целым рядом новых значений
и стало употребляться в различных сферах
деятельности, а одно из значений (долгосрочное
вложение капитала в какое-либо предприятие)
в силу массовости стало общеупотребительным.
Именно с таким значением (уже как с основным)
это слово и появилось в нашем языке, определяя
смысл и значение остальных однокоренных
слов.
Традиционно
слово инвестор толкуется как вкладчик,
а инвестирования – как помещение,
вкладывание капитала.
Деятельность
любой фирмы, так или иначе, связана
с вложением ресурсов в различные
виды активов, приобретение которых
необходимо для осуществления основной
деятельности этой фирмы. Но для увеличения
уровня рентабельности фирма также может
вкладывать временно свободные ресурсы
в различные виды активов, приносящих
доход, но не участвующих в основной деятельности.
Такая деятельность фирмы называется
инвестиционной, а управление такой деятельностью
– инвестиционным менеджментом фирмы.
Процесс
инвестирования играет важную роль в
экономике любой страны. Инвестирование
в значительной степени определяет
экономический рост государства, занятость
населения и составляет существенный
элемент базы, на которой основывается
экономическое развитие общества. Поэтому
проблема, связанная с эффективным осуществлением
инвестирования заслуживает серьезного
внимания, особенно в настоящее время
– время укрупнения субъектов рыночных
отношений и передела собственности.
В
современных условиях, когда экономические
процессы протекают в соответствии с законами
рыночных отношений, необходимо стимулировать
и регулировать инвестиционные процессы
с помощью привлечения инвестиционных
ресурсов и формирования благоприятного
инвестиционного климата.
Инвестиции
представляют собой применение финансовых
ресурсов в форме долгосрочных вложений
капитала (капиталовложений). Осуществление
инвестиций – протяженный во времени
процесс. Поэтому для наиболее эффективного
применения финансовых ресурсов предприятие
разрабатывает и реализует свою инвестиционную
стратегию. Инвестиционная стратегия
представляет собой общее руководство
для действий и принятия решений, которое
облегчает достижение целей предприятия.
Именно с помощью инвестиционной стратегии
предприятие реализует свои возможности
к предвосхищению долгосрочных тенденций
экономического развития и адаптации
к ним.
1. Общее
понятие. Факторы влияющие
на формирование инвестиционной
стратегии
Понятие
инвестиционной стратегии в условиях
экономики, как правило, относится
к управлению двумя видами инвестиций:
реальными и финансовыми.
По
отношению к совокупности этих двух
видов инвестиций на предприятиях применяют
понятие инвестиционного портфеля,
а инвестиции в различные виды
активов, связанные единой инвестиционной
политикой называются портфельными
инвестициями.
В
качестве отдачи от инвестиций принимается
разность между доходами в течение
срока использования инвестиционных
ресурсов и затратами денежных средств
в том же периоде (издержки производства,
налоги и т. д.). Эта разность в итоге
является либо прибылью, либо убытками.
Все
предприятия в той или иной
степени связаны с инвестиционной
деятельностью. Принятие решений по
инвестированию осложняется следующими
факторами:
- множественность
доступных вариантов вложения капитала;
- ограниченность
финансовых ресурсов для инвестирования;
- риск, связанный
с принятием того или иного решения по
инвестированию, и т. п.
Осуществление
инвестиционной деятельности невозможно
без стратегического подхода. Модель
инвестиционной стратегии должна включать
элементы общего стратегического подхода
и инвестиционного проектирования.
Необходимость
исследования внешней среды обусловлена
основными принципами стратегического
подхода. Поэтому параметры внешней
среды рассматриваются с точки
зрения инструментов влияния на деятельность
предприятия и с позиций субъектов воздействия
на него. В первом случае параметры внешней
среды включают в себя среду — экономическую,
социальную, технологическую, правовую,
государственно-политическую.
Во
втором случае внешнее окружение предприятия
состоит из потребителей, поставщиков
ресурсов, конкурентов, общественных организаций,
проводников государственной экономической
политики.
Благоприятные
факторы и угрозы со стороны внешней
среды влияют на формирование инвестиционной
стратегии.
В
первую очередь, внешняя среда влияет
на систему целей предприятия. Предприятие
должно инвестировать в те проекты,
которые будут решать проблему замкнутости
рыночного и стратегического
пространства предприятия. Решение
этой проблемы находится в области
сбалансирования рыночной и ресурсной
ориентации предприятия. Следующий шаг
в формировании инвестиционной стратегии
— выбор содержания, который состоит из
выбора направлений инвестиционной деятельности
и источников инвестирования.
Приоритетными
направлениями инвестирования на предприятии
можно выделить:
- развитие интегральных
связей по территориальному и/или отраслевому
признаку;
- развитие маркетинговой
сети предприятия;
- повышение таких
видов потенциала, как кадровый, финансовый,
организационный;
- реализация энергосберегающих
технологий.
Причины, обуславливающие
необходимость инвестиций, могут
быть различны, однако в целом их
можно объединить по принципу получения
дохода:
- реальные инвестиции
проводятся с целью снижения затрат на
производство продукции;
- финансовые инвестиции
проводятся с целью получения дохода от
курсовой разницы или дивидендов.
- обновление имеющейся
материально-технической базы,
- наращивание объемов
производственной деятельности,
- освоение новых
видов деятельности.
Важным
также является вопрос о размере
предполагаемых инвестиций, так как
от этого зависит глубина аналитической
проработки экономической стороны
инвестиционного проекта, которая
предшествует принятию решения.
Основными источниками
инвестирования могут быть следующие:
- средства регионального
фонда развития;
- средства, привлеченные
за счет закрытого размещения акций;
- средства, получаемые
в процессе создания стратегических альянсов
с другими предприятиями;
- налоговые льготы.
На
многих предприятиях и во многих фирмах
становится обыденной практика дифференциации
права принятия решений инвестиционного
характера, т. е. ограничивается максимальная
величина инвестиций, в рамках которой
тот или иной руководитель может принимать
самостоятельные решения.
Нередко
решения должны приниматься в
условиях, когда имеется ряд альтернативных
или взаимно независимых инвестиционных
возможностей. В этом случае необходимо
сделать выбор одного или нескольких
вариантов, основываясь на принятых
критериях. Очевидно, что таких критериев
может быть несколько, а вероятность того,
что какой-то вариант будет предпочтительнее
других, как правило, меньше единицы.
Степень
ответственности за принятие инвестиционного
проекта в рамках того или иного
направления различна. Так, если речь
идет о замещении имеющихся производственных
мощностей, решение может быть принято
достаточно безболезненно, поскольку
руководство предприятия ясно представляет
себе, в каком объеме и с какими характеристиками
необходимы новые основные средства. Задача
осложняется, если речь идет об инвестициях,
связанных с расширением основной деятельности,
поскольку в этом случае необходимо учесть
ряд новых факторов: возможность изменения
положения фирмы на рынке товаров, доступность
дополнительных объемов материальных,
трудовых и финансовых ресурсов, возможность
освоения новых рынков и т.д.
В
условиях рыночной экономики возможностей
для инвестирования довольно много.
Вместе с тем любое предприятие
имеет ограниченные свободные финансовые
ресурсы, доступные для инвестирования.
Поэтому возникает задача оптимизации
инвестиционного портфеля.
Здесь
весьма существенен фактор риска. Инвестиционная
деятельность всегда осуществляется в
условиях неопределенности, степень
которой может значительно варьироваться.
Например, в момент приобретения новых
основных средств никогда нельзя точно
предсказать экономический эффект этой
операции. Поэтому нередко решения принимаются
на интуитивной логической основе, но,
тем не менее, они должны подкрепляться
экономическим расчетом.
Определение
инвестиционных возможностей является
отправной точкой для деятельности, связанной
с инвестированием. В конечном счете, это
может стать началом мобилизации инвестиционных
средств.
Рисковые
инвестиции или «венчурный капитал»
– это термин, применяемый для обозначения
капиталовложений, для которых трудно
оценить возможные доходы и сопутствующие
расходы. Венчурный капитал представляет
собой инвестиции в новые сферы деятельности,
связанные с большим риском. Как правило,
венчурный капитал инвестируется в несвязанные
между собой проекты в расчете на быструю
окупаемость вложенных средств.
За
рубежом обычно создаются специализированные
независимые венчурные компании,
которые привлекают средства других
инвесторов и создают фонд венчурного
капитала. Этот фонд имеет непостоянный
объем средств, который управляющая фондом
венчурная фирма распределяет по проектам.
Поскольку всем вкладчикам заранее известно,
что вложение капитала представляет собой
венчурный, то есть высокорискованный,
характер, то целью венчурной фирмы является
получение максимального дохода практически
без учета риска. Единственным способом
снижения риска является высокая диверсификация
проектов.
Специализируясь
на финансировании проектов с высокой
степенью неопределенности результата,
венчурные фирмы предоставляют инвестиции
не в форме ссуды, а в обмен на большую
часть акционерного капитала создаваемого
венчурного предприятия. Это позволяет
жестко контролировать финансовое состояние,
финансовые результаты, а также ход работ
по венчурному проекту.
Таким
образом, основная задача инвестиций –
принести инвестору предполагаемый доход
при минимальном уровне риска, который
достигается путем формирования диверсифицированного
инвестиционного портфеля.
Учет
риска инвестора осуществляется
путем увеличения используемого банками
реальной процентной ставки на величину
«премии за риск».
Стратегическое
планирование инвестиций следует рассматривать
как механизм разработки инвестиционной
стратегии предприятия. Под стратегическим
планом понимается развернутый во времени,
сбалансированный по ресурсам перечень
стратегических мероприятий. Алгоритм
формирования инвестиционной стратегии
может быть представлен в виде следующей
схемы (рис.1).
Рис.
1
Под
инвестиционной стратегией предприятия
понимается определение в стратегическом
плане основных инвестиционных целей
и задач предприятия и утверждение
курса действия и распределения
ресурсов, необходимых для достижения
этих стратегических целей.
Экономическая
постановка задачи разработки инвестиционной
стратегии промышленного предприятия
понимается как выбор наиболее эффективного
распределения стратегических ресурсов,
обеспечивающих достижение стратегических
целей предприятия. Применительно к такой
постановке задачи должны рассматриваться
основные особенности инвестиционной
стратегии — учет основных параметров
внешней среды и учет потенциальных внутренних
сильных и слабых сторон промышленного
предприятия.
2. Цикл
реального инвестиционного
проекта.
Разработка
и реализация реального инвестиционного
проекта – от первоначальной идеи
до эксплуатации предприятия – может
быть представлена в виде цикла, состоящего
из трех отдельных фаз: предынвестиционной,
инвестиционной и эксплуатационной (рис.
4). Каждая из этих фаз, в свою очередь, подразделяется
на стадии, и некоторые из них содержат
такие важные виды деятельности, как консультирование,
проектирование и производство.
stud24.ru
Факторы, влияющие на формирование инвестиционной стратегии — Мегаобучалка
Очень многие факторы оказывают влияние на определение стратегии организации. Взаимодействие этих факторов носит специфический характер для каждой отрасли и организации и всегда изменяется во времени. Поэтому руководителю необходимо оценивать совокупность внешних и внутренних факторов, прежде чем начать выбор стратегии.
Инвестиционная стратегия — это комплекс долгосрочных целей в области капиталовложений и вложений в финансовые активы, развития производства, формирования оптимальной структуры инвестирования, а также совокупность действий по их достижению.
В общем виде инвестиционная стратегия реализуется в разработке плана и программы его осуществления на данном этапе развития предприятия; формируется с учетом существующих источников и форм инвестирования, их доступности и потенциальной эффективности использования.
Предпосылкой формирования инвестиционной стратегии является общая стратегия экономического развития предприятия, по отношению к которой инвестиционная стратегия носит подчиненный характер. Управление инвестиционной деятельностью, т.е. инвестиционная стратегия получает свою дальнейшую конкретизацию в процессе тактического управления этой деятельностью путем формирования инвестиционного портфеля компании. Это формирование относится к среднесрочному управлению, которое завершается реализацией отдельных инвестиционных программ и проектов. Таким образом, разработка инвестиционной стратегии является только первым этапом процесса управления инвестиционной деятельностью компании.
Формирование инвестиционной стратегии компании (фирмы) является довольно сложным творческим процессом, требующим высокой квалификации исполнителей. Прежде всего, формирование стратегии базируется на прогнозировании отдельных условий осуществления инвестиционной деятельности (инвестиционного климата) и конъюнктуры инвестиционного рынка как в целом, так и в разрезе отдельных его сегментов. Кроме того, она требует периодической корректировки с учетом меняющихся внешних условий и новых возможностей роста компании.
Инвестиционная стратегия предусматривает достижение следующих целей:
— максимизации прибыли от инвестиционной деятельности;
— минимизации инвестиционных рисков.
Для этого необходимо организовать:
-исследование внешней инвестиционной среды и прогнозирование конъюнктуры инвестиционного рынка;
-технические и маркетинговые исследования;
-поиск новых, более прибыльных инвестиционных возможностей;
-оценку привлекательности инвестиционных проектов и финансовых инструментов с отбором наиболее эффективных из них;
-разработку капитального бюджета;
-формирование оптимальной структуры инвестирования.
На выбор инвестиционной стратегии предприятия влияет ряд факторов.
К их числу относится общая стратегия развития, которая предусматривает:
— проникновение на рынок и обеспечение выживаемости при убыточной деятельности;
— закрепление на рынке и обеспечение безубыточной деятельности;
— существенное расширение своего сегмента на рынке и обеспечение систематического роста прибыли с выходом на оптимальный уровень;
— диверсификация деятельности и обеспечение сбалансированного роста прибыли на оптимальном уровне;
— обеспечение стабилизации объема деятельности путем сохранения прибыли, платежеспособности и финансовой устойчивости;
— обновление форм и направлений деятельности, обеспечение условий для высоких темпов роста прибыли.
Финансовое состояние предприятия, уровень технического и организационного потенциала определяют его конкурентную позицию на рынке сбыта. Наличие временно свободных денежных средств позволяет предприятию инвестировать их в долго-, средне- и краткосрочные реальные и финансовые активы.
Принятие решений по инвестированию осложняется следующими факторами:
— множественность доступных вариантов вложения капитала;
— ограниченность финансовых ресурсов для инвестирования;
— риск, связанный с принятием того или иного решения по инвестированию, и т. п.
Осуществление инвестиционной деятельности невозможно без стратегического подхода. Модель инвестиционной стратегии должна включать элементы общего стратегического подхода и инвестиционного проектирования.
Необходимость исследования внешней среды обусловлена основными принципами стратегического подхода. Поэтому параметры внешней среды рассматриваются с точки зрения инструментов влияния на деятельность предприятия и с позиций субъектов воздействия на него.
Благоприятные факторы и угрозы со стороны внешней среды влияют на формирование инвестиционной стратегии.
В первую очередь, внешняя среда влияет на систему целей предприятия. Предприятие должно инвестировать в те проекты, которые будут решать проблему замкнутости рыночного и стратегического пространства предприятия. Решение этой проблемы находится в области сбалансирования рыночной и ресурсной ориентации предприятия. Следующий шаг в формировании инвестиционной стратегии — выбор содержания, который состоит из выбора направлений инвестиционной деятельности и источников инвестирования.
Приоритетными направлениями инвестирования на предприятии можно выделить:
— развитие интегральных связей по территориальному и/или отраслевому признаку;
— развитие маркетинговой сети предприятия;
— повышение таких видов потенциала, как кадровый, финансовый, организационный;
— реализация энергосберегающих технологий.
Причины, обуславливающие необходимость инвестиций, могут быть различны, однако в целом их можно объединить по принципу получения дохода:
— реальные инвестиции проводятся с целью снижения затрат на производство продукции;
— финансовые инвестиции проводятся с целью получения дохода от курсовой разницы или дивидендов.
Важным также является вопрос о размере предполагаемых инвестиций, так как от этого зависит глубина аналитической проработки экономической стороны инвестиционного проекта, которая предшествует принятию решения.
На многих предприятиях и во многих фирмах становится обыденной практика дифференциации права принятия решений инвестиционного характера, т. е. ограничивается максимальная величина инвестиций, в рамках которой тот или иной руководитель может принимать самостоятельные решения.
В условиях рыночной экономики возможностей для инвестирования довольно много. Вместе с тем любое предприятие имеет ограниченные свободные финансовые ресурсы, доступные для инвестирования. Поэтому возникает задача оптимизации инвестиционного портфеля.
Здесь весьма существенен фактор риска. Инвестиционная деятельность всегда осуществляется в условиях неопределенности, степень которой может значительно варьироваться. Поэтому нередко решения принимаются на интуитивной логической основе, но, тем не менее, они должны подкрепляться экономическим расчетом.
Рисковые инвестиции или «венчурный капитал» – это термин, применяемый для обозначения капиталовложений, для которых трудно оценить возможные доходы и сопутствующие расходы. Венчурный капитал представляет собой инвестиции в новые сферы деятельности, связанные с большим риском. Как правило, венчурный капитал инвестируется в несвязанные между собой проекты в расчете на быструю окупаемость вложенных средств.
Специализируясь на финансировании проектов с высокой степенью неопределенности результата, венчурные фирмы предоставляют инвестиции не в форме ссуды, а в обмен на большую часть акционерного капитала создаваемого венчурного предприятия. Это позволяет жестко контролировать финансовое состояние, финансовые результаты, а также ход работ по венчурному проекту.
Таким образом, основная задача инвестиций – принести инвестору предполагаемый доход при минимальном уровне риска, который достигается путем формирования диверсифицированного инвестиционного портфеля.
Учет риска инвестора осуществляется путем увеличения используемого банками реальной процентной ставки на величину «премии за риск».
Стратегическое планирование инвестиций следует рассматривать как механизм разработки инвестиционной стратегии предприятия. Под стратегическим планом понимается развернутый во времени, сбалансированный по ресурсам перечень стратегических мероприятий.
Под инвестиционной стратегией предприятия понимается определение в стратегическом плане основных инвестиционных целей и задач предприятия и утверждение курса действия и распределения ресурсов, необходимых для достижения этих стратегических целей.
Экономическая постановка задачи разработки инвестиционной стратегии промышленного предприятия понимается как выбор наиболее эффективного распределения стратегических ресурсов, обеспечивающих достижение стратегических целей предприятия. Применительно к такой постановке задачи должны рассматриваться основные особенности инвестиционной стратегии — учет основных параметров внешней среды и учет потенциальных внутренних сильных и слабых сторон промышленного предприятия.
Таким образом, процесс привлечения иностранного капитала имеет существенное значение для всех стран, в том числе и Российской Федерации, поскольку носит универсальный характер. Привлечение иностранных инвестиций в российскую экономику приобрело в настоящее время особое значение, а формирование благоприятного инвестиционного климата в стране обусловливает необходимость кардинальных преобразований в инвестиционной политике, проводимой государством.
megaobuchalka.ru



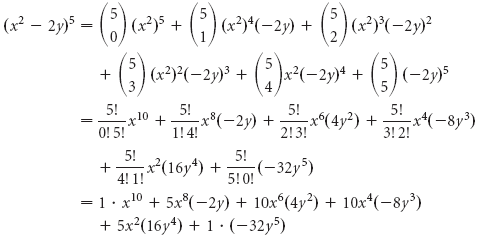
 и называются биномиальными коэффициентами . Таблица биномиальных коэффициентов для целых значений и
и называются биномиальными коэффициентами . Таблица биномиальных коэффициентов для целых значений и  в пределах имеет вид:
в пределах имеет вид:
 эти формулы всегда дают однозначный ответ в форме конечного числа. Биномы целых положительных степеней были известны очень давно, и Ньютон не сказал бы ничего нового в этом отношении, если бы он не совершил исключительно оригинальный по тем временам шаг. Этот шаг состоял в переходе от целых значений числа в биномах к дробным и отрицательным значениям. Хотя правомерность такого перехода не была обоснована строго математически, она дала большой толчок развитию теории числовых и функциональных рядов. Спустя 150 лет Н. Абель доказал правомерность такого перехода строго математически.
эти формулы всегда дают однозначный ответ в форме конечного числа. Биномы целых положительных степеней были известны очень давно, и Ньютон не сказал бы ничего нового в этом отношении, если бы он не совершил исключительно оригинальный по тем временам шаг. Этот шаг состоял в переходе от целых значений числа в биномах к дробным и отрицательным значениям. Хотя правомерность такого перехода не была обоснована строго математически, она дала большой толчок развитию теории числовых и функциональных рядов. Спустя 150 лет Н. Абель доказал правомерность такого перехода строго математически. <1.
<1. и за пределами этого радиуса не воспроизводят исходную функцию, хотя она существует за этими пределами вплоть до и до .
и за пределами этого радиуса не воспроизводят исходную функцию, хотя она существует за этими пределами вплоть до и до .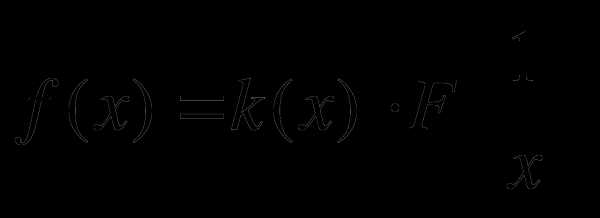 . Такая запись ориентирует на преобразование исходной функции к произведению двух функций
. Такая запись ориентирует на преобразование исходной функции к произведению двух функций 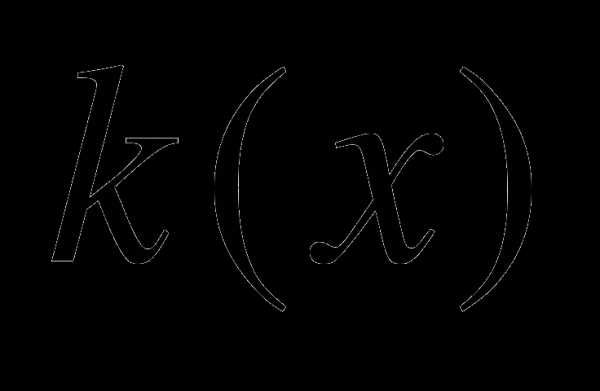 и
и  . Последняя функция
. Последняя функция 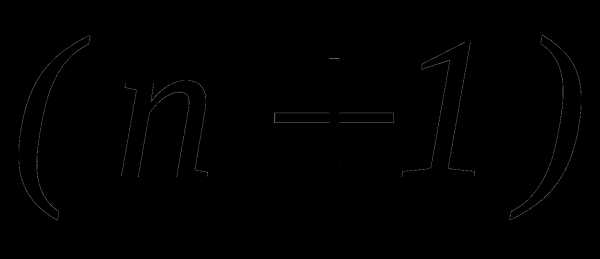
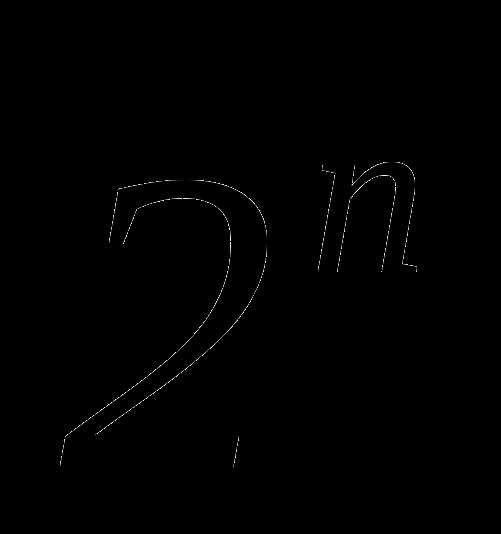
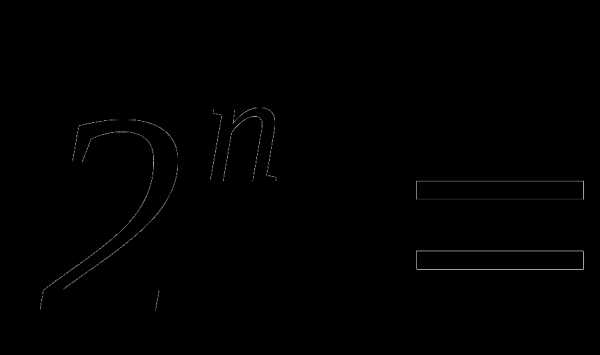
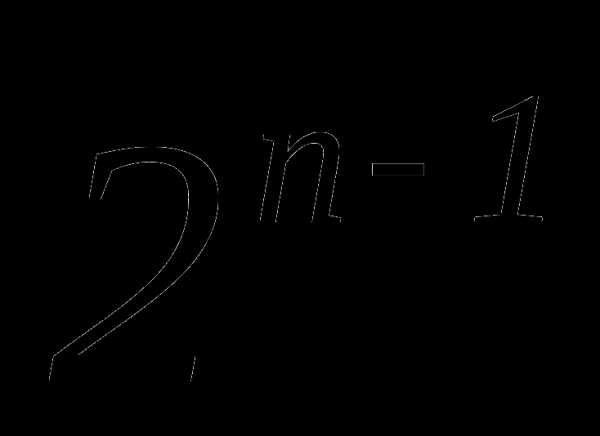
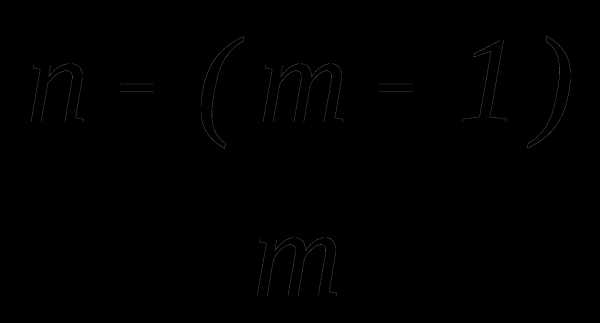
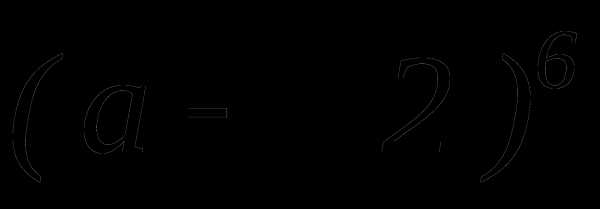
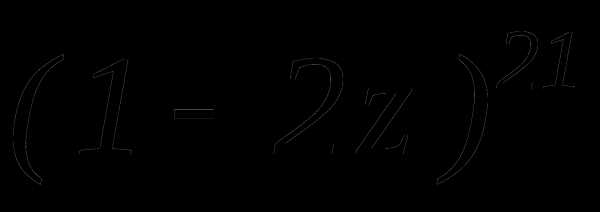
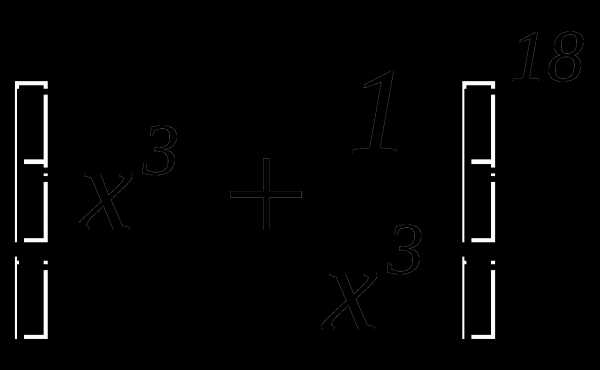 найти член разложения, не содержащий х
найти член разложения, не содержащий х
 верно неравенство Бернулли:
верно неравенство Бернулли:
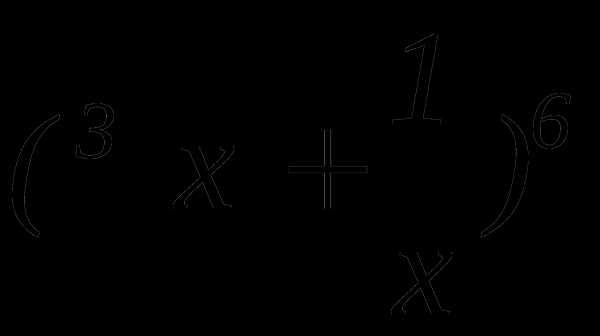 ,
не содержащего х.
,
не содержащего х.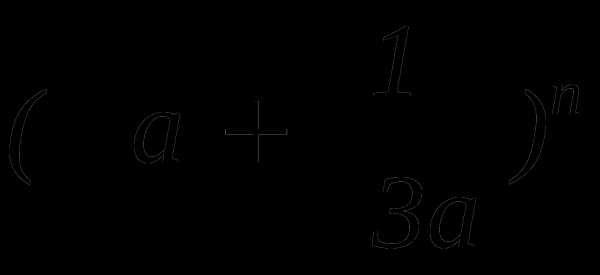 .
. ,
если биномиальный коэффициент третьего
члена на 9 больше биномиального
коэффициента второго члена.
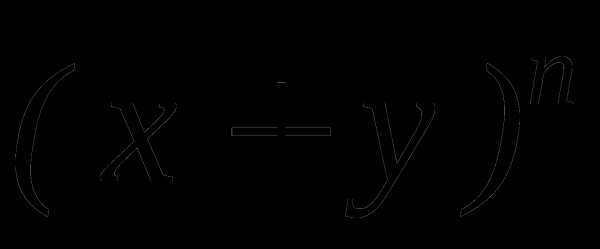
,
если биномиальный коэффициент третьего
члена на 9 больше биномиального
коэффициента второго члена.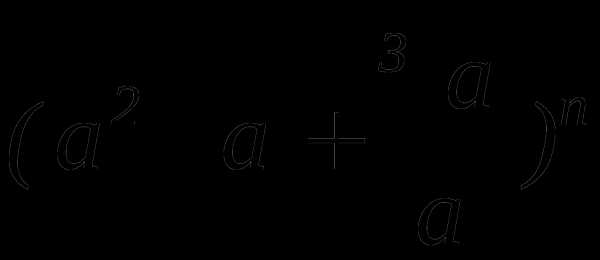 ,
если биномиальный коэффициент третьего
члена равен 36.
,
если биномиальный коэффициент третьего
члена равен 36. .
.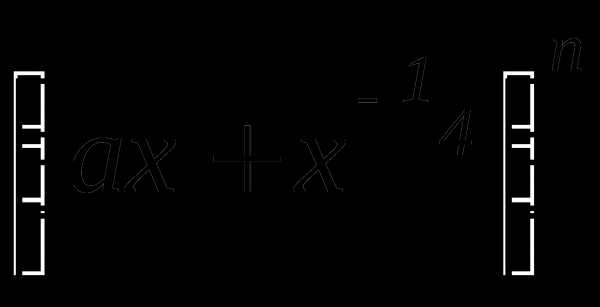 равна 512. Найти слагаемое, не содержащее х.
равна 512. Найти слагаемое, не содержащее х.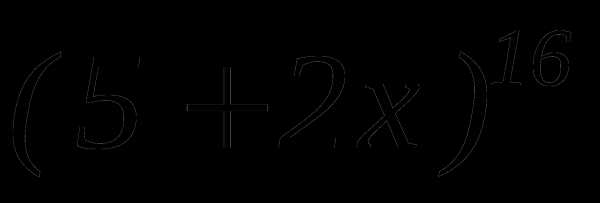 больше двух соседних с ним слагаемых?
больше двух соседних с ним слагаемых? чтобы отношение четвертого слагаемого
разложения к третьему было равно
чтобы отношение четвертого слагаемого
разложения к третьему было равно  ?
?

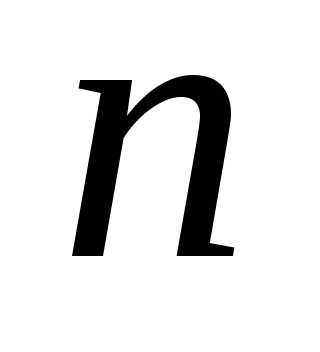 элементов. Любое подмножество
элементов. Любое подмножество (включая и пустое подмножество), содержащее
(включая и пустое подмножество), содержащее элементов, называетсясочетаниемпо
элементов, называетсясочетаниемпо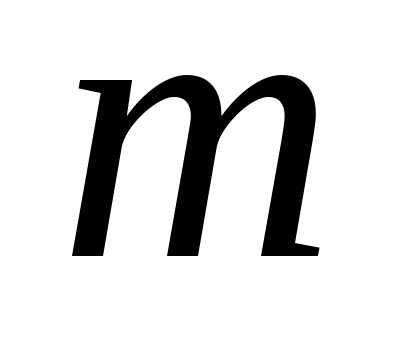 элементов из
элементов из 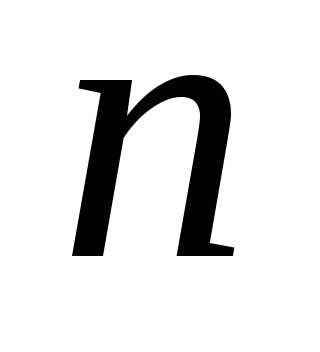 (или комбинацией по
(или комбинацией по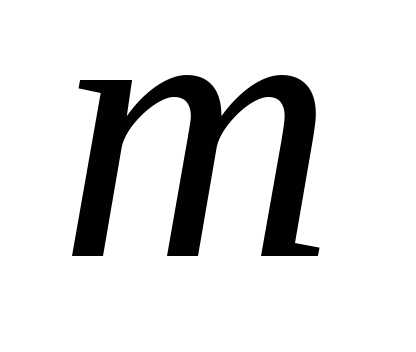 элементов из
элементов из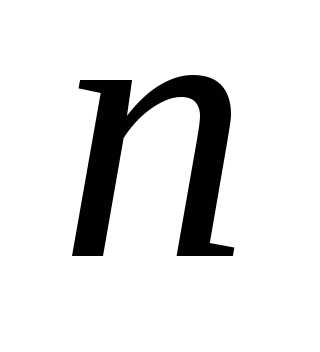 ),
при этом, разумеется,,
т.е.
),
при этом, разумеется,,
т.е.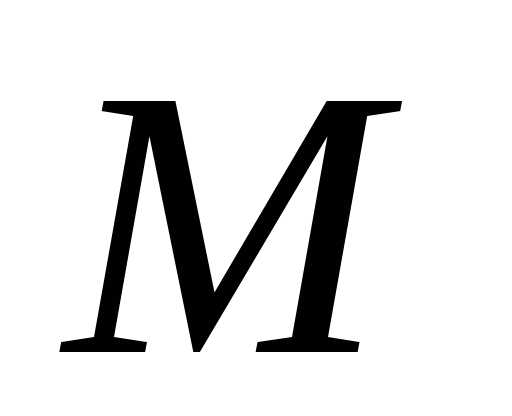 заданное
множество, состоящее из
заданное
множество, состоящее из элементов,
элементов, —
какое либо подмножество
—
какое либо подмножество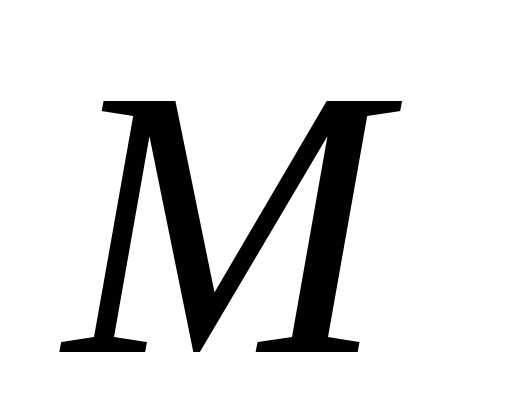 ,
содержащее
,
содержащее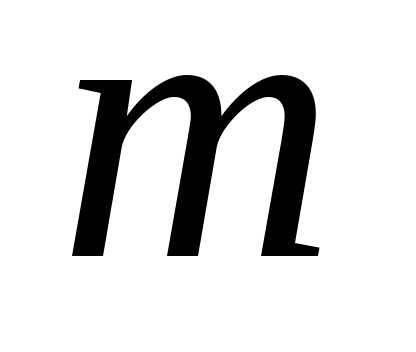 элементов. Составим всевозможные
перестановки из элементов
элементов. Составим всевозможные
перестановки из элементов ,
получим
,
получим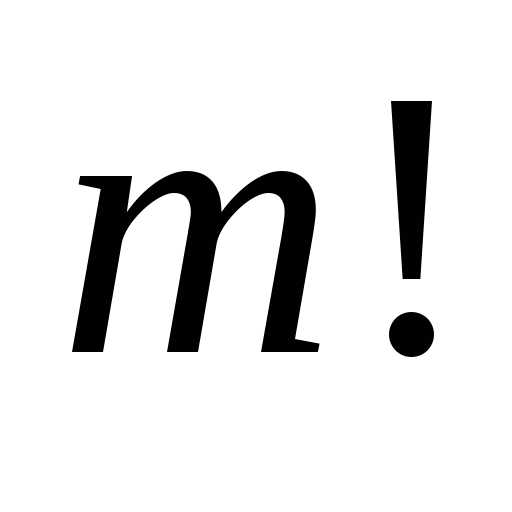 различных строк длиной
различных строк длиной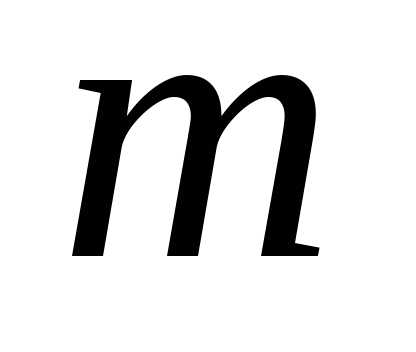 .
Если указанную операцию произвести с
каждым
.
Если указанную операцию произвести с
каждым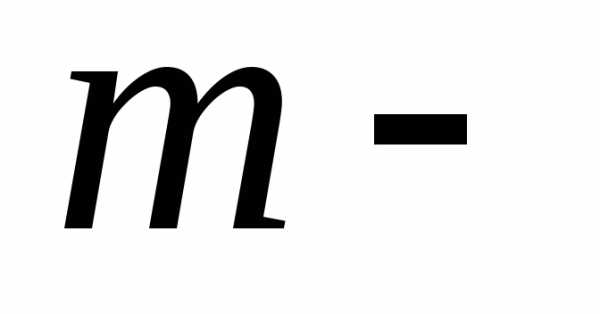 элементным
подмножеством множества
элементным
подмножеством множества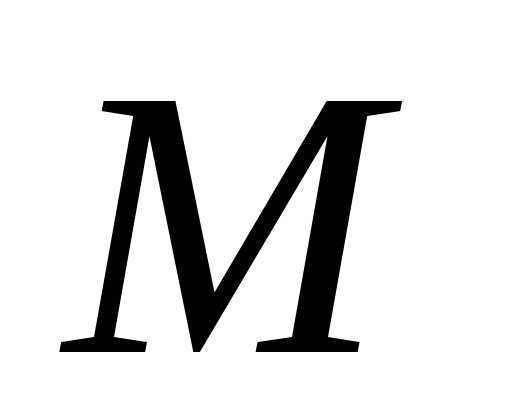 ,
то получим всего
,
то получим всего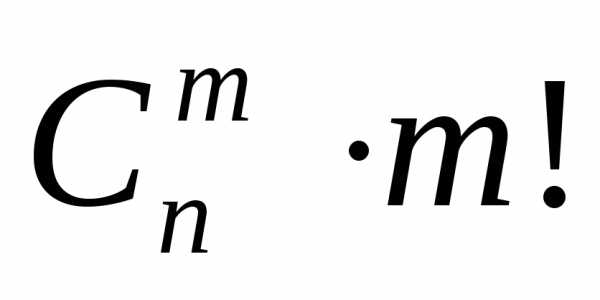 различных строк длиной
различных строк длиной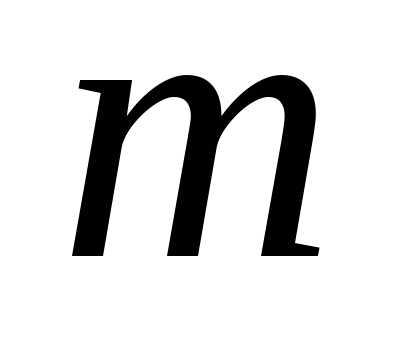 .
Естественно, таким способом должны
получиться без исключения все строки
.
Естественно, таким способом должны
получиться без исключения все строки без
повторений, которые можно составить из
элементов множества
без
повторений, которые можно составить из
элементов множества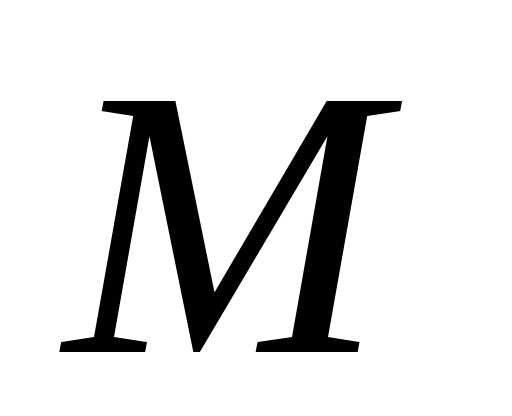 .
Поскольку, по теореме 1, число таких
строк
.
Поскольку, по теореме 1, число таких
строк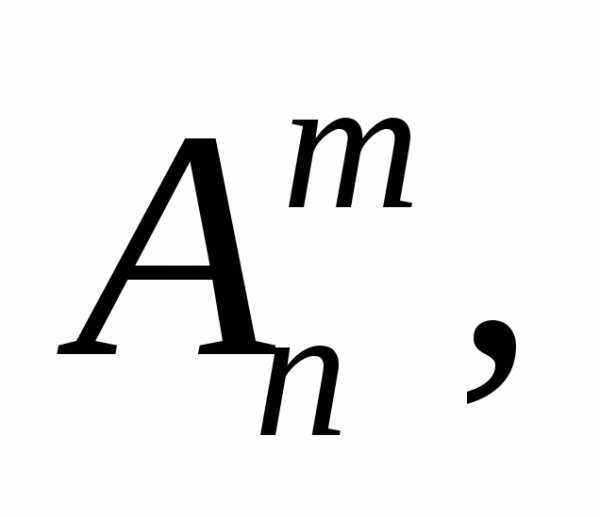 то имеем равенство
то имеем равенство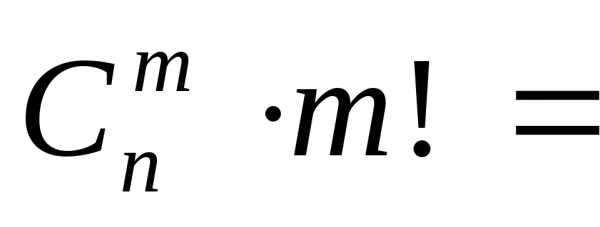
 ,
из которого следует доказательство
теоремы.Подчеркнем, что
числа размещений, перестановок и
сочетаний связаны равенствами
,
из которого следует доказательство
теоремы.Подчеркнем, что
числа размещений, перестановок и
сочетаний связаны равенствами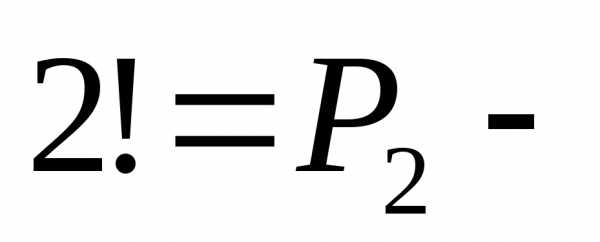 число
перестановок). Следовательно, общее
число партий (пар) будет в 2! меньше, чем
число размещений.
Поэтому, общее число партий равно.
число
перестановок). Следовательно, общее
число партий (пар) будет в 2! меньше, чем
число размещений.
Поэтому, общее число партий равно.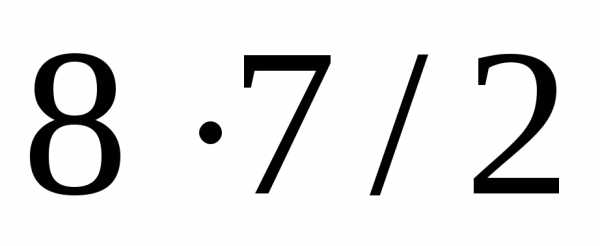 .
. и
и такие величины, для которых имеет место
равенство.
Из школьного курса известны алгебраические
тождества:
такие величины, для которых имеет место
равенство.
Из школьного курса известны алгебраические
тождества: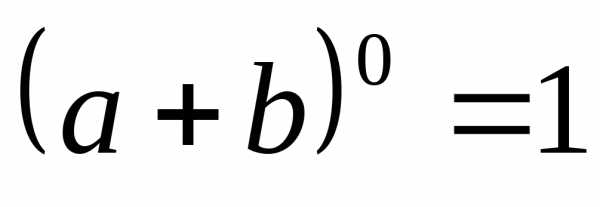 ,
,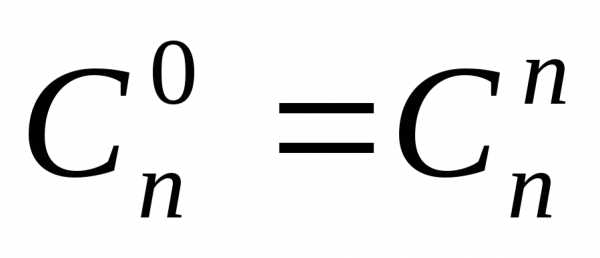 =1.
Неотрицательные целые числа
=1.
Неотрицательные целые числа (обычно называют их биномиальными
коэффициентами) определены равенствами:
(обычно называют их биномиальными
коэффициентами) определены равенствами: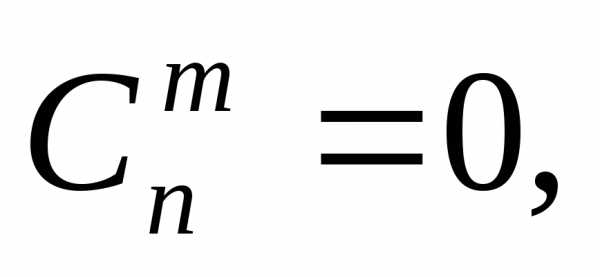 при остальных значениях
при остальных значениях .
Напомним, что принято 0!=1.
.
Напомним, что принято 0!=1.
 содержится
содержится слагаемых.
слагаемых. убывает отnдо 0,
напротив, показатель степени
убывает отnдо 0,
напротив, показатель степени возрастает от 0 до n,
в любом случае сумма показателей
степени величин (параметров)
возрастает от 0 до n,
в любом случае сумма показателей
степени величин (параметров) и
и равнаn – показателю
степени бинома.
равнаn – показателю
степени бинома.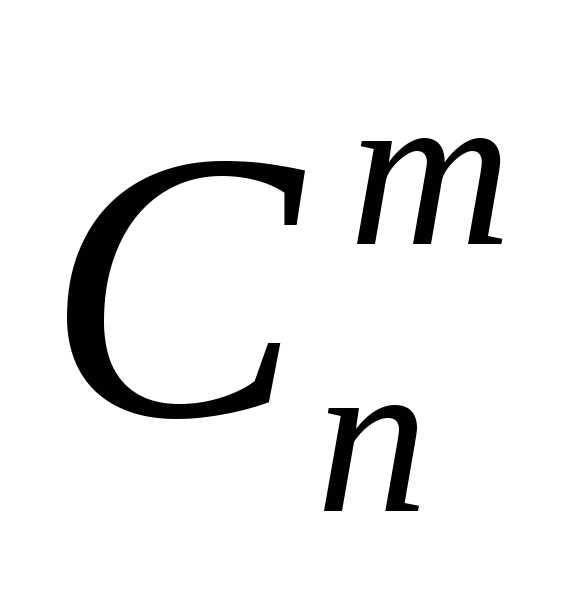 верно равенство
верно равенство ,
т.е. верна формула
,
т.е. верна формула ,
получим равенство
,
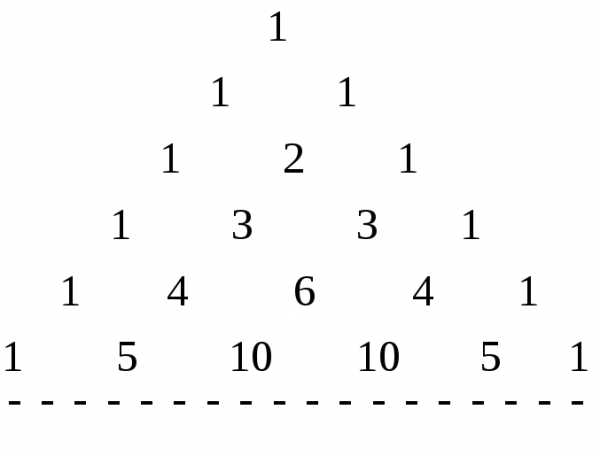
получим равенство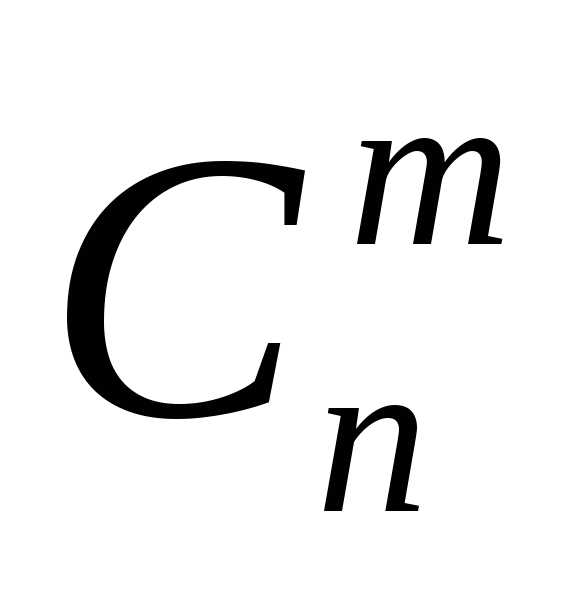 могут быть вычислены с помощью так
называемого «треугольника Паскаля»
могут быть вычислены с помощью так
называемого «треугольника Паскаля»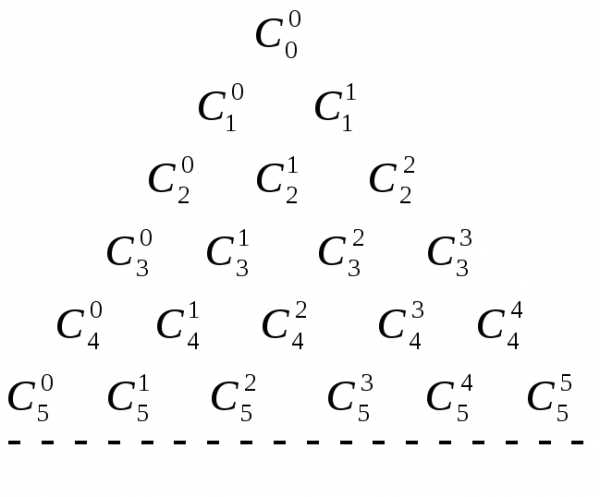
 )
– ое слагаемое
)
– ое слагаемое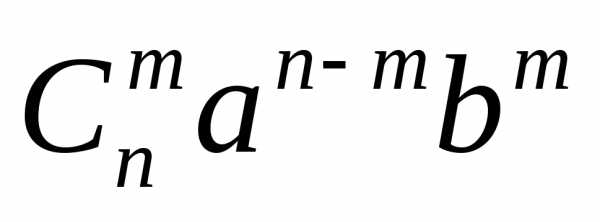 считать
считать  – им членом разложения, и обозначается:
– им членом разложения, и обозначается: найти
шестое слагаемое.
найти
шестое слагаемое.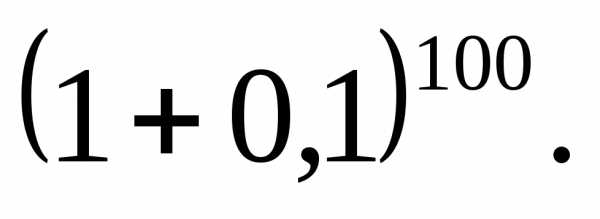
 выполняется неравенства:
выполняется неравенства: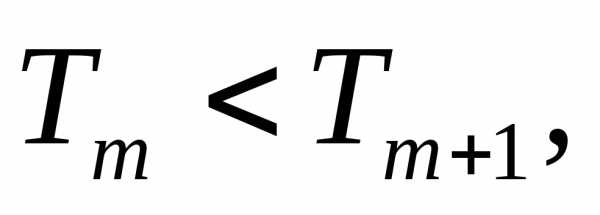
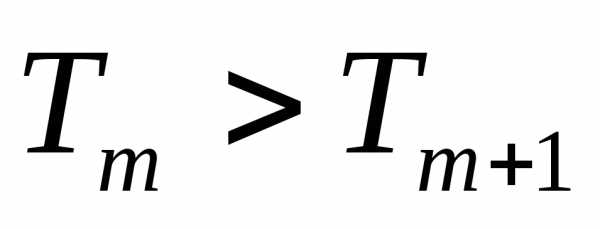 .
.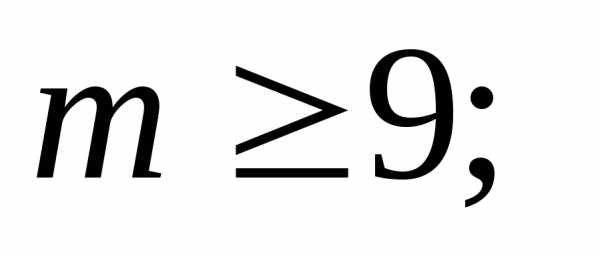 коэффициенты убывают. Значит, для номеранаибольший
член разложения бинома и он же будетдесятым слагаемым
коэффициенты убывают. Значит, для номеранаибольший
член разложения бинома и он же будетдесятым слагаемым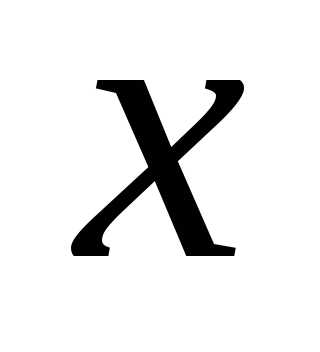 (т.е. найти слагаемое содержащее
(т.е. найти слагаемое содержащее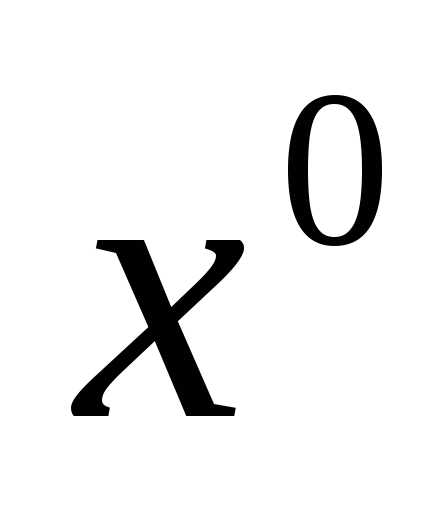 ).
). ,
после несложных упрощений получим:
,
после несложных упрощений получим: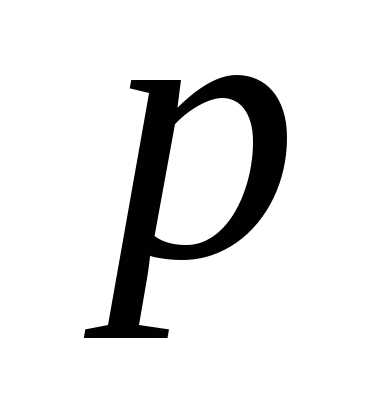 биномиальные
коэффициенты
биномиальные
коэффициенты  делятся
на число
.
делятся
на число
. ,
еслилюбое
нечётное простое число..
,
еслилюбое
нечётное простое число.. 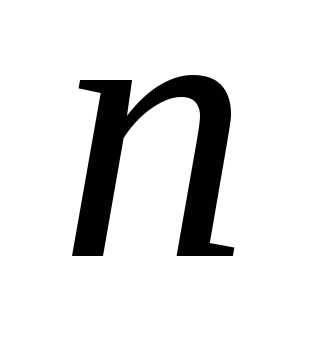 ,
определим классическую функцию Мебиуса
,
определим классическую функцию Мебиуса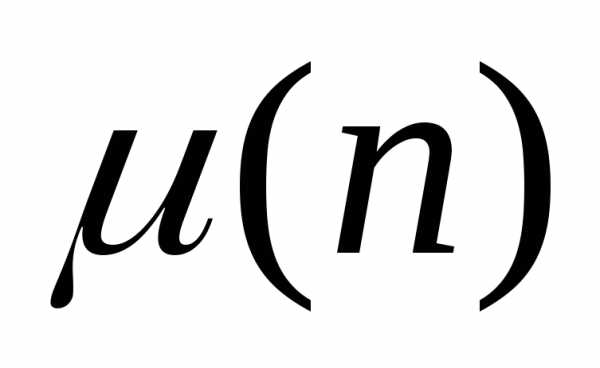 с помощью комбинаторных коэффициентов
с помощью комбинаторных коэффициентов равенством:
равенством:

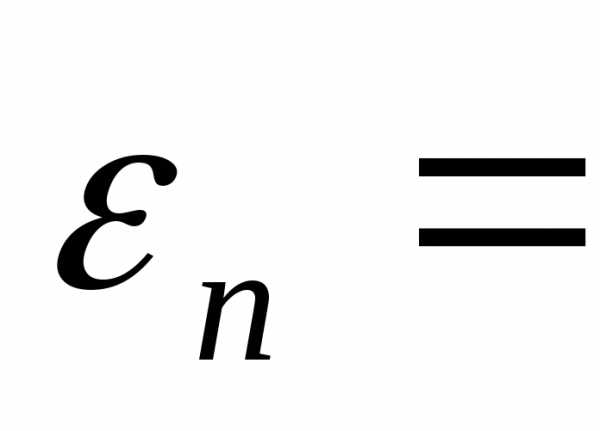
 (свойство ортогональности)
(свойство ортогональности) .
.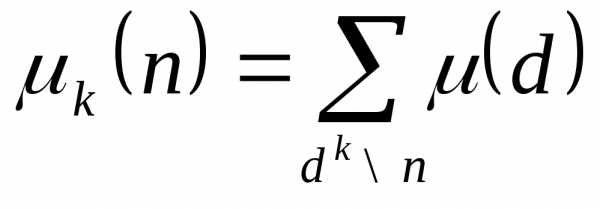 ,
, на
на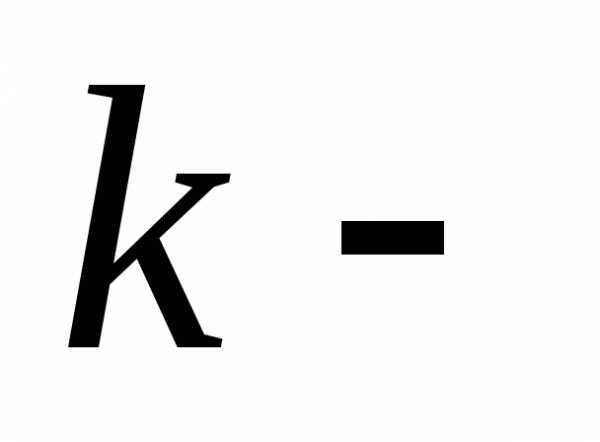 тую степень числа,
а также других арифметических функций,
связанные с функцией Мебиуса). Подробные
сведения о функции Мебиуса и её свойства
можно найти в учебниках по теории чисел
[3;4].
тую степень числа,
а также других арифметических функций,
связанные с функцией Мебиуса). Подробные
сведения о функции Мебиуса и её свойства
можно найти в учебниках по теории чисел
[3;4].  .
Состав строки. Размещение
данного состава. Рассмотрим
наборы (строки)
и.
Очевидно, что они различны, но имеют
один и тот же «состав»
— в каждую из них входят три буквы
.
Состав строки. Размещение
данного состава. Рассмотрим
наборы (строки)
и.
Очевидно, что они различны, но имеют
один и тот же «состав»
— в каждую из них входят три буквы  и две буквы
и две буквы .
Далее, уточним понятиесостава
строки. Пусть
некоторое
.
Далее, уточним понятиесостава
строки. Пусть
некоторое  членное
множество,
членное
множество, 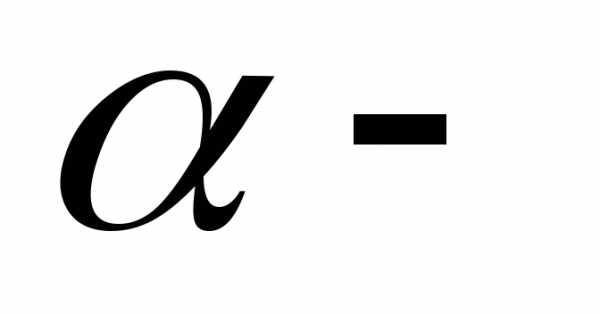 строка длиной
строка длиной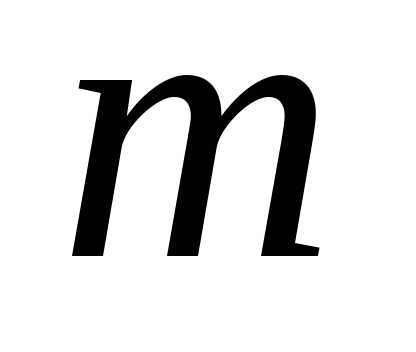 ,
составленная из элементов множества
,
составленная из элементов множества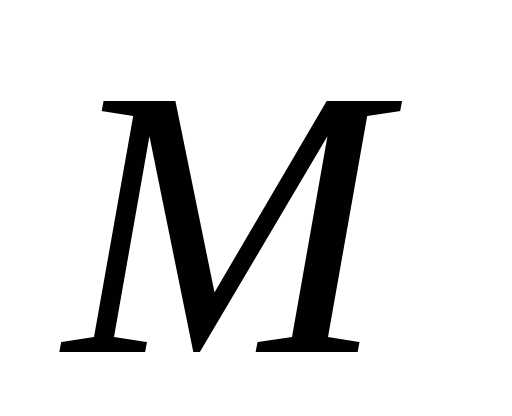 .
Тогда каждому номеру
.
Тогда каждому номеру из совокупности
из совокупности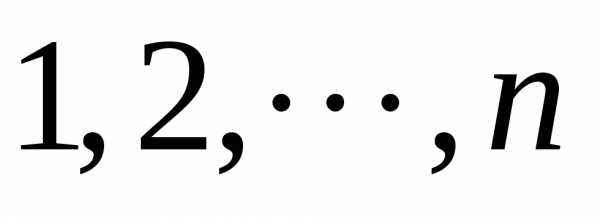 будет
соответствовать число
будет
соответствовать число 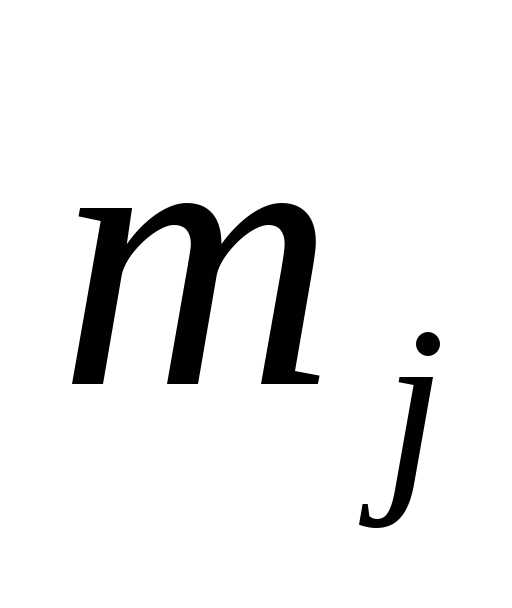 указывающее, на количество участия
элементов
указывающее, на количество участия
элементов в строке
в строке  .
Выписывая по порядку эти числа, получаем
новую строку,
которую и называют составом строки
.
Выписывая по порядку эти числа, получаем
новую строку,
которую и называют составом строки .
. имеет следующий состав
имеет следующий состав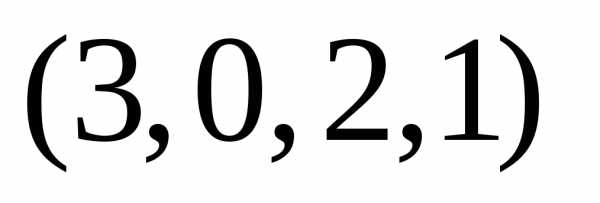 .
Следовательно, в строке
.
Следовательно, в строке элемент
элемент участвует три раза, элемент
участвует три раза, элемент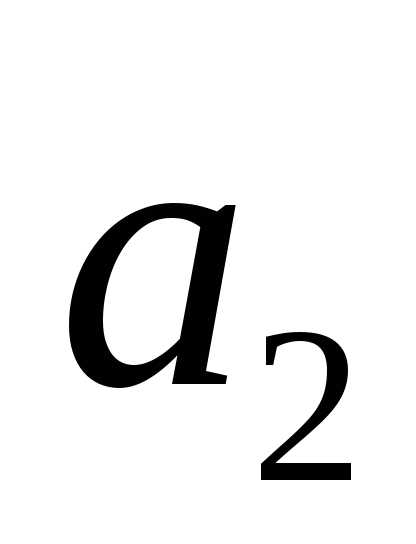 не участвует, элемент
не участвует, элемент участвует два раза, элемент
участвует два раза, элемент участвует один раз. Две строки, имеющие
один и тот же состав, могут отличаться
друг от друга лишь порядков элементов.
Их называютразмещениями
с повторениями данного состава.
участвует один раз. Две строки, имеющие
один и тот же состав, могут отличаться
друг от друга лишь порядков элементов.
Их называютразмещениями
с повторениями данного состава.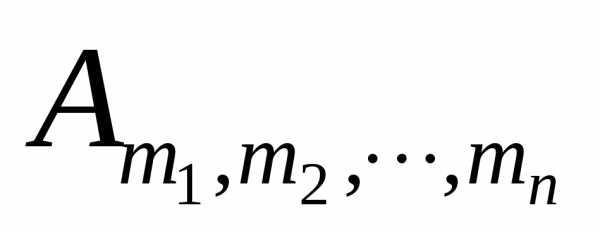 — различных
последовательностей (составов), составленных из элементов , в которых
каждый элемент
— различных
последовательностей (составов), составленных из элементов , в которых
каждый элемент  встречается
встречается 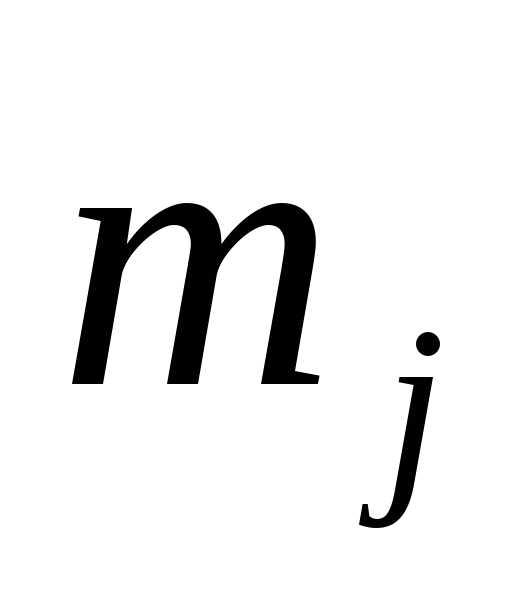 раз (равно
раз (равно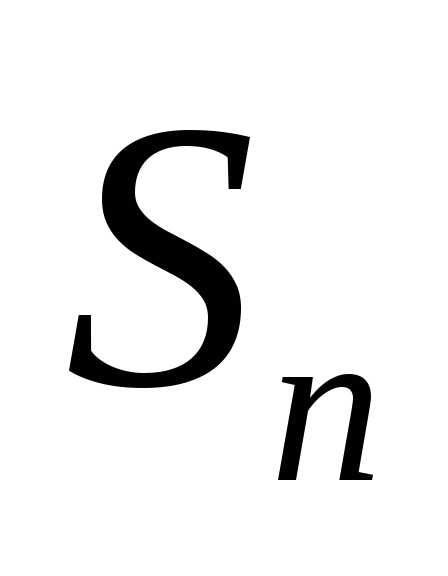 .
А так же, положим.
Введём в рассмотрение
.
А так же, положим.
Введём в рассмотрение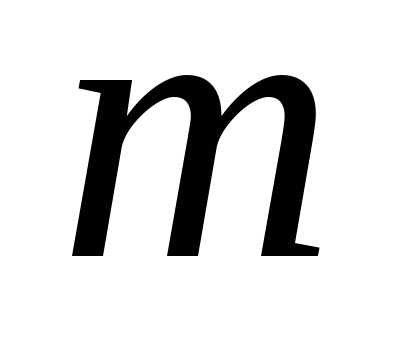 произвольных
различных элементов:
произвольных
различных элементов: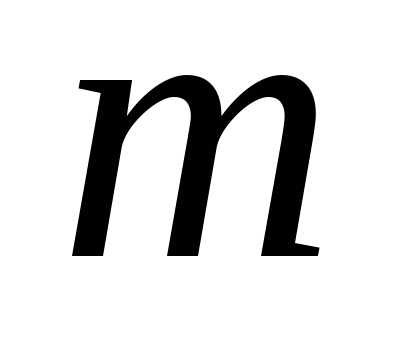 элементов, заменяя элементы по следующему
правилу. На тех местах исходной
последовательности, где стояло одно и
то же
элементов, заменяя элементы по следующему
правилу. На тех местах исходной
последовательности, где стояло одно и
то же (этот элемент встречался
(этот элемент встречался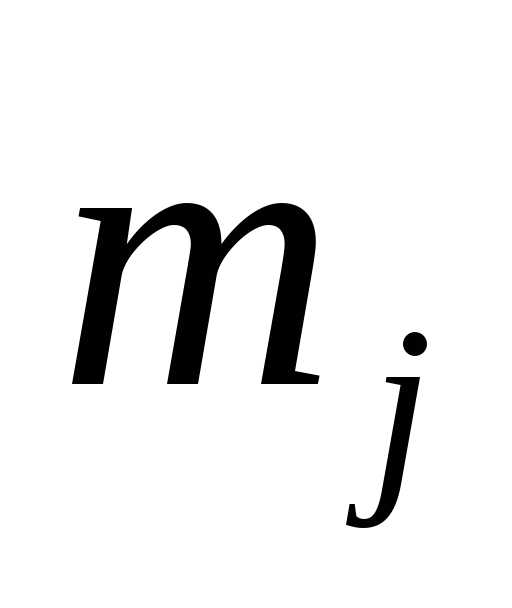 раз), записываем какой-нибудь перестановку
из
раз), записываем какой-нибудь перестановку
из элементов
.
Согласно
равенству (2) такое действие для одного
элементов
.
Согласно
равенству (2) такое действие для одного  можно осуществлять в точности
можно осуществлять в точности различными способами. Проделав такое
действие для каждого
различными способами. Проделав такое
действие для каждого (),
мы получим некоторую перестановку из
(),
мы получим некоторую перестановку из из указанных выше элементов. На основании
формулы умножения (см. пункт
из указанных выше элементов. На основании
формулы умножения (см. пункт )
для любой последовательности строки
получим всего указанным способом
различных перестановок из
)
для любой последовательности строки
получим всего указанным способом
различных перестановок из  элементов. Для различных исходных
последовательностей вышеуказанным
способом мы, естественно, получаем
различные перестановки из взятых
элементов. Для различных исходных
последовательностей вышеуказанным
способом мы, естественно, получаем
различные перестановки из взятых элементов.
При этом любая из выбранных
элементов.
При этом любая из выбранных элементов может быть получена этим
способом, если в качестве начальной
последовательности выбрать ту строку,
которая образуется в результате замены
всех элементов
во
взятой перестановке одним элементом
элементов может быть получена этим
способом, если в качестве начальной
последовательности выбрать ту строку,
которая образуется в результате замены
всех элементов
во
взятой перестановке одним элементом  для кахдого.
Таким образом, с учётом равенства (2)
получаем:
для кахдого.
Таким образом, с учётом равенства (2)
получаем: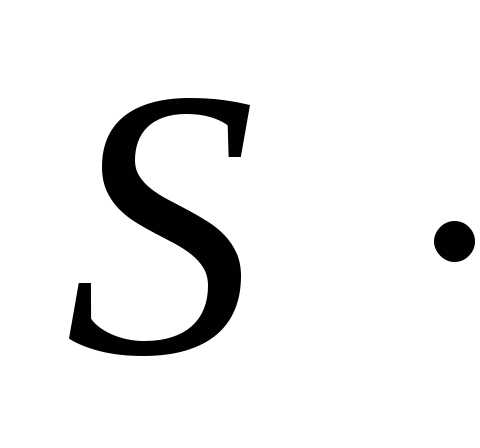 ,
следовательно,
,
следовательно,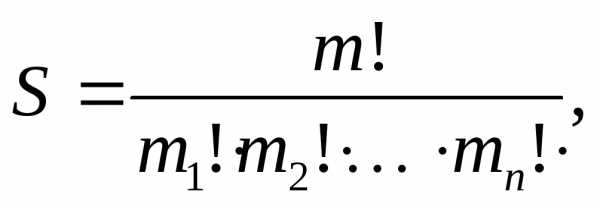
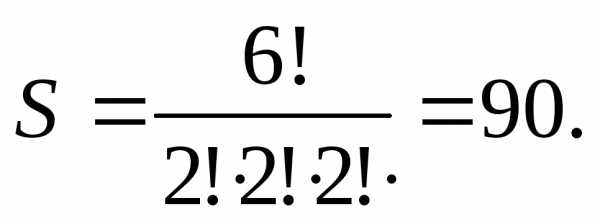
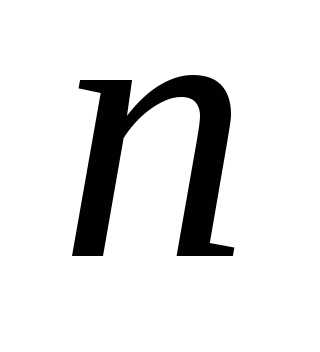 различных наименований, причём по
различных наименований, причём по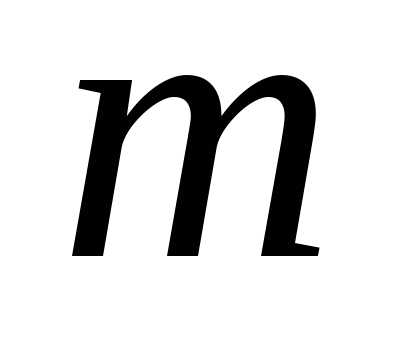 экземпляров книг каждого наименования,
то все
экземпляров книг каждого наименования,
то все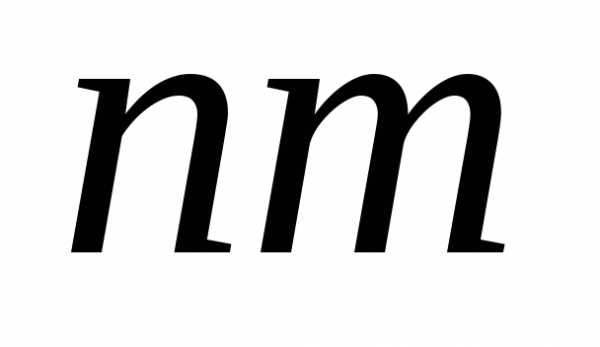 экземпляров
книг могут быть размещены на полке
экземпляров
книг могут быть размещены на полке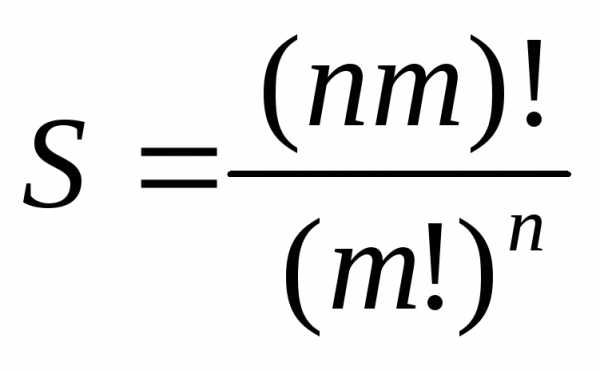
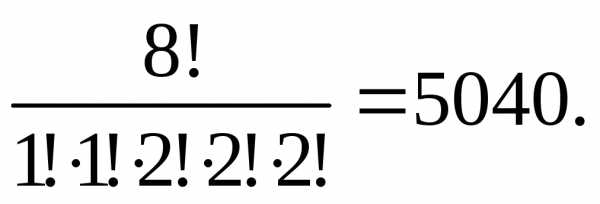
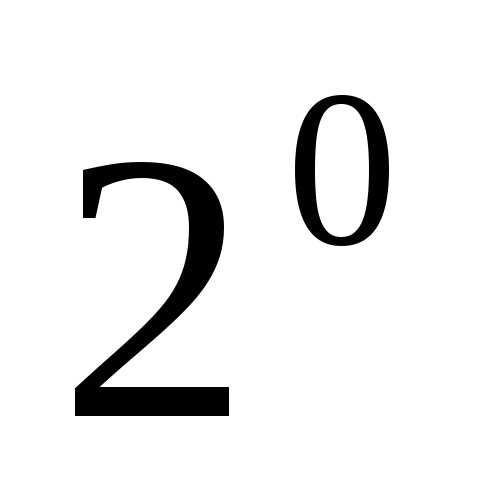 .
Полиномиальная формула. Обобщением
формулы Бинома Ньютона является так
называемая полиномиальная формула,
которую приведём без доказательства.
.
Полиномиальная формула. Обобщением
формулы Бинома Ньютона является так
называемая полиномиальная формула,
которую приведём без доказательства.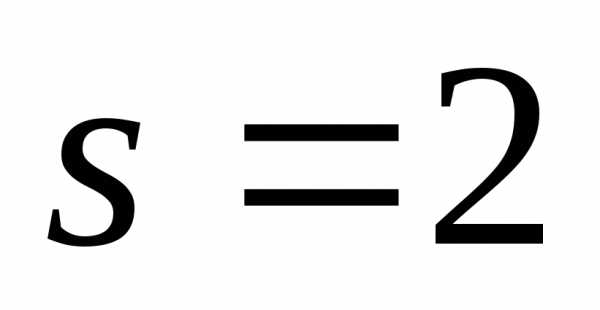 имеет
место равенство
имеет
место равенство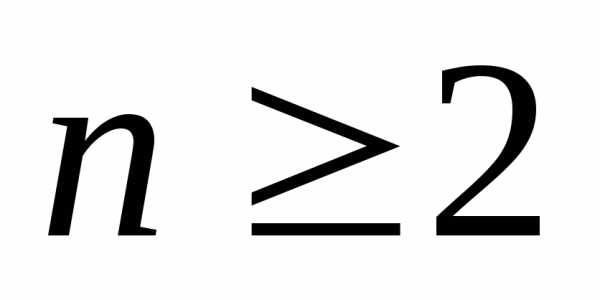 справедливо
неравенство
справедливо
неравенство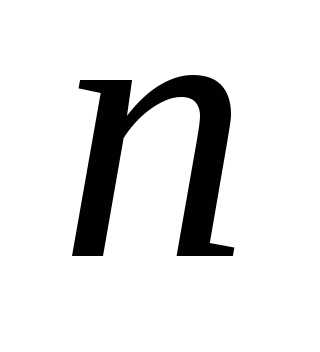 .
В частности, из неё вытекает, что
.
В частности, из неё вытекает, что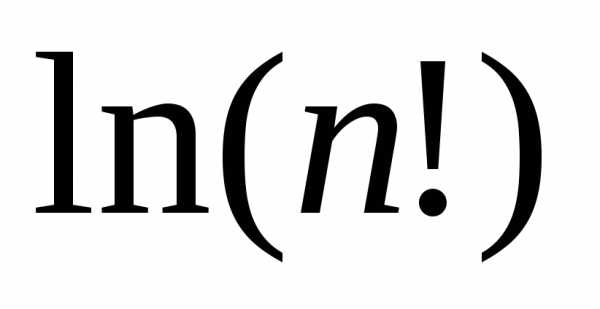 с точностью до
с точностью до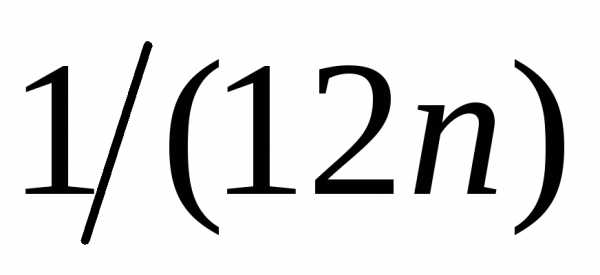 приближается выражением
приближается выражением




 Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.
Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.
 Последний был в принципе согласен со множеством фактов, предлагаемых основателем величины, но считал, что положительный и отрицательный показатели должны быть равны. В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.
Последний был в принципе согласен со множеством фактов, предлагаемых основателем величины, но считал, что положительный и отрицательный показатели должны быть равны. В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.












 Добавить
Добавить