Распределительный метод решения транспортной задачи
Наиболее трудоемким этапом в методе потенциалов является этап построения цикла пересчета для переменной, которая имеет отрицательную косвенную стоимость.
Если бы не трудоемкость этого этапа, можно было бы поступить по-другому: сначала для свободной переменной построить цикл пересчета, а после этого принять решение, следует ли эту переменную вводить в состав базисных переменных нового опорного решения или нет. То есть, вообще отказаться от вычисления потенциалов.
На этом построен распределительный метод решения транспортной задачи.
Пусть имеется
некоторое опорное решение и  — свободная переменная, а
— свободная переменная, а — базисная
переменная.
— базисная
переменная.
Построим цикл
пересчета для 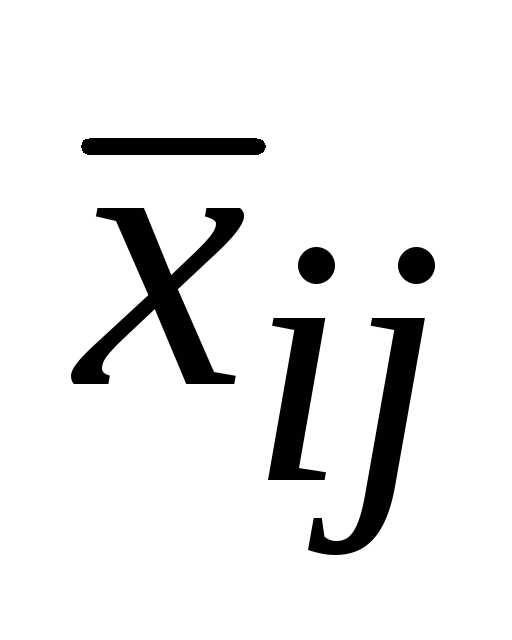 .
.
Что касается 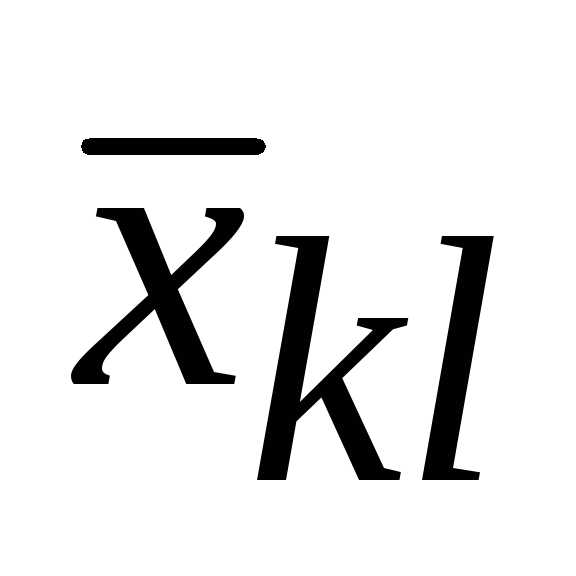 ,
возможны следующие ситуации.
,
возможны следующие ситуации.
 соответствует
положительной вершине;
соответствует
положительной вершине; соответствует
отрицательной вершине;
соответствует
отрицательной вершине; в цикл не входит.
в цикл не входит.
Если
 соответствуетположительной вершине,
то при переходе к новому опорному
решению
соответствуетположительной вершине,
то при переходе к новому опорному
решению увеличитсяна ту же величину,
что и
увеличитсяна ту же величину,
что и .
То есть, если выразить базисные переменные
через свободные, переменная
.
То есть, если выразить базисные переменные
через свободные, переменная войдет в выражение для
войдет в выражение для с коэффициентом «+1»;
с коэффициентом «+1»;Если
 соответствуетотрицательной вершине,
то при переходе к новому опорному
решению
соответствуетотрицательной вершине,
то при переходе к новому опорному
решению уменьшитсяна ту же величину,
на которую увеличится
уменьшитсяна ту же величину,
на которую увеличится .
То есть, если выразить базисные переменные
через свободные, переменная
.
То есть, если выразить базисные переменные
через свободные, переменная войдет в выражение для
войдет в выражение для с коэффициентом «-1«;
с коэффициентом «-1«;Если
 не входит в цикл пересчета, то
при переходе к новому опорному решению
значение
не входит в цикл пересчета, то
при переходе к новому опорному решению
значение не изменится. То есть, если выразить
базисные переменные через свободные,
переменная
не изменится. То есть, если выразить
базисные переменные через свободные,
переменная войдет в выражение для
войдет в выражение для с коэффициентом «0«.
с коэффициентом «0«.
Схематично эти ситуации можно представить следующим образом:
 = +1
= +1 +…….
+……. = -1
= -1 +…….
+……. = 0
= 0 +…….
+…….
Выразим теперь ЦФ через свободные переменные.
Как подсчитать, с
каким коэффициентом переменная 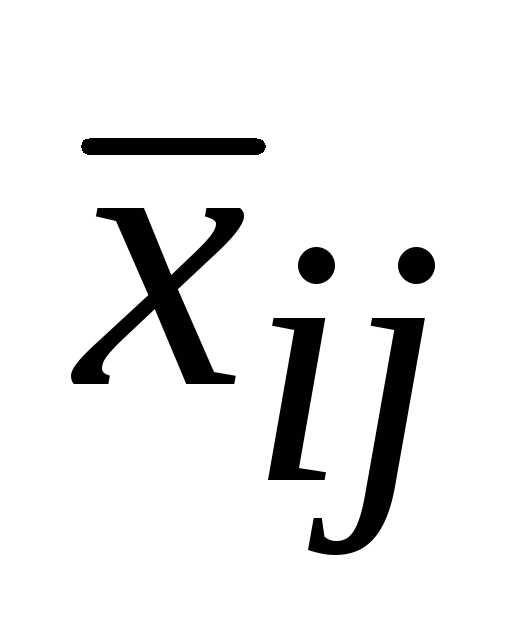 войдет
в ЦФ?
войдет
в ЦФ?
Она войдет в
соответствующее выражение непосредственно
(с коэффициентом  )
и через посредство тех и только тех
базисных переменных, которые входят в
цикл пересчета.
)
и через посредство тех и только тех
базисных переменных, которые входят в
цикл пересчета.
Но  входит в выражение для
входит в выражение для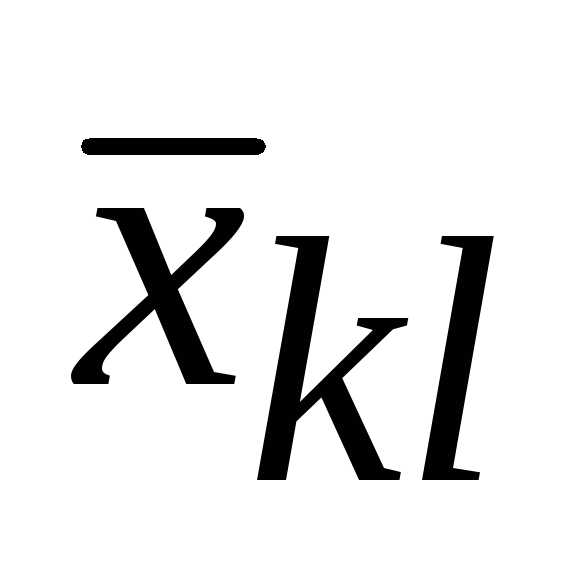 только с одним из двух коэффициентов:
+1 или -1 , в зависимости
от того, является ли вершина
только с одним из двух коэффициентов:
+1 или -1 , в зависимости
от того, является ли вершина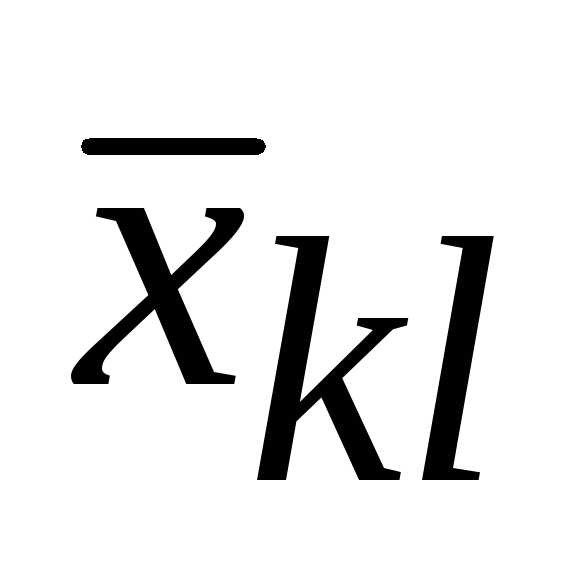 положительной
или отрицательной. А
положительной
или отрицательной. А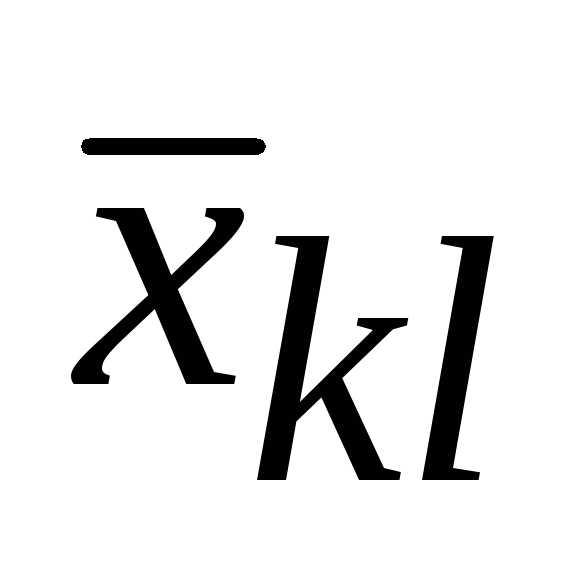 входит
в ЦФ с коэффициентом
входит
в ЦФ с коэффициентом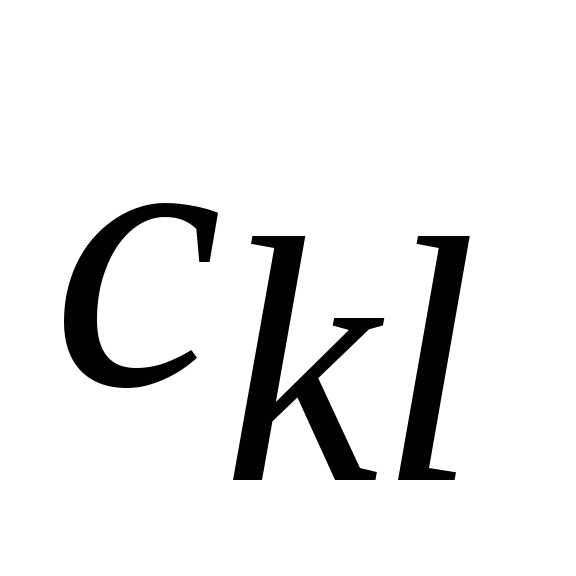 .
То есть, посредством
.
То есть, посредством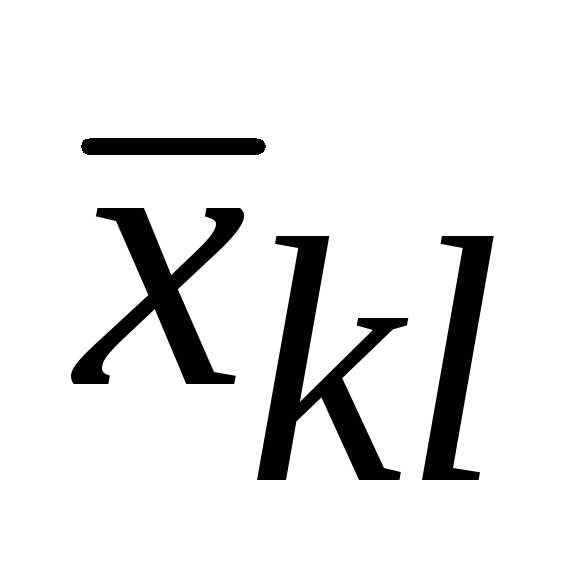 (входящей в цикл) переменная
(входящей в цикл) переменная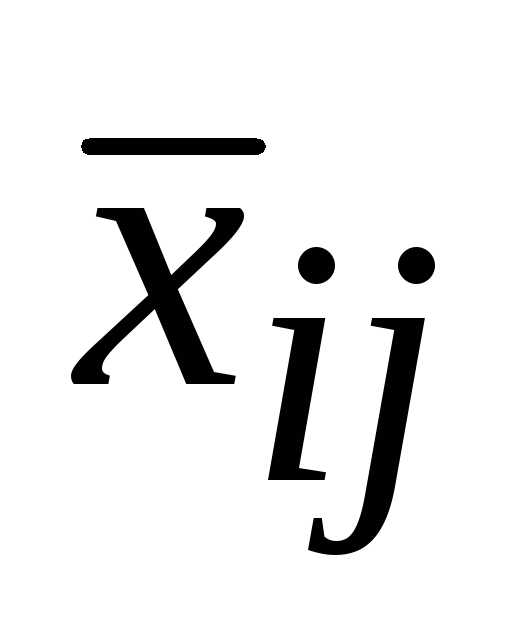 войдет в ЦФ с коэффициентом
+
войдет в ЦФ с коэффициентом
+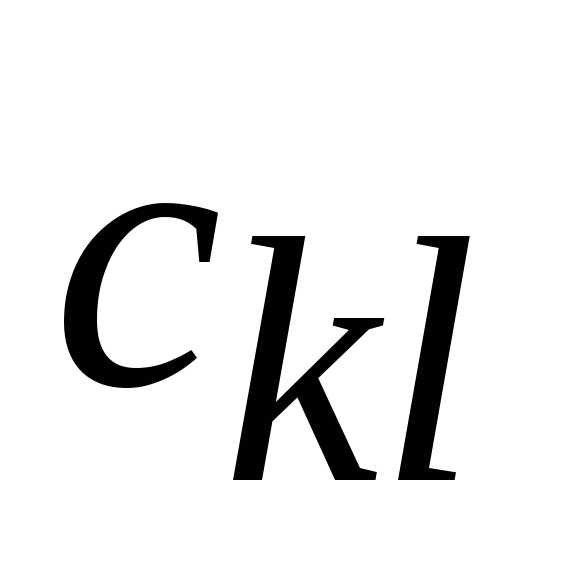 или —
или —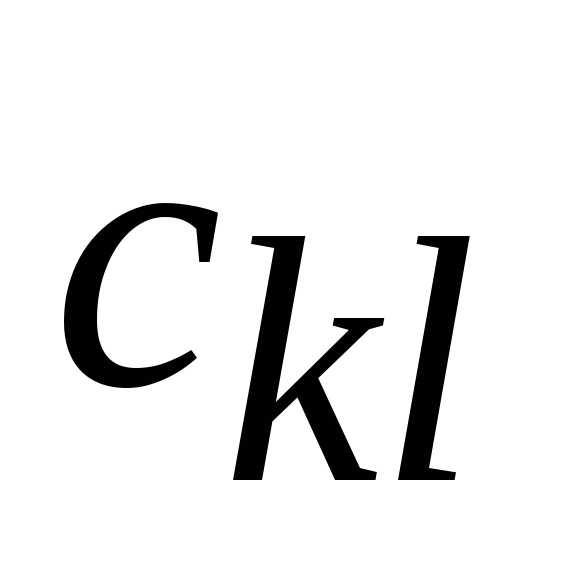 в
зависимости от того, является ли вершина
в
зависимости от того, является ли вершина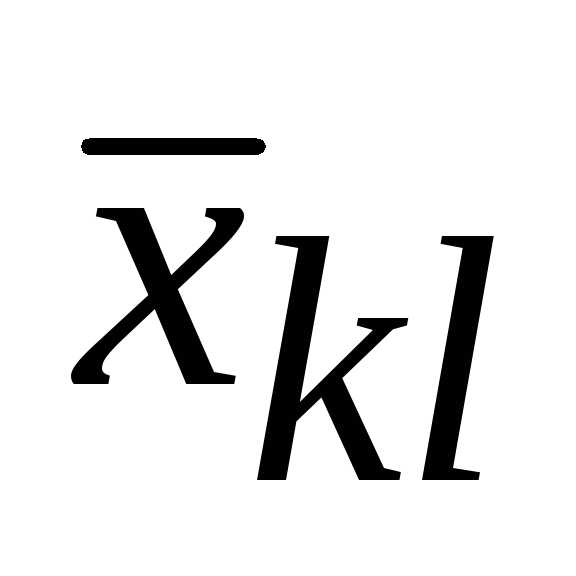 положительной
или отрицательной.
положительной
или отрицательной.
Схематично эту ситуацию можно представить следующим образом:
Z=
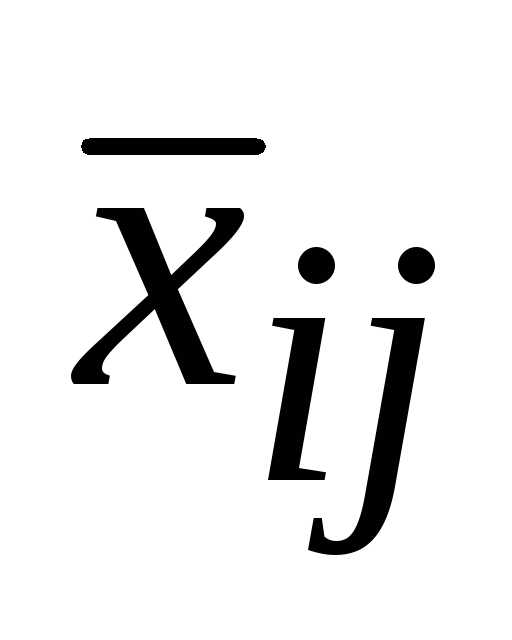 +
+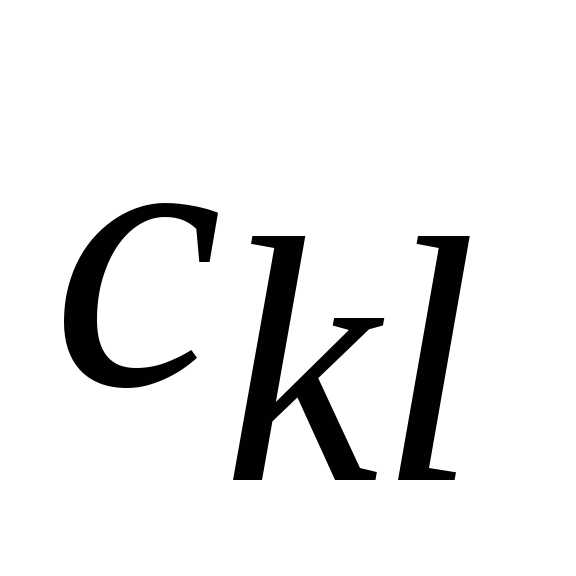
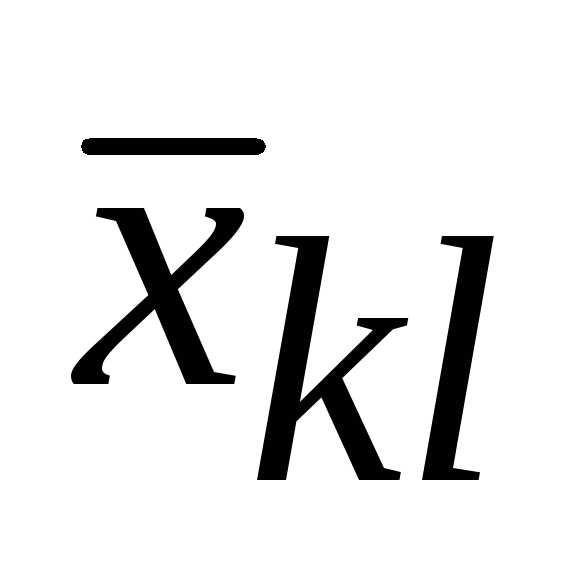 +…
+…
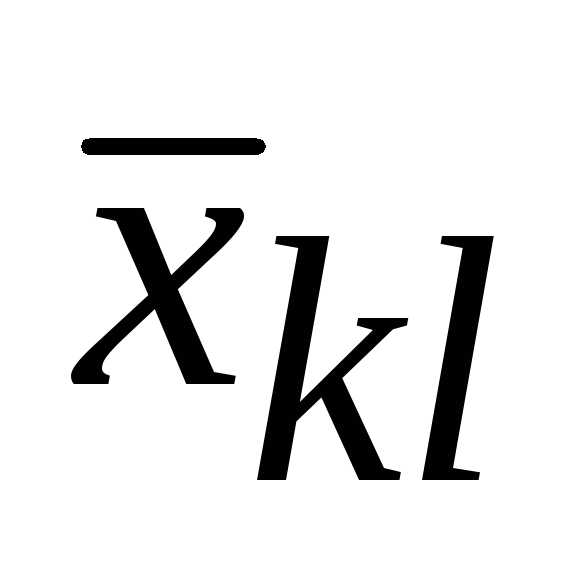 =
=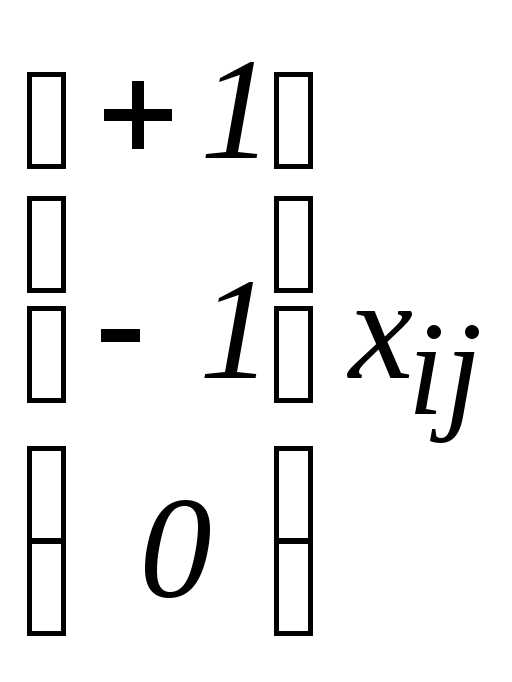 +…
+…
Z=
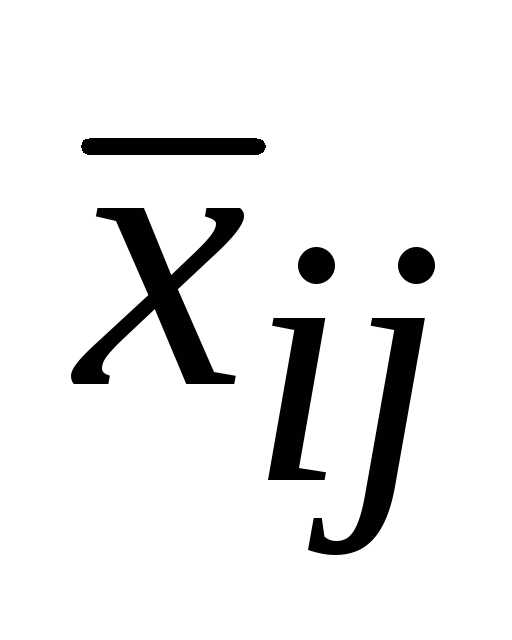 +
+ (
(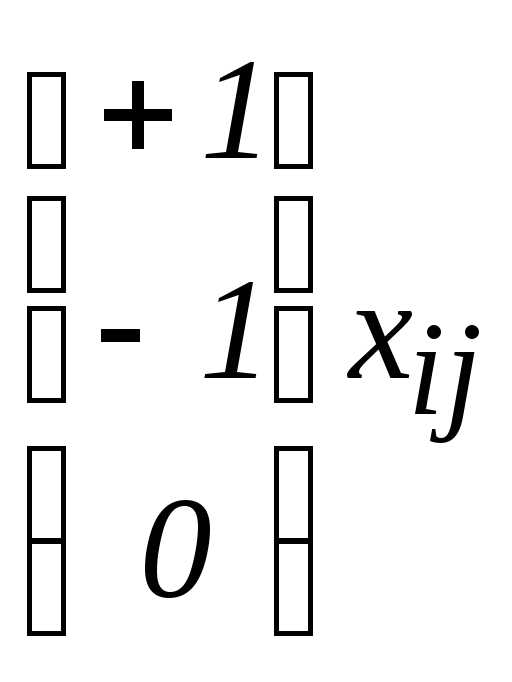 +…)+…
+…)+…
Z=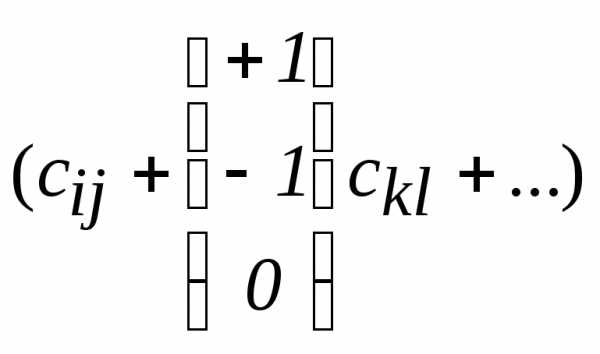
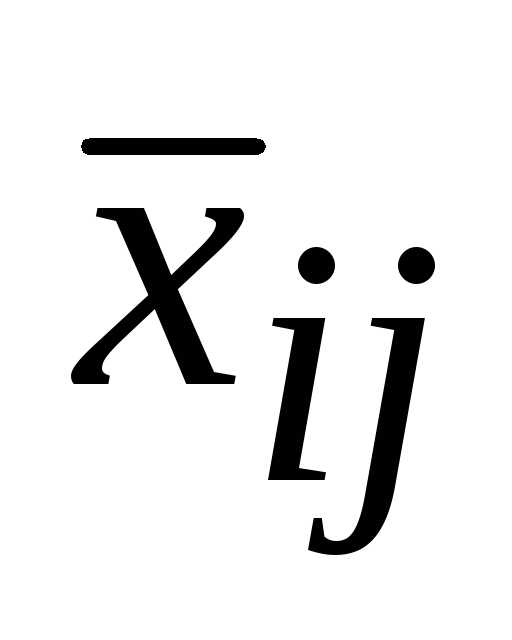 +…
+…
Как видно из этого выражения, в круглых скобках записана алгебраическая сумма всех стоимостей, которым соответствуют вершинам цикла пересчета.
Таким образом,
коэффициент, с которым свободная
переменная 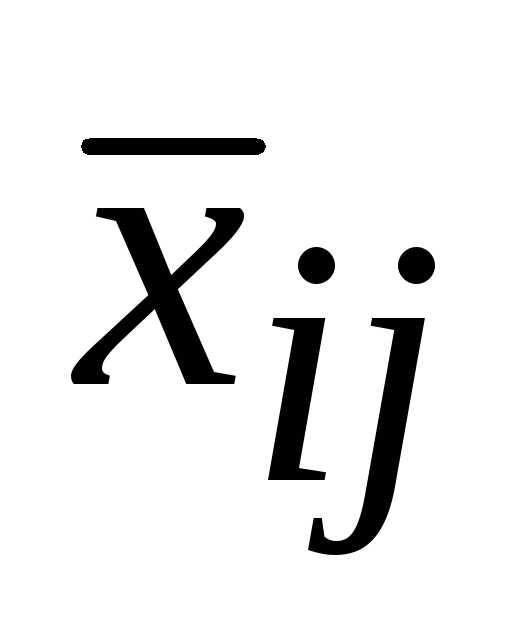 входит в ЦФ, равен алгебраической сумме
всех стоимостей, соответствующих
вершинам цикла, включая вершину, в
которой находится свободная переменная.
входит в ЦФ, равен алгебраической сумме
всех стоимостей, соответствующих
вершинам цикла, включая вершину, в
которой находится свободная переменная.
То есть, косвенную
стоимость свободной переменной 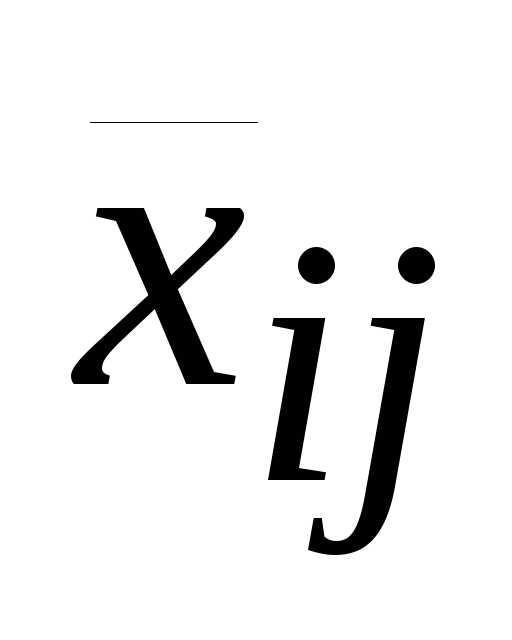 можно определить не по формуле,
а другим путем. Нужно построить для этой
переменной цикл пересчета и подсчитать
алгебраическую сумму всех стоимостей,
которым соответствуют вершинам цикла
пересчета.
можно определить не по формуле,
а другим путем. Нужно построить для этой
переменной цикл пересчета и подсчитать
алгебраическую сумму всех стоимостей,
которым соответствуют вершинам цикла
пересчета.
Алгоритм распределительного метода
Имеется некоторое опорное решение.
Шаг 1. Для данного опорного решения организуем последовательный просмотр списка свободных клеток (переменных).
Шаг 2. Для
очередной свободной клетки (пусть это
будет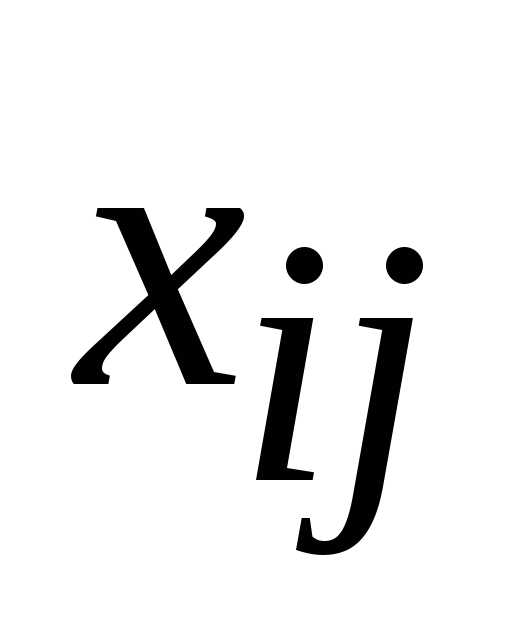 ),
строим цикл пересчета и подсчитываем
алгебраическую сумму стоимостей по
всем вершинам цикла (
),
строим цикл пересчета и подсчитываем
алгебраическую сумму стоимостей по
всем вершинам цикла (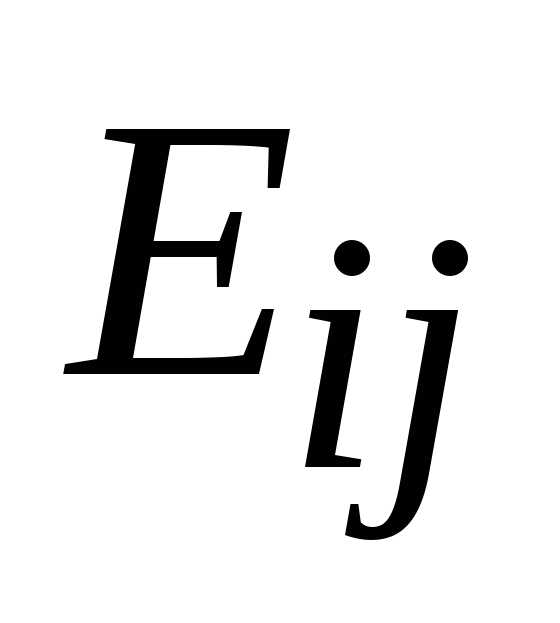 ).
).
Шаг 3. Если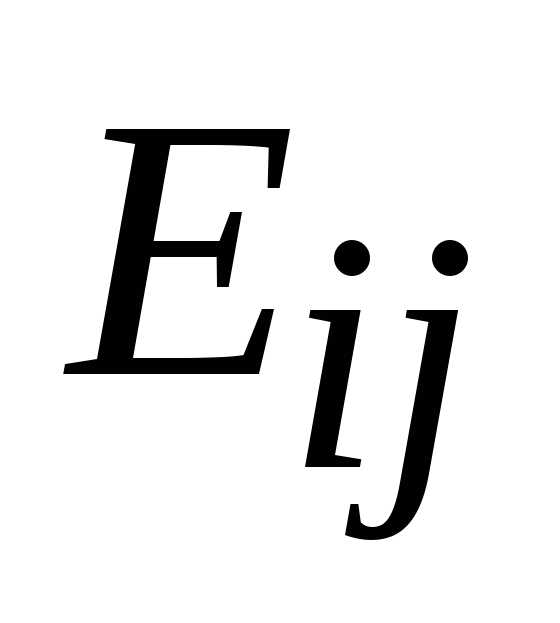 < 0,
выполняемшаг 4. В противном
случае проверяем, все ли свободные
клетки просмотрены. Если да, то очередное
решениеоптимальное.Конец.
В противном случае выполняемшаг 2.
< 0,
выполняемшаг 4. В противном
случае проверяем, все ли свободные
клетки просмотрены. Если да, то очередное
решениеоптимальное.Конец.
В противном случае выполняемшаг 2.
Шаг 4. Переменную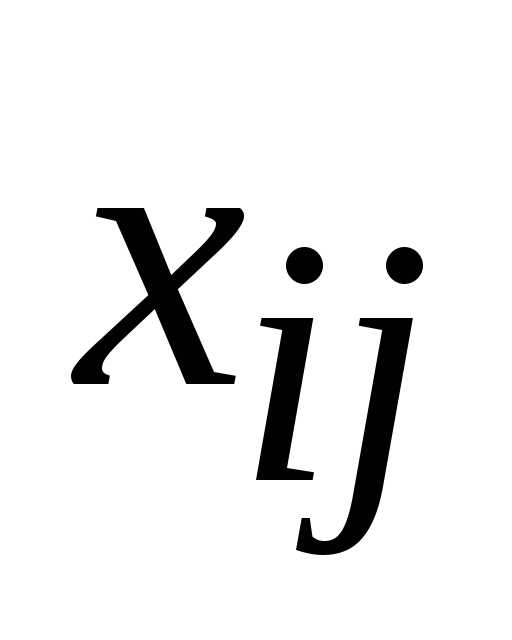 вводим в состав базисных переменных.
Для этого среди отрицательных вершин
находим вершину с минимальным значением
соответствующей базисной переменной.
Пусть это будет
вводим в состав базисных переменных.
Для этого среди отрицательных вершин
находим вершину с минимальным значением
соответствующей базисной переменной.
Пусть это будет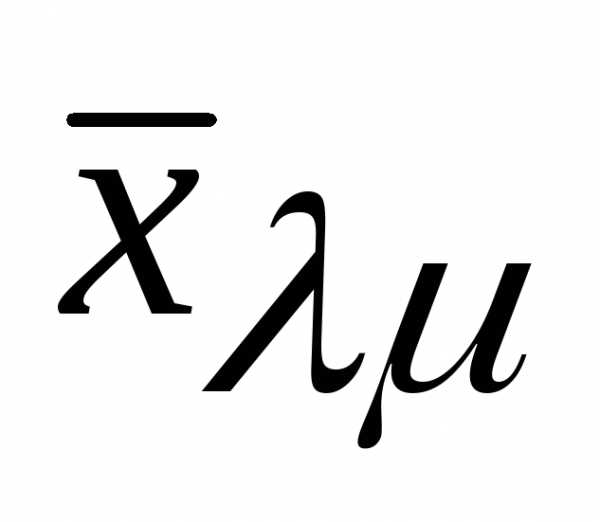 .
Производим сдвиг по циклу пересчета.
Переменная
.
Производим сдвиг по циклу пересчета.
Переменная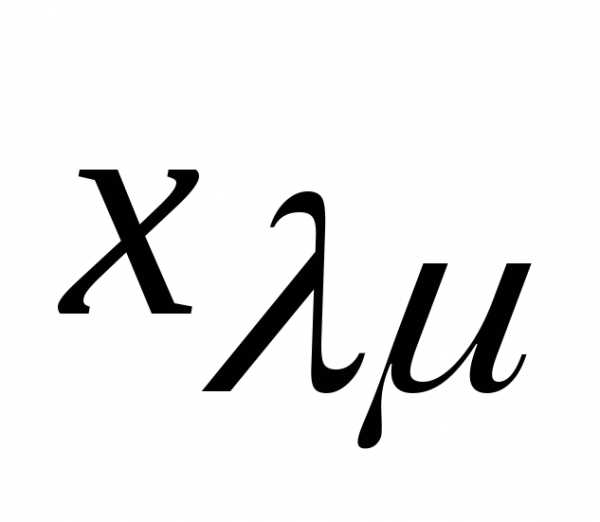 выводится из состава базисных переменных.
Имеем новое опорное решение. Выполняемшаг 1.
выводится из состава базисных переменных.
Имеем новое опорное решение. Выполняемшаг 1.
Основной недостаток метода – большое количество циклов пересчета, которые приходится строить на каждой итерации. Достоинство – не нужно специально вычислять потенциалы строк и столбцов.
Если нет эффективной процедуры построения цикла пересчета, предпочтение отдается методу потенциалов.
Пример. Дана транспортная задача и известно ее опорное решение. Определить косвенные стоимости переменных x32,x34, x46.
15 50 | 20 | 25 | 15 | 10 | 10 10 | 20 | |
5 20 | 5 | 1 30 | 4 | 2 50 | 1 | 15 | |
E32=0 | 3 | 5 | 5 | 1 | 4 | 5 40 | 2 |
20 | 7 100 | 5 | 1 20 | 3 | 5 | 4 | |
20 | 1 40 | 2 30 | 3 | 4 | 6 | 6 100 |
15 50 | 20 | 25 | 15 | 10 | 10 10 | 20 | |
5 20 | 5 | 1 30 | 4 | 2 50 | 1 | 15 | |
E34=2 | 3 | 5 | 5 | 1 | 4 | 5 40 | 2 |
20 | 7 100 | 5 | 1 20 | 3 | 5 | 4 | |
20 | 1 40 | 2 30 | 3 | 4 | 6 | 6 100 |
15 50 | 20 | 25 | 15 | 10 | 10 10 | 20 | |
5 20 | 5 | 1 30 | 4 | 2 50 | 1 | 15 | |
E46=-2 | 3 | 5 | 5 | 1 | 4 | 5 40 | 2 |
20 | 7 100 | 5 | 1 20 | 3 | 5 | 4 | |
20 | 1 40 | 2 30 | 3 | 4 | 6 | 6 100 |
studfiles.net
7.3. Распределительный метод решения транспортной задачи
Распределительный метод использует исходное базисное решение, полученное методом северо-западного угла или наименьшей стоимости, и заключается в преобразовании матрицы перевозок таким образом, что каждый последующий пересчет таблицы приближается к оптимальному решению.
Для преобразования таблицы используется понятие цикла.
Циклом в матрице называется ломаная с вершинами в клетках и звеньями, лежащими вдоль строк и столбцов матрицы, удовлетворяющая требованиям:
– замкнутости;
– в каждой вершине должно встречаться два звена.
Если в любом цикле вершинам приписать при обходе в одном направлении поочередно знаки «+» и «–», то в каждой строке (столбце) число положительных вершин будет равно числу отрицательных.
При решении задач используется операция сдвига по циклу. Эта операция заключается в увеличении элементов в положительных вершинах и уменьшении в отрицательных на одно и то же число.
Например, для свободной клетки с координатами (3,3) левой матрицы строится цикл, приведенный на рисунке, и осуществляется сдвиг по циклу на величину 8. В результате получаются новые значения перевозок, приведенные на правой матрице. Клетки, не являющиеся вершинами цикла, при этом остаются без изменений.
+ 10 | — 20 | 18 | 12 | |||
8 | 6 | Сдвиг по циклу на 8 | 8 | 6 | ||
— 8 | + | 0 | 8 |
Для оптимизации решения важно знать, с каким коэффициентом выбранная свободная неизвестная входит в выражение для базисных неизвестных. Это определяется следующим правилом:
– коэффициент равен 0, если соответствующая базисная клетка не является вершиной цикла пересчета данной свободной клетки;
– коэффициент равен 1, если базисная клетка является положительной вершиной цикла пересчета данной свободной клетки;
– коэффициент равен –1, если базисная клетка является отрицательной вершиной пересчета данной свободной клетки.
Например, матрица перевозок имеет 4 пункта отправления и 4 пункта назначения. В ней записано некоторое базисное решение в заштрихованных клетках x11 , x12 , x23 , x24 , x32 , x41 и x43 , число которых должно быть r=m+n—1=7. При этом в каждой строке и каждом столбце таблицы должна быть как минимум одна базисная клетка.
В1 | В2 | В3 | В4 | |
А1 | – | + | ||
А2 | + | – | ||
А3 | ||||
А4 | + | – |
Таким образом, можно по теореме утверждать, что клетка x14 входит в выражение для неизвестных базисных со знаками:
.
Аналогично можно найти коэффициенты для других свободных неизвестных.
У распределительного метода существуют промежуточные базисные решения, каждое из которых постепенно приближается к оптимальному.
Найденное любым методом допустимое базисное решение вносится в матрицу перевозок и занимает r=m+n—1 клеток. Вносятся и нулевые базисные решения. Далее меняются местами базисные и свободные переменные для приближения к оптимальному решению.
Во-первых, определяется свободная неизвестная, переводимая в число базисных.
Рассмотрим способ определения свободных неизвестных, которые целесообразно перевести в число базисных на конкретном примере. Возьмем базисное решение, найденное методом северо-западного угла со стоимостью перевозок
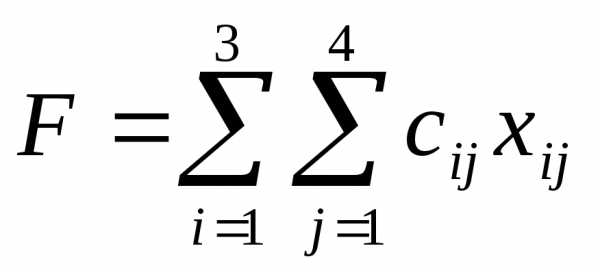 =220
+ 310
+ 220
+ 520
+ 210
+ 610
= 290.
=220
+ 310
+ 220
+ 520
+ 210
+ 610
= 290.
Теперь необходимо построить циклы пересчета для всех свободных переменных (свободных клеток) и определить сумму стоимостей по циклам пересчета ij для всех свободных неизвестных, чтобы найти, какую из них перевести в число базисных для уменьшения целевой функции.
В1 | В2 | В3 | В4 | ai | |
A1 | 2 20 | 3– 10 | 2 + | 4 | 30 |
A2 | 3 | 2 + 20 | 5 – 20 | 1 | 40 |
A3 | 4 | 3 | 2 10 | 6 10 | 20 |
bj | 20 | 30 | 30 | 10 |
Определяем сумму стоимостей по циклу пересчета для каждой свободной клетки, подставляя соответствующие стоимости перевозок из базисных клеток в вершинах цикла:
х13 13 = с13 — с23 + с22 — с12 = 2 — 5 + 2 — 3 = -4 ,
х14 14 = с14 — с24 +с33 – с23 + с22 — с12 = 4 – 6 + 2 — 5 + 2 — 3 = -6 ,
х21 21 = с21 — с11 + с12 — с22 = 3 — 2+ 3 — 2 = 2 ,
аналогично 24 = — 8, 31 = 6, 32 = 4.
Выбираем те из свободных переменных, которые имеют отрицательное значение суммы стоимости по циклу пересчета. В рассматриваемом примере это х13, х14, х24.
Во-вторых, определяется базисная переменная, переводимая в число свободных.
Для этого необходимо проанализировать цикл пересчета, соответствующий выбранной свободной неизвестной. В нашем примере это может быть цикл для переменной х13.
Производя преобразования по циклу, мы должны получить нуль в одной из базисных переменных. Кроме того, необходимо учитывать, что переменные не могут принимать отрицательных значений. Поэтому выбирается та базисная переменная, которая имеет наименьшее значение из всех базисных переменных, расположенных в отрицательных вершинах цикла пересчета. В нашем примере это будет х12=10.
Для получения нового допустимого базисного решения осуществляем сдвиг по циклу пересчета выбранной свободной переменной х13 на величину значений выбранной базисной переменной х12=10, которая после сдвига переводится в свободные.
При этом получим новую таблицу матрицы перевозок.
В1 | В2 | В3 | В4 | ai | |
A1 | 2 20 | 3 | 2 10 | 4 | 30 |
A2 | 3 | 2 30 | 5 10 | 1 | 40 |
A3 | 4 | 3 | 2 10 | 6 10 | 20 |
bj | 20 | 30 | 30 | 10 |
Сдвиг по циклу привел к новому допустимому базисному решению:
х11=20, х13=10, х22=30, х23=10, х33=10, х34=10, остальные xij=0.
Новое решение дает значение целевой функции F=250, меньшее предыдущего, т. е. ближе к оптимальному значению.
Если в отрицательных вершинах с минимальными перевозками окажется две базисных клетки с одинаковыми значениями, то после сдвига по циклу в число свободных переводится только одна из них, а вторая остается в числе базисных с нулевыми перевозками. И в дальнейших расчетах эта клетка фигурирует как базисная со всеми их характеристиками.
Для нового базисного решения также подсчитываются суммы стоимостей по циклам пересчета для каждой свободной неизвестной: 12=4, 14=2, 12=4, 21= — 2,24= — 8, 31= 2, 23= 4.
Выбираются новые свободная и базисная переменные для сдвига по новым циклам, и все повторяется. Операция продолжается до тех пор, пока не получится, что все стоимости по циклам пересчета больше нуля (ij > 0), что является признаком оптимальности решения, полученного распределительным методом.
Для рассматриваемого примера оптимальным решением является следующее:
х11=20, х13=10, х22=30, х24=10, х33=10, х12=0, остальные xij=0. Стоимость оптимальной перевозки F=170, и уменьшить ее дальше невозможно.
studfiles.net
3. Распределительный метод решения транспортной задачи
Распределительный метод использует исходное базисное решение, полученное методом северо-западного угла или наименьшей стоимости, и заключается в преобразовании матрицы перевозок таким образом, что каждый последующий пересчет таблицы приближается к оптимальному решению.
Для преобразования таблицы используется понятие цикла.
Циклом в матрице называется ломаная с вершинами в клетках и звеньями, лежащими вдоль строк и столбцов матрицы, удовлетворяющая требованиям:
– замкнутости;
– в каждой вершине должно встречаться два звена.
Если в любом цикле вершинам приписать при обходе в одном направлении поочередно знаки «+» и «–», то в каждой строке (столбце) число положительных вершин будет равно числу отрицательных.
При решении задач используется операция сдвига по циклу. Эта операция заключается в увеличении элементов в положительных вершинах и уменьшении в отрицательных на одно и то же число.
Например, для свободной клетки с координатами (3,3) левой матрицы строится цикл, приведенный на рисунке, и осуществляется сдвиг по циклу на величину 8. В результате получаются новые значения перевозок, приведенные на правой матрице. Клетки, не являющиеся вершинами цикла, при этом остаются без изменений.
Рис. 2
Для оптимизации решения важно знать, с каким коэффициентом выбранная свободная неизвестная входит в выражение для базисных неизвестных. Это определяется следующим правилом:
– коэффициент равен 0, если соответствующая базисная клетка не является вершиной цикла пересчета данной свободной клетки;
– коэффициент равен 1, если базисная клетка является положительной вершиной цикла пересчета данной свободной клетки;
– коэффициент равен –1, если базисная клетка является отрицательной вершиной пересчета данной свободной клетки.
Например, матрица перевозок имеет 4 пункта отправления и 4 пункта назначения. В ней записано некоторое базисное решение в заштрихованных клетках x11 , x12 , x23 , x24 , x32 , x41 и x43 , число которых должно быть r=m+n-1=7. При этом в каждой строке и каждом столбце таблицы должна быть как минимум одна базисная клетка.
Рис. 3
Построим цикл пересчета для свободной клетки x14 так, чтобы все остальные вершины лежали в базисных клетках. Такой цикл существует только один и приведен в таблице, при этом свободной клетке x14 присваивается знак «+», а знаки всех последующих вершин чередуются при их обходе по циклу в одном направлении.
Таким образом, можно по теореме утверждать, что клетка x14 входит в выражение для неизвестных базисных со знаками:
.
Аналогично можно найти коэффициенты для других свободных неизвестных.
У распределительного метода существуют промежуточные базисные решения, каждое из которых постепенно приближается к оптимальному.
Найденное любым методом допустимое базисное решение вносится в матрицу перевозок и занимает r=m+n-1 клеток. Вносятся и нулевые базисные решения. Далее меняются местами базисные и свободные переменные для приближения к оптимальному решению.
Во-первых, определяется свободная неизвестная, переводимая в число базисных.
Рассмотрим способ определения свободных неизвестных, которые целесообразно перевести в число базисных на конкретном примере. Возьмем базисное решение, найденное методом северо-западного угла со стоимостью перевозок
=220 + 310 + 220 + 520 + 210 + 610 = 290.
Теперь необходимо построить циклы пересчета для всех свободных переменных (свободных клеток) и определить сумму стоимостей по циклам пересчета ij для всех свободных неизвестных, чтобы найти, какую из них перевести в число базисных для уменьшения целевой функции.
Рис. 4
Определяем сумму стоимостей по циклу пересчета для каждой свободной клетки, подставляя соответствующие стоимости перевозок из базисных клеток в вершинах цикла:
х13 13 = с13 — с23 + с22 — с12 = 2 — 5 + 2 — 3 = -4 ,
х14 14 = с14 — с24 +с33 – с23 + с22 — с12 = 4 – 6 + 2 — 5 + 2 — 3 = -6 ,
х21 21 = с21 — с11 + с12 — с22 = 3 — 2+ 3 — 2 = 2 ,
аналогично 24 = — 8, 31 = 6, 32 = 4.
Выбираем те из свободных переменных, которые имеют отрицательное значение суммы стоимости по циклу пересчета. В рассматриваемом примере это х13, х14, х24.
Во-вторых, определяется базисная переменная, переводимая в число свободных.
Для этого необходимо проанализировать цикл пересчета, соответствующий выбранной свободной неизвестной. В нашем примере это может быть цикл для переменной х13.
Производя преобразования по циклу, мы должны получить нуль в одной из базисных переменных. Кроме того, необходимо учитывать, что переменные не могут принимать отрицательных значений. Поэтому выбирается та базисная переменная, которая имеет наименьшее значение из всех базисных переменных, расположенных в отрицательных вершинах цикла пересчета. В нашем примере это будет х12=10.
Для получения нового допустимого базисного решения осуществляем сдвиг по циклу пересчета выбранной свободной переменной х13 на величину значений выбранной базисной переменной х12=10, которая после сдвига переводится в свободные.
При этом получим новую таблицу матрицы перевозок.
Таблица 7
В1 | В2 | В3 | В4 | ai | |
A1 | 2 20 | 3 | 2 10 | 4 | 30 |
A2 | 3 | 2 30 | 5 10 | 1 | 40 |
A3 | 4 | 3 | 2 10 | 6 10 | 20 |
bj | 20 | 30 | 30 | 10 |
Сдвиг по циклу привел к новому допустимому базисному решению:
х11=20, х13=10, х22=30, х23=10, х33=10, х34=10, остальные xij=0.
Новое решение дает значение целевой функции F=250, меньшее предыдущего, т. е. ближе к оптимальному значению.
Если в отрицательных вершинах с минимальными перевозками окажется две базисных клетки с одинаковыми значениями, то после сдвига по циклу в число свободных переводится только одна из них, а вторая остается в числе базисных с нулевыми перевозками. И в дальнейших расчетах эта клетка фигурирует как базисная со всеми их характеристиками.
Для нового базисного решения также подсчитываются суммы стоимостей по циклам пересчета для каждой свободной неизвестной: 12=4, 14=2, 12=4, 21= — 2,24= — 8, 31= 2, 23= 4.
Выбираются новые свободная и базисная переменные для сдвига по новым циклам, и все повторяется. Операция продолжается до тех пор, пока не получится, что все стоимости по циклам пересчета больше нуля (ij> 0), что является признаком оптимальности решения, полученного распределительным методом.
Для рассматриваемого примера оптимальным решением является следующее:
х11=20, х13=10, х22=30, х24=10, х33=10, х12=0, остальные xij=0. Стоимость оптимальной перевозки F=170, и уменьшить ее дальше невозможно.
studfiles.net
21. Распределительный метод решения транспортной задачи
Решение задачи включает
— предварительный этап,
— проверку на оптимальность
— составление оптимальных планов.
Предварительный этап – составляем предварительный опорный план прикрепления.
Способ «северо-западного угла» (диагональный способ).
Распределение поставок производят с верхнего левого угла и далее по строкам по мере исчерпывания плана.
Способ двойного предпочтения
Суть данного метода в том, что по строкам отмечается минимальные значения. Далее по столбцам, не обращая внимания на отметки по строкам. Вписывание поставок начинается с клеток отмеченных дважды и далее по принципу от меньшего к большему значению коэффициента.
Проверка предварительного плана на оптимальность распределительным методом.
Суть данного метода состоит в том, для каждой свободной слетки проверяемого планом составляются контура (цепочки) по следующим правилам:
Начало контура цепочки в свободной клетке
Контур представляет собой многоугольник с четным числом вершин.
Первая вершина – свободная клетка, остальные вершины(повороты) в клетках предварительного плана.
Отдельные отрезки контура принадлежат или одной строке или одному столбцу.
Отрезки контура могут проходить как через свободные клетки, так и через занятые.
Отрезки могут пересекаться
Отдельные отрезки (стороны контура) могут пересекаться
По составленным многоугольникам (цепочка, контурам) можно создать цепочку из цифр:
Первая цифра – коэффициент стоящий в свободной клетке
Коэффициенты стоящие в углах многоугольника в углах поворота.
На основании цепочек вычисляются характеристики контуров (свободных клеток). Характеристика представляет собой алгебраическую сумму коэффициентов стоящих в вершинах. Предварительно проставляются знаки: знак + получает коэффициент в свободной клетке, далее знаки чередуются.
После вычисления характеристик незагруженных клеток производиться их анализ, если среди характеристик незагруженных клеток нет отрицательных значений анализируемый план можно считать оптимальным. Наличие хотя бы одной отрицательной характеристики свидетельствует о возможности улучшения плана, причем в план прикрепления поставщиков потребителям должна быть введена клетка имеющая отрицательную характеристику.
Для введения клетки в план прикрепления поставщиков потребителем необходимо в нем сделать перераспределение поставок, для этого контур с отрицательной характеристикой выносим за пределы матрицы и делаем в нем перераспределение: проставляем знаки по тому же принципу: знак плюс – свободная клетка и т.д. После этого из отрицательных клеток выбирается та в которой поставка минимальна.
После внесенных изменений в предварительный план необходимо снова проверить его на оптимальность путем вычисления характеристик не загруженных клеток.
22. Применение метода потенциалов для решения транспортной задачи.
Решение задачи включает
— предварительный этап,
— проверку на оптимальность
— составление оптимальных планов.
Предварительный этап – составляем предварительный опорный план прикрепления.
Способ «северо-западного угла» (диагональный способ).
Распределение поставок производят с верхнего левого угла и далее по строкам по мере исчерпывания плана.
Способ двойного предпочтения
Суть данного метода в том, что по строкам отмечается минимальные значения. Далее по столбцам, не обращая внимания на отметки по строкам. Вписывание поставок начинается с клеток отмеченных дважды и далее по принципу от меньшего к большему значению коэффициента.
Проверка предварительного плана на оптимальность методом потенциалов
Суть данного метода состоит в том, что к строкам и столбцпм матрицы подбираются вспомогательные числа (потенциалы α – потенциал строки и β – потенциал столбца)
Из условия, что для занятых клеток сумма потенциалов строки и столбца равны коэффициенту стоящему в этой клетке.
–для занятых клеток
Составляется система уравнений для занятых клеток и рассчитается значение потенциалов. Задается потенциал равным нулю, вследствие не достаточного количества уравнений в системе.
Далее в качестве проверки рассчитаем характеристики незагруженных клеток по формуле:
–для незагруженных клеток
Наличие отрицательного значения характеризующего пустую клетку свидетельствует о возможности улучшения плана.
Для введения клетки в план прикрепления поставщиков потребителем необходимо для ячейки сделать контур как в распределительном методе и в этом контуре сделать перераспределение поставок, для этого контур с отрицательной характеристикой выносим за пределы матрицы и делаем в нем перераспределение: проставляем знаки по тому же принципу: знак плюс – свободная клетка и т.д. После этого из отрицательных клеток выбирается так в которой поставка минимальна.
После внесенных изменений в предварительный план необходимо снова проверить его на оптимальность путем вычисления характеристик не загруженных клеток.
studfiles.net
РАСПРЕДЕЛИТЕЛЬНЫЙ МЕТОД РЕШЕНИЯ ТРАНСПОРТНОЙ ЗАДАЧИ Мы научились
 РАСПРЕДЕЛИТЕЛЬНЫЙ МЕТОД РЕШЕНИЯ ТРАНСПОРТНОЙ ЗАДАЧИ
РАСПРЕДЕЛИТЕЛЬНЫЙ МЕТОД РЕШЕНИЯ ТРАНСПОРТНОЙ ЗАДАЧИ
 Мы научились находить первоначальный план поставок. Теперь надо выяснить является ли найденный план оптимальным и, если нет то как его оптимизировать. Для этого надо составить матри цу оценок. Оценка клетки (J, j) вычисляется по следующему правилу: оценка i й строки + оценка j-го столбца + число в левом верхнем углу клетки (i, j) Оценки строки и столбца выбираются таким образом, чтобы оценки всех отмеченных клеток были равны нулю. После этого оценки всех клеток записываются в виде матрицы — матрицы оценок. Если матрица оценок не содержит отрицательных чисел, то получен оптимальный план поставок. Иначе проводится оптимизация плана поставок.
Мы научились находить первоначальный план поставок. Теперь надо выяснить является ли найденный план оптимальным и, если нет то как его оптимизировать. Для этого надо составить матри цу оценок. Оценка клетки (J, j) вычисляется по следующему правилу: оценка i й строки + оценка j-го столбца + число в левом верхнем углу клетки (i, j) Оценки строки и столбца выбираются таким образом, чтобы оценки всех отмеченных клеток были равны нулю. После этого оценки всех клеток записываются в виде матрицы — матрицы оценок. Если матрица оценок не содержит отрицательных чисел, то получен оптимальный план поставок. Иначе проводится оптимизация плана поставок.
 Двигаясь из клетки с отрицательной оценкой по отмеченным клеткам (причем запрещается делать два последовательных шага в одной строке или в одном столбце), строят так называемый цикл пересчета. Внутри этого цикла перераспределяют поставки. Для полученной таблицы находят матрицу оценок и т. д. Рассмотрим подробнее эту схему на конкретном примере.
Двигаясь из клетки с отрицательной оценкой по отмеченным клеткам (причем запрещается делать два последовательных шага в одной строке или в одном столбце), строят так называемый цикл пересчета. Внутри этого цикла перераспределяют поставки. Для полученной таблицы находят матрицу оценок и т. д. Рассмотрим подробнее эту схему на конкретном примере.
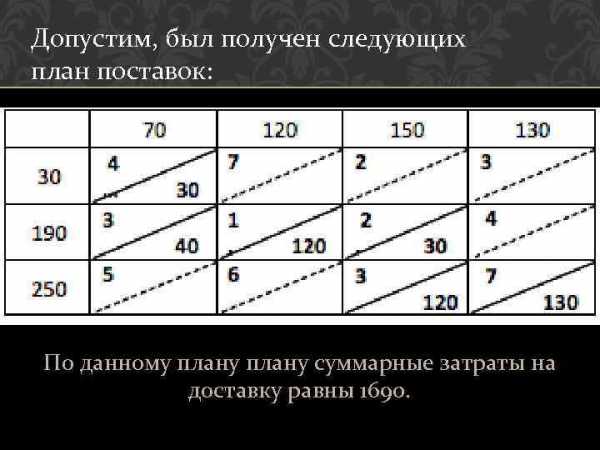 Допустим, был получен следующих план поставок: По данному плану суммарные затраты на доставку равны 1690.
Допустим, был получен следующих план поставок: По данному плану суммарные затраты на доставку равны 1690.
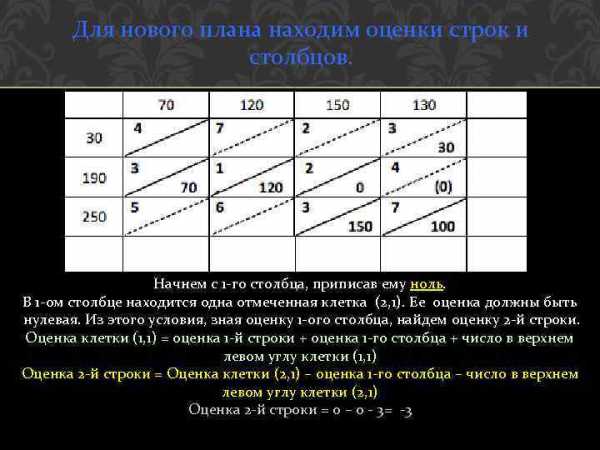
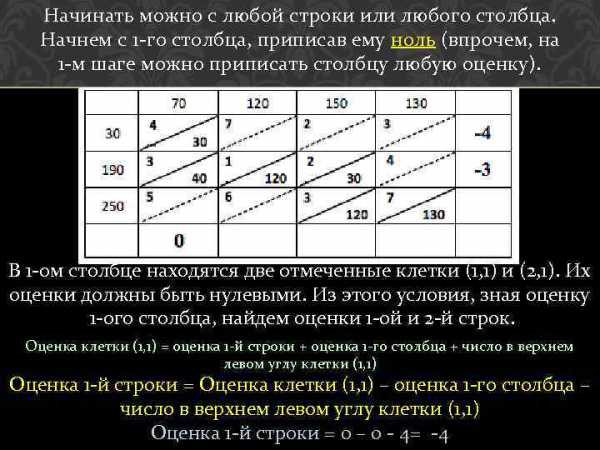 Начинать можно с любой строки или любого столбца. Начнем с 1 -го столбца, приписав ему ноль (впрочем, на 1 -м шаге можно приписать столбцу любую оценку). В 1 -ом столбце находятся две отмеченные клетки (1, 1) и (2, 1). Их оценки должны быть нулевыми. Из этого условия, зная оценку 1 -ого столбца, найдем оценки 1 -ой и 2 -й строк. Оценка клетки (1, 1) = оценка 1 -й строки + оценка 1 -го столбца + число в верхнем левом углу клетки (1, 1) Оценка 1 -й строки = Оценка клетки (1, 1) – оценка 1 -го столбца – число в верхнем левом углу клетки (1, 1) Оценка 1 -й строки = 0 – 0 — 4= -4
Начинать можно с любой строки или любого столбца. Начнем с 1 -го столбца, приписав ему ноль (впрочем, на 1 -м шаге можно приписать столбцу любую оценку). В 1 -ом столбце находятся две отмеченные клетки (1, 1) и (2, 1). Их оценки должны быть нулевыми. Из этого условия, зная оценку 1 -ого столбца, найдем оценки 1 -ой и 2 -й строк. Оценка клетки (1, 1) = оценка 1 -й строки + оценка 1 -го столбца + число в верхнем левом углу клетки (1, 1) Оценка 1 -й строки = Оценка клетки (1, 1) – оценка 1 -го столбца – число в верхнем левом углу клетки (1, 1) Оценка 1 -й строки = 0 – 0 — 4= -4
 Так же найдем оценку 2 -й строки: Оценка клетки (2, 1) = оценка 2 -й строки + оценка 1 -го столбца + число в верхнем левом углу клетки (2, 1) Оценка 2 -й строки = Оценка клетки (2, 1) – оценка 1 -го столбца – число в верхнем левом углу клетки (2, 1) Оценка 2 -й строки = 0 – 0 — 3= -3
Так же найдем оценку 2 -й строки: Оценка клетки (2, 1) = оценка 2 -й строки + оценка 1 -го столбца + число в верхнем левом углу клетки (2, 1) Оценка 2 -й строки = Оценка клетки (2, 1) – оценка 1 -го столбца – число в верхнем левом углу клетки (2, 1) Оценка 2 -й строки = 0 – 0 — 3= -3
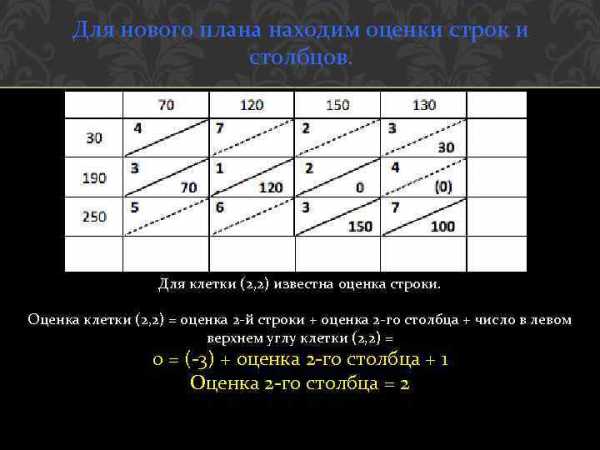
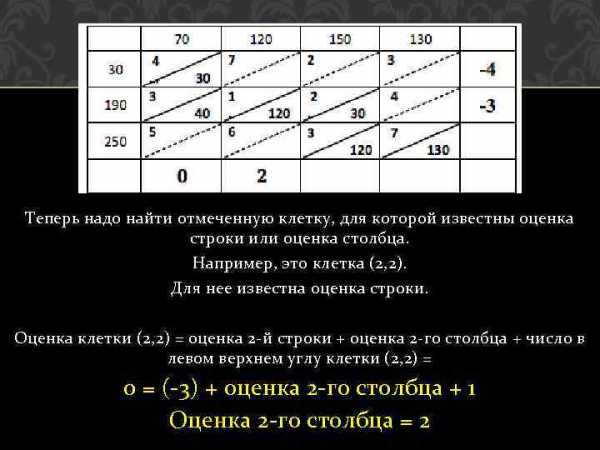 Теперь надо найти отмеченную клетку, для которой известны оценка строки или оценка столбца. Например, это клетка (2, 2). Для нее известна оценка строки. Оценка клетки (2, 2) = оценка 2 -й строки + оценка 2 -го столбца + число в левом верхнем углу клетки (2, 2) = 0 = (-3) + оценка 2 -го столбца + 1 Оценка 2 -го столбца = 2
Теперь надо найти отмеченную клетку, для которой известны оценка строки или оценка столбца. Например, это клетка (2, 2). Для нее известна оценка строки. Оценка клетки (2, 2) = оценка 2 -й строки + оценка 2 -го столбца + число в левом верхнем углу клетки (2, 2) = 0 = (-3) + оценка 2 -го столбца + 1 Оценка 2 -го столбца = 2
 Для отмеченной клетки (2, 3) мы знаем только оценку строки. Попробуйте найти оценку 3 -го столбца. Оценка клетки (2, 3) = оценка 2 -й строки + оценка 3 -го столбца + 2 = 0 ? ?
Для отмеченной клетки (2, 3) мы знаем только оценку строки. Попробуйте найти оценку 3 -го столбца. Оценка клетки (2, 3) = оценка 2 -й строки + оценка 3 -го столбца + 2 = 0 ? ?
 Оценка клетки (2, 3) = оценка 2 -й строки + оценка 3 -го столбца + 2 = 0 Оценка 2 -й строки = 1 Получаем следующую таблицу: Попробуйте самостоятельно найти оценку 3 -й строки и оценку 4 -го столбца.
Оценка клетки (2, 3) = оценка 2 -й строки + оценка 3 -го столбца + 2 = 0 Оценка 2 -й строки = 1 Получаем следующую таблицу: Попробуйте самостоятельно найти оценку 3 -й строки и оценку 4 -го столбца.
 Найдены оценки всех строк и столбцов. Вычислим оценки всех клеток и составим матрицу оценок.
Найдены оценки всех строк и столбцов. Вычислим оценки всех клеток и составим матрицу оценок.
 Для упрощения подсчета можно составить таблицу: Попробуйте рассчитать оценки клеток.
Для упрощения подсчета можно составить таблицу: Попробуйте рассчитать оценки клеток.
 Так как матрица оценок содержит отрицательные числа, то наш план является неоптимальным. Проведем его оптимизацию. Выбираем клетку с наименьшей оценкой. Это клетка (1, 4). Ее оценка -4. Наша задача – построить цикл пересчета. Выходя из клетки (1, 4) и двигаясь ТОЛЬКО ПО ОТМЕЧЕННЫМ КЛЕТКАМ, нужно вернуться в стартовую клетку (1, 4). При этом запрещается делать два последовательных шага в одной строке или в одном столбце.
Так как матрица оценок содержит отрицательные числа, то наш план является неоптимальным. Проведем его оптимизацию. Выбираем клетку с наименьшей оценкой. Это клетка (1, 4). Ее оценка -4. Наша задача – построить цикл пересчета. Выходя из клетки (1, 4) и двигаясь ТОЛЬКО ПО ОТМЕЧЕННЫМ КЛЕТКАМ, нужно вернуться в стартовую клетку (1, 4). При этом запрещается делать два последовательных шага в одной строке или в одном столбце.
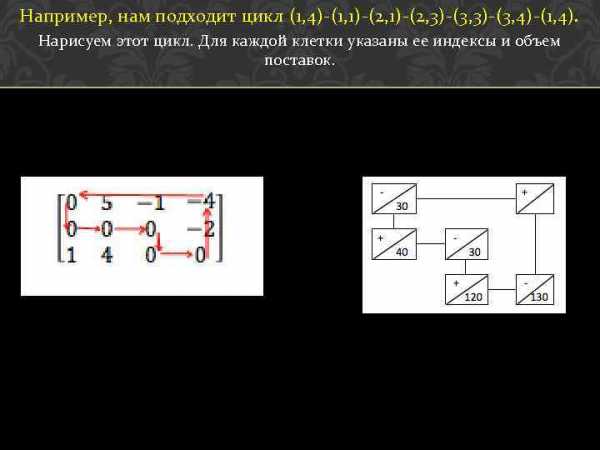 Например, нам подходит цикл (1, 4)-(1, 1)-(2, 3)-(3, 4)-(1, 4). Нарисуем этот цикл. Для каждой клетки указаны ее индексы и объем поставок.
Например, нам подходит цикл (1, 4)-(1, 1)-(2, 3)-(3, 4)-(1, 4). Нарисуем этот цикл. Для каждой клетки указаны ее индексы и объем поставок.
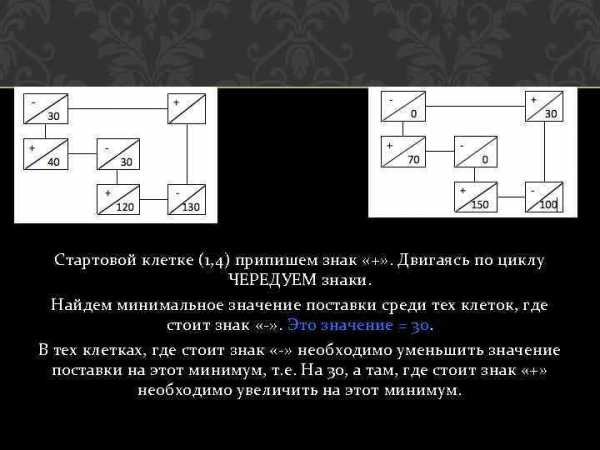 Стартовой клетке (1, 4) припишем знак «+» . Двигаясь по циклу ЧЕРЕДУЕМ знаки. Найдем минимальное значение поставки среди тех клеток, где стоит знак «-» . Это значение = 30. В тех клетках, где стоит знак «-» необходимо уменьшить значение поставки на этот минимум, т. е. На 30, а там, где стоит знак «+» необходимо увеличить на этот минимум.
Стартовой клетке (1, 4) припишем знак «+» . Двигаясь по циклу ЧЕРЕДУЕМ знаки. Найдем минимальное значение поставки среди тех клеток, где стоит знак «-» . Это значение = 30. В тех клетках, где стоит знак «-» необходимо уменьшить значение поставки на этот минимум, т. е. На 30, а там, где стоит знак «+» необходимо увеличить на этот минимум.
 Если получена одна клетка с нулевой поставкой, то она становится пустой. У нас таких клеток две: (1, 1) и (2, 3). Пустой объем поставим там, где наибольший тариф на доставку, т. е. В клетку (1, 1). Это делается для того, чтобы выполнялось соотношение: число отмеченных клеток = число строк + число столбцов -1 Получаем новый план поставок.
Если получена одна клетка с нулевой поставкой, то она становится пустой. У нас таких клеток две: (1, 1) и (2, 3). Пустой объем поставим там, где наибольший тариф на доставку, т. е. В клетку (1, 1). Это делается для того, чтобы выполнялось соотношение: число отмеченных клеток = число строк + число столбцов -1 Получаем новый план поставок.
 Для нового плана находим оценки строк и столбцов. Начнем с 1 -го столбца, приписав ему ноль. В 1 -ом столбце находится одна отмеченная клетка (2, 1). Ее оценка должны быть нулевая. Из этого условия, зная оценку 1 -ого столбца, найдем оценку 2 -й строки. Оценка клетки (1, 1) = оценка 1 -й строки + оценка 1 -го столбца + число в верхнем левом углу клетки (1, 1) Оценка 2 -й строки = Оценка клетки (2, 1) – оценка 1 -го столбца – число в верхнем левом углу клетки (2, 1) Оценка 2 -й строки = 0 – 0 — 3= -3
Для нового плана находим оценки строк и столбцов. Начнем с 1 -го столбца, приписав ему ноль. В 1 -ом столбце находится одна отмеченная клетка (2, 1). Ее оценка должны быть нулевая. Из этого условия, зная оценку 1 -ого столбца, найдем оценку 2 -й строки. Оценка клетки (1, 1) = оценка 1 -й строки + оценка 1 -го столбца + число в верхнем левом углу клетки (1, 1) Оценка 2 -й строки = Оценка клетки (2, 1) – оценка 1 -го столбца – число в верхнем левом углу клетки (2, 1) Оценка 2 -й строки = 0 – 0 — 3= -3
 Для нового плана находим оценки строк и столбцов. Для клетки (2, 2) известна оценка строки. Оценка клетки (2, 2) = оценка 2 -й строки + оценка 2 -го столбца + число в левом верхнем углу клетки (2, 2) = 0 = (-3) + оценка 2 -го столбца + 1 Оценка 2 -го столбца = 2
Для нового плана находим оценки строк и столбцов. Для клетки (2, 2) известна оценка строки. Оценка клетки (2, 2) = оценка 2 -й строки + оценка 2 -го столбца + число в левом верхнем углу клетки (2, 2) = 0 = (-3) + оценка 2 -го столбца + 1 Оценка 2 -го столбца = 2

 Составляем матрицу оценок: План является неоптимальным, т. к. Оценка клетки (2, 4) меньше 0. Строим для него цикл пересчета. Min = 0. Клетка (2. 3) становится пустой, а клетка (2, 4) – ОТМЕЧЕННОЙ (нулевая поставка).
Составляем матрицу оценок: План является неоптимальным, т. к. Оценка клетки (2, 4) меньше 0. Строим для него цикл пересчета. Min = 0. Клетка (2. 3) становится пустой, а клетка (2, 4) – ОТМЕЧЕННОЙ (нулевая поставка).
 Получаем новый план поставок: Найдите оценки клеток. Оценка клетки (J, j) вычисляется по следующему правилу: оценка i й строки + оценка j-го столбца + число в левом верхнем углу клетки (i, j)
Получаем новый план поставок: Найдите оценки клеток. Оценка клетки (J, j) вычисляется по следующему правилу: оценка i й строки + оценка j-го столбца + число в левом верхнем углу клетки (i, j)
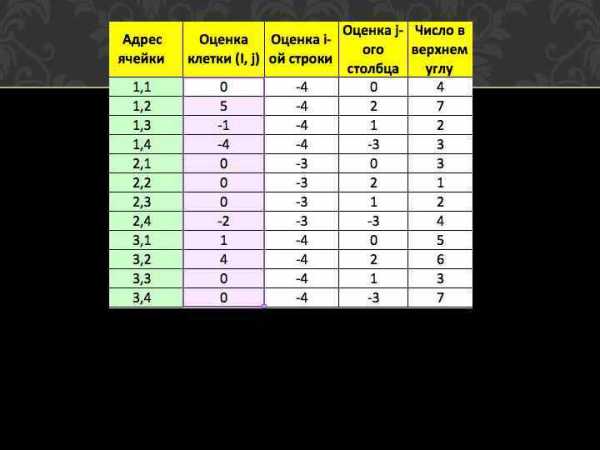
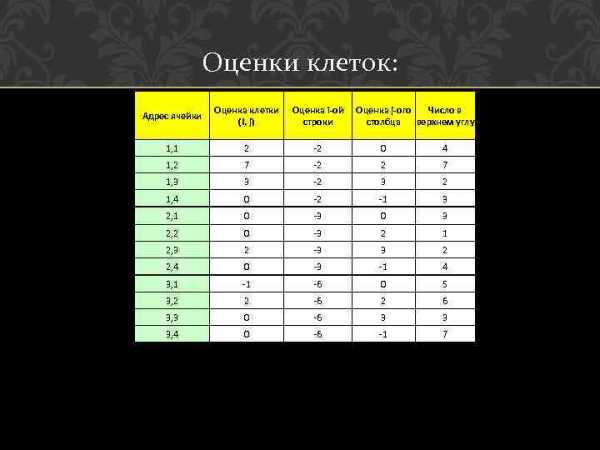 Оценки клеток: Адрес ячейки Оценка клетки (I, j) Оценка i-ой строки Оценка j-ого Число в столбца верхнем углу 1, 1 2 -2 0 4 1, 2 7 -2 2 7 1, 3 3 -2 3 2 1, 4 0 -2 -1 3 2, 1 0 -3 0 3 2, 2 0 -3 2 1 2, 3 2 -3 3 2 2, 4 0 -3 -1 4 3, 1 -1 -6 0 5 3, 2 2 -6 2 6 3, 3 0 -6 3 3 3, 4 0 -6 -1 7
Оценки клеток: Адрес ячейки Оценка клетки (I, j) Оценка i-ой строки Оценка j-ого Число в столбца верхнем углу 1, 1 2 -2 0 4 1, 2 7 -2 2 7 1, 3 3 -2 3 2 1, 4 0 -2 -1 3 2, 1 0 -3 0 3 2, 2 0 -3 2 1 2, 3 2 -3 3 2 2, 4 0 -3 -1 4 3, 1 -1 -6 0 5 3, 2 2 -6 2 6 3, 3 0 -6 3 3 3, 4 0 -6 -1 7
 Получаем следующую матрицу оценок: План является неоптимальным, т. к. Оценка клетки (3, 1) меньше 0. Постройте цикл пересчета. Нам подходит цикл (3, 1)-(2, 4)-(3, 1) Минимум (70, 100) = 70. В клетках со знакам «+» поставки увеличиваются на 70, а в клетках со знаком «-» поставки уменьшаются на 70. Клетка (2, 1) становится пустой.
Получаем следующую матрицу оценок: План является неоптимальным, т. к. Оценка клетки (3, 1) меньше 0. Постройте цикл пересчета. Нам подходит цикл (3, 1)-(2, 4)-(3, 1) Минимум (70, 100) = 70. В клетках со знакам «+» поставки увеличиваются на 70, а в клетках со знаком «-» поставки уменьшаются на 70. Клетка (2, 1) становится пустой.
 Поучаем новый план поставок: Составим матрицу оценок: 3 7 3 0 1 0 2 0 0 Матрица оценок не содержит отрицательных чисел. Получен оптимальный план поставок.
Поучаем новый план поставок: Составим матрицу оценок: 3 7 3 0 1 0 2 0 0 Матрица оценок не содержит отрицательных чисел. Получен оптимальный план поставок.
 Суммарные затраты на перевозку груза равны: Напомню, что суммарные затраты на перевозку груза 1690.
Суммарные затраты на перевозку груза равны: Напомню, что суммарные затраты на перевозку груза 1690.
 ОКТРЫТАЯ МОДЕЛЬ Открытая модель сводится к закрытой. Если суммарная мощность поставщиков больше суммарного спроса потребителей, то вводится фиктивный потребитель, которому приписывается спрос, равный разнице между суммарной мощностью поставщиков и суммарным спросом потребителей. Полученная закрытая модель решается.
ОКТРЫТАЯ МОДЕЛЬ Открытая модель сводится к закрытой. Если суммарная мощность поставщиков больше суммарного спроса потребителей, то вводится фиктивный потребитель, которому приписывается спрос, равный разнице между суммарной мощностью поставщиков и суммарным спросом потребителей. Полученная закрытая модель решается.
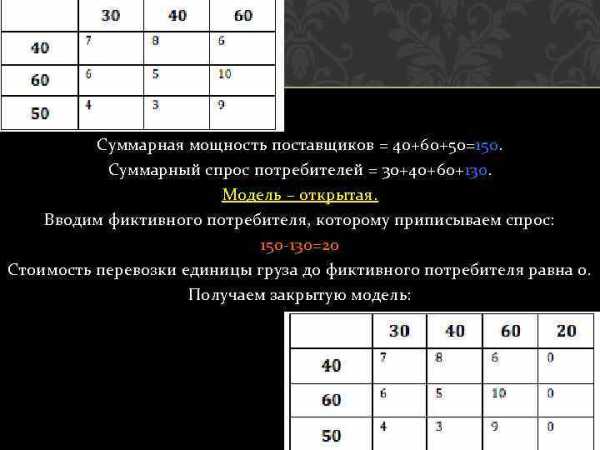 Суммарная мощность поставщиков = 40+60+50=150. Суммарный спрос потребителей = 30+40+60+130. Модель – открытая. Вводим фиктивного потребителя, которому приписываем спрос: 150 -130=20 Стоимость перевозки единицы груза до фиктивного потребителя равна 0. Получаем закрытую модель:
Суммарная мощность поставщиков = 40+60+50=150. Суммарный спрос потребителей = 30+40+60+130. Модель – открытая. Вводим фиктивного потребителя, которому приписываем спрос: 150 -130=20 Стоимость перевозки единицы груза до фиктивного потребителя равна 0. Получаем закрытую модель:
present5.com
3.3. Распределительный метод решения транспортной задачи
Рассмотрим способ определения свободных неизвестных, которые целесообразно перевести в число базисных на конкретном примере. Возьмем базисное решение, найденное методом северо-западного угла со стоимостью перевозок
=250 + 325 + 250 + 550 + 225 + 625 = 725.
Теперь необходимо построить циклы пересчета для всех свободных переменных (свободных клеток) и определить сумму стоимостей по циклам пересчета ij для всех свободных неизвестных, чтобы найти, какую из них перевести в число базисных для уменьшения целевой функции.
В1 | В2 | В3 | В4 | ai | |
A1 | 2 50 | 3– 25 | 2 + | 1 | 75 |
A2 | 4 | 2 + 50 | 5 – 50 | 2 | 100 |
A3 | 1 | 3 | 2 25 | 6 25 | 50 |
bj | 50 | 75 | 75 | 25 |
Определяем сумму стоимостей по циклу пересчета для каждой свободной клетки, подставляя соответствующие стоимости перевозок из базисных клеток в вершинах цикла:
х13 13 = с13 — с23 + с22 — с12 = 2 — 5 + 2 — 3 = — 4 ,
х14 14 = с14 — с24 +с33 – с23 + с22 — с12 = 1 – 2 + 2 — 5 + 2 — 3 = -5 ,
х21 21 = с21 — с11 + с12 — с22 = 4 – 2 + 3 — 2 = 3 ,
х24 24 = с24 — с14 + с12 — с22 = 2 — 1+ 2 — 4 = -1 ,
аналогично 31 = 6, 32 = 4.
Выбираем те из свободных переменных, которые имеют отрицательное значение суммы стоимости по циклу пересчета. В рассматриваемом примере это х13, х14, х24.
Во-вторых, определяется базисная переменная, переводимая в число свободных.
Для этого необходимо проанализировать цикл пересчета, соответствующий выбранной свободной неизвестной. В нашем примере это может быть цикл для переменной х13.
Производя преобразования по циклу, мы должны получить нуль в одной из базисных переменных. Кроме того, необходимо учитывать, что переменные не могут принимать отрицательных значений. Поэтому выбирается та базисная переменная, которая имеет наименьшее значение из всех базисных переменных, расположенных в отрицательных вершинах цикла пересчета. В нашем примере это будет х12=10.
Для получения нового допустимого базисного решения осуществляем сдвиг по циклу пересчета выбранной свободной переменной х13 на величину значений выбранной базисной переменной х12=10, которая после сдвига переводится в свободные.
При этом получим новую таблицу матрицы перевозок.
В1 | В2 | В3 | В4 | ai | |
A1 | 1 20 | 2 | 3 10 | 4 | 75 |
A2 | 2 | 4 30 | 1 10 | 3 | 100 |
A3 | 4 | 3 | 2 10 | 1 10 | 50 |
bj | 50 | 75 | 75 | 25 |
Сдвиг по циклу привел к новому допустимому базисному решению:
х11=20, х13=10, х22=30, х23=10, х33=10, х34=10, остальные xij=0.
Новое решение дает значение целевой функции F=250, меньшее предыдущего, т. е. ближе к оптимальному значению.
studfiles.net
Распределительный метод решения транспортной задачи
После того как получен первоначальный план поставок необходимо выяснить, является ли найденный план оптимальным и, если нет, то оптимизировать его. Для этого надо составить матрицу оценок.
Оценка клетки (i, j) вычисляется по следующему правилу: оценка i-ой строки + оценка j-го столбца + число в левом верхнем углу клетки (i, j). Оценки строки и столбца выбираются таким образом, чтобы оценки всех отмеченных клеток были равны 0. После этого оценки всех клеток записываются в виде матрицы – матрицы оценок. Если матрица оценок не содержит отрицательных чисел, то получен оптимальный план поставок. Иначе проводится оптимизация плана поставок.
Двигаясь из клетки с наименьшей отрицательной оценкой по отмеченным клеткам (причем запрещается делать два последовательных шага в одной строке или столбце), строят так называемый цикл пересчета. Внутри этого цикла перераспределяют поставки. Для полученной таблицы находят матрицу оценок и т. д. Рассмотрим подробнее эту схему на конкретном примере.
Пример. В предыдущем примере методом северо-западного угла был получен следующий план поставок. Исследуем его на оптимальность.
Начинать можно с любой строки или любого столбца. Начнем с 1-го столбца, приписав ему 0. В 1-м столбце находятся две отмеченные клетки (1, 1) и (1, 2). Их оценки должны быть нулевыми. Из этого условия, зная оценку первого столбца, найдем оценки 1-й и 2-й строк.
Оценка клетки (1, 1) = оценка 1-й строки + оценка 1-го столбца + число в левом верхнем углу клетки (1, 1) = оценка 1-й строки + 0 + 4= 0. Отсюда оценка 1-й строки = -4.
Оценка клетки (2, 1) = оценка 2-й строки + оценка 1-го столбца + число в левом верхнем углу клетки (2, 1) = оценка 2-й строки + 0 + 3= 0. Отсюда оценка 2-й строки = -3.
Найденные оценки столбцов записываем под таблицей, найденные оценки строк – справа от таблицы.
После этого шага получаем следующую таблицу:
| -4 | |||||
| -3 | |||||
Теперь надо найти отмеченную клетку, для которой известны оценки строки или столбца. Например, это клетка (2, 2). Для нее известна оценка строки. Оценка клетки (2, 2) = оценка 2-й строки + оценка 2-го столбца + число в левом верхнем углу клетки (2, 2) = = (-3) + оценка 2-го столбца + 1 = 0. Отсюда оценка 2-го столбца = 2.
После этого шага получаем следующую таблицу:
| -4 | |||||
| -3 | |||||
Для отмеченной клетки (2, 3) известна только оценка строки. Оценка клетки (2, 3) = оценка 2-й строки + оценка 3-го столбца + число в левом верхнем углу клетки (2, 3) = = (-3) + оценка 3-го столбца + 2 = 0. Отсюда оценка 3-го столбца = 1. После этого шага получаем следующую таблицу:
| -4 | |||||
| -3 | |||||
Оценка клетки (3, 3) = оценка 3-й строки + оценка 3-го столбца + число в левом верхнем углу клетки (3, 3) = оценка 3-й строки + 1 + 3= 0. Отсюда оценка 3-й строки = -4. После этого шага получаем следующую таблицу:
| -4 | |||||
| -3 | |||||
| -4 | |||||
Оценка клетки (3, 4) = оценка 3-й строки + оценка 4-го столбца + число в левом верхнем углу клетки (3, 4) = (-4) + оценка 4-го столбца + 7 = 0. Отсюда оценка 4-го столбца = -3. После этого шага получаем следующую таблицу:
| -4 | |||||
| -3 | |||||
| -4 | |||||
| -3 |
Найдены оценки всех строк и столбцов. Вычислим оценки всех клеток и составим матрицу оценок.
Оценка клетки (1, 2) = оценка 1-й строки + оценка 2-го столбца + число в левом верхнем углу клетки (1, 2) = (-4) + 2+ 7 = 5.
Оценка клетки (1, 3) = оценка 1-й строки + оценка 3-го столбца + число в левом верхнем углу клетки (1, 3) = (-4) + 1+ 2 = -1. И т. д.
Получаем следующую матрицу оценок:
Так как матрица оценок содержит отрицательные числа, то план поставок является неоптимальным. Проведем его оптимизацию. Выберем клетку с наименьшей оценкой. Это клетка (1, 4). Ее оценка равна -4. Наша задача – построить цикл пересчета. Выходя из клетки (1, 4) и двигаясь только по отмеченным клеткам, нужно вернуться в стартовую клетку (1, 4). При этом запрещается делать два последовательных шага в одной строке или в одном столбце. Например, подходит цикл (1, 4) – (1, 1) – (2,1) – (2,3) – (3,3) – (3,4) – (1,4). Нарисуем этот цикл. Для каждой клетки указаны ее индексы и объем поставок.
Стартовой клетке (1, 4) припишем знак «+». Двигаясь по циклу, чередуем знаки. Среди поставок в клетки со знаком «-» найдем минимальную: min (30, 30, 130) = 30. После этого в клетках со знаком «-» уменьшим поставки на этот минимум, а клетках со знаком «+» увеличим на этот минимум. Клетка (1, 4) становится отмеченной. Если получена одна клетка с нулевой поставкой, то она становится пустой. У нас таких клеток две – (1, 1), (2,3). Поэтому пустой объявим одну из них с наибольшим тарифом – клетку (1, 1). В клетку (2, 3) будет сделана нулевая поставка, и она становится отмеченной. Это делается для выполнения соотношения: число отмеченных клеток = число строк+число столбцов-1.
Нужно следить, чтобы суммы поставок по строкам и столбцам были равны мощностям поставщиков и спросу потребителей соответственно.
| -0 | |||||
| -3 | |||||
| -4 | |||||
| -3 |
Для нового плана находим оценки строк и столбцов. Затем получим матрицу оценок:
План является неоптимальным, так как оценка клетки (2, 4) меньше нуля. Строим для нее цикл пересчета: (2, 4) – (3, 4) – (3, 3) – (2, 3) (2, 4).
min (0, 100) = 0. Клетка (2, 3) становится пустой, а клетка (2, 4) – отмеченной (нулевая поставка). Новый план поставок:
| -2 | |||||
| -3 | |||||
| -6 | |||||
| -1 |
Для нового плана находим оценки строк и столбцов. Затем получим матрицу оценок клеток:
План является неоптимальным, так как оценка клетки (3, 1) меньше нуля. Строим для нее цикл пересчета: (3, 1) – (2, 1) – (2, 4) – (3, 4) – (3, 1).
min (70, 100) = 70. В клетках с «+» поставки увеличиваются на 70, а в клетках с «-» поставки уменьшаются на 70. Клетка (2, 1) становится пустой. Новый план поставок:
| -1 | |||||
| -2 | |||||
| -5 | |||||
| -2 |
Находим оценки строк и столбцов. Получаем матрицу оценок:
Матрица оценок не содержит отрицательных чисел. Получен оптимальный план поставок. Суммарные затраты на перевозку груза равны: 3*30+1*120+4*70+5*70+3*150+7*30=1500 (Для первоначального плана эта сумма была равна 1690).
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru

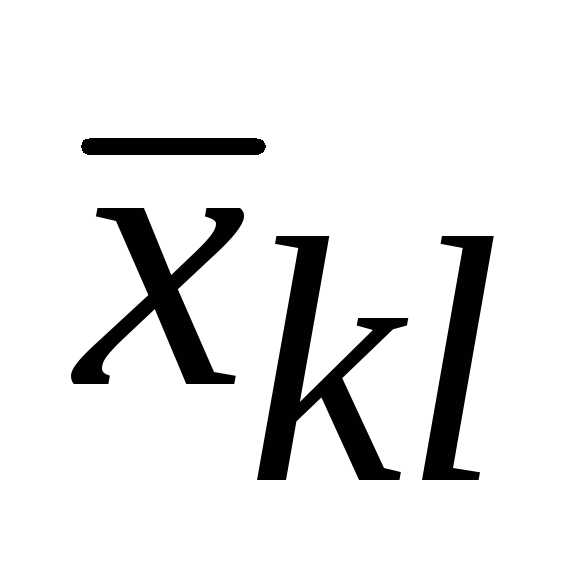 соответствует
положительной вершине;
соответствует
положительной вершине;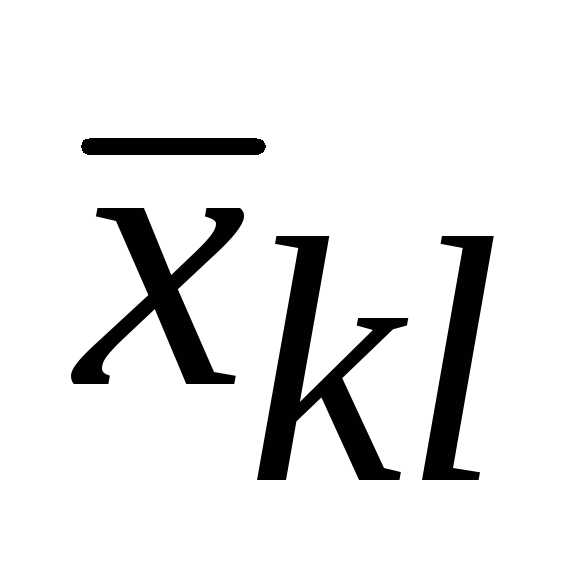 соответствует
отрицательной вершине;
соответствует
отрицательной вершине;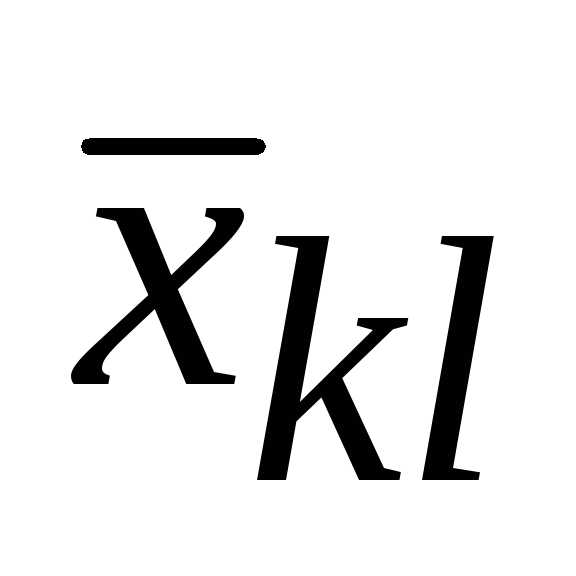 в цикл не входит.
в цикл не входит.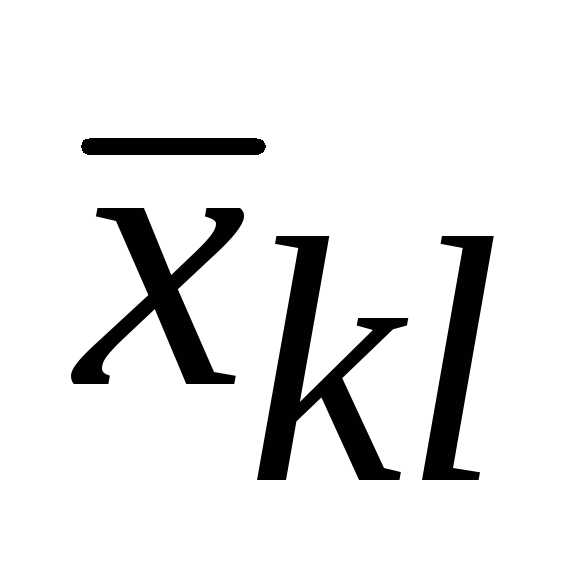 соответствуетположительной вершине,
то при переходе к новому опорному
решению
соответствуетположительной вершине,
то при переходе к новому опорному
решению увеличитсяна ту же величину,
что и
увеличитсяна ту же величину,
что и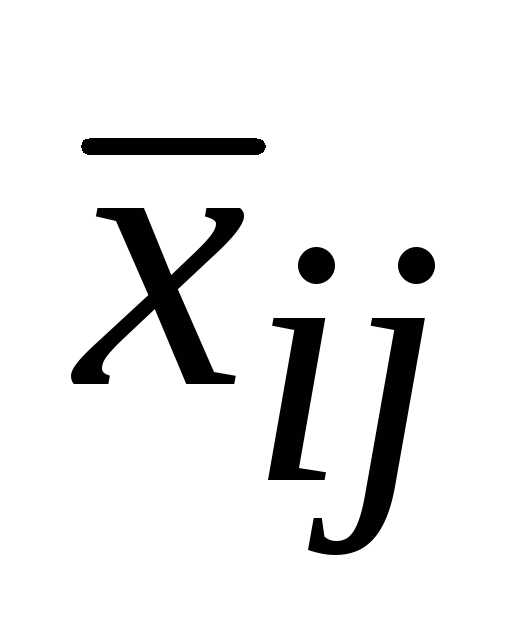 .
То есть, если выразить базисные переменные
через свободные, переменная
.
То есть, если выразить базисные переменные
через свободные, переменная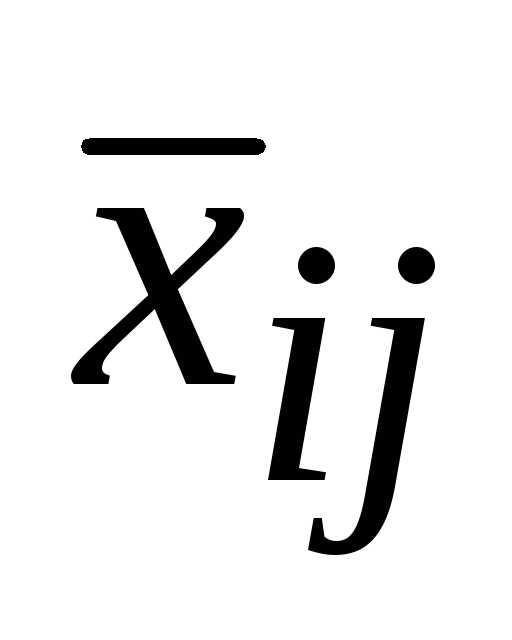 войдет в выражение для
войдет в выражение для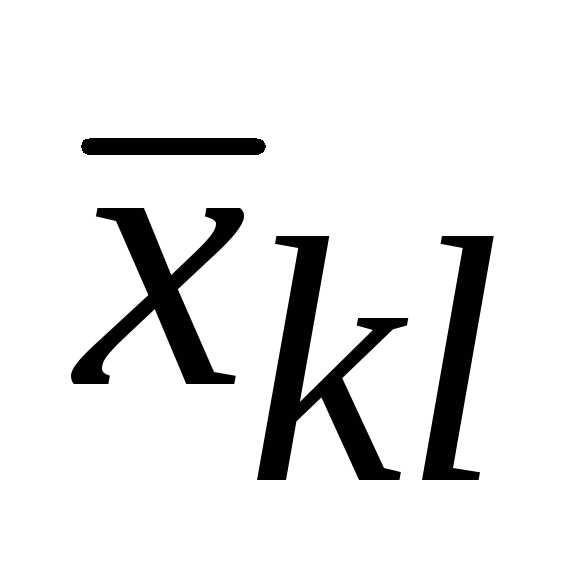 с коэффициентом «+1»;
с коэффициентом «+1»;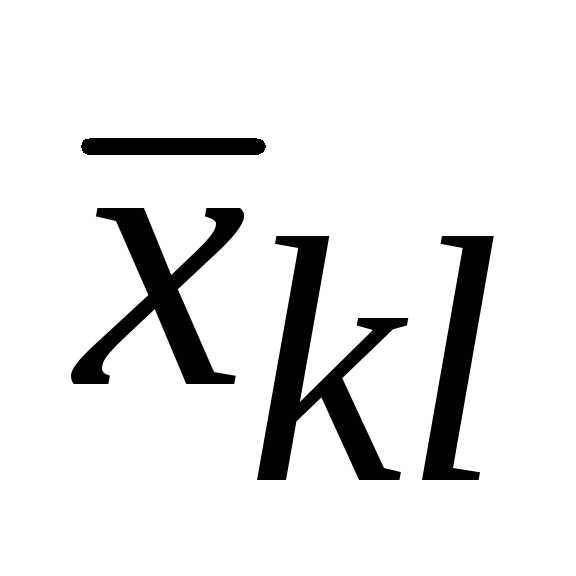 соответствуетотрицательной вершине,
то при переходе к новому опорному
решению
соответствуетотрицательной вершине,
то при переходе к новому опорному
решению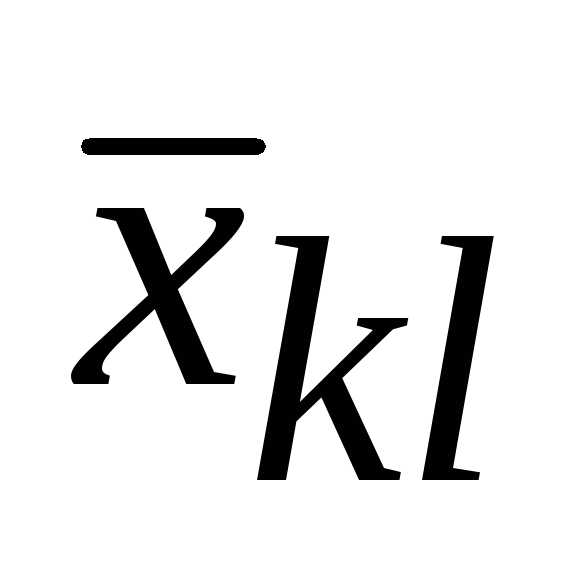 уменьшитсяна ту же величину,
на которую увеличится
уменьшитсяна ту же величину,
на которую увеличится .
То есть, если выразить базисные переменные
через свободные, переменная
.
То есть, если выразить базисные переменные
через свободные, переменная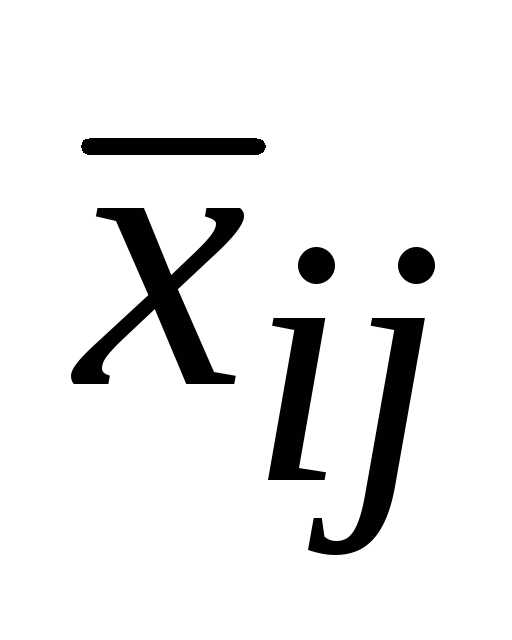 войдет в выражение для
войдет в выражение для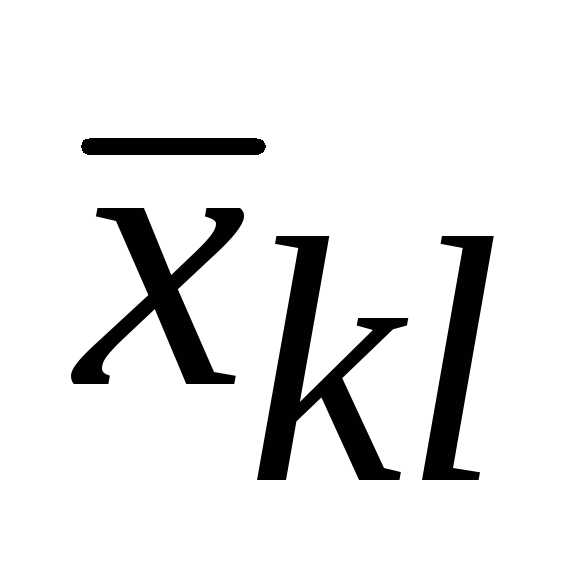 с коэффициентом «-1«;
с коэффициентом «-1«;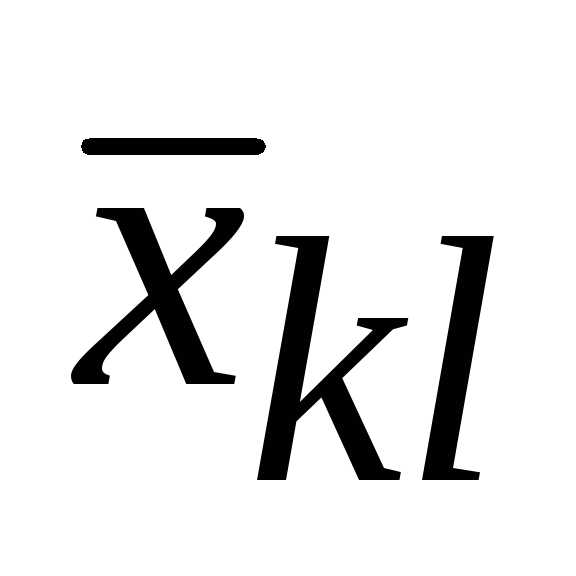 не входит в цикл пересчета, то
при переходе к новому опорному решению
значение
не входит в цикл пересчета, то
при переходе к новому опорному решению
значение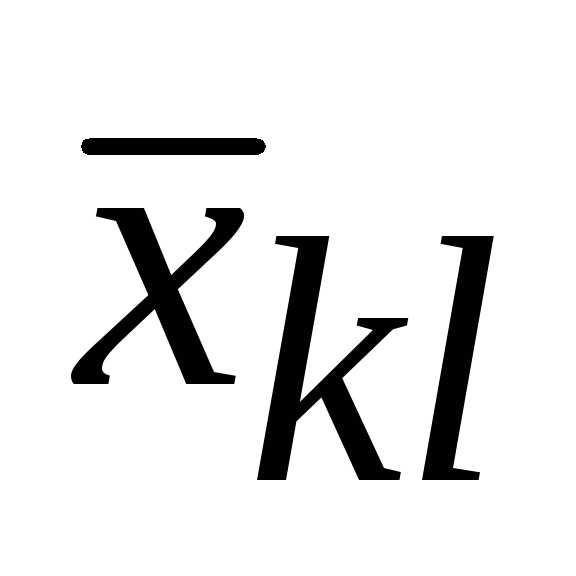 не изменится. То есть, если выразить
базисные переменные через свободные,
переменная
не изменится. То есть, если выразить
базисные переменные через свободные,
переменная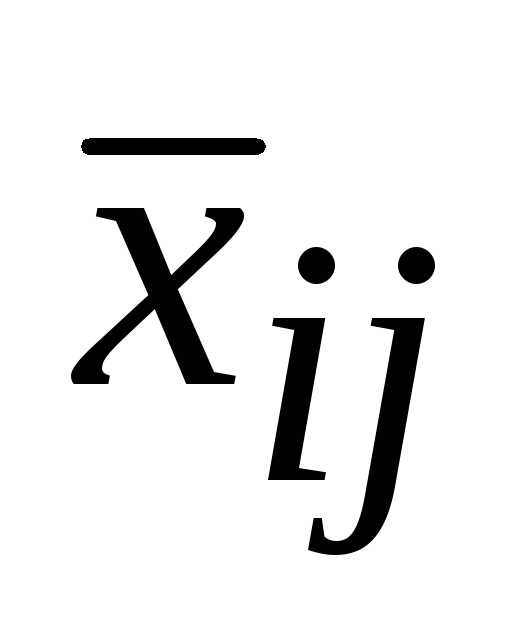 войдет в выражение для
войдет в выражение для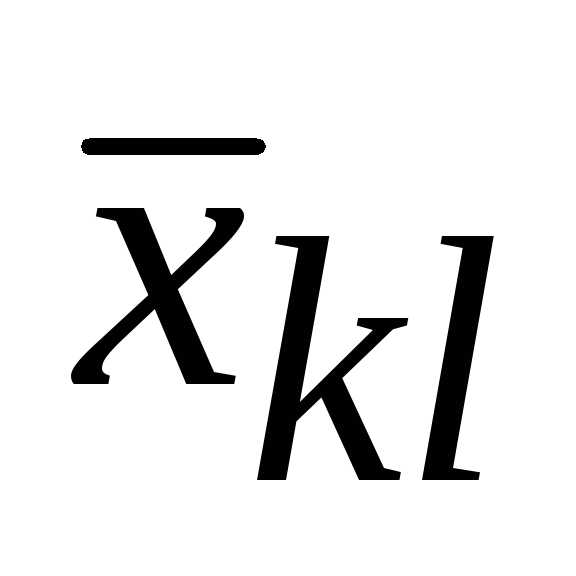 с коэффициентом «0«.
с коэффициентом «0«.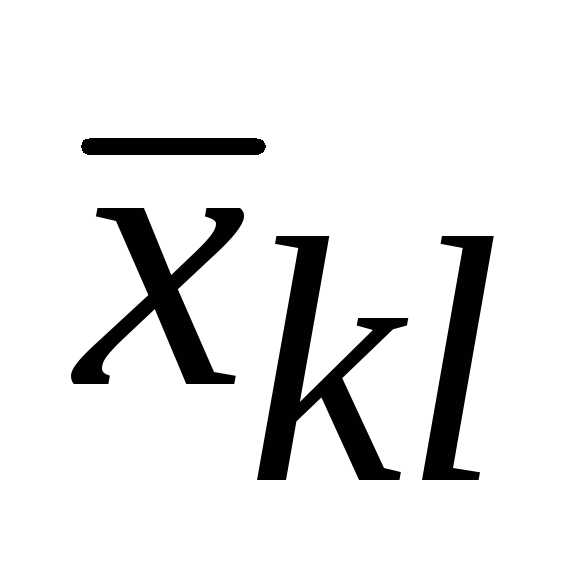 = +1
= +1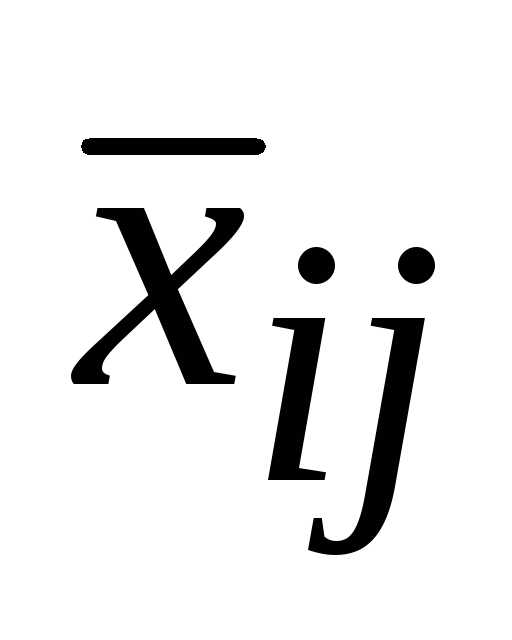 +…….
+…….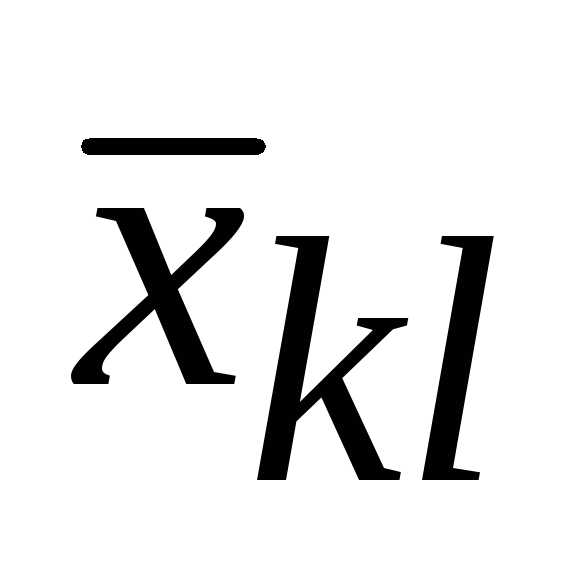 = -1
= -1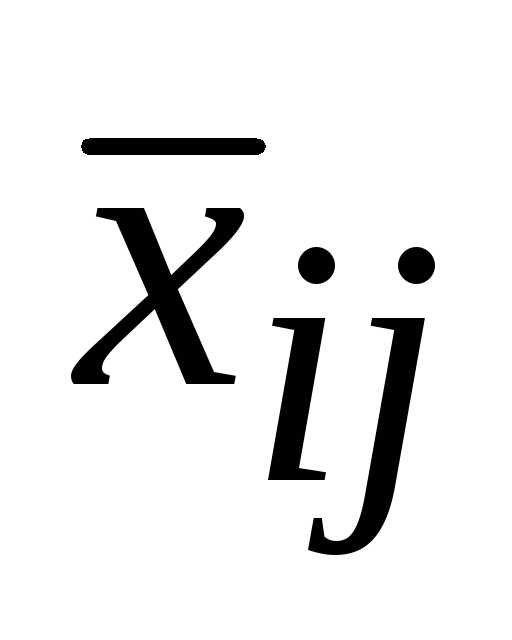 +…….
+…….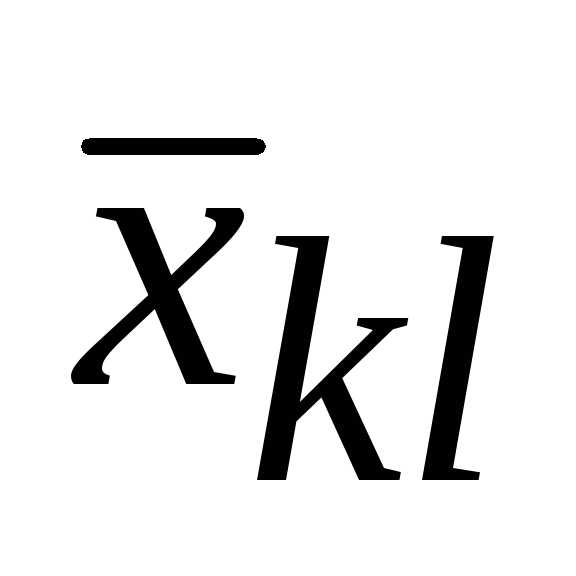 = 0
= 0 +…….
+……. Наибольшее значение функции
Наибольшее значение функции 

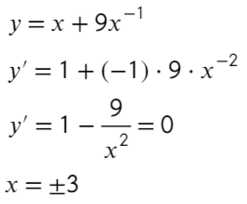




 рисунок
1 Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0. Это
наглядно показано на рисунке 2:
рисунок
1 Определение. Точка
x0 называется
точкой максимума функции f, если для
всех x из некоторой окрестности
x0 выполняется
неравенство f(x) ≤ f(x0. Это
наглядно показано на рисунке 2:  рисунок
2 По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно). В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно). Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже: Слева
направо: a — точка максимума; a — точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума. Для
точек минимума и максимума функции есть
общее определение — точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название — экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума — xmin.
рисунок
2 По
определению значение функции f в точке
x0 является
наибольшим среди значений функции в
окрестности этой точки, поэтому график
функции в окрестности x0 имеет
обычно либо вид гладкого холма, либо
вид острого пика (рис. 1 а) и б)
соответственно). В
окрестности точки минимума графики
изображаются в виде загругленной или
острой впадины (рис. 2 а) и б)
соответственно). Другие
примеры поведения графиков функций в
точках максимума и минимума приведены
на рисунке ниже: Слева
направо: a — точка максимума; a — точка
минимума; каждая точка из промежутка
[-1; 0] является как точкой максимума, так
и точкой минимума. Для
точек минимума и максимума функции есть
общее определение — точки
экстремума.
Значение функции в этих точках
соответственно назывется максимумом
или минимумом этой функции.
Общее название — экстремум
функции.
Точки максимума обычно обозначают xmax,
а точки минимума — xmin. Источник:
Источник:

















 6 2х – 4 3 Решение: решим каждое неравенство отдельно 5х + 1 6 2х – 4 3 5х 6 -1 2х 5х 5 2х х 1 х 3,5 1 3,5 х Ответ: (1; 3,5) решаем каждое неравенство системы отдельно изображаем полученные решения на числовой прямой и смотрим пересечения этих решений. Эта общая часть и является решением данной системы неравенств. «
6 2х – 4 3 Решение: решим каждое неравенство отдельно 5х + 1 6 2х – 4 3 5х 6 -1 2х 5х 5 2х х 1 х 3,5 1 3,5 х Ответ: (1; 3,5) решаем каждое неравенство системы отдельно изображаем полученные решения на числовой прямой и смотрим пересечения этих решений. Эта общая часть и является решением данной системы неравенств. «

 0 Решение: решим каждое неравенство отдельно х ² — 3х + 2 0 2х ² — 3х – 5 0 Найдем корни соответствующих квадратных уравнений х ² — 3х + 2 = 0 2х ² — 3х – 5 = 0 По свойствам коэффициентов имеем: х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5 Изобразим метод интервала на числовой оси: -1 1 2 2,5 х Ответ: (-1;1) υ (2;2,5) «
0 Решение: решим каждое неравенство отдельно х ² — 3х + 2 0 2х ² — 3х – 5 0 Найдем корни соответствующих квадратных уравнений х ² — 3х + 2 = 0 2х ² — 3х – 5 = 0 По свойствам коэффициентов имеем: х 1 = 1 х 2 = 2 х 1 = -1 х 2 = 5/2= 2,5 Изобразим метод интервала на числовой оси: -1 1 2 2,5 х Ответ: (-1;1) υ (2;2,5) «
 0 2) х-3у =6 2у-5х = -4 3) 5(х+у)-7(х-у) = 54 4(х+у)+3(х-у) = 51 «
0 2) х-3у =6 2у-5х = -4 3) 5(х+у)-7(х-у) = 54 4(х+у)+3(х-у) = 51 «

 0 «
0 «
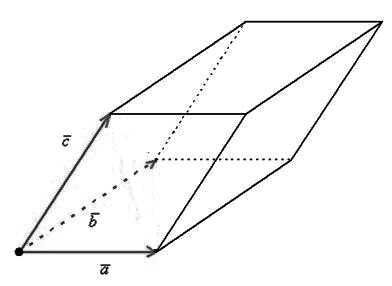
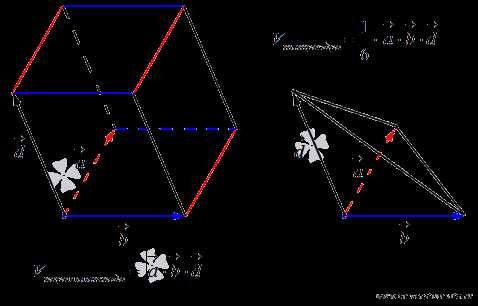 Смешанным
произведением трех векторов называется
число, равное векторному произведению
первых двух векторов,,
умноженному скалярно на вектор.
Векторами это можно представить так
Смешанным
произведением трех векторов называется
число, равное векторному произведению
первых двух векторов,,
умноженному скалярно на вектор.
Векторами это можно представить так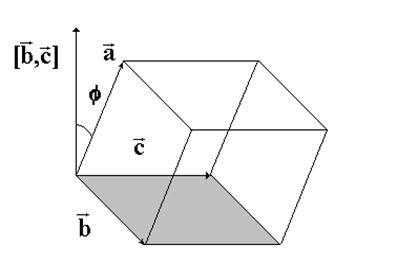 Рис.
1. К доказательству теоремы 1.
геометрический
смысл векторного произведения векторов ,
получаем, что
Рис.
1. К доказательству теоремы 1.
геометрический
смысл векторного произведения векторов ,
получаем, что Рис.
2. К доказательству теоремы 1.
Рис.
2. К доказательству теоремы 1.
 и
и 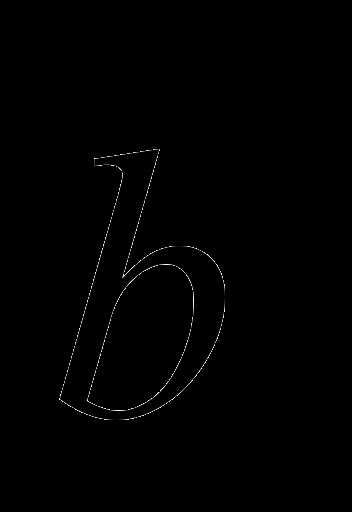 называется вектор
называется вектор  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям: перпендикулярен векторам
перпендикулярен векторам  и
и 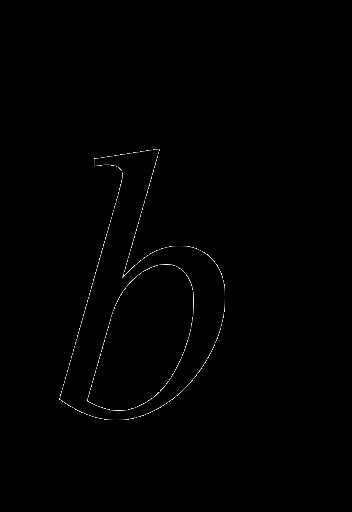 .
. кратчайший поворот от вектора
кратчайший поворот от вектора  ко второму вектору
ко второму вектору  виден против часовой стрелки.
виден против часовой стрелки. а) правая
а) правая  б) левая
б) левая


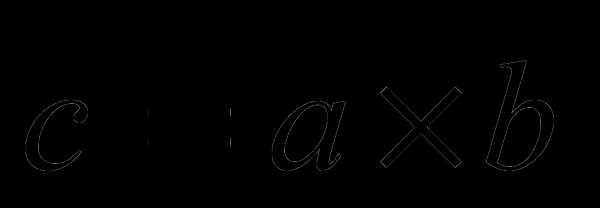 или
или 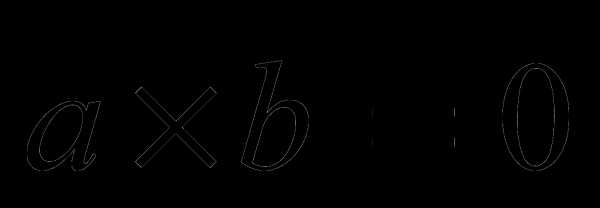 , где
, где 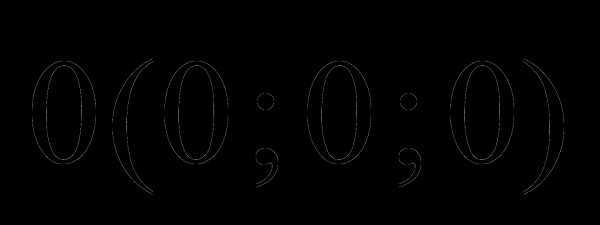 , если
, если  и
и  коллинеарные или по крайней мере один из сомножителей является нулевым вектором.
коллинеарные или по крайней мере один из сомножителей является нулевым вектором. является правой.
является правой.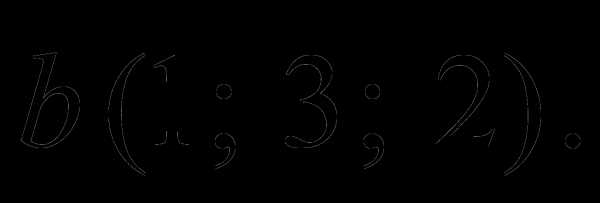 Найти площадь параллелограмма, построенного на этих векторах.
Найти площадь параллелограмма, построенного на этих векторах.
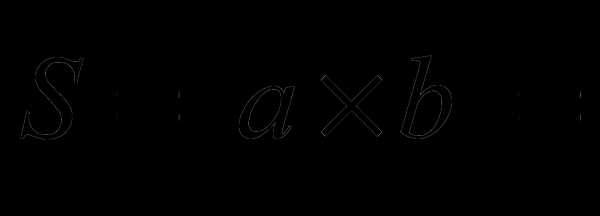
 и
и 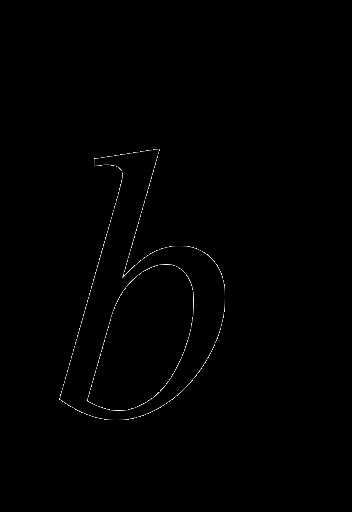 будет равна
будет равна  .
. вычисляется по формуле
вычисляется по формуле (3)
(3) относительно координатных осей. z
относительно координатных осей. z
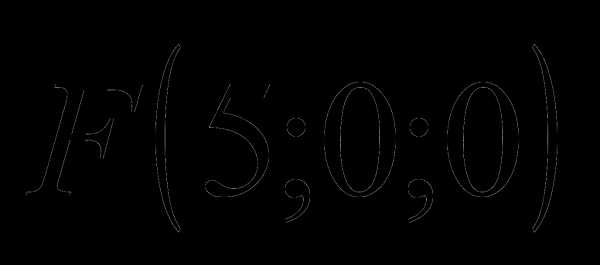 . Требуется найти моменты
. Требуется найти моменты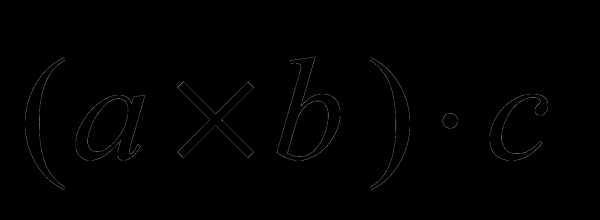 называется смешанным и обозначается
называется смешанным и обозначается 
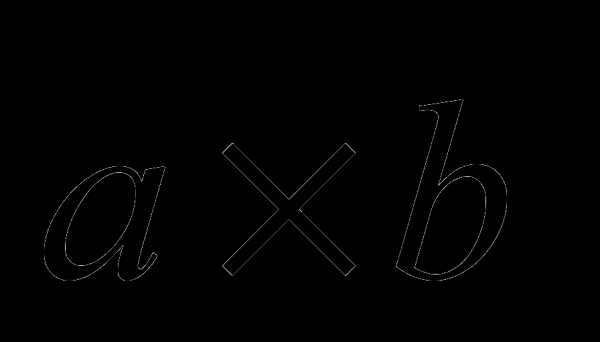

 Его объем равен в
Его объем равен в 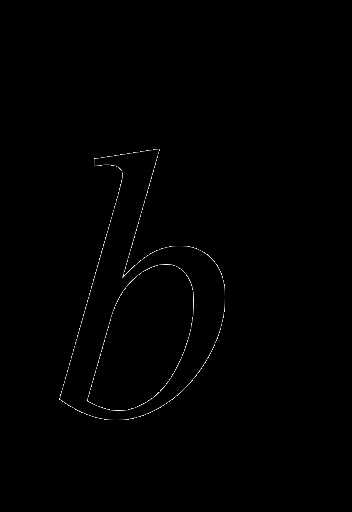
 h
h

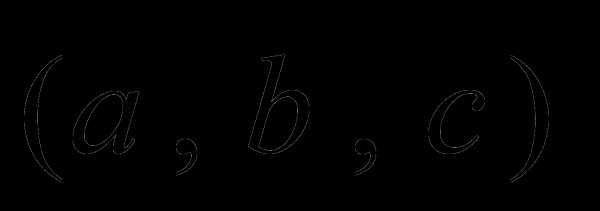 совпадает со знаком
совпадает со знаком  и поэтому смешанное произведение положительно, если вектора
и поэтому смешанное произведение положительно, если вектора 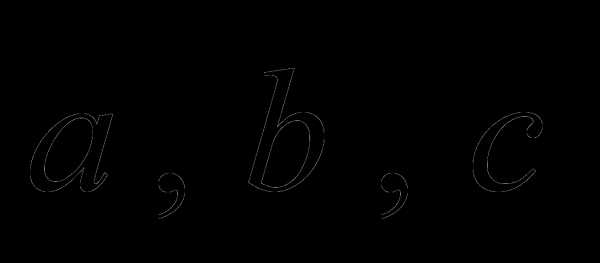 образуют правую тройку.
образуют правую тройку.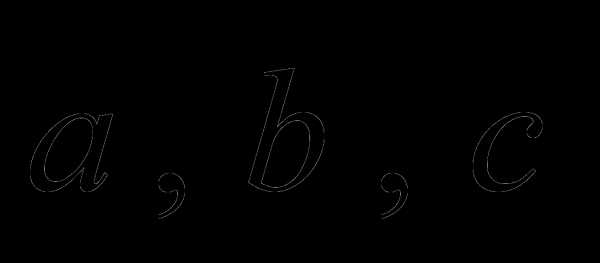 по модулю равно объёму параллелепипеда, построенного на этих векторах. Оно поло-жительно, если тройка векторов правая и отрицательно, если левая.
по модулю равно объёму параллелепипеда, построенного на этих векторах. Оно поло-жительно, если тройка векторов правая и отрицательно, если левая. является нулевым, то векторы компланарны;
является нулевым, то векторы компланарны; коллинеарны компланарны;
коллинеарны компланарны;
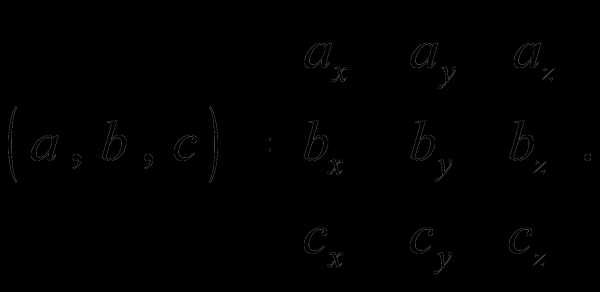 (5)
(5) и в одной плоскости, т.е. являются ли они компланарными.
и в одной плоскости, т.е. являются ли они компланарными. ,
,  и
и  лежат в одной плоскости, т.е. являются компланарными.
лежат в одной плоскости, т.е. являются компланарными. на ее высоту Н, т.е. В
на ее высоту Н, т.е. В равна половине площади параллелограмма
равна половине площади параллелограмма 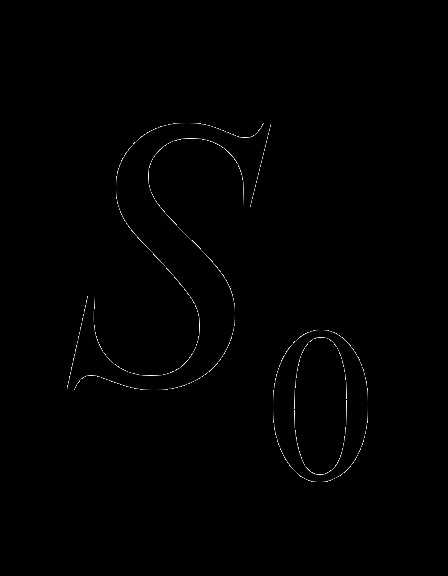 ), а высота пирамиды равна высоте соответствующего параллелепипеда.
), а высота пирамиды равна высоте соответствующего параллелепипеда.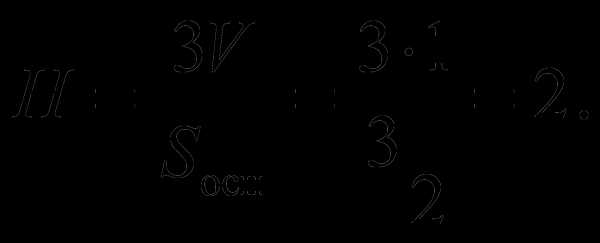


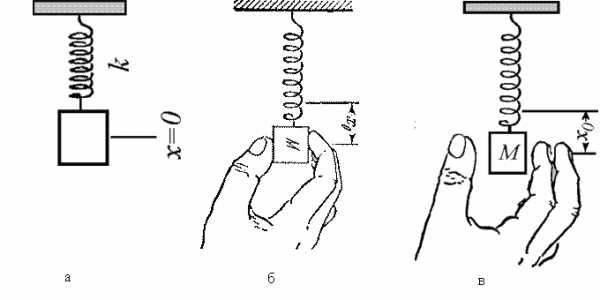
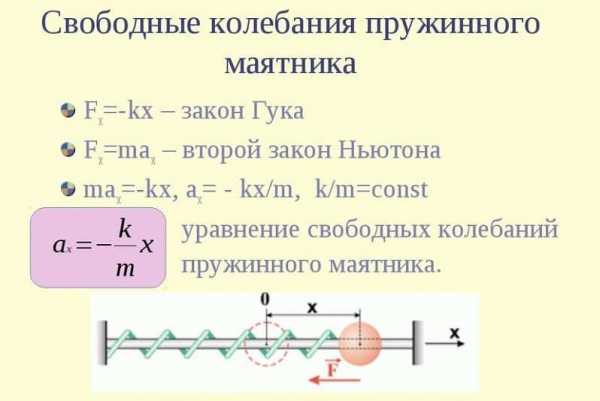


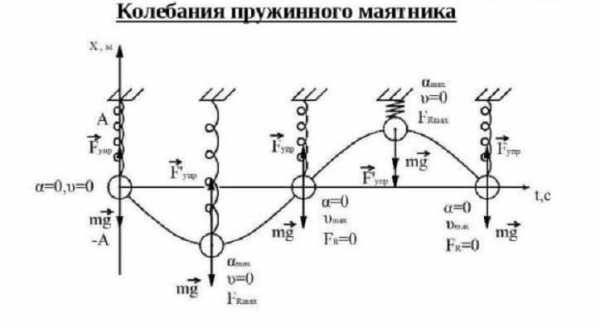
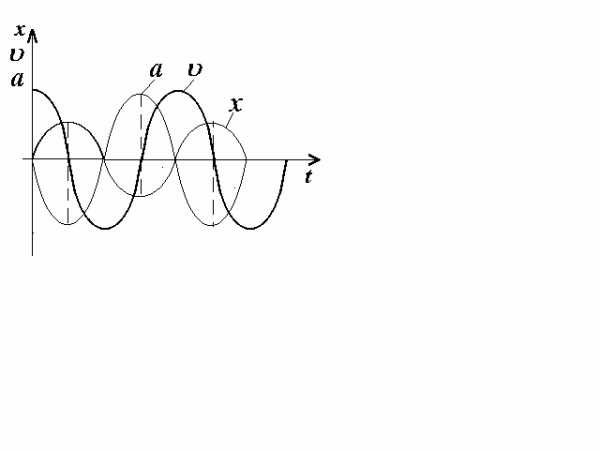
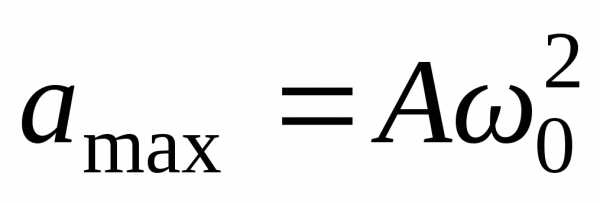 (см. формулу (1.5)). ТогдаFmax=mAω02.
Из уравнения колебания следует, что
(см. формулу (1.5)). ТогдаFmax=mAω02.
Из уравнения колебания следует, что Подставим числовые значения:Fmax=5∙10-3 0,1∙4 = 2∙10-3Н = 2мН.
Подставим числовые значения:Fmax=5∙10-3 0,1∙4 = 2∙10-3Н = 2мН.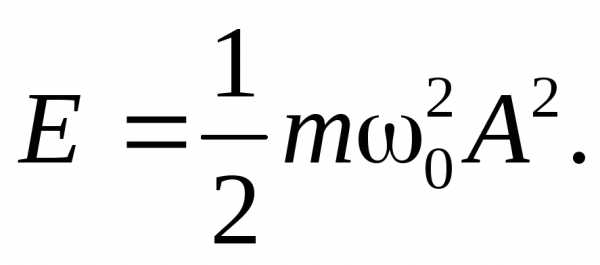 В итогеE= 0,5∙5∙10-3∙4∙10-2= 10-4Дж.
В итогеE= 0,5∙5∙10-3∙4∙10-2= 10-4Дж.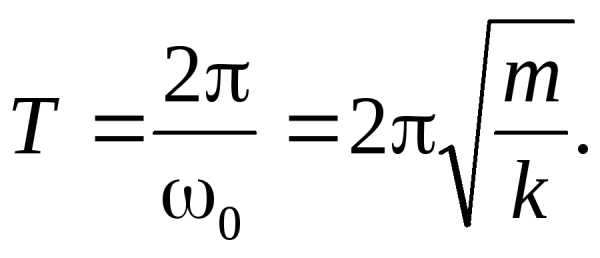 (1.8)
(1.8)
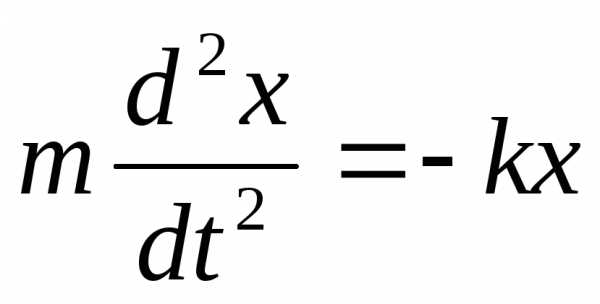 или
или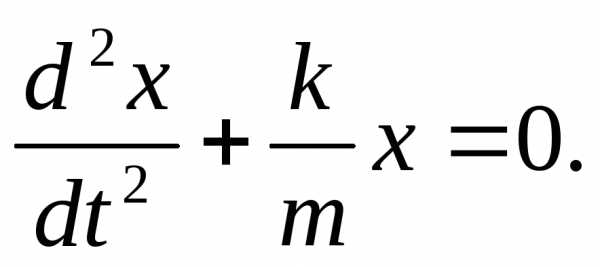
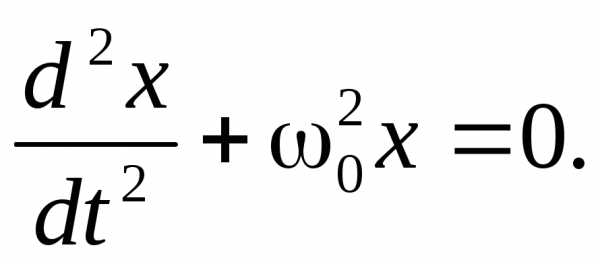 (1.9)
(1.9) .
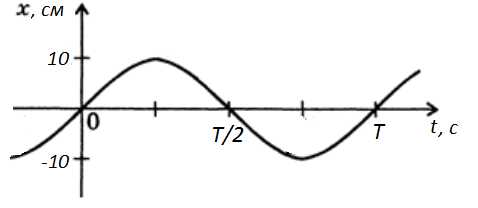
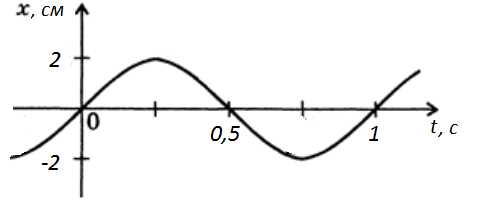
Найти частоту и период этих колебаний.
.
Найти частоту и период этих колебаний.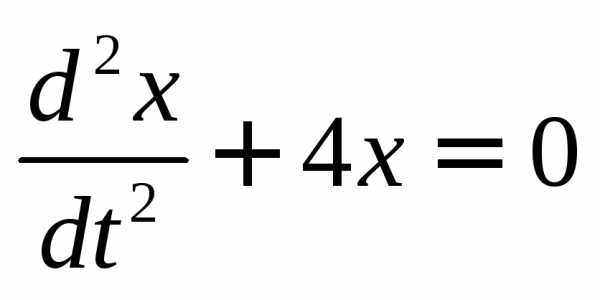 .
.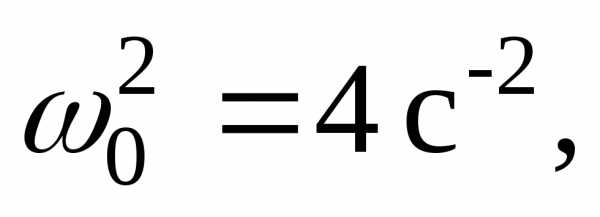 а
а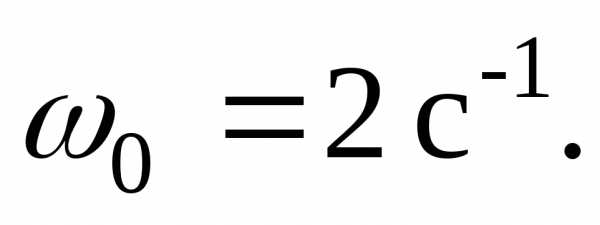 Период колебаний определяется по
формуле:Следовательно,Т= 2∙3,14/2 = 3,14 с.
Период колебаний определяется по
формуле:Следовательно,Т= 2∙3,14/2 = 3,14 с.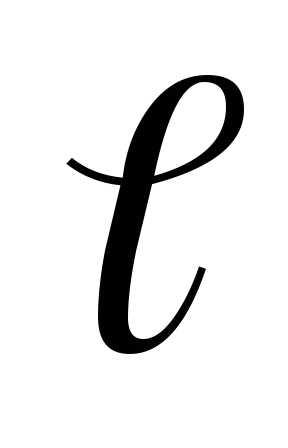 — длина физическогомаятника(pасстояние от точки подвеса до центpа
масс маятника
— длина физическогомаятника(pасстояние от точки подвеса до центpа
масс маятника 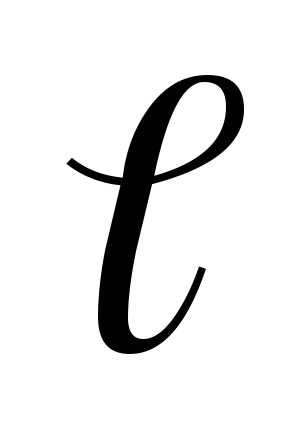 = OC).
= OC).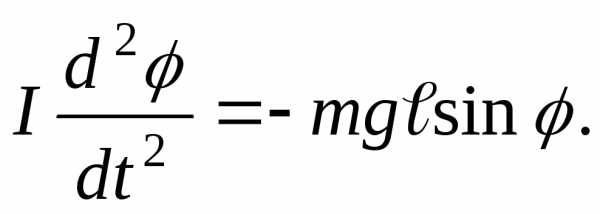 ЗдесьI– момент
инерции маятника относительно оси,
проходящей через точку подвесаО, — угловое ускорение.
ЗдесьI– момент
инерции маятника относительно оси,
проходящей через точку подвесаО, — угловое ускорение. (1.10)
(1.10) (1.11)
(1.11)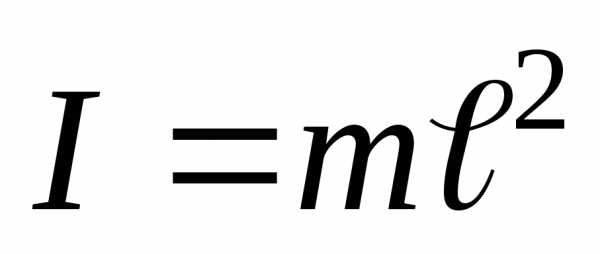 ,
получим
,
получим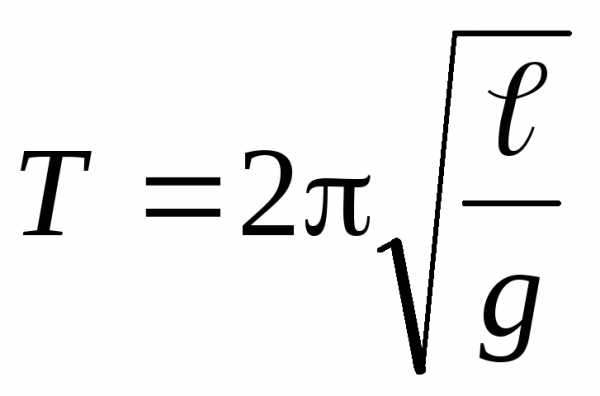
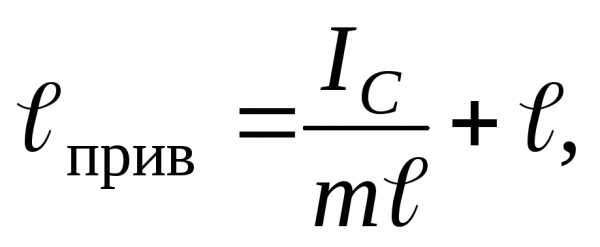
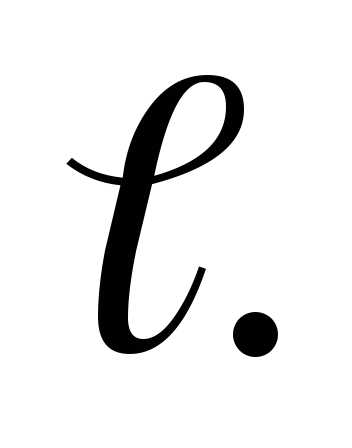
 (см. рис. 1.5), то найдём точкуО1,
которая называетсяцентром качания.
Точка подвеса и центр качания являются
сопряженными. Это значит, что маятник,
подвешенный за центр качанияО1,
не изменит периода колебаний, а точкаOсделается новым центром качания.
(см. рис. 1.5), то найдём точкуО1,
которая называетсяцентром качания.
Точка подвеса и центр качания являются
сопряженными. Это значит, что маятник,
подвешенный за центр качанияО1,
не изменит периода колебаний, а точкаOсделается новым центром качания.











 Анимация перегруппировки
Анимация перегруппировки