Год тысяча девятьсот сорок первый. 10 тысяч путей к победе
Год тысяча девятьсот сорок первый. 10 тысяч путей к победеВикиЧтение
10 тысяч путей к победеЛукашев Михаил Николаевич
Содержание
Год тысяча девятьсот сорок первый
Заметно поредевшая в последних боях рота, где служил старшина Евгений Чумаков, вошла в деревню Верхняя Сосновка за полночь. Здесь с переменным успехом уже несколько дней шли упорные бои, и было похоже, что фашистов все-таки удалось выбить из этого покинутого жителями селения. Немцы, вероятно, отошли в сторону леса, сумев при этом оторваться от наших частей.
Чумаков и его товарищи устало шагали по ночным деревенским улочкам, освещенным трепещущими багровыми отсветами пожарищ: перед отступлением фашисты успели поджечь несколько домов.
Утомленные дальним переходом солдаты начали было размещаться на ночлег по уцелевшим избам, как вдруг из темноты разноцветным трассирующим пунктиром ударила очередь немецкого пулемета. Потом сразу же еще одна и еще… Неожиданной атакой фашисты пытались снова отбить утраченную ими деревню.
Потом сразу же еще одна и еще… Неожиданной атакой фашисты пытались снова отбить утраченную ими деревню.
В суматохе внезапно вспыхнувшего ночного боя старшина старался помочь командиру организовать оборону: собирал успевших разойтись по избам красноармейцев в единый кулак.
— Чумаков, — приказал командир, — проверь: в этой избе ни кого из наших не осталось?!
Старшина понимал: бойцы так сильно уставали, что кого-то могла и не разбудить начавшаяся в деревне перестрелка. Он поспешно взбежал на крыльцо, рванул незапертую дверь и шагнул в непроглядную темноту сеней.
— Ребята! Есть здесь кто? — крикнул во всю силу легких. — Мигом все на улицу!
Никто не отозвался, в доме по-прежнему тихо, только вроде бы что-то шевельнулось в отдалении. Старшина двинулся туда и снова крикнул, но голос его осекся на полуслове: чьи-то сильные руки железной профессиональной хваткой стиснули горло. А из темноты на помощь нападавшему уже ринулось еще несколько человек: Чумаков слышал это…
Такое нередко бывало на фронте: в подходящий момент внезапно схватывали неприятельского солдата так, чтобы не мог ни выстрелить, ни подать голоса, и бесшумно в одну секунду приканчивали ножом или душили руками.
Расчет затаившихся в доме до поры фашистов был безошибочно точным: все заранее предопределено в этой заведомо неравной борьбе. Неосмотрительно вошедший русский надежно взят проверенной мертвой хваткой, и так неожиданно, что у него не оставалось абсолютно никакой возможности к сопротивлению в этом набитом немецкими солдатами доме.
В темноте лишь прозвучал шум тяжело рухнувшего на пол тела и громыханье сшибленных им с печи чугунков…
Старшина Чумаков не обладал ни богатырским сложением, ни природной геркулесовой силой, был среднего роста и обычного телосложения. И все-таки наперекор, казалось бы, явно неизбежной гибели он сумел провести эту внезапно обрушившуюся на него смертельную схватку вопреки точно рассчитанному немецкому сценарию. Не ему, а напавшему на него фашисту пришлось «тара-нить» головой деревенские кухонные чугунки. Спасла быстрота реакции: неотразимую подсечку Чумаков успел сделать мгновенно, сразу же в темп внезапного вражеского захвата за горло, хотя, разумеется, совершенно не ожидал его. А стремительно выскочить после этого на улицу было уже несложным делом.
А стремительно выскочить после этого на улицу было уже несложным делом.
Всем смертям назло старшина сумел уйти от грозившей ему гибели и успел предупредить своих товарищей о тех, кто затаился в избе, готовясь нанести им неожиданный удар с тыла…
Глава V. Тысяча девятьсот третий год. Лирическое интермеццо
Глава V. Тысяча девятьсот третий год. Лирическое интермеццо Я всё жду чего-то, как будто над нами должен обвалиться дом. А. Чехов. Вишневый сад Не раздобыть надежной славы, Покуда кровь не пролилась. Б. Окуджава Отшумел 1902 год, когда товарищу Сосо впервые в его удалой жизни
Глава IX. Эпизод четвертый. Одна тысяча девятьсот тринадцатый год, или Венский вальс
Глава IX. Эпизод четвертый. Одна тысяча девятьсот тринадцатый год, или Венский вальс Несмотря на то, что в этой главе имеются ретроспективные картины 1906 года, и, кроме того, часть описанных в ней событий относится к 1912 году, в ее название вынесен 1913 год, как переломный в
Сорок первый год
Сорок первый год Сорок первый, хмурый и уставший, В окруженье раненным попавший… Сорок первый, без вести пропавший, Мертвых в спешке не похоронивший, Под Москвой врага остановивший, Ты несешь и горестно, и свято Имя неизвестного
Полковник Туров — на фронте с сорок первого по сорок пятый
Полковник Туров — на фронте с сорок первого по сорок пятый
Я участвовал в боях на северных подступах к Сталинграду с 23 августа по 12 сентября. Таких ожесточенных боев мне видеть не приходилось. С рассвета и до вечера бомбежки, артобстрел, танковые атаки.
Жара, дым, грохот.
Таких ожесточенных боев мне видеть не приходилось. С рассвета и до вечера бомбежки, артобстрел, танковые атаки.
Жара, дым, грохот.
Авраменко Александр Михайлович О начале и причинах поражения Сорок первый. Неудачи и успехи
Авраменко Александр Михайлович О начале и причинах поражения Сорок первый. Неудачи и успехи О причинах поражений Красной Армии в начальный период тысяча девятьсот сорок первого года говорилось уже очень много. Каких только составляющих поражения не называлось — тут и
А. Сорок и сорок — рубль сорок
А. Сорок и сорок — рубль сорок О скандинавской торговле норманисты говорят исключительно в возвышенных тонах. Объёмы её определяются столь впечатлительные, что иногда перестаёшь понимать, о каком времени речь идёт. К примеру, Г. С. Лебедев считает, что «общий объём
Глава XVI Сорок первый: Считал ли Сталин все потерянным после 22 июня?
Глава XVI
Сорок первый: Считал ли Сталин все потерянным после 22 июня?
Кто борется — может проиграть. Кто не борется — уже проиграл.
(афоризм)
Но и после страшных потерь в первые дни войны СССР был невероятно силен. И мог бы быть еще сильнее, если бы с самого начала перешел к
Кто не борется — уже проиграл.
(афоризм)
Но и после страшных потерь в первые дни войны СССР был невероятно силен. И мог бы быть еще сильнее, если бы с самого начала перешел к
Сорок первый
Сорок первый Вопрос 5.1 «Двадцать второго июня, Ровно в четыре часа, Киев бомбили, нам объявили, Что началася война». Так в песне поется. А теперь попробуем уточнить: что произошло в 3 часа 15 минут, что — в 3.40 и что — в 4.15.Вопрос 5.2Наряду с немецкими соединениями на Советский
Сорок первый
Сорок первый Ответ 5.1В 3.15 началась артиллерийская подготовка противника.В 3.40 произошел первый налет пикирующих бомбардировщиков.В 4.15 началась переправа через Буг передовых частей 17-й и 18-й танковых дивизий вермахта.Ответ 5.2Соответственно: Румыния, Финляндия, Венгрия и
Шесть тысяч девятьсот два тома
Шесть тысяч девятьсот два тома Газета “Санкт-Петербургские ведомости” известила читателей, что“отлично славный нашего века писатель, господин Вольтер, владетель маркизантства фернейского, изнемог напоследок под бременем своих лет и мучительных болезней” и что“он
Глава 6 Тысяча девятьсот пятый год
Глава 6
Тысяча девятьсот пятый год
Мне кажется, что тогда мир был озабочен политической ситуацией на Дальнем Востоке и вероятностью войны с Японией. Если нам и разрешали слушать подобные разговоры, то я об этом не помню. Но когда в конце января 1904 года война была на самом
Если нам и разрешали слушать подобные разговоры, то я об этом не помню. Но когда в конце января 1904 года война была на самом
Глава 7 ГОД ТЫСЯЧА ДЕВЯТЬСОТ СОРОКОВОЙ…
Глава 7 ГОД ТЫСЯЧА ДЕВЯТЬСОТ СОРОКОВОЙ… Завидуем внукам и правнукам нашим, которым суждено видеть Россию в 1940 году, стоящую во главе образованного мира, дающую законы в науке и искусстве и принимающую благоговейную дань уважения от просвещенного человечества. В. Г.
Роковой сорок первый
Роковой сорок первый Наступил роковой сорок первый. Поток информации о предстоящем нападении немцев возрастал. Вместе с тем информация зачастую была отрывочной и противоречивой, особенно в отношении сроков нападения. Естественно, что Сталину докладывался далеко не
Очерк сорок первый Евреи в русско-японской войне.
 Погромы 1904–1905 гг. «Смутное» время. Октябрьские погромы 1905 г.
Погромы 1904–1905 гг. «Смутное» время. Октябрьские погромы 1905 г.Очерк сорок первый Евреи в русско-японской войне. Погромы 1904–1905 гг. «Смутное» время. Октябрьские погромы 1905 г. Практически после каждого разгрома еврейские общины взывали к милосердию: «Требуется безотлагательная помощь! Пожертвования просят направлять по адресу». А
Тысяча девятьсот сорок первый | это… Что такое Тысяча девятьсот сорок первый?
У этого термина существуют и другие значения, см. 1941 (значения).
«Ты́сяча девятьсо́т со́рок пе́рвый» (или «1941», 1979) — американский художественный фильм, сатирическая комедия Стивена Спилберга.
Содержание
|
Сюжет
Действие фильма разворачивается в Лос-Анджелесе в декабре 1941 года, вскоре после нападения японской авиации на Пёрл-Харбор. Многие жители Лос-Анджелеса абсолютно уверены, что следующий удар японцы нанесут по их городу и всеми силами готовятся к обороне.
Многие жители Лос-Анджелеса абсолютно уверены, что следующий удар японцы нанесут по их городу и всеми силами готовятся к обороне.
Коварные японцы действительно послали к побережью Калифорнии подводную лодку под командованием коммандера Акиро Митамура (Тосиро Мифуне) с заданием «разрушить что-нибудь важное». Эту старую субмарину подарила Японии фашистская Германия, поэтому японцев, которые плохо знакомы с немецкой техникой, консультирует опытный подводник капитан Вольфганг фон Кляйншмидт (Кристофер Ли). Однако даже его опыт не может помочь, когда на лодке выходит из строя компас и японцы обнаруживают, что заблудились, не зная, что находятся всего в паре сотен метров от американского берега. На всплывшую в ночном тумане лодку буквально натыкается пловчиха из калифорнийского клуба «моржей».
Тем временем в Лос-Анджелесе объявлено о предстоящем проведении в одном из клубов города танцевального конкурса, к которому страстно готовится танцор-любитель Уолли Стивенс (Бобби Ди Чикко). Он намерен выиграть конкурс вместе со своей девушкой Бетти Дуглас (Дайанна Кей) и не подозревает, что всех девушек из патриотических соображений обязали танцевать только с военными. Военные не заставляют себя ждать — в городе просто уйма моряков и армейцев.
Он намерен выиграть конкурс вместе со своей девушкой Бетти Дуглас (Дайанна Кей) и не подозревает, что всех девушек из патриотических соображений обязали танцевать только с военными. Военные не заставляют себя ждать — в городе просто уйма моряков и армейцев.
В это время в Долине Смерти, на шоссе возле бензозаправки, приземляется истребитель безбашенного лётчика капитана «Дикого Билла» Келсо (Джон Белуши). «Дикий Билл» требует заправить ему самолёт и пугает местных жителей рассказами о том, что он вот уже несколько суток гоняется за летающей над Америкой японской эскадрильей. Внезапно мотор его самолёта сам собой заводится и Келсо бросается вслед за своим истребителем по шоссе, паля в воздух из пистолета. Одна из пуль, срикошетив, поджигает бензин и заправка за спиной капитана взлетает на воздух.
В Лос-Анджелес прибывает новый командующий гарнизоном генерал Джозеф Стилвелл (Роберт Стэк), флегматичный и трезвый военный, который совершенно не верит в японскую угрозу и всем делам предпочитает просмотр нового диснеевского мультфильма «Дамбо». Вместе с ним приезжает его секретарь Донна Страттон (Нэнси Аллен), которая помешана на самолётах. Об этой её слабости знает адъютант Стилвелла, сексуально озабоченный штабной капитан Лумис Беркхед (Тим Матесон), который всеми силами пытается соблазнить Донну, затащив её в какой-нибудь самолёт. Забравшись в один из стоящих на лётном поле B-17, они по неосторожности сбрасывают авиабомбу, которая падает на асфальт и катится в сторону дающего пресс-конференцию генерала — как раз когда он произносит, что «пока он тут командует, ни одна бомба в Калифорнии не взорвётся». Бомба, однако, взрывается, лишь по счастью никого не убив.
Вместе с ним приезжает его секретарь Донна Страттон (Нэнси Аллен), которая помешана на самолётах. Об этой её слабости знает адъютант Стилвелла, сексуально озабоченный штабной капитан Лумис Беркхед (Тим Матесон), который всеми силами пытается соблазнить Донну, затащив её в какой-нибудь самолёт. Забравшись в один из стоящих на лётном поле B-17, они по неосторожности сбрасывают авиабомбу, которая падает на асфальт и катится в сторону дающего пресс-конференцию генерала — как раз когда он произносит, что «пока он тут командует, ни одна бомба в Калифорнии не взорвётся». Бомба, однако, взрывается, лишь по счастью никого не убив.
Уолли пытается убедить Бетти, чтобы она танцевала с ним на конкурсе. Всё это происходит возле дома отца Бетти — Уорда Дугласа, комичного патриота-энтузиаста, который не любит Уолли из-за того, что тот разбил его машину. Уолли прячется от отца Бетти в гараже. Возле дома появляется зенитка сержанта Фрэнка Три (Дэн Эйкройд), которому дан приказ установить орудие на участке Уорда Дугласа. Соблюдая требования техники безопасности, сержант показывает помешанному на оружии хозяину дома, что нельзя делать, чтобы зенитка случайно не выстрелила — то есть фактически инструктирует его, как надо из неё стрелять. В это время капрал Ситарски (Трит Уильямс) обнаруживает Бетти, мгновенно «западает» на неё и не даёт ей проходу. В гараже он сталкивается с Уолли. Завязывается драка, в результате которой сопротивляющегося Уолли насильно выносят на помойку.
Соблюдая требования техники безопасности, сержант показывает помешанному на оружии хозяину дома, что нельзя делать, чтобы зенитка случайно не выстрелила — то есть фактически инструктирует его, как надо из неё стрелять. В это время капрал Ситарски (Трит Уильямс) обнаруживает Бетти, мгновенно «западает» на неё и не даёт ей проходу. В гараже он сталкивается с Уолли. Завязывается драка, в результате которой сопротивляющегося Уолли насильно выносят на помойку.
Тем временем, командир японской субмарины, который никак не может сориентироваться, высаживает на берег в пригороде Лос-Анджелеса разведгруппу, чтобы взять «языка» и узнать, где они находятся. Группа захватывает торговца рождественскими ёлками Холлиса (Холли) Вуда (Слим Пикенс), а заодно — и его древний радиоприёмник. Японцы допрашивают придурковатого торговца, всё время путаясь из-за созвучия его имени и с названием города Голливуд. В конце концов, они решают, что Голливуд, «сердце Америки», совсем близко и они смогут его разрушить. Во время обыска они находят у Вуда в пачке с чипсами маленький игрушечный компас. Поняв, что игрушка представляет для врага интерес, Вуд героически её проглатывает. Японцы поят его слабительным, но Вуд страдает запором и добыть из его желудка компас оказывается не так легко. В результате Вуду удаётся застать японцев врасплох и сбежать с подводной лодки — правда, оказавшись в море и не зная, в какой стороне берег.
Во время обыска они находят у Вуда в пачке с чипсами маленький игрушечный компас. Поняв, что игрушка представляет для врага интерес, Вуд героически её проглатывает. Японцы поят его слабительным, но Вуд страдает запором и добыть из его желудка компас оказывается не так легко. В результате Вуду удаётся застать японцев врасплох и сбежать с подводной лодки — правда, оказавшись в море и не зная, в какой стороне берег.
Ближе к ночи в комплексе ярмарочных аттракционов на берегу на вершину колеса обозрения поднимается ночной дозор, который должен наблюдать за небом и сообщать о возможном авианалёте. Один из дозорных панически боится высоты, а второй — ярмарочный чревовещатель, у которого в мешке живёт похожая на него кукла, разговорами с которой он в случае чего развлекается.
Всё это время чокнутый Билл Келсо гоняет над Америкой воображаемую японскую эскадрилью, постепенно приближаясь к Лос-Анджелесу.
Генералу Стилвеллу мешают смотреть мультфильм, докладывая, что командующий законсервированной авиабазой полковник Мэдмен Мэддокс уверен, что японцы высадили десант для захвата его базы и срочно требует подкреплений. Для того, чтобы успокоить Мэддокса, генерал посылает капитана Лумиса Беркхеда; сопровождать его вызывается Донна Страттен.
Для того, чтобы успокоить Мэддокса, генерал посылает капитана Лумиса Беркхеда; сопровождать его вызывается Донна Страттен.
Вечером в клубе начинается танцевальный конкурс, на который Уолли удаётся проникнуть после того, как он оглушает военного полицейского и забирает его форму. Он танцует с Бетти, одновременно отбиваясь от капрала Ситарски, зарабатывает первый приз и провоцирует грандиозную драку между моряками и пехотинцами. Драку останавливает прибывший на харизматичном танке M3 Lee сержант Три, который произносит пламенную патриотическую речь.
На авиабазе Мэддокса капитан Биркхед сажает Донну в самолёт, потому что соблазнить её на земле у него не получается, и они летят на нём в сторону Лос-Анджелеса. На старом бомбардировщике нет радио, силам ПВО опознать его в темноте не удаётся, самолёт принимают за японский и по всему штату объявляется воздушная тревога. Начинается беспорядочная стрельба в небо из зениток и всех видов стрелкового оружия, которая наносит ущерб прежде всего высотным постройкам и рекламным плакатам. Сержант Три, который пулемётным огнём гасит демаскирующую город иллюминацию, ушиблен упавшей на него гигантской фигурой Санта-Клауса и находится в невменяемом состоянии.
Сержант Три, который пулемётным огнём гасит демаскирующую город иллюминацию, ушиблен упавшей на него гигантской фигурой Санта-Клауса и находится в невменяемом состоянии.
Слетевшая с катушек Донна в пилотской кабине бомбардировщика занимается любовью с Беркхедом, который одновременно пытается управлять самолётом. В это время на перехват выходит истребитель «Дикого Билла» Келсо. Он преследует почти неуправляемый бомбардировщик над Лос-Анджелесом и ведёт с ним огневой бой буквально между домами бульвара Сансет. Подбитый самолёт Беркхеда падает неподалёку от парка отдыха, прямо в смоляное озеро. Довольный победой, «Дикий Билл» Келсо разворачивается над океаном и тут замечает японскую подлодку. Однако в следующий момент его самолёт из винтовки подбивают наблюдатели на колесе обозрения. Капитан Келсо с трудом садится в центре города и сообщает всем о субмарине, после чего отбирает у военного курьера мотоцикл и мчится к побережью. Туда же отправляется и танк, экипаж которого по дороге подбирает всё ещё одетого в армейскую форму Уолли и, из-за сержантских погон на ней, назначает его командиром.
Всплывшую японскую субмарину замечает и Уорд Дуглас. Поскольку возле зенитки в этот момент нет расчёта, он самостоятельно направляет её на подлодку и открывает огонь, не обращая внимания на то, что стреляет при этом сквозь собственный дом. В это время его дети, которым поручено спустить дозорных с ярмарочного колеса, вместо этого включают иллюминацию парка развлечений. Коммандер Митамура решает, что на берегу сверкает огнями какой-то индустриальный центр, и открывает огонь из пушек по колесу обозрения. Снаряд сбивает колесо со стойки, оно катится по пирсу и под ликующие вопли японцев сваливается в воду.
На пирсе появляется танк сержанта Три, который открывает по лодке огонь из орудия. Коммандер Митамура отвечает торпедным залпом, который сносит пирс вместе с танком. Последним по разрушающемуся пирсу проносится мотоцикл «Дикого Билла» Келсо, который, видимо, пытается с разгону таранить им подводную лодку, но не долетает до цели и падает в воду.
Дозорные с колеса обозрения и экипаж танка плывут к берегу, а «Дикий Билл» Келсо — к японской субмарине. Взобравшись на неё, он врывается внутрь до того, как она успевает погрузиться, и требует от остолбеневших японцев, чтобы они отвезли его в Токио.
Взобравшись на неё, он врывается внутрь до того, как она успевает погрузиться, и требует от остолбеневших японцев, чтобы они отвезли его в Токио.
На следующее утро возле остатков дома Дугласов появляется генерал Стилвелл и собираются все персонажи фильма, сохранившие способность передвигаться. Уорд Дуглас произносит прочувствованную патриотическую речь и пытается прибить к входной двери рождественский венок — символ мира и спокойствия. После первого же удара молотком остатки его дома сползают в океан.
Интересные факты
| В этом разделе не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. |
- В фильме есть пародийные цитаты из предыдущих фильмов Спилберга.
- Всё построение вступительного эпизода пародирует начало фильма «Челюсти», и даже девушку из клуба «моржей» в начальном эпизоде фильма сыграла Сьюзан Бэклайни, игравшая также первую жертву чудовищной акулы.

- Истребитель Дикого Билла Келсо садится возле заправочной станции, где происходило действие одного из эпизодов фильма «Дуэль».
- Всё построение вступительного эпизода пародирует начало фильма «Челюсти», и даже девушку из клуба «моржей» в начальном эпизоде фильма сыграла Сьюзан Бэклайни, игравшая также первую жертву чудовищной акулы.
- Ссылка на катящееся колесо обозрения, на котором сидели дозорные, присутствует в фильме Тимура Бекмамбетова «Дневной дозор».
- Джон Уэйн не только отказался от роли генерала Стилвелла, но и пытался отговорить Спилберга от постановки «непатриотичного» фильма.
- В качестве членов команды японской подлодки снимались жители Калифорнии азиатского происхождения, которых приглашали для участия в массовке. Игравший капитана подлодки Тосиро Мифуне был так раздосадован их недисциплинированностью, что выпросил у Спилберга разрешение «привести их в форму» своими средствами. Войдя в образ, он принялся орать на них, как на новобранцев, и вскоре добился образцовой дисциплины.
- Некоторые из сцен фильма были такими шумными, что Спилбергу приходилось вместо крика «Стоп!», которого никто из актёров не слышал, стрелять холостыми очередями в воздух из взятого у реквизитора пулемёта.

- Режиссёр Джон Лэндис сыграл эпизодическую роль курьера-мотоциклиста, с ног до головы заляпанного грязью.
- Спецэффекты в этом фильме стали последней работой в кино легендарного мастера комбинированной съёмки А. Д. Флауэрса.
- Съёмки фильма продолжались 247 дней, отснятый материал составил около 300 тысяч метров плёнки.
- Предварительный трейлер фильма сосредотачивал внимание зрителя на персонаже Джона Белуши, которого в трейлере называли «Дикий Уэйн Келсо». В окончательном монтаже фильма его героя звали «Дикий Билл Келсо». В первоначальной версии сценария эта роль была совсем незначительной, но она была существенно расширена, когда играть Келсо согласился Белуши.
- Первоначально планировалось завершать каждую часть фильма, как это было принято в военное время, призывом к аудитории покупать бонды военного займа. Потом Спилберг от этой идеи отказался.
- Фильм вышел в прокат в США 14 декабря 1979 года.
- Фильм собрал в американском прокате лишь около 32 миллионов долларов, однако более чем окупился по итогам мирового проката, собрав за пределами США более 60 миллионов долларов[1].

- Расширенный монтаж фильма был впоследствии сделан Спилбергом для показа по телевидению и выпущен на коллекционном DVD-издании.
- В одной из не вошедших в фильм сцен Холлис Вуд ожидает, что сейчас его будут пытать. Появляется капитан Вольфганг фон Кляйншмидт, который держит в руках странное приспособление, похожее на пыточный инструмент. В следующую секунду оказывается, что это складные плечики для плаща. Спилберг так жалел, что сцену пришлось удалить, что поклялся любой ценой вставить этот гэг в один из следующих фильмов. В итоге эта шутка появилась в «Искателях потерянного ковчега».
- Фильм номинировался на «Оскар» в трёх номинациях — за лучшую работу оператора, за лучшие визуальные эффекты и за лучший звук.
Примечания
- ↑ 1941 (1979) — Box Office Mojo
Ссылки
- «1941» (англ.) на сайте Internet Movie Database
- «Тысяча девятьсот сорок первый» на российском фан-сайте Стивена Спилберга
1 574 147 030,82 (один миллиард, [. ..]
пятьсот семьдесят четыре мельницы ио н , сто сорок семь тысяч , т привет рты евро, [.. .] ..]
пятьсот семьдесят четыре мельницы ио н , сто сорок семь тысяч , т привет рты евро, [.. .]восемьдесят два цента) на выплату дивидендов, из которых (а) на общую сумму inversores.bbva.com inversores.bbva.com | (mil quinientos sete nt a y […] c ua tro mill on es ci ent o cuarenta y siete mi l t rei nta e ur os con ochenta […]y dos cntimos) al pago […]дивиденды, убытки (а) и общая сумма импорта 1.011.951.662,67 inversores.bbva.com inversores.bbva.com |
г) На конец периода имеются обязательства по закупке […]инвентарь, машины и оборудование […] примерно te l y сто сорок семь m i ll ион шестьсот [. ..] ..]девяносто тысяч долларов США (сто […]и пятнадцать миллионов четыреста тысяч долларов США в 2000 году). gmodelo.com gmodelo.com | d) Al cierre del ejercicio se tienen compromisos […]в сравнении с […] inventarios, maq ui naria y оборудовать o por cie nto cuarenta y siete m ill one s sei sc ientos […]noventa mil dlare s американо ( ciento айва миллионес cuatrocientos […]миллионов американских долларов в 2000 г.), приблизительно. gmodelo.com gmodelo.com |
| МЕТ НО Д : Сто сорок семь w o me n посещение […] аппараты визуализации молочных желез в Университетской больнице Вест-Индии [. ..] ..]и 127 посещающих радиологию West были опрошены, чтобы определить факторы, связанные с участием в маммографическом скрининге. caribbean.scielo.org caribbean.scielo.org | M T ODO : Ciento cuarenta y siete mu jer es que a si […] по номеру в Университетской больнице […]West Indies, y 127 que asistan a Radiology West, fueron entrevistadas a fin de determinar los factores relacionados con su participacin en el pesquisaje mamogrfico. caribbean.scielo.org caribbean.scielo.org |
дополнительные государства ратифицировали Конвенцию или присоединились к ней, в результате чего […]общее количество государств, официально принявших обязательства […] Конвенции n t o сто сорок семьdaccess-ods.un.org daccess-ods. | el aumento del nmero de Estados que han ratificado la Convencin o se han adherido a ella, gracias a lo cual el nmero total […]de Estados que han aceptado oficialmente las obligaciones estipuladas en […] la Co nv enci n asciend e a ciento cuarenta y sietedaccess-ods.un.org daccess-ods.un.org |
Подтверждает Конвенцию 1951 г. о статусе беженцев4 и Протокол к ней 1967 г.5 в качестве основы международного режима защиты беженцев, признает важность их полного и эффективного применения […]признание государств-участников и ценности, которые они воплощают, […] с удовлетворением отмечает -й а т сто сорок семь S t at es теперь являются участниками одного […]документ или к обоим, поощряет государства-неучастники [. ..] ..]рассмотреть вопрос о присоединении к этим документам, подчеркивает, в частности, важность полного соблюдения принципа невыдворения и признает, что ряд государств, не являющихся участниками международных документов о беженцах, продемонстрировали великодушный подход к приему беженцев daccess-ods.un.org daccess-ods.un.org | 4. Reafirma que la Convencin sobre el Estatuto de los Refugiados de 19514 y su Protocolo de 19675 son la base del rgimen internacional de proteccin de los refugiados, reconoce la importancia de que los Estados partes los […]apliquen plena y eficazment e y r espeten los valores que encarnan, observa […] с по sfac cin q ue ciento cuarenta y siete E sta dos son часть 90 010 es en uno de es os инструменты […]o en ambos, alienta [… ] ]a los Estados que no son partes a рассматривать su adhesin a esos tools, subraya en частности la importancia de que se respete plenam ente el principio de la no devolucin, y reconoce que un cierto nmero de Estados que no son partes en los toolsos internacionales relativos a los refugiados han dado pruebas de generosidad acogiendo a refugiados daccess-ods.un.org daccess-ods.un.org |
| ( c ) Сто сорок семь c h ур […] объединений, внесенных в Реестр церквей и других религиозных организаций […]Объединения на основании Закона от 17 мая 1989 г. «О гарантиях свободы совести и вероисповедания». daccess-ods.un.org daccess-ods.un.org | c ) Ciento cuarenta y siete i gle sia s y o rg anizaciones […] religiosas que estn inscritas en el Registro de iglesias y otras organizaciones [. ..] ..]religiosas, en virtud de la Ley de garantas de la libertad de conciencia y de religin. daccess-ods.un.org daccess-ods.un.org |
сто девяносто государств и одна региональная экономическая интеграция […]организация ратифицировала […] Конвенция и -й а т сто сорок семь С т в эс и один региональный […]организация экономической интеграции […]ратифицировали Картахенский протокол по биобезопасности к Конвенции о биологическом разнообразии2 daccess-ods.un.org daccess-ods.un.org | que ciento noventa Estados y una organizacin Regional de […]интеграцин экономический han […] ratificado el Co nveni o y qu e ciento cuarenta y siete Es ta dos y un a организация [. ..] ..]региональный отдел интеграции […]econmica han ratificado el Protocolo de Cartagena sobre Seguridad de la Biotecnologa del Convenio sobre la Diversidad Biolgica2 daccess-ods.un.org daccess-ods.un.org |
Уставный капитал […] СТО А N D СОРОК ДЕВЯТЬ M I LL ION, SIX HUN DR E D И СОРОК ОДИН , СЕМЬСОТ И S E VE N (149 641 707) ЕВРО […]и полностью подписан и оплачен. агбар.es агбар.es | Эль Капитал […] социальный e s de CIENTO CUARENTA Y NUEVE MILL ONES S E IS CIENT OS CUARENTA Y UN MIL SETECIE NTOS SIETE (149 .641 . 7 07) ЕВРО […] 7 07) ЕВРО […]y est ntegramente sucrit o y d esembolsado. agbar.es agbar.es |
4.3 Сумма данного проектного тендера, в соответствии с установленной в статье 168.4 […]ЛКСП, приходит […] до двух мил ли o n сто сорок тысяч e i gh т сот а н д двадцать семь e u ro s и пятьдесят […]центов (2 144 827,50 […]‘), плюс соответствующий НДС, общая сумма, эквивалентная сумме премий за участие в тендере, указанном в пункте 4.1 настоящей Папки, и оценочной стоимости контракта на оказание услуг, связанного с решением тендер, который впоследствии может быть одобрен JCCM. toletumvisigodo.eu toletumvisigodo.eu | 4.3. La cuanta del presente concurso de proyectos, asciende, de acuerdo con lo establecido en el [. ..] ..]арткуло 168.4 де ла […] LCSP a dos mil lo nes ci ent o cuarenta y cu atr o mil o 900 09 chocien tos veintisiete евро os c на […]центов (2.144.827,50 […]‘), ms el IVA, что соответствует, cantidad total que equivale a la suma de las primas de participacin en el concurso a que hace referencia la estipulacin 4.1 del presente Pliego, y del valor estimado del contrato de servicios asociado a la resolucin del concurso que pueda adjudicarse posteriormente por la JCCM. toletumvisigodo.eu toletumvisigodo.eu |
Совершено в Лондоне шестнадцатого числа […] день ноября be r , одна тысяча девятьсот сорок — f i ve , за один […]копия на английском и французском языках, [… ] ], из которых заверенные копии будут направлены правительством Соединенного Королевства в unesdoc.unesco.org unesdoc.unesco.org | Hecho en Londres, a diecisis […] de no vi embre de mil novecien tos cuarenta y c 900 09 inc o, e n un s olo ej emplar [… ]en franc s y en ingls, del cual entregar […]Эль-Гобьерно-дель-Рейно Унидо копиас debidamente certificadas в лос-гобиернос-де-тодос-лос-Эстадос Миемброс де лас Насьонес Унидас. unesdoc.unesco.org unesdoc.unesco.org |
Совершено в Риме двадцать пятого дня […] Март уе а р одна тысяча девятьсот пятьдесят семь .eur-lex.europa.eu eur-lex.europa.eu | Hecho en Roma, эл. [. ..]
veinticinco de m arzo de mil nov ecient os cincuen ta и место . ..]
veinticinco de m arzo de mil nov ecient os cincuen ta и место .eur-lex.europa.eu eur-lex.europa.eu |
| tw en t y — один m i lli o n семьсот t w en t y — девять тысяч t ( 2 1, 729 240) акции […] Banco de Andaluca, представляющий […]100% уставного капитала имеют номинальную стоимость 0,75 bancopopular.es bancopopular.es | L as veintin mi ll one s setecientas v eintinueve mil 9 0009 dosci ent as cuarenta (2 1.7 29. 240) ac […] Банко де Андалука, представители [. ..] ..]del 100% de su capital social, son de 0,75 bancopopular.es bancopopular.es |
Количество ДВАДЦАТЬ […] МИЛЛИОН FI V E СТО СОРОК ОДНА ТЫСЯЧА , ВОСЕМЬСОТ A N D СЕМЬДЕСЯТ ДЕВЯТЬ […]ЕВРО И ПЯТЬ ЦЕНТОВ […](’20 541 879,05) в добровольные резервы. vocento.com vocento.com | La cantidad de VEINTE M IL LONES QUIN IEN TOS CUARENTA Y UN M IL O 900 09 ШОК IE NTOS SETENTA Y […] NUEVE EUROS CON CINCO CENTIMOS (20.541.879,05 ‘) a reservas voluntarias. vocento.com vocento.com |
В результате таких приобретений ТЕЛЕФНИКА теперь […]напрямую владеет четырьмя миллиардами, […] пять миллионов девять гун др e d тысяч , семьсот сорок девять ( 4 ,0 05 900 749) акции [. ..] ..]TELEFNICA MVILES, что составляет 92,50% акционерного капитала. telefonica.com telefonica.com | Como consecuencia de tales adquisiciones, TELEFNICA es Ahora […]титульный, по форме […] directa, de c ua tro mil cin co millones novec ie ntas mil setecie nta s cuarenta y nu eve (4.00 900 09 5. 900.749) […]acciones de TELEFNICA […]MVILES, представитель 92,50% капитала соц. telefonica.com telefonica.com |
СОВЕРШЕНО в городе Сан-Франциско двадцать шестого числа […] день J un e , одна тысяча девятьсот сорок — f i ve 9001 0 .un.org un.org | FIRMADA en la ciudad de San Francisco, a los veintisis [. ..]
das del mes d e jun io de mil noveciento s cuarenta y ci код . ..]
das del mes d e jun io de mil noveciento s cuarenta y ci код .un.org un.org |
На дату настоящего отчета уставный капитал […]Tubacex, S.A. составляет пятьдесят девять миллионов, […] восемь гун др е d и сорок тысяч , ф o 90 010 у р сто пятьдесят один E u r o s и 9001 0 n i ne тыс. центов (’59 840 451,90), разделить на t o сто т ч ир тыдве мельница ио н 9 0009 , девять ч у ndr e d и s e ve 90 010 нты-е иг ч т тыс. , семьсот и восемьдесят — t w o обыкновенных акций (132 978 782) по сорок пять центов (‘0,45) номинальной стоимости каждая, пронумерованных начиная с и t или сто т ч ир ты-два мельница ио н , девять h u nd красный и семьдесят восемь […] , семьсот и восемьдесят — t w o обыкновенных акций (132 978 782) по сорок пять центов (‘0,45) номинальной стоимости каждая, пронумерованных начиная с и t или сто т ч ир ты-два мельница ио н , девять h u nd красный и семьдесят восемь […]тысяч семьсот восемьдесят два, […]включительно, и все того же класса и серии. тубаксекс тубаксекс | A la fecha de emisin del Presente Informe, el Capital […]социальный де TUBACEX, S.A. es де […] cincuenta y nuevemillon es ocho cie nto s cuarenta m il cua troci en to s cincuenta y uno con n ov enta cntimos de euro (59. 840.451,90 ‘), представитель por ciento treinta y dos millone s novecientos s etenta y o cho mil setecientas ochenta 9001 0 y do s (132.978.782) acciones iguales, ordinarias, de valor номинальная 0,45 евро cada una, numeradas correlativamen te del uno al c т.е. nto treint a y 90 009 d os millo ne s […] 840.451,90 ‘), представитель por ciento treinta y dos millone s novecientos s etenta y o cho mil setecientas ochenta 9001 0 y do s (132.978.782) acciones iguales, ordinarias, de valor номинальная 0,45 евро cada una, numeradas correlativamen te del uno al c т.е. nto treint a y 90 009 d os millo ne s […]новеньентос с и энта и очо мил сетечентас […]ochenta y dos, ambas inclusive, que forman una sola serie y clase. тубакс.es тубакс.es |
План слияния гласит, что на дату Плана Telefnica прямо или косвенно […]четыре тысячи […] три миллиона девять гуннов др е d тысяч семьсот сорок девять ( 4 ,0 03 900 749) акций […] Telefnica Mviles, что составляет 92,457% акционерного капитала. telefonica.com telefonica.com | Telefnica hace constar en el Proyecto de Fusin que, a la fecha de Formulacin del Mismo, er titular […]прямое или косвенное […] de cu at ro mil tr es millones noveci en tas mil setecie nta s cuarenta y ню накануне ( 4.003 .9 00.749) [ …]Acciones de Telefnica […]Мвиле представитель 92,457% от капитала соц. telefonica.com telefonica.com |
Они должным образом зарегистрированы в […]соответствующая книга учета запасов, которая […] в настоящее время показывает всего 267 574 941 (двести s ix t y — семь m 9000 9 i ll ion пятьсот семьдесят- fo u р тысяч девятьсот сорок один ) e nt ries, пронумерованные в порядке номеров от 1 до 267 574 941, [. ..] ..]номинальной стоимостью 1 евро каждая. cepsa.com cepsa.com | Se encuentran debidamente inscritas в корреспондентском Registro Contable, en el que figuran Actualmente anotadas un […]всего 267.574.941 […] (дознайт ОС sese nta y siete mi llo nes q ui nientas setent a y cuatr o mil n ovec ien tas cuarenta y u na) uni da des de cuenta, numeradas correlativamente del 1 al 267.574.941, ambos inclusiv e, 900 09 de 1 (un) евро de доблесть […]номинальное cada una de ellas. cepsa.com cepsa.com |
Одна тысяча t h r e e 9000 — девять г р и ц для разных уровней образования были розданы а мес н г семьсот н я ne ty семей в Испании и Латинской [. ..] ..]Америка, включая гранты для учащихся специальных учебных заведений. focus.abengoa.es focus.abengoa.es | Sealamo s en p rimer lugar […] la co nc esin de mil tre scien ta s n ov 90 009 enta y nueve A yudas d e Estudios para los diversos niveles de enseanza distribui da s en tre setecientas nov enta fa mi lias de […]Испания и Ибероамрика, […]destacando las asignadas para Educacin Especial. focus.abengoa.es focus.abengoa.es |
Увеличение капитала завершено в […] в конце апреля с подпиской и оплатой 1 310 482 акций, в результате чего было привлечено одиннадцать миллионов ли o n сто т ч ир т у — девять тысяч девяносто семь e u ro (‘11,139,097). zeltia.es zeltia.es | A finales de abril se cerr la ampliacin con la […] suscri pc in y des em bol so de un tot al de 1. 310.482 acciones, ca pt ndos e un t otal de Once Millo ne sciento t rei nta y nueve mil noven ta y siete eu ro s (1 1.13 9. 097′).zeltia.es zeltia.es |
Эта цифра состоит из: ДВЕСТИ ВОСЕМЬДЕСЯТ СЕМЬ МИЛЛИОНОВ ДЕВЯТЬСОТ ПЯТЬДЕСЯТ ВОСЕМЬ ТЫСЯЧ ДВЕСТИ […]ПЯТЬДЕСЯТ ШЕСТЬ БОЛИВАРОВ (Bs. […] 287 958 256), относящиеся к Venpre ca r , и СЕМЬСОТ СОРОК — S 90 009 E VE N МИЛЛИОН ДВЕСТИ СОРОК ПЯТЬ […]ТЫСЯЧА ДЕВЯНОСТО БОЛИВАРОВ […] (747 245 090 шиллингов), относящийся к Orinoco Iron. ibh.com.ve ibh.com.ve | Dicha cifra est compuesta por: DOSCIENTOS OCHENTA Y SIETE MILLONES NOVECIENTOS CINCUENTA Y OCHO MIL DOSCIENTOS CINCUENTA Y SEIS BOLVARES (Bs. […]287.958.256,оо) […] корреспондент es a Ve npr eca r, y SE TEC IEN T 900 09 OS CUARENTA Y SIETE MI LLON ES DOS CI ENTO S CUARENTA Y CIN CO MIL NOVENTA […]БОЛВАРЕС (Bs.747.245.090,oo) […]корреспонденции в железной дороге Ориноко. ibh.com.ve ibh.com.ve |
Средства акционеров Банка составляют ОДИН МИЛЛИАРД ВОСЕМЬСОТ ТРИДЦАТЬ ШЕСТЬ МИЛЛИОНОВ ПЯТЬСОТ ЧЕТЫРЕ ТЫСЯЧИ ВОСЕМЬСОТ ШЕСТЬДЕСЯТ ДЕВЯТЬ ЕВРО […]ДВАДЦАТЬ ДЕВЯТЬ ЕВРОЦЕНТОВ […] (‘1 836 504 869,29), представленный ТРИ БИЛЛ IO N , СЕМЬСОТ СОРОК СЕДЬМОЙ 9000 9 M I LLIO N , ДЕВЯТЬСОТ ДЕВЯТЬ ТЫСЯЧ , СТО A N D ДВАДЦАТЬ ОДИН ( 3 90 010 ,7 47 969 121) акций по СОРОК ДЕВЯТИ (49) ЕВРОЦЕНТОВ [. ..] ..]номинал каждый, […]все того же класса и серии, полностью подписанные и оплаченные. inversores.bbva.com inversores.bbva.com | El Capital Social del Banco es de MIL OCHOCIENTOS TREINTA Y SEIS MILLONES QUINIENTOS CUATRO MIL OCHOCIENTOS SESENTA Y NUEVE EUROS CON VEINTINUEVE CNTIMOS DE EURO […](1.836.504.869,29 ‘), представитель […] por TRE S MIL SETE CIE NT OS CUARENTA Y SIETE M ILL ONE S NOV EC IENTAS SESENTA Y NUEVE MIL CIENTO VEINTIUNA (3 .747.969.121) accion es de CUARENTA Y NUEVE (49) CNTIMOS DE EURO de valor номинал ca da una, t od as ellas […]де ла мисма класе у […]серия, totalmente sucritas y desembolsadas. inversores.bbva.com inversores.bbva.com |
Куарента | Перевод с испанского на английский
cuarenta
кВтч
—
rehn 90 007
—
тах
)Прилагательное — это слово, описывающее существительное (например, большая собака) .
прилагательное1. (число)
а. forty (cardinal)La montaña está a cuarenta millas de aquí. Гора находится в сорока милях отсюда.
б. сороковой (порядковый номер)Celebraron su cuarenta aniversario de boda.Они отпраздновали сороковую годовщину свадьбы.
Существительное мужского рода используется с артиклями и прилагательными мужского рода (например, el hombre guapo, el sol amarillo).
мужской род существительное2. (число)
а. сорок Diez por cuatro es igual a cuarenta. Десять раз четыре равно сорок.
Десять раз четыре равно сорок.
3. (декада)
а. fortiesLa última vez que un proyecto de infraestructura se completó en la ciudad fue en los años cuarenta. В последний раз крупный инфраструктурный проект был завершен в городе в сороковых годах.
Copyright © Curiosity Media Inc. cuarentaCopyright © 2006 Harrap Publishers Limited сорок; (cuadragésimo) сороковой
los (años) cuarenta сороковой; los cuarenta rugientes Ревущие сороковые; «Los cuarenta Principales» (Рад) (ТВ) «Сорок лучших» испанского хит-парада; (Испанский хит-парад)
cantar las cuarenta (Naipes), чтобы иметь короля и королеву козырей
cantar las cuarenta a algn рассказать кому-нибудь несколько домашних истин; скажи кое-что
esas son otras cuarenta (Arg) (Perú) это совсем другая история
hasta el cuarenta de mayo no te quits el sayo ne’er качать до мая
seis
Collin с Полный электронный словарь испанского языка © HarperCollins Publishers, 2011 г. пять
пятьМашинные переводчики
Перевод cuarenta с помощью машинных переводчиков
См.



 un.org
un.org


 Преобразование Conholdate изображения в Excel будет анализировать файлы изображений с помощью функции OCR и извлекать текст и данные таблиц. Извлеченные данные можно сохранить в различных форматах, таких как Excel, OpenOffice и других.
Преобразование Conholdate изображения в Excel будет анализировать файлы изображений с помощью функции OCR и извлекать текст и данные таблиц. Извлеченные данные можно сохранить в различных форматах, таких как Excel, OpenOffice и других.

 Конвертируйте файлы документов из одного формата в другой бесплатно, онлайн и без загрузки дополнительного программного обеспечения.
Конвертируйте файлы документов из одного формата в другой бесплатно, онлайн и без загрузки дополнительного программного обеспечения.
 д. в качестве полезного файла, который можно открывать, сохранять и редактировать при необходимости.
д. в качестве полезного файла, который можно открывать, сохранять и редактировать при необходимости.
 Начните преобразование
Начните преобразование Первоначально он был разработан в 1998 году, и этот формат претерпел множество итераций, прежде чем в 2005 году AT&T, наконец, остановилась на формате, который мы знаем и используем сегодня. Сам файл содержит отсканированный документ, состоящий из мультимедиа или текста. Сжатие означает, что он до 10 раз меньше, чем JPEG, и поэтому обычно используется теми, кто занимается графикой и хочет отображать высококачественные плакаты, книги, журналы или страницы в физической печатной форме, но которые хотят опубликовать. их в Интернет в цифровом виде. Причина, по которой файлы DJVU намного меньше, чем файлы JPG, заключается в том, что этот формат может разбивать изображения на отдельные изображения и сжимать каждое из них по отдельности. Чтобы открыть файл DJVU, вам понадобится специальная программа. Sumatara PDF является одним из таких примеров и является бесплатным, в то время как DjVulibre также будет работать.
Первоначально он был разработан в 1998 году, и этот формат претерпел множество итераций, прежде чем в 2005 году AT&T, наконец, остановилась на формате, который мы знаем и используем сегодня. Сам файл содержит отсканированный документ, состоящий из мультимедиа или текста. Сжатие означает, что он до 10 раз меньше, чем JPEG, и поэтому обычно используется теми, кто занимается графикой и хочет отображать высококачественные плакаты, книги, журналы или страницы в физической печатной форме, но которые хотят опубликовать. их в Интернет в цифровом виде. Причина, по которой файлы DJVU намного меньше, чем файлы JPG, заключается в том, что этот формат может разбивать изображения на отдельные изображения и сжимать каждое из них по отдельности. Чтобы открыть файл DJVU, вам понадобится специальная программа. Sumatara PDF является одним из таких примеров и является бесплатным, в то время как DjVulibre также будет работать.

 От пяти отнимаем один и ставим I перед цифрой V.
От пяти отнимаем один и ставим I перед цифрой V.
 Амадеусу — 7 лет, Бенедикта старше Амадеуса на 4 года, а Констанций младше Бенедикты на 2 года.
Амадеусу — 7 лет, Бенедикта старше Амадеуса на 4 года, а Констанций младше Бенедикты на 2 года.



 до н.э. до падения в 476 г. н.э. Римская империя завоевала и объединила десятки культур.
до н.э. до падения в 476 г. н.э. Римская империя завоевала и объединила десятки культур. Считается, что город-государство Рим был первоначально образован сельскими жителями Лациума, объединившимися с поселенцами с окрестных холмов в ответ на нашествие этрусков. Неясно, собрались ли они вместе для защиты или в результате того, что попали под власть этрусков. Археологические данные указывают на то, что около 600 г. до н.э. произошли большие изменения и объединения, которые, вероятно, привели к тому, что Рим стал настоящим городом.
Считается, что город-государство Рим был первоначально образован сельскими жителями Лациума, объединившимися с поселенцами с окрестных холмов в ответ на нашествие этрусков. Неясно, собрались ли они вместе для защиты или в результате того, что попали под власть этрусков. Археологические данные указывают на то, что около 600 г. до н.э. произошли большие изменения и объединения, которые, вероятно, привели к тому, что Рим стал настоящим городом.
 до н.э. После отставки Суллы в 79 г. до н.э. республика вернулась в состояние волнений. В то время как Рим продолжал управляться как республика еще 50 лет, переход к империализму начал материализоваться в 60 г. до н.э., когда к власти пришел Юлий Цезарь.
до н.э. После отставки Суллы в 79 г. до н.э. республика вернулась в состояние волнений. В то время как Рим продолжал управляться как республика еще 50 лет, переход к империализму начал материализоваться в 60 г. до н.э., когда к власти пришел Юлий Цезарь. н.э. В течение этого периода Рим пережил несколько десятилетий. мира, процветания и расширения. К 117 году нашей эры Римская империя достигла своего максимального размера, охватив три континента, включая Малую Азию, северную Африку и большую часть Европы.
н.э. В течение этого периода Рим пережил несколько десятилетий. мира, процветания и расширения. К 117 году нашей эры Римская империя достигла своего максимального размера, охватив три континента, включая Малую Азию, северную Африку и большую часть Европы.




 Тогда
Тогда  Получим
Получим Дженнифер, 20 лет
Дженнифер, 20 лет 20.
20.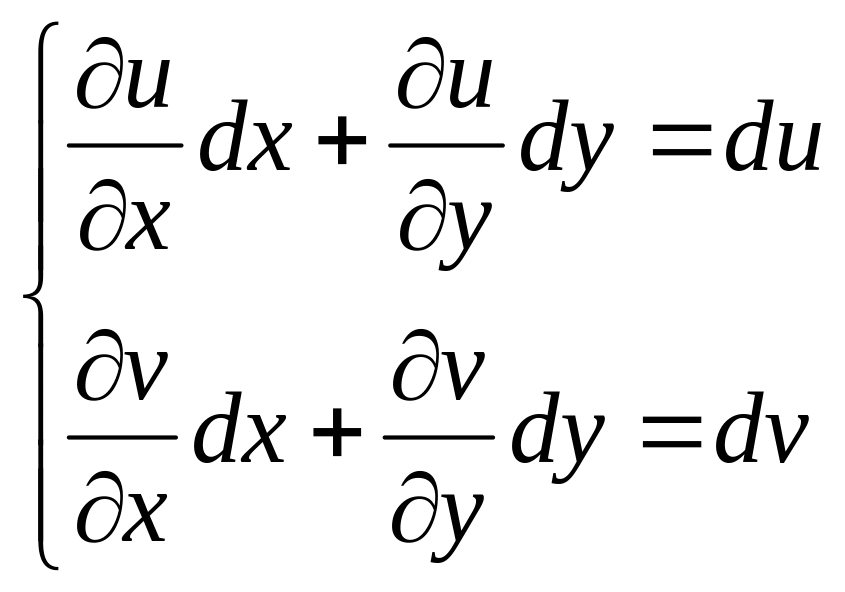



 Полная производная никогда не аппроксимирует функцию с одной переменной, если в функции присутствуют две или более переменных. Иногда полная производная совпадает с частной производной или обыкновенной производной функции.
Полная производная никогда не аппроксимирует функцию с одной переменной, если в функции присутствуют две или более переменных. Иногда полная производная совпадает с частной производной или обыкновенной производной функции.
 Пусть функция f(x,y) , где x — независимая переменная, а y — зависимая переменная x .
Пусть функция f(x,y) , где x — независимая переменная, а y — зависимая переменная x . (1)
(1)
 Это также относится к тому, что означает $\frac{d}{dx}$. Для конкретных выражений выше я бы просто использовал это. 92$. Переменные, фигурирующие в определении функции, строго говоря, невидимы для остального мира. Это просто удобный способ заявить, что «$f$ — это функция, которая принимает два аргумента. Она возводит в квадрат первый, возводит в квадрат второй и возвращает сумму квадратов». Вместо того, чтобы записывать это предложение (что люди должны были делать, прежде чем изобрести лучшую нотацию), вы можете вместо этого дать имена аргументам $f$, чтобы вы могли легко ссылаться на них при определении $f$.
Это также относится к тому, что означает $\frac{d}{dx}$. Для конкретных выражений выше я бы просто использовал это. 92$. Переменные, фигурирующие в определении функции, строго говоря, невидимы для остального мира. Это просто удобный способ заявить, что «$f$ — это функция, которая принимает два аргумента. Она возводит в квадрат первый, возводит в квадрат второй и возвращает сумму квадратов». Вместо того, чтобы записывать это предложение (что люди должны были делать, прежде чем изобрести лучшую нотацию), вы можете вместо этого дать имена аргументам $f$, чтобы вы могли легко ссылаться на них при определении $f$.
 Если бы мы обрабатывали вещи чисто символически, то определение $g$ могло бы также быть
Если бы мы обрабатывали вещи чисто символически, то определение $g$ могло бы также быть


 Общий делить 8 и 36 — 4. Это число не нужно записывать.
Общий делить 8 и 36 — 4. Это число не нужно записывать.
 НОД = 12
НОД = 12 Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.
Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей. Сократите обыкновенную дробь
Сократите обыкновенную дробь  Сократите дробь
Сократите дробь Дробь приведена к несократимому виду: =
Дробь приведена к несократимому виду: = Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.
Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами. Множители 17 и 34 равны 1, 17 и 1, 2, 17, 34 соответственно. Существует 3 широко используемых метода нахождения НОК 17 и 34: деление в длину, алгоритм Евклида и разложение на простые множители.
Множители 17 и 34 равны 1, 17 и 1, 2, 17, 34 соответственно. Существует 3 широко используемых метода нахождения НОК 17 и 34: деление в длину, алгоритм Евклида и разложение на простые множители.
 Найдите наибольшее число, которое точно делит 17 и 34.
Найдите наибольшее число, которое точно делит 17 и 34. 
 ☛ Простое число
☛ Простое число Давайте прыгать!
Давайте прыгать!



 И еще одно уравнение:
И еще одно уравнение:  В таких случаях искать дискриминант не обязательно. Можно решить проще.
В таких случаях искать дискриминант не обязательно. Можно решить проще.

 Умножить обе части уравнения на 100! Получим:
Умножить обе части уравнения на 100! Получим: На этот раз речь пойдёт о до боли знакомых квадратных уравнениях и их свойствах, о которых нет времени поговорить в школе.
На этот раз речь пойдёт о до боли знакомых квадратных уравнениях и их свойствах, о которых нет времени поговорить в школе.
 Если дискриминант отрицателен, то парабола расположена над осью и не пересекает её. В этом случае решений не будет. Если дискриминант положителен, минимум находится под осью и парабола неизбежно пересечёт эту ось в двух точках.
Если дискриминант отрицателен, то парабола расположена над осью и не пересекает её. В этом случае решений не будет. Если дискриминант положителен, минимум находится под осью и парабола неизбежно пересечёт эту ось в двух точках.
 Не буду здесь вдаваться в подробности расчёта, приведу конечный результат: доля нерешаемых уравнений составляет .
Не буду здесь вдаваться в подробности расчёта, приведу конечный результат: доля нерешаемых уравнений составляет .
 Каждая точка здесь — пара коэффициентов (b, c).
Каждая точка здесь — пара коэффициентов (b, c). Так что можно ожидать, что доля целочисленных решений будет падать пропорционально , если и . Численный эксперимент показывает, что на очень больших сказывается отличие от обратной пропорциональности, но это уже такие тонкости, в которых возиться большого смысла нет.
Так что можно ожидать, что доля целочисленных решений будет падать пропорционально , если и . Численный эксперимент показывает, что на очень больших сказывается отличие от обратной пропорциональности, но это уже такие тонкости, в которых возиться большого смысла нет.

 Корень при этом кратный, и равен
Корень при этом кратный, и равен

 При этом области, лежащие выше и ниже линии кратных корней отображаются в одну и ту же область коэффициентов, лежащую ниже линии кратных корней.Здесь чёрная линия соответствует кратным корням, а на параболоид проецируется решётка целочисленный корней.
При этом области, лежащие выше и ниже линии кратных корней отображаются в одну и ту же область коэффициентов, лежащую ниже линии кратных корней.Здесь чёрная линия соответствует кратным корням, а на параболоид проецируется решётка целочисленный корней.

 Этот метод не всегда можно использовать, потому что не все многочлены факторизуемы, но он используется везде, где возможно факторинг.
Этот метод не всегда можно использовать, потому что не все многочлены факторизуемы, но он используется везде, где возможно факторинг.
 В этом тексте мы будем использовать набор обозначений.
В этом тексте мы будем использовать набор обозначений.
 Произведение двух множителей равно нулю. Поэтому воспользуемся теоремой из предыдущего раздела.
Произведение двух множителей равно нулю. Поэтому воспользуемся теоремой из предыдущего раздела.  Проверьте эти решения.
Проверьте эти решения.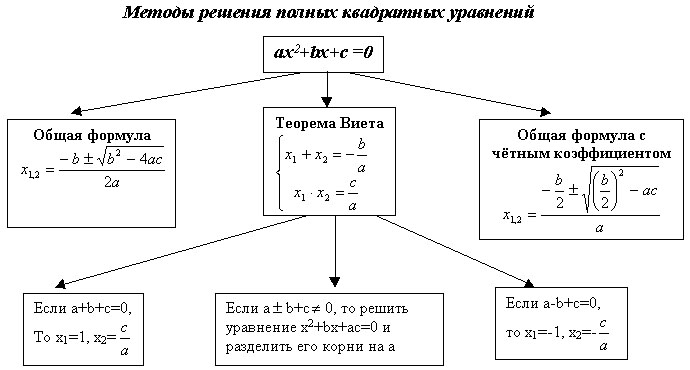






 В некотором смысле тогда ax 2 + bx + c = 0 представляет все квадратичные числа. Если вы сможете решить это уравнение, вы получите решение всех квадратных уравнений.
В некотором смысле тогда ax 2 + bx + c = 0 представляет все квадратичные числа. Если вы сможете решить это уравнение, вы получите решение всех квадратных уравнений.
 Процесс определения и постановки задачи такой же, как описано в главе 5, но с задачами, решаемыми с помощью квадратичных вычислений, вы должны быть очень осторожны, проверяя решения в самой задаче. Физические ограничения внутри проблемы могут исключить одно или оба решения.
Процесс определения и постановки задачи такой же, как описано в главе 5, но с задачами, решаемыми с помощью квадратичных вычислений, вы должны быть очень осторожны, проверяя решения в самой задаче. Физические ограничения внутри проблемы могут исключить одно или оба решения.
 Найдите целое число.
Найдите целое число.
 Этот метод основан на теореме: если AB = 0, то A = 0 или B = 0. Чтобы использовать эту теорему, мы придаем уравнению стандартную форму, множитель и устанавливаем каждый множитель равным нулю.
Этот метод основан на теореме: если AB = 0, то A = 0 или B = 0. Чтобы использовать эту теорему, мы придаем уравнению стандартную форму, множитель и устанавливаем каждый множитель равным нулю. Все решения должны быть упрощены.
Все решения должны быть упрощены.

 Умножьте первый коэффициент на последний член и перечислите множители.
Умножьте первый коэффициент на последний член и перечислите множители. Подставьте эти значения в квадратное уравнение, чтобы найти x.
Подставьте эти значения в квадратное уравнение, чтобы найти x. Когда Билли будет в 1,5 раза старше Джонни?
Когда Билли будет в 1,5 раза старше Джонни?
 Угадать и проверить было бы довольно эффективным способом решения этой задачи, но составление уравнения было бы еще быстрее. Однако сначала нам нужно выяснить, что представляет собой наша переменная. Мы знаем текущий возраст Билли и Джонни; нам просто нужно выяснить их будущий возраст. Одна переменная всегда лучше двух, поэтому вместо использования двух разных переменных для представления их соответствующего будущего возраста мы будем использовать одну переменную для представления количества лет, которые мы должны добавить к каждому из их текущих возрастов, чтобы сделать Билли 1,5 года. раз старше Джонни. Назовем эту переменную «x».
Угадать и проверить было бы довольно эффективным способом решения этой задачи, но составление уравнения было бы еще быстрее. Однако сначала нам нужно выяснить, что представляет собой наша переменная. Мы знаем текущий возраст Билли и Джонни; нам просто нужно выяснить их будущий возраст. Одна переменная всегда лучше двух, поэтому вместо использования двух разных переменных для представления их соответствующего будущего возраста мы будем использовать одну переменную для представления количества лет, которые мы должны добавить к каждому из их текущих возрастов, чтобы сделать Билли 1,5 года. раз старше Джонни. Назовем эту переменную «x». Напомним, что:
Напомним, что:
 Назовите групповой реагент и перечислите катионы, входящие в IV группу.
2. Укажите цвет гидроксидов катионов IV
Назовите групповой реагент и перечислите катионы, входящие в IV группу.
2. Укажите цвет гидроксидов катионов IV
 И все мы хорошо его запомнили и применяем в жизни, не задаваясь вопросом: «Почему?». Но вот мы выросли, у нас появились дети, и пришло время объяснять им те самые простейшие правила так, чтобы было понятно и запомнилось навсегда. Как это сделать? Какие слова подобрать? Будем разбираться.
И все мы хорошо его запомнили и применяем в жизни, не задаваясь вопросом: «Почему?». Но вот мы выросли, у нас появились дети, и пришло время объяснять им те самые простейшие правила так, чтобы было понятно и запомнилось навсегда. Как это сделать? Какие слова подобрать? Будем разбираться. При выполнении сложения и вычитания с нулём обычно проблем и сложностей не возникает. Здесь всё просто.
При выполнении сложения и вычитания с нулём обычно проблем и сложностей не возникает. Здесь всё просто.  В этом действии участвуют два составляющих компонента — множимое и множитель. Результат их умножения называют произведением. То есть для натуральных чисел умножением, по сути, является многократное сложение. Таким образом, чтобы умножить число a на число b, необходимо b раз сложить a.
В этом действии участвуют два составляющих компонента — множимое и множитель. Результат их умножения называют произведением. То есть для натуральных чисел умножением, по сути, является многократное сложение. Таким образом, чтобы умножить число a на число b, необходимо b раз сложить a. 
 В любом случае произведение будет нулевым.
В любом случае произведение будет нулевым.
 Единственное ограничение — ноль не может быть делителем для любого действительного числа. В арифметике подобные действия считаются невозможными и бессмысленными.
Единственное ограничение — ноль не может быть делителем для любого действительного числа. В арифметике подобные действия считаются невозможными и бессмысленными.
 Математическая функция деления работает иначе. Это применимо даже тогда, когда деление просто обратное умножению. Итак, если бы вы разделили число на ноль, результирующий ответ не был бы равен нулю, поскольку деление на 0 не определено.
Математическая функция деления работает иначе. Это применимо даже тогда, когда деление просто обратное умножению. Итак, если бы вы разделили число на ноль, результирующий ответ не был бы равен нулю, поскольку деление на 0 не определено. Нулевое свойство умножения применяется ко всем числам, включая отрицательные числа. Таким образом, если -75 умножить на 0, в результате получится 0,9.0003
Нулевое свойство умножения применяется ко всем числам, включая отрицательные числа. Таким образом, если -75 умножить на 0, в результате получится 0,9.0003 Из приведенных выше вариантов
Из приведенных выше вариантов  Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. е. 1,45 .
е. 1,45 . Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций: 

 Так возникают ошибки.
Так возникают ошибки. При этом главное помнить, что после введения замены в некоторое уравнение это уравнение должно:
При этом главное помнить, что после введения замены в некоторое уравнение это уравнение должно:
 Ну а основное свойство отрицательной степени записывается следующим образом:
Ну а основное свойство отрицательной степени записывается следующим образом: Кроме того, нужно отметить, что если используется запись со значком математического корня, то показатель степени этого корня может быть только целым числом, причем это число должно быть больше либо равно двум:
Кроме того, нужно отметить, что если используется запись со значком математического корня, то показатель степени этого корня может быть только целым числом, причем это число должно быть больше либо равно двум: Если под корнем квадратным имеется произведение двух отрицательных величин (т.е. по итогу величина положительная, а значит корень существует), то этот корень раскладывается на множители следующим образом:
Если под корнем квадратным имеется произведение двух отрицательных величин (т.е. по итогу величина положительная, а значит корень существует), то этот корень раскладывается на множители следующим образом:
 А если же мы возведем в четную степень, то получится уравнение, которое будет следствие данного, именно из-за этого возможно появление посторонних корней решения уравнений.
А если же мы возведем в четную степень, то получится уравнение, которое будет следствие данного, именно из-за этого возможно появление посторонних корней решения уравнений.
 Иррациональные числа, как правило, имеют бесконечные неповторяющиеся цифры после запятой. Возьмем такой пример: √8= 2,828.
Иррациональные числа, как правило, имеют бесконечные неповторяющиеся цифры после запятой. Возьмем такой пример: √8= 2,828.

 Следовательно, рациональные числа одинаково закрыты для умножения, вычитания и деления, если делитель не равен нулю.
Следовательно, рациональные числа одинаково закрыты для умножения, вычитания и деления, если делитель не равен нулю. Частные таких делений называются конечными десятичными дробями.
Частные таких делений называются конечными десятичными дробями.


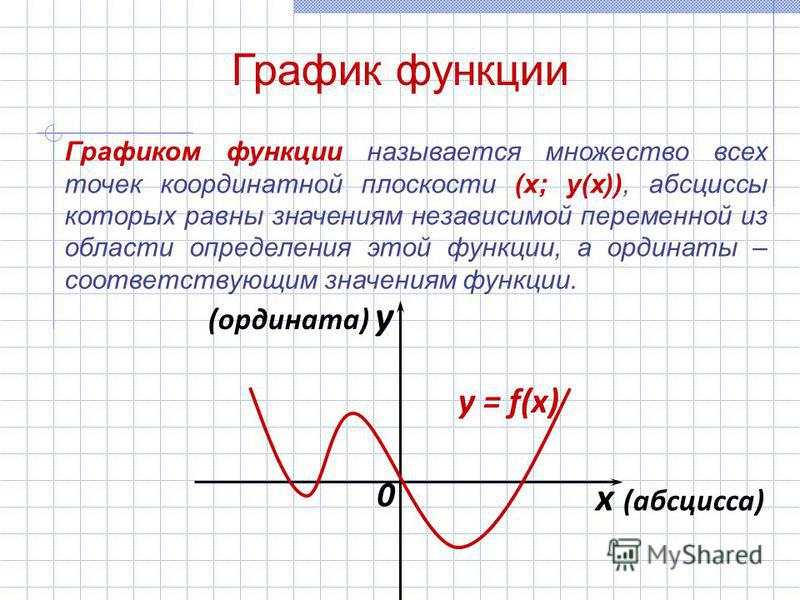 Всевозможные значения Y называются областью значений функции.
Скорее всего так)
Удачи! Читать далее
Всевозможные значения Y называются областью значений функции.
Скорее всего так)
Удачи! Читать далее 2
2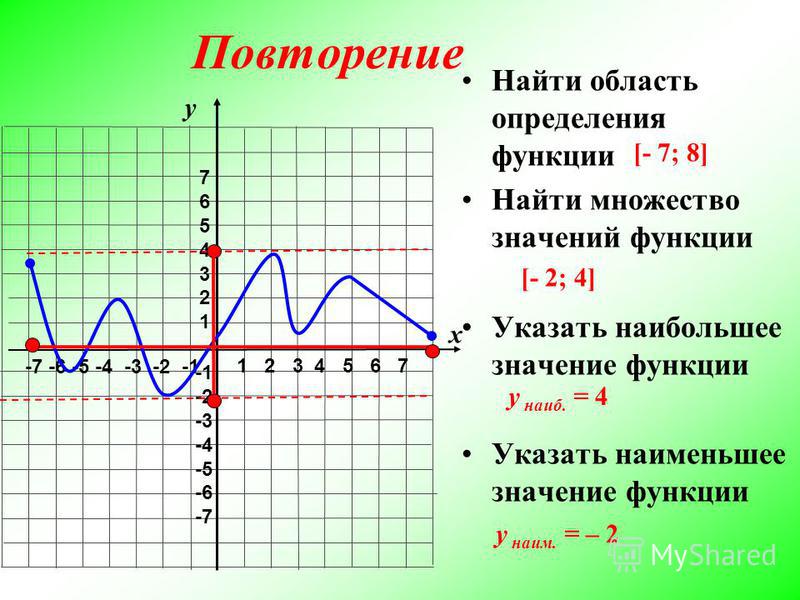 2
не входит в диапазон, так как в домене нет буквы, которая сопоставляется с
2
.
2
не входит в диапазон, так как в домене нет буквы, которая сопоставляется с
2
.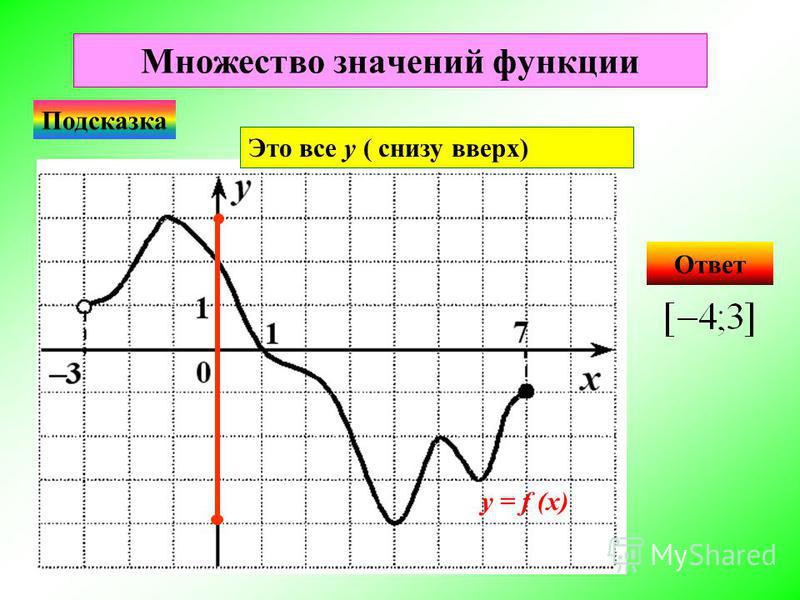

 у
-значения варьируются от
0
вплоть до
1
(включая
0
, но не включая
1
). Таким образом, область действия функции
у
-значения варьируются от
0
вплоть до
1
(включая
0
, но не включая
1
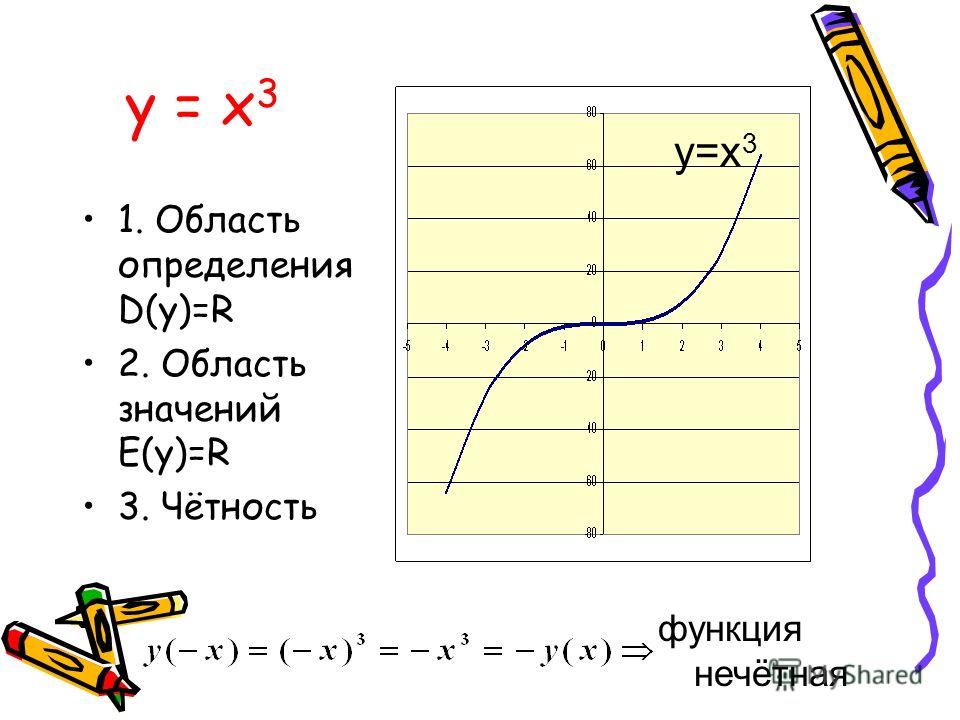
). Таким образом, область действия функции Таким образом, областью определения f(x) = x 2 являются все значения x. Затем, глядя на график или тестируя несколько значений x, мы видим, что любое значение x, которое мы подставляем, приведет к положительному значению y. Таким образом, диапазон f(x) = x 2 — все положительные значения y.
Таким образом, областью определения f(x) = x 2 являются все значения x. Затем, глядя на график или тестируя несколько значений x, мы видим, что любое значение x, которое мы подставляем, приведет к положительному значению y. Таким образом, диапазон f(x) = x 2 — все положительные значения y.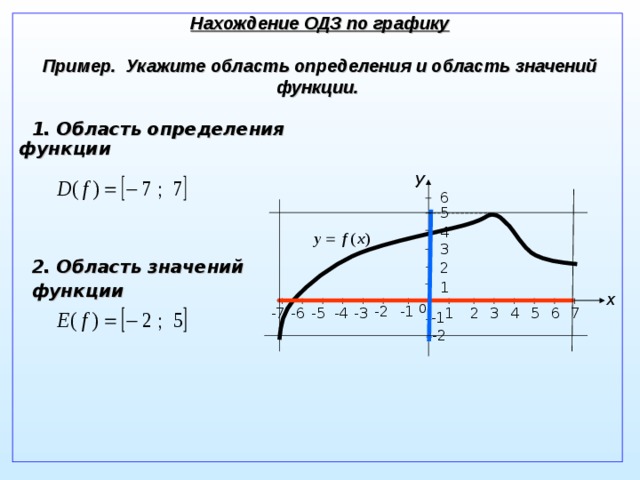
 Символ объединения можно прочитать как «или», и он используется в различных областях математики. В контексте обозначения интервала это просто означает объединение двух заданных интервалов. Например, рассмотрим функцию:
Символ объединения можно прочитать как «или», и он используется в различных областях математики. В контексте обозначения интервала это просто означает объединение двух заданных интервалов. Например, рассмотрим функцию: