| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.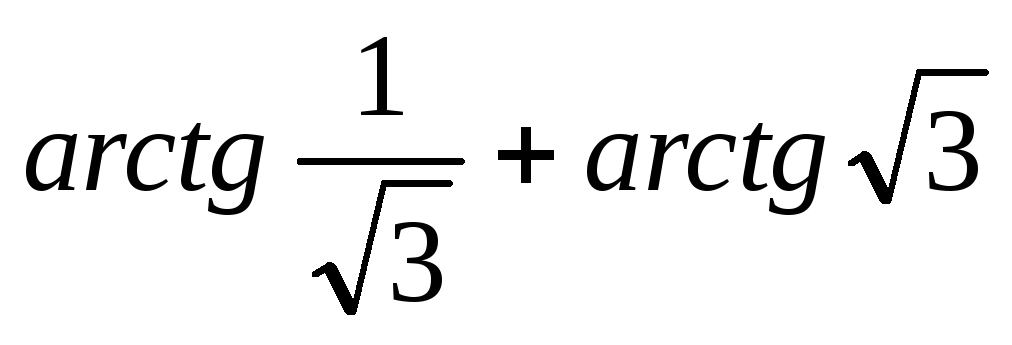 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
3 arctg 0
3 arctg 0Вы искали 3 arctg 0? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 4 arctg 1, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «3 arctg 0».
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «3 arctg 0».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 3 arctg 0,4 arctg 1,4 арктангенс 1,6 arctg,arccos онлайн,arctg 0,arctg 0 1,arctg 0 2,arctg 0 25,arctg 0 3,arctg 0 4,arctg 0 5,arctg 0 6,arctg 0 arctg 1,arctg 0 равен,arctg 1 0,arctg 1 2 в градусах,arctg 1 4,arctg 1 5,arctg 1 6,arctg 1 arctg 0,arctg 1 в градусах,arctg 10,arctg 2 0,arctg 2 3 в градусах,arctg 2 5,arctg 2 в градусах,arctg 3 0,arctg 3 5,arctg 3 в градусах,arctg 4,arctg 4 1,arctg 4 3 в градусах,arctg 4 5,arctg 4 в градусах,arctg 5,arctg 5 2,arctg 5 3,arctg 5 4,arctg 6,arctg 7,arctg 8,arctg в градусах,arctg как вычислить,arctg как найти,arctg калькулятор,arctg калькулятор онлайн,arctg калькулятор онлайн в градусах,arctg онлайн,arctg онлайн калькулятор,arctg онлайн калькулятор в градусах,arctg таблица,arctg таблица значений,arctg4,online arctg,арккотангенс онлайн,арктангенс 0,арктангенс 0 1,арктангенс 0 25,арктангенс 0 4,арктангенс 0 5,арктангенс 0 75,арктангенс 0 чему равен,арктангенс 1 2,арктангенс 1 2 в градусах,арктангенс 1 3,арктангенс 1 3 в градусах,арктангенс 1 4,арктангенс 1 5,арктангенс 1 в градусах,арктангенс 1 в радианах,арктангенс 2 3,арктангенс 2 в градусах,арктангенс 3,арктангенс 3 2,арктангенс 3 4 в градусах,арктангенс 3 в градусах,арктангенс 4 в градусах,арктангенс 45,арктангенс 5,арктангенс 8,арктангенс в градусах,арктангенс в градусах калькулятор,арктангенс вычислить,арктангенс вычислить онлайн,арктангенс как вычислить,арктангенс как посчитать,арктангенс калькулятор,арктангенс калькулятор в градусах,арктангенс калькулятор онлайн,арктангенс калькулятор онлайн в градусах,арктангенс калькулятор онлайн в градусах и минутах,арктангенс на калькуляторе,арктангенс найти,арктангенс нуля,арктангенс онлайн,арктангенс онлайн калькулятор,арктангенс онлайн калькулятор в градусах,арктангенс онлайн калькулятор в градусах и минутах,арктангенс посчитать,арктангенс посчитать онлайн,арктангенс равен 1,арктангенс угла,арктангенс числа онлайн,арктангенсы таблица,вычисление арккосинуса онлайн,вычисление арктангенса,вычисление арктангенса онлайн,вычислить arctg онлайн калькулятор,вычислить арккосинус онлайн,вычислить арктангенс,вычислить арктангенс онлайн,инженерный онлайн калькулятор с арктангенсом,как вычислить arctg,как вычислить арктангенс,как найти арктангенс,как найти арктангенс числа,как посчитать арктангенс,как считать арктангенс,калькулятор arctg,калькулятор arctg онлайн,калькулятор arctg онлайн в градусах,калькулятор арккосинус в градусах онлайн,калькулятор арктангенс,калькулятор арктангенс в градусах,калькулятор арктангенса,калькулятор арктангенса онлайн,калькулятор арктангенсов,калькулятор арктангенсов в градусах онлайн,калькулятор арктангенсов онлайн,калькулятор арктангенсов онлайн в градусах,калькулятор онлайн arctg,калькулятор онлайн арктангенс,калькулятор онлайн арктангенс в градусах,калькулятор онлайн с арктангенсом,калькулятор онлайн с арктангенсом онлайн,калькулятор с арктангенсом,калькулятор с арктангенсом онлайн,на калькуляторе арктангенс,найти арктангенс,найти арктангенс онлайн,онлайн арктангенс числа,онлайн вычисление арктангенса,онлайн калькулятор arccos в градусах,онлайн калькулятор arctg,онлайн калькулятор arctg в градусах,онлайн калькулятор арктангенс,онлайн калькулятор арктангенса,онлайн калькулятор арктангенсов,онлайн калькулятор арктангенсов в градусах,онлайн калькулятор с арктангенсом,онлайн калькулятор с арктангенсом онлайн,онлайн расчет арктангенса,онлайн считать арктангенс,перевод арктангенса в градусы,перевод арктангенса в градусы онлайн,посчитать арккосинус онлайн,посчитать арктангенс,посчитать арктангенс в градусах онлайн,посчитать арктангенс онлайн,посчитать арктангенс онлайн в градусах,расчет арктангенса онлайн,таблица arctg,таблица арков,таблица брадиса arctg,таблица значений арктангенс,чему равен arctg,чему равен арктангенс 1. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 3 arctg 0. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 4 арктангенс 1).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 3 arctg 0. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 4 арктангенс 1).
Решить задачу 3 arctg 0 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор — arctan(-1.5) — Солуматы
Арктан, расчет онлайн
Резюме:
Функция арктангенса позволяет вычислить арктангенс числа.
Функция арктангенса является обратной функцией функции тангенса.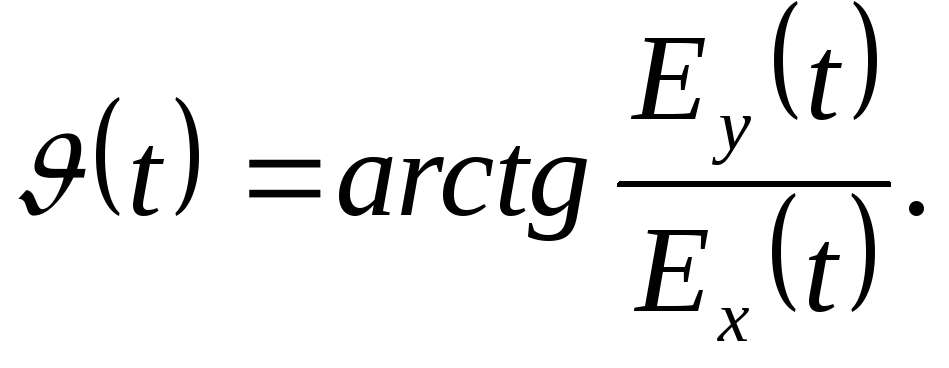
Описание:
Функция arctan является обратной функцией касательная функция, это вычисляет арктангенс числа онлайн .
- Расчет арктангенса
- Пределы арктангенса Пределы арктангенса существуют при `-oo` (минус бесконечность) и `+oo` (плюс бесконечность):
Чтобы вычислить арктангенс числа, просто введите число и примените арктанг функция.
Например, чтобы вычислить арктангенс следующего числа 10, введите arctan(`10`), или сразу 10, если кнопка arctan уже появляется, возвращается результат 1.4711276743. 92)`.
- Функция арктангенса имеет предел в `-oo`, который равен `pi/2`.
- Функция арктангенса имеет предел в `+oo`, который равен `-pi/2`.

- `lim_(x->-oo)arctan(x)=pi/2`
- `lim_(x->+oo)arctan(x)=-pi/2`
| arctan(`-1`) | `3*pi/4` |
| arctan(`-sqrt(3)/3`) | `5*pi/6` |
| арктический (`-sqrt(3)`) | `2*pi/3` |
| arctan(`0`) | `0` |
| arctan(`sqrt(3)`) | 9 0070 `пи /3`|
| arctan(`1`) | `pi/4` |
| arctan(`sqrt(3)/3`) | `pi/6` |
теория, практика и инфраструктура в опционной торговле · IT Global LLC
четверг, 24 ноября 2016 г.
Века назад мореходы чертили карты, по небу строили путь и прогнозы погод, плыли навстречу золоту, специям и шелкам в обход мелей и пиратов. В программе юбилейной Х Народной опционной конференции мы собрали самых ярких и бывалых, проверенных штормами обвалов, штилями волатильности, непредсказуемостью налогового и валютного законодательства. Будем чертить общие карты!
10 декабря в 11:00 (регистрация с 10:15) ждем вас в Синем зале Геологического музея им.Вернадского по адресу ул. Моховая 11, стр. 11. Метро Охотный ряд или Библиотека им. Ленина.
Cвет, крыша, еда и комфортные кресла – с участием старых друзей Option Workshop (IT Global) и международного брокера Freedom Finance.
| Время | Доклад | Докладчик |
|---|---|---|
| 10:15 – 11:00 | Регистрация | |
| Секция 1: Универсальные опционные техники | ||
| 11:00–11:30 | Сравнение стратегий дельта-хеджирования с позиции применения на модельных рядах. Мой выбор. Мой выбор. | Андрей Агапов, частный алготрейдер |
| 11:30–12:00 | Опционный арбитраж вмененных волатильностей индексов и товаров | Алексей Всемирнов, частный трейдер и управляющий, преподаватель |
| 12:00–12:30 | Торговля дисперсией и корреляцией – индексный арбитраж в работе маркет-мейкера | Дмитрий Кулешов, управляющий активами |
| 12:30–13:00 | Арбитражные роботы и торговля волатильностью на США (опционы, акции, валюта) | Сергей Елисеев, трейдер и управляющий, создатель Option-Lab |
| 13:00–13:30 | Торговля VIX на рынке США | Олег Анферов, алгоритмический трейдер, Anderida Financial Group |
| 13:30–14:30 | Обед | |
| Секция 2: Опционный практикум | ||
| 14:30–14:50 | Обзор нового релиза Option Workshop. Результаты запуска на российском рынке. Применение на зарубежных рынках. Результаты запуска на российском рынке. Применение на зарубежных рынках. | Павел Корякин, IT Global, создатель Option Workshop |
| 14:50–16:00 | Блиц-турнир опционных стратегий, каждому 10 минут: как зарабатываю, доходность-просадка, стратегия, рынок, пример | Модератор: Андрей Кузнецов, управляющий активами в Ryal Capital Advisors, основатель Wild Bear Capital |
| — Примеры торговли с софтом Option Workshop на рынках США | Андрей Кузнецов | |
| — Применение фьючерсно-опционного баланса на Мосбирже | Альберт Бурага, трейдер и управляющий, эксперт YouTrade.TV (Краснодар) | |
| — Алгоритмическая торговля в опционах | Илья Гадаскин, управляющий партнер компании Финстрит, (Воронеж) | |
| — Торгую новости и волатильность на недельных опционах США | Егор Романюк, управляющий на США, основатель Barna Capital Group (Барнаул) | |
| “Свободный микрофон” | +2-3 выступления, заявки на alina@lowrisk. ru ru | |
| 16:00–16:30 | Полдник | |
| Секция 3: Инфраструктура | ||
| 16:30–17:30 | Круглый стол по налогообложению дохода от торговли через российских и зарубежных брокеров | — Денис Шушин, советник государственной гражданской службы; |
| — Олег Харитонов, управляющий; | ||
| — Арсен Яковлев, частный алготрейдер; | ||
| — Дмитрий Кулешов, управляющий активами; | ||
| — Андей Агапов (модерация) | ||
| 17:30–18:00 | Валютный контроль при торговле на зарубежном брокерском счете | Виктория Курзаева, представитель валютного контроля банка Открытие |
| 18:10–18:30 | Организация торговли на рынках США через российского брокера | Игорь Клюшнев, глава департамента торговых операций Freedom Finance |
| 18:30–19:00 | Кое-что о Срочном рынке Московской биржи | пока секрет |
| 19:00 | **Кулуары и вино в кафе Геологического музея ** |
LowRisk. ru & AllDerivatives Café – лучший сайт об опционах и торговых стратегиях. Народная опционная конференция, Четверги, Субботы и мастер-классы для трейдеров и управляющих в AllDerivatives | Школе срочного рынка. Диалоги о финансовой карьере для студентов МГИМО.
ru & AllDerivatives Café – лучший сайт об опционах и торговых стратегиях. Народная опционная конференция, Четверги, Субботы и мастер-классы для трейдеров и управляющих в AllDerivatives | Школе срочного рынка. Диалоги о финансовой карьере для студентов МГИМО.
семинар выступления option-workshop uncategorized Постоянная ссылка
Шифр— Тайна NOC +10
6 марта 2015 года был создан канал на YouTube под названием «Noc +10» . С того дня этот канал загружает действительно мрачные загадочные видео. Я начну говорить кое-что о названии этого канала, которое действительно довольно странно: введя в Google «NOC +10», вы легко обнаружите, что оно может относиться к Naval Operation Concept 2010 , также представленному с аббревиатура «НОК 10».
1. Первый контакт — 7 марта 2015 г.
0101 0101 0000 0001 Первое видео , загруженное Noc +10 7 марта 2015 года, называется 0101 01001 0 006 : это сразу же позволяет нам думать о каком-то двоичном коде. Он разделен на блоки по четыре бита, но мы не знаем его смысла. Это видео состоит из странного дисплея, похожего на старый осциллограф, на котором отображаются некоторые искаженные буквы и слова. Давайте разберем это:
- Он начинает отображать строку
NOC+10, с фоновой фортепианной музыкой, которую легко узнать: это Nocturne Op. 27 № 1 до-минор Фредерика Шопена. - Экран на некоторое время становится черным, музыка останавливается, начинается низкочастотный шум: появляется слово
СТАРТ. - Отображается ряд букв, произнесенных женским компьютеризированным голосом:
JKnjGvPaITB, которым предшествует строка?v=.
- Когда голос закончит произносить буквы, слово 9Появляется 0005
END, и видео останавливается через несколько секунд.
Глядя на строку ?v=JKnjGvPaITB , мы можем легко представить идентификатор какого-то видео на YouTube , но сама строка зашифрована, и видео с таким идентификатором не существует. Кстати, применив к этому идентификатору знаменитый шифр Цезаря , мы можем его расшифровать и найти идентификатор GHkgDsMxFQY , который является действительным идентификатором видео YouTube.
При просмотре этого видео у меня возникло много других вопросов: "Noc" как-то связан с "Nocturne"? Что означает песня? И т. д.
2. Первое скрытое видео - 7 марта 2015 г. тот же канал под названием
0101 0101 0000 0010 . Первое, что мы замечаем, это то, что название видео почти совпадает с предыдущим, но на самом деле последние 4 бита отличаются: 0010 . Название видео изменилось с окончания
Название видео изменилось с окончания 0001 на 0010 : ясно, что два названия этих видео являются последовательными двоичными числами . Давайте посмотрим, что внутри этого второго видео:Видео начинается с высокочастотного шума, и отображается строка
NOC+10.Затем внезапный обрыв видео подводит нас к длинной цепочке явно случайных заглавных букв, заканчивающейся кучей нулей:
РКХОХККДГДВВХДПЕРДВ ВКХВВХДПЕРДВКДГДЕХОО ZKHQKHOHQZHQWWRKHDYHQ WKHVWHDPERDWZHQWWRKHOO 00000000000000000000000
Та же фоновая музыка воспроизводится вместе с тем же женским голосом, произносящим эту последовательность букв.
- Видео заканчивается через несколько секунд после того, как голос закончил произносить весь код.
Снова применив к коду шифр Цезаря , мы можем его расшифровать:
RKKHOHQKDGDVWHDPERDW -> OHHELENHADASTEAMBOAT WKHVWHDPERDWKDGDEHOO -> ПАРОВАЯ ЛОДКА HADABELL ZKHQKHOHQZHQWWRKHDYHQ -> КОГДА ПОШЛА НА НЕБЕСА WKHVWHDPERDWZHQWWRKHOO -> ПАРОВАЯ ЛОДКА ПОШЛА В АД 0000000000000000000000 -> Эти нули, похоже, не имеют никакого значения
Разделив код на нужные части, мы можем различить нечто вроде вирши, которая гласит:
У О Хелен был пароход
У парохода был колокол
Когда Хелен попала в рай
Пароход отправился в ад
Эти рифмы, особенно первый куплет, заставляют нас задуматься о Мисс Сьюзи, американской школьной стишке , может быть, это ее вариация? Глядя на Википедию на странице мисс Сьюзи, мы можем найти связанную статью: 900:05 Трагедия SS Sultana (1865 г. ), величайшая морская катастрофа в истории Соединенных Штатов. Ну, скажем так: выглядит чертовски загадочно и мрачно!
), величайшая морская катастрофа в истории Соединенных Штатов. Ну, скажем так: выглядит чертовски загадочно и мрачно!
3. Второй контакт - 12 марта 2015 г.
0101 0101 0000 0011 0101 0101 0000 0011 . Если бы у нас были подозрения, что названия видеороликов представляют собой последовательных двоичных чисел , теперь понятно! Опять же, давайте проанализируем это третье видео так же, как и предыдущие:
Оно начинается с обычной строки
NOC+10с той же музыкой Шопена на заднем плане.На экране отображается длинная строка цифр и букв:
6D3248656C6C6F4166776F726C645156 68656C656E79324937367761697459
Это наводит нас на мысль о какой-то шестнадцатеричной строке, поскольку буквы, встречающиеся в этой строке, не превосходят букву F, которая является наибольшей допустимой шестнадцатеричной цифрой.
- Мужской голос издает 16 одинаковые и неузнаваемые звуки, пока на экране отображается вышеуказанная строка, и видео заканчивается: это подтверждает наш тезис о шестнадцатеричной строке.

Применение шифра Цезаря на этот раз не работает, но я попытался перевести его из шестнадцатеричных пар символов в символы ASCII, и результат оказался еще более жутким, чем предыдущий:↓ m2HelloAfworldQVheleny2I76waitY
Кажется, это какой-то текст, чередующийся с двухсимвольными строками, вставленными для разделения слов. Результат удаления лишних символов:
привет мир Хелен я жду
А как же удаленные персонажи? Выглядят знакомо: m2AfQVy276Y , ДА! Они представляют другой идентификатор видео YouTube!
4. Второе скрытое видео - 12 марта 2015 г.
0101 0101 0000 0100 Четвертое видео , найденное с идентификатором, извлеченным из третьего, отсутствует в списке и было загружено Noc +10 ранее в тот же день, что и предыдущее. Его название 0101 0101 0000 0100 . Эти последовательных двоичных чисел продолжаются. Это видео также содержит намного больше информации, чем другие :
Это видео также содержит намного больше информации, чем другие :
Оно начинается с того же вступления
NOC+10, играет та же музыка Шопена.В видеофрагменте показан еще один кадр с текстом, на этот раз не зашифрованным:
СИСТЕМА 00033 МЕРТВЫЙ СИСТЕМА 01090 УМЕРЛА СИСТЕМА 00010 ЖИВА
Начинает играть другая песня: похоже на старую песню 70-х.
Затем более длинный и подробный текст:
ВОДОНЕПРОНИЦАЕМЫЙ СТАБИЛЬНЫЙ ПОД ДАВЛЕНИЕМ СЕКТОР 1 СТАБИЛЬНЫЙ СЕКТОР 2 СТАБИЛЬНЫЙ СЕКТОР 3 СТАБИЛЬНЫЙ РАЗДЕЛ 4 ПРИНЦИП ЗАПОЛНЕНИЯ СЕКТОР 5 СТАБИЛЬНЫЙ СЕКТОР 6 ОТСУТСТВУЕТ СИГНАЛ СЕКТОР 7 СТАБИЛЬНЫЙ
Теперь появляется фраза
ЗДЕСЬ ЕЩЕ ОДНА МАТЬ СПИТ, и мужской голос произносит буквыЛ-И-О-У-Й, после чего видео заканчивается.
Это видео кажется самым важным на данный момент: оно явно полно связей и загадок, которые нужно разгадать . Это также приводит к большому количеству других вопросов:
Это также приводит к большому количеству других вопросов:
- На что ссылаются эти
SYSTEM? - это
СЕКТОРчасть корабля? Может СС Султана? - Что означает
LIOUY? - Может, под "еще одной спящей матерью" имеется в виду еще одна умершая система?
- Имеют ли эти два экрана какое-либо отношение к трагедии СС Султана?
Посмотрим, сможем ли мы ответить на некоторые из них:
Строка
LIOUYиспользовалась как старый коммерческий код телеграммы, означающий "Почему вы не отвечаете на мой вопрос?" .Частичная анаграмма фразы
ЗДЕСЬ СПАТЬ ЕЩЕ ОДНА МАТЬдает нам:ОШИБКА ТЕРМОСТАТА НЕТ СНА
Это также похоже, что знаменитая трагедия SS Sultana связана с этими последними видео. Цитата со страницы Википедии (ссылка выше):
[.
..] Около 2 часов ночи 27 апреля 1865 года, когда «Султана» находилась всего в семи милях к северу от Мемфиса, ее котлы внезапно взорвались. Сначала взорвался один котел, а через долю секунды еще два. Причина взрыва Слишком большое давление и мало воды в котлах . Были основания полагать, что допустимое рабочее давление пара было превышено при попытке преодолеть весеннее течение реки. Мощный взрыв сбросил некоторых пассажиров на палубе в воду и разрушил большую часть лодки. [...]
По ходу этой истории я все больше и больше склоняюсь к мысли, что эти SYSYEM и SECTOR относятся к SS Sultana.
5. Третий контакт - 19 марта, 2015
0101 0101 0000 0101 Пятое видео загружено Noc +10 через семь дней после предыдущего. Это видео под названием 0101 0101 0000 0101 является третьим общедоступным видео и было загружено 19 марта.
Еще раз:
Женский голос, если проиграть в обратном направлении, кажется, произносит P. , послушать можно здесь *ссылка может истечь . Могут ли эти две буквы обозначать $\pi$ (иррациональное число Pi)? I.
I.
Похоже, что код, указанный в этом видео, содержит другой идентификатор видео YouTube, а именно oYzXqoELKjE , но видео с таким идентификатором нет. Кроме того, применение к нему шифра Цезаря не дает действительного идентификатора видео. Может быть, в трех других символах A 14 есть какая-то скрытая информация, какая-то информация о том, как расшифровать идентификатор?
Общие моменты
Все видео начинаются с одинакового введения . Все заголовков видео представлены возрастающим двоичным числом 9.0006 разделен на 4 блока по 4 бита. Если мы переведем числа в десятичную систему счисления, то получим числа 5501, 5502, 5503 и т.д. . Похоже, что последовательность общедоступных настроек видео такова: общедоступный, незарегистрированный, общедоступный, незарегистрированный и т. . Все видео, не включенные в список, были обнаружены при декодировании данных, предоставленных предыдущими общедоступными видео, это заставляет нас поверить, что есть шестое скрытое видео, которое нужно найти, анализируя данные последнего видео . д.
д.
Сможете ли вы взломать код последнего видео и найти идентификатор следующего?
Это краткий обзор событий, произошедших с момента обнаружения первого видео:
#1 0101 0101 0000 0001 - 03.07.2015 - общедоступный | |- URL видео: youtube.com/watch?v=NCAUPuXzn4U |- Зашифрованные данные: "?v=JKnjGvPaITB" |- Расшифровано (ROT23): "?v=GHkgDsMxFQY" | |- Расшифрованный идентификатор видео приводит нас к видео № 2. #2 0101 0101 0000 0010 - 03.07.2015 - нет в списке | |- URL видео: youtube.com/watch?v=GHkgDsMxFQY |- Зашифрованные данные: [длинные, см. выше] |- Расшифровано (ROT23): "У Елены был пароход..." рифмы | |- Неизвестное значение расшифрованных данных #3 0101 0101 0000 0011 - 03.12.2015 - публичный | |- URL видео: youtube.com/watch?v=AHtiPxfPSu4 |- Зашифрованные данные: [длинные, см. выше] |- Расшифрованные данные (HEX в ASCII): | |- Фраза "Hello world helen I жду" | |- Идентификатор другого видео: "m2AfQVy276Y" | |- Неизвестное значение фразы |- Расшифрованный идентификатор видео приводит нас к видео № 4. #4 0101 0101 0000 0100 - 03.12.2015 - нет в списке | |- URL видео: youtube.com/watch?v=m2AfQVy276Y |- Простые данные: [очень долго, см. выше] | |- Неизвестное значение данных №5 0101 0101 0000 0101 - 2015/19/03 - публичный | |- URL видео: youtube.com/watch?v=-qrtM4LdHH0 |- Зашифрованные данные: "A oYzXqoELKjE 14" | |- Неизвестный метод шифрования |- Неизвестное значение данных | ------ Тайна разгадана ------ | |- Ключ расшифровки: | |- Десятичные цифры числа Пи от 10-й до 20-й, на что указывают два шестнадцатеричных числа «А» и «14». | |- Расшифровано (шифр Гронсфельда): идентификатор видео "jQqQhlCICfY"
В ожидании других откровений
Я потратил кучу времени на это, но так и не смог определить следующее видео (если оно есть). Кстати, эта серия загадок мне кажется очень интересной и сложной!
Кстати, эта серия загадок мне кажется очень интересной и сложной!
Первая ветка 4chan об этом , к сожалению, заархивирована, но содержит много полезной информации о первых четырех видео. Еще одна тема была открыта 19 марта 2015 года относительно пятого видео, и она может быть полезна для поиска дополнительных скрытых подсказок.
Этот чат был создан для того, чтобы обсудить тему и обсудить некоторые идеи, чтобы найти следующее видео. Чат был заморожен за неактивность 24 мая 2015 года. Кстати, вы все еще можете читать существующие сообщения.
Обновления
- 20 марта 2015 г. - обновление №1: добавлена ссылка на вторую ветку 4chan о пятом видео; добавлен раздел "общие точки"; добавлено резюме прогресса, достигнутого до сих пор.
- 20 марта 2015 г. - обновление № 2: добавил цитату со страницы Википедии SS Sultana в четвертый раздел видео: похоже, это связано с этой тайной.

- 20 марта 2015 г. — обновление №3: добавлена ссылка на чат, созданный Бобсоном (спасибо!). Всем заинтересованным добро пожаловать!
- 24 марта 2015 г. - обновление №4: удалена вторая ветка 4chan.
- 13 апреля 2015 г. — обновление № 4: первая ветка 4chan была удалена.
- 22 октября 2015 г. — обновление № 5: чат заморожен из-за бездействия.
Примечания
Я оставлю этот пост активным и обновлю его, если будет какой-либо важный шаг вперед к разгадке тайны NOC+10.
Следующая часть тайны исследуется в этой теме: Тайна Нока +10, часть 2
шифр - Тайна НОК +10, часть 2
Это просто краткое изложение информации, которую мы получили о его последнем видео, список неудачных попыток и потенциально актуальных элементы для новых подходов.
Элементы, содержащиеся в видео:
- Название видео: 0101 0101 0000 0111
- Обычная вступительная музыка
- Сюита № 3 ре мажор Иоганна Себастьяна Баха, также известная как « Воздух на струне G "
- Строка " ISL 4$$$$3 xEFTvZ "
Анализ этих элементов:
Название видео, как обычно, двоичное число.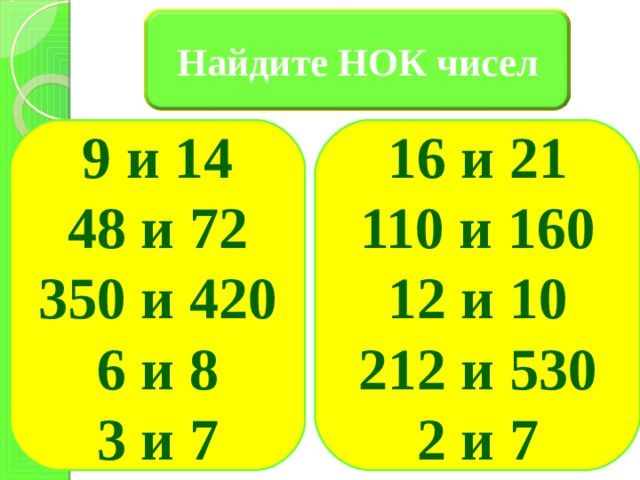 Номера заголовков всегда идут подряд, в данном случае 0101 0101 0000 0111, что означает 5507 в десятичном виде. Кажется, в названии нет намека.
Номера заголовков всегда идут подряд, в данном случае 0101 0101 0000 0111, что означает 5507 в десятичном виде. Кажется, в названии нет намека.
Кроме того, у нас есть типичная интро-музыка, в основном фирменная NOC. Здесь нет информации!
Затем слушаем "Сюиту №3 ре мажор". Что в нем может быть полезного? Ну, у нас есть цифра 3 и заглавная буква D, но эта информация кажется совершенно неуместной.
Настоящая информация, скорее всего, содержится во втором названии этой музыки, которое звучит как "Эфир на струне соль". Слова «Air» и «string» имеют одинаковую длину «ISL» и «xEFTvZ», что предполагает прямое соответствие между ними.
Кроме того, слово «Вкл.» может быть интерпретировано как «1» (ВКЛ.=1, ВЫКЛ.=0), так что теперь обе строки можно идеально выровнять. А как же "Г"? Написанная строчными буквами «g» визуально похожа на цифру «9», даже если это выглядит придирчиво.
Итак, у нас есть ядро головоломки, строка ISL 4 $ $ $ $ 3 xEFTvZ.
Наиболее примечательными особенностями этой строки являются наличие ровно 11 буквенно-цифровых символов, как и во всех идентификаторах видео на Youtube (идентификатор видео — это то, что мы на самом деле ожидаем найти), предложение «IS LEFT Z», образованное заглавными буквами. , безмолвное разделение между «4» и «3» (моя линейка показывает, что она состоит из 3 пробелов). Как было сказано ранее, эти слова очень хорошо сочетаются с названием музыки.
Кто-то также указал, что в музыке играется ровно 11 нот. Это может быть отличным намеком, если подтвердится!
, безмолвное разделение между «4» и «3» (моя линейка показывает, что она состоит из 3 пробелов). Как было сказано ранее, эти слова очень хорошо сочетаются с названием музыки.
Кто-то также указал, что в музыке играется ровно 11 нот. Это может быть отличным намеком, если подтвердится!
Возможные стратегии:
Почти очевидно, что мы имеем дело с шифром, как мы уже делали ранее. Шифр Цезаря был бы слишком тривиален, мы уже разгадывали такой шифр в предыдущем видео. Шифр
Виженера — главный кандидат на решение этой загадки, поскольку мы имеем дело с двумя строками одинаковой длины.
Должны ли мы добавлять или вычитать строки? Мы действительно не знаем, попробуйте оба!
Зашифрованный текст:
" ISL 4 $ $ $ $ 3 xEFTvZ "
Потенциально полезные ключи:
AIR 1 G STRING
AIR 1 9 STRING
AIR ? ? STRING где ? означает любую цифру/букву между 0-9/A-Z.
AIRAIRAIRAIRAIRAIRAIRAIRAIR
Кроме того, 11 заметок в видео могли бы быть ключом, если бы мы только могли найти их названия
Что, если ничего из этого не сработает?
Ну, нам определенно нужна новая идея! также, возможно, придется покопаться в его 3 предыдущих общедоступных видео в поисках дополнительных подсказок.

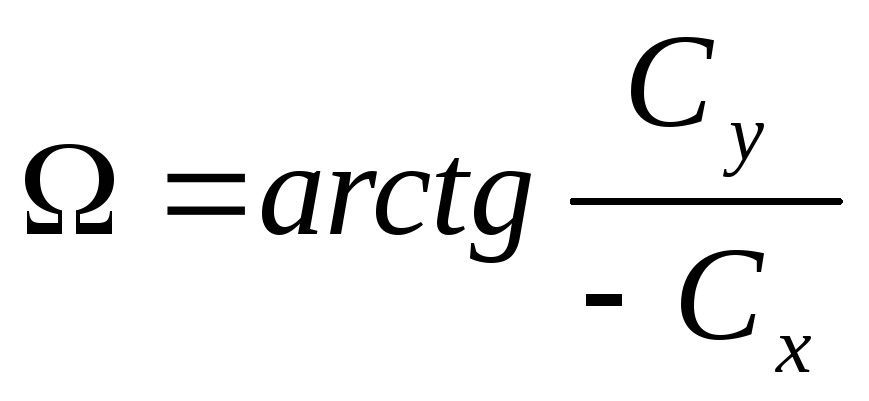

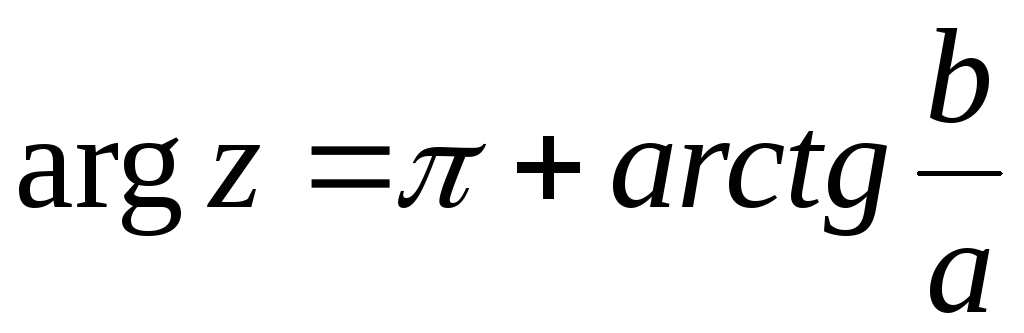 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.


 ..] Около 2 часов ночи 27 апреля 1865 года, когда «Султана» находилась всего в семи милях к северу от Мемфиса, ее котлы внезапно взорвались. Сначала взорвался один котел, а через долю секунды еще два. Причина взрыва Слишком большое давление и мало воды в котлах . Были основания полагать, что допустимое рабочее давление пара было превышено при попытке преодолеть весеннее течение реки. Мощный взрыв сбросил некоторых пассажиров на палубе в воду и разрушил большую часть лодки. [...]
..] Около 2 часов ночи 27 апреля 1865 года, когда «Султана» находилась всего в семи милях к северу от Мемфиса, ее котлы внезапно взорвались. Сначала взорвался один котел, а через долю секунды еще два. Причина взрыва Слишком большое давление и мало воды в котлах . Были основания полагать, что допустимое рабочее давление пара было превышено при попытке преодолеть весеннее течение реки. Мощный взрыв сбросил некоторых пассажиров на палубе в воду и разрушил большую часть лодки. [...] 12.2015 - публичный
|
|- URL видео: youtube.com/watch?v=AHtiPxfPSu4
|- Зашифрованные данные: [длинные, см. выше]
|- Расшифрованные данные (HEX в ASCII):
| |- Фраза "Hello world helen I жду"
| |- Идентификатор другого видео: "m2AfQVy276Y"
|
|- Неизвестное значение фразы
|- Расшифрованный идентификатор видео приводит нас к видео № 4.
#4 0101 0101 0000 0100 - 03.12.2015 - нет в списке
|
|- URL видео: youtube.com/watch?v=m2AfQVy276Y
|- Простые данные: [очень долго, см. выше]
|
|- Неизвестное значение данных
№5 0101 0101 0000 0101 - 2015/19/03 - публичный
|
|- URL видео: youtube.com/watch?v=-qrtM4LdHH0
|- Зашифрованные данные: "A oYzXqoELKjE 14"
|
|- Неизвестный метод шифрования
|- Неизвестное значение данных
|
------ Тайна разгадана ------
|
|- Ключ расшифровки:
| |- Десятичные цифры числа Пи от 10-й до 20-й, на что указывают два шестнадцатеричных числа «А» и «14».
|
|- Расшифровано (шифр Гронсфельда): идентификатор видео "jQqQhlCICfY"
12.2015 - публичный
|
|- URL видео: youtube.com/watch?v=AHtiPxfPSu4
|- Зашифрованные данные: [длинные, см. выше]
|- Расшифрованные данные (HEX в ASCII):
| |- Фраза "Hello world helen I жду"
| |- Идентификатор другого видео: "m2AfQVy276Y"
|
|- Неизвестное значение фразы
|- Расшифрованный идентификатор видео приводит нас к видео № 4.
#4 0101 0101 0000 0100 - 03.12.2015 - нет в списке
|
|- URL видео: youtube.com/watch?v=m2AfQVy276Y
|- Простые данные: [очень долго, см. выше]
|
|- Неизвестное значение данных
№5 0101 0101 0000 0101 - 2015/19/03 - публичный
|
|- URL видео: youtube.com/watch?v=-qrtM4LdHH0
|- Зашифрованные данные: "A oYzXqoELKjE 14"
|
|- Неизвестный метод шифрования
|- Неизвестное значение данных
|
------ Тайна разгадана ------
|
|- Ключ расшифровки:
| |- Десятичные цифры числа Пи от 10-й до 20-й, на что указывают два шестнадцатеричных числа «А» и «14».
|
|- Расшифровано (шифр Гронсфельда): идентификатор видео "jQqQhlCICfY"



 Перевод градусов в радианы и обратно, формулы, примеры
Перевод градусов в радианы и обратно, формулы, примеры С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.
С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.
 Для каждой из указанных функций
существует обратная
тригонометрическая функция.
Для каждой из указанных функций
существует обратная
тригонометрическая функция. Поэтому, приведенные
выше определения тригонометрических
функций в приложении к прямоугольному
треугольнику формулируются таким
образом: Синусом угла α называется отношение противолежащего
катета к гипотенузе. Косинусом угла α называется отношение прилежащего
катета к гипотенузе. Тангенсом угла α называется противолежащего катета
к прилежащему. Котангенсом угла α называется прилежащего катета к
противолежащему.
Поэтому, приведенные
выше определения тригонометрических
функций в приложении к прямоугольному
треугольнику формулируются таким
образом: Синусом угла α называется отношение противолежащего
катета к гипотенузе. Косинусом угла α называется отношение прилежащего
катета к гипотенузе. Тангенсом угла α называется противолежащего катета
к прилежащему. Котангенсом угла α называется прилежащего катета к
противолежащему. единицах Конвертер магнитодвижущей силы Конвертер напряженности магнитного поля Конвертер магнитного потока Конвертер магнитной индукции Радиация. Конвертер мощности поглощенной дозы ионизирующего излучения Радиоактивность. Конвертер радиоактивного распада Радиация. Конвертер экспозиционной дозы Радиация. Конвертер поглощённой дозы Конвертер десятичных приставок Передача данных Конвертер единиц типографики и обработки изображений Конвертер единиц измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева
единицах Конвертер магнитодвижущей силы Конвертер напряженности магнитного поля Конвертер магнитного потока Конвертер магнитной индукции Радиация. Конвертер мощности поглощенной дозы ионизирующего излучения Радиоактивность. Конвертер радиоактивного распада Радиация. Конвертер экспозиционной дозы Радиация. Конвертер поглощённой дозы Конвертер десятичных приставок Передача данных Конвертер единиц типографики и обработки изображений Конвертер единиц измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева Лучи называются сторонами угла. У углов много интересных свойств, например, сумма всех углов в параллелограмме — 360°, а в треугольнике — 180°.
Лучи называются сторонами угла. У углов много интересных свойств, например, сумма всех углов в параллелограмме — 360°, а в треугольнике — 180°. Они равны.
Они равны.
 В Марокко существует похожий геометрический стиль мозаики, зулляйдж или зилидж. Форма терракотовых изразцов, из которых складывают эту мозаику, не соблюдается так строго, как в гирихе, и изразцы часто более причудливой формы, чем строгие геометрические фигуры в гирихе. Несмотря на это, мастера зулляйджа также используют углы для создания контрастных и причудливых узоров.
В Марокко существует похожий геометрический стиль мозаики, зулляйдж или зилидж. Форма терракотовых изразцов, из которых складывают эту мозаику, не соблюдается так строго, как в гирихе, и изразцы часто более причудливой формы, чем строгие геометрические фигуры в гирихе. Несмотря на это, мастера зулляйджа также используют углы для создания контрастных и причудливых узоров. Эти башни находятся в Куала-Лумпуре в Малайзии и в их проектировании участвовал премьер-министр страны.
Эти башни находятся в Куала-Лумпуре в Малайзии и в их проектировании участвовал премьер-министр страны.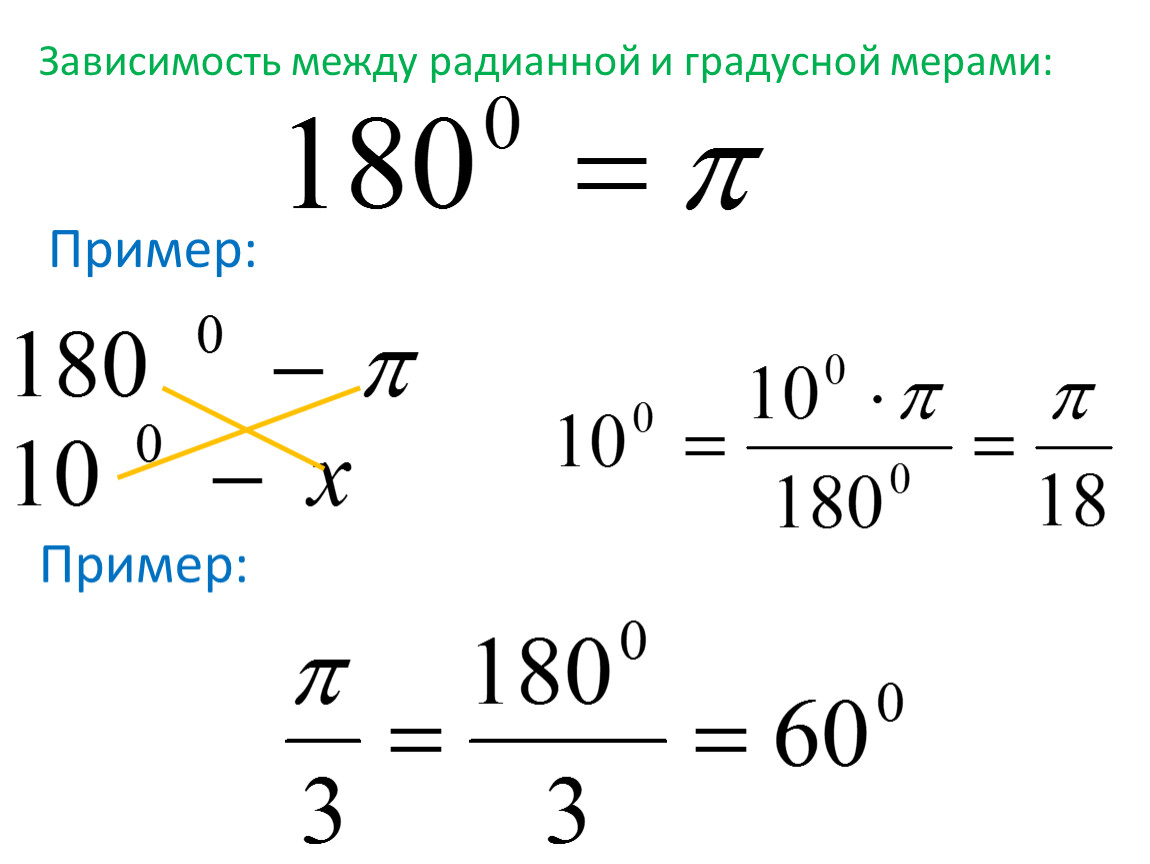 Один из примеров наклонных зданий — Тадж-Махал в Индии. Четыре минарета, которые окружают главное строение, построены с наклоном от центра, чтобы в случае землетрясения они упали не вовнутрь, на мавзолей, а в другую сторону, и не повредили основное здание. Иногда здания строят под углом к земле в декоративных целях. Например, Падающая башня Абу-Даби или Capital Gate наклонена на 18° к западу. А одно из зданий в Мире Головоломок Стюарта Лэндсборо в городе Ванка в Новой Зеландии наклоняется к земле на 53°. Это здание так и называется, «Падающая башня».
Один из примеров наклонных зданий — Тадж-Махал в Индии. Четыре минарета, которые окружают главное строение, построены с наклоном от центра, чтобы в случае землетрясения они упали не вовнутрь, на мавзолей, а в другую сторону, и не повредили основное здание. Иногда здания строят под углом к земле в декоративных целях. Например, Падающая башня Абу-Даби или Capital Gate наклонена на 18° к западу. А одно из зданий в Мире Головоломок Стюарта Лэндсборо в городе Ванка в Новой Зеландии наклоняется к земле на 53°. Это здание так и называется, «Падающая башня». 5°до 4°. Башня церкви СуурХусен в Германии тоже наклонена из-за того, что ее деревянный фундамент прогнил с одной стороны после осушения болотистой почвы, на которой она построена. На данный момент эта башня наклонена больше, чем Пизанская — примерно на 5°.
5°до 4°. Башня церкви СуурХусен в Германии тоже наклонена из-за того, что ее деревянный фундамент прогнил с одной стороны после осушения болотистой почвы, на которой она построена. На данный момент эта башня наклонена больше, чем Пизанская — примерно на 5°. ..
.. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее… Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона?
Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее… Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона? Никогда.
Никогда. Но…
Но… На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°.
На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°. В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает.
В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает. Получаем, что один градус равен:
Получаем, что один градус равен: Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…
Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…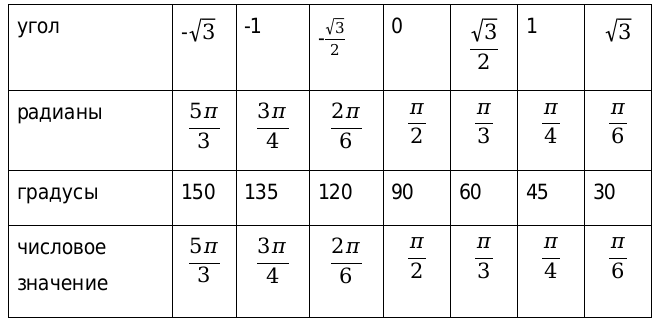 Смотрим, какие синусы у этих углов. Короче, всё, как в конце темы про тригонометрический круг расписано. На круге (даже самом кривом!) будет чётко видно, что sin60° существенно больше, чем sin1,05° .
Смотрим, какие синусы у этих углов. Короче, всё, как в конце темы про тригонометрический круг расписано. На круге (даже самом кривом!) будет чётко видно, что sin60° существенно больше, чем sin1,05° . А то некоторые этот угол никак на круге найти не могут… И, соответственно, в тригонометрических функциях нуля путаются… Другое дело, что положение подвижной стороны в нуле градусов совпадает с положением в 360°, так совпадения на круге — сплошь и рядом.
А то некоторые этот угол никак на круге найти не могут… И, соответственно, в тригонометрических функциях нуля путаются… Другое дело, что положение подвижной стороны в нуле градусов совпадает с положением в 360°, так совпадения на круге — сплошь и рядом. ) Но перевод углов — это первый шаг к постижению тригонометрии. Там же ещё с синусами-косинусами работать надо. Да и с тангенсами, котангенсами тоже…
) Но перевод углов — это первый шаг к постижению тригонометрии. Там же ещё с синусами-косинусами работать надо. Да и с тангенсами, котангенсами тоже… ..)
..) ..
..  Градус = рад*57,295779513082
Градус = рад*57,295779513082  Радианы — это единица измерения угла, а градусы — это единица измерения угла. Поэтому знание того, как сделать преобразование между ними, является важным навыком для любого изучающего математику и геометрию. Давайте посмотрим, что такое радианы и градусы и как их можно преобразовать друг в друга.
Радианы — это единица измерения угла, а градусы — это единица измерения угла. Поэтому знание того, как сделать преобразование между ними, является важным навыком для любого изучающего математику и геометрию. Давайте посмотрим, что такое радианы и градусы и как их можно преобразовать друг в друга. Эта формула берет наше уравнение длины дуги выше и решает его для градусов вместо длины; таким образом, позволяя нам легко конвертировать из радианов в градусы. Просто подставив наши известные значения в это уравнение, мы можем легко выполнять преобразования между этими двумя единицами измерения. Например, если бы мы хотели узнать, сколько градусов эквивалентно 3π/4 радианам, то мы подставили бы 3π/4 в наше уравнение следующим образом: Измерение градусов = 3π/4 x (180/π) = 135°. Следовательно, Меры 3π/4 радиана были бы эквивалентны измерениям градусов 135 °.
Эта формула берет наше уравнение длины дуги выше и решает его для градусов вместо длины; таким образом, позволяя нам легко конвертировать из радианов в градусы. Просто подставив наши известные значения в это уравнение, мы можем легко выполнять преобразования между этими двумя единицами измерения. Например, если бы мы хотели узнать, сколько градусов эквивалентно 3π/4 радианам, то мы подставили бы 3π/4 в наше уравнение следующим образом: Измерение градусов = 3π/4 x (180/π) = 135°. Следовательно, Меры 3π/4 радиана были бы эквивалентны измерениям градусов 135 °.

 Также квадратом числа называется результат его возведение в степень 2 (во вторую степень)
Также квадратом числа называется результат его возведение в степень 2 (во вторую степень) Например, 5 — это квадратный корень из 25, потому что 5 2 = 5•5 = 25, -5 — это квадратный корень из 25, потому что (-5) 2 = (-5)•(-5) = 25. При написании математических выражений люди часто используют sqrt(x) для обозначения квадратного корня из x. Подробнее о квадратном корне читайте здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
Например, 5 — это квадратный корень из 25, потому что 5 2 = 5•5 = 25, -5 — это квадратный корень из 25, потому что (-5) 2 = (-5)•(-5) = 25. При написании математических выражений люди часто используют sqrt(x) для обозначения квадратного корня из x. Подробнее о квадратном корне читайте здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram 828
828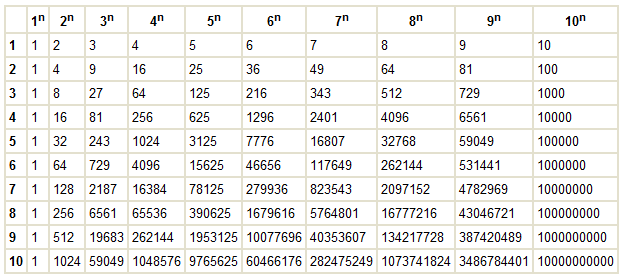 385
385 000
000 185
185 487
487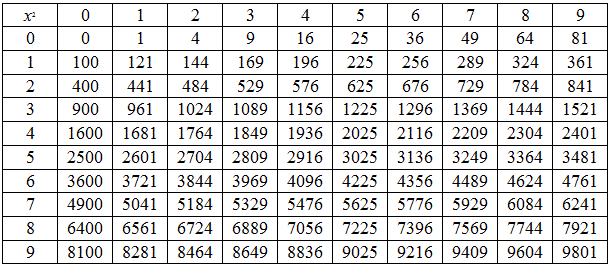 См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя. 000
000 899
899 141
141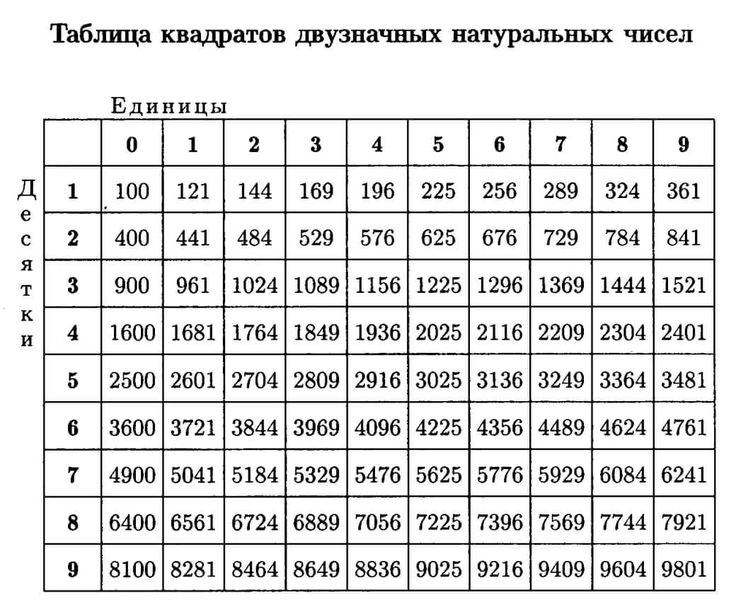
 Одним из преимуществ исключения Гаусса является то, что его можно легко реализовать в компьютерных алгоритмах, что делает его полезным для решения крупномасштабных систем уравнений в различных областях. В целом, исключение Гаусса — это мощный метод решения систем линейных уравнений, который имеет широкий спектр приложений в математике и других областях.
Одним из преимуществ исключения Гаусса является то, что его можно легко реализовать в компьютерных алгоритмах, что делает его полезным для решения крупномасштабных систем уравнений в различных областях. В целом, исключение Гаусса — это мощный метод решения систем линейных уравнений, который имеет широкий спектр приложений в математике и других областях.
 Это особенно полезно в инженерных и научных приложениях, где линейные уравнения используются для моделирования физических систем.
Это особенно полезно в инженерных и научных приложениях, где линейные уравнения используются для моделирования физических систем.
 Wolfram|Alpha способна решать самые разные системы уравнений.
Wolfram|Alpha способна решать самые разные системы уравнений.

 Нулевой уклон означает горизонтальную поверхность. Уклон в 100% означает подъём на 1 метр на каждый метр расстояния, т.е. угол наклона 45 градусов. Вертикальная линия имеет бесконечное значение уклона.
Нулевой уклон означает горизонтальную поверхность. Уклон в 100% означает подъём на 1 метр на каждый метр расстояния, т.е. угол наклона 45 градусов. Вертикальная линия имеет бесконечное значение уклона. Com понравилось. Приходите снова!
Com понравилось. Приходите снова!
 Физический смысл уклона — отношение перепада высот к длине участка, на котором это наблюдается. По сути — тангенс угла: превышение 12 метров на отрезке дороги в сто метров выражается величиной 0,12 (тангенс) = 12% = 120 ‰. То есть чтобы сделать расчёт уклона в промилле, надо умножить процентный показатель на десять.
Физический смысл уклона — отношение перепада высот к длине участка, на котором это наблюдается. По сути — тангенс угла: превышение 12 метров на отрезке дороги в сто метров выражается величиной 0,12 (тангенс) = 12% = 120 ‰. То есть чтобы сделать расчёт уклона в промилле, надо умножить процентный показатель на десять.
 Как посчитать уклон в процентах — определено выше: высоту конька делят на половину ширины чердачного перекрытия, если скаты равной величины. Или на проекцию каждой из поверхностей кровли, когда размеры сторон различаются. Можно заметить, что это и есть тангенс уже определённого в градусах угла. Чтобы перейти к процентному выражению уклона, надо выполнить действие: значение tg *100, и результат получится в процентах.
Как посчитать уклон в процентах — определено выше: высоту конька делят на половину ширины чердачного перекрытия, если скаты равной величины. Или на проекцию каждой из поверхностей кровли, когда размеры сторон различаются. Можно заметить, что это и есть тангенс уже определённого в градусах угла. Чтобы перейти к процентному выражению уклона, надо выполнить действие: значение tg *100, и результат получится в процентах.
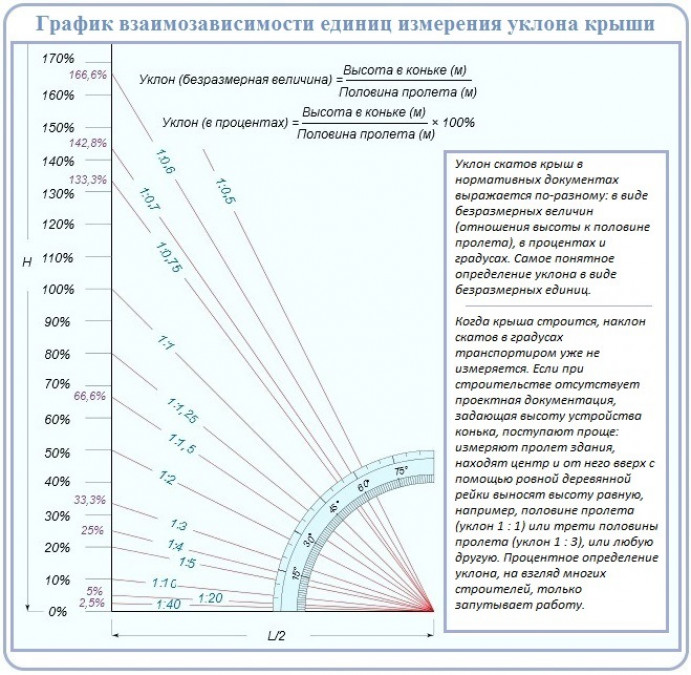 При необходимости вычислить точные показатели, пользуются современными измерительными приборами.
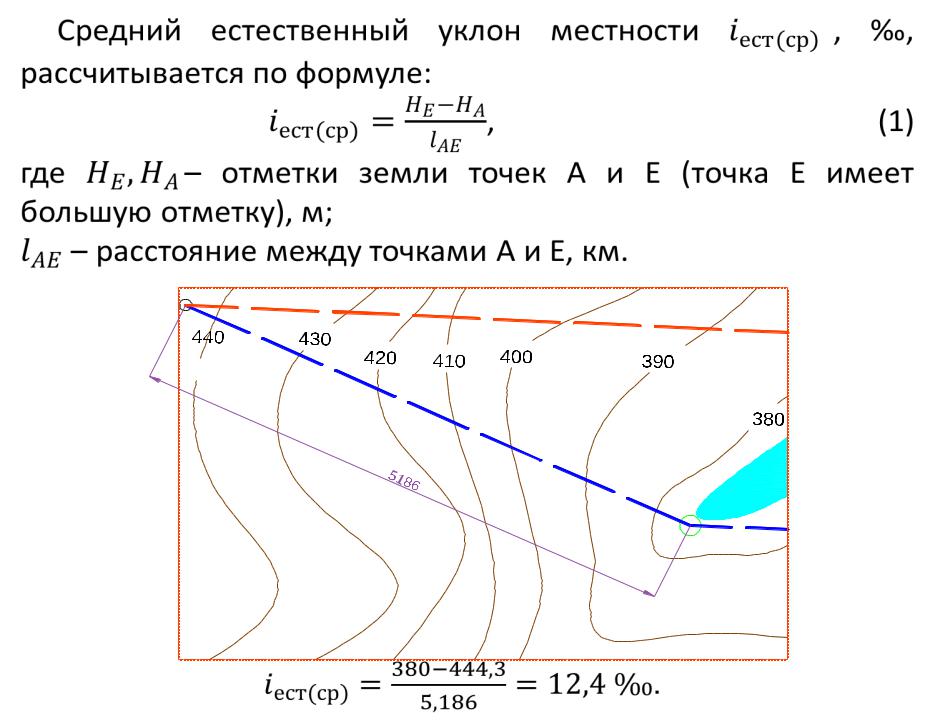
При необходимости вычислить точные показатели, пользуются современными измерительными приборами.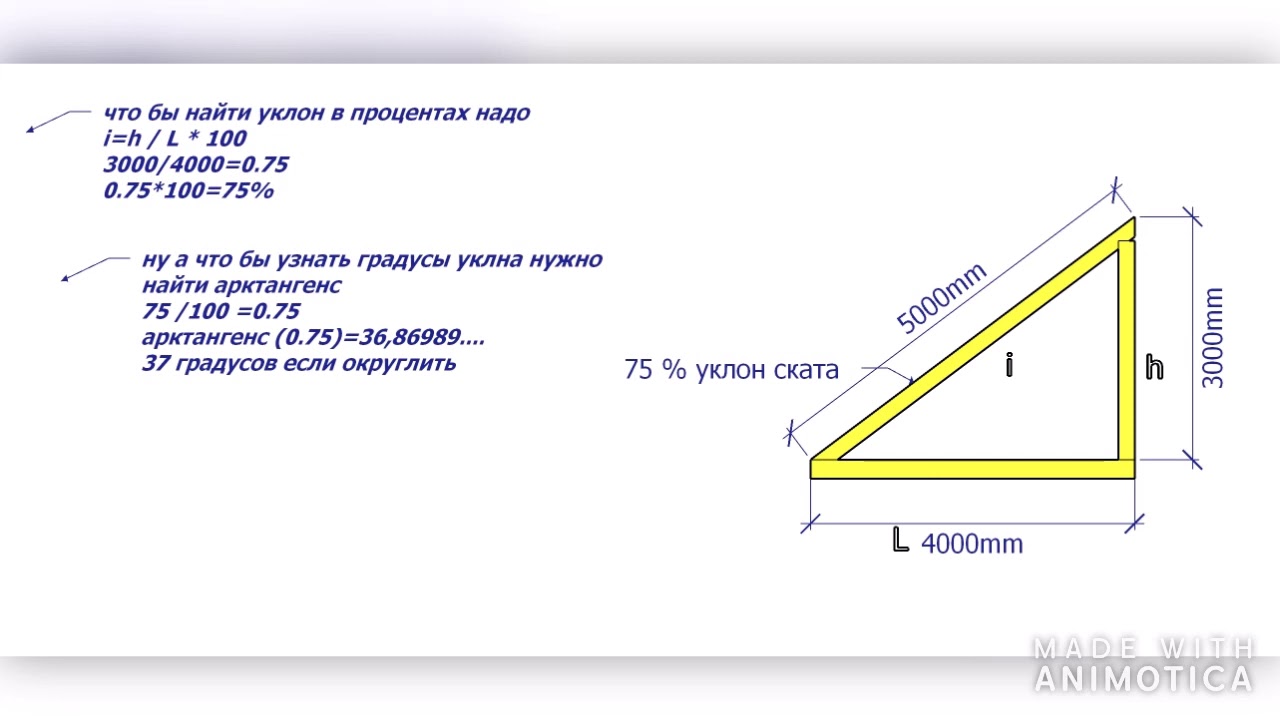 Он также включает приведенные ниже таблицы преобразования.
Он также включает приведенные ниже таблицы преобразования. 087
087 4996
4996

 Как уже упоминалось, многие люди здесь со своими аквариумами с растениями работают рядом с КН на благо растений, поэтому практически нет необходимости тестировать его, пока ситуация с баком понятна и исходная вода проверена. Рифовые аквариумы SW и аквариумы с цихлидами — это отдельная история, конечно, поддержание высокого KH потребует больше усилий, чем поддержание нуля.
Как уже упоминалось, многие люди здесь со своими аквариумами с растениями работают рядом с КН на благо растений, поэтому практически нет необходимости тестировать его, пока ситуация с баком понятна и исходная вода проверена. Рифовые аквариумы SW и аквариумы с цихлидами — это отдельная история, конечно, поддержание высокого KH потребует больше усилий, чем поддержание нуля. .. удачное время!
.. удачное время! Так что я акклиматизирую всех FW-животных, которые, как я сомневаюсь, резко приспособятся к низким параметрам моего аквариума. В любом случае, я хочу сказать, что твердость может очень сильно варьироваться от растения к растению, даже в местных городах/пригородах. Если вы находитесь в пригороде, таком как мой, где есть очистные сооружения с севера, юга, востока и запада, убедитесь, что вы читаете правильный отчет для своего района.
Так что я акклиматизирую всех FW-животных, которые, как я сомневаюсь, резко приспособятся к низким параметрам моего аквариума. В любом случае, я хочу сказать, что твердость может очень сильно варьироваться от растения к растению, даже в местных городах/пригородах. Если вы находитесь в пригороде, таком как мой, где есть очистные сооружения с севера, юга, востока и запада, убедитесь, что вы читаете правильный отчет для своего района.
 Я использую только набор для тестирования Freshwater Master Test Kit от API (пока). Моя флора и фауна такие же, как в моей подписи, за исключением того, что пока я построил свои Кадиналы только до 9. Все довольны и хорошо растут.
Я использую только набор для тестирования Freshwater Master Test Kit от API (пока). Моя флора и фауна такие же, как в моей подписи, за исключением того, что пока я построил свои Кадиналы только до 9. Все довольны и хорошо растут. Теперь я даже никогда не проверяю воду. Я думаю, неоднократно демонстрировалось, что почти вся рыба, которую мы можем купить, может быть легко акклиматизирована к любым параметрам нашей местной водопроводной воды. Конечно, есть места с очень плохой водой, но большинству из нас повезло больше.
Теперь я даже никогда не проверяю воду. Я думаю, неоднократно демонстрировалось, что почти вся рыба, которую мы можем купить, может быть легко акклиматизирована к любым параметрам нашей местной водопроводной воды. Конечно, есть места с очень плохой водой, но большинству из нас повезло больше.
 Рыба прекрасно адаптируется к любому постоянному уровню pH. Стабильный pH совпадает с стабильным KH, что, в свою очередь, означает стабильный GH, а стабильная общая жесткость означает, что клеточные стенки вашей рыбы не взрываются во время осмотического шока. Возможно, теперь вы понимаете, почему в последнее время я не тестирую ничего, кроме гормона роста. Я могу позвонить маме и попросить ее папу написать мне, какого цвета небо, или я могу просто посмотреть в окно. Скорее всего, рыба, которую вы получите, будет куплена/отправлена в воде, которая не соответствует ее естественной среде обитания, это то, что есть в магазине у заводчика/дистрибьютора/продавца, что также означает, что параметры могут постоянно меняться, когда рыба переходит из рук в руки. Большинство этих рыб, которых мы держим, по-прежнему используются в качестве хобби из-за их прекрасной способности адаптироваться к стрессу перемен.
Рыба прекрасно адаптируется к любому постоянному уровню pH. Стабильный pH совпадает с стабильным KH, что, в свою очередь, означает стабильный GH, а стабильная общая жесткость означает, что клеточные стенки вашей рыбы не взрываются во время осмотического шока. Возможно, теперь вы понимаете, почему в последнее время я не тестирую ничего, кроме гормона роста. Я могу позвонить маме и попросить ее папу написать мне, какого цвета небо, или я могу просто посмотреть в окно. Скорее всего, рыба, которую вы получите, будет куплена/отправлена в воде, которая не соответствует ее естественной среде обитания, это то, что есть в магазине у заводчика/дистрибьютора/продавца, что также означает, что параметры могут постоянно меняться, когда рыба переходит из рук в руки. Большинство этих рыб, которых мы держим, по-прежнему используются в качестве хобби из-за их прекрасной способности адаптироваться к стрессу перемен. aquahobby.com/articles/e_adjusting_pH.php
aquahobby.com/articles/e_adjusting_pH.php
 Действия в скобках
Действия в скобках Онлайн калькулятор расстояния между точками
Онлайн калькулятор расстояния между точками Найди правильный ответ.
Найди правильный ответ.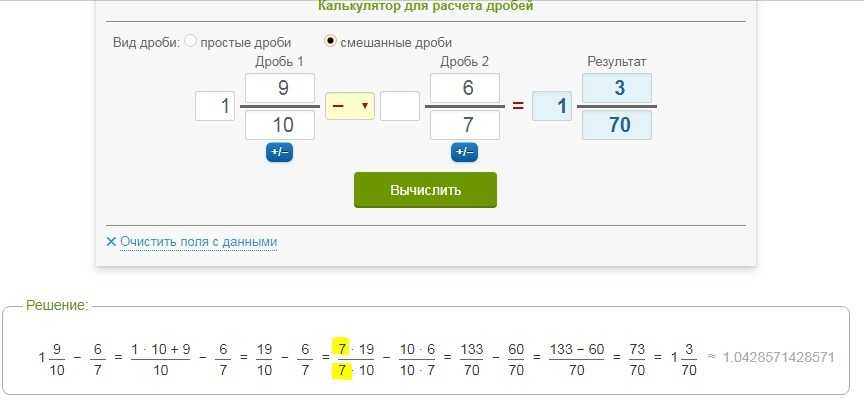 Калькулятор вычисления силы, массы и ускорения.
Калькулятор вычисления силы, массы и ускорения.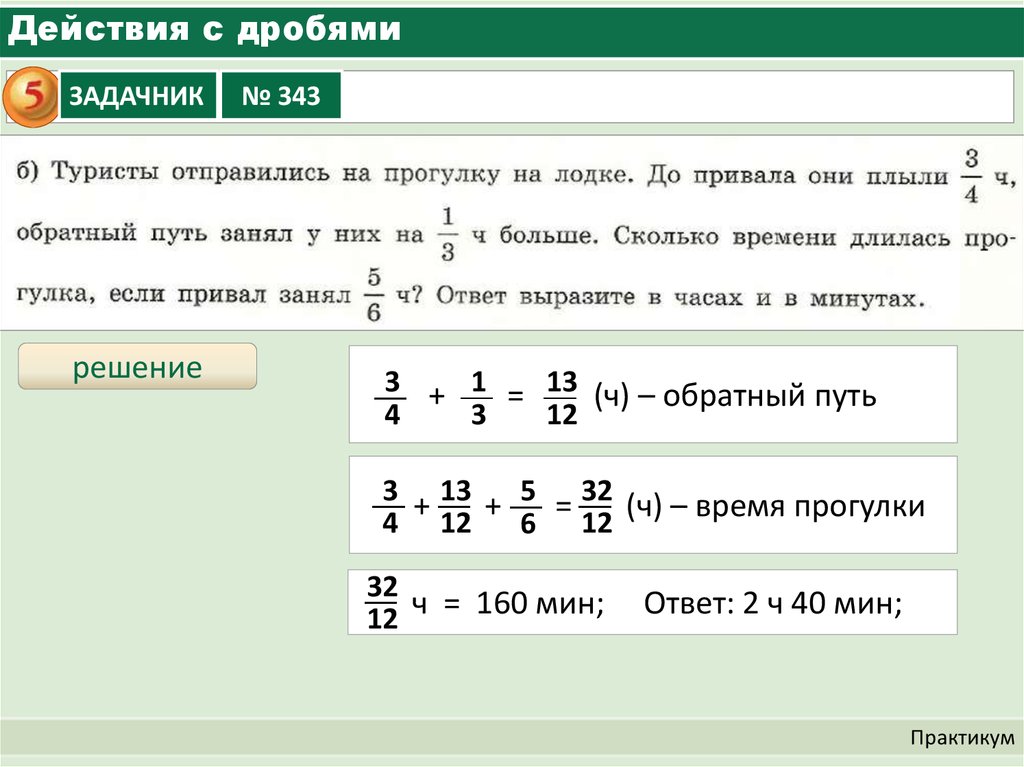 Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов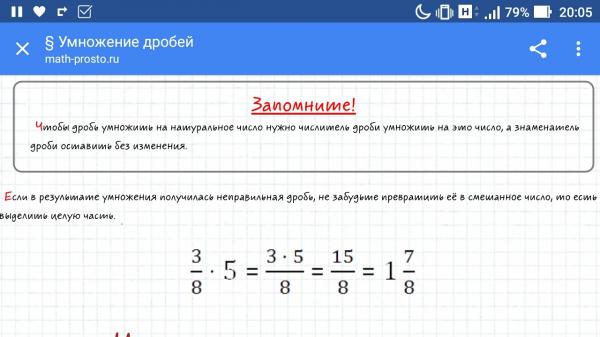
 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Какая часть носков Макса коричневого или черного цвета?
Какая часть носков Макса коричневого или черного цвета?
 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
 Начнём с —2у, это попроще будет.
Начнём с —2у, это попроще будет.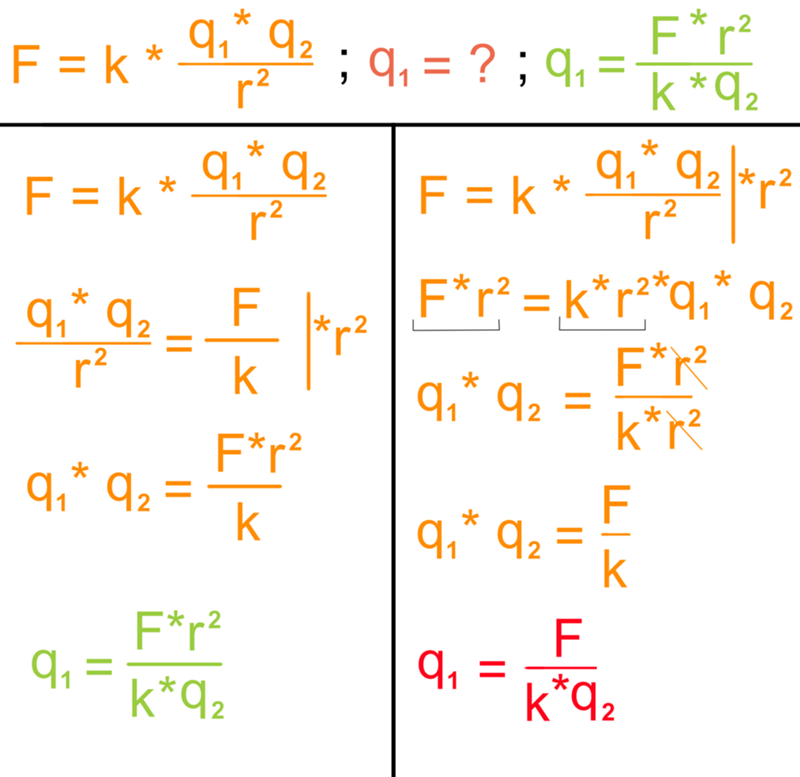 Самое главное — не порядок применения тождественных преобразований, а их правильность!
Самое главное — не порядок применения тождественных преобразований, а их правильность!
 Осталось переписать равенство в привычном виде, слева направо и — ответ готов:
Осталось переписать равенство в привычном виде, слева направо и — ответ готов: Вот этим и займёмся. Смотрим на формулу:
Вот этим и займёмся. Смотрим на формулу: )
)

 Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с-1, а центростремительное ускорение равно 289 м/с2.
Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 8,5 с-1, а центростремительное ускорение равно 289 м/с2. ..
.. е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):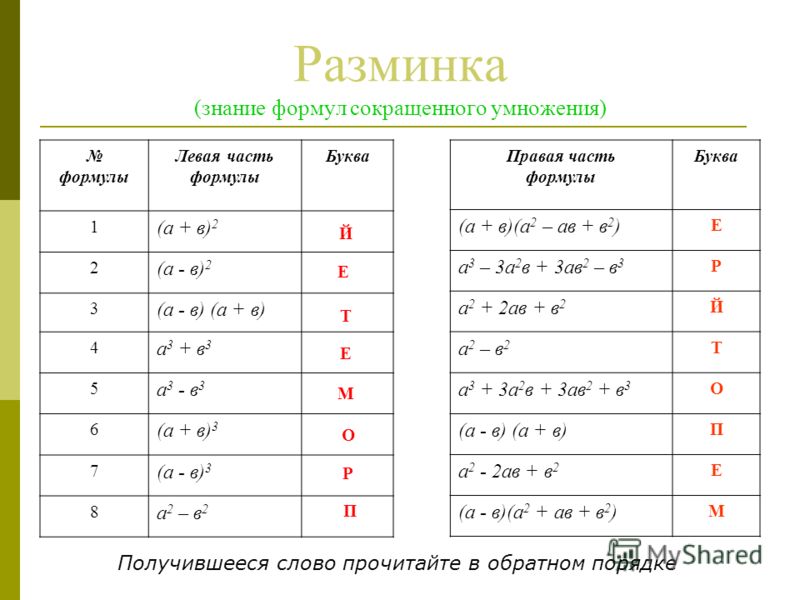 ..
.. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:
Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется: Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот): Закон Бойля-Мариотта:
Закон Бойля-Мариотта: При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При парообразовании поглощается, а при конденсации выделяется количество теплоты равное: Изохорный процесс (V = const):
Изохорный процесс (V = const): В этом случае высота столба жидкости в капилляре станет равной:
В этом случае высота столба жидкости в капилляре станет равной: е. определение электрического напряжения может быть задано формулой:
е. определение электрического напряжения может быть задано формулой: ..
.. Он может быть рассчитан по формуле:
Он может быть рассчитан по формуле: ..
.. Действующее значение силы тока:
Действующее значение силы тока: ч. света) в среде и в вакууме также связаны между собой формулой:
ч. света) в среде и в вакууме также связаны между собой формулой: ..
.. ..
.. ..
..



 (Опыт работы с VBA не требуется.)
(Опыт работы с VBA не требуется.) ..
.. (Опыт работы с VBA не требуется.)
(Опыт работы с VBA не требуется.) Значения ASCII заглавных букв английского алфавита от 65 (A) до 9.0 (З). Итак, чтобы получить код заглавной буквы A, вы добавляете 1 к 64; чтобы получить код символа верхнего регистра B, вы добавляете 2 к 64 и так далее.
Значения ASCII заглавных букв английского алфавита от 65 (A) до 9.0 (З). Итак, чтобы получить код заглавной буквы A, вы добавляете 1 к 64; чтобы получить код символа верхнего регистра B, вы добавляете 2 к 64 и так далее. 
 Затем функция Split разбивает возвращаемую строку на отдельные элементы, используя знак $ в качестве разделителя, и мы возвращаем элемент (1), который является буквой столбца.
Затем функция Split разбивает возвращаемую строку на отдельные элементы, используя знак $ в качестве разделителя, и мы возвращаем элемент (1), который является буквой столбца. Полная формула примет следующий вид:
Полная формула примет следующий вид:
 В нашем случае ячейки данных находятся в строках с 3 по 8, поэтому мы используем следующую формулу:
В нашем случае ячейки данных находятся в строках с 3 по 8, поэтому мы используем следующую формулу:
 , постоянно совершенствуется и изменяется. До 1 января 1999 г. общие принципы построения налоговой системы были установлены Законом Российской Федерации от 27 декабря 1991 г. №2118-1 «Об основах налоговой системы в Российской Федерации». Порядок исчисления и уплаты различных налогов определялся множеством законов и нормативных актов. Для этого периода характерны частые изменения в области налогообложения. С 1 января 1999 г. действует часть первая Налогового кодекса Российской Федерации (НК РФ), которая позволила решить многие назревшие к тому времени налоговые проблемы и значительно повысила защищенность добросовестных налогоплательщиков. Этим документом регулируются отношения между государством и его гражданами по вопросам взимания налогов и сборов. Частью первой НК РФ установлены система налогов, взимаемых на территории Российской Федерации, права и обязанности налогоплательщиков и налоговых органов, формы и методы контроля и ответственность за совершение налоговых правонарушений. В данном сборнике задач названным вопросам посвящены главы 1, 2 и 8.
, постоянно совершенствуется и изменяется. До 1 января 1999 г. общие принципы построения налоговой системы были установлены Законом Российской Федерации от 27 декабря 1991 г. №2118-1 «Об основах налоговой системы в Российской Федерации». Порядок исчисления и уплаты различных налогов определялся множеством законов и нормативных актов. Для этого периода характерны частые изменения в области налогообложения. С 1 января 1999 г. действует часть первая Налогового кодекса Российской Федерации (НК РФ), которая позволила решить многие назревшие к тому времени налоговые проблемы и значительно повысила защищенность добросовестных налогоплательщиков. Этим документом регулируются отношения между государством и его гражданами по вопросам взимания налогов и сборов. Частью первой НК РФ установлены система налогов, взимаемых на территории Российской Федерации, права и обязанности налогоплательщиков и налоговых органов, формы и методы контроля и ответственность за совершение налоговых правонарушений. В данном сборнике задач названным вопросам посвящены главы 1, 2 и 8.
 Кроме того, тесты составлены так, чтобы при поиске правильного ответа возникало меньше затруднений при работе с НК РФ и другими законодательными и нормативными актами.
Кроме того, тесты составлены так, чтобы при поиске правильного ответа возникало меньше затруднений при работе с НК РФ и другими законодательными и нормативными актами. Представлены тесты и задачи различной степени сложности, что позволяет применять их для проверки знаний в зависимости от глубины изучения предмета.
Представлены тесты и задачи различной степени сложности, что позволяет применять их для проверки знаний в зависимости от глубины изучения предмета. Налоговый контроль
Налоговый контроль Г. — Учебник
Г. — Учебник Анализ, представленный в этом отчете, был подготовлен до вспышки COVID-19.пандемии и вызванного ею экономического кризиса.
Анализ, представленный в этом отчете, был подготовлен до вспышки COVID-19.пандемии и вызванного ею экономического кризиса.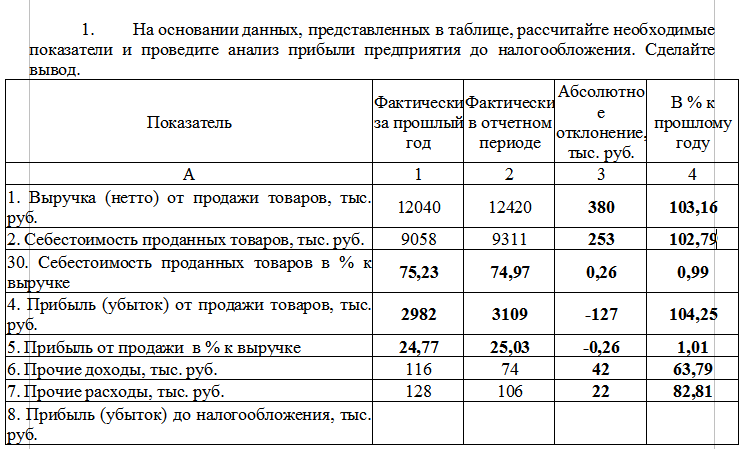 Эта реформа требует принятия мер по усилению функционирования налоговой администрации, включая введение налоговой декларации по итогам года.
Эта реформа требует принятия мер по усилению функционирования налоговой администрации, включая введение налоговой декларации по итогам года.


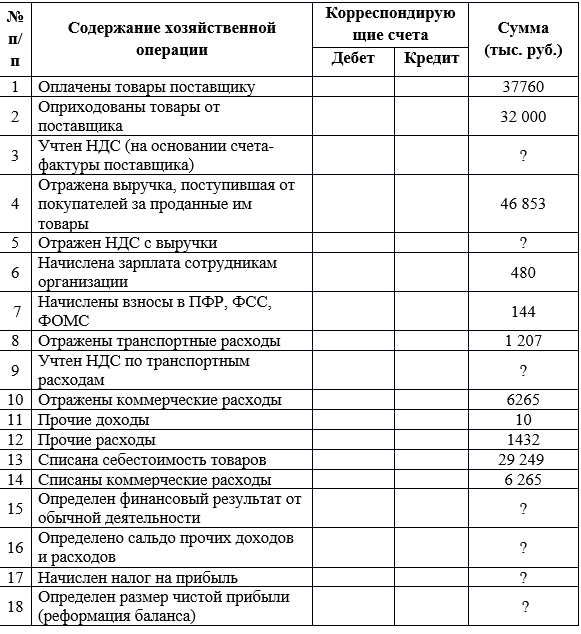


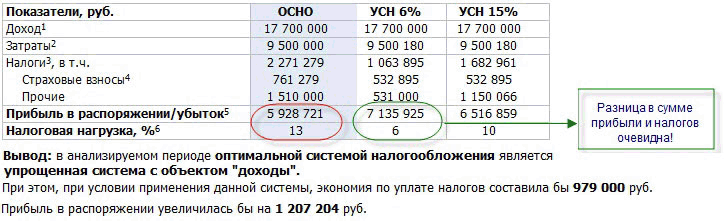 – 21,5%;
– 21,5%;

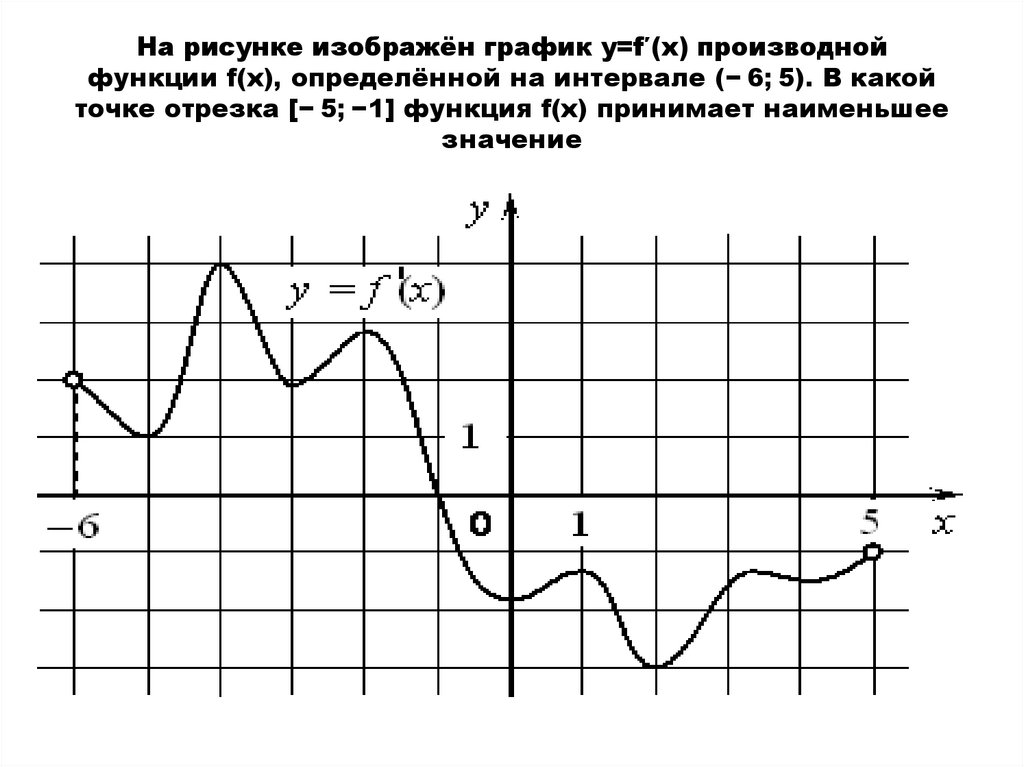
 Таким образом, значение производной отрицательно во всех точках нашего графика.
Для убывающей функции выполняет следующее неравенство: f'(x) ≤ 0, для любой точки x.
Таким образом, значение производной отрицательно во всех точках нашего графика.
Для убывающей функции выполняет следующее неравенство: f'(x) ≤ 0, для любой точки x.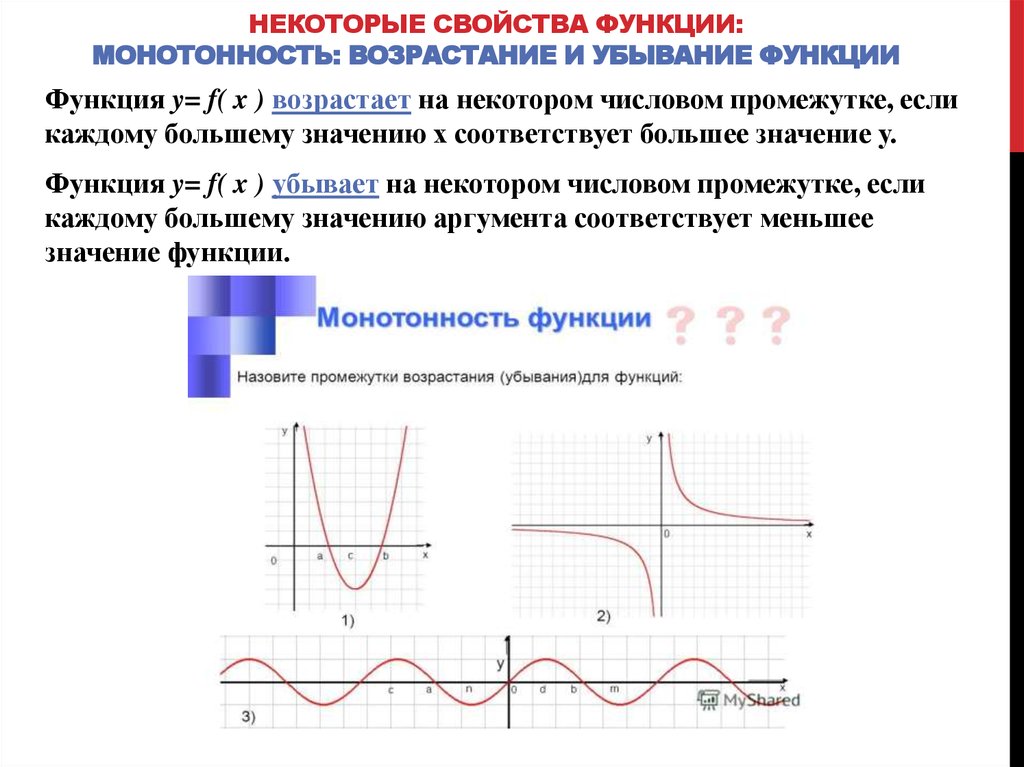

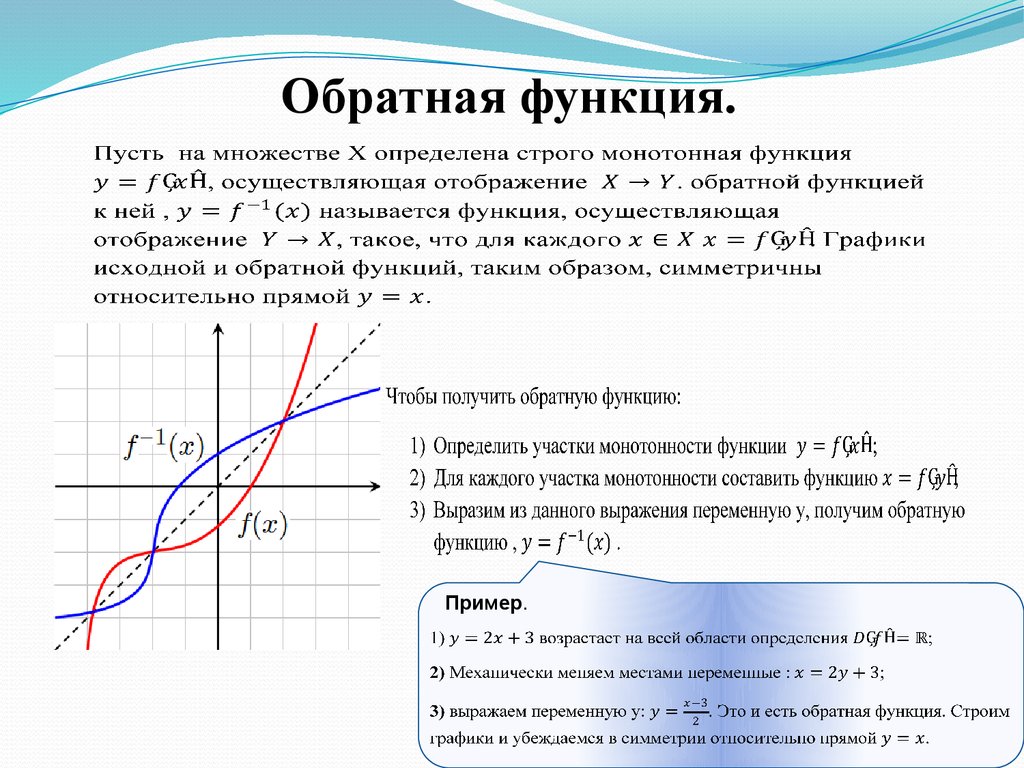
 {3}$ возрастает на всей действительной оси.
{3}$ возрастает на всей действительной оси.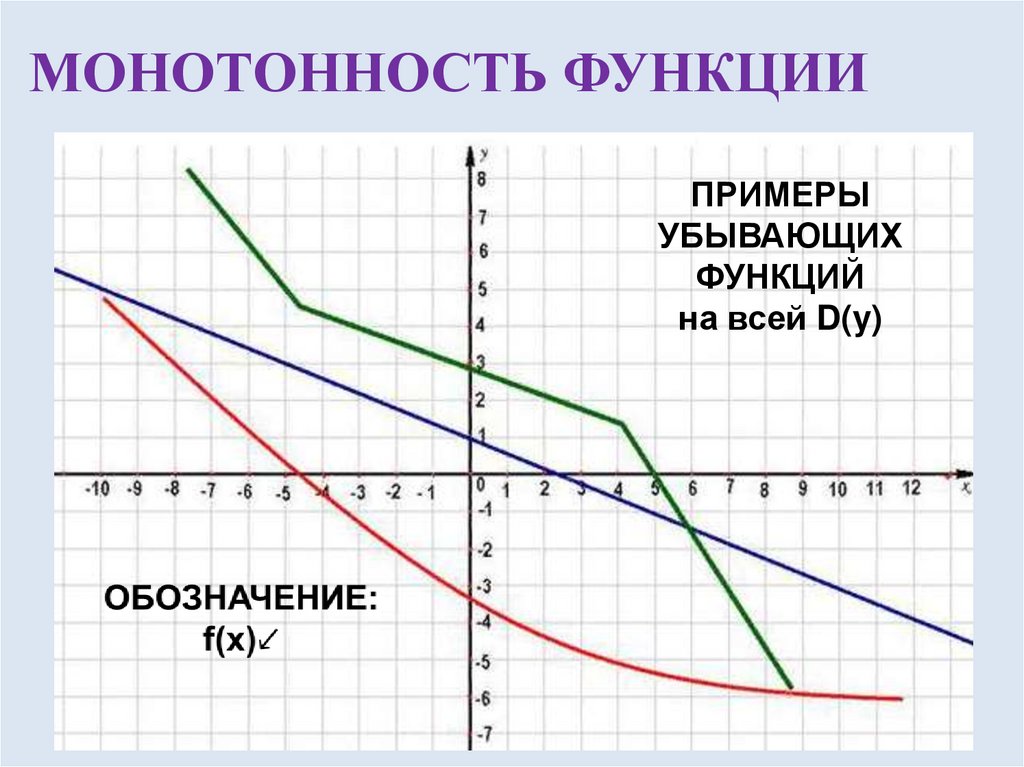 Итак, чтобы доказать немонотонность функции, достаточно доказать, что f ′ имеет разные знаки в разных точках.
Итак, чтобы доказать немонотонность функции, достаточно доказать, что f ′ имеет разные знаки в разных точках.
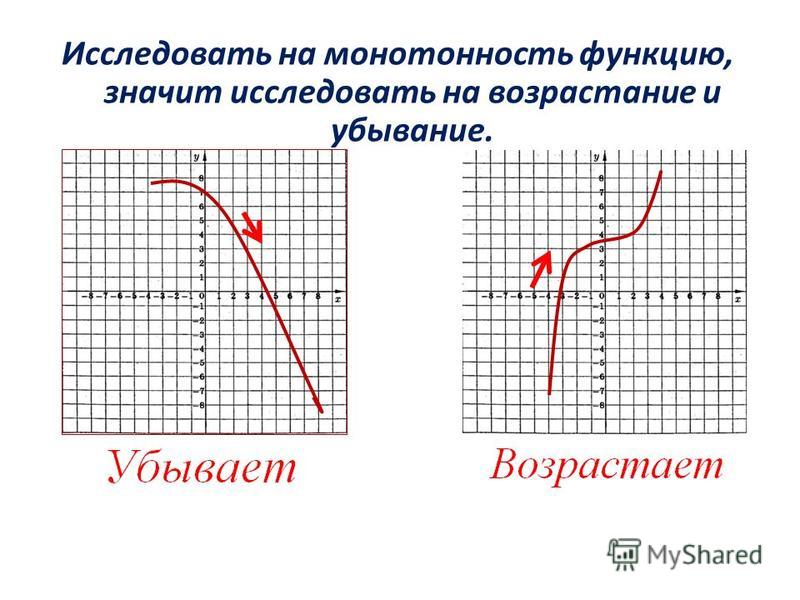 .. Мне нужен подарок завтра в классе 🙁
.. Мне нужен подарок завтра в классе 🙁