Ответ
Проверено
258,3 тыс. Когда ученик переходит в старшую школу, математика разделяется на 2 предмета: алгебру и геометрию. Понятий становится все больше, задания все сложнее. У некоторых возникают трудности с восприятием дробей. Пропустили первый урок по этой теме, и вуаля. дроби? Вопрос, который будет мучить на протяжении всей школьной жизни. Начнем с определения. Под алгебраической дробью понимается выражения P/Q, где P является числителем, а Q — знаменателем. Под буквенной записью может скрываться число, числовое выражение, численно-буквенное выражение. Прежде чем задаваться вопросом, как решать алгебраические дроби, для начала нужно понимать, что подобное выражение — часть целого. Как правило, целое — это 1. Число в знаменателе показывает, на сколько частей разделили единицу. Числитель необходим для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Когда учащиеся проходят данную тему в школе, им дают примеры на закрепление. Чтобы правильно их решать и находить различные пути из сложных ситуаций, нужно применять основное свойство дробей. Оно звучит так: Если умножить и числитель, и знаменатель на одно и то же число или выражение (отличные от нуля), то значение обыкновенной дроби не изменится. Частным случаем от данного правила является разделение обеих частей выражения на одно и то же число или многочлен. Подобные преобразования называются тождественными равенствами. Ниже будет рассмотрено, как решать сложение и вычитание алгебраических дробей, производить умножение, деление и сокращение дробей. Рассмотрим, как решать, основное свойство алгебраической дроби, как применять его на практике. Так, для операции сложения и вычитания следует найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби даны с одинаковыми выражениями Q, то нужно опустить этот пункт. Когда общий знаменатель найден, как решать алгебраические дроби? Нужно сложить или вычесть числители. Но! Нужно помнить, что при наличии знака «-» перед дробью все знаки в числителе меняются на противоположные. Иногда не следует производить каких-либо подстановок и математических операций. Достаточно поменять знак перед дробью. Часто используется такое понятие, как сокращение дробей . Это означает следующее: если числитель и знаменатель разделить на отличное от единицы выражение (одинаковое для обеих частей), то получается новая дробь. Делимое и делитель меньше прежних, но в силу основного правила дробей остаются равными изначальному примеру. Целью этой операции является получение нового несократимого выражения. Решить данную задачу можно, если сократить числитель и знаменатель на наибольший общий делитель. Алгоритм операции состоит из двух пунктов: Ниже показана таблица, в которой расписаны формулы. Для удобства ее можно распечатать и носить с собой в тетради. Однако, чтобы в будущем при решении контрольной или экзамена не возникло трудностей в вопросе, как решать алгебраические дроби, указанные формулы нужно выучить наизусть. С теоретической точки зрения рассмотрен вопрос, как решать алгебраические дроби. Примеры, приведенные в статье, помогут лучше усвоить материал. 1. Преобразовать дроби и привести их к общему знаменателю. 2. Преобразовать дроби и привести их к общему знаменателю. После изучения теоретической части и расссмотрения практической вопросов больше возникнуть не должно. Данная статья продолжает тему преобразования алгебраических дробей: рассмотрим такое действие как сокращение алгебраических дробей. Дадим определение самому термину, сформулируем правило сокращения и разберем практические примеры. Yandex.RTB R-A-339285-1 В материалах об обыкновенной дроби мы рассматривали ее сокращение. Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель. Сокращение алгебраической дроби представляет собой аналогичное действие. Определение 1 Сокращение алгебраической дроби – это деление ее числителя и знаменателя на общий множитель. При этом, в отличие от сокращения обыкновенной дроби (общим знаменателем может быть только число), общим множителем числителя и знаменателя алгебраической дроби может служить многочлен, в частности, одночлен или число. К примеру, алгебраическая дробь 3 · x 2 + 6 · x · y 6 · x 3 · y + 12 · x 2 · y 2 может быть сокращена на число 3 , в итоге получим: x 2 + 2 · x · y 6 · x 3 · y + 12 · x 2 · y 2 . Эту же дробь мы можем сократить на переменную х, и это даст нам выражение 3 · x + 6 · y 6 · x 2 · y + 12 · x · y 2 . Также заданную дробь возможно сократить на одночлен 3 · x или любой из многочленов x + 2 · y , 3 · x + 6 · y , x 2 + 2 · x · y или 3 · x 2 + 6 · x · y . Конечной целью сокращения алгебраической дроби является дробь более простого вида, в лучшем случае – несократимая дробь. Опять же из материалов об обыкновенных дробях мы знаем, что существуют сократимые и несократимые дроби. Несократимые – это дроби, не имеющие общих множителей числителя и знаменателя, отличных от 1 . С алгебраическими дробями все так же: они могут иметь общие множители числителя и знаменателя, могут и не иметь. Наличие общих множителей позволяет упростить исходную дробь посредством сокращения. В общих случаях по заданному виду дроби довольно сложно понять, подлежит ли она сокращению. Конечно, в некоторых случаях наличие общего множителя числителя и знаменателя очевидно. Например, в алгебраической дроби 3 · x 2 3 · y совершенно понятно, что общим множителем является число 3 . В дроби — x · y 5 · x · y · z 3 также мы сразу понимаем, что сократить ее возможно на х, или y , или на х · y . И все же гораздо чаще встречаются примеры алгебраических дробей, когда общий множитель числителя и знаменателя не так просто увидеть, а еще чаще – он попросту отсутствует. Например, дробь x 3 — 1 x 2 — 1 мы можем сократить на х — 1 , при этом указанный общий множитель в записи отсутствует. А вот дробь x 3 — x 2 + x — 1 x 3 + x 2 + 4 · x + 4 подвергнуть действию сокращения невозможно, поскольку числитель и знаменатель не имеют общего множителя. Таким образом, вопрос выяснения сократимости алгебраической дроби не так прост, и зачастую проще работать с дробью заданного вида, чем пытаться выяснить, сократима ли она. Правило сокращения алгебраических дробей состоит из двух последовательных действий: Самым удобным методом отыскания общих знаменателей является разложение на множители многочленов, имеющихся в числителе и знаменателе заданной алгебраической дроби. Это позволяет сразу наглядно увидеть наличие или отсутствие общих множителей. Само действие сокращения алгебраической дроби базируется на основном свойстве алгебраической дроби, выражаемой равенством undefined , где a , b , c – некие многочлены, причем b и c – ненулевые. Первым шагом дробь приводится к виду a · c b · c , в котором мы сразу замечаем общий множитель c . Несмотря на некоторую очевидность, уточним про частный случай, когда числитель и знаменатель алгебраической дроби равны. Подобные дроби тождественно равны 1 на всей ОДЗ переменных этой дроби: 5 5 = 1 ; — 2 3 — 2 3 = 1 ; x x = 1 ; — 3 , 2 · x 3 — 3 , 2 · x 3 = 1 ; 1 2 · x — x 2 · y 1 2 · x — x 2 · y ; Поскольку обыкновенные дроби являются частным случаем алгебраических дробей, напомним, как осуществляется их сокращение. Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются). К примеру, 24 1260 = 2 · 2 · 2 · 3 2 · 2 · 3 · 3 · 5 · 7 = 2 3 · 5 · 7 = 2 105 Произведение простых одинаковых множителей возможно записать как степени, и в процессе сокращения дроби использовать свойство деления степеней с одинаковыми основаниями. Тогда вышеуказанное решение было бы таким: 24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 — 2 3 2 — 1 · 5 · 7 = 2 105 (числитель и знаменатель разделены на общий множитель 2 2 · 3 ). 24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 2 2 · 3 3 2 · 1 5 · 7 = 2 1 · 1 3 · 1 35 = 2 105 По аналогии осуществляется сокращение алгебраических дробей, у которых в числителе и знаменателе имеются одночлены с целыми коэффициентами. Пример 1 Задана алгебраическая дробь — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z . Необходимо произвести ее сокращение. Решение Возможно записать числитель и знаменатель заданной дроби как произведение простых множителей и переменных, после чего осуществить сокращение: 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 · 3 · 3 · a · a · a · a · a · b · b · c · z 2 · 3 · a · a · b · b · c · c · c · c · c · c · c · z = = — 3 · 3 · a · a · a 2 · c · c · c · c · c · c = — 9 · a 3 2 · c 6 Однако, более рациональным способом будет запись решения в виде выражения со степенями: 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 3 · a 5 · b 2 · c · z 2 · 3 · a 2 · b 2 · c 7 · z = — 3 3 2 · 3 · a 5 a 2 · b 2 b 2 · c c 7 · z z = = — 3 3 — 1 2 · a 5 — 2 1 · 1 · 1 c 7 — 1 · 1 = · — 3 2 · a 3 2 · c 6 = · — 9 · a 3 2 · c 6 . Ответ: — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 9 · a 3 2 · c 6 Когда в числителе и знаменателе алгебраической дроби имеются дробные числовые коэффициенты, возможно два пути дальнейших действий: или отдельно осуществить деление этих дробных коэффициентов, или предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на некое натуральное число. Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»). Пример 2 Задана дробь 2 5 · x 0 , 3 · x 3 . Необходимо выполнить ее сокращение. Решение Возможно сократить дробь таким образом: 2 5 · x 0 , 3 · x 3 = 2 5 3 10 · x x 3 = 4 3 · 1 x 2 = 4 3 · x 2 Попробуем решить задачу иначе, предварительно избавившись от дробных коэффициентов – умножим числитель и знаменатель на наименьшее общее кратное знаменателей этих коэффициентов, т. 2 5 · x 0 , 3 · x 3 = 10 · 2 5 · x 10 · 0 , 3 · x 3 = 4 · x 3 · x 3 = 4 3 · x 2 . Ответ: 2 5 · x 0 , 3 · x 3 = 4 3 · x 2 Когда мы сокращаем алгебраические дроби общего вида, в которых числители и знаменатели могут быть как одночленами, так и многочленами, возможна проблема, когда общий множитель не всегда сразу виден. Или более того, он попросту не существует. Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители. Пример 3 Задана рациональная дробь 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 . Необходимо ее сократить. Решение Разложим на множители многочлены в числителе и знаменателе. Осуществим вынесение за скобки: 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · (a 2 + 14 · a + 49) b 3 · (a 2 — 49) Мы видим, что выражение в скобках возможно преобразовать с использованием формул сокращенного умножения: 2 · b 2 · (a 2 + 14 · a + 49) b 3 · (a 2 — 49) = 2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7) Хорошо заметно, что возможно сократить дробь на общий множитель b 2 · (a + 7) . 2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7) = 2 · (a + 7) b · (a — 7) = 2 · a + 14 a · b — 7 · b Краткое решение без пояснений запишем как цепочку равенств: 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · (a 2 + 14 a + 49) b 3 · (a 2 — 49) = = 2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7) = 2 · (a + 7) b · (a — 7) = 2 · a + 14 a · b — 7 · b Ответ: 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · a + 14 a · b — 7 · b . Случается, что общие множители скрыты числовыми коэффициентами. Тогда при сокращении дробей оптимально числовые множители при старших степенях числителя и знаменателя вынести за скобки. Пример 4 Дана алгебраическая дробь 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 . Необходимо осуществить ее сокращение, если это возможно. Решение На первый взгляд у числителя и знаменателя не существует общего знаменателя. Однако, попробуем преобразовать заданную дробь. 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2 Теперь видна некая схожесть выражения в скобках и выражения в знаменателе за счет x 2 · y . Вынесем за скобку числовые коэффициенты при старших степенях этих многочленов: x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2 = x · — 2 7 · — 7 2 · 1 5 + x 2 · y 5 · x 2 · y — 1 5 · 3 1 2 = = — 2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10 Теперь становится виден общий множитель, осуществляем сокращение: 2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10 = — 2 7 · x 5 = — 2 35 · x Ответ: 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = — 2 35 · x . Сделаем акцент на том, что навык сокращения рациональных дробей зависит от умения раскладывать многочлены на множители. Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter Основано на их основном свойстве: если числитель и знаменатель дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь. Сокращать можно только множители! Члены многочленов сокращать нельзя! Чтобы сократить алгебраическую дробь, многочлены, стоящие в числителе и знаменателе, нужно предварительно разложить на множители. Рассмотрим примеры сокращения дробей. В числителе и знаменателе дроби стоят одночлены. Они представляют собой произведение (чисел, переменных и их степеней), множители сокращать можем. Числа сокращаем на их наибольший общий делитель, то есть на наибольшее число, на которое делится каждое из данных чисел. Для 24 и 36 это — 12. После сокращения от 24 остается 2, от 36 — 3. Степени сокращаем на степень с наименьшим показателем. Сократить дробь — значит, разделить числитель и знаменатель на один и тот же делитель, а показатели вычитаем. a² и a⁷ сокращаем на a². При этом в числителе от a² остается единица (1 пишем только в том случае, когда кроме нее после сокращения других множителей не осталось. От 24 осталась 2, поэтому 1, оставшуюся от a², не пишем). b и b сокращаем на b, полученные в результате единицы не пишем. c³º и с⁵ сокращаем на с⁵. От c³º остается c²⁵, от с⁵ — единица (ее не пишем). Таким образом, Числитель и знаменатель данной алгебраической дроби — многочлены. Сокращать члены многочленов нельзя! (нельзя сократить, к примеру, 8x² и 2x!). Чтобы сократить эту дробь, надо . В числителе есть общий множитель 4x. Выносим его за скобки: И в числителе, и в знаменателе есть одинаковый множитель (2x-3). Сокращаем дробь на этот множитель. В числителе получили 4x, в знаменателе — 1. По 1 свойству алгебраических дробей, дробь равна 4x. Сокращать можно только множители (сократить данную дробь на 25x² нельзя!). Поэтому многочлены, стоящие в числителе и знаменателе дроби, нужно разложить на множители. В числителе — полный квадрат суммы, в знаменателе — разность квадратов. После разложения по формулам сокращенного умножения получаем: Сокращаем дробь на (5x+1) (для этого в числителе зачеркнем двойку в показатель степени, от (5x+1)² при этом останется (5x+1)): В числителе есть общий множитель 2, вынесем его за скобки. В результате разложения в числителе и знаменателе получили одинаковый множитель (9+3a+a²). Сокращаем дробь на него: Многочлен в числителе состоит из 4 слагаемых. первое слагаемое со вторым, третье — с четвертым и выносим из первых скобок общий множитель x². Знаменатель раскладываем по формуле суммы кубов: В числителе вынесем за скобки общий множитель (x+2): Сокращаем дробь на (x+2): В этой статье мы подробно остановимся на сокращении алгебраических дробей . Сначала разберемся, что понимают под термином «сокращение алгебраической дроби», и выясним, всегда ли алгебраическая дробь сократима. Дальше приведем правило, позволяющее проводить это преобразование. Наконец, рассмотрим решения характерных примеров, которые позволят уяснить все тонкости процесса. Навигация по странице. Изучая , мы говорили про их сокращение. мы назвали деление ее числителя и знаменателя на общий множитель. Под сокращением алгебраической дроби понимают аналогичное действие. Сократить алгебраическую дробь – это значит разделить ее числитель и знаменатель на общий множитель. Но если общим множителем числителя и знаменателя обыкновенной дроби может быть только число, то общим множителем числителя и знаменателя алгебраической дроби может быть многочлен , в частности, одночлен или число. Например, алгебраическую дробь можно сократить на число 3
, что даст дробь . Также можно выполнить сокращение на переменную x
, что приведет к выражению . Исходную алгебраическую дробь можно подвергнуть сокращению на одночлен 3·x
, а также на любой из многочленов x+2·y
, 3·x+6·y
, x 2 +2·x·y
или 3·x 2 +6·x·y
. Конечная цель сокращения алгебраической дроби состоит в получении дроби более простого вида, в лучшем случае – несократимой дроби. Нам известно, что обыкновенные дроби подразделяются на . Алгебраические дроби также могут иметь общие множители числителя и знаменателя, а могут и не иметь. При наличии общих множителей возможно сокращение алгебраической дроби. Если же общих множителей нет, то упрощение алгебраической дроби посредством ее сокращения невозможно. В общем случае по внешнему виду алгебраической дроби достаточно сложно определить, возможно ли выполнить ее сокращение. Несомненно, в некоторых случаях общие множители числителя и знаменателя очевидны. Например, хорошо видно, что числитель и знаменатель алгебраической дроби имеют общий множитель 3
. Также несложно заметить, что алгебраическую дробь можно сократить на x
, на y
или сразу на x·y
. Но намного чаще общего множителя числителя и знаменателя алгебраической дроби сразу не видно, а еще чаще – его просто нет. К примеру, дробь возможно сократить на x−1
, но этот общий множитель явно не присутствует в записи. Вообще, вопрос о сократимости алгебраической дроби очень непростой. И порой проще решить задачу, работая с алгебраической дробью в исходном виде, чем выяснить, можно ли эту дробь предварительно сократить. Но все же существуют преобразования, которые в некоторых случаях позволяют с относительно небольшими усилиями найти общие множители числителя и знаменателя, если таковые имеются, либо сделать вывод о несократимости исходной алгебраической дроби. Эта информация будет раскрыта в следующем пункте. Информация предыдущих пунктов позволяет естественным образом воспринять следующее правило сокращения алгебраических дробей , которое состоит из двух шагов: Указанные шаги озвученного правила нуждаются в разъяснении. Самый удобный способ отыскания общих заключается в разложении на множители многочленов , находящихся в числителе и знаменателе исходной алгебраической дроби. При этом сразу становятся видны общие множители числителя и знаменателя, либо становится видно, что общих множителей нет. Если общих множителей нет, то можно делать вывод о несократимости алгебраической дроби. Если же общие множители обнаружены, то на втором шаге они сокращаются. В результате получается новая дробь более простого вида. В основе правила сокращения алгебраических дробей лежит основное свойство алгебраической дроби , которое выражается равенством , где a
, b
и c
– некоторые многочлены, причем b
и c
– ненулевые. На первом шаге исходная алгебраическая дробь приводится к виду , из которого становится виден общий множитель c
, а на втором шаге выполняется сокращение – переход к дроби . Переходим к решению примеров с использованием данного правила. На них мы и разберем все возможные нюансы, возникающие при разложении числителя и знаменателя алгебраической дроби на множители и последующем сокращении. Для начала нужно сказать про сокращение алгебраических дробей, числитель и знаменатель которых одинаковые. Такие дроби тождественно равны единице на всей ОДЗ входящих в нее переменных, например, Теперь не помешает вспомнить, как выполняется сокращение обыкновенных дробей – ведь они являются частным случаем алгебраических дробей. Натуральные числа в числителе и знаменателе обыкновенной дроби , после чего общие множители сокращаются (при их наличии). Например, . Произведение одинаковых простых множителей можно записывать в виде степеней, а при сокращении пользоваться . В этом случае решение выглядело бы так: , здесь мы числитель и знаменатель разделили на общий множитель 2 2 ·3
. Или для большей наглядности на основании свойств умножения и деления решение представляют в виде . По абсолютно аналогичным принципам проводится сокращение алгебраических дробей, в числителе и знаменателе которых находятся одночлены с целыми коэффициентами. Пример. Сократите алгебраическую дробь . Решение. Можно представить числитель и знаменатель исходной алгебраической дроби в виде произведения простых множителей и переменных, после чего провести сокращение: Но более рационально решение записать в виде выражения со степенями: Ответ: . Что касается сокращения алгебраических дробей, имеющих дробные числовые коэффициенты в числителе и знаменателе, то можно поступать двояко: либо отдельно выполнять деление этих дробных коэффициентов, либо предварительно избавляться от дробных коэффициентов, умножив числитель и знаменатель на некоторое натуральное число. Про последнее преобразование мы говорили в статье приведение алгебраической дроби к новому знаменателю , его можно проводить в силу основного свойства алгебраической дроби. Разберемся с этим на примере. Пример. Выполните сокращение дроби . Решение. Можно сократить дробь следующим образом: . А можно было предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на знаменателей этих коэффициентов, то есть, на НОК(5, 10)=10
. Ответ: . Можно переходить к алгебраическим дробям общего вида, у которых в числителе и знаменателе могут быть как числа и одночлены, так и многочлены. При сокращении таких дробей основная проблема заключается в том, что общий множитель числителя и знаменателя далеко не всегда виден. Более того, он не всегда существует. Для того, чтобы найти общий множитель или убедиться в его отсутствии нужно числитель и знаменатель алгебраической дроби разложить на множители. Пример. Сократите рациональную дробь . Решение. Для этого разложим на множители многочлены в числителе и знаменателе. Начнем с вынесения за скобки: . Очевидно, выражения в скобках можно преобразовать, используя Деление и числителя и знаменателя дроби на их общий делитель , отличный от единицы, называют сокращением дроби . Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число. Это число является наибольшим общим делителем числителя и знаменателя данной дроби. Возможны следующие формы записи решения примеров на сокращение обыкновенных дробей. Учащийся вправе выбрать любую форму записи. Примеры. Упростить дроби. Сократим дробь на 3 (делим числитель на 3; делим знаменатель на 3). Сокращаем дробь на 7. Выполняем указанные действия в числителе и знаменателе дроби. Полученную дробь сокращаем на 5. Сократим данную дробь 4) на 5·7³ — наибольший общий делитель (НОД) числителя и знаменателя, который состоит из общих множителей числителя и знаменателя, взятых в степени с наименьшим показателем. Разложим числитель и знаменатель этой дроби на простые множители. Получаем: 756=2²·3³·7 и 1176=2³·3·7² . Определяем НОД (наибольший общий делитель) числителя и знаменателя дроби 5) . Это произведение общих множителей, взятых с наименьшими показателями. НОД(756; 1176)=2²·3·7 . Делим числитель и знаменатель данной дроби на их НОД, т. е. на 2²·3·7 получаем несократимую дробь 9/14 . А можно было записать разложения числителя и знаменателя в виде произведения простых множителей, не применяя понятие степени, а затем произвести сокращение дроби, зачеркивая одинаковые множители в числителе и знаменателе. Когда одинаковых множителей не останется — перемножаем оставшиеся множители отдельно в числителе и отдельно в знаменателе и выписываем получившуюся дробь 9/14 . И, наконец, можно было сокращать данную дробь 5) постепенно, применяя признаки деления чисел и к числителю и к знаменателю дроби. Рассуждаем так: числа 756 и 1176 оканчиваются четной цифрой, значит, оба делятся на 2 . Сокращаем дробь на 2 . Числитель и знаменатель новой дроби — числа 378 и 588 также делятся на 2 . Сокращаем дробь на 2 . Замечаем, что число 294 — четное, а 189 — нечетное, и сокращение на 2 уже невозможно. (1+8+9)=18 делится на 3 и (2+9+4)=15 делится на 3, следовательно, и сами числа 189 и 294 делятся на 3 . Сокращаем дробь на 3 . Далее, 63 делится на 3, а 98 — нет. Перебираем другие простые множители. Оба числа делятся на 7 . Сокращаем дробь на 7 и получаем несократимую дробь 9/14 . Главная›Калькуляторы›Математические калькуляторы›Упроститель дробей Калькулятор фракций
Упрощение дробей
Преобразователь дробей Введите дробь Результат упрощенной дроби Расчет * gcf = наибольший общий делитель Калькулятор дробей ► Когда вы держите iPhone вертикально в стандартном портретном режиме и используете встроенное приложение «Калькулятор», у вас будет возможность выполнять основные математические уравнения, такие как сложение, вычитание и тому подобное. Тем не менее, вы можете улучшить тип математических уравнений, которые вы можете проводить, наклонив калькулятор вашего iPhone вбок, чтобы получить доступ к раскладке научного калькулятора в ландшафтном режиме, что позволяет вам выполнять математические формулы, такие как дроби или квадратные корни. Вот как это сделать. 1. 2. После запуска приложения поверните iPhone на бок, чтобы перевести его в ландшафтный режим. В левой части экрана появятся дополнительные функции. 3. Когда вы будете готовы вычислять дроби, введите число, которое вы хотите преобразовать в дробь. Затем вы можете нажать кнопку 1/x, чтобы поместить это число в знаменатель (числитель будет равен 1) и получить значение дроби. 4. Значение дроби, в числителе которой нет 1, можно вычислить с помощью кнопки деления. В частности, формулу можно выполнить, введя значение числителя, нажав клавишу деления, а затем введя значение знаменателя. Когда вы нажмете кнопку равенства (=), вы получите значение дроби.
от 0 p.
от 70 p.
от 0 p. Посмотреть всех экспертов из раздела Учеба и наука В каком году была сформулирована теория — предшественница кислородной теории горения. В 150 мл воды растворили 33,6л аммиака (н. у) . Найдите массовую долю аммиака в полученном растворе. Структурная формула всех изомеров С7Н16 Решено помогите срочно решить задачу: при сжигании 4,4 г углеводорода получили 13,2 г оксида углерода (IV). Решено KMnO4+h3O2=MnO2+KOH+O2+h3O
Объясните, как уравнять, пожалуйста Пользуйтесь нашим приложением By Бисваруп Чандра Дей КМnО4 является сильным окислителем и может реагировать с молекулами, имеющими более высокий восстановительный потенциал. Рассмотрим подробно механизм его реакции с h3SO4. Перманганат калия представляет собой твердую молекулу пурпурного цвета и является мощным реагентом, поскольку центральный металл Mn имеет степень окисления +7. Он может реагировать с холодной и концентрированной формой серной кислоты и образовывать различные продукты окисления. В этой реакции KMnO4 действует как самокатализатор. О механизме реакции между серной кислотой и железом, энтальпии реакции, типе реакции, образовании продукта и т.д. поговорим в следующей части статьи. Сульфат марганца и сульфат калия образуются в качестве основных продуктов, когда H2SO4 и KMnO4 реагируют вместе. Молекулы воды и газообразный кислород также выделяются в результате их реакции.Продукт реакции H2SO4 + Реакция KMnO4 является примером реакции двойного замещения наряду с окислительно-восстановительными реакциями и реакциями осаждения. Это также реакция выделения кислорода наряду с реакцией гидролиза. H2SO4 + КМnО4 = МnSO4 + К2SO4 + H2О + О2 Мы должны сбалансировать уравнение следующим образом: Чтобы оценить количество калия или марганца, мы можем выполнить титрование между KMnO4 и H2SO4 Для этого титрования нам потребуются бюретка, коническая колба, держатель бюретки, мерная колба и стаканы. H2SO4 по сравнению с KMnO4, H2SO4 акты в качестве титранта, который берется в бюретку и анализируется молекула KMnO4 который отбирают в коническую колбу. Все титрование проводят в кислой среде, так как концентрация H2SO4 высока, и для этой реакции KMnO4 действует как самоиндикатор, потому что это окрашенный раствор и при разном pH он меняет цвет. Бюретка заполнялась стандартизированным H2SO4 и KMnO4 отбирали в коническую колбу вместе с соответствующим индикатором. Мы повторяем титрование несколько раз для получения лучших результатов, а затем оцениваем количество калия и марганца по формуле V1S1 V =2S2. Чистое ионное уравнение между H2SO4 + КМnО4 как следует, 2H+ + ТАК42- + K+ + MnO4– = Мн2+ + K+ + SO42- + H+ + OH– + О2 В реакции Н2SO4 + КМnО4 сопряженные пары будут соответствующими депротонированными и протонированными формами этого конкретного вида, которые перечислены ниже: Межмолекулярная сила между H2SO4 представляет собой электростатическую ковалентную силу. В реакции Н2SO4 + КМnО4 энтальпия реакции составляет -4400.4 кДж/моль, что можно получить по формуле энтальпия продуктов – энтальпия реагентов, причем изменение энтальпии положительно. Реакция между H2SO4 + KMnO4 дает буферный раствор и им можно регулировать рН раствора. Реакция между H2SO4 + КМnО4 является полной реакцией, потому что она дает два полных продукта MnSO4 и K2SO4 вместе с О2 газ. Реакция H2SO4 + KMnO4 экзотермичен с точки зрения первого закона термодинамики. Таким образом, реакция высвобождает больше энергии и температуры в окружающую среду, поэтому мы должны быть более осторожный, где δH всегда отрицательно. Реакция между H2SO4 + КМnО4 — это окислительно-восстановительная реакция потому что в этой реакции многие элементы восстанавливаются и окисляются.Окислительно-восстановительная схема Реакция Н2SO4 + КМnО4 является реакцией осаждения, потому что он осаждается в растворе и не растворяется в реакционной смеси. Реакция между H2SO4+ KMnO4 необратим, потому что мы получаем O2 газ как товар. Когда в ходе реакции образуется газ, энтропия реакции увеличивается, и равновесие реакции смещается только в правую сторону. Реакция между H2SO4+ КМnО4 это пример одинарное перемещение реакция, потому что в приведенной выше реакции Mn и K замещаются H+ в H2SO4 И O2 газ освобождается от реакции.Одиночная реакция смещения H2SO4 и KMnO4 реакция в основном дает нам K2SO4 и MnSO4 наряду с газообразным кислородом, так что это коммерчески важная реакция для производства газообразного кислорода. Кроме того, количественный анализ H2SO4 и KMnO4 укажите количество Mn и K в соответствующем образце. Узнайте больше о 11 фактов о h3SO4 + Al(OH)3. Узнайте больше фактов о h3SO4: 31 мая 2018 г. Хлорид натрия и перманганат калия реагируют друг с другом в кислой среде (NaCl KMnO4 h3SO4) с образованием свободного хлора. Это окислительно-восстановительная реакция. Поскольку вы ищете баланс этой реакции, это означает, что вы уже знаете, что такое окислительно-восстановительная реакция. Простым языком можно сказать, что это реакция, в которой реагенты передают между собой электроны. Теперь давайте поговорим о беспокоящей реакции. Эта конкретная химическая реакция является окислительно-восстановительной , т.е. окислительно-восстановительной реакцией, поскольку степень окисления Mn в KMnO4 равна +7, а после реакции степень окисления Mn становится +2. С другой стороны, степень окисления Fe в реагентах равна +2, тогда как в продуктах +3. Из этого обсуждения мы ясно видим, что в этой реакции происходит перенос электрона. Поэтому, конечно, это окислительно-восстановительная реакция. Чтобы уравновесить эту реакцию, мы должны использовать ионно-электронный метод. окислитель и восстановитель в реагенте. Для вышеуказанной реакции KMnO4 действует как агент окисления, а NaCl действует как агент восстановления. Окислитель: KMnO 4 или (исключая зрительный ион) MnO 4 -1 Восстановитель : NaCl или Cl -1 (исключая зрительный ион) Окислитель принимает электроны и восстанавливается так же, как окисляет восстановитель. ⇒ MnO 4 -1 +5e – + 8H + = 4H 2 O + Mn 2+ … …. …. …. (1) С другой стороны, поскольку окисление-восстановление является одновременным процессом, полуреакция окисления протекает вместе с полуреакцией восстановления, показанной в уравнении (1). На этот раз окислитель Cl -1 высвобождает один электрон, чтобы восстановиться, а также стать свободным атомом Cl. Таким образом, полуреакция окисления — Cl -1 – e – = Cl 0 … … … … … (2) В это время мы должны умножить номер уравнения (2) 5 раз, а затем добавить его с номером уравнения ( 1). уравнение (1) + (2)x5, MnO 4 -1 +5e – + 8H + = 4H 2 O + Mn 2- ⇒ MnO 4 -1 + 5Cl -1 + 8H + = 5Cl 0 + Mn 2- + 4H 2 O или MnO 4 -1 + 5Cl -1 + 8H + = 5 / 2 Cl 2 + Mn 2- + 4H 2 O или, 2MnO 4 -1 + 10Cl -1 + 16H + = 5Cl 2 + 2Mn 2- + 8H 2 O (умножая обе стороны на 2) Теперь, добавляя необходимые ионы и радикалы, получаем Cl+ 8H 2 SO 4 = 5Cl 2 + 2MnSO 4 + 8H 2 O + 5Na 2 SO 4 +K 2 SO 4 Большое спасибо за прочтение статьи. Следуйте за нами на Twitter, Facebook, Linkedin и Tumblr Подробнее FeSO4 + KMnO4 + h3SO4 = Fe2(SO4) 3 + MnSO4 + h3O + K2SO4 FeSO4 + KMnO4 + h3SO4 = Fe2(SO4)3 + MnSO4 + h3O + K2SO4 Окислительно-восстановительные (ОВП) реакции Тим Ким Пхонг Трин Хоа Хок ✖Площадь прямоугольника — это общее количество плоскостей, ограниченных границей прямоугольника.ⓘ Площадь прямоугольника [A] акрАкко (служба США)НаходятсяАрпентамбарКарроКруговая дюймаКруговая MilCuerdaарамДунамРаздел электрон КрестаГаусадьбаMuпингплощадьPyongклочок землиСабинРазделКвадратный АнгстремПлощадь СантиметрПлощадь цепи Площадь декаметровойквадратный дециметрКвадратный футКвадратный фут (служба США)Площадь гектометровыеКвадратный дюймквадратный километрКвадратный метрПлощадь микрометраПлощадь MilКвадратная миляКвадратная миля (римская)Квадратная миля (Статут)Квадратная миля (служба США)Площадь МиллиметрПлощадь NanometreМера площадиПлощадь полюсаПлощадь РодКвадратный Rod (служба США)Квадратный дворрастяжениегородокВарас Castellanas CuadВарас Conuqueras Cuad +10% -10% ✖Длина прямоугольника — это любая из пары параллельных сторон, которая длиннее оставшейся пары параллельных сторон. створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр +10% -10%
✖Периметр прямоугольника — это общая длина всех граничных линий прямоугольника.
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр
⎘ копия
👎
Формула
сбросить
👍
ШАГ 0: Сводка предварительного расчета ШАГ 1. Площадь прямоугольника: 48 Квадратный метр —> 48 Квадратный метр Конверсия не требуется ШАГ 2: Оцените формулу ШАГ 3: Преобразуйте результат в единицу вывода 28 метр —> Конверсия не требуется
Периметр прямоугольника по площади и тупому углу между диагоналями
Идти
Периметр прямоугольника = 2*sqrt(Площадь прямоугольника*cosec((pi-Тупой угол между диагоналями прямоугольника)/2)*sec((pi-Тупой угол между диагоналями прямоугольника)/2)+(2*Площадь прямоугольника))
Периметр прямоугольника по радиусу окружности и углу между диагональю и шириной
Идти
Периметр прямоугольника = 4*Окружность прямоугольника*sqrt(1+(2*sin((pi/2)-Угол между диагональю и шириной прямоугольника)*cos((pi/2)-Угол между диагональю и шириной прямоугольника)))
Периметр прямоугольника по диагонали и углу между диагональю и шириной
Идти
Периметр прямоугольника = 2*Диагональ прямоугольника*sqrt(1+(2*sin((pi/2)-Угол между диагональю и шириной прямоугольника)*cos((pi/2)-Угол между диагональю и шириной прямоугольника)))
Периметр прямоугольника по радиусу окружности и тупому углу между диагоналями
Идти
Периметр прямоугольника = 4*Окружность прямоугольника*sqrt(1+(2*sin((pi-Тупой угол между диагоналями прямоугольника)/2)*cos((pi-Тупой угол между диагоналями прямоугольника)/2)))
Периметр прямоугольника по диагонали и тупому углу между диагоналями
Идти
Периметр прямоугольника = 2*Диагональ прямоугольника*sqrt(1+(2*sin((pi-Тупой угол между диагоналями прямоугольника)/2)*cos((pi-Тупой угол между диагоналями прямоугольника)/2)))
Периметр прямоугольника по площади и углу между диагональю и шириной
Идти
Периметр прямоугольника = 2*sqrt((Площадь прямоугольника*sec(Угол между диагональю и шириной прямоугольника)*cosec(Угол между диагональю и шириной прямоугольника))+(2*Площадь прямоугольника))
Периметр прямоугольника с заданной площадью и углом между диагональю и длиной
Идти
Периметр прямоугольника = 2*sqrt((Площадь прямоугольника*sec(Угол между диагональю и длиной прямоугольника)*cosec(Угол между диагональю и длиной прямоугольника))+(2*Площадь прямоугольника))
Периметр прямоугольника по площади и острому углу между диагоналями
Идти
Периметр прямоугольника = 2*sqrt(Площадь прямоугольника*cosec(Острый угол между диагоналями прямоугольника/2)*sec(Острый угол между диагоналями прямоугольника/2)+(2*Площадь прямоугольника))
Периметр прямоугольника с учетом диаметра окружности и угла между диагональю и длиной
Идти
Периметр прямоугольника = 2*Диаметр окружности прямоугольника*sqrt(1+(2*sin(Угол между диагональю и длиной прямоугольника)*cos(Угол между диагональю и длиной прямоугольника)))
Периметр прямоугольника по радиусу окружности и острому углу между диагоналями
Идти
Периметр прямоугольника = 4*Окружность прямоугольника*sqrt(1+(2*sin(Острый угол между диагоналями прямоугольника/2)*cos(Острый угол между диагоналями прямоугольника/2)))
Периметр прямоугольника по диагонали и острому углу между диагоналями
Идти
Периметр прямоугольника = 2*Диагональ прямоугольника*sqrt(1+(2*sin(Острый угол между диагоналями прямоугольника/2)*cos(Острый угол между диагоналями прямоугольника/2)))
Периметр прямоугольника по радиусу окружности и углу между диагональю и длиной
Идти
Периметр прямоугольника = 4*Окружность прямоугольника*sqrt(1+(2*sin(Угол между диагональю и длиной прямоугольника)*cos(Угол между диагональю и длиной прямоугольника)))
Периметр прямоугольника по диагонали и углу между диагональю и длиной
Идти
Периметр прямоугольника = 2*Диагональ прямоугольника*sqrt(1+(2*sin(Угол между диагональю и длиной прямоугольника)*cos(Угол между диагональю и длиной прямоугольника)))
Периметр прямоугольника по ширине и диаметру окружности
Идти
Периметр прямоугольника = 2*(Ширина прямоугольника+sqrt(Диаметр окружности прямоугольника^2-Ширина прямоугольника^2))
Периметр прямоугольника по длине и диаметру окружности
Идти
Периметр прямоугольника = 2*(Длина прямоугольника+sqrt(Диаметр окружности прямоугольника^2-Длина прямоугольника^2))
Периметр прямоугольника по ширине и радиусу окружности
Идти
Периметр прямоугольника = 2*(Ширина прямоугольника+sqrt((4*Окружность прямоугольника^2)-Ширина прямоугольника^2))
Периметр прямоугольника по длине и радиусу окружности
Идти
Периметр прямоугольника = 2*(Длина прямоугольника+sqrt((4*Окружность прямоугольника^2)-Длина прямоугольника^2))
Периметр прямоугольника по диагонали и ширине
Идти
Периметр прямоугольника = 2*(sqrt(Диагональ прямоугольника^2-Ширина прямоугольника^2)+Ширина прямоугольника)
Периметр прямоугольника по диагонали и длине
Идти
Периметр прямоугольника = 2*(Длина прямоугольника+sqrt(Диагональ прямоугольника^2-Длина прямоугольника^2))
Периметр прямоугольника с заданной площадью и длиной
Идти
Периметр прямоугольника = (2*(Площадь прямоугольника+Длина прямоугольника^2))/Длина прямоугольника
Периметр прямоугольника по площади и ширине
Идти
Периметр прямоугольника = 2*((Площадь прямоугольника/Ширина прямоугольника)+Ширина прямоугольника)
Периметр прямоугольника по площади и диаметру окружности
Идти
Периметр прямоугольника = 2*sqrt(Диаметр окружности прямоугольника^2+(2*Площадь прямоугольника))
Периметр прямоугольника по площади и радиусу окружности
Идти
Периметр прямоугольника = 2*sqrt((2*Площадь прямоугольника)+(4*Окружность прямоугольника^2))
Периметр прямоугольника по площади и диагонали
Идти
Периметр прямоугольника = 2*sqrt(Диагональ прямоугольника^2+(2*Площадь прямоугольника))
Периметр прямоугольника
Идти
Периметр прямоугольника = 2*(Длина прямоугольника+Ширина прямоугольника)
Периметр прямоугольника = (2*(Площадь прямоугольника+Длина прямоугольника^2))/Длина прямоугольника
Прямоугольник — это двумерная геометрическая фигура, имеющая четыре стороны и четыре угла. Share
Copied!
Тема урока: «Периметр прямоугольника» Цели урока: познакомить с понятием «периметр прямоугольника», совершенствовать вычислительные навыки и умения решать задачи, развивать умение рассуждать, сопоставлять, сравнивать. Планируемые результаты: — Предметные: учить находить периметр прямоугольника разными способами, развивать геометрические представления, совершенствовать умение решать текстовые задачи. — Личностные: определять личностный смысл изучения темы, применять новые знания на практике. Тип урока: изучение нового материала. Оборудование: учебник по Математике 2 класс 2 часть 2015 год; Программа «Школа России»; М.И. Моро, М.А.Бантова. № Этап урока Метод и приемы Хро-нометраж Содержание урока. Деятельность учителя. Деятельность ученика УУД 1. Включение в учебную деятельность Словес.: слово учителя. ≈ 3 Приветствие. (слайд 1 ) Давайте, ребята. Учиться считать, Делить, умножать, Прибавлять, вычитать. Запомните все, Что без точного счета Не сдвинется с места Любая работа. Чтение слов Меркушевича (слайд 2) Приветствовать учителя, настраиваться на работу. Р.: принимают и сохраняют уч. задачу. К.: участвуют в учебном диалоге; формулируют ответы и выводы; обмениваются мнениями; строят реч. 2. 3. 4 5. 6. 7. 8. 9. 10. Актуализация знаний Практич: устный счет. Практич.: логическая разминка Практич.: работа с фигурами. Самоопределение к деятельности Словес.: ответы на вопросы. Словес.: определение темы и цели урока. Практич: писм. задание. Практич.: нахождение периметра. Практич.: анализ и решение задачи. Практич: сам. Работа. Первичное усвоение новых знаний. Физминутка Включение нового в систему знаний. Сравнение с эталоном. Реализация построенного проекта Закрепление с проговариванием во внешней речи. Самостоятельная работа по повторению. Рефлексия 5 5 6 1 1 5 6 10 1 Устный счёт Запишите число, классная работа. — Прочитайте слова , расположив ответы в порядке возрастания 15-(6+5) (У) 17-(18-9) (Н) 4+8-7 (М) (90+5)-(43-40) (А) (46-40)+(58-8) (Ц) (3+8)+(12-6) (И) — Какие выражения можно заменить умножением? Почему? 3+3+3+3 а+а+а 5+5+4+4 а+в+а+в 7+5+3 — Расставьте вместо звездочек знаки + и – та, чтобы получилось верное равенство. 2*6*3*4*5*8=12 (2+6-3+4-5+8) Сегодня мы совершим ещё одно путешествие в страну Геометрия. Что означает это слово? Посмотрите на этот замок(слайд3) — Из каких геометрических фигур состоит замок? — На какие 2 группы можно разделить все эти фигуры?(многоугольники и круг) -Если круг убрать? — Как теперь можно разделить фигуры на 2 группы?(треугольники и четырехугольники) Если треугольники убрать. — Как назвать одним словом оставшиеся фигуры?(четырехугольники) — На какие 2 группы их можно разделить?(фигуры с прямыми и без прямых углов) — Какие фигуры остались?(прямоугольники) — Докажите, что оставшиеся фигуры-прямоугольники. — Сколько пар одинаковых сторон у прямоугольника?(2) — Что можно узнать, зная длину сторон прямоугольника? (периметр) -Давайте измерим стороны этого прямоугольника и найдём его периметр. ( Р= 5+11+5+11 (см)) -Можно ли эту сумму заменить произведением? — Как вы это определили? (если слагаемые одинаковые, то сложение можно заменить умножением) — Сколько произведений по ним можно составить?(2) — Тогда скажите, о чем мы с вами сегодня поговорим на уроке? — Какие цели поставим на уроке?(учиться находить периметр прямоугольника разными способами) (слайд 4) — Хорошо. — А теперь постройте у себя в тетрадях прямоугольник со сторонами 3 см и 6 см и подпишите длину его сторон. — Что такое периметр?(сумма длин всех сторон) -А сейчас мы в этом потренируемся. — Найдите периметр прямоугольника.(3+6+3+6=18(см)) — Это первый способ нахождения периметра прямоугольника. (слайд 5) — Сумму каких слагаемых можно заменить умножение?(3+3 и 6+6) — Замените. (3*2+6*2=18 (см)) — Это 2 способ нахождения периметра прямоугольника. Но можно по-другому записать это решение. — Посмотрите на свой прямоугольник. Сколько разных сторон у него?(2:длина и ширина) — Как эти стороны называются?(длина и ширина) — Запишите их сумму?(3+6) — Сколько раз в прямоугольнике повторяются эти стороны?(2) Учитель делает запись на доске, а учащиеся в тетрадях. (3+6)*2=18 (см) — Это 3 способ нахождения периметра. — Обозначим длину прямоугольника латинской буквой а, а ширину – буквой в. Поставим в наши решения. — Мы получили три формулы нахождения периметра прямоугольника. Р=а+в+а+в Р=а*2+в*2 Р=(а+в)*2 (слайд6) №1(стр.52)(слайд7) — Посмотрите, как находили периметр прямоугольника. — Совпадает ли решение с теми формулами, которые мы с вами только что вывели? №2(стр.52)(слайд 6) — Сколько способов нахождения периметра вы знаете? — Прочитайте условие. — Найдите самостоятельно периметр этого прямоугольника разными способами. 1)Нахождение периметра прямоугольника ( по эталону) Работа в тетради по вариантам. Найдите периметр прямоугольника по формуле: 1 вариант – Р=а+в+а+в 2 вариант – Р=а*2+в*2 2)Проверка по эталону. -Как найти периметр прямоугольника? -Для чего нужно находить периметр прямоугольника? -Людям каких профессий это необходимо? -Пользуются ли ваши родители нахождением периметра? №3 — Прочитайте условие задачи. — Что нужно узнать? №7 (Самостоятельное выполнение 1 группа -1 и 2 примеры, 2 группа – 3 и 4 примеры. (работа в группах) (слайд7) 82-46=36 37+58=95 49-38=11 65+35=100 Ребята, как вы думаете, пригодится ли нам в жизни знание формул периметра прямоугольника? Давайте мы ещё раз их запишем на доске и в тетрадях. Вычислять. Отвечать на вопросы. Доказывать. Определять тему, ставить цели. Отвечать на вопросы. Находить 2 способ нахождения периметра. Записывать решение в тетрадь. Находить 3 способ вычисления периметра. Находить периметр, записывать решение. Записывать решение задачи. Производить вычисления. Делать выводы, отвечать на вопросы. Р.: принимают и сохраняют уч. задачу при выполнении заданий; действуют с уче-том выделенных учителем ориентиров; применяют освоенные способы действия. К. : участвуют в учебном диалоге; формулируют ответы и выводы; обмениваются мнениями; строят реч. высказывания. К. : участвуют в учебном диалоге; формулируют ответы и выводы; обмениваются мнениями; строят реч. высказывания. . Р.: принимают и сохраняют уч. задачу при выполнении заданий; действуют с уче-том выделенных учителем ориентиров; применяют освоенные способы действия. К. : участвуют в учебном диалоге; формулируют ответы и выводы; обмениваются мнениями; строят реч. высказывания. П: извлекать необходимую информацию из текста учителя, ориентировать в системе знаний. Р.: осмысляют уч. материал; действуют с учетом выделенных учителем ориентиров 11. 12. Итог урока. (предметная). Словес.: ответы на вопросы, самоанализ Домашнее задание ≈1 1 — Чем мы с вами занимались на уроке? — Какие поставили в начале урока цели? — Достигли их? — Какое открытие мы сделали на уроке? — Оцените свою работу на уроке. (слайд 8) Домашнее задание с. 52 №4, 8 Повторить формулы нахождение периметра прямоугольника. (Слайд 9) Делать вывод, отвечать на вопросы. Записывать домашнее задание Р.: осмысляют уч. материал; действуют с учетом выделенных учителем ориентиров; адекватно воспринимают оценку учителя. Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/251217-perimetr-prjamougolnika-2-klass Геометрия Джесслин М. Подписаться Подробнее Отчет Автор:
Лучшие новыеСамые старые Уиз С.
ответил 28.08.19 Репетитор Новое в Византе Опытный и терпеливый репетитор по математике Смотрите таких репетиторов Смотрите таких репетиторов Периметр прямоугольника равен 30 футов. Ширина на 5 футов больше, чем длина. Какая ширина и длина? => ширина = w длина = l = w+5 2(l+w) =p 2(w+5+w) = 30 2(2w+5)=30 2w +5 =15 2w =10 w =5 ширина = w= 5 футов длина = l = w+5 =5+5 =10 футов Голосовать за 1 Понизить Подробнее Отчет Захари В. Репетитор 5,0
(134) Я физик, который хочет, чтобы все знали физику! Об этом репетиторе › Об этом репетиторе › Мы знаем, что периметр прямоугольника равен сумме всех сторон. У прямоугольника четыре стороны, но два набора одинаковых размеров. Таким образом, мы можем записать периметр (P) как сумму длин (L) и ширин (W), или: П = Д + Д + Ш + Ш = 2Л + 2Ш. Нам дали две части информации: 1. что периметр (P) прямоугольника составляет 30 футов, и 2. что ширина (W) на 5 футов больше, чем длина (L). Мы можем выразить эту информацию с помощью следующих двух уравнений: P = 2L + 2W = 30 футов W = L + 5 футов Теперь у нас есть два неизвестных. Мы не знаем ни длины (L), ни ширины (W) прямоугольника, но у нас есть два линейно независимых уравнения, то есть такое же количество неизвестных, что и у нас, поэтому мы можем найти ширину (W) и длина (L) прямоугольника. W = L + 5 футов 2L + 2W = 30 футов Используя уравнение W = L + 5 футов, мы можем подставить его в уравнение периметра и получить: 2L + 2(L + 5 футов) = 30 футов Теперь разделите обе части уравнения на 2: L + (L + 5 футов) = 15 футов Группировка общих терминов: 2L + 5 футов = 15 футов Вычитание 5 футов из обеих частей уравнения: 2L + 5 футов — 5 футов = 15 футов — 5 футов 2L = 10 футов И разделив обе стороны на 2, получим: L = 5 футов . Теперь, используя новое найденное значение L и соотношение W = L + 5 футов, мы можем найти ширину (W): W = (5 футов) + 5 футов W = 10 футов . Итак, мы нашли длину (L) и ширину (W) прямоугольника, и они равны: L = 5 футов W = 10 футов Голосовать за 0 Понизить Подробнее Отчет Все предметы Математика Литература Алгебра Русский язык Геометрия Английский язык Физика Биология Другие предметы История Обществознание Окружающий мир География Українська мова Информатика Українська література Қазақ тiлi Экономика Музыка Беларуская мова Французский язык Немецкий язык Психология Оʻzbek tili Кыргыз тили Астрономия Физкультура и спорт Вариант I Na + Cl2 → NaCl Al + Cl2 → А1С13 FeCl2 + Cl2 → FeCl3 С3Н6 + 02 → C02 + h30 Fe(OH)3 → Fe203 + Н20 Al + CuBr2 → АlBr3 + Сu Ca(OH)2 + Na3P04 → Ca3(P04)2 + NaOH К20 + Н20→ КОН N02 → NO + 02 В2Н6 + 02 → В2О3 + Н20 С5Н10 + 02→ С02 + Н20 Ответ дан Irinkaaaaaaaaaaa Ответ: 2Na+Cl2=2NaCl 2Al+3Cl2=2AlCl3 2FeCl2+Cl2=2FeCl3 2C3h3+9O2=6CO2+6h3O 2Cu+O2=2CuO 2Fe(OH)3=Fe2O3+3h3O 2Al+3CuBr2=2AlBr3+3Cu 3Ca(OH)2+2NA3PO4=Ca3(PO4)2+5NaOH K2O+h3O=2KOH 2NO2=2NO+O2 B2H6+3O2=B2O3+B2O3+3h3O 2C5h20+15O2=10CO2+10h3O Уравновешенные уравнения и химические реакции Существует четыре основных типа химических реакций. Na (т) + Cl 2 (г) NaCl (т) Реагенты находятся слева от стрелки, а продукт(ы) справа. Это может означать, что реагенты, натрий и хлор, будут реагировать с образованием одного продукта, хлорида натрия. В приведенном выше химическом уравнении (s) обозначает твердое вещество, а (g) обозначает газ, что указывает на то, в каком состоянии вещества находится вещество. Иногда стрелка читается как «урожайность». Глядя на это уравнение, возникает естественный вопрос: почему с одной стороны уравнения три атома, а с другой только два? Что случилось с лишним атомом хлора? Хороший вопрос. 2Na (т) + Cl 2 (г) 2NaCl (т) Это можно понять, сказав, что два атома натрия соединяются с одной двухатомной молекулой хлора, образуя две ионные единицы хлорида натрия. Другим аспектом химических реакций являются физические свойства соединений или то, как атомы и молекулы соединяются друг с другом. Если мы посмотрим на кристаллическую структуру NaCl, то заметим, что это плотно упакованный куб. Все реакции — это просто перераспределение материи более устойчивым образом. натрий + хлор → хлорид натрия 2 Na(т) + Cl 2 (г) 2 NaCl(т) 2 моля + 1 моль = 2 моля 2(23 а.е.м.) + 2(35 а.е.м.) = 2(58 а.е.м.) 46 а.е.м. + 70 а.е.м. = 116 а.е.м. 116 а.е.м. = 116 а.е.м. Используя атомные веса из таблицы Менделеева, вы можете увидеть, что два атома натрия весят 46 атомных единиц массы. Одна молекула хлора весит 70 атомных единиц массы. Две единицы кристалла хлорида натрия весят 116 атомных единиц массы. Суммарная масса реагентов должна равняться общей массе продукта. Натрий, очень активный металл, который вступает в реакцию с газообразным хлором с образованием хлорида натрия, нейтральной соли. Мы знаем, что натрий является очень активным металлом, а хлор также является очень активным неметаллом. Обычно металлы любят удалять электроны, а неметаллы, такие как галогены, любят принимать электроны. Натрий легко устраняет свои последние электроны оболочки, превращаясь в катион Na + , и хлор принимает это
электрон с образованием аниона Cl — . Na + Cl 2 → 2NaCl Два моля газообразного хлора реагируют с одним молем натрия с образованием двух молей хлорида натрия. Эту реакцию легче сбалансировать методом контроля, чем окислительно-восстановительным методом. Окислительно-восстановительный метод займет
много времени. Но это полезно для балансировки больших окислительно-восстановительных уравнений. Это очень простая окислительно-восстановительная реакция для балансировки, и если вы новичок в уравнениях балансировки, это также
хороший пример, чтобы начать балансировку окислительно-восстановительной реакции. Натрий окисляется от степени окисления 0 до степени окисления +1. Хлор восстанавливается до степени окисления -1.
от 0 степени окисления. Напишите степени окисления, если каждый атом близок к атомам. Проверить число атомов окисленного и восстановленного в реакции (левая и правая часть) и уравновесить их, если
они не сбалансированы, как следующий шаг. В левой части два атома хлора. Чтобы сбалансировать их, сделайте два
хлорида натрия справа. Тогда в правой части реакции два атома натрия, а в левой только один.
сторона. Следовательно, сделайте два атома натрия слева. Затем найдите разность степеней окисления окисленных атомов (натрий в ион натрия) и восстановленных атомов (хлор
к хлориду). Твердый реагент натрия реагирует с зелено-желтым газообразным хлором с образованием твердого хлорида натрия
который представляет собой белое кристаллическое твердое вещество. Эта реакция протекает с высокой скоростью, поскольку оба реагента очень реакционноспособны. Натрий – металл 1 группы,
любит удалять свои внешние электроны, а хлор хочет забирать электроны извне. Реакция натрия и хлора экзотермическая (в результате реакции выделяется тепло).
Энтальпию реакции принимают за энтальпию образования двух молей хлорида натрия. Стандартная энтальпия реакции = -411,12 кДж Энтропия реакции (298 0 Кл) = 72,10 Дж/(К моль) Проведем простой расчет. Вы собираетесь смешать 4 моля натрия и 2 моля газообразного хлора. Определение стандартной энтальпии образования хлорида натрия: При образовании 1 моль хлорида натрия наружу выделяется 411,120 кДж. При образовании 2 моль хлорида натрия наружу выделяется 411,120*2 кДж. Теперь вы знаете, что выделяемое тепло зависит от количества образовавшегося хлорида натрия. Теперь вам предстоит выяснить, сколько хлорида натрия вырабатывается в этом вопросе. По стехиометрии для реакции с 1 моль газообразного хлора требуется 2 моля натрия. Из-за этого для реакции с 2 молями газообразного хлора требуется 4 моля натрия, а в начале реакции имеется 4 моля. Если вы смешаете значительное количество газообразного хлора и натрия, вы увидите, что идет реакция, потому что реакционный стакан будет красного цвета из-за выделения большого количества тепла. Вопросы Когда натрий реагирует с газообразным хлором, в качестве продукта образуется хлорид натрия (NaCl). Да. Это реакция соединения, потому что два соединения соединяются вместе и дают одно соединение в качестве продукта. Во-первых, в какой фазе нужен хлорид натрия? Твердый или водный или жидкий NaCl? Вы должны планировать свой метод в соответствии с физическим состоянием хлорида натрия. Реакция натрия и хлора является прямым способом получения хлорида натрия, если вам нужен твердый NaCl. Во втором способе можно приготовить хлорид натрия в водном состоянии. Так что вам нужно удалить воду методом разделения, если вам нужен твердый хлорид натрия.
Если вам нужен водный раствор хлорида натрия, это лучший способ сделать это. Да. Калий реагирует с хлором с образованием хлорида калия. 2K + Cl 2 → 2KCl Натрий + газообразный хлор → хлорид натрия Литий реагирует с газообразным хлором так же, как и натрий. Таким образом, уравнение очень похоже на реакцию газообразного натрия и хлора. 2Li + Cl 2 → 2LiCl Да.
Если вы студент, особенно заочник, то вас наверняка заинтересуют готовые контрольные работы по информатике. В этом разделе их пока немного, но я постараюсь по мере возможности добавлять новые.
Информатика: Контрольная работа № 1
Информатика: Контрольная работа № 2
Информатика: Виды носителей информации. Хранение информации. Реферат.
Информационные технологии. Программная анимация в ADOBE FLASH CS3 PROFESSIONAL
Теперь, когда вы ознакомились со списком готовых контрольных работ по информатике, скажу ещё пару-тройку слов по этой теме.
Сначала хочу обратить ваше внимание на то, что все эти контрольные сделаны лично мной. Некоторые во времена моей учёбы в университете (то есть это реальные контрольные, которые я сдавал, причём успешно). Ну а некоторые сделаны уже позже исключительно для помощи студентам (кто-то попросил помочь, кому-то сделал за деньги — и такое бывало).
Сам я учился заочно и нисколько об этом не пожалел. Хотя бытует мнение, что заочное обучение — это ничто. Я с этим, конечно, не согласен. На момент написания этой статьи я работаю руководителем инженерного отдела, и мне приходится принимать на работу, в том числе, и студентов очников. И, скажу я вам — их разум — это чистое поле. Даже не засеянное.
Так что для того, чтобы из такого очника сделать хоть какого-то специалиста, мне надо ещё минимум года три. Так что имеет значение не то, на какой форме обучения и где вы учились, а то — как вы учились.
Что касается информатики, то это очень интересная тема. Я уже написал об этом немало статей. Сегодня информатика применяется везде, в любой сфере деятельности. И, если вы плохо знаете информатику, то хорошим специалистом вы не станете.
Так что контрольные, конечно, скачивайте — для этого они здесь и выложены. Но я всё-таки рекомендую их использовать только как примеры. А выполнять задания именно ваших контрольных надо всё-таки самостоятельно.
Удачи на экзаменах!
Никто не будет спорить, что информатика – очень важная учебная дисциплина, без базовых знаний в которой практически невозможно найти работу. А чтобы найти хорошую работу, нужно для начала хорошо писать контрольные. Поговорим о том, как эффективно подготовиться к контрольной по информатике. Подпишитесь на наш телеграм, чтобы регулярно получать полезную рассылку. А если хотите сделать заказ со скидкой – обязательно прочекайте акции для клиентов на нашем втором канале. Даже если ваша специальность очень отдаленно связана с компьютерами, контрольную по информатике все равно писать придется. В зависимости от учебной программы это может быть большая итоговая контрольная по курсу «Информатика», либо промежуточный контроль знаний. Чаще всего контрольная по информатике имеет практический характер. Например, нужно перевести число из двоичного кода в десятичный, написать небольшую программу в Pascal или Delphi и объяснить, как она работает. Если вы проходите информатику лишь поверхностно, на котрольной работе могут быть задания на знание базовых программ, таких как Word, Excel, Power Point. Так, вас могут попросить нарисовать рамку в ворде или подготовить презентацию. Также контрольная по информатике может быть в виде проверочного онлайн-теста. Контрольная по информатике для заочников чаще бывает в виде теоретического реферата, но к ней в приложениях все равно нужно прикрепять листинг написанных программ или скриншоты выполненных заданий. Подготовка к контрольной работе по информатике не вызывает затруднений, если вы внимательно слушали преподавателя и читали учебник. Но даже если это не так, вы можете подготовиться к контрольной и самостоятельно. Например, если вы знаете, что вам предстоит решать контрольную по информатике, установите на свой ноутбук нужные программы и потренируйтесь выполнять типовые задачи дома. Чтобы итоговый балл не снизили, внимание нужно уделить не только правильности решения, но и оформлению. В контрольной все должно быть оформлено по госту: Чтобы вы не мучались, мы подготовили для вас подробный гайд по оформлению конрольных. С его помощью вы сможете оформить любую контрольную по ГОСТу. Нужна помощь в выполнении контрольных? Обратитесь за ней к специалистам профессионального сервиса для студентов. Автор:
Иван Иван Колобков, известный также как Джони. С появлением больших данных и увеличением числа людей, имеющих медицинскую страховку, возрастает потребность в систематизации и анализе медицинской информации. В результате карьера в области информатики здравоохранения растет. В области информатики здравоохранения существует множество карьерных возможностей: от специалиста по информатике в области здравоохранения и медсестры-информатика до должности менеджера по информатике и директора. Ознакомьтесь со списком профессий в области информатики здравоохранения, навыками, необходимыми для информатики здравоохранения, и ожидаемой заработной платой ниже. Специалист по информатике в области здравоохранения — это профессия, которая фокусируется на сборе, передаче и использовании медицинской информации в различных медицинских учреждениях. Благодаря переходу на электронные медицинские карты, установленному федеральным законодательством, карьерный путь специалиста по информатике в области здравоохранения является многообещающим. Вы можете начать с младшей степени в области информатики в области здравоохранения, чтобы подготовить вас к должности начального уровня в качестве медицинского работника или специалиста по информатике. Как правило, степень бакалавра необходима для управленческих должностей, таких как менеджер информационных систем. По мере роста вашего опыта и образования вы сможете подняться до должности аналитика медицинской информации, собирая и интерпретируя данные из различных источников. Более высокие степени, такие как магистр медицинской информатики , могут подготовить вас к руководящей роли в этой профессии. Специалист по информатике в области здравоохранения является ценным сотрудником в самых разных учреждениях здравоохранения, от больниц и исследовательских центров до консультантов. Те, у кого есть опыт работы в сфере здравоохранения, например медсестры, могут быть лучше подготовлены к руководящим должностям в этой развивающейся области. Специалисты по информатике в области здравоохранения взаимодействуют с врачами, медсестрами, специалистами и ИТ-специалистами. Ежедневные обязанности специалистов по информатике различаются, но большинство из них будут включать сбор и анализ данных, разработку рабочих процессов, измерение воздействия, обучение и обучение конечных пользователей, управление системами и управление дискуссиями между конечными пользователями и разработчиками программного обеспечения. Некоторые из наиболее распространенных навыков в области информатики здравоохранения включают решение проблем и общение. Вас могут попросить разработать новые инструменты для сбора и анализа данных, которые помогут старшим администраторам здравоохранения и поставщикам медицинских услуг принимать стратегические решения. Консультант по информатике в области здравоохранения работает с организацией здравоохранения, чтобы обеспечить соблюдение федеральных правил, обучает и поддерживает персонал в области технологий и процедур, а также поддерживает связь на нескольких уровнях организации. Люди с этим титулом могут работать полный рабочий день на работодателя или могут работать в консалтинговом агентстве с различными клиентами. Как правило, степень бакалавра является минимумом, необходимым для работы в роли консультанта. Специалисты по клинической информатике обычно имеют степень бакалавра и некоторый клинический опыт. Если у вас уже есть степень бакалавра, при подаче заявления вы можете рассмотреть возможность получения степени магистра в области медицинской информатики, поскольку обычно предпочтение отдается степени магистра (PDF, 910 КБ) от работодателей. Область сестринской информатики охватывает сестринское дело, информатику и информатику для поддержки практики сестринского дела. Организации здравоохранения обращаются к медсестрам-информатикам для управления клиническими результатами и повышения экономической эффективности. После завершения программы информатики для медсестер вы будете готовы обрабатывать сложную медицинскую информацию в больницах, домах престарелых, фирмах общественного здравоохранения и исследовательских лабораториях. Эта карьера, как правило, для тех, кто уже является медсестрой. Специалист по информатике аптек использует медицинские знания и информационные технологии для улучшения результатов лечения пациентов. Новые технологии, такие как электронные медицинские записи и компьютеризированный ввод рецептов, заменяют бумажные записи в аптечной практике, открывая двери для более тесного сотрудничества с врачами. В области общественного здравоохранения специалисты в области информатики обеспечивают эффективное принятие решений, связывая и интерпретируя данные для практикующих врачей. Расширяя возможности профилактики заболеваний и вмешательства, информатика общественного здравоохранения ведет к улучшению здоровья сообществ и отдельных лиц. Поскольку информатика здравоохранения сочетает в себе технологии и медицину, специалисты должны развивать ряд навыков от программирования до управления, чтобы быть более конкурентоспособными на должностях в области информатики здравоохранения. Некоторые люди начинают с клинической подготовки и проходят обучение информационным технологиям. Другие начинают с противоположного направления, добавляя медицинское образование к своему опыту в области ИТ. Помимо знаний в области здравоохранения, некоторые общие навыки, необходимые, если вы хотите продолжить карьеру в области информатики здравоохранения, могут включать: Знание систем данных о здоровье: Специалисты в области информатики здравоохранения анализируют, разрабатывают, оценивают, тестируют и поддерживают системы данных о здоровье. Знание программирования: Хотя не все специалисты по информатике уделяют время программированию, многие должности требуют знания ряда компьютерных языков. Например, вам могут пригодиться Java, Python, C, SQL и другие языки для создания баз данных и управления ими. Навыки анализа данных: Специалист может также создавать диаграммы, графики и презентации для информирования менеджеров и практиков о результатах и тенденциях, основанных на данных. Некоторые навыки анализа данных в Excel или Tableau могут быть полезны для визуализации этих результатов. Самостоятельное решение проблем : Поддерживая систему здравоохранения и работая с большими данными, специалисты могут решать множество неожиданных задач, от защиты данных до обслуживания систем. Способность решать проблемы помогает профессионалам находить решения, отвечающие потребностям всех заинтересованных сторон. Навыки общения и сотрудничества: Эти навыки являются одними из наиболее ценных для специалистов по информатике в области здравоохранения, поскольку они взаимодействуют с людьми из разных слоев своей организации, а также с группами заинтересованных сторон. Возможность извлекать выводы из сложной информации с помощью навыков управления данными так же важна, как и донесение этих выводов до заинтересованных сторон. Поскольку отрасль продолжает внедрять требования к ведению электронной документации, карьерные перспективы специалистов по информатике в здравоохранении будут благоприятными до середины 2020-х годов. Средняя заработная плата варьируется от 45 240 долларов США в год для специалистов по медицинской документации и медицинской информации, которым обычно требуется диплом о высшем образовании, до 126 830 долларов США для ученых, занимающихся компьютерными и информационными исследованиями, со степенью магистра, согласно данным Бюро статистики труда за май 2020 года ( БЛС). Ожидается, что к 2030 году количество рабочих мест для специалистов по медицинской документации и медицинской информации увеличится на 9%, а количество рабочих мест для ученых, занимающихся компьютерными и информационными исследованиями, вырастет на 22%. Кабинет врача: Поставщики медицинских услуг должны защищать данные пациентов, а также собирать и анализировать данные для улучшения результатов в отношении здоровья. В зависимости от размера практики вы можете работать полный рабочий день или в качестве консультанта. Специализированная практика: Медицинские специальности полагаются на точные, легкодоступные записи пациентов для эффективного оказания помощи. Ваша аналитика данных может улучшить результаты лечения пациентов и повысить качество жизни многих людей. Аптека: Данные — это источник жизненной силы аптеки, а информатика позволяет аптеке безопасно и эффективно взаимодействовать с другими поставщиками медицинских услуг. Больница: Менеджеры здравоохранения регулярно сверяются с данными, чтобы принимать клинические и коммерческие решения, и они полагаются на специалистов по информатике для беспрепятственного предоставления информации. Часто специалисты по информатике общаются через ведомственные барьеры из-за междисциплинарного характера области. Агентство общественного здравоохранения: Вы можете сотрудничать с агентствами, чтобы улучшить показатели здоровья неблагополучных слоев населения или помочь справиться со вспышками заболеваний. ИТ-консультант: Консультанты работают с клиентами над внедрением и улучшением их программ в области информатики. Вы можете помочь решить проблемы в больнице или установить новую систему в медицинской практике. Существует множество профессий в области информатики здравоохранения, где студенты могут сочетать здравоохранение с технологиями для эффективного улучшения результатов лечения пациентов. Информация последний раз обновлялась в сентябре 2021 г. Специалисты клинической информатики работают с информационными технологиями в здравоохранении. Их цель — повысить качество оказания помощи пациентам путем анализа информации, собираемой организациями здравоохранения. Специалисты по клинической информатике необходимы для позитивных преобразований в сфере здравоохранения. Хотя у них много ролей, они сосредоточены на улучшении ухода за пациентами, улучшении результатов в отношении здоровья и укреплении отношений между врачом и пациентом. Те, кто увлечен здравоохранением и улучшением медицинского обслуживания, найдут эту карьеру чрезвычайно полезной. Специалисты по клинической информатике работают с данными в клиниках. Они часто имеют опыт работы как в области здравоохранения, так и в области клинической информатики. Они тесно сотрудничают с системами ввода данных и хранения визуальных изображений для сбора информации о существующих практиках. Они также обучают персонал тому, как использовать системы данных, создавать интерфейсы и устранять неполадки в программном обеспечении. Во многих случаях они начинают работать медсестрами в системе здравоохранения. Наблюдая и понимая клинический рабочий процесс, терминологию и медицинскую практику, медсестры могут применить свои знания, чтобы стать специалистами в области клинической информатики. Не все из них начинают работать медицинскими работниками. Некоторые специалисты переходят на эту должность, имея опыт работы в информационных системах (ИТ), потому что эта должность требует обширных знаний о данных и методах кодирования. Им потребуется опыт работы в области здравоохранения и данных, а также степень магистра в области клинической информатики. Это не входная позиция и требует опыта работы в различных областях. Узнайте о вариантах получения степени Специалисты по клинической информатике управляют информационными технологиями в здравоохранении. Они являются мостом между клиницистами и данными. Типичный день специалиста по клинической информатике может включать: Большую часть их работы составляет общение. Они также несут ответственность за программы устранения неполадок, чтобы гарантировать, что все будет работать максимально гладко в течение дня. Специалисты по клинической информатике играют важную роль в принятии решений, связанных с ИТ, вместе с руководством больницы. Они представят данные и обсудят, какую пользу новые системы принесут как пациентам, так и сотрудникам больницы. Специалисты по клинической информатике должны иметь опыт работы в области здравоохранения или информационных технологий, чтобы их рассматривали на должность в медицинском учреждении. Для многих рабочих мест требуется только степень бакалавра в области управления медицинской информацией. Эта степень даст вам важные знания и полномочия как в области здравоохранения, так и в области данных, а также в том, как они связаны. Для нынешних медсестер, которые хотят расширить свои карьерные возможности, идеально подойдет MSN с упором на информатику для медсестер. Эта степень идеально подходит для тех, кто имеет опыт работы в области здравоохранения и хочет перейти в область информатики. MSN в области информатики для медсестер будет уделять больше внимания анализу данных, моделированию и пониманию систем управления. Эти навыки будут иметь ключевое значение, помогая вам продвигаться вперед в роли клинической информатики. Сертификаты могут выступать в качестве подтверждения третьей стороной, чтобы показать, что кандидат на работу обладает навыками, которые ищет работодатель. Во многих случаях наличие сертификата помогает подтвердить навыки кандидата и выделить его среди конкурентов. Некоторые полезные сертификаты включают: Экзамен RHIA рекомендуется лицам со степенью бакалавра, которые заинтересованы в управлении медицинской информацией пациентов. Сертификация представляет собой четырехчасовой экзамен со 180 вопросами с несколькими вариантами ответов и должна продлеваться каждые три года. Экзамен RHIA сдают около 71 % тестировщиков, впервые пришедших на тест. Те, кто сдает экзамен CAHIMS, должны иметь как минимум аттестат о среднем образовании и не менее 45 часов непрерывного образования в области медицинских информационных технологий или цифрового здравоохранения. Эта сертификация предназначена для тех, кому не хватает опыта и подготовки, но они стремятся их получить. CAHIMS — это двухчасовой тест со 115 вопросами с несколькими вариантами ответов, который необходимо продлевать каждые три года. Программа для будущих лидеров HIM:… Программа для будущих лидеров HIM:… Программа для будущих лидеров HIM: Некоторые профессии и рабочие места, к которым вас подготовит эта степень: 9 Сравните с B.S. Бизнес – Управление здравоохранением Программа обучения медсестер, которая расширяет возможности медсестер, работающих с данными, которые… Программа обучения медсестер, которая расширяет возможности… Программа обучения медсестер, которая расширяет возможности медсестер, работающих на основе данных, которые уже имеют BSN, но стремятся к успеху, который может принести только степень магистра: Некоторые профессии и рабочие места, к которым вас подготовит эта степень: Развитие данных и информатики в здравоохранении будет постоянно открывать возможности для медсестер, выбравших этот путь. Программа медсестер, позволяющая медсестрам, работающим на данных, перейти от RN… их BSN по пути: Некоторые профессии и рабочие места, к которым вас подготовит эта степень: Развитие данных и информатики в здравоохранении будет постоянно открывать возможности для дипломированных медсестер, выбравших этот путь. Следующая дата начала Начните 1-го числа любого месяца — как только вы завершите регистрацию! Узнайте о поступлении в колледж через Интернет в WGU. В WGU есть множество вариантов получения степени. Специалист в области клинической информатики или информации должен обладать рядом качеств и навыков, которые помогут ему преуспеть в быстро меняющейся среде. Некоторые из наиболее важных навыков включают: Специалисты по клинической информации должны быть профессионалами как в сфере здравоохранения, так и в мире информационных технологий. Дополнительные навыки, такие как моделирование и анализ данных, необходимы для успешной карьеры. Специалисты по клинической информатике получают среднюю зарплату 80 306 долларов в год, примерно 38 долларов в час. Заработная плата варьируется в зависимости от штата, опыта и уровня образования. Например, специалист по клинической информации со степенью бакалавра, скорее всего, заработает меньше, чем человек со степенью магистра. Лучшие 10% специалистов по клинической информации могут зарабатывать более 100 000 долларов в год, а нижние 10 % — менее 60 000 долларов в год. Бюро статистики труда США предполагает, что к 2031 году количество рабочих мест для техников медицинской информации вырастет на 8%, что выше, чем в среднем по стране. Население Соединенных Штатов продолжает стареть по мере увеличения продолжительности жизни и снижения рождаемости. Бюро переписи населения США прогнозирует, что к 2035 году пожилых людей будет больше, чем детей. Стареющее население нуждается в большем количестве медицинских услуг, и для улучшения ухода потребуется большее количество специалистов по клинической информации. Специалисты по клинической информатике работают в медицинских учреждениях, чтобы улучшить впечатления каждого пациента, входящего в здание. Однако это не означает, что они ограничены больницами и отделениями неотложной помощи. Специалисты по клинической информатике могут работать во многих учреждениях, таких как: Больницы: большие и малые больницы в значительной степени полагаются на специалистов-клиницистов для предоставления новых идей и систем. Они играют большую роль в сокращении больничных расходов и делают поездки в больницу более приятными для пациентов. Частная практика. Частная практика помогает пациентам в меньшем масштабе, но ее влияние не менее важно. Клинические специалисты могут помочь небольшим клиникам улучшить уход за пациентами. Учреждения по уходу: Учреждения по уходу отвечают за помощь пожилым людям, бездомным или тем, кто не может позаботиться о себе. Этим учреждениям нужны клинические специалисты для обеспечения бесперебойной работы систем. Американская ассоциация медицинской информатики (AMIA) определяет клиническую информатику как «применение информатики и информационных технологий для оказания медицинских услуг». Чтобы получить работу специалиста по клинической информатике, вам потребуется опыт работы в области ИТ или здравоохранения и, как правило, степень бакалавра. Также полезно, если ваша степень бакалавра связана с управлением медицинской информацией, так как это требуется для многих профессий. Средняя общенациональная зарплата медсестер информатики составляет 77 971 долларов США.
Сократить дробь онлайн калькулятор с буквами: Калькулятор для сокращения дробей
Сокращение дробей с буквами. Выполнение сокращения дробей
Понятие алгебраической дроби
 Допускается запись дробного выражения в качестве математической операции «Деление». В таком случае числитель — делимое, знаменатель — делитель.
Допускается запись дробного выражения в качестве математической операции «Деление». В таком случае числитель — делимое, знаменатель — делитель.Основное правило обыкновенных дробей
Математические операции с дробями
 Если нужно перемножить две дроби, сложить их, разделить одну на другую или произвести вычитание, нужно всегда придерживаться правил.
Если нужно перемножить две дроби, сложить их, разделить одну на другую или произвести вычитание, нужно всегда придерживаться правил.
Несколько примеров с решениями

Смысл сокращения алгебраической дроби

Все ли алгебраические дроби подлежат сокращению?
 Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.
Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.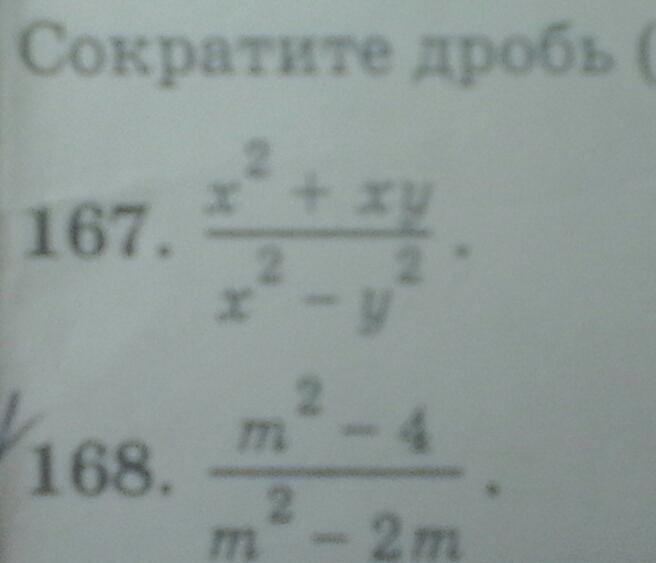 При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.
При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.Правило сокращения алгебраических дробей
 Вторым шагом – выполняем сокращение, т.е. переход к дроби вида a b .
Вторым шагом – выполняем сокращение, т.е. переход к дроби вида a b .Характерные примеры
 Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:
Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:
 е. на НОК (5 , 10) = 10 . Тогда получим:
е. на НОК (5 , 10) = 10 . Тогда получим: Произведем сокращение:
Произведем сокращение: Вынесем за скобки множитель х в числителе:
Вынесем за скобки множитель х в числителе:
 От a⁷ после сокращения остается a⁵.
От a⁷ после сокращения остается a⁵. В знаменателе — формула разности кубов:
В знаменателе — формула разности кубов:Что значит сократить алгебраическую дробь?
 Например, обыкновенную дробь 30/54
можно сократить на 6
(то есть, разделить на 6
ее числитель и знаменатель), что приведет нас к дроби 5/9
.
Например, обыкновенную дробь 30/54
можно сократить на 6
(то есть, разделить на 6
ее числитель и знаменатель), что приведет нас к дроби 5/9
.Любая ли алгебраическая дробь подлежит сокращению?
 Несократимые дроби не имеют отличных от единицы общих множителей в числителе и знаменателе, следовательно, не подлежат сокращению.
Несократимые дроби не имеют отличных от единицы общих множителей в числителе и знаменателе, следовательно, не подлежат сокращению. А алгебраическую дробь сократить невозможно, так как ее числитель и знаменатель не имеют общих множителей.
А алгебраическую дробь сократить невозможно, так как ее числитель и знаменатель не имеют общих множителей.Правило сокращения алгебраических дробей


Характерные примеры
и т.п.
 В этом случае имеем .
В этом случае имеем .

 Проверим признак делимости чисел 189 и 294 на 3 .
Проверим признак делимости чисел 189 и 294 на 3 . Упрощение дробей
Упрощение дробей Дробь в упрощенную таблицу дробей
Дробь Упрощенный
Дробь 1/2 1/2 1/3 1/3 2/3 2/3 1/4 1/4 2/4 1/2 3/4 3/4 1/5 1/5 2/5 2/5 3/5 3/5 4/5 4/5 1/6 1/6 2/6 1/3 3/6 1/2 4/6 2/3 5/6 5/6 1/7 1/7 2/7 2/7 3/7 3/7 4/7 4/7 5/7 5/7 6/7 6/7 1/8 1/8 2/8 1/4 3/8 3/8 4/8 1/2 5/8 5/8 6/8 3/4 7/8 7/8 1/9 1/9 2/9 2/9 3/9 1/3 4/9 4/9 5/9 5/9 6/9 2/3 7/9 7/9 8/9 8/9 1/10 1/10 2/10 1/5 3/10 3/10 4/10 2/5 5/10 1/2 6/10 3/5 7/10 7/10 8/10 4/5 9/10 9/10 См.
 также
также Напишите, как улучшить эту страницу
МАТЕМАТИЧЕСКИЕ КАЛЬКУЛЯТОРЫ
RAPID TABLES
Как делать дроби на калькуляторе iPhone двумя способами

 Запустите приложение «Калькулятор», расположенное на вашем iPhone.
Запустите приложение «Калькулятор», расположенное на вашем iPhone.
Как изменить сеть Wi-Fi в Центре управления на iPhone с iOS 13
Как поделиться паролем Wi-Fi или получить его на iPhone несколькими нажатиями и присоединиться к новой сети Wi-Fi.

Nacl h2so4 kmno4: KMnO4 + NaCl + H2SO4 = Cl2 + . — Спрашивалка
Zn+NaAsO2+HCl=ZnCl2+NaCl+Ash4+h3O ; K2MnO4+h3SO4=MnO2+K2SO4+KMnO4+h3O; C6h5(OH)2+J2+KOH=KJ+h3O+C6h5O2 ОВР,методом электронного баланса(по целым веществам, например,AsO2 и — вопрос №3496271
Ответы
Ирина Владимировна
30.  10.19
10.19
Михаил Александров
Читать ответы
Андрей Андреевич

Читать ответы
Eleonora Gabrielyan

Читать ответы
Похожие вопросы  Относительная плотность вещества по воздухуравна 1,52. Определите молекулярную формулу этого вещест
Относительная плотность вещества по воздухуравна 1,52. Определите молекулярную формулу этого вещестчто, как сбалансировать и часто задаваемые вопросы —

1. Чему равно произведение H
2SO4 и KMnO4?
между Н2SO4 и KMnO42. Какой тип реакции Н
2SO4 + КМnО4?3. Как сбалансировать H
2SO4 + КМnО4?4.
 Ч2SO4 + КМnО4 титрование
Ч2SO4 + КМnО4 титрованиеИспользуемый аппарат
Титр и титрант
Индикаторные
Процедура
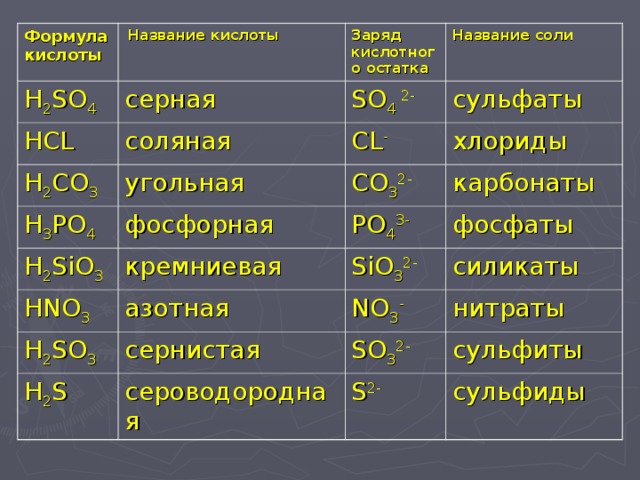 H2SO4 добавляют по каплям в коническую колбу и колбу постоянно встряхивают. Через определенное время, когда конечная точка прибыла KMnO4 меняет свой цвет.
H2SO4 добавляют по каплям в коническую колбу и колбу постоянно встряхивают. Через определенное время, когда конечная точка прибыла KMnO4 меняет свой цвет.5. Ч
2SO4+ КМnО4 чистое ионное уравнение
6. Ч
2SO4+ КМnО4 сопряженные пары7. Ч
2SO4 и KMnO4 межмолекулярные силы Для КМnО4 это ионное взаимодействие, а для MnSO4 и K2SO4 ионное взаимодействие связано с кулоновской силой. Н-связь присутствует в воде, а сила Ван-дер-Ваальса действует в O.2 молекулы.
Для КМnО4 это ионное взаимодействие, а для MnSO4 и K2SO4 ионное взаимодействие связано с кулоновской силой. Н-связь присутствует в воде, а сила Ван-дер-Ваальса действует в O.2 молекулы.
Межмолекулярные силымолекула и.о.
силаH2SO4 электростатический,
Ван дер Вааль
Диполь
взаимодействиеКМnО4 Ионные, металлические и
электростатическийK2SO4 / МнSO4 Кулоновская сила,
сильное ионное взаимодействиеH2O ковалентный,
Н-связьO2 Сила Ван-дер-Ваала,
Лондонская сила8.
 ЧАС2SO4 + КМnО4 энтальпия реакции
ЧАС2SO4 + КМnО4 энтальпия реакции
Энтальпия реагентовмолекула энтальпия
(кДж/моль)KMnO4 -813 H2SO4 -814 MnSO4 -1130 K2SO4 -1437.8 H2O -68 O2 0
и продукты9.
 Н2SO4 + КМnО4 буферный раствор?
Н2SO4 + КМnО4 буферный раствор?10. Н
2SO4 + КМnО4 полная реакция?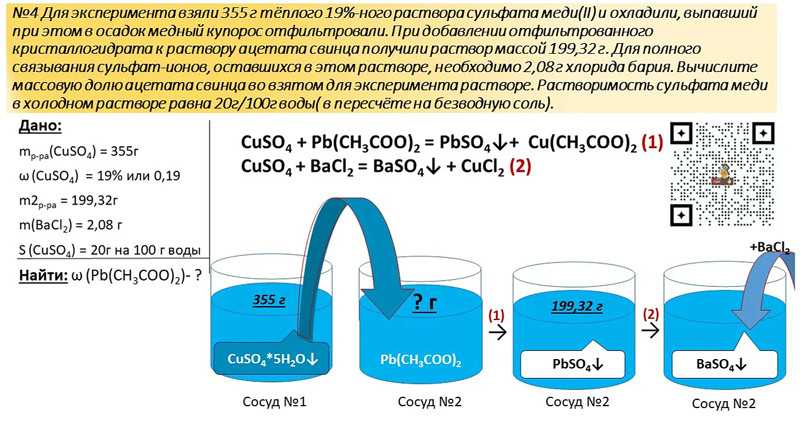
12. Н
2SO4 + КМnО4 окислительно-восстановительная реакция?
H2SO4 и KMnO4 реакция13. Н
2SO4 + КМnО4 реакция осаждения14. Н
2SO4 + КМnО4 обратимая или необратимая реакция?
15. Н
2SO4 + КМnО4 реакция смещения?Заключение
NaCl + KMnO4 + h3SO4 = Cl2 + MnSO4 + Na2SO4 + K2SO4 + h3O
 Туба для обучения
Химическая реакция
0
Туба для обучения
Химическая реакция
0 2KMnO
4 + 10NaCl+ 8H 2 SO 4 = 5Cl 2 + 2MnSO 4 + 5Na 2 SO 4 + K 2 SO 4 + 8H 2 O Реакция хлорида натрия с перманганатом калия и серной кислотой
 Потому что ионно-электронный метод — самый популярный и простой способ уравновесить окислительно-восстановительную реакцию. Для этого мы должны принять во внимание скелетную формулу реакции. что такое-
Потому что ионно-электронный метод — самый популярный и простой способ уравновесить окислительно-восстановительную реакцию. Для этого мы должны принять во внимание скелетную формулу реакции. что такое- NaCl + KMnO4 + h3SO4 = Cl2
+ MnSO4+ Na2SO4 + K2SO4+ h3O или,
NaCl + KMnO
4 + H 2 SO 4 = Cl 2 + MnSO 4 + Na 2 SO 4 + K 2 SO 4 + H 2 O Половина реакции восстановления
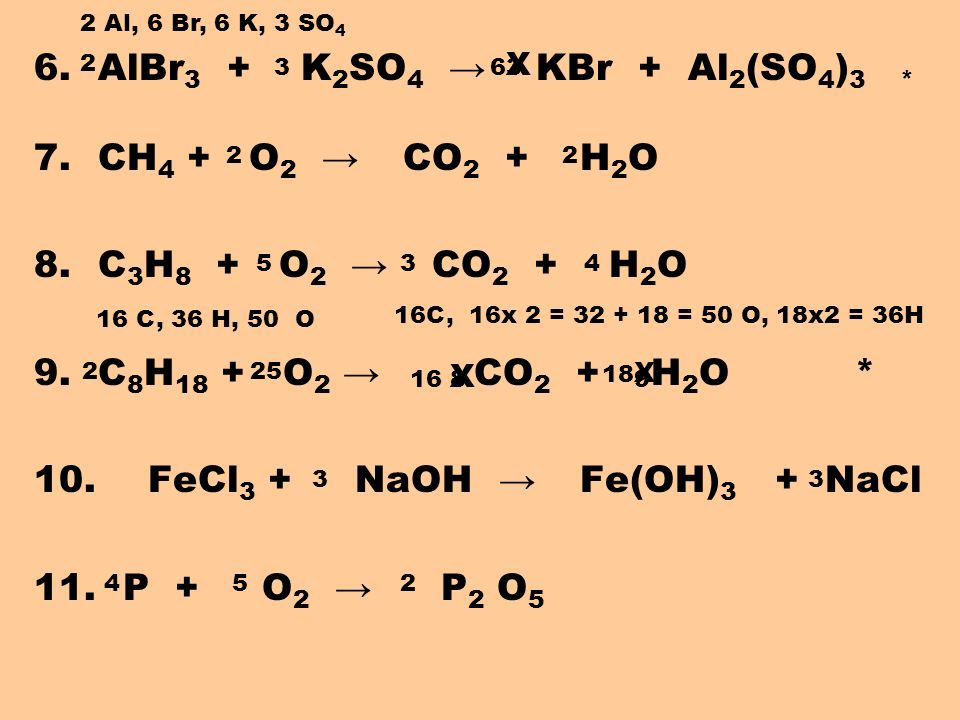 Потому что окисление и восстановление — одновременные процессы. В этой реакции Mn принимает 5 электронов, и степень окисления становится +2 с +7. Таким образом, восстановительная полуреакция для приведенной выше окислительно-восстановительной реакции выглядит следующим образом:0007
Потому что окисление и восстановление — одновременные процессы. В этой реакции Mn принимает 5 электронов, и степень окисления становится +2 с +7. Таким образом, восстановительная полуреакция для приведенной выше окислительно-восстановительной реакции выглядит следующим образом:0007 Полуреакция окисления
 Поскольку окислитель забирает 5 электронов из реакции, но есть только один вид, который не принимает более одного электрона. По этой причине для восстановления одного окислителя требуется пять восстановителей. Теперь сделаем так-
Поскольку окислитель забирает 5 электронов из реакции, но есть только один вид, который не принимает более одного электрона. По этой причине для восстановления одного окислителя требуется пять восстановителей. Теперь сделаем так- «Ответ»
⇒ 2KMnO
4 + 10NaCl+ 8H 2 SO 4 = 5Cl 2 + 2MnSO 4 + 5Na 2 SO 4 + 8H 2 O + K 2 SO 4  Надеюсь, что эта статья была полезна для вашего обучения. Если вы считаете, что мы делаем отличную работу, подпишитесь на нас и поделитесь статьей с друзьями.
Надеюсь, что эта статья была полезна для вашего обучения. Если вы считаете, что мы делаем отличную работу, подпишитесь на нас и поделитесь статьей с друзьями. h3so4+kmno4+nacl → cl2+h3o+mnso4+na2so4+k2so4Tất cả phương trình điều chế từ h3so4+kmno4+nacl ra cl2+h3o+mnso4+na2so4+k2so4
h3so4+kmno4+nacl → cl2+h3o+mnso4+na2so4+k2so4Tất cả phương trình điều chế từ h3so4+kmno4+nacl ra cl2+h3o+mnso4+na2so4+k2so4 org/ListItem»> Транг чо
Hãy nhập vào chất tham gia hoặc/và chất sản phẩm để bắt đầu tìm kiem Тим Ким Нхом Хок Мьен Пхи Онлайн Facebook Lưu ý: mỗi chất cách nhau 1 khoảng trắng, ví dụ: h3 O2 Tổng hợp đầy đủ và chi tiết nhất can bằng phương trình điều chế từ h3so4+kmno4+nacl ra cl2+h3o+mnso4+na2so4+k2so4. Đầy đủ trạng thai, máu sắc chất và tính số mol trong phản ứng hóa học.

Периметр прямоугольника это что: Периметр — урок. Математика, 2 класс.
Периметр прямоугольника с заданной площадью и длиной Калькулятор
 ⓘ Длина прямоугольника [l]
ⓘ Длина прямоугольника [l]
 ⓘ Периметр прямоугольника с заданной площадью и длиной [P]
ⓘ Периметр прямоугольника с заданной площадью и длиной [P]
Периметр прямоугольника с заданной площадью и длиной Решение
 Преобразование входов в базовый блок
Преобразование входов в базовый блок
Длина прямоугольника: 8 метр —> 8 метр Конверсия не требуется
<
25 Периметр прямоугольника Калькуляторы
<
6 Периметр прямоугольника Калькуляторы
Периметр прямоугольника с заданной площадью и длиной формула
P = (2*(A+l^2))/l
Что такое прямоугольник?
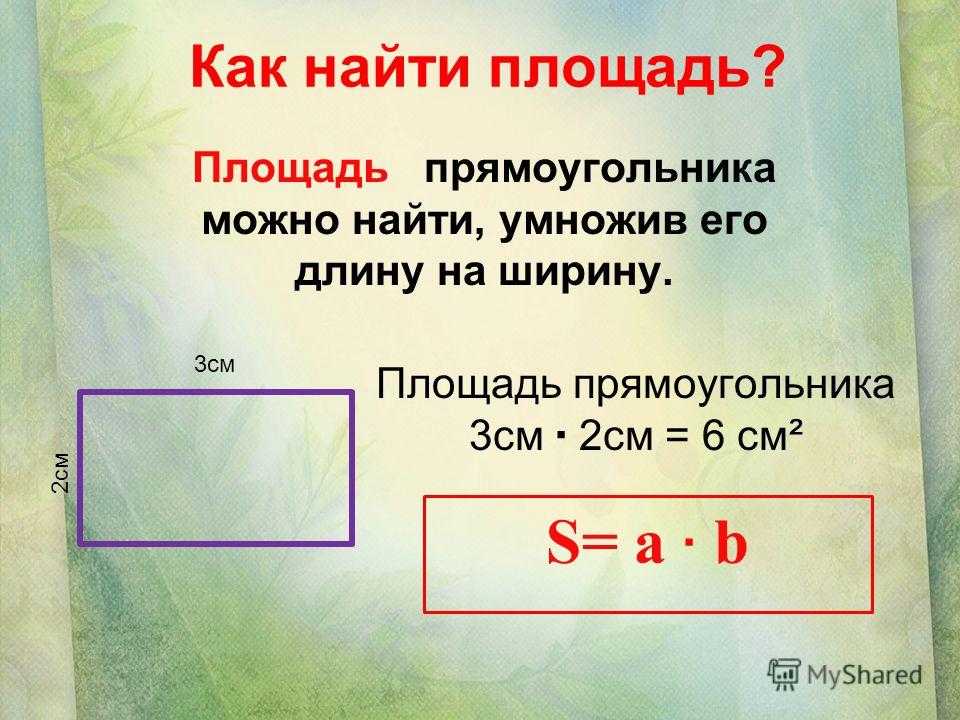 Четыре стороны разделены на две пары, в которых каждая пара линий равна по длине и параллельна друг другу. А соседние стороны перпендикулярны друг другу. Обычно двумерные фигуры с четырьмя граничными ребрами называются четырехугольниками. Итак, прямоугольник — это четырехугольник, у которого все углы прямые.
Четыре стороны разделены на две пары, в которых каждая пара линий равна по длине и параллельна друг другу. А соседние стороны перпендикулярны друг другу. Обычно двумерные фигуры с четырьмя граничными ребрами называются четырехугольниками. Итак, прямоугольник — это четырехугольник, у которого все углы прямые.
Периметр прямоугольника 2 класс

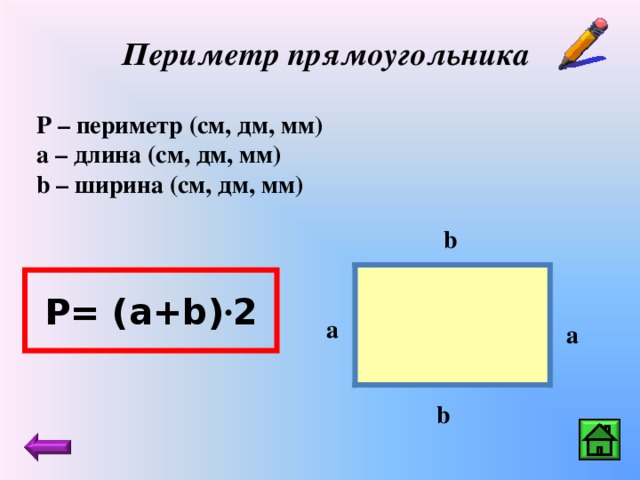 высказывания.
высказывания. 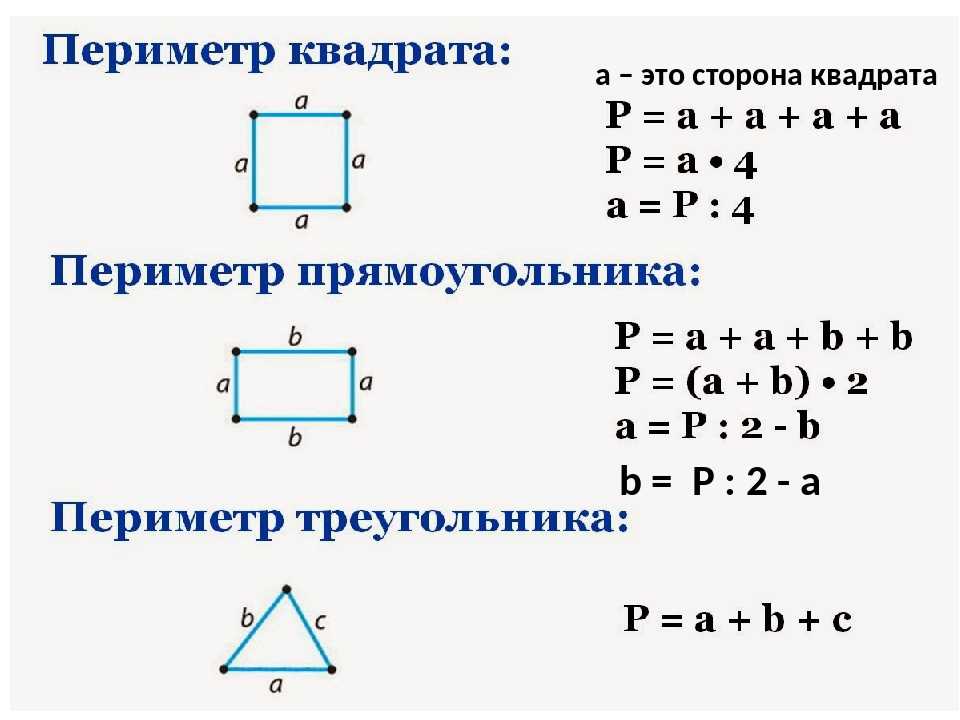
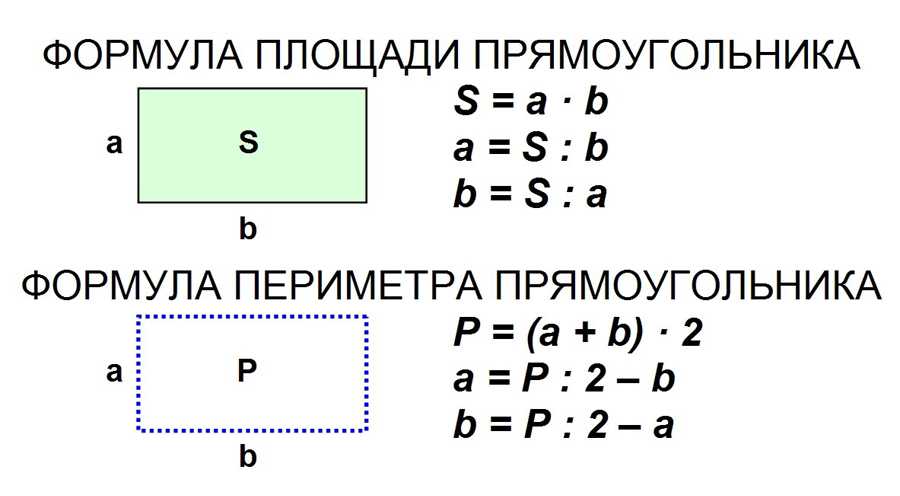 (4 стороны, 4 угла, все углы прямые, противоположные стороны равны)
(4 стороны, 4 угла, все углы прямые, противоположные стороны равны)

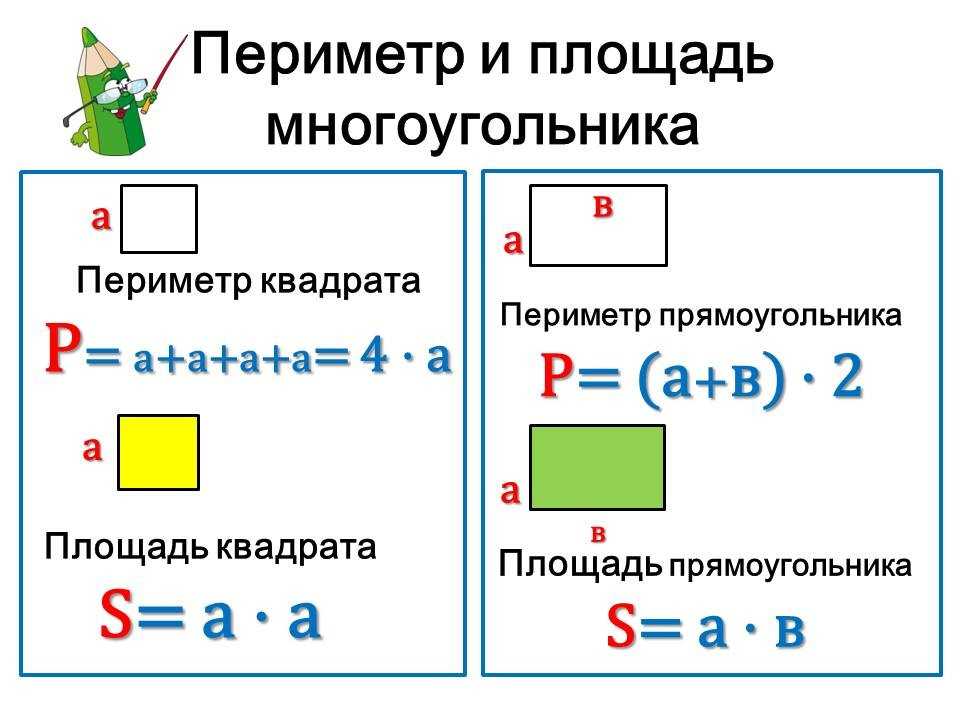
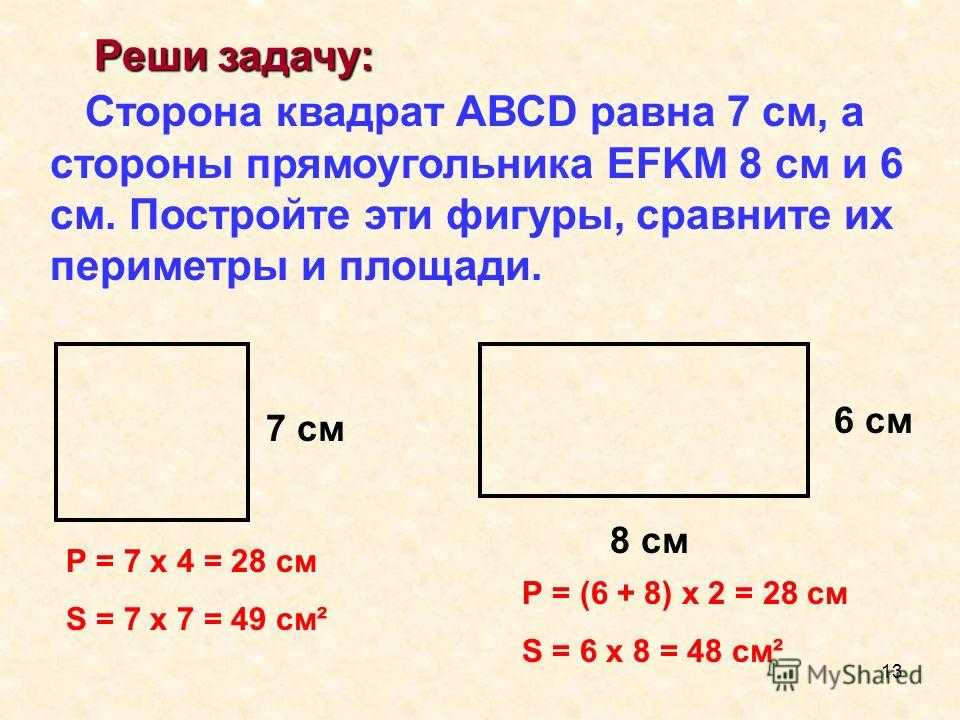
Мэтуэй | Популярные задачи
1 Найти том сфера (5) 2 Найти площадь круг (5) 3 Найдите площадь поверхности сфера (5) 4 Найти площадь круг (7) 5 Найти площадь круг (2) 6 Найти площадь круг (4) 7 Найти площадь круг (6) 8 Найти том сфера (4) 9 Найти площадь круг (3) 10 9(1/2) 11 Найти простую факторизацию 741 12 Найти том сфера (3) 13 Оценить 3 квадратный корень из 8*3 квадратный корень из 10 14 Найти площадь круг (10) 15 Найти площадь круг (8) 16 Найдите площадь поверхности сфера (6) 17 Найти простую факторизацию 1162 18 Найти площадь круг (1) 19 Найдите окружность круг (5) 20 Найти том сфера (2) 21 Найти том сфера (6) 22 Найдите площадь поверхности сфера (4) 23 Найти том сфера (7) 24 Оценить квадратный корень из -121 25 Найти простую факторизацию 513 26 Оценка квадратный корень из 3/16* квадратный корень из 3/9 27 Найти том коробка (2)(2)(2) 28 Найдите окружность круг (6) 29 Найдите окружность круг (3) 30 Найдите площадь поверхности сфера (2) 31 Оценить 2 1/2÷22000000 32 Найдите Том коробка (5)(5)(5) 33 Найти том коробка (10)(10)(10) 34 Найдите окружность круг (4) 35 Преобразование в проценты 1,7 36 Оценить (5/6)÷(4/1) 37 Оценить 3/5+3/5 38 Оценить ф(-2) 92 40 Найти площадь круг (12) 41 Найти том коробка (3)(3)(3) 42 Найти том коробка (4)(4)(4) 92-4*-1+2 45 Найти простую факторизацию 228 46 Оценить 0+0 47 Найти площадь круг (9) 48 Найдите окружность круг (8) 49 Найдите окружность круг (7) 50 Найти том сфера (10) 51 Найдите площадь поверхности сфера (10) 52 Найдите площадь поверхности сфера (7) 53 Определить, является простым или составным 5 60 Преобразование в упрощенную дробь 2 1/4 61 Найдите площадь поверхности сфера (12) 62 Найти том сфера (1) 63 Найдите окружность круг (2) 64 Найти том коробка (12)(12)(12) 65 Добавить 2+2= 66 Найдите площадь поверхности коробка (3)(3)(3) 67 Оценить корень пятой степени из 6* корень шестой из 7 68 Оценить 7/40+17/50 69 Найти простую факторизацию 1617 70 Оценить 27-(квадратный корень из 89)/32 71 Оценить 9÷4 72 Оценка 92 74 Оценить 1-(1-15/16) 75 Преобразование в упрощенную дробь 8 76 Оценка 656-521 9-2 79 Оценить 4-(6)/-5 80 Оценить 3-3*6+2 81 Найдите площадь поверхности коробка (5)(5)(5) 82 Найдите площадь поверхности сфера (8) 83 Найти площадь круг (14) 84 Преобразование в десятичное число 5 ноября 85 9-2 88 Оценить 1/2*3*9 89 Оценить 4/4-17/-4 90 Оценить 11.  02+17.19
02+17.19 91 Оценить 3/5+3/10 92 Оценить 4/5*3/8 93 Оценить 6/(2(2+1)) 94 Упростить квадратный корень из 144 95 Преобразование в упрощенную дробь 725% 96 Преобразование в упрощенную дробь 6 1/4 97 Оценить 7/10-2/5 98 Оценить 6÷3 99 Оценить 5+4 100 Оценить квадратный корень из 12- квадратный корень из 192 периметр прямоугольника равен 30 футов.
 Ширина на 5 футов больше, чем длина. Какая ширина и длина?
Ширина на 5 футов больше, чем длина. Какая ширина и длина? 2 ответа от опытных наставников
Лучший
Новейшие
Самый старый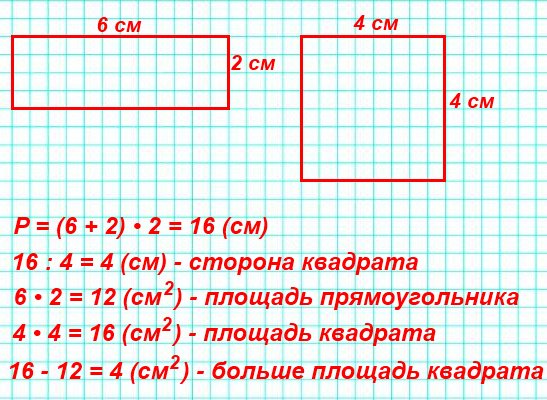 ответил 28.08.19
ответил 28.08.19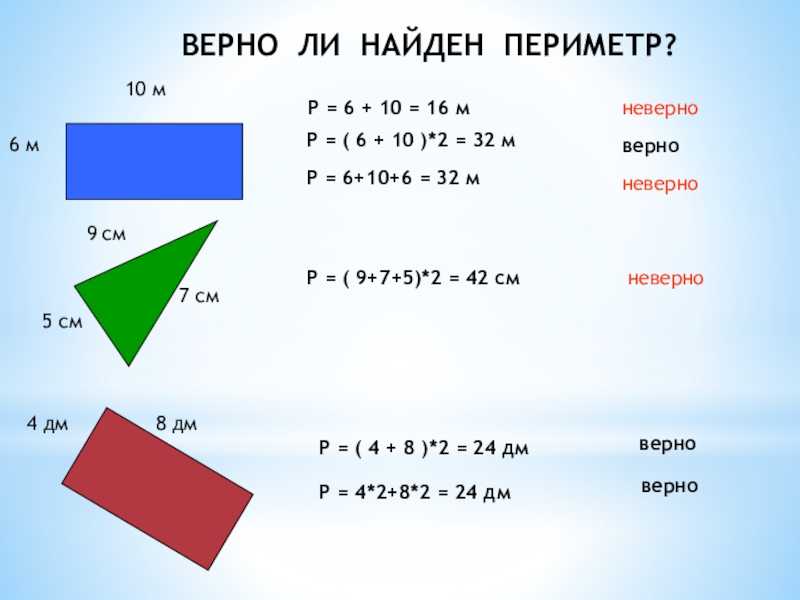
Все еще ищете помощь? Получите правильный ответ, быстро.

Na cl2 nacl: Расставить коэффициенты методом электронного баланса. 1) NA+CL2=NACL 2) LI+N2=LI3N 3) CU+HNO3=CU(NO3)2+NO+H2O
Mathway | Популярные задачи
1 Найти число нейтронов H 2 Найти массу одного моля H_2O 3 Баланс H_2(SO_4)+K(OH)→K_2(SO_4)+H(OH) 4 Найти массу одного моля H 5 Найти число нейтронов Fe 6 Найти число нейтронов Tc 7 Найти конфигурацию электронов H 8 Найти число нейтронов Ca 9 Баланс CH_4+O_2→H_2O+CO_2 10 Найти число нейтронов C 11 Найти число протонов H 12 Найти число нейтронов O 13 Найти массу одного моля CO_2 14 Баланс C_8H_18+O_2→CO_2+H_2O 15 Найти атомную массу H 16 Определить, растворима ли смесь в воде H_2O 17 Найти конфигурацию электронов Na 18 Найти массу одного атома H 19 Найти число нейтронов Nb 20 Найти число нейтронов Au 21 Найти число нейтронов Mn 22 Найти число нейтронов Ru 23 Найти конфигурацию электронов O 24 Найти массовую долю H_2O 25 Определить, растворима ли смесь в воде NaCl 26 Найти эмпирическую/простейшую формулу H_2O 27 Найти степень окисления H_2O 28 Найти конфигурацию электронов K 29 Найти конфигурацию электронов Mg 30 Найти конфигурацию электронов Ca 31 Найти число нейтронов Rh 32 Найти число нейтронов Na 33 Найти число нейтронов Pt 34 Найти число нейтронов Be Be 35 Найти число нейтронов Cr 36 Найти массу одного моля H_2SO_4 37 Найти массу одного моля HCl 38 Найти массу одного моля Fe 39 Найти массу одного моля C 40 Найти число нейтронов Cu 41 Найти число нейтронов S 42 Найти степень окисления H 43 Баланс CH_4+O_2→CO_2+H_2O 44 Найти атомную массу O 45 Найти атомное число H 46 Найти число нейтронов Mo 47 Найти число нейтронов Os 48 Найти массу одного моля NaOH 49 Найти массу одного моля O 50 Найти конфигурацию электронов Fe 51 Найти конфигурацию электронов C 52 Найти массовую долю NaCl 53 Найти массу одного моля K 54 Найти массу одного атома Na 55 Найти число нейтронов N 56 Найти число нейтронов Li 57 Найти число нейтронов V 58 Найти число протонов N 59 Упростить H^2O 60 Упростить h*2o 61 Определить, растворима ли смесь в воде H 62 Найти плотность при стандартной температуре и давлении H_2O 63 Найти степень окисления NaCl 64 Найти атомную массу He He 65 Найти атомную массу Mg 66 Найти число электронов H 67 Найти число электронов O 68 Найти число электронов S 69 Найти число нейтронов Pd 70 Найти число нейтронов Hg 71 Найти число нейтронов B 72 Найти массу одного атома Li 73 Найти эмпирическую формулу H=12% , C=54% , N=20 , , 74 Найти число протонов Be Be 75 Найти массу одного моля Na 76 Найти конфигурацию электронов Co 77 Найти конфигурацию электронов S 78 Баланс C_2H_6+O_2→CO_2+H_2O 79 Баланс H_2+O_2→H_2O 80 Найти конфигурацию электронов P 81 Найти конфигурацию электронов Pb 82 Найти конфигурацию электронов Al 83 Найти конфигурацию электронов Ar 84 Найти массу одного моля O_2 85 Найти массу одного моля H_2 86 Найти число нейтронов K 87 Найти число нейтронов P 88 Найти число нейтронов Mg 89 Найти число нейтронов W 90 Найти массу одного атома C 91 Упростить na+cl 92 Определить, растворима ли смесь в воде H_2SO_4 93 Найти плотность при стандартной температуре и давлении NaCl 94 Найти степень окисления C_6H_12O_6 95 Найти степень окисления Na 96 Определить, растворима ли смесь в воде C_6H_12O_6 97 Найти атомную массу Cl 98 Найти атомную массу Fe 99 Найти эмпирическую/простейшую формулу CO_2 100 Найти число нейтронов Mt 8 класс.
 расстановка коэффициентов вариант i na + cl2 → nacl al + cl2 → а1с13 fecl2 + cl2 → fecl3 с3н6 + 02 → c02 + h30 cu + 02 → cuo fe(oh)3 → fe203 + н20 al + cubr2 → аlbr3 + сu ca(oh)2 + na3p04 → ca3(p04)2 + naoh к20 + н20→ кон n02 → no + 02 в2н6 + 02 → в2о3 + н20 с5н10 + 02→ с02 + н20 — Школьные Знания.net
расстановка коэффициентов вариант i na + cl2 → nacl al + cl2 → а1с13 fecl2 + cl2 → fecl3 с3н6 + 02 → c02 + h30 cu + 02 → cuo fe(oh)3 → fe203 + н20 al + cubr2 → аlbr3 + сu ca(oh)2 + na3p04 → ca3(p04)2 + naoh к20 + н20→ кон n02 → no + 02 в2н6 + 02 → в2о3 + н20 с5н10 + 02→ с02 + н20 — Школьные Знания.net
Cu + 02 → CuO Химия
 Первый является самым простым и известен как синтез или композиционная реакция. Этот тип реакции объединяет два или более веществ с образованием по крайней мере одного нового соединения. Один пример уже приводился, когда металлический натрий в твердом состоянии соединяется с газообразным хлором с образованием хлорида натрия. Реакцию можно представить следующим образом:
Первый является самым простым и известен как синтез или композиционная реакция. Этот тип реакции объединяет два или более веществ с образованием по крайней мере одного нового соединения. Один пример уже приводился, когда металлический натрий в твердом состоянии соединяется с газообразным хлором с образованием хлорида натрия. Реакцию можно представить следующим образом: Это уравнение не является сбалансированным уравнением, и материя не просто исчезает и появляется. Более точно можно правильно представить эту реакцию следующим образом:
Это уравнение не является сбалансированным уравнением, и материя не просто исчезает и появляется. Более точно можно правильно представить эту реакцию следующим образом:
Кристаллическая структура хлорида натрия имеет каждый атом с шестью его ближайшими соседями в октаэдрической геометрической структуре. Ионы Na окрашены в светло-голубой цвет, а ионы Cl — в темно-зеленый цвет для контраста. Новая материя никогда не создается, и никакая материя никогда не уничтожается. Это известно как закон сохранения материи ; материя не может быть ни создана, ни уничтожена, она просто меняет форму.
Новая материя никогда не создается, и никакая материя никогда не уничтожается. Это известно как закон сохранения материи ; материя не может быть ни создана, ни уничтожена, она просто меняет форму. Реакция натрия и газообразного хлора
 Натрий окисляется до катиона натрия (Na + ), а газообразный хлор восстанавливается до хлорид-анионов (Cl —).
Натрий окисляется до катиона натрия (Na + ), а газообразный хлор восстанавливается до хлорид-анионов (Cl —).
Механизм реакции
Сбалансированное химическое уравнение Na + Cl
2 реакция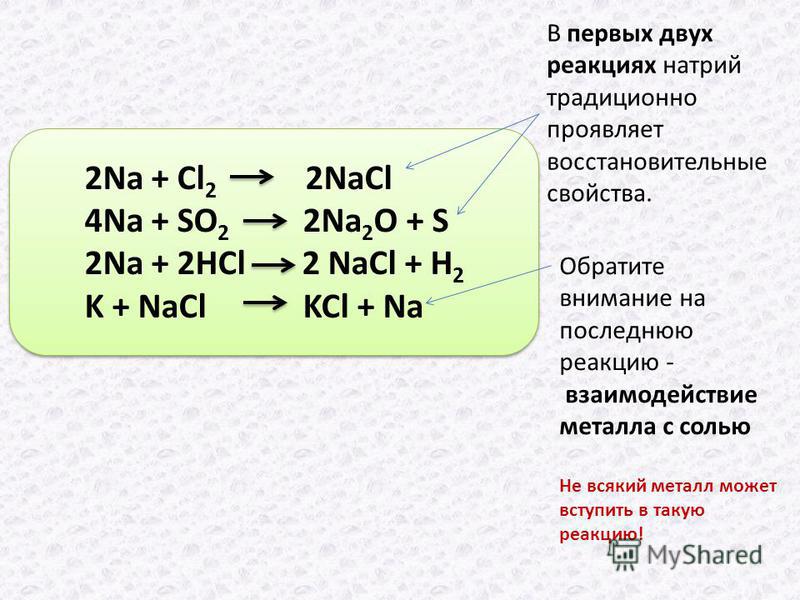
Как сбалансировать реакцию окислительно-восстановительного метода?
 Разница степеней окисления натрия составляет два, а для хлора — два. Так они же
и компенсируют друг друга.
Разница степеней окисления натрия составляет два, а для хлора — два. Так они же
и компенсируют друг друга.
Физические изменения реакции
Энтальпия реакции натрия и хлора
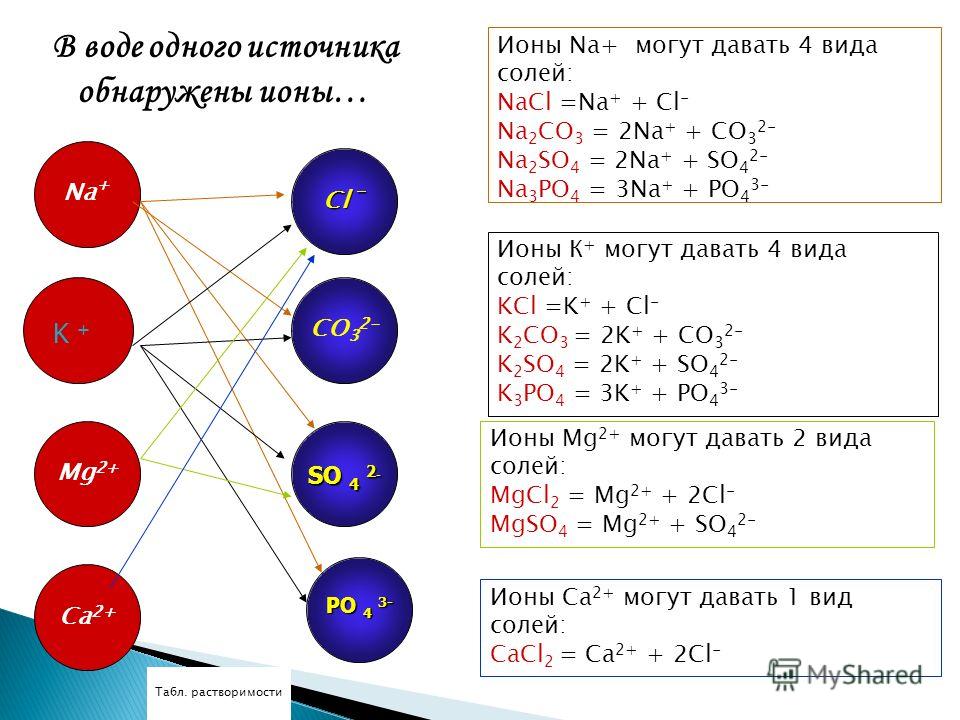 Сколько энергии выделится в результате реакции? Стандартная энтальпия образования хлорида натрия = -411,120 кДж/моль
Сколько энергии выделится в результате реакции? Стандартная энтальпия образования хлорида натрия = -411,120 кДж/моль
Как узнать, произошла ли реакция?
 Если количество реагентов мало, выполните
качественный анализ ионов натрия и хлористых ионов.
Если количество реагентов мало, выполните
качественный анализ ионов натрия и хлористых ионов. продукт реакции металлического натрия с газообразным хлором в реакции композиции
Я хочу получить хлорид натрия по реакции. Я изучил несколько реакций, возможных для производства хлорида натрия. Одним из способов является реакция газообразного натрия и хлора. Другой способ — реакция соляной кислоты и реакция водного гидроксида натрия. Я хочу знать, как лучше всего приготовить хлорид натрия из этих двух методов?
 Но эта реакция слишком опасна, потому что она выделяет большое количество энергии, а хлор — смертельно ядовитый газ.
Но эта реакция слишком опасна, потому что она выделяет большое количество энергии, а хлор — смертельно ядовитый газ. Что насчет калия и хлора? Это похоже на реакцию натрия и хлора?
формула натрия и хлора?
реакция металлического лития с газообразным хлором уравнение
твердый натрий реагирует с газообразным хлором с образованием твердого хлорида натрия, верно ли это?
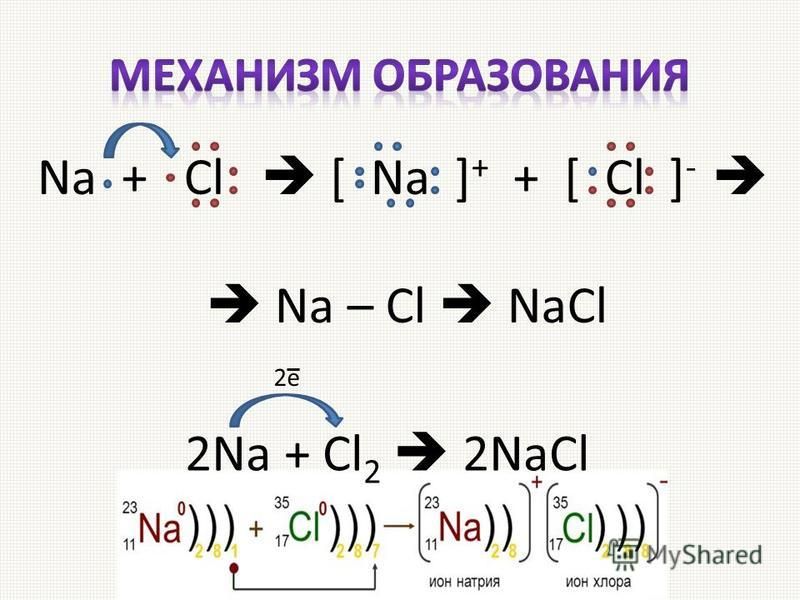
Работы по информатике: Контрольная работа по информатике на заказ, заказать контрольную по информатике
Готовые контрольные работы по информатике
Путь к файлу. bat-файл. Расчёт максимально возможного количества кластеров рабочей области логического диска.
Определение максимально возможного количества файлов на дискете.
Алгоритм работы процедуры восстановления файлов.
Подробнее…
Линейный адрес. Сегментный адрес. Базовый адрес. Сегмент. Смещение. Сумматор адреса.
Функциональное назначение областей памяти. Алгоритм работы программы обработки прерывания № 9.
Управляющие клавиши.
Подробнее…
Реферат на тему «Виды носителей информации. Хранение информации». Описаны основные носители информации, история их создания.
Рассмотрены наиболее распространённые файловые системы и способы хранения данных на компьютере.
Подробнее…
Хранение информации». Описаны основные носители информации, история их создания.
Рассмотрены наиболее распространённые файловые системы и способы хранения данных на компьютере.
Подробнее…
Краткое описание Adobe Flash CS3 Professional. Основы работы в среде Adobe Flash CS3 Professional.
Основные возможности языка Action Script на примере простого приложения.
В итоге пишем простую игрушку. Исходные коды и флэш-ролик прилагаются.
Подробнее…
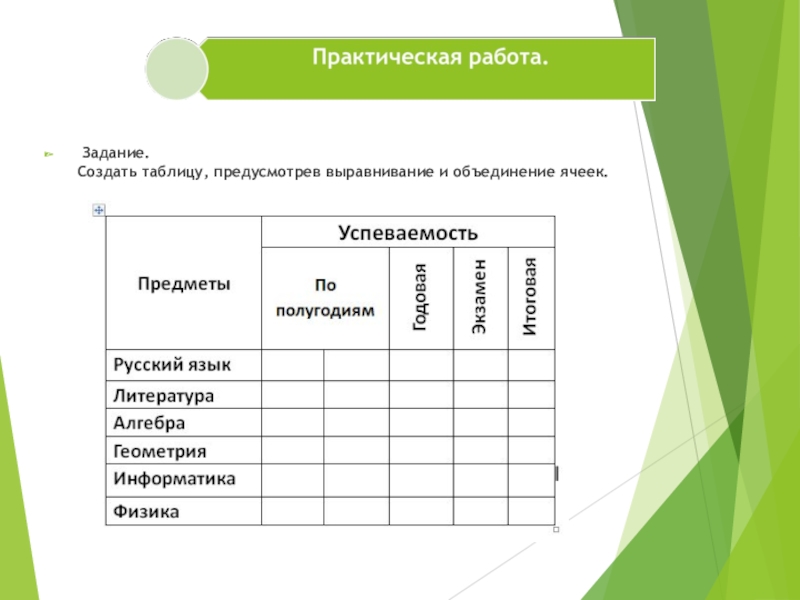

как подготовиться и выполнить на отлично
Контрольная работа по информатике

Как готовиться к контрольной по информатике

Как оформить контрольную по информатике
 Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски. 6 Медицинская информатика Карьера, должностные обязанности и ресурсы
 Это междисциплинарный подход, сочетающий информационные технологии с коммуникациями и здравоохранением. Цель перехода на цифровые технологии – более эффективное оказание медицинской помощи на более высоком уровне.
Это междисциплинарный подход, сочетающий информационные технологии с коммуникациями и здравоохранением. Цель перехода на цифровые технологии – более эффективное оказание медицинской помощи на более высоком уровне.
 Специалисты по информатике в области здравоохранения также часто управляют и защищают данные пациентов, такие как лечение, результаты анализов и другие истории пациентов, в соответствии с правилами и политиками компании.
Специалисты по информатике в области здравоохранения также часто управляют и защищают данные пациентов, такие как лечение, результаты анализов и другие истории пациентов, в соответствии с правилами и политиками компании. Люди на этой должности тесно сотрудничают с поставщиками медицинских услуг, чтобы обеспечить надлежащее функционирование клинических информационных систем и обеспечить адекватную поддержку миссии.
Люди на этой должности тесно сотрудничают с поставщиками медицинских услуг, чтобы обеспечить надлежащее функционирование клинических информационных систем и обеспечить адекватную поддержку миссии.
 Им необходимо учиться и помогать оптимизировать новые системы по мере развития технологий.
Им необходимо учиться и помогать оптимизировать новые системы по мере развития технологий.

 Вы можете специализироваться в области существующего опыта или перейти в новую область здравоохранения. Для медицинских работников, которые ищут новые вызовы, карьера специалиста по информатике в области здравоохранения может стать привлекательным и полезным вариантом для вашего будущего. Если вы планируете получить ученую степень для ее получения и не хотите бросать работу, вам может подойти онлайн-программа магистра информатики в области здравоохранения.
Вы можете специализироваться в области существующего опыта или перейти в новую область здравоохранения. Для медицинских работников, которые ищут новые вызовы, карьера специалиста по информатике в области здравоохранения может стать привлекательным и полезным вариантом для вашего будущего. Если вы планируете получить ученую степень для ее получения и не хотите бросать работу, вам может подойти онлайн-программа магистра информатики в области здравоохранения. Что такое специалист по клинической информатике?

 Те, кто разбирается в бизнесе и технологиях, также могут стать специалистами в области клинической информатики после получения дополнительного образования.
Те, кто разбирается в бизнесе и технологиях, также могут стать специалистами в области клинической информатики после получения дополнительного образования.  Они тесно сотрудничают с управленческими командами, чтобы наблюдать, как данные используются на практике. Наблюдая за управленческими командами и наблюдая за тем, как ИТ-системы влияют на пациентов, они изменят свои планы относительно будущих компьютерных программ.
Они тесно сотрудничают с управленческими командами, чтобы наблюдать, как данные используются на практике. Наблюдая за управленческими командами и наблюдая за тем, как ИТ-системы влияют на пациентов, они изменят свои планы относительно будущих компьютерных программ. 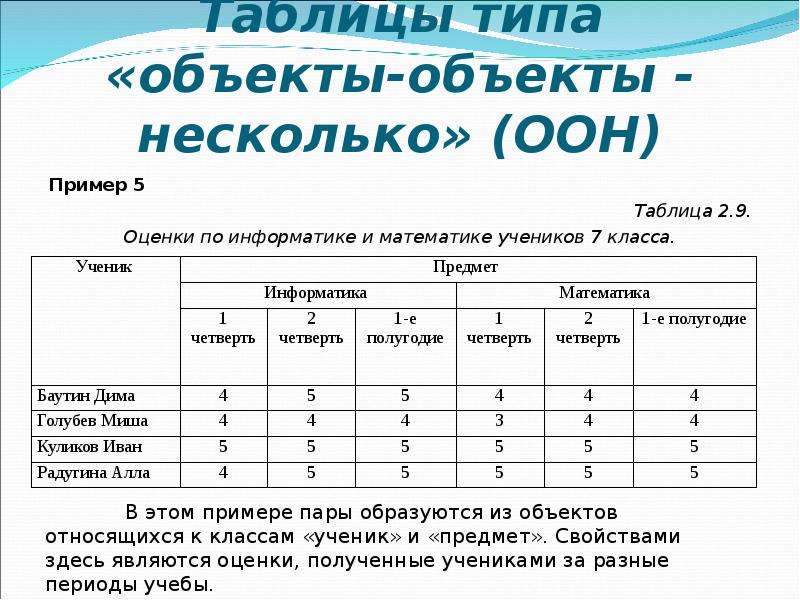
Зарегистрированный администратор медицинской информации (RHIA)
 Экзамен проверяет ваши знания медицинских, этических и правовых стандартов и гарантирует, что все тестируемые знают, как защитить конфиденциальность пациентов.
Экзамен проверяет ваши знания медицинских, этических и правовых стандартов и гарантирует, что все тестируемые знают, как защитить конфиденциальность пациентов. Certified Associate in Healthcare Information and Management Systems (CAHIMS)
Управление медицинской информацией – B.
 S.
S. Сестринское дело – Информатика сестринского дела (BSN-to-MSN) – M.S.
Сестринское дело – Информатика сестринского дела (RN–to–MSN) – M.S.
Нет необходимости ждать весеннего или осеннего семестра. В WGU круглый год начинается школьная пора. Начните, поговорив с консультантом по зачислению сегодня, и вы будете на пути к осуществлению своей мечты о степени бакалавра или магистра — раньше, чем вы думаете!
Сравните варианты получения степени
 Сравните их, чтобы найти наиболее подходящий для вас.
Сравните их, чтобы найти наиболее подходящий для вас.
Сколько зарабатывают специалисты по клинической информатике?
80 306 долларов
Каков прогнозируемый рост числа рабочих мест?
7%
Где работают специалисты по клинической информатике?
Варьируется

Часто задаваемые вопросы специалиста по клинической информатике

Делить корень из х на х: Mathway | Популярные задачи
Введение в задачи с параметром: решение уравнений с параметром
На этой странице вы узнаете- Игра в прятки: как значение одной переменной может помочь найти другую?
- Парадокс: как стоять на месте и бежать с любой скоростью одновременно?
- Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром?
Мы привыкли, что в уравнении коэффициенты не меняются. Но возможно ли из одного уравнения составить бесконечное множество различных его вариантов? Узнаем об этом в статье.
Что такое параметрУтром на термометре было некоторое количество градусов, которое мы обозначим за х. В обед температура воздуха изменилась в несколько раз. Во сколько раз должна была измениться температура воздуха, чтобы на термометре было 20 градусов?
Такие задачи достаточно легко решаются. Если бы изначально было пять градусов, то искомое число было бы равно \(\frac{20}{5} = 4\). А если было 10 градусов, то искомое число было бы равно \(\frac{20}{10} = 2\).
А если было 10 градусов, то искомое число было бы равно \(\frac{20}{10} = 2\).
Но не все так просто. Мы не знаем, какой изначально была температура. Также мы не знаем, во сколько раз она изменилась. То есть мы получили уравнение с двумя неизвестными переменными.
Обозначим вторую переменную a, у нас получится уравнение вида ax=20. Только что введенная нами переменная “a” называется параметр.
Параметр — это условная буква, вместо которой можно подставить число.
То есть параметр — это еще одна переменная, которая может принять несколько значений.
Как решать уравнения с параметром, если у нас целых две (а то и больше) неизвестных переменных? Нужен иной подход, чем при решении обычного уравнения.
Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется.
Мы ищем не единственное значение параметра, а все возможные его значения для заданного условия.
| Игра в прятки: как значение одной переменной может помочь найти другую? Поскольку параметр — переменная в уравнении, которая является коэффициентом, его значение задает и корни уравнения. |
Вернемся к нашей погоде. У нас получилось уравнение ax = 20. Как найти, сколько градусов было изначально? Разделить все уравнение на число a.
\(x = \frac{20}{a}\)
Какие значения может принимать параметр? Любые. Например, при a = 1 x = 20.
При a = 2 x = 10.
При a = 40 x = 0,5
Что, если a=0? Мы получаем уравнение \(x = \frac{20}{0}\), у которого нет решения, поскольку на 0 делить нельзя.
Если мы не будем преобразовывать изначальное уравнение, то получится 0*x=20, то есть уравнение не будет выполняться: какое бы число мы ни умножили на 0, получится 0.
Получается, решение есть при любых значениях a, кроме 0. Таким образом, мы и нашли ответ: при a = 0 решений нет, при a \(\neq\) 0 — x = 20a.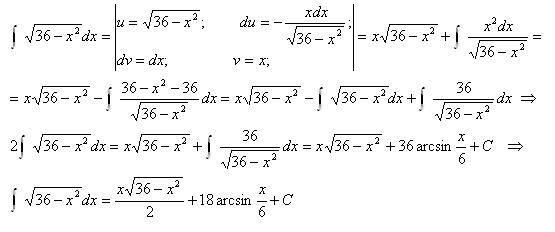
Добавим немного теории. Представим наше уравнение в виде ax = b, где a, b — действительные числа. Рассмотрим несколько случаев.
1) b \(\neq\) 0.
Предположим, Пете необходимо в несколько раз увеличить скорость х, пробежать дистанцию и поставить рекорд. Чтобы поставить рекорд, он должен бежать со скоростью 15 км/ч — это и будет коэффициент b.
Получаем уравнение ax = 15. Как найти начальную скорость Пети? \(x = \frac{15}{a}\).
Такое уравнение мы уже решали выше. Получаем два случая:
- Если a = 0 — решений нет.
- Если a \(\neq\) 0, то изначальная скорость Пети была равна \(x = \frac{15}{a}\).
| Парадокс: как стоять на месте и бежать с любой скоростью одновременно? Когда Пете нужно увеличить скорость в 0 раз, получается парадокс. |
2) b = 0.
Мы получаем уравнение ax = 0. Также разберем два случая значений параметра:
- a = 0. Мы получаем уравнение 0 * x = 0. Какое значение х нужно подставить, чтобы уравнение выполнялось?
Какое бы число мы ни умножили на 0, получим 0. Получаем бесконечное множество решений.
- a \(\neq\) 0. Здесь получается, что равен 0 уже х: \(x = \frac{0}{a} = 0\).
Подведем итог. Как можно решить уравнение вида ax = b?
- Если a = 0, b = 0 — бесконечное множество решений.
- Если a = 0, b \(\neq\) 0 — решений нет.
- Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\).
Прежде чем приступать к изучению следующего материала, рекомендуем ознакомиться с понятием квадратного уравнения в статье «Линейные, квадратные и кубические уравнения». Также важно ориентироваться в графиках параболы из статьи «Основные элементарные функции».
Квадратное уравнение имеет вид ax2 + bx + c = 0, а графиком функции y = ax2 + bx + c будет парабола.
Как работать с такими уравнениями, если в них присутствует параметр? В первую очередь, важны рассуждения. Любое задание с параметром можно решить, проанализировав функцию.
Решение квадратного уравнения опирается на понятие дискриминанта. В зависимости от его значений может получиться разное количество корней:
- При D > 0 уравнение имеет два корня.
- При D = 0 уравнение имеет один корень.
- При D < 0 уравнение не имеет корней.
Как это проверить на графике? Корни уравнения — это точки, в которых парабола пересекает ось абсцисс, то есть ось х.
Рассмотрим три уравнения.
1) x2 — x — 2 = 0
Решим уравнение с помощью дискриминанта.
D = 12 — 4 * 1 * (-2) = 1 + 8 = 9
Поскольку дискриминант больше 0, то уравнение имеет два корня.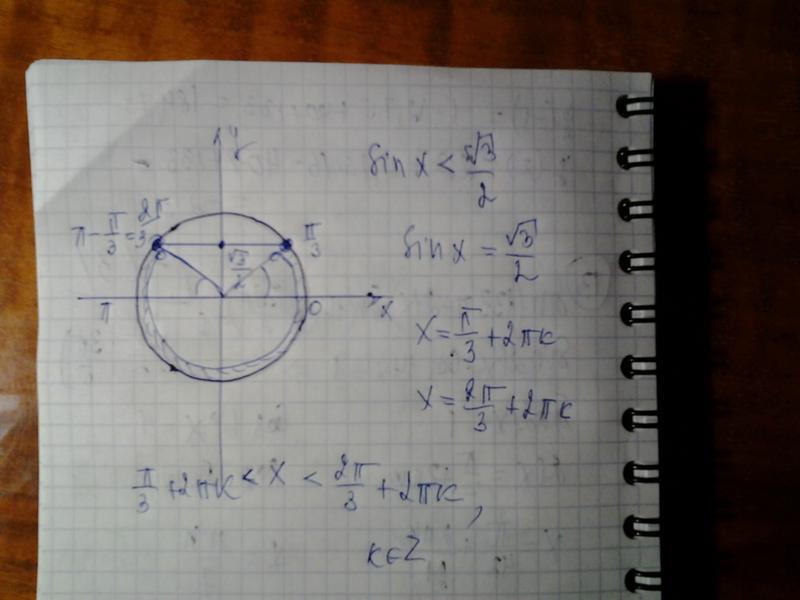
\(x_1 = \frac{1 + 3}{2} = 2\)
\(x_2 = \frac{1 — 3}{2} = -1\)
Проверим с помощью графика функции. Построим параболу и заметим, что она действительно дважды пересекает ось абсцисс, а координаты этих точек равны (−1; 0) и (2; 0) .
2) x2 -4x + 4 = 0
Решим уравнение с помощью дискриминанта.
D = 16 — 4 * 1 * 4 = 16 — 16 = 0
Поскольку дискриминант равен 0, у уравнения всего один корень.
\(x = \frac{4}{2} = 2\)
Проверим на графике. И действительно, парабола касается оси х только один раз в вершине, координаты которой (2; 0).
3) x2 — 5x + 7 = 0
Решим уравнение с помощью дискриминанта.
D = 25 — 4 * 1 * 7 = 25 — 28 = -3
Поскольку дискриминант отрицательный, у уравнения нет корней. И это отлично видно, если посмотреть на график функции: парабола лежит выше оси х и никогда ее не пересечет.
Где можно применить эти знания, решая параметры?
Пример 1. Найдите все значения параметра a, при которых уравнение x2 + (3a + 11)x + 18,25 + a = 0 имеет два различных решения.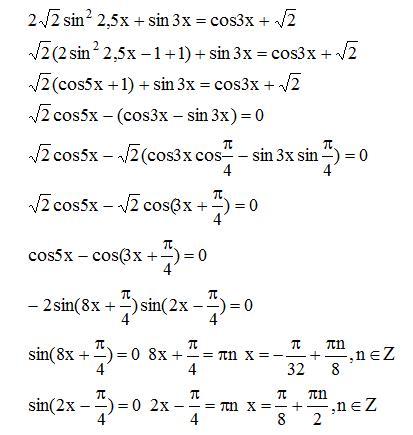
Решение. Перед нами квадратное уравнение с коэффициентами b = 3a + 11, c = a + 18,25. В каких случаях это уравнение будет иметь два различных корня?
Квадратное уравнение имеет два корня, если D > 0. Нужно найти все значения параметра, при которых дискриминант будет положительным.
1. Для начала найдем сам дискриминант.
D = (3a + 11)2 — 4 * 1 * (a + 18,25) = 9a2 + 66a + 121 — 4a — 73 = 9a2 + 62a + 48
2. Поскольку дискриминант должен быть больше 0, то получаем неравенство 9a2 + 62a + 48 > 0
3. Решим его «Методом интервалов».
9a2 + 62a + 48 = 0
D = 3844 — 1728 = 2116
\(a_1 = \frac{-62 + 46}{18} = -\frac{16}{18} = -89\)
\(a_2 = \frac{-62 — 46}{18} = -\frac{108}{18} = -6\)
4. Дискриминант будет положительным при \(a \in (-\infty; -6) \cup (-\frac{8}{9}; +\infty)\). Это и будет ответ.
Ответ: \(a \in (-\infty; -6) \cup (-\frac{8}{9}; +\infty)\).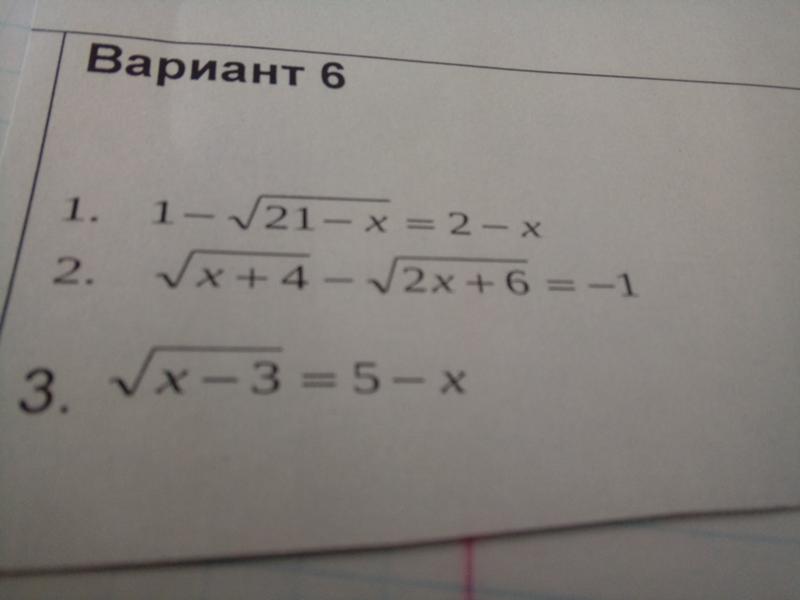
Важно: в уравнении мы указываем не сами решения уравнения, а значения параметра, при которых уравнение имеет два решения.
Пример 2. При каких значениях параметра a уравнение (2a + 1)x2 — ax + 3a + 1 = 0 имеет два различных решения?
Решение. Этот пример похож на предыдущий, однако здесь есть одна важная особенность. Что произойдет с уравнением, если 2a+1 = 0?
Мы получим уравнение 0,5x — 0,5 = 0, то есть линейное уравнение. У уравнения будет всего одно решение, что уже не подходит под условие задачи.
| Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром? Если перед x2 стоит коэффициент, обязательно проверить, чтобы он не был равен 0. В противном случае уравнение из квадратного превращается в линейное, а это уже совершенно другой алгоритм решений уравнений. |
1. Поскольку по условию должно быть 2 решения, мы получаем, что a \(\neq\) -0,5. 2 + 20a + 4 = 23(a — \frac{2\sqrt{2} — 10}{23})(a — \frac{-2\sqrt{2} — 10}{23})\)
2 + 20a + 4 = 23(a — \frac{2\sqrt{2} — 10}{23})(a — \frac{-2\sqrt{2} — 10}{23})\)
5. Получаем неравенство:
\(23(a — \frac{2\sqrt{2} — 10}{23})(a — \frac{-2\sqrt{2} — 10}{23} < 0\)
6.Тогда \(a \in (\frac{-2\sqrt{2} — 10}{23}; \frac{2\sqrt{2} — 10}{23})\). Вспомним, что a \(\neq\) -0,5, следовательно, мы получаем ответ \(a \in (\frac{-2\sqrt{2} — 10}{23}; -0,5) \cup (-0,5; \frac{2\sqrt{2} — 10}{23})\).
Ответ: \(a \in (\frac{-2\sqrt{2} — 10}{23}; -0,5) \cup (-0,5; \frac{2\sqrt{2} — 10}{23})\)
Теорема ВиетаДискриминант — не единственный способ решить квадратное уравнение. Обратимся к теореме Виета. Если нам дано уравнение ax2 + bx + c = 0, то его корни можно найти с помощью следующей системы:
Теорему Виета удобно использовать, если на корни уравнения наложены дополнительные ограничения.
Пример 3. При каких значениях параметра a корни уравнения x2 — 3ax — a(a — 1) = 0 удовлетворяют условию x1 = 5x2. 2 — 4a = 0 \rightarrow a(9a — 4) = 0 \rightarrow a = 0, a = \frac{4}{9}\)
2 — 4a = 0 \rightarrow a(9a — 4) = 0 \rightarrow a = 0, a = \frac{4}{9}\)
5. Мы нашли значения параметра, при которых выполняется условие. Осталось проверить, чтобы при этих значениях у уравнения было два корня.
a = 0 не подходит, поскольку ограничение \(a \in (-\infty; 0) \cup (\frac{4}{13}; +\infty)\) не включает точку 0.
\(a = \frac{4}{9}\) подходит, поскольку \(\frac{4}{9} > \frac{4}{13}\).
Ответ: \(a = \frac{4}{9}\)
Условия на корни квадратного трехчленаОднако могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев.
1. Корни квадратного трехчлена меньше, чем число N.
Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз.
Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N.
Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту.
Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка.
Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа.
Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы.
Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N.
В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов.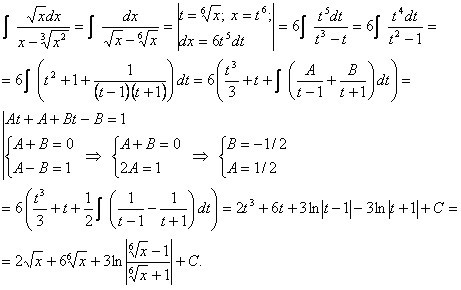
А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними.
В этом случае смотровая площадка окажется между привалами.
Аналогичным способом можно проследить изменение условий при любом положении точки N на графике.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий:
Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг.
Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы.
Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий:
2. Корни квадратного трехчлена больше, чем число N.
Корни квадратного трехчлена больше, чем число N.
Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы.
Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий:
Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий:
С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько.
| Алгоритм: как задать любые условия для корней квадратных уравнений с помощью графика? Достаточно начертить примерный график функции и расставить на оси х нужные точки. 1. Определить, куда направлены ветви параболы и задать условие для коэффициента перед x2. |
В итоге должна получиться система, с помощью которой можно решить задачу.
Фактчек- Параметр — это буква a, вместо которой можно подставить число. Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется.
- При решении линейного уравнения ax=b в зависимости от значения коэффициентов может получиться несколько вариантов решений. Если a = 0, b = 0 — бесконечное множество решений. Если a = 0, b \(\neq\) 0 — решений нет.
 Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\).
Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\). - При решении квадратного уравнения обязательно проверять коэффициент перед x2. Если коэффициент будет равен 0, то уравнение станет линейным.
- При решении квадратного уравнения важно учитывать значение дискриминанта: если он строго больше 0, то корней у уравнения два, если дискриминант равен 0, то у уравнения один корень, если дискриминант меньше 0, то у уравнения нет корней.
- Решить квадратное уравнение можно и с помощью теоремы Виета.
- Если в задаче даны дополнительные условия на корни уравнения (например, они должны быть больше или меньше определенного числа), то задать их можно с помощью системы. Неравенства в системе можно составить с помощью анализа примерного графика функций.
Задание 1.
Что такое параметр?
- Это буква a, вместо которой можно подставить число.

- Это коэффициент перед x2 в квадратном уравнении.
- Это переменная х.
- Это значение функции в определенной точке.
Задание 2.
Дано уравнение ax = b. Сколько решений оно имеет, если a = 0 и b = 0?
- Решений нет.
- Одно решение.
- Бесконечное множество решений.
- Невозможно определить количество решений.
Задание 3.
При каких значениях дискриминанта уравнение будет иметь корни?
- D > 0
- D = 0
- D < 0
- D \(\neq\) 0
Задание 4.
Корни квадратного уравнения меньше числа А. Где будет лежать вершина параболы относительно точки А?
- Справа.
- Слева.
- Совпадать с точкой А.
- Невозможно определить расположение вершины.
Задание 5.
Меньший корень квадратного уравнения больше числа А, но меньше числа В. Ветви параболы направлены вниз. Чему будет равно значение функции в точке В?
- Значение функции в точке В будет меньше 0.

- Значение функции в точке В будет равно 0.
- Значение функции в точке В будет больше 0.
- Невозможно определить значение функции.
Ответы: 1. — 1 2. — 3 3. — 4 4. — 2 5. — 3.
3-8Функция квадратного корня в Python — Real Python
Смотреть сейчас Это руководство содержит соответствующий видеокурс, созданный командой Real Python.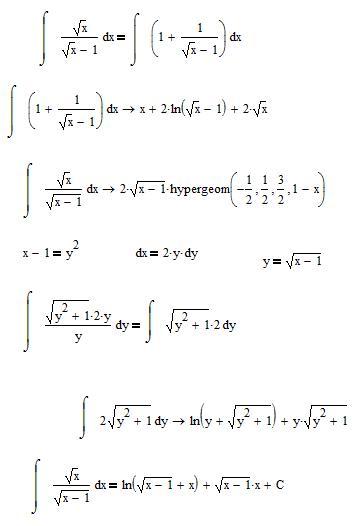 Посмотрите его вместе с письменным учебным пособием, чтобы углубить свое понимание: Функция извлечения квадратного корня в Python
Посмотрите его вместе с письменным учебным пособием, чтобы углубить свое понимание: Функция извлечения квадратного корня в Python
Вы пытаетесь решить квадратное уравнение? Возможно, вам нужно вычислить длину одной стороны прямоугольного треугольника. Для этих и других типов уравнений функция квадратного корня Python, sqrt() поможет вам быстро и точно рассчитать ваши решения.
К концу этой статьи вы узнаете:
- Что такое квадратный корень
- Как использовать функцию квадратного корня Python,
sqrt() - Когда
sqrt()может быть полезен в реальном мире
Начинаем!
Python Pit Stop: Это руководство представляет собой быстрое и практическое способов найти нужную информацию, чтобы вы быстро вернулись к своему проекту!
Бесплатный бонус: Нажмите здесь, чтобы получить нашу бесплатную памятку по Python, которая покажет вам основы Python 3, такие как работа с типами данных, словарями, списками и функциями Python.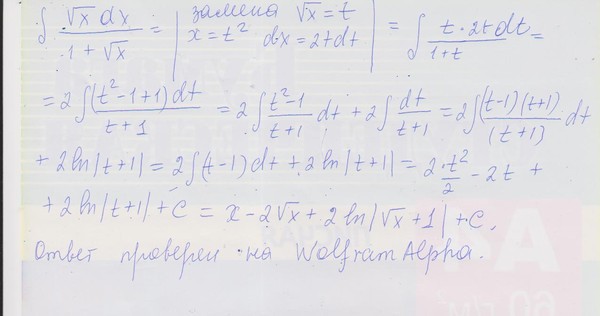
Квадратные корни в математике
В алгебре квадрат , x , является результатом числа, n , умноженного на себя: x = n²
Вы можете вычислять квадраты с помощью Python:
>>>
>>> n = 5 >>> х = п ** 2 >>> х 25
Оператор Python ** используется для вычисления степени числа. В этом случае 5 в квадрате или 5 в степени 2 равно 25.
Таким образом, квадратный корень — это число n , которое при умножении само на себя дает квадрат x .
В этом примере n , квадратный корень равен 5.
25 является примером идеальный квадрат . Совершенные квадраты — это квадраты целых чисел:
.>>>
>>> 1 ** 2 1 >>> 2 ** 2 4 >>> 3 ** 2 9
Возможно, вы запомнили некоторые из этих правильных квадратов, когда изучали таблицу умножения на уроке элементарной алгебры.
Если вам дан маленький идеальный квадрат, может быть достаточно просто вычислить или запомнить его квадратный корень. Но для большинства других квадратов этот расчет может стать немного более утомительным. Часто оценка достаточно хороша, когда у вас нет калькулятора.
К счастью, у вас как у разработчика Python есть калькулятор, а именно интерпретатор Python!
Удалить рекламу
Функция квадратного корня Python
Модуль Python math в стандартной библиотеке может помочь вам решить связанные с математикой задачи в коде. Он содержит множество полезных функций, таких как Reостатка() и factorial() . Он также включает функцию квадратного корня Python, sqrt() .
Вы начнете с импорта математика :
>>>
>>> импорт математики
Это все, что нужно! Теперь вы можете использовать math. для вычисления квадратных корней.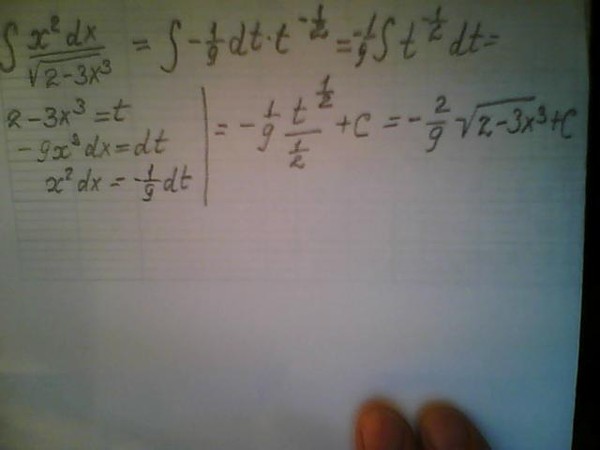 sqrt()
sqrt()
sqrt() имеет простой интерфейс.
Он принимает один параметр, x , который (как вы видели ранее) обозначает квадрат, для которого вы пытаетесь вычислить квадратный корень. В предыдущем примере это будет 25 .
Возвращаемое значение sqrt() — это квадратный корень из x в виде числа с плавающей запятой. В примере это будет 5.0 .
Давайте рассмотрим несколько примеров того, как (и как не следует) использовать sqrt() .
Квадратный корень из положительного числа
Один тип аргумента, который вы можете передать в sqrt() , является положительным числом. Сюда входят типы int и float .
Например, вы можете найти квадратный корень из 9.0913 49 с использованием sqrt() :
>>>
>>> math.sqrt(49) 7,0
Возвращаемое значение — 7,0 (квадратный корень из 49 ) в виде числа с плавающей запятой.
Наряду с целыми числами вы также можете передать значений с плавающей запятой :
>>>
>>> math.sqrt(70.5) 8.396427811873332
Вы можете проверить точность этого квадратного корня, вычислив его обратную величину:
>>>
>>> 8.396427811873332 ** 2 70,5
Квадратный корень из нуля
Даже 0 является допустимым квадратом для передачи в функцию квадратного корня Python:
>>>
>>> math.sqrt(0) 0,0
Хотя вам, вероятно, не придется часто вычислять квадратный корень из нуля, вы можете передавать в функцию sqrt() переменную, значение которой на самом деле вам неизвестно. Итак, хорошо знать, что в таких случаях он может обрабатывать ноль.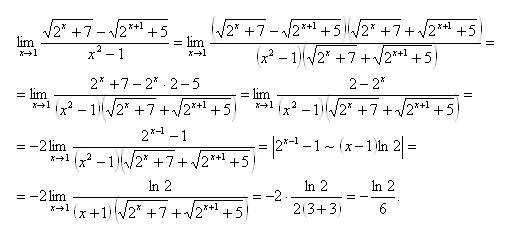
Удалить рекламу
Квадратный корень из отрицательных чисел
Квадрат любого действительного числа не может быть отрицательным. Это связано с тем, что отрицательный продукт возможен только в том случае, если один фактор положительный, а другой отрицательный. Квадрат по определению является произведением числа и самого себя, поэтому отрицательный действительный квадрат невозможен:
.>>>
>>> math.sqrt(-25) Traceback (последний последний вызов): Файл "", строка 1, в ValueError: ошибка математического домена
Если вы попытаетесь передать отрицательное число в sqrt() , вы получите ValueError , потому что отрицательные числа не находятся в области возможных действительных квадратов. Вместо этого квадратный корень из отрицательного числа должен быть сложным, что выходит за рамки функции квадратного корня Python.
Квадратные корни в реальном мире
Чтобы увидеть реальное применение функции квадратного корня Python, давайте обратимся к теннису.
Представьте, что Рафаэль Надаль, один из самых быстрых игроков в мире, только что нанес удар справа из дальнего угла, где базовая линия встречается с боковой линией теннисного корта:
Теперь предположим, что его противник контратаковал броском (таким, при котором мяч будет коротким с небольшим импульсом вперед) в противоположный угол, где другая боковая линия встречается с сеткой:
Какое расстояние должен пробежать Надаль, чтобы достать мяч?
По нормативным размерам теннисного корта вы можете определить, что длина базовой линии составляет 27 футов, а боковой линии (с одной стороны сетки) — 39 футов.ноги длинные. Итак, по сути, это сводится к нахождению гипотенузы прямоугольного треугольника:
. Используя ценное уравнение из геометрии, теорему Пифагора, мы знаем, что a² + b² = c² , где a и b — катеты прямоугольного треугольника, а c — гипотенуза.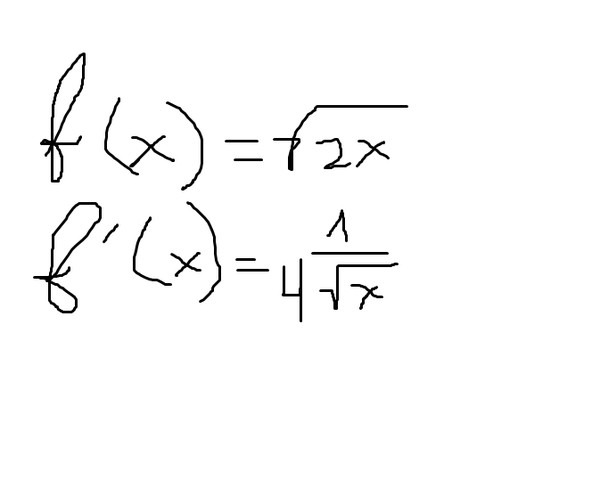
Следовательно, мы можем рассчитать расстояние, которое должен пробежать Надаль, переставив уравнение для решения c :
.Вы можете решить это уравнение, используя функцию квадратного корня Python:
>>>
>>> а = 27 >>> б = 39 >>> math.sqrt(a ** 2 + b ** 2) 47.434164569
Итак, Надаль должен пробежать примерно 47,4 фута (14,5 метра), чтобы дотянуться до мяча и сохранить очко.
Заключение
Поздравляем! Теперь вы знаете все о функции квадратного корня Python.
Вы охватили:
- Краткое введение в квадратные корни
- Все плюсы и минусы функции квадратного корня Python,
кв() - Практическое применение
sqrt()на реальном примере
Умение использовать sqrt() — это только полдела. Понимание того, когда его использовать, — это другое. Теперь вы знаете и то, и другое, так что идите и примените свое новообретенное мастерство в функции квадратного корня Python!
Смотреть сейчас Это руководство содержит связанный с ним видеокурс, созданный командой Real Python.

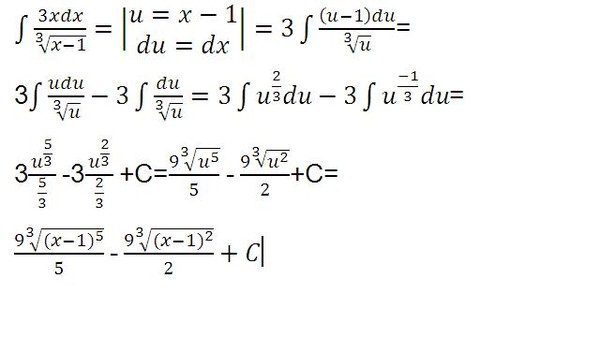 То есть переменные а и х зависят друг от друга так же, как и зависят корни обычного уравнения от его коэффициентов.
То есть переменные а и х зависят друг от друга так же, как и зависят корни обычного уравнения от его коэффициентов. 
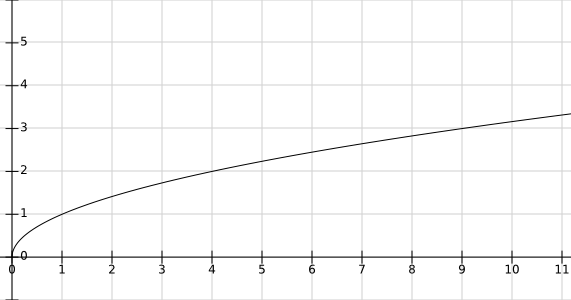 Чтобы составить систему, необходимо:
Чтобы составить систему, необходимо: 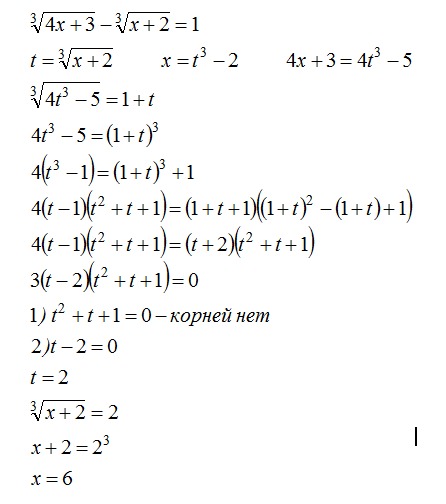 Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\).
Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\). 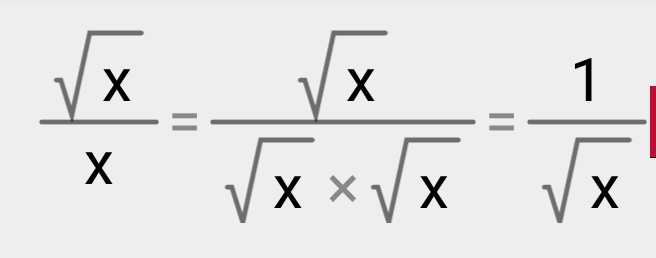
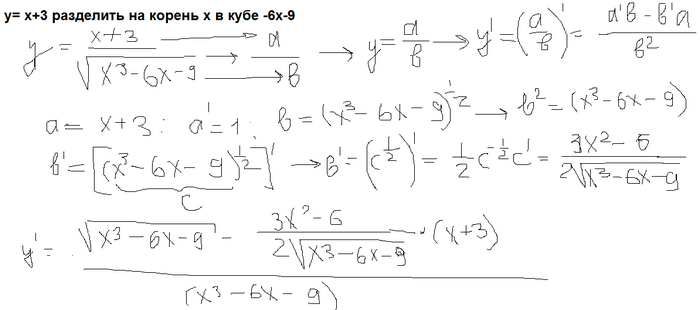
 sqrt(49)
7,0
sqrt(49)
7,0

 Если не знаете — есть отличный шанс погуглить его.
Если не знаете — есть отличный шанс погуглить его. Единственная вещь, о который ты должен думать — это на сколько креативное и необычное твое решение.
Единственная вещь, о который ты должен думать — это на сколько креативное и необычное твое решение.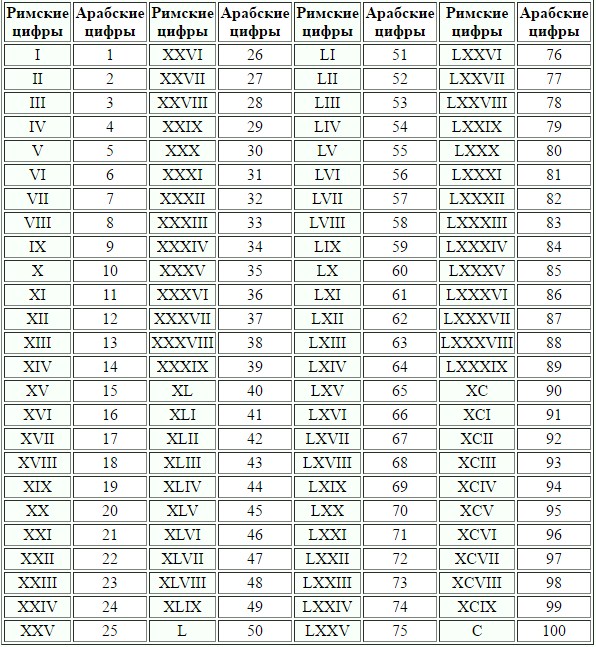 join(roman(n)).upper()
join(roman(n)).upper()
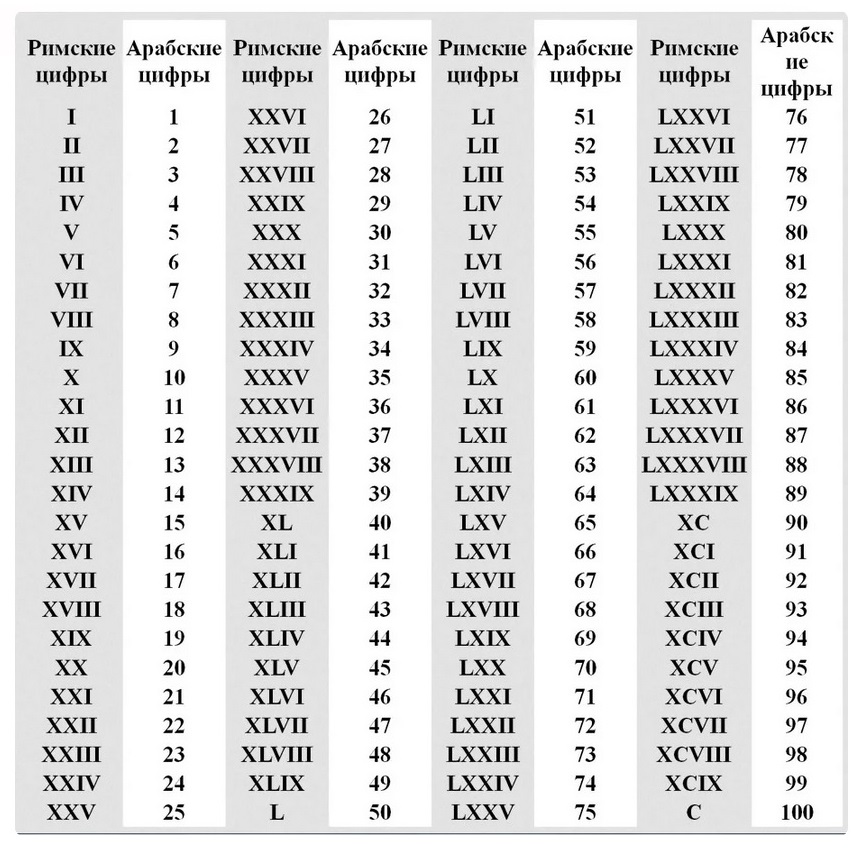 Перейдя по ним, вы можете прочитать код-ревью других пользователей либо написать свое.
Перейдя по ним, вы можете прочитать код-ревью других пользователей либо написать свое.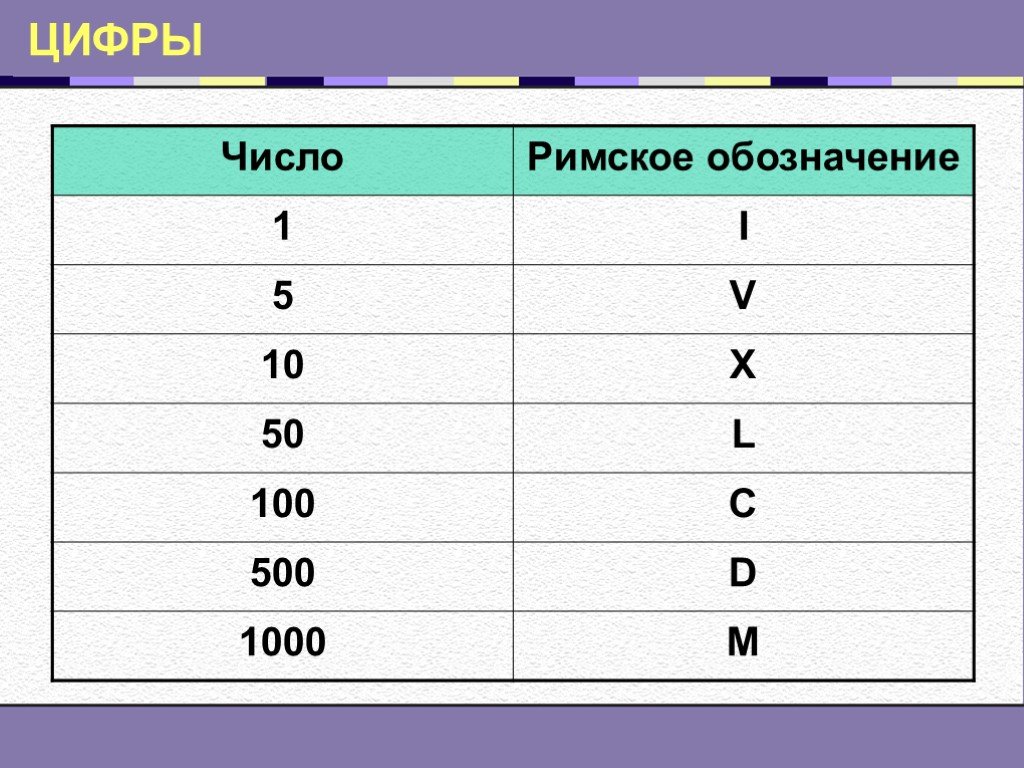 По понятным причинам я могу вам показать только ссылку.
По понятным причинам я могу вам показать только ссылку.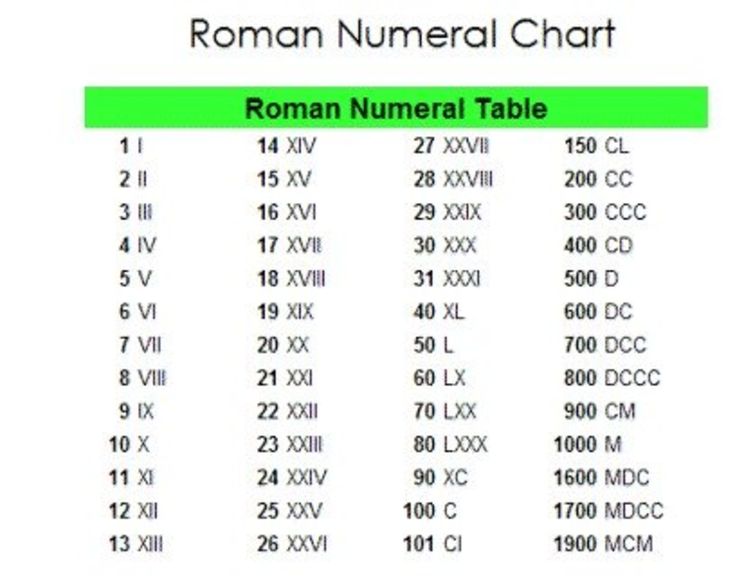
 Следовательно, 3000 будет МММ, а 4000 будет I̅V̅. 5000 — это V̅. 10 000 — это X̅, а 100 000 — это C̅. 1 000 000 – это M̅. Этот вариант намного проще, чем вышеописанный, и поэтому многие предпочитают его.
Следовательно, 3000 будет МММ, а 4000 будет I̅V̅. 5000 — это V̅. 10 000 — это X̅, а 100 000 — это C̅. 1 000 000 – это M̅. Этот вариант намного проще, чем вышеописанный, и поэтому многие предпочитают его.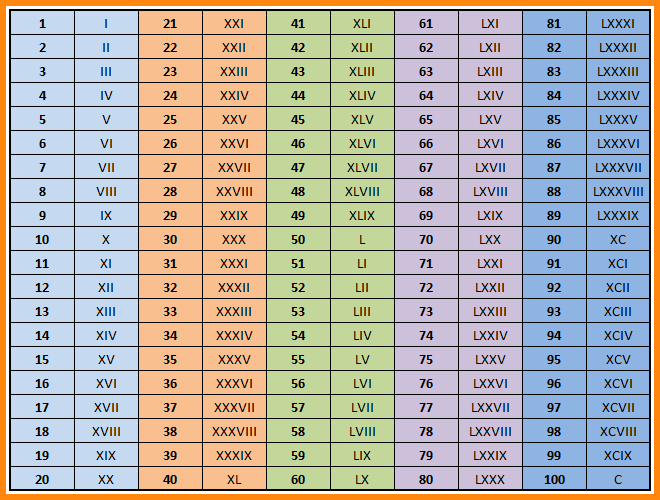 Они также применяются к цифрам со значением от b4+1{\displaystyle {\frac {b}{4}}+1}до b2−1{\displaystyle {\frac {b}{2}}-1}. как 3b4+1{\displaystyle {\frac {3b}{4}}+1}до 3b2−1{\displaystyle {\frac {3b}{2}}-1}.
Они также применяются к цифрам со значением от b4+1{\displaystyle {\frac {b}{4}}+1}до b2−1{\displaystyle {\frac {b}{2}}-1}. как 3b4+1{\displaystyle {\frac {3b}{4}}+1}до 3b2−1{\displaystyle {\frac {3b}{2}}-1}.
 0053 CXIV
0053 CXIV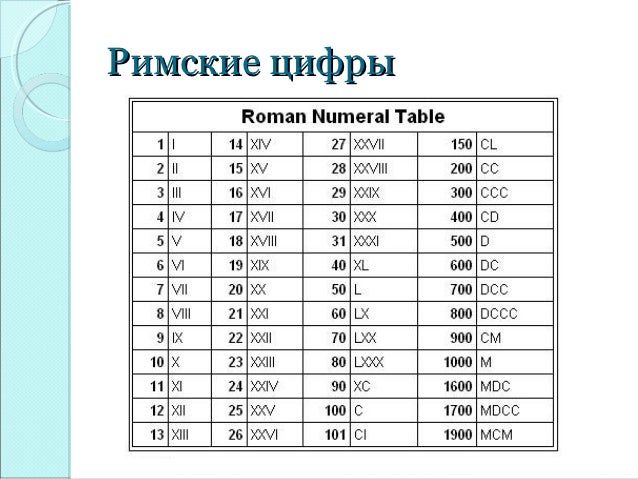 0054
0054 Как вы можете видеть, это очень циклично: длина увеличивается по мере того, как цифра I добавляется поэтапно, а затем уменьшается, когда она проходит кратность пяти, заменяясь символом с более высоким значением.
Как вы можете видеть, это очень циклично: длина увеличивается по мере того, как цифра I добавляется поэтапно, а затем уменьшается, когда она проходит кратность пяти, заменяясь символом с более высоким значением.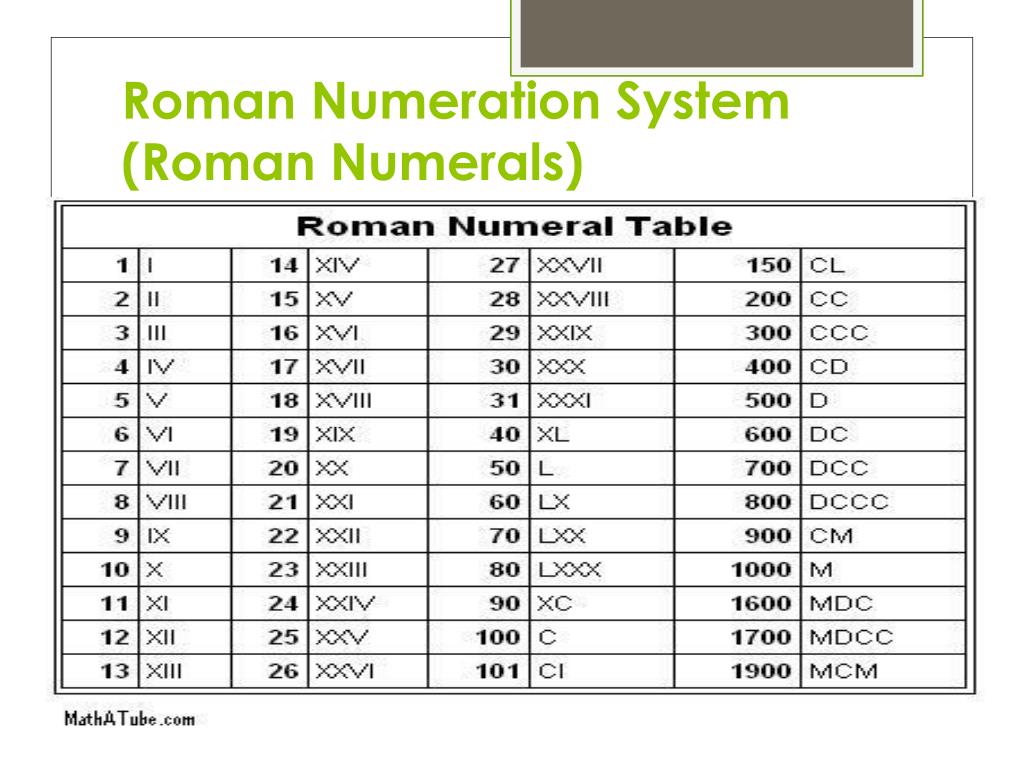
 Advanced Grapher обладает инструментарием для расчета производных и первообразных функций. К тому же, программа умеет отображать их на графике.
Advanced Grapher обладает инструментарием для расчета производных и первообразных функций. К тому же, программа умеет отображать их на графике.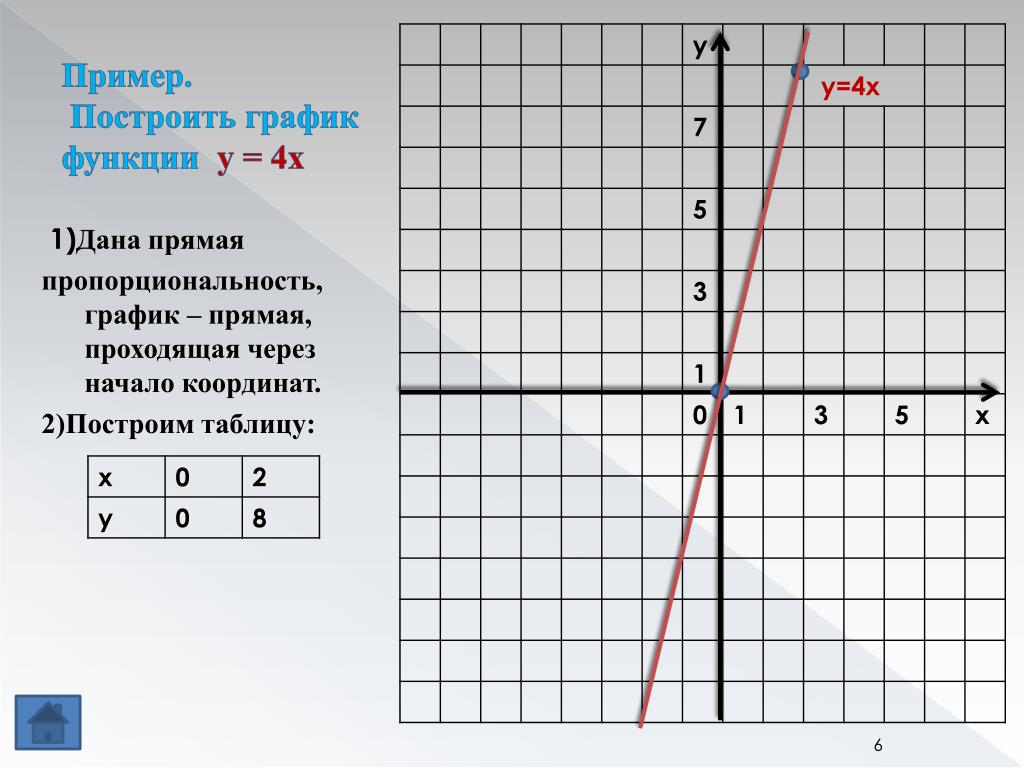 Можно создавать как 3D, так и 2D модели.
Можно создавать как 3D, так и 2D модели.
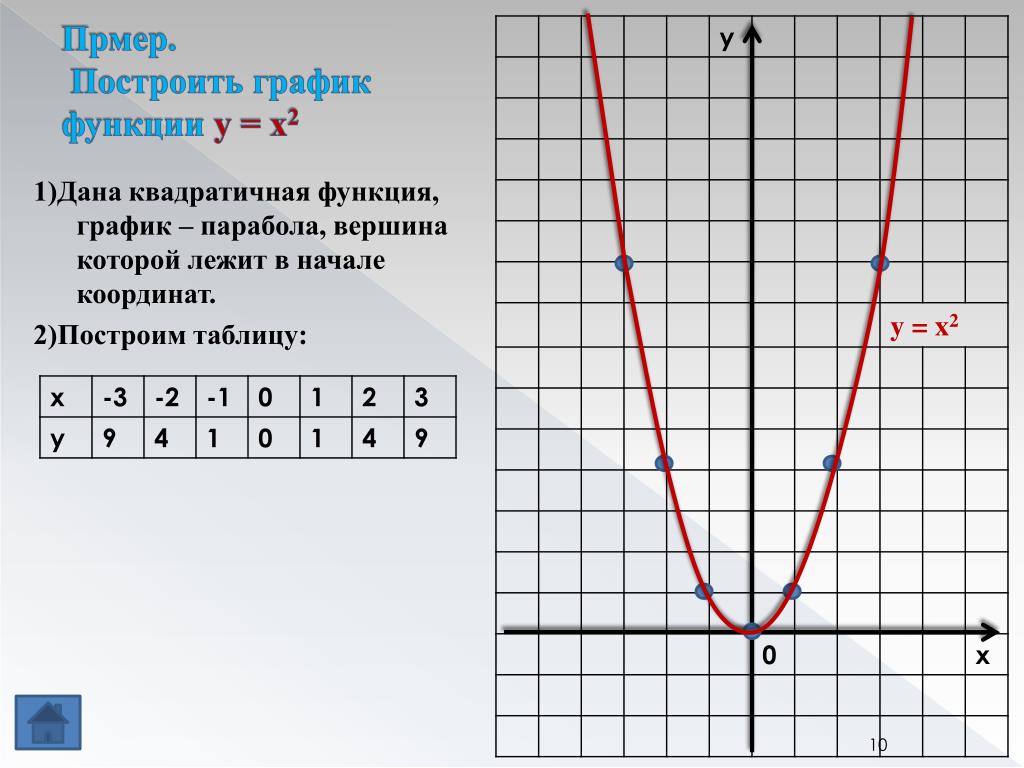
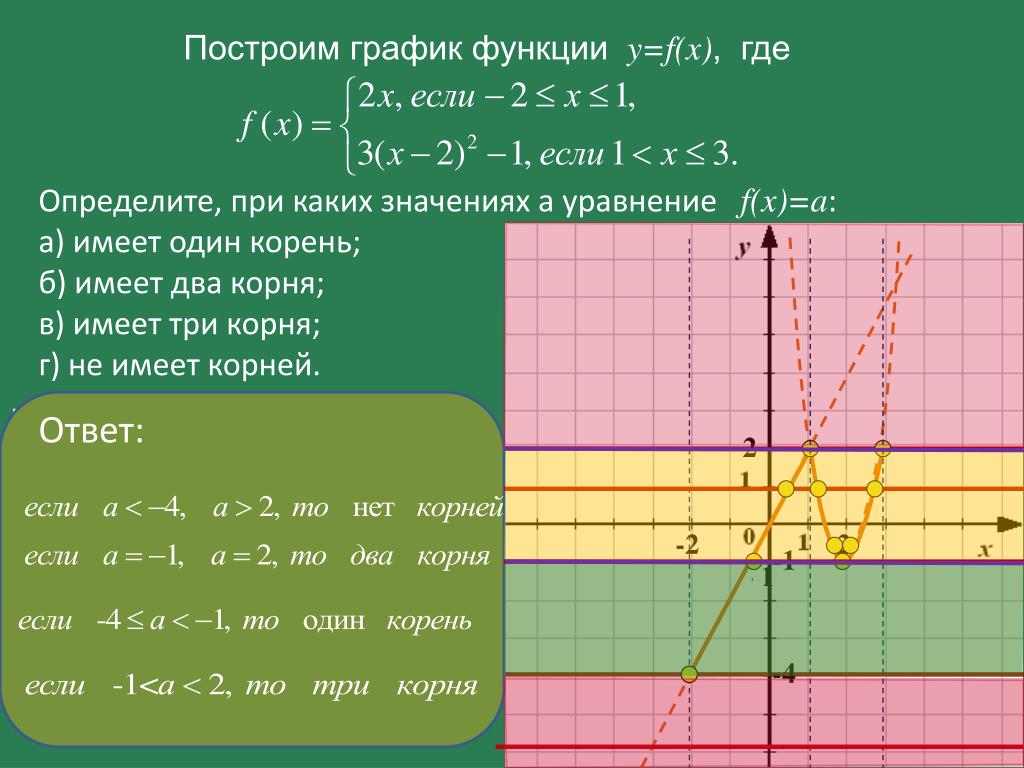 Единственным недостатком можно считать немного непонятное отображение 3D графиков.
Единственным недостатком можно считать немного непонятное отображение 3D графиков.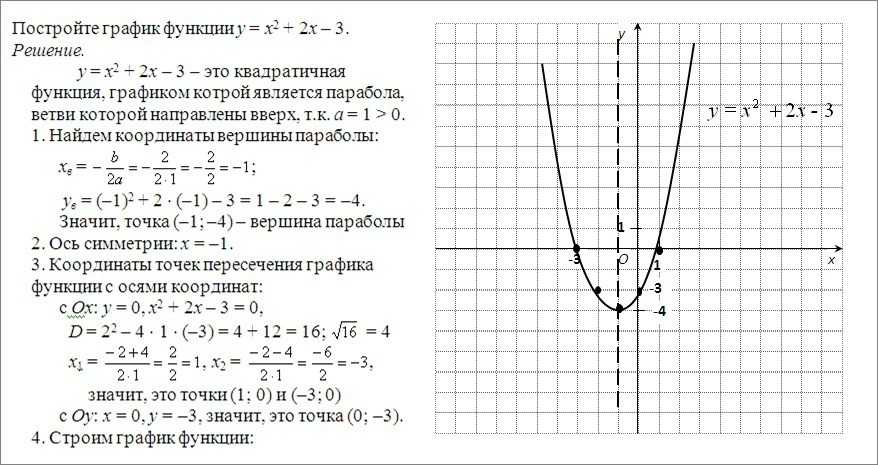 Однако она не отличается слишком уж богатым функционалом и не умеет строить трехмерные графики. Зато работает очень быстро и совершенно бесплатна.
Однако она не отличается слишком уж богатым функционалом и не умеет строить трехмерные графики. Зато работает очень быстро и совершенно бесплатна.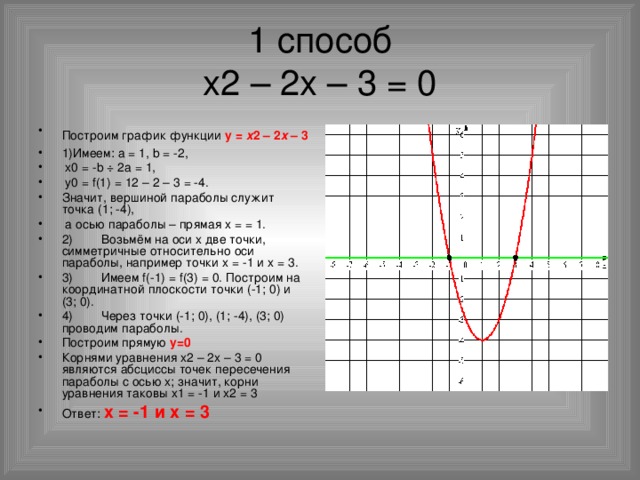
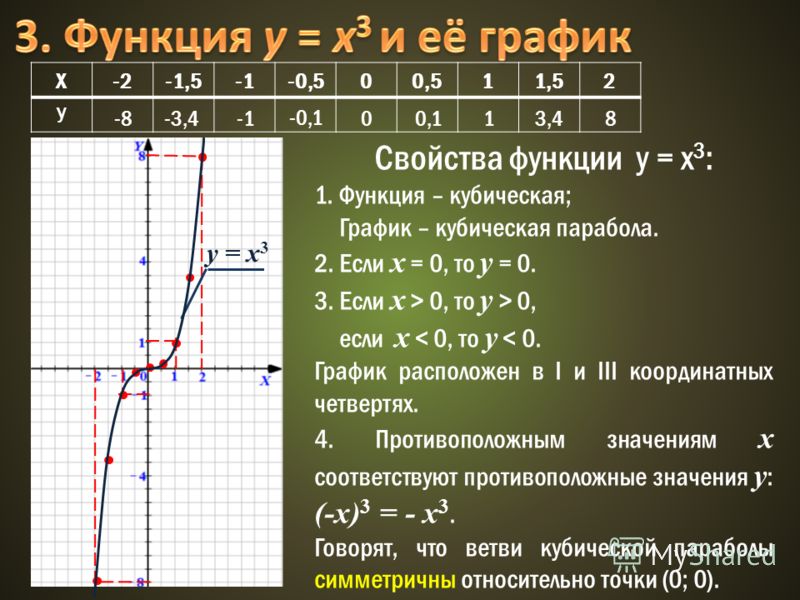 В нем присутствует русский язык и имеется графическое управление функциями. Скачать данную утилиту можно очень легко на официальном сайте компании Microsoft.
В нем присутствует русский язык и имеется графическое управление функциями. Скачать данную утилиту можно очень легко на официальном сайте компании Microsoft.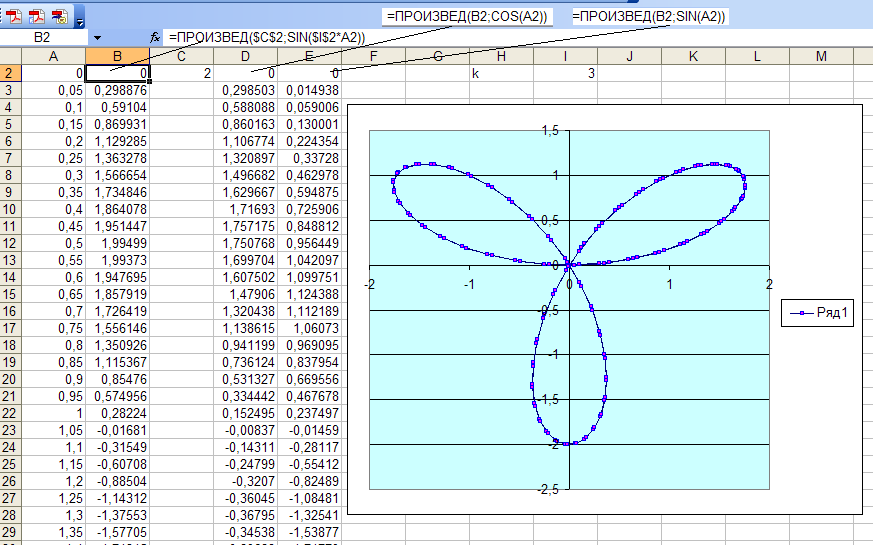 Продукт является полностью бесплатным. Его можно скачать на сайте разработчика.
Продукт является полностью бесплатным. Его можно скачать на сайте разработчика.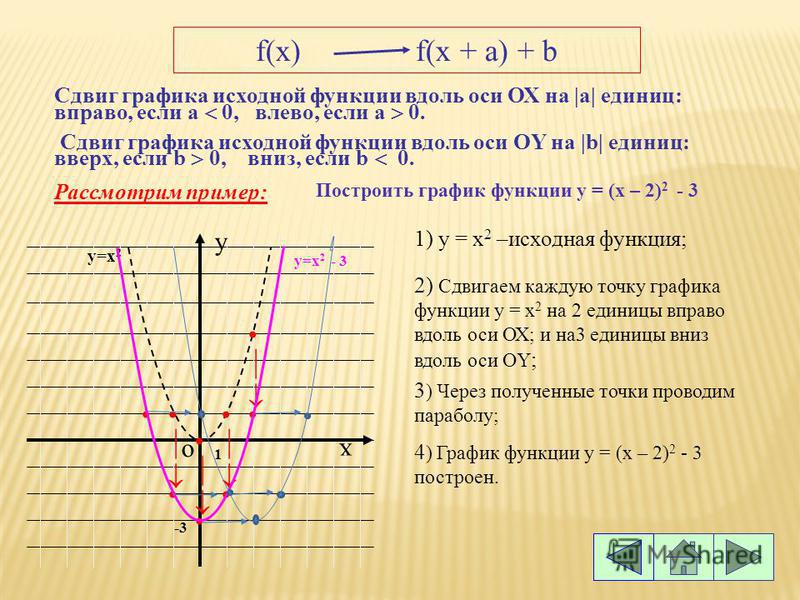
 Отлично работает практически со всеми математическими функциями и обладает простым интерфейсом.
Отлично работает практически со всеми математическими функциями и обладает простым интерфейсом.
 Урок 15: Построение графиков
Урок 15: Построение графиков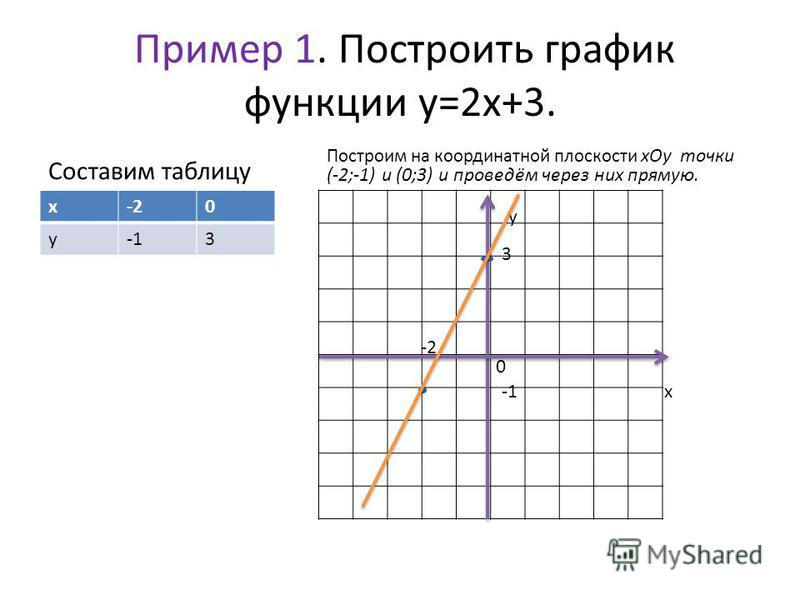 5
5 Рассмотрим некоторые из них более подробно.
Рассмотрим некоторые из них более подробно. plot(x, y, z, label='parametric curve')
plot(x, y, z, label='parametric curve')

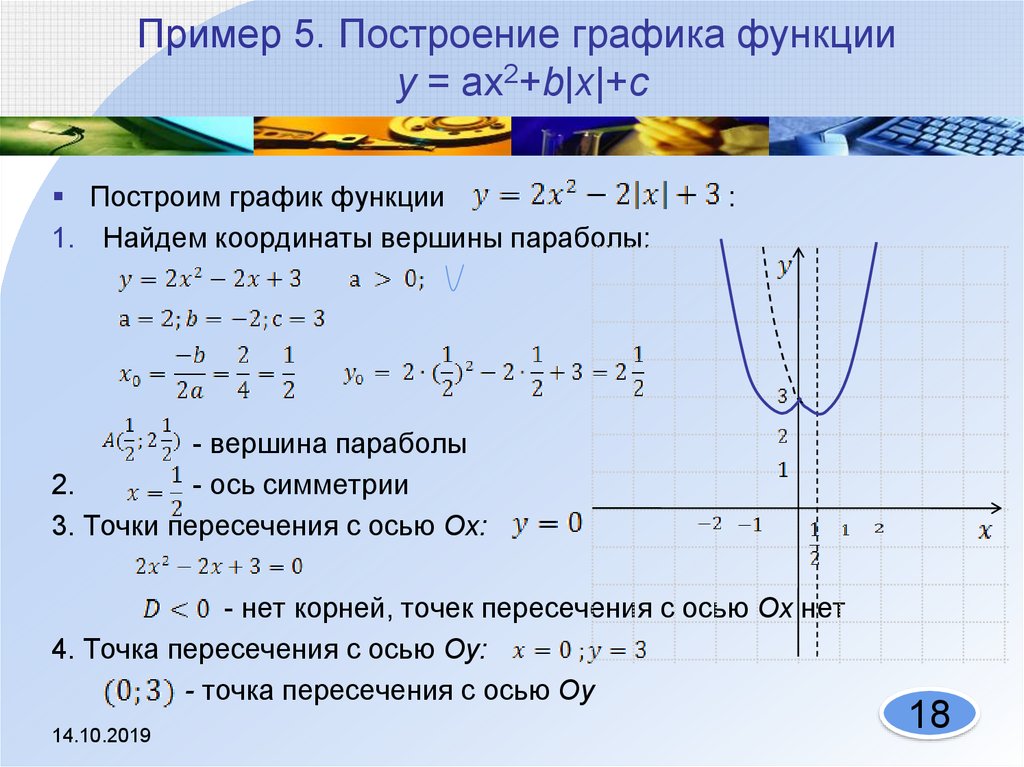
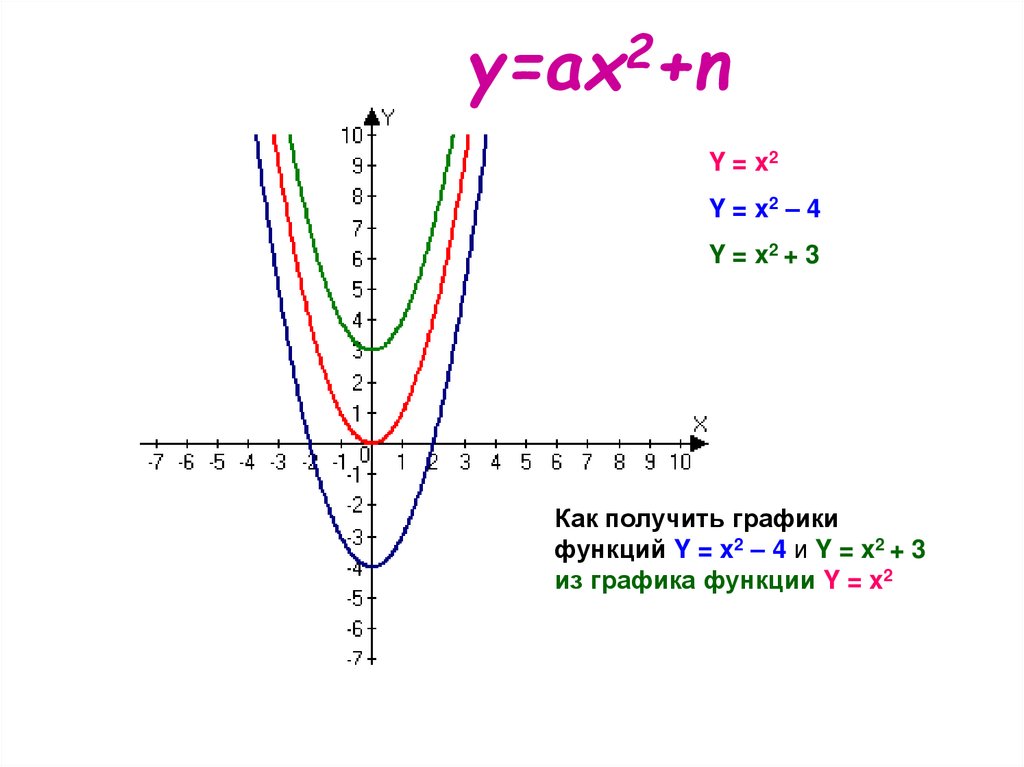
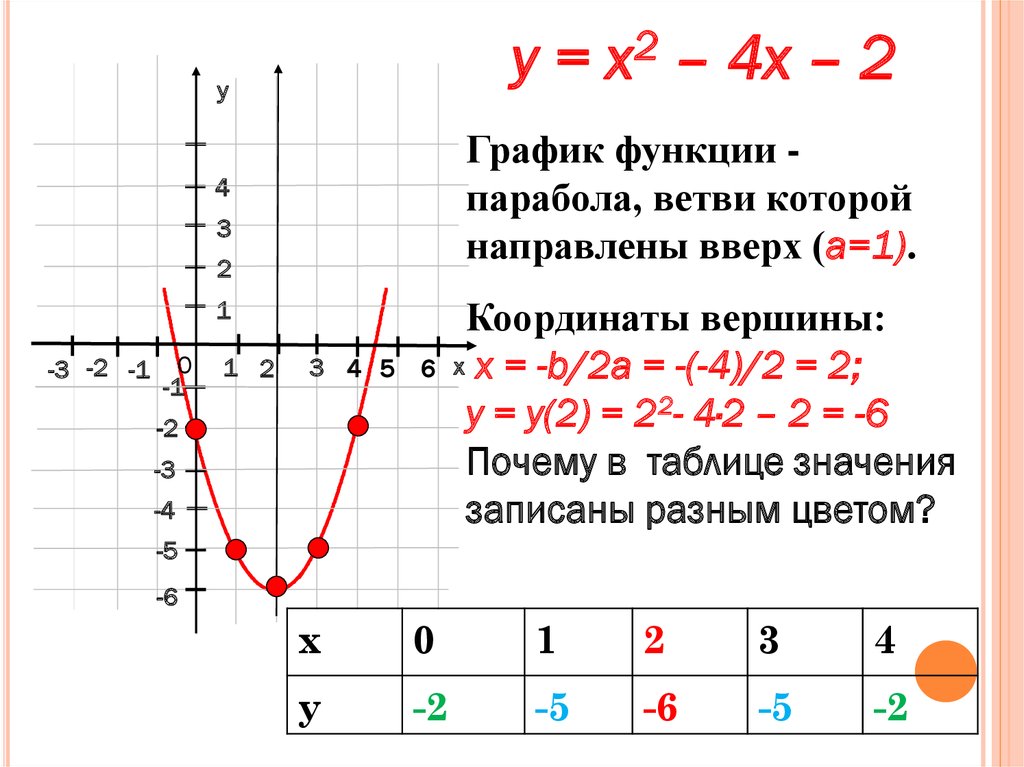 Вы получите образец, указанный ниже:
Вы получите образец, указанный ниже: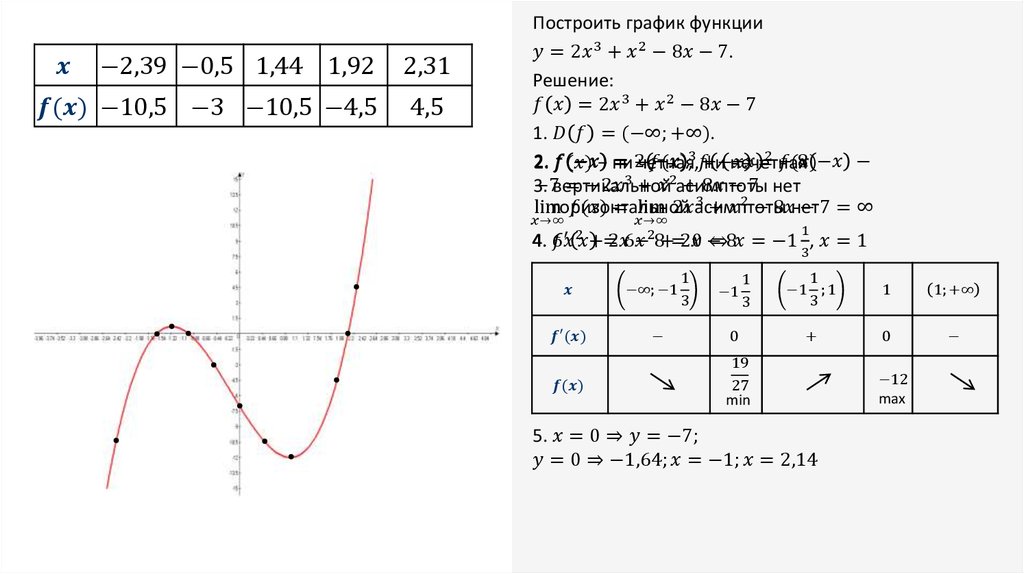 В диалоговом окне установите From , To равным -127 , -65 . Нажмите кнопку ОК.
В диалоговом окне установите From , To равным -127 , -65 . Нажмите кнопку ОК.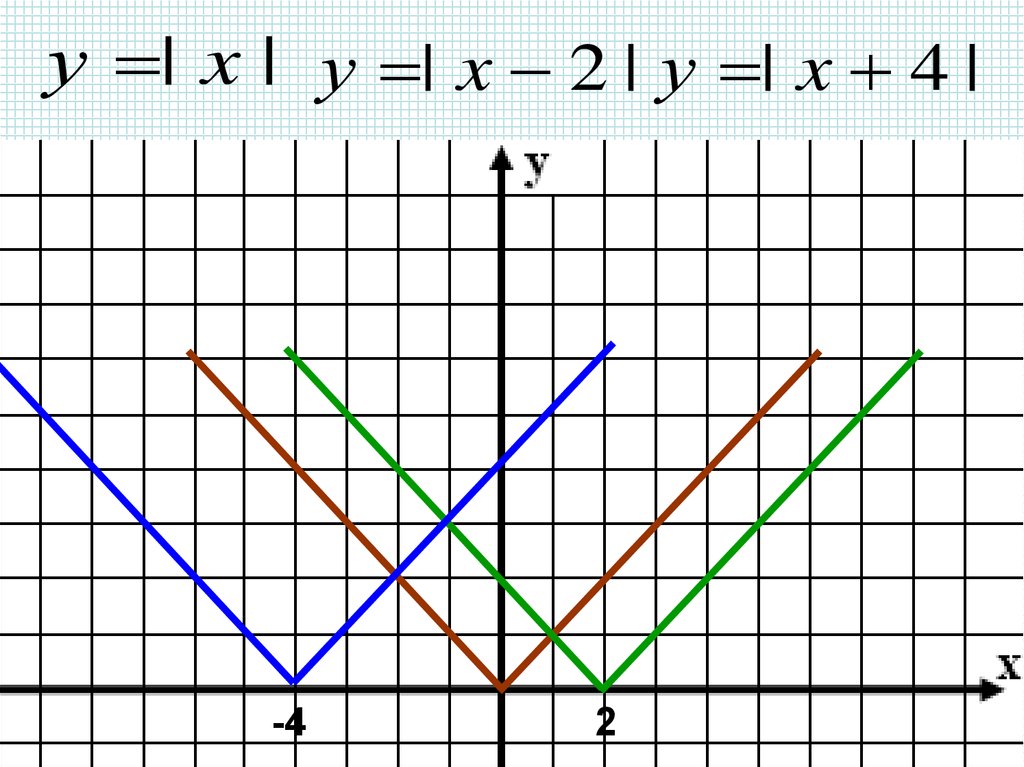 Щелкните заголовок Lines , убедитесь, что выбран параметр Show on Major Levels Only . Выберите 9Установите флажок 0073 Color под Apply to All и выберите LT Grey из раскрывающегося списка в качестве цвета контурной линии. Нажмите OK , чтобы закрыть диалоговое окно.
Щелкните заголовок Lines , убедитесь, что выбран параметр Show on Major Levels Only . Выберите 9Установите флажок 0073 Color под Apply to All и выберите LT Grey из раскрывающегося списка в качестве цвета контурной линии. Нажмите OK , чтобы закрыть диалоговое окно.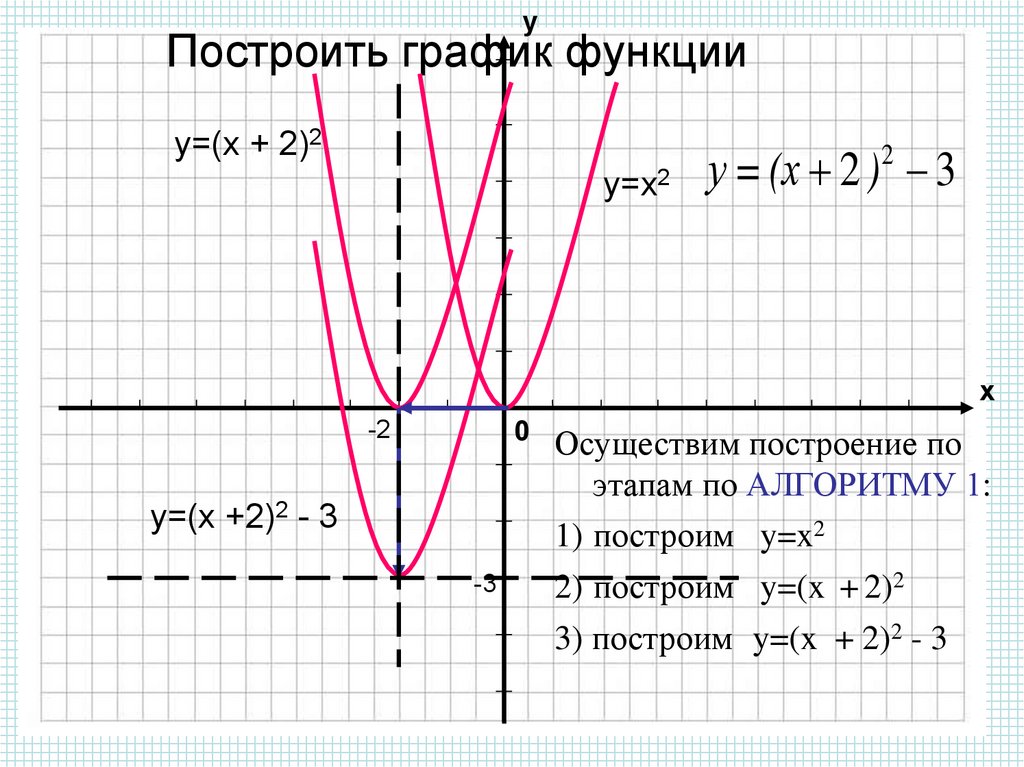
 Можно рисовать поверхностные, гистограммы и точечные графики. Данные
должны быть легко представлены в виде регулярной сетки. Эта процедура предполагает
что элементы сетки являются значениями оси Z, полученными из функции
F(x,y) путем его вычисления через регулярные интервалы X и Y. Сетка
Предполагается, что они размещены в матрице данных таким образом, что столбцы соответствуют значениям
переменной Y, а строки соответствуют значениям переменной X. Для
Например, ячейка (5,2) блока данных должна содержать значение F(x(5),y(2)),
т. е. значение двумерной функции, оцененное на пятом шаге X
переменная и второй шаг переменной Y.
Можно рисовать поверхностные, гистограммы и точечные графики. Данные
должны быть легко представлены в виде регулярной сетки. Эта процедура предполагает
что элементы сетки являются значениями оси Z, полученными из функции
F(x,y) путем его вычисления через регулярные интервалы X и Y. Сетка
Предполагается, что они размещены в матрице данных таким образом, что столбцы соответствуют значениям
переменной Y, а строки соответствуют значениям переменной X. Для
Например, ячейка (5,2) блока данных должна содержать значение F(x(5),y(2)),
т. е. значение двумерной функции, оцененное на пятом шаге X
переменная и второй шаг переменной Y. Если вы хотите построить явную функцию двух переменных F (x, y)
это проще сделать в процедуре График 3D-функций, без необходимости генерировать
сначала сетка.
Если вы хотите построить явную функцию двух переменных F (x, y)
это проще сделать в процедуре График 3D-функций, без необходимости генерировать
сначала сетка.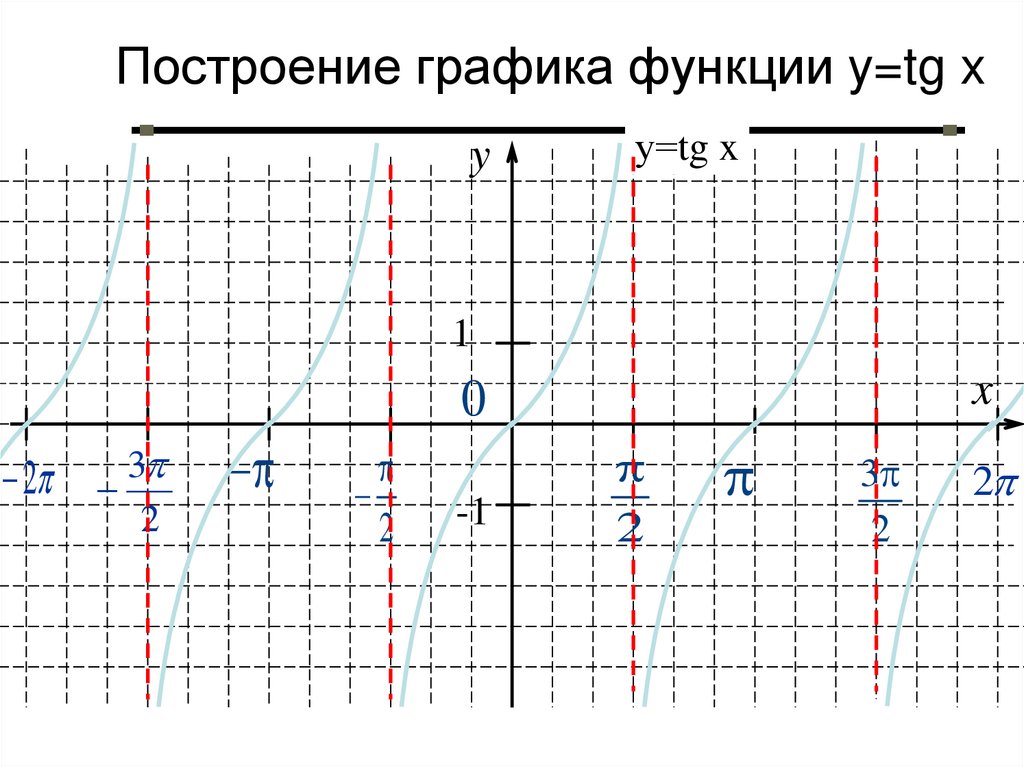

 Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.
Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.
 Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
 е. коэффициенты при неизвестных и свободные члены пропорциональны.
е. коэффициенты при неизвестных и свободные члены пропорциональны.

 Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко
ходить не надо.
Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко
ходить не надо. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения! Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи. В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
 Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
 По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.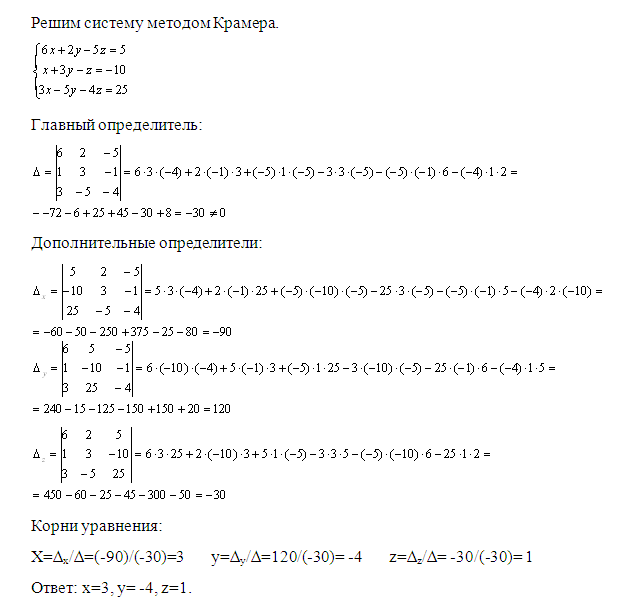
 Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
 В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
 В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
 Соответствующие ссылки будут даны по ходу объяснений.
Соответствующие ссылки будут даны по ходу объяснений. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:



