3DNews Технологии и рынок IT. Новости интересности из мира хай-тек Casio анонсировала новую линейку инженер… Самое интересное в обзорах 08.12.2014 [08:02], Дмитрий Приходько Эпоха классических калькуляторов в виде отдельных устройств постепенно становится частью истории, их место заняли многофункциональные приложения на мобильных устройствах. Учитывая то, что удобные для сложных математических вычислений сенсорные телефоны с большой площадью дисплея стали доступными всем слоям населения, потребность в обычных калькуляторах практически исчезла. Однако не дать кануть в лету столь знаковому изобретению XX столетия делает попытки небезызвестная компания Casio. В своё время, как впрочем и сегодня, инженерные калькуляторы японского производителя являются эталоном эргономичности, максимально возможной за указанную стоимость функциональности, которой пользовались студенты и специалисты различных областей знаний. Флагманское устройство, а также его упрощённая модификация fx-570EX, впервые обладают поддержкой функции электронной таблицы, информация в которой отображается на LCD-дисплее в 12 096 точек. Разрешение выполненного по технологи film-compensated super-twisted nematic (FSTN) экрана на основе монохромной пассивной матрицы с пленочной компенсацией, необходимой для расширения углов обзора, в четыре раза превышает данный параметр прошлых моделей. Это позволяет работать со сложными формулами и большим количеством математических символов на маленьком дисплее со значительно большим комфортом, нежели прежде. Главной особенностью Casio fx-991EX, как уже было отмечено выше, стала поддержка таблиц, которые значительным образом упростят взаимодействие с калькулятором при работе с рекуррентными формулами и заполнением статистических показателей. В дополнение к вышесказанному владелец Casio fx-991EX сможет передавать на дисплей смартфона или планшета введённые на калькуляторы формулы и готовые результаты. Для этого потребуется воспользоваться опцией преобразования формул на экране калькулятора в QR-код, который можно распознать камерой мобильного устройства в тандеме со специальным ПО, чтобы отобразить его в первоначальном виде. Собственно, ознакомиться с руководством пользователя для Casio fx-991EX можно, в том числе, именно таким способом. Используемой в калькуляторе батарейки типа LR44 и миниатюрной солнечной панели, по заявлению производителей, хватит на 2 года работы, исходя из одного часа работы ежедневно. На данный момент стоимость новинки пока что остаётся неизвестной, но в продажу калькулятор должен поступить уже в I квартале 2015 года. Источник: Если вы заметили ошибку — выделите ее мышью и нажмите CTRL+ENTER. Материалы по теме Постоянный URL: https://3dnews.ru/906293 Рубрики: Новости Hardware, интересности из мира хай-тек, Теги: casio, калькулятор, анонс, модель, математика, вычисления, электронная, таблица, устройство ← В прошлое В будущее → |
4 лучших графических калькулятора для инженеров (2023)
Взгляд инженера
Содержание
Введение
Давайте будем честными, графические калькуляторы стоят дорого. Важно найти правильный, который соответствует вашим потребностям в классе или на вашем рабочем месте в качестве инженера.
Эта статья расскажет о наиболее важных функциях графического калькулятора и поможет вам определить, какой калькулятор лучше всего подходит для ваших конкретных нужд.
4 лучших графических калькулятора для инженеров и студентов инженерных специальностей
Вот лучшие графические калькуляторы для инженера или студента инженерного факультета:
- Графический калькулятор Texas Instruments TI-84 Plus CE (Лучший в целом) 9 0026
- CASIO fx-9750GII Графический калькулятор (самый доступный/дешевый)
- Texas Instruments TI-Nspire CX CAS (лучший расширенный)
- Графический калькулятор HP Prime G2 (CAS) (Лучший сенсорный экран)
Графический калькулятор Texas Instruments TI-84 Plus CE (самый доступный/самый дешевый)
Предоставлено: Texas Instruments
Проверить цену на Amazon
Резюме: Мы выбрали TI-84 CE как лучший графический калькулятор из-за надежного программного обеспечения и разумной цены. CE — это более современная версия старых выпусков TI-84, но с лучшей скоростью обработки (в 2,5 раза быстрее), временем автономной работы, разрешением экрана и в целом более гладким и компактным внешним видом.
CE — это более современная версия старых выпусков TI-84, но с лучшей скоростью обработки (в 2,5 раза быстрее), временем автономной работы, разрешением экрана и в целом более гладким и компактным внешним видом.
Цена ПРОВЕРИТЬ ЦЕНУ ЗДЕСЬ 900 05 | Цветной Да (дисплей с подсветкой) | ||
| 900 61 Хранение 3,0 МБ ПЗУ / 154 КБ ОЗУ | Разрешение 320 x 240 пикселей 140 точек на дюйм; 16-битный цвет | ||
Питание Аккумулятор емкостью 1200 мАч (~1 месяц использования без подзарядки) | Размер 19,05 x 8,69 x 1,57 см | ||
Вес 340,19 г | Процессор Zilog eZ80 @ 48 МГц |
Отличительные особенности
- Впечатляющий дисплей: Возможность видеть безупречный цветной дисплей с подсветкой, когда вам нужно отобразить несколько функций и извлечь информацию, очень полезна.
 Поверьте нам в этом.
Поверьте нам в этом. - Много места для хранения: Будучи студентом инженерного факультета, вам придется вычислять множество смехотворно длинных формул, а наличие места для программирования этих уравнений и констант в вашем графическом калькуляторе может иметь решающее значение для своевременной сдачи выпускного экзамена.
- Очень легкий вес. Он примерно на 30 % легче, чем его предыдущие модели TI-84 (очень тонкий дизайн), и это важно, когда вы таскаете с собой задания, заметки и учебники.
- Цена: это невероятная цена за программное обеспечение, которое предлагает эта машина: скорость обработки 48 МГц и 3 МБ ПЗУ.
- Прием в среднюю школу: PSAT*, SAT* и ACT*, AP*, IB
Графический калькулятор CASIO fx-9750GII (самый доступный/самый дешевый)
90 005 Предоставлено: CASIO
Проверить цену на Amazon. Входит по низкой цене до ~$70 , это один из самых дешевых графических калькуляторов на рынке.
Этот калькулятор позволяет программировать на Python. Учитывая популярность языка программирования почти во всех инженерных дисциплинах, это, безусловно, выдающаяся функция по цене калькулятора.
Учитывая популярность языка программирования почти во всех инженерных дисциплинах, это, безусловно, выдающаяся функция по цене калькулятора.
Одним из самых больших преимуществ является то, насколько он удобен для пользователя, что отчасти связано с отсутствием причудливых функций, которые большинство людей, вероятно, никогда не будут использовать (например, трехмерные графики, электронные таблицы, периодические таблицы).
ЦЕНА ПРОВЕРИТЬ ЦЕНУ ЗДЕСЬ 9000 5 | Цветной №: монохромный ЖК-экран | ||
Хранение 0,26 МБ ОЗУ, 62 000 байт памяти | Разрешение 64 x 128 пикселей | Мощность AAA (примерно 230 часов) | Размер 18,54 x 2,54 x 8,89 см |
Вес 226,8 г | Процессор Zilog Z80 @ 6 МГц |
Отличительные особенности
- Цена: цена здесь является самой привлекательной чертой.

- Удобный для пользователя: охватывает все основы с тем, что нужно графическому калькулятору без большого количества наворотов. В конечном итоге это должно сделать кривую обучения менее крутой, а некоторые важные программы, такие как приложение Solver, менее сложными в использовании.
- Разрешение экрана: Разрешение не самое лучшее, что затрудняет различение графических элементов, таких как асимптоты в графических функциях, особенно без какой-либо цветовой кодировки.
- Прием в среднюю школу: Вступительные экзамены в колледж PSAT, SAT и ACT, тесты IB и AP.*
Texas Instruments TI-Nspire CX CAS (Лучший продвинутый)
Предоставлено: Texas InstrumentsПроверить цену на Amazon
Резюме: TI-Nspire CX CAS — это совершенно другая машина. При впечатляюще легком весе в 242 грамма этот калькулятор имеет безумную скорость обработки 132 МГц, что для справки почти в 9 раз больше, чем у классического TI-84 в раз. Это то, что даст вам невероятно быстрое графическое время без каких-либо задержек. Вы также получите исходное качество изображения с высокой плотностью пикселей, что очень полезно при построении нескольких кривых или сложных моделей.
Это то, что даст вам невероятно быстрое графическое время без каких-либо задержек. Вы также получите исходное качество изображения с высокой плотностью пикселей, что очень полезно при построении нескольких кривых или сложных моделей.
Имея впечатляющие 64 МБ ОЗУ и 100 МБ флэш-памяти, эта красавица сможет сохранять что угодно, от множества графических функций до документов TI-Nspire. Если деньги не имеют значения или вам требуется высокая функциональность и широкий спектр приложений, то калькулятор TI-Nspire CX CAS — это то, что вам нужно.
ЦЕНА ПРОВЕРИТЬ ЦЕНУ ЗДЕСЬ | Цвет Да (дисплей с подсветкой) | ||
Хранение 100 МБ памяти / 64 МБ оперативной памяти | Разрешение 125 DPI; 16-битный цвет | ||
Питание Аккумулятор 1200 мАч | 9 № 0063 | Размер 18,5 x 1,5 x 8 см | |
Вес 242 грамма | 90 061 Процессор ARM9 @ 132 МГц |
Отличительные особенности
- Приложения и функции: CAS Калькуляторы — это в основном графические компьютеры.
 Расчеты можно сохранять в виде документов так же, как это делается на компьютере, что обязательно пригодится во время тестов, если вы хотите сослаться на какие-либо расчеты, используемые при решении практических задач. Одной из наших любимых функций является функция создания ползунка для графического отображения различных функций. Это особенно полезно, если вы хотите увидеть, насколько влиятельна переменная в уравнении. Это полезно в химической инженерии в таких курсах, как проектирование реакторов, где можно изучать двухмерные функции, чтобы понять важность определенных переменных.
Расчеты можно сохранять в виде документов так же, как это делается на компьютере, что обязательно пригодится во время тестов, если вы хотите сослаться на какие-либо расчеты, используемые при решении практических задач. Одной из наших любимых функций является функция создания ползунка для графического отображения различных функций. Это особенно полезно, если вы хотите увидеть, насколько влиятельна переменная в уравнении. Это полезно в химической инженерии в таких курсах, как проектирование реакторов, где можно изучать двухмерные функции, чтобы понять важность определенных переменных. - Режим экзамена: Несмотря на то, что это калькулятор CAS, который может вызвать сложности при экзаменах, существует «режим экзамена», который позволяет вашему учителю ограничивать определенные функции с помощью пароля на время экзамена.
- Очень легкий вес: он примерно на 30 % легче, чем его предыдущие модели TI-84 (очень тонкий дизайн)
- Впечатляющее время автономной работы: Производитель хвастается «Один месяц использования» на одном заряде
- Цена: цена очевидно, на более высоком уровне, так что это минус.

- Прием в старшие классы: экзамены SAT, AP и PSAT/NMSQT с высокими ставками. Он также одобрен для некоторых государственных экзаменов.
Взгляд инженера
CAS и не-CAS
Проверьте, есть ли в калькуляторе слово «CAS», что означает «система компьютерной алгебры». Калькуляторы CAS Graphing — это невероятные устройства, способные решать, разлагать на множители и манипулировать уравнениями, и они могут быть вашими лучшими друзьями до тех пор, пока их не допустят к экзамену.
Графический калькулятор HP Prime G2 (CAS) (лучше всего подходит для сенсорного экрана)
Кредит: HP
Проверить цену на Amazon
Резюме: В мире, где почти каждое портативное устройство оснащено сенсорным экраном, этот калькулятор отличается от других калькуляторов «наведи и щелкни». Этот калькулятор очень похож на TI-Nspire CX как по дизайну, так и по программному обеспечению. Высокая скорость обработки, прочный металлический корпус и сенсорный экран — все это отличные функции, которые значительно улучшают работу пользователя.
О, и еще одна интересная функция — темный режим, которого мы не видели ни на одном другом калькуляторе; определенно отлично подходит для тех долгих ночей наедине с калькулятором.
ЦЕНА ПРОВЕРИТЬ ЦЕНУ ЗДЕСЬ | Цвет Да | ||
| 900 61 Хранение 256 МБ ОЗУ 512 МБ ПЗУ | Разрешение 320×240 пикселей 900 61 16-битный цветной, мультитач | ||
Питание 1 Литиевый ионные батареи | Размер 9,3 x 1,6 x 18,5 | ||
Вес 226,8 г | Процессор Ядро Cortex A7 с частотой 528 МГц |
Отличительные особенности
90 022 Основным преимуществом невероятного процессора является отсутствие задержек при использовании функции сенсорного экрана для поворота 3D-графиков.
Основным преимуществом невероятного процессора является отсутствие задержек при использовании функции сенсорного экрана для поворота 3D-графиков.Взгляд инженера
Нужен ли он мне?
Помните, что иногда графические калькуляторы могут даже не понадобиться. Например, если он вам нужен только для 1 курса на получение степени, возможно, стоит просто одолжить его у друга и купить прочный научный калькулятор за 20 долларов.
Подробное руководство покупателя
Существует 6 основных моментов, которые необходимо учитывать при покупке графического калькулятора:
- Цена
- Память
- Мощность/Б батарея
- Вес/Размер
- Экран Качество (цвет, разрешение, размер)
- Одобрение экзамена
1.
 Цена
ЦенаСтоимость большинства калькуляторов обычно превышает 100 долларов. Хотя графические калькуляторы являются технологией начала 2000-х годов, динамика спроса и предложения работает в их пользу и оказывает огромное влияние на их высокую цену.
При этом лучше всего рассматривать покупку графического калькулятора как инвестицию в академическую и профессиональную инженерную карьеру.
Как и при любых инвестициях, вы хотите получить наилучшее соотношение цены и качества. В то время как более дешевые калькуляторы обеспечивают функциональность, необходимую для большинства инженерных курсов, им обычно не хватает качества оборудования, и они более подвержены повреждениям.
Мы также рекомендуем приобрести футляр для калькулятора, чтобы продлить срок службы ваших инвестиций.
Взгляд инженера
Помните, что вы всегда можете купить бывшие в употреблении калькуляторы
Посмотрим правде в глаза, для бедных студентов колледжей новые модные калькуляторы могут быть дорогими. Покупка бывших в употреблении калькуляторов — отличный вариант при ограниченном бюджете. Проверьте, есть ли в вашей школе онлайн-группа по покупке/продаже, или поищите выгодные предложения на Kijiji.
Покупка бывших в употреблении калькуляторов — отличный вариант при ограниченном бюджете. Проверьте, есть ли в вашей школе онлайн-группа по покупке/продаже, или поищите выгодные предложения на Kijiji.
Есть два ведущих бренда в игре с графическим калькулятором; Texas Instruments и Casio . Обе компании производят и продают свои графические калькуляторы уже более 30 лет.
Ведущим брендам можно доверять. Гораздо безопаснее инвестировать в покупку калькулятора у компании с многолетним опытом и знаниями в области продукции. Большинство моделей калькуляторов, продаваемых как Casio, так и Texas Instruments, прошли несколько итераций и имеют оптимизированные функции для визуализации сложных функций и проблем, с которыми вы столкнетесь в своей инженерной карьере.
2. Память
Память графических калькуляторов находится в RAM (оперативная память) и FlashROM (постоянная память). Оперативная память является самой быстрой из обеих памяти и используется при запуске программ, но легко очищается после сбоев. Флэш-ПЗУ более надежна в долгосрочной перспективе и обычно называется архивной памятью.
Флэш-ПЗУ более надежна в долгосрочной перспективе и обычно называется архивной памятью.
Вы хотите быть уверены, что ваш калькулятор имеет достаточно оперативной памяти, чтобы вы могли выполнять вычисления без стресса во время теста, и достаточно флэш-памяти для восстановления сохраненных приложений и программ.
Взгляд инженера
RAM
Очищайте ОЗУ вашего калькулятора перед каждым тестом, чтобы избежать ненужной паники. Последнее, что вы хотите увидеть перед тестом, это то, что у вашего калькулятора недостаточно памяти!
3. Питание/аккумулятор
Все графические калькуляторы не одинаковы. Некоторые поставляются с батареями, а другие требуют покупки батарей. Некоторые из них имеют встроенные аккумуляторы, которые можно перезаряжать.
Исходя из нашего личного опыта и опыта, мы обнаружили, что графические калькуляторы, для которых требуются батареи, обычно более надежны, особенно в сценариях экзаменов. При обычном использовании такие калькуляторы, как графический калькулятор Texas Instruments TI-84 Plus CE, обычно работают около года, а их резервные батареи обычно работают от 2 до 5 лет, что устраняет любые немедленные беспокойства.
При этом перезаряжаемым графическим калькуляторам обычно требуется около 4 часов для полной зарядки батарей, но полностью заряженного калькулятора, такого как TI-Nspire CX, обычно хватает примерно на 2 недели при полной зарядке. На самом деле, калькулятор цветной графики TI-Nspire CX II CAS предоставляется с двухнедельной зарядкой!
4. Качество экрана
При выборе качества экрана необходимо учитывать три момента
- Цвет
- Разрешение
- Размер
Мы предпочитаем цветные экраны более распространенным монохромным ЖК-дисплеям. Это делает обучение более визуально стимулирующим. Говоря более научным языком, наш мозг использует цвет для развития распознавания образов, памяти и усвоения информации. Представьте, как это может быть полезно во время продолжительных ночных занятий!
Разрешение
Большинство калькуляторов с цветным экраном обычно имеют более высокое разрешение, около 360 x 240 пикселей, по сравнению с их монохромными аналогами без подсветки. Это означает, что калькуляторы, такие как TI-Nspire CX или TI-Nspire CX II CAS Color Graphing Calculator будут идеальным выбором, если вы хотите оптимизировать разрешение в качестве соображений.
Это означает, что калькуляторы, такие как TI-Nspire CX или TI-Nspire CX II CAS Color Graphing Calculator будут идеальным выбором, если вы хотите оптимизировать разрешение в качестве соображений.
Существует причина, по которой размеры экранов большинства портативных устройств с годами увеличились. Мы хотим видеть больше и, в буквальном смысле, получить более широкую картину. Вот почему размер экрана является важным фактором при покупке графического калькулятора.
Меньший размер экрана создаст трудности при расшифровке точек пересечения на графиках функций или может привести к тому, что меню программы будет выглядеть слишком сжатым.
Большинство калькуляторов CAS предлагают увеличенный размер экрана, чтобы оптимизировать отображение широкого спектра имеющихся у них функций. Если вы считаете размер экрана важным фактором в процессе принятия решений, мы рекомендуем HP Prime G2 Graphing Calculator . Его диагональ 3,5 дюйма/8,9 см в сочетании с впечатляюще чувствительным сенсорным дисплеем делают работу пользователя еще более приятной!
5.
 Размер и вес
Размер и весМы рекомендуем выбирать графический калькулятор со встроенными перезаряжаемыми батареями, такими как TI-Nspire CX II CAS Color Graphing Calculator , так как батареи AAA или AA имеют тенденцию увеличивать вес калькулятора.
6. Утверждение экзамена
Последнее, что вы хотите, это купить графический калькулятор на предстоящий учебный год и понять, что вы не сможете воспользоваться ни одной из его уникальных функций.
Хотя большинство обычных графических калькуляторов разрешены на уровне средней школы для сдачи экзаменов SAT, PSAT, ACT, AP и IB. На университетском уровне лучше подтвердить, что вам разрешено использовать эти калькуляторы со своими преподавателями до учебного года для таких курсов, как линейная алгебра, исчисление I и II, численные методы и т. д.
Почему графический калькулятор важен в технике?
Графические калькуляторы позволяют нам строить графики функций, которые являются строительными блоками для моделирования этих явлений. Инженерия по своей природе заключается в использовании моделей для понимания и управления аспектами мира природы.
Инженерия по своей природе заключается в использовании моделей для понимания и управления аспектами мира природы.
Как быстро научиться пользоваться графическим калькулятором?
Усовершенствованные графические калькуляторы могут делать так много, что иногда сложно понять их. Тем не менее, стоит потратить дополнительное время на изучение некоторых из этих функций, поскольку они могут быть очень полезны на экзаменах.
Вот несколько отличных способов использовать все возможности графического калькулятора:
Видео графического калькулятора на YouTube
Наш любимый канал для Texas Instruments называется Texas Instruments Education.
Руководство по эксплуатации
Эти руководства можно найти на официальном сайте конкретной модели калькулятора. Они предлагают подробное руководство по функциям и возможностям вашего калькулятора.
Веб-сайты/Сообщения в блогах
Существует множество веб-сайтов (например, dummies. com, sciencing.com), которые предоставляют отличные ресурсы и шпаргалки о том, как использовать ваш калькулятор.
com, sciencing.com), которые предоставляют отличные ресурсы и шпаргалки о том, как использовать ваш калькулятор.
Используют ли инженеры графические калькуляторы на работе?
Да . Графические калькуляторы могут быть очень полезны работающему инженеру, но это очень зависит от типа работы, которую вы выполняете . Многие компании используют программное обеспечение корпоративного уровня для расширенного моделирования и расчетов (Minitab, Python, Excel), однако всегда безопасно иметь собственный надежный графический калькулятор для выполнения любых необходимых проверок.
Заключение
Калькуляторы — это инвестиции, которые требуют обдумывания перед покупкой. Проведите исследование и следуйте нашему руководству, чтобы найти идеальное сочетание для вас.
6 лучших калькуляторов для инженеров в 2023 году
Раскрытие информации: этот пост содержит партнерские ссылки, и я могу получить небольшую комиссию, если вы сделаете покупку по этим ссылкам.
До появления электронных калькуляторов механические калькуляторы, изобретенные в конце 17 века, имели решающее значение, помогая инженерам решать уравнения. Сегодня электронные калькуляторы развились не только для обработки сложных уравнений, но и для высокой скорости и точности. Ученые и инженеры во всем мире используют их для быстрого и точного выполнения сложных математических уравнений.
Существует множество разновидностей калькуляторов, которые инженеры могут использовать в своих проектах. Большинство из них многофункциональны, с подключением через USB, возможностью построения графиков, хранением данных и памяти, возможностями программирования и т. д.
В этом руководстве мы рассмотрим пять лучших калькуляторов для инженеров, представленных на рынке в 2023 году, включая типы и основные факторы, которые необходимо учитывать перед покупкой.
Вот некоторые из лучших моделей калькуляторов, доступных на рынке, основанные на последних данных о настроениях клиентов и рекомендациях нашего собственного сообщества инженеров-металлургов со всего мира:
| | 👑 ЛУЧШИЙ ОБЩИЙ | 🛠️ ЛУЧШИЙ ВТОРОЙ ВАРИАНТ | 🛋️ ДЛЯ СТУДЕНТОВ |
|---|---|---|---|
| | Texas Instruments TI-84 | HP PRIME G2 | Техас Инструменты TI-89 |
| 3 | 3,0 МБ ПЗУ / 154 КБ ОЗУ | 256 МБ флэш-памяти | ОЗУ 188 КБ и флэш-память 2,7 МБ |
| ПИТАНИЕ 🕒 | 1 литий-металлические батареи (в комплекте) | 1 литий-металлические батареи (в комплекте) | 4 А батареи (в комплекте) |
| РАЗМЕР ЭКРАНА📏 | 3,2 дюйма | 3,5 дюйма | 100 x 160 пикселей |
| ВЕС ⚖️ | 7 унций | 4,8 унции | 9 0796 10,24 унции|
| ПЛЮСЫ 👍 | Большой экран упрощает чтение и доступ к меню | Он имеет 30 КБ памяти и более 800 независимых регистров хранения | Он поставляется с прикрепленной твердой задвижной крышкой для защиты в случае падения |
| МИНУСЫ 👎 | Это дорого по сравнению с некоторыми другими калькуляторами | Это делает не имеют подсветки, что затрудняет использование в условиях низкой освещенности | Тем, кто работает в профессиональной среде, может потребоваться больше функций |
| ЦЕНА 💵 | 117,00 $ | 128,50 $ | 129,00 $ |
Texas Instruments TI- Графический калькулятор 84 Plus CE — идеальный выбор для студентов, изучающих математику и естественные науки. Благодаря 480 КБ ПЗУ, 24 КБ ОЗУ и полноцветному дисплею с подсветкой высокого разрешения он обеспечивает мощные и интуитивно понятные графические возможности.
Благодаря 480 КБ ПЗУ, 24 КБ ОЗУ и полноцветному дисплею с подсветкой высокого разрешения он обеспечивает мощные и интуитивно понятные графические возможности.
Устройство является перезаряжаемым и поставляется с рядом предварительно загруженных приложений и изображений, которые позволяют настраивать графики с использованием различных стилей линий, форм, цветов и т. д. Он также имеет четырнадцать интерактивных функций масштабирования, функцию математической печати для ввода уравнений в формате учебника и семь стилей графиков для дифференциации ваших графиков.
Этот калькулятор доступен в различных забавных цветах, и клиенты могут получить версию на Python, пока есть в наличии. Упаковка может отличаться. Приготовьтесь вывести свои математические и научные исследования на новый уровень с графическим калькулятором Texas Instruments TI-84 Plus CE!
Отличительные особенности:
- 3,0 МБ ПЗУ и 154 КБ ОЗУ для больших наборов данных
- Полноцветный дисплей высокого разрешения с подсветкой
- Аккумулятор
- Предустановленные приложения и изображения
- 14 интерактивных функций масштабирования
Что нам нравится:
- Он прост в использовании благодаря 7,5-дюймовому цветному экрану, что упрощает чтение и доступ к меню.

- Калькулятор поставляется с перезаряжаемой батареей.
Что нам не нравится:
- Дорого по сравнению с некоторыми другими калькуляторами.
Распродажа
Калькулятор цветных графиков Texas Instruments TI-84 Plus CE, черный 7,5 дюйма
- Полноцветный дисплей высокого разрешения с подсветкой
- Аккумулятор
- Предварительно загруженные приложения и изображения. Четырнадцать функций интерактивного масштабирования
- Функция MathPrint. забавных цветов, клиенты могут получить версию для Python, пока есть в наличии.
2. HP PRIME G2 —
Great Second Option HP PRIME G2 — это научный калькулятор с интуитивно понятным черным дизайном, надежной памятью и мощными функциями. Он имеет RPN и алгебраическую логику системы ввода для простого переключения режимов, 30 КБ памяти, 800 независимых регистров хранения и большой 1-дюймовый ЖК-экран для хорошего изображения. Идеальный карманный исполнитель.
Идеальный карманный исполнитель.
HP Solve предлагает множество функций, в том числе 100 встроенных функций, расширенный режим дробей, 42 встроенных физических константы, статистические и математические пакеты для инженерных приложений, регулируемый контрастный двухстрочный дисплей, а также редактирование/отмену/удаление. способность. Используйте все эти инструменты для быстрого и точного хранения уравнений и решения переменных!
Научный калькулятор HP PRIME G2 — идеальный выбор для инженеров. Он легкий, работает от литий-металлического аккумулятора и имеет выступающие защитные края, что делает его надежным и точным вариантом для выполнения сложных вычислений.
Выделенные функции:
- 30 КБ флэш-памяти
- Более 800 независимых регистров хранения
- 42 встроенных физических константы
- Полная библиотека преобразований единиц измерения
- Он имеет расширенный режим дробей, статистику и математические пакеты.

- Большой двухстрочный дисплей с регулируемой контрастностью.
Что нам нравится:
- Он весит всего 4,8 унции, идеально подходит для мобильных профессионалов
- Он имеет 30 КБ памяти и более 800 независимых регистров хранения.
Что нам не нравится:
- У него нет подсветки, что затрудняет использование в условиях низкой освещенности.
Распродажа
2AP18AA#ABA Hp Prime Graphing Calculator II
- Утвержденный экзамен на получение диплома IB
- Гладкий тонкий корпус из полированного металла, который отлично выглядит и работает еще лучше. Защитите калькулятор, когда он не используется, с помощью съемной крышки
- Наслаждайтесь многофункциональными вычислениями благодаря знакомой буквенно-цифровой клавиатуре HP и большому мультисенсорному дисплею диагональю 3,5 дюйма
- Литий-ионная аккумуляторная батарея, флэш-память 256 МБ Prime Wireless Kit1 и HP Connectivity Kit
TI-89 Titanium — необходимый инженерный инструмент. Он оснащен дисплеем с разрешением 100 x 160 пикселей с разделенным экраном, что позволяет легко просматривать все ваши данные в одном месте. Этот продвинутый графический калькулятор легко справляется с исчислением, алгеброй, матрицами и статистическими функциями. Он также совместим с системой CBL 2, датчиком движения CBR 2, системами vernier easylink и vernier easytemp, что обеспечивает беспрепятственный сбор и анализ данных.
Он оснащен дисплеем с разрешением 100 x 160 пикселей с разделенным экраном, что позволяет легко просматривать все ваши данные в одном месте. Этот продвинутый графический калькулятор легко справляется с исчислением, алгеброй, матрицами и статистическими функциями. Он также совместим с системой CBL 2, датчиком движения CBR 2, системами vernier easylink и vernier easytemp, что обеспечивает беспрепятственный сбор и анализ данных.
188 КБ ОЗУ и 2,7 МБ флэш-памяти упрощают хранение функций, программ и данных. Эта модель также поставляется с редактором программ, поэтому вы можете создавать собственные приложения. Он также оснащен регулируемым 3-дюймовым ЖК-экраном, который можно четко просматривать при любых условиях освещения. USB-порт и кабель позволяют обмениваться файлами с другими устройствами, а порт ввода-вывода и кабель позволяют синхронизировать данные с другими калькуляторами.
TI-89 Titanium также поставляется с твердой задвижной крышкой для дополнительной защиты. При весе 10,2 унции он работает от батареек 4А (входят в комплект). Он подкреплен годовой гарантией, гарантирующей, что вы хорошо застрахованы. Когда дело доходит до покупки калькулятора для инженерных целей, ТИ-89Титаниум — отличный выбор. Благодаря своим расширенным функциям, превосходным возможностям памяти и регулируемому ЖК-экрану, это идеальный инструмент расчета для любого инженера.
Он подкреплен годовой гарантией, гарантирующей, что вы хорошо застрахованы. Когда дело доходит до покупки калькулятора для инженерных целей, ТИ-89Титаниум — отличный выбор. Благодаря своим расширенным функциям, превосходным возможностям памяти и регулируемому ЖК-экрану, это идеальный инструмент расчета для любого инженера.
Отличительные особенности:
- 188 КБ ОЗУ и 2,7 МБ флэш-памяти
- Регулируемый ЖК-экран, обеспечивающий четкое изображение при любом освещении
- Весит 10,2 унции
- Работает от батарей 4А (в комплекте)
- Совместим с несколькими системами, такими как система CBL 2, датчик движения CBR 2 и другими.
Что нам нравится:
- На этот калькулятор распространяется годовая гарантия, гарантирующая вам надежную защиту.
- Поставляется с твердой защитной крышкой на случай падения
Что нам не нравится:
- Размер и вес калькулятора затрудняют его переноску.

Texas Instruments TI-89 Titanium Graphing Calculator (упаковка может отличаться)
- Графический калькулятор обрабатывает вычисления, алгебру, матрицы и статистические функции
- 188 КБ ОЗУ и 2,7 МБ флэш-памяти для скорости; много места для хранения функций, программ, данных
- Большой дисплей с разрешением 100 x 160 пикселей для разделения экрана. Совместимость с системой CBL 2, датчиком движения CBR 2, системами vernier easylink и vernier easytemp для сбора и анализа реальных данных.
- Технология USB on-the-go для обмена файлами с другими калькуляторами и подключения к ПК. Операции с матрицами, в том числе обратные, детерминантные, транспонированные, аугментационные, операции с элементарными строками и сокращенная эшелонированная форма строк; матричные элементы могут быть вещественными или комплексными, числовыми или символьными
- Гарантия 1 год.
TI-Nspire CX II — мощный калькулятор, идеально подходящий для математических и научных задач. Его функции включают в себя цветной экран, перезаряжаемую батарею, встроенные математические шаблоны, шесть стилей графиков, 15 цветов на выбор, динамические значения коэффициентов и анимированный график пути. Экран диагональю 3,5 дюйма имеет разрешение 125 точек на дюйм и отображает до 16 бит цвета для большей четкости.
Его функции включают в себя цветной экран, перезаряжаемую батарею, встроенные математические шаблоны, шесть стилей графиков, 15 цветов на выбор, динамические значения коэффициентов и анимированный график пути. Экран диагональю 3,5 дюйма имеет разрешение 125 точек на дюйм и отображает до 16 бит цвета для большей четкости.
TI-Nspire CX II оснащен программным обеспечением TI-Inspire CX Student для расширенных графических функций и других возможностей. Он тонкий и легкий, имеет удобную навигацию с помощью сенсорной панели и быстрые альфа-клавиши для ввода уравнений и формул. Кроме того, его перезаряжаемая батарея работает до двух недель без подзарядки, что снижает риск неожиданного отключения питания.
TI-Nspire CX II от Texas Instruments — отличный выбор благодаря надежной работе и большому количеству функций. Он имеет интуитивно понятный дизайн, динамические значения коэффициентов и анимированный график пути, чтобы помочь с самыми сложными вычислениями.
Выделенные функции:
- Цветной экран — 320 x 240 пикселей
- 125 точек на дюйм; 16-битный цвет
- Аккумулятор в комплекте
- Комплект программного обеспечения для портативных устройств
- Тонкий и легкий
- Значки приложений, поддерживаемые экранными вкладками с цветовой кодировкой, для удобной навигации и использования
Что нам нравится:
- Он имеет встроенный аккумулятор и поставляется с адаптером переменного тока
- прост в использовании и имеет интуитивно понятное меню, которое упрощает навигацию по калькулятору.

Что нам не нравится:
- Интерфейс иногда может быть немного запутанным для начинающих пользователей.
Распродажа
Калькулятор цветных графиков Texas Instruments TI-Nspire CX II CAS с программным обеспечением для учащихся (ПК/Mac)
- Цветной экран. Размер экрана 320 x 240 пикселей (диагональ 3,5 дюйма), разрешение экрана 125 точек на дюйм; 16-битный цвет
- Аккумулятор в комплекте. Может работать до двух недель без подзарядки
- Портативный комплект программного обеспечения. Включает программное обеспечение TI-Inspire CX Student, обеспечивающее расширенные возможности построения графиков и другие функции.
- Тонкий и легкий дизайн с удобной навигацией с помощью сенсорной панели. Клавиши быстрого доступа к альфа-каналу
- Шесть различных стилей графиков и 15 цветов на выбор для различения внешнего вида каждого нарисованного графика
TI-Nspire CX идеально подходит для занятий по математике и естественным наукам благодаря расширенным функциям. Его полноцветный экран имеет разрешение 320 x 240 пикселей (диагональ 3,5 дюйма) с разрешением 125 точек на дюйм для кристально чистого изображения уравнений, объектов, точек и линий. Он оснащен перезаряжаемой батареей, которой хватает на две недели без подзарядки, а его тонкий дизайн и малый вес позволяют легко брать его с собой.
Его полноцветный экран имеет разрешение 320 x 240 пикселей (диагональ 3,5 дюйма) с разрешением 125 точек на дюйм для кристально чистого изображения уравнений, объектов, точек и линий. Он оснащен перезаряжаемой батареей, которой хватает на две недели без подзарядки, а его тонкий дизайн и малый вес позволяют легко брать его с собой.
TI-Nspire CX имеет большой объем памяти (100 МБ) и оперативной памяти (64 МБ). С программным обеспечением для учащихся вы можете выполнять работу вне школы. Вы также можете просматривать цифровые изображения и даже использовать свои собственные фотографии, чтобы усилить связи между уравнениями и графиками.
Исследуйте связи в реальном мире и участвуйте в занятиях по математике и естественным наукам с помощью TI-Nspire CX. Его расширенные функции, уравнения с цветовой кодировкой и легкий дизайн делают обучение интересным, наглядным и увлекательным на ходу! Получите TI-Nspire CX сегодня, чтобы получить более увлекательный образовательный опыт.
Выделенные функции:
- Цветной экран с разрешением 320 x 240 пикселей
- 16-битное цветовое разрешение
- Аккумуляторная батарея
- Тонкий и легкий
- 100 МБ памяти для хранения / 64 МБ оперативной памяти
- Уравнения цветового кода, объекты, точки и линии на полноцветном дисплее с подсветкой
Что нам нравится:
- Простота использования.

- Высокая прочность.
Что нам не нравится:
- Не поставляется с достаточным количеством инструкций по эксплуатации, что создает проблемы для начинающих пользователей
Распродажа
Графический калькулятор Texas Instruments TI-Nspire CX
- Цветной экран. Размер экрана 320 x 240 пикселей (диагональ 3,5 дюйма), разрешение экрана 125 точек на дюйм; 16-битный цвет
- Аккумулятор в комплекте. Работает до двух недель без подзарядки
- Тонкий и легкий дизайн с удобной сенсорной панелью навигации
- 100 МБ памяти / 64 МБ оперативной памяти
Калькулятор Construction Master Pro предлагает мощные решения для макетов, планов, предложений и оценок. Он поддерживает преобразование между распространенными форматами размеров, такими как футы-дюймы-доли, десятичные футы-дюймы, ярды и метрические площади/объемы. Кроме того, пользователи могут воспользоваться возможностями преобразования веса на объем и D:M:S в десятичные градусы.
Кроме того, пользователи могут воспользоваться возможностями преобразования веса на объем и D:M:S в десятичные градусы.
Construction Master Pro помогает сэкономить время и избежать дорогостоящих отходов материалов благодаря встроенным решениям для прямых углов, стропил, наклонных стен, откосов, арок, арок, кругов, колонн и многого другого. Он также имеет функции оценки кровли, гипсокартона, шпилек и блоков, а также специальные функции составного угла, которые помогают в проектах по формованию венца.
Калькулятор Construction Master Pro от Calculated Industries незаменим для профессионалов в области строительства. Он быстро и точно решает любые математические задачи, экономя ваше время и деньги.
Выделенные функции:
- Быстрое и точное решение всех многомерных математических операций
- Встроенные функции для прямых углов
- Составные функции под углом
- Полная компоновка лестницы и передовые решения
- Ограниченная гарантия сроком на один год
Что нам нравится:
- Высокая точность
- Легко читаемый
Что не нравится:
- Нет подсветки
Распродажа
Calculated Industries 4065 Construction Master Pro Усовершенствованный математический калькулятор для подрядчиков, сметчиков, строителей, монтажников, ремонтников, ремонтников и плотников
- РЕШИТЕ ВСЕ СВОИ МАТЕМАТИЧЕСКИЕ РАЗМЕРЫ быстро и точно с помощью удостоенного наград мощного строительного калькулятора CM Pro встроенные решения для заполнения макетов, планов, предложений, смет и многого другого непосредственно в предпочитаемых вами строительных единицах
- ПОЗВОЛЯЕТ ЛЕГКО РАБОТАТЬ И ПРЕОБРАЗОВАТЬ между всеми общепринятыми форматами размеров зданий: футы-дюймы-доли, десятичные футы-дюймы, ярды и метрические единицы, включая площадь и объем.
 Плюс вес на объем и преобразование D:M:S в десятичные градусы. , наклоны, углы и многое другое. Плюс полная компоновка лестницы, передовые решения для арок, арок, кругов, колонн и т. д.
Плюс вес на объем и преобразование D:M:S в десятичные градусы. , наклоны, углы и многое другое. Плюс полная компоновка лестницы, передовые решения для арок, арок, кругов, колонн и т. д. - ПРЕДОТВРАЩАЕТ ОТХОД ДОРОГИХ МАТЕРИАЛОВ благодаря встроенным решениям для оценки кровли, гипсокартона, стоек, блоков, бетонных фундаментов и пиломатериалов из досок. Дополнительные функции под углом помогают избежать ошибок при работе с лепниной и другими дорогостоящими столярными изделиями.
Типы калькуляторов для инженеров
Базовые калькуляторыБазовый калькулятор идеально подходит для большинства основных расчетов и решения простых инженерных задач. Он должен уметь обрабатывать сложные уравнения и давать быстрые и точные ответы.
Графические калькуляторы Графические калькуляторы более специализированы, чем обычные калькуляторы, и могут выполнять более сложные математические вычисления. Обычно они программируемые, что позволяет инженерам создавать свои приложения для решения конкретных задач. Большинство графических калькуляторов имеют сенсорные экраны, что упрощает их использование.
Большинство графических калькуляторов имеют сенсорные экраны, что упрощает их использование.
Предназначены для решения сложных инженерных задач. Они могут обрабатывать сложные уравнения, вычисления и другие математические операции. Обычно они имеют дополнительные функции, такие как графические возможности и программируемость.
Калькуляторы с печатьюКалькуляторы с печатью лучше всего подходят для инженеров, которым необходимо распечатывать результаты или уравнения. Они обеспечивают более высокую скорость вычислений и лучшую точность, чем обычные калькуляторы и возможности печати.
Финансовые калькуляторы Финансовые калькуляторы незаменимы для любого инженера, занимающегося финансовым анализом или задачами бюджетирования. Большинство этих устройств имеют предварительно запрограммированные финансовые формулы и специализированные функции, такие как расчет текущей или будущей стоимости.
Какие факторы необходимо учитывать при покупке инженерного калькулятора?
Цена:Цена является основным фактором при покупке калькулятора. В то время как продвинутые модели часто могут быть дорогими, некоторые модели по разумной цене обладают всеми необходимыми функциями.
Размер дисплея:Ищите калькулятор с удобным для чтения дисплеем, который позволит вам просматривать свои расчеты. Большие дисплеи обычно легче читать и предоставляют больше места для ввода чисел.
Срок службы батареи:При выборе калькулятора учитывайте срок службы батареи. Выбирайте модели с аккумуляторами длительного действия для надежного использования на улице или в дороге. Это гарантирует, что ваш калькулятор не разрядится в середине задачи.
Возможности подключения: Некоторые модели оснащены Bluetooth и USB-подключением, что позволяет передавать данные или подключаться к принтеру или компьютеру. Если вы планируете выполнять какие-либо сложные расчеты или анализ, ищите модели с этими функциями.
Если вы планируете выполнять какие-либо сложные расчеты или анализ, ищите модели с этими функциями.
Интуитивно понятный пользовательский интерфейс упрощает ввод данных и доступ к ним. Ищите модели с настраиваемым меню, кнопками и функциями, которые можно настроить в соответствии с вашими предпочтениями.
Память:Функция памяти позволяет пользователям сохранять свои расчеты, уравнения и другие данные для дальнейшего использования. Это удобно при работе со сложными формулами и уравнениями, требующими нескольких шагов и входных данных. Перед покупкой обязательно проверьте, сколько памяти предлагает ваш калькулятор.
Долговечность: Из-за суровых условий, в которых часто работают инженеры, очень важно иметь прочный калькулятор. Ознакомьтесь с обзорами и рейтингами, чтобы убедиться, что модель, которую вы покупаете, выдерживает незначительные падения без сбоев или потери точности.
Ищите калькуляторы, которые предлагают ряд встроенных функций, таких как экспоненциальные калькуляторы, калькуляторы интегрирования и различные преобразования единиц измерения. Это сэкономит время и поможет упростить сложные вычисления.
Эргономика:Инженерам нужны правильные инструменты для быстрых и точных расчетов. Эргономичный дизайн калькулятора обеспечивает удобство при длительном использовании, что делает его идеальным для инженерных задач. Это позволяет инженерам выполнять свои расчеты с легкостью и точностью.
Часто задаваемые вопросыВ. Инженеры все еще используют калькуляторы?
А. Да, инженеры до сих пор используют калькуляторы. И хотя компьютерные программы стали более мощными, калькуляторы остаются важным инструментом для инженеров.
В. Нужен ли мне инженерный калькулятор для инженерных наук?
A: Научный калькулятор необходим инженерам, поскольку он обеспечивает быстрое и точное решение задач благодаря своим дополнительным функциям, таким как логарифмы и тригонометрические функции.
В. Нужен ли инженерам графический калькулятор?
A. Графические калькуляторы используются инженерами для построения графиков и выполнения сложных расчетов. Высококачественные модели имеют такие функции, как символьные вычисления, которые могут быть полезны для передовых инженерных исследований.
В. В чем разница между калькуляторами MS и ES?
A. Калькуляторы MS и ES представляют собой два различных типа научных калькуляторов. MS являются универсальными, оснащены базовыми арифметическими вычислениями и более сложными функциями, такими как тригонометрия и логарифмирование. Однако ES специально разработан для инженерных приложений с такими функциями, как расширенное графическое и символьное вычисление.
В. Сколько стоят калькуляторы для инженеров? (50$- 300$)
A: Калькуляторы для инженеров стоят от 50 до 300 долларов США, в зависимости от типа и функций.

 И несмотря на то, что за окном 2014 год, Casio не изменяет своим традициям и анонсирует новую серию научных калькуляторов — топовую инженерную модель fx-991EX, а также более доступные версии fx-570EX, fx-350EX, fx-82EX.
И несмотря на то, что за окном 2014 год, Casio не изменяет своим традициям и анонсирует новую серию научных калькуляторов — топовую инженерную модель fx-991EX, а также более доступные версии fx-570EX, fx-350EX, fx-82EX.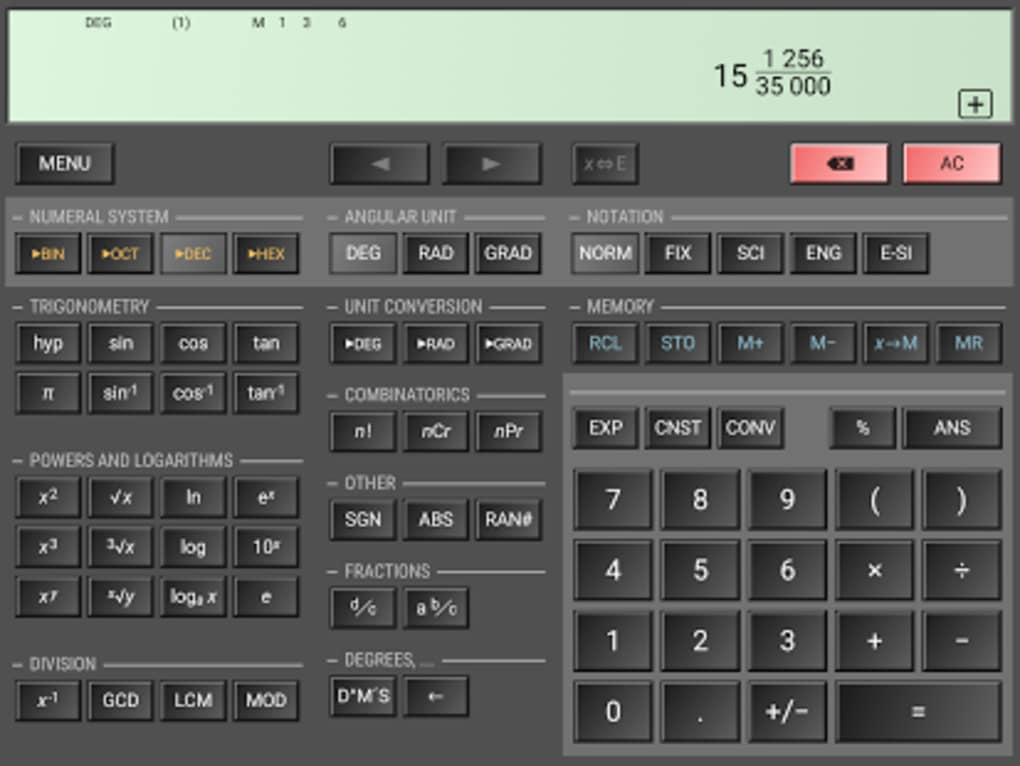 К тому же данная опция обеспечит автоматический вывод результатов более сложных расчётов, что даёт новинке преимущество перед предыдущими версиями инженерных калькуляторов от Casio.
К тому же данная опция обеспечит автоматический вывод результатов более сложных расчётов, что даёт новинке преимущество перед предыдущими версиями инженерных калькуляторов от Casio.
 Поверьте нам в этом.
Поверьте нам в этом.
 Расчеты можно сохранять в виде документов так же, как это делается на компьютере, что обязательно пригодится во время тестов, если вы хотите сослаться на какие-либо расчеты, используемые при решении практических задач. Одной из наших любимых функций является функция создания ползунка для графического отображения различных функций. Это особенно полезно, если вы хотите увидеть, насколько влиятельна переменная в уравнении. Это полезно в химической инженерии в таких курсах, как проектирование реакторов, где можно изучать двухмерные функции, чтобы понять важность определенных переменных.
Расчеты можно сохранять в виде документов так же, как это делается на компьютере, что обязательно пригодится во время тестов, если вы хотите сослаться на какие-либо расчеты, используемые при решении практических задач. Одной из наших любимых функций является функция создания ползунка для графического отображения различных функций. Это особенно полезно, если вы хотите увидеть, насколько влиятельна переменная в уравнении. Это полезно в химической инженерии в таких курсах, как проектирование реакторов, где можно изучать двухмерные функции, чтобы понять важность определенных переменных.





 Плюс вес на объем и преобразование D:M:S в десятичные градусы. , наклоны, углы и многое другое. Плюс полная компоновка лестницы, передовые решения для арок, арок, кругов, колонн и т. д.
Плюс вес на объем и преобразование D:M:S в десятичные градусы. , наклоны, углы и многое другое. Плюс полная компоновка лестницы, передовые решения для арок, арок, кругов, колонн и т. д. кол-во каналов: 8
кол-во каналов: 8 кол-во каналов: 8
кол-во каналов: 8 Это свойство
обеспечивает прочное связывание
биометалов с белками. Но соли Pb, As, Hg,
Cb
отличаются высокой токсичностью.
(Люизит) при отравлении тяжелыми
металами противоядием служат
тиолы,содержащие более 1группы SH
обеспечивающие уменьшение концентрации
иона метала в результате обр-я
нерастворимого сульфида (антиплоизит).
Это свойство
обеспечивает прочное связывание
биометалов с белками. Но соли Pb, As, Hg,
Cb
отличаются высокой токсичностью.
(Люизит) при отравлении тяжелыми
металами противоядием служат
тиолы,содержащие более 1группы SH
обеспечивающие уменьшение концентрации
иона метала в результате обр-я
нерастворимого сульфида (антиплоизит). H
H ПОДЕЛИТЬСЯ
ПОДЕЛИТЬСЯ просмотров
просмотров . [IIT 2003]
а) Одноосновная и слабая кислота Льюиса
б) Одноосновная и слабая кислота Бренстеда
c) M…
. [IIT 2003]
а) Одноосновная и слабая кислота Льюиса
б) Одноосновная и слабая кислота Бренстеда
c) M… ..
.. ..
..
 . Общий результат представляет собой реакцию \(S_n1\).
. Общий результат представляет собой реакцию \(S_n1\).
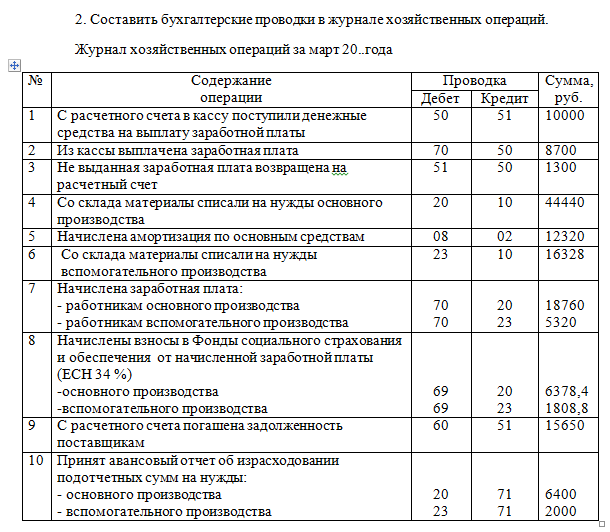
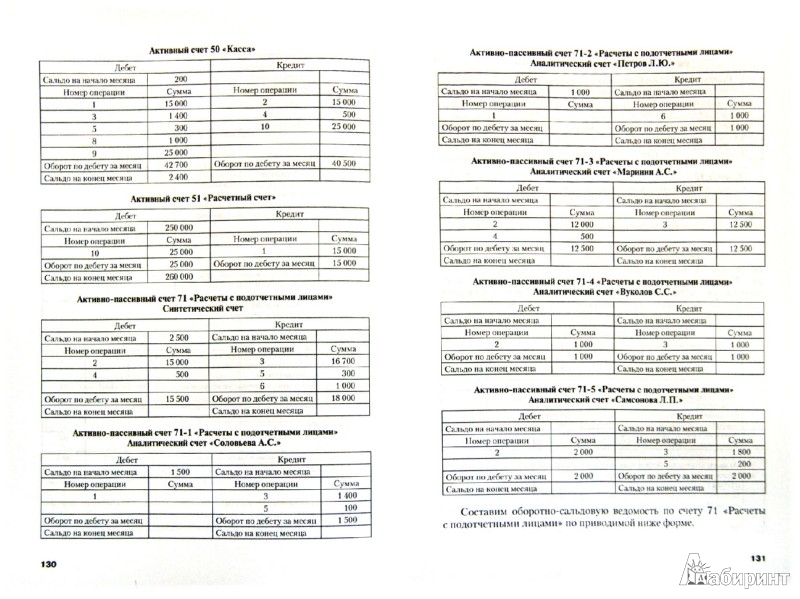
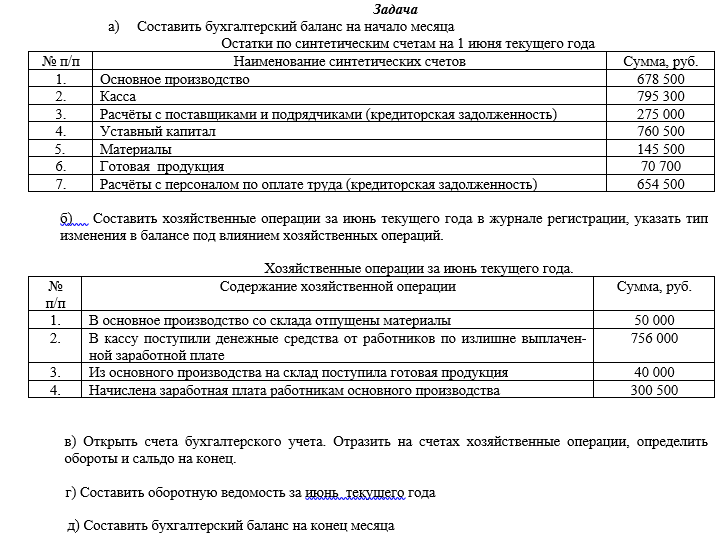
 Решить задачу по бухучету могут помочь вам наши специалисты, которым не составит труда рассчитать все правильно и быстро, применив двойную запись. После того, как вы получите уже решенное задание, вам будет легче понять, кто в данной задаче есть кто. Ведь дебитор является должником, тому, кто предоставляет ему кредит. И уже определив дебитора, становится ясно, что такое кредит. Но ранее было сказано, чтобы решение задач по бухгалтерскому учету было правильным следует знать две вещи. Второй проблемой, что может возникнуть у вас при решении задачи может стать составление баланса. Для этого нужно уметь разбивать все счета на активные и пассивные. Так, активными счетами можно назвать те, что являют собой информацию об активах организации. Пассивные же учитывают источники образования данных активов. Если же у вас возникнут вопросы в процессе решения заданной вам задачи, то вы можете заказать бухучет. И таким образом, у вас на руках будут уже правильно решенные задачи, на примере которых разобраться с балансом, дебетом и кредитом будет гораздо легче.
Решить задачу по бухучету могут помочь вам наши специалисты, которым не составит труда рассчитать все правильно и быстро, применив двойную запись. После того, как вы получите уже решенное задание, вам будет легче понять, кто в данной задаче есть кто. Ведь дебитор является должником, тому, кто предоставляет ему кредит. И уже определив дебитора, становится ясно, что такое кредит. Но ранее было сказано, чтобы решение задач по бухгалтерскому учету было правильным следует знать две вещи. Второй проблемой, что может возникнуть у вас при решении задачи может стать составление баланса. Для этого нужно уметь разбивать все счета на активные и пассивные. Так, активными счетами можно назвать те, что являют собой информацию об активах организации. Пассивные же учитывают источники образования данных активов. Если же у вас возникнут вопросы в процессе решения заданной вам задачи, то вы можете заказать бухучет. И таким образом, у вас на руках будут уже правильно решенные задачи, на примере которых разобраться с балансом, дебетом и кредитом будет гораздо легче. А может Вам нужно пройти тест по бухучету за деньги прямо на сайте дистанционного обучения?
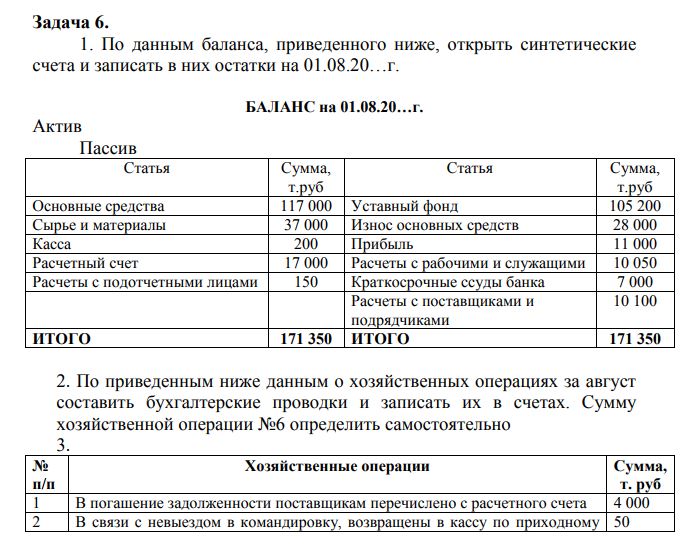
А может Вам нужно пройти тест по бухучету за деньги прямо на сайте дистанционного обучения? А также пользователям внешнего сектора, среди которых могут быть инвесторы, кредиторы и прочее.
А также пользователям внешнего сектора, среди которых могут быть инвесторы, кредиторы и прочее.

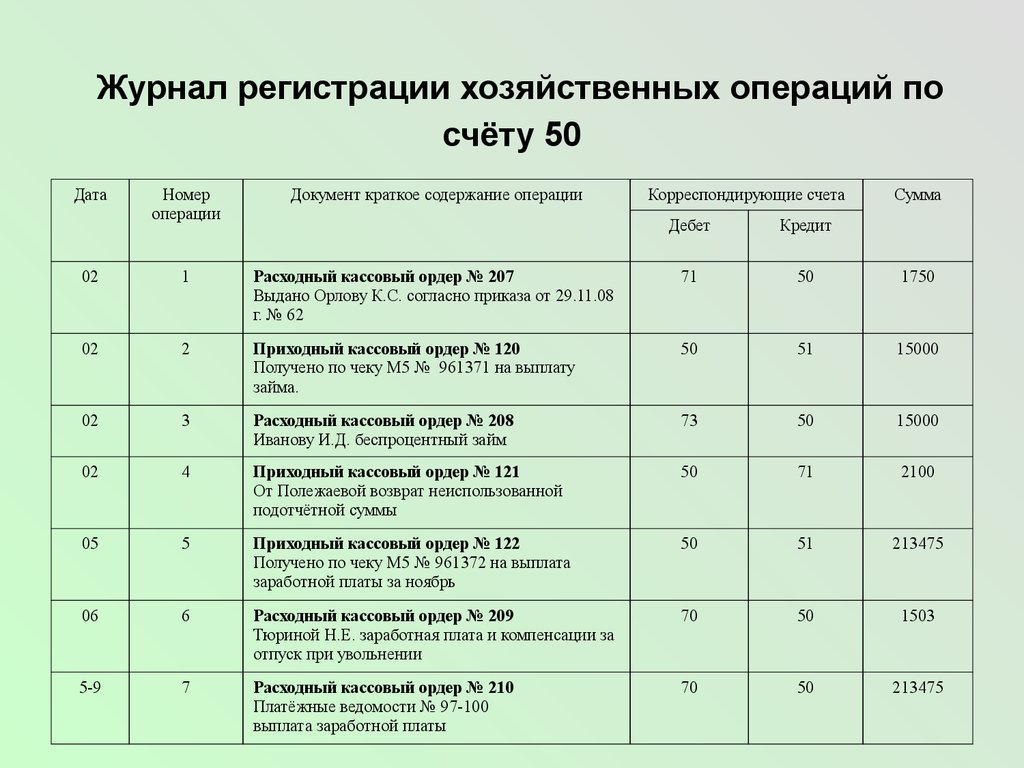 Следите за такими показателями, как расходы, просроченные счета и операционный денежный поток. Ежедневное создание и отслеживание кассовых отчетов может помочь вам планировать будущее, потому что вы будете видеть изменения или колебания, которые вы можете использовать для информирования других решений.
Следите за такими показателями, как расходы, просроченные счета и операционный денежный поток. Ежедневное создание и отслеживание кассовых отчетов может помочь вам планировать будущее, потому что вы будете видеть изменения или колебания, которые вы можете использовать для информирования других решений.
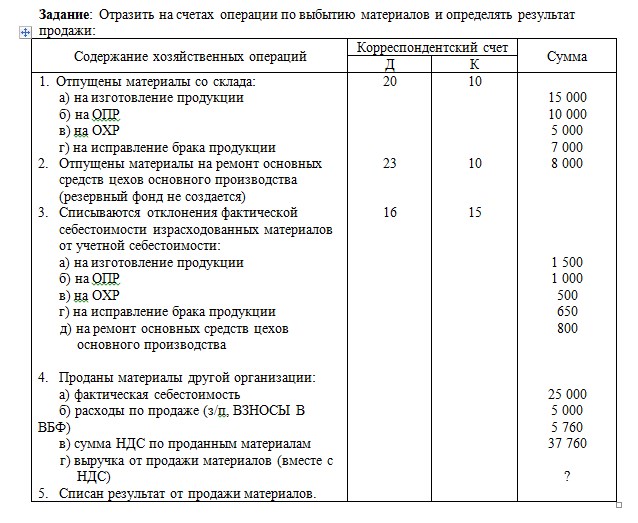 Помощь бухгалтерам в развитии технических навыков и навыков межличностного общения, чтобы лучше применять свои знания в предметной области для бизнес-стратегии, поскольку все больше транзакционных задач автоматизируется, будет иметь решающее значение для удержания кадров в 2023 году9.0003
Помощь бухгалтерам в развитии технических навыков и навыков межличностного общения, чтобы лучше применять свои знания в предметной области для бизнес-стратегии, поскольку все больше транзакционных задач автоматизируется, будет иметь решающее значение для удержания кадров в 2023 году9.0003 Облачное программное обеспечение для бухгалтерского учета, бюджетирования, прогнозирования, анализа данных и инструменты визуализации создают основу для автоматизации бухгалтерского учета.
Облачное программное обеспечение для бухгалтерского учета, бюджетирования, прогнозирования, анализа данных и инструменты визуализации создают основу для автоматизации бухгалтерского учета. Предложение непрерывного образования и обучения также имеет дополнительное преимущество, заключающееся в повышении морального духа сотрудников и их удержании. В компаниях, получивших высокие оценки по обучению сотрудников, уровень текучести кадров ниже на 53%, чем в компаниях с более низким рейтингом.
Предложение непрерывного образования и обучения также имеет дополнительное преимущество, заключающееся в повышении морального духа сотрудников и их удержании. В компаниях, получивших высокие оценки по обучению сотрудников, уровень текучести кадров ниже на 53%, чем в компаниях с более низким рейтингом.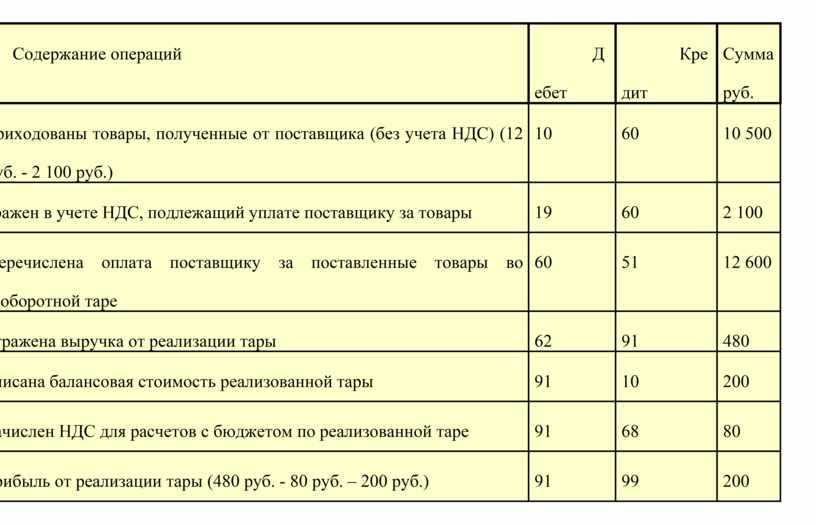 Бухгалтерские службы уделяют первостепенное внимание изменениям в налогообложении, особенно пониманию общих налоговых обязательств и навигации по изменяющейся торговой и тарифной политике.
Бухгалтерские службы уделяют первостепенное внимание изменениям в налогообложении, особенно пониманию общих налоговых обязательств и навигации по изменяющейся торговой и тарифной политике.
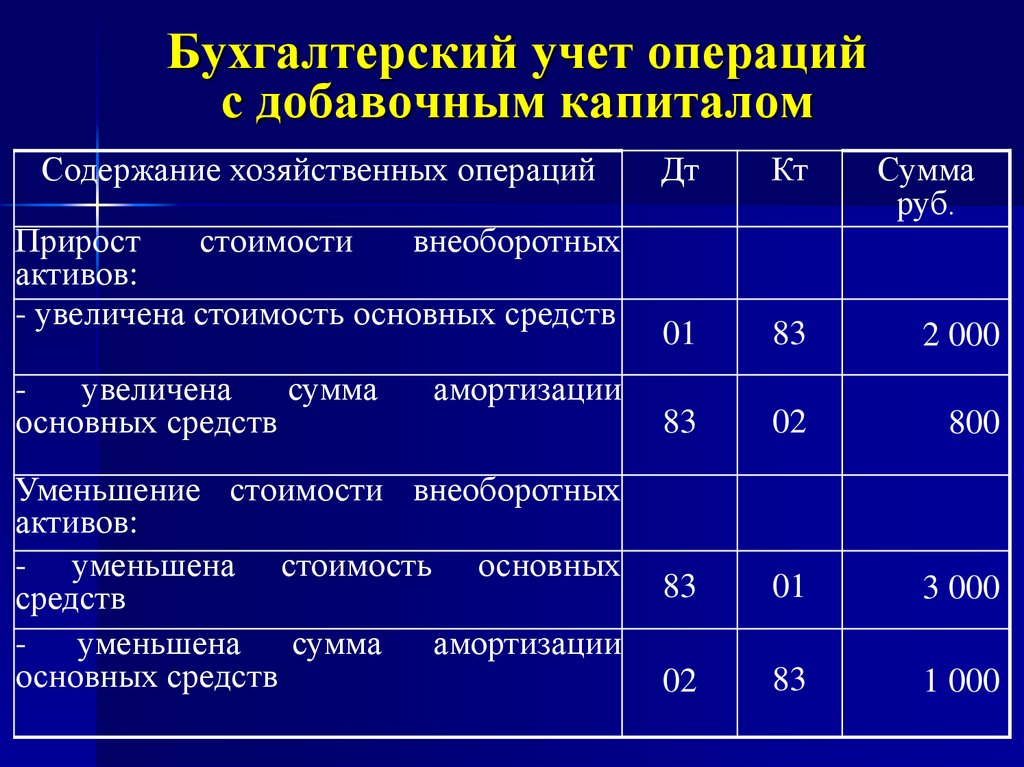 Проверьте систему внутреннего контроля и рассмотрите возможность дальнейшей автоматизации процесса управления расходами с помощью программного обеспечения, чтобы предотвратить мошеннические расходы и автоматически помечать сомнительные расходы.
Проверьте систему внутреннего контроля и рассмотрите возможность дальнейшей автоматизации процесса управления расходами с помощью программного обеспечения, чтобы предотвратить мошеннические расходы и автоматически помечать сомнительные расходы.
 Около 77% специалистов по бухгалтерскому учету хотели бы продолжать работать удаленно. Но удаленная работа создает проблемы для бухгалтерских и финансовых отделов, которые десятилетиями выполняли такие задачи, как закрытие месяца, проводя долгие ночи в офисе. Удаленная работа также усугубляет риск кибератак: IBM обнаружила, что 70% компаний, внедривших удаленную работу во время пандемии, ожидают, что это увеличит затраты на утечку данных.
Около 77% специалистов по бухгалтерскому учету хотели бы продолжать работать удаленно. Но удаленная работа создает проблемы для бухгалтерских и финансовых отделов, которые десятилетиями выполняли такие задачи, как закрытие месяца, проводя долгие ночи в офисе. Удаленная работа также усугубляет риск кибератак: IBM обнаружила, что 70% компаний, внедривших удаленную работу во время пандемии, ожидают, что это увеличит затраты на утечку данных. И эта технология часто превосходила даже VPN с доступом к локальному программному обеспечению.
И эта технология часто превосходила даже VPN с доступом к локальному программному обеспечению. Менеджеры имеют огромное влияние на моральный дух своих сотрудников. Держите открытыми линии связи между бухгалтерией и руководством. Прислушивайтесь к их мнению не только по финансовым вопросам, но и по стратегическим решениям. Предоставьте им инструменты, необходимые для совместной работы. И автоматизируйте утомительные части своей работы, чтобы освободить время.
Менеджеры имеют огромное влияние на моральный дух своих сотрудников. Держите открытыми линии связи между бухгалтерией и руководством. Прислушивайтесь к их мнению не только по финансовым вопросам, но и по стратегическим решениям. Предоставьте им инструменты, необходимые для совместной работы. И автоматизируйте утомительные части своей работы, чтобы освободить время. Поскольку очень многое меняется очень быстро, доступ к аналитике в реальном времени является ключевым. Вот что будет иметь значение при построении финансовых моделей, учитывающих исторические тенденции, текущие условия и лучшие, худшие и наиболее вероятные сценарии.
Поскольку очень многое меняется очень быстро, доступ к аналитике в реальном времени является ключевым. Вот что будет иметь значение при построении финансовых моделей, учитывающих исторические тенденции, текущие условия и лучшие, худшие и наиболее вероятные сценарии. Но многие компании работают с устаревшими локальными системами учета, которые уже устарели. Технологии влияют на финансовую отчетность, управление денежными средствами, кредиторскую задолженность и процессы закрытия месяца, и в ближайшем будущем они останутся ключевыми компонентами программного обеспечения для автоматизации и облачного учета.
Но многие компании работают с устаревшими локальными системами учета, которые уже устарели. Технологии влияют на финансовую отчетность, управление денежными средствами, кредиторскую задолженность и процессы закрытия месяца, и в ближайшем будущем они останутся ключевыми компонентами программного обеспечения для автоматизации и облачного учета. Поскольку технологии упростили эту задачу, бухгалтерам приходится бороться с правилами и нормами, преобладающими как в стране их происхождения, так и на рынках, на которых они работают. Местная экономическая нестабильность, стандарты кибербезопасности и изменения налогового законодательства в этих странах потребуют адаптируемых бухгалтерских групп. и технологии, которые облегчают проблемы.
Поскольку технологии упростили эту задачу, бухгалтерам приходится бороться с правилами и нормами, преобладающими как в стране их происхождения, так и на рынках, на которых они работают. Местная экономическая нестабильность, стандарты кибербезопасности и изменения налогового законодательства в этих странах потребуют адаптируемых бухгалтерских групп. и технологии, которые облегчают проблемы.
 д. — это распространенные проблемы, которые могут возникнуть в учет.
д. — это распространенные проблемы, которые могут возникнуть в учет.

 Устаревшее программное обеспечение для бухгалтерского учета
Устаревшее программное обеспечение для бухгалтерского учета Недостаточный финансовый анализ
Недостаточный финансовый анализ



 Для системы уравнений две неизвестные функции — это x(t) и y(t) с независимой переменной t.
Для системы уравнений две неизвестные функции — это x(t) и y(t) с независимой переменной t. по умолчанию это ODE первого порядка.
по умолчанию это ODE первого порядка.  Рассмотрим дифференциальное уравнение в частных производных дробного времени с дифференциальным временем дробного порядка.
Приведенные выше уравнения диффузии и волновые уравнения можно заменить уравнениями дробной диффузии и волновыми уравнениями.
путем изменения порядка времени на дробный порядок, например. 0,5 порядка.
Рассмотрим дифференциальное уравнение в частных производных дробного времени с дифференциальным временем дробного порядка.
Приведенные выше уравнения диффузии и волновые уравнения можно заменить уравнениями дробной диффузии и волновыми уравнениями.
путем изменения порядка времени на дробный порядок, например. 0,5 порядка. 2.
В таблице 2 показано, что все решения уравнений постоянного порядка имеют один и тот же формат exp(k x). Когда порядок дифференциальных уравнений уменьшился с 2 до 0,5, их общее решение увеличилось с exp(sqrt(2)*x) до exp(4x).
При уменьшении порядка интегральных уравнений с -0,5 до -2 их общее решение также увеличилось с exp(1/4 x) до exp(1/sqrt(2) x), но все их частные решения не изменились.
90,5 у = 2у)`
2.
В таблице 2 показано, что все решения уравнений постоянного порядка имеют один и тот же формат exp(k x). Когда порядок дифференциальных уравнений уменьшился с 2 до 0,5, их общее решение увеличилось с exp(sqrt(2)*x) до exp(4x).
При уменьшении порядка интегральных уравнений с -0,5 до -2 их общее решение также увеличилось с exp(1/4 x) до exp(1/sqrt(2) x), но все их частные решения не изменились.
90,5 у = 2у)`  Ошибки Вольфрама [12].
Ошибки Вольфрама [12]. Матем. Эду. науч. Техн., 1992, 23(1), 160-165.
Матем. Эду. науч. Техн., 1992, 23(1), 160-165.
 mathepower.com › функции преобразования
mathepower.com › функции преобразования
 Они могут помочь определить зависимости между задачами и визуализировать критический путь проекта.
Они могут помочь определить зависимости между задачами и визуализировать критический путь проекта.

 png
png
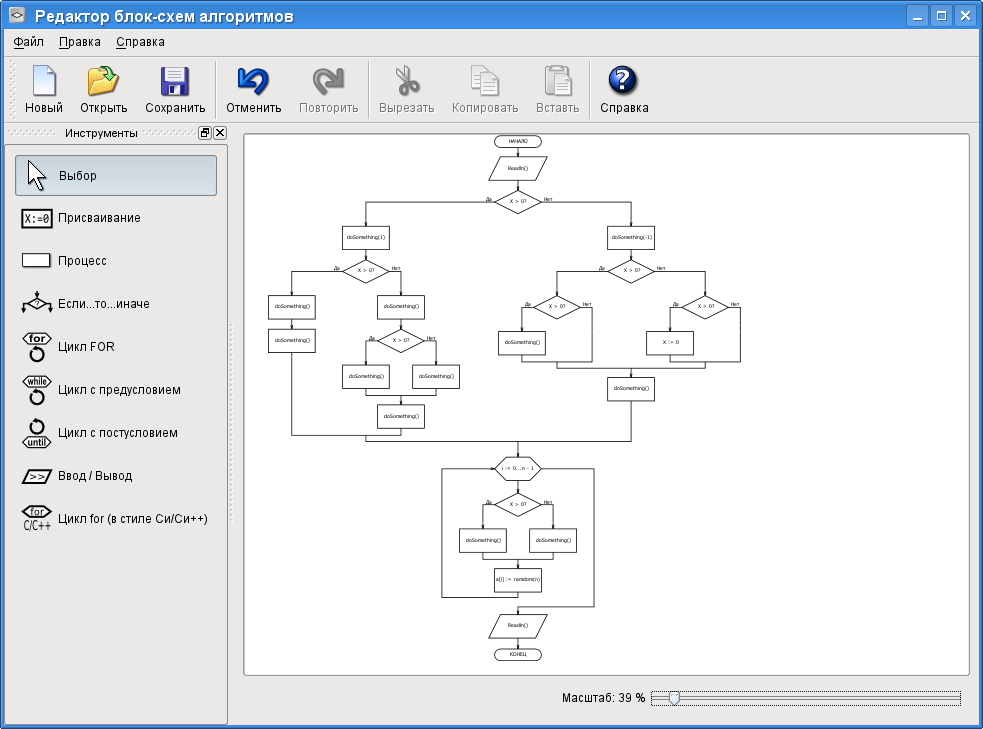
 В IT схемы используют, чтобы показать логику работы программы или спланировать командную работу.
В IT схемы используют, чтобы показать логику работы программы или спланировать командную работу. Кроме того, в Miro доступны канбан-доски и интеграция с сервисами Jira и Asana, Dropbox, Google Suite, Slack и Sketch.
Кроме того, в Miro доступны канбан-доски и интеграция с сервисами Jira и Asana, Dropbox, Google Suite, Slack и Sketch.
 Одна из фишек сервиса — горячие клавиши.
Одна из фишек сервиса — горячие клавиши. Используйте запятую «,» в качестве разделителя
Используйте запятую «,» в качестве разделителя Список краев имеет неправильный формат. Нажмите кнопку «исправить», чтобы исправить список краев, или кнопку «Справка», чтобы открыть справку о формате
Список краев имеет неправильный формат. Нажмите кнопку «исправить», чтобы исправить список краев, или кнопку «Справка», чтобы открыть справку о формате
 ..
..
 Нажмите на любой узел графа
Нажмите на любой узел графа J. Fruchterman, E. Reingold
J. Fruchterman, E. Reingold Процесс. лат.
Процесс. лат.



 Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!
Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее! Это абсциссы точек пересечения графика функции с осью Ох.
Это абсциссы точек пересечения графика функции с осью Ох. График нечетной функции симметричен относительно начала координат.
График нечетной функции симметричен относительно начала координат. {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы: {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.

 {2}+1}
. Подставьте в нее следующие значения x {\displaystyle x}
:
{2}+1}
. Подставьте в нее следующие значения x {\displaystyle x}
: {2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
{2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени. (-x))=- h(x). Следовательно, h(x) — нечетная.
(-x))=- h(x). Следовательно, h(x) — нечетная. 2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.
2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество. Назовем ее функцией общего
вида.
Назовем ее функцией общего
вида.




 org/contents/[email protected]
org/contents/[email protected]














 Умение понимать эмоциональное состояние учащихся относиться к умениям:
Умение понимать эмоциональное состояние учащихся относиться к умениям:
 ..
..

 Специфической формой деятельности ученика, направленной на усвоение знаний, овладение умениями и навыками, а также на его развитие является:
Специфической формой деятельности ученика, направленной на усвоение знаний, овладение умениями и навыками, а также на его развитие является:
 Л. С. Выготский рассматривает проблему соотношения обучения и развития:
Л. С. Выготский рассматривает проблему соотношения обучения и развития: Целью развивающего обучения является:
Целью развивающего обучения является:


 Новым общим знаменателем будет произведение знаменателей первой и второй дроби.
Новым общим знаменателем будет произведение знаменателей первой и второй дроби. Найди правильный ответ.
Найди правильный ответ.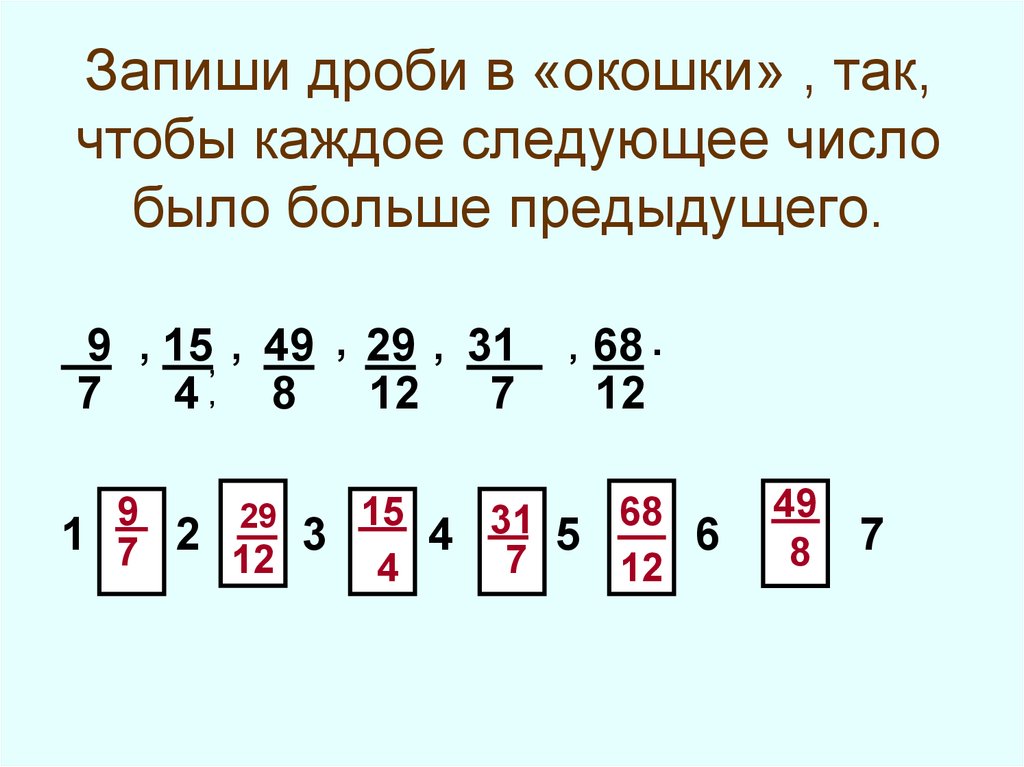 Калькулятор вычисления силы, массы и ускорения.
Калькулятор вычисления силы, массы и ускорения.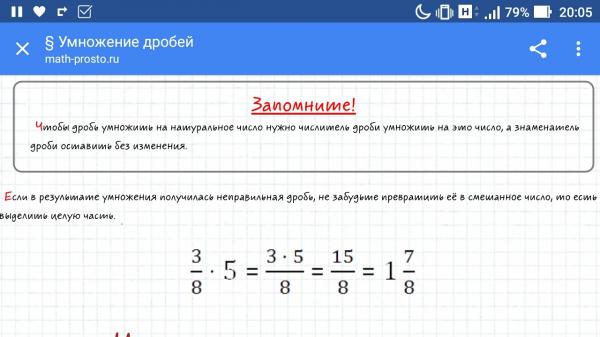 Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов

 Он также преобразует дробь в десятичное число и в неправильную дробь (если возможно).
Он также преобразует дробь в десятичное число и в неправильную дробь (если возможно).

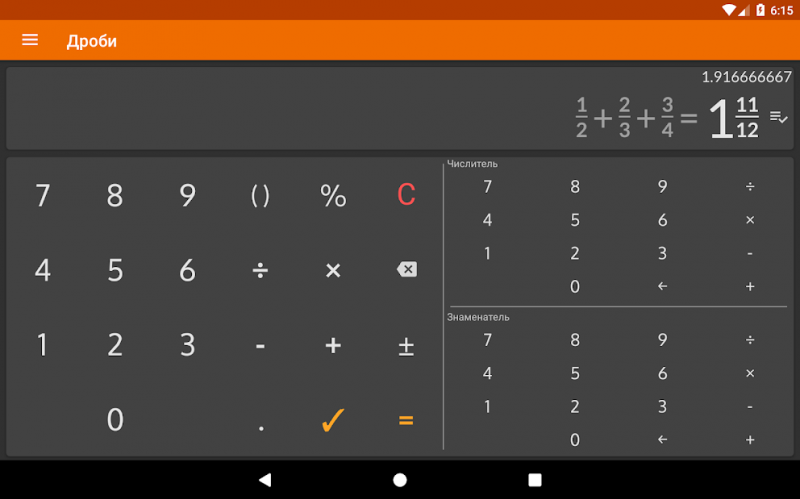 Что такое дроби
Что такое дроби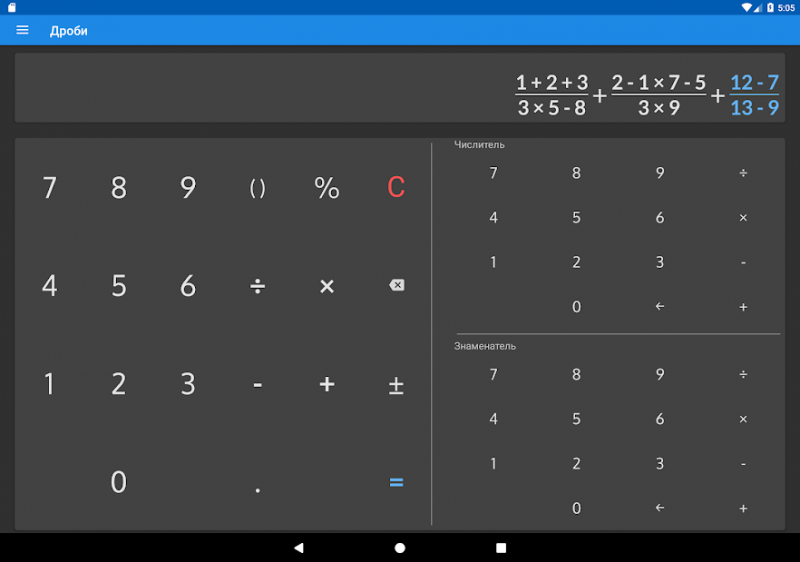
 Мы также можем выполнить деление, разделив числитель (верхнее число) одной дроби на знаменатель (нижнее число) другой дроби.
Мы также можем выполнить деление, разделив числитель (верхнее число) одной дроби на знаменатель (нижнее число) другой дроби.
 Вот таким образом:
Вот таким образом: Вычитание без перехода через десяток и вычитание с переходом через десяток — как выполняется.
Вычитание без перехода через десяток и вычитание с переходом через десяток — как выполняется. Понимание – основа знания.
Понимание – основа знания.
 Научив отличать числа в порядке «больше – меньше», можно учить дошкольника отвечать на вопросы: «Насколько больше/меньше это число?».
Научив отличать числа в порядке «больше – меньше», можно учить дошкольника отвечать на вопросы: «Насколько больше/меньше это число?».
 Для начального этапа обучения можно использовать кубики, палочки или попробовать учиться на счетах, а потом уже приучать малыша считать в уме. В возрасте 5 или 6 лет он должен уметь считать без помощи пальцев и других посторонних предметов.
Для начального этапа обучения можно использовать кубики, палочки или попробовать учиться на счетах, а потом уже приучать малыша считать в уме. В возрасте 5 или 6 лет он должен уметь считать без помощи пальцев и других посторонних предметов. д.
д.
 д.
д. При правильной реализации учащийся сможет перенести эти навыки в другие области математики и в реальные ситуации.
При правильной реализации учащийся сможет перенести эти навыки в другие области математики и в реальные ситуации.

 На данный момент она прочитала 9. Сколько еще книг ей нужно прочитать?» Эти и подобные текстовые задачи проверят знания ваших учеников о сложении и вычитании в пределах двадцати.
На данный момент она прочитала 9. Сколько еще книг ей нужно прочитать?» Эти и подобные текстовые задачи проверят знания ваших учеников о сложении и вычитании в пределах двадцати.
 Они даже могут получать награды за свою математическую практику, чтобы добавить их в свой «футляр с трофеями», чтобы вы могли отпраздновать их достижения в классе!
Они даже могут получать награды за свою математическую практику, чтобы добавить их в свой «футляр с трофеями», чтобы вы могли отпраздновать их достижения в классе! Создавайте список классов и добавляйте в него своих учеников, назначайте уникальные имена пользователей и пароли всем своим ученикам, давайте разные задания на уроки отдельным ученикам, следите за успеваемостью учащихся с помощью подробных отчетов об успеваемости, изменяйте основные настройки урока, распечатывайте, загружайте и отправляйте по электронной почте успеваемость учащихся отчеты и многое другое!
Создавайте список классов и добавляйте в него своих учеников, назначайте уникальные имена пользователей и пароли всем своим ученикам, давайте разные задания на уроки отдельным ученикам, следите за успеваемостью учащихся с помощью подробных отчетов об успеваемости, изменяйте основные настройки урока, распечатывайте, загружайте и отправляйте по электронной почте успеваемость учащихся отчеты и многое другое!