Калькулятор растра (Spatial Analyst)—ArcMap | Документация
Доступно с лицензией Spatial Analyst.
- Сводка
- Иллюстрация
- Использование
- Синтаксис
- Параметры среды
- Информация о лицензиях
Сводка
Строит и выполняет выражение Алгебры карт с использованием синтаксиса Python в интерфейсе, подобном калькулятору.
Более подробно о работе инструмента Калькулятор растра
Иллюстрация
Пример диалогового окна инструмента Калькулятор растраИспользование
Инструмент Калькулятор растров (Raster Calculator) позволяет создать и выполнить выражение Алгебра карт (Map Algebra), которое произведет вывод растра.

-
Используйте список Слои и переменные (Layers and variables) для выбора наборов данных и переменных, которые будут использоваться в выражении. В выражение можно добавить числовые значения и математические операторы, щелкнув соответствующие кнопки в диалоговом окне инструмента. Предоставляется перечень часто используемых условных и математических инструментов, позволяющий легко добавить их в выражение.
Полные пути к данным или данные, существующие в заданном параметре среды текущей рабочей области можно ввести в кавычках («»). Числа и масштабы можно ввести прямо в выражение.
Операторы диалогового окна инструмента Калькулятор растра:
/
(Деление)
==
(Равно)
!=
(Не равно)
и
(Булев оператор And)
*
(Умножение)
>
(Больше)
>=
(Больше или равно)
|
(Булев оператор Or)
—
(Вычитание)
(Изменить знак)
<
(Меньше)
<=
(Меньше или равно)
^
(Булев оператор исключающее XOr)
+
(Сложение)
~
(Булев оператор Not)
Операторы Алгебры карт Многие инструменты и операции геообработки могут быть созданы как выражение алгебры карт с использованием стандартного синтаксиса Python.

Внимание:
При вводе имен инструментов обязательно проверяйте синтаксис имени. Если регистр букв неверен, выражение будет недействительно, и его не удастся выполнить, так как Python чувствителен к регистру.
Пример общего формата выражения алгебры карт с использованием инструментов геообработки:
Con(IsNull(«streams»), 0, «streams»)
Этот инструмент поддерживает стандартный синтаксис алгебры карт, который используется в скриптах Python. Единственные отличия:
- Вам не нужно помещать выходное имя растра или знак = в выражение, т. к. выходное имя задано в параметре Выходной растр (Output raster).
- Не нужно оценивать входные данные как объект растра при использовании операторов.
Не составляет труда вырезать набор растровых данных, сформировав среду экстента и указав имя входного растра в выражении. extent environment «>extent environment and specifying the input raster name in the expression. При выполнении инструмента, выходные данные результирующего растра будут вырезаны на основе заданного экстента.
 , |) выше, чем у реляционных операторов (<, <=, >, >=, ==, !=). Поэтому, если в одном выражении используются Булевы и реляционные операторы, в первую очередь выполняются булевы операторы. Чтобы изменить порядок выполнения, используйте скобки.
, |) выше, чем у реляционных операторов (<, <=, >, >=, ==, !=). Поэтому, если в одном выражении используются Булевы и реляционные операторы, в первую очередь выполняются булевы операторы. Чтобы изменить порядок выполнения, используйте скобки.Если Булевы и/или реляционные операторы последовательно используются в одном выражении, в некоторых случаях его выполнение может завершиться неудачей. Во избежание потенциальных проблем, используйте соответствующие скобки в выражении, чтобы четко определить порядок выполнения операторов. Для получения более подробной информации см. Правила комплексного оператора.
Выполнение операции может быть повышено за счет возможностей отсроченной оценки Алгебры карт. Отсроченная оценка – это метод оптимизации, где отдельные компоненты выражения разумно обрабатываются так, чтобы свести к минимуму создание промежуточных наборов данных на диске.
Только операторы и инструменты, которые обрабатывают по принципу «ячейка за ячейкой», могут воспользоваться этой возможностью.
 Операторы и инструменты, которые поддерживают отсроченную оценку, сами включены инструмент калькулятора растров, либо представлены в виде кнопки, либо в списке предоставленных инструментов.
Операторы и инструменты, которые поддерживают отсроченную оценку, сами включены инструмент калькулятора растров, либо представлены в виде кнопки, либо в списке предоставленных инструментов.Инструмент Калькулятор растра может быть использован в ModelBuilder, но помните следующее:
- В ModelBuilder, следующие типы переменных являются корректными входными данными для выражения:
- String
- Boolean
- Числовые (двойной точности и длинное целое)
- Данные (набор растровых данных, растровый слой, канал растра, файла слоя .lyr)
- Инструмент Калькулятор растра, как правило, придерживается стандартного поведения связности моделей в ModelBuilder, отдельные исключения обусловлены требованиями к формулированию допустимого выражения алгебры карт. К ним относятся:
- Переменные связаны с инструментом Калькулятор растров (Raster Calculator), если они выбираются из перечня переменных. Все переменные автоматически перечислены в списке Переменные этого инструмента.

- Если в выражении используется набор данных или переменная, будет создана связь между переменной и инструментом. Если вы удалите переменную из выражения, связь между переменной и инструментом также будет удалена.
- Если вы удалите связь с переменной, переменная не удалится из выражения.
- Не следует переименовывать переменную, соединенную с инструментом, т.к. переменная не будет переименована в выражении. Если вы переименуете ее, выражение будет некорректным.
- Переменные связаны с инструментом Калькулятор растров (Raster Calculator), если они выбираются из перечня переменных. Все переменные автоматически перечислены в списке Переменные этого инструмента.
- В ModelBuilder, следующие типы переменных являются корректными входными данными для выражения:
Конкретные Параметры среды хранения растра могут применяться к этому инструменту, если форматом входных растровых данных является не Esri Grid.
- Для параметров среды Статистика растра (Raster statistics) поддерживается только задание значения параметра Вычислить статистику (Calculate Statistics).
- В параметрах среды Сжатие поддерживается только тип Сжатия. Параметры среды применяются только для выходных целочисленных данных. Сжатие не поддерживается растрами с плавающей точкой, поэтому данный параметр применим только для выходных целочисленных данных.

- Параметр среды Размер листа поддерживается только для выходных растров в следующих форматах: TIFF, файловая база геоданных или многопользовательская база геоданных.
Примечание:
Инструмент Калькулятор растра предназначен для использования в приложении только в качестве диалогового окна инструмента GP или в ModelBuilder. Он не предназначен для использования в скриптах и не доступен в модуле ArcPy Spatial Analyst.
Синтаксис
RasterCalculator(expression, output_raster)
| Параметр | Объяснение | Тип данных |
expression | Примечание:В Python, выражения алгебры карт необходимо создавать и выполнять с модулем Spatial Analyst, который дополняет функциональность библиотеки ArcPy языка Python. Смотрите Алгебра карт в Spatial Analyst, чтобы узнать о выполнении анализа в Python. | Raster Calculator Expression |
output_raster | Примечание:Более подробную информацию о создании выходных данных из выражения алгебры карт в Python см. Создание выходных данных из выражений алгебры карт (Creating output from Map Algebra). | Raster Dataset |
Параметры среды
- Автоматическое подтверждение
- Размер ячейки
- Метод проецирования размера ячейки
- Сжатие
- Текущая рабочая область
- Экстент
- Географические преобразования
- Маска
- Выходное ключевое слово CONFIG
- Выходная система координат
- Временная рабочая область
- Растр привязки
- Размер листа
Информация о лицензиях
- Basic: Требуется Spatial Analyst
- Standard: Требуется Spatial Analyst
- Advanced: Требуется Spatial Analyst
Связанные разделы
[Страница 19/36] — Инструкция по эксплуатации: Инженерный калькулятор ASSISTANT AC–3612
стр. 54
Таким образом, легко можно увидеть, что графики этих двух функций
имеют две точки пересечения. Приблизительные координаты для этих
двух точек пересечения могут быть найдены с помощью функции
масштабирования «Zoom» и функции прослеживания точек графика
«Trace», которые описаны в следующем разделе.
Примечание: При построении графика встроенной функции поверх
графика другой функции обязательно вводите в формулу Х, как описано
выше. Если во вторую функцию не вводится Х, то при построении второго
графика первый график удаляется с дисплея.
6.3. ИСПОЛЬЗОВАНИЕ ГРАФИКОВ
6.3.1. Функция прокручивания графика
Сразу после построения графика его изображение на дисплее
можно прокрутить. Для прокручивания графика вправо, влево, вверх
и вниз используйте соответствующие кнопки управления курсором
[
→], [←], [↑] и [↓].
При прокручивании графика параметры области отображения
графика меняются.
6.3.2. Функция масштабирования «Zoom»
Данная функция позволяет увеличивать или уменьшать масштаб
графика.
Перед увеличением масштаба переместите с помощью кнопок [
→],
[
←], [↑] и [↓] в центр дисплея ту часть изображения, масштаб которой
необходимо увеличить.
Для увеличения масштаба графика нажимайте кнопки [SHIFT]
[Zoom xf].
Для уменьшения масштаба графика нажимайте кнопки [SHIFT]
[Zoom x 1/f].
Для возвращения к исходному масштабу нажмите последовательно
кнопки [SHIFT] [Zoom Org].
Масштаб графиков увеличивается или уменьшается в соответствии
с установленными коэффициентами масштабирования. Для установки
коэффициентов масштабирования нажмите последовательно кнопки
[SHIFT] [Factor], введите коэффициент масштабирования по оси
х, нажмите [=], введите коэффициент масштабирования по оси у,
после чего нажмите [=] еще раз. Для выхода из режима установки
Для выхода из режима установки
коэффициентов масштабирования нажмите последовательно кнопки
[SHIFT] [Factor].
стр. 19
. . . В А Ш И П О М О Щ Н И К И
Представление шестнадцатеричных значений
Представление числа АBCDEF12
(-1412567278)
Представление шестидесятеричных значений (в формате
градусы-минуты-секунды)
Представление 12
° 34′ 56.78″
Градусы Минуты Секунды
1.7. ДОПОЛНИТЕЛЬНАЯ ИНФОРМАЦИЯ
1.7.1. Порядок выполнения операций
Данный калькулятор при вычислении выражений использует
законы алгебраической логики и следующий порядок приоритетности
операций:
1. Преобразование координат: Pol (x, y) Rec (r,
θ)
2. Функции типа А, для которых сначала вводится аргумент, а затем
нажимается функциональная кнопка: х
2
, х
-1
, х!, ˚,
r
,
g
, ˚ ‘ «;
Инженерные символы: х
1
, x
2
, ŷ
1
, ŷ
2
Угловые преобразования
3. Возведение в степень/извлечение корня: (x
Возведение в степень/извлечение корня: (x
y
),
x
√
4. Операции с дробями: a
b/c
5. Операции сокращенного умножения перед переменными, π, е,
скобками (2
π, 4А, 3е и т. д.)
6. Функции типа В, при вводе которых требуется сначала нажать
соответствующую функциональную кнопку, а затем ввести аргумент,
например,
√,
3
√, log, ln, 10
x
, e
x
, sin, cos, tan, sin
-1
, cos
-1
, tan
-1
, sinh, cosh,
tanh, sinh
-1
, cosh
-1
, tanh
-1
, (-).
7. Операции сокращенного умножения перед функциями типа В:
2
√3, А log2 и т. д.
8. Десятичная запятая.
9. ×, ÷
10. +, –
р
BASE-N
h
A
A
B
B
C
C
D
D
E
E
F
F 12
р
D
12 34′ 56. 78″
78″
Log Base 2 Calculator
Создано Maciej Kowalski, кандидатом наук
Отредактировано Steven Wooding
Последнее обновление: 22 мая 2023 г.
Содержание:- Что такое логарифм?
- Двоичный логарифм
- Часто задаваемые вопросы
Добро пожаловать в калькулятор Omni с основанием 2 . Ваш любимый инструмент для вычисления значения log₂(x) для произвольных (положительных) x . Операция является частным случаем логарифмирования, т.е. когда основание лога равно 2 . Таким образом, мы иногда называем его двоичным логарифмом . Если вы хотите узнать более общий случай, воспользуйтесь нашим логарифмическим калькулятором.
Так что же такое, например, лог с основанием 2 из 8 ? Или log₂ 16 ? Или log₂ 32 ? Что ж, давайте сразу перейдем к статье и узнаем!
Что такое логарифм?
Как только человечество научилось складывать числа, оно нашло способ упростить запись числа , добавив ту же цифру несколько раз: умножение.
5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 8 × 5
Тогда возник очевидный вопрос: как записать , умножив одно и то же число несколько раз? И снова пришли какие-то умные математики, которые ввели показатели степени.
5 × 5 × 5 × 5 × 5 × 5 × 5 × 5 = 5⁸
Однако всегда найдется тот один любопытный человек , который задает самые дикие вопросы. В этом случае они задавались вопросом, есть ли способ инвертировать все эти операции . К счастью для нас, математики и всего мира науки, другие любопытные люди нашли ответ.
Для сложения это было легко: обратная операция это вычитание . Для умножения все еще довольно просто: это деление. Однако для экспонентов история становится более сложной . Ведь мы знаем, что 5 + 8 = 8 + 5 и 5 × 8 = 8 × 5 , но 5⁸ сильно отличается от 8⁵ . Так что же должна дать обратная операция? Если у нас есть 5⁸ , должен ли он вернуть 5 или 8 ?
Так что же должна дать обратная операция? Если у нас есть 5⁸ , должен ли он вернуть 5 или 8 ?
Логарифм (по основанию 5 ) будет операцией, если мы выберем вариант 8 . Другими словами, это функция, которая сообщает вам показатель степени, необходимый для получения значения . Символически мы можем записать определение так:
💡 logₐ(b) дает вам мощность, до которой вам нужно поднять a , чтобы получить b . Обратите внимание, однако, что в общем случае это может быть дробная экспонента!
Для сравнения, обратная операция, которая вернет 5 из 5⁸ , будет просто корнем ( 8 -th). Если бы мы хотели получить немного более техничным , то мы могли бы сказать, что, вообще говоря, если бы у нас было выражение xʸ , то корень — это обратная операция для x , а логарифм — это операция для и . И если бы мы хотели получить еще более технически , мы бы сказали, что первый инвертирует полиномиальную функцию, а второй инвертирует экспоненциальную.
И если бы мы хотели получить еще более технически , мы бы сказали, что первый инвертирует полиномиальную функцию, а второй инвертирует экспоненциальную.
Прежде чем мы двинемся дальше, давайте составим красивый список с несколькими жизненно важными сведениями о нашем новом друге, функции логарифма .
Существуют два особых случая логарифма , которые имеют уникальные обозначения: натуральный логарифм и логарифм с основанием 9.0017 10 . Обозначим их ln(x) и log(x) (второй просто без маленькой 10 ), а их основаниями являются соответственно числа Эйлера e и (сюрприз, сюрприз!) номер 10 .
Хотя последнее очевидно, с первым могут возникнуть проблемы. Если вы не знаете, что такое число e , воспользуйтесь нашим электронным калькулятором.
Логарифмическая функция определена только для положительных чисел.
 Другими словами, всякий раз, когда мы пишем logₐ(b) , мы требуем, чтобы b было положительным.
Другими словами, всякий раз, когда мы пишем logₐ(b) , мы требуем, чтобы b было положительным.Независимо от основания, логарифм 1 равен 0 . В конце концов, что бы мы ни возводили в степень 0 , мы получаем 1 .
Логарифмы чрезвычайно важны. И мы имеем в виду ЧРЕЗВЫЧАЙНО важное. Помимо математики, они используются в статистике 9.0018 (например, логнормальное распределение), экономика (например, индекс ВВП), медицина (например, индекс QUICKI) и химия (например, период полураспада). Кроме того, вполне некоторые физические единицы основаны на логарифмах, например, шкала Рихтера, шкала рН и шкала дБ.
Сегодня мы сосредоточимся на — очень частном случае логарифма , то есть на основании 2 , которое мы иногда называем двоичным логарифмом 9. 0018 . По сути, мы сосредоточимся на том, чтобы взять силы 2 и… Хорошо, если подумать, почему бы нам не посвятить этому целый раздел?
0018 . По сути, мы сосредоточимся на том, чтобы взять силы 2 и… Хорошо, если подумать, почему бы нам не посвятить этому целый раздел?
Двоичный логарифм
Как упоминалось в конце предыдущего раздела, двоичный логарифм является частным случаем логарифмической функции с основанием 2 . Это означает, что у нас будут выражения вида log₂(x) , и мы спросим себя, в какой степени мы должны возвести 2 , чтобы получить х . Например, легко заметить, что log₂ 4 = 2 .
По-видимому, 2 — это такое же число, как и любое другое . Однако он обладает некоторыми интересными свойствами. Например, это наименьшее простое число и единственное четное. Более того, это база для любых компьютерных операций через двоичное представление.
Поскольку это так важно, давайте вспомним несколько основных сил 2 . Помните, что показатель степени также может быть равен 9.0017 0 или даже отрицательный.
Помните, что показатель степени также может быть равен 9.0017 0 или даже отрицательный.
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
2 x | ⅛ | ¼ | ½ | 1 | 2 | 4 | 8 | 16 | 32 | 9000 2 64 | 128 | 256 |
Теперь мы можем увидеть больше примеров , чем просто log₂ 4 = 2 сверху. Например, мы можем сказать, что журнал с основанием 2 из 8 это 3 .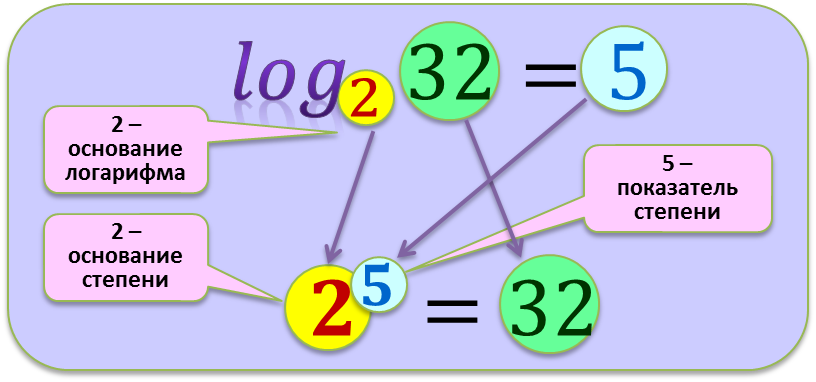 Аналогично, log₂ 16 = 4 или log₂ 32 = 5 .
Аналогично, log₂ 16 = 4 или log₂ 32 = 5 .
Но что такое, скажем, log₂ 5? Конечно, 5 не является степенью числа 2 .
Если быть точным, это не целая степень числа 2 . Мы должны помнить, что есть и дробные показатели степени, и действительно, здесь нам нужен один из них. К сожалению, не так просто угадать . В некоторых случаях мы можем попробовать использовать приемы, такие как изменение базового правила, но в целом лучше всего использовать внешний инструмент — что-то вроде нашего log base 2 калькулятор или калькулятор изменения базовой формулы.
В нем вы можете увидеть два окна переменных : x и log₂(x) . Надеюсь, обозначение понятно. Например, если вы хотите найти log₂ 16 , вам нужно ввести 16 под x , и калькулятор выдаст ответ в другом окне. Если вам требуется log₂ 32 , введите 32 . Также обратите внимание на то, как калькулятор Omni с основанием 2 логарифма работает в обоих направлениях : вы можете либо ввести значение x и получить log₂(x) , либо наоборот.
Если вам требуется log₂ 32 , введите 32 . Также обратите внимание на то, как калькулятор Omni с основанием 2 логарифма работает в обоих направлениях : вы можете либо ввести значение x и получить log₂(x) , либо наоборот.
На сегодняшний урок хватит. Иди, мой юный падаван, и обязательно поиграй с калькулятором или любым другим инструментом, связанным с алгеброй, который мы предлагаем.
Часто задаваемые вопросы
Как вычислить логарифм по основанию 2?
Чтобы вычислить логарифм по основанию 2, вам, вероятно, понадобится калькулятор. Однако, если вы знаете результат натурального логарифма или логарифма по основанию 10 того же аргумента, вы можете выполнить эти простые шаги, чтобы найти результат. Для числа x :
Найдите результат
log10(x)илиln(x).Разделить результата предыдущего шага на соответствующее значение между:
Результат деления
log2(x).
Какой логарифм по основанию 2 числа 256?
Логарифм по основанию 2 числа 256 равен 8 . Чтобы найти этот результат, рассмотрим следующую формулу:
2 x = 256
Логарифм соответствует следующему уравнению:
log2(256) = x
2, чтобы посмотреть, сможем ли мы найти значение x : 2 0 = 1 , 2 1 = 2 , 2 2 = 4 , …, 900 17 2 7 = 128 и 2 8 = 256 .
Поскольку мы нашли аргумент нашего логарифма, мы можем написать, что:
log2(256) = 8 .
Почему важен логарифм по основанию 2?
В компьютерном мире двоичный код имеет огромное значение: слова, числа, изображения и все остальное можно свести к строке из нулей и единиц. Поскольку в двоичном коде используются только две цифры , число 2 постоянно появляется в информатике.
Широкое распространение log2 в компьютерных науках не имеет сильной математической причины (поскольку логарифмы могут менять основание при умножении), но может быть полезным. Например, использование log2 для вычисления энтропии позволяет нам получить результат, выраженный в битах, которые являются естественной единицей.
В чем разница между ln и log2?
Разница между ln и log2 заключается в базе . Логарифм — это обратная операция возведения в степень , то есть степени числа, и он отвечает на вопрос: «Какой показатель степени дает данный результат?».
Основанием логарифма является число, к которому применяется показатель степени: в случае ln это число равно e , число Непера. Для log2 необходимо учитывать число 2 . Подытожим:
- Если b = ln(x) , то e b = x ; и
- Если c = log2(x) , то 2 c = x .

Maciej Kowalski, PhD кандидат
log₂(x)
Ознакомьтесь с 14 похожими калькуляторами показателей степени и логарифмов 🇪
AntilogChange of base FormulaКонденсированные логарифмы… Еще 11
Log Base 2 Калькулятор
РЕКЛАМА
Введите x для расчета журнала 2 x:
РЕКЛАМАРЕКЛАМА
Содержание
Получите виджет!
Добавьте этот калькулятор на свой сайт, чтобы пользователи могли выполнять простые расчеты.
Получить код
Обратная связь
Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам!
ОБРАТНАЯ СВЯЗЬ
Калькулятор по основанию 2 вычисляет логарифм по основанию 2 числа «x». Число обычно записывается как log2(x) или lb(x).
Для точного расчета логарифма основания 2 следуйте приведенным ниже инструкциям:
Ввод:
- Введите значение «x»
- Нажмите кнопку «Рассчитать»
Выход:
- Журнал в базу 2
Логарифм по основанию 2 также известен как двоичный логарифм и имеет основание 2. Двоичный логарифм x — это степень, в которую нужно возвести число 2, чтобы определить значение Икс. Вам нужно вычислить журнал по основанию 2 для нахождения двоичного логарифма любого числа. Кроме того, еще одна система счисления, которая поможет вам понять сложный журнал с основанием 16, — это метод шестнадцатеричных чисел, который можно решить с помощью шестнадцатеричного калькулятора.
Пример журнала на основе 2: Например, двоичный журнал 1 равен «0», а двоичный журнал 2 равен «1». Журнал по основанию 2 обычно используется в информатике и информационных технологиях. Калькулятор логарифмической базы 2 можно использовать для вычисления значений логарифмической базы 2 или любого заданного значения.
Калькулятор логарифмической базы 2 можно использовать для вычисления значений логарифмической базы 2 или любого заданного значения.
| Бревно 2 (х) | Подписка | Обозначение | Значение |
|---|---|---|---|
| Бревно 2 (1) | журнал базы 2 из 1 | фунтов(1) | 0 |
| Бревно 2 (2) | журнал базы 2 из 2 | фунтов(2) | 1 |
| Бревно 2 (3) | основание бревна 2 3 | фунтов(3) | 1,58496 |
| Бревно 2 (4) | журнал основания 2 из 4 | фунтов(4) | 2 |
| Бревно 2 (5) | журнал базы 2 из 5 | фунтов(5) | 2,321928 |
| Бревно 2 (6) | журнал основания 2 из 6 | фунтов(6) | 2,584963 |
| Бревно 2 (7) | журнал основания 2 из 7 | фунтов(7) | 2. 807355 807355 |
| Бревно 2 (8) | бревно 2 8 | фунтов(8) | 3 |
| Бревно 2 (9) | журнал основания 2 из 9 | фунтов(9) | 3.169925 |
| Бревно 2 (10) | журнал базы 2 из 10 | фунтов(10) | 3.321928 |
| Бревно 2 (11) | журнал базы 2 из 11 | фунтов(11) | 3.459432 |
| Бревно 2 (12) | журнал основания 2 из 12 | фунтов(12) | 3,584963 |
| Бревно 2 (13) | журнал базы 2 из 13 | фунтов(13) | 3.70044 |
| Бревно 2 (14) | журнал основания 2 из 14 | фунтов(14) | 3.807355 |
| Бревно 2 (15) | журнал основания 2 из 15 | фунтов(15) | 3. | 1
| Бревно 2 (16) | лог база 2 из 16 | фунтов(16) | 4 |
| Бревно 2 (17) | журнал базы 2 из 17 | фунтов(17) | 4.087463 |
| Бревно 2 (18) | бревно основание 2 из 18 | фунтов(18) | 4.169925 |
| Бревно 2 (19) | журнал базы 2 из 19 | фунтов(14) | 4.247928 |
| Бревно 2 (20) | журнал базы 2 из 20 | фунтов(14) | 4.321928 |
Вы можете вычислить логарифмическое основание 2 любого значения с помощью калькулятора логарифмического основания 2, поскольку двоичные значения логарифма обычно используются в информационных технологиях.
Как перейти с Log10 на Log2?
Вы можете рассчитать логарифм по основанию 2 из логарифма по основанию 10 по следующей формуле: 17 2 )]
Обобщенная формула для изменения основания из одной формы в другую: журнал по основанию 10 в логарифм по основанию 2 по вышеуказанной формуле.


 , |) выше, чем у реляционных операторов (<, <=, >, >=, ==, !=). Поэтому, если в одном выражении используются Булевы и реляционные операторы, в первую очередь выполняются булевы операторы. Чтобы изменить порядок выполнения, используйте скобки.
, |) выше, чем у реляционных операторов (<, <=, >, >=, ==, !=). Поэтому, если в одном выражении используются Булевы и реляционные операторы, в первую очередь выполняются булевы операторы. Чтобы изменить порядок выполнения, используйте скобки. Операторы и инструменты, которые поддерживают отсроченную оценку, сами включены инструмент калькулятора растров, либо представлены в виде кнопки, либо в списке предоставленных инструментов.
Операторы и инструменты, которые поддерживают отсроченную оценку, сами включены инструмент калькулятора растров, либо представлены в виде кнопки, либо в списке предоставленных инструментов.


 Другими словами, всякий раз, когда мы пишем logₐ(b) , мы требуем, чтобы b было положительным.
Другими словами, всякий раз, когда мы пишем logₐ(b) , мы требуем, чтобы b было положительным.

 В конце учебника приводится список литературы, дополняющей его.
В конце учебника приводится список литературы, дополняющей его.
 Макарычев Ю.Н. (7-9)
Макарычев Ю.Н. (7-9) ..
.. ..
..


 Факториал — это произведение всех положительных целых чисел, меньших n.
Факториал — это произведение всех положительных целых чисел, меньших n. Итак, 5! можно записать так: 5! = 5 * 4 * 3 * 2 * 1 = 120. Точно 6! = 6 * 5 * 4 * 3 * 2 * 1 = 720. Обратите внимание на все повторения здесь… получается 6! = 6 * 5! Это важно, потому что вы можете переписать (n+1)! как (n+1) * n! Итак, когда вы делите (n+1)! по н! как у вас в первом члене, n! сокращается как в числителе, так и в знаменателе, оставляя только (n+1). Итак, как указывает Роберт, вычитание n из первого члена оставит 1, а не 0. Таким образом, кажется, что второй член должен быть (n + 1), чтобы быть действительным.
Итак, 5! можно записать так: 5! = 5 * 4 * 3 * 2 * 1 = 120. Точно 6! = 6 * 5 * 4 * 3 * 2 * 1 = 720. Обратите внимание на все повторения здесь… получается 6! = 6 * 5! Это важно, потому что вы можете переписать (n+1)! как (n+1) * n! Итак, когда вы делите (n+1)! по н! как у вас в первом члене, n! сокращается как в числителе, так и в знаменателе, оставляя только (n+1). Итак, как указывает Роберт, вычитание n из первого члена оставит 1, а не 0. Таким образом, кажется, что второй член должен быть (n + 1), чтобы быть действительным. Пример 4! = 4 х 3 х 2 х 1
Пример 4! = 4 х 3 х 2 х 1

 Оказывается, есть очень просто решение!
Оказывается, есть очень просто решение!
 Далее разберем на примерах.
Далее разберем на примерах.
 Если у вас есть какие-либо вопросы о пересечении множеств, я буду более чем счастлив ответить на них.
Если у вас есть какие-либо вопросы о пересечении множеств, я буду более чем счастлив ответить на них. 24
учащимся не нравился ни один из предметов, 9понравилась математика только , 16
нравились науки только , 9 нравились гуманитарные науки только , 12 нравились математика и
гуманитарные науки, 7 любили математику и естественные науки и 9 любили гуманитарные и
наука.
24
учащимся не нравился ни один из предметов, 9понравилась математика только , 16
нравились науки только , 9 нравились гуманитарные науки только , 12 нравились математика и
гуманитарные науки, 7 любили математику и естественные науки и 9 любили гуманитарные и
наука. Но когда я складываю новые числа (3 + 9 + 4), я получаю 16, и я не могу сделать 9 — 16 (что равно -5, ОТРИЦАТЕЛЬНОЕ ЧИСЛО!!!). Может кто-нибудь, пожалуйста, дайте мне знать, что у меня есть сделано неправильно, и как, черт возьми, я должен вычислить пересечение трех наборов?! Любая помощь будет принята с благодарностью.
Но когда я складываю новые числа (3 + 9 + 4), я получаю 16, и я не могу сделать 9 — 16 (что равно -5, ОТРИЦАТЕЛЬНОЕ ЧИСЛО!!!). Может кто-нибудь, пожалуйста, дайте мне знать, что у меня есть сделано неправильно, и как, черт возьми, я должен вычислить пересечение трех наборов?! Любая помощь будет принята с благодарностью. Тогда ваша реальная диаграмма Венна выглядит так:
Тогда ваша реальная диаграмма Венна выглядит так: Или если есть 12$, которые любят математику и гуманитарные науки и могут любить или не любить науку.
Или если есть 12$, которые любят математику и гуманитарные науки и могут любить или не любить науку.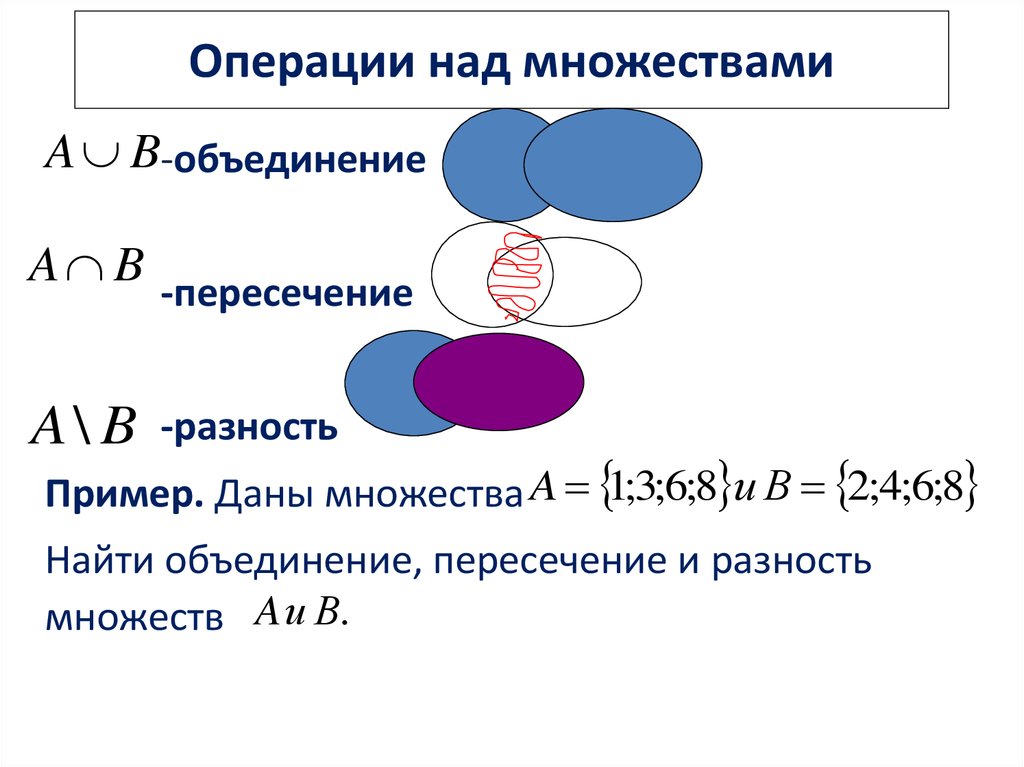


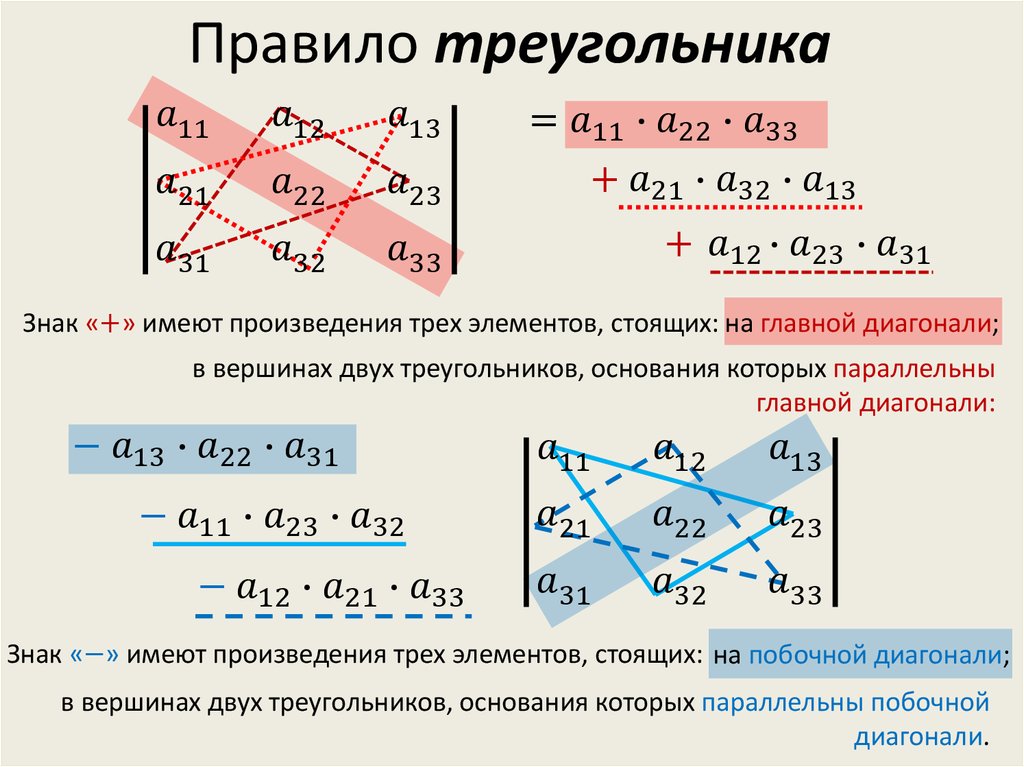 На рисунке изображаем указанные в задаче плоскости
На рисунке изображаем указанные в задаче плоскости
 Найдем косинус угла между заданными плоскостями.
Найдем косинус угла между заданными плоскостями. На рисунке изображаем указанные в задаче прямую и плоскость (прямой
На рисунке изображаем указанные в задаче прямую и плоскость (прямой

 1.
1. ndet(B-A)$%, где n это размер матриц, значит это равенство выполняется только при четном n.
ndet(B-A)$%, где n это размер матриц, значит это равенство выполняется только при четном n. TB$%… то есть при нечётном $%n$% определитель из левой части равенства равен нулю…
TB$%… то есть при нечётном $%n$% определитель из левой части равенства равен нулю…

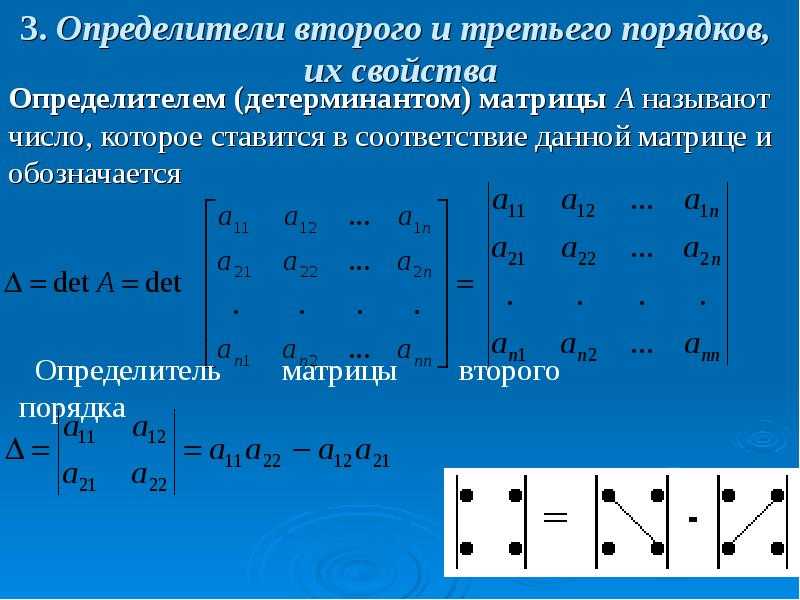
 В аналитической геометрии определители выражают знаковые
В аналитической геометрии определители выражают знаковые


 Миноры, полученные удалением всего одной строки и одного столбца из квадратных матриц (первые миноры), необходимы для вычисления матрицы кофакторов.
Миноры, полученные удалением всего одной строки и одного столбца из квадратных матриц (первые миноры), необходимы для вычисления матрицы кофакторов. 
 В противном случае он равен аддитивной величине, обратной своему минору:
В противном случае он равен аддитивной величине, обратной своему минору: 


 е. квадратная матрица, действительная, когда система имеет единственное решение. Он выражает решение через определители (квадратной) матрицы коэффициентов и матриц, полученных из нее путем замены одного столбца вектором правых частей уравнений.
е. квадратная матрица, действительная, когда система имеет единственное решение. Он выражает решение через определители (квадратной) матрицы коэффициентов и матриц, полученных из нее путем замены одного столбца вектором правых частей уравнений. 0005
0005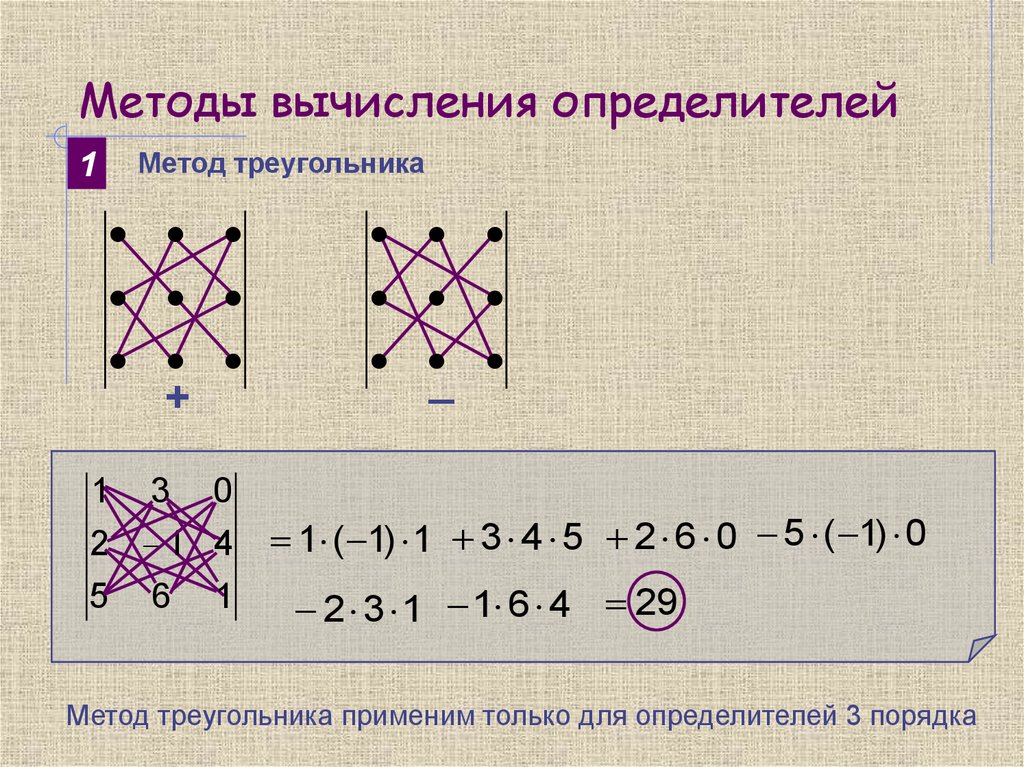 Решите систему с помощью правила Крамера:
Решите систему с помощью правила Крамера:
 Лицензия : CC BY-SA: Кофактор Attribution-ShareAlike
Лицензия : CC BY-SA: Кофактор Attribution-ShareAlike  Определитель матрицы
Определитель матрицы  Ниже приведены некоторые примеры:
Ниже приведены некоторые примеры:

 Існує чимало варіацій в плані організації самих конструкцій. Часто вся конструкція зосереджується на відкритому дворі, який також служить світлим колодязем для нижніх поверхів. Простори, що виходять на саму вулицю, часто використовувалися для меркантильних функцій.
Існує чимало варіацій в плані організації самих конструкцій. Часто вся конструкція зосереджується на відкритому дворі, який також служить світлим колодязем для нижніх поверхів. Простори, що виходять на саму вулицю, часто використовувалися для меркантильних функцій.
 Ці споруди, незважаючи на вітрувіанський ентузіазм, не обійшлися без своїх небезпек і недоліків. Оскільки пожежа була частою небезпекою в стародавньому місті, висотна квартира була особливо ризикованою, особливо для тих, хто проживав на верхніх поверхах. Умови життя в деяких випадках також могли бути менш ідеальними. Інсула як архітектурний тип демонструє різноманітність римської архітектури і надає ще один набір важливих даних про римську побутову забудову.
Ці споруди, незважаючи на вітрувіанський ентузіазм, не обійшлися без своїх небезпек і недоліків. Оскільки пожежа була частою небезпекою в стародавньому місті, висотна квартира була особливо ризикованою, особливо для тих, хто проживав на верхніх поверхах. Умови життя в деяких випадках також могли бути менш ідеальними. Інсула як архітектурний тип демонструє різноманітність римської архітектури і надає ще один набір важливих даних про римську побутову забудову. 1-156.
1-156. 31) (Рим: Американська академія в Римі, 1971).
31) (Рим: Американська академія в Римі, 1971). Навчальна дисципліна спрямована на засвоєння українськими студентами-юристами понять, категорій, усталених формулювань сучасної європейської юриспруденції латинською мовою.
Навчальна дисципліна спрямована на засвоєння українськими студентами-юристами понять, категорій, усталених формулювань сучасної європейської юриспруденції латинською мовою.
 О., Харитонова О.І.Принципи DCFR: сутність та значення для гармонізації цивільного законодавства України з правом Європейського Союзу // Часопис цивілістики. 2015.Вип.18. с.164-170.
О., Харитонова О.І.Принципи DCFR: сутність та значення для гармонізації цивільного законодавства України з правом Європейського Союзу // Часопис цивілістики. 2015.Вип.18. с.164-170. Wołodkiewicz W., Zabłocka M. Prawo rzymskie. Instytucje// Kopia pliku Kopia pliku Prawo rzymskie. instytucje [PDF] | Online Book Share (docero.tips)
Wołodkiewicz W., Zabłocka M. Prawo rzymskie. Instytucje// Kopia pliku Kopia pliku Prawo rzymskie. instytucje [PDF] | Online Book Share (docero.tips)


 Авраам объявляется праведным через веру.
Авраам объявляется праведным через веру. Тем не менее такое хвастовство ничто перед Богом ( , но не перед Богом ).
Тем не менее такое хвастовство ничто перед Богом ( , но не перед Богом ). Раввины утверждали, что Авраам в совершенстве соблюдал закон до того, как он был дан, соблюдал его интуитивно или предвидя.
Раввины утверждали, что Авраам в совершенстве соблюдал закон до того, как он был дан, соблюдал его интуитивно или предвидя. (Запад)
(Запад)
 Вместо этого дается тому, кто верит в Того, Кто оправдывает нечестивых .
Вместо этого дается тому, кто верит в Того, Кто оправдывает нечестивых . Это сосредоточено на том, что Бог возлагает на нас (праведность Иисуса), а не на том, что мы делаем для Бога.
Это сосредоточено на том, что Бог возлагает на нас (праведность Иисуса), а не на том, что мы делаем для Бога.
 Павел настаивает на том, что для того, чтобы Авраам был вашим отцом, вы должны ходить по стопам веры , в который вошел Авраам.
Павел настаивает на том, что для того, чтобы Авраам был вашим отцом, вы должны ходить по стопам веры , в который вошел Авраам. Павел от всего сердца согласился с этим принципом и распространил принцип оправдания верой на все дела Авраама.0131 духовные потомки, верующие, также идущие по стопам веры Авраама.
Павел от всего сердца согласился с этим принципом и распространил принцип оправдания верой на все дела Авраама.0131 духовные потомки, верующие, также идущие по стопам веры Авраама. (Ньюэлл)
(Ньюэлл) Прежде чем Адам согрешил, он сломал доверься Богу — поэтому Божий план искупления сосредоточен на отношениях доверительной любви — веры — вместо соблюдения закона. Когда мы сосредотачиваем наши отношения с Богом на соблюдении закона вместо того, чтобы доверять любви, мы идем против всего Его плана.
Прежде чем Адам согрешил, он сломал доверься Богу — поэтому Божий план искупления сосредоточен на отношениях доверительной любви — веры — вместо соблюдения закона. Когда мы сосредотачиваем наши отношения с Богом на соблюдении закона вместо того, чтобы доверять любви, мы идем против всего Его плана.

 Пример Авраама также помогает нам понять природу веры. Зачатие сына Авраама Исаака было чудом, но не непорочным зачатием. Вера Авраама не означала, что он ничего не делал и просто ждал, пока Бог сотворит ребенка в утробе Сарры. Авраам и Сарра состояли в браке и доверились Богу в чудесном результате. Это показывает нам, что вера означает не делать ничего , а делать все с доверием и упованием на Бога.
Пример Авраама также помогает нам понять природу веры. Зачатие сына Авраама Исаака было чудом, но не непорочным зачатием. Вера Авраама не означала, что он ничего не делал и просто ждал, пока Бог сотворит ребенка в утробе Сарры. Авраам и Сарра состояли в браке и доверились Богу в чудесном результате. Это показывает нам, что вера означает не делать ничего , а делать все с доверием и упованием на Бога. (Трапп)
(Трапп) Иногда он делился с кафедры своей собственной борьбой в этой области, но хотел дать понять, что его борениям в вере никогда не следует потакать: «Всякий раз, когда вы, дорогие слушатели, застанете кого-либо из нас, учителей, в сомнении и страхе, не жалейте нас, но ругайте нас. У нас нет права находиться в Замке Сомнений. Пожалуйста, не посещайте нас там. Следуйте за нами, насколько мы следуем за Христом, но если мы попадем в страшную Трясину Уныния, придите и вытащите нас за волосы, если нужно, но сами в нее не попадайте». (Сперджен)
Иногда он делился с кафедры своей собственной борьбой в этой области, но хотел дать понять, что его борениям в вере никогда не следует потакать: «Всякий раз, когда вы, дорогие слушатели, застанете кого-либо из нас, учителей, в сомнении и страхе, не жалейте нас, но ругайте нас. У нас нет права находиться в Замке Сомнений. Пожалуйста, не посещайте нас там. Следуйте за нами, насколько мы следуем за Христом, но если мы попадем в страшную Трясину Уныния, придите и вытащите нас за волосы, если нужно, но сами в нее не попадайте». (Сперджен) О Боже, дай служителям Твоим больше веры! Поверим тебе твердо!» (Сперджен)
О Боже, дай служителям Твоим больше веры! Поверим тебе твердо!» (Сперджен) (Кальвин)
(Кальвин) Это вменится нам, верующим в Того, Кто воскресил из мертвых Иисуса, Господа нашего, Который был предан за наши преступления и воскрес для нашего оправдания.
Это вменится нам, верующим в Того, Кто воскресил из мертвых Иисуса, Господа нашего, Который был предан за наши преступления и воскрес для нашего оправдания. 

 Её не с чем перемножать, поэтому она остаётся без изменений. Записываем её как есть к новому одночлену:
Её не с чем перемножать, поэтому она остаётся без изменений. Записываем её как есть к новому одночлену:
 Это будет коэффициент одночлена:
Это будет коэффициент одночлена:/Dopolnitelnye%20zadaniya/8%20klass/Kontrolnye%20raboty%20ris/Kontrolnaya%20rabota%20(8kl)%201.jpg)

 Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.
Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части. Перемножить одночлены −5a2bc и 2a2b4
Перемножить одночлены −5a2bc и 2a2b4 При этом используется правило деления степеней.
При этом используется правило деления степеней. Записываем в частном b после a
Записываем в частном b после a
 Делается это с целью упростить выражение.
Делается это с целью упростить выражение.
 Для этого используют правило возведения степени в степень.
Для этого используют правило возведения степени в степень. Записывают только минус и потом остальные сомножители одночлена. В приведенном примере сначала получился одночлен −1a10b5c15, затем он был заменён на тождественно равный ему одночлен −a10b5c15.
Записывают только минус и потом остальные сомножители одночлена. В приведенном примере сначала получился одночлен −1a10b5c15, затем он был заменён на тождественно равный ему одночлен −a10b5c15.

 Приведите одночлен −2aba к стандартному виду.
Приведите одночлен −2aba к стандартному виду.
 Перемножьте одночлены −8x и 5x3
Перемножьте одночлены −8x и 5x3 Возведите одночлен xy2z3 в пятую степень.
Возведите одночлен xy2z3 в пятую степень. Возведите одночлен −x2yz3 в пятую степень.
Возведите одночлен −x2yz3 в пятую степень. Представьте одночлен −a3b6 в виде одночлена, возведённого в куб.
Представьте одночлен −a3b6 в виде одночлена, возведённого в куб. Например, 3 · 3 · 3 · 3 можно записать как показатель степени 3 4 : число 3 было умножено само на себя 4 раз.
Например, 3 · 3 · 3 · 3 можно записать как показатель степени 3 4 : число 3 было умножено само на себя 4 раз. Все показатели степени состоят из двух частей: основание , которое является умножаемым числом; и в степени , то есть количество раз, которое вы умножаете на основание.
Все показатели степени состоят из двух частей: основание , которое является умножаемым числом; и в степени , то есть количество раз, которое вы умножаете на основание. К счастью, эти показатели степени подчиняются простым правилам:
К счастью, эти показатели степени подчиняются простым правилам: В алгебре вас часто будут просить выполнять вычисления с показателями степени с переменными в качестве основы. К счастью, эти показатели легко складывать, вычитать, умножать и делить.
В алгебре вас часто будут просить выполнять вычисления с показателями степени с переменными в качестве основы. К счастью, эти показатели легко складывать, вычитать, умножать и делить. Это потому, что вы можете добавлять показатели только в том случае, если их основания и показатели равны 9.0913 точно такой же . Таким образом, вы можете добавить их ниже, потому что оба термина имеют одну и ту же переменную ( r ) и одинаковую степень (7):
Это потому, что вы можете добавлять показатели только в том случае, если их основания и показатели равны 9.0913 точно такой же . Таким образом, вы можете добавить их ниже, потому что оба термина имеют одну и ту же переменную ( r ) и одинаковую степень (7):


 Следовательно, когда вы повышаете степень в степени можно умножить на показатели степени .
Следовательно, когда вы повышаете степень в степени можно умножить на показатели степени .
 Расстановка коэффициентов в ОВРСхема реакции: As2S3 + HNO3 + h3O → h4AsO4 + h3SO4 + NO
Расстановка коэффициентов в ОВРСхема реакции: As2S3 + HNO3 + h3O → h4AsO4 + h3SO4 + NO Расстановка коэффициентов в ОВРМетод полуреакций (ионно-электронный)
Расстановка коэффициентов в ОВРМетод полуреакций (ионно-электронный) Приводим подобные члены в обеих частях уравнения:
Приводим подобные члены в обеих частях уравнения:






 Субтопические: Оксимизируются и Reduciting Agentsizing & Reduciting Agentsizing & Reducitizing & Reduciting Agentsizing & Reducitizing & REDUCINGISTISISISISISISISISISISISISISISISISISISISISISISISISISISIZING & REDUCINGISISISISISISISISISISISISISISISISISISISISISION
Субтопические: Оксимизируются и Reduciting Agentsizing & Reduciting Agentsizing & Reducitizing & Reduciting Agentsizing & Reducitizing & REDUCINGISTISISISISISISISISISISISISISISISISISISISISISISISISISISIZING & REDUCINGISISISISISISISISISISISISISISISISISISISISISION
 8 и 35,6
8 и 35,6 ..
..
 2\frac{\alpha}2}\)
2\frac{\alpha}2}\) В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.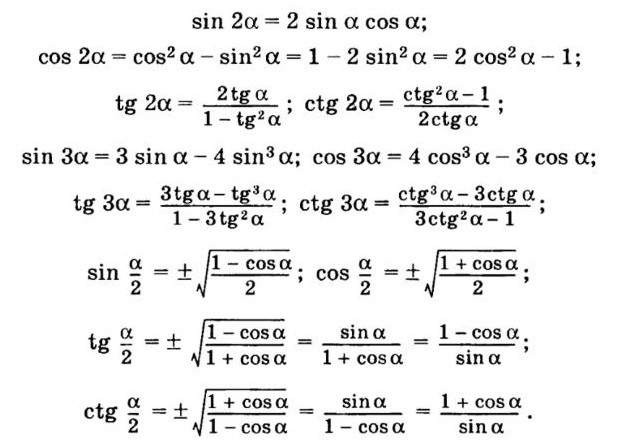 Формулу для tg любого угла αопределяет tgα2, значение угла α≠π+2π·z при z равном любому целому числу ( выражение 1+cosα с таким же значением α не должно принимать значение 0). Формула ctg угла считается справедливой для любого угла α, где половинный угол имеет место быть, α≠2π·z.
Формулу для tg любого угла αопределяет tgα2, значение угла α≠π+2π·z при z равном любому целому числу ( выражение 1+cosα с таким же значением α не должно принимать значение 0). Формула ctg угла считается справедливой для любого угла α, где половинный угол имеет место быть, α≠2π·z.
 Для этого вспомним, что угол в 15 градусов принадлежит первой четверти. Там косинус угла имеет положительное значение ( чтобы вспомнить знаки тригонометрических функций, необходимо повторить теорию знаков синуса, косинуса, тангенса и котангенса по четвертям). Следуя из вышесказанного, имеем cos215°=2+34, тогда cos 15°=2+34=2+32. Ответ: cos 15°=2+32.
Для этого вспомним, что угол в 15 градусов принадлежит первой четверти. Там косинус угла имеет положительное значение ( чтобы вспомнить знаки тригонометрических функций, необходимо повторить теорию знаков синуса, косинуса, тангенса и котангенса по четвертям). Следуя из вышесказанного, имеем cos215°=2+34, тогда cos 15°=2+34=2+32. Ответ: cos 15°=2+32. Необходимо внимательно следить за значениями углов тригонометрических функций и их нахождение в четвертях для определения знака для выражения.
Необходимо внимательно следить за значениями углов тригонометрических функций и их нахождение в четвертях для определения знака для выражения. Это исследование того, как связаны стороны и углы прямоугольного треугольника. Тригонометрия состоит из слов «Тригонон» и «Метрон», которые обозначают треугольник и измерение соответственно. Применение уравнений и тождеств, основанных на этой связи, облегчает оценку неизвестных размеров прямоугольного треугольника.
Это исследование того, как связаны стороны и углы прямоугольного треугольника. Тригонометрия состоит из слов «Тригонон» и «Метрон», которые обозначают треугольник и измерение соответственно. Применение уравнений и тождеств, основанных на этой связи, облегчает оценку неизвестных размеров прямоугольного треугольника.


 Если тангенс θ = 12/5, найти значение кроватки θ/2 по формуле половинного угла.
Если тангенс θ = 12/5, найти значение кроватки θ/2 по формуле половинного угла. 
 \]
\]


 При некоторых специальных
видах неоднородности это частное решение
можно подобрать по известной схеме.
При некоторых специальных
видах неоднородности это частное решение
можно подобрать по известной схеме.
 Найдем частное решение, соответствующее
неоднородностиf1(x)
= 3x.
Так как λ = 0 – корень характеристического
уравнения, частное решение имеет вид
(21)
Найдем частное решение, соответствующее
неоднородностиf1(x)
= 3x.
Так как λ = 0 – корень характеристического
уравнения, частное решение имеет вид
(21)

 Дифференцируя
это равенство, получим
Дифференцируя
это равенство, получим Таким
образом, общее решение уравнения имеет
вид
Таким
образом, общее решение уравнения имеет
вид com › dif
com › dif net › онлайн › исчисление › ода
net › онлайн › исчисление › ода

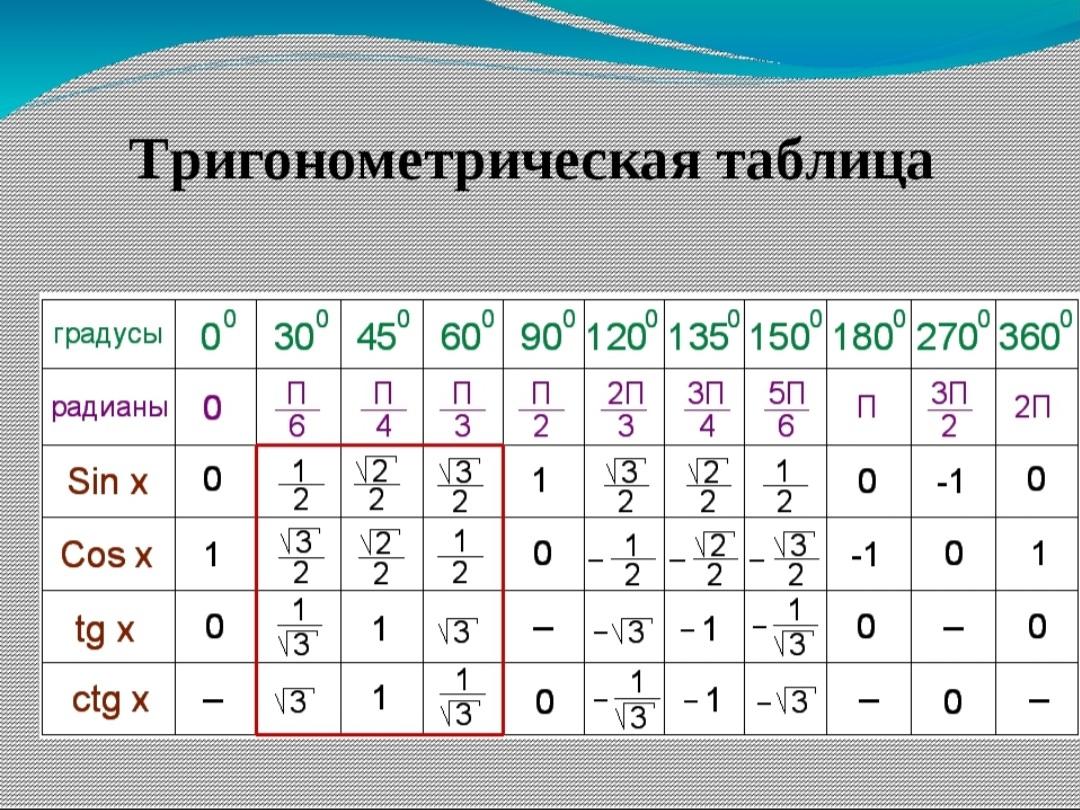
 Таким образом: 2π радиан = 360° 1 радиан = (360/2π) градусов = (180/π) градусов
Таким образом: 2π радиан = 360° 1 радиан = (360/2π) градусов = (180/π) градусов

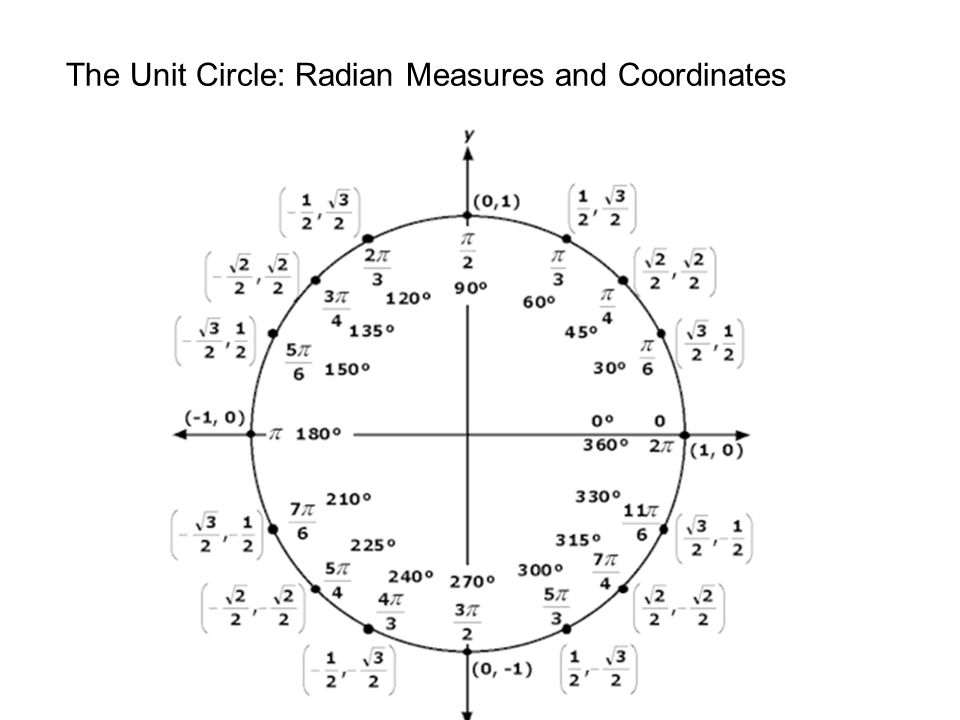 0471975512 рад
0471975512 рад
 В этой статье мы обсудим методы определения значения csc pi/6 на примерах.
В этой статье мы обсудим методы определения значения csc pi/6 на примерах.

 Найдите значение csc pi/6, если sin pi/6 равен 0,5.
Найдите значение csc pi/6, если sin pi/6 равен 0,5. 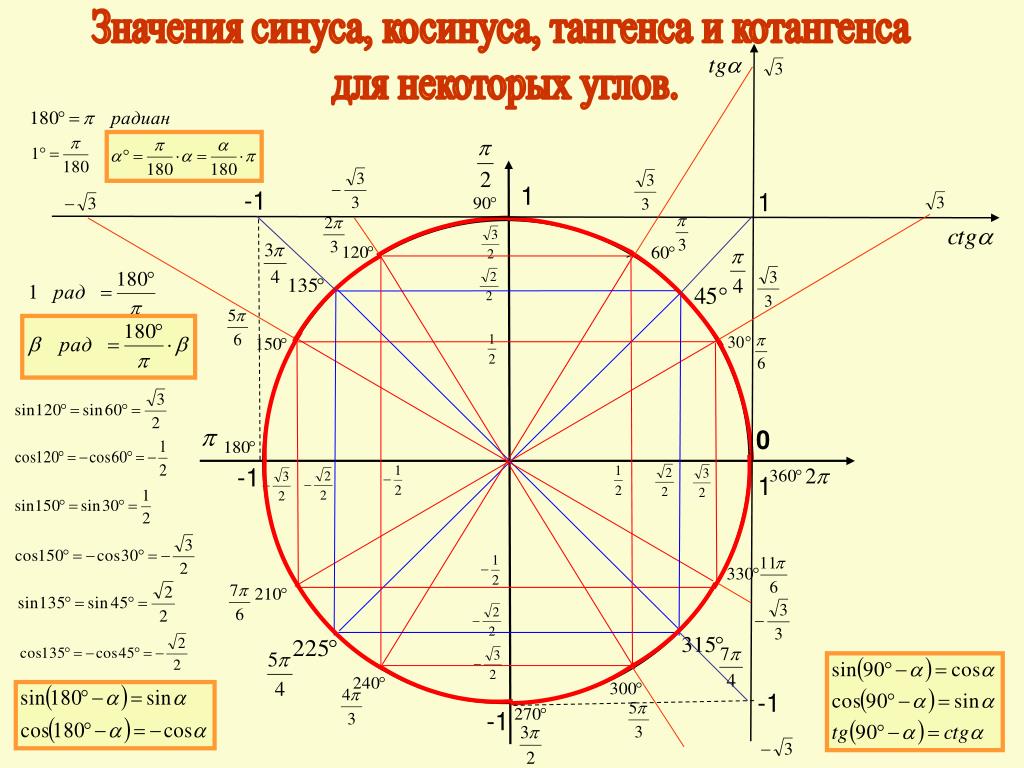 Значение сек пи/6 равно 1,1547.
Значение сек пи/6 равно 1,1547.

 Вот таблица значений общего синуса :
Вот таблица значений общего синуса :

 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.