калькулятор онлайн решение логарифмических уравнений
Вы искали калькулятор онлайн решение логарифмических уравнений? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и логарифмические уравнения онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «калькулятор онлайн решение логарифмических уравнений».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как калькулятор онлайн решение логарифмических уравнений,логарифмические уравнения онлайн,логарифмическое уравнение онлайн,онлайн калькулятор решение логарифмических уравнений,онлайн решение логарифмических уравнений,онлайн решение логарифмических уравнений онлайн,онлайн решение логарифмических уравнений онлайн с подробным решением,онлайн решение уравнений с логарифмами,решение логарифмических,решение логарифмических уравнений онлайн,решение логарифмических уравнений онлайн с подробным решением,решение уравнений онлайн с логарифмами,решение уравнений с логарифмами онлайн,решение уравнений с логарифмами онлайн с подробным решением,решить логарифмическое уравнение онлайн,решить онлайн логарифмическое уравнение,решить уравнение онлайн с логарифмами,решить уравнение с логарифмами онлайн,уравнение с логарифмами решение онлайн,уравнения онлайн логарифмы,уравнения с логарифмами онлайн. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор онлайн решение логарифмических уравнений. Просто введите задачу в окошко и нажмите
«решить» здесь (например, логарифмическое уравнение онлайн).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор онлайн решение логарифмических уравнений. Просто введите задачу в окошко и нажмите
«решить» здесь (например, логарифмическое уравнение онлайн).
Где можно решить любую задачу по математике, а так же калькулятор онлайн решение логарифмических уравнений Онлайн?
Решить задачу калькулятор онлайн решение логарифмических уравнений вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Легкий способ решения логарифмических уравнений
Алгебра Учебники
Решение логарифмических уравнений — это то, что вам нужно сделать часто при работе с алгебраическими процедурами, и стоит разрабатывать конкретную стратегию для их решения.
То, что вы узнаете в этом руководстве, являются основными стратегиями, которые вам необходимо следовать для решения логарифмических уравнений.
Что такое логарифмическое уравнение?
Первое, что нам нужно, это определить, что является логарифмическим уравнением.
Логарифмическое уравнение — это уравнение, которое включает в себя по меньшей мере одну неизвестную переменную, где логарифмическое выражение появляется в по меньшей мере, в одной стороне уравнения Отказ
Пример логарифмического уравнения
\[\ln x = 2\ln x — \ln 3\]или также
\[ \ln(3x-1) — \ln(2x + 1) = 1\]Обратите внимание, что логарифмическое уравнение может содержать более одного неизвестного, как, например,
\[ \ln(x-1) = \ln(2y + 1)\]Стратегии решения логарифмических уравнений
Первый отказ от ответственности состоит в том, что нет пуленезных способов решения логарифмического уравнения, ни общего уравнения для этого вопроса. Причина для этого все методы предполагают определенную структуру в уравнении, что не обязательно там во всех уравнениях.
Причина для этого все методы предполагают определенную структуру в уравнении, что не обязательно там во всех уравнениях.
Итак, мы не можем найти способ решения логарифмических уравнений, потому что нет ни одного способа, который будет иметь дело со всеми возможными случаями.
Тем не менее, есть пару стратегий, которые следует следовать, что даст вам лучший шанс пройти через уравнение и найти решение, если кто-то существует.
Во-первых, попробуйте группировать все логарифмическое выражение в одно логарифмическое выражение.
Это достигается, как правило, используя наиболее распространенные
ПРАВИЛА ЖУРНАЛА. , что позволяет вам компактно компактное выражение логарифмического значения, если структура выражения позволяет так.
, что позволяет вам компактно компактное выражение логарифмического значения, если структура выражения позволяет так.
Во-вторых, как только логарифмические выражения будут максимально уплотнены, вы избавитесь от них, как правило, применяя экспоненциальную функцию для обеих сторон равенства.
Надеюсь, этот последний шаг удалит все логарифмы с картинки, и она позволит вам решить для неизвестных (ы).
Так, другими словами, решение логарифмического уравнения состоит из группировки логарифмических выражений, устраняя их путем применения экспоненциальных, а затем решить уравнение в качестве регулярного уравнения.
Очевидно, что когда вы избавились от логарифмов, вы сталкиваетесь с уравнением, которое может иметь свои проблемы.
Решение различных примеров логарифмических уравнений
Нет лучшего способа узнать, как решать уравнения, чем на самом деле практиковать их:
Пример 1:
Решите следующее уравнение:
\[\large 4 \log(\sqrt x) = \log(6x-1)\]ОТВЕЧАТЬ:
Давайте будем следовать стратегиям. 2-4(1)(1)}}{2(1)}\]
\[\large \Rightarrow x = \frac{6 \pm \sqrt{36-4}}{2}\]
\[\large \Rightarrow x = \frac{6 \pm \sqrt{32}}{2}\]
\[\large \Rightarrow x = \frac{6 \pm 4\sqrt{2}}{2}\]
\[\large \Rightarrow x = 3 \pm 2\sqrt 2\]
2-4(1)(1)}}{2(1)}\]
\[\large \Rightarrow x = \frac{6 \pm \sqrt{36-4}}{2}\]
\[\large \Rightarrow x = \frac{6 \pm \sqrt{32}}{2}\]
\[\large \Rightarrow x = \frac{6 \pm 4\sqrt{2}}{2}\]
\[\large \Rightarrow x = 3 \pm 2\sqrt 2\]
Итак, __xxyz_a__ и \(x_2 = 3 — 2\sqrt 2\).Технически необходимо проверить, являются ли эти два решения исходного уравнения, поэтому чтобы убедиться, что они принадлежат к области логарифмических выражений.
В этом случае как \(x_1 = 3 + 2\sqrt 2\) и \(x_2 = 3 — 2\sqrt 2\) являются решениями исходного уравнения.
Пример 2:
Решить следующую логарифмическое уравнение:
\[\large \ln 5 — \ln(6-x) = \ln x\]ОТВЕЧАТЬ:
Использование правил журнала мы можем компактные выражения журнала, мы получаем это
\[\large \ln 5 — \ln(6-x) = \ln x\] \[\large \displaystyle \Rightarrow \ln\left(\frac{5}{6-x}\right) = \ln x\] \[\large \displaystyle \Rightarrow e^{\ln\left(\frac{5}{6-x}\right)} = e^{\ln x}\] \[\large \displaystyle \Rightarrow \frac{5}{6-x} = x\]
Потому что мы знаем, что \(e^{\ln a} = a\), который является одним из основных правил журнала. 2 -6x + 5 = 0\]
\[\large \displaystyle \Rightarrow (x-1)(x-5) = 0\]
2 -6x + 5 = 0\]
\[\large \displaystyle \Rightarrow (x-1)(x-5) = 0\]
Итак, __xxyz_a__ и \(x_2 = 5\).Давайте подключим эти значения в исходное уравнение, чтобы увидеть, на самом деле это решения:
Для \(x_1 = 1\):
\[\large \ln 5 — \ln(6-1) = \ln 1\]что такое же, как:
\[\large \ln 5 — \ln(5) = 0\]что верно, поэтому уравнение владеет.
Для \(x_1 = 5\):
\[\large \ln 5 — \ln(6-5) = \ln 5\]что такое же, как:
\[\large \ln 5 — \ln(1) = \ln(5)\]
что верно, поэтому уравнение владеет.
Следовательно, решения уравнения \(x_1 = 1\) и \(x_2 = 5\).
Подробнее о решении логарифмических уравнений
Одна вещь, о которой учащиеся самые обеспокоены тем, как вы избавитесь от войти в уравнение.Но мы видели, что это на самом деле легкая часть.То, что сложнее, на самом деле алгебраически работают выражение, так что журналы могут быть удалены.
Это поднимает вопрос о том, как бороться с разными базами, которые требуют свой собственный абзац.
Решение логарифмических уравнений с разными базами
В приведенных выше примерах мы имели дело только с __xxyz_a__ (logarithm с базой 10) и \(\ln\) (logarithm с базой \(e\)). x\).Простое право ??
x\).Простое право ??
Действительно, устранение логарифма — это легкая часть уравнений решавления журнала.Чем усердная часть процесса состоит в том, чтобы сгруппировать и компактные логарифмические выражения в форме, которую вы их устраняете.
Вы можете узнать больше о том, как работает логарифмическая функция, увидев Своства Его Графика и изучение Основные Правила Журнала Отказ
Как решить логарифмические уравнения Решение о уравнениях журнала Решение логарифмических уравнений
Решение логарифмических уравнений с помощью экспонент
Использование DefinitionCalculators и т. д.
д.
Purplemath
Второй тип логарифмического уравнения требует использования Отношения:
—Отношения—
900 02 г = б х ……….. эквивалентно …………
(означает то же самое, что и)
log b ( y ) = x
В анимированной форме два уравнения связаны, как показано ниже:
Содержание продолжается ниже
MathHelp.com
Решение логарифмических уравнений
Обратите внимание, что основание как в экспоненциальной форме уравнения, так и в логарифмической форме уравнения равно «b», но что x и y поменяйте сторону, когда вы переключаетесь между двумя уравнениями. Если вы помните, что независимо от того, что было аргументом журнала, оно становится «равным», а любое , если было «равным», становится показателем экспоненты, и наоборот, — тогда у вас не должно быть слишком много проблемы с решением логарифмических уравнений.
Журнал решения
2 ( x ) = 4
Поскольку это уравнение имеет форму «логарифм (чего-то) равен числу», а не «логарифм (чего-то) равен журналу (чего-то другого)», я могу решить уравнение, используя отношение:
log 2 ( х ) = 4
2 4 = х
16 = х
Журнал решения
2 (8) = x .
Я могу решить это, преобразовав логарифмическое выражение в его эквивалентную экспоненциальную форму, используя соотношение: = 8
Но 8 = 2 3 , поэтому я могу приравнять степени двойки:
2 x = 2 3
x = 3
Обратите внимание, что это также можно было решить, работая непосредственно с определением логарифма.
Какая мощность при значении «2» даст вам 8? Мощность 3, конечно!
Если вы хотите уделить себе много работы, вы также можете сделать это в своем калькуляторе, используя формулу изменения основания:
log 2 (8) = ln(8) / ln(2 )
Вставьте это в свой калькулятор, и вы получите «3» в качестве ответа. Хотя этот метод смены базы не особенно полезен в данном случае, вы можете видеть, что он работает. (Попробуйте это на своем калькуляторе, если вы еще этого не сделали, чтобы быть уверенным, что знаете, какие клавиши нажимать и в каком порядке.) Эта техника понадобится вам в последующих задачах.
Я не говорю, что вы обязательно захотите, чтобы решала уравнения, используя формулу замены основания, всегда используя определение бревен или любой другой конкретный метод. Но я предлагаю вам убедиться, что вы знакомы с различными методами, и что вы не должны паниковать, если вы и ваш друг использовали совершенно различных методов для решения одного и того же уравнения.
Я пока ничего не могу сделать с этим уравнением, потому что у меня еще нет его в форме «логарифм (чего-то) равен числу». Поэтому мне нужно использовать правила журнала, чтобы объединить два члена в левой части уравнения:
log 2 ( x ) + log 2 ( x − 2) = 3
log 2 [( x )( x — 2)] = 3
log 2 ( x 2 − 2 x ) = 3
Теперь уравнение удобно организовано. В этот момент я могу использовать Отношения, чтобы преобразовать логарифмическую форму уравнения в соответствующую экспоненциальную форму, а затем я могу решить результат:
log 2 ( х 2 — 2 х ) = 3
2 3 = х 2 — 2 х 90 003
8 = х 2 − 2 х
0 = x 2 — 2 x — 8
0 = ( x — 4)( x + 2)
x 9001 4 = 4, −2
Но если x = −2, то «log 2 ( x )» из исходного логарифмического уравнения будет иметь отрицательное число в качестве аргумента (как и термин «log 2 ( x − 2)»). Поскольку журналы не могут иметь нулевые или отрицательные аргументы, то решение исходного уравнения не может быть x = −2.
Поскольку журналы не могут иметь нулевые или отрицательные аргументы, то решение исходного уравнения не может быть x = −2.
Тогда мое решение:
x = 4
Имейте в виду, что вы всегда можете проверить свои ответы на любое «решающее» упражнение, подставив эти ответы обратно в исходное уравнение и проверив, что решение «работает». В этом случае я подставлю значение своего решения в любую часть исходного уравнения и убедитесь, что каждая сторона дает одно и то же число:
левая сторона:
log 2 ( x ) + log 2 ( x − 2)
= log 2 (4) + лог 2 (4 − 2 )3
= лог 2 (4) + лог 2 (2)
= лог 2 (2 2 ) + лог 2 (2 9001 5 1 )
= 2 + 1 = 3
Правая часть исходного уравнения уже была упрощена до «3», так что это решение соответствует действительности.
Это уравнение может показаться слишком сложным, но это просто еще одно логарифмическое уравнение. Чтобы решить эту проблему, мне нужно дважды применить Отношения. Я начинаю с исходного уравнения и работаю с «внешним» журналом:
Чтобы решить эту проблему, мне нужно дважды применить Отношения. Я начинаю с исходного уравнения и работаю с «внешним» журналом:
log 2 (log 2 ( x )) = 1
Отношение преобразует приведенное выше в:
2 1 = log 2 ( x )
2 = log 2 ( x )
Теперь я применю соотношение во второй раз:
х = 2 2
х = 4
Тогда решение:
х = 4
9 0049Во-первых, я расширю квадрат справа, чтобы он явный продукт двух журналов:
log 2 ( x 2 ) = [log 2 ( x )] 2
90 002 журнал 2 ( x 2 ) = [логарифм 2 ( x )] [логарифм 2 ( x )]Затем я применю правило логарифма, чтобы переместить «квадрат» из бревна в левую часть уравнения, вынеся его перед этим бревном в качестве множителя:
2 · log 2 ( x ) = [log 2 ( x )] [log 2 ( x )]
9 0002 Тогда я перенесу этот термин слева часть уравнения в правую часть:0 = [log 2 ( x )] [log 2 ( x )] − 2·log 2 ( x )
Это уравнение может выглядеть плохо, но присмотритесь внимательно. На данный момент это не более чем упражнение по факторингу. Итак, я факторизую, а затем решу множители с помощью отношения:
На данный момент это не более чем упражнение по факторингу. Итак, я факторизую, а затем решу множители с помощью отношения:
0 = [log 2 ( x )] [log 2 ( x ) − 2]
log 2 ( x ) = 0 или log 2 ( x ) − 2 = 0
2 0 = x или log 2 ( x ) = 2
1 = x или 2 2 = x
1 = x или 4 = x
Тогда мое решение :
x = 1, 4
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении логарифмических уравнений (или пропустить виджет и продолжить урок). Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления. )
)
Страница 1Страница 3
Решатель логарифмических уравнений — Googlesuche
AlleBilderVideosMapsNewsShoppingBüchersuchoptionen
Калькулятор логарифмических уравнений — Symbolab
www.symbolab.com › … › Алгебра › Уравнения
Бесплатный калькулятор логарифмических уравнений — шаг за шагом решайте логарифмические уравнения.
Калькулятор и решение логарифмических уравнений — SnapXam
www.snapxam.com › калькуляторы › логарифмическое уравнение…
Калькулятор логарифмических уравнений онлайн с решением и шагами. Подробные пошаговые решения ваших задач Логарифмические уравнения с помощью нашего математического решателя …
Калькулятор логарифмов — Mathway
www.mathway.com › Калькулятор › Калькулятор логарифмов
Бесплатный калькулятор логарифмов — пошаговые решения, помогающие упростить логарифмические выражения.
Калькулятор уравнения логарифма
www. calculatorsoup.com › Алгебра
calculatorsoup.com › Алгебра
Этот калькулятор решит основное уравнение логарифма logbx = y для любой одной из переменных, если вы введете две другие. Логарифмическое уравнение решается …
Решение логарифмических уравнений — YouTube
www.youtube.com › смотреть
01.02.2018 · Этот видеоурок по алгебре объясняет, как решать логарифмические уравнения с логарифмами с обеих сторон …
Dauer: 25:27
Прислан: 01.02.2018
900 02 Решение Логарифмические уравнения… Как? (NancyPi) – YouTube
www.youtube.com › смотреть
07.10.2018 · Выпускник Массачусетского технологического института показывает, как решать логарифмические уравнения, используя LOG PROPERTIES для упрощения и решения. Кому …
Дауэр: 15:05
Прислан: 07.10.2018
Ähnliche Fragen
Как вручную решать логарифмические уравнения?
Решение логарифмических уравнений — ChiliMath
www.chilimath.com › Уроки › Усовершенствованная алгебра
Если у вас есть один логарифм в каждой части уравнения с одинаковым основанием, вы можете установить аргументы равными друг другу и затем решить.

 Так, например, минор элемента есть определитель
Так, например, минор элемента есть определитель 2 Сумма произведений элементов какой- либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.
2 Сумма произведений элементов какой- либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.
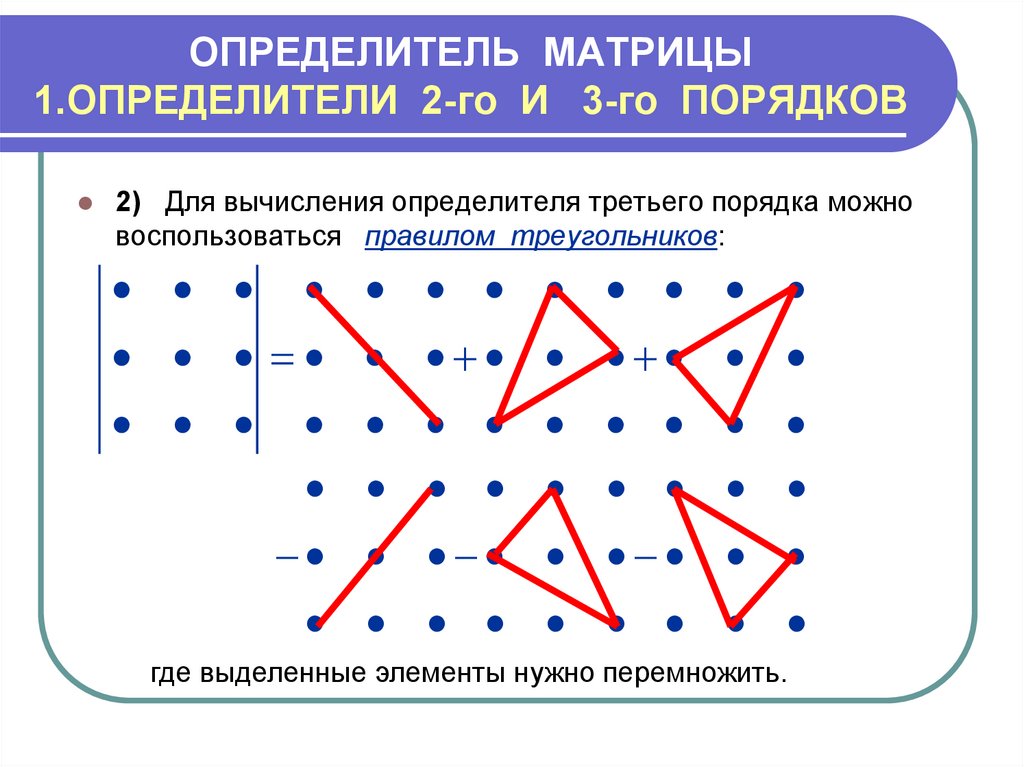
 Возьмем со знаком плюс произведение элементов, стоящих на главной диагонали определителя, а также произведения элементов, стоящих на двух параллельных к ней линиях, содержащих по три элемента.
Возьмем со знаком плюс произведение элементов, стоящих на главной диагонали определителя, а также произведения элементов, стоящих на двух параллельных к ней линиях, содержащих по три элемента. Например,
Например,

 Шаги для нахождения определителей матриц приведены ниже:
Шаги для нахождения определителей матриц приведены ниже: С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами. 2& 6& 2.3\\ -5& 1.3 & 3 \end{bmatrix}\) и проверьте это с помощью онлайн-калькулятора определителя.
2& 6& 2.3\\ -5& 1.3 & 3 \end{bmatrix}\) и проверьте это с помощью онлайн-калькулятора определителя.
 01.20210003 5 видео
01.20210003 5 видео

 д.
д. \circ-\angle BA_1B_1=\angle BAB_1\).
\circ-\angle BA_1B_1=\angle BAB_1\).

 Покажем, теперь, что стороны одного треугольника пропорциональны сходственным сторонам другого треугольника, т. е. выполнено равенство (2).
Покажем, теперь, что стороны одного треугольника пропорциональны сходственным сторонам другого треугольника, т. е. выполнено равенство (2). Пусть заданы два треугольника и и пусть , . Докажем, что (Рис.3).
Пусть заданы два треугольника и и пусть , . Докажем, что (Рис.3). статью Треугольники. Признаки равенства треугольников). Тогда , а поскольку , то . Следовательно, по второму признаку подобия треугольников, треугольники и подобны: .
статью Треугольники. Признаки равенства треугольников). Тогда , а поскольку , то . Следовательно, по второму признаку подобия треугольников, треугольники и подобны: .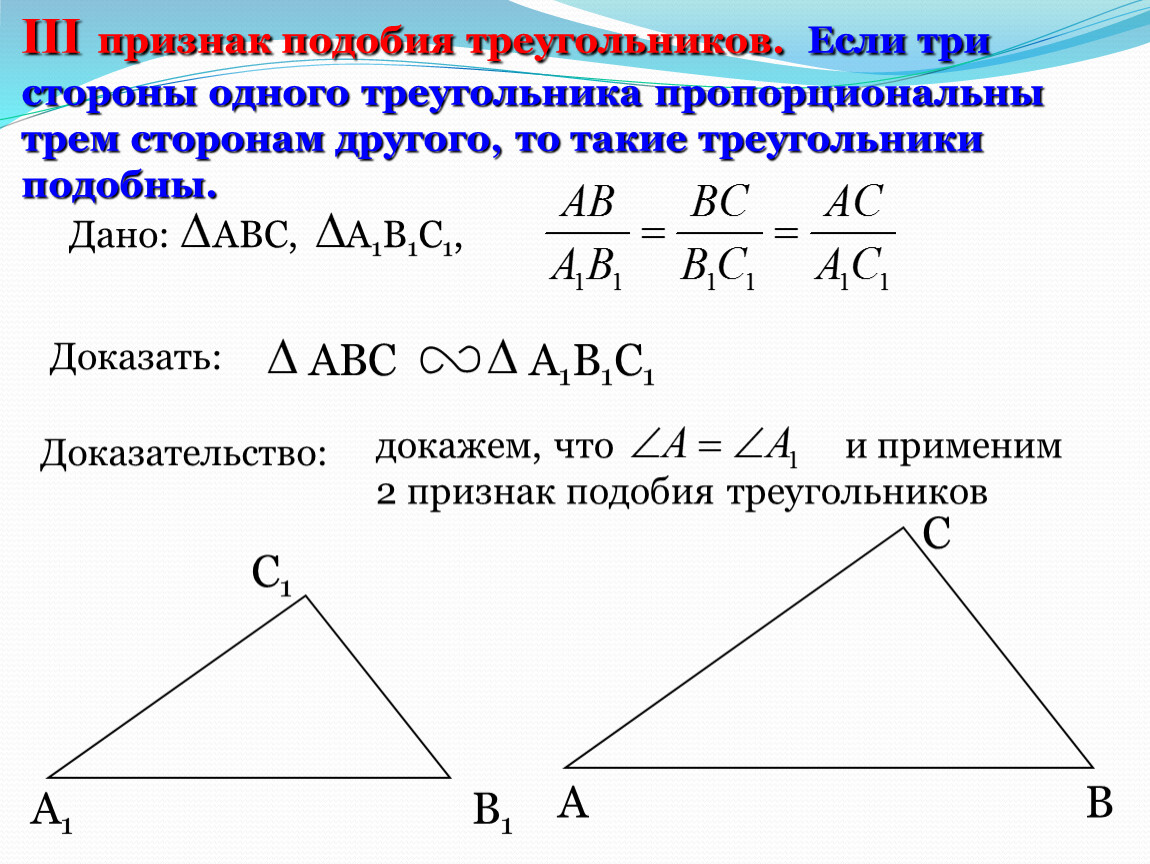 )
) Площадь и подобие
Площадь и подобие э. 2 sin(A) x 2
э. 2 sin(A) x 2 
 Для подобных треугольников три стороны двух треугольников должны быть пропорциональны. Например, если один треугольник имеет стороны 3, 5 и 6 дюймов, а второй треугольник имеет стороны 9, 15 и 18 дюймов, каждая из сторон большего треугольника в три раза длиннее одной из сторон меньшего треугольника. Стороны пропорциональны друг другу, а треугольники подобны.
Для подобных треугольников три стороны двух треугольников должны быть пропорциональны. Например, если один треугольник имеет стороны 3, 5 и 6 дюймов, а второй треугольник имеет стороны 9, 15 и 18 дюймов, каждая из сторон большего треугольника в три раза длиннее одной из сторон меньшего треугольника. Стороны пропорциональны друг другу, а треугольники подобны. Но есть и другие возможные комбинации боковых углов, которые могут гарантировать или не гарантировать сходство.
Но есть и другие возможные комбинации боковых углов, которые могут гарантировать или не гарантировать сходство.

 Делится ли произведение на 9?
Делится ли произведение на 9?
 Делимость произведения
Делимость произведения

 Я понятия не имею, смогу ли я объяснить это понятным образом, но, думаю, мне придется попытаться.
Я понятия не имею, смогу ли я объяснить это понятным образом, но, думаю, мне придется попытаться. )
)
 Обратите внимание, что правый хук
Обратите внимание, что правый хук  Это
Это 
 Если дать им две функции
Если дать им две функции  2 + 4
p' < ------------------
q ( г - SR (3))
Оценка этого неравенства почленно дает
д р р 4
p' < ------ + --- ------- + ----------
р-SR(3) q r-SR(3) q(r-SR(3))
Поскольку 2 < r < q, второе слагаемое должно быть меньше 2,366.., а
третий член меньше 0,788... Поэтому имеем
д
p' < ------- + 3,154...
р-СР(3)
что показывает, что p' < q для всех q > 15. Проверка случаев с
2 < r < q < 15 показывает, что в этом диапазоне нет решений, поэтому p' должно
быть меньше q. Отсюда следует, что p',q,r является другим решением в
различные положительные целые числа с меньшим наибольшим членом, чем p,
противоречащее предположению.
Это завершает доказательство того, что не существует четырех (или меньше) простых чисел.
произведение которых делится на сумму их квадратов. Однако,
существует много наборов из пяти простых чисел с этим свойством.
наименьший пример [3,5,11,192
Для любого такого набора простых чисел мы ссылаемся на отношение наибольшего к
наименьшее, как «соотношение сторон», поэтому соотношение сторон выше
например 23/3 = 7,666.
2 + 4
p' < ------------------
q ( г - SR (3))
Оценка этого неравенства почленно дает
д р р 4
p' < ------ + --- ------- + ----------
р-SR(3) q r-SR(3) q(r-SR(3))
Поскольку 2 < r < q, второе слагаемое должно быть меньше 2,366.., а
третий член меньше 0,788... Поэтому имеем
д
p' < ------- + 3,154...
р-СР(3)
что показывает, что p' < q для всех q > 15. Проверка случаев с
2 < r < q < 15 показывает, что в этом диапазоне нет решений, поэтому p' должно
быть меньше q. Отсюда следует, что p',q,r является другим решением в
различные положительные целые числа с меньшим наибольшим членом, чем p,
противоречащее предположению.
Это завершает доказательство того, что не существует четырех (или меньше) простых чисел.
произведение которых делится на сумму их квадратов. Однако,
существует много наборов из пяти простых чисел с этим свойством.
наименьший пример [3,5,11,192
Для любого такого набора простых чисел мы ссылаемся на отношение наибольшего к
наименьшее, как «соотношение сторон», поэтому соотношение сторон выше
например 23/3 = 7,666.

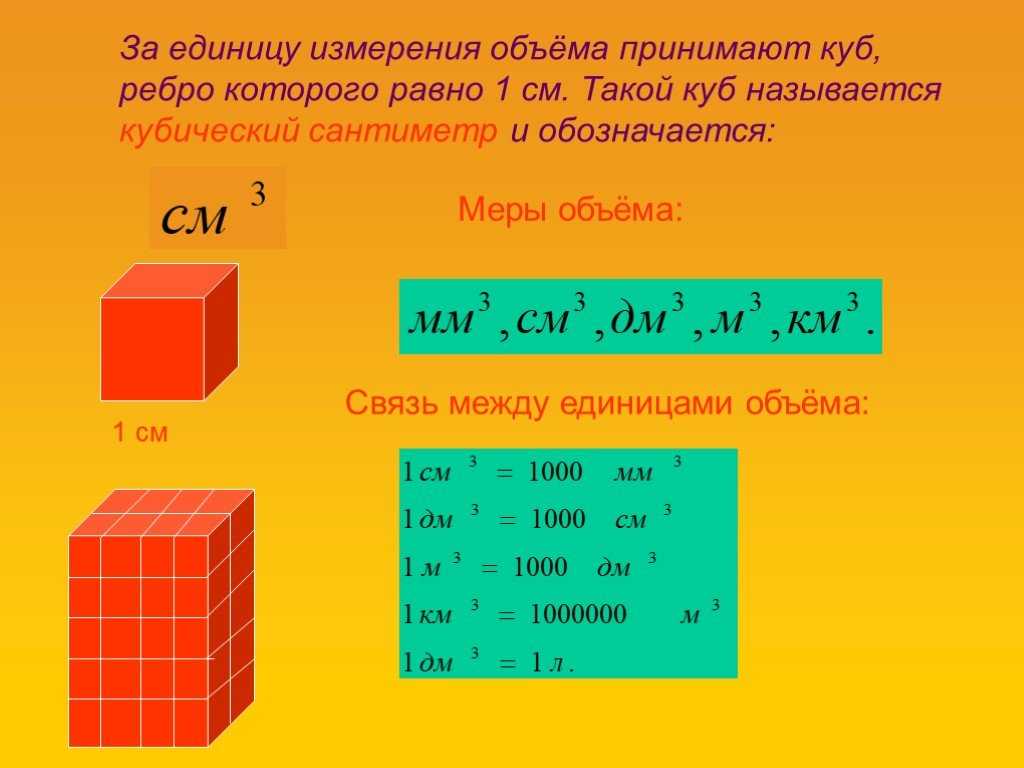
 10 3 или 10 в кубе, например, будет набором блоков 10 в высоту, 10 в ширину и 10 в глубину. Одна грань куба будет иметь набор 10 93 = 1000 \]
10 3 или 10 в кубе, например, будет набором блоков 10 в высоту, 10 в ширину и 10 в глубину. Одна грань куба будет иметь набор 10 93 = 1000 \] 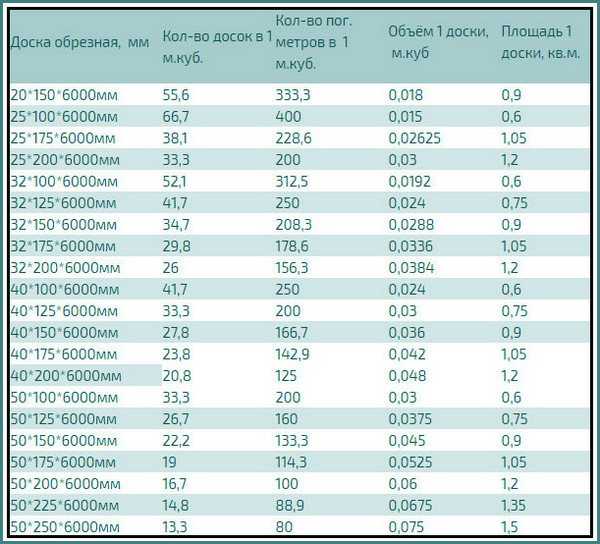 наш список первых 100 идеальных кубов.
наш список первых 100 идеальных кубов.  Например, при четных показателях и отрицательном знаке круглые скобки влияют на результат.
Например, при четных показателях и отрицательном знаке круглые скобки влияют на результат. 
 Например, куб числа 3 можно вычислить, умножив 3 трижды (3 × 3 × 3).
Например, куб числа 3 можно вычислить, умножив 3 трижды (3 × 3 × 3). 
 {2}\ –\ 20x + 36 = 0 \\ \end{matrix} \right.\ \)
{2}\ –\ 20x + 36 = 0 \\ \end{matrix} \right.\ \)


 Также в цепочке преобразований был переход от уравнения к уравнению x+2=9, при котором расширилась ОДЗ, что тоже могло привести к появлению посторонних корней. Так что проведем отсеивание посторонних корней. Сделаем это через проверку подстановкой. Подставим найденный корень в иррациональное уравнение , имеем
Также в цепочке преобразований был переход от уравнения к уравнению x+2=9, при котором расширилась ОДЗ, что тоже могло привести к появлению посторонних корней. Так что проведем отсеивание посторонних корней. Сделаем это через проверку подстановкой. Подставим найденный корень в иррациональное уравнение , имеем е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.  Причина в том, что в большинстве случаев мы на самом деле приходим к решению квадратного уравнения. Однако подход существенно отличается, поэтому в этом курсе мы разделим две темы на разные разделы.
Причина в том, что в большинстве случаев мы на самом деле приходим к решению квадратного уравнения. Однако подход существенно отличается, поэтому в этом курсе мы разделим две темы на разные разделы. 

 92}\]
92}\]
 2} — z — 2\\ & 0 = \left( {z — 2 } \right)\left( {z + 1} \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,\,\,z = — 1,\,\,\, \,z = 2\конец{выравнивание*}\]
9? 2\\ 4 — 2 & = 2\hspace{0,25 дюйма}{\mbox{OK}}\end{align*}\]
2} — z — 2\\ & 0 = \left( {z — 2 } \right)\left( {z + 1} \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,\,\,z = — 1,\,\,\, \,z = 2\конец{выравнивание*}\]
9? 2\\ 4 — 2 & = 2\hspace{0,25 дюйма}{\mbox{OK}}\end{align*}\]

 2} — 18x + 65 & = 0 \\ \left( {x — 13} \right)\left( {x — 5} \right) & = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}x = 13,\,\,\ ,х = 5\конец{выравнивание*}\]
9? \sqrt 9 \\ 1 + 2 & = 3\hspace{0,25 дюйма}{\mbox{OK}}\end{align*}\]
2} — 18x + 65 & = 0 \\ \left( {x — 13} \right)\left( {x — 5} \right) & = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}x = 13,\,\,\ ,х = 5\конец{выравнивание*}\]
9? \sqrt 9 \\ 1 + 2 & = 3\hspace{0,25 дюйма}{\mbox{OK}}\end{align*}\]


 6.2
6.2 

 {m \cdot n}\), мы имеем, например, 9{4}\)
{m \cdot n}\), мы имеем, например, 9{4}\)


 Часто проще всего сначала выделить более сложный радикал. 9{3}\)
Часто проще всего сначала выделить более сложный радикал. 9{3}\) 



 При необходимости нарисуйте рисунок и подпишите его с помощью данной информации.
При необходимости нарисуйте рисунок и подпишите его с помощью данной информации. 

 6.11
6.11  Используйте формулу \(s=\sqrt{24d}\), чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых.
Используйте формулу \(s=\sqrt{24d}\), чтобы найти скорость автомобиля до включения тормозов. Округлите ответ до десятых. 
 9{2}}\конец{массив}\)
9{2}}\конец{массив}\)


 Подчеркнем повторяющиеся одночлены и запишем их друг за другом.
Затем вынесем общий множитель у каждой группы одночленов.
Подчеркнем повторяющиеся одночлены и запишем их друг за другом.
Затем вынесем общий множитель у каждой группы одночленов.

 Разложение многочлена имеет смысл тогда, когда его степень не ниже второй. Многочлен с первой степенью называют линейным.
Разложение многочлена имеет смысл тогда, когда его степень не ниже второй. Многочлен с первой степенью называют линейным. ..·(x-x3)x2+px+q , где x2+px+q=(x-x1)(x-x2).
..·(x-x3)x2+px+q , где x2+px+q=(x-x1)(x-x2).

 Большинство всех случаев основано на следствии из теоремы Безу. Для этого необходимо подбирать значение корня x1 и понизить его степень при помощи деления на многочлена на 1 делением на (x-x1) . Полученный многочлен нуждается в нахождении корня x2 , причем процесс поиска цикличен до тех пор, пока не получим полное разложение.
Большинство всех случаев основано на следствии из теоремы Безу. Для этого необходимо подбирать значение корня x1 и понизить его степень при помощи деления на многочлена на 1 делением на (x-x1) . Полученный многочлен нуждается в нахождении корня x2 , причем процесс поиска цикличен до тех пор, пока не получим полное разложение.
 Можно провести проверку по схеме Горнера. Она очень удобная и позволяет быстро получить коэффициенты разложения многочлена:
Можно провести проверку по схеме Горнера. Она очень удобная и позволяет быстро получить коэффициенты разложения многочлена:
 Получаем, что
Получаем, что Для этого необходимо пользоваться специальными способами для нахождения множителей. Но не все многочлены можно разложить или представить в виде произведения.
Для этого необходимо пользоваться специальными способами для нахождения множителей. Но не все многочлены можно разложить или представить в виде произведения. Для этого нам понадобится произвести разложение на множители. получаем, что
Для этого нам понадобится произвести разложение на множители. получаем, что После того, как были произведены преобразования, можно выстроить строчку, состоящую из треугольника Паскаля, иначе их называют биномом Ньютона.
После того, как были произведены преобразования, можно выстроить строчку, состоящую из треугольника Паскаля, иначе их называют биномом Ньютона. Получаем, что
Получаем, что







 0110 2
0110 2 



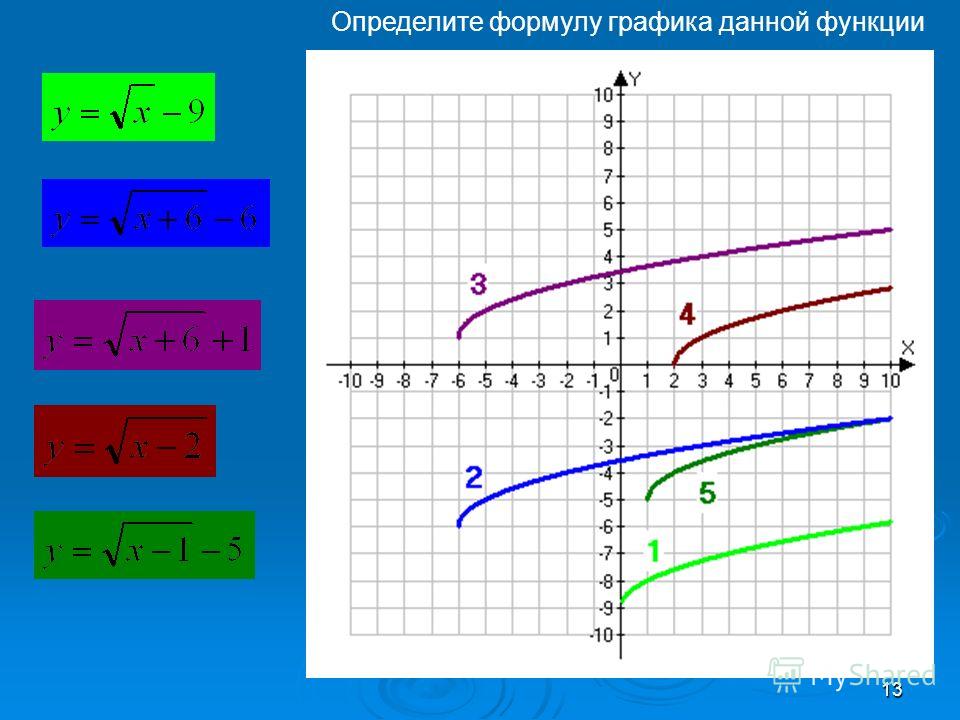 Функция
Функция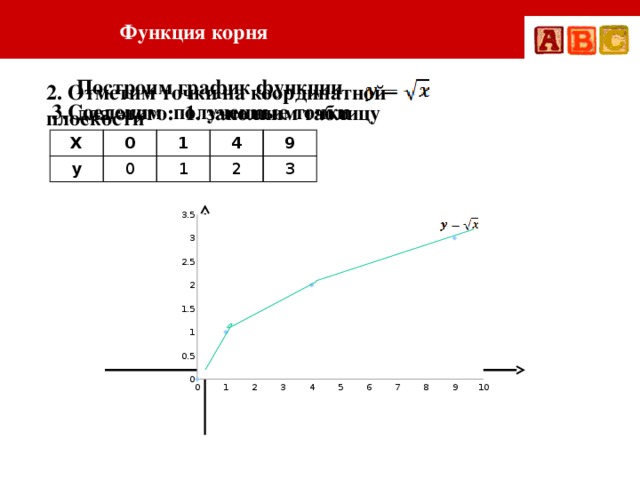 =3
=3
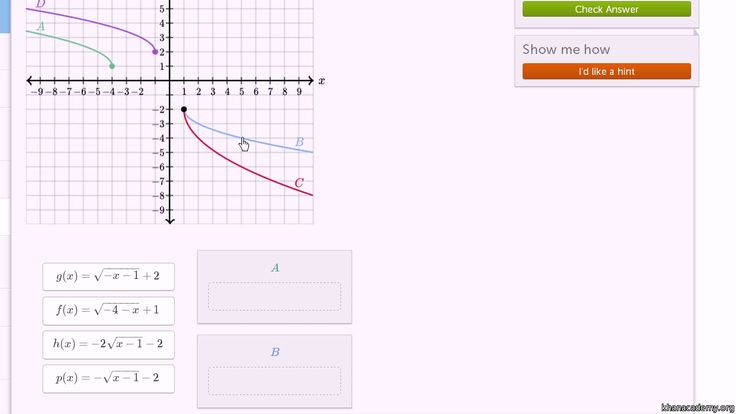 вверх.
вверх.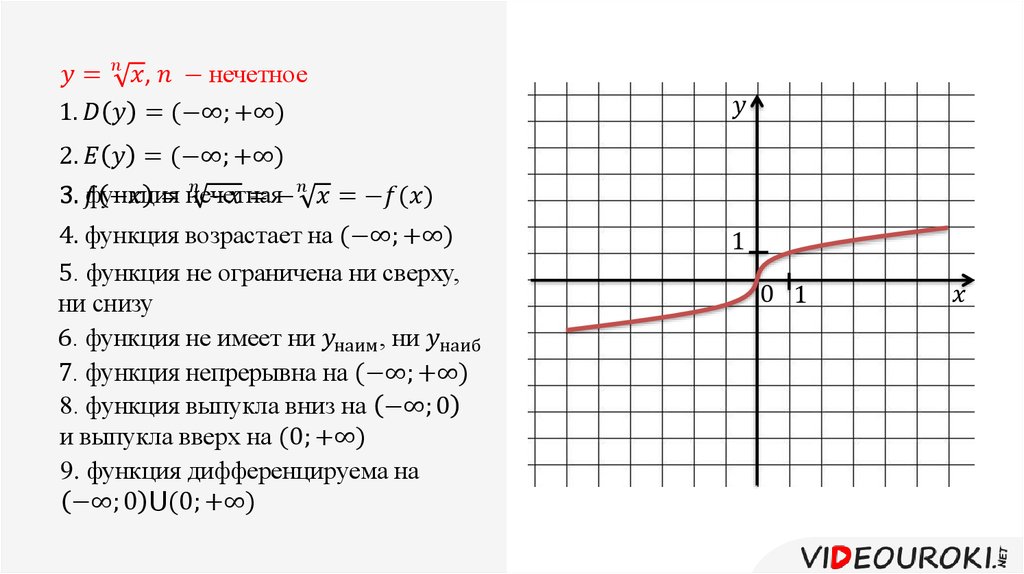


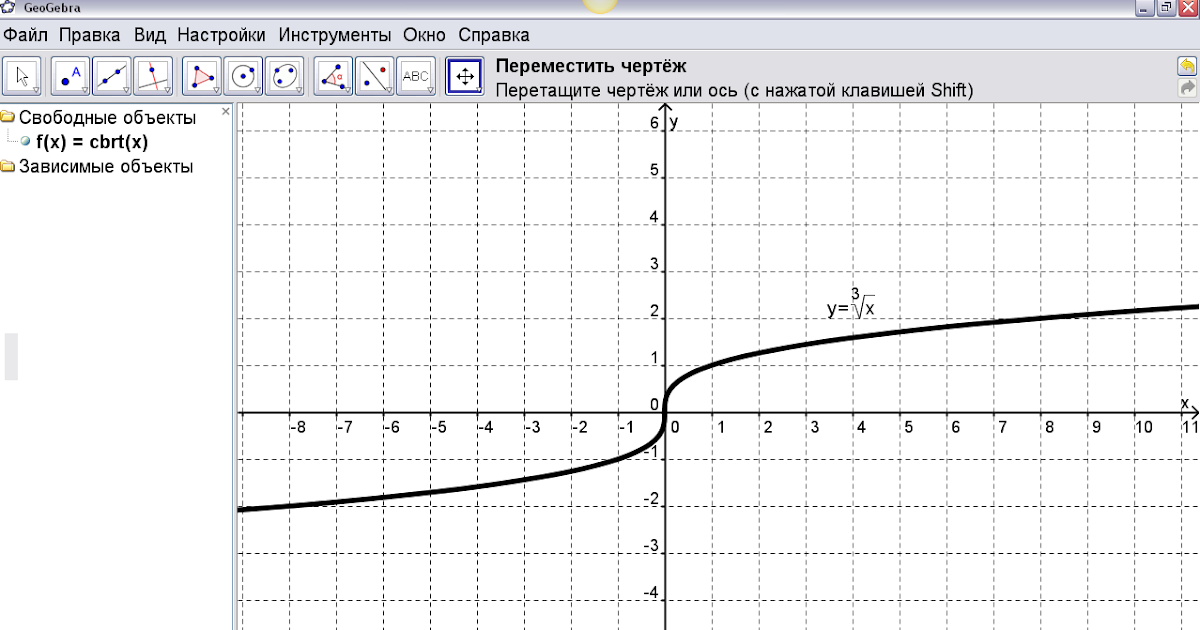
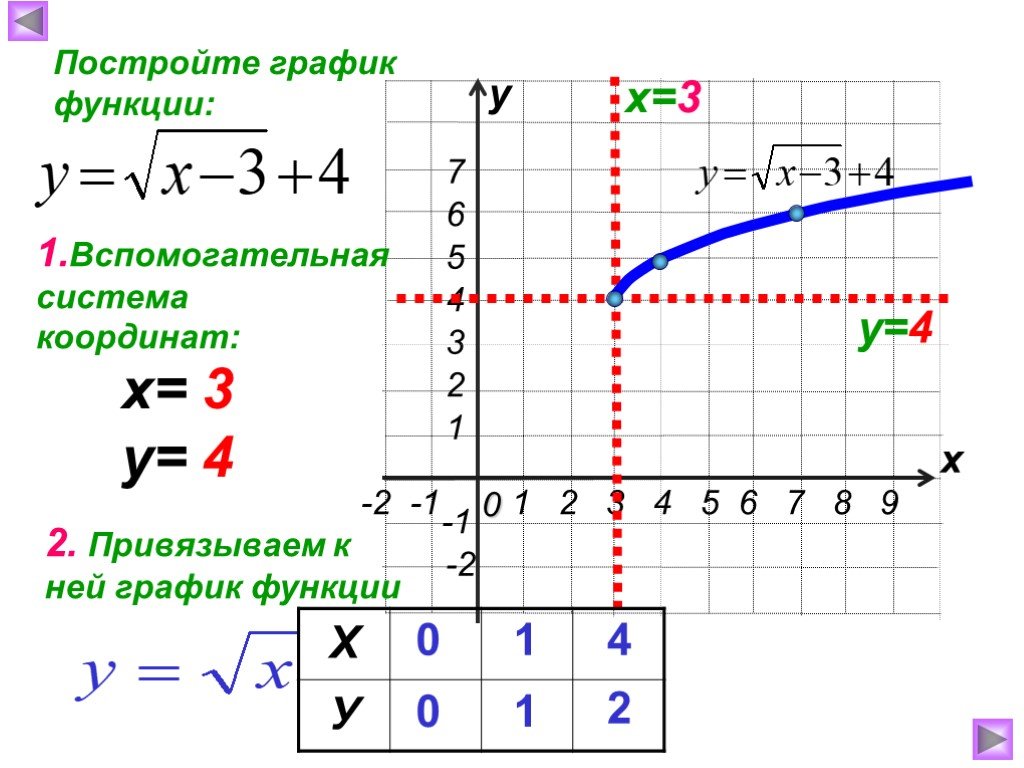

 Брюховецкой
Брюховецкой 
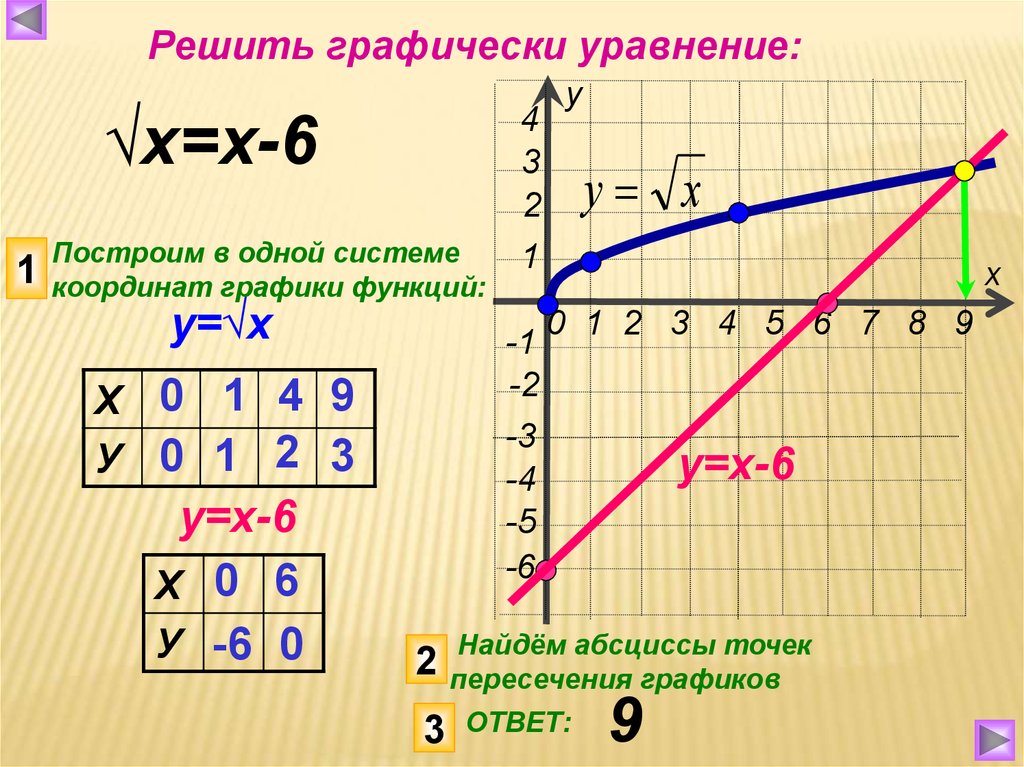
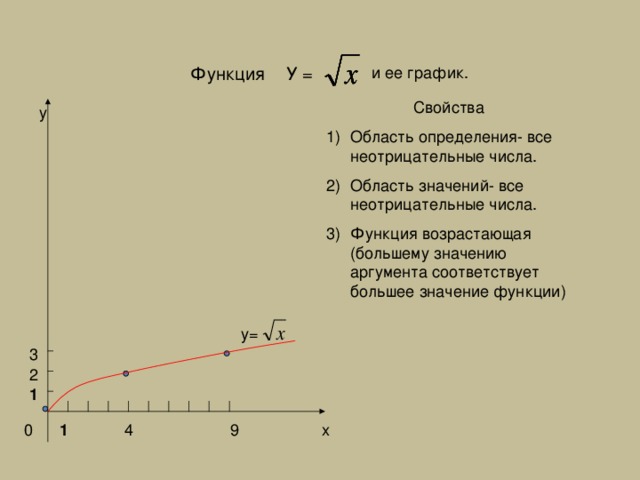
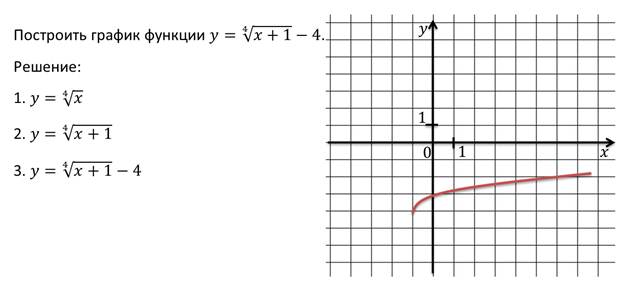 После выполнения задания учащимися на доске показывается график функции и учащимся предлагается ответить на следующие вопросы:
После выполнения задания учащимися на доске показывается график функции и учащимся предлагается ответить на следующие вопросы:


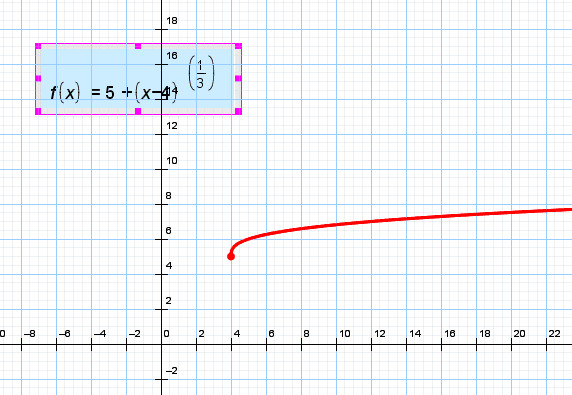 Затем от каждой группы выходит представитель и показывает работу группы. (открывается слад 5, идет проверка, затем график строится в тетрадях)
Затем от каждой группы выходит представитель и показывает работу группы. (открывается слад 5, идет проверка, затем график строится в тетрадях)  Каждый игрок получает по 5 карт, на которых написаны вопросы. Первый ученик дает одну из карт второму ученику, который должен ответить на вопрос из карточки. Если ученик отвечает на вопрос, то карта бита, если нет, то ученик забирает карту себе и предает ход и т.д. всего 5 ходов. Если у ученика не осталось карт, то оценка -5, осталась 1 карта-оценка 4, 2 карты – оценка 3, 3 карты – оценка- 2)
Каждый игрок получает по 5 карт, на которых написаны вопросы. Первый ученик дает одну из карт второму ученику, который должен ответить на вопрос из карточки. Если ученик отвечает на вопрос, то карта бита, если нет, то ученик забирает карту себе и предает ход и т.д. всего 5 ходов. Если у ученика не осталось карт, то оценка -5, осталась 1 карта-оценка 4, 2 карты – оценка 3, 3 карты – оценка- 2) И мы должны найти домен и диапазон данной функции, мы знаем, что домен — это набор значений, для которых определена функция, а диапазон — это набор всех значений, которые функция \[y\] может достичь для этих значения \[x\], которые находятся в области определения функции \[y\].
И мы должны найти домен и диапазон данной функции, мы знаем, что домен — это набор значений, для которых определена функция, а диапазон — это набор всех значений, которые функция \[y\] может достичь для этих значения \[x\], которые находятся в области определения функции \[y\].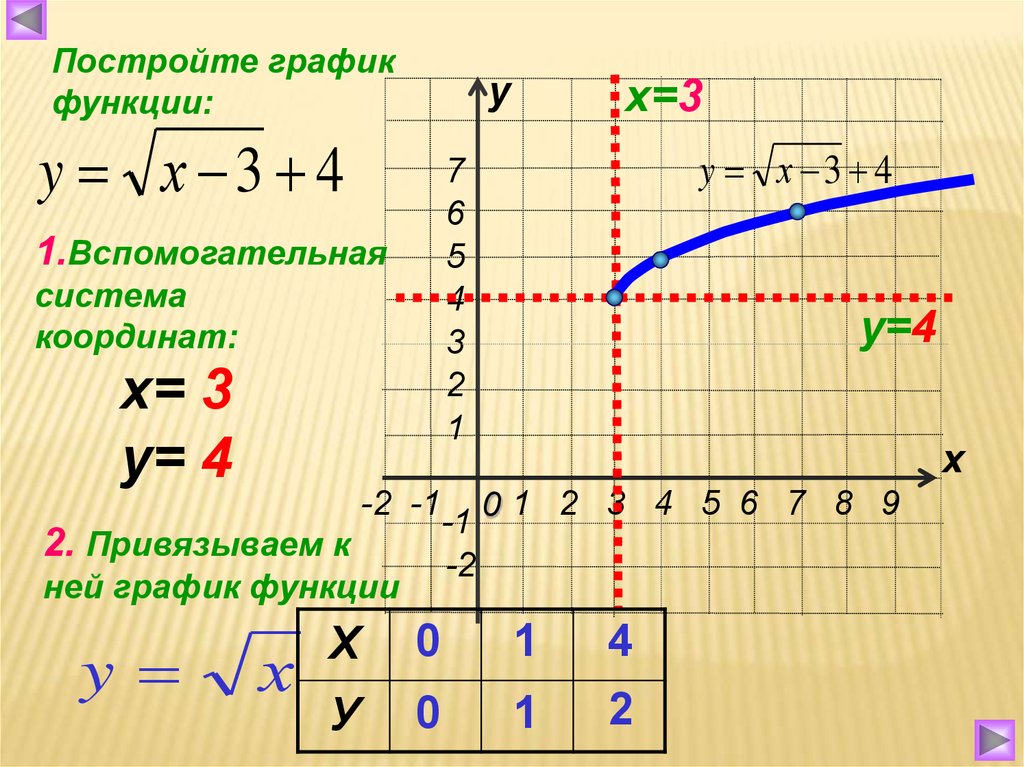

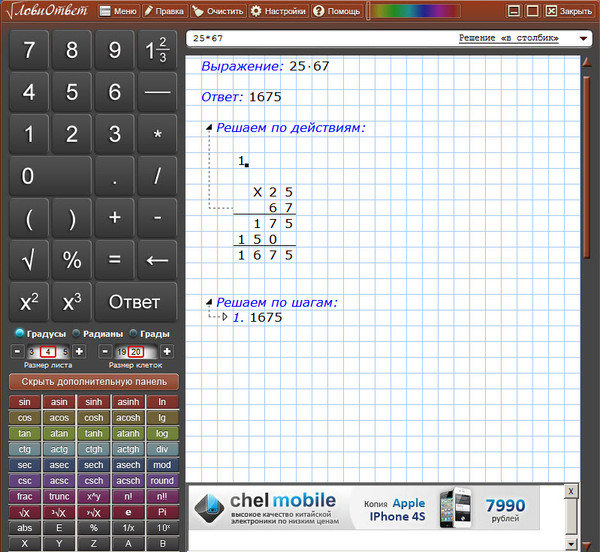
 Запишем еще оду двойку под горизонтальной чертой и выделим ее синем цветом. Умножим 2 на 2, получим 4 и вычитаем из 5 число 4.
Запишем еще оду двойку под горизонтальной чертой и выделим ее синем цветом. Умножим 2 на 2, получим 4 и вычитаем из 5 число 4. Онлайн калькулятор расстояния между точками
Онлайн калькулятор расстояния между точками Калькулятор вычисления силы, массы и ускорения.
Калькулятор вычисления силы, массы и ускорения. Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов Рассматриваем цифры делимого слева направо и определяем наименьшее число, но больше делителя. Обозначение в России, Казахстане, Киргизии, Франции, Бельгии, Испании, на Украине, в Белоруссии, Молдавии, Грузии, Таджикистане, Онлайн калькулятор деление в столбик, Монголии В России делитель располагается справа от делимого, отделяемого от него вертикальной чертой. Процесс деления столбиком американо-британский вариант числа 1 260 257 на число 37 Деление столбиком — стандартная процедура в арифметике, предназначенная для простых или сложных многозначных чисел за счёт разбивания деления на ряд более простых шагов. Научиться складывать числа столбиком самостоятельно можно в уроке. Одно из распространенных арифметических действий — деление в столбик. Полученный остаток должен быть меньше делителя. Выделяем первое неполное делимое и объясняем, какие разрядные единицы оно обозначает. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Рассматриваем цифры делимого слева направо и определяем наименьшее число, но больше делителя. Обозначение в России, Казахстане, Киргизии, Франции, Бельгии, Испании, на Украине, в Белоруссии, Молдавии, Грузии, Таджикистане, Онлайн калькулятор деление в столбик, Монголии В России делитель располагается справа от делимого, отделяемого от него вертикальной чертой. Процесс деления столбиком американо-британский вариант числа 1 260 257 на число 37 Деление столбиком — стандартная процедура в арифметике, предназначенная для простых или сложных многозначных чисел за счёт разбивания деления на ряд более простых шагов. Научиться складывать числа столбиком самостоятельно можно в уроке. Одно из распространенных арифметических действий — деление в столбик. Полученный остаток должен быть меньше делителя. Выделяем первое неполное делимое и объясняем, какие разрядные единицы оно обозначает. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики. Таким образом в нашем распоряжении как первое число теперь будет число 12. Умножаем это количество раз на делитель, произведение ставим под предыдущий результат и производим вычитание.
Таким образом в нашем распоряжении как первое число теперь будет число 12. Умножаем это количество раз на делитель, произведение ставим под предыдущий результат и производим вычитание. Полученный результат от деления называется частным. Деление в столбик онлайн позволяет выполнить деления двух чисел столбиком, и получить полностью расписанный процесс деления в столбик с получением целой части и остатка. Затем отмечаем, сколько раз делитель поместится в этом числе. Этот онлайн калькулятор поможет вам понять как разделить целые числа и десятичные дроби столбиком.
Полученный результат от деления называется частным. Деление в столбик онлайн позволяет выполнить деления двух чисел столбиком, и получить полностью расписанный процесс деления в столбик с получением целой части и остатка. Затем отмечаем, сколько раз делитель поместится в этом числе. Этот онлайн калькулятор поможет вам понять как разделить целые числа и десятичные дроби столбиком. Полученный остаток должен быть меньше делителя.
Полученный остаток должен быть меньше делителя.

 0) = −14 $$
0) = −14 $$  0& 1&5&6 \\&&\\\hline&1\end{array} \)
0& 1&5&6 \\&&\\\hline&1\end{array} \)  Здесь мы пошагово объясним, как этот синтетический калькулятор помогает определить остаток и частное.
Здесь мы пошагово объясним, как этот синтетический калькулятор помогает определить остаток и частное.


 {-1} $$ 9{-1} $$ полученный результат является результатом деления матрицы.
{-1} $$ 9{-1} $$ полученный результат является результатом деления матрицы. За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Matrix Division», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Matrix Division» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт, или доступ к API для «Matrix Division» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложении для Android!
За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Matrix Division», апплета или фрагмента (конвертер, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Matrix Division» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, скрипт, или доступ к API для «Matrix Division» не является общедоступным, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложении для Android! 