Прогнозирование и планирование Тест с ответами
1. Метод, наиболее предпочтительный в системе регионального прогнозирования
• сценарный
2. Наиболее эффективная конкурентная стратегия при прогнозировании параметров материального производства
• низких издержек
3. Наиболее точный показатель эффективности инвестиций в условиях рыночных отношений
• чистая дисконтированная стоимость
4. Базовое направление при разработке региональной территориально-отраслевой модели прогноза
• индикативное снизу вверх
5. Метод, наиболее часто используемый при прогнозировании развития аграрно-промышленного комплекса
• балансовый
6. Фактор, наиболее существенно влияющий на положение кривой спроса
• доходы населения
7. Метод, наиболее оптимально прогнозирующий темпы роста реальных доходов населения
• корректировки по индексу цен
8. Виды ресурсов, учет и использование которых предполагает балансовый метод в планировании
Виды ресурсов, учет и использование которых предполагает балансовый метод в планировании
• материальные
9. Миссия экономического субъекта в процессе разработки стратегического плана
• ориентиры, цели и задачи
10. Критерий, по которому наиболее предпочтительно оценивать эффективность функционирования экономического субъекта
• издержки производства
11. Стратегия, определяемая на этапе стратегического анализа в процессе стратегического планирования
• развития
12. Метод, применяемый при прогнозировании развития транспортных перевозок
• укрупненных нормативов
13. Товары эластичного спроса имеют коэффициент эластичности …
• больше единицы
14. Матричный метод стратегического анализа является … методом
• простым
15. Определяющее значение при прогнозировании промышленного развития на микроуровне имеет . ..
..
• спрос и заказ
16. Базовыми параметрами в прогнозировании строительного комплекса служат …
• потребности в мощностях
17. Фактор, оказывающий наиболее существенное влияние на прогнозирование реальных доходов населения
• индекс цен
18. Стратегия, определяемая на этапе конкурентного анализа в процессе стратегического планирования
• конкурентная
19. Содержание прогнозирования промышленного развития определяется по …
• объему и структуре
20. Методы, получившие наибольшее распространение при прогнозировании спроса на промышленную продукцию
• экстраполяции
21. Определяющее значение при прогнозировании промышленного развития на макроуровне имеют …
• приоритеты развития
22. Стратегия, определяемая на этапе стратегического анализа при использовании способа ликвидации разрыва
• развития
23. Метод, наиболее эффективный при прогнозировании эффективности предприятия
Метод, наиболее эффективный при прогнозировании эффективности предприятия
• сценарный
24. Способы, получившие наибольшее применение при использовании метода экстраполяции в прогнозирование
• экспоненциального сглаживания
25. Стратегическое планирование разрабатывается как …
• самостоятельное
26. Характер разрабатываемых прогнозов
• альтернативный
27. Бизнес-планирование отличается от других видов планирования по …
• структуре
28. Стратегия прогнозирования научно-технического прогресса экономики в целом базируется на основе …
• комплексного прогноза
29. Методы, наиболее предпочтительные при прогнозировании спроса на потребительские товары
• экспертных оценок
30. Рост доходов покупателей вызывает сдвиг кривой спроса …
• вправо
«Макроэкономическое планирование и прогнозирование» Ответы Тест Синергия — Тест Синергия — Ответы на тесты Синергия
«Макроэкономическое планирование и прогнозирование» Ответы Тест Синергия
Тип: Тест Синергия
Предмет: Макроэкономическое планирование и прогнозирование
Год сдачи: 2021
Итоговая оценка: 90 баллов
47 вопросов
Правильные ответы выделены маркером для удобного поиска. Тест сдан на оценку «отлично» (90 из 100), скриншот с результатом прилагается к работе.
Тест сдан на оценку «отлично» (90 из 100), скриншот с результатом прилагается к работе.
1. При использовании простой скользящей средней выравнивание на каждом актив-ном участке производится по полиному … порядка
первого
2. Тенденция изменения среднегодовой численности промышленно-производственного персонала предприятия описывается моделью , согласно которой среднегодовой темп прироста численности
2,2%
31%
22%
12,2%
102,2%
3. Методология планирования – это система
— экономических показателей для планирования
— принципов, показателей, методик и методов разработки и обоснования плановых решений
— статистических показателей и методик для разработки прогнозов
— принципов, показателей, методик и методов разработки и обоснований прогнозов
4. При расчете взвешенной скользящей средней весовые коэффициенты на каждом участке сглаживания удовлетворяют условию о том, что …
— сумма весовых коэффициентов с учетом множителя за скобками равна 1
— все весовые коэффициенты положительны
— имеет место симметричность относительно центрального уровня
— все весовые коэффициенты по модулю больше 1
-все весовые коэффициенты отрицательны
5. Представление уровней временного ряда yt(t = 1, 2, …, n) в виде yt = ut * st + εt, где ut – трендовая компонента, st – сезонная компонента, εt – случайная компонен-та, соответствует …
Представление уровней временного ряда yt(t = 1, 2, …, n) в виде yt = ut * st + εt, где ut – трендовая компонента, st – сезонная компонента, εt – случайная компонен-та, соответствует …
— аддитивной модели
— адаптивной модели
— мультипликативной модели
— модели смешанного типа
6. Представление уровней временного ряда yt (t = 1, 2, …, n) в виде yt = ut * vt * st * εt , где ut – трендовая компонента, vt – циклическая компонента, st – сезонная ком-понента, εt – случайная компонента, соответствует …
— аддитивной модели
— адаптивной модели
— мультипликативной модели
-модели смешанного типа
7. Представление уровней временного ряда yt (t = 1, 2, …, n) в виде yt = ut + vt + st + εt , где ut – трендовая компонента, vt – циклическая компонента, st – сезонная ком-понента, εt – случайная компонента, соответствует …
— аддитивной модели
— адаптивной модели
— мультипликативной модели
— модели смешанного типа
8. Прогноз с периодом упреждения 6 лет относят к … прогнозам
Прогноз с периодом упреждения 6 лет относят к … прогнозам
— дальнесрочным
— краткосрочным
— долгосрочным
— оперативным
— среднесрочным
9. Исходя из ежеквартальной динамики процентной ставки банка (представлена в таблице), прогноз процентной ставки банка в 6 квартале, рассчитанный с помощью среднего темпа роста с точностью до десятых, равен …
Текущий номер квартала t 1 2 3 4 5
yt, % 7,3 8 8,8 9,7 10,7
— 11,8 %
— 11,6 %
— 10,9 %
— 11,5 %
— 11,1%
10. Если уровни временного ряда y1,у2…,yt…,yn изменяются примерно с по-стоянным темпом роста, то прогноз на один шаг вперед с помощью среднего темпа роста может быть сделан по формуле …
11. Макроэкономическое планирование и прогнозирование – это …
— задача государственного регулирования экономики
— функция государства
— функция субъектов экономики
— задача государства
12. Расчет 7-членной взвешенной скользящей средней на каждом активном участке сглаживания yt–3, yt–2, yt-1, yt+1, yt+2, yt+3 осуществляется по формуле …
Расчет 7-членной взвешенной скользящей средней на каждом активном участке сглаживания yt–3, yt–2, yt-1, yt+1, yt+2, yt+3 осуществляется по формуле …
—
—
—
—
13. К основным показателям, характеризующим потенциал экономического разви-тия, следует отнести …
— Состав и долю отраслей национальной экономики
— производительность труда
— ВВП или ВНП
— продолжительность жизни населения
14. Метод экстраполяции в прогнозировании предполагает …
— распространение тенденций будущего на настоящий период
— нахождение прогнозных значений внутри анализируемого отрезка времени
— распространение тенденций в настоящем на будущий период
— распространение тенденции в прошлом на будущий период
15. Весовые коэффициенты при расчете взвешенной скользящей средней одинаковы при сглаживании каждого участка, как по полиному второго порядка, так и по полиному … порядка
Третьего
16. Для планирования экономического роста используют …
Для планирования экономического роста используют …
— абсолютные показатели
— относительные показатели
— средние показатели
— систему статистических показателей
17. Для планирования и прогнозирования экономического роста используют …
— абсолютные показатели
— относительные показатели
— систему показателей
— средние показатели
18. Для прогнозирования экономического роста необходимо измерить его, исполь-зуя … показатели
— порядковые
— альтернативные
— номинальные
— количественные
19. экономическая политика опирается на оптимизацию рыночной экономики с по-мощью антиинфляционной политики и развития достижений научно-технического прогресса
— Неоклассическая
— Неокейнсианская
— Кейнсианская
— Классическая
20. прогнозы предполагают использование информации о будущем при принятии решений
— Познавательные
— Долгосрочные
— Управленческие
— Все
21. … прогнозы имеют цель описать возможные или желательные перспективы со-стояния будущего
… прогнозы имеют цель описать возможные или желательные перспективы со-стояния будущего
— Все
— Познавательные
— Долгосрочные
— Управленческие
22. При сглаживании временного ряда 11-членной скользящей средней теряются … уровней
— только последние 11
— только первые 11
— только первые 5
— первые и последние 5
— первые и последние 11
23. Если при использовании скользящей средней были потеряны 3-го уровня в начале и 3-го уровня в конце временного ряда, то для сглаживания использовалась … скользящая средняя
— 11-членная
— 5-членная
— 19-членная
— 3-членная
— 7-членная
23. При сглаживании временного ряда 7-членной скользящей средней будут поте-ряны … уровней
только первые 3
первые и последние 7
только первые 7
первые и последние 3
24. Стратегия стимулирования экономического роста на основе неоклассической теории характеризуется … подходом
— макроэкономическим
— микроэкономическим
— международным
— региональным
25. Если уровни временного ряда y1,у2…yt…yn изменяются примерно с постоянным темпом роста, то прогноз на L шагов вперед с помощью среднего темпа роста может быть сделан по формуле
Если уровни временного ряда y1,у2…yt…yn изменяются примерно с постоянным темпом роста, то прогноз на L шагов вперед с помощью среднего темпа роста может быть сделан по формуле
26. Если ежеквартальная динамика процентной ставки банка представлена в табли-це ниже, то процентная ставка банка в 6 квартале, рассчитанная с помощью средне-го абсолютного прироста с точностью до десятых, составит
Текущий номер квартала t 1 2 3 4 5
yt, % 7,3 8 8,8 9,7 10,5
— 11,3 %
— 11,6 %.
— 11,1 %
— 10,9 %
27. Экономическая структура – это …
— макроэкономический рост
— взаимосвязи между элементами экономической системы
— соотношения между элементами экономической системы
— динамика развития элементов экономической системы
28. При сглаживании временного ряда скользящей средней при длине интервала сглаживания l =2p+1 теряются … уровней
— первые и последние p
— только последние l
— первые и последние l
— только первые l
— только первые p
29. Основная проблема, вызывающая необходимость планирования и прогнозиро-вания на государственном уровне, – это …
Основная проблема, вызывающая необходимость планирования и прогнозиро-вания на государственном уровне, – это …
— нехватка природных ресурсов
— рост социальной напряженности в обществе
— удовлетворение постоянно растущих потребностей
— политические и экономические кризисы
30. К главным факторам экономического роста следует отнести …
— численность населения
— размер инвестиций
— стимулирование спроса
— численность населения, размер инвестиций и стимулирование спроса
31. Прогнозирование – это
— математическая модель
— количественная и качественная оценка развития экономического объекта
— качественная оценка будущего развития экономического объекта
— количественная оценка будущего развития экономического объекта
32. Макроэкономическое планирование – это научное предвидение уровня развития и результатов функционирования …
— отраслей и регионов
— экономики
— экономики мировой
— экономики фирм и организаций
33. Основным показателем для планирования и прогнозирования с точки зрения кейнсианской теории являются факторы, определяющие …
Основным показателем для планирования и прогнозирования с точки зрения кейнсианской теории являются факторы, определяющие …
— уровень социального напряжения в обществе
— личные сбережения и инвестиции
— уровень и динамику спроса и предложения на рынке
— уровень и динамику национального дохода
34. … опираются на использование математического аппарата
— Алгоритмические методы прогнозирования
— Аналитические методы прогнозирования
— Интуитивные методы прогнозирования
— Методы экспертных оценок
35. Отрезок времени от момента, для которого имеются последние статистические данные об изучаемом объекте, до момента, к которому относится прогноз, называ-ется …
— ретроспективным участком
— периодом адаптации
— периодом наблюдения
— временем упреждения прогноза
36. Структурные кризисы в экономике вызывают необходимость …
— планирования и прогнозирования в экономике
— стимулирования предложения
— невмешательства государства в экономику
— стимулирования спроса
37. … относятся к микроэкономическим прогнозам
… относятся к микроэкономическим прогнозам
— Макроэкономические прогнозы
— Межрегиональные и межотраслевые прогнозы
— Прогнозы предприятий и организаций
— Региональные прогнозы
38. Оценка будущего состояния развития экономических процессов лежит в основе … прогноза
— нормативно-целевого
— целевого
— поискового
— нормативного
39. Оценка необходимых ресурсов для развития экономических процессов лежит в основе … прогноза
— нормативного
— целевого
— нормативно-целевого
— поискового
40. Более гладкий временной ряд будет получен при использовании … — простой скользящей средней
— 3-членной
— 5-членной
— 19-членной
— 7-членной
— 11-членной
41. Предмет изучения дисциплины «Макроэкономическое планирование и прогно-зирование» – это …
— совокупность макроэкономических показателей
— совокупность методов планирования и прогнозирования макроэкономических по-казателей
— федеральные министерства и ведомства, составляющие планы и прогнозы
— макроэкономика
42. Наибольшей эффективностью характеризуется такой тип экономического роста, как … рост
Наибольшей эффективностью характеризуется такой тип экономического роста, как … рост
— интенсивно-экстенсивный
— интенсивный
— экстенсивный
— макроэкономический
43. Макроэкономическое развитие – это …
— рост качества и уровня жизни
— экономический рост, структурные изменения в экономике, рост уровня жизни населения
— экономический рост
— структурные изменения в экономике
43. Главной отличительной чертой современной рыночной экономической системы является …
— минимальное воздействие государства на развитие национальной экономики
— отсутствие воздействия государства на развитие национальной экономики
— активное воздействие государства на развитие национальной экономики
— то, что рыночная система не предполагает вмешательство государства в экономи-ку
44. В странах с рыночной экономикой инструментом воздействия на экономику яв-ляется … планирование
— директивное
— интуитивное
— нормативное
— индикативное
45. Если ежемесячная динамика показателя описывается аддитивной моделью с ли-нейным трендом и сезонными фиктивными переменными, то число фиктивных пе-ременных в модели не может превышать …
Если ежемесячная динамика показателя описывается аддитивной моделью с ли-нейным трендом и сезонными фиктивными переменными, то число фиктивных пе-ременных в модели не может превышать …
— 11
— 4
— 6
— 3
— 10
46. Отраслевая структура развитых стран характеризуется повышением доли …
— тяжелой промышленности
— сферы услуг
— сельского и лесного хозяйства
— добывающих отраслей
47. Прогнозирование – это …
— количественная оценка будущего развития экономического объекта
— качественная оценка будущего развития экономического объекта
— количественная и качественная оценка развития экономического объекта
— математическая модель
Просмотры: 1307
Раскройте свою реальную политику планирования и прогнозирования запасов, ответив на эти 10 вопросов
В другом блоге мы задали вопрос: Как вы можете быть уверены, что у вас действительно есть политика планирования запасов и прогнозирования спроса? Мы объяснили, как отсутствие у организации понимания основ (как создается прогноз, как определяются резервные запасы и как/почему корректируются эти значения) способствует низкой точности прогнозов, нерациональному распределению запасов и отсутствию доверия ко всему. процесс.
процесс.
В этом блоге мы рассмотрим 10 конкретных вопросов, которые вы можете задать, чтобы узнать, что на самом деле происходит в вашей компании. Мы подробно описываем типичные ответы, которые дают, когда политики прогнозирования/планирования запасов на самом деле не существует, объясняем, как интерпретировать эти ответы, и предлагаем несколько четких советов, что с этим делать.
Всегда начинайте с простого гипотетического примера . Сосредоточение внимания на конкретной проблеме, с которой вы только что столкнулись, обязательно вызовет защитные ответы, скрывающие всю историю. Цель состоит в том, чтобы раскрыть фактический подход, используемый для планирования запасов и прогнозов, который был встроен в ментальную математику или электронные таблицы. Вот пример:
Предположим, у вас есть 100 единиц в наличии, время пополнения составляет 3 месяца, а среднемесячная потребность составляет 20 единиц? Когда следует заказывать больше? Сколько бы вы заказали? Как изменится ваш ответ, если запланировано получение ожидаемых поступлений в размере 10 в месяц? Как изменится ваш ответ, если товар относится к категории A, B или C, стоимость товара высокая или низкая, время выполнения заказа длинное или короткое? Проще говоря, когда вы планируете производственное задание или размещаете новый заказ у поставщика, почему вы это делаете? Что послужило толчком к решению получить больше? Какие входные данные планирования учитывались?
При получении ответов на вышеуказанный вопрос сосредоточьтесь на поиске ответов на следующие вопросы :
1. Каков основной подход к пополнению запасов? Как правило, это будет одно из следующих значений: Мин./Макс., Прогноз/Запас, Точка повторного заказа/Количество заказа, Периодический просмотр/Заказ до или даже какая-то нечетная комбинация
Каков основной подход к пополнению запасов? Как правило, это будет одно из следующих значений: Мин./Макс., Прогноз/Запас, Точка повторного заказа/Количество заказа, Периодический просмотр/Заказ до или даже какая-то нечетная комбинация
точек, или Мин./Макс., фактически рассчитано ? Недостаточно знать, что вы используете Min/Max. Вы должны точно знать, как рассчитываются эти значения. Такие ответы, как «Мы используем историю» или «Мы используем среднее значение», недостаточно конкретны. Вам понадобятся ответы, которые четко описывают, как используется история. Например, «Мы берем среднее значение за последние 6 месяцев, делим его на 30, чтобы получить среднее значение за день, а затем умножаем на время выполнения заказа в днях. Затем для позиций «А» мы умножаем среднее время выполнения заказа на 2, а для позиций «В» используем множитель 1,5». (Хотя это и не очень хороший технический подход, по крайней мере, в нем есть четкая логика.)
Когда у вас есть четко определенная политика, вы можете определить ее слабые стороны, чтобы улучшить ее. Но если предоставленный ответ не идет дальше «Мы используем историю», то у вас нет политики для начала. Ответы часто показывают, что разные планировщики используют историю по-разному. Некоторые могут учитывать только самый последний спрос, другие могут хранить запасы в соответствии со средним значением периодов самого высокого спроса и т. д. Другими словами, вы можете обнаружить, что на самом деле у вас есть несколько непродуманных «политик».
Но если предоставленный ответ не идет дальше «Мы используем историю», то у вас нет политики для начала. Ответы часто показывают, что разные планировщики используют историю по-разному. Некоторые могут учитывать только самый последний спрос, другие могут хранить запасы в соответствии со средним значением периодов самого высокого спроса и т. д. Другими словами, вы можете обнаружить, что на самом деле у вас есть несколько непродуманных «политик».
3. Используются ли прогнозы для планирования пополнения запасов, и если да, то как? Многие компании говорят, что они прогнозируют, но их прогнозы рассчитываются и используются по-разному. Используется ли прогноз для прогнозирования того, какие запасы будут в наличии в будущем, что приведет к запуску заказа? Или он используется для определения точки повторного заказа, но не для прогнозирования времени заказа (т. е. я предсказываю, что мы будем продавать 10 в неделю, поэтому, чтобы защититься от дефицита, я буду заказывать больше, когда в наличии будет 15)? Используется ли он в качестве ориентира для планировщика, чтобы помочь субъективно определить, когда им следует заказать больше? Используется ли он для создания общих заказов у поставщиков? Некоторые используют его для управления MRP. Вам нужно знать эти особенности. Подробный ответ на этот вопрос может выглядеть так: «Мой прогноз — 10 в неделю, а время выполнения заказа — 3 недели, поэтому я делаю точку повторного заказа кратной этому прогнозу, обычно умножая спрос на время выполнения в 2 раза или 60 единиц для важных товаров, и я использую меньший множитель для менее важных товаров. (Опять же, не очень технический подход, но ясный.)
Вам нужно знать эти особенности. Подробный ответ на этот вопрос может выглядеть так: «Мой прогноз — 10 в неделю, а время выполнения заказа — 3 недели, поэтому я делаю точку повторного заказа кратной этому прогнозу, обычно умножая спрос на время выполнения в 2 раза или 60 единиц для важных товаров, и я использую меньший множитель для менее важных товаров. (Опять же, не очень технический подход, но ясный.)
4. Какой метод фактически используется для создания прогноза? Это усредненная модель тренда, такая как двойное экспоненциальное сглаживание, сезонная модель? Зависит ли выбор метода изменения от типа данных о спросе или от того, когда будут доступны новые данные о спросе? (Запасные части и крупносерийные товары имеют очень разные модели спроса.) Как вы подходите к выбору модели прогноза? Этот процесс автоматизирован? Как часто пересматривается выбор модели? Как часто пересчитываются параметры модели? Какой процесс используется для пересмотра вашего подхода? Ответ здесь документирует, как составляются базовые прогнозы. После определения можно провести анализ, чтобы определить, повысят ли точность прогноза другие методы прогнозирования. Если вы не документируете точность прогнозов и не проводите анализ «прогнозируемой добавленной стоимости», вы не в состоянии должным образом оценить, являются ли производимые прогнозы лучшими, какими они могут быть. Вы упустите возможность улучшить процесс, повысить точность прогнозов и рассказать бизнесу о том, какой тип ошибки прогноза является нормальным и которого следует ожидать.
После определения можно провести анализ, чтобы определить, повысят ли точность прогноза другие методы прогнозирования. Если вы не документируете точность прогнозов и не проводите анализ «прогнозируемой добавленной стоимости», вы не в состоянии должным образом оценить, являются ли производимые прогнозы лучшими, какими они могут быть. Вы упустите возможность улучшить процесс, повысить точность прогнозов и рассказать бизнесу о том, какой тип ошибки прогноза является нормальным и которого следует ожидать.
5. Как вы используете страховой запас? Обратите внимание, что вопрос был не «Используете ли вы страховой запас?» В этом контексте и для простоты термин «страховой запас» означает запас, используемый для защиты запасов от изменчивости спроса и предложения. Все компании так или иначе используют подходы к буферизации. Однако есть некоторые исключения. Может быть, вы производитель мастерской, который закупает все детали на заказ, и ваши клиенты совершенно спокойно ждут недели или месяцы, пока вы получите материал, изготовите, проверите качество и отгрузите. Или, может быть, вы являетесь крупным производителем с огромной покупательной способностью, поэтому ваши поставщики создали местные склады, которые полностью заполнены и готовы предоставить вам запасы практически немедленно. Если эти описания не описывают вашу компанию, у вас определенно будет некий буфер для защиты от изменчивости спроса и предложения. Вы можете не использовать поле «страховой запас» в своей ERP, но вы определенно буферизуетесь.
Или, может быть, вы являетесь крупным производителем с огромной покупательной способностью, поэтому ваши поставщики создали местные склады, которые полностью заполнены и готовы предоставить вам запасы практически немедленно. Если эти описания не описывают вашу компанию, у вас определенно будет некий буфер для защиты от изменчивости спроса и предложения. Вы можете не использовать поле «страховой запас» в своей ERP, но вы определенно буферизуетесь.
Могут быть предоставлены такие ответы, как «Мы не используем страховой запас, потому что делаем прогнозы». К сожалению, хороший прогноз будет иметь шансы 50/50 быть выше/ниже фактического спроса. Это означает, что в 50% случаев вы будете получать запасы без добавления резервного запаса в прогноз. Прогнозы идеальны только тогда, когда нет случайности. Поскольку всегда есть случайность, вам нужно будет буферизоваться, если вы не хотите иметь ужасные уровни обслуживания.
Если ответ не найден, вы можете немного больше узнать о том, как различные рычаги пополнения используются для добавления возможных буферов, что приводит к вопросам 6 и 7.
6. Вы когда-нибудь увеличивали время выполнения заказа или заказы раньше, чем это действительно необходимо?
В нашем гипотетическом примере вашему поставщику обычно требуется 4 недели для доставки, и он довольно постоянен. Но для защиты от дефицита ваш покупатель обычно заказывает 6 недель вместо 4 недель. Поле страхового запаса в вашей ERP-системе может быть установлено равным нулю, потому что «мы не используем страховой запас», но на самом деле подход покупателя к заказу просто добавил 2 недели буферного запаса.
7. Вы уточняете прогноз спроса?
В нашем примере планировщик рассчитывает потреблять 10 единиц в месяц, но «на всякий случай» вводит прогноз 20 в месяц. Поле страхового запаса в системе MRP осталось пустым, но теперь замаскированный буферный запас был внесен в прогноз спроса. Это ошибка, которая вносит «предвзятость прогноза». Мало того, что ваши прогнозы будут менее точными, но если систематическая ошибка не будет учтена и другие отделы добавят страховой запас, у вас возникнет избыточный запас.
Индивидуальный характер вышеуказанных подходов усугубляет проблемы, поскольку не учитывается фактический спрос или изменчивость предложения товара. Например, планировщик может просто установить эмпирическое правило, которое удваивает прогноз времени выполнения важных заказов. Единый размер не подходит всем, когда речь идет об управлении запасами. Этот подход приведет к значительному избытку предсказуемых товаров и существенному дефициту товаров, пользующихся периодическим спросом. Вы можете прочитать «Остерегайтесь простых эмпирических правил управления запасами», чтобы узнать больше о том, почему этот тип подхода является таким дорогостоящим.
Специализированный характер подходов также игнорирует то, что происходит, когда компания сталкивается с огромным избытком или отсутствием запасов. При попытке понять, что произошло, будут изучены заявленные политики. В случае избытка система покажет нулевой страховой запас. Бизнес-лидеры решат, что у них нет никакого страхового запаса, почешут затылки и, в конце концов, просто сваливают вину на прогноз, заявляют: «Наш бизнес нельзя предсказать» и спотыкаются. Они могут даже обвинить поставщика в том, что он отгрузил слишком рано и заставил их хранить больше, чем нужно. В случае нехватки запасов они будут думать, что у них недостаточно запасов, и произвольно добавляют больше запасов по многим товарам, не понимая, что на самом деле существует много дополнительных резервных запасов, запеченных в процессе. Это увеличивает вероятность того, что запасы придется списывать в будущем.
Они могут даже обвинить поставщика в том, что он отгрузил слишком рано и заставил их хранить больше, чем нужно. В случае нехватки запасов они будут думать, что у них недостаточно запасов, и произвольно добавляют больше запасов по многим товарам, не понимая, что на самом деле существует много дополнительных резервных запасов, запеченных в процессе. Это увеличивает вероятность того, что запасы придется списывать в будущем.
8. Какая точная терминология инвентаризации используется ? Определите, что вы подразумеваете под страховым запасом, минимальным запасом, точкой заказа, EOQ и т. д. Хотя существуют стандартные технические определения, возможно, что-то отличается, и недопонимание здесь будет проблематичным. Например, некоторые компании относятся к минимальному количеству запасов, необходимому для удовлетворения спроса во время выполнения заказа, в то время как некоторые могут определять минимальное значение как включающее как спрос во время выполнения заказа, так и страховой запас для защиты от изменчивости спроса. Другие могут означать минимальный объем заказа.
Другие могут означать минимальный объем заказа.
9. Соответствуют ли наличные запасы политике? Когда ваша детективная работа завершена и все задокументировано, откройте электронную таблицу или систему ERP и посмотрите на количество в наличии. Оно должно более или менее соответствовать вашим параметрам планирования (например, если минимальное/максимальное значение составляет 20/40, а типичная потребность во времени составляет 10, то в любой момент времени у вас должно быть примерно от 10 до 40 единиц продукции. Удивительно, но для многих компаний часто существует огромное несоответствие. Мы наблюдали ситуации, когда параметр Min/Max равен 20/40, но запасы в наличии составляют 300+. Это указывает на то, что какая-либо предписанная политика просто не соблюдается. Это большая проблема
10. Что ты собираешься делать дальше?
Прогнозирование спроса и политика складского хранения должны быть четко определенными процессами, понятными и принятыми всеми участниками. Должна быть нулевая тайна .
Должна быть нулевая тайна .
Чтобы сделать это правильно, изменчивость спроса и предложения должна быть проанализирована и использована для расчета надлежащих уровней страхового запаса. Добавлять буферы без неявного понимания того, что каждая дополнительная единица буферного запаса покупает вам с точки зрения обслуживания, все равно, что произвольно добавлять горсть ингредиентов в рецепт торта. Небольшое изменение ингредиентов может оказать огромное влияние на то, что выйдет из духовки: один кусок будет слишком сладким, а другой — слишком кислым. То же самое и с управлением запасами. Немного больше здесь, немного меньше там, и довольно скоро вы обнаружите, что у вас есть дорогостоящий излишек запасов в одних областях, болезненный дефицит в других, вы понятия не имеете, как вы этого добились, и у вас мало указаний о том, как улучшить ситуацию.
Современное программное обеспечение для оптимизации запасов и планирования спроса с его передовой аналитикой и прочной основой для прогнозного анализа может помочь в решении этой проблемы. Но даже самое лучшее программное обеспечение не поможет, если оно используется непоследовательно.
Но даже самое лучшее программное обеспечение не поможет, если оно используется непоследовательно.
Smart Software и менеджер по инвентаризации и логистике APS представят сессию USMA 2023, посвященную проекту преобразования цепочки поставок APS и роли технологии оптимизации запасов в их новом процессе.
Если вы в последнее время были с высоко поднятой головой, вы, возможно, заметили еще одно безумие за пределами баскетбольной площадки: крах Silicon Valley Bank. Те из нас, кто занимается цепочками поставок, возможно, отмахнулись от банкротства банка как от чьей-то чужой проблемы, но этот печальный эпизод также является важным уроком для нас: важность правильно проведенного стресс-тестирования.
Что такое эффект покачивания? Это когда ваш статистический прогноз неверно предсказывает взлеты и падения, наблюдаемые в вашей истории спроса, когда на самом деле нет закономерности. Важно убедиться, что ваши прогнозы не колеблются, если нет реальной закономерности. Вот стенограмма от недавнего клиента, где обсуждался этот вопрос:
Вот стенограмма от недавнего клиента, где обсуждался этот вопрос:
IBM Planning Analytics | IBM
Аналитика планирования IBMСоздавайте точные планы и прогнозы с помощью простого в использовании программного обеспечения для планирования, аналитики и отчетности
Запросить демо Решите самые насущные проблемыНачните с одного отдела. Практически без помощи ИТ-отдела вы можете легко изменить свои бизнес-модели и добавить новые функции.
Программное обеспечение IBM Planning Analytics — идеальная платформа для реализации интегрированных решений бизнес-планирования. В сочетании с элегантной панелью управления рабочей областью и интерфейсом Excel он подходит как для пользователей, занимающихся аналитикой, так и для обычных пользователей отчетов.
Расширьте возможности планирования и анализа (xP&A) из FP&A, продаж, цепочки поставок и других областей.
Прочитать краткий обзор решения (850 КБ) Изучите демонстрацию продуктаIBM Planning Analytics — это многофункциональное интегрированное решение для управления производительностью с собственной надстройкой Microsoft Excel. С помощью решения на основе искусственного интеллекта вы можете автоматизировать ключевые процессы, постоянно планировать, расширять возможности человеческого интеллекта и использовать возможности прогнозирования для создания более точных, последовательных и своевременных бюджетов и прогнозов, не требуя специалиста по данным.
Запросить демоИсследование Forrester Total Economic Impact™ Обрабатывайте данные планирования на 80 % быстрее Читать историю
Аналитическое исследованиеIBM признана лидером рынка в рейтинге BARC Score 2023 Integrated Planning & Analytics (IP&A)
БлогIBM Planning Analytics as a Service — доступный всем и везде — теперь доступен на AWS
Преимущества Автоматизируйте и ускоряйте Ручной сбор данных, проверка, агрегирование и финансовая консолидация.
Анализ тысяч многомерных точек данных из нескольких источников.
Делайте точные прогнозыПрежде чем принимать решения, проверьте свои предположения с помощью неограниченных сценариев «что, если».
Функции С помощью IBM Planning Analytics, созданного на основе технологии TM1, вы получите ориентированную на ячейки базу данных с собственной надстройкой Microsoft Excel. Получите доступ к наиболее знакомым вам функциям, а также воспользуйтесь преимуществами быстродействующего инструмента бизнес-аналитики с искусственным интеллектом. IBM Planning Analytics можно развернуть локально, в облаке или как услугу, доступную на AWS. Просмотр функций Встроенная отчетность Получите глубокие знания с помощью надежных информационных панелей. Создавайте системы показателей и метрики, включая специальные отчеты и привлекательные визуализации.
Создавайте системы показателей и метрики, включая специальные отчеты и привлекательные визуализации.
Не обновлять более 100 электронных таблиц. С Planning Analytics for Excel (PAX/PAfE) любая корректировка будет применяться в режиме реального времени ко всем представлениям.
Оптимизируйте шаблоны рабочих процессов планирования и создавайте более точные прогнозы с помощью простых в использовании средств прогнозирования и возможностей искусственного интеллекта.
Посмотреть видео (02:11) Простая интеграция Простое подключение различных источников данных, включая существующие приложения для планирования, составления бюджета и прогнозирования на основе электронных таблиц, а также ERP, CRM и любой API.
Анализ многомерных данных в реальном времени гарантируется единственной в своем роде базой данных в оперативной памяти и вычислительным механизмом, построенным на технологии TM1.
Читать блог Интуитивно понятные пользовательские интерфейсыОткройте мир расширенной аналитики для всех бизнес-пользователей — создавайте планы и отчеты и управляйте ими в удобной рабочей области Planning Analytics.
Читать блогСлучаи использования
Финансовое планирование и анализ Преодолейте ограничения ручного планирования с помощью упрощенного интегрированного финансового планирования и анализа. Достигайте консенсуса между отчетами о прибылях и убытках, балансами и денежными потоками.
Узнайте больше о планировании и анализе
Цепочка поставок
Объедините расширенную аналитику иерархии и неограниченную песочницу анализа сценариев «что, если» в процессы цепочки поставок. Благодаря дальновидности быстрого поворота вы можете превратить сбои в возможности.
Узнайте больше о планировании цепочки поставок
Планирование устойчивого развития
Используйте IBM Planning Analytics для планирования устойчивого развития, составления отчетов, моделирования и оптимизации на любом уровне детализации — даже для расчета углеродного следа продукта (PCF).
Узнать больше
Продажи
Отслеживайте и анализируйте данные о производительности торговых представителей и объемах продаж в режиме реального времени.
Достигайте консенсуса между отчетами о прибылях и убытках, балансами и денежными потоками.
Узнайте больше о планировании и анализе
Цепочка поставок
Объедините расширенную аналитику иерархии и неограниченную песочницу анализа сценариев «что, если» в процессы цепочки поставок. Благодаря дальновидности быстрого поворота вы можете превратить сбои в возможности.
Узнайте больше о планировании цепочки поставок
Планирование устойчивого развития
Используйте IBM Planning Analytics для планирования устойчивого развития, составления отчетов, моделирования и оптимизации на любом уровне детализации — даже для расчета углеродного следа продукта (PCF).
Узнать больше
Продажи
Отслеживайте и анализируйте данные о производительности торговых представителей и объемах продаж в режиме реального времени. Используйте возможности искусственного интеллекта для оптимизации эффективных процессов продаж, повышения производительности и достижения целей по доходам. Автоматизируйте распределение ресурсов и планирование территории, чтобы получить конкурентное преимущество и увеличить долю рынка.
Узнать больше о планировании продаж
HR и рабочая сила
Автоматизируйте и оптимизируйте процессы управления персоналом — планирование найма, заработной платы, премий, численности персонала и льгот — все на одной платформе. Разрабатывайте точные планы и прогнозы рабочей силы с помощью ИИ на основе изменений в штатном расписании, местоположении, возвращении на работу, вознаграждении, удержании, уровне оттока и многом другом.
Узнайте больше о планировании рабочей силы
ИТ-планирование
Поддерживайте бизнес-стратегию и принимайте более эффективные решения в области ИТ.
Используйте возможности искусственного интеллекта для оптимизации эффективных процессов продаж, повышения производительности и достижения целей по доходам. Автоматизируйте распределение ресурсов и планирование территории, чтобы получить конкурентное преимущество и увеличить долю рынка.
Узнать больше о планировании продаж
HR и рабочая сила
Автоматизируйте и оптимизируйте процессы управления персоналом — планирование найма, заработной платы, премий, численности персонала и льгот — все на одной платформе. Разрабатывайте точные планы и прогнозы рабочей силы с помощью ИИ на основе изменений в штатном расписании, местоположении, возвращении на работу, вознаграждении, удержании, уровне оттока и многом другом.
Узнайте больше о планировании рабочей силы
ИТ-планирование
Поддерживайте бизнес-стратегию и принимайте более эффективные решения в области ИТ. Обеспечьте согласованность между ИТ-отделом и другими организационными целями, получая представление о распределении ресурсов, расходах, жизненных циклах, владельцах и данных об использовании активов в режиме реального времени.
Узнать больше
Тематические исследования
10%
Повышенная производительность
Обеспечьте согласованность между ИТ-отделом и другими организационными целями, получая представление о распределении ресурсов, расходах, жизненных циклах, владельцах и данных об использовании активов в режиме реального времени.
Узнать больше
Тематические исследования
10%
Повышенная производительностьКомпания Mawgif увеличила операционную эффективность на 10 % за счет оптимизации доходов и эффективности в результате анализа данных и управления ими в режиме реального времени.
50% Более быстрая отчетностьICBC Аргентина сократила время, необходимое для проведения обязательных стресс-тестов банка, с четырех недель до двух, что означает экономию времени на 50%.
83% Снижение усилий по прогнозированию Благодаря постоянному развертыванию и внедрению в компании Novolex сократила шестинедельный процесс прогнозирования до менее чем одной недели — сокращение на 83 %, даже с учетом изменений.
Размещение IBM Planning Analytics в IBM Cloud было простым решением… мы хорошо знали о высокой производительности, доступности, гибкости и безопасности…
Фредрик Ларссон
Групповой бизнес-контролер
Бравикда
Узнать больше
Мы можем построить любой отчет, который нам нужен, в [IBM Planning Analytics], тогда как другие решения потребуют гораздо более сложной разработки.
Олли Нииранен
Бизнес-контролер
Хуурре
Узнать больше
Это сэкономило нам часы каждый раз, когда мы запускаем отчет, потому что нам не нужно проверять его. Мы знаем, что у нас есть правильные цифры.
Джеймс Морган
Генеральный директор по финансам и технологиям
Coronado Curragh Pty. Ltd.
Узнать больше
Мы знаем, что у нас есть правильные цифры.
Джеймс Морган
Генеральный директор по финансам и технологиям
Coronado Curragh Pty. Ltd.
Узнать больше
Признание и награды Лидер в отчете G2 Winter 2023 Grid по планированию спроса, планированию продаж и операций и планированию цепочки поставок См. обзоры G2
Отзывы о товаре
Ресурсы
IDC MarketScape: 2022 Исследование Vendor Assessment Analyst
Узнайте, почему IDC признает IBM Planning Analytics лидером в области корпоративного планирования, бюджетирования и прогнозирования.
Получить отчет IDC Опрос бизнес-аналитики и аналитики 2023 г.
Изучите опрос BARC, чтобы выяснить, почему пользователи считают IBM Planning Analytics выдающимся решением для бизнес-аналитики и аналитики.
Получить отчет Интегрированный отчет по планированию и аналитике BARC Score 2023Узнайте, почему компания BARC назвала решения IBM Business Analytics лидером благодаря комплексной платформе для анализа данных, обширным возможностям бюджетирования, планирования и прогнозирования, а также другим преимуществам.
Получить отчет BARC Индекс плановой стоимости Ventana 2022Узнайте, почему Ventana назвала IBM Planning Analytics образцовым поставщиком в ключевых категориях, отражающих потребности покупателей.
Получить отчет VentanaНа дворе 2023 год… вы все еще планируете и составляете отчеты из электронных таблиц?
Узнайте, как IBM Planning Analytics помогает организациям применять современный комплексный подход к планированию и отчетности.
Узнайте, как IBM Planning Analytics использовалась для создания модели распределения для Revelwood, которую можно было добавить в их существующую модель планирования и отчетности.
Читать блог Расширенное планирование и анализ (xP&A) в действииУзнайте, как компании используют IBM Planning Analytics в качестве универсального решения для финансового планирования, планирования цепочки поставок и управления персоналом.
Читать блог Как IBM Planning Analytics может помочь исправить вашу цепочку поставок Узнайте, как IBM Planning Analytics может улучшить управление цепочками поставок посредством планирования, составления бюджета и прогнозирования.
Планирование и анализ спроса
Узнайте больше о гибком планировании цепочки поставок с помощью IBM Planning Analytics.
Посмотреть видео (10:59) Родословная: делает FP&A в IBM Cloud частью своей ДНК Узнайте, как Ancestry.com использовала IBM Planning Analytics для масштабирования своего роста и организационной сложности.
Откройте для себя инновационные функции IBM Business Analytics с помощью этого всеобъемлющего обзора с момента запуска продукта.
Посмотреть видео (03:23:42)Сделайте следующий шаг
См.

 Было решено сварить компот из любых двух фруктов. Сколько всего различных компотов можно сварить?
Было решено сварить компот из любых двух фруктов. Сколько всего различных компотов можно сварить?



 Если такие совпадения
имеются, правило сложения в ранее
сформулированной форме утрачивает
силу, и мы получаем m + n – k способов
выбора, где k — число совпадений.
Если такие совпадения
имеются, правило сложения в ранее
сформулированной форме утрачивает
силу, и мы получаем m + n – k способов
выбора, где k — число совпадений. е. 16 чисел в первой сотне делится
на 6. Итак, количество чисел в первой
сотне, делящихся на 2 или на 3, равно 50 +
33 – 16 = 67. Все остальные не делятся ни на
2, ни на 3. Этих чисел 100 – 67 = 33.
е. 16 чисел в первой сотне делится
на 6. Итак, количество чисел в первой
сотне, делящихся на 2 или на 3, равно 50 +
33 – 16 = 67. Все остальные не делятся ни на
2, ни на 3. Этих чисел 100 – 67 = 33. В классе 25 человек. Сколькими способами:
В классе 25 человек. Сколькими способами: е.
чтобы какое-то число очков встретилось
на обеих костях)?
е.
чтобы какое-то число очков встретилось
на обеих костях)?
 Пусть, кроме того, из города А в город D
можно попасть двумя путями, из D в C —
четырьмя (рис.1). Сколькими способами
можно добраться из А в С?
Пусть, кроме того, из города А в город D
можно попасть двумя путями, из D в C —
четырьмя (рис.1). Сколькими способами
можно добраться из А в С? Если вопрос можно перефразировать словом «или», это обычно указывает на то, что применяется правило суммы.
Если вопрос можно перефразировать словом «или», это обычно указывает на то, что применяется правило суммы. Если Рави может выбрать только одно животное в качестве питомца, сколько у него есть вариантов для питомца?
Если Рави может выбрать только одно животное в качестве питомца, сколько у него есть вариантов для питомца? Затем
Затем \( _\квадрат \)
\( _\квадрат \)

 Санджит хочет полететь из Калифорнии во Францию, а затем в Индию.
Санджит хочет полететь из Калифорнии во Францию, а затем в Индию. Если у него есть деньги только на \(1\) из этих концессий, сколько у него есть способов добраться до Милуоки?
Если у него есть деньги только на \(1\) из этих концессий, сколько у него есть способов добраться до Милуоки?  После посадки четвертого человека на пятое место у нас есть выбор любого из оставшихся 2 друзей. После посадки пятого человека, на шестое место у нас есть выбор только из 1 оставшегося друга. Следовательно, по правилу произведения существует \( 6 х 5 х 4 х 3 х 2 х 1 = 720) способов рассадить этих 6 человек. \(_\квадрат\) 9b\), где \( a\) и \( b\) — целые числа, удовлетворяющие \( 0 \leq a \leq 4, 0 \leq b \leq 3\). Есть 5 возможностей для \(a\) и 4 возможности для \(b\), и, следовательно, есть \( 5 \times 4 = 20\) (правило произведения) положительных делителей 2000 во всех. \(_\квадрат\)
После посадки четвертого человека на пятое место у нас есть выбор любого из оставшихся 2 друзей. После посадки пятого человека, на шестое место у нас есть выбор только из 1 оставшегося друга. Следовательно, по правилу произведения существует \( 6 х 5 х 4 х 3 х 2 х 1 = 720) способов рассадить этих 6 человек. \(_\квадрат\) 9b\), где \( a\) и \( b\) — целые числа, удовлетворяющие \( 0 \leq a \leq 4, 0 \leq b \leq 3\). Есть 5 возможностей для \(a\) и 4 возможности для \(b\), и, следовательно, есть \( 5 \times 4 = 20\) (правило произведения) положительных делителей 2000 во всех. \(_\квадрат\)
 Если Наэма хочет только одну банку или кувшин сока, сколько у нее есть вариантов?
Если Наэма хочет только одну банку или кувшин сока, сколько у нее есть вариантов? org. Он планирует сделать это следующим образом:
org. Он планирует сделать это следующим образом:

 Функции бывают монотонными, немонотонными и постоянными.
Функции бывают монотонными, немонотонными и постоянными.

 Это можно записать так: функция убывает при х∈ (– ∞ ;0) ∪ (0; + ∞). Подытожим эту информацию небольшой схемой.
Это можно записать так: функция убывает при х∈ (– ∞ ;0) ∪ (0; + ∞). Подытожим эту информацию небольшой схемой.

 Отвечаем: к сожалению, нет. Эти значения иногда могут совпадать, но часто определяются разными точками.
Отвечаем: к сожалению, нет. Эти значения иногда могут совпадать, но часто определяются разными точками.


 Для этого пройдем по этим шагам:
Для этого пройдем по этим шагам: Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной. Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
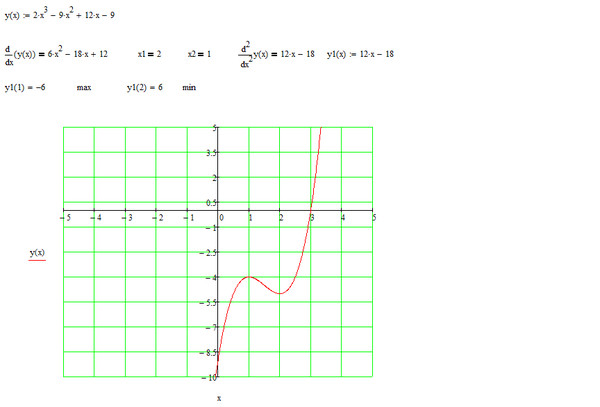
Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной. Причем, если вторая производная больше нуля (f »(x) > 0), то точкой минимума, а если вторая производная меньше нуля (f »(x) < 0), то точкой максимума.
Причем, если вторая производная больше нуля (f »(x) > 0), то точкой минимума, а если вторая производная меньше нуля (f »(x) < 0), то точкой максимума.

 3).
3). 7).
7).
 Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.:ил.
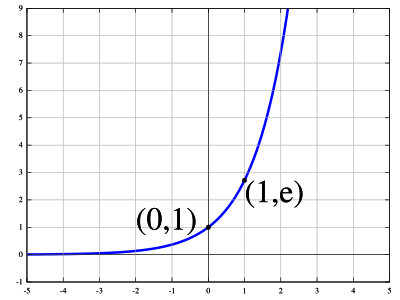
Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.:ил. Записывается как d(e x )/dx = e x .
Записывается как d(e x )/dx = e x . Математически это обозначается как d(e x )/dx = e x . e в степени x является экспоненциальной функцией с основанием, равным «e», которое известно как «число Эйлера». Оно записывается как f(x) = e x , где e — число Эйлера, а его значение приблизительно равно 2,718. Дифференцирование e в степени x может быть выполнено с использованием различных методов, таких как первый принцип дифференцирования и производная х .
Математически это обозначается как d(e x )/dx = e x . e в степени x является экспоненциальной функцией с основанием, равным «e», которое известно как «число Эйлера». Оно записывается как f(x) = e x , где e — число Эйлера, а его значение приблизительно равно 2,718. Дифференцирование e в степени x может быть выполнено с использованием различных методов, таких как первый принцип дифференцирования и производная х . Мы знаем, что для двух экспоненциальных функций, если основания одинаковы, мы складываем степени. Для доказательства производной e в степени x воспользуемся следующими формулами показательных функций и производных:
Мы знаем, что для двух экспоненциальных функций, если основания одинаковы, мы складываем степени. Для доказательства производной e в степени x воспользуемся следующими формулами показательных функций и производных: Производная показательной функции f(x) = a x равно f'(x) = (ln a) a x . Используя эту формулу и подставляя значение a = e в f'(x) = (ln a) a x , мы получаем дифференцирование e в степени x, которая определяется выражением f'(x) = (ln e) e x = 1 x e x = e x [Поскольку по правилам журнала, ln e = 1]. Следовательно, производная от e в степени x равна e x .
Производная показательной функции f(x) = a x равно f'(x) = (ln a) a x . Используя эту формулу и подставляя значение a = e в f'(x) = (ln a) a x , мы получаем дифференцирование e в степени x, которая определяется выражением f'(x) = (ln e) e x = 1 x e x = e x [Поскольку по правилам журнала, ln e = 1]. Следовательно, производная от e в степени x равна e x .
 Математически это обозначается как d(e x )/dx = e x .
Математически это обозначается как d(e x )/dx = e x .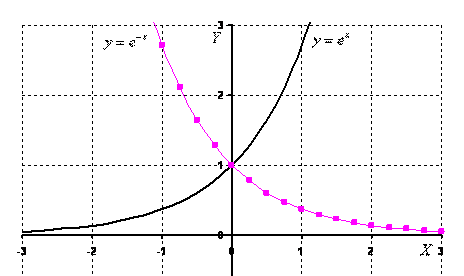 x.$$ 9х$$
является примером экспоненциального распада. Он быстро уменьшается по мере увеличения $x$, как показано на его графике.
x.$$ 9х$$
является примером экспоненциального распада. Он быстро уменьшается по мере увеличения $x$, как показано на его графике.



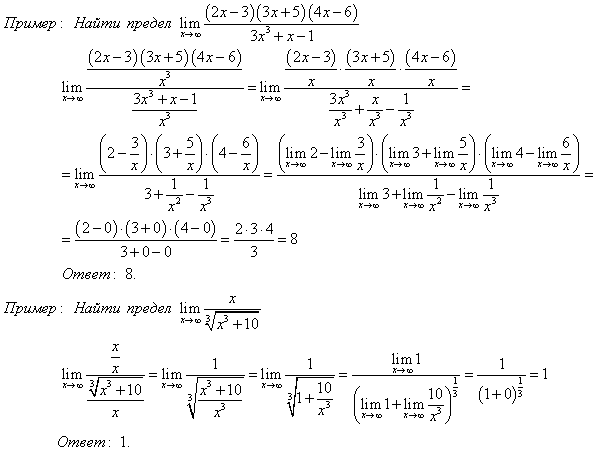 В точке x=1
обнуляется и числитель, и знаменатель. Чтобы найти предел в этой точке,
сократим дробь на (x−1). Получится выражение 1/(x+1). Оно имеет предел,
равный 1/2 при x→1. Значит, вертикальной асимптоты x=1 у функции
нет.
В точке x=1
обнуляется и числитель, и знаменатель. Чтобы найти предел в этой точке,
сократим дробь на (x−1). Получится выражение 1/(x+1). Оно имеет предел,
равный 1/2 при x→1. Значит, вертикальной асимптоты x=1 у функции
нет. Говорят,
что предел функции f(x) при x стремящемся к плюс бесконечности равен
b, если для всякого ε>0 найдётся такое C, что для всех x>C
верно неравенство |f(x)−b|<ε.
Говорят,
что предел функции f(x) при x стремящемся к плюс бесконечности равен
b, если для всякого ε>0 найдётся такое C, что для всех x>C
верно неравенство |f(x)−b|<ε.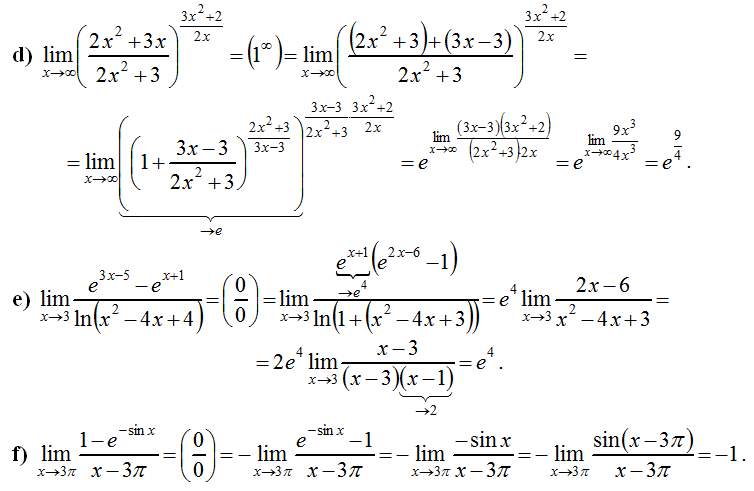 Такая прямая
называется горизонтальной асимптотой.
Такая прямая
называется горизонтальной асимптотой.
 Можно скрестить ужа с ежом и получить бесконечные пределы
при x стремящемся к бесконечности.
Можно скрестить ужа с ежом и получить бесконечные пределы
при x стремящемся к бесконечности.

 (12.1)(12.2)
При этом они обязаны равняться указанным значениям (k и b).
(12.1)(12.2)
При этом они обязаны равняться указанным значениям (k и b). ∎
∎ Для начала, как я могу сделать так, чтобы ограничения начинались с начала символа lim, а не перед ним? Это означает, что символ предела и пределы не должны быть центрированы.
Для начала, как я могу сделать так, чтобы ограничения начинались с начала символа lim, а не перед ним? Это означает, что символ предела и пределы не должны быть центрированы. Выравнивание задается параметром режима (
Выравнивание задается параметром режима ( 



 )
) )
) )
) )
) )
) )
) )
) )
) Темы, содержащиеся в статье, рассматриваются в соответствии с кодификатором, задающим элементы содержания заданий для выпускников образовательных организаций.
Темы, содержащиеся в статье, рассматриваются в соответствии с кодификатором, задающим элементы содержания заданий для выпускников образовательных организаций.
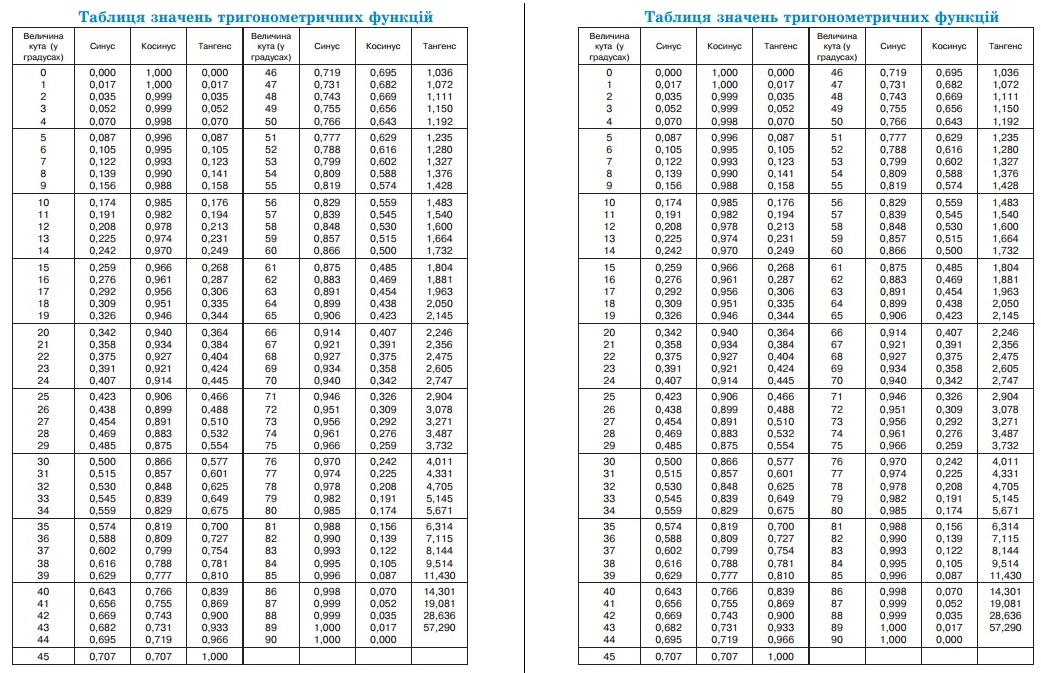
 Отрицательным тангенс является в четвёртой и второй четвертях.
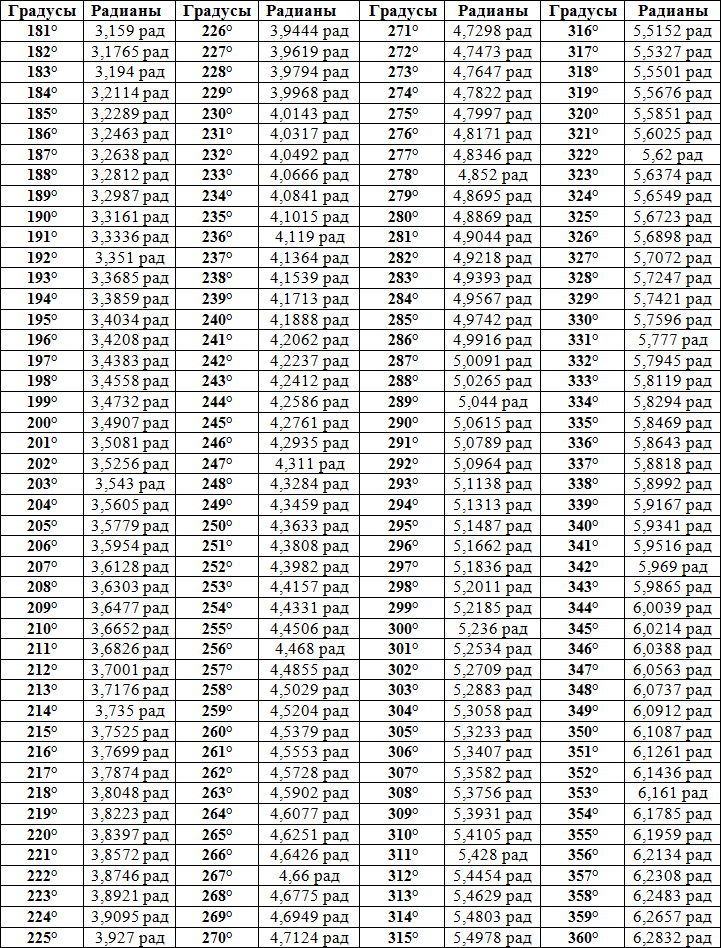
Отрицательным тангенс является в четвёртой и второй четвертях.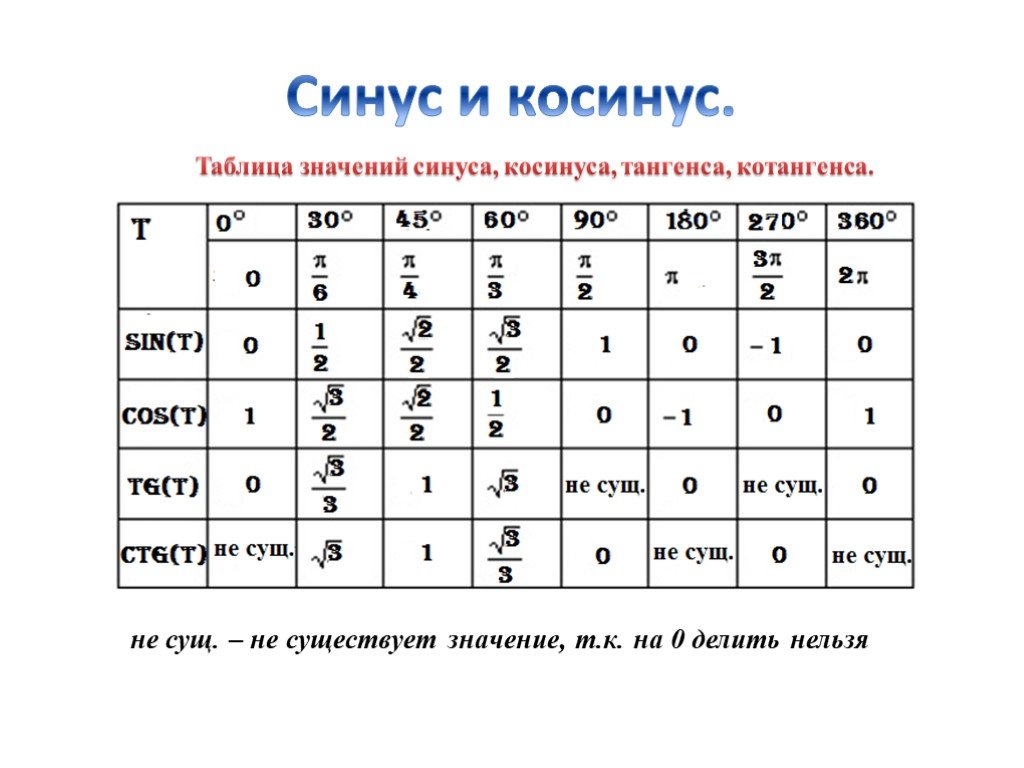 Один градус будет равен п 180 радиан. Один радиан соответственно, будет равен 180п. При этом, окружность будет равняться 2п.
Один градус будет равен п 180 радиан. Один радиан соответственно, будет равен 180п. При этом, окружность будет равняться 2п.

 . . Тангенс 1 градус в радианах записывается как тангенс (1° × π/180°), т. е. тангенс (0,017453…). В этой статье мы обсудим методы определения значения тангенса 1 градуса на примерах.
. . Тангенс 1 градус в радианах записывается как тангенс (1° × π/180°), т. е. тангенс (0,017453…). В этой статье мы обсудим методы определения значения тангенса 1 градуса на примерах.  Поскольку функция тангенса положительна в первом квадранте, значение тангенса 1° = 0,0174550. . .
Поскольку функция тангенса положительна в первом квадранте, значение тангенса 1° = 0,0174550. . .  998) точки пересечения (0,9998, 0,0175) единичной окружности и r.
998) точки пересечения (0,9998, 0,0175) единичной окружности и r. 
 Здесь значение sin 1° равно 0,0175.
Здесь значение sin 1° равно 0,0175.  Мы здесь, чтобы помочь вам понять, что означают эти уравнения и как их решать.
Мы здесь, чтобы помочь вам понять, что означают эти уравнения и как их решать.  Префикс
Префикс 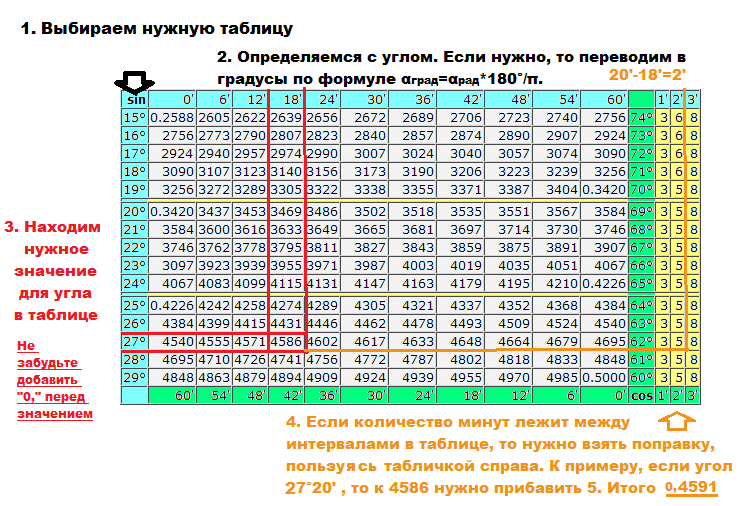 Вот они:
Вот они: 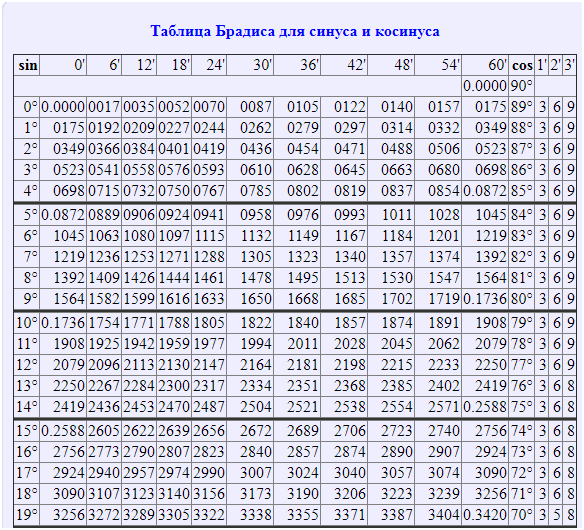
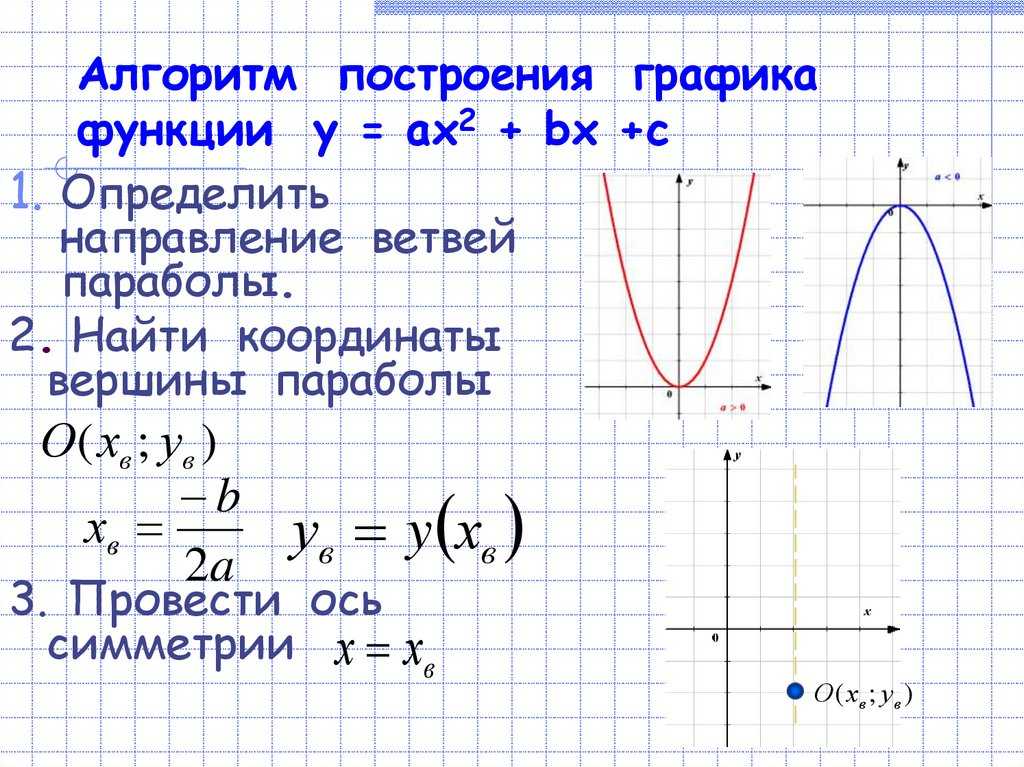 Любая точка на кривой находится на одинаковом расстоянии от фиксированной точки и фиксированной прямой линии. Результат выглядит как половина эллипса или дуги, образованной, когда объект подбрасывается в воздух и падает на небольшое расстояние. Поскольку это не математическая программа, Microsoft Word не может построить график на основе введенных вами данных, но благодаря большому набору инструментов для рисования вы можете нарисовать параболу после того, как рассчитаете ее форму.
Любая точка на кривой находится на одинаковом расстоянии от фиксированной точки и фиксированной прямой линии. Результат выглядит как половина эллипса или дуги, образованной, когда объект подбрасывается в воздух и падает на небольшое расстояние. Поскольку это не математическая программа, Microsoft Word не может построить график на основе введенных вами данных, но благодаря большому набору инструментов для рисования вы можете нарисовать параболу после того, как рассчитаете ее форму. 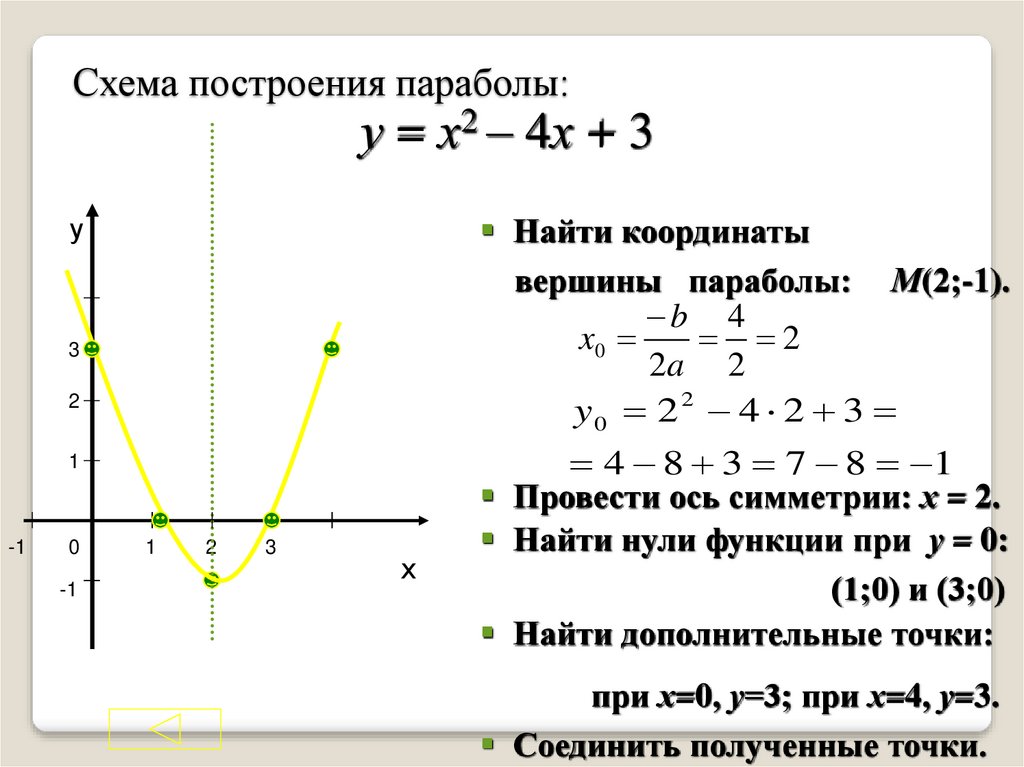 Эта вкладка содержит все команды рисования Word, но появляется только при выборе объекта рисования.
Эта вкладка содержит все команды рисования Word, но появляется только при выборе объекта рисования. 
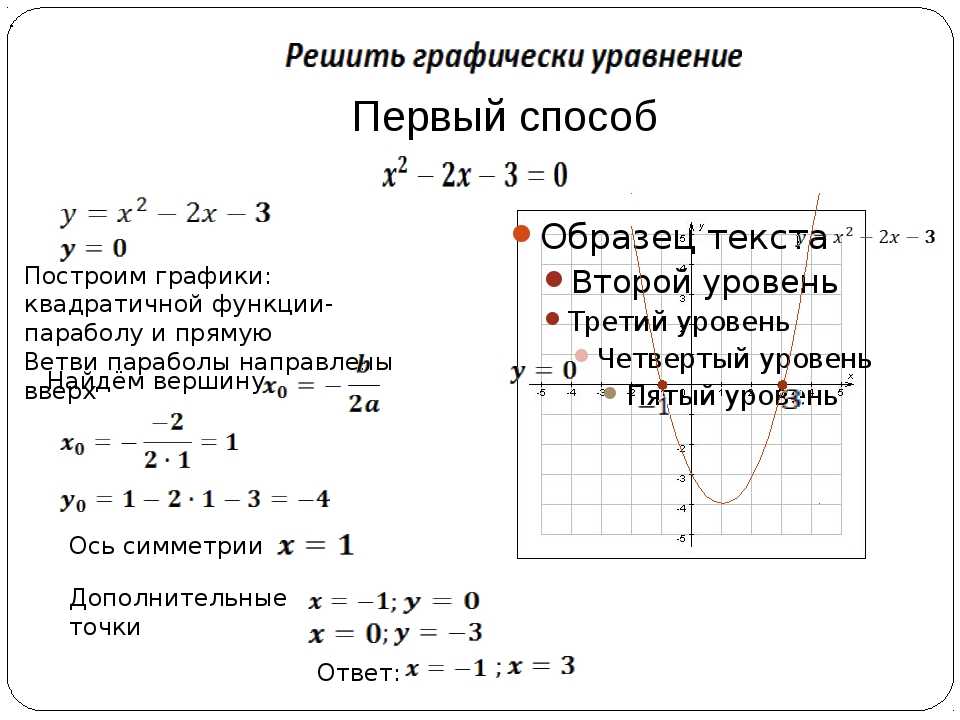


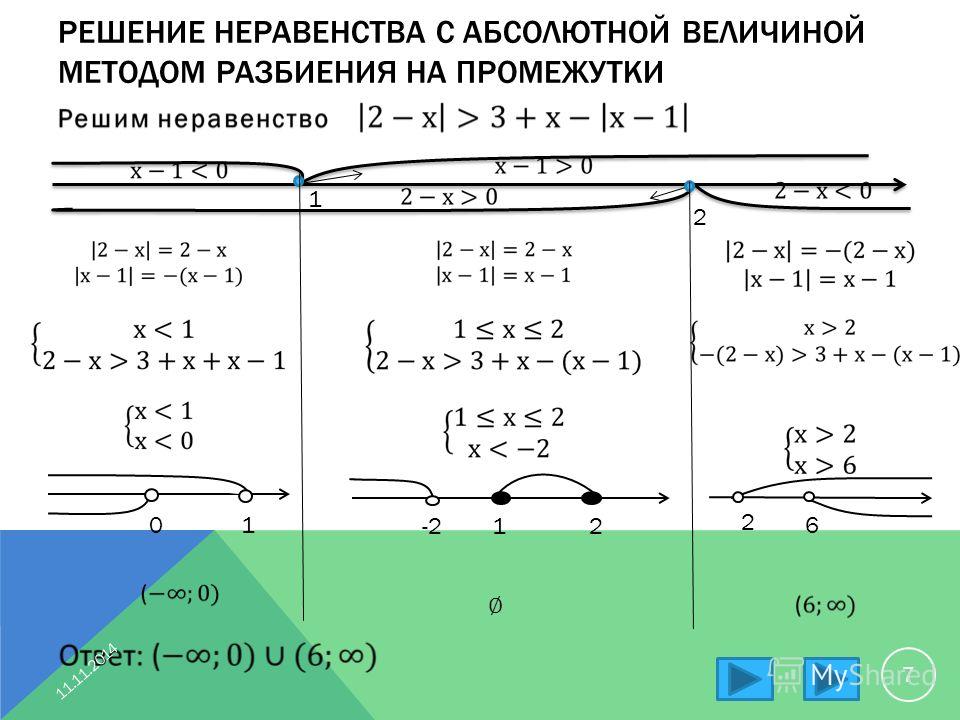
 Этот способ часто применяют в классе на уроке алгебры и при решении домашних заданий.
Этот способ часто применяют в классе на уроке алгебры и при решении домашних заданий. Для этого сначала вычислим нули выражений, которые записаны под знаком модуля:
Для этого сначала вычислим нули выражений, которые записаны под знаком модуля:

 Xartli formulasi, kompyuterning ishlashining mantiqiy, 11 A sinf , Noaniq integral haqida ma’ruza va yechish usullari , 1-Test, xosmas integrallarning geometriya va fizikaga tatbiqlari, 2013, 1367254467.0182english-grammar-tests, ielts speaking, art-spok, fizika oqitish metodikasi, Algoritmlash va dasturlash ingliz tili
Xartli formulasi, kompyuterning ishlashining mantiqiy, 11 A sinf , Noaniq integral haqida ma’ruza va yechish usullari , 1-Test, xosmas integrallarning geometriya va fizikaga tatbiqlari, 2013, 1367254467.0182english-grammar-tests, ielts speaking, art-spok, fizika oqitish metodikasi, Algoritmlash va dasturlash ingliz tili Иначе вы рискуете вообще не понять материал сегодняшнего урока.
Иначе вы рискуете вообще не понять материал сегодняшнего урока.

 Исследуйте книгу Купить на Amazon
Исследуйте книгу Купить на Amazon  Абсолютное значение всегда должно быть нулевым или положительным (единственное, что меньше отрицательных чисел, — это другие отрицательные числа). Например, абсолютное неравенство |2 x – 1| < –3 не имеет решения, потому что неравенство меньше отрицательного числа.
Абсолютное значение всегда должно быть нулевым или положительным (единственное, что меньше отрицательных чисел, — это другие отрицательные числа). Например, абсолютное неравенство |2 x – 1| < –3 не имеет решения, потому что неравенство меньше отрицательного числа.  Любое действительное число, которое вы подставите в это уравнение, работает.
Любое действительное число, которое вы подставите в это уравнение, работает. 



 Затем мы решаем каждую отдельно.
Затем мы решаем каждую отдельно.



 Наибольший из них – 15 – является самым большим. Это и есть НОД.
Наибольший из них – 15 – является самым большим. Это и есть НОД. В данном случае – 10.
В данном случае – 10. е. представим каждое число как произведения простых чисел. Множители большего числа запишем сверху:
е. представим каждое число как произведения простых чисел. Множители большего числа запишем сверху:
 У нас также есть несколько вопросов, основанных на наименьшем общем кратном, которое может ответить ваш ребенок, и все, чтобы помочь ему (и вам) быстро освоить математику!
У нас также есть несколько вопросов, основанных на наименьшем общем кратном, которое может ответить ваш ребенок, и все, чтобы помочь ему (и вам) быстро освоить математику!

 Например, чтобы вычислить 3/5 + 1/6, нам нужно найти общий знаменатель, вычислив наименьшее общее кратное 5 и 6 (30). Затем мы можем преобразовать дроби в 18/30 + 5/30 = 23/30.
Например, чтобы вычислить 3/5 + 1/6, нам нужно найти общий знаменатель, вычислив наименьшее общее кратное 5 и 6 (30). Затем мы можем преобразовать дроби в 18/30 + 5/30 = 23/30.
 значения в обоих списках): 12, 24, …
значения в обоих списках): 12, 24, …


 Для других – сделает изучение хотя бы не столь противным (что тоже немаловажно, так как многие дети просто не хотят учить таблицу умножения). Для третьих мало что изменится в ходе заучивания, но зато запомнится все гораздо более устойчиво.
Для других – сделает изучение хотя бы не столь противным (что тоже немаловажно, так как многие дети просто не хотят учить таблицу умножения). Для третьих мало что изменится в ходе заучивания, но зато запомнится все гораздо более устойчиво.
 Все это будет размещаться в разделе КАРП-ВИДЕО.
Все это будет размещаться в разделе КАРП-ВИДЕО. Страницы
Страницы  Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7.
Например, опишите контекст, в котором общее количество объектов может быть выражено как 5 × 7.  Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?
Например, определите неизвестное число, которое делает уравнение истинным в каждом из уравнений 8 × ? = 48, 5 = _ ÷ 3, 6 × 6 = ?  Math.Content.3.OA.C. 7 Свободно умножайте и делите в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел.
Math.Content.3.OA.C. 7 Свободно умножайте и делите в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например, зная, что 8 × 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. К концу 3 класса знать наизусть все произведения двух однозначных чисел. 

 Или нажмите «Файл», затем «Печать». Страницы
Или нажмите «Файл», затем «Печать». Страницы 
 К концу 3 класса знать наизусть все произведения двух однозначных чисел.
К концу 3 класса знать наизусть все произведения двух однозначных чисел.  Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.  Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.  Наши рабочие листы и печатные формы для разделения на основе навыков помогают учащимся с третьего по пятый класс поднять свои математические навыки на ступеньку выше. Изучите анатомию задач на деление и попрактикуйтесь в многозначном делении и дробях с манипуляциями, используя эти рабочие листы деления и печатные формы!
Наши рабочие листы и печатные формы для разделения на основе навыков помогают учащимся с третьего по пятый класс поднять свои математические навыки на ступеньку выше. Изучите анатомию задач на деление и попрактикуйтесь в многозначном делении и дробях с манипуляциями, используя эти рабочие листы деления и печатные формы!