 2}4.
$$
2}4.
$$Заметно сложнее угадать формулу для суммы четвертых степеней. В отличие от предыдущих случаев, у $S_4(n)$ практически не видно общих делителей с $S_1(n)$ (кроме двойки). Зато можно заметить, что 14 и 98 делятся на 7, 55 и 979 на 11… Посмотрим на отношение $S_4/S_2$.
| $n$ | 1 | 2 | 3 | 4 | 5 | 6 |
| $S_2$ | 1 | 5 | 14 | 30 | 55 | 91 |
| $S_4$ | 1 | 17 | 98 | 354 | 979 | 2275 |
| $S_4/S_2$ | 1 | 17/5 | 7 | 59/5 | 89/5 | 25 |
Видно, что после домножения этого отношения на 5 получится последовательность целых чисел: 5, 17, 35, 59, 89, 125… Тут уже нельзя сказать, что разность соседних чисел неизменна… Все же посмотрим на эти разности: 12, 18, 24, 30… — закономерность сразу видна!
Таким образом, гипотеза состоит в том, что
$$
S_4(n)/S_2(n)=
\frac{5+6\cdot2+6\cdot3+\ldots+6n}5=
\frac{6\frac{n(n+1)}2-1}5=
\frac{3n^2+3n-1}5,
$$
и соответственно
$$
S_4(n)=\frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}. 2}6$ (т. е. значений
знаменитой дзета-функции), и в комбинаторике, и в теории
чисел, и в топологии…
2}6$ (т. е. значений
знаменитой дзета-функции), и в комбинаторике, и в теории
чисел, и в топологии…
Литература
- Д. Пойа. Математика и правдоподобные рассуждения (М.: Наука, 1975)
http://ilib.mccme.ru/djvu/polya/rassuzhdenija.htm
Мало где можно прочитать не о конкретной области математики, а о том, как вообще решать новую для себя математическую задачу. Подсказки и решение выше по существу следуют главе 7 этой замечательной книги. - Интервью с академиком И. М. Гельфандом // Квант, 1989, № 1, 3–12
http://kvant.mccme.ru/1989/01/akademik_izrail_moiseevich_gel.htm
В решении выше сделана попытка объяснить, как некоторые формулы для сумм степеней мог бы искать любой человек. Интересующимся математикой может быть интересно прочитать, как такую задачу решал в школьные годы один из выдающихся математиков 20 века (собственно про это — небольшой фразмент на стр. 8–9, но все интервью интересное). - В. С. Абрамович. Суммы одинаковых степеней натуральных чисел // Квант, 1973, № 5, 22–25
http://kvant. n)?
n)?06.02.2018, 13:13
25/11/08
449
Как можно посчитать сумму ряда ? С чего начинать? |
| pogulyat_vyshel |
| |||
27/12/17 |
| |||
| ||||
| B@R5uk |
| ||
26/05/12 |
| ||
| |||
| grizzly |
| |||
09/09/14 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 5 ] |
Модераторы: Модераторы Математики, Супермодераторы
Ряды
Ряды — это просто бесконечные суммы. Мы с ними уже несколько раз сталкивались
— например, когда обсуждали, что некоторые функции оказываются равны своим рядам
Тейлора (см. замечание 2 из
лекции 22). Пришло время поговорить про ряды
подробнее.
Мы с ними уже несколько раз сталкивались
— например, когда обсуждали, что некоторые функции оказываются равны своим рядам
Тейлора (см. замечание 2 из
лекции 22). Пришло время поговорить про ряды
подробнее.
28.1Сходящиеся и расходящие ряды
28.1.1Определения и примеры
Пусть есть какая-то последовательность {ak}.
Определение 1. Бесконечным рядом (или просто рядом) называется такая бесконечная сумма:
∞∑k=1ak=a1+a2+a3+….
Если вместо бесконечности взять первые n слагаемых, получится частичная сумма ряда:
Sn:=n∑k=1ak=a1+a2+…+an.
По определению, суммой ряда называется предел частичных сумм:
∞∑k=1ak:=limn→∞Sn=limn→∞n∑k=1ak.
Конечно, этот предел может существовать, а может не существовать. В первом случае ряд называется сходящимся, во втором — расходящимся.
Пример 1. Ряд
Ряд
∞∑k=112k=12+14+18+…
сходится. Это геометрическая прогрессия со знаменателем, по модулю меньшим 1, но сходимость здесь можно увидеть и непосредственно. Если у вас была одна шоколадка, вы съели от неё половину, потом половину от оставшейся половины (то есть четверть), потом половины от того, что осталось (то есть одну возьмую) и т.д. — в пределе ничего не останется, но и больше, чем целую шоколадку, вы не съедите. Значит, сумма съеденных кусочков стремится к единице.
Рис. 28.1: Сумма бесконечной геометрической прогрессии «на шоколадках»
Пример 2. Ряд
∞∑k=1k2=1+4+9+16+…
расходится: поскольку все слагаемые больше или равны 1, частичные суммы неограничены: Sn≥n, и значит расходятся. Можно сказать, что сумма равна плюс бесконечности:
∞∑k=1k2=+∞.
28.1.2Геометрическая прогрессия
Важным примером рядов являются суммы геометрических прогрессий, то есть
последовательностей вида {b0qk}, где q называется знаменателем прогрессии.
Поскольку я никогда не могу запомнить формулу для суммы членов геометрической прогрессии и каждый раз вывожу её заново, приведу этот вывод и здесь.
Утверждение 1. Для всяких b0∈R, q≠1 и n∈N справедливо утверждение
n∑k=1b0qk=b0q1−qn1−q.
Доказательство. Вынесем b0q за знак суммирования, а потом сделаем замену индекса суммирования m=k−1:
n∑k=1b0qk=b0qn∑k=1qk−1=b0qn−1∑m=0qm.
Остаётся найти, чему равна сумма ∑n−1m=0qm. Обозначим её через S. Тогда
S=1+q+q2+…+qn−1qS=q+q2+…+qn−1+qn
Вычитая из первого равенства второе, получаем:
S−qS=1−qn,
откуда
S=1−qn1−q.
∎
Следствие 1. При |q|<1,
∞∑k=1b0qk=b0q1−q
поскольку в этом случае qn стремится к нулю при n стремящемся к
бесконечности. При |q|>1 при b0≠0 ряд расходится, поскольку qn
стремится к бесконечности. При q=1 последовательность является постоянной
и ряд расходится при b0≠0.
При |q|>1 при b0≠0 ряд расходится, поскольку qn
стремится к бесконечности. При q=1 последовательность является постоянной
и ряд расходится при b0≠0.
В примере 1, b0=1 и q=1/2, значит сумма равна
∞∑k=112k=1⋅121−12=1,
как и ожидалось.
28.1.3«Телескопические суммы»
Вообще есть мало сколь-нибудь универсальных способов нахождения бесконечных сумм в явном виде. Но чтобы вам не казалось, что нет никаких поддающихся анализу рядов, кроме геометрической прогрессии, обсудим ещё один тип.
Пример 3. Найдём сумму ряда
∞∑k=11k(k+1).(28.1)
Для этого заметим, что
1k(k+1)=1k−1k+1.
Дальше хочется сделать такую штуку:
∞∑k=11k(k+1)=∞∑k=1(1k−1k+1)=(11−12)+(12−13)+(13−14)+…==11+(−12+12)+(−13+13)+…=11+0+0+…=1.
∞∑k=11k(k+1)=∞∑k=1(1k−1k+1)==(11−12)+(12−13)++(13−14)+…==11+(−12+12)++(−13+13)+…==11+0+0+…=1.
Это преобразование выглядит реалистично — в самом деле, нас учили, что при суммировании неважно, как расставлять скобки — однако таит в себе опасность. Рассмотрим, например, такой ряд:
∞∑k=1(−1)k=−1+1−1+…(28.2)
Его частичными суммами Sn будут числа −1 (при нечётных n) и 0 — при чётных. Мы знаем, что предела у такой последовательности нет. Однако, казалось бы, можно записать:
∞∑k=1(−1)k=−1+1−1+1−…=(−1+1)+(−1+1)+…=0+0+…=0.
∞∑k=1(−1)k=−1+1−1+1−…==(−1+1)+(−1+1)+…==0+0+…=0.
Впрочем, с тем же успехом мы могли бы получить и −1, если бы сгруппировали слагаемые иначе (первое оставили отдельно, а второе сгруппировали с третьим, четвертой с пятым и т.д.)
Пример с рядом ∑∞k=1(−1)k показывает, что бесконечные суммы
могут быть коварными — привычные нам операции типа группировки слагаемых
могут менять результат. Как же всё-таки найти сумму ряда (28. 1)?
1)?
Если мы не уверены, что некоторое преобразование сработает с бесконечным рядом, мы можем вернуться в ту область, где всё просто и понятно — в область конечных сумм. Давайте рассмотрим частичные суммы этого ряда:
n∑k=11k(k+1)=11−12+12−13+…+1n−1−1n+1n−1n+1.
n∑k=11k(k+1)=11−12+12−13+…++1n−1−1n+1n−1n+1.
Тут уже скобки не важны, потому что группировка слагаемых в конечных суммах не меняет их значения. Мы видим, что слагаемые (−1/2) и 1/2 сокращаются, и дальше сократятся все пары слагаемых, заканчивая (−1/n) и 1/n. Останется только первое и последнее слагаемое. (Если вы чувствуете малейшие сомнения в этом месте, подставьте какое-нибудь небольшое конкретное n — например, n=3, и проследите, как это работает.) Итак:
n∑k=1=11−1n+1
и значит предел частичных сумм равен 1. То есть наше вычисление дало
правильный результат, и теперь мы это аккуратно обосновали. (Проверьте, что
будет, если попытаться применить то же самое рассуждение к ряду
(28. 2).)
2).)
Суммы такого вида, у которых слагаемые последовательно сокращаются, иногда называют «телескопическими» — в процессе сокращения сумма как бы складывается, как складная подзорная труба или телескоп.
28.1.4Простейшие свойства
Как показвает пример с рядом (28.2), не все привычные нам операции с конечными суммами можно применять к рядам. Однако, некоторые всё-таки можно.
Утверждение 2. Пусть ряды ∑∞k=1ak и ∑∞k=1bk сходятся и c∈R — какая-то константа. Тогда
- ∞∑k=1(ak+bk)=∞∑k=1ak+∞∑k=1bk.
- ∞∑k=1(cak)=c∞∑k=1ak.
Доказательство. Это прямое следствие из аналогичных свойств пределов. Докажем, например, первое свойство. Рассмотрим n-ю частичную сумму:
n∑k=1(ak+bk)=(a1+b1)+(a2+b2)+…+(an+bn)=…
n∑k=1(ak+bk)=(a1+b1)+(a2+b2)+…++(an+bn)=…
Это конечная сумма, в ней можно раскрывать скобки и переставлять слагаемые,
как нас учат в школе. Поэтому можно продолжить равенство:
Поэтому можно продолжить равенство:
…=(a1+a2+…+an)+(b1+b2+…+bn)=n∑k=1ak+n∑k=1bk.
…=(a1+a2+…+an)++(b1+b2+…+bn)==n∑k=1ak+n∑k=1bk.
Значит
∞∑k=1(ak+bk)=limn→∞n∑k=1(ak+bk)=limn→∞(n∑k=1ak+n∑k=1ak)==limn→∞n∑k=1ak+limn→∞n∑k=1bk=∞∑k=1ak+∞∑k=1bk.
∞∑k=1(ak+bk)=limn→∞n∑k=1(ak+bk)==limn→∞(n∑k=1ak+n∑k=1ak)==limn→∞n∑k=1ak+limn→∞n∑k=1bk==∞∑k=1ak+∞∑k=1bk.
В третьем равенства мы использовали теорему о пределе суммы.
Второе свойство доказывается аналогично, запишите доказательство самостоятельно.∎
28.2Признаки сходимости и расходимости
28.2.1Необходимое условие сходимости: члены стремятся к нулю
Утверждение 3. Если ряд ∑∞k=1ak сходится, то
limn→∞an=0.
Доказательство. Обозначим через Sn частичную сумму нашего ряда:
Sn:=n∑k=1ak.
Тогда для всех n>1
an=Sn−Sn−1.
Рассмотрим предел последовательности {an}:
limn→∞an=limn→∞(Sn−Sn−1)=limn→∞Sn−limn→∞Sn−1,
но пределы Sn и Sn−1 — это фактически один и тот же предел (во втором случае последовательность просто сдвинута на один элемент вправо, но предел от этого не изменился). И оба предела существуют, потому что по определению, предел частичных сумм — это сумма ряда, а ряд сходится. Обозначим сумму ряда за S. Тогда
limn→∞an=S−S=0.
∎
28.2.2Гармонический ряд
Условие an→0 является необходимым для сходимости ряда, но является ли оно достаточным? Оказывается, нет. Приведём в качестве примере известный гармонический ряд.
Утверждение 4. Ряд
∞∑k=11k=11+12+13+…(28.3)
расходится.
Доказательство. Заметим, что
12≥1213+14≥2⋅14=1215+16+17+18≥4⋅18=1219+110+111+112+113+114+115+116≥8⋅116=12
12≥1213+14≥2⋅14=1215+16+17+18≥4⋅18=1219+110+111+112+113+114+115+116≥8⋅116=12
Каждая из сумм в левой части не меньше, чем своё последнее слагаемое (самое
маленькое) умножить на число слагаемых. Понятно, что так можно продолжать и
дальше. Для произвольного натурального m возьмём слагаемые с номерами от
2m+1 до 2m+1. Их количество равно разности между этими двумя
числами, плюс один. (Потому что и первое и последнее число включатся в
подсчёт: например, если бы эти числа совпадали, разность равнялась нулю, но
при этом одно слагаемое мы бы взяли.) Значит, общее число слагаемых равно
Понятно, что так можно продолжать и
дальше. Для произвольного натурального m возьмём слагаемые с номерами от
2m+1 до 2m+1. Их количество равно разности между этими двумя
числами, плюс один. (Потому что и первое и последнее число включатся в
подсчёт: например, если бы эти числа совпадали, разность равнялась нулю, но
при этом одно слагаемое мы бы взяли.) Значит, общее число слагаемых равно
2m+1−(2m+1)+1=2m+1−2m=2m(21−1)=2m
2m+1−(2m+1)+1=2m+1−2m==2m(21−1)=2m
и каждое слагаемое не меньше последнего, то есть 1/2m+1. Итак:
2m+1∑k=2m+11k≥2m12m+1=12.(28.4)
Возьмём первые 2N слагаемых ряда (28.3). В них есть первое слагаемое, равное 1/1, и ещё N «блоков» вида (28.4), каждый из которых не меньше 1/2. Значит, их сумма не меньше, чем N12+1 и стремится к бесконечности. Значит, ряд расходится.∎
28.2.3Признак сравнения
Ну хорошо, у нас есть необходимое условие сходимости — может быть, есть и
какие-то достаточные? Да, есть.
Теорема 1. Рассмотрим два ряда:
∞∑k=1ak,∞∑k=1bk.
Если известно, что для всех натуральных k верны неравенства
0≤ak≤bk(28.5)
и ряд
∞∑k=1bk(28.6)
сходится, то ряд
∞∑k=1ak(28.7)
тоже сходится.
Доказательство. Доказательство полностью аналогично доказательству похожей теоремы для несобственных интегралов. Попробуйте написать его самостоятельно.
Узнать ответ
Верный ответ.
Обозначим сумму ряда (28.6) через B, частичные суммы
ряда (28.6) через Bn, а частичные суммы ряда
(28.7) через An. Поскольку все слагаемые
неотрицательны, обе последовательности {An} и {Bn}
неубывают. Также в силу (28.5), для всех n, An≤Bn. С другой стороны, в силу неубывания, все элементы Bn не
превосходят предела B (если бы какой-то элемент перескочил
через предел, все следующие элементы были бы отделены от предела
и не могли бы к нему стремиться). Значит, для всех n, An≤Bn≤B и значит последовательность {An} является
неубывающей и ограниченной. Значит, по теоремe
Вейерштрасса, у неё есть предел.
Значит, для всех n, An≤Bn≤B и значит последовательность {An} является
неубывающей и ограниченной. Значит, по теоремe
Вейерштрасса, у неё есть предел.
∎
Пример 4. Докажем, что ряд
∞∑k=11kk
сходится. Действительно, для всех k≥2, kk≥2k и следовательно 1/kk≤1/2k. Никакое конечное число начальных членов на сходимость ряда не влияет и значит в признаке сравнения достаточно выполнения неравенства для всех k, начиная с некоторого. А ряд
∞∑k=112k
сходится. Значит, и наш ряд сходится.
Пример 5. Докажем, что ряд
∞∑k=1lnkk(28.8)
расходится. Действительно, для всех k≥3, lnk≥1 и следовательно
1k≤lnkk.
Но если бы ряд (28.8) сходился, тогда и ограниченный им ряд
∑∞k=11/k тоже сходился бы. Но мы знаем, что последнее
неверно. Значит, наш ряд расходится.
Значит, наш ряд расходится.
28.2.4Интегральный признак сходимости
Как мы уже отмечали, между несобственными интегралами и рядами много общего. При этом анализировать интегралы часто проще, чем ряды — есть разнообразные способы преобразования интегралов, которые к рядам применяются плохо. К счастью, есть теорема, которая позволяет переносить результаты о сходимости интегралов на ряды и наоборот.
Теорема 2. Пусть функция f:[1,+∞)→R невозрастает, неотрицательна и интегрируема на любом отрезке [a,t], t>a. В этих условиях ряд
n∑k=1f(k)(28.9)
сходится тогда и только тогда, когда сходится несобственный интеграл
∫∞1f(x)dx.(28.10)
Доказательство.
Если интеграл сходится, то и ряд тоже сходится. Построим график
функции y=f(x). Мы хотим представить сумму ряда (28.9) в виде
некоторой площади, чтобы сравнить её с площадью, которая соответствует
интегралу (28. 10). Для этого над каждым отрезком [k−1,k]
построим прямоугольник высотой f(k), k=1,2,….
10). Для этого над каждым отрезком [k−1,k]
построим прямоугольник высотой f(k), k=1,2,….
Рис. 28.3: Интеграл оценивает сумму ряда, начиная со второго слагаемого
Площадь k-го прямоугольника равна f(k), сумма всех площадей равна сумме ряда. Все прямогольники, кроме первого, находятся не выше графика функции: в силу неубывания на каждом отрезке [k−1,k] значение функции не меньше f(k). Разобьём наш ряд в сумму первого члена и всех остальных:
∞∑k=1=f(1)+∞∑k=2f(k).
Слагаемое f(1) не меняет сходимости ряда, и значит достаточно изучить сходимость ∑∞k=2f(k). Любая частичная сумма этого ряда не превосходит значение интеграла (28.10) и последовательность частичных сумм неубывает в силу неотрицательности f. Значит, последовательность частичных сумм имеет предел и ряд сходится.
Формально можно записать так. Заметим, что
∞∑k=2f(k)=∫+∞1f(⌈x⌉)dx,(28.11)
где ⌈x⌉ — окугление «вверх» от числа x. Этот интеграл равен
площади суммы всех прямоугольников, которую мы обсуждали выше (на каждом
полуинтервале (k−1,k] мы интегрируем константу f(k)). С другой стороны,
⌈x⌉≥x и значит f(⌈x⌉)≤f(x). По признаку
сравнения для интегралов, если интеграл (28.10)
сходится, то и интеграл (28.11) сходится.
С другой стороны,
⌈x⌉≥x и значит f(⌈x⌉)≤f(x). По признаку
сравнения для интегралов, если интеграл (28.10)
сходится, то и интеграл (28.11) сходится.
Если ряд сходится, то и интеграл сходится. Доказательство полностью аналогично, только всю картинку с прямоугольниками нужно сдвинуть на одну позицию вправо. То есть на отрезке [k,k+1] нужно построить прямоугольник высотой f(k). Теперь верхние стороны наших прямуогльники будут ограничивать график функции y=f(x) сверху, и из сходимости ряда будет следовать сходимость интеграла.
Рис. 28.4: Сумма ряда оценивает интеграл сверху
Формально, можно записать:
∞∑k=1f(k)=∫+∞1f(⌊x⌋)dx,(28.12)
гда ⌊x⌋ — округление вниз числа x, и использовать неравенство f(⌊x⌋)≥f(x). Значит ряд ограничивает интеграл и из сходимости ряда следует сходимость интеграла.∎
Пример 6. Докажем, что ряд
∞∑k=11k2(28.13)
сходится.
Действительно, этот ряд можно представить в виде ряда ∑∞k=1f(k), где f(x)=1/x2 — невозрастающая неотрицательная функция. Значит сходимость этого ряда эквивалентна сходимости интеграла
∫∞11x2dx.
Но мы уже доказывали, что этот интеграл сходится. Значит, ряд тоже сходится.
28.2.5Знакочередующиеся ряды
Признаки сравнения, обсуждающиеся выше, применимы к рядам с неотрицательными членами. Легко придумать их аналоги для рядов, чьи члены всегда неположительны. Если условие знакопостоянства верно для всех членов, начиная с некоторого, эти признаки тоже работают: никакое конечное число первых членов на сходимость ряда не влияют.
Можно ли что-то сказать в том случае, когда среди членов ряда есть бесконечно много положительных и бесконечно много отрицательных членов (такие ряды называют знакопеременными)? В некоторых случаях — можно.
Определение 2. Пусть ak — некоторая последовательность с положительными членами. Рассмотрим ряд
Рассмотрим ряд
∞∑k=1(−1)k+1ak.(28.14)
Он называется знакочередующимся. Также можно поставить коэффициент (−1)k, получится тоже знакочередующийся ряд.
Про знакочередующиеся ряды обычно просто сказать, сходятся они или нет: необходимое условие сходимости в этом случае почти совпадает с достаточным (но не совсем совпадает, нужно дополнительное условие).
Теорема 3. (Признак Лейбница.) Пусть для знакочередующегося ряда (28.14) модули членов невозрастают, то есть для всех k, ak+1≤ak. Если при этом
limk→∞ak=0,
то ряд сходится.
Доказательство. Обозначим частичные суммы ряда через Sn. Тогда S1=a1, S2=a1−a2, S3=a1−a2+a3 и т.д. Будем откладывать эти точки на числовой прямой, см. рис. 28.5.
Вот мы отложили точку S1. Затем нужно сдвинуться влево на a2, чтобы
получить S2. Отсюда нужно сдвинуться вправо на a3, чтобы получить
S3. Может ли оказаться, что мы «перескочим» при этом S1? Нет, потому
что последовательность ak невозрастает, и значит a3≤a2, то есть
сдвиг от S2 до S3 не превосходит длину отрезка [S2,S1]. Значит
точка S3 лежит в отрезке [S2,S1].
Может ли оказаться, что мы «перескочим» при этом S1? Нет, потому
что последовательность ak невозрастает, и значит a3≤a2, то есть
сдвиг от S2 до S3 не превосходит длину отрезка [S2,S1]. Значит
точка S3 лежит в отрезке [S2,S1].
Рис. 28.5: Частичные суммы знакочередующегося ряда с убывающими членами
Следующий шаг должен быть влево, и поскольку a4≤a3, точка S4 лежит на отрезке [S2,S3]. И так далее.
Можно построить последовательность вложенных отрезков {Ik}, определяемых следующим образом:
Ik=[min(Sk,Sk+1),max(Sk,Sk+1)],
то есть концы k-го отрезка — это просто частичные суммы
(k-я и k+1-я), записанные в правильном порядке (та, что больше, справа,
а та, что меньше, слева).
Тогда
I1=[S2,S1],I2=[S2,S3],I3=[S4,S3],I4=[S4,S5],
и т.д. По построению, Ik+1⊂Ik и |Ik|=ak+1→0 при
k→0. Значит по лемме о вложенных
отрезках существует единственная точка c,
принадлежащая всем Ik, и концы отрезков стремятся к c. Но концами
являются наши предельные суммы и значит если они стремятся к c, то ряд
сходится к c.∎
Но концами
являются наши предельные суммы и значит если они стремятся к c, то ряд
сходится к c.∎
Пример 7. Ряд
∞∑k=1(−1)k+1k(28.15)
является сходящимся.
28.3Абсолютная и условная сходимость
Определение 3. Рассмотрим ряд
∞∑k=1ak.(28.16)
Если ряд из модулей
∞∑k=1|ak|
сходится, ряд (28.16) называется абсолютно сходящимся.
Утверждение 5. Если ряд сходится абсолютно, то он сходится. (Звучит забавно, но, действительно, в определении абсолютной сходимости ничего не сказано про то, сходится сам ряд, или нет — сказано только про ряд из модулей.)
Доказательство. Докажите самостоятельно. Подсказка: пусть bn=an+|an|. Тогда bn≥0 и bn≤2|an|. Но an=bn−|an|.∎
Определение 4. Если ряд сходится, но не является абсолютно сходящимся, говорят, что он сходится условно.
Пример 8. Ряд (28.15) сходится условно, потому что соответствующий ему ряд из модулей является гармоническим (см. (28.3)) и расходится.
Оказывается, что абсолютно и условно сходящиеся ряды ведут себя существенно по-разному — некоторые естественные операции можно безопасно делать с абсолютно сходящимися рядами, но нельзя с условно сходящимися. В частности, для условно сходящихся рядов не действует принцип «от перемены мест слагаемых сумма не меняется».
Определение 5. Биективное отображение φ:N→N называется перестановкой натурального ряда.
Если задана какая-то перестановка натурального ряда φ, с её помощью можно из ряда
∞∑k=1ak
изготовить ряд
∞∑k=1aφ(k),
то есть ряд, члены которого совпадают с {ak}, но их порядок изменён с помощью перестновки φ.
Теорема 4. В результате перестановок членов абсолютно сходящегося ряда его сумма не меняется.
Набросок доказательства. Если ряд имеет только положительные элементы, легко показать, что частичные
суммы переставленного ряда оцениваются частичными суммами исходного, и
наоборот. Ряд с положительными и отрицательными членами можно представить
как разность двух рядов с положительными членами.∎
Если ряд имеет только положительные элементы, легко показать, что частичные
суммы переставленного ряда оцениваются частичными суммами исходного, и
наоборот. Ряд с положительными и отрицательными членами можно представить
как разность двух рядов с положительными членами.∎
Теорема 5. (Римана) Пусть есть какой-то условно сходящийся ряд ∑∞k=1ak. Тогда выбором подходящей перестановки его членов можно получить ряд с любой заранее заданной суммой. Иными словами, для всякого c найдётся такая перестановка φ, что в результате этой перестановки получается ряд, сумма которого равна c.
Доказательство.
Положительные и отрицательные члены. Будем для простоты считать, что в исходном ряду нет нулевых членов — если они есть, на сумму они никак не влияют, и в силу расходимости ряда из модулей, количество ненулевых членов не может быть конечным.
Ключевой момент доказательства состоит в том, чтобы отдельно рассмотреть
положительные и отрицательные члены ряда. Для этого введём такие
обозначения:
Для этого введём такие
обозначения:
a+k:={ak,ak>0,0,ak<0,,a−k:={0,ak>0,ak,ak<0.
Тогда ряд
∞∑k=1a+k(28.17)
состоит только из его положительных слагаемых исходного ряда, а
∞∑k=1a−k(28.18)
только из отрицательных. Заметим, что
ak:=a+k+a−k,|ak|=a+k−a−k.
Докажем, что оба ряда (28.17) и (28.18) расходятся. Действительно, пусть, например, ряд ∑∞k=1a+k сходится (другой случай рассматривается так же). Тогда
∞∑k=1a−k=∞∑k=1(ak−a+k)=∞∑k=1ak−∞∑k=1a+k
тоже сходится, как разность сходящихся рядов (см. утверждение 2). Но в этом случае и ряд
∞∑k=1|ak|=∞∑k=1(a+k−a−k)=∞∑k=1a+k−∞∑k=1a−k
тоже сходится, а это противоречит предположению, что исходный ряд ∑∞k=1ak сходится лишь условно, а не абсолютно.
Итак, оба ряда (28.18) и (28.17) расходятся. Первый состоит
только из неотрицательных слагаемых. Единственный способ, каким он может
расходиться, то есть не иметь предела — это стремиться к плюс бесконечности.
Действительно, последовательность частичных сумм {S+N} неубывает.
Она не может быть ограниченной сверху, поскольку неубывающая ограниченная
сверху последовательность имеет предел по теореме
Вейерштрасса 2. Значит, она не является ограниченной, то
есть для всякого C найдётся такое N, что S+N>C. Но в силу
неубывания, для всех n>N, S+n≥S+N>C. Значит, S+n→+∞ при n→∞.
Первый состоит
только из неотрицательных слагаемых. Единственный способ, каким он может
расходиться, то есть не иметь предела — это стремиться к плюс бесконечности.
Действительно, последовательность частичных сумм {S+N} неубывает.
Она не может быть ограниченной сверху, поскольку неубывающая ограниченная
сверху последовательность имеет предел по теореме
Вейерштрасса 2. Значит, она не является ограниченной, то
есть для всякого C найдётся такое N, что S+N>C. Но в силу
неубывания, для всех n>N, S+n≥S+N>C. Значит, S+n→+∞ при n→∞.
Аналогично доказывается, что ряд (28.18) стремится к минус бесконечности.
Точная подгонка. Пусть из последовательности {a+k} выкинули все нулевые члены. Подпоследовательность, составленную из оставшихся членов, назовём {b+m}. Порядок следования членов последовательности {b+m} — такой же, как в {a+k}, просто все нулевые пропущены.
Аналогично определим последовательность {b−l} — последовательность
из всех ненулевых членов {a−k}, идущих в том же порядке, в котором они
были.
Иными словами, {b+m} и {b−l} — это последовательности положительных и отрицательных членов исходной последовательности {ak}.
Эта лекция читается в конце декабря, так что можно представить себе, что {b+m} — это мешок с бесконечным количеством подарков, каждый подарок имеет свой размер, влияющий на то, насколько повышается настроение у человека, которому вы его дарите. Про этот мешок вы знаете, что подарки в нём пронумерованы, и что мешок этот бесконечно большой, подарков в нём достаточно, чтобы поднять настроение на любой уровень.
Тогда {b−l} — это мешок антиподарков, которые снижают настроение, а не повышают его. Подарки в нём также пронумерованы и имеют в совокупности неограниченный потенциал для снижения настроения.
Пусть теперь нам задано какое-то число c∈R. Мы будем
выписывать элементы последовательностей b+m и b−l таким образом,
чтобы сумма выписанных элементов стремилась к c. Каждый элемент будет
выписан ровно один раз, и до любого элемента мы рано или поздно доберёмся.
Алгоритм устроен так. Допустим, c≥0, обратный случай рассматривается аналогично. Мы начинаем из точки 0 и будем выписывать элементы из последовательности {b+m} по порядку, до тех пор, пока сумма выписанных элементов не превзойдёт c. Если в какой-то момент эта сумма попала ровно в c, выпишем ещё один элемент. Визуально это соответствует тому, что мы делаем скачки вправо на величину b+1, b+2 и т.д., до тех пор, пока не «перескочим» через c.
Как только это произошло, мы меняем направление. Теперь будем выписывать элементы из последовательности {b−l} по порядку. Они отрицательные, поэтому сумма всех выписанных элементов будет каждый раз сдвигаться влево на модуль очередного выписанного элемента. В какой-то момент мы перескочим через c (теперь в обратном направлении, слева направо). Сразу после этого нужно снова сменить направление движения.
Теперь мы опять должны выписывать элементы из {b+m}, продолжая ровно
с того места, где остановились в прошлый раз. Если последний выписанный нами
на предыдущем этапе элемент был {b+m1}, то начать надо с элемента
{b+m1+1}. И снова мы выписываем элементы из {b+m} до тех
пор, пока сумма всех элементов (включая все выписанные ранее) не превзойдёт
c. В этот момент мы снова переключимся, и будем так продолжать до
бесконечности.
И снова мы выписываем элементы из {b+m} до тех
пор, пока сумма всех элементов (включая все выписанные ранее) не превзойдёт
c. В этот момент мы снова переключимся, и будем так продолжать до
бесконечности.
Почему этот алгоритм работает.
Я утверждаю, что описанный нами алгоритм реализует искомую перестановку — а именно, что получится последовательность, которая является перестановкой исходной последовательности {ak}, и что предел её частичных сумм равен c.
Во-первых, этот алгоритм никогда не остановится, и будет делать бесконечное
количество переключений между движением вправо и движением влево. Почему
так? Потому что сумммы (28.17) и (28.18) расходятся, и
значит в наших «мешках с подарками и антиподарками» подарков достаточно,
чтобы сделать сколь угодно хорошее и сколь угодно плохое настроение. Более
того, поскольку начальные члены ряда не влияют на сумму, эти свойства
сохранятся и после того, как какое-то конечное количество слагаемых из
последовательностей {b+m} и {b−l} было выписано. Значит мы
всегда можем взять достаточно много элементов из «хвостов» этих
последовательностей, чтобы сдвинуться как угодно далеко вправо или как
угодно далеко влево. Значит, нам всегда удастся перескочить через c и
сменить направление движения.
Значит мы
всегда можем взять достаточно много элементов из «хвостов» этих
последовательностей, чтобы сдвинуться как угодно далеко вправо или как
угодно далеко влево. Значит, нам всегда удастся перескочить через c и
сменить направление движения.
В ходе каждого этапа движения вправо или влево из соответстующей последовательности берётся по крайней мере один элемент. По построению, мы не пропускаем никакие элементы и не повторяем одни и тот же элемент дважды. Поскольку этапов бесконечно много, это означает, что любой элемент рано или поздно будет выписан, причём ровно один раз. Это означает, что новая последовательность — перестановка старой.
Наконец, почему предел её частичных сумм стремится к c? Заметим,
что в силу необходимого условия сходимости, ak→0 при k→∞ и значит a+k→0 и a−k→0. Это
означает, что limm→∞b+m=0 и liml→∞b−l=0. То есть скачки, которые мы совершаем каждый раз, стремятся к нулю.
Однако, расстояние от c до очередной частичной суммы не превосходит
модуля длины последнего скачка, после которого мы перескочили через c. Этот скачок равен соответствующему элементу последовательности ak, и его
номер стремится к бесконечности, поскольку при каждом проходе «вправо» мы
берём как минимум один элемент из последовательности положительных членов, а
при проходе «влево» берём как минимум один элемент из последовательности
отрицательных членов. Значит, k как минимум не меньше, чем число проходов
вправо и влево. Поэтому расстояние от c до очередной частичной суммы
стремится к нулю.
Этот скачок равен соответствующему элементу последовательности ak, и его
номер стремится к бесконечности, поскольку при каждом проходе «вправо» мы
берём как минимум один элемент из последовательности положительных членов, а
при проходе «влево» берём как минимум один элемент из последовательности
отрицательных членов. Значит, k как минимум не меньше, чем число проходов
вправо и влево. Поэтому расстояние от c до очередной частичной суммы
стремится к нулю.
Теорема доказана.∎
28.4Заключение
Ряды естественным образом возникают в ситуациях, когда есть какая-то величина,
меняющаяся дискретно (в отдельные моменты времени), и нас интересует, как это
величина накапливается. Сложные проценты в финансах, расчёты платежей в теории
игр, математические ожидания дискретных случайных величин в теории вероятностей
— во всех этих областях появляются ряды. Особенно важно понимать, какие ряды
сходятся, а какие нет — и мы подробно обсудили несколько достаточно
универсальных признаков, применимых в широком спектре ситуаций. К сожалению,
нахождение значений рядов — задача ещё более сложная, чем нахождение сумм
интегралов. Впрочем, если вы хотите углубиться в эту тему, могу рекомендовать
книгу «Конкретная математика. Основание информатики» (Р. Грэхем, Д. Кнут, О.
Поташник). Там эта тема обсуждается подробно.
К сожалению,
нахождение значений рядов — задача ещё более сложная, чем нахождение сумм
интегралов. Впрочем, если вы хотите углубиться в эту тему, могу рекомендовать
книгу «Конкретная математика. Основание информатики» (Р. Грэхем, Д. Кнут, О.
Поташник). Там эта тема обсуждается подробно.
А мы подходим к концу курса. Осталась буквально одна тема. И это будет что-то новое!
← Предыдущая глава Следующая глава →
Сумма ряда на практике
Вычислить сумму ряда можно только в случае, когда ряд сходится. Если ряд расходится то сумма ряда бесконечна и нет смысла что-то вычислять. Ниже приведены примеры из практики нахождения суммы ряда, которые задавали в Львовском национальном университете имени Ивана Франка. Задания на ряды подобраны так, что условие сходимости выполняется всегда, однако проверку на сходимость мы выполнять будем. Эта и следующие за ней статьи составляют решение контрольной работы по анализе рядов.
Пример 1. 4 Вычислить сумму рядов:
4 Вычислить сумму рядов:
а)
Вычисления: Поскольку граница общего члена ряда при номере следующему до бесконечности равна 0
то данный ряд сходится. Вычислим сумму ряда. Для этого преобразуем общий член, разложив его на простейшие дроби I и II типа. Методика разложения на простые дроби здесь приводиться не будет (хорошо расписана при интегрировании дробей), а лишь запишем конечный вид разложения
В соответствии с этим можем сумму расписать через сумму ряда образованного из простейших дробей, а дальше из разницы сумм рядов
Далее расписываем каждый ряд в явную сумму и выделяем слагаемые (подчеркивание), которые превратятся 0 после сложения. Таким образом сумма ряда упростится к сумме 3 слагаемых (обозначены черным), что в результате даст 33/40.
На этом базируется вся практическая часть нахождения суммы для простых рядов.
Примеры на сложные ряды сводятся к сумме бесконечно убывающих прогрессий и рядов, которые находят через соответствующие формулы, но здесь такие примеры рассматривать не будем.
б)
Вычисления: Находим границу n-го члена суммы
Она равна нулю, следовательно заданный ряд сходится и имеет смысл искать его сумму. Если граница отличная от нуля, то сумма ряда равна бесконечности со знаком «плюс» или «минус».
Найдем сумму ряда. Для этого общий член ряда который является дробью превратим методом неопределенных коэффициентов к сумме простых дробей I типа
Далее по инструкции которая приводилась ранее записываем сумму ряда через соответствующие суммы простейших дробей
Расписываем суммы и выделяем слагаемые, которые станут равными 0 при суммировании.
В результате получим сумму нескольких слагаемых (выделенные черным) которая равна 17/6.
Пример 1.9 Найти сумму ряда:
а)
Вычисления: Вычислениям границы
убеждаемся что данный ряд сходится и можно находить сумму. Далее знаменатель функции от номера n раскладываем на простые множители, а весь дробь превращаем к сумме простых дробей I типа
Далее сумму ряда в соответствии с расписанием записываем через два простые
Ряды записываем в явном виде и выделяем слагаемые, которые после добавления дадут в сумме ноль. Остальные слагаемые (выделенные черным) и представляет собой конечную сумму ряда
Остальные слагаемые (выделенные черным) и представляет собой конечную сумму ряда
Таким образом, чтобы найти сумму ряда надо на практике свести под общий знаменатель 3 простых дроби.
б)
Вычисления: Граница члена ряда при больших значениях номера стремится к нулю
Из этого следует что ряд сходится, а его сумма конечна. Найдем сумму ряда, для этого сначала методом неопределенных коэффициентов разложим общий член ряда на три простейшего типа
Соответственно и сумму ряда можно превратить в сумму трех простых рядов
Далее ищем слагаемые во всех трех суммах, которые после суммирования превратятся в ноль. В рядах, содержащих три простых дроби один из них при суммировании становится равным нулю (выделен красным). Это служит своеобразной подсказкой в вычислениях
Сумма ряда равна сумме 3 слагаемых и равна единице.
Пример 1.15 Вычислить сумму ряда:
а)
Вычисления: При общем член ряда стремящемся к нулю
данный ряд сходится. Преобразуем общий член таким образом, чтобы иметь сумму простейших дробей
Преобразуем общий член таким образом, чтобы иметь сумму простейших дробей
Далее заданный ряд, согласно формулам расписания, записываем через сумму двух рядов
После записи в явном виде большинство членов ряда в результате суммирования станут равны нулю. Останется вычислить сумму трех слагаемых.
Сумма числового ряда равна -1/30.
б)
Вычисления: Поскольку граница общего члена ряда равна нулю,
то ряд сходится. Для нахождения суммы ряда разложим общий член на дроби простейшего типа.
При разложении использовали метод неопределенных коэффициентов. Записываем сумму ряда из найденного расписание
Следующим шагом выделяем слагаемые, не вносящие никакого вклада в конечную сумму и остальные оставшиеся
Сумма ряда равна 4,5.
Пример 1.25 Вычислить сумму рядов:
а)
Вычисления: Находим границу общего члена ряда
Поскольку она равна нулю то ряд сходится. Можем найти сумму ряда. Для этого по схеме предыдущих примеров раскладываем общий член ряда через простейшие дроби
Это позволяет записать ряд через сумму простых рядов и, выделив в нем слагаемые, упростив при этом суммирование.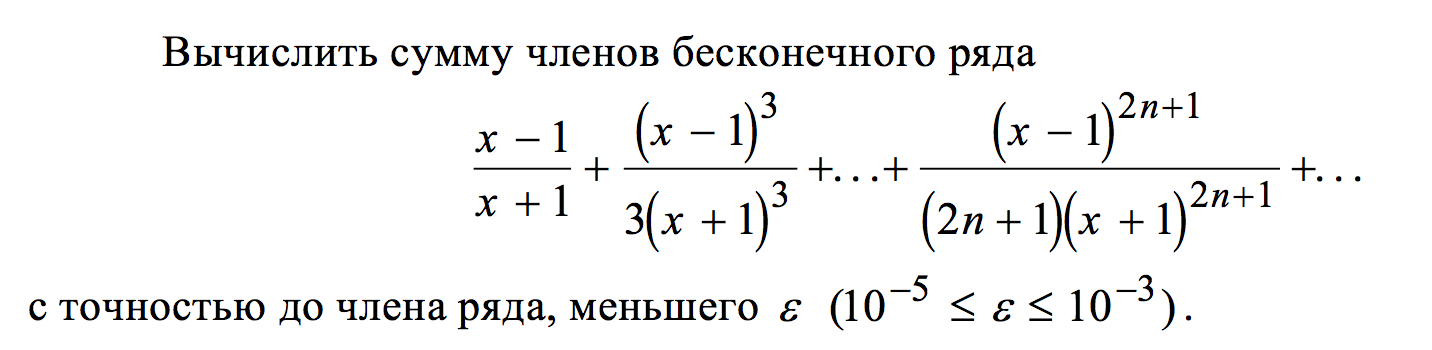
В этом случае останется одно слагаемое которое равен единице.
б)
Вычисления: Находим границу общего члена ряда
и убеждаемся что ряд сходится. Далее общий член числового ряда методом неопределенных коэффициентов раскладываем на дроби простейшего типа.
Через такие же дроби расписываем сумму ряда
Записываем ряды в явном виде и упрощаем к сумме 3 слагаемых
Сумма ряда равна 1/4.
На этом ознакомление со схемами суммирования рядов завершено. Здесь еще не рассмотрены ряды, которые сводятся к сумме бесконечно убывающей геометрической прогрессии, содержащие факториалы, степенные зависимости и подобные. Однако и приведенный материал будет полезен для студентов на контрольных и тестах.
- Назад
- Вперёд
Сумма ряда x в степени n – dj-sensor.ru
Содержание
- Введите данные для подчета суммы ряда
- Сходимость ряда
- Правила ввода выражений и функций
- Лучшие эксперты в этом разделе
Введите данные для подчета суммы ряда
Найдем сумму ряда чисел. Если не получается ее найти, то система вычисляет сумму ряда с определенной точностью.
Если не получается ее найти, то система вычисляет сумму ряда с определенной точностью.
Сходимость ряда
Данный калькулятор умеет определять – сходится ли ряд, также показывает – какие признаки сходимости срабатывают, а какие – нет.
Также умеет определять сходимость степенных рядов.
Также строится график ряда, где можно увидеть скорость сходимости ряда (или расходимости).
Правила ввода выражений и функций
© Контрольная работа РУ – калькуляторы онлайн
Проверить сходимость ряда можно несколькими способами. Во-первых можно просто найти сумму ряда. Если в результате мы получим конечное число, то такой ряд сходится. Например, поскольку
то ряд сходится. Если нам не удалось найти сумму ряда, то следует использовать другие методы для проверки сходимости ряда.
Одним из таких методов является признак Даламбера, который записывается следующим образом:
здесь и соответственно n-ый и (n+1)-й члены ряда, а сходимость определяется значением D: Если D 1 – расходится.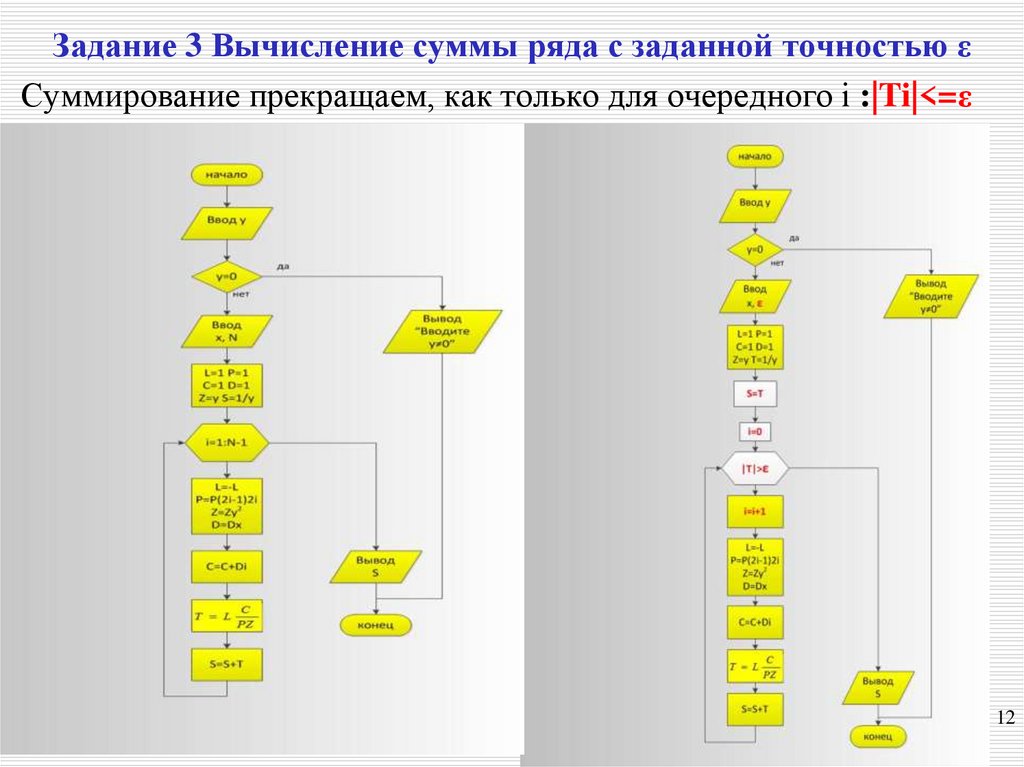 При D = 1 – данный признак не даёт ответа и нужно проводить дополнительные исследования.
При D = 1 – данный признак не даёт ответа и нужно проводить дополнительные исследования.
В качестве примера, исследуем сходимость ряда с помощью признака Даламбера. Сначала запишем выражения для и . Теперь найдем соответствующий предел:
Поскольку , в соответствии с признаком Даламбера, ряд сходится.
Еще одним методом, позволяющим проверить сходимость ряда является радикальный признак Коши, который записывается следующим образом:
здесь n-ый член ряда, а сходимость, как и в случае признака Даламбера, определяется значением D: Если D 1 – расходится. При D = 1 – данный признак не даёт ответа и нужно проводить дополнительные исследования.
В качестве примера, исследуем сходимость ряда с помощью радикального признака Коши. Сначала запишем выражение для . Теперь найдем соответствующий предел:
Читайте также: Что означает три точки в математике
Поскольку 1′ title=’15625/64>1′ /> , в соответствии с радикальным признаком Коши, ряд расходится.
Стоит отметить, что наряду с перечисленными, существуют и другие признаки сходимости рядов, такие как интегральный признак Коши, признак Раабе и др.
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет протестировать сходимость ряда. При этом, если калькулятор в качестве суммы ряда выдает конкретное число, то ряд сходится. В противном случае, необходимо обращать внимание на пункт «Тест сходимости ряда». Если там присутствует словосочетание «series converges», то ряд сходится. Если присутствует словосочетание «series diverges», то ряд расходится.
Ниже представлен перевод всех возможных значений пункта «Тест сходимости ряда»:
Консультации и решение задач по алгебре, геометрии, анализу, дискретной математике.
Лучшие эксперты в этом разделе
| Коцюрбенко Алексей Владимирович Статус: Модератор Рейтинг: 1690 | w3.org/2000/svg’%20viewBox=’0%200%200%200’%3E%3C/svg%3E» data-lazy-src=»https://rfpro.ru/images/nouser0.jpg»/> | epimkin Статус: Бакалавр Рейтинг: 386 | Roman Chaplinsky / Химик CH Статус: Модератор Рейтинг: 380 |
| Перейти к консультации №: |
Уважаемые эксперты! Пожалуйста, ответьте на вопрос:Укажите, чему равна сумма ряда х в степени n:
1) е в степени x (x-любое)
2) 1/(x+1) (-1 Последнее редактирование 17.11.2016, 16:03 Лысков Игорь Витальевич (Старший модератор)
Состояние: Консультация закрыта
Здравствуйте, Алексей Валентинович!
По-моему, правильный ответ 5).
P. S. Как Вы сами правильно заметили в мини-форуме консультации, всё-таки правильный ответ 3), а не 5).
0
Отправлять сообщения
модераторам могут
только участники портала.
ВОЙТИ НА ПОРТАЛ »
регистрация »
Елена Васильевна
Бакалавр
ID: 398750
Прикрепите фото задания
Гордиенко Андрей Владимирович
Специалист
ID: 17387
Известны следующие “стандартные” разложения:
Профессионал
ID: 304951
Мне не переслать фото.Там написан такой ряд: Сигма от 0 до бесконечности x в степени n. И сумма этого ряда равна одному из четырёх вариантов. Извините, забыл написать пятый вариант
5) Среди предложенных вариантов ответа нет верного
Читайте также: Что значит значок якоря в ворде
Гордиенко Андрей Владимирович
Специалист
ID: 17387
Тогда, по-моему, правильный ответ 5).
Гордиенко Андрей Владимирович
Специалист
ID: 17387
Почему-то невозможно отправить ответ и в этой консультации. 3+. при -1 Специалист
3+. при -1 Специалист
ID: 17387
Даже стыдно стало. Прошу извинить! Ответ, с Вашего согласия, исправлю. На будущее учту.
Возможность оставлять сообщения в мини-форумах консультаций доступна только после входа в систему.
Воспользуйтесь кнопкой входа вверху страницы, если Вы зарегистрированы или пройдите простую процедуру регистрации на Портале.
- Автор: Мария Сухоруких
- Распечатать
Оцените статью:
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Методы сложения чисел от 1 до 100 – BetterExplained
Существует популярная история о том, что у Гаусса, выдающегося математика, был ленивый учитель. Так называемый воспитатель хотел занять детей, чтобы он мог вздремнуть; он попросил класс сложить числа от 1 до 100.
Гаусс подошел со своим ответом: 5050. Так скоро? Учитель заподозрил обман, но нет. Сложение вручную было для лохов, и Гаусс нашел формулу, позволяющую обойти проблему:
Сложение вручную было для лохов, и Гаусс нашел формулу, позволяющую обойти проблему:
Давайте поделимся несколькими объяснениями этого результата и действительно поймем его интуитивно. Для этих примеров мы добавим 1 к 10, а затем посмотрим, как это применимо к 1 к 100 (или 1 к любому числу).
Техника 1: Парные номера
Парные номера — распространенный подход к этой проблеме. Вместо того, чтобы записывать все числа в один столбец, давайте обернем числа так:
1 2 3 4 5 10 9 8 7 6
Возникает интересный паттерн: сумма каждого столбца равна 11 . По мере увеличения верхней строки нижняя строка уменьшается, поэтому сумма остается прежней.
Поскольку 1 находится в паре с 10 (наше n), мы можем сказать, что в каждом столбце есть (n+1). А сколько у нас пар? Итак, у нас есть 2 равных строки, у нас должно быть n/2 пар.
, что является формулой выше.
Подождите, а как насчет нечетного количества предметов?
Ах, я рад, что вы подняли эту тему. Что, если мы сложим числа от 1 до 9? У нас нет четного количества предметов, которые можно соединить. Многие объяснения просто дадут объяснение выше и остановятся на этом. я не буду.
Что, если мы сложим числа от 1 до 9? У нас нет четного количества предметов, которые можно соединить. Многие объяснения просто дадут объяснение выше и остановятся на этом. я не буду.
Складываем числа от 1 до 9, но вместо того, чтобы начинать с 1, давайте считать с 0:
0 1 2 3 4 9 8 7 6 5
Считая от 0, мы получаем «дополнительный элемент» (всего 10), поэтому у нас может быть четное количество строк. Однако наша формула будет выглядеть немного иначе.
Обратите внимание, что сумма каждого столбца равна n (а не n+1, как раньше), поскольку 0 и 9 сгруппированы. И вместо того, чтобы иметь ровно n элементов в 2 строках (всего n/2 пар), у нас есть n + 1 элемент в 2 строках (всего (n + 1)/2 пар). Если вы подставите эти числа, вы получите:
, что является той же формулой, что и раньше. Меня всегда раздражало, что одна и та же формула работает и для нечетных, и для четных чисел — дробь не получится? Да, вы получаете ту же формулу, но по другим причинам.
Способ 2: Использование двух рядов
Описанный выше метод работает, но вы по-разному обрабатываете нечетные и четные числа. Разве нет лучшего способа? Да.
Вместо того, чтобы зацикливать числа, давайте запишем их в два ряда:
1 2 3 4 5 6 7 8 910 10 9 8 7 6 5 4 3 2 1
Обратите внимание, что у нас есть 10 пар, и каждая пара в сумме дает 10+1.
Сумма всех приведенных выше чисел равна
Но нам нужна сумма только одной строки, а не обеих. Итак, мы делим приведенную выше формулу на 2 и получаем:
Вот это круто (настолько круто, насколько могут быть ряды чисел). Это работает для нечетного или четного количества предметов одинаково!
Техника 3: Создание прямоугольника
Недавно я наткнулся на другое объяснение, свежий подход к старому объяснению спаривания. Разные объяснения работают лучше для разных людей, и мне это нравится больше.
Вместо того, чтобы писать числа, представьте, что у нас есть бобы. Мы хотим добавить 1 боб к 2 бобам, к 3 бобам… вплоть до 5 бобов.
Мы хотим добавить 1 боб к 2 бобам, к 3 бобам… вплоть до 5 бобов.
х х х х х х х х х х х х х х х
Конечно, мы могли бы использовать 10 или 100 бобов, но с 5 вы поняли идею. Как нам посчитать количество бобов в нашей пирамиде?
Ну, сумма явно 1 + 2 + 3 + 4 + 5. Но давайте посмотрим на это по-другому. Допустим, мы зеркально отразим нашу пирамиду (я буду использовать «о» для отраженных бобов), а затем опрокинем ее:
х о х о о о о о х х о о х х о о о о х х х о о о => х х х о о о х х х х о о о о х х х х о о х х х х х о о о о о х х х х х х о
Круто, да? Если вам интересно, действительно ли это совпадает, то это так. Взгляните на нижний ряд правильной пирамиды с 5′x (и 1°). В следующем ряду пирамиды на 1 x меньше (всего 4) и на 1 больше (всего 2), чтобы заполнить пробел. Так же, как и в паре, одна сторона увеличивается, а другая уменьшается.
Теперь пояснение: сколько у нас всего бобов? Ну, это просто площадь прямоугольника.
У нас есть n строк (количество строк в пирамиде мы не меняли), а ширина нашей коллекции (n + 1) единиц, так как 1 «о» стоит в паре со всеми «иксами».
Обратите внимание, что на этот раз нам все равно, будет ли n нечетным или четным — формула общей площади работает просто отлично. Если n нечетно, у нас будет четное количество элементов (n+1) в каждой строке.
Но, конечно, нам не нужна общая площадь (количество иксов и ноликов), нам нужно только количество иксов. Поскольку мы удвоили x, чтобы получить o, x сами по себе составляют лишь половину общей площади:
И мы вернулись к нашей первоначальной формуле. Опять же, количество x в пирамиде = 1 + 2 + 3 + 4 + 5 или сумма от 1 до n.
Метод 4. Усреднение
Все мы знаем, что
среднее = сумма / количество элементов
, что мы можем преобразовать в
сумма = среднее * количество элементов
Чтобы получить среднее значение, обратите внимание, что все числа распределены поровну. Для каждого большого числа на другом конце есть маленькое число. Давайте посмотрим на небольшой набор:
Для каждого большого числа на другом конце есть маленькое число. Давайте посмотрим на небольшой набор:
1 2 3
Среднее значение равно 2. 2 уже находится посередине, а 1 и 3 «сокращаются», поэтому их среднее значение равно 2.
Для четного числа предметов
1 2 3 4
среднее между 2 и 3 — это 2,5. Несмотря на то, что у нас есть дробное среднее, это нормально — поскольку у нас есть даже элементов, когда мы умножаем среднее значение на количество, эта уродливая дробь исчезнет.
Обратите внимание, что в обоих случаях 1 находится по одну сторону от среднего, а N одинаково далеко по другую. Таким образом, мы можем сказать, что среднее значение всего набора на самом деле является средним значением 1 и n: (1 + n)/2.
Подставляем это в нашу формулу
И вуаля! У нас есть четвертый способ думать о нашей формуле.
Так почему же это полезно?
Три причины:
1) Быстрое сложение чисел может быть полезным для оценки. Обратите внимание, что формула расширяется до этого:
Обратите внимание, что формула расширяется до этого:
Допустим, вы хотите сложить числа от 1 до 1000: предположим, вы получаете 1 дополнительного посетителя на свой сайт каждый день — сколько всего посетителей будет через 1000 дней? Так как тысяча в квадрате = 1 миллион, мы получаем миллионов / 2 + 1000/2 = 500 500 .
2) Эта концепция сложения чисел от 1 до N проявляется и в других местах, например, при вычислении вероятности парадокса дня рождения. Твердое понимание этой формулы поможет вашему пониманию во многих областях.
3) Самое главное, этот пример показывает, что есть много способов понять формулу. Может быть, вам нравится метод сопряжения, может быть, вы предпочитаете технику прямоугольника, или, может быть, есть другое объяснение, которое вам подходит. Не отказывайтесь от , если вы не понимаете — попробуйте найти другое объяснение, которое работает. Счастливая математика.
Кстати, есть более подробная информация об истории этой истории и возможной технике, которую использовал Гаусс.
Вариации
Вместо 1 до n, как насчет 5 до n?
Начните с обычной формулы (1 + 2 + 3 + … + n = n * (n + 1) / 2) и вычтите ненужную часть (1 + 2 + 3 + 4 = 4 * (4 + 1) / 2 = 10).
Сумма для 5 + 6 + 7 + 8 + … n = [n * (n + 1) / 2] – 10
И для любого начального числа a:
Сумма от a до n = [n * (n + 1) / 2] – [(a - 1) * a / 2]
Мы хотим избавиться от всех чисел от 1 до — 1.
Как насчет четных чисел, таких как 2 + 4 + 6 + 8 + … + n?
Просто удвойте обычную формулу. Чтобы сложить четные числа от 2 до 50, найдите 1 + 2 + 3 + 4 … + 25 и удвойте его:
Сумма 2 + 4 + 6 + … + n = 2 * (1 + 2 + 3 + … + n/ 2) = 2 * п/2 * (п/2 + 1) / 2 = п/2 * (п/2 + 1)
Итак, чтобы получить четные числа от 2 до 50, нужно сделать 25 * (25 + 1) = 650
Как насчет нечетных чисел, например 1 + 3 + 5 + 7 + … + n?
Это то же самое, что и четная формула, за исключением того, что каждое число на 1 меньше своего аналога (у нас есть 1 вместо 2, 3 вместо 4 и т. д.). Получаем следующее по величине четное число (n + 1) и убираем лишнее (n + 1)/2 «-1″ предметов:
д.). Получаем следующее по величине четное число (n + 1) и убираем лишнее (n + 1)/2 «-1″ предметов:
Сумма 1 + 3 + 5 + 7 + … + n = [(n + 1)/2 * ((n + 1)/2 + 1)] – [(n + 1) / 2]
Чтобы добавить 1 + 3 + 5 + … 13, возьмите следующее наибольшее четное (n + 1 = 14) и выполните
[14/2 * (14/2 + 1)] – 7 = 7 * 8 – 7 = 56 – 7 = 49
Комбинации: четы и смещения
Допустим, вам нужны четы из 50 + 52 + 54 + 56 + … 100. Найдите все четы
2 + 4 + 6 + … + 100 = 50 * 51
и вычесть ненужные
2 + 4 + 6 + … 48 = 24 * 25
Итак, сумма из 50 + 52 + … 100 = (50 * 51) – (24 * 25) = 1950
Фу! Надеюсь это поможет.
Рубиновые умники: вы можете проверить это, используя
(50..100).select {|x| х % 2 == 0 }.inject(:+)
1950 г.
Специалисты по Javascript, сделайте это:
[...Array(51).keys()].map(x => x + 50).filter(x => x % 2 == 0).reduce(( х, у) => х + у) 1950 г. // Примечание: имеется 51 число от 50 до 100 включительно.Забор!
Другие сообщения из этой серии
- Методы сложения чисел от 1 до 100
- Переосмысление арифметики: визуальное руководство
- Quick Insight: интуитивное значение подразделения
- Quick Insight: вычитание отрицательных чисел
- Удивительные закономерности в квадратных числах (1, 4, 9, 16…)
- Развлечение с модульной арифметикой
- Учимся считать (избегая проблемы с ограждением)
- Причудливое введение в системы счисления
- Еще один взгляд на простые числа
- Интуиция для золотого сечения
- Различные интерпретации числа ноль
Как суммировать в Excel Примеры и видео
Примеры показывают, как суммировать в Microsoft Excel с помощью простой функции СУММ или формул, которые суммируют на основе одного или нескольких критериев.
Во-первых, для быстрого обзора посмотрите видео: 7 способов суммирования в Excel. Затем прокрутите вниз, чтобы увидеть больше видеороликов о функции Sum, письменных инструкций и бесплатных книг Excel. Кроме того, внизу страницы есть список тем, если вы ищете конкретную тему «Как суммировать».
Кроме того, внизу страницы есть список тем, если вы ищете конкретную тему «Как суммировать».
Автор: Дебра Далглиш
Обзор: 7 способов суммирования в экселеЧтобы получить краткий обзор 7 различных способов суммирования чисел с помощью функций Excel, вы можете посмотреть это 9-минутное видео. Под видео есть письменные шаги и снимки экрана для всех примеров. Временная шкала видео (синие ссылки ведут к письменным шагам под видео)
|
Суммирование диапазона ячеек — Функция СУММ
Самый быстрый и простой способ суммирования диапазона ячеек – использовать кнопку Excel AutoSum. Он автоматически вводит функцию СУММ Excel в выбранной ячейке. Функция СУММ суммирует одно или несколько чисел в диапазоне ячеек.
В первом примере ниже показано, как использовать функцию автосуммы
- Выберите пустую ячейку в строке под ячейками, которые вы хотите
сумма, ячейка A5 в этом примере.

- Щелкните команду AutoSum на вкладке «Главная» ленты,
или используйте сочетание клавиш: Alt + = - В активной ячейке появится формула СУММ со ссылкой на
ячейки выше. На снимке экрана ниже есть формула СУММ в
ячейка А5: =СУММ(A1:A4)
ПРИМЕЧАНИЕ. Если все ячейки не включаются автоматически, можно расширить кадр, чтобы выбрать их. - Нажмите клавишу Enter, чтобы завершить ввод.
Настройка функции SUM
Вместо использования команды AutoSum для вставки функции SUM можно введите функцию вручную.
Настройка функции СУММ (синтаксис): СУММ(число1 , [число2],…).
- Имеет один обязательный аргумент: число1
- Он также имеет необязательные аргументы (заключенные в квадратные
скобки): [номер2],..

Эти аргументы могут быть ссылками на ячейки или могут быть введены в формулу.
В приведенном выше примере ( =СУММ(A1:A4) ) есть один аргумент — ссылка на ячейки A1:A4.
Исправить числа, которые не складываютсяНекоторые значения Excel выглядят как числа, но не складываются, так как Excel думает, что это текст. Иногда вы можете решить проблему с помощью Paste Специальный. Посмотрите этот короткий видеоурок, чтобы увидеть шаги Для получения письменных инструкций и других способов решения проблемы перейдите на страницу «Числа не складываются». Общий итог по диапазону ячеек Одним быстрым шагом вы можете вычислить строку, столбец и общие итоги для
диапазон ячейки. Посмотрите этот короткий Excel
Видео Grand Totals, чтобы увидеть, как это сделать. Быстрый общий итог для диапазона ячеек
|
ИтогоЧтобы увидеть промежуточный итог в каждой строке списка Excel, вы можете использовать Функция SUM с блокировкой начальной строки как абсолютной ссылки. Ниже приведены немного другие шаги,
Промежуточный итог в списке рабочих листов Для списка рабочих листов (не именованной таблицы Excel) в этом видео показано, как настроить формулу промежуточного итога и заблокировать начальную строку. Промежуточный итог — список рабочих листовДля списка рабочих листов (не именованной таблицы Excel) выполните следующие действия, чтобы создать промежуточный итог. На приведенном ниже снимке экрана суммы вводятся в столбец C, а текущий итог рассчитывается в столбце D.
Как работает формулаФормула использует абсолютную ссылку на строку 2 в качестве отправной точки — C$2 — и относительная ссылка на конечную точку — C2 Это гарантирует, что начальная точка не изменится при копировании
формулу до строк ниже.
Промежуточный итог в таблице ExcelДля именованной таблицы Excel нельзя использовать формулу списка рабочих листов из предыдущего раздела. Сначала я покажу вам задачу с этой формулой, а затем вы увидите формулу, которая работает в именованной таблице. Проблема с промежуточным итогомПосле того, как вы введете формулу в ячейку D2 указанной таблицы Excel, она автоматически заполнится, и промежуточный итог будет выглядеть правильно. Но, как только вы начинаете новую строку внизу таблицы, формула в последней строке меняется. Перед добавлением строки в ячейке D6 была следующая формула:
Как только в строке 7 была запущена следующая запись, формула в D6 автоматически изменилась.
По мере добавления каждой новой строки формулы в нижних строках продолжают изменяться, чтобы показать номер последней строки. Формула промежуточного итога для именованной таблицыЧтобы избежать этой проблемы, мы будем использовать немного другую формулу для промежуточного итога в именованной таблице Excel. На приведенном ниже снимке экрана суммы вводятся в столбце C, а текущий итог рассчитывается в столбце D.
Как работает формулаФормула использует абсолютную ссылку на ячейку заголовка в качестве отправной точки — 1 канадский доллар
Для конечной точки есть ссылка на структурированную таблицу — [@Amt]
На этом снимке экрана показано, что при запуске новой строки в ячейке C6 по-прежнему отображается исходная формула, а суммы промежуточных сумм в каждой строке верны |
Суммирование диапазона ячеек — OFFSET Если вы вставите строку непосредственно над функцией СУММ в предыдущем примере,
новая строка не может быть включена в SUM.
|
Сумма ячеек, соответствующих критериям — СУММЕСЛИВот 3 способа суммирования ячеек, соответствующих критериям, с помощью функции СУММЕСЛИ в Excel: — Точное соответствие критерию — Критерий совпадения в строка – Критерий соответствия с использованием оператор Совет : Для примеров того, как суммировать на основе нескольких критериев, перейдите к ячейкам суммы с сложный раздел множественных критериев , ниже. Настройка функции СУММЕСЛИНастройка функции СУММЕСЛИ (синтаксис): СУММЕСЛИ(диапазон , критерии , [ диапазон_суммы ])
Эти аргументы могут быть ссылками на ячейки или могут быть введены в формулу. Точное соответствие критерию Вы можете рассчитать итог для строк, соответствующих определенному критерию.
Примечание : Вместо того, чтобы вводить критерий в формулу, вы можете указать
в ячейку. Вы можете добавить ячейки, содержащие критерий, как часть содержимого ячейки. В этом примере все заказы Pen, Gel Pen и Pencil будут суммироваться, потому что они содержат строку «ручка».
Примечание : Вместо того, чтобы вводить критерий в формулу, вы можете указать
в ячейку. Например, формула на шаге 9выше можно изменить на: |
Критерий и оператор Вы можете использовать оператор с условием. В приведенных ниже примерах см.
как объединить их в формуле СУММЕСЛИ. Пример 1 Пример 2 Пример 1 — сумма строк больше заданного значенияВ этом примере только строки, в которых количество торговых представителей больше больше или равно десяти, будут включены в общую сумму.
Примечание : Вместо того, чтобы вводить критерий в формулу, вы можете указать
в ячейку. Например, формула на шаге 9выше можно изменить на: Пример 2 — скользящие итоги за 12 месяцев В этом примере только строки за предыдущие 11 месяцев и текущий
месяц, будут включены в общую сумму. Даты находятся в столбце A, и список должен быть отсортирован по дате. Ежемесячный суммы указаны в столбце B.
Как это работает Формула проверяет даты в столбце A, начиная со строки 2 (A$2), и вниз к текущей строке (A2) =СУММЕСЛИ( A$2:A2 Функция ДАТА вычисляет дату на 11 месяцев раньше даты. в текущей строке ДАТА(ГОД(A2),МЕСЯЦ(A2)-11,ДЕНЬ(A2)) Оператор >= проверяет даты, которые больше или равны эта дата, «>=» & ДАТА(ГОД(A2),МЕСЯЦ(A2)-11,ДЕНЬ(A2)) Для строк, соответствующих критерию, формула суммирует суммы в столбце B, начиная со строки 2 (B$2) и заканчивая текущей строкой (B2) B$2:B2 |
Сумма ячеек, соответствующих нескольким критериям — СУММЕСЛИМН В Excel 2007 и более поздних версиях вы можете использовать функцию СУММЕСЛИМН для
вычислить итог для строк, которые соответствуют двум или более критериям. Полную расшифровку видео можно найти на странице суммирования сумм по 2 критериям. СУММЕСЛИМН Настройка функцииНастройка функции СУММЕСЛИМН (синтаксис): СУММЕСЛИМН(диапазон , критерии , [ диапазон_суммы ])
Эти аргументы могут быть ссылками на ячейки или могут быть введены в формулу. Соответствие нескольким критериямВ этом примере функция СУММЕСЛИМН суммирует суммы в столбце D на основе 2 критериев :
Эти критерии вводятся в ячейки F6 (Отправлено) и G6 (10) Выполните следующие действия, чтобы создать формулу СУММЕСЛИМН:
|
Формулы со ссылками на таблицы Если вы создаете формулы со ссылками на таблицы, а затем пытаетесь скопировать эти формулы в соседние столбцы, вы можете столкнуться с проблемами. Проблемы со ссылками на таблицыВ этой сводке продаж есть формула СУММЕСЛИМН в ячейке C5, которая показывает правильную сумму продаж батончиков в Восточном регионе. =СУММЕСЛИМН(Данные_продаж[Количество], Данные_продаж[Регион],$B5, Данные_продаж[Категория],4C$) Однако, если вы наведете указатель на маркер заполнения в ячейке C5 и перетащите вправо, формула покажет неверный итог в ячейке D5. Если вы проверите формулу в ячейке D5, все ссылки на таблицы сместятся на один столбец вправо, потому что формула была перетащена на один столбец вправо. =СУММЕСЛИМН(Данные_продаж[Общая стоимость],Данные_продаж[Категория],$B5, Данные_продаж[Продукт],D$4)
 Ни один из этих критериев не найден, поэтому результат равен нулю. Чтобы предотвратить эту проблему смещения ссылок на таблицы, не перетаскивайте маркер заполнения для копирования. Вместо этого используйте один из следующих методов:
Заполнить справа
Копировать и вставить
 |
СУММЕСЛИМН с несколькими критериями И/ИЛИВ приведенном ниже списке можно использовать формулу СУММЕСЛИМН для суммирования строк, где:
И
Формула в ячейке G9 будет:
Формула с несколькими критериями для И/ИЛИОднако вместо одной категории мы хотели бы рассчитать общее количество для двух и более категорий. В этом примере мы посчитаем общую сумму где:
ИЛИ
Две категории вводятся в ячейки G6:G7 рабочего листа. Массивная формулаЧтобы вычислить итог, мы добавим в формулу СУММЕСЛИМН функцию СУММ, и введите формулу в виде массива.
|
| Сумма ячеек соответствует нескольким критериям —
СУММПРОДУКТ Соответствие нескольким критериям В Excel 2003 и более ранних версиях можно использовать функцию СУММПРОИЗВ для вычисления
общее количество строк, соответствующих двум или более критериям. В этом примере только строки со статусом «Активно». и количество посещений больше или равно десяти будет включено в сумме.
|
Сумма первых 5 номеров в спискеИспользуйте вместе функцию СУММ и функции НАИБОЛЬШИЙ, чтобы сложить наибольшую номера в списке. Версия 1 — несколько лучших номеров Если нужно просуммировать несколько чисел, напр. топ 3, вы можете ввести цифры
в формулу. =СУММ(НАИБОЛЬШИЙ(A1:A7,{1,2,3})) Результат: 70+60+50 = 180 Примечание : Вторые 50 не включаются в результат, хотя он делит 3-е место. Версия 2 — Много лучших номеровЕсли необходимо суммировать много верхних чисел, вы можете включить функцию ДВССЫЛ. в формуле с функцией СУММ. В функции ДВССЫЛ используйте строку числа, которые представляют числа, которые вы хотите включить. В этом примере используются строки 1:10, поэтому первые 10 чисел в указанном диапазоне будут суммироваться.
Версия 3 — Переменные верхние номера Если необходимо суммировать переменное количество верхних чисел, вы можете включить
функция ДВССЫЛ в формуле с функцией СУММ, как показано выше,
и обратитесь к ячейке, содержащей переменную.
|
Сумма сумм в диапазоне датЧтобы суммировать суммы на основе диапазона дат, вы можете использовать функцию СУММЕСЛИМН. в Excel 2007 или более поздних версиях. Посмотрите это видео, чтобы увидеть шаги, и письменные инструкции находятся под видео. Сумма сумм в диапазоне дат Чтобы суммировать суммы за определенный диапазон дат, используйте функцию СУММЕСЛИМН.
(Excel 2007 и более поздние версии) или функцию СУММЕСЛИ. — Всего с СУММЕСЛИМН — Всего с SUMIF В этом примере на лист вводятся даты начала и даты окончания. Даты указаны в столбце A, а проданные единицы — в столбце B. Дополнительные примеры диапазона дат см. на странице Сумма или количество для диапазона дат. Использование СУММЕСЛИМН для вычисления итогового значения для диапазона датВ Excel 2007 и более поздних версиях можно использовать функцию СУММЕСЛИМН для рассчитать итог на основе нескольких критериев. Мы будем использовать формулу СУММЕСЛИМН чтобы суммировать все единицы, где дата продажи:
Вот формула, которая вводится в ячейку D5: =СУММЕСЛИМН($B$2:$B$9,$A$2:$A$9,»>=» & $D$2, $A$2:$A$9,»<=" и $Е$2)
В этом примере результат для выбранного диапазона дат составляет всего Продано 494 единицы. Чтобы проверить, вы можете выбрать ячейки B3: B6 и посмотреть на общее количество отображается в строке состояния Excel. Чтобы получить общее количество единиц для другого диапазона дат, измените дату начала
в ячейке D2 и/или Дата окончания в ячейке E2. Использование СУММЕСЛИ для вычисления итогового значения для диапазона датВ Excel 2003 и более ранних версиях можно использовать функцию СУММЕСЛИ для рассчитать итог по одному критерию. Мы будем использовать одну формулу СУММЕСЛИ чтобы суммировать все единицы, где дата продажи:
Затем мы воспользуемся другой формулой СУММЕСЛИ, чтобы вычесть любые значения, где есть дата
Вот формула, которая вводится в ячейку D5: =СУММЕСЛИ($A$2:$A$9,»>=»
&$D$2,$B$2:$B$9)
В этом примере результат для выбранного диапазона дат составляет всего
Продано 494 единицы. Чтобы получить общее количество единиц для другого диапазона дат, измените дату начала. в ячейке D2 и/или Дата окончания в ячейке E2. |
Суммируйте отфильтрованный список с промежуточным итогомПосле того, как вы отфильтруете строки в списке, вы можете использовать функцию ПРОМЕЖУТОЧНЫЕ.ИТОГИ, вместо функции СУММ для суммирования чисел в видимых строках.
Примечание . В Excel 2003 и более поздних версиях можно использовать формулу: Промежуточные номера функцийПервый аргумент в функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ – это номер функции, который указывает, как числа должны быть рассчитаны. Есть 11 функций который вы можете использовать в качестве первого аргумента в функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ. Список в алфавитном порядке, так что это может помочь вам запомнить некоторые цифры, без обращения к справке Excel каждый раз. Каждая из функций указана дважды. Первая группа функций
под номерами 1-11. Каждая из функций указана дважды. Вторая группа функций номер 101-111. |
Суммировать отфильтрованный список с АГРЕГАТОМФункция АГРЕГАТ, представленная в Excel 2010, аналогична ПРОМЕЖУТОЧНОМУ ИТОГУ. функция, но она имеет больше функций и может игнорировать значения ошибок, а также как скрытые строки в данных. Посмотрите это видео, чтобы узнать, как настроить формулу АГРЕГАТ, и письменные инструкции находятся под видео. Суммирование отфильтрованного списка с AGGREGATE После фильтрации строк в списке можно использовать функцию АГРЕГАТ,
вместо функции СУММ для суммирования чисел в видимых строках. Этот
функция была представлена в Excel 2010. Аналогично функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ, АГРЕГАТ игнорирует скрытые строки и предлагает несколько функций, таких как SUM или AVERAGE, для выбранных данных. Однако у него 19функций по сравнению с ПРОМЕЖУТОЧНЫМИ ИТОГОМИ 11 функций. В отличие от функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ, АГРЕГАТ может быть настроен на игнорирование ошибок, а также скрытые строки и вложенные функции ПРОМЕЖУТОЧНЫЕ.ИТОГИ и АГРЕГАТ. Чтобы суммировать значения в отфильтрованном списке и игнорировать скрытые строки и ошибки:
Завершенная формула: =АГРЕГАТ(9,3,D2:D7) |
Сумма конкретных элементов в отфильтрованном спискеПример 1 Лоран Лонгр создал формулу, позволяющую работать с видимыми строками
после фильтра. Для получения информации см. Техника формулы мощности в этой статье.
на веб-сайте Джона Уокенбаха (больше не доступен). Используя этот метод, СУММПРОИЗВ можно использовать для суммирования видимых элементов. в отфильтрованной таблице. В следующем примере столбец D был отфильтрован для сумм, превышающих 100. Следующая формула суммирует общее количество суммы в строках, содержащих «ручка» в столбце A.
Пример 2 Еще один пример совместного использования СУММПРОИЗВ и ПРОМЕЖУТОЧНЫЙ ИТОГ см. в моем блоге Промежуточный итог и Суммарное произведение с фильтром. В рабочей книге Сэма есть список с полями «Продукт», «Регион» и «Количество». Он создал динамические именованные диапазоны для записей в каждом поле, используя ИНДЕКС и СЧЕТЧИК. Вы можете получить рабочую тетрадь Сэма в разделе «Загрузки» ниже. |
Получить образцы файлов
|
Как суммировать в Excel — Список тем
Вот темы, посвященные суммированию на этой странице
Обзор: 7 способов суммирования в Excel не суммировать
Общая сумма диапазон ячеек
Промежуточный итог
Сумма диапазона ячеек — СМЕЩЕНИЕ
Сумма ячеек, соответствующих одному критерию
0Sum -ячейки, которые соответствуют множественным критериям
Формулы с Ссылками на таблицы
Сумма с множественными и/или критериями
Сумма с Комплексными номерами
Sum TOP 5 номеры в списке
Sum TOP 5 в списке
SUM TOP 5 в списке
SUM TOP 5 в списке
Sum
Сумма сумм в диапазоне дат
Сумма отфильтрованного списка с ПРОМЕЖУТОЧНЫЙ ИТОГ
Сумма отфильтрованного списка с АГРЕГАТ
Сумма конкретных элементов в Отфильтрованный список
Получить образец рабочей книги
Дополнительные руководства по функциям
Список функций
Опции расчета
Формулы, Приступая к работе
Функция ПРОМЕЖУТОЧНЫЙ ИТОГ
СРЕДНЕЕ
СЧЁТ / СЧЁТЕСЛИ
Сумма sql для данных в нескольких столбцах и по строкам с суммой и процентом
Мы видели, как функция суммы используется для получения общего значения столбца в таблице MySQL. Теперь мы узнаем, как получить запрос на сумму в нескольких столбцах и для каждой записи таблицы. Для лучшего понимания немного изменим нашу таблицу учеников, добавив оценки по разным предметам для каждой записи. Теперь таблица будет такой.
Теперь мы узнаем, как получить запрос на сумму в нескольких столбцах и для каждой записи таблицы. Для лучшего понимания немного изменим нашу таблицу учеников, добавив оценки по разным предметам для каждой записи. Теперь таблица будет такой.| id | name | class | social | science | math | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | John Deo | Four | 75 | 84 | 78 | ||||||||||||||||||
| 2 | Max Ruin | Три | 54 | 67 | 85 | ||||||||||||||||||
| 3 | Три | 6 | Krish Star | Four | 50 | 51 | 53 | ||||||||||||||||
| 5 | John Mike | Four | 80 | 78 | 89 | ||||||||||||||||||
| 6 | Alex John | Four | 78 | 60 | 60 | ||||||||||||||||||
| 7 | My John Rob | Five | 77 | 68 | 83 | ||||||||||||||||||
| 8 | Asruid | Five | 55 | 50 | 55 | ||||||||||||||||||
| 9 | Tes Qry | Six | 68 | 60 | 62 | ||||||||||||||||||
| 10 | Big John | Four | 65 | 66 | 76 |
youtube.com/embed/QTmEfTUkhXk» title=»Sum of values of columns in MySQL table with GROUP BY , IN and CASE» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>
Мы напишем запрос для отображения суммы всех оценок каждого ученика. Обратите внимание, что здесь мы не будем использовать функцию sum sql внутри нашего запроса. Вот код.
ВЫБЕРИТЕ идентификатор, имя, класс, (общественное + наука + математика) КАК итого ОТ student_sum
| id | name | class | total |
|---|---|---|---|
| 1 | John Deo | Four | 237 |
| 2 | Max Ruin | Three | 206 |
| 3 | Арнольд | Три | 233 |
| 4 | Криш Стар | Четыре | 154 |
| 5 | John Mike | Four | 247 |
| 6 | Alex John | Four | 198 |
| 7 | My John Rob | Five | 228 |
| 8 | Asruid | Five | 160 |
| 9 | Tes Qry | Six | 190 |
| 10 | Big John | Четыре | 207 |
Несколько столбцов SUM
Связанный учебник
СУММА MySQL
MySQL Макс
MySQL Мин. Среднее значение MySQL
Среднее значение MySQL
ВЫБЕРИТЕ сумму (социальное + математика + естествознание) как общее ОТ student_sum
| всего |
| 2060 |
Расчет процента оценок
Предположим, что полная оценка по каждому предмету равна 95. Итак, чтобы получить процентную оценку каждого учащегося, мы должны умножить 95 на 3 (для трех предметов), а затем разделить это от общего числа и умножить на 100. Вот запрос.ВЫБЕРИТЕ имя, (( социальные сети + естественные науки + математика)/(95*3) * 100) в процентах ОТ `student_sum`
Отображение общей оценки в процентах
И общую оценку, и процент мы можем отобразить следующим образом.
ВЫБЕРИТЕ идентификатор, имя, класс (социальные науки + математика) как общее количество, (( социальные + науки + математика)/(95*3) * 100) AS процент ОТ `student_sum`Выход здесь.
| id | имя | класс | Всего | процент |
|---|---|---|---|---|
| 1 | John Deo | Four | 237 | 83.1579 |
| 2 | Max Ruin | Three | 206 | 72.2807 |
| 3 | Arnold | Three | 233 | 81.7544 |
| 4 | Krish Star | Four | 154 | 54.0351 |
| 5 | John Mike | Four | 247 | 86.6667 |
| 6 | Alex John | Four | 198 | 69.4737 |
| 7 | My John Rob | Five | 228 | 80. 0000 0000 |
| 8 | Asruid | Five | 160 | 56.1404 |
| 9 | Tes Qry | Six | 190 | 66.6667 |
| 10 | Big John | Четыре | 207 | 72,6316 |
ВЫБЕРИТЕ идентификатор, имя, класс (социальные науки + математика) как общее количество, ФОРМАТ((( социальные + естествознание + математика)/(95*3) * 100),2) в процентах ОТ `student_sum`
Сумма данных строки каждой записи
Теперь попробуем отобразить все оценки и их сумму для каждого ученика с помощью группировки. Обратите внимание, что id — уникальный столбец значения в нашей таблице. Вот запросВЫБЕРИТЕ идентификатор, имя, класс, социальные сети, математика, наука, сумма (социальные + математика + наука) как Total from student_sum GROUP BY idВыход здесь
| id | name | class | social | math | science | Total |
|---|---|---|---|---|---|---|
| 1 | John Deo | Four | 75 | 78 | 84 | 237 |
| 2 | Max Ruin | Three | 54 | 85 | 67 | 206 |
| 3 | Arnold | Three | 78 | 90 | 65 | 233 |
| 4 | Krish Star | Четыре | 50 | 53 | 51 | 154 |
| 154 | ||||||
| 154 | ||||||
. 0296 0296 | 89 | 78 | 247 | |||
| 6 | Alex John | Four | 78 | 60 | 60 | 198 |
| 7 | My John Rob | Five | 77 | 83 | 68 | 228 |
| 8 | Asruid | Five | 55 | 55 | 50 | 160 |
| 9 | Tes Qry | Six | 68 | 62 | 60 | 190 |
| 10 | Big John | Four | 65 | 76 | 66 | 207 |
Отображение от наибольшего к наименьшему
Мы можем перечислить, начиная с самой высокой оценки до самой низкой оценки, используя Order By Query.ВЫБЕРИТЕ идентификатор, имя, класс, социальные сети, математика, наука, сумма (социальные + математика + наука) как Total from student_sum GROUP BY id ORDER BY Total DESC
Отображение наивысшей и самой низкой оценки по всем предметам каждого учащегося
ВЫБЕРИТЕ id,name,GREATEST(социальные,науки,математика) как максимальное, НАИМЕНЕЕ(социальные,науки,математика) как min FROM student_sum;
| id | name | max | min |
|---|---|---|---|
| 1 | John Deo | 84 | 75 |
| 2 | Max Ruin | 85 | 54 |
| 3 | Arnold | 90 | 65 |
| 4 | Krish Star | 53 | 50 |
| 5 | John Mike | 89 | 78 |
| 6 | Alex John | 78 | 60 |
| 7 | My John Rob | 83 | 68 |
| 8 | Asruid | 55 | 50 |
| 9 | Tes Qry | 68 | 60 |
| 10 | Big John | 76 | 65 |
Displaying sum of all columns at last row
Как и в MS Excel, мы можем отобразить сумму всех столбцов и сумму всех оценок по предметам, используя UNION. Обратите внимание, что мы должны поддерживать одинаковое количество столбцов при использовании запроса UNION.
Обратите внимание, что мы должны поддерживать одинаковое количество столбцов при использовании запроса UNION.ВЫБЕРИТЕ идентификатор, имя, класс, социальные сети, математика, наука, сумма (социальные + математика + наука) как Total from student_sum GROUP BY id СОЮЗ ВЫБЕРИТЕ '','','Всего',сумма(социальные),сумма(математика),сумма(наука), сумма(социальная)+сумма(математика)+сумма(наука) от student_sumВывод (смотрите последнюю строку)
| id | name | class | social | math | science | Total |
|---|---|---|---|---|---|---|
| 1 | John Deo | Four | 75 | 78 | 84 | 237 |
| 2 | Макс Руин | Три | 54 | 85 | 67 | 206 |
| 3 | Three | 78 | 90 | 65 | 233 | |
| 4 | Krish Star | Four | 50 | 53 | 51 | 154 |
| 5 | John Mike | Four | 80 | 89 | 78 | 247 |
| 6 | Alex John | Four | 78 | 60 | 60 | 198 |
| 7 | My John Rob | Five | 77 | 83 | 68 | 228 |
| 8 | Asruid | Five | 55 | 55 | 50 | 160 |
| 9 | Tes Qry | Six | 68 | 62 | 60 | 190 |
| 10 | Big John | Four | 65 | 76 | 66 | 207 |
| Total | 680 | 731 | 649 | 2060 |
Show Grade based on the total mark ( using CASE statement )
Мы можем отобразить оценку учащегося, используя оператор CASE в нашем запросе. MySQL Case запрос выполняет оператор на основе условия соответствия. Здесь мы сравним общую оценку с установленными оценками для разных уровней оценки и соответственно присвоим ей оценку.
MySQL Case запрос выполняет оператор на основе условия соответствия. Здесь мы сравним общую оценку с установленными оценками для разных уровней оценки и соответственно присвоим ей оценку.Подробнее об операторе CASE WHEN THEN читайте здесь.
Вот наш запрос.ВЫБЕРИТЕ идентификатор, имя, класс, социальные сети, математика, наука, сумма (социальные + математика + наука) как Total , СЛУЧАЙ, КОГДА сумма (социальное + математика + наука) >= 225 THEN 'A' КОГДА сумма (социальное + математика + наука) >=200 ТО 'B' КОГДА сумма (социальное + математика + наука) >=170 ТО 'C' ИНАЧЕ "НЕУДАЧА" КОНЕЦ КАК from student_sum GROUP BY idВыход здесь.
| id | name | class | social | math | science | Total | grade | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | John Deo | Four | 75 | 78 | 84 | 237 | A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Max Ruin | Three | 54 | 85 | 67 | 206 | B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Arnold | Three | 78 | 90 | 65 | 233 | A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Krish Star | Four | 50 | 53 | 51 | 154 | FAIL | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | John Mike | Четыре | 80 | 89 | 78 | 247 | A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | ALECK JOHLE JOHN | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. 0296 0296 | 198 | C | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | My John Rob | Five | 77 | 83 | 68 | 228 | A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Asruid | Five | 55 | 55 | 50 | 160 | FAIL | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Tes Qry | Six | 68 | 62 | 60 | 190 | C | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Большой Джон | Четырехместный | 65 | 76 | 66 | 207 | B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| id | имя | социальная | математика | наука | всего< /й>"; foreach ($dbo->query($count) as $row) { echo " | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $row[id] | $row[name] | $row[social] | $row[math]< /td> | $row[наука] | $row[total] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Имя аргумента | Описание |
|---|---|
номер1 Обязательно | Первый номер, который вы хотите добавить. |
номер2-255 Дополнительно | Это второй номер, который вы хотите добавить. Таким образом можно указать до 255 номеров. |
В этом разделе обсуждаются некоторые рекомендации по работе с функцией СУММ. Многое из этого можно применить и для работы с другими функциями.
Метод =1+2 или =A+B. Хотя вы можете ввести =1+2+3 или =A1+B1+C2 и получить полностью точные результаты, эти методы подвержены ошибкам по нескольким причинам:
- org/ListItem»>
#ЗНАЧ! ошибки от ссылки на текст вместо цифр
Если вы используете формулу вроде:
Ваша формула может не работать, если в ячейках, на которые ссылаются, есть какие-либо нечисловые (текстовые) значения, которые вернут #ЗНАЧ! ошибка. SUM будет игнорировать текстовые значения и даст вам сумму только числовых значений.

#ССЫЛКА! ошибка при удалении строк или столбцов
Если вы удалите строку или столбец, формула не будет обновлена, чтобы исключить удаленную строку, и она вернет #ССЫЛКА! error, когда функция СУММ будет автоматически обновляться.
Формулы не будут обновлять ссылки при вставке строк или столбцов
Если вы вставите строку или столбец, формула не будет обновляться, чтобы включить добавленную строку, где автоматически обновится функция СУММ (если вы не выходите за диапазон, указанный в формуле). Это особенно важно, если вы ожидаете, что ваша формула обновится, а она не обновится, так как это оставит вас с неполными результатами, которые вы можете не уловить.

СУММ с отдельными ссылками на ячейки в сравнении с диапазонами
Используя формулу типа:
=СУММ(А1,А2,А3,В1,В2,В3)
В равной степени подвержен ошибкам при вставке или удалении строк в указанном диапазоне по тем же причинам. Гораздо лучше использовать отдельные диапазоны, например:
=СУММ(A1:A3;B1:B3)
Который будет обновляться при добавлении или удалении строк.

Опечатка . Представьте, что вы пытаетесь ввести больше и/или гораздо большие значения, например:
.Затем попробуйте проверить правильность введенных данных. Гораздо проще поместить эти значения в отдельные ячейки и использовать формулу СУММ. Кроме того, вы можете форматировать значения, когда они находятся в ячейках, что делает их более читабельными, чем когда они находятся в формуле.
Я просто хочу складывать/вычитать/умножать/разделять числа Посмотрите эту серию видео об основах математики в Excel или используйте Excel в качестве калькулятора.
Как показать больше/меньше десятичных разрядов? Вы можете изменить формат номера. Выберите нужную ячейку или диапазон и используйте Ctrl+1 , чтобы вызвать диалоговое окно Формат ячеек , затем щелкните вкладку Число и выберите нужный формат, обязательно указав количество десятичных разрядов, которое вы хотите.
org/ListItem»>Как получить разницу между датами? Как и в случае со временем, вы можете добавлять и вычитать даты. Вот очень распространенный пример подсчета количества дней между двумя датами. Это так же просто, как =B2-A2 . Ключом к работе как с датами, так и с временем является то, что вы начинаете с даты/времени окончания и вычитаете дату/время начала.
Дополнительные способы работы с датами см. в разделе Вычисление разницы между двумя датами.
Как суммировать только видимые ячейки? Иногда, когда вы вручную скрываете строки или используете автофильтр для отображения только определенных данных, вы также хотите суммировать только видимые ячейки.
 Вы можете использовать функцию ПРОМЕЖУТОЧНЫЙ ИТОГ. Если вы используете итоговую строку в таблице Excel, любая функция, выбранная вами в раскрывающемся списке «Итого», будет автоматически введена как промежуточный итог. Узнайте больше о том, как суммировать данные в таблице Excel.
Вы можете использовать функцию ПРОМЕЖУТОЧНЫЙ ИТОГ. Если вы используете итоговую строку в таблице Excel, любая функция, выбранная вами в раскрывающемся списке «Итого», будет автоматически введена как промежуточный итог. Узнайте больше о том, как суммировать данные в таблице Excel.
Как добавить или вычесть время? Вы можете складывать и вычитать время несколькими способами. Например, чтобы получить разницу между 8:00 и 12:00 для целей расчета заработной платы, вы должны использовать: =(«12:00 PM»-«8:00 AM»)*24 , взяв время окончания минус время начала. Обратите внимание, что Excel вычисляет время как часть дня, поэтому вам нужно умножить на 24, чтобы получить общее количество часов. В первом примере мы используем =((B2-A2)+(D2-C2))*24 , чтобы получить сумму часов от начала до конца, за вычетом обеденного перерыва (всего 8,50 часов).
Если вы просто добавляете часы и минуты и хотите отображать их таким образом, то вы можете суммировать и не нужно умножать на 24, поэтому во втором примере мы используем =СУММ(A6:C6) , поскольку нам просто нужно общее количество часов и минут для поставленных задач (5:36 или 5 часов 36 минут).
Для получения дополнительной информации см. : Добавление или вычитание времени.
: Добавление или вычитание времени.
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
См. также
Узнать больше о СУММ
Функция СУММЕСЛИ складывает только те значения, которые соответствуют одному критерию.
Функция СУММЕСЛИМН складывает только те значения, которые соответствуют нескольким критериям.
Функция СЧЁТЕСЛИ подсчитывает только те значения, которые соответствуют одному критерию. здесь k — может принимать любые целые значения, поэтому говорят, что логарифм комплексного числа многозначен. Для практических целей используется главное значение(k=0) Формула расчета экспоненты комплексного числа тоже Таким образом у нас есть всё, что бы рассчитать на практике комплексную степень комплексного числа. Если используете XMPP клиент: step_i <запрос> Если используете этот сайт: <запрос> где запрос — состоит из двух чисел. Сначала идет основание потом в другом окне степень. Основание может быть как действительным числом так и комплексным, положительным или отрицательным Комплексное значение пишется как x:y где х- действительная часть числа, а y- мнимая часть, но можно написать и в нормальном виде через символ i Степень может быть быть целым числом,как положительным так и отрицательным. Степень может быть выражена также степенью двух целых чисел например 1/2 или -5/7. Например: взять степень 2/5 от комплексного числа 1-2.5i Пишем 1:-2.5 2/5 или если делаете запрос через Jabber step_i 1:-2.5 2/5 Ответ получим Комплексное число 1:-2.5 в степени 2/5 равно Действительная часть: 1.3209 Комплексная часть: -0.6812 Интересно, а чему будет равна мнимая единица в степени мнимой единицы? пишем i i и получаем что возведем еще одно число в комплексную степень. число 1+i в комплексную степень 1-i результат вот такой Обновление: На 12 сентября 2017 года, упрощен ввод данных.2}\) Данный бот еще может использовать пятую операцию — возведение в степень, а так же все основные тригонометрические функции (синус, косинус, тангенс), обратные тригонометрические функции, взятие логарифма и экспоненты. Заметьте, эти функции могут использовать как действительные аргументы, так и комплексные, что открывает широкие возможности по вычислению выражений. Возведение в степень осуществляется по известной формуле Муавра. Степень числа, может быть как действительным так и мнимым. Калькулятор работает, исправен, и не допускает ошибки при корректном вводе выражения. Как уже было сказано, выражение по сложности может быть неограниченным по размерам и иметь множество скобок. Если используете Jabber или любой другой XMPP клиент: calc_i <строка> Если используете данный сайт: <строка> Строкой может быть любое выражение без каких либо функций. Могут воспользоватся следующие операции: + сложение — вычитание * умножение / деление ^ возведение в степень синус(sin) косинус(cos) натуральный логарифм(ln) тангенс(tan) артангенс(atan) арксинус(asin) арккосинус(acos) гиперболический синус(sinh) гиперболический косинус(cosh) гиперболический тангенс(tanh) Число в выражении может быть как действительным, которое записывается в привычном виде, так и комплексным числом которое обозначается символом i Просьба по возможности оборачивать каждое комплексное число в круглые скобки, если первый символ в нём является минус (-) (-4-1i)/((-5-2i)+7-1.(1/2)) Результат выражения Действительная часть 0.66468285388895 Мнимая часть 1.0051451851734 Как видите, сложность выражения может быть произвольной и включать в себя комплексные числа. Вы искали 1 2i 1 i? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 2i 3 i, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «1 2i 1 i». Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 1 2i 1 i,1 2i 3 i,1 4i 1 i,1 i 1 2i,1 i 12,1 i 2 3i,1 i 2 5i,1 i 2 i,1 i 25,1 i 3,1 i 4,1 i 8,1 i x 1 i y 3 i,1 i z,1 i равно,1 i решение,1i,2 3i 1 i,2 i 1 3i,2 i 1 i,2 i 3 2i,2i 1 i,2i i,3 2i 1 i,3 2i 5 i,3 2i 7 i,3 i 1,3 i 1 2i,3 i 2 i,3 i 5 2i,3 i z 2 i,3 i комплексные числа,3i2 ru,5 i 2 i,i 0 i 3 i,i 1 12,i 1 3,i 2 i 3,i 3 1,i 3 вычислить,i 3 комплексные числа,i i2 i3 i4,i i2 i3 i4 i5,i z 1,i в 3 степени комплексные числа,i в степени 3 комплексные числа,z 1 2i,z 1 i 1 2i,z 1 i 2 i,z 2 2i,z 2 3i,z 2 3i 2,z 2 i,z 2i,z 3 i 2 i,z 3i z 2,z i,z i 2,z i 3 1,z i z 2,z1 1 i,z1 2 i,z1 2 i решение,z1 z2 комплексные числа,выполните действия над комплексными числами,выполнить действия с комплексными числами,выполнить действия с комплексными числами онлайн,вычисление комплексных чисел,вычисление комплексных чисел онлайн,вычислите 2 i 1 i,вычислите i 1 i,вычислите i 3,вычислите i i2 i3 i4,вычислить 3 i,вычислить i 3,вычислить комплексное число,вычислить комплексное число онлайн с подробным решением,вычислить комплексные числа,вычислить комплексные числа онлайн,вычислить онлайн комплексные числа,вычислить по формуле муавра онлайн калькулятор,вычитание и сложение комплексных чисел онлайн,даны комплексные числа,даны комплексные числа z1 и z2 решить онлайн,действие с комплексными числами,действия комплексные числа,действия над комплексными числами в алгебраической форме онлайн калькулятор,действия над комплексными числами калькулятор онлайн,действия над комплексными числами онлайн,действия над комплексными числами онлайн калькулятор,действия с комплексными числами,действия с комплексными числами онлайн,действия с комплексными числами онлайн калькулятор,деление комплексные числа онлайн,деление комплексных чисел калькулятор,деление комплексных чисел калькулятор онлайн,деление комплексных чисел онлайн,деление комплексных чисел онлайн калькулятор,записать комплексное число в алгебраической форме онлайн калькулятор,как комплексные числа решать онлайн,калькулятор действительных чисел,калькулятор деление комплексных чисел,калькулятор для комплексных чисел,калькулятор для комплексных чисел онлайн,калькулятор комплексного числа,калькулятор комплексные числа,калькулятор комплексных,калькулятор комплексных чисел,калькулятор комплексных чисел в показательной форме онлайн,калькулятор комплексных чисел деление,калькулятор комплексных чисел онлайн,калькулятор комплексных чисел онлайн с подробным решением,калькулятор комплексных чисел онлайн с решением,калькулятор комплексных чисел онлайн с решением в показательной форме,калькулятор комплексных чисел с подробным решением онлайн,калькулятор комплексных чисел с решением,калькулятор комплексных чисел умножение онлайн,калькулятор мнимой единицы,калькулятор мнимых чисел,калькулятор мнимых чисел онлайн,калькулятор онлайн для комплексных чисел,калькулятор онлайн комплексные числа,калькулятор онлайн комплексные числа с решением,калькулятор онлайн с комплексными числами,калькулятор онлайн с мнимой единицей,калькулятор решение комплексных чисел,калькулятор с комплексными числами,калькулятор с комплексными числами онлайн,калькулятор с мнимой единицей,калькулятор с мнимой единицей онлайн,калькулятор с решением комплексных чисел,комплексного числа калькулятор,комплексное число вычислить,комплексное число калькулятор онлайн,комплексное число онлайн,комплексное число онлайн калькулятор,комплексные числа i 3,комплексные числа i в степени 3,комплексные числа z1 z2,комплексные числа вычислить,комплексные числа вычислить онлайн,комплексные числа действия,комплексные числа калькулятор,комплексные числа калькулятор онлайн,комплексные числа калькулятор онлайн с подробным решением,комплексные числа калькулятор онлайн с решением,комплексные числа онлайн,комплексные числа онлайн вычислить,комплексные числа онлайн деление,комплексные числа онлайн калькулятор,комплексные числа онлайн калькулятор с подробным решением,комплексные числа онлайн калькулятор с решением,комплексные числа онлайн решение,комплексные числа онлайн решить,комплексные числа онлайн решить уравнение,комплексные числа посчитать онлайн,комплексные числа примеры с решением онлайн,комплексные числа решение онлайн,комплексные числа решить онлайн,комплексные числа решить уравнение онлайн,комплексный калькулятор,комплексный калькулятор онлайн,комплексный онлайн калькулятор,найдите разность z1 z2 комплексных чисел,найдите сумму комплексных чисел,найти произведение комплексных чисел,найти сумму разность произведение и частное комплексных чисел z1 и z2,найти частное двух комплексных чисел полученное число представить,найти частное комплексных чисел 1 i,онлайн вычисление комплексных чисел,онлайн вычитание комплексных чисел,онлайн действия над комплексными числами,онлайн действия с комплексными числами,онлайн калькулятор действия над комплексными числами,онлайн калькулятор для комплексных чисел,онлайн калькулятор комплексное число,онлайн калькулятор комплексных чисел,онлайн калькулятор комплексных чисел деление,онлайн калькулятор комплексных чисел с подробным решением,онлайн калькулятор комплексных чисел умножение,онлайн калькулятор мнимых чисел,онлайн калькулятор решение уравнений с комплексными числами,онлайн калькулятор с комплексными числами,онлайн калькулятор с мнимой единицей,онлайн калькулятор умножение комплексных чисел,онлайн комплексное число,онлайн произведение комплексных чисел онлайн,онлайн расчет комплексных чисел,онлайн решение комплексных уравнений,онлайн решение комплексных чисел,онлайн решение комплексных чисел с решением,операции с комплексными числами онлайн,посчитать комплексные числа онлайн,расчет комплексных чисел онлайн,решение комплексные числа онлайн,решение комплексных уравнений калькулятор онлайн,решение комплексных уравнений онлайн калькулятор,решение комплексных чисел онлайн,решение комплексных чисел онлайн с подробным решением,решение комплексных чисел онлайн с решением,решение комплексных чисел с подробным решением онлайн,решение онлайн комплексные числа,решение онлайн комплексных чисел,решение уравнений с комплексными числами онлайн,решение уравнений с комплексными числами онлайн калькулятор,решить комплексные числа онлайн,решить онлайн комплексные числа,решить уравнение комплексные числа онлайн,решить уравнение онлайн комплексные числа,решить уравнение с комплексными числами онлайн,сложение комплексных чисел онлайн,умножение комплексных чисел онлайн,умножение комплексных чисел онлайн калькулятор,уравнения с комплексными числами онлайн,формула муавра онлайн калькулятор с решением. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 1 2i 1 i. Просто введите задачу в окошко и нажмите
«решить» здесь (например, 1 4i 1 i). Решить задачу 1 2i 1 i вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора. Факториал натурального числа n — произведение первых по счету,n натуральных чисел от 1 до n включительно, обозначается n!
n! = 1 • 2 • 3 • 4 • 5 • … • n
Факториа́л числа – это число, умноженное на «себя минус один», затем на «себя минус два» и так далее, до единицы.
n! = n • (n — 1) • (n — 2) • … • 1
Для приближённого вычисления факториала и гамма-функции используется формула Стирлинга . Названа в честь Джеймса Стирлинга и Абрахама де Муавра, последний считается автором формулы Вычисление факториала числа (n!) по формуле в Стирлинга. Этот калькулятор может быть использован для вычисления значений n больше 100. Приближенное значение не ограничено по колличеству n Точное значение, ограниченное по колличеству n n! ≈ √(2π) × n(n+1/2) × e -n Примеры значений для разных n:
1! = 1 По общепринятой договоренности 0! = 1 (факториал нуля равен единице). Этот факт важен, к примеру, для вычисления биномиальных коэффициентов. Факториал числа, функцию от натурального аргумента можно продолжить на все действительные числа с помощью т.н. Гамма-функции (важно отметить, что для этого требуется определенный математический аппарат). В таком случае, мы сможем посчитать факториал любого действительного числа. Например, факториал (или, Гамма-функция, что математически правильнее) числа Пи. π! приблизительно равен 2.28803779534. Факториал числа Эйлера, другого трансцендентного числа, Γ(e) ~ 1.567468255 (упрощенно, факториал числа e). Чтобы быстро и правильно выполнить операцию с комплексными числами, воспользуйтесь данным онлайн калькулятором, для этого необходимо: Числа вида a+bi называются комплексными (мнимыми) числами, где a,b — вещественные (или действительные) числа, i — мнимая единица — число, для которого выполняется равенство: i2 = -1, т.е. мнимая единица в квадрате является отрицательным числом, равным -1. Комплексные числа расширяют понятие действительного числа, позволяют в удобной форме описывать математические модели всевозможных прикладных процессов. Комплексное число z можно представить в алгебраической, тригонометрической или показательной (экспоненциальной) форме. 1. Алгебраическая запись: z = a + bi, где a и b являются вещественными числами, причем, a — действительная часть, bi — мнимая, i — мнимая единица. 2. Тригонометрическая запись: z = r (cos + i sin φ), где r — модуль комплексного числа, z — расстояние от точки на комплексной плоскости до начала координат. Модуль комплексного числа — вещественное число |z|, равное корню квадратному из суммы квадратов вещественных чисел (a и b): r = |z| = √a2 + b2 Аргумент комплексного числа z — угол φ, образованный радиус-вектором точки, соответствующей комплексному числу. Значение аргумента находится в диапазоне (-π…π], для всех целых k определяется с точностью 2πk: φ = Аrg (z) = arctg (b/a). Для z, равного нулю, аргумент не определен. 3. Для сокращения Эйлер ввел Показательную запись: z = rеiφ 1. Сложение: z1 + z2 = (а1 + а2) + (b1 + b2) i, где z1 = а1 + b1i; z2 = а2 + b2i. При сложении комплексных чисел складываются их реальные и мнимые части, причем, сумма не изменится от перемены мест слагаемых. 2. Вычитание: z1 — z2 = (а1 — а2) + (b1 — b2) i. При вычитании комплексных чисел вычитаются их реальные и мнимые части. 3. Умножение: z1z2 = (а1а2 — b1b2) + (а1b2 + а2b1) i, зная что i*i=-1. Умножение комплексных чисел выполняется по правилам умножения многочленов. 4. Деление: z1 / z2 = (a + bi) / (c + di) = (ac + bd) / (c2 + d2) + ((bc — ad) / (c2 + d2)) i, где z1 = a + bi; z2 = c + di. Деление выполняется путем умножения числителя и знаменателя на выражение, сопряженное знаменателю. 5. Возведение в целую степень. Для возведения комплексного числа во вторую степень можно записать степень, как произведение двух множителей и выполнить операцию умножения по правилу умножения многочленов. Для возведения комплексного числа в большую степень проще воспользоваться показательной формой: zn = rneinφ полученной из формулы Муавра: (cos (х) + isin (х))n = cos (nх) + isin (nх). 6. Вычисление корня n-ой степени: , где k — целое число в диапазоне 0…n-1 Возводить в натуральную степень $n$, если она
достаточно велика, комплексные числа проще всего в
тригонометрической форме, то есть если число
$z=a+b i$ задано в
алгебраической форме, то
его изначально надо записать в тригонометрической.{2}}},}
3. Применение
Начиная с XVI века математики столкнулись с необходимостью специальных чисел, также известных в настоящее время как комплексные числа. Комплексное число — это число вида a + bi, где a, b — действительные числа, а i — мнимая единица, является решением уравнения: i 2 = -1. Интересно проследить эволюцию взглядов математиков на задачи со сложными числами. Вот цитаты из древних работ по этой теме: Используется по-разному при определении комплексных чисел. Покажем троих , , — это упрощенная версия полярной формы, полученная из формулы Эйлера. Цифры после десятичной точки: 2 Главное значение аргумента (рад) Главное значение аргумента (градусы) Комплексная плоскость Файл очень большой.Во время загрузки и создания может произойти замедление работы браузера. Скачать закрыть content_copy Ссылка сохранить Сохранить расширение Виджет Аргумент комплексного числа является многозначной функцией для целого числа k. Главное значение аргумента — это единственное значение в открытом периоде (-π..π]. Все элементарные арифметические операции определены для комплексного числа: Цифры после десятичной точки: 2 Файл очень большой. Во время загрузки и создания может произойти замедление работы браузера. Скачать закрыть content_copy Ссылка сохранить Сохранить расширение Виджет Одно комплексное число может быть добавлено к другому так же, как и многочлены: Используя определение комплексного числа i * i = -1, мы можем легко объяснить формулу умножения комплексного числа: Чтобы вывести формулу деления комплексных чисел, мы умножаем числитель и знаменатель на сопряженное комплексное число (чтобы исключить мнимую единицу в знаменателе): Используя форму Эйлера, это просто: По формуле Де Муавра корни n n степени z (степень 1 / n) даются по формуле: Наш калькулятор комплексных чисел (также известный как калькулятор мнимых чисел) — отличный инструмент для решения основных операций с комплексными числами. Читайте дальше, чтобы найти ответ на вопрос: «Что такое комплексное число?», Узнать об алгебраической и полярной форме комплексных чисел и овладеть навыками умножения и деления комплексных чисел.В конце этого текста вы также можете найти информацию о свойствах комплексных чисел (большинство из которых основаны на сопряженных или абсолютных значениях комплексных чисел) и даже о некоторых их практических применениях. Чтобы ответить на вопрос, что такое комплексное число, мы должны сначала спросить: «Что такое мнимое число?». Мнимое число — это квадратный корень из отрицательного числа .Основное мнимое число обозначается буквой Определение комплексного числа Здесь и Другой способ записать две части комплексного числа — Сопряжение комплексного числа определяется как: Как мы видим, сопряжение комплексного числа не влияет на действительную часть, в то время как мнимая часть имеет знак, противоположный исходному. Комплексные числа имеют много общего с декартовой системой координат, потому что они представляют собой пары чисел на декартовой комплексной плоскости . Полезно представить комплексные числа как векторы на этой комплексной плоскости. Формулы, которые преобразуют комплексные числа из декартовой формы в полярную форму, точно такие же, как и классические преобразования координат: , где Зная это, мы можем написать любое комплексное число, используя его полярные координаты на этой плоскости: Здесь sin и cos — основные тригонометрические функции. Эти формулы получены из соотношений в прямоугольном треугольнике на комплексной плоскости. Другими словами, комплексное число можно записать как: Есть также другой способ переписать это число, используя формулу Эйлера : , где , где Полярная форма комплексных чисел очень полезна в различных вычислениях, включая умножение, деление и даже некоторые более сложные вычисления. Экспоненциальная форма особенно удобна, если вы недостаточно разбираетесь в тригонометрических законах или просто предпочитаете работать со степенями. При выполнении простых операций с комплексными числами полезно думать о них как о векторах.Затем довольно просто добиться как сложения, так и вычитания комплексных чисел. Обозначим первое число как , где Аналогично можно найти разницу этих чисел: и теперь Вы помните, как складывать или вычитать два 2D-вектора? Это точно так же, как мы делаем это в этом калькуляторе комплексных чисел — вам просто нужно добавить (или вычесть) каждую пару компонентов отдельно, и все! Теперь давайте перейдем к чему-то более сложному — мы хотим выяснить, как работает умножение комплексных чисел. Следуя обозначениям из предыдущего раздела, мы можем написать: На этот раз действительная часть может быть записана как Умножение комплексных чисел не так уж и страшно, правда? Так что насчет деления комплексных чисел? Давайте посмотрим на расчеты с пошаговыми подсказками: Получаем следующие результаты: Мы также можем рассмотреть описанные выше операции в полярной записи, например , и мы видим, что: Комплексные числа делятся почти так же, как и в этой записи: , переписывая результат как: Похоже, что вторая попытка намного проще, поэтому иногда стоит подумать об изменении формы наших выражений перед началом вычислений . Мы всегда можем вернуться от полярных обозначений к алгебраическим. Если вам это не нравится, просто воспользуйтесь нашим калькулятором комплексных чисел, чтобы убедиться, что результат правильный. Мы можем сделать краткий обзор того, как вычислить некоторые более сложные операции с комплексными числами.G . Тогда абсолютное значение будет: Логарифм комплексного числа (также известный как комплексный логарифм ) можно вычислить следующим образом: Одно критическое замечание: поскольку фазы Инструмент действительно прост в использовании. Все, что вам нужно сделать, это написать действительную и мнимую части двух чисел. Если число является чисто реальным или чисто мнимым, установите другой компонент равным 0.Вот и все. В результате вы получите полярную форму комплексных чисел, сумму, разность, произведение, частное, а также первое число в степени второго и логарифм первого числа. Существует несколько свойств комплексных чисел, включая сопряжение или абсолютное значение комплексных чисел, которые могут быть полезны при вычислении некоторых упражнений. Комплексные числа иногда действительно полезны с алгебраическими выражениями, особенно если они связаны с тригонометрическими функциями. Многие физические задачи выигрывают от силы комплексных чисел. Одна из основных областей использования комплексных чисел — это мир волновых функций и гармонического движения. Множественные задачи из электроники можно значительно упростить с помощью комплексных чисел. Вы можете проверить, как это делается на практике, с помощью калькулятора делителя напряжения. Процесс математической индукции можно использовать для доказательства очень важной теоремы в математике, известной как теорема Де Муавра . Если комплексное число z = r (cos α + i sin α), то Предыдущий образец можно расширить с помощью математической индукции до теоремы Де Муавра. Если z = r (cos α + i sin α) и n — натуральное число, то Пример 1: Запишите в виде s + bi . Сначала определите радиус: Так как cos α = и sin α = ½, α должен находиться в первом квадранте и α = 30 °. Следовательно, Пример 2: Запишите в форме a + bi . Сначала определите радиус: Так как cos и sin, α должно быть в четвертом квадранте и α = 315 °. Следовательно, Задачи, связанные со степенями комплексных чисел, можно решить с помощью биномиального разложения, но применение теоремы Де Муавра обычно более прямое. Теорема Де Муавра может быть расширена на корни комплексных чисел, давая теорему о корне n-й степени . Учитывая комплексное число z = r (cos α + i sinα), все корни n -й степени из z равны где k = 0, 1, 2,…, (n — 1) Если k = 0, эта формула сокращается до Этот корень известен как главный корень n-й степени из z .Если α = 0 ° и r = 1, то z = 1 и корни n-й степени из единицы даются как , где k = 0, 1, 2,…, ( n — 1) Пример 3: Какие пять корней пятой степени выражены в тригонометрической форме? Поскольку cos и sin α = ½, α находится в первом квадранте и α = 30 °. Следовательно, поскольку синус и косинус периодические, и применяя теорему n о корне , пять корней пятой степени из z даются как , где k = 0, 1, 2, 3 и 4 Таким образом, пять корней пятой степени равны Обратите внимание на равномерное расстояние между пятью корнями по кругу на Рисунке 1. Рисунок 1 Процесс использования нормальной кривой для оценки формы биномиального распределения известен как нормальное приближение. Объясните происхождение центральной предельной теоремы для биномиальных распределений Биномиальное распределение можно использовать для решения таких задач, как: «Если честная монета подбрасывается 100 раз, какова вероятность выпадения 60 или более орлов?» Вероятность того, что точно [latex] \ text {x} [/ latex] выпадет из [latex] \ text {N} [/ latex] флипов, вычисляется по формуле: [латекс] \ displaystyle \ text {P} \ left (\ text {x} \ right) = \ frac {\ text {N}! } {\ text {x}! \ left (\ text {N} — \ text {x} \ right)! } {\ pi} ^ {\ text {x}} {\ left (1- \ pi \ right)} ^ {\ text {N} — \ text {x}} [/ latex] где [latex] \ text {x} [/ latex] — это количество головок (60), [latex] \ text {N} [/ latex] — это количество флипов (100), а [latex] \ pi [/ latex] — вероятность выпадения головы (0.5). Следовательно, чтобы решить эту проблему, вы вычисляете вероятность 60 орлов, затем вероятность 61 орла, 62 орла и т. Д. И складываете все эти вероятности. Абрахам де Муавр, статистик 18 -го -го века и консультант игроков, часто был приглашен для выполнения этих длительных вычислений. де Муавр отметил, что, когда количество событий (подбрасываний монеты) увеличивалось, форма биномиального распределения приближалась к очень плавной кривой. Поэтому де Муавр рассуждал, что, если бы он мог найти математическое выражение для этой кривой, он бы гораздо легче мог решать такие задачи, как определение вероятности 60 или более решек из 100 подбрасываний монеты.Именно это он и сделал, и обнаруженная им кривая теперь называется нормальной кривой. Процесс использования этой кривой для оценки формы биномиального распределения известен как нормальное приближение. Нормальное приближение : Нормальное приближение к биномиальному распределению для 12 подбрасываний монеты. Плавная кривая — нормальное распределение. Обратите внимание, насколько хорошо он аппроксимирует биномиальные вероятности, представленные высотой синих линий. Важность нормальной кривой проистекает прежде всего из того факта, что распределение многих природных явлений, по крайней мере, приблизительно нормально распределено.Одним из первых применений нормального распределения был анализ ошибок измерения, сделанных в астрономических наблюдениях, ошибок, возникающих из-за несовершенных инструментов и несовершенных наблюдателей. Галилей в 17 -м веках отмечал, что эти ошибки были симметричными и что небольшие ошибки возникали чаще, чем большие ошибки. Это привело к нескольким гипотетическим распределениям ошибок, но только в начале 19 -го -го века было обнаружено, что эти ошибки следовали нормальному распределению.Независимо друг от друга математики Адриан (в 1808 г.) и Гаусс (в 1809 г.) разработали формулу для нормального распределения и показали, что ошибки хорошо вписываются в это распределение. Это же распределение было открыто Лапласом в 1778 году, когда он вывел чрезвычайно важную центральную предельную теорему. Лаплас показал, что даже если распределение не имеет нормального распределения, средние значения повторных выборок из распределения будут почти нормальными, и чем больше размер выборки, тем ближе распределение будет к нормальному распределению.Большинство статистических процедур проверки различий между средними значениями предполагают нормальное распределение. Поскольку распределение средних очень близко к нормальному, эти тесты работают хорошо, даже если само распределение лишь приблизительно нормальное. Объем нормального приближения зависит от размера нашей выборки и становится более точным по мере увеличения размера выборки. Объясните, как центральная предельная теорема применяется в нормальном приближении Инструмент нормальной аппроксимации позволяет нам аппроксимировать вероятности случайных величин, для которых нам неизвестны все значения, или для очень большого диапазона потенциальных значений, вычисление которых было бы очень трудным и длительным. Мы делаем это, преобразовывая диапазон значений в стандартизованные единицы и находя площадь под нормальной кривой. Проблема возникает, когда имеется ограниченное количество выборок или рисунков в случае данных, «извлеченных из коробки». Гистограмма вероятности такого набора может не напоминать нормальную кривую, и поэтому нормальная кривая не будет точно представлять ожидаемые значения случайных величин.Другими словами, объем нормального приближения зависит от размера нашей выборки, становясь более точным по мере увеличения размера выборки. Эта характеристика следует из статистических тем закона больших чисел и центральной предельной теоремы (см. Ниже). Закон больших чисел : Иллюстрация закона больших чисел с использованием конкретной серии бросков одного кубика. По мере увеличения количества бросков в этом прогоне среднее значение всех результатов приближается к 3.5. В то время как разные серии будут иметь разную форму при небольшом количестве бросков (слева), при большом количестве бросков (справа) они будут очень похожи. Закон больших чисел (LLN) — это теорема, описывающая результат многократного выполнения одного и того же эксперимента. Согласно закону, среднее значение результатов, полученных в результате большого количества испытаний, должно быть близко к ожидаемому значению и будет иметь тенденцию становиться ближе по мере проведения большего количества испытаний. Закон больших чисел важен, потому что он «гарантирует» стабильные долгосрочные результаты для средних значений случайных событий. Например, в то время как казино может потерять деньги за одно вращение колеса рулетки, его доходы будут иметь тенденцию к предсказуемому проценту на большом количестве вращений. Любая выигрышная серия игрока в конечном итоге будет преодолена параметрами игры. Важно помнить, что LLN применяется (как указывает название) только тогда, когда учитывается большое количество наблюдений.Не существует принципа, согласно которому небольшое количество наблюдений будет совпадать с ожидаемым значением или что полоса одного значения будет немедленно «уравновешена» другими. Центральная предельная теорема (ЦПТ) утверждает, что при определенных условиях среднее значение достаточно большого числа независимых случайных величин, каждая из которых имеет четко определенное среднее значение и четко определенную дисперсию, будет приблизительно нормально распределено. Центральная предельная теорема имеет несколько вариантов.В обычном виде случайные величины должны быть одинаково распределены. В вариантах сходимость среднего к нормальному распределению также происходит для неидентичных распределений, при условии, что они соответствуют определенным условиям. 2 [/ latex].{2}} {\ text {n}} [/ латекс]. Полезность теоремы заключается в том, что распределение [латекса] \ sqrt {\ text {n}} ({\ text {S}} _ {\ text {n}} — \ mu) [/ latex] приближается к нормальному, независимо от форма распределения отдельных [латекс] \ text {X} _ \ text {i} [/ latex]. Центральная предельная теорема : распределение «сглаживается» суммированием, показывая исходную плотность распределения и три последующих суммирования В этом атоме мы приводим пример того, как вычислить нормальное приближение для биномиального распределения.2 = \ text {Np} (1- \ text {p}) = 10 \ cdot 0,5 \ cdot 0,5 = 2,5 [/ латекс]; поэтому стандартное отклонение составляет 1,5811. Ниже приводится пример того, как вычислить нормальное приближение для биномиального распределения.2 = \ text {Np} (1- \ text {p}) = 10 \ cdot 0,5 \ cdot 0,5 = 2,5 [/ latex]. Таким образом, стандартное отклонение составляет 1,5811. Всего 8 голов: [латекс] \ displaystyle \ frac {8-5} {1,5811} = 1,8973 [/ латекс] Стандартные отклонения выше среднего значения распределения. Тогда возникает вопрос: «Какова вероятность того, что значение будет на 1,8973 стандартного отклонения выше среднего?» Вы можете быть удивлены, узнав, что ответ — 0 (вероятность получения любой конкретной точки равна 0). Проблема в том, что биномиальное распределение — это дискретное распределение вероятностей, тогда как нормальное распределение — это непрерывное распределение. Решение состоит в том, чтобы округлить и рассмотреть любое значение от 7,5 до 8,5, чтобы представить результат из 8 решек. Используя этот подход, мы вычисляем площадь под нормальной кривой от 7,5 до 8,5. Зеленая область на рисунке представляет собой приблизительную вероятность получения 8 голов. Нормальное приближение : Приближение вероятности выпадения 8 голов с нормальным распределением. Чтобы вычислить эту площадь, сначала мы вычисляем площадь ниже 8,5, а затем вычитаем площадь ниже 7.5. Это можно сделать, найдя оценки [latex] \ text {z} [/ latex] и используя таблицу оценок [latex] \ text {z} [/ latex]. Здесь для удобства мы использовали онлайн-калькулятор нормальной площади. Результаты представлены на следующих рисунках: Нормальная область 2 : На этом графике показана область ниже 7,5. Нормальная область 1 : На этом графике показана область ниже 8,5. [latex] \ text {z} [/ latex] -Score Таблица : Таблица [latex] \ text {z} [/ latex] -score используется для вычисления вероятностей для стандартного нормального распределения. Разница между площадями составляет 0,044, что является приближением биномиальной вероятности. Для этих параметров приближение очень точное. Если бы у нас не было калькулятора нормальной площади, мы могли бы найти решение, используя таблицу стандартного нормального распределения (таблица [latex] \ text {z} [/ latex]) следующим образом: Та же логика применяется при вычислении вероятности диапазона результатов. Например, чтобы рассчитать вероятность от 8 до 10 переворотов, вычислите площадь от 7.5 до 10,5. Чтобы рассмотреть нормальное распределение или нормальное приближение, необходима стандартная шкала или стандартные единицы. Объясните значение нормализации рейтингов и вычислите эту нормализацию Чтобы рассмотреть нормальное распределение или нормальное приближение, необходима стандартная шкала или стандартные единицы. В простейших случаях нормализация рейтингов означает приведение значений, измеренных в разных шкалах, к условно общей шкале, часто до усреднения. В более сложных случаях нормализация может относиться к более сложным корректировкам, цель которых состоит в том, чтобы привести в соответствие все распределения вероятностей скорректированных значений. В случае нормализации оценок в образовательной оценке может быть намерение привести распределения в соответствие с нормальным распределением.Другой подход к нормализации вероятностных распределений — это квантильная нормализация, при которой квантили различных показателей приводятся в соответствие. Нормализация также может относиться к созданию смещенных и масштабированных версий статистики, где цель состоит в том, что эти нормализованные значения позволяют сравнивать соответствующие нормализованные значения для разных наборов данных. Некоторые типы нормализации включают только изменение масштаба для получения значений, относящихся к некоторой переменной размера. Стандартный балл — это количество стандартных отклонений, при которых наблюдение или данные превышают среднее значение. Таким образом, положительная стандартная оценка представляет собой данные выше среднего, а отрицательная стандартная оценка представляет собой данные ниже среднего. Это безразмерная величина, полученная путем вычитания среднего значения совокупности из индивидуальной исходной оценки и последующего деления разницы на стандартное отклонение совокупности. Этот процесс преобразования называется стандартизацией или нормализацией. Стандартные оценки также называются [latex] \ text {z} [/ latex] -values, [latex] \ text {z} [/ latex] -scores, нормальные оценки и стандартизованные переменные. Использование «[latex] \ text {Z} [/ latex]» связано с тем, что нормальное распределение также известно как «распределение [latex] \ text {Z} [/ latex]». Чаще всего они используются для сравнения образца со стандартным нормальным отклонением (стандартное нормальное распределение, при котором [latex] \ mu = 0 [/ latex] и [latex] \ sigma = 1 [/ latex]). Оценка [latex] \ text {z} [/ latex] определяется только в том случае, если известны параметры популяции.Если имеется только набор образцов, то аналогичное вычисление с выборочным средним и стандартным отклонением выборки дает статистику Стьюдента [latex] \ text {t} [/ latex]. Стандартная оценка необработанной оценки [latex] \ text {x} [/ latex] составляет: [латекс] \ displaystyle \ text {z} = \ frac {\ text {x} — \ mu} {\ sigma} [/ latex] Где [латекс] \ му [/ латекс] — среднее значение для генеральной совокупности, а — стандартное отклонение для генеральной совокупности. Абсолютное значение [latex] \ text {z} [/ latex] представляет собой расстояние между исходной оценкой и средним значением генеральной совокупности в единицах стандартного отклонения.[latex] \ text {z} [/ latex] отрицательно, когда необработанная оценка ниже среднего, положительная, когда выше. Ключевым моментом является то, что для вычисления [latex] \ text {z} [/ latex] требуется среднее значение генеральной совокупности и стандартное отклонение генеральной совокупности, а не выборочное среднее или отклонение выборки. Это требует знания параметров совокупности, а не статистики выборки, взятой из интересующей совокупности. Однако знание истинного стандартного отклонения совокупности часто нереально, за исключением таких случаев, как стандартизованное тестирование, когда измеряется вся совокупность.В случаях, когда невозможно измерить каждого члена генеральной совокупности, может использоваться случайная выборка. Значение [latex] \ text {Z} [/ latex] измеряет сигма-расстояние фактических данных от среднего и обеспечивает оценку того, насколько нецелевой процесс работает. Нормальное распределение и шкалы : сравнивает различные методы классификации в нормальном распределении. Включает: стандартные отклонения, совокупные проценты, процентильные эквиваленты, баллы [latex] \ text {Z} [/ latex], баллы [latex] \ text {T} [/ latex] и стандартные девять. Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от устройства (для их просмотра должна быть возможность прокручивать), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. В этом разделе мы рассмотрим действительно хороший способ быстрого вычисления целочисленных степеней и корней комплексных чисел. {i \ frac {\ pi} {4}}} \] Обратите внимание, что мы использовали главное значение аргумента для экспоненциальной формы, хотя в этом и не было необходимости.n} = 1 \] Ясно (надеюсь) \ (z = 1 \) — одно из решений. Мы хотим определить, есть ли другие решения. Для этого мы будем использовать факт из предыдущих разделов, который гласит, что \ ({z_1} = {z_2} \) тогда и только тогда, когда Итак, давайте начнем с преобразования обеих частей уравнения в комплексную форму, а затем вычислим степень в левой части.n} = 1 \ hspace {0,5 дюйма} n \ theta = 0 + 2 \ pi k \, \ hspace {0,25 дюйма} k = 0, \ pm 1, \ pm 2, \ ldots \] Теперь \ (r \) является положительным целым числом (в предположении экспоненциальной / полярной формы), и поэтому решение дает, Тогда решения уравнения: Вспомните из нашего обсуждения полярной формы (и, следовательно, экспоненциальной формы), что эти точки будут лежать на окружности радиуса \ (r \).Итак, наши точки будут лежать на единичной окружности, и они будут равномерно разнесены на единичной окружности на каждые \ (\ frac {{2 \ pi}} {n} \) радианы. Обратите внимание, что это также говорит нам о том, что существует \ (n \) различных корней, соответствующих \ (k = 0,1,2, \ ldots, n — 1 \), поскольку мы вернемся туда, откуда начали, как только достигнем \ (k = п \) Следовательно, имеется \ (n \) n -го корня из единицы, и они равны, , а в мире действительных чисел мы знаем, что решение этой проблемы \ (z \) = 1. Однако из вышеприведенной работы мы знаем, что в этом случае имеется 3 n th корней из единицы. Проблема здесь в том, что оставшиеся два являются комплексными решениями, и о них обычно не думают при поиске реального решения этого уравнения, что обычно является тем, что мы хотели до этого момента. Итак, давайте продолжим и найдем n -го корней из единицы для \ (n \) = 3.2 & = \ exp \ left ({i \, \, \ frac {{4 \ pi}} {3}} \ right) \\
& = \ cos \ left ({\ frac {{2 \ pi}} {3}} \ right) + i \ sin \ left ({\ frac {{2 \ pi}} {3}} \ right) & \ hspace {0,5 дюйма} & = \ cos \ left ({\ frac {{4 \ pi}} {3}} \ right) + i \ sin \ left ({\ frac {{4 \ pi}} {3}} \верно)\\
& = — \ frac {1} {2} + \ frac {{\ sqrt 3}} {2} i & & = — \ frac {1} {2} — \ frac {{\ sqrt 3}} {2} я \ конец {выравнивание *} Я оставлю это на ваше усмотрение, чтобы убедиться, что если вы кубите последние два значения в куб, вы фактически получите 1.{i \, \, {\ theta _0}}} \] Итак, это говорит нам, что Таким образом, различные решения \ (\ eqref {eq: eq5} \) равны Итак, мы можем видеть, что точно так же, как было n n -е корня из единицы, так же есть n n -й корень из \ ({z_0} \).{\ frac {1} {3}}} \) Показать все решения Скрыть все решения Показать решение Первое, что нужно сделать, это записать экспоненциальную форму комплексного числа, от которого мы извлекаем корень. Итак, если мы используем \ ({\ theta _0} = \ frac {\ pi} {2} \), мы можем использовать \ (\ eqref {eq: eq6} \) для записи корней. Подключение для \ (k \) дает, Я оставлю это на ваше усмотрение, чтобы убедиться, что если вы возведете оба квадрата в квадрат, то получите 2 \ (i \). Вот экспоненциальная форма числа, Используя \ (\ eqref {eq: eq6} \), корни равны, Подключение для \ (k \) дает, Как и в предыдущей части, я оставлю вам проверить, что если вы кубите каждый из них, вы получите \ (\ sqrt 3 — i \). В предыдущей части курса мы увидели, что биномиальные вероятности могут использоваться для решения таких задач, как «Если честная монета подбрасывается 2 раза, какова вероятность выпадения 2 орлов?» Вероятность выпадения ровно k орлов из N подбрасываний может быть вычислена с помощью формулы ИЛИ с использованием онлайн-калькулятора здесь: Если мы хотим узнать вероятность того, что определенное количество орлов или более, то решить задачу немного сложнее. решить.Чтобы решить такую задачу для большого N (скажем, 100) и большого количества орлов (скажем, 60), вы вычисляете вероятность 60 орлов, затем вероятность 61 орла, 62 голов и т. Д. И складываете все эти вероятности. Представьте, сколько времени потребовалось для вычисления биномиальных вероятностей до появления калькуляторов и компьютеров! Абрахам де Муавр, статистик 18 века и консультант игроков, часто привлекался для выполнения этих длительных вычислений. де Муавр отметил, что, когда количество событий (подбрасываний монеты) увеличивалось, форма биномиального распределения приближалась к очень плавной кривой.Биномиальные распределения для 2, 4 и 12 флипов показаны на рисунке 1. Рисунок 1. Примеры биномиальных распределений. Высота синих столбцов представляет вероятности. де Муавр рассуждал, что, если бы он мог найти математическое выражение для этой кривой, ему было бы намного легче решать такие задачи, как определение вероятности 60 или более решек из 100 подбрасываний монеты. Именно это он и сделал, и обнаруженная им кривая теперь называется «нормальной кривой».« Рис. 2. Нормальное приближение к биномиальному распределению для 12 подбрасываний монеты. Плавная кривая — нормальное распределение. Обратите внимание, насколько хорошо он аппроксимирует биномиальные вероятности, представленные высотой синих линий. Важность нормальной кривой проистекает прежде всего из того факта, что распределения многих природных явлений, по крайней мере, ПРИМЕРНО нормально распределены. Одним из первых применений нормального распределения был анализ ошибок измерения, сделанных в астрономических наблюдениях, ошибок, возникающих из-за несовершенных инструментов и несовершенных наблюдателей.Галилей в 17 веке отмечал, что эти ошибки были симметричными и что небольшие ошибки возникали чаще, чем большие ошибки. Это привело к нескольким гипотетическим распределениям ошибок, но только в начале 19 века было обнаружено, что эти ошибки следовали нормальному распределению. Независимо от этого математики Адрейн в 1808 г. и Гаусс в 1809 г. разработали формулу нормального распределения и показали, что это распределение хорошо соответствует ошибкам. Это же распределение было открыто Лапласом в 1778 году, когда он вывел чрезвычайно важную центральную предельную теорему, которая стала темой более позднего раздела этого чтения.Лаплас показал, что даже если распределение не является нормально распределенным, средние значения повторных выборок из распределения будут почти нормально распределены, и что чем больше размер выборки, тем ближе распределение средних будет к нормальному распределению. Большинство статистических процедур проверки различий между средними значениями предполагают нормальное распределение. Поскольку распределение средних очень близко к нормальному, эти тесты работают хорошо, даже если исходное распределение лишь приблизительно нормальное. Quételet был первым, кто применил нормальное распределение к человеческим характеристикам. Он отметил, что такие характеристики, как рост, вес и сила, распределялись нормально. Площади под частями нормального распределения могут быть вычислены с помощью исчисления. Поскольку это нематематическая обработка статистики, мы будем полагаться на компьютерные программы и таблицы для определения этих областей. На рисунке 3 показано нормальное распределение со средним значением 50 и стандартным отклонением 10.Заштрихованная область между 40 и 60 составляет 68% распределения. Рис. 3. Нормальное распределение со средним значением 50 и стандартным отклонением 10. 68% площади находится в пределах одного стандартного отклонения (10) от среднего (50). На рисунке 4 показано нормальное распределение со средним значением 100 и стандартным отклонением 20. Как показано на рисунке 3, 68% распределения находится в пределах одного стандартного отклонения от среднего. Рис. 4. Нормальное распределение со средним значением 100 и стандартным отклонением 20.68% площади находится в пределах одного стандартного отклонения (20) от среднего (100). Нормальные распределения, показанные на рисунках 3 и 4, являются конкретными примерами общего правила, согласно которому 68% площади любого нормального распределения находится в пределах одного стандартного отклонения от среднего. Вам следует знать следующие правила: 1) 34% площади при нормальном распределении находится между средним значением и 1 стандартным отклонением выше среднего 2) 14% площади при нормальном распределении находится между 1 и 2 стандартными отклонениями выше среднего 3) 2% площади при нормальном распределении более чем на 2 стандартных отклонения выше среднего A можно использовать для расчета площадей при нормальном распределении.Например, вы можете использовать его, чтобы найти долю нормального распределения со средним значением 90 и стандартным отклонением 12, превышающим 110. Установите для среднего значения 90 и стандартного отклонения 12. Затем введите «110» в поле поле справа от переключателя «Вверху». Внизу экрана вы увидите, что заштрихованная область равна 0,0478. Посмотрим, сможете ли вы использовать калькулятор, чтобы определить, что область между 115 и 120 составляет 0,0124. Рис. 5. Дисплей калькулятора, показывающий область выше 110. Ниже ссылка на обычный калькулятор. Используйте его, чтобы проверить три приведенных выше правила. Попробуйте! Ниже приведено видео с информацией, содержащейся в этом чтении. Идите и проверьте это. Приложение-справочник по математике IB со множеством калькуляторов и решателей, предназначенное для IB математики высшего уровня, стандартного уровня, математических исследований и других математических образовательных программ того же уровня. Он используется тысячами студентов каждый день и включает почти все необходимое для успешной сдачи экзаменов IB по математике. Это ваш личный репетитор по математике. Это приложение призвано помочь учащимся пересмотреть и понять основные математические темы своих учебных планов. В этой версии рассматриваются следующие темы: Полезные тождества Округление значащих чисел с помощью калькулятора Формулы Виета Прямые линии Квадратичные уравнения и решения неравенств Квадратичные функции Калькулятор Экспоненты и логарифмы Экспоненциальные и логарифмические функции Арифметические последовательности и ряды с помощью калькулятора, который используется для вычисления n-го члена и суммы первого n термины.Геометрические последовательности и ряды с калькулятором, который используется для вычисления n-го члена, суммы первых n элементов и суммы до бесконечности. Калькулятор сложных процентов. Калькулятор расширения биномиальной теоремы Математические преобразования функций индукции (горизонтальный перенос, вертикальный перенос, горизонтальное растяжение — сжатие, вертикальное растяжение — сжатие, отражения, преобразования абсолютных значений, график обратной функции) Тригонометрия (тригонометрические уравнения, тригонометрические функции, тригонометрические тождества и т. Дифференциация решателя треугольников (производная, правила дифференцирования, таблицы производных, неявное дифференцирование, касательные и нормали, стационарные точки, точки перегиба, построение кривой, графики f (x) и ее производной) Интегрирование (неопределенный интеграл, определенный интеграл, интегральная таблица, Методы интеграции) Приложения интеграции (область между кривой и осью x, площадь между кривой и осью y, площадь между двумя кривыми, объем вращения, кинематика) Комплексные числа (операции с комплексными числами, комплексные сопряжения, уравнения, декартовы уравнения) форма, полярная форма, экспоненциальная форма, диаграмма Аргана, модуль и аргумент, Де Муав Теорема Ре, корни комплексных чисел) Векторы, линии, плоскости с калькулятором Вектор и скалярная проекция с калькулятором Точечное произведение с калькулятором Скрещенное произведение с калькулятором Множества и вероятность (множества, вероятность, условная вероятность, независимые события, теорема Байеса) Калькулятор комбинаций, перестановок и расстановок.Условный калькулятор вычисляет вероятность возникновения события A, учитывая, что событие B произошло, и наоборот. Калькулятор нормального распределения. Калькулятор биномиального распределения. Калькулятор распределения Пуассона. Статистика и статистика двух переменных, а также содержание математических исследований. Мы периодически предоставляем обновления, чтобы улучшить производительность и функциональность приложения. Никаких данных или подключения к Wi-Fi не требуется, кроме видеоуроков. Мы любим отзывы. Итак, присылайте свои мысли или задайте нам вопрос, связавшись с нами здесь: admin @ Mathematics4u.com УСЛОВИЯ ИСПОЛЬЗОВАНИЯ Информация, представленная в этом приложении, предназначена для образовательных целей, и ее точность не гарантируется. Содержание этого приложения было исследовано и опубликовано с особой тщательностью и вниманием, однако нельзя исключать ошибки в процессе. Присылайте любые комментарии и исправления по адресу admin@mat Mathematics4u. В современном мире арабские цифры считаются общепризнанным стандартом исчисления. Десятичная система знаков используется для подсчетов и нумерации во всех развитых странах мира. При этом от римских цифр, которые использовались в непозиционной системе счисления древних римлян, полностью не отказались. Часто можно видеть, что с их помощью нумеруются разделы в книгах, отмечаются века в исторической литературе, указывается группа крови и многие другие параметры, для которых обозначение римскими цифрами стало стандартным. При работе за компьютером с браузером, текстовыми редакторами и другими приложениями может понадобиться ввести некоторые значения римскими цифрами. Отдельный цифровой блок с ними отсутствует на стандартном устройстве ввода, но есть сразу несколько способов, как написать римские цифры на клавиатуре быстро. Лишь малая часть разработчиков приложений предусматривают удобные способы ввода в своих продуктах римских цифр при помощи клавиатуры. На любом компьютере по умолчанию одним из доступных языков является английский. На него можно быстро переключиться за счет комбинации клавиш Alt+Shift или Windows+Пробел (в Windows 10). Английский алфавит полностью закрывает потребность в отдельной цифровой клавиатуре для ввода римских цифр, поскольку все их аналоги могут быть набраны с его помощью заглавными буквами. Следующие буквы английского алфавита заменяют римские цифры: Еще в школе обучают, каким образом необходимо использовать римские цифры, чтобы вводить различные цифры. Например: Чтобы ввести число 33, потребуется использовать 10+10+10+1+1+1. Соответственно, в римской вариации число 33 будет записано следующим образом: XXXIII. Также имеются некоторые особые правила ввода римских цифр, позволяющие укоротить написание больших чисел. В операционной системе Windows поддерживаются ASCII-коды, предназначенные для ввода различных символов. Они могут использоваться, в том числе, для ввода римских цифр. ASCII – это американская таблица кодирования, в которой приведены самые популярные печатные и непечатные символы в виде цифровых комбинаций. Чтобы использовать символы из данной таблицы на стандартной клавиатуре для ввода римских цифр, необходимо применить цифровой блок NUM – расположенный в правой части клавиатуры. Активируйте работу дополнительного цифрового блока при помощи кнопки Num Lock. Следующие комбинации дополнительного цифрового блока идентичны римским цифрам: Способ ввода римских цифр с использованием ASCII-кодов нельзя назвать удобным, но он может применяться, например, когда по тем или иным причинам отключена английская раскладка на клавиатуре. Компания Microsoft при разработке офисного пакета и приложения Word учла, что пользователям, которые работают с текстами, может потребоваться ввести римские цифры. Поскольку делать это с помощью английской раскладки или ASCII-кодов не особо удобно, корпорация Microsoft ввела в Word поддержку специальной команды, автоматически переводящей арабские цифры в римские. Для обозначения цифр в латинском языке приняты комбинации следующих семи знаков: I (1), V (5), X (10), L (50), С (100), D (500), М (1000). Для запоминания буквенных обозначений цифр в порядке убывания придумано мнемоническое правило: Мы Dарим Сочные Lимоны, Хватит Vсем Iх (соответственно M, D, C, L, X, V, I). Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее число следует прибавлять к большему, если слева, то вычитать, а именно: VI — 6, т.е. 5 + 1 Возможно различное обозначение одного и того же числа. Например, число 80 можно обозначить как LXXX (50 + 10 + 10 + 10) и как ХХС (100 — 20). Для записи чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц. I (1) — unus (унус) Если вдруг любознательный человек спросит, почему для обозначения цифр 50, 100, 500 и 1000 были выбраны латинские буквы V, L, С, D, М, то сразу скажем, что это вовсе не латинские буквы, а совсем иные знаки. Дело в том, что основой для латинского алфавита послужил алфавит западногреческий. Именно к нему восходят три знака L, С и М. Здесь они обозначали придыхательные звуки, которых не было в латинском языке. Когда оформлялся латинский алфавит, именно они оказались лишними. Их и приспособили для обозначения чисел в латинской графике. Позднее они по написанию совпали с латинскими буквами. Так, знак С (100) стал похож на первую букву латинского слова centum (сто), а М (1000) — на первую букву слова mille (тысяча). Что же касается знака D (500), то он представлял собой половину знака Ф (1000), а потом уж стал похож на латинскую букву. Знак V (5) являлся всего навсего верхней половиной знака X (10). Мы все пользуемся римскими цифрами – отмечаем ими номера веков или месяцев года. Римская система счета в ее современном варианте состоит из следующих базовых знаков: I 1 Чтобы запомнить цифры, непривычные для нас, пользующихся арабской системой, существует несколько специальных мнемонических фраз на русском и английском языках: Система расположения этих цифр друг относительно друга такова: числа до трех включительно образуются при помощи сложения единиц (II, III), — четырехкратное повторение любой цифры запрещено. Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления — после, (4 = IV), та же логика действует и с другими цифрами (90 = XC). Важно, что любая цифра не должна повторять больше трех раз, таким образом, самое длинное число до тысячи – 888 = DCCCLXXXVIII (500+100+100+100+50+10+10+10+5+1+1+1). Запрет на четвертое использование одной и той же цифры подряд стал появляться только в XIX веке. Поэтому в старинных текстах можно увидеть варианты IIII и VIIII вместо IV и IX, и даже IIIII или XXXXXX вместо V и LX. Остатки этого написания можно увидеть на часах, где четыре часто отмечается именно с помощью четырех единиц. В старых книгах также нередки случаи двойных вычитаний – XIIX или IIXX вместо стандартных в наши дни XVIII. Также в Средневековье появилась новая римская цифра – ноль, который обозначался буквой N (от латинского nulla, ноль). Большие числа отмечались специальными знаками: 1000 — ↀ (или C|Ɔ),5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ). Миллионы получаются при двойном подчеркивании стандартных цифр. На данный момент не существует единой теории происхождения римских цифр. Одна из самых популярных гипотез гласит, что этрусско-римские цифры произошли от системы счета, которая использует вместо цифры штрихи-зарубки. Таким образом, цифра «I» — это не латинская или более древняя буква «и», а насечка, напоминающая форму этой буквы. Каждую пятую насечку обозначали скосом – V, а десятую перечеркивали – Х. Число 10 выглядело в этом счете следующим образом: IIIIΛIIIIX. Именно благодаря такой записи цифр подряд мы обязаны особой системе сложения римских цифр: со временем запись числа 8 (IIIIΛIII) могла сократиться до ΛIII, что убедительно демонстрирует, каким образом римская система счета получила свою специфику. Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Альтернативная теория принадлежит Альфреду Куперу, который предположил рассмотреть римскую систему счета с точки зрения физиологии. Купер считает, что I, II, III, IIII – это графическое представление количества пальцев правой руки, выкидываемых торговцем при назывании цены. V – это отставленный большой палец, образующий вместе с ладонью подобную букве V фигуру. Именно поэтому римские цифры суммируют не только единицы, но и складывают их с пятерками – VI, VII и т.п. – это откинутый большой палец и другие выставленные пальцы руки. Число 10 выражали с помощью перекрещивания рук или пальцев, отсюда пошел символ X. Еще один вариант – цифру V попросту удвоили, получив X. Большие числа передавали с помощью левой ладони, которая считала десятки. Так постепенно знаки древнего пальцевого счета стали пиктограммами, которые затем начали отождествлять с буквами латинского алфавита. Сегодня в России римские цифры нужны, в первую очередь, для записи номера века или тысячелетия. В разных странах римские цифры употребляются немножко по-разному: в СССР было принято указывать с помощью них месяц года (1.XI.65). На западе римскими цифрами часто пишут номер года в титрах фильмов или на фасадах зданий. В части Европы, в особенности в Литве, нередко можно встретить обозначение римскими цифрами дней недели (I – понедельник и так далее). В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр. В России при письме рукой принято подчеркивать римские числа снизу и сверху одновременно. Однако часто в других странах подчеркивание сверху значило увеличение регистра числа в 1000 раз (или 10000 раз при двойном подчеркивании). Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой). Римская
система нумерации с помощью букв была
распространена в Древнем Риме и Европе
на протяжении двух тысяч лет. Только в
позднем средневековье ее сменила более
удобная для вычислений десятичная
система цифр, заимствованная у арабов
(1,2,3,4,5…). Но,
до сих пор римскими цифрами обозначаются
даты на монументах, время на часах и (в
англо-американской типографической
традиции) страницы книжных предисловий,
размеры одежды, главы монографий и
учебников. Для
обозначения чисел применялось 7 букв
латинского алфавита (первая буква слов
– пять, десять, пятьдесят, сто, пятьсот,
тысяча): I
= 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000 С
(100) -это первая буква латинского слова
centum (сто) а
М — (1000) — на первую букву слова mille (тысяча). Что
же касается знака D (500), то он представлял
собой половину знака Ф (1000) Знак
V (5) является верхней половиной знака Х
(10) Промежуточные
числа образовывались путем прибавления
нескольких букв справа или слева. Сначала
пишутся тысячи и сотни, затем десятки
и единицы. Таким образом, число 24 пишется
как XXIV Натуральные
числа записываются при помощи повторения
этих цифр. При
этом, если большая цифра стоит перед
меньшей, то они складываются (принцип
сложения), если же меньшая — перед большей,
то меньшая вычитается из большей (принцип
вычитания). Другими
словами — если знак, обозначающий меньшее
число, стоит справа от знака, обозначающего
большее число, то меньшее прибавляют к
большему; если слева — то вычитают:
VI
— 6, т.е. 5+1
IV — 4, т.е. 5-1
LX — 60, т.е. 50+10
XL
— 40, т.е. 50-10
CX — 110, т.е.100+10
XC — 90, т.е.
100-10
MDCCCXII — 1812, т.е. 1000+500+100+100+100+10+1+1 Последнее
правило применяется только во избежание
четырёхкратного повторения одной и той
же цифры. Во
избежание 4-х кратного повторения число
3999 записывается как MMMIM. Возможно
различное обозначение одного и того же
числа. Так, число 80 можно представить
как LXXX (50+10+10+10) и как XXC(100-20). Например,
I, Х, С ставятся соответственно перед Х,
С, М для обозначения 9, 90, 900 или перед V,
L, D для обозначения 4, 40, 400. Например,
VI = 5+1 = 6, IV = 5 — 1 = 4 (вместо IIII). XIX
= 10 + 10 — 1 = 19 (вместо XVIIII), XL
= 50 — 10 =40 (вместо XXXX), XXXIII
= 10 + 10 + 10 + 1 + 1 + 1 = 33 и т.д. Римские
цифры MCMLXXXIV Примечание: Основные
римские цифры:
I(1) — unus (унус)
II(2) — duo
(дуо)
III(3) — tres (трэс)
IV(4) — quattuor
(кваттуор)
V(5) — quinque (квинквэ)
VI(6) — sex
(сэкс)
VII (7) — septem (сэптэм)
VIII (8) — octo
(окто)
IX (9) — novem (новэм)
X (10) — decem (дэцем)
и т. В настоящее время большинство людей используют систему арабские цифры за то, что было проще. В этом руководстве мы стремимся научить вас этой системе нумерации, которая все еще используется в некоторых вещах (например, в фильмах: Звездные войны IV, V, VI), и объясните вам, чтобы вы могли легко выучить. Прежде всего, если вы уже знакомы с теорией и хотите использовать конвертер, вы можете использовать его отсюда: Содержание Сегодня римские цифры — это редко используемая система счисления. Они составлены заглавные буквы для представления чисел. Объединение этих букв добавляется или вычитается, чтобы освободить место для другого числа. Все буквы используются следующие: Например, число 1 представлено буква I «, и два посредством суммы 2 «II». Как только эти эквивалентности будут поняты, ниже мы объясним, как писать римские цифры. Чтобы написать римские цифры, вы должны освоить сложение и вычитание. Если две буквы равны или первая больше второй, сложить, в противном случае (если первая буква меньше второй), вычитаются. Например: Если вы хотите использовать число, равное или больше 4, вам нужно будет разместить строку с именем связь; вверху букв. Это будет означать, что число умножается на 1. Например, 4.000 римскими цифрами представлен так: Число 10.000 представлен так: И, наконец, тот, который может быть сложным, 50.000 римскими цифрами записывается следующим образом: Раньше не было необходимости в очень больших количествах, таких как млн. Число 5 (V) и его кратные, 50 и 500 (L, D), их нельзя использовать для вычитания. Неверно писать «VC» для обозначения Число 95. Правильная форма: XCV. Поскольку у вас есть представление о том, как писать римские цифры, удобно видеть полный список с числа от 1 до 1000, и еще одна серия с более высокими числами. Так вы познакомитесь с ними ближе и сможете лучше их понять. В предыдущих списках мы достигли числа 1. Мы размещаем случайные числа, потому что считаем, что нумерация их всех будет ненужное и неэффективное. Понаблюдайте за ними и посмотрите, какую структуру мы используем для их записи, а еще лучше придумайте другой способ представления того же числа. Тогда мы расскажем почему они могут быть написаны только так. Эта информация вам очень поможет. По общему признанию, арифметические операции с римскими цифрами несколько сложны, по сути, это одна из причины почему эта система нумерации не использовалась. Способ решения этих операций состоит из следующих шагов, как и в случае с арабскими цифрами, однако процесс с римскими цифрами Это дольше. Здесь мы объясним, как сложить, вычесть, умножить и dividir с номерами древнего рима. Чтобы добавить 2 римские цифры, выполните следующие действия: Вычитание легче сложения. Для его выполнения выполните следующие действия. Чтобы умножить римские цифры, вы должны знать сложите их, а арабские числа разделите и умножьте на 2. Вы также должны сделать стол, разместив римскую цифру справа, а другую — слева. Затем выполните следующие шаги. Мы собираемся сослаться на «А» как числа слева уже «B» как те, что справа. Посмотрите пример умножения двух римских цифр. Теперь удаляем все строки, в которых в левой части стоит четное число. Теперь нам нужно только сложить числа справа, как мы уже сделали. Деления римскими цифрами они были не очень успешными, кроме того, нет никаких известных правил их удаления. Единственное, что известно, это то, что вам нужно вычесть делитель на дивиденд пока не дойдете до числа меньше делителя. Например: 10/3. Здесь дивиденд равен 10, а делитель равен 3. Для вычисления деления римскими цифрами необходимо следующее: Остаток равен 1, а частное равно 3. Вы должны проделать тот же процесс с латинскими буквами, и вы получите результат в этой системе счисления. Чтобы вам было понятно, что это за информация, мы покажем вам больше вещей, которые вы должны принять во внимание при использовании этих чисел. Мы уверены, что так вы их полностью поймете. Римские цифры используются очень редко, хотя их изучение важно. Вы часто увидите их написанными в следующих случаях: Записывать даты римскими цифрами очень просто. Все, что вам нужно сделать, это разделить дату на подгруппы и преобразовать их в римские цифры. Например, если мы хотим преобразовать дату 01-02-2018 или другую дату, 1 февраля 2018. Сначала мы конвертируем день 1, который будет I, затем мы конвертируем месяц, 2, который будет II, и, наконец, мы конвертируем год, 2018, который будет MMXVIII. Затем мы повторно группируем каждую из частей в наш традиционный формат: I-II-MMXVIII. Если у вас есть какие-либо вопросы по поводу этого процесса, вы можете оставить нам комментарий в конце статьи. Многие из вас задавали нам этот вопрос, и мы постараемся ответить на него наилучшим образом. Прежде всего, если вы хотите написать 1 римскими цифрами в текстовом редакторе Word, вам просто нужно написать букву I в верхнем регистре. От 1 до 4000 все числа могут быть представлены буквами, которые мы обычно используем. Если вы хотите написать большее число, например 5000, вы должны использовать уздечка как мы уже прокомментировали, этого можно достичь, выполнив следующие шаги: Готовый! Вы уже умеете писать римские цифры в Word. С другой стороны, если вы хотите, чтобы в списке использовались римские цифры вместо обычных чисел, используется следующая опция: В любом случае, если у вас есть какие-либо вопросы, вы можете оставить нам комментарий ниже, и мы ответим как можно скорее. Далее мы подготовили для вас несколько упражнений, чтобы вы могли проверить свои знания римских цифр. Вы можете без проблем просмотреть то, что мы узнали на протяжении всей статьи, важно, чтобы вы соблюдали основы и основы 🙂 Удачи! Римские цифры актуальны и по сей день, несмотря на то, что в повседневной жизни их применение усложнило бы жизнь для большинства профессий, если бы их использовали вместо уже привычных арабских. Большие цифры выглядят довольно устрашающими, например, число 3 999 на римский лад будет MMMCMXCIX. Это число является последним, которое можно записать таким образом. Содержание Римские цифры использовали в древнем Риме в непозиционной системе счисления. В раннем периоде римляне записывали и большие цифры. В то время максимальным числом являлось 399 999. Цифры записывались в следующей последовательности: сначала записывались сотни тысяч, затем десятки тысяч, тысячи, сотни, десятки и единицы. Часто для того, чтобы выделить в тексте числа, их записывали с чертой сверху. Иногда записывались числа с чертой и сверху, и снизу. Такая запись применялась в русском рукописном тексте. В типографии римские цифры записывались без черт из-за возникновения технических сложностей. Иногда авторы применяли черту сверху над римским числом для увеличения его значения в тысячу раз. Это интересно: римские цифры от 1 до 10. До 19 века число 4 на римский манер записывалось как IIII. Затем число изменили, и оно обрело новый, упрощенный вид — IV (5 — 1). Меньшие цифры могут стоять перед большими. В этом случае они отнимаются от большего. И наоборот, если единицы стоят после десятков, то они суммируются, например, VI (5 + 1) — это цифра 6. При этом вычесть можно только цифру, обозначающую один или степени десятки. Уменьшаемые могут быть только ближайшие к вычитаемому в числовом ряду две цифры.Нельзя повторять меньшие цифры в числе. Из этого следует только 6 примеров правила вычитания: Например, число 94 римскими цифрами будет XCIV, то есть: 100 — 10 + 5 — 1. Некоторые фирмы по производству часов до сих пор используют запись четверки как IIII. Скорее всего делают они это скорее по эстетическим соображениям. Есть несколько версий о том, почему такая форма более приемлема. По одной из версий запись IV является в имени бога дневного света и неба Юпитера первой буквой — IVPITER. Арабские цифры: Римские цифры: 1 I 2 II 3 III 4 IV 5 V 6 VI 7 VII 8 VIII 9 IX 10 X 11 XI 12 XII 13 XIII 14 XIV 15 XV 16 XVI 17 XVII 18 XVIII 19 XIX 20 XX 21 XXI 22 XXII 23 XXIII 24 XXIV 25 XXV 26 XXVI 27 XXVII 28 XXVIII 29 XXIX 30 XXX 31 XXXI 32 XXXII 33 XXXIII 34 XXXIV 35 XXXV 36 XXXVI 37 XXXVII 38 XXXVIII 39 XXXIX 40 XL 41 XLI 42 XLII 43 XLIII 44 XLIV 45 XLV 46 XLVI 47 XLVII 48 XLVIII 49 XLIX 50 L 51 LI 52 LII 53 LIII 54 LIV 55 LV 56 LVI 57 LVII 58 LVIII 59 LIX 60 LX 61 LXI 62 LXII 63 LXIII 64 LXIV 65 LXV 66 LXVI 67 LXVII 68 LXVIII 69 LXIX 70 LXX 71 LXXI 72 LXXII 73 LXXIII 74 LXXIV 75 LXXV 76 LXXVI 77 LXXVII 78 LXXVIII 79 LXXIX 80 LXXX 81 LXXXI 82 LXXXII 83 LXXXIII 84 LXXXIV 85 LXXXV 86 LXXXVI 87 LXXXVII 88 LXXXVIII 89 LXXXIX 90 XC 91 XCI 92 XCII 93 XCIII 94 XCIV 95 XCV 96 XCVI 97 XCVII 98 XCVIII 99 XCIX 100 C 101 CI Пользователям достаточно сложно запомнить все римские цифры от 1 до 100 и более. Итак: Под формой ввода находятся примеры записи веков римским цифрами. Еще один удобный сервис для перевода любого арабского числа в римское. Здесь есть 2 поля ввода. Он находится по адресу http://infofaq.ru/perevod-v-rimskie-chisla.html. Пользоваться им также достаточно просто: Читайте также: арабские цифры от 1 до 10. Чаще всего римские цифры сегодня применяются для записи тысячелетия или веков. Их используют для придания роману или другому тексту оттенок архаичности. Часто такие цифры используются в исторических книгах и учебниках. Применяются цифры и в написаниях исторических имен для обозначения порядкового номера, к примеру, Петр l, Рамсес ll. Киноиндустрия США часто употребляет римские цифры для обозначения части фильмов и телесериалов. Некоторые европейские страны записывают так дни недели. А в Голландии железнодорожные промежутки пути имеют обозначения каждого сотого метра римскими цифрами. Есть заблуждение, что западные швейные фирмы используют римские цифры для обозначения размеров — L, M, S, XL, но это не так. На самом деле это сокращения от английских слов: Large (большой), eXtra (весьма, очень), Small (маленький). Чаще всего в странах СНГ применяются римские цифры от 1 до 100. В настоящее время римская система счисления утратила былое значение. Большинство западных стран полагаются на арабские цифры, азиатские страны имеют собственную цифровую систему, а в арабской культуре применяется типографика, отличная от классических арабских цифр. Однако в часовом деле римские цифры являются одним из классических элементов дизайна и продолжают широко использоваться. Их можно встретить на циферблатах часов разных эпох, начиная от карманного антиквариата и заканчивая современными моделями Glashütte Original, Lange, Ulysse Nardin, Blancpain, Cartier или даже Rolex. Иногда владельцы часов с римскими цифрами замечают нечто странное и необычное: в то время как в римской системе счисления цифра «4» пишется как «IV», в большинстве часов используется написание «IIII». Обычно римские цифры пишутся так: I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII и т.д. Числа в римской системе представлены комбинациями букв латинского алфавита. Они возникли в Древнем Риме примерно в 1000 г. до н.э. и оставались привычным способом написания чисел в Европе вплоть до позднего средневековья. В 14 веке, с началом эпохи Возрождения римские цифры утратили актуальность (как и латинский язык) и их постепенно заменили современными (и более удобными) арабскими цифрами. В раннем варианте римского счисления применялись обозначения «IIII» для 4 (вместо «IV») и «VIIII» для 9 (вместо «IX»), но их часто путали с похожими «III» и «VIII». Уже после падения Римской империи начальная аддитивная система римских числовых обозначений трансформировалась в более привычную нам субтрактивную систему. Первые механические часы появились в Европе в 13 веке. В те времена часы устанавливались на церквях, а латынь была официальным католическим языком. Таким образом, присутствие римских цифр на циферблатах старинных часов вполне логично. Однако причина, по которой часовые мастера применяли написание «IIII» вместо «IV», когда она уже вышла из обращения, остается неясной. Древние римляне пользовались солнечными часами, основанными на концепции теневых часов из античной Вавилонской астрономии (около 1500 г. до н.э.). Нельзя забывать, что часовое дело произошло от астрономии. При раскопках в Риме были найдены античные солнечные часы и даже их карманные варианты с выгравированными римскими цифрами. Причина, по которой в те времена практиковалось написание «IIII», объясняется древней римской мифологией, где главным божеством считался Юпитер — бог неба, дневного света и грозы (на латыни IVPPITER). Было бы богохульством использовать первые буквы имени бога в качестве цифры, поэтому обозначение «IIII» выглядело предпочтительнее. Современная субтрактивная система внедрялась постепенно, и у ранних часовщиков был выбор, какой из вариантов написания «четверки» применять на практике. Как уже упоминалось, первые часы устанавливались на церквях, соборах и других публичных зданиях. В средневековье распространение грамотности ограничивалось небольшой группой духовенства и горожан, а большинство населения было неграмотно. Этим можно объяснить использование «IIII», так как понимание «IV» требует знаний элементарной математики. Одна из теорий касается французского короля Людовика XIV по прозвищу «Король-солнце», объединившего вокруг своей персоны всю систему абсолютного монархического правления во Франции. Считавший себя представителем бога на земле, Людовик XIV не хотел, чтобы часть его имени писали на циферблатах солнечных часов. Эта теория кажется весьма неправдоподобной, ведь обозначение «IIII» уже существовало в различных областях при правлении многих других монархов, чьи имена не содержали «IV». Последнее возможное объяснение является наиболее рациональным и логичным из вышеперечисленных. Причиной использования «IIII» может быть способ достижения большего визуального баланса циферблата. Многие винтажные и современные часы полагаются на сочетание аддитивной и субтрактивной систем (где 4-IIII, а 9-IX). В этом случае циферблат имеет следующие цифры: I, II, III, IIII, V, VI, VII, VIII, IX, X, XI, XII. Их можно разделить на три равных области, в каждой из которых используется уникальный набор числовых обозначений: в первой трети — только «I», второй — только «V» и, наконец, в последней трети — цифры с «X». С помощью такого разделения достигается элегантный и гармоничный вид циферблата. Более того, «IIII» легче читается, особенно в перевернутом виде, поскольку все цифры ориентируются на центр циферблата. Видимо, не единственный точный ответ, а совокупность старинных традиций и практических решений смогут лучше всего объяснить, почему часовая индустрия по-прежнему предпочитает «IIII» на циферблатах с римскими цифрами.
20 710
Таким образом, VI = 6 (V + I), цель IV = 4 (V – I). Отсюда, как вы пишете римские цифры в vi? Следовательно, 6 римскими цифрами записывается как VI = 6. Почему цифра 4 на часах с римскими цифрами неверна? Причина не так уж и надуманная. Использование четырех I вместо IV для «четырех» из-за процесса литья цифр. Так как некоторые цифры были отлиты из металла или вырезаны из дерева или кости, вам понадобится 20 I, 4 V и 4 X, четные числа каждого, если вы используете четыре I для «четырех». Дополнительно Как вы меняете IX на 6? Также известно, что буква х символизирует умножение. Следовательно, IX6=6 (1×6=6), или 1, умноженный на 6, равно 6. Альтернативный ответ: добавьте букву S перед IX, чтобы читать SIX. Добавьте «S» перед IX, чтобы получилось ШЕСТЬ. Что означает III VI IX XII? Римская цифра «XII» появляется над лицом, римская цифра «III» появляется справа от лица, римская цифра «VI» появляется под лицом и римская цифра «IX» появляется слева от лица. Римские цифры пишутся с использованием семь разных букв: I, V, X, L, C, D и M представляют собой числа 1, 5, 10, 50, 100, 500 и 1,000. Мы используем эти семь букв, чтобы составить тысячи других. Например, римская цифра для двоих записывается как «II», что означает, что две единицы соединяются вместе. Что такое римские числа? Символы В римской системе счисления используется всего семь символов: I, V, X, L, C, D и M. I представляет число 1, V представляет число 5, X равно 10, L равно 50, C равно 100, D равно 500 и M равно 1,000. Различные расположения этих семи символов представляют разные числа. Можете ли вы написать 4 как IIII? IIII был самым ранним способом написать 4 Обычно римские цифры пишутся так: I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII и так далее. … Однако, несмотря на то, что в настоящее время широко признано, что 4 надо писать IV, первоначальный и самый древний образец римских цифр не был таким, каким мы его знаем сегодня. 2021 римскими цифрами — это MMXXI. Также Почему 49 римскими цифрами не так? Формирование цифр Вы бы сложили все отдельные значения символов вместе, чтобы получить общее значение. … Например, римскими цифрами 49 будет XLIX (50-10 = 40 и 10-1 = 9), а не IL. Кроме того, для вычитания вы можете поместить только одну меньшую цифру перед большой. Что нужно добавить к 9, чтобы получилось 6? При просмотре номера 9 с планшета заблокируйте автоповорот экрана перед поворотом на 180 градусов. Это превратит 9 в 6. Наконец, добавьте букву S к римской цифре девять так, чтобы С + IX = ШЕСТЬ. Римская цифра 9 (9) Что означает Тиффани Атлас? С эстетикой, которая с годами приобрела безошибочную привлекательность Tiffany, Atlas® коллекция названа в честь мифологический греческий титан который изображен на деревянной статуе с часами над главными дверями флагманского магазина Tiffany & Co. Какое число XVI? Значащие числа от одного до тысячи Что означает VII XII? XII = 12 и VII = 7 в цифрах. Почему 2020 римскими цифрами написано как MMXX? Мы знаем, что римскими цифрами мы пишем 10 как Х, а 1000 как М. Следовательно, 2020 римскими цифрами записывается как 2020 = 2000 + 20 = ММ + ХХ = ММХХ. Какое римское число равно 400? Римские цифры от 1 до 1000 Как написать 0 римскими цифрами? Согласно истории римских цифр, римская система не имела никакого значения для обозначения нуля. Какое римское число равно 100? 100 римскими цифрами C тогда как 31 — это XXXI. 100 – 31 = 69. Римляне никогда не использовали свои цифры для арифметики., что позволяет избежать необходимости оставлять столбец пустым с нулевым символом. … Вместо этого сложение и вычитание выполнялись на счетах или счетной рамке. Какое число LLL записано римскими цифрами? Решение: римская цифра III 3 а я 1. Почему IIII изменился на IV? Когда Римская империя использовала римские цифры, имя верховного божества римлян, Юпитера, записывалось на латыни как IVPPITER. Там возникло ощущение, что использование начала имени Юпитера на циферблате часов, перевернутого туда, где оно упало, было бы неуважением к божеству. Почему Rolex использует IIII вместо IV? Глядя на древние артефакты, мы видим, что римляне использовали «IIII» вместо «IV». Это означает, что Используемые сегодня римские цифры на часах являются исторически действительными римскими цифрами.. Римляне использовали сложение и вычитание для составления чисел из латинских букв. В то время как в математике они ставили «IV», они выгравировали «IIII» на своих солнечных часах. Замечательную систему цифр придумали древние арабы! Практически везде на нашей планете ею пользуются достаточно успешно различные люди вот уже несколько веков. Но и римские цифры пока не утратили свою актуальность. Непозиционная система счисления от древних римлян используется в письме для обозначения веков и тысячелетий, порядковых номеров монархов и номеров томов в энциклопедиях, при обозначении валентности химических элементов, нумерации циферблатов наручных часов. Только вот задача набрать римские цифры на клавиатуре у тех, кто этого никогда ранее не делал может вызвать некоторые затруднения. Сначала вам покажется, что римская система чисел достаточно громоздкая и неудобная, использовать ее для записи конкретных дат сложно, читать тоже. Но вы научитесь со временем набирать римские цифры быстро. Как набрать римские цифры на компьютерной клавиатуре Чтобы быстро набрать римские цифры на клавиатуре, перейдите на английский язык. Нажмите на CapsLock, чтобы набирались заглавные буквы. Цифра 1 – это буква I . Цифре 2 соответствуют две буквы II и так далее до трех. Цифре 5 соответствует буква V . Цифра 4 в римской системе это «5-1», значит набираем IV . При наборе меньшее число пишется перед большим. Цифра 6=5+1, то есть VI . При наборе меньшее число пишется после большего. Цифра 10 – это X . Цифра 50 обозначается на письме буквой L . А вот 40=50-10, значит, XL . Цифра 60 – это 50+10, значит, LX . Буква С – это сотня (легко запоминается, если провести ассоциацию с центнером), буква D – 500, буква М – тысяча. Если требуется записать сложное число, такое, как 178, например, то справа пишем меньшее число, слева побольше: 178=100+70+8, значит СLXXVIII . Если ваш день рождения в арабской нумерации 23.06.1977, то записанный римскими цифрами он будет выглядеть как XXIII.VI.MCMLXXVII . В некоторых случаях при записи больших чисел римскими цифрами могут возникать некоторые затруднения. Чтобы их успешно преодолеть рекомендуем воспользоваться одним из конвертеров римских чисел в арабские. Один из таких конвертеров представлен на сайте . Кстати, римская система исчисления была популярна в Европе более 2 тысяч лет. В вордовском документе ставить рисские цифры приходится каждому второму пользователю. Особенно это пригождается студентам, кто во время учебы пишет немало научных работ: курсовых, рефератов, диссертаций и дипломов. В них римские цифры используются для обозначения разделов и глав. В нашей статье вы сможете узнать, как поставить римские цифры в Ворде , сделав это максимально быстро и просто. Под римскими цифрами принято понимать цифры, которые использовались еще древними римлянами. У них есть свои способы написания, запомнить их относительно несложно. Однако, несмотря на частоту использования римских цифр, на компьютерной клавиатуре они не размещены, поэтому у пользователей, особенно начинающих, возникает вопрос: «А как же поставить римские цифры в Ворде?». Обо всем по порядку. Для данной версии текстового редактора Ворд принято выделять два способа написания римских цифр. Например: V (5), X (10), L (50), C (100), D (500 Второй способ написания римских цифр в Ворде – при помощи формулы перевода арабских цифр в римские, которая имеется в программе Microsoft Word. Для этого пользователю необходимо в нужном месте вордовского документа нажать сочетание двух — клавиш Ctrl+F9. При этом должны появиться две фигурные скобки, которые будут выделены серым цветом. Далее, в выделенной области между фигурными скобками вводим код. Выглядит он следующим образом: {=число\* Roman}. Например, если пользователю необходимо написать число 1500, то вводится код {=1500\* Roman}. Затем нажимаем на клавиатуре клавишу F9 и получаем написанное число уже римскими цифрами. Какому способу лучше всего отдать предпочтение? Выбирать первый вариант написания римских цифр лучше всего тем, кто знает как правильно писать то или иное число. Либо римское число находится перед глазами пользователя. А вот второй способ удобен в случае, когда пользователь в написании римских цифр не силен. Для более свежих версий текстового редактора Word могут применяться как вышеописанные способы, так и еще один, о котором мы прямо сейчас расскажем. В этом варианте пользователем применяется способ, в котором выбирается нужный формат нумерации. Как же это сделать? Для начала пользователь заходит во вкладку «Главная» на панели инструментов. Далее – в раздел «Абзац» и «Нумерация». После в последнем разделе выбираем необходимый нам раздел. Благодаря клавише «Enter», нужная нам нумерация будет сохраняться от пункта к пункту. Последний метод тоже вряд ли кого-то затруднит, он также прост и удобен в исполнении. Печатая в Ворде зачастую необходимо по содержанию текста воспользоваться римскими цифрами. Это может быть оформление оглавления, перечисления и просто вставка нужного числа в контексте. Особенно римские цифры необходимы в текстах где приводятся исторические события. В Word существует несколько вариантов вставки необходимых римских цифр. Просто перейдя на английский язык, заглавными буквами печатаем необходимое римское число. Ведь латиница, которую используют для их написания, совпадает с ним. Единицы здесь отображаются «I», пять «V», десятки «X», сотни «C», тысячи «M». При таком способе необходимо знать как правильно написать нужное число. Для начала напечатать весь текст, который впоследствии должен быть пронумерован римскими цифрами. Произвести его выделение. А затем наведя на него курсор кликнуть правую клавишу мыши. Появиться меню, в котором необходимо выбрать «Нумерация», а в открывшемся подменю «Библиотека нумерации» выбрать квадрат с римской нумерацией. Произойдет автоматическое выставление нужного количества номеров. Можно проделать это на первом предложении, тогда нумерация следующей строки будет происходить автоматически при нажатии «ENTER». Зайдите в ленте панели меню «Вставка» и откройте «Символы». В «Набор» выберите «основная латиница». Вставьте нужную комбинацию символов, соответствующую необходимой римской цифре. Также, если сначала сверху листа вставить все необходимые символы, можно в дальнейшем пользоваться через их «Копирование» и в нужном месте «Вставка». Примените сочетание функциональных клавиш. В процессе работы с текстовым редактором Microsoft Word пользователям приходится сталкиваться с разнообразными заданиями и трудностями. Некоторые из них могут быть достаточно банальными. Довольно часто пользователи интересуются, как поставить римские цифры в Word. Этому вопросу и посвящена данная статья. Давайте разбираться. Поехали! Для вставки дополнительных символов есть свои комбинации клавиш Первый способ — набрать вручную. Если необходимо сделать такую нумерацию для списка, то кликнув по кнопке нумерации, выберите из списка вариант с нумерацией римскими цифрами. Суть следующего варианта заключается в написании формулы. Такой способ считается более правильным. Установите значок курсора на том месте, где хотите поставить число и воспользуйтесь комбинацией клавиш Ctrl+F9. В появившихся фигурных скобках без кавычек введите следующее: «=арабская цифра\*ROMAN» и нажмите F9. Если вы напишите «roman» маленькими буквами, то и полученное число также будет нижнего регистра. Рассмотрим четыре способа, как напечатать римские цифры в Word. Римские цифры можно писать по-разному, в зависимости от цели. Римские цифры в списке Word. Если римские числа нужны для нумерации в списке, то можно воспользоваться функциями Word создания нумерованного списка. На закладке «Главная» в разделе «Абзац» нажимаем на кнопку «Нумерация» в Word 2013, а в Word 2007 это кнопа – «Создание нумерованного списка». Выбираем в появившемся окне кнопку с римскими числами. Как написать римские цифры в Word. Пишем римские цифры английскими большими буквами. Переключаем клавиатуру на английскую раскладку и печатаем большими (заглавными) буквами. Вспоминаем, чтобы написать буквы заглавными нужно: a)Или нажимаем клавишу «Caps Lock». Чтобы написать римскую цифру 1, нажимаем на клавишу буквы «I» (и английской). Римская цифра 2 – II. Здесь приведена таблица написания римских чисел. Как сделать римские цифры в Word. Применим формулу, которая будет переводить арабские числа в римские. Ставим курсор в то место, где нужно написать римское число. Нажимаем сочетание клавиш «Ctrl» + «F9». Внимание! Если это сочетание клавиш не работает (в Word 2013), то попробуйте нажать такое сочетание клавиш – «Ctrl» + «Fn» + «F9». Появится серое поле в фигурных скобках. В этом поле пишем формулу, которая преобразует арабские цифры в римские. Мы будем преобразовывать число 2015. Пояснение к формуле. Сначала ставим всегда знак «Равно». Пишем число, которое нужно преобразовать. Пишем косую черточку (слеш), наклоненную в лево (). Она ставится так – нажимаем на клавишу черточек, без нажатия дополнительных кнопок, русская раскладка клавиатуры. Пишем английскими буквами слово «ROMAN». Тогда число римскими буквами будет написано большими цифрами. Если в формуле напишем слово «roman» маленькими буквами, то и римское число будет написано маленькими цифрами. Нажимаем на клавишу «F9» (или сочетание клавиш – «Fn» + «F9»). Чтобы откорректировать формулу, изменить число в формуле, т.д., нажимаем на эту цифру и нажимаем правую кнопку мыши. Из появившегося диалогового окна выбираем функцию «Коды/значения полей». Вместо числа появилась формула. Меняем число 2015 на 10. Снова нажимаем клавишу «F9» (или «Fn» + «F9»). Как вставить римские числа в Word. Вставить символы. На закладке «Вставка» В разделе «Символы» нажимаем на кнопку «Символ». Затем, нажимаем на кнопку «Другие символы». Выбираем нужный символ. В диалоговом окне «Символ» указан код этого символа. Можно поставить этот символ кодом. Использование предлога in в английском языке Употребление и произношение in LearnPracticeDownload 6 римскими цифрами — это VI. Чтобы преобразовать 6 в римские цифры, мы запишем 6 как сумму чисел 5 и 1, то есть 6 = 5 + 1, после чего заменим преобразованные числа соответствующими римскими цифрами, мы получим 6 = V + I = VI. В этой статье мы объясним, как правильно преобразовать 6 в римские цифры. Римскую цифру 6 можно получить, используя метод, указанный ниже: ☛ Также проверьте: Калькулятор римских цифр Римские цифры могут показаться отличными от цифр, но они похожи. Например, 6 римскими цифрами эквивалентно VI. Римские цифры для чисел, относящихся к 6, приведены ниже: Пример 1. Найдите разницу между 86 и 6 римскими цифрами. Решение: Решение данной задачи, 86 — 6 = 80 Пример 2: Найдите значение (20 — 24) + 6 римскими цифрами. Решение: Решение (20 — 24) + 6 = -4 + 6 = 2. Теперь запишем ответ, то есть 2 = II. Пример 3: Найдите значение 3908 — 6. Решение: Решение данной задачи, 3908 — 6 = 3902 Пример 4. Чему равно частное при делении XVIII на VI? Решение: XVIII = 18 и VI = 6 в цифрах. перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду Готовы увидеть мир глазами математика? Математика лежит в основе всего, что мы делаем. Забронируйте бесплатный пробный урок Чтобы записать 6 римскими цифрами, мы сначала представим 6 как сумму чисел 5 и 1, а затем запишем их соответствующие эквивалентные римские буквы, чтобы применить «аддитивную запись», т. е. 6 = 5 + 1 = V + я = VI. Следовательно, 6 в римских числах выражается как VI. 6 римскими цифрами — это VI, а 4 — это IV. 6 — 4 = 2. Следовательно, чтобы получить 6, к 4 нужно прибавить 2. Теперь, чтобы перевести 2 в римские числа, выразим его в виде суммы двух единиц, то есть 2 = 1 + 1 = I + I = II. Решение (76 — 79) + 6 = -3 + 6 = 3. Чтобы выразить (76 — 79) + 6 римскими цифрами, запишем ответ, то есть 3, как сумму трех единиц и соединим эквивалентные римские цифры, т. Чтобы преобразовать 6 в римские цифры, преобразование включает в себя разбиение числа на сумму 2 чисел, так что мы можем применить «аддитивную запись», то есть 6 = 5 + 1 = V + I = VI. Согласно правилам написания римских цифр, мы знаем, что когда большая буква предшествует меньшей, буквы добавляются. В случае 6 это будет VI = V + I = 5 + 1 = 6. Поэтому мы обозначаем 6 римскими цифрами как VI. ☛ Статьи по теме: Рабочие листы по математике и LearnPracticeDownload Римские цифры VI можно записать в виде чисел, комбинируя преобразованные римские цифры, т. Числовое значение римских цифр VI может быть получено с помощью любого из двух методов, приведенных ниже: Метод 1: В этом методе мы разбиваем римские цифры на отдельные буквы, пишем числовое значение каждой буквы и добавить/убрать их. Метод 2: В этом методе мы рассматриваем группы римских цифр для сложения или вычитания, например, Следовательно, числовое значение римских цифр VI равно 6. ☛ Также проверьте: Калькулятор римских цифр Римские цифры использовались в Древнем Риме и представляли собой комбинации букв латинского алфавита I, V, X, L, C, D и M. Может показаться, что они отличаются от цифр, но они похожи. Например, VI римские цифры эквивалентны числу 6. Римские цифры, относящиеся к VI, приведены ниже: Пример 1: Найдите сумму римских цифр MMMDXXII и VI. Решение: MMMDXXII = 3000 + 500 + 20 + 2 = 3522 и VI = 6 Пример 2. Найдите произведение римских цифр VI и CDLIII. Решение: VI = 6 и CDLIII = 400 + 50 + 3 = 453 Пример 3: Найдите разницу между римскими цифрами VI и II. Решение: Римская цифра VI равна 6, а II равна 2. Пример 4. Найдите частное деления 12 на 2 с помощью римских цифр VI. Решение: Римская цифра XII равна 12, а II равна 2. перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду Готовы увидеть мир глазами математика? Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем. Запишитесь на бесплатный пробный урок Мы будем писать римские цифры VI как VI = V + I = 5 + 1 = 6. Следовательно, значение римских цифр VI равно 6. Сначала запишем MCCLXXXI и VI цифрами, т. е. VI = 6 и MCCLXXXI = 1281. Теперь 1281 — 6 = 1275. И 1275 = MCCLXXV. Следовательно, MCCLXXV следует добавить к римским цифрам VI, чтобы получить MCCLXXXI. Мы знаем, что римскими цифрами 6 записывается как VI. Чтобы преобразовать римские цифры VI в числа, необходимо разбить римские цифры следующим образом: VI Римские цифры = 6. При делении 6 на 6 получается остаток 0. Теперь 6 = VI Следовательно, когда VI делится на VI, остаток равен 0, но частное 1 в римских цифрах равно I ☛ Статьи по теме: Рабочие листы по математике и визуальный учебный план Римские цифры используют семь букв: I, V, X, L, C, D и M для обозначения чисел 1, 5, 10, 50 , 100, 500 и 1000. Римские цифры записываются семью разными буквами: I, V, X, L, C, D и M, они представляют числа 1, 5, 10, 50, 100 , 500 и 1000. Мы используем эти семь букв, чтобы составить тысячи других. Например, римская цифра «два» записывается как «II», что означает просто два сложенных вместе. Число двенадцать — это XII, то есть просто X (10) + II (2). Если мы сделаем еще один шаг, то число двадцать семь запишется как XXVII, что в разбивке выглядит как XX (20) + V (5) + II (2) — в сумме получается двадцать семь. Римские цифры обычно пишутся слева направо от большего к меньшему. Однако это не всегда так. Римляне не любили писать четыре одинаковых числительных подряд, поэтому они разработали систему вычитания. Римская цифра три пишется III, а четыре не IIII. Вместо этого используется принцип вычитания. Число четыре пишется как «IV». Здесь у нас есть I (1) перед V (5), и поскольку меньшее число стоит перед большим числом, мы знаем, что здесь нужно вычесть, что дает IV четыре. В шести случаях используется вычитание: Число 994 — прекрасный пример этого правила — оно написано CMXCIV. В разбивке имеем СМ = 900, ХС = 90 и IV = 4; добавление всего этого возвращает нас к 994. Чтобы написать 16 цифрами, берем 10 (X), 5 (V) и 1 (I), чтобы получилось XVI. Чтобы написать 27 цифрами, берем 20 (XX), 5 (V) и 2 (II), чтобы получилось XXVII. Чтобы написать 32 цифрами, мы берем 30 (XXX) и 2 (II), чтобы получилось XXXII. Чтобы написать 58 цифрами, берем 50 (L), 5 (V) и 3 (III), чтобы получилось LVIII. Чтобы написать 183 цифрами, мы берем 100 (С), 50 (L), 30 (XXX) и 3 (III), чтобы получить CLXXXIII. Чтобы написать 555 цифрами, берем 500 (Д), 50 (Л) и 5 (В), чтобы получилось ДЛВ. Чтобы записать 1582 цифрами, мы берем 1000 (М), 500 (Д), 50 (Л), 30 (ХХХ) и 2 (II), чтобы получить MDLXXXII. Годы, написанные римскими цифрами, могут быть довольно длинными и страшными, но, разбив их, мы увидим, что на самом деле они довольно простые. Давайте рассмотрим несколько примеров. Годы в 21 веке приятны и легки. Сначала мы начинаем с MM (1000 + 1000), а затем добавляем все, что нам нужно. Если мы хотим написать 2020 цифрами, мы начинаем с ММ и добавляем XX (20), чтобы получить MMXX. Годы из 20 века тоже достаточно простые. Мы начинаем с MCM (1900), а затем аналогичным образом добавляем все, что нам нужно. Например, 1985 будет записано как MCM (1900) + LXXX (80) + V (5), что при записи будет MCMLXV. Здесь года цифрами с 2010 по 2029: Поскольку самой большой буквой, используемой в римских цифрах, является M, и мы можем сложить вместе только три одинаковых цифры, наибольшее число, которое вы можете записать, используя стандартные цифры, будет 3999 (MMMCMXCIX). Но можно написать числа больше 3999. Если мы проведем линию через верхнюю часть числа, то мы умножим его на 1000. Например, римская цифра 5000 записывается как V̅ (5 x 1000 ). Точно так же один миллион записывается как M̅ (1000 x 1000). Если мы хотим написать 1 550 000 римскими цифрами, это будет выглядеть так: M̅ D̅ L̅. Если мы разобьем его, число 1 000 000 будет M̅, число 500 000 — D̅, а число 50 000 — L̅. Интересно, что нет нулевой цифры. Это связано с тем, что цифры были разработаны для целей торговли, и в нуле не было необходимости, вместо этого использовалось латинское слово «nulla». В валюте часто использовались дроби. Наиболее распространенными дробями были двенадцатые и половинки. Двенадцатый был представлен одной точкой «•», известной как «uncia». Половинки обозначались буквой «S», сокращенно от «полуфабрикаты». Без числительного, обозначающего ноль, это немного усложняет любую сложную математику, но сложение и вычитание находятся в пределах возможностей. При сложении цифр совет номер один — игнорировать принцип вычитания, т. е. вместо того, чтобы писать четыре как IV, записывайте их как IIII. Возьмем простой пример. Чтобы сложить IX (9) и XI (11) вместе, мы: При вычитании числительных мы также игнорируем принцип вычитания. Возьмем почти страшную задачу CCLXXXVIII (288) – CCLXXI (271): Римские цифры можно найти повсюду в современном обществе, вот пять примеров: Список можно продолжать и продолжать, цифры можно найти в книгах для нумерации вводных страниц, в юридических контрактах для обозначения разделов и подразделов, для обозначения войн (Первая и Вторая мировые войны) и так далее, и так далее… До появления римлян другие цивилизации разработали свои собственные системы счета. Распространенная теория состоит в том, что цифры обозначают сигналы рукой. Цифры один, два, три и четыре обозначаются эквивалентным количеством пальцев. Пятерка представлена разделением большого пальца и остальных пальцев в форме буквы «V». Цифры от шести до девяти показаны одной рукой, показывающей пять, а другой — соответствующим количеством пальцев. Десять изображается скрещиванием рук или больших пальцев в форме буквы «Х». Другая теория предполагает, что цифры произошли от насечек, выгравированных на счетных палочках. Эти палочки для подсчета использовались за столетия до римлян для основного счета; на самом деле они все еще использовались пастухами в Европе до 19 века.век. Цифры один, два, три и четыре были представлены эквивалентным количеством прямых линий, выгравированных на дереве. Эта система следовала тем же принципам, что и цифры. Семь на счетной палочке будет выглядеть так: IIIIVII, что будет сокращено до VII. Возьмем другой пример: семнадцать в полной форме будет выглядеть как IIIIVIIIIXIIIIVII, а в краткой форме: XVII. Теория предполагает, что римляне разработали эту систему, добавляя буквы «L», «C», «D» и «M» для обозначения 50, 100, 500 и 1000. Многие другие цивилизации древнего мира уже придумали свои собственные системы счисления и методы счета. Мы быстро рассмотрим египетскую и вавилонскую системы счета. Одна из древнейших систем счисления происходит из Египта, разработана более 5000 лет назад! Их система была очень всеобъемлющей по сравнению с другими; у них даже был символ бесконечности! В отличие от римлян, у египтян был символ нуля. Египтяне не использовали принцип вычитания, и без символа пять это означало, что число девять отображалось как девять выписанных I. Вавилонская система чисел также была довольно сложной; они фактически переняли и адаптировали свою систему от более ранних шумеров. Подобно египтянам, не было символа для пяти, что означает, что девять также записывались как девять единиц (см. Таблицу ниже). Одна вещь, общая для вавилонской системы с римской, заключалась в отсутствии символа, обозначающего ноль. часы с римскими цифрами Смотреть все медиа Просмотреть весь связанный контент → Популярные вопросы Что такое римские цифры? Римские цифры — это символы, используемые в системе числового обозначения, основанной на древнеримской системе. Какие римские цифры используются сегодня? Примеры использования римских цифр сегодня включают обозначение глав книг, название ежегодного Суперкубка Национальной футбольной лиги, а также названия летних и зимних Олимпийских игр и маркировку часов на циферблатах. Как работают римские цифры? В римской системе счисления символы I, V, X, L, C, D и M обозначают соответственно 1, 5, 10, 50, 100, 500 и 1000 в индийско-арабской системе счисления. Символ, размещенный после другого равного или большего значения, добавляет свою ценность. Символ, помещенный перед символом большего значения, вычитает его значение. Полоса, расположенная над числом, умножает его значение на 1000. Откуда взялись римские цифры? Как и во всех подобных вопросах, происхождение римской системы счисления неясно, хотя изменения в их формах с 3 века до н. По-прежнему важно учить римские цифры? Несмотря на непрактичность использования римских цифр для математических расчетов, что привело к широкому использованию индийско-арабской системы счисления, которую мы знаем сегодня, некоторые люди все еще спорят о важности преподавания римских цифр в школах. Сторонники считают, что римские цифры имеют непреходящую культурную значимость, о чем свидетельствует их постоянное использование в названиях спортивных мероприятий и главах книг. Учить больше. Римская цифра , любой из символов, используемых в системе числовых обозначений, основанной на древнеримской системе. Символы I, V, X, L, C, D и M обозначают соответственно 1, 5, 10, 50, 100, 500 и 1000 в индийско-арабской системе счисления. Символ, размещенный после другого равного или большего значения, добавляет свою ценность; например, II = 2 и LX = 60. Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена Эриком Грегерсеном. Римские цифры — это система счисления, возникшая в Древнем Риме. Они используются для представления чисел в десятичной системе, но не используются для математических операций. В этой системе символы используются для обозначения различных чисел, где I обозначает 1, V обозначает 5, X обозначает 10, L обозначает 50, C обозначает 100, D обозначает 500, а M обозначает 1000. Вот таблица символов, используемых в римской системе счисления: Значение цифры определяется ее положением по отношению к другим символам. Например, числительное VI или 6 будет читаться как «пять плюс один» (5 + 1), а XI или 11 — как «десять плюс один» (10 + 1). Но способы представления 4 и 9 особенные. Римская цифра IV, или 4, читалась бы как «на единицу меньше 5» (5 — 1). Кроме того, числительное IX или 9 будет читаться как «на один меньше 10» (10 — 1). Вот таблица чисел и их римских эквивалентов, за которыми следуют более подробные объяснения того, как выполнять преобразования. Просто прокрутите таблицу или используйте Ctrl/Cmd + f, чтобы найти нужное значение: Поскольку римские цифры часто располагаются в порядке от наибольшего к наименьшему, разбейте преобразуемое число на группы тысяч, сотен, десятков и единиц и выполните преобразование на каждая группа. Например, если вы хотите преобразовать число 2014 (год основания freeCodeCamp) в римские цифры, разбейте число следующим образом: Затем выполните преобразование для каждой группы и объедините их, чтобы получить эквивалент римской цифры: РЕКЛАМА Возможно, вы заметили, что в приведенной выше таблице используются значения только от 1 до 3,9.99. Это связано с особыми способами представления 4 и 9, упомянутыми выше. Если вы посмотрите таблицу выше, вы увидите, что всякий раз, когда появляется 4 или 9 (включая 40, 90, 400, 900), римские цифры упорядочены определенным образом, поэтому меньший символ вычитается из большего значения. сразу после. Поскольку римские цифры никогда не были полностью стандартизированы, число 4000 может быть представлено как ММММ. Это работает, но многие считают это недействительным, так как 4 (и 9) имеют специальные представления в меньших числах. Вместо этого одним из наиболее распространенных способов представления более крупных римских цифр является винкулум или прямая горизонтальная линия над одним или несколькими символами. Если вы видите символ римской цифры с горизонтальной чертой над ним, это просто означает умножение этого символа на 1000. Вот римские цифры с нанесенным винкулумом: С этим расширенным набором символов римских цифр число 4000 будет представлено следующим образом: IV А вот таблица больших чисел и их представления римскими цифрами для начала: РЕКЛАМА Для вас, разработчиков, самый простой способ добавить винкулум к римским цифрам онлайн — это обернуть символы в элемент и использовать немного CSS . Например, чтобы добавить горизонтальную линию над символами IV в IVIII, вы можете поместить их в элемент IVIII Что будет отображать следующее: IVIII РЕКЛАМА Если эта разбивка римских цифр показалась вам полезной, поделитесь ею с друзьями, чтобы больше людей могли извлечь из нее пользу. Кроме того, не стесняйтесь обращаться к Twitter и дайте мне знать, что вы думаете. Научитесь программировать бесплатно. Учебная программа freeCodeCamp с открытым исходным кодом помогла более чем 40 000 человек получить работу в качестве разработчиков. Начать РЕКЛАМА Римские цифры — это символы I, V, X, L, C, D и M, которые обозначают числа 1, 5, 10, 50, 100, 500 и 1000 соответственно. Количество и порядок этих букв определяли значение конечного числа, а это означает, что древние римляне записывали числа комбинацией всего семи букв! На первый взгляд они могут показаться запутанными по сравнению с нашим современным способом выражения чисел (который основан на ранних арабских цифрах), но римские цифры на самом деле основаны на базовой единице 10, как и современные числа. Одно из возможных объяснений этого заключается в том, что люди начали считать пальцами (дополнительную информацию см. В разделе «Происхождение римских цифр» ниже). Как упоминалось выше, римские цифры записываются с помощью комбинации семи букв. Это: Римская цифра Номер I 1 В 5 Х 10 л 50 С 100 Д 500 М 1000 В своей простейшей форме числа выражаются путем объединения букв вместе, что фактически создает небольшую математическую задачу, которую необходимо решить путем сложения букв (или, точнее, чисел, которые они представляют, вместе). Перевод римских цифр в числа может быть запутанным и трудным, когда вы только начинаете, и даже опытным ученым часто приходится тратить время на то, чтобы разобраться с этим! Начните с просмотра таблицы римских цифр ниже, чтобы увидеть ее в действии. Однако вы можете обнаружить, что некоторые числа записываются не так, как вы ожидаете, и почему большие числа не записываются в виде очень длинной строки букв? Более подробное объяснение можно найти под диаграммой. В приведенной ниже таблице показаны римские цифры для чисел от 1 до 25 и большой выбор других. Показаны выбранные числа выше 4000, однако обязательно прочтите также раздел «Было ли 3999 самым большим числом, которое могли сосчитать римляне?»! Арабский или современный Латинская или римская Форма цифр Порядковый номер . . пример — раз, два, три… пример — первый, второй, третий… 1 I унус — уна — унум примус 2 II дуэт — дуэт — дуэт секунды 3 III трес-триа третичный 4 IV quattuor кварт 5 В квинке квинтус 6 ВИ секс секст 7 VII сентябрь септимус 8 VIII окто октавус 9 IX ноябрь нонус 10 Х декум децим 11 XI ундецим десятая десятая 12 XII дуодецим двенадцатиперстный 13 XIII тредецим десятичный терций 14 XIV кватурдецим кварта десятичная 15 XV пятизначная цифра десятичная пятая десятка 16 XVI седецим десятичный секст 17 XVII семеричный септимус десятичный 18 XVIII дуодевигинти дуоустройствосимус 19 XIX недеджинти ундецисимус 20 ХХ вигинти вице-симус 21 XXI вигинти унус вице-примус 22 XXII вигинти дуэт vicesimus secundas 23 XXIII вигинти триа vicesimus tertius 24 XXIV четыре четверти vicesimus quartus 25 ХХV вигинти пятый vicesimus quintus 30 ХХХ тригинта тройной 40 XL квадрагинта квадр. 50 л пятиместный пятидесятиричный 60 LX сексагинта шестидесятеричный 70 LXX септуагинта септуагесимус 80 LXXX восьмигранный октогесимус 90 ХС нонагинта нестареющий 100 С центум центезимуса 200 СС дученти дуцентезимус 300 ССС Треценти трецентезимус 400 CD квадрингенти четырехзначный 500 Д квингенти квинтэсимус 600 DC сесценгенты сесцентесимус 700 ДКК сегменты septingentesimus 753 DCCLIII сепингенти квинквагинта триа Год основания Рима – 753 г. 800 DCCC Октингенти восьмизначный 900 СМ негенти негентезимус 1000 М милле миллисимус 1900 МКМ тысячелетие миллеснонгентесимус 2000 ММ Дуомилия бисмилисимус 2100 ММС дуомилия центум бисмилле сотенных 3000 МММ тресмилиа тремиллесимус 4000 ММММ квадрамилия четырехугольный 5000 В квинмилия пятимиллионный 6000 ВМ семилия единицы с точностью до секунды 7000 ВММ септуамилия семимиллионный 8000 ВМММ октомилия восьмидесятилетний 9000 МХ нонамилия нонамилессимус 10 000 Х декэм милиа десятитысячных миллисимуса 11 000 ХМ ундецим милиа десятая миллисимус 12 000 XMM двенадцатиперстная кишка двенадцатеричный миллезимус 50 000 л пятая миля пятитысячник 60 000 LX половые органы тысячекратный секс 80 000 LXXX октомилия восьмитысячное число 90 099 XCXCIX нона милис новагинта новем нона миллесимус нонус 100 000 С центум милиа миллисимуса центов 200 000 СС Милия дуцента дуцента тысячелистная 200 100 ССС дуцента милиа центум дуцента тысячелистная цента 200 510 CCDX дуцента милиа квиндесем квиндесем 500 000 Д квингенти милиа квингенти миллесимус 600 000 DC sescenti milia sescenti Millesimus 700 000 ДКК сепуцентная милиа сепценты миллесимуса 1 000 000 М Милли милиа миллисимус Этот удобный список римских цифр содержит наиболее распространенные числа и полезные ориентиры. Однако что происходит с другими числами, такими как 4, которые пишутся IV? Не следует ли писать как IIII? А если сложить буквы, как пишется (IV), не будет ли это равно 6 (I + V)? Ответ известен как принцип вычитания. Римлянам не нравилось, когда четыре последовательных буквы одного и того же значения шли вместе. Предположительно, это было связано с тем, что наличие большого количества букв одного типа затрудняло легкое определение значения. Выражение числа 8, например, как IIIIIIIII означало бы, что человеку пришлось бы индивидуально считать каждое «I», чтобы понять, что это за число. Чтобы преодолеть это, римляне писали числа, используя принцип вычитания или понятие вычитания , при котором первая буква последовательности вычитается из большей. Снова взглянув на таблицу с римскими цифрами, мы видим, что число 9 пишется как IX. По существу это означает 10 минус 1, что равняется 9. Если бы это не было выражено так, это было бы записано как VIIII (5 + 1 + 1 + 1 + 1). Хотя это по-прежнему имело бы смысл, чтение заняло бы немного больше времени и привело бы к большему количеству ошибок, если бы люди пропустили одну из букв «I» при их подсчете. Имейте в виду, что это был период времени задолго до появления электроники, поэтому цифры не были аккуратно напечатаны и напечатаны. Они должны были быть нарисованы, вырезаны, выгравированы на поверхностях и т. д. Скорее всего, они были далеко не четкими и четкими в своем шрифте, поэтому важно сделать последовательности настолько короткими, насколько это практически возможно. В системе, которая, на первый взгляд, сводится к сложению чисел, представленных буквами, понять, когда нужно вычесть число, может быть непросто. Простой ответ заключается в том, что число нужно вычесть, если оно появляется перед большим. Для этого вам нужно будет обратиться к таблице семи букв, используемых в римских цифрах, в верхней части этой страницы. Используя диаграмму, мы можем видеть, что X больше (10), чем V (5), которые больше, чем I (1). Посмотрите, как это относится к числам ниже: XI = 11. I (1) стоит после большего числа X (10), что означает, что их нужно сложить, чтобы получить 11. IX = 9. I стоит перед X, что означает, что 1 нужно вычесть из 10, что дает 9. Если мы просто сложим числа, которые представляют буквы, оба результата будут 11 (X = 10 плюс я = 1). Вот почему так важно, идет ли меньшее число до или после большего числа. В числах, содержащих более двух букв, нужно вычесть только число, которое следует за меньшим числом. Это выделено в примере ниже: XXIX = 29. Сумма равна 10 (Х) + 10 (Х) + 9 (IX). Римские цифры читаются слева направо, поэтому предшествующие буквы складываются вместе, а затем вычитается меньшее число из большего, следующего за ним. Только с ограниченным количеством букв и числами, основанными на единице 10, на самом деле это может произойти только в шести случаях: Наибольшее число, которое может быть выражено римскими цифрами, — это 3999, которое записывается как MMMCMXCIX. Это связано с тем, что число 4000 должно быть написано как ММММ, что противоречит принципу отсутствия четырех последовательных букв одного и того же типа вместе. Винкулум — это горизонтальная линия, используемая в математике над или под значением для обозначения определенной цели, такой как группировка или повторяющееся десятичное значение. В современной математике его часто заменяют круглыми скобками. В Средние века число свыше 4000 обычно выражали римскими цифрами с помощью линии винкулума над буквами. Эта строка представляла число, кратное 1000, и могла охватывать все или только начальную часть выражения с римскими цифрами. Это становится более понятным, если взглянуть на примеры ниже: Это может работать аккуратно, однако существует много споров о том, действительно ли эта система использовалась древними римлянами, или она была просто продуктом более поздних поколений и цивилизаций. Следует помнить, для чего на самом деле римляне использовали свою систему счисления. Основное использование было в торговле и коммерции, и для среднего торговца было крайне маловероятно, что у него когда-либо было более 3999 чего-либо, будь то предметы, деньги и т. д. Сегодня это может показаться нам крайне чуждым, с единицами валюты, где мы могут потратить десятки или даже сотни тысяч из них за один раз на крупные покупки, или огромные корпорации, которые могут производить и отгружать миллионы товаров, но тогда это было не так уж распространено. Хотя, возможно, реже приходилось иметь дело с числами от 4000 и выше или с необходимостью записывать их, все же маловероятно, что римляне не имели дело с некоторыми вещами, превышающими это количество. В современном обществе мы растем и живем в мире больших, полных чисел. У нас есть определенная сумма долларов в банке, это около 238 855 миль до Луны 1 , в 2019 году ВВП США составил $21,43 трлн 2 , в Соединенном Королевстве проживает около 68 млн человек 3 и т.д. Огромные, общие цифры. Но хотя древним римлянам не о чем было думать в таких числах (если только они не думали о количестве песчинок на пляже или о чем-то еще), вполне вероятно, что они думали о числах с точки зрения групп, а не как реальных общее количество, как мы делаем. Подсказки можно найти в том, как определенные элементы структурированы в римском мире. Например, римская армия была сильно разделена на части, которые сами состояли из других частей. Может ли эта организация посредством группировки отражать образ мышления римлян? Если это так, то вместо того, чтобы Юлий Цезарь размышлял перед битвой о том, что у него есть армия из 24 000 человек, он, возможно, с большей вероятностью просто думал, что у него 6 легионов. Даже если бы он подумал о числе 24 000, если бы он где-нибудь его записал, то было бы гораздо проще написать «VI», чем цифры, эквивалентные 24 000! История римских цифр и римской математики плохо документирована. Поскольку люди, вероятно, начали считать, используя самые простые доступные вещи — пальцы, — математика развивалась в базовой единице 10. Как и многое в ранней римской культуре, многое было основано на более ранних цивилизациях, существовавших в Средиземноморском регионе, которые в то время превосходили расцветающую Римскую империю. Одна из систем нумерации, наиболее похожая на ту, что использовалась римлянами, использовалась этрусками. В этом нет ничего удивительного, поскольку этрусская цивилизация покрывала большую часть северной Италии и оказала значительное влияние на развитие римлян на юге. Во всех буквах и цифрах, которые сейчас вертятся у вас в голове, когда вы пытаетесь разобраться в этой древней системе счисления, вы могли заметить или не заметить, что нигде не упоминается ноль. При торговле на рынке никто не подходил к булочнику и не просил буханки хлеба (а если и просил, то пекарь быстро их прогонял за трату времени!) Практической пользы от этого было мало. Конечно, понятие нуля существовало в виде 9.4027 nulla (лат. Ничего), чтобы выразить отсутствие чего-либо, но в отличие от современной системы счисления, в которой для обозначения значения нужны нули (10, 403 и т. д.), римляне могли составить все свои числа из комбинации семи букв, перечисленных вверху. страницы. Несмотря на то, что они довольно громоздки по сравнению с современными цифрами от 0 до 9, римские цифры по-прежнему встречаются в удивительно большом количестве мест. Одной из возможных причин этого является просто их возраст. Довольно часто люди думают, что элементы из прошлого более стильны, чем современный вкус, и использование римских цифр часто может придать внешнему виду элегантность. Существует множество других примеров, когда римские цифры до сих пор используются в описаниях и ссылках. К ним относятся: Римские цифры до сих пор используются как часть системы анализа, используемой музыкантами для разбора и интерпретации музыкальных произведений. Система определяет степень гаммы основной ноты, качество и любые расширения или инверсии, которые может включать аккорд. Узнайте больше на нашей странице о теории и анализе музыки с римскими цифрами. Говоря о римских цифрах в фильмах и телепередачах, если вы хотите узнать, когда был снят тот фильм или передача, которую вы только что посмотрели, вы можете решить это самостоятельно, используя приведенное выше объяснение… или просто воспользуйтесь удобным списком дат показа ниже. с 1990 года! Используйте инструмент преобразования римских цифр ниже, чтобы преобразовать римские цифры в современные числа или наоборот. Номер: Римская цифра: Этот бесплатный скрипт предоставлен Умножение и деление в Excel не представляют никаких сложностей: достаточно создать простую формулу. Не забывайте, что все формулы в Excel начинаются со знака равенства (=), а для их создания можно использовать строку формул. Предположим, требуется определить количество бутылок воды, необходимое для конференции заказчиков (общее число участников × 4 дня × 3 бутылки в день) или сумму возмещения транспортных расходов по командировке (общее расстояние × 0,46). Существует несколько способов умножения чисел. Для выполнения этой задачи используйте арифметический оператор * (звездочка). Например, при вводе в ячейку формулы =5*10 в ячейке будет отображен результат 50. Предположим, необходимо умножить число в каждой из семи ячеек в столбце на число, которое содержится в другой ячейке. В данном примере множитель — число 3, расположенное в ячейке C2. Введите =A2*$B$2 в новом столбце таблицы (в примере выше используется столбец D). Не забудьте ввести символ $ в формуле перед символами B и 2, а затем нажмите ввод.
Примечание: Использование символов $ указывает Excel, что ссылка на ячейку B2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку B2. Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения. Перетащите формулу вниз в другие ячейки столбца.
Примечание: В Excel 2016 для Windows ячейки заполняются автоматически. Функцию PRODUCT можно использовать для умножения чисел, ячеек и диапазонов. Функция ПРОИЗВЕД может содержать до 255 чисел или ссылок на ячейки в любых сочетаниях. Например, формула =ПРОИЗВЕДЕНИЕ(A2;A4:A15;12;E3:E5;150;G4;h5:J6) перемножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазона (A4:A15, E3:E5 и h5:J6). Предположим, что вы хотите узнать, сколько человеко-часов потребовалось для завершения проекта (общее время проекта ÷ всего людей в проекте) или фактический километр на лилон для вашего последнего меж страны(общее количество километров ÷ лилонов). Деление чисел можно разделить несколькими способами. Для этого воспользуйтесь арифметическим оператором / (косая черта). Например, если ввести =10/5 в ячейке, в ячейке отобразится 2.
Важно: Не забудьте ввести в ячейку знак равно(=)перед цифрами и оператором /. в противном случае Excel интерпретирует то, что вы введите, как дату. Например, если ввести 30.07.2010, Excel может отобразить в ячейке 30-июл. Если ввести 36.12.36, Excel сначала преобразует это значение в 01.12.1936 и отобразит в ячейке значение «1-дек».
Примечание: В Excel нет функции DIVIDE. Вместо того чтобы вводить числа непосредственно в формулу, можно использовать ссылки на ячейки, такие как A2 и A3, для обозначения чисел, на которые нужно разделить или разделить числа.
Пример:
Чтобы этот пример проще было понять, скопируйте его на пустой лист.
Копирование примера
Создайте пустую книгу или лист. Выделите пример в разделе справки.
Примечание: Не выделяйте заголовки строк или столбцов.
Выделение примера в справке Нажмите клавиши CTRL+C. Выделите на листе ячейку A1 и нажмите клавиши CTRL+V. Чтобы переключиться между просмотром результатов и просмотром формул, которые возвращают эти результаты, нажмите клавиши CTRL+’ (ударение) или на вкладке «Формулы» нажмите кнопку «Показать формулы».
A
B
C
1
Данные
Формула
Описание (результат)
2
15000 =A2/A3 Деление 15000 на 12 (1250).
3
12 Предположим, вам нужно разделить каждую ячейку в столбце из семи чисел на число, которое содержится в другой ячейке. В этом примере число, на которые нужно разделить, составляет 3, содержалось в ячейке C2.
A
B
C
1
Данные
Формула
Константа
2
15000 =A2/$C$2 3
3
12 =A3/$C$2
4
48 =A4/$C$2
5
729 =A5/$C$2
6
1534 =A6/$C$2
7
288 =A7/$C$2
8
4306 =A8/$C$2 В ячейке B2 введите =A2/$C$2. Не забудьте в формуле включить символ $ перед символами C и 2. Перетащите формулу в ячейке B2 вниз в другие ячейки в столбце B.
Примечание: Символ $ указывает Excel, что ссылка на ячейку C2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали в формуле символы $ и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3/C3, которая не будет работать, так как в ячейке C3 нет значения. Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Умножение столбца чисел на одно и то же число
Умножение на процентное значение
Создание таблицы умножения
Операторы вычислений и порядок операций
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними. Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи: В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. Вернемся к обыкновенным дробям позже, а сейчас обсудим десятичные дроби. Их знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так: Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено. Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой. Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например: Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны: Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части. Пример 1. Перевести обыкновенную дробь 16/10 в десятичную. Как решаем: Ответ: 16/10 = 1,6. Пример 2. Перевести 37/1000 в десятичную дробь. Как решаем: Ответ: 37/1000 = 0,037. Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой: Сохраняй наглядную картинку, чтобы быстрее запомнить. С десятичными дробями можно производить те же действия, что и с любыми другими числами: складывать и вычитать, делить и умножать. В этом блоке узнаем, как умножать дроби. Умножение десятичных дробей друг на друга можно упростить и просто умножить натуральные числа. Главное — правильно поставить запятую в ответе. Если в задаче даны десятичные дроби с разными знаками — используем правило умножения отрицательных чисел. Как быстро запомнить: Числа с единицей и нулями (10, 100, 1000 и т. д.) называются разрядными единицами, так как цифра 1 — единственная значимая цифра в числе и от ее местоположения зависит количественное значение числа. Важно запомнить правила для умножения и деления на разрядную единицу: Чтобы перемножить десятичные дроби нужно сделать три шага: Пример 1. Перевести 5,4 в смешанное число. Как решаем: Получаем: 311 ∗ 001 = 311. Ответ: 3,11 ∗ 0,01 = 0,0311. Чтобы закрепить тему, смотрите видео «Умножение десятичных дробей». Умножение десятичных дробей на обычные числа происходит так же, как и умножение между десятичными дробями. Чтобы считать быстрее, умножайте их в столбик по правилам выше. А вот и примерчики! Пример 1. Умножить десятичную дробь 2,27 на целое число 15. Как решаем: умножить столбиком данные числа и отделить два знака запятой. Ответ: 15 ∗ 2,27 = 34,05. Пример 2. Умножить 11 на 0,005. Как решаем: умножить столбиком данные числа и отделить три знака запятой. Ответ: 11 ∗ 0,005 = 0,055. Пример 3. Умножить 0,1557.. на 3. Как решаем: Ответ: 0,1557.. ∗ 3 ≈ 0468.. Чтобы умножить десятичную дробь на 10, 100, 1000, нужно просто перенести запятую в дроби вправо на столько знаков, сколько нулей стоит во втором множителе. Лишние нули слева можно отбросить. А если цифр не хватает — дописываем нули. Примеры: Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, нужно перенести запятую в дроби влево на столько знаков, сколько нулей стоит перед единицей. Ноль целых — тоже считаем. Если цифр не хватает — просто дописываем дополнительный ноль — один или несколько — после запятой. Примеры: Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем. Пример 1. Умножить 3/5 на 0,9. Как решаем: Записать 0,9 в виде обыкновенной дроби: Ответ: 3/5 ∗ 0,9 = 0,54. Пример 2. Умножить 0,18 на 3 1/4. Как решаем: Записать 3 1/4 в виде десятичной дроби: Произвести умножение в столбик или при помощи калькулятора: Ответ: 0,18 ∗ 3 1/4 = 0,585. А если нужно решить примеры с десятичными дробями быстро — поможет онлайн-калькулятор. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников: Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых. Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе? Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4. 4 + 4 + 4 = 12. Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах. Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц. Для записи умножения используется знак 4 х 3 или 4 · 3 Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак 4 · 3 = 12. Умножение – это краткая запись сложения одинаковых слагаемых. Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести: 6 + 6 + 6 + 6 + 6 = 30. Сократим запись, заменив сложение на умножение: 6 · 5 = 30. Оба выражения равны: 6 + 6 + 6 + 6 + 6 = 6 · 5 = 30, но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух. Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи: 4 · 3, 4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых. Произведение — это число, которое получается в результате умножения. Например, в записи: 4 · 3 = 12, 12 — это произведение. При этом сама запись 4 · 3 тоже называется произведением. Эту запись можно прочитать так: Множимое и множитель иначе называются множителями или сомножителями. Рассмотрим выражение: 4 · 3 = 12, где 4 — это множимое, 3 — это множитель, а 12 — произведение. Чтобы узнать правильно ли было выполнено умножение, можно:
12 : 3 = 4. 12 : 4 = 3. Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно. Производитель Мощность максимальная полная кВт Мощность топки или горелки теплового агрегата, например, котла. Чтобы узнать полезную мощность — реальное количество тепла, которое вы получите, необходимо этот показатель умножить на КПД агрегата. Используется для расчета потребления топлива. кВт Тип топлива Выберите только те типы топлива, которые вам нужны одновременно. Если выбрать слишком много типов, такого оборудования может не быть. Количество ступеней горелки Модулируемая горелка — автоматическая регулировка мощности по датчику температуры или давления, или по внешнему сигналу. Пламенная голова Подбирается в зависимости от толщины дверки топки. Условный показатель, так как отличается у разных производителей. Газовая рампа Арматура, необходимая для присоединения горелки к газопроводу. Включает в себя реле минимального давления, фильтр-стабилизатор и предохранительный клапан, может включать реле максимального давления. Также называется мультиблоком. Диаметр присоединения газа мм (дюйм) Для промышленного оборудования указывается минимально возможный диаметр. Возможна комплектация на 1, 2, 3 типоразмера больше. мм (дюйм) Страна производитель Диаметр сопла Мощность минимальная полная кВт Минимально возможная мощность горелки агрегата, например, котла. кВт Напряжение В Значение питающего напряжения. Через черту / указаны пределы или возможные варианты. В Высота Глубина Ширина Гарантия 147 параллельный перевод They took with them eight lovely adolescent girls to serve as victims for their criminal desires plus four women well versed in debauchery whose narrative skills would serve to stimulate their already jaded appetites whenever interest flagged Они захватили с собой восемь нежнейших невиннейших дев чтобы те пали жертвой их преступной похоти да ещё четырёх прожжёных дам, искушённых в пьяных дебошах чьё искусство болтовни могло разогреть и увлечь их пресыщенные организмы лишь только они дадут им знак. It’s too clear that I won. Four plus four, eight. Четыре и четыре — восемь. The Cylons have three base ships confirmed, plus four squadrons from Gamoray. ои йукымес евоум 3 пкоиа-басеис йаи 4 лоияес стом цйалояез. «What’s four plus four?» «Jell-O.» «Сколько будет четыре плюс четыре?» «Мармеладка.» Three plus four is seven. Seven and six are 13. 3 плюс 4 это 7… 7 и 6 это 13. Plus four fifths. Плюс четыре пятых. And in related news four plus four is eight. И в последующих новостях, четыре плюс четыре — восемь! 14 is one plus four which equals five. 14 это один плюс четыре, то есть, пять There’ll definitely be a regional news team filming our arrival, plus four local papers. — Regional news? Наше прибытие точно будут снимать региональные новости, плюс четыре местных газеты. — Or two plus four is what? Или 2 плюс 4, сколько? One plus two, plus three, plus four : Один плюс два, плюс три, плюс четыре : десять. Four plus four. Четыре плюс четыре. Four times a year, plus the annual stockholders’meeting. Четыре раза в год, плюс ежегодное собрание акционеров. You want two plus two to be four. Тебе нужно дважды два — четыре. Two, four, six, and three is nine, plus two is 11. Два, четыре, шесть, и еще три это девять, плюс два это одиннадцать. Four plus three, seven. — Четыре и три — семь. — Да. Выиграл Агостино. This is 07. Four plus three. Говорит 07. 4 плюс 3. Even in this corner of the galaxy, captain, two plus two equals four. Даже в этой части галактики, капитан, 2 плюс 2 равно 4. You can have the licence. The price is 250,000 dollars. Plus five per cent of the gross monthly, of all four hotels, Mr Corleone. Цена 250 тысяч долларов плюс ежемесячная плата в размере пяти процентов от прибыли… от всех четырёх отелей… You couldn’t help him, you couldn’t help your father, two plus two makes four. Вы не могли помочь ему, вы не могли помочь вашему отцу, Два плюс два четыре. Four, including me. Plus two dogs they gave us to follow tracks. И ещё две собаки, якобы, ищейки. «is the freedom to say two plus two equals four.» «свобода сказать два плюс два равно четыре.» «Freedom is the freedom to say two plus two equals four»? «Свобода — это свобода сказать два плюс два равно четыре»? Four bucks, plus tax. Четыре доллара плюс налог. — Steve plus three or four. — Стив плюс три или четыре. Two plus two is four. Два плюс два — четыре. Two plus two is four. Two plus two is four. Два плюс два — четыре… Two plus two is four. Два плюс два — четыре… About four, or three, plus a driver. Сколько нужно людей? I can’t stand by and let you think that one plus one might equal three or four or yellow! Я не могу позволить тебе думать, что 1 + 1 может быть равно трем или четырем или быть желтым In the last eighteen hours, I’ve seen four people get abducted by a space alien, watched Ducky try to drown himself, plus I spent like 387 bucks on CDs at Aran’s. За последние 18 часов я видел, как четырех человек похитили пришельцы, как Даки пытался утопиться, еще я потратил 387 баксов на СиДи в музыкальном магазине. The four of us, plus Odo. Четверо нас, плюс Одо. Four here, plus that one in the control room. Четыре здесь и один в комнате управления. Two plus two equaled seven or even one hundred, but never four. Два плюс два равнялось семи или даже ста, но не четырём. Four, plus the taker. — Четверо, плюс захватчик. Sergeant Major Plumley made all four combat jumps in the 82nd Airborne during World War II. Sicily, Salerno, Normandy and Holland, plus one more in Korea. Старший сержант Пламли… во время второй мировой войны… высаживался на Сицилии, в Салерно, в Нормандии… и в Голландии. Some of you know I’ve had nine pictures under my subspecies, four in the «South Beach Strumpet» series alone, each with 30,000-plus DVDs in print. Некоторые из вас в курсе, что я принимал участие в съемках девяти картин. Лично выпустил четыре серии «Пляжной проститутки». Тираж — более 30 тысяч копий на Ди-Ви-Ди. I mean, A-sub-N equals N plus one over four. Эмм, я имела в виду, в скобках N равняется N плюс 1 и поделить на 4. And out of 30-plus songs, only four songs got all four votes. И из 30 с лишним песен, только 4 песни получили по 4 голоса. Our top story this morning two plus two is four. Наше самое актуальное сообщение этим утром. Два плюс два — четыре. That suite is crowded enough with the four of us, plus the Jolly Green Giant and everyone else passing through there. — Эти апартаменты достаточно наполнены нами, плюс Веселый Зеленый Великан. и все остальные, что ходят туда-сюда. Она должна съехать. Seven plus one is… — Four. — Сколько это? Two plus two equals four. Два плюс два равно четыре. Kidnapping Corey is 10 years each. If you kill him tonight it’s 1st degree murder for the shooter, it’s 2nd degree for the other. That’s 25 to life, plus another 100 or so for the four rapes. Похищение Кори 10 лет каждому. еще 100 или около за 4 изнасилования. Plus, who runs four 250 Mercs off a deep-V hull? — У кого 4 меркури по 250 сил? What’s four times five plus six times seven? Сколько будет, 4 умножить на 5 плюс 6 умножить на 7? Four plus 19 is 23. 4 плюс 19 — это 23. Plus two gunshot wounds, four stab wounds, and a tire track across the upper torso. Плюс два огнестрельных ранения, четыре ножевых ранения, и следы от автомобиля на верхней части тела. I can probably just do it for four bucks plus tax. — Ну, может, за 4 доллара плюс налоги. You’ve got there before me, because in first place, and this may be a first for first place, with plus four is Alan Davies! А значит наш ушедший вразнос неудачник с — 37 очками — Джимми Карр. Two times two, two plus two, two to the power of two and therefore four. Два во второй степени, и все равно четыре. Слишком просто. Дата выпуска продукта. Литография указывает на полупроводниковую технологию, используемую для производства интегрированных наборов микросхем и отчет показывается в нанометре (нм), что указывает на размер функций, встроенных в полупроводник. Количество ядер — это термин аппаратного обеспечения, описывающий число независимых центральных модулей обработки в одном вычислительном компоненте (кристалл). Поток или поток выполнения — это термин программного обеспечения, обозначающий базовую упорядоченную последовательность инструкций, которые могут быть переданы или обработаны одним ядром ЦП. Базовая частота процессора — это скорость открытия/закрытия транзисторов процессора. Базовая частота процессора является рабочей точкой, где задается расчетная мощность (TDP). Частота измеряется в гигагерцах (ГГц) или миллиардах вычислительных циклов в секунду. Максимальная тактовая частота в режиме Turbo — это максимальная тактовая частота одноядерного процессора, которую можно достичь с помощью поддерживаемых им технологий Intel® Turbo Boost и Intel® Thermal Velocity Boost. Частота измеряется в гигагерцах (ГГц) или миллиардах вычислительных циклов в секунду. Кэш-память процессора — это область быстродействующей памяти, расположенная в процессоре. Интеллектуальная кэш-память Intel® Smart Cache указывает на архитектуру, которая позволяет всем ядрам совместно динамически использовать доступ к кэшу последнего уровня. Интерфейс Intel® Ultra Path Interconnect (UPI) представляет собой высокоскоростной канал взаимодействия процессоров, обеспечивающий повышенную пропускную способность и производительность по сравнению с Intel® QPI. Расчетная тепловая мощность (TDP) указывает на среднее значение производительности в ваттах, когда мощность процессора рассеивается (при работе с базовой частотой, когда все ядра задействованы) в условиях сложной нагрузки, определенной Intel. Ознакомьтесь с требованиями к системам терморегуляции, представленными в техническом описании. Доступные варианты для встраиваемых систем указывают на продукты, обеспечивающие продленную возможность приобретения для интеллектуальных систем и встроенных решений. Спецификация продукции и условия использования представлены в отчете Production Release Qualification (PRQ). Обратитесь к представителю Intel для получения подробной информации. Поиск продукции с Доступные варианты для встраиваемых систем Макс. объем памяти означает максимальный объем памяти, поддерживаемый процессором. Процессоры Intel® поддерживают четыре разных типа памяти: одноканальная, двухканальная, трехканальная и Flex. От количества каналов памяти зависит пропускная способность приложений. Поддержка памяти ECC указывает на поддержку процессором памяти с кодом коррекции ошибок. Память ECC представляет собой такой типа памяти, который поддерживает выявление и исправление распространенных типов внутренних повреждений памяти. Обратите внимание, что поддержка памяти ECC требует поддержки и процессора, и набора микросхем. Поиск продукции с Поддержка памяти ECC ‡ Энергонезависимая память Intel® Optane™ DC — это революционный уровень энергонезависимой памяти, который находится между памятью и устройством хранения данных для создания большого, доступного объема памяти, сопоставимого по производительности с DRAM. Формируя большой объем памяти системного уровня в сочетании с традиционной памятью DRAM, энергонезависимая память Intel Optane DC предназначена для преобразования важных, использующих память рабочих процессов — облачных вычислений, баз данных, аналитических операций в памяти, виртуализации и сетей доставки информации. Поиск продукции с Поддержка энергонезависимой памяти Intel® Optane™ DC Редакция PCI Express — это версия, поддерживаемая процессором. PCIe (Peripheral Component Interconnect Express) представляет собой стандарт высокоскоростной последовательной шины расширения для компьютеров для подключения к нему аппаратных устройств. Различные версии PCI Express поддерживают различные скорости передачи данных. Полоса PCI Express (PCIe) состоит из двух дифференциальных сигнальных пар для получения и передачи данных, а также является базовым элементом шины PCIe. Количество полос PCI Express — это общее число полос, которое поддерживается процессором. Разъемом называется компонент, которые обеспечивает механические и электрические соединения между процессором и материнской платой. Критическая температура — это максимальная температура, допустимая в интегрированном теплораспределителе (IHS) процессора. Новый набор встраиваемых процессорных технологий, предназначенный для ускорения глубинного обучения искусственного интеллекта. Он дополняет Intel AVX-512 новыми командами VNNI (Vector Neural Network Instruction), что значительно повышает производительность обработки данных глубинного обучения в сравнении с предыдущими поколениями. Возможность конфигурации работы процессора в трех отдельных точках. Дает пользователям возможность повысить гарантированную базовую частоту на определенных ядрах (ядра с высоким приоритетом) и понизить базовую частоту на оставшихся ядрах (ядра с низким приоритетом). Повышает общую производительность за счет увеличения тактовой частоты текущих используемых ядер. Технология Intel® Resource Director Technology формирует новый уровень доступности и управления общими ресурсами, например, использование кэша последнего уровня (LLC) и пропускной способности памяти приложениями, виртуальными машинами и контейнерами. Технология Intel® Speed Shift использует аппаратно-управляемые P-состояния для обеспечения повышенной оперативности при обработке одного потока данных и кратковременных рабочих нагрузок, таких как веб-поиск, позволяя процессору быстрее выбирать нужную частоту и напряжение для поддержания оптимальной производительности и энергоэффективности. Технология Intel® Turbo Boost Max 3.0 определяет лучшую производительность ядер в процессоре и обеспечивает увеличенную производительность в ядрах с помощью возрастающей по мере необходимости частоты, пользуясь преимуществом резерва мощности и температуры. Технология Intel® Turbo Boost динамически увеличивает частоту процессора до необходимого уровня, используя разницу между номинальным и максимальным значениями параметров температуры и энергопотребления, что позволяет увеличить эффективность энергопотребления или при необходимости «разогнать» процессор. Intel® Hyper-Threading Technology (Intel® HT Technology) обеспечивает два потока обработки для каждого физического ядра. Многопоточные приложения могут выполнять больше задач параллельно, что значительно ускоряет выполнение работы. Поиск продукции с Технология Intel® Hyper-Threading ‡ Технология Intel® Virtualization для направленного ввода/вывода (VT-x) позволяет одной аппаратной платформе функционировать в качестве нескольких «виртуальных» платформ. Технология улучшает возможности управления, снижая время простоев и поддерживая продуктивность работы за счет выделения отдельных разделов для вычислительных операций. Поиск продукции с Технология виртуализации Intel® (VT-x) ‡ Технология Intel® Virtualization Technology для направленного ввода/вывода дополняет поддержку виртуализации в процессорах на базе архитектуры IA-32 (VT-x) и в процессорах Itanium® (VT-i) функциями виртуализации устройств ввода/вывода. Технология Intel® Virtualization для направленного ввода/вывода помогает пользователям увеличить безопасность и надежность систем, а также повысить производительность устройств ввода/вывода в виртуальных средах. Поиск продукции с Технология виртуализации Intel® для направленного ввода/вывода (VT-d) ‡ Intel® VT-x с технологией Extended Page Tables, известной также как технология Second Level Address Translation (SLAT), обеспечивает ускорение работы виртуализованных приложений с интенсивным использованием памяти. Технология Extended Page Tables на платформах с поддержкой технологии виртуализации Intel® сокращает непроизводительные затраты памяти и энергопотребления и увеличивает время автономной работы благодаря аппаратной оптимизации управления таблицей переадресации страниц. Intel® Transactional Synchronization Extensions New Instructions (Intel® TSX-NI) представляют собой набор команд, ориентированных на масштабирование производительности в многопоточных средах. Эта технология помогает более эффективно осуществлять параллельные операции с помощью улучшенного контроля блокировки ПО. Архитектура Intel® 64 в сочетании с соответствующим программным обеспечением поддерживает работу 64-разрядных приложений на серверах, рабочих станциях, настольных ПК и ноутбуках.¹ Архитектура Intel® 64 обеспечивает повышение производительности, за счет чего вычислительные системы могут использовать более 4 ГБ виртуальной и физической памяти. Поиск продукции с Архитектура Intel® 64 ‡ Расширения набора команд — это дополнительные инструкции, с помощью которых можно повысить производительность при выполнении операций с несколькими объектами данных. К ним относятся SSE (Поддержка расширений SIMD) и AVX (Векторные расширения). Intel® Advanced Vector Extensions 512 (AVX-512), новые расширения набора команд, имеющие максимально широкие возможности векторных операций (512 бит) с использованием до 2 команд FMA (Fused Multiply Add) для повышения производительности наиболее ресурсоемких вычислительных задач. Усовершенствованная технология Intel SpeedStep® позволяет обеспечить высокую производительность, а также соответствие требованиям мобильных систем к энергосбережению. Стандартная технология Intel SpeedStep® позволяет переключать уровень напряжения и частоты в зависимости от нагрузки на процессор. Усовершенствованная технология Intel SpeedStep® построена на той же архитектуре и использует такие стратегии разработки, как разделение изменений напряжения и частоты, а также распределение и восстановление тактового сигнала. Технология Intel® Volume Management Device (VMD) обладает основными возможностями надежного управления функциями оперативной замены со светодиодным интерфейсом для твердотельных накопителей типа NVMe. Команды Intel® AES-NI (Intel® AES New Instructions) представляют собой набор команд, позволяющий быстро и безопасно обеспечить шифрование и расшифровку данных. Команды AES-NI могут применяться для решения широкого спектра криптографических задач, например, в приложениях, обеспечивающих групповое шифрование, расшифровку, аутентификацию, генерацию случайных чисел и аутентифицированное шифрование. Поиск продукции с Новые команды Intel® AES Технология Intel® Trusted Execution расширяет возможности безопасного исполнения команд посредством аппаратного расширения возможностей процессоров и наборов микросхем Intel®. Эта технология обеспечивает для платформ цифрового офиса такие функции защиты, как измеряемый запуск приложений и защищенное выполнение команд. Это достигается за счет создания среды, где приложения выполняются изолированно от других приложений системы. Поиск продукции с Технология Intel® Trusted Execution ‡ Бит отмены выполнения — это аппаратная функция безопасности, которая позволяет уменьшить уязвимость к вирусам и вредоносному коду, а также предотвратить выполнение вредоносного ПО и его распространение на сервере или в сети. Технология Intel® Run Sure содержит функции, обеспечивающие высокую надежность и отказоустойчивость платформ (RAS), для максимального продления времени бесперебойной работы серверов, осуществляющих обработку важных задач. Управление выполнением на основе режимов может использоваться для проверки надежности и целостности кода ядра. Эдит Р. Запишите следующее уравнение Артуро О.
ответил • 04.09.18 Опытный учитель физики Репетиторство по физике Выберите эксперта и познакомьтесь онлайн.
Никаких пакетов или подписок, платите только за необходимое время. Ханна П. Шесть умноженное на число плюс 4 совпадает с числом минус 11 Лорен Х.
ответил • 19.09.18 Опытный учитель химии в старших классах Шесть раз число плюс 4 совпадает с числом минус 11 6x + 4 = x — 11 вычтите x с каждой стороны; прибавить 11 к каждой стороне 5x = -15 разделить каждую сторону на 5 x = -3 Выберите эксперта и познакомьтесь онлайн.
Никаких пакетов или подписок, платите только за необходимое время. Подробнее о математике в The Times Стивен Строгац Чтобы помочь учащимся в США запомнить этот порядок операций, учителя вставляют в них аббревиатуру PEMDAS: скобки, показатели, умножение, деление, сложение, вычитание.Другие учителя используют эквивалентную аббревиатуру BODMAS: скобки, порядки, деление и умножение, а также сложение и вычитание. Третьи советуют своим ученикам запомнить маленькую частушку: «Прошу прощения, моя дорогая тетя Салли». [ Эта математическая задача — не первый раз, когда Интернет раскололся. Помните Янни и Лорел? Как насчет цвет этого платья ? ] А теперь поймите, что следование за тетей Салли — это чисто условный вопрос.В этом смысле PEMDAS произвольна. Более того, по моему опыту математика, выражения вроде 8 ÷ 2 × 4 выглядят абсурдно надуманными. Ни один профессиональный математик никогда не написал бы что-то столь явно неоднозначное. Мы бы вставили круглые скобки, чтобы обозначить наш смысл и указать, следует ли сначала выполнить деление или умножение. В последний раз, когда это появилось в Твиттере, я отреагировал возмущенно: казалось смешным, что мы тратим так много времени в школьной программе на такую софизму.Но теперь, будучи просветленным некоторыми из моих компьютерных друзей в Твиттере, я пришел к пониманию того, что условности важны и от них могут зависеть жизни. Мы знаем это всякий раз, когда выезжаем на шоссе. Если все остальные едут по правой стороне дороги (как в США), вам будет разумно последовать их примеру. То же самое, если все остальные едут слева, как в Соединенном Королевстве. Неважно, какая конвенция будет принята, если все ее соблюдают. Точно так же важно, чтобы каждый, кто пишет программное обеспечение для компьютеров, электронных таблиц и калькуляторов, знал правила порядка операций и следовал им.Для остальных из нас сложности PEMDAS менее важны, чем более крупный урок о том, что условности имеют свое место. Это двойная желтая линия по центру дороги — бесконечный знак равенства — и общее соглашение о понимании друг друга, совместной работе и избежании лобовых столкновений. В конечном счете, 8 ÷ 2 (2 + 2) — это не столько утверждение, сколько кирпичная кладка; это все равно, что написать фразу «ест побеги и листья» и прийти к выводу, что язык капризен. Ну да, при отсутствии знаков препинания это так; вот почему мы изобрели этот материал. Итак, от имени всех учителей математики, пожалуйста, извините нас за то, что вы натренируете себя в юности на этой скуке. Мои дочери тратили на это несколько недель каждый учебный год в течение нескольких лет обучения, как будто готовились стать автоматами. Неудивительно, что так много студентов начинают рассматривать математику как бесчеловечный и бессмысленный набор произвольных правил и процедур. Очевидно, что если этот последний приступ беспорядка в Интернете является каким-либо признаком, то многие студенты не могут усвоить более глубокий и важный урок. Возможно, пора перестать извинять дорогую тетю Салли и вместо этого обнять ее. При умножении положительных и отрицательных чисел существует меньше правил, чем при сложении и вычитании положительных и отрицательных чисел. Следует запомнить всего три правила: Это умножение, которое вы делали все время: положительные числа, умноженные на положительные числа, равны положительным числам. Например, 5 x 3 = 15.5 — положительное число, 3 — положительное число, а умножение дает положительное число: 15. Ответ 5 x 3 = 15. Когда вы умножаете отрицательное число на положительное, ваш ответ — отрицательное число. Не имеет значения, в каком порядке вы умножаете положительные и отрицательные числа, ответ всегда будет отрицательным. Например: -2 x 4, что по сути то же самое, что -2 + (-2) + (-2) + (-2) Ответ: -2 х 4 = -8. И, как мы уже сказали, если около 4 x -2 наоборот, ответ все тот же: -8. Ответ: 4 х -2 = -8. Два отрицательных числа дают положительное число, поэтому умножение отрицательного числа на отрицательное число дает положительное число. Если вы посмотрите на него на числовой прямой, идя назад и повернувшись лицом в отрицательном направлении, вы двинетесь в положительном направлении. Например.-2 x -4 отрицательны, поэтому мы знаем, что ответ будет положительным. Ответ: -2 x -4 = 8. Вот общее правило, которое следует помнить при умножении положительных и отрицательных чисел: Два одинаковых знака дают положительный знак: Два непохожих знака образуют знак минус: Если вы все еще не понимаете, почему отрицательное число, умноженное на отрицательное, дает положительное число, Диана Браун с факультета математики Университета Джорджии объясняет это разными способами в этой статье. Скотт из About.com также собрал удобное видео о том, как создать шпаргалку для умножения отрицательных и положительных чисел (прокрутите страницу вниз, и вы найдете видео). Количество позиций: 1 Сэкономьте деньги и распечатайте фотографии дома с помощью этой упаковки из 100 фотобумаги от Canon.Photo Paper Plus Glossy II Vidid Colours обеспечивает глянцевую поверхность и исключительно насыщенные цвета, придавая вашим изображениям внешний вид традиционной фотографии. Каждый лист фотобумаги размером 4 x 6 дюймов имеет стандартный размер, который легко помещается в любой принтер. Обеспечивая качественную домашнюю печать, эта бумага позволит еще проще делиться любимыми фотографиями с друзьями и семьей. О компании Canon: Новый стандарт фотобумаги Canon. Красивый блеск фотопечати на фотобумаге настолько экономичен, что вы можете наслаждаться ее блеском и яркими цветами в любое время. Canon с гордостью объявляет о выпуске Photo Paper Plus Glossy II PP-201, фотобумаги, улучшенной по сравнению с Photo Paper Plus Glossy PP-101, и устанавливает новый стандарт качества изображения и экономичности. Используя технологию нанесения покрытия для струйной печати, оригинальное применение светочувствительных материалов, Canon удалось разделить слои отложения чернил по функциям.Там, где раньше был сформирован только один слой покрытия для струйной печати, эта технология создает два отдельных слоя: слой для воспроизведения цвета и поглощающий слой. Blacker Blacks Фотографии получаются великолепно, потому что краситель фиксируется близко к поверхности бумаги. Новый слой воспроизведения цвета фиксирует краситель на поверхности бумаги. Условия измерения Soma Tech Intl предлагает портативный рентгеновский аппарат GE AMX 4 Plus
до 50% ниже цен OEM с тем же обслуживанием и гарантией, что и новые.Портативный рентгеновский аппарат GE AMX 4 Plus не только технически отремонтирован, но и обновлен косметически, чтобы он работал и выглядел как новый. Когда начинается процесс восстановления рентгеновского аппарата, он тщательно проверяется и тестируется нашими собственными биомедицинскими инженерами, обладающими высокой квалификацией и сертифицированными для работы с рентгеновскими лучами. При необходимости детали заменяются, чтобы убедиться, что все аспекты портативного рентгеновского аппарата GE AMX 4 Plus работают должным образом. Как только все будет в рабочем состоянии, устройство снова откалибровано в соответствии с исходными техническими характеристиками производителя.Это гарантирует, что устройство будет работать так же, как оно было изначально оставлено производителем. После того, как портативный рентгеновский аппарат GE AMX 4 Plus заработал как новый, он подвергается специальной косметической реставрации. Он очищен, устранены мелкие царапины и вмятины, окрашен, при необходимости заменены новые декали Переносной рентгеновский аппарат GE AMX 4 Plus. После этого кропотливого процесса восстановления устройство функционирует и выглядит как новый. Soma Tech Intl имеет сертификат ISO 13485 и гарантирует высочайшее качество всего продаваемого ими основного медицинского оборудования.Прежде чем портативный рентгеновский аппарат GE AMX 4 Plus будет отмечен как готовый к пациенту и упакован для отправки, он проходит последний тест контроля качества, который гарантирует, что все аспекты снова работают должным образом. Если вы хотите купить отремонтированный портативный рентгеновский аппарат GE AMX 4 Plus
свяжитесь с Soma по адресу [адрес электронной почты защищен] aTechnology.com или позвоните нам по телефону 1-800-GET-SOMA. Soma Tech Intl также активно ищет возможности приобрести Siemens Siremobil Compact C-Arm.
Если вы или ваше учреждение хотите продать свой портативный рентгеновский аппарат GE AMX 4 Plus / a>, обязательно свяжитесь с Soma Tech Intl.В Soma есть специализированный и опытный отдел закупок, который поможет вам на протяжении всего процесса. Продажа подержанного или бывшего в употреблении портативного рентгеновского аппарата GE AMX 4 Plus компании Soma Tech Intl устраняет посредника в уравнении. Это также гарантирует, что ваше медицинское учреждение получит большие деньги за ваше оборудование. Soma на 100% соответствует требованиям HIPPA и гарантирует, что ваше оборудование попадет на наш объект в том же состоянии, в каком оно оставило ваше. Soma Tech Intl также предоставляет возможность обмена вашего медицинского оборудования в кредит.Если вы или ваше предприятие хотите освободить место для нового оборудования, или если вы хотите обновить свое текущее оборудование, свяжитесь с отделом закупок Soma Techn Intl по адресу [адрес электронной почты защищен] или отправьте нам сообщение на нашем href = «https: // www.somatechnology.com/Sell-to-Soma/ «target =» _ blank «> Продать на веб-сайт Soma. Есть вопросы о портативном рентгеновском аппарате? Soma Tech Intl предлагает широкий спектр
портативный рентгеновский аппарат. Если у вас есть какие-либо вопросы по любому из наших портативных рентгеновских аппаратов или вам нужно быстрое предложение, позвоните по телефону 1-800-GET-SOMA и одному из наших
знающие торговые представители помогут вам. Первые несколько чисел, кратных 4, находятся в таблице умножения на четыре: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48. Мы можем продолжить прибавлять 4 к этим числам, чтобы найти следующие числа, кратные 4. 48 + 4 = 52, поэтому 52 является следующим кратным 4. Затем снова добавляем 4, получаем 56 и так далее. Вот список всех кратных от 4 до 100. 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100. Вот список всех кратных от 4 до 100, представленных в числовой сетке. Мы видим, что числа всегда появляются в определенных столбцах. Кратные 4 появляются только в столбцах с четными числами, номера которых заканчиваются на 0, 2, 4, 6 или 8. Однако мы видим, что не все числа , заканчивающиеся на 2, 4, 6, 8 или 0, кратны 4. Чтобы найти число, кратное 4, просто умножьте число на четыре. Например, чтобы найти 5-е кратное 4, умножьте 5 на 4. 5 × 4 = 20 Итак, пятое число, кратное четырем, равно 20. Таблица умножения: Итак, кратные четырем: Все числа, кратные 4, оканчиваются одними и теми же цифрами: 0, 4, 8, 2, 6. Правильные ответы обозначены + 1.Тест. За унитарным предприятием закрепляется имущество: — На правах долгосрочной аренды — На правах собственности + На правах оперативного управления либо хозяйственного ведения 2. Присущ ли риск предпринимательству? + Да, риск – это неотъемлемая составляющая предпринимательства — Да, но лишь в условиях кризисов и инфляции — Нет 3. Целью предпринимательства является: — Удовлетворение потребностей населения в товарах и услугах — Пополнение бюджета государства налоговыми поступлениями + Систематическое получение прибыли 4. Ключевые слова, определяющие понятие «предпринимательство»: — Риск, прибыль, потребности, конкуренция + Риск, прибыль, инициатива, инновации — Конкуренция, прибыль, налоги 5. Важнейшими чертами предпринимательства являются: + Риск и неопределенность, самостоятельность и свобода деятельности, опора на инновации — Постоянный поиск новых идей, риск, экономическая зависимость от макроэкономической ситуации в стране — Самостоятельность, оглядка на конкурентов, опора на инновации 6. — Торговля продуктами питания — Организация регулярных пассажирских перевозок + Эмиссия ценных бумаг и торговля ими Тест.7. Субъектами предпринимательства могут быть: — Физические лица + Физические и юридические лица — Юридические лица 8. Предпосылки, предопределяющие становление предпринимательства в России: + Политические, экономические, юридические, психологические — Политические, экономические, социальные — Политические, экономические, юридические, культурные 9. Какие бывают формы предпринимательства? — Частное, общее, государственное + Индивидуальное, партнерское, корпоративное — Индивидуальное, совместное 10. Предпринимательство выполняет следующие функции: — Социально-экономическую, направляющую, распределительную, организаторскую — Экономическую, политическую, правовую, социально-культурную + Общеэкономическую, политическую, ресурсную, организаторскую, социальную, творческую 11. + Унитарные муниципальные предприятия — Стратегически важные предприятия и учреждения — Банковские структуры 12. Основу акционерного предпринимательства составляет: — Четкое разграничение ответственности между акционерами — Обязательное вхождение в состав акционерного общества доли государственной собственности + Акционерная собственность на средства производства 13. Что является основами свободного предпринимательства? — Рыночный механизм, частная собственность и совершенная конкуренция + Диалектическая взаимосвязь производительных сил, производственных отношений и хозяйственного механизма, действующих в условиях частной собственности на средства производства, свободы предпринимательства и свободной конкуренции — Производительные силы, материальные и трудовые ресурсы, находящиеся в свободном для предпринимателей доступе 14. + Четкая направленность на получение финансового результата — Желание максимально удовлетворить потребности общества в товарах и услугах — Желание занять максимально перспективную нишу на рынке 15. Коллективное предпринимательство осуществляется группой граждан на основе: — Четкого разделения ответственности в зависимости от доли участия в предприятии + Личных интересов каждого из них — Равноценного участия в деятельности предприятия 16. Производственное предпринимательство — вид бизнеса, основу которого составляет: — Материальное производство — Материальное производство и оказание услуг + Материальное, интеллектуальное и духовное производство 17. Экономической основой индивидуального предпринимательства является … собственность. + Частная — Общественная — Государственная 18 — тест. — Частная — Коллективная + Муниципальная 19. Финансовое предпринимательство — вид бизнеса, основу которого составляют: — Ценные бумаги + Деньги, в том числе иностранная валюта, ценные бумаги — Движимое имущество 20. Семейное предпринимательство может осуществляться на основе: + Совместного владения крестьянским (фермерским) хозяйством и/или приватизированным жильем — Юридически подтвержденных родственных связей — Долевого владения производительными силами 21. Предпринимательство на основе частичной занятости предполагает: — Вынужденное занятие иными видами деятельности, приносящими доход — Одновременную реализацию нескольких коммерческих проектов + Совмещение или чередование занятия предпринимательством с другими видами производственной и непроизводственной трудовой деятельности 22. — Постоянное желание рисковать, потребность во влиянии + Стремление к успеху, внедрение инноваций — Удовлетворение от самостоятельного ведения дел, постоянное желание рисковать 23. Укажите вид предпринимательства, который предусматривает постоянные торгово-обменные операции по купле-продаже товаров: + Коммерческое — Финансовое — Производственное 24. Предпринимателю необходимы навыки: — Экономические, производственные, концептуальные + Экономические, коммуникативные, технологические — Коммуникативные, экономические 25. Что является источниками формирования предпринимательской идеи? — Конкуренция, инновации, товарный рынок — Экономическая нестабильность, товарный рынок, конкуренция + Конкуренция, географические и структурные «разрывы», достижения НТП 26. — Юридическое лицо + Физическое лицо — Совместная деятельность 27. Финансовыми ресурсами производства являются: — Здания и оборудование — Трудоспособное население + Деньги 28. Кого относят к юридическим лицам? + Фирмы, предприятия, организации — Работников — Безработных 29. Укажите форму ответственности для индивидуальных предпринимателей. — Субсидиарная ответственность принадлежащим ему имуществом + Полная ответственность принадлежащим ему имуществом — Ответственность в виде штрафов и административных взысканий 30. Соглашение между предпринимателями одной отрасли о ценах, разделе рынков сбыта и доли в общем рынке – это: — Корпорация + Картель — Коммандитное товарищество 31. Согласно определению Д. Макклелланда, предприниматель – это: + Энергичный человек, который действует в условиях умеренного риска — Ключевая фигура бизнеса — Человек, получающий прибыль благодаря имеющимся у него организаторским способностям 32. — Стремление к личной независимости — Продолжение традиций семьи + Накопленные личные сбережения 33. Сколько участников может состоять в открытом акционерном обществе? — Не менее 2 — Не менее 10 + Любое количество 34. Полное товарищество могут организовать: + Индивидуальные предприниматели и коммерческие организации — Индивидуальные предприниматели и некоммерческие организации — Юридические лица 35. Участники закрытого акционерного общества – это: — Экзекуторы — Товарищи + Акционеры 36. В каком случае невозможен отказ от регистрации предприятия? — Доказанная экономическая нецелесообразность производства данного продукта — Несоответствие учредительных документов требованиям законодательства + Нарушен установленный законом порядок создания предприятия 37. — Валоризация + Предпринимательский доход — Обеспечение 38. Какое из перечисленных направлений не является формой государственной поддержки и регулирования предпринимательской деятельности? — Совершенствование системы финансовой поддержки малого предпринимательства — Формирование нормативно-правовой базы поддержки и развития предпринимательства + Формирование государственной программы производства экологически чистых продуктов 39. Кто автор слов «Доход предпринимателя – это плата за риск?» + Р. Кантильон — А. Каминка — И. Шумпетер 40. Укажите минимальное количество учредителей общества с ограниченной ответственностью: + 1 — 2 — 10 Последний раз тест пройден более 24 часов назад.
Для учителя
Вопрос 1 из 10 верно только А верно только Б верны оба определения оба определения ложны Правильный ответ Неправильный ответ В вопросе ошибка? Вопрос 2 из 10 верно только А верно только Б верны оба определения оба определения ложны Правильный ответ Неправильный ответ В вопросе ошибка? Вопрос 3 из 10 верно только А верно только Б верны оба определения оба определения ложны Правильный ответ Неправильный ответ В вопросе ошибка? Вопрос 4 из 10 партнерство дружба нескольких десятков предпринимателей союз вкладчиков объединение финансовых средств Правильный ответ Неправильный ответ В вопросе ошибка? Вопрос 5 из 10 верно только А верно только Б верны оба определения оба определения ложны Правильный ответ Неправильный ответ В вопросе ошибка? Вопрос 6 из 10 редко используемая организационно-правовая форма для организаций крупного и среднего бизнеса предприятие или организация, уставный капитал которого разделен на определенное число акций, распределенных между акционерами распространенная организационно-правовая форма для мелких частных компаний предприятие или организация, уставный капитал которого разделен между акционерами в зависимости от их авторитета Правильный ответ Неправильный ответ В вопросе ошибка? Вопрос 7 из 10 корпорация индивидуальное предприятие совместное хозяйство товарищество Правильный ответ Неправильный ответ В вопросе ошибка? Вопрос 8 из 10 верно только А верно только Б верны оба высказывания оба определения неправильные Правильный ответ Неправильный ответ В вопросе ошибка? Вопрос 9 из 10 Правильный ответ Неправильный ответ В вопросе ошибка? Вопрос 10 из 10 штрафы действия ценные бумаги банкноты Правильный ответ Неправильный ответ В вопросе ошибка? Доска почёта Чтобы попасть сюда — пройдите тест. Саша Скрыпник 10/10 Данил Лимонов 10/10 Данил Майор 9/10 Эльмин Мехралиев 10/10 Алиса Шварц 9/10 3.8 Средняя оценка: 3.8 Всего получено оценок: 792. А какую оценку получите вы? Чтобы узнать — пройдите тест. Главная / Экономика /
Основы предпринимательства / Тест 1 Упражнение 1: Номер 1 Ответ:  (1) все перечисленное верно   (2) получение максимальной прибыли при минимальном риске   (3) соблюдение социальных гарантий   (4) самостоятельность и независимость хозяйствующих субъектов  Номер 2 Ответ:  (1) получение максимальной прибыли при минимальном риске   (2) самостоятельность и независимость хозяйствующих субъектов   (3) хозяйственный риск и ответственность   (4) соблюдение социальных гарантий  Номер 3 Ответ:  (1) в эпоху правления Петра I   (2) в эпоху существования Киевской Руси   (3) в эпоху существования Советского Союза   (4) в досоветское время  Упражнение 2: Номер 1 Ответ:  (1) коммерческая деятельность   (2) предпринимательство   (3) инновационное предпринимательство  Номер 2 Ответ:  (1) в коммандитном товариществе   (2) в обществе с ограниченной ответственностью   (3) в обществе с дополнительной ответственностью   (4) в хозяйственном обществе  Номер 3 Ответ:  (1) иметь в собственности обособленное имущество   (2) монополизировать рынки сбыта продукции   (3) от своего имени заключать гражданско-правовые договоры на все виды деятельности   (4) предъявлять иски и выступать в суде в качестве ответчика  Упражнение 3: Номер 1 Ответ:  (1) унитарное предприятие   (2) хозяйственное общество   (3) хозяйственное товарищество   (4) коммандитное товарищество  Номер 2 Ответ:  (1) простые акции   (2) привилегированные акции   (3) простые и привилегированные акции  Номер 3 Ответ:  (1) синдикат   (2) финансово-промышленная группа (ФПГ)   (3) картель   (4) концерн  Упражнение 4: Номер 1 Ответ:  (1) объединение сбыта продукции предпринимателями одной отрасли с целью устранения излишней конкуренции между ними   (2) объединение предпринимателей с целью совместного проведения финансовой операции   (3) форма добровольного объединения экономически самостоятельных предприятий, организаций, которые одновременно могут входить и в другие образования   (4) многоотраслевое акционерное общество, контролирующее предприятия через систему участия  Номер 2 Ответ:  (1) товарная биржа   (2) финансовый рынок   (3) фондовая биржа   (4) торговая биржа  Номер 3 Ответ:  (1) не может оказывать существенного влияния на перспективы развития   (2) осуществляется в достаточном объеме   (3) закреплена в Законе о развитии малого и среднего бизнеса  Упражнение 5: Номер 1 Ответ:  (1) могут существовать во всех сферах и отраслях народного хозяйства   (2) могут осуществлять любые виды хозяйственной деятельности без специального разрешения, выдаваемого компетентными государственными органами власти   (3) не могут самостоятельно распоряжаться выпускаемой продукцией   (4) не являются юридическими лицами  Номер 2 Ответ:  (1) коммунанты   (2) патиенты   (3) эксплеренты  Номер 3 Ответ:  (1) в сферах торговли и общественного питания   (2) как производители ресурсоемкой продукции   (3) в добывающем секторе экономики России   (4) в перерабатывающей сфере  Упражнение 6: Номер 1 Ответ:  (1) является единовременной   (2) является поэтапной   (3) не может быть пересмотрена по инициативе инвестора   (4) все перечисленное верно  Номер 2 Ответ:  (1) коммерческое инвестирование   (2) инновационное предпринимательство   (3) хозяйственное предпринимательство   (4) венчурное инвестирование  Номер 3 Ответ:  (1) связано с высокой долей предпринимательского риска   (2) связано с минимальной долей предпринимательского риска   (3) имеет высокую долю среди видов предпринимательской деятельности   (4) обладает высокой инвестиционной привлекательностью  Упражнение 7: Номер 1 Ответ:  (1) коммерческое инвестирование   (2) венчурное инвестирование   (3) инновационное предпринимательство   (4) хозяйственное предпринимательство  Номер 2 Ответ:  (1) поглощение компании другой фирмой   (2) выкуп акций остальными собственниками финансируемой компании   (3) выпуск акций посредством первичного размещения капитала   (4) синдицирование инвестиций  Номер 3 Ответ:  (1) деятельность по производству товаров первой необходимости   (2) предпринимательская деятельность, связанная с финансовыми и капитальными вложениями в промышленное производство товаров   (3) предпринимательская деятельность, связанная с финансовыми и капитальными вложениями в инновацию   (4) предпринимательская деятельность, направленная на использование и коммерциализацию результатов научных исследований и разработок для расширения и обновления номенклатуры, улучшения качества выпускаемой продукции (работ, услуг), совершенствования технологий их изготовления с последующим внедрением и эффективной реализацией на рынке  Упражнение 8: Номер 1 Ответ:  (1) близость к местным рынкам и приспособление к запросам клиентуры   (2) производство и торговля малыми партиями   (3) исключение лишних звеньев управления   (4) большое число звеньев управления  Номер 2 Ответ:  (1) не более 5 человек   (2) не более 15 человек   (3) от 16 до 100 человек   (4) не более 10 человек  Упражнение 9: Номер 1 Ответ:  (1) товарищества и общества   (2) кооперативы   (3) артели   (4) концерны, ассоциации, консорциумы, синдикаты, картели, финансово-промышленные группы  Номер 2 Ответ:  (1) товарищество   (2) консорциум   (3) общество   (4) кооператив  Упражнение 10: Номер 1 Ответ:  (1) хозяйственное общество   (2) кооперативное предприятие (артель)   (3) унитарное предприятие   (4) хозяйственное товарищество  Номер 2 Ответ:  (1) наличие обособленного имущества   (2) способность отвечать по обязательствам своим имуществом   (3) возможность предъявлять иски и выступать в качестве ответчика в суде, арбитражном суде   (4) способность выступать в хозяйственном обороте от имени любого другого юридического лица  Упражнение 11: Номер 1 Ответ:  (1) все перечисленное верно   (2) экономическая заинтересованность   (3) хозяйственный риск и ответственность   (4) мобильность и динамичность предпринимательских действий  Номер 2 Ответ:  (1) личный риск   (2) реакция на финансовые возможности   (3) способность внести организованность в неструктурированную организацию   (4) желание долго и упорно работать, не отдыхая  Главная / Экономика /
Основы предпринимательства / Тест 1 1. инновации + конкуренция инициативность + риск + платежеспособность прибыль + 2. Укажите объекты предпринимательской деятельности в зависимости от видов предпринимательства: 1. производственное А. купля-продажа товаров 2. финансовое Б. страхование сделок 3. коммерческое В. преобразование ресурсов в общественно-полезный продукт Ответ: 1-В, 2 –Б, 3 –А 3. Какое количество волн выделяют в развитии процесса научного осмысления практики предпринимательства: одну две три + 4. Отметьте побудительные мотивы деятельности предпринимателя, выделенные Й.Шумпетером: потребность в господстве, влиянии получение максимальной прибыли внедрение инноваций + стремление к успеху + радость творчества при самостоятельном ведении дел. 5. Укажите хозяйственные операции сельскохозяйственного предпринимателя, которые относятся к производственному предпринимательству: наем работников для выполнения различных коммерческих операций организация эмиссии простых акций ремонтно-строительные работы в животноводстве + аренда торговых складов плата процентов за краткосрочный кредит рекламная деятельность приобретение семян + 6. наем работников для выполнения различных коммерческих операций + организация эмиссии простых акций ремонтно-строительные работы в животноводстве аренда торговых складов + плата процентов за кредит рекламная деятельность + приобретение семян 7. Укажите хозяйственные операции сельскохозяйственного предпринимателя, которые относятся к финансовому предпринимательству: наем работников для выполнения различных коммерческих операций организация эмиссии простых акций + ремонтно-строительные работы в животноводстве аренда торговых складов плата процентов за кредит + рекламная деятельность приобретение семян 8. Какой вид предпринимательства предусматривает торгово-обменные операции по купле-продаже товаров: производственное коммерческое + финансовое 9. «Акула» + «Рак» «Дельфин» 10. Как называется энергичный предприниматель с положительной социальной ориентацией: «Акула» «Рак» «Дельфин» + 11. Как называется малоэнергичный предприниматель с отрицательной социальной ориентацией: «Акула» «Рак» + «Дельфин» 12. Как называется предприниматель с позитивными общественными поступками и умеренной или низкой деловой активностью: «Акула» «Рыба» + «Дельфин» 13. Укажите три основные группы навыков, необходимые предпринимателю: технологические + концептуальные позитивные экономические + коммуникативные + 14.Отметьте разновидности посредников в финансовом предпринимательстве: дилеры брокеры + агенты маклеры + 15. Отметьте разновидности посредников в коммерческом предпринимательстве: дилеры + брокеры агенты + маклеры 16. 17. Спекулянтов на бирже называют: дилеры брокеры + агенты 18. Спекулянты, играющие на повышении цены называются: «Быки» + «Медведи» 19. Спекулянты, играющие на понижении цены называются: «Быки» «Медведи»+ 20. Дополните ответ: Предпринимательская идея – это ____________________________присущего потребителю желания иметь товары и услуги определенного качества и ассортимента. Ответ: «отражение в сознании предпринимателя» 21. Отметьте источники формирования предпринимательских идей: достижения науки и техники + товарный рынок конкуренция + географические и структурные «разрывы» + фондовые биржи 22. Укажите положительные стороны выбора формы хозяйствования в виде индивидуального предпринимательства: регистрация проще, чем юридического лица + небольшая сумма стартового капитала упрощенная отчетность + упрощенная форма налогообложения + 23. юридического лица физического лица + 24. Отметьте недостатки и слабые стороны индивидуального предпринимательства (ИП): ответственность по обязательствам своим имуществом+ необходимость выполнять несколько производственно-хозяйственных функций одному человеку+ финансово-экономическая уязвимость бизнеса сориентированного на одного человека наличие основных и дополнительных участников в форме хозяйствования. 25. Каковы недостатки акционерной формы хозяйствования: □ обязательства бессрочной выплаты дивидендов + □ ответственность участников АО своим имуществом □ громоздкость управления+ □ часть держателей акций не участвуют трудом в деятельности общества+ □ число участников не должно быть меньше пяти человек 26. Укажите, какие сферы предпринимательства являются наиболее предпочтительными в настоящее время: □ оказание деловых услуг □ строительство дорог □ торговля потребительскими товарами + □ службы автосервиса + □ общественное питание + 27. Организации, имеющие в качестве основной цели своей деятельности получение прибыли называются ___________________________________________________ Ответ: коммерческими 28. Дополните ответ: Организации, не имеющие основной целью своей деятельности получение прибыли называются ___________________________________________________ Ответ: некоммерческими 29. Установите виды ответственности в организациях следующих правовых форм: 1. Открытое акционерное общество 2. Полное товарищество 3. Общество с ограниченной ответственностью Виды ответственности: А. имущественная ответственность участника Б. ответственность в пределах суммы вклада в уставный капитал В.участник не несет ответственности, так как имеет права на основе договора Ответ: 1 — В, 2 –А, 3 — Б 30. Дополните ответ: Предпринимательство – это самостоятельная, инициативная деятельность физических и юридических лиц, для которой характерны____________________, ответственность, инновации с целью получения прибыли. Ответ: риск 31. Предпринимательство – это самостоятельная, инициативная деятельность физических и юридических лиц, осуществляемая с целью: □ получения прибыли+ □ помощи нуждающимся □ удовлетворения амбиций Поделиться с друзьями: Adblock Авторам 8-800-333-85-44 Оформить заявку Вход Выполним любые типы работ Юридические дисциплины Юридические дисциплины Юридические дисциплины Юридические дисциплины Юридические дисциплины Юридические дисциплины Юридические дисциплины Юридические дисциплины Юридические дисциплины Контрольная работа от 1 дня
/ от 100 руб Курсовая работа от 5 дней
/ от 1800 руб Реферат от 1 дня
/ от 700 руб Онлайн-помощь от 1 дня
/ от 300 руб Оставляй заявку — и мы пройдем все тесты за тебя! Планирование – это: функция управления, включающая следующий комплекс работ: анализ ситуаций и факторов внешней среды; прогнозирование, оценка и оптимизация альтернативных вариантов достижения целей, сформулированных на стадии стратегического маркетинга; разработка плана; реализация плана. Хотите лучше понять, кто вы? Этот тест измеряет знаменитые черты личности «Большой пятерки». Пройдите тест Узнайте, притягивают ли ваши черты характера ушибленные пальцы ног, сломанные кости и множество бинтов. Пройдите тест Выявляет ли вождение самые худшие качества? Узнайте, подвержены ли вы риску агрессивного поведения на дороге, с помощью этого теста. Пройти тест EQ — это не прихоть. Это ключ к более счастливой и успешной жизни. Оцените свои эмоциональные компетенции здесь. Пройдите тест Умеете ли вы обращаться со словами? Используйте свою болтливость, многословие и словоохотливость с пользой в этом тесте. Пройди тест Трехмерные фигуры, сложные слова и головоломки с числами. Пройти тест Нужна проверка отношений? Оцените свой уровень доверия, сексуальную совместимость и многое другое с помощью этого теста. Пройти тест Довольны ли вы каждым аспектом ваших отношений или что-то нужно исправить? Узнайте с помощью этого теста. Пройти тест Довольны ли вы своими отношениями и своим партнером, или есть что-то, что вы хотели бы изменить? Пройти тест Административная работа — это не только ответы на телефонные звонки и набор электронных писем. Пройти тест Вы думаете об инвестировании во франчайзинг и управлении им? Оцените свои способности в этой области прямо здесь. Пройти тест Обучение юных умов — ваше призвание? Узнайте, есть ли у вас необходимые навыки и качества, чтобы стать педагогом. Пройти тест Вы авангардистка или предпочитаете более традиционные гендерные роли? Узнайте с помощью этого теста. Пройти тест Являются ли ваши взгляды на гендерные роли более современными или они прочно укоренились в традициях? Узнайте, где вы стоите. Пройди тест Откладываешь ли ты дела, которые тебе не нравятся? Мы настоятельно рекомендуем пройти этот тест сейчас, а не позже. Пройти тест Вы приходите в норму после жизненных взлетов и падений или они подрывают вас? Испытайте свои душевные силы. Пройти тест Многие люди не осознают, что их чувства влияют на их привычки в еде. Ваш голод физический или эмоциональный? Пройти тест Ваши симптомы ПМС едва заметны или вызывают физические, эмоциональные и психологические потрясения? Пройти тест Профессиональные оценки Queendom проходят тщательное исследование и анализ. В этом разделе вы найдете тесты, охватывающие
все, от психического здоровья до отношений, IQ, карьерных способностей и многого другого. Подробнее Вы драматург, метросексуал, хороший сосед? Что бы вы сделали за 10 миллионов долларов? Королевские предложения
широкий ассортимент забавных, познавательных и наводящих на размышления тестов. Посмотреть еще Ваш мозг подобен мускулу: вы должны поддерживать его в форме! Queendom предлагает множество сложных и запутанных логических, вербальных,
пространственные и математические головоломки, которые заставят вас прыгать через умственные обручи. Посмотреть еще Знаете ли вы, что такое «Бургермейстер»? Кто написал Доктор Джекил и мистер Хайд ? Проверьте свои знания о
история, литература, география, поп-культура и многое другое с нашими мелочами. Посмотреть еще Как вы относитесь к патриотизму, пластической хирургии и полигамии? Вы чистите зубы так же часто, как средний человек?
Отдайте свой голос и просмотрите результаты всех наших опросов. Пусть ваш голос услышат! Подробнее Почувствуйте вдохновение, силу, самовыражение и живите полной жизнью с самородками Queendom
мудрости. Посмотреть еще Нужен совет? Квалифицированные консультанты предлагают рекомендации по всем вопросам, от вопросов психического здоровья до секса.
Вопросы и ответы к причудам личности. Прочитайте более тысячи ответов от прошлых посетителей или задайте свой вопрос. Подробнее Блогер Queen D делится пикантными фактами и глубокими выводами из исследований Queendom, а также личными
истории и мудрость, которые она собрала на своем пути к самосознанию. Посмотреть еще Эти семь личностных тестов помогут вам понять свои сильные стороны как предпринимателя. Тест личности может стать ценным инструментом, который поможет вам обрести самосознание и стать предпринимателем. [Подробнее: 6 черт личности, которые делают великого предпринимателя] Тест личности предпринимателя — это бесплатная оценка, предлагаемая Psychology Today. Это хороший вариант для тех, кому интересно, подходит ли их личность для предпринимательства. Тест основан на книге Билла Вангера « Предприниматель по соседству ». После прохождения теста вы получите бесплатный обзор и резюме своего отчета. Если вам нужны полные результаты, вы можете приобрести их за 9 долларов.0,95. Если вы поклонник личностных тестов, то наверняка слышали об индикаторе типа Майерс-Бриггс (MBTI). Этот тест часто считают золотым стандартом личностных тестов, но, к сожалению, он платный. Но лучше всего подойдет 16 Personalities — бесплатная версия MBTI. Тест описывает 16 различных типов личности, разбитых на четыре категории: Аналитики, Дипломаты, Стражи и Исследователи. Вы можете использовать свои результаты, чтобы понять свои сильные и слабые стороны, улучшить отношения и стать лучшим владельцем бизнеса. Эннеаграмма — это тест личности, ставший популярным в духовных и деловых кругах за последние пять лет. Тест гораздо более глубокий, чем другие личностные тесты, и рассматривает мотивы человека, лежащие в основе того, почему он делает определенные вещи. Эннеаграмма не только дает обзор вашего типа личности, но также объясняет: Прохождение теста стоит 12 долларов, но вы можете найти бесплатные версии в Интернете. Вы можете использовать свои результаты, чтобы понять свои сильные и слабые стороны,
улучшить свои отношения и стать лучшим владельцем бизнеса. Тест HIGH5 — это бесплатная версия теста Gallup CliftonStrengths. Этот тест может помочь вам раскрыть свои сильные стороны и развить эти сильные стороны в бизнесе и жизни. Тест доступен для отдельных лиц, но вы также можете поручить его пройти своей команде. Эта информация может помочь вам раскрыть сильные стороны каждого из ваших сотрудников, чтобы они могли полностью раскрыть свой потенциал. Тест HIGH5 также может помочь вашей команде открыть для себя новые способы общения и совместной работы. [Подробнее: Что такое CliftonStrengths Assessment и как он работает?] Цветовой личностный тест — это бесплатный тест, который измеряет вашу индивидуальность на основе четырех различных цветов: синего, оранжевый, желтый и зеленый. Skills You Need — это бесплатная самооценка, которая может помочь вам улучшить свои навыки межличностного общения, которые имеют решающее значение для любого предпринимателя. Тест измеряет, насколько хорошо вы работаете в следующих категориях: Этот тест поможет вам оценить, насколько хорошо вы взаимодействуете с другими людьми, и определить возможности для улучшения. [Подробнее: Наем на личностные тесты для поиска лучших кандидатов] Карьерный личностный профайл — это бесплатный тест, предлагаемый Truity. Это также может помочь вам узнать, какие задачи вы любите делать, а каких избегаете. И это может помочь вам увидеть, как вы сохраняете мотивацию, работаете в командной среде и решаете сложные проблемы. Когда вы закончите сдавать тест, вы получите бесплатный обзор своих результатов. CO— стремится вдохновить вас от ведущих
уважаемые специалисты. Однако, прежде чем принимать какое-либо деловое решение, вы
следует проконсультироваться со специалистом, который может дать вам совет на основе вашего
индивидуальная ситуация. Подпишитесь на нас в Instagram , чтобы узнать больше советов экспертов и историй владельцев бизнеса. Чтобы быть в курсе всех новостей, влияющих на ваш малый бизнес, перейдите сюда для всех наших последних новостей и обновлений малого бизнеса. CO — стремится помочь вам начать, управлять и развивать свой малый бизнес. Узнайте больше о преимуществах членства малого бизнеса в Торговой палате США здесь. Сообщение от Вас приглашают присоединиться к частной сети генеральных директоров. Узнайте, как 45 000 руководителей развивают свой бизнес. Свяжитесь с проверенными компаниями в безопасной частной сети, чтобы найти новых клиентов, собрать деньги и найти надежные решения для любого бизнес-приоритета. Советы экспертов по бизнесу, новости и тенденции, доставляемые еженедельно Регистрируясь, вы соглашаетесь с Политикой конфиденциальности CO. Вы можете отказаться в любое время. Опубликовано 06 августа 2021 г. В сфере занятости используется несколько различных тестов для определения надлежащей классификации работника. Первоначально, еще в 1800-х годах, тест использовался для целей ответственности агентства ( responseeat Superior ) – контрольный тест. Контрольный тест используется в нескольких федеральных законах, и соответствующие административные органы используют контрольный тест для определения классификации работника по причинам, не связанным с деликтной ответственностью: Закон о возрастной дискриминации при приеме на работу (ADEA), Закон об американцах-инвалидах (ADA), пенсионное страхование сотрудников. Контрольный тест считает, что работник является наемным работником, если нанимающая организация «контролировала или имела право контролировать способы и средства» работы работника. Чтобы сделать это определение, совокупность обстоятельств рассматривается при взвешивании длинного списка факторов, которые исходят из повторного заявления (второго) агентства: Налоговое управление использует форму контрольного теста и фокусируется на трех категориях независимости: поведенческой, финансовой и типе отношений. См. IRS, независимый подрядчик (самозанятый) или сотрудник? Тест экономических реалий в настоящее время используется для целей FLSA (минимальная заработная плата, сверхурочная работа и страхование по безработице). 1- Степень права предполагаемого работодателя контролировать способ выполнения работы; 2- возможность предполагаемого работника получить прибыль или убыток в зависимости от его управленческих навыков; 3- инвестиции предполагаемого работника в оборудование или материалы, необходимые для его работы, или наем им помощников; 4- требует ли оказываемая услуга особого мастерства; 5- степень постоянства трудовых отношений; и 6- является ли оказанная услуга неотъемлемой частью бизнеса предполагаемого работодателя. При администрации Трампа Министерство труда изменило тест, используемый для целей FLSA. Тест на предпринимательские возможности в настоящее время используется для целей NLRA и, в частности, окружным судом округа Колумбия. Рассмотрение предпринимательских возможностей обычно требует рассмотрения того, есть ли у работников «значительные предпринимательские возможности для получения прибыли или убытков». Симфонический оркестр Ланкастера против N.L.R.B. , 822 F.3d 563, 565-66 (округ округа Колумбия, 2016 г.) «При рассмотрении предпринимательских возможностей [суд] . . . рассмотрите [s] возможности, создаваемые положением «взять на себя [] экономический риск и иметь [иметь] соответствующую возможность получить прибыль, работая умнее, а не просто усерднее». Id. Этот тест является спорным, и в настоящее время федеральное правительство рассматривает возможность использования теста ABC для целей NLRA, поэтому мы отложим обсуждение этого вопроса до тех пор, пока не получим больше ясности. Многие штаты используют так называемый тест ABC для определенных целей классификации работников. Некоторые используют его только для целей выплаты пособий по безработице, поэтому обязательно проверьте свою юрисдикцию. Тест ABC описывает презумпцию статуса сотрудника, если нанимающая организация не может доказать все три элемента. Если элементы доказаны, рабочий является независимым подрядчиком. Ниже приведен тест ABC штата Массачусетс: Лицо, оказывающее любую услугу… считается наемным работником, за исключением случаев, когда: (1) это лицо свободно от контроля и руководства в связи с оказанием услуги, как в соответствии с его контрактом на оказание услуги, так и фактически; и (2) услуга оказывается за рамками обычной деятельности работодателя; и (3) физическое лицо обычно занимается независимо установленной торговлей, занятием, профессией или бизнесом того же характера, что и выполняемая услуга. МГЛ С.149§148B Калифорния приняла тест ABC, но изменила его в соответствии со своими потребностями. Бизнес-курсы Пройдите этот комплексный курс подготовки к экзамену, чтобы подготовиться к экзамену TECEP Introduction to Entrepreneurship и получить зачет по курсу. Вы можете пройти курс за несколько недель, чтобы освоить все предпринимательские концепции, по которым вас будут тестировать. Попробуйте бесплатно в течение 30 дней Создайте учетную запись Попробуйте без риска в течение 30 дней Создайте учетную запись Экспертный участник:
Брианна Уайтинг Брианна имеет степень магистра образования в области лидерства в образовании, степень бакалавра делового администрирования и степень бакалавра наук в области зоотехники. раскрыть все
|
свернуть все Практический тест Проверьте свои знания по этому курсу с помощью практического теста из 50 вопросов. Пройти практический тест Просмотреть все практические тесты в этом курсе Неделя {{::cp. Перейти к главе Введение в предпринимательство Глава 1 Практический тест
Практический тест: Введение в предпринимательство Неделя {{::cp.getGoalWeekForTopic(1, 17)}} Перейти к главе Основы бизнеса для предпринимательства Глава 2 Практический тест
Практический тест: основы бизнеса для предпринимательства Неделя {{::cp. Перейти к главе Генерация бизнес-идей Глава 3 Практический тест
Практический тест: Генерация бизнес-идей Неделя {{::cp. Перейти к главе Оценка возможностей в бизнесе Глава 4 Практический тест
Практический тест: оценка возможностей в бизнесе Неделя {{::cp.getGoalWeekForTopic(4, 17)}} Перейти к главе Типы собственности бизнеса Глава 5 Практический тест
Практический тест: Типы владения бизнесом Неделя {{::cp.getGoalWeekForTopic(5, 17)}} Перейти к главе Введение в бизнес-модели Глава 6 Практический тест
Практический тест: Введение в бизнес-модели Неделя {{::cp. Перейти к главе Разработка бизнес-плана Глава 7 Практический тест
Практический тест: разработка бизнес-плана Неделя {{::cp. Перейти к главе Этические и правовые основы бизнеса Глава 8 Практический тест
Практический тест: Этические и правовые основы бизнеса Неделя {{::cp. Перейти к главе Работа с Business Advisors Неделя {{::cp.getGoalWeekForTopic(9, 17)}} Перейти к главе Обзор финансовой отчетности Глава 10 Практический тест
Практический тест: Обзор финансовой отчетности Неделя {{::cp.getGoalWeekForTopic(10, 17)}} Перейти к главе Экономическая среда и рынки Глава 11 Практический тест
Практический тест: экономическая среда и рынки Неделя {{::cp.getGoalWeekForTopic(11, 17)}} Перейти к главе Деньги и финансовые учреждения Глава 12 Практический тест
Практический тест: Деньги и финансовые учреждения Неделя {{::cp. Перейти к главе Финансирование малого бизнеса Глава 13 Практический тест
Практический тест: Финансирование малого бизнеса Неделя {{::cp.getGoalWeekForTopic(13, 17)}} Перейти к главе Теории и функции менеджмента Глава 14 Практический тест
Практический тест: теории и функции управления Неделя {{::cp. Перейти к главе Маркетинг, маркетинговые исследования и брендинг Глава 15 Практический тест
Практический тест: маркетинг, маркетинговые исследования и брендинг Неделя {{::cp.getGoalWeekForTopic(15, 17)}} Перейти к главе Закон об интеллектуальной собственности Глава 16 Практический тест
Практический тест: Закон об интеллектуальной собственности Неделя {{::cp.getGoalWeekForTopic(16, 17)}} Перейти к главе TECEP Введение в предпринимательство Flashcards TECEP Введение в предпринимательство: учебное пособие и практический тест для подготовки к экзамену Знаете ли вы… У нас есть более 220 курсов колледжа, которые подготовят вас к заработку
кредит на экзамене, который принимается более чем 1500 колледжей и университетов. Вы можете протестировать первые два года обучения в колледже и сэкономить
тысячи от вашей степени. Любой может получить кредит за экзамен, независимо от возраста или уровня образования. Чтобы узнать больше, посетите нашу страницу Earning Credit Page Проверьте свои знания по этому курсу с помощью практического теста из 50 вопросов. Пройдя тест, вы получите
подробный отчет об экзамене с вашей личной статистикой и даже конкретными уроками, на которых стоит сосредоточиться!
Пройдите пробный тест прямо сейчас TECEP Введение в предпринимательство: учебное пособие и практический тест для подготовки к экзамену Гл. Введение в тест на предпринимательскую практику Гл. 2 Основы бизнеса для практического теста предпринимательства Гл. 3 Генерация бизнес-идей Практический тест Гл. 4 Оценка возможностей в тесте деловой практики Гл. 5 Типы тестов на владение бизнесом Гл. 6 Введение в практический тест бизнес-моделей Гл. 7 Разработка практического теста бизнес-плана Гл. 8 Этические и правовые основы тестирования деловой практики Гл. 9 Работа с бизнес-консультантами Гл. 10 Обзор финансовой отчетности Практический тест Гл. 11 Практический тест экономической среды и рынков Гл. 12 Практический тест по деньгам и финансовым учреждениям Гл. 13 Практический тест по финансированию малого бизнеса Гл. 14 Теории управления и практический тест функций Гл. 15 Тест по маркетингу, исследованию рынка и брендингу Гл. Практический тест по праву интеллектуальной собственности Гл. 17 Карточки TECEP Introduction to Entrepreneurship Это была самая полезная услуга по обучению, которую я когда-либо получал. Я пробовал несколько сервисов, много учился самостоятельно и использовал флеш-карты. Я терпел неудачу много раз и не мог добиться большего. Это было то, что помогло мне больше всего, и в конце концов я, наконец, прошел. Мария об успешной подготовке к экзамену через TrustPilot 4.6 1128 Отзывы Это была самая полезная услуга по обучению, которую я когда-либо получал. Я пробовал несколько сервисов, много учился самостоятельно и использовал флеш-карты. Я терпел неудачу много раз и не мог добиться большего. Это было то, что помогло мне больше всего, и в конце концов я, наконец, прошел. Приложение простое, а тренировочные тесты помогли мне точно определить, что мне нужно изучать. Идеально подходит для того, для чего он мне нужен! Тесты и уроки были тщательными, и я прошел несколько практических тестов перед моим настоящим. Уроки были актуальными и понятными. Мне понравилось, что я мог смотреть видео и использовать аудиорежим для прослушивания во время вождения или других дел. Этот веб-сайт был отличным ресурсом для меня, когда я готовился к своим сертификационным тестам. Study.com помог мне сдать тесты, и я не знаю, смог бы я добиться этого без этого ресурса! Отличный контент. Это было напрямую связано с моим тестом. Study.com действительно хорошо поработал над тем, чтобы добраться до сути контента. Это фантастическая услуга! Я не только сдал все экзамены, к которым готовился, но и научился кое-чему во время учебы, а не просто запоминал скучные факты, которые потом будут потеряны в мозговой свалке. Содержание, контекст и несколько способов представления, которые они обеспечивают, очень эффективны и приятны! Если бы не Study. Просмотр Просмотр по теме Журнальная статья Себастьян Дёрр Себастьян Дорр Ищите другие работы этого автора на: Оксфордский академический Google ученый Примечания автора Review of Finance , Volume 25, Issue 5, September 2021, Pages 1609–1637, https://doi.org/10.1093/rof/rfab007 Published: February Получено: 02 июля 2020 г. Принято: 11 февраля 2021 г. Опубликовано: 15 февраля 2021 г. Исправлено и набрано: 04 октября 2021 г. Фильтр поиска панели навигации
Обзор финансовВ этом выпускеG20 — Общие сведенияG21 — Банки; Депозитарные учреждения; микрофинансовые организации; ИпотекаL26 — ПредпринимательствоФинансовые учреждения и услугиФинансовые рынкиКнигиЖурналыOxford Academic
Термин поиска мобильного микросайта Закрыть Фильтр поиска панели навигации
Обзор финансовВ этом выпускеG20 — Общие сведенияG21 — Банки; Депозитарные учреждения; микрофинансовые организации; ИпотекаL26 — ПредпринимательствоФинансовые учреждения и услугиФинансовые рынкиКнигиЖурналыOxford Academic
Термин поиска на микросайте Advanced Search В этой статье показано, что посткризисные стресс-тесты отрицательно сказываются на предпринимательстве и инновациях в молодых фирмах. Финансовый кризис 2007–2008 годов привел к серьезной рецессии и показал, что банки брали на себя чрезмерный риск в преддверии этого кризиса. Регуляторы ввели ежегодные стресс-тесты для мониторинга инвестиционных портфелей системно значимых банков в США. Стресс-тесты предполагают неблагоприятные экономические сценарии, например рост безработицы и падение цен на жилье. Для каждого сценария внутренняя модель прогнозирует гипотетические убытки банков с учетом их портфелей активов. Эти потери затем проецируются на минимальные коэффициенты достаточности капитала, которые потребуются банкам, чтобы выдержать спад. Если финансовые учреждения не проходят тест, они должны скорректировать свой капитал и не могут распределять капитал в течение следующих кварталов. В этой статье утверждается, что банки, прошедшие стресс-тестирование, сократили кредитование предпринимателей, тем самым сократив занятость и инновации в молодых фирмах. Используя уникальную особенность географически дезагрегированных данных по ипотечному кредитованию, я установил, что банки, подвергшиеся посткризисным стресс-тестам, резко сократили кредитование малого бизнеса под залог собственного капитала. Поскольку кредитование собственного капитала является важным источником финансирования для предпринимателей, в округах, в которых банки, прошедшие стресс-тестирование, имели более высокую докризисную долю рынка, во время восстановления наблюдалось относительное снижение занятости в молодых фирмах. Эмпирический анализ начинается с демонстрации того, что банки, подвергающиеся стресс-тестам, сокращают ссуды малым предприятиям, которые обеспечены собственным капиталом. Чтобы выявить в данных ссуды под залог жилья, связанные с бизнесом, я использую уникальную особенность данных на уровне ссуд по жилищному ипотечному кредитованию, представленную в данных Закона о раскрытии информации о жилищной ипотеке (HMDA). В данных HMDA банки должны сообщать коды этнической принадлежности и пола как неприменимые, если заявитель или созаявитель не является физическим лицом, то есть если заявителем является компания (Avery, Brevoort, and Canner, 2007). Чтобы оценить влияние стресс-тестов на предложение кредита, я сравниваю кредитование банков, прошедших стресс-тестирование, с банками, не прошедшими стресс-тестирование, в до- и посткризисный период. Банки, прошедшие стресс-тестирование, сократили кредитование собственного капитала, связанного с бизнесом, примерно на 30% больше, чем банки, не прошедшие стресс-тестирование, в период стресс-тестирования. Детализированные данные на уровне округа-банка позволяют мне изолировать предложение кредита, включив изменяющиеся во времени фиксированные эффекты на уровне округа-заемщика, которые контролируют ненаблюдаемые характеристики округа, например, спрос на кредит. На совокупном уровне банков я также показываю, что банки, прошедшие стресс-тестирование, сократили свои кредиты малому бизнесу, обеспеченные залогом недвижимости, на 36% больше, чем банки, не прошедшие стресс-тестирование. Они сократили необеспеченные кредиты для малого бизнеса на незначительные 13%. Сравнение внутри банка позволяет мне контролировать изменяющиеся во времени искажающие факторы на уровне банка с помощью фиксированных эффектов банка*время. Их включение существенно не влияет на результаты. Падение кредитования собственного капитала, связанного с бизнесом, вероятно, является непреднамеренным побочным эффектом стресс-тестов из-за предполагаемого падения цен на жилье, которое, хотя и направлено на снижение риска на рынке жилищной ипотеки, представляет собой дополнительные расходы на обеспеченные кредиты для малого бизнеса. На втором этапе я анализирую последствия сокращения предложения кредита для реальной экономики. Для каждого округа США до кризиса подверженность банкам, прошедшим стресс-тестирование, измеряет долю депозитов округа, хранящихся в филиалах прошедших стресс-тестирование банков. Риск отражает географические различия в значимости банков, прошедших стресс-тестирование, на местных рынках США. Сначала я установил, что совокупное кредитование собственного капитала, связанное с бизнесом, снижается в округах с более высоким риском. Банки, не прошедшие стресс-тестирование, не компенсируют сокращение обеспеченных кредитов для малого бизнеса банками, прошедшими стресс-тестирование. Затем я показываю, что в округах с более высоким уровнем риска наблюдается значительное снижение занятости среди молодых фирм в посткризисный период по сравнению с округами с низким уровнем риска. В округах с 75-м процентилем воздействия наблюдается на 6% более сильное снижение занятости в молодых фирмах по сравнению с округами с 25-м процентилем. Поскольку молодые фирмы непрозрачны и часто полагаются на личные активы для обеспечения кредитов (Steijvers and Voordeckers, 2009), сильное сокращение кредитования малого бизнеса, обеспеченного собственным капиталом, должно непропорционально сильно повлиять на молодые фирмы, которые больше полагаются на такое финансирование. Используя Опрос владельцев бизнеса 2007 года, я подсчитал долю молодых фирм в отрасли, которые используют собственный капитал или личные активы для открытия или расширения своего бизнеса. В отраслях, находящихся в верхнем терциле зависимости от собственного капитала, негативное воздействие воздействия на предпринимательство почти в три раза больше, чем в отраслях, находящихся в нижнем терциле. В отраслях с интенсивным использованием собственного капитала занятость снижается на 11% больше в округах с 75-м процентилем воздействия по сравнению с округами с 25-м процентилем; их доля в общей занятости снижается еще на 0,8 процентных пункта (п.п.). Снижение занятости в округах с высокой подверженностью риску превышает одну треть общего поперечного снижения: средняя доля занятости в молодых фирмах снизилась примерно на 2,2 п. Воздействие также оказывает сильное и существенное негативное влияние на инновации в молодых фирмах, измеряемое по заявкам на патенты. В посткризисный период в округах, находящихся в 75-м процентиле воздействия, наблюдается 17-процентное снижение числа патентных заявок молодых фирм, взвешенных по цитируемости, по сравнению с округами в 25-м процентиле. 2 На долю молодых фирм приходится около четверти всех патентных заявок, поэтому снижение их патентной активности на 17% означает сокращение общего количества патентов примерно на 4%. Молодые фирмы вносят непропорционально большой вклад в рост совокупной производительности (Haltiwanger, 2015), поэтому мои результаты поднимают вопрос о том, способствовало ли финансовое регулирование посткризисному замедлению производительности. Действительно, средняя заработная плата (показатель производительности труда) снижается значительно сильнее в уязвимых округах и особенно в отраслях с более высокой зависимостью от финансирования собственного капитала. Эмпирический анализ сталкивается с различными проблемами. Посткризисный период пронизан регуляторными инициативами и государственными программами, поэтому я провожу дополнительные тесты, чтобы изолировать роль стресс-тестов. Во-первых, я ограничиваю выборку банками с активами не менее 20 миллиардов долларов. Сужение контрольной группы существенно не влияет на результаты. Во-вторых, я показываю, что обеспеченное и необеспеченное банковское кредитование следует одной и той же тенденции до кризиса среди банков, прошедших стресс-тестирование; также нет дифференциального предтренда между банками, прошедшими и не прошедшими стресс-тестирование. В-третьих, в выборке банков, прошедших стресс-тестирование, я использую квазиэкзогенные дефицит капитала , рассчитанный Cortés et al. (2020) между прогнозируемым и нормативным минимальным коэффициентом капитала. Основная проблема идентификации при установлении реальных последствий заключается в контроле ненаблюдаемых потрясений, которые затрагивают молодые фирмы и коррелируют с подверженностью округа. Я решаю эту проблему, используя вариацию страны, отрасли и времени, а также включаю гранулярный фиксированный эффект. Контроль фиксированных эффектов округа*отрасли для ненаблюдаемой и неизменной во времени неоднородности округа и отрасли. Фиксированные эффекты округа*по времени позволяют шокам неоднородно воздействовать на каждый округ в каждый момент времени и контролировать ненаблюдаемые во времени фундаментальные показатели округа (например, цены на жилье или безработицу). Кроме того, фиксированные отраслевые*временные эффекты смягчают опасения, что отраслевые изменения могут повлиять на молодые фирмы. Кроме того, метод инструментальной переменной (IV) использует экзогенную вариацию докризисной доли банков на рынке по странам. На первом этапе я прогнозирую географическое распределение депозитов банков по округам с помощью гравитационной модели, основанной на расстоянии между головными офисами банков и округами филиалов, а также относительном размере их рынка (Goetz, Laeven, and Levine, 2013, 2016). . На втором этапе прогнозируемые депозиты корректируются с помощью индекса поэтапного дерегулирования банковской деятельности между штатами с учетом того, что штаты в той или иной степени ограничили доступ банков из других штатов (Rice and Strahan, 2010). Повторно вычисляя риск округа на основе прогнозируемых отложений, я показываю, что инструментальный риск значительно снижает занятость в молодых фирмах. Коэффициенты IV аналогичны по знаку и значимости регрессиям методом наименьших квадратов (OLS), но больше по величине, что может указывать на то, что инструмент разрешает выбор банков, прошедших стресс-тестирование, в округа с более сильными ненаблюдаемыми фундаментальными показателями (как предполагает регрессия с фиксированными эффектами) . Это также может отражать, что IV преодолевает погрешность затухания в спецификациях OLS, если есть ошибка измерения в экспозиции округа (Pancost and Schaller, 2020). Я провожу дополнительные тесты на надежность. Основной вклад этой статьи заключается в освещении реального воздействия стресс-тестов на предпринимательство и инновации. Ключевой особенностью анализа является построение нового набора данных о кредитовании банками собственного капитала, связанного с бизнесом, на детализированном уровне банка-округа на основе данных HMDA. Основываясь на этих данных, результаты показывают, что банки, прошедшие стресс-тестирование, сокращают кредиты малому бизнесу, обеспеченные собственным капиталом, значительно больше, чем банки, не прошедшие стресс-тест; кредитование собственного капитала на уровне округа, связанное с бизнесом, также снижается. Предпринимательство падает больше в округах с более высоким риском воздействия банков, прошедших стресс-тестирование, и особенно в отраслях, которые больше полагаются на финансирование собственного капитала. Эта статья относится к литературе, в которой исследуется влияние стресс-тестов на малый бизнес. Кортес и др. (2020) сосредоточены на влиянии стресс-тестов на предложение банковских кредитов. Используя данные Закона о реинвестициях сообщества (CRA) по кредитованию малого бизнеса, они показывают, что банки, более затронутые стресс-тестами, сокращают кредитование малого бизнеса, особенно в более рискованных областях. Они обнаружили, что более мелкие банки частично компенсируют снижение кредитования малого бизнеса банками, прошедшими стресс-тестирование. Вместо этого мои результаты показывают, что вызванное стресс-тестом влияние предложения на кредитование собственного капитала имеет значение в совокупности: в то время как необеспеченное кредитование малого бизнеса в основном восстановилось после кризиса, обеспеченное кредитование малого бизнеса не восстановилось. Мои результаты не означают, что стресс-тесты снижают благосостояние, поскольку стресс-тесты также снижают готовность банков идти на риск (Acharya, Berger, and Roman, 2018). Укрепление финансовой стабильности может потребовать сокращения кредитования молодых фирм, если банки будут неосмотрительно кредитовать рискованных предпринимателей в преддверии кризиса. Тем не менее, как я расскажу более подробно ниже, существует мало свидетельств того, что банки занимались чрезмерным кредитованием стартапов. После финансового кризиса 2007–2008 годов регулирующие органы США ввели стресс-тесты для крупнейших финансовых учреждений. Первый стресс-тест был проведен в 2009 году в рамках Программы оценки надзорного капитала, а в 2011 году они стали регулярными в рамках Комплексного анализа и обзора капитала (CCAR). Результат решения публично раскрывается в сводном отчете CCAR. Если банки не соответствуют критериям надзора, им не разрешается производить какое-либо распределение капитала в следующих кварталах. По сути, стресс-тесты представляют собой перспективные требования к капиталу с целью убедиться, что у банков достаточно капитала, и ограничить принятие ими рисков. В 2009 году стресс-тесты прошли девятнадцать учреждений с активами, превышающими 100 миллиардов долларов. Считается, что стресс-тесты эффективны для изменения кредитного поведения банков с целью снижения риска (Acharya, Berger, and Roman, 2018). Тем не менее, они могут сократить кредит, доступный малым фирмам, по двум основным причинам. Во-первых, малые предприятия процикличны и зависят от местного спроса, что делает их чувствительными к изменениям совокупных макроэкономических условий и, следовательно, более рискованными. Поскольку банки могут ослабить свои требования к капиталу за счет снижения риска в своем кредитном портфеле, кредитование малого бизнеса становится более дорогим для банков, прошедших стресс-тестирование (Bordo, Cole, and Duca, 2019).; Кортес и др. , 2020). Во-вторых, молодые и малые фирмы непрозрачны, поэтому банки требуют залога, чтобы преодолеть асимметричную информацию о качестве заемщиков (Berger et al. , 2011). Чтобы проанализировать влияние стресс-тестов на предложение кредита на обеспеченные кредиты для малого бизнеса, я использую функцию данных на уровне кредита по жилищному ипотечному кредитованию, представленную в данных HMDA. HMDA собирает данные о заявках на ипотеку, охватывая подавляющее большинство заявок и утвержденных кредитов в США. Ежегодные данные включают результат подачи заявки, сумму кредита и доход заемщика. Кроме того, они содержат подробную информацию о расе, поле и этнической принадлежности заявителя. Федеральная корпорация по страхованию депозитов (FDIC) предоставляет подробные данные банковского баланса, а также информацию о обеспеченных и необеспеченных кредитах для малого бизнеса в своей статистике депозитных учреждений (SDI). Окончательная выборка содержит 169 061 наблюдение банка-округа-год; 3195 банков обслуживают 2373 округа. Таблица I, панели (a) и (b), среднее значение отчета, стандартное отклонение (SD) и дополнительные статистические данные для ключевых переменных на уровне банка и округа с 2002 по 2016 год. Таблица I. Описательная статистика Эта таблица показывает описательную статистику для основных переменных. Определения переменных см. в тексте. Открыть в новой вкладке Таблица I. Описательная статистика Эта таблица показывает описательную статистику для основных переменных. Определения переменных см. в тексте. Открыть в новой вкладке Сводка депозитов FDIC предоставляет ежегодную информацию о банковских депозитах в каждом округе. Я рассчитываю подверженность банкам, прошедшим стресс-тестирование, по состоянию на 2007 г. как подверженность рискуc,07=∑b=1Bдепозитыc,bдепозитыsc×1(стресс-тестированныеb), (1) , где депозитыc,b обозначают банк b’ s депозиты в округе c в 2007 году, а 1(тестирование на стрессb) является индикатором со значением 1, если банк b принадлежит банковской холдинговой компании, прошедшей стресс-тестирование . Высокая подверженность риску означает, что большая часть депозитов графства хранится в офисах банков, прошедших стресс-тестирование, в то время как низкая подверженность риску означает, что большая доля депозитов находится в отделениях банков, не прошедших стресс-тестирование. Экспозиция варьируется от [0,1]. Квартальные показатели рабочей силы содержат данные за 4-й квартал на уровне уездов-отраслей по занятости на конец квартала по возрасту компаний. PatentsView предоставляет патентные заявки на уровне округов и отраслей. «Отрасль» относится к Международной патентной классификации (МПК) патента. Я отношу патенты к округу изобретателя и определяю молодые фирмы как правопреемники, которые впервые подали патенты не более 5 лет назад. Молодые фирмы часто используют собственный капитал или личные активы для финансирования расширения операций (Meisenzahl, 2014; Adelino, Schoar, and Severino, 2015; Schmalz, Sraer, and Thesmar, 2017; Bahaj, Foulis, и Пинтер, 2020). Опрос владельцев бизнеса, проведенный в 2007 году, предоставляет информацию на уровне компаний об источниках капитала для открытия и расширения бизнеса с разбивкой по отраслям с двузначным числом NAICS. домашнего капиталаi,07=∑f=1Fi1 (использует домашний капиталf) Fi. (2) В таблице I, панели (c) и (d), представлены сводные статистические данные по основным переменным округа по полной выборке из 2 644 округов с 2002 по 2016 год. уровень и панель (d) для уровня округа-отрасли-года. Среднее воздействие равно 0,36 со стандартным отклонением 0,24 и межквартильным диапазоном 0,39.. По выборке средняя доля занятых в молодых фирмах от общей численности занятых составляет 7%. В среднем по отрасли 17,6% молодых фирм используют собственный капитал при стандартном отклонении 4%. 9 В этом разделе представлена эмпирическая стратегия и представлены основные результаты. Во-первых, я установил, что банки, прошедшие стресс-тестирование, сокращают кредитование малого бизнеса под залог собственного капитала. Затем я показываю, что сокращение предложения кредита наносит ущерб предпринимателям: в округах с большей зависимостью от банков, прошедших стресс-тестирование, наблюдается относительное снижение занятости в молодых фирмах. Наконец, я исследую влияние воздействия на инновации и производительность. Чтобы исследовать, как прошедшие стресс-тесты банки корректируют свое кредитование по сравнению с другими банками во время восстановления, я оцениваю следующую панельную регрессию с 2002 по 2016 год: ln(amt)b,c, t=γhmda стресс-тестированныеb,t+контролиb,t−1+θb,c+τc,t+ϵb,t, (3) , где ln(amt)b,c,t обозначает логарифмический объем домашнего HMDA ссуды в виде капитала малым предприятиям банком b округу c в год t . Коэффициент γ hmda в уравнении (3) отражает изменения предложения банковских кредитов, а также спроса на кредиты. В округах, где банки, прошедшие стресс-тестирование, выдают больше кредитов, мелкие фирмы могут требовать меньше кредита по причинам, не связанным со стресс-тестированием. Дезагрегированные данные банка по округам позволяют включить фиксированные эффекты округ*время (τc,t), которые поглощают любые ненаблюдаемые изменения в характеристиках заемщиков по округам. При допущении, что малые предприятия зависят от местного спроса, включая фиксированные эффекты округа *, изолирующие изменения в предложении кредита. Таким образом, сравнение коэффициентов с фиксированными эффектами округов и без них дает представление о величине и направлении систематической ошибки, возникающей из-за несовершенного контроля характеристик округов. Одно из возможных предостережений заключается в том, что банки, не прошедшие стресс-тестирование, могут увеличить кредитование в ответ на сокращение своего кредита, прошедшего стресс-тестирование. Таблица II показывает, что банки, прошедшие стресс-тестирование, сокращают предложение обеспеченных кредитов для малого бизнеса. Столбец (1) показывает, что банки, прошедшие стресс-тестирование, сократили кредитование собственного капитала, связанного с бизнесом, на 35,9% больше в течение периода стресс-тестирования, чем банки, не прошедшие стресс-тестирование. Таблица II. Кредитование малого бизнеса банками, прошедшими стресс-тестирование, снижается В этой таблице показаны результаты уравнений (3) и (4) на уровне округов и банков. Зависимая переменная в столбцах (1) и (2) представляет собой журнал кредитования малого бизнеса HMDA на уровне банка и округа. Зависимые переменные в столбцах (3) и (4) представляют собой необеспеченное и обеспеченное кредитование малого бизнеса банками на уровне банка. Таблица II. Кредитование малого бизнеса банками, прошедшими стресс-тестирование, снижается В этой таблице показаны результаты уравнений (3) и (4) на уровне округов и банков. Зависимая переменная в столбцах (1) и (2) представляет собой журнал кредитования малого бизнеса HMDA на уровне банка и округа. Зависимые переменные в столбцах (3) и (4) представляют собой необеспеченное и обеспеченное кредитование малого бизнеса банками на уровне банка. Столбцы (5)–(7) относятся к типу банковского кредита и годам, и в качестве зависимой переменной используется логарифм суммы кредита (обеспеченный или необеспеченный). Стресс-тестирование — это фиктивная переменная со значением 1, если банк проходил стресс-тестирование в данном году, и 1 (2009 г.).−16) является фиктивной величиной, равной единице, для 2009–2016 годов. Обеспеченный является фиктивным значением, равным единице, если тип кредита равен обеспеченным кредитам для малого бизнеса, и нулю, если тип кредита равен необеспеченным кредитам для малого бизнеса. Данные HMDA охватывают подмножество общего объема кредитования малого бизнеса банками. Они также охватывают только часть кредиторов, которые сообщают о своих заявках HMDA. Чтобы увидеть, относится ли снижение обеспеченных бизнес-кредитов также к совокупному банковскому кредитованию, я использую данные FDIC SDI об общем обеспеченном и необеспеченном кредитовании малого бизнеса на уровне банка за год. На рис. 1 показано, что оба типа кредитов развивались сходным образом до 2009 года, но с тех пор разошлись. На графике (а) показано, что, несмотря на то, что после кризиса в банках, прошедших стресс-тестирование, наблюдалось снижение общего объема кредитования малого бизнеса (серая пунктирная линия), к 2016 г. объем необеспеченного кредитования малого бизнеса (красная пунктирная линия) восстановился, в то время как кредиты, обеспеченные недвижимость (синяя сплошная линия) упала более чем на 40% по сравнению с докризисным пиком. Рисунок 1. Открыть в новой вкладкеСкачать слайд Кредитование малого бизнеса под залог. ( a ) Показано общее, необеспеченное и обеспеченное кредитование малого бизнеса банками, прошедшими стресс-тестирование, нормализованное до 1 в 2009 году. ( b ) Доля обеспеченных кредитов в общем объеме кредитов малому бизнесу для прошедших стресс-тестирование (синяя сплошная линия) и не прошедших стресс-тестирование (черная пунктирная линия) банков. Для более подробного изучения этой закономерности я оцениваю следующие регрессии: yb,t=γ стресс-испытаниеb,t+контрольb,t−1+θb+τt1+ϵb,t (4) yb,l,t=δ1 стресс-тестированиеb,t+δ2 защищенноеl+δ3 стресс-тестированиеb, t×securedl+controlsb,t−1+θb,l+τt2+ϵb,l,t. (5) В уравнении (4)yb,t обозначает логарифмический объем обеспеченных или необеспеченных кредитов малому бизнесу банком b в год t . После включения базового банковского контроля, а также банковских ( θ b ) и временных (τt1) фиксированных эффектов коэффициент γ показывает, сокращают ли банки, прошедшие стресс-тестирование, кредитование в большей степени, чем банки, не прошедшие стресс-тестирование, по сравнению с соответствующие им докризисные тенденции. Чтобы упростить идентификацию, уравнение (5) сравнивает обеспеченное и необеспеченное кредитование одним и тем же банком. С этой целью я выполняю регрессии на уровне типа банковского кредита (l)-год, где yb,l,t обозначает логарифмический объем кредита типа необеспеченного или обеспеченного банком b в год t . Пустышка под залог принимает значение единицы для обеспеченных кредитов для малого бизнеса. Столбцы (3)–(7) в Таблице II показывают, что сокращение обеспеченного кредитования малого бизнеса банками, прошедшими стресс-тестирование, также сохраняется на совокупном уровне банка. Для уравнения (4) в столбце (3) банки, прошедшие стресс-тестирование, сокращают необеспеченное кредитование малого бизнеса на 12,5% больше, чем банки, не прошедшие стресс-тестирование, с момента введения стресс-тестов в 2009 году. В столбцах (5)–(7) представлены результаты регрессии для уравнения (5). В столбце (5) банки, прошедшие стресс-тестирование, сократили обеспеченное кредитование малого бизнеса еще на 37,7% по сравнению с необеспеченным кредитованием. Включение фиксированных эффектов банка*время и тип кредита*время в столбцах (6) и (7) не влияет на коэффициент каким-либо статистически или экономически значимым образом. В совокупности результаты, представленные в Таблице II, показывают, что банки, прошедшие стресс-тестирование, сокращают кредитование малого бизнеса, особенно если оно обеспечено залогом. После Великой рецессии создание рабочих мест молодыми фирмами разочаровало (Siemer, 2016). Рисунок 2. Открыть в новой вкладкеСкачать слайд Работа в молодой фирме. ( a ) Общее создание рабочих мест молодыми фирмами (возраст 0–1 год) и всеми другими фирмами (возраст ≥2 лет) во время Великой рецессии (заштрихованная область) и после ее восстановления. Чтобы более подробно изучить динамику занятости, я оцениваю ) где yc,t – соответствующая переменная результата в округе c в году t . риск означает риск округа в банках, прошедших стресс-тестирование, как определено в уравнении (1). Post — это фиктивный параметр со значением 1 для стресс-тестирования 2009 года.–16. Базовый контроль округа включает логарифмическое население, уровень безработицы, рост цен на жилье, долю чернокожего населения и долю населения старше 65 лет, а также логарифмический доход на душу населения, все с запозданием на один период. Согласно результатам на уровне банков, сильное сокращение обеспеченных кредитов должно особенно сильно ударить по молодым фирмам, которые используют собственный капитал. Таким образом, я оцениваю следующую спецификацию на уровне округа-отрасли-года: yc,i,t=γ1 экспозицияc+γ2 postt+γ3 экспозицияc×postt+γ4 домашний капиталi+γ5 экспозицияc×домовой капиталi+γ6 домашний капиталi×postt+γ7 экспозицияc×домовой капиталi×postt+θc,i+τc,t +τi,t+ϵc,i,t, (7) где yc,i,t — либо логарифм занятости фирм в возрасте от нуля до одного года, либо логарифм средней заработной платы в округе c и отрасли i в году т . Идентификация — фиксированные эффекты Эмпирический аргумент основывается на предположении, что в округах с более высоким риском наблюдается относительный спад молодых фирм и инноваций, потому что банки, прошедшие стресс-тестирование , предоставляют меньше кредитов. Таким образом, основная задача идентификации заключается в контроле характеристик, влияющих на молодые фирмы, помимо изменения предложения кредита банками, прошедшими стресс-тестирование. Идентификация — гравитационная модель и дерегулирование Воздействие основано на распределении депозитов по округам, но доли депозитов банков потенциально эндогенны для ненаблюдаемых характеристик округа. депозитная доляb,B,c,t=γ1 ln(distanceb,c)+γ2 ln(populationc,tpopulationB,t)+ϵb,B,c,t, (8) , где b обозначает банк , B округ штаб-квартиры банка и c округ назначения (филиала). Гравитационная модель предсказывает, что γ1>0,γ2>0. Следуя Goetz, Laeven, and Levine (2016), я использую дробную логит-модель для оценки уравнения (8) для 2007 года. Таблица III, столбец (1), показывает сильное и значительное негативное влияние расстояния на долю депозитов банков в данном округе. Размер рынка входит положительно, предполагая, что банки держат более высокую долю депозитов на более крупных рынках. В столбцах (2)–(5) используются регрессии МНК и добавляются фиксированные эффекты, чтобы проверить, чувствительны ли эффекты к ненаблюдаемым характеристикам домашнего (округ штаб-квартиры банка) или принимающего (округ филиала банка) рынка. Столбец (2) показывает, что результаты аналогичны для МНК и логит-регрессии. Столбец (3) добавляет фиксированные эффекты принимающего округа, а столбец (4) — фиксированные эффекты родного округа. Столбец (5) также включает фиксированные эффекты штата происхождения * принимающего округа и сравнивает доли депозитов банков, расположенных в одном штате, кредитующих один и тот же округ. Таблица III. Уравнение силы тяжести В этой таблице показаны результаты уравнения (8) на уровне банка и округа за 2007 год. Зависимой переменной является доля депозитов банка b в округе c (от общего объема банковских депозитов). log (1+ расстояние ) обозначает логарифм единицы плюс расстояние между округом штаб-квартиры банка и округом филиала банка. log (соотношение населения ) — это логарифмическое отношение домашнего (штаб-квартира банка) к населению принимающего (отделение банка) округа. В столбце (1) используется дробная логит-модель. Столбцы (2)–(4) добавляют фиксированные эффекты для учета ненаблюдаемых характеристик округов в головных офисах банков и округах филиалов. Открыть в новой вкладке Таблица III. Уравнение гравитации В этой таблице показаны результаты уравнения (8) на уровне банка и округа за 2007 г. Зависимой переменной является доля депозитов банка b в округе c (от общего объема банковских депозитов). log (1+ расстояние ) обозначает логарифм единицы плюс расстояние между округом штаб-квартиры банка и округом филиала банка. log (соотношение населения ) — это логарифмическое отношение домашнего (штаб-квартира банка) к населению принимающего (отделение банка) округа. Открыть в новой вкладке Гравитационная модель не учитывает, что штаты налагают ограничения на вход иностранных банков. Райс и Страхан (2010) показывают, что даже после отмены государственного регулирования де-юре после принятия Закона об эффективности банковских операций и отделений между штатами в 1994, большинство штатов использовали инструменты политики для защиты отечественных банков от внешней конкуренции. Со временем государства ослабили эти ограничения. Регулирование местных банковских рынков принимало одну или несколько из следующих форм: (1) минимальный возраст целевого банка; (2) de novo филиал без явного согласия государственных органов; (3) приобретение отдельных филиалов без приобретения всего банка; и (4) ограничение общей суммы депозитов в масштабах штата, контролируемых одним банком или БХК. Хотя ненаблюдаемые факторы могут быть связаны с расстоянием между штаб-квартирой и отделением в гравитационной модели, заданной уравнением (8), вариации запретов на отделение в разных состояниях и во времени обеспечивают квазиэкзогенное изменение способности банков войти в другие состояния. Таким образом, идентифицирующее допущение состоит в том, что воздействие на округcIV, основанное на местных отложениях, предсказанных с помощью гравитационной модели и скорректированных с учетом поэтапного снятия ограничений на разветвления до кризиса, определяет изменение наблюдаемого воздействия, которое, вероятно, является экзогенным по отношению к другим (ненаблюдаемым) характеристикам округа, например, разница в ценах на жилье или безработица. Результаты В Таблице IV показано, что более высокая подверженность округам связана с относительным снижением совокупного кредитования и занятости среди молодых фирм. В столбцах (1) и (2) представлены регрессии на уровне округов-годов для уравнения (6). Зависимой переменной является логарифм кредитования малого бизнеса под залог собственного дома. Столбец (1) показывает негативное и весьма существенное влияние подверженности риску на совокупное кредитование в течение периода стресс-тестирования. Перемещение округа с 25-го на 75-й процентиль с точки зрения воздействия приводит к относительному снижению совокупного кредита на (0,39×0,267=) 10,4%. Столбец (2) отражает подверженность риску и показывает, что более высокая прогнозируемая подверженность значительно снижает совокупное кредитование малого бизнеса. Этот результат означает, что банки, не прошедшие стресс-тестирование, не в состоянии полностью компенсировать снижение кредитования банками, прошедшими стресс-тестирование. Таблица IV. Сокращение числа занятых в молодых фирмах в незащищенных округах В этой таблице показаны результаты для уравнений (6) и (7) на уровне округа и на уровне округа-отрасли. Зависимой переменной является логарифм кредитования собственного капитала в столбцах (1) и (2) и логарифм занятости молодых фирм (возраст 0–1) в столбцах (3)–(7). риск означает докризисный риск округа перед банками, прошедшими стресс-тестирование, как определено в уравнении (1). 1 (2009 г.−16) — фиктивная переменная со значением единицы для 2009–2016 годов, то есть лет после введения стресс-тестов. Собственный капитал — это доля молодых фирм в каждой двузначной отрасли, которая использует финансирование собственного капитала для начала или расширения операций. Столбцы (5) и (7) используют изменяющиеся во времени фиксированные эффекты на уровне округа и отрасли. В столбцах (2), (6) и (7) показано воздействие округа с прогнозируемым воздействием на основе гравитационной модели. Таблица IV. Сокращение числа занятых в молодых фирмах в незащищенных округах В этой таблице показаны результаты для уравнений (6) и (7) на уровне округа и на уровне округа-отрасли. Зависимой переменной является логарифм кредитования собственного капитала в столбцах (1) и (2) и логарифм занятости молодых фирм (возраст 0–1) в столбцах (3)–(7). риск означает докризисный риск округа перед банками, прошедшими стресс-тестирование, как определено в уравнении (1). 1(2009–2016) — фиктивная переменная со значением 1 для 2009–2016 годов, то есть лет после введения стресс-тестов. Собственный капитал — это доля молодых фирм в каждой двузначной отрасли, которая использует финансирование собственного капитала для начала или расширения операций. Столбцы (5) и (7) используют изменяющиеся во времени фиксированные эффекты на уровне округа и отрасли. В столбцах (2), (6) и (7) показано воздействие округа с прогнозируемым воздействием на основе гравитационной модели. Ценности Андерсона-Рубина F — статистика в столбцах (2), (6) и (7) равна 67,38, 53,00 и 44,27 соответственно. Открыть в новой вкладке В столбцах (3)–(7) анализируется влияние воздействия стресс-тестов на (логарифмическую) занятость молодых фирм (см. уравнение (7)). Столбец (3) показывает, что перемещение округа с 25-го на 75-й процентиль с точки зрения воздействия приводит к относительному сокращению занятости молодых фирм на 1,8%. В столбцы (4) и (5) добавлены взаимодействующие условия воздействия с долей фирм, использующих собственный капитал в каждой отрасли. Столбцы (6) и (7) фактические данные прибора с прогнозируемым воздействием. 13 Оценки IV подтверждают, что более высокая экспозиция снижает занятость среди молодых фирм, особенно в отраслях с интенсивным использованием собственного капитала. Оценки IV больше, чем оценки OLS: в столбце (6) перемещение округа с 25-го на 75-й процентиль с точки зрения воздействия приводит к относительному сокращению занятости молодых фирм на 6%. Предприниматели имеют первостепенное значение для инноваций и совокупной производительности (Haltiwanger, 2015). Таблица V, столбцы (1)–(5), показывают, что в округах с более высоким риском воздействия банков, прошедших стресс-тестирование, наблюдается снижение количества патентных заявок от молодых фирм. В каждом столбце используется журнал патентов молодых фирм в качестве зависимой переменной на уровне округа-МПК-год. 14 Колонка (1) включает фиксированные эффекты за год и показывает, что патентные заявки молодых фирм значительно снижаются в округах с более высоким риском. Добавление контроля округа в столбец (2) и изменяющихся во времени фиксированных эффектов на уровне штатов и ИПК-отрасли в столбце (3) не оказывает существенного влияния на размер или значимость коэффициента. Во всех спецификациях наблюдается значительное негативное влияние воздействия на патентные заявки молодых фирм. Таблица V. Снижение количества патентов в экспонированных округах В этой таблице показаны результаты на уровне округов-IPC. Зависимой переменной является журнал патентных заявок молодых фирм в столбцах (1)–(5) и старых фирм в столбцах (6) и (7). риск означает докризисный риск округа перед банками, прошедшими стресс-тестирование, как определено в уравнении (1). 1(2009–2016) — фиктивная переменная со значением 1 для 2009–2016 годов, то есть лет после введения стресс-тестов. цит. взвешенный означает патенты, взвешенные по цитированию. Столбцы (1) и (2) представляют базовые регрессии, а столбцы (3)–(5) используют изменяющиеся во времени фиксированные эффекты на уровне штата и отрасли. В столбцах (5) и (7) показано воздействие округа с прогнозируемым воздействием, основанным на гравитационной модели. Столбцы (6) и (7) повторяют столбцы (4) и (5), но используют журнал взвешенных по цитированию патентов старых фирм в качестве зависимой переменной. Ценности Андерсона-Рубина F — статистика в столбцах (5) и (7) равна 22,93 и 0,40 соответственно. Открыть в новой вкладке Таблица V. Снижение количества патентов в экспонированных округах В этой таблице показаны результаты на уровне округов-IPC. Зависимой переменной является журнал патентных заявок молодых фирм в столбцах (1)–(5) и старых фирм в столбцах (6) и (7). риск означает докризисный риск округа перед банками, прошедшими стресс-тестирование, как определено в уравнении (1). 1 (2009 г.−16) — фиктивная переменная со значением единицы для 2009–2016 годов, то есть лет после введения стресс-тестов. цит. взвешенный означает патенты, взвешенные по цитированию. Столбцы (1) и (2) представляют базовые регрессии, а столбцы (3)–(5) используют изменяющиеся во времени фиксированные эффекты на уровне штата и отрасли. В столбцах (5) и (7) показано воздействие округа с прогнозируемым воздействием, основанным на гравитационной модели. Столбцы (6) и (7) повторяют столбцы (4) и (5), но используют журнал взвешенных по цитированию патентов старых фирм в качестве зависимой переменной. Ценности Андерсона-Рубина F — статистика в столбцах (5) и (7) равна 22,93 и 0,40 соответственно. Открыть в новой вкладке Не все патенты полезны: если их не используют другие компании, сокращение числа патентов молодыми фирмами не будет иметь большого значения. Таблица V, следовательно, предполагает, что в округах с более высоким риском воздействия банков, прошедших стресс-тестирование, наблюдается снижение инноваций молодых фирм, но не наблюдается значительного увеличения числа патентов старых фирм. Сокращение занятости и инноваций в молодых компаниях может привести к снижению производительности. В Таблице VI исследуется связь между стресс-тестами и производительностью труда на уровне округа-отрасли-года (см. уравнение (7)). 15 Зависимой переменной является логарифм средней заработной платы, показатель производительности труда. Столбец (1) показывает, что более высокий риск связан с относительным снижением средней заработной платы в период стресс-тестирования. Столбцы (2) и (3) показывают, что спад сконцентрирован в отраслях, которые в большей степени полагаются на финансирование собственного капитала. Таблица VI. В незащищенных округах наблюдается снижение средней заработной платы В этой таблице показаны результаты уравнения (7) на уровне округа-отрасли. Зависимой переменной является логарифм средней заработной платы. риск означает докризисный риск округа перед банками, прошедшими стресс-тестирование, как определено в уравнении (1). 1(2009–2016) — это фиктивная переменная со значением 1 за период с 2009 по 2016 год, то есть годы после введения стресс-тестов. Собственный капитал — это доля молодых фирм в каждой двузначной отрасли, которая использует финансирование собственного капитала для начала или расширения операций. Столбцы (1) и 2) представляют базовые регрессии с фиксированными эффектами округ*отрасль и год. Столбец (3) добавляет изменяющиеся во времени фиксированные эффекты округа и отрасли. Открыть в новой вкладке Таблица VI. В незащищенных округах наблюдается снижение средней заработной платы В этой таблице показаны результаты уравнения (7) на уровне округа-отрасли. Зависимой переменной является логарифм средней заработной платы. риск означает докризисный риск округа перед банками, прошедшими стресс-тестирование, как определено в уравнении (1). 1(2009–2016) — это фиктивная переменная со значением 1 за период с 2009 по 2016 год, то есть годы после введения стресс-тестов. Собственный капитал — это доля молодых фирм в каждой двузначной отрасли, которая использует финансирование собственного капитала для начала или расширения операций. Столбцы (1) и 2) представляют базовые регрессии с фиксированными эффектами округ*отрасль и год. Столбец (3) добавляет изменяющиеся во времени фиксированные эффекты округа и отрасли. В столбцах (4) и (5) представлены данные о воздействии на округа с прогнозируемым воздействием, основанным на гравитационной модели. Ценности Андерсона-Рубина F — статистика в столбцах (4) и (5) равна 14,02 и 15,65 соответственно. Открыть в новой вкладке Оценки в Таблице VI показывают, что более высокая подверженность вредит производительности труда в отраслях с более высокой долей молодых фирм, использующих финансирование собственного капитала, именно там, где занятость молодых фирм сокращается сильнее. В Таблице VII представлены дополнительные данные о влиянии стресс-тестов на кредитование малого бизнеса банками. Все регрессии контролируют ненаблюдаемые характеристики округа с помощью фиксированных эффектов округ*время. Столбцы (1) и (2) разлагают логарифм общего объема кредита на логарифм количества (nr) кредитов и среднего размера кредита (avg). В то время как коэффициент при испытании на фиктивное напряжение отрицательный в обоих столбцах, он значим только в столбце (1). Таблица VII. Надежность банка В этой таблице показаны проверки надежности для регрессий на уровне банка и округа. Зависимые переменные в столбцах (1) и (2) представляют собой логарифм количества кредитов малому бизнесу HMDA и среднего размера кредита; в столбцах (3)–(6) зависимая переменная — логарифм кредитования малого бизнеса HMDA; а в столбцах (7)–(11) это логарифмическое изменение кредитования малого бизнеса HMDA. стресс-тестирование — это фиктивная переменная со значением 1 за каждый год, когда банк подвергался стресс-тестированию. Воздействие стресс-теста означает отклонение прогноза банков от требуемого минимального коэффициента капитала. Колонка (3) ограничивает выборку банками с общим размером активов (по состоянию на 2008 г.) не менее 20 миллиардов долларов. Столбец (4) исключает повторные транзакции. Колонны (9)–(11) ограничить выборку стресс-тестами 2012–2016 годов. Открыть в новой вкладке Таблица VII. Надежность банка В этой таблице показаны проверки надежности для регрессий на уровне банка и округа. Зависимые переменные в столбцах (1) и (2) представляют собой логарифм количества кредитов малому бизнесу HMDA и среднего размера кредита; в столбцах (3)–(6) зависимая переменная — логарифм кредитования малого бизнеса HMDA; а в столбцах (7)–(11) это логарифмическое изменение кредитования малого бизнеса HMDA. стресс-тестирование — это фиктивная переменная со значением 1 за каждый год, когда банк подвергался стресс-тестированию. Воздействие стресс-теста означает отклонение прогноза банков от требуемого минимального коэффициента капитала. Колонка (3) ограничивает выборку банками с общим размером активов (по состоянию на 2008 г.) не менее 20 миллиардов долларов. Столбец (4) исключает повторные транзакции. Колонны (9)–(11) ограничить выборку стресс-тестами 2012–2016 годов. Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне банковской холдинговой компании. Открыть в новой вкладке Банки, прошедшие стресс-тестирование, включают в себя крупнейшие банки с совокупными активами не менее 50 миллиардов долларов. Кредитование собственного капитала, связанного с бизнесом, основанное на данных HMDA, может включать транзакции застройщиков, то есть кредиты, которые следуют иному процессу андеррайтинга, чем средний кредит для молодых или малых предприятий. Таким образом, я повторно строю выборку кредитов под залог жилья, связанных с бизнесом, но исключаю все кредиты, которые были приобретены в течение предыдущего года, что исключает, например, деятельность по «перепродаже». Столбец (4) показывает, что исключение повторных транзакций существенно не влияет на знак, размер или значимость коэффициента на стресс-тест . Чтобы пролить свет на роль местного риска, я следую Cortés et al. (2020) и определить риск округа как средневзвешенную по занятости бета-версию отрасли, то есть долгосрочную чувствительность занятости отрасли к изменениям совокупной занятости. Столбцы (7)–(11) используют логарифмическое изменение суммы кредита в качестве зависимой переменной. Столбец (7) показывает, что банки, прошедшие стресс-тестирование, отмечают более медленный рост кредитов в течение периода стресс-тестирования в более рискованных странах. Включение фиксированных эффектов банка*время в колонку (8) не оказывает существенного влияния на результаты. Обратите внимание, что хотя R 2 увеличивается более чем на 30 п.п. при включении фиксированных эффектов банка * время коэффициент взаимодействия остается значительным и имеет одинаковую величину для всех спецификаций. Это говорит о том, что эффект стресс-тестирования в рискованных округах ортогонален широкому набору ненаблюдаемых и наблюдаемых характеристик банков (Oster, 2019). Столбцы (9)–(11) ограничивают выборку банками, прошедшими стресс-тестирование за период 2012–2016 годов. В этой группе воздействие стресс-теста обозначает квазиэкзогенный разрыв капитала банков, то есть расстояние прогнозируемого от требуемого минимального коэффициента капитала (дополнительные подробности приведены в Cortes et al. [2020]). Столбец (9) показывает, что среди прошедших стресс-тестирование банков те, которые показали относительно худшие результаты в стресс-тестах, отмечают сильное и значительное снижение роста кредитования малого бизнеса под залог жилья. В столбцах (10) и (11) воздействие стресс-теста взаимодействует с риском округа. Как и в случае с полной выборкой, темпы роста кредита снижаются в большей степени в рискованных округах. Добавление фиксированных эффектов банка*время уменьшает размер коэффициента, но остается значимым на уровне 5%. Рост цен на недвижимость увеличивает стоимость залога и ослабляет финансовые ограничения через залоговый канал (Adelino, Schoar, and Severino, 2015; Bahaj, Foulis, and Pinter, 2020). В таблице VIII более подробно исследуется боковой канал. Столбцы (1) и (2) включают изменение цен на дома в графствах во время бума (с 2000 по 2007 год) и периода спада (с 2007 по 2010 год), поскольку дополнительные регрессоры взаимодействовали с собственным капиталом и постдамми. Обе переменные входят значительно и с ожидаемым знаком (более выраженный бум и спад снижают занятость молодых фирм в посткризисный период), но коэффициент при экспозиция × собственный капитал ×1 (2009 – 16) остается таким же по знаку, размеру и значению, что и базовая спецификация. Таблица VIII. Надежность округа В этой таблице показаны результаты для уравнения (7) на уровне округа-отрасли. Зависимой переменной является логарифм занятости молодых фирм. риск означает докризисный риск округа перед банками, прошедшими стресс-тестирование, как определено в уравнении (1). Собственный капитал — это доля молодых фирм в каждой двузначной отрасли, которая использует финансирование собственного капитала для начала или расширения операций. 1(2009–2016) — это фиктивная переменная со значением 1 за период с 2009 по 2016 год, то есть годы после введения стресс-тестов. ΔHPI 00−07 и ΔHPI 07−10 — изменения цен на окружные дома с 2000 по 2007 и с 2007 по 2010 годы; собственность 10 округа доля домовладельцев в 2010 году; Δ HPI – это годовой рост цен на окружное жилье. Темпы роста представляют собой логарифмические различия. top-4-exposition означает подверженность округов четырем крупнейшим банкам США с точки зрения совокупных активов по состоянию на 2007 год. Открыть в новой вкладке Таблица VIII. Надежность округа В этой таблице показаны результаты для уравнения (7) на уровне округа-отрасли. Зависимой переменной является логарифм занятости молодых фирм. Открыть в новой вкладке Chen, Hanson, and Stein (2017) обнаружили, что четыре крупнейших банка США сократили кредитование малого бизнеса после кризиса. Контроль влияния округов на четыре ведущих банка в столбце (6) или ограничение выборки округами, не представленными в четырех крупнейших банках в столбце (7), не оказывает существенного влияния на процентный коэффициент. Это говорит о том, что последствия воздействия (и, следовательно, стресс-тестов) не связаны исключительно с сокращением кредитования четырьмя крупнейшими банками. В дополнительном приложении сообщается о дополнительных тестах на надежность. Он показывает, что результаты устойчивы к учету отраслевого риска или ненаблюдаемых тенденций, характерных для фирм разных возрастных групп. Кроме того, результаты аналогичны, когда риск строится на основе данных о кредитах CRA, а не на данных о депозитах; и при перерасчете доли собственного капитала на государственно-отраслевом уровне. В этой статье представлены новые доказательства того, что банки, прошедшие стресс-тестирование, сокращают кредитование малого бизнеса, обеспеченное собственным капиталом, и что сокращение кредитного предложения имеет реальные последствия. Используя географические различия в подверженности округов банкам, прошедшим стресс-тестирование, я обнаружил, что в округах с более высокой подверженностью риску наблюдается относительное снижение занятости в молодых фирмах во время восстановления. Более высокий риск сильнее бьет по предпринимателям в отраслях, которые в большей степени полагаются на финансирование собственного капитала, то есть в секторах, в большей степени зависящих от кредитования под залог. Регулирование капитала в целом и стресс-тесты, в частности, направлены на снижение рисков, принимаемых банками, и повышение устойчивости финансового сектора. Если стресс-тесты снижают чрезмерно рискованное кредитование молодых фирм, снижение уровня предпринимательства является долгожданным побочным эффектом: молодые фирмы, которые финансировались до проведения стресс-тестов, не должны были финансироваться при разумном управлении рисками. Стресс-тесты исправили бы сбой рынка и однозначно повысили бы благосостояние. Однако более высокие требования к капиталу, особенно для проциклических кредитов, таких как кредиты для малого бизнеса, обеспеченные залогом недвижимости, также могли снизить кредитные возможности банков. Перемещение банковского кредита от молодых фирм имело негативные побочные эффекты, а предприниматели стали побочным ущербом. Хотя оценить общие последствия для благосостояния сложно, некоторые данные подтверждают мнение о том, что предприниматели столкнулись с непропорциональным сокращением предложения кредита, даже несмотря на то, что стресс-тесты сделали финансовую систему более безопасной. Во-первых, формирование фирм неуклонно снижалось еще до начала стресс-тестов. Это трудно согласовать с мнением о том, что банки занимались безрассудным кредитованием стартапов, которые нуждались в исправлении. Во-вторых, рост банковского кредитования малого бизнеса до кризиса был ничтожным по сравнению с ростом в других сегментах, таких как ипотечное кредитование, что еще раз свидетельствует о том, что избыточное кредитование молодых фирм было незначительным. И в-третьих, мои результаты показывают, что постоянный спад в кредитовании стартапов привел к сокращению инноваций и потенциально способствовал замедлению производительности после кризиса. Даже если стресс-тесты сократили банковский кредит некоторым чрезмерно рискованным фирмам, средняя пострадавшая молодая фирма действительно была инновационной. Снижение волатильности и частоты кризисов может потребовать сокращения рискованного кредитования, в том числе для молодых фирм. Тем не менее, возможное непреднамеренное воздействие стресс-тестов на предпринимательство следует учитывать при оценке общих последствий более высоких требований к капиталу, особенно в свете текущих дебатов о снижении динамизма и замедлении производительности. Дополнительные данные доступны по адресу Review of Finance онлайн. 1 Дополнительное приложение проверяет наличие потенциальных побочных эффектов от банков, прошедших стресс-тестирование, к банкам, не прошедшим стресс-тестирование, в спецификациях с фиксированными эффектами округ*время (Berg and Streitz, 2019). 2 Расчетный эффект выше, когда патенты взвешиваются по цитируемости, что предполагает, что инновационные фирмы, производящие широко цитируемые патенты, получают меньше финансирования. 3 Расхождение в результатах совокупного кредитования по сравнению с моей статьей может возникнуть еще и потому, что базовые данные различаются: по совокупным кредитам под залог собственного капитала, связанным с бизнесом, на основе данных HMDA в среднем около 11% от общего объема CRA малого бизнеса банков. кредитование, которое включает общее обеспеченное и необеспеченное кредитование малого бизнеса. Банки, прошедшие стресс-тестирование, сокращают обеспеченное кредитование малого бизнеса более чем в три раза по сравнению с необеспеченным кредитованием, поэтому обеспеченное кредитование также снижается в совокупности. Кроме того, мои результаты могут свидетельствовать о том, что более мелкие фирмы, которые зависят от кредитов под залог собственного жилья, не могут найти другие источники финансирования, в то время как средние предприятия имеют больше возможностей получить финансирование от банков, не прошедших стресс-тестирование. 4 Ачарья, Бергер и Роман (2018 г. 5 Результаты показывают отсутствие роста патентования старыми фирмами в незащищенных округах, что может свидетельствовать о том, что они не увеличили свою патентную активность в той же степени, в какой снизилась активность молодых фирм. 6 Как было предложено Avery, Brevoort, and Canner (2007), в 2004 году эта классификация относилась только к кредитам, для которых гендерный код был указан как неприменимый. 7 При классификации не учитываются бизнес-кредиты, которые не заявлены как таковые (т. е. заявитель не берет кредит от имени своего бизнеса). 8 Онлайн-приложение содержит дополнительную информацию о построении данных и сводной статистике. Кредиты под залог жилья, связанные с бизнесом, сильно коррелируют с кредитами для малого бизнеса, охватываемыми данными CRA или SBA, и меняются вместе с изменениями местных цен на жилье. 9 Онлайн-приложение содержит дополнительную сводную статистику. 10 Если s равно штату головного офиса банка, то дерегулирование s = 1, поскольку банки не сталкиваются с ограничениями на расширение в своем собственном штате. Кумулятивный прирост отражает то, что у «иностранных» банков было больше времени, чтобы войти в государства, которые ранее отменили регулирование. 11 Онлайн-приложение показывает, что значительная корреляция достигается в регрессиях с фиксированными эффектами штата и контролем на уровне округа. 12 F-статистика первой стадии равна 67,38. Этот вывод отличается от Cortés et al. (2020), которые не обнаружили значительного влияния стресс-тестов на совокупное кредитование малого бизнеса на основе данных CRA, отражающих обеспеченное и необеспеченное кредитование. Поскольку банки, прошедшие стресс-тестирование, сокращают обеспеченное кредитование малого бизнеса более чем в три раза по сравнению с необеспеченным кредитованием малого бизнеса, это может объяснить, почему совокупное кредитование собственного капитала небольшим фирмам значительно сокращается, даже если общее кредитование малого бизнеса не происходит. 13 F-статистика первой стадии составляет 53,00 и 44,27 соответственно. 14 Отрасли различаются по интенсивности патентования. 15 Литературу о влиянии предложения кредитов на производительность см. в Manaresi and Pierri (2017), Doerr, Raissi, and Weber (2018) и Duval, Hong, and Timmer (2020). 16 Онлайн-приложение показывает, что нет систематической связи между подверженностью округа стресс-тестированным банкам и местным восстановлением стоимости жилья. 17 По сравнению с Chen, Hanson, and Stein (2017), моя схема отличается по двум важным аспектам: во-первых, они используют долю предприятий малого бизнеса, которые расширились в данном году, в качестве переменной результата, в то время как в моей статье используется занятость среди стартапов. Во-вторых, их уровень агрегирования — это уровень округа, в то время как я использую данные на уровне округа-отрасли и сосредотачиваюсь на влиянии воздействия на отрасли с интенсивным использованием собственного капитала. Acharya V. V. , Berger A. N. , Roman R. A. ( 2018 ): Lending implications of U.S. bank stress tests: costs or benefits ? . Аделино М. , SCHOAR A. , Searino F. ( 2015 ): цены на жилые помещения, Solutheral and Selfemortment , . 117 , 288 – 306 . Эйвери Р. Б. , Бревоорт К. П. , Каннер G. B. ( 2007 ): Opportunities and issues in using HMDA data , Journal of Real Estate Research 29 , 351 – 380 . BAHAJ S. , FOILIS A. , Pinter G. ( 2020 ): ( 2020 ): . , Американское экономическое обозрение 110 , 2225 – 2270 . Berg T., Reisinger, M., , Streitz D. ( предстоящий ): Spillover Corporate Finance. Бергер А. Н. , Эспиноса-Вега М. А. , Рама С. В. , Миллер Н. Х. ( 2011 Berrospide J. M. , Edge R. M. ( 2019 ): Влияние буферов банковского капитала на банковское кредитование и деятельность компаний: что мы можем узнать из пятилетних результатов стресс-тестов? Серия дискуссий по финансам и экономике 2019-050. Вашингтон: Совет управляющих Федеральной резервной системы. BORD V. M. , Ivashina V. , Taliaferro R. D. ( 2018 ). Рабочий документ NBER 25184, Национальное бюро экономических исследований. Bordo M. D. , Cole R. A. , DUCA J. V. ( 2019 ). Влияние DOD-FRANK. Рабочий документ NBER 24501, Национальное бюро экономических исследований. Célerier C. , Matray A. ( 2019 ): , Обзор финансовых исследований 32 , 4767 – 4809 . Chen B. S. , Hanson S. , Stein J. C. ( 2017 ). кредит и рынок труда. Рабочий документ NBER 23843, Национальное бюро экономических исследований. Расчетная палата ( 2017 ): Ограничивают ли стресс-тесты надзорного банка кредитование малого бизнеса? Исследовательская записка Май. Connolly M. F. ( 2018 ): реальный эффект стресс-тестирования. Неопубликованный рабочий документ. Кортес К.Р. , Демяник Ю.С. , Ли Л. 3 30013 Loutskina E. , Strahan P. E. ( 2020 ): Стрессовые испытания и малые бизнеса , Ст. 260 – 279 . Доерр С. , Раисси М. , Вебер А. ( 2018 ): Credit-supply shocks and firm productivity in Italy , Journal of International Money and Finance 87 , 155 – 171 . Duval R. , Hong G. H. , Timmer Y. ( 2020 : ( 2020 ): ( 2020 ): ( 2020 ): . , Обзор финансовых исследований 33 , 475 – 503 . Goetz M. R. , Laeven L. , Levine R. ( 2013 ). от географической диверсификации банков США , Обзор финансовых исследований 26 , 1787 – 1823 . Goetz M. R. , Laeven L. , Levine R. ( 2016 ). , Журнал финансовой экономики 120 , 346 – 362 . Gourio F. , Messer T. , Siemer M. ( 2016 ): Firm entry and macroeconomic dynamics: a state-level analysis . Гранха J. , Leuz C. ( 2019 ): Смерть регулятора: Строгий надзор, банковское кредитование и деловая активность. Рабочий документ NBER 24168, Национальное бюро экономических исследований. Gropp R. , Mosk T. , Ongena S. , Wix C. ( 2019 ): Banks реакция на более высокие требования к капиталу: данные квазиестественного эксперимента , Обзор финансовых исследований 32 , 266 – 299 . Haltiwanger J. C. ( 2015 ): Создание рабочих мест, разрушение рабочих мест и рост производительности: роль молодых предприятий , Годовой обзор экономики . Годовой обзор экономики , . – 358 . Хименес Г. , Онгена С. , Пейдро Ж.-Л. , Saurina J. ( 2014 ): Опасные времена для денежно-кредитной политики: что двадцать три миллиона банковских кредитов говорят о влиянии кредитно-денежной политики на риск? , Эконометрика 82 , 463 – 505 . Manaresi F. , Pierri N. ( 2018 ): Предложение кредита и рост производительности. Meisenzahl R. R. ( 2014 ): Проверка состояния ограничений финансирования: данные об американском бизнес -кредитах , Журнал «Экономическая динамика и контроль », Журнал «Экономическая динамика и контроль », журнал о экономических динамиках и контроле , журнал о экономических динамиках и контроле , .0013 43 , 58 – 77 . Mian A. , Sufi A. , Trebbi F. ( 2015 ): Foreclosures, house prices, and the real economy , Журнал финансов 70 , 2587 – 2634 . Остер E. ( 2019 ): Unobservable selection and coefficient stability: theory and evidence , Journal of Business & Economic Statistics 37 , 187 – 204 . Pancost Нет данных , Schaller G. ( 2020 ): Погрешность измерения. Pierret D. , Steri R. ( 2020 ): Напряженные банки. Неопубликованный рабочий документ. Рис T. , Strahan P. E. ( 2010 Влияет ли кредитование на конкуренцию малых фирм? , Журнал финансов 65 , 861 – 889 . Schmalz M. C. , SRAER D. A. , THESMAR D. ( 2017 D. ( 2017 ). 72 , 99 – 132 . Siemens M. ( 2016 ): Устойчивый вход и динамика занятости в период Великой рецессии. Неопубликованный рабочий документ. STEIJVERS T. , Voordeckers W. ( 2009 ): СОВЕТА И КРЕДИТА. Журнал экономических обзоров 23 , 924 – 946 . * Я хотел бы поблагодарить Вимала Баласубраманиама, Тобиаса Берга, Хосе Берроспиде, Мартина Брауна, Кристл Ромеро Кортес, Юлию Демяник, Дэвида Дорна, Леонардо Гамбакорта, Эмилию Гарсиа-Аппендини, Жоао Гранха, Дениса Громб, Дэвид Хемус, Кэтрин Кох, Адриен Матрей, Ральф Мейзенцаль, Карстен Мюллер, Стивен Онгена, Хосе-Луис Пейдро, Дайан Пьерре, Каспер Росбах, Флориан Шойер, Джоэл Шапиро, Франк Сметс, Роберто Стери, Рене Штульц, Хавьер Суарес и Иоахим Вот , а также участники конференций и семинаров на SFI Research Days, Swiss Winter Conference on Financial Intermediation, Annual Meeting European Finance Association, Chicago Financial Institutions Conference, European System of Central Banks’ Day-Ahead Conference, Financial Management Association Annual Meeting, NYU , HEC Paris, HEC Lausanne, Oxford Saïd Business School, ETH Zurich, Амстердамский университет, Роттердамский университет Эразма, Боннский университет, Джорджтаунский университет y, Банк международных расчетов, Норвежская школа бизнеса BI, Копенгагенская школа бизнеса, Копенгагенский университет, Университет Боккони, Совет Федеральной резервной системы, Цюрихский университет, а также команда UBS по тестированию рисков и стрессу. © Автор(ы), 2021 г. Опубликовано Oxford University Press от имени Европейской финансовой ассоциации. Все права защищены. Для получения разрешений обращайтесь по электронной почте: [email protected] © Авторы, 2021 г. Опубликовано издательством Oxford University Press от имени Европейской финансовой ассоциации. Все права защищены. Для получения разрешений обращайтесь по электронной почте: [email protected] JEL G20 — GeneralG21 — банки; Депозитарные учреждения; микрофинансовые организации; ИпотекаL26 — Предпринимательство Раздел выпуска: Статьи Скачать все слайды Дополнительные данные rfab007_Supplementary_Data — pdf файл Реклама Дополнительная информация о метриках Оповещение об активности статьи Предварительные уведомления о статьях Оповещение о новой проблеме Предупреждение о классификации JEL Оповещение о теме Получайте эксклюзивные предложения и обновления от Oxford Academic Риск неявных гарантий: данные теневых банков в Китае Социальное взаимодействие в семье: данные Investors’ Security Holdings Пересмотр долга вне кризиса Налог на прирост капитала, венчурный капитал и инновации в стартапах Финансовое посредничество, накопление капитала и восстановление после кризиса Реклама Что вас мотивирует и движет ? Может быть, вы считаете себя – интуитивным, творческим и отличным инициатором, навыки как пойманные спонтанно , или – хороший планировщик, любит эффективность, целостно ориентированный , или – Гибкость, часто может сочетать чувства и аналитические способности при принятии решений, или – Инновационные, ориентированные на детали навыки, способность действовать в соответствии со своими импульсами или, как вы это называете – интуиция , или – Эффективный, целостный и часто ориентированный на клиента, или вы видите себя таким, как – Эмоции, а также ментальные мотивы, сама работа дает вам стимулы и стимулы, Что движет самосознанием, любопытством? Попробуйте пройти тест EPT и посмотрите. Здесь мы находим инсайты и узнаем больше о наших или чьих-то мотиваторах (если вы используете их, например, для построения команды) и какие движущие силы у вас есть, и описываем, почему вы, а также почему мы действуем так, как поступаем в разных ситуациях. Самосознание повышает вашу и всех способность работать и сотрудничать с другими людьми. Как внутреннее самосознание, так и внешнее самосознание. То есть то, что вы знаете или с чем знакомы, то, что другие видят в вас. Это понимание ценно во всех ситуациях, но не в последнюю очередь в повседневной работе. Развивая свое самосознание, вы можете объективно увидеть, какое решение вы приняли, чтобы добраться туда, где вы находитесь сегодня. Благодаря ЭПТ и его обратной связи вы можете научиться лучше управлять своими состояниями, эмоциями и импульсами. И тем самым предстоящие решения принимать. Самопознание часто упоминается как разделяющий фактор. Улучшая самосознание и выявляя факторы мотивации и возможности для улучшений, мы можем улучшить себя и тем самым наши компании и организации. Лучше понять, как поощрять как персонал, так и лидеров и менеджеров для экономического развития в наших организациях, а также личного роста и радости. Мы все понимаем, что улучшение самосознания может быть чрезвычайно полезным для предпринимателей, которые хотят улучшить свою работу и эффективность своих компаний. Точно так же, как и для тех, кто собирается начать свой первый корпоративный путь. Знание или осознание своего предпринимательского профиля и его движущих сил во многих случаях имеет решающее значение. Если характер бизнеса, которым вы занимаетесь, не соответствует характеру вашего предпринимательского типа, вы рискуете потерять и свой бизнес, и деньги — и напрасно. Развитие успешной компании требует развития организации. Для предпринимательской компании этот процесс начинается с предпринимателя, или, как показывают наши исследования, предприниматель должен развиваться. Но получить информацию, необходимую для этого развития, непросто. На основе нашего исследования мы разработали набор профилей ( дополнительных исследований по Стефану Линдстрему researchgate.net), которые значительно облегчают процесс выявления и мотивации этого развития. Вы найдете свой набор инструментов под Как использовать ваш результат или получить личный отзыв, а также добровольный план профессионального роста, связавшись с нами. Чтобы найти свой профиль и начать путь к совершенствованию, пройдите тест, который даст вам это понимание, как уже сделали более 27 800 других. Вы также получаете личностный профиль, который можете использовать для своего личного развития, а также для развития команды, развития персонала, управления персоналом, коучинга, наставничества и т. Рекрутинг, узнайте, какой профиль лучше всего подходит для вашего бизнеса и, возможно, будущих потребностей при наборе персонала. Удачи и наслаждайтесь результатами. Stefan Lindström 2010 © 0298 Почему мы это делаем? Формат записи даты рождения: ДЕНЬ.МЕСЯЦ.ГОД Пример: Если Вам посчастливилось родится 8 апреля 1991 года. То найдя нужные ячейки в ниже приведённых табличках, у Вас в итоге должна получится такая запись: VIII.IV.MCMXCI Автор: Bill4iam
Римские цифры — цифры
, использовавшиеся древними римлянами в своей непозиционной системе счисления. Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая — перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры. Римские цифры появились около 500 лет до нашей эры у этрусков. Для закрепления в памяти буквенных обозначений цифр в порядке убывания существует мнемоническое правило: М ы D арим С очные L имоны, Х ватит V сем I х. Соответственно M, D, C, L, X, V, I Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц. Существует «сокращённый способ» для записи больших чисел, таких как 1999. Он не рекомендуется, но иногда используется для упрощения. Отличие состоит в том, что для уменьшения цифры слева от неё может писаться любая цифра: Повсеместно записывать число «четыре» как «IV» стали только в XIX веке, до этого наиболее часто употреблялась запись «IIII». Однако запись «IV» можно встретить уже в документах манускрипта «Forme of Cury», датируемых 1390 годом. На циферблатах часов в большинстве случаев традиционно используется «IIII» вместо «IV», главным образом, по эстетическим соображениям: такое написание обеспечивает визуальную симметрию с цифрами «VIII» на противоположной стороне, а перевёрнутую «IV» прочесть труднее, чем «IIII». В русском языке римские цифры используются в следующих случаях: В других языках сфера применения римских цифр может иметь особенности, например, в западных странах римскими цифрами иногда записывается номер года. Стандарт Юникод определяет символы для представления римских цифр, как часть Числовых форм (англ. Number Forms ), в области знаков с кодами с U+2160 по U+2188. Например, MCMLXXXVIII может быть представлено в форме ⅯⅭⅯⅬⅩⅩⅩⅧ
. Этот диапазон включает как строчные, так и прописные цифры от 1 (Ⅰ
или I) до 12 (Ⅻ
или XII), в том числе и комбинированные глифы для составных чисел, таких как 8 (Ⅷ
или VIII), главным образом для обеспечения совместимости с восточноазиатскими наборами символов в таких промышленных стандартах, как JIS X 0213
, где эти символы определены. Комбинированные глифы используются для представления чисел, которые ранее составлялись из отдельных символов (например, Ⅻ
вместо его представления как Ⅹ
и Ⅱ
). В дополнение к этому, глифы существуют для архаичных форм записи чисел 1000, 5000, 10 000, большой обратной C (Ɔ
), поздней формы записи 6 (ↅ
, похожей на греческую стигму: Ϛ
), ранней формы записи числа 50 (ↆ
, похожей на стрелку, указывающую вниз ↓⫝⊥
), 50 000, и 100 000. Следует отметить, что маленькая обратная c, ↄ
не включена в символы римских цифр, но включена в стандарт Юникод как прописная клавдиева буква Ↄ
. Символы в диапазоне U+2160-217F присутствуют только для совместимости с другими стандартами, которыми определены эти символы. В обиходе применяются обычные буквы латинского алфавита. Отображение таких символов требует наличия программного обеспечения, поддерживающего стандарт Юникод, и шрифта, содержащего соответствующие этим символам глифы. Римские цифры — цифры, использовавшиеся древними римлянами в своей непозиционной системе счисления. История римских цифр Римские цифры появились за 500 лет до нашей эры у этрусков, которые могли заимствовать часть цифр у прото-кельтов. Римская система нумерации с помощью букв была распространена в Европе на протяжении двух тысяч лет. Только в позднем средневековье ее сменила более удобная для вычислений десятичная система цифр, заимствованная у арабов. Но до сих пор римскими цифрами обозначаются даты на монументах, время на часах и (в англо-американской типографической традиции) страницы книжных предисловий. Кроме того, в русском языке римскими цифрами принято обозначать порядковые числительные. Римские цифры 1 — I (лат. unus) В русском языке для закрепления в памяти буквенных обозначений цифр в порядке убывания существуют мнемонические правила: М ы D арим С очные L имоны, Х ватит V сем I х. Соответственно M, D, C, L, X, V, I. Правила записи римских цифр Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая — перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры. Например, I, Х, С ставятся соответственно перед Х, С, М для обозначения 9, 90, 900 или перед V, L, D для обозначения 4, 40, 400. Например, VI = 5+1 = 6, IV = 5 — 1 = 4 (вместо IIII). XIX = 10 + 10 — 1 = 19 (вместо XVIIII), XL = 50 — 10 = 40 (вместо XXXX), XXXIII = 10 + 10 + 10 + 1 + 1 + 1 = 33 и т.д. Выполнение арифметических действий над многозначными числами в этой записи весьма неудобно. Например, 1368=MCCCLXIIX=M+C+C+C+L+X+(X-I-I), где 1000=М, 300=ССС, 60=LX, 8=IIX. Система римских цифр настоящее время не применяется, за исключением в отдельных случаях обозначения веков (XV век и т.д.), годов н.э. (MCMLXXVII и т.д.) и месяцев при указании дат (например, 1. V. 1975), порядковых числительных, а также иногда производных небольших порядков, больших трёх: yIV, yV и т.д. С помощью римских цифр можно записывать и большие числа. Для этого над теми цифрами, которые обозначают тысячи, ставится черта, а над цифрами, которые обозначают миллионы, — двойная черта. Как через интернет бесплатно отправить смс абоненту сотового оператора Теле2 Что такое укачивание Что такое литературная гипербола Какие существуют принципы организации системы доходов бюджета Какие помещения в многоквартирном доме признаны нежилыми Как правильно поздравлять: с Восьмым марТА или Восьмым мартОМ Как проявляется аматофобия С какого года бег на 5000 метров (5 километров) является Олимпийской дисциплиной лёгкой атлетики для мужчин Где сдать кровь в Приморском крае Какие фигуры называются геральдическими Как перевести веб страницу Мы все пользуемся римскими цифрами – отмечаем ими номера веков или месяцев года. Римские цифры находятся на часовых циферблатах, в том числе на курантах Спасской башни. Мы их используем, но знаем про них не так много. Римская система счета в ее современном варианте состоит из следующих базовых знаков: I 1 Чтобы запомнить цифры, непривычные для нас, пользующихся арабской системой, существует несколько специальных мнемонических фраз на русском и английском языках: Система расположения этих цифр друг относительно друга такова: числа до трех включительно образуются при помощи сложения единиц (II, III), — четырехкратное повторение любой цифры запрещено. Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления — после, (4 = IV), та же логика действует и с другими цифрами (90 = XC). Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам. Важно, что любая цифра не должна повторять больше трех раз, таким образом, самое длинное число до тысячи – 888 = DCCCLXXXVIII (500+100+100+100+50+10+10+10+5+1+1+1). Запрет на четвертое использование одной и той же цифры подряд стал появляться только в XIX веке. Поэтому в старинных текстах можно увидеть варианты IIII и VIIII вместо IV и IX, и даже IIIII или XXXXXX вместо V и LX. Остатки этого написания можно увидеть на часах, где четыре часто отмечается именно с помощью четырех единиц. В старых книгах также нередки случаи двойных вычитаний – XIIX или IIXX вместо стандартных в наши дни XVIII. Также в Средневековье появилась новая римская цифра – ноль, который обозначался буквой N (от латинского nulla, ноль). Большие числа отмечались специальными знаками: 1000 — ↀ (или C|Ɔ),5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ). Миллионы получаются при двойном подчеркивании стандартных цифр. Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::. На данный момент не существует единой теории происхождения римских цифр. Одна из самых популярных гипотез гласит, что этрусско-римские цифры произошли от системы счета, которая использует вместо цифры штрихи-зарубки. Таким образом, цифра «I» — это не латинская или более древняя буква «и», а насечка, напоминающая форму этой буквы. Каждую пятую насечку обозначали скосом – V, а десятую перечеркивали – Х. Число 10 выглядело в этом счете следующим образом: IIIIΛIIIIX. Именно благодаря такой записи цифр подряд мы обязаны особой системе сложения римских цифр: со временем запись числа 8 (IIIIΛIII) могла сократиться до ΛIII, что убедительно демонстрирует, каким образом римская система счета получила свою специфику. Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи. Альтернативная теория принадлежит Альфреду Куперу, который предположил рассмотреть римскую систему счета с точки зрения физиологии. Купер считает, что I, II, III, IIII – это графическое представление количества пальцев правой руки, выкидываемых торговцем при назывании цены. V – это отставленный большой палец, образующий вместе с ладонью подобную букве V фигуру. Именно поэтому римские цифры суммируют не только единицы, но и складывают их с пятерками – VI, VII и т.п. – это откинутый большой палец и другие выставленные пальцы руки. Число 10 выражали с помощью перекрещивания рук или пальцев, отсюда пошел символ X. Еще один вариант – цифру V попросту удвоили, получив X. Большие числа передавали с помощью левой ладони, которая считала десятки. Так постепенно знаки древнего пальцевого счета стали пиктограммами, которые затем начали отождествлять с буквами латинского алфавита. Сегодня в России римские цифры нужны, в первую очередь, для записи номера века или тысячелетия. Римские цифры удобно ставить рядом с арабскими – если написать век римскими цифрами, а затем год – арабскими, то в глазах не будет рябить от обилия одинаковых знаков. Римские цифры имеют некоторый оттенок архаичности. С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида. В разных странах римские цифры употребляются немножко по-разному: в СССР было принято указывать с помощью них месяц года (1.XI.65). На западе римскими цифрами часто пишут номер года в титрах фильмов или на фасадах зданий. В части Европы, в особенности в Литве, нередко можно встретить обозначение римскими цифрами дней недели (I – понедельник и так далее). В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр. В России при письме рукой принято подчеркивать римские числа снизу и сверху одновременно. Однако часто в других странах подчеркивание сверху значило увеличение регистра числа в 1000 раз (или 10000 раз при двойном подчеркивании). Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой). Для обозначения цифр в латинском языке приняты комбинации следующих семи знаков: I (1), V (5), X (10), L (50), С (100), D (500), М (1000). Для запоминания буквенных обозначений цифр в порядке убывания придумано мнемоническое правило: Мы Dарим Сочные Lимоны, Хватит Vсем Iх (соответственно M, D, C, L, X, V, I). Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее число следует прибавлять к большему, если слева, то вычитать, а именно: VI — 6, т.е. 5 + 1 Возможно различное обозначение одного и того же числа. Например, число 80 можно обозначить как LXXX (50 + 10 + 10 + 10) и как ХХС (100 — 20). Для записи чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц. I (1) — unus (унус) Если вдруг любознательный человек спросит, почему для обозначения цифр 50, 100, 500 и 1000 были выбраны латинские буквы V, L, С, D, М, то сразу скажем, что это вовсе не латинские буквы, а совсем иные знаки. Дело в том, что основой для латинского алфавита послужил алфавит западногреческий. Именно к нему восходят три знака L, С и М. Здесь они обозначали придыхательные звуки, которых не было в латинском языке. Когда оформлялся латинский алфавит, именно они оказались лишними. Их и приспособили для обозначения чисел в латинской графике. Позднее они по написанию совпали с латинскими буквами. Так, знак С (100) стал похож на первую букву латинского слова centum (сто), а М (1000) — на первую букву слова mille (тысяча). Что же касается знака D (500), то он представлял собой половину знака Ф (1000), а потом уж стал похож на латинскую букву. Знак V (5) являлся всего навсего верхней половиной знака X (10). Для обозначения цифр в латинском языке приняты комбинации следующих семи знаков: I (1), V (5), X (10), L (50), С (100), D (500), М (1000). Для запоминания буквенных обозначений цифр в порядке убывания придумано мнемоническое правило: М ы D арим С очные L имоны, Х ватит V сем I х (соответственно M, D, C, L, X, V, I ). Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее число следует прибавлять к большему, если слева, то вычитать, а именно: VI — 6, т.е. 5 + 1 Возможно различное обозначение одного и того же числа. Например, число 80 можно обозначить как LXXX (50 + 10 + 10 + 10) и как ХХС (100 — 20). Для записи чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц. I (1) — unus (унус) Если вдруг любознательный человек спросит, почему для обозначения цифр 50, 100, 500 и 1000 были выбраны латинские буквы V, L, С, D, М, то сразу скажем, что это вовсе не латинские буквы, а совсем иные знаки. Дело в том, что основой для латинского алфавита послужил алфавит западногреческий. Именно к нему восходят три знака L, С и М. Здесь они обозначали придыхательные звуки, которых не было в латинском языке. Когда оформлялся латинский алфавит, именно они оказались лишними. Их и приспособили для обозначения чисел в латинской графике. Позднее они по написанию совпали с латинскими буквами. Так, знак С (100) стал похож на первую букву латинского слова centum (сто), а М (1000) — на первую букву слова mille (тысяча). Что же касается знака D (500), то он представлял собой половину знака Ф (1000), а потом уж стал похож на латинскую букву. Знак V (5) являлся всего навсего верхней половиной знака X (10). Вот и вся история с этими римскими цифрами. Обратите внимание на обозначение трех дат. Здесь зашифрованы римскими цифрами годы рождения Александра Пушкина, Александра Герцена и Александра Блока, Решите сами, какому Александру принадлежит какая дата. MDCCCXH На сайте собраны калькуляторы, конвертеры, формулы, справочники, таблицы и много другой полезной и нужной информации для учёбы и работы. Формат записи даты рождения ДЕНЬ.МЕСЯЦ.ГОД Пример Если Вам посчастливилось родится 8 апреля 1991 года. То найдя нужные ячейки в ниже приведённых табличках, у Вас в итоге должна получится такая запись: VIII.IV.MCMXCI Поделитесь с другими: Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями! Читать по теме Интересные статьи В одном километре содержится тысяча метров. 1 км = 1000 м Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки. Парциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре. Невозможно создать круговой процесс, результатом которого станет исключительно превращение теплоты, которое получено от нагревателя, в работу. Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними. Один морской узел равен одной тысяче восемьсот пятьдесят двум метрам или одному километру восемьсот пятьдесят двум метрам Число Римское Число Римское обозначение Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц. Часы марки Tissot с традиционным написанием «IIII» И НИКАКИЕ ОНИ не РИМСКИЕ — ЭТРУССКИЕ ! В античные времена римляне были очень активны в торговле и коммерции, и как только она обрели письменность они стали нуждаться в обозначении чисел.
Система, которую они изобрели для обозначения цифр и чисел, активно использовалась на протяжении многих веков, и даже сейчас она находит свое применение во многих специальных случаях написания чисел. Римские числа традиционно обозначают порядок правителей или людей имеющие одинаковое имя (например, Екатерина II , Николай II , Людовик XIV ). Они так же иногда используются для обозначения дат в издательском деле или на зданиях, для указания года постройки, или на надгробных камнях, когда есть желание создать впечатление, ощущение классической почести, дани уважения. Римские числа и цифры (вся целая система) так е живет в нашем языке, который до сих пор использует корни Латинских заимствованных слов для отображения тех или иных численных идей или значений. Несколько примеров: duo — двойной, quadricep — четырёхглавая мышца, decade — группа из десяти, десяток или десятилетие, milliliter — миллилитр, одна тысячная литра и т.п. Одно большое различие между римскими и арабскими числами (те которые мы используем повседневно сейчас) это то, что Римская система исчислений не имеет символа нуля, и второе, что положение цифры в записи может означать не сложение, но иногда и вычитание. Римские числа математически конвертируются в арабские числа путём простого назначения каждой цифре Римского числа соответствующего целочисленного значения в арабской системе с автоматическим суммированием: M=1000 | D=500 | C=100 | L=50 | X=10 | V=5 | I=1. Ниже приводятся детальное описание всех основных римских цифр: 1901 = MCMI 1911 = MCMXI 1921 = MCMXXI 1931 = MCMXXXI 1941 = MCMXLI 1951 = MCMLI 1961 = MCMLXI 1971 = MCMLXXI 1981 = MCMLXXXI 2001 = MMI Вводите все буквы в римской записи числа, как они указаны на вашем экспонате: Для корректной работы Dates Calculator Online, вам необходимо включить поддержку JavaScript в своем обозревателе (IE, Firefox, Opera)! Мы все пользуемся римскими цифрами – отмечаем ими номера веков или месяцев года. Римские цифры находятся на часовых циферблатах, в том числе на курантах Спасской башни. Мы их используем, но знаем про них не так много. Римская система счета в ее современном варианте состоит из следующих базовых знаков: I 1 Чтобы запомнить цифры, непривычные для нас, пользующихся арабской системой, существует несколько специальных мнемонических фраз на русском и английском языках: Система расположения этих цифр друг относительно друга такова: числа до трех включительно образуются при помощи сложения единиц (II, III), — четырехкратное повторение любой цифры запрещено. Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления — после, (4 = IV), та же логика действует и с другими цифрами (90 = XC). Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам. Важно, что любая цифра не должна повторять больше трех раз, таким образом, самое длинное число до тысячи – 888 = DCCCLXXXVIII (500+100+100+100+50+10+10+10+5+1+1+1). Запрет на четвертое использование одной и той же цифры подряд стал появляться только в XIX веке. Поэтому в старинных текстах можно увидеть варианты IIII и VIIII вместо IV и IX, и даже IIIII или XXXXXX вместо V и LX. Остатки этого написания можно увидеть на часах, где четыре часто отмечается именно с помощью четырех единиц. В старых книгах также нередки случаи двойных вычитаний – XIIX или IIXX вместо стандартных в наши дни XVIII. Также в Средневековье появилась новая римская цифра – ноль, который обозначался буквой N (от латинского nulla, ноль). Большие числа отмечались специальными знаками: 1000 — ↀ (или C|Ɔ),5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ). Миллионы получаются при двойном подчеркивании стандартных цифр. Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::. На данный момент не существует единой теории происхождения римских цифр. Одна из самых популярных гипотез гласит, что этрусско-римские цифры произошли от системы счета, которая использует вместо цифры штрихи-зарубки. Таким образом, цифра «I» — это не латинская или более древняя буква «и», а насечка, напоминающая форму этой буквы. Каждую пятую насечку обозначали скосом – V, а десятую перечеркивали – Х. Число 10 выглядело в этом счете следующим образом: IIIIΛIIIIX. Именно благодаря такой записи цифр подряд мы обязаны особой системе сложения римских цифр: со временем запись числа 8 (IIIIΛIII) могла сократиться до ΛIII, что убедительно демонстрирует, каким образом римская система счета получила свою специфику. Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи. Альтернативная теория принадлежит Альфреду Куперу, который предположил рассмотреть римскую систему счета с точки зрения физиологии. Купер считает, что I, II, III, IIII – это графическое представление количества пальцев правой руки, выкидываемых торговцем при назывании цены. V – это отставленный большой палец, образующий вместе с ладонью подобную букве V фигуру. Именно поэтому римские цифры суммируют не только единицы, но и складывают их с пятерками – VI, VII и т.п. – это откинутый большой палец и другие выставленные пальцы руки. Число 10 выражали с помощью перекрещивания рук или пальцев, отсюда пошел символ X. Еще один вариант – цифру V попросту удвоили, получив X. Большие числа передавали с помощью левой ладони, которая считала десятки. Так постепенно знаки древнего пальцевого счета стали пиктограммами, которые затем начали отождествлять с буквами латинского алфавита. Сегодня в России римские цифры нужны, в первую очередь, для записи номера века или тысячелетия. Римские цифры удобно ставить рядом с арабскими – если написать век римскими цифрами, а затем год – арабскими, то в глазах не будет рябить от обилия одинаковых знаков. Римские цифры имеют некоторый оттенок архаичности. С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида. В разных странах римские цифры употребляются немножко по-разному: в СССР было принято указывать с помощью них месяц года (1.XI.65). На западе римскими цифрами часто пишут номер года в титрах фильмов или на фасадах зданий. В части Европы, в особенности в Литве, нередко можно встретить обозначение римскими цифрами дней недели (I – понедельник и так далее). В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр. В России при письме рукой принято подчеркивать римские числа снизу и сверху одновременно. Однако часто в других странах подчеркивание сверху значило увеличение регистра числа в 1000 раз (или 10000 раз при двойном подчеркивании). Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой). Римские цифры — цифры, использовавшиеся древними римлянами в своей непозиционной системе счисления. История римских цифр Римские цифры появились за 500 лет до нашей эры у этрусков, которые могли заимствовать часть цифр у прото-кельтов. Римская система нумерации с помощью букв была распространена в Европе на протяжении двух тысяч лет. Только в позднем средневековье ее сменила более удобная для вычислений десятичная система цифр, заимствованная у арабов. Но до сих пор римскими цифрами обозначаются даты на монументах, время на часах и (в англо-американской типографической традиции) страницы книжных предисловий. Кроме того, в русском языке римскими цифрами принято обозначать порядковые числительные. Римские цифры 1 — I (лат. unus) В русском языке для закрепления в памяти буквенных обозначений цифр в порядке убывания существуют мнемонические правила: М ы D арим С очные L имоны, Х ватит V сем I х. Соответственно M, D, C, L, X, V, I. Правила записи римских цифр Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая — перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры. Например, I, Х, С ставятся соответственно перед Х, С, М для обозначения 9, 90, 900 или перед V, L, D для обозначения 4, 40, 400. Например, VI = 5+1 = 6, IV = 5 — 1 = 4 (вместо IIII). XIX = 10 + 10 — 1 = 19 (вместо XVIIII), XL = 50 — 10 = 40 (вместо XXXX), XXXIII = 10 + 10 + 10 + 1 + 1 + 1 = 33 и т.д. Выполнение арифметических действий над многозначными числами в этой записи весьма неудобно. Например, 1368=MCCCLXIIX=M+C+C+C+L+X+(X-I-I), где 1000=М, 300=ССС, 60=LX, 8=IIX. Система римских цифр настоящее время не применяется, за исключением в отдельных случаях обозначения веков (XV век и т.д.), годов н.э. (MCMLXXVII и т.д.) и месяцев при указании дат (например, 1. V. 1975), порядковых числительных, а также иногда производных небольших порядков, больших трёх: yIV, yV и т.д. С помощью римских цифр можно записывать и большие числа. Для этого над теми цифрами, которые обозначают тысячи, ставится черта, а над цифрами, которые обозначают миллионы, — двойная черта. Как через интернет бесплатно отправить смс абоненту сотового оператора Теле2 Что такое укачивание Что такое литературная гипербола Какие существуют принципы организации системы доходов бюджета Какие помещения в многоквартирном доме признаны нежилыми Как правильно поздравлять: с Восьмым марТА или Восьмым мартОМ Как проявляется аматофобия С какого года бег на 5000 метров (5 километров) является Олимпийской дисциплиной лёгкой атлетики для мужчин Где сдать кровь в Приморском крае Какие фигуры называются геральдическими Как перевести веб страницу Римские цифры, придуманные более 2500 лет тому назад, использовались европейцами на протяжении двух тысячелетий, затем были вытеснены арабскими цифрами. Это произошло потому, что римские цифры записать достаточно сложно, да и любые арифметические действия в римской системе выполнять гораздо сложнее, чем в арабской системе исчисления. Не смотря на то, что сегодня римская система не часто используется, это вовсе не значит, что она стала неактуальна. В большинстве случаев века римскими цифрами обозначают, а вот годы или точные даты принято писать арабскими цифрами. Римскими цифры также используются при написании порядковых номеров монархов, энциклопедических томов, валентности различных химических элементов. На циферблатах ручных часов также часто используются цифры римской системы исчисления. Римские цифры представляют собой определенные знаки, с помощью которых записывают десятичные разряды и их половины. Используют для этого всего семь заглавных букв латинского алфавита. Числу 1 соответствует римская цифра I, 5 – V, 10 – X, 50 – L, 100 – C, 500 – D, 1000 – M. При обозначении натуральных чисел эти цифры повторяются. Так 2 можно написать, используя два раза I, то есть 2 – II, 3 — три буквы I, то есть 3 – III. Если меньшая цифра стоит перед большей, то используется принцип вычитания (меньшая цифра вычитается из большей).
Так, цифра 4 изображается как IV (то есть 5-1). В случае, когда большая цифра стоит впереди меньшей, их складывают, например 6 записывается в римской системе, как VI (то есть 5+1). Если Вы привыкли записывать числа арабскими цифрами, то могут возникнуть некоторые затруднения в том случае, когда нужно записать века римскими цифрами, какое-либо число или дату. Перевести любое число из арабской системы в римскую систему исчисления и наоборот можно очень легко и очень быстро, воспользовавшись удобным конвертером на нашем сайте. На клавиатуре компьютера достаточно перейти на английский язык, чтобы без труда записать любое число римскими цифрами. По всей видимости, древние римляне отдавали предпочтение прямым линиям, поэтому все их цифры прямые и строгие. Однако, римские цифры представляют собой ни что иное, как упрощенное изображение пальцев человеческой руки. Цифры с одного до четырех напоминают вытянутые пальцы, цифру пять можно сравнить с раскрытой ладонью, где большой палец оттопырен. А цифра десять напоминает две скрещенные руки. В европейских странах при счете принято разгибать пальцы, а вот в России, наоборот, загибать. Понравился калькулятор? Поделитесь с друзьями: Дорогие друзья! 2020 год для нас чрезвычайно знаковый, потому что мы отмечаем 70-летие бренда Tokina. В ознаменование этого большого события мы решили выпустить специальный материал, который проливает свет на практически неизвестную историю бренда и раскрывает много интересных фактов о компании, в том числе полную хронологию истории объективов Tokina и новый юбилейный состав Tokina 2020 года. Мало кто знает, но есть книга под названием «30 лет истории Tokina», изданная еще в 1980 году. Книга рассказывает, что история Tokina восходит к 31 мая 1950 года. В этот день в Токио в районе Синдзюку было создано производство оптического оборудования (на японском языке — Tokyo Koki Seisakusho). Основанная г-ном Кавагути Денкики, компания начала свою деятельность в качестве субподрядчика с полировки плоских зеркал, линз для биноклей и слайд-проекторов. Первые 5 лет были непростыми для компании из-за экономической ситуации, когда страна только начинала восстанавливаться после окончания Второй мировой войны, а заказы были довольно нестабильными. В 1959 году, после реструктуризации, компания сменила название на Tokyo Optical Equipment (Tokyo Koki). В то время компания начала разрабатывать объективы для зеркальных камер, поскольку Nikon и многие другие японские производители камер демонстрировали резкий рост продаж. Руководство компании осознало, что японские производители камер, вероятно, будут управлять рынком камер в будущем. В качестве отправной точки Tokyo Koki начала выпускать объективы для зарубежных заказчиков, одновременно задумываясь о выпуске собственных объективов. Согласно записям, первыми объективами, разработанными компанией Tokyo Optical Equipment, были 135mm f/3.5 и 100mm f/4 для бренда HANIMEX (Австралия). Это было время, когда для экспорта оптической продукции за пределы Японии JCII (Японский институт по проверке и тестированию фотоаппаратов и оптических инструментов) обязывал производителей отправлять продукцию под собственными зарегистрированными брендами. Чтобы наладить бесперебойный процесс производства объективов, компания Tokyo Optical Equipment создала и зарегистрировала свой собственный бренд в 1960 году. На протяжении многих лет ходили слухи о происхождении бренда Tokina. Вероятно, сейчас самое подходящее время, чтобы приблизить истину: президент компании г-н Кавагути Денкичи и его команда мечтали иметь возможность продемонстрировать свои объективы на знаменитой выставке Photokina в Германии. Они решили воплотить эту мечту в жизнь и взяли «Tokina» у Photokina и зарегистрировали её как фирменный знак для своих сменных объективов. Позже, в 1974 году, компания выставила свой стенд на Photokina (фото ниже). В 1971 году спрос на сменные объективы для зеркальных камер во всем мире значительно вырос, и компания заложила основу для своего бренда, изменив название на Tokina Optics Co., Ltd. и инвестировав в будущие технологии. 1981 год ознаменовался выпуском двух серий объективов: Tokina AT-X (сокращение от «ADVANCED TECHNOLOGY X») в высоком ценовом сегменте и Tokina SZ-X (сокращение от «SYSTEM ZOOM X») в бюджетном сегменте. Обе римские цифры X в названиях обозначали 10 — поскольку Tokina планировала выпустить не менее 10 объективов для каждой серии. В 1985 году Minolta потрясла рынок фотоаппаратов, выпустив новейшие камеры α-7000 с системой автофокусировки нового поколения. Эта система автофокусировки была намного эффективнее, точнее и быстрее существующих. Tokina, наряду с другими марками объективов, которые в то время производили в основном объективы с ручной фокусировкой, пережили довольно трудные времена. Чтобы не остаться в стороне, Tokina начала разработку автофокусных объективо для системы Minolta AF и вскоре после этого выпустила свой самый первый объектив с поддержкой автофокуса в серии AT-X AT-X 270 AF (28-70mm f/2.8) в 1988 году. Говоря об объективах Tokina 80-х годов, важную роль в истории компании сыграли две модели с ручной фокусировкой: телеобъектив AT-X 828 (80-200mm f/2.8) (выпущен в 1983 году) и стандартный автофокусный зум AT-X 270 AF (28-70mm f/2.8) (выпущен в 1988 году). Заблуждение, которое в настоящее время широко распространено среди фотографов всего мира, связано с создателем известного, современного и очень удобного телеобъектива. Самым первым объективом с диапазоном 70-200 мм с постоянной светосилой f/2.8 ошибочно считают Tokina. Хотя это очень лестно, эта деталь на самом деле не совсем точна. За два года до того, как Tokina выпустила объектив AT-X 828 (80-200mm f/2.8), Nikon выпустила свой Nikkor 80-200mm f/2.8. То есть Nikkor 80-200mm стал своего рода «родителем» для Tokina 70-200mm f/2.8. Nikkor 80-200mm f/2.8 был дорогим (в то время 420000 JPY) и тяжелым объективом (1900 г), в то время как Tokina весил всего 1080 г по цене менее половины от прежней (120000 JPY). Благодаря этим уникальным характеристикам Tokina AT-X 828 ошибочно считается основоположником нынешнего стандарта 70-200mm f/2.8. Другая модель, которая внесла значительный вклад в процесс создания Tokina как всемирно известного бренда объективов, была AT-X 270 AF (28-70mm f/2.8). Последний был первым в серии AT-X, поддерживающим автофокус. В то время как у конкурентов был объектив 35-70mm f/2.8 с всего 35mm в самом широком положении, у Tokina 28-70mm был больший диапазон фокусных расстояний, начиная с 28mm. Представленный Tokina диапазон фактически стал стандартом для современных среднефокусных объективов, выпускаемых большинством производителей. Оба вышеупомянутых объектива были перевыпущены в серии AT-X PRO в 1994 году и в дальнейшем закрепили за маркой Tokina репутацию известного мирового производителя светосильных стандартных зум-объективов. В начале 2000-х цифровая революция была на грани прорыва. В то время как первые цифровые зеркальные камеры были чрезвычайно дорогими, Canon EOS D60 (выпущенный в 2000 году) и Nikon D100 (выпущенный в 2002 году) сделали фотографию более доступной как для любителей, так и для профессиональных фотографов. Tokina медленно, но методично начала пересматривать основные технические характеристики и разрабатывать объективы, предназначенные исключительно для цифровых зеркальных камер. Еще одна знаменательная веха произошла в 2004 году, когда Tokina выпустила легендарный объектив AT-X 124 AF PRO DX (12-24mm f/4) для зеркальных камер формата APS-C. Широкоугольники, которые сформировали золотой стандарт в части оптической схемы, включали в конструкцию дорогие асферические элементы как композитного, так и стеклянного типа. Tokina преуспела в разработке эксклюзивного, высококачественного, недорогого и высокоэффективного асферического элемента, в результате чего был выпущен объектив, который по характеристикам не уступал конкурентам, но был вдвое дешевле! Хотя вышеуказанный AT-X 124 AF PRO DX, действительно, был легендарным объективом среди фотографов, однако, еще больший вклад в становление Tokina, как глобального производителя, сделал объектив AT-X 116 PRO DX (11-16mm f/2.8), выпущенный в 2008 году, который был признан также и среди видеооператоров во всем мире. Технологии, которые Tokina разрабатывала в течение долгого периода своей истории, до сих пор применяются в современных моделях, и благодаря этому бренд Tokina прочно удерживает на рынке позиции ведущего мирового производителя широкоугольных объективов. Римские цифры (I, V, X, L, C, D, M) образуют систему счисления, которая использовалась в Древнем Риме, где буквы обозначают числа. Они использовались в Европе до позднего средневековья. Это контрастирует с арабскими цифрами, которые являются современной системой счисления, используемой во всем мире (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Наш вышеупомянутый инструмент позволяет конвертировать арабские цифры в римские. Римские цифры и их арабские аналоги можно найти в таблице ниже: Традиционная римская система счисления использовалась только для чисел до 3999, которые представлены как MMMCMXCIX. Теоретически вы можете добавить больше «M» в начало, что добавляет 1000 для каждой «M», но более простой способ — добавить римские цифры с чертой. Верхняя черта над римской цифрой означает, что вы умножаете ее на 1000, поэтому V̅ составляет 5 * 1000 = 5000. Римские цифры обычно не используются в наши дни, но есть некоторые ограниченные сценарии, в которых вы можете столкнуться с ними.Вы можете использовать наш генератор римских цифр для этих различных случаев использования. Обычно римские цифры используются в приглашениях, циферблатах часов и в названии ежегодного Суперкубка. Они также использовались в королевских титулах, чтобы указать, какой король или королева. Вот текущая дата и время, написанные римскими цифрами.Поскольку в римской системе счисления нет нуля, час, минута и секунда в метках времени иногда становятся пустыми. 1950 год начался в воскресенье и не был високосным. Здесь вы можете узнать больше о том, что произошло в 1950 году. Число 1950 делится на 2, 3, 5, 6, 10, 13, 15, 25, 26, 30, 39, 50, 65, 75, 78, 130, 150, 195, 325, 390, 650 и 975 и можно разложить на простые множители в 2 × 3 × 5 2 × 13. 1950 как двоичное число: 11110011110 Ниже приведены числа с 1947 по 1953 год, которые близки к 1950 году. В правом столбце показано, как каждая римская цифра складывается в общую сумму. Римские цифры происходят, как следует из названия, из Древней Римской империи.В отличие от нашей системы координат с основанием 10, римская система основана на сложении (а иногда и вычитании) семи различных значений. Эти символы используются для обозначения этих значений: Например, чтобы выразить число 737 римскими цифрами, вы пишете DCCXXXVII, то есть 500 + 100 + 100 + 10 + 10 + 10 + 5 + 1 + 1. Однако для чисел 4 и 9 вместо сложения используется вычитание. , а меньшее число пишется перед большим числом: e.грамм. 14 записывается как XIV, то есть 10 + 5 — 1, а 199 выражается как CXCIX, т.е. 100 + 100 — 10 + 10 — 1. Можно утверждать, что 199 было бы легче записать как CIC, но согласно наиболее распространенному По определению, вы можете вычесть только число, которое на порядок меньше, чем числа, из которых вы вычитаете, а это означает, что IC для 99 неверно. Римские цифры часто используются в пронумерованных списках, на зданиях, чтобы указать год, когда они были построены, и в именах регентов, таких как Людовик XVI из Франции. Не стесняйтесь ссылаться на этот сайт, если найдете его полезным. Также можно напрямую ссылаться на определенные числа, такие как roman-numerals.info/XXXVII или roman-numerals.info/37. Вы также можете ссылаться на интервалы, например, roman-numerals.info/1-100 или roman-numerals.info/1980-2020, чтобы увидеть числа в формате списка. Римские цифры — это древний способ написания чисел, зародившийся в Древнем Риме. Он все еще используется сегодня, но в основном для дат (например, Super Bowl L для Super Bowl 50) или для фильмов.
сериал (Звездные войны IV — Новая надежда). Вот основные используемые символы: Для чисел, превышающих 1000, вы ставите тире над римской цифрой, чтобы указать умножение на 1000. Чтобы преобразовать 1950 в римские цифры, нам нужно разделить его на разрядные значения (единицы, десятки, сотни и т. Д.), вот так: Обратите внимание, мы пропустили разрядные значения, равные 0. Затем вы объединяете их все вместе (начиная сверху), чтобы получить MCML . Вы, вероятно, встречали римские цифры в своей повседневной жизни и задавались вопросом, почему мы все еще чувствуем необходимость использовать их сегодня. В конце концов, разве нет более простого способа записывать числа? В этой статье мы объясним, как работают римские цифры, и предоставим вам несколько таблиц преобразования римских цифр, , которые вы можете использовать, чтобы изучить и просмотреть эту древнюю систему счисления.Мы также дадим вам три метода, которые вы можете использовать для запоминания римских цифр. Римские цифры — это древняя система счисления, зародившаяся в Риме (отсюда и название «римская»). Как вы, наверное, знаете, они сильно отличаются от того, что сегодня используют большинство людей и культур, а именно арабских цифр или цифр 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. В отличие от арабских цифр, римские цифры представляют собой жесткую систему, состоящую всего из семи символов, , которые вы можете комбинировать для образования новых чисел с помощью специальных правил сложения и вычитания (мы объясним, как эти правила работают буквально через мгновение). Вот семь римских цифр и их значение: Это основные числа, которые обозначают римские цифры, когда они используются по отдельности. Чтобы сформировать другие числа с помощью этой системы, вы размещаете цифры рядом, чтобы обозначить сложение. Если число идет после числа, которое больше или равно по значению, то к числу перед ним нужно прибавить . Например, если вы хотите написать 3 римскими цифрами, вы просто напишите I три раза так: III. Это означает I + I + I (или 1 + 1 + 1). Или, скажем, вы хотите написать число 56 римскими цифрами. Чтобы сделать это, вы должны начать с самой большой единицы, представленной римской цифрой — в данном случае это 50, которая представлена буквой L.Затем вы добавляете V (5), а затем I (1), чтобы получилось 6. Это даст вам LVI, или 56. Главное правило, которое следует запомнить: нельзя складывать вместе более трех одинаковых римских цифр. Здесь и вступает в игру вычитание. Меньшая цифра, помещенная перед , большая цифра означает вычитание этой меньшей цифры из большей. Например, чтобы получить число 4, вы не можете просто написать IIII, потому что вы не можете сложить вместе более трех I.Что вам нужно сделать, это вычесть 1 из 5 (I из V). Чтобы изобразить вычитание римскими цифрами, вы должны поставить меньшую цифру непосредственно перед цифрой , из которой она вычитается. Для 4 это будет IV (то есть V — I или 5 — 1). Обратите внимание, что нельзя вычесть более одного значения из римской цифры. Вот еще один пример. Допустим, вы хотите записать число 719 римскими цифрами. Для начала вам нужно найти самую большую ценность — сотни.Помните, что D означает 500, а C означает 100, поэтому вы можете просто сложить эти символы вместе, чтобы получить 700: DCC. Теперь нам нужно получить 19. Если вы сложите вместе 10 (X) и 5 (V), вы получите 15. Но вы не можете добавить четыре I после этого, чтобы получить 19 , так как это будет больше. чем три одинаковых числа. Вместо этого вы можете использовать два X и вычесть I из второго X. Это даст XIX. Буквально это означает X + (X — I) или 10 + (10-1), что, как известно, равно 19. Теперь соедините эти две части вместе, чтобы получить комбинацию римских цифр для 719: DCCXIX. Вычитание используется только для определенных чисел и числовых комбинаций. Это любых чисел, заканчивающихся цифрами 4 или 9, а также числами 40, 90, 400 и 900: Правильная римская цифра (с вычитанием) НЕПРАВИЛЬНАЯ римская цифра (с использованием сложения) Значение IV IIII * 4 IX VIIII 9 XL XXXX 40 XC LXXXX 90 CD CC 400 СМ DCCCC 900 * Хотя обычно считается неправильным использование, IIII иногда используется вместо IV на часах. Как вы, наверное, заметили выше, римские цифры увеличиваются только до M (1000). Согласно правилам сложения и вычитания это означает, что — наибольшее число, которое мы можем сформировать римскими цифрами, — это MMMCMXCIX, или 3,999. Но есть — это способов представить числа даже выше этого. Один из способов — это нарисовать горизонтальную линию или полосу поперек римской цифры (или комбинации цифр), чтобы умножить ее на 1000. Например, если вы хотите написать 5000, вы должны написать V. Другой, менее распространенный способ написания еще больших чисел включает помещения рамки или прямоугольника, открытого снизу вокруг римской цифры, чтобы умножить ее на 100 000. Итак, I с рамкой вокруг него означает 100000, тогда как IV с рамкой вокруг него означает 400000. Римские цифры до сих пор используются в самых разных ситуациях, поэтому очень важно, чтобы вы понимали, как их читать. Вот три основных примера использования римских цифр: Хотя арабские цифры намного превосходят римские цифры (каламбур) с точки зрения широты ситуаций, в которых они используются, определенно стоит потратить некоторое время, чтобы сесть и научиться использовать римские цифры, особенно если вы планируете пойти в путь. в футбол или кинопроизводство! На этой таблице преобразователя римских цифр показаны все основные выписанные римские цифры: Римская цифра Значение Римская цифра Значение Я 1 LX 60 II 2 LXX 70 III 3 LXXX 80 IV 4 XC 90 В 5 С 100 VI 6 CC 200 VII 7 CCC 300 VIII 8 CD 400 IX 9 D 500 Х 10 постоянного тока 600 ХХ 20 DCC 700 XXX 30 DCCC 800 XL 40 СМ 900 л 50 м 1 000 Это основные числа, которые вы можете написать с помощью семи римских цифр. Но если вы хотите записать еще большие числа, вот таблица для преобразования римских цифр. Напомним, что столбик сверху умножает число на 1000. Римская цифра Значение M или I 1 000 MM или II 2 000 МММ или III 3 000 IV 4 000 В 5 000 Х 10 000 л 50 000 С 100 000 D 500 000 м 1 000 000 CORNERSTONES of NY / Flickr Многим людям интересно, как выглядят годы , представленные римскими цифрами, , поскольку это обычная практика, используемая на зданиях (обычно для обозначения даты постройки), в фильмах и для выделения дней рождения и других важных дат на такие вещи, как кольца и татуировки. Ниже приведена таблица преобразователя даты в римские цифры, которую вы можете использовать, чтобы быстро понять, как разные годы выглядят римскими цифрами: Римская цифра Год MCM 1900 MCMX 1910 MCMXX 1920 MCMXXX 1930 MCMXL 1940 MCML 1950 MCMLX 1960 MCMLXX 1970 MCMLXXX 1980 MCMXC 1990 ММ 2000 MMX 2010 MMXX 2020 У вас не всегда будет доступ к диаграммам преобразования римских цифр, подобным тем, которые мы дали вам выше, так как же вы можете убедиться, что понимаете, как правильно читать римские цифры? Вот три метода, которые помогут вам запомнить римские цифры и то, как они работают. Многие студенты считают, что легче всего запомнить семь римских цифр, используя простой мнемонический прием. Такое устройство может помочь вам запомнить римские цифры, напоминая вам буквы, используемые для их обозначения от наименьшего к наибольшему или наоборот. Еще раз эти буквы следующие: Не стесняйтесь делать свои собственные мнемонические приемы, если они вам не нравятся или их трудно запомнить. Некоторые люди предпочитают запоминать римские цифры, придумывая определенные ассоциации с буквами и цифрами, которые они представляют, или придумывая определенные слова / фразы (не обязательно мнемонические приемы). Например, один популярный трюк состоит в том, чтобы думать, что римская цифра M (что означает 1000) означает «Миллениум», и римскую цифру C (что означает 100) означает «век».» Другие люди мыслят терминами словесных ассоциаций или сокращений. Например, римские цифры L, C и D могут напоминать вам ЖК-монитор компьютера. Знание этой ассоциации может помочь вам запомнить правильный (возрастающий) порядок этих цифр. Попробуйте найти свои собственные ассоциации, которые помогут вам запомнить римские цифры. Последний способ помочь вам запомнить римские цифры — это использовать так называемый трюк с руками, который можно использовать для запоминания первых трех римских цифр (I, V и X). Начните с того, что поднимите только один палец, чтобы получилась фигура, похожая на римскую цифру I. Итак, один палец = I. Достаточно просто, не так ли? Теперь сделайте V-образную форму одной рукой, оттолкнув большой палец от четырех других пальцев. Пять пальцев в форме буквы V должны напоминать вам, что римская цифра V равна 5. Наконец, сделайте крестик обеими руками. Вы должны увидеть, что 10 пальцев в форме X соответствуют римской цифре X или 10. Прежде чем мы завершим эту статью, давайте проведем небольшую викторину по преобразованию римских цифр, чтобы увидеть, насколько хорошо вам удалось запомнить римские цифры и как они работают (ответы ниже). Напишите следующие числа римскими цифрами: Ответы: Вот краткая таблица преобразователя числа дней рождения римскими цифрами, которую вы можете использовать в качестве справки: Год Римская цифра Год Римская цифра 2019 MMXIX 2004 MMIV 2018 MMXVIII 2003 MMIII 2017 MMXVII 2002 MMII 2016 MMXVI 2001 MMI 2015 MMXV 2000 ММ 2014 MMXIV 1999 MCMXCIX 2013 MMXIII 1998 MCMXCVIII 2012 MMXII 1997 MCMXCVII 2011 MMXI 1996 MCMXCVI 2010 MMX 1995 MCMXCV 2009 MMIX 1994 MCMXCIV 2008 MMVIII 1993 MCMXCIII 2007 MMVII 1992 MCMXCII 2006 MMVI 1991 MCMXCI 2005 MMV 1990 MCMXC Остин Кирк / Flickr Хотя римские цифры возникли в Древнем Риме и сегодня мало используются в повседневной жизни, они все еще важны, особенно если вы хотите уметь читать старые -модели аналоговые часы и годы для таких вещей, как выпуск фильмов. Римская система счисления основана на семи основных числах: I, V, X, L, C, D и M (1, 5, 10, 50, 100, 500 и 1000, соответственно). Римские цифры пишутся слева направо, начиная с самой большой единицы. Цифры можно складывать вместе для образования новых чисел (например, III = I + I + I = 3), но нельзя складывать вместе не более трех одинаковых цифр. Кроме того, чтобы сформировать любые числа, оканчивающиеся на 4 или 9 или числа 40, 90, 400 и 900, вы должны вычесть из большей единицы , потому что вы не можете сложить более трех одинаковых чисел.Например, IV = V — I = 5 — 1 = 4. Чтобы представить очень большое число (1000+), добавьте горизонтальную черту над цифрой, чтобы умножить ее на 1000. Итак, X = 10 * 1000 = 10000. Есть много способов помочь себе запомнить римские цифры. Вот три метода: Теперь вы должны знать все, что нужно знать о римских цифрах! В числах есть гораздо больше, чем римские цифры. Ознакомьтесь с нашими руководствами, чтобы узнать, как округлять числа с десятичными знаками в них, как преобразовывать десятичные дроби в дроби, а также как складывать и вычитать дроби. Хотите узнать о больших числах? Мы объясняем, что следует за триллионом, и даем вам названия тонн больших чисел. Мы также выясняем, сколько нулей в миллионе, миллиард и триллион. Мы производим вычисления в десятичной системе счисления с использованием индо-арабских цифр.Но как быть с римскими цифрами и без знака нуля в аддитивной системе счисления, если нет ручных счётов? (См. Также сообщение ACM : Как римляне рассчитывали?). Предварительные замечания При расчетах римскими цифрами порядок цифр не имеет значения. Исключения: если меньшая единица находится слева от большей единицы, она вычитается из большей единицы: IV, IX, IL, IC, ID, IM; ВЛ, ВК, ВД, ВМ; XL, XC, XD, XM; LD, LM, а также CD и CM. Дополнение Огенд и добавление складываются так же, как и счеты (см. Табл. 1–2). При необходимости числовые обозначения необходимо объединить (связать). Табл. 1: Сложение в римской системе счисления 1 Табл. 2: Сложение в римской системе счисления 2 Вычитание Вычитаемое вычитается из уменьшаемого аналогично счетам (см. Таблицу 3).При необходимости числовые знаки необходимо разрешить (разобрать). Числа, которые встречаются как в убывающем, так и в вычитаемом, могут быть удалены. Табл. 3: Вычитание в римской системе счисления Умножение Умножение — это повторное сложение. Множитель 23 складывается 6 раз (см. Таблицу 4). Таким же образом вы производите вычисления на счетах, и большинство механических калькуляторов используют аналогичную процедуру.В средние века были и другие методы, такие как удвоение (дублирование), метод гелосии (решеточное умножение) и египетское умножение (эфиопское умножение). Табл. 4: Умножение в римской системе счисления Отдел Деление — это последовательное вычитание. Делитель 7 можно вычесть 8 раз из дивиденда 56 (см. Таблицу 5). Таким же образом вы производите вычисления на счетах, и большинство механических калькуляторов используют аналогичную процедуру.В средние века были и другие методы, например деление пополам (медитация). Табл. 5: Деление в римской системе счисления Римский письменный калькулятор Шеннона В музее Массачусетского технологического института в Кембридже, штат Массачусетс, хранится релейная машина Клода Шеннона, которая производит вычисления в римской системе счисления (см. Рис. 1). Рис.1 : Тробак Шеннона (любезно предоставлен Музеем Массачусетского технологического института, Кембридж, Массачусетс) Throbac ( Thr ifty Ro man-numeral ba ckard looking c computer) — настольный калькулятор, который рассчитывает полностью в римской системе счисления.Он выполняет четыре основных арифметических операции (сложение, вычитание, умножение и деление) и работает так же, как используемый в то время электромеханический настольный калькулятор. Машина принимает разные варианты написания (IV или IIII, IL или XLIX). IIIIIV интерпретируется как 0. Умножение выполняется как повторное сложение, деление — как повторяющееся вычитание. При умножении 7 x 8 сначала вводится множимое VII, затем число множителя на число I, I, I, V. См. Также https: // www.Engage-csedu.org/find-resources/shannons-throbac. Ссылки Шеннон, Клод Э .: Throbac I, Bell Laboratories Memorandum, 9 апреля 1953 г. (Клод Элвуд Шеннон: сборник статей, изд. NJA Sloane, Aaron D. Wyner, Piscataway, NJ: IEEE Press 1993, стр. 695-698) Уильямс, Майкл Рой: История компьютерных технологий, издательство IEEE Computer Society Press, Лос-Аламитос, Калифорния 1997, страницы 7–8 Благодарности Большое спасибо Дебби Дуглас и Ариэль Вайнберг из Массачусетского технологического института. Герберт Брудерер — бывший преподаватель дидактики информатики в Высшей технической школе Цюриха. Совсем недавно он стал историком технологий. [email protected], [email protected] Записей не найдено Если вы действительно
потеряли, вы можете найти номер по алфавиту 1450 = MCDL Добро пожаловать в Brand Breakdown, серию исчерпывающих, но легко усваиваемых руководств для ваших любимых компаний, с идеями и информацией, которые вы не найдете на обычной странице «О компании». Джовани Панерай открыл свою первую часовую мастерскую во Флоренции, Италия, в 1860 году, и вскоре его деятельность расширилась, включив в себя оживленную мастерскую и первый во Флоренции центр обучения часовому искусству. К началу 20 века Panerai заключила контракты с Королевским флотом Италии, а в 1916 году Panerai получила важный патент на Radiomir, светящуюся краску на основе радия. Как и многие фирмы, застрявшие в фашистских странах, Panerai во время Второй мировой войны разрабатывала часы для не той стороны, но диктаторские полномочия и большие карманы Муссолини подтолкнули Panerai к быстрым инновациям.Они разработали кристалл Perspex (1936 г.), массивные светящиеся сэндвич-циферблаты (1938 г.), интегрированные проушины с пружинными стержнями (1940 г.) и механизм с 8-дневным запасом хода для уменьшения износа уплотнений заводной головки (также 1940 г.). После падения фашистов компания Panerai разработала свою знаменитую люминесцентную люминесцентную лампу на основе трития под названием Luminor (1949 г.) и фирменный замок заводной головки с рычажным приводом (1950 г.). Panerai Panerai не пользовались широкой аудиторией, пока в 1993 году они не представили гражданскую коллекцию и не получили одобрения Сильвестра Сталлоне.К 1997 году Panerai стала настолько успешной, что Vendome Group (позже Richemont Group) приобрела фирму, перенесла производство в Швейцарию и превратила Panerai в компанию роскошных спортивных часов, которую мы знаем сегодня. Panerai потребовалось некоторое время, чтобы избавиться от бравады Слая Рокки / Рэмбо и рассказать свою историю более прямо, но как только это произошло, компания предложила более тонкую форму хулиганства, основанную на морских приключениях. Италия почти полностью занимает побережье, а ее флот славится инновационными морскими технологиями и техникой.Panerai тут же создавала дайверские часы, датчики и компасы для этих первооткрывателей бездны. Между тем, компания поддерживает тесные отношения с гонками на яхтах, в том числе на старинных деревянных яхтах. Несмотря на перемещение производства в Швейцарию, стиль Panerai остается верным оригинальным итальянским образцам начала и середины 20 века, и сегодняшняя коллекция намного разнообразнее, чем когда-либо прежде. Panerai Обширный и разнообразный каталог Иногда различие между моделями заключается просто в материале корпуса или цвете циферблата, но покупка Panerai является обычным явлением, потому что предпочтительный внешний вид и посадка не всегда сопровождаются механизмом / функциями, которые вы предпочитаете, или наоборот. -versa. Мы стремимся максимально упростить навигацию по этому плотному каталогу. Номера Panerai Мануфактурные механизмы Panerai имеют номера калибра в следующем формате: P.xxxx. Лучший способ разделить и завоевать обширный каталог Panerai — это начать с интересующей вас коллекции, а затем выбрать размер корпуса, который вам подойдет лучше всего (помните, что Panerais предназначены для носить смело). Используя фильтр на сайте бренда, вы увидите, что, хотя в семействе Luminor есть 150 моделей, поэтому, если вы знаете, что размер 42 мм для вас, он легко сужает его до 6 (на момент написания).Затем вам нужно рассмотреть несколько цветов циферблата и усложнения. Однако большая часть разнообразия Panerai обусловлена его механизмами и усложнениями. Типичным примером Panerai, вполне возможно, является Luminor на 44 мм, но существует более 100 моделей, которые соответствуют этому описанию, поэтому, помимо сужения выбора по материалам корпуса, у вас также будет множество доступных функций. Для самых простых и начальных вариантов ознакомьтесь с линейкой Base Logo. Начиная с конца 1940-х годов, Panerai перешла от Radiomir lume к смеси на основе трития, запатентованной как Luminor.В 1950 году Panerai представила свой фирменный заводной замок. Линия Luminor отличается этим замком заводной головки, интегрированными ушками и формой амортизатора, которая уходит своими корнями в прошлое, но также была немного модернизирована для первой гражданской коллекции 1993 года. Сегодня это самый узнаваемый образ Panerai. МАГАЗИН ПРЕДНАЗНАЧЕННЫЙ В НАЛИЧИИ Panerai Panerai Luminor Base Logo PAM01086 Это классический образ Panerai за минимальные деньги, и он даже поставляется с мануфактурным механизмом.Базовый логотип — это самый простой логотип бренда, его несколько вариантов есть в коллекциях Luminor и Radiomir. Вы можете узнать время двумя стрелками с помощью простого механизма с ручным заводом и раскрашенного циферблата, а не фирменного «сэндвич-циферблата». В более новых моделях есть собственные механизмы, но были получены более старые. Диаметр : 44 мм Panerai Panerai Luminor Marina PAM02392 Заголовок здесь 42 мм .Многие люди находят большую часть каталога Panerai диаметром 44 мм, 45 мм и 47 мм просто громоздкой, несмотря на то, что им нравится все остальное в часах. Многие обрадовались, когда эта новая версия была представлена в TKTK, предлагая полный пакет — только в меньшем размере и более удобном для ношения. Обратите внимание, что они водонепроницаемы до 100 м, а не 300 м традиционных часов для дайвинга, но более чем достаточны для большинства нужд. Диаметр : 42 мм Panerai Panerai Luminor Power Reserve PAM00423 PAM 432 — удачный представитель мужских 47-миллиметровых часов марки, а также пример усложнений.Здесь у нас есть индикатор запаса хода, который вы найдете во многих других моделях, особенно полезный, поскольку здесь механизм заводится вручную. Вы также найдете другие усложнения, такие как GMT и хронографы с обратным ходом, часто в комбинации. Диаметр : 47 мм Panerai Panerai Luminor Marina Carbotech PAM01118 Panerai силен в стиле, но бренд демонстрирует его часовую сущность, предлагая перспективные и экспериментальные часы с использованием передовых материалов, сложных усложнений и отделки высокого класса, а также экзотических техник.Здесь бренд объединил свой запатентованный углеродный композитный материал Carbotech с люминесцентным светом, встроенным в корпус в неожиданных и нестандартных местах. Диаметр : 44 мм Хотя обычно он меньше, тоньше и выглядит немного «красивее», Due («двойка» по-итальянски) выглядит как Подколлекция линейки Luminor и отличается знакомым дизайном и механизмом блокировки защиты заводной головки. Понятно, что бренд хотел отделить его от знаменитого прочного Luminor с его происхождением часов для дайвинга, поскольку у Due есть только уровень водонепроницаемости на 30 м и более тонкий профиль.Линия Due, представленная в 2018 году, является ответом Panerai на потребности как в меньших, так и в более женственных моделях. МАГАЗИН ПРЕДНАЗНАЧЕННЫЙ В НАЛИЧИИ Panerai Panerai Luminor Due PAM00927 Имея схожий внешний вид и размер с 42-миллиметровыми моделями Luminor, поначалу может быть трудно сказать, что делает это должным. У него меньшая водонепроницаемость и более тонкий корпус, а эта конкретная модель предлагает такие функции, как матовый титан и автоматический механизм с 3-дневным запасом хода, а также в целом элегантное исполнение, основанное на винтажных моделях. Диаметр : 42 мм Panerai Panerai Piccolo Due PAM01029 Эти миниатюрные Panerais толщиной всего 38 мм из коллекции Luminor Due называются Piccolo Due. Самый маленький Panerai, который вы найдете, по-прежнему имеет привлекательный вид (без присутствия) и показывает, что харизма бренда не зависит от его размера.Эта модель изготовлена из золотого сплава Goldtech, но есть и более доступные версии из стали. Диаметр : 38 мм Ссылаясь на самые ранние военные часы Panerai 1930-х годов, модели Radiomir выделяются среди остальных коллекций по нескольким причинам. Во-первых, им не хватает выдающейся защиты заводной головки и механизма блокировки, которые почти определяют бренд и являются отличительной чертой всех остальных коллекций.У них также есть несколько стилей корпусов либо с проушинами, которые отсоединяются для замены ремешка, либо модели Radiomir 1940 со встроенными проушинами и пружинными стержнями. Часы Radiomir могут выглядеть относительно классически и по-старинному, но помните, что многие из них имеют размер, обеспечивающий очень заметное присутствие, в основном диаметром 45 или 47 мм. МАГАЗИН ПРЕДНАЗНАЧЕННЫЙ В НАЛИЧИИ Panerai Panerai Radiomir Base Logo PAM00753 Как и логотип Luminor Base, представленный выше, это самая простая и доступная модель Radiomir, а также общая точка входа для бренда.Никакого «сэндвич-циферблата» или автоматического подзавода, но вы получаете мануфактурный механизм, водонепроницаемость на 100 м и яркую форму запястья на 45 мм. Диаметр : 45 мм Panerai Panerai Radiomir California PAM00931 Без логотипа или текста на циферблате, только огромный стальной корпус диаметром 47 мм и циферблат California. Бренд немного поигрался с дизайном циферблатов в своей коллекции Radiomir, а Panerai — одна из часовых компаний, известных своими калифорнийскими циферблатами (наполовину римскими, наполовину арабскими цифрами).Эта конкретная модель имеет проволочные проушины, луковичную корону и светло-коричневый циферблат с градиентным эффектом. Внутри он оснащен мануфактурным механизмом с ручным заводом, показывающим только часы и минуты, но красиво оформленным и видимым через заднюю крышку. Диаметр : 47 мм Panerai Panerai Radiomir 1940 Tourbillon GMT Oro Rosso PAM00558 Это пример корпуса Radiomir 1940 со встроенными ушками, а также демонстрирующий взгляд бренда на классическое часовое искусство высокого класса.Несмотря на то, что он имеет относительно традиционный внешний вид, пара выдающихся особенностей не сразу бросается в глаза: во-первых, на задней крышке корпуса виден турбийон и индикатор запаса хода, а простой циферблат отображает время по Гринвичу и функции день / ночь. Наконец, он в массивном 48-миллиметровом корпусе из фирменного сплава Goldtech. Диаметр : 48 мм В 2019 году Panerai завершила свое специальное погружение часы в эту новую категорию, что значительно упростило их каталог.В то время как другие часы Panerai могут технически заслуживать названия часов для дайвинга из-за их происхождения и водонепроницаемости, у них есть такие особенности, как вращающиеся безели, которые мы склонны ассоциировать с современными дайверами. Он также отличается от других коллекций такими элементами, как дизайн циферблата и скелетонизированные стрелки. МАГАЗИН ПРЕДНАЗНАЧЕННЫЙ В НАЛИЧИИ Panerai Погружной аппарат Panerai PAM00973 Как и другие коллекции, многие часы Panerai Submersible для дайвинга имеют внушительные размеры, поэтому, когда бренд представил новую версию с диаметром 42 мм, многие люди были довольны.Его размер правильный, он водонепроницаем до 300 м и оснащен отличным автоматическим механизмом с 3-дневным запасом хода. Его цена соответствует вашим деньгам Submariner, но, несомненно, он предлагает более сильную и самобытную личность. Диаметр : 42 мм Panerai Panerai Luminor Submersible 1950 3-дневный автомат Bronzo PAM00382 Еще одна особенность Panerai — это раннее использование бронзы и соблазнительное название часов, сделанных из нее: Bronzo.Эти массивные 47-миллиметровые часы для дайвинга выглядят так, как будто они пришли из затонувшего корабля и готовы вернуться, чтобы исследовать его, только лучше и прочнее, чем их бронзовый корпус с патиной. Он также оснащен одним из самых привлекательных механизмов бренда с трехдневным запасом хода и автоматическим заводом. Диаметр : 47 мм Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты.Вы можете найти больше информации об этом и подобном контенте на сайте piano.io. Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу. Деление – интересная операция, в чем мы и убедимся с вами в этой статье! Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек. Записывается это так: 9:3, ответом будет цифра 3. Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное». Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12. Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше. Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2). Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется: Найти сумму цифр делимого. Поделить на 3 или 9 (в зависимости от того, что вам нужно). Если ответ получается без остатка, то и число поделится без остатка. Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка. Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет. Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей. Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель. В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки: Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой? Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок? Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук? Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже: Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача. Рассмотрим пример, 512:8. 1 шаг . Запишем делимое и делитель следующим образом: Частное будет записано в итоге под делителем, а расчеты под делимым. 2 шаг . 3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого: Теперь 51 больше 8. Это неполное частное. 4 шаг . Ставим точку под делителем. 5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку: 6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем: 7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»: 8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3. * 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3: 10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4. Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица. Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа. Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5): Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7. Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа. Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания. Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме. Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше. Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше. Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше. Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше. Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика. Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач. Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту. Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать. После прохождения курса ребенок сможет: Мозгу, как и телу нужен фитнес. Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их. Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон. Для деления чисел из двух и более цифр (знаков) применяют деление в столбик . По традиции, разбираться как делить столбиком будем на примере. Вычислить: Для начала запишем делимое и делитель в столбик. Выглядеть это будет так: Их частное (результат) будем записывать под делителем. У нас это цифра «8
». Начинаем делить «512
» на «8
» следующим образом: Берём «5
».
Цифра «5
» меньше «8
», значит нужно взять еще одну цифру из делимого. Запомните! Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном. Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас
после «51
» стоит только одно цифра
«2
». Значит и добавляем в результат ещё одну точку. Записываем «48
» под «51
». Запомните! При записи под неполном частным самая правая цифра неполного
частного должна стоять над самой правой цифрой произведения. Между «51
» и «48
» слева поставим «−
» (минус). Вычтем по правилам
вычитания в столбик «48
» и под чертой запишем результат. Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком . Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту: За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту: Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное: Под делимым будут записываться промежуточные вычисления: Полностью форма записи деления столбиком выглядит следующим образом: Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению: Деление столбиком выполняется поэтапно. это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него: В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого. Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр. Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка: Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше. К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль: Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем: Рассмотрим пример, когда в частном получаются нули. Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают: Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают: Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого: Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль: Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело: Рассмотрим пример, когда делимое оканчивается нулями. Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно: Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0: Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело: Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело: Пусть нам требуется разделить 1340 на 23. Определяем неполное делимое — это число 134. Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6: Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6: 1340: 23 = 58 (остаток 6) Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3: 3: 10 = 0 (остаток 3) Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить. Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения. Я уже писала о том, Эта статья может стать для вас полезной. На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи. Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению. Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением. Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно. Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель. Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения! По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик. Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел. Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить. Шаг 1 . Записываем числа, разделив их «уголком». Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1. Шаг 3. Переходим к оформлению деления столбиком: Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2. Записываем результат. Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик. Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2. Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28. Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134. Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост. Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Для того чтобы легко научить ребёнка операции деления нужно: Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях. Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т. Преподаватель, специалист детского развивающего центра Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик: Деление «уголком» — это, на мой взгляд, самая тяжелая, самая нудная тема во всей школьной математике. Тут нам придется всерьез поднапрячься. Пусть, однако, нас вдохновляет мысль, что весь последующий материал будет значительно легче и приятнее. Прежде всего, рассмотрим деление на однозначное число. Допустим, мы хотим вычислить значение выражения $648 / 2$. Пользуясь свойствами умножения, мы можем расписать делимое таким образом: $648 =$ $6$ $\,\cdot\,100~+$ $4$ $\,\cdot\,10~+~$ $8$ $~=$ $3$ $\,\cdot\,$ $2$ $\,\cdot\,100~+~$ $2$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $4$ $\,\cdot\,$ $2$ $~=$ $($ $3$ $\,\cdot\,100~+~$ $2$ $\,\cdot\,10~+~$ $4$ $)\,\cdot\,$ $2$ $~=$ $3$ $2$ $4$ $\,\cdot\,$ $2$ . После этого становится очевидно, что частное от деления равно $648 / 2 = 324$. Но это мы взяли самый что ни на есть простейший случай, когда каждую отдельно взятую цифру делимого можно поделить на делитель. А вот пример несколько посложнее: $156 / 2 =$ ? Здесь первая цифра оказалась меньше делителя. Поэтому, расписывая делимое, мы не будем отрывать ее от второй цифры: $156~=$ $15$ $\,\cdot\,10~+~$ $6$ . Поскольку число $15$ не делится нацело на $2$, придется нам прибегнуть к делению с остатком. Представим результат такого деления в виде: $15$ $~=~$ $7 \cdot 2$ $~+~$ $1$ $~=~$ $14$ $~+~$ $1$ . Теперь мы можем продолжать расписывать наше делимое дальше: $156 =$ $15$ $\,\cdot\,10~+~$ $6$ = ( $14$ $~+~$ $1$ )$\,\cdot\,10~+~$ $6$ $~=$ $14$ $\,\cdot\,10~+~$ $1$ $\,\cdot\,10~+~$ $6$ $~=$ $14$ $\,\cdot\,10~+~$ $16$ $~=$ $7$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $8$ $\,\cdot\,$ $2$ $~=$ ( $7$ $\,\cdot\,10~+~$ 8 )$\,\cdot\,$ $2$ $~=$ $7$ $8$ $\,\cdot\,$ $2$ . Отсюда моментально получаем ответ: $156 / 2 = 78$. Такого рода расчеты можно проводить в уме и сразу же писать ответ. Но мы сейчас перепишем их в виде краткой таблицы. Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто. Делимое и делитель запишем так: $1$ $5$ $6$ $2$ При делении первых двух разрядов ( $15$ ) на двойку получается $7$ плюс еще какой-то остаток. С этим остатком мы разберемся чуть позже, а пока запишем семерку под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ): $1$ $5$ $6$ $2$ $7$ Умножаем на эту семерку наш делитель ( $2$ ) и записываем ответ ( $14$ ) под первыми двумя разрядами делимого ( $15$ ): $1$ $5$ $6$ $2$ $1$ $4$ $7$ Теперь настало время вычислить остаток от деления $15$ на $2$ . $15$ $~-~$ $2$ $\,\cdot\,$ $7$ $~=~$ $15$ $~-~$ $14$ . У нас уже всё подготовлено, чтобы выполнить это вычитание «столбиком»: $1$ $5$ $6$ $2$ $1$ $4$ $7$ $1$ У нас получается единица , к которой мы приписываем шестерку из следующего разряда делимого: $1$ $5$ $6$ $2$ $1$ $4$ $7$ $1$ $6$ В результате такого приписывания у нас получается число $16$ . $1$ $5$ $6$ $2$ $1$ $4$ $7$ $8$ $1$ $6$ Ответ мы получили, однако правила составления таблицы таковы, что нам надо добавить в нее еще две строки. Мы должны формальным образом убедиться, что не потеряли остаток от деления. Умножаем делитель ( $2$ ) на последнюю цифру ответа ( $8$ ), приписываем результат ( $16$ ) снизу к нашей таблице в последние два разряда делимого: $1$ $5$ $6$ $2$ $1$ $4$ $7$ $8$ $1$ $6$ $1$ $6$ Вычитаем последнюю строку из предпоследней и получаем $0$: $1$ $5$ $6$ $2$ $1$ $4$ $7$ $8$ $1$ $6$ $1$ $6$ $0$ Этот последний ноль есть не что иное, как остаток от деления, который образовался бы в том случае, если бы мы рассматривали деление с остатком: $156 : 2 = 78~(\text{ост. Чтобы получше это понять, возьмем похожий пример, в котором, однако, остаток не равен нулю: $157 : 2 = 78~(\text{ост.}~1)$. Таблица для этого примера выглядит так: $1$ $5$ $7$ $2$ $1$ $4$ $7$ $8$ $1$ $7$ $1$ $6$ $1$ Здесь, опять-таки, остаток стоит в последней строке. $157~=$ $14$ $\,\cdot\,10~+~$ $17$ $~=$ $7$ $\,\cdot\,$ $2$ $\,\cdot\,10~+~$ $8$ $\,\cdot\,$ $2$ $~+~1~=$ ( $7$ $\,\cdot\,10~+~$ $8$ )$\,\cdot\,$ $2$ $~+~1~=$ $7$ $8$ $\,\cdot\,$ $2$ $~+~1$ Теперь мы готовы к тому, чтобы делить (нацело или с остатком) на многозначные числа. Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком: $135674 : 259~=~$? Приступаем к заполнению таблицы: $1$ $3$ $5$ $6$ $7$ $4$ $2$ $5$ $9$ В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого ( $1356$ ) и получившееся число поделить (с остатком) на делитель ( $259$ ). $1356$ : $259$ = ? Тут нам помогут приближенные вычисления, для которых, как мы знаем, вовсе необязательно, чтобы числа делились друг на друга нацело: $1356$ / $259$ $~\approx 1356 / 300 \approx 1500 / 300 = 15 / 3~=~$ $5$ . Зная результат приближенного деления, мы можем предположить, что, скорее всего, $1356$ : $259$ = $5$ (остаток — пока неважно какой). Конечно, абсолютной уверенности у нас нет. Здесь вместо пятерки вполне может стоять четверка или шестерка , однако вряд ли мы ошиблись больше, чем на одну единицу. Имея это в виду, тем не менее берем эту пятерку и заносим ее в нашу таблицу в строку ответа. После этого умножаем на нее делитель ( $259$ ) и при этом записываем ответ под делимым в подходящие разряды: $1$ $3$ $5$ $6$ $7$ $4$ $2$ $5$ $9$ $1$ $2$ $4$ $259$ $~\cdot~$ $5$ = $1$ $2$ $9$ $5$ $5$ Здесь «маленькие» цифры — это побочный продукт процедуры умножения: мы познакомились с ними, когда учились умножать «в столбик». Теперь выполняем вычитание в столбик и получаем: $1$ $3$ $5$ $6$ $7$ $4$ $2$ $5$ $9$ $1$ $2$ $4$ $259$ $~\cdot~$ $5$ = $1$ $2$ $9$ $5$ $5$ $6$ $1$ Внимательно приглядимся к полученной разности ( $61$ ). $1356$ : $259$ = $5$ (ост. $61$ ). Возвращаемся к таблице. К нашему остатку ( $61$ ) приписываем семерку из следующего разряда делимого и приступаем к нахождению второй цифры ответа. Это делается с помощью точно такой же процедуры, что и раньше. Потом — очередь за третьей цифрой. В конце концов таблица принимает такой вид: $1$ $3$ $5$ $6$ $7$ $4$ $2$ $5$ $9$ $1$ $2$ $4$ $259$ $~\cdot~$ $5$ = $1$ $2$ $9$ $5$ $5$ $2$ $3$ $6$ $1$ $7$ $1$ $1$ $259$ $~\cdot~$ $2$ $~=~$ $5$ $1$ $8$ $9$ $9$ $4$ $1$ $2$ $259$ $~\cdot~$ $3$ $~=~$ $7$ $7$ $7$ $2$ $1$ $7$ Можно выписывать окончательный ответ: $135674 : 259 = 523~(\text{ост}. Самая большая неприятность в делении «уголком» состоит в том, что приближенные вычисления, к которым приходится прибегать по ходу дела, не дают сразу гарантированно правильного результата и нуждаются иногда в последующей коррекции. Впрочем, по мере тренировки, у нас выработается особое чутье и мы будем уже сразу почти наверняка знать, какие цифры следует писать в строке ответа, чтобы потом ничего больше не надо было исправлять и переделывать. Разумеется, нам будут попадаться случаи, когда частное содержит нули. Каждый такой ноль позволит сделать в таблице небольшие сокращения. Вот пример такой таблицы: $2$ $6$ $2$ $7$ $4$ $0$ $8$ $7$ $2$ $2$ $2$ $6$ $1$ $3$ $0$ $2$ $0$ $1$ $7$ $4$ $1$ $1$ $1$ $7$ $4$ $0$ Как и в случае умножения «в столбик», для того чтобы было удобнее писать «маленькие» цифры, нам может понадобиться лист со специальной линовкой для вычислений (формат pdf). Теперь остается только тренироваться, тренироваться и тренироваться. Конспект Деление «уголком». Рассмотрим пример: делимое : делитель = частное (остаток такой-то). Наша задача — найти частное и остаток, если известны делимое и делитель. Решаем эту задачу в несколько шагов, на каждом из которых мы находим одну цифру частного. Шаг первый. Берем в делимом столько цифр спереди, чтобы они составляли число, которое при делении на делитель дает однозначное число и еще какой-то (промежуточный) остаток. Выполнив такое деление, выписываем полученное однозначное число в качестве первой цифры частного, а к промежуточному остатку приписываем в конец первую из оставшихся цифр делимого. В результате такого приписывания мы получаем число, которое мы передаем для дальнейшей «обработки» во второй шаг. Шаг второй. Число, поступившее для «обработки» из предыдущего шага, делим на делитель. В результате получаем однозначное число и какой-то еще промежуточный остаток. Описание последующих шагов в точности совпадает с описанием второго шага. Мы останавливаемся, когда в делимом больше не остается цифр для приписывания к очередному промежуточному остатку. К этому времени частное оказывается полностью выписанным, а последний промежуточный остаток и есть окончательный остаток в нашем исходном примере. Из «бесконечного» сборника типовых упражнений Деление нацело на однозначное число Деление с остатком на однозначное число Деление с остатком на однозначное число с возможным «приписыванием» нулей Деление нацело на двузначное число Деление с остатком на двузначное число Деление нацело на трехзначное число Деление с остатком на трехзначное число При делении с остатком на двузначное число рассуждают также, как и при делении без остатка. Объясни, как выполнено деление с остатком. Надо 324 разделить на 62. Надо 526 разделить на 74. Надо 793 разделить на 83. 211. Найди частное и остаток, проверь решение. — 156 |48 Проверка: 144 + 12 = 156 — 278 |62 Проверка: 248 + 30 = 278 — 346 |56 Проверка: 336 + 10 = 346 — 445 |73 Проверка: 438 + 7 = 445 212. 1 сутки = 24 часа — 290 |24 213. Площадь первого участка 120 м2, второго 160 м2. При одинаковой норме высева на 1 м2 на первом участке высеяли семян ржи на 1 кг меньше, чем на втором. Объясни, что означают выражения. 160 — 120 — разница между площадями участков 214. В международном автопробеге участвовало 350 машин. Экипаж каждой машины состоял из трёх спортсменов. До финиша не дошли 105 машин. Сколько машин и сколько спортсменов прибыли к финишу? 1) 350 – 105 = 245 (м. 215. Составь по задачам уравнения и реши их. 1) x — 28 = 58 + 37 2) x • 8 = 80 • 12 3) x : 28 = 300 — 203 216. 384 : 96 192 : 48 648 : 72 352 • 46 — 5840 : 80 — 384 |96 — 192 |48 — 648 |72 352 • 46 — 5840 : 80 = 16192 — 73 = 16119 _16192 217. 360 : 1 = 360 360 • 1 = 360 218. Выложи из палочек такую фигуру. Какие углы в этой фигуре? Переложи 4 палочки так, чтобы получилось два остроугольных треугольника. Будут ли эти треугольники равнобедренными? равносторонними? 399 : 57 236 : 59 475 : 95 609 • 27 — 4320 : 60 — 399 |57 — 236 |59 — 475 |95 609 • 27 — 4320 : 60 = 16443 — 72 = 16371 _16443 ЗАДАНИЕ НА ПОЛЯХ ГДЗ по математике. Учебник. Математика. 4 класс Содержание Инструкция Сначала проверьте навыки ребенка в умножении. Если ребенок нетвердо знает таблицу умножения, то с делением у него тоже могут быть проблемы. Тогда при объяснении деления можно разрешить подглядывать в шпаргалку, но таблицу все-таки придется выучить. Запишите делимое и делитель через разделительную вертикальную черту. Под делителем вы будете записывать ответ — частное, отделив его горизонтальной чертой. Возьмите первую цифру числа 372 и спросите у ребенка, сколько раз число шесть «помещается» в тройке. Правильно, нисколько. Тогда возьмите уже две цифры — 37. Для наглядности можно выделить их уголком. Снова повторите вопрос – сколько раз число шесть содержится в 37. Запишите 36 под цифрой 37, подведите чертой. Для наглядности в записи можно использовать знак . Под чертой поставьте остаток – 1. Теперь «спустите» следующую цифру числа, двойку, к единице – получилось 12. Объясните ребенку, что цифры всегда «спускаются» по одной. Опять спросите, сколько «шестерок» содержит 12. Ответ – 2, на этот раз без остатка. Напишите вторую цифру частного рядом с первой. Окончательный результат – 62. Также подробно рассмотрите случай деления . Например, 167/6 = 27, остаток 5. Скорее всего, ваш отпрыск про простые дроби пока ничего не слышал. Но если он будет задавать вопросы, что делать с остатком дальше, можно объяснить на примере яблок. 167 яблок разделили между шестью людьми. То есть результат можно записать так: 27 5/6. Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает. Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик. Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид: Пусть нам нужно разделить 6105 на 55 , запишем: Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так: Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений. Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это: Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Итак, сначала запишем делимое и делитель согласно методу деления в столбик. Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель. Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге. Вернемся к примеру. 2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8 Итак, мы сразу получили число, равное делимому. Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 . Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка. Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 . В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате: 3 · 0 = 0 7 Под делимым записываем число, полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 . В завершение операции вычитаем 6 из 7 и получаем: Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 . Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные. Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком. 1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 . 2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль: 0 , 1 , 2 , 3 и так далее. В соответствии с алгоритмом имеем: 4 · 0 = 0 14 . Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 . 4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Важно! Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком. 2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем: Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение. 3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 . 4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 . Принимаем это число за рабочее и снова выполняем пункты алгоритма. 2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом. 4 · 0 = 0 2 Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 . 4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа. Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма. Проделав все по правилам, получаем результат: Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем: В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена. Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно. Приведем другие примеры деления чисел в столбик и примеры записи решений. Пример 1. Деление натуральных чисел в столбик Разделим натуральное число 7136 на натуральное число 9 . После второго, третьего и четвертого шага алгоритма запись примет вид: Повторим цикл: Последний проход, и поучаем результат: Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 . При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев. Пример 2. Деление натуральных чисел в столбик Разделим число 7042035 на 7 . Ответ: 1006005 Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными. Перемножать большие числа, записывая их в строку, рано или поздно становится довольно сложным и утомительным процессом. Гораздо проще воспользоваться специальным алгоритмом по умножению в столбик: вам не придется держать числа в своей голове и что-либо запоминать. Вы можете делать пометки над столбиком, чтобы всегда видеть, как числа вам нужно перенести. Если вы пытаетесь обучить такому способу ребенка, то очень важно, чтобы таблица умножения отскакивала у него от зубов, иначе, процесс затянется надолго, а сам малыш совершит много ошибок, которые вереницей потянутся по всему примеру. Внимательно прочитайте статью и возьмите такой алгоритм себе на вооружение. Запишите пример в строчку и посмотрите: какой из множителей меньше? Меньший окажется ниже в записи умножения в столбик, а большой множитель будет стоять наверху. Запишите пример по такому принципу, как указано на картинке ниже. Если в примере есть множитель, который оканчивается на ноль или несколько нолей, то его следует записывать так: В таком случае, вы просто переносите это количество нолей сразу в ответ. Если ноли имеются и у первого множителя, и у второго, то сложите их количество и запишите в ответ. Теперь начинайте расчёт по такому принципу: Как только вы перемножите верхнее число на последнюю цифру нижнего и запишите свой ответ, начинайте перемножать следующее. По такому же принципу умножьте всё верхнее число на вторую с конца цифру нижнего. Также записывайте числа переноса, однако, ответ вам следует записать под первым решением, но сдвинув запись на одну клеточку левее. У вас получится столбик с выступающей влево строкой. Как вы уже догадались, вам нужно перемножить верхнее число на все цифры нижнего, начиная с конца. Каждый раз запись ответа переносится на одну клетку левее. Перемножьте таким образом все числа между собой. Теперь снова проведите черту под столбиком. Между всеми решениями поставьте знак сложения. Теперь вам осталось выполнить сложение в столбик, которое вы уже должны уметь делать: Под некоторыми числами вовсе не будет других – в таком случае, вы просто записываете это число в ответ. Не забывайте переносить в ответ все нули, которые стоят в конце множителей. Выполнять умножение в столбик очень удобно и быстро, особенно, если требуется перемножить большие числа. Вы легко можете проверить правильность умножения, просто разделив ответ на один из множителей. Для этого используйте калькулятор, либо способ деления уголком. На первых порах такое умножение занимает значительную долю времени, но с опытом, всё действие происходит всего за пару секунд. Азы деления столбиком и в уме дети изучают в начальной школе: в 3-м или 4-м классе. Но вникают в материал быстро и легко далеко не все третьеклассники. Дома нужно много практиковаться, решать тренировочные примеры. Но сначала лучше еще раз объяснить деление уголком, с остатком, выявить пробелы в детских знаниях. Как стать суперучителем без специальной подготовки и помочь ребенку с этой трудной темой, расскажем подробнее. Деление столбиком с остатком и без него нельзя начинать без подготовки. Сначала ребенок должен хорошо уметь и знать следующее: Отработайте все обозначенные умения до автоматизма. Затем приступайте к делению маленьких цифр на примере таблицы умножения в уме. Например, ребенок выучил, как умножать цифру 6: Смело предлагайте такие примеры: Через пару уроков школьник будет выполнять такие задания легко. Можно разнообразить занятия по устному счету играми на деление. На заметку! Все начальные математические навыки хорошо автоматизируются с помощью онлайн-тестов, где ребенок получает мгновенный результат своей работы. Интересные математические игры на деление помогают детям закрепить навык, узнать законы работы с цифрами, освоить устный счет. 45:9 120:60 14:7 Школьник должен вычислять результат к каждому заданию, а потом складывать все числа между собой. Получится так: Ребенок должен найти дерево под номером 9. Для игры можно использовать цветные пуговицы и ставить их на занятые деревья. Развлечение подходит для командных соревнований. После устной работы с делением натуральных чисел можно показать ребенку порядок записи примеров столбиком. Если педагогического опыта у вас нет, посмотрите видеоурок на эту тему, вспомните теорию сами. Теперь можно приступать к объяснению сложного материала школьнику. Есть несколько методик домашнего обучения делению: Родителям придется ненадолго стать педагогами. Оборудовать доску, купить мел или маркеры. Заранее вспомнить школьный материал. Объяснить пошагово теорию и закрепить ее на практике с помощью большого количества самостоятельных, карточек, контрольных работ. Например, это: Затем нужно обсуждать с малышом материал, закреплять навык на практике несколько недель. Деление не самая сложная тема в школьной программе. В начальных классах можно легко обойтись без платных уроков с педагогом. Этот вариант оставим на крайний случай. На заметку! Обязательно противопоставляйте деление умножению. Проверяйте результат обоих действий противоположным. Сначала стоит доходчиво объяснить, что такое деление на простом примере. Суть математического действия — разложить число поровну. В 3-м классе дети хорошо учатся на доступных примерах: раздают кусочки торта гостям, рассаживают кукол по 2 машинам. Когда малыш усвоит суть деления, покажите его запись на листке. Используйте уже знакомые задания с простыми числами: Желательно научить третьеклассника рассуждать в процессе вычисления вслух, выполнять действия на черновике. На заметку! Приучайте малыша постоянно проверять себя. Школьник должен понимать, что величина остатка вычитания в столбике деления должен всегда быть меньше делителя. Возьмите листок и ручку, посадите ребенка рядом. Сначала запишите пример уголком сами. Для деления на однозначное число выбирайте такие цифры, которые дают результат без остатка (полный ответ). Первый урок можно построить так: Для закрепления запишите еще 3–5 примеров на деление на этом же листочке. Не отходите далеко от школьника, образец не прячьте, не превращайте урок в проверочную работу. Малыш только учится делить. На этом этапе помогайте ему, подсказывайте и наталкивайте на правильное решение для повышения уверенности в себе. На заметку! Для автоматизации навыка деления столбиком можно составить небольшую памятку, где прописан каждый этап математического действия. Разрешайте школьнику смотреть в нее до тех пор, пока он сам не забудет об образце. Когда ученик 3-го класса усвоил деление на однозначное число, можно приступать к следующему этапу — работе с двузначными цифрами. Начинайте с простых, явных примеров, чтобы малыш понял алгоритм действий. Например, возьмите числа 196 и 28 и объясните принцип: Еще один вариант обучения: деление на двузначное число уголком. Для проверки правильности решение произведите умножение: 74х55=4070. Есть мнение! Иметь в доме решебник с ГДЗ многие родители считают недопустимым. А зря. С помощью готовых заданий ребенок может легко проверить себя. Главное — правильно объяснить школьнику назначение сборника ДЗ с ответами. Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы: При обучении решению задач с крупными числами действуйте поэтапно: Найдите неполное частное в примерах: 369:28; 897:12; 698:36. На заметку! Примеры с семизначными цифрами с третьеклассниками решать не нужно. Это лишнее. Достаточно остановиться на заданиях с пятизначными числами (до 10 000). Деление миллионов дети проходят в старших классах. Завершающим этапом уроков на закрепление навыка деления будет решение заданий с остатком. Они обязательно встретятся в решебнике для 3–4-го класса. В гимназиях с математическим уклоном школьники изучают не только неполные числа, но и десятичные дроби. Форма записи примера уголком останется прежней, отличаться будет только ответ. Примеры на деление с остатком берите несложные, можно преобразовывать уже решенные задания с целым числом в ответе, прибавляя к делимому единицу. Это очень удобно для ребенка, он сразу увидит, чем примеры похожи и чем отличаются. Урок может выглядеть так: На заметку! Отделять целое число от остатка запятой, делать из него дробное на начальном этапе обучения делению не нужно. Записывайте остаток отдельно, чтобы школьник видел конечный результат разности в столбике. Проверка деления производится с помощью умножения: делитель умножается на делитель. Теперь проверим: Для проверки деления с остатком нужно: 34+1 (остаток) =35 Алгоритм проверки правильности решения примера деления не изменяется от разрядности цифр. Важно! Первое время просите ребенка расписывать проверку умножением подробно, чтобы проверить и закрепить знание таблицы. Научиться быстро решать примеры с делением помогают тренировочные задания. Карточками может оканчиваться каждый урок после прохождения новой темы. В качестве домашнего математического тренажера используйте карточки с примерами. В них включайте разные случаи: с однозначными и многозначными числами, деление с полным результатом и остатком. Скачать карточки можно бесплатно. Раздаточный материал обязательно следует напечатать для проверочной работы. Ошибки с делением у детей в начальной школе встречаются довольно часто. Уделите этой теме максимум внимания и времени, чтобы усвоение последующего материала проходило без запинок. Используйте карточки, видеоуроки, постоянную тренировку навыка и повторение пройденных тем в игровой форме. Тогда домашние уроки не навеют на ребенку скуку и пройдут с максимальной пользой. ВАЖНО ! *при копировании материалов статьи обязательно указывайте активную ссылку на перво Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу. Деление – интересная операция, в чем мы и убедимся с вами в этой статье! Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно. Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное». Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12. Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше. Например, поделим 17 на 5. Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1). Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется: Найти сумму цифр делимого. Поделить на 3 или 9 (в зависимости от того, что вам нужно). Если ответ получается без остатка, то и число поделится без остатка. Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка. Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет. Умножение и деление – это противоположные друг другу операции. Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей. Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель. В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки: Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой? Задача 2 . Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково? Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук? Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже: Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача. Рассмотрим пример, 512:8. 1 шаг . Запишем делимое и делитель следующим образом: Частное будет записано в итоге под делителем, а расчеты под делимым. 2 шаг . Деление начинаем слева направо. Сначала берем цифру 5: 3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого: Теперь 51 больше 8. Это неполное частное. 4 шаг . Ставим точку под делителем. 5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку: 6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем: 7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»: 8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3. * 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3: 10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4. Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица. Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа. Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5): Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7. Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа. Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания. Презентация – еще один способ наглядно показать тему деления. Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме. Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше. Игра «Упрощение» развивает мышление и память. Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше. Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше. Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше. Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика. Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач. Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту. Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек. Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их. Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон. Напомним, что разделить натуральное число a на натуральное число b – это значит представить число a в виде: a = bc + r , где частное c и остаток r – целые неотрицательные числа, причем остаток r удовлетворяет неравенству: Если друг на друга делить многочлены, то возникает похожая ситуация. Действительно, при выполнении над многочленами операций сложения, вычитания и умножения результатом всегда будет многочлен. В частности, при перемножении двух многочленов, отличных от нуля, степень произведения будет равна сумме степеней сомножителей. Однако в результате деления многочленов многочлен получается далеко не всегда. Говорят, что один многочлен нацело (без остатка) делится на другой многочлен, если результатом деления является многочлен. Если же один многочлен не делится нацело на другой многочлен, то всегда можно выполнить деление многочленов с остатком, в результате которого и частное, и остаток будут многочленами. Определение. Разделить многочлен a(x) на многочлен b(x) с остатком – это значит представить многочлен a(x) в виде a(x) = b(x) c(x) + r(x) , где многочлен c(x) – частное, а многочлен r(x) – остаток, причем, степень остатка удовлетворяет неравенству: Очень важно отметить, что формула a(x) = b(x) c(x) + r(x) является тождеством, т. При делении (с остатком или без остатка) многочлена на многочлен меньшей степени в частном получается многочлен, степень которого равна разности степеней делимого и делителя. Один из способов деления многочленов с остатком – это деление многочленов «уголком», что представляет собой полную аналогию с тем, как это происходит при делении целых чисел. К описанию этого способа деления многочленов мы сейчас и переходим. Пример. Заранее расположив многочлены по убывающим степеням переменной, разделим многочлен 2x4 – x3 + 5x2 – 8x + 1 на многочлен x2 – x + 1 . Решение. Опишем алгоритм деления многочленов «уголком» по шагам: 2x4 – 2x3 + 2x2 пишем под делимым 2x4 – x3 + 5x2 – 8x + 1 . x3 + 3x2– 8x . Если бы этот остаток был равен нулю, или был многочленом, степень которого меньше, чем степень делителя ( в данном случае меньше 2), то процесс деления был бы закончен. Однако это не так, и деление продолжается. x3 – x2 + x пишем под первым остатком x3 + 3x2– 8x . 4x2 – 9x + 1 . Если бы этот остаток был бы равен нулю, или был многочленом, степень которого меньше, чем степень делителя, то процесс деления был бы закончен. Однако это не так, и деление продолжается. 4x2 – 4x + 4 пишем под вторым остатком. – 5x – 3 . Степень этого остатка равна 1, что меньше, чем степень делителя. Следовательно, процесс деления закончен. 2x4 – x3 + 5x2 – 8x + 1 = где Запись изложенного процесса деления многочленов «уголком» имеет следующий вид: На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике. Как делить десятичные дроби на натуральные числа? Рассмотрим правило и его применение на примерах. Чтобы разделить десятичную дробь на натуральное число, надо: 1) разделить десятичную дробь на число, не обращая внимания на запятую; 2) когда закончится деление целой части, в частном поставить запятую. Примеры. Разделить десятичные дроби: Чтобы разделить десятичную дробь на натуральное число, делим, не обращая внимания на запятую. 5 на 6 не делится, поэтому в частном ставим нуль. Деление целой части окончено, в частном ставим запятую. Сносим нуль. 50 делим на 6. Берем по 8. 6∙8=48. От 50 вычитаем 48, в остатке получаем 2. Сносим 4. 24 делим на 6. Получаем 4. В остатке — нуль, значит, деление окончено: 5,04: 6 = 0,84. 2) 19,26: 18 Делим десятичную дробь на натуральное число, не обращая внимания на запятую. Делим 86 на 25. Берем по 3. 25∙3=75. От 86 вычитаем 75. В остатке — 11. Деление целой части окончено, в частном ставим запятую. Сносим 5. Берем по 4. 25∙4=100. От 115 вычитаем 100. Остаток — 15. Сносим нуль. 150 делим на 25. Получаем 6. Деление окончено: 86,5: 25 = 3,46. 4) 0,1547: 17 Нуль на 17 не делится, в частном пишем нуль. Деление целой части окончено, в частном ставим запятую. Сносим 1. 1 на 17 не делится, в частном пишем нуль. Сносим 5. 15 на 17 не делится, в частном пишем нуль. Сносим 4. Делим 154 на 17. Берем по 9. 17∙9=153. От 154 вычитаем 153. В остатке — 1. Сносим 7. Делим 17 на 17. Получаем 1. Деление окончено: 0,1547: 17 = 0,0091. 5) Десятичная дробь может получиться и при делении двух натуральных чисел. При делении 17 на 4 берем по 4. И еще пара примеров на деление десятичных дробей на натуральные числа: В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий. Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней. Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение. Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще. Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению: Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ. Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае. Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую. Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33: До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату? После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным. Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже: Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами. Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Рассмотреть такое деление можно на примере — 12082: 863. Ответом в примере будет число 14. Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80. Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше. Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше. Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду. Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число. Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами. В качестве примера: 28,4 делим на 3,2: Деление закончено. Результат примера 28,4:3,2 равен 8,875. Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями. Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части. При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части). Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули. В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам. Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9. Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму. Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным. Деление столбиком неотъемлемая часть школьной программы и необходимое знание для ребенка. Чтобы избежать проблем на уроках и с их выполнением, следует давать ребенку основные знания еще с маленького возраста. Гораздо легче объяснять ребенку определенные вещи и процессы в игровой форме, а не в формате стандартного урока (хотя на сегодняшний день существует достаточно разнообразных методик обучения в разных формах). Из этой статьи вы узнаете Дети постоянно сталкиваются с разными математическими терминами, даже не подозревая, откуда они. Ведь многие мамочки, в форме игры, объясняют ребенку, что папы больше тарелка, в садик ходить дальше, чем в магазин и другие незамысловатые примеры. Всё это представляет ребенку первоначальное впечатление о математике, еще до похода ребёнка в первый класс. Чтобы научить ребёнка делить без остатка, а позже с остатком, необходимо прямо предложить поиграть малышу в игры с делением. Разделите, например, конфеты между собой, а затем по очереди добавляйте следующих участников. Сначала ребенок будет делить конфеты, отдавая каждому участнику по одной. А в конце вместе сделаете вывод. Следует пояснить, что «разделить» — значит всем одинаковое число конфет. Если Вам необходимо растолковать этот процесс с помощью цифр, то можно привести пример в форме игры. Можно сказать, что цифра – это конфета. Следует объяснить, что число конфет, которые нужно делить между участниками – делимое. А количество человек, на которых делят эти конфеты – это делитель. Потом следует показать это все наглядно, привести «живые» примеры, чтобы быстрее научить кроху делить. Играя, он намного быстрее все поймет и усвоит. Пока алгоритм объяснить будет сложно, и сейчас это не нужно. Объяснение крохе разных математических действий – это хорошая подготовка к походу в класс, особенно математический класс. Если Вы решили перейти к обучению ребенка делению столбиком, значит такие действия как сложение, вычитание, и что такое таблица умножения он уже усвоил. Если же это у него все еще вызывает некоторые сложности, то нужно подтянуть все эти знания. Стоит напомнить алгоритм действий предыдущих процессов, научить свободно пользоваться своими знаниями. Для облегчения понимания этого, сейчас есть таблица деления для малышей. Принцип у нее такой же, как и у таблиц умножения. Но нужна ли уже такая таблица, если малыш знает таблицу умножения? Это зависит от школы и учителя. При формировании понятия «деление» нужно обязательно делать все в игровой форме, приводить все примеры на знакомых ребенку вещах и предметах. Очень важно, чтобы все предметы были четного числа, чтобы малышу было ясно, что итогом являются равные части. Это будет правильно, поскольку позволит крохе осознать, что деление — процесс обратный умножению. Если предметы будут нечетного количества, то итог выйдет с остатком и малыш запутается. При объяснении малышу взаимосвязи между умножением и делением, необходимо это все наглядно показывать на каком-либо примере. Например: 5 х 3 = 15. Вспомните, что итог умножения это произведение двух чисел. И только после этого, объясняйте, что это обратный процесс к умножению и продемонстрируйте это наглядно с помощью таблицы. Скажите, что нужно поделить результат «15» — на какой-то из множителей («5»/ «3»), и итогом будет постоянно иной, не принимавший участие в делении, множитель. Также необходимо растолковать малышу, как правильно называются категории, которые выполняют деление: делимое, делитель, частное. И снова с помощью примера покажите, что из них является конкретной категорией. Деление столбиком вещь не очень сложная, у нее есть свой легкий алгоритм, которому малыша нужно научить. После закрепления всех этих понятий и знаний, можно переходить к дальнейшему обучению. В принципе, родителям стоит выучить с любимым чадом таблицу умножения в обратном порядке, и наизусть ее запомнить, так как это будет нужным при обучении делению столбиком. Это делать необходимо до похода в первый класс, чтобы ребенку в школе было намного легче освоиться, и успевать за школьной программой, и чтобы класс из-за небольших неудач не начал дразнить ребенка. Прежде чем приступить к занятию, нужно вспомнить названия цифр при делении. Что такое делитель, делимое и частное. Ребенок должен без ошибок делить эти цифры на правильные категории. Самое главное при обучении деления столбиком, это усвоить алгоритм, который, в общем, довольно простой. Но сначала объясните ребенку значение слова «алгоритм», если он забыл его или до этого не изучал. В том случае, если кроха прекрасно разбирается в таблице умножения и обратного деления, у него не будет никаких сложностей. Однако на полученном результате долго задерживаться нельзя, необходимо регулярно тренировать приобретенные умения и навыки. Двигайтесь далее, как только станет ясно, что малыш понял принцип метода. Необходимо научить малыша делить столбиком без остатка и с остатком, чтобы ребенок не пугался, что у него что-то не получилось разделить правильно. Чтобы было проще обучить малыша процессу деления необходимо: Нужно побуждать интерес малыша к математическим процессам, чтобы этот урок в школе приносил ему удовольствие и желание учиться, и не мотивировать его на одних на уроках, но и в жизни. Ребенок должен носить разные инструменты для уроков математики, учиться ими пользоваться. Однако если ребенку тяжело все носить, то не стоит его перегружать. Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор. Главной особенностью программы является уникальность расчета математических операций. Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками: Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради. Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком: Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании. Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит. Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях. Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Деление – интересная операция, в чем мы и убедимся с вами в этой статье! Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек. Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно. Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное». Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12. Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше. Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2). Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1). Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется: Найти сумму цифр делимого. Поделить на 3 или 9 (в зависимости от того, что вам нужно). Если ответ получается без остатка, то и число поделится без остатка. Например, число 18. Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет. Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки. Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей. Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки: Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой? Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок? Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково? Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук? Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача. Рассмотрим пример, 512:8. 1 шаг . Запишем делимое и делитель следующим образом: Частное будет записано в итоге под делителем, а расчеты под делимым. 2 шаг . Деление начинаем слева направо. Сначала берем цифру 5: 3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого: Теперь 51 больше 8. Это неполное частное. 4 шаг . Ставим точку под делителем. 5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку: 6 шаг . Начинаем операцию деления. 7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»: 8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3. * 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3: 10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4. Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица. Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа. Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7. Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни. Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа. Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания. Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите! Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме. Игра «Угадай операцию» развивает мышление и память. Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше. Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше. Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше. Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика. Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач. Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям. Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня. Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек. Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их. Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал. Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление». Итак, как объяснить ребенку деление столбиком : Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе. Начинайте с простого — деление на однозначное число: Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться. Например, 256 разделить на 4: Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа. Выполните вместе такое простое действие: 184:23 — как нужно объяснять: Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит. Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа: Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число. Например: Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно. Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему. Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3): После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3: Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал. Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление. Алгоритм деления чисел заключается в следующем: По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее). Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например: Для закрепления результата можно использовать такие игры на деление: Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту. Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Деление – интересная операция, в чем мы и убедимся с вами в этой статье! Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек. Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно. Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное». Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12. Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше. Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2). Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1). Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется: Найти сумму цифр делимого. Поделить на 3 или 9 (в зависимости от того, что вам нужно). Если ответ получается без остатка, то и число поделится без остатка. Например, число 18. Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет. Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки. Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей. Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки: Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой? Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок? Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково? Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук? Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача. Рассмотрим пример, 512:8. 1 шаг . Запишем делимое и делитель следующим образом: Частное будет записано в итоге под делителем, а расчеты под делимым. 2 шаг . Деление начинаем слева направо. Сначала берем цифру 5: 3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого: Теперь 51 больше 8. Это неполное частное. 4 шаг . Ставим точку под делителем. 5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку: 6 шаг . Начинаем операцию деления. 7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»: 8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3. * 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3: 10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4. Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица. Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа. Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7. Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни. Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа. Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания. Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите! Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме. Игра «Угадай операцию» развивает мышление и память. Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше. Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше. Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше. Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика. Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач. Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям. Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня. Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек. Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их. Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Деление многозначных или многоразрядных чисел удобно производить письменно в столбик . Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого. Итак, поделим 354 на 2 . Для начала разместим эти числа как показано на рисунке: Делимое размещаем слева, делитель справа, а частное будем записывать под делителем. Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое , для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем. 3 больше 2 , значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3. 2 × 1
= 2
(2 2 × 2 = 4 (4 > 3) 2 меньше 3 , а 4 больше, значит, берем первый пример и множитель 1 . Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым: Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем: Полученное значение сравниваем с делителем. 15 больше 2 , значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15 : 2 × 7
= 14
(14 2 × 8 = 16 (16 > 15) Искомый множитель 7 , записываем его в частное на место второй точки (в десятки). Продолжаем деление, для чего находим третье неполное делимое . Спускаем следующий разряд делимого: Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления: 2 × 7
= 14 Результат деления третьего неполного делимого на делитель пишем в частное, находим разность: Разность мы получили равную нулю, значит деление произведено правильно . Усложним задачу и приведем другой пример: 1020 ÷ 5 Запишем наш пример в столбик и определим первое неполное частное: Разряд тысяч делимого составляет 1 , сравниваем с делителем: 1 Добавляем в неполное делимое разряд сотен и сравниваем: 10 > 5 – мы нашли неполное делимое. Делим 10 на 5 , получаем 2 , записываем результат в частное. Разность между неполным делимым и результатом умножения делителя и найденного разряда частного. 10 – 10 = 0 0 мы не пишем, опускаем следующий разряд делимого – разряд десятков: Сравниваем второе неполное делимое с делителем. 2 Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0 : 20 ÷ 5 = 4 Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0 , значит пример решён правильно . И ещё 2 правила деления в столбик: 1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например: Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя. 2. Если в делимом после деления остались нули, то их следует перенести в частное: Итак, сформулируем последовательность действий при делении в столбик. а) выделяем в неполный делитель старший разряд делимого; б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в) , если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4 ; в) добавляем в неполное делимое следующий разряд и переходим к пункту (б) . а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4; б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0; в) переходим к пункту (а). 10. Если мы выполняли деление без остатка и последняя найденная разность равна 0 , то мы правильно выполнили деление . Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично: Вычитание многозначных чисел обычно выполняют столбиком, записывая числа друг под другом (уменьшаемое сверху, вычитаемое снизу) так, чтобы цифры одинаковых разрядов стояли друг под другом (единицы под единицами, десятки под десятками и т. д.). Слева между числами ставится знак действия. Под вычитаемым проводят черту. Вычисление начинают с разряда единиц: из единиц вычитают единицы, затем из десятков — десятки и т. д. Результат вычитания записывают под чертой: Рассмотрим пример, когда в каком-либо разряде цифра уменьшаемого меньше цифры вычитаемого: От 2 мы не можем отнять 9, что нам делать в этом случае? В разряде единиц у нас нехватка, но в разряде десятков у уменьшаемого аж 7 десятков, поэтому мы можем один из этих десятков перекинуть в разряд единиц: В разряде единиц у нас было 2, мы перекинули десяток, стало 12 единиц. Вычитание столбиком обычно не записывают так подробно, вместо этого, над цифрой разряда, у которого будет занята единица, ставят точку, чтобы не запоминать, у какого разряда надо будет дополнительно вычесть единицу: При этом говорят так: из 2 вычесть 9 нельзя, занимаем единицу, из 12 вычитаем 9 — получим 3, пишем 3, в разряде десятков у нас было 7 единиц, мы одну перекинули, осталось 6, пишем 6 . Теперь рассмотрим вычитание столбиком из чисел, содержащих нули: Начинаем вычитать. От 7 отнимаем 3, пишем 4. От нуля мы не можем отнять 5, поэтому мы вынуждены занять единицу в старшем разряде, но в старшем разряде у нас тоже 0, поэтому и для этого разряда мы вынуждены занять в более старшем разряде. Занимаем единицу из разряда тысяч, получаем 10 сотен: Одну из единиц разряда сотен мы занимаем в младший разряд, получаем 10 десятков. В разряде сотен у нас осталось 9 единиц поэтому, от 9 отнимаем 6, пишем 3. В разряде тысяч у нас была единица, но мы её потратили на младшие разряды, поэтому здесь остаётся нуль (его записывать не надо). В результате мы получили число 354: Такая подробная запись решения была приведена, чтобы было проще понять, как выполняется вычитание столбиком из чисел содержащих нули. Как уже упоминалось, на практике решение обычно записывается так: А все упомянутые действия выполняются в уме. Чтобы было легче выполнять вычитание, запомните простое правило: Если при вычитании столбиком над нулём стоит точка, нуль превращается в 9. Данный калькулятор поможет вам выполнить вычитание чисел столбиком. Просто введите уменьшаемое и вычитаемое и нажмите кнопку Вычислить. Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком . Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту: Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное: Под делимым будут записываться промежуточные вычисления: Полностью форма записи деления столбиком выглядит следующим образом: Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению: Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого: это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него: В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого. Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр. Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка: Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6: Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль: Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем: Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9. Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают: Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого: Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль: Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело: Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6. Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно: Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0: Сносим следующую цифру делимого — 0. Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело: Пусть нам требуется разделить 1340 на 23. Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19: Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6: Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6: 1340: 23 = 58 (остаток 6) Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. 3: 10 = 0 (остаток 3) Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить. Главная >
Образование >
Математика >
МАТЕМАТИКА «С НУЛЯ» (учебник) > << Назад | Оглавление | Далее >> Деление «уголком» — это, на мой взгляд, самая тяжелая, самая нудная тема во всей школьной математике. Тут нам придется всерьез поднапрячься. Пусть, однако, нас вдохновляет мысль, что весь последующий материал будет значительно легче и приятнее. Прежде всего, рассмотрим деление на однозначное число. Допустим, мы хотим вычислить значение выражения 648 / 2. Пользуясь свойствами умножения, мы можем расписать делимое таким образом: 648 = 6 ∙ 100 + 4 ∙ 10 + 8 = 3 ∙ 2 ∙ 100 + 2 ∙ 2 ∙ 10 + 4 ∙ 2 = ( 3 ∙ 100 + 2 ∙ 10 + 4 ) ∙ 2 = 324 ∙ 2 . После этого становится очевидно, что частное от деления равно 648 / 2 = 324. Но это мы взяли самый что ни на есть простейший случай, когда каждую отдельно взятую цифру делимого можно поделить на делитель. А вот пример несколько посложнее: 156 / 2 = ? Здесь первая цифра оказалась меньше делителя. Поэтому, расписывая делимое, мы не будем отрывать ее от второй цифры: 156 = 15 ∙ 10 + 6 . Поскольку число 15 не делится нацело на 2, придется нам прибегнуть к делению с остатком. Представим результат такого деления в виде: 15 = 7 ∙ 2 + 1 = 14 + 1 . Теперь мы можем продолжать расписывать наше делимое дальше: 156 = 15 ∙ 10 + 6 = ( 14 + 1 ) ∙ 10 + 6 = 14 ∙ 10 + 1 ∙ 10 + 6 = 14 ∙ 10 + 16 = 7 ∙ 2 ∙ 10 + 8 ∙ 2 = ( 7 ∙ 10 + 8 ) ∙ 2 = 78 ∙ 2 . Отсюда моментально получаем ответ: 156 / 2 = 78. Такого рода расчеты можно проводить в уме и сразу же писать ответ. 1 5 6 2 При делении первых двух разрядов ( 15 ) на двойку получается 7 плюс еще какой-то остаток. С этим остатком мы разберемся чуть позже, а пока запишем семерку под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ): 1 5 6 2 7 Умножаем на эту семерку наш делитель ( 2 ) и записываем ответ ( 14 ) под первыми двумя разрядами делимого ( 15 ): 1 5 6 2 1 4 7 Теперь настало время вычислить остаток от деления 15-ти на 2 . 15 − 2 ∙ 7 = 15 − 14 . У нас уже всё подготовлено, чтобы выполнить это вычитание «столбиком»: 1 5 6 2 1 4 7 1 У нас получается единица , к которой мы приписываем шестерку из следующего разряда делимого: 1 5 6 2 1 4 7 1 6 В результате такого приписывания у нас получается число 16 . 1 5 6 2 1 4 7 8 1 6 Ответ мы получили, однако правила составления таблицы таковы, что нам надо добавить в нее еще две строки. Мы должны формальным образом убедиться, что не потеряли остаток от деления. Умножаем делитель ( 2 ) на последнюю цифру ответа ( 8 ), приписываем результат ( 16 ) снизу к нашей таблице в последние два разряда делимого: 1 5 6 2 1 4 7 8 1 6 1 6 Вычитаем последнюю строку из предпоследней и получаем 0: 1 5 6 2 1 4 7 8 1 6 1 6 0 Этот последний нуль есть не что иное, как остаток от деления, который образовался бы в том случае, если бы мы рассматривали деление с остатком: 156 : 2 = 78 (ост. Чтобы получше это понять, возьмем похожий пример, в котором, однако, остаток не равен нулю: 157 : 2 = 78 (ост. 1). Таблица для этого примера выглядит так: 1 5 7 2 1 4 7 8 1 7 1 6 1 Здесь, опять-таки, остаток стоит в последней строке. Для полноты картины распишем наше делимое в таком виде: 157 = 14 ∙ 10 + 17 = 7 ∙ 2 ∙ 10 + 8 ∙ 2 + 1 = ( 7 ∙ 10 + 8 ) ∙ 2 + 1 = 7 8 ∙ 2 + 1 Теперь мы готовы к тому, чтобы делить (нацело или с остатком) на многозначные числа. 135674 : 259 = ? Приступаем к заполнению таблицы: 1 3 5 6 7 4 2 5 9 В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого ( 1356 ) и получившееся число поделить (с остатком) на делитель ( 259 ). Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( 135 ) оказалось бы меньше делителя ( 259 ), а это совсем не то, из чего можно было бы извечь полезную информацию. 1356 : 259 = ? Тут нам помогут приближенные вычисления, для которых, как мы знаем, вовсе необязательно, чтобы числа делились друг на друга нацело: 1356 / 259 ≈ 1356 / 300 ≈ 1500 / 300 = 15 / 3 = 5 . Зная результат приближенного деления, мы можем предположить, что, скорее всего, 1356 : 259 = 5 (остаток — пока неважно какой). Конечно, абсолютной уверенности у нас нет. Здесь вместо пятерки вполне может стоять четверка или шестерка , однако вряд ли мы ошиблись больше, чем на одну единицу. Имея это в виду, тем не менее берем эту пятерку и заносим ее в нашу таблицу в строку ответа. После этого умножаем на нее делитель ( 259 ) и при этом записываем ответ под делимым в подходящие разряды: 1 3 5 6 7 4 2 5 9 1 2 4 259 ∙ 5 = 1 2 9 5 5 Здесь «маленькие» цифры — это побочный продукт процедуры умножения: мы познакомились с ними, когда учились умножать «в столбик». Теперь выполняем вычитание в столбик и получаем: 1 3 5 6 7 4 2 5 9 1 2 4 259 ∙ 5 = 1 2 9 5 5 6 1 Внимательно приглядимся к полученной разности ( 61 ). 1356 : 259 = 5 (ост. 61 ). Возвращаемся к таблице. К нашему остатку ( 61 ) приписываем семерку из следующего разряда делимого и приступаем к нахождению второй цифры ответа. Это делается с помощью точно такой же процедуры, что и раньше. Потом — очередь за третьей цифрой. В конце концов таблица принимает такой вид: 1 3 5 6 7 4 2 5 9 1 2 4 259 ∙ 5 = 1 2 9 5 5 2 3 6 1 7 1 1 259 ∙ 2 = 5 1 8 9 9 4 1 2 259 ∙ 3 = 7 7 7 2 1 7 Можно выписывать окончательный ответ: 135674 : 259 = 523 (ост. Самая большая неприятность в делении «уголком» состоит в том, что приближенные вычисления, к которым приходится прибегать по ходу дела, не дают сразу гарантированно правильного результата и нуждаются иногда в последующей коррекции. Впрочем, по мере тренировки, у нас выработается особое чутье и мы будем уже сразу почти наверняка знать, какие цифры следует писать в строке ответа, чтобы потом ничего больше не надо было исправлять и переделывать. Разумеется, нам будут попадаться случаи, когда частное содержит нули. Каждый такой нуль позволит сделать в таблице небольшие сокращения. Вот пример такой таблицы: 2 6 2 7 4 0 8 7 2 2 2 6 1 3 0 2 0 1 7 4 1 1 1 7 4 0 Как и в случае умножения «в столбик», для того чтобы было удобнее писать «маленькие» цифры, нам может понадобиться лист со специальной линовкой для вычислений (формат pdf).
\((x-1)(x-2)(x-\sqrt{2})(x+\sqrt{2})≥0\)
Вот сейчас все готово для применения метода интервалов.
Запишем ответ.
Ответ: \((-∞;-\sqrt{2}]∪[1;\sqrt{2}]∪[2;∞)\).
Скачать статью Делить десятичные дроби в столбик немного сложнее, чем целые числа из-за плавающей точки, еще задачу усложняет надобность деления остатка. Поэтому если вы хотите упростить этот процесс или проверить свой результат, можно воспользоваться онлайн-калькулятором, который не только выведет ответ, но и покажет всю процедуру решения. Читайте также: Конвертеры величин онлайн Подходящих под эту цель онлайн-сервисов существует большое количество, однако практически все они мало чем отличаются друг от друга. Сайт OnlineMSchool был разработан для изучения математики. Сейчас на нем присутствует не только множество полезной информации, уроков и задач, но и встроенные калькуляторы, один из которых мы сегодня задействуем. Деление в столбик десятичных дробей в нем происходит так: Перейти на сайт OnlineMSchool Перед тем как делить остаток, внимательно изучите условие задачи. Часто этого делать не нужно, иначе ответ могут засчитать неправильным. Всего за семь простых шагов мы смогли поделить десятичные дроби в столбик с помощью небольшого инструмента на сайте OnlineMSchool. Онлайн-сервис Rytex также помогает в изучении математики, предоставляя примеры и теорию. Однако сегодня нас интересует присутствующий в нем калькулятор, переход к работе с которым осуществляется следующим образом: Перейти на сайт Rytex Как видите, рассмотренные нами сервисы практически не отличаются между собой, разве что только внешним видом. Поэтому можно сделать вывод – нет разницы, какой веб-ресурс использовать, все калькуляторы считают правильно и предоставляют развернутый ответ по вашему примеру. Читайте также: Мы рады, что смогли помочь Вам в решении проблемы. ДА НЕТ Разделите \ (8932 \) на \ (7 \) — \ ((8932 \ div 7) \). Следовательно, \ (8932 \ div 7 = 1276 \) Теперь попробуйте ответить на вопрос, приведенный ниже. Разделите \ (346 \) на \ (8 \) — \ ((346 \ div 8) \) Следовательно \ (346 \ div 8 = 43 \ cdot 25 \) NULLIF, WHERE Вы хотите выполнить деление в своем SQL-запросе, но знаменатель — это выражение, которое может быть нулевым. База данных выдаст вам ошибку, когда знаменатель фактически равен нулю. В нашей базе данных есть таблица с именем Давайте разделим цену за акцию на разницу между доходами и расходами, чтобы определить коэффициент P / E (соотношение цены и прибыли) для каждого года. Этот запрос возвращает коэффициент P / E для каждого года, как описано в формулировке задачи: Если разница между доходами и расходами равна нулю (как в случае с 2017 годом), функция Если вы хотите изящно обрабатывать деление на ноль, вы можете использовать функцию Эту функцию можно использовать для обработки потенциального деления на ноль, заключив знаменатель в обращение к Конечно, в некоторых ситуациях вы можете использовать более простое решение: просто избегайте деления на ноль, используя Обратите внимание, что с решением Перегородка может быть добавлена в дистилляционную колонну для повышения эффективности разделения трех или более продуктов. ▲ Рис. 1. Стандартная колонна с перегородкой (DWC) имеет стенку, разделяющую колонну на две части. Потоки пара и жидкости показаны синими стрелками и красными стрелками соответственно. Колонны с перегородкой (DWC) — это тип дистилляционной колонны, которая может разделять смеси нескольких компонентов на три или более высокочистых потока (рис. 1). DWC требует гораздо меньше энергии, капиталовложений и производственного пространства, чем обычные колонны в последовательной или параллельной конфигурации. Фактически, требования к капитальным затратам для DWC могут быть на 20–30% ниже, чем у традиционных градирен (1–5) . Обычные дистилляционные колонны являются неотъемлемой частью нефтеперерабатывающей и химической промышленности. Концепция DWC хорошо известна, и большое количество литературы посвящено моделированию и контролю этих столбцов (1, 6, 7) . В нескольких публикациях обсуждались промышленные применения DWC в различных массовых и модернизированных приложениях (8, 9) . Технология достаточно универсальна, и нет двух абсолютно одинаковых приложений DWC. Таким образом, сложно разработать стандартный протокол для проектирования этих столбцов. DWC используются в различных сферах, например, в газовых установках, в установках для разделения нафты и разделителях риформинга. В этой статье описаны три основных типа DWC. Когда-нибудь в некоторых ваших электронных таблицах Microsoft Excel отображалась ошибка # DIV / 0 в различных ячейках? Ошибка Excel возникает, когда формула электронной таблицы пытается разделить на 0 или пустую ячейку. В этом руководстве я объясню, как можно предотвратить появление этих ошибок, добавив простой аргумент функции ЕСЛИ. Это логическая ошибка, которая возникает, когда возникает одно из этих условий: Предположим, вы должны были щелкнуть одну из # DIV / 0! ячеек вы увидите всплывающую подсказку Excel, которая гласит: « Используемая формула или функция — деление на ноль или пустые ячейки. Пример # DIV / 0! ошибка и всплывающая подсказка Я получил ошибку Excel в ячейке E7 , потому что я попытался разделить свое значение Cost в C7 на мое Счетчик каталогов в D7 . Я запустил объявление стоимостью 77,45 доллара и произвел 0 запросов в каталог. Другими словами, я просил Microsoft Excel разделить 77,45 доллара на ноль. Ой. Вторая причина, по которой Excel отображает эту ошибку для ячейки E11 , заключалась в том, что ячейка D11 пуста.Трудно увидеть, потому что всплывающая подсказка перекрывает значение ячейки. Хотя может показаться, что эта ошибка отображается только при делении, ее можно унаследовать от диапазона. В приведенном ниже примере я попытался ввести СУММ столбец E. Я также получаю сообщение об ошибке, потому что было # DIV / 0! в диапазоне ячеек. # DIV / 0! в ячейках отображаются ошибки. Вероятно, вы задаетесь вопросом, как удалить ошибку # div / 0. В конце концов, пустые ячейки и нули — допустимые записи.Есть несколько способов исправить эту ошибку, включая функцию ЕСЛИОШИБКА. Однако я предпочитаю использовать функцию ЕСЛИ. ЕСЛИОШИБКА может замаскировать все ошибки, помимо этого раздражения. Это логическая функция, в которой вы можете указать Excel выполнить одно действие IF , условие ИСТИНА и другое действие, если условие ЛОЖНО . В этом случае я хочу, чтобы Excel выполнил другое действие, ЕСЛИ у меня счетчик каталога «0». В противном случае Excel может продолжить работу в обычном режиме.В частности, я хочу заменить сообщение об ошибке на 0,00 долларов США. Логический тест для ячейки = 0 Вы можете увидеть это в примере ниже. В каждом случае, когда у меня был «0» или пустая ячейка в столбце D (количество каталогов), Excel оставил значение Conv Cost в столбце E равным 0,00 долларов США. Эта функция также зафиксировала значение моей суммы в ячейке E14. Обратите внимание, как # div / 0! ошибки исчезли Вскоре вы начнете вводить эту функцию прямо в строке формул Excel, а не использовать диалоговое окно Вставить функцию . Точно так же, как некоторым людям не нравятся сообщения об ошибках деления на ноль, другие могут возражать против значений пустых ячеек или ссылки 0,00 доллара США. Они могут предпочесть что-то вроде текстового значения или даже содержимого другой ячейки. Вы можете подставить текст или ссылку на ячейку вместо того, чтобы значение ячейки было 0,00 долларов США. Например, я мог бы использовать «NA». или оставлено пустым или использовалось другое значение ячейки В этом последнем примере Excel вместо этого вставит значение Cost в ячейку Conv Cost.В зависимости от вашей ситуации это может быть более точным. В моем примере стоимости преобразования каталога лучше использовать значение «Стоимость», чем «0» или пустое поле. Другое решение от читателей упомянуло, что метод ERROR.TYPE работает хорошо. Корпорация Майкрософт присвоила этому примеру # DIV / 0 значение ошибки «2». Более подробную информацию об ERROR.TYPE можно найти на сайте Microsoft. Как видите, есть несколько способов исправить ошибку деления на ноль в Excel. Скорее всего, какой бы метод вы ни выбрали, он будет меньше раздражать ваших пользователей, чем просмотр # DIV / 0! Заявление об отказе от ответственности: изображения из API рекламы продуктов Amazon. Хотя «формулы умножения Excel» не существует, существует несколько способов умножения в Excel. Например, вы используете звездочку (*) для умножения, но ударяетесь о кирпичную стену, когда применяете другие арифметические операторы? А как насчет быстрых клавиш для умножения множества чисел за один шаг? Прочтите, чтобы узнать о трех эффективных способах вычисления формулы умножения в Excel. 1.). В этих случаях помните, что Excel выполняет операции в порядке PEMDAS: сначала скобки, затем показатели, умножение, деление, сложение и вычитание. В следующей формуле «= 2 * 3 + 5 * 6» Excel сначала выполняет две операции умножения, получая 6 + 30, и складывает произведения, чтобы получить 36. Что делать, если вы хотите сложить 3 + 5 перед умножением? Используйте круглые скобки. Excel всегда будет оценивать все, что указано в скобках, прежде чем возобновить оставшиеся вычисления после PEMDAS. Если у вас возникли проблемы с запоминанием порядка PEMDAS, используйте мнемонический прием тети Салли: используйте первые буквы предложения: «Пожалуйста, извините мою дорогую тетю Салли». 2. Умножение с функцией ПРОДУКТ Если вам нужно умножить несколько чисел, вы можете оценить сокращенную формулу ПРОДУКТ, которая умножает все числа, указанные в скобках. = ПРОДУКТ (3,5 + 2,8,3,14) Это эквивалентно = 3 * (5 + 2) * 8 * 3,14. = ПРОДУКТ (A3, C3, D3, F3). Это эквивалентно = A3 * C3 * D3 * F3. = ПРОДУКТ (F3: F25), , что эквивалентно = F3 * F4 * F5 * (и так далее, вплоть до) * F25, или: = ПРОДУКТ (F3: F25, h5: h45). В каждом случае Excel умножает все числа, чтобы найти произведение. Если ячейка в диапазоне пуста или содержит текст, Excel не учитывает значение этой ячейки в вычислениях. Если ячейка в диапазоне равна нулю, продукт будет равен нулю. 3. Умножение диапазонов с помощью функции СУММПРОИЗВ Рассмотрим следующий счет. Формула в столбце E (с формулой, показанной справа от таблицы) умножает количество на цену, чтобы получить расширенную цену.Сумма в ячейке E7 суммирует расширенные цены. Но что, если вы не хотите, чтобы расширенные цены отображались как отдельные расчеты? Что, если вы хотите сделать все за один шаг? Попробуйте функцию СУММПРОИЗВ, которая умножает ячейки в двух диапазонах и суммирует результаты. СУММПРОИЗВ (D2: D5, C2: C5) умножает D2 * C2, D3 * C3 и т. Д. И суммирует результаты. Обратите внимание, что результат 84,50 такой же, как в предыдущем примере. Эта функция неоценима для расчета средневзвешенных значений, таких как оценки в классе или цены на основе переменного государственного налога, при котором диапазон значений умножается на диапазон, содержащий веса. Следующие шаги Это всего лишь три метода умножения чисел в формулах Excel. Когда вы освоите их, попробуйте формулу PRODUCTIF, которая умножает все числа в диапазоне, если выполняется условие. А пока попробуйте смешать и сопоставить формулы умножения, используя любую комбинацию вместе с другими арифметическими функциями, чтобы создать сложные математические модели. Функция MOD выполняет операцию по модулю.Он принимает число и делитель и возвращает остаток после деления. В этой формуле мы вычитаем один результат MOD из другого. Для первого МОДа мы используем число … . Время в Excel — это дробное значение, равное 24 часам. Один час времени равен 1/24, а 1 минута времени составляет 1 / (24 * 60) = 1/1440. Время в Excel — это дробное значение числа 1.Итак, 12:00 — это 24.12 = 0,5, 6:00 — это 24.06 = 0,25 и так далее. Итак, чтобы преобразовать время по заданному числу, вам нужно разделить количество часов на 24, чтобы получить необходимое … Формулы, в которых используется понятие «день недели», основаны на идее, что каждый день недели имеет определенное число. По умолчанию Excel присваивает 1 воскресенью и 7 субботе. В формуле примера B6 — это дата … Первое, что делает эта формула, — сравнивает дату в столбце B с датой начала: = ЕСЛИ (B4> = начало Если дата не больше даты начала, формула возвращает ноль.Если дата больше или равна … Ядром этой формулы является функция MOD. MOD принимает число и делитель и возвращает остаток после деления, что делает его полезным для формул, которые должны делать что-то каждый n-й раз. В этом случае … Эта формула использует функции MOD и COLUMN для фильтрации значений не в n-м столбцах, а затем запускает MAX для результата. Порядковые номера представляют собой позицию или ранг в последовательном порядке. Обычно они пишутся с использованием номера + буквенного суффикса: 1-й, 2-й, 3-й и т. Д. Чтобы получить порядковый суффикс для небольшого набора чисел, вы можете использовать … Когда вы используете формулу для применения условного форматирования, формула вычисляется для каждой ячейки в выделенном фрагменте. В этом случае в формуле нет адресов, поэтому для каждой ячейки в данных это СТРОКА и ЕДИНИЦА… Функция СУММПРОИЗВ работает напрямую с массивами. Одна вещь, которую вы можете довольно легко сделать с помощью SUMPRODUCT, — это выполнить тест на массиве, используя один или несколько критериев, а затем подсчитать результаты. В этом случае мы запускаем … Функция MOD возвращает остаток после деления. Если делитель равен 1, MOD вернет ноль для любого целого числа. Мы используем этот факт, чтобы построить простую формулу, которая проверяет результат MOD. По сути, эта формула вычитает время начала из времени окончания, чтобы получить продолжительность в часах. Это делается для расчета рабочего времени и времени перерыва. MOD (C6-B6,1) // получаем время работы
MOD (E6-D6,1) // получаем время перерыва Далее … Сложность подсчета количества часов между двумя моментами времени проистекает из времени, которое пересекает полночь. Это потому, что время, которое пересекает полночь, часто имеет время начала позже, чем время окончания (т.е. начать с … Excel обрабатывает даты и время, используя систему, в которой даты — это порядковые номера, а время — дробные значения. Например, 1 июня 2000 г. 12:00 представлено в Excel как число 36678,5, где 36678 — это дата … Время в Excel — это дробное значение, равное 24 часам. Один час времени равен 1/24, а 1 минута времени составляет 1 / (24 * 60) = 1/1440. В результате, если у вас есть десятичное значение для 6 часов и время в A1, вы можете добавить 6 часов… Применимо к Sisense в Linux и Microsoft Windows Сводные таблицы — один из самых полезных виджетов для визуализации данных. В средах Windows и Linux используются разные версии виджета сводной таблицы. Sisense в Windows использует Pivot1, а Sisense в Linux использует Pivot2.В целом Pivot1 и Pivot2 одинаковы, но есть небольшие различия в функциях и поведении. Например, когда Sisense развернут в Linux, вы можете выбрать отображение HTML в ячейках Pivot2 в виде HTML или обычного текста (Pivot1 всегда отображает HTML). Это полезно, например, для отображения гиперссылок. Для этого: Чтобы сравнить функции Pivot1 и Pivot2, см. Sisense в Windows и Linux. Начиная с Sisense V8.2.1 для развертываний Linux, максимальное количество видимых столбцов в сводных таблицах по умолчанию установлено равным 70. Это экономит время и повышает производительность. Чтобы изменить эти максимальные настройки: Примечание. Эти настройки применяются ко всем сводным таблицам в учетной записи. Выберите данные, которые будут отображаться в сводной таблице. Вы можете добавлять общие и промежуточные итоги в свои таблицы и определять, как рассчитывать промежуточные итоги. Чтобы добавить общие и промежуточные итоги в строки: Если вы выбрали отображение промежуточных итогов, выберите метод их вычисления. Щелкните меню «Значение» на панели данных, затем щелкните «Подытог по» и выберите метод. Параметр по умолчанию — Авто, который объединяет все данные, отправляя отдельный запрос в модель данных.Это означает, что Sisense применяет одну и ту же формулу, заданную в мере, ко всем данным. Другие настраиваемые параметры (Sum, Min, Max и т. Д.) Вычисляют только значения в строках над промежуточным итогом на основе данных, представленных в сводной таблице, вместо исходной формулы, установленной в мере. Рассмотрим следующее: В верхнем примере при использовании параметра Авто промежуточный итог для среднего дохода объединяет все данные о продажах и доходах. В нижнем примере среднее значение используется для вычисления промежуточного итога и, следовательно, вычисляет среднее значение всех средних значений дохода в строках над промежуточным итогом. Общие итоги объединяют строки в сводной таблице. Для сложения общих итогов: Если определено, на общие итоги влияют промежуточные итоги.В следующем примере общая сумма средних продаж равна 10, что соответствует средним продажам для двух регионов (Азии и Европы). В приведенном ниже примере для параметра «Средние продажи» для параметра «Промежуточный итог» (см. Выше) установлено значение «Сумма», поэтому общий итог — это сумма строк выше. В некоторых случаях может показаться, что общая сумма или промежуточная сумма рассчитываются неправильно. В других случаях вы можете рассчитывать средневзвешенные значения в общих и промежуточных итогах вместо среднего арифметического, которое используется системой. Чтобы исправить проблемы с общими и промежуточными итогами: Чтобы вычислить средневзвешенные значения в общих и промежуточных итогах: Настройте внешний вид таблицы PIVOT с помощью следующих инструментов. Условное форматирование можно использовать для выделения исключений в сводной таблице. См. Раздел «Выбор цветов в виджетах» для получения дополнительной информации. Примечание. Дополнительные параметры стиля, включая стиль и цвета шрифта, см. В этой статье. Чтобы успешно экспортировать сводные таблицы, разделите большую сводную таблицу с множеством столбцов, чтобы разделить сводные таблицы меньшего размера. . Те, кто в школе относился к урокам математики с пренебрежением, наверняка хотя бы несколько раз в жизни бывали в неловкой ситуации. Как посчитать, сколько оставить на чай или сумму коммунального платежа? Если знать пару простых приёмов, это займёт у вас буквально секунду. А уж во время экзамена знание правил умножения больших чисел может помочь сэкономить критически недостающее время. «Мел» совместно с Creu делится простыми секретами вычислений. Все мы знаем, что при умножении на десять к числу добавляется ноль, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он: Возьмите исходное число и представьте промежуток между двумя знаками (в этом примере мы используем число 52): 5_2 Теперь сложите два числа и запишите их посередине: 5_(5+2)_2. Таким образом, ваш ответ: 572.Если при сложении чисел в скобках получается двузначное число, просто запомните вторую цифру, а единицу прибавьте к первому числу: 9_(9+9)_9 (9+1)_8_9 10_8_9 1089. Этот приём поможет быстро возвести в квадрат двузначное число, которое заканчивается на пять. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и всё! 252 = (2x(2+1)) & 25 2×3 = 6 625 Большинству очень просто даётся таблица умножения на пять, но когда приходится иметь дело с большими числами, сделать это становится сложнее. Этот приём невероятно прост. Возьмите любое число и поделите пополам. Если в результате получилось целое число, припишите ноль в конце. Если нет, не обращайте внимание на запятую и в конце добавьте пять. Это срабатывает всегда: 2682×5 = (2682 / 2) & 5 или 0 2682 / 2 = 1341 (целое число, поэтому добавьте 0) 13410 Давайте попробуем другой пример: 5887×5 2943,5 (дробное число, пропустите запятую, добавьте 5) 29435 Это просто. Чтобы умножить любое число от одного до девяти на девять, посмотрите на руки. Это очень простой приём, хотя очевидный лишь для некоторых. Хитрость в том, что нужно просто умножить на два, а затем опять умножить на два: 58×4 = (58×2) + (58×2) = (116) + (116) = 232. Если вам нужно оставить 15% чаевых, есть простой способ сделать это. Высчитайте 10% (разделите число на десять), а потом добавьте получившееся число к его половине и получите ответ: 15% от $25 = (10% от 25) + ((10% от 25) / 2) $2.50 + $1.25 = $3.75 Если вам нужно умножать большие числа, причём одно из них — чётное, вы можете просто перегруппировать их, чтобы получить ответ: 32×125 всё равно что: 16×250 всё равно что: 8×500 всё равно что: 4×1000 = 4,000 На самом деле делить большие числа на пять очень просто. Нужно просто умножить на два и перенести запятую: 195 / 5 1. 195 * 2 = 390 2. Переносим запятую: 39,0 или просто 39. 2978 / 5 1. 2978 * 2 = 5956 2. 595,6 Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом. Отнимите от девяти все цифры, кроме последней. А последнюю цифру отнимите от десяти: 1000-648 1. От 9 отнимите 6 = 3 2. От 9 отнимите 4 = 5 3. От 10 отнимите 8 = 2 Ответ: 352 Умножение на 5: Умножьте на 10 и разделите на 2. Умножение на 6: Иногда проще умножить на 3, а потом на 2. Умножение на 9: Умножьте на 10 и отнимите исходное число. Умножение на 12: Умножьте на 10 и дважды прибавьте исходное число. Умножение на 13: Умножьте на 3 и 10 раз прибавьте исходное число. Умножение на 14: Умножьте на 7, а затем на 2. Умножение на 15: Умножьте на 10 и 5 раз прибавьте исходное число, как в предыдущем примере. Умножение на 16: Если хотите, 4 раза умножьте на 2. Или умножить на 8, а потом на 2. Умножение на 17: Умножьте на 7 и 10 раз прибавьте исходное число. Умножение на 18: Умножьте на 20 и дважды отнимите исходное число. Умножение на 19: Умножьте на 20 и отнимите исходное число. Умножение на 24: Умножьте на 8, а потом на 3. Умножение на 27: Умножьте на 30 и 3 раза отнимите исходное число. Умножение на 45: Умножьте на 50 и 5 раз отнимите исходное число. Умножение на 90: Умножьте на 9 и припишите 0. Умножение на 98: Умножьте на 100 и дважды отнимите исходное число. Умножение на 99: Умножьте на 100 и отнимите исходное число. Вычислить 7% от 300. Сперва нужно понять значение слова «процент» (percent). Итак, получается, что 7% от 100 будет семь. (Семь для каждой сотни, только одной сотни). 8% от 100 = 8. 35,73% от 100 = 35,73 Но как это может быть полезным? Вернёмся к задачке 7% от 300. 7% от первой сотни равно 7. 7% от второй сотни — то же 7, и 7% от третьей сотни — все те же 7. Итак, 7 + 7 + 7 = 21. Если 8% от 100 = 8, то 8% от 50 = 4 (половина от 8). Дробите каждое число, если нужно вычислить проценты из 100, если же число меньше 100, просто перенесите запятую влево. Примеры: 8%200 =? 8 + 8 = 16. 8%250 =? 8 + 8 + 4 = 20, 8%25 = 2,0 (Передвигаем запятую влево). 15%300 = 15+15+15 =45 15%350 = 15+15+15+7,5 = 52,5 Также полезно знать, что вы всегда можете поменять числа местами: 3% от 100 — то же самое, что 100% от 3. Источник: Creu Урок 9. Математический диктант.
Вычислите сумму чисел 45 и 60 и уменьшите её на 4 десятка.
Вычислите разность чисел 330 и 220 и уменьшите её на 50.
Найдите частное чисел 450 и 9.
Известна сумма 750 и первое слагаемое 200. Чему равно второе
слагаемое?
Известна разность между числами — 300 и уменьшаемое 770.
Чему равно вычитаемое?
Известно частное 6 и делитель 30. Чему равно делимое?
Найдите частное чисел 360 и 6.
Найдите второе слагаемое, если первое слагаемое 20, а сумма
900.
Произведение 720, первый множитель 8. Чему равен второй
множитель?
Частное 6, делитель 50. Урок 10. Самостоятельная работа.1 вариант
2 вариант
Решить задачу:
В 6 одинаковых домах 24 подъезда. Сколько подъездов в 12 таких
же домах?
Решить задачу:
От 4 коров получили за день 40 л молока, от каждой поровну.
Сколько коров при том же надое дадут 90 л молока?
Выполни вычисления:
105 x 5 425 x 2 856 : 4 504 + 139
2 x 128 959 : 7 585 : 9 603 — 427
Выполни вычисления:
748 : 2 648 : 4 913 x 3 704 — 328
987 : 3 507 x 2 5 x 329 405 + 249
Найти значения выражений:
(30 + 160 : 4) : 2 280 — 40 : 2 + 100
Найти значения выражений:
(400 — 160 : 8) : 2 900 — 50 x 2 + 140
Найти периметр и площадь
прямоугольника со сторонами 5 см и 4 см. Найти периметр и площадь
квадрата со стороной 6 см.
Урок 11. Входная контрольная работа. №1
Урок 13. Контрольный устный счёт.
92 : 23 84 : 6 200 x 4 + 200
68 : 17 91 : 7 900 — 400 : 2
57 : 19 75 : 3 1000 : 2 + 500
64 : 16 85 : 5 1000 : 5 — 200
Урок 15. Проверочная работа.
(Печатная тетрадь, стр. 4 — 7)
Урок 21. Контрольный устный счёт.
30 000 : 100 200 x 10 84 x 1 000 : 10
5 000 : 1 000 307 x 100 47 x 100 x 100
371 x 100 810 : 10 43 x 1 000 : 100
35 x 1 000 3 500 : 100 582 x 100 : 10
Урок 23. Проверочная работа.
(Печатная тетрадь, стр. 16 — 17)
Урок 24. Самостоятельная работа.Вариант
Решить задачу:
В 12 лодках можно перевезти 48 человек, размещая людей в лодках
поровну в каждой. Сколько людей перевезли в 7 таких лодках ?
Решить задачу:
В санаторий привезли 100 кг картофеля в 5 одинаковых мешках. Выполни вычисления:
328 + 243 984 — 638 215 x 4
739 + 1 10 000 — 1 843 972 — 3 000
546 x 1 000 849 600 : 10 67 800 + 90
Выполни вычисления:
436 + 259 792 — 456 828 : 3
69 + 1 30 000 — 1 709 318 — 300
680 x 1 000 95 800 : 100 138 000 + 45
Сравни : числа и поставь нужный знак(>,<,=):
039 и 270 039 12 650 и 12 065
Сравни : числа и поставь нужный знак(>,<,=):
0 и 405 070 25 390 и 25 309
Запиши наименьшее пятизначное
число и число, которое следует за ним при счёте. Запиши наибольшее пятизначное
число и число, которое следует за ним при счёте.
5*. Запиши 2 числа, произведение
которых равно 100, а частное 1.
5*. Запиши 2 числа, произведение
которых равно 100, а разность 0.
Урок 25. Контрольная работа. №2вариант
2 вариант
Реши задачу:
Токарь за семичасовой рабочий день вытачивает 63 детали, а его
ученик за 6 ч вытачивает 30 таких деталей. На сколько больше
деталей вытачивает за 1 ч рабочий, чем его ученик?
Реши задачу:
Рабочий за семичасовой рабочий день изготавливает 56 деталей, а
его ученик за 4 ч изготавливает 24 такие детали. Сколько всего
деталей изготавливают за 1 ч рабочий и его ученик вместе?
Вычисли:
000 : 1 000 7 800 x 10
3 000 + 400 + 50 + 9 400 376 — 400 000 — 70
5 000 + 60 + 2 605 — 500 000 — 600
9 000 + 5 43 879 — 43 000 — 800
Вычисли:
84 000 : 1 000 5 300 x 100
7 000 + 500 + 60 + 3 800 231 — 800 000 — 1
6 000 + 500 + 1 657 908 — 600 000 — 50 000 7 000 + 7 65 997 — 65
000 — 70
Запиши числа 3 798 до 3 806. Запиши числа 5 697 до 5 703.
Запиши число, в котором:
а) 15 единиц IV класса, 30 единиц III класса, 567
единиц II класса, 306 единиц I класса;
б) 168 миллионов 48 тысяч 30 единиц;
в) 27 миллионов 27 тысяч 27 единиц;
г) 3 миллиарда 430 миллионов 5 тысяч
50 единиц.
Запиши число, в котором:
а) 7 единиц IV класса, 31 единица III класса, 907 единиц II
класса, 36 единиц I класса;
б) 22 миллиарда 40 миллионов 16 тысяч 20 единиц;
в) 118 миллионов 18 тысяч 80 единиц;
г) 35 миллионов 35 тысяч 35 единиц.
Реши уравнения:
: a = 9 b : 3 = 11 14 x c = 42
Реши уравнения:
96 : a = 8 b : 4 = 11 13 x c = 52
6*. котором единиц на 3 больше, чем десятков, а сумма цифр равна 15.
6*. Запиши двузначное число, в
котором единиц на 4 меньше, чем десятков, а сумма цифр равна 18.
Урок 26. Проект «Числа вокруг нас. Наш город в числах и
величинах». (стр. 32)
Урок 30. Математический диктант.
800 кв. дм = . . . кв. м
60 000 кв. см = . . . кв. м
2 кв. км = . . . кв. м
2 кв. см 10 кв. мм = . . . кв. мм
6 кв. дм 05 кв. см = . . . кв. см
2 кв. м 50 кв. дм = . . . кв. дм
Сравнить: 1 кв. м и 99 кв. дм
Сравнить: 1 кв. км и 999 999 кв. м
Найти площадь прямоугольника со сторонами 10 см и 30 см.
Найти площадь квадрата со стороной 90 см. Урок 38. Проверочная работа.
(Печатная тетрадь, п\р, стр. 28 — 29 )
Урок 39. Самостоятельная работа.
(Печатная тетрадь, п\р, стр. 30 — 31)
Урок 40. Контрольная работа. №3 (сборник к\р, синенькая)1
вариант
2 вариант
Реши задачу:
В магазин привезли 32 коробки конфет, по 9 кг в каждой, и 36
коробок вафель, по 8 кг в каждой. Каких сладостей привезли больше и
на сколько килограммов больше?
Реши задачу:
Один мастер изготовил 6 ниток бус, по 38 бусинок в каждой, а
другой — 7 ниток бус , по 36 бусинок в каждой. Какой мастер
использовал больше бусинок и на сколько?
Вычисли:
618 + 4 536 7 518 x 3
879 — 19 586 16 002 : 7
Вычисли:
42 731 + 23 895 8 416 x 4
586 — 33 569 32 568 : 6
Выполни вычисления и сделай проверку:
км 640 м — 9 км 890 м
Выполни вычисления и сделай проверку:
29 т 350 кг + 18 т 980 кг
Реши уравнение:
X — 180 = 20 x 6
Реши уравнение:
X + 60 = 16 x 6
5*. 3 7 9
+ 6
6 5 8
5*.Восстанови пропущенные цифры:
2 8 6
+ 1
1 1 5 4
Урок 42. Тест. (Печатная тетрадь, п\р, стр. 32 — 35)
Урок 43. Контрольный устный счёт.
(учебник, 4 кл. I часть, стр. 58 — 59)
Урок 46. Математический диктант.
К какому числу прибавили 560 и получили 840?
Сумму чисел 370 и 630 разделите на 100.
Сколько вычли из 341, если получили 333?
Найдите произведение чисел 320 и 3.
Какое число в 5 раз больше числа 200?
Уменьшите 600 на 3.
Частное чисел 320 и 40 увеличьте в 5 раз.
Из какого числа нужно вычесть 135, чтобы получилось 70?
Из 100 000 вычтите 5. 900 разделите на 100.
Урок 50. Математический диктант.
— Запишите цифрами числа.
Шесть тысяч триста восемьдесят шесть. (6 386)
Семь миллионов двести пятьдесят четыре тысячи сорок восемь.
(7 254 048)
Пятнадцать миллионов две тысячи триста двадцать. (15 002 320
Двести четырнадцать миллионов пятьдесят шесть. (214 000 056)
Шесть миллиардов четыре миллиона семь. (6 004 000 007)
— Увеличьте каждое число на 7 000.
(13 386, 7 261 048, 15 009 320, 214 007 056, 6 004 007 007).
— Уменьшите каждое из полученных чисел на 200.
(13 186, 7 260 848, 15 009 120, 214 006 856, 6 004 006 807).
Урок 51. Проверочная работа.
(Печатная тетрадь, п\р, стр. 36 — 39 )
Урок 52. Контрольная работа. 2 вариант
Реши задачу:
На комбинате в декабре изготовили 7 163 л сока, а в январе — на
678 литров меньше. Из всего сока 9 789 литров разлили в пакеты, а
остальной сок — в бутылки. Сколько литров сока разлили в бутылки?
Реши задачу:
Зимой в магазине продали 3 486 кукол, весной — на 697 кукол
меньше. Из всех проданных кукол 4 486 кукол были в платьях, а
остальные — в спортивных костюмах. Сколько было кукол в спортивных
костюмах?
Выполни вычисления и сделай проверку:
700 000 — 24 618 312 879 — 179 542
804 608 + 96 395 730 406 + 1 962
Выполни вычисления и сделай проверку:
600 600 — 24 863 529 631 — 181 479
143 807 + 57 296 320 504 + 5 893
Вычисли, записывая вычисления в столбик :
28 км 640 м — 9 км 890 м
18 т 360 кг + 16 т 740 кг
Вычисли, записывая вычисления в столбик:
16 т 230 кг — 9 т 750 кг
км 560 м — 19 км 540 м
Реши уравнения:
290 + X = 640 — 260 b x 13 = 78
Реши уравнения:
400 — X = 275 + 25 а : 5 = 90
5*. 3 7 9
+ 4 3 1
5 6 0
5 6 8
5*.Вставь пропущенные цифры:
6 7 1
+ 5 8 3
7 6 9
6 2 6
6*.Вставь пропущенные цифры:
а : b — c x d + k x m : n
6*.Вставь пропущенные цифры:
а : (b — c) x d + k x (m : n)
Урок 53. Тест. (учебник, 4 кл. I часть, стр. 74 — 75)
Урок 60. Контрольный устный счёт.
0 : 145 400 x 8 0 дес. x 5 + 3 дес.
312 x 1 1 x 19 050 4 тыс. + 0 тыс. x 7
0 x 195 375 : 375 4 800 : = 60
805 x 10 4 200 : 3 x 10 = 3 500
Урок 62. Самостоятельная работа.
(Печатная тетрадь, п\р, стр. 48 — 49)
Урок 65. Математический диктант.
Запишите число, которое на 1 единицу больше, чем 85 699, 50
000 009.
Запишите число, которое на 1 единицу меньше, чем 555 500, 10
000, 999 999. Запишите число, которое состоит из 3 542 десятков.
Из цифр 9, 8, 7, 5, 0 составьте наименьшее число.
Запишите число 50 000, а рядом число в 50 раз меньше его.
Сколько всего сотен в числе 6 668 956?
Сколько цифр надо для записи числа 5 591 116?
Найди двадцатую часть от 840.
Выразите в сутках 360 часов.
Выразите в тоннах 336 000 кг.
Урок 67. Проверочная работа.
(Печатная тетрадь, п\р, стр. 44 — 47)
Урок 68. Контрольная работа. №5
(учебник, 4 кл. I часть, стр. 96 — 99) иливариант
вариант
Реши задачу:
С одного поля собрали 1 т 800 кг картофеля, а с другого — в 3
раза меньше. Реши задачу:
В первый день в санаторий приехало 900 человек, а во второй — в
9 раз меньше, чем в первый. Всех отдыхающих поселили в комнаты, по
2 человека в каждой. Сколько комнат заняли все отдыхающие?
Выполни вычисления:
6 234 x 2 8 334 : 6
32 542 x 7 6 985 : 5
80 020 x 5 1 520 : 4
907 x 9 — 852 : 3
Выполни вычисления:
5 124 x 2 9 522 : 6
23 452 x 7 2 367 : 3
20 080 x 9 1 806 : 6
840 x 6 — 795 : 3
Вычисли периметр и площадь
прямоугольника со сторонами 2 см и 4 см.
Вычисли периметр и площадь
прямоугольника со сторонами 7 см и 3 см. Реши уравнения:
90 + X = 1 800 : 10
Реши уравнения:
470 — X = 30 x 4
Урок 72. Самостоятельная работавариант
вариант
Реши задачу:
Какое расстояние проедет всадник за 3 ч, если скорость его
движения 13 км/ч?
Реши задачу:
За 2 ч велосипедист проехал 28 км. С какой
скоростью ехал велосипедист?
Выполни вычисления:
234 x 600 2 380 x 40 3 405 x 300
500 x (2 357 — 2 000)
Выполни вычисления:
457 x 500 3 160 x 30 2 608 x 400
400 + 600 x 1 358
3. Реши задачу:
Слон и слонёнок начали двигаться одновременно навстречу друг
другу. 3. Реши задачу:
Две черепахи начали двигаться одновременно навстречу друг другу,
когда находились на расстоянии 66 м. Скорость одной черепахи 5
м/мин, а другой — 6 м/мин. Через сколько минут черепахи встретятся?
4*. Периметр квадрата равен 16 см.
Из трёх таких квадратов сложили один прямоугольник. Найди
периметр и площадь этого прямоугольника.
4*. Периметр квадрата равен 24 см. Из
трёх таких квадратов сложили один прямоугольник. Найди периметр
и площадь этого прямоугольника.
Урок 73. Контрольный устный счёт.
Скорость грузового поезда 35 км/час. Поезд был в пути 2
часа. Какое расстояние он прошёл?
Велосипедист проехал 36 км за 2 часа. С какой скоростью он
двигался?
Охотник верхом на лошади проехал 28 км со скоростью 14
км/час. Расстояние от города до посёлка 30 км. Сколько времени
потребуется пешеходу, чтобы пройти это расстояние со скоростью
6 км/час?
Мальчик пробежал 20 м за 10 сек. С какой скоростью бежал
мальчик?
Крейсер проплыл 80 км со скоростью 40 км/час. Сколько
времени он затратил?
Муха летела со скоростью 5 м/сек 15 секунд. Какое расстояние
она пролетела?
Грач пролетел 100 м со скоростью 10 м/сек. Сколько времени
он был в пути?
За 3 сек сокол пролетел 78 м. Какова скорость сокола?
Орёл летел со скоростью 30 м/сек 6 секунд. Сколько метров
пролетел орёл?
Урок 74. Проверочная работа.
(Печатная тетрадь, п\р, стр. 54 — 55)
Урок 83. вариант
Реши задачу:
От двух пристаней, находящихся на рас-стоянии 90 км друг от
друга, одновремен-но отправились навстречу друг другу два теплохода
и встретились через 2 ч. Скорость одного из них 21 км/ч. С какой
скоростью шёл второй теплоход?
Реши задачу:
Две девочки одновременно вышли из своих домов навстречу друг
другу и встретились через 3 мин. Скорость первой девочки 60 м/мин,
а второй девочки — 70 м/мин Каково расстояние между их домами?
Вычисли, выполнив запись столбиком:
00 x 5 540 x 700
3 400 x 30 80 x 356
Вычисли, выполнив запись столбиком :
2 300 x 90 640 x 800
64 000 x 3 70 x 365
Вырази в указанных единицах измерения:
45 м 2 дм = . 7 сут. 14 ч = . . . ч 20 000 кв.см = . . . кв.м
Вырази в указанных единицах измерения:
34 000 кв.дм = . . . кв.м 36 ц 5 кг = . . . кг
7 кв.м 14 кв.см = . . . кв.см 4 ч 23 мин = . . . мин
Реши уравнения:
X — 546 = 35 + 64 X x (500 : 100) = 125
Реши уравнения:
376 — X = 7 x 9 у : 3 = 720 : 9
5*. Запиши такое числовое равенство, в котором произведение
будет равно одному из множителей.
5*. Запиши такое числовое равенство, в котором делитель будет
равен частному.
Урок 86. Контрольный устный счёт.
— Ответ предыдущего примера является первым числом следующего.
2 000 : 2 = 30 000 : 1 000 = 9 000 : 1 000 =
x 7 = x 10 = x 100 =
: 100 = : 3 = : 9 =
: 7 = x 60 = x 50 =
x 50 = : 100 = : 5 =
: 100 = x 10 = x 8 =
x 1 000 = : 6 = : 8 =
Урок 90. вариант
Реши задачу:
От одной платформы одновременно в противоположных направлениях
отошли два поезда. Скорость движения одного поезда 40 км/ч, а
другого — 30 км/ч. Через сколько часов расстояние между поездами
будет 280 км ?
Реши задачу:
Из одной деревни одновременно в разных направлениях выехали
велосипедист и мотоциклист. Скорость велосипедиста 12 км/ч, а
мотоциклиста 38 км/ч. Какое расстояние будет между ними через 3 ч ?
Выполни вычисления:
44 820 : 60 269 100 : 900 72 800 : 700
x (2 357 — 2 000)
Выполни вычисления:
12 700 : 50 248 800 : 800 98 100 : 900
400 + 600 x 1 358
Реши уравнение:
: X = 99 : 9
Реши уравнение:
у x 40 = 640 + 560
4*. 3 варианта.
4*. Запиши 2 числа, при умножении которых получается 104. Найди
3 варианта.
Урок 92. Математический диктант.
Найдите произведение чисел 700 и 4.
Делимое 800, делитель 80. Чему равно частное?
Какое число меньше, чем число 560, в 80 раз?
Во сколько раз 4 тысячи больше 2 сотен?
Чему равно частное от деления чисел 3 200 и 800?
Увеличьте число 22 в 30 раз.
Первый множитель 400, второй 30. Чему равно произведение?
Уменьшите число 7 200 в 80 раз.
Произведение чисел 15 и 400 уменьшите в 100 раз.
Делимое 560, делитель 70. Найти частное.
Урок 93. (Печатная тетрадь, п\р, стр. 64 — 65)
Урок 94. Контрольная работа. №7вариант
вариант
Реши задачу:
Из двух городов, расстояние между которыми 330 км, одновременно
навстречу друг другу выехали два автобуса и встретились через 3 ч.
Первый автобус ехал со средней скоростью 60 км/ч. С какой средней
скоростью ехал второй автобус?
Реши задачу:
Из двух городов, расстояние между которыми 560 км, одновременно
навстречу друг другу выехали два поезда и встретились через 4 ч.
Первый поезд ехал со средней скоростью 65 км/ч. С какой средней
скоростью ехал второй поезд?
Выполни вычисления:
65 700 : 900 36 200 : 40
2 374 x 50 843 x 600
Выполни вычисления :
800 : 800 18 270 : 30
3 643 x 70 659 x 700
Выполни деление с остатком:
7 360 : 800 11 970 : 400
Выполни деление с остатком:
3 380 : 600 13 590 : 300
Найди ширину прямоугольника,
если известно, что его площадь равна 7 200 кв. Найди длину прямоугольника, если
известно, что его площадь равна 4 800 кв. дм, а ширина — 80 дм.
5*. Вставь пропущенные знаки
арифметических действий и расставь скобки так, чтобы равенство
стало верным.
6 6 6 6 6 6 6 =100
5*. Вставь пропущенные знаки
арифметических действий и расставь скобки так, чтобы равенство
стало верным.
5 5 5 5 5 = 100
Урок 100. Проверочная работа.
(Печатная тетрадь, п\р, стр. 70 — 71)
Урок 101. Контрольный устный счёт.
360 : 3 560 : 80 2 300 : 100
120 x 6 770 : 7 99 x 10
780 : 6 5 200 : 260 3 200 : 800
35 x 20 450 : 9 63 x 2
25 x 30 85 x 2 240 : 120
9 000 : 30 68 x 3 1 000 — 1
Урок 103. Математический диктант.
Какое число надо разделить на 1 000, чтобы получить 527
Увеличьте 9 789 в 100 раз. Найдите произведение чисел 1300 и 5.
На сколько надо разделить 15 300, чтобы получить 5 100?
Запишите все числа от 55 068 до 55 498, которые делятся на
100 без остатка.
Найдите шестую часть от числа 4 800.
Найдите одну восьмую от разности чисел 600 и 40.
Какое число уменьшили в 120 раз и получили 40?
Из 6000 вычтите произведение чисел 150 и 20.
Составьте наибольшее четырёхзначное число при помощи цифр 1,
0, 8, 4. Цифры в числе не повторяются.
Урок 107. Контрольная работа. №8вариант
вариант
Реши задачу:
Из двух городов, расстояние между которыми 200 км, одновременно
в противоположных направлениях выехали два автомобиля. Реши задачу:
Из двух посёлков, расстояние между которыми 40 км, одновременно
в противоположных направлениях вышли два пешехода. Скорость одного
5 км/ч, а другого — 6 км/ч . Какое расстояние будет между ними
через 3 ч?
Выполни вычисления:
654 x 98 8 104 x 65
738 x 52 7 415 x 32
x 780 3 004 x 401
Выполни вычисления :
357 x 48 5 702 x 37
812 x 64 6 814 x 820
x 702 8 003 x 231
Реши уравнение:
а + 120 = 4 000 : 5
Реши уравнение:
а + 970 = 69 x 32
Найди значение выражения. 000 — 424 x 76 : 4
Найди значение выражения.
8 000 — 568 x 14 : 2
5*. Реши задачу.
Оля вышла на прогулку на 3 мин раньше, чем Алёша. Алёша вышел на
2 мин позже, чем Саша. Кто из детей вышел раньше всех и на сколько
минут?
5*. Реши задачу.
Врач прописал больному 5 уколов — по
уколу через каждые полчаса. Сколько потребуется времени, чтобы
сделать все уколы?
Урок 114. Математический диктант.
Сколько нулей нужно записать после цифры 3, чтобы она
обозначала десятки тысяч?
Увеличьте в 2 раза разность чисел 880 и 630.
Запишите число, которое состоит из 45 десятков, и увеличьте
его в 100 раз.
Наибольшее трёхзначное число увеличьте в 1 000 раз?
Не выполняя деления, определите, сколько цифр будет в
частном при делении числа 308 на 28. Найдите одну седьмую часть от числа 4 200.
Какое число увеличили в 120 раз, если получили 9 600?
Произведение двух чисел равно 8 844. Одно из чисел 4. Чему
равно второе число?
Во сколько раз уменьшили 8 004, если получили 2 001?
Какое число может быть частным от деления числа 486 на 54 -
6, 8 или 9?
Урок 117. Проверочная работа.
(Печатная тетрадь, п\р, стр. 77 — 76)
Урок 118. Контрольный устный счёт.
360 : 18 600 : 15 810 : 27
520 : 13 880 : 22 480 : 12
960 : 80 715 : 15 700 : 35
770 : 77 780 : 26 680 : 17
270 : 27 320 : 16 840 : 21
510 : 17 500 : 25 930 : 31
Урок 121. Самостоятельная работавариант
вариант
Реши задачу:
Если в каждом зале помещать по 28 картин, то все
картины займут 48 залов. Реши задачу:
Если на каждую страницу помещать 32 строки, то весь текст займёт
52 страницы. Сколько страниц займёт этот текст, если на каждую
страницу помещать 26 строк?
Выполни деление:
288 648 : 72 243 452 : 503
61 983 : 97 166 520 : 724
Выполни деление:
25 543 : 89 760 518 : 253
27 360 : 38 985 312 : 328
Сравни : числа и поставь нужный знак(>,<,=):
430дм 34м 3т 917кг 3т 719кг
Сравни : числа и поставь нужный знак(>,<,=):
72 т 720 ц 3 км 615 м 4 651 м
4*. Восстанови пропущенные числа.
X 2 8 7 9
9 6
4*. Восстанови пропущенные числа. X 5 7
3 6 3 6
Урок 124. Контрольная работа. №9вариант
вариант
Реши задачу:
Из питомника привезли 3 600 луковиц тюльпанов, а луковиц ирисов
— в 5 раз меньше. Двенадцатую часть всех ирисов посадили на
городские клумбы, а остальные отдали в детские сады. Сколько ирисов
посадят в детских садах?
Реши задачу:
В теплице собрали 2 352 кг помидоров, а огурцов — в 7 раз
меньше. Седьмую часть всех огурцов отправили на консервный завод, а
остальные продали. Сколько килограммов огурцов продали?
Вычисли значения выражений и сделай проверку:
654 x 209 2 844 840 : 471
Вычисли значения выражений и сделай проверку:
898 x 306 760 760 : 364
Реши уравнение:
112 : x = 48 : 6
Реши уравнение:
112 : x = 48 : 8
Выполни действия, вставь пропущенные числа. 33 м 49 см + 22 м 68 см = м см
8 мин 10 с — 7 мин 45 с = мин с
3 т 2 ц 75 кг — 8 ц 98 кг = т ц кг
Выполни действия, вставь пропущенные числа.
8 м 7 см — 5 дм 9 см = м дм см
2 мин 52 с + 43 с = мин с
2 т 2 ц 88 кг + 7 ц 86 кг = т ц кг
5*. Реши задачу.
Сколько нужно досок длиной 3 м и шириной 2 дм, чтобы настелить
пол в квадратной комнате, сторона которой 6 м?
5*. Реши задачу.
Сколько нужно досок длиной 4 м и шириной 4 дм, чтобы настелить
пол в квадратной комнате, сторона которой 8 м?
Урок 125. Самостоятельная работавариант
вариант
Реши задачу:
В 7 одинаковых по массе пакетах 28 кг
мандаринов. Сколько потребуется таких пакетов, чтобы так же
разложить 64 кг мандаринов?
Реши задачу:
За 5 одинаковых коробок пластилина заплатили 70 р. Выполни вычисления:
65 000 — 8 679 5 098 X 27
56 387 + 47 918 19 712 : 64
150 131 — 25 942 : 7 X 27
Выполни вычисления:
60 079 — 7 385 6 098 X 45
59 346 + 18 958 35 958 : 78
100 — 18 534) : 6 X 25
Реши уравнение:
456 — x = 7 X 8
Реши уравнение:
у : 12 = 42 + 58
Длина участка прямоугольной
формы 8 м, а ширина в 2 раза меньше. Найди площадь этого
участка.
Ширина парника прямоугольной
формы 6 м, а длина на 2 м больше его ширины. Найди площадь этого
парника.
5*. произведения двух множителей, каждый из которых делится на 100.
5*. Представь число 40 000 в виде
произведения двух множителей, каждый из которых делится на 100.
Урок 127. Математический диктант.
Увеличьте число 569 в 1 000 раз.
Найдите частное чисел 8 000 и 50.
Найдите сумму чисел 8 300 и 1 700. Уменьшите её в 1 000 раз.
Найдите произведение чисел 140 и 50.
Найдите одну третью часть от суммы чисел 240 и 360.
Сколько сантиметров в пяти метрах трёх дециметрах?
Запишите пятизначное число, сумма цифр которого равна 8.
Чему равна половина от числа 740?
Сколько центнеров в 90 000 килограммов?
Сколько часов в двух сутках и десяти часах?
Урок 130. (Печатная тетрадь, п/р, стр. 78 — 79)
Урок 131. Итоговая контрольная работа.вариант
вариант
Реши задачу:
Из двух городов одновременно навстречу друг другу отправились
скорый и товарный поезда. Они встретились через 13 ч. Каково
расстояние между городами, если известно, что скорость скорого
поезда 100 км/ч, а скорость товарного поезда составляет половину от
его скорости?
Реши задачу:
Из двух городов, расстояние между которыми 918 км, выехали
одновременно навстречу друг другу два скорых поезда. Скорость
одного поезда 65 км/ч. Какова скорость другого поезда, если поезда
встретились через 6 ч?
Вычисли значения выражений:
654 x 204 — (8 963 + 68 077) : 36
9 676 + 12 237 — 8 787 x 2 : 29
Вычисли значения выражений:
587 x 706 + (213 956 — 41 916) : 34
735 148 — 86 499 + 56 763 : 9 x 45
Реши уравнение:
x — 8 700 = 1 700
Реши уравнение:
500 — у = 1 500
Сравни величины. 5 400 кг 54 ц 4 ч 20 мин 420 мин
970 см 97 м 3 кв. дм 7кв. см 307 кв.см
Сравни величины.
4 т 56 кг 456 кг 4 мин 30с 430 с
870 см 8дм 7см 8 кв. см 6 кв. мм 86 кв.мм
Реши задачу.
Участок прямоугольной формы, ширина которого в 2 раза меньше
длины, засеяли овсом. Периметр участка 1 140 м. Чему равна его
площадь?
Реши задачу.
Длина поля 130 м, ширина 70 м. Две пятые части участка засеяны
картофелем. Сколько квадратных метров площади засеяно картофелем?
5*. Оля и Алёша познакомились 7 лет
назад. Сколько лет тогда было Оле, если через 5 лет Алёше будет
17 лет и он старше Оли на 2 года?
5*. Аня и Ира познакомились 5 лет
назад. Сколько лет тогда было Ире, если через 6 лет Ане будет 18
лет и она младше Иры на 2 года?
Урок 133. 860 : 430 2 500 : 125 555 000 : 555
660 : 330 66 000 : 220 77 700 : 111
936 : 234 8 400 : 210 32 000 : 160
780 : 260 5 400 : 108 60 000 : 150
848 : 212 7 400 : 185 6 000 : 400
968 : 121 52 500 : 105 640 000 : 320
Запутались в длинном делении? К концу этой статьи вы сможете разделить 648 на 4, используя деление в длинную сторону, и сможете применить ту же технику к любой другой задаче на деление в длинную сторону! Давайте взглянем. Хотите быстро научиться или показать учащимся, как решать число 648, разделенное на 4, с помощью деления в большую сторону? Включи это очень быстрое и веселое видео прямо сейчас! Итак, первое, что нам нужно сделать, это уточнить термины, чтобы вы знали, что представляет собой каждая часть деления: Здесь мы разберем каждый шаг процесса длинного деления на 648, разделенного на 4, и объясним каждый из них, чтобы вы точно поняли, что происходит. Первым шагом является настройка нашей задачи деления с делителем в левой части и делимым в правой части, как показано ниже: Мы можем выяснить, что делитель (4) входит в первую цифру делимого (6), 1 раз. Теперь, когда мы это знаем, мы можем поставить 1 вверху: Если мы умножим делитель на результат предыдущего шага (4 x 1 = 4), то теперь мы можем добавить этот ответ под делимым: Далее из второй цифры делимого (6 — 4 = 2) вычтем результат предыдущего шага и запишем этот ответ ниже: Move the second digit of the dividend (4) down like so: Если мы умножим делитель на результат предыдущего шага (4 x 6 = 24), то теперь мы можем добавить этот ответ под делимым: Далее отнимаем результат предыдущего шага от третьей цифры делимого2 (20 — : Делитель (4) входит в нижнее число (8), 2 раза, поэтому мы можем поставить 2 сверху: . Далее вычтем результат предыдущего шага из четвертой цифры делимого (8 — 8 = 0) и запишем этот ответ ниже: Если вы дочитали до этого урока, молодец! Больше не осталось цифр, чтобы двигаться вниз от делимого, а это значит, что мы решили задачу деления в длинную сторону. Ваш ответ — это верхнее число, а любой остаток будет нижним числом. Итак, для 648, разделенных на 4, окончательное решение: 162 Остаток 0 Теперь вы изучили метод деления 648 на 4, вот несколько других способов, которыми вы можете выполнить вычисления: Введите еще одну задачу на деление на длинное деление Хотите еще больше деления на длинное деление, но не хотите вводить два числа в калькулятор выше? Без проблем. Чему равно 648, разделенное на 5 в длинное деление? Если вы добрались до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите задачи на длинное деление, а? Ниже приведена куча случайно сгенерированных вычислений для вашего долгого деления удовольствия: Чему равно 445, разделенное на 477 в длинное деление? Чему равно 235, разделенное на 274 в длинное деление? Чему равно 597, разделенное на 751 в длинном делении? Чему равно 26, разделенное на 452 в длинное деление? Чему равно 560, разделенное на 725 с использованием длинного деления? Сколько 274 разделить на 465 с помощью деления в большую сторону? Чему равно 877, разделенное на 929 в длинное деление? Чему равно 671, разделенное на 701 с использованием длинного деления? Чему равно 267, разделенное на 816 в длинное деление? Чему равно 775, разделенное на 781 с использованием длинного деления? Чему равно 40, разделенное на 480 в длинное деление? Чему равно 550, разделенное на 617 с использованием длинного деления? Чему равно 81, разделенное на 311 в длинное деление? Чему равно 521, разделенное на 628 с использованием длинного деления? Чему равно 417, разделенное на 653 в длинное деление? Сколько 104 разделить на 954 в длинное деление? Чему равно 872, разделенное на 886 с использованием длинного деления? Сколько 32 разделить на 153 с помощью деления в длинное число? Чему равно 975, разделенное на 988 с помощью деления в большую сторону? Чему равно 365, разделенное на 695 в длинное деление? Чему равно 835, разделенное на 912 с использованием длинного деления? Чему равно 788, разделенное на 983 в длинное деление? Чему равно 414, разделенное на 527 с использованием длинного деления? Чему равно 669, разделенное на 998 в длинное деление? Чему равно 472, разделенное на 728 в длинное деление? Чему равно 556, разделенное на 783 в длинное деление? Что такое 279разделить на 865 с использованием длинного деления? Чему равно 144, разделенное на 263 в длинном делении? Чему равно 921, разделенное на 963 в длинное деление? Сколько 908 разделить на 923 в длинное деление? Чему равно 128, разделенное на 731 в длинном делении? Чему равно 785, разделенное на 794 в длинное деление? Чему равно 958, разделенное на 997 в длинное деление? Чему равно 716, разделенное на 802 с использованием длинного деления? Сколько 132 разделить на 539?используя длинное деление? Чему равно 620, разделенное на 674 в длинное деление? Чему равно 542, разделенное на 592 в длинное деление? Чему равно 65, разделенное на 850 с использованием длинного деления? Чему равно 232, разделенное на 822 в длинное деление? Чему равно 596, разделенное на 818 в длинном делении? Чему равно 946, разделенное на 952 в длинное деление? Чему равно 879, разделенное на 900 с использованием длинного деления? Чему равно 710, разделенное на 862 с использованием длинного деления? Чему равно 75, разделенное на 313 с использованием длинного деления? Чему равно 490, разделенное на 934 в длинное деление? Чему равно 921, разделенное на 959 с использованием длинного деления? Чему равно 785, разделенное на 931 с использованием длинного деления? Чему равно 710, разделенное на 731 с использованием длинного деления? Чему равно 705, разделенное на 902 с использованием длинного деления? Чему равно 398, разделенное на 582 с использованием длинного деления? Чему равно 69, разделенное на 545 в длинное деление? Чему равно 645, разделенное на 814 с использованием длинного деления? Чему равно 909, разделенное на 931 с использованием длинного деления? Чему равно 350, разделенное на 735 с использованием длинного деления? Сколько 122 разделить на 732 в длинное деление? Чему равно 607, разделенное на 657 в длинное деление? Чему равно 480, разделенное на 594 с использованием длинного деления? Сколько 512 разделить на 973 в длинное деление? Чему равно 977, разделенное на 986 в длинное деление? Чему равно 95, разделенное на 884 с использованием длинного деления? Чему равно 641, разделенное на 654 в длинное деление? Чему равно 138, разделенное на 929 в длинное деление? Чему равно 567, разделенное на 935 в длинное деление? Чему равно 737, разделенное на 966 с использованием длинного деления? Чему равно 451, разделенное на 834 с использованием длинного деления? Чему равно 928, разделенное на 932 в длинное деление? Сколько 912 разделить на 919 в длинное деление? Чему равно 932, разделенное на 987 с использованием длинного деления? Чему равно 931, разделенное на 932 с использованием длинного деления? Что такое 963 разделить на 971 с использованием длинного деления? Чему равно 344, разделенное на 367 в длинное деление? Чему равно 285, разделенное на 456 в длинном делении? Чему равно 204, разделенное на 882 в длинное деление? Чему равно 927, разделенное на 981 с использованием длинного деления? Чему равно 588, разделенное на 596 в длинное деление? Чему равно 506, разделенное на 669 в длинное деление? Чему равно 378, разделенное на 889 в длинное деление? Сколько будет 221 разделить на 900 с использованием длинного деления? Чему равно 975, разделенное на 984 с использованием длинного деления? Чему равно 679, разделенное на 795 в длинное деление? Чему равно 719, разделенное на 734 с использованием длинного деления? Чему равно 224, разделенное на 532 в длинном делении? Сколько 313 разделить на 437 в длинное деление? Сколько 369 разделить на 391 с помощью деления в большую сторону? Сколько 321 разделить на 372 в длинное деление? Чему равно 355, разделенное на 406 с использованием длинного деления? Сколько 178 разделить на 270 в длинное деление? Чему равно 876, разделенное на 968 в длинное деление? Чему равно 482, разделенное на 886 в длинное деление? Чему равно 412, разделенное на 952 с использованием длинного деления? Чему равно 805, разделенное на 980 с использованием длинного деления? Сколько 804 разделить на 927 с помощью деления в большую сторону? Чему равно 716, разделенное на 828 с использованием длинного деления? Чему равно 966, разделенное на 969 в длинное деление? Чему равно 588, разделенное на 824 в длинное деление? Чему равно 675, разделенное на 968 в длинное деление? Чему равно 414, разделенное на 574 в длинное деление? Чему равно 241, разделенное на 550 в длинное деление? Чему равно 740, разделенное на 865 с использованием длинного деления? Чему равно 920, разделенное на 997 с использованием длинного деления? Чему равно 962, разделенное на 993 в длинное деление? (А) Этот раздел применяется к соглашению о запланированной зоне застройки или району зонирования.
требования этого раздела заменяют противоречащие положения запланированного развития
территориальное соглашение или постановление, если таковые имеются. (Б) Планируемая застройка территории не может создавать опасных или нежелательных элементов, т.к.
описанных в этом разделе или административном регламенте города. (С) Опасные или нежелательные элементы включают опасные, вредные, вредные или нежелательные
шум, дым, пыль, запах, загрязнение воздуха, жара, влажность, жидкие или твердые отходы или
отходы, свет или блики или другое вещество, состояние, излучение или элемент, которые неблагоприятно
затрагивает имущество или использование имущества в непосредственной близости. Это исключает восстановление ресурсов
системы, использующие твердые отходы. (Д) Опасный или нежелательный элемент измеряется в порядке, установленном настоящим
подраздел. (1) Шум, вибрация, свет, блики, запах или излучение измеряются в точке на
линия исходного свойства, которая имеет самые высокие показания, или в любой другой точке, где
существование элементов может быть более очевидным. (2) Дым или токсичные или вредные вещества измеряются в месте выброса в атмосферу. (3) Для открытых промышленных операций, описанных в подразделе (E)(6), концентрация пыли
измеряется на уровне земли или на жилой высоте, а также на границе участка
или за его пределами, в зависимости от того, что приводит к наивысшему измерению. (Е) Опасный или нежелательный элемент не может превышать пределы, установленные настоящим
подраздел. (1) За исключением шума от транспортного средства или строительных работ, шум не может
превышать 55 децибел по локальной сети в светлое время суток и 45 децибел по локальной сети в ночное время
часы. (2) Колебания земли не должны превышать: (а) пределы в колонке I ниже; или же (б) если точка измерения является границей жилого района или находится в пределах 80 футов
линии границы жилой застройки, расположенной на полосе отчуждения улицы,
пределы в колонке II ниже. (3) Легкая или прямая сварочная вспышка не может превышать 0,4 фут-свечи поперек источника. (4) Дымить нельзя: (а) таким же темным или более темным по оттенку, как обозначенный № 0 на диаграмме Ринглеманна, как
опубликован Горным бюро США; или же (б) непрозрачности, которая затемняет поле зрения наблюдателя до степени, равной или превышающей
дым, описанный в подразделе (E)(4)(a). (5) Выбросы твердых частиц на каждый акр земли в запланированной застройке
площадь не может превышать: (а) для частиц размером 44 микрона или меньше — один фунт в течение любого часа; а также (б) для частиц размером более 44 микрон – 0,05 фунта в течение любого часа. (6) Открытые промышленные операции с пылеобразующим оборудованием, включая пескоструйную обработку,
распыление краски, дозирование гравия и бетона и подобные операции могут не производить
пыль в концентрации, превышающей один миллион частиц на каждый кубический фут в
точка измерения. (Ф) Планируемая территория застройки должна соответствовать требованиям по хранению, использованию,
и производство взрывчатых веществ и опасных материалов в Главе 6-2 (
Опасные материалы
) а также
Глава 25-12,
Статья 7 (
Единый пожарный кодекс
). Alcoholism & Substance Abuse Prevention-Education & Referral — Four Rivers Alliance HFM Prevention Council Координатор грантов …………………………………………Патрик Крауз Преподаватель по профилактике ……………………………….. … Лора Ли Лаурия Государственный защитник 102 County View Drive Государственный защитник ……………………………….. ……………….Стерлинг Гудспид _________________________________________________________________________ Совет по этике Почтовый индекс Box 205 Председатель …………………. …………..Джек Фиттерер – Индиан Лейк Роберт Лимперт — Ариетта P.O. Box 168 Предотвращение злоупотребления психоактивными веществами 143 White Birch Lane Клерк, округ Гамильтон 102 County View Drive, P.O. Box 204 Автомобиль — лицензии, регистрация и сделки. Сделки с землей — подача и запись. Судебные документы — верховный, окружной и уголовный. Залоги и судебные решения. Лицензии на охоту, рыбалку, отлов. Карты обследования. Лицензии на пистолет. Нотариальная информация и документы. «Ведение бизнеса как» и корпоративные документы. Важные формы: Для получения записей о рождении, браке или смерти, а также разрешений на использование собак обращайтесь к своему секретарю в ГОРОД. НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ СКАЧАТЬ СЧЕТ НАЖМИТЕ ЗДЕСЬ — Отчет о передаче недвижимого имущества RP-5217 Персонал: Комиссар присяжных заседателей Здание суда округа Гамильтон Общественные службы 143 White Birch Lane Часы работы: с понедельника по пятницу с 8:30 до 16:30 Психиатрическая служба: Кризисная служба и служба «горячей линии». Психиатрические услуги. Психологические службы. Индивидуальная, семейная, парная и групповая терапия Директор ……………………………………………… ………… Роберт Клеппанг, LMSW, ACSW Расширение кооператива Корнелла «Помогая людям помочь себе» Просветительская деятельность и образование в следующих областях: Дом и территория – Выбор и идентификация растений, идентификация вредителей, включая насекомых и животных, тестирование почвы и рекомендации по исправлению положения. Овощеводство. Старший руководитель отдела ……………………………………… Джамиля Пейдж Коронеры: Район № 1 Район № 2 District #3 District #4 Окружной прокурор и помощник окружного прокурора Окружной прокурор Помощник прокурора округа Судебные канцелярии и палаты 139 White Birch Lane, P.O. Box 780 Адреса электронной почты: Главный клерк ………………………………………….. …….. Ариана К. Элдридж *Все судебные заседания проходят по адресу: Lake Pleasant Courthouse, 102 County View Drive, Lake Pleasant, NY 12108 Судья по семейным делам, окружным и суррогатным судам Судья…………………………………………… ………… Достопочтенный. Татьяна Н. Коффингер Главный прокурор суда…………………………….. Линн Пуччарелли Окружной прокурор 139 Уайт Берч Лейн, П.О. Box 277 ДОРОЖНЫЕ БИЛЕТЫ: Чтобы подать заявку на возможное снижение штрафа за нарушение правил дорожного движения, нажмите на ссылку ниже и Следуйте всем инструкциям. НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ запросить снижение стоимости транспортных средств и дорожного движения Экономическое развитие 102 County View Drive Директор . Агентство промышленного развития округа Гамильтон 102 County View Drive Поддержка малого бизнеса. Стартапы. Расширение. Финансирование. Кредиты. Совет. Бизнес и маркетинговые планы. Государственное агенство. Регуляторная помощь. www.hamiltoncounty.com/economic-development/ida Исполнительный директор ………………………………………… ….Кристи Л. Уилт Выборы, Совет 102 County View Drive Зарегистрироваться для голосования, Изменить регистрацию партии, Адрес (почтовый) Изменить, ОТЧЕТ ОБ УЧАСТОКЕ ИЗБИРАТЕЛЬСТВА ЧТОБЫ ЗАГРУЗИТЬ РЕГИСТРАЦИОННУЮ ФОРМУ, ФОРМУ ИЗМЕНЕНИЯ РЕГИСТРАЦИИ И ИЛИ АДРЕСА, НАЗНАЧЕНИЕ/НЕЗАВИСИМУЮ ПЕТИЦИЮ, ЗАКОН О ВЫБОРАХ NYS OPEN HOW TO ALL IN OFFICE, ФОРМУ ОТСУТСТВУЮЩЕГО ЗАЯВЛЕНИЯ, ПОСЕТИТЕ СЛЕДУЮЩИЙ ВЕБ-САЙТ: www.elections.ny.gov Персонал: Избирательная комиссия округа Гамильтон, информация Управление по чрезвычайным ситуациям План уменьшения опасности округа Гамильтон нажмите ЗДЕСЬ Персонал: Телефон: (518) 548-6223 Факс: (518) 548-3392 Консультативный совет по пожарной безопасности Президент ……………………………….. Винс Лаурия Вице-президент…………………….. Мэтт О’Брейн Консультативный совет по пожарной безопасности НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПОЛУЧИТЬ ПРАВИЛА И ПОЛОЖЕНИЯ Встречи проводятся по телефонам: Историк Генеалогические файлы. Информацию об услугах, ресурсах, коллекциях и часах работы можно найти на веб-сайте историка округа: www.hamiltoncountyhistorian.org ЧАСЫ — четверг с 9:00 до 11:10: 00:00 и с 13:00 до 16:00 Жилищная помощь Joseph E. Mastrianni, Inc. Услуги по охране психического здоровья 148 White Birch Lane Директор ……………………………………………… …………………………..Роберт Клеппанг Департамент транспортных средств Офис для пожилых людей 1340 State Route 9, Lake George, NY 12845 Директор ……………………………………………… …. Дина Парк Официальная газета Единый рабочий источник Округ Гамильтон OneWorkSource предлагает широкий спектр услуг, помогающих поддерживать как работодателей, так и сотрудников. Это универсальный центр карьеры, предоставляющий услуги предприятиям и соискателям округа Гамильтон. Почтовый индекс Box 725 Отдел кадров Заявление о приеме на государственную службу: НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ СКАЧАТЬ (Заявка на обследование) Прием заявлений для: Уборщица в Индиан-Лейк Объявленные осмотры: Справочник сотрудника округа Гамильтон Офицер. Почтовый индекс Box 174 Hours of Рабочий: Отдел пробации Подготовка досудебных расследований. Отчеты для уголовных судов. Надзор за преступниками, осужденными на условный срок. Директор ………………………………………………………. …….. Эми Грейнджер, Часы работы: Пн-Пт – Обычно с 8:30 до 16:30 Доступность офиса может меняться в зависимости от надзора на местах и обязанностей суда. Общественное здравоохранение Агентство по охране здоровья на дому 0 Сестринские услуги Box 250, White Birch Lane Директор по работе с пациентами …………………………..Carriann Grexa-Allen DSS Public Health & Community Services: Департамент общественных работ Главный офис — 2558 State Route 8 Суперинтендант……………….. .. ……… ОТДЕЛ ШОССЕ: Техническое обслуживание дорог округа. Удаление снега и льда. Ремонт мостов и техническое обслуживание водопропускных труб на всех дорогах города и округа. Позвоните по номеру 518-548-7141, чтобы сообщить о любом небезопасном мусоре на дорогах округа. Чтобы получить Карты Графства — Стоимость $4,00 каждая. НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПОЛУЧИТЬ: Заявление о разрешении на проезд. НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПОЛУЧИТЬ ИНСТРУКЦИЮ ПО РАЗРЕШЕНИЮ НА РАБОТУ НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ РАЗРЕШИТЬ НА РАБОТУ Гараж на озере Плезант…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………… ..…Грегг Бойер Гараж в Индиан-Лейк……………………………..(518) 648-6128 Гараж Лонг-Лейк………………………………..(518) 624-2186 ОТДЕЛ ТВЕРДЫХ ОТХОДОВ: Предприятия, расположенные в Индиан-Лейк и Лейк-Плезант, принимают твердые отходы и материалы для вторичной переработки от жителей и городов округа Гамильтон. НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ Ознакомиться с Правилами и положениями станции перегрузки твердых отходов Справочный лист рекомендаций по переработке Пересадочная станция Лейк-Плезант Перегрузочная станция Индиан-Лейк Щелкните здесь, чтобы ознакомиться с Законом штата Нью-Йорк о переработке аккумуляторов Нажмите здесь, чтобы ознакомиться с Законом штата Нью-Йорк о переработке и повторном использовании электронного оборудования ЗДАНИЯ ОТДЕЛ: Служба налогообложения недвижимости Информация об оценке: инвентаризация имущества, оценочная стоимость, выравнивающие ставки и т. д. НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ — Загрузить платежную ведомость Директор ………………………………………………………. ……………………..Barry L. Baker Электронная почта: [email protected] Департамент шерифа Шериф ………………………………………………………. …………………….. Карл Г. Абрамс Отдел социальных услуг Временная помощь (TA), талоны на питание (FS), медицинская помощь (MA), программа пособий по планированию семьи, Family Health Plus, сберегательная программа Medicare (Buy-IN), программа помощи в оплате электроэнергии на дому (HEAP), отдел сбора алиментов ( SCU), услуги для взрослых, уход за приемными родителями, услуги по усыновлению, защита детей, профилактика детей, насилие в семье, домохозяйка/услуги по уходу за собой (PC), расширенные услуги на дому для пожилых людей (EISEP), информационный и справочный уход за детьми, летняя молодежная программа (SYP) и Программа трудоустройства и базовых навыков (JOBS). Персонал: PO Box 725, 139 White Birch Lane Конфиденциальная телефонная линия по борьбе с мошенничеством Если вы подозреваете, что совершается мошенническое действие, позвоните на горячую линию конфиденциальной информации о мошенничестве по телефону: 1-866-448-6662. Звонящие могут оставаться анонимными DSS округа Гамильтон предоставляет субсидию по уходу за детьми , чтобы помочь покрыть расходы по уходу за детьми для квалифицированных семей, пока родитель/опекун занят работой. Эта субсидия зависит от дохода. Дополнительную информацию можно получить на веб-сайте Управления по делам детей и семьи (OCFS.ny.gov) или связавшись с Конни по телефону DSS округа Гамильтон (518) 648-6131. Для получения помощи по программе HEAP или SNAP — https://www.mybenefits.ny.gov Скидка на широкополосный доступ.. . Программа экстренной помощи широкополосной связи (getemergencybroadband.org) Веб-сайт службы здравоохранения и социальных служб округа Гамильтон: НАЖМИТЕ ЗДЕСЬ Район охраны почв и водных ресурсов Мониторинг качества озерной и паровой воды. Для получения дополнительной информации о наших программах посетите веб-сайт Округа охраны почв и водных ресурсов округа Гамильтон по адресу: www.hcswcd.com Персонал: Часы работы: понедельник – Пятница: с 8:00 до 16:30 103 County View Drive Остановка D.W.I. Программы Почтовый индекс Box 210 Туризм Директор ………………………………………………………. ……………………..Кристи Л. Уилт Казначей, графство Гамильтон 102 County View Drive ДЛЯ ОПЛАТЫ СБОРОВ НАЖМИТЕ ЗДЕСЬ.1064 Оплатите налоги на имущество моей просроченной задолженности Оплатите налоги Центральной школы Лейк-Плезант за 2018/2019 годы здесь: Veteran’s Service Agency (контракт с Fulton Co.) Home » Office of Information Policy » Подайте запрос по Закону о свободе информации в DOJ Переключение видов Антимонопольный отдел Кеннет Хендрикс Центр обслуживания запросов по Закону о свободе информации: (202) 514-2692 Представитель по связям с общественностью по Закону о свободе информации: Уэйн Фостер, (202) 514-2692 Бюро по алкоголю, табаку, огнестрельному оружию и взрывчатым веществам Адам С. Сайпл Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 648-8740 Представитель по связям с общественностью по Закону о свободе информации: Зина Корнегай, (202) 648- 7390 Гражданский отдел Элизабет А. Центр обслуживания запросов по Закону о свободе информации: (202) 514-2319 Представитель по связям с общественностью по Закону о свободе информации: Стефани Б. Логан, (202) 514-2319 Отдел гражданских прав Килиан Б. Кагл, начальник Служба по связям с общественностью Шон Голидей Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 305-2935 Представитель по связям с общественностью по Закону о свободе информации: Шон Голидей, (202) 431-1277 Криминальный отдел Кристина Батлер 3 Представитель по связям с общественностью по Закону о свободе информации: Сара Вестенберг, (202) 616-0307 Управление по борьбе с наркотиками Келли Миллер, начальник Отдел окружающей среды и природных ресурсов Чарльз Смиролдо Представитель по связям с общественностью по Закону о свободе информации: Эмбер Блаха, (202) 616-5515 Исполнительный отдел иммиграционного контроля Джозеф Р. Шааф FOIA 900 Центр: Связь с общественностью по Закону о свободе информации: Административное управление по борьбе с организованной преступностью Целевые группы по борьбе с наркотиками Кристин Бруди-Эверетт Отправить запрос: ocdetf. Исполнительный офис прокуроров США Арла Витте-Симпсон Форма онлайн-запроса Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 252-6020 Связь с общественностью по Закону о свободе информации)05 36-6022)05 36-6022 Исполнительный офис попечителей США Исполнительный офис попечителей США Randi Meth Представитель по связям с общественностью по Закону о свободе информации: Елизавета Ференцевич, (202) 307-1399 Федеральное бюро расследований Майкл Г. Зайдель, начальник отдела Центр обслуживания запросов по Закону о свободе информации: (540) 868-1535 Представитель по связям с общественностью по Закону о свободе информации: Джозеф Бендер, (540) 868-2101 Федеральное бюро тюрем Юджин Байме Комиссия США по урегулированию иностранных претензий Джереми Р. ЛаФрансуа Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 616-6975 Представитель по связям с общественностью по Закону о свободе информации: Джереми Р. ЛаФрансуа, (202) 616-6975 ИНТЕРПОЛ (Национальное центральное бюро США) Дэниел Дембковски Центр обслуживания запросов по Закону о свободе информации: (202) 616-0201 Представитель по связям с общественностью по Закону о свободе информации: Даниэль Дембковски, (202) 616-0201 Отдел управления правосудием Карен Макфадден Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3101 Представитель по связям с общественностью по Закону о свободе информации: Карен Макфадден, 5 (202) -3101 Отдел национальной безопасности Арнетта Мэллори Представитель по связям с общественностью по Закону о свободе информации: Патрисия Мэтьюз, (202) 233-2639 Управление общественной полицейской службы Николь Ли, сотрудник Закона о свободе информации Управление информационной политики Дуглас Хиббард Форма онлайн-запроса FO 9000 Служба запроса Центр: (202) 514-3642 FOIA Представитель по связям с общественностью: Валери Вильянуэва, (202) 514-3642 Управление программ юстиции Моника Поттер-Джонсон Офис юрисконсульта Мелисса Голден Управление правовой политики Дуглас Хиббард Форма онлайн-запроса Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3642 Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, 5, (20) -3642 Управление по законодательным вопросам Дуглас Хиббард Форма онлайн-запроса Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3642 Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, (202) 514-3642 Управление профессиональной ответственности Кармен Смит Картер, помощник советника по законам о свободе информации и конфиденциальности Представитель по связям с общественностью по Закону о свободе информации: Аннетт Уормли, (202) 514-3365 Управление по связям с общественностью Дуглас Хиббард Онлайн-форма запроса Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3642 Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, (202) 514-36042 2 Офис помощника генерального прокурора Дуглас Хиббард Форма онлайн-запроса Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3642 Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, (202) 514-3642 Генеральная прокуратура Дуглас Хиббард Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-3642 Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, (202) 514-3642 Канцелярия заместителя Генерального прокурора Дуглас Хиббард Центр обслуживания запросов по Закону о свободе информации: (202) 514-3642 Представитель по связям с общественностью по Закону о свободе информации: Валери Вильянуэва, (202) 514-3642 Офис Генерального инспектора Дебора Уоллер Центр обслуживания запросов по Закону о свободе информации: (202) 616-0646 Представитель по связям с общественностью по Закону о свободе информации: Дебора М. Уоллер, (202) 616-0646 Прокуратура по помилованию Лиза Поркари, советник прокурора Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 616-6070 Представитель по связям с общественностью по Закону о свободе информации: Малави Уэллс, (202) 616-6070 Office of the General Solicitor Valerie H. Yancey Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 616-9406 Представитель по связям с общественностью по Закону о свободе информации: Валери Х. Янси, (202) 514-2203 Управление племенного правосудия Арла Витте-Симпсон Онлайн-форма запроса Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 259-60200003 Связь с общественностью по Закону о свободе информации: (202) 252-6036 Управление по борьбе с насилием в отношении женщин Кэтрин Постон Представитель по связям с общественностью по Закону о свободе информации: Кэтрин Постон, (202) 307-6026 Консультативный отдел по вопросам профессиональной ответственности Маргерит А. Дриссен Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 514-0458 Представитель по связям с общественностью по Закону о свободе информации: Квадира Зелеке, (202) 514-0458 Налоговый отдел Кармен М. Банерджи Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 307-6423 Представитель по связям с общественностью по Закону о свободе информации: Кармен М. Банерджи, (202) 307-6423 Адвокаты США Арла Витте-Симпсон Форма онлайн-запроса Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 252-6020 Связь с общественностью по Закону о свободе информации)05 36-6022)05 36-6022 Служба маршалов США Служба маршалов США Шарлотта М. Лакстон Связь с общественностью по Закону о свободе информации: (703) 740-3943 Комиссия США по условно-досрочному освобождению Анисса Бэнкс Была ли эта страница полезной? I.T. проектные решения и то, как они принимаются, неизбежно формируют нашу судьбу. Сделайте их правильно, и мы поднимем бизнес… Джек Кин, 15 мая 2003 г. НЕ СМОТРИТЕ СЕЙЧАС, но новое оптическое волокно с низкими потерями — с зеркальной сердцевиной — может проводить интенсивный поток лазерного света, который… Джон Эдвардс, 15 мая 2003 г. Разочарованный генеральный менеджер быстрорастущего подразделения фармацевтической компании из списка Fortune 100 решил поиграть с ИТ своей корпорации … Майкл Шраге, 15 мая 2003 г. Возраст: 51 год Зарплата: 133 660 долларов Предыдущее место работы: 30 лет работал в Verizon в штате Делавэр, занимая должность директора правительство, образование … Трейси Мэйор, 1 мая 2003 г. оп, Бисмарк, Н.Д. Взяли на работу… Трейси Мэйор, 1 мая 2003 г. Представлено Microsoft Новый подход к оценке ERP В этом техническом документе представлена структура для оценки современной ERP и того, как она может улучшить результаты бизнеса. Доступ сейчас Как ИТ-директору вам знаком следующий сценарий: вы вложили 900 000 долларов в систему прогнозирования, которая, как ожидается, будет стоить 1 доллар… Меридит Левинсон, 1 мая 2003 г. В среду, 29 января 2003 г., полиция арестовала 69-летнего Джеральда Ф. Мейсона за убийство двух патрульных из Эль-Сегундо, Калифорния. … Бен Уортен, 1 мая 2003 г. Управление портфелем позволяет получить целостный взгляд на ИТ-портфель компании. В нем сравниваются инвестиции в технологии с точки зрения риска и … Автор Lorraine Cosgrove WareMay, 1 2003 С ростом аутсорсинга ИТ-директора находятся в центре морального кризиса. Они видят, как многие их работники борются со стрессом на работе. Лучшие лидеры учатся помогать сотрудникам сейчас и удерживать их в будущем. Стефани Оверби, 1 мая 2003 г. В Париже трудно представить день без смарт-карт. By Susannah Patton May, 1 May, 2003 Безопасность является главной заботой повсюду, но в Европе эта забота не отражается в решениях по бюджетированию. Безопасность заняла третье место в … Кэтлин Карр, 1 мая 2003 Рон Кифер, вице-президент по управлению программами в DHL Americas, является ветераном типичного планирования проектов и портфелей? или … Тодд Datz, 1 мая 2003 г. Алексей Зоглин (слева) отправился в путь. В прошлом месяце он покинул свой пост технического директора Orbitz после трехлетнего … By Meridith Levinson, 1 мая 2003 Нет ничего более раздражающего, чем незнакомец, звонящий во время ужина, чтобы продать вас Джули Хэнсон, 1 мая 2003 г. Статья Cigna не соответствует действительностиВаша статья от 15 марта [«Самостоятельные раны Cigna»] об инициативе Cigna HealthCare по преобразованию для интеграции службы поддержки клиентов… By CIO Staff, 1 мая 2003 г. Охотники Луи Фриссор управляет дата-центрами. Александр Седроне, менеджер хранилища данных, обеспечивает работу CRM. Сьюзен Брэдли — специалист по кадрам … Майкл Голдберг, 1 мая 2003 г. По данным исследования AMR Research, 75% компаний не имеют четкого постоянного контроля над портфелями своих ИТ-проектов… Автор Richard Pastore, 1 мая 2003 г. Дебби Янг, 1 мая 2003 г. Точно так же, как удовлетворенность клиентов является ключевой целью для компаний, обеспечение удовлетворенности конечных пользователей является важной обязанностью … Моханбир Сохни, 1 мая 2003 г. утечки ниже и ответьте «верно», если они соответствуют описанию, или «ложно», если они… ориентироваться в меняющемся ландшафте новых законодательных и нормативных директив, влияющих на ИТ и … Эбби Лундберг, 15 апреля 2003 г. До сих пор ИТ-директор уважаемой исследовательской организации в Калифорнии понятия не имеет, как кто-то взломал его … By Sarah D ScaletApr, 15 2003 ШИРОКОПОЛОСНЫЙ ИНТЕРНЕТ через каждую электрическую розетку? Технология существует. Кристофер Линдквист, 15 апреля 2003 г. Служебные вычисления — скромный термин для большой идеи: архитектуры, в которой управление сетью сведено к … Автор Фред Хэпгуд, 15 апр. Страница не найдена [404] | Расширение сотрудничества UGA Публикации 4-H Молодежное развитие
Встречи округов и клубов, экологическое просвещение, программы животноводства, достижения проекта, летний лагерь Животноводство
Аквакультура, говядина, пчелы, молочные продукты, лошади, мелкие жвачные, птица и яйца, свиноводство Окружающая среда и природные ресурсы
Инвазивные виды, предотвращение загрязнения, лесное хозяйство, вода и засуха, погода и климат, дикая природа Деньги, семья и дом
Развитие взрослых и семьи, развитие младенцев, детей и подростков, деньги, жилье и домашняя среда Полевые культуры, производство кормов и газонов
Кукуруза, хлопок, фураж, конопля, арахис, мелкозерновые, соевые бобы, табак, газонная трава Еда и здоровье
Сохранение пищевых продуктов, коммерческая и домашняя безопасность пищевых продуктов, пищевая наука и производство, питание и здоровье Производство фруктов, овощей и декоративных растений
Черника, виноград, декоративное садоводство, лук, персики, орехи пекан, мелкие фрукты, овощи Газон, сад и ландшафт
Домашние сады, уход за газонами, декоративные растения, ландшафтный дизайн Сорняки, болезни и вредители
Болезни животных и паразиты, муравьи, термиты, вши и другие вредители, вредные животные, борьба с вредителями и болезнями растений, сорняки Актуальные и актуальные темы
Последние обновления, инициативы и программы от UGA Extension. Избранные программы Классы, семинары и клубные встречи
UGA Extension предлагает множество персонализированных услуг
как семинары, классы, консультации, сертификаты, лагеря и педагог
Ресурсы. Углы Углы Углы Углы Угол Cos Угол Cos Угол Cos Угол Cos Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций Доп. Инфо: У меня есть проблема в вычислении с matlab . Я знаю, что pi — это плавающее число и не является точным. Итак, в matlab sin(pi) не совсем ноль. Мой вопрос заключается в том, что если pi не… У меня возникли проблемы с правильным построением графика sin(x)/(x). В частности, когда x = 0, возвращает NaN в Matlab. Однако при применении правила L’hôpital фактическое значение равно y = 1. мой… Я пытаюсь создать быстрое приближение sin и cos в MATLAB, которое является текущим узким местом в моей программе. Существует ли более быстрый метод, чем встроенная процедура? Узкое место: на каждой… Stack Overflow на русском — это сайт вопросов и ответов для программистов. Присоединяйтесь! Регистрация займёт не больше минуты.
Любой может задать вопрос
Любой может ответить
Лучшие ответы получают голоса и поднимаются наверх
Вопрос задан
Просмотрен
3k раза
ответ дан 12 сен ’17 в 15:34
62.6k55 золотых знаков4444 серебряных знака103103 бронзовых знака
lang-py
Ваша конфиденциальность
Нажимая «Принять все файлы cookie» вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей [Политикой в отношении файлов cookie] (https://stackoverflow.com/legal/cookie-policy).
Принять все файлы cookie
Настроить параметры
20.07.2021 Для того, чтобы ваш частный дом был действительно уютным и тёплым даже при самых сильных морозах, обязательно потребуется наличие в нём собственной отопительной системы, если нет возможности подключения к централизованной… 16.07.2021 Назначение дымохода – выведение продуктов горения от камина, печки или котла отопления. Главный из них – дым. При его формировании необходимо учитывать множество факторов, так как в случае дефектов можно… 12.07.2021 Сезон пикников и домашнего шашлыка на собственном участке находится в полном разгаре, что не может не радовать любителей такого вида отдыха. Лето в этом году весьма своеобразное в плане погоды… 02.07.2021 На современном рынке сантехнического оборудования выбрать действительно качественный смеситель достаточно тяжело ввиду огромного разнообразия и наличия большого количества моделей. Как во многих других направлениях, здесь перед покупателем обязательно встанет выбор:… 28.06.2021 Поликарбонат, вне зависимости от того, является он сотовым или обладает монолитной структурой, является материалом, изготовленным из синтетического полимера. В основе самого полимера, имеющего отличные эксплуатационные характеристики, лежит смесь полимерного фенола… 23.06.2021 Шумоизоляция помещения помогает добиться максимального уровня комфорта, повысить качество проживания, работы. Согласно исследованиям, проводимых ВОЗ, шумовые раздражители являются проблемой, которая имеет серьезной влияние на здоровье человека. Применение материалов, обладающих шумоизоляционными… 17.06.2021 Если вы в поисках качественных резервуаров для личных целей или потребностей производства, рекомендуем обратить внимание на изделия от компании «АКПОЛ». Большой ассортимент емкостей «АКПОЛ» в магазине «СтройСила» позволяет подобрать изделия… 15.06.2021 Приятные ощущения при посещении ванной комнаты, прежде всего, обусловлены особенностями и функциональностью наполнения. Главный ее элемент – ванная, но все чаще сегодня ее заменяют душевые кабины. В магазине «СтройСила» в… 10.06.2021 Тепло в доме – это правильно организованная система отопления, и конечно, радиаторы в ней. На нашем сайте предлагаем подобрать радиаторы отопления в магазине «СтройСила», которые повлияют на создание благоприятного климата… 08.06.2021 При обустройстве ванной комнаты уделяется внимание не только дизайну самой ванны, материалу из которого она изготовлена. Нельзя забывать о внешнем оформлении ее пространства, так как сегодня его можно сделать его… Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств. Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций. Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции. Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа). Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами: Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам: Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла. Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 . Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще. cos (α — β) = cos α · cos β + sin α · sin β sin (α + β) = sin α · cos β + sin β · cos α sin (α — β) = sin α · cos β — sin β · cos α Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций: Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла. Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов. Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла. Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов. Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов. Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α . Тригонометрическая окружность наглядно показывает отношения синуса и косинуса при различных значениях угла α . Угол α начинает раскрываться с правой стороны оси косинуса. Если исследовать значения синуса, то в первой и второй четверти графика они будут положительны, так как находятся выше оси косинуса, то есть выше нуля, а в третьей и четвертой четверти графика синус станет отрицательным, так как точки окружности опускаются ниже нуля. Поэтому синус угла от 0° до 180° будет со знаком плюс, а синус угла от 180° до 360° будет со знаком минус, как видно из таблицы ниже. В таблице приведены все значения синусов углов от 0° до 360° с точностью до 1 градуса. Наиболее часто встречающиеся тригонометрические формулы: (lacktriangleright) Основные тождества: [egin <|l|l|>hline sin^2 alpha+cos^2 alpha =1& mathrm, alpha cdot mathrm, alpha =1 \ &(sinalpha (lacktriangleright) Формула вспомогательного аргумента: [egin <|c|>hline ext<Частный случай>\ hline \ sinalphapm cosalpha=sqrt2cdot sin<left(alphapm dfrac<pi>4 Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести. Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”. (lacktriangleright) Вывод формулы косинуса разности углов (cos<(alpha -eta)>=cosalphacoseta+sinalphasineta) Рассмотрим тригонометрическую окружность и на ней углы (alpha) и (eta) .2alpha=dfrac<1-cos2alpha>2) Заметим, что в данных формулах степень синуса/косинуса равна (2) в левой части, а в правой части степень косинуса равна (1) . (lacktriangleright) Вывод формул произведения функций: 1) Сложим формулы косинуса суммы и косинуса разности двух углов: Получим: (cos(alpha+eta)+cos(alpha-eta)=2cosalphacoseta Rightarrow cosalphacoseta=dfrac12Big(cos(alpha-eta)+cos(alpha+eta)Big)) 2) Если вычесть из формулы косинуса суммы косинус разности, то получим: 3) Сложим формулы синуса суммы и синуса разности двух углов: (lacktriangleright) Вывод формул суммы/разности функций: Обозначим (alpha+eta=x, alpha-eta=y) . Тогда: (alpha=dfrac2, eta=dfrac2) . Подставим эти значения в предыдущие три формулы: Получили формулу суммы косинусов. Получили формулу разности косинусов. Получили формулу суммы синусов. 4) Формулу разности синусов можно вывести из формулы суммы синусов: Аналогично выводится формула суммы котангенсов.2=dfrac=1) Таким образом, можно утверждать, что существует такой угол (phi) , для которого, например, (cos phi=a_1, sin phi=b_1) . Тогда наше выражение примет вид: (sqrt,ig(cos phi sin x+sin phicos xig)=sqrt,sin (x+phi)) (по формуле синуса суммы двух углов) Значит, формула выглядит следующим образом: [<large,sin (x+phi),>> quad ext <где >cos phi=dfrac a<sqrt>] Заметим, что мы могли бы, например, принять за (cos phi=b_1, sin phi=a_1) и тогда формула выглядела бы как [asin x+bcos x=sqrt,cos (x-phi)] (lacktriangleright) Рассмотрим некоторые частные случаи формул вспомогательного угла: (a) sin xpmcos x=sqrt2,left(dfrac1<sqrt2>sin xpmdfrac1<sqrt2>cos x (b) sqrt3sin xpmcos x=2left(dfrac<sqrt3>2sin xpm dfrac12cos x (c) sin xpmsqrt3cos x=2left(dfrac12sin xpmdfrac<sqrt3>2cos x Эта функция, обозначенная, определяется как комбинация функции квадрата и функции косинуса.Явно это карта: Для краткости запишем как. В математике функция косинуса (cos) — это функция, которая связывает внутренний угол треугольника с длиной его сторон. Функция косинуса, а также функция синуса и тангенса являются тремя основными тригонометрическими функциями. В прямоугольном треугольнике косинус угла равен отношению стороны, прилегающей к углу, к длине гипотенузы прямоугольного треугольника. Математически это: cos (A) = смежный / гипотенуза Функция косинуса принимает угловые измерения в качестве входных данных и возвращает отношение в качестве выходных данных.Когда угол A = 0 °, функция косинуса принимает значение: cos (0) = 1 Косинус угла в ноль градусов равен 1. Чтобы понять, почему, рассмотрим, что происходит с прямоугольным треугольником. когда один из его углов стремится к 0. По мере приближения угла к 0 противоположная сторона становится все меньше и меньше. По мере уменьшения этого угла длины гипотенузы и стороны, прилегающей к углу, становятся все ближе и ближе. Как только значение угла достигнет 0, гипотенуза и прилегающая сторона будут идеально лежать друг на друге, попадая в соотношение 1: 1.Таким образом, косинус 0 равен 1. Три триггерные функции представляют собой общее соответствие между внутренними углами треугольника и длинами его сторон. Тот факт, что существует повторяющееся соотношение между сторонами и углами прямоугольного треугольника, является следствием того факта, что подобные треугольники поддерживают соотношение между своими сторонами. Прямоугольный треугольник 3-4-5 имеет те же пропорции, что и треугольник 6-8-10; последнее является целым кратным первому.Таким образом, любые соотношения между длинами сторон двух треугольников будут точно такими же. Рассмотрим простой прямоугольный треугольник: Начиная с некоторого угла A, стороны треугольника помечены следующим образом: Гипотенуза — это сторона, противоположная прямому углу. Гипотенуза всегда является самой длинной стороной треугольника. Противоположная сторона — это сторона, находящаяся прямо напротив интересующего угла. смежная сторона — это сторона, непосредственно следующая за углом, который не является гипотенузой. Следуя этим обозначениям, мы можем определить три основные триггерные функции следующим образом: sin (A) = противоположный / гипотенуза cos (A) = смежный / гипотенуза tan (A) = противоположный / смежный Поскольку одинаковые треугольники имеют одинаковые пропорции, значения этих функций не зависят от размера прямоугольного треугольника, только угол оценки (A) равен.Хорошей мнемоникой для запоминания определений триггерных функций является аббревиатура SOH-CAH-TOA (произносится «со-ка-тоа») Давайте добавим несколько цифр к этим абстрактным формулам. Скажем, у нас есть прямоугольный треугольник со сторонами 3 и 4 и гипотенуза длиной 5: Мы можем вычислить значения триггерных функций относительно угла A следующим образом: sin (A) = противоположное / гипотенуза = 4/5 = 0,8 cos (A) = смежный / гипотенуза = 3/5 = 0,6 tan (A) = противоположный / смежный = 4/3 = 1.3 Обратите внимание, что функции синуса и косинуса эквивалентны с учетом разных углов. Установив угол B в качестве интересующего нас угла, мы можем вычислить триггерные функции следующим образом: sin (B) = 3/5 = cos (A) = 0,6 cos (B) = 4/5 = sin (A) = 0,8 Это приводит нас к общему правилу, что для любого прямоугольного треугольника, где углы A и B не являются прямым углом: sin (A) = cos (B) и sin (B) = cos (A) В дополнение к 3 основным функциям триггера есть 3 взаимные триггерные функции.Обратные функции являются обратными базисным функциям и называются секансом, косекансом и котангенсом. Их можно определить как: сек (A) = 1 / sin (A) = гипотенуза / противоположная косекунд (A) = 1 / cos (A) = гипотенуза / смежная котан (A) = 1 / tan (A) = смежный / противоположный Допустим, вам дано только измерение угла, и вас просят вычислить синус этого угла только из этого значения. К сожалению, для этого не существует простого алгоритма.Вычисление значений sin вручную под заданным углом требует много времени и сложных вычислений. Вместо этого большинство калькуляторов используют справочные таблицы, таблицы со списком измерений углов и соответствующих значений sin. Эти таблицы были рассчитаны с высочайшей точностью. Однако есть интересный способ концептуализации угловых измерений, который делает вычисление некоторых значений триггерных функций интуитивно понятным и простым. Внутреннюю работу триггерных функций можно понять по структуре единичной окружности на координатной плоскости.Единичный круг — это круг радиуса один, центр которого находится в начале координатной плоскости (0,0). Перетаскивание радиуса вокруг исходной точки приведет к появлению круга, длина окружности которого составляет ровно 2π единицы. По теореме Пифагора этот круг представляет собой набор всех точек (x, y), таких что x 2 + y 2 = 1 Углы могут быть измерены в терминах длины дуги на окружности, которую угол выводит наружу. Эти единицы называются радианами. Поскольку окружность единичной окружности равна точно 2π, угловая мера 2π в радианах соответствует 360 °.Аналогично, π / 2 радиан соответствует 90 °, π радиан — 180 °, π / 3 радиан — 60 ° и так далее. Любая точка на единичной окружности может быть представлена как конечная точка линии, идущей от центральной точки под углом θ с центром в начале координат. Значения x и y этой точки соответствуют сторонам прямоугольного треугольника. Это понимание приводит к некоторым интересным свойствам триггерных функций.Поскольку по определению единичный круг имеет радиус 1, sin (θ) = y и cos (θ) = x. Согласно теореме Пифагора и определению единичной окружности, верно, что cos 2 (θ) + sin 2 (θ) = 1. Что произойдет с прямоугольным треугольником, если мы изменим угол луча от происхождения? Изменение угла, на который линия простирается от начала координат, приводит к соответствующему изменению других сторон треугольника. Чем меньше угол, тем меньше и сторона, противоположная углу.а соседняя сторона становится больше. По мере увеличения угла противоположная сторона становится больше, а соседняя — меньше. Таким образом, когда мы меняем угол, мы можем визуализировать, как изменяется соотношение сторон треугольника. Сразу обратите внимание на несколько вещей. Что происходит, когда угол равен 0? Какое соотношение сторон друг к другу? По мере приближения угла к 0 синус угла (противоположный / гипотенуза) становится все меньше и меньше.Когда угол достигает 0, длина противоположной стороны достигает 0, поэтому полное отношение между противоположной стороной и гипотенузой равно 0. Итак, мы знаем, что sin (0) = 0. Что насчет того, когда мы сделаем угол больше? По мере увеличения угла противоположная сторона увеличивается в длине, пока мы не дойдем до π / 2 рад (90 °), после чего противоположная сторона и гипотенуза станут равной длины. Если стороны равны по длине, то их отношение равно 1, поэтому мы знаем, что sin (π / 2) = 1. Рассмотрим функцию косинуса.Что происходит со значением косинуса при уменьшении угла? По мере приближения к 0 отношение между соседней стороной и гипотенузой увеличивается, пока смежная сторона и гипотенуза не станут равными, когда угол равен 0. Итак, мы знаем, что cos (0) = 1. Аналогичным образом, когда угол приближается π / 2, соседняя сторона становится все меньше и меньше относительно гипотенузы, пока не станет равной 0; таким образом, cos (π / 2) = 0 А как насчет касательной функции? Когда угол равен 0, отношение противоположной стороны к соседней стороне также равно 0, поэтому мы можем определить, что tan (0) = 0. По мере увеличения угла противоположная сторона становится больше, а соседняя — меньше, пока не достигнет точки, в которой две стороны имеют одинаковую длину. Прямоугольный треугольник может иметь только две стороны равной длины, если оба непрямых угла равны 45 °. Это означает, что под углом 45 ° длины двух сторон равны, и поэтому их отношение равно 1. 45 ° равно π / 4 рад, поэтому мы знаем, что тангенс (π / 4) = 1 А как насчет значения tan (π / 2)? Обратите внимание, что по мере того, как угол увеличивается и приближается к π / 2 рад, противоположная сторона становится больше, а соседняя сторона сжимается до 0.Это означает, что tan (π / 2) равен выражению 1/0. Деление на 0 не определено, поэтому функция tan (π / 2) не определена и не имеет допустимого значения. Осмысление угловых измерений в радианах единичной окружности также объясняет еще одно интересное свойство триггерной функции; их периодичность. Значения триггерных функций колеблются между фиксированными выходами от входов от 0 до 2π, поскольку угловые измерения, превышающие 2π, могут быть представлены как кратные 2π. Графическое изображение выходных данных функций sin и косинуса дает красивый высокий волнообразный узор: Вершины и впадины приведенных выше графиков представляют выходные значения 1 и -1 соответственно. Интересно отметить, что функции синуса и косинуса идентичны по форме, но функция косинуса смещена от функции синуса на половину длины волны. Периодичность триггерной функции (в частности, синуса и косинуса) делает их полезными в науке для моделирования периодических явлений, таких как механические или электромагнитные волны. Была ли эта статья полезной? Затем рассмотрим углы 30 ° и 60 °. В прямоугольном треугольнике 30 ° -60 ° -90 ° отношения
сторон равны 1: √3: 2. Отсюда следует, что
sin 30 ° = cos 60 ° = 1/2, и
sin 60 ° = cos 30 ° = √3 / 2. Эти результаты занесены в эту таблицу. 30. b = 2,25 метра и cos A = 0,15. Найдите a и c. 33. b = 12 футов и cos B = 1/3. Найдите c и a. 35. b = 6,4, c = 7,8. Найдите A и a. 36. A = 23 ° 15 ‘, c = 12.15. Найдите a и b. 30. Косинус A связывает b с гипотенузой c, , поэтому сначала вы можете вычислить c. Если вы знаете b, и c, , вы можете найти a по теореме Пифагора. 33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух сторон, которых вы не знаете, а именно a / c. Тем не менее, это дает вам уравнение, с которым можно работать: 1/3 = a / c. Тогда c = 3 a. Из теоремы Пифагора тогда следует, что a 2 + 144 = 9 a 2 . Вы можете решить это последнее уравнение для a , а затем найти c. 35. b и c дают A по косинусам и a по теореме Пифагора. 36. A и c дают по синусам и b по косинусам. 30. c = b / cos A = 2,25 / 0,15 =
15 метров; a = 14,83 метра. 33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a равно 4,24 ‘или 4’3 «. 35. cos A = b / c = 6,4 / 7,8 = 0,82. Следовательно, A = 34,86 ° = 34 ° 52 ‘, или около 35 °. 36. a = c sin A = 12,15 sin 23 ° 15 ‘= 4,796. Тождество в математике — это всегда верное уравнение. Все пифагорейские тождества включают число 1, и его пифагорейские аспекты можно ясно увидеть при доказательстве теорем о единичной окружности. В этом вопросе мы собираемся исследовать пифагорейские тождества. Вы можете обратиться к приведенному ниже списку формул, когда имеете дело с 3 пифагорейскими тождествами. Давайте исследуем пифагорейские тождества. В первом из этих трех состояний синус в квадрате плюс косинус в квадрате равняется единице. Второй утверждает, что квадрат касательной плюс один равен квадрату секущей. Что касается последнего, он утверждает, что один плюс квадрат котангенса равен квадрату косеканса. В следующем вопросе мы попытаемся использовать единичный круг, чтобы доказать первое пифагорейское тождество: синус в квадрате плюс косинус в квадрате равняется единице.2 \ тета = 1cos2θ + sin2θ = 1 С чего начать? Вы помните свойства единичного круга? Мы рассмотрели единичный круг в предыдущем разделе. Вкратце, единичный круг — это просто круг с радиусом в одну единицу, то есть радиус должен быть равен единице. См. Изображение выше. Мы обозначим точку на окружности в X, Y. Здесь координата X равна X, а координата Y — Y. С этого момента проведем перпендикулярную линию к оси X.Мы сосредоточимся на этом треугольнике. Воспользуйтесь моментом, чтобы вспомнить, что на этом изображении? означает. На самом деле это опорный угол, верно? Это один из самых важных углов в тригонометрии. Что означает опорный угол, если координата X равна X? Это означает, что длина сегмента X равна X. Аналогичным образом, если координата Y равна Y, это означает, что длина вертикального сегмента треугольника будет равна Y. Давайте продемонстрируем это на реальных цифрах, чтобы проиллюстрировать эту концепцию. В приведенном выше примере есть точка 3,5. Если мы рисуем треугольник, тройка обозначает координату X. Это означает, что длина этого сегмента равна 3. Теперь, если координата Y равна 5, что это значит? Длина вертикального отрезка треугольника должна составлять пять. Возвращаясь к предыдущей иллюстрации единичного круга, давайте сосредоточимся на прямоугольном треугольнике и применим теорему Пифагора.Что такое теорема Пифагора? Пифагор говорит нам, что X в квадрате плюс Y в квадрате равняется квадрату гипотенузы. Гипотенуза в данном случае равна единице, поскольку мы используем единичную окружность. Итак, здесь X в квадрате плюс Y в квадрате равняется одному квадрату. Одна из замечательных особенностей единичного круга заключается в том, что его координата X также может быть представлена в терминах угла тета. Координата X может быть представлена как косинус-тета, а ее координата Y может быть представлена как синус-тета. Имейте в виду, что это только для единичного круга.2 \ тета = 1 cos2θ + sin2θ = 1 Ответ становится очевидным благодаря использованию единичного круга. Один квадрат — это всего лишь один. Координата X также может быть представлена как косинус тета. Координата Y может быть представлена как синус-тета. И вуаля! Мы сделали. Используя единичную окружность, мы успешно доказали, что возведенный в квадрат косинус плюс квадрат синуса равны единице, взяв одно из трех тождеств Пифагора. Тригонометрическая функция cos вычисляет косинус угла в радианах,
градусы или градианы. Калькулятор позволяет использовать большинство тригонометрических функций , можно вычислить косинус ,
синус
и касательная
угла через одноименные функции .. Тригонометрическая функция косинус отмечен cos ,
позволяет вычислить
косинус угла онлайн , можно использовать разные угловые единицы:
градусы, градианы и радианы, которые являются угловыми единицами по умолчанию. Калькулятор косинуса позволяет через функцию cos вычислить онлайн косинус угла в радианах, сначала необходимо
выберите желаемую единицу измерения, нажав кнопку параметров модуля расчета.
После этого можно приступать к расчетам. Чтобы вычислить косинус числа «пи / 6» онлайн, введите
cos (`pi / 6`), после вычисления результат
sqrt (3) / 2 возвращается. Обратите внимание, что функция косинуса способна распознавать некоторые особые углы и делать
вычисления со специальными связанными значениями в точной форме. Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу
нажав на кнопку опций модуля расчета. После этого вы можете приступить к расчету. Чтобы вычислить косинус 90, введите cos (90), после вычисления
restults 0 возвращается. Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать желаемую единицу измерения.
нажав на кнопку опций модуля расчета. После этого вы можете приступить к расчету. Чтобы вычислить косинус 50, введите cos (50), после вычисления
возвращается результат sqrt (2) / 2. Обратите внимание, что функция косинуса способна распознавать некоторые особые углы и выполнять
исчисление со специальными связанными точными значениями. Косинус допускает некоторые особые значения, которые калькулятор может определять в точной форме. Вот список
специальные значения косинуса : Производная косинуса равна -sin (x). Первообразная косинуса равна sin (x). Функция косинуса является четной функцией для каждого действительного x: `cos (-x) = cos (x)`.
Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии. В калькуляторе есть решающая программа, позволяющая решать
уравнение с косинусом
имеет вид cos (x) = a .Расчеты для получения результата детализированы, поэтому можно будет решить такие уравнения, как
`cos (x) = 1 / 2`
или же
`2 * cos (x) = sqrt (2)`
с шагами расчета. Чтобы дифференцировать функцию косинуса онлайн,
можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса Производная от cos (x) — это производная_вычислителя (`cos (x)`) = `-sin (x)` Калькулятор первообразной функции косинуса. Первообразная от cos (x) — это первообразная_производной (`cos (x)`) = `sin (x)` Калькулятор пределов позволяет вычислить пределы функции косинуса. Предел для cos (x) — limit_calculator (`cos (x)`) Обратная функция от косинуса — это функция арккосинуса, отмеченная как arccos. Графический калькулятор может строить функцию косинуса в интервале ее определения. Касательная функция — это
периодический
функция, которая очень важна в тригонометрии. Есть несколько значений синуса и косинуса, которые следует запомнить, исходя из
30
°
—
60
°
—
90
°
треугольники и
45
°
—
45
°
—
90
°
треугольники.На их основе вы можете определить соответствующие значения для тангенса. грех
(
θ
) потому что
(
θ
) загар
(
θ
) Обратите внимание, что: Вы можете нанести эти точки на координатную плоскость, чтобы показать часть функции, часть между
0
и
2
π
. Для значений
θ
меньше, чем
0
или больше чем
2
π
вы можете найти ценность
θ
с использованием
опорный угол
. График функции в более широком интервале показан ниже. Обратите внимание, что область действия функции — это вся действительная линия, а диапазон —
—
∞
≤
у
≤
∞
. Бесплатный онлайн калькулятор Контур.Бухгалтерии вам поможет и подскажет, какое количество дней прошло между двумя заданными датами. Кроме того, если у вас возникла необходимость, вы можете посчитать сколько календарных, выходных или рабочих дней (часов) содержит указанный период года или нескольких лет. Вы просто задаете конкретный день начала и конца и через доли секунд получаете расчет. Все данные онлайн-калькулятор считает самостоятельно. Если вы изменяете исходные дни недели, результат автоматически пересчитывается, с учетом високосного года. Важно: нельзя брать из расчетов за прошлые года показатели рабочих дней/часов за месяц и предоставлять в качестве расчетов — данные будут различаться. Поэтому, лучше воспользуйтесь калькулятором. Итак, порядок действий: Вы — бухгалтер. Руководитель попросил вас в ближайшие пару минут предоставить данные по количеству рабочих часов, которые должны отработать все сотрудники компании в феврале. Количество работников вы можете легко определить — у вас перед глазами цифры. Решение: просто воспользуйтесь нашим виджетом. Всю информацию вы получите автоматически, вам не нужны настольные календари и калькуляторы. Хотите вести бухучет, отправлять отчетность и делать расчеты в удобном и простом веб-сервисе? Попробуйте бесплатно целый месяц Контур.Бухгалтерию! Мы быстро вас научим, как сервисом пользоваться и ответим на все вопросы! Если на листе Excel Вы работаете не только с числами, графиками, рисунками, но и с датами, то, наверняка, сталкивались с ситуацией, когда необходимо было посчитать разницу между ними. Например, нужно определить количество дней или месяцев за определенный период времени, или посчитать возраст человека так, чтобы результат получился в днях, месяцах и годах, а может, требуется вычислить именно рабочие дни. Статья про расчет разницы в Эксель на сайте уже есть, и в ней я немного затрагивала даты. Но сейчас давайте рассмотрим данный вопрос подробнее и разберемся, как посчитать количество дней между двумя датами простым способом или используя функцию РАЗНДАТ(), и как определить количество именно рабочих дней. Начнем с самого простого – это отнимем от одной даты вторую, и получим нужное нам значение. Перед этим убедитесь, что формат ячеек, в которые вписаны числа, выбран «Дата»
. Если еще не заполняли их, тогда выделите диапазон, с которым хотите работать и нажмите напротив названия группы «Число»
на маленькую стрелочку. В открывшемся окне слева выберите подходящий нам формат, а потом в основной области определитесь с типом: 14.03.12, 14 мар 12 или другой. Нажимайте «ОК»
. В те ячейки, для которых только что поменяли формат, вводите данные. Я заполнила А1
и В1
. Теперь нужно выбрать любую ячейку (D1
), в которой установлен общий формат данных, иначе расчеты будут некорректные. Для этого выделите ячейку, в которой будет результат (В3
), и посмотрите, чтобы для нее был выбран общий формат. Для вычисления дней будем использовать функцию РАЗНДАТ()
. В нее входят три аргумента: дата начальная и конечная, единица. Единица – это в чем мы хотим получить результат. Сюда подставляется: «d»
– количество дней; Ставим в В3
знак равенства, пишем РАЗНДАТ
и открываем скобку. Затем выделяем раннюю дату (А1
), потом позднюю (В1
), ставим в кавычках подходящую единицу и закрываем скобку. Между всеми аргументами ставьте «;»
. Для расчета, нажмите «Enter»
. У меня получилась такая формула: РАЗНДАТ(A1;B1;»d») Выбрав в качестве единицы «d»
, я получила результат – 111. Если изменить данное значение, например, на «md»
, тогда формула посчитает разницу между 5 и 24 без учета месяцев и годов. Меняя таким образом данный аргумент, получится вывести точный возраст человека. В одной ячейке будут года «y»
, второй месяцы «ym»
, третьей дни «md» Для примера возьмем такую табличку. В столбце А
у нас начало месяца или начальная дата отсчета, в В
– конец месяца или отсчета. Данная функция считает рабочие дни без учета субботы и воскресенья, но в месяцах есть еще и праздники, поэтому столбец С
заполним соответствующими датами. ЧИСТРАБДНИ(A5;B5;C5) В качестве аргументов указываем начальную дату (А5
), потом конечную (В5
). Последний аргумент – это праздники (С5
). Разделяем их «;»
. Нажав «Enter»
появится результат, в примере ячейка D5
– 21 день. Теперь рассмотрим, если в месяце несколько праздников. Например, в январе Новый год и Рождество. Выделяем ячейку (D6
) и ставим в нее равно. Потом нажимаем в строке формул на букву «f»
. Откроется окно «Вставка функции»
. В поле «Категория»
выберите «Полный алфавитный перечень»
и найдите в списке нужную функцию. Жмите «ОК»
. Дальше необходимо выбрать аргументы функции. В «Нач_дата»
выбираем начальное значение (А6
), в «Кон_дата»
– конечное (В6
). В последнем поле вписываем даты праздников в скобках {}
и кавычках «»
. Потом нажимайте «ОК»
. В результате мы получим такую функцию и значение будет посчитано без учета выходных и указанных праздников: ЧИСТРАБДНИ(A6;B6;{«01.01.17″;»07.01.17»}) Чтобы не прописывать праздники вручную, можно указать в соответствующем поле определенный диапазон. У меня это С6:С7
. Рабочие дни посчитаются, и функция будет иметь вид: ЧИСТРАБДНИ(A6;B6;C6:C7) Теперь сделаем подсчет для последнего месяца. ЧИСТРАБДНИ(A8;B8;C8) В феврале получилось 19 рабочих дней. Про другие функции даты и времени в Эксель , я написала отдельную статью, и ее можно прочесть, перейдя по ссылке. Калькулятор достаточно простой, но тем не менее на мой взгляд очень удобный, для подсчета количества рабочих дней между произвольными датами. Калькулятор использует данные о переносе рабочих дней и праздничных днях, которые содержатся в ежегодных постановлениях Правительства РФ. Таких калькуляторов конечно же много и мы в этом не оригинальны, но есть несколько изюминок которые я думаю Вам понравятся, и могут использоваться для создания других калькуляторов. Первая изюминка: Мы можем не учитывать праздничные даты которые содержатся в постановлениях Правительства РФ, а учитывать только выходные дни(для России суббота и воскресенье) Вторая изюминка: Для тех стран, у которых, выходными днями являются другие дни недели (например в Израиле, выходные дни это пятница и суббота), можно указать какие дни недели будут являться выходными. Это удобно не только для других стран, но и для местного применения, когда известно что работаем по сменам, каждые четверг, субботу и вторник. Третья изюминка: Мы можем использовать совершенно произвольную систему выходных, заданную в определенном виде (отображение этой функции нет на сайте, хотя функционал рабочий) и для всех желающих, построить производственный календарь для Беларусии, Казахстана или Сербии не составит затруднения. Побочным приятным эфектом этого калькулятора является еще и расчет количества дней между двумя датами. Причем разницу она высчитывает так, как это делается в бухгалтерии и отделе кадров. В отличии от математических и астрономических калькуляторов, где при тех же данных получается 7 суток. Эта ошибка в одни сутки появляется из-за того что в кадровых решениях последний день, он всегда явлется рабочим и его надо учитывать, а в точных и абстрактных калькуляторах считается, что 8 июля наступает в полночь (0:0:0) и разница между полночью 1 июля и полночью 8 июля (или 23 часа 59 минут 59 секунд 999 милисекунд, 999999 микросекунд и т.д 7 июля) составит ровно 7 суток. Основной принцип, котрого придерживается бот, это периодичность выходных в течении недели. Если это соблюдается, калькулятор выдаст реузультат, на который вы рассчитывали. Очень жаль, что в постановлениях Правительства РФ до сих пор не внедряют QR-код, где для машинной обработки были бы указаны все праздники на текущий код. Это бы упростило бы работу определенному кругу лиц. Праздники и переносы на территории РФ учитываются с 2010 по 2019 год включительно. Для пользователей кому необходимо рассчитать первую рабочую дату после отпуска или командировки или другого промежутка времени, обратите внимание на вот этот калькулятор Дата выхода на работу из отпуска, декрета онлайн Для Jabber клиентов rab_d дата.начала; дата.конца;неделя неделя — дает полную информацию о том, как рассчитывать рабочие дни и часы. Неделя состоит из семи символов 0 или 1, где каждый символ несет свою роль. 0- человек работает, 1 — человек не работает(выходной). Если неделя пустая, то используется код 0000011 — то есть суббота и воскресенье выходной. Хотелось бы заметить, что это календарная неделя и этот показатель показывает, как в течении недели вы отдыхаете. Нумерация недели у нас начинается с нуля и это день — понедельник, потом идет вторник -1, среда-2 и т.д. дата начала — дата в виде ДД/ММ/ГГГГ — обозначает начало диапазона, для которого рассчитывается количество рабочих дней дата конца — дата в виде ДД/ММ/ГГГГ — обозначает конец диапазона, для которого рассчитывается количество рабочих дней ВНИМАНИЕ! Дата может быть введена и через точку или через слеш. rab_d 1/1/2014;31/12/2014 в ответ получим Количество суток между двумя указанными датами 365 Количество рабочих дней 247 Количество выходных и праздничных дней 118 rab_d 2/7/2010;25/10/2013 В ответ получим Количество суток между двумя указанными датами 1212 Количество рабочих дней 827 Количество выходных и праздничных дней 385 rab_d 20/1/2010;10/2/2014;0101001 В ответ получаем Количество суток между двумя указанными датами 1483 Количество рабочих дней 797 Количество выходных и праздничных дней 686 Предыдущий пример, только не учитывать государственные праздники. Как вариант использования сменные дежурства, охрана и т.п. исходная дата дни между датами века между датами конечная дата рабочие дни между датами * годы между датами месяцы между датами часы между датами минуты между датами секунды между датами годы месяцы сутки часы минуты Число минут и секунд в дате не может превышать 60, Вы ввели. О-о! Извините! Перед Вами простой онлайн расчетчик, осознающий свои, увы, скромные возможности, а не астрономическая программа! Пожалуйста, введите другое число. На основе этого небольшого табло создан . Сейчас расчетная таблица настроена на подсчет дней до начала лета. Чтобы расчитать, сколько дней прошло или пройдет между интересующими Вас датами, просто введите их в соответствующие поля таблицы. Интервал времени можно изменять точно так же как и даты, при этом отсчет будет вестись от «Даты 1», а изменяться будет «Дата 2». Если на табло Вы видите самый судьбоопределяющий для нашей страны период истории — дни между датами Великой Отечественной войны, то, значит, в Вашем браузере отключен Jawa Script и для проведения расчетов его необходимо включить. * В пределах 2019 года расчет рабочих дней ведется с учетом праздников России и утвержденной правительством РФ схемы переноса выходных дней. При больших промежутках времени между датами, расчеты количества рабочих дней ведутся в предположении пятидневной рабочей недели, праздники не учитываются . Sergey Ov (Seosnews9
) Справочная информация: «Производственный календарь на 2021 год для пятидневной рабочей недели» Количество дней (календарных/рабочих/выходных и праздничных) и нормы рабочего времени в 2021 году 2021 год Количество дней Рабочее время (в часах) Календарные дни Рабочие дни Выходные и праздничные дни при 40-часовой рабочей неделе при 39-часовой рабочей неделе при 36-часовой рабочей неделе при 35-часовой рабочей неделе при 33-часовой рабочей неделе при 30-часовой рабочей неделе при 24-часовой рабочей неделе при 20-часовой рабочей неделе при 18-часовой рабочей неделе Январь 31 15 16 120 117 108 105 99 90 72 60 54 Февраль 28 19 9 151 147,2 135,8 132 124,4 113 90,2 75 67,4 Март 31 22 9 176 171,6 158,4 154 145,2 132 105,6 88 79,2 I квартал 90 56 34 447 435,8 402,2 391 368,6 335 267,8 223 200,6 Апрель 30 22 8 175 170,6 157,4 153 144,2 131 104,6 87 78,2 Май 31 19 12 152 148,2 136,8 133 125,4 114 91,2 76 68,4 Июнь 30 21 9 167 162,8 150,2 146 137,6 125 99,8 83 74,6 II квартал 91 62 29 494 481,6 444,4 432 407,2 370 295,6 246 221,2 1-е полугодие 181 118 63 941 917,4 846,6 823 775,8 705 563,4 469 421,8 Июль 31 22 9 176 171,6 158,4 154 145,2 132 105,6 88 79,2 Август 31 22 9 176 171,6 158,4 154 145,2 132 105,6 88 79,2 Сентябрь 30 22 8 176 171,6 158,4 154 145,2 132 105,6 88 79,2 III квартал 92 66 26 528 514,8 475,2 462 435,6 396 316,8 264 237,6 Октябрь 31 21 10 168 163,8 151,2 147 138,6 126 100,8 84 75,6 Ноябрь 30 20 10 159 155 143 139 131 119 95 79 71 Декабрь 31 22 9 176 171,6 158,4 154 145,2 132 105,6 88 79,2 IV квартал 92 63 29 503 490,4 452,6 440 414,8 377 301,4 251 225,8 2-е полугодие 184 129 55 1031 1005,2 927,8 902 850,4 773 618,2 515 463,4 2021 год 365 247 118 1972 1922,6 1774,4 1725 1626,2 1478 1181,6 984 885,2 Среднемесячное количество рабочих часов 164,3 160,2 147,9 143,8 135,5 123,2 98,5 82,0 73,8 Производственный календарь на 2021 год (для пятидневной рабочей недели)
Комментарий к производственному календарю на 2021 год Течка у собак июня 02, 2022 Течка, или по-научному, — эструс, это период полового цикла собаки, во время которого она готова к спариванию и оплодотворению. Первая течка начинается в возрасте от 6 до 18 месяцев. Это может зависеть от породы и размера собаки. У собак мелких пород течка, как правило, наступает раньше, в возрасте 6-9 месяцев. У собак средних и крупных пород – ближе к году, а иногда и после года. Если у вашей собаки нет течки до 1,5 лет, не стоит пугаться, это тоже вариант нормы, у некоторых собак первая течка начинается ближе к 2 годам. Если же течка не началась и после этого времени, стоит обратиться к ветеринарному врачу. Возможно, у животного имеются какие-то гормональные нарушения или патология развития органов репродуктивной системы. В таком случае стоит обратиться к врачу-репродуктологу. В среднем течка длится 3 недели. Период течки можно разделить на несколько фаз. Проэструс (предтечка) длится 7-10 дней. В этот период может наблюдаться изменение поведения собаки. Животное становится менее управляемым, может проявлять агрессию, активно метить территорию, не выполнять команды, которые обычно не вызывали затруднений. Некоторые животные, наоборот, становятся более вялыми, апатичными, пугливыми. Также самки могут активно реагировать на кобелей, но при этом не подпускать их к себе, и при попытке приблизиться будут огрызаться и отходить в сторону. Наружные половые органы в этот период также претерпевают изменения. Вульва (петля) набухает за счет прилива крови, и слизистые оболочки наружных половых органов могут приобретать более интенсивный цвет (ярко-розовый или даже синюшный). Появляются кровянистые выделения из петли. Зачастую именно по наличию кровянистых выделений владелец может определить, что у собаки началась течка. Поскольку выделения могут быть достаточно обильными, чтобы избежать загрязнения поверхностей в доме (ковры, диваны), можно надевать на собаку специальные трусы. По возможности рекомендуется обходиться без подобных приспособлений. Собаки постоянно вылизываются, и таким образом, осуществляют гигиенический уход за собой, а наличие трусов будет этому препятствовать. Чтобы избежать нежелательного загрязнения полов и диванов, ковры на период течки можно свернуть и не разрешать животному запрыгивать на диван, а лежать только на своем месте. Следующая фаза — эструс, непосредственно фаза половой охоты. Длится она 7-9 дней. Эта фаза, во время которой происходит овуляция, а соответственно, возможно наступление беременности. Обычно это 11-13 день от момента начала течки. Третья фаза цикла — диэструс (метэструс). Она длится примерно 60 дней. В этот период выделения прекращаются, отечность петли спадает, и она приобретает обычный цвет и размер. В это время возможно наступление ложной щенности. Обычно данное состояние проявляется набуханием молочных желез и выделением из них секрета (он может быть прозрачным или беловатым, как молоко; если секрет приобретает коричневый оттенок, это может быть признаком мастита, в таком случае рекомендуется обратиться к врачу). Собака может быть более вялой, апатичной, отказываться от еды. Иногда животное начинает искать место, как будто готовится к родам, копать подстилку, таскать игрушки. Следующая фаза цикла — анэструс. Это период полового покоя, который длится до начала следующей течки, его продолжительность может составлять от 4 до 6 месяцев. С возрастом период между течками может увеличиваться. Симптомы течки у пожилых собак могут быть менее выражены, но это не исключает возможности наступления беременности. Также существует такое понятие, как расщепленная течка. У животного наблюдаются симптомы, характерные для первой фазы — кровянистые выделения, набухание вульвы и так далее, но через несколько дней эти признаки исчезают и возобновляются через несколько недель. Владельцы могут подумать, что у животного прошло две течки подряд. Для молодого животного до двух лет это вариант нормы, в более старшем возрасте это может быть признаком нарушения работы яичников. В таком случае лучше обратиться к специалисту. У некоторых животных наблюдается так называемая скрытая течка. Как уже упоминалось выше, течка у собак сопровождается кровянистыми выделениями. Животные могут оставлять следы на полу или мебели. Если вы не хотите, чтобы собака испачкала в этот период ковры и мебель, либо используйте специальные трусы, либо ограничьте ее передвижения по дому такой территорией, где будет легко за ней убрать. Поведение животного в период течки может значительно меняться. Некоторые животные становятся более вялыми, пассивными, хуже едят. Другие становятся менее управляемыми, агрессивными по отношению к другим животным, возбужденными. В любом случае, в этот период не рекомендуется отпускать собаку с поводка. В результате незапланированной вязки у собаки может наступить беременность. Если кобель был крупнее, могут возникнуть проблемы во время родов. Если плоды очень крупные, собака не сможет сама разродиться, и потребуется проведение оперативного вмешательства (кесарево сечение). Другим следствием незапланированной вязки может быть воспаление матки (эндометрит, пиометра), что потребует проведения лечения, а возможно даже оперативного вмешательства. Есть ряд инфекций, передающихся половым путем, которые могут приводить к воспалению и даже бесплодию. Не рекомендуется во время течки позволять собаке плавать в открытых водоемах, давать ей возможность сидеть на земле или загрязненных участках. В этот период половые пути самки более открыты, вследствие чего туда легче проникают бактерии, что в свою очередь может приводить к воспалению в органах мочеполовой системы (цистит, эндометрит). Признаки цистита — учащенное мочеиспускание небольшими порциями, моча может приобретать резкий специфический запах, может появляться кровь в моче. Эндометрит — это воспаление внутренней оболочки матки. Это заболевание может проявляться появлением выделений слизистого, слизисто-гнойного или кровянистого характера из наружных половых путей. Если вовремя не провести лечение, эндометрит может привести к развитию пиометры — гнойного воспаления матки. Это очень серьезное системное заболевание. Если при этом шейка матки остается закрытой, то весь этот гной скапливается в полости матки, токсические вещества всасываются в кровь и оказывают влияние на весь организм. Если шейка матки остается открытой, то вы можете заметить гнойные или кровянисто-гнойные выделения из петли, иногда с неприятным запахом, шерсть вокруг петли, области хвоста и внутренней поверхности бедер может быть испачкана этими выделениями. Животное может стать более вялым, апатичным, больше пить, отказываться от еды, у него может повыситься температура. В период течки рекомендуется избегать посещения выставок, прогулок на собачьих площадках, где возможно скопление большого количества животных, по причинам, которые упоминались выше. Не рекомендуется проводить плановую вакцинацию в период течки, рекомендуется дождаться ее окончания. При содержании разнополых животных в одной квартире, на период течки лучше их разделять. Разместить животных по отдельным комнатам недостаточно. Кобели чувствуют запах суки в течке за несколько километров. Лучший вариант на время одно из животных увезти в другой дом. Наличие в доме самки в течке является сильным стрессом для кобеля. Животное становится неуправляемым, может отказываться от еды, скулить, царапать дверь и всячески стараться добраться до самки. Конечно, самый эффективный и действенный способ — это стерилизация собаки. После проведения операции течки прекращаются, поскольку удаляется матка и яичники. Если такой вариант для владельцев неприемлем, или это племенное животное, существуют различные спреи, маскирующие или устраняющие запах в период течки. Животное необходимо обрабатывать несколько раз в день перед каждой прогулкой. Рекомендуется начинать обработки за несколько дней до предполагаемой даты начала течки. Обрабатывают область крупа, хвоста, внутренней поверхности бедер собаки. Следует избегать попадания спрея непосредственно на слизистые оболочки. Также некоторые производители рекомендуют обрабатывать и одежду хозяина, поскольку на ней может сохраняться запах. Период течки — непростое время как для животного, так и для владельца. Вот основные моменты, которые должен запомнить хозяин про период течки у собаки: В норме течка начинается в возрасте 6-18 месяцев. Если владельцы хотят получить от своей собаки потомство, рекомендуется вязать животное на 2-3 течку, в возрасте 24-36 месяцев. Время наступления первой течки не соответствует времени физиологической зрелости. Оптимальные сроки вязки — это 11-13 день от начала течки. Для более точного определения времени наступления овуляции проводятся специальные анализы — цитологическое исследование (мазок) и анализы на гормоны. В период течки рекомендуется гулять на поводке и максимально избегать контактов с другими животными, чтобы избежать нежелательных последствий (см. выше). Если произошла незапланированная вязка, рекомендуется как можно быстрее обратиться к врачу. Существуют препараты для предотвращения нежелательной беременности, которые вводятся в определенные дни после внеплановой вязки. Не рекомендуется купать животное в водоемах, разрешать залезать в грязь и так далее. В плане кормления в этот период не существует каких-то специальных рекомендаций. Собака может капризничать и отказываться от привычного корма, но не стоит идти у нее не поводу. Рекомендуется кормить животное полнорационным кормом в соответствии с породой и возрастом. PRO PLAN® OPTIBALANCE® для взрослых собак средних пород, с курицей Средние породы (собаки весом весом от 10 до 25 кг) составляют наиболее… PRO PLAN® OPTIBALANCE® для взрослых собак средних пород, с курицей Средние породы (собаки весом весом от 10 до 25 кг) составляют наиболее. PRO PLAN® DENTAL PRO BAR для взрослых собак для поддержания здоровья полости рта Для поддержания здоровья полости рта у собак. PRO PLAN® DENTAL PRO BAR для взрослых собак для поддержания здоровья полости рта Для поддержания здоровья полости рта у собак. PRO PLAN® OPTIBALANCE® для взрослых собак мелких и карликовых пород с курицей В рейтинге факторов, влияющих на долголетие собаки, правильное кормление… PRO PLAN® OPTIBALANCE® для взрослых собак мелких и карликовых пород с курицей В рейтинге факторов, влияющих на долголетие собаки, правильное кормление… Корм консервированный полнорационный диетический PRO PLAN® Veterinary Diets HA Hypoallergenic для щенков и взрослых собак для снижения пищевой непереносимости ингредиентов и питательных веществ PURINA® PRO PLAN® VETERINARY DIETS (Пурина Про План Ветеринари Даетс) HA. Корм консервированный полнорационный диетический PRO PLAN® Veterinary Diets HA Hypoallergenic для щенков и взрослых собак для снижения пищевой непереносимости ингредиентов и питательных веществ PURINA® PRO PLAN® VETERINARY DIETS (Пурина Про План Ветеринари Даетс) HA. Корм… Понимание удивительной трансформации, которую переживает котенок от рождения до взрослого возраста, поможет вам обеспечить ему подходящее сбалансированное питание на каждом этапе развития. Сразу после рождения следует позаботиться о том, чтобы котята начали получать материнское молоко. В первые часы и дни после рождения мать вместе с молоком передает новорожденным необходимые питательные вещества, которые способствуют здоровому развитию котят. После появления на свет котята должны сразу подползать к матери и начинать сосать молоко. Так они получают молозиво — компонент материнского молока, который богат антителами и укрепляет иммунную систему. При рождении котята подвержены риску двух типов: Во-первых, из-за отслойки плаценты они могут страдать от недостатка кислорода в течение разных периодов времени. Во-вторых, после рождения они вступают в непосредственный контакт с бактериями и вирусами окружающей среды. Заводчик должен принять все меры предосторожности, тщательно подготовить родильный манеж и контролировать рождение котят, чтобы снизить риск нарушений здоровья новорожденных. Хотя котята рождаются глухими и слепыми, они проявляют ряд рефлекторных поведенческих реакций на раннем этапе. Котята уже способны ориентироваться в пространстве, полагаясь на обоняние и осязание. Они могут греться, прижимаясь к матери, и сосать ее молоко, чтобы утолить голод. Вес новорожденных котят должен составлять примерно 2–3 % от веса их матери. В первые дни их ежедневный прирост в весе составляет примерно 10 % от веса при рождении. Самцы обычно весят больше и растут быстрее. Котята рождаются слепыми и глухими. Они тянутся к матери в поисках защиты и питания. Новорожденные котята должны постоянно находиться рядом с матерью, которая согревает, кормит и вылизывает их. В их манеже нужно поддерживать температуру около 30 °C, чтобы снизить риск переохлаждения, а также стремиться поддерживать влажность на уровне 65–70%. Новорожденные котята находятся под защитой и в тепле рядом с матерью и другими котятами своего помета. Основную часть времени они спят и едят. В первые дни жизни котят ответственный заводчик должен обеспечить их осмотр ветеринарным врачом. Ветеринарный врач проверит, есть ли у котят врожденные дефекты или проблемы со здоровьем, требующие лечения. На этом этапе иммунная система котенка по-прежнему в значительной степени поддерживается за счет материнского молока, обеспечивающего его организм основными белками, необходимыми для развития. На этом этапе котята спят большую часть дня — примерно 90 % времени в первые несколько недель. Они двигаются только, чтобы подползти к матери за теплом и молоком. Котята уже умеют мурлыкать и издавать другие звуки. В возрасте примерно пяти дней котята открывают глаза. Пуповина отпадает приблизительно через неделю после рождения. В это же время котята начинают прибавлять в весе от 10 до 30 граммов в день. В первые недели жизни котенка основные требования к условиям содержания — это чистота, тишина и тепло. Физическое развитие котят ускоряется, и начинается процесс отлучения от матери. Это важный этап, на котором котенок учится, наблюдая за матерью и общаясь с другими котятами. По мере развития молочных зубов для котенка начинается процесс отъема (отлучения от матери). Через некоторое время котята проявляют первый интерес к твердому корму, который получает их мать, и тогда можно начинать вводить твердый корм в их рацион. Из-за незрелой пищеварительной системы котятам очень важно получать легкоусвояемый корм, учитывающий их особые потребности на данном этапе. На этом этапе происходит ослабление иммунитета. На данном этапе котята начинают больше взаимодействовать и вылизывать шерсть друг друга. Они начинают активно играть, бегать, атаковать и имитировать охоту. На этой стадии зрение котят полностью сформировано. К четвертой неделе слух и обоняние хорошо развиты. К концу шестой-седьмой недель начинают формироваться модель сна и моторика, характерные для взрослых животных. Ключевые социальные навыки вырабатываются в процессе общения с однопометниками, а обучение происходит путем наблюдения за поведением матери. Поскольку в этом возрасте котята проявляют все больше любопытства и становятся все более активными, необходимо сделать окружающее пространство безопасным для них. Котенок начинает понимать, что от него требуется, и вырабатывает поведение, которое уже не изменится в течение жизни. Примерно восьминедельный возраст идеален для первой вакцинации котенка, последующая обязательная ревакцинация — через 3-5 недель. Это важный процесс, обеспечивающий котенка защитой от опасных заболеваний во взрослой жизни. Обратитесь к ветеринарному врачу, чтобы составить план вакцинации. Некоторые питательные вещества котенок еще не способен усваивать, поэтому важно, чтобы он получал корм, учитывающий индивидуальные потребности на конкретном этапе его развития. На этом этапе на поведение котенка больше всего влияет его окружение, в том числе котята из его помета, другие домашние питомцы и люди. Кроме того, котенок начинает понимать, какое место он занимает в доме, и у него может формироваться доминирующее или подчиненное поведение в зависимости от его опыта и воспитания. Это ключевой этап в развитии взаимоотношений, поэтому стабильность, поддержка и эмоциональная привязанность очень важны. Эффективная социализация на этом этапе поможет вырастить воспитанную и счастливую кошку. Котят можно забирать от матери и знакомить с новым домом с 8-недельного возраста. В зависимости от заводчика этот срок может увеличиться до 12 недель. Перед тем как принести котенка домой, важно убедиться, что квартира полностью готова к его появлению: следует спрятать электрические провода и закрыть розетки, обезопасить окна, балконы и лестницы, убрать все острые и мелкие предметы. По мере взросления котенок постепенно достигает полной физической зрелости. В этот период кошки начинают метить территорию, где они живут, мочой и секретом лицевых желез: они трутся головой о предметы, других животных и людей. Это признак начала полового созревания. Теперь следует обсудить с ветеринарным врачом необходимость стерилизации (кастрации). По мере достижения котенком физической зрелости и приближения к весу взрослого животного его необходимо постепенно переводить на рацион для взрослых кошек и соответствующим образом адаптировать размеры порций. Баланс питательных веществ в составе корма зависит от возраста кошки и таких факторов, влияющих на метаболизм, как образ жизни (бывает ли животное на улице) и кастрация (было ли животное кастрировано). По мере того как кошка взрослеет, она все больше стремится к доминированию в вашей семье. На этом этапе у котенка происходит смена зубов на 30 постоянных. Если котенок не стерилизован, в шесть месяцев наступает половая зрелость, сопровождаемая половыми циклами и брачным поведением. К восьми месяцам котенок достигает 80 % веса взрослого животного. В зависимости от размера породы, взросление наступает в период от 12 до 15 месяцев. Если котята получили все необходимые прививки, примерно с возраста шести месяцев вы можете выпускать их на улицу. Лучше всего действовать поэтапно. До тех пор, пока котята не привыкнут к новой обстановке, оставайтесь на улице рядом с ними. Когда они почувствуют себя увереннее, они начнут активнее исследовать окружающее пространство. Вес взрослого животного в 40–50 раз больше веса новорожденного котенка. Котята становятся взрослыми примерно через 12 месяцев после рождения, а кошки более крупных пород достигают зрелости только в возрасте 15 месяцев. Когда кошка становится взрослой, следует постепенно перевести ее на корм, который сможет удовлетворить ее потребности в питании с учетом породы и образа жизни. Питание ROYAL CANIN® для котят поддерживает рост и развитие вашего питомца, обеспечивая организм животного всеми питательными веществами, необходимыми для его здоровья в первый год жизни. Корма для котят Формулы наших продуктов удовлетворяют потребности взрослых кошек и учитывают их возраст, породу, размер и образ жизни. Корма для кошек Нормальное развитие детей раннего возраста в значительной степени определяется правильным уходом за ними. Процесс приучения к горшку – важный этап в развитии и взрослении ребенка, а также в формировании его отношений с родителями. Многие родители склонны проявлять излишнее беспокойство, когда их ребенок не развивается в соответствии с их представлениями. Практикуемые до недавнего времени методы «раннего приучения к горшку» (в течение первого года жизни) следует признать устаревшими и нефизиологическими, поскольку при их использовании не учитывается степень зрелости мышц и нервной системы ребенка (в частности, иннервация мочевого пузыря и кишечника). Описываемые методы раннего приучения к горшку относятся к рефлекторным, то есть, основанным на выработке условного рефлекса, а не сознательного навыка. Чтобы процесс приучения к горшку проходил быстро и легко, родители должны быть проинформированы о методе, «ориентированном на ребенка. «Ориентированный на ребенка» или физиологический метод туалетного обучения, является методом, учитывающим степень зрелости центральной нервной системы. Именно ЦНС обеспечивает иннервацию мышц, органов мочеполовой системы и желудочно-кишечного тракта детей. Данный подход помогает родителям правильно понять ребенка и направить процесс приучения к горшку в соответствие с уровнем развития ребенка. Согласно этому методу ребенок становится главной фигурой, повышается его уверенность в себе и самоуважение. Обучение, согласно такой методике, призвано не просто выработать у ребенка рефлекс, а ускорить усвоение соответствующей информации или навыков, в случае с приучением к горшку – знакомство ребенка с собственным телом. Физиологическая модель учитывает три ведущие составляющие детского развития: физиологическую зрелость (укрепление мышц сфинктера мочевого пузыря и кишечника, необходимое развитие ЦНС), психологическую и эмоциональную готовность (понимание и желание следовать инструкциям). Вверх
Приучая ребенка к горшку, Вы должны знать, что успех обучения полностью зависит от того, насколько его организм готов к этому. Доказано, что детский организм готов к приучению к горшку в среднем не раньше 18 месяцев. Ребенок может осознанно ходить в туалет только тогда, когда у него развивается связь между нервной системой и мышцами. Эта связь окончательно формируется приблизительно в возрасте 18 месяцев и представляет собой многочисленные нервные структуры, соединяющие спинной мозг с мочевым пузырем и кишечником. Когда мочевой пузырь или кишечник наполняются, по нервам передается сигнал в спинной мозг, оттуда — в головной мозг, и малыш понимает, что он хочет писать или какать. Только после этого ребенок может осознанно сесть на горшок и сделать свое дело. Вверх
Правда, очень многим терпеливым и активным родителям удается добиться прекрасных результатов уже на первом году жизни. Сплошь и рядом произносятся гордые заявления о том, что ребенок в 10, 9, 8 даже в 7 месяцев писает по команде «пи-пи», а какает исключительно после «а-а». И в этом нет совершенно ничего удивительного. Многократным пипиканьем и ааканьем несложно добиться возникновения условного рефлекса, только рефлекс этот — не совсем то, что нам нужно. Почему? Да потому, что это связь между процессом опорожнения мочевого пузыря и звуком «пи-пи». Приучение к горшку в возрасте около 18 месяцев Приучение к горшку в более раннем возрасте Ребенок осознанно контролирует все процессы Процесс основывается полностью на рефлексах Приобретенные навыки не теряются При любых переменах в жизни ребенка он быстро забывает все, чему научился Приучение проходит быстрее и легче Приучение дольше и сложнее для ребенка Ребенок наслаждается своими успехами и самим процессом Частые промашки, больше стресса для ребенка Расплата за ранние успехи приходит на втором году жизни. Вверх
Для того, чтобы процесс прошел максимально гладко, следует знать некоторые признаки, указывающие на психическую и физиологическую готовность организма ребенка к познанию туалетной науки. К таким признакам относятся: И, наконец, самый достоверный признак: умение любым способом — словом, мимикой, жестами — передать родителям слово «хочу». И не потому что так будет легче для мамы и она успеет усадить ребенка на горшок — это свидетельствует о том, что малыш научился общаться! Вверх
Вашему малышу уже около 18 месяцев? Вы заметили в его поведении какие-либо из приведенных выше признаков готовности? Значит, можно начинать овладение новой сложной наукой. 1. Помимо готовности ребенка должна быть и готовность взрослых. Очевидно, что на этапе перехода от подгузника к горшку затраты времени на непосредственное общение с малышом заметно увеличиваются. Нельзя вырабатывать туалетные навыки лишь по воскресеньям или только в те дни, когда ожидается официальный визит бабушки. 2. Ребенок, как, впрочем, и всякий взрослый человек, склонен к переменам в настроении. Ранний этап туалетного обучения лучше проводить тогда, когда все члены семьи здоровы и жизнерадостны. 3. Купите удобный и … теплый горшок — холодное посадочное место может надолго испортить отношения с горшком. Сидение должно повторять анатомические изгибы, желательно наличие удобной спинки (такие горшки называют физиологичными). Первым делом вымойте горшок и поставьте его в комнате у крохи, чтобы он стал привычным для него предметом. 4. Знакомимся с горшком. Предлагаем его ребенку тогда, когда вероятность «процесса» максимальна — после сна, после еды, когда он показывает своим поведением, что ему пора. 5. В случае успеха — очень-очень хвалим. Вслучае неудачи — изо всех сил стараемся не огорчаться, а если огорчаемся — огорчения не показываем. 6. Фиксируем внимание не только на самом горшке, но и на действиях, непосредственно предшествующих общению с горшком и расставанию с ним: как горшок достать, как его открыть, как снять трусы, как одеть трусы, как и куда вылить содержимое из горшка, как помыть горшок, как закрыть горшок и поставить его на место. Реализация всего перечисленного с легкостью превращается в интересную игру. Замечательно, если после каждого удачно осуществленного действия родители не скупятся на похвалы — весь процесс в таком случае сопровождают положительные эмоции, а это, пожалуй, главное на переходном этапе. 7. Постепенно организовываем встречи с горшком не только тогда, когда ребенку пора, а тогда, когда этого требует распорядок дня. Например, в обязательном порядке усаживаемся перед сном, перед прогулкой. 8. Расставаться с подгузниками окончательно и бесповоротно не следует. прогулке в прохладное время года, поначалу и во время дневного сна. Но всякий раз, когда проснулись сухие и быстренько уселись на горшок — обращаем внимание на то, какие мы молодцы, и в подтверждение этого очевидного факта демонстрируем сухой подгузник. 9. Важно, чтобы горшок воспринимался не как игрушка, а в качестве предмета совершенно определенного назначения. И в этой связи не стоит поощрять просто игры с горшком. «Вот это стул. На нем сидят» — и, по аналогии, — «Это горшок, на нем писают и какают». 10. Не принципиально: горшок или унитаз (подразумевается наличие специального детского сиденья). Тут уж как Вам удобнее. С учетом того, что, особенно на первых порах, процесс может затягиваться, горшок сподручнее, поскольку общаться в комнате приятнее, чем в тесном туалетном пространстве. Совмещать горшок с унитазом — вполне приемлемый вариант, особенно для мальчиков. Специальная табуреточка в туалете, а с нее пописать — это же просто удовольствие и осознанное приобщение к миру взрослых. Вверх
«Нам уже один годик. Наша Анюта может очень долго сидеть на горшочке, играть, смотреть книжки, но того, что надо, не делает. Как нам быть?» Мария
Не стоит переживать по этому поводу. Ваша дочь еще слишком мала для приучения к горшку. Начинать приучать ребенка можно только тогда, когда его организм физиологически готов к этому — то есть приблизительно в возрасте 18 месяцев. Только к этому возрасту у него формируется нервная система и он начинает осознавать, что хочет в туалет. А сейчас, когда Вашей дочке 1 год и она начинает ходить, очень важно помочь ей развивать равновесие и укреплять мышцы спины — для этого очень бы подошли упражнения на гимнастическом мяче (покачивания малыша, лежаще- го спинкой или животиком на мяче) или перешагивания через препятствия (через игрушки на полу). «Мы начали приучать нашего малыша ходить на горшок около 3 недель назад, он вроде бы сразу все понял и делал все как надо, а потом стал отказываться, и теперь не хочет даже приближаться к нему. Такое часто случается, и в этом нет ничего страшного. Постарайтесь вспомнить, после чего ребенок стал отказываться от горшка. Может, что-то его напугало, или горшок был холодный. Обратите внимание на обстановку в семье, задумайтесь, что изменилось в жизни малыша и не переживает ли он стресс? И если Вы поймете причину, постарайтесь устранить ее. Ни в коем случае не заставляйте его садиться на горшок. Лучше всего приостановить процесс обучения на несколько недель и окружить ребенка вниманием и лаской. Обычно после такой передышки дети готовы заново знакомиться с горшком. «Наша Катюша в свои 1 год и 7 месяцев не ходит на горшок. Но она очень интересуется всем, что происходит в туалетной комнате. Когда кто-то из нас заходит туда, она каждый раз пытается ворваться и посмотреть, что мы там делаем. Нормально ли это?» Дарья
Не волнуйтесь! Это абсолютно нормально, более того, этот интерес Вашей дочери свидетельствует о ее готовности к приучению к горшку. Вы все делаете правильно. А если где-то была допущена ошибка и горшок теперь вызывает у ребенка отрицательные эмоции, прервитесь и начните обучение заново. Воспользуйтесь ее любопытством к поведению взрослых. Известно, что малыши очень любят подражать взрослым. Купите дочери детское сидение для унитаза и покажите ей, как использовать туалет. После этого скорее всего она сама захочет вести себя, как взрослая, и делать то же самое. Вверх
1.«Мне кажется что чем раньше я начну учить малыша использовать горшок, тем быстрее он научится это делать. Так ли это?»
Вы, как и все родители, хотите для своего ребенка только самого лучшего и стараетесь развивать все его способности как можно раньше. Но в таком деле, как приучение к горшку, торопиться не стоит. Чем раньше Вы начнете, тем дольше и сложнее для ребенка будет этот процесс. 2.«Правда ли, что если малыш все время носит одноразовые подгузники, в которых не чувствует, что он мокрый, то приучить его использовать горшок сложнее?»
Независимо от того, какие подгузники носит малыш и носит ли он их вообще, он научится ходить на горшок, когда его организм будет готов. В подтверждение этому есть результаты исследований, сравнивших поведение двух групп детей — в первой группе малыши с рождения носили традиционные марлевые подгузники, а во второй — одноразовые подгузники. В обеих группах возраст, в котором малыши перестали полностью нуждаться в подгузниках, был совершенно одинаковым — в среднем 27 месяцев (E.Takanashi, 1988 г., Япония). Поэтому можно с уверенностью сказать, что использование одноразовых подгузников с сухой поверхностью никак не сказывается на способности малышей научиться использовать горшок и возрасте, когда они могут это сделать. 3.«Я боюсь одевать подгузники на своего 3-месячного сынишку, так как слышала, что из-за парникового эффекта они могут привести к бесплодию»
Во-первых, репродуктивная система у мальчиков начинает развиваться только в 7-9 лет. В 7 лет появляются клетки-предшественнки сперматозойдов, а сами спермотозойды могут быть обнаружены не раньше, чем в 10 лет, но как правило, значительно позднее. Из этого понятно, что подгузники никак не могут влиять на качество спермы — ее у мальчиков в этом возрасте нет в принципе. Также существует ряд исследований, которые подтверждают, что одноразовые подгузники не создают парникового эффекта — температура под подгузником практически не отличается от температуры кожи в обычных пеленках, а уровень влажности под подгузником значительно ниже, чем при использовании пеленок. Поэтому подводим итог: одноразовые подгузники и мальчики совместимы. 4.«Моей дочке 1 годик. Я знаю, что ее еще рано приучать к горшку, но я очень переживаю, что мы не успеем научиться до детского сада. Независимо от того, в каком возрасте Вы начнете приучать своего ребенка к горшку, нет никакой гарантии, что она научится это делать до детского сада. Ведь все дети приучаются к горшку примерно в одно и то же время. Поэтому если начать приучение в раннем возрасте, это не поможет ускорить процесс, а наоборот обучение затянется — ребенок не будет понимать, чего от него хотят, она будет расстраиваться из-за этого, да и Вы тоже. А если начинать, когда организм ребенка готов к этому, то Вы и Ваш малыш добьетесь успеха значительно быстрее и легче, и ребенок будет уже понимать, что это его достижение и сможет гордиться этим. 5.«Многие из моих подруг во дворе говорят, что их малыши ходят на горшказ в возрасте 9, 8, и даже в 6 месяцев. Моей дочке 1 годик, я пыталась ее научить, но ничего не выходит. Может я что-то делаю не так? Почему мой ребенок не может так же быстро научиться, как и остальные дети?»
Татьяна, я понимаю, что Вы, как и все остальные родители, сравниваете своего ребенка с чужими детьми и стараетесь доказать, что Ваш не хуже. Ваши подруги скорее всего умалчивают о том, что их малыши сидят на горшке и слушают нескончаемые «пись-пись» и «а-а» по 30-40 минут, а к этому времени у ребенка даже пустой мочевой пузырь наполняется, и они писают в горшок. И приводит это к вырабатыванию условного рефлекса на просьбы мамы пописать или покакать. Но на втором году жизни этот рефлекс неожиданно для родителей пропадает. И только тогда ребенок начинает осознанно учиться ходить на горшок. Так что помните — всему, особенно тому, что касается горшка, свое время. 6.«Моя мама считает, что использование пеленок более полезно для здоровья нашего малыша, чем подгузники. Такие предубеждения старшего поколения по отношению к подгузникам связаны с тем, что раньше эти средства гигиены были попросту недоступны. И сегодня бабушкам, которые часто с подозрением смотрят на все новое, трудно оценить достоинства подгузников. Хотя, если сравнивать подгузники c пеленками, то преимущества первых налицо — мокрая поверхность пеленок вызывает раздражения и заболевания кожи, а в холодную погоду продолжительность прогулок малыша в пеленках значительно сокращается. Союз Педиатров России проводил клинические исследования, и результаты показали, что в подгузниках влажность кожи ребенка значительно ниже, чем в пеленках. Также в ходе исследований выяснилось, что одноразовые подгузники помогают устранить раздражение на детской коже, даже если у малыша пеленочный дерматит, чего не могут сделать пеленки. Поэтому врачи СПР рекомендуют мамам с самого рождения малыша регулярно использовать одноразовые подгузники. Вверх
Истории На продолжительность беременности влияет множество факторов даже в рамках одного вида: например, время года, пол и количество детенышей и т. Все ныне живущие представители семейства опоссумов населяют Новый Свет, хотя ископаемые формы встречаются на территории Европы. Хотя продолжительность жизни большинства мышиных, как правило, составляет менее двух лет, они обладают высоким репродуктивным потенциалом, и их популяция быстро растет, а затем резко сокращается, когда пищевые ресурсы истощаются. Как полагают ученые, плохая память некоторых видов белок помогает сохранять леса, так как они закапывают орехи в землю и забывают про них, а из проросших семян появляются новые деревья. Волки моногамны, для них типичен образ жизни семейными группами, состоящими из пары родителей и их детей, а также пришлых одиноких волков. Бобрята появляются на свет полузрячими. Они хорошо опушенные, через 2 суток уже могут плавать, но нырять и скрываться от опасности еще не способны. Лосята могут вставать через несколько минут после рождения, через 3 дня свободно передвигаются. Молочное кормление продолжается до 4 месяцев. Беременность коровы длится чуть дольше 9 месяцев, однако сами роды у здоровых животных продолжаются всего 30 минут. Уже через 10—15 минут после появления на свет жеребенок самостоятельно встает на ноги, через час начинает сосать молоко. Обычно первые 2-3 дня самка никого не подпускает к детенышу, чтобы он запомнил индивидуальный рисунок на ее теле и отличал потом ее от других зебр. Роды происходят в позиции стоя, так что малышу первым делом предстоит упасть с двухметровой высоты. Самка обычно приносит одного малыша. Уже через сутки он может сопровождать мать, через неделю начинает питаться травой, но до года не бросает сосать молоко. Обычно слоны образуют группы из самок и детенышей, возглавляемых старой и опытной самкой. Слонята рождаются весом около 100 кг и ростом около 1 метра, но без бивней. Теги Сегодня читают Что будет, если каждый день пить томатный сок? Объясняет гастроэнтеролог 10 красивых имен со всего света, которые приносят богатство Что будет, если перестать пить спиртное: исследования ученых Художник спрятал 3 совят среди школьников: сумеете их отыскать? Что будет, если есть кабачки каждый день? 6 фактов про пользу и вред «кустовой тыквы» Сколько 18 месяцев? Сколько будет 18 месяцев в днях? Преобразование 18 мес в д. От
СтолетияДниДесятилетияЧасыЧасы:Минуты:СекундыМикросекундыМилленияМиллисекундыМинутыМесяцыНаносекундыСекундыНеделиРабочие неделиГоды До
CenturiesDaysDecadesHoursHours:Minutes:SecondsMicrosecondsMilleniaMillisecondsMinutesMonthsNanosecondsSecondsWeeksWork WeeksYears единицы обмена ↺ Сумма 18 месяцев = 547,86375 Дни (точный результат) Показать результат как
NumberFraction (точное значение) Месяц составляет 1/12 -го года. В григорианском календаре в среднем в месяце ровно 30,436875 дней. Первоначально он был основан на времени, которое требуется Луне, чтобы вращать Землю. День — это приблизительное время, за которое Земля совершает один оборот. Он определяется как ровно 86 400 секунд. Преобразование месяцев в дни (некоторые результаты округлены) 18 месяцев равно
547,864 дня Сумма От
сантиметры (см) футы (футы) дюймы (дюймы) километры (км) метры (м) мили (ми) дециметры (дм) миллиметры (мм) ярды (ярды) граммы (г) унции (унции) фунты (фунты) килограммы ( кг)дни (d)месяцы (mo)годы (год)часы (hr)минуты (min)секунды (s)недели (wk)футы в секунду (ft/s)километры в час (km/h)узлы (kt) метры в секунду (м/с)миль в час (миль/ч)кубические сантиметры (см3)кубические футы (ft3)кубические дюймы (in3)кубические метры (м3)стаканы (cup)децилитры (dL)галлоны (gal)литры (L) миллилитры (мл)жидкие унции (жидкие унции)пинты (pt)кварт (qt)столовые ложки (tbsp)чайные ложки (tsp) Кому
сантиметры (см) футы (футы) дюймы (дюймы) километры (км) метры (м) мили (ми) дециметры (дм) миллиметры (мм) ярды (ярды) граммы (г) унции (унции) фунты (фунты) килограммы ( кг)дни (d)месяцы (mo)годы (год)часы (hr)минуты (min)секунды (s)недели (wk)футы в секунду (ft/s)километры в час (km/h)узлы (kt) метры в секунду (м/с)миль в час (миль/ч)кубические сантиметры (см3)кубические футы (ft3)кубические дюймы (in3)кубические метры (м3)стаканы (cup)децилитры (dL)галлоны (gal)литры (L) миллилитры (мл)жидкие унции (жидкие унции)пинты (pt)кварт (qt)столовые ложки (tbsp)чайные ложки (tsp) Коэффициент перевода месяцев в дни равен 30,436875, что означает, что 1 месяц равен 30,436875 дням: 1 мес = 30,436875 д Чтобы преобразовать 18 месяцев в дни, мы должны умножить 18 на коэффициент преобразования, чтобы получить количество времени из месяцев в дни. 1 мес → 30.436875 д 18 мес → Т (г) Решите приведенную выше пропорцию, чтобы получить время Т в днях: T (г) = 18 мес × 30,436875 д Т (г) = 547,86375 д Окончательный результат: 18 мес → 547,86375 д Мы заключаем, что 18 месяцев эквивалентны 547,86375 дням : 18 месяцев = 547,86375 дней Мы также можем преобразовать, используя обратное значение коэффициента преобразования. В этом случае 1 день равен 0,0018252713379923 × 18 месяцев . Другой способ сказать, что 18 месяцев равно 1 ÷ 0,0018252713379923 дней . Для практических целей мы можем округлить наш окончательный результат до приблизительного числового значения. Мы можем сказать, что восемнадцать месяцев примерно пятьсот сорок семь целых восемь целых шесть четыре дня : 18 мес ≅ 547,864 д Альтернативой также является то, что один день равен примерно нулю целых ноль целых два раза восемнадцать месяцев . Для быстрого ознакомления ниже приведена таблица преобразования, которую можно использовать для преобразования месяцев в дни В этом преобразовании участвуют месяцы и дни. Месяц (обозначение: мес) — это единица времени, используемая в календарях, которая примерно равна естественному периоду, связанному с движением Луны; месяц и Луна являются родственными. Традиционная концепция возникла с циклом лунных фаз; такие месяцы (лунные месяцы) являются синодическими месяцами и длятся примерно 29,53 дня. Из раскопанных палочек для подсчета исследователи пришли к выводу, что люди считали дни по фазам Луны еще в эпоху палеолита. Синодические месяцы, основанные на периоде обращения Луны относительно линии Земля-Солнце, до сих пор являются основой многих календарей и используются для деления года. День (обозначение: d) — единица времени. В обычном использовании это либо интервал, равный 24 часам, либо дневное время, последовательный период времени, в течение которого Солнце находится над горизонтом. 18 месяцев =
547.864 дней Сумма От
Сантиметры (см)Футы (футы)Дюймы (дюймы)Километры (км)Метры (м)Мили (мили)Морские мили (нми)Миллиметры (мм)Нанометры (нм)Ярды (ярды)Граммы (г)Миллиграммы (мг)Унции (oz)Фунты (lb)Стоуны (st)Длинные тонны (uk tn)Метрические тонны (t)Короткие тонны (us tn)Килограммы (kg)Дни (d)Десятилетия (decade)Месяцы (mo)Годы (yr)Часы ( ч)Миллисекунды (мс)Минуты (мин)Наносекунды (нс)Секунды (с)Недели (нед)Цельсий (°C)Фаренгейты (°F)Кельвины (K)Акры (акр)Гектары (га)Квадратные футы (ft2)Квадрат Дюймы (in2)Квадратные километры (km2)Квадратные метры (m2)Квадратные мили (mi2)Квадратные ярды (yd2)Британские термальные единицы (BTU)Фут-фунты (ft-lb)Джоули (J)Килокалории (kcal)Килоджоули (kJ)Киловатты Часы (кВтч) Термы (термы) Ватт-часы (Втч) Гигагерцы (ГГц) Герцы (Гц) Килогерцы (кГц) Мегагерцы (МГц) Терагерцы (ТГц) Футы в секунду (фут/с) Километры в час (км/ч) Узлы (kt) Метры в секунду (m/s) Мили в час (mph) Нефтяные баррели (bbl) Кубические сантиметры (cm3) Кубические футы (ft3) Кубические дюймы (in3) Кубические метры (m3) Британские кубки (uk cup) Чашки ( чашка)Имперские галлоны (британские галлоны)Галлоны (галлоны )Литры (л)Миллилитры (мл)Английские жидкие унции (uk fl oz)Жидкие унции (fl oz)Английские пинты (uk pt)Пинты (pt)Английские кварты (uk qt)Кварты (qt)Английские столовые ложки (uk tbsp)Столовые ложки (tbsp)Имперские чайные ложки (uk tsp)Чайные ложки (tsp)Биты (b)Байты (B)Гигабиты (Gb)Гигабайты (GB)Килобиты (kb)Килобайты (KB)Мегабиты (Mb)Мегабайты (MB)Петабиты (Pb)Петабайты (PB)Терабиты (Tb)Терабайты (TB)Биты/секунды (bps)Байты/секунды (Bps)Гигабиты/секунды (Gbps)Гигабайты/секунды (GBps)Килобиты/секунды (kbps)Килобайты/секунды (kBps)Мегабиты/секунды (Мбит/с)Мегабайт в секунду (МБ/с)Терабит/секунду (Тбит/с)Терабайт/секунду (ТБ/с) Кому
Сантиметры (см)Футы (футы)Дюймы (дюймы)Километры (км)Метры (м)Мили (мили)Морские мили (нми)Миллиметры (мм)Нанометры (нм)Ярды (ярды)Граммы (г)Миллиграммы (мг)Унции (oz)Фунты (lb)Стоуны (st)Длинные тонны (uk tn)Метрические тонны (t)Короткие тонны (us tn)Килограммы (kg)Дни (d)Десятилетия (decade)Месяцы (mo)Годы (yr)Часы ( ч)Миллисекунды (мс)Минуты (мин)Наносекунды (нс)Секунды (с)Недели (нед)Цельсий (°C)Фаренгейты (°F)Кельвины (K)Акры (акр)Гектары (га)Квадратные футы (ft2)Квадрат Дюймы (in2)Квадратные километры (km2)Квадратные метры (m2)Квадратные мили (mi2)Квадратные ярды (yd2)Британские термальные единицы (BTU)Фут-фунты (ft-lb)Джоули (J)Килокалории (kcal)Килоджоули (kJ)Киловатты Часы (кВтч) Термы (термы) Ватт-часы (Втч) Гигагерцы (ГГц) Герцы (Гц) Килогерцы (кГц) Мегагерцы (МГц) Терагерцы (ТГц) Футы в секунду (фут/с) Километры в час (км/ч) Узлы (kt) Метры в секунду (m/s) Мили в час (mph) Нефтяные баррели (bbl) Кубические сантиметры (cm3) Кубические футы (ft3) Кубические дюймы (in3) Кубические метры (m3) Британские кубки (uk cup) Чашки ( чашка)Имперские галлоны (британские галлоны)Галлоны (галлоны )Литры (л)Миллилитры (мл)Английские жидкие унции (uk fl oz)Жидкие унции (fl oz)Английские пинты (uk pt)Пинты (pt)Английские кварты (uk qt)Кварты (qt)Английские столовые ложки (uk tbsp)Столовые ложки (tbsp)Имперские чайные ложки (uk tsp)Чайные ложки (tsp)Биты (b)Байты (B)Гигабиты (Gb)Гигабайты (GB)Килобиты (kb)Килобайты (KB)Мегабиты (Mb)Мегабайты (MB)Петабиты (Pb)Петабайты (PB)Терабиты (Tb)Терабайты (TB)Биты/секунды (bps)Байты/секунды (Bps)Гигабиты/секунды (Gbps)Гигабайты/секунды (GBps)Килобиты/секунды (kbps)Килобайты/секунды (kBps)Мегабиты/секунды (Мбит/с)Мегабайт в секунду (МБ/с)Терабит/секунду (Тбит/с)Терабайт/секунду (ТБ/с) Чтобы преобразовать 18 месяцев в дни, нужно умножить 18 на 30,436875, поскольку 1 месяц равен 30,436875 дням. 18 мес. × 30,436875 = 547,864 дня 18 мес = 547,864 д Мы заключаем, что восемнадцать Месяцев эквивалентны пятистам сорока семи целых восемь десятых шесть четыре Дня: 18 месяцев равно 547,864 дням. Таким образом, если вы хотите рассчитать, сколько дней в 18 месяцах, вы можете сделать это, используя приведенную выше формулу преобразования. Ниже приведена таблица перевода месяцев в дни Давайте посмотрим, как определяются обе единицы в этом преобразовании, в данном случае месяцы и дни: Месяц (обозначение: мес) — это единица времени, используемая в календарях, которая примерно равна естественному периоду, связанному с движением Луны; месяц и Луна являются родственными. Традиционная концепция возникла с циклом лунных фаз; такие месяцы (лунные месяцы) являются синодическими месяцами и длятся примерно 29,53 дня. Из раскопанных палочек для подсчета исследователи пришли к выводу, что люди считали дни по фазам Луны еще в эпоху палеолита. Синодические месяцы, основанные на периоде обращения Луны относительно линии Земля-Солнце, до сих пор являются основой многих календарей и используются для деления года. День (обозначение: d) — единица времени. В обычном использовании это либо интервал, равный 24 часам, либо дневное время, последовательный период времени, в течение которого Солнце находится над горизонтом. Период времени, за который Земля совершает один оборот относительно Солнца, называется солнечными сутками. Несколько определений этого универсального человеческого понятия используются в зависимости от контекста, необходимости и удобства. В 1960 году секунда была переопределена с точки зрения орбитального движения Земли и стала базовой единицей времени в системе СИ. Единица измерения «день», переопределенная в 1960 как 86 400 секунд СИ и обозначенное символом d, не является единицей СИ, но допускается для использования с СИ. Гражданский день обычно составляет 86 400 секунд плюс или минус возможная дополнительная секунда по всемирному скоординированному времени (UTC), а иногда плюс или минус час в тех местах, которые переходят на летнее время или на него. Основные факты Найдите количество лет, месяцев, недель и дней между датами. Нажмите «Настройки», чтобы определить праздники. года месяца недели дня расчет в рабочих днях Григорианский календарь сегодня является наиболее распространенным. Григорианский календарь — это реформированная версия юлианского календаря, который сам по себе был модификацией древнеримского календаря. Древний римский календарь считался наблюдательным лунным календарем, основанным на циклах лунных фаз. Тогда считалось, что римляне приняли 10-месячный календарь с 304 днями, оставив оставшиеся 50 или около того дней в виде неорганизованной зимы. В этом календаре летние и зимние месяцы были совершенно неуместны, что привело к принятию более точных календарей. Республиканский календарь, позже использовавшийся Римом, следовал греческому календарю в его предположениях о 29,5 днях в лунном цикле и 12,5 синодических месяцах в солнечном году, которые выравниваются каждый четвертый год после добавления вставочных месяцев января и февраля. Несмотря на все усилия, юлианский календарь все еще нуждался в дальнейшей реформе, так как календарь смещался относительно равноденствий и солнцестояний примерно на 11 минут в год. К 1582 году это привело к разнице в 10 дней с ожидаемой. Папа Григорий XIII решил эту проблему, фактически пропустив 10 дней в дате, сделав день после 4 октября 1582 года 15 октября. Также была внесена корректировка в алгоритм юлианского календаря, который изменил, какие столетние годы будут считаться високосными. Принятие григорианского календаря происходило медленно, в течение столетий, и, несмотря на множество предложений по дальнейшей реформе календаря, григорианский календарь по-прежнему преобладает как наиболее часто используемая система датирования во всем мире. Праздник – это день, который по обычаю или по закону откладывается таким образом, что обычная деятельность, такая как посещение работы или учебы, приостанавливается или, по крайней мере, сокращается. Термин «праздник» может трактоваться по-разному, в зависимости от региона. В США оплачиваемый отпуск обычно называют «отпуском», а выходные дни, связанные с национальными, религиозными или культурными традициями, — исключительно «отпуском». Однако в некоторых регионах, таких как Соединенное Королевство или бывшие британские колонии, термин «отпуск» также может относиться к оплачиваемому отпуску. Как правило, праздники предназначены для ознаменования какого-либо события, человека или группы, имеющих культурное или религиозное значение. Хотя некоторые праздники, такие как Рождество и Новый год, широко отмечаются во всем мире, в большинстве стран есть свой собственный набор праздников, специфичных для страны, и даже одни и те же праздники могут отмечаться в разных странах по-разному: некоторые из них могут получить полную приостановку. типичных повседневных занятий, в то время как другие могут получать только частичные выходные дни. В некоторых странах есть праздники, которые фактически закрывают почти все предприятия. Например, в Бразилии Carnaval do Brasil приводит к тому, что почти целую неделю работают только промышленное производство, торговые предприятия или предприятия, связанные с карнавалом. Этот калькулятор в основном ориентирован на праздники в США, но праздники, характерные для данной страны, можно ввести вручную. Некоторые праздники также могут быть исключены. Некоторые праздники, такие как Новый год, называются «фиксированными праздниками», поскольку каждый год они выпадают на одно и то же число. Другие, такие как день рождения Мартина Лютера Кинга-младшего, не имеют фиксированной даты, потому что они приходятся на «плавающий понедельник»; в данном конкретном случае праздник приходится на третий понедельник января. Другой широко отмечаемый праздник в США, День Благодарения, приходится на «плавающий четверг», четвертый четверг ноября, поэтому даты этих праздников меняются в зависимости от года. Федеральные праздники США в 2022 году Федеральные праздники США в 2023 году Из
Столетия (c.) Дни (d) Десятилетия (dec) Часы (hr) Тысячелетия (mil.) Миллисекунды (ms) Минуты (min) Месяцы (mo) Наносекунды (ns) Секунды (s) Недели (wk) Рабочие недели (work) wk) Лет (год) К
Столетия (c.) Дни (d) Десятилетия (dec) Часы (hr) Тысячелетия (mil.) Миллисекунды (ms) Минуты (min) Месяцы (mo) Наносекунды (ns) Секунды (s) Недели (wk) Рабочие недели (work) нед) Лет (год) Количество Показать результат как
DecimalScientific Notation Результат Вопрос: Что находится в или сколько ? Ответ: равно . Эта таблица преобразования показывает, как длина по сравнению с другими единицами площади. Задание №7 из ОГЭ прошлых лет, рекомендованные как тренировочные. Задача № 1 Уравнение x2 + px + q = 0 имеет корни: −5; 7. Найдите q. Решение Из условия задачи известно, что данное уравнение имеет два корня: х1 = -5 х2 = 7 Составим систему уравнений, в которую подставим имеющиеся корни: Из первого уравнения выразим q: q = 5p — 25 (1) Полученное выражение подставим во второе уравнение: 49 + 7p + (5p — 25) = 0 49 + 7p + 5p — 25 = 0 7p + 5p = 25 — 49 12p = — 24 p = -2 Полученное значение «p» подставим в (1): q = 5· (- 2) — 25 = — 10 — 25 = — 35 Ответ: −35. Задача № 2 Найдите корни уравнения x2 + 7x — 18 = 0 Если корней несколько, запишите их в ответ без пробелов в порядке возрастания. Решение Перед нами классическое квадратное уравнение. Решим его через нахождение дискриминанта: D = b2 – 4ac = 72 – 4 · 1 · (-18) = 49 + 72 = 121 Значение дискриминанта больше нуля, следовательно, уравнение имеет два корня. Тогда корни можем найти по формуле: Запишем получившиеся корни в порядке возрастания: -92 Ответ: −92 Задача № 3 Найдите корни уравнения х2 + 4 = 5х Если корней несколько, запишите их в ответ без пробелов в порядке возрастания. Решение Преобразуем уравнение и запишем в виде: х2 — 5х + 4 = 0 Решим его через нахождение дискриминанта: D = b2 – 4ac = 52 – 4 · 1 · 4 = 25 — 16 = 9 Значение дискриминанта больше нуля, следовательно, уравнение имеет два корня. Тогда, корни можем найти по формуле: Запишем получившиеся корни в порядке возрастания: 14 Ответ: 14 Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас! Запишитесь на бесплатное тестирование знаний! Наши преподаватели
Репетитор по математике
Белорусский государственный педагогический университет им. Максима Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 3-8 классов. Я люблю математику, потому что нахожу ее очень увлекательной. В преподавании придерживаюсь гуманистического и личностно-ориентированного методов обучения. Всегда стараюсь найти общий язык с учеником, стать для него товарищем и поддержкой в процессе обучения. Я гарантирую позитивное и познавательное погружение в увлекательный мир математики!
Репетитор по математике
Крымский федеральный университет им. Вернадского
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-4 классов.
Я люблю математику потому, что в ней всё
подчиняется определенным правилам, которые легко понять и которые одинаковы абсолютно для всех. Математика имеет свои неизменные законы, которые действуют во все времена и во всех странах.
Со мной , Ваш ребенок, не будет получать скучные знания в душных кабинетах, а с удовольствием проведёт досуг познания «царицы наук» в игровой форме, не выходя из зоны комфорта , ведь математика — это весело !
Со мной будет интересно , обещаю ; )
Репетитор по математике
Барнаульский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Придерживаюсь знаменитых слов Ломоносова В.М. » Математику за то учить надо, что она ум в порядок приводит»!
Мои ученики – девятиклассники успешно сдают ОГЭ. А ребята младших классов повышают свои успехи в изучении интересной, но сложной науки «Математика». Направления моей педагогической деятельности:
-Систематизация и совершенствование знаний при изучении математики для улучшения успеваемости по предмету, при подготовки к школе : развитие внимания, логического мышления, изучение основных понятий математики для поступления в школу.
-Ликвидация пробелов изучения математики у учащихся и непонимания тем, помощь в выполнении домашних заданий.
-Подготовка к ОГЭ и ВПР по математике.
Похожие статьи 1) 4×2 − 12 = 0; 3) x2 − 6x − 16 = 0; 5) x2 − 7x + 4 = 0; 2) 7×2 + 5x = 0; 4) 15×2 − 4x − 3 = 0; 6) x2 + 5x + 9 = 0. 2. Составьте приведённое квадратное уравнение, сумма корней которого равна числу 4, а произведение — числу −3. 3. Одна из сторон прямоугольника на 3 см больше другой. Найдите стороны прямоугольника, если его площадь равна 88 см2. 4. Число −3 является корнем уравнения 5×2 + mx − 12 = 0. Найдите второй корень уравнения и значение m. 5. При каком значении a уравнение 3×2 − 6x + a = 0 имеет единственный корень? 6. Известно, что x1 и x2 — корни уравнения x2 + 6x − 13 = 0. Не решая уравнения, найдите значение выражения . Вариант 4 1. Решите уравнение: 1) 3×2 − 18 = 0; 3) x2 − x − 20 = 0; 5) x2 + 6x − 2 = 0; 2) 8×2 − 3x = 0; 4) 3×2 − 2x − 8 = 0; 6) x2 − 4x + 6 = 0. 2. Составьте приведённое квадратное уравнение, сумма корней которого равна числу −6, а произведение — числу 3. 3. Одна из сторон прямоугольника на 6 см меньше другой. Найдите стороны прямоугольника, если его площадь равна 72 см2. 4. Число 5 является корнем уравнения 4×2 + 6x + k = 0. Найдите второй корень уравнения и значение k. 5. При каком значении a уравнение 4×2 + 8x + a = 0 имеет единственный корень? 6. Известно, что x1 и x2 — корни уравнения x2 + 10x + 4 = 0. Не решая уравнения, найдите значение выражения . Тест составлен по теме «Квадратные уравнения» и предназначен для обучающихся 8 класса. Разработанные задания могут быть использованы педагогами при организации обобщающего повторения по названной теме, а также для подготовки обучающихся к итоговой аттестации самостоятельно либо непосредственно на уроке. Государственное учреждение «Михайловская средняя школа» Мендыкаринского района Костанайской области Республики Казахстан Интерактивный тест по алгебре Тема: «Квадратные уравнения» для обучающихся 8 класса Автор разработки: с. Михайловка 2012 год Пояснительная записка: Задания, которые содержатся в данном тесте, позволят не только отработать тему «Квадратные уравнения», но и помогут обучающимся научиться уверенно решать задания разного характера (как стандартные, так и нестандартные). Важность представленного теста обусловлена еще и тем, что задания, связанные с нахождением корней квадратных уравнений, встречаются в материалах ГИА (Россия) или материалах ВОУД (Казахстан). Тест может быть полезен как для обучающихся с повышенной мотивацией к изучению математики, так и для обучающихся, которые стремятся повысить уровень своих знаний по математике. Тест состоит из 20 заданий по 4 варианта. По трудности варианты между собой равноценны. Каждое задание теста имеет 4 варианта ответов, из которых только один является верным. Методические рекомендации по применению интерактивного теста в работе: Интерактивный тест создан с помощью свободно распространяемой программы E-Publish «Конструктор сайтов». Для корректной работы интерактивного теста на Вашем компьютере должны быть установлены браузеры Google Chrom или Firefox (желательно открывать в браузере Google Chrom). Итак, … На главной странице расположен теоретический материал по теме «Квадратные уравнения» с определениями и формулами. На боковой панели расположены гиперссылки: «Главная», «Тест №1. Вариант 1», «Тест №1. Вариант 2», «Тест №1. Вариант 3», «Тест №1. Вариант 4» для навигации. На страницах с названием «Тест №1. Вариант 1-4» размещены интерактивные тесты по данной теме. Каждый тест предполагает выполнение в течение 30-45 минут. В каждом вопросе теста должен быть проставлен один правильный ответ. По окончании теста нажмите кнопку «Ответить». Результаты появятся в виде списка вопросов с 1-го по 20-ый в форме «правильно» / «неправильно». Чтобы поставить себе оценку, на каждой странице перед тестом даны критерии оценивания, по которым и выставляется оценка за пройденный тест. Тест по теме «Квадратные уравнения» 8 класс 1) А) Приведите уравнение (3х-1)2— 5х2 = 10 — 8х к виду ах2+bx +c =0: а) 14x2+2x+11=0; б) 4x2+2x-9=0; в) 4x2-2x+9=0; г) 4x2-14x-9=0. Б) Приведите уравнение х 2 +11x=(5-х)(5+x)– 17 к виду ах2+bx +c =0: а) 2х2+11x -8 =0; б) 2х2-11x +8 =0; в) х2-11x +8 =0; г) 2х2+11x +8 =0. В) Приведите уравнение (х+7)2 — 31= 4х2 — х к виду ах2+bx +c =0: а) 5х2-15x +18 =0; б) 3х2-13x +18 =0; в) -3х2+15x +18 =0; г) 3х2-15x -18 =0. Г) Приведите уравнение 6х 2 —13x=(2х-3)(x+1) к виду ах2+bx +c =0: а) 4х2+12x -5 =0; б) 8х2-12x +5 =0; в) 8х2-12x -5 =0; г) 4х2-12x +3 =0. 2) А) Составьте уравнение ах2+bx +c =0, если а= -3; b=8; c=5: а) 3х2+8x +5 =0; б) -3х2+8x -5 =0; в) -3х2+8x +5 =0; г) -3х2-8x +5 =0. Б) Составьте уравнение ах2+bx +c =0, если а= -2; b=4; c= -3: а) -2х2-4x +3 =0; б) 2х2-4x -3 =0; в) -2х2+4x -3 =0; г) -2х2+4x +3 =0. В) Составьте уравнение ах2+bx +c =0, если а= -5; b= -7; c=4: а) -5х2-7x +4 =0; б) -5х2+7x +4 =0; в) 5х2-7x -4 =0; г) 5х2-7x +4 =0. Г) Составьте уравнение ах2+bx +c =0, если а=6; b= -2; c= -3: а) 6х2-2x +3 =0; б) -6х2-2x +3 =0; в) 6х2-2x -3 =0; г) 6х2+2x -3 =0. 3) А) Найдите коэффициенты и свободный член уравнения 7х2-0,1x -2 =0: а) а=7; b=0,1; c= -2; б) а=7; b=0,1; c= 2; в) а=-7; b=-0,1; c= 2; г) а=7; b= -0,1; c= -2. Б) Найдите коэффициенты и свободный член уравнения 11х2-8x -2 =0: а) а= -11; b= -8; c= -2; б) а= 11; b= -8; c= -2; в) а= -11; b= 8; c= 2; г) а= 11; b= 8; c= -2. В) Найдите коэффициенты и свободный член уравнения 19х2+2x -1 =0: а) а= -19; b= -2; c= -1; б) а= 19; b= -2; c= 1; в) а= -19; b= 2; c= -1; г) а= 19; b= 2; c= -1. Г) Найдите коэффициенты и свободный член уравнения -х2+5x +4 =0: а) а= -1; b= -5; c= -4; б) а= -1; b= 5; c= 4; в) а= 1; b= 5; c= 4; г) а= -1; b= -5; c= 4. 4) А) Приведите уравнение 2х 2 +15=(х-3)2 к виду х2+px +q =0 а) х2+6x +6 =0; б) х2-6x +24 =0; в) 3х2+6x -1 =0; г) -х2+6x +6 =0. Б) Приведите уравнение 3х 2 —x=2(х-2)(x+2) к виду х2+px +q =0 а) х2-x -8 =0; б) 4х2-x +8 =0; в) х2-x +8 =0; г) х2+x +8 =0. В) Приведите уравнение x(4-х)=15-2x2 к виду х2+px +q =0 а) 3х2-4x -15 =0; б) х2-4x +15 =0; в) х2+4x -15 =0; г) х2+4x +15=0. Г) Приведите уравнение (5+х) 2 -10=7х+1 к виду х2+px +q =0 а) х2+3x -14 =0; б) х2+3x +14 =0; в) х2+3x +16 =0; г) х2+3x +15 =0. 5) А) Какое число является корнем уравнения -2х2+5x -2 =0. а) 1; б) -2; в) 2; г) 0? Б) Какое число является корнем уравнения х2+7x -30 =0. а) -1; б) 2; в) -3; г) 3? В) Какое число является корнем уравнения х2-3x -10 =0. а) -3; б) -5; в) 3; г) -2? Г) Какое число является корнем уравнения -4х2+9x +13=0. а) -1; б) 1; в) 13; г) -12? 6) А) Решите уравнение -5х2+3x +8=0: а) 1,6;-1; б) 1;-1,6; в) -5; 8; г) 8; -5. Б) Решите уравнение 3х2-4x -4=0: а) 2;-; б) ;-2; в) 1; ; г) -3; 2. В) Решите уравнение -7х2+2x +5=0: а) 1;; б) -1;-; в) 1; -; г) -1; -. Г) Решите уравнение 8х2+5x -3=0: а) -; 1; б) -; 3; в) -1; ; г) -;8. 7) А) Решите уравнение x(x-2)=2x+12: а) -6; 2; б) 4; -3; в) 6; -2; г) 3; 4. Б) Решите уравнение (x-1)2=36-4x: а) 7; -5; б) 1; 35; в) 5; -7; г) 1; -35. В) Решите уравнение 24—x=х(x+4): а) 8; -3; б) -8; 3; в) -4; 6; г) -2; 12. Г) Решите уравнение (x+1)2-21=20-x: а) 4; -10; б) -5; 8; в) -8; 5; г) -2; 20. 8) А) При каких значениях х значение выражения 11х2-3х равно нулю: а) -; 0; б) ; 0; в) 0; ; г) ? Б) При каких значениях х значение выражения 12х2-3 равно нулю: а) ; б) ; в) ; г) 12? В) При каких значениях х значение выражения х2-х равно нулю: а) 0; 2; б) 0; -0,5; в) 0; 0,5; г) 0; 0,2? Г) При каких значениях х значение выражения х2-7 равно нулю: а) 0; ; б) 0; -; в) ; г) ? 9) А) Решите уравнение : а) 3; -9; б) -3; 9; в) 1; -27; г) -1; 27. Б) Решите уравнение : а) 4; -8; б) -4; 8; в) 2; -16; г) -2; 16. В) Решите уравнение : а) 1; -11; б) -1; 11; в) 1; 12; г) -12; 1. Г) Решите уравнение : а) 2; -13; б) -2; 13; в) 2; 13; г) -26; 1. 10) А) Решите уравнение (x+2)2+3=5-0,5x: а) 2; -0,5; б) -4; -0,5; в) 0,5; 4; г) 2; -1. Б) Решите уравнение (x-2)2-5=0,8x: а) 0,2; -5; б) 0,2; 5; в) -0,2; 5; г) 2; -0,5. В) Решите уравнение (x+2,5)2+0,7х=8,05: а) -6; -0,3; б) 6; 0,3; в) 0,3; -6; г) 0,6; -3. Г) Решите уравнение (x-1)2+0,4х=1,8: а) 8; -0,1; б) -0,4; 2; в) -0,2; 4; г) -0,8; 1. 11) А) Найдите отрицательный корень уравнения —х2+4x +32 =0: а) -4; б) -6; в) -8; г) -16. Б) Найдите отрицательный корень уравнения х2+10x -11 =0: а) -1; б) -11; в) -10; г) -2. В) Найдите отрицательный корень уравнения —х2-11x +26 =0: а) -13; б) -2; в) -1; г) -26. Г) Найдите отрицательный корень уравнения —х2+6x +27 =0: а) -1; б) -27; в) -9; г) -3. 12) А) Найдите положительный корень уравнения х2-4,8x -1 =0: а) 0,2; б) 2; в) 1; г) 5. Б) Найдите положительный корень уравнения х2+5,7x -1,8 =0: а) 0,3; б) 6; в) 0,6; г) 3. В) Найдите положительный корень уравнения х2-1,6x -0,8 =0: а) 8; б) 0,1; в) 0,4; г) 2. Г) Найдите положительный корень уравнения х2+3,5x -2 =0: а) 10; б) 0,5; в) 4; г) 0,2. 13) А) Составьте квадратное уравнение, если корни и -5: а) х2+4,5x -2,5 =0; б) х2-4,5x -2,5 =0; в) х2+5,5x -25 =0; г) х2-4,5x +2,5 =0. Б) Составьте квадратное уравнение, если корни и 3: а) х2+3,25x -7,5 =0; б) х2-3,25x -0,75=0; в) х2+3,25x +7,5 =0; г) х2-3,25x +0,75 =0. В) Составьте квадратное уравнение, если корни — и 6: а) х2+6,2x -1,2 =0; б) х2-5,8x -1,2 =0; в) х2-6,2x +1,2 =0; г) х2 +5,8x -1,2 =0. Г) Составьте квадратное уравнение, если корни и -3: а) х2-2,9x -0,3 =0; б) х2+2,9x -0,3 =0; в) х2-2,9x +0,3 =0; г) х2-2,9x -3 =0. 14) А) При каких значениях х значения дробей и равны: а) -10;2; б) 4; 5; в) -5; -4; г) -10; -2? Б) При каких значениях х значения дробей и равны: а) -24; 2; б) -8; 6; в) -6; 8; г) -3; 16? В) При каких значениях х значения дробей и равны: а) -1; 35; б) -35; 1; в) -5; 7; г) -7; 5? Г) При каких значениях х значения дробей и равны: а) -6; -5; б) -2; -15; в) 6; 5; г) 2; 15? 15) А) Если х1—меньший корень, х2— больший корень уравнения х2-3,25x +0,75 =0, то найдите значение выражения 2х2-4х1: а) 7; б) 5; в) -5; г) 6. Б) Если х1—отрицательный корень, х2— положительный корень уравнения х2-5,8x -1,2 =0, то найдите значение выражения 10х1-2х2: а) -10; б) 14; в) -14; г) -12. В) Если х1— положительный корень, х2— отрицательный корень уравнения х2+2,9x -0,3 =0, то найдите значение выражения 20х1+5х2: а) 17; б) -13; в) 13; г) -17. Г) Если х1— положительный корень, х2— отрицательный корень уравнения х2+4,5x -2,5 =0, то найдите значение выражения 8х1-2х2: а) -6; б) 14; в) 6; г) -14. 16) А) Напишите квадратное уравнение, если один корень равен 7, а второй коэффициент = 3: а) х2-3x +4 =0; б) х2+3x -4 =0; в) х2+3x +70 =0; г) х2 +3x -70 =0. Б) Напишите квадратное уравнение, если один корень равен 11, а свободный член = -66: а) х2-5x +66 =0; б) х2+5x -66 =0; в) х2-66x -5 =0; г) х2 -5x -66 =0. В) Напишите квадратное уравнение, если один корень равен 9, а второй коэффициент = -14: а) х2-14x +45 =0; б) х2+14x +45 =0; в) х2-14x -40 =0; г) х2 -14x -45 =0. Г) Напишите квадратное уравнение, если один корень равен -8, а свободный член = 56: а) х2-15x +56 =0; б) х2+15x -56 =0; в) х2+15x +56 =0; г) х2 -8x +56 =0. 17) А) Одна сторона прямоугольника на 4 см больше другой, а диагональ равна см. Найдите площадь прямоугольника: а) 9 см2; б) 21 см2; в) 49 см2; г) 24 см2. Б) Одна сторона прямоугольника на 6 см больше другой, а диагональ равна см. Найдите площадь прямоугольника: а) 24 см2; б) 32 см2; в) 20 см2; г) 16 см2. В) Одна сторона прямоугольника на 5 см больше другой, а диагональ равна см. Найдите площадь прямоугольника: а) 66 см2; б) 24 см2; в) 14 см2; г) 6 см2. Г) Одна сторона прямоугольника на 5 см больше другой, а диагональ равна см. Найдите площадь прямоугольника: а) 3 см2; б) 8 см2; в) 22 см2; г) 24 см2. 18) А) Найдите два числа, если одно меньше другого на 4 и сумма их квадратов равна 136: а) 7; 8; б) 7; 11; в) 3; 7; г) 6; 10. Б) Найдите два числа, если одно меньше другого на 8 и сумма их квадратов равна 130: а) 2; 10; б) 3; 11; в) 1; 9; г) 4; 12. В) Найдите два числа, если одно меньше другого на 5 и сумма их квадратов равна 37: а) 7; 2; б) 1; 6; в) 3; 8; г) 2; -7. Г) Найдите два числа, если одно меньше другого на 5 и сумма их квадратов равна 97: а) 2; 7; б) 4; 9; в) 5; 10; г) 3; 8. 19) А) Периметр прямоугольного треугольника равен 48 м, а гипотенуза – 20 м. Найдите катеты: а) 12; 20; б) 16; 12; в) 8; 6; г) 3; 7. Б) Периметр прямоугольного треугольника равен 60 м, а гипотенуза – 25 м. Найдите катеты: а) 15; 20; б) 10; 20; в) 15; 10; г) 20; 5. В) Периметр прямоугольного треугольника равен 36 м, а гипотенуза – 15 м. Найдите катеты: а) 13; 8; б) 12; 9; в) 9; 15; г) 10; 11. Г) Периметр прямоугольного треугольника равен 24 м, а гипотенуза – 10 м. Найдите катеты: а) 5; 9; б) 9; 1; в) 12; 7; г) 6; 8. 20) А) Знаменатель дроби на 3 больше числителя. Если к этой дроби прибавить обратную ей дробь, то получим . Найдите первоначальную дробь: а) ; б) ; в) ; г) . Б) Знаменатель дроби на 5 больше числителя. Если к этой дроби прибавить обратную ей дробь, то получим . Найдите первоначальную дробь: а) ; б) ; в) ; г) . В) Знаменатель дроби на 3 больше числителя. Если к этой дроби прибавить обратную ей дробь, то получим . Найдите первоначальную дробь: а) ; б) ; в) ; г) . Г) Знаменатель дроби на 1 больше числителя. Если к этой дроби прибавить обратную ей дробь, то получим . Найдите первоначальную дробь: а) ; б) ; в) ; г) . Ключ к тесту № задания Ответ А Ответ Б Ответ В Ответ Г 1 б а в г 2 в в а в 3 г б г б 4 а в в г 5 в г г а 6 а а в в 7 в в б в 8 в в в в 9 а а б а 10 б в в б 11 а б а г 12 г а г б 13 а г б б 14 г б в в 15 б в б б 16 а г а в 17 б г в г 18 г б б б 19 б а б г 20 б в г а Список литературы и сайтов: Решение приведенного квадратного уравнения выделением квадрата двучлена x2+4x-5=0 (x2+2∙2∙x+4)-4-5=0 x+22-9=0 x+22=9 x+2=3 или x+2=-3 x=1 x=-5 Ответ: -5;1. Класс разбился на группы. Группам было предложено домашнее задание: решить квадратные уравнения и ответы записать в виде пар (x1;x2) так, чтобы x1>x2, руководителям групп проверить решение и по координатам этих точек построить на координатной плоскости рисунок. 2. Проверка домашнего задания и выставление оценок (оценки выставляются руководителями групп). Ответ: -16 . Ответ: 16 . Решение: * 5 * 5 * 5 * 5 * 5 * Удачи тебе на экзаменах! У тебя всё получится — мы в тебя верим! Поделись этой информацией с помощью кнопок ниже (облегчи учёбу другим ученикам, и будет тебе плюс в карму!) Задание 15 № 507658 Решите неравенство Решение. Сделаем замену: Тогда Неравенство принимает вид: откуда Это неравенство выполняется тогда и только тогда, когда Получаем: Ответ: Примечание. Задача допускает решение без замены переменной: тождественными преобразованиями данное неравенство приводится к откуда также получается ответ Задание 15 № 508212 Решите неравенство: Решение. Используя метод интервалов, получаем: Ответ: Задание 15 № 507491 Решите неравенство: Решение. Перепишем неравенство в виде: Множество решений исходного неравенства: Ответ: Задание 15 № 508213 Решите неравенство: Решение. Используя метод интервалов, получаем: Ответ: Задание 15 № 508345 Решите неравенство: Решение. Приведём выражение к общему знаменателю: Предпоследнее преобразование верно, так как модуль не может принимать отрицательных значений. Получаем или Ответ: Задание 15 № 508347 Решите неравенство: Решение. Пусть получаем: Возвращаясь к исходной переменной, получаем: или Ответ: Задание 15 № 508348 Решите неравенство: Решение. Сделав замену получаем: Возвращаясь к исходной переменной, получаем: Ответ: Задание 15 № 508355 Решите неравенство: Решение. Преобразуем неравенство: Решения неравенства: или Ответ: Задание 15 № 508360 Решите неравенство: Решение. Решим неравенство методом интервалов: Ответ: Задание 15 № 508364 Решите неравенство: Решение. Решим первое неравенство: Ответ: Задание 15 № 508367 Решите неравенство: Решение. Решим неравенство методом интервалов: Ответ: Задание 15 № 508371 Решите неравенство: Решение. Решим неравенство методом интервалов: Ответ: Задание 15 № 508381 Решите неравенство: Решение. Решим второе неравенство: Ответ: Задание 15 № 508429 Решите неравенство: Решение. Сделав замену получаем: Значит, и Ответ: Задание 15 № 508432 Решите неравенство: Решение. Решим неравенство методом интервалов: Ответ: Задание 15 № 508434 Решите неравенство: Решение. Решим неравенство методом интервалов: Ответ: Задание 15 № 508442 Решите неравенство: Решение. По теореме Виета, сумма корней уравнения равна , а их произведение равно Поэтому корни этого уравнения — числа и Тогда неравенство можно решить так: Ответ: Задание 15 № 508447 Решите неравенство: Решение. Преобразуем неравенство: Ответ: Задание 15 № 508449 Решите неравенство: Решение. Заметим, что поэтому неравенство выполнено при всех , кроме и Ответ: Задание 15 № 508530 Решите неравенство: Решение. Последовательно получаем: Ответ: Задание 15 № 512484 Решите неравенство Решение. Преобразуем неравенство: Учитывая, что при всех значениях x выражение x2 + 3 положительно, получаем откуда Ответ: Задание 15 № 507203 Решите неравенство Решение. Сделаем замену Получим Следовательно, Ответ: Задание 15 № 515707 Решите неравенство Решение. Решим неравенство: Ответ: Задание 15 № 516402 Решите неравенство Решение. Преобразуем неравенство: Ответ: Задание 15 № 521996 Решите неравенство Решение. Решим неравенство методом интервалов: откуда и Ответ: Задание 15 № 522124 Решите неравенство Решение. Решим неравенство методом интервалов: откуда и Ответ: Задание 15 № 523996 Решите неравенство Решение. Сделаем замену Получим: Отсюда после обратной замены получаем: Ответ: Задание 15 № 526726 Решите неравенство Решение. Преобразуем неравенство: Решая полученное неравенство методом интервалов (см. рис.), находим ответ: Ответ: Задание 15 № 530384 Решите неравенство: Решение. Заметим, что Применим эту формулу к каждому слагаемому левой части, получим: Ответ: Задание 15 № 530457 Решите неравенство Решение. Запишем исходное неравенство в виде: Ответ: Задание 15 № 530674 Решите неравенство Решение. Запишем исходное неравенство в виде: Ответ: Задание 15 № 530701 Решите неравенство: Решение. Разложим разность по формуле разности кубов, получим: Вынесем в знаменателе общий множитель за скобки: Ответ: 1.1 Факторинг x 2 + 7x-18 Первый член равен x 2 его коэффициент равно 1. Шаг-1: Умножьте коэффициент первого члена на константу 1 • -18 = -18 Шаг-2: Найдите два множителя -18, сумма которых равен коэффициенту среднего члена, равному 7. Шаг 4: сложите первые 2 члена, вычитая одинаковые множители: 2.1 Произведение нескольких членов равно нулю. Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю. Теперь мы решим каждый член = 0 отдельно Другими словами, мы собираемся решить столько уравнений, сколько членов есть в произведении. Любое решение для члена = 0 также решает продукт = 0. 2.2 Решите: x + 9 = 0 Вычтите 9 из обеих частей уравнения: 2.3 Решите: x-2 = 0 Добавьте 2 к обеим сторонам уравнения: Ранее мы разложили этот многочлен на множители, разделив средний член. давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу 3.1 Найдите вершину y = x 2 + 7x-18 Параболы имеют наибольшее значение или самая низкая точка называется Вершиной.Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля). Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы. То есть, если парабола действительно имеет два реальных решения. Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины. Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A). В нашем случае координата x равна -3.5000 Подставляя в формулу параболы -3,5000 для x, мы можем вычислить координату y: Корневой график для: y = x 2 + 7x-18 3.2 Решение x 2 + 7x-18 = 0, заполнив квадрат. Добавьте 18 к обеим сторонам уравнения: Теперь умный бит: возьмите коэффициент при x, равный 7, разделите его на два, получив 7/2, и возведите его в квадрат. давая 49/4 Добавьте 49/4 к обеим частям уравнения: Сложение 49/4 завершает левую часть в виде полного квадрата: Мы будем называть это уравнение уравнением. # 3.2.1 Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны. Обратите внимание, что квадратный корень из Теперь, применяя принцип квадратного корня к уравнению.# 3.2.1 получаем: Вычтем 7/2 с обеих сторон, чтобы получить: Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное Обратите внимание, что √ 121/4 можно записать как 3.3 Решение x 2 + 7x-18 = 0 по квадратичной формуле. Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, дается как: В нашем случае A = 1 Соответственно B 2 — 4AC = Применение квадратичной формулы: -7 ± √ 121 Можно ли упростить √ 121? Да! Разложение на простые множители 121 равно Германия отправила гессиан для поддержки британских солдат Есть четыре красных сердца и шесть розовых сердечек. 4/6 = 2/3 Ответ: Пошаговое объяснение: Треугольник особенный — это квадрат, разрезанный пополам по диагонали. Ноги (стороны, образующие угол 90 градусов) равны. Гипотенуза — это катет, умноженный на квадратный корень из 2. Итак Удалите равные части каждого уравнения и сложите. — 6 x + 10 = 3 x + 1 — 6 x + 10 = 3 x + 1 Переместите все члены, содержащие x x , в левую часть уравнения. Вычтем 3 x 3 x из обеих частей уравнения. — 6 x + 10 — 3 x = 1 — 6 x + 10 — 3 x = 1 y = 3 x + 1 y = 3 x + 1 3 x 3 x из — 6 x — 6 x . — 9 x + 10 = 1 — 9 x + 10 = 1 y = 3 x + 1 y = 3 x + 1 Переместите все члены, не содержащие x x , в правую часть уравнения . Вычтем 10 10 из обеих частей уравнения — 9 x = 1 — 10 — 9 x = 1 — 10 y = 3 x + 1 y = 3 x + 1 Вычесть 10 из 1 1 . — 9 x = — 9 — 9 x = — 9 y = 3 x + 1 y = 3 x + 1 Разделите каждый член на — 9 — 9 и упростите. Разделите каждый член на — 9 x = — 9 — 9 x = — 9 на — — 9 . — 9 x — 9 = — 9 — 9 — 9 x — = — 9 — 9 y = 3 x + 1 y = 3 x + 1 Уменьшить выражение путем отмены общих факторов x = — 9 — 9 x = — 9 — 9 y = 3 x + 1 y = 3 x + 1 Деление — 9 — 9 по 9 — 9 . x = 1 x = 1 y = 3 x + 1 Заменить все вхождения x x на решение найдено путем решения последнего уравнения для x x . В этом случае подставляемое значение будет 1 1 . x = 1 x = 1 y = 3 ( 1 ) + 1 y = 3 ( 1 ) + 1 Упрощение 3 ( 1 ) + 1 3 ( ) 1 ( ) 1 + 1 . Нажмите, чтобы уменьшить количество шагов … Умножьте 3 3 на 1 1 . x = 1 x = 1 y = 3 + 1 y = 3 + 1 Складываем 3 3 и 1 1 . x = 1 x = 1 y = 4 y = 4 Решение системы уравнений можно представить в виде точка. ( 1 , 4 ) ( 1 , 4 ) Результат может быть представлен в нескольких формах. Точечная форма: ( 1 , 4 ) ( 1 , 4 ) Форма уравнения: x = 1 , и = 4 Следовательно, \ [\ sqrt {\ text {3}} \] и \ [{\ text {4}} \] являются а не корни данного уравнения. Примечание: Квадратное уравнение с действительным или комплексным коэффициентом имеет два решения, называемых корнями. $ $ Решите квадратные уравнения, используя квадратный корень $ $ \ color {# FF6800 } {x} \ color {# FF6800} {-} \ color {# FF6800} {\ dfrac {7} {2}} = \ pm \ sqrt {\ color {# FF6800} {\ dfrac {121} {4} }} $ $ \ color {# FF6800} {x} \ color {# FF6800} {-} \ color {# FF6800} {\ dfrac {7} {2}} = \ pm \ sqrt {\ color {# FF6800} {\ dfrac {121} {4}}} $ $ $ Решите решение для $ x $ $ \ color {# FF6800} {x} = \ pm \ color {# FF6800} {\ dfrac { 11} {2}} \ color {# FF6800} {+} \ color {# FF6800} {\ dfrac {7} {2}} $ $ \ color {# FF6800} {x} = \ pm \ color { # FF6800} {\ dfrac {11} {2}} \ color {# FF6800} {+} \ color {# FF6800} {\ dfrac {7} {2}} $ $ $ Разделить ответ $ $ \ begin {array} {l} \ color {# FF6800} {x} = \ color {# FF6800} {\ dfrac {7} {2}} \ color {# FF6800} {+} \ color {# FF6800} {\ dfrac {11} {2}} \\ \ color {# FF6800} {x} = \ color {# FF6800} {\ df rac {7} {2}} \ color {# FF6800} {-} \ color {# FF6800} {\ dfrac {11} {2}} \ end {array} $ $ \ begin {array} {l} \ color {# FF6800} {x} = \ color {# FF6800} {\ dfrac {7} {2}} \ color {# FF6800} {+} \ color {# FF6800} {\ dfrac {11} {2} } \\ \ color {# FF6800} {x} = \ color {# FF6800} {\ dfrac {7} {2}} \ color {# FF6800} {-} \ color {# FF6800} {\ dfrac {11} {2}} \ end {array} $ $ $ Организуйте выражение $ $ \ begin {array} {l} \ color {# FF6800} {x} = \ color {# FF6800} {9} \ \ \ color {# FF6800} {x} = \ color {# FF6800} {-} \ color {# FF6800} {2} \ end {array} $ Научиться решать уравнения — одна из наших основных целей в алгебре.До этого момента мы решали линейные уравнения степени 1. В этом разделе мы изучим технику, которую можно использовать для решения некоторых уравнений степени 2. Квадратичное уравнение Полиномиальное уравнение с одной переменной степени 2. — любое уравнение, которое можно записать в стандартной форме Квадратичное уравнение, записанное в виде ax2 + bx + c = 0. , где a , b и c — действительные числа и a 0. Ниже приведены некоторые примеры квадратных уравнений, все из которых будут решены в этом разделе: Решение квадратного уравнения в стандартной форме называется корневым решением квадратного уравнения в стандартной форме.. Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь реального решения. Квадратное уравнение x2 + x − 6 = 0 имеет два решения, а именно x = −3 и x = 2. Пример 1: Убедитесь, что x = −3 и x = 2 являются решениями x2 + x − 6 = 0. Решение: Чтобы проверить решения, подставьте значения для x , а затем упростите, чтобы увидеть, является ли результат истинным. Ответ: Оба значения дают верные утверждения.Следовательно, они оба являются решениями уравнения. Наша цель — разработать алгебраические методы нахождения решений квадратных уравнений. Первый метод требует свойства нулевого продукта: любой продукт равен нулю тогда и только тогда, когда хотя бы один из факторов равен нулю .: Другими словами, если какой-либо продукт равен нулю, то один или оба переменных фактора должны быть равны нулю. Пример 2: Решить: (x − 8) (x + 7) = 0. Решение: Это уравнение состоит из произведения двух величин, равных нулю; следовательно, применяется свойство нулевого продукта. Одно или оба количества должны быть равны нулю. Чтобы убедиться, что это решения, подставьте их вместо переменной x . Обратите внимание, что каждое решение дает коэффициент, равный нулю. Ответ: Решения 8 и −7. Квадратное уравнение не может быть дано в его факторизованной форме. Пример 3: Решить: x2 + 3x − 10 = 0. Решение: Цель состоит в том, чтобы произвести продукт, равный нулю. Мы можем сделать это, факторируя трехчлен в левой части уравнения. Затем примените свойство нулевого произведения и установите каждый коэффициент равным нулю. Это оставляет нам два линейных уравнения, каждое из которых может быть решено относительно x. Проверьте решения, подставив их в исходное уравнение, чтобы убедиться, что мы получаем истинные утверждения. Ответ: Решения — 5 и 2. Использование свойства нулевого произведения после факторизации квадратного уравнения в стандартной форме является ключом к этому методу. Однако квадратное уравнение не может быть дано в стандартной форме, и поэтому перед факторизацией могут быть предприняты некоторые предварительные шаги.Шаги, необходимые для решения путем факторизации Процесс решения уравнения, равного нулю, путем факторизации и последующего установления каждого переменного коэффициента равным нулю. описаны в следующем примере. Пример 4: Решить: 2×2 + 10x + 20 = −3x + 5. Раствор: Шаг 1: Выразите квадратное уравнение в стандартной форме. Для применения свойства нулевого продукта квадратное выражение должно быть равно нулю.Используйте свойства сложения и вычитания равенства, чтобы объединить противоположные стороны, похожие на члены, и получить ноль на одной стороне уравнения. В этом примере прибавьте 3x и вычтите 5 с обеих сторон. Шаг 2: Разложите квадратное выражение на множители. Шаг 3: Примените свойство нулевого произведения и установите каждый переменный коэффициент равным нулю. Шаг 4: Решите полученные линейные уравнения. Ответ: Решения: −5 и −3/2. Проверка не обязательна. Пример 5: Решить: 9×2 + 1 = 6x. Решение: Запишите это в стандартной форме, вычтя 6x с обеих сторон. После того, как уравнение имеет стандартную форму, коэффициент равен нулю. Это трехчлен в виде полного квадрата. Следовательно, установка каждого коэффициента равным нулю приводит к повторному решению. Повторяющееся решение называется двойным корнем Корень, который повторяется дважды. и не нужно писать дважды. Ответ: Решение 1/3. Попробуй! Решите: x2−3x = 28. Ответ: x = −4 или x = 7 Не все квадратные уравнения в стандартной форме являются трехчленами. Мы часто сталкиваемся с двучленами. Пример 6: Решить: x2−9 = 0. Решение: Это квадратное уравнение дается в стандартной форме, где бином в левой части представляет собой разность квадратов. Фактор: Затем установите каждый коэффициент равным нулю и решите. Ответ: Решениями являются 3 и −3, которые также можно записать как ± 3. Пример 7: Решить: 5×2 = 15x. Решение: Посмотрев, мы видим, что x = 0 является решением этого квадратного уравнения.Поскольку деление на ноль не определено, мы не хотим делить обе части этого уравнения на x . В общем, мы не хотим делить обе части любого уравнения на переменную или выражение, содержащее переменную. Мы обсудим это более подробно позже. Первый шаг — переписать это уравнение в стандартной форме с нулем на одной стороне. Затем разложите выражение на множители. Обратите внимание, что бином слева имеет GCF 5x. Установите каждый коэффициент равным нулю. Ответ: Решения 0 и 3. Пример 8: Решите: (2x + 1) (x + 5) = 11. Решение: Это квадратное уравнение, по-видимому, учитывается; следовательно, может возникнуть соблазн установить каждый коэффициент равным 11. Однако это приведет к неверным результатам. Мы должны переписать уравнение в стандартной форме, равной нулю, чтобы мы могли применить свойство нулевого произведения. Когда он будет в стандартной форме, мы можем разложить на множители, а затем установить каждый фактор равным нулю. Ответ: Решения: 1/2 и −6. Пример 9: Решить: 15×2−25x + 10 = 0. Решение: Начнем с факторинга GCF 5. Затем разложим полученный трехчлен на множители. Затем мы устанавливаем каждый переменный коэффициент равным нулю и решаем для x . Обратите внимание, что коэффициент 5 не является переменным фактором и, следовательно, не вносит вклад в набор решений. Ответ: Решения 2/3 и 1. Пример 10: Фактор: 52×2 + 76x − 13 = 0. Решение: Очистите дроби, умножив обе части уравнения на ЖК-дисплей, который равен 6. На данный момент у нас есть эквивалентное уравнение с целочисленными коэффициентами, которое, как обычно, можно разложить на множители. Начнем с множителей 15 и 2. Коэффициент при среднем члене равен 7 = 3 (−1) +5 (2).Фактор: Установите каждый коэффициент равным нулю и решите. Ответ: Решения — 2/3 и 1/5. Попробуй! Решить: 4×2−9 = 0. Ответ: −3/2 и 3/2 Состояние нулевого продукта, Верно и обратное: В этом случае мы можем написать следующее: Мы используем это свойство, чтобы находить уравнения по решениям.Для этого шаги решения путем факторинга выполняются в обратном порядке. Пример 11: Найдите квадратное уравнение с решениями −7 и 2. Решение: Имея решения, мы можем определить два линейных фактора. Произведение этих линейных множителей равно нулю, когда x = −7 или x = 2: Умножьте биномы и представьте уравнение в стандартной форме. Ответ: x2 + 5x − 14 = 0. Мы можем проверить наше уравнение, подставив данные ответы, чтобы увидеть, получим ли мы истинное утверждение. Кроме того, приведенное выше уравнение не является уникальным, поэтому проверка становится важной, когда наше уравнение отличается от чужого. Это оставлено как упражнение. Пример 12: Найдите квадратное уравнение с целыми коэффициентами, учитывая решения 1/2 и −3/4. Решение: Чтобы избежать дробных коэффициентов, мы сначала очищаем дроби, умножая обе части на знаменатель. Примените свойство нулевого произведения и умножьте. Ответ: 8×2 + 2x − 3 = 0 Попробуй! Найдите квадратное уравнение с целыми коэффициентами при решениях −1 и 2/3. Ответ: 3×2 + x − 2 = 0 Свойство нулевого произведения верно для любого числа факторов, составляющих уравнение.Если выражение равно нулю и может быть разложено на линейные коэффициенты, тогда мы сможем установить каждый коэффициент равным нулю и решить для каждого уравнения. Пример 13: Решить: 3x (x − 5) (3x − 2) = 0. Решение: Установите каждый переменный коэффициент равным нулю и решите. Ответ: Решения: 0, 5 и 2/3. Конечно, нельзя ожидать, что уравнение будет дано в факторизованной форме. Пример 14: Решите: x3 + 2×2−9x − 18 = 0. Решение: Начните с полного факторизации левой стороны. Установите каждый коэффициент равным нулю и решите. Ответ: Решения: −2, −3 и 3. Обратите внимание, что степень многочлена равна 3, и мы получили три решения. В общем, для любого полиномиального уравнения с одной переменной степени n фундаментальная теорема алгебры гарантирует, что будет столько же (или меньше) действительных решений многочлена с одной переменной, сколько его степени.гарантирует n реальных решений или меньше. Мы видели, что многие многочлены не множатся. Это не означает, что уравнения, включающие эти неактивируемые многочлены, не имеют реальных решений. Фактически, многие полиномиальные уравнения, не учитывающие множителей, имеют действительные решения. Мы узнаем, как решать эти типы уравнений, продолжая изучать алгебру. Попробуй! Решите: −10×3−18×2 + 4x = 0. Ответ: −2, 0, 1/5 Часть A: Решения квадратных уравнений Определите, является ли данный набор значений решениями квадратного уравнения. 1. {−3, 5}; x2−2x − 15 = 0 2. {7, −1}; x2−6x − 7 = 0 3. {−1/2, 1/2}; х2−14 = 0 4. {−3/4, 3/4}; х2−916 = 0 5. {−3, 2}; х2-х-6 = 0 6. {−5, 1}; x2−4x − 5 = 0 Решить. 7. (x − 3) (x + 2) = 0 8. (x + 5) (x + 1) = 0 9. (2x − 1) (x − 4) = 0 10.(3x + 1) (3x − 1) = 0 11. (x − 2) 2 = 0 12. (5x + 3) 2 = 0 13. 7x (x − 5) = 0 14. −2x (2x − 3) = 0 15. (x − 12) (x + 34) = 0 16. (x + 58) (x − 38) = 0 17. (14x + 12) (16x − 23) = 0 18. (15x − 3) 2 = 0 19. −5 (x + 1) (x − 2) = 0 20. 12 (x − 7) (x − 6) = 0 21. (x + 5) (x − 1) = 0 22.(х + 5) (х + 1) = 0 23. −2 (3x − 2) (2x + 5) = 0 24. 5 (7x − 8) 2 = 0 Часть B: Решить факторингом Решить. 25. x2 − x − 6 = 0 26. x2 + 3x − 10 = 0 27. y2−10y + 24 = 0 28. y2 + 6y − 27 = 0 29. x2−14x + 40 = 0 30. x2 + 14x + 49 = 0 31. x2−10x + 25 = 0 32.3×2 + 2x − 1 = 0 33. 5×2−9x − 2 = 0 34. 7y2 + 20y − 3 = 0 35. 9×2−42x + 49 = 0 36. 25×2 + 30x + 9 = 0 37. 2y2 + y − 3 = 0 38. 7×2−11x − 6 = 0 39. 2×2 = −15x + 8 40. 8x − 5 = 3×2 41. x2−36 = 0 42. x2−100 = 0 43. 4×2-81 = 0 44. 49×2−4 = 0 45.х2 = 4 46. 9y2 = 1 47. 16y2 = 25 48. 36×2 = 25 49. 4×2−36 = 0 50. 2×2−18 = 0 51. 10×2 + 20x = 0 52. −3×2 + 6x = 0 53. 25×2 = 50x 54. x2 = 0 55. (x + 1) 2−25 = 0 56. (x − 2) 2−36 = 0 57. 5x (x − 4) = — 4 + x 58.(x − 1) (x − 10) = 22 59. (x − 3) (x − 5) = 24 60. −2x (x − 9) = x + 21 61. (x + 1) (6x + 1) = 2x 62. (x − 2) (x + 12) = 15x 63. (х + 1) (х + 2) = 2 (х + 16) 64. (x − 9) (2x + 3) = 2 (x − 9) Очистите дроби, сначала умножив обе части на ЖК-дисплей, а затем решив. 65. 115×2 + 13x + 25 = 0 66. 114×2−12x + 37 = 0 67.32×2−23 = 0 68. 52×2−110 = 0 69. 314×2−212 = 0 70. 13×2−15x = 0 71. 132×2−12x + 2 = 0 72. 13×2 + 56x − 12 = 0 73. Стороны квадрата имеют размер x + 3 единицы. Если площадь составляет 25 квадратных единиц, найдите x . 74. Высота треугольника на 2 единицы больше его основания. Если площадь 40 квадратных единиц, то найдите длину основания. 75. Стороны прямоугольного треугольника имеют меры, являющиеся последовательными целыми числами. Найдите длину гипотенузы. (Подсказка: гипотенуза — самая длинная сторона. Примените теорему Пифагора.) 76. Прибыль в долларах от производства и продажи нестандартных ламп x определяется функцией P (x) = — 10×2 + 800x − 12000. Сколько ламп нужно продать и произвести, чтобы обеспечить безубыточность? (Подсказка: мы выходим на уровень безубыточности, когда прибыль равна нулю.) Предполагая сухие дорожные условия и среднее время реакции, безопасный тормозной путь d футов среднего автомобиля определяется по формуле d = 120v2 + v , где v представляет скорость машина в милях в час.Для каждой приведенной ниже проблемы, учитывая тормозной путь, определите безопасную скорость. 77.15 футов 78. 40 футов 79. 75 футов 80. 120 футов Часть C: Нахождение уравнений с заданными решениями Найдите квадратное уравнение с целыми коэффициентами, имея следующие решения. 81. −3, 1 82.−5, 3 83. −10, −3 84. −7, −4 85. −1, 0 86,0, 3/5 87. −2, 2 88. −1/2, 1/2 89. −4, 1/3 90. 2/3, 2/5 91. −1/5, −2/3 92. −3/2, 3/4 93,3, двойной корень 94. −5, двойной корень Часть D. Решение полиномиальных уравнений Решить. 95. 7x (x + 5) (x − 9) = 0 96. (x − 1) (x − 2) (x − 3) = 0 97. −2x (x − 10) (x − 1) = 0 98. 8x (x − 4) 2 = 0 99. 4 (x + 3) (x − 2) (x + 1) = 0 100. −2 (3x + 1) (3x − 1) (x − 1) (x + 1) = 0 101. x3 − x2−2x = 0 102. 2×3 + 5×2−3x = 0 103. 5×3−15×2 + 10x = 0 104. −2×3 + 2×2 + 12x = 0 105.3×3−27x = 0 106. −2×3 + 8x = 0 107. x3 + x2 − x − 1 = 0 108. x3 + 2×2−16x − 32 = 0 109. 8×3−4×2−18x + 9 = 0 110. 12×3 = 27x Часть E: Темы дискуссионной доски 111. Объясните, почему 2 (x + 5) (x − 5) = 0 имеет два решения, а 2x (x + 5) (x − 5) = 0 имеет три решения. 112. Составьте собственное квадратное уравнение и разместите его вместе с решениями на доске обсуждений. 113. Объясните своими словами, как решить квадратное уравнение в стандартной форме. 1: Есть 3: Есть 5: № 7: −2, 3 9: 1/2, 4 11: 2 13: 0, 5 15: −3/4, 1/2 17: -2, 4 19: -1, 2 21: −5, 1 23: −5/2, 2/3 25: −2, 3 27: 4, 6 29: 4, 10 31: 5 33: -1/5, 2 35: 7/3 37: −3/2, 1 39: −8, ½ 41: −6, 6 43: −9/2, 9/2 45: -2, 2 47: −5/4, 5/4 49: −3, 3 51: −2, 0 53: 0, 2 55: −6, 4 57: 1/5, 4 59: -1, 9 61: -1/2, -1/3 63: −6, 5 65: −3, −2 67: −2/3, 2/3 69: ± 7 71: 8 73: 2 шт. 75: 5 шт. 77: 10 миль в час 79:30 миль в час 81: x2 + 2x − 3 = 0 83: x2 + 13x + 30 = 0 85: х2 + х = 0 87: x2−4 = 0 89: 3×2 + 11x − 4 = 0 91: 15×2 + 13x + 2 = 0 93: x2−6x + 9 = 0 95: −5, 0, 9 97: 0, 1, 10 99: −3, −1, 2 101: -1, 0, 2 103: 0, 1, 2 105: −3, 0, 3 107: -1, 1 109: −3/2, 1/2, 3/2 Приведем еще несколько примеров. Я не только не могу применить квадратичную формулу на данном этапе, но и не могу использовать множители. Почему? Потому что это уравнение пока что в правильном виде. И я, , конечно же, не могу с невозмутимым видом утверждать, что « x = 4, x — 2 = 4», потому что это , а не , как работает «решение с факторингом». Независимо от того, какой метод решения я собираюсь использовать — факторизирую ли я на множители или использую квадратичную формулу, чтобы найти свои ответы — я должен сначала преобразовать уравнение в форму «(квадратичный) = 0». Первое, что я сделаю здесь, это умножу на левую часть, а затем переместу 4 из правой части в левую: x ( x — 2) = 4 x 2 -2 x = 4 x 2 -2 x -4 = 0 Поскольку нет множителей при (1) (- 4) = –4, которые в сумме дают –2, то эта квадратичная величина не множится.(Другими словами, невозможно, чтобы решение с искусственным факторингом « x = 4, x — 2 = 4» могло быть хоть немного правильным.) Значит, факторинг не сработает, но я могу использовать квадратичную формулу; в этом случае я подставляю значения a = 1, b = –2 и c = –4: Тогда ответ: x = –1.24, x = 3,24 с округлением до двух десятичных знаков. Для справки, вот как выглядит график соответствующей квадратичной, y = x 2 -2 x -4, выглядит так: Как видите, решения квадратичной формулы совпадают с интерцепциями x . Точки пересечения графика с осью x дают значения, которые решают исходное уравнение. Существует еще одна связь между решениями из квадратичной формулы и графиком параболы: вы можете определить, сколько интервалов x вы получите, исходя из значения внутри квадратного корня. Аргумент (то есть содержание) квадратного корня, являющийся выражением b 2 — 4 ac , называется «дискриминантом», потому что, используя его значение, вы можете «различать» (что уметь различать) различные типы решений. В данном случае значение дискриминанта b 2 -4 ac было 20; в частности, значение было , а не ноль, и было , а не отрицательным. Поскольку значение не было отрицательным, уравнение должно было иметь по крайней мере одно (действительное) решение; поскольку значение не было нулевым, два решения должны были быть разными (то есть они должны были отличаться друг от друга). Используя a = 9, b = 12 и c = 4, квадратичная формула дает мне: Тогда ответ: В первом примере на этой странице я получил два решения, потому что значение дискриминанта (то есть значение внутри квадратного корня) было ненулевым и положительным.В результате часть формулы «плюс-минус» дала мне два различных значения; один для «плюсовой» части числителя и другой для «минусовой» части. Однако в этом случае квадратный корень уменьшился до нуля, поэтому плюс-минус ни для чего не учитывался. Такое решение, при котором вы получаете только одно значение, потому что «плюс или минус ноль» ничего не меняет, называется «повторяющимся» корнем, потому что x равно Вы можете лучше увидеть это повторение, если разложите квадратичный множитель (и, поскольку решения были хорошими аккуратными дробями, квадратичный должен множить ): 9 x 2 + 12 x + 4 = (3 x + 2) (3 x + 2) = 0, поэтому первый множитель дает нам 3 x + 2 = 0, поэтому Каждый раз, когда вы получаете ноль внутри квадратного корня квадратной формулы, вы получаете только одно решение уравнения в смысле получения одного числа, которое решает уравнение. Но вы получите два решения в том смысле, что одно значение будет подсчитано дважды. Другими словами, дискриминант (то есть выражение b 2 — 4 ac ) с нулевым значением означает, что вы получите одно «повторяющееся» значение решения. Ниже показан график связанной функции, y = 9 x 2 + 12 x + 4, выглядит так: Парабола только касается оси x при Поскольку нет множителей при (3) (2) = 6, которые в сумме дают 4, эта квадратичная величина не множится. Но квадратичная формула всегда работает; в этом случае я вставлю значения a = 3, b = 4 и c = 2: На данный момент у меня есть отрицательное число внутри квадратного корня.Если вы еще не узнали о комплексных числах, вам придется остановиться на этом, и ответ будет «нет решения»; если вы знаете комплексные числа, то можете продолжить вычисления: Таким образом, в зависимости от вашего уровня обучения, ваш ответ будет одним из следующих: решений с реальными числами: нет решения комплексно-числовых решений: Партнер Но знаете ли вы о комплексах или нет, вы знаете, что вы не можете изобразить свой ответ, потому что вы не можете изобразить квадратный корень из отрицательного числа на правильном декартовом месте.На оси x таких значений нет. Поскольку вы не можете найти графическое решение квадратичной функции, разумно не должно быть никаких перехватов x (потому что вы можете построить график перехвата x ). Вот график связанной функции, y = 3 x 2 + 4 x + 2: Как видите, график не пересекает ось x и даже не касается ее.Это соотношение всегда верно: если вы получите отрицательное значение внутри квадратного корня, тогда не будет решения действительного числа и, следовательно, не будет перехватов x . Другими словами, если дискриминант (являющийся выражением b 2 — 4 ac ) имеет отрицательное значение, то у вас не будет графических нулей. (взаимосвязь между дискриминантом (являющимся значением внутри квадратного корня), типом решения (два различных решения, одно повторяющееся решение или отсутствие графифицируемых решений) и числом x -перехватываний на графике (два , один или нет) сведены в диаграмму на следующей странице. {2} + b x + c = 0 \) как уравнение вида Этот процесс называется , завершение квадрата 4 .{2} = \ color {Cerulean} {1} \) Чтобы завершить квадрат, добавьте \ (1 \) к обеим сторонам, завершите квадрат и затем решите, извлекая корни. На этом этапе разделите «плюс или минус» на два уравнения и решите каждое отдельно. Ответ : Решения: \ (- 8 \) и \ (6 \). Примечание В предыдущем примере решения — целые числа. Если это так, то исходное уравнение будет учитываться. Если уравнение множится, мы можем решить его путем факторизации.{2} — 10 х + 26 = 0 \). Раствор Начните с вычитания \ (26 \) из обеих частей уравнения. Здесь \ (b = -10 \), и мы определяем значение, завершающее квадрат, следующим образом: Чтобы завершить квадрат, добавьте \ (25 \) к обеим сторонам уравнения. {2} + 18 \), где \ (t \) представляет время через секунды после падения объекта.{2} + 50 \), где \ (t \) представляет время в секундах после падения объекта. Сколько времени нужно, чтобы объект упал на землю? (Округлите до ближайшей сотой доли секунды.) 1. \ (\ pm 9 \) 3. \ (\ pm \ frac {1} {3} \) 5. \ (\ pm 2 \ sqrt {3} \) 7. \ (\ pm \ frac {3} {4} \) 9. \ (\ pm \ frac {\ sqrt {2}} {2} \) 11. \ (\ pm 2 \ sqrt {10} \) 13. \ (\ pm i \) 15. \ (\ pm \ frac {\ sqrt {5}} {5} \) 17. \ (\ pm \ frac {\ sqrt {2}} {4} i \) 19.\ (\ pm 2 i \) 21. \ (\ pm \ frac {2} {3} \) 23. \ (\ pm 2 \ sqrt {2} \) 25. \ (\ pm 2 i \ sqrt {2} \) 27. \ (\ pm \ frac {\ sqrt {10}} {5} \) 29. \ (- 9, -5 \) 31. \ (5 \ pm 2 \ sqrt {5} \) 33. \ (- \ frac {2} {3} \ pm \ frac {\ sqrt {6}} {3} i \) 35. \ (\ frac {- 2 \ pm 3 \ sqrt {3}} {6} \) 37. \ (\ frac {1} {3} \ pm \ frac {\ sqrt {6}} {6} i \) 39.{2} = 3 (3 т + 1) \) 1. \ (- 15 \ pm \ sqrt {10} \) 3. 1 \ (\ pm 2 \ sqrt {2} \) 5. 1 \ (\ pm i \ sqrt {3} \) 7. \ (- 15,5 \) 9. \ (- \ frac {1} {3}, 1 \) 11. \ (\ frac {-1 \ pm \ sqrt {5}} {2} \) 13. \ (\ frac {-3 \ pm \ sqrt {17}} {2} \) 15. \ (- \ frac {3} {2} \ pm \ frac {\ sqrt {11}} {2} i \) 17.\ (\ frac {7 \ pm 3 \ sqrt {3}} {2} \) 19. \ (\ frac {1 \ pm \ sqrt {17}} {4} \) 21. \ (\ frac {2 \ pm \ sqrt {5}} {2} \) 23. \ (\ frac {-3 \ pm \ sqrt {6}} {3} \) 25. \ (\ frac {-1 \ pm \ sqrt {10}} {3} \) 27. \ (\ frac {3 \ pm 2 \ sqrt {6}} {2} \) 29. 1 \ (\ pm 2 i \) 31. \ (\ frac {1 \ pm \ sqrt {17}} {4} \) 33. \ (\ frac {-1 \ pm \ sqrt {7}} {3} \) 35. 2 \ (\ pm 2 \ sqrt {5} \) 37.{2} -6 (6 x + 1) = 0 \) 1. \ (0.19,1.31 \) 3. \ (- 0,45,1,12 \) 5. \ (0,33,0,67 \) Упражнение \ (\ PageIndex {11} \)
Вычислить по формуле муавра онлайн калькулятор: Формула Муавра, возведение в степень комплексного числа
Синтаксис
 5{/tex}
5{/tex}Примеры
Действительная часть: 1.0560 Комплексная часть: 1.0457
Действительная часть: -0.6682 Комплексная часть: 1.3275
Действительная часть: -1.4690 Комплексная часть: -0.2253
Действительная часть: -0.2396 Комплексная часть: -1.4667Универсальный калькулятор комплексных чисел онлайн
Вы ввели следующее выражение Окончательный результат выражения Синтаксис
Примеры
1 2i 1 i
Где можно решить любую задачу по математике, а так же 1 2i 1 i Онлайн?
Калькулятор онлайн для расчета факториала числа
Расчет факториала по формуле Джеймса Стирлинга
Расчет факториала от 0 до 100
Формула Джеймса Стирлинга для расчета факториала
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
4! = 4 × 3 × 2 × 1 = 24
5! = 5 × 4 × 3 × 2 × 1 = 120Не стоит забывать
Полезный факт
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsboxКалькулятор комплексных чисел: сложение, вычитание, деление, умножение
Действия над комплексными числами
Возведение комплексного числа в степень, теория и примеры
где z = cos nx + i sin nx.
Таким образом, Sn справедливо для всего множества целых чисел n.
Аналогичная формула применима также и при вычислении корней n -й степени из ненулевого комплексного числа:
z 1 / n =
Дата публикации:
05-16-2020
Дата последнего обновления:
05-16-2020
Онлайн-калькулятор: Комплексные числа
Алгебраическая форма
где a и b — действительные числа, i — мнимая единица, так что i 2 = -1. а — соответствует действительной части, б — мнимой части. Полярная форма
где r — модуль комплексного числа:
— расстояние между точкой 0 и комплексной точкой на комплексной плоскости, а φ — угол между положительной действительной осью и комплексным вектором (аргументом). Экспоненциальная форма (форма Эйлера)
Комплексное число
Точность вычисления
Главное значение может быть вычислено из алгебраической формы по следующей формуле:
Этот алгоритм реализован в javascript Math.atan2 функция. Элементарные операции с комплексным числом
OperationAddSubtractMultiplyDivideExponentiateTake n-й корень Точность вычисления Сложение комплексного числа
Умножение комплексных чисел
Деление комплексных чисел
Сопряжение определяется как:
Итак, окончательная формула деления: Возведение в степень комплексного числа
Эта формула получена из формулы Де Муавра: корень n-й степени
,
корней n, где k = 0..n-1 — корневой целочисленный индекс. Корни могут отображаться на комплексной плоскости как вершины правого многоугольника. Калькулятор комплексных чисел
Что такое комплексное число? — Определение комплексного числа
i (иногда j , например, в электронике) и определяется как: i = √ (-1) . z — это комбинация действительной a и мнимой b * i частей, так что: г = а + би . a , и b являются классическими действительными числами. Когда b = 0 , число чисто реальное, а если a = 0 , мы имеем чисто мнимое число.Вы можете использовать этот калькулятор комплексных чисел как калькулятор мнимых чисел — просто введите действительный компонент, равный 0. Re и Im , так что Re (z) = a , а Im (z) = b . На самом деле, есть числа с более мнимыми частями: кватернионы. К счастью, здесь нам не о чем беспокоиться. z = а - би . Полярная форма комплексных чисел
| z | = a² + b² , тангенс (φ) = b / a , | z | — это модуль / абсолютное значение комплексного числа , φ известен как аргумент или фаза (иногда мы используем обозначение arg (z) = φ ), а tan является тангенсом данный аргумент.Точно так же длина вектора в двумерной евклидовой плоскости — это расстояние между его концом и началом системы координат. Угол φ отсчитывается от оси X против часовой стрелки и может изменяться от 0 до 2π или от -π до π (в зависимости от соглашения, поскольку оба они эквивалентны). a = | z | * cosφ , b = | z | * sinφ . z = | z | * (cosφ + i * sinφ) . z = | z | * ехр (i * φ) , exp () — экспоненциальная функция, в основе которой лежит число e .Благодаря свойству периодичности мы можем видеть, что: ехр (iφ) = ехр (i (φ + 2kπ)) , k — любое целое число. Основные операции с комплексными числами — сумма и разность
F = a + bi , а второе как G = c + di . Тогда сумма двух комплексных чисел будет: F + G = a + bi + c + di = (a + c) + (b + d) * i , Re (F + G) = a + c — действительная часть суммы, а Im (F + G) = b + d — мнимая. F - G = a + bi - c + di = (a - c) + (b - d) * i , Re (F - G) = a - c и Im (F - G) = b - d . Умножение и деление комплексных чисел
F * G = (a + bi) * (c + di) = a * c + a * d * i + b * c * i + b * d * i * i = (a * c - b * d ) + (а * г + Ь * в) * я . Re (F * G) = a * c - b * d , а мнимая часть — как Im (F * G) = a * d + b * c . Обратите внимание, что в действительной части стоит знак минус, поскольку в какой-то момент мы столкнулись с умножением двух мнимых чисел i * i , что по определению равно -1 . F / G = (a + bi) / (c + di) = , дополнить числитель и знаменатель конъюгатом комплексного числа последнего. = (a + bi) * (c - di) / ((c + di) * (c - di)) = , выполнить стандартные умножения. = (a * c - a * d * i + b * c * i - b * d * i * i) / (c² - (di) ²) = , снова используйте тот факт, что i * я = -1 . = (a * c + b * d + (b * c - a * d) * i) / (c² + d²) . Re (F / G) = (a * c + b * d) / (c² + d²) , Im (F * G) = (b * c - a * d) / (c² + d²) . Конечно, деление возможно только при G 0 . F = | z₁ | * exp (iφ₁) , G = | z₂ | * exp (iφ₂) . Тогда умножение комплексных чисел дает: F * G = | z₁ | * exp (iφ₁) * | z₂ | * exp (iφ₂) = | z₁ * z₂ | * ехр (я (φ₁ + φ₂)) , | F * G | = | z₁ * z₂ | и arg (F * G) = φ₁ + φ₂ . F / G = | z₁ | * exp (iφ₁) / | z₂ | * exp (iφ₂) = | z₁ / z₂ | * ехр (я (φ₁-φ₂)) , | F / G | = | z₁ / z₂ | и arg (F / G) = φ₁-φ₂ .Используя эту форму, ясно видно, что результирующий модуль представляет собой просто отношение абсолютных значений обоих чисел. Комплексная мощность и комплексный логарифм
F G = (a + bi) (c + di) = , поскольку не очевидно, как расширить это выражение, мы можем записать F в полярной форме комплексных чисел. = (| z₁ | * exp (iφ₁)) (c + di) = , теперь произведение любой степени суммы — это произведение каждого элемента на каждый компонент в отдельности. = | z₁ | ᶜ * exp (iφ₁ * c) * | z₁ | ᵈⁱ * exp (-φ₁ * d) = , мы можем использовать известное свойство экспоненты: x n = exp (n * ln (x)) , где ln — натуральный логарифм. знак равно | z₁ | ᶜ * ехр (-φ₁ * d) * ехр (i (φ₁ * c + d * ln | z₁ |)) . | F G | = | z₁ | ᶜ * exp (-φ₁ * d) , а аргумент: arg (F G ) = φ₁c + d * ln | z₁ | . Хотя мы смешиваем две разные нотации, это нормально. Мы также можем изменить их, как вам нравится — это все, что вам нужно. ln (F) = ln (| z₁ | * exp (iφ₁)) = ln (| z₁ |) + iφ₁ . φ₁ и φ₁ + 2kπ эквивалентны, комплексный логарифм имеет бесконечное число решений, и общий результат дается как: ln (| z₁ |) + i (φ₁ + 2kπ) . Как пользоваться калькулятором комплексных чисел
Свойства комплексных чисел
Re (z) = Re (z) , Im (z) = -Im (z) , z * z = | z | ² , | z₁ + z₂ | ≤ | z₁ | + | z₂ | , | z₁ * z₂ | = | z₁ | * | z₂ | , | z₁ / z₂ | = | z₁ | / | z₂ | , z = 0 , то и a = 0 , и b = 0 . Реальные комплексные числа
Теорема Де Муавра
Рисунок для примера 3. Нормальное приближение | Безграничная статистика
Нормальное приближение к биномиальному распределению
Цели обучения
Основные выводы
Ключевые моменты
Ключевые термины
Объем нормального приближения
Цели обучения
Основные выводы
Ключевые моменты
Ключевые термины
Закон больших чисел
Центральная предельная теорема
Расчет нормального приближения
Ключевые термины
Изменение шкалы
Цели обучения
Основные выводы
Ключевые моменты
Ключевые термины
Нормализация
Стандартный балл
Праймер для комплексных чисел
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Полномочия и корни
b Показать решение Психология 2300: Определения
IB для iPhone, iPad, Android, Windows Phone | Математика 4у
Римская цифра 6 как пишется: Ошибка 404: страница не найдена
Римская цифра 6 как пишется. Как устроены римские цифры
Римские цифры на клавиатуре в любом приложении
 Большая часть программ не имеет специальной функциональности для работы с непозиционной системой счисления, что требует проявления смекалки от пользователя для ввода римских цифр в них. Можно выделить два удобных способа, как ввести римские цифры с клавиатуры в любой программе.
Большая часть программ не имеет специальной функциональности для работы с непозиционной системой счисления, что требует проявления смекалки от пользователя для ввода римских цифр в них. Можно выделить два удобных способа, как ввести римские цифры с клавиатуры в любой программе.Замена римских цифр английскими буквами
 Принцип простой: до нужного числа добираются римские цифры максимально большие подходящие в данной ситуации.
Принцип простой: до нужного числа добираются римские цифры максимально большие подходящие в данной ситуации.Использование ASCII-кодов для ввода римских цифр
 После этого зажмите левый ALT на клавиатуре и вводит комбинации римских цифр на правом цифровом блоке. После ввода каждого символа, нужно отпустить ALT, чтобы символ отобразился в поле для ввода. Далее вновь ALT требуется зажать и можно вводить следующий символ.
После этого зажмите левый ALT на клавиатуре и вводит комбинации римских цифр на правом цифровом блоке. После ввода каждого символа, нужно отпустить ALT, чтобы символ отобразился в поле для ввода. Далее вновь ALT требуется зажать и можно вводить следующий символ.Как напечатать римские цифры в Word

IV — 4, т.е. 5 — 1
XI — 11, т.е. 10 + 1
IX — 9, т.е. 10 — 1
LX — 60, т.е. 50 + 10
XL — 40, т.е. 50 — 10
СХ — 110, т.е. 100 + 10
ХС — 90, т.е. 100-10
MDCCCXII — 1812, т.е. 1000 + 500 + 100 + 100 + 100 + 10 + 1 + 1.
II (2) — duo (дуо)
III (3) — tres (трэс)
IV (4) — quattuor (кваттуор)
V (5) — quinque (квинквэ)
VI (6) — sex (сэкс)
VII (7) — septera (сэптэм)
VIII (8) — octo (окто)
IX (9) — novem (новэм)
X (10) — decern (дэцем)
XI (11) — undecim (ундецим)
XII (12) — duodecim (дуодэцим)
ХШ (13) — tredecim (трэдэцим)
XIV (14) — quattuordecim (кваттуордэцим)
XV (15) — quindecim (квиндэцим)
XVI (16) — sedecim (сэдэцим)
XVII (17) — septendecim (сэптэндэцим)
XVIII (18) — duodeviginti (дуодэвигинти)
XIX (19) — undeviginti (ундэвигинти)
XX (20) — viginti (вигинти)
XXI (21) — unus et viginti или viginti unus
XXII (22) — duo et viginti или viginti duo и т.д.
XXVIII (28) — duodetriginta (дуодэтригинта)
XXIX (29) — undetriginta (ундэтригинта)
XXX (30) : triginta (тригинта)
XL (40) — quadraginta (квадрагинта)
L (5O) — quinquaginta (квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX (70) — septuaginta (сзлтуагинта)
LXXX180) — octoginta (октогинта)
КС (90) — nonaginta (нонагинта)
C (100) centum (центум)
CC (200) — ducenti (дуценти)
CCC (300) — trecenti (трэценти)
CD (400) — quadrigenti (квадригэнти)
D (500) — quingenti (квингэнти)
DC (600) — sescenti(сэсценти) или sexonti (сэксцонти)
DCC (700) — septigenti (сэптигэнти)
DCCC (800) — octingenti (октингэнти)
CV (DCCC) (900) — nongenti (нонгэнти)
M (1000) — mille (милле)
ММ (2000) — duo milia (дуо милиа)
V (5000) — quinque milla (квинквэ милиа)
X (10 000) — decem milia (дэцем милиа)
XX (20000) — viginti milia (вигинти милиа)
C (100000) — centum milia (центум милиа)
XI (1000000) — decies centena milia (дэциэс центэна милиа).
![]() Римские цифры находятся на часовых циферблатах, в том числе на курантах Спасской башни. Мы их используем, но знаем про них не так много.
Римские цифры находятся на часовых циферблатах, в том числе на курантах Спасской башни. Мы их используем, но знаем про них не так много.Как устроены римские цифры
V 5
X 10
L 50
C 100
D 500
M 1000
Мы Dарим Сочные Lимоны, Хватит Vсем Iх
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам
I Value Xylophones Like Cows Dig Milk Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.Альтернативные варианты
 Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::.
Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::.Происхождение
 Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.
Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.Современное применение
 Римские цифры удобно ставить рядом с арабскими – если написать век римскими цифрами, а затем год – арабскими, то в глазах не будет рябить от обилия одинаковых знаков. Римские цифры имеют некоторый оттенок архаичности. С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида.
Римские цифры удобно ставить рядом с арабскими – если написать век римскими цифрами, а затем год – арабскими, то в глазах не будет рябить от обилия одинаковых знаков. Римские цифры имеют некоторый оттенок архаичности. С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида.
 Кроме того, в русском языке
римскими цифрами принято обозначать
порядковые числительные. Система Римских
цифр в настоящее время применяется при
обозначения веков (XV век и т.д.), годов
н. э. (MCMLXXVII т. д.) и месяцев при указании
дат (например, 1. V.1975), в исторических
памятниках права как номера статей
(Каролина и др)
Кроме того, в русском языке
римскими цифрами принято обозначать
порядковые числительные. Система Римских
цифр в настоящее время применяется при
обозначения веков (XV век и т.д.), годов
н. э. (MCMLXXVII т. д.) и месяцев при указании
дат (например, 1. V.1975), в исторических
памятниках права как номера статей
(Каролина и др)

 д.
XX (20) — viginti (вигинти)
XXI (21) —
unus et viginti или viginti unus
XXII (22) — duo et viginti или
viginti duo и т.д.
XXVIII (28) — duodetriginta
(дуодэтригинта)
XXIX (29) — undetriginta
(ундэтригинта)
XXX (30) — triginta (тригинта)
XL
(40) — quadraginta (квадрагинта)
L (50) — quinquaginta
(квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX
(70) — septuaginta (сэптуагинта)
LXXX (80) — octoginta
(октогинтна)
XC (90) — nonaginta (нонагинта)
C
(100) — centum (центум)
CC (200) — ducenti (дуценти)
CCC
(300) — trecenti (трэценти)
CD (400) — quadrigenti
(квадригэнти)
D (500) — quingenti (квингэнти)
DC
(600) — sexcenti (сэксценти)
DCC (700) — septigenti
(сэптигэнти)
DCCC(800) — octingenti (октигенти)
CM
(DCCCC) (900) — nongenti (нонгэнти)
M (1000) — mille
(милле)
MM (2000) — duo milia (дуо милиа)
V (5000)
— quinque milia (квинквэ милиа)
X (10000) — decem
milia (дэцем милиа)
XX (20000) — viginti milia (вигинти
милиа)
C (1000000) — centum milia (центум милиа)
XI
(1000000) — decies centena milia (дэциэс центэна милиа)»
д.
XX (20) — viginti (вигинти)
XXI (21) —
unus et viginti или viginti unus
XXII (22) — duo et viginti или
viginti duo и т.д.
XXVIII (28) — duodetriginta
(дуодэтригинта)
XXIX (29) — undetriginta
(ундэтригинта)
XXX (30) — triginta (тригинта)
XL
(40) — quadraginta (квадрагинта)
L (50) — quinquaginta
(квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX
(70) — septuaginta (сэптуагинта)
LXXX (80) — octoginta
(октогинтна)
XC (90) — nonaginta (нонагинта)
C
(100) — centum (центум)
CC (200) — ducenti (дуценти)
CCC
(300) — trecenti (трэценти)
CD (400) — quadrigenti
(квадригэнти)
D (500) — quingenti (квингэнти)
DC
(600) — sexcenti (сэксценти)
DCC (700) — septigenti
(сэптигэнти)
DCCC(800) — octingenti (октигенти)
CM
(DCCCC) (900) — nongenti (нонгэнти)
M (1000) — mille
(милле)
MM (2000) — duo milia (дуо милиа)
V (5000)
— quinque milia (квинквэ милиа)
X (10000) — decem
milia (дэцем милиа)
XX (20000) — viginti milia (вигинти
милиа)
C (1000000) — centum milia (центум милиа)
XI
(1000000) — decies centena milia (дэциэс центэна милиа)»Римские цифры от 1 до 1000: список, переводчик и упражнения
 Хотя в остальное время было иначе. Много лет назад Римская империя он доминировал на больших территориях в течение нескольких столетий. Обладая огромным мастерством, он повсюду распространял свою философию и знания, Римские цифры.
Хотя в остальное время было иначе. Много лет назад Римская империя он доминировал на больших территориях в течение нескольких столетий. Обладая огромным мастерством, он повсюду распространял свою философию и знания, Римские цифры.  1 Сума
1 СумаПереводчик римских цифр (конвертер)
ИСХОД: ИСХОД: Что такое римские цифры?
Как пишутся римские цифры?
 Остальное — простые правила, которые мы вам покажем. Для начала вы должны знать, что подряд может быть не более 3-х одинаковых букв.
Остальное — простые правила, которые мы вам покажем. Для начала вы должны знать, что подряд может быть не более 3-х одинаковых букв. А римлянам было все равно. Тем не менее, их можно написать, поместив линию под и над буквами. В этом смысле, если бы мы хотели сослаться на 5 000 000, мы использовали бы формат:
А римлянам было все равно. Тем не менее, их можно написать, поместив линию под и над буквами. В этом смысле, если бы мы хотели сослаться на 5 000 000, мы использовали бы формат:Список римских цифр
1 50 к
Número Римская цифра 1 I 2 II 3 III 4 IV 5 V 6 VI 7 VII 8 VIII 9 IX 10 X 11 XI 12 XII 13 XIII 14 XIV 15 XV 16 XVI 17 XVII 18 XVIII 19 XIX 20 XX 21 XXI 22 XXII 23 XXIII 24 XXIV 25 XXV 26 XXVI 27 XXVII 28 XXVIII 29 XXIX 30 XXX 31 XXXI 32 XXXII 33 XXXIII 34 XXXIV 35 XXXV 36 XXXVI 37 XXXVII 38 XXXVIII 39 XXXIX 40 XL 41 XLI 42 XLII 43 XLIII 44 XLIV 45 XLV 46 XLVI 47 XLVII 48 XLVIII 49 XLIX 50 L 1 100 к
Número Римская цифра 1 I 2 II 3 III 4 IV 5 V 6 VI 7 VII 8 VIII 9 IX 10 X 11 XI 12 XII 13 XIII 14 XIV 15 XV 16 XVI 17 XVII 18 XVIII 19 XIX 20 XX 21 XXI 22 XXII 23 XXIII 24 XXIV 25 XXV 26 XXVI 27 XXVII 28 XXVIII 29 XXIX 30 XXX 31 XXXI 32 XXXII 33 XXXIII 34 XXXIV 35 XXXV 36 XXXVI 37 XXXVII 38 XXXVIII 39 XXXIX 40 XL 41 XLI 42 XLII 43 XLIII 44 XLIV 45 XLV 46 XLVI 47 XLVII 48 XLVIII 49 XLIX 50 L 51 LI 52 ЛИИ 53 LIII 54 LIV 55 LV 56 LVI 57 LVII 58 LVIII 59 LIX 60 LX 61 LXI 62 LXII 63 LXIII 64 LXIV 65 LXV 66 LXVI 67 LXVII 68 LXVIII 69 LXIX 70 LXX 71 LXXI 72 LXXII 73 LXXXIII 74 LXXIV 75 LXXV 76 LXXVI 77 LXXVII 78 LXXVIII 79 LXXXIX 80 LXXX 81 LXXXI 82 LXXXII 83 LXXXIII 84 LXXXIV 85 LXXXV 86 LXXXVI 87 LXXXVII 88 LXXXVIII 89 LXXXIX 90 XC 91 XCI 92 XII 93 XCIII 94 XCIV 95 XCV 96 XCVI 97 XVII 98 XCVIII 99 ХХIХ 100 C 1 500 к
Número Римская цифра 1 I 2 II 3 III 4 IV 5 V 6 VI 7 VII 8 VIII 9 IX 10 X 11 XI 12 XII 13 XIII 14 XIV 15 XV 16 XVI 17 XVII 18 XVIII 19 XIX 20 XX 21 XXI 22 XXII 23 XXIII 24 XXIV 25 XXV 26 XXVI 27 XXVII 28 XXVIII 29 XXIX 30 XXX 31 XXXI 32 XXXII 33 XXXIII 34 XXXIV 35 XXXV 36 XXXVI 37 XXXVII 38 XXXVIII 39 XXXIX 40 XL 41 XLI 42 XLII 43 XLIII 44 XLIV 45 XLV 46 XLVI 47 XLVII 48 XLVIII 49 XLIX 50 L 51 LI 52 ЛИИ 53 LIII 54 LIV 55 LV 56 LVI 57 LVII 58 LVIII 59 LIX 60 LX 61 LXI 62 LXII 63 LXIII 64 LXIV 65 LXV 66 LXVI 67 LXVII 68 LXVIII 69 LXIX 70 LXX 71 LXXI 72 LXXII 73 LXXXIII 74 LXXIV 75 LXXV 76 LXXVI 77 LXXVII 78 LXXVIII 79 LXXXIX 80 LXXX 81 LXXXI 82 LXXXII 83 LXXXIII 84 LXXXIV 85 LXXXV 86 LXXXVI 87 LXXXVII 88 LXXXVIII 89 LXXXIX 90 XC 91 XCI 92 XII 93 XCIII 94 XCIV 95 XCV 96 XCVI 97 XVII 98 XCVIII 99 ХХIХ 100 C 101 CI 102 CII 103 C-III 104 CIV 105 CV 106 ХВН 107 CVII 108 CVIII 109 CIX 110 CX 111 CXI 112 CXII 113 СXIII 114 CXIV 115 CXV 116 CXVI 117 СXVII 118 CXVIII 119 CIX 120 СХХ 121 CXXI 122 CXXII 123 CXXXIII 124 CXXIV 125 CXXV 126 CXXVI 127 CXXVII 128 CXXVIII 129 CXXIX 130 CXXX 131 CXXXI 132 CXXXII 133 CXXXIII 134 CXXXIV 135 CXXXV 136 CXXXVI 137 CXXXVII 138 CXXXVIII 139 CXXXIX 140 CXL 141 CXLI 142 CXLII 143 CXLIII 144 CXLIV 145 CXLV 146 CXLVI 147 CXLVII 148 CXLVIII 149 CXLIX 150 CL 151 CLI 152 CLII 153 КЛIII 154 КЛИВ 155 CLV 156 КЛВИ 157 CLVII 158 CLVIII 159 КЛИКС 160 CLX 161 CLXI 162 CLXII 163 CLXIII 164 CLXIV 165 CLXV 166 CLXVI 167 CLXVII 168 CLXVIII 169 CLXIX 170 CLXX 171 CLXXI 172 CLXXII 173 CLXXIII 174 CLXXIV 175 CLXXV 176 CLXXVI 177 CLXXVII 178 CLXXVIII 179 CLXXXIX 180 CLXXX 181 CLXXXI 182 CLXXXII 183 CLXXXIII 184 CLXXXIV 185 CLXXXV 186 CLXXXVI 187 CLXXXVII 188 CLXXXVIII 189 CLXXIX 190 СХС 191 CXCI 192 CXCII 193 CXCIII 194 CXCIV 195 CXCV 196 CXCVI 197 CXCVII 198 CXCVIII 199 CXCIX 200 CC 201 CCI 202 IICC 203 CCIII 204 CCVI 205 ККТ 206 CCVI 207 CCVII 208 CCVIII 209 CCIX 210 CCX 211 CCXI 212 CCXII 213 CCXIII 214 CCXIV 215 CCXV 216 CCXVI 217 CCXVII 218 CCXVIII 219 CXXIX 220 CCXX 221 CCXXI 222 CCXXII 223 CCXXIII 224 CCXXIV 225 CCXXV 226 CCXXVI 227 CCXXVII 228 CCXXVIII 229 CCXXIX 230 CCXXX 231 CCXXXI 232 CCXXXII 233 CCXXXIII 234 CCXXXIV 235 CCXXXV 236 CCXXXVI 237 CCXXXVII 238 CCXXXVIII 239 CCXXXIX 240 CCXL 241 CCXLI 242 CCXLII 243 CCXLIII 244 CCXLIV 245 CCXLV 246 CCXLVI 247 CCXLVII 248 CCXLVIII 249 CCXLIX 250 CCL 251 CCLI 252 CCLII 253 CCIII 254 CCLIV 255 CCLV 256 CCLVI 257 CCLVII 258 CCLVIII 259 ССЛИКС 260 CCLX 261 CCLXI 262 CCLXII 263 CCLXIII 264 CCLXIV 265 CCLXV 266 ССLXVI 267 CCLXVII 268 ССLXVIII 269 CCLXIX 270 CCLXX 271 CCLXXI 272 CCLXXII 273 ККЛ XXIII 274 CCXXIV 275 CCLXXV 276 CCLXXVI 277 CCLXXVII 278 CCLXXVIII 279 CCXXIX 280 CCLXXX 281 CCLXXXI 282 CCLXXXII 283 CCLXXXIII 284 CCLXXXIV 285 CCLXXXV 286 CCLXXXVI 287 CCLXXXVII 288 CCLXXXVIII 289 CCLXXXIX 290 CCXC 291 CCXCI 292 CCXCII 293 CCXCIII 294 CCXCIV 295 CCXCV 296 CCXCVI 297 CCXCVII 298 CCXCVIII 299 CCXCIX 300 CCC 301 CCCI 302 CCII 303 СССIII 304 CCIV 305 CC CV 306 CCCVI 307 СССVII 308 СССVIII 309 CCCIX 310 CCCX 311 CCXI 312 CCXII 313 CCXIII 314 CCXIV 315 CCXV 316 СССXVI 317 СССXVII 318 CCXVIII 319 CCXIX 320 СССХХ 321 CCCXXXI 322 СССXXII 323 СССXXIII 324 CCXXIV 325 CCCXXV 326 CCXXVI 327 СССXXVII 328 CCCXXXVIII 329 CCXXIX 330 СССХХХ 331 CCCXXXI 332 CCXXXII 333 СССXXXIII 334 CCXXXIV 335 CCXXXV 336 CCXXXVI 337 CCXXXVII 338 CCXXXVIII 339 CCXXXIX 340 CCXL 341 CCXLI 342 CCXLII 343 CCXLIII 344 CCXLIV 345 CCXLV 346 CCCXLVI 347 CCXLVII 348 CCXLVIII 349 CCXLIX 350 CCCL 351 CCCLI 352 CCCL II 353 CCCL III 354 CCCL IV 355 CCLV 356 CCCLVI 357 CCLVII 358 CCCLVIII 359 CCCLIX 360 CCCLX 361 CCCLXI 362 CCCLXII 363 CCCLXIII 364 CCCLXIV 365 CCCLXV 366 CCCLXVI 367 CCCLXVII 368 CCCLXVIII 369 CCCLXIX 370 CCCLXX 371 CCCLXXI 372 CCCLXXII 373 CCCLXXIII 374 CCCLXXIV 375 CCCLXXV 376 CCCLXXVI 377 CCCLXXVII 378 CCCLXXVIII 379 CCCLXXIX 380 CCCLXXX 381 CCCLXXXI 382 CCCLXXXII 383 CCCLXXXIII 384 CCCLXXXIV 385 CCCLXXXV 386 CCCLXXXVI 387 CCCLXXXVII 388 CCCLXXXVIII 389 CCCLXXXIX 390 CCCXC 391 CCCXCI 392 CCCXCII 393 CCCXCIII 394 CCCXCIV 395 CCCXCV 396 CCCXCVI 397 CCCXCVII 398 CCCXCVIII 399 CCCXCIX 400 CD 401 CDI 402 МКБ 403 CDIII 404 IVCD 405 CDV 406 CDVI 407 CDVII 408 CDVIII 409 CDIX 410 CDX 411 CDXI 412 CDXII 413 CDXIII 414 CDXIV 415 CDXV 416 CDXVI 417 CDXVII 418 CDXVIII 419 CDXIX 420 CDXX 421 CDXXI 422 CDXXII 423 CDXXIII 424 CDXXIV 425 CDXXV 426 CDXXVI 427 CDXXVII 428 CDXXVIII 429 CDXXXIX 430 CDXXX 431 CDXXXI 432 CDXXXII 433 CDXXXIII 434 CDXXXIV 435 CDXXXV 436 CDXXXVI 437 CDXXXVII 438 CDXXXVIII 439 CDXXXIX 440 CDXL 441 CDXLI 442 CDXLII 443 CDXLIII 444 CDXLIV 445 CDXLV 446 CDXLVI 447 CDXLVII 448 CDXLVIII 449 CDXLIX 450 CDL 451 CDLI 452 CDLII 453 КДЛ III 454 CDLIV 455 CDLV 456 CDLVI 457 CDLVII 458 CDLVIII 459 CDLIX 460 CDLX 461 CDLXI 462 CDLXII 463 CDLXIII 464 CDLXIV 465 CDLXV 466 CDLXVI 467 CDLXVII 468 CDLXVIII 469 CDLXIX 470 CDLXX 471 CDLXXI 472 CDLXXII 473 CDLXXIII 474 CDLXXIV 475 CDLXV 476 CDLXXVI 477 CDLXVII 478 CDLXXVIII 479 CDLXXIX 480 CDLXXX 481 CDLXXXI 482 CDLXXXII 483 CDLXXXIII 484 CDLXXXIV 485 CDLXXXV 486 CDLXXXVI 487 CDLXXXVII 488 CDLXXXVIII 489 CDLXXXIX 490 CDXC 491 CDXCI 492 CDXCII 493 CDXCIII 494 CDXCIV 495 CDXCV 496 CDXCVI 497 CDXCVII 498 CDXCVIII 499 CDXCIX 500 D 1 1000 к
Número Римская цифра 1 I 2 II 3 III 4 IV 5 V 6 VI 7 VII 8 VIII 9 IX 10 X 11 XI 12 XII 13 XIII 14 XIV 15 XV 16 XVI 17 XVII 18 XVIII 19 XIX 20 XX 21 XXI 22 XXII 23 XXIII 24 XXIV 25 XXV 26 XXVI 27 XXVII 28 XXVIII 29 XXIX 30 XXX 31 XXXI 32 XXXII 33 XXXIII 34 XXXIV 35 XXXV 36 XXXVI 37 XXXVII 38 XXXVIII 39 XXXIX 40 XL 41 XLI 42 XLII 43 XLIII 44 XLIV 45 XLV 46 XLVI 47 XLVII 48 XLVIII 49 XLIX 50 L 51 LI 52 ЛИИ 53 LIII 54 LIV 55 LV 56 LVI 57 LVII 58 LVIII 59 LIX 60 LX 61 LXI 62 LXII 63 LXIII 64 LXIV 65 LXV 66 LXVI 67 LXVII 68 LXVIII 69 LXIX 70 LXX 71 LXXI 72 LXXII 73 LXXXIII 74 LXXIV 75 LXXV 76 LXXVI 77 LXXVII 78 LXXVIII 79 LXXXIX 80 LXXX 81 LXXXI 82 LXXXII 83 LXXXIII 84 LXXXIV 85 LXXXV 86 LXXXVI 87 LXXXVII 88 LXXXVIII 89 LXXXIX 90 XC 91 XCI 92 XII 93 XCIII 94 XCIV 95 XCV 96 XCVI 97 XVII 98 XCVIII 99 ХХIХ 100 C 101 CI 102 CII 103 C-III 104 CIV 105 CV 106 ХВН 107 CVII 108 CVIII 109 CIX 110 CX 111 CXI 112 CXII 113 СXIII 114 CXIV 115 CXV 116 CXVI 117 СXVII 118 CXVIII 119 CIX 120 СХХ 121 CXXI 122 CXXII 123 CXXXIII 124 CXXIV 125 CXXV 126 CXXVI 127 CXXVII 128 CXXVIII 129 CXXIX 130 CXXX 131 CXXXI 132 CXXXII 133 CXXXIII 134 CXXXIV 135 CXXXV 136 CXXXVI 137 CXXXVII 138 CXXXVIII 139 CXXXIX 140 CXL 141 CXLI 142 CXLII 143 CXLIII 144 CXLIV 145 CXLV 146 CXLVI 147 CXLVII 148 CXLVIII 149 CXLIX 150 CL 151 CLI 152 CLII 153 КЛIII 154 КЛИВ 155 CLV 156 КЛВИ 157 CLVII 158 CLVIII 159 КЛИКС 160 CLX 161 CLXI 162 CLXII 163 CLXIII 164 CLXIV 165 CLXV 166 CLXVI 167 CLXVII 168 CLXVIII 169 CLXIX 170 CLXX 171 CLXXI 172 CLXXII 173 CLXXIII 174 CLXXIV 175 CLXXV 176 CLXXVI 177 CLXXVII 178 CLXXVIII 179 CLXXXIX 180 CLXXX 181 CLXXXI 182 CLXXXII 183 CLXXXIII 184 CLXXXIV 185 CLXXXV 186 CLXXXVI 187 CLXXXVII 188 CLXXXVIII 189 CLXXIX 190 СХС 191 CXCI 192 CXCII 193 CXCIII 194 CXCIV 195 CXCV 196 CXCVI 197 CXCVII 198 CXCVIII 199 CXCIX 200 CC 201 CCI 202 IICC 203 CCIII 204 CCVI 205 ККТ 206 CCVI 207 CCVII 208 CCVIII 209 CCIX 210 CCX 211 CCXI 212 CCXII 213 CCXIII 214 CCXIV 215 CCXV 216 CCXVI 217 CCXVII 218 CCXVIII 219 CXXIX 220 CCXX 221 CCXXI 222 CCXXII 223 CCXXIII 224 CCXXIV 225 CCXXV 226 CCXXVI 227 CCXXVII 228 CCXXVIII 229 CCXXIX 230 CCXXX 231 CCXXXI 232 CCXXXII 233 CCXXXIII 234 CCXXXIV 235 CCXXXV 236 CCXXXVI 237 CCXXXVII 238 CCXXXVIII 239 CCXXXIX 240 CCXL 241 CCXLI 242 CCXLII 243 CCXLIII 244 CCXLIV 245 CCXLV 246 CCXLVI 247 CCXLVII 248 CCXLVIII 249 CCXLIX 250 CCL 251 CCLI 252 CCLII 253 CCIII 254 CCLIV 255 CCLV 256 CCLVI 257 CCLVII 258 CCLVIII 259 ССЛИКС 260 CCLX 261 CCLXI 262 CCLXII 263 CCLXIII 264 CCLXIV 265 CCLXV 266 ССLXVI 267 CCLXVII 268 ССLXVIII 269 CCLXIX 270 CCLXX 271 CCLXXI 272 CCLXXII 273 ККЛ XXIII 274 CCXXIV 275 CCLXXV 276 CCLXXVI 277 CCLXXVII 278 CCLXXVIII 279 CCXXIX 280 CCLXXX 281 CCLXXXI 282 CCLXXXII 283 CCLXXXIII 284 CCLXXXIV 285 CCLXXXV 286 CCLXXXVI 287 CCLXXXVII 288 CCLXXXVIII 289 CCLXXXIX 290 CCXC 291 CCXCI 292 CCXCII 293 CCXCIII 294 CCXCIV 295 CCXCV 296 CCXCVI 297 CCXCVII 298 CCXCVIII 299 CCXCIX 300 CCC 301 CCCI 302 CCII 303 СССIII 304 CCIV 305 CC CV 306 CCCVI 307 СССVII 308 СССVIII 309 CCCIX 310 CCCX 311 CCXI 312 CCXII 313 CCXIII 314 CCXIV 315 CCXV 316 СССXVI 317 СССXVII 318 CCXVIII 319 CCXIX 320 СССХХ 321 CCCXXXI 322 СССXXII 323 СССXXIII 324 CCXXIV 325 CCCXXV 326 CCXXVI 327 СССXXVII 328 CCCXXXVIII 329 CCXXIX 330 СССХХХ 331 CCCXXXI 332 CCXXXII 333 СССXXXIII 334 CCXXXIV 335 CCXXXV 336 CCXXXVI 337 CCXXXVII 338 CCXXXVIII 339 CCXXXIX 340 CCXL 341 CCXLI 342 CCXLII 343 CCXLIII 344 CCXLIV 345 CCXLV 346 CCCXLVI 347 CCXLVII 348 CCXLVIII 349 CCXLIX 350 CCCL 351 CCCLI 352 CCCL II 353 CCCL III 354 CCCL IV 355 CCLV 356 CCCLVI 357 CCLVII 358 CCCLVIII 359 CCCLIX 360 CCCLX 361 CCCLXI 362 CCCLXII 363 CCCLXIII 364 CCCLXIV 365 CCCLXV 366 CCCLXVI 367 CCCLXVII 368 CCCLXVIII 369 CCCLXIX 370 CCCLXX 371 CCCLXXI 372 CCCLXXII 373 CCCLXXIII 374 CCCLXXIV 375 CCCLXXV 376 CCCLXXVI 377 CCCLXXVII 378 CCCLXXVIII 379 CCCLXXIX 380 CCCLXXX 381 CCCLXXXI 382 CCCLXXXII 383 CCCLXXXIII 384 CCCLXXXIV 385 CCCLXXXV 386 CCCLXXXVI 387 CCCLXXXVII 388 CCCLXXXVIII 389 CCCLXXXIX 390 CCCXC 391 CCCXCI 392 CCCXCII 393 CCCXCIII 394 CCCXCIV 395 CCCXCV 396 CCCXCVI 397 CCCXCVII 398 CCCXCVIII 399 CCCXCIX 400 CD 401 CDI 402 МКБ 403 CDIII 404 IVCD 405 CDV 406 CDVI 407 CDVII 408 CDVIII 409 CDIX 410 CDX 411 CDXI 412 CDXII 413 CDXIII 414 CDXIV 415 CDXV 416 CDXVI 417 CDXVII 418 CDXVIII 419 CDXIX 420 CDXX 421 CDXXI 422 CDXXII 423 CDXXIII 424 CDXXIV 425 CDXXV 426 CDXXVI 427 CDXXVII 428 CDXXVIII 429 CDXXXIX 430 CDXXX 431 CDXXXI 432 CDXXXII 433 CDXXXIII 434 CDXXXIV 435 CDXXXV 436 CDXXXVI 437 CDXXXVII 438 CDXXXVIII 439 CDXXXIX 440 CDXL 441 CDXLI 442 CDXLII 443 CDXLIII 444 CDXLIV 445 CDXLV 446 CDXLVI 447 CDXLVII 448 CDXLVIII 449 CDXLIX 450 CDL 451 CDLI 452 CDLII 453 КДЛ III 454 CDLIV 455 CDLV 456 CDLVI 457 CDLVII 458 CDLVIII 459 CDLIX 460 CDLX 461 CDLXI 462 CDLXII 463 CDLXIII 464 CDLXIV 465 CDLXV 466 CDLXVI 467 CDLXVII 468 CDLXVIII 469 CDLXIX 470 CDLXX 471 CDLXXI 472 CDLXXII 473 CDLXXIII 474 CDLXXIV 475 CDLXV 476 CDLXXVI 477 CDLXVII 478 CDLXXVIII 479 CDLXXIX 480 CDLXXX 481 CDLXXXI 482 CDLXXXII 483 CDLXXXIII 484 CDLXXXIV 485 CDLXXXV 486 CDLXXXVI 487 CDLXXXVII 488 CDLXXXVIII 489 CDLXXXIX 490 CDXC 491 CDXCI 492 CDXCII 493 CDXCIII 494 CDXCIV 495 CDXCV 496 CDXCVI 497 CDXCVII 498 CDXCVIII 499 CDXCIX 500 D 501 DI 502 ДИИ 503 ДIII 504 DIV 505 DV 506 DVI 507 ДВII 508 ДВIII 509 DIX 510 DX 511 DXI 512 DXII 513 DXIII 514 DXIV 515 DXV 516 DXVI 517 DXVII 518 DXVIII 519 DXIX 520 DXX 521 DXXI 522 DXXII 523 DXXIII 524 DXXIV 525 DXXV 526 DXXVI 527 DXXVII 528 DXXVIII 529 DXXIX 530 Dxxx 531 DXXXI 532 DXXXII 533 DXXXIII 534 DXXXIV 535 DXXXIV 536 DXXXVI 537 DXXXVII 538 DXXXVIII 539 DXXXIX 540 DXL 541 DXLI 542 DXLII 543 DXLIII 544 DXLIV 545 DXLV 546 DXLVI 547 DXLVII 548 DXLVIII 549 DXLIX 550 DL 551 РМИ 552 ДЛИИ 553 ДЛIII 554 ДЛИВ 555 DLV 556 ДЛВИ 557 DLVII 558 DLVIII 559 DLIX 560 DLX 561 DLXI 562 DLXII 563 DLXIII 564 DLXIV 565 DLXV 566 DLXVI 567 ДЛXVII 568 DLXVIII 569 DLXIX 570 DLXX 571 DLXXI 572 DLXXII 573 ДЛ XXIII 574 DLXXIV 575 DLXXV 576 DLXXVI 577 DLXXVII 578 DLXXVIII 579 DLXXXIX 580 DLXXX 581 DLXXXI 582 DLXXXII 583 DLXXXIII 584 DLXXXIV 585 DLXXXV 586 DLXXXVI 587 DLXXXVII 588 DLXXXVIII 589 DLXXXIX 590 DXC 591 DXCI 592 DXCII 593 DXCIII 594 DXCIV 595 DXCV 596 DXCVI 597 DXCVII 598 DXCVIII 599 DXCIX 600 DC 601 DCI 602 DCII 603 DCIII 604 IVCD 605 DCV 606 DCVI 607 DCVII 608 АДВIII 609 DCIX 610 DCX 611 DCXI 612 DCXII 613 ADXIII 614 DCXIV 615 XV нашей эры 616 ADXVI 617 ADXVII 618 ADXVIII 619 ADXIX 620 DCXX 621 DCXXI 622 DCXXXII 623 XXIII н.  э.
э.624 DCXXIV 625 DCXXV 626 DCXXVI 627 ADXXVII 628 ADXXVIII 629 DCXXXIX 630 DCXXX 631 DCXXXI 632 DCXXXII 633 DCXXXIII 634 DCXXXIV 635 DCXXXV 636 DCXXXVI 637 DCXXXXVII 638 ADXXXVIII 639 DCXXXIX 640 DCXL 641 DCXLI 642 DCXLII 643 DCXLIII 644 DCXLIV 645 DCXLV 646 DCXLVI 647 DCXLVII 648 DCXLVIII 649 DCXLIX 650 DCL 651 DCLI 652 DCLII 653 ДКЛIII 654 DCLIV 655 DCLV 656 ДЦЛВИ 657 DCLVII 658 DCLVIII 659 ДКЛИКС 660 DCLX 661 DCLXI 662 DCLXII 663 DCLXIII 664 DCLXIV 665 DCLXV 666 ДКЛXVI 667 ДКЛXVII 668 ДКЛXVIII 669 ДКЛXIX 670 ДКЛХХ 671 DCLXXI 672 ДКЛXXII 673 ДКЛXXIII 674 ДКЛXXIV 675 DCLXXV 676 ДКЛXXVI 677 ДКЛXXVII 678 DCLXXVIII 679 ДКЛXXIX 680 ДКЛХХХ 681 DCLXXXI 682 DCLXXXII 683 DCLXXXIII 684 DCLXXXIV 685 DCLXXXV 686 DCLXXXVI 687 DCLXXXVII 688 DCLXXXVIII 689 ДКЛXXXIX 690 DCXC 691 DCXCI 692 DCXCII 693 DCXCIII 694 DCXCIV 695 DCXCV 696 DCXCVI 697 DCXCVII 698 DCXCVIII 699 DCXCIX 700 DCC 701 DCCI 702 DCCII 703 ДКК III 704 DCCIV 705 DCCV 706 DCCVI 707 DCCV II 708 DCCVIII 709 DCCIX 710 DCCX 711 DCCXI 712 ДКК XII 713 ДКК XIII 714 DCCXIV 715 DCCXV 716 DCCXVI 717 DCCXVII 718 DCCXVIII 719 DCCXIX 720 DCCXX 721 DCCXXI 722 DCCXXII 723 ДКК XXIII 724 ДКК XXIV 725 DCCXXV 726 DCCXXVI 727 DCCXXVII 728 DCCXXVIII 729 DCCXXIX 730 DCCXXX 731 DCCXXXI 732 DCCXXXII 733 DCCXXXIII 734 DCCXXXIV 735 DCCXXXV 736 DCCXXXVI 737 DCCXXXVII 738 DCCXXXVIII 739 DCCXXXIX 740 DCCXL 741 DCCXLI 742 DCCXLII 743 DCCXLIII 744 DCCXLIV 745 DCCXLV 746 DCCXLVI 747 DCCXLVII 748 DCCXLVIII 749 DCCXLIX 750 ДЦКЛ 751 DCCLI 752 DCCL II 753 ДЦКЛ III 754 ДЦКЛ IV 755 DCCLV 756 DCCLVI 757 DCCLVII 758 DCCLVIII 759 DCCLIX 760 DCCLX 761 DCCLXI 762 DCCLXII 763 DCCLXIII 764 DCCLXIV 765 DCCLXV 766 DCCLXVI 767 DCCLXVII 768 DCCLXVIII 769 DCCLXXIX 770 DCCLXX 771 DCCLXXI 772 DCCLXXII 773 DCCLXXIII 774 DCCLXXIV 775 DCCLXXV 776 DCCLXXVI 777 DCCLXXVII 778 DCCLXXVIII 779 DCCLXXIX 780 DCCLXXX 781 DCCLXXXI 782 DCCLXXXII 783 DCCLXXXIII 784 DCCLXXXIV 785 DCCLXXXV 786 DCCLXXXVI 787 DCCLXXXVII 788 DCCLXXXVIII 789 DCCLXXXIX 790 DCCXC 791 DCCXCI 792 DCCXCII 793 DCCXCIII 794 DCCXCIV 795 DCCXCV 796 DCCXCVI 797 DCCXCVII 798 DCCXCVIII 799 DCCXCIX 800 DCCC 801 DCCCI 802 DCCC II 803 DCCC III 804 DCCC IV 805 DCCCV 806 DCCCVI 807 DCCCVII 808 DCCCVIII 809 DCCCIX 810 DCCCX 811 DCCCXI 812 DCCCXII 813 DCCCXIII 814 DCCCXIV 815 DCCCXV 816 DCCCXVI 817 DCCCXVII 818 DCCCXVIII 819 DCCCXIX 820 DCCCXX 821 DCCCXXXI 822 DCCCXXII 823 DCCC XXIII 824 DCCCXXIV 825 DCCCXXV 826 DCCCXXVI 827 DCCCXXVII 828 DCCCXXVIII 829 DCCCXXIX 830 DCCCXXX 831 DCCCXXXI 832 DCCCXXXII 833 DCCCXXXIII 834 DCCCXXXIV 835 DCCCXXXV 836 DCCCXXXVI 837 DCCCXXXVII 838 DCCCXXXVIII 839 DCCCXXXIX 840 DCCCXL 841 DCCCXLI 842 DCCCXLII 843 DCCCXLIII 844 DCCCXLIV 845 DCCCXLV 846 DCCCXLVI 847 DCCCXLVII 848 DCCCXLVIII 849 DCCCXLIX 850 ДКККЛ 851 DCCCLI 852 DCCCLII 853 ДКККЛ III 854 ДККЛИВ 855 DCCCLV 856 DCCCLVI 857 DCCCLVII 858 DCCCLVIII 859 DCCCLIX 860 DCCCLX 861 DCCCLXI 862 DCCCLXII 863 DCCCLXIII 864 DCCCLXIV 865 DCCCLXV 866 DCCCLXVI 867 DCCCLXVII 868 DCCCLXVIII 869 DCCCLXIX 870 DCCCLX 871 DCCCLXXI 872 DCCCLXXII 873 DCCCLXXIII 874 DCCCLXIV 875 DCCCLXXV 876 DCCCLXXVI 877 DCCCLXXVII 878 DCCCLXXVIII 879 DCCCLXXIX 880 DCCCLXXX 881 DCCCLXXXI 882 DCCCLXXXII 883 DCCCLXXXIII 884 DCCCLXXXIV 885 DCCCLXXXV 886 DCCCLXXXVI 887 DCCCLXXXVII 888 DCCCLXXXVIII 889 DCCCLXXXIX 890 DCCCXC 891 DCCCXCI 892 DCCCXCII 893 DCCCXCIII 894 DCCCXCIV 895 DCCCXCV 896 DCCCXCVI 897 DCCCXCVII 898 DCCCXCVIII 899 DCCCXCIX 900 CM 901 CMI 902 CMII 903 СМIII 904 ИВМК 905 CMV 906 ЦМВИ 907 ЦМВII 908 ЦМВIII 909 CMIX 910 CMX 911 CMXI 912 СМХ II 913 CMXIII 914 СМХ IV 915 CMXV 916 CMXVI 917 СМXVII 918 CMXVIII 919 CMXIX 920 CMXX 921 CMXXI 922 CMXXII 923 CMXXIII 924 CMXXIV 925 CMXXV 926 CMXXVI 927 CMXXVII 928 CMXXVIII 929 CMXXIX 930 СМХХХ 931 CMXXXI 932 CMXXXII 933 CMXXXIII 934 CMXXXIV 935 CMXXXV 936 CMXXXVI 937 CMXXXXVII 938 CMXXXVIII 939 CMXXXIX 940 CMXL 941 CMXLI 942 CMXLII 943 CMXLIII 944 CMXLIV 945 CMXLV 946 CMXLVI 947 CMXLVII 948 CMXLVIII 949 CMXLIX 950 CML 951 CMLI 952 CMLII 953 ХМЛ III 954 СМЛИВ 955 ЦМЛВ 956 СМЛВИ 957 CMLVII 958 CMLVIII 959 СМЛИКС 960 CMLX 961 CMLXI 962 CMLXII 963 CMLXIII 964 CMLXIV 965 CMLXV 966 CMLXVI 967 CMLXVII 968 CMLXVIII 969 CMLXIX 970 СМЛХХ 971 CMLXXI 972 CMLXXII 973 CMLXXIII 974 CMLXXIV 975 CMLXXV 976 CMLXXVI 977 CMLXXVII 978 CMLXXVIII 979 CMLXXIX 980 СМЛХХХ 981 CMLXXXI 982 CMLXXXII 983 CMLXXXIII 984 CMLXXXIV 985 CMLXXXV 986 CMLXXXVI 987 CMLXXXXVII 988 CMLXXXVIII 989 CMLXXXIX 990 CMXC 991 CMXCI 992 CMXCII 993 CMXCIII 994 CMXCIV 995 CMXCV 996 CMXCVI 997 CMXCVII 998 CMXCVIII 999 CMXCIX 1000 M от 1 и выше
 000, которое обозначено буквой M. Ниже мы представляем другие более высокие числа, которые могут вас заинтересовать.
000, которое обозначено буквой M. Ниже мы представляем другие более высокие числа, которые могут вас заинтересовать.Правила с римскими цифрами
Сума
вычитание
 Например: от CCXLI (241) до CCXXXXI. Неважно, повторяется ли буква более 3 раз.
Например: от CCXLI (241) до CCXXXXI. Неважно, повторяется ли буква более 3 раз.умножение


деление
 (потому что мы вычитали 3 раза). Итак, ответ — 3, однако это не совсем так, так как 10/3 = 3,33333 …
(потому что мы вычитали 3 раза). Итак, ответ — 3, однако это не совсем так, так как 10/3 = 3,33333 …
Даты римскими цифрами

Как поставить римские цифры в Word?
 Например, для числа 5002 у нас будет:
Например, для числа 5002 у нас будет:Сверлить
Римские цифры от 1 до 100
 Поэтому чаще всего применяют римские цифры по шкале от одного до сто. О них и будет идти речь в этой статье.
Поэтому чаще всего применяют римские цифры по шкале от одного до сто. О них и будет идти речь в этой статье.Немного истории
 Например, римская цифра 5 с чертой наверху — V̅, обозначала 5 000.
Например, римская цифра 5 с чертой наверху — V̅, обозначала 5 000.Формирование римских цифр – счёт от 1 до 100
 Стоить заметить, что другие методы вычитания применять ранее было недопустимо. Запись арабской цифры 99 должно выглядеть так: XCIX, а не IC. Но в наши дни в популярном текстовом редакторе Microsoft Word и Microsoft Excel применяются упрощенные числа. Здесь допустимо использоваться конструкцию IC, а также другие — VC (95), вместо XCV и так далее.
Стоить заметить, что другие методы вычитания применять ранее было недопустимо. Запись арабской цифры 99 должно выглядеть так: XCIX, а не IC. Но в наши дни в популярном текстовом редакторе Microsoft Word и Microsoft Excel применяются упрощенные числа. Здесь допустимо использоваться конструкцию IC, а также другие — VC (95), вместо XCV и так далее.Сервисы по преобразованию арабских цифр в римские
 Тем более принципы их образования. Этого делать и не нужно. Есть специальные конвертеры, которые помогут вам преобразовать любые арабские цифры в римские и обратно. Одним из таких сервисов является calc.ru. Здесь вы сможете перевести арабские, римские или индийские цифры в разной последовательности. Переводить можно только целые числа.
Тем более принципы их образования. Этого делать и не нужно. Есть специальные конвертеры, которые помогут вам преобразовать любые арабские цифры в римские и обратно. Одним из таких сервисов является calc.ru. Здесь вы сможете перевести арабские, римские или индийские цифры в разной последовательности. Переводить можно только целые числа.![]()
Применение в наши дни

Почему в часах используют римскую цифру «IIII» вместо «IV»
 Но попадаются и исключения, например, лондонский Биг-Бен. Почему так происходит? До сих пор никто не знает точного ответа. В этой статье мы рассмотрим наиболее вероятные объяснения такой странной нумерации.
Но попадаются и исключения, например, лондонский Биг-Бен. Почему так происходит? До сих пор никто не знает точного ответа. В этой статье мы рассмотрим наиболее вероятные объяснения такой странной нумерации.«IIII» — ранний вариант обозначения цифры «4»

Оскорбление бога Юпитера
 Впоследствии его, возможно, продолжили применять просто как дань традиции.
Впоследствии его, возможно, продолжили применять просто как дань традиции.Упрощение для неграмотного населения
Людовик XIV «Король-солнце»

Визуальный баланс
 И, конечно, всегда будут исключения из правил…
И, конечно, всегда будут исключения из правил…Что такое римская цифра VI? – Обзоры Вики
 Все римские цифры отображаются темно-синим цветом.
Все римские цифры отображаются темно-синим цветом.Как вы пишете римские цифры?

Как написать 2021 римскими цифрами?
Что это за IX?
 на Пятой авеню.
на Пятой авеню. римские цифры арабские цифры верхний регистр в нижнем регистре XV xv 15 XVI XVI 16 XVII XVII 17 Почему 2020 MMXX римскими цифрами?
Номера Римские числа 200 CC 300 CCC 400 CD 500 D  Нуль представляется с помощью слово nulla. Согласно латинскому языку, слово nulla означает отсутствие. До сих пор не существует определенного символа или буквы для обозначения нуля в римской системе счисления.
Нуль представляется с помощью слово nulla. Согласно латинскому языку, слово nulla означает отсутствие. До сих пор не существует определенного символа или буквы для обозначения нуля в римской системе счисления.Почему в римских цифрах нет нуля?
 , поэтому вместо него был введен IIII.
, поэтому вместо него был введен IIII.три способа на все случаи

У вас, конечно, имеется стандартная клавиатура, где присутствуют буквы английского алфавита, то ввести в любой текст римские цифры особого труда не составит. Только надо знать, какие буквы какому числу соответствуют. С девяткой поступаем так же, как и с четверкой. 9=10-1, значит, пишем IX .
С девяткой поступаем так же, как и с четверкой. 9=10-1, значит, пишем IX . Только в эпоху позднего Средневековья арабы заменили ее на упрощенную систему, которой мы пользуемся сейчас. К счастью, в Интернете римская система чисел встречается редко.
Только в эпоху позднего Средневековья арабы заменили ее на упрощенную систему, которой мы пользуемся сейчас. К счастью, в Интернете римская система чисел встречается редко.Как поставить римские цифры в Ворде 2007 года
 Первый из них – ручной. Что для этого необходимо сделать?
Первый из них – ручной. Что для этого необходимо сделать?
Как поставить римские цифры в Word свежей версии?
Римские цифры: третий способ постановки
 Для начала пользователь должен открыть вкладку под названием «Вставка», найти в нем пункт «Символ», а затем нажать кнопку «Другие символы». После, в появившемся на экране окне нужно найти необходимый символ. Когда это будет сделано – нажать кнопку «Вставить». Этот способ доступен практически на всех версиях текстового редактора Word.
Для начала пользователь должен открыть вкладку под названием «Вставка», найти в нем пункт «Символ», а затем нажать кнопку «Другие символы». После, в появившемся на экране окне нужно найти необходимый символ. Когда это будет сделано – нажать кнопку «Вставить». Этот способ доступен практически на всех версиях текстового редактора Word.Латиница и римские цифры
Автонумерация римскими цифрами
Вставка римской цифры через символы
Сочетание клавиш для вставки римских цифр
 В этом случае знать как пишется римское число необязательно. Нажав Ctrl+F9, в местоположении курсора появятся фигурные скобки. В которые нужно вписать {=нужное число\*ROMAN}, и нажать F9, автоматически появиться соответствующее римское число. Его впоследствии можно корректировать наведя курсор и кликнув правой кнопкой мыши. В появившемся меню выбрать «Коды/значения полей» которое вернет к исходному варианту. Изменив число и нажав F9 получите искомый результат. Пример: {=2137\*ROMAN} соответствует MMCXXXVII. Здесь нужно учесть что набрав roman получится mmcxxxvii.
В этом случае знать как пишется римское число необязательно. Нажав Ctrl+F9, в местоположении курсора появятся фигурные скобки. В которые нужно вписать {=нужное число\*ROMAN}, и нажать F9, автоматически появиться соответствующее римское число. Его впоследствии можно корректировать наведя курсор и кликнув правой кнопкой мыши. В появившемся меню выбрать «Коды/значения полей» которое вернет к исходному варианту. Изменив число и нажав F9 получите искомый результат. Пример: {=2137\*ROMAN} соответствует MMCXXXVII. Здесь нужно учесть что набрав roman получится mmcxxxvii. Этот вариант самый простой. Римские цифры выглядят как некоторые латинские буквы. Поэтому достаточно переключить язык на «Английский», включить CAPS LOCK или зажать клавишу Shift и ставить цифры в нужном формате, комбинируя между собой буквы «i», «v» и «x». Для составления крупных чисел вам понадобятся буквы «m», «c», «e», «l». Из этого можно составить все необходимые значения : I, II, III, IV, V, VI, VII, VIII, IX, X, и так далее.
Этот вариант самый простой. Римские цифры выглядят как некоторые латинские буквы. Поэтому достаточно переключить язык на «Английский», включить CAPS LOCK или зажать клавишу Shift и ставить цифры в нужном формате, комбинируя между собой буквы «i», «v» и «x». Для составления крупных чисел вам понадобятся буквы «m», «c», «e», «l». Из этого можно составить все необходимые значения : I, II, III, IV, V, VI, VII, VIII, IX, X, и так далее. Например, вводим {=1234\*ROMAN}, нажимаем F9 и получаем MCCXXXIV. Очень удобно использовать такой подход, если вам требуется указать крупное число, но вы не знаете, как оно должно выглядеть в римском формате. Используя такой подход, можно переводить любые арабские значения, без ограничений, вплоть до 1000, 10000 и более крупных.
Например, вводим {=1234\*ROMAN}, нажимаем F9 и получаем MCCXXXIV. Очень удобно использовать такой подход, если вам требуется указать крупное число, но вы не знаете, как оно должно выглядеть в римском формате. Используя такой подход, можно переводить любые арабские значения, без ограничений, вплоть до 1000, 10000 и более крупных.Первый способ.
Второй способ.
b)Или нажимаем и удерживаем нажатой во время набора букв, клавишу «Shift».
Римская цифра 3 – III.
Римская цифра 4 – IV (большие английские буквы I и V).
Римская цифра 5 – V.
Римская цифра 6 – VI.
Римская цифра 7 – VII.
Римская цифра 8 – VIII.
Римская цифра 9 – IX (большие английские буквы I и X).
Римская цифра 10 – X.
Римская цифра 50 – L.
Римская цифра 100 – C.
Римская цифра 500 – D.
Римская цифра 1000 – M.Третий способ.

Четвертый способ.
6 римскими цифрами — Как написать 6 римскими цифрами?
1. 
Как написать 6 римскими цифрами? 2. Основные правила 3. Номера, относящиеся к 6 4. Часто задаваемые вопросы о 6 римскими цифрами Как написать 6 римскими цифрами?
В этом методе мы разбиваем 6 на сумму чисел 5 и 1, чтобы применить «аддитивную запись». В нем говорится, что всякий раз, когда буква большего размера предшествует букве меньшего размера, буквы будут добавляться. Таким образом, мы можем получить римскую цифру для 6, разбив ее на сумму 5 и 1 и написав их соответствующие эквивалентные римские буквы и объединив их, то есть 6 = 5 + 1 = V + I = VI.
Следовательно, значение 6 в римских цифрах равно VI. Основные правила интерпретации римских цифр
 Например: CX, C > X, поэтому CX = C + X = 100 + 10 = 110.
Например: CX, C > X, поэтому CX = C + X = 100 + 10 = 110. 6 римскими цифрами Примеры
Чтобы определить значение 86 — 6 римскими цифрами, выразим 80 как LXXX.
Для определения значения 3908 — 6 римскими цифрами выразим 3902 в развернутом виде, т.е. 3902 = 3000 + 900 + 2 = МММ + СМ + II = МММСМII.
Разделив 18 на 6, мы получим 3 в качестве частного.
Теперь 3 = III
.
Следовательно, когда XVIII делится на VI, в частном получается III. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем. Часто задаваемые вопросы о 6 римскими цифрами
Что означает 6 римскими цифрами?
Что нужно добавить к 4, чтобы получить 6? Запишите ответ римскими цифрами.
Каково значение (76 — 79) + 6 в римских цифрах?
 е. 3 = 1 + 1 + 1 = I + I + I = III
е. 3 = 1 + 1 + 1 = I + I + I = III Чему равно число 6 римскими цифрами?
Почему 6 римскими цифрами пишется как VI?
наглядный учебный план VI Римские цифры | Как написать ВП цифрами?
 е. VI = V + I = 5 + 1 = 6. Старшие римские цифры предшествуют младшим цифрам, что обеспечивает правильный перевод VI римских цифр. В этой статье мы объясним, как преобразовать римские цифры VI в правильный перевод числа.
е. VI = V + I = 5 + 1 = 6. Старшие римские цифры предшествуют младшим цифрам, что обеспечивает правильный перевод VI римских цифр. В этой статье мы объясним, как преобразовать римские цифры VI в правильный перевод числа. Как писать римские цифры VI?
Каковы основные правила написания римских цифр?
 Например: ML, M > L, поэтому ML = M + L = 1000 + 50 = 1050
Например: ML, M > L, поэтому ML = M + L = 1000 + 50 = 1050 Числа, связанные с римскими цифрами VI
VI Примеры римских цифр

Теперь MMMDXXII + VI = 3522 + 6 = 3528
.
Так как MMMDXXVIII = 3000 + 500 + 20 + 8 = 3528
Следовательно, сумма римских цифр MMMDXXII и VI равна MMMDXXVIII
Теперь VI × CDLIII = 6 × 453 = 2718
Так как MMDCCXVIII = 2000 + 700 + 10 + 8 = 2718
Следовательно, VI × CDLIII = MMCCXVIII
Теперь VI — II = 6 — 2 = 4
Так как 4 = IV
Следовательно, VI — II = IV
Теперь, когда мы делим XII на II, т.е. 12 ÷ 2, в частном получается 6.
Так как 6 = VI
Следовательно, XII ÷ II = VI Часто задаваемые вопросы о римских цифрах VI
Каково значение римских цифр VI?
Что нужно добавить к римским цифрам VI, чтобы получить MCCLXXXI?
Почему 6 пишется римскими цифрами как VI?
 Следовательно, 6 римскими цифрами записывается как VI = 6.
Следовательно, 6 римскими цифрами записывается как VI = 6. Как преобразовать римские цифры VI в арабские числа?
Какой остаток при делении VI на VI в римских цифрах?
Римские цифры: руководство, таблица и конвертер
 Эти семь букв составляют тысячи цифр. Прочтите наше полное руководство ниже или воспользуйтесь конвертером и диаграммой, чтобы быстро проверить числовое значение.
Эти семь букв составляют тысячи цифр. Прочтите наше полное руководство ниже или воспользуйтесь конвертером и диаграммой, чтобы быстро проверить числовое значение. Преобразователь цифр
Таблица цифр
1 I 34 XXXIV 67 LXVII 2 II 35 XXXV 68 LXVIII 3 III 36 XXXVI 69 LXIX 4 IV 37 ХХXVII 70 LXX 5 В 38 XXXVIII 71 LXXI 6 VI 39 XXXIX 72 LXXII 7 VII 40 XL 73 LXXIII 8 VIII 41 XLI 74 LXXIV 9 IX 42 XLII 75 LXXV 10 Х 43 XLIII 76 LXXVI 11 XI 44 XLIV 77 LXXVII 12 XII 45 XLV 78 LXXVIII 13 XIII 46 XLVI 79 LXXXIX 14 XIV 47 XLVII 80 LXXX 15 XV 48 XLVIII 81 LXXXI 16 XVI 49 XLIX 82 LXXXII 17 XVII 50 л 83 LXXXIII 18 XVIII 51 ЛИ 84 LXXXIV 19 XIX 52 ЛИИ 85 LXXXV 20 ХХ 53 LIII 86 LXXXVI 21 XXI 54 ЛИВ 87 LXXXVII 22 XXII 55 ЛВ 88 LXXXVIII 23 XXIII 56 LVI 89 LXXXIX 24 XXIV 57 LVII 90 ХС 25 ХХV 58 LVIII 91 XCI 26 ХХVI 59 LIX 92 XCII 27 XXVII 60 LX 93 XCIII 28 XXVIII 61 LXI 94 XCIV 29 XXIX 62 LXII 95 XCV 30 ХХХ 63 LXIII 96 XCVI 31 XXXI 64 LXIV 97 XCVII 32 XXXII 65 LXV 98 XCVIII 33 XXXIII 66 LXVI 99 XCIX 100 С Содержание страницы
Видеогид
youtube.com/embed/ByVrkHakTm0″> Основы
 Тот же принцип применим к числу девять, которое пишется как IX.
Тот же принцип применим к числу девять, которое пишется как IX.
Годы и даты
2010 MMX 2020 ММХХ 2011 MMXI 2021 MMXXI 2012 MMXII 2022 MMXXII 2013 MMXIII 2023 MMXXIII 2014 MMXIV 2024 MMXXIV 2015 ММХВ 2025 MMXXV 2016 MMXVI 2026 ММХXVI 2017 ММXVII 2027 ММХXVII 2018 ММXVIII 2028 ММХXVIII 2019 MMXIX 2029 ММХХIX Большие числа

Нули и дроби
Сложение и вычитание

Дополнение
Вычитание
Современное использование
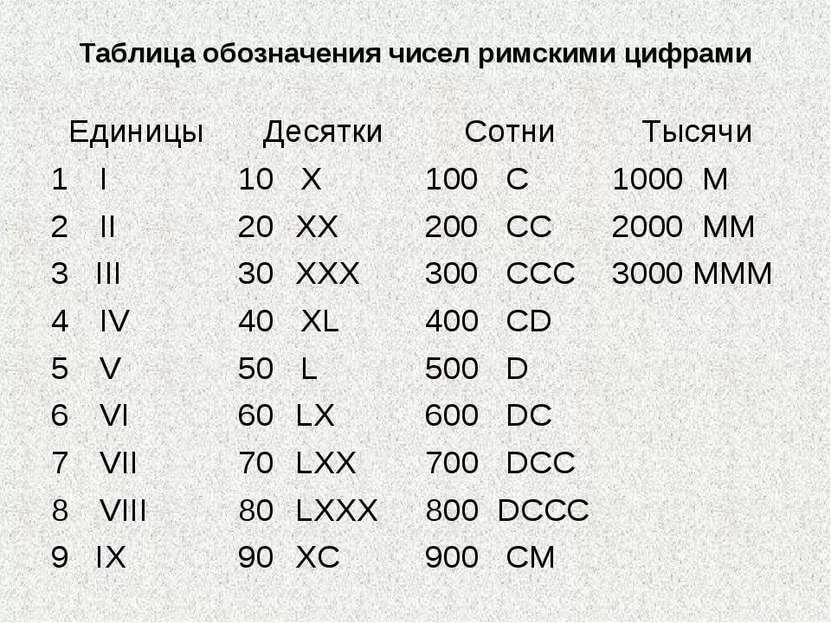 Например; Генрих VIII Англии и Людовик XVI Франции.
Например; Генрих VIII Англии и Людовик XVI Франции. Происхождение римских цифр
 Этруски, оккупировавшие центральную Италию до прихода римлян, разработали аналогичную систему, но с использованием других символов.
Этруски, оккупировавшие центральную Италию до прихода римлян, разработали аналогичную систему, но с использованием других символов. Теория 1
Теория 2
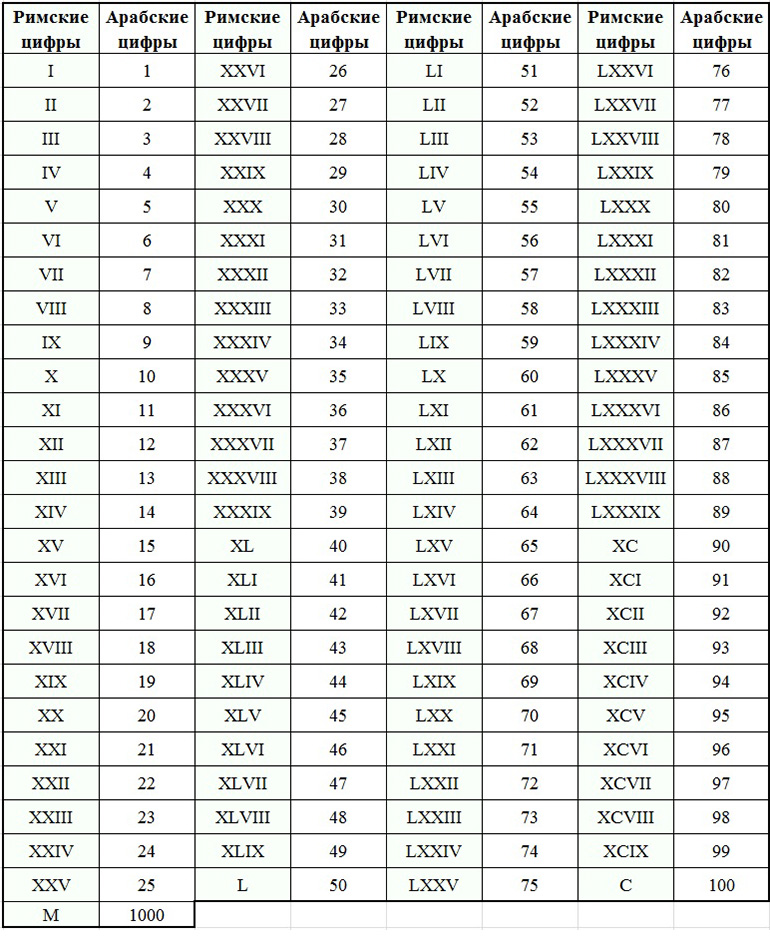 Пять были показаны как перевернутая буква «V», а десять — как «X».
Пять были показаны как перевернутая буква «V», а десять — как «X». Другие системы счисления и счета
Египетские числа: 3000-1600 гг. до н.э.
 Возьмем другой пример: 1700 записывалось как:
Возьмем другой пример: 1700 записывалось как: Вавилонские числа: 1750 г. до н.э.
Поделиться этой страницей
Библиография
Часто задаваемые вопросы
Родственные страницы
Римская цифра | Диаграмма и факты
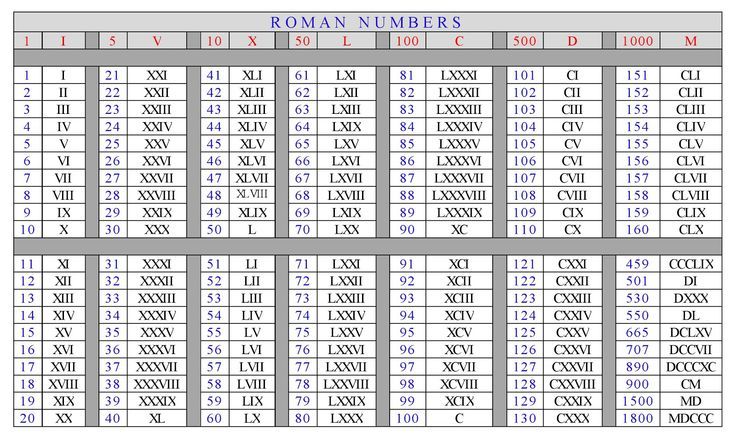 Символы I, V, X, L, C, D и M обозначают соответственно 1, 5, 10, 50, 100, 500 и 1000.
Символы I, V, X, L, C, D и M обозначают соответственно 1, 5, 10, 50, 100, 500 и 1000.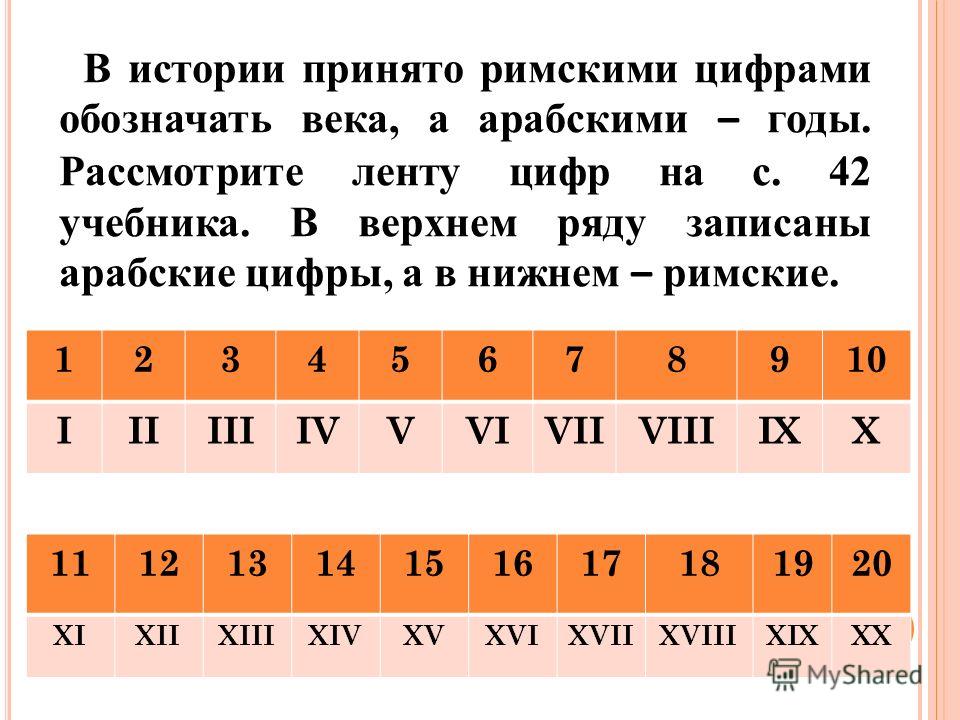 э. хорошо известны. Римские цифры, вероятно, были разработаны в результате необходимости общего метода подсчета для лучшего ведения торговли.
э. хорошо известны. Римские цифры, вероятно, были разработаны в результате необходимости общего метода подсчета для лучшего ведения торговли.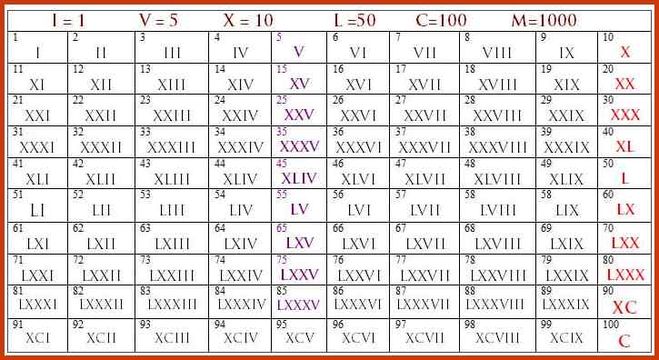 Символ, помещенный перед символом большего значения, вычитает его значение; например, IV = 4, XL = 40 и CD = 400. Черта, помещенная над числом, умножает его значение на 1000.
Символ, помещенный перед символом большего значения, вычитает его значение; например, IV = 4, XL = 40 и CD = 400. Черта, помещенная над числом, умножает его значение на 1000. арабский Римский 1 я 2 II 3 III 4 IV 5 В 6 VI 7 VII 8 VIII 9 IX 10 Икс 11 XI 12 XII 13 XIII 14 XIV 15 XV 16 XVI 17 XVII 18 XVIII 19 XIX 20 ХХ 21 XXI 22 XXII 23 XXIII 24 XXIV 30 ХХХ 40 XL 50 л 60 LX 70 LXX 80 LXXX 90 ХС 100 С 101 КИ 102 СII 200 CC 300 ССС 400 CD 500 Д 600 ОКРУГ КОЛУМБИЯ 700 ДКК 800 DCCC 900 СМ 1000 М 1001 Ми 1002 МИИ 1003 МIII 1900 МКМ 2000 мм 2001 MMI 2002 MMII 2100 ММС 3000 М-М-М 4000 ММММор М
В 5000 В 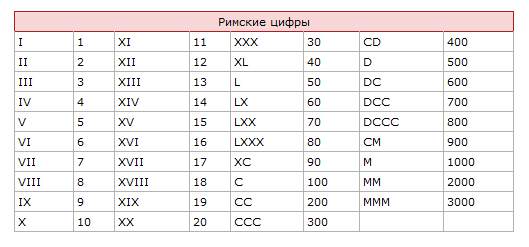
Римские цифры – римские цифры для 4, 6, 9 и др.
1 5 10 50 100 500 1000 I В х л С Д М  Когда символ равного или меньшего значения помещается после другого символа, их значения складываются. Но когда определенные символы меньшей стоимости помещаются перед другим символом, их значения вычитаются.
Когда символ равного или меньшего значения помещается после другого символа, их значения складываются. Но когда определенные символы меньшей стоимости помещаются перед другим символом, их значения вычитаются. Число Римская цифра 1 я 2 II 3 III 4 IV 5 В 6 ВИ 7 VII 8 VIII 9 IX 10 х 11 XI 12 XII 13 XIII 14 XIV 15 XV 16 XVI 17 XVII 18 XVIII 19 XIX 20 ХХ 21 ХХI 22 XXII 23 XXIII 24 XXIV 25 ХХV 30 ХХХ 40 XL 50 л 60 ЛХ 70 ЛХХ 80 LXXX 90 ХС 100 С 101 ДИ 102 СИИ 103 СIII 104 ЦИВ 105 Резюме 200 СС 300 ССС 400 КД 500 Д 600 DC 700 ДКК 800 ДККК 900 см 1000 М 1 001 МИ 1 002 МИИ 1 003 МIII 1 004 МИВ 1 005 МВ 1 900 МКМ 2000 ММ 3000 МММ 3 999 MMMCMXCIX Как преобразовать число в римские цифры

2014 = 2000 + 10 + 4
* 2000 = MM
* 10 = Х
* 4 = IV
2014 = 2000 + 10 + 4 = MMXIV
Как представлять большие числа римскими цифрами

1000 5000 10 000 50 000 100 000 500 000 1 000 000 М или I В х л С Д М Номер Римская цифра 4000 IV 4 001 ИВИ 4 002 IVII 4 003 IVIII 5 000 В 6000 ВИ 7 000 VII 8 000 VIII 9000 IX 10 000 х 40 000 XL 90 000 ХС 400 000 компакт-диск 900 000 см 1 000 000 М Как добавить винкулум или горизонтальную линию над римскими цифрами с помощью HTML и CSS

span и установить для его свойства text-decoration значение overline :
Таблица римских цифр, информация, происхождение, современное использование
Что такое римские цифры?

Содержание:
Как читать римские цифры
 Наличие таких букв, как V и X для 5 и 10, важно, иначе такое число, как 27, было бы выражено путем написания 27 отдельных букв «I»!
Наличие таких букв, как V и X для 5 и 10, важно, иначе такое число, как 27, было бы выражено путем написания 27 отдельных букв «I»!
Римские цифры Таблица


 до н.э.
до н.э. Глядя на график, некоторые цифры очевидны. Сами буквы соответствуют числу, которое они представляют (например, I = 1, V = 5 и т. д.). Кроме того, многие числа имеют смысл, например, 3 — это III (I + I + I).
Глядя на график, некоторые цифры очевидны. Сами буквы соответствуют числу, которое они представляют (например, I = 1, V = 5 и т. д.). Кроме того, многие числа имеют смысл, например, 3 — это III (I + I + I).
Принцип вычитания
 Как только вы привыкнете к этому, римские цифры станут намного легче быстро читать, поскольку они короче, чем могли бы быть в противном случае.
Как только вы привыкнете к этому, римские цифры станут намного легче быстро читать, поскольку они короче, чем могли бы быть в противном случае. Как узнать, что число следует вычесть?
 Итак, как вы узнаете, когда добавлять или вычитать буквы, когда выясняете, какое число представляет уравнение с римскими цифрами?
Итак, как вы узнаете, когда добавлять или вычитать буквы, когда выясняете, какое число представляет уравнение с римскими цифрами? Простой пример

Более сложный пример – большие числа
Было ли 3999 максимальным значением, которое могли сосчитать римляне?

Решение этой проблемы с помощью Vinculum
 Если это так, то это означает, что римляне не умели считать больше 3,9.99. Это может показаться невозможным для нас сегодня и нашего современного образа мыслей, но это не так странно, как кажется.
Если это так, то это означает, что римляне не умели считать больше 3,9.99. Это может показаться невозможным для нас сегодня и нашего современного образа мыслей, но это не так странно, как кажется. Если римляне действительно не использовали винкулум для записи чисел таким образом, объяснение можно было бы найти в фактическом способе количественной оценки предметов , а не в самих числах.
Если римляне действительно не использовали винкулум для записи чисел таким образом, объяснение можно было бы найти в фактическом способе количественной оценки предметов , а не в самих числах. Как мы видели из структуры имперского легиона, один легион, обычно насчитывавший 6000 человек, состоял из 10 когорт. Из них каждая когорта состояла из 6 центурий . Каждая центурия состояла из 10 contubernium (палаточных групп), из которых по 8 человек на палатку.
Как мы видели из структуры имперского легиона, один легион, обычно насчитывавший 6000 человек, состоял из 10 когорт. Из них каждая когорта состояла из 6 центурий . Каждая центурия состояла из 10 contubernium (палаточных групп), из которых по 8 человек на палатку.
Происхождение римских цифр
 Активно участвуя в торговле и использовании денежных единиц, римляне нуждались в системе, в которой счет был бы не только пальцами. Развитие числовых символов, возможно, изначально было тесно связано с формой руки: I для одного пальца, V для всей вытянутой руки, X для обеих рук таким же образом.
Активно участвуя в торговле и использовании денежных единиц, римляне нуждались в системе, в которой счет был бы не только пальцами. Развитие числовых символов, возможно, изначально было тесно связано с формой руки: I для одного пальца, V для всей вытянутой руки, X для обеих рук таким же образом. А Зеро? Не пропал ли номер?!
 Аналогично тому, почему римская система счисления не превышала 3999, число ноль не использовалось римлянами просто потому, что они мало им пользовались!
Аналогично тому, почему римская система счисления не превышала 3999, число ноль не использовалось римлянами просто потому, что они мало им пользовались!
Современное использование римских цифр
 Обычный пример этого можно найти в богато украшенных часах и часах, которые используют римские цифры на циферблате или циферблате вместо 1-12.
Обычный пример этого можно найти в богато украшенных часах и часах, которые используют римские цифры на циферблате или циферблате вместо 1-12.
Лет римскими цифрами
Конвертер римских цифр
 Конечно, этот инструмент точен только до числа 3999… если вы дочитали эту статью до конца, то поймете, почему! Это особенно удобно для определения даты создания того или иного фильма, если дата указана римскими цифрами, если он был снят до 1990 года и отсутствует в списке выше, или для определения года вашего рождения римскими цифрами.
Конечно, этот инструмент точен только до числа 3999… если вы дочитали эту статью до конца, то поймете, почему! Это особенно удобно для определения даты создания того или иного фильма, если дата указана римскими цифрами, если он был снят до 1990 года и отсутствует в списке выше, или для определения года вашего рождения римскими цифрами.
JavaScript Kit Связанные страницы:
Знаете ли вы, что…
Первое свидетельство существования нуля относится к шумерской культуре в Месопотамии около 5000 лет назад. Символ менялся со временем по мере того, как позиционное обозначение, для которого ноль имел решающее значение, попало в Вавилонскую империю, а оттуда в Индию и к грекам.
4 умножить на 4 плюс 4: 4 ПЛЮС 4 УМНОЖИТЬ НА 4 ПОМОГИТЕ
Умножение и деление чисел в Excel
Умножение чисел
Умножение чисел в ячейке
Умножение столбца чисел на константу
Перемножение чисел в разных ячейках с использованием формулы
Деление чисел
Деление чисел в ячейке
Деление чисел с помощью ссылок на ячейки
Деление столбца чисел на константу
Дополнительные сведения
См. также
Умножение десятичных дробей — примеры, правила как умножать в 5 классе
Понятие десятичной дроби
Свойства десятичных дробей
Основные свойства Как записать десятичную дробь
Как читать десятичную дробь
Сколько цифр после запятой? Читается, как одна цифра — десятых; 1,3 — одна целая, три десятых; две цифры — сотых 2,22 — две целых, двадцать две сотых; три цифры — тысячных; 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; четыре цифры — десятитысячных; 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; и т.д. Принципы умножения десятичных дробей
Свойства умножения десятичных дробей
ab = ba
(ab)c = a(bc)
a(b + c) = ab + ac
a(b — c) = ab — ac«−−» минус на минус дает плюс «−+» минус на плюс дает минус «+−» плюс на минус дает минус «++» плюс на плюс дает плюс Как умножать десятичные дроби в столбик
Примеры умножения десятичных дробей столбиком: Как умножать десятичные дроби на натуральные числа
Как умножать десятичные дроби на 10, 100, 1000
Как умножать десятичные дроби на 0,1, 0,01, 0,001
Как умножить десятичную дробь на обыкновенную
3/5 ∗ 9/10 = 27/50 = 0,54.Умножение чисел. Множимое, множитель и произведение
х
(косой крест) или ·
(точка), который ставится между числами. Например:=
(равно), после которого записывается полученный результат:Множимое, множитель и произведение
произведение четырёх и трёх равно двенадцати
, четыре умножить на три равно двенадцати
, по четыре взять три раза, получится двенадцать
.Проверка умножения
Газовая горелка Elco VECTRON G 4 Duo Plus VG4.460 DP KL d1″1/4
Elco Мощность максимальная полная 460 кВт Тип топлива газ, сжиженный газ Количество ступеней горелки
Плавно-двухступенчатую горелку можно модернизировать в модулируемую. плавно-двухступенчатая Пламенная голова
Как правило, длинная используется у стальных котлов и печей, короткая у теплогенераторов и чугунных котлов.
Точная информация по запросу. длинная Газовая рампа есть Диаметр присоединения газа 32 [1 1/4″] мм (дюйм) Швейцария 150 мм Мощность минимальная полная 100 кВт Напряжение 220 В 730 мм 1000 мм 465 мм 1 лет Plus four — перевод на русский | английский-русский
Translate.vc
EnglishespañolFrançaisPortuguêsрусскийTürkçeПроцессор Intel® Xeon® Gold 6240R (35,75 МБ кэш-памяти, 2,40 ГГц) Спецификации продукции
Дата выпуска
Литография
Количество ядер
Количество потоков
Базовая тактовая частота процессора
Максимальная тактовая частота с технологией Turbo Boost
Кэш-память
Количество каналов UPI
Расчетная мощность
Доступные варианты для встраиваемых систем
Макс. объем памяти (зависит от типа памяти)
Типы памяти
Макс. число каналов памяти
Поддержка памяти ECC
‡Поддержка энергонезависимой памяти Intel® Optane™ DC
Редакция PCI Express
Макс. кол-во каналов PCI Express
Поддерживаемые разъемы
T
CASEТехнология Intel® Deep Learning Boost (Intel® DL Boost)
Технология Intel® Speed Select Technology (Intel® SST) — профиль производительности
Технология Intel® Speed Select Technology (Intel® SST) — базовая частота
Технология Intel® Resource Director Technology (Intel® RDT)
Технология Intel® Speed Shift
Технология Intel® Turbo Boost Max 3.0
‡Технология Intel® Turbo Boost
‡Технология Intel® Hyper-Threading
‡Технология виртуализации Intel® (VT-x)
‡Технология виртуализации Intel® для направленного ввода/вывода (VT-d)
‡Intel® VT-x с таблицами Extended Page Tables (EPT)
‡Intel® TSX-NI
Архитектура Intel® 64
‡Расширения набора команд
Количество модулей AVX-512 FMA
Enhanced Intel SpeedStep® Technology (Усовершенствованная технология Intel SpeedStep®)
Технология Intel® Volume Management Device (VMD)
Новые команды Intel® AES
Технология Intel® Trusted Execution
‡Функция Бит отмены выполнения
‡Технология Intel® Run Sure
Управление выполнением на основе режимов (MBE)
Четырехкратное число минус 4 равно трехкратному числу плюс 6
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчас
¢
€
£
¥
‰
µ
·
•
§
¶
SS
‹
›
«
» <
> ≤
≥
—
—
¯
‾
¤
¦
¨
¡
¿
ˆ
˜
°
—
±
÷
⁄
×
ƒ
∫
∑
∞
√
∼
≅
≈
≠
≡
∈
∉
∋
∏
∧
∨
¬
∩
∪
∂
∀
∃
∅
∇
*
∝
∠
´
¸
ª
º
†
‡
А
Á
Â
Ã
Ä
Å
Æ
Ç
È
É
Ê
Ë
Я
Я
Я
Я
Ð
Ñ
Ò
Ó
Ô
Õ
Ö
Ø
Œ
Š
Ù
Ú
Û
Ü
Ý
Ÿ
Þ
à
á
â
ã
ä
å
æ
ç
è
é
ê
ë
я
я
я
я
ð
ñ
ò
ó
ô
х
ö
ø
œ
š
ù
ú
û
ü
ý
þ
ÿ
Α
Β
Γ
Δ
Ε
Ζ
Η
Θ
Ι
Κ
Λ
Μ
Ν
Ξ
Ο
Π
Ρ
Σ
Τ
Υ
Φ
Χ
Ψ
Ω
α
β
γ
δ
ε
ζ
η
θ
ι
κ
λ
μ
ν
ξ
ο
π
ρ
ς
σ
τ
υ
φ
χ
ψ
ω
ℵ
ϖ
ℜ
ϒ
℘
ℑ
←
↑
→
↓
↔
↵
⇐
⇑
⇒
⇓
⇔
∴
⊂
⊃
⊄
⊆
⊇
⊕
⊗
⊥
⋅
⌈
⌉
⌊
⌋
〈
〉
◊ Шестикратное число плюс4 совпадает с числом минус 11
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчас
¢
€
£
¥
‰
µ
·
•
§
¶
SS
‹
›
«
» <
> ≤
≥
—
—
¯
‾
¤
¦
¨
¡
¿
ˆ
˜
°
—
±
÷
⁄
×
ƒ
∫
∑
∞
√
∼
≅
≈
≠
≡
∈
∉
∋
∏
∧
∨
¬
∩
∪
∂
∀
∃
∅
∇
*
∝
∠
´
¸
ª
º
†
‡
А
Á
Â
Ã
Ä
Å
Æ
Ç
È
É
Ê
Ë
Я
Я
Я
Я
Ð
Ñ
Ò
Ó
Ô
Õ
Ö
Ø
Œ
Š
Ù
Ú
Û
Ü
Ý
Ÿ
Þ
à
á
â
ã
ä
å
æ
ç
è
é
ê
ë
я
я
я
я
ð
ñ
ò
ó
ô
х
ö
ø
œ
š
ù
ú
û
ü
ý
þ
ÿ
Α
Β
Γ
Δ
Ε
Ζ
Η
Θ
Ι
Κ
Λ
Μ
Ν
Ξ
Ο
Π
Ρ
Σ
Τ
Υ
Φ
Χ
Ψ
Ω
α
β
γ
δ
ε
ζ
η
θ
ι
κ
λ
μ
ν
ξ
ο
π
ρ
ς
σ
τ
υ
φ
χ
ψ
ω
ℵ
ϖ
ℜ
ϒ
℘
ℑ
←
↑
→
↓
↔
↵
⇐
⇑
⇒
⇓
⇔
∴
⊂
⊃
⊄
⊆
⊇
⊕
⊗
⊥
⋅
⌈
⌉
⌊
⌋
〈
〉
◊ Математическое уравнение, которое пыталось поставить в тупик Интернет
Умножение положительных и отрицательных чисел: 3 простых правила
Правило 1. Положительное число, умноженное на положительное число, равняется положительному числу.
Правило 2: Отрицательное число, умноженное на положительное, равняется отрицательному числу.
Правило 3: Отрицательное число, умноженное на отрицательное число, равняется положительному числу.
Amazon.com: Canon Photo Paper Plus Glossy II, 4 x 6 дюймов, 100 листов (2311B023): Фотобумага: Офисные продукты
Amazon.com
Первоначально базирующаяся в Японии, Canon превратилась в одну из ведущих мировых компаний, специализирующихся на производстве изображений и оптических продуктов, от высококачественных фотоаппаратов до копировальных аппаратов и компьютерных принтеров.Благодаря своей обширной линейке продуктов и цифровых решений они продолжают помогать компаниям и потребителям во всем мире собирать, хранить и распространять информацию. От производителя
Глянцевая бумага — высочайшая цветопередача: Photo Paper Plus Glossy II PP-201.
Глубокий, насыщенный черный — это черный цвет, который выглядит действительно черным для глаз, а не сероватым или голубоватым. Насыщенный, глубокий черный цвет важен не только для воспроизведения глубоких черных областей на фотографиях.Они также способствуют общей плотности, контрастности и четкости фотографии. Светлые серовато-черные цвета ослабляют эффектность фотографии, делая ее обыкновенной и невзрачной. С Photo Paper Plus Glossy II PP-201 краситель закрепляется ближе к поверхности бумаги, обеспечивая насыщенный, глубокий черный цвет на отпечатанных фотографиях.
Слой, принимающий чернила, принимает красители, содержащиеся в чернилах, и помещает их на поверхность бумаги.Если этот слой слишком толстый, красители рассеиваются слишком редко, уменьшая плотность цвета и создавая размытые тусклые цвета. Если она слишком тонкая, вода в чернилах может вылиться из поверхности бумаги, вызывая образование бисера и кровотечение.
Photo Paper Plus Glossy II PP-201 решает эту дилемму с помощью инновационной технологии нанесения покрытия для струйной печати. При использовании этой технологии принимающий чернила слой разделяется на два слоя : слой для воспроизведения цвета, на котором закреплен краситель, и поглощающий слой, который впитывает избыток водного растворителя.
Эта многослойная структура позволяет закрепить краситель ближе к поверхности бумаги, улучшая плотность черных чернил по сравнению с Photo Paper Plus Glossy PP-101. Эта новая технология обеспечивает насыщенный, глубокий черный цвет и яркие, живые фотографические результаты. В то же время впитывающий слой быстро удаляет излишки водного растворителя, обеспечивая четкое и резкое изображение.
Более полная, более яркая цветопередача.
Чем шире цветовой охват, тем больше цветов может быть воспроизведено. Photo Paper Plus Glossy II PP-201 по всей гамме цветов CMY и RGB улучшает воспроизводимый диапазон Photo Paper Plus Glossy PP-101. Эта фотобумага передает все выразительные возможности PIXMA для неизменно великолепной цветопередачи.
Оптическая плотность сразу после печати выше, чем когда-либо.Смотрите настоящие цвета ваших фотографий прямо сейчас.
При использовании обычной бумаги для струйных принтеров качество печати прямо из принтера немного нечеткое, цвета тусклые. Цвета проявляются постепенно, поэтому вам нужно подождать несколько минут, чтобы узнать, соответствует ли отпечаток цвету, контрасту и другим характеристикам исходного изображения. Если ваша семья или друзья ждут готовых отпечатков, или если вы тестируете исправления в фотографиях, ожидание может показаться вечностью.
Photo Paper Plus Glossy II PP-201 — это совершенно другой опыт.Оптическая плотность (плотность цвета) высокая сразу после печати, а цветопередача происходит быстро. За меньшее время, чем когда-либо, воспроизведение цветов исходной фотографии будет завершено. По завершении печати изображения становятся яркими и живыми.
Графики и фотографические образцы, используемые в этом руководстве, были подготовлены с использованием следующих условий измерения.
Модель: PIXMA MP970 / MP610
Бумага: (Photo Paper Plus Glossy II PP-201) Режим печати по умолчанию при выборе Photo Paper Plus Glossy II.
(Photo Paper Plus Glossy PP-101) Режим печати по умолчанию, когда выбран Photo Paper Plus Glossy.
Образцы фотографий создаются путем сканирования образцов печати на каждой фотобумаге. В результате цвета на образцах фотографий, представленных в этом руководстве, отличаются от фактических цветов при печати. GE AMX 4 Plus Портативный рентгеновский аппарат GE
Восстановленный портативный рентгеновский аппарат GE AMX 4 Plus GE
, кратное 4 — математика с мамой
Кратное 4 — это числа, которые можно разделить на четыре точно, не оставляя остатка. Кратное 4 начинается с таблицы умножения четырех и продолжается, добавляя четыре, чтобы перейти к следующему числу. Как найти кратное 4
Обучение кратному 4
Тесты по предпринимательству: Тесты по основам предпринимательства с ответами
Тесты по основам предпринимательства с ответами
 К предпринимательству не относится деятельность:
К предпринимательству не относится деятельность: Основой государственного предпринимательства являются:
Основой государственного предпринимательства являются: Что лежит в основе любого предпринимательства?
Что лежит в основе любого предпринимательства? Экономической основой государственного предпринимательства является … собственность.
Экономической основой государственного предпринимательства является … собственность. Экономист И. Шумпетер выделял следующие побудительные мотивы деятельности предпринимателя:
Экономист И. Шумпетер выделял следующие побудительные мотивы деятельности предпринимателя: В какой форме регистрируют индивидуальное предпринимательство?
В какой форме регистрируют индивидуальное предпринимательство? Что из перечисленного нельзя отнести к стимулам для начала собственного дела?
Что из перечисленного нельзя отнести к стимулам для начала собственного дела? Как называется разница между ожидаемой (прогнозной) денежной выручкой фирмы и ее реальной величиной?
Как называется разница между ожидаемой (прогнозной) денежной выручкой фирмы и ее реальной величиной?Тест Предпринимательство по обществознанию онлайн

Выберите правильное определение для термина «бизнес»: А) экономическая деятельность, направленная на систематическое получение прибыли от производства и продажи товаров, оказания услуг Б) деятельность, направленная на систематическое получение прибыли от пользования имуществом, продажи товаров, выполнения работ или оказания услуг, которая осуществляется самостоятельно на свой риск лицом, зарегистрированным в установленном законом порядке в качестве индивидуального предпринимателя.
Подсказка
Выберите правильную характеристику предпринимательства: А) экономическая деятельность, направленная на систематическое получение прибыли от производства и продажи товаров, оказания услуг Б) важнейшее свойство рыночной экономики, пронизывающее все её институты.

Подсказка
Фирма – это: найдите правильную формулировку понятия: А) единица предпринимательской деятельности, оформленная юридически и реализующая собственные интересы посредством производства и продажи товаров и услуг с использованием различных факторов производства. Б) коммерческая организация, приобретающая факторы производства с целью создания и продажи благ и получения на этой основе прибыли.
Подсказка
Товарищество – это:
Подсказка
Выберите правильное определение термина: А) Товарищество – это форма организации предпринимательской деятельности, основанной на объединении (обычно паевого) имущества различных владельцев Б) Товарищество — вид организации, при котором происходит объединение лиц, несущих полную ответственность за деятельность созданной формы.

Подсказка
Акционерное общество – это:
Подсказка
Что не является формой предпринимательской деятельности:
Подсказка
Найдите верное высказывание: А) Малая форма бизнеса – это один человек, являющийся и руководителем, и исполнителем прибыльных действий Б) Малая форма чаще используется в сельском хозяйстве для открытия фермерских хозяйств
Подсказка
Найти лишний термин:
Подсказка
Акции – это:
Подсказка

Рейтинг теста
Основы предпринимательства — тест 1
Что из перечисленного можно отнести к важнейшим чертам предпринимательства?
Формула предпринимательства
Наибольшее развитие предпринимательства в России в исторической ретроспективе происходило
Как называется процесс создания чего-то нового, обладающего ценностью; процесс, поглощающий время и силы, предполагающий принятие на себя финансовой, моральной и социальной ответственности; приносящий в результате денежный доход и личное удовлетворение от достигнутого?
В какой организации часть партнеров может обладать неограниченной, а часть — ограниченной в ответственностью?
Юридическое лицо не имеет право
Какая из перечисленных организаций создается по соглашению не менее двух граждан либо юридических лиц путем объединения их вкладов (как в денежной, так и натуральной форме) в целях осуществления хозяйственной деятельности?
Какие акции дают право на участие в управлении обществом?
Как называется соглашение между предприятиями одной отрасли о ценах на продукцию, услуги, о разделе рынков сбыта, долях в общем объеме производства?
Что называется консорциумом?
Как называется разновидность оптового товарного рынка без предварительного осмотра покупателем образцов и заранее установленных минимальных партий товара?
Государственная поддержка малого и среднего бизнеса в Российской Федерации
Малые предприятия
Как называются венчурные фирмы или инновационные предприятия, которые занимаются в основном научными, конструкторскими разработками, коммерческим освоением технических открытий, производством опытных партий товаров?
Малые, средние и микропредприятия получили особое развитие
Схема вложения венчурного капитала
Как называется предпринимательская деятельность, связанная с финансовыми и капитальными вложениями в инновацию?
Инновационное предпринимательство
Как называется предпринимательская деятельность, направленная на использование и коммерциализацию результатов научных исследований и разработок для расширения и обновления номенклатуры, улучшения качества выпускаемой продукции (работ, услуг), совершенствования технологий их изготовления с последующим внедрением и эффективной реализацией на рынке?
Какого способа выхода венчурных инвесторов из капитала финансируемых компаний не существует?
Что понимается под венчурным инвестированием?
Что из перечисленного не является преимуществом малых форм бизнеса по сравнению с крупным производством?
Какова численность работников микропредприятий?
К основным организационно-экономическим формам предпринимательства можно отнести
Что не относится к организационно-правовым формам предпринимательства?
Как называется коммерческая организация, не наделенная правом собственности на закрепленное за ней имущество?
Что из перечисленного не является признаком юридического лица?
Что относится к важнейшим чертам предпринимательства?
Что из перечисленного не относится к основным характеристикам предпринимателя?
Тест с ответами по дисциплине Основы предпринимательства
 Ключевые слова, определяющие понятие «предпринимательство»:
Ключевые слова, определяющие понятие «предпринимательство»: Укажите хозяйственные операции сельскохозяйственного предпринимателя, которые относятся к коммерческому предпринимательству:
Укажите хозяйственные операции сельскохозяйственного предпринимателя, которые относятся к коммерческому предпринимательству: Как называется энергичный предприниматель с отрицательной социальной ориентацией
Как называется энергичный предприниматель с отрицательной социальной ориентацией
 Индивидуальное предпринимательство регистрируется в форме:
Индивидуальное предпринимательство регистрируется в форме: Дополните ответ:
Дополните ответ:
detectorРазвитие предпринимательства. Тест для самопроверки № 1 – пройти тест онлайн бесплатно
Узнай бесплатно стоимость работыосновы предпринимательства ответы на тесты | Упражнения и задачи Бизнес или Основы предпринимательства
 Многосторонние сделки – это: сделки, число сторон, в которых составляет не менее трех, причем действия сторон не противостоят друг другу, а направлены на достижение одних и тех же целей. Баланс состоит из следующих разделов: все ответы верны. Индивидуальный трудовой договор (ИТД)- это: двустороннее соглашение между работником и работодателем, заключаемое в письменной форме, по которому работник обязуется выполнять работу по определенной специальности, квалификации или должности с исполнением актов работодателя, а работодатель обязуется своевременно и в полном объеме выплачивать работнику заработную плату и иные, предусмотренные законодательством и соглашением сторон, денежные выплаты, обеспечивать условия труда, предусмотренные законодательством о труде и коллективным договором. По срокам выполнения планы бывают: долгосрочные, среднесрочные, краткосрочные. Когда вышел Указ Президента страны № 3589 «О приоритетных и региональных программах поддержки и развития малого предпринимательства в Республике Казахстан»: 7 июля 1997г.
Многосторонние сделки – это: сделки, число сторон, в которых составляет не менее трех, причем действия сторон не противостоят друг другу, а направлены на достижение одних и тех же целей. Баланс состоит из следующих разделов: все ответы верны. Индивидуальный трудовой договор (ИТД)- это: двустороннее соглашение между работником и работодателем, заключаемое в письменной форме, по которому работник обязуется выполнять работу по определенной специальности, квалификации или должности с исполнением актов работодателя, а работодатель обязуется своевременно и в полном объеме выплачивать работнику заработную плату и иные, предусмотренные законодательством и соглашением сторон, денежные выплаты, обеспечивать условия труда, предусмотренные законодательством о труде и коллективным договором. По срокам выполнения планы бывают: долгосрочные, среднесрочные, краткосрочные. Когда вышел Указ Президента страны № 3589 «О приоритетных и региональных программах поддержки и развития малого предпринимательства в Республике Казахстан»: 7 июля 1997г. Трудовые правоотношения – это: юридическая связь между работником и работодателем, на основании которой стороны получают определенный комплекс прав и обязанностей. Формы планирования в зависимости от длительности планового периода: все ответы верны. Любой контракт состоит из: преамбулы, основной части, заключительной части. Предпринимательство – это: инициативная, самостоятельная, осуществляемая от своего имени, на свой риск, под свою имущественную ответственность деятельность граждан, физических и юридических лиц, направленная на систематическое получение дохода, прибыли от пользования имуществом, продажи товаров, выполнения работ, оказания услуг. Предпринимательство – это: инициативная, самостоятельная, осуществляемая от своего имени, на свой риск, под свою имущественную ответственность деятельность граждан, физических и юридических лиц, направленная на систематическое получение дохода, прибыли от пользования имуществом, продажи товаров, выполнения работ, оказания услуг. Главной целью планирования является: обеспечение эффективного функционирования и развития предприятия.
Трудовые правоотношения – это: юридическая связь между работником и работодателем, на основании которой стороны получают определенный комплекс прав и обязанностей. Формы планирования в зависимости от длительности планового периода: все ответы верны. Любой контракт состоит из: преамбулы, основной части, заключительной части. Предпринимательство – это: инициативная, самостоятельная, осуществляемая от своего имени, на свой риск, под свою имущественную ответственность деятельность граждан, физических и юридических лиц, направленная на систематическое получение дохода, прибыли от пользования имуществом, продажи товаров, выполнения работ, оказания услуг. Предпринимательство – это: инициативная, самостоятельная, осуществляемая от своего имени, на свой риск, под свою имущественную ответственность деятельность граждан, физических и юридических лиц, направленная на систематическое получение дохода, прибыли от пользования имуществом, продажи товаров, выполнения работ, оказания услуг. Главной целью планирования является: обеспечение эффективного функционирования и развития предприятия. Существует три вида планов: все ответы верны. Партнерство – это: юридическая форма организации совместной экономической деятельности нескольких физических или юридических лиц. Контокоррентный кредит – это: кредит по специальному контокоррентному (текущему) счету. По срокам выполнения планы бывают: долгосрочные, среднесрочные, краткосрочные. Товарищество с ограниченной ответственностью (ТОО) – это: товарищество, которое наряду с одним или более участниками, несущими дополнительную ответственность по обязательствам товарищества всем своим имуществом, включает также одного или более участников, ответственность которых ограничена суммой вклада и которые не принимают участия в предпринимательской деятельности. форма организации предприятий, при которой его участники отвечают по его обязательствам своими вкладами в уставный фонд, а при недостаточности этих сумм – дополнительно принадлежащим им имуществом в размере, пропорциональном внесенным вкладам. форма организации предприятий, при которой его участники отвечают по его обязательствам в размере своих вкладов в уставный фонд.
Существует три вида планов: все ответы верны. Партнерство – это: юридическая форма организации совместной экономической деятельности нескольких физических или юридических лиц. Контокоррентный кредит – это: кредит по специальному контокоррентному (текущему) счету. По срокам выполнения планы бывают: долгосрочные, среднесрочные, краткосрочные. Товарищество с ограниченной ответственностью (ТОО) – это: товарищество, которое наряду с одним или более участниками, несущими дополнительную ответственность по обязательствам товарищества всем своим имуществом, включает также одного или более участников, ответственность которых ограничена суммой вклада и которые не принимают участия в предпринимательской деятельности. форма организации предприятий, при которой его участники отвечают по его обязательствам своими вкладами в уставный фонд, а при недостаточности этих сумм – дополнительно принадлежащим им имуществом в размере, пропорциональном внесенным вкладам. форма организации предприятий, при которой его участники отвечают по его обязательствам в размере своих вкладов в уставный фонд. товарищество, участники которого при недостаточности имущества несут солидарную ответственность по его обязательствам всем своим личным имуществом. добровольное объединение граждан на основе членства для совместной трудовой деятельности. Субъектами предпринимательства могут быть: отдельные частные лица. объединения партнеров. отдельные частные лица, так и объединения партнеров. все ответы верны. любые люди Оборотный капитал необходим: для инвестиций в непрерывное (незавершенное) производство. все ответы верны. для инвестиций в готовую продукцию. для покрытия разницы между дебиторской задолженностью и кредиторской задолженностью. для закупок сырья. Производственным кооперативом признается: товарищество, участники которого при недостаточности имущества несут солидарную ответственность по его обязательствам всем своим личным имуществом. форма организации предприятий, при которой его участники отвечают по его обязательствам своими вкладами в уставный фонд, а при недостаточности этих сделки, число сторон, в которых составляет не менее трех, причем действия сторон не противостоят друг другу, а направлены на достижение одних и тех же целей.
товарищество, участники которого при недостаточности имущества несут солидарную ответственность по его обязательствам всем своим личным имуществом. добровольное объединение граждан на основе членства для совместной трудовой деятельности. Субъектами предпринимательства могут быть: отдельные частные лица. объединения партнеров. отдельные частные лица, так и объединения партнеров. все ответы верны. любые люди Оборотный капитал необходим: для инвестиций в непрерывное (незавершенное) производство. все ответы верны. для инвестиций в готовую продукцию. для покрытия разницы между дебиторской задолженностью и кредиторской задолженностью. для закупок сырья. Производственным кооперативом признается: товарищество, участники которого при недостаточности имущества несут солидарную ответственность по его обязательствам всем своим личным имуществом. форма организации предприятий, при которой его участники отвечают по его обязательствам своими вкладами в уставный фонд, а при недостаточности этих сделки, число сторон, в которых составляет не менее трех, причем действия сторон не противостоят друг другу, а направлены на достижение одних и тех же целей. Капитал амортизационный – это: капитал, предназначенный для воспроизводства основных средств, образуемый за счет амортизационных отчислений. Лица, виновные в нарушении законодательства Республики Казахстан о труде, несут ответственность, установленную законами Республики Казахстан и привлекаются к: все ответы верны. Предприятие муниципальное – это: Выберите один ответ: предприятие, имеющее одного хозяина, основанное на частной собственности индивидуального лица, владельца и распорядителя основных средств, капитала предприятия. предприятие, в работе которого участвуют фирмы других стран, организационно оформленное как единое, общее предприятие. коммерческая организация, не наделенная правом собственности на закрепленное за ним собственником имущество. нет правильного ответа. предприятие, средства производства которого находятся в муниципальной собственности. Капитал гомогенный – это: капитал, однородный по возрастной структуре. Факторинг – это: Выберите один ответ: форма торговых операций по купле-продаже (аренде, лицензированию) прав на марку товара, фирменную упаковку, имя (название) фирмы; особый способ продажи товара, метод маркетингового исследования и т.
Капитал амортизационный – это: капитал, предназначенный для воспроизводства основных средств, образуемый за счет амортизационных отчислений. Лица, виновные в нарушении законодательства Республики Казахстан о труде, несут ответственность, установленную законами Республики Казахстан и привлекаются к: все ответы верны. Предприятие муниципальное – это: Выберите один ответ: предприятие, имеющее одного хозяина, основанное на частной собственности индивидуального лица, владельца и распорядителя основных средств, капитала предприятия. предприятие, в работе которого участвуют фирмы других стран, организационно оформленное как единое, общее предприятие. коммерческая организация, не наделенная правом собственности на закрепленное за ним собственником имущество. нет правильного ответа. предприятие, средства производства которого находятся в муниципальной собственности. Капитал гомогенный – это: капитал, однородный по возрастной структуре. Факторинг – это: Выберите один ответ: форма торговых операций по купле-продаже (аренде, лицензированию) прав на марку товара, фирменную упаковку, имя (название) фирмы; особый способ продажи товара, метод маркетингового исследования и т. п. формирование спроса и стимулирование сбыта. покупка у торговых предприятий требований по товарным поставкам, т.е. дебиторской задолженности. система скупки факторинг-фирмой (фактором) дебиторских задолженностей у торговых предприятий. процесс и результат разделения штучного, сыпучего и жидкого товара на порции определенного размера (веса, емкости) и размещения его в соответствующую упаковку; фасовка необходима для удобства продажи, транспортировки и потребления. Проблемы развития сектора микрокредитования: все ответы верны. неотработанная схема сотрудничества этой сферы с госорганами; отсутствие развитой системы мониторинга; отсутствие ресурсной базы и др. отсутствие методологии и обучающих программ для участников системы; Трудовые правоотношения – это: юридическая связь между работником и работодателем, на основании которой стороны получают определенный комплекс прав и обязанностей. Существует три вида планов: все ответы верны. Обеспечение текущих потребностей бизнеса: финансирование оборотных средств и выполнение долговых обязательств.
п. формирование спроса и стимулирование сбыта. покупка у торговых предприятий требований по товарным поставкам, т.е. дебиторской задолженности. система скупки факторинг-фирмой (фактором) дебиторских задолженностей у торговых предприятий. процесс и результат разделения штучного, сыпучего и жидкого товара на порции определенного размера (веса, емкости) и размещения его в соответствующую упаковку; фасовка необходима для удобства продажи, транспортировки и потребления. Проблемы развития сектора микрокредитования: все ответы верны. неотработанная схема сотрудничества этой сферы с госорганами; отсутствие развитой системы мониторинга; отсутствие ресурсной базы и др. отсутствие методологии и обучающих программ для участников системы; Трудовые правоотношения – это: юридическая связь между работником и работодателем, на основании которой стороны получают определенный комплекс прав и обязанностей. Существует три вида планов: все ответы верны. Обеспечение текущих потребностей бизнеса: финансирование оборотных средств и выполнение долговых обязательств. Акционерное общество (закрытое и открытое) – это: организация, созданная по соглашению юридическими и физическими лицами путем объединения их вкладов через выпуск и продажу акций в целях осуществления хозяйственной деятельности. Инвесторы обращают внимание на четыре «Д» предпринимателя: все ответы верны. Лица, виновные в нарушении законодательства Республики Казахстан о труде, несут ответственность, установленную законами Республики Казахстан и привлекаются к: все ответы верны. Оборотный капитал необходим: все ответы верны. По срокам выполнения планы бывают: долгосрочные, среднесрочные, краткосрочные. Предпринимательство – это: инициативная, самостоятельная, осуществляемая от своего имени, на свой риск, под свою имущественную ответственность деятельность граждан, физических и юридических лиц, направленная на систематическое получение дохода, прибыли от пользования имуществом, продажи товаров, выполнения работ, оказания услуг. Проблемы развития сектора микрокредитования: все ответы верны.
Акционерное общество (закрытое и открытое) – это: организация, созданная по соглашению юридическими и физическими лицами путем объединения их вкладов через выпуск и продажу акций в целях осуществления хозяйственной деятельности. Инвесторы обращают внимание на четыре «Д» предпринимателя: все ответы верны. Лица, виновные в нарушении законодательства Республики Казахстан о труде, несут ответственность, установленную законами Республики Казахстан и привлекаются к: все ответы верны. Оборотный капитал необходим: все ответы верны. По срокам выполнения планы бывают: долгосрочные, среднесрочные, краткосрочные. Предпринимательство – это: инициативная, самостоятельная, осуществляемая от своего имени, на свой риск, под свою имущественную ответственность деятельность граждан, физических и юридических лиц, направленная на систематическое получение дохода, прибыли от пользования имуществом, продажи товаров, выполнения работ, оказания услуг. Проблемы развития сектора микрокредитования: все ответы верны. отсутствие ресурсной базы и др. отсутствие развитой системы мониторинга; отсутствие методологии и обучающих программ для участников системы; неотработанная схема сотрудничества этой сферы с госорганами; Предпринимательский контракт – это: волеизъявление сторон по поводу не организации, а осуществления самого предпринимательского процесса, не предполагающее объединение договаривающихся сторон в какую-либо единую организационно-правовую структуру. Формы планирования в зависимости от содержания плановых решений: все ответы верны. Оборотный капитал необходим: все ответы верны. Лизингодатель – это: компания, приобретающая оборудование за свой счет и сдающая его в аренду на несколько лет. Существует два типа внешнего долгосрочного финансирования: кредитование и акционерное финансирование. Когда был принят закон «Об индивидуальном предпринимательстве» в РК: 19 июня 1997 г. Капитал гибкий – это: капитал, легко поддающийся замещению Планирование – это: функция управления, включающая следующий комплекс работ: анализ ситуаций и факторов внешней среды; прогнозирование, оценка и оптимизация альтернативных вариантов достижения целей, сформулированных на стадии стратегического маркетинга; разработка плана; реализация плана.
отсутствие ресурсной базы и др. отсутствие развитой системы мониторинга; отсутствие методологии и обучающих программ для участников системы; неотработанная схема сотрудничества этой сферы с госорганами; Предпринимательский контракт – это: волеизъявление сторон по поводу не организации, а осуществления самого предпринимательского процесса, не предполагающее объединение договаривающихся сторон в какую-либо единую организационно-правовую структуру. Формы планирования в зависимости от содержания плановых решений: все ответы верны. Оборотный капитал необходим: все ответы верны. Лизингодатель – это: компания, приобретающая оборудование за свой счет и сдающая его в аренду на несколько лет. Существует два типа внешнего долгосрочного финансирования: кредитование и акционерное финансирование. Когда был принят закон «Об индивидуальном предпринимательстве» в РК: 19 июня 1997 г. Капитал гибкий – это: капитал, легко поддающийся замещению Планирование – это: функция управления, включающая следующий комплекс работ: анализ ситуаций и факторов внешней среды; прогнозирование, оценка и оптимизация альтернативных вариантов достижения целей, сформулированных на стадии стратегического маркетинга; разработка плана; реализация плана. Корпорация – это: правовая форма бизнеса, отличающаяся и отделенная от конкретных лиц, ими владеющих. Производственным кооперативом признается: добровольное объединение граждан на основе членства для совместной трудовой деятельности. Бизнес-план – это: документ, определяющий тактические действия организации, как правило, на ближайший год в развитие его стратегии. Капитал активный – это: капитал, свободный от обязательств и долгов Субъектами предпринимательства могут быть: отдельные частные лица, так и объединения партнеров. Товарищество с дополнительной ответственностью (ТДО) – это: форма организации предприятий, при которой его участники отвечают по его обязательствам своими вкладами в уставный фонд, а при недостаточности этих сумм – дополнительно принадлежащим им имуществом в размере, пропорциональном внесенным вкладам. Абстрактные сделки – это: сделки характеризуются тем, что доказывать основание сделки запрещено. сделка, в которой одна сторона получает какое либо благо, не отдавая ничего взамен.
Корпорация – это: правовая форма бизнеса, отличающаяся и отделенная от конкретных лиц, ими владеющих. Производственным кооперативом признается: добровольное объединение граждан на основе членства для совместной трудовой деятельности. Бизнес-план – это: документ, определяющий тактические действия организации, как правило, на ближайший год в развитие его стратегии. Капитал активный – это: капитал, свободный от обязательств и долгов Субъектами предпринимательства могут быть: отдельные частные лица, так и объединения партнеров. Товарищество с дополнительной ответственностью (ТДО) – это: форма организации предприятий, при которой его участники отвечают по его обязательствам своими вкладами в уставный фонд, а при недостаточности этих сумм – дополнительно принадлежащим им имуществом в размере, пропорциональном внесенным вкладам. Абстрактные сделки – это: сделки характеризуются тем, что доказывать основание сделки запрещено. сделка, в которой одна сторона получает какое либо благо, не отдавая ничего взамен. сделки, действительность которых зависит от наличия основания сделки. сделки, считающиеся заключенными с момента, когда между сторонами достигнуто согласие. сделки, для совершения которых необходимы: 1) соглашение; 2) действие, выраженное в передаче вещей. Многосторонние сделки – это: . сделки, число сторон, в которых составляет не менее трех, причем действия сторон не противостоят друг другу, а направлены на достижение одних и тех же целей. Правовые условия – это:
сделки, действительность которых зависит от наличия основания сделки. сделки, считающиеся заключенными с момента, когда между сторонами достигнуто согласие. сделки, для совершения которых необходимы: 1) соглашение; 2) действие, выраженное в передаче вещей. Многосторонние сделки – это: . сделки, число сторон, в которых составляет не менее трех, причем действия сторон не противостоят друг другу, а направлены на достижение одних и тех же целей. Правовые условия – это: Добро пожаловать в Квиндом! Хотели бы вы узнать больше о себе? Вы пришли в нужное место!
Тесты личности
Тест личности Большой пятерки

Тест на склонность к несчастным случаям
Тест на вождение автомобиля
IQ-тесты
Тест эмоционального интеллекта
Тест на вербально-лингвистический интеллект
Классический тест IQ
 Не лучший научно-фантастический фильм, но отличный тест на IQ!
Не лучший научно-фантастический фильм, но отличный тест на IQ! Тесты на отношения
Диагностический тест любви
Тест на здоровье в отношениях (для пар с детьми)
Тест на здоровье в отношениях (для пар без детей)
Карьерные тесты
Тест на офисные навыки и пригодность к работе
 Проверьте свои способности с помощью этой оценки.
Проверьте свои способности с помощью этой оценки. Тест на пригодность франчайзи
Тест на пригодность учителя
Тесты отношения и образа жизни
Тест гендерных ролей (для женщин)
Тест на определение гендерных ролей (для мужчин)
Тест на прокрастинацию

Тесты на здоровье
Тест на выносливость
Тест на эмоциональное питание
Тест на ПМС
Научно разработанные тесты
Популярное сегодня
Веселые тесты и викторины

Популярное сегодня
Реклама
Растяжка мозга
Популярные сегодня
Викторины
 Бросьте вызов своей семье и друзьям!
Бросьте вызов своей семье и друзьям! Популярные сегодня
Опросы
Популярные сегодня
Жизненные советы
 Узнайте, как изгнать скуку, арканную ревность, простить и забыть, и извлеките уроки из жизни.
Узнайте, как изгнать скуку, арканную ревность, простить и забыть, и извлеките уроки из жизни. Популярное сегодня
КУШЕТКА ТЕРАПЕВТА
Популярное сегодня
Наш блог

Популярное сегодня
Реклама
Бесплатные личностные тесты для предпринимателей
Развиваться » Процветать
Автор:
Джейми Джонсон, автор
Хотя результаты личностных тестов не обязательно должны полностью определять вас, они являются хорошим способом определить, в чем заключаются ваши сильные стороны или какие возможности вам следует изучить. — Getty Images/филадендрон Информация, которую вы получаете, может помочь вам развить свои сильные стороны, управлять командой и более эффективно общаться с другими. Эти семь бесплатных личностных тестов — хорошие варианты для предпринимателей.
Информация, которую вы получаете, может помочь вам развить свои сильные стороны, управлять командой и более эффективно общаться с другими. Эти семь бесплатных личностных тестов — хорошие варианты для предпринимателей. Тест личности предпринимателя
16 Личности

Эннеаграмма

Тест HIGH5
Цветовой личностный тест
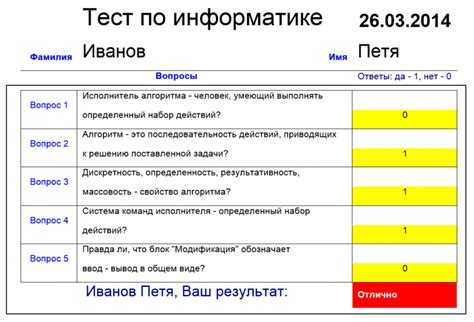 Вы можете использовать тест, чтобы помочь вам понять такие характеристики, как:
Вы можете использовать тест, чтобы помочь вам понять такие характеристики, как: Skills You Need
Карьерный личностный профайл
 В ходе этой 15-минутной оценки рассматриваются различные варианты карьеры, которые могут подойти вам в зависимости от вашего темперамента и личностных качеств.
В ходе этой 15-минутной оценки рассматриваются различные варианты карьеры, которые могут подойти вам в зависимости от вашего темперамента и личностных качеств.
Подпишитесь на нашу рассылку Midnight Oil
Тесты – Предпринимательское право: Создание компании
 Независимо от того, какой тест используется, есть некоторая общность по всем направлениям. Все тесты представляют собой тесты фактов и обстоятельств, которые будут рассматривать всю ситуацию (и применять факторы или элементы), чтобы установить истинный характер отношений. Если работодатель отправляет 1099 вместо W-2 работнику, что не свидетельствует об истинном характере отношений. Аналогичным образом, если работник подписывает контракт, в котором говорится, что он является независимым подрядчиком, контракт может быть только частью рассматриваемого доказательства. Использование «отраслевого стандарта» в качестве оправдания неправильной классификации также не работает. Факторы взвешивания или проверка на соответствие элементам — это то, что вы увидите в приведенных ниже тестах.
Независимо от того, какой тест используется, есть некоторая общность по всем направлениям. Все тесты представляют собой тесты фактов и обстоятельств, которые будут рассматривать всю ситуацию (и применять факторы или элементы), чтобы установить истинный характер отношений. Если работодатель отправляет 1099 вместо W-2 работнику, что не свидетельствует об истинном характере отношений. Аналогичным образом, если работник подписывает контракт, в котором говорится, что он является независимым подрядчиком, контракт может быть только частью рассматриваемого доказательства. Использование «отраслевого стандарта» в качестве оправдания неправильной классификации также не работает. Факторы взвешивания или проверка на соответствие элементам — это то, что вы увидите в приведенных ниже тестах. Закон (ERISA), Федеральный закон о налоге на безработицу (FUTA), Федеральный закон о страховых взносах (FICA), Налоговый кодекс (IRC), Национальный закон о трудовых отношениях (NLRA), Закон о безопасности и гигиене труда (OSHA), Раздел VII Гражданского Закон о правах 1964 и Закон об уведомлении об адаптации и переподготовке работников (WARN). Законы и суды нескольких штатов также по-разному используют контрольный тест. Фактически, многие суды используют его по умолчанию, когда термин «работник» не определен законом.
Закон (ERISA), Федеральный закон о налоге на безработицу (FUTA), Федеральный закон о страховых взносах (FICA), Налоговый кодекс (IRC), Национальный закон о трудовых отношениях (NLRA), Закон о безопасности и гигиене труда (OSHA), Раздел VII Гражданского Закон о правах 1964 и Закон об уведомлении об адаптации и переподготовке работников (WARN). Законы и суды нескольких штатов также по-разному используют контрольный тест. Фактически, многие суды используют его по умолчанию, когда термин «работник» не определен законом.
 Этот тест основан на деле Верховного суда США 1947 года, Rutherford Food Corp. против McComb , 331 U.S. 722, 730 (1947). Рабочий является наемным работником, если «в экономической реальности рабочий следует обычным путем наемного работника и зависит от предприятия, которому он или она служит». Следующие факторы входят в состав Теста экономических реалий:
Этот тест основан на деле Верховного суда США 1947 года, Rutherford Food Corp. против McComb , 331 U.S. 722, 730 (1947). Рабочий является наемным работником, если «в экономической реальности рабочий следует обычным путем наемного работника и зависит от предприятия, которому он или она служит». Следующие факторы входят в состав Теста экономических реалий: Администрация Байдена откатывает модификацию, и мы должны быть в поиске чего-то нового в классификации рабочих для целей FLSA на горизонте.
Администрация Байдена откатывает модификацию, и мы должны быть в поиске чего-то нового в классификации рабочих для целей FLSA на горизонте.
 Нюанс — это доброе слово. 📖 Прочтите The AB5 Experiment статьи, страницы 10-22, и вы увидите, насколько запутанной Калифорния сделала свой закон о классификации рабочих. Вы также можете увидеть, что произошло с Предложением 22. В последнем разделе статьи обсуждаются научные предложения по улучшению способов определения классификации работников.
Нюанс — это доброе слово. 📖 Прочтите The AB5 Experiment статьи, страницы 10-22, и вы увидите, насколько запутанной Калифорния сделала свой закон о классификации рабочих. Вы также можете увидеть, что произошло с Предложением 22. В последнем разделе статьи обсуждаются научные предложения по улучшению способов определения классификации работников. TECEP Введение в предпринимательство: учебное пособие и курс подготовки к экзаменам — онлайн-видеоуроки
Краткое содержание курса

, чтобы начать этот курс сегодня
Попробуйте без риска в течение 30 дней Образец урока
17 глав в TECEP Введение в предпринимательство: учебное пособие и подготовка к экзаменам
 getGoalWeekForTopic(0, 17)}}
getGoalWeekForTopic(0, 17)}} Прогресс курса Лучший результат Урок 1 — Распространенные формы предпринимательства
Распространенные формы предпринимательства видео пройти тест academyAssetId»> пройти тест Урок 2 — Как стать успешным предпринимателем
Как стать успешным предпринимателем Текстовый урок пройти тест Урок 3 — Предприниматели: типы личности и характеристики
Предприниматели: типы личности и характеристики lessonToPreview.academyAssetId}»> видео пройти тест Урок 4 — Предприниматели: необходимые навыки и компетенции
Предприниматели: необходимые навыки и компетенции видео пройти тест Урок 5 — Привычки успешных предпринимателей
Привычки успешных предпринимателей lessonToPreview.academyAssetId}»> Текстовый урок пройти тест Урок 6 — Предпринимательство и экономика: определение и важность
Предпринимательство и экономика: определение и значение видео пройти тест Урок 7.  Демография предпринимателей в США.
Демография предпринимателей в США
Демография предпринимателей в США.
Демография предпринимателей в США Текстовый урок пройти тест Урок 8 — Управление человеческими ресурсами в малых и предпринимательских фирмах
Управление человеческими ресурсами в малых и предпринимательских фирмах lessonToPreview.academyAssetId}»> видео пройти тест Прогресс курса Лучший результат Урок 1 — Открытие бизнеса: факторы, процедуры и проблемы
Открытие бизнеса: факторы, процедуры и проблемы lessonToPreview.academyAssetId}»> видео пройти тест Урок 2 — Выбор места для бизнеса
Выбор места для бизнеса видео пройти тест Урок 3.  Разработка продукта и рост бизнеса: процессы и стратегии
Разработка продукта и рост бизнеса: процессы и стратегии
Разработка продукта и рост бизнеса: процессы и стратегии
Разработка продукта и рост бизнеса: процессы и стратегии видео пройти тест Урок 4 — Что такое бизнес-цели? — Определение и примеры
Что такое бизнес-цели? — Определение и примеры lessonToPreview.academyAssetId}»> видео пройти тест Урок 5. Понимание бизнес-тенденций: прошлое, настоящее и будущее
Понимание бизнес-тенденций: прошлое, настоящее и будущее видео пройти тест  getGoalWeekForTopic(2, 17)}}
getGoalWeekForTopic(2, 17)}} Прогресс курса Лучший результат Урок 1. Творчество, инновации, изменения и экономика знаний
Творчество, инновации, изменения и экономика знаний видео пройти тест Урок 2 — Креативность и инновации в бизнесе: экологические факторы и препятствия
Креативность и инновации в бизнесе: экологические факторы и препятствия lessonToPreview.academyAssetId}»> Текстовый урок пройти тест Урок 3 — Инновации в бизнесе: важность, типы и примеры
Инновации в бизнесе: значение, типы и примеры видео пройти тест Урок 4.  Техники творчества при разработке продукта: определения и типы
Методы творчества в разработке продукта: определения и типы
Техники творчества при разработке продукта: определения и типы
Методы творчества в разработке продукта: определения и типы Текстовый урок пройти тест Урок 5 — Шесть шляп мышления де Боно: резюме и примеры
Шесть шляп мышления де Боно: резюме и примеры lessonToPreview.academyAssetId}»> видео пройти тест Урок 6 — Что такое генерация идей? — Определение, процесс и методы
Что такое Генерация идей? — Определение, процесс и методы видео пройти тест  getGoalWeekForTopic(3, 17)}}
getGoalWeekForTopic(3, 17)}} Ход курса Лучший результат Урок 1 — ТЭО проекта: определение и этапы
ТЭО проекта: определение и этапы видео пройти тест Урок 2 — ТЭО для малого бизнеса
ТЭО для малого бизнеса lessonToPreview.academyAssetId}»> видео пройти тест Урок 3 — Анализ отрасли для бизнес-планов
Отраслевой анализ для бизнес-планов видео пройти тест Урок 4 — Цели анализа конкурентов: стратегии и действия
Цели анализа конкурентов: стратегии и действия lessonToPreview.academyAssetId}»> видео пройти тест Урок 5 — Как проводить анализ конкурентов
Как провести анализ конкурентов видео пройти тест Урок 6.  Структура анализа конкурентов Портера
Структура анализа конкурентов Портера
Структура анализа конкурентов Портера
Структура анализа конкурентов Портера видео пройти тест Прогресс курса Лучший результат Урок 1 — Что такое индивидуальный предприниматель? — Определение, преимущества, недостатки и примеры
Что такое Индивидуальное Предприятие? — Определение, преимущества, недостатки и примеры lessonToPreview.academyAssetId}»> видео пройти тест Урок 2 — Основы партнерства: типы и примеры
Основы партнерства: типы и примеры видео пройти тест Урок 3 — Основы ООО: компании с ограниченной ответственностью
Основы ООО: компании с ограниченной ответственностью lessonToPreview.academyAssetId}»> видео пройти тест Урок 4 — Корпорации: типы, преимущества, недостатки и примеры
Корпорации: типы, преимущества, недостатки и примеры видео пройти тест Урок 5 — Корпоративное расширение: слияния и поглощения
Корпоративное расширение: слияния и поглощения lessonToPreview.academyAssetId}»> видео пройти тест Урок 6 — Франшизы: возможности и проблемы
Франшизы: возможности и вызовы видео пройти тест Урок 7 — Роль кооперативов в бизнесе
Роль кооперативов в бизнесе lessonToPreview.academyAssetId}»> видео пройти тест Ход курса Лучший результат Урок 1 — Что такое бизнес-модель? — Определение и связь с операциями
Что такое бизнес-модель? — Определение и связь с операциями lessonToPreview.academyAssetId}»> видео пройти тест Урок 2. Инновационные и имитационные бизнес-модели
Инновационные и имитационные бизнес-модели Текстовый урок пройти тест Урок 3 — Корпорации: характеристики и процесс запуска
Корпорации: характеристики и процесс запуска lessonToPreview.academyAssetId}»> видео пройти тест Урок 4 — Электронный бизнес: типы и примеры
Электронный бизнес: типы и примеры видео пройти тест  getGoalWeekForTopic(6, 17)}}
getGoalWeekForTopic(6, 17)}} Прогресс курса Лучший результат Урок 1 — Почему важны бизнес-планы?
Почему важны бизнес-планы? видео пройти тест Урок 2 — Как написать бизнес-план
Как написать бизнес-план lessonToPreview.academyAssetId}»> видео пройти тест Урок 3 — Бизнес-планы: как разработать заявление о бизнес-миссии
Бизнес-планы: как разработать заявление о бизнес-миссии видео пройти тест Урок 4 — Бизнес-планы: как разработать ТЭО
Бизнес-планы: как разработать технико-экономический план lessonToPreview.academyAssetId}»> видео пройти тест Урок 5. Важность профилей ключевых лиц в бизнес-плане
Важность профилей ключевых лиц в бизнес-плане видео пройти тест Урок 6 — Анализ рынка для бизнес-планов: пример и определение
Анализ рынка для бизнес-планов: пример и определение lessonToPreview.academyAssetId}»> видео пройти тест Урок 7. Описание компании как расширенная презентация в лифте
Описание компании как расширенная презентация в лифте видео пройти тест  getGoalWeekForTopic(7, 17)}}
getGoalWeekForTopic(7, 17)}} Ход курса Лучший результат Урок 1 — Деловая этика в современном бизнесе
Деловая этика в современном бизнесе видео пройти тест Урок 2.  Почему в бизнесе возникают этические проблемы
Почему в бизнесе возникают этические проблемы
Почему в бизнесе возникают этические проблемы
Почему в бизнесе возникают этические проблемы видео пройти тест Урок 3 — Этический климат в организации: определение, проблемы и улучшения
Организационный этический климат: определение, проблемы и улучшения lessonToPreview.academyAssetId}»> видео пройти тест Урок 4 — Важность политики этики, программ обучения и отчетности на рабочем месте
Важность политики этики, программ обучения и отчетности на рабочем месте видео пройти тест Урок 5 — Разница между этикой на рабочем месте и законом
Разница между этикой на рабочем месте и законом lessonToPreview.academyAssetId}»> видео пройти тест Урок 6 — Правовые факторы, влияющие на бизнес
Правовые факторы, влияющие на бизнес видео пройти тест  getGoalWeekForTopic(8, 17)}}
getGoalWeekForTopic(8, 17)}} Прогресс курса Лучший результат Урок 1. Государственные менторские организации для бизнеса
Государственные менторские организации для бизнеса Текстовый урок пройти тест Урок 2 — Нетворкинг для карьерного успеха: как установить профессиональные контакты
Нетворкинг для карьерного успеха: как установить профессиональные контакты lessonToPreview.academyAssetId}»> видео пройти тест Прогресс курса Лучший результат Урок 1 — Что такое финансовая отчетность? — Определение, цель и важность
Что такое финансовая отчетность? — Определение, цель и важность lessonToPreview.academyAssetId}»> видео пройти тест Урок 2 — Назначение примечаний к финансовой отчетности
Цель примечаний к финансовой отчетности видео пройти тест Урок 3 — Бухгалтерский баланс: цель, компоненты и формат
Бухгалтерский баланс: цель, компоненты и формат lessonToPreview.academyAssetId}»> видео пройти тест Урок 4 — Что такое отчет о прибылях и убытках? — Цель, компоненты и формат
Что такое отчет о прибылях и убытках? — Цель, компоненты и формат видео пройти тест Урок 5 — Отчет о движении денежных средств: цель, формат и примеры
Отчет о движении денежных средств: цель, формат и примеры lessonToPreview.academyAssetId}»> видео пройти тест Урок 6 — Отчет об изменениях в капитале: цель и примеры
Отчет об изменениях в капитале: цель и примеры видео пройти тест Урок 7 — Интегрированная отчетность: определение, цель и структура
Интегрированная отчетность: определение, цель и структура lessonToPreview.academyAssetId}»> видео пройти тест Прогресс курса Лучший результат Урок 1 — Что такое экономическая среда в бизнесе? — Определение, важность и факторы
Что такое экономическая среда в бизнесе? — Определение, важность и факторы lessonToPreview.academyAssetId}»> видео пройти тест Урок 2 — Финансовые рынки и товарные рынки
Финансовые рынки и товарные рынки видео пройти тест Урок 3 — Прогнозирование: стратегическая роль, компоненты и типы
Прогнозирование: стратегическая роль, компоненты и типы lessonToPreview.academyAssetId}»> видео пройти тест Прогресс курса Лучший результат Урок 1. Четыре основные функции денег
Четыре основные функции денег lessonToPreview.academyAssetId}»> видео пройти тест Урок 2 — Деньги и эффект мультипликатора: формула и соотношение резервов
Деньги и эффект мультипликатора: формула и соотношение резервов видео пройти тест Урок 3 — Частные инвестиции и реальные процентные ставки
Частные инвестиции и реальные процентные ставки lessonToPreview.academyAssetId}»> видео пройти тест Урок 4 — Что такое Федеральная резервная система?
Что такое Федеральная резервная система? видео пройти тест Урок 5 — Резервные требования, операции на открытом рынке и учетная ставка
Резервные требования, операции на открытом рынке и учетная ставка lessonToPreview.academyAssetId}»> видео пройти тест Урок 6 — Учреждения банковской системы США
Учреждения банковской системы США видео пройти тест Урок 7 — Как правительство защищает ваши деньги во время финансового кризиса
Как правительство защищает ваши деньги во время финансового кризиса lessonToPreview.academyAssetId}»> видео пройти тест Урок 8. Как технологии делают банковскую деятельность более эффективной
Как технологии делают банковское дело более эффективным видео пройти тест Урок 9 — Международные банковские услуги и услуги
Международные банковские услуги и услуги lessonToPreview.academyAssetId}»> видео пройти тест Урок 10 — Всемирный банк, МВФ и другие международные банковские организации
Всемирный банк, МВФ и другие международные банковские организации видео пройти тест  getGoalWeekForTopic(12, 17)}}
getGoalWeekForTopic(12, 17)}} Прогресс курса Лучший результат Урок 1 — Бюджет стартапа: определение и пример
Стартовый бюджет: определение и пример видео пройти тест Урок 2 — Возможности финансирования для предпринимателей
Возможности финансирования для предпринимателей lessonToPreview.academyAssetId}»> видео пройти тест Урок 3. Начальная загрузка: определение, метод, приемы и пример
Начальная загрузка: определение, метод, методы и пример видео пройти тест Урок 4 — Кредитование под залог активов: определение и использование
Кредитование под залог активов: определение и использование lessonToPreview.academyAssetId}»> видео пройти тест Урок 5 — Ангельское инвестирование: определение, преимущества и риски
Ангельское инвестирование: определение, преимущества и риски видео пройти тест Урок 6 — Источники краткосрочного финансирования
Источники краткосрочного финансирования lessonToPreview.academyAssetId}»> видео пройти тест Урок 7 — Источники долгосрочного финансирования
Источники долгосрочного финансирования видео пройти тест Урок 8 — Процесс финансового планирования
Процесс финансового планирования lessonToPreview.academyAssetId}»> видео пройти тест Прогресс курса Лучший результат Урок 1. Роли и принципы управления
Роли и принципы управления lessonToPreview.academyAssetId}»> г. видео пройти тест Урок 2 — Навыки управления: определение и примеры
Навыки управления: определение и примеры г. видео пройти тест Урок 3 — Фредерик Тейлор: теории, принципы и вклад в менеджмент
Фредерик Тейлор: теории, принципы и вклад в менеджмент lessonToPreview.academyAssetId}»> видео пройти тест Урок 4 — Принципы управления Анри Файоля: управление организацией задач отдела
Принципы управления Анри Файоля: управление организацией задач отдела видео пройти тест Урок 5 — Планирование как функция управления
Планирование как функция управления lessonToPreview.academyAssetId}»> видео пройти тест Урок 6. Организация как функция управления
Организация как функция управления видео пройти тест Урок 7.  Лидерство как функция менеджмента
Лидерство как функция управления
Лидерство как функция менеджмента
Лидерство как функция управления видео пройти тест Урок 8 — Контроллинг как функция менеджмента
Контроллинг как функция менеджмента видео пройти тест Урок 9 — Координация как функция управления
Координация как функция управления lessonToPreview.academyAssetId}»> видео пройти тест Урок 10 — Управление человеческими ресурсами: найм и укомплектование персоналом
Управление человеческими ресурсами: найм и укомплектование персоналом видео пройти тест  getGoalWeekForTopic(14, 17)}}
getGoalWeekForTopic(14, 17)}} Прогресс курса Лучший результат Урок 1 — Введение в маркетинг: определение и применение
Введение в маркетинг: определение и приложения видео пройти тест Урок 2.  Комплекс маркетинга: продукт, место, цена и продвижение
Комплекс маркетинга: продукт, место, цена и продвижение
Комплекс маркетинга: продукт, место, цена и продвижение
Комплекс маркетинга: продукт, место, цена и продвижение видео пройти тест Урок 3 — Что такое Интернет-маркетинг? — Определение и преимущества перед печатью
Что такое Интернет-маркетинг? — Определение и преимущества перед печатью lessonToPreview.academyAssetId}»> видео пройти тест Урок 4 — Стратегия продаж и маркетинговая стратегия
Стратегия продаж и маркетинговая стратегия видео пройти тест Урок 5 — Количественные и качественные исследования в маркетинге
Количественные и качественные исследования в маркетинге lessonToPreview.academyAssetId}»> видео пройти тест Урок 6. Сегментация рынка: почему рыночные сегменты важны для маркетологов
Сегментация рынка: почему сегменты рынка важны для маркетологов видео пройти тест Урок 7.  Сегментация рынка: географическая, демографическая, психологическая и др.
Сегментация рынка: географическая, демографическая, психологическая и др.
Сегментация рынка: географическая, демографическая, психологическая и др.
Сегментация рынка: географическая, демографическая, психологическая и др. видео пройти тест Урок 8 — Что такое маркетинговый план? — Определение и образец
Что такое маркетинговый план? — Определение и образец lessonToPreview.academyAssetId}»> видео пройти тест Урок 9 — Что такое маркетинг взаимоотношений? — Определение и стратегии
Что такое маркетинг взаимоотношений? — Определение и стратегии видео пройти тест Урок 10 — Что такое поведение потребителей в маркетинге? — Факторы, модель и определение
Что такое потребительское поведение в маркетинге? — Факторы, модель и определение lessonToPreview.academyAssetId}»> видео пройти тест Урок 11. Влияние на решения потребителей о покупке: культура, ценности и многое другое
Влияние на решения потребителей о покупке: культура, ценности и многое другое видео пройти тест Урок 12 — Брендинг и капитал бренда в бизнес-маркетинге
Брендинг и капитал бренда в бизнес-маркетинге lessonToPreview.academyAssetId}»> видео пройти тест Урок 13 — Что такое лояльность к бренду в маркетинге? — Определение и примеры
Что такое лояльность к бренду в маркетинге? — Определение и примеры видео пройти тест Урок 14 — Что такое стратегия бренда? — Определение, примеры и развитие
Что такое стратегия бренда? — Определение, примеры и развитие lessonToPreview.academyAssetId}»> видео пройти тест Прогресс курса Лучший результат Урок 1 — Что такое право интеллектуальной собственности? — Определение и права
Что такое право интеллектуальной собственности? — Определение и права lessonToPreview.academyAssetId}»> видео пройти тест Урок 2 — Нарушение прав на товарный знак: законы и санкции
Нарушение прав на товарный знак: законы и санкции видео пройти тест Урок 3 — Патентные нарушения: определение и дела
Патентные нарушения: определение и случаи lessonToPreview.academyAssetId}»> видео пройти тест Урок 4. Что такое нарушение авторских прав? — Понимание закона об авторском праве
Что такое нарушение авторских прав? — Понимание закона об авторском праве видео пройти тест Урок 5 — Коммерческая тайна и патентная защита: защита интеллектуальной собственности
Коммерческая тайна и патентная защита: защита интеллектуальной собственности lessonToPreview.academyAssetId}»> видео пройти тест Ход курса Лучший результат Карточки — генерация бизнес-идей lessonToPreview.academyAssetId}»> Карточки Карточки — оценка возможностей в бизнесе Карточки Карточки — Типы владения бизнесом lessonToPreview.academyAssetId}»> Карточки Карточки — Введение в бизнес-модели Карточки Карточки — Разработка бизнес-плана lessonToPreview.academyAssetId}»> Карточки Карточки — Этические и правовые основы бизнеса Карточки Карточки — Деньги и финансовые институты lessonToPreview.academyAssetId}»> Карточки Карточки — Финансирование малого бизнеса Карточки Карточки — Теории и функции управления lessonToPreview.academyAssetId}»> Карточки Карточки — Маркетинг, исследование рынка и брендинг Карточки Карточки — Закон об интеллектуальной собственности lessonToPreview.academyAssetId}»> Карточки Earning College Credit
 1
1 16
16 Я с честью сдал экзамен благодаря Study.com!
Я с честью сдал экзамен благодаря Study.com! com, я бы точно не знал, что мне нужно изучать. Это ОПРЕДЕЛЕННО было причиной того, что я прошел три суперсложных теста!
com, я бы точно не знал, что мне нужно изучать. Это ОПРЕДЕЛЕННО было причиной того, что я прошел три суперсложных теста! Ознакомьтесь с нашей библиотекой из более чем 84 000 уроков
Поиск курсов и уроков
Поиск Поиск по теме
Стресс-тесты, предпринимательство и инновации* | Обзор финансов
1
История статьи

Abstract
 Используя уникальные данные о кредитах под залог недвижимости, связанных с бизнесом, в Законе о раскрытии информации об ипотечном кредитовании, я показываю, что банки, прошедшие стресс-тестирование, резко сократили кредиты для малого бизнеса, обеспеченные собственным капиталом, важным источником финансирования для предпринимателей. Меньшее предложение кредита приводит к относительному сокращению предпринимательства в округах с большей подверженностью банкам, прошедшим стресс-тестирование. Снижение сильнее в секторах с более высокой долей молодых фирм, использующих финансирование собственного капитала, то есть в тех, в которых сокращение кредита ударит сильнее всего. В более уязвимых округах также наблюдается снижение количества патентных заявок от молодых фирм, а также снижение производительности труда, что отражает непропорциональный вклад молодых фирм в рост.
Используя уникальные данные о кредитах под залог недвижимости, связанных с бизнесом, в Законе о раскрытии информации об ипотечном кредитовании, я показываю, что банки, прошедшие стресс-тестирование, резко сократили кредиты для малого бизнеса, обеспеченные собственным капиталом, важным источником финансирования для предпринимателей. Меньшее предложение кредита приводит к относительному сокращению предпринимательства в округах с большей подверженностью банкам, прошедшим стресс-тестирование. Снижение сильнее в секторах с более высокой долей молодых фирм, использующих финансирование собственного капитала, то есть в тех, в которых сокращение кредита ударит сильнее всего. В более уязвимых округах также наблюдается снижение количества патентных заявок от молодых фирм, а также снижение производительности труда, что отражает непропорциональный вклад молодых фирм в рост. 1. Введение
 Чтобы избежать повторения, политики ввели новые правила, стремясь повысить устойчивость банков к потрясениям и сделать финансовую систему более безопасной. Более высокие требования к капиталу стали наиболее заметным инструментом: новые правила, такие как Базель III или нормативные стресс-тесты, предписывают значительно более высокие коэффициенты капитала для банков. Однако эти меры не бесспорны, и наблюдатели опасаются непреднамеренных побочных эффектов для реальной экономики.
Чтобы избежать повторения, политики ввели новые правила, стремясь повысить устойчивость банков к потрясениям и сделать финансовую систему более безопасной. Более высокие требования к капиталу стали наиболее заметным инструментом: новые правила, такие как Базель III или нормативные стресс-тесты, предписывают значительно более высокие коэффициенты капитала для банков. Однако эти меры не бесспорны, и наблюдатели опасаются непреднамеренных побочных эффектов для реальной экономики. Хотя стресс-тесты являются макропруденциальным инструментом, предназначенным для укрепления финансовой стабильности, общее беспокойство вызывает то, что они повышают стоимость кредитования малого бизнеса за счет более высоких коэффициентов неявного риска (Bordo, Cole, and Duca, 2019).; Кортес и др. , 2020).
Хотя стресс-тесты являются макропруденциальным инструментом, предназначенным для укрепления финансовой стабильности, общее беспокойство вызывает то, что они повышают стоимость кредитования малого бизнеса за счет более высоких коэффициентов неявного риска (Bordo, Cole, and Duca, 2019).; Кортес и др. , 2020). Важно отметить, что сокращение занятости происходит в большей степени в отраслях, в которых более высокая доля молодых фирм зависит от финансирования собственного капитала. В округах с более высокой долей рынка банков, прошедших стресс-тестирование, также наблюдается относительное снижение количества патентных заявок от молодых фирм, а также производительности труда, что отражает огромное значение молодых фирм для инноваций и роста (Haltiwanger, 2015).
Важно отметить, что сокращение занятости происходит в большей степени в отраслях, в которых более высокая доля молодых фирм зависит от финансирования собственного капитала. В округах с более высокой долей рынка банков, прошедших стресс-тестирование, также наблюдается относительное снижение количества патентных заявок от молодых фирм, а также производительности труда, что отражает огромное значение молодых фирм для инноваций и роста (Haltiwanger, 2015). Сосредоточив внимание на рефинансированных кредитах, я определяю кредиты для малого бизнеса, обеспеченные собственным капиталом. Таким образом, HMDA предоставляет подробные ежегодные данные о кредитовании собственного капитала, связанного с бизнесом, с разбивкой по банкам и округам. Насколько мне известно, этот богатый источник данных о кредитовании, связанном с бизнесом, до сих пор игнорировался в литературе.
Сосредоточив внимание на рефинансированных кредитах, я определяю кредиты для малого бизнеса, обеспеченные собственным капиталом. Таким образом, HMDA предоставляет подробные ежегодные данные о кредитовании собственного капитала, связанного с бизнесом, с разбивкой по банкам и округам. Насколько мне известно, этот богатый источник данных о кредитовании, связанном с бизнесом, до сих пор игнорировался в литературе. Включение фиксированных эффектов округа * времени уменьшает размер эффекта, но коэффициенты остаются экономически и статистически значимыми, что позволяет предположить, что банки сокращают предложение кредитов. 1
Включение фиксированных эффектов округа * времени уменьшает размер эффекта, но коэффициенты остаются экономически и статистически значимыми, что позволяет предположить, что банки сокращают предложение кредитов. 1  .
.
 п. относительно докризисного периода.
п. относительно докризисного периода. Этот вывод свидетельствует о том, что стресс-тесты могли негативно повлиять на производительность труда во время восстановления.
Этот вывод свидетельствует о том, что стресс-тесты могли негативно повлиять на производительность труда во время восстановления. Банки, столкнувшиеся с меньшим дефицитом капитала, имеют значительно более низкие темпы роста кредитования собственного капитала, связанного с бизнесом, в период с 2012 по 2016 год. последствия.
Банки, столкнувшиеся с меньшим дефицитом капитала, имеют значительно более низкие темпы роста кредитования собственного капитала, связанного с бизнесом, в период с 2012 по 2016 год. последствия. По сути, я сравниваю занятость в молодых фирмах в одном и том же округе и в одной и той же отрасли для разных уровней воздействия и зависимости от собственного капитала (Хименес 9).0297 и др. , 2014). Коэффициенты остаются значимыми в конкретных действиях с фиксированными эффектами; в целом размер эффекта увеличивается, что говорит о том, что банки, прошедшие стресс-тестирование, обслуживают округа с более сильными ненаблюдаемыми показателями.
По сути, я сравниваю занятость в молодых фирмах в одном и том же округе и в одной и той же отрасли для разных уровней воздействия и зависимости от собственного капитала (Хименес 9).0297 и др. , 2014). Коэффициенты остаются значимыми в конкретных действиях с фиксированными эффектами; в целом размер эффекта увеличивается, что говорит о том, что банки, прошедшие стресс-тестирование, обслуживают округа с более сильными ненаблюдаемыми показателями. Межгосударственные и временные вариации запретов на открытие филиалов до финансового кризиса обеспечивают экзогенные вариации способности банков входить в другие состояния. Таким образом, прогнозируемые отложения, вероятно, ортогональны ненаблюдаемым характеристикам округа во время добычи.
Межгосударственные и временные вариации запретов на открытие филиалов до финансового кризиса обеспечивают экзогенные вариации способности банков входить в другие состояния. Таким образом, прогнозируемые отложения, вероятно, ортогональны ненаблюдаемым характеристикам округа во время добычи. Борд, Ивашина и Талиаферро (2018) показывают, что банки, более пострадавшие от падения цен на недвижимость во время Великой рецессии, в большей степени сокращают кредитование малых фирм. Учет докризисного жилищного бума, снижения цен на жилье во время рецессии или различий в собственности на жилье не учитывает влияние на предпринимательство подверженности округов банкам, прошедшим стресс-тестирование. Наоборот, стресс-тесты затронули молодые фирмы в ущерб каналу залога. Кроме того, Chen, Hanson и Stein (2017) показывают, что четыре крупнейших банка США сократили кредитование малого бизнеса в посткризисный период. Хотя финансовое регулирование может объяснить их выводы, они не предоставляют прямых доказательств. Я показываю, что влияние стресс-тестов на банковское кредитование не ограничивается четырьмя крупнейшими банками, но также присутствует среди более мелких банков, прошедших стресс-тестирование, и когда я ограничиваю выборку округами, не представленными в четырех крупнейших банках.
Борд, Ивашина и Талиаферро (2018) показывают, что банки, более пострадавшие от падения цен на недвижимость во время Великой рецессии, в большей степени сокращают кредитование малых фирм. Учет докризисного жилищного бума, снижения цен на жилье во время рецессии или различий в собственности на жилье не учитывает влияние на предпринимательство подверженности округов банкам, прошедшим стресс-тестирование. Наоборот, стресс-тесты затронули молодые фирмы в ущерб каналу залога. Кроме того, Chen, Hanson и Stein (2017) показывают, что четыре крупнейших банка США сократили кредитование малого бизнеса в посткризисный период. Хотя финансовое регулирование может объяснить их выводы, они не предоставляют прямых доказательств. Я показываю, что влияние стресс-тестов на банковское кредитование не ограничивается четырьмя крупнейшими банками, но также присутствует среди более мелких банков, прошедших стресс-тестирование, и когда я ограничиваю выборку округами, не представленными в четырех крупнейших банках. Наконец, при учете отраслевого риска или различий в чувствительности молодых и старых фирм к общим потрясениям результаты практически не изменяются.
Наконец, при учете отраслевого риска или различий в чувствительности молодых и старых фирм к общим потрясениям результаты практически не изменяются. Молодые фирмы также сокращают свою патентную деятельность в незащищенных странах. Таким образом, отсутствие кредита и связанные с ним реальные последствия могли способствовать слабому восстановлению стартапов после Великой рецессии.
Молодые фирмы также сокращают свою патентную деятельность в незащищенных странах. Таким образом, отсутствие кредита и связанные с ним реальные последствия могли способствовать слабому восстановлению стартапов после Великой рецессии. Этот вывод, вероятно, отражает то, что предполагаемый обвал цен на жилье увеличивает стоимость обеспеченного кредитования малого бизнеса. 3 Bordo, Cole, and Duca (2019) используют агрегированные данные на уровне банков и предоставляют доказательства временных рядов, чтобы показать, что стресс-тесты привели к ужесточению банковских кредитных стандартов в отношении кредитов малым фирмам. Они также дают наводящие доказательства того, что ужесточение кредитных стандартов могло повлиять на появление новых заведений. 4
Этот вывод, вероятно, отражает то, что предполагаемый обвал цен на жилье увеличивает стоимость обеспеченного кредитования малого бизнеса. 3 Bordo, Cole, and Duca (2019) используют агрегированные данные на уровне банков и предоставляют доказательства временных рядов, чтобы показать, что стресс-тесты привели к ужесточению банковских кредитных стандартов в отношении кредитов малым фирмам. Они также дают наводящие доказательства того, что ужесточение кредитных стандартов могло повлиять на появление новых заведений. 4  Формирование фирм уже до кризиса неуклонно снижалось; рост банковского кредитования малого бизнеса затмевается ростом в других сегментах (таких как ипотечное кредитование). Таким образом, мои результаты показывают, что предприниматели могли столкнуться с непропорциональным сокращением предложения кредита, что могло снизить динамизм и инновации во время восстановления, даже если стресс-тесты сделали финансовую систему более безопасной в целом. 5 Этот возможный непреднамеренный побочный эффект стресс-тестов необходимо учитывать при оценке общего воздействия посткризисного финансового регулирования.
Формирование фирм уже до кризиса неуклонно снижалось; рост банковского кредитования малого бизнеса затмевается ростом в других сегментах (таких как ипотечное кредитование). Таким образом, мои результаты показывают, что предприниматели могли столкнуться с непропорциональным сокращением предложения кредита, что могло снизить динамизм и инновации во время восстановления, даже если стресс-тесты сделали финансовую систему более безопасной в целом. 5 Этот возможный непреднамеренный побочный эффект стресс-тестов необходимо учитывать при оценке общего воздействия посткризисного финансового регулирования. 2. Институциональная основа и данные
 цены на дома. Регуляторы предлагают банкам различные сценарии, имитирующие все более враждебную экономическую среду. Например, крайне неблагоприятный сценарий 2014 г. предполагает рост уровня безработицы до 12% и падение цен на жилье на 35%. Банки должны разрабатывать годовые планы капитала и поддерживать достаточный капитал, чтобы выдержать эти сценарии. Они представляют свои планы капиталовложений на рассмотрение регулирующему органу, включая планируемые эмиссии и распределения капитала. Основываясь на внутренних моделях, Федеральная резервная система решает, прошли ли банки тесты или нет.
цены на дома. Регуляторы предлагают банкам различные сценарии, имитирующие все более враждебную экономическую среду. Например, крайне неблагоприятный сценарий 2014 г. предполагает рост уровня безработицы до 12% и падение цен на жилье на 35%. Банки должны разрабатывать годовые планы капитала и поддерживать достаточный капитал, чтобы выдержать эти сценарии. Они представляют свои планы капиталовложений на рассмотрение регулирующему органу, включая планируемые эмиссии и распределения капитала. Основываясь на внутренних моделях, Федеральная резервная система решает, прошли ли банки тесты или нет. К 2014 году тесты включали более мелкие учреждения с активами более 50 миллиардов долларов и охватили в общей сложности 32 банка.
К 2014 году тесты включали более мелкие учреждения с активами более 50 миллиардов долларов и охватили в общей сложности 32 банка. Стресс-тесты моделируют сильное снижение цен на жилье (залоговая стоимость) в дополнение к снижению экономической активности (слабый местный спрос). Таким образом, обеспеченное кредитование малого бизнеса подвержено как снижению спроса, так и снижению стоимости залога во время стресс-тестов, что предполагает высокие требования к капиталу и может сделать его менее прибыльным для банков, прошедших стресс-тестирование (Clearinghouse, 2017).
Стресс-тесты моделируют сильное снижение цен на жилье (залоговая стоимость) в дополнение к снижению экономической активности (слабый местный спрос). Таким образом, обеспеченное кредитование малого бизнеса подвержено как снижению спроса, так и снижению стоимости залога во время стресс-тестов, что предполагает высокие требования к капиталу и может сделать его менее прибыльным для банков, прошедших стресс-тестирование (Clearinghouse, 2017). 2.1 Данные HMDA
 Особенностью записи данных HMDA является то, что, если заявитель или созаявитель не является физическим лицом (т. и Каннер, 2007). 6 Эта классификация позволяет мне идентифицировать кредиты, связанные с бизнесом, обеспеченные собственным капиталом, путем ограничения выборки рефинансированными кредитами, для которых заявитель и/или созаявитель по этнической принадлежности, расе и полу кодируются как недоступные. 7 Я исключаю все наблюдения за ссудой, сумма ссуды которой превышает 1 миллион долларов, а затем агрегирую до уровня банка-округа-года. Я держу только пары банк-округ по крайней мере с тремя наблюдениями (ссудами) в год, чтобы устранить шумные колебания, возникающие из-за незначительных сумм ссуд, выданных на месте. Кроме того, поскольку HMDA плохо охватывает сельские районы, я ограничиваю выборку заемщиками, проживающими в столичных статистических районах.
Особенностью записи данных HMDA является то, что, если заявитель или созаявитель не является физическим лицом (т. и Каннер, 2007). 6 Эта классификация позволяет мне идентифицировать кредиты, связанные с бизнесом, обеспеченные собственным капиталом, путем ограничения выборки рефинансированными кредитами, для которых заявитель и/или созаявитель по этнической принадлежности, расе и полу кодируются как недоступные. 7 Я исключаю все наблюдения за ссудой, сумма ссуды которой превышает 1 миллион долларов, а затем агрегирую до уровня банка-округа-года. Я держу только пары банк-округ по крайней мере с тремя наблюдениями (ссудами) в год, чтобы устранить шумные колебания, возникающие из-за незначительных сумм ссуд, выданных на месте. Кроме того, поскольку HMDA плохо охватывает сельские районы, я ограничиваю выборку заемщиками, проживающими в столичных статистических районах. 2.2 Банковские данные
 Я определяю кредиты для малого бизнеса как непогашенные кредиты с суммой выдачи 1 миллион долларов или меньше. Обеспеченные коммерческие кредиты определяются как «нежилищные кредиты (за исключением сельскохозяйственных кредитов), в основном обеспеченные недвижимостью, находящейся в местных офисах», и не включают кредиты на строительство. Каждому банку присваивается фиктивный стресс-тест со значением один в каждый год, когда его банковская холдинговая компания (BHC) проходит стресс-тесты. Далее я собираю данные за второй квартал каждого года по совокупным активам банков, коэффициенту капитала первого уровня, непроцентным доходам и общему доходу, общему объему инвестиционных ценных бумаг, накладным расходам (коэффициенту эффективности), просроченным кредитам, рентабельности активов и общей сумме депозитов.
Я определяю кредиты для малого бизнеса как непогашенные кредиты с суммой выдачи 1 миллион долларов или меньше. Обеспеченные коммерческие кредиты определяются как «нежилищные кредиты (за исключением сельскохозяйственных кредитов), в основном обеспеченные недвижимостью, находящейся в местных офисах», и не включают кредиты на строительство. Каждому банку присваивается фиктивный стресс-тест со значением один в каждый год, когда его банковская холдинговая компания (BHC) проходит стресс-тесты. Далее я собираю данные за второй квартал каждого года по совокупным активам банков, коэффициенту капитала первого уровня, непроцентным доходам и общему доходу, общему объему инвестиционных ценных бумаг, накладным расходам (коэффициенту эффективности), просроченным кредитам, рентабельности активов и общей сумме депозитов. Доля обеспеченных кредитов для малого бизнеса составляет в среднем 58%. , с большим стандартным отклонением 0,24. С точки зрения сводной выборочной статистики, на банки, прошедшие стресс-тестирование, приходится 65% (58%) от общего объема банковских активов (кредитов) и 35% (31%) от общего объема (обеспеченных) кредитов малому бизнесу (по состоянию на 2008 г.). Средняя (медианная) сумма кредита для связанных с бизнесом кредитов под домашний капитал составляет 176 000 долларов США (119 долларов США).000), который подобен в размере к средним обеспеченным банкам ссуды малого бизнеса сообщают в их отчетах о звонка. В совокупности кредиты под залог собственного капитала, связанные с бизнесом, составляют около 11% от общего объема кредитования малого бизнеса CRA банками. 8
Доля обеспеченных кредитов для малого бизнеса составляет в среднем 58%. , с большим стандартным отклонением 0,24. С точки зрения сводной выборочной статистики, на банки, прошедшие стресс-тестирование, приходится 65% (58%) от общего объема банковских активов (кредитов) и 35% (31%) от общего объема (обеспеченных) кредитов малому бизнесу (по состоянию на 2008 г.). Средняя (медианная) сумма кредита для связанных с бизнесом кредитов под домашний капитал составляет 176 000 долларов США (119 долларов США).000), который подобен в размере к средним обеспеченным банкам ссуды малого бизнеса сообщают в их отчетах о звонка. В совокупности кредиты под залог собственного капитала, связанные с бизнесом, составляют около 11% от общего объема кредитования малого бизнеса CRA банками. 8 . 
Среднее
. SD
. Мин.
. Макс.
. Количество
. Panel (a): bank Share secured SB loans 0.58 0.24 0.00 1.00 94,510 Log (активы) 14,93 1,38 9.72 24.14 94,510 Nonperforming loans (%) 0.30 0.63 –0.75 3.58 94,510 Return on assets (%) 0.80 1.04 –4.40 4,23 94,510 Депозиты/активы (%) 0,93 0,07 0,93 0,07 0, 9 0,07 888888989 0,07 888888880, 989.  0589
0589 Liquidity (%) 0.07 0.05 0.01 0.30 94,510 Tier 1 capital (%) 0.18 0.10 0.04 0.80 94,510 Noninterest income (%) 0.76 0.88 –0.56 6.67 94,510 Efficiency (%) 0.72 0.23 0.30 1.92 94,510 Panel (b): Bank-county Home equity amount 148.75 122.27 0.30 534.90 169,061 Log(home equity amount) 6.95 0.89 1.10 8.58 169,061 Panel (c): County Exposure 0.  36
36 0.24 0.00 1.00 91,999 Exposure (predicted) 0,33 0,17 –0,02 0,94 91,906 log (популяция) 2,45 9888888888888888888888888888 гг.0589 2.78 91,999 Population share black 0.10 0.12 0.00 0.70 91,999 Population share elderly 0.14 0.04 0.02 0.33 91,999 Часть рабочей силы. скорость 0,94 0,02 0,81 1,06 91 999 Unemployment rate 0.06 0.02 0.01 0.19 91,999 Δ House price index 0.02 0.07 –0.  30
30 0.34 91,999 Log(income per capita) 10.49 0.29 9.61 11.81 91,999 Panel (d): County-industry Log(employment young firms) 3.55 1.64 0.00 10.99 293,868 Share empl. young firms 0.07 0.08 0.00 0.50 293,868 Log(average wage) 6.84 0.85 4.34 8.77 293,868 . Среднее
. SD
. Мин.
. Макс.
. Количество
. Panel (a): bank Share secured SB loans 0.  58
58 0.24 0.00 1.00 94,510 Log(assets) 14.93 1.38 9.72 24.14 94,510 Nonperforming loans (%) 0.30 0.63 –0.75 3.58 94,510 Return on assets (%) 0.80 1.04 –4.40 4.23 94,510 Deposits/assets (%) 0.93 0.07 0.07 1.00 94,510 Liquidity (%) 0.07 0.05 0.01 0.30 94,510 Tier 1 capital (%) 0.18 0.10 0.04 0.80 94,510 Noninterest income (%) 0.76 0.88 –0.  56
56 6.67 94,510 Efficiency (%) 0.72 0.23 0.30 1.92 94,510 Panel (b): Bank-county Сумма домаров 148,75 122,27 0 122,27 0,30589 122,27 0,30589 122,27 0,30589 122,27 ,75999 122,27 ,75 122,27 ,75 122,27 ,0576 Log(home equity amount) 6.95 0.89 1.10 8.58 169,061 Panel (c): County Exposure 0,36 0,24 0,00 1,00 91,999 (прогнозировано) 0,33 88888880,17 0,33 9888888888880,17 0,33 88888880,17888888880 гг.  0589
0589 0.94 91,906 Log(population) 2.45 0.11 1.81 2.78 91,999 Population share black 0.10 0.12 0.00 0.70 91,999 Доля населения пожилой пожилой.0588 Часть рабочей силы. rate 0.94 0.02 0.81 1.06 91,999 Unemployment rate 0.06 0.02 0.01 0.19 91,999 Δ House price index 0.02 0,07 –0,30 0,34 91 999 Log(доход на душу населения) 10,49 9.61 11.81 91,999 Panel (d): County-industry Log(employment young firms) 3.  55
55 1.64 0.00 10,99 293 868 молодые фирмы 0,07 0,08 0,00 0,50 293 868 Log(average wage) 6.84 0.85 4.34 8.77 293,868 . Среднее
. сд
. Мин.
. Макс.
. Количество
. Panel (a): bank Share secured SB loans 0.  58
58 0.24 0.00 1.00 94,510 Log (активы) 14,93 1,38 9.72 24.14 94,510 Nonperforming loans (%) 0.30 0.63 –0.75 3.58 94,510 Return on assets (%) 0.80 1.04 –4.40 4,23 94,510 Депозиты/активы (%) 0,93 0,07 0,93 0,07 0, 9 0,07 888888989 0,07 888888880, 989.0589 Liquidity (%) 0.07 0.05 0.01 0.30 94,510 Tier 1 capital (%) 0.18 0.10 0.04 0.80 94,510 Noninterest income (%) 0.  76
76 0.88 –0.56 6.67 94,510 Efficiency (%) 0.72 0.23 0.30 1.92 94,510 Panel (b): Bank-county Home equity amount 148.75 122.27 0.30 534.90 169,061 Log(home equity amount) 6.95 0.89 1.10 8.58 169,061 Panel (c): County Exposure 0.36 0.24 0.00 1.00 91,999 Exposure (predicted) 0,33 0,17 –0,02 0,94 91,906 log (популяция) 2,45 9888888888888888888888888888 гг.  0589
0589 2.78 91,999 Population share black 0.10 0.12 0.00 0.70 91,999 Population share elderly 0.14 0.04 0.02 0.33 91,999 Часть рабочей силы. скорость 0,94 0,02 0,81 1,06 91 999 Unemployment rate 0.06 0.02 0.01 0.19 91,999 Δ House price index 0.02 0.07 –0.30 0.34 91,999 Log(income per capita) 10.49 0.29 9.61 11.81 91,999 Panel (d): County-industry Log(employment young firms) 3.  55
55 1.64 0.00 10.99 293,868 Share empl. young firms 0.07 0.08 0.00 0.50 293,868 Log(average wage) 6.84 0.85 4.34 8.77 293,868 . Среднее
. SD
. Мин.
. Макс.
. Количество
. Panel (a): bank Share secured SB loans 0.58 0.24 0.00 1.00 94,510 Log(assets) 14.93 1.38 9.72 24.14 94,510 Nonperforming loans (%) 0.  30
30 0.63 –0.75 3.58 94,510 Return on assets (%) 0.80 1.04 –4.40 4.23 94,510 Deposits/assets (%) 0.93 0.07 0.07 1.00 94,510 Liquidity (%) 0.07 0.05 0.01 0.30 94,510 Tier 1 capital (%) 0.18 0.10 0.04 0.80 94,510 Noninterest income (%) 0.76 0.88 –0.56 6.67 94,510 Efficiency (%) 0.72 0.23 0.30 1.92 94,510 Panel (b): Bank-county Сумма домаров 148,75 122,27 0 122,27 0,30589 122,27 0,30589 122,27 0,30589 122,27 ,75999 122,27 ,75 122,27 ,75 122,27 ,0576 Log(home equity amount) 6.  95
95 0.89 1.10 8.58 169,061 Panel (c): County Exposure 0,36 0,24 0,00 1,00 91,999 (прогнозировано) 0,33 88888880,17 0,33 9888888888880,17 0,33 88888880,17888888880 гг.0589 0.94 91,906 Log(population) 2.45 0.11 1.81 2.78 91,999 Population share black 0.10 0.12 0.00 0.70 91,999 Доля населения пожилой пожилой.0588 Часть рабочей силы. rate 0.94 0.02 0.  81
81 1.06 91,999 Unemployment rate 0.06 0.02 0.01 0.19 91,999 Δ House price index 0.02 0,07 –0,30 0,34 91 999 Log(доход на душу населения) 10,49 9.61 11.81 91,999 Panel (d): County-industry Log(employment young firms) 3.55 1.64 0.00 10,99 293 868 молодые фирмы 0,07 0,08 0,00 0,50 293 868 Log(average wage) 6.84 0.85 4.34 8.77 293,868 2.
 3 Данные округа
3 Данные округа Для каждой двузначной ячейки «отрасль-графство» молодые фирмы (или предприниматели) определяются как компании нулевого или годовалого возраста (Gourio, Messer, and Siemer, 2016). Всеобъемлющие данные о создании фирм доступны с 2002 по 2016 год. Контроль округа включает логарифмическое население, долю чернокожего населения и долю населения старше 65 лет, уровень безработицы, рост цен на жилье и логарифмический доход на душу населения. Соответствующими источниками данных являются: оценки населения Бюро переписи населения, статистика безработицы по местным районам Бюро статистики труда, индекс цен на жилье Федерального агентства по финансированию жилищного строительства и личный доход местного района Бюро экономического анализа.
Для каждой двузначной ячейки «отрасль-графство» молодые фирмы (или предприниматели) определяются как компании нулевого или годовалого возраста (Gourio, Messer, and Siemer, 2016). Всеобъемлющие данные о создании фирм доступны с 2002 по 2016 год. Контроль округа включает логарифмическое население, долю чернокожего населения и долю населения старше 65 лет, уровень безработицы, рост цен на жилье и логарифмический доход на душу населения. Соответствующими источниками данных являются: оценки населения Бюро переписи населения, статистика безработицы по местным районам Бюро статистики труда, индекс цен на жилье Федерального агентства по финансированию жилищного строительства и личный доход местного района Бюро экономического анализа. Средняя выборочная доля патентов молодых фирм в общем количестве патентов страны составляет 21%, что близко к их совокупной доле 25%. Средняя заработная плата на уровне уезд-отрасль-год, полученная из квартальной переписи занятости и заработной платы, косвенно отражает производительность труда округа. Для каждой двузначной отрасли NAICS я получаю данные о заработной плате за 4-й квартал каждого года. Наконец, я объединяю кредиты под залог собственного капитала, связанные с бизнесом, чтобы получить обеспеченное кредитование малого бизнеса на уровне округа.
Средняя выборочная доля патентов молодых фирм в общем количестве патентов страны составляет 21%, что близко к их совокупной доле 25%. Средняя заработная плата на уровне уезд-отрасль-год, полученная из квартальной переписи занятости и заработной платы, косвенно отражает производительность труда округа. Для каждой двузначной отрасли NAICS я получаю данные о заработной плате за 4-й квартал каждого года. Наконец, я объединяю кредиты под залог собственного капитала, связанные с бизнесом, чтобы получить обеспеченное кредитование малого бизнеса на уровне округа. 2.4 Отраслевые данные
 Для каждой отрасли i я вычисляю среднюю долю молодых фирм9.0297 f i среди всех фирм F i , которые сообщают об использовании финансирования собственного капитала или личных активов (далее домашний капитал ) для открытия или расширения своего бизнеса как
Для каждой отрасли i я вычисляю среднюю долю молодых фирм9.0297 f i среди всех фирм F i , которые сообщают об использовании финансирования собственного капитала или личных активов (далее домашний капитал ) для открытия или расширения своего бизнеса как 3.
 Эмпирическая стратегия и результаты
Эмпирическая стратегия и результаты 3.1 Стресс-тесты и кредитование под залог собственного капитала
 стресс-тестирование — это фиктивная переменная со значением, равным единице за каждый год, в течение которого банк проходит стресс-тестирование, и нулем в противном случае. Банковский контроль включает в себя журнал общих активов, рентабельность активов, депозиты к общим активам, соотношение капитала 1-го уровня, накладные расходы, долю необслуживаемых кредитов в общем объеме кредитов, долю непроцентного дохода и банковскую ликвидность (денежные средства плюс рыночные ценные бумаги по сравнению с активами). ). Все элементы управления отстают на один период, чтобы избежать эндогенности. Стандартные ошибки группируются на уровне банковского холдинга. Каждая регрессия включает фиксированные эффекты банк*округ (θb,c) и использует вариации в каждой комбинации банк–округ относительно ее среднего значения. Если γhmda<0, банки, прошедшие стресс-тестирование, сокращают кредитование в большей степени, чем банки, не прошедшие стресс-тест, по сравнению с их соответствующими докризисными тенденциями.
стресс-тестирование — это фиктивная переменная со значением, равным единице за каждый год, в течение которого банк проходит стресс-тестирование, и нулем в противном случае. Банковский контроль включает в себя журнал общих активов, рентабельность активов, депозиты к общим активам, соотношение капитала 1-го уровня, накладные расходы, долю необслуживаемых кредитов в общем объеме кредитов, долю непроцентного дохода и банковскую ликвидность (денежные средства плюс рыночные ценные бумаги по сравнению с активами). ). Все элементы управления отстают на один период, чтобы избежать эндогенности. Стандартные ошибки группируются на уровне банковского холдинга. Каждая регрессия включает фиксированные эффекты банк*округ (θb,c) и использует вариации в каждой комбинации банк–округ относительно ее среднего значения. Если γhmda<0, банки, прошедшие стресс-тестирование, сокращают кредитование в большей степени, чем банки, не прошедшие стресс-тест, по сравнению с их соответствующими докризисными тенденциями. Время ( τ t ) фиксированные эффекты учитывают обычные шоки.
Время ( τ t ) фиксированные эффекты учитывают обычные шоки. Эти побочные эффекты, в дополнение к лечебному эффекту, будут учтены коэффициентом γ hmda . Добавление фиксированных эффектов округ*время для сравнения кредитования банками в одном округе может еще больше усилить эти вторичные эффекты (Berg and Streitz, 2019). Дополнительное приложение выполняет дополнительные тесты для изучения наличия побочных эффектов. Он показывает, что оценки коэффициентов остаются схожими в спецификациях с фиксированными эффектами округа*времени и без них при исключении округов, в которых банки, не прошедшие стресс-тестирование, имеют значительную долю рынка, или в регрессионном анализе, который использует только вариации внутри группы банков, прошедших стресс-тестирование.
Эти побочные эффекты, в дополнение к лечебному эффекту, будут учтены коэффициентом γ hmda . Добавление фиксированных эффектов округ*время для сравнения кредитования банками в одном округе может еще больше усилить эти вторичные эффекты (Berg and Streitz, 2019). Дополнительное приложение выполняет дополнительные тесты для изучения наличия побочных эффектов. Он показывает, что оценки коэффициентов остаются схожими в спецификациях с фиксированными эффектами округа*времени и без них при исключении округов, в которых банки, не прошедшие стресс-тестирование, имеют значительную долю рынка, или в регрессионном анализе, который использует только вариации внутри группы банков, прошедших стресс-тестирование. Эффекты зависят от банковского контроля, фиксированных эффектов банка * округа и фиксированных эффектов года. Чтобы выделить изменения в предложении кредита, в колонке (2) представлены фиксированные эффекты округа*времени. Коэффициент процента сохраняет знак и значение; банки, прошедшие стресс-тестирование, сокращают предложение кредитов на 26,7% больше, чем банки, не прошедшие стресс-тестирование. Уменьшение размера коэффициента свидетельствует о том, что банки, прошедшие стресс-тестирование, кредитуют страны с более слабым спросом на кредиты в посткризисный период.
Эффекты зависят от банковского контроля, фиксированных эффектов банка * округа и фиксированных эффектов года. Чтобы выделить изменения в предложении кредита, в колонке (2) представлены фиксированные эффекты округа*времени. Коэффициент процента сохраняет знак и значение; банки, прошедшие стресс-тестирование, сокращают предложение кредитов на 26,7% больше, чем банки, не прошедшие стресс-тестирование. Уменьшение размера коэффициента свидетельствует о том, что банки, прошедшие стресс-тестирование, кредитуют страны с более слабым спросом на кредиты в посткризисный период. Столбцы (5)–(7) относятся к типу банковского кредита и годам, и в качестве зависимой переменной используется логарифм суммы кредита (обеспеченный или необеспеченный). Стресс-тестирование — это фиктивная переменная со значением 1, если банк проходил стресс-тестирование в данном году, и 1 (2009 г.).−16) является фиктивной величиной, равной единице, для 2009–2016 годов. Обеспеченный является фиктивным значением, равным единице, если тип кредита равен обеспеченным кредитам для малого бизнеса, и нулю, если тип кредита равен необеспеченным кредитам для малого бизнеса. Колонка (1) включает банковский контроль, а также фиксированные эффекты банка * округа и года (T). Столбец (2) включает фиксированные эффекты округ*время (C*T). Столбцы (3) и (4) включают фиксированные эффекты банка и года. Столбцы (5)–(7) используют фиксированные эффекты банка*типа кредита и добавляют фиксированные эффекты банка*время (B*T) и тип кредита*время (L*T). Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне банковской холдинговой компании.
Столбцы (5)–(7) относятся к типу банковского кредита и годам, и в качестве зависимой переменной используется логарифм суммы кредита (обеспеченный или необеспеченный). Стресс-тестирование — это фиктивная переменная со значением 1, если банк проходил стресс-тестирование в данном году, и 1 (2009 г.).−16) является фиктивной величиной, равной единице, для 2009–2016 годов. Обеспеченный является фиктивным значением, равным единице, если тип кредита равен обеспеченным кредитам для малого бизнеса, и нулю, если тип кредита равен необеспеченным кредитам для малого бизнеса. Колонка (1) включает банковский контроль, а также фиксированные эффекты банка * округа и года (T). Столбец (2) включает фиксированные эффекты округ*время (C*T). Столбцы (3) и (4) включают фиксированные эффекты банка и года. Столбцы (5)–(7) используют фиксированные эффекты банка*типа кредита и добавляют фиксированные эффекты банка*время (B*T) и тип кредита*время (L*T). Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне банковской холдинговой компании. Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1.
Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. Зам.вар.:
. лог (амм. HMDA)
. незащищенный
. защищенный
. лог(амт)
. Stress tested –0.359*** –0.267*** –0.125* –0.358*** –0.053 (0.088) (0,094) (0,075) (0,074) (0,047) Stress tested × secured –0.  377***
377*** –0.377*** –0.421*** (0.092) (0.092) (0.096) Observations 169,061 169,061 94,230 94,230 188,460 188,460 188,460 R 2 0.567 0.752 0.906 0.895 0.896 0.958 0.959 Bank controls ✓ ✓ ✓ ✓ ✓ ✓ ✓ Bank*County FE ✓ ✓ – – – – – Bank FE – – ✓ ✓ – – – Bank*Sec FE – – – – ✓ ✓ ✓ Time FE T C*T T T T B*T B*T + L*T . 
(1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. Зам.вар.:
. журнал (амт HMDA)
. незащищенный
. защищенный
. лог(амт)
. Stress tested –0.359*** –0.267*** –0.125* –0.358*** –0.053 (0.088) (0,094) (0,075) (0,074) (0,047) проверено 9084 0589 –0.377*** –0.377*** –0.421*** (0.  092)
092) (0.092) ( 0.096) Observations 169,061 169,061 94,230 94,230 188,460 188,460 188,460 R 2 0.567 0.752 0.906 0.895 0.896 0.958 0.959 Bank controls ✓ ✓ ✓ ✓ ✓ ✓ ✓ Банк*округ FE ✓ ✓ — — — — — 9 898
8
88898888888888888888888888888888888888888888 гг.0589 – ✓ ✓ – – – Bank*Sec FE – – – – ✓ ✓ ✓ ВРЕМЯ FE T C*T T T T B*T B*T+L*T B*T+L*T 4999 9.  4999
4999 9.
Открыть в новой вкладке  Колонка (1) включает банковский контроль, а также фиксированные эффекты банка * округа и года (T). Столбец (2) включает фиксированные эффекты округ*время (C*T). Столбцы (3) и (4) включают фиксированные эффекты банка и года. Столбцы (5)–(7) используют фиксированные эффекты банка*типа кредита и добавляют фиксированные эффекты банка*время (B*T) и тип кредита*время (L*T). Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне банковской холдинговой компании. Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1.
Колонка (1) включает банковский контроль, а также фиксированные эффекты банка * округа и года (T). Столбец (2) включает фиксированные эффекты округ*время (C*T). Столбцы (3) и (4) включают фиксированные эффекты банка и года. Столбцы (5)–(7) используют фиксированные эффекты банка*типа кредита и добавляют фиксированные эффекты банка*время (B*T) и тип кредита*время (L*T). Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне банковской холдинговой компании. Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. Зам.вар.:
. лог (амм. HMDA)
. незащищенный
. защищенный
. 
лог(амт)
. Stress tested –0.359*** –0.267*** –0.125* –0.358*** –0.053 (0.088) (0,094) (0,075) (0,074) (0,047) Stress tested × secured –0.377*** –0.377*** –0.421*** (0.092) (0.092) (0.096) Observations 169,061 169,061 94,230 94,230 188,460 188,460 188,460 R 2 0.567 0.752 0.  906
906 0.895 0.896 0.958 0.959 Bank controls ✓ ✓ ✓ ✓ ✓ ✓ ✓ Bank*County FE ✓ ✓ – – – – – Bank FE – – ✓ ✓ – – – Bank*Sec FE – – – – ✓ ✓ ✓ Time FE T C*T T T T B*T B*T + L*T . (1)
. (2)
. (3)
. (4)
. 
(5)
. (6)
. (7)
. Зам.вар.:
. журнал (амт HMDA)
. незащищенный
. защищенный
. лог(амт)
. Stress tested –0.359*** –0.267*** –0.125* –0.358*** –0.053 (0.088) (0,094) (0,075) (0,074) (0,047) проверено 9084 0589 –0.377*** –0.377*** –0.421*** (0.092) (0.092) ( 0.096) Observations 169,061 169,061 94,230 94,230 188,460 188,460 188,460 R 2 0.  567
567 0.752 0.906 0.895 0.896 0.958 0.959 Bank controls ✓ ✓ ✓ ✓ ✓ ✓ ✓ Банк*округ FE ✓ ✓ — — — — — 9 898
8
88898888888888888888888888888888888888888888 гг.0589 – ✓ ✓ – – – Bank*Sec FE – – – – ✓ ✓ ✓ ВРЕМЯ FE T C*T T T T B*T B*T+L*T B*T+L*T 4999 9.  4999
4999 9.
Открыть в новой вкладке  Обеспеченное и необеспеченное кредитование следует той же тенденции до рецессии. На панели (b) показано, что сокращение обеспеченного кредитования малого бизнеса приводит к сильному падению его доли в общем объеме кредитования малого бизнеса для банков, прошедших стресс-тестирование (синяя сплошная линия). Для банков, не прошедших стресс-тестирование (серая пунктирная линия), доля остается стабильной и близкой к докризисному уровню. До 2009 г. различий между группами не наблюдалось..
Обеспеченное и необеспеченное кредитование следует той же тенденции до рецессии. На панели (b) показано, что сокращение обеспеченного кредитования малого бизнеса приводит к сильному падению его доли в общем объеме кредитования малого бизнеса для банков, прошедших стресс-тестирование (синяя сплошная линия). Для банков, не прошедших стресс-тестирование (серая пунктирная линия), доля остается стабильной и близкой к докризисному уровню. До 2009 г. различий между группами не наблюдалось..
 Следовательно, коэффициент δ 3 указывает, сокращает ли банк обеспеченные кредиты в большей или меньшей степени, чем необеспеченные кредиты. θb,l обозначают фиксированные эффекты типа банка*кредита. τt2 — это либо год, банк*год, либо банк*год и тип кредита*год с фиксированными эффектами. Контроль фиксированных эффектов банк*год для всех наблюдаемых и ненаблюдаемых изменяющихся во времени характеристик банка. Фиксированные эффекты типа кредита*года дополнительно контролируют факторы, влияющие на обеспеченные и необеспеченные кредиты по-разному во всех банках с течением времени. Стандартные ошибки группируются на уровне BHC.
Следовательно, коэффициент δ 3 указывает, сокращает ли банк обеспеченные кредиты в большей или меньшей степени, чем необеспеченные кредиты. θb,l обозначают фиксированные эффекты типа банка*кредита. τt2 — это либо год, банк*год, либо банк*год и тип кредита*год с фиксированными эффектами. Контроль фиксированных эффектов банк*год для всех наблюдаемых и ненаблюдаемых изменяющихся во времени характеристик банка. Фиксированные эффекты типа кредита*года дополнительно контролируют факторы, влияющие на обеспеченные и необеспеченные кредиты по-разному во всех банках с течением времени. Стандартные ошибки группируются на уровне BHC. Коэффициент значим на уровне 10%. В столбце (4) в качестве зависимой переменной используется логарифмическое обеспеченное кредитование малого бизнеса и показано относительное снижение на 35,8% для банков, прошедших стресс-тестирование, то есть в три раза больше, чем у необеспеченного аналога.
Коэффициент значим на уровне 10%. В столбце (4) в качестве зависимой переменной используется логарифмическое обеспеченное кредитование малого бизнеса и показано относительное снижение на 35,8% для банков, прошедших стресс-тестирование, то есть в три раза больше, чем у необеспеченного аналога. 3.2 Воздействие округа и предпринимательство
 Рисунок 2, панель (а), показывает, что молодые фирмы (синяя сплошная линия) столкнулись с 30-процентным сокращением валового создания рабочих мест во время недавнего кризиса, падение по величине аналогично старым фирмам (черная пунктирная линия). С тех пор создание рабочих мест старыми фирмами почти вернулось к докризисному уровню, а молодые фирмы не восстановились. Панель (b) разделяет округа на округа с экспозицией в верхнем («высоком») и нижнем («низком») терциле. Занятость снижается в одинаковой степени в обеих группах во время кризиса. Тем не менее, с года первого раунда стресс-тестов в 2009 г.далее в округах с высоким уровнем воздействия наблюдается дальнейшее снижение, в то время как округа с низким уровнем воздействия вступают на путь восстановления.
Рисунок 2, панель (а), показывает, что молодые фирмы (синяя сплошная линия) столкнулись с 30-процентным сокращением валового создания рабочих мест во время недавнего кризиса, падение по величине аналогично старым фирмам (черная пунктирная линия). С тех пор создание рабочих мест старыми фирмами почти вернулось к докризисному уровню, а молодые фирмы не восстановились. Панель (b) разделяет округа на округа с экспозицией в верхнем («высоком») и нижнем («низком») терциле. Занятость снижается в одинаковой степени в обеих группах во время кризиса. Тем не менее, с года первого раунда стресс-тестов в 2009 г.далее в округах с высоким уровнем воздействия наблюдается дальнейшее снижение, в то время как округа с низким уровнем воздействия вступают на путь восстановления. Ряды нормированы по их докризисному пику ( Источник : Таблицы данных о характеристиках фирм Census BDS). ( б ) Эволюция логарифмической занятости среди фирм возрастом 0–1 год для округов в верхней (синяя сплошная линия) и нижней (черная пунктирная линия) терцилях округа, подвергающихся стресс-тестированным банкам. Оба ряда нормализованы к 100 в 2007 г.
Ряды нормированы по их докризисному пику ( Источник : Таблицы данных о характеристиках фирм Census BDS). ( б ) Эволюция логарифмической занятости среди фирм возрастом 0–1 год для округов в верхней (синяя сплошная линия) и нижней (черная пунктирная линия) терцилях округа, подвергающихся стресс-тестированным банкам. Оба ряда нормализованы к 100 в 2007 г. Стандартные ошибки группируются на уровне округов. Если γc<0, то в округах с более высоким докризисным риском воздействия банков, прошедших стресс-тестирование, наблюдается более сильное снижение переменных результатов, чем в округах с низким уровнем воздействия в течение периода стресс-тестирования.
Стандартные ошибки группируются на уровне округов. Если γc<0, то в округах с более высоким докризисным риском воздействия банков, прошедших стресс-тестирование, наблюдается более сильное снижение переменных результатов, чем в округах с низким уровнем воздействия в течение периода стресс-тестирования. собственный капиталi обозначает долю молодых фирм в отрасли i , которые используют финансирование собственного капитала для расширения операций, как определено в уравнении (2). Основной процентный коэффициент ( γ 7 ) показывает, наблюдается ли в округах с более высоким риском более сильное снижение важности молодых фирм или заработной платы (по сравнению с округами с низким уровнем воздействия) в отраслях, которые больше полагаются на финансирование собственного капитала.
собственный капиталi обозначает долю молодых фирм в отрасли i , которые используют финансирование собственного капитала для расширения операций, как определено в уравнении (2). Основной процентный коэффициент ( γ 7 ) показывает, наблюдается ли в округах с более высоким риском более сильное снижение важности молодых фирм или заработной платы (по сравнению с округами с низким уровнем воздействия) в отраслях, которые больше полагаются на финансирование собственного капитала. Я преодолел эту проблему в уравнении (7), включив гранулярные фиксированные эффекты. Во-первых, фиксированные эффекты округа*отрасли (θc,i) используют вариации внутри одной и той же комбинации «страна-отрасль» с течением времени и контролируют ненаблюдаемую и неизменную во времени неоднородность округа и отрасли (например, чувствительность к деловому циклу или важность отрасль в округе). Во-вторых, фиксированные эффекты округа*времени (τc,t) контролируют ненаблюдаемые во времени характеристики округа (такие как цены на жилье, безработица или спрос на кредит). В-третьих, фиксированные эффекты отрасли*времени (τi,t) поглощают изменяющиеся во времени шоки, характерные для отраслей с двузначным числом, например, долгосрочный спад в обрабатывающей промышленности. После поглощения изменений в характеристиках округа и отрасли оставшаяся вариация, вероятно, отражает изменения в предложении кредита.
Я преодолел эту проблему в уравнении (7), включив гранулярные фиксированные эффекты. Во-первых, фиксированные эффекты округа*отрасли (θc,i) используют вариации внутри одной и той же комбинации «страна-отрасль» с течением времени и контролируют ненаблюдаемую и неизменную во времени неоднородность округа и отрасли (например, чувствительность к деловому циклу или важность отрасль в округе). Во-вторых, фиксированные эффекты округа*времени (τc,t) контролируют ненаблюдаемые во времени характеристики округа (такие как цены на жилье, безработица или спрос на кредит). В-третьих, фиксированные эффекты отрасли*времени (τi,t) поглощают изменяющиеся во времени шоки, характерные для отраслей с двузначным числом, например, долгосрочный спад в обрабатывающей промышленности. После поглощения изменений в характеристиках округа и отрасли оставшаяся вариация, вероятно, отражает изменения в предложении кредита. Детализированные фиксированные эффекты, изменяющиеся во времени, уменьшают опасения по поводу выбора и ненаблюдаемости. Тем не менее, если смешанные факторы на уровне округа систематически изменяются в зависимости от интенсивности собственного капитала отраслей, они будут искажать коэффициенты. Таким образом, я разрабатываю и IV на основе депозитов, предсказанных с помощью гравитационной модели банковского расширения (Goetz, Laeven, and Levine, 2013, 2016) и индекса межгосударственного банковского дерегулирования (Rice and Strahan, 2010). Я оцениваю следующее уравнение «нулевой стадии»:
Детализированные фиксированные эффекты, изменяющиеся во времени, уменьшают опасения по поводу выбора и ненаблюдаемости. Тем не менее, если смешанные факторы на уровне округа систематически изменяются в зависимости от интенсивности собственного капитала отраслей, они будут искажать коэффициенты. Таким образом, я разрабатываю и IV на основе депозитов, предсказанных с помощью гравитационной модели банковского расширения (Goetz, Laeven, and Levine, 2013, 2016) и индекса межгосударственного банковского дерегулирования (Rice and Strahan, 2010). Я оцениваю следующее уравнение «нулевой стадии»: Затем я прогнозирую долю депозитов для каждой комбинации банка и округа на основе расстояния и размера рынка. Я устанавливаю отрицательные предсказанные значения равными нулю.
Затем я прогнозирую долю депозитов для каждой комбинации банка и округа на основе расстояния и размера рынка. Я устанавливаю отрицательные предсказанные значения равными нулю. Учет ненаблюдаемых характеристик существенно не влияет на процентный коэффициент, предполагая, что влияние расстояния на местные депозиты ортогональны наблюдаемым и ненаблюдаемым характеристикам дома и принимающего округа.
Учет ненаблюдаемых характеристик существенно не влияет на процентный коэффициент, предполагая, что влияние расстояния на местные депозиты ортогональны наблюдаемым и ненаблюдаемым характеристикам дома и принимающего округа. Столбец (5) использует различия между банками, расположенными в одном и том же штате, которые кредитуют один и тот же округ. Значения в скобках обозначают стандартные ошибки, сгруппированные в округе проживания. Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1.
Столбец (5) использует различия между банками, расположенными в одном и том же штате, которые кредитуют один и тот же округ. Значения в скобках обозначают стандартные ошибки, сгруппированные в округе проживания. Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. Зам.вар.:
. логит
. депозитная доля
. log(1+distance) –0.960*** –0.136*** –0.138*** –0.138*** –0.159*** (0.006) (0.004) (0.003) (0.003) (0.002) log(population ratio) 0.  267***
267*** 0.003 –0.008** (0,009) (0,003) (0.003) Observations 27,601 27,601 27,470 27,105 22,619 R 2 – 0.729 0.785 0.830 0,850 Графство графства FE — — ✓ ✓ — — 988 ✓ — 78888888888888888888 гг.0589 – – – ✓ ✓ Home State*Host County FE – – – – ✓ . (1)
. (2)
.
(3)
. (4)
. (5)
. отд.вар.:
. логит
. депозитная доля
. log (1+расстояние) –0,960 *** –0,136 *** –0,138 *** –0,1388888 8888 8888 8888 8888 8888 8888 8888 8888 8888 8888 8888 8888 888 8888 888 8888888 **0588 **0588 –0,138 *** **0588 **0588 –0,138 *** 9058 8888888*. (0,006) (0,004) (0,003) (0,003) (0,002) log(доля населения) 9 0.267*** 0.003 –0.008** (0.009) (0.003) (0.003) Observations 27,601 27,601 27,470 27,105 22,619 R 2 – 0.  729
729 0.785 0.830 0.850 Host County FE – – ✓ ✓ – Home County FE – – – ✓ ✓ Home State* Принимающий округ FE – – – – ✓  В столбце (1) используется дробная логит-модель. Столбцы (2)–(4) добавляют фиксированные эффекты для учета ненаблюдаемых характеристик округов в головных офисах банков и округах филиалов. Столбец (5) использует различия между банками, расположенными в одном и том же штате, которые кредитуют один и тот же округ. Значения в скобках обозначают стандартные ошибки, сгруппированные в округе проживания. Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1.
В столбце (1) используется дробная логит-модель. Столбцы (2)–(4) добавляют фиксированные эффекты для учета ненаблюдаемых характеристик округов в головных офисах банков и округах филиалов. Столбец (5) использует различия между банками, расположенными в одном и том же штате, которые кредитуют один и тот же округ. Значения в скобках обозначают стандартные ошибки, сгруппированные в округе проживания. Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. Зам.вар.:
. логит
. депозитная доля
. log(1+distance) –0.960*** –0.136*** –0.138*** –0.138*** –0.  159***
159*** (0.006) (0.004) (0.003) (0.003) (0.002) log(population ratio) 0.267*** 0.003 –0.008** (0,009) (0,003) (0.003) Observations 27,601 27,601 27,470 27,105 22,619 R 2 – 0.729 0.785 0.830 0,850 Графство графства FE — — ✓ ✓ — — 988 ✓ — 78888888888888888888 гг.0589 – – – ✓ ✓ Home State*Host County FE – – – – ✓ . 
(1)
. (2)
. (3)
. (4)
. (5)
. отд.вар.:
. логит
. депозитная доля
. log (1+расстояние) –0,960 *** –0,136 *** –0,138 *** –0,1388888 8888 8888 8888 8888 8888 8888 8888 8888 8888 8888 8888 8888 888 8888 888 8888888 **0588 **0588 –0,138 *** **0588 **0588 –0,138 *** 9058 8888888*. (0,006) (0,004) (0,003) (0,003) (0,002) log(доля населения) 9 0.267*** 0.003 –0.008** (0.009) (0.003) (0.003) Observations 27,601 27,601 27,470 27,105 22,619 R 2 – 0.  729
729 0.785 0.830 0.850 Host County FE – – ✓ ✓ – Home County FE – – – ✓ ✓ Home State* Принимающий округ FE – – – – ✓  Для каждого штата я сначала строю годовой индекс, который находится в диапазоне от 0 до 4, чтобы отразить каждое измерение ограничений на ветвление на уровне штата, аналогично Célerier and Matray (2019).× дерегулирование × общий объем банковских депозитовb. На последнем этапе я вычисляю риск cIV в соответствии с уравнением (1), но на основе прогнозируемых отложенийc,bIV. Коэффициент регрессии фактического воздействия на прогнозируемое на уровне уезда значим на уровне 1% (см. Дополнительное приложение). 11
Для каждого штата я сначала строю годовой индекс, который находится в диапазоне от 0 до 4, чтобы отразить каждое измерение ограничений на ветвление на уровне штата, аналогично Célerier and Matray (2019).× дерегулирование × общий объем банковских депозитовb. На последнем этапе я вычисляю риск cIV в соответствии с уравнением (1), но на основе прогнозируемых отложенийc,bIV. Коэффициент регрессии фактического воздействия на прогнозируемое на уровне уезда значим на уровне 1% (см. Дополнительное приложение). 11 
 12
12  Значения статистики Андерсона–Рубина F в столбцах (2), (6) и (7) равны 67,38, 53,00 и 44,27 соответственно. Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1.
Значения статистики Андерсона–Рубина F в столбцах (2), (6) и (7) равны 67,38, 53,00 и 44,27 соответственно. Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. Зам.вар.:
. лог(HMDA амт)
. лог(эмп молодой)
. . ОЛС
. IV
. ОЛС
. . . IV
. . воздействие ×1(2009-16) –0,267*** –0,859*** –0,045*** *** 0, 589 –0.  154***
154*** (0.040) (0.113) (0.014) (0.060) (0.021) home equity ×1 (2009-16) –2.419*** (0.147) exposure × home equity ×1(2009–16) –1.504*** –2.052*** –3.307*** (0.336) (0.338) (0.499) Observations 24,638 24,638 293,868 293,868 293,868 293,534 293,534 R 2 0.  778
778 – 0.809 0.810 0.817 – – County FE ✓ ✓ – – – – – County*Industry FE – – ✓ ✓ ✓ ✓ ✓ Time FE ✓ ✓ ✓ ✓ – ✓ – County*Time FE – – – – ✓ – ✓ Industry*Time FE – – – – ✓ – ✓ . (1)
. (2)
. (3)
. 
(4)
. (5)
. (6)
. (7)
. Зам.вар.:
. лог(HMDA амт)
. лог(эмп молодой)
. . ОЛС
. IV
. ОЛС
. . . IV
. . Экспозиция × 1 (2009-16) –0,267 *** –0,859 *** –0.045 *** .2068 888888888888888888888888 гг. (0.040) (0.113) (0.014) (0.060) (0.021) home equity ×1(2009-16) –2.419*** (0.  147)
147) exposure × home equity ×1(2009–16) –1.504*** –2.052*** –3.307*** (0.336) (0.338) (0.499) Observations 24,638 24,638 293,868 293,868 293,868 293,534 293,534 R 2 0.778 – 0.809 0.810 0.817 – – County FE ✓ ✓ – – – – – County*Industry FE – – ✓ ✓ ✓ ✓ ✓ Time FE ✓ ✓ ✓ ✓ – ✓ – County*Time FE – – – – ✓ – ✓ Промышленность*Время FE — — — — ✓ — Iла 98 8 8 8 8 8 89898 8
8888 — ✓ — Iла
Открыть в новой вкладке IX 1679 = MDCLXXVIII 
 Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1.
Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. Зам.вар.:
. лог(HMDA амт)
. лог(эмп молодой)
. . ОЛС
. IV
. ОЛС
. . . IV
. . Экспозиция × 1 (2009-16) –0,267 *** –0,859 *** –0,045 *** 9058 8.2068888888888888888888888888 гг. 
(0.040) (0.113) (0.014) (0.060) (0.021) home equity ×1(2009-16) –2.419*** (0.147) exposure × home equity ×1(2009–16) –1.504*** –2.052*** –3.307*** (0.336) (0.338) (0.499) Observations 24,638 24,638 293,868 293,868 293,868 293,534 293,534 R 2 0.  778
778 – 0.809 0,810 0,817 — — округ FE ✓ ✓ — ✓ — ✓ — ✓ — ✓ — ✓ — ✓ — .0589 – – – County*Industry FE – – ✓ ✓ ✓ ✓ ✓ Time FE ✓ ✓ ✓ ✓ – ✓ – County*Time FE – – – – ✓ – ✓ Industry*Time FE – – – – ✓ – ✓ . 
(1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. отд.вар.:
. лог(HMDA амт)
. лог(эмп молодой)
. . ОЛС
. IV
. ОЛС
. . . IV
. . экспозиция ×1 (2009 г.-16) –0.267*** –0.859*** –0.045*** 0.206*** –0.154*** (0.040) (0.113) (0.014) (0.060) (0.021) home equity ×1(2009-16) –2.  419***
419*** (0.147) exposure × home equity ×1(2009–16) –1.504*** –2.052*** –3.307*** (0.336) (0.338) (0.499) Observations 24,638 24,638 293,868 293,868 293,868 293,534 293,534 R 2 0.778 – 0.809 0.810 0.817 – – округа FE ✓ ✓ — — — — — — — — .  0589
0589 – – ✓ ✓ ✓ ✓ ✓ Time FE ✓ ✓ ✓ ✓ – ✓ – County*Time FE – – – – ✓ – ✓ Industry*Time FE – – – – ✓ – ✓  Столбец (4) поглощает общие шоки через фиксированные годовые эффекты, а столбец (5) добавляет детализированные данные округа*время и отрасль*фиксированное время. Коэффициент при тройном члене взаимодействия является отрицательным и значимым: снижение занятости молодых фирм сильнее в отраслях с более высокой долей фирм, использующих собственный капитал для открытия или расширения операций. Включение фиксированных эффектов для контроля эффектов спроса не меняет знака или значения процентного коэффициента. Однако коэффициент увеличивается по величине, что говорит о том, что округа с более высокой подверженностью риску имеют более сильные фундаментальные показатели.
Столбец (4) поглощает общие шоки через фиксированные годовые эффекты, а столбец (5) добавляет детализированные данные округа*время и отрасль*фиксированное время. Коэффициент при тройном члене взаимодействия является отрицательным и значимым: снижение занятости молодых фирм сильнее в отраслях с более высокой долей фирм, использующих собственный капитал для открытия или расширения операций. Включение фиксированных эффектов для контроля эффектов спроса не меняет знака или значения процентного коэффициента. Однако коэффициент увеличивается по величине, что говорит о том, что округа с более высокой подверженностью риску имеют более сильные фундаментальные показатели. В отраслях с интенсивным использованием собственного капитала в столбце (7) относительное снижение составляет 11%. В соответствии со спецификациями с фиксированными эффектами увеличение размера коэффициента может свидетельствовать о том, что в округах с высоким уровнем воздействия более сильные фундаментальные показатели. Это может также отражать смещение затухания в спецификации OLS. Объясняющая переменная Воздействие является косвенным показателем доли на местном рынке банков, прошедших стресс-тестирование, и может быть измерено с ошибкой, что приведет к смещению оценок OLS в сторону нуля. Как показывают Pancost and Schaller (2020), IV могут помочь преодолеть смещение затухания, возникающее из-за ошибки измерения независимой переменной. В заключение в Таблице IV показано, что кредитование под залог жилья и предпринимательство, связанные с бизнесом, снижаются в затронутых округах.
В отраслях с интенсивным использованием собственного капитала в столбце (7) относительное снижение составляет 11%. В соответствии со спецификациями с фиксированными эффектами увеличение размера коэффициента может свидетельствовать о том, что в округах с высоким уровнем воздействия более сильные фундаментальные показатели. Это может также отражать смещение затухания в спецификации OLS. Объясняющая переменная Воздействие является косвенным показателем доли на местном рынке банков, прошедших стресс-тестирование, и может быть измерено с ошибкой, что приведет к смещению оценок OLS в сторону нуля. Как показывают Pancost and Schaller (2020), IV могут помочь преодолеть смещение затухания, возникающее из-за ошибки измерения независимой переменной. В заключение в Таблице IV показано, что кредитование под залог жилья и предпринимательство, связанные с бизнесом, снижаются в затронутых округах. 3.3 Инновации и производительность
 В этом разделе анализируется, способствует ли спад предпринимательства из-за подверженности банкам, прошедшим стресс-тестирование, замедлению посткризисных инноваций и роста.
В этом разделе анализируется, способствует ли спад предпринимательства из-за подверженности банкам, прошедшим стресс-тестирование, замедлению посткризисных инноваций и роста.
 Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1.
Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. . . . . цит. взвешенный
. Зам.вар.:
. бревно(патенты молодые)
. журнал(патенты старые)
. . ОЛС
. IV
. ОЛС
. IV
. Экспозиция × 1 (2009-16) –0,116 *** –0,150 *** –0,133 *** 9058 –0,2548 *** 888 –0588 **088 –0544 **088 –0548 –0,2548 –0548 –0,2548 –0588 –0588 –0588* 0,044 0,070 (0,025) (0,027) (0,031) (0,041) 9889 (0,041) 9889 (0,041) 9 9889 (0,041) 9 9889 (0,041) (0,031) (0,041) (0,031) (0,041) (0,031). 
Observations 91,999 91,999 91,999 91,999 91,906 91,999 91,906 R 2 0.795 0.799 0.801 0.521 – 0.727 – County Controls – ✓ ✓ ✓ ✓ ✓ ✓ County*Industry FE ✓ ✓ ✓ ✓ ✓ ✓ ✓ Time FE ✓ ✓ – – – – – State*Time FE – – ✓ ✓ ✓ ✓ ✓ Промышленность*Время FE — — ✓ ✓ ✓ ✓ ✓ 9998 898 8 8 8 8
888
888
88889888 Iла
. 
(1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. . . . . цит. взвешенный
. Зам.вар.:
. бревно(патенты молодые)
. журнал(патенты старые)
. . ОЛС
. IV
. ОЛС
. IV
. Экспозиция × 1 (2009-16) –0,116 *** –0,150 *** –0,133 *** 9058 –0,2548 *** 888 –0588 **088 –0544 **088 –0548 –0,2548 –0548 –0,2548 –0588 –0588 –0588* 0.044 0.  070
070 (0.025) (0.027) (0.031) (0.041) (0.094) (0.030) (0.110) Observations 91,999 91,999 91,999 91,999 91,906 91,999 91,906 R 2 0.795 0.799 0.801 0.521 – 0.727 – County Controls — ✓ ✓ ✓ ✓ ✓ ✓ 888888888888 гг.0589 ✓ ✓ ✓ ✓ ✓ ✓ ✓ Time FE ✓ ✓ – – – – – State*Time FE – – ✓ ✓ ✓ ✓ ✓ Industry*Time FE – – ✓ ✓ ✓ ✓ ✓ 
 Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1.
Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. . . . . цит. взвешенный
. Зам.вар.:
. бревно(патенты молодые)
. журнал(патенты старые)
. . ОЛС
. IV
. ОЛС
. IV
. Экспозиция × 1 (2009-16) –0,116 *** –0,150 *** –0,133 *** 9058 –0,2548 *** 888 –0588 **088 –0544 **088 –0548 –0,2548 –0548 –0,2548 –0588 –0588 –0588* 0,044 0,070 (0,025) (0,027) (0,031) (0,041) 9889 (0,041) 9889 (0,041) 9 9889 (0,041) 9 9889 (0,041) (0,031) (0,041) (0,031) (0,041) (0,031). 
Observations 91,999 91,999 91,999 91,999 91,906 91,999 91,906 R 2 0.795 0.799 0.801 0.521 – 0.727 – County Controls – ✓ ✓ ✓ ✓ ✓ ✓ County*Industry FE ✓ ✓ ✓ ✓ ✓ ✓ ✓ Time FE ✓ ✓ – – – – – State*Time FE – – ✓ ✓ ✓ ✓ ✓ Промышленность*Время FE — — ✓ ✓ ✓ ✓ ✓ 9998 898 8 8 8 8
888
888
88889888 Iла
. 
(1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. . . . . цит. взвешенный
. Зам.вар.:
. бревно(патенты молодые)
. журнал(патенты старые)
. . ОЛС
. IV
. ОЛС
. IV
. Экспозиция × 1 (2009-16) –0,116 *** –0,150 *** –0,133 *** 9058 –0,2548 *** 888 –0588 **088 –0544 **088 –0548 –0,2548 –0548 –0,2548 –0588 –0588 –0588* 0.044 0.  070
070 (0.025) (0.027) (0.031) (0.041) (0.094) (0.030) (0.110) Observations 91,999 91,999 91,999 91,999 91,906 91,999 91,906 R 2 0.795 0.799 0.801 0.521 – 0.727 – County Controls — ✓ ✓ ✓ ✓ ✓ ✓ 888888888888 гг.0589 ✓ ✓ ✓ ✓ ✓ ✓ ✓ Time FE ✓ ✓ – – – – – State*Time FE – – ✓ ✓ ✓ ✓ ✓ Industry*Time FE – – ✓ ✓ ✓ ✓ ✓  Столбец (4) показывает, что влияние воздействия на патенты сильнее, когда я взвешиваю патенты по цитированию, то есть когда я учитываю их важность. По сравнению со столбцом (3) размер эффекта почти удваивается, что позволяет предположить, что фирмы в округах, которые производят широко цитируемые патенты, особенно страдают. Этот вывод подтверждается в колонке (5), которая учитывает фактическое воздействие с прогнозируемым воздействием: перемещение округа с 25-го на 75-й процентиль с точки зрения воздействия приводит к относительному снижению количества патентов, взвешенных по цитированию, на 17,2%. Наконец, столбцы (6) и (7) повторяют столбцы (4) и (5), но используют журнал взвешенных патентов старых фирм в качестве зависимой переменной. Отмечается незначительное и слабо положительное влияние воздействия на патенты старых фирм.
Столбец (4) показывает, что влияние воздействия на патенты сильнее, когда я взвешиваю патенты по цитированию, то есть когда я учитываю их важность. По сравнению со столбцом (3) размер эффекта почти удваивается, что позволяет предположить, что фирмы в округах, которые производят широко цитируемые патенты, особенно страдают. Этот вывод подтверждается в колонке (5), которая учитывает фактическое воздействие с прогнозируемым воздействием: перемещение округа с 25-го на 75-й процентиль с точки зрения воздействия приводит к относительному снижению количества патентов, взвешенных по цитированию, на 17,2%. Наконец, столбцы (6) и (7) повторяют столбцы (4) и (5), но используют журнал взвешенных патентов старых фирм в качестве зависимой переменной. Отмечается незначительное и слабо положительное влияние воздействия на патенты старых фирм. Этот вывод может свидетельствовать о том, что даже если банки, прошедшие стресс-тестирование, перешли к кредитованию старых фирм, это не увеличило их патентование в той же степени, в какой сократилось патентование молодых фирм. Поскольку на долю молодых фирм приходится около четверти всех патентных заявок, снижение их патентной активности на 17% означает сокращение общего количества патентов примерно на 4%.
Этот вывод может свидетельствовать о том, что даже если банки, прошедшие стресс-тестирование, перешли к кредитованию старых фирм, это не увеличило их патентование в той же степени, в какой сократилось патентование молодых фирм. Поскольку на долю молодых фирм приходится около четверти всех патентных заявок, снижение их патентной активности на 17% означает сокращение общего количества патентов примерно на 4%. Этот результат устойчив к включению фиксированных эффектов округа*время и отрасли*время в столбце (3), а также при использовании инструментального воздействия в столбцах (4) и (5).
Этот результат устойчив к включению фиксированных эффектов округа*время и отрасли*время в столбце (3), а также при использовании инструментального воздействия в столбцах (4) и (5). В столбцах (4) и (5) представлены данные о воздействии на округа с прогнозируемым воздействием, основанным на гравитационной модели. Ценности Андерсона-Рубина F — статистика в столбцах (4) и (5) равна 14,02 и 15,65 соответственно. Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1.
В столбцах (4) и (5) представлены данные о воздействии на округа с прогнозируемым воздействием, основанным на гравитационной модели. Ценности Андерсона-Рубина F — статистика в столбцах (4) и (5) равна 14,02 и 15,65 соответственно. Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. отл.вар.:
. журнал(средняя заработная плата)
. . ОЛС
. IV
. exposure ×1(2009–16) –0.016* 0.276*** –0.  052***
052*** (0.009) (0.050) (0,014) home equity ×1(2009–16) 1.149*** (0.121) exposure × home equity ×1(2009–16) –1.623*** –1.493*** –0.926** (0.257) (0.260) ( 0,390) Observations 293,868 293,868 293,868 293,534 293,534 R 2 0.710 0.710 0.723 – – County *Индустрия FE ✓ ✓ ✓ ✓ ✓ время Fe Iла 8 FE Iла 8888 8888 8888 8888 8888888 8888888. 
– ✓ – County*Time FE – – ✓ – ✓ Industry*Time FE – – ✓ – ✓ . (1)
. (2)
. (3)
. (4)
. (5)
. Зам.вар.:
. журнал(средняя заработная плата)
. . ОЛС
. IV
. exposure ×1(2009–16) –0.016* 0.276*** –0.052*** (0.009) (0.050) (0.014) home equity ×1(2009–16) 1.  149***
149*** (0.121) exposure × home equity ×1(2009–16) –1.623*** –1.493*** –0.926** (0.257) ( 0,260) (0.390) Observations 293,868 293,868 293,868 293,534 293,534 R 2 0.710 0.710 0.723 – — графство*промышленность FE ✓ ✓ ✓ ✓ ✓ 88888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888880589 ✓ ✓ – ✓ – County*Time FE – – ✓ – ✓ Industry*Time FE – – ✓ – ✓ 
 Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1.
Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. отл.вар.:
. журнал(средняя заработная плата)
. . ОЛС
. IV
. exposure ×1(2009–16) –0.016* 0.276*** –0.052*** (0.009) (0.050) (0,014) home equity ×1(2009–16) 1.149*** (0.  121)
121) exposure × home equity ×1(2009–16) –1.623*** –1.493*** –0.926** (0.257) (0.260) ( 0,390) Observations 293,868 293,868 293,868 293,534 293,534 R 2 0.710 0.710 0.723 – – County *Индустрия FE ✓ ✓ ✓ ✓ ✓ время Fe Iла 8 FE Iла 8888 8888 8888 8888 8888888 8888888. – ✓ – County*Time FE – – ✓ – ✓ Industry*Time FE – – ✓ – ✓ . 
(1)
. (2)
. (3)
. (4)
. (5)
. Зам.вар.:
. журнал(средняя заработная плата)
. . ОЛС
. IV
. exposure ×1(2009–16) –0.016* 0.276*** –0.052*** (0.009) (0.050) (0.014) home equity ×1(2009–16) 1.149*** (0.121) exposure × home equity ×1(2009–16) –1.623*** –1.  493***
493*** –0.926** (0.257) ( 0,260) (0.390) Observations 293,868 293,868 293,868 293,534 293,534 R 2 0.710 0.710 0.723 – — графство*промышленность FE ✓ ✓ ✓ ✓ ✓ 88888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888880589 ✓ ✓ – ✓ – County*Time FE – – ✓ – ✓ Industry*Time FE – – ✓ – ✓  Аналогичная картина эволюции занятости и производительности в подверженных риску странах может свидетельствовать о том, что нехватка молодых фирм является ключевым фактором замедления экономического роста. Тем не менее, важное предостережение заключается в том, что стресс-тесты могут повлиять на производительность не только через финансирование стартапов в условиях общего равновесия. Это предостережение необходимо иметь в виду при интерпретации величины коэффициентов.
Аналогичная картина эволюции занятости и производительности в подверженных риску странах может свидетельствовать о том, что нехватка молодых фирм является ключевым фактором замедления экономического роста. Тем не менее, важное предостережение заключается в том, что стресс-тесты могут повлиять на производительность не только через финансирование стартапов в условиях общего равновесия. Это предостережение необходимо иметь в виду при интерпретации величины коэффициентов. 4. Надежность
4.1 Надежность банка
 Стресс-тесты: банки выдают меньше кредитов вместо того, чтобы снижать среднюю сумму.
Стресс-тесты: банки выдают меньше кредитов вместо того, чтобы снижать среднюю сумму. Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне банковской холдинговой компании. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1.
Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне банковской холдинговой компании. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. (8)
. (9)
. (10)
. (11)
. . . . >20 миллиардов
. Без повтора
. . . . . . . . Зам.вар.:
. журнал(номер)
. 
журнал (среднее)
. журнал (амт HMDA)
. Δ HMDA в т.ч.
. Стресс-тест –0,204** –0,063 –0,278*** –0,2589** 9 9 0.385** (0.081) (0.049) (0.100) (0.127) (0.359) (0.187) Stress tested × county risk –0.595 –0.544*** –0.398** –0.428*** (0.439) (0.162) (0.190) (0.158) Stress-tested exposure –0.  114**
114** –0.043 (0.046) (0.056) Stress-tested exposure × county risk –0.079*** –0.059** (0.020) (0.021) Observations 169,061 169,061 131,295 83,735 117,870 112,815 111,396 111,396 21,344 21,344 21,344 R 2 0.713 0.  803
803 0.867 0.737 0.868 0.948 0.532 0.835 0.347 0.348 0.535 Bank Controls ✓ ✓ ✓ ✓ ✓ – ✓ – ✓ ✓ – Bank*County FE ✓ ✓ ✓ ✓ ✓ ✓ – – – – – County*Time FE ✓ ✓ ✓ ✓ ✓ – ✓ ✓ ✓ ✓ ✓ Bank*Time FE – – – – – ✓ – ✓ – – ✓ . 
(1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. (8)
. (9)
. (10)
. (11)
. . . . >20 миллиардов
. Без повтора
. . . . . . . . Зам.вар.:
. журнал(номер)
. журнал (среднее)
. журнал (амт HMDA)
. Δ HMDA в т.ч.
. Stress tested –0.  204**
204** –0.063 –0.278*** –0.289** 0.188 0.385** (0,081) (0,049) (0.100) (0.127) (0.359) (0.187) Stress tested × county risk –0.595 –0.544*** –0.398** –0.428*** (0.439) (0.162) (0.190) (0.158) Stress-tested exposure –0.  114 **
114 ** –0.043 (0.046) (0.056) Stress-tested exposure × county risk –0.079*** –0.059** (0.020) (0.021) Observations 169,061 169,061 131,295 83,735 117,870 112,815 111,396 111,396 21,344 21,344 21,344 R 2 0.713 0.  803
803 0.867 0.737 0.868 0.948 0.532 0.835 0.347 0.348 0.535 Bank Controls ✓ ✓ ✓ ✓ ✓ – ✓ – ✓ ✓ – Bank*County FE ✓ ✓ ✓ ✓ ✓ ✓ – – – – – County*Time FE ✓ ✓ ✓ ✓ ✓ – ✓ ✓ ✓ ✓ ✓ Bank*Time FE – – – – – ✓ – ✓ – – ✓ 
 Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1.
Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. (8)
. (9)
. (10)
. (11)
. . . . >20 миллиардов
. Без повтора
. . . . . . . . Зам.вар.:
. журнал(номер)
. журнал (среднее)
. журнал (амт HMDA)
. Δ HMDA в т.  ч.
.
ч.
. Стресс-тест –0,204** –0,063 –0,278*** –0,2589** 9 9 0.385** (0.081) (0.049) (0.100) (0.127) (0.359) (0.187) Stress tested × county risk –0.595 –0.544*** –0.398** –0.428*** (0.439) (0.162) (0.190) (0.158) Stress-tested exposure –0.  114**
114** –0.043 (0.046) (0.056) Stress-tested exposure × county risk –0.079*** –0.059** (0.020) (0.021) Observations 169,061 169,061 131,295 83,735 117,870 112,815 111,396 111,396 21,344 21,344 21,344 R 2 0.713 0.  803
803 0.867 0.737 0.868 0.948 0.532 0.835 0.347 0.348 0.535 Bank Controls ✓ ✓ ✓ ✓ ✓ – ✓ – ✓ ✓ – Bank*County FE ✓ ✓ ✓ ✓ ✓ ✓ – – – – – County*Time FE ✓ ✓ ✓ ✓ ✓ – ✓ ✓ ✓ ✓ ✓ Bank*Time FE – – – – – ✓ – ✓ – – ✓ . 
(1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. (8)
. (9)
. (10)
. (11)
. . . . >20 миллиардов
. Без повтора
. . . . . . . . Зам.вар.:
. журнал(номер)
. журнал (среднее)
. журнал (амт HMDA)
. Δ HMDA в т.ч.
. Stress tested –0.  204**
204** –0.063 –0.278*** –0.289** 0.188 0.385** (0,081) (0,049) (0.100) (0.127) (0.359) (0.187) Stress tested × county risk –0.595 –0.544*** –0.398** –0.428*** (0.439) (0.162) (0.190) (0.158) Stress-tested exposure –0.  114 **
114 ** –0.043 (0.046) (0.056) Stress-tested exposure × county risk –0.079*** –0.059** (0.020) (0.021) Observations 169,061 169,061 131,295 83,735 117,870 112,815 111,396 111,396 21,344 21,344 21,344 R 2 0.713 0.  803
803 0.867 0.737 0.868 0.948 0.532 0.835 0.347 0.348 0.535 Bank Controls ✓ ✓ ✓ ✓ ✓ – ✓ – ✓ ✓ – Bank*County FE ✓ ✓ ✓ ✓ ✓ ✓ – – – – – County*Time FE ✓ ✓ ✓ ✓ ✓ – ✓ ✓ ✓ ✓ ✓ Bank*Time FE – – – – – ✓ – ✓ – – ✓  Чтобы сузить группу сравнения, столбец (3) ограничивает контрольную группу банками с совокупными активами не менее 2 миллиардов долларов США по состоянию на 2008 год. Процентный коэффициент остается почти идентичным с точки зрения знака, размера и значимости исходным результатам.
Чтобы сузить группу сравнения, столбец (3) ограничивает контрольную группу банками с совокупными активами не менее 2 миллиардов долларов США по состоянию на 2008 год. Процентный коэффициент остается почти идентичным с точки зрения знака, размера и значимости исходным результатам. Столбцы (5) и (6) показывают, что сокращение кредитования малого бизнеса под залог недвижимости особенно сильно проявляется в более рискованных округах. В то время как величины одинаковы в обоих столбцах, включение фиксированных эффектов берег*время для контроля ненаблюдаемых характеристик берега в столбце (6) повышает точность оценки.
Столбцы (5) и (6) показывают, что сокращение кредитования малого бизнеса под залог недвижимости особенно сильно проявляется в более рискованных округах. В то время как величины одинаковы в обоих столбцах, включение фиксированных эффектов берег*время для контроля ненаблюдаемых характеристик берега в столбце (6) повышает точность оценки. ).
). 4.2 Надежность округа
 В то время как фиксированные эффекты округа * года контролируют общие шоки для всех фирм в округе, изменения местных цен на недвижимость могут повлиять на отрасли в зависимости от интенсивности их собственного капитала. Например, если цены на жилье восстанавливались после Великой рецессии медленнее в округах с более высоким риском, пониженная стоимость залогового обеспечения снизит спрос на кредит в большей степени в отраслях, которые полагаются на собственный капитал. Кроме того, Миан, Суфи и Требби (2015) показывают, что докризисный бум цен на жилье и последовавший за ним спад оказали долгосрочное воздействие на домовладельцев и местную экономику.
В то время как фиксированные эффекты округа * года контролируют общие шоки для всех фирм в округе, изменения местных цен на недвижимость могут повлиять на отрасли в зависимости от интенсивности их собственного капитала. Например, если цены на жилье восстанавливались после Великой рецессии медленнее в округах с более высоким риском, пониженная стоимость залогового обеспечения снизит спрос на кредит в большей степени в отраслях, которые полагаются на собственный капитал. Кроме того, Миан, Суфи и Требби (2015) показывают, что докризисный бум цен на жилье и последовавший за ним спад оказали долгосрочное воздействие на домовладельцев и местную экономику. Учет доли собственников жилья по состоянию на 2010 г. в колонке (3) также не оказывает существенного влияния на процентный коэффициент. Столбец (4) включает взаимосвязь с одновременным ростом местных цен на жилье. Коэффициент воздействия не меняется статистически или экономически значимым образом, что позволяет предположить, что воздействие воздействия на занятость молодых фирм не объясняется потенциально более слабым восстановлением жилья. 16 Столбец (5) показывает, что воздействие воздействия на занятость молодых фирм остается значительным и весьма значимым в скачках со всеми переменными, связанными с жильем. Стабильность основного эффекта предполагает, что результаты не связаны с нарушением местного коллатерального канала и, следовательно, указывают на механизм, отличный от Bord, Ivashina и Taliaferro (2018). Вместо этого риск, вероятно, отражает падение предложения кредитов банками, прошедшими стресс-тестирование, которое не зависит от характеристик и динамики местных рынков жилья.
Учет доли собственников жилья по состоянию на 2010 г. в колонке (3) также не оказывает существенного влияния на процентный коэффициент. Столбец (4) включает взаимосвязь с одновременным ростом местных цен на жилье. Коэффициент воздействия не меняется статистически или экономически значимым образом, что позволяет предположить, что воздействие воздействия на занятость молодых фирм не объясняется потенциально более слабым восстановлением жилья. 16 Столбец (5) показывает, что воздействие воздействия на занятость молодых фирм остается значительным и весьма значимым в скачках со всеми переменными, связанными с жильем. Стабильность основного эффекта предполагает, что результаты не связаны с нарушением местного коллатерального канала и, следовательно, указывают на механизм, отличный от Bord, Ivashina и Taliaferro (2018). Вместо этого риск, вероятно, отражает падение предложения кредитов банками, прошедшими стресс-тестирование, которое не зависит от характеристик и динамики местных рынков жилья.
 Столбец (7) не включает округа с высокой долей рынка четырех крупнейших банков США. Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1.
Столбец (7) не включает округа с высокой долей рынка четырех крупнейших банков США. Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** p < 0,01, ** p < 0,05, * p < 0,1. . (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. . . . . . . . без верха4
. Зам.вар.:
. журнал (эмп молодой)
. Экспозиция × Home Equity × 1 (2009–16) –1,697 *** –1,415 *** –2.071 *** 9058 —–2. 9058 — 071 ***
071 *** –2.071 *** 9058 —. ** –1,897*** –2,525*** (0,349) (0,356) (0,351) (0,338) (0,367) (0,408) (0,629). –2.089*** –0.786 (0.411) (0.547) Δ House Price Индекс 07-10 × собственный капитал × 1 (2009 г.–16) 3.677*** 2.842*** (0.555) (0.722) Ownership 10 × home equity ×1(2–09-16) 0.005 0.005 (0.  010)
010) (0.010) Δ House Price Index × home equity ×1(2009–16) 3.173*** 3.206*** (0.251) (0.258) Top-4 exposure × home equity ×1(2009–16) –0.720 (0.933) Observations 276,889 287,127 287,314 286,847 276,833 293 868 145 586 Р 2 0,814 9,815890588 0.815 0.815 0.  814
814 0.815 0.676 County*Industry FE ✓ ✓ ✓ ✓ ✓ ✓ ✓ County*Time FE ✓ ✓ ✓ ✓ ✓ ✓ ✓ Industry*Time FE ✓ ✓ ✓ ✓ ✓ ✓ ✓ . (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. . . . . . . . без верха4
. Зам.  вар.:
.
вар.:
. журнал (эмп молодой)
. Экспозиция × Home Equity × 1 (2009–16) –1,697 *** –1,415 *** –2.071 *** 9058 —–2.071 *** 9058 — –2.071 *** 9058 —. ** –1,897*** –2.525*** (0.349) (0.356) (0.351) (0.338) (0.367) (0.408) (0.629) Δ House Price Index 00-07 × home equity ×1(2009–16) –2.089*** –0.786 (0.411) (0,547) Δ House Price Index 07-10 × home equity ×1(2009–16) 3.677*** 2.  842***
842*** (0.555) (0.722) Ownership 10 × home equity ×1(2–09-16) 0.005 0.005 (0.010) (0.010) Δ House Price Index × home equity ×1(2009–16) 3.173*** 3.206*** (0.251) (0.258) Top-4 exposure × home equity ×1(2009–16) –0.720 (0.  933)
933) Observations 276,889 287,127 287,314 286,847 276,833 293,868 145,586 R 2 0.814 0.815 0.815 0.815 0.814 0.815 0.676 County*Industry FE ✓ ✓ ✓ ✓ ✓ ✓ ✓ . Industry*Time FE ✓ ✓ ✓ ✓ ✓ ✓ ✓  риск означает докризисный риск округа перед банками, прошедшими стресс-тестирование, как определено в уравнении (1). Собственный капитал — это доля молодых фирм в каждой двузначной отрасли, которая использует финансирование собственного капитала для начала или расширения операций. 1 (2009 г.−16) — это фиктивная переменная со значением 1 за период с 2009 по 2016 год, то есть годы после введения стресс-тестов. ΔHPI 00−07 и ΔHPI 07−10 — изменения цен на окружные дома с 2000 по 2007 и с 2007 по 2010 годы; собственность 10 округа доля домовладельцев в 2010 году; Δ HPI – это годовой рост цен на окружное жилье. Темпы роста представляют собой логарифмические различия. top-4-exposition означает подверженность округов четырем крупнейшим банкам США с точки зрения совокупных активов по состоянию на 2007 год. Столбец (7) не включает округа с высокой долей рынка четырех крупнейших банков США. Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1.
риск означает докризисный риск округа перед банками, прошедшими стресс-тестирование, как определено в уравнении (1). Собственный капитал — это доля молодых фирм в каждой двузначной отрасли, которая использует финансирование собственного капитала для начала или расширения операций. 1 (2009 г.−16) — это фиктивная переменная со значением 1 за период с 2009 по 2016 год, то есть годы после введения стресс-тестов. ΔHPI 00−07 и ΔHPI 07−10 — изменения цен на окружные дома с 2000 по 2007 и с 2007 по 2010 годы; собственность 10 округа доля домовладельцев в 2010 году; Δ HPI – это годовой рост цен на окружное жилье. Темпы роста представляют собой логарифмические различия. top-4-exposition означает подверженность округов четырем крупнейшим банкам США с точки зрения совокупных активов по состоянию на 2007 год. Столбец (7) не включает округа с высокой долей рынка четырех крупнейших банков США. Значения в скобках обозначают стандартные ошибки, сгруппированные на уровне округов. Ключ: *** р < 0,01, ** р < 0,05, * р < 0,1.
. (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. . . . . . . . без верха4
. Зам.вар.:
. журнал (эмп молодой)
. Экспозиция × Home Equity × 1 (2009–16) –1,697 *** –1,415 *** –2.071 *** 9058 —–2.071 *** 9058 — –2.071 *** 9058 —. ** –1,897*** –2.525*** (0.349) (0.356) (0.351) (0.338) (0.  367)
367) (0.408) (0.629) Δ House Price Index 00-07 × home equity ×1(2009–16) –2.089*** –0.786 (0.411) (0,547) Δ House Price Index 07-10 × home equity ×1(2009–16) 3.677*** 2.842*** (0.555) (0.722) Ownership 10 × home equity ×1(2–09-16) 0.005 0.005 (0.010) (0.010) Δ House Price Index × home equity ×1(2009–16) 3.  173***
173*** 3.206*** (0.251) (0.258) Top-4 exposure × home equity ×1(2009–16) –0.720 (0.933) Observations 276,889 287,127 287,314 286,847 276,833 293,868 145,586 R 2 0.814 0.815 0.815 0.815 0.814 0.815 0.676 County*Industry FE ✓ ✓ ✓ ✓ ✓ ✓ ✓ . 
Industry*Time FE ✓ ✓ ✓ ✓ ✓ ✓ ✓ . (1)
. (2)
. (3)
. (4)
. (5)
. (6)
. (7)
. . . . . . . . без верха4
. Зам.вар.:
. журнал (эмп молодой)
. Подверженность кредиту × собственный капитал × 1 (2009–2016 годы) –1,697*** –1.415*** –2.071*** –2.116*** –1.405*** –1.  897***
897*** –2.525*** (0.349) (0.356) (0.351) (0.338) (0.367) (0.408) (0.629) Δ House Price Index 00-07 × home equity ×1(2009–16) –2,089*** –0,786 (0.411) (0.547) Δ House Price Index 07-10 × home equity ×1(2009–16) 3.677** * 2.842*** (0.555) (0.722) Ownership 10 × home equity ×1(2 –09-16) 0.005 0.005 (0.  010)
010) (0.010) Δ House Price Index × home equity ×1(2009–16) 3.173*** 3.206*** (0.251) (0.258) Top-4 exposure × home equity ×1(2009–16) –0.720 (0.933) Observations 276,889 287,127 287,314 286,847 276,833 293,868 145,586 R 2 0.814 0.815 0.815 0.  815
815 0.814 0.815 0.676 County*Industry FE ✓ ✓ ✓ ✓ ✓ ✓ ✓ *ВРЕМЯ FE 88888888888888 8888 гг. ✓ ✓ ✓ ✓ ✓ ✓ Industry*Time FE ✓ ✓ ✓ ✓ ✓ ✓ ✓  17
17 5. Заключение
 Более высокая экспозиция также снижает количество патентных заявок и производительность труда во время восстановления, отражая чрезмерное значение молодых фирм для совокупных инноваций и роста.
Более высокая экспозиция также снижает количество патентных заявок и производительность труда во время восстановления, отражая чрезмерное значение молодых фирм для совокупных инноваций и роста.

Дополнительные материалы
Сноски

 ), Коннолли (2018 г.) и Пьерет и Стери (2020 г.) используют данные о синдицированных кредитах, чтобы изучить, как стресс-тесты влияют на принятие банками рисков или кредитование. Дополнительные документы о требованиях к капиталу и стресс-тестах см. в Berrospide and Edge (2019), Granja and Leuz (2019) и Gropp et al. (2019).
), Коннолли (2018 г.) и Пьерет и Стери (2020 г.) используют данные о синдицированных кредитах, чтобы изучить, как стресс-тесты влияют на принятие банками рисков или кредитование. Дополнительные документы о требованиях к капиталу и стресс-тестах см. в Berrospide and Edge (2019), Granja and Leuz (2019) и Gropp et al. (2019). Однако регрессии используют различия в кредитовании разными банками одного и того же округа. Чтобы ошибочная классификация ссуд привела к искажению результатов, ее необходимо было бы систематически соотносить не с характеристиками на уровне округа, а с типом кредитора. Другими словами, заемщики, которые объединяются с банками, прошедшими стресс-тестирование, должны систематически с большей или меньшей вероятностью не брать кредиты от имени своей компании по сравнению с заемщиками из банков, не прошедших стресс-тестирование, проживающих в том же округе.
Однако регрессии используют различия в кредитовании разными банками одного и того же округа. Чтобы ошибочная классификация ссуд привела к искажению результатов, ее необходимо было бы систематически соотносить не с характеристиками на уровне округа, а с типом кредитора. Другими словами, заемщики, которые объединяются с банками, прошедшими стресс-тестирование, должны систематически с большей или меньшей вероятностью не брать кредиты от имени своей компании по сравнению с заемщиками из банков, не прошедших стресс-тестирование, проживающих в том же округе. Существуют значительные различия в подверженности округов в США, а также в отдельных штатах. В общей сложности 805 округов не подвержены рискам банков, прошедших стресс-тестирование. Среди неторгуемых (торгуемых) отраслей доля собственного капитала составляет в среднем 20% (17%). Отрасли с самой высокой интенсивностью собственного капитала — это производство, размещение и питание, а с самой низкой — образовательные и профессиональные, научные и технические услуги.
Существуют значительные различия в подверженности округов в США, а также в отдельных штатах. В общей сложности 805 округов не подвержены рискам банков, прошедших стресс-тестирование. Среди неторгуемых (торгуемых) отраслей доля собственного капитала составляет в среднем 20% (17%). Отрасли с самой высокой интенсивностью собственного капитала — это производство, размещение и питание, а с самой низкой — образовательные и профессиональные, научные и технические услуги. Таким образом, IV объясняет распределение банковских депозитов между штатами и внутри них и делает это в значительной степени независимо от характеристик округов.
Таким образом, IV объясняет распределение банковских депозитов между штатами и внутри них и делает это в значительной степени независимо от характеристик округов. Изменяющиеся во времени фиксированные эффекты на уровне МПК*год учитывают изменения в наблюдаемых и ненаблюдаемых различиях между отраслями, например патентная активность или рост доли непатентованных инноваций.
Изменяющиеся во времени фиксированные эффекты на уровне МПК*год учитывают изменения в наблюдаемых и ненаблюдаемых различиях между отраслями, например патентная активность или рост доли непатентованных инноваций. Тем не менее, мои результаты говорят об их выводах: более широкое присутствие четырех крупнейших банков оказывает негативное влияние на формирование фирм, но этот эффект связан со стресс-тестами.
Тем не менее, мои результаты говорят об их выводах: более широкое присутствие четырех крупнейших банков оказывает негативное влияние на формирование фирм, но этот эффект связан со стресс-тестами. References

 0013
0013



 0013
0013

13
13
 341
341 Рабочие документы BIS 711.
Рабочие документы BIS 711.
 Неопубликованный рабочий документ.
Неопубликованный рабочий документ.
Примечания автора
 Высказанные здесь взгляды принадлежат только авторам и не обязательно принадлежат Банку международных расчетов.
Высказанные здесь взгляды принадлежат только авторам и не обязательно принадлежат Банку международных расчетов. Дополнительные данные
Цитаты
Altmetric
Оповещения по электронной почте
Ссылки на статьи по телефону
Последний
Самые читаемые
Самые цитируемые
Тест профиля предпринимателя — узнайте, что вас мотивирует и движет.




 д. Самосознание увеличивает свои способности.
д. Самосознание увеличивает свои способности.
Римскими цифрами 1950: напишите цифры 1950 и 1963 римскими цифрами и разъясните
Как написать дату рождения (Год, Месяц, День) римскими цифрами?
Год (Арабскими цифрами) Год (Римскими цифрами) 2030 MMXXX 2029 MMXXIX 2028 MMXXVIII 2027 MMXXVII 2026 MMXXVI 2025 MMXXV 2024 MMXXIV 2023 MMXXIII 2022 MMXXII 2021 MMXXI 2020 MMXX 2019 MMXIX 2018 MMXVIII 2017 MMXVII 2016 MMXVI 2015 MMXV 2014 MMXIV 2013 MMXIII 2012 MMXII 2011 MMXI 2010 MMX 2009 MMIX 2008 MMVIII 2007 MMVII 2006 MMVI 2005 MMV 2004 MMIV 2003 MMIII 2002 MMII 2001 MMI 2000 MM 1999 MCMXCIX 1998 MCMXCVIII 1997 MCMXCVII 1996 MCMXCVI 1995 MCMXCV 1994 MCMXCIV 1993 MCMXCIII 1992 MCMXCII 1991 MCMXCI 1990 MCMXC 1989 MCMLXXXIX 1988 MCMLXXXVIII 1987 MCMLXXXVII 1986 MCMLXXXVI 1985 MCMLXXXV 1984 MCMLXXXIV 1983 MCMLXXXIII 1982 MCMLXXXII 1981 MCMLXXXI 1980 MCMLXXX 1979 MCMLXXIX 1978 MCMLXXVIII 1977 MCMLXXVII 1976 MCMLXXVI 1975 MCMLXXV 1974 MCMLXXIV 1973 MCMLXXIII 1972 MCMLXXII 1971 MCMLXXI 1970 MCMLXX 1969 MCMLXIX 1968 MCMLXVIII 1967 MCMLXVII 1966 MCMLXVI 1965 MCMLXV 1964 MCMLXIV 1963 MCMLXIII 1962 MCMLXII 1961 MCMLXI 1960 MCMLX 1959 MCMLIX 1958 MCMLVIII 1957 MCMLVII 1956 MCMLVI 1955 MCMLV 1954 MCMLIV 1953 MCMLIII 1952 MCMLII 1951 MCMLI 1950 MCML 1949 MCMXLIX 1948 MCMXLVIII 1947 MCMXLVII 1946 MCMXLVI 1945 MCMXLV 1944 MCMXLIV 1943 MCMXLIII 1942 MCMXLII 1941 MCMXLI 1940 MCMXL 1939 MCMXXXIX 1938 MCMXXXVIII 1937 MCMXXXVII 1936 MCMXXXVI 1935 MCMXXXV 1934 MCMXXXIV 1933 MCMXXXIII 1932 MCMXXXII 1931 MCMXXXI 1930 MCMXXX 1929 MCMXXIX 1928 MCMXXVIII 1927 MCMXXVII 1926 MCMXXVI 1925 MCMXXV 1924 MCMXXIV 1923 MCMXXIII 1922 MCMXXII 1921 MCMXXI 1920 MCMXX 1919 MCMXIX 1918 MCMXVIII 1917 MCMXVII 1916 MCMXVI 1915 MCMXV 1914 MCMXIV 1913 MCMXIII 1912 MCMXII 1911 MCMXI 1910 MCMX 1909 MCMIX 1908 MCMVIII 1907 MCMVII 1906 MCMVI 1905 MCMV 1904 MCMIV 1903 MCMIII 1902 MCMII 1901 MCMI 1900 MCM 1899 MDCCCXCIX 1898 MDCCCXCVIII 1897 MDCCCXCVII 1896 MDCCCXCVI 1895 MDCCCXCV 1894 MDCCCXCIV 1893 MDCCCXCIII 1892 MDCCCXCII 1891 MDCCCXCI 1890 MDCCCXC … Порядковый номер месяца (Арабскими цифрами) Номер месяца (Римскими цифрами) 1 (Январь) I 2 (Февраль) II 3 (Март) III 4 (Апрель) IV 5 (Май) V 6 (Июнь) VI 7 (Июль) VII 8 (Август) VIII 9 (Сентябрь) IX 10 (Октябрь) X 11 (Ноябрь) XI 12 (Декабрь) XII День месяца (Арабскими цифрами) День месяца (Римскими цифрами) 1 I 2 II 3 III 4 IV 5 V 6 VI 7 VII 8 VIII 9 IX 10 X 11 XI 12 XII 13 XIII 14 XIV 15 XV 16 XVI 17 XVII 18 XVIII 19 XIX 20 XX 21 XXI 22 XXII 23 XXIII 24 XXIV 25 XXV 26 XXVI 27 XXVII 28 XXVIII 29 XXIX 30 XXX 31 XXXI Римская восемь как пишется. Римские цифры или как правильно написать дату римскими цифрами для тату
Применение Римских цифр
Римские цифры в Юникод
Код 0 1 2 3 4 5 6 7 8 9 A B C D E F Значение 1 2 3 4 5 6 7 8 9 10 11 12 50 100 500 1 000 U+2160 Ⅰ
2160Ⅱ
2161Ⅲ
2162Ⅳ
2163Ⅴ
2164Ⅵ
2165Ⅶ
2166Ⅷ
2167Ⅸ
2168Ⅹ
2169Ⅺ
216AⅫ
216BⅬ
216CⅭ
216DⅮ
216EⅯ
216FU+2170 ⅰ
2170ⅱ
2171ⅲ
2172ⅳ
2173ⅴ
2174ⅵ
2175ⅶ
2176ⅷ
2177ⅸ
2178ⅹ
2179ⅺ
217Aⅻ
217Bⅼ
217Cⅽ
217Dⅾ
217Eⅿ
217FЗначение 1 000 5 000 10 000 — — 6 50 50 000 100 000 U+2160! U+2180 ↀ
2180ↁ
2181ↂ
2182Ↄ ↄ ↄ ↄ ↄ ↄ
5 — V (лат. quinque)
10 — X (лат. decem)
50 — L (лат. quinquaginta)
100 — (C лат. centum)
500 — (D лат. quingenti)
1000 — (M лат. mille)
M ы D аем C оветы L ишь X орошо V оспитанным I ндивидуумам.
Для обозначения чисел применялось 7 букв латинского алфавита: I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000. Промежуточные числа образовывались путем прибавления нескольких букв справа или слева. Сначала писались тысячи и сотни, затем десятки и единицы. Таким образом, число 24 изображалось как XXIV. Горизонтальная линия над символом означала умножение на тысячу.
Полезная информация — Как через интернет бесплатно отправить смс абонентам других операторов сотовой связи? TELE2 Официальный сайт компании TELE2 — tele2.ru На этих страничках можно отправить смс на телефоны абонентов TELE2 в различных регионах: — Белгородская область — префиксы: +7904, нумерация: 530-
Укачивание (кинетоз или болезнь движения) — болезненное состояние, возникающее во время качки на море (морская болезнь), при полете на самолетах и вертолетах (воздушная болезнь), при движении на других видах транспорта. Может появиться при катании на карусели или на качелях, иногда во время танца с элементами кружения. Укачиванию подвержено большое количество люд
Гипербола (в литературе, риторике)Гипербола (греч. hyperbole — избыток, преувеличение; от hyper — через, сверх и bole — бросок, метание) — стилистическая фигура явного и намеренного преувеличения, с целью усиления выразительности и подчёркивания сказанной мысли, например «я
Доходы бюджета Доходы бюджета представляют собой часть бюджетных отношений, связанных с формированием фондов денежных средств, находящихся в распоряжении органов государственной власти и местного самоуправления. По своему материальному воплощению — денежные средства, поступающие в безвозмездном и безвозвратном порядке в соответствии с законодательством РФ в б
Нежилыми помещениями в многоквартирном доме признаются помещения, являющиеся недвижимым имуществом, и предназначенные для общего пользования гражданами, а также жилые помещения, установленные в законном порядке непригодными для проживания. Нежилые помещения могут находиться в собственности как жителей многоквартирного дома (входить в состав общего имущества собственников квартир
Как правильно поздравлять: с Восьмым марТА или Восьмым мартОМ? Правильно: с Восьмым марта. Марта здесь — зависимое слово (восстановим опущенные слова: восьмое число месяца марта), оно не изменяется по падежам при изменении слова Восьмое: Восьмого марта, Восьмому марта и т. д. Как правильно: «поздравляю с 8 Марта» или &laqu
Аматофобия (греч. amathos — пыль, phobos — страх) — навязчивый страх, боязнь пыли. Фобии различного происхождения сопровождают людей повсюду, некоторые из них незаметны окружающим и спокойно дремлют, дожидаясь подходящего момента, чтобы вдруг появиться из темных глубин подсознания
Бег на 5000 метров — стадионная дисциплина лёгкой атлетики, относится к бегу на длинные дистанции. Исторически в Великобритании была популярна дистанция 3 мили (4828 метров), которая позже стала более популярной метрической дистанцией 5000 метров. Является Олимпийской дисциплиной лёгкой атлетики для мужчин с 1912 года, для женщин с 199
Предоставляется наиболее подробный список станций переливания крови в Приморской области. Контактные телефоны можно узнать, воспользовавшись телефонной справочной интересуещего региона, либо можно воспользоваться прямой ссылкой:Станции Службы крови в Приморской области Арсеньевский филиал ГУЗ Краевая станция переливания крови: Адрес: г. Арсеньев, ул. Ломоносова, 11; Владивостокский филиал ГУЗ Краевая станц
Геральдический щит (гербовый щит) — это условно изображённый стилизованный щит признанной в геральдической традиции формы, либо характерной конструкции (павеза), несущий на своей лицевой поверхности (в гербовом поле) определённый набор гербовых фигур. Является основой любого герба. Щиты бывают разной формы и в зависимости от этого получили разные названия. Самой
На сегодняшний день online — перевод Web — страницы можно произвести совершенно бесплатно на следующих ресурсах:Translate.ru: translate.ru — английский, немецкий, русский, испанский, итальянский, португальский, французский.Google Translate: google.comКак устроены римские цифры
V 5
X 10
L 50
C 100
D 500
M 1000
Мы Dарим Сочные Lимоны, Хватит Vсем Iх
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам
I Value Xylophones Like Cows Dig MilkАльтернативные варианты
Происхождение
Современное применение
IV — 4, т.е. 5 — 1
XI — 11, т.е. 10 + 1
IX — 9, т.е. 10 — 1
LX — 60, т.е. 50 + 10
XL — 40, т.е. 50 — 10
СХ — 110, т.е. 100 + 10
ХС — 90, т.е. 100-10
MDCCCXII — 1812, т.е. 1000 + 500 + 100 + 100 + 100 + 10 + 1 + 1.
II (2) — duo (дуо)
III (3) — tres (трэс)
IV (4) — quattuor (кваттуор)
V (5) — quinque (квинквэ)
VI (6) — sex (сэкс)
VII (7) — septera (сэптэм)
VIII (8) — octo (окто)
IX (9) — novem (новэм)
X (10) — decern (дэцем)
XI (11) — undecim (ундецим)
XII (12) — duodecim (дуодэцим)
ХШ (13) — tredecim (трэдэцим)
XIV (14) — quattuordecim (кваттуордэцим)
XV (15) — quindecim (квиндэцим)
XVI (16) — sedecim (сэдэцим)
XVII (17) — septendecim (сэптэндэцим)
XVIII (18) — duodeviginti (дуодэвигинти)
XIX (19) — undeviginti (ундэвигинти)
XX (20) — viginti (вигинти)
XXI (21) — unus et viginti или viginti unus
XXII (22) — duo et viginti или viginti duo и т.д.
XXVIII (28) — duodetriginta (дуодэтригинта)
XXIX (29) — undetriginta (ундэтригинта)
XXX (30) : triginta (тригинта)
XL (40) — quadraginta (квадрагинта)
L (5O) — quinquaginta (квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX (70) — septuaginta (сзлтуагинта)
LXXX180) — octoginta (октогинта)
КС (90) — nonaginta (нонагинта)
C (100) centum (центум)
CC (200) — ducenti (дуценти)
CCC (300) — trecenti (трэценти)
CD (400) — quadrigenti (квадригэнти)
D (500) — quingenti (квингэнти)
DC (600) — sescenti(сэсценти) или sexonti (сэксцонти)
DCC (700) — septigenti (сэптигэнти)
DCCC (800) — octingenti (октингэнти)
CV (DCCC) (900) — nongenti (нонгэнти)
M (1000) — mille (милле)
ММ (2000) — duo milia (дуо милиа)
V (5000) — quinque milla (квинквэ милиа)
X (10 000) — decem milia (дэцем милиа)
XX (20000) — viginti milia (вигинти милиа)
C (100000) — centum milia (центум милиа)
XI (1000000) — decies centena milia (дэциэс центэна милиа).
IV — 4, т.е. 5 — 1
XI — 11, т.е. 10 + 1
IX — 9, т.е. 10 — 1
LX — 60, т.е. 50 + 10
XL — 40, т.е. 50 — 10
СХ — 110, т.е. 100 + 10
ХС — 90, т.е. 100-10
MDCCCXII — 1812, т.е. 1000 + 500 + 100 + 100 + 100 + 10 +
1 + 1.
II (2) — duo (дуо)
III (3) — tres (трэс)
IV (4) — quattuor (кваттуор)
V (5) — quinque (квинквэ)
VI (6) — sex (сэкс)
VII (7) — septera (сэптэм)
VIII (8) — octo (окто)
IX (9) — novem (новэм)
X (10) — decem (дэцем)
XI (11) — undecim (ундецим)
XII (12) — duodecim (дуодэцим)
ХШ (13) — tredecim (трэдэцим)
XIV (14) — quattuordecim (кваттуордэцим)
XV (15) — quindecim (квиндэцим)
XVI (16) — sedecim (сэдэцим)
XVII (17) — septendecim (сэптэндэцим)
XVIII (18) — duodeviginti (дуодэвигинти)
XIX (19) — undeviginti (ундэвигинти)
XX (20) — viginti (вигинти)
XXI (21) — unus et viginti или viginti unus
XXII (22) — duo et viginti или viginti duo и т.д.
XXVIII (28) — duodetriginta (дуодэтригинта)
XXIX (29) — undetriginta (ундэтригинта)
XXX (30) : triginta (тригинта)
XL (40) — quadraginta (квадрагинта)
L (5O) — quinquaginta (квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX (70) — septuaginta (сзлтуагинта)
LXXX180) — octoginta (октогинта)
КС (90) — nonaginta (нонагинта)
C (100) centum (центум)
CC (200) — ducenti (дуценти)
CCC (300) — trecenti (трэценти)
CD (400) — quadrigenti (квадригэнти)
D (500) — quingenti (квингэнти)
DC (600) — sescenti(сэсценти) или sexonti (сэксцонти)
DCC (700) — septigenti (сэптигэнти)
DCCC (800) — octingenti (октингэнти)
CV (DCCC) (900) — nongenti (нонгэнти)
M (1000) — mille (милле)
ММ (2000) — duo milia (дуо милиа)
V
(5000) — quinque milla (квинквэ милиа)
X
(10 000) — decem milia (дэцем милиа)
XX
(20000) — viginti milia (вигинти милиа)
C
(100000) — centum milia (центум милиа)
XI
(1000000) — decies centena milia (дэциэс центэна милиа).Задание для закрепления пройденного материала
MDCCXCIX
MDCCCLXXXКак написать дату рождения (Год, Месяц, День) римскими цифрами?
Все онлайн калькуляторыКак правильно записать год рождения римскими цифрами?
Год (Арабскими цифрами)
Год (Римскими цифрами)
2030
MMXXX
2029
MMXXIX
2028
MMXXVIII
2027
MMXXVII
2026
MMXXVI
2025
MMXXV
2024
MMXXIV
2023
MMXXIII
2022
MMXXII
2021
MMXXI
2020
MMXX
2019
MMXIX
2018
MMXVIII
2017
MMXVII
2016
MMXVI
2015
MMXV
2014
MMXIV
2013
MMXIII
2012
MMXII
2011
MMXI
2010
MMX
2009
MMIX
2008
MMVIII
2007
MMVII
2006
MMVI
2005
MMV
2004
MMIV
2003
MMIII
2002
MMII
2001
MMI
2000
MM
1999
MCMXCIX
1998
MCMXCVIII
1997
MCMXCVII
1996
MCMXCVI
1995
MCMXCV
1994
MCMXCIV
1993
MCMXCIII
1992
MCMXCII
1991
MCMXCI
1990
MCMXC
1989
MCMLXXXIX
1988
MCMLXXXVIII
1987
MCMLXXXVII
1986
MCMLXXXVI
1985
MCMLXXXV
1984
MCMLXXXIV
1983
MCMLXXXIII
1982
MCMLXXXII
1981
MCMLXXXI
1980
MCMLXXX
1979
MCMLXXIX
1978
MCMLXXVIII
1977
MCMLXXVII
1976
MCMLXXVI
1975
MCMLXXV
1974
MCMLXXIV
1973
MCMLXXIII
1972
MCMLXXII
1971
MCMLXXI
1970
MCMLXX
1969
MCMLXIX
1968
MCMLXVIII
1967
MCMLXVII
1966
MCMLXVI
1965
MCMLXV
1964
MCMLXIV
1963
MCMLXIII
1962
MCMLXII
1961
MCMLXI
1960
MCMLX
1959
MCMLIX
1958
MCMLVIII
1957
MCMLVII
1956
MCMLVI
1955
MCMLV
1954
MCMLIV
1953
MCMLIII
1952
MCMLII
1951
MCMLI
1950
MCML
1949
MCMXLIX
1948
MCMXLVIII
1947
MCMXLVII
1946
MCMXLVI
1945
MCMXLV
1944
MCMXLIV
1943
MCMXLIII
1942
MCMXLII
1941
MCMXLI
1940
MCMXL
1939
MCMXXXIX
1938
MCMXXXVIII
1937
MCMXXXVII
1936
MCMXXXVI
1935
MCMXXXV
1934
MCMXXXIV
1933
MCMXXXIII
1932
MCMXXXII
1931
MCMXXXI
1930
MCMXXX
1929
MCMXXIX
1928
MCMXXVIII
1927
MCMXXVII
1926
MCMXXVI
1925
MCMXXV
1924
MCMXXIV
1923
MCMXXIII
1922
MCMXXII
1921
MCMXXI
1920
MCMXX
1919
MCMXIX
1918
MCMXVIII
1917
MCMXVII
1916
MCMXVI
1915
MCMXV
1914
MCMXIV
1913
MCMXIII
1912
MCMXII
1911
MCMXI
1910
MCMX
1909
MCMIX
1908
MCMVIII
1907
MCMVII
1906
MCMVI
1905
MCMV
1904
MCMIV
1903
MCMIII
1902
MCMII
1901
MCMI
1900
MCM
1899
MDCCCXCIX
1898
MDCCCXCVIII
1897
MDCCCXCVII
1896
MDCCCXCVI
1895
MDCCCXCV
1894
MDCCCXCIV
1893
MDCCCXCIII
1892
MDCCCXCII
1891
MDCCCXCI
1890
MDCCCXC
…
Порядковый номер месяца (Арабскими цифрами)
Номер месяца (Римскими цифрами)
1 (Январь)
I
2 (Февраль)
II
3 (Март)
III
4 (Апрель)
IV
5 (Май)
V
6 (Июнь)
VI
7 (Июль)
VII
8 (Август)
VIII
9 (Сентябрь)
IX
10 (Октябрь)
X
11 (Ноябрь)
XI
12 (Декабрь)
XII
В вашем браузере отключен Javascript. День месяца (Арабскими цифрами)
День месяца (Римскими цифрами)
1
I
2
II
3
III
4
IV
5
V
6
VI
7
VII
8
VIII
9
IX
10
X
11
XI
12
XII
13
XIII
14
XIV
15
XV
16
XVI
17
XVII
18
XVIII
19
XIX
20
XX
21
XXI
22
XXII
23
XXIII
24
XXIV
25
XXV
26
XXVI
27
XXVII
28
XXVIII
29
XXIX
30
XXX
31
XXXI
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!Больше интересного в телеграм @calcsbox
Римские цифры. Запись натуральных чисел.: greenn007 — LiveJournal
обозначение
1 I
5 V
10 X
50 L
100 C
500 D
1000 M
0 —
4 IV
8 VIII
9 IX
31 XXXI
46 XLVI
99 XCIX
666 DCLXVI
888 DCCCLXXXVIII
1668 MDCLXVIII
1989 MCMLXXXIX
2009 MMIX
3999 MMMCMXCIX
Пример: число 1988. Одна тысяча M, девять сотен CM, восемьдесят LXXX, восемь VIII. Запишем их вместе: MCMLXXXVIII.
Довольно часто, чтобы выделить числа в тексте, над ними рисовали черту: LXIV. Иногда черту рисовали и сверху, и снизу: XXXII — в частности, так принято выделять римские цифры в русском рукописном тексте (в типографском наборе это не используют из-за технической сложности). У других авторов черта сверху могла обозначать увеличение значения цифры в 1000 раз: VM = 6000.
Существует «сокращённый способ» для записи больших чисел, таких как 1999. Он не рекомендуется, но иногда используется для упрощения. Отличие состоит в том, что для уменьшения цифры слева от неё может писаться любая цифра:
999. Тысяча (M), вычтем 1 (I), получим 999 (IM) вместо CMXCIX. Следствие: 1999 — MIM вместо MCMXCIX
95. Сто (C), вычтем 5 (V), получим 95 (VC) вместо XCV
1950: Tысяча (M), вычтем 50 (L), получим 950 (LM). Следствие: 1950 — MLM вместо MCML
впрочем как и АРАБСКИЕ — на самом деле — ИНДИЙСКИЕ !
а ещё есть — ДАЖЕ ЧУВАШСКИЕ Древние цифры(из тюркской рунической письменности)
и 20-ричная система счисления майя…
:)))
источник
http://ru.wikipedia.org/wiki/%D0%90%D1%80%D0%B0%D0%B1%D1%81%D0%BA%D0%B8%D0%B5_%D1%86%D0%B8%D1%84%D1%80%D1%8B
http://ru.wikipedia.org/wiki/%D0%A0%D0%B8%D0%BC%D1%81%D0%BA%D0%B8%D0%B5_%D1%86%D0%B8%D1%84%D1%80%D1%8BРимские цифры все по порядку с переводом. Римские цифры (Roman numerals)
Простой принцип расчета
I
Самый простой способ записать маленькие числа это нарисовать «зазубрины» — цифра один: I. Две палочки II означают два, III — три. Однако, для большего числа количество становиться очень большим и абсолютно не читаемым…. 20-ый век
1902 = MCMII
1903 = MCMIII
1904 = MCMIV
1905 = MCMV
1906 = MCMVI
1907 = MCMVII
1908 = MCMVIII
1909
= MCMIX
1910 = MCMX
1912 = MCMXII
1913 = MCMXIII
1914 =
MCMXIV
1915 = MCMXV
1916 = MCMXVI
1917 = MCMXVII
1918 =
MCMXVIII
1919 = MCMXIX
1920 = MCMXX
1922 = MCMXXII
1923 = MCMXXIII
1924 =
MCMXXIV
1925 = MCMXXV
1926 = MCMXXVI
1927 = MCMXXVII
1928 =
MCMXXVIII
1929 = MCMXXIX
1930 = MCMXXX
1932 = MCMXXXII
1933 = MCMXXXIII
1934
= MCMXXXIV
1935 = MCMXXXV
1936 = MCMXXXVI
1937 = MCMXXXVII
1938
= MCMXXXVIII
1939 = MCMXXXIX
1940 = MCMXL
1942 = MCMXLII
1943 = MCMXLIII
1944 =
MCMXLIV
1945 = MCMXLV
1946 = MCMXLVI
1947 = MCMXLVII
1948 =
MCMXLVIII
1949 = MCMXLIX
1950 = MCML
1952 = MCMLII
1953 = MCMLIII
1954 =
MCMLIV
1955 = MCMLV
1956 = MCMLVI
1957 = MCMLVII
1958 =
MCMLVIII
1959 = MCMLIX
1960 = MCMLX
1962 = MCMLXII
1963 = MCMLXIII
1964 =
MCMLXIV
1965 = MCMLXV
1966 = MCMLXVI
1967 = MCMLXVII
1968 =
MCMLXVIII
1969 = MCMLXIX
1970 = MCMLXX
1972 = MCMLXXII
1973 = MCMLXXIII
1974
= MCMLXXIV
1975 = MCMLXXV
1976 = MCMLXXVI
1977 = MCMLXXVII
1978
= MCMLXXVIII
1979 = MCMLXXIX
1980 = MCMLXXX
1982 = MCMLXXXII
1983 = MCMLXXXIII
1984 = MCMLXXXIV
1985 = MCMLXXXV
1986 = MCMLXXXVI
1987 =
MCMLXXXVII
1988 = MCMLXXXVIII
1989 = MCMLXXXIX
1990 = MCMXC
1991 = MCMXCI
1992 = MCMXCII
1993 = MCMXCIII
1994 =
MCMXCIV
1995 = MCMXCV
1996 = MCMXCVI
1997 = MCMXCVII
1998 =
MCMXCVIII
1999 = MCMXCIX
2000 = MM21-ый век
2002 = MMII
2003 = MMIII
2004 = MMIV
2005 = MMV
2006 =
MMVI
2007 = MMVII
2008 = MMVIII
2009 =
MMIX
2010 = MMX 2011 = MMXI
2012 = MMXII
2013 =
MMXIII
2014 = MMXIV
2015 = MMXV
2016 = MMXVI
2017 = MMXVII
2018
= MMXVIII
2019 = MMXIX
2020 = MMXXV
Таким образом, появилась число 5 — V. Расположение перед ним единички: IV — или расположение любого другого меньшего числа, чем последующий (в нашем случае символ пять) — означает вычитание. Таким образом, IV означает 4. После V можно указать меньшие цифры, тогда это будет означать складывание — VI означает 6, VII означает 7, VIII равно 8. X
X означает 10. Но что насчет 9? Аналогичное используется правило как с пятёркой. IX означает вычитание I из X, и это равно 9. Числа первого десятка, второго десятка и третьего формируются таким же образом, только с X-ами означающие количество десятков в числе. Таким образом, мы получаем, что XXXI — 31, а XXIV это 24. L
Значение L равно 50. Основываясь на том, что вы уже прочитали выше, вы уже можете догадаться, как будет записано число 40. Если вы думаете, что это будет XL, то вы правы = 10 отнимается от 50-и. И другие числа 60, 70, и 80 будут выглядеть как LX, LXX и LXXX. C
Цифра C пошла от слова centum , латинского слова означающее 100. centurion означает 100 людей. Мы по-прежнему используем такие слова, как «century » (столетие) и «cent » (цент). Как и с L, вычитание десятка означает понижение основной последующей цифры: 90 будет записано, как 100 минус 10 = XC. Несколько подряд цифр C будет означать соответствующее количество сотен: CCCLXIX равно 369. D
D указывает на значение равное 500. По аналогии, CD означает 400. CDXLVIII равное 448. M
M это 1000. Это цифра очень часто попадается, так как римские числа в основном используются для записи года. MMX — 2010 год. V
Более большие числа в Римском исчислении записываются при помощи горизонтальной линии расположенной над цифрами, что будет означать умножение данных цифр на тысячу.
Отсюда выходит, что V с горизонтальной линией над этой цифрой будет означать 5000. Конвертирование римских чисел онлайн
Как устроены римские цифры
V 5
X 10
L 50
C 100
D 500
M 1000
Мы Dарим Сочные Lимоны, Хватит Vсем Iх
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам
I Value Xylophones Like Cows Dig MilkАльтернативные варианты
Происхождение
Современное применение
5 — V (лат. quinque)
10 — X (лат. decem)
50 — L (лат. quinquaginta)
100 — (C лат. centum)
500 — (D лат. quingenti)
1000 — (M лат. mille)
M ы D аем C оветы L ишь X орошо V оспитанным I ндивидуумам.
Для обозначения чисел применялось 7 букв латинского алфавита: I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000. Промежуточные числа образовывались путем прибавления нескольких букв справа или слева. Сначала писались тысячи и сотни, затем десятки и единицы. Таким образом, число 24 изображалось как XXIV. Горизонтальная линия над символом означала умножение на тысячу.
Полезная информация — Как через интернет бесплатно отправить смс абонентам других операторов сотовой связи? TELE2 Официальный сайт компании TELE2 — tele2.ru На этих страничках можно отправить смс на телефоны абонентов TELE2 в различных регионах: — Белгородская область — префиксы: +7904, нумерация: 530-
Укачивание (кинетоз или болезнь движения) — болезненное состояние, возникающее во время качки на море (морская болезнь), при полете на самолетах и вертолетах (воздушная болезнь), при движении на других видах транспорта. Может появиться при катании на карусели или на качелях, иногда во время танца с элементами кружения. Укачиванию подвержено большое количество люд
Гипербола (в литературе, риторике)Гипербола (греч. hyperbole — избыток, преувеличение; от hyper — через, сверх и bole — бросок, метание) — стилистическая фигура явного и намеренного преувеличения, с целью усиления выразительности и подчёркивания сказанной мысли, например «я
Доходы бюджета Доходы бюджета представляют собой часть бюджетных отношений, связанных с формированием фондов денежных средств, находящихся в распоряжении органов государственной власти и местного самоуправления. По своему материальному воплощению — денежные средства, поступающие в безвозмездном и безвозвратном порядке в соответствии с законодательством РФ в б
Нежилыми помещениями в многоквартирном доме признаются помещения, являющиеся недвижимым имуществом, и предназначенные для общего пользования гражданами, а также жилые помещения, установленные в законном порядке непригодными для проживания. Нежилые помещения могут находиться в собственности как жителей многоквартирного дома (входить в состав общего имущества собственников квартир
Как правильно поздравлять: с Восьмым марТА или Восьмым мартОМ? Правильно: с Восьмым марта. Марта здесь — зависимое слово (восстановим опущенные слова: восьмое число месяца марта), оно не изменяется по падежам при изменении слова Восьмое: Восьмого марта, Восьмому марта и т. д. Как правильно: «поздравляю с 8 Марта» или &laqu
Аматофобия (греч. amathos — пыль, phobos — страх) — навязчивый страх, боязнь пыли. Фобии различного происхождения сопровождают людей повсюду, некоторые из них незаметны окружающим и спокойно дремлют, дожидаясь подходящего момента, чтобы вдруг появиться из темных глубин подсознания
Бег на 5000 метров — стадионная дисциплина лёгкой атлетики, относится к бегу на длинные дистанции. Исторически в Великобритании была популярна дистанция 3 мили (4828 метров), которая позже стала более популярной метрической дистанцией 5000 метров. Является Олимпийской дисциплиной лёгкой атлетики для мужчин с 1912 года, для женщин с 199
Предоставляется наиболее подробный список станций переливания крови в Приморской области. Контактные телефоны можно узнать, воспользовавшись телефонной справочной интересуещего региона, либо можно воспользоваться прямой ссылкой:Станции Службы крови в Приморской области Арсеньевский филиал ГУЗ Краевая станция переливания крови: Адрес: г. Арсеньев, ул. Ломоносова, 11; Владивостокский филиал ГУЗ Краевая станц
Геральдический щит (гербовый щит) — это условно изображённый стилизованный щит признанной в геральдической традиции формы, либо характерной конструкции (павеза), несущий на своей лицевой поверхности (в гербовом поле) определённый набор гербовых фигур. Является основой любого герба. Щиты бывают разной формы и в зависимости от этого получили разные названия. Самой
На сегодняшний день online — перевод Web — страницы можно произвести совершенно бесплатно на следующих ресурсах:Translate.ru: translate.ru — английский, немецкий, русский, испанский, итальянский, португальский, французский.Google Translate: google.com21-й XXI 20-й XX 19-й XIX 18-й XVIII 17-й XVII 16-й XVI 15-й XV 14-й XIV 13-й XIII 12-й XII 11-й XI 10-й X 9-й IX 8-й VIII 7-й VII 6-й VI 5-й V 4-й IV 3-й III 2-й II 1-й I Перевод в римские цифры онлайн
Онлайн калькулятор перевода римских цифр в русские числа (арабские цифры), двоичной системы счисления. Для конвертации числа, в римские числа, введите нужное число для перевода в десятичной системе и нажмите, перевести.Таблица
Арабские цифры (русские) Римские
Арабские цифры (русские) Римские
1
I
30
XXX 2
II
40
XL 3
III
50
L 4
IV
60
LX 5
V
70
LXX 6
VI
80
LXXX 7
VII
90
XC 8
VIII
100
C 9
IX
200
CC 10
X
300
CCC 11
XI
400
CD 12
XII
500
D 13
XIII
600
DC 14
XIV
700
DCC 15
XV
800
DCCC 16
XVI
900
CM 17
XVII
1000
M 18
XVIII
1950
MCML 19
XIX
2325
MMCCCXXV 20
XX
2550
MMDL История Tokina с 1950 по 2020 гг
1950 римскими цифрами: 1950 = MCML — Генератор римских цифр
Что такое римские цифры?
Когда используются римские цифры?
римских цифр: 1950 = MCML
. Текущая дата и время римскими цифрами
2021-07-22 07:21:16 MMXXI-VII-XXII VII: XXI: XVI 1950 год
Номер 1950
1950 как восьмеричное число: 3636
1950 как шестнадцатеричное число: 79E Числа близкие к 1950
1947 = MCMXLVII = 1000 + 1000-100 + 50-10 + 5 + 1 + 1 1948 = MCMXLVIII = 1000 + 1000 — 100 + 50-10 + 5 + 1 + 1 + 1 1949 = MCMXLIX = 1000 + 1000-100 + 50-10 + 10-1 1950 = MCML = 1000 + 1000-100 + 50 1951 = MCMLI = 1000 + 1000-100 + 50 + 1 1952 = MCMLII = 1000 + 1000 — 100 + 50 + 1 + 1 1953 = MCMLIII = 1000 + 1000 — 100 + 50 + 1 + 1 + 1 О римских цифрах
Каким образом 1950 записывается римскими цифрами?
Почему 1950 написано римскими цифрами как MCML?
Основные символы римских цифр
1 5 10 50 100 500 1 000 I В х л С D млн Базовые комбинации
1 2 3 4 5 6 7 8 9 I II III IV В VI VII VIII IX 10 20 30 40 50 60 70 80 90 X ХХ ХХХ XL л LX LXX LXXX XC 100 200 300 400 500 600 700 800 900 С CC CCC CD D постоянного тока DCC DCCC СМ большие числа
5 000 10 000 50 000 100 000 500 000 1 000 000 В х л С D млн Как преобразовать 1950 в римские цифры?
Значение места Число Римская цифра Тысячи 1,000 M Сотни 900 CM Десятки 50 L Как числа около 1950 написаны римскими цифрами?
Как преобразовать римские цифры: 3 простых метода
Что такое римские цифры и как они работают?
Римская цифра I В X л С D M Арабская цифра 1 5 10 50 100 500 1 000 Почему вы должны знать, что такое римские цифры?
Таблицы преобразования римских цифр
Как запоминать римские цифры: 3 метода
# 1: Запоминание мнемонического устройства
Вот некоторые распространенные мнемонические устройства: # 2: Придумывайте свои собственные ассоциации
# 3: Используйте трюк с руками
Обзор: Викторина о преобразователе римских цифр
Заключительные слова: почему вы должны учить римские цифры
Что дальше?
Посчитать римскими цифрами не так уж и сложно | блог @ CACM
Герберт Брудерер
18 марта, 2019
Комментарии римских цифр — преобразование из арабских в римские (II)
римских цифр — преобразование из арабских в римские (II) 1450-2100
Преобразование для меньших чисел 1-1449
1451 = MCDLI
1452 = MCDLI
1453 = MCDLIII
1454 = MCDLIV
1455 = MCDLV
1456 = MCDLVI
1457 = MCDLVII
1458 = MCDLVIII
1459 = MCDLIX
1459 = MCDLIX
1459 = MCDLIX
1459 = MCDLIX
1459 = MCDLXII
1463 = MCDLXIII
1464 = MCDLXIV
1465 = MCDLXV
1466 = MCDLXVI
1467 = MCDLXVII
1468 = MCDLXVIII
1469 = MCDLXIX
1470 = MCDLXX
1471 1471 1470 = MCDLXX
1471 1471 1470 = MCDLXX
1471 1471 1470 = MCDLXX
1471 1471 1470 MCDLXXXX
1471 1471 = MCDLXXXX
1471 1471
1475 = MCDLXXV
1476 = MCDLXXVI
1477 = MCDLXXVII
1478 = MCDLXXVIII
1479 = MCDLXXIX
1480 = MCDLXXX
1481 = MCDLXXXI 900X71 1482 = MCDLXXXIII 1482 1482 = MCDLXXXIII 1482 1482 = MCDLXXXII71 1482 = MCDLXXXIII 1482 = MCDLXXXIII 1482 1482 = MCDLXXXII71 1482 = MCDLXXXII71 1482 = MCDLXXXII71 1482 1482 = MCDLXXXII71 148 = MCDLXXXVII
1488 = MCDLXXXVIII
1489 = MCDLXXXIX
1490 = MCDXC
1491 = MCDXCI
1492 = MCDXCII
1493 = MCDXCIII
1494 = MCDXCIV
1495 = MCDXCV
CVI
1497 = MCDXCVII
1498 = MCDXCVIII
1499 = MCDXCIX
1500 = MD
1501 = MDI
1502 = MDII
1503 = MDIII
1504 = MDIV
1505 = MDV
1506 = MDVI
1507 = MDVII
15071 = MDVII
15071 = MDVII
15071 = MDVII
15071 = MDVII
15071 1509 = MDIX
1510 = MDX
1511 = MDXI
1512 = MDXII
1513 = MDXIII
1514 = MDXIV
1515 = MDXV
1516 = MDXVI
1517 = MDXVII
1518 = MDXVIII
1519 = 1521 MDXIX
1520 = MDX
1520 = MDX 900 MDXXI
1522 = MDXXII
1523 = MDXXIII
1524 = MDXXIV
1525 = MDXXV
1526 = MDXXVI
1527 = MDXXVII
1528 = MDXXVIII
1529 = MDXXIX
1530 = MDXXX
1531 = MDXXX
1531 = MDXXX
1531 = MDXXX 900X 1534 = MDXXXIV
1535 = MDXXXV
1536 = MDXXXVI
1537 = MDXXXVII
1538 = MDXXXVIII
1539 = MDXXXIX
1540 = MDXL
1541 = MDXLI
1542 = MDXLII
1543 = MDXLII
1543 = MDXXXVI
1543 = MDXXLII
1543 = MDXXLII
1543 = MDXLII
1543 = MDXLII
1543 = MDXLII
1543 = MDXLII
1543 = MDXLII
1543 = MDXLII MDXLVI
1547 = MDXLVII
1548 = MDXLVIII
1549 = MDXLIX
1550 = MDL
1551 = MDLI
1552 = MDLII
1553 = MDLIII
1554 = MDLIV
1555 = MDLV
1556 = MDLVI
1557 = MDLVII
1571 = 1571 = 1571 1560 = MDLX
1561 = MDLXI
1562 = MDLXII
1563 = MDLXIII
1564 = MDLXIV
1565 = MDLXV
1566 = MDLXVI
1567 = MDLXVII
1568 = MDLXVIII
1569 = MDLXIX
1571 = 1571X = MDLXI 900XI
1570 = MDLXI 900XI
1570 = 1570 MDLXXII
1573 = MDLXXIII
1574 = MDLXXIV
1575 = MDLXXV
1576 = MDLXXVI
1577 = MDLXXVII
1578 = MDLXXVIII
1579 = MDLXXIX
1580 = 1580 MDLXXX
1581IX = 1581X 1581X 900III 1581IX = MDLXXX
1581IX = MDLXXX
1581IX1 1585 = MDLXXXV
1586 = MDLXXXVI
1587 = MDLXXXVII
1588 = MDLXXXVIII
1589 = MDLXXXIX
1590 = MDXC
1591 = MDXCI
1592 = MDXCII
1593 = MDLXCIII
1594 = MDXCII
1593 = MDXCIII
C =
1594C =
1594V MDXCVI
1597 = MDXCVII
1598 = MDXCVIII
1599 = MDXCIX
1600 = MDC
1601 = MDCI
1602 = MDCII
1603 = MDCIII
1604 = MDCIV
1605 = MDCV
1606 = MDCVI
16071 = MDCV
1606 = MDCVI
160VI7 = MDC 1609 = MDCIX
1610 = MDCX
1611 = MDCXI
1612 = MDCXII
1613 = MDCXIII
1614 = MDCXIV
1615 = MDCXV
1616 = MDCXVI
1617 = MDCXVII
1618 = MDCXVIII IX 1619 = 1620X 900XVIII IX 1619 = 1620X 1619 = 1620X MDCXXI
1622 = MDCXXII
1623 = MDCXXIII
1624 = MDCXXIV
1625 = MDCXXV
1626 = MDCXXVI
1627 = MDCXXVII
1628 = MDCXXVIII
1629 = MDCXXIX
163071XIIC 1629 = MDCXXIX
163071 = MDXIIC 1629 = MDCXXIX
163071 = MDXIIC 1629 = MDCXXIX
163071 = MDXX31 1634 = MDCXXXIV
1635 = MDCXXXV
1636 = MDCXXXVI
1637 = MDCXXXVII
1638 = MDCXXXVIII
1639 = MDCXXXIX
1640 = MDCXL
1641 = MDCXLI
1642 = MDCXLI
1642 = MDCXLI
1642 = MDCXXLI
1642 = MDCXLI
1642 = MDCXLI
1642 = MDC43IIIXL 1 645 = MDCXLV
1646 = MDCXLVI
1647 = MDCXLVII
1648 = MDCXLVIII
1649 = MDCXLIX
1650 = MDCL
1651 = MDCLI
1652 = MDCLII
1653 = MDCLIII
1654 = MDCLIV
1671 1655 = MDCLIII
1654 = MDCLIV
1655 = MDCLIV
1655 = MDCLIV
1655 = 900V57 1655 MDCLVII
1658 = MDCLVIII
1659 = MDCLIX
1660 = MDCLX
1661 = MDCLXI
1662 = MDCLXII
1663 = MDCLXIII
1664 = MDCLXIV
1665 = MDCLXV
1666 = MDCLXVI
1667 = MDCLXVI
1667 = MDCLXVII
1667 = MDCLXVII
= MDCLXVII
= MDCLXVII
= MDCLXVII
1670 = MDCLXX
1671 = MDCLXXI
1672 = MDCLXXII
1673 = MDCLXXIII
1674 = MDCLXXIV
1675 = MDCLXXV
1676 = MDCLXXVI
1677 = MDCLXCLVII
1678 = MDCLXXVIII
1671XCL 1678 = MDCLXXVIII
1679 = MDCLXXVIII
1679 = 1679X MDCLXXXII
1683 = MDCLXXXIII
1684 = MDCLXXXIV
1685 = MDCLXXXV
1686 = MDCLXXXVI
1687 = MDCLXXXVII
1688 = MDCLXXXVIII
1689 = MDCLXXXIX
1690 = MDCXC
1690 = 991CXC 0071 1692 = MDCXCII
1693 = MDCXCIII
1694 = MDCXCIV
1695 = MDCXCV
1696 = MDCXCVI
1697 = MDCXCVII
1698 = MDCXCVIII
1699 = MDCXCIX
17071 MDCXCIX
1700 = MDCC
II1 = MDCXCIX 9004 170CC3 170CC3 170CC3 170CC3 170CC3 170CC3 170CC3 170CC3 170CC3 170CC3 170CC3 170CC3 170CCI1 =
170CC2 = MDCCIV
1705 = MDCCV
1706 = MDCCVI
1707 = MDCCVII
1708 = MDCCVIII
1709 = MDCCIX
1710 = MDCCX
1711 = MDCCXI
1712 = MDCCXII
1713 = MDCCXIII
1714 = MDCCXIV
1715 = MDCCXIII
1714 = MDCCXIV
1715XV = MDCCXIV
1715 = MDCCXI
1717 = MDCCXVII
1718 = MDCCXVIII
1719 = MDCCXIX
1720 = MDCCXX
1721 = MDCCXXI
1722 = MDCCXXII
1723 = MDCCXXIII
1724 = MDCCXXIV
1725 = MDCCXXXV
1726ICC 1725 = MDCCXXV
1730 = MDCCXXX
1731 = MDCCXXXI
1732 = MDCCXXXII
1733 = MDCCXXXIII
1734 = MDCCXXXIV
1735 = MDCCXXXV
1736 = MDCCXXXVI
1737 = MDCCX 17XXVIICC
XXVIII
1739 = MDCCXXXIX
1740 = MDCCXL
1741 = MDCCXLI
1742 = MDCCXLII
1743 = MDCCXLIII
1744 = MDCCXLIV
1745 = MDCCXLV
1746 = MDCCXLVI
1747 = MDCCXLVI
1747 = MDCCXLVI
1747 = MDCCXLVI
1747 = MDCCXLVI
1747 = MDCCXLVII 900CC 1747 = MDCCXLVIICC 900CC 1747 = MDCCXLVIICC 900CC 1747 = MDCCXLVII 900CC 1747 = MDCCXLVIICC 9007 1751 = MDCCLI
1752 = MDCCLII
1753 = MDCCLIII
1754 = MDCCLIV
1755 = MDCCLV
1756 = MDCCLVI
1757 = MDCCLVII
1758 = MDCCLVIII
1759 = MDCCLIX
1760 = MDCCLX 900LII71 1761 = MDCCLIX
1760 = MDCCLX 900LII71 1761 = 900CCLX 900LII71 17CC = MDCCLX 900LII71 = 1760 MDCCLXIII
1764 = MDCCLXIV
1765 = MDCCLXV
1766 = MDCCLXVI
1767 = MDCCLXVII
1768 = MDCCLXVIII
1769 = MDCCLXIX
1770 = MDCCLXX
1771 = MDCCLXXI
1772CC 1771XXXXXI
1772CC 1771 = MDCCLXXI
1772CC 1772CC 1776 = MDCCLXXVI
1777 = MDCCLXXVII
1778 = MDCCLXXVIII
1779 = MDCCLXXIX
1780 = MDCCLXXX
1781 = MDCCLXXXI
1782 = MDCCLXXXII
1783 = MDCCLXXX III
1784 = MDCCLXXXIV
1785 = MDCCLXXXV
1786 = MDCCLXXXVI
1787 = MDCCLXXXVII
1788 = MDCCLXXXVIII
1789 = MDCCLXXXIX
1790 = MDCCXC
1791 = MDCCXC
1791CC 1790 = MDCCXC
1791CC = MDCCXXC
1791 = MDCCXXC
1791 = MDCCXXC
CC 1792CC = 1792CCICC 900IIICC = 1792CC 1791CC = 1792CCICC 1796 = MDCCXCVI
1797 = MDCCXCVII
1798 = MDCCXCVIII
1799 = MDCCXCIX
1800 = MDCCC
1801 = MDCCCI
1802 = MDCCCII
1803 = MDCCCIII
1804 = MDCCCIV
1805 = MDCCCI
1805 = MDCCCI
1805 = MDCCCVI
1805 = MDCCCI
1805 = MDCCCVI
1805 = MDCCCVI
1805 = MDCCCVII 9007 =
1805 MDCCCVIII
1809 = MDCCCIX
1810 = MDCCCX
1811 = MDCCCXI
1812 = MDCCCXII
1813 = MDCCCXIII
1814 = MDCCCXIV
1815 = MDCCCXV
1816 = MDCCCXVI
1817 = MDCCCXVIIC
1817 = MDCCCXVIICC 9001 1817 = MDCCCXVIICC 1821 = MDCCCXXI
1822 = MDCCCXXII
1823 = MDCCCXXIII
1824 = MDCCCXXIV
1825 = MDCCCXXV
1826 = MDCCCXXVI
1827 = MDCCCXXVII
1828 = MDCCC XXVIII
1829 = MDCCCXXIX
1830 = MDCCCXXX
1831 = MDCCCXXXI
1832 = MDCCCXXXII
1833 = MDCCCXXXIII
1834 = MDCCCXXXIV
1835 = MDCCCXXXV
1836 = MDCCCXXXV
1836 = MDCCCXXXXV
1836 = MDCCCXXXXV
1836 = MDCCXXXXV
1836 = MDCCXXXXV 1841 = MDCCCXLI
1842 = MDCCCXLII
1843 = MDCCCXLIII
1844 = MDCCCXLIV
1845 = MDCCCXLV
1846 = MDCCCXLVI
1847 = MDCCCXLVII
1848 = MDCCCXLVIII
LVII
1848 = MDCCCXLVIII
LVII
1848 = MDCCCXLVIII
LVII
1848 = MDCCCXLVIII
LVII = MDCC 900CC
1849CC 900CCC
1849CCC 900CCC
1849CCC 900CCC
1849CCC 900CCC
1849CCC 900CCC 1849CCC 900CCC
1849CCC 900CCC
1849CCC 900CCC MDCCCLIII
1854 = MDCCCLIV
1855 = MDCCCLV
1856 = MDCCCLVI
1857 = MDCCCLVII
1858 = MDCCCLVIII
1859 = MDCCCLIX
1860 = MDCCCLX
1861 = MDCCCLXI
1862 = MDCCCLXI
1862 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1863 = MDCCCLXII
1866 = MDCCCLXVI
1867 = MDCCCLXVII
1868 = MDCCCLXVIII
1869 = MDCCCLXIX
1870 = MDCCCLXX
1871 = MDCCCLXXI
1872 = MDCCCLXXII
1873 = MDCCCLXXIII
1874 = MDCCCLXXIV
1875 = MDCCCLXXV
1876 = MDCCCLXXVI
1877 = MDCCCLXXVII
1878 = MDCCCLXXVIII
1879X81 MDCCCLXXIX
MDXXVIII
1879X81 MDXCLXXIX
1880CCICCICCI
1880 = MDXIICCICCI MDCCCLXXXIV
1885 = MDCCCLXXXV
1886 = MDCCCLXXXVI
1887 = MDCCCLXXXVII
1888 = MDCCCLXXXVIII
1889 = MDCCCLXXXIX
1890 = MDCCCXC
1891 = MDCCCXCI
1892 = MDCCCXCII
1893 = MDCCCXCIII
1894 = MDCCCXCIV
1895 = MDCCCXCV
1896 = MDCCCXCVI
1897 = MDCCCXCVII
1898 = MDCCCXCVIII
1899 = MDCCCXCIX
1900 = MCM
1901 = MCMI
1902 = MCMII
1903 = MCMIII
1904 = MCMIV
1905 = MCMV
1906 = MCMVI
1907 = MCMVII
1907 = MCMVII 900 MCMIX
1910 = MCMX
1911 = MCMXI
1912 = MCMXII
1913 = MCMXIII
1914 = MCMXIV
1915 = MCMXV
1916 = MCMXVI 900 71 1917 = MCMXVII
1918 = MCMXVIII
1919 = MCMXIX
1920 = MCMXX
1921 = MCMXXI
1922 = MCMXXII
1923 = MCMXXIII
1924 = MCMXXIV
1925 = MCMXXV
1926 = MCMXII900 MCMXXV
1926 = MCMXIIXV
1926 = MCMXIIXV = MCMXXIX
1930 = MCMXXX
1931 = MCMXXXI
1932 = MCMXXXII
1933 = MCMXXXIII
1934 = MCMXXIV
1935 = MCMXXXV
1936 = MCMXXXVI 900XXXXV
1936 = MCMXXXVI 900XMIX 1937 = MCMXXXVIIM 900XXVI 1937 = MCMXXXVII71
1942 = MCMXLII
1943 = MCMXLIII
1944 = MCMXLIV
1945 = MCMXLV
1946 = MCMXLVI
1947 = MCMXLVII
1948 = MCMXLVIII
1949 = MCMXLIX
19571 1950 = MCML
1951 = MCML 900ML
MCMLI
= MCML 9007 = MCMLIV
1955 = MCMLV
1956 = MCMLVI
1957 = MCMLVII
1958 = MCMLVIII
1959 = MCMLIX
1960 = MCMLX
1961 = MCMLXI
1962 = MCMLXII
1963 = MCMLXIII
1964 = MCMLX IV
1965 = MCMLXV
1966 = MCMLXVI
1967 = MCMLXVII
1968 = MCMLXVIII
1969 = MCMLXIX
1970 = MCMLXX
1971 = MCMLXXI
1972 = MCMLXXII
1973 = MCMLXXIII
1974 = MCMLXXII
1973 = MCMLXXIII
1974 MCMLXXIVML
1974 MCMLXXIV 900I 1977 = MCMLXXVII
1978 = MCMLXXVIII
1979 = MCMLXXIX
1980 = MCMLXXX
1981 = MCMLXXXI
1982 = MCMLXXXII
1983 = MCMLXXXIII
1984 = MCMLXXXIV
1985 = MCMLXXXV
1986 = MCMLXIIXV
1986 = MCMLXIIXV
MCMLXXXV
1986 = MCMLXIIXV MCMLXXXIX
1990 = MCMXC
1991 = MCMXCI
1992 = MCMXCII
1993 = MCMXCIII
1994 = MCMXCIV
1995 = MCMXCV
1996 = MCMXCVI
1997 = MCMXCVII
1998 = MCMXCVIII
1999 = MCMCVIII
1999 = MCMCVIII
200071 1998 = MCMXCVIII
1999 = MCMC
1999 = MCMC
2002 = MMII
2003 = MMIII
2004 = MMIV
2005 = MMV
2006 = MMVI
2007 = MMVII
2008 = MMVIII
2009 = MMIX
2010 = MMX
2011 = MMXI
2012 = MM XII
2013 = MMXIII
2014 = MMXIV
2015 = MMXV
2016 = MMXVI
2017 = MMXVII
2018 = MMXVIII
2019 = MMXIX
2020 = MMXX
2021 = MMXXI
2022 = MMXXII
2023 = MMXXIII
2024 = MMXXIV
2024 = MMXXIV 2025 = MMXXV
2026 = MMXXVI
2027 = MMXXVII
2028 = MMXXVIII
2029 = MMXXIX
2030 = MMXXX
2031 = MMXXXI
2032 = MMXXXII
2033 = MMXXXIII
2034 = 2034 = MMXXXIV
2034 = MMXXXIV MMXXXVII
2038 = MMXXXVIII
2039 = MMXXXIX
2040 = MMXL
2041 = MMXLI
2042 = MMXLII
2043 = MMXLIII
2044 = MMXLIV
2045 = MMXLV
2046 = MMXLVI 900VI 20471 2046 = MMXLVI 900VI 20471 2050 = MML
2051 = MMLI
2052 = MMLII
2053 = MMLIII
2054 = MMLIV
2055 = MMLV
2056 = MMLVI
2057 = MMLVII
2058 = MMLVIII
2059 = MMLIX
2060 = MMLX
2061 = 2062MLX MMLXII 900 71 2063 = MMLXIII
2064 = MMLXIV
2065 = MMLXV
2066 = MMLXVI
2067 = MMLXVII
2068 = MMLXVIII
2069 = MMLXIX
2070 = MMLXX
2071 = MMLXXI
2071 MMLXXI
2072 = MMLXIIML
2072 = MMLXIIML
2072 = MMLXIIML = MMLXXV
2076 = MMLXXVI
2077 = MMLXXVII
2078 = MMLXXVIII
2079 = MMLXXIX
2080 = MMLXXX
2081 = MMLXXXI
2082 = MMLXXXI
2082 = MMLXXXII
2083 = MMLXXXIIIML X71 2083 = MMLXXXIIIML 2084 2083 = MMLXXX86ML 2084
2088 = MMLXXXVIII
2089 = MMLXXXIX
2090 = MMXC
2091 = MMXCI
2092 = MMXCII
2093 = MMXCIII
2094 = MMXCIV
2095 = MMXCV
2096 = MMXCVI
2097 = 2098X71 MMXCVI
2097 = 2098X71 MMXCVI
2097 = 2098X71 MMXCVII
2097 = MMXCVII = MMC
Весь материал на этих страницах — Пол Льюис 1997-2005 гг. Полное руководство по покупке Panerai: описание каждой текущей модели
Разбитая на четыре коллекции, Panerai предлагает более 20 мануфактурных механизмов, а также ряд механизмов, созданных на базе сторонних производителей, и эти калибры присутствуют в более чем 200 отдельных моделях часов, доступных из стали. , бронза, титан, золото, платина и фирменные материалы корпуса, такие как BMG-TECH (объемное металлическое стекло), Carbotech (полиэфирэфиркетон) и Panerai Composite (синтетическая керамика с использованием микродугового окисления).
Каждым часам присваивается индивидуальный номер или PAM-номер: PAMxxxxx. В разговорной речи ссылочные номера часто упоминаются без нулей между PAM и числами в конце.
Механизмы компании, построенные на базе Unitas / ETA, имеют римские цифры калибра, которые начинаются с OP (например, OPXXII). Четыре категории моделей Panerai
Panerai Luminor
Механизм : Руководство Panerai P.6000
Механизм : Panerai P.9010 автоматический
Механизм : Руководство Panerai P.3002
Механизм : Panerai P.9010 с автоматическим подзаводом Panerai Luminor Due
Механизм : Panerai P.900 автоматический
Механизм : Panerai P.900 с автоподзаводом Panerai Radiomir
Механизм : Руководство Panerai P.6000
Механизм : Panerai P.3000 manual
Механизм : механическая коробка Panerai P.2005, турбийон, время по Гринвичу, запас хода, am / pm, запас хода на 6 дней Panerai Submersible
Механизм : Panerai P.900 автоматический
Механизм : Panerai P.9000 автоматический, 3-дневный запас хода 648 разделить на 4 в столбик: Разделить столбиком 648 на 4
Как правильно объяснить ребёнку деление в столбик. Деление в столбик 648 разделить на 6 в столбик объяснение
Деление чисел
 То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.Деление с остатком
 А записывается: 22:7=3(1).
А записывается: 22:7=3(1).Деление на 3 и 9
Умножение и деление
 Там же найдете таблицу умножения и примеры для тренировки.
Там же найдете таблицу умножения и примеры для тренировки.Деление 3 класс
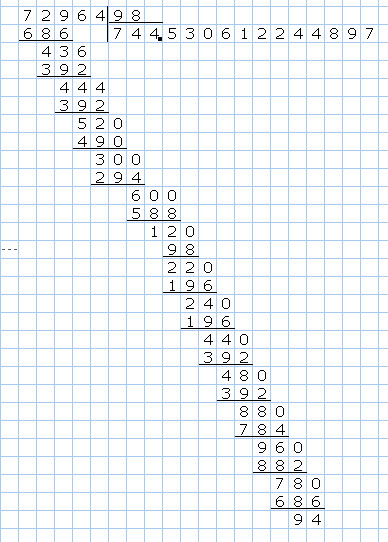 Сколько каждый получит яблок, если нужно поделить их одинаково?
Сколько каждый получит яблок, если нужно поделить их одинаково?Деление 4 класс
Деление в столбик
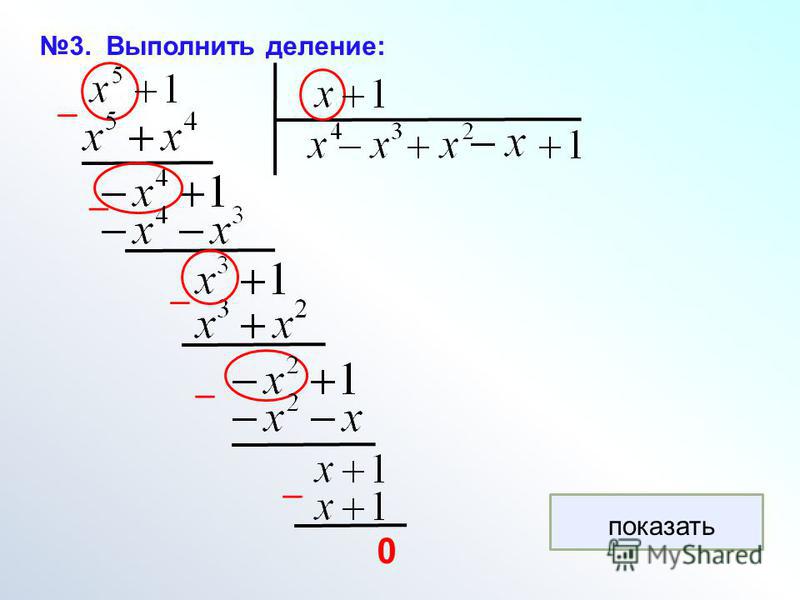 Деление начинаем слева направо. Сначала берем цифру 5:
Деление начинаем слева направо. Сначала берем цифру 5:
Деление трехзначных
Деление дробей
Деление числа на классы
 В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.Деление натуральных чисел
Деление презентация
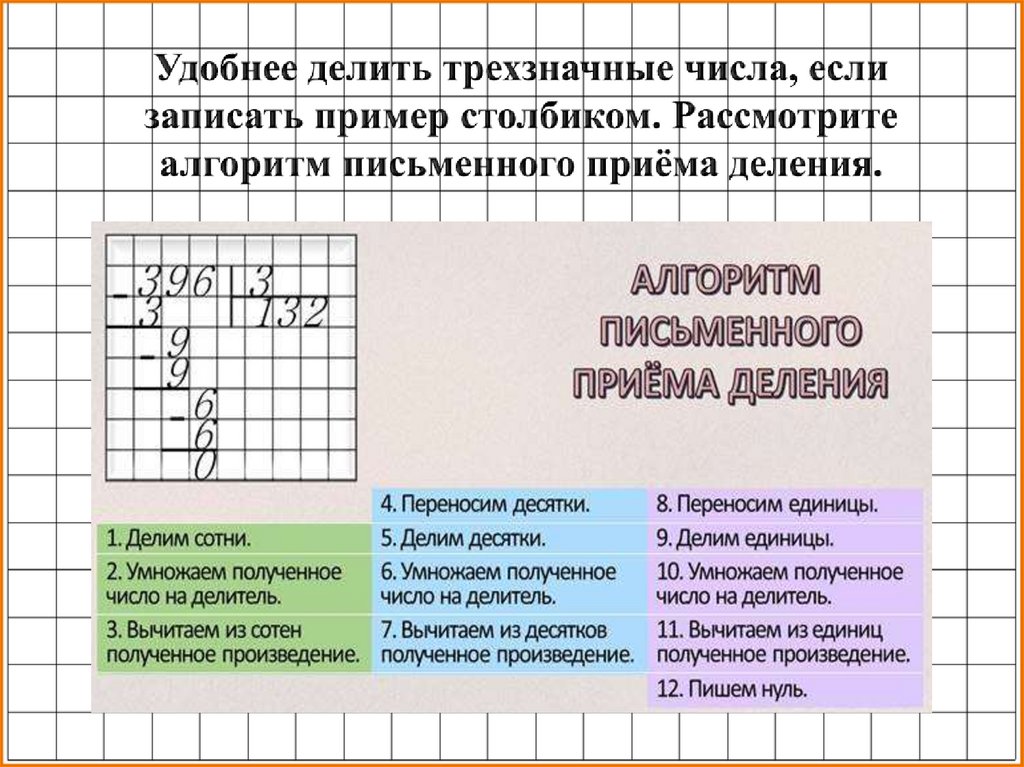 Время зря не потратите, а свои знания закрепите!
Время зря не потратите, а свои знания закрепите!Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Игра «Угадай операцию»
Игра «Упрощение»
 Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.Игра «Быстрое сложение»
Игра «Визуальная геометрия»
 Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.Игра «Копилка»
Игра «Быстрое сложение перезагрузка»
Развитие феноменального устного счета
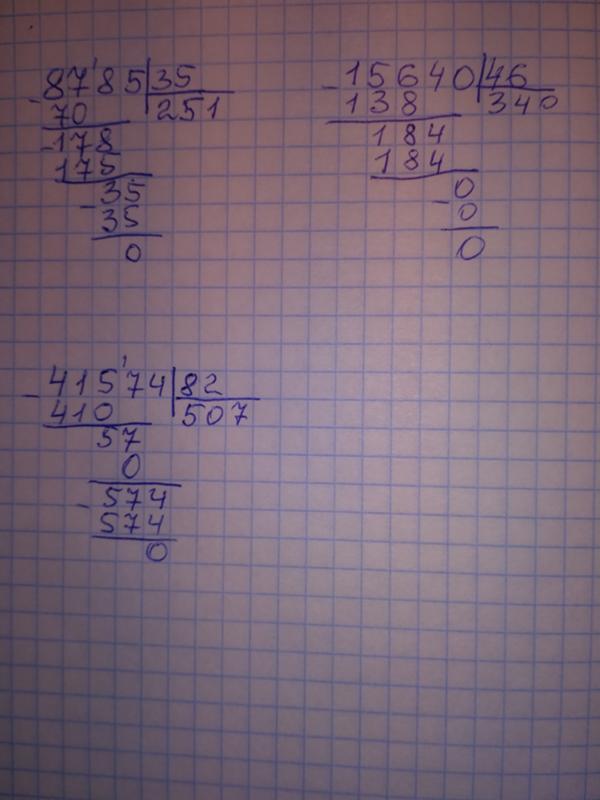
Скорочтение за 30 дней
Развитие памяти и внимания у ребенка 5-10 лет
 Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.Деньги и мышление миллионера

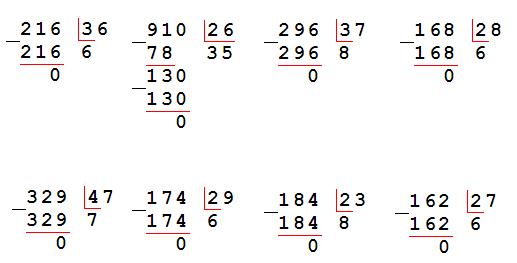
«6 · 8 = 48
»
Записываем цифру «6
» в частное.Как делить столбиком
 Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого: Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6: Допустим нам нужно разделить 9027 на 9.
Допустим нам нужно разделить 9027 на 9. Пусть нам требуется разделить 3000 на 6.
Пусть нам требуется разделить 3000 на 6.Деление столбиком с остатком
 Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:Калькулятор деления столбиком
 Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?Осваиваем операцию разделения (деления) на части в игровой форме
 Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.Умножаем и делим, используя таблицу умножения

Делим столбиком – приведем пример

Объясняем наглядно
 Приписываем 3 к полученному числу 2.
Приписываем 3 к полученному числу 2.Как научить ребенка делению – закрепляем навык
 А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода. д.) во время конструирования, игр и наблюдений за природой.
д.) во время конструирования, игр и наблюдений за природой.
Дружинина Елена
специально для проекта сайт Математика. Деление уголком | Сайт Леонида Некина

 Он равен, очевидно,
Он равен, очевидно, Мы делим его на наш делитеть ( $2$ ) и получаем $8$ . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
Мы делим его на наш делитеть ( $2$ ) и получаем $8$ . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
 }~0)$.
}~0)$. Для полноты картины распишем наше делимое в таком виде:
Для полноты картины распишем наше делимое в таком виде: Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( $135$ ) оказалось бы меньше делителя ( $259$ ), а это не то, что нам надо. Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:
Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( $135$ ) оказалось бы меньше делителя ( $259$ ), а это не то, что нам надо. Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком: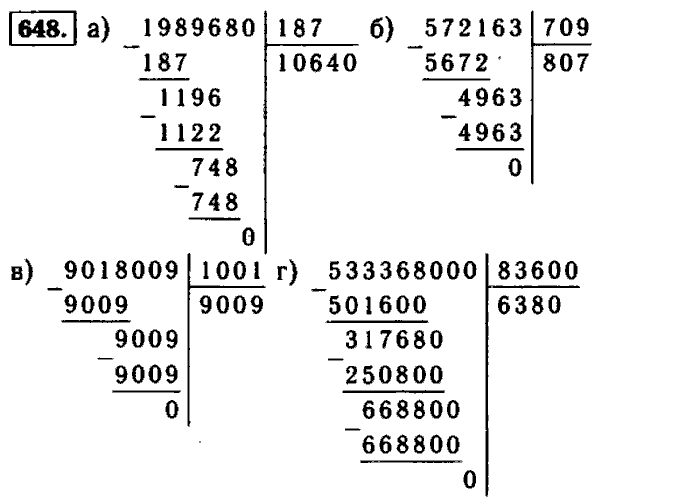 После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение $259$ ∙ $5$ , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения $1295$ оказался меньше записанного над ним числа $1356$ , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение $259$ ∙ $5$ , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения $1295$ оказался меньше записанного над ним числа $1356$ , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется. Очень важно, что она оказалась меньше делителя ( $259$ ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
Очень важно, что она оказалась меньше делителя ( $259$ ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что, ~217)$.
~217)$.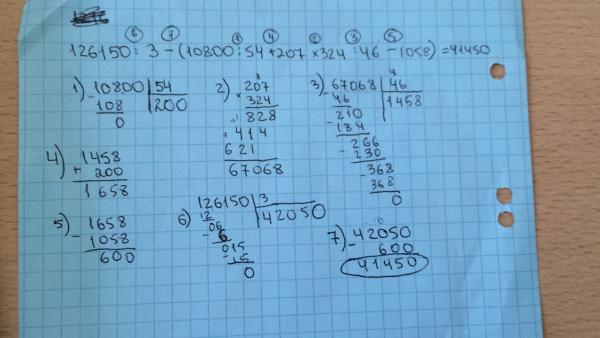
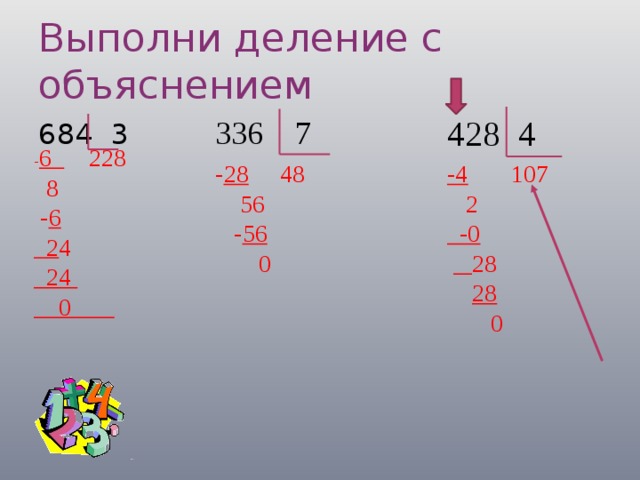 Однозначное число мы записываем в качестве следующей цифры частного, а к промежуточному остатку приписываем в конец первую из оставшихся цифр делимого и передаем получившееся число для дальнейшей «обработки» в следующий шаг.
Однозначное число мы записываем в качестве следующей цифры частного, а к промежуточному остатку приписываем в конец первую из оставшихся цифр делимого и передаем получившееся число для дальнейшей «обработки» в следующий шаг.4 класс.
 Моро. Учебник №2. Ответы к стр. 58
Моро. Учебник №2. Ответы к стр. 58Числа от 1 до 1000
Деление на двузначное и трёхзначное число
Письменное деление на двузначное число
Ответы к стр. 58
_ 324 |62 _ 526 |74 _ 793 |83
310 |5 518 |7 474 |9
14 8 46
Разделю 324 не на 62, а на 60, чтобы легче было найти цифру частного. Для этого разделю 32 на 6, получу 5. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 5.
Умножу 62 на 5, получится 310. Вычту: 324 — 310 = 14, 14 меньше 62, значит, цифра 5 подходит, а 14 — остаток. Теперь её можно записать в частном.
Теперь её можно записать в частном.
Разделю 526 не на 74, а на 70, чтобы легче было найти цифру частного. Для этого разделю 52 на 7, получу 7. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 7.
Умножу 74 на 7, получится 518. Вычту: 526 — 518 = 8, 8 меньше 74, значит, цифра 7 подходит, а 8 — остаток. Теперь её можно записать в частном.
Разделю 793 не на 83, а на 80, чтобы легче было найти цифру частного. Для этого разделю 79 на 8, получу 9. Это пробная цифра, её нельзя сразу записать в частном — сначала надо проверить, подходит ли цифра 9.
Умножу 83 на 9, получится 747. Вычту: 793 — 747 = 46, 46 меньше 83, значит, цифра 9 подходит, а 46 — остаток. Теперь её можно записать в частном.
156 : 48 278 : 62 346 : 56 445 : 73
144 |3 × 48
12 3
144
248 |4 × 62
30 4
248
336 |6 × 56
10 6
336
438 |6 × 73
7 6
438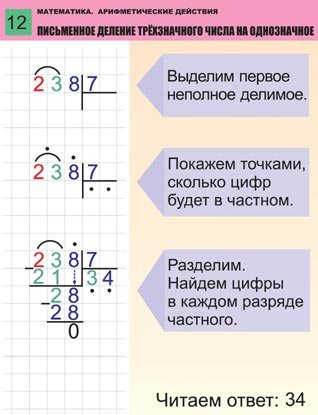 Космонавты были в полёте 290 ч. Сколько это суток и часов?
Космонавты были в полёте 290 ч. Сколько это суток и часов?
24 |12 — суток
_50
48
2 — часа
О т в е т: 12 суток и 2 часа.
160 — 120 1000 : (160 — 120) 1000 : (160 — 120) • 160
1000 : (160 — 120) — столько грамм семян высеяли на 1 м2
1000 : (160 – 120) • 160 – столько грамм семян высеяли на втором участке ) — дошли до финиша
) — дошли до финиша
2) 245 • 3 = 735 (с.) — прибыли к финишу
О т в е т: 245 машин и 735 спортсменов.
1) Какое число надо уменьшить на 28, чтобы получить число, равное сумме чисел 58 и 37?
2) Какое число надо увеличить в 8 раз, чтобы получить число, равное произведению чисел 80 и 12?
3) Какое число надо уменьшить в 28 раз, чтобы получить число, равное разности чисел 300 и 203?
x — 28 = 95
x = 95 + 28
x = 123
x • 8 = 960
x = 960 : 8
x = 120
x : 28 = 97
x = 97 • 28
x = 2716
384 |4 192 |4
0 0
648 |9
0
× 352 — 5840|80
46 560 |73
+ 2112 —240
1408 240
16192 0
73
16119 Найди значения выражений 360 : с и 360 • с, если с = 1; c = 3; c = 4; c = 6; c = 10.
Найди значения выражений 360 : с и 360 • с, если с = 1; c = 3; c = 4; c = 6; c = 10.
Наблюдай, как при этом изменяется частное, как изменяется произведение.
360 : 3 = 120 360 • 3 = 1080
360 : 4 = 90 360 • 4 = 1440
360 : 6 = 60 360 • 6 = 2160
360 : 10 = 36 360 • 10 = 3600
Значение частного уменьшается, а значение произведения увеличивается.
В этой фигуре все углы тупые.
Эти треугольники будут и равнобедренными и равносторонними. Равнобедренный треугольник — это треугольник, у которого две стороны равны по длине. Условие равенства двух сторон является необходимым и достаточным, чтобы считать треугольник равнобедренным. Это условие в равностороннем треугольнике выполняется всегда. Следовательно равносторонний треугольник всегда является равнобедренным.
Это условие в равностороннем треугольнике выполняется всегда. Следовательно равносторонний треугольник всегда является равнобедренным.
399 |7 236 |4
0 0
475 |5
0
× 609 — 4320|60
27 420 |72
+ 4263 —120
1218 120
16443 0
72
16371
МАГИЧЕСКИЙ КВАДРАТ 4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
4 класс. Часть 2. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.Онлайн калькулятор. Умножение столбиком. — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
правило, примеры. Калькулятор умножения столбиком
 Чтобы сосчитать быстро, пригодится . Подберите ответ вместе: 6*4 = 24 – совсем непохоже; 6*5 = 30 – близко к 37. Но 37-30 = 7 – шесть «поместится» еще раз. Наконец, 6*6 = 36, 37-36 = 1 – подходит. Первая цифра частного найдена – это 6. Напишите ее под делителем.
Чтобы сосчитать быстро, пригодится . Подберите ответ вместе: 6*4 = 24 – совсем непохоже; 6*5 = 30 – близко к 37. Но 37-30 = 7 – шесть «поместится» еще раз. Наконец, 6*6 = 36, 37-36 = 1 – подходит. Первая цифра частного найдена – это 6. Напишите ее под делителем. Каждому досталось 27 штук, и пять яблок остались неподеленными. Можно поделить и их, разрезав каждое на шесть долек и раздав поровну. Каждому человеку досталась одна долька от каждого яблока – 1/6. А так как яблок было пять штук, то и долек у каждого оказалось по пять – 5/6.
Каждому досталось 27 штук, и пять яблок остались неподеленными. Можно поделить и их, разрезав каждое на шесть долек и раздав поровну. Каждому человеку досталась одна долька от каждого яблока – 1/6. А так как яблок было пять штук, то и долек у каждого оказалось по пять – 5/6.
 Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .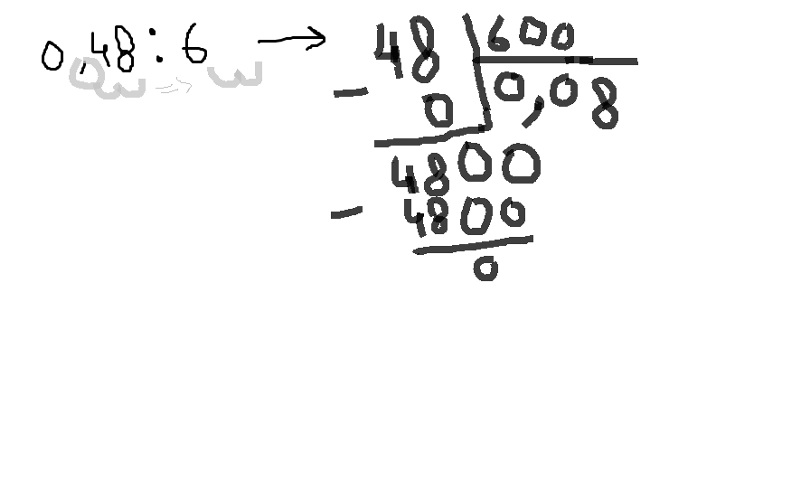 Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
 Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делителем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следующую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
3. Выполняем операцию вычитания и под чертой записываем результат.
Деление многозначных натуральных чисел столбиком
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе. Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.



Как научиться делить столбиком
Игровые задания
 Напишите в тетради 3–5 примеров на деление с ответами. Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные с помощью устного счета.
Напишите в тетради 3–5 примеров на деление с ответами. Все, кроме одного, должны быть решены неверно. Нужно быстро найти тот пример, который содержит правильный ответ. Затем исправить остальные с помощью устного счета. Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей.
Укажите время на решение, например 5 минут. Поставьте перед ребенком песочные часы. После выполнения контрольной верно поощрите школьника походом в зоопарк, кино, покупкой книги, сладостей.1.
 Мама-учитель
Мама-учитель2. Посмотреть вместе с ребенком обучающее видео
3. Нанять репетитора
Как объяснить деление столбиком

 Сначала проговаривайте алгоритм вместе, потом только слушайте ученика и помогайте исправить ошибки.
Сначала проговаривайте алгоритм вместе, потом только слушайте ученика и помогайте исправить ошибки.Деление на однозначное число
 Ответ: 1.
Ответ: 1.
Деление на двузначное число
 Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:
Такой способ больше подходит для работы с числами от четырех разрядов, то есть тысяч. Приведем простой пример:
Многозначные числа
 В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.
В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.
Деление с остатком
Как делать проверку
 Делать это можно столбиком:
Делать это можно столбиком:Примеры для тренировки
Однозначные
Двузначные
Многозначные
Скачать карточки

Деление чисел
 То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.Деление с остатком
 Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).Деление на 3 и 9
Умножение и деление
 Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.Деление 3 класс
 На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?Деление 4 класс
Деление в столбик


Деление трехзначных
Деление дробей
Деление числа на классы
 Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.Деление натуральных чисел
Деление презентация
 Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Игра «Угадай операцию»
Игра «Упрощение»
 Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.Игра «Быстрое сложение»
Игра «Визуальная геометрия»
 Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.Игра «Копилка»
Игра «Быстрое сложение перезагрузка»
Развитие феноменального устного счета

Скорочтение за 30 дней
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Деньги и мышление миллионера
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

 е. равенством, справедливым при всех значениях переменной x .
е. равенством, справедливым при всех значениях переменной x . Получаем первый член частного 2x2 .
Получаем первый член частного 2x2 . Получаем второй член частного x .
Получаем второй член частного x .
= (x2 – x + 1) (2x2 + x +
+ 4) – 5x – 3 ,
Калькулятор столбиком умножение деление вычитание прибавление. Как делить в столбик? Как объяснить ребенку деление столбиком? Деление на однозначное, двузначное, трехзначное число, деление с остатком
 Делим 19 на 18. Берем по 1. Деление целой части окончено, в частном ставим запятую. Вычитаем от 19 18. В остатке — 1. Сносим 2. 12 на 18 не делится, в частном пишем нуль. Сносим 6. 126 делим на 18, получаем 7. Деление окончено: 19,26: 18 = 1,07.
Делим 19 на 18. Берем по 1. Деление целой части окончено, в частном ставим запятую. Вычитаем от 19 18. В остатке — 1. Сносим 2. 12 на 18 не делится, в частном пишем нуль. Сносим 6. 126 делим на 18, получаем 7. Деление окончено: 19,26: 18 = 1,07. Деление целой части окончено, в частном ставим запятую. 4∙4=16. От 17 вычитаем 16. Остаток — 1. Сносим нуль. 10 делим на 4. Берем по 2. 4∙2=8. От 10 вычитаем 8. В остатке — 2. Сносим нуль. 20 делим на 4. Берем по 5. Деление окончено: 17: 4 = 4,25.
Деление целой части окончено, в частном ставим запятую. 4∙4=16. От 17 вычитаем 16. Остаток — 1. Сносим нуль. 10 делим на 4. Берем по 2. 4∙2=8. От 10 вычитаем 8. В остатке — 2. Сносим нуль. 20 делим на 4. Берем по 5. Деление окончено: 17: 4 = 4,25.
Как умножаются в столбик натуральные числа?
 Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.Алгоритм умножения в столбик десятичных дробей
С чего начать обучение делению?
 Второе (на него делят) — делитель. Ответ — частное.
Второе (на него делят) — делитель. Ответ — частное.Алгоритм деления чисел в столбик
 Обычно оно состоит из одной цифры, максимум из двух.
Обычно оно состоит из одной цифры, максимум из двух.Как решать деление в столбик, если в делителе больше одной цифры?
 Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.Как быть, если делимое заканчивается на ноль?
 Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.Что делать, если разделить нужно десятичную дробь?
 Иногда это нужно для того, чтобы доделить числа до конца.
Иногда это нужно для того, чтобы доделить числа до конца.Деление двух десятичных дробей

Что делать, если делитель равен 10, 100, 0,1, или 0,01?
 То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.Деление периодических дробей

Если в примере разные дроби…

Принцип деления для малышей

Как обучить малыша делению в столбик
 В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.
В противном случае малыш просто запутается во всех процессах, и перестанет что-либо понимать.Умножаем и делим с помощью таблицы

 Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.
Таблица умножения есть и в школе, и в тетрадях, поэтому носить отдельную таблицу в школу не придется.Делим с помощью столбика

Особенности
 Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Достоинства и недостатки
 2 и более поздней версией.
2 и более поздней версией. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.Деление чисел

Деление с остатком
Деление на 3 и 9
 Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.Умножение и деление
 Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.Деление 3 класс
Деление 4 класс
 Что же такое деление в столбик? Ответ можете найти ниже:
Что же такое деление в столбик? Ответ можете найти ниже:Деление в столбик
 Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:Деление трехзначных
Деление дробей
 То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):Деление числа на классы
Деление натуральных чисел

Деление презентация
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Игра «Угадай операцию»
 Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.Игра «Упрощение»
Игра «Быстрое сложение»
 Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.Игра «Визуальная геометрия»
Игра «Копилка»
Игра «Быстрое сложение перезагрузка»
 Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.Развитие феноменального устного счета
Скорочтение за 30 дней
 В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.Развитие памяти и внимания у ребенка 5-10 лет
Супер-память за 30 дней

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Деньги и мышление миллионера
 Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.Решение по действиям в столбик. Деление натуральных чисел столбиком, примеры, решения
 Если малыш плохо знает умножение, он не поймет деление.
Если малыш плохо знает умножение, он не поймет деление.
Письменное деление на двузначное число
 Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры. Записываем 3 в ответ под чертой справа
Записываем 3 в ответ под чертой справа Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4 Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
 Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.Деление чисел

Деление с остатком
Деление на 3 и 9
 Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.Умножение и деление
 Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.Деление 3 класс
Деление 4 класс
 Что же такое деление в столбик? Ответ можете найти ниже:
Что же такое деление в столбик? Ответ можете найти ниже:Деление в столбик
 Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:Деление трехзначных
Деление дробей
 То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):Деление числа на классы
Деление натуральных чисел

Деление презентация
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Игра «Угадай операцию»
 Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.Игра «Упрощение»
Игра «Быстрое сложение»
 Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.Игра «Визуальная геометрия»
Игра «Копилка»
Игра «Быстрое сложение перезагрузка»
 Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.Развитие феноменального устного счета
Скорочтение за 30 дней
 В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.Развитие памяти и внимания у ребенка 5-10 лет
Супер-память за 30 дней

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Деньги и мышление миллионера
 Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни: Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
 Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.

Как вычитать столбиком
 Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63:
Теперь мы легко можем от 12 отнять 9. Записываем под чертой в разряде единиц 3. В разряде десятков у нас было 7 единиц, одну из них мы перекинули в простые единицы, осталось 6 десятков. Записываем под чертой в разряде десятков 6. В результате мы получили число 63: Из 10 вычитаем 5, пишем 5:
Из 10 вычитаем 5, пишем 5:Калькулятор вычитания столбиком
 Сначала записываем делимое и справа от него ставим вертикальную черту:
Сначала записываем делимое и справа от него ставим вертикальную черту:Как делить столбиком

 Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают: Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:Деление столбиком с остатком
 Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:Калькулятор деления столбиком
Математика. Деление уголком | Сайт Леонида Некина

 Но мы сейчас перепишем их в виде краткой таблицы. Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто. Делимое и делитель запишем так:
Но мы сейчас перепишем их в виде краткой таблицы. Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто. Делимое и делитель запишем так: Он равен, очевидно,
Он равен, очевидно, Мы делим его на наш делитеть ( 2 ) и получаем 8 . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
Мы делим его на наш делитеть ( 2 ) и получаем 8 . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
 0).
0). Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком:
Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком: Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:
Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком: После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение 259 ∙ 5 , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения ( 1295 ) оказался меньше записанного над ним числа 1356 , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение 259 ∙ 5 , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения ( 1295 ) оказался меньше записанного над ним числа 1356 , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется. Очень важно, что она оказалась меньше делителя ( 259 ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
Очень важно, что она оказалась меньше делителя ( 259 ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что, 217).
217). 2=(a-b)(a+b)\).
2=(a-b)(a+b)\).
Онлайн-калькулятор для деления в столбик десятичных дробей
Делим в столбик десятичные дроби с помощью онлайн-калькулятора
 Сегодня мы подготовили для вас два разных варианта вычисления, а вы, ознакомившись с инструкциями, выберите тот, который будет наиболее подходящим.
Сегодня мы подготовили для вас два разных варианта вычисления, а вы, ознакомившись с инструкциями, выберите тот, который будет наиболее подходящим.Способ 1: OnlineMSchool
 Если нет, измените ее, воспользовавшись всплывающим меню.
Если нет, измените ее, воспользовавшись всплывающим меню.Способ 2: Rytex
 На ней кликните по надписи «Онлайн калькуляторы».
На ней кликните по надписи «Онлайн калькуляторы».
Сложение систем счисления онлайн
Перевод из восьмеричной в десятичную онлайн
Перевод из десятичной в шестнадцатеричную систему онлайн
Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.Помогла ли вам эта статья?
Общий метод — Дивизион — Национальная версия 4 по математике
Как обрабатывать деление на ноль в SQL
База данных:
Операторы:
Проблема:
Пример:
investor_data с данными в следующих столбцах: id , investor_year , price_per_share , доход и расходы . id investor_year price_per_share доход расходы 1 2016 20 3200 2300 2 2017 130 2000 2000 3 2018 40 200 100 4 2019 15 5900 4900  Обратите внимание, что бывают случаи, когда доход равен расходам, поэтому их разница будет равна нулю. Таким образом, нам нужно найти способ избежать деления на ноль.
Обратите внимание, что бывают случаи, когда доход равен расходам, поэтому их разница будет равна нулю. Таким образом, нам нужно найти способ избежать деления на ноль. Решение:
ВЫБЕРИТЕ инвестор_год,
price_per_share / NULLIF (доходы-расходы, 0) AS P_E_ratio
ИЗ данных инвестора;
инвестор_год P_E_ratio 2016 0.0222 2017 НЕТ 2018 0,4000 2019 0,0150 NULLIF изменяет ноль на значение NULL. Следовательно, деление на ноль дает результат NULL. Обсуждение:
NULLIF .
NULLIF принимает два аргумента: интересующее выражение и значение, которое вы хотите переопределить. Если первый аргумент равен второму, то NULLIF возвращает NULL; в противном случае возвращается первый аргумент. NULLIF . В нашем примере, если разница между доходами и расходами равна нулю, это значение будет изменено на NULL, а знаменатель в делении будет NULL, а не ноль. Решение 2. Используйте
ГДЕ WHERE с оператором сравнения. В нашем примере мы могли бы проверить, отличается ли доход-расходы от 0. Если это так, расчет будет возвращен.
ВЫБЕРИТЕ инвестор_год,
price_per_share / (доходы-расходы) AS P_E_ratio
ИЗ данных инвестора
ГДЕ (доходы-расходы) 0;
WHERE вы получите меньше строк, чем в таблице investor_date . Строки, в которых доходы и расходы равны, в конечном результате отображаться не будут.
Строки, в которых доходы и расходы равны, в конечном результате отображаться не будут. Знакомство с колоннами с перегородкой | AIChE
 Модернизация существующих колонн с помощью перегородки для повышения эффективности разделения является частью более масштабного стремления к интенсификации процессов в этих отраслях. Интенсификация процесса (PI) направлена на резкое повышение стоимости и энергоэффективности за счет переосмысления традиционных схем работы. DWC — один из примеров усовершенствованной технологии.
Модернизация существующих колонн с помощью перегородки для повышения эффективности разделения является частью более масштабного стремления к интенсификации процессов в этих отраслях. Интенсификация процесса (PI) направлена на резкое повышение стоимости и энергоэффективности за счет переосмысления традиционных схем работы. DWC — один из примеров усовершенствованной технологии. Пример демонстрирует, как добавление перегородки может улучшить чистоту бокового потока без необходимости добавления второй колонны.
Пример демонстрирует, как добавление перегородки может улучшить чистоту бокового потока без необходимости добавления второй колонны. Как удалить # DIV / 0 в Excel • Портфолио производительности
Что значит # DIV / 0! Имеете ввиду в Excel?
 ”Вы можете увидеть пример на скриншоте ниже, используя Microsoft Office 365.
”Вы можете увидеть пример на скриншоте ниже, используя Microsoft Office 365.
Добавьте простую логику в формулу Excel
Как показать ноль вместо # DIV / 0!
 в столбце E)
в столбце E)
Другие замены формул для # DIV / 0!
 Обратите внимание на кавычки, иначе вы можете получить ошибки в формулах.
Обратите внимание на кавычки, иначе вы можете получить ошибки в формулах. = ЕСЛИ (D2 = 0, "NA", C2 / D2)
= ЕСЛИ (D2 = 0, "", C2 / D2)
= ЕСЛИ (D2 = 0, C2, C2 / D2)
Вам также могут понравиться эти учебные пособия по Excel
 Я могу получить партнерскую комиссию за эти продукты, если вы их купите. Обновлено: 2021-05-05
Я могу получить партнерскую комиссию за эти продукты, если вы их купите. Обновлено: 2021-05-05 3 способа умножения в Excel
 В случае «= 3 * (3 + 5) * 6» Excel сначала складывает 3 и 5, в результате получается 8. Затем он умножает 3 * 8 * 6 и достигает 144.
В случае «= 3 * (3 + 5) * 6» Excel сначала складывает 3 и 5, в результате получается 8. Затем он умножает 3 * 8 * 6 и достигает 144.
Аргументы могут быть:

Как использовать функцию Excel MOD
 В результате, если у вас есть десятичное значение для 15 минут и время в A1, вы можете добавить 15 минут …
В результате, если у вас есть десятичное значение для 15 минут и время в A1, вы можете добавить 15 минут … Ключ в этом фрагменте: MOD (COLUMN (B5: K5) -COLUMN (B5) + 1, L5) = 0 Здесь в формуле используется КОЛОНКА…
Ключ в этом фрагменте: MOD (COLUMN (B5: K5) -COLUMN (B5) + 1, L5) = 0 Здесь в формуле используется КОЛОНКА… Когда результат …
Когда результат … Pivot | Sisense | Документация
 Они позволяют быстро обобщать и анализировать большие объемы данных.
Они позволяют быстро обобщать и анализировать большие объемы данных. Сводные таблицы в Windows и Linux

Видимые столбцы таблицы (Linux)

Добавление данных в сводную таблицу
Примечание. Когда Sisense развернут в Linux, вы можете отображать HTML в ячейках Pivot 2 как HTML или обычный текст. Чтобы выбрать «Администратор»> «Управление системой», затем в области «Сводная таблица» установите переключатель «Разрешить отображение содержимого сводной таблицы в формате HTML». Когда переключатель включен, Sisense отображает HTML как HTML, а когда он отключен, Sisense отображает HTML как простой текст.
Когда переключатель включен, Sisense отображает HTML как HTML, а когда он отключен, Sisense отображает HTML как простой текст.
Если выбрано несколько строк, они разбиваются на подстроки (группы). Например, ниже показано условие, добавленное как вторая строка:
Вы можете перетащить поля, добавленные в столбцы, в область строк и наоборот.
Совет. Щелкните значение правой кнопкой мыши, чтобы добавить гистограммы в сводную таблицу. Общие и промежуточные итоги

Примечание. Промежуточные итоги доступны только в том случае, если у вас более одной строки в таблице.
Примечание. В каждом поле можно выбрать разные промежуточные итоги. Для этого щелкните заголовок нужного значения в таблице, щелкните «Подытог по» и выберите метод.  Это истинный промежуточный итог среднего дохода по азиатскому региону.
Это истинный промежуточный итог среднего дохода по азиатскому региону. Всего
Устранение проблем с общими и промежуточными итогами
 Причиной может быть как раз выбранный метод расчета.
Причиной может быть как раз выбранный метод расчета.
Например, см. Нижеприведенный вариант использования (из Образца информационной панели Healthcare) с использованием взвешенного агрегирования:
Здесь используются два связанных поля: деление. ID и Rooms.Division_ID. Эти два поля используются из таблицы измерений в строке «Строки» и ее эквивалента в таблице фактов в формуле.
ID и Rooms.Division_ID. Эти два поля используются из таблицы измерений в строке «Строки» и ее эквивалента в таблице фактов в формуле.
В этом примере мы подсчитываем койки в подразделении, суммируем результаты и делим этот результат на сумму комнат в подразделении. Рассматривая конкретное деление, это то же самое, что и подсчет коек / комнат, но в целом это 10/59 (сумма / сумма) — средневзвешенное значение.
Более подробный пример см. Здесь. Разработка сводной таблицы
Выберите способ выделения строк и столбцов сводной таблицы. Выделение исключений
 Например, как показано ниже:
Например, как показано ниже: Ограничения

10 математических
секретов, которые
научат легко
считать в уме
1. Умножение на 11
 Это срабатывает всегда.
Это срабатывает всегда.2. Быстрое возведение в квадрат
3. Умножение на пять
4. Умножение на девять
 Загните палец, который соответствует умножаемому числу (например, 9×3 — загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 — это два), затем посчитайте после загнутого пальца (в нашем случае — семь). Ответ — 27.
Загните палец, который соответствует умножаемому числу (например, 9×3 — загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 — это два), затем посчитайте после загнутого пальца (в нашем случае — семь). Ответ — 27.5. Умножение на четыре
6. Подсчёт чаевых
7. Сложное умножение
8.
 Деление на пять
Деление на пять9. Вычитание из 1000
10. Систематизированные правила умножения

БОНУС: проценты
 Первая часть слова — про (per). Per = для каждого. Вторая часть — цент (cent), это как 100. Например, столетие = 100 лет. 100 центов в одном долларе и так далее. Итак, процент = для каждой сотни.
Первая часть слова — про (per). Per = для каждого. Вторая часть — цент (cent), это как 100. Например, столетие = 100 лет. 100 центов в одном долларе и так далее. Итак, процент = для каждой сотни. А 35% от 8 — то же самое, что и 8% от 35.
А 35% от 8 — то же самое, что и 8% от 35.Контрольные и проверочные работы по математике 4 класс
 Чему равно делимое?
Чему равно делимое?

 Сколько килограммов картофеля в 3 таких мешках?
Сколько килограммов картофеля в 3 таких мешках?


 Запиши двузначное число, в
Запиши двузначное число, в

 Восстанови пропущенные цифры:
Восстанови пропущенные цифры:

 №4 (методичка, с. 376)вариант
№4 (методичка, с. 376)вариант
 Вставь пропущенные цифры:
Вставь пропущенные цифры:

 Весь картофель разложили в мешки, по 40 кг в каждый.
Сколько мешков с картофелем получили?
Весь картофель разложили в мешки, по 40 кг в каждый.
Сколько мешков с картофелем получили?

 Скорость слона 60 м/мин, скорость слонёнка 20 м/мин. Слоны
встретились через 10 мин. Какое расстояние было между ними сначала?
Скорость слона 60 м/мин, скорость слонёнка 20 м/мин. Слоны
встретились через 10 мин. Какое расстояние было между ними сначала?
 Сколько времени он потратил на дорогу?
Сколько времени он потратил на дорогу?
 Контрольная работа. №61 вариант
Контрольная работа. №61 вариант
 . . дм 8 т 5 ц = . . . кг
. . дм 8 т 5 ц = . . . кг
 Самостоятельная работавариант
Самостоятельная работавариант
 Запиши 2 числа, при умножении которых получается 105. Найди
Запиши 2 числа, при умножении которых получается 105. Найди
 Проверочная работа.
Проверочная работа.
 дм, а длина — 80
дм.
дм, а длина — 80
дм.

 Скорость
одного 65 км/ч, а другого — 35 км/ч . Какое расстояние будет между
ними через 2 ч?
Скорость
одного 65 км/ч, а другого — 35 км/ч . Какое расстояние будет между
ними через 2 ч?


 Сколько залов займут все эти картины, если
в каждый зал помещать по 24 картины?
Сколько залов займут все эти картины, если
в каждый зал помещать по 24 картины?


 Сколько таких
коробок пластилина можно купить на 98 р.?
Сколько таких
коробок пластилина можно купить на 98 р.?
 Представь число 60 000 в виде
Представь число 60 000 в виде
 Проверочная работа.
Проверочная работа.

 Контрольный устный счёт.
Контрольный устный счёт.
Сколько 648 разделить на 4 с использованием длинного деления?

648 разделить на 4 пошаговое руководство
Шаг 1
Шаг 2
Шаг 3
1 4 6 4 8 8 4 Шаг 4
0 1 4 6 4 8 — 4 2 Step 5
1 4 6 4 8 — 4 2 4 40035 40032 (Diving 6).  (s), поэтому мы можем поставить 6 сверху:
(s), поэтому мы можем поставить 6 сверху: 1 6 4 6 4 8 — 4 2 4 Шаг 7
1 6 4 6 4 8 — 4 2 4 2 4 Шаг 8
1 6 4 6 4 8 — 4 2 4 — 2 4 0 0 .  0002 Move the third digit of the dividend (8) down like so:
0002 Move the third digit of the dividend (8) down like so: 1 6 4 6 4 8 — 4 2 4 — 2 4 8 Шаг 10
5 6 2 4 6 4 8 — 4 2 4 — 2 4 8 Шаг
 can now add that answer below the dividend:
can now add that answer below the dividend: 1 6 2 4 6 4 8 — 4 2 4 — 2 4 8 8 Шаг 12
1 6 2 4 6 4 8 — 4 2 4 — 2 4 8 — 8 0 Чему равно число 4, разделенное на 4?

Дополнительные вычисления для вас
Калькулятор деления на длинное деление
Следующая задача на деление на длинное деление
 Вот следующая задача, которую вам нужно решить:
Вот следующая задача, которую вам нужно решить: Случайные задачи на длинное деление
§ 25-2-648.
 НОРМЫ ПОКАЗАТЕЛЕЙ ТЕРРИТОРИИ ПЛАНИРУЕМОЙ ЗАСТРОЙКИ (ТРЗ)., Раздел 5. Объединение и наложение районов., Статья 3. ДОПОЛНИТЕЛЬНЫЕ ТРЕБОВАНИЯ К ОТДЕЛЬНЫМ РАЙОНАМ., Подглава С. ПРАВИЛА ИСПОЛЬЗОВАНИЯ И ЗАСТРОЙКИ., Глава 25-2. ЗОНИРОВАНИЕ., Раздел 25. ЗЕМЕЛЬНОЕ РАЗВИТИЕ., Кодекс землеустройства, Остин
НОРМЫ ПОКАЗАТЕЛЕЙ ТЕРРИТОРИИ ПЛАНИРУЕМОЙ ЗАСТРОЙКИ (ТРЗ)., Раздел 5. Объединение и наложение районов., Статья 3. ДОПОЛНИТЕЛЬНЫЕ ТРЕБОВАНИЯ К ОТДЕЛЬНЫМ РАЙОНАМ., Подглава С. ПРАВИЛА ИСПОЛЬЗОВАНИЯ И ЗАСТРОЙКИ., Глава 25-2. ЗОНИРОВАНИЕ., Раздел 25. ЗЕМЕЛЬНОЕ РАЗВИТИЕ., Кодекс землеустройства, Остин
 Уровни шума определяются в соответствии
с информацией об уровнях шума в окружающей среде, необходимых для защиты здоровья населения
и благосостояние с достаточным запасом прочности, Агентство по охране окружающей среды, 1974.
Уровни шума определяются в соответствии
с информацией об уровнях шума в окружающей среде, необходимых для защиты здоровья населения
и благосостояние с достаточным запасом прочности, Агентство по охране окружающей среды, 1974.

Колонка I Колонка II Частота циклов в секунду Рабочий объем (дюймы) Рабочий объем (дюймы) от 0 до 1 .  0020
0020 .0008 от 1 до 10 .0010 .0004 от 10 до 20 .0008 .0002 от 20 до 30 .  0005
0005 .0001 от 30 до 40 .0004 .0001 40 лет и старше .0003 .0001  линия собственности. Свет от этих источников должен быть экранирован от соседней собственности.
линия собственности. Свет от этих источников должен быть экранирован от соседней собственности.

Отделы и услуги | Hamilton County NY
88 Bridge Street — Suite 5
Johnstown, N.Y. 12095
Office: (518) 736-8188 доб. 107
Электронная почта: [email protected]
Офис: (518) 774-0372
Электронная почта: [email protected]
Офис: (518) 921-8113
Эл. ……………………..Эванджелин Уэллс
Офис: (518) 648 -5355
Lake Pleasant, NY 12108
Офис: (518) 548-6810 или (518) 251-2702
Электронная почта: Defender@hamiltoncountyny. gov
gov
Помощник государственного защитника……………………. ……………. Мартин Позефски
Lake Pleasant, NY 12108
(518) 548-6651
Секретарь ………………………………………………………. ………. Лаура Абрамс, Ариетта
Шон Карри — Лонг Лейк
Дэвид Скрэнтон — Инлет
Манро Колли Смит — Спекулянт
НАЖМИТЕ ЗДЕСЬ, чтобы ознакомиться с Кодексом этики
НАЖМИТЕ ЗДЕСЬ, чтобы ознакомиться с формой жалобы на нарушение этических норм
Сотрудник по бюджету
Lake Pleasant, NY 12108
(518)548-5531
Офицер . ………………………………. ……………………………….. Барри Л. Бейкер
………………………………. ……………………………….. Барри Л. Бейкер
Indian Lake, NY 12842
Офис: (518) 648-5355
Директор ………………………………… ……………………….. Роберт Клеппанг
Lake Pleasant, New York 12108
Телефон: (518) 548-7111
Факс: (518) 548-9740
Электронная почта: [email protected]
[email protected] Обзор оценки мелких претензий
Обзор оценки мелких претензий
Посетите веб-сайт www.dmv.ny.gov
MV-44 Заявление о выдаче водительского удостоверения, водительского удостоверения или удостоверения личности
MV-44EDL Заявление о выдаче расширенного/реального удостоверения личности, водительского удостоверения или удостоверения личности
ID-44 Как подать заявление на получение нового York Learner Permit, Driver License, Non-Driver ID
MV-619 Отчет о проверке зрения
MV-82 Заявление о регистрации транспортного средства/право собственности
MV-82B Заявление о регистрации лодки
ID-82 Удостоверение личности
DTF-802 Налоговая форма
DTF -803 Форма 9 освобождения от налога с продаж0003
Джейн С. Зареки, клерк округа
Зареки, клерк округа
Хизер А. Фарбер, заместитель клерка округа
Эйлин Хиггинс, помощник заместителя клерка — Автомобили с 8:30 до 16:00
Records Room с 8:30 до 16:30
102 County View Drive, PO Box 701
Lake Pleasant, NY 12108
Телефон: (518) 285-6188
Комиссия по электронной почте: swilt.0gover91 …………………………………………. ………………… Сэди С. Уилт
Indian Lake, NY 12842
. Службы управления делами. Службы поддержки семьи. Консультирование по созависимости. Дневные услуги/отдых. Координация CCSI. Детская СПОА. Услуги по профилактике психического здоровья. Услуги по профилактике употребления алкоголя, табака и других наркотиков (химической зависимости). Программа Trailblazer. Информационно-просветительская деятельность. Справочные услуги для домашней и общественной программы Wavier. Помощь амбулаторному лечению. Оценки, назначенные судом. Услуги молодежного совета. Передышка. Направление на услуги, не предоставляемые в округе (например, жилье, RTF, дневное лечение и программы проживания, SPOA для взрослых). Направление для лечения химической зависимости, лечения от азартных игр и услуг OMRDD.
Координация CCSI. Детская СПОА. Услуги по профилактике психического здоровья. Услуги по профилактике употребления алкоголя, табака и других наркотиков (химической зависимости). Программа Trailblazer. Информационно-просветительская деятельность. Справочные услуги для домашней и общественной программы Wavier. Помощь амбулаторному лечению. Оценки, назначенные судом. Услуги молодежного совета. Передышка. Направление на услуги, не предоставляемые в округе (например, жилье, RTF, дневное лечение и программы проживания, SPOA для взрослых). Направление для лечения химической зависимости, лечения от азартных игр и услуг OMRDD.
Кризисная служба: 24/7 1-800-533-8443
Телефон: (518) 648-5355 Факс (518) 648-6437
E- почта: [email protected]

Энергетическое образование.
Растущие здоровые дети.
Большой подсчет птиц на заднем дворе.
Урожай Адирондака.
Неместные инвазивные виды.
Часы работы: Пн-Пт — с 8:30 до 16:30
Телефон (518) 548-6191 Факс (518) 548-7803
Мэтью Дж. Миллер
PO Box 76, Inlet, NY 13360
Домашний: (315) 357-3418 или сотовый: (315) 369-5432
Электронная почта: [email protected]
Тимоти Смит
P.O. Box 667, Lake Pleasant, NY 12108
Домашний: (518) 548-3634 или сотовый: (757)705-9081
Электронная почта: [email protected]
John Anderson
141 Little Amsterdam Road
P.O. Box 87, Wells, NY 12190
Мобильный: (518) 332-0941
Электронная почта: coroner3@hamiltoncountyny. gov
gov
Carl E. Turner
1188 Main Street
Long Lake, NY 12847-2204
Мобильный телефон: (518) 636-8808
Эл.
Charles R. Getty, Jr.
320 North George Street
P.O. Box 950
Rome, NY 13442-0950
Офис: (315) 336-3900
Факс (315)336-3239
Электронная почта: [email protected]
Кристин Э. Николелла, эсквайр
PO Box 395
Delanson, NY 12053
Телефон: (518) 895-2111
Эл.
Офис секретаря суда — Суд по семейным делам, окружной и суррогатный суд
Indian Lake, NY 12842
Телефон: (518) 648-5411
[email protected] hamiltonfamily@nycourts. gov [email protected]
gov [email protected]
Заместитель главного клерка………………….. ……… Мишель ДеШо
P.O.Box 780 139 White Birch Lane
Indian Lake, NY 12842
Телефон: (518)648-5966
Электронная почта: [email protected]
Секретарь судьи…. ……………………………… Наташа Гэдвей
Indian Lake, NY 12842
Телефон: (518) 648-5113 Факс: (518) 648-5724
Эл. …………………………………………. Кристофер С. Шамбо
…………………………………………. Кристофер С. Шамбо
Ассистент Окружной прокурор ……………………………….. Сьюзан Хартманн
Если вам было предъявлено обвинение в нарушении правил дорожного движения, отличном от вождения в состоянии алкогольного опьянения или вождения в состоянии инвалидности, вы можете иметь право на снижение суммы обвинения.
P.O. Box 57
Lake Pleasant, NY 12108
Офис: (518) 548-3078 Факс: (518) 548-3091
E-mail: [email protected] ……………………………………………………… …………..Кристи Л. Уилт
……………………………………………………… …………..Кристи Л. Уилт
Помощник ……………………………… …………………………..РаШель Мартц
Lake Pleasant, NY 12108
Телефон: (518) 548-3078 Факс: (518) 548-3091
www.adirondackgoodlife.com
Электронная почта: [email protected]
P.O. Box 175
Lake Pleasant, NY 12108
Телефон: 518-548-4684
баллотирование на политические посты, подача петиций о назначении и независимых петиций, раскрытие финансовой информации, проверка выборов и обучение хранителей машины для голосования в день выборов, заочное голосование, посещение средних школ для регистрации (18 лет).
Джейд Шерман, комиссар по выборам демократов
Гейл П. Тил, комиссар по выборам республиканцев
Виктория Э. Фиш, заместитель комиссара по выборам республиканцев
2558 State Route 8
Lake Pleasant, NY 12108
Что вы знаете о планах по уменьшению опасности вашего округа? Что ж, мы случайно знаем, где можно узнать больше! Присоединяйтесь к Департаменту по чрезвычайным ситуациям округа Гамильтон в партнерстве с Отделом внутренней безопасности и служб экстренной помощи штата Нью-Йорк и лабораторией AVAIL Университета в Олбани, когда мы разрабатываем законопроект округа Гамильтон 9. 1064 Мультиюрисдикционный план смягчения последствий всех опасностей (HMP). Проект плана находится по адресу https://hamilton.mitigateny.org/. Пожалуйста, расскажите нам о своем опыте борьбы со стихийными бедствиями и о том, как лучше всего справляться с этими опасностями, приняв участие в опросе общественного мнения. Заранее спасибо за участие в опросе! Вы вносите свой вклад в обеспечение безопасности вашего сообщества! Вопросы можно направлять по адресу:[email protected].
1064 Мультиюрисдикционный план смягчения последствий всех опасностей (HMP). Проект плана находится по адресу https://hamilton.mitigateny.org/. Пожалуйста, расскажите нам о своем опыте борьбы со стихийными бедствиями и о том, как лучше всего справляться с этими опасностями, приняв участие в опросе общественного мнения. Заранее спасибо за участие в опросе! Вы вносите свой вклад в обеспечение безопасности вашего сообщества! Вопросы можно направлять по адресу:[email protected].
Директор аварийно-спасательных служб ……………… Джилл Данхэм
Электронная почта: [email protected]
Координатор службы неотложной помощи ……………………………..Avis Warner
Электронная почта: [email protected]
Координатор пожарной охраны ……………………………….. Джей Гриффин
Электронная почта: [email protected]
Для экстренных случаев используйте: 518-548-6111 (депеша шерифа)
P. O. Box 44
O. Box 44
Lake Pleasant, NY 12108
Телефон: (518)924-4401 или Электронная почта: [email protected]
Секретарь……… …………………………… Крис Хейс
Электронная почта: [email protected] Бенсон Джеймс Льюек Озеро Блу Маунтин Шеф Грег Джордж, заместитель начальника Чарльз Брузо Надежда Ass’t Chief Эрик Робинсон, Гарри Даунинг Индиан Лейк Крис Митчелл Вход Шеф Деннис Хадсон, Тодд Марло Лейк-Плезант Шеф Билл Уортон, заместитель начальника Крис Хейс Лонг Лейк Шеф Мартин Пирс, первый заместитель начальника Джон Уокер Морхаус Шеф Джеймс Лак, Брайан Тейлор Писеко Стивен Воэрле, Дон Пинкертон Ракетт Лейк Майкл Лэмпхер Спекулянт Мэтт О’Брайен, Майк Трейси Колодцы Шеф Винс Лаурия, Тимоти О’Нил
Департамент добровольной пожарной охраны Лейк-Плезант, 114 S Shore Rd Lake Pleasant, NY 12108
(518) 548-3760
и:
Byron Park Building — 8284 NY IndianLake
(518)-648-6483
Все собрания открыты для публики и начинаются в 19:00
 Карты, книги и тематические файлы. Фотографии
Карты, книги и тематические файлы. Фотографии
102 County View Drive
P.O. Box 205, Lake Pleasant, NY 12108
* Если что-то нужно в любой другой день, просто оставьте сообщение на рабочем телефоне или отправьте электронное письмо *
Окружной историк …………………………………………. ………….. Эрнест Д. Вирджил
Телефон: (518) 548-5526
Cell: (518) 420-8339
Электронная почта: историксы @hamiltoncountyny.gov
11 Federal Street
Saratoga Springs, NY 12866
Телефон: (518) 372-4739
Indian Lake, N. Y. 12842
Y. 12842
Телефон: (518) 648-5355 Факс: (518) 648-6437
Электронная почта: [email protected]
102 County View Drive
P.O. Box 204
Lake Pleasant, NY 12108
Телефон: (518) 548-7111 Факс: (518) 548-9740
Электронная почта: [email protected]
Телефон: (518) 761-6347
Факс: (518) 761-6344
Бухгалтерский учет ……………………………….. ….. Джеффри Хейнс
Гамильтон Каунти Экспресс
PO Box 659, 2942 State Route 28
Old Forge, NY 13420
Телефон: (315) 369-2237
Эл. …………………………………………. ……………….. Джефф Дилонг
…………………………………………. ……………….. Джефф Дилонг
Indian Lake, NY 12842
Телефон: (518) 648-6131 Факс: (518) 648-5257
Часы работы: с понедельника по пятницу, с 8:30 до 15:30
Для получения информации о нашей универсальной карьере Щелкните по центру ЗДЕСЬ
Полицейский
Сертифицированный медицинский помощник на дому
Заместитель шерифа
Бухгалтерский клерк
Социальный работник
Координатор семейных медицинских услуг
Координатор общественного здравоохранения и готовности к чрезвычайным ситуациям
Зарегистрированная медсестра
Директор общественных служб
Cleaner-Lake Clinic1 Социальный работник (MHSA)
Директор по обслуживанию пациентов
Заместитель шерифа
Полицейский ………………………………………….. ………………….Кимберли Бирн
………………………………………….. ………………….Кимберли Бирн
Клерк………………….. ……………………………………… Хайде Томсон
102 County View Drive Route 8,
Court House Lake Pleasant, NY 12108
Телефон: (518) 548-6375 Факс: (518) 548-3108
Электронная почта: [email protected]
с понедельника по пятницу с 8:30 до 16:30
Экзамены проводятся по субботам в течение года.
, сотрудник службы пробации………………….. …. John Boya
Телефон: (518) 648-5040 Факс: (518) 648-0359
Электронная почта: probation@hamiltoncountyny. gov
gov
P.O. Box 666
Indian Lake, NY 12842
Сестринские услуги
Телефон: (518) 648-6141
Дети с особыми медицинскими потребностями
Телефон: (518) 648-6497
Indian Lake, NY 12842
Телефон: (518) 648-6497 Факс: (518) 648-6143
Эл. ……… Эрика Махони
Электронная почта: [email protected]
E-mail: Carriann.Grexaallen [email protected]
Программы общественного здравоохранения — (518) 648-6497
Сертифицированное агентство по охране здоровья на дому — (518) 648-6141
Веб-сайт: www. hamiltoncounty.com/health-human-services
hamiltoncounty.com/health-human-services
P.O. Box 56
Lake Pleasant, NY 12108
Офис: (518) 548-7141 Факс: (518) 548-4308
Электронная почта: highway@
Административный менеджер… ………………….
Road Supervisor III …………………..  Это должно быть
Это должно быть
представлено и одобрено суперинтендантом шоссе округа до 9.1064 действительно.
Дорожный инспектор II………………………….. ..…..Роберт Берджесс
Дорожный инспектор II……………………… ..……….Джон Уокер
Часы работы с 8:00 до 16:00 с понедельника по субботу
2297 State Route 8 Lake Pleasant, NY 12108
Джозеф Блэквуд, техник полигона
Телефон: (518) 548-3867
Часы работы: с 8:00 до 4:00 с четверга по понедельник
Чейн-Лейк-роуд, Индиан-Лейк, Нью-Йорк 12842
Рэнди Делонг, техник полигона
Телефон: (518) 648-0223
НАЖМИТЕ ЗДЕСЬ, чтобы ознакомиться с проектом плана обращения с твердыми отходами
Руководитель строительных проектов…………………………. Марк Стюарт
Марк Стюарт
(518) 548-5200
Налоговая информация: налоговые ставки, налоговые сборы, городские/окружные/школьные/деревенские налоги и т. д.
История участка. Данные о продажах
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ — Поиск Parcel & GIS
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ — информация о том, как оспорить оценку
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ — Отчет о передаче недвижимого имущества RP-5217
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ — Данные и информация о недвижимости
Тел.: (518) 548 — 5531
Факс: (518) 548-7064 P.
Карты ГИС: www.hamcomaps.net
www.hamiltoncounty.com/municipalities/town-assessment-rolls
Тюрьма
102 County View Drive
P.O. Box 210
Lake Pleasant, NY 12108
Тюрьма: (518) 548-3113 Факс: (518) 548-4619
Офис: (518) 548-3113 Факс: (518) 548-10604 .gov
Электронная почта: [email protected]
Младший шериф ………………………………………… Кевин Брауниус
Электронная почта: [email protected] 
Комиссар ……………………………………… ……………Роберта А. Блай
Эшли Сноу, социальный работник (обслуживание взрослых и детей)
Эбигейл Эйхлер, старший социальный работник (DV, EISEP, ПК)
ЭваДжин Андерссон, социальный работник
Эллисон Махони (HEAP)
Бет Кинг, эксперт по социальному обеспечению (MA &FS)
Виктория Мур, эксперт по социальному обеспечению
Дайан Кротти, координатор CSE (SCU и IT)
Стефани Хатчинс, главный бухгалтер
Конни Махони, эксперт по социальному обеспечению (TA/трудоустройство/уход за детьми)
Indian Lake, New York 12842-0725
Телефон: (518) 648-6131 Факс: (518) 648-5257
Часы работы: с 8:00 до 16:30
Федеральные и государственные правила проживания в домах престарелых и престарелых Информационно-просветительская работа по инвазивным видам и управление ими. Борьба с эрозией отложений, включая гидропосев. Продажа деревьев и кустарников. Помощь в управлении озером и береговой линией. Техническая поддержка. Стабилизация береговой эрозии. Частные испытания скважин в течение всего лета. Образовательная программа по охране природы среди студентов и местных сообществ. День охраны окружающей среды Энвиротон. Студенческий опыт обучения на свежем воздухе. Информация о ливневых и альтернативных септических системах. Ежемесячный уголок охраны природы и ежегодный информационный бюллетень.
Информационно-просветительская работа по инвазивным видам и управление ими. Борьба с эрозией отложений, включая гидропосев. Продажа деревьев и кустарников. Помощь в управлении озером и береговой линией. Техническая поддержка. Стабилизация береговой эрозии. Частные испытания скважин в течение всего лета. Образовательная программа по охране природы среди студентов и местных сообществ. День охраны окружающей среды Энвиротон. Студенческий опыт обучения на свежем воздухе. Информация о ливневых и альтернативных септических системах. Ежемесячный уголок охраны природы и ежегодный информационный бюллетень.
Найдите нас на Facebook и Vimeo
Районный менеджер …………………………………………. ..Кейтлин Стюарт
Техник по консервации……………………………. Ленни Крут
Ленни Крут
Lake Pleasant, NY 12108
Телефон: (518) 548-3991 Факс: (518) 548-5602
Электронная почта: [email protected]
Lake Pleasant, NY 12108
Телефон: (518) 548-3113 Факс: (518) 548-5407
Координатор ………………….. ………………….Шериф Карл Г. Абрамс
102 County View Drive
P.O. Box 57
Lake Pleasant, NY 12108
Офис: 518-548-3076 Факс: 518-548-3091
Электронная почта: [email protected]
Веб-сайт — www.AdirondackExperience.com
Помощник……………… ………………………………. ………… ……..RaChelle Martz
………… ……..RaChelle Martz
Маркетинг — Региональное управление устойчивого туризма (ROOST) …….. 518-523-2445
P.O. Box 206
Lake Pleasant, NY 12108
Телефон: (518) 548-7911
Факс: (518) 548-4519
Эл. …………………………………………. Бет Хант
Заместитель казначея…………………………………………… …… Джоди Смолл
Электронная почта: [email protected]
Оплатите налоги Центральной школы Лейк-Плезант за 2018/2019 годы
102 County View Drive
Lake Pleasant, NY 12108
Телефон: (518) 548-6651 или (518) 736-5651 Факс 9104:5688 -7608
Электронная почта: ветераны@fultoncountyny. gov
gov
Меры и весы
Почтовый индекс Box 392
Inlet, NY 13360
Домашний: (315) 357-3309 Сотовый: (315) 369-8771
Электронная почта: [email protected]
Директор…………… ……………………………….. Герберт В. Шмид Найдите контактное лицо по Закону о свободе информации в Министерстве юстиции | OIP
Найдите контактное лицо по Закону о свободе информации в Министерстве юстиции | ОИП | Департамент правосудия
Перейти к основному содержанию You are here
Начальник отдела FOIA/PA
Антимонопольный отдел
Министерство юстиции
Здание Liberty Square
Suite 1000, 450 5th Street, N. W.
W.
Washington, DC 20530-0001
Телефон: (202) 514-2692
Факс: (202) 616-4529
Электронная почта: [email protected]
Начальник отдела управления информацией и конфиденциальностью
Бюро по алкоголю, табаку, огнестрельному оружию и взрывчатым веществам
Министерство юстиции
Комната 4.E-301
99 Нью-Йорк Авеню, Н.В.
Вашингтон, округ Колумбия 20226
Телефон: (202) 648-8740
Портал FOIA: https://www.securerelease.us/ Вуд
Вуд
Закон о свободе информации и конфиденциальности
Гражданский отдел
Министерство юстиции
Комната 8314
1100 L Street, NW
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 514-2319 Факс: 910 (202) 514-2319 Факс: (910) 202) 514-7866
Электронная почта: [email protected]
4CON, комната 6.153
950 Pennsylvania Ave., N.W.
Washington, DC 20530
Телефон: (202) 514-4210
Эл. Служба по связям с общественностью
Координатор Закона о свободе информации/PA
Служба по связям с общественностью
Министерство юстиции
145 N Street NE
Suite 5E300
Вашингтон, округ Колумбия 20530
Телефон: (202) 3095-10645 CRSFOIA @ usdoj. gov
gov
Исполняющий обязанности начальника, FOIA/PA Unit
Отдел уголовных преступлений
Министерство юстиции
Комната 803, здание Кини
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 616-0307
Факс: (202) 514-6117
Электронная почта: [email protected]2 Центр обслуживания лиц, подавших запросы по Закону о свободе информации: (202) 616-0307
Закон о свободе информации и конфиденциальности, раздел
Drug Enforcement Administration
8701 Morrissette Drive
Springfield, Virginia 22152
Телефон: (571) 776-2300
Эл. : Дешелия Уоллес, (571) 776-2300
: Дешелия Уоллес, (571) 776-2300
Координатор Закона о свободе информации
Министерство юстиции
Отдел окружающей среды и природных ресурсов
Law and Policy Section
950 Pennsylvania Avenue, NW
Washington, DC 20530-0001
Телефон: (202) 514-0424
Эл.
Главный юрисконсульт
Административно-правовой отдел
Исполнительный отдел иммиграционного контроля
Департамент юстиции
Suite 1903, 5107 Leesburg Pike
Falls Church, VA 22041
Телефон: (703) 605-1297
Факс: (703) 605-0570
Электронная почта: [email protected]
(703) 605-1297
Crystal Souza, (703) 605-1297
Целевые группы по борьбе с организованной преступностью по борьбе с наркотиками
Министерство юстиции США
441 G Street NW
Suite 6B13
Washington, DC 20530 [email protected]
[email protected]
FOIA Представитель по связям с общественностью: Кристин Бруди-Эверетт, ) 514-0296
Служба связи с общественностью
Исполнительный офис прокуроров США
Министерство юстиции
175 N Street, N.E.
Suite 5.400
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 252-6036
Советник по Закону о свободе информации
Офис главного юрисконсульта
Исполнительный офис попечителей США
Министерство юстиции
441 G Street, NW, Suite 6150
Washington, DC 20530
Телефон: (202) 307-1399
Факс: (202) 307-2397
Эл. : (202) 307-1399
: (202) 307-1399
Отдел документации/распространения информации
Отдел управления документами
Федеральное бюро расследований
Министерство юстиции
200 Конституция Драйв
Винчестер, Вирджиния 22602
Телефон: (540) 868-4593
Факс: (540) 868-4997
Онлайн-форма запроса: https://efoia.fbi.gov
Надзорный прокурор
Запросы Закона о свободе информации/Закона о конфиденциальности
Федеральное бюро тюрем
Министерство юстиции
Комната 924, здание HOLC
320 First Street, N. W.
W.
Washington, DC 20534
Телефон: (202) 514-6655
Эл. 202) 616-7750
Главный административный советник
Комиссия по урегулированию иностранных претензий
Министерство юстиции
441 G Street, NW Room 6330
Washington, DC 20579
Телефон: (202) 616-6975
Факс: (202) 616-6993
Электронная почта: info.fcc @usdoj.gov
Специалист по правительственной информации
Офис главного юрисконсульта
Интерпол-Национальное центральное бюро США
Министерство юстиции
Вашингтон, округ Колумбия 20530
Телефон: (202) 616-0201
Электронная почта: Interpol-USNCB. [email protected]
[email protected]
FOIA Контактное лицо
Управление юстиции
Министерство юстиции
Комната 1111 RFK, 950 Pennsylvania Avenue, N.W.
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 514-3101
Электронная почта: [email protected]
Специалист по правительственной информации
Отдел национальной безопасности
Министерство юстиции
3 Площадь Конституции
175 N Street N. E., 12th Floor
E., 12th Floor
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 233-2639
Эл. : (202) 233-2639
Юридический отдел
Управление общественной полиции
Министерство юстиции
Площадь Две Конституции
145 N Street. Н.Э.
Washington, DC 20530-0001
Телефон: (202) 514-1873
Факс: (202) 514-3456
Эл. Представитель FOIA по связям с общественностью: Мелисса Фиери-Фетров, (202) 514-1873
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA
Специалист по правительственной информации
Управление программ юстиции
Министерство юстиции
Комната 5400, 810 7th Street, N. W.
W.
Washington, DC 20531
Телефон: (202) 307-6235
Факс: (202) 307-1419
Эл. Чандрия Слотер, (202) 307-6235
Ведущий помощник юриста и специалист FOIA
Министерство юстиции
, комната 5517, Пенсильвания-авеню, 950, северо-запад.
Washington, DC 20530-0001
Телефон: (202) 514-2053
Эл. ) 514-2053
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA
Управление профессиональной ответственности
Министерство юстиции
950 Pennsylvania Avenue, N. W.
W.
Suite 3241
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-3365
Факс: (202) 514-5050
Эл.
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA2 Канцелярия помощника генерального прокурора
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-FOIA
Начальник отдела первоначального запроса
Управление информационной политики
Министерство юстиции
6-й этаж
441 G St NW
Вашингтон, округ Колумбия 20530
Телефон: (202) 514-3 FOIA Форма онлайн-запроса
Специалист по правительственной информации
Офис Генерального инспектора
Министерство юстиции
Комната 4726
950 Pennsylvania Avenue, N. W.
W.
Washington, DC 20530-0001
Телефон: (202) 616-0646
Факс: (202) 616-9152
Электронная почта: [email protected]
Прокуратура по помилованию
Министерство юстиции
950 Pennsylvania Avenue, N.W.
Washington, DC 20530
Телефон: (202) 616-6070
Факс: (202) 616-6069
Сотрудник по Закону о свободе информации и исполнительный директор
Office General Solicitor
Министерство юстиции
950 Pennsylvania Avenue, N. W., Room 6627
W., Room 6627
Washington, DC 20530-0001
Телефон: (2022020202020202020202020202020202020202020300001
) 616-9406
Электронная почта: [email protected]
Служба по связям с общественностью по Закону о свободе информации
Исполнительный офис прокуроров США
Министерство юстиции
175 N Street, N.E.
Suite 5.400
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 252-6036
Факс: (202) 252-6048
Советник адвоката
145 N Street NE
Suite 10W. 121
121
Вашингтон, округ Колумбия 20530
Телефон: (202) 307-6026
Эл. Центр обслуживания заявителей: (202) 307-6026
Адвокат-консультант
Консультативный отдел по вопросам профессиональной ответственности
Министерство юстиции
441 G Street, NW
6-й этаж
Вашингтон, округ Колумбия 20530
Телефон: (202) 5814-00 202) 353-7483
Электронная почта: [email protected]
Старший юрисконсульт отдела по вопросам Закона о свободе информации и Федерального закона
Налоговый отдел
Министерство юстиции
Почтовый ящик 227
Ben Franklin Station
Washington, DC 20044
Телефон: (202) 307-10643 9 : TaxDiv. [email protected]
[email protected]
Отдел по связям с общественностью по Закону о свободе информации
Исполнительный офис прокуроров США
Министерство юстиции
175 N Street, N.E.
Suite 5.400
Вашингтон, округ Колумбия 20530-0001
Телефон: (202) 252-6036
Офицер Закона о свободе информации
Служба маршалов США
Офис главного юрисконсульта
CG-3 15th Floor
Washington, DC 20530-0001
Телефон: (703) 740-3943
Эл. 703) 740-3943
703) 740-3943
Специалист по Закону о свободе информации/PA
Комиссия США по условно-досрочному освобождению
Министерство юстиции
90 K Street NE
3rd Floor
Washington, DC 20530
Телефон: (202) 346-7030
Эл. 202) 346-7030 Была ли эта страница полезной?
Да
№ Другие полезные истории от ИТ-директора — стр. 648
Как выбрать правильные ИТ-проекты
Последние разработки в волоконной оптике

Знакомство с услугами с оплатой по факту использования перед регистрацией
Профиль Томаса Джарретта, секретаря Департамента технологий и информации и директора по информационным технологиям
Вопросы и ответы с Дэном Ариели: почему хорошие ИТ-директора принимают плохие решения

База данных отпечатков пальцев ФБР помогла раскрыть дело об убийстве 45-летней давности
Почему стоит управлять ИТ как портфелем
Оповещение для сотрудников
Использование смарт-карт в Париже
 Маленькие пластиковые карты, изобретенные во Франции в 1979 году…
Маленькие пластиковые карты, изобретенные во Франции в 1979 году… Европейские фирмы не сосредотачиваются на расходах на ИТ-безопасность
Правильное управление портфелем
Перемещение ИТ-директора, май 2003 г.
FTC создаст реестр «Не звонить»

Отзывы читателей Февраль, март 2003 г. Выпуски журнала CIO Magazine: Cigna, Передовой опыт в области ИТ, Открытый исходный код
Экономическое обоснование управления ИТ-портфелем
ВОЗМОЖНО, вы узнаете знаменитые телефоны Polycom с треугольным динамиком, серые коммуникаторы, которые сидят на столах в конференц-залах по всему миру.
 …
… Как сохранить удовлетворенность ваших ИТ-клиентов
Индустрия развлечений против музыкального и кинопиратства
Широкополосный доступ в Интернет скоро появится в ближайшей к вам розетке?
 Но индустрия широкополосной связи по линиям электропередач все еще сталкивается с внедрением, регулированием …
Но индустрия широкополосной связи по линиям электропередач все еще сталкивается с внедрением, регулированием … Долгосрочные результаты служебных вычислений


Cos 0 в квадрате: Решите уравнение cos(x^2)=0 (косинус от (х в квадрате) равно 0)
Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов.
Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°.
cos(0°)=cos(360°)=1; точная, но чуть более сложная таблица ( с точностью до 1″) здесь.
таблица косинусов, косинусы углов в угловых градусах ,cos α, cosinus, сколько составляет косинус?, узнать косинус, косинус градусов
1° — 90°
91 ° — 180°
181° — 270°
271 ° — 360°
1°
cos= 0.9998
2°
cos= 0.9994
3°
cos= 0.9986
4°
cos= 0.9976
5°
cos= 0.9962
6°
cos= 0.9945
7°
cos= 0.9925
8°
cos= 0.9903
9°
cos= 0.9877
10°
cos= 0.9848
11°
cos= 0.9816
12°
cos= 0.9781
13°
cos= 0.9744
14°
cos= 0.9703
15°
cos= 0.9659
16°
cos= 0.9613
17°
cos= 0.9563
18°
cos= 0.9511
19°
cos= 0.9455
20°
cos= 0.9397
21°
cos= 0.9336
22°
cos= 0.9272
23°
cos= 0.9205
24°
cos= 0.9135
25°
cos= 0.9063
26°
cos= 0.8988
27°
cos= 0.891
28°
cos= 0.8829
29°
cos= 0.8746
30°
cos= 0.866
31°
cos= 0.8572
32°
cos= 0.848
33°
cos= 0.8387
34°
cos= 0.829
35°
cos= 0.8192
36°
cos= 0.809
37°
cos= 0.7986
38°
cos= 0.788
39°
cos= 0.7771
40°
cos= 0.766
41°
cos= 0.7547
42°
cos= 0.7431
43°
cos= 0.7314
44°
cos= 0.7193
45°
cos= 0.7071
46°
cos= 0.6947
47°
cos= 0.682
48°
cos= 0.6691
49°
cos= 0.6561
50°
cos= 0.6428
51°
cos= 0.6293
52°
cos= 0.6157
53°
cos= 0.6018
54°
cos= 0.5878
55°
cos= 0.5736
56°
cos= 0.5592
57°
cos= 0.5446
58°
cos= 0.5299
59°
cos= 0.515
60°
cos= 0.5
61°
cos= 0.4848
62°
cos= 0.4695
63°
cos= 0.454
64°
cos= 0.4384
65°
cos= 0.4226
66°
cos= 0.4067
67°
cos= 0.3907
68°
cos= 0.3746
69°
cos= 0.3584
70°
cos= 0.342
71°
cos= 0.3256
72°
cos= 0.309
73°
cos= 0.2924
74°
cos= 0.2756
75°
cos= 0.2588
76°
cos= 0.2419
77°
cos= 0.225
78°
cos= 0.2079
79°
cos= 0.1908
80°
cos= 0.1736
81°
cos= 0.1564
82°
cos= 0.1392
83°
cos= 0.1219
84°
cos= 0.1045
85°
cos= 0.0872
86°
cos= 0.0698
87°
cos= 0.0523
88°
cos= 0.0349
89°
cos= 0.0175
90°
cos= 0
91°
cos= -0.0175
92°
cos= -0.0349
93°
cos= -0.0523
94°
cos= -0.0698
95°
cos= -0.0872
96°
cos= -0.1045
97°
cos= -0.1219
98°
cos= -0.1392
99°
cos= -0.1564
100°
cos= -0.1736
101°
cos= -0.1908
102°
cos= -0.2079
103°
cos= -0.225
104°
cos= -0.2419
105°
cos= -0.2588
106°
cos= -0.2756
107°
cos= -0.2924
108°
cos= -0.309
109°
cos= -0.3256
110°
cos= -0.342
111°
cos= -0.3584
112°
cos= -0.3746
113°
cos= -0.3907
114°
cos= -0.4067
115°
cos= -0.4226
116°
cos= -0.4384
117°
cos= -0.454
118°
cos= -0.4695
119°
cos= -0.4848
120°
cos= -0.5
121°
cos= -0.515
122°
cos= -0.5299
123°
cos= -0.5446
124°
cos= -0.5592
125°
cos= -0.5736
126°
cos= -0.5878
127°
cos= -0.6018
128°
cos= -0.6157
129°
cos= -0.6293
130°
cos= -0.6428
131°
cos= -0.6561
132°
cos= -0.6691
133°
cos= -0.682
134°
cos= -0.6947
135°
cos= -0.7071
136°
cos= -0.7193
137°
cos= -0.7314
138°
cos= -0.7431
139°
cos= -0.7547
140°
cos= -0.766
141°
cos= -0.7771
142°
cos= -0.788
143°
cos= -0.7986
144°
cos= -0.809
145°
cos= -0.8192
146°
cos= -0.829
147°
cos= -0.8387
148°
cos= -0.848
149°
cos= -0.8572
150°
cos= -0.866
151°
cos= -0.8746
152°
cos= -0.8829
153°
cos= -0.891
154°
cos= -0.8988
155°
cos= -0.9063
156°
cos= -0.9135
157°
cos= -0.9205
158°
cos= -0.9272
159°
cos= -0.9336
160°
cos= -0.9397
161°
cos= -0.9455
162°
cos= -0.9511
163°
cos= -0.9563
164°
cos= -0.9613
165°
cos= -0.9659
166°
cos= -0.9703
167°
cos= -0.9744
168°
cos= -0.9781
169°
cos= -0.9816
170°
cos= -0.9848
171°
cos= -0.9877
172°
cos= -0.9903
173°
cos= -0.9925
174°
cos= -0.9945
175°
cos= -0.9962
176°
cos= -0.9976
177°
cos= -0.9986
178°
cos= -0.9994
179°
cos= -0.9998
180°
cos= -1
181°
cos=-0.9998
182°
cos=-0.9994
183°
cos=-0.9986
184°
cos=-0.9976
185°
cos=-0.9962
186°
cos=-0.9945
187°
cos=-0.9925
188°
cos=-0.9903
189°
cos=-0.9877
190°
cos=-0.9848
191°
cos=-0.9816
192°
cos=-0.9781
193°
cos=-0.9744
194°
cos=-0.9703
195°
cos=-0.9659
196°
cos=-0.9613
197°
cos=-0.9563
198°
cos=-0.9511
199°
cos=-0.9455
200°
cos=-0.9397
201°
cos=-0.9336
202°
cos=-0.9272
203°
cos=-0.9205
204°
cos=-0.9135
205°
cos=-0.9063
206°
cos=-0.8988
207°
cos=-0.891
208°
cos=-0.8829
209°
cos=-0.8746
210°
cos=-0.866
211°
cos=-0.8572
212°
cos=-0.848
213°
cos=-0.8387
214°
cos=-0.829
215°
cos=-0.8192
216°
cos=-0.809
217°
cos=-0.7986
218°
cos=-0.788
219°
cos=-0.7771
220°
cos=-0.766
221°
cos=-0.7547
222°
cos=-0.7431
223°
cos=-0.7314
224°
cos=-0.7193
225°
cos=-0.7071
226°
cos=-0.6947
227°
cos=-0.682
228°
cos=-0.6691
229°
cos=-0.6561
230°
cos=-0.6428
231°
cos=-0.6293
232°
cos=-0.6157
233°
cos=-0.6018
234°
cos=-0.5878
235°
cos=-0.5736
236°
cos=-0.5592
237°
cos=-0.5446
238°
cos=-0.5299
239°
cos=-0.515
240°
cos=-0.5
241°
cos=-0.4848
242°
cos=-0.4695
243°
cos=-0.454
244°
cos=-0.4384
245°
cos=-0.4226
246°
cos=-0.4067
247°
cos=-0.3907
248°
cos=-0.3746
249°
cos=-0.3584
250°
cos=-0.342
251°
cos=-0.3256
252°
cos=-0.309
253°
cos=-0.2924
254°
cos=-0.2756
255°
cos=-0.2588
256°
cos=-0.2419
257°
cos=-0.225
258°
cos=-0.2079
259°
cos=-0.1908
260°
cos=-0.1736
261°
cos=-0.1564
262°
cos=-0.1392
263°
cos=-0.1219
264°
cos=-0.1045
265°
cos=-0.0872
266°
cos=-0.0698
267°
cos=-0.0523
268°
cos=-0.0349
269°
cos=-0.0175
270°
cos=0
271°
cos=0.0175
272°
cos=0.0349
273°
cos=0.0523
274°
cos=0.0698
275°
cos=0.0872
276°
cos=0.1045
277°
cos=0.1219
278°
cos=0.1392
279°
cos=0.1564
280°
cos=0.1736
281°
cos=0.1908
282°
cos=0.2079
283°
cos=0.225
284°
cos=0.2419
285°
cos=0.2588
286°
cos=0.2756
287°
cos=0.2924
288°
cos=0.309
289°
cos=0.3256
290°
cos=0.342
291°
cos=0.3584
292°
cos=0.3746
293°
cos=0.3907
294°
cos=0.4067
295°
cos=0.4226
296°
cos=0.4384
297°
cos=0.454
298°
cos=0.4695
299°
cos=0.4848
300°
cos=0.5
301°
cos=0.515
302°
cos=0.5299
303°
cos=0.5446
304°
cos=0.5592
305°
cos=0.5736
306°
cos=0.5878
307°
cos=0.6018
308°
cos=0.6157
309°
cos=0.6293
310°
cos=0.6428
311°
cos=0.6561
312°
cos=0.6691
313°
cos=0.682
314°
cos=0.6947
315°
cos=0.7071
316°
cos=0.7193
317°
cos=0.7314
318°
cos=0.7431
319°
cos=0.7547
320°
cos=0.766
321°
cos=0.7771
322°
cos=0.788
323°
cos=0.7986
324°
cos=0.809
325°
cos=0.8192
326°
cos=0.829
327°
cos=0.8387
328°
cos=0.848
329°
cos=0.8572
330°
cos=0.866
331°
cos=0.8746
332°
cos=0.8829
333°
cos=0.891
334°
cos=0.8988
335°
cos=0.9063
336°
cos=0.9135
337°
cos=0.9205
338°
cos=0.9272
339°
cos=0.9336
340°
cos=0.9397
341°
cos=0.9455
342°
cos=0.9511
343°
cos=0.9563
344°
cos=0.9613
345°
cos=0.9659
346°
cos=0.9703
347°
cos=0.9744
348°
cos=0.9781
349°
cos=0.9816
350°
cos=0.9848
351°
cos=0.9877
352°
cos=0.9903
353°
cos=0.9925
354°
cos=0.9945
355°
cos=0.9962
356°
cos=0.9976
357°
cos=0.9986
358°
cos=0.9994
359°
cos=0.9998
360°
cos=1
почему в matlab sin (pi) не является точным, но sin(pi/2) является точным?
Построение графика sin (x)/(x) в Matlab
Быстрая аппроксимация для sin/cos в MATLABpython — как возвести cos в квадрат в пайтоне?
python — как возвести cos в квадрат в пайтоне? — Stack Overflow на русском
Всё ещё ищете ответ? Посмотрите другие вопросы с метками python python-3.x или задайте свой вопрос.
Леска д/триммера с металлической крошкой,15м,квадрат,3,0 мм
Синус угла в квадрате
Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:Простейшие тригонометрические тождества
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Формулы универсальной тригонометрической подстановки
Тригонометрические тождества преобразования половины угла
Тригонометрические формулы сложения углов
cos (α + β) = cos α · cos β — sin α · sin βФормулы преобразования суммы или разности тригонометрических функций
Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
Формулы преобразования произведения тригонометрических функций
Формулы приведения тригонометрических функций
e 0, cosalpha
e 0)\[0.2, alpha>\&\ cosalpha
e 0 & sinalpha
e 0\ hline end]
ight)>\\ sqrt3sinalphapm cosalpha=2sin<left(alphapm dfrac<pi>6
ight)>\\ sinalphapm sqrt3cosalpha=2sin<left(xpm dfrac<pi>3
ight)>\\ hline ext<Общий случай>\ hline\ asinalphapm bcosalpha=sqrtcdot sin<(alphapm phi)>, cosphi=dfrac a<sqrt>, sinphi=dfrac b<sqrt>\\ hline end]
ight)=sqrt2, sin left(xpmdfrac<pi>4
ight))
ight)=2, sin left(xpmdfrac<pi>6
ight))
ight)=2,sinleft(xpmdfrac<pi>3
ight)) Mathway | Популярные задачи
1 Найдите производную — d / dx натуральное журнал x 2 Оцените интеграл интеграл натурального логарифма x относительно x 3 Найдите производную — d / dx е ^ х 4 Оцените интеграл интеграл от e ^ (2x) относительно x 5 Найдите производную — d / dx 1 / х 6 Найдите производную — d / dx х ^ 2 7 Найдите производную — d / dx 1 / (х ^ 2) 8 Найдите производную — d / dx грех (х) ^ 2 9 Найдите производную — d / dx сек (x) 10 Оцените интеграл интеграл e ^ x относительно x 11 Оцените интеграл интеграл x ^ 2 относительно x 12 Оцените интеграл интеграл квадратного корня x относительно x 13 Найдите производную — d / dx соз (х) ^ 2 14 Оцените интеграл интеграл от 1 / x по отношению к x 15 Оцените интеграл интеграл sin (x) ^ 2 относительно x 16 Найдите производную — d / dx х ^ 3 17 Найдите производную — d / dx сек (x) ^ 2 18 Оцените интеграл интеграл cos (x) ^ 2 относительно x 19 Оцените интеграл интеграл от sec (x) ^ 2 относительно x 20 Найдите производную — d / dx е ^ (х ^ 2) 21 Оцените интеграл интеграл от 0 до 1 кубического корня из 1 + 7x относительно x 22 Найдите производную — d / dx грех (2x) 23 Найдите производную — d / dx загар (x) ^ 2 24 Оцените интеграл интеграл 1 / (x ^ 2) относительно x 25 Найдите производную — d / dx 2 ^ х 26 График натуральное бревно из 27 Найдите производную — d / dx cos (2x) 28 Найдите производную — d / dx хе ^ х 29 Оцените интеграл интеграл от 2x относительно x 30 Найдите производную — d / dx (натуральный логарифм x) ^ 2 31 Найдите производную — d / dx натуральный логарифм (x) ^ 2 32 Найдите производную — d / dx 3x ^ 2 33 Оцените интеграл интеграл xe ^ (2x) относительно x 34 Найдите производную — d / dx 2e ^ x 35 Найдите производную — d / dx натуральное бревно 2x 36 Найдите производную — d / dx -sin (х) 37 Найдите производную — d / dx 4x ^ 2-x + 5 38 Найдите производную — d / dx y = 16 корень четвертой степени из 4x ^ 4 + 4 39 Найдите производную — d / dx 2x ^ 2 40 Оцените интеграл интеграл e ^ (3x) относительно x 41 Оцените интеграл интеграл cos (2x) относительно x 42 Найдите производную — d / dx 1 / (квадратный корень из x) 43 Оцените интеграл интеграл e ^ (x ^ 2) относительно x 44 Оценить e ^ бесконечность 45 Найдите производную — d / dx х / 2 46 Найдите производную — d / dx -cos (x) 47 Найдите производную — d / dx грех (3x) 48 Найдите производную — d / dx 1 / (х ^ 3) 49 Оцените интеграл интеграл tan (x) ^ 2 относительно x 50 Оцените интеграл интеграл 1 по x 51 Найдите производную — d / dx х ^ х 52 Найдите производную — d / dx x натуральное бревно x 53 Найдите производную — d / dx х ^ 4 54 Оценить предел предел, когда x приближается к 3 из (3x-5) / (x-3) 55 Оцените интеграл интеграл x ^ 2 натуральный логарифм x относительно x 56 Найдите производную — d / dx f (x) = квадратный корень из x 57 Найдите производную — d / dx х ^ 2sin (х) 58 Оцените интеграл интеграл sin (2x) относительно x 59 Найдите производную — d / dx 3e ^ x 60 Оцените интеграл интеграл xe ^ x относительно x 61 Найдите производную — d / dx у = х ^ 2 62 Найдите производную — d / dx квадратный корень из x ^ 2 + 1 63 Найдите производную — d / dx грех (x ^ 2) 64 Оцените интеграл интеграл от e ^ (- 2x) относительно x 65 Оцените интеграл интеграл натурального логарифма квадратного корня x относительно x 66 Найдите производную — d / dx е ^ 2 67 Найдите производную — d / dx х ^ 2 + 1 68 Оцените интеграл интеграл sin (x) относительно x 69 Найдите производную — d / dx арксин (х) 70 Оценить предел предел, когда x приближается к 0 of (sin (x)) / x 71 Оцените интеграл интеграл e ^ (- x) относительно x 72 Найдите производную — d / dx х ^ 5 73 Найдите производную — d / dx 2 / х 74 Найдите производную — d / dx натуральное бревно из 3х 75 Найдите производную — d / dx х ^ (1/2) 76 Найдите производную — d / d @ VAR f (x) = квадратный корень из x 77 Найдите производную — d / dx соз (x ^ 2) 78 Найдите производную — d / dx 1 / (х ^ 5) 79 Найдите производную — d / dx кубический корень из x ^ 2 80 Оцените интеграл интеграл cos (x) относительно x 81 Оцените интеграл интеграл e ^ (- x ^ 2) относительно x 82 Найдите производную — d / d @ VAR е (х) = х ^ 3 83 Оцените интеграл интеграл от 0 до 10 из 4x ^ 2 + 7 по x 84 Оцените интеграл интеграл (натуральный логарифм x) ^ 2 относительно x 85 Найдите производную — d / dx журнал x 86 Найдите производную — d / dx арктан (x) 87 Найдите производную — d / dx натуральное бревно 5x 88 Найдите производную — d / dx 5e ^ x 89 Найдите производную — d / dx cos (3x) 90 Оцените интеграл интеграл x ^ 3 относительно x 91 Оцените интеграл интеграл от x ^ 2e ^ x относительно x 92 Найдите производную — d / dx 16 корень четвертой степени из 4x ^ 4 + 4 93 Найдите производную — d / dx х / (е ^ х) 94 Оценить предел предел, когда x приближается к 3 от arctan (e ^ x) 95 Оцените интеграл интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x 96 Найдите производную — d / dx 3 ^ х 97 Оцените интеграл интеграл xe ^ (x ^ 2) относительно x 98 Найдите производную — d / dx 2sin (х) 99 Оценить сек (0) ^ 2 100 Найдите производную — d / dx натуральный логарифм x ^ 2 Функция косинуса в квадрате — исчисление
Эта статья посвящена конкретной функции от подмножества действительных чисел к действительным числам.Информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференциации и интеграции, представлена в статье.
Просмотрите полный список определенных функций в этой вики. Для функций, включающих углы (тригонометрические функции, обратные тригонометрические функции и т. Д.), Мы следуем соглашению, согласно которому все углы измеряются в радианах. Так, например, угол измеряется как.
Определение
Основные данные
Товар Стоимость Домен по умолчанию все действительные числа, т. Е. Все из. диапазон , т.е. период , т.е. локальные максимальные значения и точки достижения Все локальные максимальные значения равны 1 и достигаются при целых кратных. локальные минимальные значения и точки достижения Все локальные минимальные значения равны 0 и достигаются с нечетным целым числом, кратным. точки перегиба (обе координаты) нечетных кратных, со значением в каждой точке производная то есть отрицательная функция синусоиды двойного угла. вторая производная Высшие производные раз выражение, которое равно или, в зависимости от остатка от mod 4. первообразная среднее значение за период выражение как синусоидальная функция плюс постоянная функция важные симметрии четная функция
В более общем смысле имеет зеркальную симметрию относительно всех вертикальных линий, целое число.
Также имеет симметрию на пол-оборота относительно всех точек формы, то есть всех точек перегиба. описание интервала на основе увеличения / уменьшения и вогнутости вверх / вниз Для каждого целого числа интервал от до подразделяется на четыре части:
: убывающая и вогнутая вниз
: убывающая и вогнутая вверх
: увеличивающаяся и вогнутая вверх
: увеличивающаяся и вогнутая вниз. Чему равен cos (0)?
Кредит: WikiCommons CC0 1.0 Основы триггерных функций
Числовые значения триггерных функций
Триггерные функции и единичная окружность
Косинусы
Угол Градусы Радианы косинус синус 90 ° π /2 0 000 000000 000 /3 1/2 √3 / 2 45 ° π /4 √2 / 2 √2 / 2 000 π /6 √3 / 2 1/2 0 ° 0 1 0 Упражнения
Все эти упражнения относятся к прямоугольным треугольникам со стандартной маркировкой. Подсказки
ответы
c = 3 a , что равно 12.73 ‘или 12’9 «.
a 2 = 7,8 2 — 6,4 2 = 19,9, поэтому составляет около 4,5.
b = c cos A = 12,15 cos 23 ° 15 ‘= 11.17. Пифагорейские тождества | StudyPug
Каковы пифагорейские тождества?
Пифагорейские тождества
Калькулятор — cos (0) — Solumaths
Резюме:
Описание:
Косинус для вычисления угла в радианах
Вычислить косинус угла в градусах
Вычислить косинус угла в градусах
Тригонометрическая функция cos вычисляет косинус угла в радианах,
градусы или градианы. Синтаксис:
cos (x), где x — мера угла в градусах, радианах или градианах. Примеры:
cos (`0`), возвращает 1 Производный косинус:
Первоначальный косинус:
Предельный косинус:
Косинус обратной функции:
Графический косинус:
Свойство функции косинус:
Функция косинуса является четной функцией.
Рассчитать онлайн с cos (косинусом) Касательная функция
грех
(
0
°
)
знак равно
0 потому что
(
0
°
)
знак равно
1 загар
(
0
°
)
знак равно
0
1
знак равно
0 грех
(
30
°
)
знак равно
1
2 потому что
(
30
°
)
знак равно
3
2 загар
(
30
°
)
знак равно
1
2
⋅
2
3
знак равно
3
3 грех
(
45
°
)
знак равно
2
2 потому что
(
45
°
)
знак равно
2
2 загар
(
45
°
)
знак равно
2
2
⋅
2
2
знак равно
1 грех
(
60
°
)
знак равно
3
2 потому что
(
60
°
)
знак равно
1
2 загар
(
60
°
)
знак равно
3
2
⋅
2
1
знак равно
3 грех
(
90
°
)
знак равно
1 потому что
(
90
°
)
знак равно
0 загар
(
90
°
)
знак равно
1
0
знак равно
undef
. Сколько в 18 месяцах дней: Сколько дней в 18 месяцах
Сколько дней в 18 месяцах. Посчитать дни, месяца и годы между двумя датами онлайн
Сколько дней в 18 месяцах. Посчитать дни, месяца и годы между двумя датами онлайн
Сколько дней между датами? Инструкция

Для чего можно использовать калькулятор
Пример:
 А вот количество часов нужно считать….А сколько там в феврале дней? А год-то високосный? А какие дни были выходными? А как определить количество дней праздников?
А вот количество часов нужно считать….А сколько там в феврале дней? А год-то високосный? А какие дни были выходными? А как определить количество дней праздников?Вам понравился этот калькулятор? Тогда попробуйте другие наши возможности

Способ 1: вычитание
 Поставьте в нее «=»
и нажмите сначала позднюю (В1
) дату, потом раннюю (А1
). Чтобы вычислить между ними количество дней, жмите «Enter»
.
Поставьте в нее «=»
и нажмите сначала позднюю (В1
) дату, потом раннюю (А1
). Чтобы вычислить между ними количество дней, жмите «Enter»
.Способ 2: использование функции
«m»
– количество полных месяцев;
«y»
– количество полных лет;
«md»
– посчитает дни без учета месяцев и годов;
«yd»
– подсчет дней без учета только годов;
«ym»
– посчитает месяцы не учитывая год.
Способ 3: считаем рабочие дни

 Вводим функцию и заполняем ее аргументы:
Вводим функцию и заполняем ее аргументы:Начало периода (или через слеш или точку) Конец периода (или через слеш или точку) Отмеченные выходные на неделе П В С
Ч П С
В Учитывать постановления Правительства РФ о переносе дней ДА Расчет рабочих дней и выходных

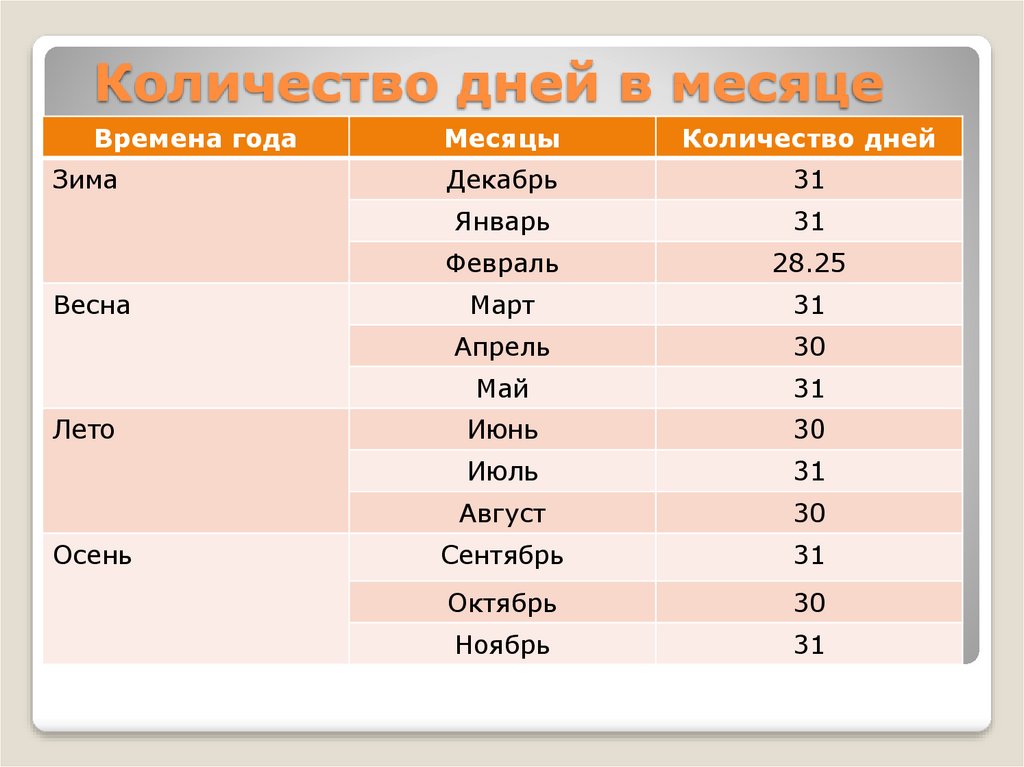 То есть если человек работает с 1 июля по 8 июля, то получается 8 дней. Так как последний день считается рабочим.
То есть если человек работает с 1 июля по 8 июля, то получается 8 дней. Так как последний день считается рабочим.
Синтаксис
 Через точку удобнее вводить на сотовых и планшетах, а через слеш удобнее на компьютере на клавиатуре справа (панели цифровой)
Через точку удобнее вводить на сотовых и планшетах, а через слеш удобнее на компьютере на клавиатуре справа (панели цифровой)Примеры использования
Календарь — это способ подсчета и отображения больших промежутков времени.
Все наши расчеты ведутся в рамках общепринятого сейчас во всем мире григорианского календаря (средняя продолжительность года 365,2425 дней).
При проведении исторических подсчетов, пожалуйста, проверяйте датировку. Разница между показаниями григорианского и юлианского календаря сейчас
составляет 13 дней,
но в ранние века количество дней между равными датами было меньшим,
тем меньше, чем ближе к началу нашей эры (). Дата 1
вс
22
. 06 . 1941
04
:
00Интервал
1417
Дата 2
вт
09
. 05 . 1945
01
:
431012
3
46
34009
2040583
122434980
3
10
17
1
43
между двумя датами  .. будут изменены еще и другие параметры даты
.. будут изменены еще и другие параметры даты
Количество часов в дате не может превышать 23, Вы ввели: … — будут изменены еще и другие параметры даты
Внимание!
Праздники России учитываются полностью, только если обе даты относятся к 2018 году
Число дней в месяце \n не может быть больше 31
Введенное Вами число относится ко временам, которые трудно себе представить…
В результатах расчета так же отображаются неизменяемые информационные величины и показатели — это дни недели (темно-серый цвет — будни, оранжево-красный — выходные) и, как итоговое резюме, интервал между датами, выраженный через годы, месяцы, дни, часы и минуты.
Справка: Достоверно известно, что в конце первого тысячелетия в Древней Руси отсчет времени велся по Юлианскому календарю, правда новый год справлялся 1 марта, отсчет времени по такому календарю называют Мартовским стилем. Разница между равными датами современного и древнего календря на 1 марта 1000 года составляла 59+6=65 дней (6 дней разница между показаниями юлианского и григорианского календаря, равными датами считаются даты с равными числами и равными номерами месяцев от начала года).
В 1492 году постановлением Московского Собора Русской православной церкви был принят календарь, согласно которому новый год (Новолетье) начинался 1 сентября (Сентябрьский стиль ), разница с современным календарем составляла 9-122=-113 дней.
Спустя два столетия в канун круглой календарной даты Петр Первый вводит календарь ведущий исчисление от Рождества Христова. Новый год в России встречают 1 января с начиная 1700 года (правда, на самом деле, по современному календарю этот новый год наступил 11 января 1700 года). Страна перешла из 7208 года в 1700! Так что, в новый тогда 18 век, наступивший в 1701 году Россия вошла почти в ногу с Европой. Почти в ногу, потому что летоисчисление, как и прежде велось по юлианскому календарю (изменилась только датировка, теперь она называется старым стилем ) , в то время как Европа уже частично перешла на григорианский календарь.
Современный григорианский календарь на территории России был принят только в 21 веке. 26 января 1918 года: Владимир Ильич Ленин подписал декрет Совнаркома о переходе на новое исчисление времени, при этом датировка сдвинулась на 13 дней. Последний государственный документ датированный по старому стилю вышел 31 января 1918 года — на следующий день наступило 14 февраля!
26 января 1918 года: Владимир Ильич Ленин подписал декрет Совнаркома о переходе на новое исчисление времени, при этом датировка сдвинулась на 13 дней. Последний государственный документ датированный по старому стилю вышел 31 января 1918 года — на следующий день наступило 14 февраля!
Так что вопрос:
«Сколько дней между двумя датами?» в историческом смысле всегда требует уточнения…Количество дней (календарных/рабочих/выходных и праздничных) и нормы рабочего времени в 2021 году \ КонсультантПлюс
Течка у собак 🐕 – сколько длится, признаки и симптомы, помощь питомцу
 То есть это период, когда вы можете повязать собаку, если хотите получить от нее щенков, или же наоборот, соблюдать дополнительные меры предосторожности, чтобы избежать внеплановой вязки.
То есть это период, когда вы можете повязать собаку, если хотите получить от нее щенков, или же наоборот, соблюдать дополнительные меры предосторожности, чтобы избежать внеплановой вязки.В каком возрасте начинается первая течка
Сколько длится течка у собак

 Такие трусы продаются в зоомагазинах. Они изготавливаются из различных материалов и могут по-разному крепиться на теле животного — с помощью ремешков, липучек или на резинке. Обычно они имеют специальный кармашек, в который вкладывается прокладка. Важно, чтобы трусы имели отверстие для хвоста, и ремешки или другие крепления не соприкасались непосредственно с половыми органами, чтобы не повредить слизистые оболочки.
Такие трусы продаются в зоомагазинах. Они изготавливаются из различных материалов и могут по-разному крепиться на теле животного — с помощью ремешков, липучек или на резинке. Обычно они имеют специальный кармашек, в который вкладывается прокладка. Важно, чтобы трусы имели отверстие для хвоста, и ремешки или другие крепления не соприкасались непосредственно с половыми органами, чтобы не повредить слизистые оболочки. Поведение собаки в этот период так же меняется. Она становится более ласковой и дружелюбной, охотно подпускает к себе кобелей, отводит хвост в сторону и замирает, демонстрируя таким поведением готовность к вязке. Выделения из петли приобретают более светлый оттенок, становятся практически прозрачными, петля становится более мягкой, но остается набухшей и увеличенной в объеме.
Поведение собаки в этот период так же меняется. Она становится более ласковой и дружелюбной, охотно подпускает к себе кобелей, отводит хвост в сторону и замирает, демонстрируя таким поведением готовность к вязке. Выделения из петли приобретают более светлый оттенок, становятся практически прозрачными, петля становится более мягкой, но остается набухшей и увеличенной в объеме. Если вы заметили подобные симптомы, рекомендуется обратиться к ветеринарному врачу.
Если вы заметили подобные симптомы, рекомендуется обратиться к ветеринарному врачу. При этом у собаки отсутствуют, либо слабо выражены симптомы течки, такие как набухание вульвы, кровянистые выделения, привлекательность для кобелей. В то же время яичники функционируют нормально, и овуляция также наступает. Поэтому, если вы планируете вязать собаку, лучше ориентироваться не на внешние признаки течки, а на результаты анализов.
При этом у собаки отсутствуют, либо слабо выражены симптомы течки, такие как набухание вульвы, кровянистые выделения, привлекательность для кобелей. В то же время яичники функционируют нормально, и овуляция также наступает. Поэтому, если вы планируете вязать собаку, лучше ориентироваться не на внешние признаки течки, а на результаты анализов.С какими проблемами, связанными с течкой, могут столкнуться владельцы
 Это поможет избежать неприятных последствий, таких как проявление агрессии к другим животным и людям, возможные травмы (животное в состоянии возбуждения может выбежать на дорогу и попасть под машину) и нежелательная вязка.
Это поможет избежать неприятных последствий, таких как проявление агрессии к другим животным и людям, возможные травмы (животное в состоянии возбуждения может выбежать на дорогу и попасть под машину) и нежелательная вязка.
 Это серьезное заболевание, которое может угрожать жизни вашего питомца! Если вы заметили подобные симптомы, это повод немедленно обратиться к врачу! Воспаление матки может возникнуть как через несколько дней после окончания течки, так и через месяц или два.
Это серьезное заболевание, которое может угрожать жизни вашего питомца! Если вы заметили подобные симптомы, это повод немедленно обратиться к врачу! Воспаление матки может возникнуть как через несколько дней после окончания течки, так и через месяц или два.
Как избавиться от внимания кобелей во время течки
Советы ветеринарного врача
 У собак мелких пород течка начинается раньше. Продолжительность течки в среднем составляет 21 день.
У собак мелких пород течка начинается раньше. Продолжительность течки в среднем составляет 21 день. В этот период рекомендуется более тщательно следить за гигиеной, особенно если собака недостаточно за собой ухаживает. По возможности рекомендуется избегать ношения специальных гигиенических трусов, поскольку это может препятствовать нормальному уходу животного за собой. При появлении признаков воспаления органов мочеполовой системы следует немедленно обратиться к ветеринарному врачу.
В этот период рекомендуется более тщательно следить за гигиеной, особенно если собака недостаточно за собой ухаживает. По возможности рекомендуется избегать ношения специальных гигиенических трусов, поскольку это может препятствовать нормальному уходу животного за собой. При появлении признаков воспаления органов мочеполовой системы следует немедленно обратиться к ветеринарному врачу.Поделиться
Сопутствующие товары
 ..
.. Корм…
Корм…Развитие котят по дням — как растут котята по неделям: рост котят по месяцам
Рождение

Рождение
Питание
Рождение
Здоровье
Рождение
Поведение

Рождение
Развитие
Рождение
Условия содержания
Неонатальный
От 0 до 3 недель
Здоровье
 Разлучение котят с матерью и однопометниками в неонатальном возрасте может привести к отставанию в физическом и умственном развитии и поведенческим проблемам, связанным с агрессией. Дегельминтизация в первые полгода жизни должна проводиться ежемесячно.
Разлучение котят с матерью и однопометниками в неонатальном возрасте может привести к отставанию в физическом и умственном развитии и поведенческим проблемам, связанным с агрессией. Дегельминтизация в первые полгода жизни должна проводиться ежемесячно.0–3 недель
Питание
0–3 недель
Поведение
От 0 до 3 недель
Развитие
0–3 недель
Условия содержания
 Чрезмерный шум и отвлекающие факторы могут привести к нарушению режимов сна и питания. Очень важно, чтобы температура тела котенка не опускалась ниже 35 °С, в противном случае он не сможет эффективно усваивать материнское молоко. А если температура тела опустится ниже 32 °С, котенок утратит сосательный рефлекс, что сделает нормальное кормление невозможным.
Чрезмерный шум и отвлекающие факторы могут привести к нарушению режимов сна и питания. Очень важно, чтобы температура тела котенка не опускалась ниже 35 °С, в противном случае он не сможет эффективно усваивать материнское молоко. А если температура тела опустится ниже 32 °С, котенок утратит сосательный рефлекс, что сделает нормальное кормление невозможным.Отъем от матери
4–8 недель
Питание
4–8 недель
Здоровье
 Это означает, что защита, обусловленная полученными от матери антителами, уже ослабла, однако количество этих антител по-прежнему достаточно большое, из-за чего вакцинация может быть неэффективна. В этот период котенок становится особенно восприимчивым к заболеваниям. Поскольку сон помогает укрепить иммунную систему котенка, очень важно обустроить для него теплое, удобное и тихое место для сна.
Это означает, что защита, обусловленная полученными от матери антителами, уже ослабла, однако количество этих антител по-прежнему достаточно большое, из-за чего вакцинация может быть неэффективна. В этот период котенок становится особенно восприимчивым к заболеваниям. Поскольку сон помогает укрепить иммунную систему котенка, очень важно обустроить для него теплое, удобное и тихое место для сна.4–8 недель
Поведение
4–8 недель
Развитие
4–8 недель
Условия содержания
 Кроме того, условия содержания играют важную роль в их обучении, поэтому позаботьтесь о том, чтобы у котят был постоянный доступ к игрушкам и другим предметам, стимулирующим развитие когнитивных функций. Регулярное общение с разными людьми поможет котятам в будущем более уверенно взаимодействовать с человеком.
Кроме того, условия содержания играют важную роль в их обучении, поэтому позаботьтесь о том, чтобы у котят был постоянный доступ к игрушкам и другим предметам, стимулирующим развитие когнитивных функций. Регулярное общение с разными людьми поможет котятам в будущем более уверенно взаимодействовать с человеком.Интенсивный рост
2–4 месяца
Здоровье
2–4 месяца
Питание
 Такой корм обеспечивает вашего питомца необходимым количеством питательных веществ и энергии, которые необходимы ему в течение этой жизненно важной стадии развития.
Такой корм обеспечивает вашего питомца необходимым количеством питательных веществ и энергии, которые необходимы ему в течение этой жизненно важной стадии развития.2–4 месяца
Поведение
2–4 месяца
Развитие
2–4 месяца
Условия содержания

Замедленный рост
Старше 4 месяцев
Здоровье
Старше 4 месяцев
Питание
Старше 4 месяцев
Поведение
 Она «испытывает на прочность» статус людей и других животных в существующей иерархии. Важно, чтобы вы как владелец поддерживали нормы поведения и распорядок дня, которые вы установите для своего питомца в первые месяцы его жизни. Стабильность обстановки позволит контролировать уровень стресса.
Она «испытывает на прочность» статус людей и других животных в существующей иерархии. Важно, чтобы вы как владелец поддерживали нормы поведения и распорядок дня, которые вы установите для своего питомца в первые месяцы его жизни. Стабильность обстановки позволит контролировать уровень стресса.Старше 4 месяцев
Развитие
Старше 4 месяцев
Условия содержания
 Как правило, коты отходят дальше от дома, чем кошки. На данном этапе важны последовательное поведение владельца и дисциплина.
Как правило, коты отходят дальше от дома, чем кошки. На данном этапе важны последовательное поведение владельца и дисциплина.Взросление вашего питомца
12–18 месяцев
Взросление вашего питомца
Питание, учитывающее особые потребности котенка
Подберите правильный корм для своей кошки

Особенности полового созревания кота
Пять ключевых этапов роста котенка
Когда котята становятся взрослыми?
Вопросы питания котенка
Половое созревание котенка
Подготовка котенка к первому посещению ветеринарного врача
Уход за кошкой в период беременности и ее кормление
Вакцинация котят
Смена зубов у котят
Приучение к горшку
Когда лучше начинать
 Как следствие, обучение становится долгим и малопродуктивным процессом. Кроме того, при их применении у детей могут возникать негативные реакции (поскольку обучение построено на давлении со стороны родителей) и соматоневрологические дисфункции, что впоследствии чревато такими проблемами, как запоры, недержание мочи/кала, многочисленные невротические реакции (включая логоневроз, тики и др.), а по достижении определенного возраста – энурез, гиперактивный мочевой пузырь и стойкий энкопрез. Принудительное приучение к горшку в любом возрасте может обернуться стрессом как для ребенка, так и для родителей. Описываемый стресс становится еще более выраженным, если ребенок не способен понять или интерпретировать полученную команду. Попытки навязать ребенку такие методы, основанные на доминировании взрослого, неизбежно приводят к затягиванию процесса обучения и низкой эффективности.
Как следствие, обучение становится долгим и малопродуктивным процессом. Кроме того, при их применении у детей могут возникать негативные реакции (поскольку обучение построено на давлении со стороны родителей) и соматоневрологические дисфункции, что впоследствии чревато такими проблемами, как запоры, недержание мочи/кала, многочисленные невротические реакции (включая логоневроз, тики и др.), а по достижении определенного возраста – энурез, гиперактивный мочевой пузырь и стойкий энкопрез. Принудительное приучение к горшку в любом возрасте может обернуться стрессом как для ребенка, так и для родителей. Описываемый стресс становится еще более выраженным, если ребенок не способен понять или интерпретировать полученную команду. Попытки навязать ребенку такие методы, основанные на доминировании взрослого, неизбежно приводят к затягиванию процесса обучения и низкой эффективности. В процессе приучения родители определяют сигналы и «язык тела» ребенка перед мочеиспусканием или дефекацией подобно тому, как приучают к туалету домашних животных. Такие приемы основаны не на реальном обучении, а на выработке рефлекса, и поэтому неэффективны. Успех процесса зависит от того, сумеет ли взрослый распознать потребность или желание ребенка сходить в туалет (при этом отсутствуют основные элементы обучения, и процесс не носит ассоциативный характер). Приобретенное ребенком «умение» имеет непостоянный характер и может быть утрачено при любой стрессовой ситуации (например, болезнь или переезд из квартиры, ссора родителей) или других неблагоприятных обстоятельствах. Поэтому попытки принудительного приучения ребенка к горшку до достижения им физической готовности и/или повышенная интенсивность обучения никоим образом не ускоряют и не приближают желаемый результат. Успешное приучение к горшку – это воспитание когнитивного (сознательного) навыка или умения, которое должно быть сосредоточено вокруг ребенка; оно должно проходить позитивно и занимательно.
В процессе приучения родители определяют сигналы и «язык тела» ребенка перед мочеиспусканием или дефекацией подобно тому, как приучают к туалету домашних животных. Такие приемы основаны не на реальном обучении, а на выработке рефлекса, и поэтому неэффективны. Успех процесса зависит от того, сумеет ли взрослый распознать потребность или желание ребенка сходить в туалет (при этом отсутствуют основные элементы обучения, и процесс не носит ассоциативный характер). Приобретенное ребенком «умение» имеет непостоянный характер и может быть утрачено при любой стрессовой ситуации (например, болезнь или переезд из квартиры, ссора родителей) или других неблагоприятных обстоятельствах. Поэтому попытки принудительного приучения ребенка к горшку до достижения им физической готовности и/или повышенная интенсивность обучения никоим образом не ускоряют и не приближают желаемый результат. Успешное приучение к горшку – это воспитание когнитивного (сознательного) навыка или умения, которое должно быть сосредоточено вокруг ребенка; оно должно проходить позитивно и занимательно. Важно помнить, что приобретенный рефлекс легко утрачивается, если не является заученной моделью поведения.
Важно помнить, что приобретенный рефлекс легко утрачивается, если не является заученной моделью поведения. Согласно литературным данным, здоровый ребенок достигает необходимой физиологической зрелости в среднем в возрасте от 18 до 24 месяцев (Американская Академия Педиатрии, 2003).
Согласно литературным данным, здоровый ребенок достигает необходимой физиологической зрелости в среднем в возрасте от 18 до 24 месяцев (Американская Академия Педиатрии, 2003).
Как устроен организм малыша
 Зная это, можно придти к очень существенным выводам , которые, впрочем, вполне очевидны. Чем раньше Вы начнете процесс приучения к горшку, тем больших усилий это от Вас потребует. Приучение к горшку тем успешнее, безболезненнее и проще, чем выше уровень физиологического развития ребенка. И если Вы начинаете приучение, когда детский организм полностью готов к этому, Вы и Ваш ребенок добьетесь успеха значительно быстрее и легче.
Зная это, можно придти к очень существенным выводам , которые, впрочем, вполне очевидны. Чем раньше Вы начнете процесс приучения к горшку, тем больших усилий это от Вас потребует. Приучение к горшку тем успешнее, безболезненнее и проще, чем выше уровень физиологического развития ребенка. И если Вы начинаете приучение, когда детский организм полностью готов к этому, Вы и Ваш ребенок добьетесь успеха значительно быстрее и легче.Ранние успехи
 И если этот звук произносится часто и подолгу, и если все равно тебя не оставят в покое, пока не пописаешь, то связь эта установится рано или поздно. Но цепочка должна быть другой: не «пи-пи» — наполнение пузыря — мочеиспускание, а наполнение пузыря — горшок — мочеиспускание. То есть побудительным мотивом к горшку должен стать физиологический процесс (наполнение пузыря), а не звуковой раздражитель («пи-пи»).
И если этот звук произносится часто и подолгу, и если все равно тебя не оставят в покое, пока не пописаешь, то связь эта установится рано или поздно. Но цепочка должна быть другой: не «пи-пи» — наполнение пузыря — мочеиспускание, а наполнение пузыря — горшок — мочеиспускание. То есть побудительным мотивом к горшку должен стать физиологический процесс (наполнение пузыря), а не звуковой раздражитель («пи-пи»).
 Якобы способный и развитый ребенок, с 9 месяцев сидящий на горшке, вдруг, по каким-то «непонятным» соображениям, перестает это делать, и активно воюет за свою свободу с озабоченными родственниками. А соображения очень даже понятные — наступает время формирования того самого нормального, естественного контроля над выделениями, о котором мы уже говорили. Мочевой пузырь пустой, а они тут лезут со своими «пи-пи»… Каких бы «поразительных успехов» Вы ни добились, но до того, как ребенок будет готов к приучению к горшку (а это приблизительно в 18 месяцев), успехи эти будут временными, а эпизоды промашек — частыми. И к этому надобно относиться весьма философски. Нет совсем ничего плохого в том, что Вам удастся познакомить ребенка с такой интересной штукой, как горшок. Но знакомство это, по крайней мере, с точки зрения медицинской науки, будет поверхностным, а выработанные навыки не стойкими.
Якобы способный и развитый ребенок, с 9 месяцев сидящий на горшке, вдруг, по каким-то «непонятным» соображениям, перестает это делать, и активно воюет за свою свободу с озабоченными родственниками. А соображения очень даже понятные — наступает время формирования того самого нормального, естественного контроля над выделениями, о котором мы уже говорили. Мочевой пузырь пустой, а они тут лезут со своими «пи-пи»… Каких бы «поразительных успехов» Вы ни добились, но до того, как ребенок будет готов к приучению к горшку (а это приблизительно в 18 месяцев), успехи эти будут временными, а эпизоды промашек — частыми. И к этому надобно относиться весьма философски. Нет совсем ничего плохого в том, что Вам удастся познакомить ребенка с такой интересной штукой, как горшок. Но знакомство это, по крайней мере, с точки зрения медицинской науки, будет поверхностным, а выработанные навыки не стойкими.Как узнать, что ребенок готов

10 правил успешного освоения горшка
 Приступаем.
Приступаем.
 Они вполне пригодятся для поездок в транспорте, ночью, на
Они вполне пригодятся для поездок в транспорте, ночью, на А если еще папа найдет время показать, как это делается…
А если еще папа найдет время показать, как это делается…«Малыш отказывается от горшка. Как быть?»
 Нам 1,5 годика.» Ирина
Нам 1,5 годика.» Ирина
 Если она сейчас игнорирует процесс обучения, внимательно посмотрите мои правила успешного освоения горшка и убедитесь, что
Если она сейчас игнорирует процесс обучения, внимательно посмотрите мои правила успешного освоения горшка и убедитесь, что6 самых распространенных заблуждений
 Ведь он сможет контроливать свой мочевой пузырь и кишечник, только когда его организм будет достаточно развит — в среднем в 18 месяцев. И если начинать обучение в правильном возрасте, то ребенок научится намного быстрее и легче и сможет гордиться своим достижением. А Вы будете гордиться им!
Ведь он сможет контроливать свой мочевой пузырь и кишечник, только когда его организм будет достаточно развит — в среднем в 18 месяцев. И если начинать обучение в правильном возрасте, то ребенок научится намного быстрее и легче и сможет гордиться своим достижением. А Вы будете гордиться им!
 »
»
 Хочу Вас успокоить — в таком раннем возрасте дети просто физически неспособны осознанно ходить на горшок. Их нервная система еще недостаточно развита, чтобы подавать сигналы о наполненном мочевом пузыре или кишечнике. До 1,5 лет они ходят в туалет, сами того не осознавая и не замечая. И Вы никак не можете повлиять на это и ускорить развитие ребенка.
Хочу Вас успокоить — в таком раннем возрасте дети просто физически неспособны осознанно ходить на горшок. Их нервная система еще недостаточно развита, чтобы подавать сигналы о наполненном мочевом пузыре или кишечнике. До 1,5 лет они ходят в туалет, сами того не осознавая и не замечая. И Вы никак не можете повлиять на это и ускорить развитие ребенка. Правда ли это?»
Правда ли это?»
От 12 дней до 22 месяцев: удивительные сроки беременности в мире животных
 д. У копытных беременность длится дольше, однако их дети появляются на свет хорошо развитыми, сразу после рождения могут передвигаться самостоятельно. У хищных длительность беременности меньше, однако первое время им требуется особая забота и защита. Рассказываем о самых удивительных сроках.
д. У копытных беременность длится дольше, однако их дети появляются на свет хорошо развитыми, сразу после рождения могут передвигаться самостоятельно. У хищных длительность беременности меньше, однако первое время им требуется особая забота и защита. Рассказываем о самых удивительных сроках.Опоссум — 12-13 дней
Мышь — 20 дней
Белка — 35 дней

Волк — 63 дня
Бобр — 106 дней
Лось — 225 дней

Корова — 300 дней
Зебра — 12 месяцев
Жираф — 14 месяцев
 Уже через несколько часов он начинает бегать. Однако в стадо детеныши допускают только через две-три недели.
Уже через несколько часов он начинает бегать. Однако в стадо детеныши допускают только через две-три недели.Белый носорог — 18 месяцев
Слон — 22 месяца
Преобразовать 18 месяцев в дни

мес д 18.  00
00 547,86 18,01 548,17 18,02 548,47 18,03 548,78 18,04 549,08 18,05 549,39 18,06 549,69 18.07 549,99 18,08 550,30 18,09 550,60 18,10 550,91 18,11 551,21 18,12 551,52 18,13 551,82 18,14 552,12 18,15 552,43 18.16 552,73 18,17 553,04 18,18 553,34 18,19 553,65 18,20 553,95 18,21 554,26 18,22 554,56 18,23 554,86 18,24 555,17 пн д 18,25 555,47 18,26 555,78 18,27 556,08 18,28 556,39 18,29 556,69 18,30 556,99 18,31 557,30 18,32 557,60 18.  33
33 557,91 18,34 558,21 18,35 558,52 18,36 558,82 18,37 559,13 18,38 559,43 18,39 559,73 18,40 560,04 18,41 560,34 18.42 560,65 18,43 560,95 18,44 561,26 18,45 561,56 18,46 561,86 18,47 562,17 18,48 562,47 18,49 562.78 мес д 18,50 563,08 18,51 563,39 18,52 563,69 18,53 564,00 18,54 564,30 18,55 564,60 18,56 564,91 18,57 565,21 18,58 565,52 18,59 565,82 18,60 566,13 18,61 566,43 18,62 566,73 18,63 567,04 18,64 567,34 18,65 567,65 18,66 567,95 18,67 568,26 18,68 568,56 18,69 568,87 18,70 569,17 18,71 569,47 18,72 569,78 18,73 570,08 18,74 570.  39
39 мес д 18,75 570,69 18,76 571,00 18,77 571,30 18,78 571,60 18,79 571,91 18,80 572,21 18,81 572,52 18,82 572,82 18,83 573,13 18,84 573,43 18,85 573,74 18,86 574,04 18,87 574,34 18,88 574,65 18,89 574,95 18,90 575,26 18,91 575,56 18,92 575,87 18,93 576,17 18,94 576,47 18,95 576,78 18,96 577,08 18,97 577,39 18,98 577,69 18,99 578.  00
00 18 месяцев в днях — Сколько дней составляет 18 месяцев?
Конвертер единиц измерения
Формула преобразования
 Мы также можем составить простую пропорцию для вычисления результата:
Мы также можем составить простую пропорцию для вычисления результата: Альтернативное преобразование
Приблизительный результат

Таблица преобразования
График месяцев в днях
месяца (мес.) дня (г) 19 месяцев 578,301 дней 20 месяцев 608 738 дней 21 месяц 639,174 дня 22 месяца 669 611 дней 23 месяца 700.048 дней 24 месяца 730 485 дней 25 месяцев 760,922 дня 26 месяцев 791,359 дней 27 месяцев 821 796 дней 28 месяцев 852,233 дня Блоки преобразования
 Вот как они определяются:
Вот как они определяются:
День  Период времени, за который Земля совершает один оборот относительно Солнца, называется солнечными сутками. Несколько определений этого универсального человеческого понятия используются в зависимости от контекста, необходимости и удобства. В 1960, секунда была переопределена с точки зрения орбитального движения Земли и обозначена как основная единица времени в системе СИ. Единица измерения «день», переопределенная в 1960 году как 86 400 секунд СИ и обозначенная символом d, не является единицей СИ, но принята для использования с СИ. Гражданский день обычно составляет 86 400 секунд плюс или минус возможная дополнительная секунда по всемирному скоординированному времени (UTC), а иногда плюс или минус час в тех местах, которые переходят на летнее время или на него.
Период времени, за который Земля совершает один оборот относительно Солнца, называется солнечными сутками. Несколько определений этого универсального человеческого понятия используются в зависимости от контекста, необходимости и удобства. В 1960, секунда была переопределена с точки зрения орбитального движения Земли и обозначена как основная единица времени в системе СИ. Единица измерения «день», переопределенная в 1960 году как 86 400 секунд СИ и обозначенная символом d, не является единицей СИ, но принята для использования с СИ. Гражданский день обычно составляет 86 400 секунд плюс или минус возможная дополнительная секунда по всемирному скоординированному времени (UTC), а иногда плюс или минус час в тех местах, которые переходят на летнее время или на него. Сколько времени составляет 18 месяцев в других единицах времени?
Преобразование последних месяцев в дни
Последние преобразования
 1 кубических сантиметров в литров
1 кубических сантиметров в литров 18 Месяцев в Дней | от 18 мес до д
Конвертер единиц измерения
Как преобразовать 18 месяцев в дни
 Результат следующий:
Результат следующий: Таблица преобразования месяцев в дни
Месяцы (мес.) Дней (г) 19 месяцев 578.301 дней 20 месяцев 608 738 дней 21 месяц 639,174 Дней 22 месяца 669 611 дней 23 месяца 700.048 дней 24 месяца 730 485 дней 25 месяцев 760.  922 Дней
922 Дней 26 месяцев 791 359 дней 27 месяцев 821.796 дней 28 месяцев 852.233 Дней Определение единиц


Часто задаваемые вопросы по переводу 18 месяцев в дни
Преобразование 18 месяцев в другие единицы времени
Преобразование последних месяцев в дни
Последние преобразования
Перевод месяцев в дни, дни в месяце
Таблица преобразования месяцев в дни
1 month 30.  42 days
42 days 2 months 60.83 days 3 months 91.25 days 4 months 121.7 days 5 months 152.1 days 6 months 182.5 days 7 months 212.9 days 8 months 243.3 days 9 months 273.8 days 10 months 304,2 дня 11 месяцев 334,6 дня 12 месяцев 365 дней 2 9 9003 40043 395.4 days 14 months 425.8 days 15 months 456.3 days 16 months 486.7 days 17 months 517.1 days 18 months 547,5 дня 19 месяцев 577,9 дня 20 месяцев 608,3 дня 8 21 months 638.  8 days
8 days 22 months 669.2 days 23 months 699.6 days 24 months 730 days 25 months 760.4 days 26 месяцев 790,8 дня 27 месяцев 821,3 дня 28 месяцев 851.7 days 29 months 882.1 days 30 months 912.5 days 31 months 942.9 days 32 months 973.3 days 33 months 1004 дня 34 месяца 1034 дня 35 месяцев 1065 дней 3604 1095 days 37 months 1125 days 38 months 1156 days 39 months 1186 days 40 months 1217 days 41 месяц 1247 дней 42 месяца 1278 дней 43 месяца 130042 дней 44 months 1338 days 45 months 1369 days 46 months 1399 days 47 months 1430 days 48 months 1460 days 49 месяцев 1490 дней 50 месяцев 1521 день 9 51 месяц 3 10043 52 months 1582 days 53 months 1612 days 54 months 1643 days 55 months 1673 days 56 months 1703 days 57 месяцев 1734 дня 58 месяцев 1764 дня 7 59 месяцев 35 дней 60 месяцев 1825 дней 61 months 1855 days 62 months 1886 days 63 months 1916 days 64 months 1947 days 65 months 1977 days 66 месяцев 2008 дней 67 months 2038 days 68 months 2068 days 69 months 2099 days 70 months 2129 days 72 months 2190 days 74 месяца 2251 день 76 месяцев 2312 дней 78 месяцев 2373 дня 80 months 2433 days 82 months 2494 days 85 months 2585 days 90 months 2738 days 95 months 2890 days 100 месяцев 3042 дня Таблица перевода дней в месяцы
1 день 0.  03288 month
03288 month 2 days 0.06575 month 3 days 0.09863 month 4 days 0.1315 month 5 days 0.1644 month 6 days 0,1973 месяц 7 дней 0,2301 месяц 8 дней 0,263 месяц 9 9days 0.2959 month 10 days 0.3288 month 11 days 0.3616 month 12 days 0.3945 month 13 days 0.4274 month 14 дней 0,4603 месяца 15 дней 0,4932 месяца 16 дней 0,526 месяца 17 days 0.5589 month 18 days 0.5918 month 19 days 0.  6247 month
6247 month 20 days 0.6575 month 21 days 0.6904 month 22 days 0.7233 month 23 days 0.7562 month 24 days 0.789 month 25 days 0.8219 month 26 days 0.8548 month 27 days 0.8877 month 28 days 0.9205 month 29 days 0,9534 месяца 30 дней 0,9863 месяца 32 дня 1,052 месяца 80042 34 days 1.118 months 36 days 1.184 months 38 days 1.249 months 40 days 1.  315 months
315 months 42 days 1.381 months 44 дня 1,447 месяца 46 дней 1,512 месяца 48 дней 1,573 мес.0038 50 дней 1,644 месяца 52 days 1.71 months 54 days 1.775 months 56 days 1.841 months 58 days 1.907 months 60 days 1.973 months 65 дней 2,137 месяца 70 дней 2.301 months 75 days 2.466 months 80 days 2.63 months 85 days 2.795 months 90 days 2.959 months 95 days 3,123 месяца 100 дней 3,288 месяца 105 дней 3,452 месяца 80042 110 days 3.  616 months
616 months 115 days 3.781 months 120 days 3.945 months 125 days 4.11 months 130 days 4.274 months 135 дней 4,438 месяца 140 дней 4,603 месяца 145 дней 4.767 months 150 days 4.932 months 155 days 5.096 months 160 days 5.26 months 165 days 5.425 months 170 days 5,589 месяцев 175 дней 5,753 месяцев 180 дней 5,918 месяцев 185 days 6.082 months 190 days 6.  247 months
247 months 200 days 6.575 months 250 days 8.219 months 300 days 9.863 months 350 дней 11,51 месяцев 400 дней 13,15 месяцев 500 дней 700 days 23.01 months 900 days 29.59 months 1000 days 32.88 months Калькулятор дат
Дней между двумя датами
Добавление или вычитание из даты
Калькулятор связанного времени | Калькулятор возраста Дата начала +– История григорианского календаря
 В рамках этого календаря стандартный год состоит из 365 дней, при этом високосный день вводится в февраль в течение високосного года. В апреле, июне, сентябре и ноябре по 30 дней, а в остальных — по 31 дню, за исключением февраля, в котором 28 дней в стандартном году и 29 — в високосном.
В рамках этого календаря стандартный год состоит из 365 дней, при этом високосный день вводится в февраль в течение високосного года. В апреле, июне, сентябре и ноябре по 30 дней, а в остальных — по 31 дню, за исключением февраля, в котором 28 дней в стандартном году и 29 — в високосном. С этого момента было предпринято множество попыток согласовать республиканский календарь с солнечным годом, включая добавление дополнительного месяца к определенным годам, чтобы заменить отсутствие дней в конкретном году. В 46 г. до н.э. календарь был дополнительно реформирован Юлием Цезарем, введя алгоритм, устранивший зависимость календарей от наблюдения за новолунием. Чтобы добиться этого, Цезарь добавил в республиканский календарь дополнительные 10 дней, в результате чего общее количество дней в году составило 365. календарь с солнечным годом.
С этого момента было предпринято множество попыток согласовать республиканский календарь с солнечным годом, включая добавление дополнительного месяца к определенным годам, чтобы заменить отсутствие дней в конкретном году. В 46 г. до н.э. календарь был дополнительно реформирован Юлием Цезарем, введя алгоритм, устранивший зависимость календарей от наблюдения за новолунием. Чтобы добиться этого, Цезарь добавил в республиканский календарь дополнительные 10 дней, в результате чего общее количество дней в году составило 365. календарь с солнечным годом. По григорианскому календарю столетние годы, не делящиеся на 400, не будут високосными. Эти изменения уменьшили ошибку с 1 дня за 128 лет до 1 дня за 3030 лет по отношению к текущему значению среднего солнечного года.
По григорианскому календарю столетние годы, не делящиеся на 400, не будут високосными. Эти изменения уменьшили ошибку с 1 дня за 128 лет до 1 дня за 3030 лет по отношению к текущему значению среднего солнечного года. Праздники

 Для дальнейшего уровня конкретности федеральные праздники в США относятся к праздникам, признанным правительством США; в эти дни второстепенные учреждения федерального правительства закрыты, и все федеральные служащие получают оплачиваемый отпуск. Однако это не обязательно верно в отношении частного сектора, и то, какие федеральные отпуска получает работник частного сектора, во многом зависит от усмотрения компании. В некоторых случаях работник, который должен работать в федеральный праздник, может получить компенсацию в виде отпускных в дополнение к своей обычной заработной плате.
Для дальнейшего уровня конкретности федеральные праздники в США относятся к праздникам, признанным правительством США; в эти дни второстепенные учреждения федерального правительства закрыты, и все федеральные служащие получают оплачиваемый отпуск. Однако это не обязательно верно в отношении частного сектора, и то, какие федеральные отпуска получает работник частного сектора, во многом зависит от усмотрения компании. В некоторых случаях работник, который должен работать в федеральный праздник, может получить компенсацию в виде отпускных в дополнение к своей обычной заработной плате. Ниже приведены две таблицы, показывающие даты федеральных праздников в США на 2022 и 2023 годы9.0003
Ниже приведены две таблицы, показывающие даты федеральных праздников в США на 2022 и 2023 годы9.0003 Преобразование 18 месяцев в рабочие недели (18 месяцев в рабочую неделю)

Сколько времени по сравнению с другими единицами времени?
месяцев в рабочие недели
пн рабочая неделя 18 = 328.71825 18.01 = 328. 1 18.02 = 329.083493 18.03 = 329.266114 18.04 = 329,448735 18,05 = 329.631356 18.06 = 329.813978 18.07 = 329.996599 18.08 = 330.17922 18.09 = 330.361841 18.1 = 330.  544463
544463 18.11 = 330,727084 18.12 = 18.12 = 18.12 = 18.12 = 18.12 = 18.12 = 330. 5 18.13 = 331.0 18.14 = 331.274948 18.15 = 331.457569 18.16 = 331.64019 18.17 = 331.822811 18.18 = 332.005433 18.19 = 18.19 = 18.19 = 18.19 = 18.19 = 18.19 = 18.19 .0043 332.188054 мес рабочая неделя 18.  2
2 = 332.370675 18.21 = 332.553296 18.22 = 332.735918 18.23 = 332. 9 18.24 = 333,10116 18.25 = 333.283781 18.26 = 333.466403 18.27 = 333.649024 18.28 = 333.831645 18.29 = 334.014266 18.3 = 334.196888 18.31 = 334.379509 18.32 = 334.56213 18.33 = 334.744751 18.34 = 334. 3 18.  35
35 = 335.109994 18.36 = 335.2 18.37 = 335.475236 18.38 = 335.657858 18,39 = 335,840479 мес рабочая неделя 18.4 = 336.0231 18.41 = 336.205721 18.42 = 336.388343 18.43 = 336.570964 18.44 = 336,753585 18.45 = 336.936206 18.46 = 337.118828 18.47 = 337.301449 18.48 = 337.48407 18.  49
49 = 337.666691 18.5 = 337.849313 18.51 = 338.031934 18.52 = 338.214555 18.53 = 338.397176 18.54 = 338.579798 18.55 = 338.762419 18.56 = 338,94504 18,57 = 339.127661 18,58 = 3339.31029.3102898 = 333.39.31029.31029.31029.31029.31029.31029.310289.58 .0043 18,59 = 339,4 мес рабочая неделя 18.6 = 339.675525 18.61 = 339.858146 18.  62
62 = 340.040768 18.63 = 340.223389 18.64 = 340.40601 18.65 = 340.588631 18.66 = 340.771253 18.67 = 340.953874 18.68 = 341.136495 18,69 = 341.319116 18,7 = 341.501738 18,7111739 18,7111143 = 18,7111143 = .0043 341.684359 18.72 = 341.86698 18.73 = 342.049601 18.74 = 342.232223 18.75 = 342.414844 18,76 = 342.  597465
597465 18,77 = 342,780086 18,78 = 18,78 = 18,78 = 18,78 = 18,78 = 18,78 = 18,78 = .0043 342,962708 18,79 = 343,145329 мес. рабочая неделя 18.8 = 343.32795 18.81 = 343.510571 18.82 = 343.693193 18.83 = 343.875814 18.84 = 344.058435 18.85 = 344.241056 18.86 = 344.423678 18.87 = 344. 
Решите уравнение x 2 7x 18 0: Решите уравнение х^2+7х-18=0 — Школьные Знания.com
ОГЭ по математике, базовый уровень. Квадратные уравнения
Курсы ЕГЭ
1) 3×2 − 18 = 0; 3) x2 − x − 20 = 0; 5) x2 + 6x − 2 = 0; 2) 8×2 − 3x = 0; 4) 3×2 − 2x − 8 = 0; 6) x2 − 4x + 6 = 0. 2. составьте приведённое квадратное уравнение, сумма корней которого равна числу −6, а произведение — числу 3. 3. одна из сторон прямоугольника на 6 см меньше другой. найдите стороны прямоугольника, если его площадь равна 72 см2. 4. число 5 является корнем уравнения 4×2 + 6x + k = 0. найдите второй корень уравнения и значение k. 5. при каком значении a уравнение 4×2 + 8x + a = 0 имеет единственный корень? 6. известно, что x1 и x2 — корни уравнения x2 + 10x + 4 = 0. не решая уравнения, найдите значение выражения . — Знания.org
Интерактивный тест по алгебре «Квадратные уравнения»
учитель математики и информатики
Ряполова Татьяна ВикторовнаКонспект урока по теме квадратные уравнения
Тронина Татьяна Сергеевна,
учитель математики МБОУ «Очёрская СОШ №1», г.Очёр
Конспект урока математики в 8 классе по теме
Тема: «Решение квадратных уравнений». Цель: Образовательная: отработка способов решения квадратных уравнений, формирование навыков решения квадратных уравнений по формуле. Развивающая: развитие внимания, памяти, умений сравнивать, обобщать. Воспитательная: воспитание трудолюбия, взаимопомощи, культуры общения.
План. 1. Повторить теорию. 2. Проверка домашнего задания (выставление оценок руководителями групп, каждому ученику, работающему в группе)- групповая работа. 3. Устная работа (тестовая форма). 4. Решение квадратных уравнений по формуле c самопроверкой. 5. Домашняя работа. 6. Итог урока. Оборудование: 1. Бланки с тестами (для устной работы). 2. Карточки с буквами А Б В Г. 3. Портреты ученых – математиков Евклида, Ф.Виета, У. Гамильтона, Л.Пизанского.
Историческая справка
III век до н. э. Древнегреческий ученый Евклид – решение квадратных уравнений графически. XIII век Европа, Леонардо Пизанский – формулы корней квадратного уравнения. XVI век Французский математик Франсуа Виет – вывод формулы корней квадратного уравнения в общем виде. XVI век Германия, Штифель (священник и математик) – систематическое употребление термина «корень уравнения». XIX век Ирландский ученый – математик Уильям Гамильто – ввел термин «дискриминант».1. Повторение теоретического материала. 1. Вывести формулы корней квадратного уравнения – работают 2 ученика на листочках. 2. Решить графически приведенное квадратное уравнение x2-2x-3=0 — один ученик выполняет задание на доске. 3. Решить приведенное квадратное уравнение выделением квадрата двучлена x2+4x-5=0 – второй ученик выполняет задание на доске.
В это время остальные дети отвечают на вопросы по теме. — Дать определение квадратного уравнения. — По какой формуле находятся корни квадратного уравнения. — Что такое дискриминант? — Как зависят корни квадратного уравнения от дискриминанта? — Дать определение приведенного квадратного уравнения, неприведенного квадратного уравнения. — Привести примеры приведенного и неприведенного квадратных уравнений. — Дать определение неполного квадратного уравнения. — Привести пример неполного квадратного уравнения 1-го вида и решить его на доске.(например, 5×2=0; x2=0;x=0). — Привести пример неполного квадратного уравнения 2-го вида и решить его на доске (например, 3×2-6x=0; x3x-6=0 ; x=0 или 3x-6=0;3x=6;x=2 Ответ: 0; 2). — Привести пример неполного квадратного уравнения 3-го вида и решить его. (например, 2×2-10=0;2×2=10; x2=5;x=5;x=-5 . Ответ: 5;-5 ).
Графическое решение приведенного квадратного уравнения x2-2x-30=0
у y=x2 0 3 хy=2x+3×2=2x+3 Построим 2 графика: y=x2 – параболу и y=2x+3 – прямую.
Эти графики пересеклись в двух точках (-1;1) и (3; 9 ). Ответ: -1; 3.
1 группа Дельфин 2 группа Мышонок
x2+4x=0 (0; -4) x2+8x-20=0 (2; -10)
x2-6x+8=0(4; 2) x2+5x-36=0 (4; -9)
x2-8x+12=0 (6; 2) x2-49=0 (7; -7)
-x2+14x-45=0 (9; 5) -x2+6x+40=0 (10; -4)
x2-11x+18=0 (9; 2) x2-7x-18=0 (9; -2)
0,5×2-7x+12=0 (12; 2) 2×2-18x=0 (9; 0)
x2-9x-112=0 (16; -7) x2-12x+20=0 (10; 2)
x2-6x-187=0 (17; -11) -x2+14x-33=0 (11; 3)
x2-5x-150=0 (15; -10) x2-17x+52=0 (13; 4)
x2-144=0 (12; -1 2) x2-18x+65=0 (13; 5)
x2-7x-98=0 (14; -7) x2-19x+78=0 (13; 6)
-x2+6x+40=0 (10; -4) 0,5×2-10x+42=0 (14; 6)
3×2+12x=0 (0; -4) x2-19x+70=0 (14; 5)
x2-2x-3=0 (3; -1) x2-20x+75=0 (15; 5)
-2×2+2x+12=0 (3; -2) 0,5×2-10x+32=0 (16; 4)
12×2-x-4=0 (4; -2) x2-21x+54=0 (18; 3)
x2-3x-4=0 (4; -1) 12×2-10x+18=0 (18; 2)
-x2+2x+3=0 (3; -1) x2-18x+32=0 (16; 2)
x2-7x=0 (7; 0) x2-17x+16=0 (16; 1)
x2-5x-14=0 (7; -2) x2-18x+17=0 (17; 1)
x2-8x-20=0 (10; -2) x2-16x=0 (16; 0)
x2+8x+9=0 (9; -1) -x2+15x=0 (15; 0)
2×2-14x=0 (7; 0) x2-12x-28=0 (14; -2)
x2-10x-39=0 (13; -3)
-x2+13x+45=0 (15; -3)
x2-9x-52=0 (13; -4)
x2-6x-40=0 (10; -4)
x2-19x+48=0 (16; 3)
4 группа Лиса 5 группа Сова 3 группа Заяц
x2-7x+10=0 (5; 2) x2-10x+9=0 (9; 1) x2-17x+60=0 (12; 5)
x2-x=0(1; 0) 2×2-16x=0 (8; 0) x2-19x+88=0 (11; 8)
2×2-8x-10=0 (5; -1) -3×2+9x=0 (3; 0) x2-19x+90=0 (10; 9)
x2-8x=0 (8; 0) x2-7x+10=0 (5; 2) -x2+17x-72=0 (9; 8)
2×2-12x-14=0 (7; -1) x2-13x+36=0 (9; 4) x2-16x+55=0 (11; 5)
-x2+6x+16=0 (8; -2) -x2+14x-40=0 (10; 4) -x2+12x-27=0 (9; 3)
3×2-24x-60=0 (10; -2) x2-14x+45=0 (9; 5) -2×2+10x-8=0 (4; 1)
x2-8x-9=0 (9; -1) x2-16x+63=0 (9; 7) x2-x-6=0 (3; -2)
-x2+7x+8=0 (8; -1) x2-18x+80=0 (10; 8) -x2+x+2=0 (2; -1)
2×2+20x=0 (10; 0) x2-17x+70=0 (10; 7) 3×2-12=0 (2; -2)
x2-10x-11=0 (11; -1) x2-19x+84=0 (18; 7) x2-16=0 (4; -4)
2×2-28x-30=0 (15; -1) -x2+20x-96=0 (12; 8) x2-5x-36=0 (9; -4)
0,5×2-7x-16=0 (16; -2) x2-20x+91=0 (13; 7) x2-5x-24=0 (8; -3)
x2-17x-38=0 (19; -2) x2-18x+65=0 (13; 5) -x2+4x+21=0 (7; -3)
x2-17x-18=0 (18; -1) 0,5×2-8x+24=0 (12; 4) 2×2-22x+20=0 (10; 1)
2×2-30x-32=0 (16; -1) x2-17x+52=0 (13; 4) x2-7x-44=0 (11; -4)
-x2+17x=0 (17; 0) -x2+19x-34=0 (17; 2) x2-8x-48=0 (12; -4)
2×2-36x=0 (18; 0) x2-19x=0 (19; 0) x2-9x-22=0 (11; -2)
x2-20x+19=0 (19; 1) 2×2-28=0 (14; 0) -x2+12x-11=0 (11; 1)
x2-20x+51=0 (17; 3) x2-14x+13=0 (13; 1) x2-14x+24=0 (12; 2)
x2-19x+34=0 (17; 2) x2-11x-26=0 (13; -2 )x2-15x+26=0 (13; 2)
-x2-19x-48=0 (16; 3) -x2+9x+36=0 (12; -3) x2-17x+42=0 (14; 3)
0,5×2-9x+16=0 (16; 2) x2-7x-78=0 (13; -6) x2-17x+60=0 (12; 5)
x2-16x+15=0 (15; 1) x2-6x-55=0 (11; -5) -x2+22x-117=0 (13; 9)
x2-15x+14=0 (14; 1) -x2+3x+54=0 (9; -6) 0,5×2-11x+56=0 (14; 8)
2×2-30x+52=0 (13; 2) x2-7x-30=0 (10; -3) 4×2-68x+225=0 (12,5; 4,5)
-x2+11x-18=0 (9; 2) 2×2-14x-36=0 (9; -2) x2-16x+48=0 (12; 4)
x2-9x+8=0 (8; 1) -2×2+20x-18=0 (9; 1) 12×2-3,5x+5=0 (5; 2) 12×2-8x+30=0 (10; 6) 2×2-37x+35=0 (17,5; 1) x2-16x+55=0 (11; 5) 0,5×2-3x+36=0 (12; 6) Рисунки, полученные при выполнении домашнего задания.
y 1 0 x
y 1 0 x
y 1 0 x
y 1 0 x
y 1 0 x
Решение приведенного квадратного уравнения выделением квадрата двучлена x2+4x-5=0 (x2+2∙2∙x+4)-4-5=0 x+22-9=0 x+22=9 x+2=3 или x+2=-3 x=1 x=-5 Ответ: -5;1. Класс разбился на группы. Группам было предложено домашнее задание: решить квадратные уравнения и ответы записать в виде пар (x1;x2) так, чтобы x1>x2, руководителям групп проверить решение и по координатам этих точек построить на координатной плоскости рисунок. 2. Проверка домашнего задания и выставление оценок (оценки выставляются руководителями групп).
3. Устная работа (дети поднимают карточки с буквами, соответствующими правильному ответу)
А Б В Г
Тест. 1. Какие из уравнений являются квадратными: А) 5-2x=0 Б) 3-7×2+4x=0 В) 5×2-1,5×3+4=0 Г) -7×2+9x=0 2. В квадратном уравнении 5-3×2+4x=0 укажите его коэффициенты А) a=5, b=-3, c=4 Б) a=4, b=5, c=-3 В) a=4, b=-3, c=5 Г) a=-3, b=4, c=5 3. Определите дискриминант в квадратном уравнении 2×2+5x-3=0 А) D=13 Б) D=47 В) D=49 Г) D=25 4. Найдите корни уравнения 3×2-9x=0 А) -3; 3 Б) 0; 3 В) 3 Г) корней нет 5. Какие из чисел являются корнями уравнения -4y2+64=0 А) 4; 0 Б) 0; -4 В) -2; -1 Г) -4; 4№ задания 1 2 3 4 5
Ответ Б Г В Б Г
4. Решите самостоятельно квадратные уравнения по формуле 1 ряд – а), 2 ряд — б) , 3 ряд – в). На доске записать решения этих примеров с ошибками и попросить детей найти эти ошибки после того, как решат сами (в решении уравнения в) ошибок нет)
а) 2×2-5x-3=0 a=2, b=-5, c=-3 D=b2-4ac= -52-4·2·-3==25-24=1>0 уравнение имеет 2корня x=-b±D2a=5±12·2; x1=5-14=44=1;
x2=5+14=64=1,5
Ответ: 1; 1,5. б) 36y2-12y+1=0 a=36, b=-12, c=1 D=b2-4ac= -122-4·36·1= =144-144=0 уравнение имеет 1корнь x=b2a=-122·36=-16;
в) 3t2-3t+1=0
a=3, b=-3, c=1 D=b2-4ac= -32-4·3·1= =9-12=-3<0 уравнение не имеет корней
Ответ: корней нет.
Решение уравнения г) записываем на доске – 1 ученик решает у доски, остальные работают в тетради.
Решение уравнений без ошибок.
а) 2×2-5x-3=0 a=2, b=-5, c=-3 D=b2-4ac= -52-4·2·-3==25+24=49>0 уравнение имеет 2корня x=-b±D2a=5±492·2; x1=5+74=3;
x2=5-74=-12
Ответ: -12; 3. б) 36y2-12y+1=0 a=36, b=-12, c=1 D=b2-4ac= -122-4·36·1= =144-144=0 уравнение имеет 1корнь x=-b2a=122·36=16;
в) 3t2-3t+1=0
a=3, b=-3, c=1 D=b2-4ac= -32-4·3·1= =9-12=-3<0 уравнение не имеет корней
Ответ: корней нет. г) x2-5x-3=2x-5 x2-5x-3-2x+5=0 x2-7x+2=0 a=1, b=-7, c=2 D=b2-4ac=(-7)2 -4·1·2= =49-8=41>0 уравнение имеет 2корня x=-b±D2a=7±412·1;
x1=7+412; x2=7-412
Ответ: 7+412; 7-4125. Подведение итога урока Загадка Я у дуба, я у зуба, Я у слов и у цветов. Я упрятан в темноту, Я не вверх, а вниз росту.
Математик без меня Не продержится и дня. Я – решенье уравненья. Это важно, без сомненья. Ответ: корень
6. Рефлексия: — Что нового узнали на уроке? — Какой из способов решения квадратных уравнений вам понравился больше? Чем?
6. Домашнее задание. 1 группа – Приготовить краткую биографию Ф.Виета и как найти корни квадратного уравнения по теореме Виета, привести примеры. 2 группа – узнать у учителей физики, какие физические явления описываются с помощью квадратного уравнения . 3группа – найти в учебнике условие, при котором один из корней равен 1 или -1, привести примеры. 4 группа – найти формулы для нахождения корней квадратного уравнения, используя четверть дискриминанта, привести примеры.2-2*x)+(7*x-19)*1/(x-3)<=(8*x+1)*1/xРешение других задач по математике на тему «Рациональные неравенства»
Пошаговое решение:
Шаг 1:
Попытка разложить на множители путем разделения среднего члена
Средний член + 7x, его коэффициент равен 7.
Последний член, «константа», равен -18-18 + 1 = -17 -9 + 2 = -7 -6 + 3 = -3 -3 + 6 = 3 -2 + 9 = 7 Вот и все
Шаг 3: Перепишите полином, разделяя средний член, используя два фактора, найденные на шаге 2 выше, -2 и 9
x 2 — 2x + 9x — 18
x • ( x-2)
Сложите последние 2 члена и вычтите общие множители:
9 • (x-2)
Шаг 5: сложите четыре члена шага 4:
(x + 9) • (x-2 )
Требуемая факторизация Уравнение в конце шага 1:
(x + 9) • (x - 2) = 0
Шаг 2:
Теория — Корни продукта:
Решение уравнения с одной переменной:
x = -9
Решение уравнения с одной переменной:
x = 2
Дополнение: Решение квадратного уравнения напрямую
Решение x 2 + 7x-18 = 0 напрямую
Парабола, найдя вершину:
y = 1,0 * -3,50 * -3,50 + 7,0 * -3,50 — 18,0
или y = -30,250 Parabola, Graphing Vertex и X-Intercepts:
Ось симметрии (пунктирная линия) {x} = {- 3,50}
Вершина в точке {x, y} = {-3,50, -30,25 }
x -Перехват (корни):
Корень 1 при {x, y} = {-9.00, 0.00}
Корень 2 при {x, y} = {2.00, 0.00} Решите квадратное уравнение, заполнив квадрат
x 2 + 7x = 18
В правой части получим:
18 + 49/4 или, (18/1) + (49/4)
Общий знаменатель две дроби равны 4. Сложение (72/4) + (49/4) дает 121/4
Таким образом, сложив обе стороны, мы, наконец, получаем:
x 2 + 7x + (49/4) = 121/4
x 2 + 7x + (49/4) =
(x + (7/2)) • (x + (7/2)) =
(x + ( 7/2)) 2
Вещи, которые равны одному и тому же, также равны друг другу.Поскольку
x 2 + 7x + (49/4) = 121/4 и
x 2 + 7x + (49/4) = (x + (7/2)) 2
, то по закону транзитивность,
(x + (7/2)) 2 = 121/4
(x + (7/2)) 2 равен
(x + (7/2)) 2/2 =
(x + (7/2)) 1 =
x + (7/2)
x + (7/2) = √ 121/4
x = -7/2 + √ 121/4
x 2 + 7x — 18 = 0
имеет два решения:
x = -7/2 + √ 121/4
или
x = -7/2 — √ 121 / 4
√ 121 / √ 4, что равно 11/2 Решите квадратное уравнение с помощью квадратичной формулы
— B ± √ B 2 -4AC
x = ————————
2A
B = 7
C = -18
49 — (-72) =
121
x = ——————
2
11 • 11
Чтобы можно было удалить что-то из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i.2 — 7x Для данного квадратного уравнения X2 7X 18 0 проверьте математику класса 10 CBSE
Подсказка: При решении квадратного уравнения
Прежде всего, мы находим два фактора, сумма которых равна коэффициенту среднего члена.{\ text {2}}} \] его коэффициент равен \ [{\ text {1}} \]
Кроме того, средний член равен \ [{\ text {- 7X}} \], его коэффициент равен \ [{\ text {- 7}} \]
Кроме того, последний член «константа» равен \ [{\ text {- 18}} \]
Здесь мы должны умножить коэффициент первого члена на константу \ [{\ text {1 \ times — 18 = — 18}} \]
Теперь нам нужно найти произведение двух множителей: \ [{\ text {- 18}} \], сумма которого равна коэффициенту среднего члена, который равен \ [{\ text {- 7}} \]
Теперь нам нужно построить это следующим образом:
\ [{\ text {- 18 + 1 = — 17}} \]
\ [{\ text {- 2 + 9 = 7}} \]
\ [{\ text {- 6 + 3 = — 3}} \]
\ [{\ text {- 9 + 2 = — 7}} \]
Здесь мы получаем \ [{ \ text {- 9 + 2 = — 7}} \]
Перепишите данное квадратное уравнение как разделение среднего члена, используя два фактора, найденные выше, а именно \ [{\ text {- 9}} \] и \ [ {\ text {2}} \]
\ [\ Rightarrow {{\ text {x}} ^ {\ text {2}}} {\ text {- 9x + 2x — 18 = 0}}…. \ left (1 \ right) \]
Теперь мы должны сложить первые два члена в \ [\ left (1 \ right) \] и вывести такие же множители: \ [{\ text {x (x — 9)}} \]
Кроме того, мы можем сложить последние два члена, извлекая аналогичные множители: \ [{\ text {+ 2 (x — 9)}} \]
Итак, мы получаем
\ [\ Rightarrow {\ text {(x + 2) (x — 9)}} {\ kern 1pt} {\ text {= 0}} \]
Это желаемая факторизация.
Также мы можем записать это как \ [{\ text {(x + 2) = 0}} \] и \ [{\ text {(x — 9)}} {\ kern 1pt} {\ text {= 0 }} \]
Теперь мы получаем корни данного квадратного уравнения.
\ [{\ text {x = — 2, x = 9}} \]
Действительные константы — это многочлены нулевой степени.
Эти два решения могут отличаться, а могут и не быть; любые они могут быть или не быть настоящими.
Метод факторизации может использоваться, когда квадратное уравнение может быть разложено на линейные множители.{\ color {# FF6800} {2}} = \ color {# FF6800} {\ dfrac {121} {4}} $ Решение уравнений с использованием факторинга
Решение квадратных уравнений с помощью факторинга
Поиск уравнений с заданными решениями
Решение полиномиальных уравнений с помощью факторинга
Основные выводы
Тематические упражнения
ответов
Квадратичная формула: решения и дискриминант
Purplemath
Решите
x ( x — 2) = 4. Округлите ответ до двух десятичных знаков. MathHelp.com
Решить 9
x 2 + 12 x + 4 = 0.Оставьте свой ответ в точной форме.

 n)?
n)? n)?
n)? 02.2018, 13:49
02.2018, 13:49  02.2018, 14:33
02.2018, 14:33  Забор!
Забор!
 Частичное совпадение суммы — совпадение с подстановочным знаком
Частичное совпадение суммы — совпадение с подстановочным знаком 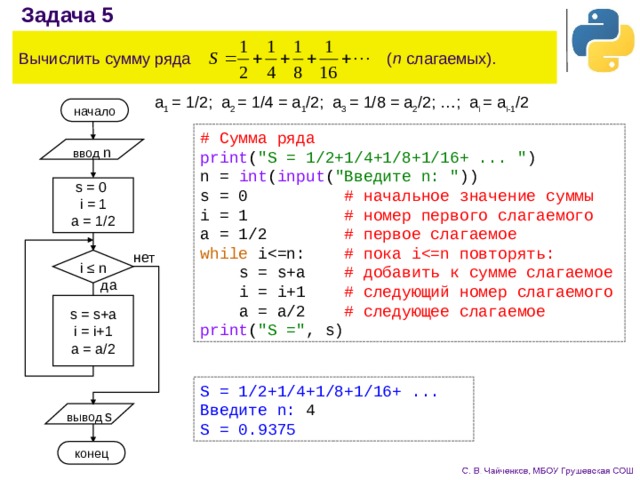

 Под видео есть письменные инструкции.
Под видео есть письменные инструкции. Письменные шаги приведены ниже. Чтобы посмотреть расшифровку видео, перейдите на страницу Running Total Video.
Письменные шаги приведены ниже. Чтобы посмотреть расшифровку видео, перейдите на страницу Running Total Video. Вот формула в ячейке D6 —
начальная точка осталась прежней, а конечная точка находится в текущей
ряд — C6
Вот формула в ячейке D6 —
начальная точка осталась прежней, а конечная точка находится в текущей
ряд — C6 Теперь у него неправильная конечная ссылка на C7 вместо C6:
Теперь у него неправильная конечная ссылка на C7 вместо C6: Он может продолжать суммировать ячейки
A1:A4 и игнорировать A5. Чтобы убедиться, что новые строки включены в итог,
вы можете использовать функцию OFFSET с функцией SUM.
Он может продолжать суммировать ячейки
A1:A4 и игнорировать A5. Чтобы убедиться, что новые строки включены в итог,
вы можете использовать функцию OFFSET с функцией SUM.
 В
В этом примере в итоговую сумму будут включены только строки с заказами пера.
В
В этом примере в итоговую сумму будут включены только строки с заказами пера. Например, формулу на шаге 9 выше можно изменить на:
Например, формулу на шаге 9 выше можно изменить на:  В этом примере
ячейки B2:B10 будут суммированы
В этом примере
ячейки B2:B10 будут суммированы

 Это создает скользящий итог.
Это создает скользящий итог. Посмотрите это короткое видео, чтобы увидеть шаги. Под видео есть письменные инструкции.
Посмотрите это короткое видео, чтобы увидеть шаги. Под видео есть письменные инструкции.
 В этом примере будут проверены ячейки B3:B10 90 218.
В этом примере будут проверены ячейки B3:B10 90 218. В этом видео показана проблема и два способа ее предотвращения. Под видео есть письменные шаги.
В этом видео показана проблема и два способа ее предотвращения. Под видео есть письменные шаги.
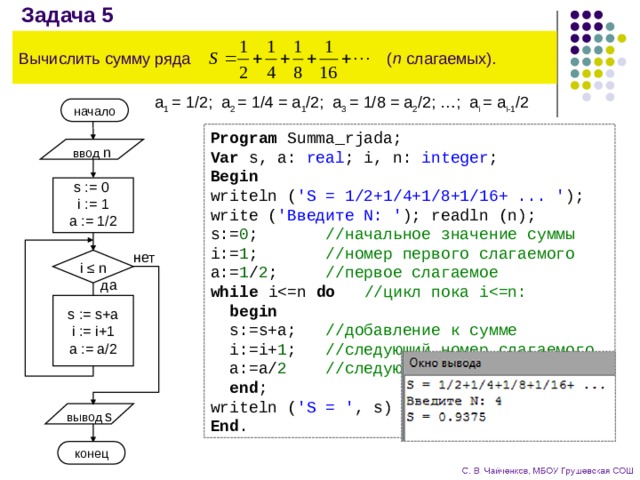 В этом примере будут проверены ячейки C4:C15 — они имеют категорию
В этом примере будут проверены ячейки C4:C15 — они имеют категорию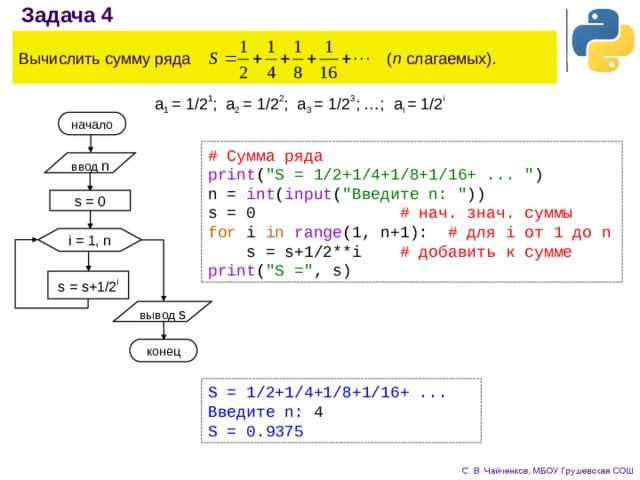 Если вы используете Excel
2007 или более поздней версии следует использовать функцию СУММЕСЛИМН, как описано в
предыдущий раздел.
Если вы используете Excel
2007 или более поздней версии следует использовать функцию СУММЕСЛИМН, как описано в
предыдущий раздел.
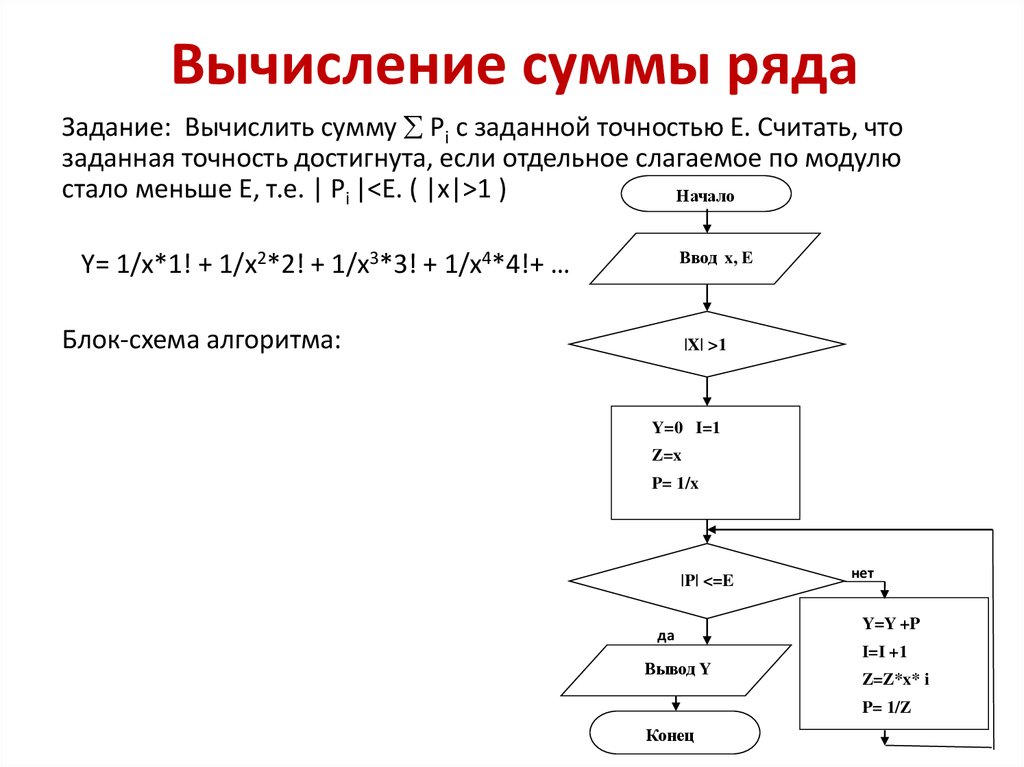 Например:
Например: .
. Ниже приведены два примера:
Ниже приведены два примера:

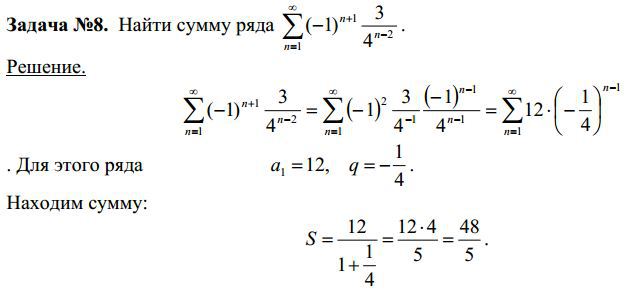 Чтобы проверить, вы можете выбрать ячейки B3: B6 и посмотреть на
общее количество отображается в строке состояния Excel.
Чтобы проверить, вы можете выбрать ячейки B3: B6 и посмотреть на
общее количество отображается в строке состояния Excel.
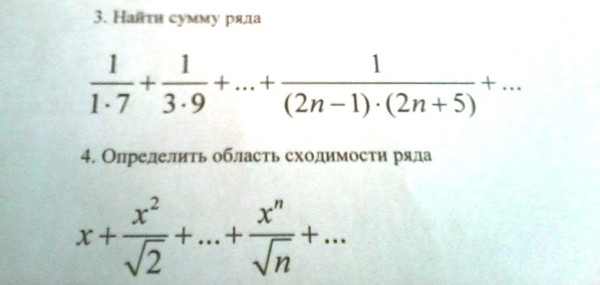


 или вариант 7. В этом примере 3 — второй аргумент, а результат
будет игнорировать скрытые строки, ошибки и вложенные функции АГРЕГАТ и ПРОМЕЖУТОЧНЫЕ ИТОГОВ.
или вариант 7. В этом примере 3 — второй аргумент, а результат
будет игнорировать скрытые строки, ошибки и вложенные функции АГРЕГАТ и ПРОМЕЖУТОЧНЫЕ ИТОГОВ.
 Сэм поделился своим методом выполнения дополнительных сумм или подсчетов на основе видимых данных в отфильтрованной таблице.
Сэм поделился своим методом выполнения дополнительных сумм или подсчетов на основе видимых данных в отфильтрованной таблице. Заархивированный файл имеет формат xlsx и не содержит макросов.
Заархивированный файл имеет формат xlsx и не содержит макросов. org/10.1093/rof/rfab007
org/10.1093/rof/rfab007