Масштаб. Измерение расстояний по планам, картам и глобусу
Содержание
Чтобы измерить расстояние по плану, карте или глобусу, нужно знать, что такое масштаб и уметь им пользоваться. Масштаб – одна из основных математических составляющих любой географической модели Земли, он показывает, во сколько раз уменьшены все расстояния на карте по сравнению с теми же расстояниями на местности.
Если масштабирование не произвести, то никакой бумаги не хватит, чтобы изобразить на ней даже небольшой участок поверхности. На старинных картах размеры и расстояния уменьшены в неодинаковое количество раз, поэтому по ним можно узнать очертания объектов, но не их величину.
Как обозначается масштаб?
Масштаб плана или карты всегда один, но указываться он может тремя разными способами. Способы обозначения масштаба следующие:
- численные;
- именованные;
- графические (линейные и поперечные).
Численный масштаб имеет вид дроби, например 1:1000, числитель которой показывает единицу измерения на карте, а знаменатель – во сколько раз она уменьшена по сравнению с действительным расстоянием, второе число называется величиной масштаба. Масштаб 1:1000 нужно читать так «один к тысячи», а обозначает он, что 1см на плане соответствует 1000 см на местности. То есть этот масштаб показывает, что действительное расстояние уменьшено в 1000 раз. Числитель и знаменатель дроби численного масштаба указываются в одинаковых единицах – в сантиметрах, ведь у дроби всегда так. Чем больше знаменатель дроби, тем меньше сама дробь, а значит, мельче масштаб. Например, масштаб 1 : 100 000 мельче, чем масштаб 1:10 000.
Масштаб 1:1000 нужно читать так «один к тысячи», а обозначает он, что 1см на плане соответствует 1000 см на местности. То есть этот масштаб показывает, что действительное расстояние уменьшено в 1000 раз. Числитель и знаменатель дроби численного масштаба указываются в одинаковых единицах – в сантиметрах, ведь у дроби всегда так. Чем больше знаменатель дроби, тем меньше сама дробь, а значит, мельче масштаб. Например, масштаб 1 : 100 000 мельче, чем масштаб 1:10 000.
Но, зная математику, мы легко можем перевести сантиметры в метры или километры. Чтобы делать это быстрее, переводя в метры, просто зачёркиваем 2 нуля, так как в 1м – 100 см, а в километры – убираем 5 нулей. Пример: 1:1000 – убираем 2 нуля и получаем 10 метров. Если масштаб один к ста тысячам, например, тогда уже можно перевести знаменатель и в километры – 1:100 000, для этого уберём 5 нулей, потому что в 1 км 100 000 см. Получим, что в 1 см на карте 10 км на местности, а это будет уже другой вид масштаба – именованный.
Именованный масштаб указывается на всех картах, он дополняется словами. В 1 см – 10 м, 10 м – это величина масштаба. Для примера переведём численный масштаб в именованный, пользуясь правилом, обсуждаемым выше:
- 1:25 000 000 – 1см-250 км;
- 1:10 000 000 – 1см-100 км;
- 1:20 000 – 1см-200 м.
При необходимости обратного перевода добавляем те же нули, при переводе километров в сантиметры добавим 5 нулей, метров в сантиметры – 2 нуля. Например:
- 1 см-300 м – это 1:30 000;
- 1см-250 км – это 1:25 000 000.
Для непосредственного определения расстояния по картам и планам служит линейный масштаб. Это график, помещаемый внизу карты в виде линейки (масштабная линейка), в России она разделёна на сантиметры. Справа от нуля у каждого деления линейки подписано истинное расстояние на местности, равное одному, двум или нескольким величинам масштаба. Слева от нуля сантиметр линейки разбивают на меньшие деления, например на миллиметры, для получения более точных результатов.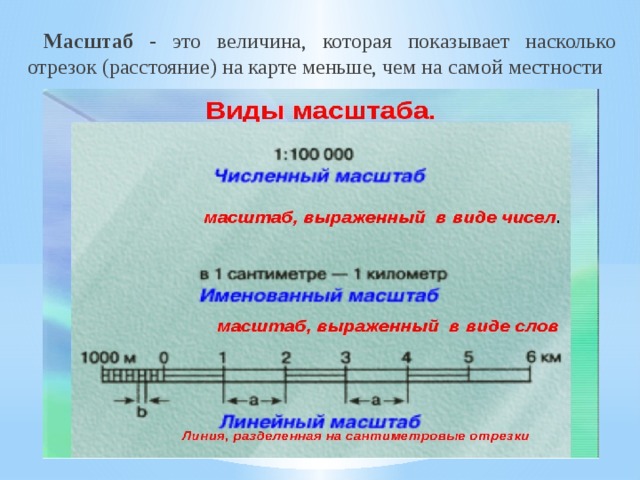
Как измерять расстояние по карте, плану или глобусу?
Измерять расстояния можно при помощи масштаба или градусной сетки (на плане её нет). Второй способ мы изучим немного позднее. Чтобы узнать расстояние на местности, нужно расстояние между двумя точками на карте или плане измерить при помощи линейки (этот способ подходит для прямых линий, для извилистых пользуются курвиметром или измерением малым раствором циркуля).
Измерения нужно производить очень точно, учитывая миллиметры. Затем полученные данные умножить на величину масштаба. Например, если при измерении мы получили расстояние 1,4 см, а масштаб карты в 1см 10 000 км, нужно умножить 1,4 на 10 000, получится 14 000 км – это и есть расстояние на местности. Нужно знать, что мы узнаём не действительное расстояние, а его проекцию. Линия на карте может иметь разные неточности в связи с углом наклона земной поверхности.
При помощи линейного масштаба измеряют расстояние линейкой или циркулем, переносят это расстояние на масштабную линейку и без дополнительных расчетов получают искомое расстояние. При этом неизбежны ошибки, которые зависят от масштаба и проекции карты. Чем крупнее масштаб карты, тем точнее измеренные расстояния.
При этом неизбежны ошибки, которые зависят от масштаба и проекции карты. Чем крупнее масштаб карты, тем точнее измеренные расстояния.
Глобус – объёмная модель Земли. Он показывает шарообразную форму нашей планеты. На нём все объекты изображены в неискажённом виде. В отличие от карты, они сохраняют свою форму, площадь, длину. Направления на глобусе совпадают с направлениями на Земле. У глобуса всюду один и тот же масштаб, который обычно надписывается в южной части Тихого океана. Масштабы школьных глобусов очень мелкие: 1:50 000 000, т. е. в 1 см – 500 км, истинное расстояние на нём уменьшается в 50 миллионов раз.
Для определения расстояний по глобусу надо ниткой или полоской бумаги измерить расстояние между заданными пунктами и, зная масштаб глобуса, вычислить истинное расстояние с помощью пропорции, как по обычной карте.
Масштаб и классификация карт по нему
Чем больший участок Земли нужно изобразить, тем в большее количество раз нужно уменьшить расстояния на карте по сравнению с действительным. На такой карте все подробности не покажешь, для этого она слишком мелкомасштабна. Приходится отбирать только те объекты, которые важны именно для цели выполняемой данной картой – этот процесс называется географической генерализацией.
На такой карте все подробности не покажешь, для этого она слишком мелкомасштабна. Приходится отбирать только те объекты, которые важны именно для цели выполняемой данной картой – этот процесс называется географической генерализацией.
Подробно можно показать небольшую площадь, посёлок, район, город. Тут будет видны уже и форма и размер зданий, расположение лесопарков, небольшие реки и др. Это возможно потому, что расстояния уменьшены несильно, масштаб карты достаточно крупный.
По масштабу карты делят на:
- мелкомасштабные (обзорные) — с масштабом менее 1: 1 000 000;
- среднемасштабные (обзорно-топографические) – в пределах 1: 200 000 до 1: 1 000 000;
- крупномасштабные (топографические) – от 1: 200 000 до 1: 10 000.
Нужно запомнить правило: чем больше величина масштаба, тем мельче масштаб карты, чем крупнее масштаб, тем подробнее карта.
Как определить масштаб: основные способы и инструкция
Отравляясь в лес или поход, мы всегда берем с собой карту. Именно с ее помощью туристы определяют свое местоположение на местности и прокладывают маршрут. Естественно, расстояния на картах показаны не в реальных показателях, а в определенном масштабе.
Именно с ее помощью туристы определяют свое местоположение на местности и прокладывают маршрут. Естественно, расстояния на картах показаны не в реальных показателях, а в определенном масштабе.
Соответственно, чтобы научиться читать карту, нужно знать, как определить масштаб в каждом конкретном случае. Именно этому вопросу и будет посвящена сегодняшняя статья.
Пошаговая инструкция, как определить масштаб
Обычно составитель указывает линейный или численный масштаб чертежа или карты, с помощью которого и определяется расстояние между объектами на местности. Но иногда топографическая карта не содержит этой информации, и определять масштаб приходится самостоятельно. В этом пригодятся некоторые знания в географии (рисунок 1).
На самом деле вычисление масштаба – простая задача, если знать, как правильно действовать. Из инструментов вам понадобится сама карта и линейка.
Самый простой способ определить масштаб – использовать километровую сетку. Она проставлена на любой карте, а стороны каждого квадрата соответствуют определенному количеству километров.
Узнать это расстояние можно по подписям у выхода линий сетки к краям карты. Например, на подписи указано, что расстояние между двумя линиями сетки составляет 1 км. Теперь измерьте это расстояние линейкой. Предположим, вы получили показатель в 2 см. Соответственно, каждый сантиметр карты соответствует 500 метрам на местности, а сам масштаб чертежа составляет 1:50000.
Понятие и виды масштабов
Чтобы научиться правильно вычислять масштаб, будет нелишним ознакомиться с самыми определением этого понятия. Итак, с научной точки зрения масштаб – это определенный показатель, по которому длина отрезка на карте, плане или схеме топосъемки соответствует действительной длине этого же отрезка на местности (рисунок 2).
Читайте также: Условные обозначения на плане местности
Существует несколько видов масштаба:
- Численный: масштаб, выполненный в виде дроби. В нем числитель – это всегда единица, а знаменатель – число, отображающее, во сколько раз уменьшено расстояние на карте.

- Линейный: масштаб, облегчающий ориентирование. Он представляет собой специальную мерную линейку, которую наносят на карты для облегчения вычисления расстояний на местности.
- Поперечный масштаб: используется для максимально точных измерений. Обычно его гравируют на металлических линейках, которые так и называют масштабными.
Самым простым считается именнованный или словесный масштаб. В данном случае на изображении карты просто указано, какому расстоянию соответствует 1 см плана (например, в 1 см 5 км).
Параметры точности масштаба
Точность масштаба на чертеже ограничена расстоянием в 0,01 см. Количество метров, соответствующее этому показателю на местности, и называется определением «графическая точность».
Чтобы узнать этот показатель, нужно воспользоваться градусной сеткой и провести некоторые вычисления. Лучше всего использовать численный масштаб. Берем его знаменатель и делим на 10 000, поскольку 1 см плана содержит 10 тысяч отрезков по 0,01 см. Полученное число и будет соответствовать размеру точности.
Берем его знаменатель и делим на 10 000, поскольку 1 см плана содержит 10 тысяч отрезков по 0,01 см. Полученное число и будет соответствовать размеру точности.
Например, если карта имеет масштаб 1:25 000, его точность на местности будет составлять 2,5 метра, а для схемы 1:100 000 – 10 метров и так далее.
Способ определения масштаба
В начале статьи мы уже описывали, как можно определить масштаб изображения с помощью километровой сетки и линейки. Но есть и другие способы установить степень уменьшения и масштабирование на конкретном плане местности (рисунок 3).
Читайте также: Ориентирование по местным признакам
Туристы обычно пользуются такими методами:
- Номенклатура карты: чтобы воспользоваться данным способом, нужно внимательно рассмотреть реквизиты карты. Фактически, номенклатура – это буквенно-числовое название листа. У каждого масштабного ряда есть свое обозначение. Например, М-35 соответствует масштабу 1:1000000, а М-35-18-А-6-1 – 1:10000.
 Конечно, для определения данным способом нужно наизусть знать номенклатурные обозначения.
Конечно, для определения данным способом нужно наизусть знать номенклатурные обозначения. - Известные расстояния: в данном случае на карте нужно найти изображения километровых столбов, которые обычно устанавливают на шоссе. Прямо на карте нужно измерить расстояние между ними. В данном случае количество сантиметров на карте будет соответствовать одному километру на местности.
- Дуга меридиана: одна минута по меридиану соответствует 1,85 км, хотя обычно эту цифру округляют до 2 км. На боковой рамке любой карты есть подписи минут и градусов, а для выделения каждой минуты используется шашечка. Если длина одной минуты равна 3,7 см, то масштаб будет составлять 1:5000, то есть одному сантиметру на карте будет соответствовать 0,5 км на местности.
На картах с масштабом 1:2000000 обычно указывается расстояние между определенными населенными пунктами в километрах. В данном случае, для определения масштаба нужно измерить расстояние на карте линейкой. Потом расстояние, указанное в километрах, следует разделить на полученное число в сантиметрах. В результате у вас получится число, которое будет соответствовать количеству километров в одном сантиметре.
Потом расстояние, указанное в километрах, следует разделить на полученное число в сантиметрах. В результате у вас получится число, которое будет соответствовать количеству километров в одном сантиметре.
Правила оформления
Если топографическая карта местности была изготовлена правильно, на ней должен обязательно быть указан масштаб. Исключение могут быть только самодельные карты или планы местности, нарисованные вручную. Во всех остальных случаях масштаб должен быть оформлен согласно ГОСТу.
Если карта была составлена правильно, находить даже уменьшенные объекты не составит труда, ведь все измерения точно соответствуют расположению на местности.
Порядок определения масштаба на готовом чертеже
Масштаб нужно не только для того, чтобы определить расстояние на карте. Он также используется при составлении чертежей (рисунок 4).
Важно правильно выбрать масштаб для чертежа детали. Например, небольшие или сборные элементы лучше выполнять в натуральную величину, то есть в масштабе 1:1.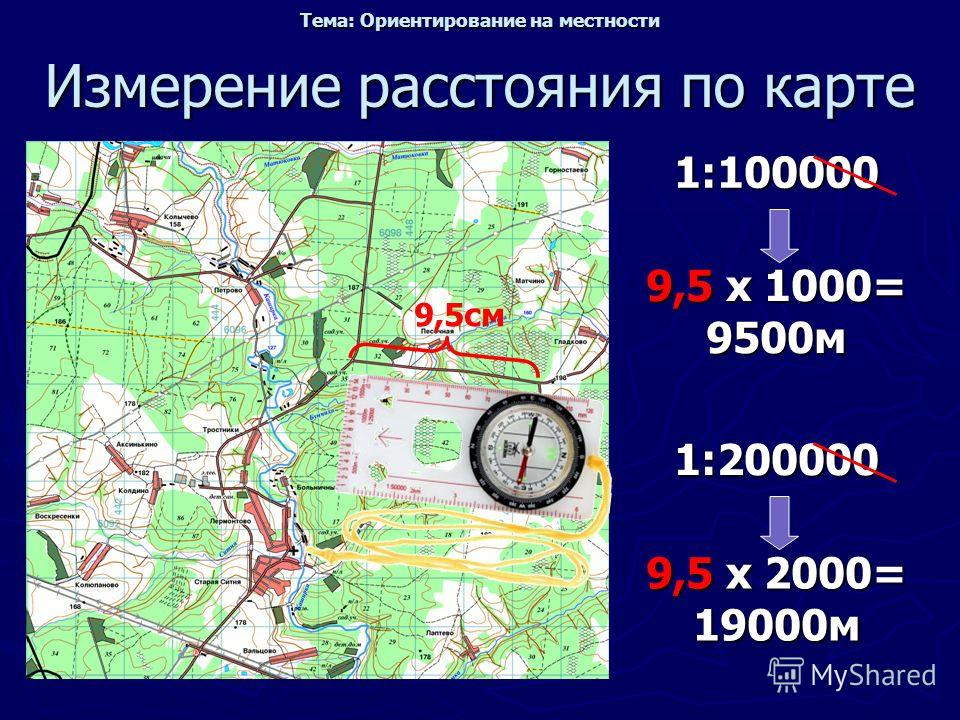 Но иногда, для удобства чтения объект, нарисованный на бумаге, уменьшают или увеличивают.
Но иногда, для удобства чтения объект, нарисованный на бумаге, уменьшают или увеличивают.
Узнать масштаб чертежа несложно, так как он определяется примерно так же, как и географический. В первую очередь нужно внимательно изучить чертеж. Согласно ГОСТу, масштаб должен быть указан в правом нижнем углу. При этом в машиностроении и приборостроении обычно используют увеличение, а на строительных чертежах – уменьшение.
Рисунок 4. Информация о размерах нарисованной детали относительно реальной обычно указывают в правом нижнем углу чертежаЕсли по каким-то причинам вы не можете найти масштаб на готовом чертеже невозможно, можно попытаться определить его. Если под рукой есть деталь, можно просто измерить ее штангенциркулем. Также можно определить масштаб по габаритным размерам детали, указанным на чертежах.
Советы бывалых
В целом, масштаб карты и топосъемки можно смело назвать весьма полезным понятием. На первый взгляд может показаться, что определять масштаб и ориентироваться с его помощью на местности сложно.
На самом деле, если научиться высчитывать расстояние, отображенное на карте, и соотносить его с объектами на местности, то отклонение будет составлять всего несколько метров.
Детальную информацию по определению масштаба вы найдете в видео.
Поделиться
Как определить масштаб карты если он не обозначен. Как определить масштаб
Понятие масштаба и его виды
Масштаб карты – это отношение длины отрезка на карте к его действительной длине на местности.
Масштаб (от немецкого Stab – палка) – это отношение длины отрезка на карте, плане, аэро- или космическом снимке к его действительной длине на местности.
Рассмотрим виды масштабов.
Численный масштаб
Это масштаб, выраженный в виде дроби, где числитель – единица, а знаменатель – число, показывающее во сколько раз уменьшено изображение.
Численный масштаб – масштаб, выраженный дробью, в которой:
- числитель равен единице,
- знаменатель равен числу, показывающему во сколько раз уменьшены линейные размеры на карте.
Именованный (словесный) масштаб
Это вид масштаба, словесное указание того, какое расстояние на местности соответствует 1 см на карте, плане, снимке.
Именованный масштаб выражается именованными числами, обозначающими длины взаимно соответствующих отрезков на карте и в натуре.
Например, в 1 сантиметре 5 километров (в 1 см 5 км).
Линейный масштаб
Это вспомогательная мерная линейка, наносимая на карты для облегчения измерения расстояний.
Масштаб плана и масштаб карты
Масштаб плана одинаков во всех его точках.
Масштаб карты в каждой точке имеет свое частное значение, зависящее от широты и долготы данной точки. Поэтому его строгой числовой характеристикой является численный масштаб – отношение длины бесконечно малого отрезка Д на карте к длине соответствующего бесконечно малого отрезка на поверхности эллипсоида земного шара.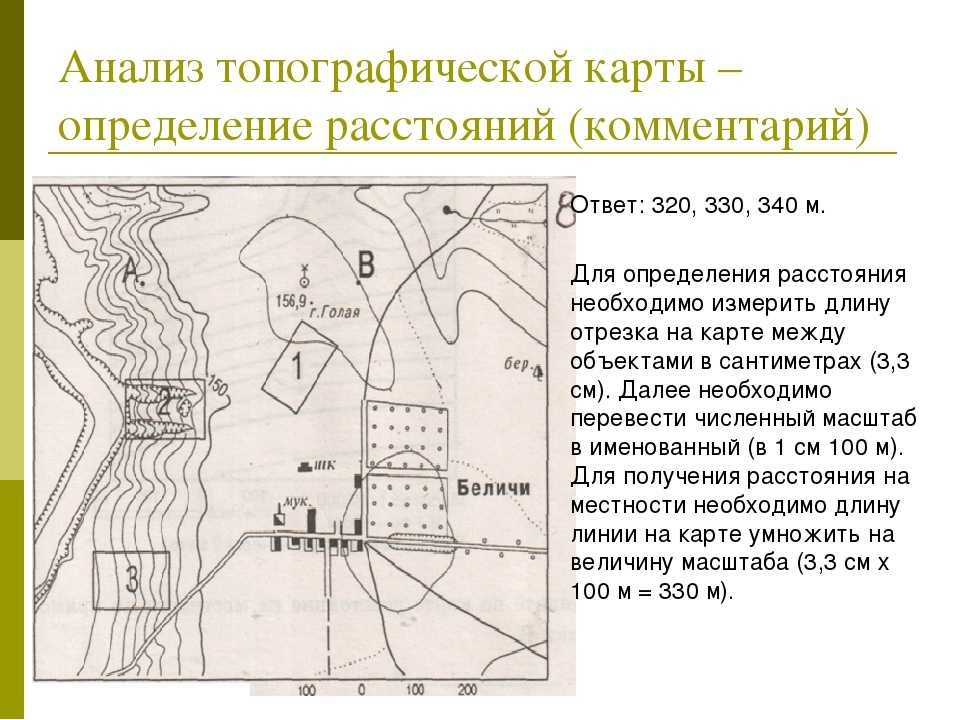
Однако при практических измерениях на карте используют её главный масштаб.
Формы выражения масштаба
Обозначение масштаба на картах и планах имеет три формы – численный, именованный и линейный масштабы.
Численный масштаб выражают дробью, в которой:
- числитель — единица,
- знаменатель М – число, показывающее, во сколько раз уменьшены размеры на карте или плане (1:М)
В России для топографических карт приняты стандартные численные масштабы
- 1:1 000 000
- 1:500 000
- 1:300 000
- 1:200 000
- 1:100 000
- 1:50 000
- 1:25 000
- 1:10 000
- для специальных целей создают также топографические карты в масштабах 1:5 000 и 1:2 000
Основные масштабы топографических планов в России
- 1:5000
- 1:2000
- 1:1000
- 1:500
В землеустроительной практике планы землепользований чаще всего составляют в масштабах 1:10 000 и 1:25 000, а иногда — 1:50 000.
При сравнении различных численных масштабов более мелким является тот, у которого больше знаменатель М, и, наоборот, чем меньше знаменатель М, тем крупнее масштаб плана или карты.
Так, масштаб 1:10000 крупнее, чем масштаб 1:100000, а масштаб 1:50000 мельче масштаба 1:10000.
Примечание
Применяемые в топографических картах масштабы установлены Приказом Министерства экономического развития РФ «Об утверждении требований к государственным топографическим картам и государственным топографическим планам, включая требования к составу сведений, отображаемых на них, к условным обозначениям указанных сведений, требования к точности государственных топографических карт и государственных топографических планов, к формату их представления в электронной форме, требований к содержанию топографических карт, в том числе рельефных карт» (№ 271 от 6 июня 2017 года с изменениями на 11 декабря 2017 года).
Именованный масштаб
Так как длины линий на местности принято измерять в метрах, а на картах и планах в сантиметрах, то масштабы удобно выражать в словесной форме, например:
В одном сантиметре 50 м. Это соответствует численному масштабу 1:5000. Поскольку 1 метр равен 100 сантиметрам, то число метров местности, содержащееся в 1 см карты или плана, легко определяют путём деления знаменателя численного масштаба на 100.
Линейный масштаб
Представляет собой график в виде отрезка прямой, разделенного на равные части с подписанными значениями соразмерных им длин линий местности. Линейный масштаб позволяет без вычислений измерять или строить расстояния на картах и планах.
Точность масштаба
Предельная возможность измерения и построения отрезков на картах и планах ограничена величиной 0.01 см. Соответствующее ей число метров местности в масштабе карты или плана представляет собой предельную графическую точность данного масштаба.
Поскольку точность масштаба выражает длину горизонтального проложения линии местности в метрах, то для ее определения следует знаменатель численного масштаба разделить на 10 000 (1 м содержит 10 000 отрезков по 0.01 см). Так, для карты масштаба 1:25 000 точность масштаба равна 2.5 м; для карты 1:100 000 — 10 м и т. п.
Масштабы топографических картчисленный масштаб карты | названиекарты | 1 см на карте соответствует на местности расстоянию | 1 см2 на карте соответствует на местности площади |
1:5 000 | пятитысячная | 50 м | 0.25 га |
1:10 000 | десятитысячная | 100 м | 1 га |
1:25 000 | двадцатипятитысячная | 250 м | 6. |
1:50 000 | пятидесятитысячная | 500 м | 25 га |
1:1100 000 | стотысячная | 1 км | 1 км2 |
1:200 000 | двухсоттысячная | 2 км | 4 км2 |
1:500 000 | пятисоттысячная, или полумиллионная | 5 км | 25 км2 |
1:1000000 | мииллионная | 10 км | 100 км2 |
Ниже приведены численные маштабы карт и соответствующие им именованые масштабы:
Масштаб 1:100 000
- 1 мм на карте – 100 м (0.1 км) на местности
- 1 см на карте – 1000 м (1 км) на местности
- 10 см на карте – 10000 м (10 км) на местности
Масштаб 1:10000
- 1 мм на карте – 10 м (0.
 01 км) на местности
01 км) на местности - 1 см на карте – 100 м (0.1 км) на местности
- 10 см на карте – 1000 м (1 км) на местности
Масштаб 1:5000
- 1 мм на карте – 5 м (0.005 км) на местности
- 1 см на карте – 50 м (0.05 км) на местности
- 10 см на карте – 500 м (0.5 км) на местности
Масштаб 1:2000
- 1 мм на карте – 2 м (0.002 км) на местности
- 1 см на карте – 20 м (0.02 км) на местности
- 10 см на карте – 200 м (0.2 км) на местности
Масштаб 1:1000
- 1 мм на карте – 100 см (1 м) на местности
- 1 см на карте – 1000 см (10 м) на местности
- 10 см на карте – 100 м на местности
Масштаб 1:500
- 1 мм на карте – 50 см (0.5 м) на местности
- 1 см на карте – 5 м на местности
- 10 см на карте – 50 м на местности
Масштаб 1:200
- 1 мм на карте – 0,2 м (20 см) на местности
- 1 см на карте – 2 м (200 см) на местности
- 10 см на карте – 20 м (0.
 2 км) на местности
2 км) на местности
Масштаб 1:100
- 1 мм на карте – 0,1 м (10 см) на местности
- 1 см на карте – 1 м (100 см) на местности
- 10 см на карте – 10 м (0.01 км) на местности
Пример 1
Переведите численный масштаб карты в именованный:
- 1:200 000
- 1:10 000 000
- 1:25 000
Решение:
Для более легкого перевода численного масштаба в именованный нужно посчитать, на сколько нулей кончается число в знаменателе.
Например, в масштабе 1:500 000 в знаменателе после цифры 5 находится пять нулей.
Если после цифры в знаменателе пятьи более нулей, то, закрыв (пальцем, авторучкой или просто зачеркнув) пять нулей, получим число километров на местности, соответствующее 1 сантиметру на карте.
Пример для масштаба 1:500 000
В знаменателе после цифры – пять нулей. Закрыв их, получим для именованного масштаба: в 1 см на карте 5 километров на местности.
Если после цифры в знаменателе менее пяти нулей, то, закрыв два нуля, получим число метров на местности, соответствующее 1 сантиметру на карте.
Если, например, в знаменателе масштаба 1:10 000 закроем два нуля, получим:
в 1 см – 100 м.
Ответы:
- в 1 см – 2 км
- в 1 см – 100 км
- в 1 см – 250 м
Используйте линейку, накладывайте на карты для облегчения измерения расстояний.
Пример 2
Переведите именованный масштаб в численный:
- в 1 см – 500 м
- в 1 см – 10 км
- в 1 см – 250 км
Решение:
Для более легкого перевода именованного масштаба в численный нужно перевести расстояние на местности, указанное в именованном масштабе, в сантиметры.
Если расстояние на местности выражено в метрах, тогда чтобы получить знаменатель численного масштаба, нужно приписать два нуля, если в километрах, то пять нулей.
Например, для именованного масштаба в 1 см – 100 м расстояние на местности выражено в метрах, поэтому для численного масштаба приписываем два нуля и получаем: 1:10 000.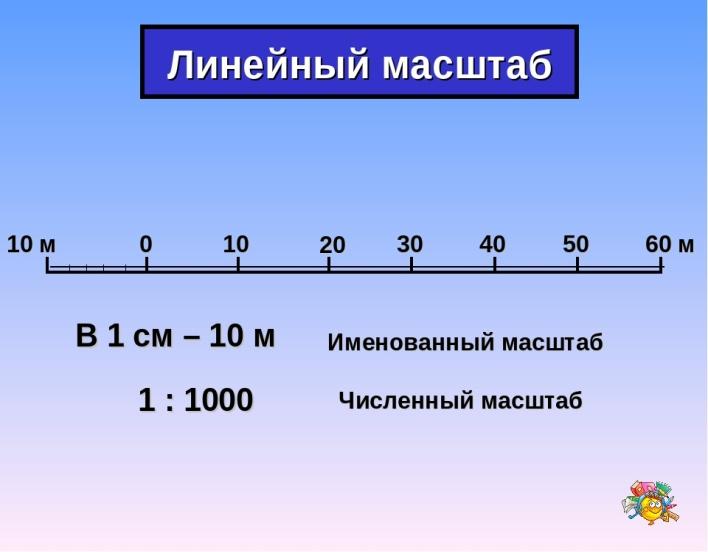
Для масштаба в 1 см – 5 км приписываем к пятерке пять нулей и получаем: 1:500 000.
Ответы:
- 1:50 000
- 1:1 000 000
- 1:25 000 000
Типы карт в зависимости от масштабов
Карты в зависимости от масштабов условно подразделяют на следующие типы:
- топографические планы 1:400 – 1:5 000
- крупномасштабные топографические карты 1:10 000 – 1:100 000
- среднемасштабные топографические карты от 1:200 000 – 1:1 000 000
- мелкомасштабные топографические карты менее 1:1 000 000
Топографическая карта
Топографическими называются такие карты, содержание которых позволяет решать по ним разнообразные технические задачи.
Карты либо являются результатом непосредственной топографической cъемки местности, либо составляются по имеющимся картографическим материалам.
Местность на карте изображается в определенном масштабе.
Чем меньше знаменатель численного масштаба, тем крупнее масштаб. Планы составляют в крупных масштабах, а карты – в мелких.
Планы составляют в крупных масштабах, а карты – в мелких.
В картах учитывается «шарообразность» земли, а в планах – нет. Из-за этого планы не составляются для территорий площадью свыше 400 км² (то есть участков земли примерно 20 км х 20 км).
- Стандартные масштабы топографических карт
В нашей стране приняты следующие масштабы топографических карт:
- 1:1 000 000
- 1:500 000
- 1:200 000
- 1:100 000
- 1:50 000
- 1:25 000
- 1:10 000
Этот ряд масштабов называется стандартным. Раньше этот ряд включал масштабы 1:300 000, 1:5000 и 1:2000.
- Крупномасштабныетопографические карты
Карты масштабов:
- 1:10 000 (1см =100 м)
- 1:25 000 (1см = 100 м)
- 1:50 000 (1см = 500 м)
- 1:100 000 (1см =1000 м)
называются крупномасштабными.
Топографические карты территории России до масштаба 1:50 000 включительно являются секретными, топографические карты масштаба 1:100 000 — ДСП (для служебного пользования), а мельче – не секретными.
В настоящее время существует методика создания топографических карт и планов любых масштабов, не имеющих грифа секретности и предназначенных для открытого пользования.
Сказка про карту в масштабе 1:1
Жил-был Капризный Король. Однажды он объехал своё королевство и увидел, как велика и прекрасна его земля. Он увидел извилистые реки, огромные озёра, высокие горы и чудесные города. Он возгордился своими владениями и захотел, чтобы весь мир узнал о них.
И вот, Капризный Король приказал картографам создать карту королевства. Картографы трудились целый год и, наконец, преподнесли Королю замечательную карту, на которой были обозначены все горные гряды, крупные города и большие озёра и реки.
Однако, Капризный Король остался недоволен. Он хотел видеть на карте не только очертания горных цепей, но и изображение каждой горной вершины. Не только крупные города, но и мелкие, и селения. Он хотел видеть небольшие речки, впадающие в реки.
Картографы вновь принялись за работу, трудились много лет и нарисовали другую карту, размером в два раза больше предыдущей. Но теперь Король пожелал, чтобы на карте были видны перевалы между горными вершинами, маленькие озерца в лесах, ручейки, крестьянские домики на окраине селений. Картографы рисовали все новые и новые карты.
Но теперь Король пожелал, чтобы на карте были видны перевалы между горными вершинами, маленькие озерца в лесах, ручейки, крестьянские домики на окраине селений. Картографы рисовали все новые и новые карты.
Капризный Король умер, так и не дождавшись окончания работы. Наследники один за другим вступали на трон и умирали в свою очередь, а карта все составлялась и составлялась. Каждый король нанимал новых картографов для составления карты королевства, но всякий раз оставался недовольным плодами труда, находя карту недостаточно подробной.
Наконец картографы нарисовали Невероятную карту! Она изображала всё королевство в мельчайших подробностях — и была точно такого же размера, как само королевство. Теперь уже никто не мог найти различия между картой и королевством.
Где же собирались хранить Капризные Короли свою замечательную карту? Ларца для такой карты не хватит. Понадобится огромное помещение вроде ангара, и в нем карта будет лежать во много слоев. Только нужна ли такая карта? Ведь карта в натуральную величину может быть с успехом заменена самой местностью ))))
Полезно ознакомиться и с этим
- Ознакомиться с используемыми в России единицами измерения площадей земельных участков можно здесь.

- Для тех, кого интересует возможность увеличения площади земельных участков для ИЖС, ЛПХ, садоводства, огродничества, находящихся в собственности, полезно ознакомиться с порядком оформления прирезок.
- С 1 января 2018 года в кадастровом паспорте должны быть зафиксированы точные границы участка, поскольку купить, продать, заложить или подарить землю без точного описания границ будет попросту невозможно. Так регламентировано поправками к Земельному кодексу. А тотальная ревизия границ по инициативе муниципалитетов началась с 1 июня 2015 г.
- С 1 марта 2015 года вступил в силу новый Федеральный закон «О внесении изменений в Земельный кодекс РФ и отдельные законодательные акты РФ» (N 171-ФЗ от 23.06.2014 г.), в соответствии с которым, частности, упрощена процедура выкупа земельных участков у муниципалитетов. Ознакомиться с основными положениями закона можно здесь.
- В отношении регистрации домов, бань, гаражей и других построек на земельных участках, находящихся в собственности граждан, улучшит ситуацию новая дачная амнистия.

Масштаб единицы измерения. Виды масштабов
Бизнес идеи
Бетуганов Астемир
Руководитель проекта:
Шопагова Алла Сергеевна
Учреждение:
МКОУ «СОШ №27» г. Нальчика
В представленной исследовательской работе по математике на тему «Масштаб и его применение» я постараюсь выяснить при каком масштабе будет удобно располагать объекты на листе А4. Работа над исследовательским проектом о масштабе поможет закрепить мне полученные знания по математике.
В моем исследовательском проекте по математике «Масштаб и его применение» мне необходимо будет уточнить и сопоставить математические расчёты с полученными данными.
В ходе исследовательской работы по математике о масштабе и его применении я надеюсь, что масштабы которые я задам, позволят расположить мне объекты на альбомном листе А4.
Также, в практической части своей работы я рассмотрю и математически решу интересные задачи на расстояние и масштаб.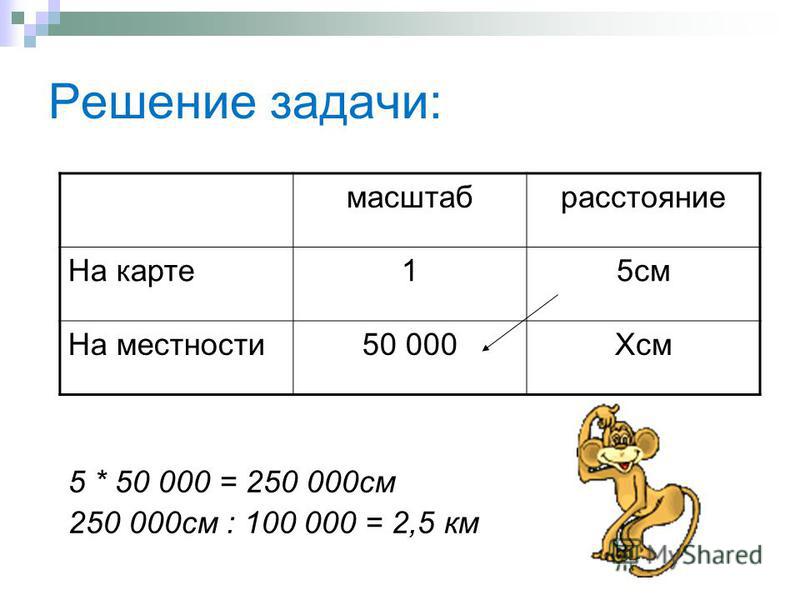
Введение
Основная часть
1. Определение масштаба.
2. Решение интересных задач на масштаб.
Выводы
Приложения.
Введение
На уроках математики в 6 классе мы проходили эту интересную тему, из которой узнали, как, используя масштаб, можно найти расстояние на местности, зная длину отрезка на карте, соответствующего этому расстоянию на местности , и наоборот.
Рисуя на бумаге изображение предметов, мы чаще всего вынуждены изменять их настоящие размеры: большие предметы приходится изображать в уменьшенном виде, а маленькие – увеличивать.
Участки земной поверхности изображают на бумаге в уменьшенном виде. Примером такого изображения служит любая карта, план. А маленькие детали изображают на чертежах в увеличенном виде.
Но чертеж, карта или план должны давать представление о настоящих размерах предметов. Поэтому на чертежах и картах делают специальную запись, показывающую отношение длины отрезка на карте или чертеже к его настоящей длине.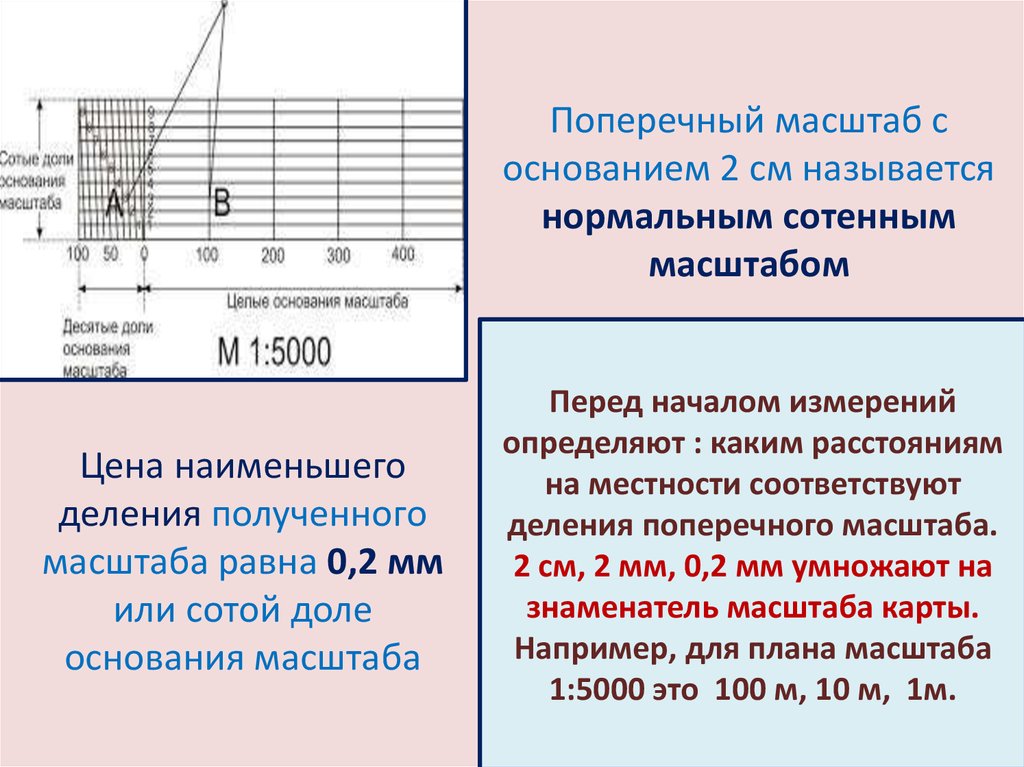
Тема моего исследовательского проекта по математике «Масштаб и его применение ».
Цель проекта: выяснить при каком масштабе будет удобно располагать объекты на листе А4.
Задачи проекта:
- закрепить школьные знания по математике;
- уточнить, сопоставимы ли математические расчёты с полученными данными.
Гипотеза: выкройки наиболее эффективно чертить 1:10, планировку квартиры 1:100; паспорт дома 1:1000; карту города 1:10000; карту района 1:100000.
Ожидаемый результат: заданные мною масштабы, позволят расположить объекты на альбомном листе.
Оборудование:
линейка, карандаш, циркуль, калькулятор, карта.
лист А 4, линейка, карандаш.
Определение масштаба
Масштаб – это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на местности.
Например: 1:1000 (одна тысячная) значит, все расстояния на местности уменьшены в тысячу раз.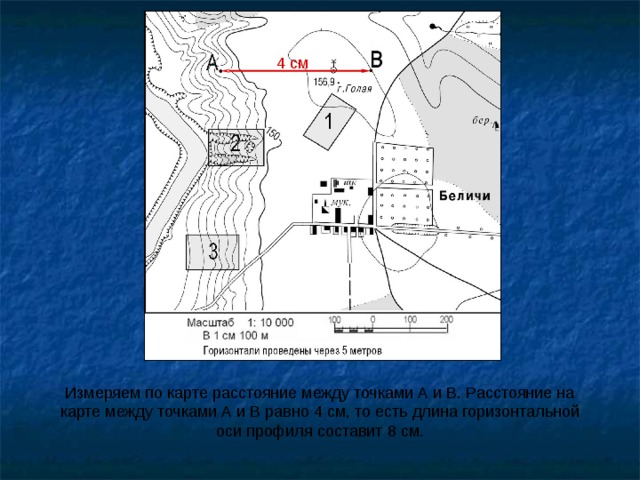 Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.
Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.
- численный , выражается в числах 1:1000;
- именованный , выражается словами, то есть см переводим в м: в 1см 10м, 10м – это величина масштаба;
- линейный , зная величину масштаба, мы можем определить расстояния.
Посмотрим на карту. Вверху указан масштаб (1: 500 000). Говорят, что карта сделана в масштабе одна пятисоттысячная. Это значит, что 1 см на карте соответствует 500 000 см на местности. Значит, отрезок на карте в 1 см соответствует отрезку на местности в 5 км.
А если я возьму на карте отрезок длиной в 3 см, то на местности это будет отрезок длиной в 15 км.
Я скачал с интернета карту Кабардино-Балкарской Республики. Карта республики с масштабом 1:10000, то есть в 1 см 100 метров, а масштаб окрестностей 1:100000 в 1 см 1 километр. Я сразу нашёл по ней мое родное село.
Итак, масштаб (нем. Maßstab , букв. «мерная палка »: Maß «мера », Stab «палка ») — в общем, отношение двух линейных размеров.
«мерная палка »: Maß «мера », Stab «палка ») — в общем, отношение двух линейных размеров.
Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта .
Понятие масштаба наиболее распространено в геодезии, картографии и проектировании — отношение натуральной величины объекта к величине его изображения.
Человек не в состоянии изобразить большие объекты, например дом, в натуральную величину, и поэтому при изображении большого объекта в рисунке, чертеже, макете и так далее, человек уменьшает величину объекта в несколько раз: в два, пять, десять, сто, тысяча и так далее раз. Число показывающее, во сколько раз уменьшен изображенный объект, есть масштаб.
Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину ее изображения в несколько раз.
Число, показывающее во сколько раз, произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.
Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе.
Правильная методика определения масштаба зависит от контекста, в котором используется изображение.
Выводы
Сравнил свои предположения, выдвинутые в моей гипотезе с надписями на выкройках, картах и технических планах дома и квартиры. Оказалось , что кое-где я ошибся в 10 и даже в 100 раз.
- выкройки наиболее эффективно чертить 1:10;
- планировку квартиры 1:100;
- паспорт дома 1:1000;
- карту города 1:10000;
- карту района 1:100000.
На самом деле, план квартиры обычно берут в масштабе 1:200; масштабы карт оказались точно такими же, как и в оригинале, но располагаются они аж на 6 альбомных листах!
Так что в который раз, я убеждаюсь, что прежде чем предполагать, нужно несколько раз пересчитать.
Таким образом , мы сформировали понятие масштаба, карты, чертежа, отрабатывали решение задач на вычисление длины отрезка на местности и на карте.
Решение задач на масштаб
Задача 1. Расстояние между двумя городами равно 400 км. Найдите длину отрезка, соединяющего эти города на карте, выполненной в масштабе 1:5000000.
Решение:
400км = 400000м = 40000000см
40000000: 5000000 = 40: 5 = 8 (см)
Задача 2. Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км от центра до центра. По автотрассе протяженность маршрута 700 км.
Во сколько раз надо уменьшить это расстояние, чтобы его можно было изобразить на слайде в виде отрезка длиной в 14 см?
Решение:
700км = 700000м = 70000000см
70000000см: 14см = 5000000(раз)
Задача 3. По физической карте России определите реальное расстояние между Москвой и Санкт-Петербургом.
М1: 20000000, если на карте расстояние равно 3 см.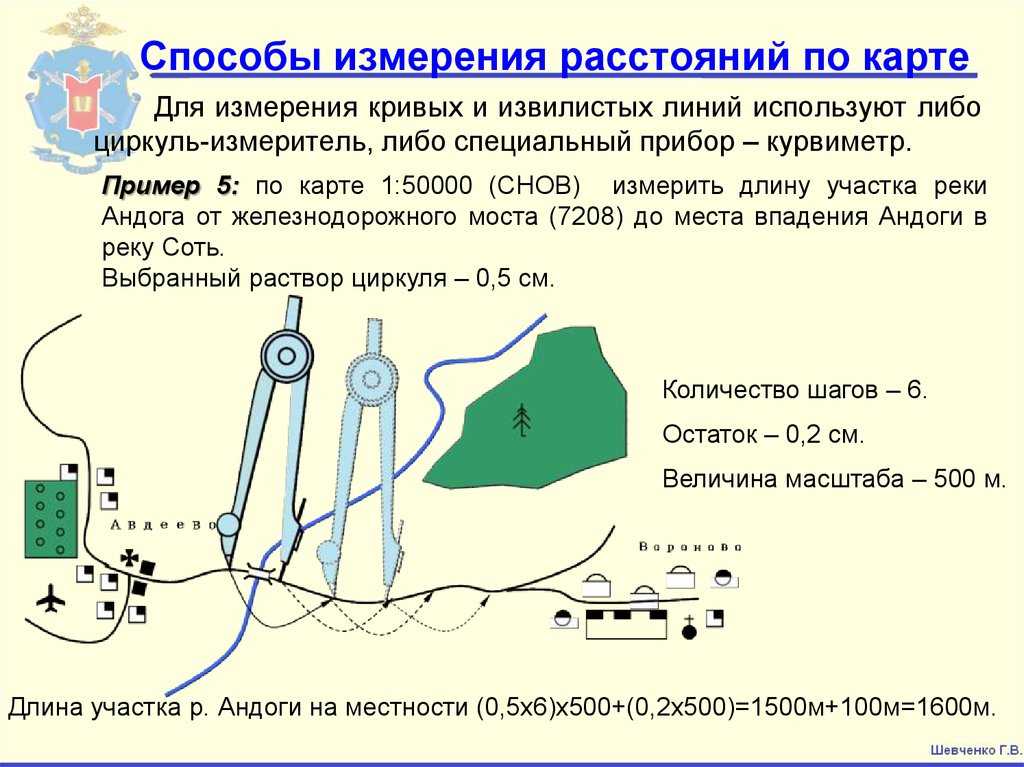
Масштаб можно написать цифрами или словами, или изобразить графически.
- Численный.
- Именованный.
- Графический.
- Линейный.
- Поперечный.
Численный масштаб
Численный масштаб подписывают цифрами внизу плана или карты. Например, масштаб «1: 1000» означает, что на плане все расстояния уменьшены в 1000 раз. 1 см на плане соответствует 1000 см на местности, или, по-скольку 1000 см =10 м, 1 см на плане соответствует 10 м на мест-ности.
Именованный масштаб
Именованный масштаб плана или карты обозначают словами. Например может быть написано «в 1 см — 10 м».
Линейный масштаб
Удобнее всего пользоваться масштабом, изображённым в виде отрезка прямой линии, разделённой на равные части, обычно сантиметры (рис. 15). Такой масштаб называется линейным , он также показывается внизу карты или плана. Обратите внимание , что при вычерчивании линейного масштаба нуль ставят, отступая на 1 см от левого конца отрезка, а первый сантиметр делят на пять частей (по 2 мм).
Возле каждого сантимет-ра подписано, какому расстоянию это соответствует на плане. Один сантиметр разделен на части, возле которых написано, како-му расстоянию на карте они соответствуют. Циркулем-измерите-лем или линейкой измеряют длину какого-либо отрезка на плане и, прикладывая этот отрезок к линейному масштабу, определяют его длину на местности.
Зная масштаб, можно определять расстояния между географи-ческими объектами, измерять сами объекты.
Если расстояние от дороги до реки на плане с масштабом 1: 1000 («в 1 см — 10 м») равно 3 см, значит, на местности оно равно 30 м. Материал с сайта
Предположим, от одного объекта до другого 780 м. По-казать в натуральную величину это расстояние на бумаге невоз-можно, поэтому придётся вычертить его в масштабе. Например, если все расстояния будут изображены в 10 000 раз меньшими, чем в дей-ствительности, т. е. 1 см на бумаге будет соответствовать 10 тыс. см (или 100 м) на местности. Тогда в масштабе расстоя-ние в нашем примере от одного объекта до другого будет равно 7 см и 8 мм.
Картинки (фото, рисунки)
На этой странице материал по темам:
Масштабом называется отвлеченное число, показывающее во сколько раз уменьшены горизонтальные проложения линий местности при изображении их на планах и картах, кратное 100 или 1000
. Обозначают 1: М. Масштаб вычисляют как отношение длины отрезка на карте к соответствующему горизонтальному отрезку на местности. (Горизонтальным проложением называется проекция наклонного расстояния на горизонтальную плоскость). Масштаб выражается в числовом, текстовом и графическом видах и соответственно называется числовым, именованным, линейным и поперечным. Числовой масштаб это дробь, числитель которой единица, а знаменатель — число с двумя и более нулями. Словами масштаб выражают как долю знаменателя: 1:500 — одна пятисотая; 1: 10000 — одна десятитысячная; 1: 50000 — одна пятидесятитысячная и т.д. Масштаб 1:М обозначает, что единице длины взятой на карте на местности соответствует М таких же единиц. Например, в масштабе 1:2000 отрезку на плане 1см на местности будет соответствовать 2000см или 20м, 1мм соотве5тствует 2000мм или 2м. Числовой масштаб позволяет решать две задачи: 1) по длине отрезка на карте (плане) определить длину соответствующего горизонтального проложения на местности: S 0 = s * М ; 2) по длине горизонтального проложения линии на местности определить его длину на карте s = S 0 / М . Числовой масштаб подписывают на картах и планах внизу листа карты (под южной стороной рамки) посередине его. Именованный масштаб – это текст, выражающий число метров или километров горизонтального отрезка на местности, соответствующее 1 сантиметру на карте (плане). Например, для масштаба 1:500 будет: в 1см 5м. Его используют для упрощения измерения расстояний по карте. Измерив линейкой расстояние между точками на карте в сантиметрах (до 0,05см) и умножив величину именованного масштаба на число сантиметров, получают расстояние между точками на местности. Линейный масштаб – это шкала с делениями, подписанными значениями расстояний на местности, соотве5тствующими числовому масштабу. Линейный масштаб вычерчивают так: на чертежной бумаге прочерчивают две параллельные линии с расстоянием между ними 1мм.
Числовой масштаб позволяет решать две задачи: 1) по длине отрезка на карте (плане) определить длину соответствующего горизонтального проложения на местности: S 0 = s * М ; 2) по длине горизонтального проложения линии на местности определить его длину на карте s = S 0 / М . Числовой масштаб подписывают на картах и планах внизу листа карты (под южной стороной рамки) посередине его. Именованный масштаб – это текст, выражающий число метров или километров горизонтального отрезка на местности, соответствующее 1 сантиметру на карте (плане). Например, для масштаба 1:500 будет: в 1см 5м. Его используют для упрощения измерения расстояний по карте. Измерив линейкой расстояние между точками на карте в сантиметрах (до 0,05см) и умножив величину именованного масштаба на число сантиметров, получают расстояние между точками на местности. Линейный масштаб – это шкала с делениями, подписанными значениями расстояний на местности, соотве5тствующими числовому масштабу. Линейный масштаб вычерчивают так: на чертежной бумаге прочерчивают две параллельные линии с расстоянием между ними 1мм. Разделяют линии на отрезки длиной обычно 2см, называемые основаниями масштаба и проводят в них перпендикуляры, выступающие на 1мм над верхней линией. Первое слева основание делят на десять частей (делений) и проводят через них перпендикуляры так же как через основания. Закрашивают половинки делений в продольном направлении через одно деление. Проводят через середины делений вертикально отрезки между линиями шкалы (через 1мм). Подписывают деления следующим образом. Над правым концом первого основания пишут 0 (ноль), а над левым — число метров или километров, соответствующее в данном масштабе основанию. Над основаниями правее нуля подписывают значения соответствующих расстояний на местности. Левее нуля подписывают значения через одно деление (Рис. 2.2)
Разделяют линии на отрезки длиной обычно 2см, называемые основаниями масштаба и проводят в них перпендикуляры, выступающие на 1мм над верхней линией. Первое слева основание делят на десять частей (делений) и проводят через них перпендикуляры так же как через основания. Закрашивают половинки делений в продольном направлении через одно деление. Проводят через середины делений вертикально отрезки между линиями шкалы (через 1мм). Подписывают деления следующим образом. Над правым концом первого основания пишут 0 (ноль), а над левым — число метров или километров, соответствующее в данном масштабе основанию. Над основаниями правее нуля подписывают значения соответствующих расстояний на местности. Левее нуля подписывают значения через одно деление (Рис. 2.2)
Рис.2.2 Линейный масштаб
По линейному масштабу расстояния измеряют с точностью 0,0 2-0,03 основания или примерно 0,5мм.
Поперечный масштаб – это график или номограмма, построенный с использованием метода пропорционального клина. Его применяют для измерений и построений на картах с повышенной точностью. Обычно его гравируют на металлических линейках или транспортирах, такие линейки называют масштабными . Он может быть построен и на чертежной бумаге. Поперечный масштаб устроен следующим образом. Он имеет вид прямоугольника, разделенного вертикальными, горизонтальными и наклонными линиями. Нижняя горизонтальная линия разделена на отрезки равные 2см, называемые основаниями масштаба , они пронумерованы: ниже линии оснований масштаба на правом краю первого основания подписан ноль, далее 1, 2, 3 и т.д., на левом краю первого основания – 1. Через концы оснований проведены перпендикуляры, которые разделены на 10 частей горизонтальными линиями с расстояниями между ними 2, 2,5 или 3мм. Нижняя и верхняя линии первого основания разделены на 10 частей. Ноль нижнего основания соединен наклонной линией с первым слева от нулевого перпендикуляра делением верхней линии, первый слева нижний со вторым слева верхним и т.
Его применяют для измерений и построений на картах с повышенной точностью. Обычно его гравируют на металлических линейках или транспортирах, такие линейки называют масштабными . Он может быть построен и на чертежной бумаге. Поперечный масштаб устроен следующим образом. Он имеет вид прямоугольника, разделенного вертикальными, горизонтальными и наклонными линиями. Нижняя горизонтальная линия разделена на отрезки равные 2см, называемые основаниями масштаба , они пронумерованы: ниже линии оснований масштаба на правом краю первого основания подписан ноль, далее 1, 2, 3 и т.д., на левом краю первого основания – 1. Через концы оснований проведены перпендикуляры, которые разделены на 10 частей горизонтальными линиями с расстояниями между ними 2, 2,5 или 3мм. Нижняя и верхняя линии первого основания разделены на 10 частей. Ноль нижнего основания соединен наклонной линией с первым слева от нулевого перпендикуляра делением верхней линии, первый слева нижний со вторым слева верхним и т. д., 9-й нижний с последним (десятым) верхним. Наклонные линии называют трансверсалями . Таким образом, левая часть графика имеет вид горизонтальных и наклонных линий. Фигуры между нулевым перпендикуляром и первой к нему трансверсалью и первым слева перпендикуляром и ближайшей к нему трансверсалью имеют вид пропорционального клина. Расстояния на горизонтальных линиях между смежными трансверсалями составляют десятую долю основания, а между нулевой вертикальной линией и трансверсалями изменяется от одной сотой на первой горизонтальной линии до одной десятой доли основания на последней – верхнем основании (рис.1б). Так как первое основание разделено на десять частей и перпендикуляр к нему разделен также на десять частей, то минимальное расстояние между вертикальной и наклонной линиями клина на горизонтальной линии составляет одну сотую долю основания, поэтому такой поперечный масштаб называют сотенным . Поперечный масштаб строят в следующем порядке. На прямой линии, как и при построении линейного масштаба, откладывают несколько раз основание масштаба равное 2см.
д., 9-й нижний с последним (десятым) верхним. Наклонные линии называют трансверсалями . Таким образом, левая часть графика имеет вид горизонтальных и наклонных линий. Фигуры между нулевым перпендикуляром и первой к нему трансверсалью и первым слева перпендикуляром и ближайшей к нему трансверсалью имеют вид пропорционального клина. Расстояния на горизонтальных линиях между смежными трансверсалями составляют десятую долю основания, а между нулевой вертикальной линией и трансверсалями изменяется от одной сотой на первой горизонтальной линии до одной десятой доли основания на последней – верхнем основании (рис.1б). Так как первое основание разделено на десять частей и перпендикуляр к нему разделен также на десять частей, то минимальное расстояние между вертикальной и наклонной линиями клина на горизонтальной линии составляет одну сотую долю основания, поэтому такой поперечный масштаб называют сотенным . Поперечный масштаб строят в следующем порядке. На прямой линии, как и при построении линейного масштаба, откладывают несколько раз основание масштаба равное 2см. Основания нумеруют: слева от нуля 1, справа – 1, 2,3 и т.д. В конечных точках основания восстанавливают перпендикуляры длиной, равной основанию, или большей длины. Крайние перпендикуляры делят на десять частей, и через полученные точки проводят
Основания нумеруют: слева от нуля 1, справа – 1, 2,3 и т.д. В конечных точках основания восстанавливают перпендикуляры длиной, равной основанию, или большей длины. Крайние перпендикуляры делят на десять частей, и через полученные точки проводят
Рис. 2.3. Линейный и поперечный масштабы
прямые линии, параллельные линии оснований. Нижнюю и верхнюю линии первого основания делят на десять равных частей. Полученные точки соединяют следующим образом: нулевую точку нижнего основания с первым верхним слева, первую нижнюю – со второй верхней и т.д. девятую нижнюю с десятой верхней, как показано на рис.1б. С помощью поперечного масштаба можно измерить длину отрезка на плане (карте) с точностью половины наименьшего деления клина, т.е. 0,1мм. Для отложения на плане измеренного на местности расстояния (горизонтального проложения), его выражают в долях основания масштаба (целых и дробных) делением на величину основания в заданном масштабе, наносят на график и с него циркулем переносят на план (карту).
Точность масштаба Невооруженным глазом с расстояния нормального зрения (25см) можно различить две точки раздельно, если расстояние между ними не менее 0,1мм. Эта величина принята в качестве критерия точности масштаба. Точностью масштаба называется горизонтальный отрезок на местности в метрах, соответствующий 0,1мм на карте, обозначают t, т.е. t = 0,1мм * М. Его проще вычислять делением знаменателя масштаба на 10000: t m = М:10000 (так как 1м равен 1000мм). Например, точность масштаба 1: 500 равна 0,1мм* 500 =50мм = 0,05м или 500: 10000 = 0,05м. Точность масштаба позволяет решать две важные задачи: 1) Определять, какие из предметов местности с известными размерами ℓ могут быть изображены в данном масштабе и какие не изобразятся. Если ℓ ³ t m , то изобразятся, а если ℓ
Классификация карт и планов
Карты различают по следующим признакам: 1) По виду картографируемого объекта — карты Земли (их называют географическими), Луны, планет и астрономические или звездного неба. 2) По пространственному охвату — карты всей поверхности Земли — мира, полушарий, материков, Мирового океана, государств и их частей. 3) По масштабу: крупномасштабные (1:100000 и крупнее), их называют крупномасштабными топографическими; среднемасштабные (1:200000, 1:500000, 1:1000000), их называют обзорно-топографическими; мелкомасштабные (мельче 1:1000000) — обзорные или общегеографические. 4) По назначению: многоцелевые и специальные. Многоцелевые предназначены для широкого круга потребителей, на них отображается совокупность всех элементов земной поверхности – ситуации и рельефа с одинаковой подробностью. Специальные (или тематические) карты предназначены для узкого круга специалистов. Основным содержанием их является отображаемая тема, природные или общественные явления. К ним относятся: научно-справочные, учебные, физико-географические, политико-административные, экономические, морские навигационные, аэронавигационные, дорожные, туристские, пропагандистские и др.
2) По пространственному охвату — карты всей поверхности Земли — мира, полушарий, материков, Мирового океана, государств и их частей. 3) По масштабу: крупномасштабные (1:100000 и крупнее), их называют крупномасштабными топографическими; среднемасштабные (1:200000, 1:500000, 1:1000000), их называют обзорно-топографическими; мелкомасштабные (мельче 1:1000000) — обзорные или общегеографические. 4) По назначению: многоцелевые и специальные. Многоцелевые предназначены для широкого круга потребителей, на них отображается совокупность всех элементов земной поверхности – ситуации и рельефа с одинаковой подробностью. Специальные (или тематические) карты предназначены для узкого круга специалистов. Основным содержанием их является отображаемая тема, природные или общественные явления. К ним относятся: научно-справочные, учебные, физико-географические, политико-административные, экономические, морские навигационные, аэронавигационные, дорожные, туристские, пропагандистские и др.
Ни один географический объект, например реку, мост, поселок, невозможно изобразить на топографическом плане в натуральную величину. В древности люди рисовали уменьшенные изображения местности, на которых разные участки уменьшались произвольно, в разной степени. Поэтому старинные чертежи местности не дают возможности понять, например, каково расстояние между берегами реки, чему равна длина реки и т. д. Чтобы был более точным, необходимо все расстояния уменьшать в одинаковое число раз с сохранением всех пропорций, делать изображение в масштабе.
В древности люди рисовали уменьшенные изображения местности, на которых разные участки уменьшались произвольно, в разной степени. Поэтому старинные чертежи местности не дают возможности понять, например, каково расстояние между берегами реки, чему равна длина реки и т. д. Чтобы был более точным, необходимо все расстояния уменьшать в одинаковое число раз с сохранением всех пропорций, делать изображение в масштабе.
Показывает, во сколько раз расстояния на плане уменьшены по отношению к реальным расстояниям.
Длина школы на плане школьного двора в 1000 раз меньше, чем в действительности. Это означает, что на данном плане все расстояния уменьшены в 1000 раз.
Численный и именованный масштабы
Масштаб пишут по-разному. В виде числа масштаб изображается так: 1:100 (это означает, что 1 см плана заменяет 100 см на местности). Это численный масштаб. 100 см — это 1 м, поэтому можно просто написать: в 1 см — 1м. Масштаб, записанный в таком виде, — именованный масштаб.
Линейный масштаб
Обычно на планах, кроме численного и именованного масштабов, помещают линейный масштаб.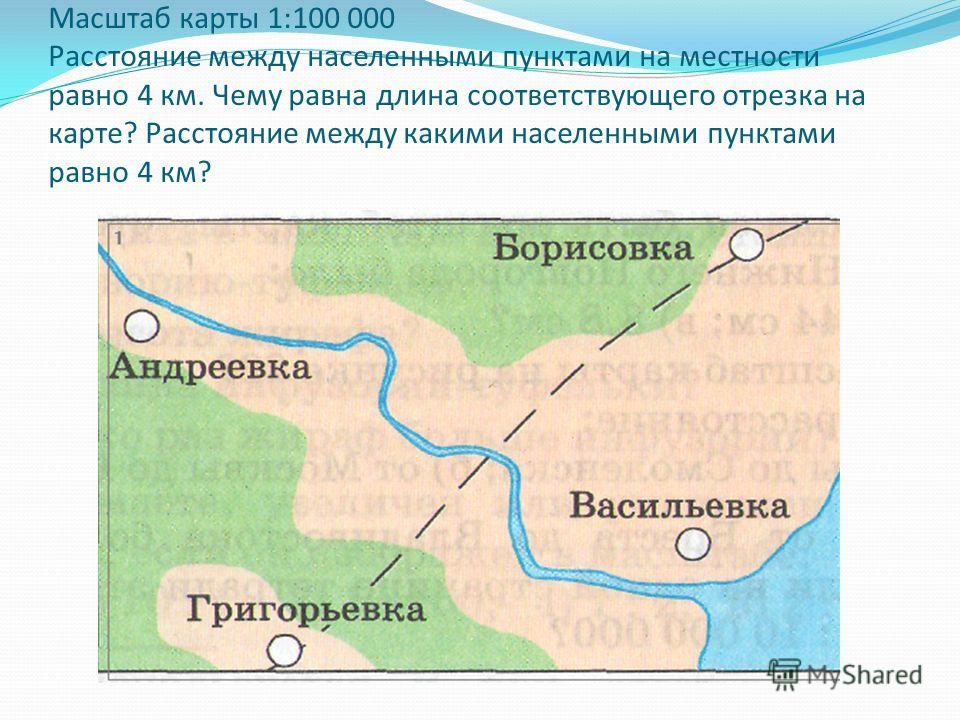 Он представляет собой линию, разделенную на равные отрезки. Отрезки справа от 0 показывают, какому расстоянию на местности соответствуют расстояния на плане в 1 см, 2 см и т. д. Отрезок слева от 0 разделен на равные мелкие части. Зная расстояние на местности, которому соответствует большой отрезок, и количество мелких отрезков, можно вычислить, какому расстоянию на местности соответствует каждый мелкий отрезок. Например, длина большого отрезка слева от 0 на рисунке равна 10м. Этот отрезок разделен на 5 мелких частей, значит, длина одной такой части составляет 10м:5=2 м.
Он представляет собой линию, разделенную на равные отрезки. Отрезки справа от 0 показывают, какому расстоянию на местности соответствуют расстояния на плане в 1 см, 2 см и т. д. Отрезок слева от 0 разделен на равные мелкие части. Зная расстояние на местности, которому соответствует большой отрезок, и количество мелких отрезков, можно вычислить, какому расстоянию на местности соответствует каждый мелкий отрезок. Например, длина большого отрезка слева от 0 на рисунке равна 10м. Этот отрезок разделен на 5 мелких частей, значит, длина одной такой части составляет 10м:5=2 м.
Линейный масштаб позволяет измерять расстояния на плане при помощи циркуля-измерителя или полоски бумаги.
При помощи линейного масштаба можно определять длину кривых линий, например реки, дороги. Для этого надо отметить на полоске бумаги небольшое расстояние или установить небольшой раствор между иглами циркуля-измерителя и переставлять бумагу с отметкой или циркуль вдоль измеряемой линии, считая число перестановок.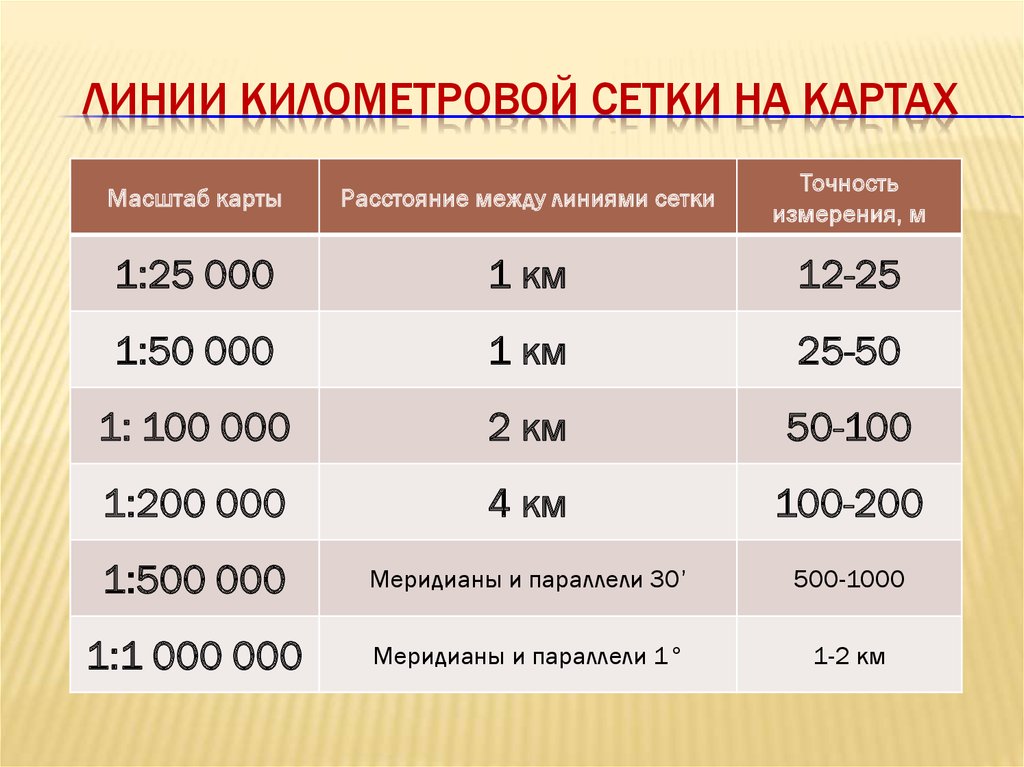 Определив при помощи линейного масштаба длину одного «шага» в метрах и умножив ее на число перестановок, мы получим длину кривой линии.
Определив при помощи линейного масштаба длину одного «шага» в метрах и умножив ее на число перестановок, мы получим длину кривой линии.
Выбор масштаба
Масштаб выбирают в зависимости от величины расстояний. Например, надо изобразить расстояние в 6 км. Тогда масштаб в 1 см — 10 м не годится, потому что это расстояние изображается линией в 600 см, то есть в 6 м; но линию в 6 м нельзя поместить на обычном листе бумаги. Удобнее взять масштаб: в 1 см — 1 км. При таком масштабе расстояние в 6 км будет соответствовать линии в 6 см.
Отношение натуральной величины объекта к величине его изображения. Человек не в состоянии изобразить большие объекты, например, дом, в натуральную величину, поэтому, при изображении большого объекта в рисунке, чертеже, макете и так далее, человек уменьшает величину объекта в несколько раз: в два, пять, десять, сто, тысяча и так далее. Число, показывающее, во сколько раз уменьшен изображенный объект, есть масштаб. Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину ее изображения в несколько раз. Число, показывающее, во сколько раз произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.
Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину ее изображения в несколько раз. Число, показывающее, во сколько раз произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.
Масштаб в геодезии, картографии и проектировании
Масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Есть три вида масштаба: численный, именованный, графический.
Масштабы на картах и планах могут быть представлены численно или графически.
Численный масштаб записывают в виде дроби , в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5 000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.
Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1 000 крупнее, чем масштаб 1:25 000.
Графические масштабы подразделяются на линейные и поперечные. Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части. Поперечный масштаб — это графический масштаб в виде номограммы , построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла.Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0. Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД = 0,2 мм, а точность — 0,1.
Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).
Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).
Масштабы изображений на чертежах должны выбираться из следующего ряда:
При проектировании генеральных планов крупных объектов допускается применять масштабы 1:2 000; 1:5 000; 1:10 000; 1:20 000; 1:25 000; 1:50 000.
В необходимых случаях допускается применять масштабы увеличения (100n):1, где n — целое число.
Масштаб в фотографии
Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе. Правильная методика определения масштаба зависит от контекста, в котором используется изображение.
Масштаб имеет важное значение при расчете глубины резко изображаемого пространства . Фотографам доступен очень широкий диапазон масштабов — от практически бесконечно малого (например, при съемке небесных тел) до очень крупного (без использования специальной оптики возможно получение масштабов порядка 10:1).
Фотографам доступен очень широкий диапазон масштабов — от практически бесконечно малого (например, при съемке небесных тел) до очень крупного (без использования специальной оптики возможно получение масштабов порядка 10:1).
Масштаб-число,показывающее, во сколько раз уменьшены или увеличены настоящие размеры на чертеже.
Примечания
Wikimedia Foundation . 2010 .
Синонимы :
Смотреть что такое «Масштаб» в других словарях:
— (нем. Masstaq, от нем. Mass мера). 1) мерило, мера линейная, принятая при чертежах в уменьшенном виде. 2) в артиллерии: медная линейка с обозначением на ней калибра орудий, снарядов и употребительнейших мер в артиллерии. Словарь иностранных слов … Словарь иностранных слов русского языка
Масштаб — – отношение длины данной линии, изображенной на чертеже, плане или карте, к длине ее в натуре. [Словарь основных терминов, необходимых при проектировании, строительстве и эксплуатации автомобильных дорог.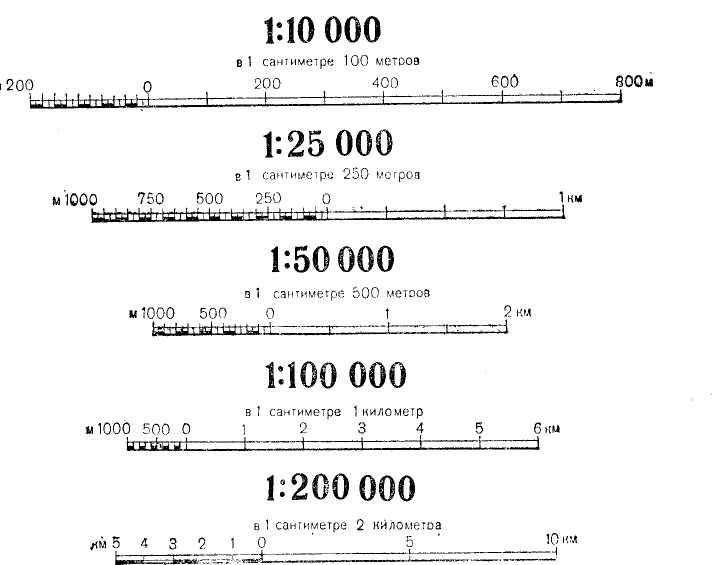 ] Масштаб – это отношение… … Энциклопедия терминов, определений и пояснений строительных материалов
] Масштаб – это отношение… … Энциклопедия терминов, определений и пояснений строительных материалов
См … Словарь синонимов
Отношение линейных размеров изображенного на карте, аэрофотоснимке и т. д предмета к его размерам в натуре. Различают масштаб уменьшения и увеличения, может быть выражен численным отношением (численный масштаб) или изображен графически… … Морской словарь
— [аш] (или маштаб), масштаба, муж. (нем. Masstab). 1. Отношение уменьшенных расстояний и размеров на карте и чертеже к действительным. Географическая карта крупного масштаба. Масштаб 10 верст в дюйме. В десятиверстном масштабе. 2. Мера. В большом … Толковый словарь Ушакова
масштаб 1:1 — полный масштаб — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом Синонимы полный масштаб EN full scale … Справочник технического переводчика
— (нем. Ma?stab) отношение длины линии на чертеже, плане или карте к длине соответствующей линии в натуре. Обозначается в виде дроби, числитель которой равен единице, а знаменатель числу, показывающему степень уменьшения длин линий (напр., 1: 100… … Большой Энциклопедический словарь
Обозначается в виде дроби, числитель которой равен единице, а знаменатель числу, показывающему степень уменьшения длин линий (напр., 1: 100… … Большой Энциклопедический словарь
— (нем. Maβstab; от Maβ мера и Stab палка * a. scale; н. Maβstab, Skala; ф. echelle; и. escala) отношение длины линии на чертеже, плане, карте, предметной модели к длине соответствующей линии в натуре. Ha геогр. картах различают главный M.… … Геологическая энциклопедия
— (от нем. Ma?stab) англ. scale; нем. Ma?stab. 1. Отношение линейных размеров объекта, изображенного на чертеже, плане, карте к его размерам в натуре. 2. Размеры, относительная величина ч. л. (напр., масштаб цен). Antinazi. Энциклопедия социологии … Энциклопедия социологии
Совет 1: Как измерять масштаб
Инструкция
Внимательно рассмотрите карту и найдите километровую сетку, которая должна быть на ней проставлена. Стороны квадратов сетки соответствуют определенному количеству , узнать это количество вы можете по подписям на выходах линии стеки у края рамки карты. К примеру, расстояние между двумя соседними линиями сетки равно 1 км. Измерьте это расстояние линейкой. Допустим, вы получили 2 см. Таким образом, масштаб карты: в 1 см 500 м или 1:50000.
К примеру, расстояние между двумя соседними линиями сетки равно 1 км. Измерьте это расстояние линейкой. Допустим, вы получили 2 см. Таким образом, масштаб карты: в 1 см 500 м или 1:50000.
Второй способ определения масштаб а – по номенклатуре карты. Внимательно рассмотрите реквизиты карты. Номенклатура представляет собой буквенно-числовое листа карты. Любой масштаб ный ряд имеет свое конкретное , по которому специалист легко определит масштаб карты. Например, номенклатурное обозначение М-35 масштаб 1:1000000; М-35-XI обозначает масштаб 1:200000; М-35-18-А-6-1 – масштаб 1:10000 и т.д. Разумеется, для определения масштаб а таким способом необходимо иметь представление о номенклатурных обозначениях и определенный опыт обращения с топографическими картами.
Третий способ определения масштаб а карты – по известным расстояниям. Найдите изображения километровых столбов на шоссейных дорогах. Измерьте по расстояние от одного столба до другого.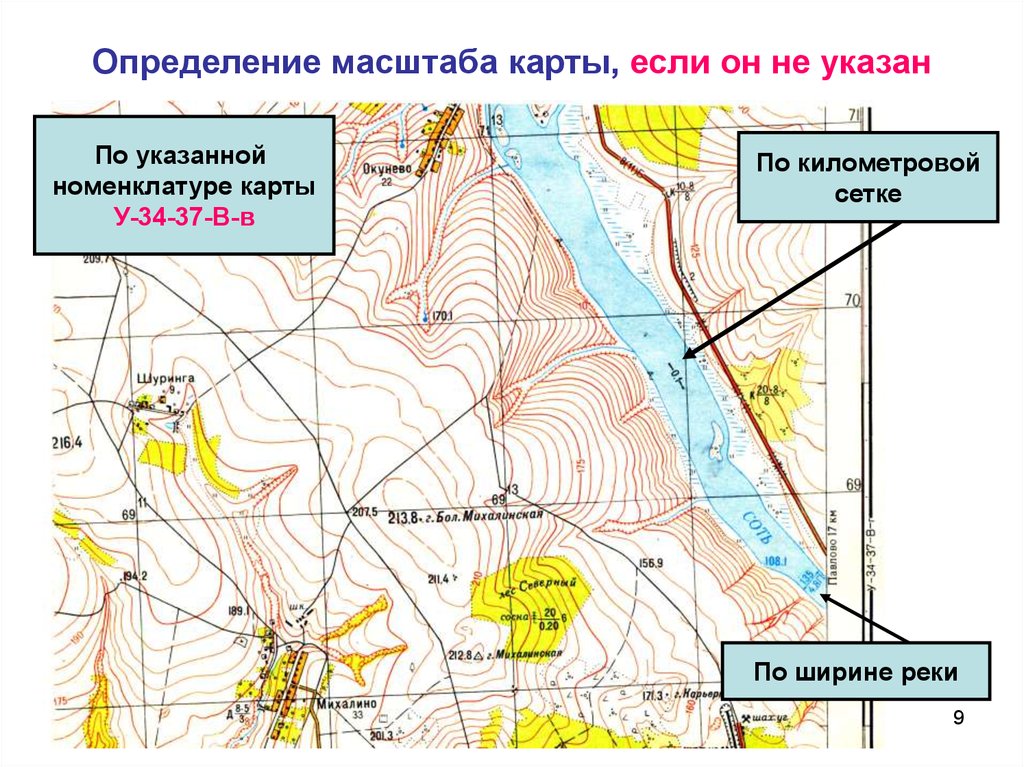 Вы сразу узнаете масштаб карты (число сантиметров карты будет соответствовать одному километру местности).
Вы сразу узнаете масштаб карты (число сантиметров карты будет соответствовать одному километру местности).
На картах масштаб а 1:200000 на дорогах обозначены расстояния между населенными пунктами в . В таком случае измерьте по карте при помощи линейки расстояние в сантиметрах от одного населенного пункта до другого, а подписанное количество километров разделите на расстояние, выраженное в сантиметрах. Таким образом, вы получили величину масштаб а карты, то есть число километров в .
Если вы находитесь на местности, которая изображена на карте, определите ее масштаб по измеренным расстояниям. Для этого измерьте расстояние между нанесенными на карту объектами.
Используйте также знание длины дуги меридиана. Одна минута по равна примерно 2 км, а более точно – 1,85 км. На боковой стороне рамки карты даны подписи градусов и минут, каждая минута шашечкой. Если, допустим, длина одной минуты равна 3,7 см, то масштаб карты будет 1:50000 (один сантиметр на карте равен 0,5 км на местности).
Источники:
- Как определить масштаб
- Точность масштаба Длины линий на местности, соответствующие
Изображение крупных обьектов можно получить на бумажном или любом другом носителе только в уменьшенном виде. Это, в первую очередь, касается различных карт местности. Масштабом карты называется отношение длины линии, нанесенной между двумя точками на плане или карте к тому же расстоянию на местности. Знать масштаб необходимо для того, чтобы измерять расстояния по карте.
Инструкция
Обычно, любой карты или указан в ее легенде – сопровождающем пояснительном тексте. Масштаб может быть изображен в виде шкалы или текста, в котором указывается, сколько метров или километров на местности равен 1 см расстояния, отложенного по данной . Масштаб 1: 50000 , что 1 см, отложенный на данной карте, равен 500 метрам или 0,5 км в натуре. Чем крупнее масштаб, тем меньшее число указывается в его числителе. Топографические карты масштаба 1:10000 и крупнее относятся к сведениям, гриф «секретно».
Если по какой-то причине масштаб карты не указан, отсутствует зарамочное или легенда, то определить его можно с помощью геоинформационных картографических серверов GoogleEarth или YandexMap, включив их в режиме «Гибрид», который позволяет одновременно со спутниковой фотографической основой видеть оцифрованное изображение местности – , границы городов, отдельно стоящие здания.
Определите географическое положение изображенной на ней местности. Выберите на ней две характерные точки, которые можно будет легко идентифицировать по спутниковому снимку данной местности. Обычно, удобно использовать для этого перекрестки магистралей или усовершенствованных шоссе, автодорог.
Найдите эти две точки по спутниковому снимку местности. Инструментом «Линейка» измерьте расстояние между ними. При активации инструмента появляется табличка, где автоматически будет высвечиваться расстояние между двумя указанными вами точками на космическом спутниковом снимке. Задайте удобные для вас единицы измерения – метры, километры.
Разделите полученное по спутниковым снимкам расстояние на количество сантиметров, измеренных по карте. Вы получите значение масштаба данной карты .
Видео по теме
Масштаб показывает, во сколько раз карта уменьшает реальную местность, которая на ней изображена. Только зная эту величину, можно откладывать на карте или схеме местности реальные расстояния. Узнать масштаб можно по маркировке на карте. Если таковой не имеется, рассчитайте его по линиям параллелей.
Вам понадобится
- — различные карты;
- — линейка;
- — калькулятор.
Инструкция
Если на плане или нанесена номенклатура листа, то по специальной таблице определите масштаб карты. Например, если на листе карты есть М-35-А, то ее масштаб составляет 1:500000. Это значит, что 1 см , на местности составляет 500000 см или 5 км.
Если маркировки нет, обратите внимание на километровую сетку, которая наносится на любую топографическую карту. Сторона квадрата такой сетки соответствует фиксированному количеству . Измерьте линейкой сторону этого квадрата в см и найдите отношение расстояния на карте к реальному. Это и будет масштаб. Например, если стека на карте 4 км, а расстояние между линиями составляет 2 см, то масштаб будет равен 2:4 км=2:400000 см=1:200000 см.
Сторона квадрата такой сетки соответствует фиксированному количеству . Измерьте линейкой сторону этого квадрата в см и найдите отношение расстояния на карте к реальному. Это и будет масштаб. Например, если стека на карте 4 км, а расстояние между линиями составляет 2 см, то масштаб будет равен 2:4 км=2:400000 см=1:200000 см.
Если более крупного с параллелями, то определите его с помощью этой сетки. Для этого измерьте расстояние между двумя нанесенными рядом параллелями в сантиметрах. На этих рядом стоящих параллелях от большего числового значения вычтите меньшее. Поскольку один параллели соответствует 111 км, непосредственно на местности, умножьте полученную разницу на это число, а также число 100000 для того, чтобы это расстояние в сантиметры.
Найдите отношение измеренного линейкой расстояния к результату вычислений. Получите масштаб карты. Например, если параллели идут 0?, 10?, 20? и т.д. найдите разницу двух близлежащих линий. Она составит 10. Затем, умножьте это число на 111 и 100000. Получите 10 111 100000=111000000. Если расстояние измеренное линейкой равно 4,5 см, получите масштаб 4,5:111000000 см?1:25000000 см. Это значит, что одном карты умещается 250 км местности.
Получите 10 111 100000=111000000. Если расстояние измеренное линейкой равно 4,5 см, получите масштаб 4,5:111000000 см?1:25000000 см. Это значит, что одном карты умещается 250 км местности.
Измеряйте масштаб по реальным расстояниям. Для этого известное расстояние отложите на карте, и соотнесите с реальным. Например, если расстояние между двумя составляет 400 км, а на карте оно равно 8 см, найдите соотношение 8:400 км=8:40000000=1:5000000. Это и есть масштаб карты.
Топографические планы и карты, составленные на их основе, являются точными изображениями земной поверхности, спроектированными на плоскость. Масштаб – отношение размера любого топографического объекта на карте к его реальному размеру на местности, позволяет производить по ней линейные и площадные измерения.
Масштабы карт и свойства масштабов—ArcGIS Pro
В ArcGIS Pro карту можно отобразить в любом масштабе. Вы также можете задать серию масштабов, которые можно быстро выбирать из списка. Список масштабов находится внизу каждого вида. Каждый вид имеет собственный, независимый масштаб. В 3D-видах список масштабов ссылается на высоту камеры над земной поверхностью.
Каждый вид имеет собственный, независимый масштаб. В 3D-видах список масштабов ссылается на высоту камеры над земной поверхностью.
Несмотря на использование единого формата масштаба, можно ввести масштаб в любом формате, а ArcGIS конвертирует его. Например, если масштабы в списке отображаются как относительные доли, а вы введи 1 см = 1.5 км, ArcGIS конвертирует его в 1:150,000.
Настройка списка масштабов карты
Вы можете настроить список стандартных масштабов, который отображается по всему проекту. Когда вы щелкаете Настроить в списке масштабов, открывается диалоговое окно Свойства масштаба. Здесь можно создать собственные масштабы карты, добавляя или удаляя их из списка, задавая псевдонимы масштабов, импортировать весь список, сохранить изменения и опубликовать их. В 2D список отображается на вкладке Стандартные масштабы, а в 3D — на вкладке Стандартные высоты.
Публикация списка масштабов
Чтобы опубликовать список масштабов карты, щелкните Сохранить в диалоговом окне Свойства масштаба.
Чтобы сделать текущий список масштабов карты списком по умолчанию, использующемся во всех ваших проектах, щелкните кнопку По умолчанию на вкладке Стандартные масштабы для карт и на вкладке Стандартные высоты — для сцен.
Загрузка списка масштабов карты
Чтобы восстановить в активной карте список стандартных масштабов по умолчанию, щелкните Загрузить > Масштабы по умолчанию профиля пользователя.
Чтобы восстановить в активной карте список стандартных масштабов Esri, использующийся по умолчанию, щелкните Загрузить > Исходные масштабы по умолчанию.
Псевдонимы масштабов
При желании можно задать псевдонимы для масштабов в списке масштабов карты. Чтобы задать псевдоним для отдельного масштаба, введите описание в столбец Псевдоним на вкладке Стандартные масштабы (2D) или Стандартные высоты (3D) диалогового окна Свойства масштаба. Выберите, как ваш список масштабов должен быть представлен в проекте, указав режим отображения в ниспадающем списке Отображение. Есть следующие варианты показа вашего списка масштабов карты:
Есть следующие варианты показа вашего списка масштабов карты:
- Масштаб: Например, 1:1,000
- Псевдоним: Например, Инженерный масштаб
- Масштаб (Псевдоним): Например, 1:1,000 (Инженерный масштаб)
- Псевдоним (Масштаб): Например, Инженерный масштаб (1:1 000)
Если у масштаба нет псевдонима, используется значение масштаба.
Использование масштабов из списка предустановленных масштабов
Для карты или сцены можно задать масштабирование только в соответствии со списком предустановленных масштабов, установив отметку в окне Отображать только эти масштабы при масштабировании. Если эта опция включена, масштабирование будет выполняться только в масштабах, указанных в этом диалоговом окне.
Масштабирование в соответствии со списком масштабов применяется при использовании поэтапных («плавных») методов навигации, к которым относятся следующие:
- Прокрутка колесика мыши
- Использование кнопок Фиксированное увеличение и Фиксированное уменьшение в группе Навигация на вкладке Карта
- Нажатие клавиш Плюс или Минус на клавиатуре
Это также относится к интерактивным методам, таким как непрерывное масштабирование с помощью правой кнопки мыши и инструмента Исследовать . Это не относится к операциям Приближение к закладке.
Это не относится к операциям Приближение к закладке.
Формат масштаба
Чтобы настроить отображение масштабов в 2D, используйте вкладку Формат масштаба в диалоговом окне Свойства масштаба.
Форматы масштаба
Существует много способов ввода значений масштаба:
Ввод числа с запятыми или без них.
Введите 1: и число.
Вставка в поле значений из буфера обмена.
Ввод относительного масштаба (например, 1 см = 100 м или 1 дюйм = 1 миля).
Префикс 1: не обязателен (например, 1000000).
В качестве разделителя вместо двоеточия (:) можно использовать дефис (-) или слово to (к).
Для разделения тысяч можно использовать запятые или отказаться от них (например, 1,000,000 или 1000000).
Если вы вводите абсолютный масштаб, можно указать его в обратном порядке (например, 5 миль в 1 дюйме).

Можно ввести число буквами, а не цифрами (например, Один дюйм = 5 милям).
Можно использовать следующие сокращения: in, pt, ft, yd, mi, nm, mm, cm, m, km, dd, dm.
Множественное число использовать необязательно (например, миля или мили).
Недавно введенные масштабы сохраняются в списке, но только в течение активного сеанса. Чтобы сохранить эти значения, необходимо вручную снова ввести их в диалоговом окне Свойства масштаба и добавить в текущий список масштабов по умолчанию. Щелкните Настройка, чтобы открыть свойства масштабов.
Две дополнительные опции масштаба
При задании масштаба, например при настройке диапазона видимости слоя, вы можете увидеть в списке опции <Нет> и <Текущий>.
<Нет> — выберите эту опцию, чтобы очистить значение масштаба, при этом никакой масштаб не будет использоваться. Также можно ввести 0, нет или <Нет>.

<Текущий> — при выборе этой опции в поле будет автоматически вставлен текущий масштаб активного вида.
Связанные разделы
Отзыв по этому разделу?
кластерный анализ | статистика | Британника
- Похожие темы:
- статистика
Просмотреть весь связанный контент →
кластерный анализ , в статистике набор инструментов и алгоритмов, который используется для классификации различных объектов по группам таким образом, что сходство между двумя объектами является максимальным, если они принадлежат к одной группе и минимальным в противном случае. В биологии кластерный анализ является важным инструментом таксономии (классификации живых и вымерших организмов). В клинической медицине его можно использовать для выявления пациентов с заболеваниями общей причины, пациентов, которые должны получать одинаковое лечение, или пациентов, у которых должен быть одинаковый уровень ответа на лечение. В эпидемиологии кластерный анализ имеет множество применений, например, для поиска значимых конгломератов регионов, сообществ или районов с аналогичными эпидемиологическими профилями, когда задействовано много переменных и не существует естественных группировок. В общем, всякий раз, когда нужно классифицировать большие объемы информации по небольшому количеству значимых категорий, может быть полезен кластерный анализ.
В эпидемиологии кластерный анализ имеет множество применений, например, для поиска значимых конгломератов регионов, сообществ или районов с аналогичными эпидемиологическими профилями, когда задействовано много переменных и не существует естественных группировок. В общем, всякий раз, когда нужно классифицировать большие объемы информации по небольшому количеству значимых категорий, может быть полезен кластерный анализ.
Исследователи часто сталкиваются с задачей сортировки наблюдаемых данных в осмысленные структуры. Кластерный анализ представляет собой индуктивный исследовательский метод в том смысле, что он раскрывает структуры, не объясняя причин их существования. Это метод генерации гипотез, а не проверки гипотез. В отличие от дискриминантного анализа, где объекты распределяются по уже существующим группам на основе статистических правил распределения, кластерный анализ создает группы или обнаруживает скрытую структуру групп в данных.
Классификация методов
В первом широком подходе методы кластерного анализа могут быть классифицированы как иерархические, если результирующая группировка имеет возрастающее число вложенных классов, напоминающих филогенетическую классификацию, или неиерархические, если результаты выражаются в виде уникального раздела всего набора объекты.
Иерархические алгоритмы могут быть разделительными или агломеративными. Разделительный метод начинается со всех случаев в одном кластере. Этот кластер постепенно разбивается на все более мелкие кластеры. Агломеративные методы обычно начинаются с одночленных кластеров, которые последовательно сливаются до тех пор, пока не образуется один большой кластер. На начальном этапе два объекта с наименьшим расстоянием (или наибольшим сходством) объединяются в кластер. На следующем этапе идентифицируется и изучается объект с наименьшим расстоянием до любого из первых двух. Если он ближе к четвертому объекту, чем к любому из первых двух, третий и четвертый объекты становятся вторым кластером из двух случаев; в противном случае третий объект включается в первый кластер. Процесс повторяется, добавляя наблюдения к существующим кластерам, создавая новые кластеры или объединяя уже возникшие до тех пор, пока каждый объект не будет исследован и не выделен в один кластер или не станет отдельным кластером сам по себе.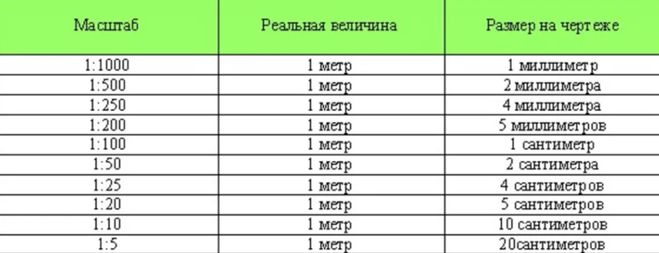 На каждом этапе процесса формируется другой раздел, вложенный в раздел, созданный на следующем этапе. Обычно исследователь выбирает тот раздел, который оказывается наиболее значимым для конкретного приложения.
На каждом этапе процесса формируется другой раздел, вложенный в раздел, созданный на следующем этапе. Обычно исследователь выбирает тот раздел, который оказывается наиболее значимым для конкретного приложения.
Расстояние и сходство являются ключевыми понятиями в контексте кластерного анализа. Большинство алгоритмов, особенно те, которые дают иерархические разбиения, начинаются с матрицы расстояния или подобия. Записи ячеек этой матрицы представляют собой расстояния или сходства между парами объектов. Существует много типов расстояний, из которых наиболее распространенным является евклидово расстояние. Евклидово расстояние между любыми двумя объектами — это квадратный корень из суммы квадратов разностей всех координат векторов, определяющих каждый объект. Его можно использовать для переменных, измеряемых на интервальной шкале. Когда для расчета расстояния используются две или более переменных, доминирует переменная с большей величиной. Чтобы избежать этого, принято сначала стандартизировать все переменные.
Выбор типа расстояния имеет решающее значение для всех алгоритмов иерархической кластеризации и зависит от характера переменных и ожидаемой формы кластеров. Например, евклидово расстояние имеет тенденцию давать сферические кластеры. К другим часто используемым расстояниям относятся манхэттенское расстояние, расстояние Чебышева, расстояние степени и процентное расхождение. Манхэттенское расстояние определяется как среднее расстояние между переменными. В большинстве случаев он дает результаты, аналогичные простому евклидову расстоянию. Однако влияние одиночных больших разностей (выбросов) ослабляется (поскольку они не возведены в квадрат). Расстояние Чебышева может быть уместно, когда объекты, отличающиеся только одной переменной, следует считать разными. Дистанция степени используется, когда важно увеличить или уменьшить прогрессивный вес, который присваивается переменным, по которым соответствующие объекты сильно различаются. Дистанция мощности контролируется двумя определяемыми пользователем параметрами, р и р .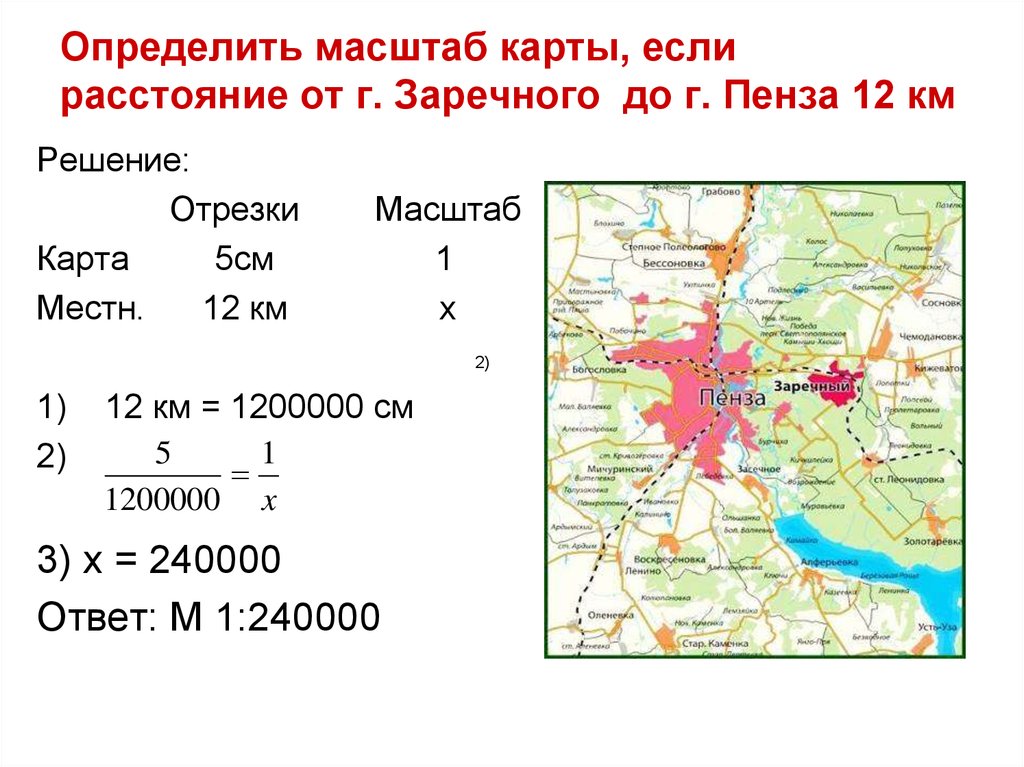 Параметр p управляет прогрессивным весом, который присваивается различиям отдельных переменных, а параметр r управляет прогрессивным весом, который присваивается большим различиям между объектами. Если r и p равны 2, то это расстояние равно евклидову расстоянию. Процент расхождений можно использовать, когда данные состоят из категориальных переменных.
Параметр p управляет прогрессивным весом, который присваивается различиям отдельных переменных, а параметр r управляет прогрессивным весом, который присваивается большим различиям между объектами. Если r и p равны 2, то это расстояние равно евклидову расстоянию. Процент расхождений можно использовать, когда данные состоят из категориальных переменных.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Правила связывания
Когда кластеры состоят из одного объекта, расстояние между ними можно рассчитать с помощью любого из вышеупомянутых расстояний. Однако когда кластеры формируются двумя или более объектами, необходимо определить правила для расчета этих расстояний.
Расстояние между двумя кластерами может быть определено как расстояние между двумя ближайшими объектами в двух кластерах. Этот подход, известный как правило ближайшего соседа, связывает объекты вместе и имеет тенденцию формировать цепные кластеры.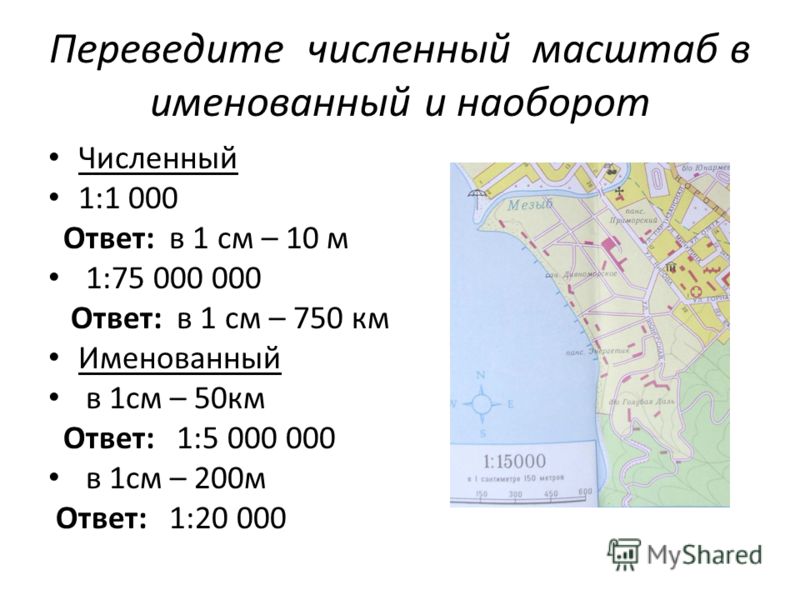
Другими популярными правилами связи являются среднее значение пары-группы и центроид пары-группы. Первое из этих правил определяется как среднее расстояние между всеми парами объектов в двух разных кластерах. Этот метод имеет тенденцию формировать естественные отчетливые группы объектов. Центроид парной группы — это расстояние между центроидами или центрами тяжести кластеров.
Наиболее часто используемым методом неиерархической кластеризации является алгоритм k средних, основанный на принципах дисперсионного анализа. На самом деле его можно рассматривать как дисперсионный анализ в обратном направлении. Если количество кластеров фиксировано как k , алгоритм начнет с k случайных кластеров, а затем переместит объекты между ними с целью минимизации изменчивости внутри кластеров и максимизации изменчивости между кластерами.
Хорхе Бакаллао Галлестей Редакторы Британской энциклопедииТипы данных и шкалы измерения
Данные являются ценным активом настолько, что это самый ценный ресурс в мире. Это делает понимание различных типов данных и роль специалиста по обработке и анализу данных более важными, чем когда-либо. В деловом мире все больше компаний пытаются понять большие числа и то, что они могут с ними сделать. Экспертиза данных пользуется большим спросом. Определение правильных данных и шкал измерения позволяет компаниям организовывать, идентифицировать, анализировать и, в конечном счете, использовать данные для обоснования стратегий, которые позволят им оказывать реальное влияние.
Это делает понимание различных типов данных и роль специалиста по обработке и анализу данных более важными, чем когда-либо. В деловом мире все больше компаний пытаются понять большие числа и то, что они могут с ними сделать. Экспертиза данных пользуется большим спросом. Определение правильных данных и шкал измерения позволяет компаниям организовывать, идентифицировать, анализировать и, в конечном счете, использовать данные для обоснования стратегий, которые позволят им оказывать реальное влияние.
Данные высшего уровня: качественные и количественные
Что такое данные? Короче говоря, это совокупность измерений или наблюдений, разделенных на два разных типа: качественные и количественные.
Качественные данные относятся к информации о качествах или к информации, которую невозможно измерить. Как правило, описательный и текстовый. Примеры включают цвет глаз человека или тип автомобиля, на котором он ездит. В опросах он часто используется для классификации ответов «да» или «нет».
Количественные данные являются числовыми. Он используется для определения информации, которую можно подсчитать. Некоторые примеры количественных данных включают расстояние, скорость, рост, длину и вес. Легко запомнить разницу между качественными и количественными данными, поскольку одни относятся к качествам, а другие — к количествам.
Книжная полка, например, может иметь 100 книг и иметь высоту 100 сантиметров. Это количественные точки данных. Цвет книжной полки — красный — является качественной точкой данных.
Что такое количественные (числовые) данные?
Количественные или числовые данные можно разделить на два типа: дискретные и непрерывные.
Дискретные данные
Дискретные данные — это целое число, которое нельзя разделить или разбить на отдельные части, дроби или десятичные дроби. Примеры дискретных данных включают количество домашних животных у кого-то — можно иметь двух собак, но не двух с половиной собак. Количество побед чьей-либо любимой команды также является формой дискретных данных, потому что у команды не может быть полувыигрыша — это либо победа, либо поражение, либо ничья.
Непрерывные данные
Непрерывные данные описывают значения, которые можно разбить на различные части, единицы, дроби и десятичные дроби. Можно измерять непрерывные точки данных, такие как рост и вес. Время также можно разбить – на полсекунды или на полчаса. Температура — еще один пример непрерывных данных.
Дискретные и непрерывные
Существует простой способ запомнить разницу между двумя типами количественных данных: данные считаются дискретными, если их можно подсчитать, и непрерывными, если их можно измерить. Кто-то может считать студентов, купленные билеты и книги, а кто-то измеряет рост, расстояние и температуру.
Что такое качественные (категориальные) данные?
Качественные данные описывают качество точек данных и не являются числовыми. Он используется для определения информации, а также может быть дополнительно разбит на подкатегории по четырем шкалам измерения.
Свойства и шкалы измерения
Шкалы измерения определяют и классифицируют переменные. Психолог Стэнли Стивенс разработал четыре общепринятые шкалы измерения: номинальные , порядковый номер , интервал и отношение . Каждая шкала измерения имеет свойства, которые определяют, как правильно анализировать данные. Оцениваются следующие свойства: идентичность , величина , равные интервалы и минимальное значение нуля .
Психолог Стэнли Стивенс разработал четыре общепринятые шкалы измерения: номинальные , порядковый номер , интервал и отношение . Каждая шкала измерения имеет свойства, которые определяют, как правильно анализировать данные. Оцениваются следующие свойства: идентичность , величина , равные интервалы и минимальное значение нуля .
Свойства измерения
Идентичность: Идентичность относится к каждому значению, имеющему уникальное значение.
Величина: Величина означает, что значения имеют упорядоченную связь друг с другом, поэтому переменные имеют определенный порядок.
Равные интервалы: Равные интервалы означают, что точки данных вдоль шкалы равны, поэтому разница между точками данных 1 и 2 будет такой же, как разница между точками данных 5 и 6.
Минимальное значение нуля: Минимальное значение нуля означает, что весы имеют истинную нулевую точку.
 Градусы, например, могут упасть ниже нуля и все еще иметь значение. Но если вы ничего не весите, вы не существуете.
Градусы, например, могут упасть ниже нуля и все еще иметь значение. Но если вы ничего не весите, вы не существуете.
Четыре шкалы измерения
Понимая масштаб измерения своих данных, специалисты по данным могут определить тип статистического теста для выполнения.
1. Номинальная шкала измерения
Номинальная шкала измерения определяет свойство идентичности данных. Эта шкала имеет определенные характеристики, но не имеет числового значения. Данные могут быть помещены в категории, но не могут быть умножены, разделены, добавлены или вычтены друг из друга. Также невозможно измерить разницу между точками данных.
Примеры номинальных данных включают цвет глаз и страну рождения. Номинальные данные можно снова разбить на три категории:
Номинал с порядком: Некоторые номинальные данные могут быть разбиты на подкатегории по порядку, например, «холодный, теплый, горячий и очень горячий».
Номинальные без порядка: Номинальные данные также могут быть подразделены на номинальные без порядка, например, мужские и женские.

Дихотомический: Дихотомические данные определяются наличием только двух категорий или уровней, таких как «да» и «нет».
2. Порядковая шкала измерения
Порядковая шкала определяет данные, которые располагаются в определенном порядке. Хотя каждое значение ранжировано, нет информации, которая бы указывала, что отличает категории друг от друга. К этим значениям нельзя ни добавить, ни вычесть.
Примером такого рода данных могут быть точки данных об удовлетворенности в опросе, где «один = счастливый, два = нейтральный и три = несчастный». Когда кто-то финишировал в гонке, также описываются порядковые данные. Хотя первое, второе или третье место показывает, в каком порядке финишировали бегуны, оно не указывает, насколько далеко финишер, занявший первое место, был впереди бегуна, занявшего второе место.
3. Интервальная шкала измерения
Интервальная шкала содержит свойства номинальных и упорядоченных данных, но разницу между точками данных можно определить количественно.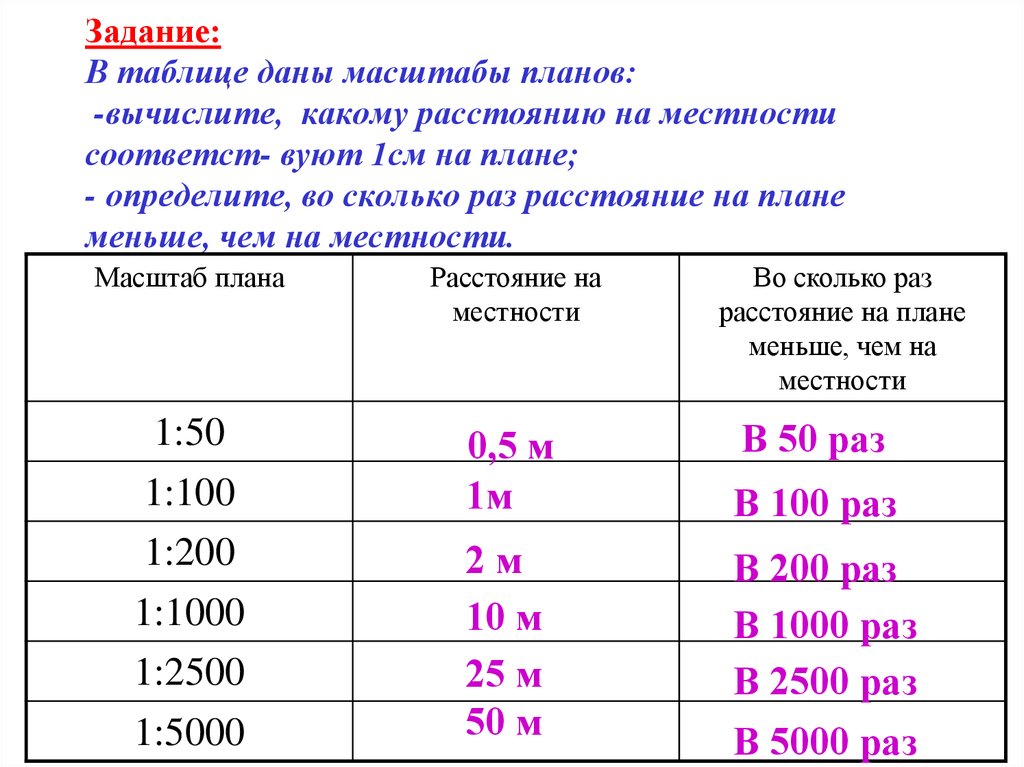 Этот тип данных показывает как порядок переменных, так и точные различия между переменными. Их можно складывать или вычитать друг из друга, но нельзя умножать или делить. Например, 40 градусов — это не 20 градусов, умноженных на два.
Этот тип данных показывает как порядок переменных, так и точные различия между переменными. Их можно складывать или вычитать друг из друга, но нельзя умножать или делить. Например, 40 градусов — это не 20 градусов, умноженных на два.
Эта шкала также характеризуется тем, что число ноль является существующей переменной. В порядковой шкале ноль означает, что данные не существуют. В интервальной шкале ноль имеет значение — например, если вы измеряете градусы, ноль имеет значение температуры.
Точки данных на шкале интервалов имеют одинаковую разницу между собой. Разница на шкале между 10 и 20 градусами такая же, как и между 20 и 30 градусами. Эта шкала используется для количественной оценки различий между переменными, тогда как две другие шкалы используются только для описания качественных значений. Другие примеры интервальных шкал включают год выпуска автомобиля или месяцы года.
4. Шкала отношений
Шкалы измерений включают свойства всех четырех шкал измерения. Данные являются номинальными и определяются тождеством, могут быть классифицированы по порядку, содержат интервалы и могут быть разбиты на точные значения. Вес, рост и расстояние — все это примеры переменных отношений. Данные в шкале отношений можно складывать, вычитать, делить и умножать.
Данные являются номинальными и определяются тождеством, могут быть классифицированы по порядку, содержат интервалы и могут быть разбиты на точные значения. Вес, рост и расстояние — все это примеры переменных отношений. Данные в шкале отношений можно складывать, вычитать, делить и умножать.
Шкалы отношений также отличаются от шкал интервалов тем, что шкала имеет «истинный ноль». Число ноль означает, что данные не имеют точки значения. Примером этого является рост или вес, поскольку кто-то не может быть ростом ноль сантиметров или весить ноль килограммов, или иметь отрицательные сантиметры или отрицательные килограммы. Примерами использования этой шкалы являются расчет акций или продаж. Из всех типов данных на шкалах измерения специалисты по данным могут больше всего сделать с точками данных отношения.
Подводя итог, номинальные весы используются для маркировки или описания значений. Порядковые шкалы используются для предоставления информации о конкретном порядке точек данных, что в основном наблюдается при использовании опросов удовлетворенности. Шкала интервалов используется для понимания порядка и различий между ними. Шкалы отношений дают больше информации об идентичности, порядке и различиях, а также разбивку числовых деталей в каждой точке данных.
Шкала интервалов используется для понимания порядка и различий между ними. Шкалы отношений дают больше информации об идентичности, порядке и различиях, а также разбивку числовых деталей в каждой точке данных.
Использование количественных и качественных данных в статистике
Как только специалисты по обработке и анализу данных получат окончательный набор данных из своей выборки, они могут начать использовать эту информацию для составления описаний и выводов. Для этого они могут использовать как описательную, так и логическую статистику.
Описательная статистика
Описательная статистика помогает продемонстрировать, представить, проанализировать и обобщить результаты, содержащиеся в образце. Они представляют данные в простой для понимания и презентабельной форме, например, в виде таблицы или графика. Без описания данные были бы в необработанном виде без пояснений.
Подсчет частоты
Один из способов, которым специалисты по данным могут описать статистику, — это использование подсчета частоты или статистики частоты, которая описывает количество раз, когда переменная присутствует в наборе данных.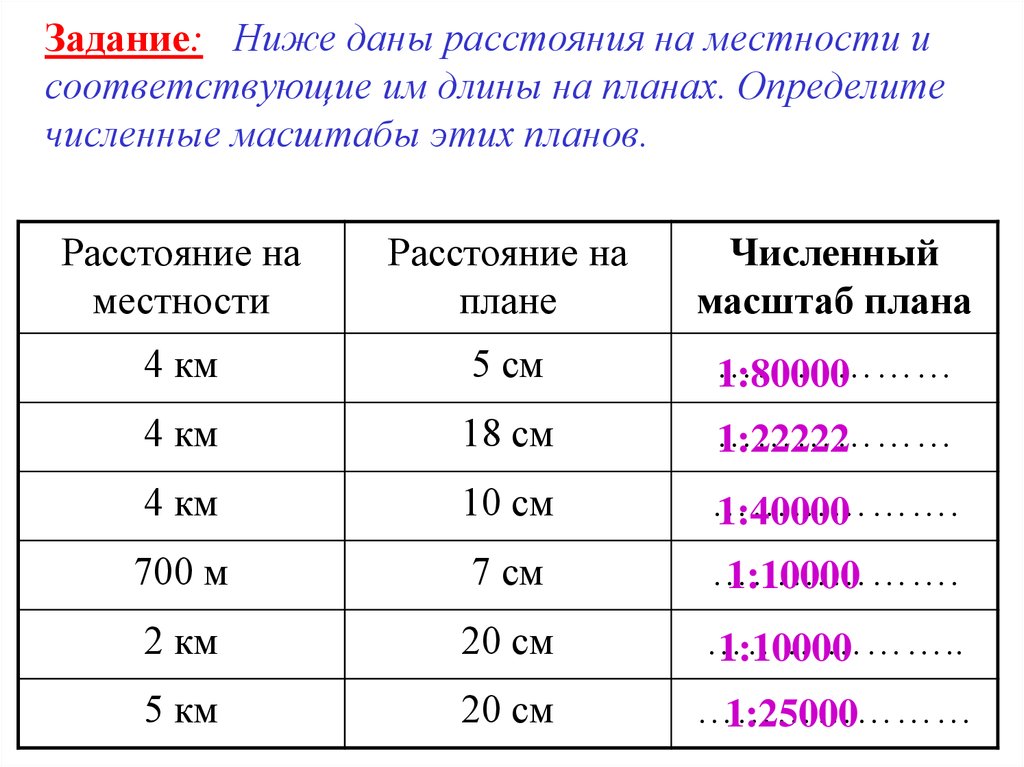 Например, количество людей с голубыми глазами или количество людей с водительскими правами в выборке можно подсчитать по частоте. Другие примеры включают квалификацию образования, такую как аттестат о среднем образовании, университетский диплом или докторскую степень, а также категории семейного положения, такие как холост, женат или разведен.
Например, количество людей с голубыми глазами или количество людей с водительскими правами в выборке можно подсчитать по частоте. Другие примеры включают квалификацию образования, такую как аттестат о среднем образовании, университетский диплом или докторскую степень, а также категории семейного положения, такие как холост, женат или разведен.
Частотные данные представляют собой форму дискретных данных, так как части значений не могут быть разбиты на части. Вместо этого для расчета непрерывных точек данных, таких как возраст, специалисты по данным могут использовать центральную статистику тенденций. Для этого они находят среднее или среднее значение точки данных. Используя пример возраста, это может сказать им средний возраст участников в выборке.
Хотя специалисты по обработке и анализу данных могут делать выводы на основе описательной статистики и представлять их в понятной форме, они не всегда могут делать выводы. Вот тут-то и приходит на помощь статистика выводов.
Логическая статистика
Логическая статистика используется для выдвижения гипотезы из набора данных. Было бы невозможно получить данные от всего населения, поэтому специалисты по данным могут использовать логическую статистику для экстраполяции своих результатов. Используя эту статистику, они могут делать обобщения и прогнозы в отношении более широкой выборки, даже если они не опросили их всех.
Примером использования логической статистики являются выборы. Еще до того, как вся страна проголосовала, специалисты по данным могут использовать подобную статистику, чтобы делать предположения относительно того, кто может победить на основе меньшего размера выборки.
Использование визуализации данных для обмена идеями
Визуализация данных описывает методы, используемые для создания графического представления выборки данных путем кодирования ее с помощью визуальных фрагментов информации. Это помогает передавать данные зрителям четким и эффективным способом.
Характеристики эффективных графических дисплеев
Эффективная визуализация может помочь людям анализировать сложные значения данных и делать выводы. Целью этого процесса является максимально четкое изложение результатов. Графический дисплей с эффективным обменом сообщениями будет четко отображать данные и позволит зрителю получить представление и тенденции из набора данных и выявить различные результаты между данными.
Примеры визуализации данных
Наилучшее визуальное представление набора данных определяется отношениями, которые специалисты по данным хотят передать между точками данных. Они хотят представить распределение с выбросами? Они хотят сравнить несколько переменных или проанализировать одну переменную во времени? Представляют ли они тенденции в вашем наборе данных? Вот некоторые из ключевых примеров визуализации данных.
Гистограмма используется для сравнения двух или более значений в категории и того, как несколько фрагментов данных соотносятся друг с другом.

Линейный график используется для визуального представления тенденций, шаблонов и колебаний в наборе данных. Линейные графики обычно используются для прогнозирования информации.
Точечная диаграмма используется для отображения взаимосвязи между точками данных в компактной визуальной форме.
Круговая диаграмма используется для сравнения частей целого.
Воронкообразная диаграмма используется для представления того, как данные перемещаются по различным шагам или стадиям процесса.
Гистограмма используется для представления данных за определенный период времени или интервал.
Количественные сообщения
Количественные сообщения описывают отношения данных. В зависимости от выборки существуют разные способы передачи количественных данных.
Номинальное сравнение: Подкатегории сравниваются по отдельности в произвольном порядке.

Временной ряд: Индивидуальная переменная отслеживается в течение определенного периода времени, обычно представленного на линейной диаграмме.
Ранжирование: Подкатегории ранжируются по порядку, обычно представленному в виде гистограммы.
Часть к целому: Подкатегории представлены в виде соотношения по сравнению с целым, обычно представленным в виде гистограммы или круговой диаграммы.
Отклонение: Подкатегории сравниваются с контрольной точкой, обычно представленной в виде гистограммы.
Частотное распределение: Подкатегории подсчитываются в интервалах, обычно представленных в виде гистограммы.
Корреляция: Два набора мер сравниваются, чтобы определить, движутся ли они в одном или противоположном направлении, обычно представленном на диаграмме рассеивания.
Расширьте свои знания в области обработки данных
Поскольку наука о данных становится все более востребованным навыком, самое время расширить свои знания о самом ценном ресурсе в мире: данных. Степень в области науки о данных позволит вам выявлять, анализировать и представлять сложные и переплетенные сети данных. Затем вы можете использовать эти идеи для прогнозирования и создания стратегий, особенно в бизнес-среде. Магистр наук о данных UNSW может дать вам навыки, необходимые для того, чтобы раскрыть всю мощь данных и помочь компаниям принимать более эффективные решения, позволяя им добиваться значительных изменений и результатов.
Степень в области науки о данных позволит вам выявлять, анализировать и представлять сложные и переплетенные сети данных. Затем вы можете использовать эти идеи для прогнозирования и создания стратегий, особенно в бизнес-среде. Магистр наук о данных UNSW может дать вам навыки, необходимые для того, чтобы раскрыть всю мощь данных и помочь компаниям принимать более эффективные решения, позволяя им добиваться значительных изменений и результатов.
Весы | Как читать измерения на весах — видео и расшифровка урока
Курсы английского языка / Основные предметы Praxis: Знание содержания (5511) Подготовка Курс / Как решать геометрические и измерительные задачи Глава
Памела Пратт-Завадил, Мэтью Бергстрессер- Автор Памела Пратт-Завадил
Памела работает учителем последние 8 лет. В течение последних 4 лет она преподавала морские науки в средней школе. Она также преподавала естествознание в 7-м классе средней школы, биологию, науки о Земле, физические науки и морскую биологию в средних школах.
Посмотреть биографию Она получила степень магистра образования в Университете Феникса, находясь за границей в армии. Она получила степень бакалавра в области гигиены окружающей среды в Университете Западной Каролины. До получения образования она работала в лабораториях и в атомной энергетике.
Она получила степень магистра образования в Университете Феникса, находясь за границей в армии. Она получила степень бакалавра в области гигиены окружающей среды в Университете Западной Каролины. До получения образования она работала в лабораториях и в атомной энергетике. - Инструктор Мэтью Бергстрессер
Мэтью имеет степень магистра гуманитарных наук в области физического образования. Он преподавал химию и физику в средней школе в течение 14 лет.
Посмотреть биографию
Поймите, что такое измерительная шкала и что она измеряет. См. примеры того, как читать линейку и весы. Научитесь читать измерения. Обновлено: 26.01.2022
Содержание
- Измерительная шкала
- Как читать шкалу
- Краткое содержание урока
Измерительные весы
Измерения используются ежедневно во многих видах деятельности. В своей простейшей форме измерение — это нахождение числа, представляющего количество чего-либо. Например, рост Стивена 5 футов, или собака весит 20 килограммов, или встреча в Zoom продлится 1 час — все это примеры измерений, и для каждого из них требуется свой инструмент для точного измерения. Приборы используются для измерения длины, веса, площади, объема, температуры или времени. В зависимости от того, что измеряется, используются разные единицы измерения. Измерительные инструменты имеют числа, разделенные приращения и единицы измерения на них. Существуют 2 основные системы измерения: 9.0349 Международная система единиц (СИ), более известная как метрическая система, используемая в большинстве стран, и имперская система , используемая в США.
Например, рост Стивена 5 футов, или собака весит 20 килограммов, или встреча в Zoom продлится 1 час — все это примеры измерений, и для каждого из них требуется свой инструмент для точного измерения. Приборы используются для измерения длины, веса, площади, объема, температуры или времени. В зависимости от того, что измеряется, используются разные единицы измерения. Измерительные инструменты имеют числа, разделенные приращения и единицы измерения на них. Существуют 2 основные системы измерения: 9.0349 Международная система единиц (СИ), более известная как метрическая система, используемая в большинстве стран, и имперская система , используемая в США.
Произошла ошибка при загрузке этого видео.
Попробуйте обновить страницу или обратитесь в службу поддержки.
Вы должны cСоздать учетную запись, чтобы продолжить просмотр
Зарегистрируйтесь, чтобы просмотреть этот урок
Вы студент или преподаватель?
Создайте учетную запись, чтобы продолжить просмотр
В качестве члена вы также получите неограниченный доступ к более чем 84 000
уроки математики, английского языка, науки, истории и многое другое. Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам
преуспеть.
Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам
преуспеть.
Получите неограниченный доступ к более чем 84 000 уроков.
Попробуй это сейчас
Настройка занимает всего несколько минут, и вы можете отменить ее в любое время.
Уже зарегистрированы? Войдите здесь для доступ
Назад
Что учителя говорят об Study.com
Попробуй это сейчас
Уже зарегистрирован? Войдите здесь для доступа
Далее: Как читать и интерпретировать масштабные чертежи
пройти викторину Смотреть Следующий урок
Повторить
Просто отмечаюсь. Вы все еще смотрите?
Да! Продолжай играть.Ваш следующий урок будет играть в 10 секунд
- 0:04 Измерение
- 0:33 Весы
- 2:14 Единиц
- 4:54 Итоги урока
Сохранить Сохранить Сохранить
Хронология
Автовоспроизведение
Автовоспроизведение
Скорость
Скорость
| Единицы СИ | Имперские единицы | |
|---|---|---|
| Длина | миллиметр, метр сантиметр, километр | дюйм, фут, ярд, миля |
| Вес | миллиграмм, грамм, килограмм | унция, фунт, тонна |
| Том | миллилитров, литров | килолитровчашка, пинта, кварта, галлон |
| Температура | по Цельсию | по Фаренгейту |
| Время | секунд, минут, часов, дней, лет, эонов | секунд, минут, часов, дней, лет, эонов |
Как читать шкалу
Измерительные устройства отмечены шкалой, чтобы обеспечить точные измерения. Они должны иметь возможность повторить измерение несколько раз и каждый раз получать один и тот же ответ. это называется точность . Большинство измерительных приборов указывают, какие единицы измерения используются (например, дюймы, миллилитры, граммы и т. д.). Некоторые инструменты, такие как часы, обычно понятны и не указывают конкретно используемые единицы измерения.
Они должны иметь возможность повторить измерение несколько раз и каждый раз получать один и тот же ответ. это называется точность . Большинство измерительных приборов указывают, какие единицы измерения используются (например, дюймы, миллилитры, граммы и т. д.). Некоторые инструменты, такие как часы, обычно понятны и не указывают конкретно используемые единицы измерения.
Рулетка, изображенная ниже, имеет большие цифры, отмечающие каждый сантиметр. Это основные рекомендации. Числа считаются на единицу. Между каждым большим числом находятся меньшие отметки. Чтобы найти приращения меньших отметок, посчитайте общее количество отметок и следующее большее число. Есть 9маленькие метки плюс следующее большое число, что дает 10 приращений между каждым числом. Каждая меньшая секция составляет одну десятую сантиметра или 1 миллиметр. При измерении размера чего-либо прочитайте последнее целое число, затем найдите ближайшую маленькую черту и посчитайте от последнего целого числа. Оценку можно произвести до еще одной значащей цифры между самыми маленькими заданными строками.
Оценку можно произвести до еще одной значащей цифры между самыми маленькими заданными строками.
Не все шкалы имеют приращение 1. Некоторые имеют приращение 10, 20 или более — некоторые измерительные приборы могут иметь приращение 50 или 100. Чтобы определить приращение, посмотрите на разницу между двумя данными последовательными числа. Вычесть меньшие числа из больших чисел. Эти мензурки измеряются в миллилитрах (мл), как указано на мензурках. Выберите 2 последовательных числа и вычтите меньшее из большего числа. Например, 200 и 400 стоят рядом. 400-200 = 200, поэтому этот стакан размечен с шагом 200 мл другой меньшей чертой посередине между цифрами. Эта линия составляет половину от 200, что составляет 100 мл. На стакане написано 800мл. Это весь путь до верха стакана. Меньший стакан на 150 мл имеет маркировку 40 мл, 80 мл и 120 мл. Таким образом, шкала имеет шаг 40 мл (80-40 = 40). Если необходимо произвести более точные измерения, может понадобиться стакан меньшего размера.
Меньший стакан на 150 мл имеет маркировку 40 мл, 80 мл и 120 мл. Таким образом, шкала имеет шаг 40 мл (80-40 = 40). Если необходимо произвести более точные измерения, может понадобиться стакан меньшего размера.
Как читать линии на весах
Весы используются для измерения веса. Вес можно измерять в граммах, килограммах, унциях или фунтах. Весы для ванной – это универсальный инструмент, используемый для измерения веса человека. Эти весы измеряют в фунтах (lbs) по внешней шкале и в килограммах (kg) по внутренней шкале:
Как читать линейку
Линейки используются для измерения длины. Эта линейка измеряет как в метрической системе, измеряемой в сантиметрах (см) с одной стороны, так и в имперской системе измерения, измеряемой в дюймах (дюймах) с другой стороны. Дюймы подразделяются на более мелкие части 1/2 дюйма, 1/4 дюйма, 1/8 дюйма и 1/16 дюйма — 15 меньших линий + следующее большее число составляют приращения между последовательными большими числами. Это делает 16 равномерно расположенных секций между каждым дюймом для точного измерения. В метрической системе для измерения используются миллиметры (мм) и сантиметры (см). Большие числа читаются в см. Есть 9меньшие миллиметровые отметки между каждым числом, что, прибавляя к следующему большому числу, составляет 10 мм в каждом сантиметре. Итак, чтобы прочитать линейку, сначала прочитайте наибольшее целое число, а затем посчитайте количество маленьких пробелов перед следующим целым числом. Например, резьба на маленьком болте не достигает отметки 1 см, поэтому она меньше 1 см. Подсчитайте меньшие приращения, чтобы найти, что резьба на маленьком болте составляет 4 мм. Резьба на большем болте 5 мм.
Итак, чтобы прочитать линейку, сначала прочитайте наибольшее целое число, а затем посчитайте количество маленьких пробелов перед следующим целым числом. Например, резьба на маленьком болте не достигает отметки 1 см, поэтому она меньше 1 см. Подсчитайте меньшие приращения, чтобы найти, что резьба на маленьком болте составляет 4 мм. Резьба на большем болте 5 мм.
Как читать инженерную шкалу
В инженерии используется множество различных инструментов. Мультиметр используется электриками для проверки напряжения, силы тока и сопротивления электрических проводов. Этот мультиметр масштабируется большими числами с шагом 10. Между каждым большим числом есть 20 меньших разделов. 10 разделить на 20 = 0,5; следовательно, каждое меньшее приращение читается как 0,5. Стрелка этого мультиметра показывает 9.5 вольт. Некоторые мультиметры имеют регулируемые шкалы для выбора шкалы, соответствующей тому, над чем работают.
Некоторые мультиметры имеют регулируемые шкалы для выбора шкалы, соответствующей тому, над чем работают.
Как считывать показания термометра.
Термометры — это приборы, используемые для измерения температуры. Их используют как в кабинетах врачей, так и дома. Две распространенные шкалы на термометре — это шкала Фаренгейта (F), используемая в США, и шкала Цельсия (C), используемая в большей части остального мира. Двумя распространенными температурами, используемыми для стандартизации термометров, являются точка замерзания воды, которая составляет 32 градуса по Фаренгейту или 0 градусов по Цельсию, и точка кипения воды, которая составляет 212 градусов по Фаренгейту или 100 градусов по Цельсию9.0009
Большинство термометров имеют красный или серебристый центр, который поднимается по шкале по мере повышения температуры. Цифры, выделенные красным цветом или со знаком «минус» впереди, означают температуру ниже 0 градусов. Оба этих термометра имеют маркировку с шагом 10 градусов с 5 равными делениями между каждым числом. Чтобы узнать, сколько стоит каждая маленькая линия, возьмите 10-градусную шкалу и разделите ее на 5 равных частей, что дает нам 2 градуса на приращение. Чтение температуры слева дало бы нам 24 градуса C; термометр справа будет 74 градуса по Фаренгейту.
Цифры, выделенные красным цветом или со знаком «минус» впереди, означают температуру ниже 0 градусов. Оба этих термометра имеют маркировку с шагом 10 градусов с 5 равными делениями между каждым числом. Чтобы узнать, сколько стоит каждая маленькая линия, возьмите 10-градусную шкалу и разделите ее на 5 равных частей, что дает нам 2 градуса на приращение. Чтение температуры слева дало бы нам 24 градуса C; термометр справа будет 74 градуса по Фаренгейту.
Как читать медицинские инструменты.
Получение точной дозы в медицине очень важно. Приборы должны давать точные дозировки и быть в состоянии многократно точно измерять дозу. Шприц отмеряет точное количество. Этот шприц имеет шкалу в миллилитрах (мл). Большие цифры на шприце увеличиваются на 1 мл каждая. Весь шприц может вместить в общей сложности 12 мл. Между каждым из больших чисел есть 5 меньших приращений. 1 мл, разделенный на 5 приращений = 0,2 мл, что означает, что каждое меньшее приращение равно 0,2 мл. Мы можем оценить еще одну цифру, оценив между наименьшими приращениями. Это даст нам точность 0,1 мл. Этот шприц вмещает 3 мл. жидкости. Жидкость набирается в шприц до тех пор, пока число на краю черного поршня, ближайшем к кончику шприца, не достигнет желаемого количества.
Весь шприц может вместить в общей сложности 12 мл. Между каждым из больших чисел есть 5 меньших приращений. 1 мл, разделенный на 5 приращений = 0,2 мл, что означает, что каждое меньшее приращение равно 0,2 мл. Мы можем оценить еще одну цифру, оценив между наименьшими приращениями. Это даст нам точность 0,1 мл. Этот шприц вмещает 3 мл. жидкости. Жидкость набирается в шприц до тех пор, пока число на краю черного поршня, ближайшем к кончику шприца, не достигнет желаемого количества.
Краткое содержание урока
Измерение — это нахождение числа, представляющего количество чего-либо. Приборы используются для измерения длины, ширины, площади, объема, температуры и времени. На измерительном приборе будут большие числа, меньшие приращения и единицы измерения. Используются две системы измерений, SI и Imperial System . Меньшие деления шкалы используются для большей точности . Чтобы определить шкалу , используемую на инструменте, найдите 2 последовательных больших числа и вычтите меньшее из большего. Чтобы найти меньшие приращений , подсчитайте общее количество меньших делений между двумя последовательными большими числами. Не все весы считают на 1с. Некоторые считают на 10, 20, 50 или 100 секунд.
Используются две системы измерений, SI и Imperial System . Меньшие деления шкалы используются для большей точности . Чтобы определить шкалу , используемую на инструменте, найдите 2 последовательных больших числа и вычтите меньшее из большего. Чтобы найти меньшие приращений , подсчитайте общее количество меньших делений между двумя последовательными большими числами. Не все весы считают на 1с. Некоторые считают на 10, 20, 50 или 100 секунд.
Весы используются для измерения веса. Они весят в граммах, кг, унциях. и фунты. При взвешивании в фунтах принято разбивать их на меньшие приращения в один десятичный знак вместо использования унций — например, 7,6 фунтов. Линейки обычно измеряют как в метрических, так и в имперских единицах измерения. Дюйм разбит на 16 равных частей, а сантиметр — на 10 равных частей. В инженерии используется множество различных инструментов, и масштаб может меняться в зависимости от того, что измеряется. Термометры — это инструменты для измерения количества тепла. Термометры используют шкалы Фаренгейта и Цельсия для считывания температуры, которая обычно обозначается красной или серой линией, которая поднимается и опускается при нагревании или охлаждении. Очень важно быть точным и воспроизводимым с медицинским инструментом. Шприцы обычно измеряются в мл.
Термометры — это инструменты для измерения количества тепла. Термометры используют шкалы Фаренгейта и Цельсия для считывания температуры, которая обычно обозначается красной или серой линией, которая поднимается и опускается при нагревании или охлаждении. Очень важно быть точным и воспроизводимым с медицинским инструментом. Шприцы обычно измеряются в мл.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свой аккаунт
Зарегистрируйтесь для просмотра этого урока
Вы студент или преподаватель?
Разблокируйте свое образование
Убедитесь сами, почему 30 миллионов человек используют Study.com
Станьте участником Study.com и начните учиться прямо сейчас.
Стать участником
Уже зарегистрированы? Войти
Назад
Что учителя говорят об Study.com
Попробуй это сейчас
Уже зарегистрирован? Войдите здесь для доступа
| 1.
Исследовательский анализ данных 1.3. Методы ЭДА 1.3.5. Количественные методы
| |||
| Масштаб, изменчивость или разброс | Фундаментальная задача многих статистических анализов состоит в том, чтобы охарактеризовать
разброс или изменчивость набора данных. Меры масштаба
являются просто попытками оценить эту изменчивость. При оценке изменчивости набора данных есть два ключевых момента: составные части:
Гистограмма является эффективным графическим
методика отображения обеих этих составляющих спреда. куда \(\bar{Y}\) — среднее значение данных. Дисперсия примерно равна среднему арифметическому квадрата расстояние от среднего. Возведение в квадрат расстояния от среднее имеет эффект придания большего веса значениям которые дальше от среднего. Например, точка 2 единицы от среднего добавляют 4 к вышеуказанной сумме, в то время как Пункт 10 единиц от среднего добавляет 100 к сумме. Хотя дисперсия предназначена для общего измерения распространения, на него может сильно повлиять хвост поведение. 9{2}/(N — 1)} \) Стандартное отклонение восстанавливает единицы спреда до исходные единицы данных (дисперсия возводит единицы).  Разброс около центра данных не фиксируется
вообще. Разброс около центра данных не фиксируется
вообще.куда \(\bar{Y}\) является средним значением данные и |Y| — абсолютное значение Д . Эта мера не возводится в квадрат расстояние от среднего, поэтому на него меньше влияет крайними наблюдениями, чем дисперсия и стандартное отклонение.
куда
\(\tilde{Y}\) — медиана данных и |Д| — абсолютное значение Д . Это вариация на
среднее абсолютное отклонение, которое еще меньше
подвержены экстремумам в хвосте, потому что данные в
хвосты меньше влияют на расчет
медианы, чем в среднем. | ||
| Почему разные меры? | Следующий пример помогает понять, почему эти альтернативные
определения распространения полезны и необходимы. На этом графике показаны гистограммы для 10 000 случайных чисел, сгенерированных из
нормальная, двойная экспонента, Коши и Тьюки-лямбда
распределение. | ||
| Нормальное распределение | Первая гистограмма представляет собой выборку из
нормальное распределение.
стандартное отклонение 0,997, среднее абсолютное отклонение составляет
0,681, а диапазон 7,87. Нормальное распределение — это симметричное распределение с
хорошие хвосты и один пик в центре распределения.
Под симметричностью мы подразумеваем, что распределение можно свернуть относительно
ось так, чтобы обе стороны совпадали. То есть ведет себя
то же самое слева и справа от некоторой центральной точки. В таком случае,
среднее абсолютное отклонение немного меньше стандартного
отклонение из-за утяжеления хвостов. Диапазон
чуть менее 8 указывает на то, что экстремальные значения попадают в
около 4 стандартных отклонений от среднего.
Если гистограмма или график нормальной вероятности указывают на
что ваши данные хорошо аппроксимируются нормальным распределением, тогда
разумно использовать стандартное отклонение в качестве спреда
оценщик. | ||
| Двойное экспоненциальное распределение | Вторая гистограмма представляет собой выборку из
двойное экспоненциальное распределение.
Стандартное отклонение составляет 1,417, медиана абсолютного
отклонение 0,706, размах 17,556. Сравнение двойной экспоненциальной и нормальной гистограмм показывает, что двойная экспонента имеет более сильный пик при центре, быстрее затухает вблизи центра и имеет гораздо более длительный хвосты. Из-за более длинных хвостов стандартное отклонение стремится быть завышенным по сравнению с обычным. С другой стороны, среднее абсолютное отклонение лишь немного больше, чем для нормальные данные. Более длинные хвосты четко отражаются на значении диапазона, который показывает, что экстремумы падают примерно на 6 стандартных отклонения от среднего по сравнению с примерно 4 для нормальных данных. | ||
| Распределение Коши | Третья гистограмма представляет собой выборку из
Распределение Коши. стандартное отклонение равно 998,389, среднее абсолютное отклонение равно
1,16, а диапазон — 118 953,6. стандартное отклонение равно 998,389, среднее абсолютное отклонение равно
1,16, а диапазон — 118 953,6.Распределение Коши является симметричным распределением с большим хвосты и один пик в центре распределения. Распределение Коши обладает интересным свойством: сбор большего количества данных не дает более точной оценки для среднего или стандартного отклонения. То есть выборка распределение средних значений и стандартное отклонение эквивалентны выборочному распределению исходных данных. Это означает, что для распределения Коши стандартное отклонение бесполезен в качестве меры распространения. Судя по гистограмме, ясно, что почти все данные находятся между примерно -5 и 5. Однако несколько очень экстремальных значений вызывают как стандартное отклонение и дальность очень велики. Тем не менее, медиана абсолютное отклонение лишь немного больше, чем для нормальное распределение. В этом случае среднее абсолютное отклонение явно является лучшей мерой распространения. Хотя распределение Коши является крайним случаем, оно
иллюстрируют важность тяжелых хвостов в измерении
распространять. | ||
| Распределение Тьюки-Лямбда | Четвертая гистограмма представляет собой выборку из
Лямбда-распределение Тьюки с
параметр формы λ = 1,2. Стандартное отклонение 0,49, медиана
абсолютное отклонение 0,427, размах 1,666. Лямбда-распределение Тьюки имеет диапазон, ограниченный (-1/ λ , 1/ λ ). То есть у него укорочены хвосты. В этом случае стандартное отклонение и среднее абсолютное отклонение имеют более близкие значения, чем для другие три примера, которые имеют значимые хвосты. | ||
| Надежность | Тьюки и Мостеллер
определил два типа устойчивости, где надежность
отсутствие восприимчивости к эффектам ненормальности.
 Среднее абсолютное отклонение и межквартильный размах являются оценочными. масштаба, которые обладают надежностью валидности. Однако они не особенно сильным для надежности эффективности. Если гистограммы и графики вероятностей показывают, что ваши данные на самом деле разумно аппроксимируются нормальным распределением, то имеет смысл использовать стандартное отклонение в качестве оценки масштаба. Однако, если ваши данные не являются нормальными, и в частности если есть длинные хвосты, то с помощью альтернативной меры, такой как среднее абсолютное отклонение, среднее абсолютное отклонение или межквартильный диапазон имеет смысл. Диапазон используется в некоторых приложений, таких как контроль качества, из-за его простоты. Кроме того, сравнение диапазона со стандартным отклонением дает индикация разброса данных в хвостах. Так как диапазон определяется двумя крайними точками в
набор данных, мы должны быть осторожны при его использовании для больших значений N . Тьюки и Мостеллер дать оценку шкалы, которая обладает как надежностью достоверности, так и надежность эффективности. Однако все сложнее и мы не приводим формулу здесь. | ||
| Программное обеспечение | Большинство статистических программ общего назначения может генерировать по крайней мере некоторые из мер масштаба обсуждалось выше. | ||
7 Типы шкал измерения данных в исследованиях
Шкалы измерения в исследованиях и статистике — это различные способы определения переменных и группировки их в разные категории. Иногда называемый уровнем измерения, он описывает характер значений, присвоенных переменным в наборе данных.
Термин «шкала измерения» происходит от двух ключевых слов в статистике, а именно; измерение и масштаб. Измерение — это процесс записи наблюдений, собранных в рамках исследования.
Масштабирование, с другой стороны, представляет собой присвоение объектам чисел или семантики. Эти два слова, объединенные вместе, относятся к взаимосвязи между назначенными объектами и записанными наблюдениями.
Эти два слова, объединенные вместе, относятся к взаимосвязи между назначенными объектами и записанными наблюдениями.
Шкала измерения используется для квалификации или количественного определения переменных данных в статистике. Он определяет тип методов, которые будут использоваться для статистического анализа.
Существуют различные виды шкал измерения, и тип собираемых данных определяет вид шкалы измерения, который будет использоваться для статистических измерений. Этих шкал измерения четыре, а именно; номинальная шкала, порядковая шкала, интервальная шкала и шкала отношений.
Шкалы измерения используются для измерения качественных и количественных данных. Номинальная и порядковая шкалы используются для измерения качественных данных, а шкалы интервалов и отношений используются для измерения количественных данных.
Характеристики шкалы измерений Идентичность Идентичность определяется как присвоение чисел значениям каждой переменной в наборе данных. Рассмотрим вопросник, в котором запрашивается пол респондента, например, с вариантами «Мужской» и «Женский». Значения 1 и 2 могут быть присвоены мужчинам и женщинам соответственно.
Рассмотрим вопросник, в котором запрашивается пол респондента, например, с вариантами «Мужской» и «Женский». Значения 1 и 2 могут быть присвоены мужчинам и женщинам соответственно.
Над этими значениями нельзя выполнять арифметические операции, поскольку они предназначены только для целей идентификации. Это характеристика номинальной шкалы.
ВеличинаВеличина определяется как размер шкалы измерения, где числа (идентичность) имеют неотъемлемый порядок от наименьшего к наибольшему. Обычно они представлены на шкале в порядке возрастания или убывания. Позиция в гонке, например, располагается от 1-го, 2-го, 3-го до наименьшего.
Этот пример измеряется по порядковой шкале, потому что он имеет как идентичность, так и величину.
Равные интервалы Равные интервалы определяются как шкала со стандартным порядком. То есть разница между каждым уровнем на шкале одинакова. Это не относится к приведенному выше примеру с порядковой шкалой.
Каждая позиция не имеет одинаковой разницы интервалов. В гонке 1-е место может завершить гонку за 20 секунд, 2-е место — за 20,8 секунды, а 3-е место — за 30 секунд.
Переменная, которая имеет идентичность, величину и равный интервал, измеряется по шкале интервалов.
Абсолютный нольАбсолютный ноль определяется как характеристика, уникальная для шкалы отношений. Это означает, что на шкале существует ноль, и он определяется отсутствием измеряемой переменной (например, без квалификации, без денег, без указания пола и т. д.
Уровни измерения данныхУровень измерения данного набора данных определяется соотношением между значениями, присвоенными атрибутам переменной данных. Например, связь между значениями (1 и 2), присвоенными атрибутам (мужской и женский) переменной (Пол), является «идентичностью». Это через. пример номинальной шкалы.
Зная различные уровни измерения данных, исследователи могут выбрать лучший метод статистического анализа. Существуют различные уровни измерения данных: номинальная, порядковая, интервальная шкала и шкала отношений 9.0009
Существуют различные уровни измерения данных: номинальная, порядковая, интервальная шкала и шкала отношений 9.0009
Номинальная шкала — это шкала измерения, используемая для идентификации. Это самый холодный и самый слабый уровень измерения данных среди четырех.
Иногда называемая категориальной шкалой, атрибутам присваиваются номера для облегчения идентификации. Однако эти числа не являются качественными по своей природе и действуют только как ярлыки.
Единственным статистическим анализом, который может быть выполнен на номинальной шкале, является подсчет процентов или частоты. Его можно проанализировать графически, используя гистограмму и круговую диаграмму.
Пример номинальной шкалы
В приведенном ниже примере популярность политической партии измеряется по номинальной шкале.
К какой политической партии вы относитесь?
- Независимый
- Республиканский
- демократ
Обозначение независимых как «1», «республиканцев» как «2» и «демократов» как «3» никоим образом не означает, что какой-либо из атрибутов лучше, чем другой. Они просто используются в качестве идентификатора для удобного анализа данных.
Они просто используются в качестве идентификатора для удобного анализа данных.
Порядковая шкала включает ранжирование или упорядочение атрибутов в зависимости от масштабируемой переменной. Элементы этой шкалы классифицируются в соответствии со степенью встречаемости рассматриваемой переменной.
Атрибуты в порядковой шкале обычно располагаются в порядке возрастания или убывания. Он измеряет степень появления переменной.
Порядковая шкала может использоваться в исследованиях рынка, рекламе и опросах удовлетворенности клиентов. Он использует квалификаторы, такие как очень, очень, больше, меньше и т. д., чтобы описать степень.
Мы можем выполнять статистический анализ, такой как медиана и мода, используя порядковую шкалу, но не среднее значение. Однако существуют и другие статистические альтернативы среднему, которые можно измерить с помощью порядковой шкалы.
Пример порядковой шкалы
Например: Компании-разработчику программного обеспечения может понадобиться спросить своих пользователей:
Как бы вы оценили наше приложение?
- Отлично
- Очень хорошо
- Хорошо
- Плохой
- Бедный
Атрибуты в этом примере перечислены в порядке убывания.
Интервальная шкала измерения данных представляет собой шкалу, в которой уровни упорядочены и каждые численно равные расстояния на шкале имеют одинаковую интервальную разность. Если это расширение порядковой шкалы, с основным отличием в наличии равных интервалов.
С помощью шкалы интервалов вы не только знаете, что данный атрибут A больше, чем другой атрибут B, но также и степень, в которой A больше, чем B. Кроме того, в отличие от порядковой и номинальной шкалы, арифметические операции могут выполняться на интервальная шкала.
Шкала времени с 5-минутным интервалом
Используется в различных областях, таких как образование, медицина, инженерия и т. д. Некоторые из этих применений включают расчет CGPA учащегося, измерение температуры пациента и т. д.
Пример интервальной шкалы
Типичным примером является измерение температуры по шкале Фаренгейта. Его можно использовать для расчета среднего значения, медианы, режима, диапазона и стандартного отклонения.
Его можно использовать для расчета среднего значения, медианы, режима, диапазона и стандартного отклонения.
Ratio Scale — пиковый уровень измерения данных. Это расширение шкалы интервалов, поэтому оно удовлетворяет четырем характеристикам шкалы измерения; идентичность, величина, равный интервал и свойство абсолютного нуля.
Этот уровень измерения данных позволяет исследователю сравнивать как различия, так и относительную величину чисел. Некоторые примеры шкал отношений включают длину, вес, время и т. д.
Применительно к маркетинговым исследованиям распространенными примерами шкал отношений являются цена, количество клиентов, конкуренты и т. д. Она широко используется в маркетинге, рекламе и коммерческих продажах. .
Шкала отношений измерения данных совместима со всеми методами статистического анализа, такими как меры центральной тенденции (среднее, медиана, мода и т. д.) и меры дисперсии (диапазон, стандартное отклонение и т. д.).
д.).
Пример шкалы отношений
Например: Опрос, который собирает веса респондентов.
К какой из следующих категорий вы относитесь? Весить
- более 100 кг
- 81 – 100 кг
- 61 – 80 кг
- 40 – 60 кг
- Менее 40 кг
Formplus — лучший инструмент для сбора номинальных, порядковых, интервальных и относительных данных. Это простой в использовании конструктор форм, который позволяет с легкостью собирать данные. Выполните следующие шаги, чтобы собрать данные о Formplus
. Шаг 1. Выберите функциюМы будем использовать вопросы с несколькими вариантами ответов для сбора данных о конструкторе форм Formplus.
- Зарегистрируйтесь или войдите в свою учетную запись на https://www.formpl.us/
- Перейдите на вкладку «Параметры выбора» в меню конструктора форм.

- Нажмите на радиокнопку.
- Нажмите кнопку редактирования, чтобы отредактировать форму.
- Отредактируйте вопрос и варианты выбора.
- Нажмите кнопку «Сохранить», чтобы сохранить изменения.
- Повторить Шаг 1 .
- Нажмите кнопку редактирования, чтобы изменить форму.
- Изменить вопрос и варианты выбора
- Присвойте значения параметрам выбора.
- Нажмите кнопку «Сохранить», чтобы сохранить изменения.
- Щелкните значок «+» внизу, чтобы добавить новую страницу.
- Повторить Шаг 1 .
- Нажмите кнопку редактирования, чтобы изменить форму.
- Отредактируйте вопрос и варианты выбора.

- Нажмите кнопку «Сохранить», чтобы сохранить изменения.
Примечание : параметры интервальных данных не имеют нулевого значения.
Данные соотношения- Повторить Шаг 1 .
- Нажмите кнопку редактирования, чтобы изменить форму.
- Отредактируйте вопрос и варианты выбора.
- Нажмите кнопку «Сохранить», чтобы сохранить изменения.
- Нажмите кнопку «Сохранить» в правом верхнем углу, чтобы сохранить форму.
Примечание: пример данных отношения имеет нулевое значение, что отличает его от шкалы интервалов.
Шаг 3. Настройка и предварительный просмотр формы Типы шкал измеренияСуществует два основных типа шкал измерения, а именно; сравнительные шкалы и несравнительные шкалы.
Сравнительные шкалы При сравнительном шкалировании респондентов просят сравнить один объект с другим. При использовании в маркетинговых исследованиях клиентов просят оценить один продукт в прямом сравнении с другими. Сравнительные шкалы можно дополнительно разделить на парное сравнение, ранговый порядок, постоянную сумму и шкалы q-сортировки.
При использовании в маркетинговых исследованиях клиентов просят оценить один продукт в прямом сравнении с другими. Сравнительные шкалы можно дополнительно разделить на парное сравнение, ранговый порядок, постоянную сумму и шкалы q-сортировки.
- Шкала парного сравнения
Шкала парного сравнения — это метод масштабирования, который представляет респондентам одновременно два объекта и предлагает им выбрать один в соответствии с заранее определенным критерием. Исследователи продуктов используют его в сравнительных исследованиях продуктов, предлагая покупателям выбрать наиболее предпочтительный для них продукт из двух тесно связанных продуктов.
Например, в последней версии программного продукта появилось 3 новых функции. Но компания планирует удалить одну из этих функций в новой версии. Поэтому исследователи продукта проводят сравнительный анализ наиболее и наименее предпочтительной функции.
- Какая функция из следующих пар наиболее предпочтительна для вас?
- Фильтр – Диктофон
- Фильтр – Видеорегистратор
- Диктофон – Видеомагнитофон
- Шкала рангов:
В методе ранжирования респондентам одновременно предоставляется несколько вариантов и предлагается ранжировать их в порядке приоритета на основе заранее определенного критерия. Он в основном используется в маркетинге для измерения предпочтения бренда, продукта или функции.
Он в основном используется в маркетинге для измерения предпочтения бренда, продукта или функции.
При использовании в конкурентном анализе респондента могут попросить ранжировать группу брендов с точки зрения личных предпочтений, качества продукции, обслуживания клиентов и т. д. Результаты сбора таких данных обычно получают в ходе совместного анализа, поскольку клиентов, чтобы различать варианты.
Шкала ранжирования является типом порядковой шкалы, поскольку она упорядочивает атрибуты от наиболее предпочтительных к наименее предпочтительным, но не имеет определенного расстояния между атрибутами.
Например:
Расположите следующие бренды от наиболее предпочитаемых до наименее предпочтительных.
- Кока-Кола
- Пепси-кола
- Доктор перец
- Маунтин Дью
- Шкала постоянной суммы
Шкала постоянной суммы — это тип шкалы измерения, в которой респондентов просят распределить постоянную сумму единиц, таких как очки, доллары, фишки или фишки, среди объектов-стимулов в соответствии с определенным критерием. Шкала с постоянной суммой присваивает каждому атрибуту фиксированное количество единиц, отражая важность, которую респондент придает ему.
Шкала с постоянной суммой присваивает каждому атрибуту фиксированное количество единиц, отражая важность, которую респондент придает ему.
Этот тип шкалы измерения можно использовать для определения того, что влияет на решение покупателя при выборе продукта для покупки. Например, вы можете определить, насколько важны цена, размер, аромат и упаковка для покупателя при выборе марки духов для покупки.
Некоторые из основных недостатков этого метода заключаются в том, что респонденты могут быть сбиты с толку и в конечном итоге присвоить больше или меньше баллов, чем указано. Исследователям остается иметь дело с группой данных, которые неоднородны и могут быть трудны для анализа.
Избегайте этого с помощью логической функции Formplus. Эта функция позволяет добавить ограничение, запрещающее респонденту добавлять больше или меньше баллов, чем указано в вашей форме.
- Шкала Q-сортировки
Шкала Q-сортировки — это тип шкалы измерения, в котором используется метод ранжирования для сортировки сходных объектов по некоторому критерию. Респонденты сортируют количество утверждений или отношений в стопки, обычно по 11.
Респонденты сортируют количество утверждений или отношений в стопки, обычно по 11.
Масштабирование Q-сортировки помогает присвоить ранги различным объектам в одной группе, и различия между группами (кучками) четко видны. Это быстрый способ облегчить различение среди относительно большого набора атрибутов.
Например, новый ресторан, который только готовит свое меню, может захотеть собрать некоторую информацию о том, что нравится потенциальным клиентам:
Предоставленный документ содержит список из 50 блюд. Пожалуйста, выберите 10 блюд, которые вам нравятся, 30 блюд, к которым вы относитесь нейтрально (ни нравится, ни не нравится) и 10 блюд, которые вам не нравятся.
Несравнительные шкалы При несравнительной шкале клиентов просят оценить только один объект. Эта оценка совершенно не зависит от других исследуемых объектов. Иногда называемая монадической или метрической шкалой, несравнительная шкала может быть далее разделена на непрерывную и детализированную рейтинговые шкалы 9. 0009
0009
- Шкала непрерывной оценки
В непрерывной шкале оценок респондентов просят оценить объекты, поставив соответствующую отметку на линии, идущей от одного крайнего значения критерия к другому переменному критерию. Также называемая графической оценочной шкалой, она дает респонденту возможность поставить оценку в любом месте в зависимости от личных предпочтений.
После получения оценок исследователь делит строку на несколько категорий, а затем присваивает баллы в зависимости от категории, к которой относятся оценки. Этот рейтинг можно визуализировать как в горизонтальном, так и в вертикальном виде.
Несмотря на простоту построения, непрерывная рейтинговая шкала имеет ряд существенных недостатков, что ограничивает ее использование в маркетинговых исследованиях.
- Детализированная рейтинговая шкала
Детализированная рейтинговая шкала — это разновидность порядковой шкалы, в которой каждому атрибуту присваиваются номера. Респондентов обычно просят выбрать атрибут, который лучше всего описывает их чувства по заранее определенному критерию.
Респондентов обычно просят выбрать атрибут, который лучше всего описывает их чувства по заранее определенному критерию.
Детализированная рейтинговая шкала далее делится на 2, а именно; Шкала Лайкерта, шкала Стапеля и семантическая шкала.
- Шкала Лайкерта
Шкала Лайкерта — это порядковая шкала с пятью категориями ответов, которая используется для упорядочивания списка атрибутов от лучшего к наименьшему. В этой шкале используются наречия степени, такие как очень сильно, сильно и т. Д., Для обозначения разных уровней.
- Шкала Stapel:
Это шкала с 10 категориями, обычно от -5 до 5 без нуля. Это вертикальная шкала с 3 столбцами, где атрибуты расположены посередине, а наименьшее (-5) и максимальное (5) — в 1-м и 3-м столбцах соответственно.
- Семантическая дифференциальная шкала
Это семибалльная оценочная шкала с конечными точками, связанными с биполярными метками (например, хороший или плохой, счастливый и т. д.). Его можно использовать для маркетинга, рекламы и на разных этапах разработки продукта.
д.). Его можно использовать для маркетинга, рекламы и на разных этапах разработки продукта.
Если по своей сути исследуется более одного элемента, его можно визуализировать в таблице с более чем 3 столбцами.
ЗаключениеВ двух словах, шкалы измерения относятся к различным мерам, используемым для количественной оценки переменных, которые исследователи используют при проведении анализа данных. Они являются важным аспектом исследований и статистики, поскольку именно уровень измерения данных определяет используемый метод анализа данных.
Понимание концепции шкал измерений является необходимым условием для работы с данными и выполнения статистического анализа. Различные шкалы измерения имеют некоторые схожие свойства, и поэтому важно правильно проанализировать данные, чтобы определить их шкалу измерения, прежде чем выбирать метод для анализа.
Для измерения одной и той же шкалы измерения доступен ряд методов масштабирования. Поэтому не существует единого способа выбора метода масштабирования для исследовательских целей.
Могу ли я повлиять на вас? Разработка шкалы для измерения воспринимаемой убедительности и два исследования, демонстрирующие использование шкалы
1. Введение
Многие вмешательства по изменению поведения были разработаны для самых разных областей. Например, «Fit4Life» (Purpura et al., 2011) пропагандирует здоровое управление весом, приложение ASICA (Smith et al., 2016) напоминает пациентам с раком кожи о необходимости самостоятельного осмотра своей кожи, приложение SUPERHUB (Wells et al. , 2014) мотивирует к экологичным путешествиям, в то время как «Порция» (Mazzotta et al., 2007) и «Дафна» (Grasso et al., 2000) способствуют здоровому питанию.
Очевидно, важно измерять эффективность таких убедительных вмешательств. Однако часто трудно измерить фактическую убедительность (O’Keefe, 2018). Возможно, основные три причины таких трудностей заключаются в следующем. Во-первых, измерение фактической убедительности, как правило, требует от участников больше времени и усилий, а также дополнительных ресурсов. Например, чтобы измерить убедительность вмешательства по здоровому питанию, участникам может потребоваться предоставить подробные дневники приема пищи, что громоздко и часто ненадежно (Cook et al., 2000), а также может потребоваться предоставление участникам весов. Кроме того, при изучении многих экспериментальных условий может быть трудно найти достаточное количество участников, готовых потратить необходимое время [например, для измерения фактической убедительности напоминаний в (Smith et al., 2016) потребовалось бы большое количество пациентов с раком кожи. ]. Во-вторых, трудно измерить фактическую убедительность из-за смешанных факторов. Например, при измерении убедительности приложения устойчивого транспорта другие факторы, такие как погода, могут влиять на поведение людей. В-третьих, могут быть этические проблемы, которые затрудняют измерение фактической убедительности. Например, если кто-то хотел исследовать убедительные эффекты различных типов сообщений, чтобы побудить учащихся больше учиться, это может быть сочтено неэтичным делать это в реальном классе, поскольку учащиеся в контрольных условиях могут быть замечены в невыгодном положении.
Например, чтобы измерить убедительность вмешательства по здоровому питанию, участникам может потребоваться предоставить подробные дневники приема пищи, что громоздко и часто ненадежно (Cook et al., 2000), а также может потребоваться предоставление участникам весов. Кроме того, при изучении многих экспериментальных условий может быть трудно найти достаточное количество участников, готовых потратить необходимое время [например, для измерения фактической убедительности напоминаний в (Smith et al., 2016) потребовалось бы большое количество пациентов с раком кожи. ]. Во-вторых, трудно измерить фактическую убедительность из-за смешанных факторов. Например, при измерении убедительности приложения устойчивого транспорта другие факторы, такие как погода, могут влиять на поведение людей. В-третьих, могут быть этические проблемы, которые затрудняют измерение фактической убедительности. Например, если кто-то хотел исследовать убедительные эффекты различных типов сообщений, чтобы побудить учащихся больше учиться, это может быть сочтено неэтичным делать это в реальном классе, поскольку учащиеся в контрольных условиях могут быть замечены в невыгодном положении. Пурпура и др. (2011) иллюстрирует некоторые этические проблемы при использовании технологий убеждения в вмешательствах по изменению поведения.
Пурпура и др. (2011) иллюстрирует некоторые этические проблемы при использовании технологий убеждения в вмешательствах по изменению поведения.
Из-за этих трудностей в измерении фактической убедительности, воспринимаемая убедительность часто используется в качестве аппроксимации или начального шага в измерении фактической убедительности (см. Таблицу 1, например, исследования, в которых использовалась воспринимаемая убедительность). Воспринимаемая убедительность может включать несколько факторов. Например, воспринимаемая эффективность изменения чьего-либо отношения может отличаться от воспринимаемой эффективности изменения поведения. Нам нужна надежная шкала, включающая несколько факторов в виде подшкал, каждая из которых состоит из нескольких пунктов. Такой шкалы еще не существует, и исследователям до сих пор приходилось использовать свои собственные меры без надлежащей проверки.
Таблица 1 . Элементы шкалы, связанные с измерением воспринимаемой убедительности, шкалой измерения, используемой для каждого элемента, и количеством точек измерения.
Таким образом, в этом документе описывается процесс разработки надежной и проверенной шкалы из нескольких пунктов и нескольких субшкал для измерения воспринимаемой убедительности. Кроме того, собранные данные будут использоваться для демонстрации полезности шкалы путем анализа влияния различных типов убедительных сообщений на разработанные коэффициенты шкалы.
2. Обзор литературы
Чтобы вдохновить элементы шкалы и показать необходимость разработки шкалы, мы сначала изучили, как исследователи измеряли воспринимаемую убедительность, изучив элементы шкалы и соответствующие измерения, которые они использовали в опубликованных исследованиях пользователей. Мы провели полуструктурированный обзор литературы, выполнив поиск в Scopus за период с 2014 по 2018 год по дисциплинам. Сначала мы провели узкий поиск, используя следующий поисковый запрос:
«разработка весов » И исследования И убеждение .
Однако это дало очень мало результатов поиска. Позже мы изменили поисковый запрос на следующий:
убеждение И (эксперименты ИЛИ исследования)
, чтобы получить более широкий спектр статей. Мы также провели поиск в материалах «Международной конференции по технологиям убеждения» за период с 2013 по 2018 год. Мы искали исследования пользователей, в которых была разработана или использовалась шкала для измерения воспринимаемой убедительности. В результате поиска было найдено 12 статей, в том числе 2 статьи, не относящиеся к компьютерным наукам, из области маркетинга и коммуникаций (Koch and Zerbac, 2013; Zhang et al., 2014). Хэм и др. (2015) и O’Keefe (2018) появились в первоначальных результатах поиска, но были исключены, поскольку они содержали метаобзоры, а не оригинальные исследования. Три статьи были добавлены к результатам методом снежного кома, учитывая, что они специально касались шкал воспринимаемой убедительности:
Мы также провели поиск в материалах «Международной конференции по технологиям убеждения» за период с 2013 по 2018 год. Мы искали исследования пользователей, в которых была разработана или использовалась шкала для измерения воспринимаемой убедительности. В результате поиска было найдено 12 статей, в том числе 2 статьи, не относящиеся к компьютерным наукам, из области маркетинга и коммуникаций (Koch and Zerbac, 2013; Zhang et al., 2014). Хэм и др. (2015) и O’Keefe (2018) появились в первоначальных результатах поиска, но были исключены, поскольку они содержали метаобзоры, а не оригинальные исследования. Три статьи были добавлены к результатам методом снежного кома, учитывая, что они специально касались шкал воспринимаемой убедительности:
• Каптейн и др. (2009), цитируется в Busch et al. (2013).
• MacKenzie and Lutz (1989), цитируется в Ham et al. (2015).
• Чжао и др. (2011), цитируется в O’Keefe (2018).
Результаты поиска литературы показаны в таблице 1, в которой перечислены 60 пунктов шкалы и их измерения, основанные на исследованиях, опубликованных в этих 15 статьях 1 .
К сожалению, в большинстве исследований не сообщается о конструкции, надежности или валидации весов. Исключения составляют Kaptein et al. (2009 г.) и Буш и др. (2013). Однако Каптейн и соавт. Шкала (2009) действительно измеряет восприимчивость участников к определенным принципам убеждения Чалдини (таким как симпатия и авторитет) (Чалдини, 2009), а не к убеждению самих сообщений. Точно так же Busch et al. (2013) направлен на измерение убедительности участников с помощью определенных стратегий убеждения (таких как социальное сравнение и вознаграждение).
Мы сократили 60 элементов, перечисленных в таблице 1, в два этапа. Во-первых, мы удалили дубликаты и объединили очень похожие элементы. Затем мы преобразовали элементы, которые еще не были связаны с сообщением, где это возможно (элементы 9, 11–13, 35–36). Например, пункт 11 «Эта функция поможет мне больше узнать о [политике]» был изменен на «Это сообщение поможет мне лучше узнать о моем поведении», а пункт 35 «Я всегда следую советам своего врача общей практики» был изменен на « Я буду следить за этим сообщением». Наконец, мы удалили пункты, для которых это было невозможно (например, пункты 37–44, которые измеряют восприимчивость человека, и такие пункты, как 10, 55). Это сократило список до 30 элементов, использованных для начальной разработки шкалы, как показано в Таблице 2, где также показано, из каких исходных элементов они были получены.
Наконец, мы удалили пункты, для которых это было невозможно (например, пункты 37–44, которые измеряют восприимчивость человека, и такие пункты, как 10, 55). Это сократило список до 30 элементов, использованных для начальной разработки шкалы, как показано в Таблице 2, где также показано, из каких исходных элементов они были получены.
Таблица 2 . Элементы шкалы, разработанные для использования в исследовании 1.
Ограничение нашего систематического обзора литературы заключается в том, что он в основном ограничивался статьями, опубликованными в период 2014–2018 гг. 2 . Кроме того, в систематическом обзоре статьи могут быть пропущены из-за используемых терминов поиска или ограничений поиска рефератов, заголовков и ключевых слов. Некоторые другие документы, связанные с измерением убедительности, были обнаружены после завершения обзора, что особенно заметно (Фелтэм, 1994; Аллен и др., 2000; Лехто и др., 2012; Попова и др., 2014; Ясек и др., 2015 г. ; Изер и др., 2015; Маклин и др., 2016). Мы обсудим, как шкалы, разработанные в этой статье, связаны с этой другой работой в нашем разделе обсуждения.
; Изер и др., 2015; Маклин и др., 2016). Мы обсудим, как шкалы, разработанные в этой статье, связаны с этой другой работой в нашем разделе обсуждения.
3. Дизайн исследования
3.1. Исследование 1: Разработка шкалы воспринимаемой убедительности
Мы провели исследование, чтобы разработать рейтинговую шкалу для измерения «воспринимаемой убедительности» сообщений. Цель состояла в том, чтобы получить шкалу с хорошей внутренней согласованностью и по крайней мере с тремя пунктами на фактор в соответствии с рекомендациями MacCallum et al. (1999) иметь не менее трех-четырех позиций с высокими нагрузками на фактор.
3.1.1. Участники
Участники этого исследования были набраны путем обмена ссылкой на исследование через социальные сети и списки рассылки. В исследовании было четыре проверочных вопроса, чтобы проверить, рандомно ли участники оценивали шкалы. После удаления таких участников всего 92 участника оценили 249 сообщений.
3.1.2. Процедура
Каждому участнику был показан набор из пяти сообщений (см. Таблицу 4), каждое из которых пропагандировало здоровое питание. Эти сообщения были основаны на различных схем аргументации 3 (Walton et al., 2008) и были получены в другом исследовании с использованием системы генерации сообщений (Thomas et al., 2018). Каждое сообщение оценивалось с использованием 34 пунктов шкалы (пункты шкалы, отмеченные *, служат проверкой достоверности) по 7-балльной шкале Лайкерта, которая варьируется от «полностью не согласен» до «полностью согласен» (см. Таблицу 2 и Рисунок 1). Наконец, участникам была предоставлена возможность оставить отзыв.
Таблицу 4), каждое из которых пропагандировало здоровое питание. Эти сообщения были основаны на различных схем аргументации 3 (Walton et al., 2008) и были получены в другом исследовании с использованием системы генерации сообщений (Thomas et al., 2018). Каждое сообщение оценивалось с использованием 34 пунктов шкалы (пункты шкалы, отмеченные *, служат проверкой достоверности) по 7-балльной шкале Лайкерта, которая варьируется от «полностью не согласен» до «полностью согласен» (см. Таблицу 2 и Рисунок 1). Наконец, участникам была предоставлена возможность оставить отзыв.
Рисунок 1 . Снимок экрана исследования 1, показывающий сообщение с оцениваемым элементом шкалы.
3.1.3. Вопрос исследования и гипотеза
Нас интересовал следующий вопрос исследования:
• RQ1: Какова надежная шкала для измерения воспринимаемой убедительности?
Кроме того, мы хотели изучить полезность шкалы, проанализировав, влияют ли различные типы сообщений на оценки разработанных факторов. Поэтому мы сформулировали следующую гипотезу:
Поэтому мы сформулировали следующую гипотезу:
• h2: Воспринимаемая убедительность каждого фактора различается для разных типов сообщений.
3.2. Исследование 2: Проверка шкалы воспринимаемой убедительности
Затем мы провели исследование, чтобы определить конструктную валидность разработанной шкалы. Мы воспроизвели масштабное тестирование в области безопасности электронной почты, используя другой набор данных.
3.2.1. Участники
Участники этого исследования были набраны путем обмена ссылкой на исследование через социальные сети и списки рассылки. После удаления недействительных участников (как и раньше) всего 134 участника оценили 573 сообщения.
3.2.2. Процедура
Каждому участнику был показан набор из пяти сообщений (см. Таблицу 5), которые способствуют безопасности электронной почты, опять же на основе схем аргументации. Каждое сообщение оценивалось по шкале (см. Таблицу 6 и Рисунок 2), полученной в ходе исследования 1. Наконец, участникам была предоставлена возможность оставить отзыв.
Рисунок 2 . Снимок экрана исследования 2, показывающий сообщение с оцениваемыми элементами шкалы.
3.2.3. Исследовательский вопрос и гипотезы
Нас интересовал следующий исследовательский вопрос:
• RQ2: Насколько обоснована разработанная шкала воспринимаемой убедительности?
Наше первое исследование «Разработка шкалы воспринимаемой убедительности» привело к созданию шкалы с тремя факторами для измерения воспринимаемой убедительности: эффективность, качество и возможности (см. раздел 4.1). Мы хотели изучить полезность этой шкалы, проанализировав, различаются ли типы сообщений по этим трем разработанным факторам. Поэтому мы сформулировали следующие гипотезы:
• h3: Воспринимаемый фактор убедительности Эффективность различается для разных типов сообщений.
• h4: Воспринимаемый фактор убедительности Качество различается для разных типов сообщений.
• h5: Воспринимаемый фактор убедительности Возможности различаются для разных типов сообщений.
• H5: Общая воспринимаемая убедительность 4 различается для разных типов сообщений.
4. Результаты
4.1. Исследование 1: Разработка шкалы воспринимаемой убедительности
Сначала мы проверили показатель адекватности выборки Кайзера-Мейера-Олкина, который был выше 0,90. В соответствии с этой мерой значения в пределах 0,90 указывают на то, что адекватность выборки является «изумительной» (Dziuban and Shirkey, 1980). Затем мы исследовали межэлементные корреляции. Для факторного анализа все пункты 7-балльной шкалы считались порядковыми показателями. Чтобы дополнительно отфильтровать элементы и определить факторы, мы провели Исследовательский факторный анализ (EFA) с использованием извлечения анализа основных компонентов и вращения Varimax с нормализацией Кайзера (Howitt and Cramer, 2014). Было использовано вращение Varimax, так как матрица была подтверждена ортогональной (матрица корреляции компонентов показывает, что большинство корреляций было меньше 0,5). Мы получили три фактора (см. табл. 2). Первый фактор мы назвали «Эффективность», поскольку его элементы связаны с поведением пользователя, изменениями отношения и достижением целей пользователя. Второй мы назвали Качеством, так как его элементы относятся к характеристикам силы сообщения, таким как достоверность и уместность. Третью мы назвали Capability, так как ее элементы относятся к потенциал для мотивации пользователей к изменению поведения. Мы удалили 13 пунктов, которые перекликаются с различными факторами (см. Таблицу 2 с пунктами шкалы, помеченными ® ). Это привело к Таблице 3, которая показывает уменьшенные элементы шкалы для трех факторов. Мы проверили альфу Кронбаха всех элементов, относящихся к трем факторам, по отдельности. Он был выше 0,9 для каждого из трех факторов, что указывает на «отличную» надежность шкалы.
Мы получили три фактора (см. табл. 2). Первый фактор мы назвали «Эффективность», поскольку его элементы связаны с поведением пользователя, изменениями отношения и достижением целей пользователя. Второй мы назвали Качеством, так как его элементы относятся к характеристикам силы сообщения, таким как достоверность и уместность. Третью мы назвали Capability, так как ее элементы относятся к потенциал для мотивации пользователей к изменению поведения. Мы удалили 13 пунктов, которые перекликаются с различными факторами (см. Таблицу 2 с пунктами шкалы, помеченными ® ). Это привело к Таблице 3, которая показывает уменьшенные элементы шкалы для трех факторов. Мы проверили альфу Кронбаха всех элементов, относящихся к трем факторам, по отдельности. Он был выше 0,9 для каждого из трех факторов, что указывает на «отличную» надежность шкалы.
Таблица 3 . Исследование 1: Предметы с уменьшенной шкалой после EFA.
Таблица 4 . Сообщения о здоровом питании, использованные в исследовании 1, с соответствующими схемами аргументации.
Таблица 5 . Сообщения безопасности электронной почты, использованные в исследовании 2, с соответствующими схемами аргументации.
Затем мы провели подтверждающий факторный анализ (CFA), чтобы определить достоверность шкалы и подтвердить факторы и элементы путем проверки соответствия модели (Hu and Bentler, 1999). На основании этих анализов 8 пунктов были удалены из-за высоких стандартизованных остаточных ковариаций с несколькими другими пунктами, которые превышали 0,4. Удаленные элементы — это элементы в таблице 3, отмеченные цифрой 9.1386® .
В таблице 6 показана результирующая шкала из 9 пунктов. Окончательный подтверждающий факторный анализ привел к следующим значениям индекса Такера-Льюиса (TLI) = 0,988, сравнительного индекса соответствия (CFI) = 0,993 и среднеквадратической ошибки аппроксимации (RMSEA) = 0,054 при извлечении трех факторов и их предметы. Пороговое значение, близкое к 0,95 для TLI и CFI (чем выше, тем лучше), и пороговое значение, близкое к 0,60 для RMSEA (чем ниже, тем лучше), необходимы для установления приемлемого соответствия модели между гипотетической моделью и наблюдаемыми данными. (Ху и Бентлер, 19 лет)99; Шрайбер и др., 2006). В полученной шкале TLI и CFI выше 0,95, а RMSEA ниже 0,60, что показывает приемлемое соответствие модели. Это отвечает на исследовательский вопрос RQ1.
(Ху и Бентлер, 19 лет)99; Шрайбер и др., 2006). В полученной шкале TLI и CFI выше 0,95, а RMSEA ниже 0,60, что показывает приемлемое соответствие модели. Это отвечает на исследовательский вопрос RQ1.
Таблица 6 . Исследование 1: Элементы уменьшенной шкалы после CFA.
4.2. Исследование 1: Влияние типов сообщений на факторы
На рисунке 3 показаны средние показатели эффективности, качества, возможностей и общей воспринимаемой убедительности типов сообщений, используемых для сообщений о здоровом питании. Общая воспринимаемая убедительность рассчитывалась как среднее значение факторов: Эффективность, Качество и Возможности.
Рисунок 3 . Сообщения о здоровом питании: среднее значение факторов и общий рейтинг по разработанной шкале для каждого типа сообщения.
Односторонние повторные измерения MANOVA с эффективностью, качеством, возможностями и общей воспринимаемой убедительностью в качестве зависимых переменных и типом сообщения в качестве независимой переменной предоставили результаты для анализа, приведенного ниже. Чтобы определить однородные подмножества, диапазон Райана-Эйнота-Габриэля-Уэлша был выбран в качестве апостериорного теста , поскольку у нас есть более 3 уровней в независимой переменной (т. Е. Тип сообщения).
Чтобы определить однородные подмножества, диапазон Райана-Эйнота-Габриэля-Уэлша был выбран в качестве апостериорного теста , поскольку у нас есть более 3 уровней в независимой переменной (т. Е. Тип сообщения).
По данным Thomas et al. (2018), схемы аргументации можно сопоставить с принципами убеждения Чалдини.
1. Принцип Чалдини: Обязательства и последовательность Аргумент от приверженности к цели Практические рассуждения с целью. Аргумент от невозвратных затрат с действием
2. Принцип Чалдини: Авторитет Аргумент от экспертного мнения с целью Аргумент от положения к знанию с целью.
Исследование, проведенное Thomas et al. (2017) утверждает, что Авторитет был значительно более убедительным, за ним следовали Обязательства и Последовательность и другие принципы Чалдини. Нам было интересно узнать, будут ли наши выводы схожими. Следовательно, анализ будет учитывать как схемы аргументации, так и принципы Чалдини при обсуждении результатов.
4.
 2.1. Влияние типов сообщений на эффективность
2.1. Влияние типов сообщений на эффективностьСогласно рис. 3, АРГУМЕНТ ОТ ОБЯЗАТЕЛЬСТВА С ЦЕЛЬЮ получил наивысшую оценку эффективности, а АРГУМЕНТ ИЗ ПОЛОЖЕНИЯ ЗНАТЬ С ЦЕЛЬЮ — самый низкий. Тип сообщения существенно влиял на эффективность [ F (4, 244) = 4,39, p < 0,01]. Существовала значительная разница между АРГУМЕНТ ОТ ПОЗИЦИИ ДО ЗНАТЬ С ЦЕЛЬЮ и другими типами сообщений ( р < 0,05). Остальные были несущественны. В таблице 7 показаны однородные подмножества. Это частично подтверждает гипотезу (h2) о том, что воспринимаемая убедительность по каждому фактору различается для разных типов сообщений.
Таблица 7 . Исследование 1: Однородные подмножества эффективности, качества и возможностей.
Как показано, два сообщения авторитета имели самые низкие оценки эффективности, хотя АРГУМЕНТ ИЗ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ не был оценен значительно ниже, чем сообщения обязательств и согласованности. Мы видим, что Эффективность всех сообщений была низкой, ниже или около средней точки шкалы. Это противоречит результатам Томаса и соавт. (2017), где сообщения об авторитете, обязательствах и последовательности были наиболее убедительными, хотя, конечно, в их исследовании учитывалась только общая воспринимаемая убедительность без использования проверенной шкалы.
Мы видим, что Эффективность всех сообщений была низкой, ниже или около средней точки шкалы. Это противоречит результатам Томаса и соавт. (2017), где сообщения об авторитете, обязательствах и последовательности были наиболее убедительными, хотя, конечно, в их исследовании учитывалась только общая воспринимаемая убедительность без использования проверенной шкалы.
4.2.2. Влияние типов сообщений на качество
Согласно рис. 3, сообщения о здоровом питании АРГУМЕНТ ОТ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ получили наивысшую оценку качества, а АРГУМЕНТ ИЗ ПОЛОЖЕНИЯ ЗНАТЬ С ЦЕЛЬЮ — самую низкую. Тип сообщения значительно влиял на качество [ F (4, 244) = 12,14, p < 0,001]. Существовала значительная разница ( p < 0,05) между:
1, АРГУМЕНТ ОТ ПОЗИЦИИ ЗНАТЬ С ЦЕЛЬЮ и сообщения других типов,
2. АРГУМЕНТ ОТ ПОТРЕБЛЕННЫХ ЗАТРАТ С ДЕЙСТВИЕМ и другие типы сообщений, кроме ПРАКТИЧЕСКОЕ ОБОСНОВАНИЕ С ЦЕЛЬЮ ,
2. 2. и другие типы сообщений, кроме АРГУМЕНТ ОТ ОБЯЗАТЕЛЬСТВА С ЦЕЛЬЮ и
2. и другие типы сообщений, кроме АРГУМЕНТ ОТ ОБЯЗАТЕЛЬСТВА С ЦЕЛЬЮ и
4. АРГУМЕНТ ОТ ОБЯЗАТЕЛЬСТВА С ЦЕЛЬЮ и другие типы сообщений, кроме АРГУМЕНТ ОТ ЭКСПЕРТНОГО МНЕНИЯ С ЦЕЛЬЮ .
В таблице 7 показаны однородные подмножества. Это частично подтверждает гипотезу (h2) о том, что воспринимаемая убедительность по каждому фактору различается для разных типов сообщений. Однако следует отметить, что одно сообщение авторитета является худшим, а другое — лучшим по качеству. Это может быть вызвано либо атрибутами самого сообщения, либо одной из схем аргументации Администрации, приводящей к сообщениям более высокого качества, чем другая.
4.2.3. Влияние типов сообщений на возможности
Согласно рис. 3, сообщение АРГУМЕНТ ОТ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ получило несколько более высокую оценку качества по сравнению с другими типами сообщений. Не было существенного влияния типа сообщения на возможности [ F (4, 244) = 0,98, p > 0,05]. В таблице 7 показаны однородные подмножества. Это не подтверждает гипотезу (h2) о том, что воспринимаемая убедительность каждого фактора различается для разных типов сообщений. Все типы сообщений одинаково хорошо показали себя с точки зрения возможности, которая была выше средней точки шкалы.
В таблице 7 показаны однородные подмножества. Это не подтверждает гипотезу (h2) о том, что воспринимаемая убедительность каждого фактора различается для разных типов сообщений. Все типы сообщений одинаково хорошо показали себя с точки зрения возможности, которая была выше средней точки шкалы.
4.2.4. Влияние типов сообщений на общую воспринимаемую убедительность
Согласно рисунку 3, АРГУМЕНТ ОТ ОБЯЗАТЕЛЬСТВА С ЦЕЛЬЮ получил наивысшую общую оценку, а АРГУМЕНТ ИЗ ПОЛОЖЕНИЯ ЗНАТЬ С ЦЕЛЬЮ — самый низкий. Было выявлено значительное влияние типа сообщения на общую воспринимаемую убедительность [ F (4, 244) = 4,98, p < 0,01]. АРГУМЕНТ ИЗ ПОЛОЖЕНИЯ ЗНАТЬ С ЦЕЛЬЮ значительно отличался от АРГУМЕНТ ОТ ЭКСПЕРТНОГО МНЕНИЯ С ЦЕЛЬЮ и АРГУМЕНТ ОТ ОБЯЗАТЕЛЬСТВА С ЦЕЛЬЮ ( p < 0,05). Остальные были несущественны. В таблице 8 показаны однородные подмножества. Это частично подтверждает гипотезу (h2) о том, что каждый фактор отличается для разных типов сообщений.
Таблица 8 . Исследование 1: Однородные подмножества для общей воспринимаемой убедительности.
4.3. Исследование 2: Валидация шкалы воспринимаемой убедительности
Чтобы определить конструктную валидность шкалы, разработанной в исследовании 1, и воспроизвести тестирование шкалы, мы:
1. Использовали раздельную проверку 80-20 на исходном наборе данных исследования 1. С этой конкретной комбинацией разработанная шкала привела к приемлемому соответствию модели на 80% (TLI = 0,975, CFI = 0,985, RMSEA = 0,081) и 20% данных (TLI = 0,975, CFI = 0,985, RMSEA = 0,080).
2. Использовали набор данных, полученный в результате проверки в исследовании 2. С этим набором данных разработанная модель дала приемлемое соответствие (TLI = 0,984, CFI = 0,990, RMSEA = 0,071).
Это ответ на исследовательский вопрос RQ2, подтверждающий правильность шкалы.
4.4. Исследование 2: Влияние типов сообщений на факторы
На рис. 4 показаны средние показатели эффективности, качества, возможностей и общей воспринимаемой убедительности типов сообщений, используемых для сообщений безопасности электронной почты. Как и прежде, общая воспринимаемая убедительность рассчитывалась как среднее значение факторов «Эффективность», «Качество» и «Возможность».
Как и прежде, общая воспринимаемая убедительность рассчитывалась как среднее значение факторов «Эффективность», «Качество» и «Возможность».
Рисунок 4 . Сообщения безопасности электронной почты: среднее значение факторов и общий рейтинг по разработанной шкале для каждого типа сообщения.
Односторонние повторные измерения MANOVA с эффективностью, качеством, возможностями и общей воспринимаемой убедительностью в качестве зависимых переменных и типом сообщения в качестве независимой переменной предоставили результаты для анализа, приведенного ниже. Для определения однородных подмножеств диапазон Райана-Эйно-Габриэля-Уэлша был выбран как апостериорный тест , поскольку у нас есть более 3 уровней в независимой переменной (т. Е. Тип сообщения).
4.4.1. Влияние типов сообщений на эффективность
Согласно рис. 4, АРГУМЕНТ ОТ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ получил наивысшую оценку эффективности, а АРГУМЕНТ ИЗ ОБЯЗАТЕЛЬСТВ С ЦЕЛЬЮ — самую низкую. Тип сообщения существенно влиял на эффективность [ F (4, 568) = 4,77, p < 0,01]. АРГУМЕНТ ИЗ ОБЯЗАТЕЛЬСТВ С ЦЕЛЬЮ значительно отличался от АРГУМЕНТ ИЗ ПОЛОЖЕНИЯ ЗНАТЬ С ЦЕЛЬЮ и АРГУМЕНТ ИЗ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ ( p < 0,05). Остальные были несущественны. В таблице 9 показаны однородные подмножества. Это частично поддерживает гипотезу h3, а именно, что воспринимаемая убедительность с точки зрения эффективности различается для разных типов сообщений.
Тип сообщения существенно влиял на эффективность [ F (4, 568) = 4,77, p < 0,01]. АРГУМЕНТ ИЗ ОБЯЗАТЕЛЬСТВ С ЦЕЛЬЮ значительно отличался от АРГУМЕНТ ИЗ ПОЛОЖЕНИЯ ЗНАТЬ С ЦЕЛЬЮ и АРГУМЕНТ ИЗ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ ( p < 0,05). Остальные были несущественны. В таблице 9 показаны однородные подмножества. Это частично поддерживает гипотезу h3, а именно, что воспринимаемая убедительность с точки зрения эффективности различается для разных типов сообщений.
Таблица 9 . Исследование 2: Однородные подмножества эффективности, качества и возможностей.
Подмножества показывают, что авторитетные сообщения в домене безопасности электронной почты показали лучшую эффективность, чем сообщения об обязательствах и непротиворечивости. Это согласуется с выводами исследования Томаса и соавт. (2017) и противоречит тому, что было обнаружено в исследовании 1 для сообщений о здоровом питании.
4.4.2. Влияние типов сообщений на качество
Согласно рис. 4, АРГУМЕНТ ОТ ЭКСПЕРТНОГО МНЕНИЯ С ЦЕЛЬЮ получил наивысшую оценку качества, в то время как АРГУМЕНТ ОТ ОБЯЗАТЕЛЬСТВ С ЦЕЛЬЮ был самым низким. Тип сообщения оказал значительное влияние на качество [ F (4, 568) = 11,97, p < 0,001]. АРГУМЕНТ ИЗ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ значительно отличался от сообщений других типов ( p < 0,05). Остальные были несущественны. В таблице 9 показаны однородные подмножества. Это частично подтверждает гипотезу h4, а именно то, что воспринимаемая убедительность с точки зрения Качества различается для разных типов сообщений.
Мы видим, что АРГУМЕНТ ИЗ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ был оценен значительно выше, чем другие типы сообщений, и что другое сообщение авторитета имело второе по величине среднее значение. Таким образом, в области безопасности электронной почты мы можем заключить, что принцип Авторитета кажется наиболее убедительным при рассмотрении Качества. Мы отмечаем, что АРГУМЕНТ ИЗ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ показал лучшие результаты по качеству в обоих исследованиях, поэтому эта схема аргументации, по-видимому, приводит к сообщениям хорошего качества. Напротив, АРГУМЕНТ ИЗ ПОЗИЦИИ ЗНАТЬ С ЦЕЛЬЮ не преуспел в области здорового питания. Возможно, это доменный эффект: люди больше доверяют людям с опытом в области кибербезопасности, чем в области здорового питания. Мы будем исследовать этот вывод в качестве будущей работы.
Мы отмечаем, что АРГУМЕНТ ИЗ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ показал лучшие результаты по качеству в обоих исследованиях, поэтому эта схема аргументации, по-видимому, приводит к сообщениям хорошего качества. Напротив, АРГУМЕНТ ИЗ ПОЗИЦИИ ЗНАТЬ С ЦЕЛЬЮ не преуспел в области здорового питания. Возможно, это доменный эффект: люди больше доверяют людям с опытом в области кибербезопасности, чем в области здорового питания. Мы будем исследовать этот вывод в качестве будущей работы.
4.4.3. Влияние типов сообщений на возможности
Согласно рисунку 4, АРГУМЕНТ ЭКСПЕРТА С ЦЕЛЬЮ получил наивысшую оценку возможностей, в то время как АРГУМЕНТ ОТ ОБЯЗАТЕЛЬСТВ С ЦЕЛЬЮ был самым низким. Тип сообщения оказал значительное влияние на возможности [ F (4, 568) = 10,84, p < 0,001]. Существовала значительная разница ( p < 0,05) между
1. АРГУМЕНТ ОТ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ и другими типами сообщений.
2. АРГУМЕНТ ОТ ОБЯЗАТЕЛЬСТВА С ЦЕЛЬЮ и АРГУМЕНТ ОТ ПОЛОЖЕНИЯ ЗНАТЬ С ЦЕЛЬЮ .
Значимых различий между АРГУМЕНТ ОТ НЕПОВТОРИМЫХ ЗАТРАТ С ДЕЙСТВИЯМИ и ПРАКТИЧЕСКОЕ ОБОСНОВАНИЕ С ЦЕЛЬЮ не было. В таблице 9 показаны однородные подмножества. Это частично подтверждает гипотезу h5 о том, что воспринимаемая убедительность с точки зрения возможности различается для разных типов сообщений.
Мы видим, что АРГУМЕНТ ИЗ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ был оценен значительно выше, чем другие типы сообщений, и что сообщение другого органа получило второе место. Таким образом, мы можем заключить, что принцип Полномочия также был наиболее убедительным при рассмотрении Способностей. Опять же, мы можем видеть доменные эффекты в этом открытии, с ARGUMENT FROM POSITION TO KNOW работает лучше по сравнению с другими типами сообщений в домене безопасности электронной почты.
4.4.4. Влияние типов сообщений на общую воспринимаемую убедительность
Согласно рис. 4, АРГУМЕНТ ОТ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ получил наивысшую оценку общей воспринимаемой убедительности, а АРГУМЕНТ ОТ ПРИНЯТИЯ ОБЯЗАТЕЛЬСТВ С ЦЕЛЬЮ — самый низкий. Было выявлено значительное влияние типа сообщения на общую воспринимаемую убедительность [9].0710 F (4, 568) = 11,24, р < 0,001]. В таблице 10 показаны однородные подмножества. Это частично подтверждает гипотезу H5 о том, что общая воспринимаемая убедительность различается для разных типов сообщений.
4, АРГУМЕНТ ОТ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ получил наивысшую оценку общей воспринимаемой убедительности, а АРГУМЕНТ ОТ ПРИНЯТИЯ ОБЯЗАТЕЛЬСТВ С ЦЕЛЬЮ — самый низкий. Было выявлено значительное влияние типа сообщения на общую воспринимаемую убедительность [9].0710 F (4, 568) = 11,24, р < 0,001]. В таблице 10 показаны однородные подмножества. Это частично подтверждает гипотезу H5 о том, что общая воспринимаемая убедительность различается для разных типов сообщений.
Таблица 10 . Исследование 2: Однородные подмножества для общей воспринимаемой убедительности.
Общие результаты воспринимаемой убедительности аналогичны результатам для «Влияние типа сообщения на возможности»; опять же, в целом авторитетные сообщения показали хорошие результаты, и даже лучше, чем в области здорового питания.
5. Обсуждение
Результатом наших исследований стала подтвержденная шкала воспринимаемой убедительности, а также понимание воспринимаемой убедительности различных типов сообщений.
5.1. Шкала воспринимаемой убедительности
Что касается шкалы, как упоминалось в ограничениях систематического обзора литературы, есть несколько других работ, в которых предлагались шкалы убедительности, которые не были частью обзора. Использование этих шкал было ограниченным, судя по тому, что они не использовались в рецензируемых документах. Тем не менее, интересно посмотреть, как эти шкалы сравниваются со шкалой, разработанной в этой статье, и рассмотреть, какие существуют совпадения/различия.
Во-первых, Feltham (1994) разработал и утвердил шкалу опросника убеждения (PDI), основанную на трех типах убеждения Аристотеля: этос, пафос и логос (см. Таблицу 11). Этос относится к достоверности источника сообщения, пафос — к аффективной привлекательности сообщения, а логос — к его рациональной привлекательности. Чтобы проверить шкалу PDI, они в основном рассматривали альфа Кронбаха, а не проводили факторный анализ, как это было сделано в этой статье. Их результаты предполагают, что между их коэффициентами масштабирования могут быть перекрестные нагрузки, поскольку они обнаружили положительную корреляцию между Логосом и Этосом. Они также не учитывали, хорошо ли работает шкала в разных областях, поскольку их повторная оценка проводилась в очень похожей области. Что касается содержания шкалы, шкала, разработанная в этой статье, имеет больше элементов, которые непосредственно исследуют воспринимаемую убедительность сообщения, а не эмоциональные и логические элементы, присутствующие в сообщениях, хотя Этос, Логос и Пафос все еще играют роль. Несколько элементов, связанных с Ethos, были включены в наши первоначальные элементы разработки шкалы, а именно: заслуживающий доверия, правдоподобный и заслуживающий доверия. Один из этих пунктов (ср. «заслуживающий доверия») остался в валидированной шкале как часть показателя «Качество». Пункт «точный», являющийся частью фактора Качества, можно интерпретировать как пересечение Этоса и Логоса, поскольку он, с одной стороны, дает ощущение надежности, а с другой — основан на фактах/рациональности/логичности. . Что касается Пафоса, то пункт «Это сообщение может вдохновить пользователей» в факторе Возможности явно связан с Пафосом (как и пункт «мотивация», который не попал в итоговую шкалу).
Они также не учитывали, хорошо ли работает шкала в разных областях, поскольку их повторная оценка проводилась в очень похожей области. Что касается содержания шкалы, шкала, разработанная в этой статье, имеет больше элементов, которые непосредственно исследуют воспринимаемую убедительность сообщения, а не эмоциональные и логические элементы, присутствующие в сообщениях, хотя Этос, Логос и Пафос все еще играют роль. Несколько элементов, связанных с Ethos, были включены в наши первоначальные элементы разработки шкалы, а именно: заслуживающий доверия, правдоподобный и заслуживающий доверия. Один из этих пунктов (ср. «заслуживающий доверия») остался в валидированной шкале как часть показателя «Качество». Пункт «точный», являющийся частью фактора Качества, можно интерпретировать как пересечение Этоса и Логоса, поскольку он, с одной стороны, дает ощущение надежности, а с другой — основан на фактах/рациональности/логичности. . Что касается Пафоса, то пункт «Это сообщение может вдохновить пользователей» в факторе Возможности явно связан с Пафосом (как и пункт «мотивация», который не попал в итоговую шкалу).
Таблица 11 . Перечень убедительных дискурсов (Фелтхэм, 1994).
Второй, Лехто и др. (2012) разработали модель с факторами, которые предсказывают воспринимаемую убедительность, и в рамках этого также рассмотрели внутреннюю согласованность элементов для измерения этих факторов. Некоторые из их факторов (например, диалоговая поддержка, эстетика дизайна) связаны не непосредственно с убедительными сообщениями как таковыми , а скорее с всеобъемлющей системой поведенческого вмешательства, которую они изучали. Целью их работы не было разработать шкалу, поэтому они не пытались разработать факторы, независимые друг от друга, а в основном интересовались тем, как факторы связаны друг с другом. На самом деле, несмотря на то, что они обнаружили адекватную внутреннюю согласованность, они обнаружили довольно много перекрестных нагрузок, при этом элементы одного фактора загружали выше 0,5 по другим факторам. Их проверка была только в области здоровья, и многие из их вопросов были конкретно связаны с их вмешательством (например, пункт поддержки основной задачи «NIV дает мне средство для похудения», пункт поддержки диалога «NIV предоставляет мне соответствующие консультации », воспринимаемый предмет доверия «НИВЛ производится профессионалами в области здравоохранения»). Таким образом, эта работа не привела к созданию шкалы с несколькими независимыми факторами, которую можно использовать в нескольких областях, как шкала, разработанная в этой статье. Учитывая факторы, которые они учитывали, Воспринимаемая достоверность перекрывается с Фактором качества в нашей шкале (см. Заслуживающий доверия). Поддержка основной задачи связана с фактором эффективности в нашей шкале (например, «помогает мне изменить [моё поведение]» связано с «вызывает изменение моего поведения»). Их фактор воспринимаемой убедительности имеет некоторое отношение к нашему фактору возможностей (например, сравните «оказывает на меня влияние» и «имеет потенциал повлиять на поведение пользователя», «заставляет меня пересмотреть [свое поведение]» и «имеет потенциал изменить поведение пользователей»).
Таким образом, эта работа не привела к созданию шкалы с несколькими независимыми факторами, которую можно использовать в нескольких областях, как шкала, разработанная в этой статье. Учитывая факторы, которые они учитывали, Воспринимаемая достоверность перекрывается с Фактором качества в нашей шкале (см. Заслуживающий доверия). Поддержка основной задачи связана с фактором эффективности в нашей шкале (например, «помогает мне изменить [моё поведение]» связано с «вызывает изменение моего поведения»). Их фактор воспринимаемой убедительности имеет некоторое отношение к нашему фактору возможностей (например, сравните «оказывает на меня влияние» и «имеет потенциал повлиять на поведение пользователя», «заставляет меня пересмотреть [свое поведение]» и «имеет потенциал изменить поведение пользователей»).
В-третьих, Allen et al. (2000) сравнили убедительность статистических и нарративных свидетельств в сообщении и разработали две шкалы для проведения этого исследования: шкалу достоверности (измеряющую степень доверия автору сообщения) и шкалу отношения (измеряющую степень доверия к автору сообщения). принимает заключение сообщения). Они проверили, что каждая шкала содержит только один фактор и что каждая шкала внутренне непротиворечива (с точки зрения альфа Кронбаха). Однако они не учитывали, передаются ли пункты одной шкалы в другую шкалу (например, пункты «Я думаю, что автор неправ» из шкалы Отношения и «Автор нечестен» из шкалы Достоверности кажутся связанными, поэтому могут возникнуть перекрестные нагрузки). Они также не удалили элемент с низкой факторной нагрузкой («стиль письма динамичен», нагрузка 0,40) из шкалы достоверности, что может свидетельствовать о плохой структуре шкалы (MacCallum et al., 19).99). Их шкалы измеряют только некоторые аспекты убедительности; например, они не измеряют способность сообщения вдохновлять или вызывать изменение поведения.
принимает заключение сообщения). Они проверили, что каждая шкала содержит только один фактор и что каждая шкала внутренне непротиворечива (с точки зрения альфа Кронбаха). Однако они не учитывали, передаются ли пункты одной шкалы в другую шкалу (например, пункты «Я думаю, что автор неправ» из шкалы Отношения и «Автор нечестен» из шкалы Достоверности кажутся связанными, поэтому могут возникнуть перекрестные нагрузки). Они также не удалили элемент с низкой факторной нагрузкой («стиль письма динамичен», нагрузка 0,40) из шкалы достоверности, что может свидетельствовать о плохой структуре шкалы (MacCallum et al., 19).99). Их шкалы измеряют только некоторые аспекты убедительности; например, они не измеряют способность сообщения вдохновлять или вызывать изменение поведения.
В-четвертых, Попова и др. (2014), Ясек и др. (2015) и Yzer et al. (2015) использовали многоэлементные шкалы, но без этапа разработки. Попова и др. (2014) использовали пять пунктов (убедительно-неубедительно, эффективно-неэффективно, правдоподобно-невероятно, реалистично-нереалистично и запоминающееся-незапоминающееся), Jasek et al. (2015) 13 (скучная, запутанная, убедительная, трудная для просмотра, информативная, заставила бросить курить, заставила закурить, заставила остановиться и подумать, значимая для меня, запоминающаяся, мощная, нелепая, ужасная) и Изер и др. (2015) 7 (убедительно, правдоподобно, запоминающе, хорошо, приятно, позитивно, для таких как я). Между этими пунктами и теми, которые мы использовали для разработки шкалы, есть значительное совпадение, хотя некоторые пункты в этих документах кажутся более связанными с удобством использования (например, «сбивает с толку»), а некоторые — с ощущениями (например, «приятный, » «ужасный»).
(2015) 13 (скучная, запутанная, убедительная, трудная для просмотра, информативная, заставила бросить курить, заставила закурить, заставила остановиться и подумать, значимая для меня, запоминающаяся, мощная, нелепая, ужасная) и Изер и др. (2015) 7 (убедительно, правдоподобно, запоминающе, хорошо, приятно, позитивно, для таких как я). Между этими пунктами и теми, которые мы использовали для разработки шкалы, есть значительное совпадение, хотя некоторые пункты в этих документах кажутся более связанными с удобством использования (например, «сбивает с толку»), а некоторые — с ощущениями (например, «приятный, » «ужасный»).
Пятый, Маклин и др. (2016) разработали шкалу из 13 пунктов для измерения убедительности сообщений с целью снижения стигмы по поводу булимии. Они провели только предварительный факторный анализ (используя рейтинги только 10 сообщений), поэтому никакой реальной проверки. Их шкала имеет два фактора; одно они описывают как убедительность, а другое как вероятность изменения отношения к булимии. Первый фактор включает такие пункты, как «правдоподобный» и «убедительный», которые были частью наших первоначальных пунктов для разработки шкалы и связаны с фактором качества в нашей шкале. Второй фактор связан с фактором возможностей нашей шкалы.
Первый фактор включает такие пункты, как «правдоподобный» и «убедительный», которые были частью наших первоначальных пунктов для разработки шкалы и связаны с фактором качества в нашей шкале. Второй фактор связан с фактором возможностей нашей шкалы.
Таким образом, шкала, разработанная в этой статье, уникальна тем, что она была разработана на основе большого набора вопросов, охватывающих широкий спектр аспектов убедительности, была разработана и утверждена в двух областях и, как было показано, состоит из трех независимых факторов с хорошей внутренней согласованностью. Сравнение содержания шкалы с содержанием других шкал показывает, что шкала также обеспечивает разумное освещение понятий, считающихся важными в литературе (например, присутствуют некоторые аспекты Этоса, Пафоса и Логоса).
5.2. Убедительность типов сообщений
В качестве побочного эффекта наших исследований мы также получили представление об убедительности типов сообщений. Было несколько других статей, исследующих это, хотя в этих исследованиях изучалось только влияние принципов Чалдини, а не более детализированные схемы аргументации. Например, Оржи и др. (2015) и Томас и соавт. (2017) исследовали убедительность принципов здорового питания Чалдини, Smith et al. (2016) для напоминания онкологическим больным, Ciocarlan et al. (2018) за поощрение небольших добрых дел, а Oyibo et al. (2017) в целом, без упоминания конкретных доменов.
Например, Оржи и др. (2015) и Томас и соавт. (2017) исследовали убедительность принципов здорового питания Чалдини, Smith et al. (2016) для напоминания онкологическим больным, Ciocarlan et al. (2018) за поощрение небольших добрых дел, а Oyibo et al. (2017) в целом, без упоминания конкретных доменов.
Томас и др. (2017) обнаружили, что сообщения авторитетов были наиболее убедительными, а сообщения «лайки» — наименее убедительными. Оржи и др. (2015) обнаружили, что приверженность и взаимность были наиболее убедительными для всех возрастов и полов, тогда как консенсус и дефицит были наименее убедительными. Они обнаружили, что женщины лучше реагировали на сообщения о взаимности, приверженности и консенсусе, чем мужчины. Они также заметили, что взрослые лучше реагировали на Обязательство, чем молодые люди, а молодые люди лучше реагировали на Дефицит, чем взрослые. Смит и др. (2016) заметили, что авторитет и симпатия были наиболее популярны для первого напоминания, а предпочтение отдавалось использованию дефицита и приверженности для второго напоминания. Чокарлан и др. (2018) обнаружили, что сообщение о дефиците работает лучше всего. Ойибо и др. (2017) заметили, что их участники были более восприимчивы к авторитету, консенсусу и симпатии.
Чокарлан и др. (2018) обнаружили, что сообщение о дефиците работает лучше всего. Ойибо и др. (2017) заметили, что их участники были более восприимчивы к авторитету, консенсусу и симпатии.
Противоречивые результаты этих исследований могут быть вызваны несколькими причинами. Во-первых, исследования проводились в разных областях. Наши исследования в этой статье показали, что убедительность типов сообщений на самом деле зависит от предметной области. Например, в домене «Здоровое питание» мы обнаружили, что некоторые из схем аргументации, связанных с авторитетом, получили плохие оценки по эффективности, а одна из них также была наихудшей по убедительности в целом, в то время как в домене безопасности электронной почты схемы аргументации, связанные с авторитетом, получили лучшие оценки. Во-вторых, в исследованиях использовались очень разные (и не проверенные) способы измерения убедительности. Таким образом, было бы интересно повторить все эти исследования в различных областях, используя шкалу, разработанную в этой статье. В-третьих, в этих исследованиях не рассматривались более мелкие схемы аргументации, а только принципы Чалдини. Возможно, что, например, сообщения Авторитета, использованные в одном исследовании, следовали другой схеме аргументации (в пределах набора Авторитетов), чем в другом исследовании. Наконец, в отличие от наших исследований, ни в одной из этих работ не рассматривались отдельные факторы убедительности, а рассматривалась только убедительность в целом. Наши исследования показывают, что тип сообщения может иметь плохие оценки по одному параметру убедительности, но хорошие по другим параметрам.
В-третьих, в этих исследованиях не рассматривались более мелкие схемы аргументации, а только принципы Чалдини. Возможно, что, например, сообщения Авторитета, использованные в одном исследовании, следовали другой схеме аргументации (в пределах набора Авторитетов), чем в другом исследовании. Наконец, в отличие от наших исследований, ни в одной из этих работ не рассматривались отдельные факторы убедительности, а рассматривалась только убедительность в целом. Наши исследования показывают, что тип сообщения может иметь плохие оценки по одному параметру убедительности, но хорошие по другим параметрам.
Таким образом, наиболее важные результаты в этой статье относительно убедительности типов сообщений заключаются в том, что (1) эта убедительность зависит от предметной области, (2) важно исследование более мелких схем аргументации, поскольку для разных схем аргументации могут быть получены разные результаты. которые связаны с одними и теми же принципами Чалдини, и (3) исследование разных факторов убедительности имеет значение, поскольку для разных факторов могут быть получены разные результаты.
6. Выводы
В этой статье мы разработали и утвердили шкалу воспринимаемой убедительности, которая будет использоваться при проведении исследований вмешательств в цифровое поведение. Мы провели два исследования в разных областях, чтобы разработать и проверить эту шкалу, а именно в области здорового питания и области безопасности электронной почты. Утвержденная шкала имеет 3 фактора (Эффективность, Качество и Возможности) и 9 пунктов шкалы, как показано в Таблице 6. Мы также обсудили, как эта шкала связана с более ранней работой над шкалами убедительности и расширяет их.
Помимо разработки шкалы и демонстрации ее полезности, мы проанализировали влияние типов сообщений на различные разработанные коэффициенты шкалы. Мы обнаружили, что тип сообщения значительно влияет на эффективность, качество и общую воспринимаемую убедительность в исследованиях как в области здорового питания, так и в области безопасности электронной почты. Мы также обнаружили значительное влияние типа сообщения на возможности в домене безопасности электронной почты. Три фактора (как показано в проверке) измеряют различные аспекты воспринимаемой убедительности. Одним из примеров, где это также можно увидеть, является АРГУМЕНТ ОТ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ тип сообщения, который относительно плохо работает в области эффективности в области здорового питания, но хорошо в отношении качества в этой области. Убедительность сообщений явно зависит от предметной области. Кроме того, наши исследования показывают, что стоит исследовать более тонкие схемы аргументации, а не только принципы Чалдини. Мы обсудили связанную работу по измерению убедительности типов сообщений и объяснили противоречивые результаты этих исследований.
Три фактора (как показано в проверке) измеряют различные аспекты воспринимаемой убедительности. Одним из примеров, где это также можно увидеть, является АРГУМЕНТ ОТ МНЕНИЯ ЭКСПЕРТА С ЦЕЛЬЮ тип сообщения, который относительно плохо работает в области эффективности в области здорового питания, но хорошо в отношении качества в этой области. Убедительность сообщений явно зависит от предметной области. Кроме того, наши исследования показывают, что стоит исследовать более тонкие схемы аргументации, а не только принципы Чалдини. Мы обсудили связанную работу по измерению убедительности типов сообщений и объяснили противоречивые результаты этих исследований.
Как показано в нашем обзоре литературы, исследователи, работающие над цифровыми поведенческими вмешательствами, склонны использовать свои собственные шкалы без надлежащей проверки этих шкал для исследования воспринимаемой убедительности. Утвержденная шкала, разработанная в этой статье, может быть использована для улучшения таких исследований и облегчит сравнение результатов разных исследований и в разных областях. Мы планируем использовать шкалу для изучения влияния персонализации сообщений в разных доменах.
Мы планируем использовать шкалу для изучения влияния персонализации сообщений в разных доменах.
Работа, представленная в этой статье, имеет несколько ограничений. Во-первых, мы проверили шкалу в двух областях (здоровое питание и безопасность электронной почты), и эту проверку необходимо распространить на большее количество областей. Во-вторых, необходимо проверить надежность весов. Чтобы исследовать это, нам нужно провести эксперимент «тест-повторное тестирование», в котором участники проходят одну и ту же шкалу по одним и тем же пунктам дважды с интервалом в несколько дней между двумя измерениями. Это также необходимо будет сделать в нескольких доменах. В-третьих, нам нужно повторить наши исследования типов сообщений воздействия с большим количеством сообщений и в большем количестве доменов.
Заявление о доступности данных
Наборы данных, созданные для этого исследования, доступны по запросу соответствующему автору.
Заявление об этике
Исследования с участием людей были рассмотрены и одобрены комитетом по этике CoPs University of Aberdeen. Многие из этих документов содержали дополнительные пункты; они обычно не были связаны с измерением убедительности. 9Общая воспринимаемая убедительность рассчитывалась как среднее значение факторов: Эффективность, Качество и Возможности.
Многие из этих документов содержали дополнительные пункты; они обычно не были связаны с измерением убедительности. 9Общая воспринимаемая убедительность рассчитывалась как среднее значение факторов: Эффективность, Качество и Возможности.
Ссылки
Allen, M., Bruflat, R., Fucilla, R., Kramer, M., McKellips, S., Ryan, D.J., et al. (2000). Проверка убедительности доказательств: сочетание повествовательной и статистической форм. Комм. Рез. 17, 331–336. doi: 10.1080/088240
388781CrossRef Full Text | Google Scholar
Анагностопулу Э., Магутас Б., Ботос Э., Шраммель Дж., Орджи Р. и Ментзас Г. (2017). «Изучение связей между убеждением, личностью и типами мобильности в персонализированных мобильных приложениях», в Технология убеждения: разработка и внедрение персонализированных технологий для изменения отношения и поведения , редакторы П. В. де Врис, Х. Ойнас-Кукконен, Л. Симонс, Н. Берлаге-де Йонг и Л. ван Гемерт-Пейнен (Cham: Springer Международное издательство), 107–118.
Google Scholar
Буш М., Патил С., Регал Г., Хохлейтнер К. и Челиги М. (2016). «Убедительная информационная безопасность: методы, помогающие сотрудникам защитить организационную информационную безопасность», в Технология убеждения , ред. А. Мещеряков, Б. Де Рюйтер, В. Фуксбергер, М. Мурер и М. Челиги (Cham: Springer International Publishing), 339–351.
Google Scholar
Буш М., Шраммель Дж. и Челиги М. (2013). Персонализированная технология убеждения – разработка и проверка шкал для измерения способности убеждать . Берлин; Гейдельберг: Springer, 33–38.
Google Scholar
Чанг Дж.-Х., Чжу Ю.-К., Ван С.-Х. и Ли Ю.-Дж. (2018). Вы бы передумали? эмпирическое исследование теории социального воздействия на Facebook. Телем. Поставить в известность. 35, 282–292. doi: 10.1016/j.tele.2017.11.009
CrossRef Полный текст | Google Scholar
Чалдини, Р. Б. (2009). Влияние: психология убеждения . Нью-Йорк, штат Нью-Йорк: электронные книги HarperCollins.
Google Scholar
Чокарлан А., Мастофф Дж. и Орен Н. (2018). «Доброта заразительна: исследуйте вовлеченность и адаптируйте убеждающие игры для благополучия», в материалах 26th Conference on User Modeling, Adaptation and Personalization , UMAP ’18 (Нью-Йорк, штат Нью-Йорк: ACM), 311–319.
Google Scholar
Кук А., Прайер Дж. и Шетти П. (2000). Проблема точности диетологических обследований. Анализ более чем 65 национальных обзоров диеты и питания в Великобритании. J. Эпидемиол. коммун. Здоровье 54, 611–616. doi: 10.1136/jech.54.8.611
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Дзюбан, К.Д., и Ширки, Э.К. (1980). Адекватность выборки и семантический дифференциал. Психология. Отчет 47, 351–357. doi: 10.2466/pr0.1980.47.2.351
CrossRef Полный текст | Google Scholar
Feltham, TS (1994). Оценка мнения зрителей о рекламе и транспортных средствах: разработка и проверка масштаба. ACR Северная Ам. Доп. 21, 531–535.
Доп. 21, 531–535.
Google Scholar
Грассо Ф., Коуси А. и Джонс Р. (2000). Диалектическая аргументация для разрешения конфликтов при даче советов: тематическое исследование по продвижению здорового питания. Междунар. Дж. Хам. вычисл. Стад. 53, 1077–1115. doi: 10.1006/ijhc.2000.0429
CrossRef Полный текст | Google Scholar
Хэм, К.-Д., Нельсон, М.Р., и Дас, С. (2015). Как измерить знание убеждения. Междунар. Дж. Реклама. 34, 17–53. doi: 10.1080/02650487.2014.994730
CrossRef Полный текст | Google Scholar
Хаммер С., Лугрин Б., Богомолов С., Яновский К. и Андре Э. (2016). «Исследование стратегий вежливости и их убедительности для робота-помощника пожилого возраста», в Технология убеждения , ред. А. Мещеряков, Б. Де Рюйтер, В. Фуксбергер, М. Мурер и М. Челиги (Cham: Springer International Publishing), 315–326.
Google Scholar
Хоссейн, М. Т., и Сайни, Р. (2014). Утром лохи, вечером скептики: влияние времени суток на бдительность потребителей в отношении манипуляций. Рынок. лат. 25, 109–121. doi: 10.1007/s11002-013-9247-0
Рынок. лат. 25, 109–121. doi: 10.1007/s11002-013-9247-0
CrossRef Полный текст | Google Scholar
Ховитт Д. и Крамер Д. (2014). Введение в статистику SPSS в психологии . Пирсон Образование.
Google Scholar
Ху Л. и Бентлер П. М. (1999). Критерии отсечки для индексов соответствия в ковариационном структурном анализе: традиционные критерии против новых альтернатив. Структура. Экв. Модель. Мультидисциплинарный. Дж. 6, 1–55. doi: 10.1080/107055190118
CrossRef Полный текст | Google Scholar
Ясек Дж. П., Джонс М., Мбамалу И., Ауэр К., Килгор Э. А. и Кансагра С. М. (2015). Одна сигарета — это слишком много: оценка кампании в СМИ, ориентированной на малокурящих. Борьба против табака 24, 362–368. doi: 10.1136/tobaccocontrol-2013-051348
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Каптейн М., Маркопулос П., де Рюйтер Б. и Аартс Э. (2009). Можно ли вас убедить? Индивидуальные различия в восприимчивости к убеждению . Берлин; Гейдельберг: Springer, 115–118.
Берлин; Гейдельберг: Springer, 115–118.
Google Scholar
Кох, Т., и Зербак, Т. (2013). Полезно или вредно? Как частое повторение влияет на воспринимаемую достоверность утверждения. Дж. Комм. 63, 993–1010. doi: 10.1111/jcom.12063
Полный текст CrossRef | Google Scholar
Лехто Т., Ойнас-Кукконен Х. и Дрозд Ф. (2012). «Факторы, влияющие на воспринимаемую убедительность системы поддержки изменения поведения», в Thirty Third International Conference on Information Systems, Orlando . Орландо.
Google Scholar
MacCallum, R.C., Widaman, K.F., Zhang, S., and Hong, S. (1999). Размер выборки в факторном анализе. Психология. Методы 4:84.
Google Scholar
Маккензи С. Б. и Лутц Р. Дж. (1989). Эмпирическое исследование структурных предпосылок отношения к рекламе в контексте предварительного тестирования рекламы. Дж. Рынок. 53, 48–65.
Google Scholar
Маззотта И., де Росис Ф. и Карофильо В. (2007). Portia: адаптированная для пользователей система убеждения в области здорового питания. IEEE Intel. Сист. 22, 42–51. doi: 10.1109/MIS.2007.115
(2007). Portia: адаптированная для пользователей система убеждения в области здорового питания. IEEE Intel. Сист. 22, 42–51. doi: 10.1109/MIS.2007.115
CrossRef Полный текст | Академия Google
Маклин, С. А., Пакстон, С. Дж., Мэсси, Р., Хэй, П. Дж., Монд, Дж. М., и Роджерс, Б. (2016). Выявление убедительных сообщений общественного здравоохранения для изменения знаний и отношения сообщества к нервной булимии. J. Health Commun. 21, 178–187. doi: 10.1080/10810730.2015.1049309
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Мещеряков А., Гартнер М., Мирниг А., Рёдель К. и Челиги М. (2016). «Опросник убедительного потенциала (PPQ): проблемы, недостатки и извлеченные уроки», в Технология убеждения , ред. А. Мещеряков, Б. Де Рюйтер, В. Фуксбергер, М. Мурер и М. Челиги (Cham: Springer International Publishing), 162–175.
Google Scholar
Одуор М. и Ойнас-Кукконен Х. (2017). «Устройства приверженности как системы поддержки изменения поведения: исследование воспринимаемой компетентности пользователей и намерения продолжать», в Технология убеждения: разработка и внедрение персонализированных технологий для изменения отношения и поведения , редакторы П. В. де Врис, Х. Ойнас-Кукконен, Л. Симонс, Н. Берлаге-де Йонг и Л. ван Гемерт-Пейнен (Cham: Springer International Publishing), 201–213.
В. де Врис, Х. Ойнас-Кукконен, Л. Симонс, Н. Берлаге-де Йонг и Л. ван Гемерт-Пейнен (Cham: Springer International Publishing), 201–213.
Google Scholar
О’Киф, ди-джей (2018). Предварительное тестирование сообщения с использованием оценок ожидаемой или предполагаемой убедительности: свидетельство о диагностике относительной фактической убедительности. Дж. Комм. 68, 120–142. doi: 10.1093/joc/jqx009
Полный текст CrossRef | Google Scholar
Оржи, Р. (2014). «Изучение убедительности стратегий поддержки изменения поведения и возможных гендерных различий», в Конференция 2-го Международного семинара по системам поддержки изменения поведения , Vol. 1153, ред. Л. ван Гемерт-Пейнен, С. Келдерс, А. Оорни и Х. Ойнас-Кукконен (Аахен: CEUR-WS), 41–57.
Google Scholar
Орджи Р., Мандрик Р. Л. и Васильева Дж. (2015). «Пол, возраст и реакция на стратегии убеждения Чалдини», в Persuasive Technology , eds T. MacTavish and S. Basapur (Cham: Springer International Publishing), 147–159.
Google Scholar
Орджи, Р., Василева, Дж., и Мандрик, Р.Л. (2014). Моделирование эффективности стратегий убеждения для разных типов игроков в серьезных играх на здоровье. Модель пользователя. Пользовательская адаптация. Взаимодействовать. 24, 453–498. doi: 10.1007/s11257-014-9149-8
CrossRef Полный текст | Google Scholar
Ойибо К., Оржи Р. и Василева Дж. (2017). «Исследование влияния черт личности на стратегии убеждения Чалдини», в материалах Proceedings of the 2nd International Workshop on Personalization in Persuasive Technology , Том. 1833 г., ред. Р. Орджи, М. Райзингер, М. Буш, А. Дейкстра, М. Каптейн и Э. Маттейс (CEUR-WS), 8–20.
Google Scholar
Попова Л., Нейландс Т.Б. и Линг П.М. (2014). Тестирование сообщений для снижения готовности курильщиков к употреблению новых бездымных табачных изделий. Борьба против табака 23, 313–321. doi: 10.1136/tobaccocontrol-2012-050723
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Пурпура С. , Шв В., Уильямс К., Стаблер В. и Сенгерс П. (2011). «Fit4life: дизайн убедительной технологии, способствующей здоровому поведению и идеальному весу», в Материалы Международной конференции по человеческому фактору в вычислительных системах, CHI 2011, Ванкувер, Британская Колумбия, Канада, 7–12 мая 2011 г. (Ванкувер: ACM), 423–432.
, Шв В., Уильямс К., Стаблер В. и Сенгерс П. (2011). «Fit4life: дизайн убедительной технологии, способствующей здоровому поведению и идеальному весу», в Материалы Международной конференции по человеческому фактору в вычислительных системах, CHI 2011, Ванкувер, Британская Колумбия, Канада, 7–12 мая 2011 г. (Ванкувер: ACM), 423–432.
Google Scholar
Шрайбер Дж. Б., Нора А., Стейдж Ф. К., Барлоу Э. А. и Кинг Дж. (2006). Отчет о моделировании структурных уравнений и подтверждающих результатах факторного анализа: обзор. Дж. Образовательный. Рез. 99, 323–338. doi: 10.3200/JOER.99.6.323-338
CrossRef Полный текст | Академия Google
Смит, К. А., Деннис, М., и Мастофф, Дж. (2016). «Персонализация напоминаний личности для самопроверки меланомы», в материалах Proceedings of the User Modeling Adaptation and Personalization 2016 (Галифакс), 85–93.
Google Scholar
Томас Р. Дж., Мастофф Дж. и Орен Н. (2017). «Адаптация сообщений о здоровом питании к личности», в Persuasive Technology. 12-я международная конференция, УБЕЖДЕНИЕ 2017, Proceedings (Амстердам: Springer), 119–132.
12-я международная конференция, УБЕЖДЕНИЕ 2017, Proceedings (Амстердам: Springer), 119–132.
Google Scholar
Томас Р. Дж., Орен Н. и Мастофф Дж. (2018). «ArguMessage: система автоматизации генерации сообщений с использованием схем аргументации», в Proceedings of the AISB Annual Convention 2018, 18th Workshop on Computational Models of Natural Argument (Ливерпуль), 27–31.
Google Scholar
Уолтон Д., Рид К. и Маканьо Ф. (2008). Схемы аргументации . Нью-Йорк, штат Нью-Йорк: Издательство Кембриджского университета.
Google Scholar
Wells, S., Kotkanen, H., Schlafli, M., Gabrielli, S., Masthoff, J., Jylhå, A., et al. (2014). На пути к прикладной модели геймификации для отслеживания, управления и поощрения устойчивого поведения в путешествиях. Одобряет EAI. Транс. Окружающая Сист. 1:e2. doi: 10.4108/amsys.1.4.e2
Полный текст CrossRef | Google Scholar
Yzer, M., LoRusso, S., и Nagler, RH (2015). О концептуальной двусмысленности, связанной с предполагаемой эффективностью сообщения.


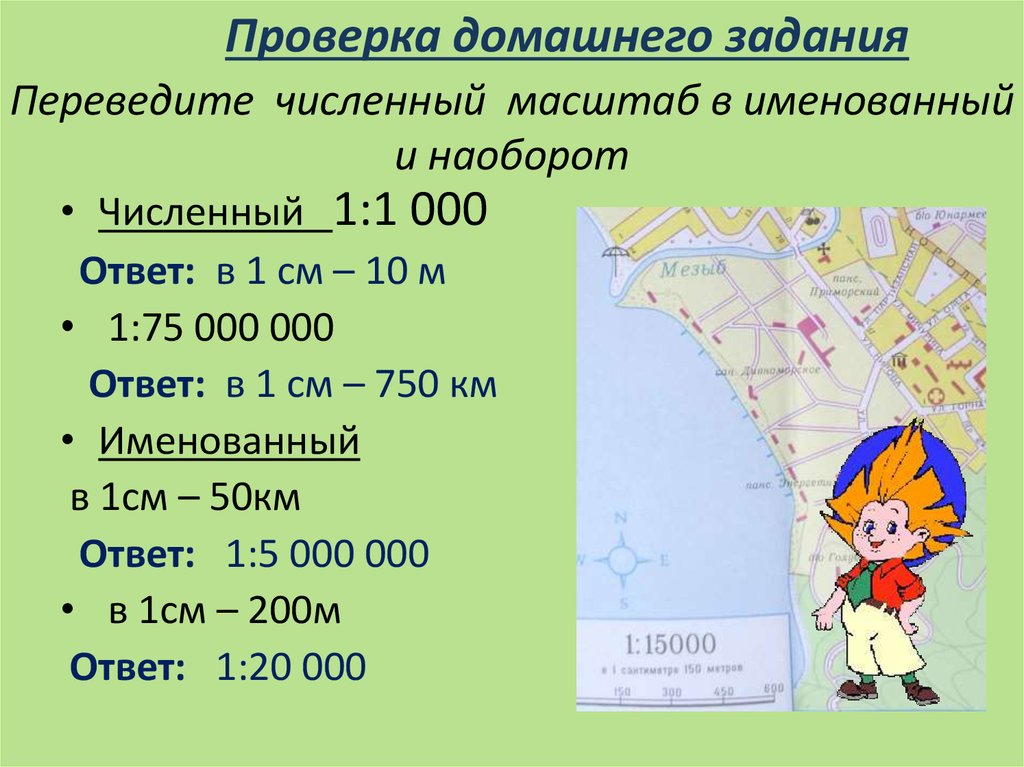 Конечно, для определения данным способом нужно наизусть знать номенклатурные обозначения.
Конечно, для определения данным способом нужно наизусть знать номенклатурные обозначения. 25 га
25 га 01 км) на местности
01 км) на местности 2 км) на местности
2 км) на местности
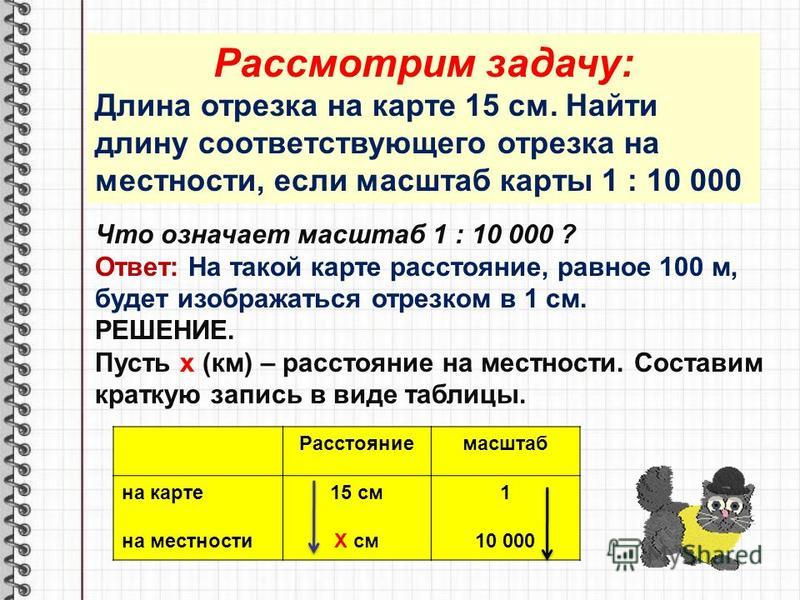
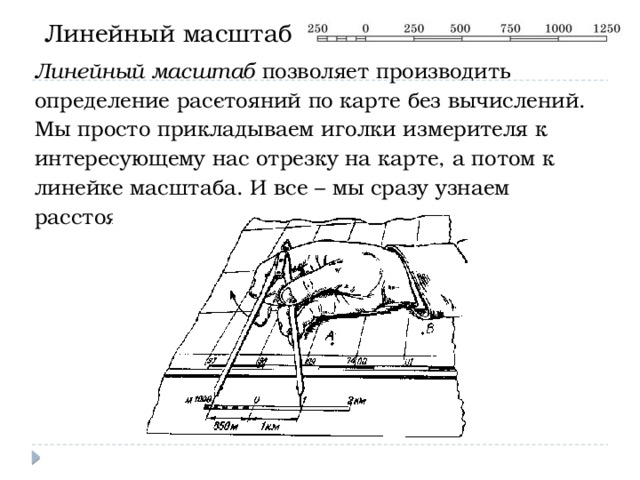
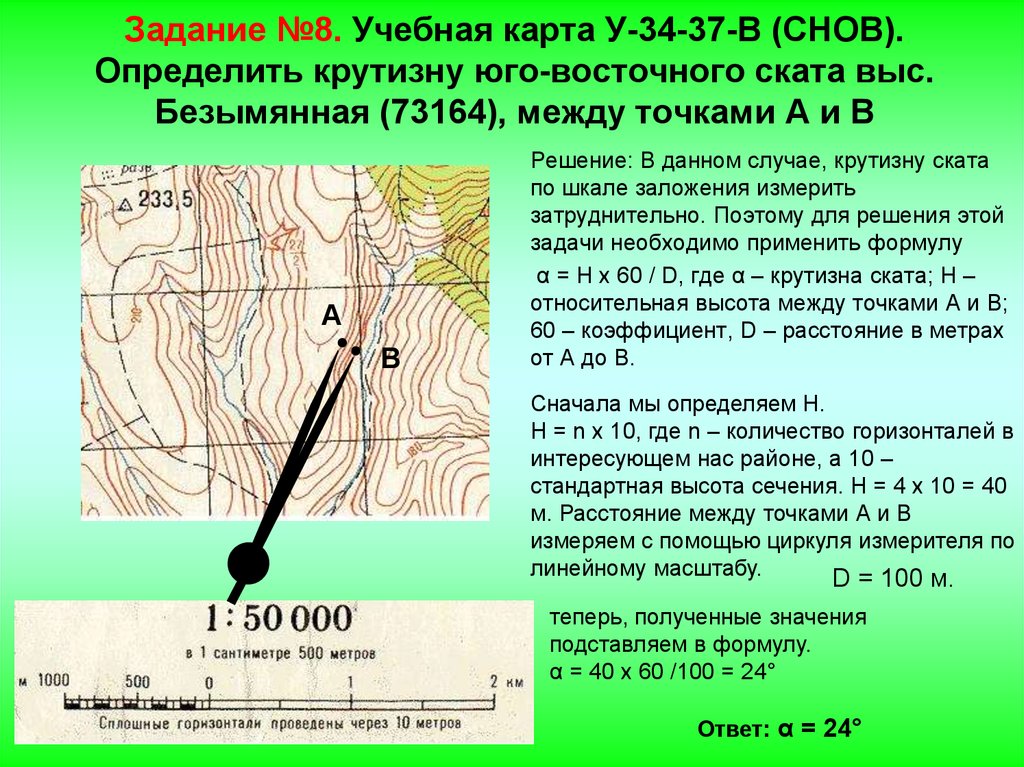
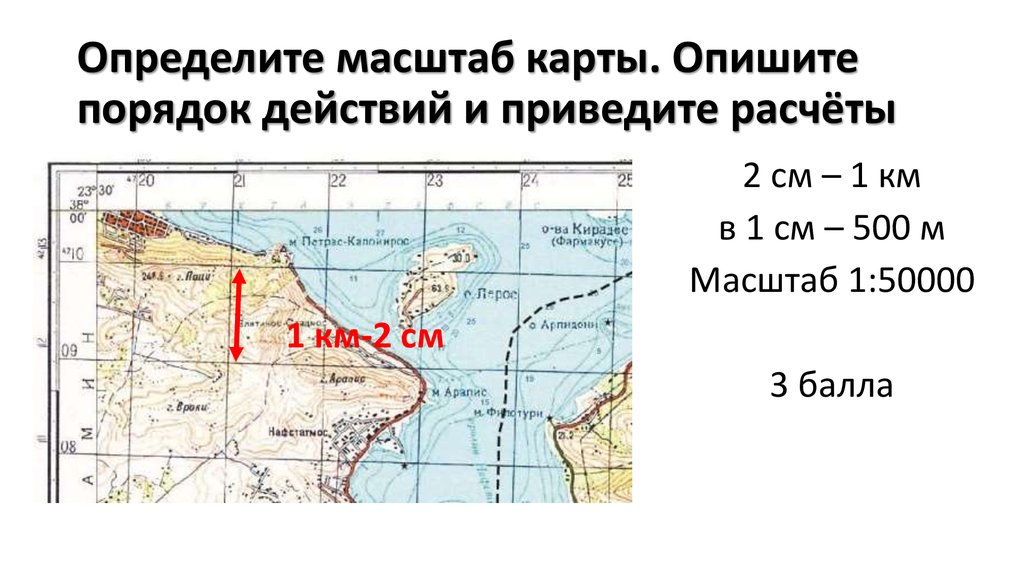 Градусы, например, могут упасть ниже нуля и все еще иметь значение. Но если вы ничего не весите, вы не существуете.
Градусы, например, могут упасть ниже нуля и все еще иметь значение. Но если вы ничего не весите, вы не существуете.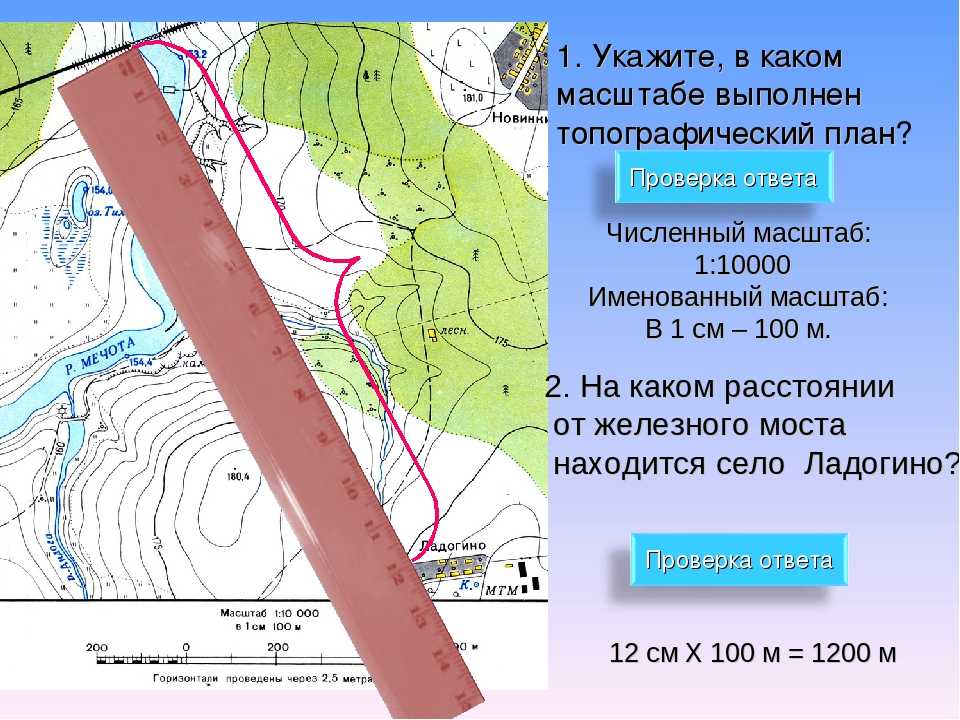
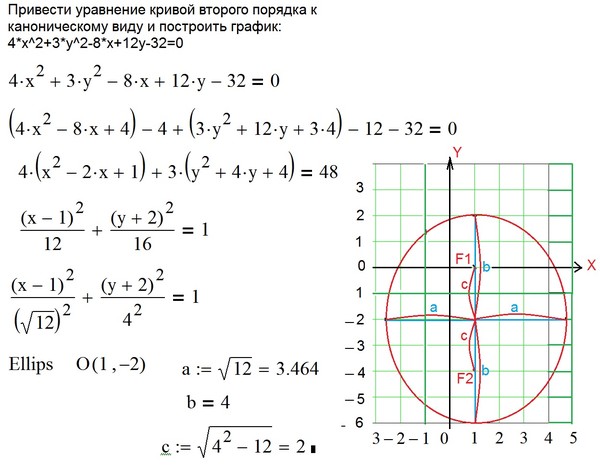 It is convenient to speak of the variable associated with the
first component of an ordered pair as the independent variable and the variable
associated with the second component of an ordered pair as the dependent variable. If the variables x and y are used in an equation, it is understood that replace-
ments for x are first components and hence x is the independent variable and
replacements for y are second components and hence y is the dependent variable.
For example, we can obtain pairings for equation
It is convenient to speak of the variable associated with the
first component of an ordered pair as the independent variable and the variable
associated with the second component of an ordered pair as the dependent variable. If the variables x and y are used in an equation, it is understood that replace-
ments for x are first components and hence x is the independent variable and
replacements for y are second components and hence y is the dependent variable.
For example, we can obtain pairings for equation It is often easier to obtain solutions if equations are first expressed in such form
because the dependent variable is expressed explicitly in terms of the independent
variable.
It is often easier to obtain solutions if equations are first expressed in such form
because the dependent variable is expressed explicitly in terms of the independent
variable.

 If the second component is positive, the point lies above the
horizontal axis; if negative, it lies below.
If the second component is positive, the point lies above the
horizontal axis; if negative, it lies below. In Section 7.2, we saw that the components of an ordered pair are the
coordinates of a point in a plane. Thus, to graph an equation in two variables, we
graph the set of ordered pairs that are solutions to the equation. For example, we
can find some solutions to the first-degree equation
In Section 7.2, we saw that the components of an ordered pair are the
coordinates of a point in a plane. Thus, to graph an equation in two variables, we
graph the set of ordered pairs that are solutions to the equation. For example, we
can find some solutions to the first-degree equation

 We will use
2 and 0 for x.
We will use
2 and 0 for x. In fact, any
ordered pair of the form (-3, y) is a solution
of (2). Graphing the solutions yields a vertical
line as shown in Figure 7.5.
In fact, any
ordered pair of the form (-3, y) is a solution
of (2). Graphing the solutions yields a vertical
line as shown in Figure 7.5. In particular, if we substitute 0 for y in Equation (1), we
get
In particular, if we substitute 0 for y in Equation (1), we
get Graphing these
points and connecting them with a straight line give us the graph of 2x — y = 6.
If the graph intersects the axes at or near the origin, the intercept method is not
satisfactory. We must then graph an ordered pair that is a solution of the equation
and whose graph is not the origin or is not too close to the origin.
Graphing these
points and connecting them with a straight line give us the graph of 2x — y = 6.
If the graph intersects the axes at or near the origin, the intercept method is not
satisfactory. We must then graph an ordered pair that is a solution of the equation
and whose graph is not the origin or is not too close to the origin.

 9. Line l1 has slope m1 = 3, and line l2 has
slope m2 = 3. In this case,
9. Line l1 has slope m1 = 3, and line l2 has
slope m2 = 3. In this case, 1 la), by the slope
formula
1 la), by the slope
formula We could also write the equation in equivalent forms y + 2x = 8,
2x + y = 8, or 2x + y — 8 = 0.
We could also write the equation in equivalent forms y + 2x = 8,
2x + y = 8, or 2x + y — 8 = 0.
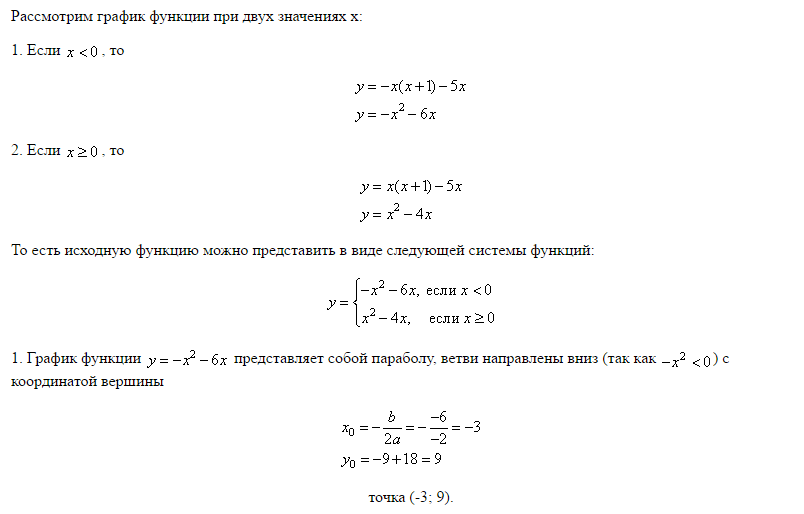
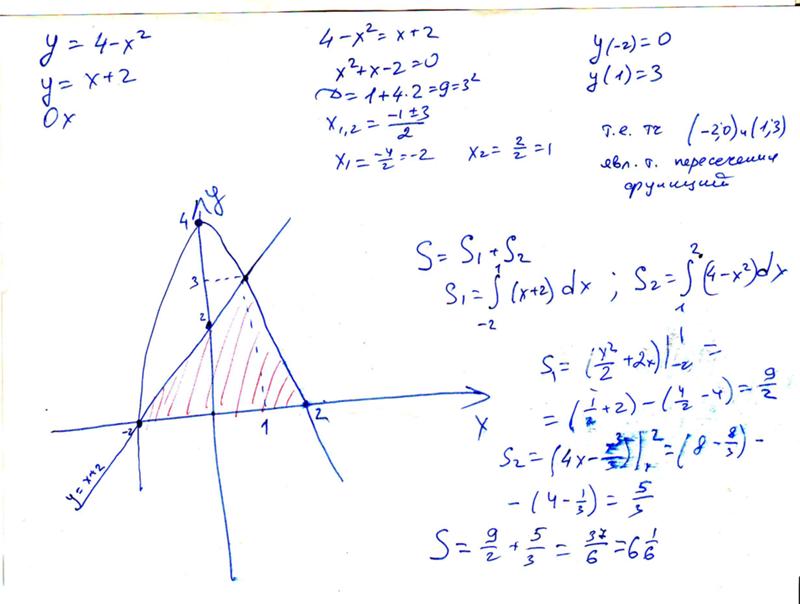 (1, 1)
(1, 1) 

 Function notation f(x) is used to name an algebraic expression in x. When x in
the symbol f(x) is replaced by a particular value, the symbol represents the value
of the expression for that value of x.
Function notation f(x) is used to name an algebraic expression in x. When x in
the symbol f(x) is replaced by a particular value, the symbol represents the value
of the expression for that value of x. However, the two solutions of an equation in two
variables that are generally easiest to find are those in which either the first or
second component is 0. The x-coordinate of the point where a line crosses the x-axis
is called the x-intercept of the line, and the y-coordinate of the point where a line
crosses the y-axis is called they-intercept of the line. Using the intercepts to graph
an equation is called the intercept method of graphing.
However, the two solutions of an equation in two
variables that are generally easiest to find are those in which either the first or
second component is 0. The x-coordinate of the point where a line crosses the x-axis
is called the x-intercept of the line, and the y-coordinate of the point where a line
crosses the y-axis is called they-intercept of the line. Using the intercepts to graph
an equation is called the intercept method of graphing.
 The solutions are the
values of the unknown variables which satisfy both equations simultaneously. In general, if there are \(n\)
unknown variables, then \(n\) independent equations are required to obtain a value for each of the \(n\)
variables.
The solutions are the
values of the unknown variables which satisfy both equations simultaneously. In general, if there are \(n\)
unknown variables, then \(n\) independent equations are required to obtain a value for each of the \(n\)
variables.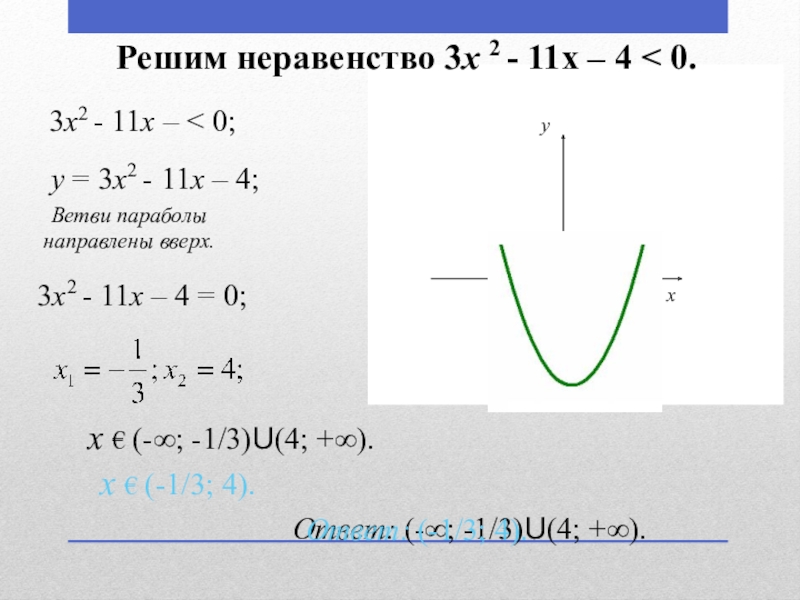 By doing this we reduce the number of equations and the
number of variables by one.
By doing this we reduce the number of equations and the
number of variables by one. Eliminate
the variable \(y\) by adding equation \(\left(1\right)\) and equation \(\left(2\right)\)
together:
Eliminate
the variable \(y\) by adding equation \(\left(1\right)\) and equation \(\left(2\right)\)
together:
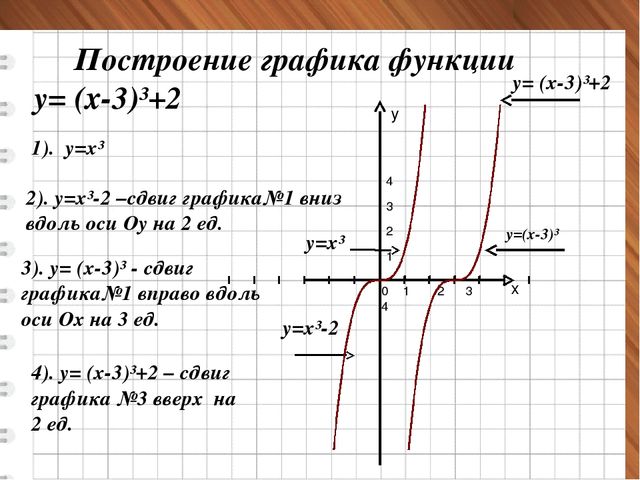 Before beginning this section it may be necessary to revise plotting graphs of linear equations with
your learners.
Before beginning this section it may be necessary to revise plotting graphs of linear equations with
your learners.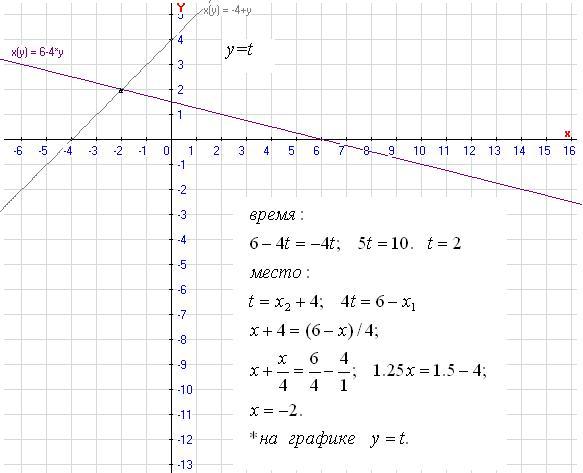
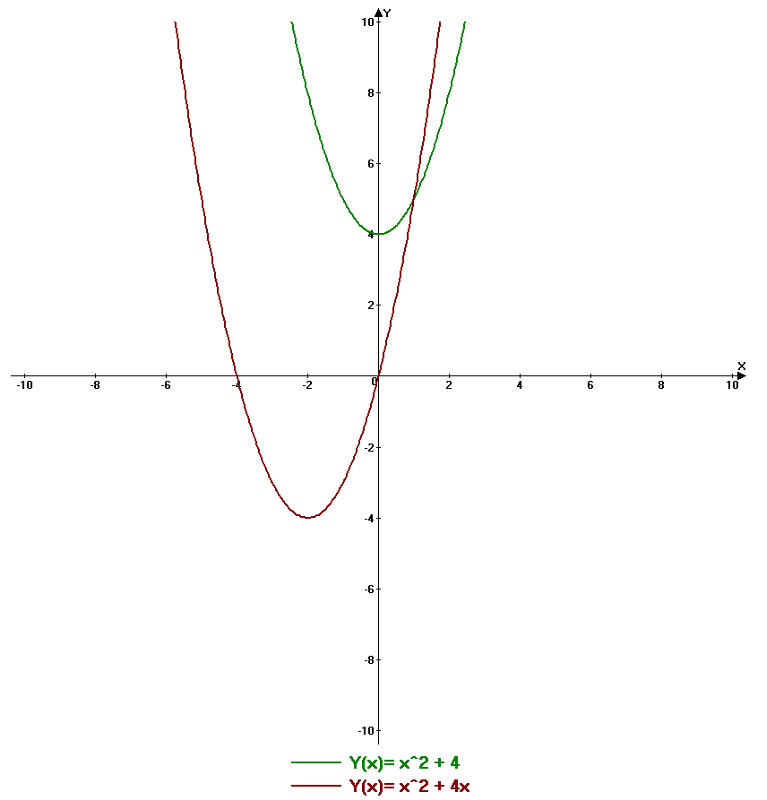 3
3








 2 &= 3 — ab
\end{align*}
2 &= 3 — ab
\end{align*}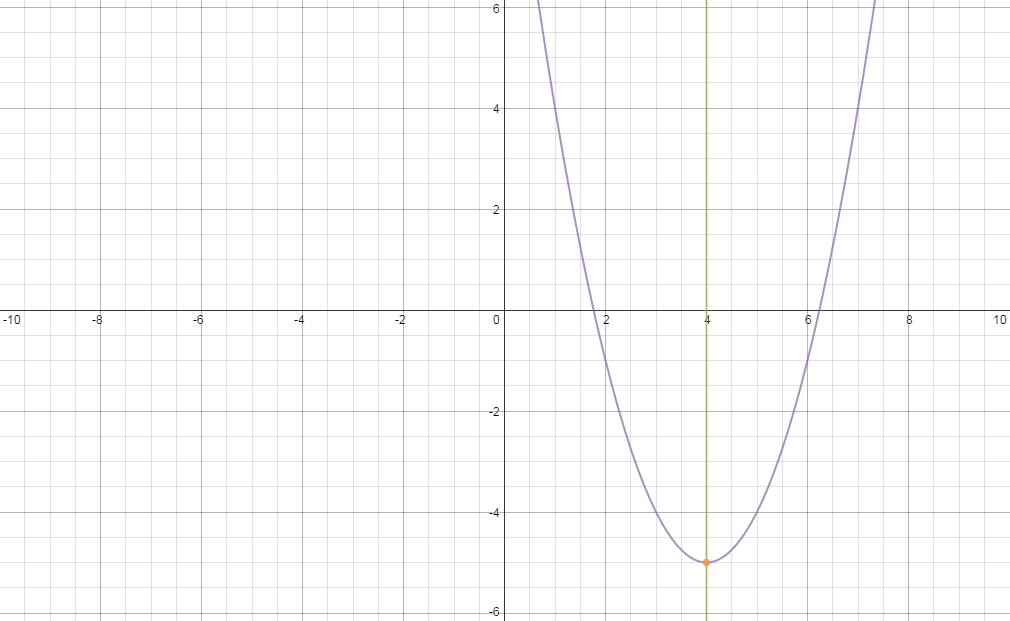
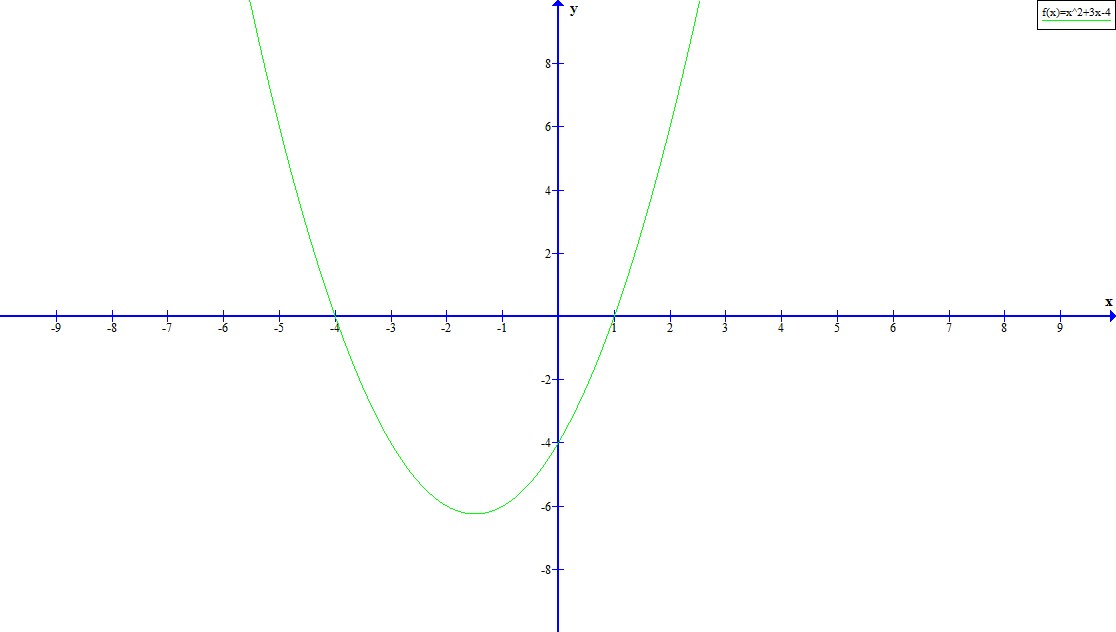

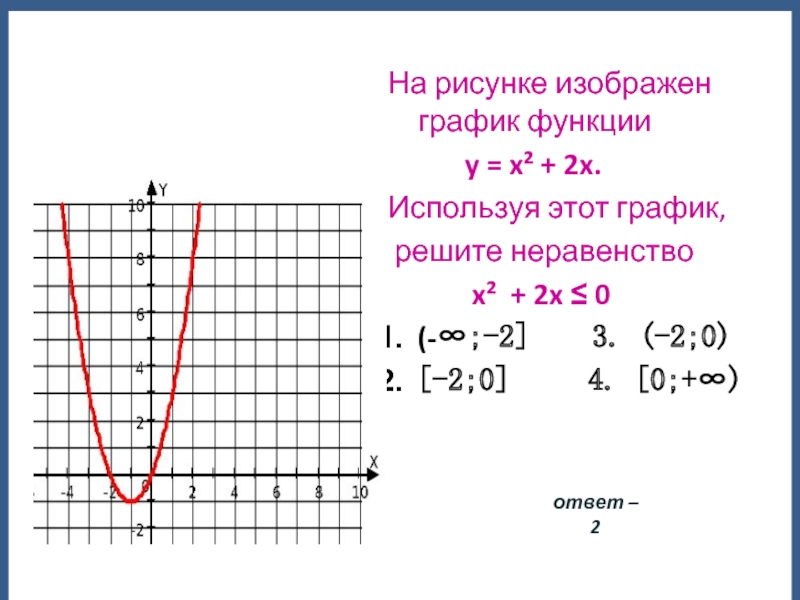
 5 Word problems
5 Word problems 2
>
Question 5
2
>
Question 5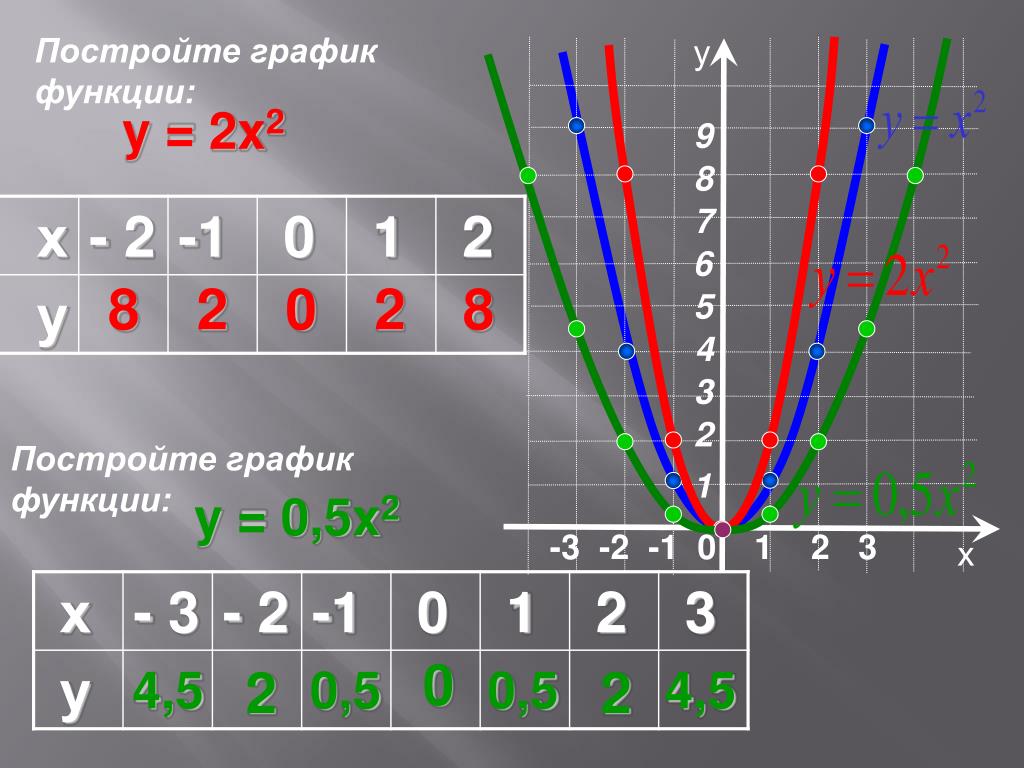 so then we find the
corresponding values of y for some
values of x
right so let us do that first
so let us take x as minus 1 0
and 2 and y will be
minus 7
so
so that is what we have to find
graphically so what we are going to do
is we are going to take 0
1 and 2 right
so we get y is equal to minus 1
minus 1 here minus 4 here
and minus 2 here
right so now let us plot the graph
so plus 2 here sorry right so 2 2
so taking the points 0 minus 4 1 minus 1
and 2
2 we plot the graph
okay and this is the graph
now this is the graph from the graph
what we can see is when x is equal to
minus 1
right the value of y will be
minus 7
and when y is equal to 5
is here x is equal to
3 right
so when x is equal to minus 1
y is equal to minus 7 and
when y is equal to 5 x will be equal to
3 isn’t that easy guys
if you still have a doubt please leave a
comment below do like the video and
subscribe to our channel
i’ll see you in our next video until
then bye guys
keep practicing»
so then we find the
corresponding values of y for some
values of x
right so let us do that first
so let us take x as minus 1 0
and 2 and y will be
minus 7
so
so that is what we have to find
graphically so what we are going to do
is we are going to take 0
1 and 2 right
so we get y is equal to minus 1
minus 1 here minus 4 here
and minus 2 here
right so now let us plot the graph
so plus 2 here sorry right so 2 2
so taking the points 0 minus 4 1 minus 1
and 2
2 we plot the graph
okay and this is the graph
now this is the graph from the graph
what we can see is when x is equal to
minus 1
right the value of y will be
minus 7
and when y is equal to 5
is here x is equal to
3 right
so when x is equal to minus 1
y is equal to minus 7 and
when y is equal to 5 x will be equal to
3 isn’t that easy guys
if you still have a doubt please leave a
comment below do like the video and
subscribe to our channel
i’ll see you in our next video until
then bye guys
keep practicing» Take 2cm = 1 unit on both axes.
Take 2cm = 1 unit on both axes. 1
1 These solutions for Linear Equations In Two Variables are extremely popular among Class 10 students for Math Linear Equations In Two Variables Solutions come handy for quickly completing your homework and preparing for exams. All questions and answers from the Mathematics Part I Solutions Book of Class 10 Math Chapter 1 are provided here for you for free. You will also love the ad-free experience on Meritnation’s Mathematics Part I Solutions Solutions. All Mathematics Part I Solutions Solutions for class Class 10 Math are prepared by experts and are 100% accurate.
These solutions for Linear Equations In Two Variables are extremely popular among Class 10 students for Math Linear Equations In Two Variables Solutions come handy for quickly completing your homework and preparing for exams. All questions and answers from the Mathematics Part I Solutions Book of Class 10 Math Chapter 1 are provided here for you for free. You will also love the ad-free experience on Meritnation’s Mathematics Part I Solutions Solutions. All Mathematics Part I Solutions Solutions for class Class 10 Math are prepared by experts and are 100% accurate.
 ….(I)
….(I) ….(III)
….(III) ….(I)
….(I)



 5).
5).

 ….I31u+27v=89 …..IIAdding I and II58u+58v=174u+v=3 …..IIISubtracting II from I4u-4v=4⇒u-v=1 …..IV
….I31u+27v=89 …..IIAdding I and II58u+58v=174u+v=3 …..IIISubtracting II from I4u-4v=4⇒u-v=1 …..IV 
 If we double the age of the father and add it to the age of his son the sum is 95. Find their present ages.
If we double the age of the father and add it to the age of his son the sum is 95. Find their present ages. Find the fraction.
Find the fraction.
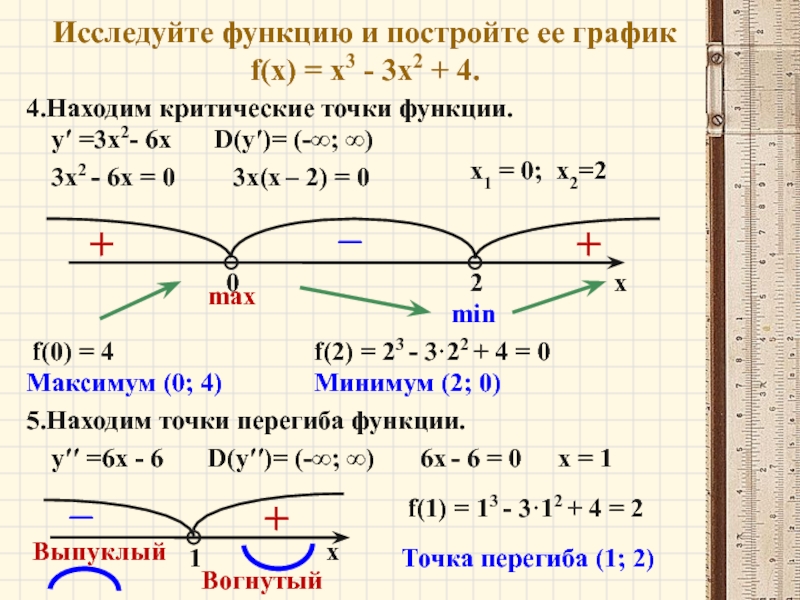
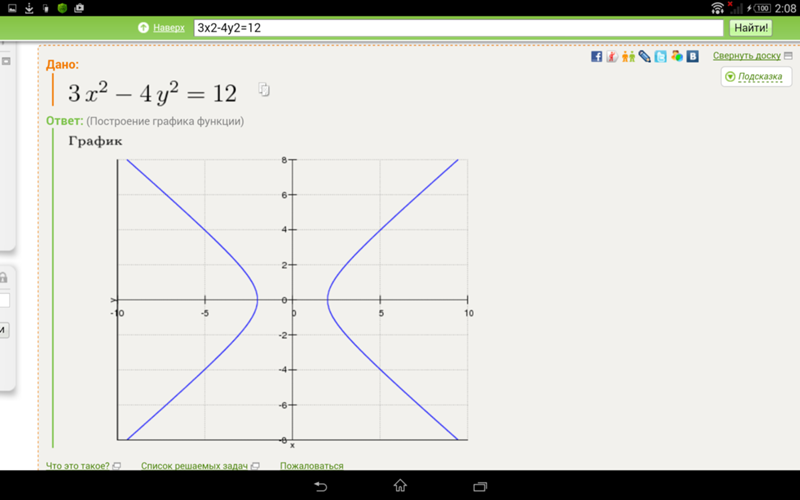


 e(3, 2).
e(3, 2). e (0, 5).
e (0, 5). e (3, 1).
e (3, 1). ….Iand x+2y-143=3x-y4⇒4x+8y-56=9x-3y⇒5x-11y=-56 …..II
….Iand x+2y-143=3x-y4⇒4x+8y-56=9x-3y⇒5x-11y=-56 …..II ….II
….II ….I5u-2v=-32⇒10u-4v=-3 …..II
….I5u-2v=-32⇒10u-4v=-3 …..II She paid Rs 880 for that. Find the rate of sugar and tea per kg.
She paid Rs 880 for that. Find the rate of sugar and tea per kg.


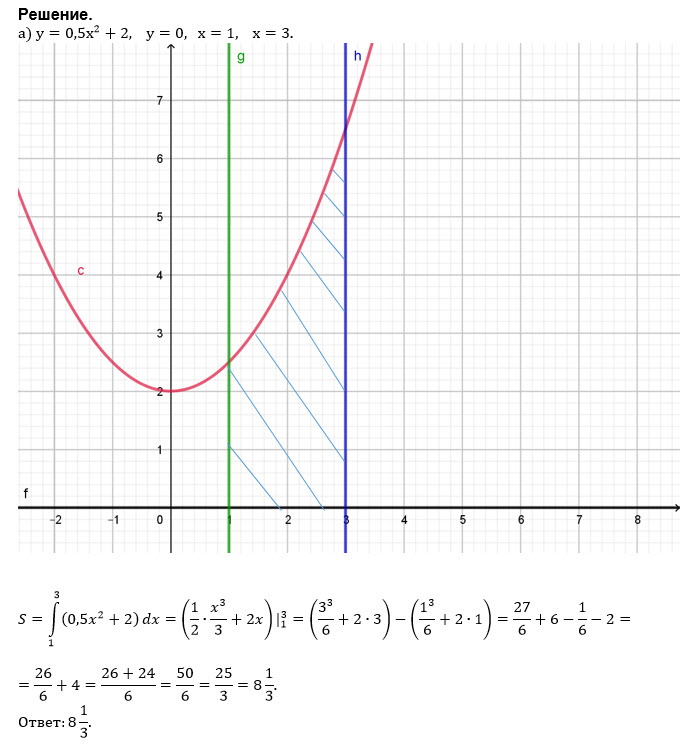 ….II
….II
 posted in the «Distance Learning» section for students of the Mokrousovsky branch in accordance with the schedule posted in the «Mokrousovsky branch» section on the technical school website. The interaction of teachers and students is carried out through e-learning and distance learning technologies.
posted in the «Distance Learning» section for students of the Mokrousovsky branch in accordance with the schedule posted in the «Mokrousovsky branch» section on the technical school website. The interaction of teachers and students is carried out through e-learning and distance learning technologies. e. f(x)=0.
e. f(x)=0.  e. x 2 >x 1 → f(x 2 )
e. x 2 >x 1 → f(x 2 )



 12 0 , x 7 x 8 0 , then 2
12 0 , x 7 x 8 0 , then 2 




 5,
5, 
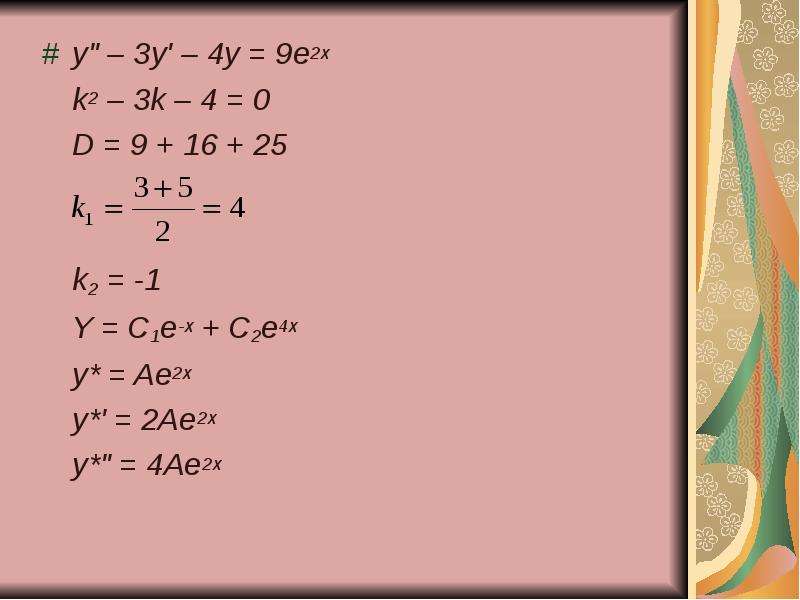




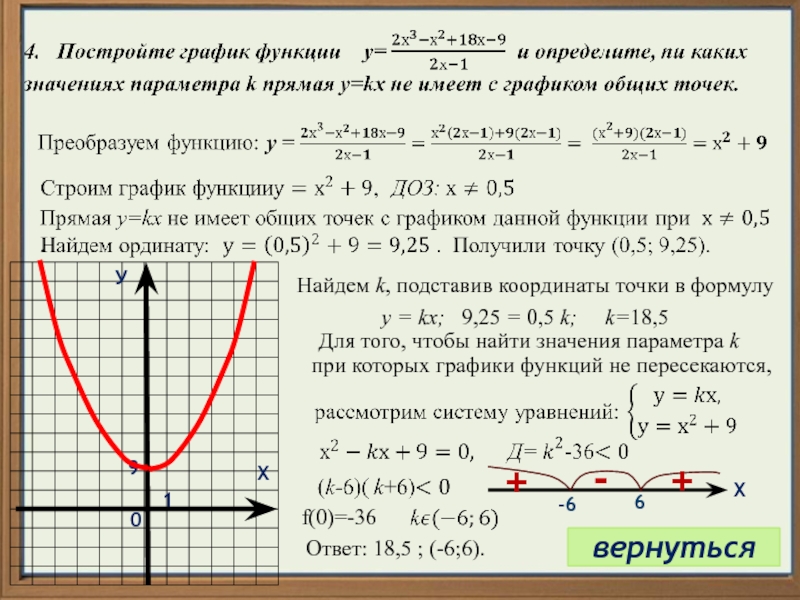


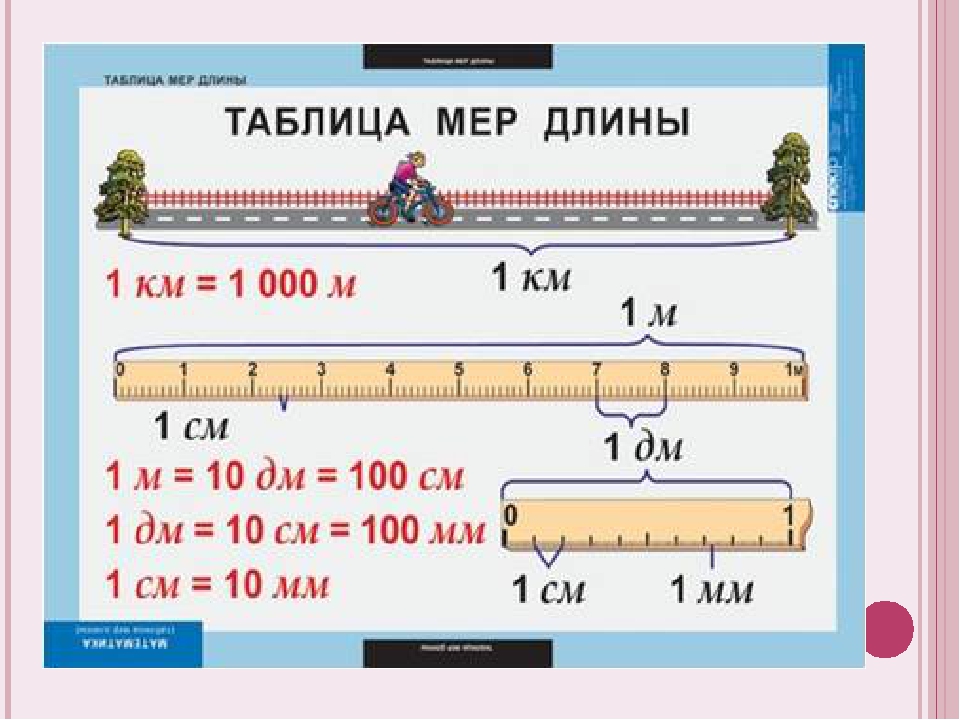 Количество осадков в миллиметрах численно равно массе воды, выпавшей на горизонтальную площадку в 1 квадратный метр
Количество осадков в миллиметрах численно равно массе воды, выпавшей на горизонтальную площадку в 1 квадратный метр Это важно знать не только для сравнения двух снегопадов, но для оценки влагонакопления за месяц или сезон, для того, чтобы оценить, сколько влаги почва получит весной, и т. д.
Это важно знать не только для сравнения двух снегопадов, но для оценки влагонакопления за месяц или сезон, для того, чтобы оценить, сколько влаги почва получит весной, и т. д. В соответствии с ним образцы ткани стирают 10 раз, чтобы приблизить их к реальным условиям эксплуатации. Затем на площади в 1 см² с помощью специального аппарата создают давление эквивалентное давлению водяного столба определённой высоты, которая измеряется в миллиметрах.
В соответствии с ним образцы ткани стирают 10 раз, чтобы приблизить их к реальным условиям эксплуатации. Затем на площади в 1 см² с помощью специального аппарата создают давление эквивалентное давлению водяного столба определённой высоты, которая измеряется в миллиметрах.  Такие показатели водостойкости обеспечат сухую внутреннюю палатку даже во время сильных, но непродолжительных осадков.
Такие показатели водостойкости обеспечат сухую внутреннюю палатку даже во время сильных, но непродолжительных осадков. 
 2\).
2\). А.М. Горького
А.М. Горького Имею высшую квалификационную категорию и педагогическое звание «Учитель — методист». В работе использую технологии развивающего, личностно-ориентированного обучения, успешно готовлю выпускников к итоговому независимому оцениванию. Я с детства люблю решать задачи. Мне кажется, что любой человек, который делает открытие, испытывает такое сильное чувство, которое хочется повторить. Любая задача, особенно трудная, позволяет испытать это чувство. Люди, которые увлекаются математикой более успешные в жизни. Ведь вся наша жизнь — это решение задач.
Имею высшую квалификационную категорию и педагогическое звание «Учитель — методист». В работе использую технологии развивающего, личностно-ориентированного обучения, успешно готовлю выпускников к итоговому независимому оцениванию. Я с детства люблю решать задачи. Мне кажется, что любой человек, который делает открытие, испытывает такое сильное чувство, которое хочется повторить. Любая задача, особенно трудная, позволяет испытать это чувство. Люди, которые увлекаются математикой более успешные в жизни. Ведь вся наша жизнь — это решение задач. С.М. Кирова
С.М. Кирова На своих уроках я применяю элементы современных образовательных технологий: здоровьесберегающие технологии, личностно-ориентированный подход, игровые технологии, технологии уровневых дифференциаций, проектное обучение, технологии проблемного обучения, также комбинирую несколько образовательных технологий в одном уроке.
С радостью жду Вас на своих занятиях!
На своих уроках я применяю элементы современных образовательных технологий: здоровьесберегающие технологии, личностно-ориентированный подход, игровые технологии, технологии уровневых дифференциаций, проектное обучение, технологии проблемного обучения, также комбинирую несколько образовательных технологий в одном уроке.
С радостью жду Вас на своих занятиях! Максима Танка
Максима Танка Я люблю математику, потому что нахожу ее очень увлекательной. В преподавании придерживаюсь гуманистического и личностно-ориентированного методов обучения. Всегда стараюсь найти общий язык с учеником, стать для него товарищем и поддержкой в процессе обучения. Я гарантирую позитивное и познавательное погружение в увлекательный мир математики!
Я люблю математику, потому что нахожу ее очень увлекательной. В преподавании придерживаюсь гуманистического и личностно-ориентированного методов обучения. Всегда стараюсь найти общий язык с учеником, стать для него товарищем и поддержкой в процессе обучения. Я гарантирую позитивное и познавательное погружение в увлекательный мир математики!
 метр. таблица единиц длины — Математика — 2 класс
метр. таблица единиц длины — Математика — 2 класс 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова А. Д. -М.: Просвещение, 2017, с.17, 18
2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова А. Д. -М.: Просвещение, 2017, с.17, 18 Сколько сантиметров помещается в данной линейке?
Сколько сантиметров помещается в данной линейке? Семьдесят сантиметров — это семь дециметров. Получается: семьдесят пять сантиметров — это семь дециметров и пять сантиметров.
Семьдесят сантиметров — это семь дециметров. Получается: семьдесят пять сантиметров — это семь дециметров и пять сантиметров. Внутренний диаметр трубы 4-1000 мм. Сколько нужно воды или антифриза или теплоносителя или, там, вазелина;) … для наполнения трубопровода.
Внутренний диаметр трубы 4-1000 мм. Сколько нужно воды или антифриза или теплоносителя или, там, вазелина;) … для наполнения трубопровода. Внутренний диаметр трубы 4-1000 мм. Масса воды в трубе. Сколько нужно воды или антифриза или теплоносителя или, там, вазелина;) … для наполнения
Внутренний диаметр трубы 4-1000 мм. Масса воды в трубе. Сколько нужно воды или антифриза или теплоносителя или, там, вазелина;) … для наполнения 1 м трубы,
1 м трубы, 1 м трубы,
1 м трубы,



 1811 дюймов
1811 дюймов
 Примеры включают мм,
дюйм, 100 кг, жидкая унция США, 6 футов 3 дюйма, 10 стоун 4, кубический см,
метры в квадрате, граммы, моль, футы в секунду и многое другое!
Примеры включают мм,
дюйм, 100 кг, жидкая унция США, 6 футов 3 дюйма, 10 стоун 4, кубический см,
метры в квадрате, граммы, моль, футы в секунду и многое другое! Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как доказать неравенство онлайн с подробным решением,иррациональные неравенства калькулятор онлайн,иррациональные неравенства онлайн калькулятор,иррациональные неравенства онлайн решение,иррациональные неравенства решение онлайн,калькулятор иррациональных неравенств,калькулятор неравенств онлайн с модулем,калькулятор неравенств с модулем онлайн,калькулятор онлайн иррациональные неравенства,калькулятор онлайн решение неравенств с модулем,калькулятор онлайн решение систем неравенств,калькулятор онлайн система неравенств,калькулятор онлайн системы неравенств,калькулятор показательных неравенств,калькулятор решение систем неравенств,калькулятор решения систем неравенств,калькулятор решите систему неравенств,калькулятор систем неравенств,калькулятор систем неравенств онлайн,калькулятор систем неравенств онлайн с решением,калькулятор систем неравенств с решением,калькулятор систем неравенств с решением онлайн,калькулятор система неравенств,калькулятор системы неравенств,калькулятор системы неравенств с решением онлайн,калькулятор тригонометрических неравенств,калькулятор тригонометрических неравенств онлайн,логарифмические неравенства онлайн калькулятор,матрицы решить неравенство,неравенства с модулем онлайн калькулятор,неравенство с модулем онлайн калькулятор с решением,онлайн калькулятор неравенств с модулем,онлайн калькулятор решение неравенств с модулем,онлайн калькулятор решение систем неравенств,онлайн калькулятор систем неравенств,онлайн калькулятор систем неравенств с решением,онлайн калькулятор системы неравенств,онлайн калькулятор системы неравенств с решением,онлайн решение иррациональных неравенств,онлайн решение иррациональных неравенств с подробным решением,онлайн решение логарифмических неравенств онлайн с подробным решением,онлайн решение модульных неравенств,онлайн решение неравенств с корнем,онлайн решение неравенств с корнями,онлайн решение неравенств с модулем онлайн,онлайн решение неравенств с модулем онлайн с подробным решением,онлайн решение неравенств система,онлайн решение систем линейных неравенств,онлайн решение систем неравенств,онлайн решение системы неравенств,онлайн решение тригонометрических неравенств с подробным решением,показательные неравенства онлайн калькулятор,построение неравенств онлайн,решатель неравенств онлайн с решением,решение двойных неравенств онлайн,решение двойных неравенств онлайн с подробным решением,решение иррациональные неравенства онлайн,решение иррациональных неравенств онлайн,решение иррациональных неравенств онлайн с подробным решением,решение линейных систем неравенств онлайн,решение логарифмических неравенств онлайн с подробным решением,решение модульных неравенств онлайн,решение неравенств графическим способом онлайн,решение неравенств онлайн с корнем,решение неравенств онлайн с корнями,решение неравенств онлайн с модулем онлайн,решение неравенств онлайн с подробным решением с корнями,решение неравенств с корнем онлайн,решение неравенств с корнями онлайн,решение неравенств с корнями онлайн с подробным решением,решение неравенств с модулем онлайн калькулятор,решение неравенств с параметром онлайн,решение неравенств с параметром онлайн с подробным решением,решение онлайн неравенств с параметром,решение онлайн неравенство с модулем,решение онлайн систем линейных неравенств,решение показательных неравенств онлайн,решение систем линейных неравенств онлайн,решение систем неравенств калькулятор,решение систем неравенств калькулятор онлайн,решение систем неравенств онлайн,решение систем неравенств онлайн калькулятор,решение систем неравенств онлайн с подробным решением,решение системы неравенств калькулятор онлайн,решение системы неравенств онлайн,решение системы неравенств онлайн калькулятор,решение системы неравенств онлайн с подробным решением,решение совокупности неравенств онлайн,решение тригонометрических неравенств онлайн,решение тригонометрических неравенств онлайн с подробным решением,решите двойное неравенство онлайн калькулятор,решите систему неравенств онлайн,решите систему неравенств онлайн с решением,решить двойное неравенство онлайн,решить иррациональное неравенство онлайн с подробным решением,решить логарифмическое неравенство онлайн с подробным решением,решить неравенство матрицы,решить неравенство онлайн с корнем,решить неравенство онлайн с параметром,решить неравенство с корнем онлайн,решить неравенство с модулем онлайн,решить онлайн показательное неравенство,решить онлайн тригонометрическое неравенство,решить показательное неравенство онлайн,решить систему неравенств калькулятор онлайн,решить систему неравенств онлайн,решить систему неравенств онлайн калькулятор,решить систему неравенств онлайн калькулятор с решением,решить систему неравенств онлайн с подробным решением,решить тригонометрическое неравенство онлайн,розв язати нерівність,система неравенств калькулятор,система неравенств калькулятор онлайн,система неравенств онлайн,система неравенств онлайн калькулятор,система решение неравенств онлайн,системы неравенств калькулятор,системы неравенств онлайн,системы неравенств онлайн калькулятор,совокупности неравенств решение онлайн,тригонометрические неравенства онлайн.
Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как доказать неравенство онлайн с подробным решением,иррациональные неравенства калькулятор онлайн,иррациональные неравенства онлайн калькулятор,иррациональные неравенства онлайн решение,иррациональные неравенства решение онлайн,калькулятор иррациональных неравенств,калькулятор неравенств онлайн с модулем,калькулятор неравенств с модулем онлайн,калькулятор онлайн иррациональные неравенства,калькулятор онлайн решение неравенств с модулем,калькулятор онлайн решение систем неравенств,калькулятор онлайн система неравенств,калькулятор онлайн системы неравенств,калькулятор показательных неравенств,калькулятор решение систем неравенств,калькулятор решения систем неравенств,калькулятор решите систему неравенств,калькулятор систем неравенств,калькулятор систем неравенств онлайн,калькулятор систем неравенств онлайн с решением,калькулятор систем неравенств с решением,калькулятор систем неравенств с решением онлайн,калькулятор система неравенств,калькулятор системы неравенств,калькулятор системы неравенств с решением онлайн,калькулятор тригонометрических неравенств,калькулятор тригонометрических неравенств онлайн,логарифмические неравенства онлайн калькулятор,матрицы решить неравенство,неравенства с модулем онлайн калькулятор,неравенство с модулем онлайн калькулятор с решением,онлайн калькулятор неравенств с модулем,онлайн калькулятор решение неравенств с модулем,онлайн калькулятор решение систем неравенств,онлайн калькулятор систем неравенств,онлайн калькулятор систем неравенств с решением,онлайн калькулятор системы неравенств,онлайн калькулятор системы неравенств с решением,онлайн решение иррациональных неравенств,онлайн решение иррациональных неравенств с подробным решением,онлайн решение логарифмических неравенств онлайн с подробным решением,онлайн решение модульных неравенств,онлайн решение неравенств с корнем,онлайн решение неравенств с корнями,онлайн решение неравенств с модулем онлайн,онлайн решение неравенств с модулем онлайн с подробным решением,онлайн решение неравенств система,онлайн решение систем линейных неравенств,онлайн решение систем неравенств,онлайн решение системы неравенств,онлайн решение тригонометрических неравенств с подробным решением,показательные неравенства онлайн калькулятор,построение неравенств онлайн,решатель неравенств онлайн с решением,решение двойных неравенств онлайн,решение двойных неравенств онлайн с подробным решением,решение иррациональные неравенства онлайн,решение иррациональных неравенств онлайн,решение иррациональных неравенств онлайн с подробным решением,решение линейных систем неравенств онлайн,решение логарифмических неравенств онлайн с подробным решением,решение модульных неравенств онлайн,решение неравенств графическим способом онлайн,решение неравенств онлайн с корнем,решение неравенств онлайн с корнями,решение неравенств онлайн с модулем онлайн,решение неравенств онлайн с подробным решением с корнями,решение неравенств с корнем онлайн,решение неравенств с корнями онлайн,решение неравенств с корнями онлайн с подробным решением,решение неравенств с модулем онлайн калькулятор,решение неравенств с параметром онлайн,решение неравенств с параметром онлайн с подробным решением,решение онлайн неравенств с параметром,решение онлайн неравенство с модулем,решение онлайн систем линейных неравенств,решение показательных неравенств онлайн,решение систем линейных неравенств онлайн,решение систем неравенств калькулятор,решение систем неравенств калькулятор онлайн,решение систем неравенств онлайн,решение систем неравенств онлайн калькулятор,решение систем неравенств онлайн с подробным решением,решение системы неравенств калькулятор онлайн,решение системы неравенств онлайн,решение системы неравенств онлайн калькулятор,решение системы неравенств онлайн с подробным решением,решение совокупности неравенств онлайн,решение тригонометрических неравенств онлайн,решение тригонометрических неравенств онлайн с подробным решением,решите двойное неравенство онлайн калькулятор,решите систему неравенств онлайн,решите систему неравенств онлайн с решением,решить двойное неравенство онлайн,решить иррациональное неравенство онлайн с подробным решением,решить логарифмическое неравенство онлайн с подробным решением,решить неравенство матрицы,решить неравенство онлайн с корнем,решить неравенство онлайн с параметром,решить неравенство с корнем онлайн,решить неравенство с модулем онлайн,решить онлайн показательное неравенство,решить онлайн тригонометрическое неравенство,решить показательное неравенство онлайн,решить систему неравенств калькулятор онлайн,решить систему неравенств онлайн,решить систему неравенств онлайн калькулятор,решить систему неравенств онлайн калькулятор с решением,решить систему неравенств онлайн с подробным решением,решить тригонометрическое неравенство онлайн,розв язати нерівність,система неравенств калькулятор,система неравенств калькулятор онлайн,система неравенств онлайн,система неравенств онлайн калькулятор,система решение неравенств онлайн,системы неравенств калькулятор,системы неравенств онлайн,системы неравенств онлайн калькулятор,совокупности неравенств решение онлайн,тригонометрические неравенства онлайн. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и доказать неравенство онлайн с подробным решением. Просто введите задачу в окошко и нажмите
«решить» здесь (например, иррациональные неравенства онлайн калькулятор).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и доказать неравенство онлайн с подробным решением. Просто введите задачу в окошко и нажмите
«решить» здесь (например, иррациональные неравенства онлайн калькулятор).
 Учебный материал включает в себя 7 модулей, в каждом из которых содержатся краткие теоретические сведения по основным разделам математики, методические указания, необходимые теоремы и формулы, видеолекции, интересные факты из математики, примеры различного уровня сложности с подробным решением, задачи для самоконтроля с ответами (домашнее задание), контрольные задания (тесты).
Учебный материал включает в себя 7 модулей, в каждом из которых содержатся краткие теоретические сведения по основным разделам математики, методические указания, необходимые теоремы и формулы, видеолекции, интересные факты из математики, примеры различного уровня сложности с подробным решением, задачи для самоконтроля с ответами (домашнее задание), контрольные задания (тесты).
 Рациональные неравенства и системы рациональных неравенств. Понятие системы и совокупности систем неравенств. Иррациональные неравенства. Некоторые нестандартные подходы к решению неравенств.
Рациональные неравенства и системы рациональных неравенств. Понятие системы и совокупности систем неравенств. Иррациональные неравенства. Некоторые нестандартные подходы к решению неравенств.
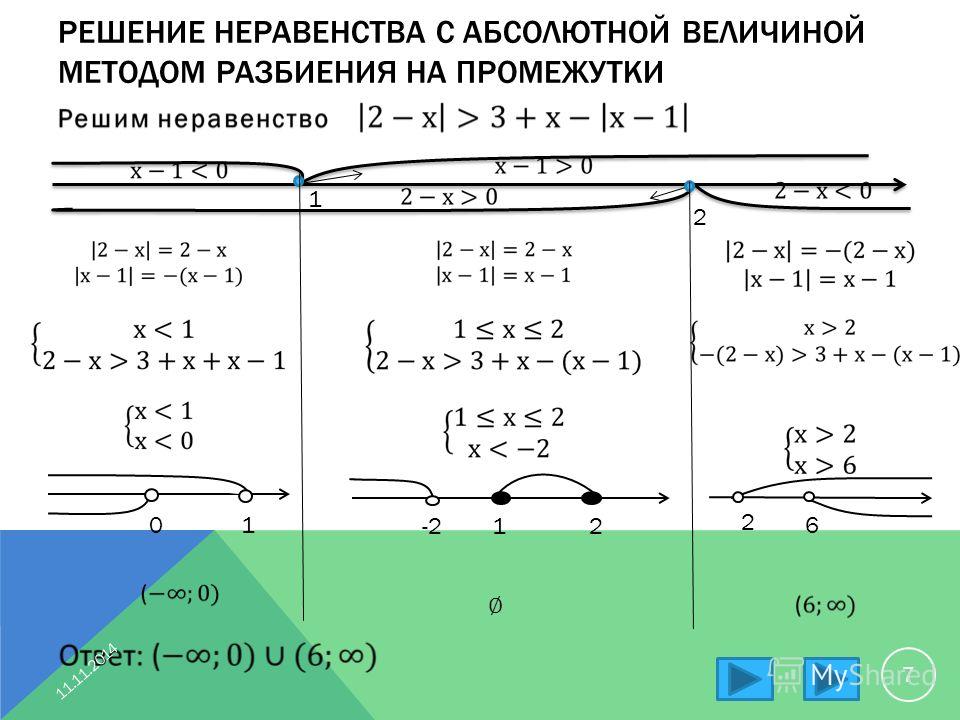 Задачи на пропорции, проценты, смеси. Задачи на целые числа. Задачи на работу. Задачи на движение.
Задачи на пропорции, проценты, смеси. Задачи на целые числа. Задачи на работу. Задачи на движение.  \)
\)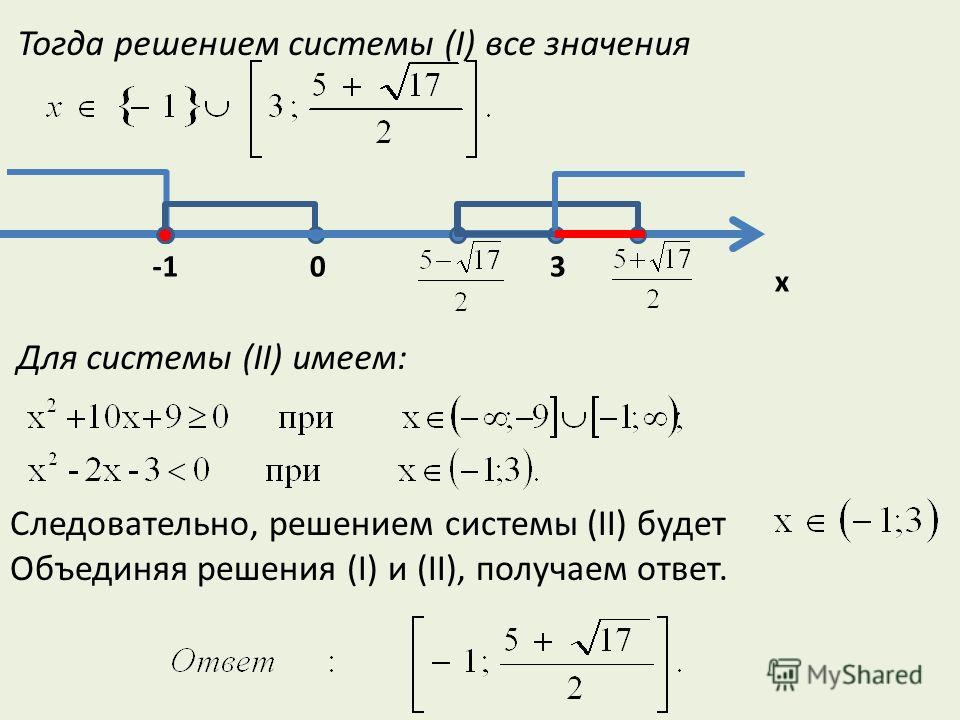 {-1}$ или $x-1<2 \Rightarrow x<3$
{-1}$ или $x-1<2 \Rightarrow x<3$ \right.$$
\right.$$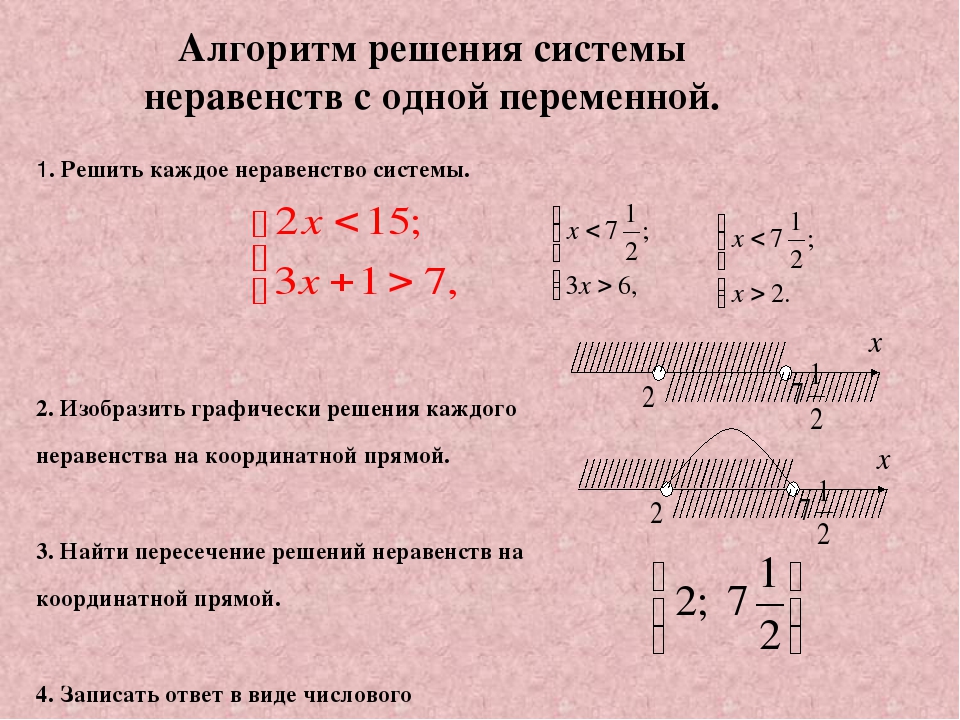 0 в области определения F(x).
0 в области определения F(x).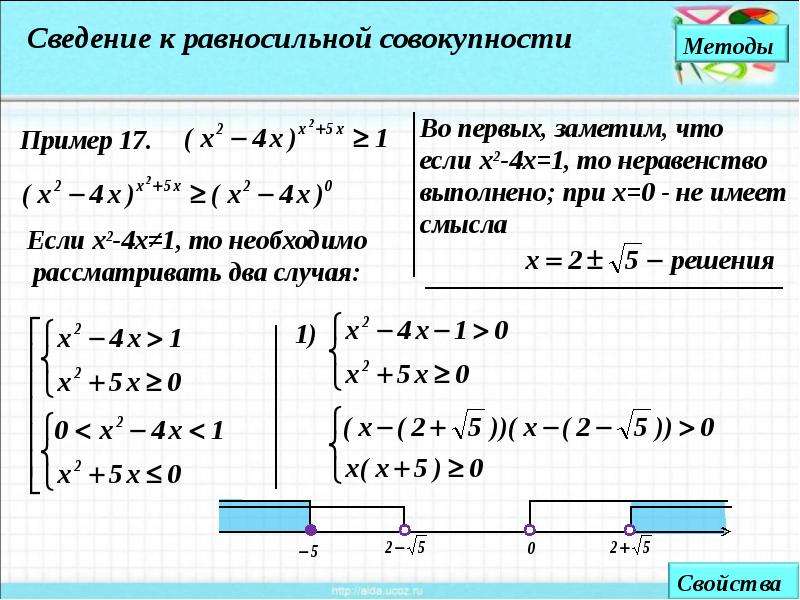
 Метод декомпозиции (рационализации)
Метод декомпозиции (рационализации) .
. Запишем неравенство в виде log2x+3×2 – 1
Запишем неравенство в виде log2x+3×2 – 1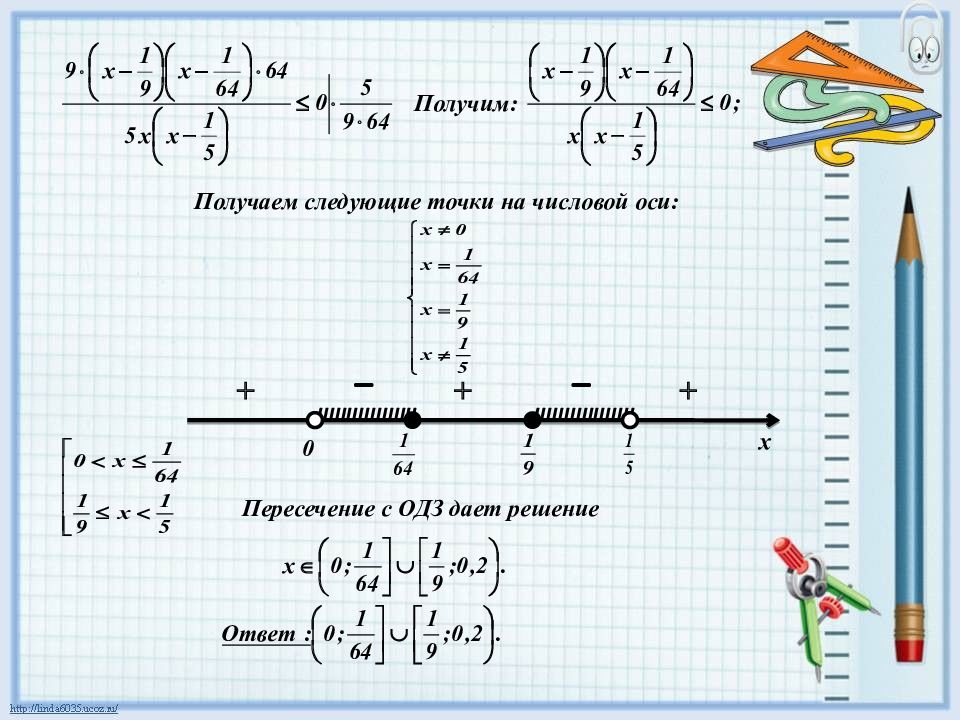




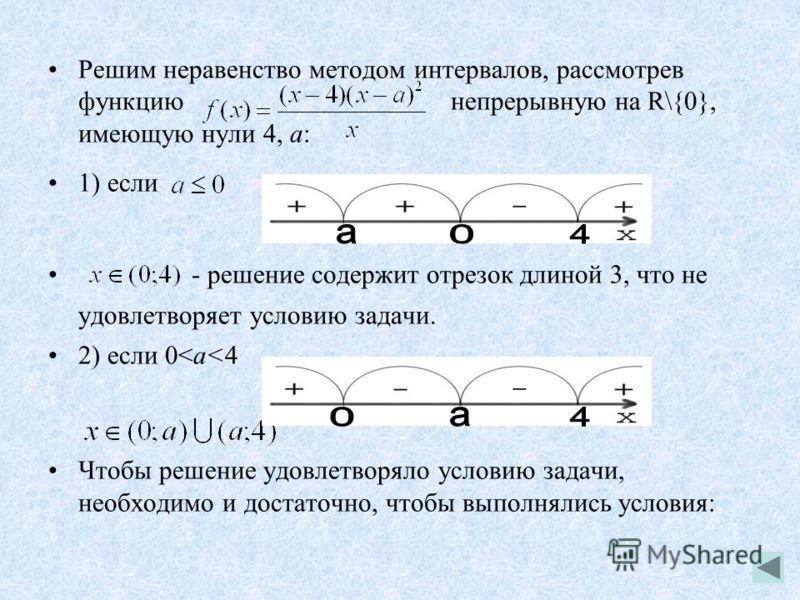
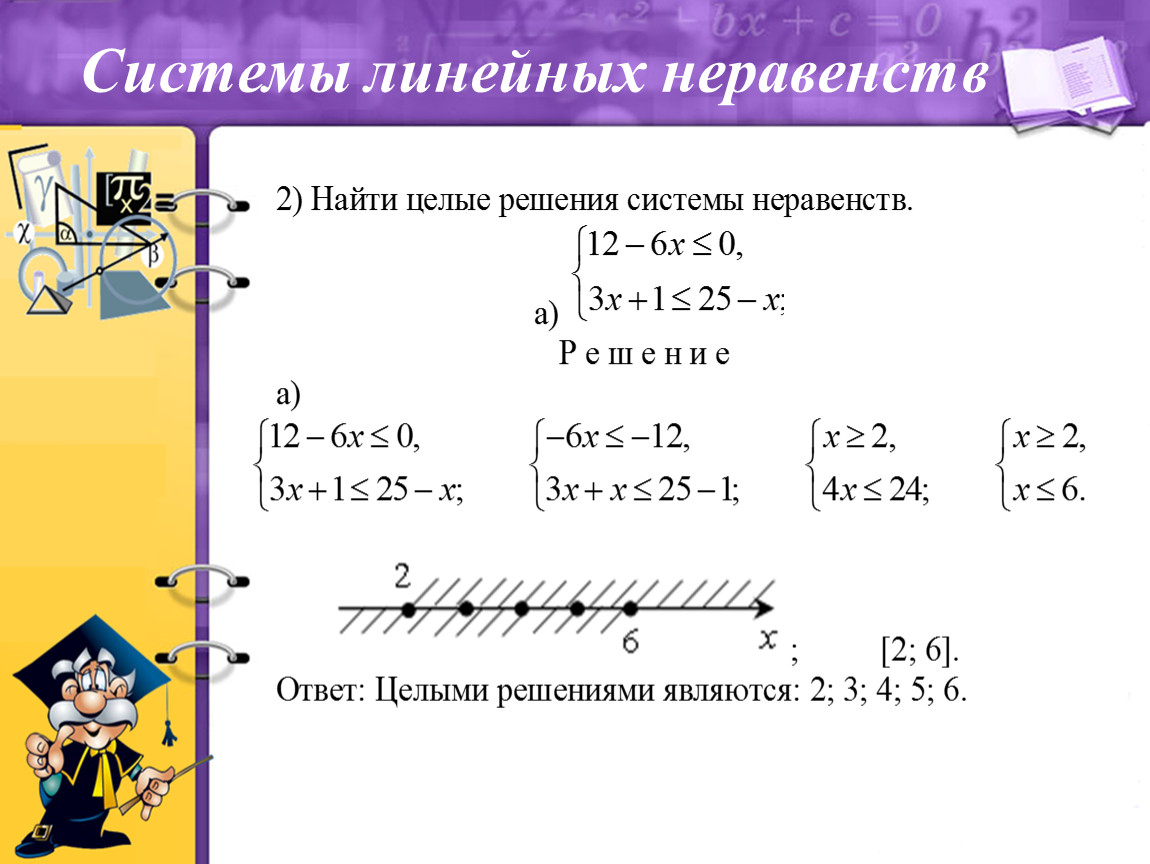 Решение
уравнений и систем уравнений (45 мин)
Решение
уравнений и систем уравнений (45 мин)
 уравнений онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
уравнений онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC! д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям. Мы предлагаем для решения заполнить два поля: само собственно уравнение и при необходимости — начальные условия (задачу Коши) — то есть информацию о граничных условиях искомой функции. Ведь как известно, диф уравнения имеют бесконечное количество решений, поскольку в ответе присутствуют константы, которые могут принимать произвольное значение. Задав задачу Коши, мы из всего множества решений выбираем частные.
д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям. Мы предлагаем для решения заполнить два поля: само собственно уравнение и при необходимости — начальные условия (задачу Коши) — то есть информацию о граничных условиях искомой функции. Ведь как известно, диф уравнения имеют бесконечное количество решений, поскольку в ответе присутствуют константы, которые могут принимать произвольное значение. Задав задачу Коши, мы из всего множества решений выбираем частные.
 В онлайн сервисах Вы такого не найдете.
В онлайн сервисах Вы такого не найдете.
 Действительные корни. Причем. x1 не равно x2
Действительные корни. Причем. x1 не равно x2 Решение квадратного уравнения с совпадением действительных корней.
Решение квадратного уравнения с совпадением действительных корней. 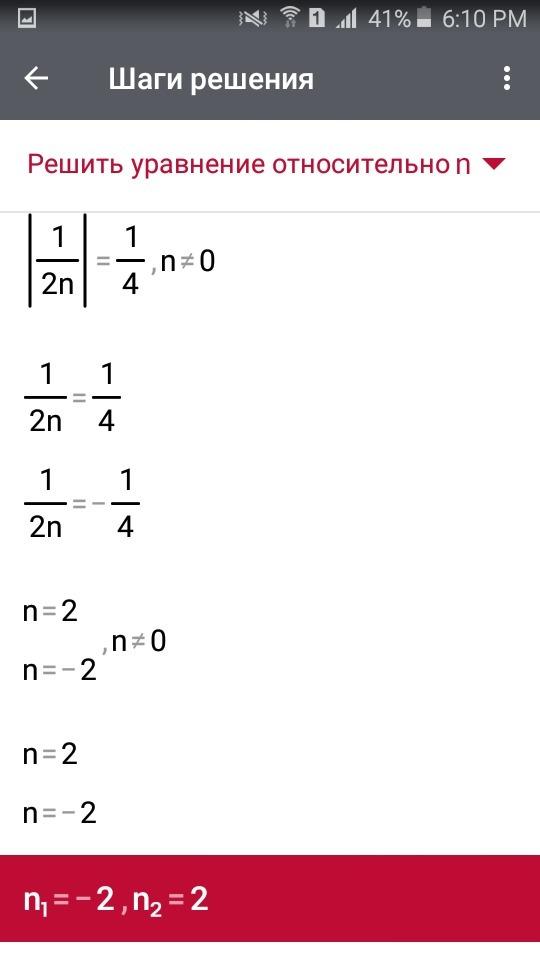 Решение простых линейных уравнений
Решение простых линейных уравнений Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:

 Например:
Например: Вывод:
Вывод:
 Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. Решение уравнения в общем виде. В таком уравнении переменные коэффициенты и искомые корни связаны между собой. Старшая степень переменной определяет порядок такого уравнения. Исходя из этого, для уравнений используют различные методы и теоремы для нахождения решений.
Польза онлайн сервиса бесценна, ведь кроме верного ответа вы получаете подробное решение каждого уравнения. Преимущества решения уравнений онлайн. Решить любое уравнение онлайн на нашем сайте вы можете абсолютно бесплатно. Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. Решение уравнения в общем виде. В таком уравнении переменные коэффициенты и искомые корни связаны между собой. Старшая степень переменной определяет порядок такого уравнения. Исходя из этого, для уравнений используют различные методы и теоремы для нахождения решений. 2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные.
2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные. После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение.
После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение. Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.
Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А. Выражаем. Из любого уравнения выражаем одну переменную.
Выражаем. Из любого уравнения выражаем одну переменную.
 Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.
Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
 . Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения.
. Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней. Решение уравнений онлайн.. Уравнения онлайн. Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени.
Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов.
Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.