Предел функции. Примеры решения
Продолжаем разбирать ответы к пределам функций и последовательностей. Примеров накопилось настолько много, что можно написать отдельную книгу — методичку по их вычислению.
В каждой публикации разжевываем методику вычислений до элементарных мелочей, при таких объяснениях каждый студент может без проблем решить подобные примеры.
Однако дальше от студентов поступают новые заказы с просьбой найти предел.
Порой нужно помочь с простыми функциями, что составляет впечатление что студенты имеют худшую подготовку, чем ученики в 11 классе, которые изучают эту тему.
Пример 11. Вычислить предел последовательности:
Решение: Подстановка большого номера в последовательность дает особенность вида бесконечность разделить на бесконечность. Для ее раскрытия в числителе и знаменателе дроби выделяем слагаемое, что вносит наибольший вклад. В скобках останутся константы + слагаемые, которые стремятся к нулю.
На общий множитель упрощаем, а константы дают значение предела последовательности.
Пример 12. Найти предел последовательности:
Решение: В предельном переходе имеем неопределенность вида бесконечность минус бесконечность. Функция представлена разницей корней. Чтобы избавиться от неопределенности, умножим и поделим разницу на сумму корней (сопряженное выражение). В результате придем к неопределенности бесконечность разделить на бесконечность. Чтобы ее раскрыть выносим множитель, что вносит наибольший вклад из числителя и знаменателя и сокращаем на него. Все что останется и будет пределом последовательности
Пример 13. Найти предел функции
Решение: При переменной стремящейся к нулю имеем неопределенность {0/0}. Для ее раскрытия разницу корней умножим и разделим на сопряженное выражение, чтобы в числителе образовать разность квадратов. В знаменателе имеем полином, который содержит особенность, поэтому разложим его на простые множители. После упрощений получим зависимость, предел которой легко находим методом подстановки
Пример 14. Вычислить предел
Вычислить предел
Решение: Переменная стремится к нулю, а функция задана долей синуса и тангенса в квадрате. В таких случаях нужно преобразовать выражение, чтобы в нем можно было легко выделить первый замечательный предел и его следствие. Для компенсации изменений в числитель и знаменатель записываем соответствующие константы. Далее переходим к произведению известных границ, вклад от каждой из которых равен единице.
Пример 15. Определить предел функции
Решение: При переменной стремящейся к нулю получим неопределенность вида единица в степени бесконечность. Для ее раскрытия выразим в степени множитель, который обратно пропорционален sin(4x).
Таким образом получим второй замечательный предел – экспоненту, а все что останется в показателе, даст степень экспоненты. Но здесь имеем долю sin(4x)/tan(3x), поэтому переходим к лимиту в показателе, а сам показатель сводим к первому замечательному пределу его следствии.
Из последнего «лимита» можно вывести простую формулу, которая может быть рассмотрена как следствие первого замечательного предела. Лимит доли тангенса к синусу (или наоборот) ровен доле их аргументов.
Лимит доли тангенса к синусу (или наоборот) ровен доле их аргументов.
Пример 16. Найти предел последовательности:
Решение: Для раскрытия особенности вида бесконечность разделить на бесконечность необходимо три раза применить правило Лопиталя. Другая схема заключается в вынесении из числителя и знаменателя наибольшего множителя, и сокращении на него. В результате останутся константы и бесконечно малые функции. Последние стремятся к нулю, поэтому лимит последовательности равен
Пример 17. Вычислить предел последовательности:
Решение: Таких лимитов в предыдущих публикациях вычислено немало и суть раскрытия подобных неопределенностей заключается в умножении на сопряженное выражение – сумму корней. На это же выражение следует разделить функцию, чтобы не изменить значение лимита. В результате в числителе дроби получим разность квадратов и таким образом избавляемся от иррациональности, а предел выражения получим через оценку максимальных множителей.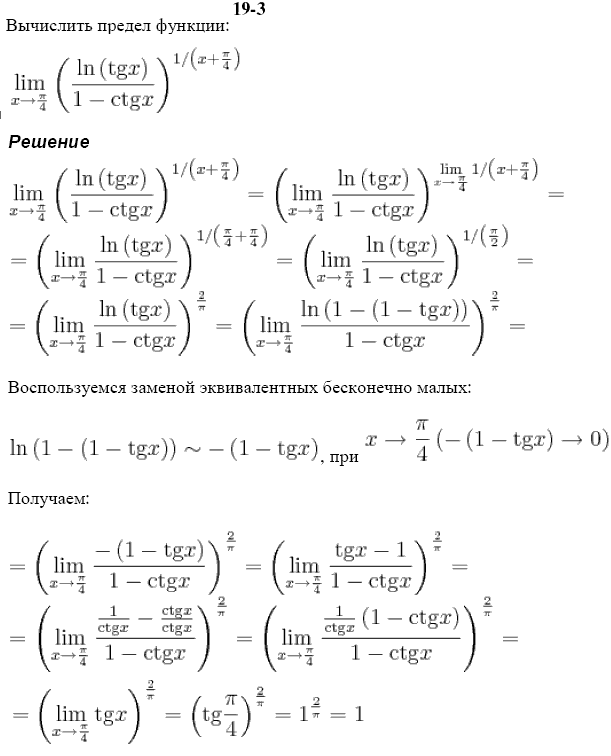
Пример 18. Определить лимит функции
Решение: Когда переменная стремится к 3 имеем неопределенность вида {0/0}. Для раскрытия неопределенности в знаменателе дроби избавляемся от иррациональности умножением на сопряженное выражение, а в числителе полином раскладываем на простые множители. В результате и тат и там получаем выражение (х-3), на которое упрощаем.
Лимит функции, что осталась, вычисляем методом подстановки.
Пример 19. Найти предел функции
Решение: Предел функции в нуле дает особенность {0/0}. Ее не так просто раскрывать, как предыдущие.
Здесь следует свести выражение к первому и второму замечательному пределу и их следствиям.
Ln(1+x)/x в предельном переходе даст единицу, так же как и tan(x)/x и sin(x)/x.
Число 4/25 и будет лимитом функции.
Пример 20. Найти лимит
Решение: Предел функции в точке имеет неопределенность вида единица в степени бесконечность. Для ее раскрытия нужно преобразовать функцию под второй замечательный предел. Для этого и в скобках, и в показателе выделяем множитель, что вносит особенность (x-3) и делаем замену переменных t=x-3.
Для этого и в скобках, и в показателе выделяем множитель, что вносит особенность (x-3) и делаем замену переменных t=x-3.
Далее переходим к экспоненте, и определяем лимит показательной функции.
Как Вы могли убедиться, задания на пределы не самые сложные в высшей математике.
Нужно знать не так много правил, чтобы без труда находить правильный ответ.
как понять, вычислить, подробное объяснение с решением
Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim — от английского limit — предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача — найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Что такое предел функции как его найти
- Общее понятие предела
- Предел функции
- Основные теоремы о пределах
- Найти предел самостоятельно, а затем посмотреть решение
- Решение пределов через раскрытие неопределённостей
- Раскрыть неопределённости самостоятельно, а затем посмотреть решения
- Решение пределов онлайн калькулятор
При каком условии Вам будут совсем не страшны любые задачи, где требуется найти предел функции? Условие следующее: у Вас есть базовый навык деления одних чисел на другие, на очень-очень маленькие числа и на очень-очень большие числа. Успех придет в процессе решения.
А теперь посмотрим, что о пределе функции гласит теория. Впрочем, можно зайти чуть-чуть вперед и сразу перейти к задачам, а потом вернуться к теории. Как удобнее.
Обобщённое понятие предела: число a есть предел некоторой переменной величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.
Поясним это на примере, который также проиллюстрируем. А после примера приведём общий алгоритм решения пределов.
В нижнюю часть равнобедренного треугольника вписана окружность. Диаметр этой
окружности обозначим как .
На рисунке диаметр проведён синим цветом. К окружности параллельно основанию первоначального
треугольника проведена касательная (она на рисунке серого цвета). В результате получен треугольник,
подобный первоначальному. В этот треугольник точно так же вписана окружность. Её диаметр —
(диаметры на рисунке
ограничены касательными). Аналогичные построения продолжаются, пока позволяет высота треугольника.
Получена последовательность уменьшающихся окружностей и соответствующая им последовательность длин
их диаметров: .
Эта последовательность длин диаметров даёт пример переменной величины
, которая с
возрастанием номера окружности x неограниченно приближается к нулю. Предел этой
последовательности равен нулю:
.
Запишем приведённый пример на языке формул. Итак, номер окружности возрастает и стремится к бесконечности, то есть . Допустим, существует такой равнобедренный треугольник, что длина диаметра каждой вписанной в него окружности расчитывается по формуле
Величина, которую нам требуется найти, будет записана так:
Lim это и есть предел, а под ним указывается переменная, которая стремится к определённому значению – нулю, любому другому числу, бесконечности.
Теперь вычислим предел, присвоив переменной x значение бесконечность (в более строгом определении это называется «доопределить функцию», с этим определением вы можете ознакомиться в последующих частях главы «Предел»). Примем, что конечная величина, поделенная на бесконечность, равна нулю:
С рассмотренной последовательностью окружностей свяжем другую переменную величину — последовательность сумм их диаметров:
Рассмотрев рисунок снова, обнаружим, что предел последовательности равен h – высоте равнобедренного треугольника. Вообще, предел может быть равен нулю, любому другому числу или бесконечности.
Вообще, предел может быть равен нулю, любому другому числу или бесконечности.
Теперь более строгие определения предела функции, которые Вас могут спросить на экзамене, и для понимания которых потребуется чуть больше внимания.
Предел функции при
Пусть функция f(x) определена на некотором множестве X и пусть дана точка . Возьмём из X последовательность точек, отличных от :
(1)
сходящуюся к . Значения функции в точках этой последовательности также образуют числовую последовательность
(2)
и можно ставить вопрос о существовании её предела.
Определение 1. Число A называется пределом функции f(x)
в точке (или при ),
если для любой сходящейся к последовательности (1)
значений аргумента x, отличных от ,
соответствующая последовательность (2) сходится к числу A.
Символически это записывается так:
Это означает: чтобы найти предел функции, нужно в функцию вместо x подставить то значение, к которому стремится x.
Пример 1. Найти предел функции при .
Решение. Подставляем вместо x значение 0. Получаем:
.
Итак, предел данной функции при равен 1.
Кроме того, решённые в этом уроке примеры и любые другие задачи на пределы, можно на проверить на калькуляторе пределов онлайн.
Предел функции при , при и при
Кроме рассмотренного понятия предела функции при существует также понятие предела функции при стремлении аргумента к бесконечности.
Определение 2. Число A называется пределом функции f(x)
при ,
если для любой бесконечно большой последовательности (1) значений аргумента соответствующая последовательность (2)
значений функции сходится к A.
Символически это записывается так: .
Определение 3. Число A называется пределом функции f(x) при (), если для любой бесконечно большой последовательности значений аргумента, элементы которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.
Символически это записывается так: ().
Это, как и в случае определения 1, означает: чтобы найти предел функции, нужно в функцию вместо x подставить бесконечность, плюс бесконечность или минус бесконечность.
Пример 2. Найти предел функции при .
Решение. Подставляем вместо x бесконечность. Получаем, что последовательность значений функции является бесконечно малой величиной и поэтому имеет предел, равный нулю:
.
Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо x супербольшое число. При делении получите супермалое число.
При делении получите супермалое число.
А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.
Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.
Теорема 2. Если функции f(x) и g(x) имеют пределы в точке , то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
(3)
2) предел произведения функций равен произведению пределов сомножителей, т.е.
(4)
3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т. е.
е.
(5)
Замечание. Формулы (3) и (4) справедливы для любого конечного числа функций.
Следствие 1. Предел постоянной равен самой постоянной, т.е.
Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.
Пример 3. Найти предел:
Решение.
А проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Пример 4. Найти предел:
Решение. Предварительно убедимся, что предел делителя не равен нулю:
Таким образом, формула (5) применима и, значит,
А проверить решение задачи на
пределы можно на калькуляторе пределов
онлайн.
Теорема 3 (о пределе сложной функции). Если существует конечный предел
а функция f(u) непрерывна в точке , то
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.
Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.
Пример 5. Найти предел:
Решение. Теорема о пределе частного здесь неприменима, так как
Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим
В числителе получим
где
корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:
Пример 6. Найти предел:
Правильное решение и ответ.
Пример 7. Найти предел:
.
Правильное решение и ответ.
Пример 8. Найти предел:
.
Правильное решение и ответ.
Пример 9. Найти предел:
.
Правильное решение и ответ.
Пример 10. Найти предел:
.
Правильное решение и ответ.
Пример 11. Найти пределы:
Правильное решение и ответ.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Предел
При решении примеров 5 и 8 нам уже встретилась неопределённость вида . Эта неопределённость и неопределённость вида — самые распространённые неопределённости, которые требуется раскрывать при решении пределов.
БОльшая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела.
Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.
Освоим эти приёмы на примерах.
Для преобразования выражений потребуются пособия Действия со степенями и корнями и Действия с дробями.
Неопределённость вида
Пример 12. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной n равна 2. Поэтому почленно делим числитель и знаменатель на :
.
Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или «супермалому числу».
Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .
Проверить решение задачи на
пределы можно на калькуляторе пределов
онлайн.
Пример 13. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:
.
Комментарий к ходу решения. В числителе загоняем «икс» под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо «икса».
Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.
Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Неопределённость вида
Пример 14. Раскрыть неопределённость и найти предел .
Раскрыть неопределённость и найти предел .
Решение. В числителе — разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:
.
В знаменателе — квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):
Запишем выражение, полученное в результате преобразований и найдём предел функции:
Проверить решение задачи на пределы можно на калькуляторе пределов онлайн.
Пример 15. Раскрыть неопределённость и найти предел
Решение. Теорема о пределе частного здесь неприменима, поскольку
Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и
сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:
Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:
Пример 16. Раскрыть неопределённость и найти предел
Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:
Пример 17. Раскрыть неопределённость и найти предел
.
Правильное решение и ответ.
Пример 18. Раскрыть неопределённость и найти предел
.
Правильное решение и ответ.
Пример 19. Раскрыть неопределённость и найти предел
.
Правильное решение и ответ.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Предел
Продолжение темы «Предел»
Первый замечательный предел
Второй замечательный предел
Бесконечно малые
Поделиться с друзьями
Вычисление простейших пределов, 11 класс (теория+практика).

Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Записывается предел следующим образом .
Вычислим предел:
Подставляем вместо х – 3.
Заметим, что предел числа равен самому числу.
Примеры: вычислите пределы
Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной (в данной точке).
Вычислим значение функции в точке x0 = 3 и значение его предела в этой точке.
Значение предела и значение функции в этой точке совпадает, следовательно, функция непрерывна в точке x0 = 3.
Но при вычислении пределов зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределённостями.
Основные виды неопределенностей:
Раскрытие неопределенностей
Для раскрытия неопределенностей используют следующее:
упрощают выражение функции: раскладывают на множители, преобразовывают функцию с помощью формул сокращенного умножения, тригонометрических формул, домножают на сопряженное, что позволяет в дальнейшем сократить и т.д., и т.п.;
если предел при раскрытии неопределенностей существует, то говорят, что функция сходится к указанному значению, если такого предела не существует, то говорят, что функция расходится.
Пример: вычислим предел.
Разложим числитель на множители
3. Вычисление пределов функции
Пример 1. Вычислите предел функции:
При прямой подстановке, получается неопределенность:
Разложим на множители числитель и знаменатель и вычислим предел.
Пример 2. Вычислите предел функции:
При прямой подстановке, получается неопределенность.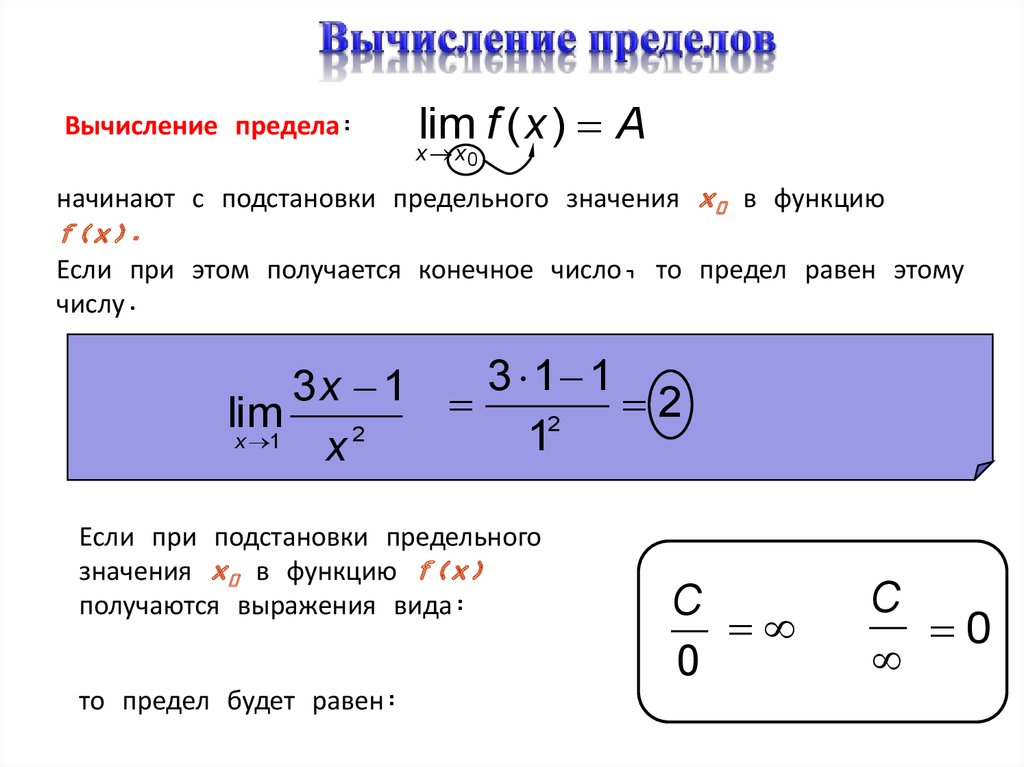
Помножим и числитель, и знаменатель на .
Учтем, что если число разделить на бесконечно большое число получится ноль. То есть предел Аналогично
Пример 3. Вычислите предел функции:
При прямой подстановке, получается неопределенность.
Помножим и числитель, и знаменатель на .
Мы учли, что
4. Самостоятельные упражнения
Вычислите пределы:
6. Домашнее задание
Домашнее задание раздается на карточках каждому ученику.
Свойства пределов функции
Предел постоянной величины равен самой постоянной величине:
Предел суммы двух функций равен сумме пределов этих функций: Аналогично предел разности двух функций равен разности пределов этих функций.
Постоянный коэффициент можно выносить за знак предела:
Предел произведения двух функций равен произведению пределов этих функций:
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
Замечание. Принято считать, что Следующие пределы считают неопределенностью: . Если в примере встретилась неопределенность, то надо найти пути для ее устранения. Общие правила:
Принято считать, что Следующие пределы считают неопределенностью: . Если в примере встретилась неопределенность, то надо найти пути для ее устранения. Общие правила:
1) если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида или , то для решения нужно разложить числитель и знаменатель на множители или разделить на максимальную степень числителя (или знаменателя) и числитель и знаменатель;2) если же в числителе или в знаменателе находятся иррациональные выражения и имеется неопределенности вида или , то для решения надо избавляться от иррациональности, помножив и числитель, и знаменатель на сопряженное выражение;3) если же в числителе или в знаменателе находятся тригонометрические выражения и имеется неопределенности вида или , то для решения используют формулу замечательного предела
Вычисление пределов функции
Пример 1.Найти предел функции:
Пример 2.Найти предел функции:
Пример 3. Найти предел функции:
Найти предел функции:
Пример 4.Найти предел функции:
Пример 5.Найти предел функции:
Пример 6.Найти предел функции:
Пример 7.Найти предел функции:
Пример 8.Найти предел функции:
Пример 9.Найти предел функции:
Пример 10.Найти предел функции: Непрерывность функции Мы интуитивно понимаем, что если функция непрерывна, то мы можем ее нарисовать, не отрывая карандаша от листа бумаги.Функция у = f (x) называется непрерывной, если она непрерывна в каждой точке своей области определения.Чтобы понять, что такое непрерывность функции в целом, сначала надо разобраться, что такое непрерывность функции в точке.Функция у = f (x) называется непрерывной в точке х = с, если предел функции в точке х = с равен значению функции в этой точке: Т.е. должны выполняться одновременно три условия:
1) функция определена и в самой точке х = с и в некоторой окрестности этой точки, причем U(с) ϵ D(f);2) существует ;3) A = f(c).
Заметим, что в случае непрерывной функции в точке x = c, на графике данная точка выколотой быть не может.Для иллюстрации, как работает данное определение, рассмотрим три функции (см. табл.). Все три условия определения выполняются только у первой функции у = х + 1. У второй — не выполняется третье условие, а у третьей функции — первое.
Непрерывная функция | Разрывная в т. х = 1 | Разрывная в т. х = 1 |
Пример 11.Найти точку разрыва функции
Решение
Найдем область определения функции: 5x + 7 ≠ 0, x ≠ -1,4.Ответ: -1,4.
Пример 12.Найти сумму значений точек разрыва функции
РешениеНайдем область определения функции: х2 + 2х — 3 ≠ 0. По теореме, обратной к теореме Виета: х1 ≠ 1, x2 ≠ -3.Далее находим сумму значений 1 + (-3) = -2.Ответ: -2.
Пример 13.Указать точку разрыва функции:
РешениеПостроим график данной функции на указанных промежутках. Видим, что целостность функции нарушается при х = 2.Ответ: 2.
Примеры решения пределов с корнями с ответами
Основные свойства пределов с корнями
Теорема
Для нахождения предела функции необходимо подставить в предел вместо Х то значение переменной, к которому стремится Х.
Нужна помощь в написании работы?
Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Правки вносим бесплатно.
Заказать работу
Примеры решений пределов с корнями
Пример №1
Задание
Найти предел
Решение
Мы имеем неопределенность вида
Первый шаг – разделить числитель и знаменатель на ”х” в высшей степени. Старшая степень для числителя в данном случае равна двум.
Со знаменателем немного сложнее. Так как у нас корень, обращаем внимание только на самое ”старшее” слагаемое –
Число (4) – это константа, его тоже отбрасываем. Находим корень
Так как числитель и знаменатель оказываются одного порядка роста, предел равен конечному числу, отличному от нуля.
Видим, что функции эквивалентны на бесконечности.
Оформляем решение:
Ответ: 1
Пример № 2
Задание
Найти предел с корнем
Решение
Подставляем
в подпредельную функцию:
Получаем неопределенность
Домножаем числитель и знаменатель на выражение, сопряженное к нему –
так как он содержит корень.
Далее, пользуясь формулой разности квадратов
и раскрывая скобки, упрощаем предел. Последний шаг – сокращение функции на
Ответ: -8
Пример №3
Задание
Решить предел с корнем
Решение
Подставляем
в предел и получаем неопределённость вида
Как и в предыдущих примерах, находим старшую степень для числителя и знаменателя, и выносим её за скобки.
И опять подставляем
в предел и решаем:
Ответ:
Пример №4
Задание
Вычислить предел корня:
Решение
Аналогично предыдущим примерам, подставляем
в предел и видим:
Находим сопряженное, в данном случае это
Как и в примере №2, пользуясь формулой разности квадратов
и раскрывая скобки, упрощаем предел:
Раскрываем скобки и упрощаем. Затем выносим х за скобки и сокращаем:
Затем выносим х за скобки и сокращаем:
Как и в начале, подставляем в предел, получаем:
Ответ:
Пример №5
Задание
Вычислить предел функции
Решение
Если подставить х=1, видно, что и числитель, и знаменатель обращаются в ноль. Получаем неопределенность вида
Как и в предыдущих примерах, первым шагом находим сопряжённое –
и домножаем на него числитель и знаменатель.
Применяем правило разности квадратов
и преобразовываем предел:
Сокращаем числитель и знаменатель на (x-1) и приходим к конечному ответу:
Ответ: 6
Пример № 6 Задание Вычислить предел: Решение: Первый шаг – подставить в предел выражение и убедиться, что выходит неопределённость вида Шаг второй – раскрываем нашу неопределенность путём умножения числителя и знаменателя на сопряжённое выражение, в данном случае – Далее, пользуясь формулой разности квадратов раскладываем числитель: Подставляем х=3 в предел и вычисляем: Ответ:
Пример №7
Задание
Вычислить предел
Решение
Как и в предыдущих заданиях, подставляем
и убеждаемся, что имеем дело с неопределённостью вида
Порядок действий стандартный. Избавляемся от иррациональности в знаменателе с помощью домножения числителя и знаменателя на сопряженное выражение. В данном примере сопряжённое выражение имеет вид –
Избавляемся от иррациональности в знаменателе с помощью домножения числителя и знаменателя на сопряженное выражение. В данном примере сопряжённое выражение имеет вид –
Перемножаем знаменатель и сокращаем в числителе и знаменателе
Подставляем, как и ранее, х=3 и находим ответ:
Ответ: 17,8
Пример №8
Задание
Определить предел функции
Решение
Смотрим на функцию, подставляем
мы имеем дело с неопределённостью вида:
Начинаем работать с функциями, содержащими корень. Умножаем числитель и знаменатель на сопряжённое выражение и упрощаем предел:
После преобразований получаем ответ:
Ответ: -2
Пример №9
Задание
Решить предел
Решение:
Подставляя
в выражение лимита, подтверждаем догадки, что перед нами неопределённость вида
Как и раньше, первый шаг – избавиться от иррациональности с помощью домножения числителя и знаменателя на соответствующее сопряженное выражение.
Раскрываем скобки и сокращаем выражения на
Неопределённости
больше нет и ничего нам не мешает вычислить пример:
Ответ:
Пример №10
Задание
Вычислить предел
Решение
Оба лимита числителя и знаменателя равны нулю, значит опять неопределённость вида
Находим сопряжённое к числителю и знаменателю число:
Домножаем на полученное выражение числитель и знаменатель, раскрываем скобки и упрощаем:
Раскладываем числитель и знаменатель:
Вычисляем предел:
Ответ:
Средняя оценка 4 / 5. Количество оценок: 4
Поставьте вашу оценку
Сожалеем, что вы поставили низкую оценку!
Позвольте нам стать лучше!
Расскажите, как нам стать лучше?
18626
Закажите помощь с работой
Не отобразилась форма расчета стоимости? Переходи по ссылке
Не отобразилась форма расчета стоимости? Переходи по ссылке
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
| Справочник по математике | Элементы математического анализа | Функции |
| Предел функции |
| Свойства пределов функций |
| Раскрытие неопределенностей типа |
| Раскрытие неопределенностей типа |
| Первый замечательный предел |
Раскрытие неопределенностей типа . Второй замечательный предел Второй замечательный предел |
Предел функции
В ряде разделов нашего справочника, где требуется применение понятия предела функции, встречаются несколько ситуаций в зависимости от того, куда стремится аргумент функции x , и того, куда при этом стремится значение функции. Определения предела функции для этих случаев удобно представить в форме таблицы. Однако таблица, описывающая все возможные случаи, должна содержать 24 строки и является слишком громоздкой. Для удобства читателей мы привели в таблице только те определения предела функции, которые использованы в нашем справочнике.
| Название | Обозначение | Определение |
Предел функции f (x) при x, стремящемся к числу a, равен числу A | Число A называют пределом функции f (x) при x, стремящемся к числу a, если для любого положительного числа ε найдется такое положительное число δ , что при всех , удовлетворяющих неравенству | x – a | < δ , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при x → a | ||
Предел функции f (x) при x, стремящемся к , равен числу A | Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при | ||
Предел функции f (x) при x, стремящемся к , равен числу A | Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при | ||
Предел функции f (x) при x, стремящемся к , равен числу A | Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x) – A | < ε . | |
f (x) → A при x → | ||
Предел функции f (x) при x, стремящемся к , равен | Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x)| > D . | |
f (x) → при x → | ||
Предел функции f (x) при x, стремящемся к , равен | Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x)| > D . | |
f (x) → при | ||
Предел функции f (x) при x, стремящемся к , равен | Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x)| > D . | |
f (x) → при | ||
Предел функции f (x) при x, стремящемся к числу a слева, равен Замечание. Когда говорят, что x стремится к a слева, то это означает, что при определении предела функции рассматриваются только те значения x , которые меньше a . | Функция f (x) стремится к , при x, стремящемся к числу a слева, если для любого положительного числа С найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a – δ < x < a , будет выполняться неравенство | f (x)| > C . | |
f (x) → при x → a – 0 | ||
Предел функции f (x) при x, стремящемся к числу a справа, равен Замечание. | Функция f (x) стремится к , при x , стремящемся к числу a справа, если для любого положительного числа С, найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a < x < a + δ , будет выполняться неравенство | f (x)| > C . | |
f (x) → при x → a + 0 |
Название: Предел функции f (x) при x, стремящемся к числу a, равен числу A Обозначения: или f (x) → A при x → a Определение: Число A называют пределом функции f (x) при x, стремящемся к числу a, если для любого положительного числа ε найдется такое положительное число δ , что при всех , удовлетворяющих неравенству | x – a | < δ , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен числу A Обозначения: или f (x) → A при Определение: Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен числу A Обозначения: или f (x) → A при Определение: Число A называют пределом функции f (x) при x , стремящемся к , если для любого положительного числа ε найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен числу A Обозначения: или f (x) → A при x → Определение: Число A называют пределом функции f (x) при x , стремящемся к, если для любого положительного числа ε найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x) – A | < ε . |
Название: Предел функции f (x) при x, стремящемся к , равен Обозначения: или f (x) → при x → Определение: Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству | x | > C , будет выполняться неравенство | f (x)| > D . |
Название: Предел функции f (x) при x, стремящемся к , равен Обозначения: или f (x) → при Определение: Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое положительное число С, что при всех x, удовлетворяющих неравенству x > C , будет выполняться неравенство | f (x)| > D . |
Название: Предел функции f (x) при x, стремящемся к , равен Обозначения: или f (x) → при Определение: Функция f (x) стремится к при x, стремящемся к , если для любого положительного числа D найдется такое отрицательное число С, что при всех x, удовлетворяющих неравенству x < C , будет выполняться неравенство | f (x)| > D . |
Название: Предел функции f (x) при x, стремящемся к числу a слева, равен Замечание. Когда говорят, что x стремится к a слева, то это означает, что при определении предела функции рассматриваются только те значения x , которые меньше a . Обозначения: или f (x) → при x → a – 0 . Определение: Функция f (x) стремится к , при x, стремящемся к числу a слева, если для любого положительного числа С найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a – δ < x < a , будет выполняться неравенство | f (x)| > C . |
Название: Предел функции f (x) при x, стремящемся к числу a справа, равен Замечание. Обозначения: или f (x) → при x → a + 0 . Определение: Функция f (x) стремится к , при x , стремящемся к числу a справа, если для любого положительного числа С, найдется такое положительное число δ что при всех x, удовлетворяющих неравенству a < x < a + δ , будет выполняться неравенство | f (x)| > C . |
Свойства пределов функций
Если у функций f (x) и g (x) при x , стремящемся к a , существуют пределы
и ,
где A и B – некоторые числа, то при x , стремящемся к a , существуют также и пределы суммы, разности и произведения этих функций, причем
* * *
* * *
Если, кроме того, выполнено условие
то при x , стремящемся к a , существует предел дроби
причем
Для любой непрерывной функции F (x) справедливо равенство
Раскрытие неопределенностей типа
Определение 1 . Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к стремятся к, то вычисление такого предела называют раскрытием неопределенности типа .
Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к стремятся к, то вычисление такого предела называют раскрытием неопределенности типа .
Часто неопределенность типа удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменале дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.
Пример 1. Найти предел функции предел функции
Решение. Вынесем за скобки «самое большое» слагаемое в каждой из скобок числителя и знаменателя дроби и, используя свойства пределов функций, получим
Ответ.
Пример 2. Найти предел функции предел функции
Решение. Преобразуем выражение, стоящее под знаком предела, к более удобному виду:
Далее, используя свойства пределов функций, находим
Ответ. 3 .
3 .
Раскрытие неопределенностей типа
Определение 2 . Если при нахождении предела дроби выясняется, что пределы числителя и знаменателя дроби равны 0 , то вычисление такого предела называют раскрытием неопределенности .
В алгебраических дробях неопределенность при x → a раскрывается при помощи разложения на множители числителя и знаменателя дроби с последующим сокращением на соответствующую степень множителя (x – a) .
Пример 3. Найти предел функции
Решение. Поскольку и числитель, и знаменатель дроби стремятся к 0 при x → – 2 , то для того, чтобы раскрыть неопределенность типа , разложим числитель и знаменатель дроби на множители. С этой целью в числителе применим формулу сокращенного умножения «сумма кубов», а в знаменателе – разложение квадратного трехчлена на множители, а затем сократим дробь на (x + 2) :
Теперь предел знаменателя дроби равен – 11 , и, воспользовавшись свойствами пределов функций, получаем
Ответ.
Пример 4. Найти предел функции
Решение. В этом примере также возникает неопределенность типа .
Поскольку знаменатель дроби является разностью двух квадратных корней, каждый из которых стремится к одному и тому же числу 5 при x → 5 , то домножим и числитель, и знаменатель дроби на сумму этих квадратных корней и применим формулу сокращенного уножения «разность квадратов»:
Разложим теперь квадратный трехчлен 4x2 – 9x – 55 на множители, а затем сократим числитель и знаменатель на (x – 5) :
Воспользовавшись свойствами пределов функций, получаем
К сожалению, из-за большого размера формул для расчета подробные вычисления на Вашем мобильном устройстве не видны. Их можно посмотреть только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах).
Указания к решению примера. Поскольку знаменатель дроби является разностью двух квадратных корней, каждый из которых стремится к одному и тому же числу 5 при x → 5 , то сначала необходимо домножить и числитель, и знаменатель дроби на сумму этих квадратных корней и применить формулу сокращенного уножения «разность квадратов». Затем, разложив квадратный трехчлен 4x2 – 9x – 55 на множители, сократить числитель и знаменатель на (x – 5) .
После этого, воспользовавшись свойствами пределов функций, получить ответ.
На Вашем мобильном устройстве отображается только результат описанных операций.
Ответ.
Первый замечательный предел
В пределах, содержащих тригонометрические функции, неопределенность раскрывается с помощью первого замечательного предела
Пример 5. Найти предел функции
Найти предел функции
Решение. Числитель и знаменатель дроби стремятся к 0 при x → 0 , поэтому для того, чтобы раскрыть неопределенность типа , разложим числитель и знаменатель дроби на множители. С этой целью в числителе вынесем за скобки x2, а в знаменателе воспользуемся формулой «разность косинусов»:
Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем
Ответ.
Пример 6. Найти предел функции
Решение. Чтобы вычислить данный предел, перейдем от переменной x к новой переменной z по формуле
.
Поскольку
,
то предел можно преобразовать к виду
Применяя формулы приведения и формулу для косинуса двойного угла, получаем
Теперь, воспользовавшись первым замечательным пределом и свойствами пределов функций, получаем
Ответ.
Раскрытие неопределенности типа . Второй замечательный предел
Определение 3. Если при нахождении предела степени некоторого выражения выясняется, что предел основания степени равен 1, а предел показателя степени равен , то вычисление такого предела называют раскрытием неопределенности .
Неопределенность раскрывается с помощью второго замечательного предела:
| (1) |
Если взять натуральный логарифм от обеих частей формулы (1), то второй замечательный предел примет вид:
| (2) |
Пример 7. Найти предел функции предел функции
Решение. Рассмотрим функцию
и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x →. Применяя свойства логарифмов, получаем
Применяя свойства логарифмов, получаем
Преобразуем выражение, стоящее под знаком логарифма к виду, удобному для применения второго замечательного предела,
и заметим, что
Поэтому, воспользовавшись вторым замечательным пределом в виде (2) и свойствами пределов функций, находим
Поэтому функцию y = ln f (x) удобно представить в сдедующем виде
Воспользовавшись вторым замечательным пределом в виде (2), находим
В пределе
и числитель, и знаменатель дроби стремятся к стремятся к, поэтому для раскрытия неопределенности вынесем за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в знаменателе дроби и, используя свойства пределов функций, получим
Следовательно,
Следовательно, воспользовавшись свойствами пределов функций, получаем
Таким образом,
Ответ.
Пример 8. Найти предел функции
Решение. Рассмотрим функцию
и, взяв от нее натуральный логарифм, найдем сначала предел функции y = ln f (x) при x → – 6 . Применяя свойства логарифмов, получаем
Чтобы вычислить предел функции y = ln f (x) при x → – 6 , перейдем от переменной x к новой переменной z по формуле
x = – 6 + z .
Поскольку
то предел (3) можно преобразовать к виду, с помощью формулы (3), получаем
Воспользовавшись вторым замечательным пределом в виде (2) и свойствами пределов функций, получаем
Следовательно,
Ответ.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Пределы — Оценка
Сначала вы должны прочитать Ограничения (Введение)
Краткое описание ограничений
Иногда мы не можем что-то решить напрямую… но мы можем увидеть, что должно быть, по мере того, как мы подходим все ближе и ближе!
Пример:
(х 2 − 1) (х — 1)
Рассчитаем для x=1:
(1 2 − 1) (1 − 1) знак равно (1 − 1) (1 − 1) знак равно 0 0
Теперь 0/0 — это сложность! На самом деле мы не знаем значения 0/0 (оно «неопределенно»), поэтому нам нужен другой способ ответить на этот вопрос.
Итак, вместо того, чтобы пытаться решить это для x = 1, давайте попробуем приближаться к все ближе и ближе:
Продолжение примера:
| x | (х 2 − 1) (х — 1) | |
| 0,5 | 1,50000 | |
| 0,9 | 1. | |
| 0,99 | 1,99000 | |
| 0,999 | 1,99900 | |
| 0,9999 | 1,99990 | |
| 0,99999 | 1,99999 | |
| … | … |
Теперь мы видим, что когда x приближается к 1, тогда (х 2 −1) (х-1) получает близко к 2
Теперь мы столкнулись с интересной ситуацией:
- Когда x=1 мы не знаем ответа (это неопределенное )
- Но мы видим, что будет 2
Мы хотим дать ответ «2», но не можем, поэтому вместо этого математики точно говорят, что происходит, используя специальное слово «предел»
предел из (х 2 −1) (х-1) по мере приближения x к 1 равно 2
И записывается символами как:
lim x→1 x 2 −1 x−1 = 2
Так что это особый способ сказать, «не обращая внимания на то, что происходит, когда мы туда добираемся, но по мере того, как мы подходим все ближе и ближе, ответ становится все ближе и ближе к 2»
На графике это выглядит так: Так что, по правде говоря, мы не можем сказать, каково значение при x=1. Но мы можем говорят, что когда мы приближаемся к 1, , предел равен 2. |
Оценка пределов
«Оценка» означает нахождение значения ( думаю e-» значение» -ating )
В приведенном выше примере мы сказали, что ограничение равно 2, потому что выглядело так, будто должно было быть . Но этого на самом деле недостаточно!
На самом деле существует много способов , чтобы получить точный ответ. Давайте посмотрим на некоторые:
1. Просто введите значение
Первое, что нужно попробовать, это просто ввести значение ограничения и посмотреть, работает ли оно (другими словами, подстановка).
Пример:
| lim x→10 x 2 | 10 2 = 5 |
Легко!
Пример:
| lim x→1 x 2 −1 x−1 | (1−1) (1−1) = 0 0 |
Не повезло. Нужно попробовать что-то другое.
Нужно попробовать что-то другое.
2. Факторы
Можем попробовать факторинг.
Пример:
lim x→1 x 2 −1 x−1
.
lim x→1 x 2 −1 x−1 = lim x→1 (x−1) (x−18) 0 (90 90−1)(x01) 0 (90 90−1)(x01) 1
= lim x→1 (x+1)
Теперь мы можем просто подставить x=1, чтобы получить предел:
lim х→1 (х+1) = 1+1 = 2
3. Конъюгат
Для некоторых дробей может помочь умножение верхнего и нижнего числа на сопряженное число.
| В сопряжении мы меняем знак в середине двух терминов, например: |
Вот пример, где это поможет нам найти предел:
lim x→4 2−√x 4-х | Оценка этого при x=4 дает 0/0, что не является хорошим ответом! |
Итак, давайте попробуем переставить:
| Умножить верх и низ на сопряжение верха: | 2−√x 4−x × 2+√x 2+√x | |
| Упростить верх, используя (a+b)(a−b) = a 2 − b 2 : | 2 2 − (√x) 2 (4−x)(2+√x) | |
| Упростить верх дальше: | 4−x (4−x)(2+√x) | |
| Отмена (4-x) сверху и снизу: | 1 2+√x |
Итак, теперь у нас есть:
LIM x → 4 2 — √x 4 -X = LIM x → 4 1 2+√x = 1 2+a 1 4
Готово!
4.
 Бесконечные пределы и рациональные функции
Бесконечные пределы и рациональные функции| Рациональная функция представляет собой отношение двух многочленов: | f(x) = P(x) Q(x) | |
| Например, здесь P(x) = x 3 + 2x — 1 и Q(x) = 6x 2 : | x 3 + 2x − 1 6x 2 |
Найдя общую степень функции, мы можем узнать, равен ли предел функции 0, бесконечности, -бесконечности или легко вычисляется из коэффициентов.
Подробнее читайте на странице Пределы бесконечности.
5. Правило Лопиталя
Правило Лопиталя может помочь нам оценить пределы, которые на первый взгляд кажутся «неопределенными», такие как 0 0 и ∞ ∞ .
Узнайте больше на сайте L’Hôpital’s Rule.
6. Формальный метод
Формальный метод доказывает, что мы можем максимально приблизить к ответу , приблизив «x» к «a».
Подробнее читайте в разделе «Пределы (формальное определение)»
Ограничения (формальное определение)
Сначала прочтите Введение в ограничения
Приближается…
Иногда мы не можем что-то решить напрямую… но мы можем увидеть, что должно быть, по мере того, как мы подходим все ближе и ближе!
Пример:
(x 2 − 1) (x − 1)
Рассчитаем для x=1:
(1 2 − 1) (1 − 1) = (1 − 1) (1 − 1) = 0 0
Теперь 0/0 — это сложность! На самом деле мы не знаем значения 0/0 (оно «неопределенно»), поэтому нам нужен другой способ ответить на этот вопрос.
Итак, вместо того, чтобы пытаться решить это для x = 1, давайте попробуем приближаться к все ближе и ближе:
Продолжение примера:
| x | (х 2 − 1) (х − 1) | |
| 0,5 | 1,50000 | |
| 0,9 | 1. | |
| 0,99 | 1,99000 | |
| 0,999 | 1,99900 | |
| 0,9999 | 1,99990 | |
| 0,99999 | 1,99999 | |
| … | … |
Теперь мы видим, что когда x приближается к 1, тогда (x 2 −1) (x−1) получает близко к 2
Теперь мы столкнулись с интересной ситуацией:
- Когда x=1 мы не знаем ответа (это неопределенное )
- Но мы видим, что будет 2
Мы хотим дать ответ «2», но не можем, поэтому вместо этого математики точно говорят, что происходит, используя специальное слово «предел»
предел из (x 2 −1) (x−1) при приближении x к 1 равно 2
И записывается символами как:
lim x→1 x 2 −1 x−1 = 2
Так что это особый способ сказать, «не обращая внимания на то, что происходит, когда мы туда добираемся, но по мере того, как мы подходим все ближе и ближе, ответ становится все ближе и ближе к 2»
На графике это выглядит так: Так что, по правде говоря, мы не можем сказать, каково значение при x=1. Но мы можем сказать, что по мере приближения к 1, предел равен 2. |
Более формальный
Но вместо того, чтобы говорить, что предел равен некоторому значению, потому что он выглядел так, как будто он приближается к , мы можем дать более формальное определение.
Итак, начнем с общей идеи.
От английского к математике
Скажем сначала по-английски:
«f(x) приближается к некоторому пределу , когда x приближается к некоторому значению»
Когда мы называем Предел «L», а значение, при котором x приближается к «a», мы можем сказать
«f(x) приближается к L, когда x приближается к a»
Расчет «Закрыть»
Итак, как математически можно сказать «близко»… можем ли мы вычесть одно значение из другого?
Пример 1: 4,01 − 4 = 0,01 (выглядит хорошо)
Пример 2: 3,8 − 4 = −0,2 ( отрицательно близко?)
Так что же нам делать с негативами? Нас не волнует положительное или отрицательное, мы просто хотим знать, как далеко. .. что является абсолютным значением.
.. что является абсолютным значением.
«Насколько близко» = |a−b|
Пример 1: |4.01−4| = 0,01
Пример 2: |3,8−4| = 0,2
И когда |a−b| мал, мы знаем, что мы близки, поэтому пишем:
«|f(x)−L| мало, когда |x−a| мало»
А эта анимация показывает, что происходит с функцией
f(x) = (x 2 −1) (x−1)
изображения/limit-lines.js
f(x) приближается к L=2, когда x приближается к a=1,
поэтому |f(x)−2| мало, когда |x−1| маленький.
Дельта и Эпсилон
Но «маленький» по-прежнему английский, а не «математический».
Выберем два значения должен быть меньше :
| δ | что |x−a| должен быть меньше | |
| ε | что |f(x)−L| должен быть меньше |
Примечание: эти две греческие буквы (δ — это «дельта» и ε — это «эпсилон») — это
, поэтому они часто используются, поэтому мы получаем фразу « дельта-эпсилон 9». 0010 »
0010 »
А у нас есть:
|f(x)−L|<ε при |x−a|<δ
Это действительно так! Итак, если вы понимаете, что понимаете ограничения…
… но чтобы было абсолютно точным , нам нужно добавить следующие условия:
- верно для любого ε>0
- δ существует и >0
- x — это , не равное a, что означает 0<|x−a|
И вот что мы получаем:
Для любого ε>0 существует δ>0, такое что |f(x)−L|<ε при 0<|x−a|<δ
Это формальное определение. На самом деле это выглядит довольно страшно, не так ли?
Но по сути там написано что-то простое:
f(x) приближается к L , когда x приближается к
Как использовать в пруфе
Чтобы использовать это определение в доказательстве, мы хотим пройти
| От кого: | Кому: | |
| 0<|x−a|<δ | |f(x)−L|<ε |
Обычно это означает поиск работающей формулы для δ (в терминах ε).
Как найти такую формулу?
Угадай и проверь!
Верно, мы можем:
- Поэкспериментируйте, пока не найдете формулу, которая может работать
- Протестируйте , чтобы увидеть, работает ли эта формула
Пример: Попробуем показать, что
lim х→3 2х+4 = 10
Используя буквы, о которых мы говорили выше:
- Значение, к которому x приближается, «a», равно 3
- Предел «L» равен 10
Итак, мы хотим знать, как нам перейти от:
0<|x−3|<δ от
до
|(2x+4)−10|<ε
Шаг 1: Поэкспериментируйте, пока не найдете формулу, по которой
может работатьНачните с: |(2x+4)−10| < ε
Упрощение: |2x−6| < ε
Шаг 2 снаружи ||: 2|х−3| < ε
Разделите обе части на 2: |х−3| < е/2
Теперь мы можем предположить, что δ=ε/2 может работать
Шаг 2:
Проверьте , чтобы увидеть, работает ли эта формула.
Итак, можем ли мы получить из 0<|x−3|<δ от до |(2x+4)−10|<ε … ?
Посмотрим…
Начните с: 0 < |х-3| < δ
Замените δ на ε/2: 0 < |х-3| < ε/2
Умножить все на 2: 0 < 2|х−3| < ε
Переместите 2 внутрь ||: 0 < |2x−6| < ε
Заменить «−6» на «+4−10»: 0 < |(2x+4)−10| < ε
Да! Мы можем перейти от 0<|x−3|<δ к |(2x+4)−10|<ε , выбрав δ=ε/2
ГОТОВО!
Итак, мы видели, что по заданному ε можно найти δ, поэтому верно, что:
Для любого ε существует такое δ, что |f(x)−L|<ε при 0<|x−a|<δ
И мы доказали, что
lim х→3 2х+4 = 10
Заключение
Это было довольно простое доказательство, но, надеюсь, оно объясняет странную формулировку «есть …» и показывает хороший подход к такого рода доказательствам.
Пределы — формула, значение, примеры
Пределы в математике определяются как значения, к которым функция приближается к выходным данным для заданных входных значений. Пределы играют жизненно важную роль в вычислениях и математическом анализе и используются для определения интегралов, производных и непрерывности. Он используется в процессе анализа и всегда касается поведения функции в конкретной точке. Предел последовательности далее обобщается в понятии предела топологической сети и связан с пределом и прямым пределом в категории теории. Обычно интегралы делятся на два типа, а именно: определенные и неопределенные интегралы. Для определенных интегралов правильно определены верхний и нижний пределы. Тогда как неопределенные интегралы выражаются без ограничений, и при интегрировании функции он будет иметь произвольную константу. Давайте подробно обсудим определение и представление пределов функции со свойствами и примерами.
Пределы играют жизненно важную роль в вычислениях и математическом анализе и используются для определения интегралов, производных и непрерывности. Он используется в процессе анализа и всегда касается поведения функции в конкретной точке. Предел последовательности далее обобщается в понятии предела топологической сети и связан с пределом и прямым пределом в категории теории. Обычно интегралы делятся на два типа, а именно: определенные и неопределенные интегралы. Для определенных интегралов правильно определены верхний и нижний пределы. Тогда как неопределенные интегралы выражаются без ограничений, и при интегрировании функции он будет иметь произвольную константу. Давайте подробно обсудим определение и представление пределов функции со свойствами и примерами.
| 1. | Что такое ограничения? |
| 2. | Ограничения и функции |
| 3. | Свойства пределов |
4. | Предел функции двух переменных |
| 5. | Пределы сложных функций |
| 6. | Пределы экспоненциальных функций |
| 9. | Часто задаваемые вопросы о лимитах |
Что такое ограничения?
Пределы в математике — это уникальные действительные числа. Рассмотрим вещественную функцию «f» и действительное число «c», предел обычно определяется как \(\lim _{x \rightarrow c} f(x)=L\). Это читается как «предел f для x, когда x приближается к c, равному L». «lim» показывает предел, а тот факт, что функция f(x) приближается к пределу L, когда x приближается к c, показан правой стрелкой. 9{+}} \mathrm{f}(\mathrm{x})=\mathrm{L}\)
Примечание: Предел функции существует между любыми двумя последовательными целыми числами.
Свойства пределов
Вот некоторые свойства пределов функции: Если пределы \( \lim _{x \rightarrow a}\) f(x) и \(\lim _{x \rightarrow a}\ ) g(x) существует, а n является целым числом, тогда
- Закон сложения: \(\lim _{x \rightarrow a}[f(x)+g(x)]=\lim _{x \rightarrow a} f(x)+\lim _{x \rightarrow a} g(x)\)
- Закон вычитания: \( \lim _{x \rightarrow a}[f(x)-g(x)]=\lim _{x \rightarrow a} f(x)-\lim _{x \rightarrow a } г(х)\)
- Закон умножения: \(\lim _{x \rightarrow a}[f(x) \cdot g(x)]=\lim _{x \rightarrow a} f(x) \cdot \lim _{x \ стрелка вправо a} g(x)\)
- Закон деления: \( \lim _{x \rightarrow a}\left[\frac{f(x)}{g(x)}\right]=\frac{\lim _{x \rightarrow a} f (x)}{\lim _{x \rightarrow a} g(x)}, \text { где } \lim _{x \rightarrow a} g(x) \neq 0\) 9{2}}\) < ∆ .
 Он определяется как \(\lim _{(x, y) \rightarrow(a, b)}\) f(x,y) = C.
Он определяется как \(\lim _{(x, y) \rightarrow(a, b)}\) f(x,y) = C.Пределы функций и непрерывность
Пределы функции и непрерывность функции тесно связаны друг с другом. Функции могут быть непрерывными и прерывистыми. Чтобы функция была непрерывной, если есть небольшие изменения на входе функции, то должны быть небольшие изменения и на выходе.
В элементарном исчислении условие f(X) →λ при x → a означает, что число f(x) может лежать сколь угодно близко к числу λ, пока мы берем число, не равное числу а, но достаточно близко к а. Что показывает, что f(a) может быть очень далеко от λ и нет необходимости даже определять f(a). Очень важный результат, который мы используем для вывода функции, таков: f'(a) данной функции f при числе a можно рассматривать как
f'(a) =\(\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}\)Пределы сложных функций
Чтобы дифференцировать функции сложной переменной, следуйте следующей формуле:
9{х}=\infty\)
Функция \(f(z)\) называется дифференцируемой в \(z=z_{0}\), если
\(\lim _{\Delta z \rightarrow 0} \frac{f\left(z_{0}+\Delta z\right)-f\left(z_{0}\right)}{\Delta z}\ ) существуют. Здесь \(\Delta \mathrm{z}=\Delta \mathrm{x}+\mathrm{i} \Delta \mathrm{y}\)
Здесь \(\Delta \mathrm{z}=\Delta \mathrm{x}+\mathrm{i} \Delta \mathrm{y}\)
☛ Также проверьте:
- Исчисление
- Формула ограничения
- Интеграция
- Производная формула
- Формулы интегрирования
Часто задаваемые вопросы о лимитах
Что такое предельная формула?
Формула пределов: Пусть y = f(x) как функция x. Если в точке х = а функция f(x) принимает неопределенный вид, то можно рассматривать значения функции, очень близкой к а. Если эти значения стремятся к некоторому определенному уникальному числу, когда x стремится к a, то полученное уникальное число называется пределом f(x) при x = a.
Что такое ограничения в вычислениях?
Предел сообщает нам значение, к которому приближается функция по мере того, как входные данные этой функции становятся все ближе и ближе (приближаются) к некоторому числу. Идея предела лежит в основе всех дифференциалов и интегралов в исчислении.
Когда предел не может существовать?
Обычная ситуация, когда предел функции не существует, — это когда односторонние пределы существуют и не равны: функция «прыгает» в точке. Предела при x→0 не существует.
Почему мы используем ограничения в математике?
Предел, математическое понятие, основанное на идее близости, используется главным образом для присвоения значений определенным функциям в точках, где значения не определены, таким образом, чтобы они соответствовали ближайшим значениям.
Как узнать, является ли ограничение односторонним?
Односторонний предел — это значение, к которому функция приближается, когда значения x приближаются к пределу *только с одной стороны*. Например, f(x)=|x|/x возвращает -1 для отрицательных чисел, 1 для положительных чисел и не определено для 0. Односторонний *правый* предел f при x=0 равен 1, и односторонний *левый* предел при x=0 равен -1.
Как пределы вычислений используются в реальной жизни?
Пределы также используются в качестве реального приближения к расчету производных. Таким образом, для выполнения расчетов инженеры будут аппроксимировать функцию, используя небольшие различия в функции, а затем пытаться вычислить производную функции, используя все меньшие и меньшие интервалы в интервалах выборки функции.
Таким образом, для выполнения расчетов инженеры будут аппроксимировать функцию, используя небольшие различия в функции, а затем пытаться вычислить производную функции, используя все меньшие и меньшие интервалы в интервалах выборки функции.
Каков предел функции синуса?
Поскольку sin(x) всегда где-то в диапазоне от -1 до 1, мы можем установить g(x) равным -1/x и h(x) равным 1/x. Мы знаем, что предел как -1/x, так и 1/x при приближении x к положительной или отрицательной бесконечности равен нулю, поэтому предел sin(x)/x при приближении x к положительной или отрицательной бесконечности равен нулю.
Как найти предел функции алгебраически
Если вам нужно найти предел функции алгебраически, у вас есть четыре метода на выбор: подстановка значения x , разложение на множители, рационализация числителя и нахождение наименьшего общий знаменатель. Лучше всего начать с первой техники. Вы можете использовать этот метод только в том случае, если функция непрерывна при значении x , при котором вы берете предел. Если функция не определена в этом x , вы должны перейти к другим методам, чтобы упростить вашу функцию, чтобы вы могли подставить приближенное значение для x.
Если функция не определена в этом x , вы должны перейти к другим методам, чтобы упростить вашу функцию, чтобы вы могли подставить приближенное значение для x.
Найдите предел, подставив значение
x Первый метод алгебраического решения для предела состоит в том, чтобы подставить число, к которому приближается x , в функцию. Если вы получаете неопределенное значение (0 в знаменателе), вы должны перейти к другому методу. Но если ваша функция непрерывна в этом x , вы получите значение, и все готово; Вы нашли свой предел! Например, с помощью этого метода вы можете найти этот предел:Предел равен 3, потому что f (5) = 3, и эта функция непрерывна при x = 5.
Найдите предел, разложив на множители
Факторинг — это метод, который стоит попробовать, когда подключение не удается, особенно когда какая-либо часть данной функции является полиномиальным выражением.Скажем, вас попросили найти этот предел:
Сначала вы пытаетесь подставить 4 в функцию, и вы получаете 0 в числителе и знаменатель, который говорит вам перейти к следующей технике. Квадратное выражение в числителе требует, чтобы вы попытались его разложить на множители. Обратите внимание, что числитель предыдущей функции равен ( x – 4)( x – 2). x – 4 сокращения сверху и снизу дроби. На этом шаге у вас останется f ( x ) = x – 2. Вы можете подставить 4 в эту непрерывную функцию, чтобы получить 2.
Квадратное выражение в числителе требует, чтобы вы попытались его разложить на множители. Обратите внимание, что числитель предыдущей функции равен ( x – 4)( x – 2). x – 4 сокращения сверху и снизу дроби. На этом шаге у вас останется f ( x ) = x – 2. Вы можете подставить 4 в эту непрерывную функцию, чтобы получить 2.
Если построить график этой функции, она будет выглядеть как прямая линия 9.0015 f ( x ) = x – 2, но у него есть дыра, когда x = 4, потому что исходная функция все еще не определена (потому что она создает 0 в знаменателе). Рисунок иллюстрирует это.
Если после того, как вы разложили на множители верхнюю и нижнюю часть дроби, член в знаменателе не сократился и искомое значение не определено, предел функции при этом значении составляет x не существует (что можно записать как DNE ).
Например, эта функция действует следующим образом:
( x – 7) вверху и внизу отменяется. Поэтому, если вас попросят найти предел функции, поскольку x приближается к 7, вы можете подставить 7 в отмененную версию и получить 11/8. Но если вы пытаетесь найти
Поэтому, если вас попросят найти предел функции, поскольку x приближается к 7, вы можете подставить 7 в отмененную версию и получить 11/8. Но если вы пытаетесь найти
предела DNE, потому что вы получите 0 в знаменателе. Таким образом, эта функция имеет предел везде, кроме случаев, когда x приближается к –1.
Найдите предел, рационализируя числитель
Третий метод, который вам нужно знать, чтобы найти пределы алгебраически, требует, чтобы вы рационализировали числитель. Функции, требующие этого метода, имеют квадратный корень в числителе и полиномиальное выражение в знаменателе. Например, вас попросили найти предел этой функции, поскольку x приближается к 13:Подстановка чисел завершается ошибкой, когда вы получаете 0 в знаменателе дроби. Факторинг терпит неудачу, потому что уравнение не имеет многочлена к фактору. В этой ситуации, если вы умножите числитель и знаменатель на сопряженное с числителем, член в знаменателе, который был проблемой, сократится, и вы сможете найти предел:
Умножьте верхнюю и нижнюю часть дроби на сопряженную.

Сопряженный числитель равен
.Умножив, вы получите такую настройку:
Умножьте члены, используя первый, внешний, внутренний, последний (FOIL) метод в числителе, чтобы получить
, что упрощается до x – 13 (два средних члена отменяются, и вы комбинируете аналогичные термины из ФОЛЬГИ).
Факторы отмены.
Отмена дает вам это выражение:
Условия ( x – 13) отменяются, оставляя вам следующий результат:
Рассчитать пределы.
Когда вы подставляете 13 в функцию, вы получаете 1/6, что является пределом.
Найдите предел, найдя наименьший общий знаменатель
Когда вам дана сложная рациональная функция, вы используете четвертый и последний алгебраический метод нахождения предела. Техника вставки не работает, потому что вы получаете 0 в одном из знаменателей. Функция неразложима, и у вас нет квадратных корней, которые можно было бы рационализировать. Поэтому вы знаете, чтобы перейти к последней технике. С помощью этого метода вы объединяете функции, находя наименьший общий знаменатель (LCD). Условия отменяются, и в этот момент вы можете найти предел.
Поэтому вы знаете, чтобы перейти к последней технике. С помощью этого метода вы объединяете функции, находя наименьший общий знаменатель (LCD). Условия отменяются, и в этот момент вы можете найти предел.Например, выполните следующие действия, чтобы найти предел:
Найдите ЖК-дисплей фракций вверху.
Распределите числители сверху.
Сложите или вычтите числители, а затем сократите члены.
Вычитание числителей дает
, который затем упрощается до
.Используйте правила дробей для дальнейшего упрощения.
Подставьте предельное значение в эту функцию и упростите.
Вы хотите найти предел, поскольку x приближается к 0, поэтому предел здесь равен –1/36.
Об этой статье
Эта статья взята из книги:
- Предварительное исчисление для чайников,
Об авторе книги:
Мэри Джейн Стерлинг, изучающая алгебру, деловое исчисление, геометрию и конечную математику в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет. Она является автором нескольких книг For Dummies, , в том числе Рабочая тетрадь по алгебре для чайников, Алгебра II для чайников, и Рабочая тетрадь по алгебре II для чайников.
Она является автором нескольких книг For Dummies, , в том числе Рабочая тетрадь по алгебре для чайников, Алгебра II для чайников, и Рабочая тетрадь по алгебре II для чайников.
Эту статью можно найти в категории:
- Предварительное исчисление,
Формула пределов – определение, свойства, формулы и примеры
Примеры пределов – одно из самых сложных понятий в математике, по мнению многих студентов. Однако благодаря более легкому пониманию и постоянной практике учащиеся могут тщательно изучить концепции пределов в математике, пример предела функции, определение пределов и свойства пределов. Предельная математика — одно из самых важных понятий в исчислении. Исчисление — это раздел математики, который занимается вычислениями, связанными с постоянно меняющимися величинами. Формула математического предела может быть определена как значение, которое функция возвращает в качестве вывода для заданных входных значений.
Что такое пределы и формула пределов в математике?
Пределы Математика очень важна в вычислениях. Это одна из основных предпосылок для понимания других концепций исчисления, таких как непрерывность, дифференцирование, формула предела интегрирования и т. Д. В большинстве случаев математические формулы предела представляют собой представление поведения функции в определенной точке. Следовательно, понятие пределов используется для анализа функции. Математическое понятие предела топологической сети обобщает предел последовательности и, следовательно, связывает математику пределов с категорией теории. Интегралы в общем подразделяются на определенные и неопределенные интегралы. Верхний и нижний пределы указываются в случае определенной формулы предела интегрирования. Однако формулы неопределенного предела интегрирования определяются без указанных пределов и, следовательно, имеют произвольную константу после интегрирования. В последующих разделах представлен краткий обзор различных концепций, необходимых для лучшего понимания формул математических пределов.
Формула пределов: Пусть y = f(x) как функция x. Если в точке х = а функция f(x) принимает неопределенный вид, то можно рассматривать значения функции, очень близкой к а. Если эти значения стремятся к некоторому определенному уникальному числу, когда x стремится к a, то полученное уникальное число называется пределом f(x) при x = a.
Пределы Математика
Предел действительнозначной функции ‘f’ относительно переменной ‘x’ может быть определен как:
\[\lim_{x\rightarrow p}f(x)=L\]
В приведенном выше уравнении слово «lim» относится к пределу.
Он обычно описывает, что функция f(x) с действительным знаком стремится достичь предела «L», когда «x» стремится к «p», и обозначается стрелкой вправо.
Мы можем прочитать это как: «предел любой заданной функции ‘f’ от ‘x’, когда ‘x’ приближается к ‘p’, равен ‘L’».
Каковы свойства или законы пределов?
Свойства пределов следующие:
Обозначение предела
Предел функции обозначается как f (x) → L как x → p или в обозначении предела как:
\[\lim_{x\rightarrow p}f(x)=L\]
Предположим, что существует \[\lim_{x\rightarrow p}f(x)\], \[\lim_{x\rightarrow p}g(x)\], \[\lim_{x\rightarrow p }f_1(x)\]……. .\[\lim_{x\стрелка вправо p}f_n(x)\]. Это предположение сделано для объяснения других свойств пределов.
.\[\lim_{x\стрелка вправо p}f_n(x)\]. Это предположение сделано для объяснения других свойств пределов.
Правило сумм
Правило сумм утверждает, что сумма индивидуальных пределов любых двух функций равна пределу суммы этих функций.
\[\lim_{x\стрелка вправо p}f(x)\] + \[\lim_{x\стрелка вправо p}g(x)\] =\[\lim_{x\стрелка вправо p}\mid f( x)+g(x)\mid \]
Расширенное правило сумм
Расширенное правило сумм совпадает с правилом сумм. Однако он определен для пределов более чем двух функций.
\[\lim_{x\стрелка вправо p}f_1(x)\] + \[\lim_{x\стрелка вправо p}f_2(x)\] +……..\[\lim_{x \rightarrow p}f_n(x)\] =\[\lim_{x\rightarrow p}\mid f_1(x)+f_2(x)+…….f_n(x)\mid \]
Правило постоянной функции
Правило постоянной функции утверждает, что предел постоянной функции равен константе.
Множественное правило констант
Предел функции, умноженный на постоянное значение, равен константе, умноженной на предел функции.
\[\lim_{x\rightarrow p}kf(x)\] = k \[\lim_{x\rightarrow p}f(x)\]
Правило произведения
Правило произведения гласит, что произведение пределов двух отдельных функций равно пределу произведения функций.
\[\lim_{x\rightarrow p}f(x)\ast \lim_{x\rightarrow p}g(x)=\lim_{x\rightarrow p}\mid f(x)\ast g(x )\mid \]
Расширенное правило продукта
Расширенное правило продукта совпадает с правилом продукта. Однако учитываются более двух функций.
\[\lim_{x\стрелка вправо p}f_1(x)\ast \lim_{x\стрелка вправо p}f_2(x)\ast . …..\lim_{x\стрелка вправо p}f_n(x) =\lim_{x\стрелка вправо p}\mid \lim_{x\стрелка вправо p}f_1(x)\ast \lim_{x\стрелка вправо p}f_2(x)\ast ……\lim_{x\ стрелка вправо p}f_n(x)\mid \]
…..\lim_{x\стрелка вправо p}f_n(x) =\lim_{x\стрелка вправо p}\mid \lim_{x\стрелка вправо p}f_1(x)\ast \lim_{x\стрелка вправо p}f_2(x)\ast ……\lim_{x\ стрелка вправо p}f_n(x)\mid \]
Правило частного
Частное частных пределов двух функций, когда предел знаменателя не равен нулю, равен пределу частного двух функций, где функция знаменателя не равна нуль.
\[\ frac {\ displaystyle \ lim \ limit_ {x \ rightarrow p} f (x)} {\ displaystyle \ lim \ limits_ {x \ rightarrow p} g (x)} = \ lim_ {x \ rightarrow p }\frac{f(x)}{g(x)}\]
Степенное правило
9n}\] Полностью сведите числитель и знаменатель к его множителям.
Теперь упростим выражение, разделив числитель и знаменатель на любой общий для них множитель.
Теперь вы можете оценить полученный лимит, не забывая о правильном домене.
Предсказать LCD двух членов в числителе для знаменателя.

Преобразуйте обе дроби в числителе так, чтобы они имели LCD в знаменателе.
Умножьте знаменатель и числитель с помощью ЖК-дисплея.
Теперь применим распределительное свойство пределов.
Упростите полученное выражение и разложите числитель.
Отменить одинаковые дроби, присутствующие в результирующем выражении.
Вычислите выражение, сохраняя пределы x в формуле.
Непосредственно вычислить частное, если оно не дано в неопределенной форме, то есть (0/0).

Вы также можете использовать метод наименьшего общего знаменателя (LCD), чтобы преобразовать два рассматриваемых частных в одно частное, взяв их сумму или разность.
Если рассматриваемый числитель также содержит корень, то рационализируйте числитель, а затем умножьте числитель и знаменатель на сопряженное число числителя.
Теперь упростим полученное выражение и оценим полученный предел.
Найдите наименьший общий знаменатель (НОД) рассматриваемой дроби.

Если вы не можете найти предел, выберите различные значения, близкие к неопределенной функции по обе стороны от входа.
Теперь вы можете использовать числовые данные для анализа ограничений с обеих сторон.
Различные свойства пределов используются для выполнения операций с пределами функции, а не с самой функцией.
Вы можете предсказать предел полиномиальной функции, вычислив сумму отдельных членов.
Предел функции, возведенной в степень, равен степени предела функции, широко известный как метод прямой подстановки.
Корень предела функции равен пределу корня функции.

Запись частного в факторизованной форме с последующим упрощением может помочь найти предел функции, выраженной в виде частного.
Можно найти предел сложной функции, найдя ее ЖК-дисплей.
Метод сопряжения можно использовать для нахождения предела функции, содержащей корень.
Метод факторинга также можно использовать для нахождения предела некоторых функций
Численное свидетельство или кусочная установка могут помочь в оценке предела частного, содержащего абсолютные значения.
Вычислить \[\lim_{x\стрелка вправо 2}\](1×3 — 3×2 + 6x -3)
- Оценка пределов: проблемы и полные решения
- Записать это число под знаком квадратного корня и разбить его цифры на «грани» по две цифры в каждой, начиная от запятой, вправо и влево. Если требуется вычислить корень с точностью до 1, то грани, расположенные направо от запятой, можно отбросить. Если требуется вычислить корень с точностью до 0,1, следует справа от запятой сохранить одну грань, при вычислении с точностью до 0,01 оставить две грани и т. д. Если при этом окажется, что цифр для заполнения нужного числа граней не хватает, приписать надлежащее количество нулей.
- Извлечь корень из старшей грани с точностью до 1, с недостатком (или точно, если это возможно). Полученное число принять за первую цифру искомого корня.
- Из старшей грани вычесть квадрат первой цифры и к полученной разности приписать вторую грань. Слева от полуденного результата провести вертикальную черту.
- Слева от черты записать удвоенную первую цифру.
- Найти целую часть частного от деления числа десятков первой разности на число, записанное слева. Если полученное число окажется больше 10, заменить числом 9.
- Полученное однозначное число подвергнуть следующему испытанию: приписать его в качестве цифры к числу, записанному слева, получившееся число умножить на испытуемое однозначное число и сравнить произведение с разностью, записанной справа от черты. Если это произведение больше указанной разности, уменьшить испытуемое число на одну единицу и вновь подвергнуть испытанию.
- Если после испытания произведение окажется меньше указанной разности, подписать его под ней и вычесть. Испытанное однозначное число принять за вторую цифру корня.
- К вновь полученной разности приписать следующую грань и определить третью цифру тем же приемом, каким била определена вторая цифра.
- Продолжать аналогичные вычисления до тех пор, пока не будет достигнута требуемая точность.
- Запятую в результате нужно поставить после того, как будут исчерпаны грани, предшествующие запятой в подкоренном числе.
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
- Состав: мука из утки (30%), мука из фазана (22%), желтый горох (20%), куриный жир (консервирован токоферолами, 8%), филе утки (5%), утиная печень (3%), яблоки (3%), крахмал из тапиоки (3%), рыбий жир лососевый (2%), морковь (1%), льняное семя (1%), нут (1%), гидролизованные панцири ракообразных (источник глюкозамина, 0,026%), экстракт хряща (источник хондроитина, 0,016%), пивные дрожжи (источник маннанолигосахаридов, 0,015%), корень цикория (источник фруктоолигосахаридов, 0,01%), юкка Шидигера (0,01%), водоросли (0,01%), псиллиум (0,01%), тимьян (0,01%), розмарин (0,01%), орегано (0,01%), клюква (0,0008%), голубика (0,0008%), малина (0,0008%).
- Аналитический состав: сырой протеин 37,0 %, сырой жир 18,0 %, сырая зола 8,5 %, сырая клетчатка 2,5 %, влага 10,0 %, кальций 1,8 %, фосфор 1,5 %.
- Пищевые добавки на 1 кг: витамин A (E672) 20 000 МЕ, витамин D3 (E671) 1 500 МЕ, витамин E (α-токоферол) (3a700) 400 мг, цинк (E6) 85 мг, железо (E1) 70 мг, марганец (E5) 35 мг, йод (E2) 0,65 мг, медь (E4) 15 мг, селен (3b8.10) 0,25 мг.
- Энергетическая ценность: 3 900 ккал/кг. Омега-3: 0,33%, Омега-6: 2,34%.
- Инструкция по кормлению: Корм давать сухим или слегка увлажненным. У собаки всегда должен быть свободный доступ к свежей питьевой воде. Ежедневные потребности в питании вашей собаки могут отличаться в зависимости от размера, возраста, уровня активности и внешней среды. Рекомендованные нормы кормления указаны в таблице. Для поддержания отличного состояния вашей собаки обеспечьте ей достаточное количество физических нагрузок и не перекармливайте. Вводя новый корм для Вашей собаки, смешайте немного нового корма с привычной едой и в течение нескольких дней постепенно увеличивайте количество нового корма.
«1» — это число, используемое для обозначения одного идентификатора.
«1» добавляется к любому целому числу, чтобы получить сразу же следующее целое число.
Когда «1» вычитается из любого целого числа, получается непосредственно предшествующее целое число.
1 — мультипликативная идентичность любого числа. т.е. когда любое число умножается само на себя, само число получается как произведение.
Мультипликативная инверсия любого числа — это значение, полученное при делении «1» на число.
Когда любое число делится на «1», ответ — это само число.
Когда число делится само на себя, получается единица.
Значение любого числа, возведенного в степень нуля, равно единице.
Решить для p, если p2 + 8 = 3
Найдите значение 7√1 — 5√1 + 2√1, используя значение под корнем 1.
«Я» — первая единица мнимых чисел. Это эквивалент числа «1» в действительных числах.
Когда отрицательная единица возведена в степень нечетных чисел, ответ будет -1, а когда отрицательная единица возведена в степень четных чисел, ответ будет +1.
Значение корня 1 в любой степени равно 1.
- Решите уравнения вида ax2 + c = 0, извлекая корни.
- Извлечение корней включает выделение квадрата и последующее применение свойства квадратного корня. После применения свойства квадратного корня у вас есть два линейных уравнения, каждое из которых можно решить. Обязательно упростите все радикальные выражения и при необходимости рационализируйте знаменатель.
, где ‘n’ — любое целое число
Аналогично, когда степени представляют собой дроби, правило степеней можно сформулировать следующим образом:
\[\lim_{x\rightarrow p}\sqrt{\ mid f(x)\mid }=\sqrt{\lim_{x\стрелка вправо p}f(x)}\]
Список формул важных пределов в пределах
Список формул математических пределов
1 | \[\lim_{x\стрелка вправо 0}\]\[sinx=0\] |
2 9n\] |
Выше приведен список формул ограничения.
Если пределы функции заданы в форме частного, как я могу ее оценить?
Если предел функции задан в виде частного, можно вычислить выражение методом факторизации. Шаги для того же:
Как я могу оценить пределы частного?
Вы можете очень легко оценить предел частного, предсказав LCD рассматриваемого выражения. Шаги, которые вы можете предпринять для такой оценки:
Как оценить предел функции, содержащей корень?
Очень легко вычислить предел функции, содержащей корень, используя сопряженный метод. Вы можете применить этот метод, просто выполнив шаги, указанные ниже:
Как я могу оценить пределы, если частное с абсолютными значениями дано?
Вы можете легко оценить пределы выражения, содержащего частное с абсолютными значениями. Следуйте инструкциям ниже, чтобы решить проблемы такого рода:
Пределы функции — краткий обзор
Ограничения Примеры и решения
Ответ:
\[\lim_{x\стрелка вправо 2}\](1×3 — 3×2 + 6x -3)
= \[\lim_{x\стрелка вправо 2}\](1×3) — \[\lim_{x\стрелка вправо 2}\](3×2) + \[\lim_{x\стрелка вправо 2} \](6x) — \[\lim_{x\стрелка вправо 2}\](3)
= 1\[\lim_{x\стрелка вправо 2}\](x3) — 3\[\lim_{x\стрелка вправо 2}\](x2) + 6\[\lim_{x\стрелка вправо 2}\](x) — (3)
= 1(2)3 — 3(2)2 +6(2) -3
= 1 х 8 — 3 х 4 + 12 — 3
= 8 — 12 + 9
= 17-12
= 5
0 Разделить на 0: решение предельных задач в математическом анализе, часть 1
ограничений, но у вас могут возникнуть проблемы с решением проблем с ограничениями в домашнем задании, особенно когда вы сначала найдете «0, деленное на 0». В этом посте мы покажем вам методы, которые вы должны знать для решения подобных проблем.
В этом посте мы покажем вам методы, которые вы должны знать для решения подобных проблем.
I. Идея пределов и
Замена (очень просто, когда работает) Вам, наверное, уже говорили что-то вроде
функция f приближается к L (даже если она никогда не равняется L ).
Вы уже на пути к пониманию пределов, если это утверждение имеет для вас смысл, и вы можете посмотреть на рисунок, подобный приведенному ниже, и сразу увидеть, что
$$\lim_{x \to 2}f(x) = 4 $$
потому что независимо от того, движемся ли мы к $x=2$ слева или справа, мы приближаемся к высоте $y = 4$.
В этом случае пределом является просто значение функции при x = 2: $\displaystyle{\lim_{x \to 2}f(x)} = f(2) = 4$.
А в некоторых домашних заданиях и тестовых вопросах (если ваш учитель чувствует себя хорошо), чтобы найти предел, вы просто подставляете значение x в функцию и находите значение в этом месте. Мы назовем этот подход Тактика №1: Замена .
Мы назовем этот подход Тактика №1: Замена .
Пример 1 .
Найдите $\displaystyle{\lim_{x \to 2}x+2}$.
Решение .
Давайте попробуем просто подставить $x=2$ в выражение:
$$\lim_{x \to 2}x+2 = 2 + 2 = 4 \quad \cmark$$
Это тот же предел, что показан на графике выше: на графике изображена функция $f(x) = x+2$, поэтому, приближаясь к $x =2$ слева или справа, мы приближаемся к фактическому значению функции в $x=2$, то есть $y = f(2) = 4$.
В этом случае простая подстановка значения x = 2 в функцию работает: вы получаете число ($f(2) =4$), и все готово. Достаточно было простой техники «Подстановки».
[Конец примера 1.]
Пример 2 .
Найдите $\displaystyle{\lim_{x \to \pi/2}\sin x}$.
Решение .
Давайте снова попробуем Подстановку и установим $x = \dfrac{\pi}{2}$:
$$\lim_{x \to \dfrac{\pi}{2}}\sin x = \sin \dfrac{ \pi}{2} = 1 \quad \cmark$$
График показывает $y = \sin x$. Когда вы приближаетесь к $x = \dfrac{\pi}{2}$ слева или справа, вы приближаетесь к высоте y = 1, которая является значением функции на $x = \dfrac {\pi}{2}$. Следовательно, предел как $x \to \dfrac{\pi}{2}$ sin x равен 1.
Когда вы приближаетесь к $x = \dfrac{\pi}{2}$ слева или справа, вы приближаетесь к высоте y = 1, которая является значением функции на $x = \dfrac {\pi}{2}$. Следовательно, предел как $x \to \dfrac{\pi}{2}$ sin x равен 1.
В этом случае снова работает подстановка: вы подставляете значение $x = \dfrac{\pi} {2}$, и вы получите число $\left(f\left(\dfrac{\pi}{2}\right) =1 \right)$. Вы закончили; легкий. 92-4}{x-2} = \frac{4-4}{2-2} = \frac{0}{0}$$
Это проблема. Давайте на мгновение остановим этот пример. . .
Почти во всех ваших домашних заданиях и тестовых вопросах, когда вы пытаетесь заменить, вы получите 0, деленное на 0. Затем вам понадобится другая тактика, чтобы найти предел.
Морщина : Нам не понадобилось бы понятие предела, если бы вы всегда могли просто подставить число и найти там значение функции. Вместо этого, правда в том, что когда вы попробуете заменить почти все свои домашние задания и контрольные вопросы, вы получите $\dfrac{0}{0}$, «ноль, деленный на ноль». Этот результат известен как неопределенный предел , что является причудливым способом сказать «еще не известно». Он говорит вам, что на самом деле ответ может быть любым — вы просто еще не знаете — и поэтому у вас есть еще над чем поработать.
Этот результат известен как неопределенный предел , что является причудливым способом сказать «еще не известно». Он говорит вам, что на самом деле ответ может быть любым — вы просто еще не знаете — и поэтому у вас есть еще над чем поработать.
В частности, результат $\dfrac{0}{0}$ указывает на необходимость использования другого метода для нахождения предела. К счастью, три простые тактики позволят вам решить большинство проблем. Давайте посмотрим на каждый.
II. Когда вы получите 0, деленное на 0, сначала попробуйте
разложить на множители. Если вы попытаетесь заменить и получите $\dfrac{0}{0}$, вашим следующим шагом будет попытка 92-4}{x-2}}$

[Конец примера 3.]
Если вы учитесь на уроках исчисления, мы гарантируем, что вы столкнетесь со многими задачами, требующими факторизации функции для нахождения предела. Действительно, на каждом экзамене по математическому анализу, который мы видели, была по крайней мере одна проблема, когда вы изначально получаете $\dfrac{0}{0}$ и должны учитывать, чтобы получить окончательный ответ. Откройте следующее поле, чтобы увидеть больше примеров.
Откройте, чтобы увидеть больше примеров факторинга для нахождения предела. 92 -3x+2} &&= \lim_{x \to 1}\frac{(x+2)(x-1)}{(x-2)(x-1)} &&= \lim_{x \to 1}\frac{x+2}{x-2} &&= \frac{1+2}{1-2} = -3 \quad \cmark
\end{align*}
[collapse]
Эти Проблемы становятся простыми, как только вы научитесь их распознавать и умеете учитывать.
Если можно, фактор.
Результат : если подстановка дает результат в виде $\dfrac{0}{0}$, первое, что вы должны попробовать, – это факторинг. Если вы можете факторизовать числитель и/или знаменатель, проблемный член в знаменателе отменяется. Гарантировано.
Если вы можете факторизовать числитель и/или знаменатель, проблемный член в знаменателе отменяется. Гарантировано.
ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ
III. Тактика № 3. Используйте
сопряженных чисел Если функция содержит квадратный корень и подстановка дает $\dfrac{0}{0}$, 0 делится на 0, затем умножьте числитель и знаменатель на
$$1 = \frac{\text{сопряжение члена (числителя или знаменателя) с корнем}}{\text{сопряжение члена (числителя или знаменателя) с корнем}}$$
Как и в случае факторинга, этот подход, вероятно, приведет к возможности отмены срока. Пример 4 иллюстрирует.
Пример 4 .
Найдите $\displaystyle{\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x}}$.
Решение .
Сначала попробуем замену:
$$\lim_{x \to 0}\frac{\sqrt{x+5} – \sqrt{5}}{x} = \frac{\sqrt{0+5}-\ sqrt{5}}{0} = \frac{0}{0}$$
Поскольку предел представлен в виде $\dfrac{0}{0}$ , он не определен – мы еще не знаем, что такое Это. Нам нужно проделать некоторую работу, чтобы привести его в форму, в которой мы сможем определить предел.
Нам нужно проделать некоторую работу, чтобы привести его в форму, в которой мы сможем определить предел.
Итак, давайте избавимся от квадратных корней, используя сопряжение, как вы тренировались в алгебре: умножьте и числитель, и знаменатель на сопряжение числителя, $\sqrt{x+5} + \sqrt{5}$.
\begin{align*}
\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x} &= \lim_{x \to 0}\dfrac{\ sqrt{x+5} – \sqrt{5}}{x} \cdot \dfrac{\sqrt{x+5} + \sqrt{5}}{\sqrt{x+5} + \sqrt{5}} \\ \\
&= \lim_{x \to 0}\dfrac{\sqrt{x+5}\sqrt{x+5} + \sqrt{x+5}\sqrt{5} — \sqrt{5 }\sqrt{x+5} -\sqrt{5}\sqrt{5}}{x[\sqrt{x+5} + \sqrt{5}]} \\ \\
&= \lim_{x \to 0}\dfrac{(x+5) – 5}{x[\sqrt{x+5} + \sqrt{5}]} \\ \\
&= \lim_{ x \to 0}\dfrac{x}{x[\sqrt{x+5} + \sqrt{5}]} \\ \\
&= \lim_{x \to 0}\dfrac{\cancel{x }}{\cancel{x}[\sqrt{x+5} + \sqrt{5}]} \\ \\
&= \lim_{x \to 0}\dfrac{1}{\sqrt{x+ 5} + \sqrt{5}} \\ \\
&=\dfrac{1}{\sqrt{0+5} + \sqrt{5}} = \dfrac{1}{2\sqrt{5}} \quad \cmark
\end{align*}
Функция, с которой мы начали, $\dfrac{\sqrt{x+5} – \sqrt{5}}{x}$, , и та, которой мы закончили (после умножение на сопряженное), $\dfrac{1}{\sqrt{x+5} + \sqrt{5}}$, одинаковы, за исключением того, что первая функция не определена в точке х = 0 (поскольку его знаменатель там равен нулю), а второй нет. Мы показали это на параллельных графиках ниже. Следовательно, их пределы такие же, как $x \to 0$, и поэтому $\displaystyle{\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x} = \ lim_{x \to 0}\dfrac{1}{\sqrt{x+5} + \sqrt{5}} = \dfrac{1}{2\sqrt{5}} }$.
Мы показали это на параллельных графиках ниже. Следовательно, их пределы такие же, как $x \to 0$, и поэтому $\displaystyle{\lim_{x \to 0}\dfrac{\sqrt{x+5} – \sqrt{5}}{x} = \ lim_{x \to 0}\dfrac{1}{\sqrt{x+5} + \sqrt{5}} = \dfrac{1}{2\sqrt{5}} }$.
[Конец примера 4.]
Как показано в примере 4, если подстановка дает вам $\dfrac{0}{0}$ и функция имеет квадратные корни, тактика умножения числителя и знаменателя на сопряженное части квадратного корня даст вам новую функцию, в которой работает подстановка. Всегда.
Откройте, чтобы увидеть другой пример с квадратными корнями.
Пример 5 .
Найдите $\displaystyle{\lim_{x \to 9}\dfrac{9-x}{3-\sqrt{x}}}$.
Решение .
Сначала попробуем замену:
$$\lim_{x \to 9}\frac{9-x}{3-\sqrt{x}} = \frac{9-9}{3-\sqrt{9}} = \frac{0}{0} $$
Поскольку предел представлен в виде $\dfrac{0}{0}$ , он не определен – мы пока не знаем, что это такое. Итак, давайте умножим числитель и знаменатель на сопряженное значение знаменателя, $3+\sqrt{x}$:
Итак, давайте умножим числитель и знаменатель на сопряженное значение знаменателя, $3+\sqrt{x}$:
\begin{align*}
\lim_{x \to 9}\frac{9-x}{3-\sqrt{x}} &= \lim_{x \to 9}\frac{9-x}{ 3-\sqrt{x}} \cdot \frac{3+\sqrt{x}}{3+\sqrt{x}} \\[8px]
&= \lim_{x \to 9}\frac{(9-x)\left(3+\sqrt{x} \right)}{9 +3 \sqrt{x} -3 \sqrt{x} -x } \\[8px]
&= \lim_{x \to 9}\frac{(9-x)\left(3+\sqrt{x} \right)}{9 -x} \\[8px]
&= \lim_{x \to 9}\frac{\cancel{(9-x)}\left(3+\sqrt{x} \right)}{\cancel{9-x}} \\[8px]
&= \lim_{x \to 9}3+\sqrt{x} \\[8px]
&= 3+ \sqrt{9} = 3+3 = 6 \quad \cmark
\end{align*}
[collapse]
Результат: Если у вас есть квадратные корни, умножьте числитель и знаменатель на сопряженную часть квадратного корня.
Мы рассмотрим больше ключевых тактик для работы с 0, разделенным на 0, в нашей следующей статье «Как решать задачи с ограничениями в исчислении — часть 2». Мы также представим несколько других ограничений, которые вы должны просто научиться распознавать. Описание товара Состав: Аналитический состав: Инструкция по кормлению: Описание товара Состав: Аналитический состав: Инструкция по кормлению: Квадратный корень легко извлекается с помощью калькулятора. Для этого достаточно набрать на нём исходное число и нажать клавишу корня √ . Если калькулятора под рукой нет, то квадратный корень извлекают пользуясь алгоритмом извлечения квадратного корня. Корнем n-й степени из числа а называется число х, n-я степень которого равна а. Например, число 2 есть корень пятой степени из 32, ибо Действие, посредством которого по данному числу а и показателю n находится корень n-й степени из а, называется извлечением корня. Показатель n называется показателем корня. Извлечение корня есть В случае квадратного корня показатель не указывается, так что квадратный корень из числа а обозначается Из определения корня следует, что Допустим, что нам дано положительное число а такое, что для него существует квадратный корень, например а = 4. Мы видим, что не одно, а целых два числа удовлетворяют определению квадратного корня из 4, именно числа 2 и —2. Действительно, Действительно, допустим, что причем х и у оба положительны. Тогда Разлагая на множители левую часть, мы придем к равенству Произведение двух чисел х—у и х + у равно нулю. Следовательно, равен нулю один из сомножителей. Однако х + у есть положительное число, как сумма двух положительных чисел. Следовательно, Положительное значение квадратного корня из положительного числа называется арифметическим значением квадратного корня. Условимся знаком Однако приняв это условие, о нем необходимо помнить, чтобы не делать ошибок при пользовании знаком квадратного корня. Так, При Извлечение квадратного корня из данного числа выполнимо далеко не всегда, если ограничиться рассмотрением рациональных чисел. Так, извлечение квадратного корня из отрицательного числа есть действие невыполнимое, ибо квадрат любого рационального числа не может быть отрицательным. Более того, далеко не из каждого рационального положительного числа можно извлечь рациональный квадратный корень. Действительно, рассмотрим таблицу квадратов целых чисел: Мы видим, что квадраты целых чисел очень быстро возрастают, так что промежутки между квадратами соседних целых чисел тоже довольно быстро растут. Целые числа, находящиеся внутри таких промежутков, не являются квадратами целых чисел. Докажем, что они не являются и квадратами дробных чисел. Для этого достаточно установить, что квадрат дробного числа не может быть числом целым. Действительно, каждое дробное число а может быть представлено в виде несократимой дроби Если Итак, числа 2, 3, 5, 6, 7, 8, 10, 11, 12… не являются ни квадратами целых чисел, ни квадратами чисел дробных. Следовательно, извлечение квадратного корня из этих чисел есть действие невыполнимое, если оставаться в области рациональных чисел. Рассмотрим теперь более подробную таблицу квадратов, придавая числу а значения через Промежуток между двумя соседними квадратами в этой таблице в среднем в 10 раз меньше, чем промежуток между соседними квадратами 1 и 4 в предшествующей таблице. Рассмотрим теперь таблицу квадратов, придавая числу а значения через По сравнению с предыдущей таблицей, промежутки между соседними квадратами еще уменьшились, в среднем в 10 раз. Таким образом, если брать значения а все более «густо», т. е. делая промежутки между соседними значениями для а все меньше и меньше, то и промежутки между соседними значениями Проследим, например, за приближениями к числу 2 посредством квадратов на протяжении составленных таблиц. Из первой таблицы мы находим, что наиболее близкие к числу 2 квадраты имеют числа 1 и 2; Если мы пожелаем еще улучшить приближения, мы можем рассмотреть квадраты чисел между 1,41 и 1,42, взяв их через 0,001. Это рассмотрение нам даст Таким образом, среди рациональных чисел не существует числа, квадрат которого равен 2, но существуют числа, квадраты которых сколь угодно близко подходят к 2. То же самое можно сказать о любом другом положительном числе, для которого точное извлечение корня в области рациональных чисел невозможно. Поэтому имеет смысл ставить вопрос о приближенном Дадим теперь строгое определение приближенных значений квадратного корня из данного положительного числа. Приближенным значением с недостатком для квадратного корня из данного положительного числа bс точностью до а называется такое положительное число а, что В свою очередь, число а + а называется приближенным значением с избытком для Для практических целей в качестве меры точности а принимаются числа 0,1, 0,01, 0,001 и т. д. В этих случаях за приближенное значение корня принимаются десятичные дроби с соответствующим числом цифр после запятой. Приближенные значения корня можно находить посредством испытаний, постепенно увеличивая точность до той, которая требуется в задаче. Рассмотрим еще один пример. Пример: Вычислить Решение: Приближения с точностью до 0,1. мы находим из приведенной выше таблицы. Приближение с недостатком есть 1,7 ибо Способом испытаний мы можем приближенно вычислять корень из любого положительного числа с любой степенью точности. Однако этот способ требует хотя и простых, но утомительных вычислений. В следующих параграфах мы познакомимся с более удобными способами вычисления квадратного корня. Отметим, что ставить вопрос о приближенном вычислении квадратного корня из отрицательного числа бессмысленно, так как приближаться к данному отрицательному числу посредством квадратов рациональных чисел невозможно. Выведенные в предшествующих параграфах свойства и особенности действия извлечения квадратного корня становятся особенно наглядными, если перейти от рассмотрения таблицы квадратов к графику зависимости Приводим снова этот график (рис. 26). Он имеет вид кривой линии, состоящей из двух бесконечных ветвей, симметричных относительно оси ординат. Эти ветви сходятся в начале координат, плавно переходя одна в другую. Как уже было сказано, эта кривая называется параболой. Задача извлечения Очевидно, что при у < 0 таких точек нет, ибо весь график расположен выше оси абсцисс, касаясь ее лишь в начале координат. При у = 0 такая точка единственна, это начало координат. Абсцисса ее равна тоже нулю. При у > 0 таких точек оказывается две, расположенных симметрично относительно оси ординат. Это соответствует тому, что квадратный корень из положительного числа имеет два значения, имеющие одинаковую абсолютную величину, но отличающиеся знаками. Выбор арифметического значения квадратного корня соответствует тому, что из двух ветвей параболы мы рассматриваем только одну, именно правую ветвь. На этой ветви точка с заданной ординатой оказывается уже единственной. Измерив абсциссу этой точки, мы получим приближенное значение Таким образом, из графика зависимости Увеличивая масштаб, мы можем построить график с любой заданной степенью точности. Следовательно, и само извлечение корня из данного положительного числа можно осуществить с любой точностью. График зависимости С этой целью следует тщательно построить график на При помощи этого графика можно также находить значения корня из любого положительного числа b. Для этого нужно найти какое либо число а, удовлетворяющее условию Следовательно, Если подобрать а так, Пусть, например, требуется найти Приступим к объяснению одной удобной арифметической схемы для приближенного извлечения квадратного корня с заданной точностью. Допустим, что нам уже известно, что число 7,236 есть Мы сможем вычислять квадратные корни с любой степенью точности, если нам удастся указать способ вычисления поправки к уже известному приближению с недостатком так, чтобы после прибавления этой поправки получалось бы снова приближение с недостатком, но значительно более точное. Для вывода удобного способа вычисления таких поправок рассмотрим задачу в общем виде. Пусть а есть приближенное значение с недостатком для Примем сначала, что a + b есть точное значение откуда Вспомним теперь, что поправку b мы ищем только приближенно. Ввиду сделанного предположения, что искомая поправка мала по сравнению с числом а мы можем отбросить в знаменателе слагаемое b, и тогда получим для b приближенное равенство В знаменателе мы отбросили положительное слагаемое, тем самым мы уменьшили знаменатель, а всю дробь увеличили. Следовательно, число Для того чтобы проверить, что вычисленная таким способом поправка дает после прибавления к а снова приближение с недостатком, надо проверить, что разность Действительно, число Рассмотрим пример на применение этих соображений. Пример. Вычислить Решение. В качестве первого приближения возьмем а = 9. В качестве поправки следует взять число, немного меньшее, чем Берем поправку b = 0,6. Эта поправка дает значение с недостатком, ибо Таким образом, число a + b = 9,6 есть приближение к Все вычисления очень удобно производить по следующей схеме: Порядок действий следующий: 1) пишем данное число под знаком корня; Пример: Вычислить Решение: Решаем этот пример, пользуясь той же схемой: При делении числа 15 на 6 мы получим, после округления, 0,8. Однако такая поправка слишком велика, так как 6,8 • 0,8 = 5,44 > 5. Примем в качестве поправки 0,7. Поправка 0,7 оказалась подходящей. Последняя разность 0,31 есть Пример: Вычислить При делении числа 2,41 на 2 получается с точностью до 0,1 число 1,2, которое явно велико в качестве поправки. Такой плохой результат получается потому, что здесь поправка совсем немала по сравнению с первым приближением, и поэтому приближенное равенство Даже 0,9 велико в качестве поправки, ибо 2,9 • 0,9 = 2,61 >2,41. Берем 0,8. Пример: Извлечь квадратный корень из числа 92,4317 с Решение: Сначала извлекаем корень с точностью до 0,1, Легко сообразить, что следует делать дальше. Примем а = 9,6 за исходное приближение и ищем для него поправку по прежнему правилу. Вычислять снова разность Последняя разность 0,0796 есть Заметим, что мы могли бы не записывать в третьей строчке две последние цифры, так как их роль сказывается только в пятой строчке. Далее, для упрощения записи можно было бы не писать запятых и Принимая все это во внимание, запись можно провести так: Продолжая вычисления, мы можем извлечь корень с точностью до 0,001; 0,0001 и т. д. Способ извлечения квадратного корня, изложенный в § 5 и 6, применялся там только к числам, заключенным между 1 и 100, т. е. к числам с однозначной или двузначной целой частью. Однако этот способ легко распространяется на любые положительные числа, целые или заданные десятичной дробью. Это следует из того, что при умножении подкоренного числа на 100 корень увеличивается в 10 раз, а при делении подкоренного числа на 100 корень уменьшается в 10 раз. Действительно, если так как ибо Умножение или деление на 100 равносильно перенесению запятой на два разряда вправо или влево. Умножение или деление на 10 равносильно перенесению запятой на один разряд. Повторное умножение или деление на 100 равносильно перенесению запятой на четное число урядов. Очевидно, что за счет такого перенесения запятой в подкоренном числе можно добиться того, чтобы целая часть нового подкоренного числа оказалась однозначным или двузначным числом. К этому числу можно применить указанный прием для извлечения квадратного корня. Чтобы получить корень из исходного числа, нужно в полученном корне перенести запятую в обратном направлении на вдвое меньшее число разрядов. Например, чтобы извлечь корень Сформулируем теперь общее правило для извлечения корня из данного числа с данным числом десятичных знаков, обобщив в этом правиле все высказанные выше соображения. Правило. Чтобы извлечь квадратный корень из данного положительного целого или записанного в виде десятичной дроби числа с, данной точностью, нужно: Целая часть, вычисляемая в п. 5 правила, может оказаться больше 9 только на первом шагу вычислений, т. е. при вычислении второй цифры. Отрицательный результат испытания в п. 6 правила довольно часто имеет место на первом шагу вычислений, когда поправка еще не очень мала, по Если подкоренное число имеет 0 целых и вслед затем следует нуль, корень имеет тоже 0 целых и затем столько нулей, сколько граней из нулей следует за запятой в подкоренном числе. Первая значащая цифра корня есть целая часть корня из первой значащей грани подкоренного числа. Мы уже не раз пользовались графиками для приближенных вычислений. Графический способ решения задач является очень полезным для приложений вследствие большой простоты и наглядности. Конечно, им следует пользоваться только в тех случаях, когда не требуется очень большой точности результата. Достоинством графического Пример: Решить приближенно уравнение Решение: Построим сначала график зависимости а затем найдем на этом графике точки, для которых у = 0. Абсциссы этих точек и дадут решения уравнения. Прежде всего вычислим таблицу значений: По этой таблице строим график (рис. 28), соединяя точки возможно более плавной линией. Из этого графика мы видим, что интересующих нас точек имеется три. Их абсциссы приближенно равны —1,8; 0,3 и 1,5. Следовательно, уравнение имеет три решения Чтобы найти более точные значения для корней уравнения, нужно построить с большей точностью и в большем масштабе участки графика, примыкающие к интересующим нас точкам. Пример: Решить приближенно систему уравнений Для решения задачи строим на одном чертеже графики зависимостей При вычислении второй таблицы мы придавали конкретные значения величине у и вычисляли соответствующие значения для х. Здесь это удобно, так как уравнение, определяющее зависимость, решено относительно х. Графики по этим таблицам изображены на рис. 29. Мы видим, что графики пересекаются в четырех точках. Следовательно, система имеет четыре решения. Приближенные решения системы даются следующими значениями для х и у: Решение заданий и задач по предметам: Дополнительные лекции по высшей математике: свежая рыба (60%), горох, куриный жир (консервированный токоферолами), нут (4%), сушеные яблоки (4 %), красная чечевица , тыква, лососевое масло (3 %), натуральный аромат, морковь, сушеная яичная скорлупа, протеин ряски (0,5%), спирулина (0,3%), сушеная облепиха (0,2%), сушеный корень имбиря (0,1%), сушеная черника (0,1%), сушеный розмарин (0,1%) сушеная клюква (0,1%), сушеный тимьян (0,1%), глюкозамин (0,026%), зеленая новозеландская мидия (0,025%), хондроитин сульфат (0,016%), пивные дрожжи (источник маннанолигосахаридов, 0,015%), корень цикория (источник фруктоолигосахаридов, 0,01%), юкка шидигера (0,01%). витамин A (3a672a) 20000 IU, витамин D3 (3a671) 1500 IU, витамин E (3a700) 400 мг, витамин C (3a312) 250 мг, таурин (3a370) 1500 мг, L-карнитин (3a310 ) 50 мг, хлорид холина (3a890) 1800 мг, ниацинамид (3a315) 20 мг, биотин (3a880) 0,5 мг, цинк (3b606) 80 мг, железо (3b106) 60 мг, марганец (3b504) 35 мг, йод ( 3b201) 0,65 мг, медь (3b406) 15 мг, селен (3b810) 0,2 мг. Содержит природные антиоксиданты: экстракты токоферола из растительных масел (1b306 (i)), аскорбил пальмитат (1b304) и экстракт розмарина. сырой протеин 25,0 %, содержание жира 15 %, влажность 10,0%, сырая зола 7,0 %, сырая клетчатка 4,0 %, кальций 1,3 %, фосфор 0,9 %, натрий 0,5 %, омега -3 0,6 %, омега-6 1,6 %, EPA (20: 5 n-3) 0,15 %, DHA (22: 6 n-3) 0,2%. 3,670 kcal/kg 1.4 kg, 4 kg, 11.4 kg {{ $root.accountingCode }}100 171547 Сбалансированный полнорационный сухой беззерновой корм для взрослых собак всех пород. Чтобы быть в отличной физической форме, взрослым собакам всех пород необходима диета, богатая высококачественными протеинами и жирными кислотами. Линейка кормов carnilove для взрослых собак разработана, чтобы максимально соответствовать природному рациону собак и их генетических предков, волков, чья диета состоит преимущественно из мяса и костей добычи, а также включает лесные ягоды, овощи и травы. Мясо и жир диких птиц и рыб содержит все жизненно необходимые взрослым собакам питательные вещества, необходимые для поддержания оптимальной физической формы и здоровой иммунной системы. Утка — это идеальный источник протеинов, с высоким содержанием полиненасыщенных жирных кислот (пнжк), которые понижают уровень холестерина в крови. Мясо утки — это фантастический источник ниацина (витамин В3), который играет важную роль в обменных процессах в организме и также помогает снизить уровень холестерина в крови. Утка содержит витамины А и С, а также важные минералы, такие как железо, кальций, селен, в то время как фазан является прекрасным источником витамина B12, фосфора и селена. Комбинация мяса утки и фазана позволило создать диетически сбалансированный и питательный продукт, содержащий все незаменимые аминокислоты. Таблица кормления: Вес собаки (кг) 5 10 15 20 25 30 40 50 60 70 80 90 Ежедневное потребление (г) 70 120 160 200 240 270 340 400 460 520 570 620 Я заметил, что иногда, когда я запускаю top , использование памяти каждым процессом в таблице процессов, по-видимому, не дает общего результата. Например, в приведенном ниже дампе top говорит, что я использую 16 Гб памяти. Однако таблица процессов показывает только два процесса, использующих чуть более 520 Мб. Как я могу узнать, что потребляет другие 15,5 Гб? (Я использую CentOS.) Правительство Российской Федерации постановляет: 1. Для определения крупного и особо крупного размера наркотических средств и психотропных веществ, обнаруженных в незаконном обороте, ответственность за который установлена статьями 228, 228(1) и 229 Уголовного кодекса Российской Федерации, утвердить прилагаемые размеры средних разовых доз наркотических средств и психотропных веществ. 2. Настоящее постановление вступает в силу с 12 мая 2004 г. Председатель Правительства Размеры средних разовых доз наркотических средств и психотропных веществ для целей статей 228, 228(1) и 229 Уголовного кодекса Российской Федерации Список наркотических средств и психотропных веществ, оборот которых в Российской Федерации запрещен в соответствии с законодательством Российской Федерации и международными договорами Российской Федерации (список I) Наркотические средства Аллилпродин 0,001 г Альфамепродин 0,001 г Альфаметадол 0,001 г Альфа-метилфентанил 0,00002 г Альфа-метилтиофентанил 0,00002 г Альфапродин 0,001 г Альфацетилметадол 0,001 г Анилэридин 0,0005 г Ацетил-альфаметилфентанил 0,00002 г Ацетилгидрокодеин 0,001 г Ацетилированный опий 0,1 г Адетилкодеин 0,001 г Ацетилметадол 0,001 г Ацеторфин 0,00002 г БДБ [L — (3,4-метилендиоксифенил) — 2-бутанамин] 0,002 г Безитрамид 0,0005 г Бензетидин 0,0002 г Бензилморфин 0,001 г Бета-гидрокси-3-метилфентанил 0,00002 г Бета-гидроксифентанил 0,00002 г Бетамепродин 0,001 г Бетаметадол 0,001 г Бетапродин 0,001 г Бетацетилметадол 0,001 г Гашиш (анаша, смола каннабиса) 0,5 г Героин (диацетилморфин) 0,1 г Гидрокодон 0,005 г Гидрокодона фосфат 0,005 г N-гидрокси-МДА 0,002 г Гидроморфинол 0,0001 г Гидроморфон 0,001 г Дезоморфин 0,0001 г Диампромид 0,0001 г Дигидроморфин 0,001 г Дименоксадол 0,001 г N-Диметил амфетамин 0,002 г Димепгептанол 0,001 г Диметилтаамбутен 0,002 г Диоксафетил бутират 0,001 г Дипипанон 0,001 г Дифеноксин 0,0002 г Диэтилтиамбутен 0,002 г ДМА (d, L — 2,5-диметокси-альфа-метил-фенил- этиламин) 0,002 г ДМГП (диметилгептилпиран) 0,0003 г ДМТ (диметилтриптамин) 0,01 г ДОБ (d, L — 2,5-диметокси-4-бром-амфетамин) 0,001 г ДОХ (d, L — 2,5-диметокси-4-хлор-амфетамин) 0,0002 г ДОЭТ (d, L — 2,5-диметокси-4-этил-амфетамин) 0,0001 г Дробетанол 0,01 г ДЭТ (N, N-диэтилтриптамин) 0,01 г Изометадон 0,001 г Каннабис (марихуана) высушенная 2 г не высушенная 14 г Кат (листья) 20 г Кетобемидон 0,5 г Клонитазен 0,00002 г Кодоксим 0,001 г Кустарно изготовленные препараты из эфедрина или из препаратов, содержащих эфедрин -сухой остаток в целом 0,3 г Кустарно изготовленные препараты из псевдоэфедрина или из препаратов, содержащих псевдоэфедрин — сухой остаток в целом 0,3 г Левометорфан 0,002 г Левоморамид 0,0005 г Леворфанол (леморан) 0,0005 г Левофенацилморфан 0,0005 г Лизергиновая кислота и ее производные 0,00005 г d-Лизергид (ЛСД, ЛСД-25) 0,0003 г Лист кока (за исключением листьев, из которых удален весь экгонин, кокаин и любые другие алколоиды экгонина) 5 г Маковая солома (опийного мака за исключением семян) высушенная 10 г не высушенная 70 г Масло каннабиса (гашишное масло) 0,1 г МБДБ [N-метил-1-(3,4-метилендиоксифенил) — 2-бутанамин] 0,002 г МДА (тенамфетамин) 0,002 г МДМА (d, L-3,4-метилендиокси-К-альфа-диметил- фенил-этиламин) 0,05 г 3-Моноацетилморфин 0,01 г 6-Моноацетилморфин 0,01 г Мескалин 0,05 г Метадон 0,05 г d-Метадон 0,05 г L-Метадон 0,05 г Метадона промежуточный продукт (4-циано-2-диметиламино-4, 4-дифенил-бутан) 0,05 г Метазоцин 0,001 г Метамфетамин 0,05 г Метиддезорфин 0,001 г Метилдигидроморфин 0,001 г 3 -метилтиофентанил 0,00002 г 3 -метилфентанил 0,00002 г N-метилэфедрон 0,0005 г Метопон 0,0002 г Мирофин 0,0005 г ММДА (2-метокси-альфа-4-метил 4, 5- (метилендиокси)-фенетиламин) 0,002 г Морамида, промежудочный продукт (2-метил- З3-морфолин-1 -дифенил-пропан-карбоновая кислота) 0,0005 г Морферидин 0,00002 г Морфин метилбромид 0,0005 г Морфин-М-окись 0,0005 г МППП (1-метил-4-фенил-4-пиперидинол пропионат (эфир) 0,0001 г Никодикодин 0,0005 г Никокодин 0,0005 г Никоморфин 0,0005 г Норациметадол 0,001 г Норкодеин 0,001 г Норлеворфанол 0,0005 г Норметадон 0,001 г Норморфин 0,0005 г Норпипанон 0,0005 г Оксикодон (текодин) 0,0002 г Оксиморфон 0,0002 г Опий (в том числе медицинский) — свернувшийся сок опийного мака 0,5 г Опийный мак (растение вида Papaver somniferum L) 8 г Орипавин 0,01 г Пара-флуорофентанил (пара-фторфентанил) 0,00002 г Парагексил 0,0002 г ПЕПАП (L-фенэтил-4-фенил-4-пиперидинол ацетат (эфир) 0,0001 г Петидин 0,005 г Петидина промежуточный продукт А (4-циано-1-метил- 4-фенилпиперидин) 0,005 г Пиминодин 0,001 г ПМА (4-метокси-альфа-метилфенил-этиламин) 0,002 г Прогептазин 0,003 г Проперидин 0,003 г Пропирам 0,003 г Псилоцибин 0,005 г Псилоцин 0,005 г Рацеметорфан 0,002 г Рацеморамид 0,0005 г Рацеморфан 0,0005 г Ролициклидин 0,0001 г 2С-В (4-бром-2,5-диметоксифенетиламин) 0,01 г СТП (ДОМ) [2-амино-1-(2,5-диметокси-4-метил) фенилпропан] 0,0005 г Тебакон 0,0007 г Теноциклидин 0,0001 г Тетрагидроканнабинол (все изомеры) 0,05 г Тиофентанил 0,00002 г ТМА (d, L-3,4,5-триметокси-альфа-метилфенил-амин) 0,03 г Фенадоксон 0,001 г Фенадон 0,01 г Феназоцин 0,003 г Фенампромид 0,0001 г Фенатин 0,0005 г Фенциклидин 0,005 г Феноморфан 0,0005 г Феноперидин 0,0002 г Фолькодин 0,001 г Фуретидин 0,005 г Экгонин, его сложные эфиры и производные, которые могут быть превращены в экгонин и кокаин 0,001 г Экстракт маковой соломы (концентрат маковой соломы — материал получаемый, когда маковая солома начала подвергаться процессу концентрации содержащихся в ней алколоидов) 0,05 г N-ЭТИЛ-МДА (d, L-N-этил-альфа-метил-3, 4- (метилендиокси)-фенетиламил) 0,002 г Этилметилтиамбутен 0,002 г Этициклидин 0,0001 г Этоксеридин 0,001 г Этонитазен 0,00002 г Эторфин 0,00002 г Этриптамин 0,005 г Эфедрон (меткатинон) 0,05 г Психотропные вещества Дексамфетамин 0,005 г Катин (d-норпсевдоэфедрин) 0,0005 г Катинон (L-альфа-аминопропиофенон) 0,0005 г Левамфетамин 0,005 г Меклоквалон 0,05 г Метаквалон 0,2 г 4-метиламинорекс 0,01 г Метилфенидат (риталин) 0,01 г Изомеры перечисленных наркотических средств и психотропных веществ (если таковые определенно не исключены) в тех случаях, когда существование таких изомеров возможно в рамках данного химического обозначения, в размере средней разовой дозы, применяемой для указанных веществ. Эфиры сложные и простые перечисленных наркотических средств и психотропных веществ в размере средней разовой дозы, применяемой для указанных веществ. Соли перечисленных наркотических средств и психотропных веществ, если существование таких солей возможно, в размере средней разовой дозы, применяемой для указанных веществ. Список наркотических средств и психотропных веществ, оборот которых в Российской Федерации ограничен и в отношении которых устанавливаются меры контроля в соответствии с законодательством Российской Федерации и международными договорами Российской Федерации (список II) (В пересчете на действующее наркотическое средство или психотропное вещество, за исключением таблеток и свечей) Наркотические средства р-Аминопропиофенон (РАРР) и его оптические изомеры (антидот против цианидов) 0,02 г Альфентанил 0,003 г Амфетамин (фенамин) и комбинированные лекарственные препараты, содержащие фенамин (амфетамин) 0,1 г Бупренорфин 0,0003 г Глютетимид (ноксирон) 0,25 г Декстроморамид 0,0005 г Декстропропоксифен (ибупроксирон, проксивон, спазмопроксивон) 0,1 г Дигидрокодеин 0,016 г Дифеноксилат 0,0025 г Кодеин 0,1 г Кодеина фосфат 0,1 г Кокаин 0,15 г Кокаина гидрохлорид 0,01 г Кодеин N-окись 0,1 г Морфин 0,01 г Морфина гидрохлорид 0,01 г Морфина сульфат 0,01 г Морфилонг 0,01 г Омнопон 0,03 г Пентазоцин 0,05 г Проперидин 0,003 г Пропирам 0,003 г Просидол 0,01 г Пиритрамид (дипидолор) 0,01 г Реазек 0,0025 г Свечи тилидина в разных дозировках 1 свеча 0,05 г Сомбревин 0,25 г Суфентанил 0,00001 г Таблетки «Алнагон» (кодеина фосфата 20 мг, кофеина 80 мг, фенобарбитала 20 мг, кислоты ацетилсалициловой 20 мг) 5 табл. Таблетки (кодеина камфосульфоната сульфагваякола калия 0,1 г, густого экстрата гринделии 0,017 г) 0,025 г, 4 табл. Таблетки кодеина 0,03 г + парацетамола 0,5 г 3 табл. Таблетки кодеина фосфата 0,015 г + сахара 0,25 г 6 табл. Таблетки кодеина 0,01 г, (0,015 г) + сахара 0,25 г 10 (6) табл. Таблетки кодеина 0,015 г + натрия гидрокарбоната 6 табл. 0,25 г Таблетки «Кодтерпин» (кодеина 0,015 г + натрия 6 табл. гидрокарбоната 0,25 г + терпингидрата 0,25 г) Таблетки от кашля. Состав: травы термопсиса в порошке — 0,01 г (0,02 г), кодеина — 0,02 г (0,01 г), натрия гидрокарбоната — 0,2 г, корня солодки в порошке — 0,2 г — 5 (10) табл. Тебаин 0,03 г Тилидин 0,05 г Тримеперидин (промедол) 0,02 г Фентанил 0,0005 г Этилформин 0,008 г Эскодол 0,05 г Эстоцин 0,06 г Эстоцина гидрохлорид 0,06 г Этилморфина гидрохлорид 0,008 г Психотропные вещества Амобарбитал (барбамил) 0,1 г Амфепрамон (фепранон, диэтилпропион) 0,025 г Кетамин 0,1 г Кетамина гидрохлорид (калипсол, кеталар) 0,1 г Таблетки (барбамила 0,15 г + бромизовала 0,15 г) 1 табл. Фенметразин 0,05 г Фентермин 0,01 г Этаминал натрия 0,2 г Хальцион (триазолам) 0,00025 г Соли перечисленных наркотических средств и психотропных веществ, если существование таких солей возможно, в размере средней разовой дозы, применяемой для указанных веществ. Список психотропных веществ, оборот которых в Российской Федерации ограничен и в отношении которых допускается исключение некоторых мер контроля в соответствии с законодательством Российской Федерации и международными договорами Российской Федерации (список III) (В пересчете на действующее психотропное вещество) Аминорекс 0,1 г Апрофен 0,025 г Бензфетамин 0,025 г Галотан (фторотан) 10 г Декстрометорфан 0,06 г Левамфетамин 0,002 г Лефетамин 0,001 г Мазиндол 0,002 г Мефенорекс 0,002 г Натрий оксибутират и другие соли оксимасляной кислоты 2 г Пентобарбитал 0,1 г Пипрадрол 0,002 г Тарен 0,2 г Фендиметразин 0,05 г Фенпропорекс 0,002 г Ципепрол 0,01 г Этиламфетамин 0,002 г Соли перечисленных наркотических средств и психотропных веществ, если существование таких солей возможно, в размере средней разовой дозы, применяемой для указанных веществ. Примечания. 1. Размеры средних разовых доз аналогов наркотических средств и психотропных веществ соответствуют размерам приведенных в настоящем перечне средних разовых доз наркотических средств и психотропных веществ. 2. Количество наркотических средств, психотропных веществ, содержащихся в пропитанных ими тампонах, марле, бинтах и т.п., определяется путем экстракции наркотического средства, психотропного вещества с последующим пересчетом его сухого остатка. кв. (0,01). Найдите квадратный корень из 0,01 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Квадратный корень 0,01 или что такое квадратный корень 0,01? Квадратный корень из числа «x» — это такое число y, что y 2 = x, другими словами, число y, квадрат которого равен y. Например, 5 — это квадратный корень из 25, потому что 5 2 = 5 • 5 = 25, -5 — квадратный корень из 25, потому что (-5) 2 = (-5) • (-5) = 25.При написании математики люди часто используют sqrt (x) для обозначения квадратного корня из x. Узнайте больше о квадратном корне здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram Вот символ квадратного корня. Он обозначается √, известным как знак корня или основание. Квадратные корни от 1 до 100 с округлением до тысячных. Здесь мы вычислим квадратный корень 0,01 (√,01) и объясним, почему квадратный корень 0,01 больше 0,01. 0,01 можно разделить на две части. Число до и число после десятичной точки. Число перед
десятичная точка — это целое число, а число после десятичной точки — это десятичная часть: 0 = целое число Число (x), где целое число не равно 0, больше, чем квадратный корень из числа (x): x> √x Это имеет смысл, потому что √x, умноженное на √x, равно x.Однако это неверно, если все число равно 0.
В этом случае все наоборот. ОК. Перво-наперво. Ниже приведен ответ на квадратный корень 0,01. √0,01 = 0,1 Как видите, 0,1 больше 0,01. Таким образом, два больших числа, умноженные вместе, равны меньшему числу!
Итак, как это возможно, что квадратный корень 0,01 больше 0,01? дивиденд ÷ делитель = частное Глядя на уравнение деления выше, вы можете сделать вывод, что если дивиденд увеличивается на большую величину, чем делитель, то
коэффициент увеличится.Кроме того, если дивиденд увеличивается на меньшую величину, чем делитель, то частное уменьшится. 1 деленное на 100 равно 0,01, поэтому мы можем преобразовать его в задачу деления следующим образом: √1 ÷ √100 = √0,01 Причина, по которой квадратный корень 0,01 больше 0,01, заключается в том, что когда вы извлекаете квадратный корень из делимого (√1), уменьшение
делимого меньше, чем уменьшение делителя, когда вы извлекаете квадратный корень из делителя (√100). Этого не было бы, если бы целое число перед десятичной запятой не было 0. Квадратный корень десятичного числа Мы получаем подозрительную активность от вас или кого-то, кто пользуется вашей интернет-сетью.Подождите, пока мы подтвердим, что вы настоящий человек. Ваш контент появится в ближайшее время.
Если вы продолжаете видеть это сообщение, напишите нам
чтобы сообщить нам, что у вас возникли проблемы. Nous avons reçu des activités suspectes venant de quelqu’un utilisant votre réseau internet.
Подвеска Veuillez Patient que nous vérifions que vous êtes une vraie personne. Вотре содержание
apparaîtra bientôt. Si vous continuez à voir ce message, veuillez envoyer un
электронная почта à
pour nous informer du désagrément. Wir haben einige verdächtige Aktivitäten von Ihnen oder von jemandem, der in ihrem
Интернет-Netzwerk angemeldet ist, festgestellt. Bitte warten Sie, während wir
überprüfen, ob Sie ein Mensch und kein Bot sind. Ihr Inhalt wird в Kürze angezeigt.
Wenn Sie weiterhin diese Meldung erhalten, informieren Sie uns darüber bitte по электронной почте:
. We hebben verdachte activiteiten waargenomen op Glassdoor van iemand of iemand die uw internet netwerk deelt.Een momentje geduld totdat, мы выяснили, что u daadwerkelijk een persoon bent. Uw bijdrage zal spoedig te zien zijn.
Als u deze melding blijft zien, электронная почта:
om ons te laten weten dat uw проблема zich nog steeds voordoet. Hemos estado detectando actividad sospechosa tuya o de alguien con quien compare tu red de Internet. Эспера
mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo
este mensaje, envía un correo electrónico
a para informarnos de
que tienes problemas. Hemos estado percibiendo actividad sospechosa de ti o de alguien con quien compare tu red de Internet. Эспера
mientras verificamos que eres una persona real. Tu contenido se mostrará en breve. Si Continúas recibiendo este
mensaje, envía un correo electrónico a
para hacernos saber que
estás teniendo problemas. Temos Recebido algumas atividades suspeitas de voiceê ou de alguém que esteja usando a mesma rede. Aguarde enquanto
confirmamos que Você é Uma Pessoa de Verdade.Сеу контексто апаресера эм бреве. Caso продолжить Recebendo esta
mensagem, envie um email para
пункт нет
informar sobre o проблема. Abbiamo notato alcune attività sospette da parte tua o di una persona che condivide la tua rete Internet.
Attendi mentre verifichiamo Che sei una persona reale. Il tuo contenuto verrà visualizzato a breve. Secontini
visualizzare questo messaggio, invia un’e-mail all’indirizzo
per informarci del
проблема. Пожалуйста, включите куки и перезагрузите страницу. Это автоматический процесс. Ваш браузер в ближайшее время перенаправит вас на запрошенный контент. Подождите до 5 секунд… Перенаправление… Код объявления: CF-102 / 673150416e0116df. 1 — самый важный элемент математики. Единица или единица в математике используются для представления единой сущности в числе, измерении или вычислении.Число «1» имеет несколько специфических свойств, которые очень важны в математических вычислениях. Это: Очень важно знать, как найти квадратный корень из 1, потому что это дает четкое представление о том, как найти квадратный корень из других целых чисел.Положительное значение единицы можно записать как 1 x 1 или 12. Итак, квадратный корень из 1 можно рассчитать как: √1 = √12 = ± 1 Формула для нахождения корней квадратного уравнения также можно использовать для нахождения квадратного корня из 1. Пусть квадрат числа «x» равен «1». Это можно записать как: x2 = 1 x = √1 → (1) Приведенное выше уравнение представляет собой квадратное уравнение, которое может быть представлено в стандартной форме как: x2 + 0 x — 1 = 0 Приведенное выше уравнение имеет вид ax2 + bx + c = 0.2} — 4x \ times 1 \ times — 1}}} {{2 \ times 1}} = \ pm \ frac {{\ sqrt 4}} {2} = \ pm \ frac {2} {2} = \ pm 1 \] → (2) Сравнивая уравнения (1) и (2), мы можем сделать вывод, что значение корня 1 равно положительной или отрицательной единице. Чаще всего значение корня 1 принимается за положительную единицу или +1. Корневое значение «-1» теоретически не существует. Это мнимое число, обозначаемое как «i». Корень -1 обычно используется для представления комплексных чисел, которые включают как действительную, так и мнимую части.Зная квадратный корень из отрицательной единицы, можно найти значение корня любого отрицательного числа. Квадратный корень из -1 — это положительная или отрицательная мнимая единица «i». Однако в большинстве случаев значение корня из -1 принимается как положительная мнимая единица «i». Число Квадрат Число Квадрат 1 ± 16 256 ± 2 4 ± 17 289 9 ± 18 324 ± 4 16 ± 19 361 25 ± 20 400 ± 6 36 ± 21 441 ± 7 49 ± 22 484 900 64 ± 23 529 ± 9 81 ± 24 576 ± 25 625 ± 11 121 ± 26 676 ± 12 ± 27 729 ± 13 169 ± 28 784 ± 14 196 ± 29 841 ± 15 33 225 30 900 Номер Квадратный корень Число Квадратный корень 1 1 6 2.4495 2 1,4142 7 2,6458 3 1,7321 4 4 2 9 3 5 2.2361 10 3.1623 Эти значения квадратного корня от 1 до 10 показаны на числовой прямой в виде спирали квадратного корня. (изображение скоро будет обновлено) Решение: p2 + 8 = 3 p2 = 3-8 p2 = — 5 p = √-5 = √-1. √5 p = √5i Решение: Значение √1 = 1 7√1 — 5√1 + 2√1 = 7 (1) — 5 (1) + 2 (1) = 7-5 + 2 = 4. Напомним, что квадратное уравнение имеет стандартную форму Любое квадратное уравнение имеет вид ax2 + bx + c = 0, где a , b и c — действительные числа и a 0. если он равен 0: , где a , b и c — действительные числа и a 0.Решение такого уравнения называется корневым решением квадратного уравнения в стандартной форме. Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь реального решения. Если квадратное выражение слева множители, то мы можем решить его путем факторизации. Обзор шагов, используемых для решения с помощью факторинга, следующий: Шаг 1: Выразите квадратное уравнение в стандартной форме. Шаг 2: Разложите квадратное выражение на множители. Шаг 3: Примените свойство нулевого произведения и установите каждый переменный коэффициент равным 0. Шаг 4: Решите полученные линейные уравнения. Например, мы можем решить x2−4 = 0, разложив на множители следующим образом: Двумя решениями являются −2 и 2. Цель этого раздела — разработать альтернативный метод, который можно использовать для простого решения уравнений, где b = 0, что дает форму Уравнение x2−4 = 0 находится в этой форме и может быть решено путем выделения x2 вначале. Если извлечь квадратный корень из обеих частей этого уравнения, мы получим следующее: Здесь мы видим, что x = −2 и x = 2 являются решениями полученного уравнения. В общем, это описывает свойство квадратного корня для любого действительного числа k , если x2 = k, то x = ± k .; для любого действительного числа к , Обозначение «±» читается как «плюс или минус» и используется как компактное обозначение, обозначающее два решения.Следовательно, утверждение x = ± k указывает, что x = −k или x = k. Применение свойства квадратного корня как средства решения квадратного уравнения называется извлечением корней Применение свойства квадратного корня как средства решения квадратного уравнения. Пример 1: Решить: x2−25 = 0. Решение: Начните с выделения квадрата. Затем примените свойство квадратного корня. Ответ: Решения — 5 и 5.Чек предоставляется читателю. Конечно, предыдущий пример можно было бы так же легко решить с помощью факторинга. Тем не менее, он демонстрирует метод, который можно использовать для решения уравнений в этой форме, которые не учитывают факторы. Пример 2: Решить: x2−5 = 0. Решение: Обратите внимание, что квадратичное выражение слева не множится. Мы можем извлечь корни, если сначала выделим главный член x2. Примените свойство квадратного корня. Для полноты проверьте, что эти два действительных решения решают исходное квадратное уравнение. Как правило, проверка не является обязательной. Ответ: Решения — 5 и 5. Пример 3: Решить: 4×2-45 = 0. Решение: Начните с изоляции x2. Примените свойство квадратного корня, а затем упростите. Ответ: Решения — 352 и 352. Иногда квадратные уравнения не имеют реального решения. Пример 4: Решить: x2 + 9 = 0. Решение: Начните с изоляции x2. После применения свойства квадратного корня у нас остается квадратный корень из отрицательного числа. Следовательно, у этого уравнения нет реального решения. Ответ: Реального решения нет Обратитесь к этому процессу, чтобы найти уравнения с заданными решениями вида ± k . Пример 5: Найдите уравнение с решениями −23 и 23. Решение: Начните с возведения в квадрат обеих частей следующего уравнения: Наконец, вычтите 12 из обеих частей и представьте уравнение в стандартной форме. Ответ: x2−12 = 0 Попробуй! Решить: 9×2−8 = 0. Ответ: x = −223 или x = 223 Рассмотрите возможность решения следующего уравнения: Чтобы решить это уравнение путем факторизации, сначала возведите в квадрат x + 2, а затем представьте его в стандартной форме, равной нулю, вычтя 25 из обеих частей. , а затем применить свойство нулевого продукта. Два решения: −7 и 3. Когда уравнение имеет такую форму, мы можем получить решения за меньшее количество шагов, извлекая корни. Пример 6: Решите: (x + 2) 2 = 25. Решение: Решите, извлекая корни. На этом этапе разделите «плюс или минус» на два уравнения и упростите каждое по отдельности. Ответ: Решения −7 и 3. В дополнение к меньшему количеству шагов этот метод позволяет нам решать уравнения, которые не учитывают множители. Пример 7: Решите: (3x + 3) 2−27 = 0. Решение: Начните с выделения квадрата. Затем извлеките корни и упростите. Решите относительно x . Ответ: Решения: −1−3 и −1 + 3. Пример 8: Решить: 9 (2x − 1) 2−8 = 0. Решение: Начните с выделения квадратного множителя. Примените свойство квадратного корня и решите. Ответ: Решения 3−226 и 3 + 226. Попробуй! Решите: 3 (x − 5) 2−2 = 0. Ответ: 15 ± 63 Пример 9: Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 2 фута, найдите размеры прямоугольника. Решение: Диагональ любого прямоугольника образует два прямоугольных треугольника. Таким образом, применима теорема Пифагора. Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы: Решить. Здесь мы получаем два решения, w = −25 и w = 25. Поскольку в задаче требовалась длина прямоугольника, мы игнорируем отрицательный ответ. Кроме того, мы рационализируем знаменатель и представим наши решения без каких-либо радикалов в знаменателе. Обратно подставьте, чтобы найти длину. Ответ: Длина прямоугольника составляет 455 футов, а ширина — 255 футов. Часть A: извлечение квадратного корня Решите с помощью факторизации, а затем извлеките корни.Проверить ответы. 1. x2−36 = 0 2. x2−81 = 0 3. 4y2−9 = 0 4. 9y2−25 = 0 5. (x − 2) 2−1 = 0 6. (x + 1) 2−4 = 0 7. 4 (y − 2) 2−9 = 0 8. 9 (y + 1) 2−4 = 0 9. −3 (t − 1) 2 + 12 = 0 10. −2 (t + 1) 2 + 8 = 0 11. (x − 5) 2−25 = 0 12. (x + 2) 2−4 = 0 Решите, извлекая корни. 13. x2 = 16 14. x2 = 1 15. y2 = 9 16. y2 = 64 17. x2 = 14 18. x2 = 19 19. y2 = 0,25 20. y2 = 0,04 21. x2 = 12 22. x2 = 18 23. 16×2 = 9 24. 4×2 = 25 25. 2t2 = 1 26.3t2 = 2 27. x2−100 = 0 28. x2−121 = 0 29. y2 + 4 = 0 30. y2 + 1 = 0 31. x2−49 = 0 32. x2−925 = 0 33. y2−0.09 = 0 34. y2−0,81 = 0 35. x2−7 = 0 36. x2−2 = 0 37. x2−8 = 0 38. t2−18 = 0 39. x2 + 8 = 0 40.х2 + 125 = 0 41. 16×2−27 = 0 42. 9×2-8 = 0 43. 2y2−3 = 0 44. 5y2−2 = 0 45. 3×2−1 = 0 46. 6×2−3 = 0 47. (x + 7) 2−4 = 0 48. (x + 9) 2−36 = 0 49. (2y − 3) 2-81 = 0 50. (2у + 1) 2−25 = 0 51. (x − 5) 2−20 = 0 52. (x + 1) 2−28 = 0 53.(3t + 2) 2−6 = 0 54. (3т − 5) 2−10 = 0 55,4 (y + 2) 2−3 = 0 56. 9 (y − 7) 2−5 = 0 57,4 (3x + 1) 2−27 = 0 58. 9 (2x − 3) 2−8 = 0 59. 2 (3x − 1) 2 + 3 = 0 60,5 (2x − 1) 2−3 = 0 61,3 (y − 23) 2−32 = 0 62. 2 (3y − 13) 2−52 = 0 Найдите квадратное уравнение стандартной формы со следующими решениями. 63. ± 7 64. ± 13 65. ± 7 66. ± 3 67. ± 35 68. ± 52 69. 1 ± 2 70,2 ± 3 Решите и округлите решения до ближайшей сотой. 71. 9x (x + 2) = 18x + 1 72. x2 = 10 (x2−2) −5 73. (x + 3) (x − 7) = 11−4x 74.(x − 4) (x − 3) = 66−7x 75. (x − 2) 2 = 67−4x 76. (x + 3) 2 = 6x + 59 77. (2x + 1) (x + 3) — (x + 7) = (x + 3) 2 78. (3x − 1) (x + 4) = 2x (x + 6) — (x − 3) Составьте алгебраическое уравнение и используйте его для решения следующих задач. 79. Если 9 вычесть из четырех квадратов числа, то результат будет 3. Найдите число. 80. Если из квадрата числа вычесть 20, то получится 4.Найдите номер. 81. Если 1 прибавить к троекратному квадрату числа, то получится 2. Найдите число. 82. Если 3 прибавить к двукратному квадрату числа, получится 12. Найдите число. 83. Если квадрат имеет площадь 8 квадратных сантиметров, найдите длину каждой стороны. 84. Если круг имеет площадь 32π квадратных сантиметра, найдите длину радиуса. 85.Объем правого кругового конуса составляет 36π кубических сантиметров при высоте 6 сантиметров. Найдите радиус конуса. (Объем правого кругового конуса равен V = 13πr2h.) 86. Площадь поверхности сферы составляет 75π квадратных сантиметров. Найдите радиус сферы. (Площадь поверхности сферы определяется как SA = 4πr2.) 87. Длина прямоугольника в 6 раз больше его ширины. Если площадь составляет 96 квадратных дюймов, найдите размеры прямоугольника. 88. Основание треугольника вдвое больше его высоты. Если площадь составляет 16 квадратных сантиметров, то найдите длину его основания. 89. Квадрат имеет площадь 36 квадратных единиц. На какую равную величину необходимо увеличить стороны, чтобы получить квадрат с удвоенной заданной площадью? 90. Круг имеет площадь 25π квадратных единиц. На какую величину нужно увеличить радиус, чтобы создать круг с удвоенной заданной площадью? 91.Если стороны квадрата равны 1 единице, то найдите длину диагонали. 92. Если стороны квадрата равны 2 единицам, найдите длину диагонали. 93. Диагональ квадрата составляет 5 дюймов. Найдите длину каждой стороны. 94. Диагональ квадрата составляет 3 дюйма. Найдите длину каждой стороны. 95. Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 10 футов, найдите размеры прямоугольника. 96. Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 8 футов, найдите размеры прямоугольника. 97. Длина прямоугольника в 3 раза больше его ширины. Если диагональ 5 метров, то найдите размеры прямоугольника. 98. Длина прямоугольника в 3 раза больше его ширины. Если диагональ составляет 2 фута, найдите размеры прямоугольника. 99. Высота в футах объекта, падающего с 9-футовой лестницы, определяется выражением h (t) = — 16t2 + 9, где t представляет время в секундах после падения объекта.Сколько времени нужно, чтобы объект упал на землю? (Подсказка: когда объект ударяется о землю, высота равна 0.) 100. Высота в футах объекта, падающего с 20-футовой платформы, определяется выражением h (t) = — 16t2 + 20, где t представляет время в секундах после падения объекта. Сколько времени нужно, чтобы объект упал на землю? 101. Высота в футах объекта, падающего с вершины 144-футового здания, определяется выражением h (t) = — 16t2 + 144, где t измеряется в секундах. а. Сколько времени потребуется, чтобы достичь половины расстояния до земли, 72 фута? г. Сколько времени потребуется, чтобы добраться до земли? Округлите до сотых долей секунды. 102. Высота в футах объекта, сброшенного с самолета на высоте 1600 футов, определяется выражением h (t) = — 16t2 + 1,600, где t — в секундах. а. Сколько времени потребуется, чтобы добраться до земли на половину расстояния? г.Сколько времени потребуется, чтобы добраться до земли? Округлить до сотых долей секунды . Часть B: Обсуждение 103. Создайте собственное уравнение, которое можно решить, извлекая корень. Поделитесь им и решением на доске обсуждений. 104. Объясните, почему метод извлечения корней значительно расширяет наши возможности решать квадратные уравнения. 105. Объясните своими словами, как решить, извлекая корни. 106. Выведите формулу диагонали квадрата через его стороны. 1: −6, 6 3: −3/2, 3/2 5: 1, 3 7: 1/2, 7/2 9: -1, 3 11: 0, 10 13: ± 4 15: ± 3 17: ± 1/2 19: ± 0.5 21: ± 23 23: ± 3/4 25: ± 22 27: ± 10 29: Реального решения нет 31: ± 2/3 33: ± 0,3 35: ± 7 37: ± 22 39: Реального решения нет 41: ± 334 43: ± 62 45: ± 33 47: −9, −5 49: −3, 6 51: 5 ± 25 53: −2 ± 63 55: −4 ± 32 57: −2 ± 336 59: Реального решения нет 61: 4 ± 326 63: x2−49 = 0 65: x2−7 = 0 67: x2−45 = 0 69: x2−2x − 1 = 0 71: ± 0.33 73: ± 5,66 75: ± 7,94 77: ± 3.61 79: −3 или 3 81: −33 или 33 83:22 сантиметра 85:32 сантиметра 87: Длина: 24 дюйма; ширина: 4 дюйма 89: −6 + 62≈2,49 ед. 91: 2 шт. 93: 522 дюйма 95: Длина: 45 футов; ширина: 25 футов 97: Длина: 3102 метра; ширина: 102 метра 99: 3/4 секунды 101: а.2,12 секунды; б. 0,88 секунды Вот почти забытое искусство: с появлением электронных
калькуляторы, скорее всего, доживут до XXI века только на бумаге и
в воспоминаниях стариков. Из какого числа вы хотите найти квадратный корень?
Вот один из них, который мы будем использовать: Сначала разделите число, которое нужно извлекать из квадратного корня, на пары цифр,
начиная с десятичной точки.То есть никакая пара цифр не должна пересекаться
десятичная точка. (Например, разделите 1225 на «12 25», а не на
«1 22 5»; 6.5536 на «6,55 36», а не на «6,5 53 6».) Затем вы можете поместить несколько линий на каждую пару цифр и полосу на
слева, что-то вроде длинного деления. Найдите наибольшее число, квадрат которого меньше или равен ведущему
пара цифр. В этом случае первая пара цифр — 4; самое большое число
квадрат которого меньше или равен 4 равен 2. Поместите это число слева, и над первой парой цифр. Теперь возведите это число в квадрат и вычтите из первой пары цифр. Выдвинуть левую скобу; умножьте последнюю (и единственную) цифру левой
число на 2, поместите его слева от разницы, которую вы только что вычислили, и
оставьте рядом с ним пустой десятичный знак. Затем опустите следующую пару цифр и поместите ее вправо
разницы. Найдите наибольшее число для этого пустого десятичного разряда, чтобы
число, умноженное на уже существующее число плюс десятичный разряд, будет меньше
чем текущая разница.Например, если 1 * 41 равно ≤ 66, то 2 * 42
≤ 66 и т. Д. В данном случае это 1. Поместите это число в оставленное вами поле,
и в следующем десятичном разряде в строке результатов вверху. Теперь вычтите продукт, который вы только что нашли. Теперь повторите, как и раньше: возьмите число в левом столбце (здесь 41) и
удвойте его последнюю цифру (что даст вам 42).Скопируйте это ниже в левый столбец и
оставьте рядом с ним пустое место. (Двойная последняя цифра с переносом: для
Например, если у вас было не 41, а 49, что составляет 40 + 9, вы должны скопировать 40 + 18
что равно 58.) Также опустите следующую пару цифр справа. Теперь найдите самую большую цифру (назовите ее #) такую, что 42 # * # ≤ 2556.Здесь,
получается, что 426 * 6 = 2556 точно. Когда разница равна нулю, у вас есть точный квадратный корень, и вы
сделано. В противном случае вы можете продолжать находить больше десятичных знаков до тех пор, пока
как ты хочешь. Вот еще один пример с меньшим количеством аннотаций. Джон Керл Текущий адрес (по состоянию на 2005 г.): Конечно, точно так же, как квадратный корень из 25 имеет два корня (+5 и -5), квадратный корень из отрицательной единицы также имеет два корня: Итак, наш ответ на проблему квадратного корня из отрицательной единицы — это два числа: + i и — i .5
Корень 0 01: Что Такое Квадратный Корень 0,01?
КАКАДУ товары для животных Carnilove ягненок и кабан 12 кг
мука из мяса дикого кабана (30%), мука из мяса ягнят, выращенных на свободном выпасе (25%), желтый горох (20%), куриный жир (консервирован токоферолами, 10%), куриная печень (3%), яблоки (3%), крахмал из тапиоки (3%), рыбий жир лососевый (2%), морковь (1%), льняное семя (1%), нут (1%), гидролизованные панцири ракообразных (источник глюкозамина, 0,026%), экстракт хряща (источник хондроитина, 0,016%), пивные дрожжи (источник маннан-олигосахаридов, 0,015%),корень цикория (источник фрукто-олигосахаридов, 0,01%), юкка Шидигера (0,01%), водоросли (0,01%), псиллиум (0,01%), тимьян (0,01%), розмарин (0,01%), орегано (0,01%), клюква (0,0008%), голубика (0,0008%), малина (0,0008%).
сырой протеин 38,0 %, сырой жир 20,0 %, сырая зола 8,0 %, сырая клетчатка 3,2 %, влага 10,0 %, кальций 1,6 %, фосфор 1,3 %. Пищевые добавки на 1 кг: витамин A (E672) 20 000 МЕ, витамин D3 (E671) 1 500 МЕ, витамин E (?-токоферол) (3a700) 400 мг, цинк (E6) 85 мг, железо (E1) 70 мг, марганец (E5) 35 мг, йод (E2) 0,65 мг, медь (E4) 15 мг, селен (3b8.10) 0,25 мг. Энергетическая ценность: 3 950 ккал/кг. Омега-3: 0,35 %, Омега-6: 2,4 %.
Корм давать сухим или слегка увлажненным. У собаки всегда должен быть свободный доступ к свежей питьевой воде. Ежедневные потребности в питании вашей собаки могут отличаться в зависимости от размера, возраста, уровня активности и внешней среды. Рекомендованные нормы кормления указаны в таблице. Для поддержания отличного состояния вашей собаки обеспечьте ей достаточное количество физических нагрузок и не перекармливайте. Вводя новый корм для Вашей собаки, смешайте немного нового корма с привычной едой и в течение нескольких дней постепенно увеличивайте количество нового корма.
Условия хранения:
Хранить при температуре от 0 до +25?С, относительной влажности воздуха не более 80%. После вскрытия пакет с кормом необходимо плотно закрывать.КАКАДУ товары для животных Carnilove ягненок и кабан 1,5 кг
мука из мяса дикого кабана (30%), мука из мяса ягнят, выращенных на свободном выпасе (25%), желтый горох (20%), куриный жир (консервирован токоферолами, 10%), куриная печень (3%), яблоки (3%), крахмал из тапиоки (3%), рыбий жир лососевый (2%), морковь (1%), льняное семя (1%), нут (1%), гидролизованные панцири ракообразных (источник глюкозамина, 0,026%), экстракт хряща (источник хондроитина, 0,016%), пивные дрожжи (источник маннан-олигосахаридов, 0,015%),корень цикория (источник фрукто-олигосахаридов, 0,01%), юкка Шидигера (0,01%), водоросли (0,01%), псиллиум (0,01%), тимьян (0,01%), розмарин (0,01%), орегано (0,01%), клюква (0,0008%), голубика (0,0008%), малина (0,0008%).
сырой протеин 38,0 %, сырой жир 20,0 %, сырая зола 8,0 %, сырая клетчатка 3,2 %, влага 10,0 %, кальций 1,6 %, фосфор 1,3 %. Пищевые добавки на 1 кг: витамин A (E672) 20 000 МЕ, витамин D3 (E671) 1 500 МЕ, витамин E (?-токоферол) (3a700) 400 мг, цинк (E6) 85 мг, железо (E1) 70 мг, марганец (E5) 35 мг, йод (E2) 0,65 мг, медь (E4) 15 мг, селен (3b8.10) 0,25 мг. Энергетическая ценность: 3 950 ккал/кг. Омега-3: 0,35 %, Омега-6: 2,4 %.
Корм давать сухим или слегка увлажненным. У собаки всегда должен быть свободный доступ к свежей питьевой воде. Ежедневные потребности в питании вашей собаки могут отличаться в зависимости от размера, возраста, уровня активности и внешней среды. Рекомендованные нормы кормления указаны в таблице. Для поддержания отличного состояния вашей собаки обеспечьте ей достаточное количество физических нагрузок и не перекармливайте. Вводя новый корм для Вашей собаки, смешайте немного нового корма с привычной едой и в течение нескольких дней постепенно увеличивайте количество нового корма.
Условия хранения:
Хранить при температуре от 0 до +25?С, относительной влажности воздуха не более 80%. После вскрытия пакет с кормом необходимо плотно закрывать.Извлечение квадратного корня в математике с примерами решения и образцами выполнения
действие, обратное действию возведения в степень. Корень n-й степени из числа а обозначается следующим образом:
несократимая дробь, ибо содержит только те простые множители, которые входят в — только те простые множители, которые входят в q а р и q общих множителей не имеют. Таким образом, не может быть целым числом.
между соседними значениями для а достаточно малыми, мы можем приблизиться посредством значений к любому положительному числу b с любой степенью точности.
вычислении квадратного корня с некоторой наперед заданной точностью. Так, числа 1 и 2 являются приближенными значениями для
недостатком)
квадратного корня заключается в
определении числа х из зависимости
при данном у. Для решения этой задачи при помощи
графика нужно на параболе
найти точки, имеющие данную ординату у, и определить абсциссы этих точек.
миллиметровой бумаге, приняв за единицу масштаба 10 см и придавая переменной х значения от 0 до 1 через каждые 0,1 (рис. 27). Тогда непосредственно по графику находятся квадратные корни чисел, заключенных между 0 и 1.
возможна ошибка на 0,02 — 0,03 в ту или другую сторону. В действительности с точностью до 0,001Извлечение квадратного корня из числа, заключенного между 1 и 100, с точностью до 0,1
приближенное значение квадратного корня из числа A= 52,365, взятое с недостатком, с точностью до 0,001. Тогда числа 7; 7,2; 7,23 и 7,236 представляют собой приближенные значения
квадратного корня из положительного числа A, и пусть b есть поправка, которую нужно добавить к числу а, чтобы получить более точное приближение к корню, тоже с недостатком. Предположим, что эта поправка мала по сравнению с самим числом а.
истинной, а поправка 0,7 и подавно. Итак, с точностью до (с недостатком).
2) определяем целую часть корня 9, возводим ее в квадрат и вычитаем из подкоренного выражения;
3) слева от полученной разности проводим вертикальную черту и слева от нее запишем
5) к числу 18 добавляем 0,6 и сумму умножаем на 0,6. Произведение записываем под ранее вычисленной разностью 11,43 и вычитаем из нее. Так как последняя разность 0,27 оказалась положительной, то вычисление заканчивается. Число 0,6 присоединяется к числу 9 в качестве поправки. Напоминаем, что последняя разность 0,27 есть разность чисел 92,43 и
точностью до 0,01.
пользуясь уже рассмотренным способом:
нулей перед значащими цифрами, имея при этом в виду, что тогда при делении
сравнению с первым приближением. На дальнейших шагах вычислений отрицательный результат испытания получается крайне редко.
способа является также его большая общность. В частности, с помощью графиков можно решать приближенно даже довольно сложные уравнения и системы уравнений. Не вдаваясь в общую теорию построения графиков и их применений* ограничимся рассмотрением двух примеров.Carnilove True Fresh — Fresh Fish with Chickpeas and Apples – Carnilove
Состав
Пищевая добавка на 1 кг
Аналитические компоненты на 1 кг
Используемая энергия
Упаковка
Product code
Корм для собак Carnilove утка и фазан 12кг
Почему использование памяти в «top» не складывается?
$ top
вверх - 12:16:34 до 45 дней, 2:28, 3 пользователя, средняя загрузка: 0,24, 0,65, 0,71
Задачи: всего 274, 1 работает, 273 спит, 0 остановлен, 0 зомби
ЦП: 2,3% США, 0,2% sy, 0,0% ni, 97,5% id, 0,0% wa, 0,0% hi, 0,0% si, 0,0% st
Память: всего 16432032k, использовано 16340144k, 91888k свободно, 21736k буферов
Обмен: всего 18481144 КБ, использовано 1112 КБ, 18480032 КБ свободно, 15624488 Кэшировано
PID USER PR NI VIRT RES SHR S% CPU% MEM TIME + КОМАНДА
18159 jsmith 15 0 260 м 31 м 4560 S 16,6 0,2 53: 35,64 питон
4795 26 15 0 260 м 6608 4220 S 2,0 0,0 0: 00,06 почтмейстер
1 корень 15 0 10344 680 568 S 0,0 0,0 0: 39,36 init
2 корень RT -5 0 0 0 S 0,0 0,0 0: 00,53 миграция / 0
3 корень 34 19 0 0 0 S 0,0 0,0 0: 00,62 ksoftirqd / 0
4 root RT -5 0 0 0 S 0.0 0.0 0: 00.00 сторожевой таймер / 0
5 root RT -5 0 0 0 S 0.0 0.0 0: 02.09 миграция / 1
6 корень 34 19 0 0 0 S 0,0 0,0 0: 01,32 ksoftirqd / 1
7 root RT -5 0 0 0 S 0.0 0.0 0: 00.00 сторожевой таймер / 1
8 корень RT -5 0 0 0 S 0,0 0,0 0: 00,99 миграция / 2
9 корень 34 19 0 0 0 S 0,0 0,0 0: 01,74 ksoftirqd / 2
10 root RT -5 0 0 0 S 0.0 0.0 0: 00.00 сторожевой таймер / 2
11 root RT -5 0 0 0 S 0.0 0.0 0: 02.16 миграция / 3
12 корень 34 19 0 0 0 S 0,0 0,0 0: 01,30 ksoftirqd / 3
13 root RT -5 0 0 0 S 0.0 0.0 0: 00.00 сторожевой таймер / 3
14 root RT -5 0 0 0 S 0,0 0,0 0: 01,94 миграция / 4
15 корень 34 19 0 0 0 S 0,0 0,0 0: 01,78 ksoftirqd / 4
16 root RT -5 0 0 0 S 0.0 0.0 0: 00.00 сторожевой таймер / 4
17 root RT -5 0 0 0 S 0.0 0.0 0: 01.92 миграция / 5
18 корень 34 19 0 0 0 S 0,0 0,0 0: 01,30 ksoftirqd / 5
19 root RT -5 0 0 0 S 0.0 0.0 0: 00.00 сторожевой таймер / 5
20 root RT -5 0 0 0 S 0.0 0.0 0: 02.06 миграция / 6
21 корень 34 19 0 0 0 S 0,0 0,0 0: 01,83 ksoftirqd / 6
22 root RT -5 0 0 0 S 0.0 0.0 0: 00.00 сторожевой таймер / 6
23 root RT -5 0 0 0 S 0.0 0.0 0: 02.31 миграция / 7
24 корень 34 19 0 0 0 S 0,0 0,0 0: 01,50 ksoftirqd / 7
25 root RT -5 0 0 0 S 0.0 0.0 0: 00.00 сторожевой таймер / 7
26 корень 10 -5 0 0 0 S 0,0 0,0 0: 00,42 события / 0
27 корень 10 -5 0 0 0 S 0,0 0,0 0: 00,28 события / 1
28 корень 10 -5 0 0 0 S 0,0 0,0 0: 00,37 события / 2
29 корень 10 -5 0 0 0 S 0,0 0,0 0: 00,21 события / 3
30 корень 10 -5 0 0 0 S 0,0 0,0 0: 00,38 события / 4
31 корень 10 -5 0 0 0 S 0,0 0,0 0: 00,27 события / 5
32 корень 10 -5 0 0 0 S 0,0 0,0 0: 00,52 события / 6
33 root 10 -5 0 0 0 S 0,0 0,0 0: 00,64 события / 7
34 корень 10 -5 0 0 0 S 0,0 0,0 0: 00,00 хелпер
Размеры средних разовых доз наркотиков — Российская газета
Российской Федерации
М. Фрадков Корень квадратный из 0,01
Что такое квадратный корень? Определение квадратного корня
квадратный символ?
Квадратный корень Таблица 1-100
число квадрат квадрат
корень 1 1 1.000 2 4 1,414 3 9 1,732 4 16 2.000 5 25 2,236 6 36 2,449 7 49 2,646 8 64 2,828 9 81 3.000 10 100 3,162 11 121 3,317 12 144 3,464 13 169 3,606 14 196 3,742 15 225 3,873 16 256 4.000 17 289 4.123 18 324 4,243 19 361 4,359 20 400 4,472 21 441 4,583 22 484 4,690 23 529 4,796 24 576 4,899 25 625 5.000 число квадрат квадрат
корень 26 676 5,099 27 729 5,196 28 784 5,292 29 841 5,385 30 900 5,477 31 961 5,568 32 1,024 5.657 33 1089 5,745 34 1,156 5,831 35 1,225 5,916 36 1,296 6.000 1296 6.000 1,369 6,083 38 1,444 6,164 39 1,521 6,245 40 1,600 6.325 41 1,681 6,403 42 1,764 6,481 43 1,849 6,557 44 1,936 6,633 6,633 2,025 6,708 46 2,116 6,782 47 2,209 6,856 48 2,304 6.928 49 2,401 7.000 50 2,500 7.071 число квадрат квадрат
корень 51 2,601 7,141 52 2,704 7,211 53 2,809 7,280 54 2,916 7.348 55 3,025 7,416 56 3,136 7,483 57 3,249 7,550 58 3,364 7,616 3,481 7,681 60 3,600 7,746 61 3,721 7,810 62 3,844 7.874 63 3,969 7,937 64 4096 8,000 65 4225 8,062 66 4,356 8,124 4,489 8,185 68 4,624 8,246 69 4,761 8,307 70 4,900 8.367 71 5,041 8,426 72 5,184 8,485 73 5,329 8,544 74 5,476 8,602 5,625 8,660 число квадрат квадрат
корень 76 5,776 8.718 77 5,929 8,775 78 6,084 8,832 79 6241 8,888 80 6,400 8,944 6,561 9,000 82 6,724 9,055 83 6,889 9,110 84 7,056 9.165 85 7,225 9,220 86 7,396 9,274 87 7,569 9,327 88 7,744 9,381 900 7921 9,434 90 8,100 9,487 91 8,281 9,539 92 8,464 9.592 93 8,649 9,644 94 8,836 9,695 95 9,025 9,747 96 9,216 9,79831 96 9,216 9,79831 9,409 9,849 98 9,604 9,899 99 9,801 9,950 100 10,000 10.000 Корень квадратный из значений около 0,01
Число Sqrt 0,11 0,332 0,21 0,458 0,31 0,557 0,41 0,640 0,41 0,640 0,51 0,714 0,61 0,781 0,71 0,843 0.81 0,900 0,91 0,954 1,01 1,005 Примеры квадратного корня
Квадратный корень 0,01 (√.01)
01 = десятичная часть
Чтобы объяснить, мы начнем с небольшого урока деления. В задаче деления есть дивиденд, делитель и частное,
например:
1 ÷ 100 = 0,01
Введите другое десятичное число ниже, чтобы получить квадратный корень из него.
Квадратный корень из 0,0101
Вот следующее десятичное число в нашем списке, для которого мы вычислили квадратный корень.
Авторские права |
Политика конфиденциальности |
Заявление об ограничении ответственности |
Контакт Безопасность | Стеклянная дверь
Nous aider à garder Glassdoor sécurisée
Unterstützen Sie uns beim Schutz von Glassdoor
квадратный корень из 1 — значение, метод расчета, решаемые примеры и ответы на часто задаваемые вопросы
Важные факты о «1»:
Квадратный корень +1.
Значение квадратного корня -1:
Квадратный корень из первых 30 целых чисел: (график скоро будет обновлен)
31025 900 900 900 0
Квадратный корень от 1 до 10:
Значения квадратного корня от 1 до 10 приведены в таблице ниже:
Пример проблемы:
Интересные факты:
Извлечение квадратного корня
Извлечение квадратного корня
Основные выводы
Тематические упражнения
ответов
Как вручную найти квадратный корень
Как вручную найти квадратный корень Как найти квадратный корень вручную
46656
+ --- ---- ----
| 4 66 56
2
+ --- ---- ----
2 | 4 66 56
2
+ --- ---- ----
2 | 4 66 56
| -4
+ ----
0
2
+ --- ---- ----
2 | 4 66 56
| -4
+ ----
4_ | 0
2
+ --- ---- ----
2 | 4 66 56
| -4
+ ----
4_ | 0 66
2 1
+ --- ---- ----
2 | 4 66 56
| -4
+ ----
41 | 0 66
2 1
+ --- ---- ----
2 | 4 66 56
| -4
+ ----
41 | 0 66
| - 41
+ --------
25
2 1
+ --- ---- ----
2 | 4 66 56
| -4
+ ----
41 | 0 66
| - 41
+ --------
42_ 25 56
2 1 6
+ --- ---- ----
2 | 4 66 56
| -4
+ ----
41 | 0 66
| - 41
+ --------
426 | 25 56
| - 25 56
+ -------------
0
7. 2 8 0 1 ...
+ ----------------------
7 | 53. 00 00 00 00 00
| 49
+ ----------------------
142 | 4 00
| 2 84
+ ----------------------
1448 | 1 16 00
| 1 15 84
+ ----------------------
14560 | 16 00
| 0
+ ----------------------
145601 | 16 00 00
| 14 56 01
+ ----------------------
| 1 43 99 00
...
john dot r dot kerl at lmco точка com
Июль 1998
[email protected]
← Прочие документы Нахождение квадратного корня из отрицательного числа 1
Решение
Затем шаблон повторяется.
Любой квадратный корень отрицательного числа будет иметь компонент i ; например, квадратный корень из -4 будет +2 i или -2 i . Комплексные числа имеют вид a + bi , где a и b являются действительными числами, а i — мнимой частью. Например, наше решение для квадратного корня из отрицательной 1 можно рассматривать как два комплексных числа: 0 + i и 0 — i .Действительные числа — это подмножество комплексных чисел, где b = 0 и a может быть любым действительным числом.
Хотя концепция квадратного корня из отрицательного возникла просто как теоретическое математическое упражнение, в итоге она нашла множество применений в современной жизни. Одно из таких применений — в области электротехники. Разработчики компьютерных плат, сотовых телефонов и планшетов используют воображаемые числа, чтобы помочь им разрабатывать все более сложные, компактные и эффективные системы, которые помогут нам привести в действие современный мир.






 {2}} &=0 \\ \frac{5}{x} &=1 \\ \left| x \right| &=64 \end{align}\]
{2}} &=0 \\ \frac{5}{x} &=1 \\ \left| x \right| &=64 \end{align}\]
 Если коэффициент $a\ne 0$, то снова никаких проблем: мы вправе поделить обе части уравнения на любое ненулевое выражение, в т.ч. на это самое $a\ne 0$:
Если коэффициент $a\ne 0$, то снова никаких проблем: мы вправе поделить обе части уравнения на любое ненулевое выражение, в т.ч. на это самое $a\ne 0$: Потому что при любом значении $x$ мы умножаем это значение на ноль и получаем ноль, который никак не может равняться 10.
Потому что при любом значении $x$ мы умножаем это значение на ноль и получаем ноль, который никак не может равняться 10.
 Существует множество способов преобразовать уравнение, но нам пока доступны лишь три элементарных преобразования и ещё вот такая хитрость:
Существует множество способов преобразовать уравнение, но нам пока доступны лишь три элементарных преобразования и ещё вот такая хитрость: Первое уравнение уже решено, а второе решается по стандартному алгоритму:
Первое уравнение уже решено, а второе решается по стандартному алгоритму: Это уравнение имеет бесконечное множество корней.
Это уравнение имеет бесконечное множество корней.



 В соответствии с (3) сделаем в уравнении (12) замену
В соответствии с (3) сделаем в уравнении (12) замену


 ..
.. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil…
Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например:
file_1_1.txt
file_1_2.txt
file_1_3.txt
file_1_4.txt
fil… На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек…
На входе сигнала подала последоватльномть с Генератора Бернули бинарного. Sample time: 1/8000. ПРи выводе сигнала на анализатор спек… 07.2022
07.2022 В данном уравнении наименьшим показателем является х. Вынесем 4х за скобки:
В данном уравнении наименьшим показателем является х. Вынесем 4х за скобки: Cледовательно: 22х=t2. Получим:
Cледовательно: 22х=t2. Получим:
 Cегодня разберёмся, как эти линейные уравнения решать.
Cегодня разберёмся, как эти линейные уравнения решать.


 Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).
Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).
 tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
 Например, уравнения $latex 4x+1=5$ и $latex 2x+12=4x-2$ являются линейными уравнениями.
Например, уравнения $latex 4x+1=5$ и $latex 2x+12=4x-2$ являются линейными уравнениями. Рекомендуется попробовать решить примеры самостоятельно, прежде чем смотреть ответ.
Рекомендуется попробовать решить примеры самостоятельно, прежде чем смотреть ответ.








 Решения для большинства алгебраических выражений ищутся с применением этого навыка. Поэтому студенты должны стать более опытными в том, как проводить операцию.
Решения для большинства алгебраических выражений ищутся с применением этого навыка. Поэтому студенты должны стать более опытными в том, как проводить операцию.


 Как только вы заметите, что переменная делится, вы можете использовать умножение для решения уравнений.
Как только вы заметите, что переменная делится, вы можете использовать умножение для решения уравнений.




 Оно имеет нет решений .
Оно имеет нет решений . Здесь возможности для значений
Икс
ограничены.
Здесь возможности для значений
Икс
ограничены.
 п.
п.
 Уравнения могут быть линейными уравнениями, квадратными уравнениями, рациональными уравнениями или радикальными уравнениями.
Уравнения могут быть линейными уравнениями, квадратными уравнениями, рациональными уравнениями или радикальными уравнениями.

 0003
0003 Квадратные многочлены имеют степень два, а нули квадратного многочлена представляют собой квадратное уравнение.
Квадратные многочлены имеют степень два, а нули квадратного многочлена представляют собой квадратное уравнение.

 Решение рационального уравнения включает следующие шаги. Приведите дроби к общему знаменателю, а затем решите уравнение числителей.
Решение рационального уравнения включает следующие шаги. Приведите дроби к общему знаменателю, а затем решите уравнение числителей.
 Примените распределительное свойство.
Примените распределительное свойство. Мы либо используем метод транспонирования, либо метод балансировки.
Мы либо используем метод транспонирования, либо метод балансировки. 3 Решение квадратных уравнений
3 Решение квадратных уравнений Для линейных уравнений существует не более одного решения уравнения.
Для линейных уравнений существует не более одного решения уравнения.



 1 Введение
1 Введение , x — уравнение, которое можно записать в стандартной форме ax+b=0, где a и b — действительные числа, а a≠ 0. Например,
, x — уравнение, которое можно записать в стандартной форме ax+b=0, где a и b — действительные числа, а a≠ 0. Например, Используя круглые скобки, мы избегаем некоторых распространенных ошибок при работе с порядком операций.
Используя круглые скобки, мы избегаем некоторых распространенных ошибок при работе с порядком операций. . Даны алгебраические выражения A и B , где c — ненулевое число:
. Даны алгебраические выражения A и B , где c — ненулевое число: Другими словами, подумайте об этом как 56 = + 8 + 12 лет. Поэтому начнем с вычитания 8 по обе стороны от знака равенства.
Другими словами, подумайте об этом как 56 = + 8 + 12 лет. Поэтому начнем с вычитания 8 по обе стороны от знака равенства.

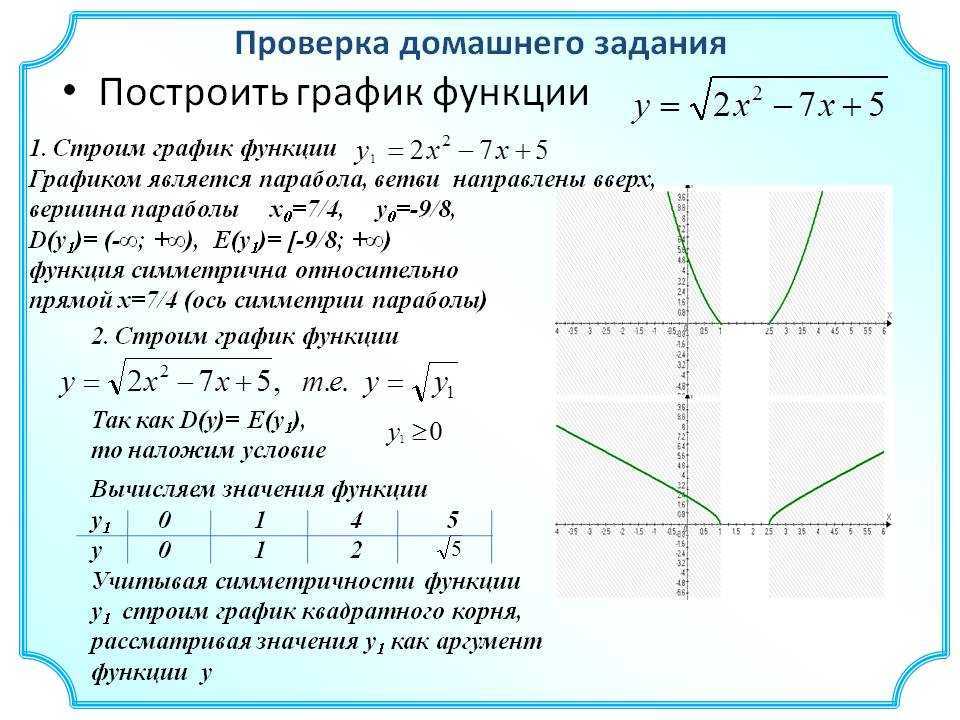 е.x \in [0;+ \infty)$
е.x \in [0;+ \infty)$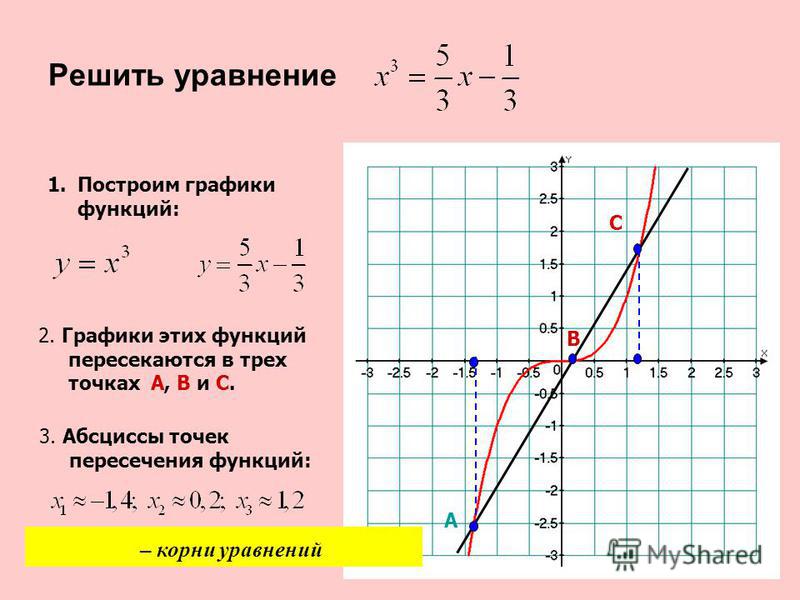 4 $
4 $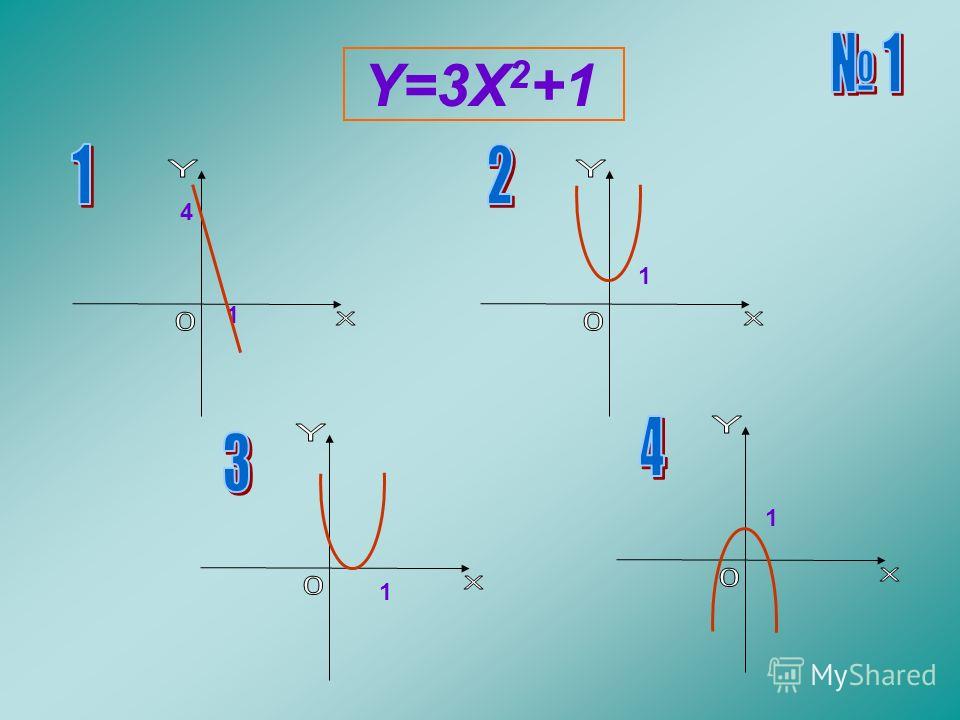 2-2x+1}$ относительно оси абсцисс OX.
2-2x+1}$ относительно оси абсцисс OX.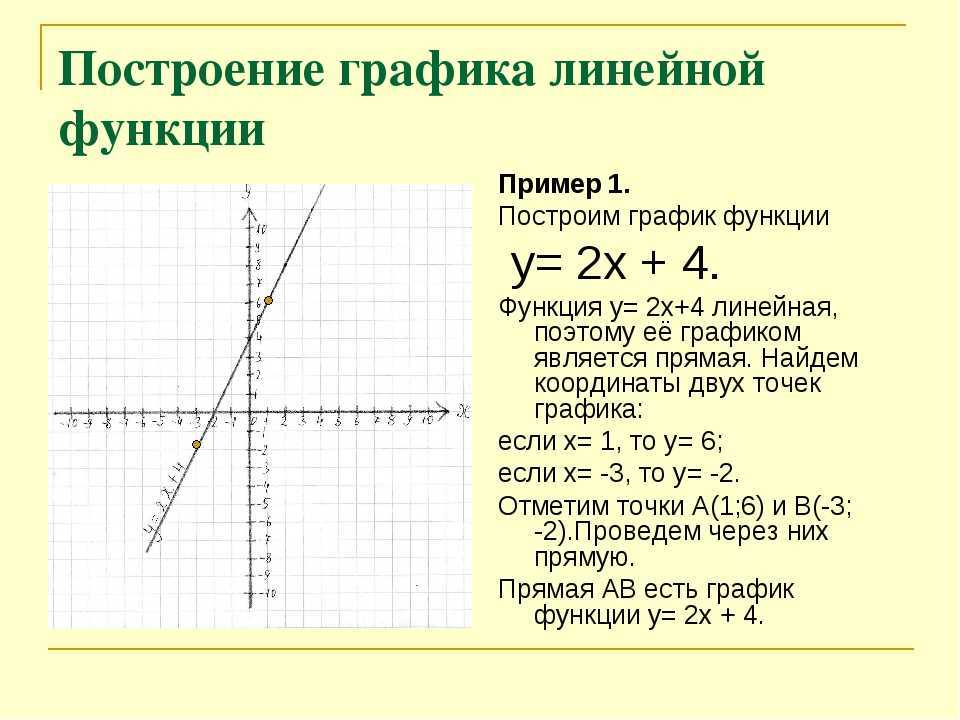
 (фронтальный
опрос)
(фронтальный
опрос)
 Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики.
Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики. Во вкладке Шрифт
установим размер шрифта 8пт.
Во вкладке Шрифт
установим размер шрифта 8пт.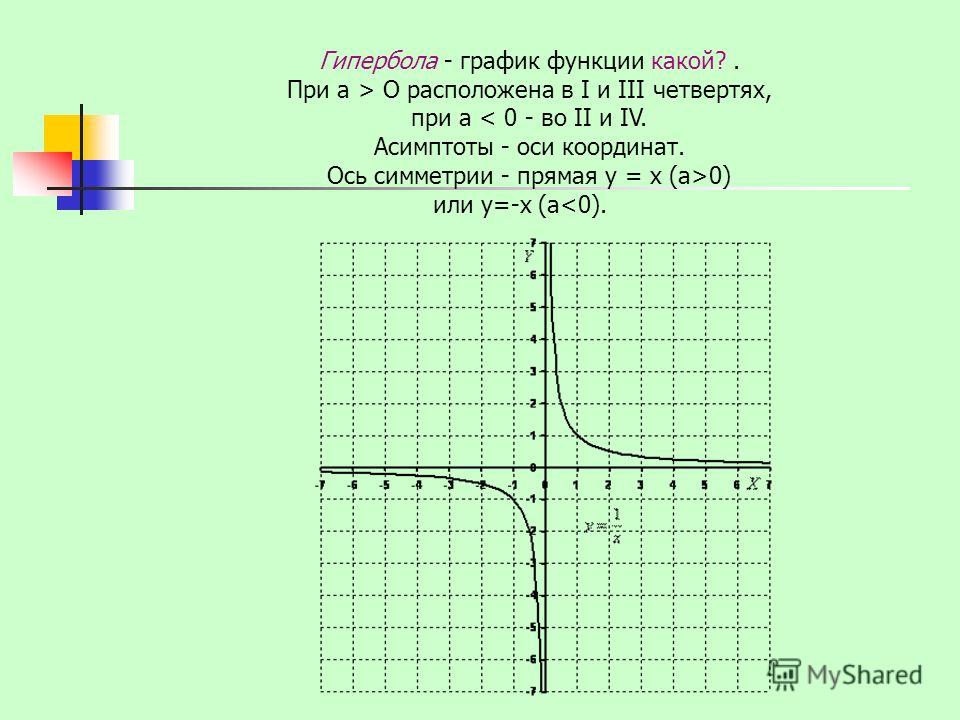 3
3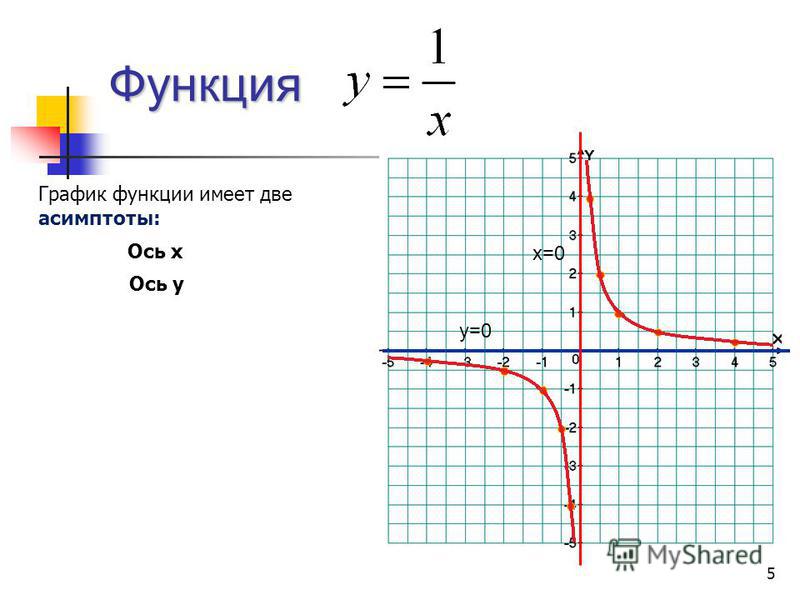 Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики.
Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики. Верхний колонтитул слева: график функции у = x3
Верхний колонтитул слева: график функции у = x3
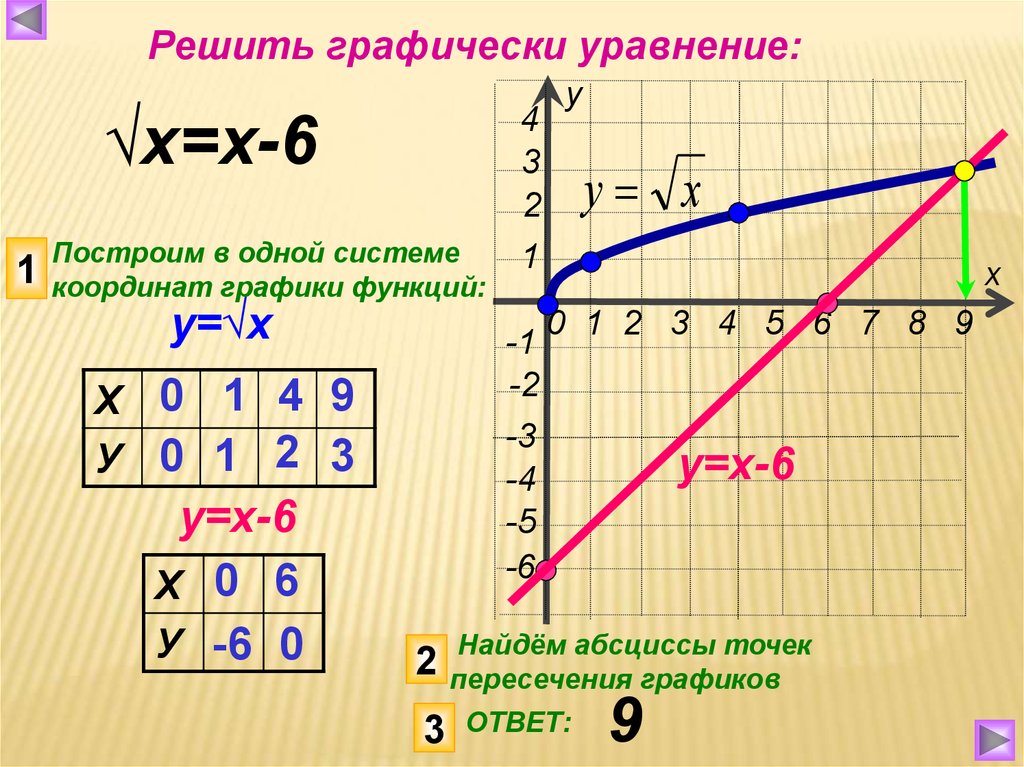 е. максимальных и минимальных значений на анализируемом промежутке времени.
е. максимальных и минимальных значений на анализируемом промежутке времени.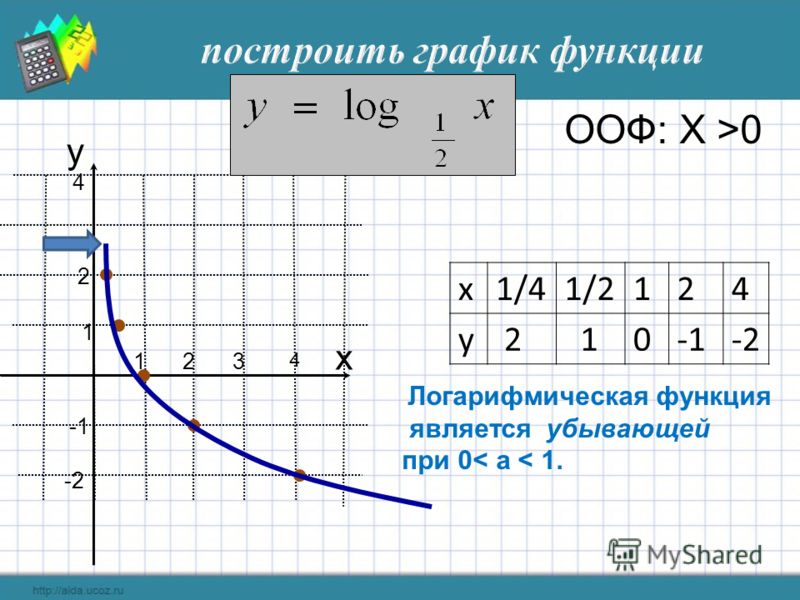 Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома
Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома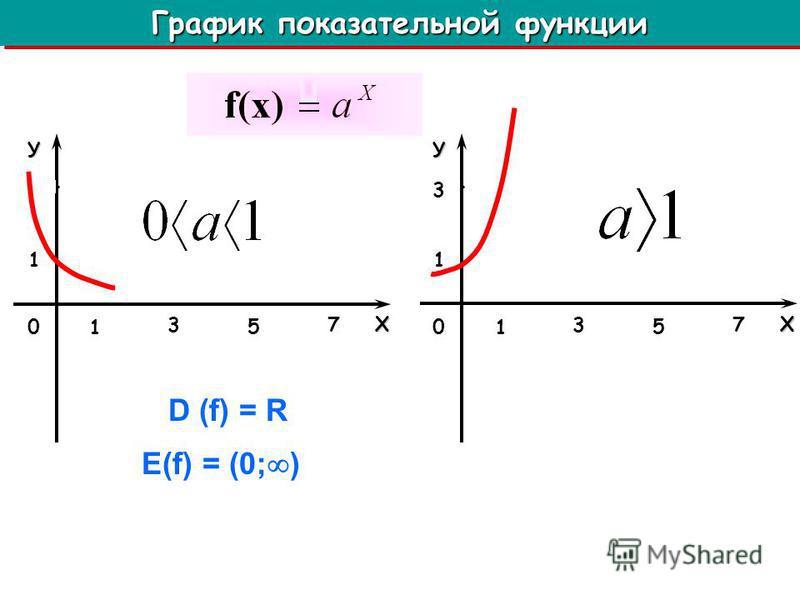 2+R7C8*RC[-3]+R8C8
2+R7C8*RC[-3]+R8C8 2+R7C8*RC[-3]+R8C8
2+R7C8*RC[-3]+R8C8
 Рассматриваем примеры на построение и нахождение свойств функций этого вида.
Рассматриваем примеры на построение и нахождение свойств функций этого вида.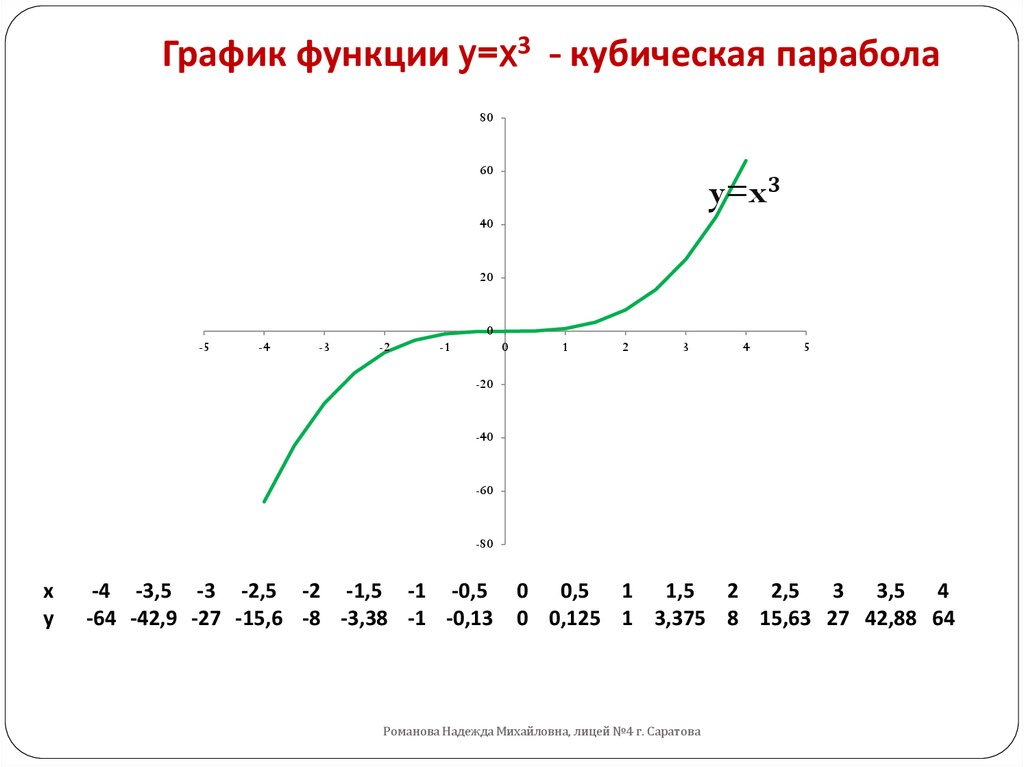

 Из курса базовой
школы мы знаем:
Из курса базовой
школы мы знаем: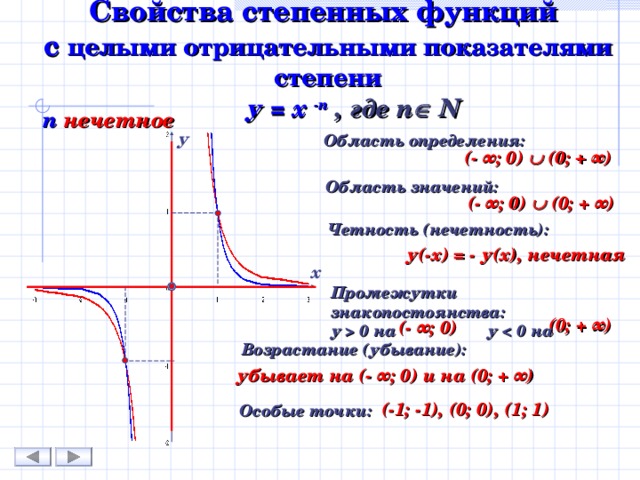
 Этот тип функции настолько разнообразен, что если вы изучаете функции, мы на 100% уверены, что вы уже встречались с типом степенной функции, не зная, что это один из них.
Этот тип функции настолько разнообразен, что если вы изучаете функции, мы на 100% уверены, что вы уже встречались с типом степенной функции, не зная, что это один из них.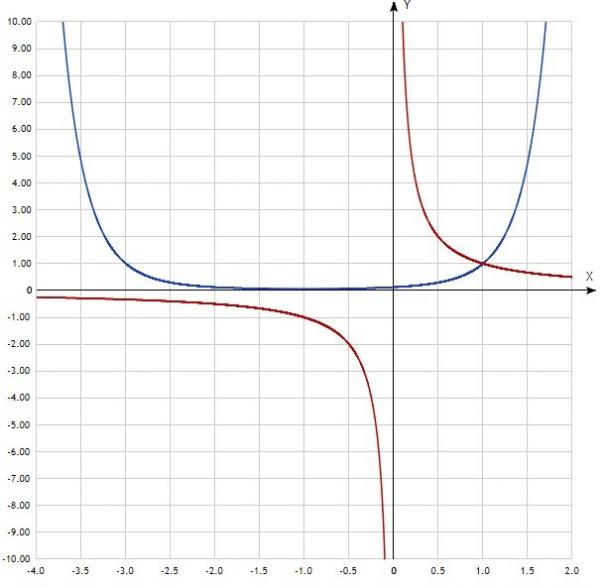 Вот общая форма степенных функций:
Вот общая форма степенных функций: Показатели степенных функций также должны быть действительными числами, поэтому давайте проверим каждый показатель из примеров, чтобы подтвердить это.
Показатели степенных функций также должны быть действительными числами, поэтому давайте проверим каждый показатель из примеров, чтобы подтвердить это.
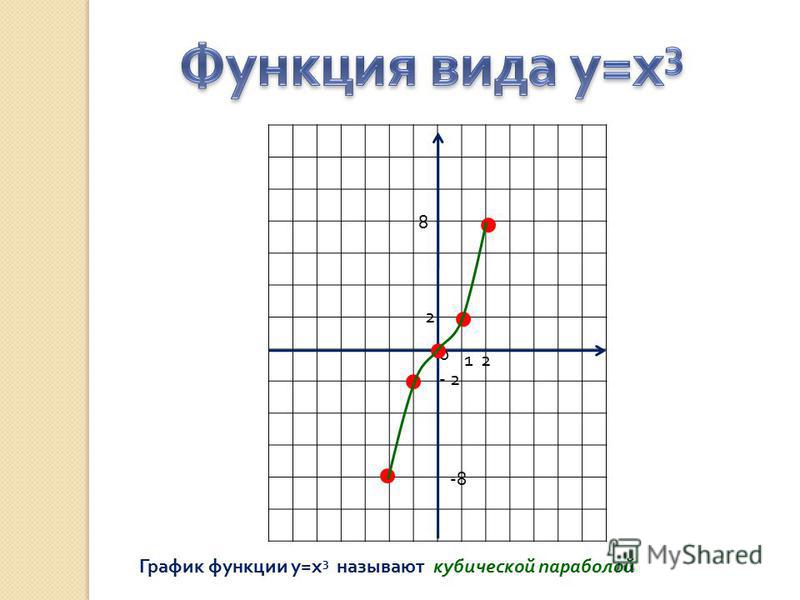 Мы также можем предсказать конечное поведение степенных функций на основе их коэффициента и мощности .
Мы также можем предсказать конечное поведение степенных функций на основе их коэффициента и мощности .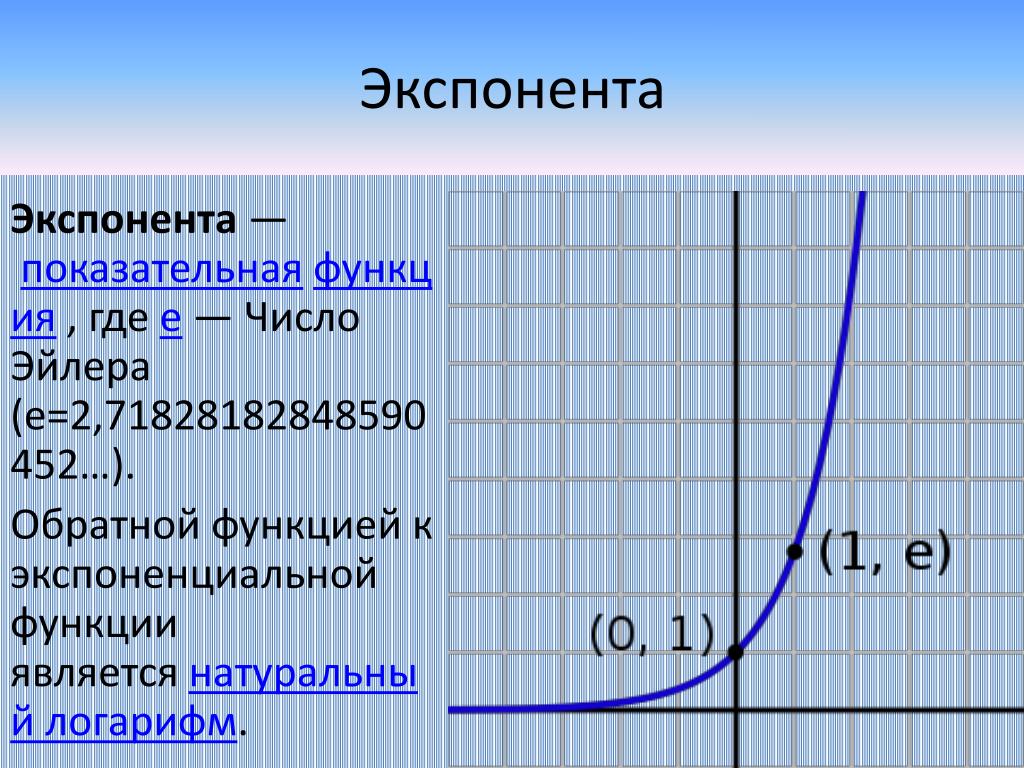

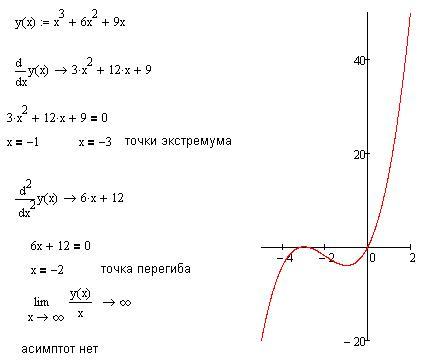
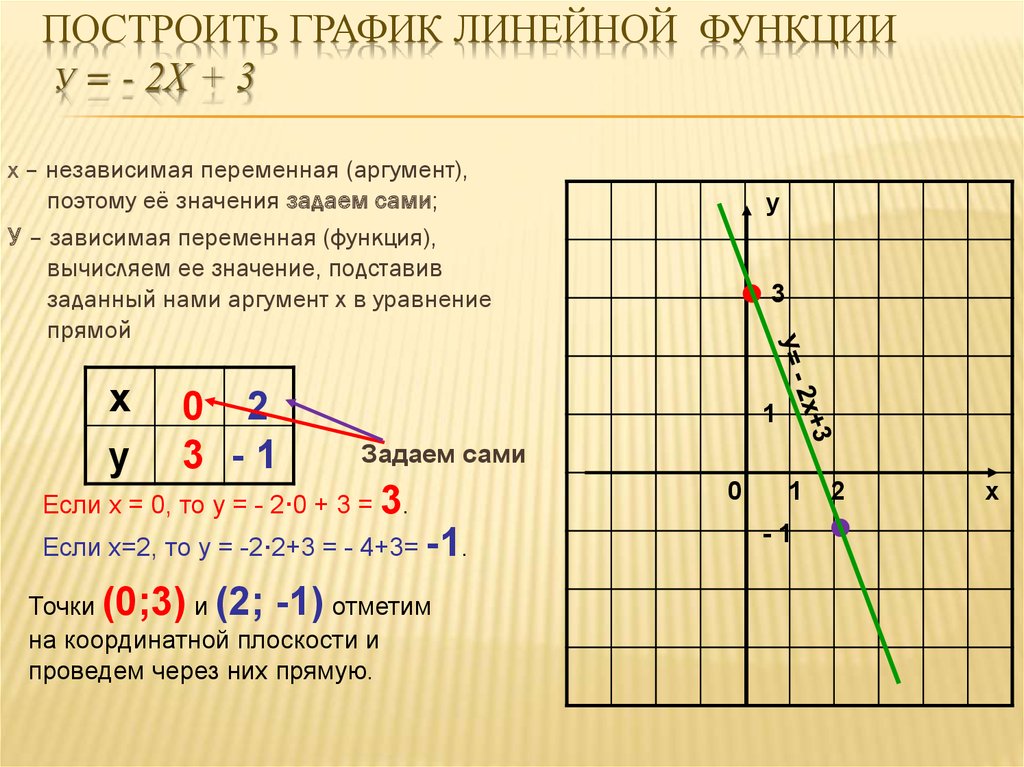
 Следовательно, a = 3,
Следовательно, a = 3,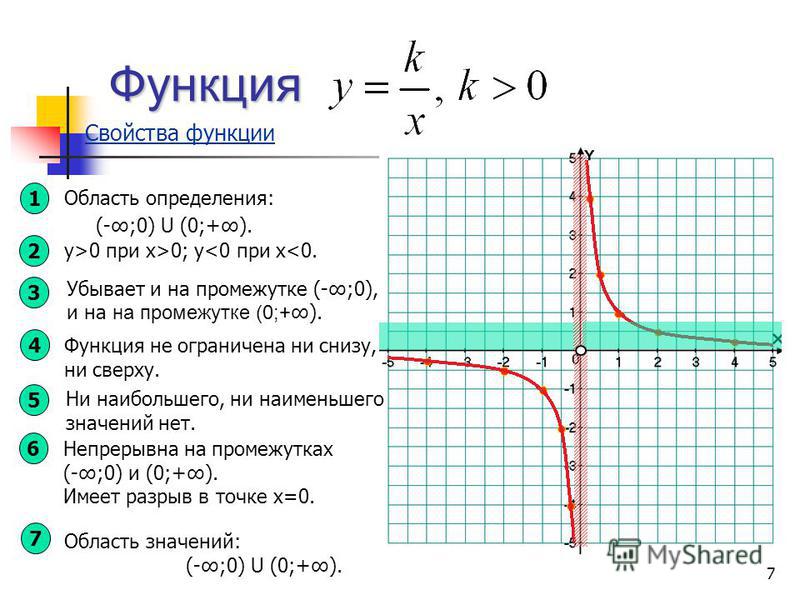
 Когда вы будете готовы, давайте продолжим и попробуем решить несколько задач!
Когда вы будете готовы, давайте продолжим и попробуем решить несколько задач!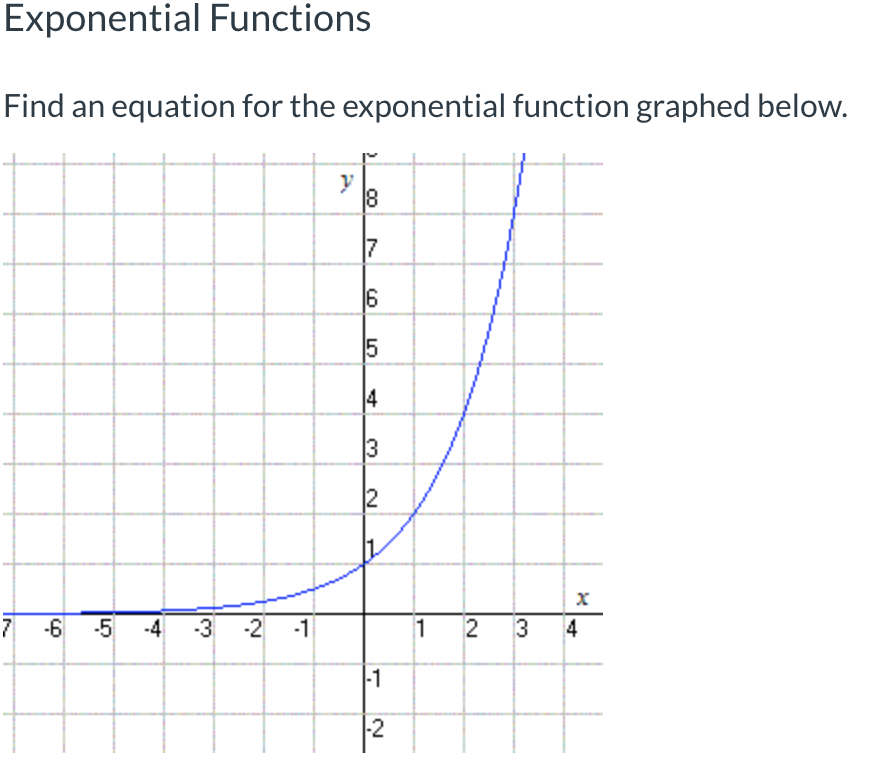 И 0,5, и π — действительные числа, поэтому h(x) также является степенной функцией .
И 0,5, и π — действительные числа, поэтому h(x) также является степенной функцией . Мы видим, что первый пример является степенной функцией, а второй — нет. Это означает, что кубические функции могут быть степенными функциями.
Мы видим, что первый пример является степенной функцией, а второй — нет. Это означает, что кубические функции могут быть степенными функциями. Используйте предоставленную нами таблицу, чтобы спрогнозировать конечное поведение.
Используйте предоставленную нами таблицу, чтобы спрогнозировать конечное поведение.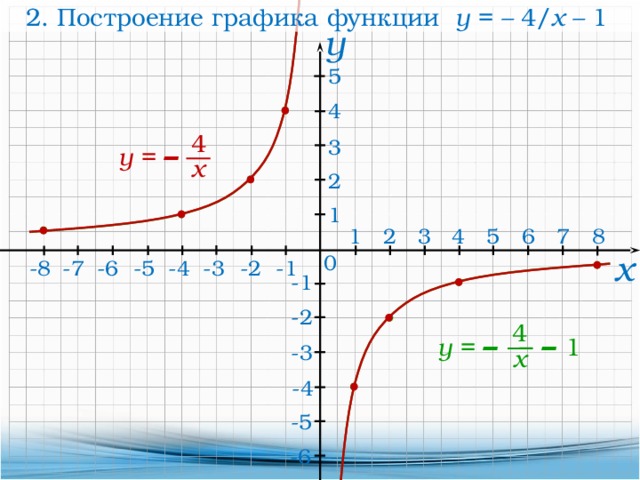


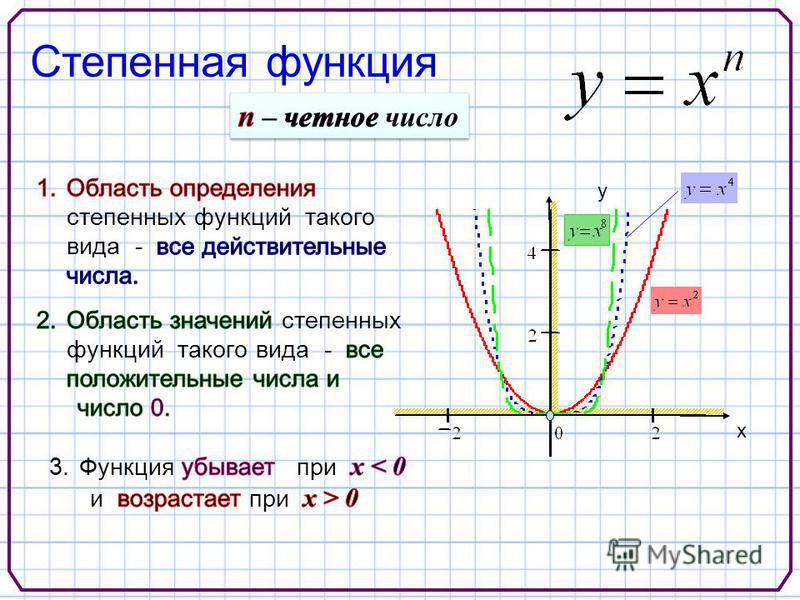
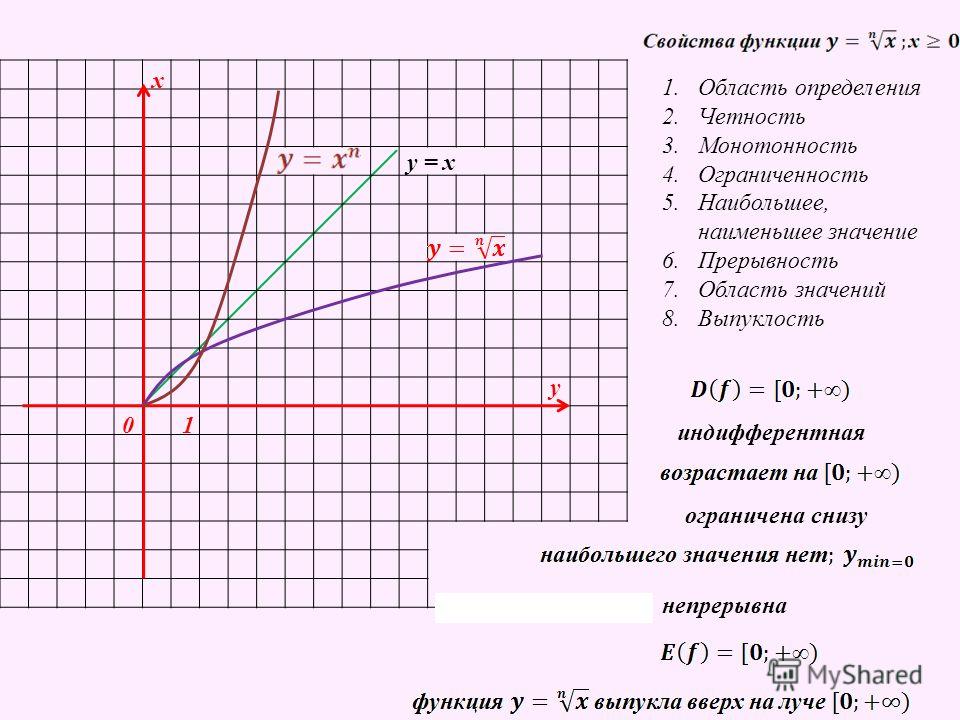 1
1 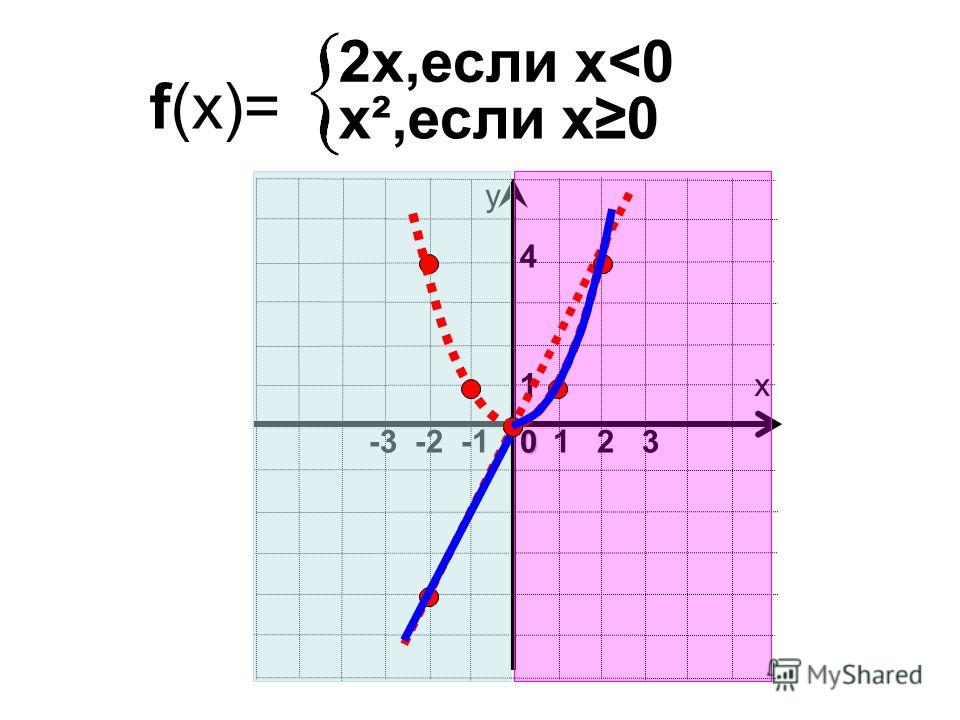 График также может подтвердить это.
График также может подтвердить это.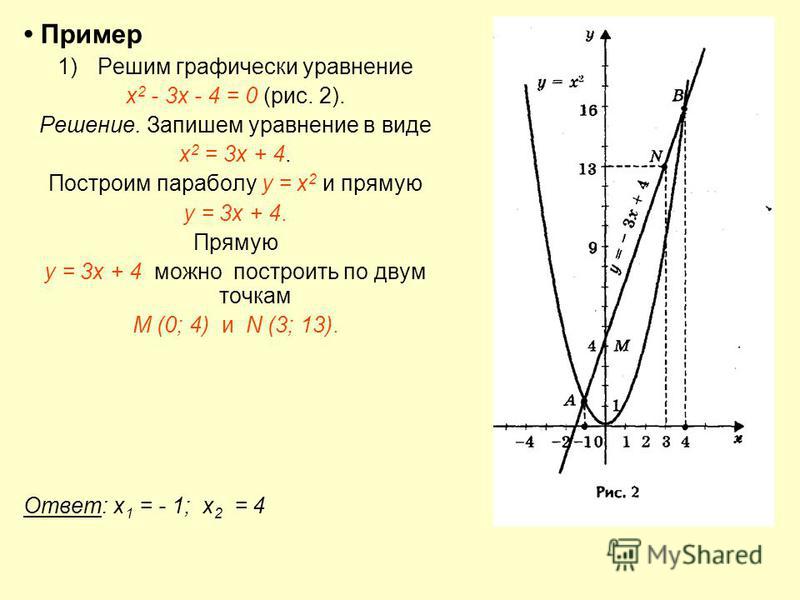
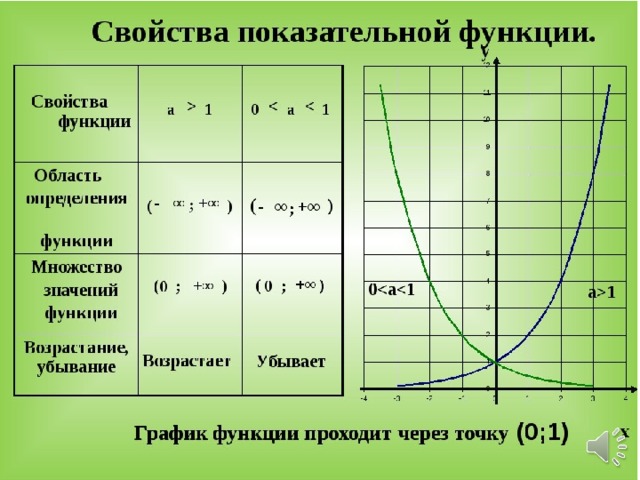
 Квадратичные функции подробно описаны здесь.
Квадратичные функции подробно описаны здесь. См. график справа.
Когда x = 0, эти функции подвергаются делению на ноль и, следовательно,
все бесконечны. Когда x большое и
положительные они маленькие и положительные. Когда x большое и отрицательное
тогда те, у которых четные степени, малы и положительны, а те, у которых
нечетные степени малы и отрицательны.
См. график справа.
Когда x = 0, эти функции подвергаются делению на ноль и, следовательно,
все бесконечны. Когда x большое и
положительные они маленькие и положительные. Когда x большое и отрицательное
тогда те, у которых четные степени, малы и положительны, а те, у которых
нечетные степени малы и отрицательны.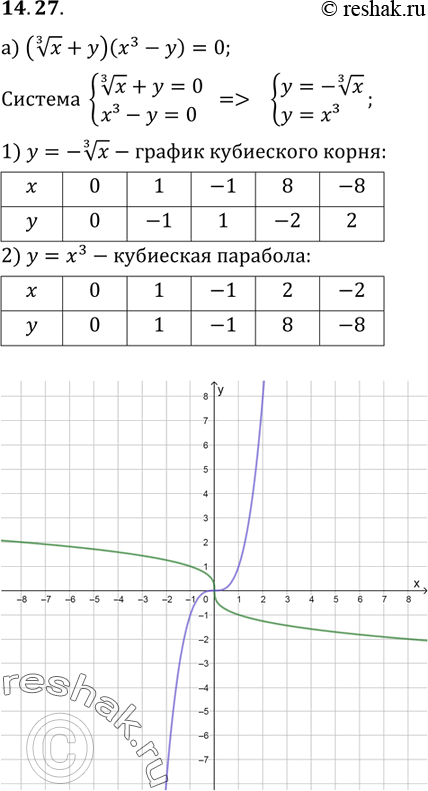 Допускаются только целые степени x .
Наивысшая степень x , которая встречается, называется степенью многочлена.
На графике показаны примеры полиномов степени 4 и степени 5.
Градус дает максимальное количество « подъемов и спадов», которые
многочлен может иметь, а также максимальное количество пересечений x ось, которую он может иметь.
Допускаются только целые степени x .
Наивысшая степень x , которая встречается, называется степенью многочлена.
На графике показаны примеры полиномов степени 4 и степени 5.
Градус дает максимальное количество « подъемов и спадов», которые
многочлен может иметь, а также максимальное количество пересечений x ось, которую он может иметь.


 {x},[/latex][латекс]\,b\,[/latex] равно постоянный коэффициент функции. Это означает, что при увеличении ввода на 1 выходное значение будет произведением базы и предыдущего вывода, независимо от значения [латекс]\,а.[/латекс] 9{х}[/латекс]
{x},[/latex][латекс]\,b\,[/latex] равно постоянный коэффициент функции. Это означает, что при увеличении ввода на 1 выходное значение будет произведением базы и предыдущего вывода, независимо от значения [латекс]\,а.[/латекс] 9{х}[/латекс]

 ( -1), 1), домен остается (0, бесконечность), а диапазон остается (-бесконечность, бесконечность). Во втором столбце показан сдвиг уравнения g(x)=log_b(x) влево, когда b>1, и отмечены следующие изменения: отраженная функция убывает по мере того, как x движется от 0 до бесконечности, асимптота остается x=0, x-пересечение изменяется на (-1, 0), ключевая точка изменяется на (-b, 1), домен изменяется на (-бесконечность, 0), а диапазон остается (-бесконечность, бесконечность)».> 9{x},[/latex][latex]\,b>1,[/latex]это
( -1), 1), домен остается (0, бесконечность), а диапазон остается (-бесконечность, бесконечность). Во втором столбце показан сдвиг уравнения g(x)=log_b(x) влево, когда b>1, и отмечены следующие изменения: отраженная функция убывает по мере того, как x движется от 0 до бесконечности, асимптота остается x=0, x-пересечение изменяется на (-1, 0), ключевая точка изменяется на (-b, 1), домен изменяется на (-бесконечность, 0), а диапазон остается (-бесконечность, бесконечность)».> 9{x},[/latex][latex]\,b>1,[/latex]это {x}[/latex] 9{x}\,[/latex] имеет пересечение y- в [latex]\,\left(0, 1\right),[/latex]домен[latex]\,\left(-\infty , \ infty \right),[/latex]range[latex]\,\left(0, \infty \right),[/latex] и горизонтальная асимптота[latex]\,y=0.\,[/latex]См. ( Фигура).
{x}[/latex] 9{x}\,[/latex] имеет пересечение y- в [latex]\,\left(0, 1\right),[/latex]домен[latex]\,\left(-\infty , \ infty \right),[/latex]range[latex]\,\left(0, \infty \right),[/latex] и горизонтальная асимптота[latex]\,y=0.\,[/latex]См. ( Фигура).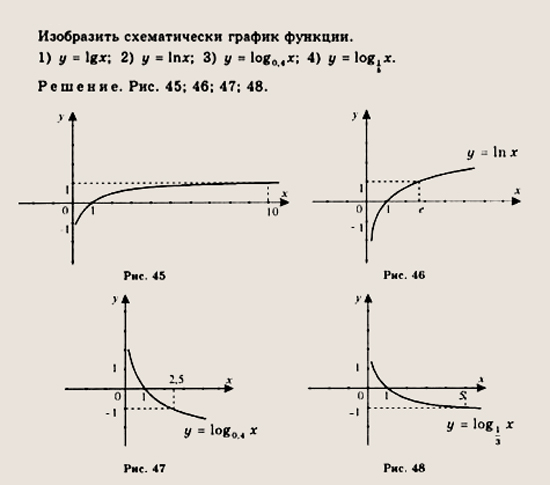 Каково уравнение новой функции,[латекс]\,г\влево(х\вправо)?\,[/латекс]Укажите ее и — точку пересечения, домен и диапазон.
Каково уравнение новой функции,[латекс]\,г\влево(х\вправо)?\,[/латекс]Укажите ее и — точку пересечения, домен и диапазон.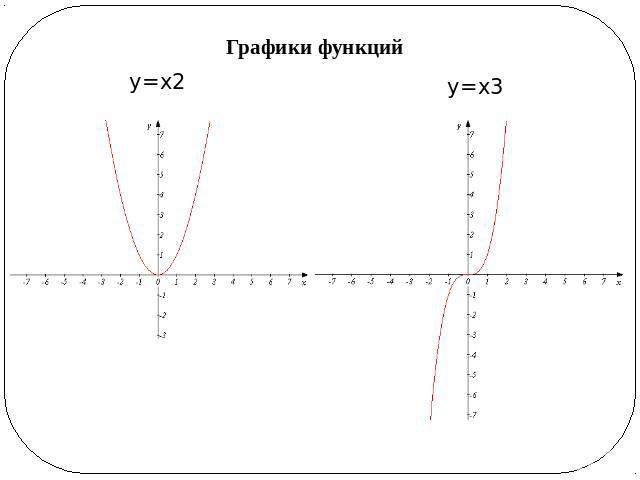
 Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Цифры могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.
Алгебра определяется как представление вычислений с использованием математических выражений, состоящих из чисел, операторов и переменных. Цифры могут быть от 0 до 9, операторы — это математические операторы, такие как +, -, ×, ÷, показатели степени и т. д., переменные, такие как x, y, z и т. д.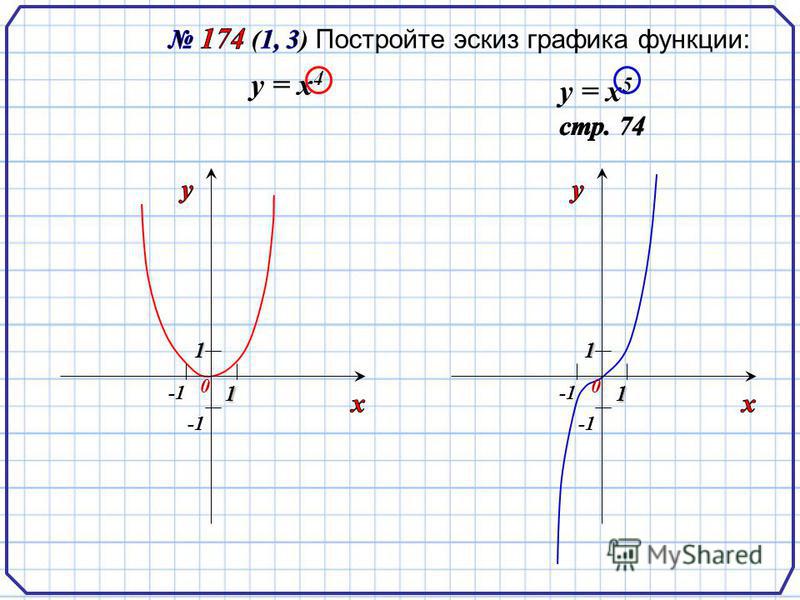 Это будет записано как
Это будет записано как Их можно представить как f(x).g(x) для умножения и f(x)/g(x) для деления.
Их можно представить как f(x).g(x) для умножения и f(x)/g(x) для деления.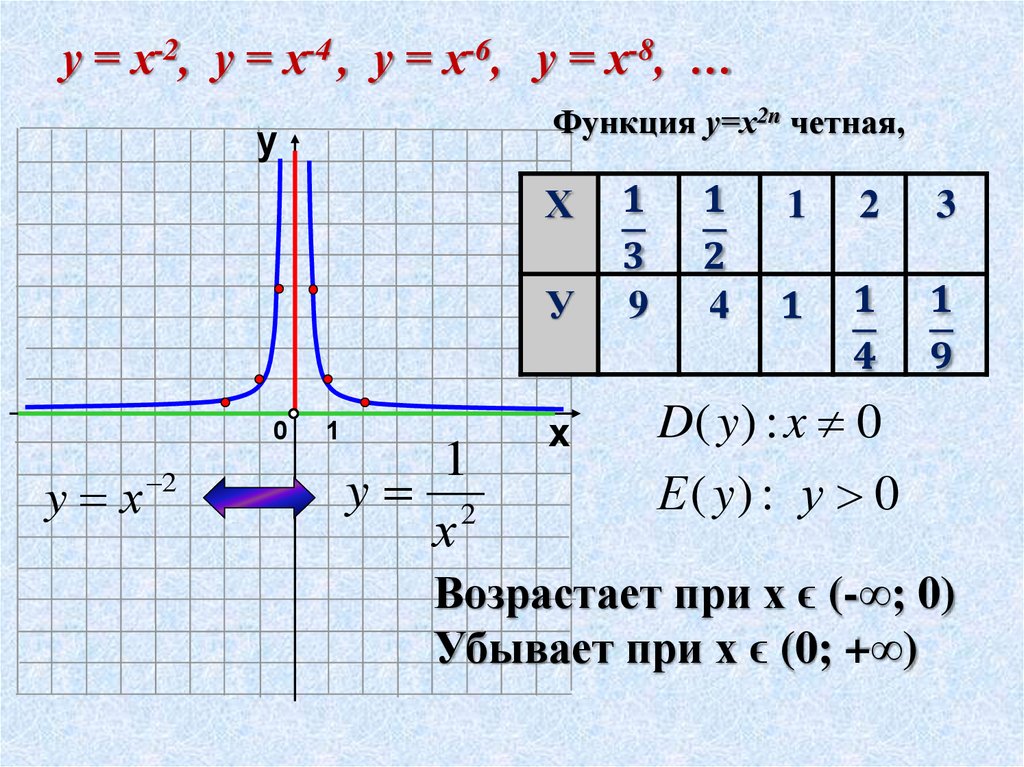 3 + 48x – 48x 2 )
3 + 48x – 48x 2 )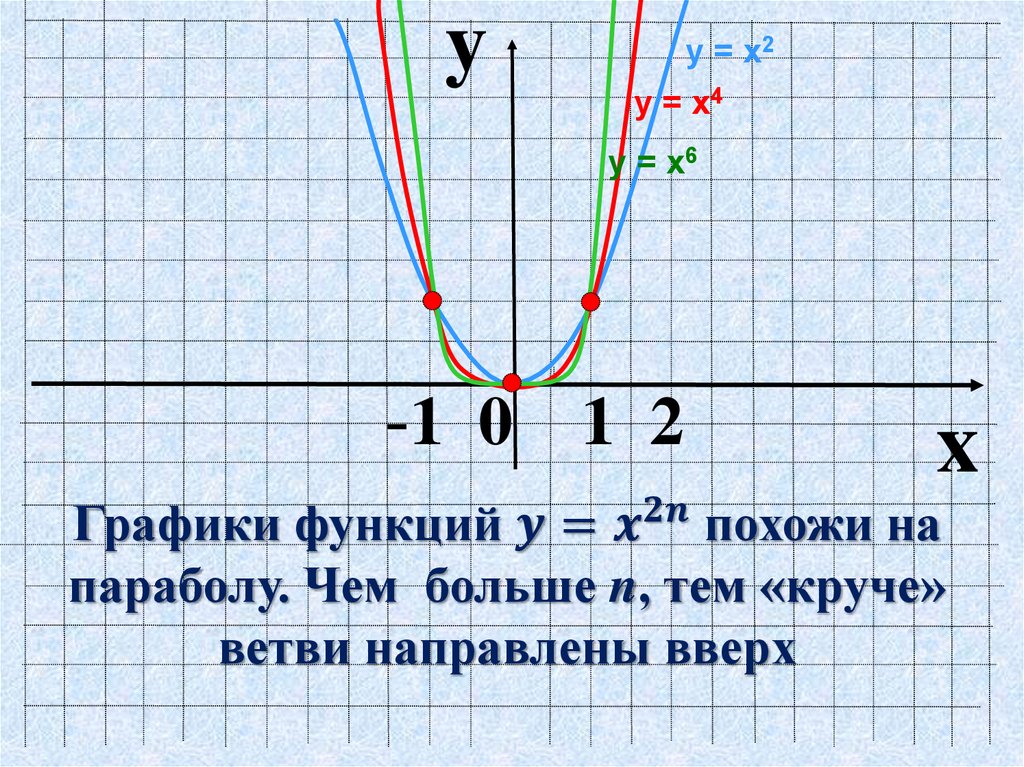

 Будем считать, что силы трения, действующие в системе, пренебрежимо малы, а значит, колебания маятника незатухающие (их амплитуда с течением времени не изменяется, а полная механическая энергия системы сохраняется). При этом потенциальная энергия деформированной пружины будет превращаться в кинетическую энергию движения тележки, и наоборот.
Будем считать, что силы трения, действующие в системе, пренебрежимо малы, а значит, колебания маятника незатухающие (их амплитуда с течением времени не изменяется, а полная механическая энергия системы сохраняется). При этом потенциальная энергия деформированной пружины будет превращаться в кинетическую энергию движения тележки, и наоборот. д.), — он определяется только характеристиками самой колебательной системы «тело — пружина». Если период Т колебаний тела и жесткость — пружины известны, можно найти массу m тела. Такой способ определения массы используют в состоянии невесомости, когда обычные весы не работают.
д.), — он определяется только характеристиками самой колебательной системы «тело — пружина». Если период Т колебаний тела и жесткость — пружины известны, можно найти массу m тела. Такой способ определения массы используют в состоянии невесомости, когда обычные весы не работают. Таким образом будет получена физическая модель — математический маятник.
Таким образом будет получена физическая модель — математический маятник. Причины, по которым математический маятник совершает свободные колебания, те же, что и в случае колебаний пружинного маятника: 1) равнодействующая сил, приложенных к телу, всегда направлена к положению равновесия; 2) колеблющееся тело инертно
Причины, по которым математический маятник совершает свободные колебания, те же, что и в случае колебаний пружинного маятника: 1) равнодействующая сил, приложенных к телу, всегда направлена к положению равновесия; 2) колеблющееся тело инертно Поэтому, измерив длину нити и период колебаний маятника, можно определить ускорение свободного падения в данной местности (см. лабораторную работу № 5).
Поэтому, измерив длину нити и период колебаний маятника, можно определить ускорение свободного падения в данной местности (см. лабораторную работу № 5). В каком положении потенциальная энергия маятника достигает максимального значения? минимального? Что можно сказать о кинетической энергии маятника в эти моменты?
В каком положении потенциальная энергия маятника достигает максимального значения? минимального? Что можно сказать о кинетической энергии маятника в эти моменты? Определите: 1) циклическую частоту и период колебаний; 2) жесткость пружины; 3) полную механическую энергию колебаний; 4) смещение, кинетическую и потенциальную энергии маятника при t = 0,025 с.
Определите: 1) циклическую частоту и период колебаний; 2) жесткость пружины; 3) полную механическую энергию колебаний; 4) смещение, кинетическую и потенциальную энергии маятника при t = 0,025 с.


 Нарисуйте равнодействующую
сил. Как меняется величина и направление
равнодействующей сил в течение периода?
Нарисуйте равнодействующую
сил. Как меняется величина и направление
равнодействующей сил в течение периода? Изобразите
математический маятник в крайней
правой точке и покажите на чертеже силы, действующие
на шарик в данной точке траектории.
Нарисуйте равнодействующую сил. Как
меняется величина и направление
равнодействующей сил в течение
периода?
Изобразите
математический маятник в крайней
правой точке и покажите на чертеже силы, действующие
на шарик в данной точке траектории.
Нарисуйте равнодействующую сил. Как
меняется величина и направление
равнодействующей сил в течение
периода?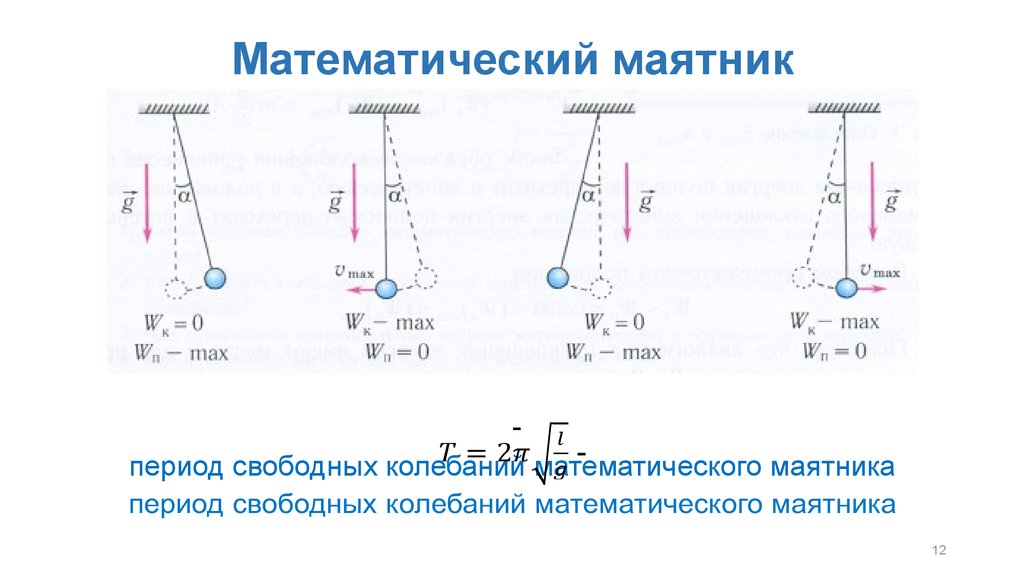 Как
будет меняться период колебаний
ведерка с водой, подвешенного на очень
длинном шнуре: А) если из отверстия в
его дне постепенно будет вытекать
вода?
Б) если увеличить длину шнура?
Какой
математический закон или формулу вы
использовали при ответе на данные
вопросы?
Как
будет меняться период колебаний
ведерка с водой, подвешенного на очень
длинном шнуре: А) если из отверстия в
его дне постепенно будет вытекать
вода?
Б) если увеличить длину шнура?
Какой
математический закон или формулу вы
использовали при ответе на данные
вопросы?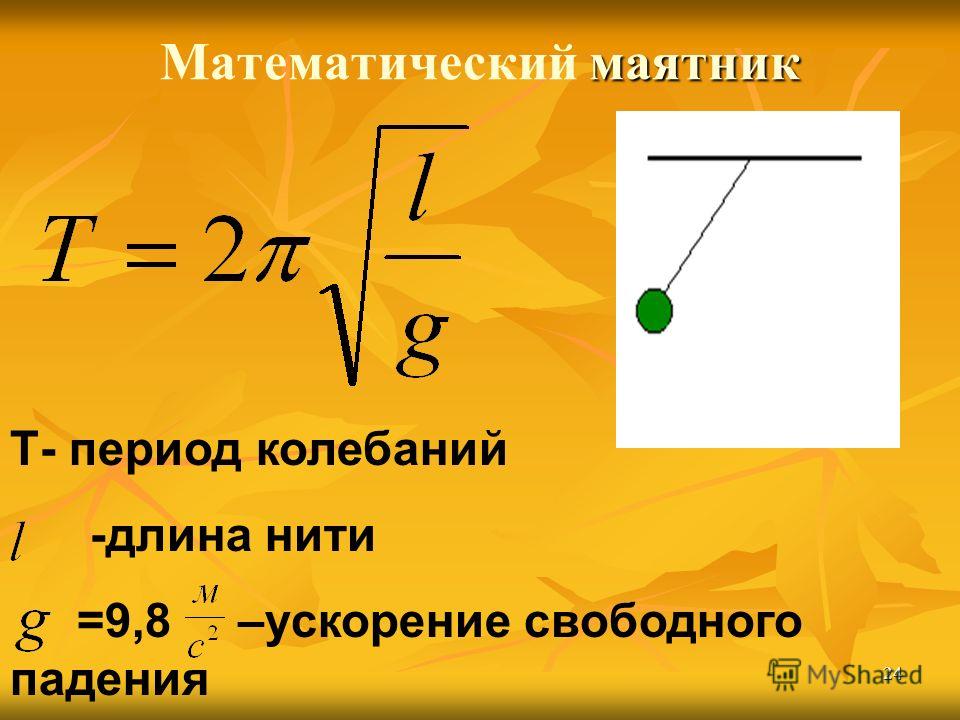
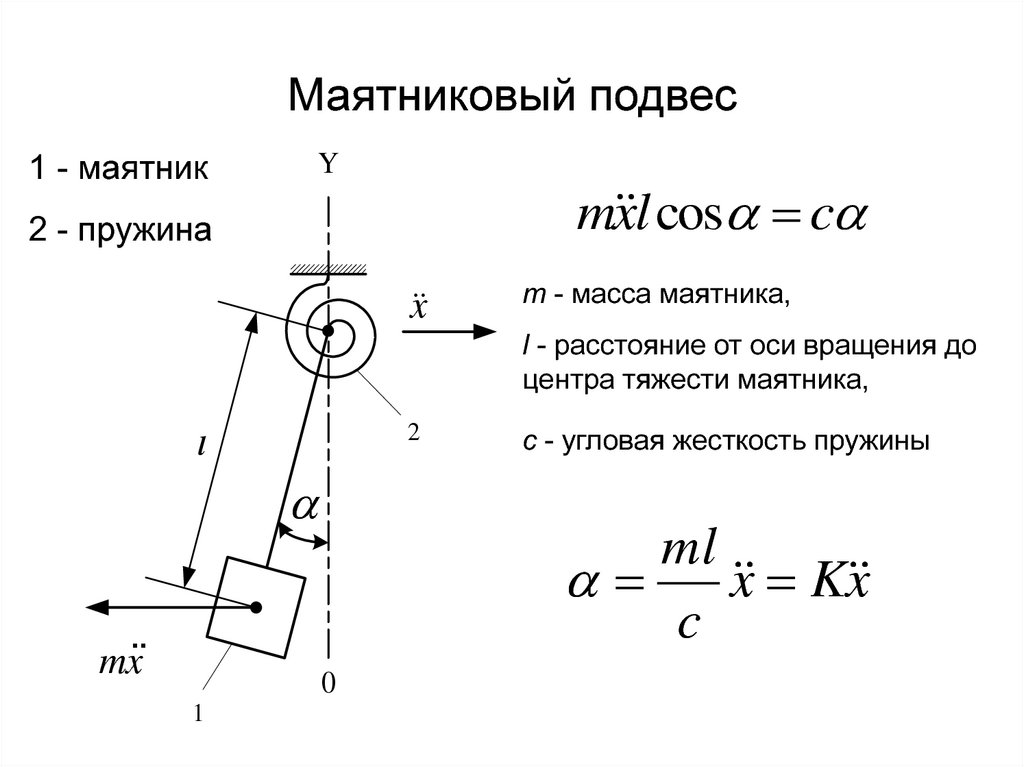 Продемонстрировать колебания нитяного и пружинного маятников.
Продемонстрировать колебания нитяного и пружинного маятников.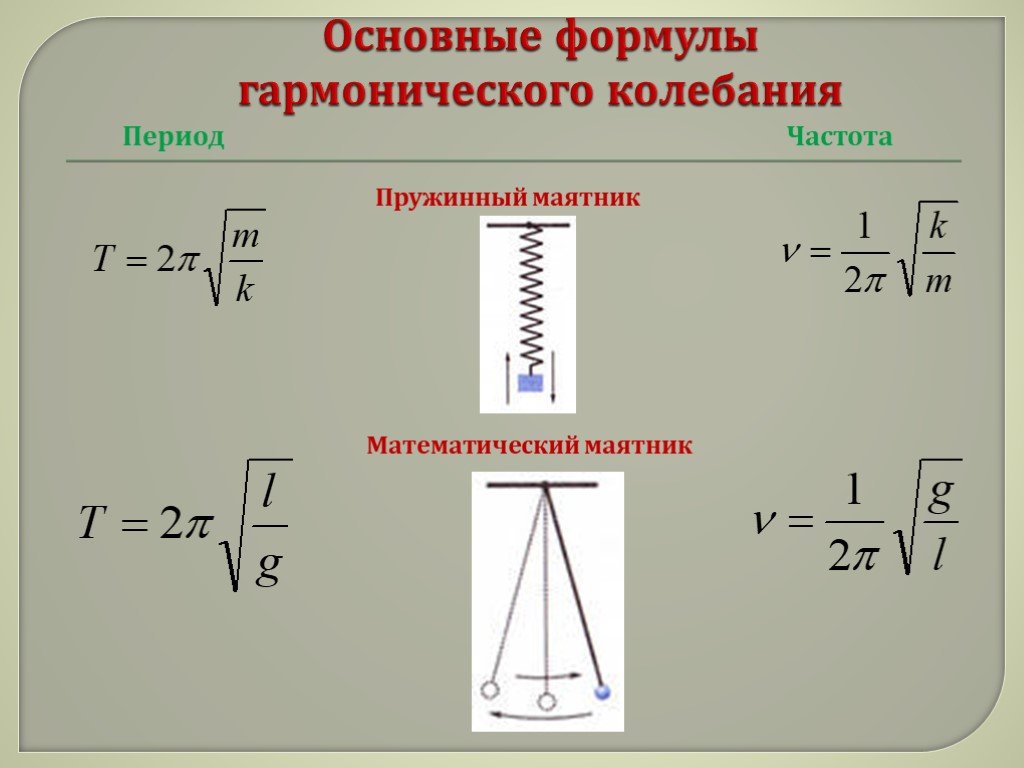

 Томсон (лорд Кельвин) и Дж. Рэлей, русские – А.С. Попов и П.Н. Лебедев, советские – А.Н. Крылов, Л.И. Мандельштам, Н.Д. Папалекси, Н.Н. Боголюбов, А.А. Андронов и другие.
Томсон (лорд Кельвин) и Дж. Рэлей, русские – А.С. Попов и П.Н. Лебедев, советские – А.Н. Крылов, Л.И. Мандельштам, Н.Д. Папалекси, Н.Н. Боголюбов, А.А. Андронов и другие.

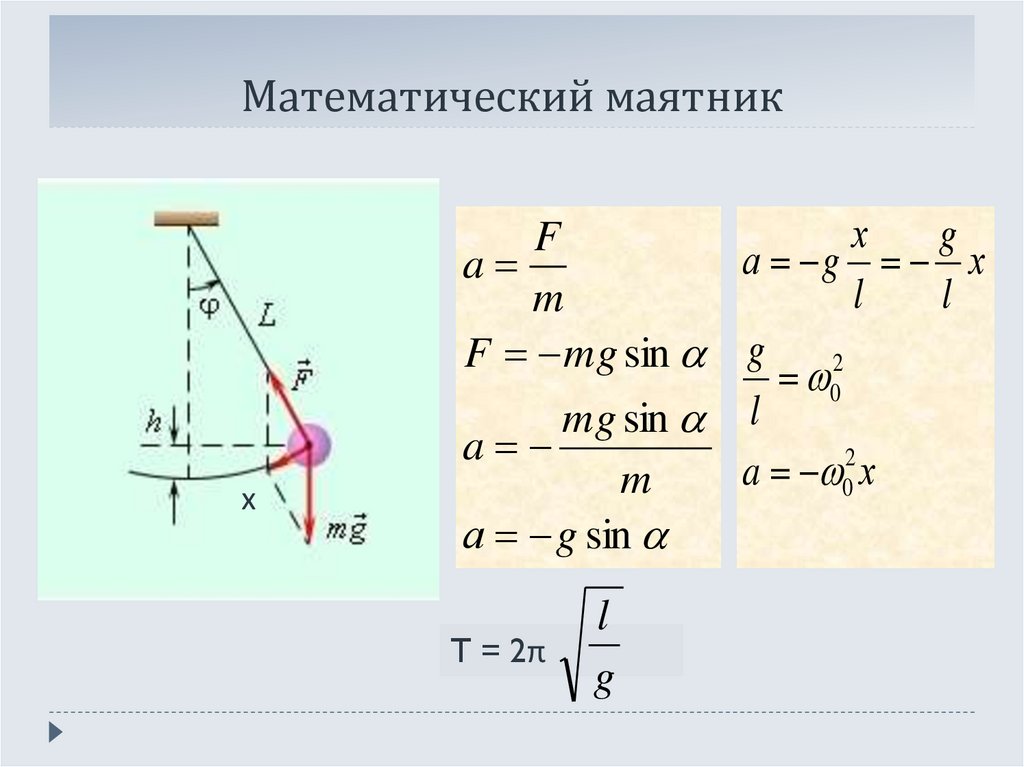 Mendeleev.upeg.net
Mendeleev.upeg.net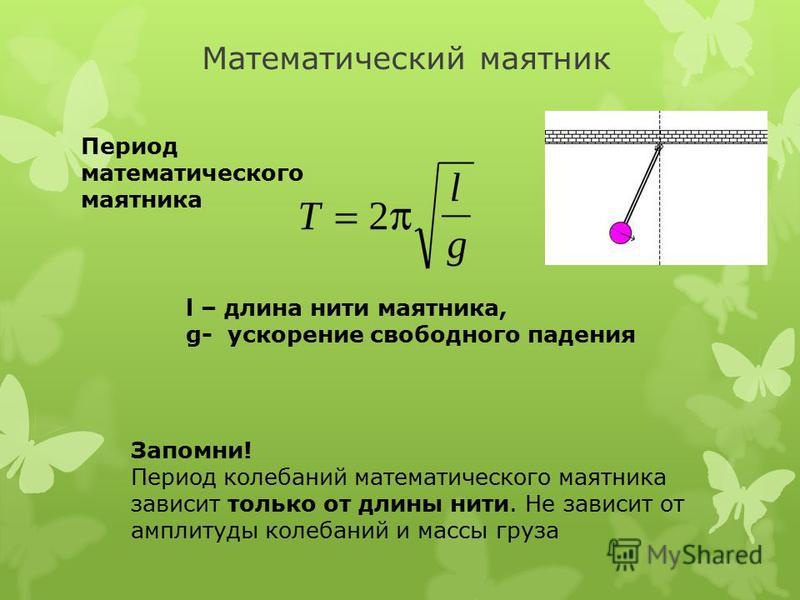 4
4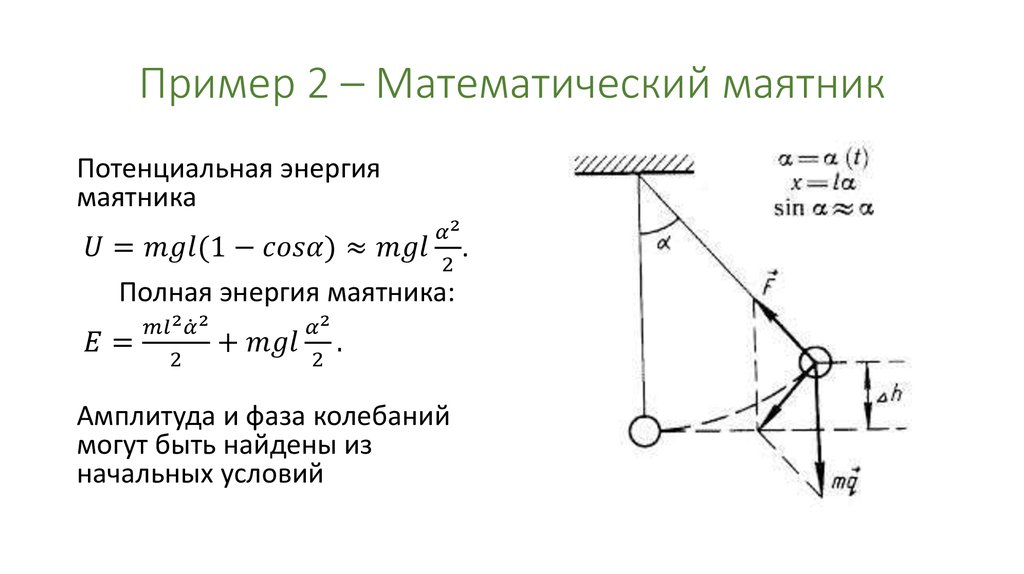 Исходя из формулы период малых колебаний маятника не зависит от амплитуды его колебаний ( Ответ на 4)
Исходя из формулы период малых колебаний маятника не зависит от амплитуды его колебаний ( Ответ на 4)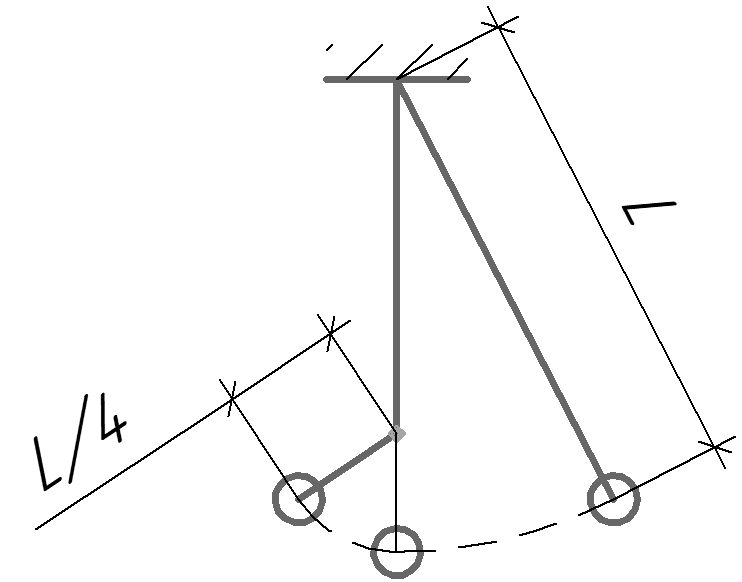 268
268
 736
736
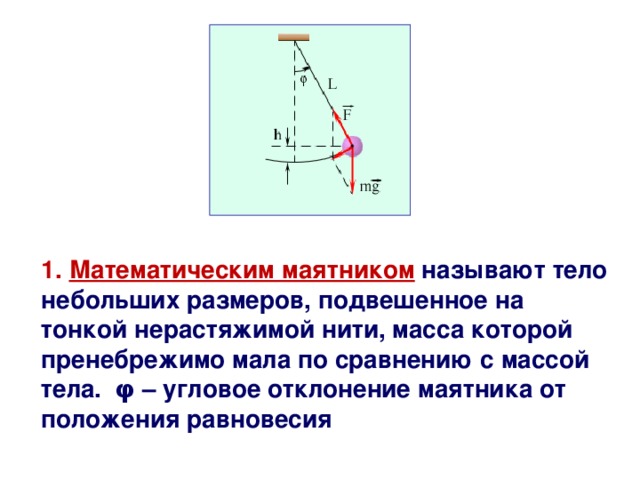 Изготовьте математический маятник длиной 1 м. Экспериментально определите период его колебаний. Результат проанализируйте и сделайте вывод.
Изготовьте математический маятник длиной 1 м. Экспериментально определите период его колебаний. Результат проанализируйте и сделайте вывод. Однако,
для этого иногда нужно построить слишком сложную теорию или выполнить громоздкие
расчеты. Поэтому бывает очень полезно определить приближенное, примерное значение
физической величины. Как говорят физики, нужно оценить физическую величину. Один
из известных наших физиков академик А.Б. Мигдал писал: “Решение большинства задач
теоретической физики начинается с применения качественных методов, которые составляют
наиболее привлекательную и красивую особенность этой науки. Под качественными
методами мы понимаем размерные оценки и оценки с помощью простых моделей”
Однако,
для этого иногда нужно построить слишком сложную теорию или выполнить громоздкие
расчеты. Поэтому бывает очень полезно определить приближенное, примерное значение
физической величины. Как говорят физики, нужно оценить физическую величину. Один
из известных наших физиков академик А.Б. Мигдал писал: “Решение большинства задач
теоретической физики начинается с применения качественных методов, которые составляют
наиболее привлекательную и красивую особенность этой науки. Под качественными
методами мы понимаем размерные оценки и оценки с помощью простых моделей” Поскольку вы делаете оценку, а не хотите знать результат точно, то
ответы 1 час 15 минут и 1 час 33 минуты будут одинаково правильными. Действительно,
ситуация, когда вам надо ждать 1 час с минутами совершенно иная, чем та, когда
надо ждать 2-3 минуты. Таким образом, числа, которые отличаются в 2 — 3 раза -
это числа одного порядка. Если же числа отличаются в 10 раз, говорят, что они
отличаются на один порядок, если в 100 — на два порядка и т.д.
Поскольку вы делаете оценку, а не хотите знать результат точно, то
ответы 1 час 15 минут и 1 час 33 минуты будут одинаково правильными. Действительно,
ситуация, когда вам надо ждать 1 час с минутами совершенно иная, чем та, когда
надо ждать 2-3 минуты. Таким образом, числа, которые отличаются в 2 — 3 раза -
это числа одного порядка. Если же числа отличаются в 10 раз, говорят, что они
отличаются на один порядок, если в 100 — на два порядка и т.д. Например, каково давление в центре Земли? С какой высоты можно прыгать
в воду, чтобы не разбиться? Какова толщина льда, при которой машина не провалится?
(Такую оценку делали физики в Ленинграде во время войны.)
Например, каково давление в центре Земли? С какой высоты можно прыгать
в воду, чтобы не разбиться? Какова толщина льда, при которой машина не провалится?
(Такую оценку делали физики в Ленинграде во время войны.) Теперь с помощью известного соотношения кинематики
находим
время движения по хорде , а значит период колебаний
.
Теперь с помощью известного соотношения кинематики
находим
время движения по хорде , а значит период колебаний
. Говорят, что большие колебания маятника неизохронны.
Говорят, что большие колебания маятника неизохронны. Тогда площадь пары крыльев S~l2. Так
как поперечные размеры комара без крылышек существенно меньше его длины, оценим
его объем как 1/10l3. Плотность голодного комара примем
равной плотности воды r. Если частота взмаха крылышек f,
то скорость крыла v~lf. Из условия равновесия комара
F~mg, используя полученные оценочные соотношения,
находим:
Тогда площадь пары крыльев S~l2. Так
как поперечные размеры комара без крылышек существенно меньше его длины, оценим
его объем как 1/10l3. Плотность голодного комара примем
равной плотности воды r. Если частота взмаха крылышек f,
то скорость крыла v~lf. Из условия равновесия комара
F~mg, используя полученные оценочные соотношения,
находим:
 На каждой
странице около сотни телефонов. Значит, число домашних телефонов, зарегистрированных
на момент создания справочника, порядка 80 тысяч.
На каждой
странице около сотни телефонов. Значит, число домашних телефонов, зарегистрированных
на момент создания справочника, порядка 80 тысяч.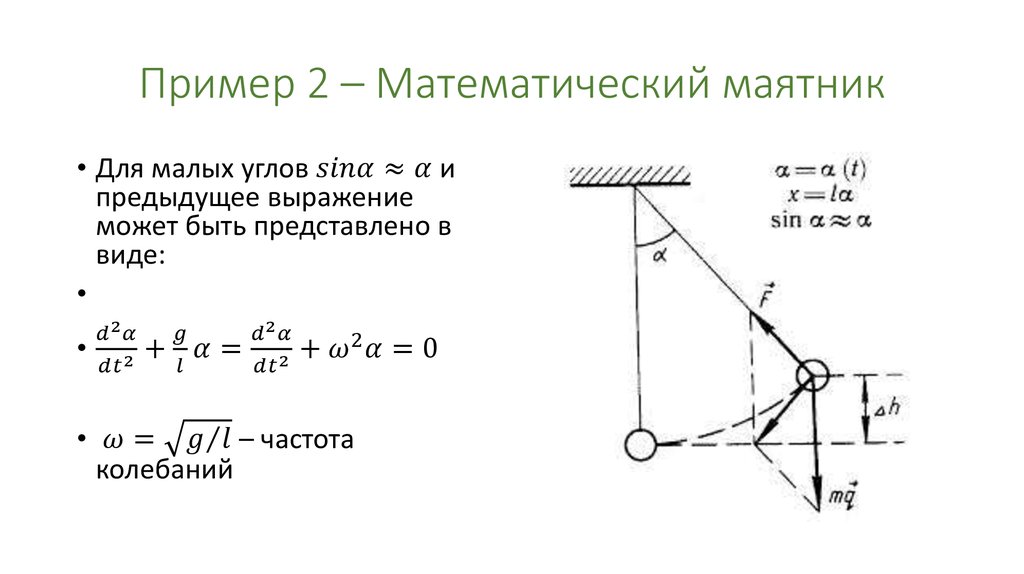 Будь смелее: ведь никому нет
дела до того, что именно ты предположил. Поэтому делай предположения быстро, интуитивно.
Удачные предположения укрепляют эту интуицию. Ошибочные предположения дают полезную
встряску». Если вернуться к началу нашего задания, то нетрудно увидеть, что
мы все время пользовались правилом Уилера, которое хорошо коррелирует с высказываниями
А.Б.Мигдала.
Будь смелее: ведь никому нет
дела до того, что именно ты предположил. Поэтому делай предположения быстро, интуитивно.
Удачные предположения укрепляют эту интуицию. Ошибочные предположения дают полезную
встряску». Если вернуться к началу нашего задания, то нетрудно увидеть, что
мы все время пользовались правилом Уилера, которое хорошо коррелирует с высказываниями
А.Б.Мигдала. Как соотносится ваш
результат с данными наблюдений с автоматических космических станций?
Как соотносится ваш
результат с данными наблюдений с автоматических космических станций? д.
На первый взгляд кажется, что размерность играет вспомогательную роль. На самом
деле это не так. Размерность — хороший помощник физика. Умение обращаться с размерностью
помогает избежать ошибок в преобразованиях, а иногда дает возможность получить
ответ к задаче, когда другие способы решения найти не удается.
д.
На первый взгляд кажется, что размерность играет вспомогательную роль. На самом
деле это не так. Размерность — хороший помощник физика. Умение обращаться с размерностью
помогает избежать ошибок в преобразованиях, а иногда дает возможность получить
ответ к задаче, когда другие способы решения найти не удается.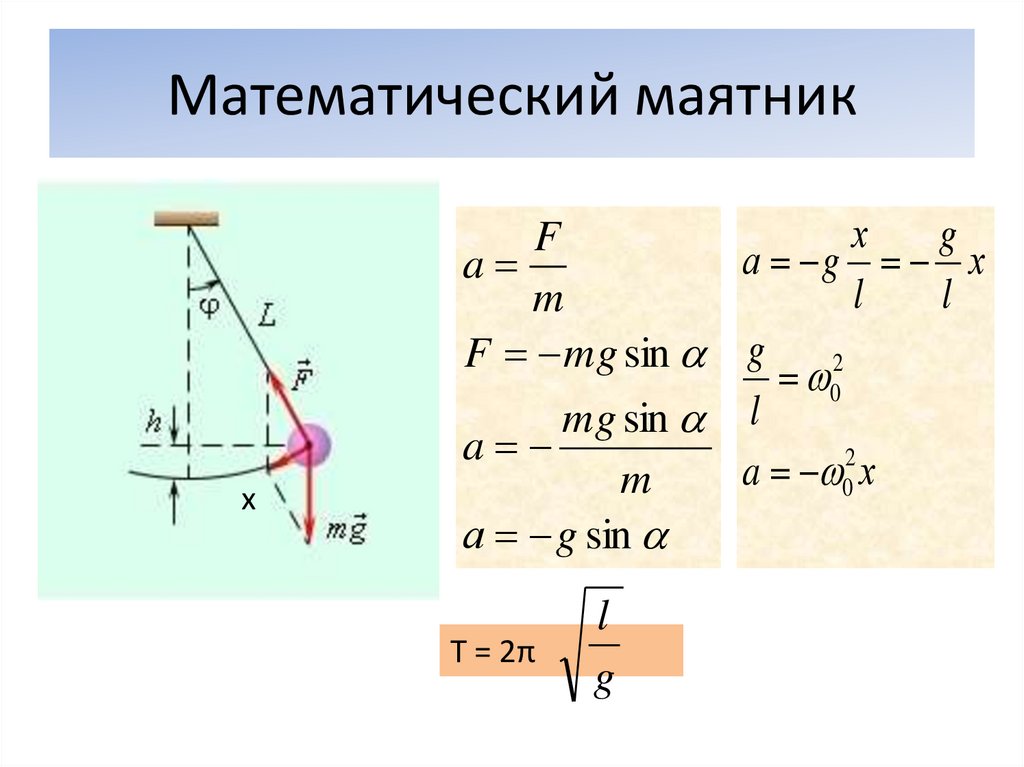 Обычно это длина, масса, время. Им соответствуют размерности
«метр», «килограмм», «секунда» или сокращенно «м»,
«кг», «с». Остальные физические величины имеют производную
размерность, например, размерность скорости — «м/с», ускорения — «м/с2«
и т.д. Вообще-то, можно придумать единицу скорости, и считать ее основной. Тогда
производной станет единица длины. Принципиальных возражений против этого нет,
но это очень неудобно.
Обычно это длина, масса, время. Им соответствуют размерности
«метр», «килограмм», «секунда» или сокращенно «м»,
«кг», «с». Остальные физические величины имеют производную
размерность, например, размерность скорости — «м/с», ускорения — «м/с2«
и т.д. Вообще-то, можно придумать единицу скорости, и считать ее основной. Тогда
производной станет единица длины. Принципиальных возражений против этого нет,
но это очень неудобно. Оказывается, анализ размерности физических величин позволяет получать новые формулы.
Соответствующий прием называют методом размерностей. Давайте научимся пользоваться
этим методом. Отыщем формулу для объема шара. Первый этап решения задачи с помощью
метода размерности состоит в том, что определяются все величины, которые могут
войти в искомую формулу. Ясно, что объем шара может зависеть только от его радиуса
R. Выпишем размерности всех интересующих нас величин:
Оказывается, анализ размерности физических величин позволяет получать новые формулы.
Соответствующий прием называют методом размерностей. Давайте научимся пользоваться
этим методом. Отыщем формулу для объема шара. Первый этап решения задачи с помощью
метода размерности состоит в том, что определяются все величины, которые могут
войти в искомую формулу. Ясно, что объем шара может зависеть только от его радиуса
R. Выпишем размерности всех интересующих нас величин: Константу C можно отыскать экспериментально, с помощью компьютерного
моделирования или строго решив задачу.
Константу C можно отыскать экспериментально, с помощью компьютерного
моделирования или строго решив задачу.
 Значит число приближенно равно 6,3. (Точное значение .)
Значит число приближенно равно 6,3. (Точное значение .)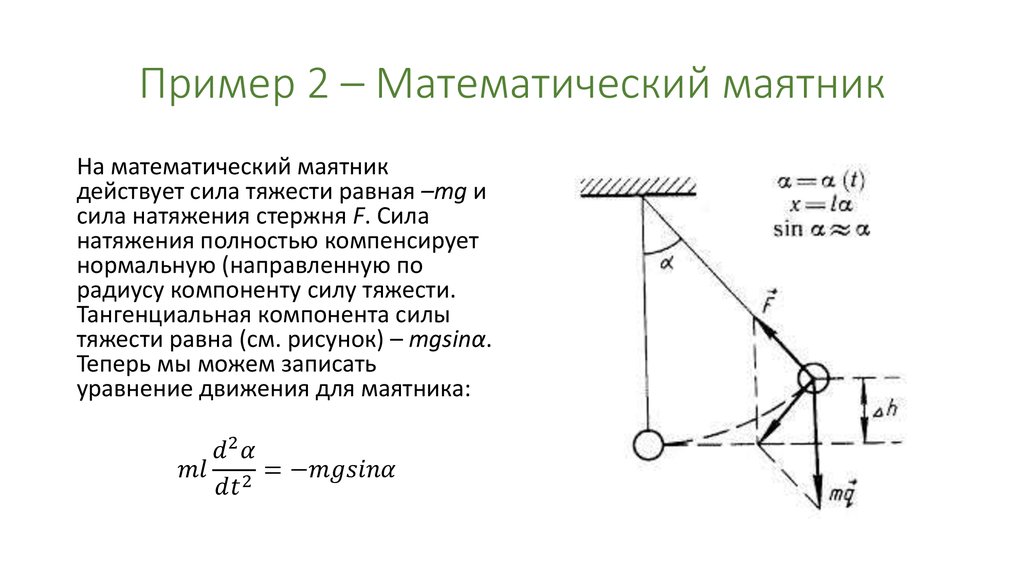 Однако ее график можно построить экспериментально. Для этого надо установить зависимость
для какой-то одной фиксированной длины l. Если затем построить график измеренной
зависимости, отложив по горизонтальной оси угол ,
а по вертикальной — комбинацию , то это и будет график функции .
Кстати, у нас обязательно при этом получится
(почему?). Кроме того, при малых значениях
функция будет почти не зависеть от
(почему?).
Однако ее график можно построить экспериментально. Для этого надо установить зависимость
для какой-то одной фиксированной длины l. Если затем построить график измеренной
зависимости, отложив по горизонтальной оси угол ,
а по вертикальной — комбинацию , то это и будет график функции .
Кстати, у нас обязательно при этом получится
(почему?). Кроме того, при малых значениях
функция будет почти не зависеть от
(почему?).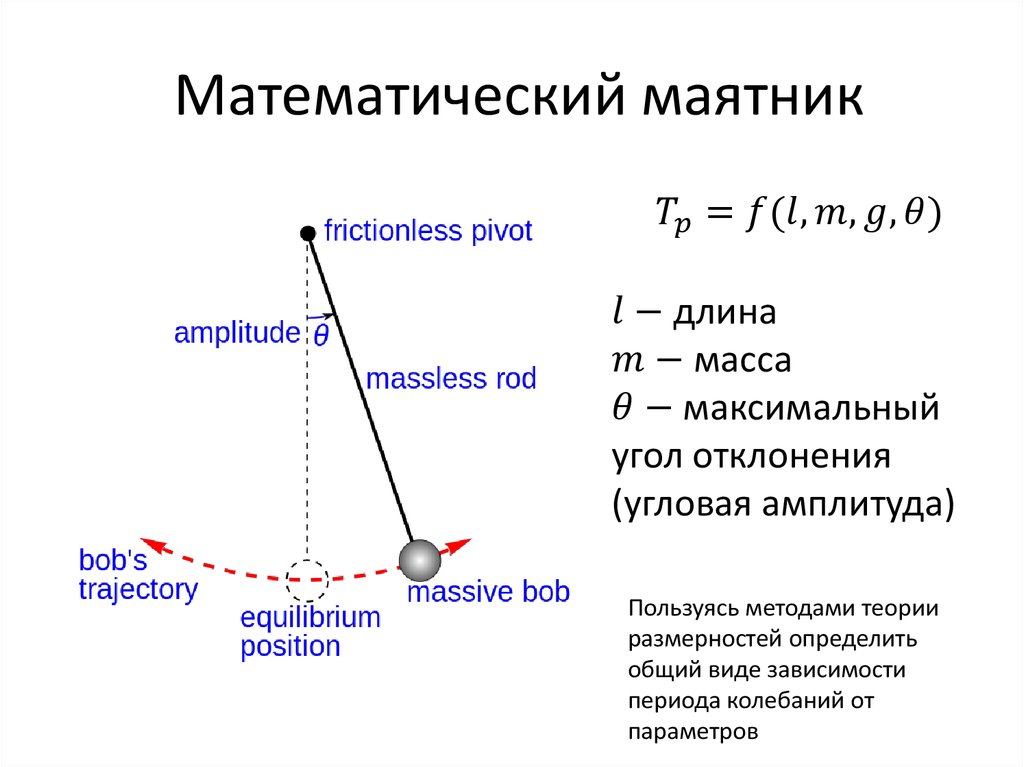 д. Тогда результаты, относящиеся к разным значениям длины, оказываются выделенными.
Получается следующая картинка. Взглянув на такой график, можно сразу сказать,
хорошо ли работает наша формула. Критерием этого является, ложатся или нет точки,
крестики, квадратики на одну кривую. Если да, то в этом случае говорят, что получилась
универсальная функция. Она является универсальной в том смысле, что она пригодна
одновременно для всех маятников, какова бы ни была длина их подвеса.
д. Тогда результаты, относящиеся к разным значениям длины, оказываются выделенными.
Получается следующая картинка. Взглянув на такой график, можно сразу сказать,
хорошо ли работает наша формула. Критерием этого является, ложатся или нет точки,
крестики, квадратики на одну кривую. Если да, то в этом случае говорят, что получилась
универсальная функция. Она является универсальной в том смысле, что она пригодна
одновременно для всех маятников, какова бы ни была длина их подвеса.
 За какое время змея, лежащая на гладкой горизонтальной поверхности вдоль прямой
линии, может свернуться, образовав кольцо? Масса змеи M, ее длина l.
За какое время змея, лежащая на гладкой горизонтальной поверхности вдоль прямой
линии, может свернуться, образовав кольцо? Масса змеи M, ее длина l. Из соображений размерности получите формулу для площади
прямоугольного треугольника. Постройте качественно универсальную функцию, характеризующую
зависимость площади прямоугольного треугольника от угла .
Из соображений размерности получите формулу для площади
прямоугольного треугольника. Постройте качественно универсальную функцию, характеризующую
зависимость площади прямоугольного треугольника от угла . Или, например, комплексными числами, которые тоже пока не изучили.
В науке же ситуация совершенно другая — можно (и нужно!) пользоваться любыми известными
знаниями. Для этого можно обращаться к справочникам, литературе, консультациями
других исследователей. На традиционных же уроках это все не разрешается. Второе,
очень существенное отличие от школьного способа обучения состоит в том, что одна
задача решается долго (неделю, месяц, год). Задачи же, которые Вы решаете в школе
и на олимпиадах совершенно другие. Урок и олимпиада скоротечны, и на каждую задачу
Вы тратите не так много времени — ведь необходимо решать их довольно большое число.
В третьих, школьная задача, как правило, имеет единственное четкое решение, именно
то, которое предполагал в учебных целях ее автор. Те же задачи, которые решает
ученый-исследователь не обладают такой степенью определенности. Можно, однако,
сформулировать задачи, содержащие традиционные для учебного курса физики ситуации,
но требующие не «ученического», а научного подхода к их решению.
Или, например, комплексными числами, которые тоже пока не изучили.
В науке же ситуация совершенно другая — можно (и нужно!) пользоваться любыми известными
знаниями. Для этого можно обращаться к справочникам, литературе, консультациями
других исследователей. На традиционных же уроках это все не разрешается. Второе,
очень существенное отличие от школьного способа обучения состоит в том, что одна
задача решается долго (неделю, месяц, год). Задачи же, которые Вы решаете в школе
и на олимпиадах совершенно другие. Урок и олимпиада скоротечны, и на каждую задачу
Вы тратите не так много времени — ведь необходимо решать их довольно большое число.
В третьих, школьная задача, как правило, имеет единственное четкое решение, именно
то, которое предполагал в учебных целях ее автор. Те же задачи, которые решает
ученый-исследователь не обладают такой степенью определенности. Можно, однако,
сформулировать задачи, содержащие традиционные для учебного курса физики ситуации,
но требующие не «ученического», а научного подхода к их решению. Наиболее
известна подборка таких задач, придуманных выдающимся ученым П.Л.Капицей для студентов
и молодых людей, поступающих в аспирантуру. Мы хотим предложить несколько задач
исследовательского характера, которые близки к научному исследованию. Из приведенных
ниже задач лучше выбрать всего одну — ту, которая Вам понравится. Значение имеет
не число решенных задач, а глубина проработки решения. Такие задачи,
можно надеяться, помогут Вам лучше понять науку, как профессию, состоящую в получении
новых результатов «своими руками».
Наиболее
известна подборка таких задач, придуманных выдающимся ученым П.Л.Капицей для студентов
и молодых людей, поступающих в аспирантуру. Мы хотим предложить несколько задач
исследовательского характера, которые близки к научному исследованию. Из приведенных
ниже задач лучше выбрать всего одну — ту, которая Вам понравится. Значение имеет
не число решенных задач, а глубина проработки решения. Такие задачи,
можно надеяться, помогут Вам лучше понять науку, как профессию, состоящую в получении
новых результатов «своими руками». Используйте
литературу — для решения некоторых задач это полезно, а решение некоторых из них
без этого и невозможно.
Используйте
литературу — для решения некоторых задач это полезно, а решение некоторых из них
без этого и невозможно.
 Покажите, что при небольших деформациях
время соударения не зависит от начальной скорости мяча. Оцените это время. Массу
мяча примите ,
радиус ,
избыточное давление внутри него равно одной атмосфере, т.е. 105 Па.
Оцените скорость мяча, при которой деформация мяча не будет малой.
Покажите, что при небольших деформациях
время соударения не зависит от начальной скорости мяча. Оцените это время. Массу
мяча примите ,
радиус ,
избыточное давление внутри него равно одной атмосфере, т.е. 105 Па.
Оцените скорость мяча, при которой деформация мяча не будет малой.
 В Пензенской области общее число мандатов осталось неизменным (89%), а в Саратовской единороссы понесли потери: если пять лет назад партия власти контролировала 80% мест в заксобрании, то сейчас — 72%.
В Пензенской области общее число мандатов осталось неизменным (89%), а в Саратовской единороссы понесли потери: если пять лет назад партия власти контролировала 80% мест в заксобрании, то сейчас — 72%. Во Владивостоке единороссы теперь контролируют 66% мандатов (было 63%), выиграв в 23 из 35 округов. В Ярославле у партии власти 89% мандатов (было 79%), ее кандидаты выиграли в 34 из 38 округов.
Во Владивостоке единороссы теперь контролируют 66% мандатов (было 63%), выиграв в 23 из 35 округов. В Ярославле у партии власти 89% мандатов (было 79%), ее кандидаты выиграли в 34 из 38 округов.
 В остальных субъектах показатели партий изменились незначительно.
В остальных субъектах показатели партий изменились незначительно. ..
.. ..
.. ст.гПа
ст.гПа Ведь наша жизнь всегда зависела от ее условий. С древних времен люди подстраивали свой образ жизни под капризы погоды: наблюдали за ней, присматривались. А потом выводили важные даты. День, когда Солнце занимает самую низкую точку относительно земного горизонта — назвали днем зимнего солнцестояния.
Ведь наша жизнь всегда зависела от ее условий. С древних времен люди подстраивали свой образ жизни под капризы погоды: наблюдали за ней, присматривались. А потом выводили важные даты. День, когда Солнце занимает самую низкую точку относительно земного горизонта — назвали днем зимнего солнцестояния. Поддерживали, так сказать, его силы пламенем.
Поддерживали, так сказать, его силы пламенем. Так же будет так же си, и тако быть. Аминь».
Так же будет так же си, и тако быть. Аминь». Пока он будет гореть, надо произнести слова:
Пока он будет гореть, надо произнести слова: В знак уважения народ разжигал костры на полях. Также было принято плести корзины из ветвей вечнозеленых растений и колосьев пшеницы. Затем туда складывались яблоки и гвоздика, которые посыпались мукой.
В знак уважения народ разжигал костры на полях. Также было принято плести корзины из ветвей вечнозеленых растений и колосьев пшеницы. Затем туда складывались яблоки и гвоздика, которые посыпались мукой.

 Прилетел в Пулково и пошел к стойке регистрации на следующий рейс узнать, когда начнется регистрация. Девушка уточнила мою фамилию и попросила чуть-чуть подождать. Тут я сразу понял, что что-то здесь не так. Ну а куда деваться?
Прилетел в Пулково и пошел к стойке регистрации на следующий рейс узнать, когда начнется регистрация. Девушка уточнила мою фамилию и попросила чуть-чуть подождать. Тут я сразу понял, что что-то здесь не так. Ну а куда деваться? Они сразу выложили свои карты: «Там твой телефон прослушивали, мессенджер читали, с какой почты ты там все это отправлял мы в курсе. И по поводу всего твоего сотрудничества с [основателем Gulagu.net Владимиром] Осечкиным последние полгода мы знаем».
Они сразу выложили свои карты: «Там твой телефон прослушивали, мессенджер читали, с какой почты ты там все это отправлял мы в курсе. И по поводу всего твоего сотрудничества с [основателем Gulagu.net Владимиром] Осечкиным последние полгода мы знаем». За то, что ты делал, ты сядешь. И с учетом того, что ты делал — ты распространил информацию про ФСИН компрометирующую, тебя там убьют. Или со шконки упадешь со второго яруса, или в камере повесишься. Найдут тебя повешенным. Перед этим ты все нам расскажешь, а когда уже будет не надо, то… То есть эта угроза вполне реальна, такое очень часто происходит на самом деле.
За то, что ты делал, ты сядешь. И с учетом того, что ты делал — ты распространил информацию про ФСИН компрометирующую, тебя там убьют. Или со шконки упадешь со второго яруса, или в камере повесишься. Найдут тебя повешенным. Перед этим ты все нам расскажешь, а когда уже будет не надо, то… То есть эта угроза вполне реальна, такое очень часто происходит на самом деле.
 Помимо этого — я ведь не улетал из России. Я летел дальше по России в Новосибирск и они, наверное, были уверены, что в случае, если я попытаюсь пересечь границу РФ в сторону Белоруссии или еще куда-то без их ведома или разрешения, тогда они увидят и смогут пресечь. Поэтому в Новосибирск я отправился оттуда. Отпустили в общем.
Помимо этого — я ведь не улетал из России. Я летел дальше по России в Новосибирск и они, наверное, были уверены, что в случае, если я попытаюсь пересечь границу РФ в сторону Белоруссии или еще куда-то без их ведома или разрешения, тогда они увидят и смогут пресечь. Поэтому в Новосибирск я отправился оттуда. Отпустили в общем. Дальше меня потащат уже куда-то по инстанциям.
Дальше меня потащат уже куда-то по инстанциям. То есть это была такая секретная операция. Это такой стресс и страх. Вот именно тогда, в тот момент, это была просто паника.
То есть это была такая секретная операция. Это такой стресс и страх. Вот именно тогда, в тот момент, это была просто паника.

 С.: Да, у меня была эта фраза, как она звучит — уже не помню, уже выпала из памяти. Я ее твердил, как заклинание, сначала одному полицейскому, он не понимал. Потом второму, потом третьему. Ну как бы ничего в конце концов и не поняли, пригласили мне переводчика, очень ему большое спасибо, очень внимательно отнесся, с пониманием, сказал, что это обычное дело, очень часто приезжают, не переживайте, это все обычная процедура, мы подпишем несколько бумаг. Несколько часов продолжалась эта процедура. Меня подержали в каком-то запертом помещении и направили в депортационный центр.
С.: Да, у меня была эта фраза, как она звучит — уже не помню, уже выпала из памяти. Я ее твердил, как заклинание, сначала одному полицейскому, он не понимал. Потом второму, потом третьему. Ну как бы ничего в конце концов и не поняли, пригласили мне переводчика, очень ему большое спасибо, очень внимательно отнесся, с пониманием, сказал, что это обычное дело, очень часто приезжают, не переживайте, это все обычная процедура, мы подпишем несколько бумаг. Несколько часов продолжалась эта процедура. Меня подержали в каком-то запертом помещении и направили в депортационный центр. Было понятно, что уже пришло положительное решение по моему вопросу, и сейчас меня выпустят в город.
Было понятно, что уже пришло положительное решение по моему вопросу, и сейчас меня выпустят в город. Сразу чем-то сбили с ног уже прямо в дверях, они прямо по мне забежали в квартиру. Здоровенный дядька в этих… берцах. То есть этот первый день, конечно, это было что то с чем-то. Это был первичный допрос, когда им еще все можно. Ну они и потом, конечно, себе очень многое позволяют, но вот в этот первый день, конечно, они оторвались неплохо на мне.
Сразу чем-то сбили с ног уже прямо в дверях, они прямо по мне забежали в квартиру. Здоровенный дядька в этих… берцах. То есть этот первый день, конечно, это было что то с чем-то. Это был первичный допрос, когда им еще все можно. Ну они и потом, конечно, себе очень многое позволяют, но вот в этот первый день, конечно, они оторвались неплохо на мне. С.: Ну, вообще да. То есть я попал в камеру третьим, там уже было два человека. Один был турок, а второй — кабардинец по-моему, уже несколько раз сидевший. Вот он начинает более-менее объяснять, что там будет дальше в следственном изоляторе, куда я дальше отправлюсь. Потому что там еще было ничего. Ну не считая того, что мы проходили следственные действия, многие из которых проходили болезненно.
С.: Ну, вообще да. То есть я попал в камеру третьим, там уже было два человека. Один был турок, а второй — кабардинец по-моему, уже несколько раз сидевший. Вот он начинает более-менее объяснять, что там будет дальше в следственном изоляторе, куда я дальше отправлюсь. Потому что там еще было ничего. Ну не считая того, что мы проходили следственные действия, многие из которых проходили болезненно. К слову. То есть будет по-тихому — проплывешь себе и поедешь дальше в зону, в зоне вообще все по-другому, там уже можно вздохнуть.
К слову. То есть будет по-тихому — проплывешь себе и поедешь дальше в зону, в зоне вообще все по-другому, там уже можно вздохнуть. Пока мне не было окончательно сформировано обвинение. После этого меня уже перевели в СИЗО №3 города Новороссийска, после этого периодически вывозили в город Крымск на судебные заседания.
Пока мне не было окончательно сформировано обвинение. После этого меня уже перевели в СИЗО №3 города Новороссийска, после этого периодически вывозили в город Крымск на судебные заседания.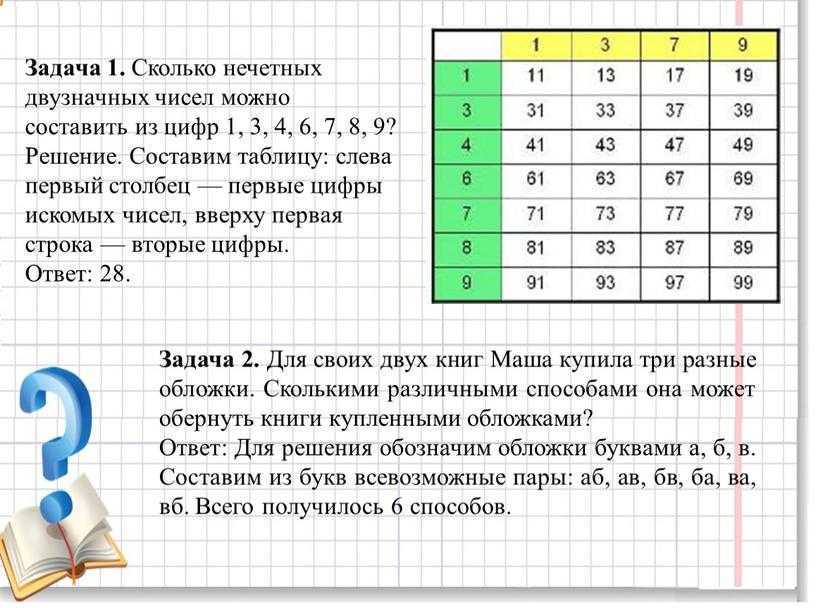 С.: Это была статья 228.1, часть 5 [незаконные производство, сбыт или пересылка наркотических средств] — и неоконченный состав преступления. То есть все вывели к тому, что я приобрел большой объем наркотических веществ с целью дальнейшего сбыта, но не довел свой умысел до конца, потому что доблестные правоохранительные органы пресекли эти действия. Мне дали всего девять лет.
С.: Это была статья 228.1, часть 5 [незаконные производство, сбыт или пересылка наркотических средств] — и неоконченный состав преступления. То есть все вывели к тому, что я приобрел большой объем наркотических веществ с целью дальнейшего сбыта, но не довел свой умысел до конца, потому что доблестные правоохранительные органы пресекли эти действия. Мне дали всего девять лет. Даже в других областях люди слышали про ОТБ-1 и про ИК-13 — самые страшные их зоны.
Даже в других областях люди слышали про ОТБ-1 и про ИК-13 — самые страшные их зоны.
 Там уже над тобой работают «активисты», сотрудники уже практически не обращают на это внимания.
Там уже над тобой работают «активисты», сотрудники уже практически не обращают на это внимания.