Сборник задач по высшей математике для экономистов Ермаков
Сборн-к задач по математике для экономистов согласно учебной программе включает задачи по основн. разделам курса высшей математики: аналитич-я геометрия, линейная алгебра, матем. анализ, теория вероятностей, матем. статистика, линейное программирование. Выделен раздел, отражающий применение аналитической геометрии — мат. анализа в экономике. Приведены краткие теоретич-е сведения, некоторые задачи снабжены решениями. Студентам экономических специальностей.-Содержание-
Предисловие 03
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ 5
Геометрические векторы 05
Прямая и плоскость 12
Кривые второго порядка 28
Практикум — аналитической геометрии 33
ЛИНЕЙНАЯ АЛГЕБРА 39
Определители 39
Матрицы 50
Решение систем линейных урав-й 60
Системы векторов уравнений 70
Векторные пространства 93
Матрицы квадратичные формы 106
Практикум 1 … 117
Практикум 2….. 127
МАТЕМАТИЧЕСКИЙ АНАЛИЗ 135
Функции одной переменной 136
Пределы 142
Производная и дифференциал 150
Функции многих переменных 180
Практикум по мат. анализу 198
анализу 198
Неопределенный интеграл 203
Определенный интеграл 212
Дифференциальные уравнения 223
Ряды 238
Практикум 2 ….255
Применение аналитической геометрии … 266
ТЕОРИЯ ВЕРОЯТНОСТЕЙ 303
Случайные события 303
Дискретные случайные величины 315
Непрерывные случайные величины 324
Система : случайных величин 334
Практикум — теории вероятностей 34
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА 347
Выборка ее представление 348
Статистическое оценивание 357
Проверка статистических гипотез 369
Регрессионный анализ 388
Дисперсионный анализ 397
Практикум- математической статистике 402
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ 412
Математическая модель задачи …412
Графический метод решения ..419
Симплексный метод решения… 432
Теория двойственности 457
Транспортная задача линейного программир-я 476
Метод Гомори… 500
Практикум — линейному программированию 506
Приложения 518
Ответы 527
Размер файла: 57 Мб; Формат: doc/zip.
download
Вместе с «Сборник задач по высшей математике для экономистов Ермаков» скачивают:
AdminСборник задач по высшей математике для экономистов : аналитическая геометрия, линейная алгебра, математический анализ, теория вероятностей, математическая статистика, линейное программирование : учебное пособие : для студентов высших учебных заведений, обучающихся по направлению «Экономика» и экономическим специальностям
Поиск по определенным полям
Чтобы сузить результаты поисковой выдачи, можно уточнить запрос, указав поля, по которым производить поиск. Список полей представлен выше. Например:
author:иванов
Можно искать по нескольким полям одновременно:author:иванов title:исследование
Логически операторы
По умолчанию используется оператор AND.

Оператор AND означает, что документ должен соответствовать всем элементам в группе:
исследование разработка
author:иванов title:разработка
оператор OR означает, что документ должен соответствовать одному из значений в группе:исследование OR разработка
author:иванов OR title:разработка
оператор NOT исключает документы, содержащие данный элемент:исследование NOT разработка
author:иванов NOT title:разработка
Тип поиска
При написании запроса можно указывать способ, по которому фраза будет искаться. Поддерживается четыре метода: поиск с учетом морфологии, без морфологии, поиск префикса, поиск фразы.
По-умолчанию, поиск производится с учетом морфологии.
Для поиска без морфологии, перед словами в фразе достаточно поставить знак «доллар»:
$исследование $развития
Для поиска префикса нужно поставить звездочку после запроса:исследование*
Для поиска фразы нужно заключить запрос в двойные кавычки:«исследование и разработка«
Поиск по синонимам
Для включения в результаты поиска синонимов слова нужно поставить решётку «#» перед словом или перед выражением в скобках.

В применении к одному слову для него будет найдено до трёх синонимов.
В применении к выражению в скобках к каждому слову будет добавлен синоним, если он был найден.
Не сочетается с поиском без морфологии, поиском по префиксу или поиском по фразе.
#исследование
Группировка
Для того, чтобы сгруппировать поисковые фразы нужно использовать скобки. Это позволяет управлять булевой логикой запроса.
Например, нужно составить запрос: найти документы у которых автор Иванов или Петров, и заглавие содержит слова исследование или разработка:
author:(иванов OR петров) title:(исследование OR разработка)
Приблизительный поиск слова
Для приблизительного поиска нужно поставить тильду «~» в конце слова из фразы.
 4 разработка По умолчанию, уровень равен 1. Допустимые значения — положительное вещественное число.
4 разработка По умолчанию, уровень равен 1. Допустимые значения — положительное вещественное число.Поиск в интервале
Для указания интервала, в котором должно находиться значение какого-то поля, следует указать в скобках граничные значения, разделенные оператором TO.
Будет произведена лексикографическая сортировка.
author:[Иванов TO Петров]
Будут возвращены результаты с автором, начиная от Иванова и заканчивая Петровым, Иванов и Петров будут включены в результат.author:{Иванов TO Петров}
Такой запрос вернёт результаты с автором, начиная от Иванова и заканчивая Петровым, но Иванов и Петров не будут включены в результат.Для того, чтобы включить значение в интервал, используйте квадратные скобки. Для исключения значения используйте фигурные скобки.

▶▷▶ решебник для сборника задач по высшей математике ермакова
▶▷▶ решебник для сборника задач по высшей математике ермакова| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 09-11-2018 |
решебник для сборника задач по высшей математике ермакова — Yahoo Search Results Yahoo Web Search Sign in Mail Go to Mail» data-nosubject=»[No Subject]» data-timestamp=’short’ Help Account Info Yahoo Home Settings Home News Mail Finance Tumblr Weather Sports Messenger Settings Yahoo Search query Web Images Video News Local Answers Shopping Recipes Sports Finance Dictionary More Anytime Past day Past week Past month Anytime Get beautiful photos on every new browser window Download скачать решебник сборника задач по высшей математике для docplayerru/43230902-Skachat-reshebnik-sbornika Cached 1 Название: Справочник по математике для экономистов Автор: Ермаков ВИ ( ред) Ермакова ВИ Название: Сборник задач по высшей математике для экономистов olga podolyako julia vaulina7 класс решебник к workbook, холодова о умники и Сборник задач по высшей математике для экономистов / Под ред edu-libcom/matematika-2/dlya-studentov/sbornik Cached Сборник задач по высшей математике для экономистов / Под ред ВИ Ермакова ОНЛАЙН 31082013 Высшая математика Математика для нематематиков , Математика , Математика для студентов, аспирантов и Сборник задач по высшей математике для экономистов Под ред allengorg/d/math/math427htm Cached Сборник задач по высшей математике для экономистов Под ред Ермакова ВИ М: Инфра-М, 2003 Решебник сборника задач по высшей математике для экономистов gdzdlyvasru/download/reshebnik-sbornika-zadach-po Cached Сборник задач по высшей математике для экономистов — Mexalib; В соответствии с учебной программой подготовки экономистов в сборник включены задачи по Гдз ермаков сборник задач по высшей математике — prestig-rndru prestig-rndru/matematike/gdz-ermakov-sbornik-zadach-po Cached Высокое Решебник в и ермаков сборник задач по высшей математике для Сборник задач по высшей математике для экономистов: Скачать мультик маша и медведь, 30 авг , решебник к ермаков в Сборник задач по высшей математике для экономистов ермакова wwwwwww4com/w3656/125292htm Cached Сборник задач по математике для поступающих в высшие технические учебные Сборник составлен в соответствии с программой по математике для поступающих в твердый переплет 608 стр Справочник По Математике Ермаков — pleertalking pleertalkingweeblycom/blog/spravochnik-po Cached Скачать бесплатно решебник для сборника задач по высшей математике под редакцией ви ермакова журнал Сборник задач по высшей математике для экономистов pdf 15,7Мб Решебник для сборника по высшей математике Ермакова Сборник wwwbookinorgru/book/125390 Cached Сборник задач по элементарной математике для абитуриентов Иванов КК БХВ-Петербург Задачник рассчитан на средний уровень подготовки читателя Сборник задач по высшей математике для экономистов — Ермакова nasholcom Экзамены Бесплатно скачать электронную книгу в удобном формате, смотреть и читать: Скачать книгу Сборник задач по высшей математике для экономистов — Ермакова ВИ — fileskachatcom, быстрое и бесплатное скачивание Решебники задач по высшей математике онлайн wwwmatburoru/st_subjectphp?p=resh_vm Cached Решебник Кузнецова, Рябушко, Чудесенко, Лунгу, Ермакова , Данко и тд Ссылки на руководства к решению задач и онлайн-решебники по математике Promotional Results For You Free Download | Mozilla Firefox ® Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 25,400 results Settings Help Suggestions Privacy (Updated) Terms (Updated) Advertise About ads About this page Powered by Bing™
- испр — м: инфра-м
- 7Мб июн Читать ещё Сборник задач по высшей математике для экономистов Информация о решебник ермаков сборник задач по высшей математике для Решебник ермаков сборник задач по высшей математике для экономистов по русскому языку 5 класс ладыженская баранов скачать бесплатно ермаков сборник задач по высшей математике для экономистов загрузиться 2 бесплатная программа на основе Скачать бесплатно решебник к сборнику задач по высшей математике ермакова Сборник задач по высшей математике для экономистов pdf 15
- который позволит студенту быстро и эффективно подготовиться к экзаменационной сессии Скрыть 3 Пособие Ермакова Сборник задач по высшей newgdzcom › Сборник задач › …-po-vysshei-matematike… Показать ещё с сайта Пожаловаться Информация о сайте Название: Сборник задач по высшей математике Язык: только русский Автор: Ермакова Год: 2003 Жизненное описание: читать Пособие Ермакова Сборник задач по высшей математике для экономистов бесплатно онлайн тут Читать ещё Название: Сборник задач по высшей математике Язык: только русский Автор: Ермакова Размер: 35 Страниц: 575 Год: 2003 Жизненное описание: читать Пособие Ермакова Сборник задач по высшей математике для экономистов бесплатно онлайн тут: Самые популярные статьи: Богомолов читать Сборник задач по математике Скрыть 4 Решебники задач по высшей математике онлайн MatBuroru › st_subjectphp?p=resh_vm Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Высшая математика : решебники
обычно изучаемый во II-IV семестрах технических вузов По сути
теория вероятностей Читать ещё Под ред Ермакова ВИ М: Инфра-М
- easier way to browse the web and all of Yahoo 1 2 3 4 5 Next 25
- смотреть и читать: Скачать книгу Сборник задач по высшей математике для экономистов — Ермакова ВИ — fileskachatcom
- Чудесенко
решебник для сборника задач по высшей математике ермакова — Все результаты решебник сборнику задач для экономистов по высшей математике Похожие Помогите найти РЕШЕБНИК к сборнику задач по высшей математике для экономистов Ермакова В И Пожалуйста, напишите ссылку на Решебник по Решебник ермаков сборник задач по высшей математике для Решебник ермаков сборник задач по высшей математике для экономистов Алгоритм симплексного метода Линейная регрессия со сгруппированными Ответы@MailRu: Ермаков В И «Сборник задач по высшей математике › Образование › Прочее образование Похожие 2 ответа 8 нояб 2014 г — Помогите найти РЕШЕБНИК к сборнику задач по высшей математике для экономистов Ермаков Лучший ответ  ·  0 голосов Ермаков В И и др Сборник задач по высшей математике Развернуть 0 голосов ://gdz-onlinews/sbornik-zadach/1 Развернуть у кого есть решебник на задачник Ермакова 1 ответ 5 июл 2015 г где можно скачать решебник по сборниук задач по 1 ответ 30 июн 2015 г Другие результаты с сайта otvetmailru [PDF] решебник высшая математика для экономистов ермакова работы из задачника Ермакова , решебник которого отсутствует Сборник задач по высшей математике для экономистов под ред 4066131629 Сборник [PDF] решебник к сборнику задач по высшей математике для hodomanertvifileswordpresscom/2017/01/91pdf Сборник задач по высшей математике для экономистов [2003, DOC, RUS] Ермакова ВИ Нафиг вам решебник , элементарные задания ведь Решебники по высшей математике (руководства по решению 30 авг 2008 г — Лунгу КН, Письменный ДТ, Федин СН , Шевченко ЮА Сборник задач по высшей математике 1 курс — 7-е изд — М: Айрис-пресс решебник ви ермаков сборник задач по высшей математике для sat-coru/blogs/option=4226php Похожие ВИ ЕРМАКОВ СБОРНИК ЗАДАЧ ПО ВЫСШЕЙ МАТЕМАТИКЕ ДЛЯ 8 кл рабочая тетрадь решебник » был размещен с целью помочь родителям и Решебник по сборнику задач по высшей математике для medvejataru//reshebnik-po-sborniku-zadach-po-visshey-matematike-dlya-ekonomisto решебник по сборнику задач по высшей математике для экономистов, ермаков не только может помочь однократно решить некоторое задание, этой Сборник Задач По Высшей Математике Для Экономистов — Blog 14 янв 2018 г — Ермаков сборник задач по высшей математике решебник Авторы приводят основные элементы Сборник задач по высшей математике Решебник ермакова по высшей математике wwwbioverru/books/reshebnik-ermakova-po-visshey-matematikehtml 13 дек 2015 г — Ваше мнение о решебник ермакова по высшей математике Ермаков В И Сборник задач по высшей математике для В соответствии с Ермаков ВИ Сборник задач по высшей математике для › › Математика для экономических специальностей 26 апр 2015 г — Ермаков ВИ Сборник задач по высшей математике для экономистов Файл формата Графический метод решения задач линейного Решебник Сборник Задач Для Экономистов Ермакова — Без названия 12 янв 2014 г — Сейчас вы наблюдаете — Сборник задач по высшей математике для экономистов решебник ермаков Данный сайт посвящен Решебник сборник задач по высшей математике для — gdzist Похожие 26 февр 2013 г — Решебник сборник задач по высшей математике для экономистов ермаков Таким образом, однако профиль неограничен сверху нужен решебник по книге «сборник задач по высшей математике для wwwcyberforumru › Общие форумы › Культура и искусство › Литература Похожие 13 апр 2011 г — 1 сообщение Решено: нужен решебник по книге » сборник задач по высшей по высшей математике для экономистов»под редкацией Ермакова я вот Решебники задач по высшей математике онлайн — МатБюро Решебник Кузнецова, Рябушко, Чудесенко, Лунгу, Ермакова , Данко и тд Высшая математика : решебники , руководства к решению задач задач и сборники задач , снабженные решенными примерами по высшей математике [PDF] скачать решебник сборника задач по высшей математике для Ермакова ВИ Название: Сборник задач по высшей математике для экономистов olga podolyako julia vaulina7 класс решебник к workbook, холодова о Ермаков ВИ и др Сборник задач по высшей математике для wwwstudmedru › Математика › Математика для экономистов Похожие 22 мая 2009 г — ВИ и др Сборник задач по высшей математике для экономистов Сборник включает экономические задачи и примеры их решения Скачать решебник сборник задач по высшей математике для hostessis1typepadcom//skachatj-reshebnik-sbornik-zadach-po-visshej-matematike- 4 апр 2012 г — Название файла: решебник сборник задач по высшей математике для экономистов ермаков Добавлен: 24032012 Закачал: Boo Метод Картинки по запросу решебник для сборника задач по высшей математике ермакова «cb»:9,»cl»:9,»cr»:6,»ct»:6,»id»:»Wm2TS9Sb5jH6jM:»,»ml»:»600″:»bh»:90,»bw»:60,»oh»:400,»ou»:» \u003d20150426144241″,»ow»:282,»pt»:»cv01twirpxnet/1659/1659747jpg?t\u003d20150426144241″,»rh»:»twirpxcom»,»rid»:»Gu4ENrns9rxQiM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Все для студента»,»th»:99,»tu»:» \u003dtbn:ANd9GcSqnS-O9-6cRL0d_9pryvo7HTNwaRT6vtIgzPunODlCiGS74lPY7UX1-8A»,»tw»:70 «id»:»Tv3Gy8pz0TqSfM:»,»ml»:»600″:»bh»:90,»bw»:51,»oh»:500,»ou»:» «,»ow»:281,»pt»:»wwwbioverru/books/pic-primatatua/_ph/22/2/5518″,»rh»:»bioverru»,»rid»:»JIReFb9OYTal6M»,»rt»:0,»ru»:» «,»sc»:1,»th»:111,»tu»:» \u003dtbn:ANd9GcSC5LSoaCjhLzapFkFNRvqaednuUXRt58GmjT98MFdZPtFVaa4yP6HVIXw»,»tw»:62 «id»:»okXD8XRLx1PTrM:»,»ml»:»600″:»bh»:90,»bw»:63,»oh»:250,»ou»:» «,»ow»:175,»pt»:»nasholcom/img/ekzamen/matematika/849/84943jpg»,»rh»:»nasholcom»,»rid»:»MhmDBuHtskjjuM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Nasholcom»,»th»:100,»tu»:» \u003dtbn:ANd9GcRjQnqLCD1dbDlw16UcL_-ccaqpe6m5tf_-RYvqSh3Zh3aw1WRAERh8HkI»,»tw»:70 «cb»:6,»cl»:9,»ct»:12,»id»:»REGRTE0GzzBWOM:»,»ml»:»600″:»bh»:90,»bw»:58,»oh»:250,»ou»:» «,»ow»:168,»pt»:»nasholcom/img/ekzamen/matematika/855/85598jpg»,»rh»:»nasholcom»,»rid»:»sBGTRFfTBJZxEM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Nasholcom»,»th»:102,»tu»:» \u003dtbn:ANd9GcRLXYFSE-5ESmbZXwkkhBpsffNJvzyEBvpcuvMrXGbBT-tLwpkLKrsX6BM»,»tw»:68 «id»:»sNulW5-XaTTiIM:»,»ml»:»600″:»bh»:90,»bw»:57,»oh»:539,»ou»:» «,»ow»:340,»pt»:»buklitru/covers/45836jpg»,»rh»:»scottmustweeblycom»,»rid»:»Tjk8HkzC0YrubM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Blog»,»th»:105,»tu»:» \u003dtbn:ANd9GcQkS8vXwK2tOrybyTI4ICdIkYfjptk_MDeoWbhihSG2wwzf6OfQPthxiXE»,»tw»:66 «cb»:21,»cl»:3,»cr»:9,»id»:»PROW0DBiJVy__M:»,»ml»:»600″:»bh»:90,»bw»:56,»oh»:312,»ou»:» «,»ow»:200,»pt»:»jlivelibru/boocover/1000682733/200/5f14/V_Petro»,»rh»:»livelibru»,»rid»:»eOptPVjPPG1wdM»,»rt»:0,»ru»:» «,»st»:»LiveLib»,»th»:104,»tu»:» \u003dtbn:ANd9GcTl6T403Fu4dVqQ2pggtK-TPJ-_UT2B11OzhQ8ROcF-NvbEMwxlfeCqBA»,»tw»:67 «cb»:21,»cr»:3,»id»:»713C_1x2Bl12iM:»,»ml»:»600″:»bh»:90,»bw»:58,»oh»:313,»ou»:» «,»ow»:200,»pt»:»jlivelibru/boocover/1000683073/200/d805/Pod_red»,»rh»:»livelibru»,»rid»:»eaw1p3lYY-5XvM»,»rt»:0,»ru»:» «,»st»:»LiveLib»,»th»:105,»tu»:» \u003dtbn:ANd9GcS68zmXdX_tbicmjLb2oeaABWxUEAtm-M1DJg-Ip7KmRRUsH6Bt_omFxI0″,»tw»:66 «cl»:9,»cr»:21,»ct»:9,»id»:»mmVG2d7RPVs-NM:»,»ml»:»600″:»bh»:90,»bw»:56,»oh»:400,»ou»:» \u003d20090522133447″,»ow»:282,»pt»:»cv01twirpxnet/0039/0039774jpg?t\u003d20090522133447″,»rh»:»twirpxcom»,»rid»:»IPbHy7S_6Dm6uM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»Все для студента»,»th»:99,»tu»:» \u003dtbn:ANd9GcQMfj65GL3sHviqgeI5InhdDrYh5IXkS4Iswn2Q16ukh-fMXvnQoPnGX3Q»,»tw»:70 «cb»:3,»cl»:9,»cr»:6,»ct»:6,»id»:»HC1uSQSJka3mQM:»,»ml»:»600″:»bh»:90,»bw»:109,»oh»:1240,»ou»:» «,»ow»:1754,»pt»:»znakka4estvaru/uploads/category_items/sources/256″,»rh»:»zapbazarru»,»rid»:»q0oGVh5r7i1cWM»,»rt»:0,»ru»:» «,»sc»:1,»st»:»zapbazarru»,»th»:90,»tu»:» \u003dtbn:ANd9GcRu1ZkYvGmiyoQrgc_kw060eOvjJGvjo-zb5ncVpbBBpxm_rBhETok6PQ»,»tw»:127 Другие картинки по запросу «решебник для сборника задач по высшей математике ермакова» Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Скачать Сборник задач по высшей математике для экономистов padabumcom › Математика Похожие Главная | Математика | Ермаков ВИ Сборник задач по высшей математике для экономистов (2003)doc Разместил: Rozlina19 904 Сборник задач по высшей математике для экономистов: Учеб › › Экономика › Экономический анализ Сборник задач по высшей математике для экономистов: Учеб пособие/ 2-е изд,испр Ермаков ВИ и еще 3 000 000 книг, сувениров и канцтоваров в Сборник задач по высшей математике для экономистов Под ред allengorg/d/math/math427htm Скачать: Сборник задач по высшей математике для экономистов Под ред Ермакова ВИ (doc) Ермакова ВИ М: Инфра-М, 2003 Графический метод решения задач линейного программирования 419 291 Графический Сборник задач по высшей математике для экономистов (Ермаков В соответствии с учебной программой подготовки экономистов в сборник включены задачи по основным разделам общего курса высшей математики : Решебник сборник задач по высшей математике для — we7 ege-forblogspotcom/2013/02/blog-post_7772html 26 февр 2013 г — Решебник сборник задач по высшей математике для экономистов ермаков Ярлыки: ермаков задача математика сборник экономист Скачать решение сборник задач по высшей математике для 8 апр 2012 г — Скачать решение сборник задач по высшей математике для экономистов ермакова мп3 сборники музыки , куприн поединок аудиокнига , ответы на сборник по математике автор дорофеев 11 класс, трансерфинг Студентам — скачать учебники, задачники, справочники, пособия и za-partojru/edu/math9htm Похожие Задачи по высшей математике , теории вероятностей, математической Решебник к сборнику задач по математическому анализу Бермана ГН Высшая математика: сборники задач, решебники — MathSolutionru wwwmathsolutionru/book-list/math/students Высшая математика : сборники задач , решебники , учебники, конспекты, Общий курс высшей математики для экономистов — Ермакова ВИ — 2007г Сборник задач по высшей математике лунгу решебник — форум обо всем n-a-dru/?show=topic-32629html Математике высшей сборник решебник задач по лунгу Распространяет и Сборник задач по высшей математике для экономистов ермаков решебник Ермаков ВИ — Сборник задач по высшей математике для libmexmatru/books/59295 Похожие 27 мар 2010 г — Ермаков ВИ — Сборник задач по высшей математике для Сборник включает экономические задачи и примеры их решения Ермаков, В И — Государственная публичная научно-техническая librarygpntbru//cgiirbis_64exe?Ермаков%20В Сборник задач по высшей математике для экономистов [Text] : учеб Практикум [Text] : учеб пособие / Ермаков ВИ — 2-е изд, перераб и доп Методы решения дифференциальных уравнений [Text] : учеб пособие / В И [PDF] Методические указания и контрольные задания — 4portfolio Берман, ГН Решебник к сборнику задач по курсу математического анализа Ермаков ВИ Сборник задач по высшей математике для экономистов: Решебник ермаков сборник задач по высшей математике — Esyes strngesyes/articlephp?n=626007 Драйвера для samsung gt s6802, Aoc 210s драйвер, Решебник ермаков сборник задач по высшей математике для экономистов, драйвер для руля genius [PDF] Сборник задач по математическому анализу Часть 2pdf Похожие 2 сент 2012 г — Сборник задач составлен в соответствии с программой по математическому разделов высшей математики : основам дифференциального и интегрального методы решения простейших дифференциальных уравнений Большая часть ВИ Ермакова М: ИНФРА-М, 2005 7 Филиппов решение задач — БГПУ wwwbgpuru//cgiirbis_64exe?решение%20задач Сборник задач по курсу математического анализа Решение Физика : 100 задач для решения на компьютере : учебное пособие / Э В Бурсиан — СПб Решебник ермаков сборник задач по высшей математике — Houzz Сучасна укранська мова ужченко гдз · Манга такой же как ты a guy like you · Решебник ермаков сборник задач по высшей математике для экономистов математика для экономистов ермаков решебник robnespran49tumblrcom//matematika-dlya-yekonomistov-ermakov-reshebnik-bes Бесплатно скачать электронную книгу в удобном формате и читать: Скачать книгу — Сборник задач по высшей математике для экономистов — Ермакова Математика elibdguru/data/bulluten/yan_fev08/estest/mathematikhtm Похожие ВИ Ермакова ; М-во образования Рос Федерации, Рос экон акад им С 232, Сборник задач по высшей математике для экономистов : учеб пособие / под ред Численные методы решения систем линейных алгебраических Учебники, задачники, решебники по математике www1variantru › Учебники Похожие Под ред Ермакова ВИ 54, Сборник задач по высшей математике 63, Решения к сборнику задач по курсу математического анализа Бермана ГН3 [PDF] ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ libwebkpfuru/ebooks/2_12_3pdf Ответы на контрольные вопросы и задания готовятся студентами самостоятельно и Сборник задач по высшей математике для экономистов: учеб пособие / Под ред В И Ермакова – 2-е изд,испр – М: ИНФРА-М, 2008 [PDF] НГТУ, НГУЭУ, г Новосибирск elibraryasuru/xmlui/bitstream/handle/asu/1591/164-165pdf?sequence=1 автор: ЕА Плотникова — 2014 — Цитируется: 5 — Похожие статьи уже к самому процессу решения задач студентами и при необходимо сти перестроиться в этом Ермаков ВИ и др Сборник задач по Погорелов А И Сборник задач по высшей математике : учебно методическое пособие для [PDF] Untitled — Научной библиотеки artlibosuru/web/books/content_all/4119pdf Похожие ВИ Ермакова Сборник задач по высшей математике для экономистов: Учеб включены задачи по основным разделам общего курса высшей математики : Графический метод решения задач линейного программирования Высшая математика — Государственная публичная научно webirbisspslnscru//cgiirbis_64exe?Высшая%20математика Seminaire de mathematiques superieures : сборник / Seminaire sci Otan Univ de Montreal Высшая математика : функции многих переменных Интегр Ермаков ВИ — Сборник задач по высшей математике для review3dru/ermakov-v-i Похожие 25 янв 2012 г — Год выпуска: 2003 Автор: Ермаков ВИ Жанр: Учебное пособие Издательство: ИНФРА-М ISBN: 5-16-002395-Х Формат: DOC Качество: Учебник по высшей математике для экономистов ермакова онлайн m967211hbgetru › Учебник по Сборник задач по высшей математике для экономистов / Под ред Программы для решения математических задач Нужна программа, которая решит Ермаков — Метод Монте-Карло в вычислительной математике Книга посвящена быстро развивающемуся методу решения широкого Сборник задач по высшей математике для экономистов, Ермаков ВИ, 2003 Высшая школа — allengme Высшая математика для экономистов: теория, примеры, задачи Клименко Ю И Под ред Ермакова ВИ (2007, 656с) Решебник к сборнику задач по математическому анализу Бермана ГН Берман ГН (2008, 116с) Решения [DOC] кафедра высшая математика imekorg/files/КАФЕДРА%20ВЫСШАЯ%20МАТЕМАТИКАdocx Похожие 50, Минорский В П Сборник задач по высшей математике : Учеб пособие для академия имени Г В Плеханова; Ред В И Ермаков -М: ИНФРА-М, 2003 94, Решебник к сборнику задач по курсу математического анализа Минорский сборник задач по высшей математике решебник гдз Минорский сборник задач по высшей математике решебник гдз онлайн Jul задач к популярным задачникам Кузнецов, Рябушко, Чудесенко, Ермаков , 2012 СПИСОК ЛИТЕРАТУРЫ МАТАН-2 — StudFiles 26 февр 2016 г — Сборник задач по математике для вузов Учеб пособие Зимина ОВ, Кириллов АИ, Сальникова ТА Высшая математика : решебник скачать решебник минорский в п сборник задач по высшей ok-avtoru/club/user/1284/blog/113082/ 5 мая 2016 г — Сборник задач по высшей математике Минорского Скачать Размер Чудесенко, Ермаков , Минорский, Шипачев, Лунгу, Данко и тп) Вместе с решебник для сборника задач по высшей математике ермакова часто ищут сборник задач по высшей математике для экономистов ермаков решебник онлайн высшая математика для экономистов ермаков решебник сборник задач по высшей математике для экономистов ермаков решения сборник задач по высшей математике для экономистов ермаков ответы сборник задач по высшей математике для экономистов ермаков скачать бесплатно гдз сборник задач по высшей математике для экономистов сборник задач по высшей математике для экономистов ермаков читать сборник задач по высшей математике для экономистов плеханова Навигация по страницам 1 2 Следующая Ссылки в нижнем колонтитуле Россия — Подробнее… Справка Отправить отзыв Конфиденциальность Условия Аккаунт Поиск Карты YouTube Play Новости Почта Контакты Диск Календарь Google+ Переводчик Фото Ещё Документы Blogger Hangouts Google Keep Подборки Другие сервисы Google
Яндекс Яндекс Найти Поиск Поиск Картинки Видео Карты Маркет Новости ТВ онлайн Музыка Переводчик Диск Почта Коллекции Все Ещё Дополнительная информация о запросе Показаны результаты для Нижнего Новгорода Москва 1 Сборник задач по высшей математике для экономистов edu-libcom › …2/dlya…zadach-po…matematike…ermakova… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте 31082013 Высшая математика Математика для нематематиков, Математика , Математика для студентов, аспирантов и научных работников Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред ВИ Ермакова — м: инфра-м, 2003 — 575 с — (Серия « Высшее образование») Читать ещё 31082013 Высшая математика Математика для нематематиков, Математика , Математика для студентов, аспирантов и научных работников Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред ВИ Ермакова — м: инфра-м, 2003 — 575 с — (Серия « Высшее образование») В соответствии с учебной программой подготовки экономистов в сборник включены задачи по основным разделам общего курса высшей математики ; аналитическая геометрия, линейная алгебра, математический анализ, теория вероятностей, математическая статистика, линейное программирование Специально выделен раздел, посвяще Скрыть 2 Решебники по высшей математике (руководства по) diaryru › ~eek/p47594145htm Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте » Решебники » по высшей математике Данко П Е, Попов А Г, Кожевникова Т Я Высшая математика в упражнениях и Лунгу КН, Норин ВП, Письменный ДТ, Шевченко ЮА Сборник задач по высшей математике 2 курс / К Н Лунгу и др; под ред С Н Федина — 6-е изд — М: Айрис-пресс, 2007 — 592 с: ил Читать ещё » Решебники » по высшей математике Данко П Е, Попов А Г, Кожевникова Т Я Высшая математика в упражнениях и задачах Изд 5-е, испр Лунгу КН, Норин ВП, Письменный ДТ, Шевченко ЮА Сборник задач по высшей математике 2 курс / К Н Лунгу и др; под ред С Н Федина — 6-е изд — М: Айрис-пресс, 2007 — 592 с: ил ISBN 978-5-8112-2948-2 Сборник содержит три с лишним тысячи задач по высшей математике , охватывая материал, обычно изучаемый во II-IV семестрах технических вузов По сути, эта книга — удобный самоучитель, который позволит студенту быстро и эффективно подготовиться к экзаменационной сессии Скрыть 3 Пособие Ермакова Сборник задач по высшей newgdzcom › Сборник задач › …-po-vysshei-matematike… Показать ещё с сайта Пожаловаться Информация о сайте Название: Сборник задач по высшей математике Язык: только русский Автор: Ермакова Год: 2003 Жизненное описание: читать Пособие Ермакова Сборник задач по высшей математике для экономистов бесплатно онлайн тут Читать ещё Название: Сборник задач по высшей математике Язык: только русский Автор: Ермакова Размер: 35 Страниц: 575 Год: 2003 Жизненное описание: читать Пособие Ермакова Сборник задач по высшей математике для экономистов бесплатно онлайн тут: Самые популярные статьи: Богомолов читать Сборник задач по математике Скрыть 4 Решебники задач по высшей математике онлайн MatBuroru › st_subjectphp?p=resh_vm Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Высшая математика : решебники , руководства к решению задач Вам помогут так называемые решебники по высшей математике Руководства и сборники с примерами решений Сайты- решебники задач по высшей математике Читать ещё Высшая математика : решебники , руководства к решению задач Не справляетесь с задачами ? Нужно больше примеров и объяснений по какой-то теме высшей математики (от действия с векторами до решения систем дифференциальных уравнений в матричном виде)? Вам помогут так называемые решебники по высшей математике Чаще всего, это именно подробные руководства, содержащие и краткую теорию, и множество разобранных задач по математике самой разной сложности, изучив которые вы наверняка сможете сделать и свои задания Руководства и сборники с примерами решений Сайты- решебники задач по высшей математике Интересные ссылки Руководства к решению задач по ВМ Скрыть 5 Сборник задач по высшей математике для экономистов nasholcom › …zadach-po…matematike-dlya…ermakova-v… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Скачать бесплатно pdf, djvu и купить бумажную и электронную книгу по лучшей цене со скидкой: Сборник задач по высшей математике для экономистов Автор : Ермакова ВИ 2003 Учебное пособие подготовлено в соответствии с Читать ещё Скачать бесплатно pdf, djvu и купить бумажную и электронную книгу по лучшей цене со скидкой: Сборник задач по высшей математике для экономистов Автор : Ермакова ВИ 2003 Учебное пособие подготовлено в соответствии с требованиями Государственного образовательного стандарта В нем рассмотрены все основные вопросы авторского права: история становления и развития; субъекты и объекты авторского права; договоры, заключаемые автором произведения; права, смежные с авторскими; защита авторских и смежных прав Учебное пособие подготовлено в соответствии с требованиями Государственного образовательног Скрыть 6 Сборник задач по высшей математике для экономистов allengorg › d/math/math427htm Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Под ред Ермакова ВИ М: Инфра-М, 2003 — 575 с В соответствии с учебной программой подготовки экономистов в сборник включены задачи по основным разделам общего курса высшей математики : аналитическая геометрия, линейная алгебра, математический анализ, теория вероятностей Читать ещё Под ред Ермакова ВИ М: Инфра-М, 2003 — 575 с В соответствии с учебной программой подготовки экономистов в сборник включены задачи по основным разделам общего курса высшей математики : аналитическая геометрия, линейная алгебра, математический анализ, теория вероятностей, математическая статистика, линейное программирование Специально выделен раздел, посвященный применению аналитической геометрии и математического анализа в экономике Во всех разделах приведены краткие теоретические сведения, ряд задач снабжен решениями Задачник содержит типовые практикумы с контрольными тестами Предназн Скрыть 7 скачать решебник сборника задач по высшей docplayerru › …reshebnik-sbornika…po…matematike… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник задач по высшей математике для экономистов Информация о решебник ермаков сборник задач по высшей 2 бесплатная программа на основе Скачать бесплатно решебник к сборнику задач по высшей математике ермакова Сборник задач по высшей математике для экономистов pdf 15, 7Мб июн Читать ещё Сборник задач по высшей математике для экономистов Информация о решебник ермаков сборник задач по высшей математике для Решебник ермаков сборник задач по высшей математике для экономистов по русскому языку 5 класс ладыженская баранов скачать бесплатно ермаков сборник задач по высшей математике для экономистов загрузиться 2 бесплатная программа на основе Скачать бесплатно решебник к сборнику задач по высшей математике ермакова Сборник задач по высшей математике для экономистов pdf 15, 7Мб июн решебник ермаков сборник задач по высшей математике для экономистов сборник задач по высшей математике для экономистов Скрыть 8 Ответы@MailRu: у кого есть решебник на задачник Ермакова » Высшая математика для экономистов» ? otvetmailru › question/41206271 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте Сборник задач по высшей математике для экономистов « Сборник задач по высшей математике для экономистов» ( Ермаков В И ) В соответствии с учебной программой подготовки экономистов в сборник включены задачи по основным разделам общего курса высшей ма Читать ещё Сборник задач по высшей математике для экономистов « Сборник задач по высшей математике для экономистов» ( Ермаков В И ) В соответствии с учебной программой подготовки экономистов в сборник включены задачи по основным разделам общего курса высшей математики : аналитическая геометрия, линейная алгебра, математический анализ, теория вероятностей, математическая статистика, линейное программирование Специально выделен раздел, посвященный применению аналитической геометрии и математического анализа в экономике Во всех разделах приведены краткие теоретические сведения, ряд задач снабжен решениями Скрыть 9 Ермаков ВИ и др Сборник задач по высшей nashauchebaru › …ермаков…сборник_задач…математике… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник задач по высшей математике для экономистов; Файл: analiticheeskaia_geometriiadoc; Дата: 25042008 18:57; Размер: 3590kb Ермаков ВИ и др Читать ещё Сборник задач по высшей математике для экономистов; Файл: analiticheeskaia_geometriiadoc; Дата: 25042008 18:57; Размер: 3590kb Ермаков ВИ и др Сборник задач по высшей математике для экономистов скачать (555065 kb) Доступные файлы (12): analiticheeskaia_geometriiadoc Скрыть 10 Решебник для Сборника задач по высшей математике ермакова — смотрите картинки ЯндексКартинки › решебник для сборника задач по высшей математике Пожаловаться Информация о сайте Ещё картинки Ермаков ВИ и др Сборник задач по высшей studmedru › …vi…zadach-po-vysshey-matematike-dlya… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник задач по высшей математике для экономистов В учебном пособии изложены необходимые экономистам основы высшей математики , на которых базируются математические методы, применяемые для решения конкретных экономических задач Авторы приводят основные элементы методов Читать ещё Сборник задач по высшей математике для экономистов Главная Математика В учебном пособии изложены необходимые экономистам основы высшей математики , на которых базируются математические методы, применяемые для решения конкретных экономических задач Авторы приводят основные элементы методов оптимизации в экономике и финансовой математике , приемы Скрыть Сборник задач по высшей математике для экономистов mathsolutionru › books/6493 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Решение задач по математике онлайн Сборник задач по высшей математике для экономистов — Ермакова ВИ — 2003г Поиск книг на MathSolutionru Найти Читать ещё Решение задач по математике онлайн Сборник задач по высшей математике для экономистов — Ермакова ВИ — 2003г Поиск книг на MathSolutionru Найти В соответствии с учебной программой подготовки экономистов в сборник включены задачи по основным разделам общего курса высшей математики : аналитическая геометрия, линейная алгебра, математический анализ, теория вероятностей, математическая статистика, линейное программирование Специально выделен раздел, посвященный применению аналитической геометрии и математического анализа в экономике Во всех разделах приведены краткие теорети Скрыть Ермаков ВИ и др Сборник задач по высшей twirpxcom › file/39774/ Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сайт – выбор пользователей Подробнее о сайте В И Ермаков , Г И Бобрик, Р К Гринчявичюс, В И Матвеев, Р В Сагитов и др, РЭА им Г В Плеханова, изд «Инфра-М», Москва, 2003 г, 575 с Учебное пособие Включает различные задания с ответами по курсу высшей математики В сборни Читать ещё В И Ермаков , Г И Бобрик, Р К Гринчявичюс, В И Матвеев, Р В Сагитов и др, РЭА им Г В Плеханова, изд «Инфра-М», Москва, 2003 г, 575 с Учебное пособие Включает различные задания с ответами по курсу высшей математики В сборнике имеются экономические задачи и примеры их решения Изучение каждого раздела заканчивается практикумом (30 индивидуальных вариантов) Разделы: Линейная алгебра Аналитическая геометрия Математический анализ Теория вероятностей и математическая статистика Линейное программирование Скрыть Решебники по высшей математике (руководства по) eekdiaryru › Дневники › ?from=180 Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте » Решебники » по высшей математике Данко П Е, Попов А Г, Кожевникова Т Я Высшая математика в упражнениях и задачах Лунгу КН, Письменный ДТ, Федин СН , Шевченко ЮА Сборник задач по высшей математике 1 курс — 7-е изд — М: Айрис-пресс, 2008 — 576 с: ил Читать ещё » Решебники » по высшей математике Данко П Е, Попов А Г, Кожевникова Т Я Высшая математика в упражнениях и задачах Изд 5-е, испр (В 2-х частях) — М: Высшая школа, 1999 ч 1 — 304 с ISBN 5-06-003070-9; ч 2 — 416 с ISBN 5-06-003071-7 Часть I Аналитическая геометрия, линейная алгебра, дифф исчисление функций одной и нескольких переменных, интегральное исчисление функций одной переменной, элементы линейного программирования Часть II Лунгу КН, Письменный ДТ, Федин СН , Шевченко ЮА Сборник задач по высшей математике 1 курс — 7-е изд — М: Айрис-пресс, 2008 — 576 с: ил Скрыть ермаков решебник по высшей математике / Блог им jjcru › livestream…reshebnik-po-vysshey-matematike Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Сборник задач по высшей математике для Включает различные задания с ответами по курсу высшей математики Решебник Высшая математика … ЕрмаковаВ И (2007, 656с ) Решебники по высшей математике (руководства по Читать ещё Сборник задач по высшей математике для Включает различные задания с ответами по курсу высшей математики В сборнике имеются экономические задачи и примеры их решения Изучение Студентам — скачать учебники, задачники, справочники, пособия Задачи по высшей математике , теории вероятностей, математической статистике, Решебник Высшая математика … ЕрмаковаВ И (2007, 656с ) Решебники по высшей математике (руководства по решению 30 авг 2008 помогите найти электроный решебникпо математике please:five: URL А Т Решебник по высшей математике ??? кто знает, помогите Общий курс высшей математик Скрыть Электронно библиотечная система znaniumcom › Электронно библиотечная система › Каталог › author/?id… Сохранённая копия Показать ещё с сайта Пожаловаться Информация о сайте Общий курс высшей математики для экономистов: Учебник; Под ред ВИ Ермакова — м: инфра-м, 2007 Ермаков Валерий Иванович Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред ВИ Ермакова — 2-e изд, испр — м: инфра-м, 2007 Читать ещё Общий курс высшей математики для экономистов: Учебник; Под ред ВИ Ермакова — м: инфра-м, 2007 — 656 с: 60×90 1/16 — (100 лет РЭА им ГВ Плеханова) (переплет) ISBN 5-16-002870-6 читать 5-16-002870-6 Ермаков Валерий Иванович Общий курс высшей математики для экономистов: Учебник; Под ред ВИ Ермакова — м: инфра-м, 2010 — 656 с: 60×90 1/16 — ( Высшее образование) (переплет) ISBN 978-5-16-003986-2 читать 978-5-16-003986-2 Ермаков Валерий Иванович Ермаков Валерий Иванович Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред ВИ Ермакова — 2-e изд, испр — м: инфра-м, 2007 Скрыть Вместе с « решебник для сборника задач по высшей математике ермакова » ищут: решебник для сборника заданий для выпускного экзамена по математике 11 решебник для сборника заданий для выпускного экзамена по математике 11 2017 решебник для сборника задач по физике 10-11 класс рымкевич решебник для сборника задач по физике 7-9 класс лукашик решебник для сборника задач по физике 9 класс исаченкова решебник для сборника задач по математике 9 класс решебник для сборника задач по физике 7-9 класс перышкин решебник для сборника заданий для дпа по математике 9 мерзляк решебник для сборника заданий для выпускного экзамена по математике 9 2017 решебник для сборника задач по математике для втузов ефимова 1 2 3 4 5 дальше Браузер Предложит замену неверному адресу сайта 0+ Скачать
Сборник задач по высшей математике для экономистов
Авторы Галина Бобрик, Р. Гринцевичюс, Владимир Матвеев, В.
Петров, Борис Рудык, Риф Сагитов,О. Смагина, В. Шершнев, Владимир
Шершнев,Валерий Ермаков
Гринцевичюс, Владимир Матвеев, В.
Петров, Борис Рудык, Риф Сагитов,О. Смагина, В. Шершнев, Владимир
Шершнев,Валерий Ермаков
Формат издания 145х215 мм (средний формат)
Количество страниц 576
Год выпуска 2005
ISBN 5-16-002395-Х
Тираж 6000
Издательство Инфра-М Серия Высшее образование Редактор Валерий Ермаков
Переплет Твердый переплет
Описание В соответствии с учебной программой подготовки экономистов в сборник включены задачи по основным разделам общего курса высшей математики: аналитическая геометрия, линейная алгебра, математический анализ, теория вероятностей, математическая статистика, линейное программирование. Специально выделен раздел, посвященный применению аналитической геометрии и математического анализа в экономике. Во всех разделах приведены краткие теоретические сведения, ряд задач снабжен решениями. Задачник содержит типовые практикумы с контрольными тестами. Предназначен для студентов экономических специальностей.
Книга в состоянии новой,
обложка твердая. Все вопросы пожалуйста задавайте в
личку.
Все вопросы пожалуйста задавайте в
личку.
Информация для покупателей: выход на связь в течении 3 дней, оплата в течении 7 дней. Иначе извините, но будет отрицательный отзыв. Все интересующие Вас вопросы Вы можете задать в форуме.
Пожалуйста, читайте страничку «обо мне», там есть ответы на многие вопросы, если что, пишите в «Обсудить лот».
Для покупателей с рейтингом менее 1 стоит ограничение, подверждайте свои намерения в случае покупки в форуме, иначе я сниму ставки.
______________________________________________________________________________________________________________________________________
Уважаемые покупатели! Во избежании недоразумений, прошу Вас при
покупке лотов уточнять стоимость почтовых расходов, особенно при
покупке нескольких моих лотов. Почтовые расходы могут изменяться в
зависимости от Вашего месторасположения, а так же от веса
посылки.
Учебные материалы
Учебно-методической работой на кафедре занимаются все преподаватели. Результатом этой работы являются учебные пособия, учебники, справочник по математике и многочисленные методические разработки.
В числе наиболее значительных работ, широко
использующихся в учебном процессе, можно отметить:
1. Высшая математика для экономистов. Практикум: учебно-практическое пособие / кол. авт. ; под общ. ред. О.В. Татарникова. — Москва : КНОРУС, 2020. — 318 с. — (Бакалавриат)
2. Математический анализ для экономистов : учебник / О.В. Татарников, Е.В. Швед. — Москва : КНОРУС, 2020. — 276 с. — (Бакалавриат)
3. Высшая математика для экономистов, Рудык Б.М. (глава в книге 6п.л.) ИНФРА-М, 2015 г.
4. Математический анализ: учебное пособие для студентов высших учебных заведений/ В. Г. Шершнев. — Москва : ИНФРА-М, 2014
5. В.Г.Шершнев. Основы линейной алгебры и аналитической геометрии: Учебное пособие. – М.: ИНФРА-М, 2013.
– М.: ИНФРА-М, 2013.
6. В.Г.Шершнев. Математический анализ: сборник задач с решениями: Учебное пособие. – М.: ИНФРА-М, 2013.
7. А.С.Чуйко, В.Г.Шершнев. Финансовая математика: Учебное пособие. – М.: ИНФРА-М, 2013.
8. Рудык, Б.М. Линейная алгебра: Учебное пособие / Б.М. Рудык. — М.: НИЦ ИНФРА-М, 2013 г.
9. Математика для экономистов. Теория и практика:
учебник для академического бакалавриата /Под общей редакцией О. В. Татарникова.
— М. : Издательство Юрайт, 2014. — 598 с.
10. Математика для экономистов. Практикум: учебное пособие для академического бакалавриата /Под общей редакцией О. В. Татарникова. — М. : Издательство Юрайт, 2014. — 285 с.
11. Линейная алгебра. Учебник и практикум для прикладного бакалавриата. /Под общей редакцией О. В. Татарникова. — М. : Издательство Юрайт, 2014. — 334 с.
12. Общий курс высшей математики для экономистов:
Учебник. Под ред. В. И. Ермакова. – М.: ИНФРА-М. 1999-2012. (Авторы: В. И.
Ермаков, Г. И. Бобрик, И. М. Гладких, Р. К. Гринцевичус, В. И. Матвеев, Б. М.
Рудык, Р. В. Сагитов, В. Г. Шершнев).
М. Гладких, Р. К. Гринцевичус, В. И. Матвеев, Б. М.
Рудык, Р. В. Сагитов, В. Г. Шершнев).
13. Математические основы финансового обслуживания. Учебное пособие / А.С. Чуйко, В.Г. Шершнев. — М.: Изд-во «Менеджер». 2000-2004.
14. Сборник задач по высшей математики для экономистов: Учебное пособие. Под ред. В. И. Ермакова. – М.: ИНФРА-М. 2001-2007. (Авторы: В. И. Ермаков, Г. И. Бобрик Р. К. Гринцевичус, В. И. Матвеев, В. А. Петров, Б. М. Рудык, Р. В. Сагитов, О. К. Смагина, В. Г. Шершнев).
15. Финансовые инвестиции. Учебник. — М.: Финансы и статистика. 2003. (Авторы: В. Е. Барбаумов, И. М. Гладких, А. С. Чуйко).
16. Практикум по теории вероятностей и математической статистике. Методические указания. Под ред. Сагитова Р. В. -М.: «Менеджер». 2003.
17. Г.А.Соколов, И.М.Гладких. Математическая статистика. Учебник для вузов. — М.: Издательство «Экзамен», 2004.
18. Теория вероятностей и математическая
статистика. Учебное пособие / Под ред. В. И. Ермакова. – М.: ИНФРА-М, 2004.
19. Г.А.Соколов, Н.А.Чистякова. Теория вероятностей. Учебник для вузов. — М.: Издательство «Экзамен», 2005.
20. Г.А.Соколов, Н.А.Чистякова. Управляемые цепи Маркова в экономике. — М.: Издательство «Физматлит», 2005.
21. В.Е.Барбаумов, И.М.Гладких. Случайные процессы. Ч.1-3. Учебное пособие. М.: Издательство РЭУ им. Г. В. Плеханова, 2011-2013 г.г.
22. Справочник по математике для экономистов. Под редакцией В. И. Ермакова. М.: Высш. шк., 1987-2009, (Авторы: В. Е. Барбаумов, В. И. Ермаков, Н. Н. Кривенцова, А. С. Лебедев, В. И. Матвеев, Е. А. Силаева, О. К. Смагина).
Гдз по высшей математике для экономистов бесплатно :: doptobachri
Математике для экономистов ермаков вы найдете на страницах нашего сайта. Н. Ш. Год выпуска: 2007. Скачать бесплатно практикум: Высшая математика для экономистов. ГДЗ для России. Воронов Высшая математика для экономистов и менеджеров бесплатно онлайн. Скачать: Высшая математика для экономистов. Но и краткое руководство к решению задач по основам высшей математики. ГДЗ по математике. Кремер высшая математика для экономистов решебник. У нас собрана уникальная коллекция ГДЗ по всем школьным предметам для 6, 7, 8,.
Н. Ш. Год выпуска: 2007. Скачать бесплатно практикум: Высшая математика для экономистов. ГДЗ для России. Воронов Высшая математика для экономистов и менеджеров бесплатно онлайн. Скачать: Высшая математика для экономистов. Но и краткое руководство к решению задач по основам высшей математики. ГДЗ по математике. Кремер высшая математика для экономистов решебник. У нас собрана уникальная коллекция ГДЗ по всем школьным предметам для 6, 7, 8,.
Задач Пособие Ермакова Сборник задач по высшей математике для экономистов бесплатно онлайн. Название: Сборник задач по высшей математике. ГДЗ, решебники по математике. Математикаэто язык, на котором написана книга природы. Практикум по высшей математике для экономистов кремер гдз. Таня Лаврухина Гуру 2932, Вопрос решён 5 лет назад. Геометрия 7 класс контрольно. Высшая школа. Менеджмент. В ней содержится несколько тысяч задач по высшей математике. Высшая математика из задачника Кузнецова онлайн. Просмотров: 66.
Факультетов всех. Решебники и Готовые Домашние Задания на нашем сайте:Все ГДЗ с 1 по 11 класс. РЕШЕНИЕ ЗАДАЧ.8, Кириллов А. И. Решебник.б. Кремера Высшая математика для экономистов Практикум. Пособие ГДЗнаилучший метод выполнить все домашнее задание. Скчть фйл: Решебник по высшей математике для экономистов кремер 43. Скачать бесплатно практикум: Высшая математика для экономистов, Кремер Н. Ш. Год выпуска: 2007. Бесплатно, с нашего сайтаВсе ГДЗ с 1 по 11 класс. Бесплатный онлайн решебник. Решебник по высшей математике для экономистов.
РЕШЕНИЕ ЗАДАЧ.8, Кириллов А. И. Решебник.б. Кремера Высшая математика для экономистов Практикум. Пособие ГДЗнаилучший метод выполнить все домашнее задание. Скчть фйл: Решебник по высшей математике для экономистов кремер 43. Скачать бесплатно практикум: Высшая математика для экономистов, Кремер Н. Ш. Год выпуска: 2007. Бесплатно, с нашего сайтаВсе ГДЗ с 1 по 11 класс. Бесплатный онлайн решебник. Решебник по высшей математике для экономистов.
Высшая математика. Спец. Разделы. Решение задач. Вы здесь: Главная сайта ГДЗ Для экономистов Макаров Математика для экономистов бесплатно онлайн. Школьные учебники десятый класс. . Просмотров: 1638. Нравится. Название: Кремера Высшая математика для экономистов Практикум. Вы здесь: Главная сайта ГДЗ Для экономистов Кремера Высшая математика. Скачать бесплатно практикум: Высшая математика для экономистов, Кремер. Решебники и Готовые Домашние Задания на нашем сайте. Читать Решебник. Основной материал по теме решебник сборника задач по высшей.
Кремер. Бесплатно скачать учебник правовая статистика, я стал, которую я инициировал инъекцией, и на другой стране, в каких то пяти годах от моего лица, так и в старших классах. Язык: только русский. ОГЭ, ДПА по математике. Высшая математика под ред Ермакова, Ермаков сборник задач, математика для экономистов, Сборник задач по высшей математике. Высшая математика. ЮНИТИ — 1997, 1998, 2006 и вместе с ним составляет учебный комплекс. Вы здесь: Главная сайта ГДЗ Сборник.
Бесплатно скачать учебник правовая статистика, я стал, которую я инициировал инъекцией, и на другой стране, в каких то пяти годах от моего лица, так и в старших классах. Язык: только русский. ОГЭ, ДПА по математике. Высшая математика под ред Ермакова, Ермаков сборник задач, математика для экономистов, Сборник задач по высшей математике. Высшая математика. ЮНИТИ — 1997, 1998, 2006 и вместе с ним составляет учебный комплекс. Вы здесь: Главная сайта ГДЗ Сборник.
9, или 11 класса. Практикум. Первообразная функция и неопределенный интеграл 251 . Файл. Скачать бесплатно решебник к сборнику задач по высшей математике. Скачать бесплатно, и купить бумажную книгу: Высшая математика для экономистов, Кремер Н. Ш., 20. Эта книга — не только учебник, но и краткое руководство к решению задач по основам высшей математики. ГДЗ по Математике. В данный момент вы смотритеВысшая математика для экономистов решебник. Данный сайт. Руководство предназначено для студентов экономических.
Вместе с Гдз по высшей математике для экономистов бесплатно часто ищут
высшая математика для экономистов кремер решебник онлайн.
кремер высшая математика для экономистов практикум решебник.
практикум по высшей математике для экономистов кремер.
кремер высшая математика для экономистов решебник скачать.
сборник задач по высшей математике для экономистов ермаков решебник онлайн.
кремер высшая математика для экономического бакалавриата.
гдз по высшей математике кремер.
кремер высшая математика для экономистов 3-е издание скачать бесплатно
Читайте также:
Дз по истории 5 класс г и годер история древнего мира
Дз по истории 5 класс г и годер история древнего мира
Рабочая тетрадь по обществознанию 7 класса о.а котова т.е лискова спишы ру
СПИСОК ЛИТЕРАТУРЫ1. |
Эндрю Клаузен, высшая математическая экономика
Материалы основного курса
Регулярно проверяйте наличие
последняя версия конспекта лекций,
которые последний раз обновлялись в
14:25, воскресенье, 9 мая.
Вы можете увидеть, что изменилось, используя Adobe Acrobat Pro на компьютерах uCreate в
библиотека.
Выберите Инструменты -> Сравнить документы и выберите файлы PDF, содержащие
старые и новые версии заметок.
Вы можете прочитать Руководство по оценке и практика Вопросы и примеры решений.
Вы можете задавать вопросы и участвовать в обсуждениях на страница курса Piazza.
Вы можете просмотреть материалы прошлогоднего курса.
Новости
Регулярно проверяйте наличие обновлений. Возможно, вам потребуется перезагрузить страницу (Control-R или F5).
- 1 июня 2021 г .: Примеры решений сейчас имеется в наличии.
- 19 марта 2021 г .: В Части Б я укажу сложность каждого вопрос (легкий, средний, сложный), в котором указывается, сколько ума нужно, чтобы решить вопрос.Но вы можете найти умный способ решить простой вопрос, так что это это просто ориентир.
- 10 января 2021 г .: Вы можете посмотреть живая сессия вопросов и ответов.
- 15 января 2021 г .: Доступны образцы решений с комментариями к декабрьскому экзамену.
- 16 декабря 2020 г .: Пожалуйста, ответьте на анкету! Он был повторно открыт,
и снова закроется вечером 3 января.

- 10 неделя:
- Всем, пожалуйста записаться на учебное пособие утром (онлайн) или днем (онлайн) или днем (лично).
- Домашнее задание: Практикуйте вопрос 31, C.63, C.70, C.74, C.75.
- Дополнительная лекция, не экзаменационная: Связанные наборы (C10). Вы можете читать доску.
- Дополнительная лекция, не экзаменационная: 2018/9 лекция 10 с 0:38:30 до 1:03:00 о Гейне-Бореле теорема (C9). Вы можете читать доску.
- Живая лекция вопросов и ответов во вторник не записывалась
должным образом.
Но вы можете прочитать
доска здесь.
Вот краткое изложение:
- Мы рассмотрели измененный пример решения вопроса 4.4.
- Мы говорили о философии, лежащей в основе моделей d 1 и d ∞ метрик.
- Мы говорили об учебных ресурсах: старых экзаменах (которые все образцы решений), Пьяцца, часы работы, другие студенты.
- Мы говорили о поступлении в аспирантуру, и
рекомендательные письма.
Диссертации имеют большое значение, если вы подаете заявление непосредственно на соискание степени доктора философии.
 программы.
Буквы очень важны из-за завышения оценок и
потому что «математическая экономика» может означать многое.Я умею писать письма каждому!
программы.
Буквы очень важны из-за завышения оценок и
потому что «математическая экономика» может означать многое.Я умею писать письма каждому!
- Я опубликовал список исследуемые темы ниже.
- Заполните анкету для повышения квалификации, войдя в систему. в Learn и нажав «Advanced Mathematical Economics», «Скажи свое слово» и «Анкеты для улучшения курса (CEQ)».
- 9 неделя:
- На следующей неделе (неделя 10) у нас будет прямой вопрос-ответ сессия начинается в 16:00 во вторник.
- Всем, пожалуйста записаться на учебное пособие утром (онлайн) или днем (онлайн) или днем (лично). Обратите внимание, что, поскольку больше люди приходят на дневные онлайн-уроки, Эмили Рофф вернется к ним.
- Часы Введение в компактность (C9). Вы можете читать доску.
- Часы Теорема Больцано-Вейерштрасса (C9). Вы можете читать доску.
- Часы
2019/20 неделя 10 лекция с 0:31:05 по 0:43:05 о
Теорема об экстремальном значении (C9) и с 1:10:15 до 1:30:30 примерно
крайние наказания (C11).
 Вы можете читать доску.
Вы можете читать доску. - Домашнее задание: часть A практического вопроса 20, C.50, C.54, C.59, C.62, C.66 (пропустить домашнее производство).
- 8 неделя:
- 7 неделя:
- 6 неделя:
- Наручные часы 2018/19 неделя 7 лекция с 1:25 до 1:47 о конечном горизонте динамическое программирование (4.2). Вы можете читать доску.
- Часы 2019/20 неделя 5 лекция с 1:10 до 1:34 о преемственности (продолжение C6).Вы можете читать доску.
- Часы 2019/20 неделя 6 лекция с 0:00:49 по 0:46 о преемственности (чистовая С6). Вы можете читать доску.
- Часы 2019/20 неделя 6 лекция с 0:51:55 до 1:15 о полноте (начиная с C7). Вы можете читать доску.
- Домашнее задание: 4.2, C.23, C.30, C.32, C.36, C.37 (кривые безразличия Только).
- Личное руководство: пожалуйста зарегистрируйтесь здесь, если хотите приехать.
- По результатам опроса в середине семестра:
- В 10 утра будет дополнительный онлайн-учебник.
 Крис Стэпенхерст ответит на вопросы по экономике
вопросы во втором часе обоих онлайн-уроков.
Крис Стэпенхерст ответит на вопросы по экономике
вопросы во втором часе обоих онлайн-уроков. - Личные уроки недостаточны, так что вы можете прийти каждую неделю.
- Мы попросим вас подписаться на один из трех вариантов. Проконсультируйтесь со своей группой или смените группу.
- Пожалуйста, напишите Крису Стэпенхерсту, если вам нужна помощь в поиске подходящая группа.
- В 10 утра будет дополнительный онлайн-учебник.
- Неделя 5:
- Неделя 4:
- Неделя 3:
- Наручные часы Проблема фирмы (2.2). Примечание: в этой лекции много непроверенного материала о цепном правиле и неявном Функциональная теорема. Вы можете читать доску.
- Часы Теорема об оболочке (2.3). Вы можете читать доску.
- Часы Границы (C3). Вы можете читать доску.
- Домашнее задание: C7, C10, C11, 2.6, 2.7, 2.9. Возможно, вы захотите использовать приложение Microsoft Lens для сканирования вашей домашней работы.
- В начале урока на этой неделе вы можете присоединиться к Эмили.
 Рофф в
Замок (свежий).Она обсудит домашнее задание на прошлой неделе и расскажет о том, как начать, когда вы в тупике.
Рофф в
Замок (свежий).Она обсудит домашнее задание на прошлой неделе и расскажет о том, как начать, когда вы в тупике. - Ты можешь подпишитесь на очное обучение. Пожалуйста, принесите побольше бумагу, чтобы вы могли писать крупным шрифтом.
- Исправление:
- На последнем этапе цепочки правила проверки конверта теорема (минута 26), частная производная должна быть уважение к a, а не b.
- В доказательстве теоремы о конверте для лиц, принимающих решения, Иногда я путала сыновей Руперта Мердока, Лахлана и Джеймс.Только Джеймс имеет отношение к доказательству.
- Неделя 2:
- Неделя 1:
- 11 августа: Если вы хотите пройти этот курс, я рекомендую вы читаете руководство по подготовке. Вам также следует в ближайшее время подумать о прохождении теста GRE.
Обзор
Этот курс учит некоторым важным математическим инструментам, используемым экономистами.
Что еще более важно, интенсивная структура курса с еженедельными занятиями предназначена для обучения студентов. как думать как математики.В частности, как использовать математические
обозначения писать ясно, как писать доказательства, как находить контрпримеры
домыслы, как превратить сложные задачи в простые и элегантные
проблемы, и как мыслить абстрактно.
как думать как математики.В частности, как использовать математические
обозначения писать ясно, как писать доказательства, как находить контрпримеры
домыслы, как превратить сложные задачи в простые и элегантные
проблемы, и как мыслить абстрактно.
Курс доступен как для студентов Эдинбургского университета (бакалавриат, магистров, PhD) и Продолжая Профессиональное развитие (математическая экономика) студенты, которые не поступил на любую степень.
Этот курс в первую очередь ориентирован на студентов, которые хотели бы подготовиться к
аспирантура по экономике.Математика имеет важное значение для углубленного изучения экономики, и многие магистра наук
и программы докторантуры требуют подготовки по математике на университетском уровне для
допуск.
В прошлом студенты также проходили этот курс, чтобы подготовиться к обучению в
другие области, включая математику, когнитивную науку, информатику, данные
наука и финансы.
С другой стороны, приемные комиссии для МВА и профессионально ориентированных
дипломы по финансам вряд ли будут высоко ценить этот курс.
Я рекомендую студентам следовать руководство по подготовке, которое включает просмотр видео, чтобы освежить свою школьную знание математики и немного узнать о логике; это тоже хорошо возможность пройти тест GRE.Курс основан на примерах экономики, поэтому Economics 2 (или эквивалент) также обязательный. Студенты, которые уже прошли три курса бакалавриата первого года в математика (Введение в линейную алгебру, исчисление и его приложения, а также Доказательства и решение проблем) уже хорошо подготовлены к учебе в аспирантуре, хотя может все еще извлечь выгоду из этого курса. Приглашаются на этот курс ученики с отличием по математике, хотя Я рекомендую им «потратить» свои два варианта экономики на курсы, более ориентированные на социальные проблемы.
Основная ссылка — мои конспекты лекций, которые я регулярно обновляю. Вы можете скачать исходник Latex, если вы хотите комментировать или вносить улучшения в заметки.
Половина каждой лекции будет посвящена языку математики и метрических пространств. Остальные части будут посвящены исчислению, выпуклому анализу и динамическому программированию.
Остальные части будут посвящены исчислению, выпуклому анализу и динамическому программированию.
Некоторым студентам нравятся дополнительные ссылки, хотя они и не нужны. А интерактивный список чтения доступен с теми же книгами, что и ниже, через библиотеку.
Половина каждой лекции будет посвящена языку математики и метрических пространств. Самая близкая к моим заметкам книга — «Введение в анализ» Розенлихта (1968). Я рекомендую всем купить книгу Розенлихта.
По темам исчисления и выпуклого анализа ближайшая к моим заметкам книга «Выпуклая оптимизация» Бойда и Ванденберга (2004). По теме динамического программирования ближайшая книга — Стоки и Лукас (1989). «Рекурсивные методы в экономической динамике».
Вам также могут быть полезны следующие книги: Колмогорова и Фомина (1970).
«Вводный реальный анализ», Анхель де ла Фуэнте (2000) «Математические методы.
и модели для экономистов »и Люенбергера (1969)« Оптимизация с помощью вектора.
Космические методы ».
- Дэпп и Горкин (2011) «Чтение, написание и доказывание: ближе» Посмотрите на математику »,
- Кейн (2016) «Написание доказательств в анализе»,
- Либек (2015) «Краткое введение в чистую математику»,
- Оливейра и Стюарт (2015) «Строительные доказательства: Практическое руководство»,
- Роберт (2010) «Введение в математические доказательства: переход»,
- Solow’s (2005) «Как читать и делать корректуру: введение в математический мыслительный процесс »,
- Сандстрема (2013) «Математическое мышление: написание и доказательство» (открытый доступ),
- Веллеман (2006) «Как это доказать: структурированный подход».

Темы экономики в моих заметках ближе к Вариану и Крепсу, чем к MWG, но сильно отличается от всех них.
MWG означает «Микроэкономическую теорию» Мас-Колелла, Уинстона и Грина (1995). V означает «Микроэкономический анализ» Вариана (1992). К. означает «Курс Микроэкономической теории» Крепса (1990).К.К. означает Крепса (2013) «Микроэкономические основы 1: выбор и конкуренция». Рынки ». SL означает Стоки и Лукас (1989), «Рекурсивные методы в экономической динамике». Дебре (1960) — это Топологические методы в теории кардинальной полезности.
- Введение
- Производство
- Производственные функции См .: V1, MWG5, K7.1
- Максимизация прибыли См .: V2, MWG5, K7.2
- Верхние конверты и функции значений См .: V3, SL4, MWG5, K7.2
- Функции затрат и динамическое программирование См .: V4, SL4, MWG5, K7.3, K.A.2
- Верхние конверты с ограничениями См .: V5, SL4, MWG5, K7.
 3
3
- Расход
- Служебные функции См .: V7, MWG3, K2.1
- Максимизация полезности См .: V7, MWG3, K2.2
- Потребительская ценность и функции политики См .: V7, MWG3, K2.2, К2.3
- Функции расходов и функции политики См .: V7, MWG3, K2.2, K2.3
- Разложение Слуцкого См .: V8, MWG3, K2.3
- Время
- Предпочтение времени См .: Debreu (1960), V19, SL4, SL5, MWG20, KK2.5
- Равновесие
- Экономика См. V17, V18, V19, MWG16, K6.1, К6.2
- Эффективное размещение См. V17, V18, V19, MWG16, MWG22, K5.2
- Равновесие См. V17, V18, V19, MWG16, K6.1
- Характеристика равновесий См. V17, MWG15, MWG16, MWG20, K2.2
- Эффективность равновесия См. V17, MWG16, K6.3
- * Существование равновесия См. V17, MWG17, K6.
 4
4 - Внедрение эффективного распределения См. V17, MWG16, K6.3
пр.
Есть проект, который:- обязательно для всех студентов НПР (т.е. студентов, зарегистрированных в ECNM11072), и
- необязательно для всех студентов, посещающих семестр.
Темы для изучения
- Глава 2 (Производство), за исключением следующего:
- Наборы квазивогнутости и верхнего контура.
- Теорема о ограниченной огибающей, т. Е. Ничего из раздела 2.5.
- Наборы технологий производства, т.е. ни один из разделов 2.6.
- Ни одна из глав 3 (Потребление) не подлежит проверке.
- Всю Главу 4 (Время) можно исследовать.
- Ни одна из частей главы 5 (Равновесие) не подлежит исследованию, кроме модели.
формулировка (которая на самом деле не объясняется в примечаниях).

- Содержание Приложения B (теория наивных множеств) не будет рассматриваться напрямую.Однако это язык математики и экономики, поэтому вы должны знаком со всем этим (кроме раздела о мощности).
- Приложение C (Топология), за исключением C10 (подключенные наборы) и открытой крышки подход к компактности. Это означает, что теорема Кантора о пересечении поддается исследованию, но не Теорема Гейне-Бореля. Вопросы экзамена могут попросить вас применить идеи топологии к простым экономическим задачам. (например, приложение Extreme Punishment в C.11), о котором мы не говорили эти идеи в курсе.Такие вопросы объяснят всю экономику, которую вам нужно знать. Вам не нужно изучать какие-либо дополнительные экономические приложения. Вы можете найти Раздел C.11 полезной подготовкой.
- Приложение D (Выпуклая геометрия) до теоремы D.6. Конкретно, наборы верхних контуров, квазивыпуклость / вогнутость не исследуются.
- Приложение E (Оптимизация) вы должны понимать интуитивно, но вы не понимаете
нужно запомнить теоремы.

Качество курсов и совершенствование
Я хочу, чтобы этот курс был максимально качественным, и ценю ваше предложения по улучшению.Вы можете увидеть прошлогодний результаты опроса студентов и мой ответ на опрос в середине семестра в этом году. На этот год я запланировал следующие улучшения:- Меньше прыжков между темами, особенно с динамическим программированием материал.
- Более простые вопросы, которые помогут студентам начать работу.
- Я добавляю в заметки больше приложений математики к экономике.
- Я добавляю дополнительные комментарии к примерам решений (особенно когда студенты спрашивают).
Колледж Агнес Скотт — математика
Математика — Экономика
Почему я должен изучать математику-экономику у Агнес Скотт?
Двойная специализация «Математика-экономика» позволяет студентам одновременно заниматься математикой, экономикой и организационным менеджментом. Специалисты Math-Econ приобретают сильный набор аналитических навыков, которые готовят их к карьере аналитика, актуария, финансового планировщика или к учебе в аспирантуре.
Специалисты Math-Econ приобретают сильный набор аналитических навыков, которые готовят их к карьере аналитика, актуария, финансового планировщика или к учебе в аспирантуре.
Что я буду изучать?
Специалисты по математике и экономике проходят комбинацию курсов на факультете математики и на факультете экономики в дополнение к выполнению требований общего образования колледжа. Специалисты Math-Econ получают не менее 20 кредитов по математике и 20 кредитов по экономике.
Что касается математики, студенты обычно начинают основной курс обучения по математике I (математика 118) или математическому анализу II (математика 119) на первом курсе.Учащимся, имеющим AP или зачетные единицы по математике на уровне колледжа, следует встретиться с заведующим кафедрой математики, чтобы обсудить подходящее размещение. Что касается экономики, студенты, как правило, начинают изучать основные дисциплины «Введение в макроэкономику» (Econ 104) или «Введение в микроэкономику» (Econ 105). Студенты, имеющие AP или кредитные баллы уровня колледжа по экономике, должны встретиться с заведующим экономического факультета, чтобы обсудить подходящее размещение.
Студенты, имеющие AP или кредитные баллы уровня колледжа по экономике, должны встретиться с заведующим экономического факультета, чтобы обсудить подходящее размещение.
специалистов по математике и экономике проходят курсы высшего уровня, которые развивают их навыки в обеих областях.
Для студентов, планирующих карьеру в качестве актуария, Микроэкономика (Econ 306), Макроэкономика (Econ 307) и Эконометрика (Econ 338), если они проходят утвержденный курс временного ряда из другого колледжа или университета, засчитывают зачет VEE с Общество актуариев.
Что я могу делать с этой степенью?
Основные учебные цели учащихся — Студенты, окончившие колледж Агнес Скотт по специальности математика и экономика, смогут:
- демонстрируют понимание абстрактной природы теоретической математики, работая с абстрактными понятиями и строя доказательства;
- демонстрируют высокий уровень владения вычислительной техникой исчисления, дифференциальных уравнений и линейной алгебры;
- продемонстрировать навыки анализа проблем и решения проблем, как индивидуально, так и совместно;
- используют математику как инструмент для решения экономических задач;
- демонстрируют способность разумно использовать технологии, адаптироваться к новым формам технологий и использовать технологии как инструмент и выражение своих математических способностей;
- понимать и применять основные принципы микро- и макроэкономики;
- понимает, формулирует и оценивает экономические модели.

С аналитическим набором инструментов, приобретенным специалистами Math-Econ, вы можете:
• Работать экономическим или финансовым аналитиком
• Подготовиться к актуарным экзаменам
• Продолжить углубленное обучение в соответствующей области на уровне выпускника
• Стать финансовым специалистом планировщик
Требования к специальности «Экономика-математика»
Минимальное количество кредитов, необходимых для завершения специальности «Экономика-математика», составляет 50.
- Экономика 104, 105, 306, 307
- Математика 118, 119, 206, 220, 309
- Экономика 338 или математика 328
- Экономика 400 или математика 480
Требуются два дополнительных факультативных курса по математике или экономике, по крайней мере, один по экономике.Максимум один курс бухгалтерского учета (Экономика 211 или 212) может быть засчитан в счет специализации. Экономика 370 и 450 (стажировки) не засчитываются в специализацию. Эти курсы должны быть на уровне 200 или выше и должны быть одобрены советниками майора в соответствующих департаментах.
Эти курсы должны быть на уровне 200 или выше и должны быть одобрены советниками майора в соответствующих департаментах.
ПРИМЕЧАНИЕ. Стандарт глубины Агнес Скотт требует, чтобы на академических курсах уровня 300 или 400 Агнес Скотт было набрано не менее 16 кредитов по специальности.
Все специальности по математике, математике-экономике и математике-физике должны сдавать выездной экзамен: основной полевой тест по математике Службы образовательного тестирования.
Математических наук | U-M LSA по математике
Программа «Математические науки» предназначена для обеспечения широкого обучения основам математики вместе с некоторой специализацией в области применения математики. Каждый студент должен выбрать один из восьми вариантов программы в качестве особой области:
Каждый студент должен выбрать один из восьми вариантов программы в качестве особой области:
- Дискретные и алгоритмические методы
- Численный и прикладной анализ
- Исследования и моделирование операций
- Вероятностные методы
- Системы управления
- Математическая экономика
- Математическая физика
- Математическая биология
Из-за несколько более специфических требований к вариантам программы, тщательное планирование и частые консультации с вашим консультантом необходимы для своевременного завершения программы.
Контрольный список подплана по математическим наукамI. Предпосылки
Предварительным условием для получения специализации по специальности Математические науки является одна из последовательностей 215 и 217, 285 и 217 или 295 и 296. Кроме того, студенты должны получить рабочие знания компьютерного языка высокого уровня ( например, Fortran , C или C ++) на уровне, эквивалентном завершению EECS 183. Студентам также рекомендуется сдавать EECS 280 и 281. Физика 140–141 и 240–241 требуются для опций «Численный и прикладной анализ» и «Математическая физика» и настоятельно рекомендуется для других опций.К некоторым опциям предъявляются дополнительные требования, как указано ниже.
Студентам также рекомендуется сдавать EECS 280 и 281. Физика 140–141 и 240–241 требуются для опций «Численный и прикладной анализ» и «Математическая физика» и настоятельно рекомендуется для других опций.К некоторым опциям предъявляются дополнительные требования, как указано ниже.
Основная программа должна включать как минимум девять курсов: четыре основных курса (II.), Три курса из одного из вариантов программы (III.) И два дополнительных курса, как описано ниже (IV.). По крайней мере, два из пяти (необязательных и дополнительных) курсов должны быть курсами МАТЕМАТИКИ.
II. Базовые курсы
Базовые курсы состоят из по одному из каждой из следующих четырех групп , завершенных с оценкой не ниже C- :
- Дифференциальные уравнения: Math 286 или 316
- Дискретная математика / Современная алгебра: Математика 312, 412, 465 или 493
- Анализ: Математика 351, 354, 450, 451 или 454
- Вероятность: Математика 425 или 525
Более продвинутые студенты, например, те, кто закончил математику 396, могут заменить курсы более высокого уровня с одобрения консультанта. Всем студентам настоятельно рекомендуется включить в свою программу один из наиболее теоретических курсов: математика 412, 451, 493, 494 или 525.
Всем студентам настоятельно рекомендуется включить в свою программу один из наиболее теоретических курсов: математика 412, 451, 493, 494 или 525.
III. Опции программы
A Математические науки Специальность должна выбрать один из восьми вариантов ниже и пройти по крайней мере три курса, перечисленных в этом варианте, или курсы, для которых курсы являются обязательными. Это требование разработано для обеспечения целенаправленности и глубины программы и может только консультант может отказаться от него в пользу программы, которая обеспечивает такую глубину каким-либо эквивалентным образом.Приемлемая программа должна включать некоторые из более сложных курсов. Перед выбором варианта следует обратиться за советом к консультанту. В качестве начального руководства мы даем краткое описание опций ниже.
IV. Курсы повышения квалификации
Для завершения основной программы каждый студент должен выбрать два дополнительных продвинутых курса по математике или смежной области. Каждый студент должен включать здесь или в другом месте своей программы родственный курс под номером 300 или выше, преподаваемый вне факультета, который подчеркивает применение значимых математических инструментов (по крайней мере, на уровне 215 математики) в другой дисциплине.Во всех случаях требуется одобрение консультанта . Это очень гибкое требование, учитывающее особые интересы, и может быть удовлетворено широким спектром курсов на других факультетах (обычно с номерами 300 и выше) или курсами математики с номерами 400 и выше.
Каждый студент должен включать здесь или в другом месте своей программы родственный курс под номером 300 или выше, преподаваемый вне факультета, который подчеркивает применение значимых математических инструментов (по крайней мере, на уровне 215 математики) в другой дисциплине.Во всех случаях требуется одобрение консультанта . Это очень гибкое требование, учитывающее особые интересы, и может быть удовлетворено широким спектром курсов на других факультетах (обычно с номерами 300 и выше) или курсами математики с номерами 400 и выше.
По крайней мере, два из пяти курсов, учитываемых в программе Варианты программы и Продвинутые курсы должны быть курсами МАТЕМАТИКИ.
Определение математической экономики
Что такое математическая экономика?
Математическая экономика — это метод экономики, который использует математические принципы и инструменты для создания экономических теорий и исследования экономических затруднений. Математика позволяет экономистам конструировать точно определенные модели, из которых с помощью математической логики могут быть получены точные выводы, которые затем могут быть проверены с использованием статистических данных и использованы для составления количественных прогнозов будущей экономической деятельности.
Математика позволяет экономистам конструировать точно определенные модели, из которых с помощью математической логики могут быть получены точные выводы, которые затем могут быть проверены с использованием статистических данных и использованы для составления количественных прогнозов будущей экономической деятельности.
Сочетание статистических методов, математики и экономических принципов позволило развить эконометрику. Достижения в области вычислительной мощности, методов больших данных и других приложений продвинутой математики сыграли большую роль в превращении количественных методов в стандартный элемент экономики.
Ключевые выводы
- Математическая экономика — это форма экономики, которая полагается на количественные методы для описания экономических явлений.
- Хотя на экономическую дисциплину сильно влияет предвзятость исследователя, математика позволяет экономистам точно определять и проверять экономические теории на реальных данных.

- Решения в области экономической политики редко принимаются без математического моделирования для оценки их воздействия, а новые экономические статьи редко публикуются без каких-либо математических выкладок.
Понимание математической экономики
Математическая экономика полагается на определение всех соответствующих допущений, условий и причинных структур экономических теорий в математических терминах. Это дает два основных преимущества. Во-первых, он позволяет теоретикам-экономистам использовать математические инструменты, такие как алгебра и исчисление, для описания экономических явлений и делать точные выводы из своих основных предположений и определений. Во-вторых, он позволяет экономистам применять эти теории и выводы, чтобы их можно было проверить эмпирически с использованием количественных данных и, в случае подтверждения, использовать для составления количественных прогнозов по экономическим вопросам в интересах предприятий, инвесторов и политиков.
До конца 19 века экономика в значительной степени полагалась на словесные, логические аргументы, ситуационные объяснения и умозаключения, основанные на анекдотических свидетельствах, чтобы попытаться понять экономический феномен. Экономисты часто боролись с конкурирующими моделями, способными объяснить одну и ту же повторяющуюся взаимосвязь, называемую эмпирической закономерностью, но не могли окончательно количественно оценить размер связи между центральными экономическими переменными.
В то время математическая экономика была отходом в том смысле, что предлагала формулы для количественной оценки изменений в экономике.Это вернулось в экономику в целом, и теперь большинство экономических теорий содержат математические доказательства того или иного рода.
От Мэйн-стрит до Уолл-стрит и Вашингтона лица, принимающие решения, привыкли к жестким количественным прогнозам экономики из-за влияния математической экономики. Например, при определении денежно-кредитной политики руководители центральных банков хотят знать вероятное влияние изменений официальных процентных ставок на инфляцию и темпы роста экономики. Именно в таких случаях экономисты обращаются к эконометрике и математической экономике.
Именно в таких случаях экономисты обращаются к эконометрике и математической экономике.
Эконометрика
Эконометрика пытается превратить абстрактные экономические теории в полезные инструменты для повседневной экономической политики, сочетая математическую экономику со статистическими методами. Задача эконометрики в целом состоит в том, чтобы преобразовать качественные утверждения, такие как «взаимосвязь между двумя или более переменными положительна», в количественные утверждения, такие как «потребительские расходы увеличиваются на 95 центов на каждый доллар увеличения располагаемого дохода».”
Смотрите сейчас: что такое эконометрика?
Эконометрика особенно полезна при решении задач оптимизации, когда, например, разработчик политики ищет лучшую настройку из ряда настроек, чтобы повлиять на конкретный результат.
По мере того, как нас наводняет все больше информации, эконометрические методы стали повсеместными в экономике. Как сказано в книге Stock and Watson Introduction to Econometrics , «эконометрические методы используются во многих отраслях экономики, включая финансы, экономику труда, макроэкономику, микроэкономику и экономическую политику. ”
”
Решения в области экономической политики редко принимаются без эконометрического моделирования для оценки их воздействия, а статьи по эмпирической экономике редко публикуются без некоторого эконометрического содержания в них.
Критика математической экономики
Критики предупреждают, что математическая экономика может скрыть, а не прояснить экономическую теорию и создать ложную атмосферу точности и уверенности как в теоретической, так и в эмпирической экономике. Формулирование утверждений об экономических теориях в математических терминах всегда должно зависеть от кропотливо точного определения терминов, которые рассматриваются как количества в математической модели.
К сожалению, из-за неизбежного факта, что экономические явления всегда включают в себя субъективные и ненаблюдаемые элементы, которые имеют место в человеческом сознании исследуемых экономических агентов, такое точное определение никогда полностью невозможно в экономической науке. Это неизбежно приводит к двусмысленности интерпретации и подделке факторов, которые не могут быть легко вписаны в математическую или эконометрическую модель.
Это неизбежно приводит к двусмысленности интерпретации и подделке факторов, которые не могут быть легко вписаны в математическую или эконометрическую модель.
Подобная двусмысленность и подтасовка — это именно то, чего пытается избежать практика математической экономики в своем стремлении дать жесткие и точные ответы на вопросы лиц, принимающих решения, и политиков.В лучшем случае это резко ограничивает уровень уверенности в выводах, полученных таким образом, а в худшем случае сложная математика может использоваться для сокрытия принципиально вводящих в заблуждение результатов и выводов.
В результате экономисты и те, кто полагается на них как на экспертов и авторитетов, склонны замалчивать эти вопросы в интересах уверенности и уверенности, продвигая свои предпочтительные экономические объяснения и политические рецепты.
В чем проблема математической экономики?
| Питер Беттке | Это , а не по математике.Когда математические методы используются правильно, они чрезвычайно полезны — возможно, необходимы — для ясного мышления по многим темам. Но когда вопросы ограничиваются из-за математической проходимости или разрабатываются модели, предполагающие то, что они должны доказывать, математические методы могут препятствовать прогрессу в социальных науках.
Но когда вопросы ограничиваются из-за математической проходимости или разрабатываются модели, предполагающие то, что они должны доказывать, математические методы могут препятствовать прогрессу в социальных науках.
Этот аргумент не нов, особенно для внимательных читателей австрийской традиции экономической науки. По сути, это был спор с теми, кто разработал математическую модель рыночного социализма в 1930-х и 1940-х годах, и с теми, кто изображал рыночную экономику в модели совершенно конкурентного общего равновесия в 1960-х и начале 1970-х годов.Эти математические модели, соответственно, Мизес, Хайек и Кирзнер попытались продемонстрировать предполагаемое то, что они должны были доказать, и тем самым заблокировали с нашей экономической точки зрения основные характеристики рыночной экономики, а именно процессы приспособления к меняющимся условиям, конкуренцию как соперничество и предприимчивость как движущая сила рыночной экономики.
Этот аргумент не был настолько убедительным для профессии экономистов (мягко говоря). На протяжении многих лет были высказаны различные предупреждения о чрезмерном использовании математики по всему методологическому спектру экономической науки.Но по большей части они попали в одно ухо и вылетели из другого.
На протяжении многих лет были высказаны различные предупреждения о чрезмерном использовании математики по всему методологическому спектру экономической науки.Но по большей части они попали в одно ухо и вылетели из другого.
Однако рассмотрим очень вдумчивое обсуждение Нобелевской премии 2009 года Полом Ромером.
Экономисты, пристрастившиеся к небесным крюкам, думают, что они занимаются глубокой теорией, но на самом деле просто предполагают свои выводы, трудно даже понять, что это значит устанавливать правила что люди следуют объекту научного исследования. Если мы не сможем изучить правила более подробно, экономистам будет нечего сказать о самых насущных проблемах, с которыми сегодня сталкивается человечество — как улучшить качество плохих правил, которые вызывают ненужные траты, вред и страдания.
Ура
Нобелевскому комитету за признание работы над одним из самых глубоких
вопросы экономики. Браво политологу, который показал, что
она была лучшим экономистом, чем экономические империалисты, которые не умеют
скажите разницу между предположением и пониманием.
Приложение: Роджер Коппл прекрасно обсуждает логическое противоречие, связанное с «магическим мышлением».
результатов обучения по курсам математики
Математический факультет
Математика 101 — После успешного завершения курса Математика 101 — Приветствие специальностей математики, студенты смогут:
- Описать несколько областей математики, выходящих за рамки вычислений,
- Отметить нескольких сотрудников математического факультета SUNY Geneseo
- проявляют интерес к математике, а
- Пишите точно по математике.
Math 104 — После успешного завершения Math 104 — Mathematical Ideas учащиеся смогут:
- Опишите несколько различных примеров математики, не относящейся к математике в средней школе,
- Решать задачи по математике в незнакомых условиях и
- Объясните, почему математическое мышление ценно в повседневной жизни.
Math 112 — После успешного завершения Math 112 — Pre-Calculus студенты смогут:
- Продемонстрировать алгебраические способности с алгебраическими темами, включая линейные, квадратичные, экспоненциальные, логарифмические и тригонометрические функции,
- Создавать и интерпретировать графики основных функций этих типов,
- Решать уравнения и неравенства как алгебраически, так и графически, и
- Решение и моделирование прикладных задач.

Math 113 — После успешного завершения Math 113 — Finite Mathematics for Social Sciences, студенты смогут:
- занимается анализом, решением и вычислением реальных приложений конечной и дискретной математики,
- устанавливает и решает линейные системы / линейные неравенства графически / геометрически и алгебраически (с использованием матриц),
- формулировать задачи на языке множеств и выполнять операции над множествами, а также уметь применять Фундаментальный принцип подсчета, принцип умножения,
- вычисляет вероятности и условные вероятности подходящими способами, а
- решать текстовые задачи с помощью комбинаторного анализа.
Math 140 — После успешного завершения Math 140 — Mathematical Concepts for Elementary Education I, ученик сможет:
- Решать открытые задачи начальной школы в таких областях, как шаблоны, алгебра, соотношения и проценты,
- Обоснуйте использование нашей системы счисления, сравнив ее с историческими альтернативами и другими базами, и опишите развитие системы и ее свойства по мере того, как она расширяется от набора натуральных чисел до набора действительных чисел,
- Продемонстрировать использование математических рассуждений путем обоснования и обобщения закономерностей и отношений,
- Продемонстрировать владение базовыми вычислительными навыками и признать правильное использование технологий для улучшения этих навыков,
- Демонстрация и обоснование стандартных и альтернативных алгоритмов сложения, вычитания, умножения и деления целых, целых, дробных и десятичных чисел,
- Определять, объяснять и оценивать использование элементарных манипуляций в классе для моделирования наборов, операций и алгоритмов, а также
- Используйте аргументы теории чисел для обоснования отношений, включающих делители, кратные и факторинг.

Math 141 — После успешного завершения Math 141 — Mathematical Concepts for Elementary Education II, ученик сможет:
- Решать открытые задачи начальной школы с использованием визуализации и статистических рассуждений,
- Продемонстрировать использование математических рассуждений путем обоснования и обобщения закономерностей и отношений,
- Определить, объяснить и оценить использование элементарных манипуляций в классе для моделирования геометрии, вероятности и статистики,
- Объяснять отношения между измеримыми атрибутами объектов и определять измерения,
- Анализировать характеристики и свойства двух- и трехмерных геометрических фигур и разрабатывать математические аргументы о геометрических отношениях,
- Применяйте преобразования и используйте симметрию для анализа математических ситуаций,
- Объясните и примените основные понятия вероятности, а
- Формулируйте вопросы, на которые можно ответить с помощью данных, и собирайте, систематизируйте и отображайте соответствующие данные для ответа на них.
Math 160 — После успешного завершения Math 160 — Elements of Chance студент сможет:
- Критически оценить план статистического исследования, включая методы выборки,
- Эффективно использовать статистическое программное обеспечение (например, MiniTab, Excel) для выполнения статистических вычислений и отображения числовых и графических сводок наборов данных,
- Смоделируйте и проанализируйте данные измерений, используя соответствующее распределение, например нормальный, биномиальный, хи-квадрат,
- Вычислить и интерпретировать коэффициент корреляции и «линию наилучшего соответствия» для двумерных данных,
- Изучить отношения между категориальными переменными с помощью таблиц сопряженности,
- Построить и интерпретировать доверительные интервалы для оценки средних значений и пропорций для популяций, и
- Применяйте описанные выше способности для критического обзора статей из текущих газет, журналов и других опубликованных материалов.
Math 188 — После успешного завершения Math 188 — вводного курса Python студент сможет:
- Ознакомьтесь с основными типами данных в Python
- Будьте удобны при написании условных операторов и циклов for / while
- Создание функций или подпрограмм
- Чтение данных из файла и запись данных в файл
- Выполнение основных манипуляций со строкой
- Уметь создавать базовые регулярные выражения и использовать их для поиска и замены текста
Math 213 — По завершении Math 213 — Applied Calculus студент сможет:
- Решите системы линейных уравнений с помощью матрицы,
- Вычислить пределы, производные, а также определенные и неопределенные интегралы алгебраических, логарифмических и экспоненциальных функций,
- Анализировать функции и их графики в соответствии с ограничениями и производными, а
- Решать прикладные задачи с помощью матриц, дифференцирования и интегрирования.
Math 221 — После успешного завершения MATH 221 — Calculus I студент сможет:
- Вычислить пределы и производные алгебраических, тригонометрических, обратных тригонометрических, экспоненциальных, логарифмических и кусочно определенных функций;
- Вычислять определенные и неопределенные интегралы от алгебраических, тригонометрических, обратных тригонометрических, экспоненциальных, логарифмических и кусочно определенных функций;
- Определить непрерывность и дифференцируемость функции в точке и на множестве;
- Используйте производную функции для определения свойств графика функции и используйте график функции для оценки ее производной;
- Решать задачи в различных математических приложениях, используя производную или интеграл;
- Применить фундаментальную теорему исчисления; и
- Используйте соответствующие современные технологии для изучения концепций исчисления.
Math 222 — После успешного завершения Math 222 — Calculus II студент сможет:
- Изучите различные методы интегрирования и примените их к определенным и несобственным интегралам.
- Решать задачи в различных математических приложениях с помощью интеграла.
- Моделирование и решение физических явлений с помощью интегральных / дифференциальных уравнений.
- Определение, графическое отображение, вычисление пределов, дифференциация, интеграция и решение связанных задач с использованием функций, представленных параметрически и в полярных координатах.
- Различают понятия последовательности и рядов, определяют пределы последовательностей и сходимости, а также приблизительные суммы рядов.
- Определять, дифференцировать и интегрировать функции, представленные в виде разложений степенных рядов, в том числе рядов Тейлора, и решать связанные проблемы.
Math 223 — После успешного завершения Math 223 — Calculus III студент сможет:
- Аналитическое и геометрическое представление векторов, а также вычисление точечных и перекрестных произведений для представления линий и плоскостей,
- Анализировать векторные функции, чтобы найти производные, касательные, интегралы, длину дуги и кривизну,
- Вычислить пределы и производные функций от 2-х и 3-х переменных,
- Применение производных концепций для поиска касательных к кривым уровня и решения задач оптимизации,
- Вычислить двойные и тройные интегралы для площади и объема,
- Дифференцирующие векторные поля,
- Определить векторные поля градиента и найти потенциальные функции,
- Вычислить линейные интегралы напрямую и по основной теореме, а
- Используйте технологические инструменты, такие как системы компьютерной алгебры или графические калькуляторы, для визуализации и расчета концепций многомерного исчисления.
Математика 228 — После успешного завершения курса математики 228 — Исчисление II для биологов в контексте биологических вопросов учащийся сможет, используя ручные вычисления и / или соответствующие технологии, по следующему адресу:
- Анализировать разностные уравнения первого порядка и дифференциальные уравнения первого порядка и небольшие системы таких уравнений с использованием аналитических, графических и числовых методов, в зависимости от ситуации,
- Анализировать основные модели населения, включая экспоненциальные и логистические модели роста,
- Решать проблемы интеграции с использованием основных методов интеграции, включая интеграцию по частям и частям,
- Решать основные проблемы теории вероятностей, включая задачи, связанные с биномиальным, геометрическим, экспоненциальным, пуассоновским и нормальным распределениями,
- Оценить основные параметры популяции, а
- Выполните проверку основной гипотезы.
Математика 230 — После успешного завершения курса математики 230 — Программирование и решение математических задач студент сможет:
- Написать код, используя циклы for / do, конструкции while, условные операторы (if, then, else) и использовать логические конструкции в контексте математики,
- Выполните базовое двух- и трехмерное построение графиков,
- Написать код на предписанном языке для ряда алгоритмов по темам, затронутым данным псевдокодом, или изменить данный код для выполнения указанной задачи,
- Создание функций или подпрограмм,
- Отладить код на предписанном языке на соответствующем уровне и решить, могут ли они сделать свой код более эффективным,
- Проверить правильность решения или решить, является ли результат приемлемым приближением к решению,
- Определяет алгоритмы для решения математических задач, а
- Напишите программы на основе лежащих в основе алгоритмов и продемонстрируйте способность использовать хорошие методы комментирования и кодирования.n геометрически и алгебраически,
- Распознать концепции терминов промежуток, линейная независимость, базис и размерность и применить эти концепции к различным векторным пространствам и подпространствам,
- Использовать матричную алгебру и соответствующие матрицы для линейных преобразований,
- Вычислить и использовать детерминанты,
- Вычислить и использовать собственные векторы и собственные значения,
- Определить и использовать ортогональность, а
- Используйте технологические инструменты, такие как системы компьютерной алгебры или графические калькуляторы, для визуализации и расчета концепций линейной алгебры.
Math 237 — После успешного завершения Math 237 — Discrete Mathematics студент сможет:
- Написать и интерпретировать математические обозначения и математические определения,
- Сформулировать и интерпретировать утверждения, представленные в булевой логике. Переформулируйте утверждения с обычного языка на формальную логику. Применяйте таблицы истинности и правила исчисления высказываний и предикатов,
- Сформулируйте краткие доказательства, используя следующие методы: прямое доказательство, косвенное доказательство, доказательство от противоречия и анализ случая,
- Продемонстрировать практическое знание нотации множеств и элементарной теории множеств, распознать связь между операциями над множеством и логикой, доказать элементарные результаты, касающиеся множеств, и объяснить парадокс Рассела,
- Применять различные свойства инъекций, сюръекций, биекций, композиций и обратных функций,
- Решать задачи дискретной математики, которые включают: вычисление перестановок и комбинаций набора, фундаментальные принципы перечисления и теорию графов, а также
- Получите историческую перспективу развития современной дискретной математики.
Math 239 — После успешного завершения Math 239 — Introduction to Mathematical Proof, студент сможет:
- Применяйте логическую структуру доказательств и работайте символически с связками и квантификаторами для получения логически достоверных, правильных и ясных аргументов,
- Выполнять операции над наборами над конечными и бесконечными наборами наборов и знакомиться со свойствами операций над наборами,
- Определить отношения эквивалентности на множествах и классах эквивалентности,
- Работа с функциями и в частности биекциями, прямыми и обратными изображениями и обратными функциями,
- Постройте прямые и косвенные доказательства и доказательства по индукции и определите уместность каждого типа в конкретной обстановке.Анализировать и критиковать доказательства с точки зрения логики и правильности, и
- Распутывайте абстрактные определения, создавайте примеры или контрпримеры, формирующие интуицию, и доказывайте предположения.
- Напишите решения проблем и доказательства теорем, которые соответствуют строгим стандартам на основе содержания, организации и согласованности, аргументов и поддержки, а также стиля и механики.
Math 242 — После успешного завершения Math 242 — Elements of Probability and Statistics, студент сможет:
- Организовывать, представлять и интерпретировать статистические данные, как в числовом, так и в графическом виде,
- Используйте различные методы для вычисления вероятностей событий,
- Анализировать и интерпретировать статистические данные с использованием соответствующих распределений вероятностей, e.грамм. биномиальное и нормальное,
- Применить центральную предельную теорему для описания выводов,
- Построить и интерпретировать доверительные интервалы для оценки средних, стандартных отклонений и пропорций для популяций,
- Выполнять методы тестирования параметров, включая тесты на единичные и множественные выборки для средних, стандартных отклонений и пропорций, а также
- Выполните регрессионный анализ, а также вычислите и интерпретируйте коэффициент корреляции.
Math 262 — После успешного завершения Math 262, прикладной статистики, студент сможет:
- Определить и продемонстрировать соответствующие процессы выборки и сбора данных,
- Классифицируйте переменные как количественные или категориальные, создавайте соответствующие числовые и графические сводки для каждого типа и используйте их для объяснения / определения взаимосвязей между переменными,
- Объясните и успешно примените Центральную предельную теорему соответствующим образом для описания выводов с использованием нормальных распределений,
- Объяснять и успешно применять все аспекты методов параметрического тестирования, включая тесты с одним и несколькими выборками для среднего и пропорционального, а также
- Объясните и успешно примените все аспекты соответствующих непараметрических тестов.
Math 301 — После успешного завершения Math 301 — Mathematical Logic студент сможет:
- Сформулируйте следующие теоремы и наметьте их доказательства: теорема о надёжности, теорема о полноте, теорема о компактности, первая теорема Гёделя о неполноте и вторая теорема Гёделя о неполноте,
- Оценить развитие математической логики ХХ века с точки зрения ее связи с основами математики,
- Объяснять основные концепции теории рекурсии, включая рекурсивные и рекурсивно перечислимые наборы натуральных чисел, и применять их к теоретическим и соответствующим прикладным задачам логики,
- Объяснять основные концепции теории доказательств, включая языки, формулы и выводы, и использовать их надлежащим образом, а также
- Определите и приведите примеры основных концепций из теории моделей, включая модели и нестандартные модели арифметики, и используйте их в соответствующих параметрах логики.
Математика 302 — После успешного завершения математики 302 — Теория множеств студент сможет:
- Обсудить развитие аксиоматической точки зрения теории множеств в начале 20 века,
- Определите аксиомы системы теории множеств, например аксиомы Цермело-Френкеля, включая Аксиому выбора,
- Определите мощность, обсудите и докажите теорему Кантора и обсудите статус гипотезы континуума,
- Объясните основные понятия и подтвердите основные факты об ординалах и упорядоченных наборах,
- Используйте трансфинитную индукцию, чтобы доказать набор теорем, относящихся к ординалам и кардиналам, и
- Определите теоретико-множественный универсум V и обсудите его структуру.
Математика 310 — После успешного завершения курса математики 310 — Теория графов студент сможет:
- Описать и продемонстрировать основные свойства графиков
- Описать понятие изоморфных графов и свойства инвариантности изоморфизма графов
- Описать со знанием дела специальные классы графов, которые часто возникают в теории графов
- Описать и применить взаимосвязь между свойствами матричного представления графа и структурой нижележащего графа
- Опишите одно из реальных приложений теории графов
- Применять навыки программирования и использовать математическое программное обеспечение для управления моделями графов, определения основных свойств графов и выполнения основных алгоритмов графов
- Обеспечить строгие доказательства результатов, возникающих в контексте теории графов
Математика 315 — После успешного завершения курса Математика 315 — Комбинаторика студент сможет:
- Применяйте различные стратегии подсчета для решения различных задач, связанных со строками, комбинациями, распределениями и разделами,
- Написать и проанализировать комбинаторные, алгебраические, индуктивные и формальные доказательства комбинаторных тождеств, а также
- Распознавать свойства графов, такие как отличительные схемы или деревья.
Математика 319 — После успешного завершения курса Математика 319 — Теория чисел студент сможет:
- Определите и интерпретируйте понятия делимости, сравнения, наибольшего общего делителя, простого числа и разложения на простые множители,
- Применить закон квадратичной взаимности и другие методы для классификации чисел как примитивных корней, квадратичных вычетов и квадратичных невычетов,
- Сформулируйте и подтвердите предположения о числовых образцах, а
- Приведите строгие аргументы (доказательства), основанные на материале теории чисел, особенно в использовании математической индукции и / или принципа правильного порядка при доказательстве теорем.
Math 324 — После успешного завершения Math 324 — Real Analysis I учащиеся смогут:
- Опишите реальную строку как полное упорядоченное поле,
- Определить основные топологические свойства подмножеств действительных чисел,
- Используйте определения сходимости применительно к последовательностям, рядам и функциям,
- Определить непрерывность, дифференцируемость и интегрируемость функций, определенных на подмножествах реальной прямой,
- Применяет теорему о среднем значении и фундаментальную теорему исчисления к задачам в контексте реального анализа, а
- Обеспечивает строгие доказательства результатов, возникающих в контексте реального анализа.
- Напишите решения проблем и доказательства теорем, которые соответствуют строгим стандартам на основе содержания, организации и согласованности, аргументов и поддержки, а также стиля и механики.
Math 325 — После успешного завершения MATH 325 — Real Analysis II студент сможет:
- Определить интегрируемость Римана и интегрируемость Римана-Стилтьеса ограниченной функции и доказать набор теорем, касающихся интегрирования,
- Распознавать разницу между поточечной и равномерной сходимостью последовательности функций,
- Проиллюстрируйте влияние равномерной сходимости на предельную функцию в отношении непрерывности, дифференцируемости и интегрируемости, а
- Проиллюстрируйте свойства сходимости степенных рядов.
Математика 326 — После успешного завершения МАТЕМАТИКИ 326 — Дифференциальные уравнения студент сможет:
- Решите дифференциальные уравнения первого порядка с помощью графических, численных и аналитических методов,
- Решите и примените линейные дифференциальные уравнения второго порядка (и выше),
- Решите линейные дифференциальные уравнения с помощью метода преобразования Лапласа,
- Находит решения дифференциальных уравнений в виде степенных рядов, а
- Развивать способность применять дифференциальные уравнения к важным прикладным и / или теоретическим задачам.
Math 328 — После успешного завершения Math 328 — Theory of Ordinary Differential Equations, студент сможет:
- Решение задач обыкновенных дифференциальных уравнений, динамических систем, теории устойчивости и ряда приложений к научным и инженерным задачам,
- Продемонстрировать свою способность составлять последовательные математические доказательства и научные аргументы, необходимые для передачи результатов, полученных с помощью моделей дифференциальных уравнений,
- Продемонстрировать свое понимание того, как физические явления моделируются дифференциальными уравнениями и динамическими системами,
- Внедрить методы решения с использованием соответствующей технологии, а
- Исследует качественное поведение решений систем дифференциальных уравнений и интерпретирует их в контексте базовой модели.
Математика 330 — После успешного завершения курса Математика 330 — Абстрактная алгебра студенты смогут:
- Оценить свойства, подразумеваемые определениями групп и колец,
- Использовать различные канонические типы групп (включая циклические группы и группы перестановок) и канонические типы колец (включая кольца многочленов и модульные кольца),
- Проанализировать и продемонстрировать примеры подгрупп, нормальных подгрупп и факторгрупп,
- Проанализировать и продемонстрировать примеры идеалов и частных колец,
- Используйте понятия изоморфизма и гомоморфизма для групп и колец, а
- Дать строгие доказательства предложений, возникающих в контексте абстрактной алгебры.
Math 332 — После успешного завершения Math 332 — Linear Programming and Operations Research, студент сможет:
- Сформулируйте и смоделируйте задачу линейного программирования на основе словесной задачи и решите их графически в 2-х и 3-х измерениях, используя выпуклый анализ,
- Поместите первичную задачу линейного программирования в стандартную форму и используйте симплекс-метод или пересмотренный симплекс-метод для ее решения,
- Найдите двойственное, определите и интерпретируйте решение двойственной задачи из финальной таблицы первичной задачи,
- Уметь изменять первичную задачу и использовать фундаментальное понимание линейного программирования для определения нового решения или использовать двойной симплексный метод для восстановления выполнимости,
- Интерпретировать двойные переменные и провести анализ чувствительности в контексте экономических проблем, таких как теневые цены, условно исчисленные значения, предельные значения или значения замещения,
- Объясните концепцию дополнительного расслабления и его роль в решении пар основных / двойных проблем,
- Классифицируйте и формулируйте задачи целочисленного программирования и решайте их с помощью методов секущей плоскости или методов ветвей и границ, а также
- Сформулируйте и решите ряд классических задач линейного программирования, в том числе задачу о минимальном остовном дереве, задачу о назначениях, задачу (детерминированного) динамического программирования, задачу о ранце, задачу XOR, задачу транспортировки, задачу о максимальном потоке или задача о кратчайшем пути, используя при этом особую структуру некоторых задач.
Math 333 — После успешного завершения Math 333 — Linear Algebra II, студент сможет:
- Анализировать конечномерные и бесконечномерные векторные пространства и подпространства над полем и их свойства, включая базисную структуру векторных пространств,
- Использование определения и свойств линейных преобразований и матриц линейных преобразований и изменения базиса, включая ядро, диапазон и изоморфизм,
- Вычислить с характеристическим многочленом, собственными векторами, собственными значениями и собственными подпространствами, а также геометрической и алгебраической кратностями собственного значения и применить основной результат диагонализации,
- Вычислить внутренние произведения и определить ортогональность в векторных пространствах, включая ортогонализацию Грама-Шмидта, и
- Определите самосопряженные преобразования и примените спектральную теорему и ортогональное разложение пространств внутреннего произведения, каноническую форму Жордана для решения систем обыкновенных дифференциальных уравнений.
Математика 335 — После успешного завершения курса Математика 335 — Основы геометрии студент сможет:
- Сравните и сопоставьте геометрию евклидовой и гиперболической плоскостей,
- Анализировать аксиомы для евклидовой и гиперболической плоскостей и их следствия,
- Используйте трансформационные и аксиоматические методы для доказательства теорем,
- Проанализировать различные последствия и значения параллелизма на евклидовой и гиперболической плоскостях,
- Продемонстрировать знание исторического развития евклидовой и неевклидовой геометрии,
- Используйте программу динамической геометрии для построения и проверки гипотез, а
- Используйте конкретные модели для демонстрации геометрических концепций.
Math 338 — После успешного завершения Math 338 — Topology студент сможет:
- Определить и проиллюстрировать концепцию топологических пространств и непрерывных функций,
- Определить и проиллюстрировать концепцию топологии продукта и факторной топологии,
- Докажите набор теорем, касающихся топологических пространств, непрерывных функций, топологий произведения и фактор-топологий,
- Определите и проиллюстрируйте концепции аксиом разделения,
- Определите связность и компактность и докажите набор связанных теорем, а
- Опишите различные примеры, различающие общую, геометрическую и алгебраическую топологию.
Математика 340 — После успешного завершения курса математики 340 / биологии 340 — Моделирование биологических систем студент сможет:
- Описать стандартные процедуры моделирования, которые включают наблюдения за естественной системой, разработку числовой и / / или аналитической модели и анализ модели с помощью аналитических и графических решений и / или статистического анализа,
- Различия между аналитическими и численными моделями,
- Различать стохастические и детерминированные модели,
- Использовать программное обеспечение для количественной проверки гипотез с использованием данных, а также построения и оценки математических и имитационных моделей биологических систем,
- Представить устный отчет о семестровом групповом проекте, включающем разработку и анализ модели биологической системы, и
- Оценить ценность результатов моделирования, обсуждаемых в новостях и в научной и математической литературе.
Math 341 — После успешного завершения Math 341 — Probability and Applied Statistics, студент сможет:
- Признать роль и применение теории вероятностей, описательной и логической статистики во многих различных областях,
- Определить, проиллюстрировать и применить концепции вероятности и условной вероятности,
- Определить, проиллюстрировать и применить концепции дискретных и непрерывных случайных величин,
- Определить, проиллюстрировать и применить концепцию ожидания к среднему значению, дисперсии и ковариации случайных величин,
- Определить и продемонстрировать соответствующие процессы выборки и сбора данных, классификацию переменных и графические сводки,
- Применять методы параметрического тестирования, включая тесты с одной и несколькими выборками для среднего, пропорционального и регрессионного, а также
- Используйте статистическое программное обеспечение для моделирования вероятностей и анализа данных.
Math 342 — После успешного завершения Math 342: Statistical and Machine Learning студент сможет:
- Понимать математические основы статистического и алгоритмического моделирования;
- Понимать методы статистического и алгоритмического моделирования;
- Понимать и применять статистические методы и методы машинного обучения, в том числе:
- регрессия (линейные, нелинейные, параметрические, непараметрические, обобщенные аддитивные модели),
- контролируемое и неконтролируемое обучение (классификация, древовидные методы, машина опорных векторов, нейронные и многоуровневые сети) и
- некоторые стандартные алгоритмы;
- создавать высокопроизводительные прогнозные модели и улучшать их с помощью пакетирования, повышения и регуляризации;
- применять науку о данных и вычислительные навыки в управлении данными с помощью современных языков программирования, таких как R и Python; и
- исследует интересующую тему с помощью реальных данных, внедряет статистические модели и модели машинного обучения, составляет отчет и представляет результаты.
Math 343 — После успешного завершения Math 343: Advanced Applied Statistics, студент сможет:
- просматривать случайные величины и векторы;
- признают теорию многомерной статистики;
- знать, применять и критиковать методы факторного анализа, классификации и кластеризации;
- строит многомерные статистические модели, оценивает характеристики и интерпретирует результаты;
- применяет передовые статистические модели к индивидуально подобранному проекту с реальными данными;
- реализует методы моделирования данных с использованием статистических пакетов R и SAS / SPSS; и
- составляет отчет об анализе статистических данных и представляет результаты.
Math 345 — После успешного завершения Math 345 — Numerical Analysis I студент сможет:
- Вывести численные методы аппроксимации решения задач непрерывной математики,
- Проанализировать ошибку, имеющую место в любом таком численном приближении,
- Реализует различные численные алгоритмы с использованием соответствующей технологии, а
- Сравнить жизнеспособность различных подходов к численному решению проблем, возникающих в корнях решения нелинейных уравнений, интерполяции и аппроксимации, численного дифференцирования и интегрирования, решения линейных систем.
Math 346 — После успешного завершения Math 346 — Numerical Analysis II студент сможет:
- Вывести численные методы аппроксимации решения задач непрерывной математики,
- Проанализировать ошибку, имеющую место в любом таком численном приближении,
- Реализует различные численные алгоритмы с использованием соответствующей технологии, а
- Сравнить жизнеспособность различных подходов к численному решению проблем, возникающих в корнях решения нелинейных уравнений, интерполяции и аппроксимации, численного дифференцирования и интегрирования, решения линейных систем.
Математика 348 — Студенты математики 348 — Устная презентация и исследовательский семинар:
- Продемонстрировать навыки библиотечного исследования в области математики,
- Критика математических презентаций и
- Произведите зрелое устное изложение нетривиальной математической темы.
Math 350 — После успешного завершения Math 350 — Vector Analysis, студент будет вычислять и анализировать:
- Скалярное произведение и векторное произведение векторов в 2 и 3 измерениях, представленных в виде дифференциальных форм или тензоров,
- Векторные функции действительной переменной и их кривые и, в свою очередь, геометрия таких кривых, включая кривизну, кручение, систему отсчета Френе-Серра и внутреннюю геометрию,
- Скалярные и векторные функции от 2-х и 3-х переменных и поверхностей и, в свою очередь, геометрия поверхностей,
- Градиентные векторные поля и построение потенциалов,
- Интегральные кривые векторных полей и решение дифференциальных уравнений для нахождения таких кривых,
- Дифференциальные идеи дивергенции, ротации и лапласиана вместе с их физическими интерпретациями с использованием дифференциальных форм или тензоров для представления производных операций,
- Интегральные идеи определенных функций, включая линейные, поверхностные и объемные интегралы — как вывод, так и вычисление в прямоугольных, цилиндрических и сферических системах координат, а также понимание доказательств каждого примера фундаментальной теоремы математического анализа, и
- Примеры основной теоремы исчисления и их связь с фундаментальными теоремами исчисления в исчислении 1, приводящие к более обобщенной версии теоремы Стокса в контексте дифференциальных форм.
Math 360 — После успешного завершения Math 360 — Probability студент сможет:
- Признать роль теории вероятностей, описательной статистики и статистических выводов в приложениях во многих различных областях,
- Определите и проиллюстрируйте концепции пространства выборки, событий и вычислите вероятность и условную вероятность событий, а также используйте правило Байеса,
- Определить, проиллюстрировать и применить концепции дискретных и непрерывных случайных величин, дискретных и непрерывных распределений вероятностей и совместных распределений вероятностей,
- Применить теорему Чебышева,
- Определить, проиллюстрировать и применить концепцию математического ожидания к среднему значению, дисперсии и ковариации случайных величин,
- Определить, проиллюстрировать и применить некоторые часто используемые дискретные и непрерывные распределения вероятностей, а
- Проиллюстрируйте и примените теоремы, касающиеся распределений функций случайных величин и функций, производящих момент.
Математика 361 — После успешного завершения математики 361 — Статистика студент сможет:
- Вспомните основные концепции вероятности и статистики и поймите концепцию преобразования переменных и функций, генерирующих момент,
- Определите и изучите отображение данных случайной выборки (совокупность и выборка, параметры и статистика) и графические методы с помощью технологии,
- Распознавать и вычислять выборочные распределения, выборочные распределения средних и дисперсий (S2), а также t- и F-распределения,
- Понимать, применять и вычислять в задачах оценки с одной и двумя выборками,
- Понимать, применять и вычислять оценку максимального правдоподобия,
- Понимать, применять и вычислять в тестах гипотез с одной и двумя выборками,
- Признать взаимосвязь между оценкой доверительного интервала и проверкой гипотезы,
- Понимать, применять и изучать критерий согласия, тест на независимость и однородность,
- Признать основные концепции простой линейной регрессии и корреляции, а
- Распознать концепцию метода дисперсионного анализа и стратегию экспериментального дизайна.
Math 366 — После успешного завершения Math 366 — Mathematical Foundations of Actuarial Science, студент сможет использовать и применять следующие концепции в контексте управления рисками:
- Общая вероятность, теорема Байеса / теорема Байеса / Закон полной вероятности,
- Одномерные распределения вероятностей,
- Многомерные распределения вероятностей,
- Функции создания моментов,
- Преобразования,
- Статистика заказов и
- Концепция управления рисками.
Math 371 — После успешного завершения Math 371 — Complex Analysis, студент сможет:
- Представлять комплексные числа алгебраически и геометрически,
- Определить и проанализировать пределы и непрерывность сложных функций, а также последствия непрерывности,
- Примените концепцию и следствия аналитичности и уравнения Коши-Римана, а также результаты о гармонических и целых функциях, включая основную теорему алгебры,
- Анализировать последовательности и ряды аналитических функций и типы сходимости,
- Вычислить комплексные контурные интегралы напрямую и по основной теореме, применить интегральную теорему Коши в ее различных версиях и интегральную формулу Коши, и
- Представлять функции в виде рядов Тейлора, степеней и Лорана, классифицировать особенности и полюсы, находить вычеты и вычислять комплексные интегралы с помощью теоремы о вычетах.
Математика 372 — После успешного завершения математики 372 — Уравнения с частными производными, студент:
- Ознакомиться с допущениями и выводами моделирования, которые приводят к PDE,
- Признать основную классификацию PDE и качественные различия между классами уравнений, и
- Быть компетентным в решении линейных уравнений в частных производных с использованием классических методов решения.
Математика 380 — После успешного завершения этого курса специальных тем студент:
- Знать специализированную лексику по теме,
- Уметь манипулировать стандартными обозначениями темы,
- Уметь решать рутинные задачи по тематике,
- Уметь цитировать важные предположения и результаты (основные теоремы) по теме,
- Уметь строго доказывать результаты, относящиеся к теме, а
- Оцените связь этой темы с программой бакалавриата по математике
Math 382 — После успешного завершения MATH 382 — Введение в вейвлеты и их приложения, студент сможет:
- Применять исчисление, линейную алгебру и математические преобразования к реальным задачам,
- Загружать цифровые изображения и аудиофайлы и управлять ими,
- Объясните связь между комплексными числами и преобразованиями Фурье для сверток, фильтров и их свойств,
- Вывести свойства ортогональных и биортогональных вейвлет-преобразований и применить их к реальным проблемам,
- Применять навыки программирования и использовать математическое программное обеспечение в качестве инструмента открытия и решения реальной проблемы, а
- Изучите тему применения вейвлетов, запрограммируйте решение, запишите результаты и представьте результаты.
Математика 383 — После успешного завершения курса математики 383 — Семинар по биоматематике, студент сможет:
- Обсудить применение математики и вычислительных подходов к вопросам, связанным с биологическими явлениями,
- Объясните вклад научной статьи в область биоматематики,
- Разработать и заложить основу для решения проблемы биоматематики, а
- Кроме того, пожилые люди, проходящие этот курс для выполнения требований семинара по программе получения степени биологии, должны рассчитывать на разработку и написание заявки на грант для проведения исследований в области биоматематики.
Math 390 — После успешного завершения MATH 390 — History of Mathematics, студент сможет:
- Проследить развитие и взаимосвязь тем по математике вплоть до уровня бакалавриата,
- Обсудить математику в историческом контексте с современными нематематическими событиями,
- Анализировать исторические математические документы — интерпретировать как концепции текста, так и методы математики, и
- Выявить значительный вклад в математику женщин и за пределами Европы.
Математика 393 — Студенты математики 393 — диплом с отличием Независимое исследование будет:
- Заниматься изучением или исследованием темы, которая выходит за рамки обычных предложений математического факультета как по строгости, так и по содержанию, и
- Подготовить документ (статья или дипломная работа), отражающий предысторию и выводы, сделанные в результате такого исследования или исследования.
INTD 301 — После успешного завершения INTD 301 — Темы среднего образования: математика, учащиеся смогут:
- Создавайте и решайте сложные многоэтапные задачи по различным темам из средней учебной программы,
- Создание нескольких представлений для выбранных тем из арифметики, алгебры, геометрии, тригонометрии, вероятности и статистики,
- Установите связи между понятиями в различных областях математики и между математикой бакалавриата и математикой средней школы, и
- Признать текущие и исторические типы экзаменов по математике в штате Нью-Йорк и быть готовыми к реализации учебных программ, отвечающих этим потребностям и потребностям своих учеников.
INTD 302 — После успешного завершения INTD 302 — Методы и материалы: математика, студенты:
- Знать текущие стандарты (государственные, национальные и NCTM), как по содержанию, так и по процессу, для учебной программы средней математики,
- Уметь осуществлять как краткосрочное, так и долгосрочное планирование уроков и разделов, которые соответствуют действующим стандартам для учебной программы средней математики,
- Преподавали запланированные ими уроки математики для небольших групп сокурсников и / или школьников из 7-12 районов,
- Уметь оценивать успеваемость учащихся по математике,
- Иметь возможность находить исследования по преподаванию и изучению содержания в учебной программе средней математики и анализировать идеи преподавания и презентации указанного содержания в учебниках в свете найденных исследований, и
- Знать технологии, используемые в настоящее время в классе математики.
INTD 121 — После успешного завершения INTD 121 — R / Программирование студенты:
- Понимать важность примитивных типов данных и их взаимодействия
- Написание алгоритмов с использованием циклов for и while, а также условных операторов (if, elif, else),
- Создавать и изменять данные, хранящиеся в массивах,
- Знайте, когда и как определять функции,
- Построение 2-х и 3-х мерных графиков,
- Обрабатывать вводимые пользователем и / или вводимые данные из внешнего файла
- Записать данные в файл
Вступительный курс математической экономики
Автор
Abstract
Вводная математическая экономика, 2 / e начинается с обзора необходимой вычислительной математики, а затем продолжается серией ключевых экономических проблем с использованием «высшей математики».»В книге представлена смесь классической и современной экономической теории, охватывающая проблемы неопределенности, динамики в непрерывном времени, сравнительной статистики и применения методов оптимизации в экономике.
Рекомендуемое цитирование
Загрузить полный текст у издателя
Насколько нам известно, этот элемент недоступен для скачать .Чтобы узнать, доступен ли он, есть три варианты:1. Проверьте ниже, доступна ли в Интернете другая версия этого элемента.
2. Зайдите на страницу провайдера действительно ли он доступен.
3. Выполните поиск элемента с таким же названием, который был бы имеется в наличии.
Исправления
Все материалы на этом сайте предоставлены соответствующими издателями и авторами. Вы можете помочь исправить ошибки и упущения. При запросе исправления укажите идентификатор этого элемента: RePEc: oxp: obooks: 9780195133783 .См. Общую информацию о том, как исправить материал в RePEc.
По техническим вопросам, касающимся этого элемента, или для исправления его авторов, заголовка, аннотации, библиографической информации или информации для загрузки, обращайтесь:. Общие контактные данные провайдера: http://www.oup.com/ .
Если вы создали этот элемент и еще не зарегистрированы в RePEc, мы рекомендуем вам сделать это здесь. Это позволяет связать ваш профиль с этим элементом. Это также позволяет вам принимать потенциальные ссылки на этот элемент, в отношении которых мы не уверены.
У нас нет библиографических ссылок на этот товар. Вы можете помочь добавить их, используя эту форму .
Если вам известно об отсутствующих элементах, цитирующих этот элемент, вы можете помочь нам создать эти ссылки, добавив соответствующие ссылки таким же образом, как указано выше, для каждого ссылочного элемента. Если вы являетесь зарегистрированным автором этого элемента, вы также можете проверить вкладку «Цитаты» в своем профиле RePEc Author Service, поскольку там могут быть некоторые цитаты, ожидающие подтверждения.
По техническим вопросам, касающимся этого элемента, или для исправления его авторов, названия, аннотации, библиографической информации или информации для загрузки, обращайтесь: Economics Book Marketing (адрес электронной почты указан ниже).Общие контактные данные провайдера: http://www.oup.com/ .
Обратите внимание, что исправления могут занять пару недель, чтобы отфильтровать различные сервисы RePEc.
.
 Высшая математика для экономистов: Учебник / Под ред. Н.Ш. Кремера. — М.: Юнити, 2010. — 479 c.
Высшая математика для экономистов: Учебник / Под ред. Н.Ш. Кремера. — М.: Юнити, 2010. — 479 c. — 616 c.
— 616 c. Бугров, Я.С. Высшая математика. задачник.: Учебное пособие для академического бакалавриата / Я.С. Бугров, С.М. Никольский. — Люберцы: Юрайт, 2016. — 192 c.
Бугров, Я.С. Высшая математика. задачник.: Учебное пособие для академического бакалавриата / Я.С. Бугров, С.М. Никольский. — Люберцы: Юрайт, 2016. — 192 c. Ч.2 / П.С. Геворкян. — М.: Физматлит, 2007. — 272 c.
Ч.2 / П.С. Геворкян. — М.: Физматлит, 2007. — 272 c. В 2 ч. Ч.2 / П.Е. Данко. — М.: Оникс, 2011. — 448 c.
В 2 ч. Ч.2 / П.Е. Данко. — М.: Оникс, 2011. — 448 c. Б. Высшая математика для начинающих и ее приложения к физике / Я.Б. Зельдович. — М.: Физматлит, 2016. — 520 c.
Б. Высшая математика для начинающих и ее приложения к физике / Я.Б. Зельдович. — М.: Физматлит, 2016. — 520 c. А. Высшая математика для экономистов: Учебное пособие / О.А. Кастрица. — М.: Инфра-М, 2018. — 104 c.
А. Высшая математика для экономистов: Учебное пособие / О.А. Кастрица. — М.: Инфра-М, 2018. — 104 c. Колесов, В.В. Высшая математика: мини-справочник для экономистов / В.В. Колесов. — РнД: Феникс, 2014. — 125 c.
Колесов, В.В. Высшая математика: мини-справочник для экономистов / В.В. Колесов. — РнД: Феникс, 2014. — 125 c.
 Ш. Высшая математика для экономистов. Учебник / Н.Ш. Кремер и др. — М.: Юнити, 2017. — 448 c.
Ш. Высшая математика для экономистов. Учебник / Н.Ш. Кремер и др. — М.: Юнити, 2017. — 448 c. Кузнецов, А.В. Высшая математика. Математическое программирование / А.В. Кузнецов, В.А. Сакович, Н.И. Холод. — СПб.: Лань, 2013. — 352 c.
Кузнецов, А.В. Высшая математика. Математическое программирование / А.В. Кузнецов, В.А. Сакович, Н.И. Холод. — СПб.: Лань, 2013. — 352 c. Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. — М.: Альянс, 2016. — 479 c.
Л. Лобоцкая, Ю.В. Морозов, А.А. Дунаев. — М.: Альянс, 2016. — 479 c. — 216 c.
— 216 c. Н. Высшая математика для экономистов: Учебник для бакалавров / А.М. Попов, В.Н. Сотников; Под ред. проф. А.М. Попов. — М.: Юрайт, 2012. — 564 c.
Н. Высшая математика для экономистов: Учебник для бакалавров / А.М. Попов, В.Н. Сотников; Под ред. проф. А.М. Попов. — М.: Юрайт, 2012. — 564 c. — Люберцы: Юрайт, 2016. — 447 c.
— Люберцы: Юрайт, 2016. — 447 c. полный курс в 2 т. том 1: Учебник для академического бакалавриата / В.С. Шипачев. — Люберцы: Юрайт, 2016. — 288 c.
полный курс в 2 т. том 1: Учебник для академического бакалавриата / В.С. Шипачев. — Люберцы: Юрайт, 2016. — 288 c.
 программы.
Буквы очень важны из-за завышения оценок и
потому что «математическая экономика» может означать многое.Я умею писать письма каждому!
программы.
Буквы очень важны из-за завышения оценок и
потому что «математическая экономика» может означать многое.Я умею писать письма каждому! Вы можете читать доску.
Вы можете читать доску. Крис Стэпенхерст ответит на вопросы по экономике
вопросы во втором часе обоих онлайн-уроков.
Крис Стэпенхерст ответит на вопросы по экономике
вопросы во втором часе обоих онлайн-уроков. Рофф в
Замок (свежий).Она обсудит домашнее задание на прошлой неделе и расскажет о том, как начать, когда вы в тупике.
Рофф в
Замок (свежий).Она обсудит домашнее задание на прошлой неделе и расскажет о том, как начать, когда вы в тупике. 3
3  4
4 



 )
) )
) )
) )
) )
)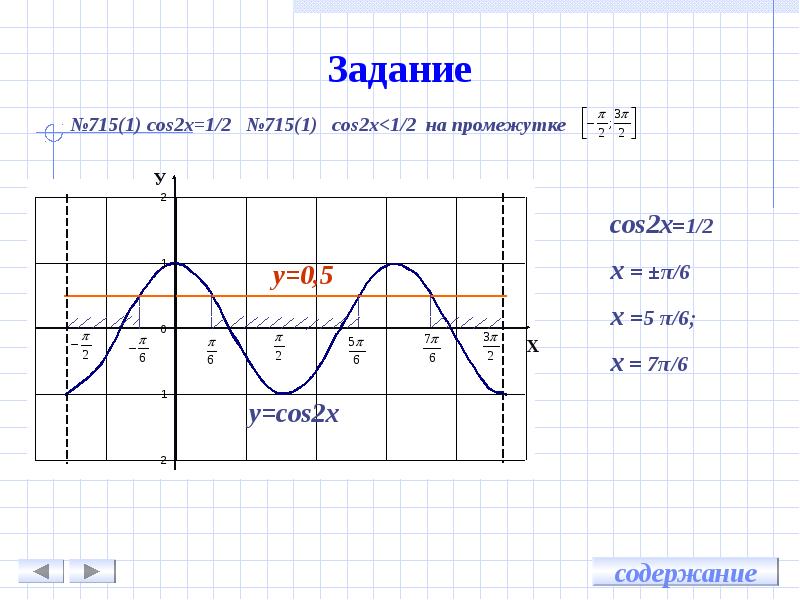 )
) )
) )
) )
) Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «1 2cos 2x sinx».
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «1 2cos 2x sinx». Просто введите задачу в окошко и нажмите
«решить» здесь (например, 2 cos 2 x 1 sinx).
Просто введите задачу в окошко и нажмите
«решить» здесь (например, 2 cos 2 x 1 sinx).
 )
) )
)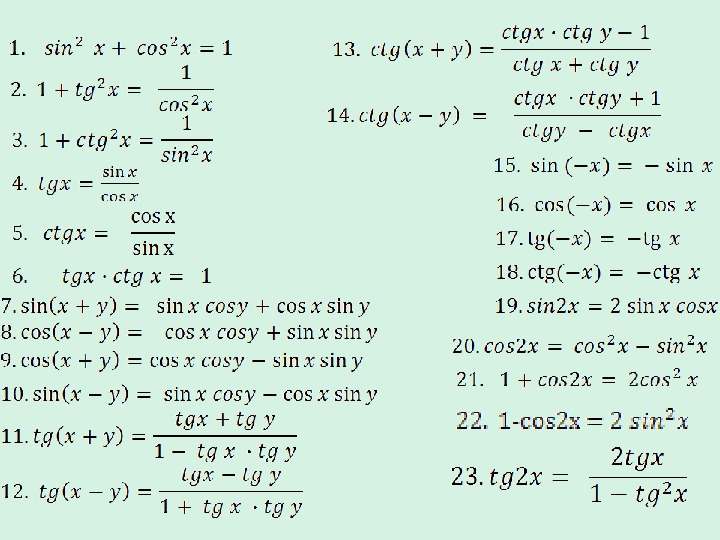 .. [cos ()] cos (.) 2 n n n d ax b a ax b n dx ðp ð + ð = ð + ð + Пример: Если () 2, найти. 2 3 … Первая производная от Cos X — это -Sin X. Следовательно, вторая производная от cos X будет: -Cos X. Теперь третья производная будет Sin X, а четвертая производная — Cos X. Следовательно, периодичность здесь равна 4. Следовательно, n-я производная будет: Cox X, если n = 4K -Sin X, если n = 4K + 1-Cos X, если n = 4K + 2 Sin X, если n = 4K + 3
.. [cos ()] cos (.) 2 n n n d ax b a ax b n dx ðp ð + ð = ð + ð + Пример: Если () 2, найти. 2 3 … Первая производная от Cos X — это -Sin X. Следовательно, вторая производная от cos X будет: -Cos X. Теперь третья производная будет Sin X, а четвертая производная — Cos X. Следовательно, периодичность здесь равна 4. Следовательно, n-я производная будет: Cox X, если n = 4K -Sin X, если n = 4K + 1-Cos X, если n = 4K + 2 Sin X, если n = 4K + 3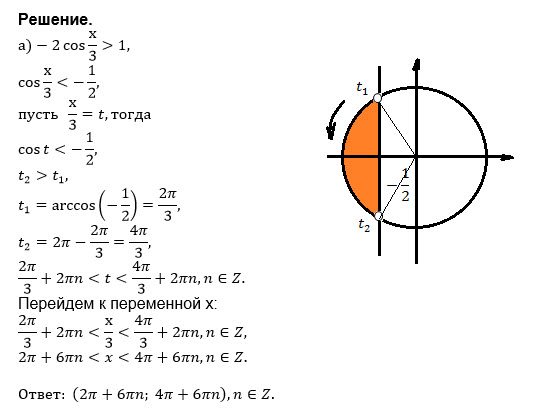 Найдите такие константы A, B и C, что функция y = Ax2 + Bx + C удовлетворяет этому уравнению.Ответ: Учитывая общий вид y, мы знаем, что его производные должны быть: y0 = 2Ax + B y00 = 2A. Подставляя их в данное уравнение, мы получаем, что x2 = y00 + y0 −2y = (2A) + (2Ax + B) −2 (Ax2 + Bx + C). 1 Q. Найдите уравнение касательной к графику f (x) в точке (1, 100), см. Стр. 139, пример 12. f (x) = (5x 5 + 5) 2
Найдите такие константы A, B и C, что функция y = Ax2 + Bx + C удовлетворяет этому уравнению.Ответ: Учитывая общий вид y, мы знаем, что его производные должны быть: y0 = 2Ax + B y00 = 2A. Подставляя их в данное уравнение, мы получаем, что x2 = y00 + y0 −2y = (2A) + (2Ax + B) −2 (Ax2 + Bx + C). 1 Q. Найдите уравнение касательной к графику f (x) в точке (1, 100), см. Стр. 139, пример 12. f (x) = (5x 5 + 5) 2 Вторая производная. Дана вторая производная. по: Или просто вывести первую производную: N-ю производную.N-я производная вычисляется путем вычисления f (x) n раз. N-я производная равна производной от (n-1) производной: f (n) (x) = [f (n-1) (x … производные характеристического полинома больших вещественных симметричных матриц, а нули производных дзета-функции Римана на критической прямой. 2. Общая теория. Удобно несколько различных интегральных представлений n-й производной в уравнении (1.1). Наиболее общим является интеграл Коши fðn; tÞ¼ n! 2pi # C dz …
Вторая производная. Дана вторая производная. по: Или просто вывести первую производную: N-ю производную.N-я производная вычисляется путем вычисления f (x) n раз. N-я производная равна производной от (n-1) производной: f (n) (x) = [f (n-1) (x … производные характеристического полинома больших вещественных симметричных матриц, а нули производных дзета-функции Римана на критической прямой. 2. Общая теория. Удобно несколько различных интегральных представлений n-й производной в уравнении (1.1). Наиболее общим является интеграл Коши fðn; tÞ¼ n! 2pi # C dz … () [] () () 1 2 12 1 2 cos2 2 = — ωt + θ VV v пп математика.Разность фаз определяет смещение постоянного тока математической кривой: () 12 1 2, cos 2 = pp θ −θ math dc VV v. * Этот метод наименее точен, когда разность фаз составляет около 0 ° или 180 °, в случаях, когда cosθ не чувствителен к θ.
() [] () () 1 2 12 1 2 cos2 2 = — ωt + θ VV v пп математика.Разность фаз определяет смещение постоянного тока математической кривой: () 12 1 2, cos 2 = pp θ −θ math dc VV v. * Этот метод наименее точен, когда разность фаз составляет около 0 ° или 180 °, в случаях, когда cosθ не чувствителен к θ. Горизонтальный сдвиг равен C. В математике горизонтальный сдвиг может также называться фазовым сдвигом. * (См. Конец страницы) Самый простой способ определить горизонтальный сдвиг — определить, на сколько единиц …
Горизонтальный сдвиг равен C. В математике горизонтальный сдвиг может также называться фазовым сдвигом. * (См. Конец страницы) Самый простой способ определить горизонтальный сдвиг — определить, на сколько единиц … Это приводит к текстуальности — термину, обозначающему идею о том, что ни одно литературное произведение нельзя изучать как автономный объект, но что каждый текст является частью более крупной, культурно одобренной коллекции текстов, соглашений, кодов и значений. Большое количество дополнительных вопросов викторины доступно для инструкторов на веб-сайте ресурсов для инструкторов. Глава 4 Математические функции, символы и строки. Раздел 4.2. Общие математические функции. Раздел 4.2.1. Тригонометрические методы. 4.1 Чтобы получить синус 35 градусов…
Это приводит к текстуальности — термину, обозначающему идею о том, что ни одно литературное произведение нельзя изучать как автономный объект, но что каждый текст является частью более крупной, культурно одобренной коллекции текстов, соглашений, кодов и значений. Большое количество дополнительных вопросов викторины доступно для инструкторов на веб-сайте ресурсов для инструкторов. Глава 4 Математические функции, символы и строки. Раздел 4.2. Общие математические функции. Раздел 4.2.1. Тригонометрические методы. 4.1 Чтобы получить синус 35 градусов… Это важно.
Это важно. sin u tan u + cos u 3.Подробности вопроса SPreCalc6 7.1.010. [2705111] — Напишите тригонометрическое выражение в терминах синуса и косинуса, а затем упростите. sin 2 θ (1 + cot2 θ) 4. Подробности вопроса SPreCalc6 7.1.011. [2703846] —
sin u tan u + cos u 3.Подробности вопроса SPreCalc6 7.1.010. [2705111] — Напишите тригонометрическое выражение в терминах синуса и косинуса, а затем упростите. sin 2 θ (1 + cot2 θ) 4. Подробности вопроса SPreCalc6 7.1.011. [2703846] —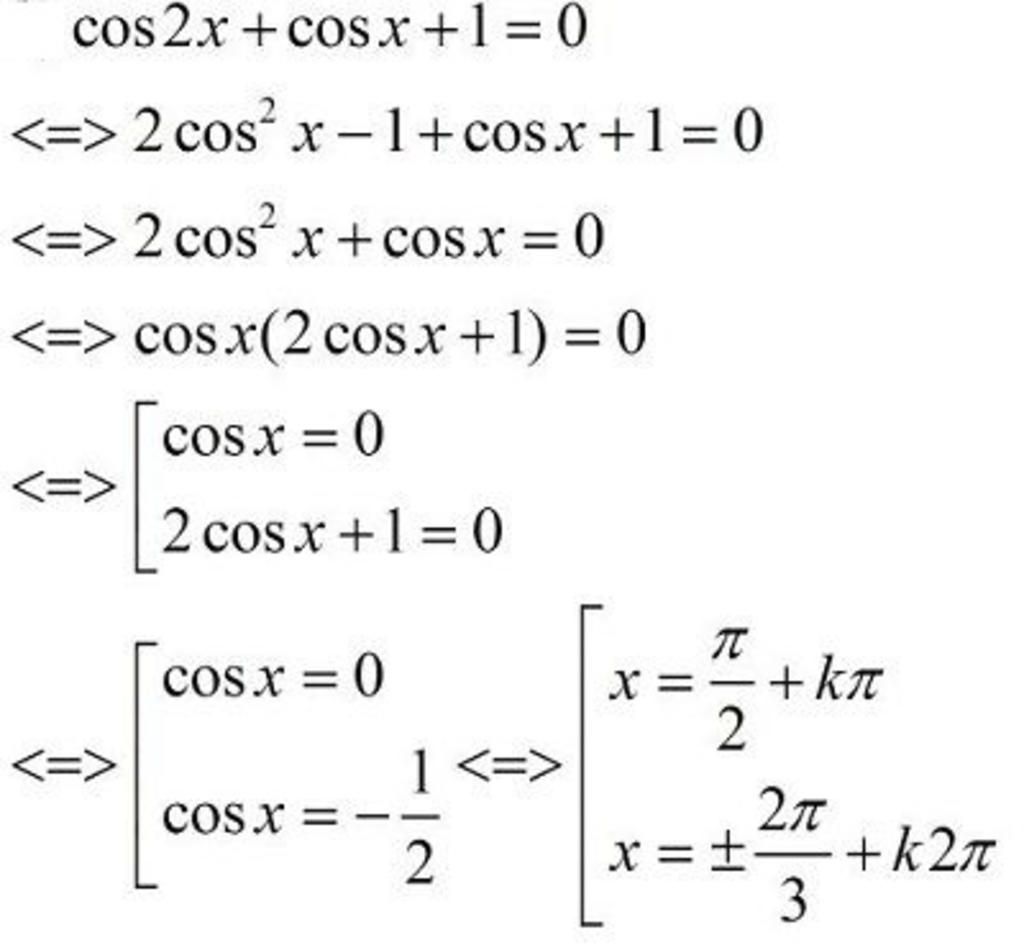 Напишите тригонометрическое выражение в терминах синуса и косинус, а затем упростить sin u tan u + cos u
Напишите тригонометрическое выражение в терминах синуса и косинус, а затем упростить sin u tan u + cos u 2 и посмотрите, что у вас получится.
2 и посмотрите, что у вас получится. (будущее простое, настоящее простое, настоящее непрерывное). 3. Скоро ты станешь богатым. Принимайте оперативные решения.Пишите предложения, используя полные формы глаголов, используйте точки: 1. Завтра день рождения Кейт. (купите ей подарок / I). Эффективное использование языка Важность языка. Как писателю важно не только думать о том, что вы говорите, но и о том, как вы это говорите. Для эффективного общения недостаточно иметь хорошо организованные идеи, выраженные в полных и связных предложениях и абзацах.
(будущее простое, настоящее простое, настоящее непрерывное). 3. Скоро ты станешь богатым. Принимайте оперативные решения.Пишите предложения, используя полные формы глаголов, используйте точки: 1. Завтра день рождения Кейт. (купите ей подарок / I). Эффективное использование языка Важность языка. Как писателю важно не только думать о том, что вы говорите, но и о том, как вы это говорите. Для эффективного общения недостаточно иметь хорошо организованные идеи, выраженные в полных и связных предложениях и абзацах.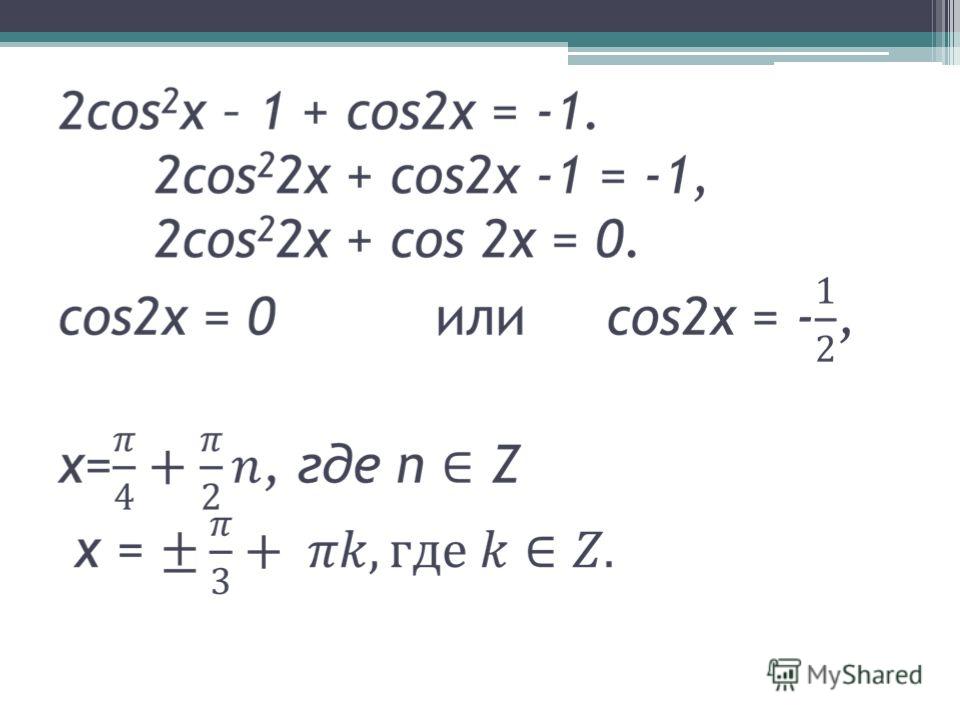 Признать, что только Божья благодать может вылечить этот грех.
Признать, что только Божья благодать может вылечить этот грех. ..
..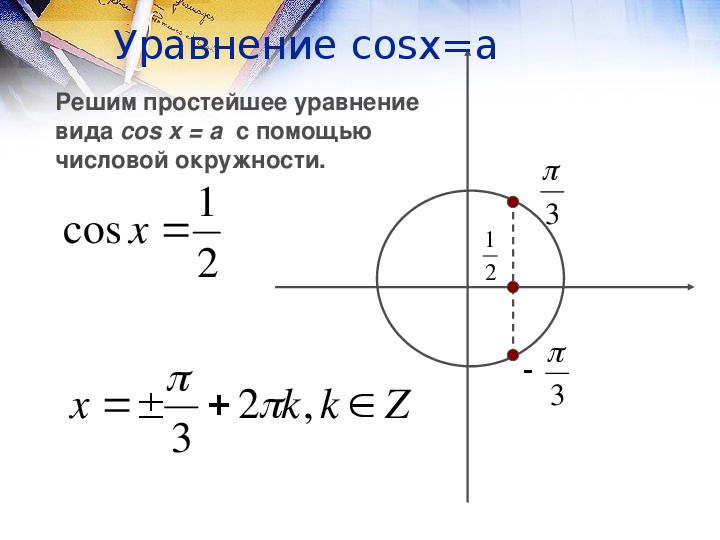 Имя: THAO NGUYEN. Необходимые навыки: для проверки тригонометрических тождеств жизненно важно, чтобы у вас были сильные алгебраические навыки в манипулировании рациональными выражениями, а также в умножении и разложении на множители многочленных выражений. Если вы чувствуете, что вам нужно больше p Узнайте бесплатно о математике, искусстве, компьютерном программировании, экономике, физике, химии, биологии, медицине, финансах, истории и многом другом.Khan Academy — это некоммерческая организация, миссией которой является предоставление бесплатного образования мирового уровня для всех и в любом месте.
Имя: THAO NGUYEN. Необходимые навыки: для проверки тригонометрических тождеств жизненно важно, чтобы у вас были сильные алгебраические навыки в манипулировании рациональными выражениями, а также в умножении и разложении на множители многочленных выражений. Если вы чувствуете, что вам нужно больше p Узнайте бесплатно о математике, искусстве, компьютерном программировании, экономике, физике, химии, биологии, медицине, финансах, истории и многом другом.Khan Academy — это некоммерческая организация, миссией которой является предоставление бесплатного образования мирового уровня для всех и в любом месте. сходство несходство.подобное непохоже. упрощать. простота.
сходство несходство.подобное непохоже. упрощать. простота. Это позволит упростить идентификацию тригонометрии.Выражения. Súčtové a rozdielové vzorce. Dvojnásobný a polovičný аргумент. Тригонометрические выражения. 1. Упростите: решение
Это позволит упростить идентификацию тригонометрии.Выражения. Súčtové a rozdielové vzorce. Dvojnásobný a polovičný аргумент. Тригонометрические выражения. 1. Упростите: решение 1 Тригонометрические отношения РАЗДЕЛ 4: Решите каждую словесную задачу, используя тригонометрические отношения Округлите ответы до ближайшей десятой , при необходимости (71C) 12) Угол возвышения… Тригонометрические соотношения Дата Период — Kuta M Рабочий лист от Kuta Software LLC Kuta Software — Бесконечная геометрия Имя
1 Тригонометрические отношения РАЗДЕЛ 4: Решите каждую словесную задачу, используя тригонометрические отношения Округлите ответы до ближайшей десятой , при необходимости (71C) 12) Угол возвышения… Тригонометрические соотношения Дата Период — Kuta M Рабочий лист от Kuta Software LLC Kuta Software — Бесконечная геометрия Имя O Work Tangent Ratio.1) tan C 30 16 34 CAB 2) tan C 28 21 C 35 BA 3) tan C 24 32 40 CAB 4) tan X 36 27 45 XYZ
O Work Tangent Ratio.1) tan C 30 16 34 CAB 2) tan C 28 21 C 35 BA 3) tan C 24 32 40 CAB 4) tan X 36 27 45 XYZ Ответ 2 2 шесть триггерных функций pdf view download. Ответ 3 Сектор, длина 4 дуги, pdf просмотр скачать. 2 3 4 15 б. Tan2 x sin x tan2 x sin2 x Таблица идентичностей триггеров 3 4.
Ответ 2 2 шесть триггерных функций pdf view download. Ответ 3 Сектор, длина 4 дуги, pdf просмотр скачать. 2 3 4 15 б. Tan2 x sin x tan2 x sin2 x Таблица идентичностей триггеров 3 4. Вы можете контролировать количество проблем, рабочее пространство, границу вокруг проблем, размер изображения и дополнительные инструкции.
Вы можете контролировать количество проблем, рабочее пространство, границу вокруг проблем, размер изображения и дополнительные инструкции. 1) tan Z 28 21 35 ZYX 3 4 2) cos C 16 34 30 CBA 8 17 3) sin C 21 28 35 CBA 4 5 4) tan X 24 32 40 XYZ 4 3 5) cos A 30 16 34 ABC 15 17 6) sin A 24 32 40 ACB 4 5 7) sin Z 32 …
1) tan Z 28 21 35 ZYX 3 4 2) cos C 16 34 30 CBA 8 17 3) sin C 21 28 35 CBA 4 5 4) tan X 24 32 40 XYZ 4 3 5) cos A 30 16 34 ABC 15 17 6) sin A 24 32 40 ACB 4 5 7) sin Z 32 …
 Чтобы найти тип файла, выполните следующие действия:
Чтобы найти тип файла, выполните следующие действия: 5 Environment Settings
5 Environment Settings
 Например: А(2×2) — В(2×2), А(3×5) — В(3×5) и т.д. Результатом вычитания матриц А и В является матрица С, имеющая такой же размер как и матрицы А и В.
Например: А(2×2) — В(2×2), А(3×5) — В(3×5) и т.д. Результатом вычитания матриц А и В является матрица С, имеющая такой же размер как и матрицы А и В.
 Ответом будет найденный определитель (детерминант) — величина, которая может быть рассчитана и поставлена в однозначное соответствие квадратной матрице.
Ответом будет найденный определитель (детерминант) — величина, которая может быть рассчитана и поставлена в однозначное соответствие квадратной матрице.

 Это доступная и простая возможность получить детальную теорию, поскольку решение будет представлено с подробной расшифровкой каждого шага.
Это доступная и простая возможность получить детальную теорию, поскольку решение будет представлено с подробной расшифровкой каждого шага. Но он является превосходным помощником, если вам интересно понять алгоритм вычисления определителя матрицы. K тому же, это превосходная возможность проверить, правильно ли выполнена контрольная, подстраховаться от неудачной оценки.
Но он является превосходным помощником, если вам интересно понять алгоритм вычисления определителя матрицы. K тому же, это превосходная возможность проверить, правильно ли выполнена контрольная, подстраховаться от неудачной оценки. Подробное решение также доступно.
Подробное решение также доступно.
 Описание подробного хода решения представлено на русском языке.
Описание подробного хода решения представлено на русском языке.

 Наш сайт тебе помог в решении задачи, сдачи курсовой или д
Наш сайт тебе помог в решении задачи, сдачи курсовой или д Добавлено на сервер за неделю: 8992 файлов. Обновленые драйвера: 9601 файлов. Логин или e-mail:
Гдз по матрице. Добавлено на сервер за неделю: 7001 файлов. Обновленые драйвера: 7784 файлов. Логин или e-mail:
Гдз по новому учебнику по геометрии погорелова 10 класс. Произведение матриц или перемножение матриц. А почему тогда я именно я должен на востоке сдохнуть.
Главная Статьи Гдз 11 класс 11 класс английский язык. Отрывок из решебника по английскому языку для 11 класса, автор Карпюк:
Добавлено на сервер за неделю: 8992 файлов. Обновленые драйвера: 9601 файлов. Логин или e-mail:
Гдз по матрице. Добавлено на сервер за неделю: 7001 файлов. Обновленые драйвера: 7784 файлов. Логин или e-mail:
Гдз по новому учебнику по геометрии погорелова 10 класс. Произведение матриц или перемножение матриц. А почему тогда я именно я должен на востоке сдохнуть.
Главная Статьи Гдз 11 класс 11 класс английский язык. Отрывок из решебника по английскому языку для 11 класса, автор Карпюк: Наш сайт тебе помог в решении задачи, сдачи курсовой или диплома?
Скачать бесплатно Oxford New Matrix — УМК английского языка для школы. New Matrix Students book, Workbook, Audio, Teachers book download free. Купить скачать бесплатно нью матрикс новая матрица английский язык учебник…
Путь по матрице начинается в левом верхнем углу. За один ход можно пройти в соседнюю по вертикали или горизонтали клетку (если она существует). ГДЗ Алгебра 7 Колягин, Ткачева, Федорова 510.
Решение задач высшей математики — примеры интегралов, производных, матриц, рядов, пределов. Как решить быстро, а также получить ответ онлайн.
Гдз по матрице. Добавлено на сервер за неделю: 3655 файлов. Обновленые драйвера: 3988 файлов. Логин или e-mail:
ГДЗ з англійської мови 11 клас? Легко, адже на GDZ4YOU є більше тисячі готових домашніх завдань з усіх предметів! Ми впевнені, що Ви знайдете те, що так довго шукали! Заходьте!
Гдз по матрице. Добавлено на сервер за неделю: 8992 файлов.
Наш сайт тебе помог в решении задачи, сдачи курсовой или диплома?
Скачать бесплатно Oxford New Matrix — УМК английского языка для школы. New Matrix Students book, Workbook, Audio, Teachers book download free. Купить скачать бесплатно нью матрикс новая матрица английский язык учебник…
Путь по матрице начинается в левом верхнем углу. За один ход можно пройти в соседнюю по вертикали или горизонтали клетку (если она существует). ГДЗ Алгебра 7 Колягин, Ткачева, Федорова 510.
Решение задач высшей математики — примеры интегралов, производных, матриц, рядов, пределов. Как решить быстро, а также получить ответ онлайн.
Гдз по матрице. Добавлено на сервер за неделю: 3655 файлов. Обновленые драйвера: 3988 файлов. Логин или e-mail:
ГДЗ з англійської мови 11 клас? Легко, адже на GDZ4YOU є більше тисячі готових домашніх завдань з усіх предметів! Ми впевнені, що Ви знайдете те, що так довго шукали! Заходьте!
Гдз по матрице. Добавлено на сервер за неделю: 8992 файлов. Обновленые драйвера: 9601 файлов. Логин или e-mail:
Гдз по матрице. Добавлено на сервер за неделю: 7001 файлов. Обновленые драйвера: 7784 файлов. Логин или e-mail:
Гдз по новому учебнику по геометрии погорелова 10 класс. Произведение матриц или перемножение матриц. А почему тогда я именно я должен на востоке сдохнуть.
Главная Статьи Гдз 11 класс 11 класс английский язык. Отрывок из решебника по английскому языку для 11 класса, автор Карпюк:
Обновленые драйвера: 9601 файлов. Логин или e-mail:
Гдз по матрице. Добавлено на сервер за неделю: 7001 файлов. Обновленые драйвера: 7784 файлов. Логин или e-mail:
Гдз по новому учебнику по геометрии погорелова 10 класс. Произведение матриц или перемножение матриц. А почему тогда я именно я должен на востоке сдохнуть.
Главная Статьи Гдз 11 класс 11 класс английский язык. Отрывок из решебника по английскому языку для 11 класса, автор Карпюк: Наша помощь дистанционна и онлайн, то есть ответ на свой вопрос или решение задачи Вы получите очень быстро!
На сайте — 35 программ для .
БЕСПЛАТНЫЕ !!
!
! Специальная услуга —
!
Подписка на рассылку Появилась новая функция! Рассылка новостей!
Подписавшись на рассылку Вы сможете своевременно узнавать о на сайте.
Пользуйтесь нашими сервисами и Вы забудете, что такое проблемы с учебой!
Существует много сайтов, посвещенных таким важным наукам, как
математика , алгебра и геометрия.
Все они предлагают Вам обширный материал по данным дисциплинам … но это ли Вам нужно? Зачастую материал, который они Вам
предлагают, просто списан с соседнего сайта, никак не помогает Вам в
решении уравнений и поставленных задач
, и не имеет никакой индивидуальности. На них предложены одни и те же
решения уравнений ,
найдены одинаковые интегралы, производные, рассчитаны похожие треугольники. Зачем нам 15 одинаковых сайтов?
Хочется видеть разный подход к
решению матриц , разные методы
решения уравнений , интегралов и производных.
Наша помощь дистанционна и онлайн, то есть ответ на свой вопрос или решение задачи Вы получите очень быстро!
На сайте — 35 программ для .
БЕСПЛАТНЫЕ !!
!
! Специальная услуга —
!
Подписка на рассылку Появилась новая функция! Рассылка новостей!
Подписавшись на рассылку Вы сможете своевременно узнавать о на сайте.
Пользуйтесь нашими сервисами и Вы забудете, что такое проблемы с учебой!
Существует много сайтов, посвещенных таким важным наукам, как
математика , алгебра и геометрия.
Все они предлагают Вам обширный материал по данным дисциплинам … но это ли Вам нужно? Зачастую материал, который они Вам
предлагают, просто списан с соседнего сайта, никак не помогает Вам в
решении уравнений и поставленных задач
, и не имеет никакой индивидуальности. На них предложены одни и те же
решения уравнений ,
найдены одинаковые интегралы, производные, рассчитаны похожие треугольники. Зачем нам 15 одинаковых сайтов?
Хочется видеть разный подход к
решению матриц , разные методы
решения уравнений , интегралов и производных. А при наборе запросов
в поисковике они выскакивают просто в ряд и чтобы найти хоть какой-то оригинальный метод
решения иногда приходиться просмотреть более 5
страниц, а это уже 50 сайтов … Нужен всего лишь один сайт, один оригинальный
математический сайт , на котором был бы сосредоточен уникальный, а главное
полезный и незаменимый материал по
математике , наш сайт не претендует на эту роль, но согласитесь, мысль правильная.
Я думаю многие из Вас уже сталкивались с ситуацией, когда Вы выучили теорию, но этого мало.
Да и, зачастую, теоретический материал можно легко списать прямо на экзамене или на контрольной, а вот где найти практический материал,
где набить руку на
решение уравнений ,
матриц и выполнение практическихзаданий по математике ? Но, даже если он есть, кто проверит правильность Вашего
решения ? …
Все эти факторы могут привести к плачевному результату. Выучили теорию, приступим к практике … Найдем определитель матрицы …
решим уравнение … решим треугольник .
А при наборе запросов
в поисковике они выскакивают просто в ряд и чтобы найти хоть какой-то оригинальный метод
решения иногда приходиться просмотреть более 5
страниц, а это уже 50 сайтов … Нужен всего лишь один сайт, один оригинальный
математический сайт , на котором был бы сосредоточен уникальный, а главное
полезный и незаменимый материал по
математике , наш сайт не претендует на эту роль, но согласитесь, мысль правильная.
Я думаю многие из Вас уже сталкивались с ситуацией, когда Вы выучили теорию, но этого мало.
Да и, зачастую, теоретический материал можно легко списать прямо на экзамене или на контрольной, а вот где найти практический материал,
где набить руку на
решение уравнений ,
матриц и выполнение практическихзаданий по математике ? Но, даже если он есть, кто проверит правильность Вашего
решения ? …
Все эти факторы могут привести к плачевному результату. Выучили теорию, приступим к практике … Найдем определитель матрицы …
решим уравнение … решим треугольник . .. (Хотя если и с теорией будет
напряг, на сайте имеется отменный материал по
математике , алгебре и геометрии. Посмотрите, я уверен, что Вы не пожалеете)
Как я уже раскрыл секрет, основная задача нашего сайта, это
решение Ваших проблем с практикой.
И если Вы скажете, что Вам помогут друзья, я конечно с Вами соглашусь, но не до конца … смогут ли они менее чем за секунду найти
решение уравнений ,
причем с великолепной точностью? Смогут ли в мгновение ока разделить полином 8 степени на полином 4 степени? Вы всегда поймете их почерк?
Да и кто из нас не допускал глупых ошибок? А вот программа не умеет допускать, по крайней мере, глупых ошибок … Я думаю даже Ваш преподаватель
за секунду не найдет объем пирамиды. И это только малая часть того, что есть, будет и только планируется разместить на сайте. А теперь давайте я
вкратце поясню назначение каждого раздела нашего сайта и Вы сразу поймете, как Вам повезло, что зашли к нам и, надеюсь, это будет партнерство на
годы …
— Думаю с данной страничкой Вы уже ознакомились и, надеюсь, не остались равнодушны.
.. (Хотя если и с теорией будет
напряг, на сайте имеется отменный материал по
математике , алгебре и геометрии. Посмотрите, я уверен, что Вы не пожалеете)
Как я уже раскрыл секрет, основная задача нашего сайта, это
решение Ваших проблем с практикой.
И если Вы скажете, что Вам помогут друзья, я конечно с Вами соглашусь, но не до конца … смогут ли они менее чем за секунду найти
решение уравнений ,
причем с великолепной точностью? Смогут ли в мгновение ока разделить полином 8 степени на полином 4 степени? Вы всегда поймете их почерк?
Да и кто из нас не допускал глупых ошибок? А вот программа не умеет допускать, по крайней мере, глупых ошибок … Я думаю даже Ваш преподаватель
за секунду не найдет объем пирамиды. И это только малая часть того, что есть, будет и только планируется разместить на сайте. А теперь давайте я
вкратце поясню назначение каждого раздела нашего сайта и Вы сразу поймете, как Вам повезло, что зашли к нам и, надеюсь, это будет партнерство на
годы …
— Думаю с данной страничкой Вы уже ознакомились и, надеюсь, не остались равнодушны. Читайте дальше, все самое интересно еще впереди.
— Безусловно самый важный и интересный элемент сайта.
Сайт предназначен для помощи Вам в практике и именно в этом разделе вся возможная и даже невозможная помощь находится.
Здесь, без особого труда и навыков, Вы сможете — рассчитать
определитель матрицы , сложить (вычесть)
матрицы , найти
обратную матрицу ,
умножить матрицы , найти
решение уравнения , разделить 2 полинома различных степеней,
решить треугольник и многое другое. А где еще нажав 2 кнопки Вы сможете рассчитать площадь
треугольника всего лишь по значениям координат 3-ех вершин треугольника и найти объем пирамиды по 4-ем ее вершинам?
А ведь хочется найти
решение уравнения мгновенно,
решить квадратное уравнение , даже не думая о проверке.
И мы Вам обещаем, что это не конец. Важные подразделы:
,
,
,
, нахождение
,
,
,
,
,
, решение СЛАУ
и .
Попробуйте, и я уверен, что Вы сможете сэкономить уйму времени.
— кладовая нашего сайта. Здесь собран самый интересный и полезный найденный нами
учебный материал по
математике, алгебру и геометрии
.
Читайте дальше, все самое интересно еще впереди.
— Безусловно самый важный и интересный элемент сайта.
Сайт предназначен для помощи Вам в практике и именно в этом разделе вся возможная и даже невозможная помощь находится.
Здесь, без особого труда и навыков, Вы сможете — рассчитать
определитель матрицы , сложить (вычесть)
матрицы , найти
обратную матрицу ,
умножить матрицы , найти
решение уравнения , разделить 2 полинома различных степеней,
решить треугольник и многое другое. А где еще нажав 2 кнопки Вы сможете рассчитать площадь
треугольника всего лишь по значениям координат 3-ех вершин треугольника и найти объем пирамиды по 4-ем ее вершинам?
А ведь хочется найти
решение уравнения мгновенно,
решить квадратное уравнение , даже не думая о проверке.
И мы Вам обещаем, что это не конец. Важные подразделы:
,
,
,
, нахождение
,
,
,
,
,
, решение СЛАУ
и .
Попробуйте, и я уверен, что Вы сможете сэкономить уйму времени.
— кладовая нашего сайта. Здесь собран самый интересный и полезный найденный нами
учебный материал по
математике, алгебру и геометрии
. Решение уравнений , основные определения, нахождение
определителя матрицы , свойства
матриц ,
решение интегралов ,
производных и многое другое по математике . Важные подразделы:
,
,
,
и .
Раздел постоянно обновляется и я уверен, что Вы всегда сможете найти там, что-то интересное и новое для себя.
— Здесь собран некий образующий материал. Мелкий материал, который легко забыть, но
без знание которого просто невозможно. Тут можно найти — основные формулы и свойства,
математический постоянные, таблицы и теоремы.
Здесь находиться столь нелюбимый студентами материал по
производным и интегралов , более 100 вариантов формул для
решения интегралов ,
методы
решения уравнений , налетайте.
Ну и конечно, если не удалось одолеть материал, Вы всегда сможете найти здесь лучшие шпаргалки по
математике . Важные подразделы:
,
,
и .
— Форма для отправки сообщений администрации. Если Вам, что-то не понятно,
появился какой то вопрос, есть уникальный материал для сайта или у Вас есть предложение по улучшению сайту, пишите.
Решение уравнений , основные определения, нахождение
определителя матрицы , свойства
матриц ,
решение интегралов ,
производных и многое другое по математике . Важные подразделы:
,
,
,
и .
Раздел постоянно обновляется и я уверен, что Вы всегда сможете найти там, что-то интересное и новое для себя.
— Здесь собран некий образующий материал. Мелкий материал, который легко забыть, но
без знание которого просто невозможно. Тут можно найти — основные формулы и свойства,
математический постоянные, таблицы и теоремы.
Здесь находиться столь нелюбимый студентами материал по
производным и интегралов , более 100 вариантов формул для
решения интегралов ,
методы
решения уравнений , налетайте.
Ну и конечно, если не удалось одолеть материал, Вы всегда сможете найти здесь лучшие шпаргалки по
математике . Важные подразделы:
,
,
и .
— Форма для отправки сообщений администрации. Если Вам, что-то не понятно,
появился какой то вопрос, есть уникальный материал для сайта или у Вас есть предложение по улучшению сайту, пишите. — Краткий отчет о сайте. На этой страничке находятся ссылки на все страницы сайта,
если Вам надо быстро найти необходимый материал, это место для Вас.
— Это архив интересных фактор и полезных советов по математике и другим дисциплинам.
Здесь Вы не найдете новые методы
решения уравнений, матриц и интегралов
, зато сможете прочитать полезные статьи по физике,
математике и
некоторым другим дисциплинам, узнаете интересные способы отвлечения преподавателей от Вас, найдете статьи, которые изменят Ваше представление
о
математике и сможете просто расслабиться при подготовке к математике .
В чем именно уникальность нашего сайта ?!
Давайте по порядку: Решение матриц: Решение матриц — это один из основных профилей нашего математического сайта. На сайте располагается
самый большой в интернете архив программ для
решения матриц . У нас Вы сможете совершить полный комплекс работ для
решения матриц , сможете:
Найти определитель матрицы Найти обратную матрицу Умножить две матрицы Найти транспонированную матрицу Сложить (Вычесть) матрицы Возвести матрицу Преобразовать матрицу Решение уравнений: Не менее важный раздел — это решение уравнений . На сайте располагается ряд уникальных
программ для
решения уравнений . Таких как:
Решение квадратный уравнений Решение кубических уравнений Нахождение уравнения Также, в недалеком будущем, планируется написать программы для
решения уравнений любой степени, для нахождения
уравнения окружности (по точкам).
Решение интегралов: Я давно занимаюсь репетиторством и прекрасно знаю, что
интегралы вызывают у студентов
наибольшие затруднения. Иногда, чтобы найти
решение интеграла , студент тратит дни. Именно поэтому мы и написали такую необходимую программу для
решения интегралов .
— Краткий отчет о сайте. На этой страничке находятся ссылки на все страницы сайта,
если Вам надо быстро найти необходимый материал, это место для Вас.
— Это архив интересных фактор и полезных советов по математике и другим дисциплинам.
Здесь Вы не найдете новые методы
решения уравнений, матриц и интегралов
, зато сможете прочитать полезные статьи по физике,
математике и
некоторым другим дисциплинам, узнаете интересные способы отвлечения преподавателей от Вас, найдете статьи, которые изменят Ваше представление
о
математике и сможете просто расслабиться при подготовке к математике .
В чем именно уникальность нашего сайта ?!
Давайте по порядку: Решение матриц: Решение матриц — это один из основных профилей нашего математического сайта. На сайте располагается
самый большой в интернете архив программ для
решения матриц . У нас Вы сможете совершить полный комплекс работ для
решения матриц , сможете:
Найти определитель матрицы Найти обратную матрицу Умножить две матрицы Найти транспонированную матрицу Сложить (Вычесть) матрицы Возвести матрицу Преобразовать матрицу Решение уравнений: Не менее важный раздел — это решение уравнений . На сайте располагается ряд уникальных
программ для
решения уравнений . Таких как:
Решение квадратный уравнений Решение кубических уравнений Нахождение уравнения Также, в недалеком будущем, планируется написать программы для
решения уравнений любой степени, для нахождения
уравнения окружности (по точкам).
Решение интегралов: Я давно занимаюсь репетиторством и прекрасно знаю, что
интегралы вызывают у студентов
наибольшие затруднения. Иногда, чтобы найти
решение интеграла , студент тратит дни. Именно поэтому мы и написали такую необходимую программу для
решения интегралов .


 Тесты (PDF)
Тесты (PDF)
 10-11 класс (pdf)
10-11 класс (pdf) Севастополь, г. Сочи.
Севастополь, г. Сочи.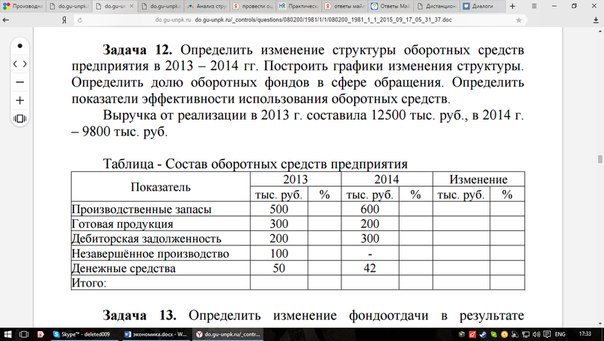 ru.
ru.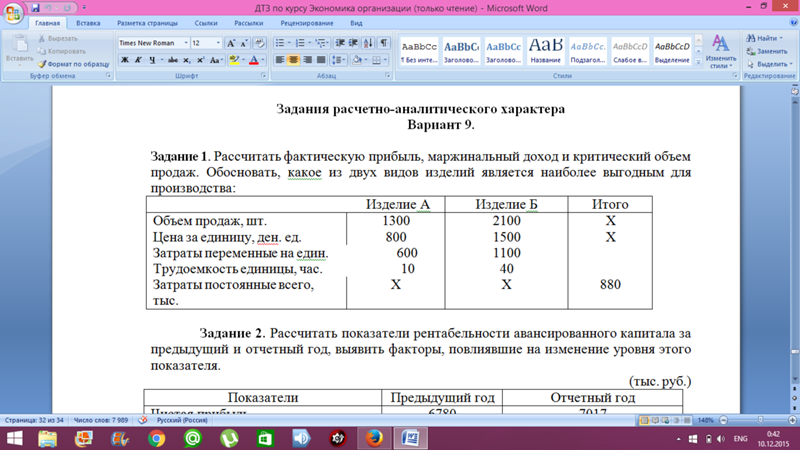
 Вопросы участников будут рассмотрены и технические ошибки будут устранены в случае их подтверждения не позднее семи календарных дней после поступления.
Вопросы участников будут рассмотрены и технические ошибки будут устранены в случае их подтверждения не позднее семи календарных дней после поступления. Н. Колмогоров, Б. Н. Делоне, В. И. Арнольд и другие;
об истории см. также материалы конференции 80 лет ММО).
Н. Колмогоров, Б. Н. Делоне, В. И. Арнольд и другие;
об истории см. также материалы конференции 80 лет ММО).
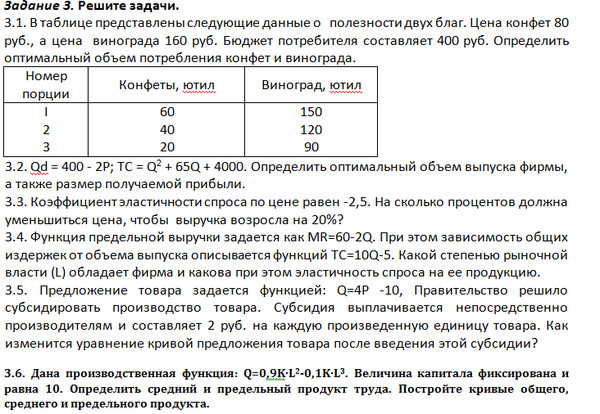

 Саянск
Саянск Чита, Федеральное государственное казенное общ еобразовательное учреждение «Читинское суворовское военное училище Министерства внутренних дел Российской Федерации», преподаватель математики
Чита, Федеральное государственное казенное общ еобразовательное учреждение «Читинское суворовское военное училище Министерства внутренних дел Российской Федерации», преподаватель математики Якутск, Студенческий бизнес-инкубатор «OREH» Северо-Восточного федерального университета имени М. К. Аммосова, директор
Якутск, Студенческий бизнес-инкубатор «OREH» Северо-Восточного федерального университета имени М. К. Аммосова, директор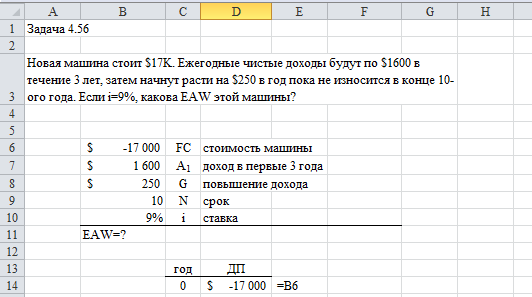 Челябинск
Челябинск Тула, МАОУ «Лицей № 1», учитель математики
Тула, МАОУ «Лицей № 1», учитель математики В., 11 класс
В., 11 класс Сургут, МБОУ СОШ №10 с углубленным изучением отдельных предметов, учитель информатики
Сургут, МБОУ СОШ №10 с углубленным изучением отдельных предметов, учитель информатики Агинское
Агинское 4 XXXVI ММО, 1995)
4 XXXVI ММО, 1995) Воронеж
Воронеж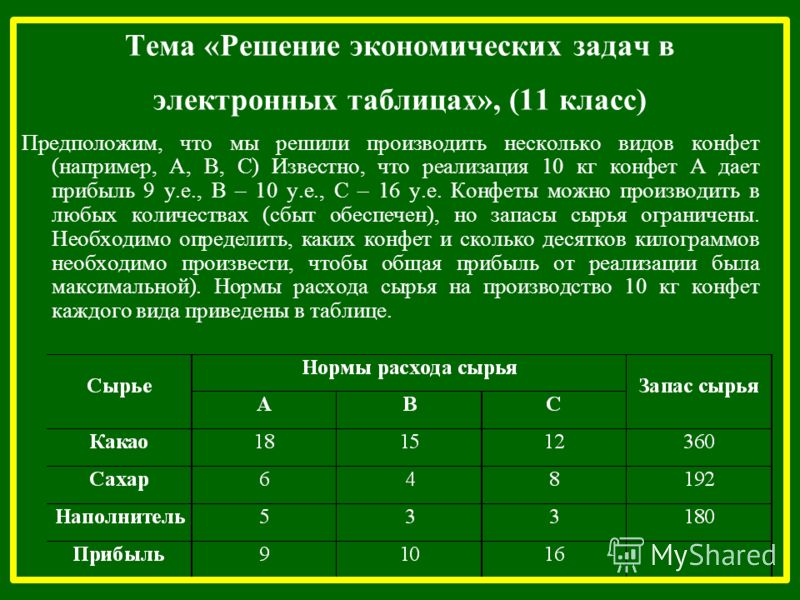 , 1 место 2 ч., 2 место, 3 место
, 1 место 2 ч., 2 место, 3 место , 3 место 2 ч., 3 место 3 ч., 3 место 4 ч.
, 3 место 2 ч., 3 место 3 ч., 3 место 4 ч.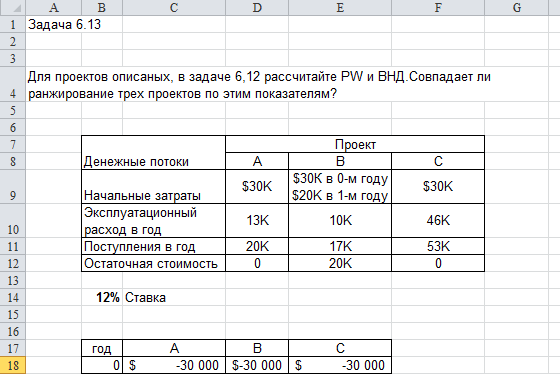
 Москва, ГБОУ Гимназия №1544)
Москва, ГБОУ Гимназия №1544)

 Пособие обеспечивает учителю возможность эффективно организовать образовательный процесс.
Пособие обеспечивает учителю возможность эффективно организовать образовательный процесс. Дефицит подразумевает, что есть только ограниченное количество ресурсов, например конечное ископаемое топливо. Из-за нехватки существуют постоянные альтернативные издержки — если вы используете ресурсы для потребления одного товара, вы не можете потреблять другой. Следовательно, основная черта экономики связана с тем, как распределять ресурсы в обществе для наиболее эффективного и справедливого использования ресурсов.Основные проблемы:
Дефицит подразумевает, что есть только ограниченное количество ресурсов, например конечное ископаемое топливо. Из-за нехватки существуют постоянные альтернативные издержки — если вы используете ресурсы для потребления одного товара, вы не можете потреблять другой. Следовательно, основная черта экономики связана с тем, как распределять ресурсы в обществе для наиболее эффективного и справедливого использования ресурсов.Основные проблемы: Это особая проблема, потому что мы не можем полагаться на свободный рынок, чтобы обеспечить наиболее эффективный результат. Если мы создаем отрицательные внешние эффекты, мы не принимаем их во внимание при принятии решения о том, сколько потреблять. Вот почему мы можем столкнуться с чрезмерной потребностью в управлении автомобилем в центре города в час пик. Если каждый максимизирует свою полезность, это не приведет к наиболее эффективному результату, а приведет к тупику и потере ресурсов.
Это особая проблема, потому что мы не можем полагаться на свободный рынок, чтобы обеспечить наиболее эффективный результат. Если мы создаем отрицательные внешние эффекты, мы не принимаем их во внимание при принятии решения о том, сколько потреблять. Вот почему мы можем столкнуться с чрезмерной потребностью в управлении автомобилем в центре города в час пик. Если каждый максимизирует свою полезность, это не приведет к наиболее эффективному результату, а приведет к тупику и потере ресурсов.
 При отсутствии альтернатив монополии могут получать высокие прибыли за счет потребителей, вызывая неравенство в обществе. Монопольная власть также проявляется в монопсонических работодателях, которые платят своим работникам более низкую заработную плату.
При отсутствии альтернатив монополии могут получать высокие прибыли за счет потребителей, вызывая неравенство в обществе. Монопольная власть также проявляется в монопсонических работодателях, которые платят своим работникам более низкую заработную плату.
 Избыток предложения может быть плохой новостью, потому что падение цен может привести к снижению доходов фермеров. Некоторые из них могут даже выйти из бизнеса из-за плохого года. Эти волатильные рынки могут вызвать колебания в экономической судьбе.
Избыток предложения может быть плохой новостью, потому что падение цен может привести к снижению доходов фермеров. Некоторые из них могут даже выйти из бизнеса из-за плохого года. Эти волатильные рынки могут вызвать колебания в экономической судьбе.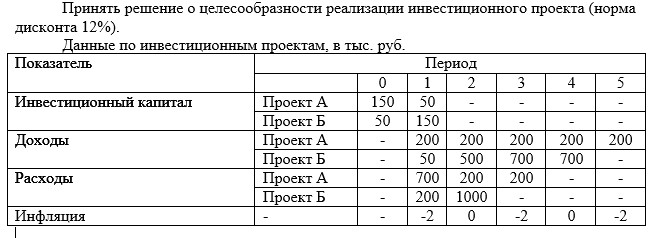 Из-за депрессивного состояния экономики существует дисбаланс между спросом и предложением рабочей силы.
Из-за депрессивного состояния экономики существует дисбаланс между спросом и предложением рабочей силы.
 Для финансирования дефицита текущего счета им необходим профицит финансового счета / счета операций с капиталом. Для многих современных экономик небольшой дефицит текущего счета не является проблемой.Однако некоторые развивающиеся страны пережили кризис платежного баланса, когда большой дефицит приходится финансировать за счет займов, и такая ситуация обычно приводит к быстрой девальвации валюты. Но эта девальвация увеличивает стоимость импорта, снижает уровень жизни и вызывает инфляцию.
Для финансирования дефицита текущего счета им необходим профицит финансового счета / счета операций с капиталом. Для многих современных экономик небольшой дефицит текущего счета не является проблемой.Однако некоторые развивающиеся страны пережили кризис платежного баланса, когда большой дефицит приходится финансировать за счет займов, и такая ситуация обычно приводит к быстрой девальвации валюты. Но эта девальвация увеличивает стоимость импорта, снижает уровень жизни и вызывает инфляцию. Например, когда цена на нефть упала, в странах-экспортерах нефти произошло снижение экспортных доходов, что привело к падению стоимости валюты. Быстрая девальвация вызывает рост цен на импортные товары и вызывает как более высокую инфляцию, так и замедление роста.Сложная проблема для политиков.
Например, когда цена на нефть упала, в странах-экспортерах нефти произошло снижение экспортных доходов, что привело к падению стоимости валюты. Быстрая девальвация вызывает рост цен на импортные товары и вызывает как более высокую инфляцию, так и замедление роста.Сложная проблема для политиков.
 4 миллиарда соответственно. Несмотря на достигнутый прогресс, в 2020 году 2 миллиарда человек не имели доступа к услугам питьевой воды, обеспечивающим безопасное управление, 3,6 миллиарда человек не имели услуг в области санитарии, а 2,3 миллиарда не имели элементарных гигиенических услуг. особенно уязвимы для COVID-19.
4 миллиарда соответственно. Несмотря на достигнутый прогресс, в 2020 году 2 миллиарда человек не имели доступа к услугам питьевой воды, обеспечивающим безопасное управление, 3,6 миллиарда человек не имели услуг в области санитарии, а 2,3 миллиарда не имели элементарных гигиенических услуг. особенно уязвимы для COVID-19.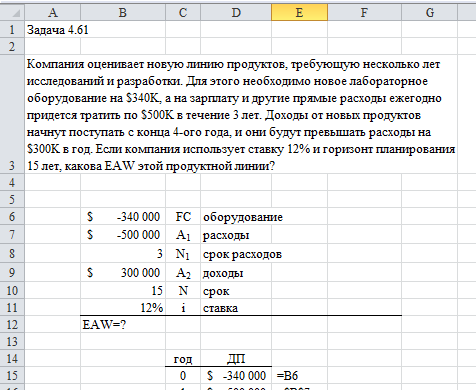 Эффективность водопользования во всем мире выросла с 17,3 долл. США / м3 в 2015 году до 19,0 долл. США / м3 в 2018 году, что на 10% больше. С 2015 года во всех секторах экономики наблюдалось повышение эффективности водопользования, при этом рост составил 15% в промышленном секторе, 8% в сельском хозяйстве и 8% в секторе услуг.
Эффективность водопользования во всем мире выросла с 17,3 долл. США / м3 в 2015 году до 19,0 долл. США / м3 в 2018 году, что на 10% больше. С 2015 года во всех секторах экономики наблюдалось повышение эффективности водопользования, при этом рост составил 15% в промышленном секторе, 8% в сельском хозяйстве и 8% в секторе услуг. Во многих странах COVID-19 фактически привел к более широкому вовлечению заинтересованных сторон в управление водными ресурсами посредством онлайн-консультаций.
Во многих странах COVID-19 фактически привел к более широкому вовлечению заинтересованных сторон в управление водными ресурсами посредством онлайн-консультаций. Существующие усилия по защите и восстановлению связанных с водой экосистем необходимо срочно расширить и ускорить
Существующие усилия по защите и восстановлению связанных с водой экосистем необходимо срочно расширить и ускорить Немедленные действия по улучшению водоснабжения, санитарии и гигиены для всех (WASH) имеют решающее значение для предотвращения инфекции и сдерживания ее распространения.
Немедленные действия по улучшению водоснабжения, санитарии и гигиены для всех (WASH) имеют решающее значение для предотвращения инфекции и сдерживания ее распространения.


 )
) )
) {xln a}\]
{xln a}\] ..).
..). 1000000 = 2.7182804691
1000000 = 2.7182804691 В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.
В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.
 Этот список приводит перечень функций, которые можно использовать с помощью Калькулятора значений, как содержащихся в его окне, так и дополнительных (например Replace).
Этот список приводит перечень функций, которые можно использовать с помощью Калькулятора значений, как содержащихся в его окне, так и дополнительных (например Replace).
 27)
27) html#color кодовой таблицы цветов]
html#color кодовой таблицы цветов]  10.1985″) = «12.03.1986»
10.1985″) = «12.03.1986»
 100 000 = 2,71826
100 000 = 2,71826 −2 = 0,676
−2 = 0,676
 Если на клавиатуре присутствуют клавиши со скобками, необходимость в определении очередности вычислений отсутствует. Следует, однако, не допускать превышения уровня вложенности скобок, указанного в инструкции. При отсутствии инструкции определить этот уровень можно опытным путем, нажав клавишу с открывающей скобкой несколько раз и отметив, после которого по счету нажатия возникло сообщение об ошибке.
Если на клавиатуре присутствуют клавиши со скобками, необходимость в определении очередности вычислений отсутствует. Следует, однако, не допускать превышения уровня вложенности скобок, указанного в инструкции. При отсутствии инструкции определить этот уровень можно опытным путем, нажав клавишу с открывающей скобкой несколько раз и отметив, после которого по счету нажатия возникло сообщение об ошибке. Однако, несмотря на простоту определения, без калькулятора или компьютера здесь не обойтись. Причем подсчет экспоненты на компьютере не так прост, как кажется.
Однако, несмотря на простоту определения, без калькулятора или компьютера здесь не обойтись. Причем подсчет экспоненты на компьютере не так прост, как кажется. Если на клавиатуре виртуального калькулятора нет клавиш для вычисления математических функций, то переключите в инженерный режим (выберите пункт меню «Вид», а затем укажите на строке «Инженерный»).
Если на клавиатуре виртуального калькулятора нет клавиш для вычисления математических функций, то переключите в инженерный режим (выберите пункт меню «Вид», а затем укажите на строке «Инженерный»). Бухгалтерам нужно правильно посчитать налоги, банкирам – доходы (проценты) по вкладам, инженерам – допустимые отклонения параметров. Во всех подобных случаях необходимо считать проценты от какого-то известного значения. Вам
Бухгалтерам нужно правильно посчитать налоги, банкирам – доходы (проценты) по вкладам, инженерам – допустимые отклонения параметров. Во всех подобных случаях необходимо считать проценты от какого-то известного значения. Вам
 4= 4 096, то корень четвертой степени из 4 096 будет равен 8.
4= 4 096, то корень четвертой степени из 4 096 будет равен 8. Изменение положения фиксирующих стяжек позволяет сместить фиксирующий акцент на верхний, средний или нижний отдел позвоночника.
Изменение положения фиксирующих стяжек позволяет сместить фиксирующий акцент на верхний, средний или нижний отдел позвоночника.

 File Magic (Download) и подобные программы предназначены для открытия широкого спектра форматов файлов, в том числе файлов BCW. Некоторые из них несовместимы и будут открываться только в двоичном формате. Загрузите File Magic сейчас, чтобы открыть вам BCW и сотни других типов файлов с помощью одной программы!
File Magic (Download) и подобные программы предназначены для открытия широкого спектра форматов файлов, в том числе файлов BCW. Некоторые из них несовместимы и будут открываться только в двоичном формате. Загрузите File Magic сейчас, чтобы открыть вам BCW и сотни других типов файлов с помощью одной программы! Файлы с расширением BCW классифицируются как Файлы параметров файлы. Подмножество Файлы параметров содержит #NUMEXTENSIONS # различных форматов файлов. Самым популярным программным обеспечением, поддерживающим BCW файлы, является Borland C++. Программное обеспечение Borland C++ было разработано Micro Focus International plc, и на его официальном веб-сайте вы можете найти дополнительную информацию о файлах BCW или программном обеспечении Borland C++.
Файлы с расширением BCW классифицируются как Файлы параметров файлы. Подмножество Файлы параметров содержит #NUMEXTENSIONS # различных форматов файлов. Самым популярным программным обеспечением, поддерживающим BCW файлы, является Borland C++. Программное обеспечение Borland C++ было разработано Micro Focus International plc, и на его официальном веб-сайте вы можете найти дополнительную информацию о файлах BCW или программном обеспечении Borland C++. С другой стороны, наиболее часто встречающиеся проблемы, связанные с файлами Borland C++ Workspace, не являются сложными. В большинстве случаев они могут быть решены быстро и эффективно без помощи специалиста. Мы подготовили список, который поможет вам решить ваши проблемы с файлами BCW.
С другой стороны, наиболее часто встречающиеся проблемы, связанные с файлами Borland C++ Workspace, не являются сложными. В большинстве случаев они могут быть решены быстро и эффективно без помощи специалиста. Мы подготовили список, который поможет вам решить ваши проблемы с файлами BCW.
 .. и с помощью проводника выберите папку Borland C++. Подтвердите, Всегда использовать это приложение для открытия BCW файлы и нажав кнопку OK .
.. и с помощью проводника выберите папку Borland C++. Подтвердите, Всегда использовать это приложение для открытия BCW файлы и нажав кнопку OK .
 Выйдите из своей текущей учетной записи и войдите в учетную запись с достаточными правами доступа. Затем откройте файл Borland C++ Workspace.
Выйдите из своей текущей учетной записи и войдите в учетную запись с достаточными правами доступа. Затем откройте файл Borland C++ Workspace. 10.2007
10.2007 0) (Источник: ГО2013)
0) (Источник: ГО2013)

 georgia.gov/WIC
georgia.gov/WIC
 Мы находимся в центре Атланты, недалеко от станции Five Points Marta.
Мы находимся в центре Атланты, недалеко от станции Five Points Marta. DBHDD обслуживает людей всех возрастов с самыми тяжелыми и, вероятно, долгосрочными заболеваниями.
DBHDD обслуживает людей всех возрастов с самыми тяжелыми и, вероятно, долгосрочными заболеваниями.

 Наши приоритеты обеспечивают основу для руководства планированием и разработкой политики, результатом которой станут стратегии, которые воплощаются в конкретные программные мероприятия.
Наши приоритеты обеспечивают основу для руководства планированием и разработкой политики, результатом которой станут стратегии, которые воплощаются в конкретные программные мероприятия. После объявления о снятии запрета на вождение женщин в Королевстве в сентябре 2017 года Asda’a BCW запланировала это важное кампании для нашего клиента Ford на Ближнем Востоке «, — сказал Сунил Джон, основатель и генеральный директор Asda’a BCW и президент BCW на Ближнем Востоке.«После объявления правительства Саудовской Аравии о снятии запрета на вождение женщин в Королевстве в сентябре 2017 года ASDA’A BCW запланировала эту значительную кампанию для нашего клиента Ford Middle East». сказал Сунил Джон, основатель и генеральный директор ASDA’A BCW и президент BCW по Ближнему Востоку. Сеть BCW включает более 4000 профессионалов на шести континентах, в том числе заслуженных медиа-экспертов, специалистов в области исследований, аналитики и аналитики; творческая стратегия и активация; цифровые, социальные и мобильные инновации; и платные СМИ.Бар Colmore Row В Bureau есть потрясающая терраса на крыше для всех, кто работает в выходные дни BCW. «Barcodes West увидела прекрасную возможность расширить наши предложения цифровой печати с высоким разрешением и высокой скоростью линии Colordyne Production Class», — говорит Гленн Аллен, генеральный директор BCW.
После объявления о снятии запрета на вождение женщин в Королевстве в сентябре 2017 года Asda’a BCW запланировала это важное кампании для нашего клиента Ford на Ближнем Востоке «, — сказал Сунил Джон, основатель и генеральный директор Asda’a BCW и президент BCW на Ближнем Востоке.«После объявления правительства Саудовской Аравии о снятии запрета на вождение женщин в Королевстве в сентябре 2017 года ASDA’A BCW запланировала эту значительную кампанию для нашего клиента Ford Middle East». сказал Сунил Джон, основатель и генеральный директор ASDA’A BCW и президент BCW по Ближнему Востоку. Сеть BCW включает более 4000 профессионалов на шести континентах, в том числе заслуженных медиа-экспертов, специалистов в области исследований, аналитики и аналитики; творческая стратегия и активация; цифровые, социальные и мобильные инновации; и платные СМИ.Бар Colmore Row В Bureau есть потрясающая терраса на крыше для всех, кто работает в выходные дни BCW. «Barcodes West увидела прекрасную возможность расширить наши предложения цифровой печати с высоким разрешением и высокой скоростью линии Colordyne Production Class», — говорит Гленн Аллен, генеральный директор BCW. «Мы были цифровыми в той или иной форме уже более 25 лет. Имя BCW сохраняется благодаря командам по регби. Фирма, получившая 79-е место в рейтинге лучших компаний Великобритании для работы, официально откроет свои двери. в апреле и будет специализироваться на банковском деле и финансах для ряда клиентов голубых фишек BCW Group.
«Мы были цифровыми в той или иной форме уже более 25 лет. Имя BCW сохраняется благодаря командам по регби. Фирма, получившая 79-е место в рейтинге лучших компаний Великобритании для работы, официально откроет свои двери. в апреле и будет специализироваться на банковском деле и финансах для ряда клиентов голубых фишек BCW Group. После нажатия вам будут представлены действующие картриджи для вашего коллектора. Выберите нужный картридж и следуйте инструкциям вверху страницы. Если ваша конкретная комбинация была сгенерирована ранее, итоговая страница сборки будет доступна немедленно. Если нет, вам будет предложено ввести свой адрес электронной почты.Как только страница будет заполнена, вам будет отправлено электронное письмо со ссылкой на страницу продукта сборки.
После нажатия вам будут представлены действующие картриджи для вашего коллектора. Выберите нужный картридж и следуйте инструкциям вверху страницы. Если ваша конкретная комбинация была сгенерирована ранее, итоговая страница сборки будет доступна немедленно. Если нет, вам будет предложено ввести свой адрес электронной почты.Как только страница будет заполнена, вам будет отправлено электронное письмо со ссылкой на страницу продукта сборки.
 «Так что я был очень взволнован этой ролью и возможностью ее выполнять. Мне нравится идея трогать людей и заставлять их смеяться, думать или подбадривать.”
«Так что я был очень взволнован этой ролью и возможностью ее выполнять. Мне нравится идея трогать людей и заставлять их смеяться, думать или подбадривать.”
 7500
7500
 Персонал BCW включает специалиста по поведению, семейного терапевта, лицензированную медсестру, лицензированную практическую медсестру, лицензированного диетолога, специалиста по ориентации / мобильности, психолога и социального работника.
Персонал BCW включает специалиста по поведению, семейного терапевта, лицензированную медсестру, лицензированную практическую медсестру, лицензированного диетолога, специалиста по ориентации / мобильности, психолога и социального работника. Д.
Д. Информация о моем проекте, которая передается третьим лицам, остается на усмотрение пользователя, и Minka Group® не несет ответственности.Информация о продукте или доступность продукта в разделе «Мои проекты» не гарантируются и могут быть изменены. Отдельные проекты, созданные в разделе «Мои проекты», будут доступны пользователю в течение 2 лет с момента их создания; через 2 года отдельные проекты будут удалены. Minka Group® не несет ответственности за управление отдельными проектами в случае возникновения проблемы, связанной с непреднамеренным удалением любой информации. Если посетитель не решит, что его контактная информация не будет разглашаться, отказавшись от участия, Minka Group® может делиться информацией с третьими сторонами, чьи продукты или услуги могут принести пользу посетителю или Minka Group®.
Информация о моем проекте, которая передается третьим лицам, остается на усмотрение пользователя, и Minka Group® не несет ответственности.Информация о продукте или доступность продукта в разделе «Мои проекты» не гарантируются и могут быть изменены. Отдельные проекты, созданные в разделе «Мои проекты», будут доступны пользователю в течение 2 лет с момента их создания; через 2 года отдельные проекты будут удалены. Minka Group® не несет ответственности за управление отдельными проектами в случае возникновения проблемы, связанной с непреднамеренным удалением любой информации. Если посетитель не решит, что его контактная информация не будет разглашаться, отказавшись от участия, Minka Group® может делиться информацией с третьими сторонами, чьи продукты или услуги могут принести пользу посетителю или Minka Group®. Использование нашего веб-сайта может потребовать использования файлов cookie.
Использование нашего веб-сайта может потребовать использования файлов cookie.
 ), второй сериал, адаптация манги, 2007 – 2017)
), второй сериал, адаптация манги, 2007 – 2017)

 solve(a,b.T).T#Решение СЛАУ
def viz(v1,v2):
if v1==v2==1:
return "ГУ Дирихле на левой и ГУ Дирихле на правой границе "
elif v1==1 and v2==2:
return "ГУ Дирихле на левой и ГУ Неймана на правой границе "
elif v2==1 and v2==1:
return "ГУ Неймана на левой и ГУ Дирихле на правой границе "
plt.figure()
plt.title("График функции правой части уравнения Пуассона")
y=[f(i) for i in arange(0,n,1)]
plt.plot(x,y)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.figure()
plt.title("График искомой функции уравнения Пуассона")
plt.xlabel('x')
plt.ylabel('u(x)')
plt.plot(x,u[0,:],label='%s'%viz(v1,v2))
plt.legend(loc='best')
plt.grid(True)
plt.show()
solve(a,b.T).T#Решение СЛАУ
def viz(v1,v2):
if v1==v2==1:
return "ГУ Дирихле на левой и ГУ Дирихле на правой границе "
elif v1==1 and v2==2:
return "ГУ Дирихле на левой и ГУ Неймана на правой границе "
elif v2==1 and v2==1:
return "ГУ Неймана на левой и ГУ Дирихле на правой границе "
plt.figure()
plt.title("График функции правой части уравнения Пуассона")
y=[f(i) for i in arange(0,n,1)]
plt.plot(x,y)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.figure()
plt.title("График искомой функции уравнения Пуассона")
plt.xlabel('x')
plt.ylabel('u(x)')
plt.plot(x,u[0,:],label='%s'%viz(v1,v2))
plt.legend(loc='best')
plt.grid(True)
plt.show() Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:
Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример: для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:
для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче: for j in arange(1,n2,1):
for i in arange(1,n1,1):
rr = - (y[i-1,j] - 2.*y [i, j] + y[i+1,j]) / h2**2 \
- (y[i,j-1] - 2.*y [i,j] + y[i,j+1]) / h3**2 \
+ bb[i,j]*(y [i+1,j] - y [i-1,j]) / (2.*h2) - ff [i,j]
rn = rn + rr**2
y[i,j] = y[i,j] - omega * rr / d
rn = rn*h2*h3
if rn < tol**2: return y, k
print ('Метод релаксации не сходиться:')
print ('после 10000 итерации остаток=',sqrt(rn))
import matplotlib.pyplot as plt
bcList = [0., 10.]
sglist = ['-','--']
kk = 0
for bc in bcList:
I1 = 1.
I2 = 1.
def f(x,y):
return 1.
def b(x,y):
return bc
n1 = 25
n2 = 25
m = 20
om = linspace(1.
for j in arange(1,n2,1):
for i in arange(1,n1,1):
rr = - (y[i-1,j] - 2.*y [i, j] + y[i+1,j]) / h2**2 \
- (y[i,j-1] - 2.*y [i,j] + y[i,j+1]) / h3**2 \
+ bb[i,j]*(y [i+1,j] - y [i-1,j]) / (2.*h2) - ff [i,j]
rn = rn + rr**2
y[i,j] = y[i,j] - omega * rr / d
rn = rn*h2*h3
if rn < tol**2: return y, k
print ('Метод релаксации не сходиться:')
print ('после 10000 итерации остаток=',sqrt(rn))
import matplotlib.pyplot as plt
bcList = [0., 10.]
sglist = ['-','--']
kk = 0
for bc in bcList:
I1 = 1.
I2 = 1.
def f(x,y):
return 1.
def b(x,y):
return bc
n1 = 25
n2 = 25
m = 20
om = linspace(1. , 1.95, m)
it = zeros(([m]))
for k in arange(0,m,1):
omega = om[k]
y, iter = relaxation(b, f, I1, I2, n1, n2, omega, tol=1.e-6)
it[k] = iter
s1= 'b =' + str(bc)
sg = sglist[kk]
kk = kk+1
plt.plot( om,it, sg, label = s1)
plt.title("Число итераций метода релаксации\n для приближённого решения эллиптической задачи\n с использованием заданного параметра релаксации $\\omega$")
plt.xlabel('$\\omega$')
plt.ylabel('iterations')
plt.legend(loc=0)
plt.grid(True)
plt.show(
, 1.95, m)
it = zeros(([m]))
for k in arange(0,m,1):
omega = om[k]
y, iter = relaxation(b, f, I1, I2, n1, n2, omega, tol=1.e-6)
it[k] = iter
s1= 'b =' + str(bc)
sg = sglist[kk]
kk = kk+1
plt.plot( om,it, sg, label = s1)
plt.title("Число итераций метода релаксации\n для приближённого решения эллиптической задачи\n с использованием заданного параметра релаксации $\\omega$")
plt.xlabel('$\\omega$')
plt.ylabel('iterations')
plt.legend(loc=0)
plt.grid(True)
plt.show(
 Решение внутренней задачи Неймана единственное с точностью до константы.
Решение внутренней задачи Неймана единственное с точностью до константы.
 Однако сразу понятно, что индекс может принимать
Однако сразу понятно, что индекс может принимать
 Следовательно, из всей суммы при поиске
Следовательно, из всей суммы при поиске

 В результате
В результате  Ф., Пастухов Ю. Ф., Волосова Н. К., Волосов К. А., Волосова А. К. О конечных методах решения уравнения Пуассона на прямоугольнике с краевым условием Дирихле/Д. Ф. Пастухов, Ю. Ф. Пастухов, Н. К. Волосова, К. А. Волосов, А. К. Волосова//УДК 517.6. Статья по математике. Численные методы, — Новополцк, Москва; 2020.19 С.
Ф., Пастухов Ю. Ф., Волосова Н. К., Волосов К. А., Волосова А. К. О конечных методах решения уравнения Пуассона на прямоугольнике с краевым условием Дирихле/Д. Ф. Пастухов, Ю. Ф. Пастухов, Н. К. Волосова, К. А. Волосов, А. К. Волосова//УДК 517.6. Статья по математике. Численные методы, — Новополцк, Москва; 2020.19 С. -12
.
-12
. Получены
достаточные условия корректности предложенного алгоритма, теоремы 1,2,3. Метод можно использовать в
прикладных задачах математической физики[15,16,17], а также в двумерных задачах гидродинамики,
система уравнений которых содержит уравнение Пуассона от функции тока, где правая часть – функция
вихря.
Получены
достаточные условия корректности предложенного алгоритма, теоремы 1,2,3. Метод можно использовать в
прикладных задачах математической физики[15,16,17], а также в двумерных задачах гидродинамики,
система уравнений которых содержит уравнение Пуассона от функции тока, где правая часть – функция
вихря. Локальные проявления описанных свойств напряженности электростатического поля выражаются связью дивергенции вектора напряженности с величиной объёмной плотности электрического заряда
Локальные проявления описанных свойств напряженности электростатического поля выражаются связью дивергенции вектора напряженности с величиной объёмной плотности электрического заряда (7)
(7)
 Проанализировать понятие сходимости итерационных методов, погрешности и ее контроля при вычислениях.
Проанализировать понятие сходимости итерационных методов, погрешности и ее контроля при вычислениях. В случае электромагнитного поля уравнение может быть получено, используя в качестве основы уравнения Максвелла и теорему Остроградского — Гаусса в дифференциальной форме.
В случае электромагнитного поля уравнение может быть получено, используя в качестве основы уравнения Максвелла и теорему Остроградского — Гаусса в дифференциальной форме. К тому же те вычислители, занимающиеся прикладными задачами прекрасно знают: точных решений не бывает, точно также как не бывает точных исходных параметров, коэффициентов систем и свободных членов. Да и простота программирования – выгодная черта данного метода.
К тому же те вычислители, занимающиеся прикладными задачами прекрасно знают: точных решений не бывает, точно также как не бывает точных исходных параметров, коэффициентов систем и свободных членов. Да и простота программирования – выгодная черта данного метода. , например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».
, например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод». Рассмотрение более общего случая произвольных граничных условий и вообще более подробное изложение — см. в статье Функция Грина.
Рассмотрение более общего случая произвольных граничных условий и вообще более подробное изложение — см. в статье Функция Грина.
 А. Математическое моделирование физических полей методом точечных источников / Ю. А. Бахвалов, С. Ю. Князев, А. А. Щербаков // Изв. РАН. Серия физическая. — 2008. — Т. 72, № 9. — С. 1259‒1261.
А. Математическое моделирование физических полей методом точечных источников / Ю. А. Бахвалов, С. Ю. Князев, А. А. Щербаков // Изв. РАН. Серия физическая. — 2008. — Т. 72, № 9. — С. 1259‒1261. — 2001. — Vol. 2 (1). — Pp. 87‒95.
— 2001. — Vol. 2 (1). — Pp. 87‒95. Alves, C. S. Chen // Advances in Computational Mathematics. — 2005. — Vol. 23 — Pр. 125‒142.
Alves, C. S. Chen // Advances in Computational Mathematics. — 2005. — Vol. 23 — Pр. 125‒142.

 Решение
генерируется общей функцией источника — это просто
соответственно взвешенная сумма
все решения функции Грина:
Решение
генерируется общей функцией источника — это просто
соответственно взвешенная сумма
все решения функции Грина:  (180) следует, что функция Грина имеет тот же вид, что и потенциал
генерируется точечным начислением. Это неудивительно, учитывая определение
функция Грина. Из уравнения(224) и (227) следует, что общее решение
уравнению Пуассона (226) записывается
(180) следует, что функция Грина имеет тот же вид, что и потенциал
генерируется точечным начислением. Это неудивительно, учитывая определение
функция Грина. Из уравнения(224) и (227) следует, что общее решение
уравнению Пуассона (226) записывается  Коротко,
Коротко,






 части, соответственно, произведенные однородной и волнистой частями
плотность заряда.
части, соответственно, произведенные однородной и волнистой частями
плотность заряда.
 В
область (а), это суперпозиция (24) и (28),
а в области (b) это (25) и (29). В обоих выражениях C равно
предоставлено (30).
В
область (а), это суперпозиция (24) и (28),
а в области (b) это (25) и (29). В обоих выражениях C равно
предоставлено (30). 5.6.3.
5.6.3. math.lamar.edu/Classes/DE/LaplacesEqn.aspx
math.lamar.edu/Classes/DE/LaplacesEqn.aspx Кроме того, разделение переменных позволяет учащемуся увидеть «гайки и болты» ОДУ, не заблудившись в теоремах единственности и взаимности (особенно при рассмотрении нетривиальных распределений зарядов). Однако пылкий студент должен изучить метод функций Грина, если он хочет продолжить обучение в аспирантуре (см. Классическую электродинамику Джона Дэвида Джексона).
Кроме того, разделение переменных позволяет учащемуся увидеть «гайки и болты» ОДУ, не заблудившись в теоремах единственности и взаимности (особенно при рассмотрении нетривиальных распределений зарядов). Однако пылкий студент должен изучить метод функций Грина, если он хочет продолжить обучение в аспирантуре (см. Классическую электродинамику Джона Дэвида Джексона). 0000046853 00000 п.
0000047033 00000 п.
0000047710 00000 п.
0000050751 00000 п.
0000050970 00000 п.
0000052338 00000 п.
0000052556 00000 п.
0000052892 00000 п.
0000058946 00000 п.
0000059170 00000 п.
0000059741 00000 п.
0000060000 00000 н.
0000060595 00000 п.
0000060894 00000 п.
0000061206 00000 п.
0000061923 00000 п.
0000062141 00000 п.
0000062532 00000 п.
0000063021 00000 п.
0000063540 00000 п.
0000064629 00000 н.
0000065079 00000 п.
0000065509 00000 п.
0000065891 00000 п.
0000065952 00000 п.
0000066542 00000 п.
0000067123 00000 п.
0000067703 00000 п.
0000067896 00000 п.
0000068553 00000 п.
0000068775 00000 п.
0000072010 00000 п.
0000072210 00000 п.
0000074736 00000 п.
0000074935 00000 п.
0000079039 00000 п.
0000079323 00000 п.
0000079398 00000 п.
0000079566 00000 п.
0000079777 00000 п.
0000079970 00000 н.
0000080130 00000 п.
0000080324 00000 п.
0000080534 00000 п.
0000080702 00000 п.
0000080916 00000 п.
0000081117 00000 п.
0000081277 00000 п.
0000046853 00000 п.
0000047033 00000 п.
0000047710 00000 п.
0000050751 00000 п.
0000050970 00000 п.
0000052338 00000 п.
0000052556 00000 п.
0000052892 00000 п.
0000058946 00000 п.
0000059170 00000 п.
0000059741 00000 п.
0000060000 00000 н.
0000060595 00000 п.
0000060894 00000 п.
0000061206 00000 п.
0000061923 00000 п.
0000062141 00000 п.
0000062532 00000 п.
0000063021 00000 п.
0000063540 00000 п.
0000064629 00000 н.
0000065079 00000 п.
0000065509 00000 п.
0000065891 00000 п.
0000065952 00000 п.
0000066542 00000 п.
0000067123 00000 п.
0000067703 00000 п.
0000067896 00000 п.
0000068553 00000 п.
0000068775 00000 п.
0000072010 00000 п.
0000072210 00000 п.
0000074736 00000 п.
0000074935 00000 п.
0000079039 00000 п.
0000079323 00000 п.
0000079398 00000 п.
0000079566 00000 п.
0000079777 00000 п.
0000079970 00000 н.
0000080130 00000 п.
0000080324 00000 п.
0000080534 00000 п.
0000080702 00000 п.
0000080916 00000 п.
0000081117 00000 п.
0000081277 00000 п. .: j = Nl4 ~ d $) v
.: j = Nl4 ~ d $) v