через диаметр и радиус. Терминология, основные формулы и характеристика фигуры
Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.
В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Обозначения величин и формулы
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
Условие. Узнать длину окружности, радиус которой равен 5 см.
Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Ответ: l = 31,4 см.
Задача вторая
Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Ответ: r = 200 мм.
Задача третья
Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.
Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.
Ответ: d = 18 см.
Задача четвертая
Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ: l 1 = 18,84 см, l 2 = 31,4 см.
Задача пятая
Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
Ответ: Белка пробегает 6,28 м.
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика.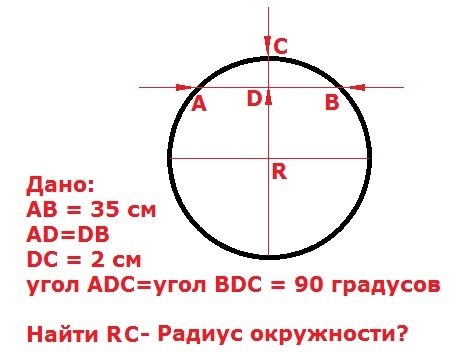 Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара.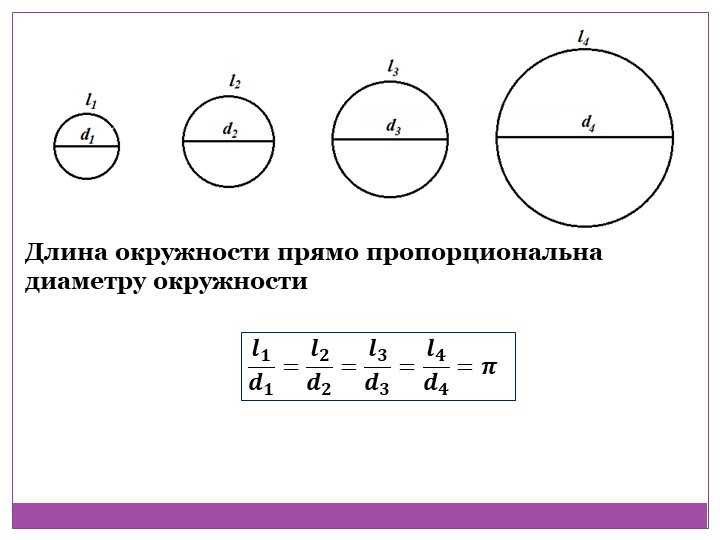 Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.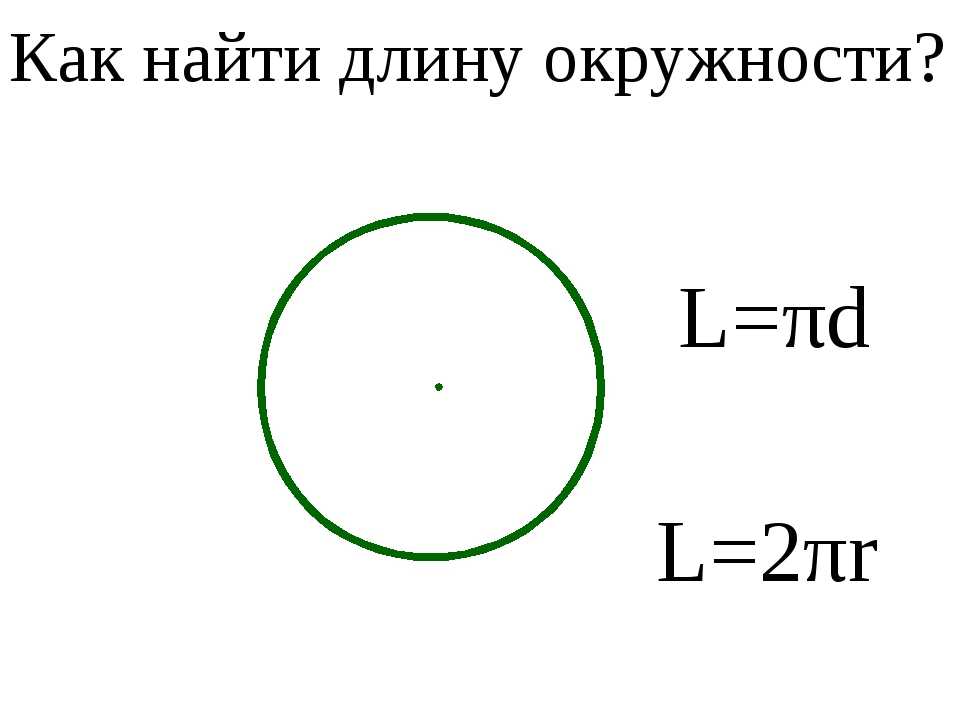
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности. 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
§ 117. Длина окружности и площадь круга.
1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис. 27).
Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.
Отрезок прямой линии (АВ), соединяющий две любые точки окружности и проходящий через её центр, называется диаметром . Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.
Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.
Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д.) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра). Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.
Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра), то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D .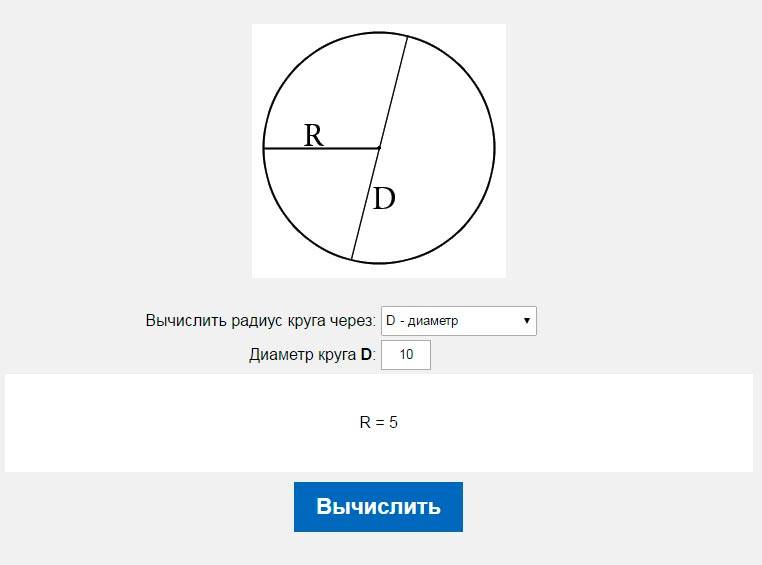 Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
В математике путём теоретических соображений установлено, что искомое отношение С: D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно 3,1416 . Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Напишем формулу для определения длины окружности.
Так как С: D = π , то
C = πD
т. е. длина окружности равна произведению числа π на диаметр.
Задача 1. Найти длину окружности (С ) круглой комнаты, если диаметр её D = 5,5 м.
Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:
5,5 3,14 = 17,27 {м).
Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.
Эта задача обратна предыдущей. Найдём диаметр колеса:
125,6: 3,14 = 40 (см).
Найдём теперь радиус колеса:
40: 2 = 20 (см).
2. Площадь круга. Чтобы определить площадь круга, можно было бы начертить на бумаге круг данного радиуса, покрыть его прозрачной клетчатой бумагой и потом сосчитать клетки, находящиеся внутри окружности (рис. 28).
Но такой способ неудобен по многим причинам. Во-первых, вблизи контура круга получается ряд неполных клеток, о величине которых судить трудно. Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу.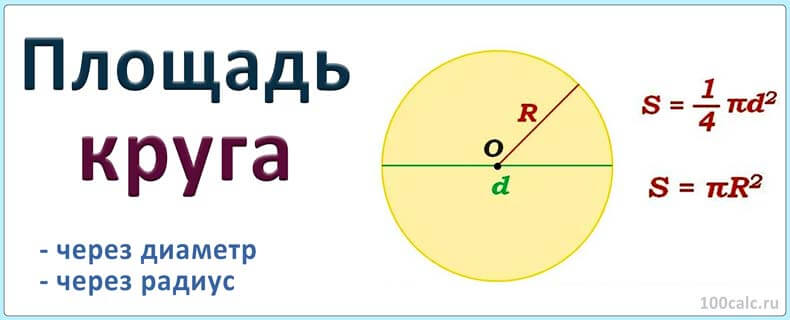 В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
Затем сложим их так, как показано на рисунке 30, т. е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.
Длина этой фигуры (основание) равна приблизительно длине полуокружности, а высота — приблизительно радиусу. Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:
которая читается так: площадь круга равна длине полуокружности, умноженной на радиус.
Задача. Найти площадь круга, радиус которого равен 4 см. Найдём сначала длину окружности, потом длину полуокружности, а затем умножим её на радиус.
1) Длина окружности С = π D = 3,14 8 = 25,12 (см).
2) Длина половины окружности C / 2 = 25,12: 2= 12,56 (см).
3) Площадь круга S = C / 2 r = 12,56 4 = 50,24 (кв. см).
§ 118. Поверхность и объём цилиндра.
Задача 1. Найти полную поверхность цилиндра, у которого диаметр основания 20,6 см и высота 30,5 см.
Форму цилиндра (рис. 31) имеют: ведро, стакан (не гранёный), кастрюля и множество других предметов.
Полная поверхность цилиндра (как и полная поверхность прямоугольного параллелепипеда) состоит из боковой поверхности и площадей двух оснований (рис. 32).
Чтобы наглядно представить себе, о чём идёт речь, необходимо аккуратно сделать модель цилиндра из бумаги. Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
1) Длина окружности: 20,6 3,14 = 64,684 (см).
2) Площадь боковой поверхности: 64,684 30,5= 1972,862(кв.см).
3) Площадь одного основания: 32,342 10,3 = 333,1226 (кв.см).
4) Полная поверхность цилиндра:
1972,862 + 333,1226 + 333,1226 = 2639,1072 (кв. см) ≈ 2639 (кв. см).
Задача 2. Найти объём железной бочки, имеющей форму цилиндра с размерами: диаметр основания 60 см и высота 110 см.
Чтобы вычислить объём цилиндра, нужно припомнить, как мы вычисляли объём прямоугольного параллелепипеда (полезно прочитать § 61).
Единицей измерения объёма у нас будет кубический сантиметр. Сначала надо узнать, сколько кубических сантиметров можно расположить на площади основания, а затем найденное число умножить на высоту.
Чтобы узнать, сколько кубических сантиметров можно уложить на площади основания, надо вычислить площадь основания цилиндра. Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:
1) Длина окружности: 60 3,14 = 188,4 (см).
2) Площадь круга: 94,2 30 = 2826 (кв. см).
3) Объём цилиндра: 2826 110 = 310 860 (куб. см).
Ответ. Объём бочки 310,86 куб. дм.
Если обозначим объём цилиндра буквой V , площадь основания S , высоту цилиндра H , то можно написать формулу для определения объёма цилиндра:
V = S H
которая читается так: объём цилиндра равен площади основания, умноженной на высоту.
§ 119. Таблицы для вычисления длины окружности по диаметру.
При решении различных производственных задач часто приходится вычислять длину окружности. Представим себе рабочего, который изготовляет круглые детали по указанным ему диаметрам. Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.
Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.
Приведём небольшую часть таких таблиц и расскажем, как ими пользоваться.
Пусть известно, что диаметр окружности равен 5 м. Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.
По этим же таблицам можно производить и обратные вычисления. Если известна длина окружности, то можно найти в таблице соответствующий ей диаметр. Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.
Таблицы, о которых здесь сказано, имеются в различных справочниках. В частности, их можно найти в книжке «Четырёхзначные математические таблицы» В. М. Брадиса. и в задачнике по арифметике С. А. Пономарёва и Н. И. Сырнева.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Калькулятор длины окружности
Калькулятор длины окружностиРассчитайте периметр круга по одному известному: диаметру, радиусу или площади круга.
Что известноДиаметрРадиусПлощадь круга
ДлинаРазмерность
СантиметрыМетрыМиллиметрыКилометры
РаcсчитатьДлина окружности равна (см):
0
Чтобы правильно интерпретировать расчёт, читайте эту информацию.
Скопировать:
ссылку link
код code
Что такое окружность?
Окружность – это замкнутая плоская кривая, ограничивающая круг.
Или, другими словами, окружность представляет собой множество точек, удаленных на одно и тоже расстояние от центра круга на длину радиуса этого круга. А длина окружности – это длина этой кривой, которую образует это множество точек и которая ограничивает собой круг. Это хорошо видно на иллюстрации выше.
Как найти длину окружности?
Чтобы вычислить длину окружности, нужно знать радиус, диаметр или площадь круга. Причём достаточно только чего-то одного из этих элементов.
По диаметру
Диаметр — это такой отрезок, который соединяет две точки на окружности и проходит через центр круга. Чтобы найти длину окружности через диаметр, просто умножаем диаметр окружности на число Пи и получаем длину окружности.
Формула будет такой:
L = π × d
Где L – длина окружности, π – константа, равная примерно 3,14, а d – это диаметр.
Например, нам нужно посчитать периметр канализационной трубы диаметром 100 мм. Окружность этой трубы можно найти весьма несложными расчётами:
L = 3,14 × 100 = 314 мм.
Кстати, у труб есть 2 окружности и 2 диметра: внутренние и внешние. Это хорошо показано на рисунке ниже.
Всегда обращайте внимание, какой именно диаметр известен и какую длину окружности вам требуется вычислить. Часто внутренний диаметр обозначается малой d или D1, а наружный просто – D или DN.
Зная радиус
Радиус окружности — это отрезок, который соединяет центр окружности с точкой на окружности. Радиус равен половине диаметра, поэтому вычисление длины окружности будет похоже на предыдущий случай: умножаем радиус на два и на число пи и получаем длину окружности.
Формула расчёта выглядит следующим образом:
L = 2π × R
Где L – длина окружности, π – константа (приблизительно 3,14), а r – это радиус.
К примеру, нужно посчитать длину внутренней окружности трубы, с внутренним радиусом 26 мм. В этом случае периметр получается следующим образом:
В этом случае периметр получается следующим образом:
L = 2 × 3,14 × 26 = 163,28 мм.
Также обратите внимание, что в число Пи взято с точностью до двух знаков после запятой, и всегда расчёт через Пи идёт с округлением и является приблизительным.
Через площадь круга
И, пожалуй, самым редким случаем калькуляции периметра круга будет тот, когда нам известна только площадь этого круга. В этом случае, чтобы рассчитать длину окружности, можно воспользоваться следующей формулой:
L = (4Sπ)1/2
Где L – длина окружности, S – площадь круга, а π – константа, равная 3,14.
То есть длина окружности равна квадратному корню произведения площади круга, числу пи, умноженному на четыре. На всякий случай, корень и степень ½ – это одно и то же.
Возьмём пример, к нам прилетели инопланетяне и оставили круги на полях.
Площадь одного из этих кругов составила аж 1146,5 квадратных метра. Чтобы рассчитать длину окружности, нужно сделать следующее:
- Умножить 4 на 3,14, и полученное произведение умножить на площадь круга 1146,5.
 Получаем 14400,04.
Получаем 14400,04. - И теперь находим квадратный корень из этого числа и получаем примерно 120 метров. Это и есть длина окружности.
Как и в прошлых случаях из-за наличия числа Пи, которое является иррациональным, ответ будет считаться с округлением.
❓Вопросы и ответы
И наконец, предлагаем вам прочитать ответы на некоторые часто задаваемые вопросы относительно вычисления длины окружности.
Что что имеет большее значение радиус, диаметр, длина окружности или площадь круга?
Площадь круга. А если выставить всё это по мере убывания, то рейтинг будет таким:
- Площадь круга
- Длина окружности
- Диаметр
- Радиус
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разные калькуляторы, в частности калькуляторы: диаметра, площади круга и длины окружности. Для последней калькулятор находится наверху данной страницы.
Для последней калькулятор находится наверху данной страницы.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Хватит ли чего-то одного (диаметра, радиуса, площади) для расчёта длины окружности?
org/Answer»>Да, хватит. Формулы и примеры расчетов периметра круга, в которых используется что-то одно из перечисленного, есть выше на данной странице.Что такое внутренняя и внешняя окружность? Чем они отличаются?
Внутренняя и внешняя окружность (а также диаметр) чаще всего используются для расчёта параметров труб, у которых есть стенки ненулевой ширины. Поэтому окружность внутри трубы всегда меньше окружности снаружи. Для окружности снаружи используется обозначение L или LN, а диаметра – D или DN. А для периметра и диаметра круга внутри добавляется нижний индекс «единица»: L1 и D1, или используются буквы в нижнем регистре (малые): l и d.
Поделитесь в соцсетях
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Как вычислить длину окружности, если я знаю диаметр?
33
33 ответа
Джеймс Фитцджеральд ответил
Чтобы вычислить это, вам нужна правильная формула. Формула длины окружности классифицируется как пи х диаметр. Его также можно записать как pi.d.
Окружность — это, по сути, расстояние или длина по окружности. _, правильно произносимое как пирог, является иррациональным числом, а это значит, что его нельзя записать в виде дроби. Поэтому, чтобы быть уверенным, хорошее приближение π равно 3,14 при использовании в конкретных формулах.
Круговая диаграмма, или число Пи, необходима для вычисления длины окружности. Убедитесь, что вы знаете, где находится центр круга. Вам нужно будет найти диаметр, который является линией, которая касается двух концов круга и центра.
Затем вы можете использовать эту линию соответственно или радиус вместе с π для вычисления длины окружности. Все, что вам нужно сделать, это умножить радиус на 2, чтобы получить диаметр.
Другие вещи, которые следует учитывать в круге, включают радиус, который представляет собой линию, которая касается внешней части круга и центра. Он не соприкасается более чем с одной частью внешней среды. Вы сможете заменить диаметр на это для альтернативной формулы. Чтобы получить радиус, вам нужно разделить диаметр на 2, чтобы получить радиус.
Есть две формулы и, учитывая, что вы уже знаете диаметр, то будет намного проще сделать окружность. В математических терминах длина окружности в алгебре описывается как:
C = π x диаметр
или
C = π x (2 x радиус)
поблагодарил автора.
брякнул это.
Оддман ответил
36*Pi ≈ 113,1
поблагодарил автора.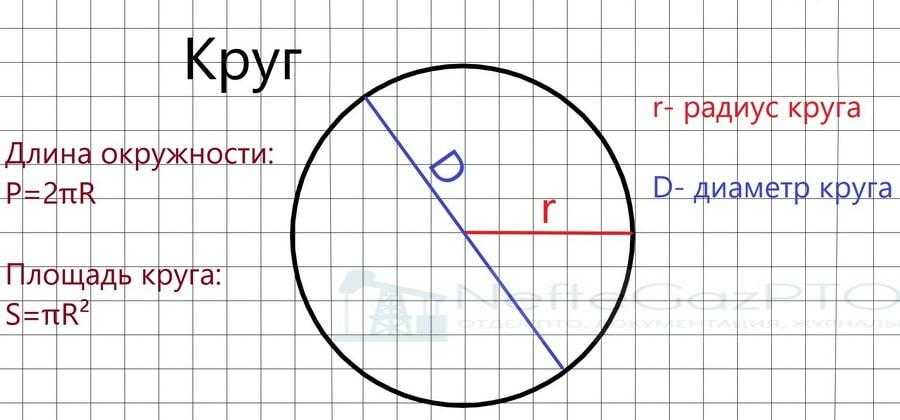
брякнул это.
Mainul Hussain ответил
113,04 дюйма, принимая pi=3,14
поблагодарил автора.
брякнул это.
Кэти Гарри ответил
Окружность на самом деле похожа на периметр круга. Формула для нахождения длины окружности:
C = Pi x r 2
Где
C = длина окружности
pi = 3,14
r = радиус
У нас есть заданный диаметр. Радиус равен половине диаметра, поэтому:
Радиус = Диаметр
2
Радиус = 28
2
Радиус = 14 дюймов
Теперь вычислим длину окружности:
C = Pi x r 2
C = 3,14 x (14) 2
C = 3,14 x 196
C = 615,4 дюйма ——ОТВЕТ
поблагодарил автора.
брякнул это.
Кэти Гарри ответила
Формула для нахождения длины окружности:
C = 2 x pi x r
Где
C = длина окружности
r = радиус
pi = 3,14
Здесь у нас нет значения радиуса, хотя оно используется в формуле.
Итак, нам нужно сначала найти радиус этой окружности. Радиус всегда равен половине диаметра, поэтому:
радиус = диаметр/2
радиус = 11/2
радиус = 5,5 футов
Теперь найдем длину окружности:
C = 2 x pi x r
C = 2 (3,14 x 5,5)
C = 2(17,27)
C = 34,54 фута
Следовательно, длина окружности этого круга составляет 34,54 фута.
поблагодарил автора.
брякнул это.
Аноним ответил
25.13
поблагодарил автора.
брякнул это.
Анонимный ответил
Чтобы найти длину окружности, зная диаметр. Все, что вам нужно сделать, это умножить диаметр на число пи (пи равно 3,14!!) и вы его получили. ХОРОШО ТЫ СДЕЛАЛА ЭТО!!!!
Все, что вам нужно сделать, это умножить диаметр на число пи (пи равно 3,14!!) и вы его получили. ХОРОШО ТЫ СДЕЛАЛА ЭТО!!!!
Формула:(пример) 3.14-pi
x 2-диаметр
»»»»»»’
6.28-длина окружности
поблагодарил автора.
брякнул это.
Робин Ротман ответила
Классическая формула для нахождения длины окружности C=2pi r или длина окружности равна 2 умножить на пи (пи равно 3,14) умножить на радиус. Радиус круга составляет половину диаметра, поэтому вы можете просто умножить диаметр на 3,14 (пи). Это ваша окружность.
поблагодарил автора.
брякнул это.
Аноним ответил
Для диаметра 36 дюймов
поблагодарил автора.
брякнул это.
Аноним ответил
25.13
поблагодарил автора.
брякнул это.
Оддман ответил
Да, и вы сможете, если умножите 8 см на число Пи.
окружность = 8*3,1416 см = 25,1328 см
поблагодарил автора.
брякнул это.
Аноним ответил
25.12
поблагодарил автора.
брякнул это.
Анонимный ответил
Если я сделаю круг диаметром 3 фута из 12-дюймовых кирпичей, сколько мне понадобится?
поблагодарил автора.
брякнул это.
янтарный Джон ответил
Длина окружности равна удвоенному произведению постоянной пи на радиус окружности.
Длина окружности = 2 * пи * радиус
Пи = 3,14
Диаметр = 2 * радиус
Радиус = Диаметр/ 2
Радиус = 14/2
Радиус = 7 единиц
Окружность = 2 * 3,14 * 7 единиц
поблагодарил автора.
брякнул это.
Анонимный ответил
Да
поблагодарил автора.
выпалил это.
Аноним ответил
Какова площадь круга, длина окружности которого равна 8
поблагодарил автора.
брякнул это.
Аноним ответил
А 6.28
поблагодарил автора.
брякнул это.
Анонимный ответил
R=5
поблагодарил автора.
брякнул это.
Аноним ответил
2 раза диаметр равен окружности
поблагодарил автора.
брякнул это.
Анонимный ответил
100,48
поблагодарил автора.
брякнул это.
Анонимный ответил
16м
поблагодарил автора.
брякнул это.
Анонимный ответил
34,54 фута
поблагодарил автора.
брякнул это.
Пэт Меррифилд ответил
Ближайший ответ, который у вас есть, d, поскольку я придумал 50,27.
поблагодарил автора.
брякнул это.
Анонимный ответил
Думаю, 2 X (круг) X r = длина окружности. Круг равен 3,14, а R — радиус, равный 1/2 диаметра.
поблагодарил автора.
брякнул это.
Анонимный ответил
Если диаметр круга равен 8, длина окружности равна 25,1327:
Окружность = (Диаметр) (пи)
= Окружность = (8) (пи)
= Окружность = 25,1327
поблагодарил автора. 2
2
поблагодарил автора.
брякнул это.
Аноним ответил
Умножить диаметр на 3,14
поблагодарил автора.
брякнул это.
Аноним ответил
Умножить на 3
поблагодарил автора.
брякнул это.
Анонимный ответил
25.13
поблагодарил автора.
брякнул это.
Анонимный ответил
Да помогите мне плз
поблагодарил автора.
брякнул это.
Мерил Харгривз ответила
Умножьте диаметр на пи (греческая буква!)
Значение приблизительно равно 22/7 или 3,1416 или даже более точно, в зависимости от того, что вам дали.
C= Pd или c=2Pr
(Нет символа пи!!)
поблагодарил автора.
брякнул это.
Майк Каталанотто-младший ответил
Периметр = пи (3,1416) x диаметр.
поблагодарил автора.
брякнул это.
Кёко Катаяма ответила
C = (pi) D; Вы делаете математику.
поблагодарил автора.
брякнул это.
Вам также может понравиться…
Ответить на вопрос
сообщите об этом объявлении
Длина окружности к диаметру — формула, значение, пример
LearnPracticeDownload
Длина окружности к диаметру круга представляет собой отношение, используемое для определения стандартного определения числа Пи (π). Окружность – это его граница или длина окружности. Принимая во внимание, что диаметр — это прямая линия, соединяющая точку с одного конца круга с точкой на другом конце, проходящая через центр. Давайте узнаем больше о длине окружности в диаметре, формулах и решим несколько примеров.
Давайте узнаем больше о длине окружности в диаметре, формулах и решим несколько примеров.
| 1. | Окружность к диаметру Определение |
| 2. | Окружность в диаметр Формула |
| 3. | Метод расчета окружности по диаметру |
| 4. | Разница между окружностью и диаметром |
| 5. | Часто задаваемые вопросы об окружности и диаметре |
Окружность к диаметру Определение
Окружность к диаметру — это отношение, в котором оно определяет π, поскольку длина окружности связана с диаметром. Мы знаем, что окружность представляет собой набор точек, равноудаленных от центральной точки O. Если известен диаметр d, вы можете легко найти длину окружности C, используя соотношение: C = πd. Итак, если окружность C поставить в отношении к диаметру d, мы получим ответ π. А стандартное определение π — это отношение длины окружности и диаметра круга.
Окружность в Диаметр Формула
Длина окружности может быть найдена с помощью радиуса или диаметра. Радиус — это отрезок, соединяющий центр с границей круга, т. е. длина равна половине диаметра. Для расчета этих трех измерений окружности используются разные формулы. Посмотрим формулы:
| Критерий | Формула |
|---|---|
| Длина окружности с радиусом | С = 2πr |
| Диаметр круга с радиусом | Д = 2р |
| Окружность круга диаметром | С = πd |
Где,
- C = Окружность
- r = радиус
- d = диаметр
- π = 22/7 или 3,142 приблизительно
Метод расчета окружности по диаметру
Чтобы вычислить длину окружности круглой формы, когда задан диаметр, нам нужно использовать формулу C = πd.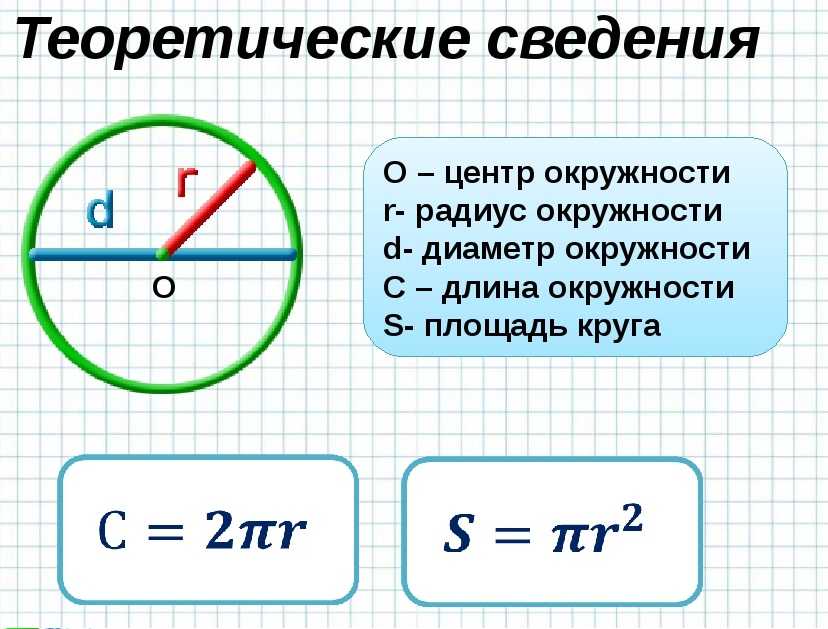 Здесь необходимо выполнить два простых шага:
Здесь необходимо выполнить два простых шага:
- Шаг 1: Указан диаметр формы. Если нет, то нам нужно вычислить его с помощью радиуса и использовать любую из приведенных выше формул.
- Шаг 2: Умножьте π на диаметр, чтобы получить окончательный результат.
Пример: Джейсон хочет покрасить внешнюю границу круглого бассейна. Он знает, что диаметр бассейна 50 футов. Чтобы рассчитать необходимое количество краски, ему нужна окружность бассейна. Давайте поможем ему вычислить это.
Решение: Дано, Диаметр (d) = 50 футов.
Используйте формулу для длины окружности C = πd = 50 × π = 50 × 3,142 = 157,1 ок.
Таким образом, окружность бассейна составляет примерно 157,1 фута.
Разница между окружностью и диаметром
Окружность и диаметр считаются двумя важными измерениями окружности. Они разделяют отношение в форме уравнения, т.е. C = πd. Посмотрите на таблицу ниже, чтобы понять окружность и диаметр.
Посмотрите на таблицу ниже, чтобы понять окружность и диаметр.
| Окружность | Диаметр |
|---|---|
| Длина одного полного круга по кругу. | Длина отрезка, который делит окружность пополам. |
| Считается внешним измерением. | Считается внутренним измерением. |
| Считается периметром круга. | Это длина двух точек на окружности окружности. |
Важные примечания
- π (Пи) — математическая константа, представляющая собой отношение длины окружности к ее диаметру. Оно приближается к π = 22/7 или 3,14.
- Мы можем найти длину окружности, используя радиус или диаметр.
- Длина окружности C и диаметр d окружности связаны соотношением C= πd
☛Связанные темы
Вот список нескольких тем, связанных с отношением длины окружности к диаметру.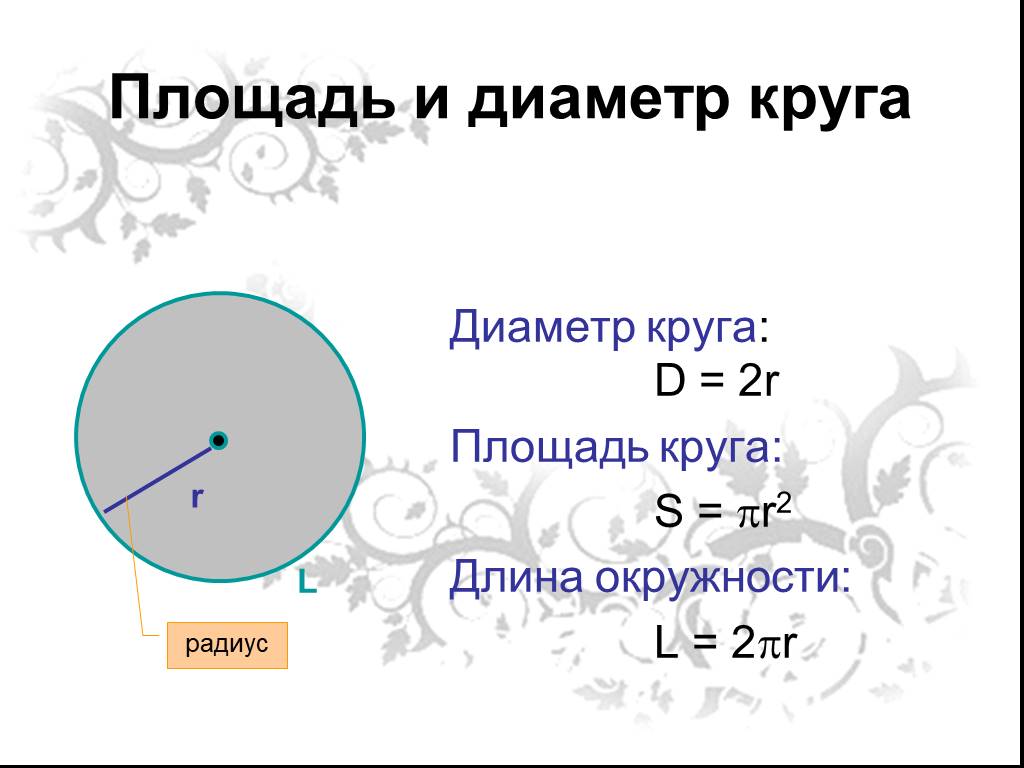
- Окружность Земли
- Калькулятор отношения диаметра к окружности
- Калькулятор окружности
- Хорды и диаметры
Окружность к диаметру Примеры
Пример 1: У Майкла есть круглый парк диаметром 21 фут перед его домом. Он хочет огородить парк. Он хочет знать длину веревки, необходимой для фехтования. Вы можете помочь ему?
Решение: Дано,
Диаметр парка d= 21 фут.
Чтобы найти длину веревки, нам понадобится длина окружности парка.
Длина окружности C футов.
C = πd
C = (22/7) × 21
C = 66
Следовательно, Михаилу понадобится веревка длиной 66 футов.
Пример 2: Джон чинит трубу в своей ванной. Диаметр трубы 2 дюйма. Можете ли вы определить длину ленты, чтобы обернуть трубу?
Решение: Дано,
Диаметр трубы d = 2 дюйма
Чтобы найти длину ленты, определим длину окружности трубы.

Длина окружности C дюймов.
C = πd
C = (22/7) × 2
C = 6,285
Следовательно, требуемая длина ленты составляет 6,285 дюйма.
Пример 3: Длина окружности колеса 440 см. Найдите его радиус и диаметр.
Решение: Дано,
Окружность колеса = 440 см
Длина окружности формула = 2πr
Давайте сначала подставим известные значения, чтобы найти радиус.
440 = 2πr
440 = 2 × (22/7) × r
радиус = 70 см
диаметр = 2 × радиус диаметр 140см.
перейти к слайдуперейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по отношению длины окружности к диаметру
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об окружности и диаметре
Как преобразовать длину окружности в диаметр?
Формула для вычисления длины окружности с диаметром: C = πd.

 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м. Получаем 14400,04.
Получаем 14400,04.

 Формат PDF / A безопаснее формата PDF и позволяет архивировать содержимое в течение более длительного периода времени. Это связано с тем, что JPG-файл может быть сильно защищен только при преобразовании в формат PDF/A. Это также поможет вам управлять изображениями в индивидуальном порядке с нужной ориентацией страницы, форматом и полями. Быстрое преобразование является еще одним фактором при использовании надежного и надежного конвертера JPG в PDF/A — PDFelement.
Формат PDF / A безопаснее формата PDF и позволяет архивировать содержимое в течение более длительного периода времени. Это связано с тем, что JPG-файл может быть сильно защищен только при преобразовании в формат PDF/A. Это также поможет вам управлять изображениями в индивидуальном порядке с нужной ориентацией страницы, форматом и полями. Быстрое преобразование является еще одним фактором при использовании надежного и надежного конвертера JPG в PDF/A — PDFelement. Выберите выходную папку и, наконец, нажмите кнопку «Сохранить».
Выберите выходную папку и, наконец, нажмите кнопку «Сохранить».
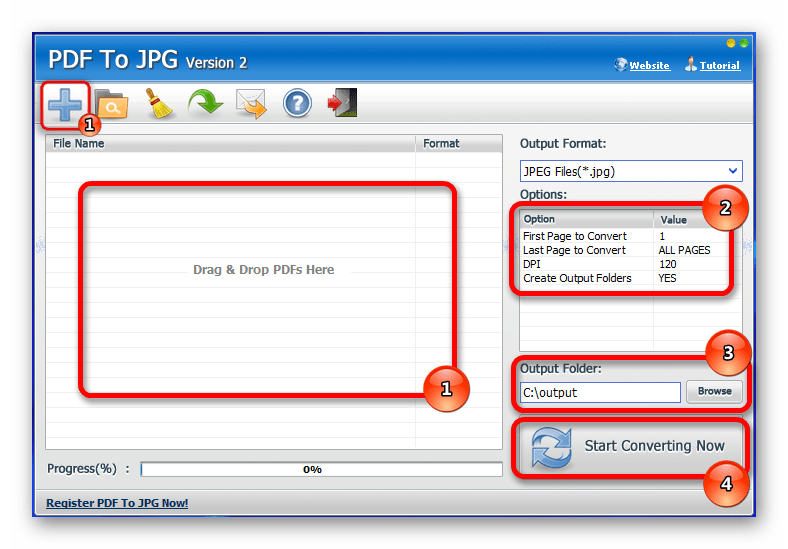 Я понятия не имею, как быстро и одновременно изменить их все. Пожалуйста, помогите мне найти правильное решение для этого процесса. Пожалуйста, объясните мне процесс преобразования PDF в JPG. Заранее спасибо.»
Я понятия не имею, как быстро и одновременно изменить их все. Пожалуйста, помогите мне найти правильное решение для этого процесса. Пожалуйста, объясните мне процесс преобразования PDF в JPG. Заранее спасибо.» 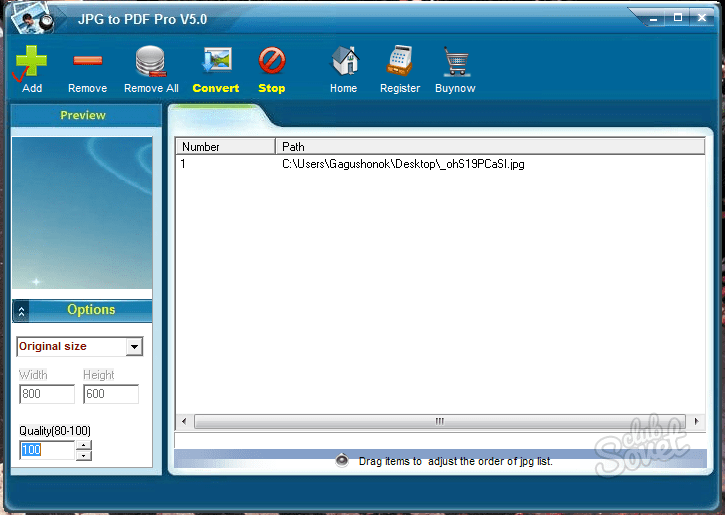 Конвертер PDF в JPEG — это прямое и быстрое программное обеспечение, которое работает только в операционных системах Windows, таких как 11, 10, 8.1, 8, 7, XP и т. д.
Конвертер PDF в JPEG — это прямое и быстрое программное обеспечение, которое работает только в операционных системах Windows, таких как 11, 10, 8.1, 8, 7, XP и т. д.
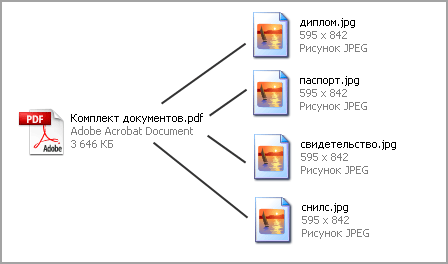 Также поддерживаются версии Adobe Reader.
Также поддерживаются версии Adobe Reader.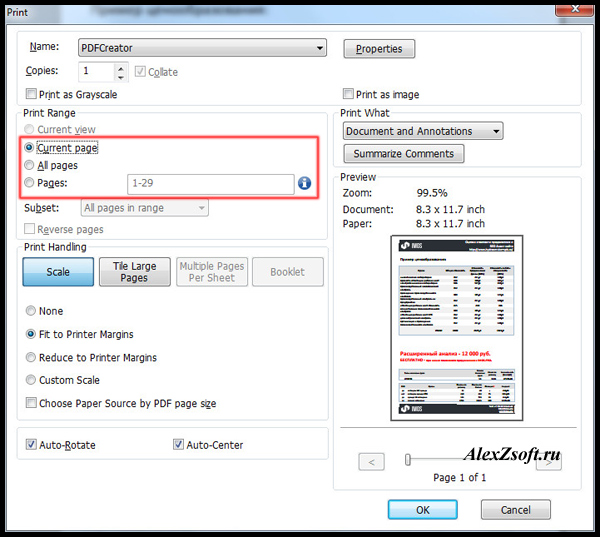 Его можно использовать без особых усилий и требуется всего несколько кликов.
Его можно использовать без особых усилий и требуется всего несколько кликов.
 Кроме того, вы можете использовать эту программу для Mac, чтобы легко создавать и настраивать PDF-файлы.
Кроме того, вы можете использовать эту программу для Mac, чтобы легко создавать и настраивать PDF-файлы.

 производные
производные 1).
1).
 1).
1).
 с. скачать
с. скачать






 Создавать PDF-файлы из изображений JPG еще никогда не было так просто!
Создавать PDF-файлы из изображений JPG еще никогда не было так просто!
 Просто загрузите файлы, и веб-инструмент автоматически сохранит изображения JPG в формате PDF.
Просто загрузите файлы, и веб-инструмент автоматически сохранит изображения JPG в формате PDF. Встроенные приложения macOS Preview и Shortcuts, а также сторонние приложения и веб-сайты легко позволяют это сделать. В этом руководстве показано, как преобразовать PDF в JPG или PNG.
Встроенные приложения macOS Preview и Shortcuts, а также сторонние приложения и веб-сайты легко позволяют это сделать. В этом руководстве показано, как преобразовать PDF в JPG или PNG.

 Вы также можете настроить значок.
Вы также можете настроить значок. Некоторые также предлагают пробный период. Если ваша работа связана с ежедневным преобразованием PDF-файлов в файлы изображений, вы можете попробовать следующие приложения:
Некоторые также предлагают пробный период. Если ваша работа связана с ежедневным преобразованием PDF-файлов в файлы изображений, вы можете попробовать следующие приложения:
 Таким образом, все скриншоты, которые вы делаете, будут одного размера.
Таким образом, все скриншоты, которые вы делаете, будут одного размера. Им нужно, чтобы преобразованное изображение JPG получилось в высоком качестве. Этот пост познакомит пользователей с тем, как конвертировать изображения PDF в JPG в высоком качестве.
Им нужно, чтобы преобразованное изображение JPG получилось в высоком качестве. Этот пост познакомит пользователей с тем, как конвертировать изображения PDF в JPG в высоком качестве. Если вам нужны фотографии в формате jpg с высоким разрешением, установите более высокое значение DPI, например 300 dpi или даже 600 dpi.
Если вам нужны фотографии в формате jpg с высоким разрешением, установите более высокое значение DPI, например 300 dpi или даже 600 dpi. Выберите PDF to Image и установите качество изображения на более высокое dpi. Вы можете конвертировать PDF в JPG с разрешением 300 dpi, 600 dpi и т. д. Нажмите «Применить».
Выберите PDF to Image и установите качество изображения на более высокое dpi. Вы можете конвертировать PDF в JPG с разрешением 300 dpi, 600 dpi и т. д. Нажмите «Применить». Вы также найдете множество функций редактирования с этим программным обеспечением. Функции редактирования в программном обеспечении включают в себя внесение изменений в различные элементы файлов PDF. Вы можете легко конвертировать PDF в JPG высокого качества с помощью PDFelement. Существует также полезная функция пакетного преобразования. Это позволяет конвертировать сразу несколько PDF-файлов в JPG.
Вы также найдете множество функций редактирования с этим программным обеспечением. Функции редактирования в программном обеспечении включают в себя внесение изменений в различные элементы файлов PDF. Вы можете легко конвертировать PDF в JPG высокого качества с помощью PDFelement. Существует также полезная функция пакетного преобразования. Это позволяет конвертировать сразу несколько PDF-файлов в JPG. Здесь вы можете контролировать преобразование PDF в JPG с точными размерами DPI от 10 до 1200 точек на дюйм. Например, если вы хотите вывести PDF в JPG с разрешением 600 точек на дюйм, PDF в JPG с разрешением 300 точек на дюйм, с помощью этого онлайн-инструмента можно получить точные результаты.
Здесь вы можете контролировать преобразование PDF в JPG с точными размерами DPI от 10 до 1200 точек на дюйм. Например, если вы хотите вывести PDF в JPG с разрешением 600 точек на дюйм, PDF в JPG с разрешением 300 точек на дюйм, с помощью этого онлайн-инструмента можно получить точные результаты. Кроме того, вы можете воспользоваться другими функциями программного обеспечения.
Кроме того, вы можете воспользоваться другими функциями программного обеспечения. Вы можете выбрать один из трех вариантов разрешения для изображений JPG.
Вы можете выбрать один из трех вариантов разрешения для изображений JPG.
 Затем в «Дополнительных настройках» введите 1200 dpi и нажмите «Преобразовать». Затем вы можете получить PDF в формате JPG в высоком качестве.
Затем в «Дополнительных настройках» введите 1200 dpi и нажмите «Преобразовать». Затем вы можете получить PDF в формате JPG в высоком качестве.
 «На данный момент самой маленькой известной звездой является RXJ-1856-37 диаметром всего 14 километров», — говорит астроном Хорхе Хорват, также из USP.
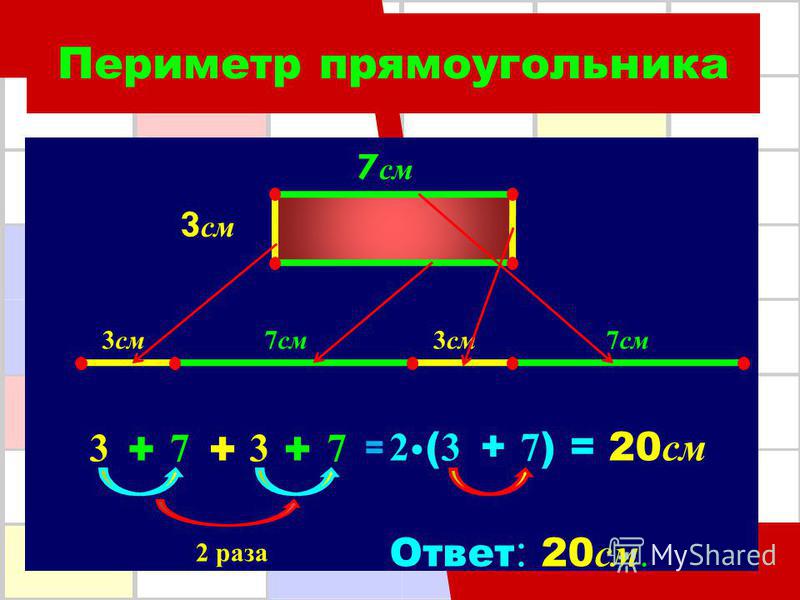
«На данный момент самой маленькой известной звездой является RXJ-1856-37 диаметром всего 14 километров», — говорит астроном Хорхе Хорват, также из USP. Периметр – это мера, наблюдаемая у плоских геометрических фигур, то есть двумерных фигур.
Периметр – это мера, наблюдаемая у плоских геометрических фигур, то есть двумерных фигур.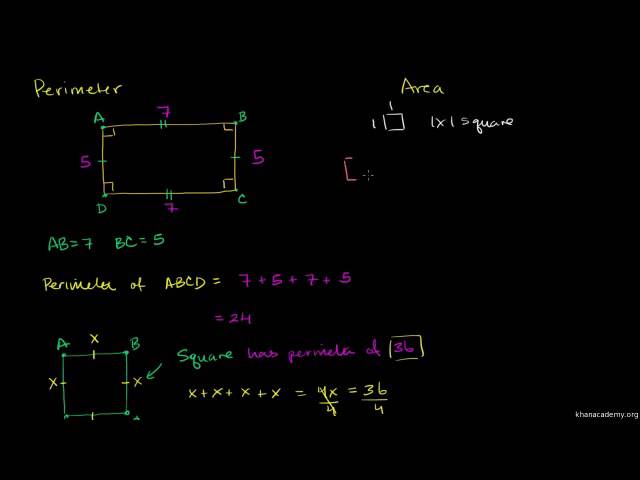

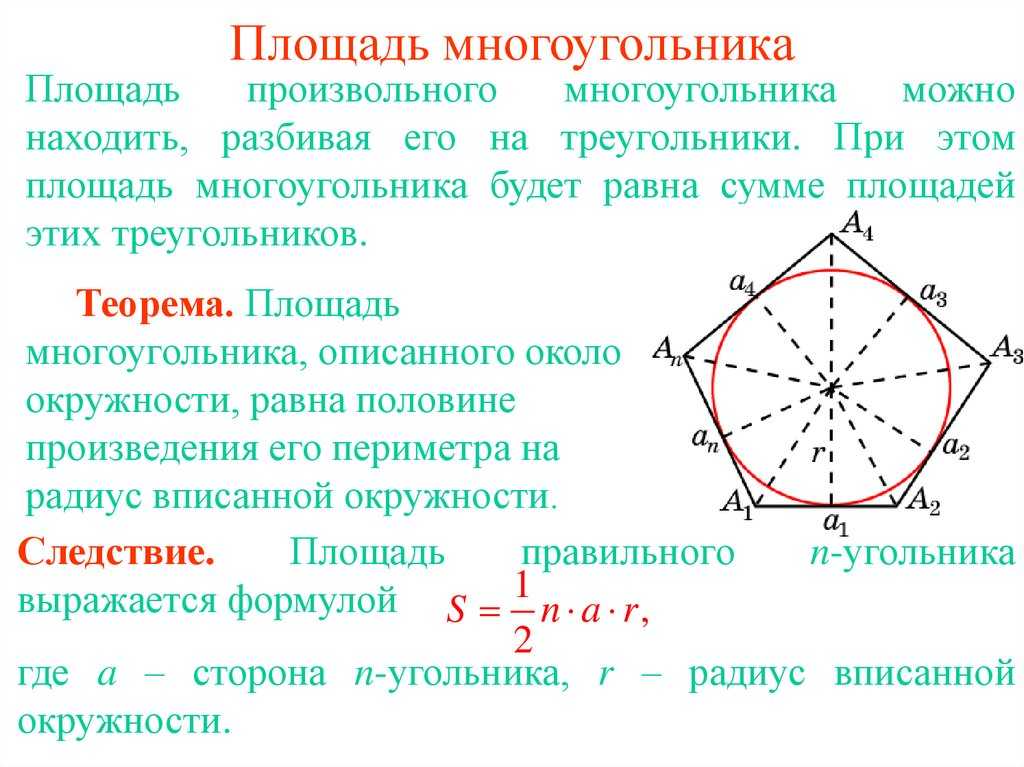
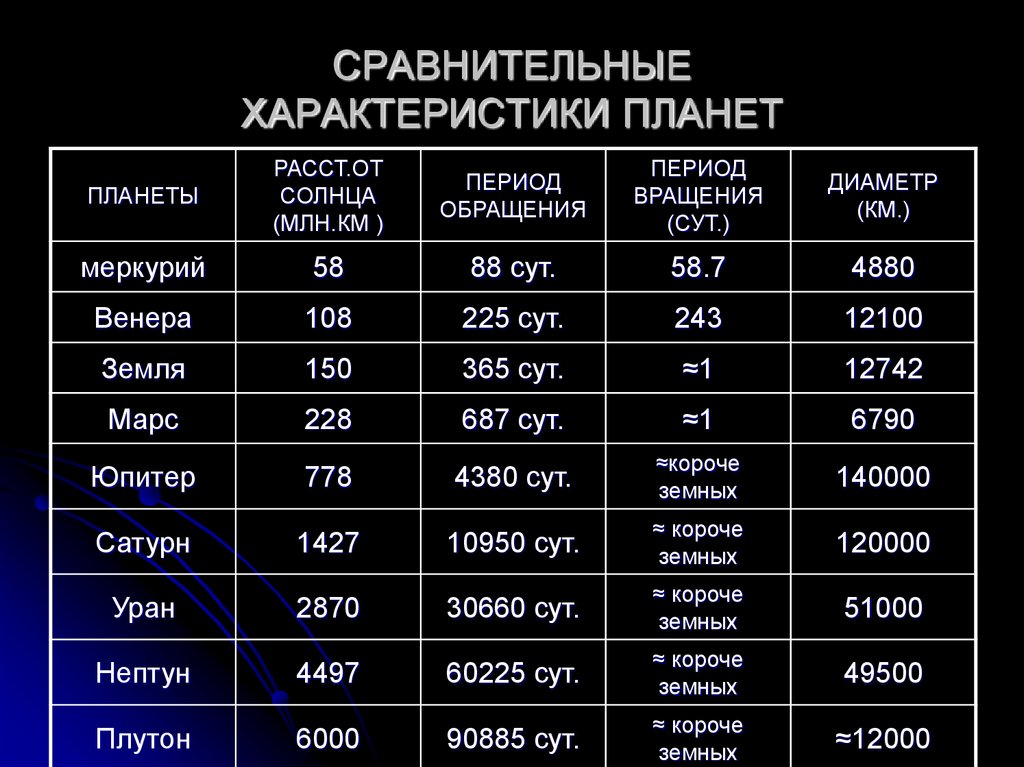 где Si — сумма внутренних углов пятиугольника.
где Si — сумма внутренних углов пятиугольника. Это самая близкая звезда к Земле, за исключением Солнца. В то время как последняя находится примерно в 150 миллионах километров от нашей планеты, Альфа Центавра находится от нас в сорока триллионах километров.
Это самая близкая звезда к Земле, за исключением Солнца. В то время как последняя находится примерно в 150 миллионах километров от нашей планеты, Альфа Центавра находится от нас в сорока триллионах километров. 500.000 XNUMX XNUMX лет.
500.000 XNUMX XNUMX лет. В случае многоугольников (таких как треугольники, квадраты, прямоугольники, пятиугольники и т. д.) периметр представляет собой сумму мер сторон.
В случае многоугольников (таких как треугольники, квадраты, прямоугольники, пятиугольники и т. д.) периметр представляет собой сумму мер сторон. е. Ближайшая звезда, Проксима Центавра, находится на расстоянии около 1,3 парсека (4,2 светового года) от Солнца.
е. Ближайшая звезда, Проксима Центавра, находится на расстоянии около 1,3 парсека (4,2 светового года) от Солнца.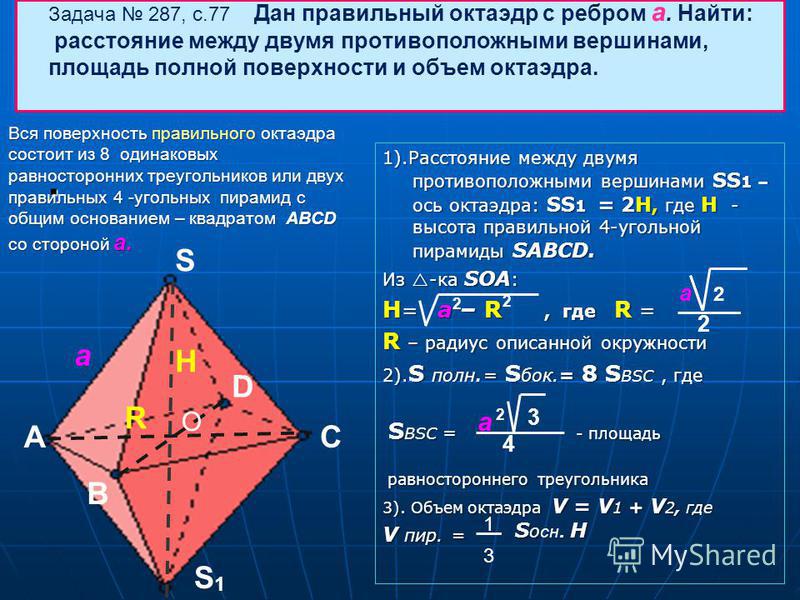 ⓘ Периметр звезды Лакшми [P]
ⓘ Периметр звезды Лакшми [P]
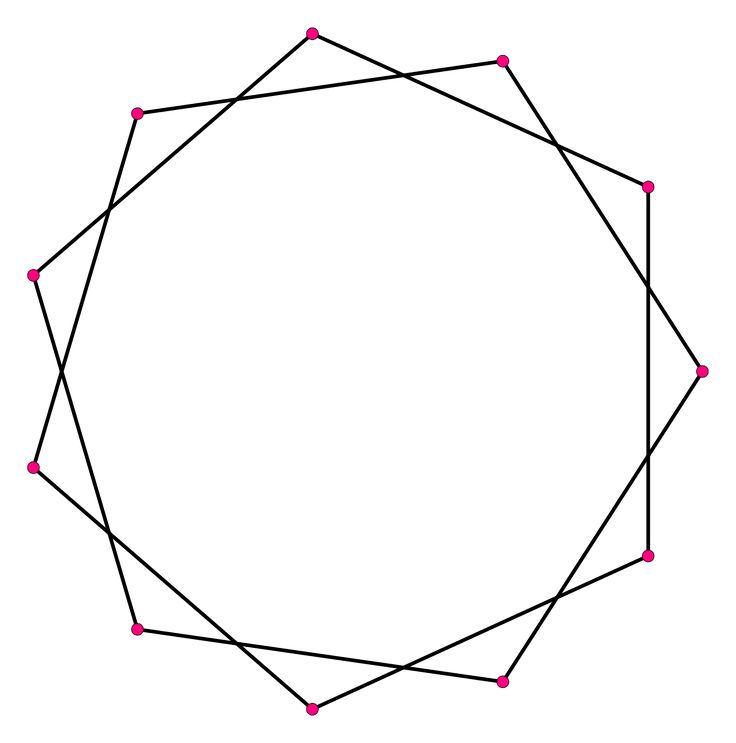 Преобразование входов в базовый блок
Преобразование входов в базовый блок
 Это происходит дважды в течение звездных суток: в нижней кульминации ее высота минимальна (часовой угол Н = 180°), а в верхней кульминации ее высота максимальна (Н = 0°). Эта последняя ситуация наиболее благоприятна для наблюдения.
Это происходит дважды в течение звездных суток: в нижней кульминации ее высота минимальна (часовой угол Н = 180°), а в верхней кульминации ее высота максимальна (Н = 0°). Эта последняя ситуация наиболее благоприятна для наблюдения.
 В случае многоугольников (таких как треугольники, квадраты, прямоугольники, пятиугольники и т. д.) периметр представляет собой сумму мер сторон.
В случае многоугольников (таких как треугольники, квадраты, прямоугольники, пятиугольники и т. д.) периметр представляет собой сумму мер сторон.
 Астрономы доказали, что могут точно рассчитать возраст звезды по скорости ее вращения. Мы знаем, что звезды со временем замедляются, но до недавнего времени было слишком мало данных для проведения точных расчетов.
Астрономы доказали, что могут точно рассчитать возраст звезды по скорости ее вращения. Мы знаем, что звезды со временем замедляются, но до недавнего времени было слишком мало данных для проведения точных расчетов.

 В свою очередь площадь геометрической фигуры соответствует мере ее поверхности.
В свою очередь площадь геометрической фигуры соответствует мере ее поверхности.
 Это происходит дважды в течение звездных суток: в нижней кульминации ее высота минимальна (часовой угол Н = 180°), а в верхней кульминации ее высота максимальна (Н = 0°). Эта последняя ситуация наиболее благоприятна для наблюдения.
Это происходит дважды в течение звездных суток: в нижней кульминации ее высота минимальна (часовой угол Н = 180°), а в верхней кульминации ее высота максимальна (Н = 0°). Эта последняя ситуация наиболее благоприятна для наблюдения.
 В случае многоугольников (таких как треугольники, квадраты, прямоугольники, пятиугольники и т. д.) периметр представляет собой сумму мер сторон.
В случае многоугольников (таких как треугольники, квадраты, прямоугольники, пятиугольники и т. д.) периметр представляет собой сумму мер сторон.
 Астрономы доказали, что могут точно рассчитать возраст звезды по скорости ее вращения. Мы знаем, что звезды со временем замедляются, но до недавнего времени было слишком мало данных для проведения точных расчетов.
Астрономы доказали, что могут точно рассчитать возраст звезды по скорости ее вращения. Мы знаем, что звезды со временем замедляются, но до недавнего времени было слишком мало данных для проведения точных расчетов.

 В свою очередь площадь геометрической фигуры соответствует мере ее поверхности.
В свою очередь площадь геометрической фигуры соответствует мере ее поверхности.
 09.2015
132818
09.2015
132818
 04.2020
5583
04.2020
5583
 02.2022
442
0
02.2022
442
0

 Математика 3 класс.
Математика 3 класс.
 Когда дети поймут их, они будут решать задачи на умножение быстрее. Кроме того, базовые задачи на умножение, такие как умножение два на один, являются первым этапом освоения умножения в столбик, и он начинается в 3-м классе.
Когда дети поймут их, они будут решать задачи на умножение быстрее. Кроме того, базовые задачи на умножение, такие как умножение два на один, являются первым этапом освоения умножения в столбик, и он начинается в 3-м классе. Эти рабочие листы заставляют детей использовать пошаговый метод решения математических задач, что очень важно для повышения их способности решать задачи.
Эти рабочие листы заставляют детей использовать пошаговый метод решения математических задач, что очень важно для повышения их способности решать задачи. Если вы продолжите использовать веб-сайт, мы поймем, что вы согласны с Условиями. Эти файлы cookie безопасны и надежны. Мы не будем передавать ваши журналы истории третьим лицам.
Показать больше
Если вы продолжите использовать веб-сайт, мы поймем, что вы согласны с Условиями. Эти файлы cookie безопасны и надежны. Мы не будем передавать ваши журналы истории третьим лицам.
Показать больше



 )
) 

 У других авторов черта сверху могла обозначать увеличение значения цифры в 1000 раз: VM = 6000.
У других авторов черта сверху могла обозначать увеличение значения цифры в 1000 раз: VM = 6000.
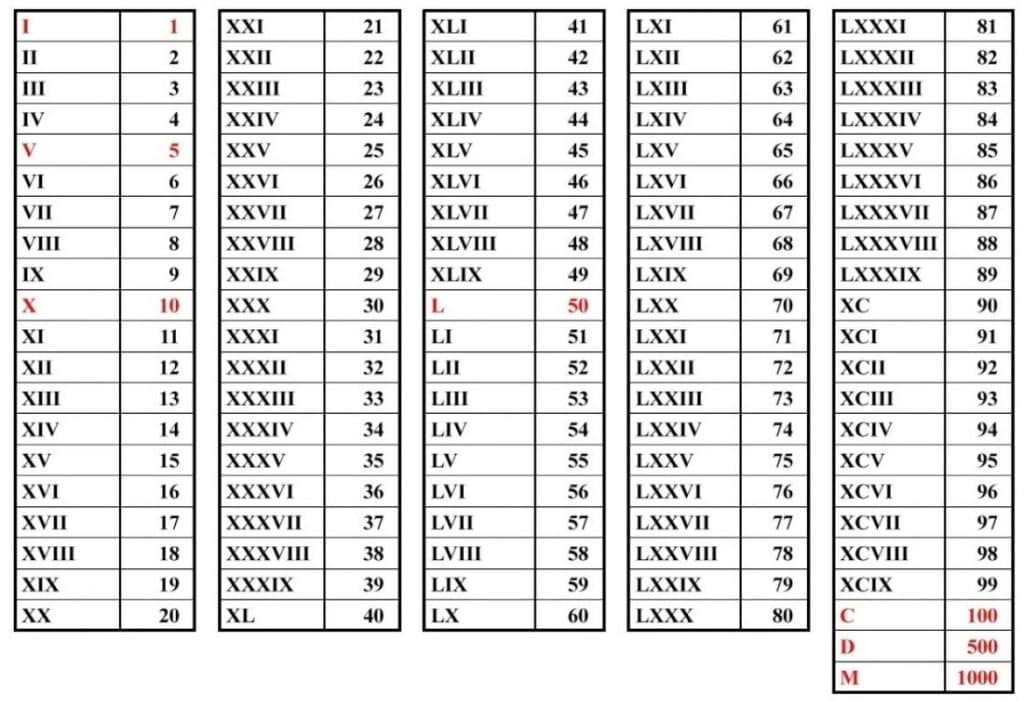
 Number Forms),[2] в области знаков с кодами с U+2160 по U+2188. Например, MCMLXXXVIII может быть представлено в форме ⅯⅭⅯⅬⅩⅩⅩⅧ. Этот диапазон включает как строчные, так и прописные цифры от 1 (Ⅰ или I) до 12 (Ⅻ или XII), в том числе и комбинированные глифы для составных чисел, таких как 8 (Ⅷ или VIII), главным образом для обеспечения совместимости с восточноазиатскими наборами символов в таких промышленных стандартах, как JIS X 0213, где эти символы определены. Комбинированные глифы используются для представления чисел, которые ранее составлялись из отдельных символов (например, Ⅻ вместо его представления как Ⅹ и Ⅱ). В дополнение к этому, глифы существуют для архаичных[2] форм записи чисел 1000, 5000, 10 000, большой обратной C (Ɔ), поздней формы записи 6 (ↅ, похожей на греческую стигму: Ϛ), ранней формы записи числа 50 (ↆ, похожей на стрелку, указывающую вниз ↓⫝⊥[3]), 50 000, и 100 000. Следует отметить, что маленькая обратная c, ↄ не включена в символы римских цифр, но включена в стандарт Юникод как прописная клавдиева буква Ↄ.
Number Forms),[2] в области знаков с кодами с U+2160 по U+2188. Например, MCMLXXXVIII может быть представлено в форме ⅯⅭⅯⅬⅩⅩⅩⅧ. Этот диапазон включает как строчные, так и прописные цифры от 1 (Ⅰ или I) до 12 (Ⅻ или XII), в том числе и комбинированные глифы для составных чисел, таких как 8 (Ⅷ или VIII), главным образом для обеспечения совместимости с восточноазиатскими наборами символов в таких промышленных стандартах, как JIS X 0213, где эти символы определены. Комбинированные глифы используются для представления чисел, которые ранее составлялись из отдельных символов (например, Ⅻ вместо его представления как Ⅹ и Ⅱ). В дополнение к этому, глифы существуют для архаичных[2] форм записи чисел 1000, 5000, 10 000, большой обратной C (Ɔ), поздней формы записи 6 (ↅ, похожей на греческую стигму: Ϛ), ранней формы записи числа 50 (ↆ, похожей на стрелку, указывающую вниз ↓⫝⊥[3]), 50 000, и 100 000. Следует отметить, что маленькая обратная c, ↄ не включена в символы римских цифр, но включена в стандарт Юникод как прописная клавдиева буква Ↄ.
 В обиходе применяются обычные буквы латинского алфавита. Отображение таких символов требует наличия программного обеспечения, поддерживающего стандарт Юникод, и шрифта, содержащего соответствующие этим символам глифы.
В обиходе применяются обычные буквы латинского алфавита. Отображение таких символов требует наличия программного обеспечения, поддерживающего стандарт Юникод, и шрифта, содержащего соответствующие этим символам глифы.

 Теперь, когда у нас есть все цифры, мы вернулись к столбцу А и вставили цифры в числовом порядке (проверив, что это возможно), что позволило нам определить, что (B, N) равно 4.
Теперь, когда у нас есть все цифры, мы вернулись к столбцу А и вставили цифры в числовом порядке (проверив, что это возможно), что позволило нам определить, что (B, N) равно 4. Затем методом проб и ошибок мы поместили оставшиеся 3 цифры числа N, начиная с правого края таблицы, и спускаясь вниз по каждому столбцу.
Затем методом проб и ошибок мы поместили оставшиеся 3 цифры числа N, начиная с правого края таблицы, и спускаясь вниз по каждому столбцу. е. цифры всегда в одном порядке: 1, 4, 2, 8, 5, 7.
е. цифры всегда в одном порядке: 1, 4, 2, 8, 5, 7.


 Если A – матрица с размерами z, x, c, транспонированная матрица AT будет иметь размер c, x, z.
Если A – матрица с размерами z, x, c, транспонированная матрица AT будет иметь размер c, x, z. Сложение и вычитание
Сложение и вычитание
 Он оперативно ответит на вопросы и в случае необходимости поможет оформить заказ по выгодной цене.
Он оперативно ответит на вопросы и в случае необходимости поможет оформить заказ по выгодной цене.  /lab7
/lab7 Чтобы правильно вычислить матричное умножение, порядок цикла не имеет значения. Однако то, как мы решаем двигаться по матрицам, может иметь большое влияние на производительность, поскольку это может нарушить предположение о пространственной локальности, которое имеет решающее значение для хорошей производительности кэша.
Чтобы правильно вычислить матричное умножение, порядок цикла не имеет значения. Однако то, как мы решаем двигаться по матрицам, может иметь большое влияние на производительность, поскольку это может нарушить предположение о пространственной локальности, которое имеет решающее значение для хорошей производительности кэша. Более формально, блокировка кеша — это метод, который пытается снизить частоту промахов кеша за счет улучшения временной и/или пространственной локальности доступа к памяти. В случае транспонирования матрицы мы рассматриваем выполнение транспонирования по одному блоку за раз.
Более формально, блокировка кеша — это метод, который пытается снизить частоту промахов кеша за счет улучшения временной и/или пространственной локальности доступа к памяти. В случае транспонирования матрицы мы рассматриваем выполнение транспонирования по одному блоку за раз. Скомпилируйте и запустите этот код. (Примечание: обязательно используйте флаг «-O3», чтобы включить оптимизацию компилятора)
Скомпилируйте и запустите этот код. (Примечание: обязательно используйте флаг «-O3», чтобы включить оптимизацию компилятора) (Подсказка: обязательно обработайте крайние случаи транспонирования: т.е. что, если мы попытаемся транспонировать приведенную выше матрицу 5 на 5 с размером блока 2?).
(Подсказка: обязательно обработайте крайние случаи транспонирования: т.е. что, если мы попытаемся транспонировать приведенную выше матрицу 5 на 5 с размером блока 2?).

 в
В случае транспонирования матриц мы рассматриваем 2D-блокировку в
выполнить транспонирование одной подматрицы
вовремя.
в
В случае транспонирования матриц мы рассматриваем 2D-блокировку в
выполнить транспонирование одной подматрицы
вовремя.



 …
…
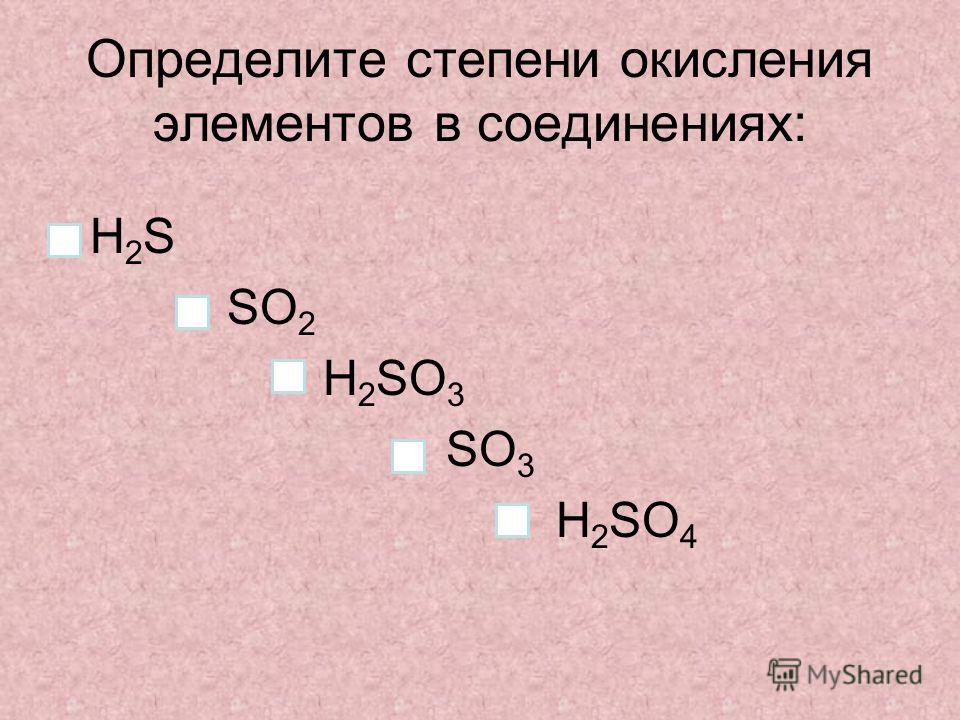
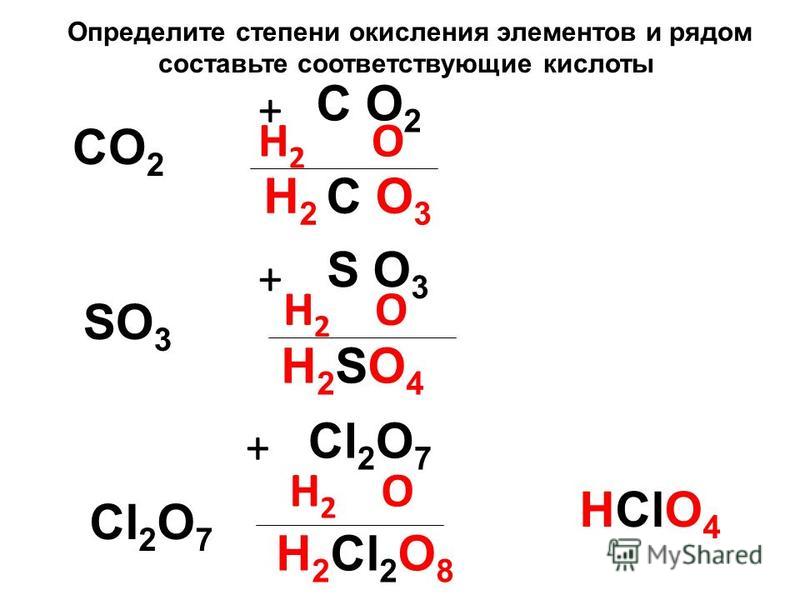
 Практические задачи
Практические задачи Степень окисления может быть положительным или отрицательным целым числом, а также может быть равна нулю.
Степень окисления может быть положительным или отрицательным целым числом, а также может быть равна нулю.