Действительное число | это… Что такое Действительное число?
Веще́ственные, или действи́тельные[1]числа — математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.
Множество вещественных чисел обозначается (Unicode: ℝ) и часто называется вещественной прямой.
Относительно операций сложения и умножения вещественные числа образуют поле. Поле вещественных чисел является важнейшим объектом математического анализа.
Содержание
|
Примеры
- Рациональные числа — 32, 36/29.
- Иррациональные числа — π, .
Определения
Существует несколько стандартных путей определения вещественных чисел:
Аксиоматическое определение
См. основную статью Аксиоматика вещественных чисел.
Множество вещественных чисел можно определить как топологически полное, упорядоченное поле, то есть поле с отношением , которое удовлетворяет следующим аксиомам:
- Отношение является отношением линейного порядка:
- Для любых или ;
- Если и , то a = b для любых ;
- Если и , то для любых ;
- Порядок согласован со структурой поля:
- Если , то для любых ;
- Если и , то .
- Порядок на удовлетворяет условию полноты:
- Пусть — непустые подмножества, такие что для любых и , тогда существует такое, что для любых и .
Примечания
Из свойства 3 следует, что у любого непустого ограниченного сверху множества (то есть такого, что для всех x из A все для некоторого ) существует точная верхняя грань (минимальная из всех), то есть число такое, что
- Для всех x из A все
- Если свойству (1) удовлетворяет также число , то .

Наличие точных верхних граней у ограниченных сверху множеств эквивалентно аксиоме полноты и часто заменяет её в аксиоматике поля .
Любые два поля с отношением порядка, удовлетворяющим этим аксиомам, изоморфны, поэтому можно говорить, что существует единственное такое поле. (На самом деле, правильней говорить, что единственна структура полного упорядоченного поля, каждое поле, которое её имеет, служит моделью множества вещественных чисел, так как любые две модели изоморфны.)
Пополнение рациональных чисел
Вещественные числа могут быть построены как пополнение множества рациональных чисел по отношению к обычной метрике .
Более точно, рассмотрим все фундаментальные последовательности рациональных чисел {ri}. На таких последовательностях можно естественным образом ввести арифметические операции: {ri} + {qi} = {ri + qi} и .
Две такие последовательности и считаются эквивалентными , если при .
Множество вещественных чисел можно определить как классы эквивалентности этих последовательностей.
Дедекиндовы сечения
См. основную статью Дедекиндово сечение.
Дедекиндово сечение — это разбиение множества рациональных чисел на два подмножества A и B такие, что:
- для любых и ;
- B не имеет минимального элемента.
Множество вещественных чисел определяется как множество дедекиндовых сечений. На них возможно продолжить операции сложения и умножения.
Например, вещественному числу соответствует дедекиндово сечение, определяемое или и и x2 > 2}. Интуитивно, можно представить себе, что для того чтобы определить мы рассекли множество на две части: все числа, что левее и все числа, что правее ; соотвеетственно, равно точной нижней грани множества B.
Бесконечные десятичные дроби
Такое задание, как правило, практикуется в школьной программе и во многом похоже на пополнение рациональных чисел.
Бесконечной десятичной дробью (со знаком) называется последовательность вида , где di являются десятичными цифрами, то есть .
Две последовательности называются эквивалентными, если они либо совпадают, либо их различающиеся «хвосты» имеют вид и , где , либо если это «нулевые» последовательности (все di равны 0), отличающиеся только знаком.
Вещественные числа определяются как классы эквивалентности десятичных дробей. Операции на десятичных дробях определяются позиционно подобно операциям над целыми числами в позиционных системах счисления.
Значение десятичной дроби формально задаётся суммой ряда .
Счетность множества
TODO:
Примечания
- ↑ Традиционно в Петербурге (СПбГУ) принято название вещественные, а в Москве (МГУ) — действительные.
Ссылки
- Кириллов, А. А. Что такое число? // Выпуск 4-й серии «Современная математика для студентов».
 — М.: Физматлит, 1993.
— М.: Физматлит, 1993. - Понтрягин, Л. С. Обобщения чисел // Серия «Математическая библиотечка». — М.: Наука, 1965.
См. также
- Комплексные числа
Числа
натуральные | целые | рациональные | вещественные | p-адические
иррациональные | алгебраические | трансцендентные
комплексные | дуальные | двойные
кватернионы | числа Кэли (октавы) | седенионы | гиперкомплексные
определение, примеры, представления, координатная прямая
Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.
Определение действительных чисел
Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?
Определение 1Действительные числа — это рациональные и иррациональные числа.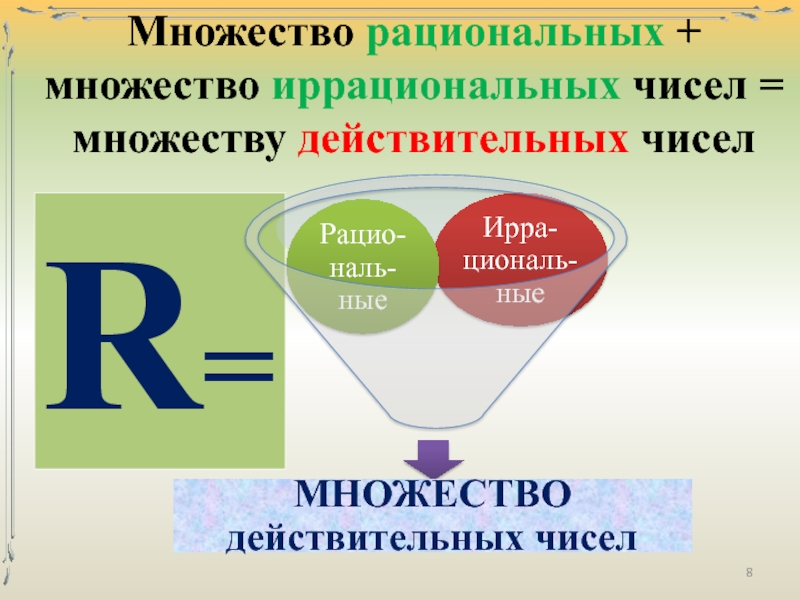 Множество действительных чисел обозначается через R.
Множество действительных чисел обозначается через R.
Данное определение можно записать иначе с учетом следующего:
- Рациональные числа можно представить в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
- Иррациональные числа представляют собой бесконечные непериодические десятичные дроби.
Действительные числа — числа, которые можно записать в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.
Действительные числа — это любые рациональные и иррациональные числа. Приведем примеры таких чисел: 0; 6; 458; 1863; 0,578; -38; 265; 0,145(3); log512.
Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.
Еще одно название для действительных чисел — вещественные числа. Эти числа позволяют описывать значение непрерывно меняющейся величины без введения эталонного (единичного) значения этой величины.
Эти числа позволяют описывать значение непрерывно меняющейся величины без введения эталонного (единичного) значения этой величины.
Координатная прямая и действительные числа
Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.
Представления действительных чисел
Под определение дейситвительных чисел попадают:
- Натуральные числа.
- Целые числа.
- Десятичные дроби.
- Обыкновенные дроби.
- Смешанные числа.
Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.
Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.
Например, значения выражений sin23π·e-285·10log32 и tg676693-8π32 — действительные числа.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Что такое числа на самом деле? Церебральная основа чувства числа
ЧТО ТАКОЕ ЧИСЛА НА САМОМ ДЕЛЕ? МОЗГОВАЯ ОСНОВА ДЛЯ ЧИСЛОВОГО ЧУВСТВА
В недавней книге, а также в жаркой дискуссии на форуме Edge математик Рубен Херш задал вопрос: «Что такое математика на самом деле?» Это извечный вопрос, который уже обсуждался в Древней Греции и озадачил Эйнштейна двадцать три века спустя. Лично я сомневаюсь, что одни только философские исследования когда-либо дадут удовлетворительный ответ (похоже, мы даже не можем договориться о том, что на самом деле означает этот вопрос!). Однако, если мы хотим использовать научный подход, мы можем обратиться к более конкретным вопросам, таким как происхождение определенных математических объектов, таких как множества, числа или функции, кто их изобрел, для какой цели они изначально использовались, их историческая эволюция. , как они усваиваются детьми и так далее. Таким образом, мы можем начать определять природу математики гораздо более конкретным способом, который открыт для научных исследований с использованием исторических исследований, психологии или даже неврологии.
Однако, если мы хотим использовать научный подход, мы можем обратиться к более конкретным вопросам, таким как происхождение определенных математических объектов, таких как множества, числа или функции, кто их изобрел, для какой цели они изначально использовались, их историческая эволюция. , как они усваиваются детьми и так далее. Таким образом, мы можем начать определять природу математики гораздо более конкретным способом, который открыт для научных исследований с использованием исторических исследований, психологии или даже неврологии.
Это именно то, что небольшая группа когнитивных нейропсихологов из разных стран и я пытались сделать в очень простой области математики, возможно, самой основной из всех: области натуральных целых чисел 1, 2, 3, 4. и т. д. Наши результаты, которые теперь основаны буквально на сотнях экспериментов, довольно удивительны: наш мозг, кажется, с рождения наделен чувством числа. Элементарная арифметика, по-видимому, является базовой, биологически детерминированной способностью, присущей нашему виду (и не только нашей собственной, поскольку мы разделяем ее со многими животными). Кроме того, у него есть специфический мозговой субстрат, набор нейронных сетей, одинаково локализованных во всех нас и хранящих знания о числах и их отношениях. Короче говоря, восприятие чисел в нашем окружении так же важно для нас, как эхолокация для летучих мышей или пение птиц для певчих птиц.
Кроме того, у него есть специфический мозговой субстрат, набор нейронных сетей, одинаково локализованных во всех нас и хранящих знания о числах и их отношениях. Короче говоря, восприятие чисел в нашем окружении так же важно для нас, как эхолокация для летучих мышей или пение птиц для певчих птиц.
Ясно, что эта теория имеет важные, непосредственные последствия для природы математики. Очевидно, что поразительный уровень математического развития, которого мы сейчас достигли, является уникальным человеческим достижением, характерным для нашего вида, одаренного языком, и в значительной степени зависящим от культурного накопления. Но утверждается, что основные понятия, лежащие в основе математики, такие как числа, множества, пространство, расстояние и т. д., возникают из самой архитектуры нашего мозга.
В этом смысле числа подобны цветам. Вы знаете, что в физическом мире нет цветов. Свет имеет различные длины волн, но длина волны — это не то, что мы называем цветом (банан по-прежнему выглядит желтым при различных условиях освещения, когда длина волны, которую он отражает, полностью меняется). Цвет — это атрибут, созданный областью V4 нашего мозга. Эта область вычисляет относительное количество света с различными длинами волн на нашей сетчатке и использует его для вычисления коэффициента отражения объектов (как они отражают падающий свет) в различных спектральных диапазонах. Это то, что мы называем цветом, но это чисто субъективное качество, созданное мозгом. Тем не менее, он очень полезен для распознавания объектов внешнего мира, потому что их цвет имеет тенденцию оставаться постоянным при различных условиях освещения, и, по-видимому, именно поэтому способность мозга к восприятию цвета развивалась таким образом.
Цвет — это атрибут, созданный областью V4 нашего мозга. Эта область вычисляет относительное количество света с различными длинами волн на нашей сетчатке и использует его для вычисления коэффициента отражения объектов (как они отражают падающий свет) в различных спектральных диапазонах. Это то, что мы называем цветом, но это чисто субъективное качество, созданное мозгом. Тем не менее, он очень полезен для распознавания объектов внешнего мира, потому что их цвет имеет тенденцию оставаться постоянным при различных условиях освещения, и, по-видимому, именно поэтому способность мозга к восприятию цвета развивалась таким образом.
Я утверждаю, что число очень похоже на цвет. Поскольку мы живем в мире, полном дискретных и подвижных объектов, нам очень полезно иметь возможность извлекать числа. Это может помочь нам отслеживать хищников или выбирать лучшие кормовые угодья, если говорить только об очень очевидных примерах. Вот почему эволюция наделила наш мозг и мозг многих видов животных простыми числовыми механизмами. У животных эти механизмы весьма ограничены, как мы увидим ниже: они приблизительны, их представление становится все более грубым по мере увеличения числа, и в них задействованы лишь простейшие арифметические действия (сложение и вычитание). Нам, людям, также посчастливилось развить способности к языку и символической записи. Это позволило нам разработать точные мысленные представления для больших чисел, а также алгоритмы для точных вычислений. Я считаю, что математика или, по крайней мере, арифметика и теория чисел — это пирамида все более абстрактных умственных построений, основанных исключительно на (1) нашей способности к символической записи и (2) нашей невербальной способности представлять и понимать числовые величины.
У животных эти механизмы весьма ограничены, как мы увидим ниже: они приблизительны, их представление становится все более грубым по мере увеличения числа, и в них задействованы лишь простейшие арифметические действия (сложение и вычитание). Нам, людям, также посчастливилось развить способности к языку и символической записи. Это позволило нам разработать точные мысленные представления для больших чисел, а также алгоритмы для точных вычислений. Я считаю, что математика или, по крайней мере, арифметика и теория чисел — это пирамида все более абстрактных умственных построений, основанных исключительно на (1) нашей способности к символической записи и (2) нашей невербальной способности представлять и понимать числовые величины.
Довольно о философии, но каковы фактические доказательства этих заявлений? Психологи начинают понимать, что большая часть нашей психической жизни основывается на работе специализированных, биологически детерминированных психических модулей, специально настроенных на ограниченные области знаний и заложенных в нашем мозгу в ходе эволюции (см. «» Стива Пинкера). Как работает разум ). Например, кажется, что у нас есть предметно-ориентированные знания о животных, еде, людях, лицах, эмоциях и многом другом. В каждом случае — и число не является исключением — психологи демонстрируют существование предметно-ориентированной системы знаний, используя следующие четыре аргумента:
«» Стива Пинкера). Как работает разум ). Например, кажется, что у нас есть предметно-ориентированные знания о животных, еде, людях, лицах, эмоциях и многом другом. В каждом случае — и число не является исключением — психологи демонстрируют существование предметно-ориентированной системы знаний, используя следующие четыре аргумента:
1) Нужно доказать, что обладание предварительными знаниями в области дает эволюционное преимущество. В случае элементарной арифметики это совершенно очевидно.
2) Должны быть предшественники способности у других видов животных. Таким образом, следует показать, что у некоторых животных есть рудиментарные арифметические способности. Должны быть систематические параллели между их способностями и способностями людей.
3) Способность должна возникать спонтанно у маленьких детей или даже младенцев, независимо от других способностей, таких как речь. Его не следует приобретать с помощью медленных, общих для предметной области механизмов обучения.
4) Следует показать, что способность имеет отчетливый нейронный субстрат. Моя книга «Чувство числа » посвящена доказательству этих четырех положений, а также исследованию их последствий для образования и философии математики. На самом деле убедительные экспериментальные данные подтверждают приведенные выше утверждения, что делает числовую область одной из областей, в которых демонстрация биологически детерминированной, специфичной для предметной области системы знаний является самой сильной. Здесь я могу привести лишь несколько примеров экспериментов.
Животные обладают элементарными числовыми способностями. Крысы, голуби, попугаи, дельфины и, конечно же, приматы могут различать зрительные паттерны или слуховые последовательности только на основе числа (каждый другой физический параметр тщательно контролируется). Например, крысы могут научиться нажимать один рычаг для двух событий, а другой — для четырех, независимо от их характера, продолжительности и интервалов, а также от того, являются ли они слуховыми или визуальными. Животные также обладают элементарными способностями к сложению и вычитанию. Эти основные способности встречаются в дикой природе, а не только у животных, обученных в лаборатории. Однако потребуются годы обучения, если кто-то хочет привить числовые символы шимпанзе. Таким образом, приблизительное манипулирование числом входит в нормальный репертуар многих видов, а точное символическое манипулирование числом — нет; это специфически человеческая способность или, по крайней мере, такая способность, которая достигает своего полного развития только у людей.
Животные также обладают элементарными способностями к сложению и вычитанию. Эти основные способности встречаются в дикой природе, а не только у животных, обученных в лаборатории. Однако потребуются годы обучения, если кто-то хочет привить числовые символы шимпанзе. Таким образом, приблизительное манипулирование числом входит в нормальный репертуар многих видов, а точное символическое манипулирование числом — нет; это специфически человеческая способность или, по крайней мере, такая способность, которая достигает своего полного развития только у людей.
Существуют систематические параллели между людьми и животными. Числовое поведение животных становится все более неточным по мере увеличения числа (эффект размера числа). То же самое верно и для людей, даже когда они оперируют арабскими цифрами: мы систематически медленнее вычисляем, скажем, 4+5, чем 2+3. Животные также испытывают трудности с различением двух близких величин, таких как 7 и 8. Мы тоже: при сравнении арабских цифр нам требуется больше времени, чтобы решить, что 9 больше, чем 8, чем принять такое же решение для 9. Vs 2 (и мы тоже делаем больше ошибок).
Vs 2 (и мы тоже делаем больше ошибок).
Невербальные человеческие младенцы также обладают элементарными вычислительными способностями. Они очень похожи на таковые у животных: младенцы могут различать два узора, основываясь только на их количестве, и они могут делать простые сложения и вычитания. Например, в возрасте 5 месяцев, когда один объект прячется за экраном, а затем добавляется другой, младенцы ожидают увидеть два объекта, когда экран опускается. Мы знаем это, потому что тщательные измерения времени их взгляда показывают, что они смотрят дольше, когда в результате трюка появляется другое количество объектов. Большее время поиска указывает на то, что они удивляются, когда видят невозможные события, такие как 1+1=1, 1+1=3 или 2-1=2. [Пожалуйста, даже если вы настроены скептически, не отбрасывайте эти данные тыльной стороной ладони, как я был встревожен, узнав, что Мартин Гарднер поступал так в недавнем обзоре моей книги для Лос-Анджелес Таймс . Разумеется, «измерять и усреднять такие времена непросто», но теперь это делается в очень строго контролируемых условиях с двойной слепой оценкой видеопленки. Я призываю вас прочитать оригинальные отчеты, например Wynn, 1992, Nature , vol. 348, pp. 749-750 (вы будете поражены уровнем детализации и экспериментального контроля, которым подвергаются такие эксперименты).
Я призываю вас прочитать оригинальные отчеты, например Wynn, 1992, Nature , vol. 348, pp. 749-750 (вы будете поражены уровнем детализации и экспериментального контроля, которым подвергаются такие эксперименты).
Подобно животным и взрослым, младенцы особенно точны в работе с небольшими числами, но они также могут более точно вычислять с большими числами. Попутно отметим, что эти эксперименты, которые очень хорошо воспроизводимы, опровергают представление Пиаже о том, что младенцы начинают свою жизнь без каких-либо знаний о числовой инвариантности. В своей книге я показываю, почему знаменитые эксперименты Пиаже по сохранению необъективны и не могут рассказать нам об истинной арифметической способности маленьких детей.
Поражения головного мозга могут привести к ухудшению восприятия чисел. Мои коллеги и я видели в больнице много пациентов, которые перенесли поражение головного мозга и, как следствие, стали неспособными обрабатывать числа. Некоторые из этих нарушений носят периферический характер и касаются способности идентифицировать слова или цифры или произносить их вслух. Другие, однако, указывают на подлинную потерю чувства числа. Поражения левой нижней теменной доли могут привести к тому, что пациент сможет читать и писать арабские цифры под диктовку, не понимая их. Один из наших пациентов не мог сделать 3 минус 1 или решить, какое число находится между 2 и 4! Однако у него не было проблем с тем, чтобы сказать нам, какой месяц приходится на период между февралем и апрелем, или какой день был незадолго до среды. Таким образом, дефицит был полностью ограничен цифрами. Место поражения, которое приводит к такому дефициту числа, хорошо воспроизводимо во всех культурах по всему миру.
Другие, однако, указывают на подлинную потерю чувства числа. Поражения левой нижней теменной доли могут привести к тому, что пациент сможет читать и писать арабские цифры под диктовку, не понимая их. Один из наших пациентов не мог сделать 3 минус 1 или решить, какое число находится между 2 и 4! Однако у него не было проблем с тем, чтобы сказать нам, какой месяц приходится на период между февралем и апрелем, или какой день был незадолго до среды. Таким образом, дефицит был полностью ограничен цифрами. Место поражения, которое приводит к такому дефициту числа, хорошо воспроизводимо во всех культурах по всему миру.
Визуализация мозга во время выполнения задач по обработке чисел выявляет весьма специфическую активацию нижней теменной доли, той самой области, которая при повреждении вызывает числовой дефицит. Теперь мы наблюдали эту активацию, используя большинство доступных в настоящее время методов визуализации. ПЭТ-сканирование и фМРТ определяют его анатомически в левой и правой внутритеменных бороздах. Электрические записи также говорят нам, что эта область активна во время таких операций, как умножение или сравнение, и что она активируется примерно через 200 мс после представления цифры на экране. Есть даже записи одиночных нейронов в теменной доле человека (в особом случае пациентов с трудноизлечимой эпилепсией), которые показывают специфическое увеличение активности во время вычислений.
Электрические записи также говорят нам, что эта область активна во время таких операций, как умножение или сравнение, и что она активируется примерно через 200 мс после представления цифры на экране. Есть даже записи одиночных нейронов в теменной доле человека (в особом случае пациентов с трудноизлечимой эпилепсией), которые показывают специфическое увеличение активности во время вычислений.
Тот факт, что в нашем мозгу существует такое биологически детерминированное представление числа, имеет много важных последствий, которые я попытался рассмотреть в этой книге. Самым важным, конечно же, является вопрос о том, как математическое образование модифицирует это представление и почему у одних детей развиваются способности к арифметике и математике, в то время как другие (многие из нас!) остаются неумеющими. Предполагая, что все мы начинаем жизнь с приблизительным представлением числа, точным только для небольших чисел и недостаточным для того, чтобы отличить 7 от 8, как мы когда-либо продвинемся дальше этой «животной» стадии? Я думаю, что овладение языком для чисел имеет решающее значение, и именно на этом этапе появляются культурные и образовательные различия. Например, китайские дети имеют преимущество в обучении счету просто потому, что их числовой синтаксис намного проще. Тогда как мы говорим «семнадцать, восемнадцать, девятнадцать, двадцать, двадцать один и т. д.», они говорят гораздо проще: «десять-семь, десять-восемь, десять-девять, два-десять, два-десять-один и т. д.». .»; следовательно, им приходится учить меньше слов и более простой синтаксис. Факты показывают, что большая простота их числовых слов ускоряет изучение последовательности счета примерно на один год! Но, спешу заметить, лучше организованы азиатские классы, как показал психолог Калифорнийского университета в Лос-Анджелесе Джим Стиглер. По мере того, как дети переходят к высшей математике, имеются убедительные доказательства того, что переход от приближения к обучению точному счету очень труден для детей и весьма утомителен даже для мозга взрослого, и что стратегии и образование имеют решающее значение.
Например, китайские дети имеют преимущество в обучении счету просто потому, что их числовой синтаксис намного проще. Тогда как мы говорим «семнадцать, восемнадцать, девятнадцать, двадцать, двадцать один и т. д.», они говорят гораздо проще: «десять-семь, десять-восемь, десять-девять, два-десять, два-десять-один и т. д.». .»; следовательно, им приходится учить меньше слов и более простой синтаксис. Факты показывают, что большая простота их числовых слов ускоряет изучение последовательности счета примерно на один год! Но, спешу заметить, лучше организованы азиатские классы, как показал психолог Калифорнийского университета в Лос-Анджелесе Джим Стиглер. По мере того, как дети переходят к высшей математике, имеются убедительные доказательства того, что переход от приближения к обучению точному счету очень труден для детей и весьма утомителен даже для мозга взрослого, и что стратегии и образование имеют решающее значение.
Почему, например, нам так трудно запомнить нашу таблицу умножения? Вероятно, потому, что наш мозг никогда не развивался для того, чтобы запоминать факты умножения, поэтому нам приходится возиться с мозговыми цепями, которые плохо приспособлены для этой цели (наша ассоциативная память заставляет нас путать восемь раз по три с восемью по четыре, а также восемь плюс три). К сожалению, умение считать может быть нашим нормальным человеческим состоянием, и нам требуются значительные усилия, чтобы научиться считать. В самом деле, многое можно объяснить в отношении неудач некоторых детей в школе и необычайных успехов некоторых идиотов-ученых в вычислениях, если обратиться к различиям в размере инвестиций и в эмоциональном состоянии, в котором они находятся, когда изучают математику. . Рассмотрев большую часть доказательств врожденных различий в математических способностях, включая гендерные различия, я не верю, что большая часть наших индивидуальных различий в математике является результатом врожденных различий в «талантах». Образование — это ключ, а положительный эффект — двигатель успеха в математике.
К сожалению, умение считать может быть нашим нормальным человеческим состоянием, и нам требуются значительные усилия, чтобы научиться считать. В самом деле, многое можно объяснить в отношении неудач некоторых детей в школе и необычайных успехов некоторых идиотов-ученых в вычислениях, если обратиться к различиям в размере инвестиций и в эмоциональном состоянии, в котором они находятся, когда изучают математику. . Рассмотрев большую часть доказательств врожденных различий в математических способностях, включая гендерные различия, я не верю, что большая часть наших индивидуальных различий в математике является результатом врожденных различий в «талантах». Образование — это ключ, а положительный эффект — двигатель успеха в математике.
Может показаться, что существование математических вундеркиндов противоречит этой точке зрения. Их выступления кажутся настолько потусторонними, что кажется, будто у них мозг, отличный от нашего. Не так, я утверждаю? или, по крайней мере, не так в начале своей жизни: они начинают жизнь с теми же дарованиями, что и все мы, — базовым числовым чувством, интуицией о числовых отношениях. Что бы ни изменилось в их взрослом мозгу, это результат успешного обучения, стратегии и запоминания. Действительно, все их подвиги, от извлечения корня до умножения многозначных чисел, можно объяснить простыми трюками, которым может научиться любой человеческий мозг, если он захочет приложить усилия.
Что бы ни изменилось в их взрослом мозгу, это результат успешного обучения, стратегии и запоминания. Действительно, все их подвиги, от извлечения корня до умножения многозначных чисел, можно объяснить простыми трюками, которым может научиться любой человеческий мозг, если он захочет приложить усилия.
Вот один пример: известный анекдот о номере такси Рамануджана и Харди. Выдающийся индийский математик Рамануджан медленно умирал от туберкулеза, когда его коллега Харди приехал навестить его и, не зная, что сказать, поразмыслил: «Такси, которое я нанял, чтобы приехать сюда, носило номер 1729. число.» «О нет, Харди, — ответил Рамануджан, — это очаровательно. Это наименьшее число, которое можно выразить двумя разными способами в виде суммы двух кубов».
На первый взгляд, мгновенное осознание этого факта на больничной койке кажется невероятным, слишком удивительно ярким, чтобы быть возможным для человека. Но на самом деле минута размышлений подсказывает простой способ, которым индийский математик мог признать этот факт. Работая десятилетиями с числами, Рамануджан, очевидно, запомнил множество фактов, включая следующий список кубов:
Работая десятилетиями с числами, Рамануджан, очевидно, запомнил множество фактов, включая следующий список кубов:
1x1x1 = 1
2x2x2 = 8
3x3x3 = 27
4x4x4 = 64
5x5x5 = 125
6x6x6 = 216
7x7x7 = 343
8x8x8 = 512
9x9x9 = 729
9 0003 10x10x10 = 100011x11x11 = 1331
12x12x12 = 1728
Теперь, если вы посмотрите на этот список, вы см., что (а) 1728 является кубом; б) 1728 — это одна единица от 1729, а 1 — тоже куб; в) 729 тоже куб; и (d) 1000 тоже куб. Следовательно, для человека, прошедшего обучение Рамануджана, совершенно ОЧЕВИДНО, что 1729 — это сумма двух кубов двумя разными способами: 1728+1 и 1000+729.. Выяснить, что это наименьшее такое число, сложнее, но это можно сделать методом проб и ошибок. В конце концов, магия этого анекдота полностью растворяется, когда узнаешь, что Рамануджан записал это вычисление в свои тетради еще подростком и, следовательно, вычислил его не под влиянием момента на больничной койке: он уже знал это!
Было бы надуманным предположить, что мы все могли бы повторить подвиг Рамануджана с достаточной подготовкой? Возможно, это предположение покажется менее абсурдным, если учесть, что любой старшеклассник, даже не считающийся особо способным, знает о математике не меньше, чем самые продвинутые ученые-математики Средневековья. Мы все начинаем жизнь с очень похожим мозгом, все наделены элементарным чувством числа, которое имеет некоторую врожденную структуру, но также и степень пластичности, которая позволяет ему формироваться культурой.
Мы все начинаем жизнь с очень похожим мозгом, все наделены элементарным чувством числа, которое имеет некоторую врожденную структуру, но также и степень пластичности, которая позволяет ему формироваться культурой.
Тогда вернемся к философии математики. Что такое числа на самом деле? Если мы допустим, что все мы рождаемся с рудиментарным чувством числа, которое в результате эволюции выгравировано в самой архитектуре нашего мозга, то, очевидно, числа следует рассматривать как конструкцию нашего мозга. Однако, в отличие от многих социальных конструкций, таких как искусство и религия, числа и арифметика не являются произвольными ментальными конструкциями. Скорее, они жестко приспособлены к внешнему миру. Откуда эта адаптация? Загадка об адекватности наших математических построений внешнему миру теряет часть своей таинственности, если принять во внимание два факта.
Во-первых, основные элементы, на которых основаны наши математические конструкции, такие как числа, множества, пространство и т. д., укоренились в архитектуре нашего мозга в результате длительного эволюционного процесса. Эволюция включила в наш разум/мозг структуры, необходимые для выживания и, следовательно, для достоверного восприятия внешнего мира. В том масштабе, в котором мы живем, число необходимо, потому что мы живем в мире, состоящем из подвижных, исчисляемых объектов. Все могло бы быть совсем иначе, если бы мы жили в чисто текучем мире или в атомном масштабе? и поэтому я согласен с некоторыми другими математиками, такими как Анри Пуанкаре, Макс Дельбрюк или Рубен Херш, в том, что они думают, что у других форм жизни могла быть математика, сильно отличающаяся от нашей.
д., укоренились в архитектуре нашего мозга в результате длительного эволюционного процесса. Эволюция включила в наш разум/мозг структуры, необходимые для выживания и, следовательно, для достоверного восприятия внешнего мира. В том масштабе, в котором мы живем, число необходимо, потому что мы живем в мире, состоящем из подвижных, исчисляемых объектов. Все могло бы быть совсем иначе, если бы мы жили в чисто текучем мире или в атомном масштабе? и поэтому я согласен с некоторыми другими математиками, такими как Анри Пуанкаре, Макс Дельбрюк или Рубен Херш, в том, что они думают, что у других форм жизни могла быть математика, сильно отличающаяся от нашей.
Во-вторых, наша математика пережила другую эволюцию, гораздо более быструю: культурную эволюцию. Математические объекты произвольно генерировались в умах математиков последних тридцати столетий (это то, что мы называем «чистой математикой»). Но затем они были выбраны за их полезность при решении реальных проблем, например, в физике. Следовательно, многие из наших нынешних математических инструментов хорошо адаптированы к внешнему миру именно потому, что они были выбраны в зависимости от этого соответствия.
Следовательно, многие из наших нынешних математических инструментов хорошо адаптированы к внешнему миру именно потому, что они были выбраны в зависимости от этого соответствия.
Многие математики являются платониками. Они думают, что Вселенная состоит из математической материи и что задача математиков — просто открывать ее. Я решительно отвергаю эту точку зрения. Однако это не означает, что я «социальный конструктивист», как хотел бы назвать меня Мартин Гарднер. Я согласен с Гарднером и вопреки многим социальным конструктивистам в том, что математические конструкции выходят за рамки конкретных человеческих культур. Однако, на мой взгляд, это связано с тем, что все человеческие культуры имеют одинаковую архитектуру мозга, которая «резонирует» с одними и теми же математическими мелодиями. Значение Пи, слава богу, не меняется вместе с культурой! (ср. дело Сокаля). Более того, я ни в коем случае не отрицаю, что внешний мир обеспечивает большую структуру, которая включается в нашу математику. Я возражаю только против того, чтобы называть строение Вселенной «математическим». Мы разрабатываем математические модели мира, но это только модели, и они никогда не бывают полностью адекватными. Планеты не движутся по эллипсам — эллиптические траектории — хорошее, но далеко не идеальное приближение. Материя состоит не из атомов, электронов или кварков — все это хорошие модели (действительно, очень хорошие), но такие, которые когда-нибудь обязательно потребуют пересмотра. Многие концептуальные трудности можно было бы прояснить, если бы математики и физики-теоретики уделяли больше внимания основному различию между моделью и реальностью, концепции, знакомой биологам.
Я возражаю только против того, чтобы называть строение Вселенной «математическим». Мы разрабатываем математические модели мира, но это только модели, и они никогда не бывают полностью адекватными. Планеты не движутся по эллипсам — эллиптические траектории — хорошее, но далеко не идеальное приближение. Материя состоит не из атомов, электронов или кварков — все это хорошие модели (действительно, очень хорошие), но такие, которые когда-нибудь обязательно потребуют пересмотра. Многие концептуальные трудности можно было бы прояснить, если бы математики и физики-теоретики уделяли больше внимания основному различию между моделью и реальностью, концепции, знакомой биологам.
Числовые строки Slide and Learn™
Перейти к содержанию Перейти к навигацииВойти Завести аккаунт
Отследить заказ Обслуживание клиентов Наша компания Способы делать покупки Колодец желаний
Связаться со службой поддержки
1-877-867-1920
С понедельника по пятницу с 9:00 до 17:00 по восточному поясному времени.
Свяжитесь с нами по электронной почте
Доступность
Товар № 157261Really Good Stuff®
Товар № 157261Really Good Stuff®
Оплата 3-мя ежемесячными платежами
Просто выберите EZ Pay на кассе. Нет сборов!12 числовых строк
Количество Готов к отправкеДобавлено в вашу корзину
Добавить в избранное
Этот товар не подлежит приоритетной доставке
Описание
Возраст: 5+ / Классы: K-1
Закрепите чувство числа с помощью этих забавных интерактивных числовых линий
Вашим учащимся понравится скользить милой маленькой лягушкой по этим прочным пластиковым числовым линиям Slide and Learn™, чтобы выделять числа от 0 до 30 и сосредотачиваться на них. Прочные числовые линии включают 12 интерактивных числовых линий, которые помогают учащимся лучше понимать числа и осваивать первые математические навыки. когда они перескакивают свои лягушки с одного числа на другое. Они идеально подходят для студенческих парт для индивидуального обучения или для работы в небольших группах, чтобы практиковать порядок чисел, сложение, вычитание и пропуск счета двойками, пятерками и десятками. В руководство «Really Good Stuff Activity Guide» включены интерактивные занятия в классе и вспомогательные воспроизводимые материалы.
Прочные числовые линии включают 12 интерактивных числовых линий, которые помогают учащимся лучше понимать числа и осваивать первые математические навыки. когда они перескакивают свои лягушки с одного числа на другое. Они идеально подходят для студенческих парт для индивидуального обучения или для работы в небольших группах, чтобы практиковать порядок чисел, сложение, вычитание и пропуск счета двойками, пятерками и десятками. В руководство «Really Good Stuff Activity Guide» включены интерактивные занятия в классе и вспомогательные воспроизводимые материалы.- ЧТО ВКЛЮЧЕНО: Набор «Числовые линейки Slide and Learn™» включает 12 прочных пластиковых числовых линеек (21 на 3 дюйма) и руководство к занятиям Really Good Stuff® с заданиями в классе и вспомогательным воспроизводимым материалом. С УНИВЕРСАЛЬНЫМ МАТЕМАТИЧЕСКИМ ИНСТРУМЕНТОМ: эти интерактивные числовые линейки идеально подходят для ознакомления, обучения и закрепления навыков работы с числовыми линейками для порядка чисел, сложения, вычитания и пропуска счета двойками, пятерками и десятками.
 -ПРАКТИКА НА ЛИНИЯХ: дайте своим учащимся новый увлекательный практический способ отработать свои навыки числовых линий с помощью практических числовых линий, которые станут любимым занятием в классе во время занятий по математике и в свободное время!
-ПРАКТИКА НА ЛИНИЯХ: дайте своим учащимся новый увлекательный практический способ отработать свои навыки числовых линий с помощью практических числовых линий, которые станут любимым занятием в классе во время занятий по математике и в свободное время! - ИДЕАЛЬНО ДЛЯ ШКОЛЫ И ДОМА: числовые линии Slide and Learn™ выделяют числа от 0 до 30 и являются удобным математическим инструментом в школе и дома, помогая учащимся лучше понимать числа, перемещая лягушку вдоль числовой линии!
- COMMON CORE READY: таблицы умножения Slide and Learn приведены в соответствие с Common Core и стандартами штата по математике. Вы можете чувствовать себя хорошо, зная, что они предназначены для работы с вашей учебной программой!
Технические характеристики
- Набор из 12 цифровых линий
- 21″ на 3″ каждый
- Руководство по работе с Really Good Stuff®
Ресурсы
Руководство по деятельностиИнструмент сопоставления стандартов
Мы знаем стандарты
Только в США почти 30% образовательных стандартов пересматриваются, пересматриваются или редактируются каждый год. Отслеживание этих изменений требует постоянного опыта, и у нас есть инструмент для управления этими стандартами, поэтому вы можете доверять нам как лидеру в согласовании стандартов. Корреляции сделаны для всех государственных, национальных и общих базовых стандартов. Кроме того, у нас есть нормативы Head Start для детей младшего возраста. А совсем недавно мы добавили как национальные стандарты STEM, так и научные стандарты следующего поколения (NGSS).
Отслеживание этих изменений требует постоянного опыта, и у нас есть инструмент для управления этими стандартами, поэтому вы можете доверять нам как лидеру в согласовании стандартов. Корреляции сделаны для всех государственных, национальных и общих базовых стандартов. Кроме того, у нас есть нормативы Head Start для детей младшего возраста. А совсем недавно мы добавили как национальные стандарты STEM, так и научные стандарты следующего поколения (NGSS).
Поиск стандартов
Описание
Возраст: 5+ / Классы: K-1
Закрепите чувство числа с помощью этих забавных интерактивных числовых линий
Вашим учащимся понравится скользить милой маленькой лягушкой по этим прочным пластиковым числовым линиям Slide and Learn™, чтобы выделять числа от 0 до 30 и сосредотачиваться на них. Прочные числовые линии включают 12 интерактивных числовых линий, которые помогают учащимся лучше понимать числа и осваивать первые математические навыки. когда они перескакивают свои лягушки с одного числа на другое. Они идеально подходят для студенческих парт для индивидуального обучения или для работы в небольших группах, чтобы практиковать порядок чисел, сложение, вычитание и пропуск счета двойками, пятерками и десятками. В руководство «Really Good Stuff Activity Guide» включены интерактивные занятия в классе и вспомогательные воспроизводимые материалы.
когда они перескакивают свои лягушки с одного числа на другое. Они идеально подходят для студенческих парт для индивидуального обучения или для работы в небольших группах, чтобы практиковать порядок чисел, сложение, вычитание и пропуск счета двойками, пятерками и десятками. В руководство «Really Good Stuff Activity Guide» включены интерактивные занятия в классе и вспомогательные воспроизводимые материалы.- ЧТО ВКЛЮЧЕНО: Набор «Числовые линейки Slide and Learn™» включает 12 прочных пластиковых числовых линеек (21 на 3 дюйма) и руководство к занятиям Really Good Stuff® с заданиями в классе и вспомогательным воспроизводимым материалом. С УНИВЕРСАЛЬНЫМ МАТЕМАТИЧЕСКИМ ИНСТРУМЕНТОМ: эти интерактивные числовые линейки идеально подходят для ознакомления, обучения и закрепления навыков работы с числовыми линейками для порядка чисел, сложения, вычитания и пропуска счета двойками, пятерками и десятками. -ПРАКТИКА НА ЛИНИЯХ: дайте своим учащимся новый увлекательный практический способ отработать свои навыки числовых линий с помощью практических числовых линий, которые станут любимым занятием в классе во время занятий по математике и в свободное время!
- ИДЕАЛЬНО ДЛЯ ШКОЛЫ И ДОМА: числовые линии Slide and Learn™ выделяют числа от 0 до 30 и являются удобным математическим инструментом в школе и дома, помогая учащимся лучше понимать числа, перемещая лягушку вдоль числовой линии!
- COMMON CORE READY: таблицы умножения Slide and Learn приведены в соответствие с Common Core и стандартами штата по математике.
 Вы можете чувствовать себя хорошо, зная, что они предназначены для работы с вашей учебной программой!
Вы можете чувствовать себя хорошо, зная, что они предназначены для работы с вашей учебной программой!
Технические характеристики
- Набор из 12 цифровых линий
- 21″ на 3″ каждый
- Руководство по работе с Really Good Stuff®
Ресурсы
Руководство по деятельностиИнструмент сопоставления стандартов
Мы знаем стандарты
Только в США почти 30% образовательных стандартов пересматриваются, пересматриваются или редактируются каждый год. Отслеживание этих изменений требует постоянного опыта, и у нас есть инструмент для управления этими стандартами, поэтому вы можете доверять нам как лидеру в согласовании стандартов. Корреляции сделаны для всех государственных, национальных и общих базовых стандартов. Кроме того, у нас есть нормативы Head Start для детей младшего возраста. А совсем недавно мы добавили как национальные стандарты STEM, так и научные стандарты следующего поколения (NGSS).
Поиск стандартов
Отзывы
19,99 $
Возраст: 5+ / классы: K-1
Укрепите чувство числа с помощью этих забавных интерактивных числовых линий
Вашим учащимся понравится скользить милой маленькой лягушкой по этим прочным пластиковым числовым линиям Slide and Learn™, чтобы выделять числа от 0 до 30 и сосредотачиваться на них. Прочные числовые линии включают 12 интерактивных числовых линий, которые помогают учащимся лучше понимать числа и осваивать первые математические навыки. когда они перескакивают свои лягушки с одного числа на другое. Они идеально подходят для студенческих парт для индивидуального обучения или для работы в небольших группах, чтобы практиковать порядок чисел, сложение, вычитание и пропуск счета двойками, пятерками и десятками. В руководство «Really Good Stuff Activity Guide» включены интерактивные занятия в классе и вспомогательные воспроизводимые материалы.
- ЧТО ВКЛЮЧЕНО: Набор «Числовые линейки Slide and Learn™» включает 12 прочных пластиковых числовых линеек (21 на 3 дюйма) и руководство к занятиям Really Good Stuff® с заданиями в классе и вспомогательным воспроизводимым материалом. С УНИВЕРСАЛЬНЫМ МАТЕМАТИЧЕСКИМ ИНСТРУМЕНТОМ: эти интерактивные числовые линейки идеально подходят для ознакомления, обучения и закрепления навыков работы с числовыми линейками для порядка чисел, сложения, вычитания и пропуска счета двойками, пятерками и десятками. -ПРАКТИКА НА ЛИНИЯХ: дайте своим учащимся новый увлекательный практический способ отработать свои навыки числовых линий с помощью практических числовых линий, которые станут любимым занятием в классе во время занятий по математике и в свободное время!
- ИДЕАЛЬНО ДЛЯ ШКОЛЫ И ДОМА: числовые линии Slide and Learn™ выделяют числа от 0 до 30 и являются удобным математическим инструментом в школе и дома, помогая учащимся лучше понимать числа, перемещая лягушку вдоль числовой линии!
- COMMON CORE READY: таблицы умножения Slide and Learn приведены в соответствие с Common Core и стандартами штата по математике.
 Вы можете чувствовать себя хорошо, зная, что они предназначены для работы с вашей учебной программой!
Вы можете чувствовать себя хорошо, зная, что они предназначены для работы с вашей учебной программой!
19,99 $
- Набор из 12 строк с цифрами
- 21″ на 3″ каждый
- Руководство по работе с Really Good Stuff®
19,99 долл. США
Руководство по деятельности19,99 долл. США
19,99 долл. США
Мы знаем стандарты
Только в США почти 30 % образовательных стандартов пересматриваются, пересматриваются или редактируются каждый год . Отслеживание этих изменений требует постоянного опыта, и у нас есть инструмент для управления этими стандартами, поэтому вы можете доверять нам как лидеру в согласовании стандартов. Корреляции сделаны для всех государственных, национальных и общих базовых стандартов. Кроме того, у нас есть нормативы Head Start для детей младшего возраста. А совсем недавно мы добавили как национальные стандарты STEM, так и научные стандарты следующего поколения (NGSS).
Поиск стандартов
Really Good Stuff предлагает продукты, которые полностью соответствуют стандартам Common Core и State Standards for Language Arts и Math. Найдите продукты, которые соответствуют нужным вам стандартам. Начните поиск, выбрав штат, класс и предметную область ниже.
Найдите продукты, которые соответствуют нужным вам стандартам. Начните поиск, выбрав штат, класс и предметную область ниже.
Стандарты поиска Соответствуют:
Slide and Learn™ Number Lines — Набор из 12
Стандарт — или — ШтатВыберите стандарт/штатВсе штаты Общие стандарты CoreHead Start Стандарты науки следующего поколения (NRCDSC)Национальные стандарты STEMАлабамаАляскаАризонаАрканзасКалифорнияКолорадоКоннектикутДелавэрДист. КолумбияФлоридаГрузияГавайиАйдахоИллинойсИндианаАйоваКанзасКентуккиЛуизианаМэнМэрилендМассачусетсМичиганМиннесотаМиссисипиМиссуриМонтанаНебраскаНевадаНью-ГэмпширНью-ДжерсиНью-МексикоНью-ЙоркСеверная КаролинаСеверная ДакотаОгайоОклахомаОрегонПенсильванияРод-АйлендЮжная КаролинаЮжная ДакотаTenne sseeТехасЮтаВермонтВирджинияВашингтонЗападная ВирджинияВисконсинВайомингУровень
Предмет
Уровень оценки
Выберите класс Начальный уровень / Раннее детствоK12345678
Предмет
Выберите предмет Начальный уровень / Раннее детствоЯзыковые искусстваМатематикаНаукаСоциальное и эмоциональное обучение
Рекомендуется для вас
Больше подобных
Предложение о бесплатной доставке действует онлайн только при минимальном заказе на сумму 39 долларов США. Максимальная экономия $500. Используйте промокод SHIP39 на кассе. Бесплатная доставка распространяется только на стандартную наземную доставку в пределах 48 континентальных штатов США. Товары со значком грузовика на странице товара не допускаются. Не действует на предыдущие заказы. Можно комбинировать с другими избранными купонами или акциями. Действительно только при минимальном заказе на сумму 39 долларов США, после применения других скидок и рекламных акций, а также без учета налогов и стоимости доставки. Предложение заканчивается 31.05.20.
Максимальная экономия $500. Используйте промокод SHIP39 на кассе. Бесплатная доставка распространяется только на стандартную наземную доставку в пределах 48 континентальных штатов США. Товары со значком грузовика на странице товара не допускаются. Не действует на предыдущие заказы. Можно комбинировать с другими избранными купонами или акциями. Действительно только при минимальном заказе на сумму 39 долларов США, после применения других скидок и рекламных акций, а также без учета налогов и стоимости доставки. Предложение заканчивается 31.05.20.
Действителен онлайн до 31.05.20, 23:59 по восточному поясному времени. Введите код купона FLAT5 во время оформления заказа, чтобы воспользоваться предложением. Заказы должны быть отправлены на один адрес в пределах Соединенных Штатов. Только стандартная доставка. Исключает товары с ограничениями по доставке. Не использовать в сочетании с любыми другими предложениями или скидками. Не может быть использован для предыдущих покупок или товаров, изготовленных по индивидуальному заказу.

 также
также
 — М.: Физматлит, 1993.
— М.: Физматлит, 1993.
 -ПРАКТИКА НА ЛИНИЯХ: дайте своим учащимся новый увлекательный практический способ отработать свои навыки числовых линий с помощью практических числовых линий, которые станут любимым занятием в классе во время занятий по математике и в свободное время!
-ПРАКТИКА НА ЛИНИЯХ: дайте своим учащимся новый увлекательный практический способ отработать свои навыки числовых линий с помощью практических числовых линий, которые станут любимым занятием в классе во время занятий по математике и в свободное время! Вы можете чувствовать себя хорошо, зная, что они предназначены для работы с вашей учебной программой!
Вы можете чувствовать себя хорошо, зная, что они предназначены для работы с вашей учебной программой! Вы можете чувствовать себя хорошо, зная, что они предназначены для работы с вашей учебной программой!
Вы можете чувствовать себя хорошо, зная, что они предназначены для работы с вашей учебной программой! Например, он может помочь узнать какие простые множители у числа 700? Выберите начальное число (например ‘700’). После чего нажмите кнопку ‘Посчитать’.
Например, он может помочь узнать какие простые множители у числа 700? Выберите начальное число (например ‘700’). После чего нажмите кнопку ‘Посчитать’. Контрольная работа по математике 6 класс с ответами. Цитаты из пособия «Контрольно-измерительные материалы по математике 6 класс» (составитель вопросов — Л.П.Попова, издательство ВАКО) использованы в учебных целях. Контрольные работы составлены по УМК Виленкин и др. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
Контрольная работа по математике 6 класс с ответами. Цитаты из пособия «Контрольно-измерительные материалы по математике 6 класс» (составитель вопросов — Л.П.Попова, издательство ВАКО) использованы в учебных целях. Контрольные работы составлены по УМК Виленкин и др. Ответы на контрольные работы адресованы родителям, которые смогут проконтролировать правильность выполнения задания.
 700 = 2*2*5*5*7, 8316 = 2*2*3*3*3*7*11.
700 = 2*2*5*5*7, 8316 = 2*2*3*3*3*7*11.




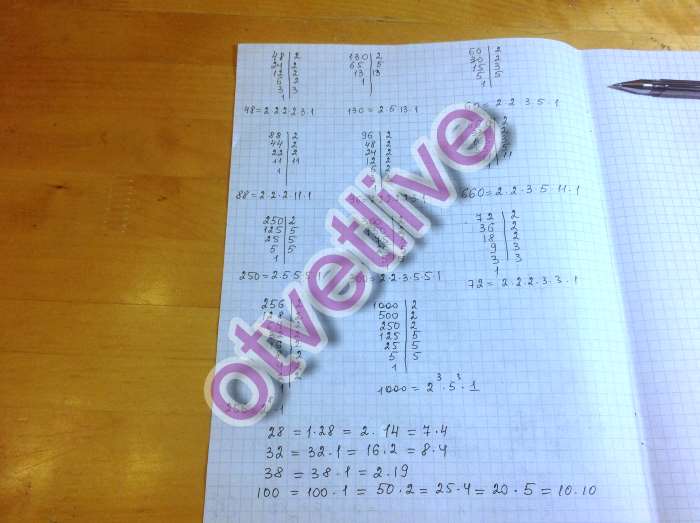
 В конце концов мы останавливаемся, если следующего простого множителя не существует или когда мы не можем дальше делить.
В конце концов мы останавливаемся, если следующего простого множителя не существует или когда мы не можем дальше делить.
 , 538.
, 538.

 Я.
Я. (Подробнее…)
(Подробнее…)

 Сравните отрезки:
Сравните отрезки:
 Я здесь не для того, чтобы плюнуть на твою нямку или рассказать тебе что-то, что ты уже знаешь.
Я здесь не для того, чтобы плюнуть на твою нямку или рассказать тебе что-то, что ты уже знаешь. Затем налейте (да, налейте! Не швырните!) немного в миску и сверху положите ваши любимые фрукты. Кусочки овса, как утки, садятся на твердую каменную поверхность, как утки на замерзшее озеро. Но вы поймете, что сделали что-то правильно, когда ваши кусочки фруктов великолепно прильнут к каше.
Затем налейте (да, налейте! Не швырните!) немного в миску и сверху положите ваши любимые фрукты. Кусочки овса, как утки, садятся на твердую каменную поверхность, как утки на замерзшее озеро. Но вы поймете, что сделали что-то правильно, когда ваши кусочки фруктов великолепно прильнут к каше. Но я буду иметь в виду и два других, так что вы должны знать различия:
Но я буду иметь в виду и два других, так что вы должны знать различия: Но овсяные хлопья быстрого приготовления просто расплющивают до следующей степени и обычно немного разбивают на более мелкие крошки. Эти овсяные хлопья настолько плоские, что их можно просто замочить в горячей воде, а не варить на медленном огне. Я не люблю их, и я действительно не знаю никого, кто любит, но они отлично подходят для пеших прогулок и занятого утра.
Но овсяные хлопья быстрого приготовления просто расплющивают до следующей степени и обычно немного разбивают на более мелкие крошки. Эти овсяные хлопья настолько плоские, что их можно просто замочить в горячей воде, а не варить на медленном огне. Я не люблю их, и я действительно не знаю никого, кто любит, но они отлично подходят для пеших прогулок и занятого утра. Но старомодные овсяные хлопья прекрасны сами по себе и лучше всего превращаются в бархатистую сливочную кашу. К сожалению, в большинстве рецептов используется слишком мало жидкости, чтобы создать текстуру, примыкающую к стальному порезу. Это приводит к скучному gloop. Лучше не пытаться заставить ваш старомодный овес вести себя как стальной овес.
Но старомодные овсяные хлопья прекрасны сами по себе и лучше всего превращаются в бархатистую сливочную кашу. К сожалению, в большинстве рецептов используется слишком мало жидкости, чтобы создать текстуру, примыкающую к стальному порезу. Это приводит к скучному gloop. Лучше не пытаться заставить ваш старомодный овес вести себя как стальной овес. Соблюдение соотношения ингредиентов на коробке с овсяными хлопьями приводит к самой липкой текстуре овсянки, которая затвердевает еще до того, как попадет в миску. Просто не хватает жидкости.
Соблюдение соотношения ингредиентов на коробке с овсяными хлопьями приводит к самой липкой текстуре овсянки, которая затвердевает еще до того, как попадет в миску. Просто не хватает жидкости. Я почти уверен, что сырость овсяных хлопьев быстрого приготовления является причиной того, что люди боятся добавлять больше жидкости в свои старомодные овсяные хлопья. Но это создает совершенно ложную дихотомию между водянистым/сырым овсом и мутным/жестким овсом. Есть кремовая альтернатива, которая ни на что не похожа.
Я почти уверен, что сырость овсяных хлопьев быстрого приготовления является причиной того, что люди боятся добавлять больше жидкости в свои старомодные овсяные хлопья. Но это создает совершенно ложную дихотомию между водянистым/сырым овсом и мутным/жестким овсом. Есть кремовая альтернатива, которая ни на что не похожа. В большинстве рецептов (включая коробочки с овсянкой) используется соотношение 1 часть овса на 2 части жидкости по объему, но я предпочитаю 1 часть овса на 4 части жидкости по объему (это примерно 1 часть овса на 9 частей).части жидкости по массе). Или, если вам не хочется заниматься математикой, просто следуйте рецепту в конце этого поста.
В большинстве рецептов (включая коробочки с овсянкой) используется соотношение 1 часть овса на 2 части жидкости по объему, но я предпочитаю 1 часть овса на 4 части жидкости по объему (это примерно 1 часть овса на 9 частей).части жидкости по массе). Или, если вам не хочется заниматься математикой, просто следуйте рецепту в конце этого поста. Так что будьте щедры с размером порции, если вы голодны. Он очень легкий, поэтому вы можете съесть большую миску, чем обычно, если хотите начать свой день с плотного завтрака.
Так что будьте щедры с размером порции, если вы голодны. Он очень легкий, поэтому вы можете съесть большую миску, чем обычно, если хотите начать свой день с плотного завтрака. Вы можете мацерировать практически любые фрукты (особенно персики, сливы, нектарины, другие ягоды и т. д.), посыпав их небольшим количеством сахара и дав соку настояться в холодильнике не менее 30 минут (лучше всего 24 часа). . Используйте сироп, который собирается умеренно (или щедро!) в качестве небольшого подсластителя.
Вы можете мацерировать практически любые фрукты (особенно персики, сливы, нектарины, другие ягоды и т. д.), посыпав их небольшим количеством сахара и дав соку настояться в холодильнике не менее 30 минут (лучше всего 24 часа). . Используйте сироп, который собирается умеренно (или щедро!) в качестве небольшого подсластителя. Как только она закипит, уменьшите огонь до среднего или средне-слабого и продолжайте варить около 15 минут, время от времени помешивая, пока жидкость не загустеет, а овсянка не станет мягкой. Сначала он будет водянистым, а в определенный момент заметно загустеет (например, пузырьки станут больше), оставаясь при этом очень текучим и кремообразным. Оставьте его открытым все время и будьте осторожны, чтобы он не пузырился.
Как только она закипит, уменьшите огонь до среднего или средне-слабого и продолжайте варить около 15 минут, время от времени помешивая, пока жидкость не загустеет, а овсянка не станет мягкой. Сначала он будет водянистым, а в определенный момент заметно загустеет (например, пузырьки станут больше), оставаясь при этом очень текучим и кремообразным. Оставьте его открытым все время и будьте осторожны, чтобы он не пузырился. Тара произнесла слова, и горшок сварил для них кашу. Тара прибежала домой с этим горшком и рассказала об этом матери.
Тара произнесла слова, и горшок сварил для них кашу. Тара прибежала домой с этим горшком и рассказала об этом матери.  Наш сегмент «Учимся дальше» отвечает на все вероятные вопросы, которые ребенок может задать из любопытства.
Наш сегмент «Учимся дальше» отвечает на все вероятные вопросы, которые ребенок может задать из любопытства.


 к _____ _____ _____
к _____ _____ _____  я вернул ей деньги
на следующий день и поблагодарил ее за помощь.
я вернул ей деньги
на следующий день и поблагодарил ее за помощь. 
 ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ: учебное пособие»,
ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ: учебное пособие», ) 2018, ПРИКЛАДНАЯ МАТЕМАТИКА. ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ: учебное пособие. Сер. 68 Профессиональное образование, 2-е изд. ред., Общество с ограниченной ответственностью «Издательство ЮРАЙТ», Москва.
) 2018, ПРИКЛАДНАЯ МАТЕМАТИКА. ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ: учебное пособие. Сер. 68 Профессиональное образование, 2-е изд. ред., Общество с ограниченной ответственностью «Издательство ЮРАЙТ», Москва. Рассмотрены вопросы построения сетевого графика, отыскания критического пути, расчета резервов времени событий и работ. Издание снабжено вариантами индивидуальных заданий, охватывающие все разобранные виды задач, задачами, приложением и библиографическим списком.
Рассмотрены вопросы построения сетевого графика, отыскания критического пути, расчета резервов времени событий и работ. Издание снабжено вариантами индивидуальных заданий, охватывающие все разобранные виды задач, задачами, приложением и библиографическим списком.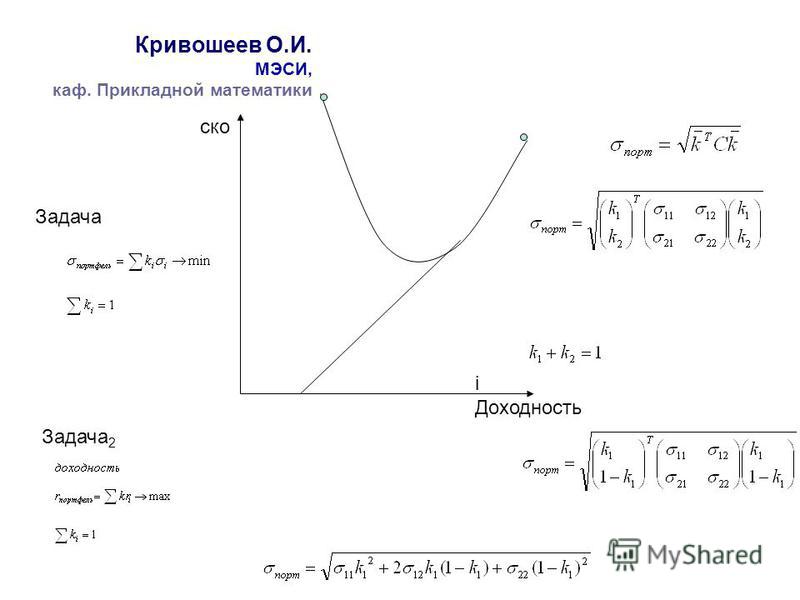 К. Крупской «Можно и нужно для задач брать примеры из окружающей жизни» и ученого математика Н. И. Лобачевского «Математике должно учить еще стой целью, чтобы познания здесь приобретаемые, были достаточными для обыкновенных потребностей жизни».
К. Крупской «Можно и нужно для задач брать примеры из окружающей жизни» и ученого математика Н. И. Лобачевского «Математике должно учить еще стой целью, чтобы познания здесь приобретаемые, были достаточными для обыкновенных потребностей жизни». 
 Нужно посчитать какую площадь нужно, чтобы поклеить комнату, если:высота стен 2.70 м, ширина(AВ и CD)-4 м, длина(АС и BD)-6 м, Sокна 2.1 м2, Sдвери-2,1 м2 ABCD
Нужно посчитать какую площадь нужно, чтобы поклеить комнату, если:высота стен 2.70 м, ширина(AВ и CD)-4 м, длина(АС и BD)-6 м, Sокна 2.1 м2, Sдвери-2,1 м2 ABCD Предоставляем работы учащихся.
Предоставляем работы учащихся. Найдём их площадь: S(a) = 4.2 * 2.6 = 10.9 м²S(a+c) = 2 * S(a) = 21.8 м²Сторона b = стороне d. Найдём их площадь: S(b) = 2.7 * 2.6 = 7.02 м²S(b+d) = 2 * S(b) = 14.04 м²S(окна) = 1.4 * 1.5 = 2.1 м²S(двери) = 0.9 * 2.1 = 1.89 м²ADBCA1 D1 B1 C1
Найдём их площадь: S(a) = 4.2 * 2.6 = 10.9 м²S(a+c) = 2 * S(a) = 21.8 м²Сторона b = стороне d. Найдём их площадь: S(b) = 2.7 * 2.6 = 7.02 м²S(b+d) = 2 * S(b) = 14.04 м²S(окна) = 1.4 * 1.5 = 2.1 м²S(двери) = 0.9 * 2.1 = 1.89 м²ADBCA1 D1 B1 C1 2
2 (По данным производителя) x1 рулон – 500 грн.x10 рулонов – 500 * 10 = 5000 грн.
(По данным производителя) x1 рулон – 500 грн.x10 рулонов – 500 * 10 = 5000 грн. Всего: 1000 г.
Всего: 1000 г. к. у нас вместо 4 картошин есть только две, а ветчины в 1.25 раза меньше, но не смотря на то что ветчины было в 1.25 раза меньше, нам пришлось уменьшить ингредиенты в два раза. Это всё для того чтобы соблюдать пропорции приготовления.
к. у нас вместо 4 картошин есть только две, а ветчины в 1.25 раза меньше, но не смотря на то что ветчины было в 1.25 раза меньше, нам пришлось уменьшить ингредиенты в два раза. Это всё для того чтобы соблюдать пропорции приготовления. Вычислите масштаб чертежа, если на нем длина сарафана будет равна 15см. Ответ: 1:5
Вычислите масштаб чертежа, если на нем длина сарафана будет равна 15см. Ответ: 1:5 «Образование не дает ростков в душе, если оно не проникает до значительной глубины» Древнегреческий философ Протагор из Абдеры (481 – 411г. до н.э.)
«Образование не дает ростков в душе, если оно не проникает до значительной глубины» Древнегреческий философ Протагор из Абдеры (481 – 411г. до н.э.) Но действительно ли тарифы настолько выгодные?Проблемный вопрос
Но действительно ли тарифы настолько выгодные?Проблемный вопрос Во всех профессиях нужна. Учителям, врачам и поварам. Бухгалтерам, певцам и продавцам. Всем математика важна. Царица всех наук она.
Во всех профессиях нужна. Учителям, врачам и поварам. Бухгалтерам, певцам и продавцам. Всем математика важна. Царица всех наук она.
 д.
д.
 be/Vb_GaXuB15c
be/Vb_GaXuB15c  be/eeGOUeX2keo
be/eeGOUeX2keo  Исключение. Равновесие твердых тел
Исключение. Равновесие твердых тел Исключение. Равновесие твердых тел
Исключение. Равновесие твердых тел






 Развивают зрительное внимание и аналитические способности мозга.
Развивают зрительное внимание и аналитические способности мозга.
 Придумай хитроумную стратегию! Прокачай внимательность, зрительную память, натренируй визуальное восприятие.
Придумай хитроумную стратегию! Прокачай внимательность, зрительную память, натренируй визуальное восприятие.
 Подходит для тренировки распределенного внимания, умения выполнять много дел сразу. Учит находить выход в сложных ситуациях. У старшего поколения Пасьянс — профилактика возрастных изменений мозга.
Подходит для тренировки распределенного внимания, умения выполнять много дел сразу. Учит находить выход в сложных ситуациях. У старшего поколения Пасьянс — профилактика возрастных изменений мозга. Увеличит количество эндорфинов — это приводит к сокращению кровяного давления и повышает стрессоустойчивость.
Увеличит количество эндорфинов — это приводит к сокращению кровяного давления и повышает стрессоустойчивость. Учит мыслить творчески и стратегически, укрепляет нервную систему и оттачивает глазомер.
Учит мыслить творчески и стратегически, укрепляет нервную систему и оттачивает глазомер.
 Для тех, кто помнит классику! Тренажер для прокачки кратковременной памяти и фокусированного внимания.
Для тех, кто помнит классику! Тренажер для прокачки кратковременной памяти и фокусированного внимания.


 д.
д. Не было ни предупреждений, ничего, сразу блок на вход. Пожалуйста, верните мне доступ, я исправлю ситуацию, больше так не буду делать в вашем приложении. Очень уважаю!
Не было ни предупреждений, ничего, сразу блок на вход. Пожалуйста, верните мне доступ, я исправлю ситуацию, больше так не буду делать в вашем приложении. Очень уважаю! Подробнее
Подробнее Эта победа вывела американского гроссмейстера на новый уровень ясно сначала.
Эта победа вывела американского гроссмейстера на новый уровень ясно сначала. Оттуда игра превратилась в сложную перестрелку. Почти на полчаса раньше Фируджа решил попробовать динамичный блеф ходом 26…Bf4.
Оттуда игра превратилась в сложную перестрелку. Почти на полчаса раньше Фируджа решил попробовать динамичный блеф ходом 26…Bf4. Тем не менее, ферзевые и второстепенные окончания могут быть богаты идеями из-за их уникального сочетания тонкостей эндшпиля и динамических возможностей. Проницательной перестановкой своих фигур Каруана создал небольшой перевес, который начал постепенно увеличиваться.
Тем не менее, ферзевые и второстепенные окончания могут быть богаты идеями из-за их уникального сочетания тонкостей эндшпиля и динамических возможностей. Проницательной перестановкой своих фигур Каруана создал небольшой перевес, который начал постепенно увеличиваться. Гири проницательно ответил, прорвавшись по центру ходом 15…d5, прежде чем Вашье-Лаграв смог упрочить свою позицию. Французский гроссмейстер продолжал прессинговать, целясь в изолированную пешку а7 и выводя коня на форпост с5. Но Гири организовал свои фигуры в стройную активно-защитную схему, ограничивающую продвижение соперника.
Гири проницательно ответил, прорвавшись по центру ходом 15…d5, прежде чем Вашье-Лаграв смог упрочить свою позицию. Французский гроссмейстер продолжал прессинговать, целясь в изолированную пешку а7 и выводя коня на форпост с5. Но Гири организовал свои фигуры в стройную активно-защитную схему, ограничивающую продвижение соперника. ..b5!?, предотвратив с4 — основной способ белых создать давление на ферзевом фланге. Чемпион мира переключил передачу, чтобы подготовить прорыв е4 в центре, но проницательная центральная игра Дуды вскоре нейтрализовала его преимущество первого хода. Игроки обменялись на ровный одноцветный слоном эндшпиль и закончили с мирным результатом.
..b5!?, предотвратив с4 — основной способ белых создать давление на ферзевом фланге. Чемпион мира переключил передачу, чтобы подготовить прорыв е4 в центре, но проницательная центральная игра Дуды вскоре нейтрализовала его преимущество первого хода. Игроки обменялись на ровный одноцветный слоном эндшпиль и закончили с мирным результатом. h5!?, присоединяется к лидерам
h5!?, присоединяется к лидерам
 🧘🏻♂️
🧘🏻♂️ Игроки дошли до эндшпиля с четным слоном и вскоре сыграли вничью.
Игроки дошли до эндшпиля с четным слоном и вскоре сыграли вничью. Когда соперники начали брать мои ладьи, знаете ли, мне пришлось изменить свою стратегию.
Когда соперники начали брать мои ладьи, знаете ли, мне пришлось изменить свою стратегию.



 Vector Magic предлагает вам содержательные настройки, понятные не только для машины, но и для людей, и их можно легко изменить.
Vector Magic предлагает вам содержательные настройки, понятные не только для машины, но и для людей, и их можно легко изменить.
 Если вам нужно конвертировать в EPS, всегда сначала пробуйте Vector Magic.
Если вам нужно конвертировать в EPS, всегда сначала пробуйте Vector Magic.
 Верните контроль над своими изображениями!
Верните контроль над своими изображениями! Векторизация или трассировка — это процесс повторной отрисовки растрового изображения как векторного.
Векторизация или трассировка — это процесс повторной отрисовки растрового изображения как векторного. Также часто используются в Интернете для экономии трафика.
Также часто используются в Интернете для экономии трафика.
 Ghostview может его очень хорошо читать, но не имеет возможности редактировать. Inkscape может только экспортировать его.
Ghostview может его очень хорошо читать, но не имеет возможности редактировать. Inkscape может только экспортировать его.

 адрес?
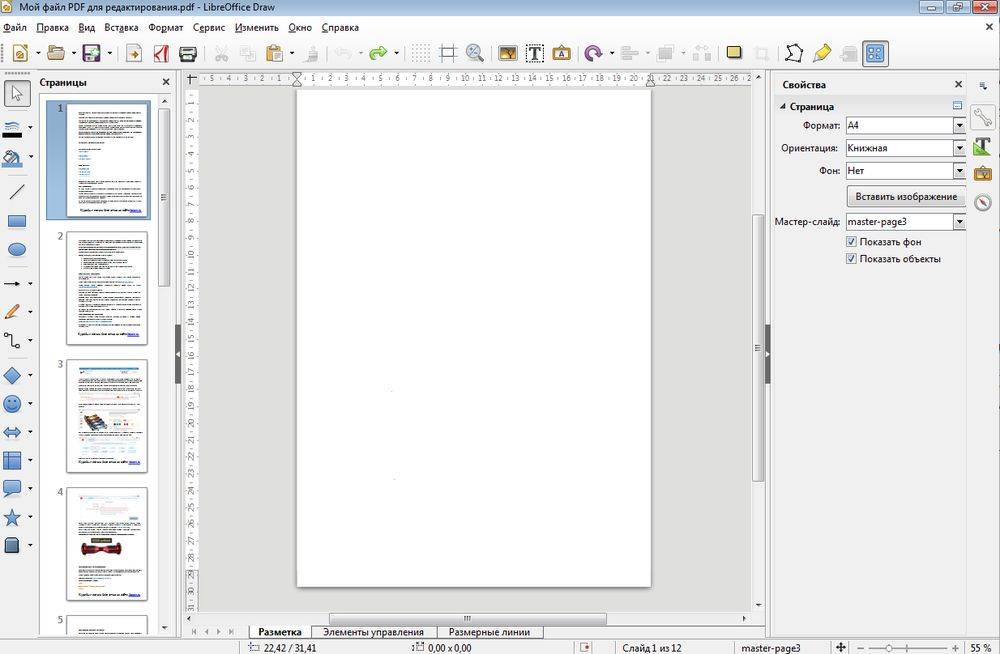
адрес? odg
odg Спецификации первоначально были разработаны Sun Microsystems. OpenDocument формат поддерживает представление документа: один XML документ и как совокупность нескольких вложенных документов в пакете.
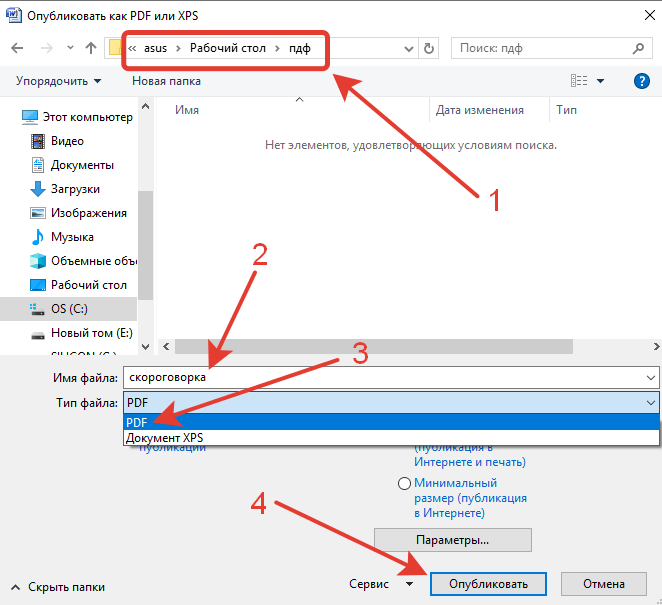
Спецификации первоначально были разработаны Sun Microsystems. OpenDocument формат поддерживает представление документа: один XML документ и как совокупность нескольких вложенных документов в пакете. pdf
pdf Он не кодирует информацию, относящуюся к программному обеспечению, аппаратному обеспечению или операционной системе, используемой для создания или просмотра документа.
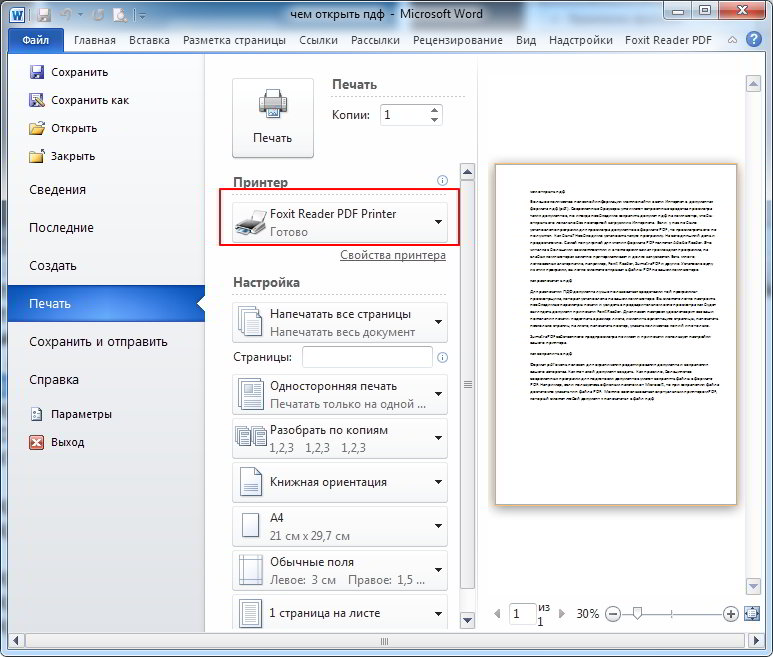
Он не кодирует информацию, относящуюся к программному обеспечению, аппаратному обеспечению или операционной системе, используемой для создания или просмотра документа. DWG в .pdf
DWG в .pdf

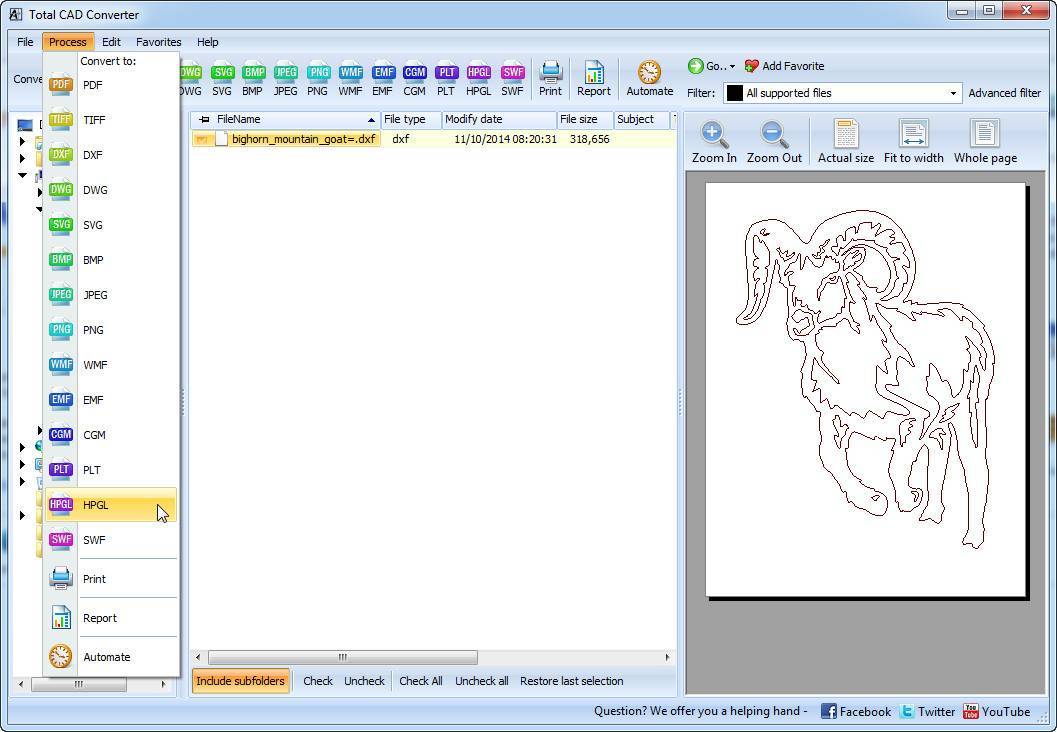
 Объединение нескольких файлов САПР в один многостраничный файл TIFF или PDF. При преобразовании нескольких папок программа может объединять выходные файлы каждой папки. т.е. вы конвертируете 2 папки с 5 файлами DWG в каждой в TIFF. Вы получаете 2 файла TIFF. Если вы хотите конвертировать файлы САПР на своем сервере, подайте заявку на серверную версию. Лицензия на сервер. Когда вы конвертируете CAD в JPEG, вы можете определить качество и сглаживание полученного изображения. Конвертируйте DWG, DXF, SVG и многие другие файлы за считанные секунды с помощью нашего понятного интерфейса в режиме мастера. Самый широкий список типов выходных файлов: PDF, TIFF, JPEG, BMP, WMF, PNG, DXF, BMP, CGM, HPGL, SVG, PS и SWF! Total CAD Converter позволяет выбрать режим сжатия, DPI изображения, фотометрическую интерпретацию для выходных изображений TIFF. Встроенная панель предварительного просмотра поможет вам быстрее найти нужный файл. Добавьте текстовые водяные знаки в верхний или нижний колонтитул выходного файла для предотвращения несанкционированного использования или добавьте информацию об авторских правах.
Объединение нескольких файлов САПР в один многостраничный файл TIFF или PDF. При преобразовании нескольких папок программа может объединять выходные файлы каждой папки. т.е. вы конвертируете 2 папки с 5 файлами DWG в каждой в TIFF. Вы получаете 2 файла TIFF. Если вы хотите конвертировать файлы САПР на своем сервере, подайте заявку на серверную версию. Лицензия на сервер. Когда вы конвертируете CAD в JPEG, вы можете определить качество и сглаживание полученного изображения. Конвертируйте DWG, DXF, SVG и многие другие файлы за считанные секунды с помощью нашего понятного интерфейса в режиме мастера. Самый широкий список типов выходных файлов: PDF, TIFF, JPEG, BMP, WMF, PNG, DXF, BMP, CGM, HPGL, SVG, PS и SWF! Total CAD Converter позволяет выбрать режим сжатия, DPI изображения, фотометрическую интерпретацию для выходных изображений TIFF. Встроенная панель предварительного просмотра поможет вам быстрее найти нужный файл. Добавьте текстовые водяные знаки в верхний или нижний колонтитул выходного файла для предотвращения несанкционированного использования или добавьте информацию об авторских правах. Хотите больше заказов? Добавьте счетчики страниц или дату на каждую страницу выходных файлов. При преобразовании DXF или DWG в PDF вы можете установить права пользователя, защитить файлы паролем или подписать их своей цифровой подписью. Доступны файлы PDF и PDF/A. Используйте его как мощный, но недорогой конвертер DWG. Пакетное преобразование файлов из DWG и в DWG для удобного обмена или импорта в другие приложения Autocad. Попробуйте использовать Total CAD ConverterX (SDK) в своем приложении ASP или PHP с ActiveX. Total CAD Converter имеет полную поддержку командной строки (получите готовую к использованию командную строку из графического интерфейса).
Хотите больше заказов? Добавьте счетчики страниц или дату на каждую страницу выходных файлов. При преобразовании DXF или DWG в PDF вы можете установить права пользователя, защитить файлы паролем или подписать их своей цифровой подписью. Доступны файлы PDF и PDF/A. Используйте его как мощный, но недорогой конвертер DWG. Пакетное преобразование файлов из DWG и в DWG для удобного обмена или импорта в другие приложения Autocad. Попробуйте использовать Total CAD ConverterX (SDK) в своем приложении ASP или PHP с ActiveX. Total CAD Converter имеет полную поддержку командной строки (получите готовую к использованию командную строку из графического интерфейса). д.). Файлы DWG содержат элементы векторного изображения и метаданные. Формат является родным для пакета САПР, хотя существуют неродные приложения САПР, с помощью которых вы можете открыть файл DWG. С момента его появления в 2000 году было разработано несколько вариантов формата DWG, и не все из них можно открыть с помощью неродного приложения.
д.). Файлы DWG содержат элементы векторного изображения и метаданные. Формат является родным для пакета САПР, хотя существуют неродные приложения САПР, с помощью которых вы можете открыть файл DWG. С момента его появления в 2000 году было разработано несколько вариантов формата DWG, и не все из них можно открыть с помощью неродного приложения.

 В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.

 Пусть точка A имеет координаты x1;y1, а точка B – координаты x2;y2.
Пусть точка A имеет координаты x1;y1, а точка B – координаты x2;y2.
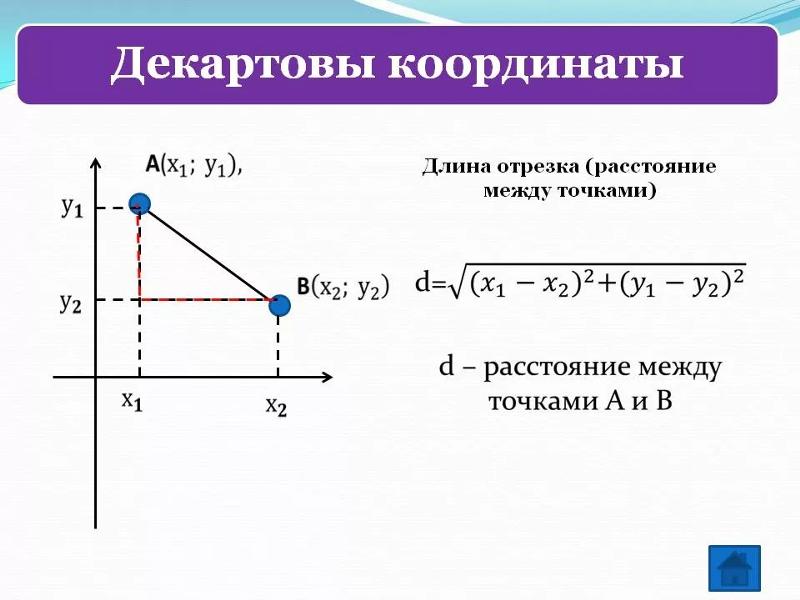 Выразим координаты x;y середины C отрезка AB через координаты его концов. Так как точка C – середина отрезка AB, то
Выразим координаты x;y середины C отрезка AB через координаты его концов. Так как точка C – середина отрезка AB, то
 Его координаты равны x2-x1;y2-y1. Следовательно, длина этого вектора может быть найдена по формуле:
Его координаты равны x2-x1;y2-y1. Следовательно, длина этого вектора может быть найдена по формуле:
 Калькулятор средней точки показывает работу, которую нужно найти:
Калькулятор средней точки показывает работу, которую нужно найти: Истинная линия в геометрии бесконечно длинна в обоих направлениях. Но отрезок прямой имеет 2 конечные точки, поэтому можно вычислить среднюю точку. Луч имеет один конец и бесконечно длинный в другом направлении.
Истинная линия в геометрии бесконечно длинна в обоих направлениях. Но отрезок прямой имеет 2 конечные точки, поэтому можно вычислить среднюю точку. Луч имеет один конец и бесконечно длинный в другом направлении.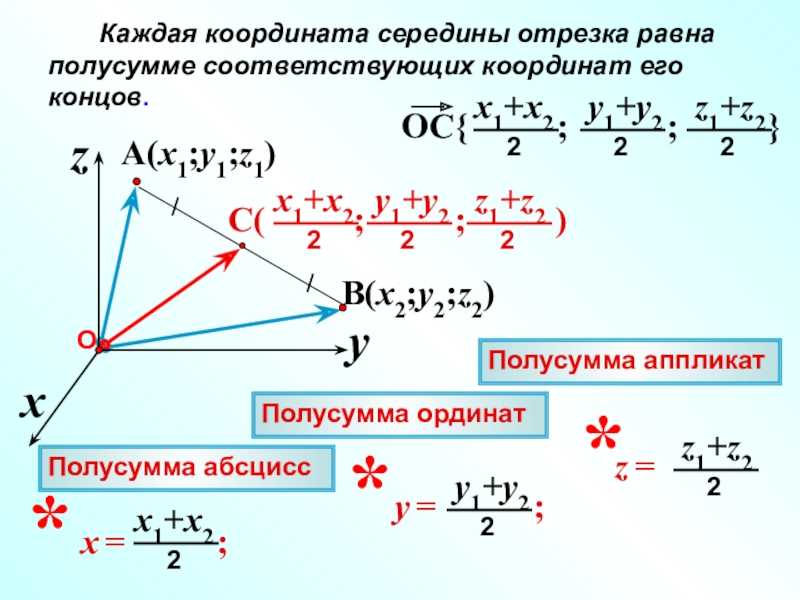 В этом примере средняя точка (9, 5).
В этом примере средняя точка (9, 5).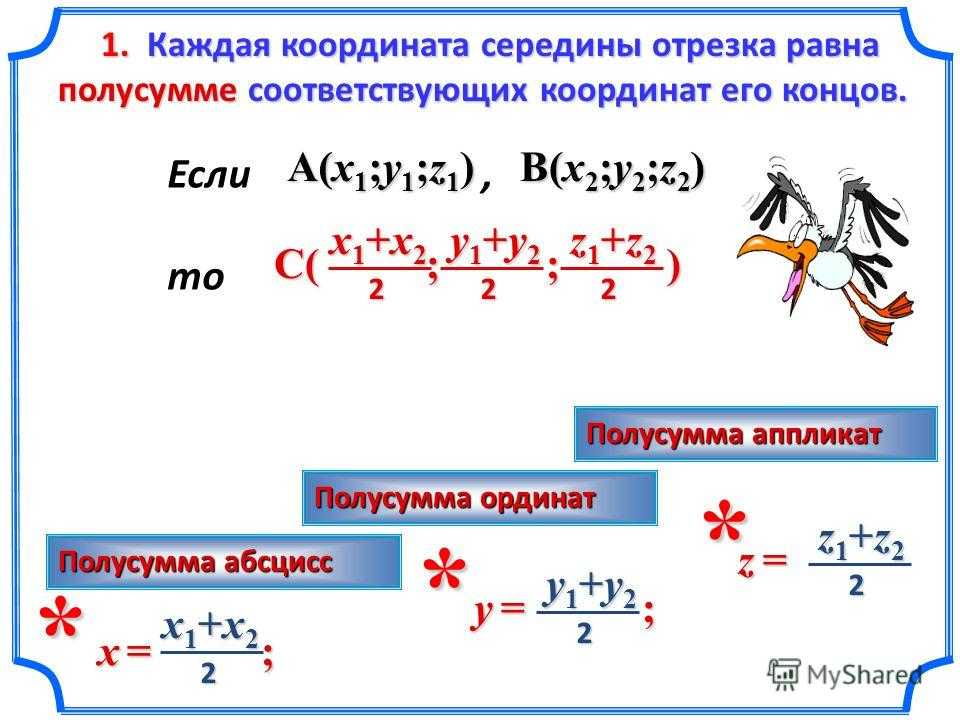 Начните с формулы средней точки сверху и определите координаты неизвестной конечной точки.
Начните с формулы средней точки сверху и определите координаты неизвестной конечной точки. Конечная точка – это (x 1 , y 1 ) координата. Середина – это (x M , y M ) координата.
Конечная точка – это (x 1 , y 1 ) координата. Середина – это (x M , y M ) координата.

 Калькулятор средней точки решит это мгновенно, если вы введете координаты. Выполните шаги, описанные выше, если рассчитываете вручную.
Калькулятор средней точки решит это мгновенно, если вы введете координаты. Выполните шаги, описанные выше, если рассчитываете вручную.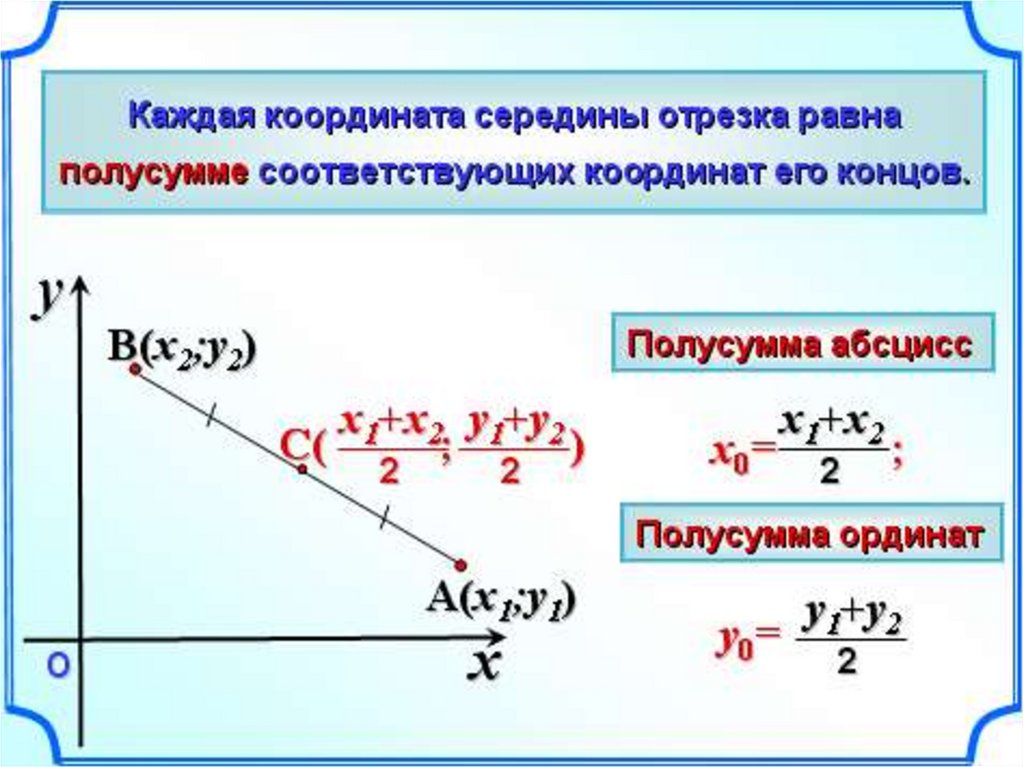 Калькулятор средней точки чрезвычайно полезен в таких случаях.
Калькулятор средней точки чрезвычайно полезен в таких случаях. Если вы знаете, как это сделать, перейдите к шагу 5 .
Если вы знаете, как это сделать, перейдите к шагу 5 . е. разделенные диаметром окружности.
е. разделенные диаметром окружности.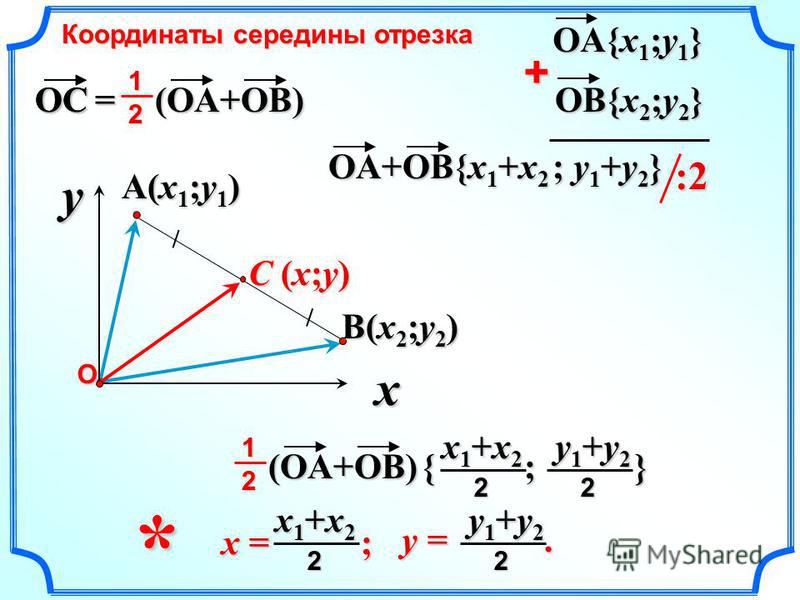


 Во многих примерах перед тем как выполнить действие нужно произвести ряд вычислений. Например, преобразовать дроби или перевести неправильную дробь в правильную.
Во многих примерах перед тем как выполнить действие нужно произвести ряд вычислений. Например, преобразовать дроби или перевести неправильную дробь в правильную. Рассмотрим конкретный случай:
Рассмотрим конкретный случай:
 Не идите сложными путями. Распланируйте все действия, решайте сначала в черновом варианте, затем переносите в школьную тетрадь.
Не идите сложными путями. Распланируйте все действия, решайте сначала в черновом варианте, затем переносите в школьную тетрадь. Тогда каждый кусочек торта, можно назвать долей. Если взять один из четырех кусков торта, то он будет одной четвертой долей.
Тогда каждый кусочек торта, можно назвать долей. Если взять один из четырех кусков торта, то он будет одной четвертой долей.

 Для этого дроби записываются запятая под запятой, и в сумме требуется лишь снести запятую вниз.
Для этого дроби записываются запятая под запятой, и в сумме требуется лишь снести запятую вниз. 30:10 = 3 — для второй. Перемножаем числители и их доп.множ. Получаем уменьшаемое 25/30 и вычитаемое 21/30. Далее выполняем вычитание числителей, а знаменатель оставляем без изменения.
30:10 = 3 — для второй. Перемножаем числители и их доп.множ. Получаем уменьшаемое 25/30 и вычитаемое 21/30. Далее выполняем вычитание числителей, а знаменатель оставляем без изменения.
 От 3,300 вычитаем 2,025. Записываем действие в столбик, запятая под запятой.
От 3,300 вычитаем 2,025. Записываем действие в столбик, запятая под запятой. Перемножаем числители и их множители, получаем сумму дробей 35/56 и 24/56. Получили сумму 59/56. Дробь неправильная, переводим ее в смешанное число.Остальные примеры решаются аналогично.
Перемножаем числители и их множители, получаем сумму дробей 35/56 и 24/56. Получили сумму 59/56. Дробь неправильная, переводим ее в смешанное число.Остальные примеры решаются аналогично. Если вы к одной такой части добавите еще две, то получится 3/7. Наглядное объяснение примера 1/7+2/7 = 3/7.
Если вы к одной такой части добавите еще две, то получится 3/7. Наглядное объяснение примера 1/7+2/7 = 3/7.

 Для наглядности возьмем пример с тортом:
Для наглядности возьмем пример с тортом:
 е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей
е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей Если у вас остались какие то вопросы по решению дробей , что то непонятно, то пишите в комментарии и мы обязательно вам ответим.
Если у вас остались какие то вопросы по решению дробей , что то непонятно, то пишите в комментарии и мы обязательно вам ответим. Знаменатели похожи, что означает, что вы можете складывать или вычитать дроби напрямую.
Знаменатели похожи, что означает, что вы можете складывать или вычитать дроби напрямую.

 У нас есть отдельные калькуляторы как для LCM, так и для расчета дробей.
У нас есть отдельные калькуляторы как для LCM, так и для расчета дробей. Например, для дробей введите «-2/3».
Например, для дробей введите «-2/3». Но это не всегда так, поскольку некоторые калькуляторы могут использовать свои собственные специальные обозначения, такие как \(abs(x)\), которые также широко используются.
Но это не всегда так, поскольку некоторые калькуляторы могут использовать свои собственные специальные обозначения, такие как \(abs(x)\), которые также широко используются.
 ..
..  8 — сумма цифр числа.
Делители: 1, 2, 4, 8.
Обратное число к 8 – 0.125.
8 — сумма цифр числа.
Делители: 1, 2, 4, 8.
Обратное число к 8 – 0.125. 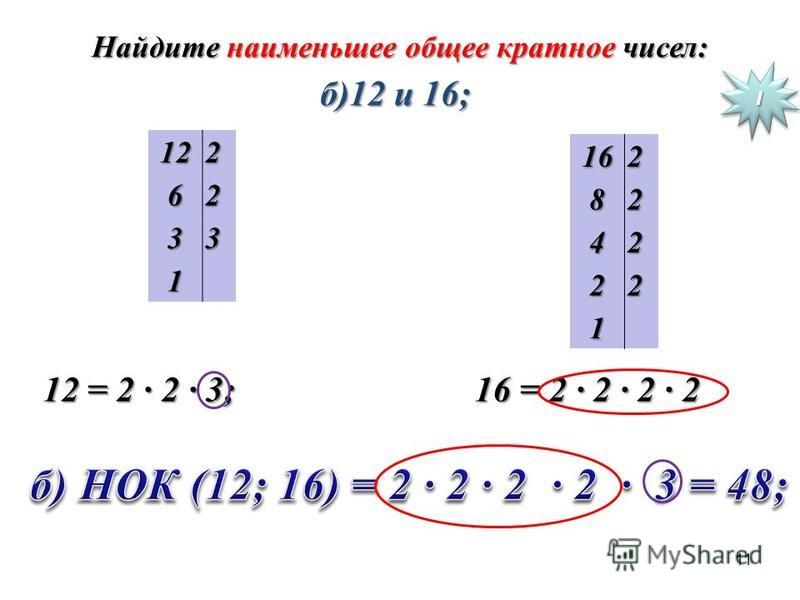
 Найдите наименьшее натуральное число R, большее единицы, чтобы отношения R:A, R:B были с остатком 1.
Найдите наименьшее натуральное число R, большее единицы, чтобы отношения R:A, R:B были с остатком 1.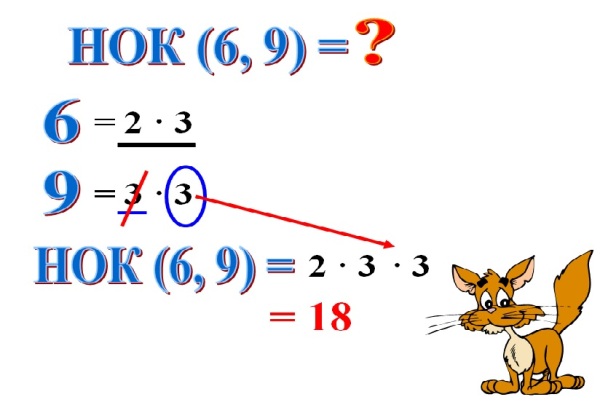 Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо?
Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо? Одна из сумм составила 679 чешских крон. Насколько велик был выигрыш?
Одна из сумм составила 679 чешских крон. Насколько велик был выигрыш? Самым простым является просто использование метода «грубой силы», который перечисляет кратные каждому целому числу.
Самым простым является просто использование метода «грубой силы», который перечисляет кратные каждому целому числу. Это также часто называют наибольшим общим фактором (GCF) среди других имен. Обратитесь к ссылке для получения подробной информации о том, как определить наибольший общий делитель. Учитывая LCM(a, b), процедура нахождения LCM с использованием НОК состоит в делении произведения чисел a и b по их GCF, т.е. (a × b)/GCF(a,b). При попытке определить НОК более двух чисел, например НОК(a, b, c), найдите НОК a и b , где результатом будет q . Затем найдите LCM c и q . Результатом будет LCM всех трех чисел. Используя предыдущий пример:
Это также часто называют наибольшим общим фактором (GCF) среди других имен. Обратитесь к ссылке для получения подробной информации о том, как определить наибольший общий делитель. Учитывая LCM(a, b), процедура нахождения LCM с использованием НОК состоит в делении произведения чисел a и b по их GCF, т.е. (a × b)/GCF(a,b). При попытке определить НОК более двух чисел, например НОК(a, b, c), найдите НОК a и b , где результатом будет q . Затем найдите LCM c и q . Результатом будет LCM всех трех чисел. Используя предыдущий пример:
 Катализаторы — это вещества, которые ускоряют темп (скорость) химической реакции, не потребляясь и не становясь частью конечного продукта.
Катализаторы не влияют на равновесные ситуации.
Катализаторы — это вещества, которые ускоряют темп (скорость) химической реакции, не потребляясь и не становясь частью конечного продукта.
Катализаторы не влияют на равновесные ситуации.

 Сделайте взвесь 2,0 г растворимого крахмала в 4 мл воды. Вылить суспензию в кипящую воду – кипятить 5 минут – разбавить до 200 мл – дать остыть.
Сделайте взвесь 2,0 г растворимого крахмала в 4 мл воды. Вылить суспензию в кипящую воду – кипятить 5 минут – разбавить до 200 мл – дать остыть. Промойте мерный цилиндр на 250 мл дистиллированной водой. Добавьте в цилиндр раствор Na 2 S 2 O 3 , 13 мл 1,0 М KI и 10 мл 1% раствора крахмала. Разбавьте смесь до 250 мл дистиллированной водой. Перелейте раствор туда и обратно между мерным цилиндром и оставшимся стаканом на 600 мл, чтобы перемешать раствор. Оставьте раствор в стакане. (Этот раствор 0,052 М в KI и 0,0032 М в Na 2 С 2 О 3 .)
Промойте мерный цилиндр на 250 мл дистиллированной водой. Добавьте в цилиндр раствор Na 2 S 2 O 3 , 13 мл 1,0 М KI и 10 мл 1% раствора крахмала. Разбавьте смесь до 250 мл дистиллированной водой. Перелейте раствор туда и обратно между мерным цилиндром и оставшимся стаканом на 600 мл, чтобы перемешать раствор. Оставьте раствор в стакане. (Этот раствор 0,052 М в KI и 0,0032 М в Na 2 С 2 О 3 .) Разведение концентрированного H 2 SO 4 является сильно экзотермическим процессом и выделяет достаточно тепла, чтобы вызвать ожоги. Поэтому при приготовлении разбавленных растворов из концентрированной кислоты всегда добавляйте кислоту в воду медленно и при перемешивании.
Разведение концентрированного H 2 SO 4 является сильно экзотермическим процессом и выделяет достаточно тепла, чтобы вызвать ожоги. Поэтому при приготовлении разбавленных растворов из концентрированной кислоты всегда добавляйте кислоту в воду медленно и при перемешивании.