| |||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||
СУНЦ УрФУ
Расписание
Электронный журнал
Поступающим
Олимпиады, турниры, конкурсы
Планы работы
Подготовительные курсы
Новости:
07.05.2023
Учимся и побеждаем!
Лицеисты заняли I и II места в Школе практического программирования.
06.05.2023
Поэзии чарующие звуки…
В СУНЦ стартует регистрация на поэтический вечер, который пройдёт 15 мая в 15:30 в актовом зале.
05.05.2023
Заключительный этап. Успех!
Наши лицеисты достойно выступили на заключительном этапе Всероссийской олимпиады школьников.
04.05.2023
Успехи на международном форуме в Кыргызстане
Лицеисты привезли из солнечного Кыргызстана золотую и бронзовую медали международного форума «Мы — интеллектуалы XXI века!».
04.05.2023
Зарядись «Энергией будущего»!
Лицеисты СУНЦ с успехом выступили на всероссийском конкурсе научно-исследовательских работ и проектов.
25.04.2023
Время зарабатывать!
Соцэки СУНЦ совершенствуют свои практические навыки.
Больше новостей
Видеогалерея:
Мужчины СУНЦ о 8 Марта (2023)
Концерт к 8 Марта (2023)
Поздравление с Днем защитника Отечества (2023)
Больше видео
О нас:
Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А. М. Горького (УрГУ).
В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями. Обучение производится по авторским программам, разработанным в соответствии с федеральными государственными образовательными стандартами; в составе СУНЦ — 8–11 классы различных профилей.
Иногородние обучающиеся проживают в уютном общежитии.
Прием производится в 8, 9, 10 и 11 классы. Работают подготовительные курсы.
Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора
по телефону +7 343 367-82-22 и в разделе нашего сайта «Поступающим».
Как нас найти:
Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝
Проезд:
- автобусами № 48, 52, 81 до остановки «Фирма Авангард»;
- автобусами № 28, 58 до остановки «Данилы Зверева», далее 7 минут пешком по улице Данилы Зверева;
- троллейбусом № 18 до остановки «Данилы Зверева», далее 14 минут пешком по улицам Сулимова, Данилы Зверева;
- троллейбусами № 4 до остановки «Сулимова», № 19, 32 до остановки «Боровая», далее 15 минут пешком по улицам Боровая, Вилонова, Данилы Зверева.
Основное исследование электронных, термодинамических и диэлектрических свойств монослоя Ca(OH)2 и Mg(OH)2
. 2022 23 мая; 12 (10): 1774.
2022 23 мая; 12 (10): 1774.
дои: 10.3390/nano12101774.
Мехрдад Ростами Осанлу 1 , Коладе А Оекан 2 , Уильям Дж. Ванденберге 2
Принадлежности
Принадлежности
- 1 Факультет физики Техасского университета в Далласе, Ричардсон, Техас 75080, США.
- 2 Факультет материаловедения и инженерии, Техасский университет в Далласе, Ричардсон, Техас 75080, США.
- PMID: 35630994
- PMCID: PMC9147085
- DOI:
10.
 3390/нано12101774
3390/нано12101774
Бесплатная статья ЧВК
Мехрдад Ростами Осанлу и др. Наноматериалы (Базель). .
Бесплатная статья ЧВК
. 2022 23 мая; 12 (10): 1774.
дои: 10.3390/nano12101774.
Авторы
Мехрдад Ростами Осанлу 1 , Коладе А Оекан 2 , Уильям Дж. Ванденберге 2
Принадлежности
- 1 Факультет физики Техасского университета в Далласе, Ричардсон, Техас 75080, США.

- 2 Факультет материаловедения и инженерии, Техасский университет в Далласе, Ричардсон, Техас 75080, США.
- PMID: 35630994
- PMCID: PMC9147085
- DOI: 10.3390/нано12101774
Абстрактный
Мы выполняем первопринципные расчеты для изучения электронных, термодинамических и диэлектрических свойств двумерных (2D) слоистых гидроксидов щелочноземельных металлов Ca(OH)2 и Mg(OH)2. Мы рассчитываем параметры решетки, энергии расслоения и фононные спектры монослоев, а также исследуем тепловые свойства этих монослоев, такие как свободная энергия Гельмгольца, теплоемкость при постоянном объеме и энтропия как функция температуры. Мы используем теорию возмущений функционала плотности (DFPT) для расчета статической диэлектрической проницаемости в плоскости и вне плоскости объемных и монослойных образцов. Мы вычисляем значения ширины запрещенной зоны и сродства к электрону с помощью функционала HSE06 и оцениваем плотность тока утечки транзисторов с монослоями Ca(OH)2 и Mg(OH)2 в качестве диэлектриков в сочетании с HfS2 и WS2 соответственно. Наши результаты показывают, что бислой Mg(OH)2 (EOT∼0,60 нм) с более низкой растворимостью в воде обеспечивает более высокие диэлектрические проницаемости вне плоскости и более низкие токи утечки, чем бислой Ca(OH)2 (EOT∼0,56 нм). Кроме того, внеплоскостная диэлектрическая проницаемость, ток утечки и EOT Mg(OH)2 превосходят двухслойный h-BN. Мы проверяем применимость правила Андерсона и делаем вывод, что бислои Ca(OH)2 и Mg(OH)2, соответственно, в паре с согласованными по решетке монослоями HfS2 и WS2 являются эффективными структурными комбинациями, которые могут привести к развитию инновационных многослойных структур.
Мы используем теорию возмущений функционала плотности (DFPT) для расчета статической диэлектрической проницаемости в плоскости и вне плоскости объемных и монослойных образцов. Мы вычисляем значения ширины запрещенной зоны и сродства к электрону с помощью функционала HSE06 и оцениваем плотность тока утечки транзисторов с монослоями Ca(OH)2 и Mg(OH)2 в качестве диэлектриков в сочетании с HfS2 и WS2 соответственно. Наши результаты показывают, что бислой Mg(OH)2 (EOT∼0,60 нм) с более низкой растворимостью в воде обеспечивает более высокие диэлектрические проницаемости вне плоскости и более низкие токи утечки, чем бислой Ca(OH)2 (EOT∼0,56 нм). Кроме того, внеплоскостная диэлектрическая проницаемость, ток утечки и EOT Mg(OH)2 превосходят двухслойный h-BN. Мы проверяем применимость правила Андерсона и делаем вывод, что бислои Ca(OH)2 и Mg(OH)2, соответственно, в паре с согласованными по решетке монослоями HfS2 и WS2 являются эффективными структурными комбинациями, которые могут привести к развитию инновационных многослойных структур. функциональные полевые транзисторы (FET).
функциональные полевые транзисторы (FET).
Ключевые слова: гетеробислой (OH)2/HfS2; двумерные диэлектрические материалы; 2D-диэлектрики с TMD-каналами; двумерные гетероструктуры для полевых транзисторов; двумерные ван-дер-ваальсовые диэлектрики; Гетеробислой Mg(OH)2/W2.
Заявление о конфликте интересов
Авторы заявляют об отсутствии конфликта интересов.
Цифры
Рисунок 1
Схематический вид…
Рисунок 1
Схематическое изображение полевого транзистора из монослойного диэлектрика M(OH) 2…
Рисунок 1 Схематическое изображение полевого транзистора, изготовленного из монослойного диэлектрика M(OH)2 и монослойного TMD-канала.
Рисунок 2
Структуры гидроксидов щелочноземельных металлов…
Рисунок 2
Структуры гидроксидов щелочноземельных металлов. Вид сбоку ( и ) и сверху…
фигура 2Структуры гидроксидов щелочноземельных металлов. Вид сбоку ( a ) и вид сверху монослоя ( d ) в дополнение к виду бислоя сбоку ( c ). ( b ) демонстрирует длину связи Ca-O/Mg-O (l1) и O-H (l2), а также углы между связями (α и β). Толщина монослоя ( t ) указана на двухслойных конструкциях.
Рисунок 3
M(OH) 2 фононная дисперсия…
Рисунок 3
M(OH) 2 Дисперсионные кривые фононов. ( a ) Фононный дисперсионный спектр…
( a ) Фононный дисперсионный спектр…
M(OH)2. ( a ) Фононный дисперсионный спектр Ca(OH)2. ( b ) Фононный дисперсионный спектр Mg(OH)2. Моды Eg (синий), A1g (красный), Eg(OH) (оранжевый) и A1g(OH) (зеленый) соответственно представляют собой поступательное движение и возвратно-поступательное движение связей O-H. На вставках визуализируются плоские и внеплоскостные колебательные моды OH. Ломаная ось показывает, что между 9 и 9 фононными ветвями нет.0 и 450 мэВ. Плоские энергетические кривые на высокоэнергетических модах (∼470 мэВ) связаны с внеплоскостными смещениями водорода и кислорода.
Рисунок 4
Термодинамические свойства Ca(OH) 2…
Рисунок 4
Термодинамические свойства Ca(OH) 2 и Mg(OH) 2 . Энтропия( S v (…
Энтропия( S v (…
Термодинамические свойства Ca(OH)2 и Mg(OH)2. Энтропия (Sv(T)), теплоемкость при постоянном объеме (Cv), внутренняя энергия ( U ( T )) и свободная энергия Гельмгольца ( A ( T )) Mg(OH)2 (Ca (OH)2) показаны сплошными (пунктирными) синими, зелеными, голубыми и красными линиями соответственно. Меньшая свободная энергия Гельмгольца означает, что с термодинамической точки зрения монослой Ca(OH)2 является лучшим материалом по сравнению с монослоем Mg(OH)2.
Рисунок 5
Структура полосы и общий DOS…
Рисунок 5
Полосная структура и суммарная ПЭС монослоя ( a ) Ca(OH) 2 и…
Рисунок 5 Зонная структура и суммарная ПЭС монослоя ( a ) Ca(OH)2 и ( b ) Mg(OH)2. Гибридные функционалы HSE06 используются для коррекции обычной недооценки ширины запрещенной зоны. Оба материала имеют прямую запрещенную зону с шириной запрещенной зоны Ca(OH)2 (5,19эВ) немного больше ширины запрещенной зоны Mg(OH)2 (4,93 эВ).
Гибридные функционалы HSE06 используются для коррекции обычной недооценки ширины запрещенной зоны. Оба материала имеют прямую запрещенную зону с шириной запрещенной зоны Ca(OH)2 (5,19эВ) немного больше ширины запрещенной зоны Mg(OH)2 (4,93 эВ).
Рисунок 6
Выравнивание полос Ca(OH) 2…
Рисунок 6
Выравнивание полос Ca(OH) 2 и Mg(OH) 2 . ( и ) В…
Рисунок 6 Выравнивание полос Ca(OH)2 и Mg(OH)2. ( a ) Смещение полос HfS2 и WS2 с Ca(OH)2, Mg(OH)2. Уровень вакуума установлен на ноль, и для сравнения включен монослой h-BN. ( b ) Средний потенциал гетероструктур (Ca(OH)2/HfS2 и Mg(OH)2/WS2) показан относительно направления z, перпендикулярного плоскости листов. Максимум зоны проводимости (CBM) и минимум валентной зоны (VBM) каждого материала показаны цветными сплошными и пунктирными линиями. CBM и VBM каждой гетероструктуры показаны длинными сплошными горизонтальными линиями. Правило Андерсона используется для расчета ширины запрещенной зоны и сродства к электрону каждой гетероструктуры.
CBM и VBM каждой гетероструктуры показаны длинными сплошными горизонтальными линиями. Правило Андерсона используется для расчета ширины запрещенной зоны и сродства к электрону каждой гетероструктуры.
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
Нитрид-галогенидные диэлектрики переходных металлов для дихалькогенидных транзисторов переходных металлов.
Ростами Осанлу М., Саадат А., Ван де Пут М.Л., Латурия А., Ванденберге В.Г. Ростами Осанлу М. и др. Наномасштаб. 2021 23 декабря; 14 (1): 157-165. дои: 10.1039/d1nr05250k. Наномасштаб. 2021. PMID: 348
Идентификация двумерных слоистых диэлектриков из первых принципов.
Осанлоо М.
 Р., Ван де Пут М.Л., Саадат А., Ванденберге В.Г.
Осанлу М.Р. и соавт.
Нац коммун. 2021 19 августа; 12 (1): 5051. doi: 10.1038/s41467-021-25310-2.
Нац коммун. 2021.
PMID: 34413289
Бесплатная статья ЧВК.
Р., Ван де Пут М.Л., Саадат А., Ванденберге В.Г.
Осанлу М.Р. и соавт.
Нац коммун. 2021 19 августа; 12 (1): 5051. doi: 10.1038/s41467-021-25310-2.
Нац коммун. 2021.
PMID: 34413289
Бесплатная статья ЧВК.Сверхвысокое внеплоскостное пьезоэлектричество, низкая теплопроводность и фотокаталитическая способность в сверхтонких двумерных ван-дер-ваальсовых гетероструктурах монофосфида бора и нитрида галлия.
Моханта М.К., Рават А., Димпл, Джена Н., Ахамед Р., Де Саркар А. Моханта М.К. и др. Наномасштаб. 21 ноября 2019 г .; 11 (45): 21880-21890. дои: 10.1039/c9nr07586k. Наномасштаб. 2019. PMID: 31697290
Структуры и характеристики атомарно тонкого ZrO 2 от монослоя к бислою и двумерного гетероперехода ZrO 2 -MoS 2 .

Венг Дж., Гао С.П. Венг Дж. и соавт. RSC Adv. 2019 16 октября; 9 (57): 32984-32994. дои: 10.1039/c9ra06074j. Электронная коллекция 2019 15 октября. RSC Adv. 2019. PMID: 35529155 Бесплатная статья ЧВК.
Сотовый монослой HfO 2 и расчет статической диэлектрической проницаемости, исключающий влияние вакуумного зазора.
Венг Дж., Гао С.П. Венг Дж. и соавт. Phys Chem Chem Phys. 2018 7 ноября; 20 (41): 26453-26462. дои: 10.1039/c8cp04743j. Epub 2018 11 октября. Phys Chem Chem Phys. 2018. PMID: 30306170
Посмотреть все похожие статьи
Рекомендации
- Гейм А.К., Новоселов К.С. Нанонаука и технологии: сборник обзоров журналов Nature.
 Всемирный научный; Сингапур: 2010 г. Расцвет графена; стр. 11–19.
Всемирный научный; Сингапур: 2010 г. Расцвет графена; стр. 11–19.
- Гейм А.К., Новоселов К.С. Нанонаука и технологии: сборник обзоров журналов Nature.
- Новоселов К.С., Фалхо В.И., Коломбо Л., Геллерт П., Шваб М., Ким К. Дорожная карта для графена. Природа. 2012; 490:192–200. дои: 10.1038/природа11458. — DOI — пабмед
- Нето А.С., Гвинея Ф., Перес Н.М., Новоселов К.С., Гейм А.К. Электронные свойства графена. Преподобный Мод. физ. 2009;81:109. doi: 10.1103/RevModPhys.81.109. — DOI
- Ванденберге В.
 Г. Определение электронных, структурных, диэлектрических, магнитных и транспортных свойств в новых электронных материалах: использование методов первых принципов. IEEE Нанотехнологии. Маг. 2021;15:68-C3. дои: 10.1109/МНАНО.2021.3113223.
—
DOI
Г. Определение электронных, структурных, диэлектрических, магнитных и транспортных свойств в новых электронных материалах: использование методов первых принципов. IEEE Нанотехнологии. Маг. 2021;15:68-C3. дои: 10.1109/МНАНО.2021.3113223.
—
DOI
- Ванденберге В.
- Гао Э., Линь С.З., Цинь З., Бюлер М.Дж., Фэн С.К., Сюй З. Механическое расслоение двумерных материалов. Дж. Мех. физ. Твердые вещества. 2018; 115: 248–262. doi: 10.1016/j.jmps.2018.03.014. — DOI
Грантовая поддержка
- 1802166/Национальный научный фонд
Растворимость гидроксидов, сульфатов и карбонатов
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3679
- Джим Кларк
- Школа Труро в Корнуолле
На этой странице обсуждается растворимость гидроксидов, сульфатов и карбонатов элементов 2-й группы — бериллия, магния, кальция, стронция и бария — в воде
Основность оксида металла группы II и растворимость гидроксида в воде увеличиваются по мере продвижения вниз по колонке. BeO и Be(OH)2 амфотерны и реагируют с кислотами и сильными основаниями, такими как NaOH. MgO является основным, а Mg(OH)2 является слабоосновным и не растворяется в растворе NaOH. Оксиды кальция, стронция и бария являются основными, а гидроксиды — сильноосновными. Растворимость гидроксидов в воде следует в следующем порядке: Be(OH)2 < Mg(OH)2 < Ca(OH)2 < Sr(OH)2 < Ba(OH)2.
BeO и Be(OH)2 амфотерны и реагируют с кислотами и сильными основаниями, такими как NaOH. MgO является основным, а Mg(OH)2 является слабоосновным и не растворяется в растворе NaOH. Оксиды кальция, стронция и бария являются основными, а гидроксиды — сильноосновными. Растворимость гидроксидов в воде следует в следующем порядке: Be(OH)2 < Mg(OH)2 < Ca(OH)2 < Sr(OH)2 < Ba(OH)2.
Оксиды металлов Основность
Оксиды металлов группы II становятся более щелочными по мере продвижения вниз по колонке. Эту тенденцию легко увидеть, если сравнить электроотрицательность металла II группы с электроотрицательностью кислорода.
| Элемент | Электроотрицательность | ∆Электроотрицательность |
|---|---|---|
| О | 3,44 | |
| Быть | 1,57 | 1,87 |
| мг | 1,31 | 2,13 |
| Са | 1,00 | 2,44 |
| Старший | 0,95 | 2,49 |
| Ба | 0,89 | 2,55 |
Как вы можете видеть, электроотрицательность металлов уменьшается вниз по столбцу, в результате чего изменение электроотрицательности увеличивается вниз по группе. Чем больше разница в электроотрицательности, тем более ионной становится связь металл-кислород. Чем более ионна связь металл-кислород, тем более основным является оксид.0003
Чем больше разница в электроотрицательности, тем более ионной становится связь металл-кислород. Чем более ионна связь металл-кислород, тем более основным является оксид.0003
Растворимость гидроксидов
Гидроксиды металлов группы II становятся более растворимыми в воде по мере продвижения вниз по колонке. Эту тенденцию можно объяснить уменьшением энергии решетки гидроксида соли и увеличением координационного числа иона металла по мере спуска по колонке.
| Элемент | Энергия решетки (кДж/моль) | Координационный номер |
|---|---|---|
| Be | 3620 | 4 |
| мг | 2998 | 6 |
| Са | 2637 | 6 |
| Старший | 2474 | 8 |
| Ба | 2330 | 8 |
Чем больше энергия решетки, тем больше энергии требуется для ее разрушения на ионы металла и гидроксида. Поскольку атомные радиусы увеличиваются вниз по группе, имеет смысл, что координационные числа также увеличиваются, потому что чем больше ион металла, тем больше места для координации с ним молекул воды.
Поскольку атомные радиусы увеличиваются вниз по группе, имеет смысл, что координационные числа также увеличиваются, потому что чем больше ион металла, тем больше места для координации с ним молекул воды.
Следующие примеры иллюстрируют эту тенденцию:
- Гидроксид магния нерастворим в воде. Однако, если его встряхнуть в воде и профильтровать, раствор будет слегка щелочным. Это свидетельствует о том, что в растворе больше гидроксид-ионов, чем в исходной воде. Это связано с тем, что часть гидроксида магния растворилась.
- Раствор гидроксида кальция называют «известковой водой». В литре чистой воды растворяется около 1 г гидроксида кальция при комнатной температуре.
- Гидроксид бария достаточно растворим для получения раствора с концентрацией около 0,1 моль дм -3 при комнатной температуре.
Растворимость сульфатов
- Сульфаты становятся менее растворимыми вниз по группе.
Эта простая тенденция верна при условии, что рассматривается гидратированный сульфат бериллия, а не безводный сульфат бериллия. В книге данных Наффилда любой водный сульфат бериллия BeSO 4 указан как нерастворимый, тогда как гидратированная форма BeSO 4 .4H 2 O растворим, с растворимостью около 39 г BeSO 4 на 100 г воды при комнатной температуре. Показатели растворимости сульфата магния и сульфата кальция также варьируются в зависимости от того, гидратирована ли соль или нет, но изменения менее значительны.
В книге данных Наффилда любой водный сульфат бериллия BeSO 4 указан как нерастворимый, тогда как гидратированная форма BeSO 4 .4H 2 O растворим, с растворимостью около 39 г BeSO 4 на 100 г воды при комнатной температуре. Показатели растворимости сульфата магния и сульфата кальция также варьируются в зависимости от того, гидратирована ли соль или нет, но изменения менее значительны.
Два распространенных примера иллюстрируют эту тенденцию:
- Известная реакция — это реакция между магнием и разбавленной серной кислотой с образованием газообразного водорода и бесцветного раствора сульфата магния. Обратите внимание, что образуется раствор, а не осадок, что означает растворимость сульфата магния.
- Сульфат бария существует в виде белого осадка в растворе. Быстрое образование осадка указывает на то, что сульфат бария совершенно нерастворим. Фактически, 1 литр воды растворяет около 2 мг сульфата бария при комнатной температуре.



 аммиака, 1780г 20% раствора щелочи потребуется для реакции.
аммиака, 1780г 20% раствора щелочи потребуется для реакции. narod.ru/
narod.ru/  3390/нано12101774
3390/нано12101774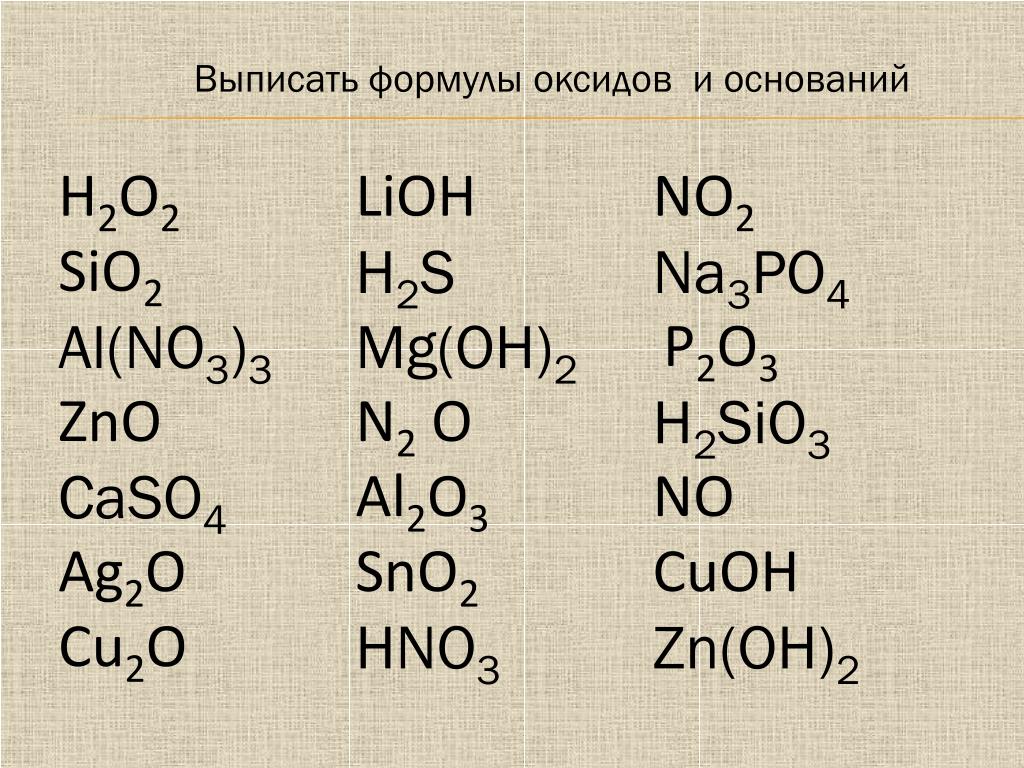
 Р., Ван де Пут М.Л., Саадат А., Ванденберге В.Г.
Осанлу М.Р. и соавт.
Нац коммун. 2021 19 августа; 12 (1): 5051. doi: 10.1038/s41467-021-25310-2.
Нац коммун. 2021.
PMID: 34413289
Бесплатная статья ЧВК.
Р., Ван де Пут М.Л., Саадат А., Ванденберге В.Г.
Осанлу М.Р. и соавт.
Нац коммун. 2021 19 августа; 12 (1): 5051. doi: 10.1038/s41467-021-25310-2.
Нац коммун. 2021.
PMID: 34413289
Бесплатная статья ЧВК.
 Всемирный научный; Сингапур: 2010 г. Расцвет графена; стр. 11–19.
Всемирный научный; Сингапур: 2010 г. Расцвет графена; стр. 11–19. Г. Определение электронных, структурных, диэлектрических, магнитных и транспортных свойств в новых электронных материалах: использование методов первых принципов. IEEE Нанотехнологии. Маг. 2021;15:68-C3. дои: 10.1109/МНАНО.2021.3113223.
—
DOI
Г. Определение электронных, структурных, диэлектрических, магнитных и транспортных свойств в новых электронных материалах: использование методов первых принципов. IEEE Нанотехнологии. Маг. 2021;15:68-C3. дои: 10.1109/МНАНО.2021.3113223.
—
DOI






 com, без риска
com, без риска Он имеет степень бакалавра физико-астрономических наук Университета Бригама Янга и степень магистра естественных наук Бостонского университета. В настоящее время он имеет лицензию преподавателя естественных наук для 8-12 классов.
Он имеет степень бакалавра физико-астрономических наук Университета Бригама Янга и степень магистра естественных наук Бостонского университета. В настоящее время он имеет лицензию преподавателя естественных наук для 8-12 классов. Вот несколько шагов для решения уравнений, содержащих скобки для неизвестной переменной.
Вот несколько шагов для решения уравнений, содержащих скобки для неизвестной переменной.
 В левой части мы можем объединить термины, содержащие x , в один термин, используя вычитание:
В левой части мы можем объединить термины, содержащие x , в один термин, используя вычитание: Мы можем переписать это уравнение как:
Мы можем переписать это уравнение как:
 🙂
🙂




 Сравнить полученные результаты.
Сравнить полученные результаты.





 Если система непротиворечива, решите систему, используя правило Крамера: 4x+y=2,12x+3y=6
Если система непротиворечива, решите систему, используя правило Крамера: 4x+y=2,12x+3y=6
 Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
 Но с ростом выборки разница исчезает.
Но с ростом выборки разница исчезает. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
 Взвешенная дисперсия (для вариационного ряда):
Взвешенная дисперсия (для вариационного ряда): (например середина интервала 159 – 165,6 = 162,3)
(например середина интервала 159 – 165,6 = 162,3) Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия. д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию). 2 раз.
2 раз. из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме.
из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме. Она провела углубленное исследование социальных и экономических вопросов, а также пересмотрела и отредактировала учебные материалы для района Большого Ричмонда.
Она провела углубленное исследование социальных и экономических вопросов, а также пересмотрела и отредактировала учебные материалы для района Большого Ричмонда.
 Например, при расчете выборочной дисперсии для оценки дисперсии совокупности знаменатель уравнения дисперсии становится равным N — 1, так что оценка является несмещенной и не занижает дисперсию совокупности.
Например, при расчете выборочной дисперсии для оценки дисперсии совокупности знаменатель уравнения дисперсии становится равным N — 1, так что оценка является несмещенной и не занижает дисперсию совокупности. Как отмечалось выше, инвесторы могут использовать стандартное отклонение, чтобы оценить, насколько постоянна доходность с течением времени.
Как отмечалось выше, инвесторы могут использовать стандартное отклонение, чтобы оценить, насколько постоянна доходность с течением времени. Извлечение квадратного корня из дисперсии дает стандартное отклонение 18% (√0,0325 = 0,180) для доходности.
Извлечение квадратного корня из дисперсии дает стандартное отклонение 18% (√0,0325 = 0,180) для доходности.
 Чем более разбросаны данные, тем больше дисперсия по отношению к среднему значению.
Чем более разбросаны данные, тем больше дисперсия по отношению к среднему значению. Вот почему стандартное отклонение часто предпочитают в качестве основной меры изменчивости.
Вот почему стандартное отклонение часто предпочитают в качестве основной меры изменчивости.
 Поскольку квадратный корень не является линейной операцией, такой как сложение или вычитание, беспристрастность формулы выборочной дисперсии не распространяется на формулу выборочного стандартного отклонения.
Поскольку квадратный корень не является линейной операцией, такой как сложение или вычитание, беспристрастность формулы выборочной дисперсии не распространяется на формулу выборочного стандартного отклонения.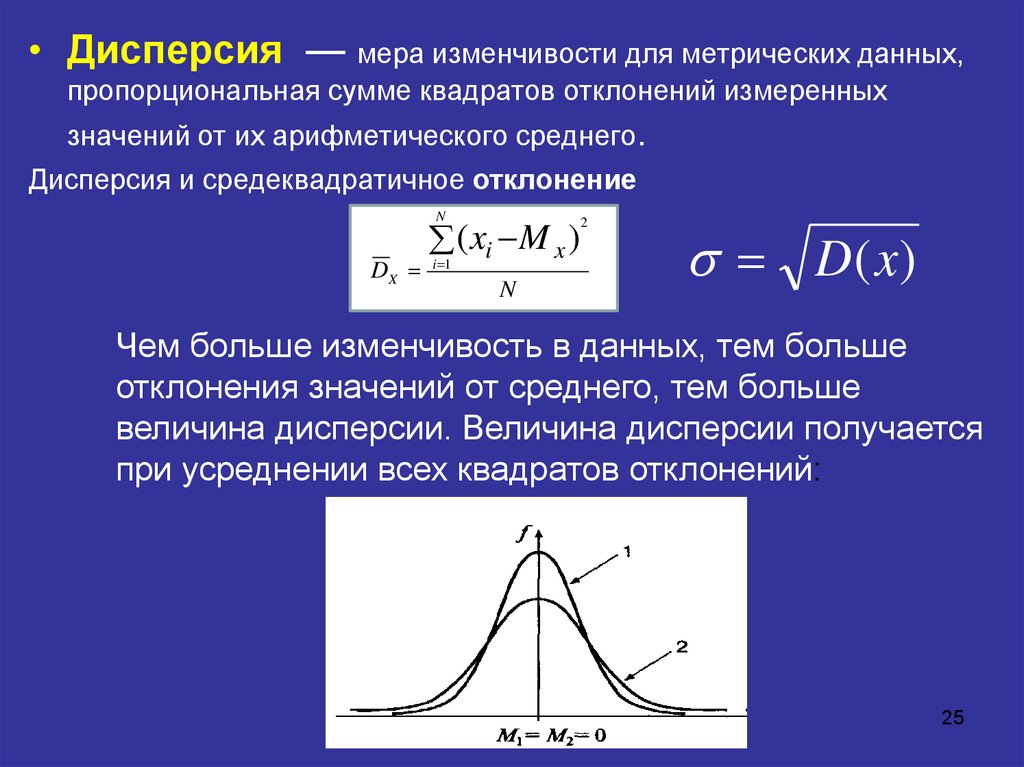 Мы будем использовать небольшой набор данных из 6 баллов, чтобы пройти по шагам.
Мы будем использовать небольшой набор данных из 6 баллов, чтобы пройти по шагам. Это приведет к положительным числам.
Это приведет к положительным числам.



 2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение… Спс
Спс ..)
..) )/3
)/3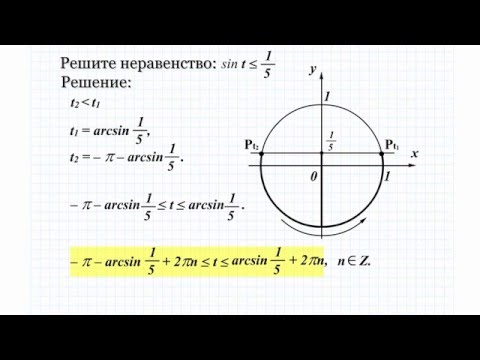 То есть $x$ — это угол, который пересекает единичную окружность в точке с горизонтальной координатой, равной $\frac{1}{\sqrt{2}}$ (не буду называть ее $x$-координатой , потому что мы уже используем $x$ для представления угла — это то, что я бы назвал плохой педагогикой). Нетрудно заметить, что таких углов два:
$$ x = \frac{\pi}{4} \qquad\text{and}\qquad x = -\frac{\pi}{4}; $$
угол $\pi/4$ пересекает единичную окружность в точке $\big(\frac{1}{\sqrt{2}}, \frac{\sqrt{3}}{2}\big)$, и угол $-\pi/4$ пересекается в точке $\big(\frac{1}{\sqrt{2}}, -\frac{\sqrt{3}}{2}\big)$.
То есть $x$ — это угол, который пересекает единичную окружность в точке с горизонтальной координатой, равной $\frac{1}{\sqrt{2}}$ (не буду называть ее $x$-координатой , потому что мы уже используем $x$ для представления угла — это то, что я бы назвал плохой педагогикой). Нетрудно заметить, что таких углов два:
$$ x = \frac{\pi}{4} \qquad\text{and}\qquad x = -\frac{\pi}{4}; $$
угол $\pi/4$ пересекает единичную окружность в точке $\big(\frac{1}{\sqrt{2}}, \frac{\sqrt{3}}{2}\big)$, и угол $-\pi/4$ пересекается в точке $\big(\frac{1}{\sqrt{2}}, -\frac{\sqrt{3}}{2}\big)$. $$
$$
 п.)
п.)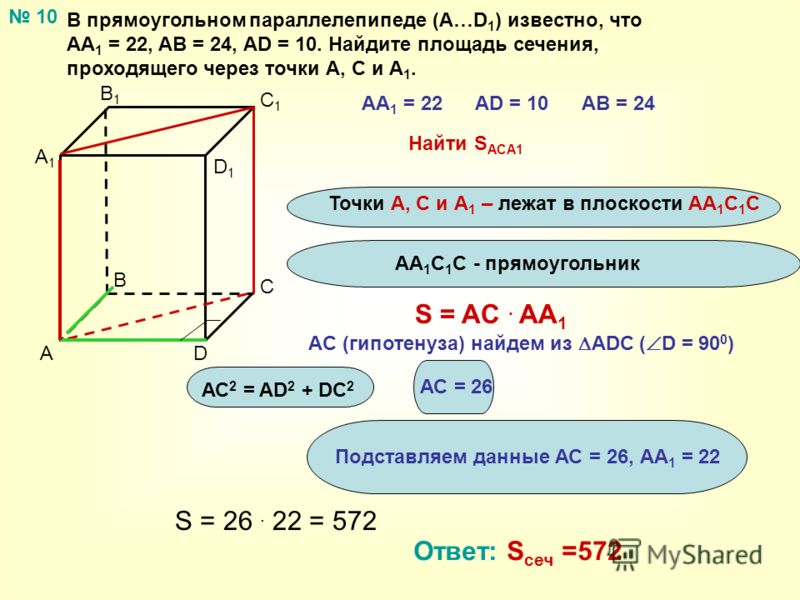


 9K
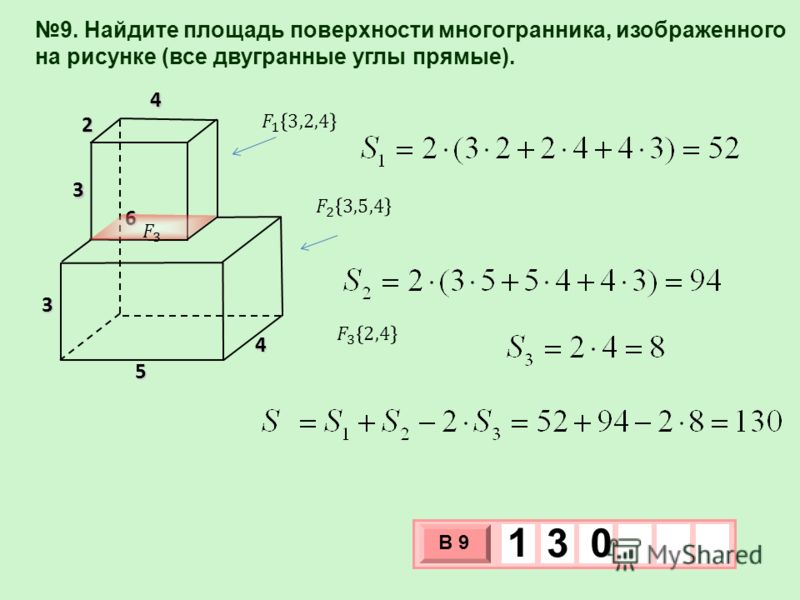
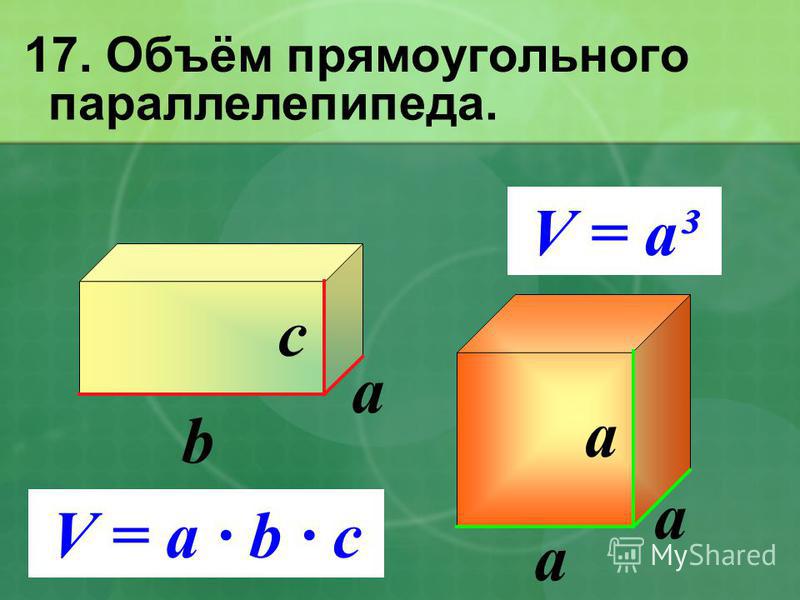
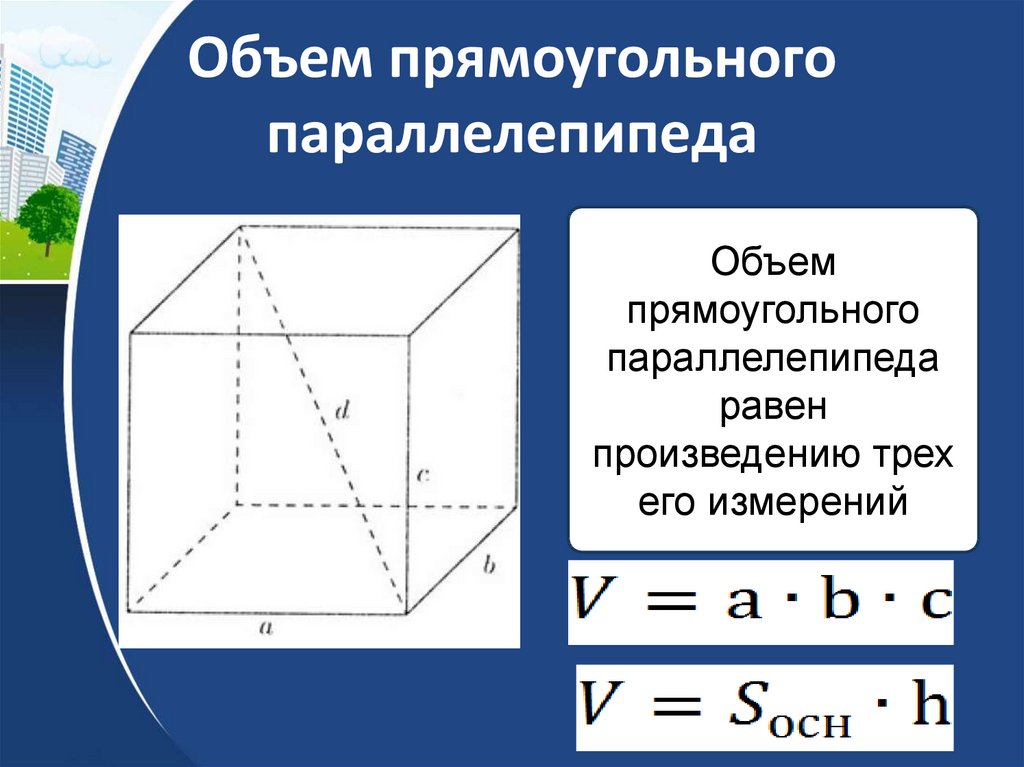
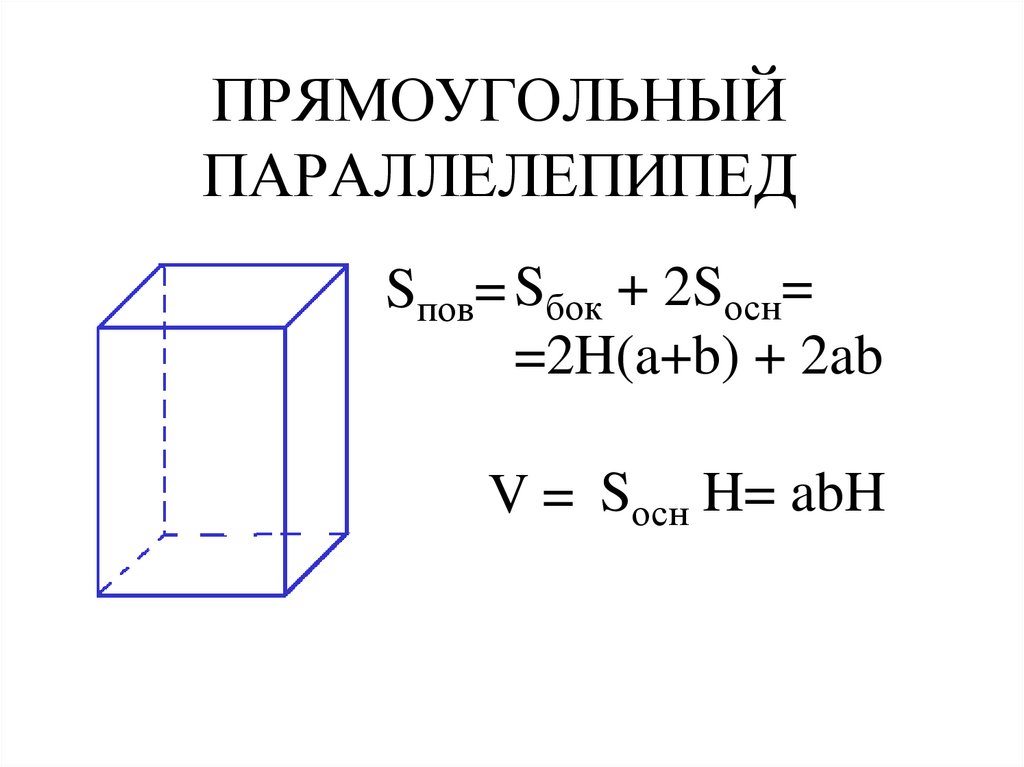
9K Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.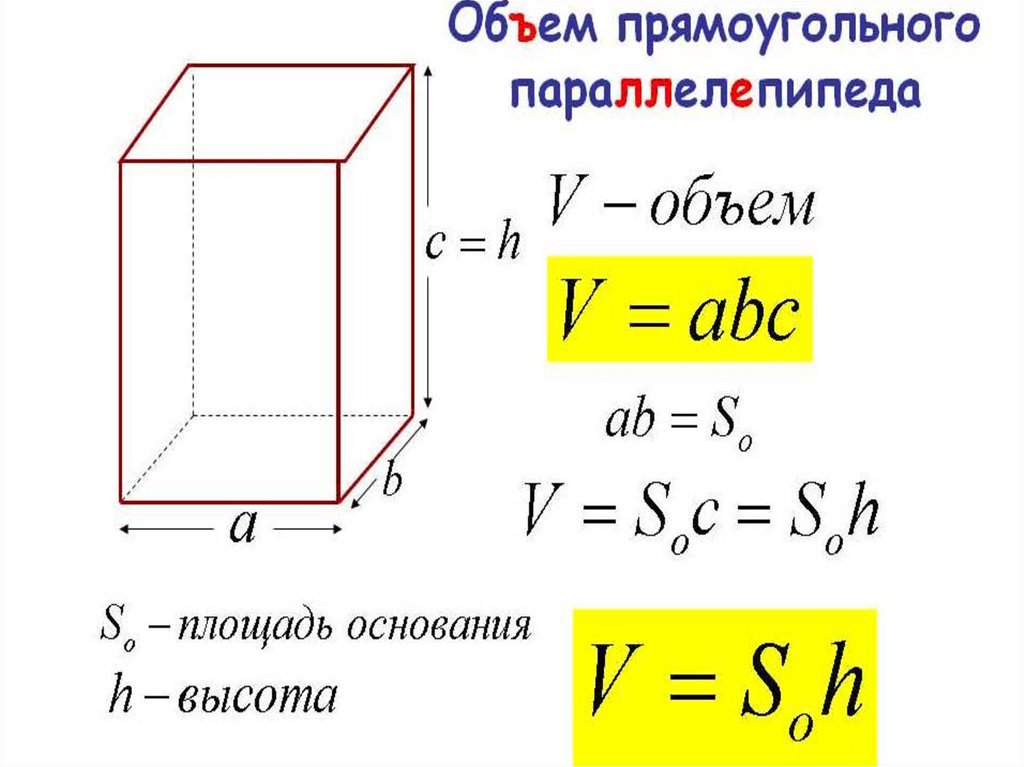 2
2

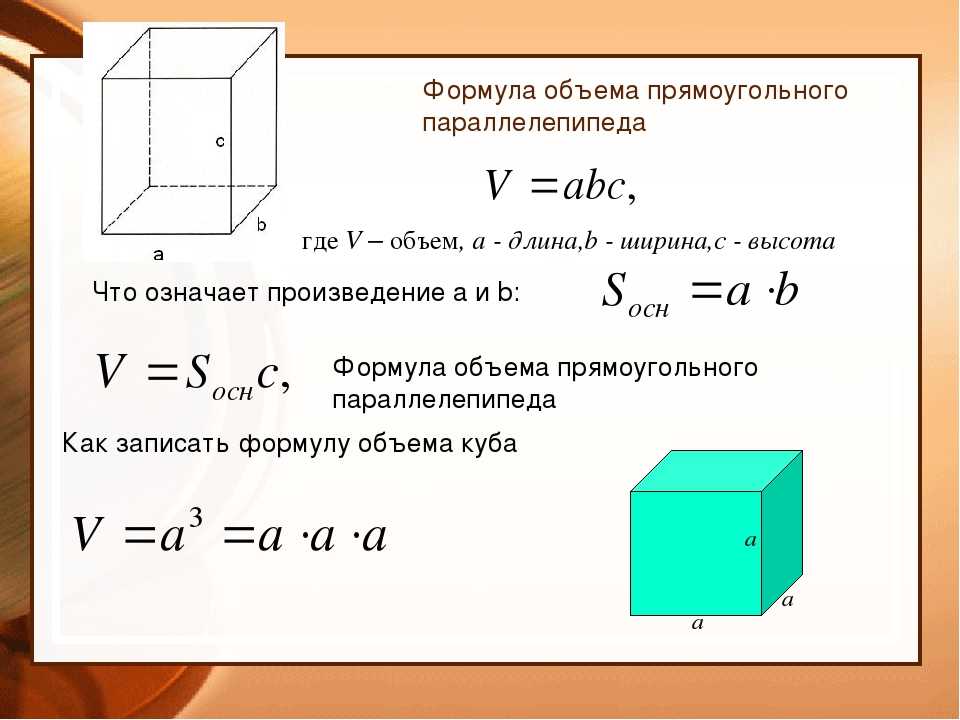
 Чтобы вычислить LSA параллелепипеда, нам нужно найти сумму площадей, занимаемых 4 боковыми гранями.
Чтобы вычислить LSA параллелепипеда, нам нужно найти сумму площадей, занимаемых 4 боковыми гранями.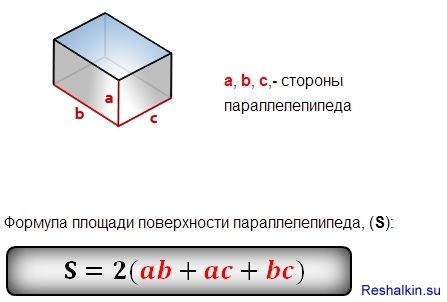 д.
д. Сколько подарочной бумаги требуется для упаковки подарочной коробки?
Сколько подарочной бумаги требуется для упаковки подарочной коробки? Параллелепипед часто называют призмой с основанием в виде параллелограмма. Куб, прямоугольный параллелепипед и ромб — все это частные случаи параллелепипеда с гранями в форме квадрата, прямоугольника и ромба соответственно.
Параллелепипед часто называют призмой с основанием в виде параллелограмма. Куб, прямоугольный параллелепипед и ромб — все это частные случаи параллелепипеда с гранями в форме квадрата, прямоугольника и ромба соответственно. Он выражается в квадратных единицах с использованием таких единиц, как квадратные дюймы, квадратные метры, квадратные футы и т. д.
Он выражается в квадратных единицах с использованием таких единиц, как квадратные дюймы, квадратные метры, квадратные футы и т. д. Трехмерные фигуры — это твердые формы или объекты, имеющие три измерения. Они измеряются по трем параметрам: длина, ширина и высота. Мы узнаем о конкретной трехмерной форме, называемой параллелепипедом, ее свойствах, формулах для общей площади, площади поверхности и объема, а также об уравнении прямоугольного параллелепипеда с решенными примерами.
Трехмерные фигуры — это твердые формы или объекты, имеющие три измерения. Они измеряются по трем параметрам: длина, ширина и высота. Мы узнаем о конкретной трехмерной форме, называемой параллелепипедом, ее свойствах, формулах для общей площади, площади поверхности и объема, а также об уравнении прямоугольного параллелепипеда с решенными примерами. Чтобы понять это, рассмотрим параллелепипед, наполненный водой. Объем воды, который помещается в параллелепипеде, является объемом параллелепипеда.
Чтобы понять это, рассмотрим параллелепипед, наполненный водой. Объем воды, который помещается в параллелепипеде, является объемом параллелепипеда. Вектор произведения перпендикулярен как \(\vec{a}\), так и \(\vec{b}\). Обратите внимание, что величина результирующего вектора \(\lvert\vec{a}\times\vec{b}\rvert\) равна площади параллелограмма, описываемого этими двумя векторами.
Вектор произведения перпендикулярен как \(\vec{a}\), так и \(\vec{b}\). Обратите внимание, что величина результирующего вектора \(\lvert\vec{a}\times\vec{b}\rvert\) равна площади параллелограмма, описываемого этими двумя векторами.


 Он находится по формуле
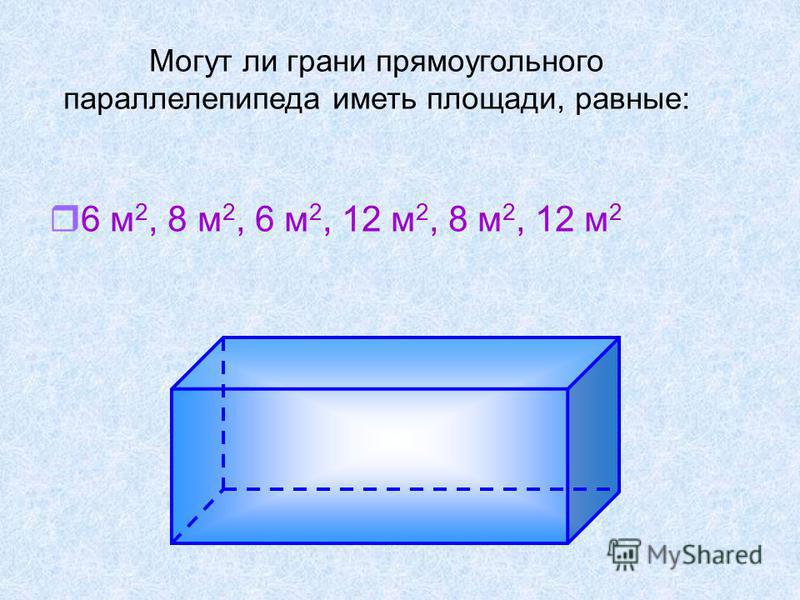
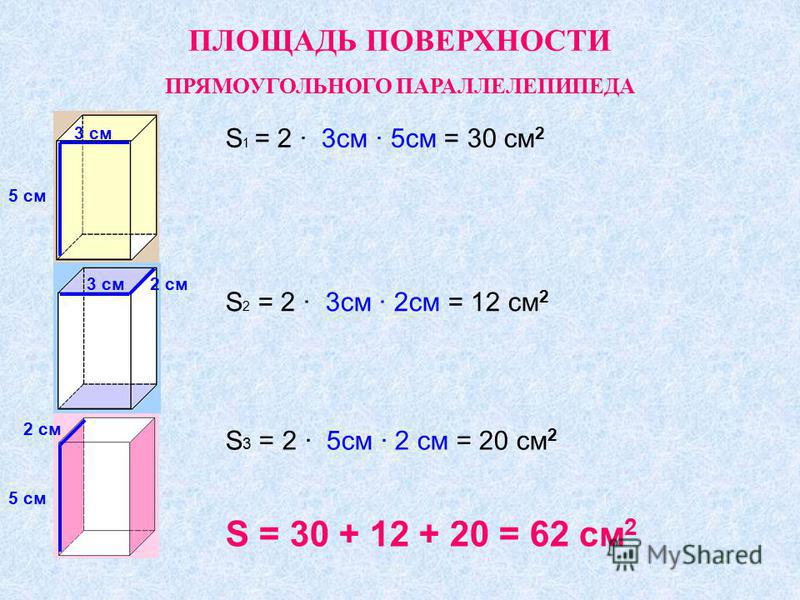
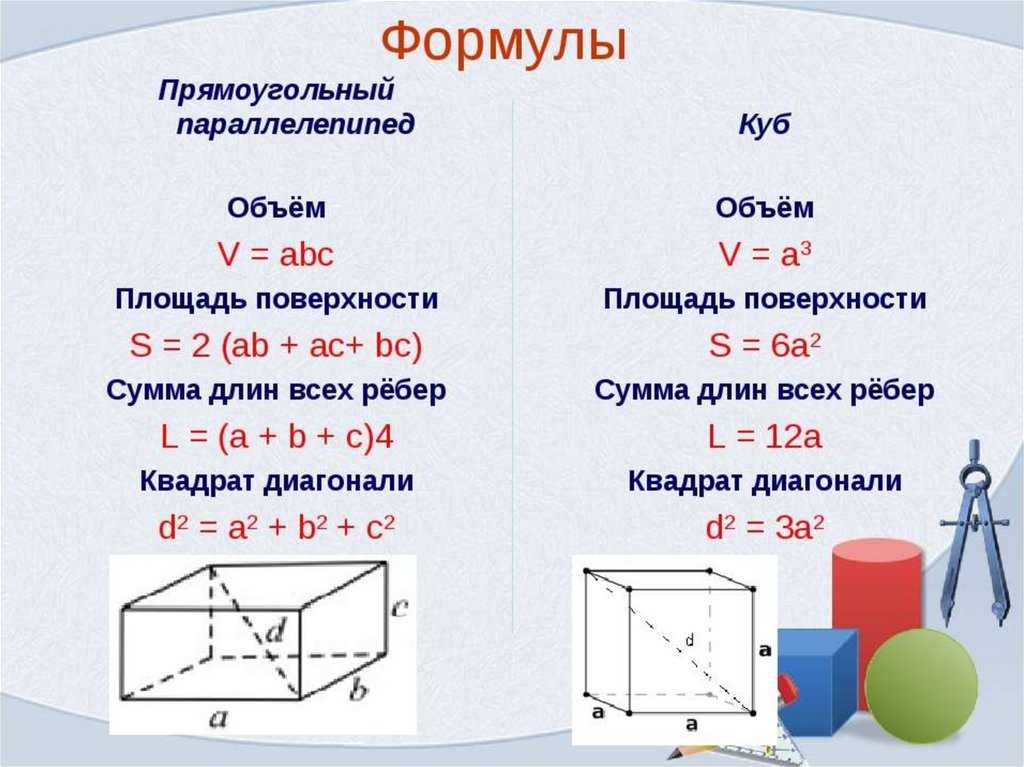
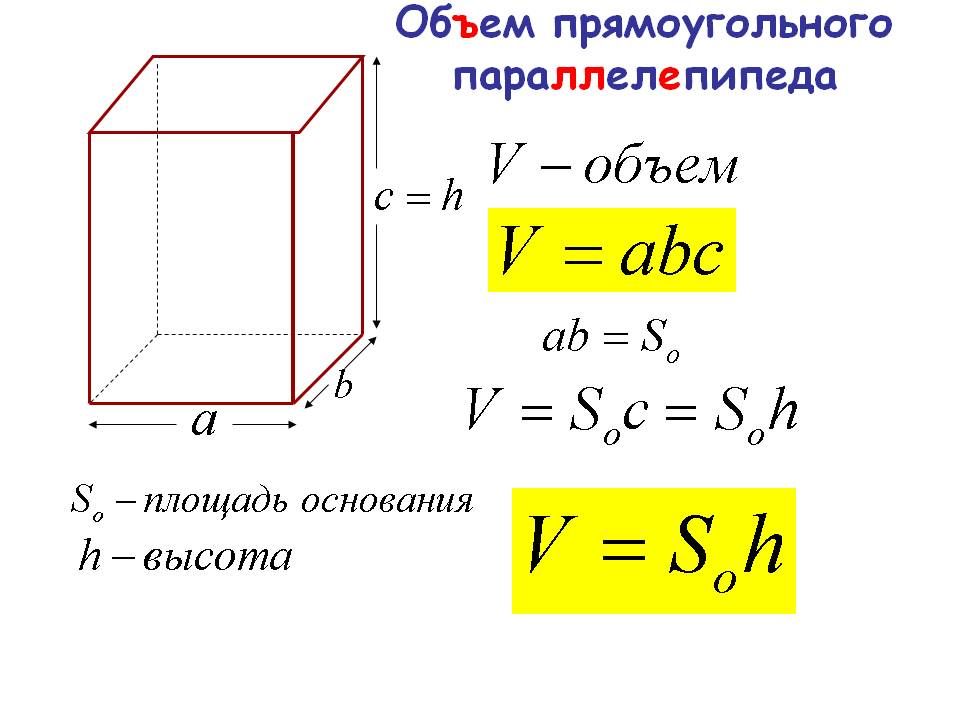
Он находится по формуле Мы должны вычислить площади шести прямоугольников, чтобы определить площадь их поверхностей (граней). Формула площади поверхности:
Мы должны вычислить площади шести прямоугольников, чтобы определить площадь их поверхностей (граней). Формула площади поверхности:
 к.:
к.: Можно предположить, что в таком случае решение будет таким:
Можно предположить, что в таком случае решение будет таким:

 е. х.
е. х.

 Как выглядит эта функция
около х = 1?
Как выглядит эта функция
около х = 1? Если
они будут идти к одному и тому же месту, тогда это место называется пределом.
Если
они будут идти к одному и тому же месту, тогда это место называется пределом. Алгебра, которая будет
работа факторинговая.
Алгебра, которая будет
работа факторинговая.
 Эти концепции также помогают нам анализировать множество функций и их поведение в исчислении. Пределы были основой почти для всех концепций исчисления. Таким образом, становится необходимым научиться вычислять пределы для различных типов функций и как обращаться с неопределенными формами пределов. Давайте посмотрим на различные методы, которые помогают нам вычислять пределы для сложных функций и выражений.
Эти концепции также помогают нам анализировать множество функций и их поведение в исчислении. Пределы были основой почти для всех концепций исчисления. Таким образом, становится необходимым научиться вычислять пределы для различных типов функций и как обращаться с неопределенными формами пределов. Давайте посмотрим на различные методы, которые помогают нам вычислять пределы для сложных функций и выражений. Цель состоит в том, чтобы найти предел этой функции при x = 2.
Цель состоит в том, чтобы найти предел этой функции при x = 2.  Необходимым условием использования этого подхода является то, что функция должна быть непрерывной, а предел не должен давать на выходе какой-либо неопределенной формы.
Необходимым условием использования этого подхода является то, что функция должна быть непрерывной, а предел не должен давать на выходе какой-либо неопределенной формы. Это удостоверение пригодится.
Это удостоверение пригодится. Его можно применять для любого типа функций, которые оцениваются в неопределенных формах с помощью метода подстановки. В этом правиле числитель и знаменатель дифференцируются до тех пор, пока предел не придет в детерминированную форму.
Его можно применять для любого типа функций, которые оцениваются в неопределенных формах с помощью метода подстановки. В этом правиле числитель и знаменатель дифференцируются до тех пор, пока предел не придет в детерминированную форму. Найти
Найти 
 , xn (x в степени n). С такими выражениями надо привыкнуть обращаться. Вот примеры:
, xn (x в степени n). С такими выражениями надо привыкнуть обращаться. Вот примеры: Переставим их так, чтобы коэффициенты и степени с одинаковыми основаниями оказались рядом, т. е.
Переставим их так, чтобы коэффициенты и степени с одинаковыми основаниями оказались рядом, т. е. е. пришлось каждый член многочлена разделить на (+3). Также, обобщая, получим:
е. пришлось каждый член многочлена разделить на (+3). Также, обобщая, получим:
 Подобные умножения легко выполнять в уме и сразу писать окончательный результат.
Подобные умножения легко выполнять в уме и сразу писать окончательный результат. Затем ищем, от каких умножений получатся члены с a² – от умножения 1-го члена (a²) на 2-ой (–5) и от умножения второго члена (–3a) на 1-ый (2a) – это указано внизу скобками; выполнив эти умножения и соединив полученные члены в один, получим –11a². Затем ищем, от каких умножений получатся члены с a в первой степени – эти умножения отмечены скобками сверху. Выполнив их и соединив полученные члены в один, получим +11a. Наконец, замечаем, что младший член произведения (+10), вовсе не содержащий a, получается от перемножения младшего члена (–2) одного многочлена на младший член (–5) другого.
Затем ищем, от каких умножений получатся члены с a² – от умножения 1-го члена (a²) на 2-ой (–5) и от умножения второго члена (–3a) на 1-ый (2a) – это указано внизу скобками; выполнив эти умножения и соединив полученные члены в один, получим –11a². Затем ищем, от каких умножений получатся члены с a в первой степени – эти умножения отмечены скобками сверху. Выполнив их и соединив полученные члены в один, получим +11a. Наконец, замечаем, что младший член произведения (+10), вовсе не содержащий a, получается от перемножения младшего члена (–2) одного многочлена на младший член (–5) другого.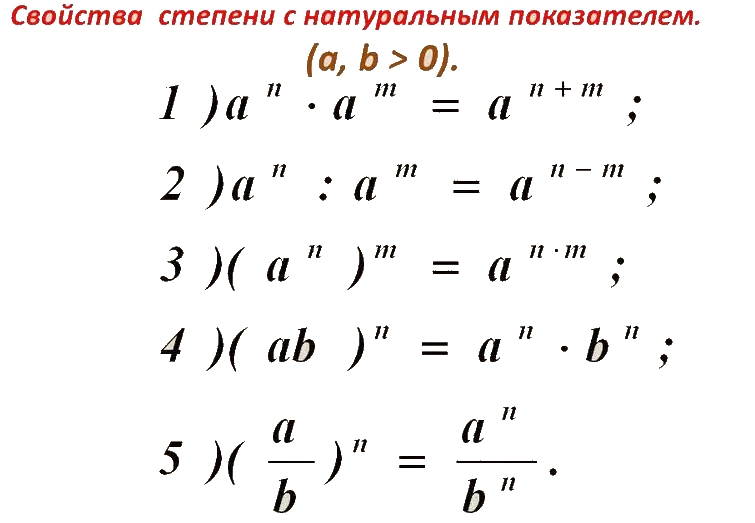

 То есть 7 ? 8 ? 9 ? 10 = 5040.
То есть 7 ? 8 ? 9 ? 10 = 5040.

 Ты сам подумай: если ты купишь землю и засеешь ее, то через год ты наверняка будешь богаче, чем сейчас, и сможешь легко отдать долг вместе с процентами.
Ты сам подумай: если ты купишь землю и засеешь ее, то через год ты наверняка будешь богаче, чем сейчас, и сможешь легко отдать долг вместе с процентами. Он сложил сто сорок флоринов и сто, получил 240 флоринов и решил, что сможет рассчитаться с банком.
Он сложил сто сорок флоринов и сто, получил 240 флоринов и решил, что сможет рассчитаться с банком. Во время очередного восстания Симпличио оказывается в первых рядах с обнаженной саблей. Дальше следы его теряются.
Во время очередного восстания Симпличио оказывается в первых рядах с обнаженной саблей. Дальше следы его теряются. По истечении одного года он должен вернуть банку
По истечении одного года он должен вернуть банку
 Затем добавьте показатели степени числа 10. Поместите новую степень числа 10 с десятичной дробью в экспоненциальной форме. Если ваше десятичное число больше 10, подсчитайте, сколько раз десятичная дробь перемещается влево, и добавьте это число к показателю степени.
Затем добавьте показатели степени числа 10. Поместите новую степень числа 10 с десятичной дробью в экспоненциальной форме. Если ваше десятичное число больше 10, подсчитайте, сколько раз десятичная дробь перемещается влево, и добавьте это число к показателю степени.
 9, ½ и т. д.).
9, ½ и т. д.).
 y = 0,5x, если x < 2.
y = 0,5x, если x < 2.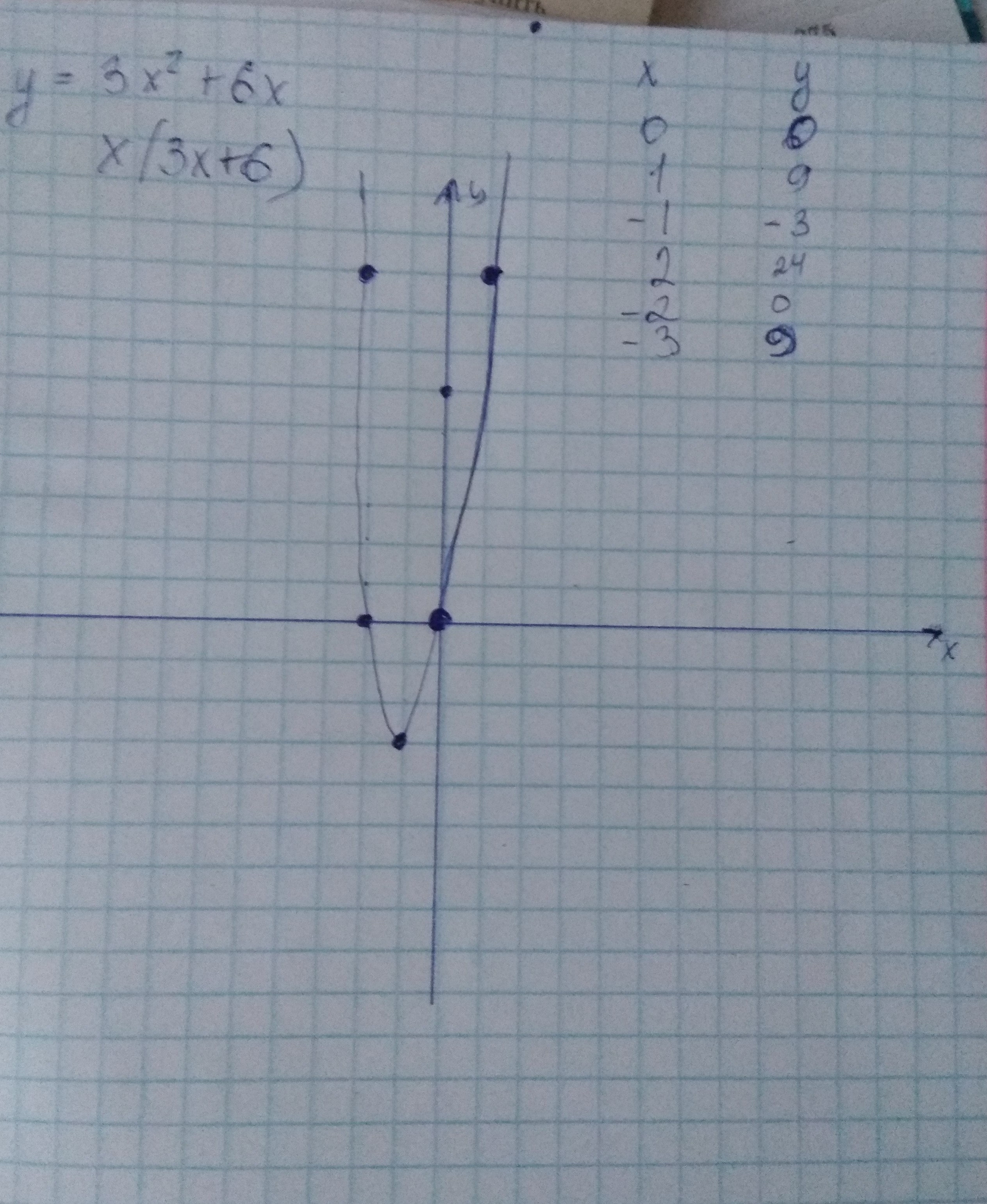 е. между кусочками функции нет разрыва.
е. между кусочками функции нет разрыва. y = 0,5x, при x < –2.
y = 0,5x, при x < –2. .
.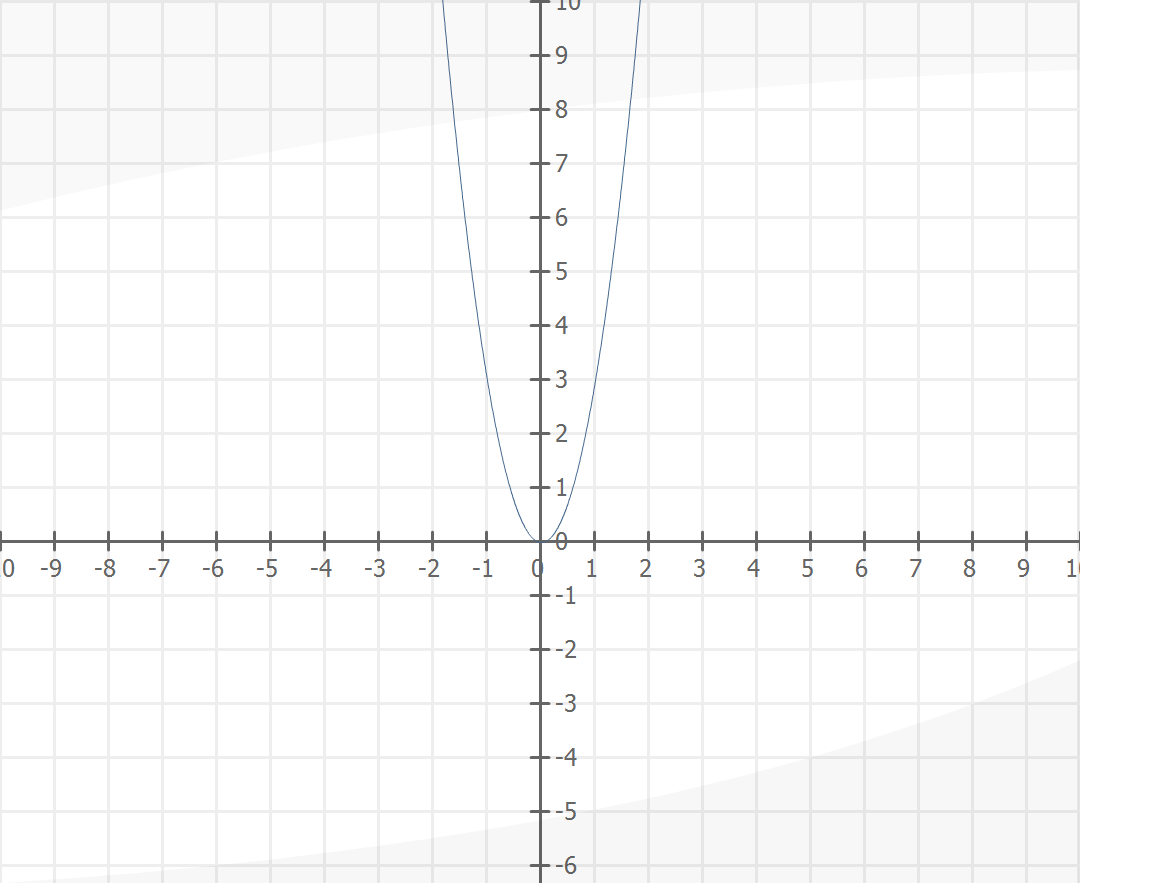 Итак, чтобы облегчить себе жизнь, я сначала решу это уравнение алгебраически.
Итак, чтобы облегчить себе жизнь, я сначала решу это уравнение алгебраически.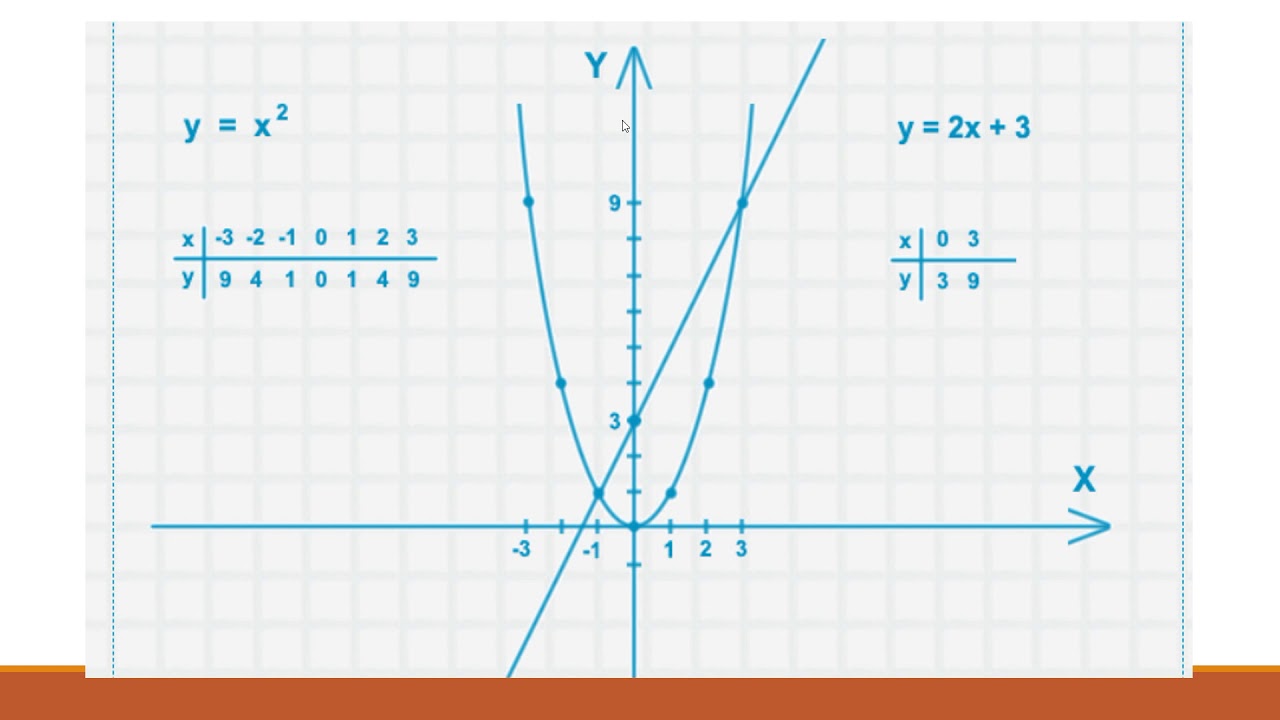 Я сделаю все, что в моих силах, для Т-диаграммы, помня, что я буду делать все, что в моих силах, когда буду строить свои точки:
Я сделаю все, что в моих силах, для Т-диаграммы, помня, что я буду делать все, что в моих силах, когда буду строить свои точки: Таким образом, я могу рассматривать это уравнение как:
Таким образом, я могу рассматривать это уравнение как:



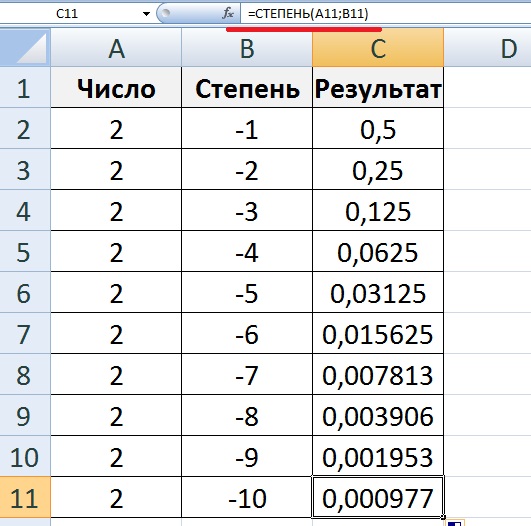 Даже если мы разделим наш доллар на 100 000 частей, доход составит:
Даже если мы разделим наш доллар на 100 000 частей, доход составит: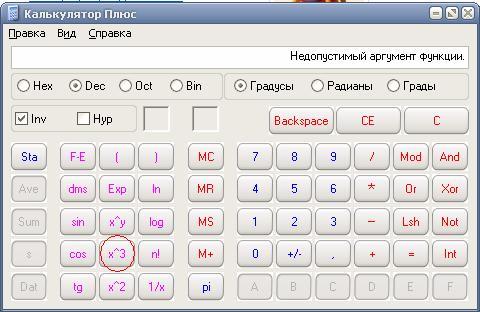 Число е – это максимально возможный результат, труднодостижимый на практике, поэтому в реальности многие процессы описываются с использованием частей экспоненты.
Число е – это максимально возможный результат, труднодостижимый на практике, поэтому в реальности многие процессы описываются с использованием частей экспоненты.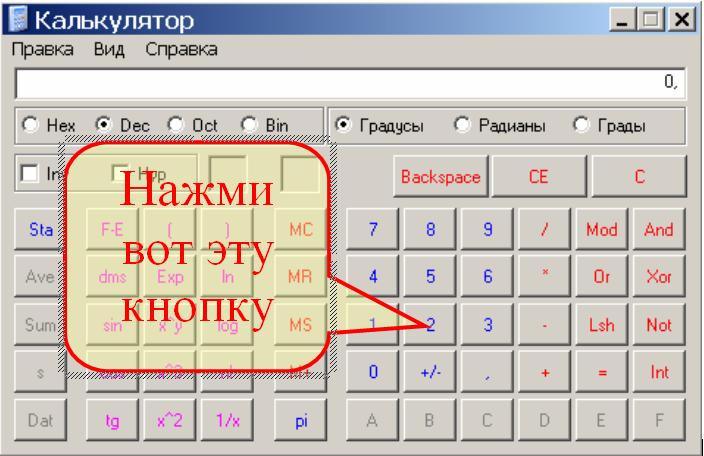
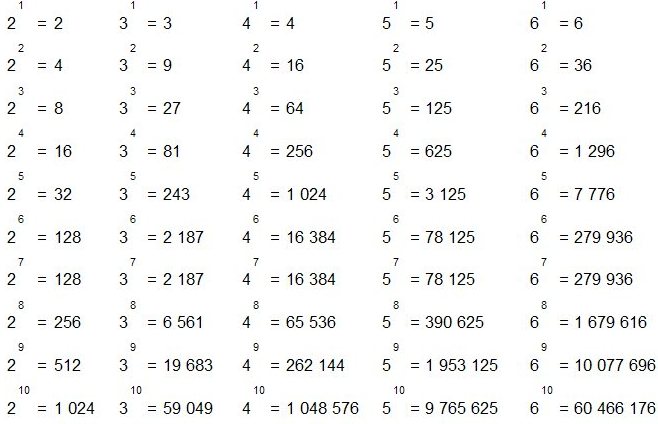 Можно поступить наоборот — сперва нажать кнопочку экспоненты ех, после этого ввести значение показателя степени и нажать кнопку равно. Для показателей степени в виде целях чисел или десятичных дробей оба варианта одинаковы. Если же показатель степени задан обыкновенной дробью, то лучше пользоваться вторым способом. Сперва нажимаете кнопку экспоненты, потом вводите числитель дроби, нажимаете кнопку деления, вводите знаменатель дроби и нажимаете кнопку равно. На этой странице мы рассмотрим первый способ.
Можно поступить наоборот — сперва нажать кнопочку экспоненты ех, после этого ввести значение показателя степени и нажать кнопку равно. Для показателей степени в виде целях чисел или десятичных дробей оба варианта одинаковы. Если же показатель степени задан обыкновенной дробью, то лучше пользоваться вторым способом. Сперва нажимаете кнопку экспоненты, потом вводите числитель дроби, нажимаете кнопку деления, вводите знаменатель дроби и нажимаете кнопку равно. На этой странице мы рассмотрим первый способ. При возведении в степень больше единицы результат будет больше первоначального. Для примера, возведем число е в не целую степень 9,876. Порядок нажимания кнопочек показан красными цифрами, результат виден на картинке.
При возведении в степень больше единицы результат будет больше первоначального. Для примера, возведем число е в не целую степень 9,876. Порядок нажимания кнопочек показан красными цифрами, результат виден на картинке. Умный калькулятор это понимает и без наших подсказок — он отлично справляется с отрицательной степенью. Для начала вычислим е в минус первой степени. Смотрим на картинку.
Умный калькулятор это понимает и без наших подсказок — он отлично справляется с отрицательной степенью. Для начала вычислим е в минус первой степени. Смотрим на картинку. Остается только предупредить, что и калькулятору полностью доверять нельзя, нужно самому анализировать результат, который он выдает.
Остается только предупредить, что и калькулятору полностью доверять нельзя, нужно самому анализировать результат, который он выдает.
 Вы можете найти как положительные, так и отрицательные показатели степени, используя наш калькулятор, возведенный в степень. Ниже мы обсудим, что такое экспоненты и калькуляторы экспонент? Как вы рассчитываете показатели степени/мощности основания вручную, а также с помощью нашего экспоненциального калькулятора?
Вы можете найти как положительные, так и отрицательные показатели степени, используя наш калькулятор, возведенный в степень. Ниже мы обсудим, что такое экспоненты и калькуляторы экспонент? Как вы рассчитываете показатели степени/мощности основания вручную, а также с помощью нашего экспоненциального калькулятора?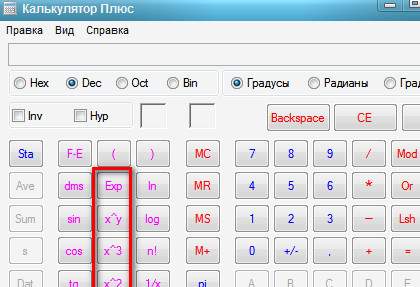 Он указывает количество обратных оснований, которые необходимо умножить на себя. Упростите такие дроби с помощью нашего калькулятора степени.
Он указывает количество обратных оснований, которые необходимо умножить на себя. Упростите такие дроби с помощью нашего калькулятора степени.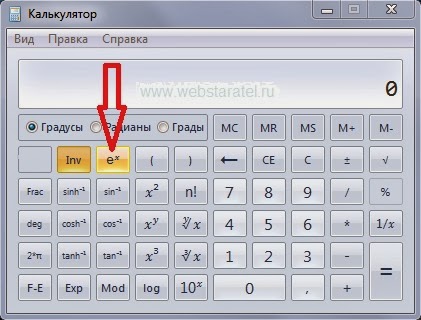 215506
215506 Если вы все еще не уверены, что такое число Эйлера, что означает e на
калькулятор, или как вычислить е в х, продолжайте читать.
Если вы все еще не уверены, что такое число Эйлера, что означает e на
калькулятор, или как вычислить е в х, продолжайте читать.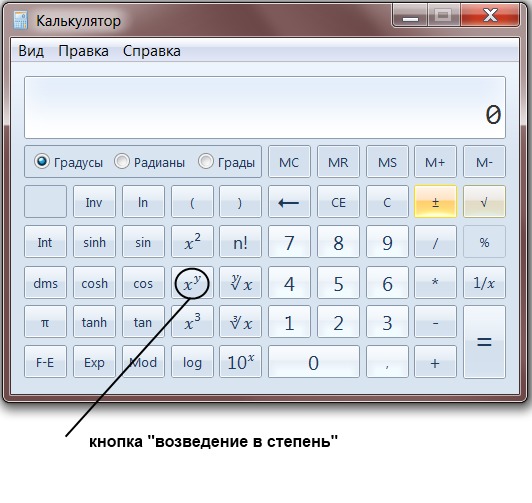 (1 + 1/н)
(1 + 1/н)