| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | Найти объем | сфера (4) | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | 2 1/2÷22000000 | |
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | Перевести в процентное соотношение | 3/9 | |
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Отображение чисел в качестве дробей
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще. ..Меньше
..Меньше
Используйте формат «Дроб», чтобы отображать или ввести числа как фактические дроби, а не в десятичных числах.
-
Выделите ячейки, которые нужно отформатировать.
-
На вкладке Главная нажмите кнопку вызова диалогового окна рядом с именем группы Число.
-
В списке Категория выберите дроби.
-
В списке Тип выберите нужный тип формата дроби.

|
Формат дроби |
В этом формате 123,456 отображается как |
|
Дробная часть с одной цифрой |
123 1/2, округление до ближайшего однозначного значения дроби |
|
Двузначная дробь |
123 26/57, округлизация до ближайшего двузначного значения дроби |
|
Трижды значок дроби |
123 57/125, округлизация до ближайшего трехзначного значения дроби |
|
Дробный в качестве дробей |
123 1/2 |
|
Дробный по кварталам |
123 2/4 |
|
Дробный в качестве частиц |
123 4/8 |
|
Дробные части в качестве шестнадцатых |
123 7/16 |
|
Дробный в качестве десятых |
123 5/10 |
|
Дробные части в качестве сотых |
123 46/100 |
Число в активной ячейке выбранного на этом сайте отображается в поле Образец, чтобы можно было просмотреть выбранные параметры форматирования.
-
После применения формата дроби к ячейке дробные числа, а также фактические дроби, которые вы в нее введите, будут отображаться как дроби. Например, если ввести 0,5 или 1/2, то при формате ячейки с типом дроби до одной цифры будет 1/2.
-
Если к ячейке не применен формат дроби и вы введите дробную часть, например 1/2,она будет отформатирована как дата. Чтобы отобразить дробную часть, применив формат дроби, а затем впечатаем ее еще раз.
-
Если вам не нужно выполнять вычисления с дробями, перед тем как ввести в нее дробную часть, можно отформать ячейку как текст, щелкнув Текст в списке Категория.
 В этом случае дробные части не будут уменьшаться или преобразовываться в десятичных. Однако математические вычисления с дробями, которые отображаются как текст, выполнять нельзя.
В этом случае дробные части не будут уменьшаться или преобразовываться в десятичных. Однако математические вычисления с дробями, которые отображаются как текст, выполнять нельзя. -
Чтобы сбросить числовом формате, в диалоговом окне Категория(диалоговое окно Формат ячеек) или Числовом формате(вкладкаГлавная, группа Число) нажмите кнопку Общий. В ячейках с форматом Общий форматирование к числам не применяется.
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | плюс | 0046 | 1/2 + 1/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | знак минус | вычитание | 1 1/2 — 2/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | звездочка | умножение | 2/3 * 3/4 9 | знак умножения | умножение | 2 /3 × 5/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | знак деления | деление | 1/2 : 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 деления 4 деления 6 | деление | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
больше задач по математике 8 Калькулятор дробей — CalcuNation.comТеперь вы можете складывать дроби, вычитать дроби, умножать дроби и делить дроби онлайн. Найдите ответ в самом простом с помощью этого онлайн-калькулятора дробей. Первая дробь / Сложение дробей Чтобы привести дробь к простейшей форме, попробуйте наш калькулятор упрощения дробей Как складывать дроби? Есть два случая относительно знаменателей, когда мы складываем обыкновенные дроби, которые показаны следующим образом: Сложение дробей с одинаковыми знаменателями:• Просто добавьте числители дробей. • Знаменатель полученной дроби будет общим знаменателем дробей. • Уменьшите полученную дробь. Например: а/б + д/б = (а + г)/б или 7/17 + 9/17 = (7 + 9)/17 Сложение дробей с разными знаменателями:• Если знаменатели не совпадают, перемножьте знаменатели вместе.• Отрегулируйте свои числители (верхние числа) соответствующим образом. Например. если удвоить знаменатель, то удвоить и числитель. • Сложите числители и поднесите эту сумму к общему знаменателю. • Упростите дробь до наименьшего возможного знаменателя, при этом числители также будут пропорционально уменьшены. Пример: a/b + c/d = (ad + cb)/bd Для сложения дробей 1/3 и 1/5, 1/3 + 1/5 = (1*5 + 1*3)/3*5 = 5+3/15 = 8/15 Сумма 8/15 уже в простейшем виде. Как вычитать дроби?Есть два случая относительно знаменателей, когда мы вычитаем обыкновенные дроби, которые показаны следующим образом с шагами: Вычитание дробей с одинаковыми знаменателями: • Просто вычтите числители дробей. Вычитание дробей с разными знаменателями: • Если знаменатели не совпадают, перемножьте знаменатели вместе. Как умножать дроби? Умножать дроби довольно просто. Урок алгебры в 9 классе по теме «Построение
графиков функции, аналитическое выражение
которых содержит знак абсолютной величины» был
построен на основе компьютерных технологии,
применяя исследовательскую деятельность
обучения. Цели урока: Обучающая: Наглядно
продемонстрировать учащимся возможности
использования компьютера при построении
графиков функции с модулями; для самоконтроля,
экономии времени при построении графиков
функций вида у=f |(х)| , у = | f (х)| , у=|f |(х)| |. Развивающая: Развитие интеллектуальных умений
и мыслительных операций — анализ и синтез
сравнение, обобщение. Формирование ИКТ
компетентности учащихся. Воспитывающая: Воспитание познавательного
интереса к предмету путем введения новейших
технологий обучения. Воспитание
самостоятельности при решении учебных задач. Оборудование: Оборудование: компьютерный
класс, интерактивная доска, презентация на тему
«Построение графиков функции, аналитическое
выражение которых содержит знак абсолютной
величины», раздаточный материал: карточки для
работы с графической моделью функций, листы для
фиксирования результатов исследования функций,
персональные компьютеры. Программное обеспечение: презентация Microsoft
PowerPoint «Построение графиков функции,
аналитическое выражение которых содержит знак
абсолютной величины» Ход урока 1. Организационный момент 2. Повторение, обобщение и систематизация. Это
этап урока сопровождается компьютерной
презентацией. Слайд 2. График функции у=f |(х)| у=f |(х)| — четная функция, т.к. | х | = | -х |, то f |-х| =
f | х | График этой функции симметричен относительно
оси координат. Следовательно, достаточно построить график
функции у=f(х) для х>0,а затем достроить его
левую часть, симметрично правой относительно оси
координат. Например, пусть графиком функции у=f(х)
является кривая, изображенная на рис.1, тогда
графиком функции у=f |(х)| будет кривая,
изображенная на рис.2. Рис.1 Рис.2 1. Исследование графика функции у= |х|
Таким образом, искомый график есть ломанная,
составленная из двух полупрямых. (Рис.3) Рис. 3 Из сопоставления двух графиков: у=х и у= |х|, учащиеся
сделают вывод, что второй получается из первого
зеркальным отображением относительно ОХ той
части первого графика, которая лежит под осью
абсцисс. Это положение вытекает из определения
абсолютной величины. Из сопоставления двух графиков: у = х и у = -х,
сделают вывод: функции у = f(|х|) получается из
графика у = f (x) при х 0 симметричным отображением
относительно оси ОУ. Можно ли применять этот метод построения
графиков для любой функции, содержащей
абсолютную величину? Слайд 3 и 4. 1. Построите график функции у=0,5 х2 — 2|х| — 2,5 1) Поскольку |х| = х при х 0, требуемый график
совпадает с параболой у=0,5 х2 — 2х — 2,5 .
Если х<0, то поскольку х2 = |х|2, |х|=-х и
требуемый график совпадает с параболой у=0,5 х2
+ 2х — 2,5. 2) Если рассмотрим график у=0,5 х2 -2х — 2,5
при х 0 и
отобразить его относительно оси ОУ мы получим
тот же самый график. Можно ли применять этот метод построения
графиков дл квадратичной функции, для графиков
обратной пропорциональности, содержащие
абсолютную величину? 2. Например: у=х2 — |х| -3 1) Поскольку |х| = х при х 0, требуемый график
совпадает с параболой у=0,25 х2 — х — 3. 2) Если рассмотрим график у=0,25 х2 — х — 3 при
х 0 и
отобразить его относительно оси ОУ мы получим
тот же самый график. (0; — 3) координаты точки пересечения графика
функции с осью ОУ. у =0, х2 -х
-3 = 0 х2 -4х -12 = 0 Имеем, х1= — 2; х2 = 6. (-2; 0) и (6; 0) — координаты точки пересечения
графика функции с осью ОХ. Если х<0, ордината точки требуемого графика
такая же, как и у точки параболы, но с
положительной абсциссой, равной |х|. Такие точки
симметричны относительно оси ОУ(например,
вершины (2; -4) и -(2; -4). Значит, часть требуемого графика,
соответствующая значениям х<0, симметрична
относительно оси ОУ его же части,
соответствующей значениям х>0. б) Поэтому достраиваю для х<0 часть графика,
симметричную построенной относительно оси ОУ. Рис. 4 На тетрадях ученики доказывают, что график
функции у = f |(х)| совпадает с графиком функции у = f
(х) на множестве неотрицательных значений
аргумента и симметричен ему относительно оси ОУ
на множестве отрицательных значений аргумента. Доказательство: Если х 0, то f |(х)|= f (х),
т.е. на множестве неотрицательных значений
аргумента графики функции у = f (х) и у = f |(х)|
совпадают. Так как у = f |(х)| — чётная функция, то её
график симметричен относительно ОУ. Таким образом, график функции у = f |(х)| можно
получить из графика функции у = f (х) следующим
образом: 1. построить график функции у = f(х) для х>0; 2. Для х<0, симметрично отразить построенную
часть относительно оси ОУ. Вывод: Для построения графика функции у = f |(х)|
1. 2. Для х<0, симметрично отразить
построенную часть относительно оси ОУ. Слайд 5 4. Исследовательская работа по построению
графика функции у = | f (х)| Построить график функции у = |х2 — 2х| Освободимся от знака модуля по определению Если х2 — 2х0,
т.е. если х
0 и х2, то |х2 -
2х|= х2 — 2х Если х2 — 2х<0, т.е. если 0<х< 2, то |х2
— 2х|=- х2 + 2х Видим, что на множестве х 0 и х2 графики функции у = х2 — 2х и у = |х2 — 2х|совпадают, а на
множестве (0;2) графики функции у = -х2 + 2х и у = |х2 — 2х|
совпадают. Построим их. График функции у = | f (х)| состоит из части
графика функции у = f(х) при у ?0 и симметрично
отражённой части у = f(х) при у <0 относительно оси
ОХ. Слайд 6 Построить график функции у = |х2 — х —6| 1) Если х2 — х -6 0, т.е. если х-2 и х3, то |х2 — х -6|= х2 — х -6. Если х2 — х -6<0, т.е. если -2<х< 3, то |х2
— х -6|= -х2 + х +6. Построим их. 2) Построим у = х2 — х -6 . Нижнюю часть
графика симметрично отбражаем относительно ОХ. Сравнивая 1) и 2), видим что графики одинаковые. Работа на тетрадях. Докажем, что график функции у = | f (х)|
совпадает с графиком функции у = f (х) для f(х) >0 и
симметрично отражённой частью у = f(х) при у <0
относительно оси ОХ. Действительно, по определению абсолютной
величины, можно данную функцию рассмотреть как
совокупность двух линий: у = f(х), если f(х)
0; у = — f(х), если f(х) <0 Для любой функции у = f(х), если f(х) >0, то | f (х)| = f(х), значит в этой части график функции у = | f (х)| совпадает с графиком самой функции у = f(х). Если же f(х) <0, то | f (х)| = — f(х),т.е. точка (х; — f(х))
симметрична точке (х; f (х)) относительно
оси ОХ. Поэтому для получения требуемого графика
отражаем симметрично относительно оси ОХ
«отрицательную» часть графика у = f(х). Слайд 7 Вывод: действительно для построения графика
функции у = |f(х) | достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней
полуплоскости, т.е., где f(х) <0, симметрично
отражаем относительно оси абсцисс. (Рис.5) Рис.5 Вывод: Для построения графика функции у=|f(х)
| 1.Построить график функции у=f(х) ; 2. На участках, где график расположен в нижней
полуплоскости, т.е., где f(х) <0, строим кривые,
симметричные построенным графикам относительно
оси абсцисс. (Рис.6, 7.) Слайды 8-13. 5. Исследовательская работа по построению
графиков функции у=|f |(х)| | Применяя определение абсолютной величины и
ранее рассмотренные примеры, построим графиков
функции: у = |2|х| — 3| у = |х2 — 5|х|| у = | |х2| — 2| и сделал выводы. Для того чтобы построить график функции у = | f
|(х)| надо: 1. Строить график функции у = f(х) для х>0. 2. Строить вторую часть графика, т. е.
построенный график симметрично отражать
относительно ОУ, т.к. данная функция четная. 3. Участки получившегося графика, расположенные
в нижней полуплоскости, преобразовывать на
верхнюю полуплоскость симметрично оси ОХ. Построить график функции у = | 2|х | — 3| (1-й
способ по определению модуля) 1. Строим у = 2|х | — 3 , для 2 |х| — 3 > 0 , |х
|>1,5 т.е. х< -1,5 и х>1,5 а) у = 2х — 3 , для х>0 б) для х<0, симметрично отражаем построенную
часть относительно оси ОУ. 2. Строим у = —2 |х| + 3, для 2|х | — 3 < 0. т.е.
-1,5<х<1,5 а) у = —2х + 3, для х>0 б) для х<0, симметрично отражаем построенную
часть относительно оси ОУ. У = | 2|х | — 3| 1) Строим у = 2х-3, для х>0. 2) Строим прямую, симметричную построенной
относительно оси ОУ. 3) Участки графика, расположенные в нижней
полуплоскости, отображаю симметрично
относительно оси ОХ. Сравнивая оба графика, видим, что они
одинаковые. 2. у = | х2 — 5|х| | 1. Строим у = х2 — 5 |х|, для х2 — 5 |х| > 0
т.е. х >5 и х<-5 а) у = х2 — 5 х, для х>0 б) для х<0, симметрично отражаем построенную
часть относительно оси ОУ. 2. Строим у = — х2 + 5 |х| , для х2 — 5 |х| <
0. т.е. -5х5 а) у = — х2 + 5 х , для х>0 б) для х<0, симметрично отражаем построенную
часть относительно оси ОУ. У = | х2 — 5|х| | а) Строим график функции у = х2 — 5 х для
х>0. Б) Строим часть графика, симметричную
построенной относительно оси ОУ в) Часть графика, расположенные в нижней
полуплоскости, преобразовываю на верхнюю
полуплоскость симметрично оси ОХ. Сравнивая оба графика, видим что они
одинаковые. (Рис.9) 3. у =| |х|2 — 2 | 1). Строим у = |х|2 — 2 , для |х|2
— 2 > 0, x>
и x< — а) у = х2 — 2, для х>0 б) для х<0, симметрично отражаю построенную
часть относительно оси ОУ. 2). Строим у = — |х|2 + 2 , для |х|2
— 2 < 0. т.е. — < x< а) у = —х2 + 2 , для х>0 б) для х<0, симметрично отражаю построенную
часть относительно оси ОУ. У = ||х|2 — 2 | а) Строим у = х2 -2 для х > 0. Б) Строим часть графика, симметричную
построенной относительно оси ОУ в) Часть графика, расположенные в нижней
полуплоскости, преобразовываю на верхнюю
полуплоскость симметрично оси ОХ. Сравнивая оба графика, видим что они
одинаковые. (Рис.10) 3. Подведение итогов урока. 14,15 слайды. Алгоритм построения графика функции у=f |(х)| 1.Построить график функции у=f(х) для х>0; 2.Построить для х<0 часть графика, симметричную
построенной относительно оси ОУ. Алгоритм построения графика функции у=|f(х) | 1.Построить график функции у=f(х) ; 2. На участках, где график расположен в нижней
полуплоскости, т.е., где f(х) <0, строить
кривые, симметричные построенным графикам
относительно оси абсцисс. Алгоритм построения графика функции у=|f |(х)|
| 1. Построить график функции у=f(х) для х>0. 2. Построить кривую графика, симметричную
построенной относительно оси ОУ, т.к. данная
функция четная. 3. Участки графика, расположенные в нижней
полуплоскости, преобразовывать на верхнюю
полуплоскость симметрично оси ОХ. 1 Вызываем Мастер диаграмм. В окне первого шага выбираем Тип диаграммы – График, вид графика – график с маркерами, помечающими точки данных. 2 В поле Диапазон, переключившись на вкладку Ряд ® Добавить. В появившемся окне ввести в поле Значение ссылку на диапазон В3 : В13, а в поле Подписи по оси Х ссылку на диапазон А3:А13. Для ввода ссылок минимизировать диалоговое окно (щелчок мыши по кнопке – минимизация, находящейся в правой части поля, после чего выделить диапазоны). 3 На вкладке Заголовки заполняем поля: Название диаграммы, Ось Х (категорий), Ось Y (значений). 4 Размещаем диаграмму на имеющемся листе. После появления диаграммы форматируем область построения диаграммы, установив для нее цвет заливки – белый (выбрать в списке Элементы диаграммы панели диаграммы значение область построения диаграммы и нажав кнопку Формат области построения, устанавливаем в диалоговом окне прозрачный тип заливки). Аналогично форматируем Ось категорий, установив на вкладке Вид переключатель метки делений в положении внизу. Форматирование элемента Ряд 1 сводится к установке на вкладке Вид флажка Сглаженная линия. В результате этих действий получится график функции, показанный на рисунке 4.40. Рисунок 4.40 – График функции Расчет минимального и максимально значений функции Установив курсор на требуемую ячейку вызываем функцию Мин, используя Мастер функций (Мастер функций ® Математические ® МИН). Аналогичные действия проделываем для нахождения максимального значения используя функцию =МАКС(). Полученные результаты и лист с формулами отображены на рисунках 4.41, 4.42. Рисунок 4.41 – Лист с расчетами Рисунок 4.42 – Лист с формулами Построение линии тренда Задание: Аппроксимировать приведенные ниже статистические данные, используя пять стандартные функции тренда. Выбрать среди них функцию, наилучшим образом описывающую исходные данные. Последовательность действий: 1 Занесите в столбец В значения X из таблицы, а в столбец С –значения Y. Измените название листа Лист1 на Данные(рис. 4.43). Рисунок 4.43 2 Пользуясь этими данными, постройте график. При построении графика укажите тип диаграммы Точечная и поместите график на отдельном листе. 3 Наведите курсор мыши на любую точку построенного графика, дождитесь появления всплывающей подсказки с параметрами этой точки и нажмите правую клавишу мыши. 5 Переместите уравнение на свободное место диаграммы, подберите размер шрифта. 6 Сформируйте заголовок диаграммы Линейная и назовите лист с диаграммой Линейная, так как показано на рисунке 4.44. Рисунок 4.44 – Диаграмма с линейной аппроксимацией 7 Выполните еще раз пункты 2, 3, 4, 5 и постройте на отдельном листе график со степенной аппроксимацией. Сформируйте заголовок диаграммы Степенная и назовите лист с диаграммой Степенная, так как показано на рисунке 4.45. Рисунок 4.45 – Диаграмма со степенной аппроксимацией 8 Выполните еще раз пункты 2,3,4,5 и постройте на отдельном листе график с логарифмической аппроксимацией. Сформируйте заголовок диаграммы Логарифмическая и назовите лист с диаграммой Логарифмическая, так как показано на рисунке 4.46. Рисунок 4.46 – Диаграмма с логарифмической аппроксимацией 9 Выполните еще раз пункты 2, 3, 4, 5 и постройте на отдельном листе график с экспоненциальной аппроксимацией. Построение двух графиков в рамках одного окна Приведем пример скрипта для построения двух графиков в рамках одного окна в MATLAB: % скрипт, строящий два графика в рамках одного окна %координаты точек… Построение диаграмм и графиков. в программе excel термин диаграмма используется для обозначения всех видов графического представления числовых данных В программе Excel термин диаграмма используется для обозначения всех видов графического представления числовых данных. Построение графического… Графики стали мощным средством моделирования и сбора данных в реальных сценариях, таких как социальные сети, веб-страницы, ссылки и местоположения. В этой статье я кратко объясню 10 основных алгоритмов работы с графами, которые очень полезны для анализа и их применения. Во-первых, давайте представим график. Граф состоит из конечного набора вершин или узлов и набора ребер , соединяющих эти вершины. Две вершины называются смежными , если они соединены друг с другом одним и тем же ребром. Некоторые основные определения, относящиеся к графикам, приведены ниже. Вы можете обратиться к рисунку 1 для примеров. Обход или поиск является одной из фундаментальных операций, которые можно выполнять на графах. В поиск в ширину (BFS), мы начинаем с определенной вершины и исследуем всех ее соседей на текущей глубине, прежде чем перейти к вершинам следующего уровня. В отличие от деревьев, графы могут содержать циклы (путь, первая и последняя вершины которого совпадают). Следовательно, мы должны отслеживать посещенные вершины. При реализации BFS мы используем структуру данных очереди. На рис. 2 показана анимация обхода BFS примера графа. Обратите внимание, как вершины обнаруживаются (желтые) и посещаются (красные). На рис. 3 показана анимация обхода в глубину того же примера графа, что и на рис. 2. Обратите внимание, как он перемещается вглубь и возвращается назад. Кратчайший путь из одной вершины в другую — это такой путь в графе, что сумма весов ребер, по которым нужно пройти, минимальна. На рис. 4 показана анимация, в которой кратчайший путь определяется из вершины 1 в вершину 6 графа. Цикл — это путь в графе, первая и последняя вершины которого совпадают. Если мы начинаем с одной вершины, идем по пути и заканчиваем в начальной вершине, то этот путь является циклом. минимальное остовное дерево — это подмножество ребер графа, которое соединяет все вершины с минимальной суммой весов ребер и состоит из циклы. На рис. 6 показана анимация, показывающая процесс получения минимального остовного дерева. Граф называется сильно связный , если каждая вершина графа достижима из любой другой вершины. На рис. 7 показан пример графа с тремя сильно связанными компонентами, вершины которых окрашены в красный, зеленый и желтый цвета. Топологическая сортировка графа представляет собой линейное упорядочение его вершин так, что для каждого направленного ребра (u, v ) в упорядочении вершина u предшествует v. На рис. 8 показан пример топологического упорядочения вершин (1, 2, 3, 5, 4, 6, 7, 8). Вы можете видеть, что вершина 5 должна идти после вершин 2 и 3. Точно так же вершина 6 должна идти после вершин 4 и 5. Окраска графа присваивает цвета элементам графа при соблюдении определенных условий. Раскраска вершин — наиболее часто используемый метод раскраски графов. При раскрашивании вершин мы пытаемся раскрасить вершины графа, используя k цветов, и любые две соседние вершины не должны иметь одинаковый цвет. Другие методы окрашивания включают окрашивание краев и окрашивание лиц . Хроматическое число графа — это наименьшее количество цветов, необходимое для раскрашивания графа. На рис. 9 показана раскраска вершин примера графа с использованием 4 цветов. Мы можем смоделировать граф как сеть потока с весами ребер в качестве пропускной способности. В задаче максимального потока мы должны найти путь потока, который может обеспечить максимально возможный расход. На рис. 10 показан анимированный пример определения максимального потока сети и определения конечного значения потока. A сопоставление в графе — это множество ребер, не имеющих общих вершин (т. е. никакие два ребра не имеют общей вершины). Сопоставление называется максимальным паросочетанием , если оно содержит максимально возможное количество ребер, соответствующих как можно большему количеству вершин. На рис. 11 показана анимация получения полного соответствия двудольного графа с двумя наборами вершин, обозначенными оранжевым и синим цветом. Я надеюсь, что вы нашли эту статью полезной как простое и обобщенное введение в алгоритмы графов. Я хотел бы услышать ваши мысли. 😇 Вы можете ознакомиться с реализациями графовых алгоритмов, найденными в networkx и igraph модули python. Вы можете прочитать о python-igraph в моей предыдущей статье «Руководство для новичков по Python-igraph». в направлении datascience.com Вы также можете ознакомиться с моими предыдущими статьями о структурах данных. по направлению datascience. по направлению к datascience.com в направлении datascience.com в направлении datascience.com Большое спасибо за прочтение. 😊 Ура! 😃 Главная/Блог/Учебники и руководства/Алгоритмы 101: Как использовать графовые алгоритмы 17 декабря 2020 г. — 11 мин чтения на собеседованиях по кодированию. Чтобы получить преимущество на собеседованиях, важно хорошо знать лучшие алгоритмы и их реализации. В сегодняшнем уроке мы будем изучать алгоритмы графа . Мы начнем с введения в теорию графов и алгоритмы графов. Далее мы узнаем, как реализовать график. Наконец, мы рассмотрим распространенные проблемы с графами, с которыми вы можете столкнуться на собеседовании по программированию. Сегодня мы узнаем: Этот кураторский путь проведет вас через все, что вам нужно знать, чтобы уверенно проходить собеседования по Python. Ace the Python Coding Interview Алгоритм — это математический процесс решения задачи с использованием четко определенного или оптимального количества шагов. Это просто базовая техника, используемая для выполнения конкретной работы. Граф — это абстрактное обозначение, используемое для представления связи между всеми парами объектов. Графы представляют собой широко используемые математические структуры, визуализируемые двумя основными компонентами: узлов и ребер . Алгоритмы графов используются для решения проблем представления графов в виде сетей, таких как рейсы авиакомпаний, способы подключения к Интернету или подключение к социальным сетям на Facebook. Они также популярны в НЛП и машинном обучении для формирования сетей. Некоторые из лучших алгоритмов графа включают: Хотя графы составляют неотъемлемую часть дискретной математики, они также находят практическое применение в компьютерных науках и программировании, в том числе в следующих областях: Граф, обозначенный G, представлен набором из вершин (V) или узлов, связанных ребрами (E) . В ориентированный граф , узлы связаны в одном направлении. Ребра здесь показывают одностороннюю связь. В неориентированном графе ребра являются двунаправленными, показывая двустороннюю связь. Пример: Хорошим примером использования неориентированного графа является алгоритм предложения друзей Facebook. Пользователь (узел) имеет ребро, идущее к другу A (другому узлу), который, в свою очередь, подключен (или имеет бегущее ребро) к другу B. Затем пользователю предлагается друг B. Существует много других сложных типов графиков, которые попадают в разные подмножества. Ориентированный граф, например, имеет компоненты сильной связности, когда каждая вершина достижима из любой другой вершины. Вершина — это точка пересечения нескольких линий. Ребро — это математический термин, используемый для обозначения линии, соединяющей две вершины. Из одной вершины может быть образовано множество ребер. Однако без вершины невозможно сформировать ребро. Для каждого ребра должны быть начальная и конечная вершины. Путь в графе G=(V,E)G = (V,E)G=(V,E) — это последовательность вершин v1, v2, …, vk, обладающая тем свойством, что являются ребрами между vivivi и vi+1vi+1vi+1. Мы говорим, что путь идет от v1v1v1 до vkvkvk. Последовательность 6,4,5,1,26,4,5,1,2 определяет путь от узла 6 к узлу 2. Подобным образом другие пути могут быть созданы путем обхода ребер графа. Путь называется простым, если все его вершины различны. Обход — это путь, но он не требует последовательности отдельных вершин. Граф является связным, если для каждой пары вершин uuu и vvv существует путь из uuu в vvv. Циклом называется путь v1, v2, …, vk, для которого верно следующее: Дерево — это связный граф, не содержащий цикла. В графе ребро, проведенное из вершины к самой себе, называется петлей. На рисунке V — это вершина, ребро которой (V, V) образует петлю. Прежде чем мы перейдем к решению задач с использованием графовых алгоритмов, важно сначала узнать, как представлять графы в коде. Графы могут быть представлены в виде матрицы смежности или списка смежности. Матрица смежности — это квадратная матрица, помеченная вершинами графа и используемая для представления конечного графа. Элементы матрицы указывают, является ли пара вершин смежной или нет в графе. В представлении матрицы смежности вам нужно будет перебрать все узлы, чтобы определить соседей узла. Список смежности используется для представления конечного графа. Представление списка смежности позволяет легко перебирать соседей узла. Каждый индекс в списке представляет вершину, а каждый узел, связанный с этим индексом, представляет соседние с ним вершины. Для класса базового графа, приведенного ниже, мы будем использовать реализацию списка смежности, так как она работает быстрее для решений алгоритмов, описанных далее в этой статье. Требования к нашей реализации графа довольно просты. Нам потребуются два члена данных: общее количество вершин в графе и список для хранения смежных вершин . Нам также нужен метод для добавления ребер или набора ребер. class AdjNode: """ Класс для представления списка смежности узла """ def __init__(self, data): 5 900 5 Constructor 02: параметр data : vertex """ self. self.next = None class Graph: """ Graph Class ADT """ """ Конструктор :param vertices : Всего вершин в графе ребро в неориентированном графе def add_edge(self, source, target): """ добавить ребро :param source: Исходная вершина :param назначение: Destination Vertex """ 5 # Добавление узла к исходному узлу node = AdjNode(destination) node.next = self.graph[source] self.graph[source] = node # Добавление исходного узла к целевому, если неориентированный граф # Намеренно закомментировал строки #node = AdjNode(source) #node.next = self.graph[destination] #self.graph[destination] = узел def print_graph(self): """ Функция распечатать график """ для i в диапазоне (self.V): print("Список смежности вершин {}\n head". temp = self.graph[i] while temp: print(" -> {} ".format(temp.vertex), end="") temp = temp.next print(" \n") # Основная программа if __name__ == "__main__": V = 5 # Всего вершин g = Graph(V) g.add_edge(0, 1) g.add_edge(0, 4) g.add_edge(1, 2) g.add_edge(1, 3) ) g.add_edge(1, 4) g.add_edge(2, 3) g.add_edge(3, 4) g.print_graph() В приведенном выше примере мы видим Python граф класса . Мы заложили основу нашего графового класса. Переменная V содержит целое число, указывающее общее количество вершин. Подготовьтесь к собеседованию по Python, не просматривая видео или документацию. Текстовые курсы Educative легко просматриваются и включают живую среду кодирования, что делает обучение быстрым и эффективным. Интервью с первоклассным программистом на Python Имея граф, представленный в виде списка смежности и начальной вершины, ваш код должен вывести строку, содержащую вершины графа, перечисленные в правильном порядке обхода. Чтобы решить эту проблему, уже добавлен ранее реализованный класс Graph. Ввод: Граф, представленный в виде списка смежности и начальной вершины Вывод: Строка, содержащая вершины графа, перечисленные в правильном порядке обхода Пример результата:4 = «02143»
или
результат = «01234» Посмотрите и разработайте пошаговый алгоритм, прежде чем переходить к реализации. Попробуйте сначала решить ее самостоятельно. Если вы застряли, вы всегда можете обратиться к решению, представленному в разделе решений. def bfs(graph, source): """ Функция для печати BFS графа :param graph: Граф :param source: начальная вершина :return: 5 "" " # Напишите здесь свой код! проход def bfs(my_graph, source): """ Функция для печати BFS графика :return: """ # Отметить все вершины как не посещенные посещенные = [False] * (len(my_graph. # Создать очередь для BFS queue = [] # Строка результата result = "" # Пометить исходный узел как # Посещенный и поставить его в очередь Удалите вершину из очереди # и распечатайте ее source = queue.pop(0) result += str(source) # Получить все смежные вершины # источника исключенных из очереди вершин. Если соседний # не был посещен, то отметьте его # посещенным и поставьте в очередь , пока my_graph.graph[source] не None: data = my_graph.graph[source].vertex если нет посещено[данные]: очередь.добавить(данные) посещено[данные] = True my_graph.graph[источник] = my_graph.graph[источник].next вернуть результат # Main для тестирования вышеуказанной программы if __name__ == "__main__": V = 5 g = Graph(V) g.add_edge(0, 1) 5 . add_edge(0, 2) g.add_edge(1, 3) g. print(bfs(g, 0)) Мы начинаем с выбранного узла и пересекаем граф по слоям. Исследуются все соседние узлы. Затем мы переходим на следующий уровень. Мы проходим по графику горизонтально, то есть по каждому слою. Граф может содержать циклы. Чтобы избежать повторной обработки одного и того же узла, мы можем использовать логический массив, который помечает посещенные массивы. Вы можете использовать очередь для хранения узла и пометить его как посещенный. Очередь должна следовать методу формирования очереди «первым пришел – первым обслужен» (FIFO). В этой задаче вам нужно реализовать обход в глубину. Для решения этой проблемы уже предусмотрен реализованный ранее класс графа. Входные данные: Граф, представленный в виде списка смежности и начальной вершины Выходные данные: Строка, содержащая вершины графа, перечисленные в правильном порядке обхода 01342″
или
результат = «02143» Посмотрите и разработайте пошаговый алгоритм, прежде чем переходить к реализации. def dfs(graph, source): """ Функция для печати DFS графа :param graph: Граф :param source: начальная вершина "" # Напишите здесь свой код! проход def dfs(my_graph, source): """ Функция для печати DFS графика График 002 :параметр источник: запуск вершина :return: возвращает обход в виде строки """ # Отметить все вершины как не посещенные посещенные = [False] * (len(my_graph.graph)) # Создать стек для DFS stack = [] # Строка результата result = "" # Поместить исходный код stack.append(source) while stack: # Извлечь вершину из стека 5 90.002 pop() , если не посещали [источник]: result += str(source) visit[source] = True # Получить все смежные вершины извлеченного источника вершин. # Если соседний не был посещен, то нажать его пока my_graph.graph[source] не None: data = my_graph.graph[source].vertex если не посещен[data]: stack.append(data) my_graph.graph[source] = my_graph.graph[source].next return result # Main для тестирования вышеуказанной программы if __name__ == "__main__": V = 5 g = Graph(V) g.add_edge(0, 1) g.add_edge(0, 2) g.ad , 3) g.add_edge(1, 4) print(dfs(g, 0)) Алгоритм поиска в глубину использует идею поиска с возвратом. Здесь «возврат» означает двигаться вперед, пока на текущем пути больше нет узлов, а затем двигаться назад по тому же пути, чтобы найти узлы для прохождения. В этой задаче вы должны реализовать функцию Ввод: Граф, источник (целое число) и пункт назначения (целое число) Вывод: Обход BFS графа с удаленным ребром между источником и местом назначения Сначала закройте рассмотрите эту проблему и разработайте пошаговый алгоритм, прежде чем переходить к реализации. Попробуйте сами, прежде чем проверять решение! def remove_edge(graph, source, target): """ Функция для удаления ребра :param graph: График :param source: Исходная вершина :param destination: Целевая вершина """ # Напишите здесь свой код! пройти Эта задача очень похожа на удаление в связанном списке, если вы с ней знакомы. Наши вершины хранятся в связанном списке. Сначала мы получаем доступ к Если ключ, который нужно удалить, находится в середине связанного списка, мы отслеживаем предыдущий узел и соединяем предыдущий узел со следующим узлом при встрече с пунктом назначения. Ниже приведены другие вопросы для интервью, которые вы можете попробовать решить: Поздравляем, вы дошли до конца. Вы должны понимать, что такое графы в Python, и понимать, что нужно подготовить к вопросам на интервью по кодированию, связанным с графами. Если вы хотите узнать больше об алгоритмах в Python, ознакомьтесь с планом обучения Educative 9.0013 Интервью по кодированию на Python . Ленг С. Автор книги, видный американский математик, профессор Колумбийского университета С. Ленг, хорошо знаком советскому читателю по двум вышедшим ранее монографиям «Алгебраические числа» и «Введение в теорию дифференцируемых многообразий» (издательство «Мир», 1966 и 1967). В книге рассмотрены все основные разделы современной алгебры (группы, кольца, модули, теория полей, линейная и полилинейная алгебра, представления грунп). Читатель найдет здесь также первоначальные сведения по гомологической алгебре и алгебраической геометрии.
Книга отражает изменения, происшедшие в алгебре за последние два десятилетия, и дает читателю возможность основательно познакомиться с областями алгебры, ставшими уже классическими. Язык категорий и функторов связывает воедино разрозненные ранее понятия и результаты.
Книга будет весьма полезной математикам различных специальностей, студентам, аспирантам и научным работникам. Она может служить основой специальных курсов по алгебре. спросил Изменено
5 лет, 3 месяца назад Просмотрено
33 тысячи раз $\begingroup$ Я пытаюсь выяснить, какие три возможности $z$ таковы, что 93 = i$, тогда
$$z = \exp\left[ i \left(\frac{\pi}{6}+\frac{2n\pi}{3}\right)\right]$$ для всех целых чисел $n$. $\endgroup$ 1 $\begingroup$ Я полагаю, что ваш «полиномиальный» подход также сработал бы, если бы вы имели в виду это: [При этом мы предполагаем, что ничего не знали о «тождестве Эйлера», теореме Де Муавра или корнях единства, всех из них обеспечивают достаточно эффективные устройства] 92 \ = \ \ frac {3} {4} \ \ \ Rightarrow \ \ a \ = \ \ pm \ frac {\ sqrt {3}} {2} \ \ \ Rightarrow \ \ z \ = \ \ frac {\ sqrt{3}}{2} + \frac{1}{2}i \ , \ -\frac{\sqrt{3}}{2} + \frac{1}{2}i \\ . Мы нашли три комплексных решения уравнения. Как говорит Дэн , (одна из форм) Фундаментальная теорема алгебры утверждает, что этот многочлен третьей степени с комплексными коэффициентами имеет всего три корня (с учетом кратностей, каждая из которых здесь равна 1). Мы, вероятно, не хотели бы использовать этот метод для более высоких степеней, поскольку алгебраическое решение стало бы более сложным. Методы, описанные на других плакатах, используются гораздо чаще. 93, 3\тета)$. Кубические корни $(r, \theta)$ равны $\left(\sqrt[3]{r}, \frac{\theta}{3}\right)$, $\left(\sqrt[3]{ r}, \frac{\theta+2\pi}{3}\right)$ и $\left(\sqrt[3]{r}, \frac{\theta+4\pi}{3}\right) $ (напомним, что добавление $2\pi$ к аргументу не меняет число). Другими словами, чтобы найти кубический корень комплексного числа, возьмите кубический корень из абсолютного значения (радиуса) и разделите аргумент (угол) на 3. $i$ находится под прямым углом от $1$ : $i = \left(1, \frac{\pi}{2}\right)$. Кубический корень из $i$ равен $A = \left(1, \frac{\pi}{6}\right)$. Два других: $B = \left(1, \frac{5\pi}{6}\right)$ и $\left(1, \frac{9\pi}{6}\right) = -i$ . Вспоминая основы тригонометрии, прямоугольные координаты $A$ равны $\left(\cos\frac{\pi}{6}, \sin\frac{\pi}{6}\right)$ (треугольник OMA равен прямоугольник в М). Таким образом, $A = \cos\frac{\pi}{6} + i \sin\frac{\pi}{6} = \frac{\sqrt{3}}{2} + i\frac{1}{ 2}$. Если вы не помните значения $\cos\frac{\pi}{6}$ и $\sin\frac{\pi}{6}$, вы можете найти их с помощью геометрии. Треугольник $OAi$ имеет две равные стороны $OA$ и $Oi$, поэтому он равнобедренный: углы $OiA$ и $OAi$ равны. Сумма углов треугольника равна $\pi$, и мы знаем, что третий угол $iOA$ равен $\frac{\pi}{2} — \frac{\pi}{6} = \frac{\ пи{3}$; поэтому $OiA = OAi = \dfrac{\pi — \frac{pi}{3}}{2} = \dfrac{\pi}{3}$. Итак, $OAi$ — равносторонний треугольник, а высота AN также является медианой, поэтому N — середина треугольника $[Oi]$: $\sin\frac{\pi}{6} = AM = ON = \frac{ 1}{2}$. Подстановка нескольких значений для $n$ дает: Установив значение $a$ в (ii), мы получаем, Если $a=0$, $b=-1$ Если $a=±b\sqrt {3}$, $ b=1/2$ Тогда $a=±b\sqrt {3}=±(1/2)\sqrt {3}=±\ sqrt {3}/2$ Итак, $(a,b)=(0,-1),(±\sqrt {3}/2,1/2)$ Теперь есть 3 значения $ з$. (1) $\sqrt [3] {i} =a+bi= 0+(-1)i= -i$ (2) $\sqrt [3] {i} =a+bi= \ dfrac {\ sqrt {3}} {2}+\ dfrac {i} {2} $ (3) $\sqrt [3] {i} =a+bi= -\dfrac {\sqrt {3}}{2}+\dfrac {i}{2}$ $\endgroup$ спросил Изменено
5 лет, 9 месяцев назад Просмотрено
4к раз $\begingroup$ Я знаю, как напрямую доказать, что комплексное число является одним из кубических корней из 1. УчебаХимия Калькулятор для уравнивания, или балансирования химических реакций. Калькулятор ниже предназначен для уравнивания химических реакций. Как известно, существует несколько методов уравнивания химических реакций: Последние два применяются для окислительно-восстановительных реакций Данный калькулятор использует математический метод — как правило, в случае сложных химических уравнений он достаточно трудоемок для ручных вычислений, но зато прекрасно работает, если все за вас рассчитывает компьютер. Математический метод основан на законе сохранения массы. Закон сохранения массы гласит, что количество вещества каждого элемента до реакции равняется количеству вещества каждого элемента после реакции. Рассмотрим этот метод на примере: Пусть дана химическая реакция: Обозначим неизвестные коэффициенты: Составим уравнения числа атомов каждого элемента, участвующего в химической реакции: Запишем их в виде общей системы: В данном случае имеем пять уравнений для четырех неизвестных, причем пятое можно получить умножением четвертого на четыре, так что его можно смело отбросить. Перепишем эту систему линейных алгебраических уравнений в виде матрицы: Эту систему можно решить методом Гаусса. Химические элементы следует писать так, как они написаны в таблице Менделеева, т. е. учитывать большие и маленькие буквы (Na3PO4 — правильно, na3po4 — неправильно). Уравнение химической реакции Сбалансированное уравнение Ссылка скопирована в буфер обмена #наука #химия баланс балансирование математический метод реакция уравнение Химия PLANETCALC, Уравнивание химических реакций Timur2020-11-03 14:19:33 Окислительно-восстановительные реакции — это процесс «перетекания» электронов от одних атомов к другим. Ключевой термин при рассмотрении окислительно-восстановительных реакций — это степень окисления, которая представляет собой условный заряд атома и количество перераспределяемых электронов. Окисление — процесс потери электронов, при котором увеличивается заряд атома. Восстановление, наоборот, представляет собой процесс присоединения электронов, при котором степень окисления уменьшается. Соответственно, окислитель принимает новые электроны, а восстановитель — теряет их, при этом такие реакции всегда происходят одновременно. Вычисление данного параметра — одна из самых популярных задач в школьном курсе химии. Поиск зарядов атомов может быть как элементарным вопросом, так и задачей, требующей скрупулезных расчетов: все зависит от сложности химической реакции и количества составляющих соединений. Хотелось бы, чтобы степени окисления указывались в периодической таблице и были всегда под рукой, однако этот параметр приходится либо запоминать, либо вычислять для конкретной реакции. Существуют химические элементы, электрический заряд которых однозначен в любых соединениях. К таким относятся: Несмотря на однозначность, существуют некоторые исключения. Фтор F —уникальный элемент, степень окисления которого всегда составляет -1. Благодаря этому свойству многие элементы изменяют свой заряд в паре с фтором. Например, кислород в соединении с фтором имеет заряд +1 (O2F2) или +2 (ОF2). Кроме того, кислород меняет свою степень в перекисных соединениях (в перекиси водорода h302 заряд равен -1). При рассмотрении окислительно-восстановительных реакций важно учитывать вещества, которые состоят из ионов. Атомы ионных химических элементов имеют степень окисления, равную заряду иона. Например, в соединении гидрида натрия NaH по идее водород имеет степень +1, однако ион натрия также имеет заряд +1. Так как соединение должно быть электрически нейтральным, то атом водорода принимает заряд -1. Отдельно в этой ситуации стоят ионы металлов, так как атомы таких элементов ионизируются на разные величины. К примеру, железо F ионизируется и на +2, и на +3 в зависимости от состава химического вещества. Для простых соединений, которые включают в себя атомы с однозначным зарядом, распределение степеней окисления не составляет труда. Например, для воды h3O атом кислорода имеет заряд -2, а атом водорода +1, что в сумме дает нейтральный нуль. В более сложных соединениях встречаются атомы, которые могут иметь разный заряд и для определения степеней окисления приходится использовать метод исключения. Сульфат натрия Na2SO4 имеет в своем составе атом серы, заряд которого может принимать значения -2, +4 или +6. Какое значение выбрать? Первым делом определяем, что ион натрия имеет заряд +1. Кислород в подавляющем большинстве случаев имеет заряд –2. Составляем простое уравнение: +1 × 2 + S + (–2) × 4 = 0 2 + S – 8 = 0 S = 8 − 2 S = 6 Таким образом, заряд серы в сульфате натрия равен +6. Теперь, когда вы знаете, как определять заряды атомов, вы можете расставлять коэффициенты в окислительно-восстановительных реакциях для их балансировки. Стандартное задание по химии: подобрать коэффициенты реакции при помощи метода электронного баланса. В этих заданиях вам нет нужды определять, какие вещества образуются на выходе реакции, так как результат уже известен. Например, определите пропорции в простой реакции: Na + O2 → Na2O Итак, определим заряд атомов. Na(0) – 1e = Na(+1) O(0) + 2e = O(–2) Для балансировки реакции требуется уравновесить кислород и добавить коэффициент 2 к оксиду натрия. Получим реакцию: Na + O2 → 2Na2O Теперь у нас дисбаланс по натрию, уравновесим его при помощи коэффициента 4: 4Na + O2 → 2Na2O Теперь количество атомов элементов совпадают с обеих сторон уравнения, следовательно, реакция сбалансирована. Все это мы проделали вручную, и это было несложно, так как реакция сама по себе элементарна. Но что делать, если требуется сбалансировать реакцию вида K2Cr2O7 + KI + H2SO4 → Cr2(SO4)3 + I2 + H2O + K2SO4? Ответ прост: используйте калькулятор. Наша программа позволяет автоматически расставить коэффициенты для самых распространенных химических реакций. Для этого вам необходимо вписать в поле программы реакцию или выбрать ее из раскрывающегося списка. Для решения выше представленной окислительно-восстановительной реакции вам достаточно выбрать ее из списка и нажать на кнопку «Рассчитать». Калькулятор мгновенно выдаст результат: K2Cr2O7 + 6KI + 7H2SO4 → Cr2(SO4)3 + 3I2 + 7H2O + 4K2SO4 Использование калькулятора поможет вам быстро сбалансировать наиболее сложные химические реакции. Умение балансировать реакции необходимо всем школьникам и студентам, которые мечтают связать свою жизнь с химией. В целом расчеты выполняются по строго определенным правилам, для понимания которых достаточно элементарных знаний по химии и алгебре: помнить, что сумма степеней окисления атомов соединения всегда равна нулю и уметь решать линейные уравнения. Ого! Wolfram|Alpha не работает без JavaScript. Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha. Примеры для Химические реакции, превращение одной молекулярной структуры в другую, происходят повсеместно в окружающем нас мире. Все, от двигателей внутреннего сгорания и сложных производственных установок до геологических процессов и самой жизни, зависит от химических реакций. Используйте Wolfram|Alpha, чтобы сбалансировать химические уравнения, определить стехиометрию реакции и предсказать продукты. Используйте Wolfram|Alpha, чтобы найти правильные коэффициенты для балансировки химической реакции. Составьте выражения, необходимые для моделирования химических равновесий. Когда вы указываете количество одного или нескольких реагентов или продуктов, Wolfram|Alpha может рассчитать свойства реакции, такие как теоретический выход, процентный выход и предельный реагент. Поиск в базе данных реакций Wolfram|Alpha. Пошаговые решения для химии Автор: Люция Заборовска, доктор медицинских наук, кандидат наук Отзыв от Bogna Szyk и Jack Bowater Последнее обновление: 17 января 2023 г. Наш калькулятор констант скорости вычисляет скорость и период полураспада реакции . Это также позволяет вам узнать константу скорости и концентрацию данного вещества, если ваш запрос основан на ставка законов , т.е. Помните, что наши калькуляторы работают в обе стороны . Что бы вы ни пытались рассчитать, мы здесь, чтобы помочь. 🙋 В статье ниже мы сосредоточимся на поиске константы скорости и теоретических основах калькулятора порядка реакции. Вначале подумайте о том, что вы пытаетесь найти — найдите все полезные данные, представленные в вашем запросе. Выберите сколько молекул взаимодействует на элементарном шаге. Выберите порядок реакции для каждой молекулы : Зеро — скорость реакции не зависит от концентрации реагента, например, 2NH₃(газ) → N₂(газ) + 3H₂(газ) , фотохимические реакции. Обратите внимание, что вы не можете установить ноль для любого из реагентов на бимолекулярной или тримолекулярной стадии. В этих случаях считайте реагент нулевого порядка несуществующим. Первый — скорость реакции зависит от концентрации одного реагента , например, C₂H₆(г) → 2CH3(г) , реакции радиоактивного распада. Вторая — Может быть описана как реакция, где скорость зависит от двух молекул . Это могут быть либо два разных реагента , либо молекула, реагирующая сама с собой, например, H₂(г) + I₂(г) → 2HI(г) или 2NO₂(г) → 2NO(г) + O₂(г) . 🙋 Знакомы ли вы с константой равновесия приведенных выше реакций? Если нет, попробуйте наш калькулятор константы равновесия! Введите концентрацию вещества. Выберите желаемый результат: Что такое период полураспада (T½)? Период полураспада – это период, в течение которого половина субстрата подвергается химическому превращению. Давайте изобразим это на быстром примере. Наша начальная концентрация [S] составляет 20 М, а Т½ = 2 мин. Введите концентрацию вещества. Выберите желаемый результат: Что такое период полураспада (T½)? Период полураспада – это период, в течение которого половина субстрата подвергается химическому превращению. Давайте изобразим это на быстром примере. Наша начальная концентрация [S] составляет 20 М, а Т½ = 2 мин. [S] 20 10 5 900 04 2,5 1,25 … 0 2 4 6 8 … Какова скорость реакции? Скорость реакции характеризует скорость реакции, выраженную в М/сек , М/мин , или моль/(сек·л) , то есть сколько молей реагирует на литр вещества в секунду. Какова константа скорости реакции? Константа скорости — это просто коэффициент пропорциональности, специфичный для данной температуры и типа реакции. Он описывается многими различными уравнениями и обычно находится экспериментально (см. Раздел ниже). 📚 Готовишься к экзамену? Попробуйте наши полезные инструменты для других типов реакций: Самый очевидный ответ на вопрос «Как найти константу скорости?» состоит в том, чтобы изменить уравнения скорости реакции или периода ее полураспада .0136 . Если вы знаете порядок реакции, концентрацию вещества или скорость/период полураспада реакции, этот метод может подойти вам. (Это также самый простой метод для реакций нулевого порядка, поскольку скорость реакции равна константе скорости! ) Зависимость константы скорости от температуры хорошо определяется уравнением Аррениуса : k = A × exp (-E / (R × T)) . Если вам интересно, как определить константу скорости обратимых реакций, вот простое уравнение, которое подходит для большинства случаев: K = k₁ / k₋₁ , где K = константа равновесия реакции, k₁ и k₋₁ = константы скорости прямой и обратной реакций соответственно. Ниже вы найдете все необходимые уравнения для расчета скорости реакции нулевого, первого и второго порядка. Посмотрите на формулы ниже и сравните их с наклонами на графиках ниже. Имейте в виду, что все эти формулы могут служить уравнениями констант скорости. Будьте осторожны с наклоном реакции первого порядка: он может выглядеть похожим на нулевой, но на самом деле он содержит натуральный логарифм от [A] по оси Y ! Чтобы найти константу скорости: Определить сколько атомов участвует в элементарной стадии реакции. Найдите порядок реакции для каждого атома, участвующего в реакции. Увеличьте начальную концентрацию каждого реагента до его порядка реакции, затем умножьте их всех вместе. Разделите скорость на результат предыдущего шага. Единицы вашей константы скорости будут зависеть от общего порядка реакции. Только температура влияет на константу скорости. Вы можете подумать, что изменение начальной концентрации повлияет на константу скорости, но это изменит только скорость. Вы можете ввести катализатор , чтобы обеспечить другой путь реакции с более низкой энергией активации, но на самом деле это будет другая реакция. Чтобы найти энергию активации из константы скорости: Найдите константу Аррениуса для реакции. Excel для Microsoft 365 Excel 2019 Excel 2016 Excel 2013 Еще…Меньше В некоторых случаях вам может потребоваться сохранить книгу в другом формате файла, например текстовом (TXT) или формате с разделителями-запятыми (CSV). Имейте в виду, что при сохранении книги в другом формате может быть утрачена часть форматирования, данных и возможностей. Внимание: При сохранении книги в любом текстовом формате теряются все элементы форматирования. Откройте книгу, которую вы хотите сохранить. На вкладке Файл выберите команду Сохранить как.
Выберите расположение, где нужно сохранить книгу.
В диалоговом окне Сохранение документа перейдите в нужное расположение. Щелкните стрелку в поле Тип файла и выберите нужный формат файла (TXT или CSV). Примечание: Список доступных форматов файлов зависит от типа активного листа в книге (лист, лист диаграммы или другой).
Примите имя, предложенное в поле Имя файла, или введите новое имя книги.
Формат
Расширение
Описание
Форматированный текст (разделители — пробелы) PRN Формат для Lotus, с разделителями — пробелами. Сохраняет только активный лист Текст (разделители — знаки табуляции) TXT Сохраняет книгу в виде текстового файла, разделенного знаками табуляции, — для использования в другой операционной системе Microsoft Windows — и гарантирует, что символы табуляции, разрывы строк и другие символы будут интерпретироваться правильно. Текст (Макинтош) TXT Сохраняет книгу в виде текстового файла, разделенного знаками табуляции, — для использования в операционной системе Макинтош — и гарантирует, что символы табуляции, разрывы строк и другие символы будут интерпретироваться правильно. Сохраняет только активный лист. Текст (MS-DOS) TXT Сохраняет книгу в виде текстового файла, разделенного знаками табуляции, — для использования в операционной системе MS-DOS — и гарантирует, что символы табуляции, разрывы строк и другие символы будут интерпретироваться правильно. Текст в кодировке Unicode TXT Сохраняет книгу в виде текста в кодировке Unicode, стандартной кодировке символов, разработанном Unicode Consortium. CSV (разделители — запятые) CSV Сохраняет книгу в виде текстового файла, разделенного знаками запятой, — для использования в другой операционной системе Windows — и гарантирует, что символы табуляции, разрывы строк и другие символы будут интерпретироваться правильно. Сохраняет только активный лист. CSV (Макинтош) CSV Сохраняет книгу в виде текстового файла, разделенного знаками запятой, — для использования в операционной системе Макинтош — и гарантирует, что символы табуляции, разрывы строк и другие символы будут интерпретироваться правильно. CSV (MS-DOS) CSV Сохраняет книгу в виде текстового файла, разделенного знаками запятой, — для использования в операционной системе MS-DOS — и гарантирует, что символы табуляции, разрывы строк и другие символы будут интерпретироваться правильно. Сохраняет только активный лист. DIF DIF Формат обмена данными. Сохраняет только активный лист. SYLK SLK Формат Symbolic Link. Здравствуйте, если вы заглянули на страничку моего блога, значит, вам нужна помощь в общении с компьютером. Помогу, чем смогу. Тема сегодняшнего обсуждения «Как создать файл txt?». Мне было удивительно видеть в комментариях к одной из статей данный вопрос, так как действия, производимые при создании основных форматов типа txt, doc, xls у меня доведены до автоматизма. И если требуется выполнить такую задачу, я просто это делаю, не задумываясь о том, как именно. Посмотрел статистику запросов в «Гугле». Выяснилось, что множество людей задают подобные вопросы — как создать txt файл на Windows 7, 10 и других операционных системах (MacOS, MS-DOS, Linux), как создать текстовый файл txt в командной строке, в папке, в «Ворде», как создать txt файл на телефоне. Порыскав в своей голове и на просторах интернета, я собрал всё, что смог найти на данную тему. Итак, поговорим о том, как создать файл.txt на компьютерах с операционной системой windows 10, 7 и более ранними, устаревшими, но вполне дееспособными версиями. Друзья, мне кажется, что будет вполне уместным сначала объяснить, что такое текстовый файл с расширением txt, а уж потом переходить к разговору о том, как его создать. Файл – это исходный элемент на компьютере, содержащий некоторую информацию. Он имеет имя и расширение. С именем, думаю, всё понятно и объяснять не стоит. Расширение – это продолжение имени, указывающее системе на формат документа и на то, какой программой его открывать. Формат – это специфика информации, которая есть в содержании, то есть текст, графика, таблицы. Текстовый файл в формате txt – это документ, содержащий только чистый текст, без какого-либо форматирования и картинок, открывается который любыми текстовыми редакторами (по умолчанию стандартной программой «Блокнот»), а как его создать в подробностях рассмотрим ниже. Самый простой и распространенный способ создать текстовый файл, которым пользуюсь я, как и большинство пользователей «Винды», содержит следующие шаги: Текстовый документ готов. Открыть его можно двумя быстрыми щелчками или через соответствующий пункт контекстного меню, которое вызывается правым щелчком мыши на документе. Друзья, хотя вышеописанным способом можно создать файл txt в любом месте, но всё-таки давайте я расскажу о том, как это сделать ресурсами конкретной папки: Как я уже упоминал, текстовый файл по умолчанию открывается программой «Блокнот», но создать документ txt можно и другими текстовыми редакторами, а также переделать из уже имеющихся документов с расширением docx. Получить из элемента doc или docx документ с заданным расширением можно тремя способами: Кстати, третий способ вполне сгодится не только для изменения расширения у имеющегося документы, но и для создания нового в требуемом формате. Создать файл txt можно и с помощью приложения cmd.exe. Это не так-то просто и не всегда понятно, а ещё необходимо знать команды. Но всё-таки я расскажу об этом вкратце, может, кому и пригодится. Итак, с помощью командной строки можно создать два вида файлов txt – пустой и заполненный, то есть имеющий содержимое. Чтобы создать пустой файл с расширением txt, посредством командной строки, необходимо для начала её запустить. Сделать это можно несколькими способами, вот самые простые: Далее, необходимо ввести команду для создания нулевого (пустого) текстового документа, их много, предлагаю вашему вниманию две самые популярные из них: Теми же командами, но с некоторыми изменениями, можно создать файл. Кстати, если вы ищете ответ на вопрос «как создать файл с расширением txt в MS-DOS?», то ознакомьтесь с описанными выше способами, так как они актуальны и для этой операционной системы. Друзья, давайте поговорим о том, как создать txt файл в операционной системе linux. Сделать это можно посредством терминала, который является аналогом командной строки в. Существует несколько команд, я расскажу о самых коротких. Итак, как и в случае с командной строкой в Windows, для создания текстового файла.txt в linux сначала потребуется запустить терминал. Для этого нажимаем одновременно три клавиши – CTRL, ALT и T. Затем вводим одну из следующих команд: Пришло время поговорить о том, как создать txt файл на устройствах с операционкой MacOs. Способов, как всегда, уйма. Поведаю самый простой: Очень часто люди спрашивают в интернете, как создать текстовый файл txt на «Андроиде». Отвечаю – ресурсами самого телефона этого не сделать. Необходимо устанавливать специальные приложения, которых навалом в сервисе Play Market – «Простой текстовый редактор» (аналог блокнота), Text Editor. Среди самых популярных поисковых запросов в «Гугле» есть и такой – «как создать txt файл в far». Расскажу в двух словах и об этом — помогу людям. Для сотворения нужного документа в FAR Manager выполняем следующие действия: Друзья, вот я и поделился всем, чем хотел. Получилось довольно много информации. Надеюсь, она кому-нибудь пригодится. Если что-то непонятно, пишите в комментариях, будем разбираться вместе. Тем более мне и самому приятен этот процесс, так как в поисках исчерпывающих ответов на ваши вопросы я узнаю много нового и полезного для себя. Обновлено: 03.09.2019, автор: Computer Hope Вы можете создать текстовый файл на своем компьютере с помощью текстового редактора. Примером текстового редактора является Блокнот, входящий в состав Microsoft Windows. Примечание Когда мы говорим о «текстовом файле», мы имеем в виду простой текстовый файл без какого-либо форматирования текста (например, жирного шрифта), изображений, различных шрифтов, размеров шрифтов и т. д. Если вам нужно создать более богатый документ с любым об этих возможностях см.: Как создать документ. Кончик Приведенные ниже рекомендации относятся к программам, включенным в операционную систему. Вы также можете загрузить и установить более мощный и бесплатный текстовый редактор, например Notepad++, для создания, просмотра и редактирования текстовых файлов. Самый простой способ создать текстовый файл в Windows — открыть программу «Блокнот» на компьютере. Блокнот — это текстовый редактор, входящий в состав Microsoft Windows. Кончик Текстовый файл считается файлом с открытым текстом, а Блокнот может создавать и редактировать только файлы с открытым текстом. Блокнот сохраняет любой текстовый файл с расширением .txt, что означает невозможность использования специального форматирования или шрифтов. Программу Блокнота Windows можно открыть одним из следующих способов. или Вы также можете создать текстовый файл, используя любую другую программу обработки текстов, например Microsoft Word или WordPad. При сохранении файла измените имя файла или тип файла от до Обычный текст , чтобы сохранить его как текстовый файл. Во многих из этих программ у вас также есть возможность сохранить файл в формате Rich Text Format. После создания и сохранения файла его также можно редактировать с помощью Блокнота или другой программы обработки текстов. Другой способ создать текстовый файл — щелкнуть правой кнопкой мыши пустую область на рабочем столе и во всплывающем меню выбрать Новый , а затем выберите Текстовый документ . Создание текстового файла таким образом открывает текстовый редактор по умолчанию с пустым текстовым файлом на рабочем столе. Вы можете изменить имя файла на что угодно. Вы можете редактировать файл в программе «Блокнот» или любой другой программе обработки текстов, например Microsoft Word. Кончик Эти же шаги можно использовать в любом другом месте на вашем компьютере, например, в другой папке. Находясь в командной строке Windows, вы также можете создать новый текстовый файл в текущем каталоге. В более ранних версиях Windows новый файл любого типа, включая текстовые файлы, можно было создать с помощью команды командной строки редактирования. Более поздние версии Windows удалили возможность использовать команду редактирования для этой цели. Вместо этого вы можете использовать команду echo в командной строке Windows, чтобы создать пустой текстовый файл в текущем каталоге. В приведенном выше примере вы используете команду echo для создания файла с именем «myfile.txt» в текущем каталоге. Обратите внимание, что между echo , точкой, знаком «больше» ( > ) и именем файла нет пробелов. Другой вариант создания текстового файла из командной строки — с помощью команды запуска, как показано в примере ниже. В этом примере вы используете команду запуска, чтобы открыть Блокнот с файлом «myfile.txt». Предполагая, что этот файл не существует, он будет создан и сохранен в вашем текущем каталоге. Если бы файл существовал, вы бы редактировали этот файл. Несколько команд могут создать текстовый файл в оболочке Linux. Одним из простых в использовании текстовых редакторов является pico. Вы можете использовать его так: После ввода вышеуказанной команды открывается редактор, в котором можно создать текстовый файл. Кончик Расширение файла .txt не требуется в Linux. Это расширение файла, наиболее часто встречающееся и используемое в Windows. Если вам не нужно, чтобы файл открывался в Windows, вы можете не иметь расширения файла или переименовать его как хотите. Как создать текстовый файл На компьютере есть множество файлов. Самый простой тип файла называется «текстовый файл». Это может иметь или не иметь «.txt»
расширение. Текстовый файл — это файл, который занимает очень мало байтов, за исключением фактического
коды символов, которые он содержит. Текстовый файл, созданный, скажем, Блокнотом, который содержит
4 слова могут быть не более 25 или 30 байт (обратите внимание, НЕ мегабайты или килобайты, а только байты!).
Сравните это с файлом Microsoft Word DOC с теми же четырьмя словами в нем — это будет как минимум
20 килобайт. Почему разница? потому что Word хранит много дополнительной информации о
документ — символы форматирования, имя автора, настройки полей, настройки шрифта и т.д. Программист должен знать, какой тип файла он создает. Все эти типы
имеют свое применение и, как правило, НЕ являются взаимозаменяемыми. Наши задания обычно говорят «создать текстовый файл». Может быть для входа
файл данных, это может быть выходной файл захвата, это может быть дизайн для программы,
это может быть тестовый план. Подсказка: если вы используете Windows,
установите свойства папки так, чтобы
вы можете увидеть расширения файлов. Это значительно облегчает понимание! Как создать текстовый файл? Есть несколько способов: Почему мы просим текстовых файлов? В заданиях по программированию будут перечислены файлы, которые вы должны сдать, и их типы. Как известно, теория обыкновенных дифференциальных уравнений начала развиваться в XVII веке одновременно с возникновением дифференциального и интегрального исчисления. Можно сказать, что необходимость решать дифференциальные уравнения для нужд механики, то есть находить траектории движений, явилась толчком для создания Ньютоном нового исчисления. Законы Ньютона позволяют строить математическую модель механического движения, которая обычно представляет собой дифференциальное уравнение. Рассмотрим, например, подробнее такую задачу. С некоторой высоты сброшено тело массой m. Требуется установить закон изменения скорости падения тела v(t), если на него действует сила сопротивления воздуха, пропорциональная скорости (коэффициент пропорциональности k). По II закону Ньютона где – ускорение движущегося тела, – сумма сил, действующих на тело – силы тяжести и силы сопротивления воздуха. Таким образом, имеем уравнение, связывающее искомую функцию v(t) и ее производную т. В математике и физике часто встречаются задачи, для решения которых требуется решить уравнение, содержащее не только неизвестную функцию и ее аргумент, но и производную неизвестной функции. Уравнение вида связывающее независимую переменную x, искомую функцию и ее производные ) , называется обыкновенным дифференциальным уравнением. Например, уравнения будут дифференциальными уравнениями первого порядка; уравнения будут дифференциальными уравнениями второго порядка; уравнение имеет третий порядок. Функция называется решением дифференциального уравнения на интервале (a,b) если при ее подстановке в это уравнение получается тождество, справедливое для всех x из интервала (a, b) Например, функция является решением дифференциального уравнения ; функция будет решением уравнения в интервале (-1;1) . Чтобы это проверить, достаточно подставить функцию в соответствующее уравнение. Уравнение задающее в неявном виде решение дифференциального уравнения, называется интегралом дифференциального уравнения. График решения (интеграла) дифференциального уравнения называется интегральной кривой. Так же если вы затрудняетесь в решении дифференциального уравнения, всегда можно воспользоваться онлайн калькулятором Процесс нахождения решений дифференциального уравнения называется интегрированием дифференциального уравнения. Это название не случайно, так как нахождение решений обычно связано с процессом интегрирования. Поскольку процесс интегрирования функции приводит к появлению множества функций, то и решений любое дифференциальное уравнение тоже будет иметь множество. Основной задачей теории дифференциальных уравнений является отыскание всех решений данного дифференциального уравнения в заданной области (в явной или неявной форме). Дифференциальное уравнение называется интегрируемым в квадратурах, если все его решения могут быть получены в результате конечной последовательности элементарных действий над известными функциями и интегрированием этих функций. Таких уравнений сравнительно немного. В нашем курсе мы рассмотрим основные типы дифференциальных уравнений, интегрируемых в квадратурах. В математике рассматриваются также уравнения, которые связывают искомую функцию нескольких переменных, ее аргументы и частные производные. Такие уравнения называются дифференциальными уравнениями в частных производных. Их интегрирование представляет собой значительно более сложную задачу, чем интегрирование обыкновенных дифференциальных уравнений. Позднее мы познакомимся с одним типом дифференциальных уравнений в частных производных. Решить онлайн дифференциальные уравнения — просто! Искусственный интеллект постоянно развивавется. Нашим
специалистам удалось научить его решать различные математические задачи. Например, стали доступны такие
раздеолы, как решение онлайн дифференциальных уравнений или производная функции онлайн. На нашем сайте вы можете решить любое дифференциальное уравнение используя Калькулятор
за пару секунд.
Пользоваться калькулятором просто. Например: Условие 1: y’=y+x Условие 2: y(0)=1 Нажав кнопку Решить вы получите подробное решение дифференциальных
уравнений. Дифференциальное уравнение (ДУ) – это уравнение с производными функции или самой
функцией, независимой
переменной и параметрами. Чтобы научиться решать дифференциальное уравнение, нужно сначала разобраться с
условными обозначениями. Производная функции обозначается символически “штрихом”. Производная функции
второго порядка отображается соответственно двумя “штрихами” и так далее. Порядок дифференциального уравнения – это порядок старшей производной в уравнении. Решение дифференциального уравнения не будет таким же, как решение обыкновенного уравнения. При решении дифференциальных уравнений, в отличие от алгебраических уравнений, ищется не число или
несколько чисел, а функция или семейство функций. Алгебраический смысл решения таковой: если вместо
функций и производных всех порядков, подставить любую функцию из семейства её решений, то получится
верное равенство. ДУ выше первого порядка возможно преобразовать в систему уравнений первого порядка, где число уравнений
равняется порядку исходного дифференциального уравнения. Таким образом дифференциальное уравнение
второго порядка преобразуется в систему функций, состоящую из двух уравнений. При решении такой задача, как дифференциальные уравнения важно помнить, что его решением
будет именно семейство функций,
так как если брать производную от константы, то она будет равняться нулю. А так как производная от
константы равняется нулю, то в исходной функции может быть такое определённое решение данного
дифференциального уравнения.
Не все калькуляторы позволяют решить дифференциальные уравнения онлайн, а только самые
“умные”. Ещё несколько
лет назад решить дифференциальное уравнение с помощью калькулятора было невозможным. Система дифференциальных уравнений, линейные дифференциальные уравнения или другое дифференциальное уравнение любой сложности будет решено нашим бесплатным решателем за
считанные секунды. Все, что вам необходимо
сделать — это просто ввести данные уравнения в калькуляторе. Так же вы можете посмотреть
видео
инструкцию и узнать, как решить дифференциальное уравнение на нашем сайте. А если у вас остались
вопросы, то
вы
можете задать их в онлайн чате на странице Калькулятора или в нашей группе
Вконтакте: pocketteacher.
Вступайте
в нашу группу, мы всегда рады помочь вам. Так же читайте нашу статью «Решить
систему
уравнений методом сложения онлайн решателем» Узнайте больше о Вышеприведенные примеры также содержат: Чтобы увидеть подробное решение, Дифференциальные уравнения Проверка решения дифференциального уравнения Последние несколько страниц этого курса будут посвящены введению в
дифференциальное уравнение. д’
+ 3xy = sin x и
x 2 y» + 3xy’ + 4y = 0 Они возникают, когда мы знаем о взаимосвязи между тем, как что-то меняется,
сколько этого чего-то есть, и как долго этот процесс продолжается.
В алгебре, когда нам говорят решить, это означает получить «у».
сам по себе в левой части и без членов «y» на
правая сторона. Если y = f(x) является
решение дифференциального уравнения, то если мы подставим «y»
в уравнение, мы получаем истинное утверждение. Часто для подключения нам нужно
сначала возьмем производные. Пример Убедитесь, что г
= е 3x является решением дифференциального уравнения г»
+ 2г’ — 15г = 0 Раствор Вычислим первые две производные. г’
= 3e 3x y»
= 9e 3x Теперь подставьте y, y’,
и y» в дифференциальное уравнение. 9e 3x + 2(3e 3x ) — 15(e 3x ) = e 3x (9 + 6
— 15) =
e 3x (0) = 0 Упражнение Убедитесь, что г
= C 1 e x + C 2 xe x является решением дифференциального уравнения г»
— 2у’ + у = 0 Особые решения В предыдущем упражнении мы видели, что общее решение включает константы.
На приведенном ниже графике показано решение для нескольких вариантов решений. Часто нам дают начальное значение или значения, которые помогут нам найти
константы. Пример В приведенном выше упражнении указано, что г
= С 1 e x + C 2 xe x является решением дифференциального уравнения г»
— 2y’ + y = 0 Если y(0) = 2 и
у'(0)
= 3 найти частное решение Раствор Подставим 0 вместо t и установим y равным 2. Матричной игрой в математической теории игр называется игра двух лиц с нулевой суммой, в которой в распоряжении каждого из них имеется конечное
множество стратегий. Правила матричной игры определяет платёжная матрица, элементы которой —
выигрыши первого игрока, которые являются также проигрышами второго игрока. Матричная игра является антагонистической игрой.
Первый игрок получает максимальный гарантированный (не зависящий от поведения второго игрока) выигрыш,
равный цене игры, аналогично, второй игрок добивается минимального гарантированного проигрыша. Под стратегией понимается совокупность правил (принципов), определяющих выбор
варианта действий при каждом личном ходе игрока в зависимости от сложившейся ситуации. Теперь обо всём по порядку и подробно. В матричной игре её правила определяет платёжная матрица. Рассмотрим игру, в которой имеются два участника: первый игрок и второй игрок. Пусть
в распоряжении первого игрока имеется m чистых стратегий, а в распоряжении второго игрока — n чистых стратегий. Поскольку рассматривается игра, естественно, что в этой игре есть выигрыши и
есть проигрыши. В платёжной матрице элементами являются числа, выражающие
выигрыши и проигрыши игроков. Выигрыши и проигрыши могут выражаться в пунктах, количестве денег или в
других единицах. Составим платёжную матрицу: . Если первый игрок выбирает i-ю чистую стратегию, а второй игрок — j-ю чистую стратегию, то выигрыш первого игрока составит aij
единиц, а проигрыш второго игрока — также aij
единиц. Так как aij + (- aij) = 0,
то описанная игра является матричной игрой с нулевой суммой. Простейшим примером матричной игры может служить бросание монеты. Правила игры следующие.
Первый и второй игроки бросают монету и в результате выпадает «орёл» или «решка». Если одновременно
выпали «орёл» и «орёл» или «решка» или «решка», то первый игрок выиграет одну единицу, а в других случаях
он же проиграет одну единицу (второй игрок выиграет одну единицу). Такие же две стратегии и в распоряжении
второго игрока. Соответствующая платёжная матрица будет следующей: . Задача теории игр — определить выбор стратегии первого игрока, которая гарантировала
бы ему максимальный средний выигрыш, а также выбор стратегии второго игрока, которая гарантировала бы ему
максимальный средний проигрыш. Вновь посмотрим на платёжную матрицу: . Сначала определим величину выигрыша первого игрока, если он использует i-ю
чистую стратегию. Если первый игрок использует i-ю чистую стратегию, то логично предположить,
что второй игрок будет использовать такую чистую стратегию, благодаря которой выигрыш первого игрока
был бы минимальным. В свою очередь первый игрок будет использовать такую чистую стратегию, которая бы
обеспечила ему максимальный выигрыш. Исходя из этих условий выигрыш первого игрока, который обозначим
как v1, называется максиминным
выигрышем или нижней ценой игры. При решении задач на цену игры и определение стратегии для этих величин у первого
игрока следует поступать следующим образом. Из каждой строки выписать значение минимального элемента и
уже из них выбрать максимальный. Теперь определим величину проигрыша второго игрока, если он использует j-ю
стратегию. В этом случае первый игрок использует такую свою чистую стратегию, при которой проигрыш
второго игрока был бы максимальным. Второй игрок должен выбрать такую чистую стратегию, при которой его
проигрыш был бы минимальным. Проигрыш второго игрока, который обозначим
как v2, называется минимаксным
проигрышем или верхней ценой игры. При решении задач на цену игры и определение стратегии для определения этих величин у второго игрока следует поступать следующим образом. Из каждого столбца
выписать значение максимального элемента и уже из них выбрать минимальный. Пример 1. Дана матричная игра с платёжной матрицей . Определить максиминную стратегию первого игрока, минимаксную стратегию второго
игрока, нижнюю и верхнюю цену игры. Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим
максимальный из них, а
снизу от матрицы — наибольшие элементы в столбцах и выберем минимальный из них: Наибольший из наименьших элементов строк — 2, это нижняя цена игры, ей соответствует первая строка,
следовательно, максиминная стратегия первого игрока первая. Теперь, когда мы научились находить нижнюю и верхнюю цену игры, максиминную и
минимаксную стратегии, пришло время научиться обозначать эти понятия формально. Итак, гарантированный выигрыш первого игрока: . Первый игрок должен выбрать чистую стратегию, которая обеспечивала бы ему
максимальный из минимальных выигрышей. Этот выигрыш (максимин) обозначается так: . Первый игрок использует такую свою чистую стратегию, чтобы проигрыш второго игрока
был максимальным. Этот проигрыш обозначается так: . Второй игрок должен выбрать свою чистую стратегию так, чтобы его проигрыш был
минимальным. Этот проигрыш (минимакс) обозначается так: . Ещё пример из этой же серии. Пример 2. Дана матричная игра с платёжной матрицей . Определить максиминную стратегию первого игрока, минимаксную стратегию второго
игрока, нижнюю и верхнюю цену игры. Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим
максимальный из них, а
снизу от матрицы — наибольшие элементы в столбцах и выберем минимальный из них: Наибольший из наименьших элементов строк — 3, это нижняя цена игры, ей соответствует вторая строка,
следовательно, максиминная стратегия первого игрока вторая. Наименьший из наибольших элементов столбцов —
5, это верхняя цена игры, ей соответствует первый столбец, следовательно, минимаксная стратегия второго
игрока — первая. Если верхняя и нижняя цена игры одинаковая, то считается, что матричная игра имеет
седловую точку. Таким образом, если ,
то — оптимальная чистая
стратегия первого игрока, а —
оптимальная чистая стратегия второго игрока. То есть равные между собой нижняя и верхняя цены
игры достигаются на одной и той же паре стратегий. В этом случае матричная игра имеет решение в чистых стратегиях. Пример 3. Дана матричная игра с платёжной матрицей . Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку? Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим
максимальный из них, а
снизу от матрицы — наибольшие элементы в столбцах и выберем минимальный из них: Нижняя цена игры совпадает с верхней ценой игры. Пример 4. Дана матричная игра с платёжной матрицей . Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку? Правильное решение и ответ. В большинстве случаев матричная игра не имеет седловой точки, поэтому соответствующая
матричная игра не имеет решений в чистых стратегиях. Но она имеет решение в оптимальных смешанных стратегиях. Для их нахождения нужно
принять, что игра повторяется достаточное число раз, чтобы на основании опыта можно было предположить,
какая стратегия является более предпочтительной. Итак, чтобы чтобы первый игрок получил
максимальный средний выигрыш и чтобы средний проигрыш второго игрока был минимальным, чистые стратегии
следует использовать с определённой вероятностью. Если первый игрок использует чистые стратегии с вероятностями
, то вектор
называется смешанной стратегией первого игрока. Иначе говоря, это «смесь» чистых стратегий. При этом
сумма этих вероятностей равна единице: . Если второй игрок использует чистые стратегии с вероятностями
, то вектор
называется смешанной стратегией второго игрока. При этом сумма этих вероятностей равна единице: . Нет времени вникать в решение? Можно заказать работу! Если первый игрок использует смешанную стратегию p, а второй игрок —
смешанную стратегию q, то имеет смысл математическое ожидание выигрыша первого игрока (проигрыша второго игрока). . Если уже подзабыто произведение матриц, то следует повторить материал. Пример 5. Дана матричная игра с платёжной матрицей . Определить математическое ожидание выигрыша первого игрока (проигрыша второго игрока),
если смешанная стратегия первого игрока ,
а смешанная стратегия второго игрока . Решение. Согласно формуле математического ожидания выигрыша первого игрока (проигрыша второго игрока)
оно равно произведению вектора смешанной стратегии первого игрока, платёжной матрицы и вектора
смешанной стратегии второго игрока: Оптимальной смешанной стратегией первого игрока
называется такая смешанная стратегия ,
которая обеспечивала бы ему максимальный средний выигрыш
, если игра повторяется
достаточное число раз. Оптимальной смешанной стратегией второго игрока
называется такая смешанная стратегия ,
которая обеспечивала бы ему минимальный средний проигрыш
, если игра повторяется
достаточное число раз. По аналогии с обозначениями максимина и минимакса в случах чистых стратегий
оптимальные смешанные стратегии обозначаются так (и увязываются с математическим ожиданием, то есть средним,
выигрыша первого игрока и проигрыша второго игрока): , . В таком случае для функции E существует седловая точка, что означает
равенство . Для того, чтобы найти оптимальные смешанные стратегии и седловую точку, то есть решить матричную игру в смешанных стратегиях, нужно свести матричную игру к задаче линейного программирования,
то есть к оптимизационной задаче, и решить соответствующую задачу линейного программирования. Для того, чтобы решить матричную игру в смешанных стратегиях, нужно составить прямую задачу линейного программирования и двойственную ей задачу. В двойственной задаче расширенная матрица,
в которой хранятся коэффициенты при переменных в системе ограничений, свободные члены и
коэффициенты при переменных в функции цели, транспонируется. При этом минимуму функции цели
исходной задачи ставится в соответствие максимум в двойственной задаче. Функция цели в прямой задаче линейного программирования: . Система ограничений в прямой задаче линейного программирования: Функция цели в двойственной задаче: . Система ограничений в двойственной задаче: Оптимальный план прямой задачи линейного программирования обозначим , а оптимальный план двойственной задачи обозначим Линейные формы для соответствующих оптимальных планов обозначим
и
, а находить их нужно как суммы соответствующих координат оптимальных планов. В соответствии определениям предыдущего параграфа и координатами оптимальных
планов, в силе следующие смешанные стратегии первого и второго игроков: , . Математики-теоретики доказали, что цена игры следующим образом выражается через
линейные формы оптимальных планов: , то есть является величиной, обратной суммам координат оптимальных планов. Нам, практикам, остаётся лишь использовать эту формулу для решения матричных игр в
смешанных стратегиях. Как и формулы для нахождения оптимальных смешанных стратегий соответственно
первого и второго игроков: , , в которых вторые сомножители — векторы. Оптимальные смешанные стратегии также, как
мы уже определили в предыдущем параграфе, являются векторами. Поэтому, умножив число (цену игры) на вектор
(с координатами оптимальных планов) получим также вектор. Пример 6. Дана матричная игра с платёжной матрицей . Найти цену игры V и оптимальные смешанные стратегии
и
. Решение. Составляем соответствующую данной матричной игре задачу линейного
программирования: Приводим задачу к канонической форме и решаем задачу и двойственную ей задачу
симплекс-методом. Получаем решение прямой задачи: . Находим линейную форму оптимальных планов как сумму найденных координат: . Получаем решение двойственной задачи: . Находим линейную форму оптимальных планов как сумму найденных координат: . Находим цену игры: . Находим оптимальную смешанную стратегию первого игрока: . Находим оптимальную смешанную стратегию второго игрока: . Пусть дана игра с платёжной матрицей Если эта матричная игра имеет седловую точку, то она имеет решение в чистых стратегиях,
как показано в параграфах 1 и 2. Если же игра не имеет седловой точки, то она имеет решение в оптимальных смешанных
стратегиях. Для этого простейшего случая матричной игры при её решениях путём сведения к задаче линейного
программирования были найдены формулы стратегий игроков и цены игры, благодаря которым такая игра
решается менее трудоёмким способом. Формула для нахождения оптимальной смешанной стратегии первого игрока: . Формула для нахождения оптимальной смешанной стратегии второго игрока: . Формула для нахождения цены игры: . Пример 7. . Найти оптимальные смешанные стратегии игроков и цену игры. Решение. Оптимальные смешанные стратегии первого игрока получаем по соответствующей из
приведённых формул: . Оптимальные смешанные стратегии второго игрока получаем также по соответствующей формуле: . Цена игры: . Матричная игра, седловая точка, чистые стратегии, смешанные стратегии… А для чего
всё это? Рассмотрим на примере, как с помощью матричных игр решаются экономические задачи. Пример 8. Составить матричную игру для следующей задачи. Предприятие может выпускать три вида продукции (A1, A2, A3),
получая при этом прибыль, зависящую от спроса, который может быть в одном из четырёх состояний
(B1, B2, B3, B4). Решение. Задача сводится к матричной игре предприятия A против спроса B. Прежде чем решать задачу, можно упростить игру, проведя анализ платёжной матрицы и
отбросив стратегии, заведомо невыгодные или дублирующие. . Далее составляется и решается задача линейного программирования. Это мы уже умеем. Нет времени вникать в решение? Можно заказать работу! К началу страницы Поделиться с друзьями Теория игр: основы. Примеры записи и решения игр из жизни Материалы по векторам и матрицам Векторы: определения и действия над векторами Произведение двух матриц Линейное программирование Задача и теоремы линейного программирования, примеры формулировки задач Симплекс-метод решения задач линейного программирования: типичный пример и алгоритм Ниже приведено условие и решение задачи. Оптимизация мощности ателье. Ателье по пошиву одежды рассчитано на выполнение не более 8 тыс. заявок в год. Будем считать, что поток заявок выражается цифрами 6, 8 тыс. в год. Накопленный опыт аналогичных предприятий показывает, что прибыль от выполнения одной заявки составляет 8 ден. ед., а потери, вызванные отказом из-за недостатка мощностей, оцениваются в 5 ден. ед., а убытки от простоя специалистов и оборудования при отсутствии заявок обходятся в 6 ден. ед. в расчете на каждую заявку. 1. Придать описанной ситуации игровую схему, установить характер игры и выявить ее 2. Составить платежную матрицу (матрицу затрат). 3. Решить задачу сведением ее к задаче линейного программирования и решить её графическим способом (т.е. найти оптимальные стратегии игроков и цену игры). Дать рекомендации о мощности ателье. Решение. 1. Одним из участников рассматриваемой в задаче ситуации является руководство предприятия, озабоченное необходимостью выполнения определенного количества заявок. Если описанной ситуации придать игровую схему, то руководство ателье выступает в ней в качестве сознательного игрока А, заинтересованного в максимизации прибыли от выполнения заказов . Вторым участником является природа — совокупность объективных факторов (П), которая реализует свои состояния по присущим ей законам. Такого рода ситуация представляется типичной для стратегической игры. Рассчитывая количество заявок, руководство предприятия может ориентироваться на величины: 6 тыс. ед. (первая чистая стратегия А1), либо 8 тыс. ед. (вторая чистая стратегия А2). Природа (совокупность объективных неопределенных факторов) может реализовать состояния П1, П2, необходимое количество заявок 6, 8 тыс. ед. соответственно. Таким образом, платежная матрица статистической игры будет иметь размерность 2х2. 2. Таблица 2.1 П1=6 П2=8 тin aj A1=6 48 48-2·5=38 18 А2=8 48-2·6=36 64 36 При расчете элементов матрицы учтена прибыль за вычетом дополнительных затрат, связанных с недостатком мощностей, а также с убытком от простоя . Заметим, что в теории игр элементы aij обычно называются выигрышами игрока A, а наилучшей для А считается стратегия, при которой выигрыш максимизируется . Рассмотрим ситуацию (а1;П2), т.е. случай, когда не хватает мощности на 2 тыс. В ситуации (А2;П1) мощность превысит потребности на 8-6=2 (вес. ед.). Поэтому затраты связанные с простоем составят 2·6=12 (ед.). Следовательно, a21 = 48-2·6=36. Рассуждая аналогично, находим и остальные элементы платежной матрицы. Определим седловой элемент: Матрица не имеет седлового элемента т.к. А ≠ В 36 ≤ v ≤ 48 3. Для определения оптимальных стратегий игроков по платежной матрице составляем пару двойственных задач. Для игрока А: f = Х1 + Х2 (min) 48Х1 +36Х2 ≥1 38Х1 +64Х2 ≥1 (1) Хj ≥0 (j=1,2) Для игрока В: φ = Y1 + Y2 (max) 48Y1 + 38Y2 ≤ 1 36Y1 + 64Y2 ≤ 1 (2) Yi ≥0 (i=1,2) Решим задачу для игрока А графическим способом. Строим прямые: 48Х1 +36Х2 =1 (I) по точкам (1/48, 0) и (0, 1/36) 38Х1 +64Х2 =1 (II) по точкам (1/38, 0) и (0, 1/64) Долее определяем область допустимых решений. На рисунке 2.1 выделена граница области допустимых решений. Разрешающая прямая fmin, перпендикулярная вектору целевой функции 0,03С, засекает область в точке А, найдем координаты точки А, решив систему уравнений: 48Х1 +36Х2 =1 (16) 38Х1 +64Х2 =1 (-9) Умножаем первое уравнение на 16, а второе на (-9), складывая, получаем: 426Х1=7, откуда Х1*=7/426 Х2* = (1 — 48∙(7/426) )/36= 5/852 fmin = 7/426 + 5/852 = 19/852 Цена игры: v = 1/fmin = 852/19. Тогда оптимальные стратегии для игрока А: Р1* = v∙X1* = (852/19)∙(7/426) = 14/19; Р1* = v∙X2* = (852/19)∙(5/852) = 5/19. Рис. 2.1 Следовательно, руководству надо ориентироваться на (6000∙14+8000∙5)/19 = 6526 заявок в год. Решим задачу для игрока В. Так как неравенства в задаче для игрока А при оптимальном решении превращаются в строгие равенства, то оптимальное решение, найдем, решив систему: 48Y1 + 38Y2 =1 (-3) 36Y1 + 64Y2 =1 (4) Умножаем первое уравнение на (-3), а второе на 4, складывая, получаем: 142Y2=1, откуда Y2*= 1/142 = 6/852 Y1* = (1 — 38∙(1/142))/48 = 104/(142∙48) = 13/852 fmin = 13/852 + 6/852 = 19/852 Цена игры: v = 1/ φ max = 852/19. Тогда оптимальные стратегии для игрока B: Q1* = v∙Y1* = (852/19)∙(13/852) = 13/19; Q1* = v∙Y2* = (852/19)∙(6/852) = 6/19. 149 500 недавних просмотров Теория игр, ставшая популярной благодаря таким фильмам, как «Игры разума», представляет собой математическое моделирование стратегического взаимодействия между рациональными (и иррациональными) агентами. Помимо того, что мы называем «играми» на обычном языке, например, шахматы, покер, футбол и т. д., сюда входит моделирование конфликтов между нациями, политических кампаний, конкуренции между фирмами и торгового поведения на таких рынках, как Нью-Йоркская фондовая биржа. Как можно было начать моделировать аукционы ключевых слов и одноранговые сети обмена файлами, не принимая во внимание стимулы людей, их использующих? Курс предоставит основы: представление игр и стратегий, расширенную форму (которую ученые-компьютерщики называют игровыми деревьями), байесовские игры (моделирование таких вещей, как аукционы), повторяющиеся и стохастические игры и многое другое. Гибкие сроки Сбрасывайте сроки в соответствии с вашим расписанием. Совместно используемый сертификат Получите сертификат по завершении 100 % онлайн Начните сразу и учитесь по собственному графику. Начальный уровень Прибл. 17 часов Английский Субтитры: арабский, французский, португальский (европейский), китайский (упрощенный), итальянский, вьетнамский, корейский, немецкий, русский, английский, испанский Гибкие сроки Сброс сроков в соответствии с вашим графиком. Общий сертификат Получите сертификат по завершении 100% онлайн Начните сразу и учитесь по собственному графику. Начальный уровень Прибл. 17 часов, чтобы закончить Английский Субтитры: арабский, французский, португальский (европейский), китайский (упрощенный), итальянский, вьетнамский, корейский, немецкий, русский, английский, испанский Экономика Компьютер Естествознание Информатика Стэнфордский младший университет Леланда, обычно называемый как Стэнфордский университет или Стэнфорд, является американским частным исследовательским университетом, расположенным в Стэнфорде, Калифорния, на территории кампуса площадью 8 180 акров (3310 га) недалеко от Пало-Альто, Калифорния, США. Университет Британской Колумбии является глобальным центром исследований и обучения. 4.6 5 звезд 71,55% 4 звезды 22,24% 3 звезды 3,92% 2 звезды 1,09% 1 звезда 1,18% by PRD 12 декабря 2018 г. Удивительный курс! Дает глубокое погружение в тему! Просто нравится, как Кевин объясняет! Мэтт действительно мог работать над своим заиканием; или, возможно, немного замедлить. by AG 5 июля 2017 г. Курс действительно хорош. Охватывает много контента. Одно из лучших мест в Интернете для изучения теории игр. Активный дискуссионный форум. Еще несколько примеров можно добавить в виде отдельных видео. от WY17 мая 2017 г. Отлично! Интересно и много одновременно. Надеюсь, что профессора разъяснят функцию стратегической полезности более четко, потому что это сложно для студентов с плохим знанием математики (забудьте о большинстве><) прямо сейчас! Еще вопросы? Посетите Справочный центр для учащихся. Равновесие по Нэшу — это концепция теории игр, согласно которой оптимальный результат достигается тогда, когда у игроков нет стимула отклоняться от своей первоначальной стратегии. В целом, человек не может получить дополнительную выгоду от изменения действий, если предположить, что другие игроки остаются неизменными в своих стратегиях. В игре может быть несколько равновесий Нэша или вообще не быть ни одного. Равновесие Нэша названо в честь его изобретателя Джона Нэша, американского математика. Это считается одним из наиболее важных понятий теории игр, которая пытается математически и логически определить действия, которые должны предпринять участники игры, чтобы обеспечить себе наилучшие результаты. Причина, по которой равновесие Нэша считается таким важным понятием теории игр, связана с его применимостью. Равновесие Нэша может быть включено в широкий спектр дисциплин, от экономики до социальных наук. Чтобы быстро найти равновесие Нэша или проверить, существует ли оно вообще, раскройте стратегию каждого игрока другим игрокам. Если никто не меняет свою стратегию, то равновесие Нэша доказано. Равновесие Нэша часто сравнивают с доминирующей стратегией, поскольку обе стратегии являются стратегиями теории игр. Доминирующая стратегия утверждает, что выбранная субъектом стратегия приведет к лучшим результатам из всех возможных стратегий, которые можно использовать, независимо от стратегии, используемой противником. Все модели теории игр работают только в том случае, если вовлеченные игроки являются «рациональными агентами», что означает, что они желают конкретных результатов, действуют, пытаясь выбрать наиболее оптимальный результат, включают неопределенность в свои решения и реалистичны в своих вариантах. Оба термина похожи, но немного отличаются. Равновесие Нэша утверждает, что ничего не выиграно, если один из игроков изменит свою стратегию, в то время как все остальные игроки сохранят свою стратегию. Доминирующая стратегия утверждает, что игрок выберет стратегию, которая приведет к наилучшему результату, независимо от стратегий, выбранных другими игроками. Представьте себе игру между Томом и Сэмом. В этой простой игре оба игрока могут выбрать стратегию А, чтобы получить 1 доллар, или стратегию Б, чтобы проиграть 1 доллар. Логически оба игрока выбирают стратегию А и получают выигрыш в размере 1 доллара. Если вы раскрыли стратегию Сэма Тому и наоборот, вы увидите, что ни один игрок не отклоняется от первоначального выбора. Знание хода другого игрока мало что значит и не меняет поведения ни одного из игроков. Результат A представляет собой равновесие Нэша. Джули Бэнг / Инвестопедия Дилемма заключенного — обычная ситуация, анализируемая в теории игр, в которой можно использовать равновесие Нэша. В этой игре двое преступников арестованы, и каждый содержится в одиночной камере, не имея возможности общаться друг с другом. Если оба заключенных предадут друг друга, каждый отбывает по пять лет тюрьмы. Если A предает B, но B хранит молчание, заключенный A освобождается, а заключенный B отбывает 10 лет тюрьмы, или наоборот. Если каждый промолчит, то каждый отбывает всего по году тюрьмы. В этом примере равновесие Нэша заключается в том, что оба игрока предают друг друга. Хотя взаимное сотрудничество приводит к лучшему результату, если один заключенный выбирает взаимное сотрудничество, а другой нет, результат одного заключенного хуже. Равновесие по Нэшу в теории игр — это ситуация, в которой игрок будет продолжать придерживаться выбранной стратегии, не имея стимула отклоняться от нее, приняв во внимание стратегию противника. Чтобы найти равновесие Нэша в игре, нужно смоделировать каждый из возможных сценариев, чтобы определить результаты, а затем выбрать оптимальную стратегию. В игре с двумя людьми это будет учитывать возможные стратегии, которые могут выбрать оба игрока. Если ни один из игроков не меняет свою стратегию, зная всю информацию, наступило равновесие Нэша. Равновесие Нэша важно, потому что оно помогает игроку определить наилучший выигрыш в ситуации, основываясь не только на своих решениях, но и на решениях других вовлеченных сторон. Равновесие Нэша можно использовать во многих сферах жизни, от бизнес-стратегий до продажи дома, от войны до социальных наук и так далее. Специальной формулы для расчета равновесия Нэша не существует. Его можно определить путем моделирования различных сценариев в данной игре, чтобы определить выигрыш каждой стратегии и выбрать оптимальную стратегию. Основным ограничением равновесия Нэша является то, что оно требует от человека знания стратегии своего противника. Равновесие Нэша может возникнуть только в том случае, если игрок решит остаться со своей текущей стратегией, если он знает стратегию своего противника. В большинстве случаев, например, на войне — будь то военная война или война торгов — человек редко знает стратегию противника или то, что он хочет, чтобы был результат. В отличие от доминирующей стратегии, равновесие Нэша не всегда приводит к наиболее оптимальному результату. Это просто означает, что человек выбирает наилучшую стратегию на основе имеющейся у него информации. Кроме того, в нескольких играх с одними и теми же противниками равновесие Нэша не принимает во внимание прошлое поведение, которое часто предсказывает будущее поведение. Равновесие Нэша — это компонент теории игр, который утверждает, что игрок будет продолжать придерживаться выбранной стратегии, зная стратегию своего противника, поскольку у него нет стимула менять курс. Общий индекс затрат на производство продукции (общий индекс товарооборота)
Анализ сезонных колебаний
Решение типовых задач
Выявление тренда методом аналитического выравнивания
Решение задач по экономике: убедитесь, что время — деньги! На экономике не экономят? Как сказать… Одним из главных вопросов относительно нашей системы высшего образования звучит так: «Чему должны учить в ВУЗах?» По какой бы специальности ни обучался студент, большая часть задач, которые он решает в ВУЗе, ему в дальнейшей деятельности не понадобится вообще. И дело даже не в том, что это за предмет, дело не в физике, не в геометрии, не в электротехнике, не в экономике или теоретической механике. Эта задача вообще лежит вне плоскости задач, входящих в курс. Главная задача современного студента (точнее сказать, метазадача) – добиться в процессе обучения максимального КПД, потратив максимум времени и усилий на профильные предметы и возможно меньше – на предметы, нужные чисто формально. Пример оформления контрольной работы по «экономической теории», выполненной нашими специалистами: Наша система образования (как и большинство систем образования) отводит очень много времени на «поиски себя». Отсюда её заведомая избыточность, отсюда множество часов на курсы, которые школьнику и студенту не пригодятся никогда в жизни, зато среди них он найдёт то, что его зацепит. Безусловно, чем больше различных знаний человек впитывает, тем легче будет найти «своё». Изучение смежных или вовсе сторонних предметов тренирует память, даёт новые подходы в мышлении, расширяет кругозор, в конце концов. И успехи советского образования и науки – лучшее тому свидетельство. Но что делать тем, кто уже в выпускных классах или первых курсах чётко определился, чего хочет? Тратить равно много времени на профильное программирование и нужную только ради оценки экономику? Вряд ли в этом есть смысл. Никто не отменяет самообразование, и впоследствии и программисту может понадобиться экономика, если он будет создавать приложения для биржевых операций или бухгалтерских нужд. Решение задач по экономике – оправдано ли оно экономически? Мы не просто так вспомнили советскую систему образования: тогдашнее время позволяло человеку развиваться всесторонне и даже требовало этого (пусть и не в такой степени, как во времена французских энциклопедистов). Сейчас условия несколько иные, объём знаний, накопленных человечеством и востребованных сейчас, просто огромен, поэтому неизбежна узкая специализация. Мало кто из студентов Гарварда или Оксфорда всерьёз ищет примеры задач по экономике, матанализу или физике в Интернете. Специализация, выбранная уже на первых курсах – отличная причина самому решать нужные задачи, набирать квалификацию и повышать профессионализм. В наших условиях, когда будущему программисту, биологу или литературоведу приходится изучать много непрофильных предметов без практической пользы, возникает вопрос: а оправдано ли морально решение экономики предприятия на заказ или решение задач по экономике онлайн? Морально – это вопрос, а экономически – однозначно да. Решение экономики на заказ – правильное решение! Вопрос, который даже трудно назвать двусмысленным: что лучше, к примеру, для программиста или вебмастера: поработать по специальности, написав коммерческую программу или сайт за вознаграждение, и потратить часть полученных денег на решение задач по экономике от профессионалов? Или упорно решать эти задачи самому, тратя время и не получая при этом необходимых знаний и навыков? В данном случае решение экономики на заказ, как ни парадоксально, будет и правильным решением практической экономической задачи, вставшей перед студентом. Умные студенты давно уже оптимизируют свою учёбу, сосредотачиваются на своём профиле, а решение задач по экономике предприятия, физике, математике и другим необязательным предметам доверяют профессионалам. Воспользуйтесь этим шансом и вы: в конце концов, это экономически правильно! Заказать нам работу! Область экономики требует от студентов критического мышления и навыков решения проблем, но, к сожалению, многие студенты не имели возможности развить такие навыки до поступления в класс экономики. Таким образом, они находят экономику пугающей. Это прискорбно, но это убедительный аргумент в пользу того, почему документированное решение проблем так хорошо подходит для курсов по экономике. Документированное решение задач эффективно использовалось в курсах по основам экономики в крупном государственном исследовательском учреждении за последние несколько лет. Он использовался с темами производственных возможностей, спроса и предложения, ценовой эластичности и потребительского спроса, рыночных структур, рынка труда, безработицы, фискальной и денежно-кредитной политики, ВВП на душу населения и экономического роста, эффективных налоговых ставок, международной торговли и многих других. . Ясно, что его можно применить практически к любому курсу экономики. Поначалу учащиеся находят этот процесс сложным, но, поскольку сам процесс не оценивается, они вскоре расслабляются и получают от него удовольствие как от инструмента, который помогает улучшить их учебный процесс. Анджело и Кросс (1993, стр. Когда учащиеся описывают, как они разбивают экономическую проблему на небольшие базовые шаги, они часто пишут: Таким образом, задокументированное решение задач дает окно, через которое преподаватель может видеть мыслительные процессы студентов. Преподавателям приятно видеть, как студенты становятся более целеустремленными и обдуманными в своем подходе к решению проблем и даже разрабатывают модели решения проблем, которые могут быть перенесены в другие области экономики и другие области обучения. Благодаря использованию задокументированного решения проблем учащиеся становятся более эффективными учениками; более экспертным в их мыслительном процессе. Документированное решение проблем хорошо работает с вопросами с множественным выбором, верно/неверно и краткими ответами. Вопросы из тестовых банков, как правило, работают и легко доступны. Кроме того, преподаватели могут написать свои собственные вопросы. Вопросы не обязательно должны быть слишком сложными, чтобы их можно было задокументировать для решения проблем, но они должны требовать многоэтапного мыслительного процесса, чтобы прийти к ответу. Для продукта XYZ эластичность спроса по цене имеет абсолютное значение 3. При прочих равных условиях , это означает, что объем спроса увеличится на: а) 1 процент за каждые 3 процента снижения цены. в) 3 процента за каждый 1 процент снижения цены. г) 3 единицы за каждый доллар снижения цены. Ответ студента: Сначала я открыл свои записи, чтобы прочитать определение ценовой эластичности спроса. Ценовая эластичность измеряет изменение величины спроса в результате изменения цены. Формула: (% изменения объема спроса) ÷ (% изменения цены). Таким образом, если ответ равен 3, 3 идет вверху (процентное изменение объема спроса) и 1 — внизу (процентное изменение цены). Действительное число отрицательное 3, потому что цена и объем спроса движутся в противоположных направлениях. Для этого вопроса, если цена вырастет на 1%, объем спроса уменьшится на 3%. Затем я посмотрел на варианты ответов, чтобы увидеть, какой из них соответствует. Если цена упадет на 1 %, то объем спроса увеличится на 3 %, поэтому правильный ответ — c. Вопросы типа определения и вопросы, в которых учащимся предлагается выбрать из списка, не являются хорошим выбором, если они просто требуют, чтобы учащиеся вспомнили заученную информацию. Какая из следующих стран ежегодно производит больше всего продукции? а) Китай б) США в) Россия г) Мексика Ответ ученика: США, потому что так написано в таблице в тексте. Однако, учитывая, что большая часть экономической науки опирается на аналитические рассуждения, легко найти множество подходящих вопросов. Большая часть информации, необходимой для начала использования документированного решения проблем, представлена на главной странице этого модуля. Теджван Петтингер Взгляд на различные виды экономической политики для преодоления экономического кризиса, например падения ВВП. В марте 2020 г. коронавирус вызвал резкое снижение спроса, что привело к рецессии. Это вызвало резкое падение цен на нефть и падение фондового рынка. Некоторые секторы экономики пострадали особенно сильно — путешествия, отдых, гиг-экономика. Неизвестно, окажется ли это временным всплеском или превратится в полномасштабную рецессию. Каков наилучший ответ на этот кризис? В какой-то степени нет никакой политики, которая могла бы предотвратить спад спроса, когда вы попадаете в такой кризис. Первой реакцией политики было снижение процентных ставок. В Великобритании ставки снизились с 5% до 0,5% Теоретически более низкие процентные ставки удешевляют заимствование, и это должно стимулировать потребление и инвестиции. В долгосрочной перспективе это может привести к более высокому росту. Однако снижение процентных ставок не было особенно эффективным в 2008/09 гг. Это произошло потому, что Правительство также оказало финансовую помощь банкам, чтобы предотвратить потерю доверия к финансовой системе. Это стало важным фактором предотвращения эскалации кризиса. В 2009 году правительство Великобритании снизило ставку НДС, чтобы обеспечить фискальный стимул. В США были скромные фискальные стимулы от администрации Обамы. США также согласились оказать финансовую помощь крупным автомобильным фирмам, которым грозило банкротство. Спасение автомобильных фирм дорого обошлось, но предотвратило дальнейший рост безработицы в автомобильной и смежных отраслях. Это помогло смягчить эффект падения доходов и обеспечить некоторое восстановление. Теоретически более низкие налоги должны увеличить располагаемый доход потребителей и, следовательно, помочь увеличить совокупный спрос (AD). Восстановление в США было более сильным, чем в еврозоне, где правительства были больше озабочены уровнем государственных заимствований, а реальных фискальных стимулов не было. Недостатком налогово-бюджетной политики является то, что развивающиеся страны могут уже иметь большие государственные долги, и поэтому они могут нервничать по поводу дополнительных заимствований. В еврозоне это было важным фактором. Фискальная политика также может быть неэффективной для повышения AD по разным причинам. См.: ограничения фискальной политики Некоторые экономические кризисы возникают из-за структурных проблем в экономике. Например, они могут включать В этих случаях странам может потребоваться не только увеличение совокупного спроса, но и реформирование предложения в экономике для повышения конкурентоспособности. Девальвация – это политика снижения стоимости обменного курса. Это дает следующие преимущества: Например, страны еврозоны, такие как Италия, Греция и Испания, пострадали от снижения конкурентоспособности, что привело к снижению темпов роста и увеличению безработицы. Недостатком девальвации является то, что она может вызвать инфляционное давление, но если экономика переживает низкий рост, то инфляция может не быть проблемой. Великобритания Государственный долг – значительно вырос во время Первой и Второй мировых войн – длительный период экономического роста позволил экономике погасить долг. Многие страны совершают ошибку, пытаясь решить долгосрочный структурный дефицит, жертвуя краткосрочным ростом. Во имя долгосрочных структурных изменений правительства дефлятируют экономику в то время, когда они должны были бы делать обратное. Великобритания и США должны разработать планы по сокращению долгосрочного дефицита, но это не должно включать краткосрочное сокращение расходов на важные капиталовложения. Эти долгосрочные меры должны включать: Такая политика является устойчивой и на самом деле имеет большое значение для долгосрочной бюджетной ситуации. Если вы распродаете активы или остановите текущие инвестиционные проекты, это будет очень ограниченной выгодой для долгосрочного бюджета. Но если вы вносите изменения в пенсионный возраст или расходы на пособия, это не просто разовая выгода, а постоянное улучшение финансового положения правительства. Доходность по облигациям Великобритании и США близка к рекордно низкому уровню. Если бы правительство выступило с планами по улучшению долгосрочной ситуации с бюджетом в течение следующих 20 лет, рынки были бы готовы кредитовать для краткосрочного восстановления экономики. В повседневной жизни мы часто пользуемся калькуляторами. Это быстро, удобно и экономит наше время. Так и у нас на сайте — стоимость продукции сразу рассчитывается в зависимости от количества, бумаги и дополнительных опций. Не нужно дозваниваться в офис или ждать ответ на отправленный запрос на расчет по почте. Подробнее о работе калькулятора расчета стоимости продукции в статье «Онлайн-калькулятор». Выбрать ВыбратьКвартальник с одним рекламным полемКвартальник с тремя рекламными полямиКвартальник с боковыми полямиКвартальный календарь с фигурным топомКвартальный календарь три в одномКарманные календари 70х100Календарь пирамидка K-16Календарь домик K-18Календарь домик квадратный K-64Календарь домик евро форматЮвелирные биркиБирка со скошенными краями 50х90 ммБирка круглая 70 ммСердечко — бирка, валентинкаБирки 95х50 с еврослотомЕврослот 120х60Стандартные визиткиЕвро визиткиВизитки из крафтаКвадратные визиткиКарты лояльностиВизитные карточки с тиснением фольгойАвтовизиткиКоробка для визиток из гофрокартонаПриглашения евро форматаПриглашение открытка-конверт с замочкомФирменные бланки компанииНастольный перекидной календарь евроНастольный квадратный календарьНастольный календарь А5 горизонтальныйНастольный календарь А5 вертикальныйКалендарь настольный перекидной пирамидкаКалендарь настольный с круглыми листамиНастольный деловой календарь с бегункомНастольный квартальный календарь с бегункомРаздаточные листовки А6Листовки А5Квадратные листовкиФлаер евро форматЛистовки А4Постер и плакатыБлокноты А6Блокноты евроБлокнот А5 на пружинеБизнес тетрадь, блокнот А5Блокнот A6 с местом под ручкуБлокнот А5 с местом под ручкуБлокнот А5 со сменным блоком и карманомЕвро конвертыКонверты С6Конверты C5 стандартныеКонверты С4 с прямым клапаном по длинной сторонеРекламный буклет в два сложения 10х21Буклет А6 вертикальныйБуклет А6 горизонтальныйКвадратные буклеты 15х15Буклет А5 вертикальныйБуклет А5 горизонтальныйМеню или программа концертаБуклет А4 в одно или два сложенияКонверт 95х60 для подарочной картыКонверт 112х72 с треугольным клапаномКонверт С6 с треугольным клапаномКонверт с треугольным клапаном 140х100Конверт С5 с треугольным клапаномКонверты С4 с треугольным клапаномКвадратные конверты с клапаном 15х15Квадратные конверты с клапаном 17х17Квадратные пригласительные конверты 12х12Квадратные конверты без клапана 15х15Календарь плакат А3Фотокалендарь складнойНастенный вертикальный календарь А3Настенный горизонтальный календарь А3Настенный деловой перекидной календарьПечать кубариковПодставка под кубарик 9 смПодставка под кубарик 5 смЕвро конверты с защитной лентой для приглашенийКартонные конверты C5 с защитной лентойКартонные конверты С4 с защитной лентойСтандартные бейджиБейджи А6Многостраничные бейджи на кольцахКонверт для подарочного сертификатаКонверт евро для приглашенияКармашек для пластиковой карты, кейхолдер для отелейКейхолдер с полукруглым вырезомКейхолдер с карманом под электронный ключ или картуКарта гостя отеля, гостиницыУпаковка для подарочной карты, кейхолдерКоробочка для карандашей и небольших подарковКоробка 50х50х50 — бонбоньеркаКоробка 60х60х100 ммКоробки с квадратным дном 100х100 ммКоробка для корпоративных подарковУпаковка сундучок для ювелирных изделийУпаковка сундучок средняяУпаковка сундучок высокая для подарковКоробка для подарков «Домик с окошками»Cамосборная коробка 120х90х25 ммУпаковка для текстильных изделийКоробка подарочная с ручкойКоробка-пирожок для ювелирных и парфюмерных изделийСредняя коробка-пирожокБольшая коробка-пирожокУпаковка-пирожок с ручкойУзкая коробка-пирожокУниверсальная коробка-пирожокУпаковка-пирожок для текстильных изделийКоробка крышка-дно для ювелирных изделийКоробка крышка-дно для браслетов и кольеКоробка крышка-дно квадратная 14х14х4Коробка крышка-дно квадратная 16х16х7Коробка крышка-дно А5Коробка крышка-дно 24х17х7Коробка крышка-дно 24х17х10Коробка крышка-дно 24х20х7Коробка крышка-дно А4Упаковка для ёлочного шара 80 ммУпаковка для ёлочного шара 100 ммУпаковка для ёлочного шара 115 ммКоробочка с откидной крышкойКоробка самосборная средняяКоробка самосборная большаяУпаковка для галстуковУпаковка для платков с тиснением фольгойКвадратная коробка 14х14х4Упаковка для пробников духовУпаковка для небольшого объёма флакончиковКонверт для визитки или пластиковой картыКонверт МИНИ 7х11 с замкомКонверт С6 с треугольным клапаномКонверт С6 с прямым клапаномКонверт С6 с лентойКвадратный конверт 15х15Коробка для вертикального хранения визитокКоробка для хранения визиток с прорезьюКоробочка для ювелирных украшенийПочтовые карточкиКарточки «Спасибо»Квадратные открытки 15х15Открытки А6Набор открыток в упаковкеОткрытка в форме сердцаПоздравительные открыткиОткрытки А5Конверт «Волна» для открытки или приглашения евроТейблтент, табличка на столТейблтент со скруглеными угламиТейблтент стандартныйТейблтент пирамидкаПапка-счёт для кафе и ресторановПапка для гарантийного и сервисного обслуживанияПапки А5 для проведения мероприятийПапка А5 с трехсторонним клапаномПапка А4 для договоровПапка А4 с широким клапаном 140 ммЭкспресс папка А4 с корешкомПапка самосборная А4Папка стандартная А4Папка А4 с логотипом для проведения мероприятийИмиджевая папка А4 с полукруглым клапаномПапка уголок А4Папка-портфель для документов из картонаДорхенгер узкийДорхенгер стандартныйПластиковый дорхенгерДорхенгер длинныйДорхенгер, крючокНекхенгер на бутылкуКорона для праздникаБумажные колпаки на праздникКороны сердце и снежинкаБабочка на шею из картонаКруглые рекламные наклейки, стикерыПодставки под кружки, чашки, стаканы с логотипомРекламная линейка 20 см или закладкаЗакладки для книг и блокнотовЮвелирный пакетик А7 брендированныйБумажный пакет А6 с логотипомПакет для ювелирных украшений и парфюмерииПодарочный пакет для небольших сувенировКвадратный пакет для дорогих подарков с лентамиПакет для ювелирных украшенийПакет А5 горизонтальный ширина 250 ммБумажный пакет с ручками трапецияБумажный пакет А5 с логотипомБумажный пакет А4 узкийБумажный пакет А4 с ручками стандартныйБумажный пакет А4+ высота 360 ммБумажные пакеты с ручками 300х400 ммПакет с тиснением фольгой из дизайнерской бумагиПакет А4 горизонтальный стандартПакет горизонтальный ширина 330 ммПакет A3 горизонтальный ширина 400 ммКвадратный бумажный пакет большойПакет под бутылку вина (для высоких узких бутылок)Подарочный пакет под бутылку винаПакет под бутылку шампанскогоВертикальный пакет 15*15 высотой 37 смУслуга ламинацииУслуги по вырубке для специалистовТиснение фольгой для специалистовСвадебные приглашения с конвертомУпаковка для шоколадки 5 г, комплимента на свадьбуЭфалин / EfalinKeaykolourТинторетто / TintorettoКолорплан / ColorplanБурано / BURANOМурилло / MURILLOМаджестик / MAJESTICКоктейль / COCKTAILБрошюра евро форматБрошюра А6 вертикальная или горизонтальнаяБрошюра А5 вертикальнаяБрошюра А5 горизонтальная на скрепкеКвадратные брошюры 21х21Квадратные брошюры 15х15Квадратные брошюры максиБрошюры А4Брошюра А4 горизонтальная на скрепкеРекламные журналы, периодические изданияУдостоверения к медалям и памятным знакамУдостоверения в твердой корочкеДипломы, грамоты, благодарностиКвалификационные и гарантийные сертификатыПодарочные сертификаты и купоны на скидкуАдресная папкаЧек бук для счета в ресторанеПлейсметы — бумажные подложки Стоимость рассчитали, теперь нужно подготовить макет для печати. Подробнее о требованиях для подготовки макетов к печати необходимо ознакомиться в статье «Технические требования». А тема данной статьи помочь понять, подходит ли Ваше изображение для печати и какого в итоге размера оно получится при разных видах печати. Для качественной печати важно не только на каком оборудовании будет производится печать, но и с каких файлов это будет делаться. Мы подготовили калькулятор для перевода размера изображения из Px в мм и обратно. Вы знаете размер картинки в мм, которую собираетесь напечатать. Например, для каталога нужна иллюстрация 50х50 мм. (Если фотография выходит за обрезное поле, то нужно добавить 3 мм с той стороны, которая будет обрезаться.) Вы задаете этот размер в калькуляторе, выбираете тип печати и соответствующий ему dpi, и получаете размер изображения в Px. У Вас есть изображение и Вы знаете его размер в пикселях. Вы вводите эти значения, выбираете тип печати и получаете максимальный размер изображения, который можно будет получить при печати. Пример: Есть фотографии, снятые на iPhone11 (можно взять любой другой телефон, а лучше фотоаппарат). Мы не будем рассматривать вопрос, связанный с качеством объектива и матрицы. Разрешение фотографии, полученной на телефон 3024х4032 pix. Вводим эти значения в калькулятор и на выходе получаем, что при 300 dpi (стандартное разрешение для качественной печати) можно напечатать изображение 256х341 мм. А это больше А4-го формата. Не так уж и мало! И наоборот. Скачанную картинку из интернета, например 700х420 pix можно напечатать качественно только 59х35 мм. Калькулятор из PIX в MM Как узнать разрешение картинки на компьютере? Во всплывающем окошке показывается размер в пикселях. Для печати картинки без белой рамки — печать навылет нужно, чтобы изображение было больше на 3 мм с каждой стороны, чем готовое изделие. Пиксель — это минимальный элемент, формирующий изображение. Одна ячейка монитора воспроизводит один пиксель. Поэтому нам кажется, что любое изображение хорошее. Но для печати это совсем не так. Вы можете сравнить печать хорошего глянцевого журнала и газеты и увидеть в газете буквально точки из которых получается изображение. dpi — это количество точек на единицу площади в дюймах (dots per inch). 300 dpi — это стандартное значение для офсетной печати и промышленных цифровых машин. 240 dpi — это минимальное значение для офсетной печати и оптимальное для среднего класса цифровых машин. РаботаИнженерныеКонвертеры Подбор формата фотографии по размерам цифрового снимка в пикселях. Вычисление используемого разрешения. Калькуляторы в этой статье посвящены теме печати цифровых фотографий. Первый калькулятор помогает подобрать формат фотографии для печати изображения известных размеров. Дано: У нас имеется цифровое изображение известных нам размеров, например, 3264 на 2448 пикселей, и набор стандартных форматов, предлагаемых сервисами фотопечати. Формат определяет линейные размеры фотографии, например, фотография формата 10х15 имеет размеры 102 на 152 миллиметра. Требуется: Выбрать из набора форматов максимально большой, на котором еще можно напечатать изображение без потери качества. Для задания форматов фотографий я создал отдельный справочник Форматы фотографий, который при необходимости можно расширять. Единственное специальное знание, которым нужно обладать для нахождения ответа, это знание того, что качественная печать цифрового изображения требует разрешения не менее 300 точек (пикселей) на дюйм (300 dpi), а более-менее приемлемая печать возможна при разрешении не менее 150 точек на дюйм (150 dpi). Все остальное — простые математические действия. Графически задача изображена на рисунке ниже Логика поиска ответа проста — линейные размеры каждого формата переводятся в дюймы, а затем в пиксели, исходя из того, что в одном дюйме 300 (150) пикселей. Из всех подходящих форматов калькулятор выбирает формат максимального размера (с печатью изображений меньшего размера проблем нет — насколько я понимаю, печатать можно и с разрешением 1200 dpi). Ширина изображения (пиксели) Высота изображения (пиксели) Рекомендованный формат для печати с разрешением 300 dpi Размер формата в пикселях для разрешения 300 dpi Рекомендованный формат для печати с разрешением 150 dpi Размер формата в пикселях для разрешения 150 dpi Второй калькулятор по размерам уже напечатанного снимка и размерам исходного изображения помогает определить получившееся разрешение снимка и обрезанную при масштабировании часть. Дано: Изображение известных размеров напечатано на снимке известных размеров. Поскольку значение соотношения высоты и ширины снимка и значение соотношения высоты и ширины цифрового изображения, как правило, не совпадают, то при печати происходит масштабирование снимка, очевидно, с сохранением пропорций. Графически это отображено на рисунке ниже. При масштабировании, как видно, возможны два варианта: Таким образом, первое, что требуется: найти получившееся разрешение снимка и часть изображения, которая не попала на снимок. Второе, соответственно, это будет разница между использованной шириной (высотой) и исходной шириной (высотой) изображения. Ширина изображения, см Ширина напечатанного изображения, см Высота изображения, см Высота напечатанного изображения, см Ширина в пикселях Ширина изображения в пикселях Высота в пикселях Высота изображения в пикселях Соотношение высоты к ширине при печати Соотношение высоты к ширине в пикселях Используемая ширина при сохранении пропорций, пикселей Используемая высота при сохранении пропорций, пикселей Разрешение при печати, в пикселях на дюйм Ссылка скопирована в буфер обмена дюйм дюймы Конвертеры печать пиксели пиксель размер разрешение формат фотография PLANETCALC, Размер снимка в пикселях и формат фотографии Timur2020-11-03 14:19:29 Сколько составляет заработная плата ваших сотрудников после уплаты налогов? Этот мощный инструмент выполняет все расчеты валовой и чистой прибыли для оценки заработной платы во всех 50 штатах. Ищете управляемый расчет заработной платы и льгот для вашего бизнеса? Получить бесплатное предложение Важное примечание о калькуляторе заработной платы: Калькулятор на этой странице предоставляется Центром ресурсов для работодателей ADP и предназначен для предоставления общих рекомендаций и оценок. На него не следует полагаться для расчета точных налогов, заработной платы или других финансовых данных. Эти калькуляторы не предназначены для предоставления налоговых или юридических консультаций и не представляют собой какие-либо услуги или решения ADP. Вам следует обратиться к профессиональному консультанту или бухгалтеру в отношении любых конкретных требований или проблем. Несмотря на то, что наш калькулятор заработной платы выполняет большую часть тяжелой работы, может оказаться полезным более подробно рассмотреть некоторые расчеты, необходимые для расчета заработной платы. Чтобы рассчитать годовой оклад, умножьте общую заработную плату (до вычета налогов) на количество периодов оплаты в году. Например, если работник зарабатывает 1500 долларов в неделю, его годовой доход составит 1500 x 52 = 78 000 долларов. Расчеты, однако, лишь часть большой картины зарплаты. Зарплата — это то, как предприятия вознаграждают сотрудников за их работу. Наиболее распространенные графики доставки — раз в две недели или раз в полгода, хотя это зависит от предпочтений работодателя и применимых законов и правил штата. Специфические для бизнеса требования, такие как коллективные договоры, касающиеся профсоюзных работников, также могут диктовать частоту выплаты заработной платы. Традиционно сотрудники получали распечатанные чеки лично или по почте, но сегодня чаще деньги вносятся на банковский счет в электронном виде. Некоторые работодатели могут также предлагать дополнительные альтернативы зарплате, такие как платежные карты, которые могут быть выгодны работникам, не имеющим банковских счетов. В отличие от справок и других документов с места работы, чеки о зарплате довольно легко расшифровать. Их прочтение — это просто вопрос проверки правильности платежной информации. В большинстве штатов сотрудники должны получать платежные квитанции. Как правило, им предоставляются платежные чеки и детали списка, такие как: Фактические платежные квитанции зависят от индивидуальных обстоятельств и штата. При анализе своей первой зарплаты те, кто только начинает работать, могут задаться вопросом, почему их заработная плата меньше, чем их валовая заработная плата. Причина в таких налогах, удержаниях и вычетах, как эти: Работодатели удерживают федеральный подоходный налог из заработной платы своих работников на основании текущих налоговых ставок и формы W-4, Свидетельства об удержании работником налога. При заполнении этой формы сотрудники, как правило, должны указать свой статус подачи и указать, заявляют ли они о каких-либо иждивенцах, работают ли они на нескольких работах или имеют ли супруга, который также работает (для целей совместной подачи в браке), или вносят какие-либо другие необходимые корректировки. FICA — двухкомпонентный налог. И работники, и работодатели платят 1,45% за Medicare и 6,2% за Social Security. Последний имеет базовый предел заработной платы в размере 160 200 долларов США, что означает, что после того, как сотрудники заработают столько, налог больше не вычитается из их доходов до конца года. Те, у кого высокий доход, также могут облагаться дополнительным налогом Medicare, который составляет 0,9% и оплачивается только работником, а не работодателем. Штатные и местные налоги сильно различаются в зависимости от географического региона, причем некоторые взимают гораздо больше, чем другие. Примеры включают: Предприятия, которые предлагают медицинское страхование, стоматологическое страхование, пенсионные сбережения и другие льготы, часто делят расходы со своими сотрудниками и удерживают их из своей заработной платы. Работодателям может потребоваться вычесть наложение ареста на заработную плату работника, если они получат соответствующее постановление суда. Это может произойти, если работник не выплачивает кредит, имеет неуплаченные налоги или обязан платить алименты или алименты. Хотя зарплатные чеки и платежные квитанции обычно выдаются вместе, это не одно и то же. Заработная плата — это директива финансовому учреждению, которая утверждает перевод средств от работодателя к работнику. С другой стороны, платежная квитанция не имеет денежной ценности и является просто пояснительным документом. Платежные ведомости обычно показывают, как был получен доход работника за определенный период оплаты, а также статьи удержанных налогов, добровольных отчислений и любых других полученных вознаграждений. Дополнительные сведения могут потребоваться властями штата или местными органами власти. Платежные квитанции используются для проверки правильности оплаты и могут быть необходимы при урегулировании споров о заработной плате/часах. По этой причине сотрудники могут захотеть сохранить свои платежные квитанции, но не обязаны это делать. Однако работодатели должны вести учет заработной платы в течение определенного периода времени, установленного федеральным правительством и правительством штата. Порядок действий зависит от причины пропущенной или задержанной зарплаты. Честно говоря, ошибки обычно можно исправить, связавшись с отделом кадров работодателя. У работодателей обычно есть два основных варианта создания чеков: Хотя наш инструмент Быстрая заработная плата и налоговые факты удобен в крайнем случае, знание тонкостей налогов на заработную плату может помочь поддерживать долгосрочные усилия по соблюдению требований В течение лет термин «налог на заработную плату» стал синонимом всех налогов, взимаемых с платежной квитанции. В действительности, однако, налоги на заработную плату отличаются от подоходных налогов и служат иной цели для общественного благосостояния. Налог на заработную плату — это налог, взимаемый федеральными, государственными или местными органами власти для финансирования государственных программ. Обычно он оплачивается за счет прямых взносов работодателей, а также вычетов из заработной платы сотрудников, отсюда и название налога на заработную плату. Примеры налога на заработную плату включают Medicare, которая обеспечивает медицинское страхование для взрослых старше 65 лет, и Social Security, которая обеспечивает пенсионный доход для взрослых в возрасте 62 лет и старше, а также для некоторых инвалидов и некоторых оставшихся в живых налогоплательщиков. Налоги на заработную плату имеют фиксированные ставки и отправляются непосредственно в программу, для которой они предназначены, например, Medicare, Social Security и т. На национальном уровне и уровне штата существует несколько видов налогов на заработную плату. Они следующие: Для сотрудников налоги на заработную плату могут быть просто строками в квитанции о заработной плате, но работодатели должны иметь более глубокое понимание связанных тем, таких как: Штатные ставки налога на пособие по безработице обычно варьируются в зависимости от предыдущих претензий работодателя. Предприятия также должны сообщить, сколько федерального налога на заработную плату они удержали и заплатили в течение года. Для налогов FICA это обычно делается ежеквартально, но в некоторых случаях, когда общая сумма налоговых обязательств невелика, это может делаться ежегодно. Депозит налога на заработную плату штата и процедуры подачи зависят от штата. Налоги на заработную плату рассчитываются путем умножения валовой налогооблагаемой заработной платы работника на применимую ставку налога на заработную плату. Например, если валовой налогооблагаемый доход за определенный период оплаты составляет 1250 долларов, то вычет по программе Medicare составит 1250 x 1,45% = 18,13 доллара, а вычет по социальному обеспечению составит 1250 x 6,2% = 77,50 доллара. Подобные расчеты налога на заработную плату обычно проще, чем расчеты подоходного налога, поскольку ставки являются фиксированными, а справки об удержании налогов не требуются. Поскольку они вычитаются из заработной платы работников и хранятся в доверительном управлении работодателем до тех пор, пока не будут переведены в соответствующее агентство, налоги FICA считаются разновидностью налога в трастовый фонд. Работодатели, которые активно управляют налогами на заработную плату, с большей вероятностью избегут штрафов, чем те, кто этого не делает. Вот несколько предупредительных советов: Сокращение налога на заработную плату или налоговые каникулы, которые произошли в соответствии с положениями Закона CARES в 2020 году, на самом деле были отсрочкой. Как правило, большинство работодателей и работников платят налоги на социальное обеспечение и Medicare. Однако исключения применяются для определенных категорий иностранцев-неиммигрантов и нерезидентов. Примеры включают студентов-неиммигрантов, ученых, учителей, исследователей и стажеров (включая медицинских стажеров), врачей, помощников по хозяйству, работников летних лагерей и других неиммигрантов, временно находящихся в Соединенных Штатах в F-1, J-1, M-1, Q. -1 или Q-2 статус. 1 Текущая ставка налога FICA составляет 15,3%. Выплачивается поровну между работодателями и работниками, это составляет 7,65% каждый за цикл расчета заработной платы. В отличие от подоходного налога, ставки налога на заработную плату являются фиксированными, что означает, что все работники платят одинаковый процент независимо от их общего дохода. Вопрос 1. Какие углы называются смежными? Вопрос 2. Докажите, что сумма смежных углов равна 180°. Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны. Из теоремы 2. Вопрос 4. Какой угол называется прямым (острым, тупым)? Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол. Вопрос 6. Вопрос 7. Докажите, что вертикальные углы равны. Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые. Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых? Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну. Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 . Вопрос 11. Что такое перпендикуляр к прямой? Вопрос 12. Объясните, в чём состоит доказательство от противного. Вопрос 13. Что называется биссектрисой угла? В процессе изучения курса геометрии понятия “угол”, “вертикальные углы”, “смежные углы” встречаются достаточно часто. Понимание каждого из терминов поможет разобраться в поставленной задаче и правильно ее решить. Что такое смежные углы и как их определять? Термин “смежные углы” характеризует два угла, образованных общим лучом и двумя дополнительными полупрямыми, лежащими на одной прямой. 1. Исходя из формулировки смежных углов, нетрудно заметить, что сумма таких углов всегда образует развернутый угол, градусная мера которого равна 180°: 2. Данное свойство углов позволяет сделать следующий вывод: угол, являющийся смежным прямому углу, также будет прямым. 3. Рассматривая тригонометрический функции (sin, cos, tg, ctg), основываясь на формулах приведения для смежных углов μ и η справедливо следующее: Пример 1 Задан треугольник с вершинами M, P, Q – ΔMPQ. смежным для угла ∠QMP будет ∠LMP, смежным для угла ∠MPQ будет ∠SPQ, смежным для угла ∠PQM будет ∠HQP. Пример 2 Величина одного смежного угла составляет 35°. Чему равна градусная мера второго смежного угла? Пример 3 Определить величины смежных углов, если известно, что градусная мера одного из низ втрое больше градусной меры другого угла. λ + 3λ = μ + η = 180°, λ = 180°/4 = 45°. Значит первый один угол ∠μ = λ = 45°, а второй угол ∠η = 3λ = 135°. Умение апеллировать терминологией, а также знание основных свойств смежных углов поможет справиться с решением многих геометрических задач. Г Л А В А I. ОСНОВНЫЕ ПОНЯТИЯ. §11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ. 1. Смежные углы. Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию. Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами. Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы. Смежные углы могут иметь самые разнообразные положения (черт. 74). Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d. Отсюда прямой угол можно определить как угол, равный своему смежному углу. Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла. Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен: 2d — 3 / 5 d = l 2 / 5 d . 2. Вертикальные углы. Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла. Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d . Таким же образом можно вычислить, чему равны / 3 и / 4. Мы видим, что / 1 = / 3 и / 2 = / 4. Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой. Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными. Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства. Доказательство можно провести следующим образом (черт. 78): / a + / c = 2d ; (так как сумма смежных углов равна 2d ). / a + / c = / b + / c (так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ). В это равенство входит один и тот же угол с . Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой. При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов. Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве. В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем. 3. Сумма углов, имеющих общую вершину. На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d . Упражнения. 1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов. 2. Доказать, что биссектрисы двух смежных углов образуют прямой угол. 3. Доказать, что если два угла равны, то равны и их смежные углы. 4. Сколько пар смежных углов на чертеже 81? 5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла? 6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла? 7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов? Как найти смежный угол? Математика — древнейшая точная наука, которую в обязательном порядке изучают в школах, колледжах, институтах и университетах. Рассмотрим подробнее определение и свойства смежных углов, а также как их вычислить по данным в задаче. Два луча, исходящие из одной точки образуют фигуру под названием «плоский угол». При этом эта точка именуется вершиной угла, а лучи являются его сторонами. Если продолжить один из лучей дальше начальной точки по прямой, то образуется еще один угол, который и называется смежным. У каждого угла в этом случае есть два смежных угла, так как стороны угла равнозначны. То есть всегда присутствует еще смежный угол в 180 градусов. К основным свойствам смежных углов относят Обычно даются три вариации задач на нахождение величины смежных углов Каждый вариант задачи имеет свое решение. Рассмотрим их. Если в задаче указана величина основного угла, то найти смежный угол очень просто. Для этого достаточно из 180 градусов вычесть величину основного угла, и вы получите величину смежного угла. Данное решение исходит из свойства смежного угла — сумма смежных углов равна всегда 180 градусам. Если же величина основного угла дана в радианах и в задаче требуется найти смежный угол в радианах, то необходимо вычесть из числа Пи величину основного угла, так как величина полного развернутого угла в 180 градусов равна числу Пи. В задаче может быть дано соотношение основного и смежного угла вместо градусов и радиан величины основного угла. Таким образом мы можем найти величину смежного угла в градусах. Однако, если необходимо найти величину в радианах, то нужно просто перевести градусы в радианы. Для этого умножаем угол в градусах на число Пи и делим все на 180 градусов. Полученное значение будет в радианах. Если в задаче не дана величина основного угла, но дана величина вертикального угла, то вычислить смежный угол можно по такой же формуле, что и в первом пункте, где дана величина основного угла. Вертикальный угол — это угол, который исходит из той же точки, что и основной, но при этом он направлен в строго противоположном направлении. Тем самым получается зеркальное отражение. Это значит, что вертикальный угол по величине равен основному. В свою очередь, смежный угол вертикального угла равен смежному углу основного угла. Благодаря этому можно вычислить смежный угол основного угла. Для этого просто вычитаем из 180 градусов величину вертикального и получаем значение смежного угла основного угла в градусах. Если же величина дана в радианах, то необходимо вычесть из числа Пи величину вертикального угла, так как величина полного развернутого угла в 180 градусов равна числу Пи. Также вы можете прочесть наши полезные статьи и . угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого известную величину основного угла α₁ = α₂ = 180°-α. Из этого имеются . Если два угла одновременно являются и смежными, и равными, то они прямые. Острый угол – это такой, градусная мера которого меньше 90 градусов, но больше 0. Тупой угол имеет градусную меру больше 90 градусов, но меньше 180. Другое свойство смежных углов формулируется так: если два угла равны, то углы, смежные с ними, также равны. Это , что если есть два угла, градусная мера для которых совпадает (например, она составляет 50 градусов) и при этом из них имеет смежный угол, то значения этих смежных углов тоже совпадают (в примере их градусная мера будет равна 130 градусам). Источники: Слово « » имеет различные толкования. В геометрии угол – это часть плоскости, ограниченная двумя лучами, выходящими из одной точки – вершины. Как и любые фигуры в геометрии, углы можно сравнивать. Равенство углов определяется с помощью движения. Угол нетрудно разделить на две равные части. Разделить на три части немного сложнее, но все же это можно сделать с помощью линейки и циркуля. Кстати, эта задача казалась довольно трудной. Описать, что один угол больше или меньше другого, геометрически несложно. В качестве единицы измерения углов принят – 1/180 Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные. Сумма смежных углов равна 180° Теорема 1. Сумма смежных углов равна 180°. Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны. Вертикальные углы равны Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2). Теорема 2. Вертикальные углы равны. Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1
∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°. Отсюда заключаем, что ∠ АОВ = ∠ COD. Следствие 1. Угол, смежный с прямым углом, есть прямой угол. Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину. АН — перпендикуляр к прямой Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра. Чертежный угольник Справедлива следующая теорема. Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один. Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5). Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны». Пример 1. Один из смежных углов равен 44°. Чему равен другой? Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1. Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС? Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1. Пример 3. Найти смежные углы, если один из них в 3 раза больше другого. Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°. Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов. Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1 В процессе изучения курса геометрии понятия “угол”, “вертикальные углы”, “смежные углы” встречаются достаточно часто. Понимание каждого из терминов поможет разобраться в поставленной задаче и правильно ее решить. Что такое смежные углы и как их определять? Термин “смежные углы” характеризует два угла, образованных общим лучом и двумя дополнительными полупрямыми, лежащими на одной прямой. 1. Исходя из формулировки смежных углов, нетрудно заметить, что сумма таких углов всегда образует развернутый угол, градусная мера которого равна 180°: 2. Данное свойство углов позволяет сделать следующий вывод: угол, являющийся смежным прямому углу, также будет прямым. 3. Рассматривая тригонометрический функции (sin, cos, tg, ctg), основываясь на формулах приведения для смежных углов μ и η справедливо следующее: Пример 1 Задан треугольник с вершинами M, P, Q – ΔMPQ. смежным для угла ∠QMP будет ∠LMP, смежным для угла ∠MPQ будет ∠SPQ, смежным для угла ∠PQM будет ∠HQP. Пример 2 Величина одного смежного угла составляет 35°. Чему равна градусная мера второго смежного угла? Пример 3 Определить величины смежных углов, если известно, что градусная мера одного из низ втрое больше градусной меры другого угла. λ + 3λ = μ + η = 180°, λ = 180°/4 = 45°. Значит первый один угол ∠μ = λ = 45°, а второй угол ∠η = 3λ = 135°. Умение апеллировать терминологией, а также знание основных свойств смежных углов поможет справиться с решением многих геометрических задач. Вопрос 1. Какие углы называются смежными? Вопрос 2. Докажите, что сумма смежных углов равна 180°. Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны. Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны. Вопрос 4. Какой угол называется прямым (острым, тупым)? Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол. Вопрос 6. Какие углы называются вертикальными? Вопрос 7. Докажите, что вертикальные углы равны. Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые. Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых? Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну. Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 . Вопрос 11. Что такое перпендикуляр к прямой? Вопрос 12. Объясните, в чём состоит доказательство от противного. Вопрос 13. Что называется биссектрисой угла? Углы, у которых одна сторона общая, а другие стороны лежат на одной прямой (на рис. углы 1 и 2 смежные). Рис. к ст. Смежные углы … Большая советская энциклопедия СМЕЖНЫЕ УГЛЫ — углы, имеющие общую вершину и одну общую сторону, а две др. их стороны лежат на одной прямой … Большая политехническая энциклопедия См. СМЕЖНЫЕ УГЛЫ, два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла … Научно-технический энциклопедический словарь См. Угол. * * * СМЕЖНЫЕ УГЛЫ СМЕЖНЫЕ УГЛЫ, см. Угол (см. УГОЛ) … Энциклопедический словарь — (Angles adjacents) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие С. углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через вершину … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона См. Угол … Естествознание. Энциклопедический словарь Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая из C и D. В геометрии, два угла называются вертикальными, если они созданы пересечением двух … Википедия Пара комплементарных углов, дополняющих друг друга до 90 градусов Комплементарные углы это пара углов, которые дополняют друг друга до 90 градусов. Пара дополнительных углов, дополняющих друг друга до 90 градусов Дополнительные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два дополнительных угла являются с … Википедия Угол – это геометрическая фигура (рис.1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла). Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми. рис. 2 На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые. рис. 3 На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C. Теорема: сумма смежных углов равна 180° Доказательство: Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол. Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°. Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом. Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла. Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым. Определение 3. Прямой угол — это угол величиной в 90 градусов. Определение 4. Угол, меньший 90 градусов, называется острым углом. Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом. Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными. Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами. рис. 4 Связь математики с музыкой «Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.» Так же предложу вашему внимаю забавную пародию про спор двух математиков =) Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов. Задание 1. 1. Вот на столе на книжной подставке стоит книга. Какой угол она образует? Задание 2. Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре. Задание 3. Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке. 1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы. 1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2. Решите задачи: 1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°? 3. Нужно найти угол, когда он втрое больше, чем смежный с ним. а) сумма 2-х углов из четырех 84°; 1. назовите углы, которые образуются при пересечении 2-х прямых? Домашнее задание: 1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго. Вопросы: Предмети > Математика > Математика 7 класс Значение слова «прилегающий» означает «рядом» или «рядом с». Примером смежности являются два соседних дома. Мы обычно считаем людей на нашей улице своими соседями. Кто тогда наш ближайший сосед? Человек, который живет в доме или квартире рядом с нами. Соседний может относиться к двум вещам, соприкасающимся друг с другом или разделяющим одну и ту же стену или границу. А как насчет двух линий, которые пересекаются в вершине многоугольника? Можно ли считать их смежными сторонами? В треугольниках и других многоугольниках две стороны, которые встречаются в вершине многоугольника, являются смежными. В математике соседними могут быть разные вещи, но смежные в основном применяются к отрезкам прямых и углам. Ниже перечислены несколько важных моментов, касающихся того, что можно считать смежным углом, а что нельзя считать смежным углом, даже если у него одна и та же вершина и сторона. Ознакомьтесь с этими интересными статьями на сайте Adjacent. Пример 1: Посмотрите на стрелки часов. Образуют ли они пару смежных углов? Решение: В данных часах часовая стрелка образует угол с секундной стрелкой, а секундная стрелка образует другой угол с минутной стрелкой. Обе эти пары углов лежат рядом друг с другом и образуют пару смежных углов. Следовательно, стрелки часов образуют пары смежных углов. Пример 2 : Смежны ли углы, отмеченные цифрами 1 и 2 на следующих рисунках? Обоснуйте свои ответы. Решение На данном рисунке Ясно, что ∠1 и ∠2 имеют общую вершину O и общее плечо OB. У них есть необщие плечи OA и OC по обе стороны от общего плеча OB. Да, ∠1 и ∠2 — смежные углы. Пример 3. Перечислите 5 пар смежных углов на следующем рисунке. Решение: Ниже приведены пять пар смежных углов. перейти к слайдуперейти к слайдуперейти к слайду Готовы увидеть мир глазами математика? Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath. Записаться на бесплатный пробный урок перейти к слайдуперейти к слайдуперейти к слайду Смежный означает, что две вещи находятся рядом или рядом друг с другом. Углы считаются смежными, если два угла имеют общую сторону и вершину и не пересекаются. Смежные углы не обязательно должны быть равными или дополнительными. Между двумя углами не должно быть зазоров или перекрытий, чтобы их можно было рассматривать как смежные углы. Смежные стороны — это стороны многоугольника, имеющие общую вершину. Например, в треугольнике PQR соседними сторонами являются PQ и QR, поскольку между обеими сторонами лежит общая вершина (то есть Q). Смежные углы не всегда должны быть равны. Нет, вертикальные углы всегда несмежные. При пересечении двух прямых образуются вертикальные углы, не являющиеся смежными углами. Эти углы имеют общую вершину, но никогда не имеют общей стороны. Да, смежные означает рядом расположенные, т. е. когда углы расположены рядом друг с другом, имеют одну и ту же вершину и одну и ту же сторону. Прилегающая сторона треугольника — это сторона, ближайшая к углу, а противоположная сторона — это сторона, расположенная напротив угла. Скачать БЕСПЛАТНЫЕ учебные материалы Рабочие листы по углам Рабочие листы по математике и Если две прямые AB и CD перпендикулярны, то их можно записать как AB $\bot$ CD. Символ $\bot$ используется для обозначения того, что линии перпендикулярны. Некоторые примеры: стороны квадрата, стрелки часов, углы доски, окна и символ Красного Креста. Перпендикулярные линии представлены символом ‘$\bot$’. Предположим, m и n две прямые, пересекающиеся под углом 90 градусов, тогда они перпендикулярны друг другу и представляются как m $\bot$ n . Точка пересечения перпендикулярных прямых называется основанием перпендикуляра. Шаг 2: Поместите транспортир на линию м так, чтобы его базовая линия совпадала с м , а его центр приходился на точку A. , Возьмите соответствующий радиус и нарисуйте дугу по обе стороны от данной точки. Шаг 2: Растяните компас шире. Шаг 3 : Используйте линейку, чтобы соединить заданную точку A и точку B, где пересекаются дуги. Дайте детям возможность наблюдать перпендикулярные линии в объектах или местах вокруг них, например, высокое дерево на земле, электрический столб на тротуаре, железнодорожный перекресток, угол двух соседних стен и высокие здания. Пример 2: Напишите отношение между сегментами линии, обозначенными стрелкой в каждой фигуре. Пример 3: Диагонали ромба перпендикулярны друг другу. Сколько прямых углов образовано при пересечении? Поскольку прямые AC и BD пересекают друг друга под углом 90 градусов, в точке пересечения имеется 4 прямых угла. $\angle \text{AED} = \angle \text{DEC} = \angle \text{CEB} = \angle \text{BEA} = 90$ градусов Пример 5: Если AB $\left|\right|$ CD и CD $\left|\right|$ EF. Если две прямые перпендикулярны одной и той же прямой, то эти две прямые параллельны друг другу. Нет, эти линии не перпендикулярны, потому что они не пересекаются под прямым углом. 1 AG и AB FE и ED FE и CD CB и AB Правильный ответ: FE и ED 2 A B C D Правильный ответ: A 3 12 часов 6 часов 3 часа 5 часов Правильный ответ: 3 часа 4 1 2 3 4 Правильный ответ: 3 5 15:40 16:00 09:00 10:10 Правильный ответ: 09:00 6 7 Мяч Шляпа на день рождения Банан Ноутбук Правильный ответ: Ноутбук Что такое перпендикулярные линии? Должны ли пересекаться перпендикулярные линии? Эти линии всегда пересекаются под прямым углом. Что такое перпендикулярный символ? Символ перпендикуляра $\left|\right|$. Он используется между двумя линиями, чтобы показать, что они перпендикулярны друг другу. В чем разница между перпендикулярными линиями и параллельными линиями? 9{\circ}$ . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 В этом случае дробные части не будут уменьшаться или преобразовываться в десятичных. Однако математические вычисления с дробями, которые отображаются как текст, выполнять нельзя.
В этом случае дробные части не будут уменьшаться или преобразовываться в десятичных. Однако математические вычисления с дробями, которые отображаются как текст, выполнять нельзя. Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Какая часть носков Макса коричневого или черного цвета?
Какая часть носков Макса коричневого или черного цвета?




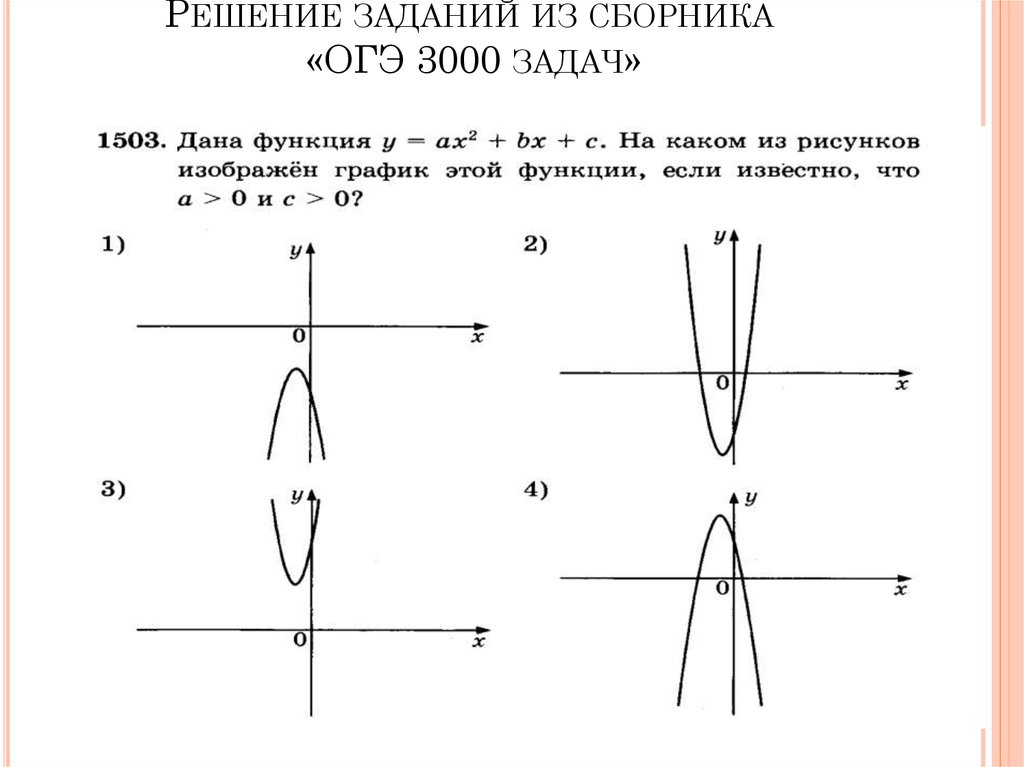 Если
х<0, то поскольку х2 = |х|2, |х|=-х и
требуемый график совпадает с параболой у=0,25 х2
+ х — 3.
Если
х<0, то поскольку х2 = |х|2, |х|=-х и
требуемый график совпадает с параболой у=0,25 х2
+ х — 3. 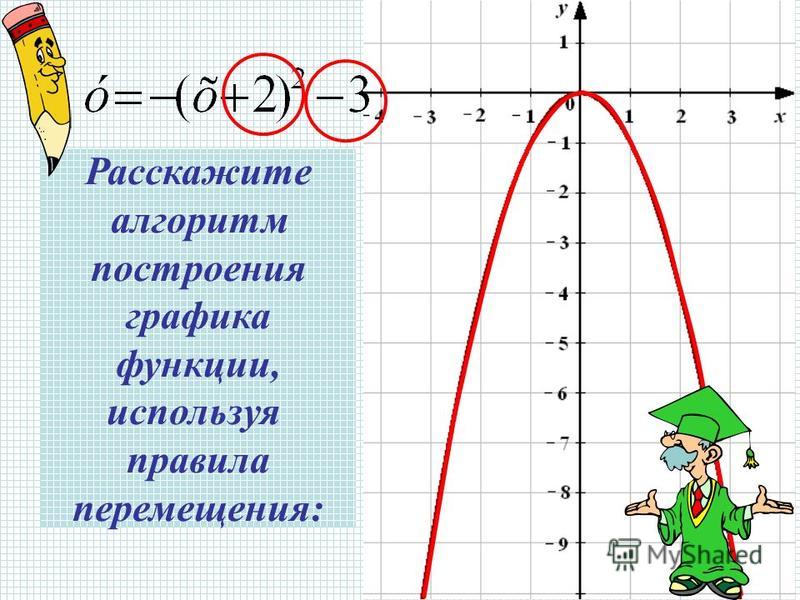
 построить график функции у = f(х) для х>0;
построить график функции у = f(х) для х>0;





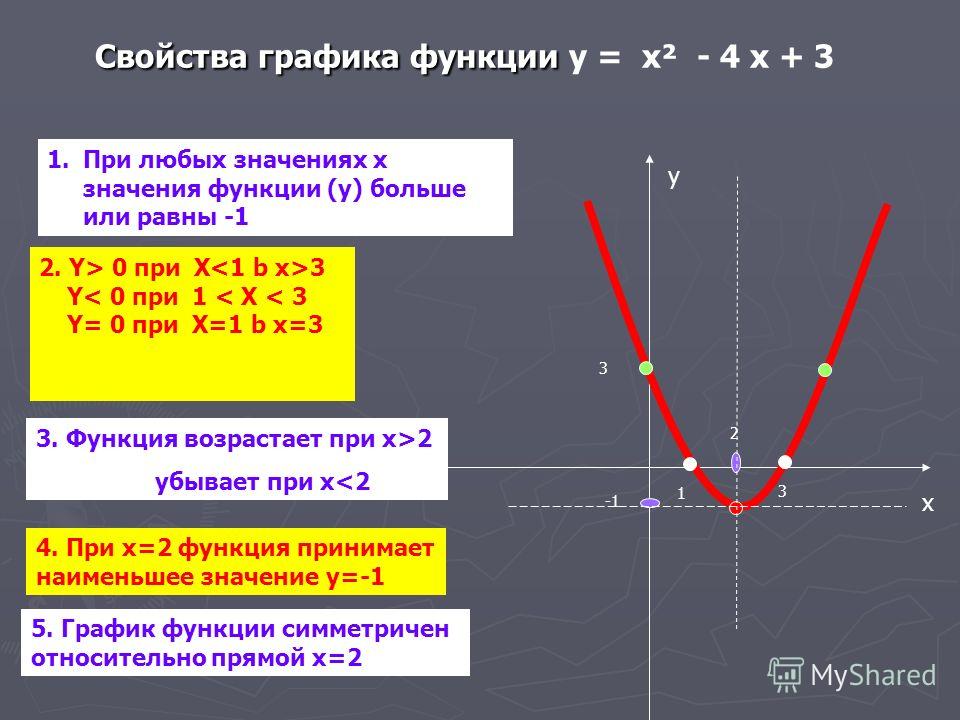
 На вкладке Линии сетки устанавливаем флажок Основные линии для оси Х, а на вкладке Легенда снимаем флажок Добавить легенду.
На вкладке Линии сетки устанавливаем флажок Основные линии для оси Х, а на вкладке Легенда снимаем флажок Добавить легенду. В появившемся диалоговом окне указываем ссылку на диапазон В3 : В13. После нажатия клавиши ОК в ячейке появляется минимальное значение функции.
В появившемся диалоговом окне указываем ссылку на диапазон В3 : В13. После нажатия клавиши ОК в ячейке появляется минимальное значение функции. 2) в положение включено и нажмите на кнопку OK.
2) в положение включено и нажмите на кнопку OK. 2) для нее наибольшая: R2 = 0,8465.
2) для нее наибольшая: R2 = 0,8465. и маршруты в GPS. Если у вас есть набор объектов, связанных друг с другом, вы можете представить их с помощью графа.
и маршруты в GPS. Если у вас есть набор объектов, связанных друг с другом, вы можете представить их с помощью графа.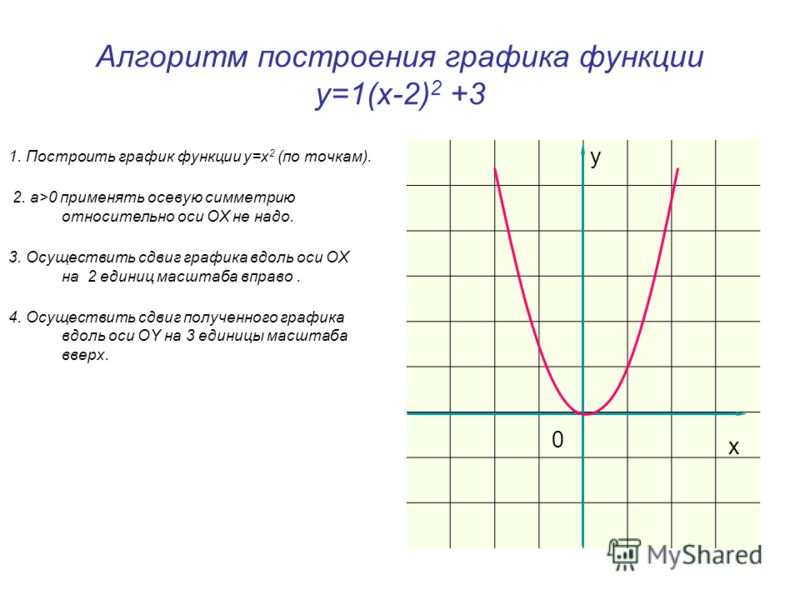 1. of Graphs (Image by Author)Рис. 2. Анимация BFS обхода графа (Image by Author)
1. of Graphs (Image by Author)Рис. 2. Анимация BFS обхода графа (Image by Author)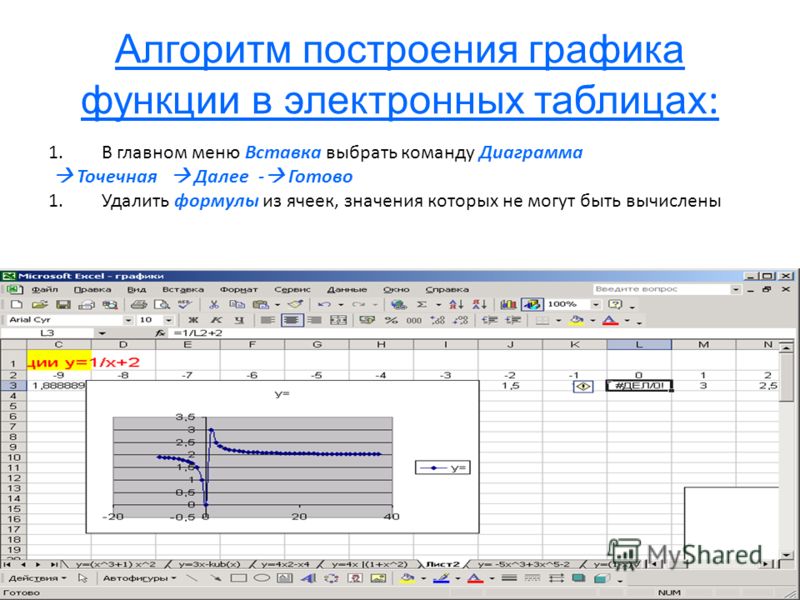

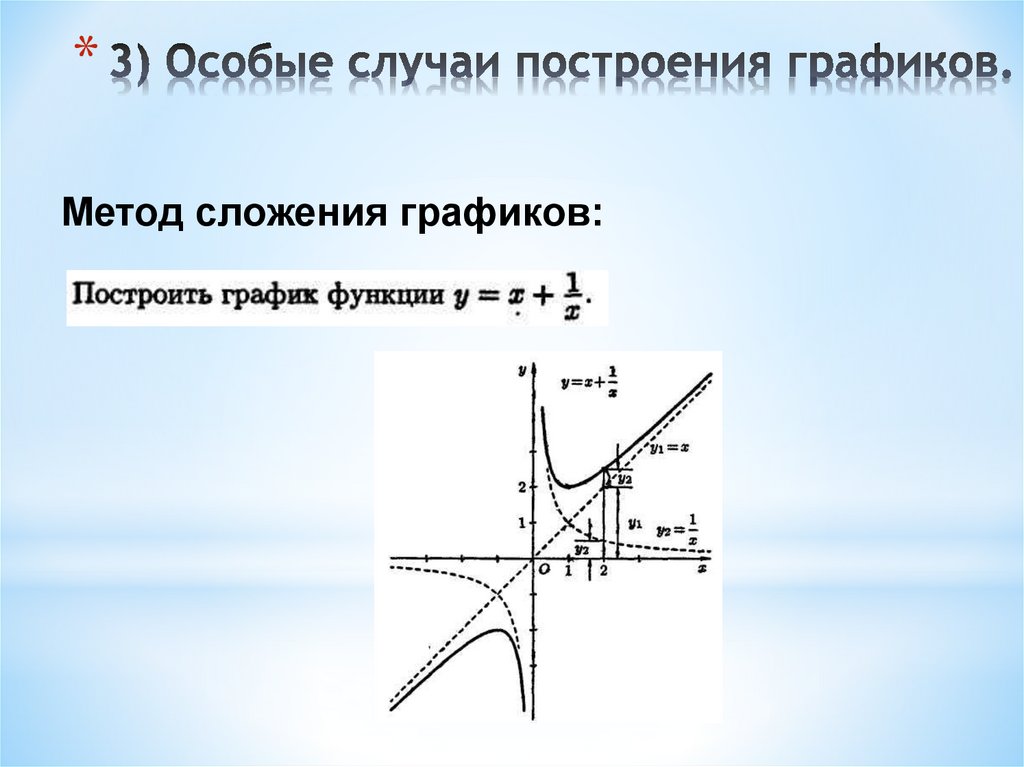 Обнаружение циклов — это процесс обнаружения этих циклов. На рис. 5 показана анимация обхода цикла.
Обнаружение циклов — это процесс обнаружения этих циклов. На рис. 5 показана анимация обхода цикла.



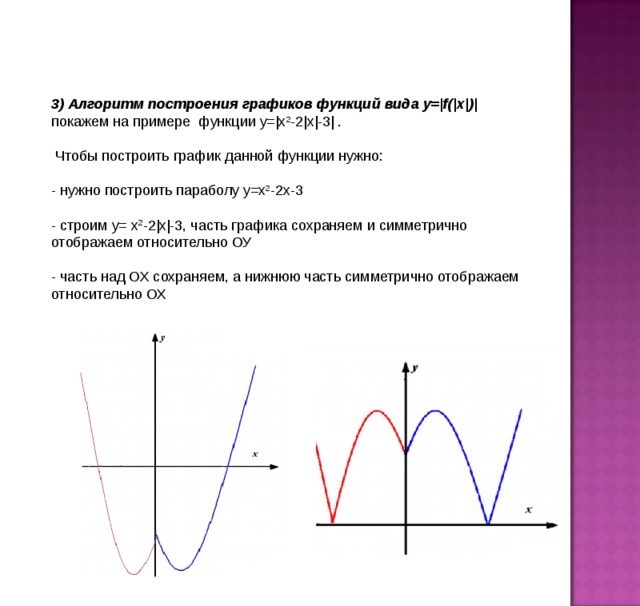

 com
com

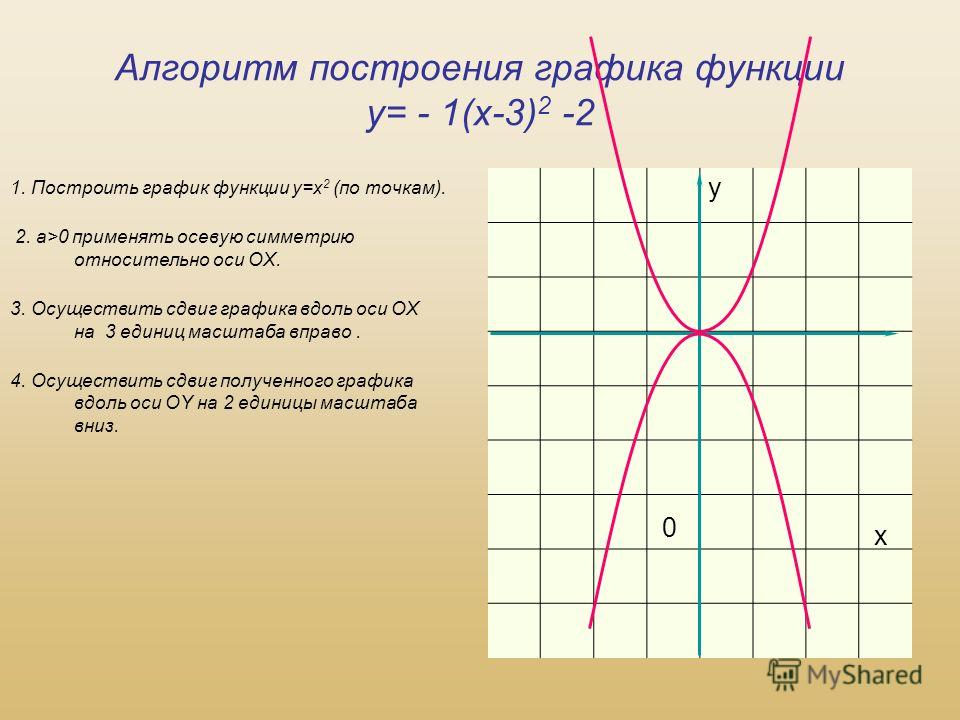 Количество ребер, которые у вас есть, зависит от вершин. Ребра могут быть направленными или ненаправленными.
Количество ребер, которые у вас есть, зависит от вершин. Ребра могут быть направленными или ненаправленными. Его еще называют узлом.
Его еще называют узлом.
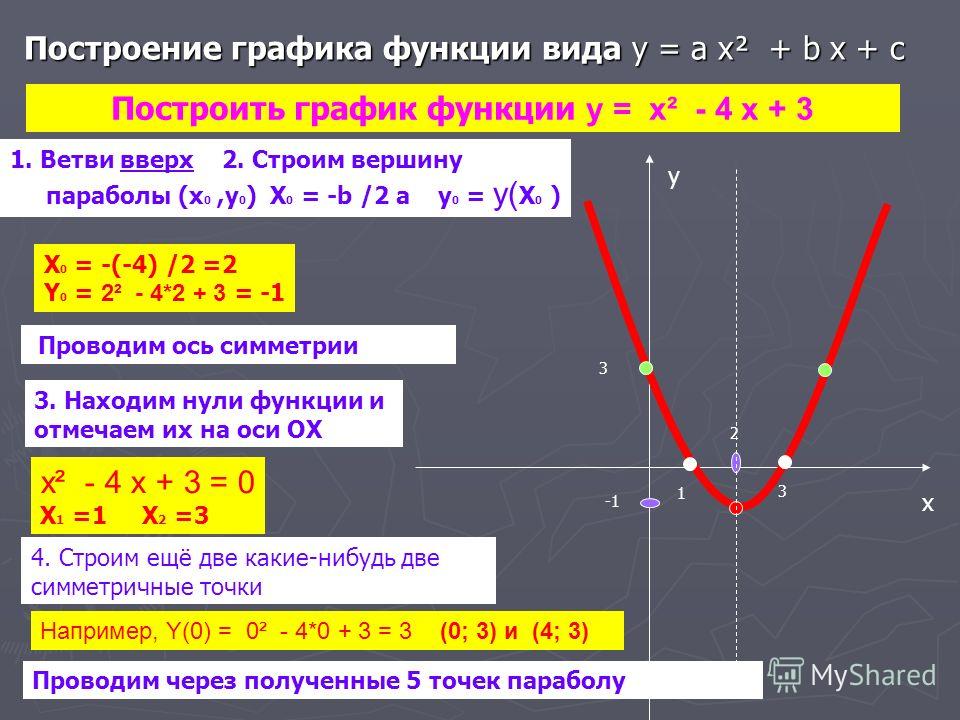
 vertex = data
vertex = data  format(i), end="")
format(i), end="")  Когда вы проходите граф от начальной вершины, вы должны сначала вывести правый потомок каждого узла, а затем левый.
Когда вы проходите граф от начальной вершины, вы должны сначала вывести правый потомок каждого узла, а затем левый. graph))
graph))  add_edge(1, 4)
add_edge(1, 4)  Попробуйте сначала решить ее самостоятельно. Если вы застряли, вы всегда можете обратиться к решению, представленному в разделе решений.
Попробуйте сначала решить ее самостоятельно. Если вы застряли, вы всегда можете обратиться к решению, представленному в разделе решений.




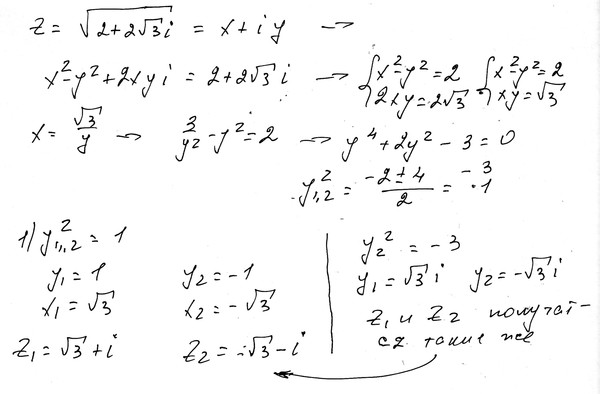 )
)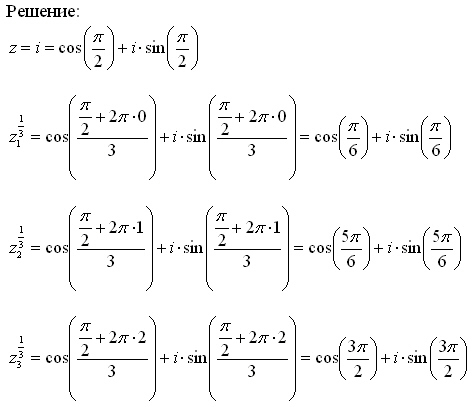 )
)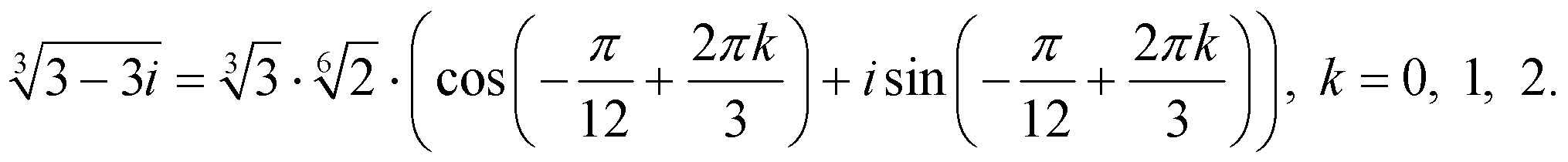 )
) )
) )
) )
) )
)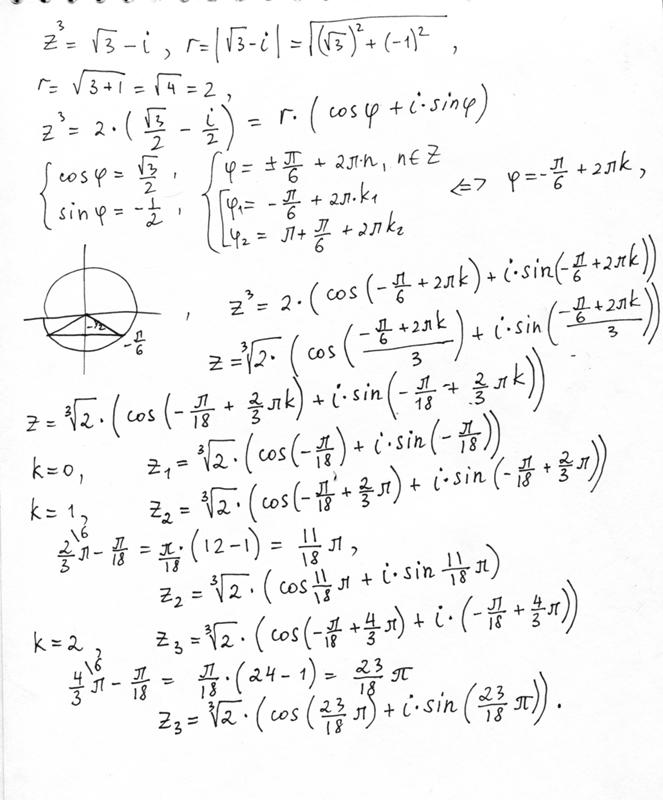 )
) Алгебра. — М.: Мир, 1968.
Алгебра. — М.: Мир, 1968.

 Эйлерова характеристика
Эйлерова характеристика n – a = 0
n – a = 0 ЛИНЕИНАЯ АЛГЕБРА И ПРЕДСТАВЛЕНИЯ
ЛИНЕИНАЯ АЛГЕБРА И ПРЕДСТАВЛЕНИЯ Полилинейные произведения
Полилинейные произведения Теорема Брауэра
Теорема Брауэра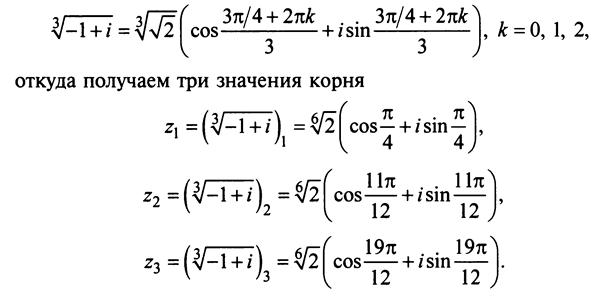 $$
$$ Графически:
Графически: 2} = \dfrac{\sqrt{3}}{2}$. 93 = i = 0 + 1i$, это означает, что $\cos(3\theta) = 0$ и $\sin(3\theta) = 1$. Решение этой системы дает $3\theta = \frac{\pi}{2} + 2\pi n$ или $\theta = \frac{\pi}{6} + \frac{2 \pi n}{3} $ для любого $n \in \mathbb{Z}$.
2} = \dfrac{\sqrt{3}}{2}$. 93 = i = 0 + 1i$, это означает, что $\cos(3\theta) = 0$ и $\sin(3\theta) = 1$. Решение этой системы дает $3\theta = \frac{\pi}{2} + 2\pi n$ или $\theta = \frac{\pi}{6} + \frac{2 \pi n}{3} $ для любого $n \in \mathbb{Z}$.
 Собственно, не всегда будет так везти, что число уравнений будет совпадать с числом неизвестных. Однако прелесть метода Гаусса в том, что он как раз и позволяет решать системы с любым числом уравнений и неизвестных. Специально для этого был написан калькулятор Решение системы линейных уравнений методом Гаусса с нахождением общего решения, который и используется при уравнивании химических реакций.
Собственно, не всегда будет так везти, что число уравнений будет совпадать с числом неизвестных. Однако прелесть метода Гаусса в том, что он как раз и позволяет решать системы с любым числом уравнений и неизвестных. Специально для этого был написан калькулятор Решение системы линейных уравнений методом Гаусса с нахождением общего решения, который и используется при уравнивании химических реакций.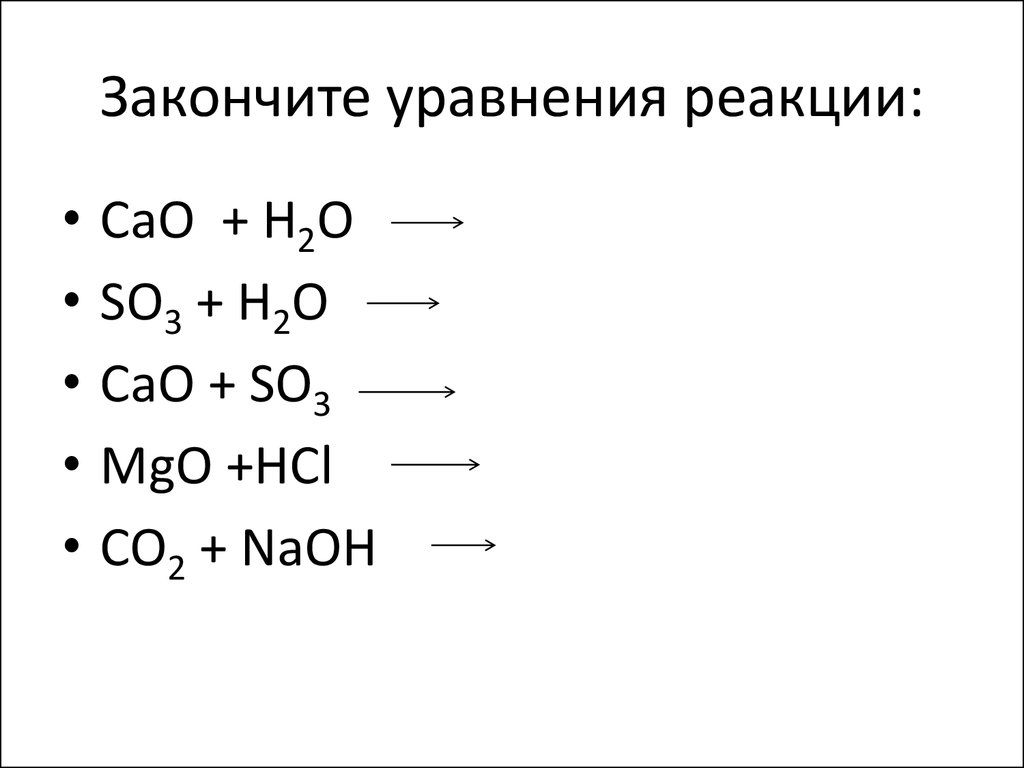 В результате происходит окисление или восстановление химических элементов, входящих в состав реагентов.
В результате происходит окисление или восстановление химических элементов, входящих в состав реагентов. Итак, существует два однозначных свойства:
Итак, существует два однозначных свойства: И, естественно, кислород имеет нулевую степень в своем простом соединении O2.
И, естественно, кислород имеет нулевую степень в своем простом соединении O2. Рассмотрим пример.
Рассмотрим пример. Так как натрий и кислород в левой части уравнения — простые вещества, то их заряд равен нулю. В оксиде натрия Na2O кислород имеет заряд -2, а натрий +1. Мы видим, что в левой части уравнения натрий имеет нулевой заряд, а в правой – положительный +1. То же самое с кислородом, который изменил степень окисления с нуля до -2. Запишем это «химическим» языком, указав в скобках заряды элементов:
Так как натрий и кислород в левой части уравнения — простые вещества, то их заряд равен нулю. В оксиде натрия Na2O кислород имеет заряд -2, а натрий +1. Мы видим, что в левой части уравнения натрий имеет нулевой заряд, а в правой – положительный +1. То же самое с кислородом, который изменил степень окисления с нуля до -2. Запишем это «химическим» языком, указав в скобках заряды элементов:






 (Молярная концентрация [M] = моль/л.)
(Молярная концентрация [M] = моль/л.)


 Сохраняет только активный лист.
Сохраняет только активный лист. Сохраняет только активный лист.
Сохраняет только активный лист. Сохраняет только активный лист.
Сохраняет только активный лист. Сохраняет только активный лист.
Сохраняет только активный лист. Так и родилась эта статья, которую я решил начать с самой распространённой операционной системы — Windows.
Так и родилась эта статья, которую я решил начать с самой распространённой операционной системы — Windows.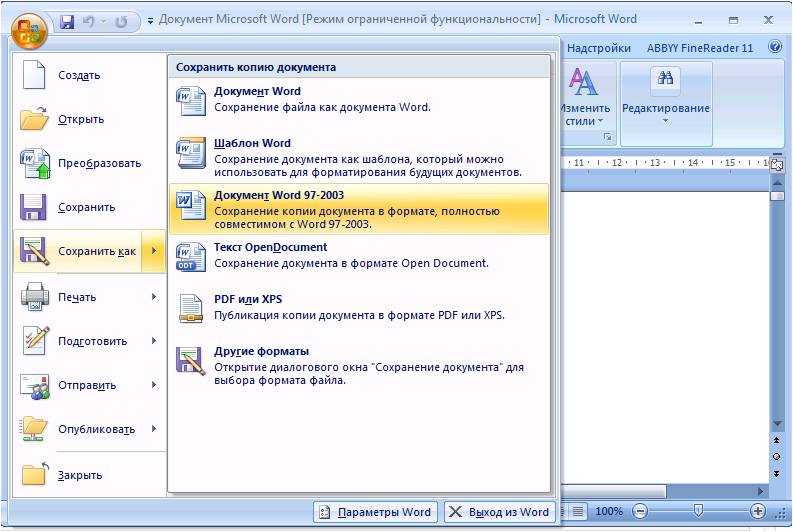
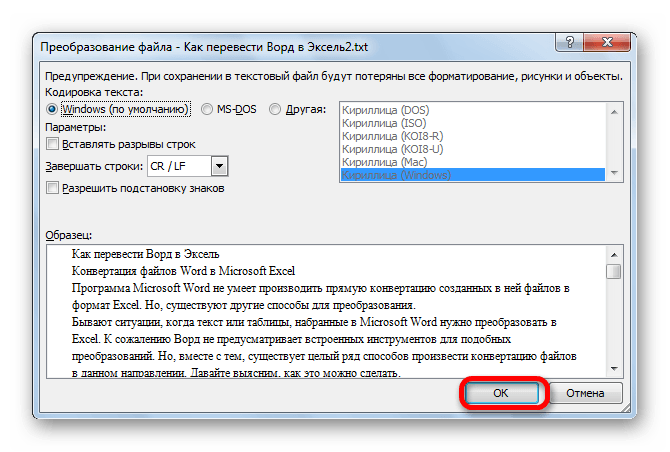


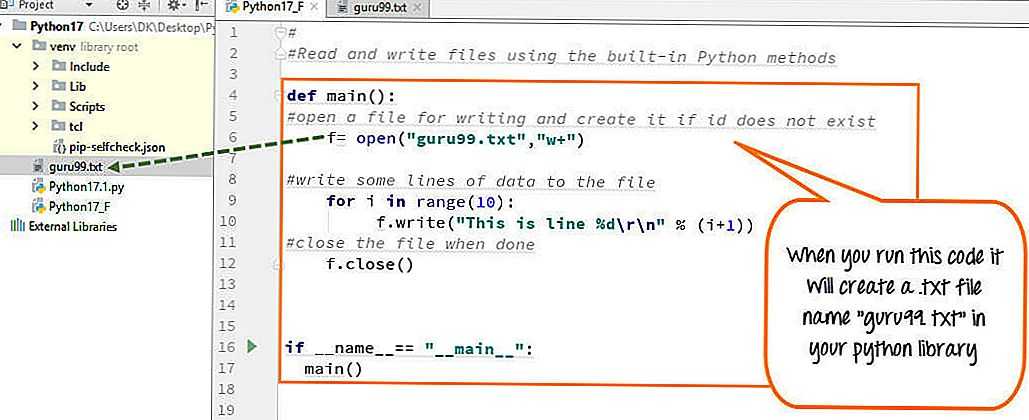 txt и сразу же записать в него данные:
txt и сразу же записать в него данные: Если нужно сотворить сразу несколько подобных документов, то вместо «> b > c > d > e > f > g» удобнее будет написать touch b c d e f g.
Если нужно сотворить сразу несколько подобных документов, то вместо «> b > c > d > e > f > g» удобнее будет написать touch b c d e f g. Есть такие, в которых текст можно надиктовывать голосом, а он будет преобразован в нужный формат (Речь текстовый редактор). Или, наоборот, выбранные фрагменты текста приложение преобразует в речь и прочтёт их в голос (Text Editor).
Есть такие, в которых текст можно надиктовывать голосом, а он будет преобразован в нужный формат (Речь текстовый редактор). Или, наоборот, выбранные фрагменты текста приложение преобразует в речь и прочтёт их в голос (Text Editor). До свиданья.
До свиданья.


 Пример использования этого показан ниже.
Пример использования этого показан ниже. Когда закончите, нажмите Ctrl + X , чтобы выйти из файла. Когда будет предложено сохранить файл, если вы хотите сохранить файл, нажмите «Y» для подтверждения.
Когда закончите, нажмите Ctrl + X , чтобы выйти из файла. Когда будет предложено сохранить файл, если вы хотите сохранить файл, нажмите «Y» для подтверждения. Вы можете просматривать файлы DOC, файлы RTF, файлы EXE, GIF, JPG,
и многие другие. Каждый из этих файлов был создан приложением, которое знало, как читать файл.
и обрабатывать его содержимое.
Вы можете просматривать файлы DOC, файлы RTF, файлы EXE, GIF, JPG,
и многие другие. Каждый из этих файлов был создан приложением, которое знало, как читать файл.
и обрабатывать его содержимое.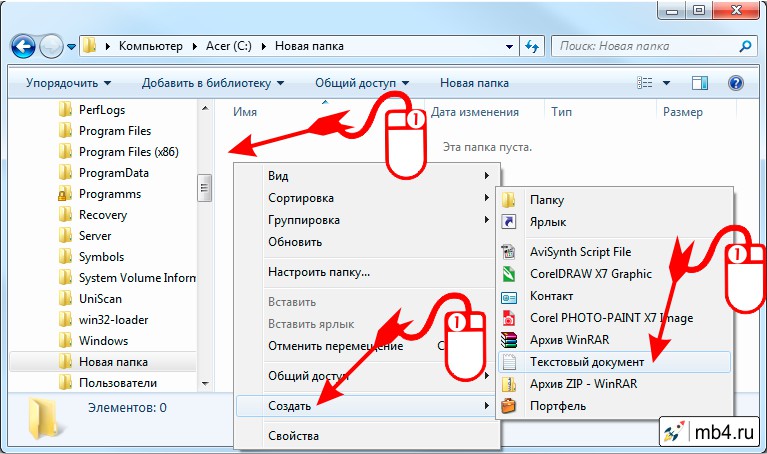
 Вы должны выбрать «Сохранить как тип» обычного текста (*.txt).
Если вы используете тип по умолчанию, вы получаете файл DOC.
В Word НЕ достаточно просто ввести имя файла «myfile.txt» в
Сохранить окно. Если ТИП файла установлен неправильно (например, «Обычный текст»),
это создаст файл с именем «myfile.txt.doc», который по-прежнему является файлом doc!
Вы должны выбрать «Сохранить как тип» обычного текста (*.txt).
Если вы используете тип по умолчанию, вы получаете файл DOC.
В Word НЕ достаточно просто ввести имя файла «myfile.txt» в
Сохранить окно. Если ТИП файла установлен неправильно (например, «Обычный текст»),
это создаст файл с именем «myfile.txt.doc», который по-прежнему является файлом doc!
 Даже в кругах исследователей – «чистых математиков» довольно долго интегрирование уравнений в квадратурах, теоретико-групповой подход к уравнениям считались тупиковой ветвью в науке. Тем не менее, теория обыкновенных дифференциальных уравнений является базой для уравнений математической физики и, кроме того, развитие современной физики показало, что именно те самые редкие и хорошо изученные случаи и представляют наибольший физический интерес. А успехи, достигнутые в ряде разделов математики – в алгебраической топологии, дифференциальной геометрии и коммутативной алгебре, позволяют надеяться на то, что общая теория уравнений с частными производными будет построена.
Даже в кругах исследователей – «чистых математиков» довольно долго интегрирование уравнений в квадратурах, теоретико-групповой подход к уравнениям считались тупиковой ветвью в науке. Тем не менее, теория обыкновенных дифференциальных уравнений является базой для уравнений математической физики и, кроме того, развитие современной физики показало, что именно те самые редкие и хорошо изученные случаи и представляют наибольший физический интерес. А успехи, достигнутые в ряде разделов математики – в алгебраической топологии, дифференциальной геометрии и коммутативной алгебре, позволяют надеяться на то, что общая теория уравнений с частными производными будет построена. Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.
Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.

 Начальные условия вводите как обычные условия. Порядок не важен.
Чтобы
ввести условие, нажмите «+условие»
Начальные условия вводите как обычные условия. Порядок не важен.
Чтобы
ввести условие, нажмите «+условие» Решением
дифференциального уравнения будет функция или семейство функций. Производные могут входить в функцию в
любом порядке и сами производные могут быть любого порядка. Производные, функции, независимые переменные
и параметры могут входить в ДУ в различных комбинациях или же могут вовсе отсутствовать. Однако в
уравнение должна входить хотя бы одна производная, иначе оно бы не будет дифференциальным.
Дифференциальным уравнением является не любое уравнение, содержащее производные неизвестной функции. К
примеру, f'(x)=f(f(x)) не является дифференциальным уравнением, а просто обозначает производную от
определённой функции.
Решением
дифференциального уравнения будет функция или семейство функций. Производные могут входить в функцию в
любом порядке и сами производные могут быть любого порядка. Производные, функции, независимые переменные
и параметры могут входить в ДУ в различных комбинациях или же могут вовсе отсутствовать. Однако в
уравнение должна входить хотя бы одна производная, иначе оно бы не будет дифференциальным.
Дифференциальным уравнением является не любое уравнение, содержащее производные неизвестной функции. К
примеру, f'(x)=f(f(x)) не является дифференциальным уравнением, а просто обозначает производную от
определённой функции.


 Дифференциальное уравнение представляет собой уравнение (вы увидите знак «=»), имеющее
производные. Некоторые примеры:
Дифференциальное уравнение представляет собой уравнение (вы увидите знак «=»), имеющее
производные. Некоторые примеры:



 Таким образом, выигрыш первого игрока будет максимальным из минимальных.
Отсюда и название — максиминный выигрыш. Номер строки этого элемента и будет номером чистой стратегии,
которую выбирает первый игрок.
Таким образом, выигрыш первого игрока будет максимальным из минимальных.
Отсюда и название — максиминный выигрыш. Номер строки этого элемента и будет номером чистой стратегии,
которую выбирает первый игрок. Таким образом, проигрыш второго
игрока будет минимальным из максимальных. Отсюда и название — минимаксный выигрыш. Номер столбца этого
элемента и будет номером чистой стратегии, которую выбирает второй игрок. Если второй игрок использует
«минимакс», то независимо от выбора стратегии первым игроком, он проиграет не более v2 единиц.
Таким образом, проигрыш второго
игрока будет минимальным из максимальных. Отсюда и название — минимаксный выигрыш. Номер столбца этого
элемента и будет номером чистой стратегии, которую выбирает второй игрок. Если второй игрок использует
«минимакс», то независимо от выбора стратегии первым игроком, он проиграет не более v2 единиц. Наименьший из наибольших элементов столбцов —
5, это верхняя цена игры, ей соответствует второй столбец, следовательно, минимаксная стратегия второго
игрока — вторая.
Наименьший из наибольших элементов столбцов —
5, это верхняя цена игры, ей соответствует второй столбец, следовательно, минимаксная стратегия второго
игрока — вторая.
 Верно и обратное утверждение: если матричная игра имеет седловую точку, то верхняя и
нижняя цены матричной игры одинаковы. Соответствующий элемент одновременно является наименьшим в строке
и наибольшим в столбце и равен цене игры.
Верно и обратное утверждение: если матричная игра имеет седловую точку, то верхняя и
нижняя цены матричной игры одинаковы. Соответствующий элемент одновременно является наименьшим в строке
и наибольшим в столбце и равен цене игры. Таким образом, цена игры равна 5.
То есть . Цена игры равна
значению седловой точки .
Максиминная стратегия первого игрока — вторая чистая стратегия, а минимаксная стратегия второго игрока —
третья чистая стратегия. Данная матричная игра имеет решение в чистых стратегиях.
Таким образом, цена игры равна 5.
То есть . Цена игры равна
значению седловой точки .
Максиминная стратегия первого игрока — вторая чистая стратегия, а минимаксная стратегия второго игрока —
третья чистая стратегия. Данная матричная игра имеет решение в чистых стратегиях. Поэтому решение связывается с понятием вероятности
и среднего (математического ожидания). В окончательном же решении есть и аналог седловой точки (то есть
равенства нижней и верхней цены игры), и аналог соответствующих им стратегий.
Поэтому решение связывается с понятием вероятности
и среднего (математического ожидания). В окончательном же решении есть и аналог седловой точки (то есть
равенства нижней и верхней цены игры), и аналог соответствующих им стратегий. Чтобы его найти, нужно перемножить вектор
смешанной стратении первого игрока (который будет матрицей из одной строки), платёжную матрицу и вектор
смешанной стратегии второго игрока (который будет матрицей из одного столбца):
Чтобы его найти, нужно перемножить вектор
смешанной стратении первого игрока (который будет матрицей из одной строки), платёжную матрицу и вектор
смешанной стратегии второго игрока (который будет матрицей из одного столбца):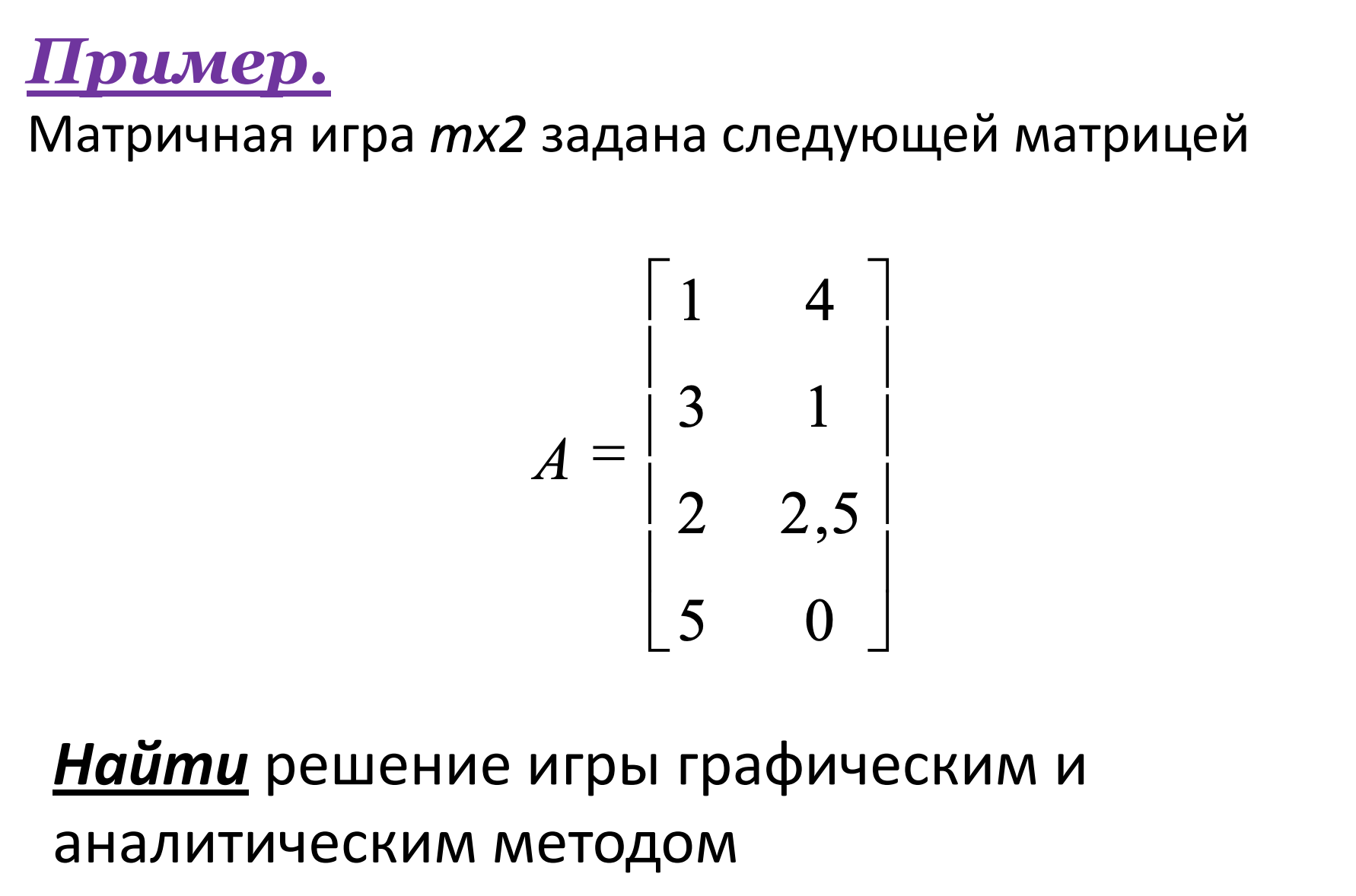




 Дана матричная игра с платёжной матрицей
Дана матричная игра с платёжной матрицей Дана матрица, элементы которой aij
характеризуют прибыль, которую получит предприятие при выпуске i-й продукции с j-м
состоянием спроса.
Дана матрица, элементы которой aij
характеризуют прибыль, которую получит предприятие при выпуске i-й продукции с j-м
состоянием спроса. Вторая стратегия (второй столбец матрицы)
является явно невыгодной для игрока B по сравнению с первой
(элементы второго столбца больше элементов первого столбца), так как цель игрока B —
уменьшить выигрыш игрока A. Поэтому второй столбец можно отбросить.
Получим следующую матрицу:
Вторая стратегия (второй столбец матрицы)
является явно невыгодной для игрока B по сравнению с первой
(элементы второго столбца больше элементов первого столбца), так как цель игрока B —
уменьшить выигрыш игрока A. Поэтому второй столбец можно отбросить.
Получим следующую матрицу: Закачка решения в формате doc начнется автоматически через 10 секунд.
Закачка решения в формате doc начнется автоматически через 10 секунд.
 Платежная матрица игры представлена в табл. 2.1.
Платежная матрица игры представлена в табл. 2.1. ед. при этом прибыль составит 64-2·5=54 . Так что «выигрыш» в этом случае равен 54 и т. д.
ед. при этом прибыль составит 64-2·5=54 . Так что «выигрыш» в этом случае равен 54 и т. д.

 Мы будем включать множество примеров, включая классические игры и несколько приложений.
Мы будем включать множество примеров, включая классические игры и несколько приложений.

 Контент был на высоте! 😉
Контент был на высоте! 😉 Игроки знают стратегию своего противника и все равно не будут отклоняться от первоначально выбранной стратегии, потому что она остается оптимальной стратегией для каждого игрока.
Игроки знают стратегию своего противника и все равно не будут отклоняться от первоначально выбранной стратегии, потому что она остается оптимальной стратегией для каждого игрока.
 Равновесие по Нэшу утверждает, что оптимальная стратегия для действующего лица состоит в том, чтобы придерживаться своей первоначальной стратегии, зная стратегию противника, и что все игроки придерживаются одной и той же стратегии.
Равновесие по Нэшу утверждает, что оптимальная стратегия для действующего лица состоит в том, чтобы придерживаться своей первоначальной стратегии, зная стратегию противника, и что все игроки придерживаются одной и той же стратегии. Доминирующая стратегия может быть включена в равновесие Нэша, тогда как равновесие Нэша может не быть лучшей стратегией в игре.
Доминирующая стратегия может быть включена в равновесие Нэша, тогда как равновесие Нэша может не быть лучшей стратегией в игре. У прокуратуры нет улик, чтобы осудить эту пару, поэтому они предлагают каждому заключенному возможность либо предать другого, дав показания о том, что другой совершил преступление, либо сотрудничать, храня молчание.
У прокуратуры нет улик, чтобы осудить эту пару, поэтому они предлагают каждому заключенному возможность либо предать другого, дав показания о том, что другой совершил преступление, либо сотрудничать, храня молчание.



 Но если вы сейчас такой потребности не ощущаете, то решение задач по экономике собственными силами – не лучший способ потратить время.
Но если вы сейчас такой потребности не ощущаете, то решение задач по экономике собственными силами – не лучший способ потратить время. Во-первых, время – деньги. Оптимизируя свой учебный процесс, вы проявляете не только правильный подход к учению, но и реалистичное понимание той самой экономики. В освободившееся время вы можете повышать квалификацию по своему профилю или зарабатывать деньги. Во-вторых, спрос определяет предложение, а спрос на решение задач по экономике у студентов очень велик. Дело именно в том, что многим надо зарабатывать деньги (по статистике работают или ищут работу сейчас четыре из пяти студентов-очников). Работу многие из них находят именно по тому профилю, по которому учатся. А значит, время надо уделять и работе, и обучению по выбранному профилю.
Во-первых, время – деньги. Оптимизируя свой учебный процесс, вы проявляете не только правильный подход к учению, но и реалистичное понимание той самой экономики. В освободившееся время вы можете повышать квалификацию по своему профилю или зарабатывать деньги. Во-вторых, спрос определяет предложение, а спрос на решение задач по экономике у студентов очень велик. Дело именно в том, что многим надо зарабатывать деньги (по статистике работают или ищут работу сейчас четыре из пяти студентов-очников). Работу многие из них находят именно по тому профилю, по которому учатся. А значит, время надо уделять и работе, и обучению по выбранному профилю.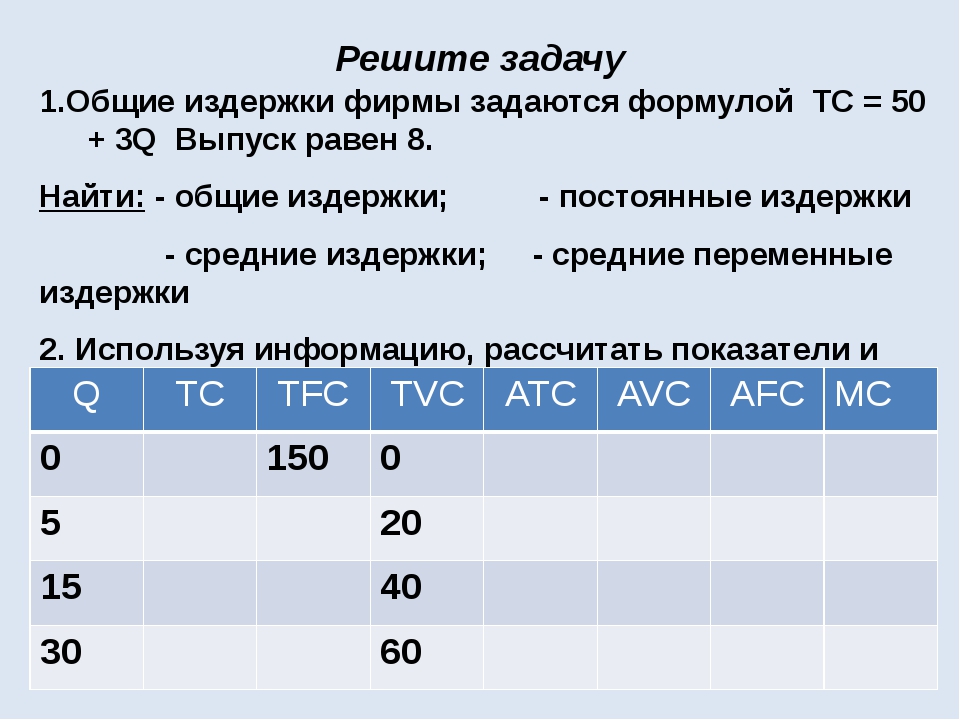 Это касается не только программистов, но и, скажем, переводчиков и журналистов (если только те не собираются работать с экономическими изданиями), врачей, биологов, других профессий.
Это касается не только программистов, но и, скажем, переводчиков и журналистов (если только те не собираются работать с экономическими изданиями), врачей, биологов, других профессий. Документированное решение проблем предоставляет учащимся основу, в которой они могут начать изучать свои стратегии решения проблем.
Документированное решение проблем предоставляет учащимся основу, в которой они могут начать изучать свои стратегии решения проблем. 222) пишут: «Чтобы стать действительно опытными в решении проблем, учащиеся должны научиться делать больше, чем просто получать правильные ответы на вопросы учебника». В какой-то момент им нужно осознать, как они решили эти проблемы и как они могут адаптировать свои процедуры решения проблем для решения запутанных, реальных проблем… Понимание и использование эффективных процедур решения проблем все, критический компонент мастерства в большинстве дисциплин». Документированное решение проблем требует от учащихся подумайте о том, как они решают проблему , а затем запишите шаги, которые они используют.
222) пишут: «Чтобы стать действительно опытными в решении проблем, учащиеся должны научиться делать больше, чем просто получать правильные ответы на вопросы учебника». В какой-то момент им нужно осознать, как они решили эти проблемы и как они могут адаптировать свои процедуры решения проблем для решения запутанных, реальных проблем… Понимание и использование эффективных процедур решения проблем все, критический компонент мастерства в большинстве дисциплин». Документированное решение проблем требует от учащихся подумайте о том, как они решают проблему , а затем запишите шаги, которые они используют.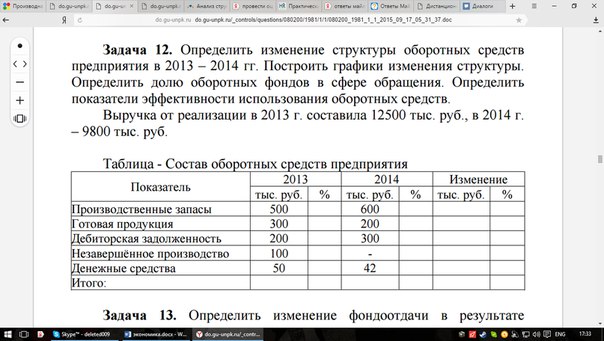 ..
..
 б) 1 единица за каждые 3 доллара снижения цены.
б) 1 единица за каждые 3 доллара снижения цены. В таком случае учащийся не может описать несколько шагов. Помните, что одна из основных причин использования задокументированного решения проблем — помочь учащимся разбить процесс решения на отдельные этапы, что в конечном итоге поможет им в развитии навыков аналитического и критического мышления.
В таком случае учащийся не может описать несколько шагов. Помните, что одна из основных причин использования задокументированного решения проблем — помочь учащимся разбить процесс решения на отдельные этапы, что в конечном итоге поможет им в развитии навыков аналитического и критического мышления.
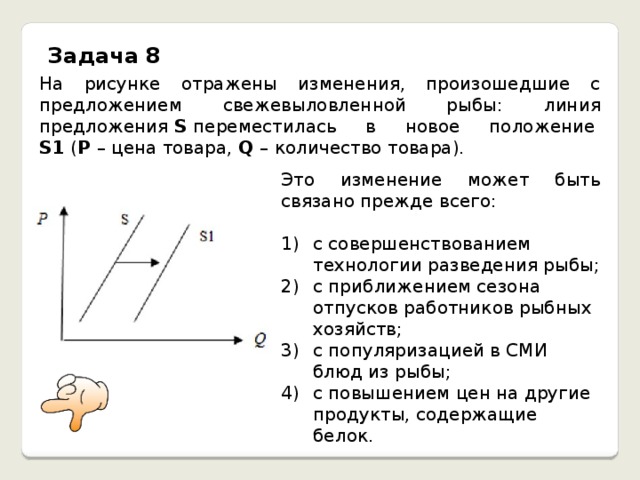
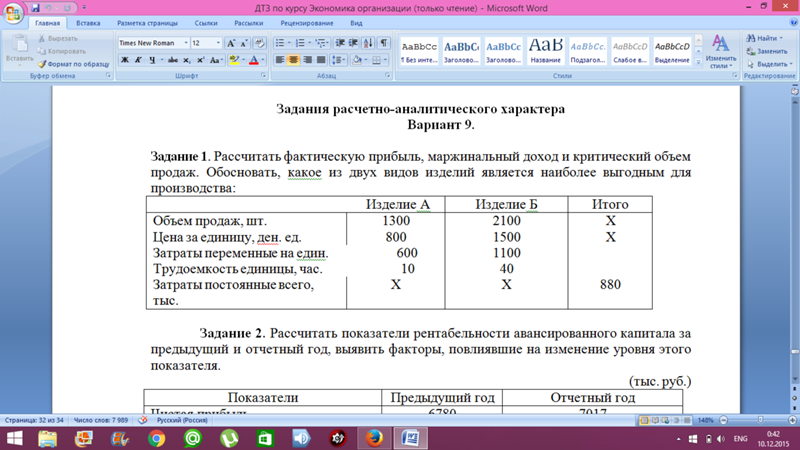 е. улучшение сбора налогов, приватизация, либерализация цен.
е. улучшение сбора налогов, приватизация, либерализация цен.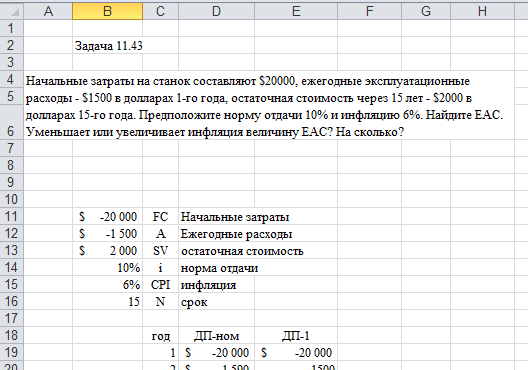 Многие работники гиг-экономики не заметят снижения процентной ставки. По сути, снижение процентной ставки перевешивает негативные настроения.
Многие работники гиг-экономики не заметят снижения процентной ставки. По сути, снижение процентной ставки перевешивает негативные настроения.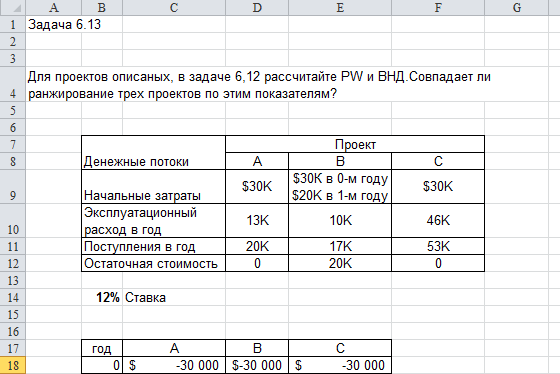
 Но правительство может
Но правительство может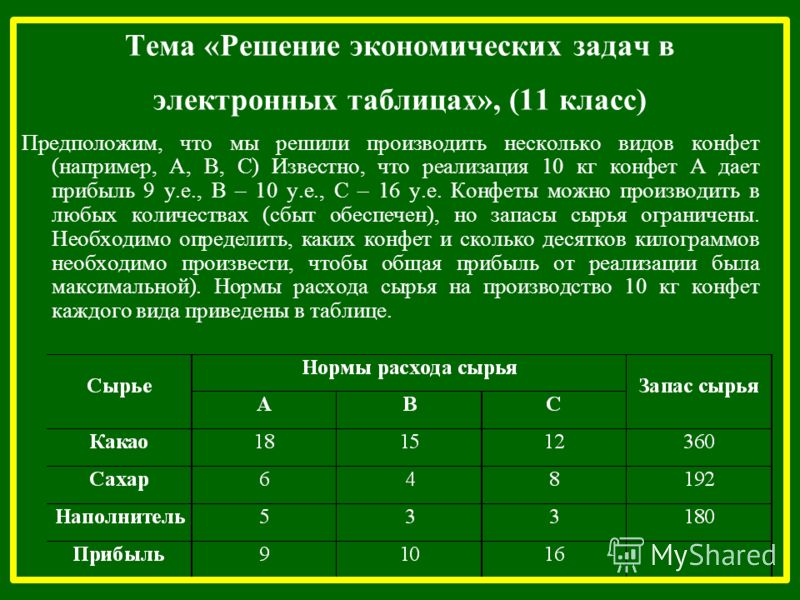

 Поэтому может возникнуть необходимость в проведении таких мер, как:
Поэтому может возникнуть необходимость в проведении таких мер, как:
 например США должны планировать повышение налога на бензин и налога на тех лиц с высоким доходом, которые выиграли от недавнего снижения налогов.
например США должны планировать повышение налога на бензин и налога на тех лиц с высоким доходом, которые выиграли от недавнего снижения налогов.
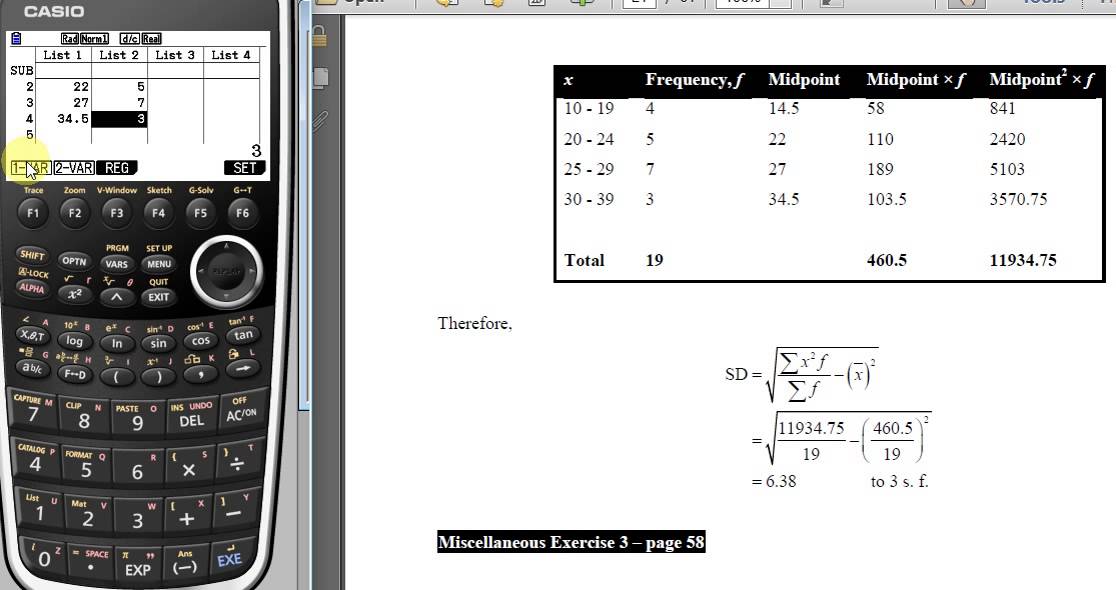 Можно скачать понравившуюся картинку из интернета и заказать печать на самой лучшей машине и получить совсем не то, что хотелось. Как понять, подходит изображение для печати? Ведь оно так красиво выглядит на экране монитора. Параметров определения качества изображений много, но начать нужно с самого простого — размер изображения.
Можно скачать понравившуюся картинку из интернета и заказать печать на самой лучшей машине и получить совсем не то, что хотелось. Как понять, подходит изображение для печати? Ведь оно так красиво выглядит на экране монитора. Параметров определения качества изображений много, но начать нужно с самого простого — размер изображения.
 Потом эти 3 мм срезаются при обрезке заготовок до готового размера изделия. Эти припуски называются вылетами, и их нужно учитывать при расчете размера изображения.
Потом эти 3 мм срезаются при обрезке заготовок до готового размера изделия. Эти припуски называются вылетами, и их нужно учитывать при расчете размера изображения.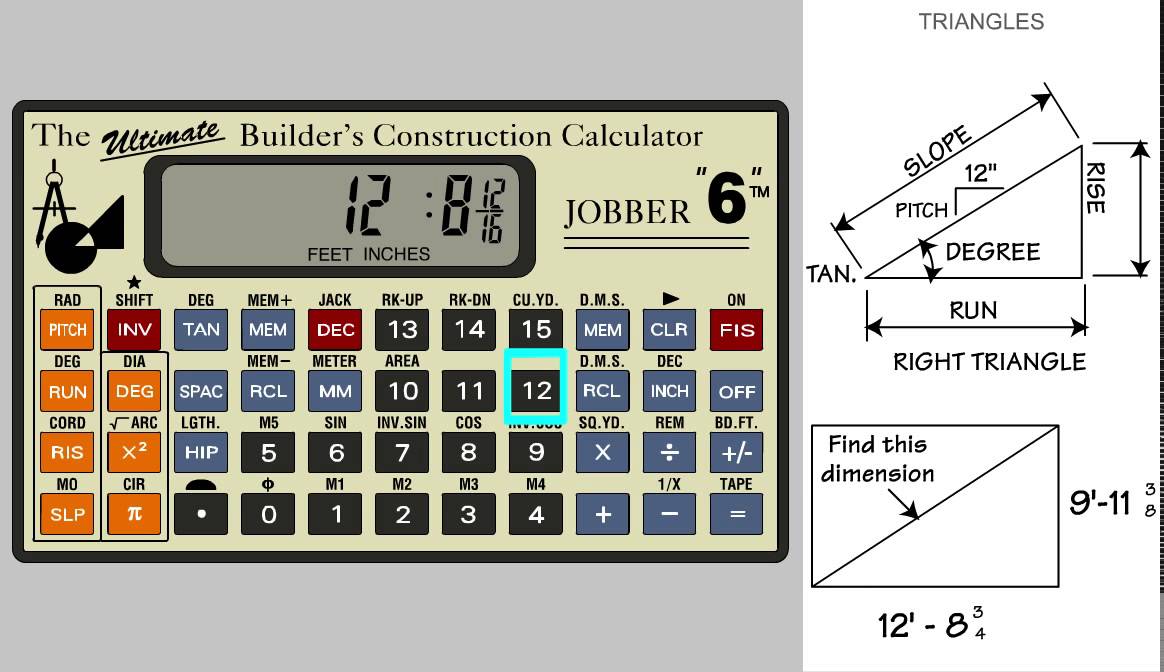 Чем больше их на единицу площади, тем лучше воспроизводится изображение.
Чем больше их на единицу площади, тем лучше воспроизводится изображение.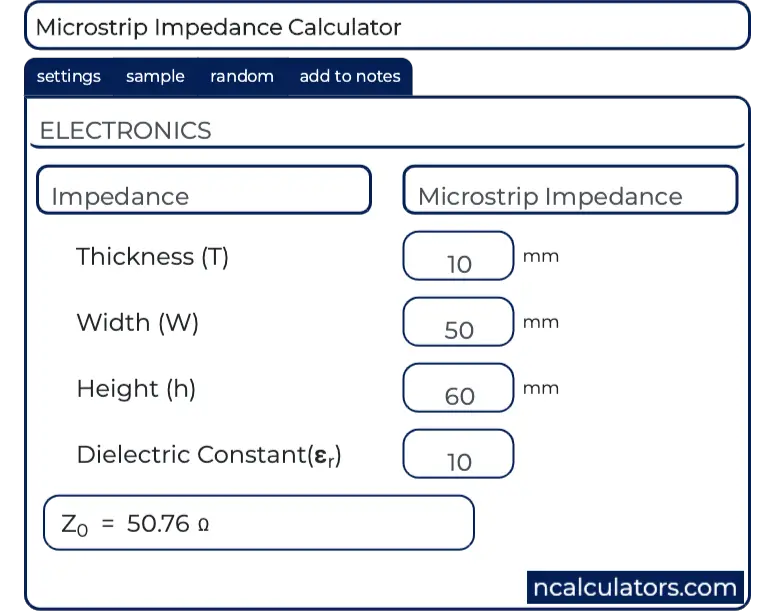 Сформулируем задачу.
Сформулируем задачу. Далее полученное число сравнивается с размером изображения (там есть определенные нюансы, связанные с отношением высоты и ширины, но об этом во второй части). Если размер формата в пикселях больше, чем размер нашего изображения (на рисунке — формат справа от фотографии), то он уже не подойдет, ибо фотографию придется растягивать, и мы получим разрешение хуже 300 (150) dpi. Если размер формата меньше, чем размер нашего изображения (на рисунке — формат справа от фотографии), то он подойдет — фотографию придется сжимать, и мы получим разрешение лучше 300 (150) dpi.
Далее полученное число сравнивается с размером изображения (там есть определенные нюансы, связанные с отношением высоты и ширины, но об этом во второй части). Если размер формата в пикселях больше, чем размер нашего изображения (на рисунке — формат справа от фотографии), то он уже не подойдет, ибо фотографию придется растягивать, и мы получим разрешение хуже 300 (150) dpi. Если размер формата меньше, чем размер нашего изображения (на рисунке — формат справа от фотографии), то он подойдет — фотографию придется сжимать, и мы получим разрешение лучше 300 (150) dpi. Сформулируем задачу.
Сформулируем задачу. Для получения дополнительной информации см. Наше руководство по расчету заработной платы.
Для получения дополнительной информации см. Наше руководство по расчету заработной платы.
 Некоторые из них предъявляют особые требования к информации, которая должна быть включена в платежную ведомость, и когда она должна быть доведена до сотрудников.
Некоторые из них предъявляют особые требования к информации, которая должна быть включена в платежную ведомость, и когда она должна быть доведена до сотрудников.
 В зависимости от типа пособия и правил, которые к нему применяются, вычет может быть доналоговым или посленалоговым. Предналог более выгоден для наемных работников, поскольку он снижает налогооблагаемый доход физического лица.
В зависимости от типа пособия и правил, которые к нему применяются, вычет может быть доналоговым или посленалоговым. Предналог более выгоден для наемных работников, поскольку он снижает налогооблагаемый доход физического лица.

 При внимательном отношении к соблюдению требований работодатели могут помочь реализовать эту общественную пользу и избежать значительных штрафов.
При внимательном отношении к соблюдению требований работодатели могут помочь реализовать эту общественную пользу и избежать значительных штрафов. д. С другой стороны, подоходные налоги имеют прогрессивные ставки, которые зависят от общего дохода и идут в США. Министерство финансов, где они могут быть использованы для финансирования различных государственных инициатив. Кроме того, некоторые налоги на заработную плату имеют ограничение на базовую заработную плату, после которого налог больше не вычитается из заработной платы работника до конца года. Подоходный налог не имеет такого предела.
д. С другой стороны, подоходные налоги имеют прогрессивные ставки, которые зависят от общего дохода и идут в США. Министерство финансов, где они могут быть использованы для финансирования различных государственных инициатив. Кроме того, некоторые налоги на заработную плату имеют ограничение на базовую заработную плату, после которого налог больше не вычитается из заработной платы работника до конца года. Подоходный налог не имеет такого предела.
 Работодатели должны уточнить у местных органов власти конкретные требования.
Работодатели должны уточнить у местных органов власти конкретные требования. Таким образом, бизнес, в котором много предыдущих сотрудников, подавших заявления на пособие по безработице, будет иметь более высокую ставку, чем бизнес, в котором их нет. Ставки других государственных и местных налогов на заработную плату различаются в зависимости от местоположения.
Таким образом, бизнес, в котором много предыдущих сотрудников, подавших заявления на пособие по безработице, будет иметь более высокую ставку, чем бизнес, в котором их нет. Ставки других государственных и местных налогов на заработную плату различаются в зависимости от местоположения. Налоги FUTA сообщаются ежегодно.
Налоги FUTA сообщаются ежегодно. Текущая ставка составляет 15,3% и распределяется следующим образом: 2,9% выплачивается Medicare, а 12,4% выплачивается Social Security. Как упоминалось ранее, Социальное обеспечение имеет предел базовой заработной платы в размере 160 200 долларов США.
Текущая ставка составляет 15,3% и распределяется следующим образом: 2,9% выплачивается Medicare, а 12,4% выплачивается Social Security. Как упоминалось ранее, Социальное обеспечение имеет предел базовой заработной платы в размере 160 200 долларов США. Это означает, что за нарушение нормативных требований предприятия могут быть оштрафованы на возврат средств в трастовый фонд (TFRP). Нарушения происходят, когда лицо (лица), ответственное за сбор, учет и уплату налогов, умышленно не делает этого. IRS определяет умышленность как осведомленность о невыплаченных налогах и либо преднамеренное игнорирование закона, либо безразличное поведение к его требованиям.
Это означает, что за нарушение нормативных требований предприятия могут быть оштрафованы на возврат средств в трастовый фонд (TFRP). Нарушения происходят, когда лицо (лица), ответственное за сбор, учет и уплату налогов, умышленно не делает этого. IRS определяет умышленность как осведомленность о невыплаченных налогах и либо преднамеренное игнорирование закона, либо безразличное поведение к его требованиям.
 Работодатели, которые не перечислили работодателю часть налога на социальное обеспечение в течение периода отсрочки, должны были сделать это позднее.
Работодатели, которые не перечислили работодателю часть налога на социальное обеспечение в течение периода отсрочки, должны были сделать это позднее.
 Какие углы называются вертикальными?
Какие углы называются вертикальными? То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a. 3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы. Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла.
Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла.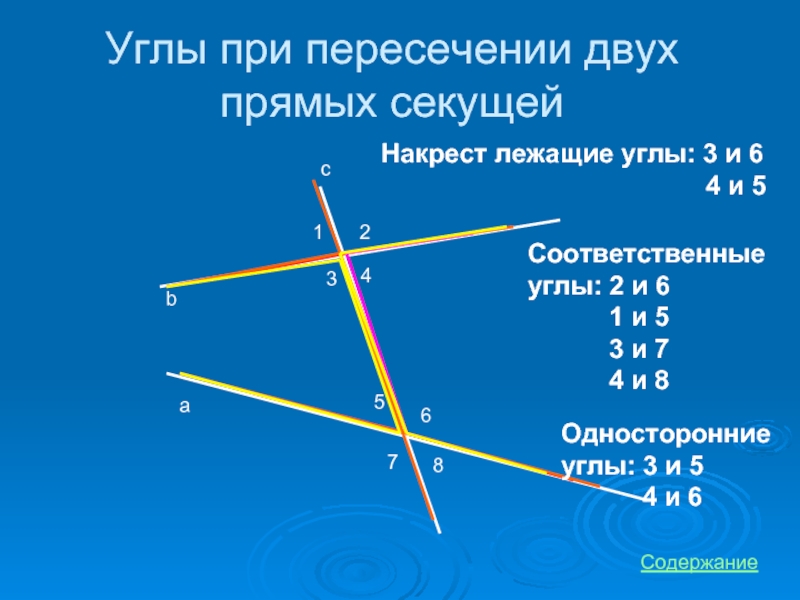 Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.
Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.

 77).
77).
 В сумме эти углы составляют развёрнутый угол, т. е.
В сумме эти углы составляют развёрнутый угол, т. е. Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.
Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.
 В этом случае решение будет выглядеть, как уравнение пропорции:
В этом случае решение будет выглядеть, как уравнение пропорции:
 Если один из смежных углов является прямым, то есть составляет 90 градусов, то другой угол тоже прямой. Если один из смежных углов острый, то другой будет тупым. Аналогично, если один из углов тупой, то второй, соответственно, будет острым.
Если один из смежных углов является прямым, то есть составляет 90 градусов, то другой угол тоже прямой. Если один из смежных углов острый, то другой будет тупым. Аналогично, если один из углов тупой, то второй, соответственно, будет острым. Когда речь идет о прямых, острых, развернутых углах, то подразумеваются именно геометрические углы.
Когда речь идет о прямых, острых, развернутых углах, то подразумеваются именно геометрические углы. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Поэтому ∠ АОВ + ∠ ВОС = 180° . Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.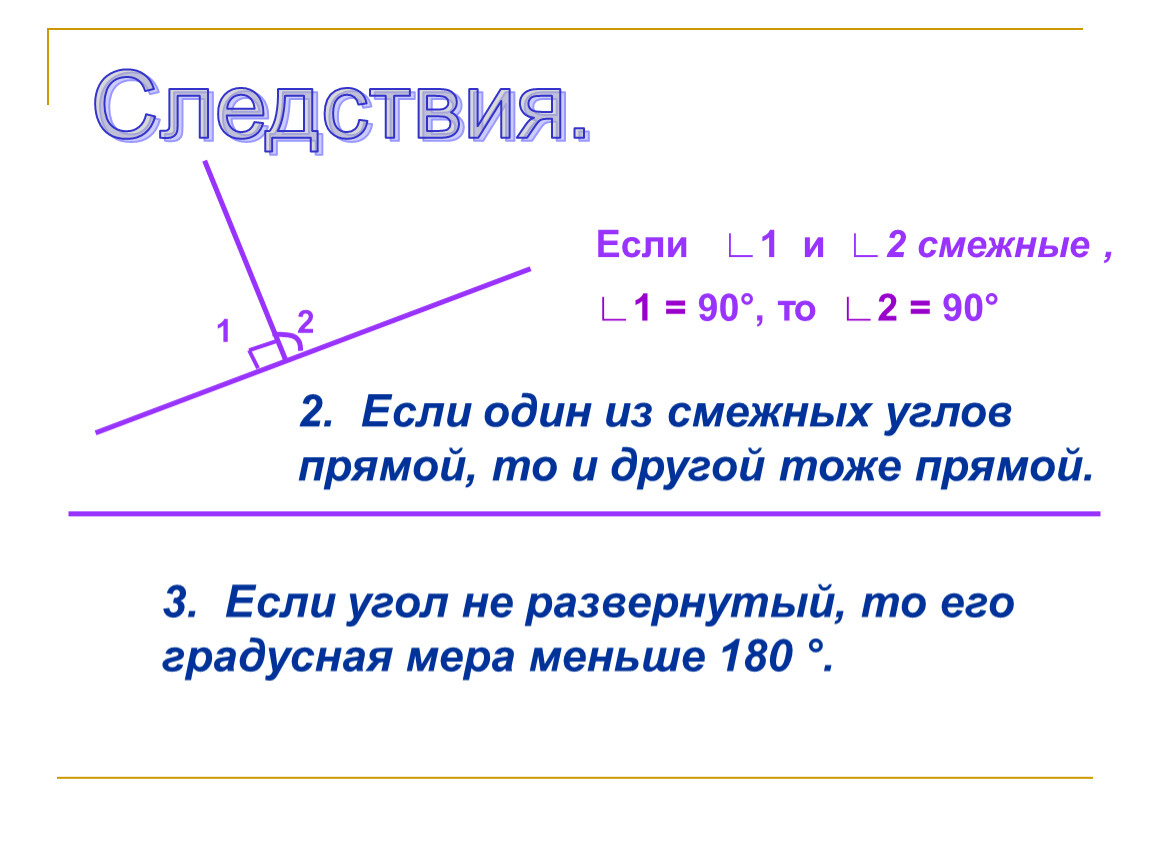 Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
 Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла.
Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла. Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.
Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.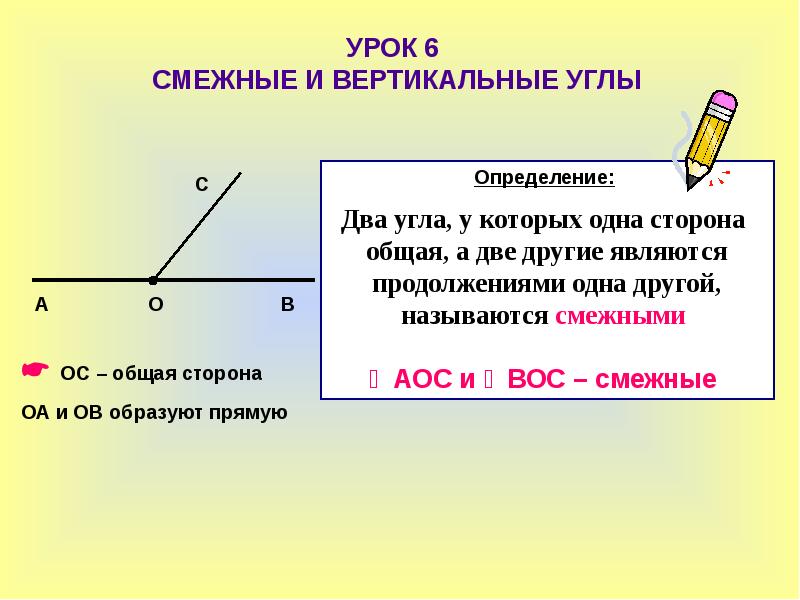


 Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать. Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы. Угол … Большой Энциклопедический словарь
Угол … Большой Энциклопедический словарь Если два комплементарных угла являются соседними (т.е. имеют общую вершину и разделяются только… … Википедия
Если два комплементарных угла являются соседними (т.е. имеют общую вершину и разделяются только… … Википедия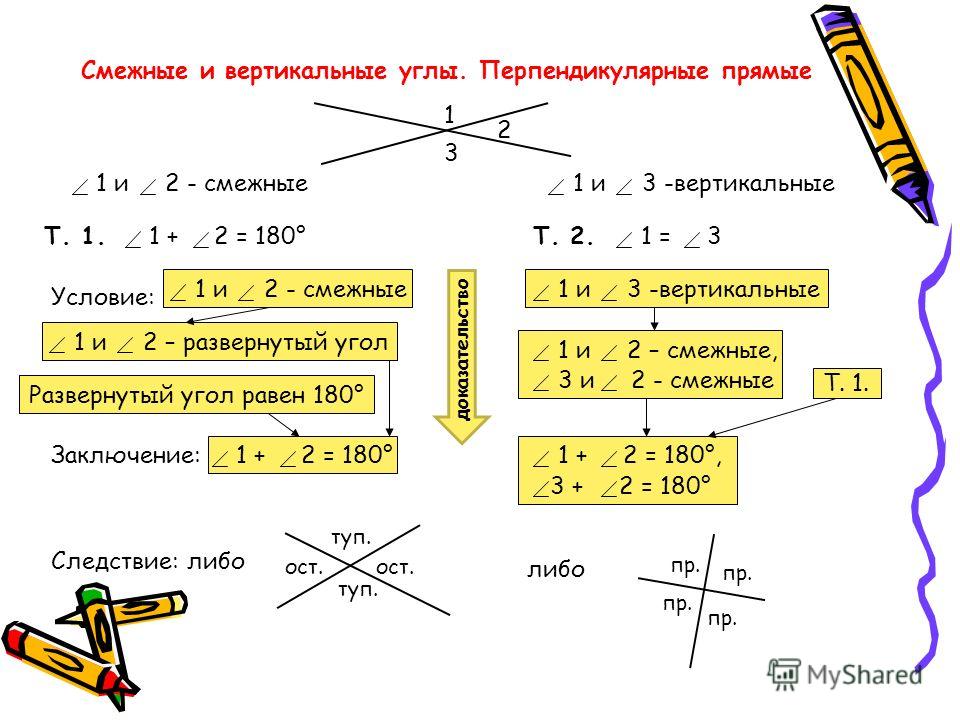
 рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана. При пересечении прямые образуют углы. Есть частные случаи:
При пересечении прямые образуют углы. Есть частные случаи:
 е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.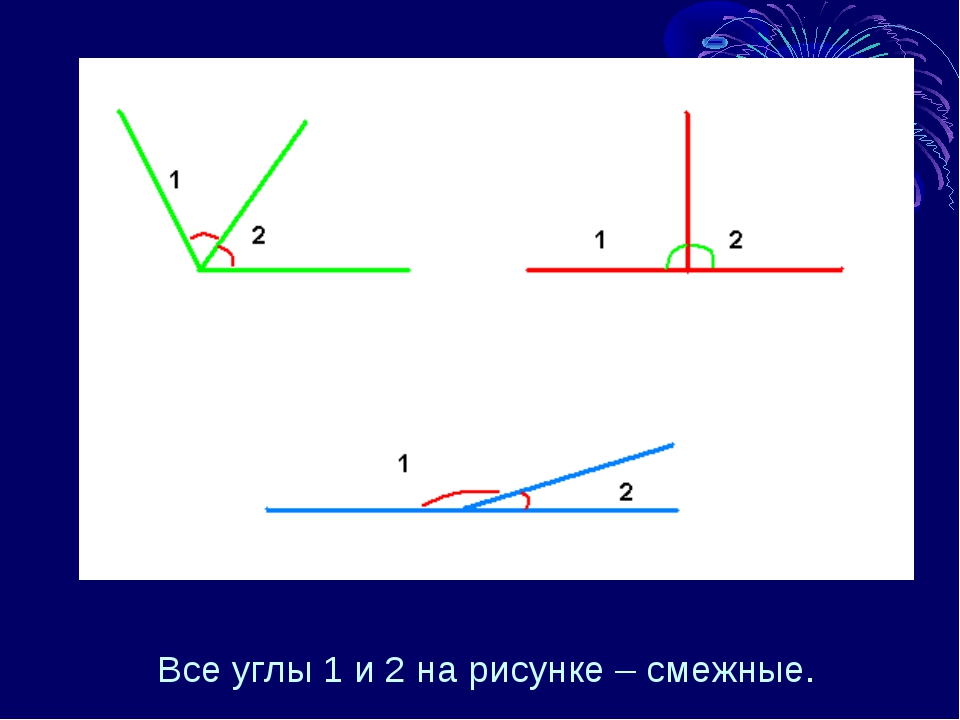 Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке. Чему равны смежные углы?
Чему равны смежные углы? Назовите эти углы.
Назовите эти углы.

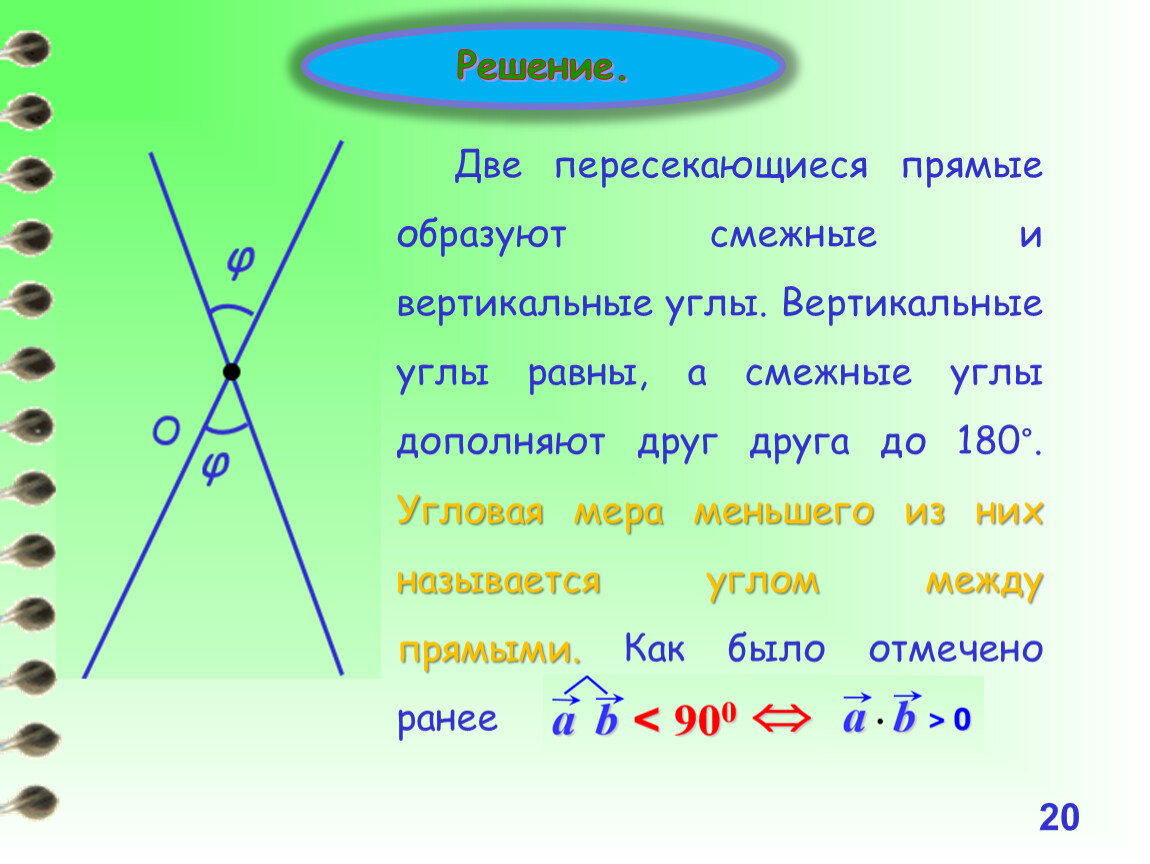 Любые два угла, имеющие общий луч или сторону, общую вершину и внутренние части которых не пересекаются, называются смежными углами. Например, посмотрите на изображение ниже: внутренности ∠ABD и ∠CBD не перекрываются и, следовательно, являются смежными углами.
Любые два угла, имеющие общий луч или сторону, общую вершину и внутренние части которых не пересекаются, называются смежными углами. Например, посмотрите на изображение ниже: внутренности ∠ABD и ∠CBD не перекрываются и, следовательно, являются смежными углами. Нажмите, чтобы узнать больше!
Нажмите, чтобы узнать больше! Итак, ∠1 и ∠2 – смежные углы.
Итак, ∠1 и ∠2 – смежные углы. В классе каждая скамья, на которой сидят 2 ученика, считается смежной. Когда состояния имеют общую границу, мы можем называть их соседними состояниями, поскольку они имеют общую границу и находятся рядом друг с другом. В математике смежный используется для обозначения двух сторон или углов, которые лежат рядом друг с другом, и мы называем их смежными сторонами и смежными углами.
В классе каждая скамья, на которой сидят 2 ученика, считается смежной. Когда состояния имеют общую границу, мы можем называть их соседними состояниями, поскольку они имеют общую границу и находятся рядом друг с другом. В математике смежный используется для обозначения двух сторон или углов, которые лежат рядом друг с другом, и мы называем их смежными сторонами и смежными углами. Два различных угла также могут считаться смежными, если они удовлетворяют всем условиям, относящимся к смежным углам. В случае квадрата или прямоугольника смежные углы равны, так как все углы равны 90º.
Два различных угла также могут считаться смежными, если они удовлетворяют всем условиям, относящимся к смежным углам. В случае квадрата или прямоугольника смежные углы равны, так как все углы равны 90º. Термин «перпендикуляр» произошел от латинского слова «perpendicularis», что означает отвес.
Термин «перпендикуляр» произошел от латинского слова «perpendicularis», что означает отвес. Поместите кончик компаса на новые точки и сделайте небольшую дугу над заданной линией. Две новые дуги пересекутся.
Поместите кончик компаса на новые точки и сделайте небольшую дугу над заданной линией. Две новые дуги пересекутся. Что вы можете сказать об AB и EF?
Что вы можете сказать об AB и EF? 
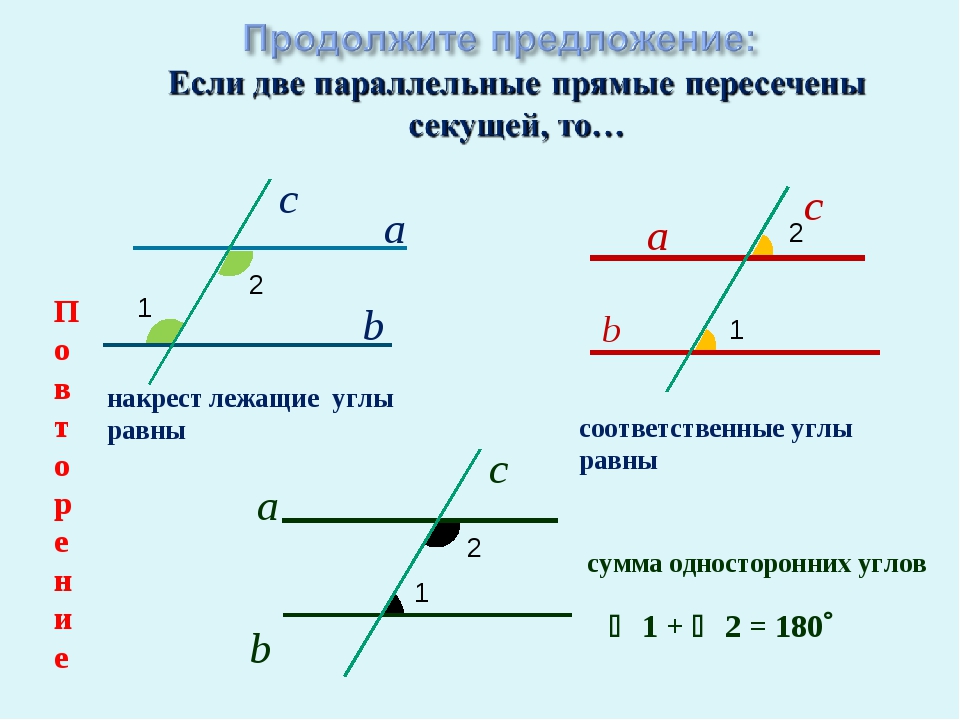 9{\circ}$ углы известны как прямые углы.
9{\circ}$ углы известны как прямые углы.