Геометрическая Пропорция
370. Но если величины находятся в геометрической пропорции, произведение её крайних членов равно произведению их средних членов.
Если a:b = c:d, ad = bc
Согласно допущению, (Статьи. 341, 359.) $\frac{a}{b } =\frac{c}{d } $
Умножив на bd, (Аксиома 3.) $\frac{abd}{b } =\frac{cbd}{d } $
Упростив дроби, ad = bc.
Так 12:8 = 15:10, поэтому 12*10 = 8*15.
Соотв: Любой множитель может быть перенесён от одной средней величины к другой, без влияния на пропорцию. Если a:mb = x:y, то a:b = mx:y. При этом произведение средних величин в обоих случаях одинаково. И если na:b = x:y, то a:b = x:ny.
371. С другой стороны, если произведение двух величин равно произведению двух других, то четыре величины сформируют пропорцию, где они сгруппированы таким образом, что одна сторона уравнения будет содержать средние члены, а другая — крайние.
Если my = nh, то m:n = h:y, то есть$\frac{m}{n } =\frac{h}{y } $
Таким образом разделив my = nh на ny, мы получим$\frac{my}{ny} =\frac{nh}{ny } $
Упростив дроби, $\frac{m}{n } =\frac{h}{y } $.
Соотв. То же самое должно быть верно по отношению любых множителей, которые образуют две стороны равенства.
Если (a + b).c = (d — m).y, то a + b:d — m = y:c.
372. Если три величины пропорциональны, то произведение их крайних членов равно квадрату средних. Таким образом одновременно пропорциональны также второй член первой пары и предыдущий член последней. (Статья. 366.) Следовательно они должны быть умножены на себя, то есть возведены в квадрат.
Если a:b = b:c, тогда умножение крайних и средних членов, ac = b2.
Следовательно, среднее пропорциональное двух величин может быть найдено путём извлечения квадратного корня из их произведения.
Если a:x = x:c, то x2 = ac, и x√ac.
373. Из Статьи. 370 следует, что соотношение любого из крайних членов равно произведению средних, разделённых на другой крайний член. И любой из средних членов равен произведению крайних членов, разделённому на другой средний член.
1. Если a:b = c:d, то ad = bc
2. Разделим на d, $a=\frac{bc}{d} $
3. Сначала разделим на c, $b=\frac{ad}{c} $
4. Разделим это на b, $c=\frac{ad}{b} $
5. Разделим на a, $d=\frac{bc}{a} $ ; Это значит, что
четвёртый член равен произведению второго и третьего, разделённому на первый.
На этом принципе основаны простые пропорции арифметики, которые часто называют Тройным Правилом. Три числа даны, чтобы найти четвёртое, которое получают путём умножения второго на третье и деления на первое.
374. Утверждение относительно произведений средних и крайних членов предоставляет очень простой и удобный критерий определения того, пропорциональны ли любые четыре величины. Нам только нужно перемножить средние и крайние члены. Если произведения равны, то величины пропорциональны. Если произведения не равны, то величины не пропорциональны.
375. В математических исследованиях, когда даны отношения нескольких величин, то они часто определены в виде пропорции. Но, как правило, необходимо, чтобы эта первая пропорция претерпела ряд трансформаций прежде, чем отчётливо выявится неизвестная величина или утверждение, которое мы хотели доказать. Она может пройти изменения, которые не окажут влияние на равенство отношений или которые обнаружат произведение средних членов равное произведению крайних.
Но, как правило, необходимо, чтобы эта первая пропорция претерпела ряд трансформаций прежде, чем отчётливо выявится неизвестная величина или утверждение, которое мы хотели доказать. Она может пройти изменения, которые не окажут влияние на равенство отношений или которые обнаружат произведение средних членов равное произведению крайних.
В первую очередь очевидно, что любая перемена в расстановке, которая не окажет влияния на эти равенство этих двух произведений, не уничтожит пропорции. Поэтому, если a:b = c:d, то порядок этих величин может варьироваться, что в любом случае приведёт к ad = bc. Отсюда,
376. Если четыре величины пропорциональны, то порядок средних членов, или крайних членов, или членов обоих пар, может быть инвертирован без разрушения пропорции.
Если a:b = c:d,
И 12:8 = 6:4
тогда
1. Инвертируя средние члены,
a:c = b:d
12:6 = 8:4
то есть
Первый относится к третьему
Как второй к четвёртому.
Другими словами, отношение предыдущих членов равно отношению последующих.
Эта инверсия средних членов часто упоминается в геометрии под названием Альтернация.
2. Инвертируя крайние члены,
d:b = c:a
4:8 = 6:12
то есть,
Четвёртый относится ко второму,
Как третий к первому.
3. Инвертируя члены каждой пары,
b:a = d:c
8:12 = 4:6
то есть,
Второй относится к первому,
Как четвёртый к третьему.
Технически это называется Инверсией.
Каждое из этого также может варьироваться, меняя порядок двух пар. (Статья. 365.)
Соотв. Порядок всей пропорции может быть инвертирован.
Если a:b = c:d, то d:c = b:a.
В каждом из данных случаев будет немедленно видно, что вычисляя произведения средних и крайних членов, у нас получается ad = bc, и 12. 4 = 8.6.
4 = 8.6.
Если члены только одной из пар инвертированы, то пропорция становится обратной. (Статья 367.)
Если a:b = c:d, то a относится к b, обратно тому, как d относится к c.
377. Разница в расположении не единственная алтернация, которую производят по отношению к членам пропорции. Часто бывает нужным умножить, разделить, возвести в степень и так далее. Во всех случаях искусство ведения исследования заключается в произведении некоторых изменений, при этом сохраняется постоянное равенство между отношением двух первых и двух последних членов. При решении уравнения, мы должны сохранять равенство сторон, так варьируя пропорцию, чтобы сохранить и равенство соотношений. И это достигается либо путём сохранения соотношений теми же, что и при альтернации членов, либо увеличивая или уменьшая одно из соотношений на столько же, как и другое. Большинство последующих доказательств направлены на чёткое выявление этого принципа и ознакомление с ним. Некоторые из утверждений могут быть доказаны более простым способом, возможно, путём умножения крайних и средних членов. Но это не даст ясного понимания природы некоторых изменений в пропорциях.
Некоторые из утверждений могут быть доказаны более простым способом, возможно, путём умножения крайних и средних членов. Но это не даст ясного понимания природы некоторых изменений в пропорциях.
Было показано, что если оба члена пары умножены или разделены на одинаковую величину, то их соотношение остаётся одинаковым (Статья. 355.) Так умножая предыдущий член (антецедента) проявится в умноженном соотношении, а деление последующего члена (консеквента) — в делении соотношения. (Статья. 352.) и следующие показывают, что умножение консеквента проявится в делении соотношения, а его деление — в произведении соотношения. (Статья. 353.) Так как соотношения в пропорции равны, то если их перемножить или разделить на одинаковую величину, то они всё ещё будут равны (Аксиома. 3.) Одно будет увеличено или уменьшено, так же как и второе. Отсюда,
378. Если четыре величины пропорциональны, два аналогичных или гомологичных члена могут быть умножены или разделены на одну и ту же величину, без нарушения пропорции.
Если аналогичные члены будут умножены или разделены, то их соотношения не поменяются. (Статья, 355.) Если гомологичные члены будут умножены или разделены, оба соотношения одинаково увеличатся или уменьшатся. (Статьи. 352, 353.)
Если a:b = c:d, то,
1. Умножая первые два члена, ma:mb = c:d
2. Умножая последние два члена, a:b = mc:md
3. Умножая два первых члена (антецедента), ma:b = mc:d
4. Умножая два последних члена (консеквента), a:mb = c:md
5. Разделив два первых члена, $\frac{a}{m}:\frac{b}{m}=c:d$
6. Разделив два последних члена, $a:b=\frac{c}{m}:\frac{d}{m }$
7. Разделив два антецедента, $\frac{a}{m}:b=\frac{c}{m}:d$ a/m:b = c/m:d
8. Разделив два консеквента, $a:\frac{b}{m}=c:\frac{d}{m}$ a:b/m = c:d/m.
Следствие. 1. Все члены могут быть умножены или разделены на одну и ту же величину.
ma:mb = mc:md, $\frac{a}{m}:\frac{b}{m}=\frac{c}{m}:\frac{d}{m} $.
Следствие. 2. В любом случае, в данной статье умножение консеквентов может быть заменено делением антецедентов той же самой пары, и деление консеквентов — умножением антецедентов. (Статья. 354, след.)
(Статья. 354, след.)
379. Часто бывает необходимо не только изменить члены пропорции и варьировать их расположение, но и сравнить одну пропорцию с другой. Из этого сравнения часто возникает новая пропорция, которая может быть необходима для решения задачи или перехода к доказательству. Один из самых важных случаев, когда сравниваемые два члена одной пропорции такие же как два в другой. Похожие члены могут исчезнуть, и новая пропорция может быть сформирована из оставшихся четырёх членов. Так,
380. Если два соотношения соответсвтенно равны третьему, то они также равны между собой.
Это не что иное, как 11ая аксиома, применяемая к соотношениям.
1. Если a:b = m:n
И c:d = m:n
тогда a:b = c:d,или a:c = b:d. (Статья.376.)
2. Если a:b = m:n
И m:n = c:d
то a:b = c:d,или a:c = b:d.
След. Если a:b = m:n
m:n > c:d
то a:b > c:d.
Так если соотношение m:n больше, чем c:d, то это показывает, что соотношение a:b, которое равно соотношению m:n, также больше чем соотношение c:d.
381. В этих примерах схожие члены двух пропорций это два первых и два последних. И порядок не важен. Порядок членов может быть изменён разными способами без влияния на равенство соотношений.
1. Похожими членами могут быть два антецедента, или два косеквента в каждой пропорции. Таким образом,
Если m:a = n:b
И m:c = n:d
тогда
Чередуем, m:n = a:b
И m:n = c:d
Отсюда a:b = c:d, или a:c = b:d, согласно последнему параграфу.
2. Антецеденты в одной пропорции, могут быть такими же как консеквенты в другой.
Если m:a = n:b
И c:m = d:n
Инветрируя и чередуя a:b = m:n
Чередуя c:d = m:n:
Поэтому a:b, и так далее как ранее.
3. Два гомологичных члена в одной из пропорций могут быть такими же, как два аналогичные члены в другой.
Если a:m = b:n
и c:d = m:n
Чередуя, a:b = m:n
И c:d = m:n
Поэтому, a:b, и так далее.
Всё это примеры равенства между соотношениями в одной пропорции с соотношениями в другой. В геометрии на предположение, к которому они принадлежат обычно ссылаются как на «ex aequo«или «ex aequali» (по справедливости). Второй случай в этой статье более всего отвечает объяснению Евклида. Но оба они все согласуются с одним и тем же принципом и часто к ним обращаются без разграничений.
В геометрии на предположение, к которому они принадлежат обычно ссылаются как на «ex aequo«или «ex aequali» (по справедливости). Второй случай в этой статье более всего отвечает объяснению Евклида. Но оба они все согласуются с одним и тем же принципом и часто к ним обращаются без разграничений.
382. Любое число пропорций может быть сравнено аналогичным способом, если два первых или два последних члена в каждой предыдущей пропорции такие же, как два первые и два последние члена в последующей.
Поэтому если a:b = c:d
И c:d = h:l
И h:l = m:n
И m:n = x:y
то a:b = x:y.
То есть два первых члена первой пропорции имеют такое же соотношение, как два последних члена последней пропорции. Это показывает, что соотношение всех пар одинаково.
И если члены не находятся в том же порядке как здесь, но могут быть упрощены к данному виду, применяется тот же самый принцип.
поэтому если a:c = b:d
И c:h = d:l
И h:m = l:n
И m:x = n:y
тогда чередуя
a:b = c:d
c:d = h:l
h:l = m:n
m:n = x:y.
Поэтому a:b = x:y, как и ранее.
Во всех примерах в этой и предшествующих статьях, два члена в одной пропорции, у которых есть равные члены в другой, не являются ни двумя средними членами, ни двумя крайними членами, а одним средним и одним крайним членом, из чего следует, что пропорция однородна и непрерывна.
383. Но если два средних или два крайних члена в одной пропорции такие же, как средние и крайние члены в другой, то оставшиеся четыре члена будут взаимно пропорциональны.
Если a:m = n:b
И c:m = n:d
тогда a:c = $\frac{1}{b}:\frac{1}{d} $, или a:c = d:b
Для ab = mn
И cd = mn
(Статья. 370) Поэтому ab = cd, и a:c = d:b.
В данном примере два средних члена в одной пропорции, такие же как те же в другой. Но принцип будет тем же, если крайние члены не равны или если крайние члены одной пропорции не равны средним членам другой.
Если m:a = b:n
И m:c = d:n
тогда a:c = d:b.
Или if a:m = n:b
И m:c = d:n
тогда a:c = d:b.
Теорема в геометрии, которая применима в данном случае обычно именуется словами «ex aequo perturbate» (по правде запутанная).
384. Другой способ варьировать члены в пропорции это сложение или вычитание.
Если к или от двух гомологичных членов пропорци вычитаются или прибавляются две другие величины, которые находятся в том же соотношении, то пропорция остаётся верной.
Соотношение не меняется, если добавить или отнять от него другое равное соотношение. (Статья. 357.)
Если a:b = c:d
И a:b = m:n
Тогда добавляя или отнимая от a и b, члены с равным соотношением m:n, мы получим
a+m:b+n = c:d, и a-m:b-n = c:d.
И добавляя или отнимая m и n к или от c и d, мы получим,
a:b = c+m:d+n, и a:b = c-m:d-n.
Здесь сложение и вычитание производится к и от аналогичных членов. Но путём чередования (Статья. 376,) эти члены будут гомологичными, и мы получим,
Но путём чередования (Статья. 376,) эти члены будут гомологичными, и мы получим,
a+m:c = b+n:d, и a-m:c = b-n:d.
След. 1. Это добавление может распространяться на любое число равных соотношений.
Таким образом, если
a:b = c:d
a:b = h:l
a:b = m:n
a:b = x:y
Тогда a:b = c+h+m+x:d+l+n+y.
След. 2. Если a:b = c:d
И m:b = n:d
тогда a+m:b = c+n:d.
Чередуем a:c = b:d
И m:n = b:d
таким образом
a+m:c+n = b:d
или a+m:b = c+n:d.
385. Из последней статьи следует, что если в любой пропорции члены прибавляются или отнимаются друг от друга, то,
Если аналогичные и гомологичные члены добавляются или отнимаются от двух других, то пропорция сохраняется верной.
Таким образом, если a:b = c:d, и 12:4 = 6:2, тогда,
1. Добавляя два последних члена к двум первым.
a+c:b+d = a:b 12+6:4+2 = 12:4
и a+c:b+d = c:d 12+6:4+2 = 6:2
или a+c:a = b+d:b 12+6:12 = 4+2:4
и a+c:c = b+d:d 12+6:6 = 4+2:2.
2. Складывая два антецедента с двумя консеквентами.
a+b:b = c+d:d 12+4:4 = 6+2:2
a+b:a = c+d:c, т.д.. 12+4:12 = 6+2:6, т.д..
Это называется Композицией.
3. Отнимая два первых члена от двух последних.
c-a:a = d-b:b
c-a:c = d-b:d, т.д..
4. Отнимая два последних члена от двух первых.
a-c:b-d = a:b
a-c:b-d = c:d, т.д..
5. Отнимая консеквенты от антецедентов.
a-b:b = c-d:d
a:a-b = c:c-d, etc.
Преобразование, показанное в последней форме называется Конверсией.
6. Отнимая антецеденты от консеквентов.
b-a:a = d-c:c
b:b-a = d:d-c, etc.
7. Добывляя и вычитая,
a+b:a-b = c+d:c-d.
То есть сумма первых двух членов относится к их разности, как сумма двух последних к их разности.
След. Если любые сложные величины, расставленые как в предыдущих примерах, пропорциональны, то простые величины, из которых они состоят также пропорциональны.
Таким образом, если a+b:b = c+d:d, то a:b = c:d.
Это называется Делением.
386. Если соответствующие члены двух или более разрядов пропорциональных величин перемножить между собой, то произведение также будет пропорционально.
Это смешанные соотношения (Статья. 347,) или смешанные пропорции. Это нужно уметь отличать от того, что называется композицией, которая является сложением членов соотношения. (Статья 385. 2.)
Если a:b = c:d 12:4 = 6:2
И h:l = m:n 10:5 = 8:4
Тогда ah:bl = cm:dn 120:20 = 48:8.
Исходя из определения пропорции два соотношения первого разряда равны, как и соотношения второго разряда. И умножение соответствующих членов является умножением соотношений, (Статья. 352. соотв.), то есть умножением равных на равные (Аксиома. 3.), так что соотношения будут всё так же равными, и поэтому все четыре произведения должны быть пропорциональны.
соотв.), то есть умножением равных на равные (Аксиома. 3.), так что соотношения будут всё так же равными, и поэтому все четыре произведения должны быть пропорциональны.
Такое же доказательство применимо к любому числу пропорций.
Если
a:b = c:d
h:l = m:n
p:q = x:y
Тогда ahp:blq = cmx:dny.
Из этого следует, что если члены пропорции перемножить на самих себя, то есть, если они возведены в какую-либо степень, то они всё равно будут пропорциональны.
Если a:b = c:d 2:4 = 6:12
a:b = c:d 2:4 = 6:12
Тогда a2:b2 = c2:d2 4:16 = 36:144
Пропорциональные величины также получаются реверсируя этот процесс, то есть вычисляя корни членов пропорции.
Если a : b:: c : d, тогда √a:√b = √c:√d.
Перемножив средние и крайние члены, ad = bc
И извлекя корень из обеих сторон, √ad = √bc
То есть, (Статья. 254, 371,) √a:√b = √c:√d.
254, 371,) √a:√b = √c:√d.
Отсюда,
387. Если некоторые величины пропорциональны, то продукты их возведения в степень или извлечения корней пропорциональны.
Если a:b = c:d
Тогда an:bn = cn:dn, и m√a:m√b = m√c:m√d.
И m√an:m√bn = m√cn:√dn, то есть, am/n:bm/n = cm/n:dm/n.
388. Если члены одного разряда пропорций разделить на соответствующие члены другого разряда, то частные будут пропорциональны.
Это иногда называют решением соотношений.
Если a:b = c:d 12:6 = 18:9
И h:l = m:n 6:2 = 9:3
Тогда $\frac{a}{h}:\frac{b}{l }=\frac{c}{m}:\frac{d}{n} $ $\frac{a}{h}:\frac{b}{l }=\frac{c}{m}:\frac{d}{n} $.
Это просто реверсия процесса в Статье. 386, и может быть доказана похожим образом.
Это нужно уметь различать от того, что в геометрии называется разделением, которое является вычитанием членов соотношения. (Статья. 385. соотв.)
389. В сложных смешанных пропорциях, равные множители или делители двух аналогичных или гомологичных членов могут быть отвергнуты.
Если
a:b = c:d 12:4 = 9:3
b:h = d:l 4:8 = 3:6
h:m = l:n 8:4 = 6:15
Тогда a:m = c:n 12:20 = 9:15.
Это правило может быть применено к случаям, к которым относятся термины «ex aequo» и «ex aequo perturbate«. Смотрите Статьи. 381 и 383. Один из методов может служить для того, чтобы подтвердить другой.
394. Изменения, которые могут быть сделаны в пропорциях без нарушения равенства соотношений, так многочислены, что они стали бы обременительны к запоминанию, если бы их нельзя было бы упростить до нескольких общих принципов. Они обычно получаются,
1. Инвертируя порядок членов, Статья. 376.
376.
2. Умножая или деля на одинаковую величину, Статья. 378.
3. Сравнивая пропорции, в которых есть схожие члены. Статьи. 380, 381, 382, 383.
4. Складывая или отнимая члены одинаковых соотношений, Статьи. 384, 385.
5. Умножая или деля одну пропорцию на другую, Статьи. 386, 387, 388.
6. Возводя в степень или извлекая корни членов, Статья. 387.
391. Когда четыре величины пропорциональны, если первая больше чем вторая, то третья будет больше чем четвёртая; если равны, то равны, а если меньше, то, соответственно, меньше.
Для одинаковых соотношений двух пар, если одно является соотношением равенства, то и второе тоже, и поэтому антецедент в каждой паре равен её консеквенту. (Статья. 345,) Если одно соотношение большего неравенства, то и второе тоже, и поэтому антецедент каждого из них больше чем соответствующий консеквент. А если одно соотношение меньшего неравенства, то и второе так же, и поэтому антецедент каждого из них меньше чем консеквент.
А если одно соотношение меньшего неравенства, то и второе так же, и поэтому антецедент каждого из них меньше чем консеквент.
Пусть a:b = c:d; тогда если
a = b, c = d
a > b, c > d
a < b, c < d.
След. 1. Если первый член больше третьего, то тогда второй больше четвёртого, если равен — то равен, если меньше — то, соответсвенно, меньше.
В случае чередования, a:b = c:d становится a:c = b:d, без какого-либо чередования величин. Таким образом, если a = b, c = d, и т.д., как и ранее.
След. 2. Если a:m = c:n
и m:b = n:d
тогда if a = b, c = d, и т.д.
Для равенства соотношений, (Статья. 381. 2.) или смешанных соотношений, (Статьи. 386, 389.)
a:b = c:d. Таким образом, если a = b, c = d, и т.д. как ранее.
След. 3. Если a:m = n:d
и m:b = c:n
тогда if a = b, c = d.
391. b. Если четыре величины пропорциональны, то обратные им величины тоже пропорциональны и наоборот.
Если a:b = c:d, тогда $\frac{a}{h}:\frac{b}{l }=\frac{c}{m}:\frac{d}{n} $.
Для каждой из этих пропорций, при сокращении получаем ad = bc.
Как решать системы уравнений в 4-5 классе
Рассмотрим уравнение с двумя неизвестными:
x + y = 10
У этого уравнения может быть много решений: x=1, y=9; x=2, y=8; x=3, y=7 и т.д.
Какое из решений выбрать — непонятно. Ситуация становится более определённой, если мы знаем, что между x и y существует ещё какая-то другая взаимосвязь. Например, мы знаем про те же самые x и y, что y-x = 2.
Итак, мы можем записать:
{
x + y = 10
y — x = 2
То, что мы записали, называется системой уравнений. Уравнения, входящие в систему, объединяются большой фигурной скобкой. Чтобы система уравнений имела решение, число уравнений должно быть равно числу неизвестных.
Так как это связанные между собой уравнения, то мы можем выразить, например, y через x в первом уравнений, и подставить получившееся выражение вместо y во второе уравнение — тем самым во втором уравнении останется только одно неизвестное (x) и мы сможем решить уравнение.
Запишем это в виде формул.
x + y = 10
y = 10 — x
Подставляем полученное выражение 10 — x вместо y во второе уравнение:
y — x = 2
10 — x — x = 2
10 — 2 = x + x
8 = 2x
x = 4
Мы нашли x. Теперь найдём y, зная, что y = 10 — x
y = 10 — 4 = 6
Мы нашли x и y. x = 4, y = 6
Проверим наше решение, подставим x и y в оба уравнения системы:
x + y = 10
y — x = 2
4 + 6 = 10
6 — 4 = 2
10 = 10
2 = 2
В обеих уравнениях левые и правые части равны, то есть x и y мы нашли правильно.
Почему мы смогли воспользоваться этим приёмом — выразить y через x в первом уравнении и подставить получившееся выражение вместо y во второе? Потому что у нас система уравнений и в этих двух уравнениях эти x и y — это одни и те же неизвестные, поэтому мы можем в одном уравнении заменять на выражения, полученные в другом
Не имеет значения — будем ли мы y выражать через x в первом уравнении и подставлять во второе, или во втором и подставлять в первое. Точно также не имеет значение, что именно мы будем подставлять — y, выраженный через x, или x, выраженные через y. Мы выражаем и подставляем то, что нам удобнее в дальнейших расчётах.
Точно также не имеет значение, что именно мы будем подставлять — y, выраженный через x, или x, выраженные через y. Мы выражаем и подставляем то, что нам удобнее в дальнейших расчётах.
Существует и другой метод решения уравнений
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
Вычитание одного уравнения из другого
Рассмотрим систему уравнений:
{
5x + 6y = 80
2x + 3y = 35
Глядя на эту систему уравнений мы понимаем, что мы не можем выразить x или y через целые числа — 80 делится на цело на 5, но не делится нацело на 6, а 35 не делится нацело ни на 2, ни на 3. Если мы не умеем работать с дробными числами, то уравнение мы можем решить по другому.
Для решения этого уравнения надо из левой части первого уравнения вычесть левую часть второго уравнения, а из правой части первого вычесть правую часть второго. При этом не принципиально вычитать именно из первого уравнения второе — можно и из второго первое. Но если мы в данной системе уравнений вычтем из правой части второго уравнения правую часть
Но если мы в данной системе уравнений вычтем из правой части второго уравнения правую часть
первого уравнения, то у нас получится 35 — 80 = -45, отрицательное число. Если с отрицательными числами мы работать ещё не умеем, то у нас остаётся только один вариант — из первого уравнения вычитать второе.
Почему мы можем вычесть из из левой части одного уравнения левую часть другого, а из правой части одного правую часть другого и при этом быть уверенными, что равенство сохранится? Потому что это свойство систем уравнений. При вычитании соответствующих частей уравнений друг из друга, равенство сохраняется.
Итак, запишем соответствующую операцию вычитания частей уравнений в виде формулы:
5x + 6y — (2x + 3y) = 80 — 35
5x + 6y — 2x — 3y = 45
3x + 3y = 45
x + y = 15
Итак, мы получили простое уравнение x + y = 15, где отсутствуют множители у x и y.
Теперь мы можем выразить x через y (или y через x — это без разницы) и подставить получившееся выражение в одно из уравнений системы.
x = 15 — y
Подставим это выражение вместо x во второе уравнение
2x + 3y = 35
2(15 — y) + 3y = 35
30 — 2y + 3y = 35
y = 35 — 30
y = 5
Мы нашли y, осталось найти x
x = 15 — y
x = 15 — 5 = 10
Наш ответ: x = 10, y = 5
Проверим наше решение, подставив найденные x и y в систему уравнений:
{
5x + 6y = 80
2x + 3y = 35
5∙10 + 6∙5 = 80
2∙10 + 3∙5 = 35
50 + 30 = 80
20 + 15 = 35
80 = 80
35 = 35
Обе части в обеих уравнениях равны друг другу, значит наше решение верное.
Ответ: x = 10, y = 5
Сложение одного уравнения с другим
Уравнения можно не только вычитать друг из друга, но и складывать.
Например:
{
5x + 3y = 71
2x + 4y = 48
Если мы просуммируем оба уравнения, то у нас в правой части у неизвестных x и y будут одинаковые коэффициенты 7 — нам будет удобно на эту 7 поделить, чтобы оставить x и y без коэффициентов.
Сложим два уравнения:
5x + 3y + 2x + 4y = 48 + 71
7x + 7y = 119
x + y = 17
x = 17 — y
Подставим x во второе уравнение:
2x + 4y = 48
Сначала разделим обе части уравнения на 2
x + 2y = 24
Подставим x:
17 — y + 2y = 24
y = 24 — 17
y = 7
x = 17 — y
x = 17 — 7 = 10
Ответ: x = 10, y = 7
Пример 1
{
2n + 3m = 19
3n – m = 12
Выразим m через n во втором уравнении:
3n – m = 12
3n – 12 = m
m = 3n – 12
Подставим 3n – 12 вместо m в первое уравнение
2n + 3m = 19
2n + 3(3n – 12) = 19
2n + 9n – 36 = 19
11n = 55
n = 5
Мы нашли n, теперь найдём m
m = 3n – 12
m = 3∙5 – 12
m = 3
Проверка решения:
2∙5 + 3∙3 = 19
3∙5 – 3 = 12
Ответ: m=3, n = 5
Пример 2
{
2x – 4y = 12
13x + 6y = 142
2x – 4y = 12
x – 2y = 6
x = 6 + 2y
13x + 6y = 142
13(6 + 2y) + 6y = 142
78 + 26y + 6y = 142
32y = 64
y = 2
x = 6 + 2y
x = 6 + 2∙2 = 10
Проверка:
2∙10 – 4∙2 = 12
13∙10 + 6∙2 = 142
Ответ: x = 10, y = 2
Пример 3
{
2x + 3y = 117
8x – 2y = 34
8x – 2y = 34
Разделим левую и правую части уравнения на 2:
4x – y = 17
4x – 17 = y
Теперь в первое уравнение вместо y подставим 4x-17:
2x + 3y = 117
2x + 3(4x – 17) = 117
2x + 12x – 51 = 117
14x = 117+51
14x = 168
x = 12
y = 4x – 17
y = 4∙12 – 17
y = 31
Ответ: x = 12, y = 31
ВИДЕОКУРС 2plus2. online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример 4
{
2x + 3y – 2z = 19
3x – 2y + 3z = 69
4z + y – x = 97
Мы имеем дело с системой уравнений, где три уравнения и три неизвестных.
Нас это не должно пугать. Для начала выразим одну неизвестную через две других, например, x через z и y. Так как в третьем уравнении у нас возле x нет никакого множителя, то именно через третье уравнение мы и будем выражать x.
4z + y – x = 97
4z + y – 97 = x
x = 4z + y – 97
Теперь подставим полученное выражение для x во второе уравнение.
3x – 2y + 3z = 69
3(4z + y – 97) – 2y + 3z = 69
12z + 3y – 291 – 2y + 3z = 69
15z + y = 360
y = 360 — 15z
Ранее мы выразили x через z и y:
x = 4z + y – 97
Теперь полученное выражение для y (y = 360 — 15z) подставим в это выражение для x
x = 4z + 360 – 15z – 97
x + 15z – 4z = 263
x + 11z = 263
x = 263 – 11z
Итак, теперь у нас есть x, выраженный через z, и y, выраженный через z.
Запишем эти выражение ещё раз:
x = 263 – 11z
y = 360 – 15z
Теперь мы можем эти выражения подставить в первое уравнение системы, и у нас получится уравнение с одним неизвестным — z
2x + 3y – 2z = 19
2(263 – 11z) + 3(360 – 15z) — 2z = 19
526 – 22z + 1080 – 45z – 2z = 19
526 + 1080 – 19 = 2z + 45z + 22z
1587 = 69z
z = 23
Теперь подставим z в выражения для x и y:
x = 263 – 11z = 263 – 11∙23 = 10
y = 360 – 15z = 360 – 15∙23 = 15
x = 10
y = 15
z = 23
Проверка:
2∙10 + 3∙15 – 2∙23 = 19
3∙10 – 2∙15 + 3∙23 = 69
4∙23 + 15 – 10 = 97
Ответ: x = 10, y = 15, z = 23
Пример 5
{
5x — z = 17
3x – 2y + 3z = 11
2x + 8y – 6z = 30
Эта система уравнений отличается от предыдущих тем, что в первом уравнении тут не три
неизвестных, а два. Но нас это не должно пугать — наоборот, нам это только упрощает задачу.
Но нас это не должно пугать — наоборот, нам это только упрощает задачу.
Выразим z через x в первом уравнении:
5x – z = 17
5x – 17 = z
z = 5x – 17
Подставим полученное выражение для z во второе уравнение.
3x – 2y + 3z = 11
3x – 2y + 3(5x – 17) = 11
3x – 2y + 15x – 51 = 11
18x – 2y = 62
9x – y = 31
9x – 31 = y
y = 9x – 31
Итак, теперь у нас есть z и y, выраженные через x. Запишем их ещё раз:
z = 5x – 17
y = 9x – 31
Теперь подставим эти выражения в третье уравнение
2x + 8y – 6z = 30
2x + 8(9x – 31) – 6(5x – 17) = 30
2x + 72x – 248 – 30x + 102 = 30
44x = 30 + 248 – 102
44x = 176
x = 4
Мы нашли x, теперь найдём z и y
z = 5x — 17
z = 5∙4 – 17 = 3
y = 9x – 31
y = 9∙4 – 31 = 5
x = 4
y = 5
z = 3
Проверка:
2∙4 + 8∙5 – 6∙3 = 30
3∙4 – 2∙5 + 3∙3 = 11
5∙4 – 3 = 17
Ответ: x = 4, y = 5, z = 3
ВИДЕОКУРС 2plus2. online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
Пример 6
{
4x + 3y = 61
4x + 5y = 75
Тут мы не можем выразить ни x, ни y, т.к. левая и правая части уравнений не делятся на цело и на 3, и на 4, ни на 5.
Поэтому воспользуемся описанным ранее способом — вычитанием частей уравнений друг из друга. Вычтем из второго уравнения первое:
4x + 5y – (4x + 3y) = 75 – 61
4x + 5y – 4x – 3y = 14
2y = 14
y = 7
Найденный y подставим в первое уравнение:
4x + 3∙7 = 61
4x + 21 = 61
4x = 40
x = 10
x = 10
y = 7
Проверка:
4∙10 + 3∙7 = 61
4∙10 + 5∙7 = 75
40 + 21 = 61
40 + 35 = 75
Ответ: x = 10, y = 7
Пример 7
{
2x + 5y = 50
3x + 7y = 71
Эту систему уравнений можно решить двумя способами.
Первый способ
Вычтем из второго уравнение первое.
3x + 7y – (2x + 5y) = 71 – 50
3x + 7y – 2x – 5y = 21
x + 2y = 21
x = 21 – 2y
Подставим выражение для x в первое уравнение.
2(21 – 2y) + 5y = 50
42 – 4y + 5y = 50
y = 8
Подставим найденный y в выражение для x
x = 21 – 2y
x = 21 – 2∙8 = 21 – 16 = 5
Проверка:
2∙5 + 5∙8 = 50
3∙5 + 7∙8 = 71
10 + 40 = 50
15 + 56 = 71
Второй способ
{
2x + 5y = 50
3x + 7y = 71
Умножим обе части первого уравнения на 3, а обе части второго уравнения на 2.
Тем самым мы в обеих уравнениях получим множитель 6 у x, после чего при вычитании одного
уравнения из другого x у нас уйдёт (6x — 6x = 0), и останется только y.
3(2x + 5y) = 3∙50
2(3x + 7y) = 2∙71
6x + 15y = 150
6x + 14y = 142
Вычтем из первого уравнения второе.
6x + 15y – (6x + 14y) = 150 – 142
6x + 15y – 6x – 14y = 8
y = 8
Подставим найденный y в первое уравнение системы:
2x + 5y = 50
2x + 5∙8 = 50
2x + 40 = 50
2x = 50 – 40
2x = 10
x = 5
В этой системе уравнений мы применили такой приём, как умножение обеих уравнений на разные числа так, чтобы у одного из неизвестных (в нашем случае у x) в обеих уравнениях оказался один и тот же множитель. После этого мы вычли одно уравнение из другого, x у нас исчез, и мы легко смогли найти y.
Ответ: x = 5, y = 8
Решение пропорций
Этот урок посвящен решению пропорций с использованием перекрестного произведения для поиска неизвестных членов.
Мы также покажем некоторые принципы, специальные приемы или сокращения, которые можно использовать для быстрого решения пропорции.
Термины, которые необходимо знать:
x, y или любая другая буква используется для обозначения неизвестного числа.
Неизвестный термин: Отсутствующее или неизвестное число в пропорции.
В уроке о пропорциях мы видели, что мы можем использовать перекрестное произведение, чтобы определить, являются ли дроби или отношения пропорциями.
Перекрестные произведения также можно использовать для нахождения неизвестного члена в пропорции. Вот как!
Если а / б «=» | с / д тогда a × d = b × c |
Если а / б «=» | с / д тогда a × d = b × c |
Проиллюстрируем это парой примеров.
Пример №1:
Найдите х, если 5 / х | «=» 10 / 16 |
Поскольку эти две дроби или отношения находятся в пропорциях, мы знаем, что перекрестный продукт должен быть равен.
Используя векторное произведение, мы получаем:
5 × 16 = x × 10
80 = 10x
Если вы знаете свою таблицу умножения, вы можете быстро получить ответ.
Если 10 × х = 80, то х должно быть равно 8, потому что 10 × 8 равно 80.
х = 8
Пропорция становится 5 / 8 | «=» 10 / 16 |
Обратите внимание, что 5 × 16 = 8 × 10 = 80
Вы также можете разбить задачу на несколько шагов, если хотите, как показано ниже:
Первое векторное произведение: 5 × 16 = 80
Второе векторное произведение: 10 × x
Приравняв векторные произведения, мы получим:
10 × х = 80
Есть более быстрый способ получить ответ при решении пропорций. Посмотрите еще раз на пропорцию:
«=» 10 / 16 |
Обратите внимание: чтобы получить 10, нужно 5 умножить на 2. Точно так же, чтобы получить 16, нужно что-то или число умножить на 2. Какое число, умноженное на 2, даст вам 16? Без сомнения, это 8!
Точно так же, чтобы получить 16, нужно что-то или число умножить на 2. Какое число, умноженное на 2, даст вам 16? Без сомнения, это 8!
Пример №2:
Решите для n, если 8 / 10 | «=» нет / 25 |
Используя векторное произведение, мы получаем:
8 × 25 = 10 × n
200 = 10n
Вместо того, чтобы спрашивать себя «10 умножить на то, что равно 200?», мы на этот раз решим уравнение, чтобы показать вы другой способ получить n.
Разделите обе стороны на 10
200 / 10 | «=» 10н / 10 |
200 разделить на 10 равно 20, а 10 разделить на 10 равно 1
20 = 1n
20 = n
Полезные эквивалентные пропорции, которые можно использовать при решении пропорций.

Принцип №1:
Если а / б | «=» с / д затем, | а + б / б | «=» в + г / д |
Доказательство:
Добавьте 1 к обеим частям уравнения и выполните математические действия, как показано:
х — 8 / 8
«=»
6 / 4
Приведенное выше уравнение становится
х — 8 + 8 / 8 | «=» 6 + 4 / 4 |
или
«=» 10 / 4 |
Приведенное выше, конечно, намного проще решить
Принцип №2:
Если х / г | «=» х / 4 тогда у = 4 |
Например, если 50 / г | «=» 50 / 100 тогда у = 100 |
Если 18 / г | «=» х / у тогда х = 18 |
Принцип №3:
Если а / б | «=» с / д затем, | а + в / б + д | «=» а / б |
а + в / б + д | «=» а / б |
Почему принцип №3 полезен при решении пропорций?
Скажи, что у тебя есть х + 2 / 8 + 4 | «=» х / 8 |
Это эквивалентно х / 8 | «=» 2 / 4 |
Опять же последний формат имеет дружественный вид и решается быстрее.
Просто помните эти 3 принципа при решении пропорций, и это облегчит вам упражнение с пропорциями. Спасибо за прочтение!
Спасибо за прочтение!
Проиллюстрируем это парой примеров.
Пример №1:
Найдите х, если 5 / х | «=» 10 / 16 |
Поскольку эти две дроби или отношения находятся в пропорциях, мы знаем, что перекрестное произведение должно быть равно.
Используя векторное произведение, мы получаем:
5 × 16 = x × 10
80 = 10x
Если вы знаете свою таблицу умножения, вы можете быстро получить ответ.
Если 10 × x = 80, то x должно быть равно 8, потому что 10 × 8 равно 80.
x = 8
Пропорция становится 5 / 8 | «=» 10 / 16 |
Обратите внимание, что 5 × 16 = 8 × 10 = 80
Вы также можете разбить проблему на несколько шагов, если хотите, как показано ниже:
Первое векторное произведение: 5 × 16 = 80
Второе векторное произведение: 10 × x
Приравняв векторные произведения, мы получим:
10 × x = 80
Есть более быстрый способ получить ответ, когда решение пропорций. Посмотрите еще раз на пропорцию:
Посмотрите еще раз на пропорцию:
«=» 10 / 16 |
Обратите внимание: чтобы получить 10, нужно 5 умножить на 2. Точно так же, чтобы получить 16, нужно что-то или число умножить на 2. Какое число, умноженное на 2, даст вам 16? Без сомнения, это 8!
Пример #2:
Решите для n, если 8 / 10 | «=» нет / 25 |
Используя векторное произведение, мы получаем:
8 × 25 = 10 × n
200 = 10n
Вместо того, чтобы спрашивать себя «10 умножить на то, что равно 200?», мы на этот раз решим уравнение, чтобы показать есть другой способ получить n
Разделите обе части на 10
200 / 10 | «=» 10н / 10 |
200 разделить на 10 равно 20, а 10 разделить на 10 равно 1 3
Принцип №1:
Если а / б | «=» с / д затем, | а + б / б | «=» в + г / д |
Доказательство:
Добавьте 1 к обеим частям уравнения и выполните математические действия, как показано:
х — 8 / 8
«=»
6 / 4
Приведенное выше уравнение становится
х — 8 + 8 / 8 | «=» 6 + 4 / 4 |
Или
«=» 10 / 4 |
Приведенное выше, конечно, намного проще решить
Принцип №2:
Если х / г | «=» х / 4 тогда у = 4 |
Например,
Если 50 / г | «=» 50 / 100 тогда у = 100 |
Если 18 / г | «=» х / у тогда х = 18 |
Принцип №3:
Если а / б | «=» с / д затем, | а + в / б + д | «=» а / б | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а + в / б + д | «=» а / б |
Почему принцип №3 полезен при решении пропорций?
Скажи, что у тебя есть х + 2 / 8 + 4 | «=» х / 8 |
Это эквивалентно х / 8 | «=» 2 / 4 |
Опять же последний формат имеет дружественный вид и решается быстрее.
Просто помните эти 3 принципа при решении пропорций, и это облегчит вам упражнение на пропорции. Спасибо, что прочитали
Спасибо, что прочитали
Решение викторины пропорций. Сможете ли вы пройти этот тест на 100%?
Треугольник 45-45-90
01, 23 мая 07:00
Что такое треугольник 45-45-90? Определение, доказательство, площадь и простые примеры из реальной жизни.
Подробнее
Теоретическая вероятность — определение, объяснение и примеры
24, 23 апреля 07:02
Узнайте, как вычислить правдоподобие или вероятность события с помощью формулы теоретической вероятности.
Подробнее
Решение пропорций и их применение
В этом разделе рассматриваются следующие темы:
- Использование определения пропорции
- Решение пропорций
- Решение приложений с использованием пропорций
- Запись процентных уравнений в виде пропорций
- Преобразование и решение процентных пропорций
 Когда два соотношения или скорости равны, уравнение, связывающее их, называется пропорцией . ПРОПОРЦИЯ
Когда два соотношения или скорости равны, уравнение, связывающее их, называется пропорцией . ПРОПОРЦИЯ Пропорция – это уравнение вида $\frac{a}{b} = \frac{c}{d}$, где $b \neq 0, d \neq 0$.
Пропорция указывает, что два соотношения или скорости равны. Пропорция читается как «$a$ к $b$, как $c$ к $d$».
Уравнение $\frac{1}{2} = \frac{4}{8}$ является пропорцией, поскольку две дроби равны. Пропорция $\frac{1}{2} = \frac{4}{8}$ читается как «$1$ к $2$, как $4$ к $8$».
Если мы сравниваем количества с единицами, мы должны быть уверены, что сравниваем их в правильном порядке. Например, в пропорции $\frac{20\ \mathrm{студенты}}{1\ \mathrm{учитель}} = \frac{60\ \mathrm{студенты}}{3\ \mathrm{учителя}}$ мы сравните количество учеников с количеством учителей. Ставим учеников в числители, а учителей в знаменатели.
Пример 1Напишите каждое предложение в виде пропорции:
- 3$ к 7$, как 15$ к 35$.

- $5$ попаданий в летучих мышах за $8$ равносильно попаданию $30$ в летучих мышей за $48$.
- $ \$1,50$ за 6$ унций эквивалентно $\$2,25$ за 9$ унций.
| Часть 1. | |
| От 3$ до 7$, а от 15$ до 35$. | |
| Напишите в виде пропорции. | $\frac{3}{7} = \frac{15}{ 35}$ |
| Часть 2. | $5$ попадает в $8$ у летучих мышей то же самое, что $30$ ударов в летучих мышах за $48$. |
| Запишите каждую дробь для сравнения попаданий с летучими мышами. | $\frac{\mathrm{hits}}{\mathrm{at-bats}} = \frac{\mathrm{hits}}{\mathrm{at-bats}}$ |
| Запишите в виде пропорции. | $\frac{5}{8} = \frac{30}{ 48}$ |
| Часть 3. | |
$ \$1,50$ за $6$ унций эквивалентно $\$2. 25$ за 9$ унций. 25$ за 9$ унций. | |
| Напишите каждую дробь, чтобы сравнить доллары с унциями. | $\frac{$}{\mathrm{унции}} = \frac{$}{\mathrm{унции}}$ |
| Запишите в виде пропорции. | $\frac{1.50}{6} = \frac{2.25}{ 9}$ |
Посмотрите на соотношение $\frac{1}{2} = \frac{4}{8}$ и $\frac{2}{3} = \frac{6}{9}$. Из нашей работы с эквивалентными дробями мы знаем, что эти уравнения верны. Но как узнать, является ли уравнение пропорцией с эквивалентными дробями, если оно содержит дроби с большими числами?
Чтобы определить, верна ли пропорция, мы находим перекрестных произведения каждой пропорции. Чтобы найти перекрестные произведения, мы умножаем каждый знаменатель на противоположный числитель (по диагонали через знак равенства). Результаты называются перекрестными произведениями из-за образовавшегося перекрестия. Взаимные произведения пропорции равны.
ПЕРЕКРЕСТНЫЕ ПРОИЗВЕДЕНИЯ ПРОПОРЦИИ Для любой пропорции вида $\frac{a}{b} = \frac{c}{d}$, где $b \neq 0, d \neq 0$, его перекрестные произведения равны.
Перекрестные произведения можно использовать для проверки правильности пропорции. Чтобы проверить, составляет ли уравнение пропорцию, мы находим перекрестные произведения. Если они равны, мы имеем пропорцию.
Пример 2Определить, является ли каждое уравнение пропорцией:
- $\frac{4}{9} = \frac{12}{28}$
- $\frac{17.5}{37.5} = \frac{7}{15}$
| Часть 1. | |
| $\frac{4}{9} = \frac{12}{28}$ | |
| Найдите перекрестные произведения. | $28 \cdot 4 = 112$ и $9 \cdot 12 =108$ |
Поскольку перекрестные произведения не равны, $28 \cdot 4 \neq 9 \cdot 12$, уравнение не является пропорцией.
| Часть 2. | ||
| . | $15 \cdot 17,5 = 262,5$ и $37,5 \cdot 7 =262,5$ |
Поскольку перекрестные произведения равны, $15 \cdot 17,5 = 37,5 \cdot 7$, уравнение является пропорцией.
Чтобы решить пропорцию, содержащую переменную, мы помним, что пропорция представляет собой уравнение. Все методы, которые мы использовали до сих пор для решения уравнений, все еще применимы. В следующем примере мы решим пропорцию путем умножения на наименьший общий знаменатель (НОД), используя свойство равенства умножения.
Пример 3Решите: $\frac{x}{63} = \frac{4}{7}$.
Решение| $\frac{x}{63} = \frac{4}{7}$ | |
| Чтобы изолировать $x$, умножьте обе части на LCD, $63$. | $63( \frac{x}{63} ) = 63( \frac{4}{7} )$ |
| Упростить. | $x= \frac{9 \cdot \cancel{7} \cdot 4}{\cancel{7}}$ |
| Разделите общие делители. | $x=36$ |
| Проверка: Чтобы проверить наш ответ, подставляем в исходную пропорцию. | |
| $\frac{x}{63} = \frac{4}{7}$ | |
| Подставить $x=36$ | $\frac{x}{63} \stackrel{? }{=} \frac{4}{7}$ |
Показать общие множители. | $\frac{4 \cdot 9}{7 \cdot 9} \stackrel{?}{=} \frac{4}{7}$ |
| Упростить. | $\frac{4}{7} = \frac{4}{7}$✓ |
Когда переменная находится в знаменателе, мы будем использовать тот факт, что перекрестные произведения пропорциональности равны, чтобы решить пропорции.
Мы можем найти перекрестные произведения пропорции и приравнять их. Затем мы решаем полученное уравнение, используя наши знакомые методы.
Пример 4Решите: $\frac{144}{a} = \frac{9}{4}$.
Решение Обратите внимание, что переменная находится в знаменателе, поэтому мы будем решать, находя перекрестные произведения и приравнивая их.
| Найдите перекрестные произведения и приравняйте их. | $4 \cdot 144 = a \cdot 9$ |
| Упрощение. | $576=9a$ |
| Разделите обе части на $9$. | $\frac{576}{9} = \frac{9a}{9}$ |
| Упростить. | $64=a$ |
| Проверьте свой ответ. | |
| $\frac{144}{a} = \frac{9}{4}$ | |
| Подставить $a=64$ | $\frac{144}{64} \stackrel{? }{=} \frac{9}{4}$ |
| Показать общие множители. | $\frac{9 \cdot 16}{4 \cdot 16} \stackrel{?}{=} \frac{9}{4}$ |
| Упростить. | $\frac{9}{4} = \frac{9}{4}$✓ |
Другим способом решения этой проблемы может быть умножение обеих сторон на LCD, $4a$. Попробуйте и убедитесь, что вы получили такое же решение.
Пример 5 Решите: $\frac{52}{91} = \frac{-4}{y}$.
| Найдите перекрестные произведения и приравняйте их. | |
| $y \cdot 52 = 91(-4)$ | |
| Упростить. | $52y=-364$ |
| Разделите обе части на $52$. | $\frac{52y}{52} = \frac{-364}{52}$ |
| Упростить. | $y=-7$ |
| Чек. | |
| $\frac{52}{91} = \frac{-4}{y}$ | |
| Замена $a=-7$ | $\frac{52}{91} \stackrel {?}{=} \frac{-4}{-7}$ |
| Показать общие факторы. | $\frac{4 \cdot 13}{7 \cdot 13} \stackrel{?}{=} \frac{-4}{-7}$ |
| Упростить. | $ \ frac {4} {7} = \ frac {4} {7} $ ✓ |
 5.3. в этой главе также работает для пропорций, так как пропорции являются уравнениями. Когда мы устанавливаем пропорцию, мы должны убедиться, что единицы измерения правильные — единицы в числителях совпадают, а единицы в знаменателях совпадают. Пример 6
5.3. в этой главе также работает для пропорций, так как пропорции являются уравнениями. Когда мы устанавливаем пропорцию, мы должны убедиться, что единицы измерения правильные — единицы в числителях совпадают, а единицы в знаменателях совпадают. Пример 6 Когда педиатры назначают детям ацетаминофен, они назначают 5 долларов США миллилитров (мл) ацетаминофена на каждые 25 долларов США фунтов веса ребенка. Если Зоя весит 80 фунтов, сколько миллилитров ацетаминофена пропишет ее врач?
Решение| Определите, что вас просят найти. | Сколько мл ацетаминофена выпишет врач |
| Выберите переменную для ее представления. | Пусть $a=$ мл ацетаминофена. |
| Напишите предложение, которое дает информацию, чтобы найти его. | Если 5$ мл прописано за каждые 25$ фунтов, сколько будет прописано за 80$ фунтов? |
| Перевести в пропорцию. | $\frac{\mathrm{ml}}{\mathrm{pounds}} = \frac{\mathrm{ml}}{\mathrm{pounds}}$ |
Подставьте указанные значения — будьте осторожны с единицами измерения . | $\frac{5}{25} = \frac{a}{80}$ |
| Умножьте обе стороны на 80$. | $80 \cdot \frac{5}{25} = 80 \cdot \frac{a}{80}$ |
| Умножьте и покажите общие множители. | $\frac{16 \cdot 5 \cdot 5}{5 \cdot 5} = \frac{80a}{80}$ |
| Упростить. | $16=a$ |
| Проверьте правильность ответа. | |
| Да. Поскольку 80 долларов — это примерно 3 доллара, умноженные на 25 долларов, стоимость лекарства должна быть примерно 3 доллара, умноженная на 5 долларов. | |
| Напишите полное предложение. | Педиатр пропишет Зои 16$ мл ацетаминофена. |
Вы также можете решить эту пропорцию, приравняв перекрестные произведения.
Пример 7Порция попкорна одной марки содержит 120 долларов США калорий. Целый пакет этого попкорна стоит 3,5 $ порции. Сколько калорий в целом пакете этого попкорна для микроволновки?
Решение Определите, что вас просят найти. | Сколько калорий в целом пакете попкорна для микроволновки? |
| Выберите переменную для ее представления. | Пусть $c=$ количество калорий. |
| Напишите предложение, которое дает информацию, чтобы найти его. | Если на порцию приходится 120$ калорий, то сколько калорий содержится в целой упаковке с порцией по 3,5$? |
| Перевести в пропорцию. | $\frac{\mathrm{калории}}{\mathrm{порция}} = \frac{\mathrm{калории}}{\mathrm{порция}}$ |
| Подставьте указанные значения. | $\frac{120}{1} = \frac{c}{3.5}$ |
| Умножьте обе части на $3,5$. | $(3.5)( \frac{120}{1} ) = (3.5) ( \frac{c}{3.5} )$ |
| Умножить. | $420=c$ |
| Проверьте правильность ответа. | |
| Да. Поскольку 3,5$ составляет от 3$ до 4$, общее количество калорий должно составлять от 360$ (3 \cdot 120)$ до 480$ (4 \cdot 120 )$. | |
Напишите полное предложение. | Весь пакет попкорна для микроволновки содержит 420$ калорий. |
Джозайя поехал в Мексику на весенние каникулы и обменял $\$325$ долларов на мексиканские песо. В то время обменный курс $\$1$ США был равен 12,54$ мексиканских песо. Сколько мексиканских песо он получил за поездку?
Решение| Определите, что вас просят найти. | Сколько мексиканских песо получил Иосия? |
| Выберите переменную для ее представления. | Пусть $p=$ количество песо. |
| Напишите предложение, которое дает информацию, чтобы найти его. | Если $ \$1$ США равен $12,54$ мексиканских песо, тогда $\$325$ сколько песо? |
| Перевести в пропорцию. | $\frac{$}{\mathrm{pesos}} = \frac{$}{\mathrm{pesos}}$ |
| Подставьте указанные значения. | $\frac{1}{12,54} = \frac{325}{p}$ |
Переменная стоит в знаменателе, поэтому найдите перекрестные произведения и приравняйте их. | $p \cdot 1 = 12,54(325)$ |
| Упростить. | $c=4 075,5$ |
| Проверить правильность ответа. | |
| Да. $ \ $ 100 $ будет $ \ $ 1,254 $ песо. $ \$325$ чуть более чем в 3$ раза превышает эту сумму. | |
| Напишите полное предложение. | У Джозайи есть 4 075,5 песо на поездку на весенние каникулы. |
Ранее мы решали процентные уравнения, применяя свойства равенства, которые мы использовали для решения уравнений в этом тексте. Некоторые люди предпочитают решать процентные уравнения, используя метод пропорций. Метод пропорций для решения процентных задач предполагает процентную пропорцию. Пропорция процентов – это уравнение, в котором процент равен эквивалентному отношению.
Например, $60 \% = \frac{60}{100}$, и мы можем упростить $\frac{60}{100} = \frac{3}{5}$. Поскольку уравнение $\frac{60}{100} = \frac{3}{5}$ показывает процент, равный эквивалентному отношению, мы называем его пропорцией процентов . Используя словарь, который мы использовали ранее:
Поскольку уравнение $\frac{60}{100} = \frac{3}{5}$ показывает процент, равный эквивалентному отношению, мы называем его пропорцией процентов . Используя словарь, который мы использовали ранее:
$\large \frac{\mathrm{amount}}{\mathrm{base}} = \frac{\mathrm{percent}}{100}$
$\large \frac{ 3}{5} = \frac{60}{100}$
ПРОЦЕНТНАЯ ПРОПОРЦИЯСумма указана к основанию, так как процент равен 100$.
$\large \frac{\mathrm{amount}}{\mathrm{base}} = \frac{\mathrm{percent}}{100}$
Если мы переформулируем задачу словами пропорции, она может быть проще настроить пропорцию:
𝑇ℎ𝑒 𝑎𝑚𝑜𝑢𝑛𝑡 𝑖𝑠 𝑡𝑜 𝑡ℎ𝑒 𝑏𝑎𝑠𝑒 𝑎𝑠 𝑡ℎ 𝑒 𝑝𝑒𝑟𝑐𝑒𝑛𝑡 𝑖𝑠 𝑡𝑜 𝑜𝑛𝑒 ℎ𝑢𝑛𝑑𝑟𝑒𝑑.
Мы могли бы также сказать:
𝑇ℎ𝑒 𝑎𝑚𝑜𝑢𝑛𝑡 𝑜𝑢𝑡 𝑜𝑓 𝑡ℎ𝑒 𝑏𝑎𝑠𝑒 𝑖 𝑠 𝑡ℎ𝑒 𝑠𝑎𝑚𝑒 𝑎𝑠 𝑡ℎ𝑒 𝑝𝑒𝑟𝑐𝑒𝑛𝑡 𝑜𝑢𝑡 𝑜𝑓 𝑜𝑛𝑒 ℎ 𝑢𝑛𝑑𝑟𝑒𝑑.
Сначала потренируемся переводить в процентную пропорцию. Позже решим пропорцию.
Пример 9 Преобразование в пропорцию. Какое число равно $75\%$ от $90$?
Какое число равно $75\%$ от $90$?
Если вы ищете слово «из», это может помочь вам определить основу.
| Определите части процентной доли. | |
| Пересчитайте в виде пропорции. | Какое число из 90$ совпадает с 75$ из 100$? |
| Установите пропорцию. Пусть $n=$ число. | $\frac{n}{90} = \frac{75}{100}$ |
Преобразование в пропорцию. $19$ равно $25\%$ от какого числа?
Решение| Определите части процентной доли. | |
| Пересчитайте в виде пропорции. | 19$ из какого числа равно 25$ из 100$? |
| Установите пропорцию. Пусть $n=$ число. | $\фракция{19}{n} = \frac{25}{100}$ |
Преобразование в пропорцию. Какой процент от 27$ составляет 9$?
Решение Определите части процентной доли. | |
| Пересчитайте в виде пропорции. | 9$ из 27$ равно какому числу из 100$? |
| Установите пропорцию. Пусть $p=$ процентов. | $\frac{9}{27} = \frac{p}{100}$ |
Теперь, когда мы записали уравнения процентов в виде пропорций, мы готовы решать уравнения.
Пример 12Переведите и решите, используя пропорции: Какое число составляет $45\%$ от $80$?
Решение| Определите части процентной доли. | |
| Пересчитайте в виде пропорции. | Какое число из 80$ совпадает с 45$ из 100$? |
| Установите пропорцию. Пусть $n=$ число. | $\frac{n}{80} = \frac{45}{100}$ |
| Найдите перекрестные произведения и приравняйте их. | 100$ \cdot n = 80 \cdot 45$ |
Упростить. | 100$n=3600$ |
| Разделите обе части на 100$. | $\frac{100n}{100} = \frac{3,600}{100}$ |
| Упростить. | $n=36$ |
| Проверить правильность ответа. | |
| Да. 45 долларов — это чуть меньше половины от 100 долларов, а 36 долларов — чуть меньше половины 80 долларов. | |
| Напишите полное предложение, отвечающее на вопрос. | $36$ равно $45\%$ 0f $80$. |
В следующем примере процент превышает 100 долл. США, что составляет более одного целого. Значит, неизвестное число будет больше основания.
Пример 13Переведите и решите, используя пропорции: 125$ \%$ от 25$ это какое число?
Решение| Определите части процентной доли. | |
| Пересчитайте в виде пропорции. | Какое число из 25$ равно 125$ из 100$? |
Установите пропорцию. Пусть $n=$ число. Пусть $n=$ число. | $\frac{n}{25} = \frac{125}{100}$ |
| Найдите перекрестные произведения и приравняйте их. | 100$ \cdot n = 25 \cdot 125$ |
| Упростить. | 100$n=3125$ |
| Разделите обе части на 100$. | $\frac{100n}{100} = \frac{3,125}{100}$ |
| Упростить. | $n=31,25$ |
| Проверить правильность ответа. | |
| Да. 125$ больше 100$, а 31,25$ больше 25$. | |
| Напишите полное предложение, отвечающее на вопрос. | $125\%$ от $25$ составляет $31,25$. |
Проценты с десятичными знаками и деньгами также используются в пропорциях.
Пример 14Переведите и решите: $6,5 \%$ из какого числа $ \$1,56$?
Решение| Определите части процентной доли. | |
Пересчитайте в виде пропорции. | $ \$1,56$ из какого числа равно $6,5$ из $100$? |
| Установите пропорцию. Пусть $n=$ число. | $\frac{1.56}{n} = \frac{6.5}{100}$ |
| Найдите перекрестные произведения и приравняйте их. | 100$(1,56) = n \cdot 6,5$ |
| Упростить. | $156=6,5n$ |
| Разделите обе части на $6,5$, чтобы изолировать переменную. | $\frac{156}{6,5} = \frac{6,5n}{16,5}$ |
| Упростить. | $24=n$ |
| Проверить правильность ответа. | |
| Да. $6,5\%$ — это небольшая сумма, а $\$1,56$ намного меньше, чем $\$24$. | |
| Напишите полное предложение, отвечающее на вопрос. | $6,5\%$ от $\$24$ составляет $\$1,56$. |
Переведите и решите, используя пропорции: Сколько процентов от 72$ составляет 9$?
Решение Определите части процентной доли. | |
| Пересчитайте в виде пропорции. | 9$ из 72$ равно какому числу из 100$? |
| Установите пропорцию. Пусть $n=$ число. | $\frac{9}{72} = \frac{n}{100}$ |
| Найдите перекрестные произведения и приравняйте их. | 72$ \cdot n = 100 \cdot 9$ |
| Упростить. | 72$n=900$ |
| Разделите обе части на 72$. | $\frac{72n}{72} = \frac{900}{72}$ |
| Упростить. | $n=12,5$ |
| Проверить правильность ответа. | |
| Да. $9$ – это $\frac{1}{8}$ из $72$, а $\frac{1}{8}$ – $12,5 \%$. | |
| Напишите полное предложение, отвечающее на вопрос. | $12,5 \%$ от $72$ составляет $9$. |
CC Лицензионный контент, оригинал
- Пересмотр и адаптация.

Сдо миэп прометей: МИЭП ответы на тесты, курсовые, дипломные, ПТК
Как войти в личный кабинет МИЭП Прометей
На чтение: 3 минОбновлено: Автор: Максим Бондаренко
Международный институт экономики и права – один из негосударственных образовательных учреждений высшего образования Москвы, успешно работающий с 1992 года. МИЭП входит в число ведущих экономических ВУЗов не только столицы, но и всей России, готовя высококвалифицированных специалистов по различным направлениям.
Секрет успеха МИЭП кроется в собственной образовательной концепции, в которой соединяются классические системы с передовыми мировыми достижениями в сфере образования. Студенты ВУЗа могут получить специальность по таким направлениям, как экономика, менеджмент, юриспруденция, государственное и муниципальное управление.
Для студентов института создана система дистанционного обучения Прометей, предоставляющая доступ к учебным материалам и практикам в онлайн режиме.
 Для этого понадобится только оформление личного кабинета МИЭП Прометей.
Для этого понадобится только оформление личного кабинета МИЭП Прометей.Содержание
- Как зарегистрироваться
- Как войти
- Восстановление пароля
- Функционал личного кабинета
- Контактная информация для связи
Как зарегистрироваться
В 2021 году абитуриентам Международного института экономики и права предоставляется удобная возможность поступить в ВУЗ в онлайн режиме. Специально для этого создана виртуальная приемная комиссия.
Для этого абитуриентам нужно перейти на страницу https://miep.ru/postupit-v-miep/ и выбрать интересующий пункт – «Зарегистрироваться, отправить документы и поступить сейчас» или «Зарегистрироваться и пройти вступительные испытания». По любым вопросам поступления абитуриенты могут написать на электронную почту [email protected].
Студенты МИЭП могут зарегистрировать личный кабинет и получить доступ к системе дистанционного обучения:
- Откройте главную страницу сайта https://miep.ru/ и выберите вкладку «Вход в личный кабинет» на верхней панели.

- Выберите пункт «Регистрация» и заполните небольшую анкету.
- Напишите серию и номер паспорта.
- Укажите табельный номер или номер зачетной книжки.
- Введите адрес электронного почтового ящика – на него будет отправлено письмо с кодом для подтверждения регистрации аккаунта.
- Составьте уникальный пароль для учетной записи, состоящий как минимум из 6 символов и продублируйте его дважды.
- Подтвердите согласие с политикой обработки персональной информации.
- Кликните кнопку «Регистрация».
После этого на указанную почту будет отправлено письмо, подтверждающее создание учетной записи. Перейдите по ссылке из письма – на этом регистрация аккаунта МИЭП считается завершенной.
Как войти
Для входа в личный кабинет МИЭП Прометей перейдите на страницу http://sdo.miep.ru/client/items. Выберите тип своего аккаунта – для персонала или студента.
Во всплывшем окошке укажите имя пользователя и пароль, затем нажмите «Вход».
 После автоматической проверки введенных данных будет открыт доступ к учетной записи МИЭП.
После автоматической проверки введенных данных будет открыт доступ к учетной записи МИЭП.Восстановление пароля
Для восстановления пароля от личного аккаунта МИЭП перейдите на страницу http://portal.miep.ru/login и кликните вкладку «Забыли свой пароль».
Укажите в открывшейся форме свою электронную почту, привязанную к кабинету и нажмите «Выслать контрольную строку». Новые данные для входа в систему Прометей будут отправлены в электронном письме.
Функционал личного кабинета
Личный кабинет МИЭП Прометей открывает учащимся круглосуточный доступ к таким онлайн функциям:
- Онлайн доступ к полному курсу методических программ – текстовым, аудио- и видеоматериалам, конспектам лекций.
- Получение практических и тестовых работ.
- Просмотр расписания занятий.
- Контроль текущей и общей успеваемости.
- Доступ к электронной библиотеке института.
- Ведение онлайн переписки с преподавателями и другими студентами.
Зарегистрированные студенты могут онлайн оплатить образовательные услуги МИЭП.
 Это можно сделать на странице https://miep.ru/payment/, указав номер договора, сумму и свои персональные данные.
Это можно сделать на странице https://miep.ru/payment/, указав номер договора, сумму и свои персональные данные.Международный институт экономики и права расположен по адресу 105082, Москва, Рубцовская наб., д. 3, стр. 1.
Абитуриенты и студенты могут обратиться за помощью к представителям ВУЗа, позвонив по номеру 8-800-775-58-58 или написать на электронную почту [email protected].
МИЭП — Нахимова 21, Смоленск (3 отзыва, телефон и режим работы)
Контакты
Сохранить контакт
Редактировать
Ещё контакты
Информация предоставлена посетителями Добавить ещё
- МИЭП
- +7 910 722-49-64
- Дзержинского, 9А (2 этаж)
Контакты верны?
Добавить описание
Как доехать
Общественный транспорт Автомобиль Велосипед Пешком
FAQ
Вы можете позвонить по номеру +7 481 265-80-64
Смоленск, Нахимова, 21 (2 этаж). Ближайшие остановки общественного транспорта: «Фабрика «Шарм»» – 300 метров, «ГТС» – 450 метров
График работы такой: ПН: 09:00-17:30, ВТ: 09:00-17:30, СР: 09:00-17:30, ЧТ: 09:00-17:30, ПТ: 09:00-17:30. Это информация от посетителей страницы.
Супер! Пользователи оценили это место на 5 (3 голоса)
Режим работы
Пн 09:00 – 17:30 Перерыв 13:00 – 14:00 Вт 09:00 – 17:30 Перерыв 13:00 – 14:00 Ср 09:00 – 17:30 Перерыв 13:00 – 14:00 Чт 09:00 – 17:30 Перерыв 13:00 – 14:00 Пт 09:00 – 17:30 Перерыв 13:00 – 14:00 Сб Вс Время в Смоленске – 14:09
Вы можете позвонить по номеру +7 481 265-80-64 и уточнить режим работы
Ошибка
Ближайшие похожие места
Очень близко
ВСН-СМОЛ.
 инфо
инфо Рекламная группа
Нахимова, 21
Очень близко
Мир кровли
Торговая компания, ООО Техноресурс
Нахимова, 21
Очень близко
Регион-Запад-Перспектива
Агентство недвижимости
Нахимова, 21
Очень близко
СпецКомплектСервис
Оптовая компания
Нахимова, 21
Очень близко
Юридическое агентство
ИП Тарасенков А.В.
Нахимова, 21
1.7 км
Мир знаний
Институт дистанционного обучения
Кирова, 17
2 км
Смоленский областной институт развития образования
Октябрьской Революции, 20а
2.1 км
Международный юридический институт
Смоленский филиал
Октябрьской Революции, 9 К1
2.
 5 км
5 кмСмоленский институт бизнеса и предпринимательства
Гагарина проспект, 22а
2.8 км
Московский институт управления и права
Смоленский филиал
Памфилова, 5
3 км
Смоленский областной институт патологии
Гагарина проспект, 27 к1
3 км
МИГУП
Московский институт государственного управления и права Смоленской области
Ново-Московская, 2/8
3.3 км
МНЮИ
Московский новый юридический институт, Смоленский филиал
Крупской, 37
4 км
Смоленский государственный институт искусств
Румянцева, 8
4.7 км
СПбИВЭСЭП
Санкт-Петербургский институт внешнеэкономических связей, экономики и права, филиал в г.
 Смоленске
СмоленскеСоболева, 105а
3 отзыва
Регистрация не требуется
Дневник молодой девушки: персонажи и цитаты
Дневник молодой девушки (1947) — научно-популярный текст всемирно известной Анны Франк. Он состоит из дневников Анны, в которых подробно описаны ужасы жизни еврея в Европе во время Второй мировой войны.
Предупреждение о содержании: пояснение ниже содержит обсуждение Холокоста и антисемитских предрассудков.
Рис. 1 – Портрет Анны Франк в школе.
Анна Франк,
Дневник молодой девушки : краткое изложениеАнне Франк родители подарили дневник на свое тринадцатилетие 12 июня 1942 года и начала писать в нем. Энн признается, что всегда хотела иметь друга, которому могла бы довериться, и надеется, что этот дневник станет для нее таким. Она подробно описывает, что, хотя ее семья родом из Франкфурта в Германии, они переехали в Амстердам в Нидерландах, чтобы избежать преследований евреев в Германии.
 Даже в Нидерландах она и ее старшая сестра Марго должны посещать школу для еврейских учащихся.
Даже в Нидерландах она и ее старшая сестра Марго должны посещать школу для еврейских учащихся.Евреи подвергались преследованиям в Германии (и Европе в целом), поскольку Германия вторглась в новые страны из-за режима Адольфа Гитлера. У Гитлера был план, известный как «Окончательное решение». Он считал, что еврейский народ по своей природе неполноценен и опасен и должен быть истреблен. Он начал собирать евреев и отправлять их в лагеря, где их либо убивали в газовых камерах, либо работали до смерти.
Гитлер считал, что те, кого он называл «чистыми» белыми немцами, были расой господ. На протяжении 19В 30-х годах антиеврейские настроения постепенно формировались в Германии с помощью средств массовой информации, политики и образования. Этот темный и ужасающий период европейской истории известен как Холокост.
Сначала в дневнике Анны записан относительно нормальный подростковый возраст. Она пишет о школе, дружбе и мальчиках, которые ей интересны. Однако преследование евреев нацистами постепенно усиливается, и в ее произведения иногда закрадываются текущие события.
 Все меняется, когда эсэсовцы вызывают Марго явиться в нацистский трудовой лагерь.
Все меняется, когда эсэсовцы вызывают Марго явиться в нацистский трудовой лагерь.SS было сокращением от Schutzstaffel. Это была хорошо обученная военная группа, которая действовала как телохранители Гитлера. Во время Второй мировой войны СС стали известны своей огромной жестокостью по отношению к евреям.
Это просто другое название концлагеря . Франки знали, что теперь им грозит серьезная опасность, и скрылись.
Концлагеря стали символом Второй мировой войны. Это были большие лагеря, созданные и построенные нацистами для размещения, жестокого обращения и убийства любых групп людей, которых они считали нежелательными. В основном это были евреи, но были также цыгане, ЛГБТ+, коммунисты и политические критики нацистской партии.
Семья Франк укрылась в скрытой пристройке, которая была частью офисного здания компании Отто Франка, отца Анны. К ним присоединились друзья семьи мистер и миссис ван Даан, их сын-подросток Питер и знакомый Отто Франка Альфред Дюссель.
 Работники предприятия Отто Франка помогали тем, кто прятался в пристройке, принося им продукты и припасы.
Работники предприятия Отто Франка помогали тем, кто прятался в пристройке, принося им продукты и припасы.На личном уровне Анне Франк очень тяжело в Пристройке. Несмотря на ее сложные и уникальные обстоятельства, она все еще борется со взрослением, часто конфликтуя с другими людьми, с которыми она живет. Она самоуверенна и признает, что много говорит. Некоторым другим взрослым, особенно миссис ван Даан, это не нравится.
Энн взрослеет на протяжении всего текста. У нее первые месячные, и она начинает задумываться о вопросах сексуальности и идентичности. Она сближается с Питером, который изначально ее мало интересовал. У них развиваются романтические отношения. Энн надеется, что нашла кого-то, кому она действительно может довериться. Эта близость длится какое-то время, но в конце концов они расходятся, и Энн снова чувствует себя одинокой и изолированной.
Помимо этих типичных подростковых забот, Энн также сильно страдает из-за войны за пределами Приложения. Не только это, но и жители пристройки становятся все более раздраженными.
 Из-за совместного проживания в таких тесных помещениях происходит много столкновений. Анна также пишет о своих мыслях о том, как быть евреем в Европе в это неспокойное время. Она не может понять, почему ее сообщество так преследуется. Анна не знает, какой стране она на самом деле принадлежит, поскольку ее немецкое гражданство было аннулировано. Жители пристройки постепенно получают новости о том, как продвигается война, многие из которых угнетают их.
Из-за совместного проживания в таких тесных помещениях происходит много столкновений. Анна также пишет о своих мыслях о том, как быть евреем в Европе в это неспокойное время. Она не может понять, почему ее сообщество так преследуется. Анна не знает, какой стране она на самом деле принадлежит, поскольку ее немецкое гражданство было аннулировано. Жители пристройки постепенно получают новости о том, как продвигается война, многие из которых угнетают их.Семья Франк переехала в Амстердам в 1934 году, спасаясь от немецких преследований. Однако в 1940 году Амстердам тоже был захвачен нацистами, несмотря на статус Нидерландов как нейтральной страны в войне. Это сделало невозможным для франков покинуть страну или остаться в безопасности.
Кажется, дела идут лучше, поскольку военные усилия союзников продвигаются вперед. Энн также слышит, что дневники, подобные ее, написанные в это время, могут быть очень ценными после окончания войны. Это дает Энн надежду, и она решает, что хочет стать журналистом, когда станет старше.

«Союзники» — это страны, сражавшиеся против вторжения нацистской Германии в Европу во время Второй мировой войны. Группа состояла из Великобритании, Франции, Советского Союза, Америки и Китая.
Последняя запись в дневнике Анны Франк датирована 1 августа 1944 года. Она описывает относительно обычный день, в котором не происходит ничего экстраординарного. На этом ее письмо заканчивается. В послесловии читателям сообщается, что через несколько дней после ее последней записи семья Франк была предана СС и схвачена. Анну и Марго отправили в концлагерь Берген-Бельзен. Анна и Марго умерли от тифа весной 1945, всего за несколько недель до того, как солдаты союзников освободили лагерь.
Рис. 2. Считается, что надгробие Анны и Марго Франк находится в Берген-Бельзене.
Персонажи в
Дневник юной девушкиЭто главные персонажи Дневник юной девушки . Люди, живущие в пристройке, пережили невообразимые травмы во время Холокоста. Это часто приводило к межличностным столкновениям и спорам.

Важно помнить, что люди в дневниках Анны Франк не обязательно персонажи. Это были настоящие люди, которых Энн записала своими глазами.
Анна Франк
Анна Франк ведет эти дневники в первые годы своего подросткового возраста. Она умная и разговорчивая девушка со многими мнениями. Ее общительная сторона часто приводит к столкновениям с другими, живущими в Пристройке.
Энн любит писать и обладает глубоким творческим талантом. Находясь в бегах, она использует письмо как утешение, облегчая чувство одиночества. По мере развития Дневник молодой девушки Энн меняется. Большая часть ее произведений кажется зрелой не по годам, но это, вероятно, связано с ужасной ситуацией, в которой она оказалась. Энн была вынуждена повзрослеть, будучи еще очень молодой женщиной.
Марго Франк
Марго не фигурирует в дневниках Анны. Она старше Анны, которая считает ее довольно сложной. Марго также более сдержанна и корректна, чем ее младшая сестра. Она подчиняется общественным традициям поведения, ожидаемого от молодых девушек, гораздо больше, чем Энн.
 Энн также отмечает, что Марго очень красивая.
Энн также отмечает, что Марго очень красивая.Отто и Эдит Франк
У Анны очень разные отношения с матерью и отцом. Энн близка со своим отцом, которого она считает похожим на себя. Энн и Отто разделяют любовь к учебе. Отто — рассудительный и прагматичный человек, который следит за порядком в Пристройке. Он глубоко заботится о своих детях и делает для них все возможное, несмотря на обстоятельства. Энн также приписывает большую часть своей уверенности в себе влиянию отца. Они разделяют большую близость.
Отношения Энн и Эдит заметно отличаются. Они постоянно конфликтуют, и Энн обвиняет свою мать во многих из этих споров. Энн считает свою мать холодной и безразличной. Она часто пишет о ней довольно резко. Однако трудно понять, сколько в этом правды. Вполне возможно, что Энн была просто подростком в одной из самых напряженных ситуаций, которые только можно себе представить, и в результате набрасывалась.
Питер ван Даан
Питер — еще один молодой человек, переживший ужасы Холокоста.
 Он застенчив и невинен, часто находит убежище в ребячестве. Энн не нравятся в нем эти черты, и она мало обращает внимания на Питера, когда они впервые входят в пристройку. Через некоторое время у нее появляется к нему интерес, и у них завязываются романтические отношения. Это длится какое-то время, но в конце концов Энн понимает, что просто идеализировала Питера, поскольку он был единственной надеждой на роман, который у нее был.
Он застенчив и невинен, часто находит убежище в ребячестве. Энн не нравятся в нем эти черты, и она мало обращает внимания на Питера, когда они впервые входят в пристройку. Через некоторое время у нее появляется к нему интерес, и у них завязываются романтические отношения. Это длится какое-то время, но в конце концов Энн понимает, что просто идеализировала Питера, поскольку он был единственной надеждой на роман, который у нее был.Г-жа ван Даан, г-н ван Даан и Альфред Дюссель
Это трое других обитателей пристройки. Ван Дааны — родители Питера. Мистер ван Даан нечасто фигурирует в дневниках Анны. Он кажется относительно самоуверенным человеком, но у Энн с ним мало стычек. Однако ее отношения с миссис ван Даан совсем другие. Энн и миссис ван Даан, мягко говоря, не ладят. Миссис ван Даан — уверенная в себе женщина, которая не боится ссориться. У них с Эдит несколько столкновений. Миссис ван Даан также не одобряет болтливость и любознательность Анны. Ей также не нравится, насколько близки Энн и Питер на какое-то время.

Альфред Дюссель — дантист, который переезжает в пристройку позже других жителей. Энн не представляет его положительного изображения в своих дневниках. Эти двое вынуждены делить комнату, и Энн находит его властным и эгоистичным. В то время как между всеми в Пристройке есть трудности из-за их стрессовых обстоятельств, Альфред кажется действительно неприятным. Он даже копит еду, несмотря на то, что запасов для всех участников очень мало.
Рис. 3 — Дверь в здание, в котором находилась пристройка, ныне музей.
Дневник девушки : темаНиже приведены ключевые темы серии Дневник девушки . Однако важно помнить, что книга Анны Франк фиксирует реальные переживания человека, страдающего от бесчеловечного режима, и читатель должен подходить к ней именно так.
Дневник молодой девушки : взрослениеАнна Франк растет и взрослеет на протяжении своих дневников. Они охватывают критический период ее ранней юности, когда она впервые исследует свою личность и сексуальность.
 Она подробно описывает более невинные отношения, которые у нее были с мальчиками в молодости. Читатели могут увидеть, как это перерастает в более серьезное влечение, когда Энн размышляет о своих чувствах к Питеру в Приложении.
Она подробно описывает более невинные отношения, которые у нее были с мальчиками в молодости. Читатели могут увидеть, как это перерастает в более серьезное влечение, когда Энн размышляет о своих чувствах к Питеру в Приложении.Взросление Анны также связано с ее растущим пониманием проблем личности. Она уверена в своем еврействе и оплакивает огромные притеснения, с которыми она сталкивается из-за этого. Однако ее немецкая идентичность является для нее более сложным вопросом. Семья Франк — немка, но их лишили гражданства, потому что они евреи. Энн также называет Нидерланды своим домом, поскольку живет там, но многие голландцы отвернулись от евреев из-за войны.
Процесс взросления Энн тормозится, задерживается и в конце концов останавливается из-за окружающих обстоятельств. Пережить Холокост молодой еврейской девушкой в Европе было невообразимо трудным положением. Энн не может познать внешний мир, поскольку ее семья должна прятаться в пристройке. Это означает, что у Анны нет сверстников, с которыми она могла бы испытать свою молодую жизнь.
 Она также живет в состоянии постоянного страха, что позиция ее семьи будет раскрыта властям. Смерть Анны в трагически молодом возрасте — одна из многих молодых жизней, оборвавшихся из-за действий нацистов.
Она также живет в состоянии постоянного страха, что позиция ее семьи будет раскрыта властям. Смерть Анны в трагически молодом возрасте — одна из многих молодых жизней, оборвавшихся из-за действий нацистов.Я мечтаю кататься на велосипеде, танцевать, свистеть, смотреть на мир, чувствовать себя молодым и знать, что я свободен, но не могу показать этого. (декабрь 1943 г.)
Дневник девушки : войнаВойна и ее различные последствия занимают центральное место в дневниках Анны Франк. Пока семья Франк прячется в пристройке, вокруг них бушует Вторая мировая война. Они находятся в постоянной опасности и ведут психологически истощающее существование. Жители пристройки регулярно собираются у своего радиоприемника, чтобы послушать сводки новостей о том, как продвигается война. Позитивные действия немецких войск вселяют страх в сердца всех слушающих. Дневники Энн показывают, какие потери война наносит ей и ее семье. Бывают времена, когда они чувствуют себя совершенно безнадежно, но Энн постоянно удается восстановить чувство надежды на то, что однажды все они будут свободны.

Каждую ночь сотни самолетов пролетают над Голландией, направляясь в немецкие города, чтобы сбросить бомбы на немецкую землю. Каждый час в России и Африке убивают сотни, а может быть, и тысячи людей. Никто не может оставаться в стороне от конфликта, весь мир находится в состоянии войны, и хотя у союзников дела идут лучше, конца не видно. (Январь 1943 г.)
Предпосылка войны также влияет на тех, кто в Приложении, особенно на юную Энн. Они прячутся только потому, что они еврейский народ. Энн знает, что за пределами их убежища тысячи евреев подвергаются пыткам и убийствам без всякой причины. Она часто испытывает чувство чувство вины за то, что они оставались скрытыми, пока они так сильно страдают.
Рис. 4. Евреев арестовывают за пределами печально известного концлагеря Освенцим.
Анна Франк:
Дневник молодой девушкиАнна Франк погибла от тифа в концентрационном лагере Берген-Бельзен где-то в марте 1945 года. Ей еще не было шестнадцати.
 Ее дневники были обнаружены сотрудником Отто, Мип Гис, после того, как власти совершили налет на пристройку. Мип собрала разбросанные рукописи и хранила их до возвращения Отто после войны. Отто был единственным выжившим членом семьи Франк.
Ее дневники были обнаружены сотрудником Отто, Мип Гис, после того, как власти совершили налет на пристройку. Мип собрала разбросанные рукописи и хранила их до возвращения Отто после войны. Отто был единственным выжившим членом семьи Франк.Немного поколебавшись, Отто прочитал дневники Энн. Он боролся с тем, публиковать их или нет. Энн хотела стать писательницей, но некоторая информация в ее дневниках была очень личной. В конце концов он решил, что их следует опубликовать для всеобщего обозрения. После некоторых трудностей голландское издательство согласилось опубликовать дневники Анны Франк. Первое издание было выпущено в 1947 году. Важность и популярность текста привели к тому, что его перевели на многие другие языки, включая английский, немецкий и французский.
В последние годы возникли разногласия по поводу цензуры дневников Анны ее отцом перед публикацией. Отто исключил отрывки, в которых Анна критиковала брак своих родителей. Он также удалил разделы, в которых Энн графически обсуждала сексуальность, мастурбацию и менструацию.
 Она писала, что испытывает какое-то влечение к представителям своего пола, но Отто вырезал это. Он также включил разделы, которые сама Анна отредактировала из своих дневников, например, ее влечение к Питеру ван Даану. Эти правки заставили некоторых задуматься о том, «Дневник молодой девушки» дал совершенно точное представление о многогранной, несовершенной и подлинной личности, которой была Анна Франк.
Она писала, что испытывает какое-то влечение к представителям своего пола, но Отто вырезал это. Он также включил разделы, которые сама Анна отредактировала из своих дневников, например, ее влечение к Питеру ван Даану. Эти правки заставили некоторых задуматься о том, «Дневник молодой девушки» дал совершенно точное представление о многогранной, несовершенной и подлинной личности, которой была Анна Франк.Анна Франк, Дневник молодой девушки: цитаты
Дневники Анны Франк были написаны ее собственными словами. Они были новаторским взглядом на жизнь молодого человека во время Холокоста. Сегодня они рассматриваются как жизненно важный исторический документ.
Цитата Запись Пояснение «Мне кажется, что в дальнейшем ни мне, ни кому-либо еще не будут интересны размышления тринадцатилетней школьницы. О, это не имеет значения. Мне хочется писать, и еще больше мне нужно избавиться от всяких вещей». 
Июнь 1942 года. Оглядываясь назад, это довольно пророческая цитата. Анна Франк никогда не могла знать, насколько важными станут ее дневники. Она подчеркивает, что она обычная девушка. Это ключевая причина популярности ее произведений. «Не могу не сказать вам, что в последнее время я стал чувствовать себя покинутым. Я окружен слишком большой пустотой. Ноябрь 1942 года. Энн говорит здесь о своем одиночестве. Вдали от сверстников она чувствует себя очень одинокой, несмотря на то, что живет в очень тесном контакте с другими обитателями пристройки. Они полностью изолированы от остального мира. ‘Ужасные вещи происходят снаружи. В любое время дня и ночи бедных беспомощных людей вытаскивают из домов. Им разрешается взять с собой только рюкзак и немного наличных, да и то по дороге отнимают эти вещи. Семьи разлучены; мужчины, женщины и дети разделены. Дети приходят домой из школы и обнаруживают, что их родители исчезли». 
Январь 1943 года. Энн подробно рассказывает об ужасах, происходящих рядом с их пристройкой. Большинство людей, которых преследуют и пытают, — евреи. Эта цитата заключает в себе тяжелую травму, которую Энн и ей подобным пришлось пережить с самого раннего возраста. «Дневник молодой девушки» — основные выводы
- «Дневник молодой девушки» (1947) — научно-популярный текст Анны Франк.
- Это дневники молодой еврейской девушки, скрывавшейся от нацистов во время Холокоста.
- Две ключевые темы в тексте — взросление и война.
- Анна Франк была умной и талантливой молодой писательницей, которая использовала свое писательство как убежище от окружавших ее ужасов.
- Отец Анны, Отто, в конце концов опубликовал ее дневники в 1947 году. Он был единственным выжившим членом семьи Франк.
Драма Nat Geo рассказывает историю семьи, которая спрятала Анну Франк ее муж Ян скрывал семью Анны Франк во время нацистской оккупации Нидерландов.

Сериал, премьера которого состоится 1 мая, рассказывает историю Мип в самые мрачные дни войны, когда она и ее муж становятся все более отчаянными под нацистской оккупацией. Но когда ее работодатель Отто Франк попросил помочь спрятать его семью от эскадронов смерти, она без колебаний соглашается. Смотрите сами в трейлере прямо сейчас вверху страницы.
В течение двух лет Мип и Ян прятали Франков, а также четырех членов семьи Пфефферов — пока их не выдали и Франков и Пфефферов, арестованных нацистской полицией, не отправили в различные концлагеря. Ги избежали ареста и казни почти по счастливой случайности, а в конце концов только Отто Франк выжил в лагерях. Однако Мип сохранила многие вещи Франков и Пфеффер, в том числе дневник Анны.
Читайте также:
Марш производственников Disney в Бербанке вместе с анимационной гильдией требуют объединения в профсоюзы«Когда мы впервые услышали замечательную историю Мип Гис, мы были потрясены и глубоко тронуты.
 Мы также были убеждены, что этот ограниченный сериал о повседневном супергерое, о котором большинство людей во всем мире никогда не слышали, нуждается в беспрецедентном развертывании», — сказала Кэролин Бернстайн, исполнительный вице-президент по сценариям и документальным фильмам в National Geographic. «Мы полны решимости донести «Маленький свет» до максимально возможной глобальной аудитории и надеемся, что это амбициозное развертывание в нескольких сетях и потоковых платформах позволит зрителям влюбиться в Miep и вдохновиться ею так же, как и мы».
Мы также были убеждены, что этот ограниченный сериал о повседневном супергерое, о котором большинство людей во всем мире никогда не слышали, нуждается в беспрецедентном развертывании», — сказала Кэролин Бернстайн, исполнительный вице-президент по сценариям и документальным фильмам в National Geographic. «Мы полны решимости донести «Маленький свет» до максимально возможной глобальной аудитории и надеемся, что это амбициозное развертывание в нескольких сетях и потоковых платформах позволит зрителям влюбиться в Miep и вдохновиться ею так же, как и мы».Произведенный ABC Signature и Keshet Studios, сериал «Маленький свет» будет запущен с одновременной трансляцией первых двух эпизодов на National Geographic, Nat Geo WILD и Lifetime. Первый эпизод выйдет на бис 6 мая в 8/7c на Freeform, а после этого премьера двух эпизодов будет каждый понедельник в 9/8c на National Geographic, а на следующий день они будут транслироваться на Disney+ и Hulu, а также на Nat Geo TV и приложения АВС.
В главных ролях Бел Паули в роли Мип и Лив Шрайбер в роли Отто Франка, в фильме «Маленький огонек» также снимались Амира Касар в роли Эдит Франк, Билли Буллет в роли Анны Франк, Эшли Брук в роли Марго Франк, Энди Найман в роли Германа ван Пелса, Кэролайн Катц в роли Огюста ван Пелс, Руди Гудман в роли Питера ван Пелса и Ной Тейлор в роли доктора Фрица Пфеффера.

Y log2x: Решить y=log2x | Microsoft Math Solver
y = log2*(|x|)
Графики функций, Построение графиков Работа проверена: sargy Время решения: 6 мин Сложность: 3.7
Дано
$$f{left (x right )} = log{left (2 right )} left|{x}right|$$
График функции
Точки пересечения с осью координат X
График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$log{left (2 right )} left|{x}right| = 0$$
Решаем это уравнение
Точки пересечения с осью X:Аналитическое решение
$$x_{1} = 0$$
Численное решение
$$x_{1} = 0$$Точки пересечения с осью координат Y
График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в log(2)*|x|.
$$log{left (2 right )} left|{0}right|$$
Результат:
$$f{left (0 right )} = 0$$
Точка:(0, 0)
Экстремумы функции
Для того, чтобы найти экстремумы, нужно решить уравнение
$$frac{d}{d x} f{left (x right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$frac{d}{d x} f{left (x right )} = $$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = 0$$
Зн. экстремумы в точках:
экстремумы в точках:(0, 0)
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_{1} = 0$$
Максимумов у функции нет
Убывает на промежутках[0, oo)
Возрастает на промежутках
(-oo, 0]
Горизонтальные асимптоты
Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
$$lim_{x to -infty}left(log{left (2 right )} left|{x}right|right) = infty$$
Возьмём предел
значит,
горизонтальной асимптоты справа не существуетНаклонные асимптоты
Наклонную асимптоту можно найти, подсчитав предел функции log(2)*|x|, делённой на x при x->+oo и x ->-oo
$$lim_{x to -infty}left(frac{left|{x}right|}{x} log{left (2 right )}right) = – log{left (2 right )}$$
Возьмём предел
значит,
уравнение наклонной асимптоты справа:
$$y = x log{left (2 right )}$$Чётность и нечётность функции
Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).

Итак, проверяем:
$$log{left (2 right )} left|{x}right| = log{left (2 right )} left|{x}right|$$
– Да
$$log{left (2 right )} left|{x}right| = – log{left (2 right )} left|{x}right|$$
– Нет
значит, функция
является
чётной
3-8
Логарифмические функции и их графики
4.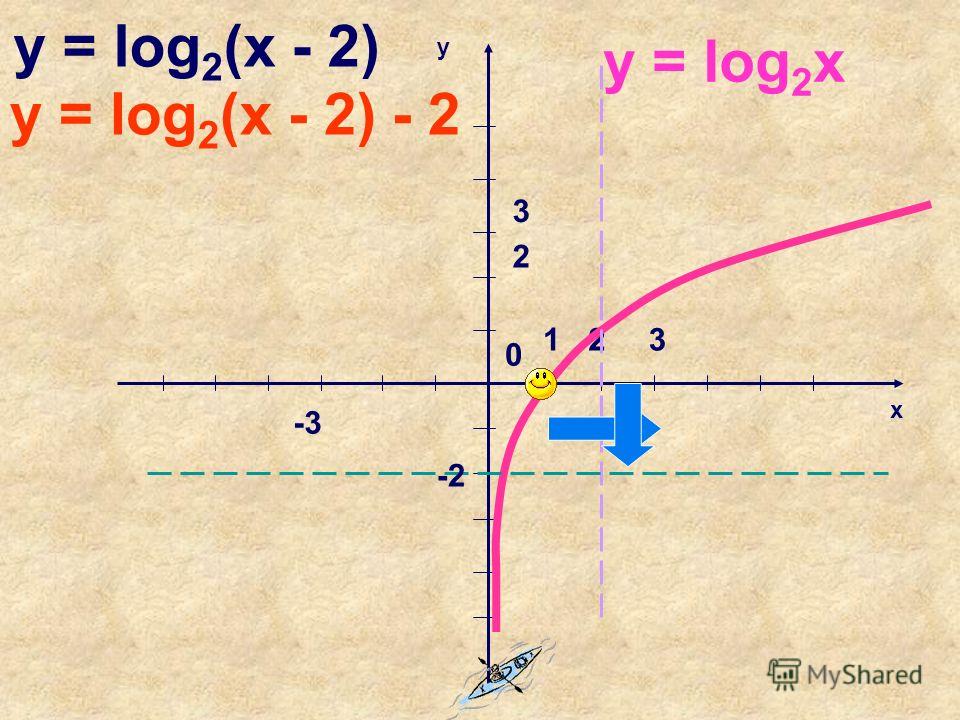 2 — Логарифмические функции и их графики
2 — Логарифмические функции и их графикиОбратная экспоненциальная функция
В разделе об экспоненциальных функциях мы заявили, что экспоненциальные функции были взаимно однозначными. Один к одному функции обладали тем особым свойством, что они имеют обратные это тоже функции. И, как многие из вас говорили в классе, и я так рад, что вы помните, функции один-к-одному могут применяться к обеим частям уравнения. Они также проходят тест горизонтальной линии.
Этот раздел посвящен обратной экспоненциальной функция. Обратной экспоненциальной функцией является логарифмическая функция. Помните, что инверсия функция получается путем переключения координат x и y. Это отражает график относительно прямой y=x. Как видно из графика справа, логарифмическая кривая является отражением экспоненциальной кривой.
В таблице ниже показано, как значения x и y точек на экспоненциальной кривую можно переключать, чтобы найти координаты точек на логарифмической изгиб.
| Точка на экспоненциальной кривой | Соответствующая точка на логарифмической кривой |
|---|---|
| (-3, 1/8) | (1/8, -3) |
| (-2, 1/4) | (1/4, -2) |
| (-1, 1/2) | (1/2, -1) |
| (0, 1) | (1, 0) |
| (1, 2) | (2, 1) |
| (2, 4) | (4, 2) |
| (3, 8) | (8, 3) |
Сравнение экспоненциальной и логарифмической функций
Давайте посмотрим на некоторые свойства
из двух функций.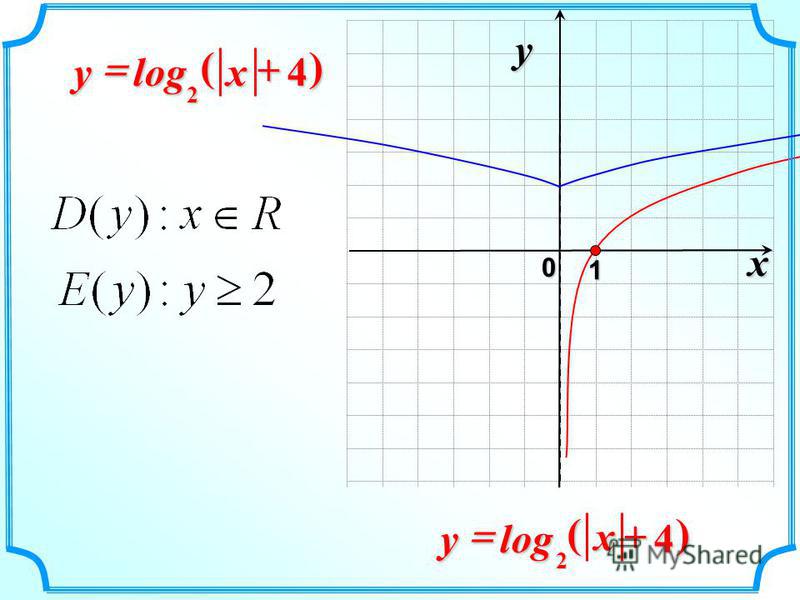
Стандартная форма логарифмической функции: y = log a x
Обратите внимание, если «а» в приведенном выше выражении не является нижним индексом (ниже, чем «лог»), тогда вам нужно обновить свой веб-браузер.
| Экспоненциальный | Логарифмический | |
|---|---|---|
| Функция | у=а х , а>0, а≠1 | у=log а х, а>0, а≠1 |
| Домен | все реалы | х > 0 |
| Диапазон | г > 0 | все реалы |
| перехват | г = 1 | х = 1 |
| увеличение | при > 1 | при > 1 |
| по убыванию | , когда 0 < а < 1 | , когда 0 < а < 1 |
| асимптота | ось x (y=0) | ось Y (x=0) |
| непрерывный | да | да |
| гладкая | да | да |
Рабочее определение логарифма
В экспоненциальной функции x был показателем степени.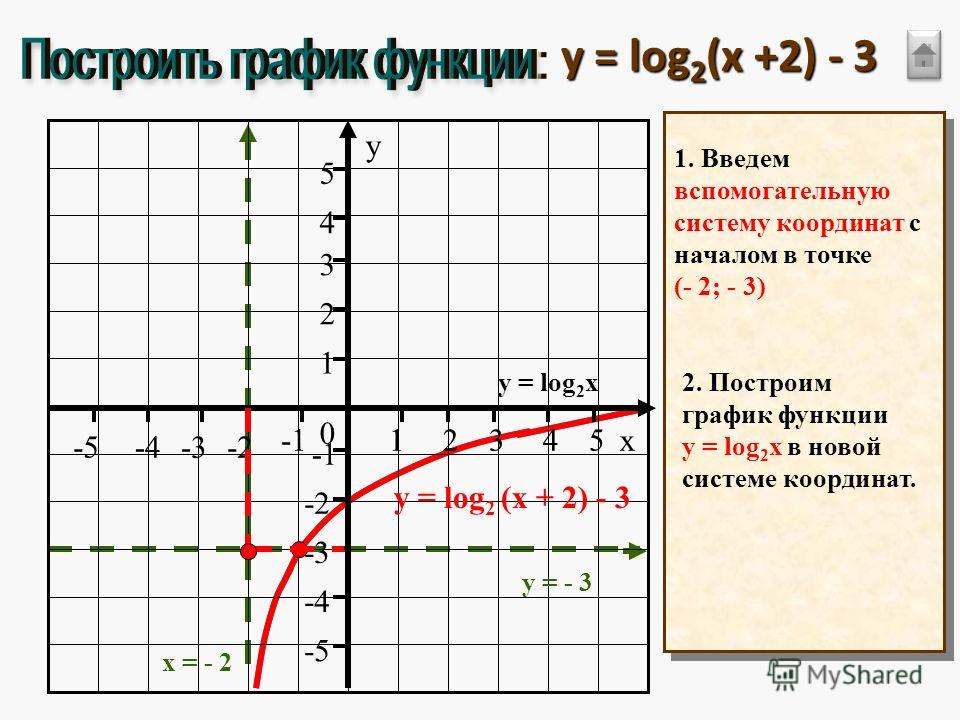 Цель обратной функции
чтобы сообщить вам, какое значение x было использовано, когда вы уже знаете значение y. Итак, целью
логарифм, чтобы сказать вам показатель степени.
Цель обратной функции
чтобы сообщить вам, какое значение x было использовано, когда вы уже знаете значение y. Итак, целью
логарифм, чтобы сказать вам показатель степени.
Таким образом, наше простое определение логарифма состоит в том, что он является показателем степени.
Другой способ взглянуть на выражение «log a x» — это «в какую степень (показатель степени) нужно возвести а получить х?»
Эквивалентные формы
Логарифмическая форма уравнения y=log a x эквивалентна экспоненциальной форме x=a y .
Чтобы переписать одну форму в другую, оставьте основу прежней и поменяйте местами две другие стороны ценности.
Свойства логарифмов
- журнал a 1 = 0, потому что a 0 = 1
- Независимо от базы, если она разрешена, логарифм 1 всегда равен 0. Это потому что логарифмические кривые всегда проходят через (1,0)
- log a a = 1, потому что a 1 = a
- Любое значение, возведенное в первую степень,
такое же значение.

- журнал а а х = х
- Основание логарифма x и a в степени x являются обратными функциями. Всякий раз, когда инверсия функции применяются друг к другу, они инвертируются, и у вас остается в аргумент, в данном случае x.
- log a x = log a y означает, что x = y
- Если два бревна с одинаковым основанием равны, то аргументы должны быть равны.
- log a x = log b x означает, что a = b
- Если два логарифма с одним и тем же аргументом равны, то основания должны быть равны.
Обычные бревна и бревна
На вашем калькуляторе есть две кнопки логарифмирования. Один помечен как «журнал» и другой отмечен «лн». Ни в одном из них не записана база. База может быть определена, однако, взглянув на обратную функцию, которая написана над ключом и доступ по 2 и ключ.
Десятичный логарифм (основание 10)
Когда вы видите написанное «журнал» без основания, примите, что основание равно 10.
То есть: log x = log 10 x.
Некоторые приложения, использующие десятичные логарифмы, относятся к pH (для измерения кислотности), децибелам. (сила звука), шкала Рихтера (землетрясения).
Интересное (возможно) примечание о рН. «Глава 50: Канализация» деревни Кодекса Форсайта требует запрещает сброс отходов с рН менее 5,5 или выше 10,5 (раздел 50.07).
Обычные журналы служат и другой цели. Каждое увеличение десятичного логарифма на 1 является результатом 10-кратного аргумента. То есть землетрясение силой 6,3 имеет 10 раз превышает величину землетрясение силой 5,3 балла. Уровень децибел громкой рок-музыки или бензопилы (115 децибел = 11,5 бел) в 10 раз громче, чем куры внутри здания (105 децибел = 10,5 бел)
Натуральные логарифмы (основание e)
Помните тот номер e , который у нас был из предыдущего раздела? Знаешь, тот, который был
примерно 2,718281828 (но не повторяется и не заканчивается). Это основа естественного
логарифм.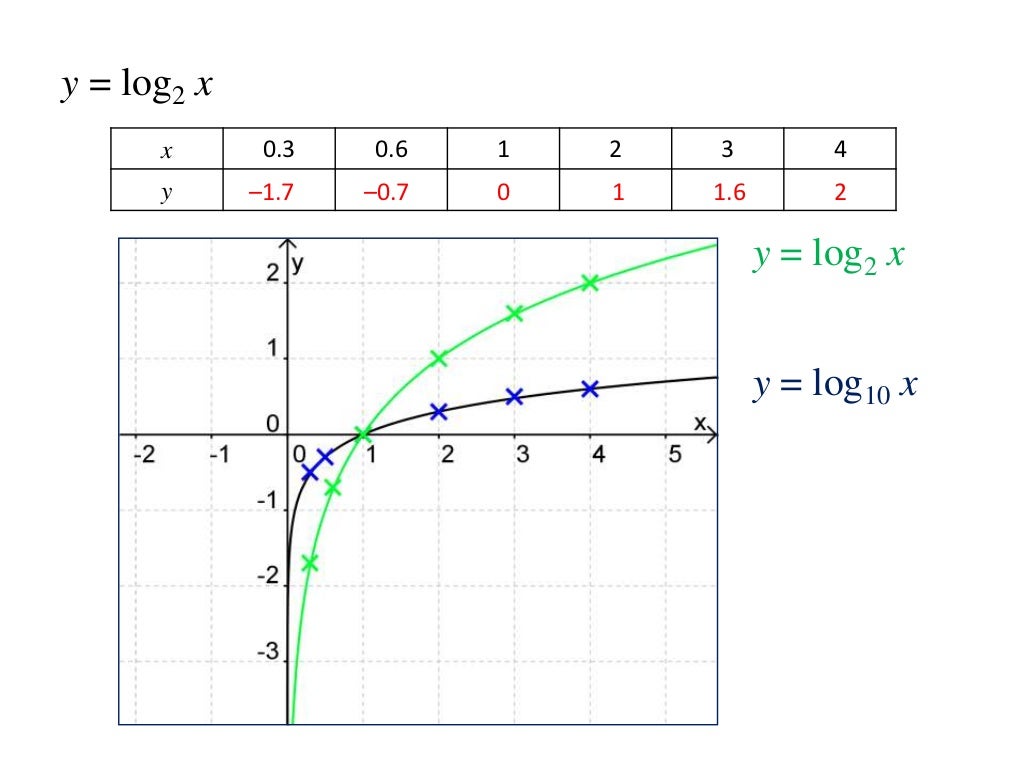
Когда вы видите написанное «ln», основание равно e .
То есть: ln x = log e x
Модели экспоненциального роста и затухания — одно из приложений, использующих натуральные логарифмы. Этот включает непрерывное накопление, радиоактивный распад (период полураспада), рост населения. Обычно приложения, в которых постоянно происходит процесс. Теперь эти приложения были первыми упоминается в экспоненциальном разделе, но вы сможете решить для других переменных участие (после раздела 4) с использованием логарифмов.
В высшей математике натуральный логарифм является предпочтительным логарифмом. Есть несколько особые свойства функции натурального логарифма и ее обратной функции, которые делают жизнь намного интереснее. проще в расчетах.
Поскольку «ln x» и « e x » являются обратными функциями друг друга, всегда, когда «ln» и «e» появляются правильно
рядом друг с другом, между которыми абсолютно ничего нет (то есть, когда они
составлены друг с другом), затем они инвертируются, и у вас остается
Аргумент.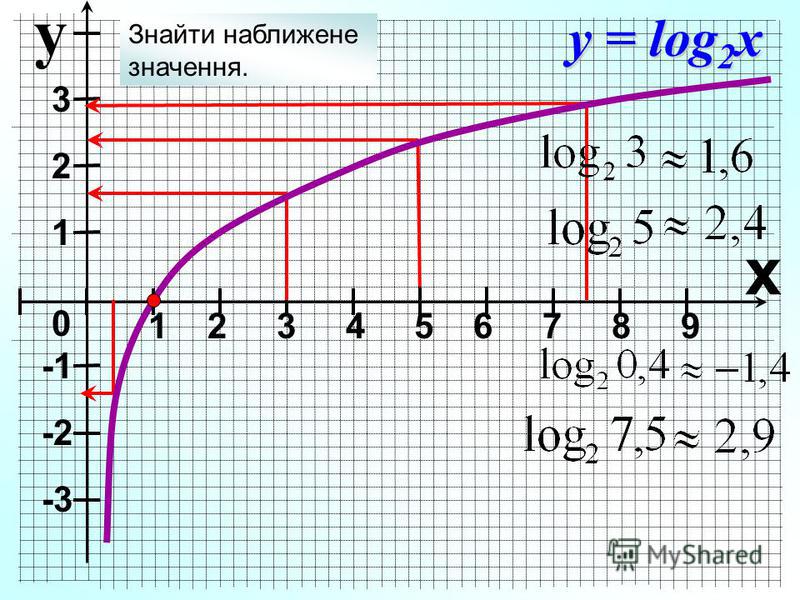

 Фактор a с правой стороны.
Фактор a с правой стороны. Фактор a из правой части
Фактор a из правой части

 После автоматической проверки введенных данных будет открыт доступ к учетной записи МИЭП.
После автоматической проверки введенных данных будет открыт доступ к учетной записи МИЭП. Это можно сделать на странице https://miep.ru/payment/, указав номер договора, сумму и свои персональные данные.
Это можно сделать на странице https://miep.ru/payment/, указав номер договора, сумму и свои персональные данные. инфо
инфо  5 км
5 км Смоленске
Смоленске Даже в Нидерландах она и ее старшая сестра Марго должны посещать школу для еврейских учащихся.
Даже в Нидерландах она и ее старшая сестра Марго должны посещать школу для еврейских учащихся. Все меняется, когда эсэсовцы вызывают Марго явиться в нацистский трудовой лагерь.
Все меняется, когда эсэсовцы вызывают Марго явиться в нацистский трудовой лагерь.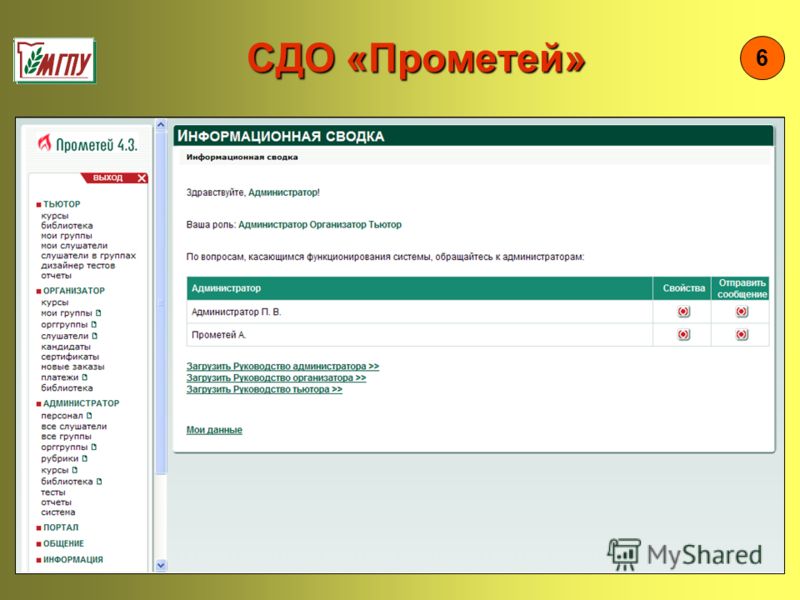 Работники предприятия Отто Франка помогали тем, кто прятался в пристройке, принося им продукты и припасы.
Работники предприятия Отто Франка помогали тем, кто прятался в пристройке, принося им продукты и припасы. Из-за совместного проживания в таких тесных помещениях происходит много столкновений. Анна также пишет о своих мыслях о том, как быть евреем в Европе в это неспокойное время. Она не может понять, почему ее сообщество так преследуется. Анна не знает, какой стране она на самом деле принадлежит, поскольку ее немецкое гражданство было аннулировано. Жители пристройки постепенно получают новости о том, как продвигается война, многие из которых угнетают их.
Из-за совместного проживания в таких тесных помещениях происходит много столкновений. Анна также пишет о своих мыслях о том, как быть евреем в Европе в это неспокойное время. Она не может понять, почему ее сообщество так преследуется. Анна не знает, какой стране она на самом деле принадлежит, поскольку ее немецкое гражданство было аннулировано. Жители пристройки постепенно получают новости о том, как продвигается война, многие из которых угнетают их.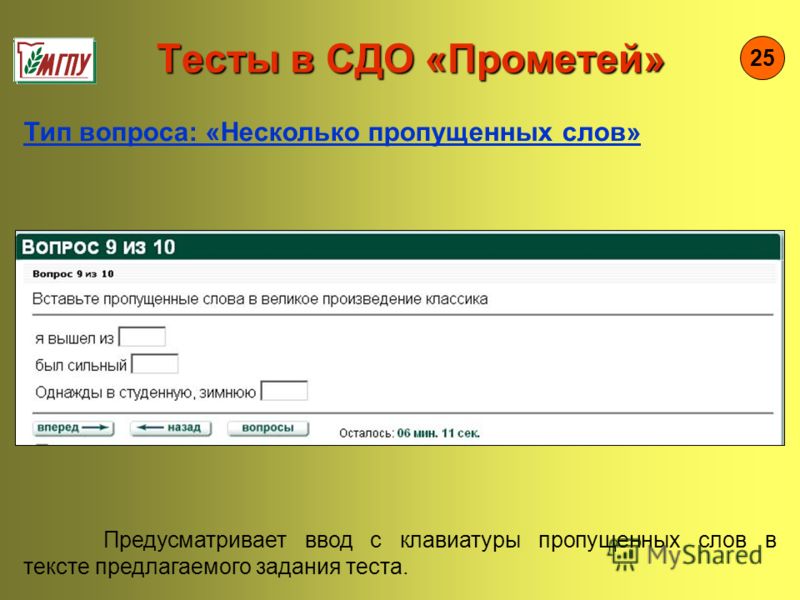

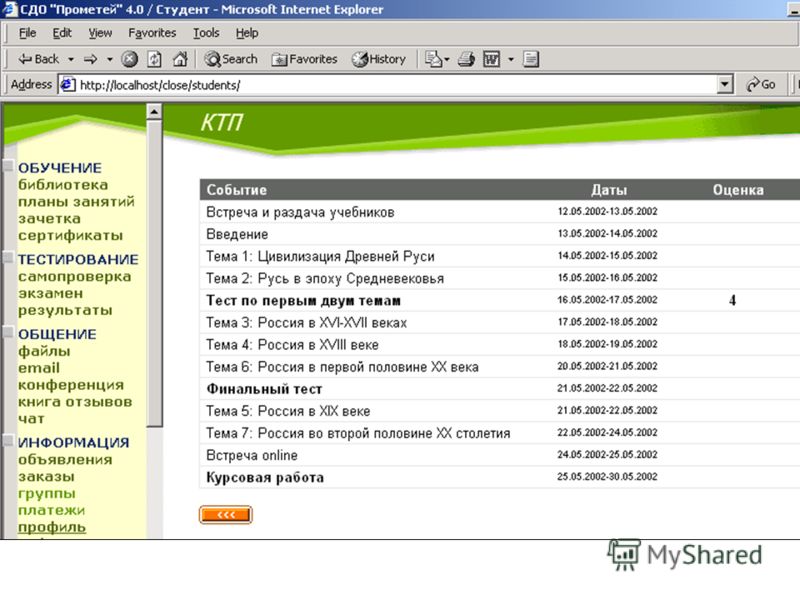 Энн также отмечает, что Марго очень красивая.
Энн также отмечает, что Марго очень красивая. Он застенчив и невинен, часто находит убежище в ребячестве. Энн не нравятся в нем эти черты, и она мало обращает внимания на Питера, когда они впервые входят в пристройку. Через некоторое время у нее появляется к нему интерес, и у них завязываются романтические отношения. Это длится какое-то время, но в конце концов Энн понимает, что просто идеализировала Питера, поскольку он был единственной надеждой на роман, который у нее был.
Он застенчив и невинен, часто находит убежище в ребячестве. Энн не нравятся в нем эти черты, и она мало обращает внимания на Питера, когда они впервые входят в пристройку. Через некоторое время у нее появляется к нему интерес, и у них завязываются романтические отношения. Это длится какое-то время, но в конце концов Энн понимает, что просто идеализировала Питера, поскольку он был единственной надеждой на роман, который у нее был.
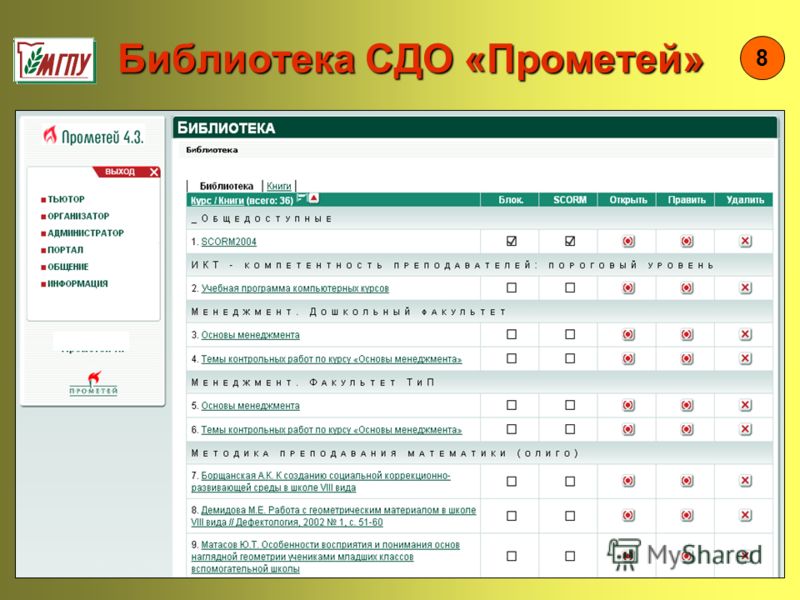 Она подробно описывает более невинные отношения, которые у нее были с мальчиками в молодости. Читатели могут увидеть, как это перерастает в более серьезное влечение, когда Энн размышляет о своих чувствах к Питеру в Приложении.
Она подробно описывает более невинные отношения, которые у нее были с мальчиками в молодости. Читатели могут увидеть, как это перерастает в более серьезное влечение, когда Энн размышляет о своих чувствах к Питеру в Приложении. Она также живет в состоянии постоянного страха, что позиция ее семьи будет раскрыта властям. Смерть Анны в трагически молодом возрасте — одна из многих молодых жизней, оборвавшихся из-за действий нацистов.
Она также живет в состоянии постоянного страха, что позиция ее семьи будет раскрыта властям. Смерть Анны в трагически молодом возрасте — одна из многих молодых жизней, оборвавшихся из-за действий нацистов.
 Ее дневники были обнаружены сотрудником Отто, Мип Гис, после того, как власти совершили налет на пристройку. Мип собрала разбросанные рукописи и хранила их до возвращения Отто после войны. Отто был единственным выжившим членом семьи Франк.
Ее дневники были обнаружены сотрудником Отто, Мип Гис, после того, как власти совершили налет на пристройку. Мип собрала разбросанные рукописи и хранила их до возвращения Отто после войны. Отто был единственным выжившим членом семьи Франк. Она писала, что испытывает какое-то влечение к представителям своего пола, но Отто вырезал это. Он также включил разделы, которые сама Анна отредактировала из своих дневников, например, ее влечение к Питеру ван Даану. Эти правки заставили некоторых задуматься о том, «Дневник молодой девушки» дал совершенно точное представление о многогранной, несовершенной и подлинной личности, которой была Анна Франк.
Она писала, что испытывает какое-то влечение к представителям своего пола, но Отто вырезал это. Он также включил разделы, которые сама Анна отредактировала из своих дневников, например, ее влечение к Питеру ван Даану. Эти правки заставили некоторых задуматься о том, «Дневник молодой девушки» дал совершенно точное представление о многогранной, несовершенной и подлинной личности, которой была Анна Франк.

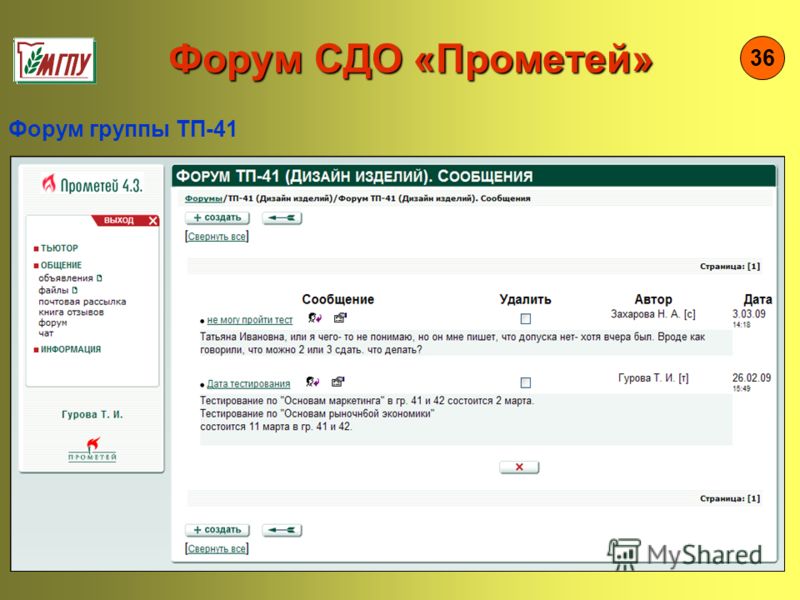
 Мы также были убеждены, что этот ограниченный сериал о повседневном супергерое, о котором большинство людей во всем мире никогда не слышали, нуждается в беспрецедентном развертывании», — сказала Кэролин Бернстайн, исполнительный вице-президент по сценариям и документальным фильмам в National Geographic. «Мы полны решимости донести «Маленький свет» до максимально возможной глобальной аудитории и надеемся, что это амбициозное развертывание в нескольких сетях и потоковых платформах позволит зрителям влюбиться в Miep и вдохновиться ею так же, как и мы».
Мы также были убеждены, что этот ограниченный сериал о повседневном супергерое, о котором большинство людей во всем мире никогда не слышали, нуждается в беспрецедентном развертывании», — сказала Кэролин Бернстайн, исполнительный вице-президент по сценариям и документальным фильмам в National Geographic. «Мы полны решимости донести «Маленький свет» до максимально возможной глобальной аудитории и надеемся, что это амбициозное развертывание в нескольких сетях и потоковых платформах позволит зрителям влюбиться в Miep и вдохновиться ею так же, как и мы».
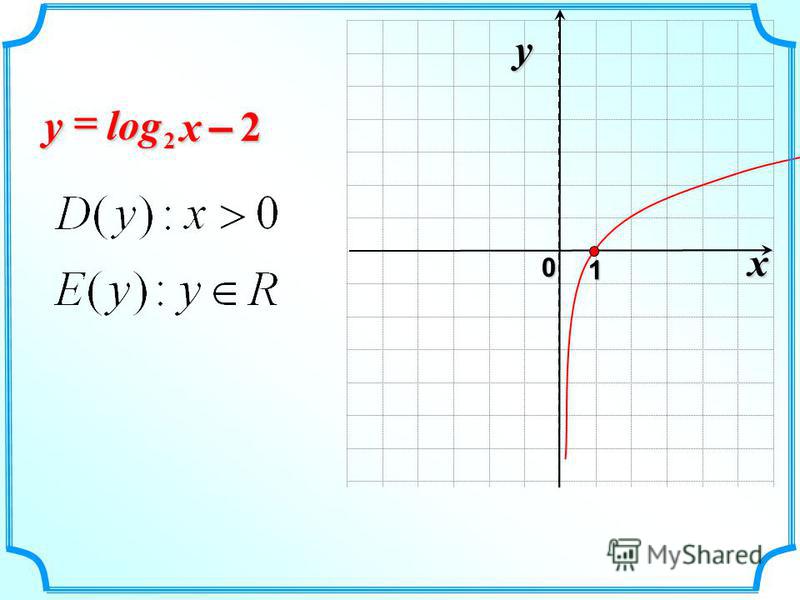

 Справедливость этой формулы доказывается как и формула логарифма произведения: так как , то по определению логарифма .
Справедливость этой формулы доказывается как и формула логарифма произведения: так как , то по определению логарифма . Тогда b p =|b| p =(a log a |b|) p =a p·log a |b|
, откуда log a b p =p·log a |b|
.
Тогда b p =|b| p =(a log a |b|) p =a p·log a |b|
, откуда log a b p =p·log a |b|
.

 Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.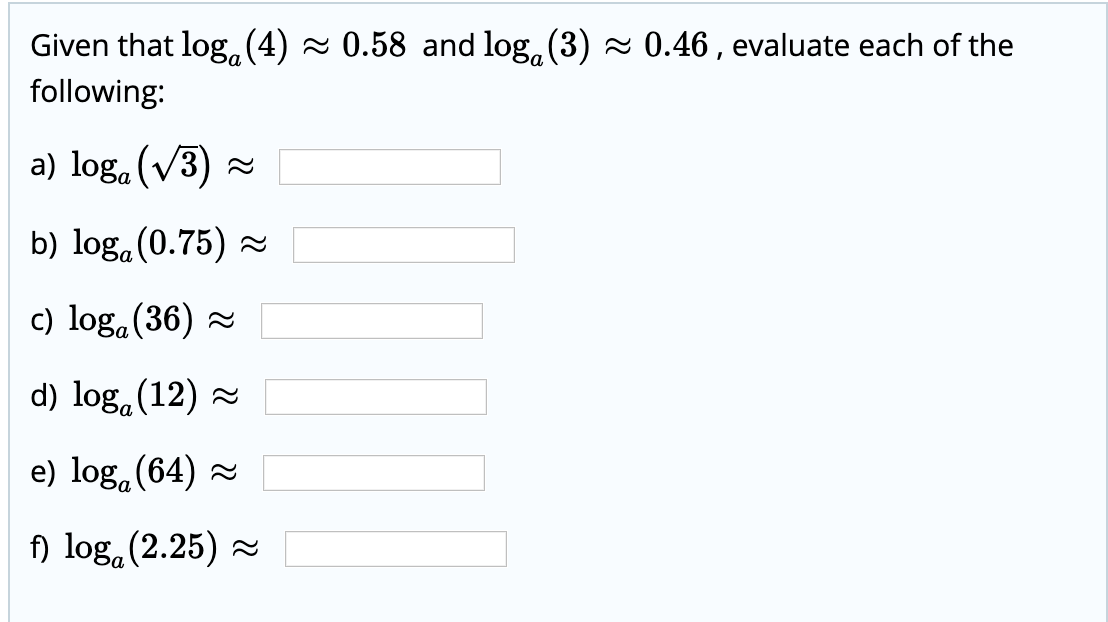






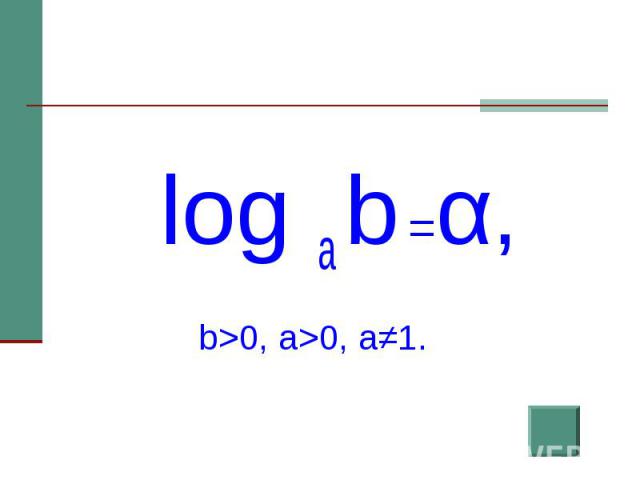 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
 .. — иррациональное число). Обозначается как ln.
.. — иррациональное число). Обозначается как ln. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: » «. Не пропустите!
Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: » «. Не пропустите!

 Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени! Попутно лучше избавиться от десятичных дробей;
Попутно лучше избавиться от десятичных дробей;
 к. множитель всего один;
к. множитель всего один;




 2 / аб) ?,
2 / аб) ?, log(c)b.log(a)c равно
log(c)b.log(a)c равно 07.2021 ) (Вопросы с несколькими вариантами ответов)
07.2021 ) (Вопросы с несколькими вариантами ответов) logca-logaa)+(logab.logcb.logcb-logbb)+(logac.logbc-logcC)=0, тогда abc равно
logca-logaa)+(logab.logcb.logcb-logbb)+(logac.logbc-logcC)=0, тогда abc равно
 Как их избежать.
Как их избежать.
 Если не известно число b.
Если не известно число b. Поэтому пишут 1 % = 0,01.
Поэтому пишут 1 % = 0,01.

 Чтобы правильно ответить на них, вам нужно внимательно изучить вопросы. Всегда убедитесь, что вы знаете, о чем спрашивают, какие операции необходимы и какие единицы, если таковые имеются, вам нужно включить в свой ответ.
Чтобы правильно ответить на них, вам нужно внимательно изучить вопросы. Всегда убедитесь, что вы знаете, о чем спрашивают, какие операции необходимы и какие единицы, если таковые имеются, вам нужно включить в свой ответ. Какой процент вопросов он ответил правильно?
Какой процент вопросов он ответил правильно? Если, например, задача со словами требует от вас найти 77 процентов от 50, вы можете просто найти 50 процентов от 77:
Если, например, задача со словами требует от вас найти 77 процентов от 50, вы можете просто найти 50 процентов от 77:




 Для умножения Python использует *, для деления – /.
Для умножения Python использует *, для деления – /. К примеру, разделив 100//40, вы получите 2.
К примеру, разделив 100//40, вы получите 2.
 Составные операторы объединяют арифметический оператор с оператором =. Например:
Составные операторы объединяют арифметический оператор с оператором =. Например:



 Это означает, что при совершении такой процедуры частное является неопределенным. Таким образом, теоретически оно может представлять собой абсолютно любое число.
Это означает, что при совершении такой процедуры частное является неопределенным. Таким образом, теоретически оно может представлять собой абсолютно любое число. Мой вопрос: «Почему на калькуляторе две разные кнопки для минуса и минуса?». Насколько мне известно, они обрабатываются точно так же, единственное отличие состоит в том, что минус является бинарным, а отрицательный — унарным. В остальном разницы не вижу. Так почему же у калькуляторов есть две отдельные кнопки для них? В языках программирования нет различия между минусом и минусом, различие делают только калькуляторы. Это по той причине, которую я назвал, или это что-то совершенно другое? Я не понимаю, как унарный или двоичный код может иметь какое-либо отношение к тому, как калькулятор что-то вычисляет, но я не могу придумать никаких других причин. Кто-нибудь знает, почему?
Мой вопрос: «Почему на калькуляторе две разные кнопки для минуса и минуса?». Насколько мне известно, они обрабатываются точно так же, единственное отличие состоит в том, что минус является бинарным, а отрицательный — унарным. В остальном разницы не вижу. Так почему же у калькуляторов есть две отдельные кнопки для них? В языках программирования нет различия между минусом и минусом, различие делают только калькуляторы. Это по той причине, которую я назвал, или это что-то совершенно другое? Я не понимаю, как унарный или двоичный код может иметь какое-либо отношение к тому, как калькулятор что-то вычисляет, но я не могу придумать никаких других причин. Кто-нибудь знает, почему? Минус вычитает число, что является совершенно другой операцией. Разница заключается в том, где вы можете его использовать, так как знак минус нельзя использовать для первого числа, которое вы пишете, так как его не из чего вычитать, и вы не можете использовать отрицание между двумя числами, так как между ними не происходит операции. их.
Минус вычитает число, что является совершенно другой операцией. Разница заключается в том, где вы можете его использовать, так как знак минус нельзя использовать для первого числа, которое вы пишете, так как его не из чего вычитать, и вы не можете использовать отрицание между двумя числами, так как между ними не происходит операции. их. -2, дают такой же результат, как если бы вы использовали ключ отрицания для отрицания. Единственное отличие, которое я смог найти до сих пор, заключается в том, что после того, как вы выполните какое-либо вычисление, а затем нажмете любую из 4 основных кнопок арифметического оператора (без предварительной очистки с помощью «AC»), калькулятор начнет новую формулу с «Ans», за которым следует Оператор. Ans относится к результату последнего вычисления. При использовании клавиши (-) калькулятор не будет вставлять «Ответ» и начнет новую формулу с нуля (оператор -). Я не нахожу это полезным, так как у меня есть привычка всегда очищать ввод с помощью кнопки AC.
-2, дают такой же результат, как если бы вы использовали ключ отрицания для отрицания. Единственное отличие, которое я смог найти до сих пор, заключается в том, что после того, как вы выполните какое-либо вычисление, а затем нажмете любую из 4 основных кнопок арифметического оператора (без предварительной очистки с помощью «AC»), калькулятор начнет новую формулу с «Ans», за которым следует Оператор. Ans относится к результату последнего вычисления. При использовании клавиши (-) калькулятор не будет вставлять «Ответ» и начнет новую формулу с нуля (оператор -). Я не нахожу это полезным, так как у меня есть привычка всегда очищать ввод с помощью кнопки AC.



 Когда вы используете ссылки на ячейки в формуле вместо значения ячейки, вы можете изменить значение, не изменяя формулу.
Когда вы используете ссылки на ячейки в формуле вместо значения ячейки, вы можете изменить значение, не изменяя формулу.
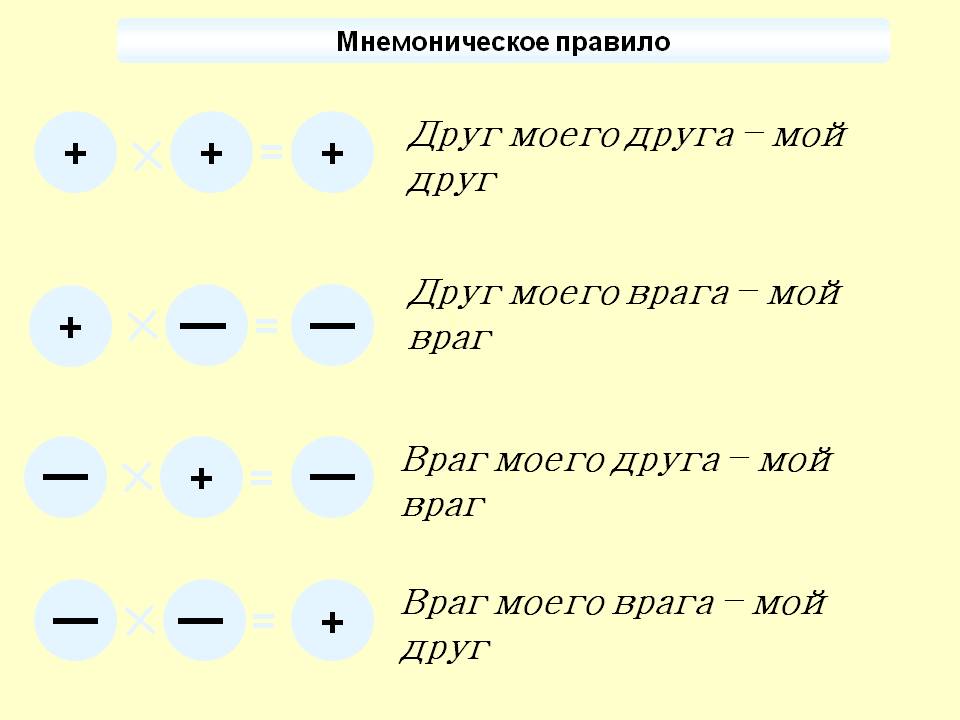
 Когда вы используете ссылки на ячейки в формуле вместо значения ячейки, вы можете изменить значение, не изменяя формулу.
Когда вы используете ссылки на ячейки в формуле вместо значения ячейки, вы можете изменить значение, не изменяя формулу. 14159..
14159..

 д.
д.
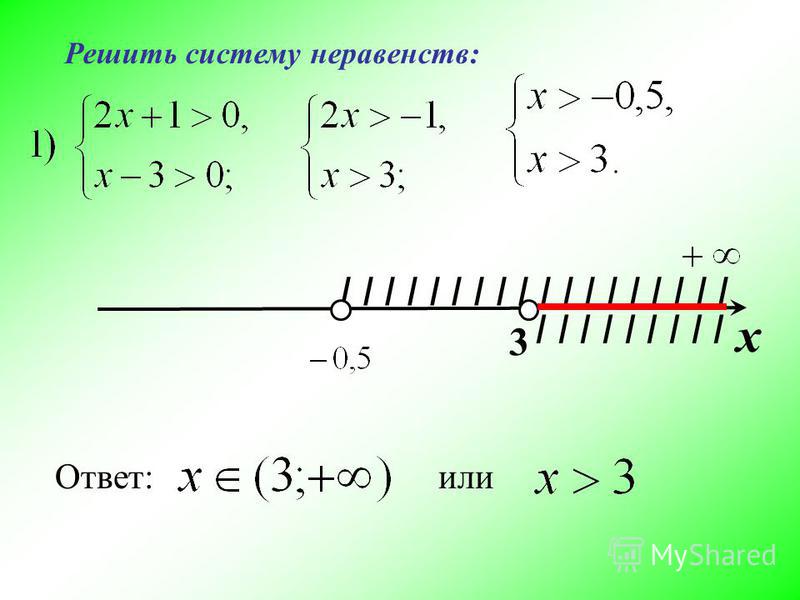
 Перед учениками ставится задача исследования количества решений системы уравнений в зависимости от значения параметра а. Затем ученики находят решения системы уравнений в каждом случае
Перед учениками ставится задача исследования количества решений системы уравнений в зависимости от значения параметра а. Затем ученики находят решения системы уравнений в каждом случае Это приводит к условиям a= или а = . После получения аналитического решения системы уравнений его можно проверить, используя приложение Калькулятор. В данном случае для получения общего решения мы использовали букву b (при использовании параметра а программа подставляет текущее численное значение для параметра и выдаёт только частное решение).
Это приводит к условиям a= или а = . После получения аналитического решения системы уравнений его можно проверить, используя приложение Калькулятор. В данном случае для получения общего решения мы использовали букву b (при использовании параметра а программа подставляет текущее численное значение для параметра и выдаёт только частное решение). Если значение функции равно нулю, то на графике будут выделены только значения х, удовлетворяющие условиям системы неравенств
Если значение функции равно нулю, то на графике будут выделены только значения х, удовлетворяющие условиям системы неравенств

 Я заменю данный символ неравенства на символ равенства, чтобы построить линию.
Я заменю данный символ неравенства на символ равенства, чтобы построить линию. Для двух приведенных выше примеров мы можем объединить оба графика и построить площадь, общую для двух неравенств.
Для двух приведенных выше примеров мы можем объединить оба графика и построить площадь, общую для двух неравенств.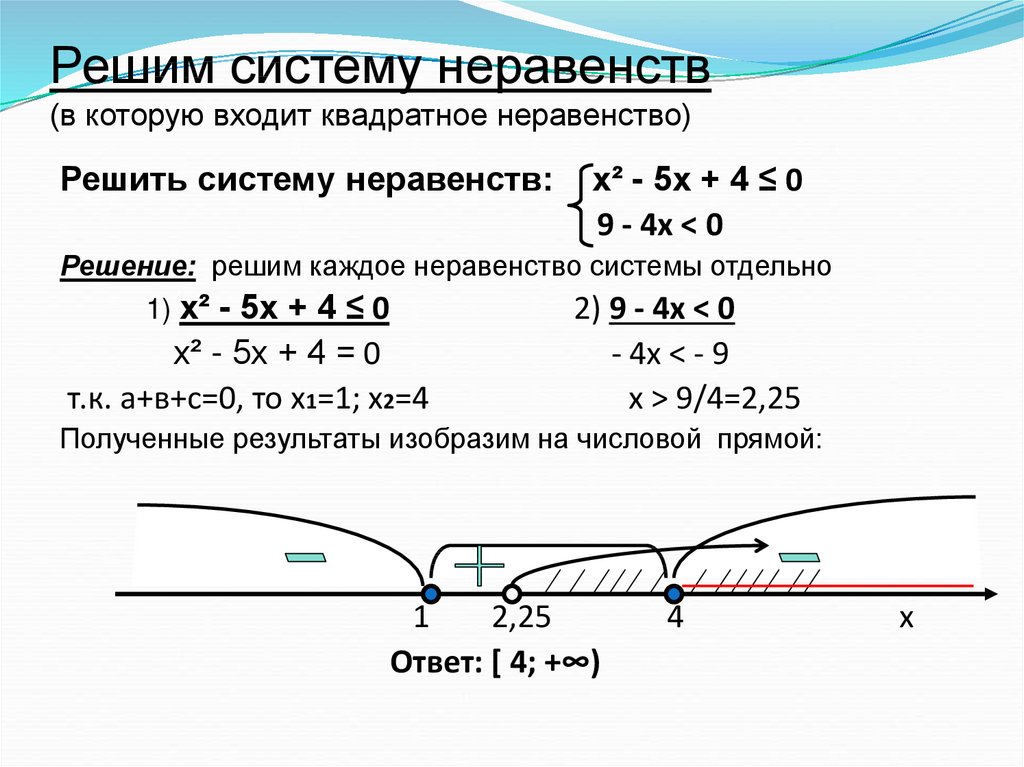 05.2006
05.2006  03.2004
03.2004  08.2001
08.2001  08.2001
08.2001 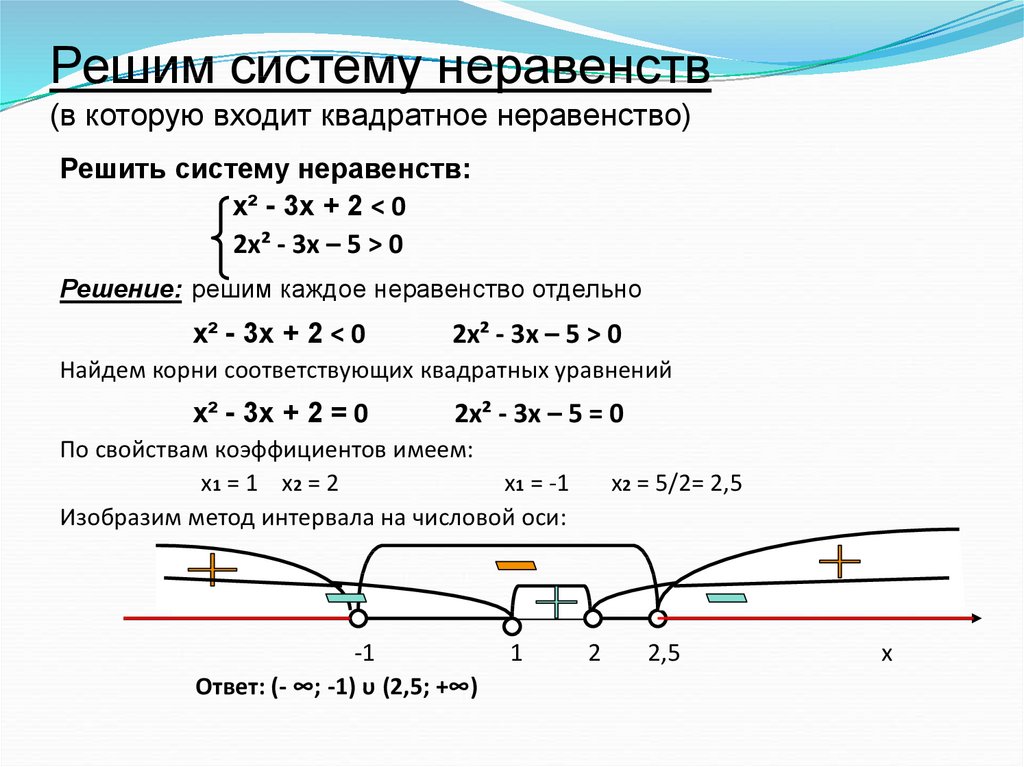

 Решить
уравнение tg x+ = 0.
Решить
уравнение tg x+ = 0.


 Решить
уравнение sin4x = 3 cos2х.
Решить
уравнение sin4x = 3 cos2х.

 В результате приходим к квадратному уравнению относительно tg2 x – 3 tg x + 2 = 0,
В результате приходим к квадратному уравнению относительно tg2 x – 3 tg x + 2 = 0, д.
д.
 Решить
уравнение
Решить
уравнение Решить
уравнение .
Решить
уравнение . Сколько
корней имеет уравнение:
Сколько
корней имеет уравнение: Решите
уравнение
Решите
уравнение Решите
уравнение
Решите
уравнение Решите
уравнение
Решите
уравнение
 :Наука. Главная редакция физико – математической
литературы,1986.
:Наука. Главная редакция физико – математической
литературы,1986. В.Белошинстая.-М.:Издательство «Экзамен»,2007.
В.Белошинстая.-М.:Издательство «Экзамен»,2007.

 Объяснение нового.
Объяснение нового. е. х2+рх+q=0
можно находить по теореме Виета:
е. х2+рх+q=0
можно находить по теореме Виета: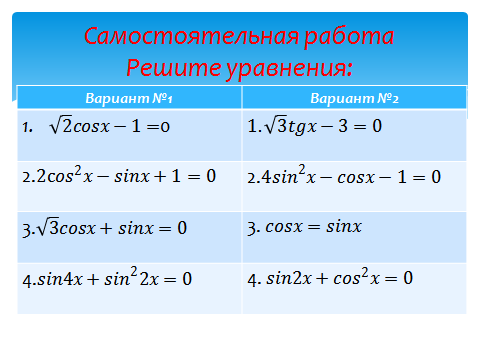 Для
этого заменим cos2 x на 1-sin2x. Получим
относительно xinx квадратное уравнение:
Для
этого заменим cos2 x на 1-sin2x. Получим
относительно xinx квадратное уравнение: №164 (в) — cамостоятельно
№164 (в) — cамостоятельно



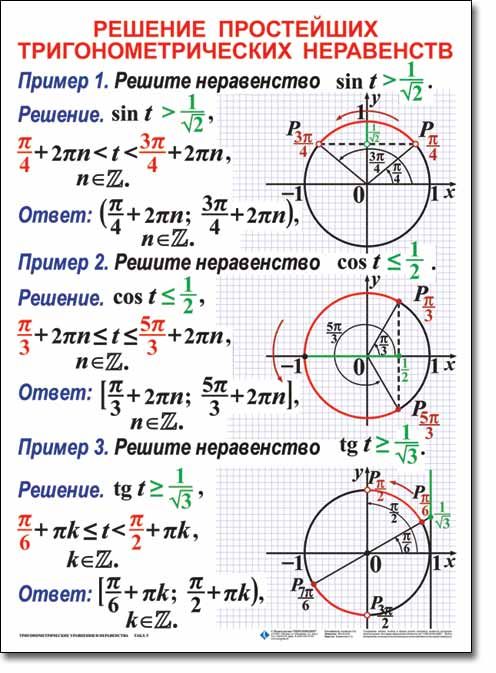
 ..} \\
& \приблизительно \текст{15,15}\текст{м}
\конец{выравнивание*}
9{2}\).
..} \\
& \приблизительно \текст{15,15}\текст{м}
\конец{выравнивание*}
9{2}\). Затем мы можем добавить
эти два угла вместе, чтобы найти \(A\hat{B}C\).
Затем мы можем добавить
эти два угла вместе, чтобы найти \(A\hat{B}C\). Гораздо разумнее использовать
тригонометрия.
Гораздо разумнее использовать
тригонометрия. ..} \\
& примерно \текст{80}
\конец{выравнивание*}
..} \\
& примерно \текст{80}
\конец{выравнивание*}

 \circ\). 9\circ} & = \frac{x}{\text{4,2}} \\
х & = \текст{9,0069…} \\
& \ приблизительно \ текст {9}
\конец{выравнивание*}
\circ\). 9\circ} & = \frac{x}{\text{4,2}} \\
х & = \текст{9,0069…} \\
& \ приблизительно \ текст {9}
\конец{выравнивание*} ..} \\
& \приблизительно \text{35,30}°
\конец{выравнивание*}
..} \\
& \приблизительно \text{35,30}°
\конец{выравнивание*}


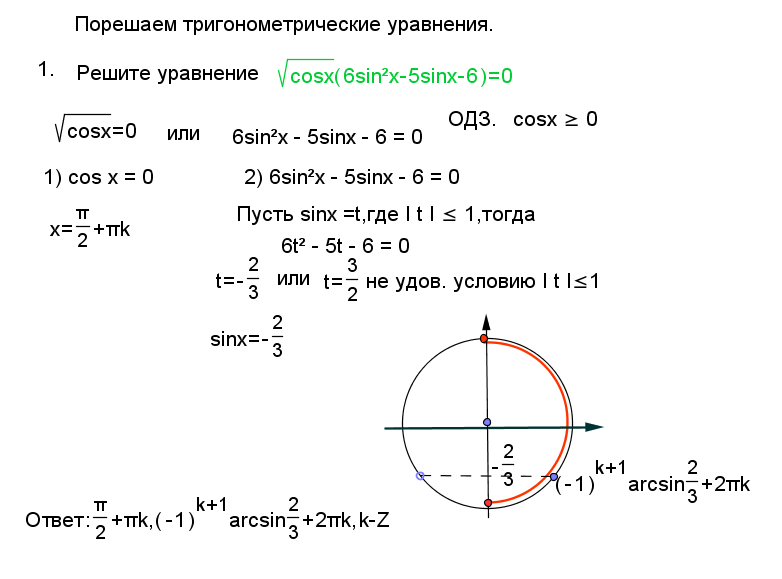


 Никто не имеет доступа к вашим файлам. Преобразование файлов (включая WORD в TXT) абсолютно безопасно.
Никто не имеет доступа к вашим файлам. Преобразование файлов (включая WORD в TXT) абсолютно безопасно. Вы получите ссылку для скачивания, как только файл будет конвертирован.
Вы получите ссылку для скачивания, как только файл будет конвертирован.
 Сначала загрузите исходный файл для преобразования: перетащите DOC в форму конвертации или нажмите кнопку «Выбрать файл». После этого нажмите кнопку «Конвертировать». Когда конвертация DOC в TXT завершится, вы сможете скачать файл TXT.
Сначала загрузите исходный файл для преобразования: перетащите DOC в форму конвертации или нажмите кнопку «Выбрать файл». После этого нажмите кнопку «Конвертировать». Когда конвертация DOC в TXT завершится, вы сможете скачать файл TXT. doc
doc Такие файлы можно просматривать и редактировать на текстовых терминалах или в простых текстовых редакторах.
Такие файлы можно просматривать и редактировать на текстовых терминалах или в простых текстовых редакторах.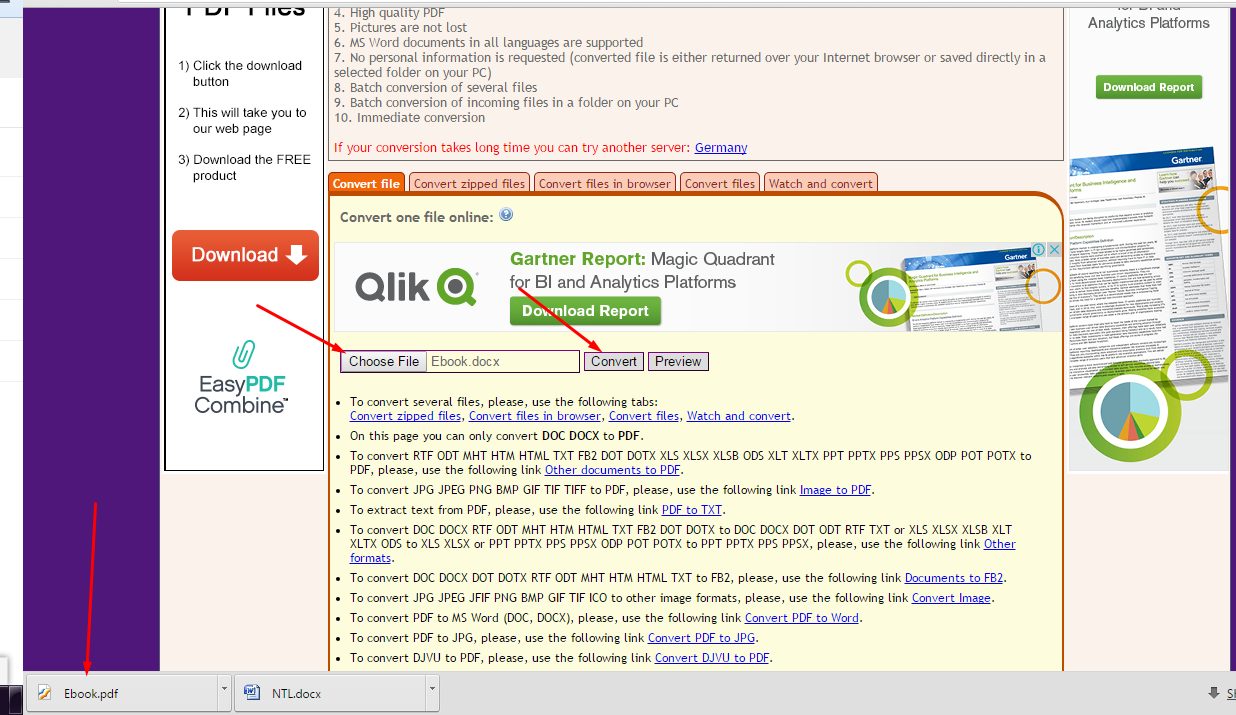 8 (145 голосов)
8 (145 голосов)






 В систему в среднем поступает 6 заказов в час. Если свободных каналов нет, следует отказ. Определить характеристики обслуживания: вероятность отказа, среднее число занятых обслуживанием линий связи, абсолютную и относительную пропускные способности, вероятность обслуживания. Найти число выделенных каналов, при котором относительная пропускная способность системы будет не менее 0,95. Считать, что потоки заявок и обслуживаний простейшие.
В систему в среднем поступает 6 заказов в час. Если свободных каналов нет, следует отказ. Определить характеристики обслуживания: вероятность отказа, среднее число занятых обслуживанием линий связи, абсолютную и относительную пропускные способности, вероятность обслуживания. Найти число выделенных каналов, при котором относительная пропускная способность системы будет не менее 0,95. Считать, что потоки заявок и обслуживаний простейшие.

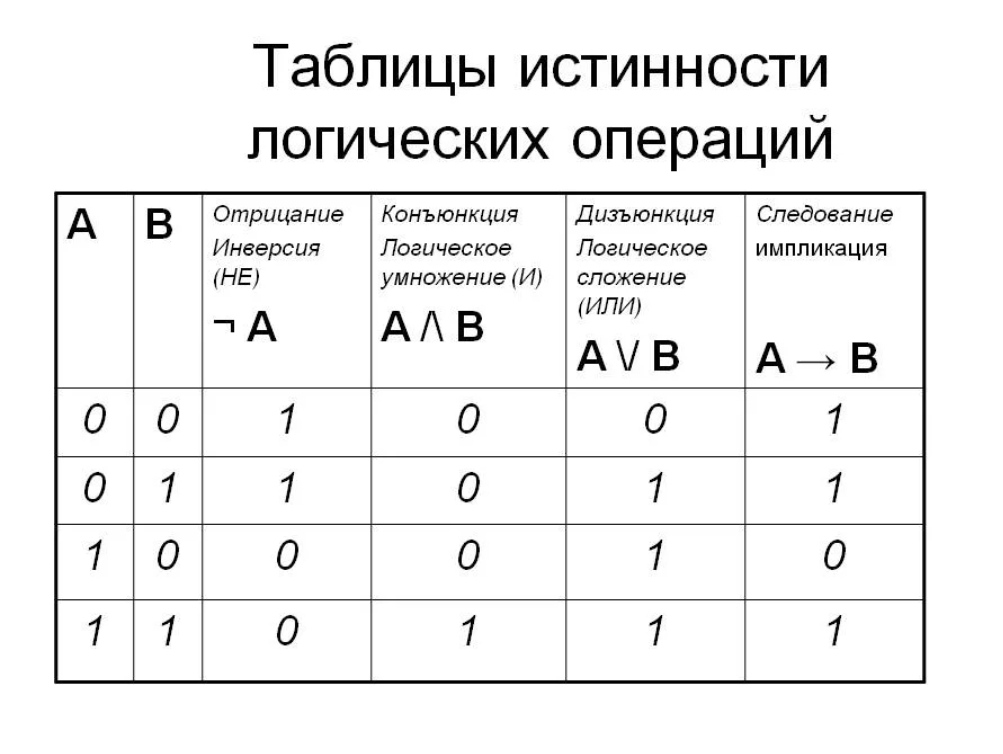 к, коэффициент простоя оборудования кn
к, коэффициент простоя оборудования кn
 Если бы делала сама, потеряла бы уйму времени и нервов. Спасибо, делаете нужное дело!
Если бы делала сама, потеряла бы уйму времени и нервов. Спасибо, делаете нужное дело! Спасибо, теперь будете помогать моему брательнику.
Спасибо, теперь будете помогать моему брательнику. Самая большая помощь – с чертежами. Автор выполнил их ОТ РУКИ, как и потребовал от меня преподаватель. Огромное за это спасибо! Очень клиентоориентированный подход.
Самая большая помощь – с чертежами. Автор выполнил их ОТ РУКИ, как и потребовал от меня преподаватель. Огромное за это спасибо! Очень клиентоориентированный подход. Обязательно порекомендую вас своим партнерам по бизнесу.
Обязательно порекомендую вас своим партнерам по бизнесу.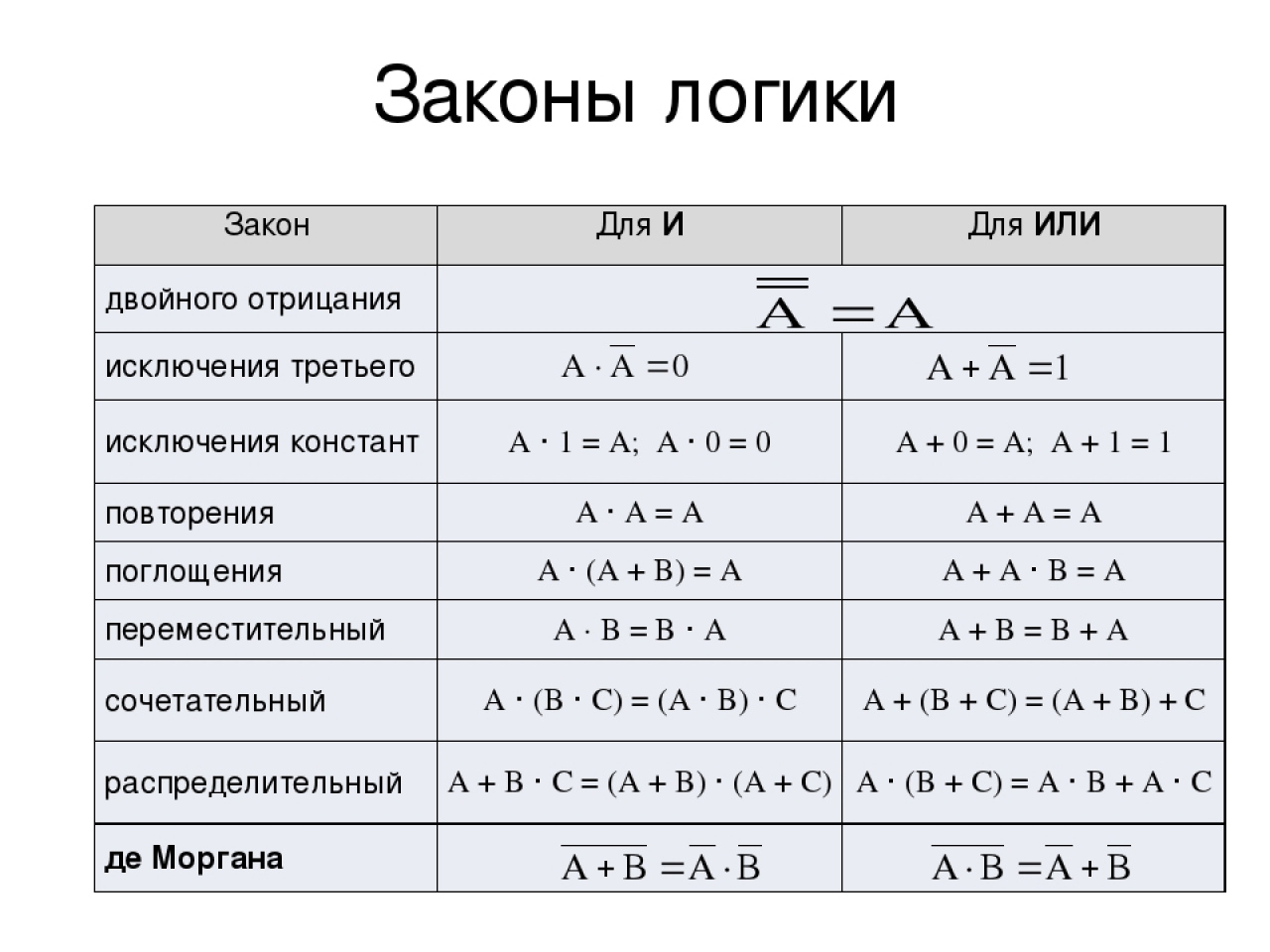 Спасибо авторам studavtor.ru. Посоветовала своим коллегам.
Спасибо авторам studavtor.ru. Посоветовала своим коллегам. Столкнулась недавно с такой необходимостью по литературе. Сестра подсказала сайт студавтор.ру. Не понравилось, что долго искали специалиста, но заказ выполнили буквально за день. Оцениваю сервис хорошо!
Столкнулась недавно с такой необходимостью по литературе. Сестра подсказала сайт студавтор.ру. Не понравилось, что долго искали специалиста, но заказ выполнили буквально за день. Оцениваю сервис хорошо! После окончания вуза и профессиональной деятельности решила открыть собственное дело, и тут опять пригодилась помощь. Заказала бизнес-план. Все необходимые документы с подробными расчетами прислали через три дня. Оперативность и качество работы, как всегда, порадовали. Начинающим предпринимателям советую этот сайт.
После окончания вуза и профессиональной деятельности решила открыть собственное дело, и тут опять пригодилась помощь. Заказала бизнес-план. Все необходимые документы с подробными расчетами прислали через три дня. Оперативность и качество работы, как всегда, порадовали. Начинающим предпринимателям советую этот сайт. Когда потребовалась помощь со статьей ВАК, сразу обратился к специалистам из СтудАвтор. Один материал немного доработал, остальные девять текстов удались на славу. Рекомендую эту компанию всем своим коллегам.
Когда потребовалась помощь со статьей ВАК, сразу обратился к специалистам из СтудАвтор. Один материал немного доработал, остальные девять текстов удались на славу. Рекомендую эту компанию всем своим коллегам. На удивление быстро нашли автора для подготовки монографии по теоретической физике. Результатом доволен. Обязательно посоветую это ресурс знакомым.
На удивление быстро нашли автора для подготовки монографии по теоретической физике. Результатом доволен. Обязательно посоветую это ресурс знакомым. Даже такую нетривиальную задачу решили специалисты этого сайта. В короткие сроки автор подготовил текст, благодаря которому меня приняли на заветную должность в сфере маркетинга. Соискателям мой опыт будет полезен, берите на вооружение!
Даже такую нетривиальную задачу решили специалисты этого сайта. В короткие сроки автор подготовил текст, благодаря которому меня приняли на заветную должность в сфере маркетинга. Соискателям мой опыт будет полезен, берите на вооружение! Решение принял заранее, компанию тоже выбирал по рекомендации бывших выпускников. Считаю, что поступил правильно. Работу сделали в срок, но выявились небольшие недочеты, которые были оперативно исправлены. Кое-что я еще сам подкорректировал. На мой взгляд, у компании адекватное соотношение цены и качества. На защите получил «четверку», но меня это вполне устроило. Если бы лучше подготовился, думаю, мог бы и на «пятерку» претендовать. В целом сотрудничеством с компанией остался доволен, могу с чистой совестью рекомендовать studavtor.ru теперь уже от своего лица.
Решение принял заранее, компанию тоже выбирал по рекомендации бывших выпускников. Считаю, что поступил правильно. Работу сделали в срок, но выявились небольшие недочеты, которые были оперативно исправлены. Кое-что я еще сам подкорректировал. На мой взгляд, у компании адекватное соотношение цены и качества. На защите получил «четверку», но меня это вполне устроило. Если бы лучше подготовился, думаю, мог бы и на «пятерку» претендовать. В целом сотрудничеством с компанией остался доволен, могу с чистой совестью рекомендовать studavtor.ru теперь уже от своего лица. Ответы даны конкретные, удобно структурированы, написаны простым понятным языком. Я считаю, это очень удобно, особенно если заказывать на несколько человек. Думаю, будем еще пользоваться услугами студавтора!
Ответы даны конкретные, удобно структурированы, написаны простым понятным языком. Я считаю, это очень удобно, особенно если заказывать на несколько человек. Думаю, будем еще пользоваться услугами студавтора! Была уверена, что и сама напишу не хуже. Но попала в неприятную ситуацию: меня «бросил» мой дипломный руководитель, пришлось найти другого, а он посоветовал мне поменять тему. Практически мне пришлось начинать все сначала. Друзья посоветовали не паниковать и найти в интернете хорошего исполнителя. Я остановила свой выбор на StudAvtor. С первых же минут прониклась к компании доверием. Менеджер выслушал мою историю и успокоил. Сказал, что как раз по моей теме есть очень хороший исполнитель, он только что сдал предыдущий заказ и пока свободен. Не могу выразить словами, как я благодарна и автору, и менеджерам. Они были со мной на связи, держали в курсе выполнения заказа, уточняли детали. Заказ был выполнен даже раньше, чем я рассчитывала. Дипломный руководитель работу похвалил, ну и защита прошла на «отлично». Рекомендую обращаться в Студавтор, если у кого-то, как у меня, возникнут проблемы с написанием диплома.
Была уверена, что и сама напишу не хуже. Но попала в неприятную ситуацию: меня «бросил» мой дипломный руководитель, пришлось найти другого, а он посоветовал мне поменять тему. Практически мне пришлось начинать все сначала. Друзья посоветовали не паниковать и найти в интернете хорошего исполнителя. Я остановила свой выбор на StudAvtor. С первых же минут прониклась к компании доверием. Менеджер выслушал мою историю и успокоил. Сказал, что как раз по моей теме есть очень хороший исполнитель, он только что сдал предыдущий заказ и пока свободен. Не могу выразить словами, как я благодарна и автору, и менеджерам. Они были со мной на связи, держали в курсе выполнения заказа, уточняли детали. Заказ был выполнен даже раньше, чем я рассчитывала. Дипломный руководитель работу похвалил, ну и защита прошла на «отлично». Рекомендую обращаться в Студавтор, если у кого-то, как у меня, возникнут проблемы с написанием диплома. В результате решил обратиться за помощью в студенческий сервис. Рекламу компании «студавтор ру» видел в интернете не так давно, поэтому и выбор пал на нее. Работа была нужно срочно, пришлось немного понервничать, пока нашелся свободный автор. С заказом он справился в срок, но я для себя сделал вывод, что лучше не затягивать с обращением, потому что времени на доскональную проверку и корректировку уже не оставалось. Преподаватель это тоже заметил, сказал, что по его ощущению эссе написано наспех. Но в целом работа его устроила, он поставил мне «хорошо», так как критичных ошибок не было. По моему мнению работа выполнена на достаточно хорошем уровне, с учетом ее срочности. Однозначно буду пользоваться услугами сайта studavtor.ru в будущем и рекомендовать друзьям.
В результате решил обратиться за помощью в студенческий сервис. Рекламу компании «студавтор ру» видел в интернете не так давно, поэтому и выбор пал на нее. Работа была нужно срочно, пришлось немного понервничать, пока нашелся свободный автор. С заказом он справился в срок, но я для себя сделал вывод, что лучше не затягивать с обращением, потому что времени на доскональную проверку и корректировку уже не оставалось. Преподаватель это тоже заметил, сказал, что по его ощущению эссе написано наспех. Но в целом работа его устроила, он поставил мне «хорошо», так как критичных ошибок не было. По моему мнению работа выполнена на достаточно хорошем уровне, с учетом ее срочности. Однозначно буду пользоваться услугами сайта studavtor.ru в будущем и рекомендовать друзьям. Это был мой первый опыт, и я остался доволен. В процессе написания НИР связывался с менеджерами, которые всегда отвечали на все мои вопросы по статусу заказа. Работу выполнили качественно, без ошибок и опечаток. Защитился на отлично. Спасибо SudAvtor за сотрудничество!
Это был мой первый опыт, и я остался доволен. В процессе написания НИР связывался с менеджерами, которые всегда отвечали на все мои вопросы по статусу заказа. Работу выполнили качественно, без ошибок и опечаток. Защитился на отлично. Спасибо SudAvtor за сотрудничество! СтудАвтор нашел в Интернете, доверился отзывам. Оказалось, что их услуги дешевле, чем у других исполнителей. Но качество очень обрадовало. Подготовили дипломную работу на сложную тему сравнительно быстро, была возможность связываться с автором и просить внести бесплатные доработки в текст. Диплом защитил на 4. Спасибо StudAvtor за работу!
СтудАвтор нашел в Интернете, доверился отзывам. Оказалось, что их услуги дешевле, чем у других исполнителей. Но качество очень обрадовало. Подготовили дипломную работу на сложную тему сравнительно быстро, была возможность связываться с автором и просить внести бесплатные доработки в текст. Диплом защитил на 4. Спасибо StudAvtor за работу! Когда потребовалось сдать лабораторную работу, сразу обратилась к сервису STUDAVTOR. Про этот сервис часто писали в чате факультета. Результат оправдал ожидания, получила «отлично». Обращайтесь, не пожалеете!
Когда потребовалось сдать лабораторную работу, сразу обратилась к сервису STUDAVTOR. Про этот сервис часто писали в чате факультета. Результат оправдал ожидания, получила «отлично». Обращайтесь, не пожалеете! Пропустила много тем по маркетингу. Препод разрешил подтянуть успеваемость с помощью доклада. Спасибо одногруппникам, что подсказали полезный сервис StudAvtor. Автора нашли не сразу, за что снижаю оценку. Работа была выполнена качественно, тест написан интересным и понятным языком. Думаю, я не единственная, кто столкнулся с подобными проблемами. Поэтому, этот ресурс рекомендую каждому!
Пропустила много тем по маркетингу. Препод разрешил подтянуть успеваемость с помощью доклада. Спасибо одногруппникам, что подсказали полезный сервис StudAvtor. Автора нашли не сразу, за что снижаю оценку. Работа была выполнена качественно, тест написан интересным и понятным языком. Думаю, я не единственная, кто столкнулся с подобными проблемами. Поэтому, этот ресурс рекомендую каждому! {n+1}F_{n} \]
{n+1}F_{n} \] Э., Искусство компьютерного программирования. Том I. Основные алгоритмы, Addison-Wesley, 19.97, Бостон, Массачусетс. стр. 79-86
Э., Искусство компьютерного программирования. Том I. Основные алгоритмы, Addison-Wesley, 19.97, Бостон, Массачусетс. стр. 79-86 д. Мы рассмотрели все формулы для связанных понятий в следующих разделах. они такие
д. Мы рассмотрели все формулы для связанных понятий в следующих разделах. они такие Круговая перестановка задается формулой (n-1)!. Подставьте полученное значение n и решите, сколько способов вы можете расположить различные объекты по кругу.
Круговая перестановка задается формулой (n-1)!. Подставьте полученное значение n и решите, сколько способов вы можете расположить различные объекты по кругу.

 е. 5 и 2, в формулу
е. 5 и 2, в формулу