Как выучить таблицу умножения быстро и легко наизусть
Содержание
Как показывает практика, даже во взрослом возрасте далеко не все могут похвастаться знанием таблицы умножения. Педагоги говорят, что это очень большое упущение.
Заучивание таблицы в детском возрасте направлено на улучшение памяти, когнитивных способностей. Это также нужно и для того, чтобы создать математический базис, без которого многие предметы, такие, как физику, геометрию, тригонометрию, химию, будет изучать значительно сложнее.
Основная проблема с таблицей умножения – изначально неправильно выбранный подход. В результате, ребенок начинает думать, что это сложно, долго, у него не получится.
В этой статье мы разберем, как быстро выучить таблицу умножения и не допустить распространенных ошибок, с которыми люди сталкиваются чаще всего.
Используйте таблицу Пифагора вместо обычной
Математики отмечают, что одна из проблем заучивания таблицы умножения заключается в том, что многие учат ее на сложных примерах, а также заучивают отдельные действия для каждой цифры. Выбирайте тетради с таблицей Пифагора, либо распечатайте ее, и все дальнейшее изучение стройте уже по ней.
Выбирайте тетради с таблицей Пифагора, либо распечатайте ее, и все дальнейшее изучение стройте уже по ней.
Выглядит таблица Пифагора так:
Таблица Пифагора значительно удобнее и проще в изучении.Пользоваться таблицей максимально просто. Все что нужно – взять цифру по оси Х и найти место ее состыковки с цифрой по оси Y или наоборот. Результат и станет ответом на задачу. Учитывая, что можно использовать как вертикальный, так и горизонтальный ряд, ребенку будет намного проще учить, объем работы сократится в два раза.
При этом решается и очень важная психологическая задача. Вы показываете, что математика значительно доступнее, чем кажется. Аналогичный подход используется и для других математических задач. Главное – не пропускать темы и формировать прочную базу для дальнейшего изучения предмета.
Используйте закономерности таблицы
Очень важно, чтобы ребенок не занимался простым механическим заучиванием, а понимал смысл выполнения умножения. Рекомендуем для понимания физического смысла, использовать следующий метод:
- Разделите таблицу на прямоугольники, каждая сторона которых соответствует цифрам, которые будете умножать друг на друга.

- Выделите первые клеточки – 2х4, обведите их красным маркером.
- Сосчитайте, сколько клеток совмещается внутри одного полученного прямоугольника. Так вы поймете, что количество клеток – 8.
Это работает, если обвести любое количество цифр и сложить их между собой. Физический смысл умножения кроется именно в этом.
Еще одно важное понимание заключается в том, что в таблице есть закономерности. Это значительно ускоряет изучение. Среди главных закономерностей есть следующие:
- Любая цифра останется прежней, если умножить ее на 1.
- При умножении на 2 к цифре прибавляется еще одна такая же.
- При любом умножении на 5 получается число, в конце которого стоит либо 5 либо 0.
- Если умножать на 9, то сумма всех чисел полученного результата будет также 9.
- Умножение на 10 самое простое – достаточно просто приписать к числу 0.
Все это показывает ребенку, что в математике есть много закономерностей и главное – научиться ими правильно пользоваться, чтобы быстро решать практически любые примеры.
Важные факторы успешности обучения
Существует три важных фактора, которые помогают значительно быстрее достичь успеха в деле изучения таблицы умножения. К ним относятся такие, как:
- Двигайтесь от простого к сложному и постепенно закрепляйте результат. Не нужно пытаться брать сразу крупные числа. Сначала работайте с умножением на 1, 2, 5 и 10. Далее можно постепенно добавлять другие числа и двигаться по таблице Пифагора.
- Не пытайтесь охватить сразу все. Таблицу нужно учить постепенно, дробить занятия. Во многих школах встречается распространенная ошибка – таблицу делят на две части и проходят за два урока. Это приводит к тому, что и во взрослом возрасте человек не может быстро умножать без калькулятора.
- Помните о важности повторения. Первоначально нужно действовать по принципам целенаправленного повторения – задавать вопросы по умножению по мере возрастания чисел.
 Затем результат закрепляется, и задачи берутся вразброс. Это имеет критическую важность для того, чтобы ребенок научился работать с разными примерами, а не просто зубрил.
Затем результат закрепляется, и задачи берутся вразброс. Это имеет критическую важность для того, чтобы ребенок научился работать с разными примерами, а не просто зубрил.
Педагоги также рекомендуют использовать наглядные обучающие материалы. Они помогают быстрее запоминать примеры. Многие дети сегодня лучше всего усваивают именно поданную наглядно информацию.
Использование геймификации как часть успеха обучения
Проще всего изучать математику в процессе игры. Существует большое количество настольных игр, а также специальных материалов, которые помогают обучаться в простой игровой форме.
Серди наиболее простых вариантов игр:
- Использование кубиков. Они могут в случайном порядке извлекаться из мешка. Все что нужно ребенку – быстро умножить полученные цифры.
- Наперегонки с калькулятором. Когда человек хорошо знает таблицу умножения, он говорит ответ быстрее, чем вы вводите данные на калькуляторе.
 Предложите малышу такую гонку и шанс проявить себя.
Предложите малышу такую гонку и шанс проявить себя. - Полезная математика. Вокруг нас много примеров вариантов применения таблицы умножения. Используйте практические задачи, чтобы показать реальную пользу предмета для ребенка в его будущей жизни.
При использовании игровой формы обучения, очень важно не забывать о поощрении. Так, если вы хотите соревноваться в счете, стоит обязательно предусмотреть для победителя небольшой приз.
5 распространенных ошибок изучения таблицы умножения
Ища ответ на вопрос о том, как выучить таблицу умножения быстро и легко, многие сталкиваются с классическими ошибками домашнего преподавания. К ним относятся такие, как:
- Занятия без мотивации. Важно, чтобы ребенок был мотивирован на изучение таблицы умножения. Если такой мотивации нет, можно не ждать каких-либо выдающихся результатов.
- Упреки. Даже если малыш ошибся, нельзя ругать его, сильно давить, угрожать. Это приводит к тому, что у человека на всю жизнь появляется неприязнь, как к учебе, так и к математике в частности.

- Использовать примеры детей из класса. Многие думают, что это стимулирует соревновательный дух. На деле, вы просто создаете у малыша ощущение неполноценности.
- Обучение в большом объеме. Каким бы ни был умным ваш ребенок, он не запомнит сразу всю таблицу умножения. А вот крупный объем задач детей обычно пугает. Потому, как мы и советовали, делите занятия на небольшие порции информации и старайтесь усвоить их постепенно.
- Игнорирование успехов. Многие родители принимают успехи ребенка в учебе как что-то само собой разумеющееся. Как результат, без вашей похвалы дети попросту не получают нужного уровня мотивации для того, чтобы показывать еще более заметные результаты. Любые успехи всегда нужно отмечать.
Еще проще обучить ребенка таблице умножения, если отдать его в специальный учебный центр. В таком случае, весь процесс обучения будет контролироваться педагогами с большим опытом, а успехов можно будет достичь намного быстрее.
Читайте также
Рубрика: Образование
Читать все новости28.10.2021
Подпишитесь на email уведомления
✖Спасибо, что оставили заявку
Мы скоро свяжемся с вами!
Подпишитесь на группу ВКонтакте
SmartyKidsКак выучить таблицу умножения ребенку легко и быстро: все способы
https://ria.ru/20221102/umnozhenie-1828522004.html
Цифры в столбик: как помочь ребенку выучить таблицу умножения
Как выучить таблицу умножения ребенку легко и быстро: все способы
Цифры в столбик: как помочь ребенку выучить таблицу умножения
Знание таблицы умножения очень пригодится школьнику на уроках математики. Однако выучить ее наизусть быстро и легко, за 5 минут, вряд ли получится. Изучением. .. РИА Новости, 02.11.2022
.. РИА Новости, 02.11.2022
2022-11-02T15:01
2022-11-02T15:01
2022-11-02T15:14
общество
образование
дети
социальный навигатор
детские вопросы
/html/head/meta[@name=’og:title’]/@content
/html/head/meta[@name=’og:description’]/@content
https://cdnn21.img.ria.ru/images/07e6/0b/01/1828498896_0:0:3072:1728_1920x0_80_0_0_66e021c56210b9307b4dc7f7d40ab85e.jpg
МОСКВА, 2 ноя – РИА Новости. Знание таблицы умножения очень пригодится школьнику на уроках математики. Однако выучить ее наизусть быстро и легко, за 5 минут, вряд ли получится. Изучением этой темы дети занимаются примерно в 8 лет, то есть во 2 и в 3 классах. Как выучить таблицу умножения и какие способы сделают процесс проще — в материале РИА Новости.Таблица умноженияВряд ли кому-то нужно объяснять, как именно выглядит таблица умножения. Именно ее ровные столбики с примерами от 1*1 до 10*10 украшают заднюю обложку многих школьных тетрадей.Умножение — одна из ключевых операций в математике. Ее суть — взять два числа, первое из которых именуется множимым, а второе (на которое и необходимо умножить первое число) — множителем. Получившийся в результате умножения результат называется произведением.Для чего нужнаДаже в современном мире, где практически у каждого человека есть при себе смартфон с калькулятором, люди нередко сталкиваются с необходимостью выполнять более или менее сложные вычисления в уме. В том числе — умножая числа одно на другое. Это может происходить как на работе, так и в бытовых ситуациях, например, в магазине или при планировании различных мероприятий.Зная назубок таблицу умножения, производить необходимые вычисления удается заметно проще и быстрее. Тем более что далеко не всегда есть время и возможность воспользоваться калькулятором.В каком возрасте учитьКак правило, первое знакомство с таблицей умножения у современных школьников происходит в начальных классах.“К изучению таблицы умножения в большинстве образовательных программ начального общего образования (за исключением системы развивающего обучения Д.
Ее суть — взять два числа, первое из которых именуется множимым, а второе (на которое и необходимо умножить первое число) — множителем. Получившийся в результате умножения результат называется произведением.Для чего нужнаДаже в современном мире, где практически у каждого человека есть при себе смартфон с калькулятором, люди нередко сталкиваются с необходимостью выполнять более или менее сложные вычисления в уме. В том числе — умножая числа одно на другое. Это может происходить как на работе, так и в бытовых ситуациях, например, в магазине или при планировании различных мероприятий.Зная назубок таблицу умножения, производить необходимые вычисления удается заметно проще и быстрее. Тем более что далеко не всегда есть время и возможность воспользоваться калькулятором.В каком возрасте учитьКак правило, первое знакомство с таблицей умножения у современных школьников происходит в начальных классах.“К изучению таблицы умножения в большинстве образовательных программ начального общего образования (за исключением системы развивающего обучения Д. Б.Эльконина-В.В.Давыдова) приступают во 2 классе. Совершенствование навыков продолжается в 3-4 классах,” — говорит учитель начальных классов, руководитель кафедры учителей начальных классов МБОУ «Гимназия № 4» города Смоленска Татьяна Мельникова.Таким образом, азы умножения ребенок постигает примерно в возрасте 7-8 лет.Теоретически объяснить ребенку основной принцип этой операции можно попробовать и в более раннем возрасте. Однако целенаправленно “зубрить” и запоминать именно таблицу умножения дошкольникам и даже первоклассникам многие эксперты все же не рекомендуют. Ведь для того, чтобы перейти к умножению, ребенку нужно уверенно научиться сложению, так как большинство методистов рассматривает умножение именно как сложение одинаковых слагаемых.“Например, до знакомства с действием умножения детям могут предложить следующие задания: посчитать предметы двойками (тройками или пятерками) или изобразить на рисунке две тарелки, на каждой из которых находится по 3 яблока, а после посчитать, сколько всего яблок на картинке”, — говорит Татьяна Мельникова.
Б.Эльконина-В.В.Давыдова) приступают во 2 классе. Совершенствование навыков продолжается в 3-4 классах,” — говорит учитель начальных классов, руководитель кафедры учителей начальных классов МБОУ «Гимназия № 4» города Смоленска Татьяна Мельникова.Таким образом, азы умножения ребенок постигает примерно в возрасте 7-8 лет.Теоретически объяснить ребенку основной принцип этой операции можно попробовать и в более раннем возрасте. Однако целенаправленно “зубрить” и запоминать именно таблицу умножения дошкольникам и даже первоклассникам многие эксперты все же не рекомендуют. Ведь для того, чтобы перейти к умножению, ребенку нужно уверенно научиться сложению, так как большинство методистов рассматривает умножение именно как сложение одинаковых слагаемых.“Например, до знакомства с действием умножения детям могут предложить следующие задания: посчитать предметы двойками (тройками или пятерками) или изобразить на рисунке две тарелки, на каждой из которых находится по 3 яблока, а после посчитать, сколько всего яблок на картинке”, — говорит Татьяна Мельникова. В каком порядке учитьПриступая к изучению таблицы умножения, стоит руководствоваться принципом “от простого — к сложному”. Соответственно, первым делом запоминается умножение на единицу, затем — на 2, следом — на 3 и так далее по возрастающей.Способы выучить таблицу умноженияПорой ребенку очень сложно выучить самостоятельно такой большой объем новой и непростой для него информации. В данном случае на помощь школьнику могут прийти родители, взяв на вооружение один из способов облегчить процесс запоминания таблицы умножения.Классический — заучиваниеПервый и, наверное, наиболее очевидный для многих способ выучить таблицу умножения — попросту заучить последовательно, один за другим, все десять столбиков. Сделать это непросто, ведь каждый ребенок по-разному запоминает один и тот же объем информации.Для того, чтобы ребенок быстрее смог запомнить всю таблицу умножения, стоит постараться, чтобы она была у него постоянно перед глазами. Это не означает, что учить таблицу необходимо целыми днями без остановки.
В каком порядке учитьПриступая к изучению таблицы умножения, стоит руководствоваться принципом “от простого — к сложному”. Соответственно, первым делом запоминается умножение на единицу, затем — на 2, следом — на 3 и так далее по возрастающей.Способы выучить таблицу умноженияПорой ребенку очень сложно выучить самостоятельно такой большой объем новой и непростой для него информации. В данном случае на помощь школьнику могут прийти родители, взяв на вооружение один из способов облегчить процесс запоминания таблицы умножения.Классический — заучиваниеПервый и, наверное, наиболее очевидный для многих способ выучить таблицу умножения — попросту заучить последовательно, один за другим, все десять столбиков. Сделать это непросто, ведь каждый ребенок по-разному запоминает один и тот же объем информации.Для того, чтобы ребенок быстрее смог запомнить всю таблицу умножения, стоит постараться, чтобы она была у него постоянно перед глазами. Это не означает, что учить таблицу необходимо целыми днями без остановки. Можно носить небольшую табличку с собой и при каждом удобном случае (например, во время поездки в общественном транспорте или на переменах) просматривать ее. Можно купить и повесить в комнате большой плакат с таблицей умножения: время от времени он непременно будет попадаться на глаза ребенку и что-то обязательно запомнится.ЛогическийПодступиться к изучению таблицы умножения можно и опираясь на принципы логики. Например, попробовать первым делом объяснить ребенку, что любой пример на умножение можно представить через сложение.Так, 7×3 — это то же самое, что 7+7+7, а 5×6, соответственно, 5+5+5+5+5+5. В случае с небольшими множителями выполнить такое сложение относительно просто (например, при умножении на 2 или на 3 сложить две или три цифры ребенок сможет достаточно быстро). Когда умножать необходимо на 7 или, например, на 9, то сложение такого количества цифр может занять немало времени.На помощь в данной ситуации приходит еще один полезный принцип, который кратко можно сформулировать так: от перестановки множителей результат не меняется.
Можно носить небольшую табличку с собой и при каждом удобном случае (например, во время поездки в общественном транспорте или на переменах) просматривать ее. Можно купить и повесить в комнате большой плакат с таблицей умножения: время от времени он непременно будет попадаться на глаза ребенку и что-то обязательно запомнится.ЛогическийПодступиться к изучению таблицы умножения можно и опираясь на принципы логики. Например, попробовать первым делом объяснить ребенку, что любой пример на умножение можно представить через сложение.Так, 7×3 — это то же самое, что 7+7+7, а 5×6, соответственно, 5+5+5+5+5+5. В случае с небольшими множителями выполнить такое сложение относительно просто (например, при умножении на 2 или на 3 сложить две или три цифры ребенок сможет достаточно быстро). Когда умножать необходимо на 7 или, например, на 9, то сложение такого количества цифр может занять немало времени.На помощь в данной ситуации приходит еще один полезный принцип, который кратко можно сформулировать так: от перестановки множителей результат не меняется. Эту мысль очень важно донести до ребенка, в некоторых случаях это может заметно облегчить ему задачу.Пример: нужно посчитать произведение для 3×7. Если пытаться представить умножение через сложение, то школьнику необходимо найти результат для 3+3+3+3+3+3+3. Это, как известно, будет 21. Но если поменять цифры местами, то пример для сложение будет куда короче: 7+7+7. А ответ по-прежнему остается 21, хотя складывать нужно уже гораздо меньше цифр.Логика пригодится и для запоминания принципов умножения на 5. Ведь ответ здесь всегда будет заканчиваться либо на 5, либо на 0. Первое — для нечетных чисел (7×5=35, 5×5=25 и так далее), второе — для примеров с четными (4×5=20, 8×5=40 и другие).С логической точки зрения можно подойти и к запоминанию столбца умножения на 9. Ведь умножение любого числа на девять — это практически то же самое, что результат умножения на 10, за вычетом одной цифры множимого. Проще говоря, 7×9 можно определить как 7×10-7 (то есть 70-7=63).На пальцахУмножение на 9 можно запомнить не только через примеры с десятками, но и при помощи “инструмента”, который у школьника всегда с собой (в отличие, например, от калькулятора или тетради с нужной таблицей, которые вполне можно забыть дома).
Эту мысль очень важно донести до ребенка, в некоторых случаях это может заметно облегчить ему задачу.Пример: нужно посчитать произведение для 3×7. Если пытаться представить умножение через сложение, то школьнику необходимо найти результат для 3+3+3+3+3+3+3. Это, как известно, будет 21. Но если поменять цифры местами, то пример для сложение будет куда короче: 7+7+7. А ответ по-прежнему остается 21, хотя складывать нужно уже гораздо меньше цифр.Логика пригодится и для запоминания принципов умножения на 5. Ведь ответ здесь всегда будет заканчиваться либо на 5, либо на 0. Первое — для нечетных чисел (7×5=35, 5×5=25 и так далее), второе — для примеров с четными (4×5=20, 8×5=40 и другие).С логической точки зрения можно подойти и к запоминанию столбца умножения на 9. Ведь умножение любого числа на девять — это практически то же самое, что результат умножения на 10, за вычетом одной цифры множимого. Проще говоря, 7×9 можно определить как 7×10-7 (то есть 70-7=63).На пальцахУмножение на 9 можно запомнить не только через примеры с десятками, но и при помощи “инструмента”, который у школьника всегда с собой (в отличие, например, от калькулятора или тетради с нужной таблицей, которые вполне можно забыть дома). Речь идет о руках, точнее, о ладонях с пальцами, которые помогут быстро найти ответ на нужный пример.Итак, первым делом нужно повернуть руки ладонями к себе и мысленно пронумеровать пальцы от 1 до 10, начиная с большого пальца левой руки. В зависимости от того, какую цифру необходимо умножить на 9, полагается согнуть определенный палец.К примеру, нужно высчитать результат для 4×9. Значит, загнуть четвертый по счету палец (то есть безымянный палец левой руки). Перед вами — ответ на заданный пример: слева от согнутого пальца — десятки, справа — единицы (прижатый палец не считается нигде). Осталось лишь посчитать их, в данном примере ответ — 36.Таблица ПифагораКлассическая таблица умножения — это десять столбиков, в которых последовательно перемножаются все цифры от 1 до 10. Однако существует и упрощенный, более понятный для многих школьников вариант — так называемая таблица Пифагора. Внешне она представляет собой квадрат, параметры которого — 11 ячеек по вертикали и столько же — по горизонтали, пронумерованные от 1 до 10.
Речь идет о руках, точнее, о ладонях с пальцами, которые помогут быстро найти ответ на нужный пример.Итак, первым делом нужно повернуть руки ладонями к себе и мысленно пронумеровать пальцы от 1 до 10, начиная с большого пальца левой руки. В зависимости от того, какую цифру необходимо умножить на 9, полагается согнуть определенный палец.К примеру, нужно высчитать результат для 4×9. Значит, загнуть четвертый по счету палец (то есть безымянный палец левой руки). Перед вами — ответ на заданный пример: слева от согнутого пальца — десятки, справа — единицы (прижатый палец не считается нигде). Осталось лишь посчитать их, в данном примере ответ — 36.Таблица ПифагораКлассическая таблица умножения — это десять столбиков, в которых последовательно перемножаются все цифры от 1 до 10. Однако существует и упрощенный, более понятный для многих школьников вариант — так называемая таблица Пифагора. Внешне она представляет собой квадрат, параметры которого — 11 ячеек по вертикали и столько же — по горизонтали, пронумерованные от 1 до 10. Порой можно встретить и еще более простой вариант, от 1 до 9, так как умножение на 10, как правило, не вызывает у ребят проблем.Пользоваться таблицей Пифагора достаточно просто: нужно лишь выбрать строчку и столбик, соответствующие перемножаемым числам — и в точке их пересечения будет указано искомое произведение. При этом неважно, как именно будут расположены числа (какое из них искать по вертикали, а какое — по горизонтали), ведь от перемены множителей результат, как уже было сказано выше, не меняется.Еще один важный принцип, который наглядно представлен в таблице Пифагора — совсем не обязательно заучивать всю таблицу умножения наизусть, достаточно запомнить чуть больше половины. Если провести диагональ через ячейки с результатами перемножения одинаковых чисел (1×1=1, 2×2=4, 3×3=9 и так далее), можно увидеть, что результаты над этой диагональю и под нею симметричны. Ведь если запомнить, что 3×4=12, то легко можно понять, что и умножение 4 на 3 дает аналогичный результат.В игровой формеЕще один эффективный способ помочь ребенку запомнить новую информацию — это превратить процесс обучения в увлекательную игру.
Порой можно встретить и еще более простой вариант, от 1 до 9, так как умножение на 10, как правило, не вызывает у ребят проблем.Пользоваться таблицей Пифагора достаточно просто: нужно лишь выбрать строчку и столбик, соответствующие перемножаемым числам — и в точке их пересечения будет указано искомое произведение. При этом неважно, как именно будут расположены числа (какое из них искать по вертикали, а какое — по горизонтали), ведь от перемены множителей результат, как уже было сказано выше, не меняется.Еще один важный принцип, который наглядно представлен в таблице Пифагора — совсем не обязательно заучивать всю таблицу умножения наизусть, достаточно запомнить чуть больше половины. Если провести диагональ через ячейки с результатами перемножения одинаковых чисел (1×1=1, 2×2=4, 3×3=9 и так далее), можно увидеть, что результаты над этой диагональю и под нею симметричны. Ведь если запомнить, что 3×4=12, то легко можно понять, что и умножение 4 на 3 дает аналогичный результат.В игровой формеЕще один эффективный способ помочь ребенку запомнить новую информацию — это превратить процесс обучения в увлекательную игру. Например, запомнить умножение на 7 помогут обычные игральные кубики. Правила игры просты: нужно взять энное количество кубиков и предложить школьнику посостязаться в том, кто быстрее посчитает количество точек, выпавшее как на верхних. так и на противоположных им нижних гранях. Сложить такого количество чисел, конечно, будет непросто, тогда можно раскрыть небольшой секрет: сумма противоположных граней на таких кубиках всегда равна 7. А значит, для получения верного ответа нужно лишь умножить 7 на количество используемых кубиков. Плюс у ребенка появился стимул: получить правильный ответ быстрее всех и выиграть.Учить таблицу умножения можно и при помощи обычной игры-ходилки, в которой, бросая кубики и продвигаясь на выпавшее число шагов, необходимо пройти путь от старта до финиша. Чтобы совместить приятное с полезным и помочь ребенку выучить таблицу умножения, можно предложить ему умножать выпавшее количество ходов на 2. И, если он даст правильный ответ, то продвинется вперед, к примеру, уже не на 6, а на 12 делений.
Например, запомнить умножение на 7 помогут обычные игральные кубики. Правила игры просты: нужно взять энное количество кубиков и предложить школьнику посостязаться в том, кто быстрее посчитает количество точек, выпавшее как на верхних. так и на противоположных им нижних гранях. Сложить такого количество чисел, конечно, будет непросто, тогда можно раскрыть небольшой секрет: сумма противоположных граней на таких кубиках всегда равна 7. А значит, для получения верного ответа нужно лишь умножить 7 на количество используемых кубиков. Плюс у ребенка появился стимул: получить правильный ответ быстрее всех и выиграть.Учить таблицу умножения можно и при помощи обычной игры-ходилки, в которой, бросая кубики и продвигаясь на выпавшее число шагов, необходимо пройти путь от старта до финиша. Чтобы совместить приятное с полезным и помочь ребенку выучить таблицу умножения, можно предложить ему умножать выпавшее количество ходов на 2. И, если он даст правильный ответ, то продвинется вперед, к примеру, уже не на 6, а на 12 делений. Так постепенно можно перейти к умножению на 3, 4 и так далее.ТренажерСуществуют и специальные тренажеры в онлайн-формате, которые помогают как изучать таблицу, так и закрепить полученные знания. Они включают различные виды заданий: самостоятельно вписать ответ на предложенные примеры, определить, в каких примерах с умножением специально допущены ошибки, и так далее. Некоторые позволяют даже выставить нужный уровень сложности или, к примеру, практиковаться в умножении на определенное число.Закрепление и проверка результатаНа то, чтобы запомнить всю таблицу умножения, у школьника может уйти немало времени. Проверить, насколько хорошо ему удалось усвоить все примеры, можно при помощи не только онлайн-тренажеров, но и другими доступными способами.К примеру, проверить, насколько уверенно ребенок ориентируется в умножении на различные числа, можно при помощи простой игры. Для этого необходимо подготовить две группы карточек. На карточках из первой группы будут написаны примеры перемножения различных чисел, карточки из второй группы будут содержать ответы.
Так постепенно можно перейти к умножению на 3, 4 и так далее.ТренажерСуществуют и специальные тренажеры в онлайн-формате, которые помогают как изучать таблицу, так и закрепить полученные знания. Они включают различные виды заданий: самостоятельно вписать ответ на предложенные примеры, определить, в каких примерах с умножением специально допущены ошибки, и так далее. Некоторые позволяют даже выставить нужный уровень сложности или, к примеру, практиковаться в умножении на определенное число.Закрепление и проверка результатаНа то, чтобы запомнить всю таблицу умножения, у школьника может уйти немало времени. Проверить, насколько хорошо ему удалось усвоить все примеры, можно при помощи не только онлайн-тренажеров, но и другими доступными способами.К примеру, проверить, насколько уверенно ребенок ориентируется в умножении на различные числа, можно при помощи простой игры. Для этого необходимо подготовить две группы карточек. На карточках из первой группы будут написаны примеры перемножения различных чисел, карточки из второй группы будут содержать ответы. Задача школьника — правильно сопоставить примеры с правильными ответами.Повторять таблицу умножения можно и в различных бытовых ситуациях. Например, в магазине, где родители могут предложить сыну или дочке посчитать, сколько яблок нужно купить, чтобы каждому члену семьи досталось по 2 фрукта, или какое количество сладостей стоит взять, чтобы угостить одноклассников и каждому из них вручить по 3 конфеты.На первом этапе стоит повторять таблицу умножения по порядку: школьник выучил умножение на 2 — повторяет этот столбик, освоил умножение на 3 — повторяет эти примеры. Только после того, как ребенок твердо усвоил всю таблицу, можно приступать к проверку вразброс.Как не стоит учить таблицу умноженияДаже если использовать упрощенный вариант таблицы умножения, то есть квадрат Пифагора, задача все равно остается для школьников достаточно непростой. А потому не стоит пытаться запомнить всю таблицу сразу и целиком, добиться результата в экстремально короткие сроки. Пусть ребенок учит ее постепенно, небольшими частями.
Задача школьника — правильно сопоставить примеры с правильными ответами.Повторять таблицу умножения можно и в различных бытовых ситуациях. Например, в магазине, где родители могут предложить сыну или дочке посчитать, сколько яблок нужно купить, чтобы каждому члену семьи досталось по 2 фрукта, или какое количество сладостей стоит взять, чтобы угостить одноклассников и каждому из них вручить по 3 конфеты.На первом этапе стоит повторять таблицу умножения по порядку: школьник выучил умножение на 2 — повторяет этот столбик, освоил умножение на 3 — повторяет эти примеры. Только после того, как ребенок твердо усвоил всю таблицу, можно приступать к проверку вразброс.Как не стоит учить таблицу умноженияДаже если использовать упрощенный вариант таблицы умножения, то есть квадрат Пифагора, задача все равно остается для школьников достаточно непростой. А потому не стоит пытаться запомнить всю таблицу сразу и целиком, добиться результата в экстремально короткие сроки. Пусть ребенок учит ее постепенно, небольшими частями. Переходить к следующей части стоит лишь при условии, что ученик хорошо запомнил предыдущий этап.Для многих детей процесс изучения таблицы умножения заметно осложняет тот факт, что для них это занятие представляется бессмысленным и бесполезным. А значит, важно найти правильную мотивацию (фразы из разряда “так нужно” или “учитель сказал надо” к таковым не относятся). Родителям необходимо убедить школьника в том, что знание таблицы умножения будет полезно и пригодится в будущем, сделает жизнь проще и поможет избежать ошибок.И, конечно, не стоит заставлять ребенка зубрить таблицу умножения, если он категорически не желает этого делать. Лучше выбрать другой момент, когда школьник будет более настроен на работу. Ведь если учить примеры через силу, любви к таблице умножения у ребенка точно не прибавится, да и добиться нужного результата тоже вряд ли получится.
Переходить к следующей части стоит лишь при условии, что ученик хорошо запомнил предыдущий этап.Для многих детей процесс изучения таблицы умножения заметно осложняет тот факт, что для них это занятие представляется бессмысленным и бесполезным. А значит, важно найти правильную мотивацию (фразы из разряда “так нужно” или “учитель сказал надо” к таковым не относятся). Родителям необходимо убедить школьника в том, что знание таблицы умножения будет полезно и пригодится в будущем, сделает жизнь проще и поможет избежать ошибок.И, конечно, не стоит заставлять ребенка зубрить таблицу умножения, если он категорически не желает этого делать. Лучше выбрать другой момент, когда школьник будет более настроен на работу. Ведь если учить примеры через силу, любви к таблице умножения у ребенка точно не прибавится, да и добиться нужного результата тоже вряд ли получится.
https://sn.ria.ru/20200228/1565311167.html
https://ria.ru/20220928/shkola-1820210067.html
РИА Новости
1
5
4. 7
7
96
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
2022
Алёна Пава
Алёна Пава
Новости
ru-RU
https://ria.ru/docs/about/copyright.html
https://xn--c1acbl2abdlkab1og.xn--p1ai/
РИА Новости
1
5
4.7
96
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
1920
1080
true
1920
1440
true
https://cdnn21.img.ria.ru/images/07e6/0b/01/1828498896_191:0:2922:2048_1920x0_80_0_0_fc7688e65386e929c36c30a0c34f2ed6.jpg1920
1920
true
РИА Новости
1
5
4.7
96
7 495 645-6601
ФГУП МИА «Россия сегодня»
https://xn--c1acbl2abdlkab1og.xn--p1ai/awards/
Алёна Пава
общество, образование, дети, социальный навигатор, детские вопросы
Общество, Образование, Дети, Социальный навигатор, Детские вопросы
Оглавление- Таблица умножения
- Для чего нужна
- В каком возрасте учить
- В каком порядке учить
- Способы выучить таблицу умножения
- Классический — заучивание
- Логический
- На пальцах
- Таблица Пифагора
- В игровой форме
- Тренажер
- Закрепление и проверка результата
- Как не стоит учить таблицу умножения
МОСКВА, 2 ноя – РИА Новости. Знание таблицы умножения очень пригодится школьнику на уроках математики. Однако выучить ее наизусть быстро и легко, за 5 минут, вряд ли получится. Изучением этой темы дети занимаются примерно в 8 лет, то есть во 2 и в 3 классах. Как выучить таблицу умножения и какие способы сделают процесс проще — в материале РИА Новости.
Знание таблицы умножения очень пригодится школьнику на уроках математики. Однако выучить ее наизусть быстро и легко, за 5 минут, вряд ли получится. Изучением этой темы дети занимаются примерно в 8 лет, то есть во 2 и в 3 классах. Как выучить таблицу умножения и какие способы сделают процесс проще — в материале РИА Новости.
Таблица умножения
Вряд ли кому-то нужно объяснять, как именно выглядит таблица умножения. Именно ее ровные столбики с примерами от 1*1 до 10*10 украшают заднюю обложку многих школьных тетрадей.
Умножение — одна из ключевых операций в математике. Ее суть — взять два числа, первое из которых именуется множимым, а второе (на которое и необходимо умножить первое число) — множителем. Получившийся в результате умножения результат называется произведением.
Для чего нужна
Даже в современном мире, где практически у каждого человека есть при себе смартфон с калькулятором, люди нередко сталкиваются с необходимостью выполнять более или менее сложные вычисления в уме. В том числе — умножая числа одно на другое. Это может происходить как на работе, так и в бытовых ситуациях, например, в магазине или при планировании различных мероприятий.
В том числе — умножая числа одно на другое. Это может происходить как на работе, так и в бытовых ситуациях, например, в магазине или при планировании различных мероприятий.
Зная назубок таблицу умножения, производить необходимые вычисления удается заметно проще и быстрее. Тем более что далеко не всегда есть время и возможность воспользоваться калькулятором.
Эксперты рассказали, почему школьникам трудно преуспеть в учебе28 февраля 2020, 10:17
В каком возрасте учить
Как правило, первое знакомство с таблицей умножения у современных школьников происходит в начальных классах.
“К изучению таблицы умножения в большинстве образовательных программ начального общего образования (за исключением системы развивающего обучения Д.Б.Эльконина-В.В.Давыдова) приступают во 2 классе. Совершенствование навыков продолжается в 3-4 классах,” — говорит учитель начальных классов, руководитель кафедры учителей начальных классов МБОУ «Гимназия № 4» города Смоленска Татьяна Мельникова.
Таким образом, азы умножения ребенок постигает примерно в возрасте 7-8 лет.
Теоретически объяснить ребенку основной принцип этой операции можно попробовать и в более раннем возрасте. Однако целенаправленно “зубрить” и запоминать именно таблицу умножения дошкольникам и даже первоклассникам многие эксперты все же не рекомендуют. Ведь для того, чтобы перейти к умножению, ребенку нужно уверенно научиться сложению, так как большинство методистов рассматривает умножение именно как сложение одинаковых слагаемых.
“Например, до знакомства с действием умножения детям могут предложить следующие задания: посчитать предметы двойками (тройками или пятерками) или изобразить на рисунке две тарелки, на каждой из которых находится по 3 яблока, а после посчитать, сколько всего яблок на картинке”, — говорит Татьяна Мельникова.
В каком порядке учить
Приступая к изучению таблицы умножения, стоит руководствоваться принципом “от простого — к сложному”. Соответственно, первым делом запоминается умножение на единицу, затем — на 2, следом — на 3 и так далее по возрастающей.
28 сентября 2022, 23:02
Способы выучить таблицу умножения
Порой ребенку очень сложно выучить самостоятельно такой большой объем новой и непростой для него информации. В данном случае на помощь школьнику могут прийти родители, взяв на вооружение один из способов облегчить процесс запоминания таблицы умножения.
Классический — заучивание
Первый и, наверное, наиболее очевидный для многих способ выучить таблицу умножения — попросту заучить последовательно, один за другим, все десять столбиков. Сделать это непросто, ведь каждый ребенок по-разному запоминает один и тот же объем информации.
Для того, чтобы ребенок быстрее смог запомнить всю таблицу умножения, стоит постараться, чтобы она была у него постоянно перед глазами. Это не означает, что учить таблицу необходимо целыми днями без остановки. Можно носить небольшую табличку с собой и при каждом удобном случае (например, во время поездки в общественном транспорте или на переменах) просматривать ее. Можно купить и повесить в комнате большой плакат с таблицей умножения: время от времени он непременно будет попадаться на глаза ребенку и что-то обязательно запомнится.
Можно купить и повесить в комнате большой плакат с таблицей умножения: время от времени он непременно будет попадаться на глаза ребенку и что-то обязательно запомнится.
Логический
Подступиться к изучению таблицы умножения можно и опираясь на принципы логики. Например, попробовать первым делом объяснить ребенку, что любой пример на умножение можно представить через сложение.
© Фото : Freepik Мама помогает ребенку выучить таблицу умножения
© Фото : Freepik
Мама помогает ребенку выучить таблицу умножения
Так, 7×3 — это то же самое, что 7+7+7, а 5×6, соответственно, 5+5+5+5+5+5. В случае с небольшими множителями выполнить такое сложение относительно просто (например, при умножении на 2 или на 3 сложить две или три цифры ребенок сможет достаточно быстро). Когда умножать необходимо на 7 или, например, на 9, то сложение такого количества цифр может занять немало времени.
На помощь в данной ситуации приходит еще один полезный принцип, который кратко можно сформулировать так: от перестановки множителей результат не меняется. Эту мысль очень важно донести до ребенка, в некоторых случаях это может заметно облегчить ему задачу.
Эту мысль очень важно донести до ребенка, в некоторых случаях это может заметно облегчить ему задачу.
Пример: нужно посчитать произведение для 3×7. Если пытаться представить умножение через сложение, то школьнику необходимо найти результат для 3+3+3+3+3+3+3. Это, как известно, будет 21. Но если поменять цифры местами, то пример для сложение будет куда короче: 7+7+7. А ответ по-прежнему остается 21, хотя складывать нужно уже гораздо меньше цифр.
Логика пригодится и для запоминания принципов умножения на 5. Ведь ответ здесь всегда будет заканчиваться либо на 5, либо на 0. Первое — для нечетных чисел (7×5=35, 5×5=25 и так далее), второе — для примеров с четными (4×5=20, 8×5=40 и другие).
С логической точки зрения можно подойти и к запоминанию столбца умножения на 9. Ведь умножение любого числа на девять — это практически то же самое, что результат умножения на 10, за вычетом одной цифры множимого. Проще говоря, 7×9 можно определить как 7×10-7 (то есть 70-7=63).
На пальцах
© Фото : Freepik Ребенок учится счету
© Фото : Freepik
Ребенок учится счету
Умножение на 9 можно запомнить не только через примеры с десятками, но и при помощи “инструмента”, который у школьника всегда с собой (в отличие, например, от калькулятора или тетради с нужной таблицей, которые вполне можно забыть дома). Речь идет о руках, точнее, о ладонях с пальцами, которые помогут быстро найти ответ на нужный пример.
Речь идет о руках, точнее, о ладонях с пальцами, которые помогут быстро найти ответ на нужный пример.
Итак, первым делом нужно повернуть руки ладонями к себе и мысленно пронумеровать пальцы от 1 до 10, начиная с большого пальца левой руки. В зависимости от того, какую цифру необходимо умножить на 9, полагается согнуть определенный палец.
К примеру, нужно высчитать результат для 4×9. Значит, загнуть четвертый по счету палец (то есть безымянный палец левой руки). Перед вами — ответ на заданный пример: слева от согнутого пальца — десятки, справа — единицы (прижатый палец не считается нигде). Осталось лишь посчитать их, в данном примере ответ — 36.
Таблица Пифагора
Классическая таблица умножения — это десять столбиков, в которых последовательно перемножаются все цифры от 1 до 10. Однако существует и упрощенный, более понятный для многих школьников вариант — так называемая таблица Пифагора. Внешне она представляет собой квадрат, параметры которого — 11 ячеек по вертикали и столько же — по горизонтали, пронумерованные от 1 до 10. Порой можно встретить и еще более простой вариант, от 1 до 9, так как умножение на 10, как правило, не вызывает у ребят проблем.
Порой можно встретить и еще более простой вариант, от 1 до 9, так как умножение на 10, как правило, не вызывает у ребят проблем.
Пользоваться таблицей Пифагора достаточно просто: нужно лишь выбрать строчку и столбик, соответствующие перемножаемым числам — и в точке их пересечения будет указано искомое произведение. При этом неважно, как именно будут расположены числа (какое из них искать по вертикали, а какое — по горизонтали), ведь от перемены множителей результат, как уже было сказано выше, не меняется.
Ученица гимназии № 1 на удалённом занятии по математике
Еще один важный принцип, который наглядно представлен в таблице Пифагора — совсем не обязательно заучивать всю таблицу умножения наизусть, достаточно запомнить чуть больше половины. Если провести диагональ через ячейки с результатами перемножения одинаковых чисел (1×1=1, 2×2=4, 3×3=9 и так далее), можно увидеть, что результаты над этой диагональю и под нею симметричны. Ведь если запомнить, что 3×4=12, то легко можно понять, что и умножение 4 на 3 дает аналогичный результат.
В игровой форме
Еще один эффективный способ помочь ребенку запомнить новую информацию — это превратить процесс обучения в увлекательную игру.
Например, запомнить умножение на 7 помогут обычные игральные кубики. Правила игры просты: нужно взять энное количество кубиков и предложить школьнику посостязаться в том, кто быстрее посчитает количество точек, выпавшее как на верхних. так и на противоположных им нижних гранях. Сложить такого количество чисел, конечно, будет непросто, тогда можно раскрыть небольшой секрет: сумма противоположных граней на таких кубиках всегда равна 7. А значит, для получения верного ответа нужно лишь умножить 7 на количество используемых кубиков. Плюс у ребенка появился стимул: получить правильный ответ быстрее всех и выиграть.
Учить таблицу умножения можно и при помощи обычной игры-ходилки, в которой, бросая кубики и продвигаясь на выпавшее число шагов, необходимо пройти путь от старта до финиша. Чтобы совместить приятное с полезным и помочь ребенку выучить таблицу умножения, можно предложить ему умножать выпавшее количество ходов на 2. И, если он даст правильный ответ, то продвинется вперед, к примеру, уже не на 6, а на 12 делений. Так постепенно можно перейти к умножению на 3, 4 и так далее.
И, если он даст правильный ответ, то продвинется вперед, к примеру, уже не на 6, а на 12 делений. Так постепенно можно перейти к умножению на 3, 4 и так далее.
© Fotolia / Peter AtkinsДевушка с детскими кубиками
© Fotolia / Peter Atkins
Девушка с детскими кубиками
Тренажер
Существуют и специальные тренажеры в онлайн-формате, которые помогают как изучать таблицу, так и закрепить полученные знания. Они включают различные виды заданий: самостоятельно вписать ответ на предложенные примеры, определить, в каких примерах с умножением специально допущены ошибки, и так далее. Некоторые позволяют даже выставить нужный уровень сложности или, к примеру, практиковаться в умножении на определенное число.
Закрепление и проверка результата
На то, чтобы запомнить всю таблицу умножения, у школьника может уйти немало времени. Проверить, насколько хорошо ему удалось усвоить все примеры, можно при помощи не только онлайн-тренажеров, но и другими доступными способами.
К примеру, проверить, насколько уверенно ребенок ориентируется в умножении на различные числа, можно при помощи простой игры. Для этого необходимо подготовить две группы карточек. На карточках из первой группы будут написаны примеры перемножения различных чисел, карточки из второй группы будут содержать ответы. Задача школьника — правильно сопоставить примеры с правильными ответами.
Повторять таблицу умножения можно и в различных бытовых ситуациях. Например, в магазине, где родители могут предложить сыну или дочке посчитать, сколько яблок нужно купить, чтобы каждому члену семьи досталось по 2 фрукта, или какое количество сладостей стоит взять, чтобы угостить одноклассников и каждому из них вручить по 3 конфеты.
Школьница учит таблицу умножения по учебнику
На первом этапе стоит повторять таблицу умножения по порядку: школьник выучил умножение на 2 — повторяет этот столбик, освоил умножение на 3 — повторяет эти примеры. Только после того, как ребенок твердо усвоил всю таблицу, можно приступать к проверку вразброс.
Как не стоит учить таблицу умножения
Даже если использовать упрощенный вариант таблицы умножения, то есть квадрат Пифагора, задача все равно остается для школьников достаточно непростой. А потому не стоит пытаться запомнить всю таблицу сразу и целиком, добиться результата в экстремально короткие сроки. Пусть ребенок учит ее постепенно, небольшими частями. Переходить к следующей части стоит лишь при условии, что ученик хорошо запомнил предыдущий этап.
Для многих детей процесс изучения таблицы умножения заметно осложняет тот факт, что для них это занятие представляется бессмысленным и бесполезным. А значит, важно найти правильную мотивацию (фразы из разряда “так нужно” или “учитель сказал надо” к таковым не относятся). Родителям необходимо убедить школьника в том, что знание таблицы умножения будет полезно и пригодится в будущем, сделает жизнь проще и поможет избежать ошибок.
И, конечно, не стоит заставлять ребенка зубрить таблицу умножения, если он категорически не желает этого делать. Лучше выбрать другой момент, когда школьник будет более настроен на работу. Ведь если учить примеры через силу, любви к таблице умножения у ребенка точно не прибавится, да и добиться нужного результата тоже вряд ли получится.
Лучше выбрать другой момент, когда школьник будет более настроен на работу. Ведь если учить примеры через силу, любви к таблице умножения у ребенка точно не прибавится, да и добиться нужного результата тоже вряд ли получится.
App Store: Визуальная таблица умножения
Скриншоты iPad
Описание
Исследуйте и изучайте таблицу умножения визуальным способом. Wired.com: «Я очень рекомендую это всем детям, которые изучают таблицу умножения».
Четыре различных способа изучения таблицы умножения:
— Таблица: изучение таблицы умножения.
— Группы: просмотрите умножение как визуализацию.
— Множители: посмотрите, как у каждого числа есть неограниченное количество кратных.
— Решить: Скремблировать и решить таблицу умножения.
Выделено Apple в списках «Новые и заслуживающие внимания» образования США и «Избранное сотрудников».
Отзыв на Wired.com:
«Я очень рекомендую это всем детям, которые изучают таблицу умножения или которым нужен более наглядный способ приблизиться к предмету».
Видео о приложении
Чтобы посмотреть видео о приложении, посетите idevbooks.com.
Appsforhomeschooling.com:
«Таблица умножения — это новаторский способ визуализации и взаимодействия с таблицей умножения. Совершенно очевидно, что она создана любителем математики, который ценит закономерности и порядок, которые можно найти в этой дисциплине. исследовательские способы взаимодействия с таблицей умножения помогут вам научить ребенка думать об умножении как о наглядном, упорядоченном и, самое главное, понятном понятии».
Другие математические приложения iDevBooks
Математические приложения iDevBooks были проверены и одобрены Wired.com, IEAR.org, Edudemic.com, Teachers with Apps и другими уважаемыми сайтами и организациями.
Некоторые из других 40 математических приложений iDevBooks включают визуальные дроби, десятичные дроби и проценты, сложение столбцов, длинное умножение, длинное деление, вычитание столбцов, вычитание частичных разностей, умножение частичных произведений, сложение частичных сумм, десятичное округление и т. д.
д.
Отзывы и запросы на новые функции
Приветствуются новые идеи по улучшению этого приложения. Пожалуйста, посетите idevbooks.com, чтобы оставить отзыв.
Конфиденциальность
В этом приложении нет рекламы или встроенных покупок, и оно не передает никаких данных во время работы приложения. Это приложение также не содержит ссылок на другие приложения или в Интернете.
Версия 4.0
— поддержка iOS 13
— новый интерфейс с поддержкой последних моделей iPad
— мелкие исправления ошибок
Рейтинги и обзоры
1 Рейтинг
Замечательный способ визуализировать математику!
Я очень рекомендую это приложение.
Мне, как визуалу, было трудно понять математику. Это приложение просто фантастическое для меня, так как я хочу проверить и отточить свои способности. Хотел бы я иметь это в детстве!
На дизайн, цвета и анимацию приятно смотреть, а пользоваться им очень интересно и интересно.
В нескольких отзывах говорилось, что приложение работает медленно. Это можно исправить, перезапустив приложение. Вы можете увидеть, что приложения «работают» в фоновом режиме, дважды нажав кнопку «Домой». Затем в нижней части экрана iPad появляется ряд значков. Вы можете перемещать строку пальцем, чтобы увидеть еще больше приложений. Это приложения, которые вы недавно использовали и которые зависли в фоновом режиме и готовы к повторному использованию. Если вы нажмете на любой из значков и будете удерживать, вы увидите, что они начинают покачиваться, а рядом со всеми ними появляется красный знак минуса. Если вы нажмете знак минус, вы закроете соответствующее приложение в фоновом режиме (приложение не будет удалено).Затем, когда вы снова запустите приложение, оно перезапустится. Поэтому, если вы обнаружите, что приложение работает медленно, выйдите и перезапустите его, как описано выше. Это снова будет быстро!
Мне нравится это приложение для визуализации математики гораздо больше, чем приложения в стиле счеты. Стоит каждой копейки!
Сделано очень творческим человеком!
Очень креативный способ визуализации таблицы умножения! Моя 10-летняя дочь была поражена этим приложением! В то время она довольно долго экспериментировала с цветами, фоном и узорами чисел, занимаясь умножением! Если ваш ребенок креативен и обладает богатой фантазией, это приложение — лучший инструмент для освоения умножения!
Великолепно!
Это приложение одновременно является произведением искусства и гениальным устройством для визуализации фактов умножения и самой концепции умножения.
Я занимаюсь домашним обучением и репетитором по математике, и меня нелегко впечатлить, но я ВПЕЧАТЛЕН этим приложением!
Разработчик, Эса Хелттула, не предоставил Apple подробностей о своей политике конфиденциальности и обработке данных. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Сведения не предоставлены
Разработчик должен будет предоставить сведения о конфиденциальности при отправке следующего обновления приложения.
Информация
- Продавец
- Эса Хелттула
- Размер
- 11,6 МБ
- Категория
- Образование
- Возрастной рейтинг
- 4+, для детей от 9 до 11 лет
- Авторское право
- © Эса Хелттула
- Цена
- 3,99 $
- Сайт разработчика
- Тех.
 поддержка
поддержка - политика конфиденциальности
Опоры
Еще от этого разработчика
Вам также может понравиться
бесплатных печатных таблиц умножения — проекты «сделай сам», выкройки, монограммы, рисунки, шаблоны
Таблицы умножения (PDF): бесплатные печатные таблицы умножения
Бесплатные печатные таблицы умножения (таблицы умножения) доступны в формате PDF. Используйте эти красочные таблицы умножения, чтобы помочь вашему ребенку обрести уверенность, осваивая факты умножения. Дополнительные идеи см. в печатной бумаге, математических упражнениях и генераторе математических задач.
Загрузите бесплатную распечатанную таблицу умножения, выбрав «Формат PDF» или «Формат PNG». Вы также можете изменить цвета, выбрав «Редактировать / Сохранить». См. примечания ниже.
См. примечания ниже.
Бесплатные печатные таблицы умножения (PDF) – таблицы умножения 1-12
- Таблица умножения.
(Альбомная ориентация)
ПУСТОЙ
12 x 12 - ○ Формат PDF
- ○ Формат PNG
- Бесплатная таблица умножения.
(Книжная ориентация)
ПУСТОЙ
1-12 - ○ Формат PDF
- ○ Формат PNG
Бесплатные печатные таблицы умножения (PDF): таблицы умножения 1-10
ПРИМЕЧАНИЕ. Вы можете указать новые цвета для таблицы умножения или таблицы умножения, нажав кнопку «Редактировать/Сохранить». После выбора новых цветов укажите высоту «3000 пикселей», чтобы обеспечить высокое разрешение и убедиться, что ваша таблица или диаграмма помещается на весь лист бумаги.
Таблицы и схемы умножения могут быть бесценными инструментами, когда дети изучают факты умножения. Используйте эти бесплатные PDF-файлы таблицы умножения дома или в школе. Просто нажмите на нужную диаграмму или таблицу, затем загрузите и распечатайте. Затем вы можете повесить диаграмму на стену или заламинировать диаграмму для долговечности. Вы также можете распечатать одну из этих таблиц умножения и вложить ее в защитную пленку, а затем добавить в папку домашнего обучения вашего ребенка. Это облегчает поиск и использование при решении математических задач. Отлично подходит для 2-х, 3-х, 4-х, 5-х и 6-х классов.
Просто нажмите на нужную диаграмму или таблицу, затем загрузите и распечатайте. Затем вы можете повесить диаграмму на стену или заламинировать диаграмму для долговечности. Вы также можете распечатать одну из этих таблиц умножения и вложить ее в защитную пленку, а затем добавить в папку домашнего обучения вашего ребенка. Это облегчает поиск и использование при решении математических задач. Отлично подходит для 2-х, 3-х, 4-х, 5-х и 6-х классов.
Больше БЕСПЛАТНОЙ бумаги для печати, математических диаграмм, рабочих листов и т. д.
Найдите бесплатную отмеченную наградами бумагу для печати, рабочие листы и рисунки, которые помогут вам и вашим детям добиться успеха. Откройте для себя бесплатную миллиметровку и бумага с координатной сеткой. Найдите большой выбор линованная бумага для печати включая широкую линейку, линейку колледжа, узкую линейку, бумагу для рукописного ввода и бумагу для детского сада. Будьте организованы в школе, дома и на работе с милыми еженедельники и ежедневники.


 Затем результат закрепляется, и задачи берутся вразброс. Это имеет критическую важность для того, чтобы ребенок научился работать с разными примерами, а не просто зубрил.
Затем результат закрепляется, и задачи берутся вразброс. Это имеет критическую важность для того, чтобы ребенок научился работать с разными примерами, а не просто зубрил. Предложите малышу такую гонку и шанс проявить себя.
Предложите малышу такую гонку и шанс проявить себя.
 Мне, как визуалу, было трудно понять математику. Это приложение просто фантастическое для меня, так как я хочу проверить и отточить свои способности. Хотел бы я иметь это в детстве!
Мне, как визуалу, было трудно понять математику. Это приложение просто фантастическое для меня, так как я хочу проверить и отточить свои способности. Хотел бы я иметь это в детстве!  Затем, когда вы снова запустите приложение, оно перезапустится. Поэтому, если вы обнаружите, что приложение работает медленно, выйдите и перезапустите его, как описано выше. Это снова будет быстро!
Затем, когда вы снова запустите приложение, оно перезапустится. Поэтому, если вы обнаружите, что приложение работает медленно, выйдите и перезапустите его, как описано выше. Это снова будет быстро!  Я занимаюсь домашним обучением и репетитором по математике, и меня нелегко впечатлить, но я ВПЕЧАТЛЕН этим приложением!
Я занимаюсь домашним обучением и репетитором по математике, и меня нелегко впечатлить, но я ВПЕЧАТЛЕН этим приложением! поддержка
поддержка исходный код
исходный код
 Нажмите эту ссылку, чтобы посетить форумы.
Нажмите эту ссылку, чтобы посетить форумы.







 Максимальный размер файла 100 МБ или регистрация
Максимальный размер файла 100 МБ или регистрация 6
6 1
1 3
3 1
1 3
3 7
7 7
7 0
0 2
2 2
2 2 (398 083 голоса)
2 (398 083 голоса) Мы поддерживаем почти все аудио, видео,
форматы документов, электронных книг, архивов, изображений, электронных таблиц и презентаций. Кроме того, вы можете использовать наш онлайн
инструмент без загрузки какого-либо программного обеспечения.
Мы поддерживаем почти все аудио, видео,
форматы документов, электронных книг, архивов, изображений, электронных таблиц и презентаций. Кроме того, вы можете использовать наш онлайн
инструмент без загрузки какого-либо программного обеспечения.
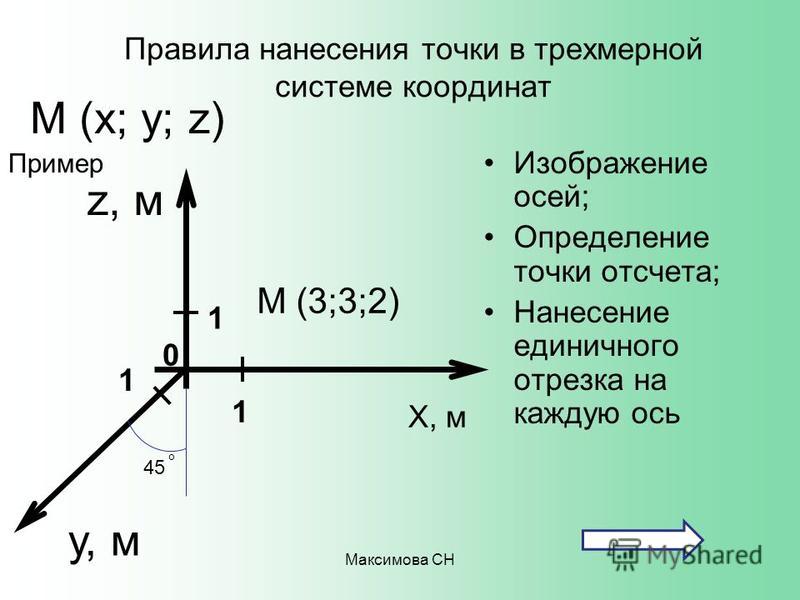 Также функцию симметричную относительно оси ординат называют четной функцией, значит, функция является четной.
Также функцию симметричную относительно оси ординат называют четной функцией, значит, функция является четной. Вместе эти координаты помогают определить точное местоположение точки.
Вместе эти координаты помогают определить точное местоположение точки.
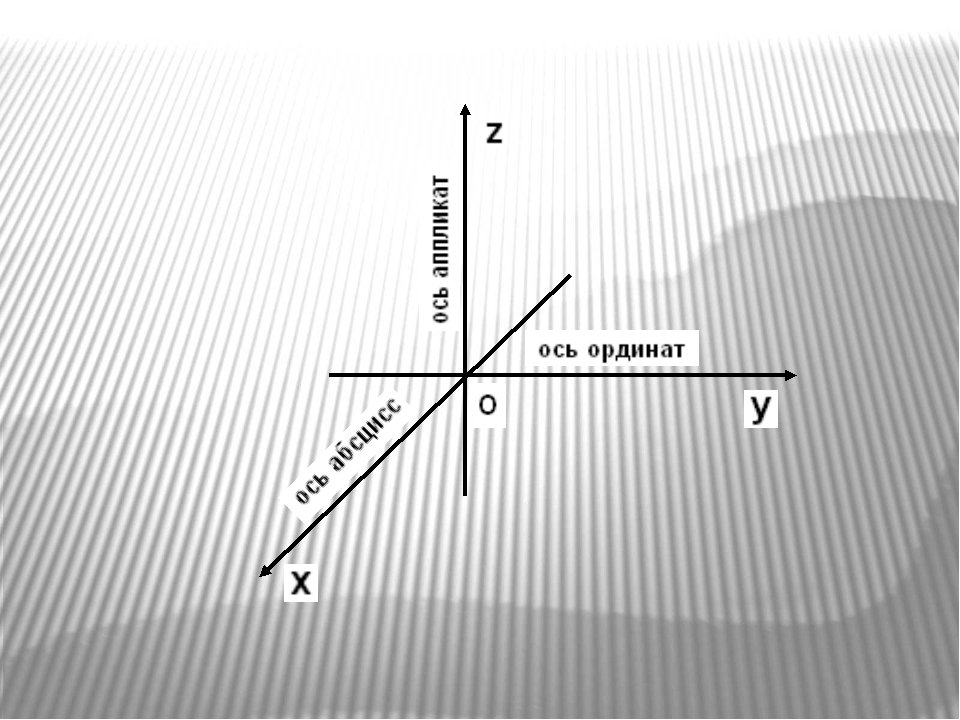
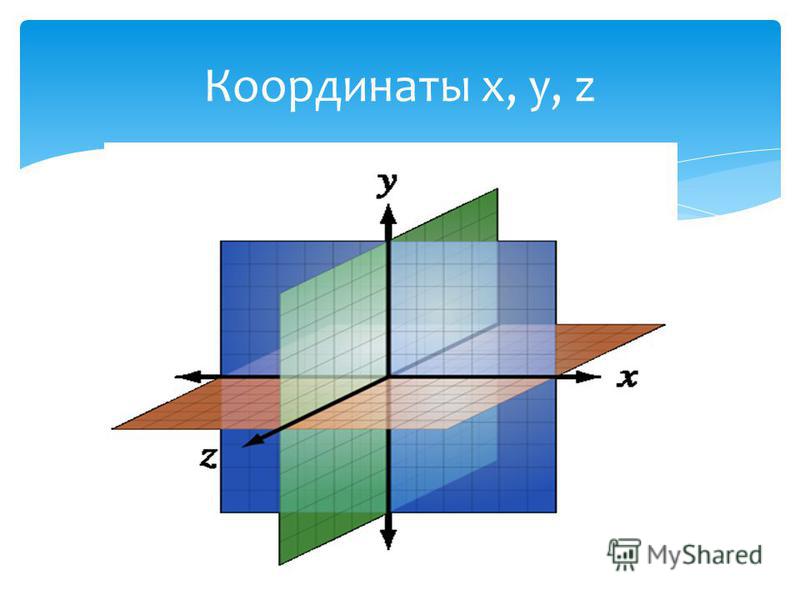
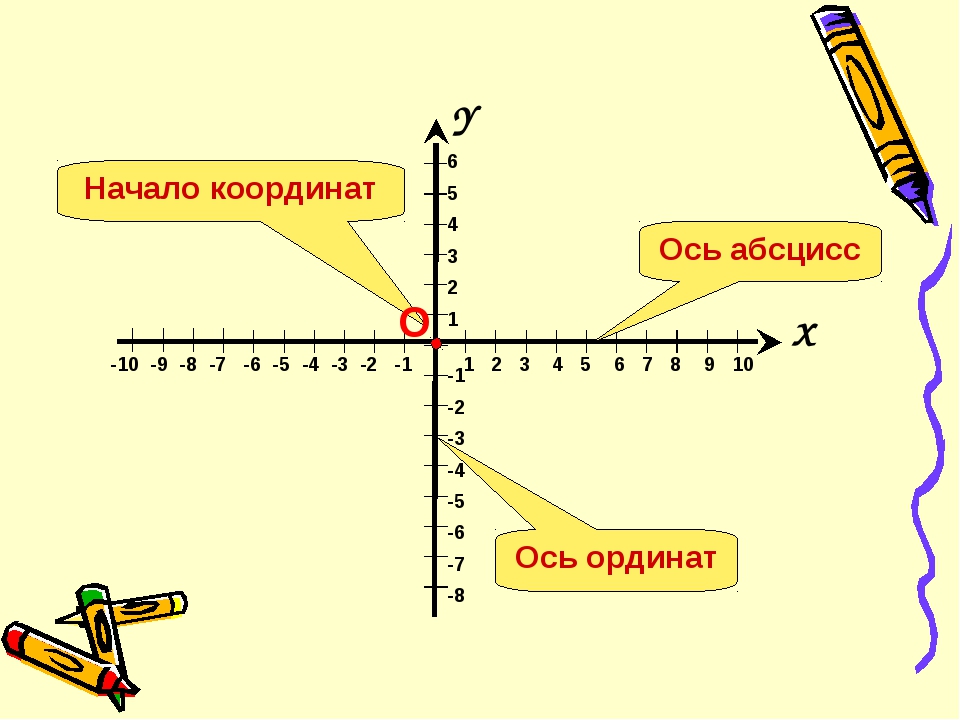
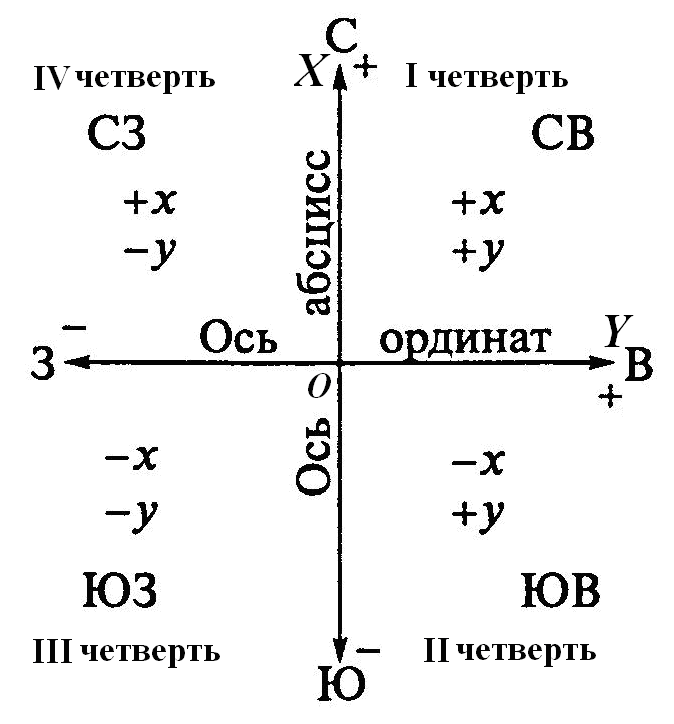

 Затем координаты x и y соединяются в прямую линию.
Затем координаты x и y соединяются в прямую линию. Он преобразует цифровые данные …
Он преобразует цифровые данные …
 ..
.. ..
..


 д. Кроме того, некоторые из других важных применений координат x и y суть в следующем.
д. Кроме того, некоторые из других важных применений координат x и y суть в следующем.
 Следовательно, x = -3 и y = 4.
Следовательно, x = -3 и y = 4.
 Поэтому для определения площади прямоугольного треугольника необходимо это произведение a ⋅ b разделить на 2. Чтобы найти площадь прямоугольного треугольника, нужно произведение его катетов разделить на 2.
Поэтому для определения площади прямоугольного треугольника необходимо это произведение a ⋅ b разделить на 2. Чтобы найти площадь прямоугольного треугольника, нужно произведение его катетов разделить на 2. S = a × a = a2, где S — площадь, a — сторона. Эту формулу проходят в 3 классе.
S = a × a = a2, где S — площадь, a — сторона. Эту формулу проходят в 3 классе. Площади двух абсолютно разных фигур могут быть одинаковыми.
Площади двух абсолютно разных фигур могут быть одинаковыми.

 В данной задаче это квадратные сантиметры. Также важно
помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.
В данной задаче это квадратные сантиметры. Также важно
помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.
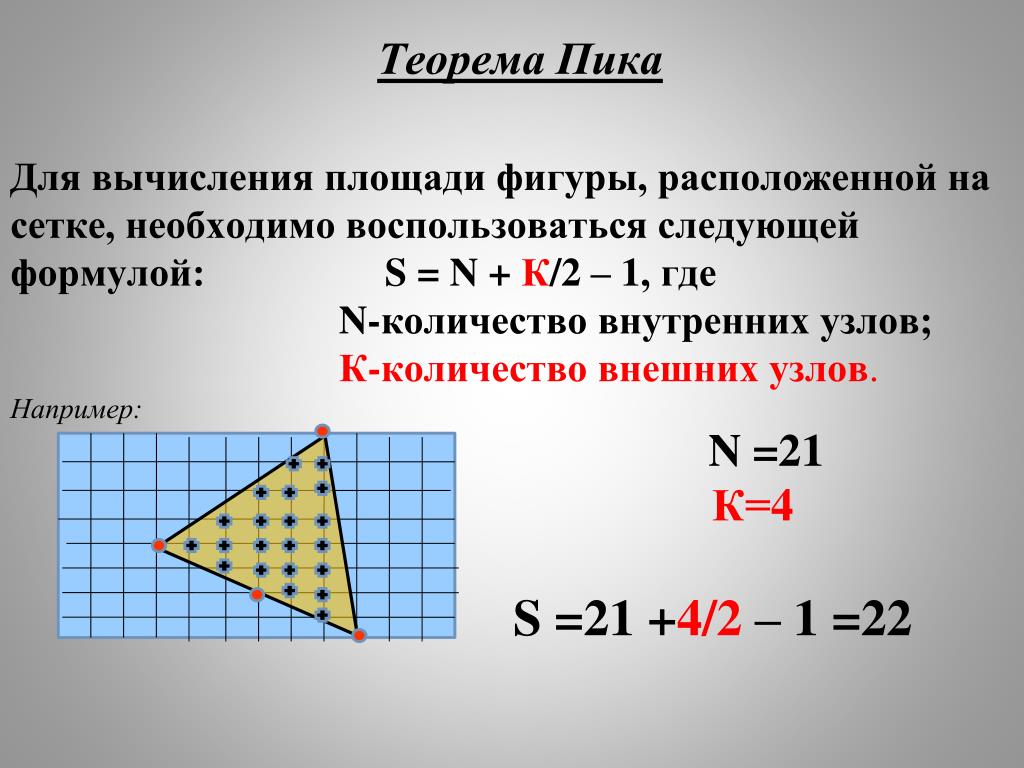
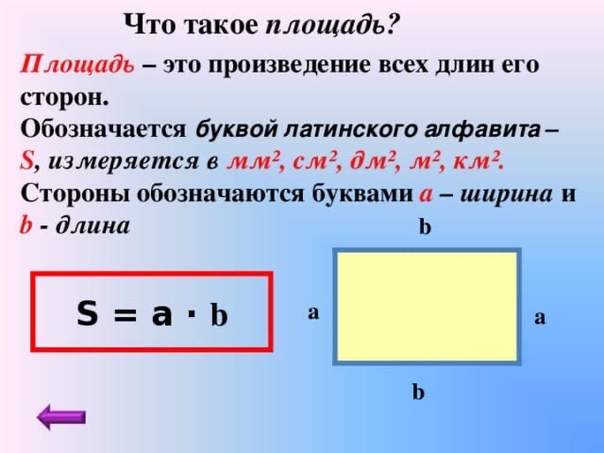
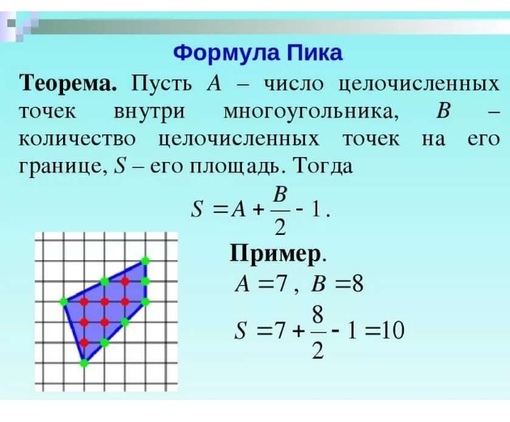 В этой статье мы рассмотрим основные теории и математические формулы, связанные с площадью прямоугольника, например, площадь прямоугольника, формулу площади прямоугольника и ее применение в повседневной жизни.
В этой статье мы рассмотрим основные теории и математические формулы, связанные с площадью прямоугольника, например, площадь прямоугольника, формулу площади прямоугольника и ее применение в повседневной жизни.
 Это математически формулируется как
Это математически формулируется как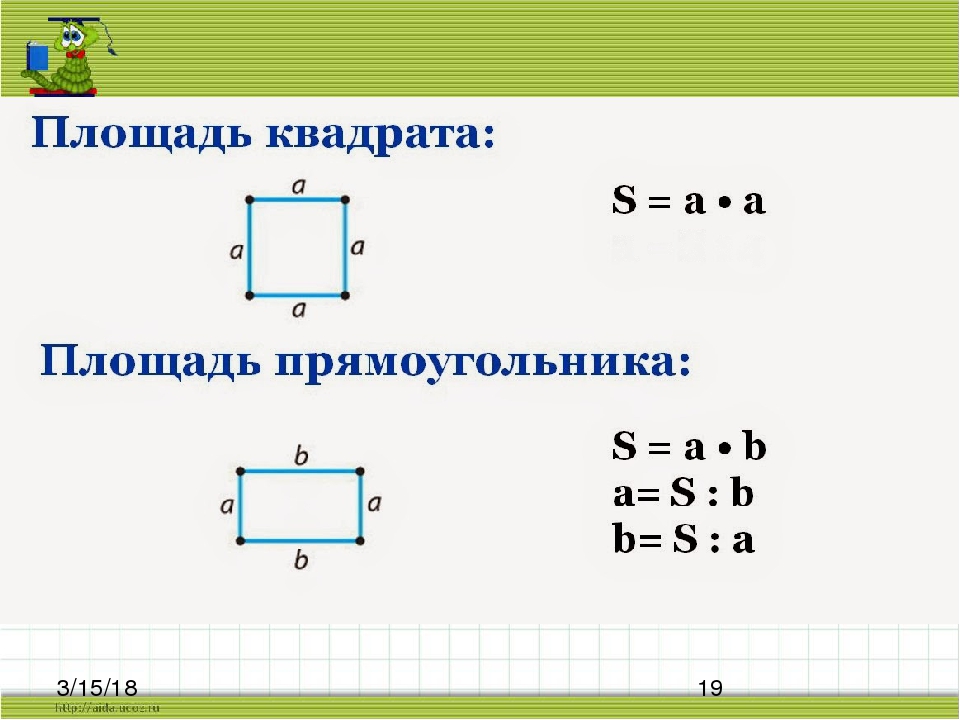 д.
д.

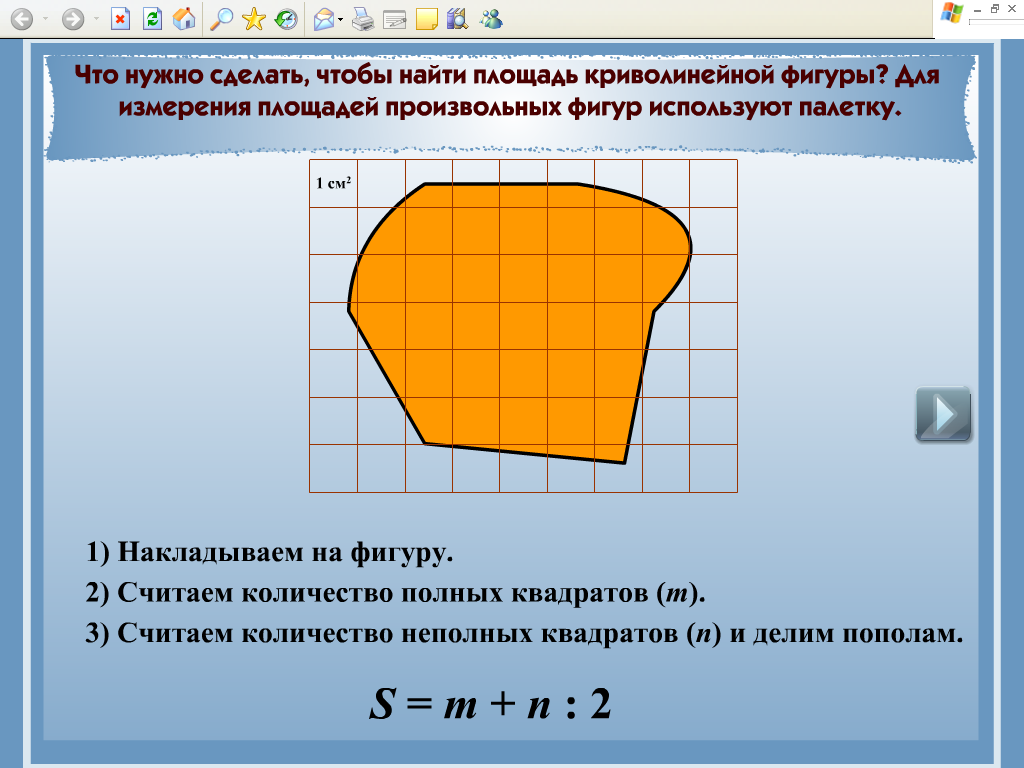 Но когда-нибудь задумывались, почему это формула? В этом разделе выведем формулу площади прямоугольника.
Но когда-нибудь задумывались, почему это формула? В этом разделе выведем формулу площади прямоугольника.

 Он использует длину и ширину прямоугольника, которые являются его сторонами.
Он использует длину и ширину прямоугольника, которые являются его сторонами. Все 4 внутренних угла прямоугольника прямые. Книга, футбольное поле, окно, дорожный чемодан — все это примеры прямоугольников.
Все 4 внутренних угла прямоугольника прямые. Книга, футбольное поле, окно, дорожный чемодан — все это примеры прямоугольников. Условно одну из длинных сторон прямоугольника принимают за основание, а одну из сторон, перпендикулярных основанию, считают высотой. В этом прямоугольнике высота равна длине AD.
Условно одну из длинных сторон прямоугольника принимают за основание, а одну из сторон, перпендикулярных основанию, считают высотой. В этом прямоугольнике высота равна длине AD. д. . Подумайте, сколько квадратных единиц необходимо, чтобы точно и исчерпывающе покрыть всю поверхность замкнутой фигуры. Эта сумма и есть площадь фигуры.
д. . Подумайте, сколько квадратных единиц необходимо, чтобы точно и исчерпывающе покрыть всю поверхность замкнутой фигуры. Эта сумма и есть площадь фигуры. Затем, когда известны и основание, и высота прямоугольника, можно вычислить площадь.
Затем, когда известны и основание, и высота прямоугольника, можно вычислить площадь.
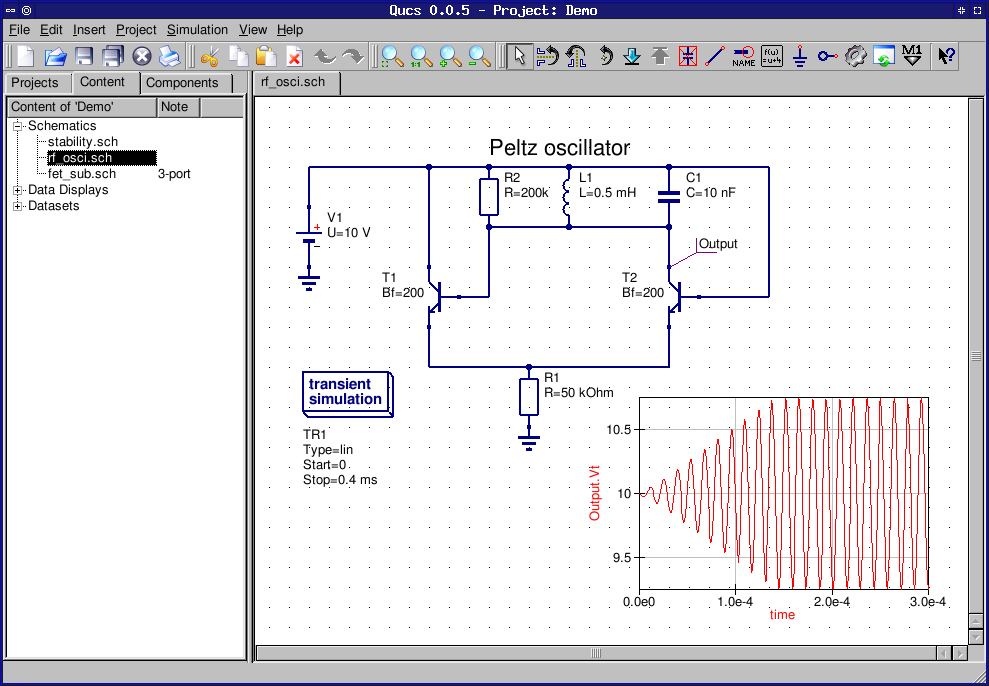
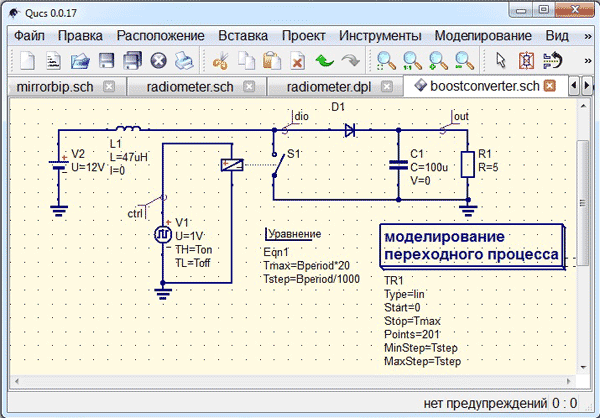
 Любая модель всегда повторяет лишь часть свойств моделируемого объекта. В частности, многие распространенные в реальной работе проблемы, например, плохой электрический контакт в разъеме, здесь воспроизвести нельзя, а между тем нечто подобное может привести к полной неработоспособности устройства. Главное предназначение данного симулятора, это быстрое моделирование простых электронных устройств, особенно в условиях, когда те или иные компоненты для их сборки недоступны. Продолжение материала связанное с Ардуино проектами читайте по ссылке. Автор обзора – Denev.
Любая модель всегда повторяет лишь часть свойств моделируемого объекта. В частности, многие распространенные в реальной работе проблемы, например, плохой электрический контакт в разъеме, здесь воспроизвести нельзя, а между тем нечто подобное может привести к полной неработоспособности устройства. Главное предназначение данного симулятора, это быстрое моделирование простых электронных устройств, особенно в условиях, когда те или иные компоненты для их сборки недоступны. Продолжение материала связанное с Ардуино проектами читайте по ссылке. Автор обзора – Denev.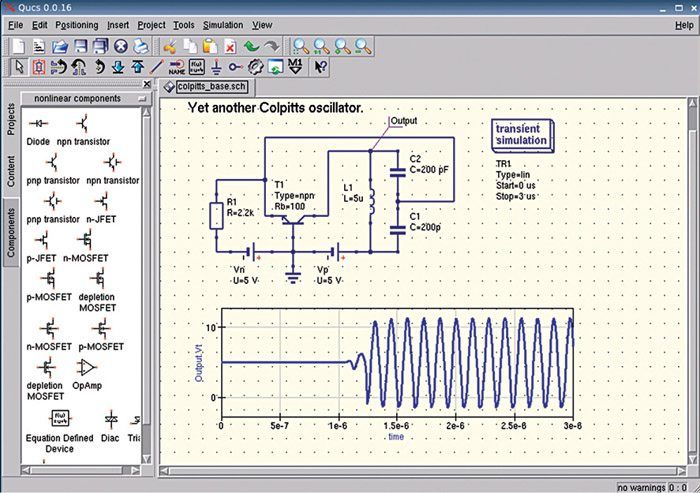
 , но он, несомненно, один из лучших, которые мы можем найти в этой области, поэтому он не отсутствует в списке. Это очень полный симулятор, с помощью которого мы сможем проектировать и экспериментировать со схемами, как в цифровом, так и в аналоговом формате. Кроме того, приложение также имеет анализ в реальном времени, что делает его идеальным инструментом, например, для студентов инженерных специальностей.
, но он, несомненно, один из лучших, которые мы можем найти в этой области, поэтому он не отсутствует в списке. Это очень полный симулятор, с помощью которого мы сможем проектировать и экспериментировать со схемами, как в цифровом, так и в аналоговом формате. Кроме того, приложение также имеет анализ в реальном времени, что делает его идеальным инструментом, например, для студентов инженерных специальностей.
 Те, которые мы создали, могут быть добавлены к символам, которые программа предлагает вам с самого начала. Таким образом, при создании контура доступен более широкий выбор.
Те, которые мы создали, могут быть добавлены к символам, которые программа предлагает вам с самого начала. Таким образом, при создании контура доступен более широкий выбор. . Это одно из самых полных приложений для создания электрических схем, доступных на рынке. В нем мы можем создавать схемы всех видов, от самых простых до гораздо более сложных, где у нас больше элементов. Кроме того, это то, что мы можем сделать быстро и без необходимости быть для этого инженером. Это делает его подходящим для всех типов пользователей.
. Это одно из самых полных приложений для создания электрических схем, доступных на рынке. В нем мы можем создавать схемы всех видов, от самых простых до гораздо более сложных, где у нас больше элементов. Кроме того, это то, что мы можем сделать быстро и без необходимости быть для этого инженером. Это делает его подходящим для всех типов пользователей.
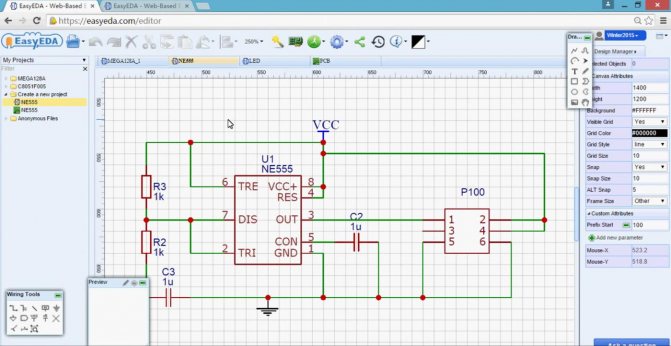
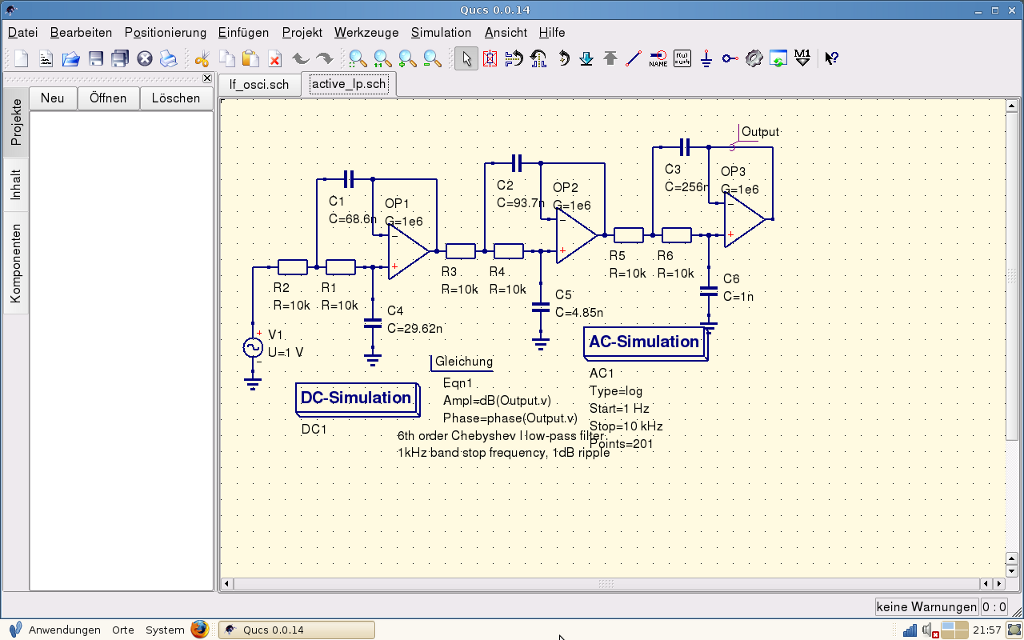 Это приложение предлагает нам надежный калькулятор, с помощью которого мы сможем выполнять все виды расчетов, которые затем позволят нам создавать эти электрические схемы. По этой причине это приложение не может отсутствовать в списке лучших приложений для создания электрических схем для Android. Приложение способно вычислять напряжение, ток, сопротивление и мощность простым способом.
Это приложение предлагает нам надежный калькулятор, с помощью которого мы сможем выполнять все виды расчетов, которые затем позволят нам создавать эти электрические схемы. По этой причине это приложение не может отсутствовать в списке лучших приложений для создания электрических схем для Android. Приложение способно вычислять напряжение, ток, сопротивление и мощность простым способом. Внутри него есть реклама, но она не является чем-то слишком агрессивным, что мы также не сможем устранить с помощью покупок. Если вы хотите попробовать это приложение на своем планшете Android, вы можете загрузить его из магазина Google Play по следующей ссылке:
Внутри него есть реклама, но она не является чем-то слишком агрессивным, что мы также не сможем устранить с помощью покупок. Если вы хотите попробовать это приложение на своем планшете Android, вы можете загрузить его из магазина Google Play по следующей ссылке:
 Форма волны RC Однако мы видели…
Форма волны RC Однако мы видели…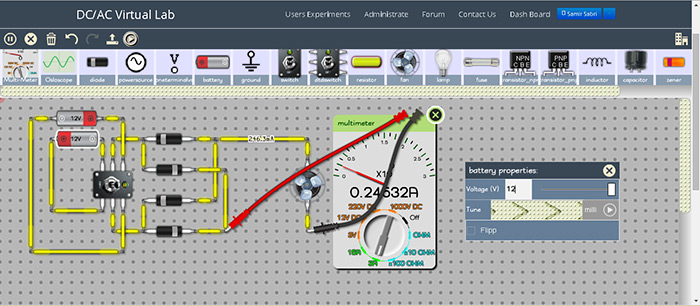 Таким образом, образовательные цели DCACLab можно резюмировать в балльной форме следующим образом с точки зрения того, что учащийся должен уметь делать в конце лабораторной работы:
Таким образом, образовательные цели DCACLab можно резюмировать в балльной форме следующим образом с точки зрения того, что учащийся должен уметь делать в конце лабораторной работы: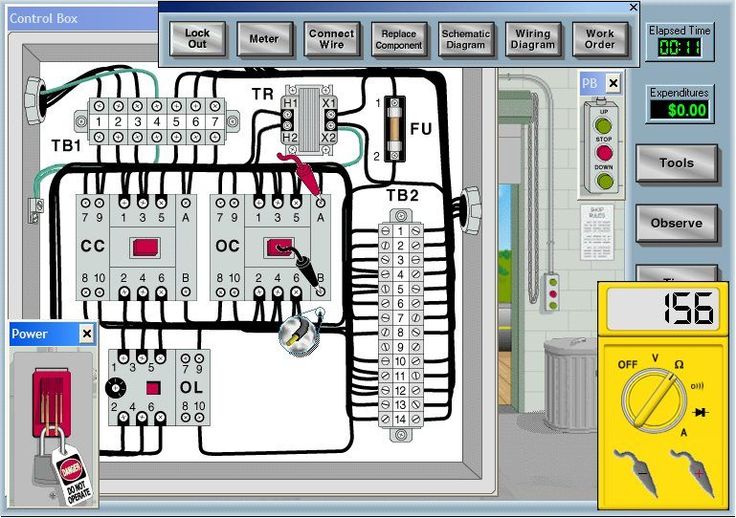 Ручку выбора можно использовать для простой установки требуемого счетчика и выбора из нескольких диапазонов значений. Измерители на выбор:
Ручку выбора можно использовать для простой установки требуемого счетчика и выбора из нескольких диапазонов значений. Измерители на выбор: DCAClab вычисляет среднеквадратичное значение путем выборки входного напряжения и вычисления суммы квадратов, имитируя высококачественные вольтметры, как измеритель переменного тока, так и осциллограф имеют среднеквадратичное значение, осциллограф рисует пунктирную линию для обозначения среднеквадратичного значения.
DCAClab вычисляет среднеквадратичное значение путем выборки входного напряжения и вычисления суммы квадратов, имитируя высококачественные вольтметры, как измеритель переменного тока, так и осциллограф имеют среднеквадратичное значение, осциллограф рисует пунктирную линию для обозначения среднеквадратичного значения.
 \)
\) 

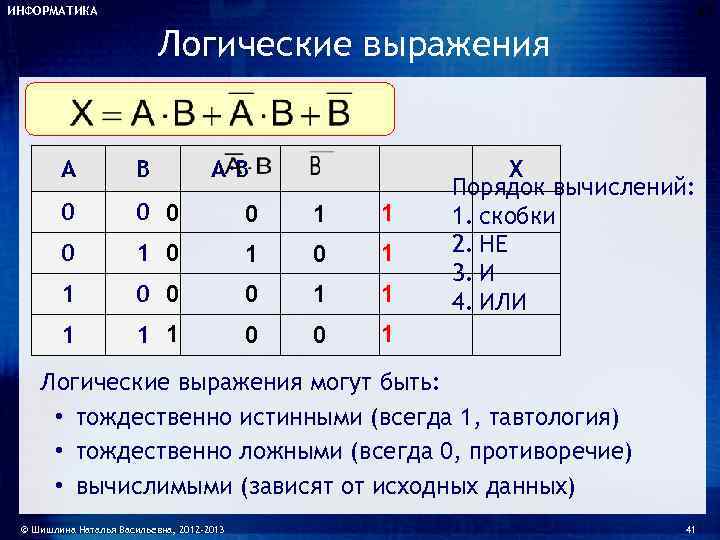
 \ \\ \ \\ \end{matrix} \right.\ \Longleftrightarrow — a < f\left( x \right) < a\)
\ \\ \ \\ \end{matrix} \right.\ \Longleftrightarrow — a < f\left( x \right) < a\) \ \\ \left\{ \begin{matrix} \ \\ x < 0 \\ x < — 1 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\ \)
\ \\ \left\{ \begin{matrix} \ \\ x < 0 \\ x < — 1 \\ \ \\ \end{matrix} \right.\ \\ \ \\ \end{matrix} \right.\ \) \ \)
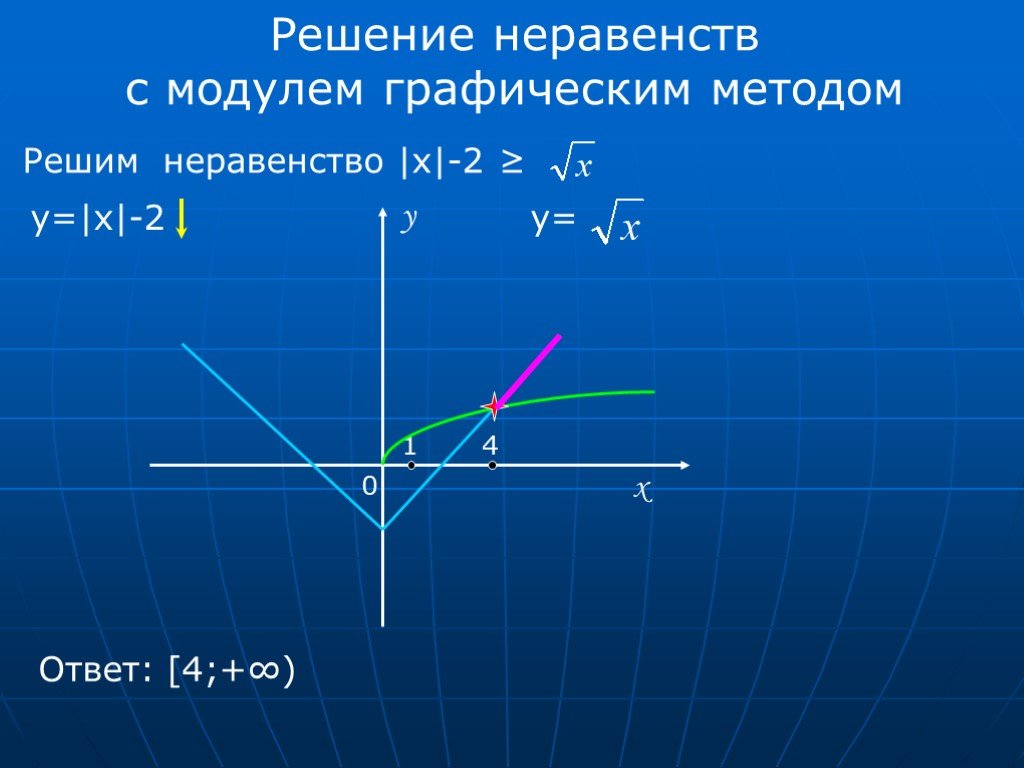
\ \)
 {2} — 2x + 1\)
{2} — 2x + 1\) Аналогично, $|x-4|=x-4$ для $x \geq 4$, тогда как $|x-4|=4-x$ для $x \leq 4$
Аналогично, $|x-4|=x-4$ для $x \geq 4$, тогда как $|x-4|=4-x$ для $x \leq 4$
 Итак, мы имеем дело с неравенством $(x-3)-(x-4)\lt x$, то есть с $1\lt x$, что заведомо верно при $x\ge 4$.
Итак, мы имеем дело с неравенством $(x-3)-(x-4)\lt x$, то есть с $1\lt x$, что заведомо верно при $x\ge 4$. Этот сложный набор условий можно обобщить гораздо проще: $x\gt -1$.
Этот сложный набор условий можно обобщить гораздо проще: $x\gt -1$.
 В результате мы можем записать значение $x$ для уравнения (b) в виде: $(-∞,+∞)$
В результате мы можем записать значение $x$ для уравнения (b) в виде: $(-∞,+∞)$
 \)
\) \end{случаи}\]
\end{случаи}\]
 \]
Здесь у нас есть два неравенства, и решением для этого случая является пересечение обоих неравенств. Это потому, что \(x\) должно удовлетворять обоим, поскольку они зависят друг от друга \((\) только потому, что \(x\geq -3\) у нас есть \(x<4)\). Следовательно, решение для этого случая равно \(-3 \leq x < 4\).
\]
Здесь у нас есть два неравенства, и решением для этого случая является пересечение обоих неравенств. Это потому, что \(x\) должно удовлетворять обоим, поскольку они зависят друг от друга \((\) только потому, что \(x\geq -3\) у нас есть \(x<4)\). Следовательно, решение для этого случая равно \(-3 \leq x < 4\). \конец{выравнивание} \]
Чтобы решить это квадратное неравенство, мы можем использовать диаграмму анализа знаков.
\конец{выравнивание} \]
Чтобы решить это квадратное неравенство, мы можем использовать диаграмму анализа знаков.


 Таким образом, когда \(-5 < x < -2 \), \(y = -3x - 9 \).
Таким образом, когда \(-5 < x < -2 \), \(y = -3x - 9 \). \(_\квадрат\)
\(_\квадрат\) \конец{выровнено}\]
\конец{выровнено}\]


 Это означает, что до этого момента осталось 31,57 недели, 5304,0 часа и 7,89 месяца. Мы используем этот расчет довольно часто в календаре, даже если
мы этого не осознаем. Обратный отсчет чьего-то дня рождения, юбилея или особой даты важен, чтобы вовремя заказать подарки!
Если 9 декабряособенный для вас, сделайте одолжение себе в будущем и установите напоминание в календаре на день раньше и
сделай это повторяющимся. Пожалуйста.
Это означает, что до этого момента осталось 31,57 недели, 5304,0 часа и 7,89 месяца. Мы используем этот расчет довольно часто в календаре, даже если
мы этого не осознаем. Обратный отсчет чьего-то дня рождения, юбилея или особой даты важен, чтобы вовремя заказать подарки!
Если 9 декабряособенный для вас, сделайте одолжение себе в будущем и установите напоминание в календаре на день раньше и
сделай это повторяющимся. Пожалуйста.
 и 29,03% в течение декабря.
и 29,03% в течение декабря. Стрелец (Стрелец)
Стрелец (Стрелец)


 Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
 Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
 Ну… почти ничего.
Ну… почти ничего.
 Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.
Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.
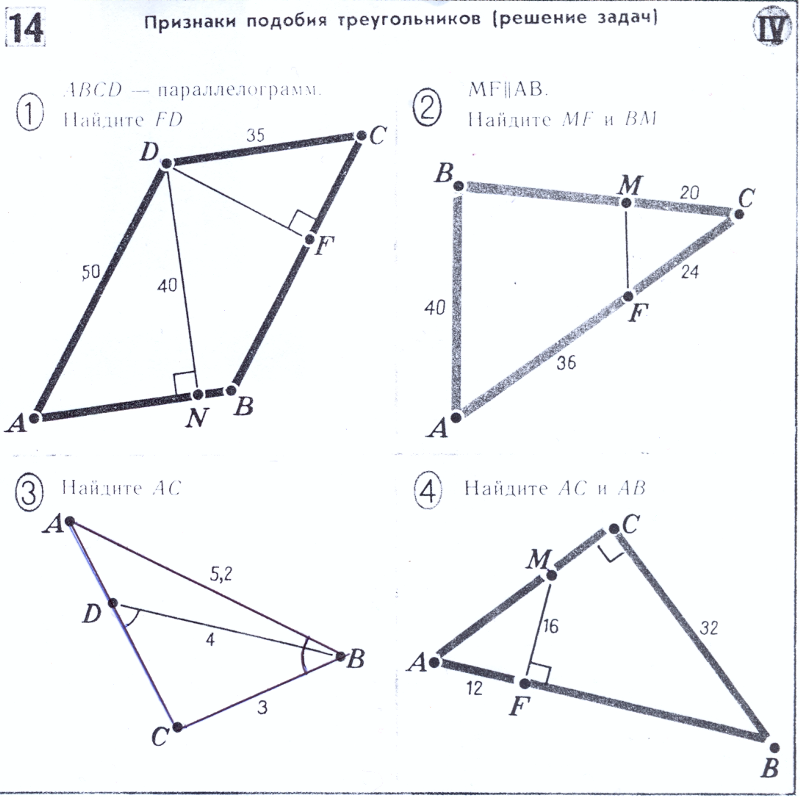 ?BDE ~ ?ABC по двум сторонам и углу между ними.
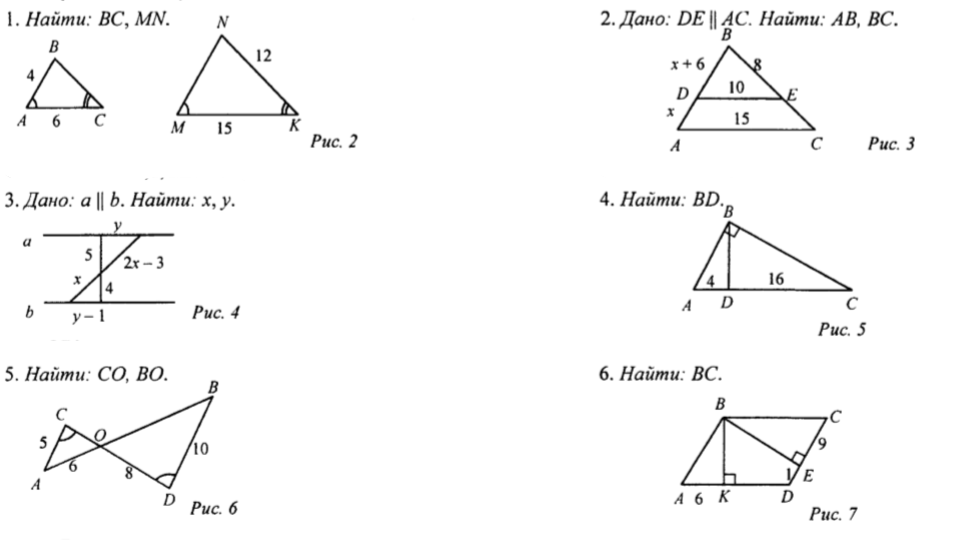
?BDE ~ ?ABC по двум сторонам и углу между ними.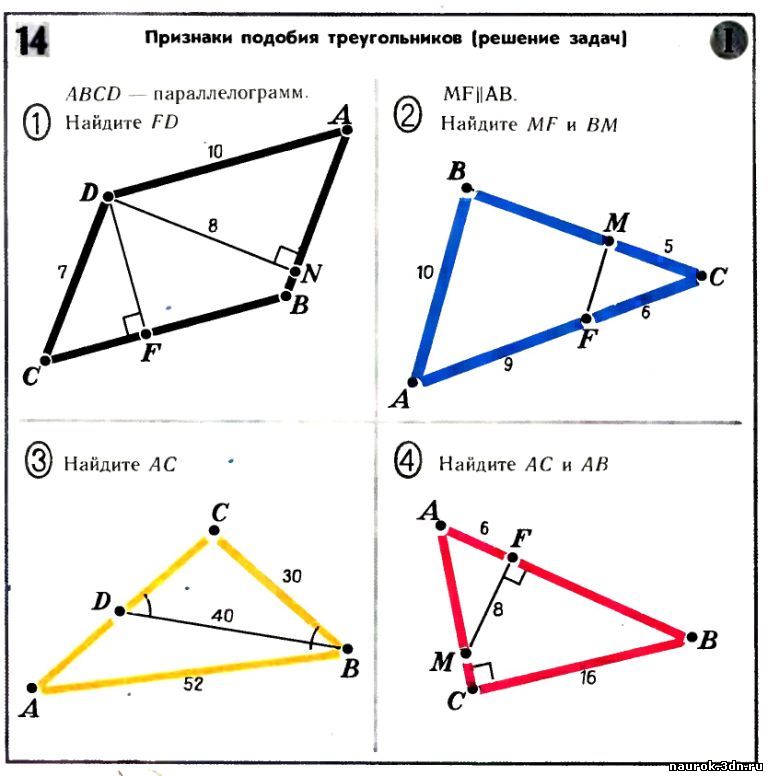 Из одной точки к окружности проведены две касательные. Длина каждой касательной равна 12 см, а расстояние между точками касания 14,4 см. Определите радиус окружности (рис. 186). (2)
Из одной точки к окружности проведены две касательные. Длина каждой касательной равна 12 см, а расстояние между точками касания 14,4 см. Определите радиус окружности (рис. 186). (2) Треугольник ONC прямоугольный, в нём ОС = 5, ON = 3. Следовательно,
Треугольник ONC прямоугольный, в нём ОС = 5, ON = 3. Следовательно, В параллелограмме ABCD проведена диагональ BD и отрезок AF (F ? ВС), пересекающий BD в точке О. Известно, что ВО = 6, OD = 18, FB = 4. Определите сторону параллелограмма AD. (1)
В параллелограмме ABCD проведена диагональ BD и отрезок AF (F ? ВС), пересекающий BD в точке О. Известно, что ВО = 6, OD = 18, FB = 4. Определите сторону параллелограмма AD. (1) Известно, что площадь треугольника ABC равна 18, площадь треугольника BPQ равна 2, а длина отрезка PQ равна 2?2. Вычислите радиус окружности, описанной около треугольника ABC. (3)
Известно, что площадь треугольника ABC равна 18, площадь треугольника BPQ равна 2, а длина отрезка PQ равна 2?2. Вычислите радиус окружности, описанной около треугольника ABC. (3)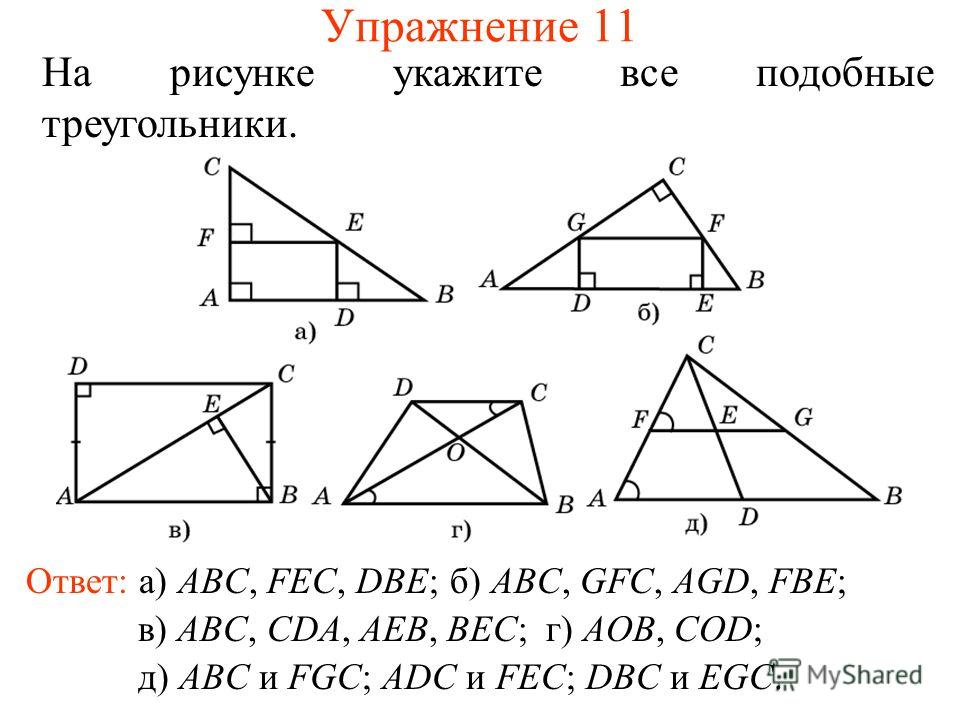
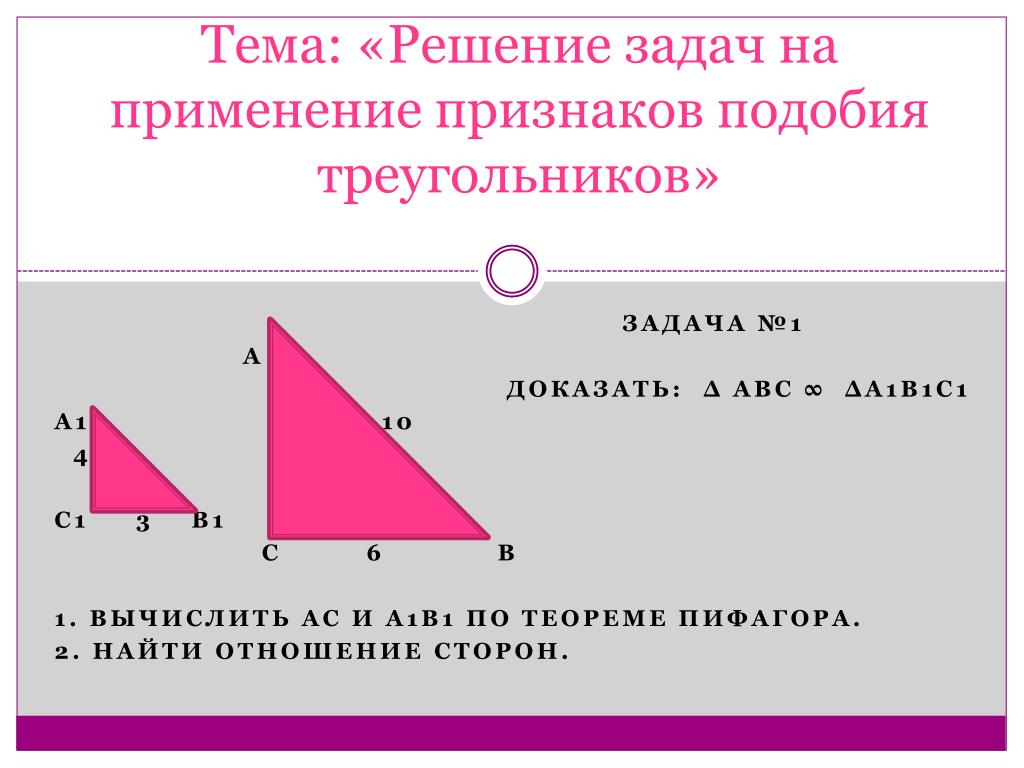


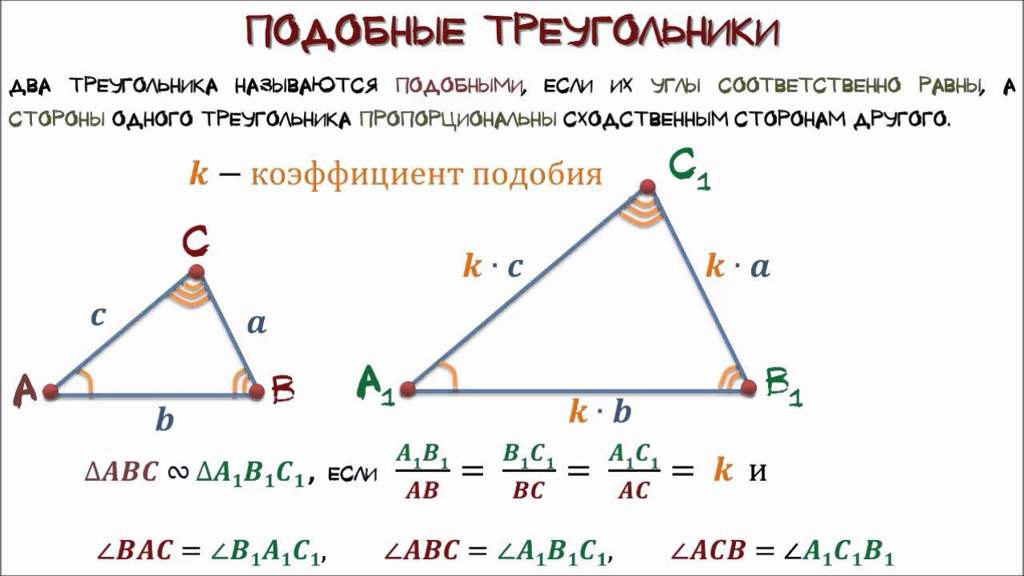
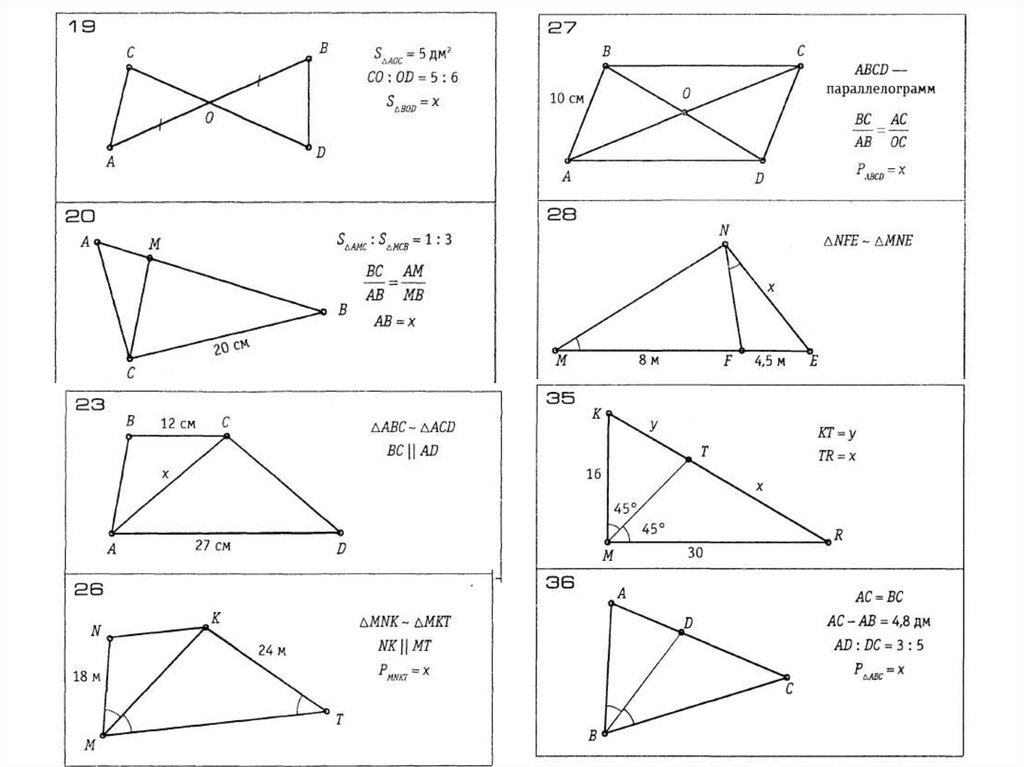 Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сторонам другого.
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сторонам другого.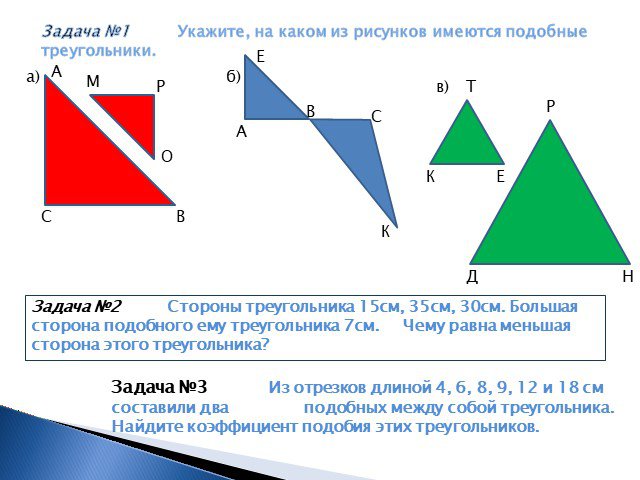 Сохранившаяся копия относится к 1629 г.
Сохранившаяся копия относится к 1629 г. 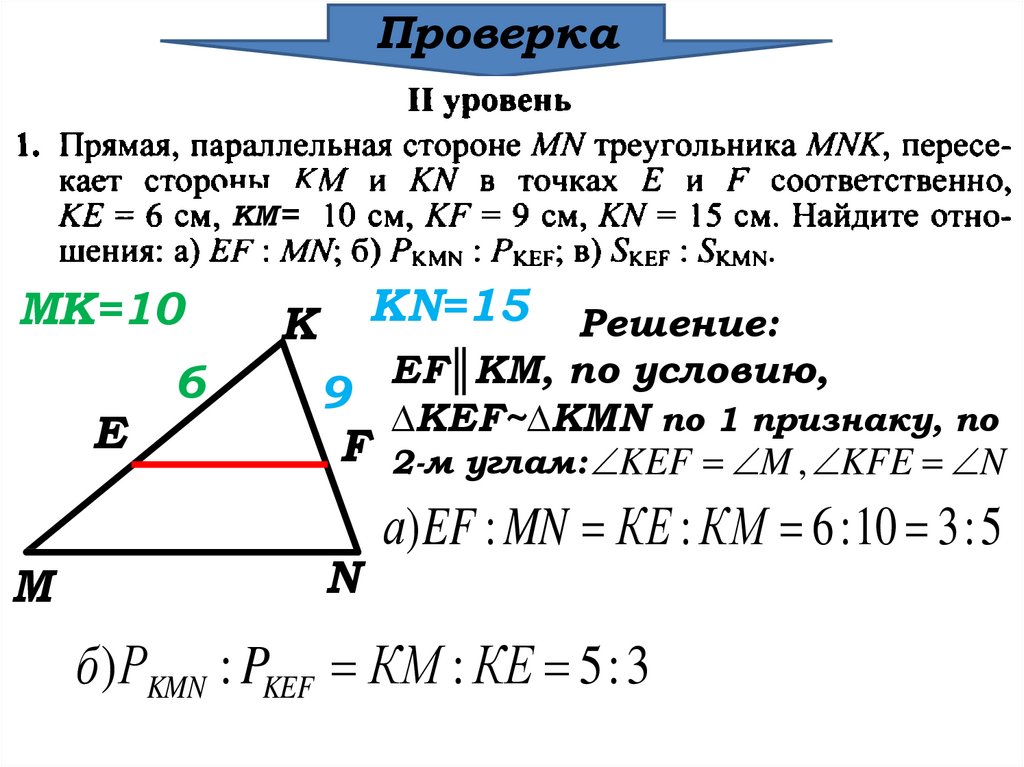
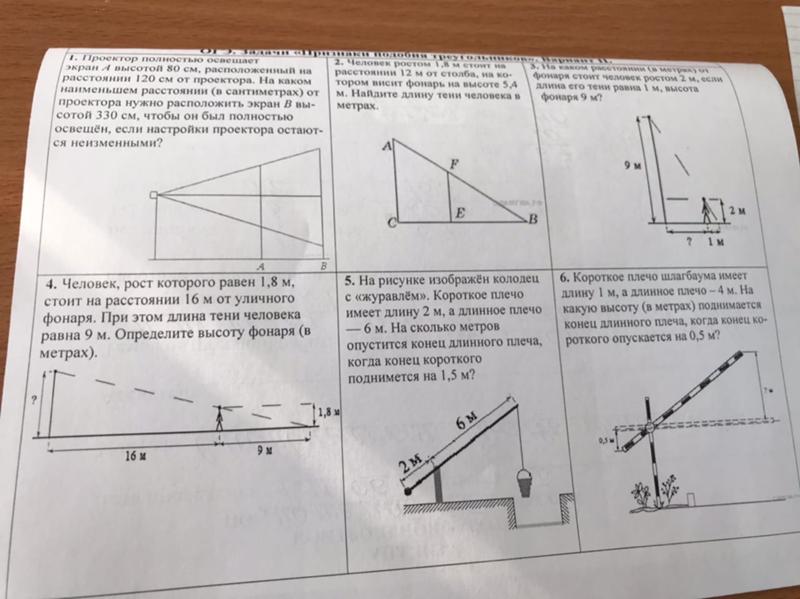
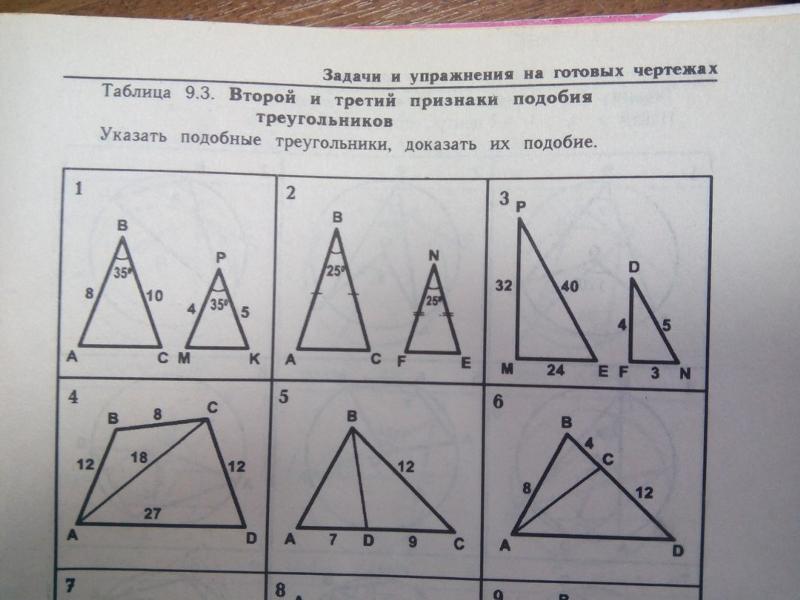 Для этого нудно рассмотреть подобие двух треугольников. Помните: солнечные лучи падают параллельно друг другу. (Ответ:15м).
Для этого нудно рассмотреть подобие двух треугольников. Помните: солнечные лучи падают параллельно друг другу. (Ответ:15м). (Ответ: х=3/4*n*10; 375м).
(Ответ: х=3/4*n*10; 375м).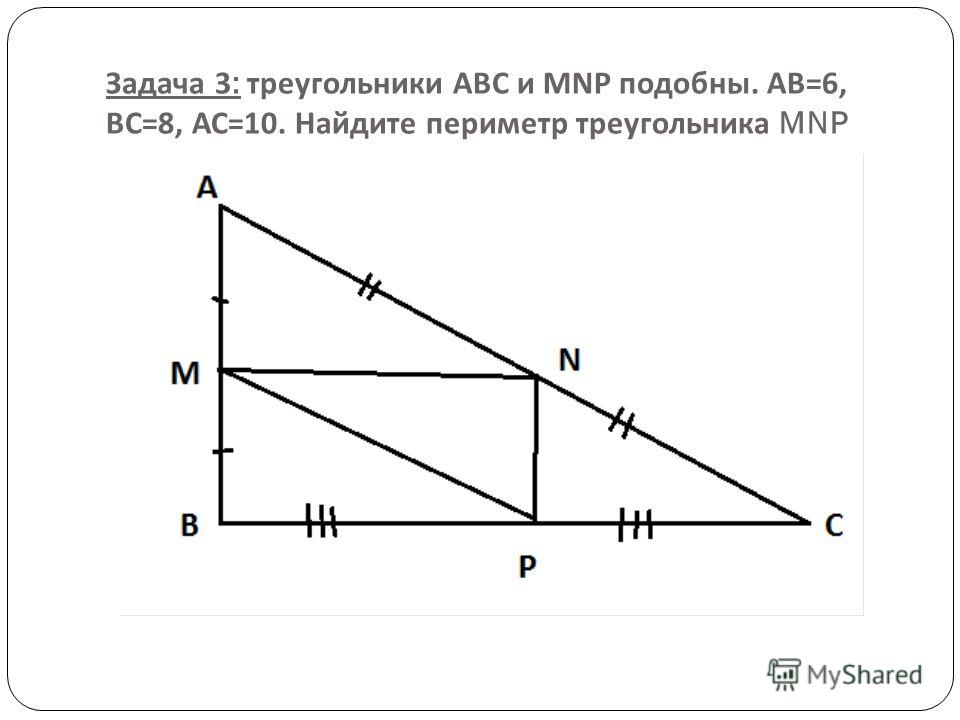

 Высота шеста – 1,5 м.
Высота шеста – 1,5 м.


 docx DLL3 МАТЕМАТИКА 9 НЕДЕЛЯ—.docx
docx DLL3 МАТЕМАТИКА 9 НЕДЕЛЯ—.docx (M9GE-IIIf-2)
Учащийся иллюстрирует подобие фигур. (M9GE-IIIg-1)
Учащийся доказывает условия подобия треугольников по теореме о подобия АА. (M9GE-IIIg-h-1)
Учащийся доказывает условия подобия треугольников по теореме подобия SSS. (M9GE-IIIg-h-1)
II.СОДЕРЖАНИЕ (предмет)
Доля
Основные теоремы
пропорция
Подобные многоугольники решают задачи, связанные с воздушным змеем. ЕЖЕНЕДЕЛЬНАЯ ВИКТОРИНА
III. ОБРАЗОВАТЕЛЬНЫЕ РЕСУРСЫ
А. Ссылки
1. Страницы руководства для учителей TG MATH 9, стр. 232-234 ТГ МАТЕМАТИКА 9, стр. 232-234 ТГ МАТЕМАТИКА 9, стр. 234-240 ТГ МАТЕМАТИКА 9, стр. 241-243 ТГ МАТЕМАТИКА 9, стр. 241-243
2. Страницы материалов для учащихся LM MATH 9, стр. 356-363 LM MATH 9, стр. 358-361 LM MATH 9, стр. 361-367 LM MATH 9, стр. 368-371 LM MATH 9, стр. 370-372
3. Страницы учебника
4. Дополнительные материалы от LRDMS
B. Другие учебные ресурсы Интернет/наглядные пособия Интернет/наглядные пособия Интернет/наглядные пособия Интернет/наглядные пособия
IV. ПРОЦЕДУРЫ Подготовительные мероприятия
1.
(M9GE-IIIf-2)
Учащийся иллюстрирует подобие фигур. (M9GE-IIIg-1)
Учащийся доказывает условия подобия треугольников по теореме о подобия АА. (M9GE-IIIg-h-1)
Учащийся доказывает условия подобия треугольников по теореме подобия SSS. (M9GE-IIIg-h-1)
II.СОДЕРЖАНИЕ (предмет)
Доля
Основные теоремы
пропорция
Подобные многоугольники решают задачи, связанные с воздушным змеем. ЕЖЕНЕДЕЛЬНАЯ ВИКТОРИНА
III. ОБРАЗОВАТЕЛЬНЫЕ РЕСУРСЫ
А. Ссылки
1. Страницы руководства для учителей TG MATH 9, стр. 232-234 ТГ МАТЕМАТИКА 9, стр. 232-234 ТГ МАТЕМАТИКА 9, стр. 234-240 ТГ МАТЕМАТИКА 9, стр. 241-243 ТГ МАТЕМАТИКА 9, стр. 241-243
2. Страницы материалов для учащихся LM MATH 9, стр. 356-363 LM MATH 9, стр. 358-361 LM MATH 9, стр. 361-367 LM MATH 9, стр. 368-371 LM MATH 9, стр. 370-372
3. Страницы учебника
4. Дополнительные материалы от LRDMS
B. Другие учебные ресурсы Интернет/наглядные пособия Интернет/наглядные пособия Интернет/наглядные пособия Интернет/наглядные пособия
IV. ПРОЦЕДУРЫ Подготовительные мероприятия
1. Молитва
2. Посещаемость/задание
3. Управление классом
Подготовительные мероприятия
1. Молитва
2. Посещаемость/задание
3. Управление классом
Подготовительные мероприятия
1. Молитва
2. Посещаемость/задание
3. Управление классом
Подготовительные мероприятия
4. Молитва
5. Посещаемость/задание
6. Управление классом
Подготовительные мероприятия
1.Молитва
2.Посещаемость/задание
3.Управление классом
A. Обзор прошлого урока или презентация
новый урок Предварительный
1. Предварительная оценка
Выразите следующее как
соотношение:
от 2 метров до 40 сантиметров
от 3 недель до 6 дней
от 25 минут до 2 часов
от 6 лет до 1,5 десятилетий
от века до десятилетия
Ответьте на каждый из следующих вопросов.
а. Когда две фигуры
конгруэнтны?
б. Проиллюстрируйте пару
конгруэнтные фигуры
в. Если ,
которые совпадают
стороны? равные углы?
2. Какие фигуры кажутся
похожий? конгруэнтны?
Анализируй-Потом Решай!
Активность:
ОТВЕТИТЬ МО, ПОКАЗАТЬ МО
B. Установление цели нового
урок
Учитель покажет разные
изображения на мониторе и
учащиеся описывают/объясняют, что
они заметили.
Молитва
2. Посещаемость/задание
3. Управление классом
Подготовительные мероприятия
1. Молитва
2. Посещаемость/задание
3. Управление классом
Подготовительные мероприятия
1. Молитва
2. Посещаемость/задание
3. Управление классом
Подготовительные мероприятия
4. Молитва
5. Посещаемость/задание
6. Управление классом
Подготовительные мероприятия
1.Молитва
2.Посещаемость/задание
3.Управление классом
A. Обзор прошлого урока или презентация
новый урок Предварительный
1. Предварительная оценка
Выразите следующее как
соотношение:
от 2 метров до 40 сантиметров
от 3 недель до 6 дней
от 25 минут до 2 часов
от 6 лет до 1,5 десятилетий
от века до десятилетия
Ответьте на каждый из следующих вопросов.
а. Когда две фигуры
конгруэнтны?
б. Проиллюстрируйте пару
конгруэнтные фигуры
в. Если ,
которые совпадают
стороны? равные углы?
2. Какие фигуры кажутся
похожий? конгруэнтны?
Анализируй-Потом Решай!
Активность:
ОТВЕТИТЬ МО, ПОКАЗАТЬ МО
B. Установление цели нового
урок
Учитель покажет разные
изображения на мониторе и
учащиеся описывают/объясняют, что
они заметили.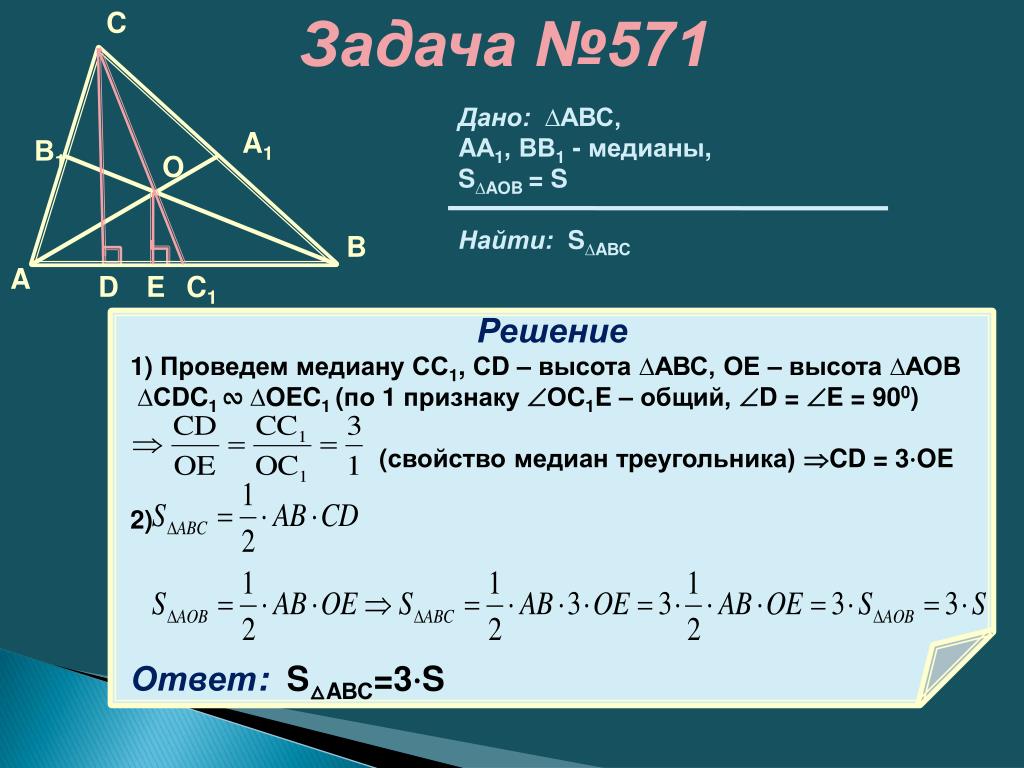 Следующие свойства показывают
несколько способов перезаписи
пропорции, не изменяющие
смысл их значений.
Посмотрите на вещи внутри
классе и выявить
похожие стороны или лица.
книги на доске
Стены Стола
1. Найдите пары фигур
в вашем классе
которые показывают сходство.
Мотивационная активность Активность:
Я БРОСАЮ ВАМ ВЫЗОВ!
Следующие свойства показывают
несколько способов перезаписи
пропорции, не изменяющие
смысл их значений.
Посмотрите на вещи внутри
классе и выявить
похожие стороны или лица.
книги на доске
Стены Стола
1. Найдите пары фигур
в вашем классе
которые показывают сходство.
Мотивационная активность Активность:
Я БРОСАЮ ВАМ ВЫЗОВ!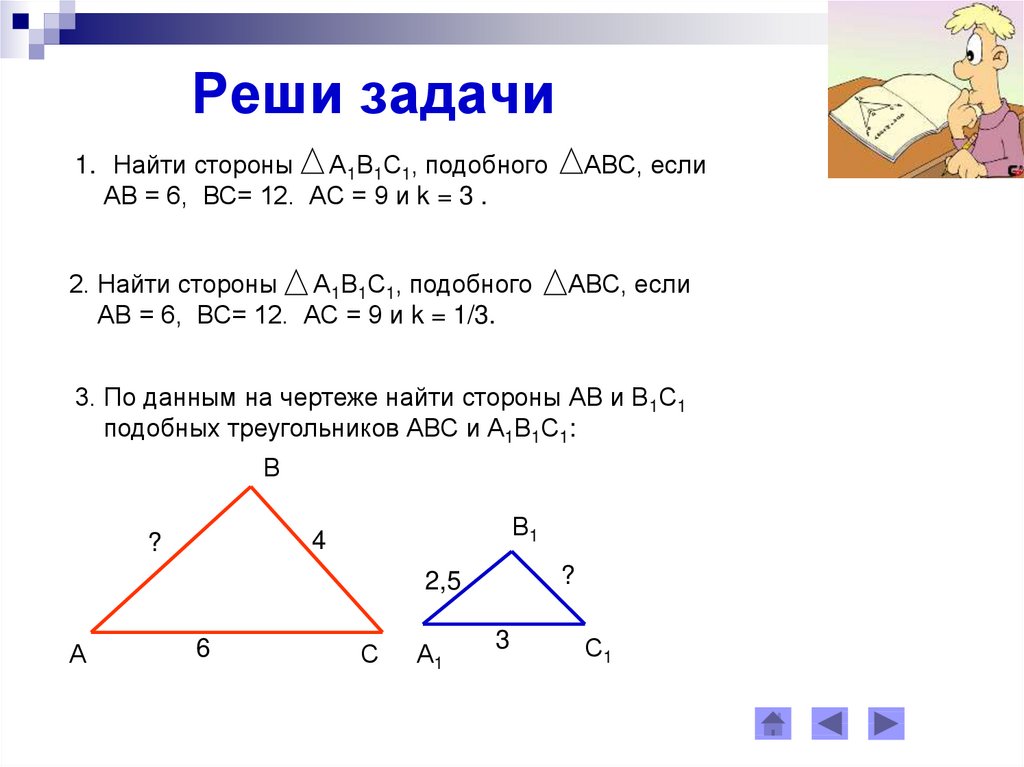 В пропорции произведение
средство равно произведению
крайности
Найдите x в пропорции.
1. =
2. =
3. =
4. 2:3 = 11: (Х+3)
(2Х + 1) : 15 = Х : 7
Активность:
а. Назовите соответствующий
сторон треугольников I и II.
б. Найдите отношение
соответствующие стороны.
в. Определить периметр
треугольники I и II
АКТИВНОСТЬ
Напишите утверждения или причины
которые оставлены пустыми в доказательстве
Теорема подобия AA.
Активность
Наводящие вопросы
D. Обсуждение новых концепций и
отработка новых навыков №2
Управляемая практика (давайте сделаем это!) Решите каждую пропорцию.
Ответить на следующие вопросы.
1. Как соотносятся
связаны углы треугольников?
2. Что вы замечаете в
длины
соответствующие стороны
треугольники I и II?
Анализ Анализ
E. Развитие мастерства (приводит к
Формирующее оценивание 3.)
Являются ли следующие соотношения
пропорциональный?
Ответьте да или нет
Если ответ отрицательный, дайте соотношение,
пропорционально любому из заданных
отношения.
Применить основной закон
пропорция, найдя недостающее
переменная.
В пропорции произведение
средство равно произведению
крайности
Найдите x в пропорции.
1. =
2. =
3. =
4. 2:3 = 11: (Х+3)
(2Х + 1) : 15 = Х : 7
Активность:
а. Назовите соответствующий
сторон треугольников I и II.
б. Найдите отношение
соответствующие стороны.
в. Определить периметр
треугольники I и II
АКТИВНОСТЬ
Напишите утверждения или причины
которые оставлены пустыми в доказательстве
Теорема подобия AA.
Активность
Наводящие вопросы
D. Обсуждение новых концепций и
отработка новых навыков №2
Управляемая практика (давайте сделаем это!) Решите каждую пропорцию.
Ответить на следующие вопросы.
1. Как соотносятся
связаны углы треугольников?
2. Что вы замечаете в
длины
соответствующие стороны
треугольники I и II?
Анализ Анализ
E. Развитие мастерства (приводит к
Формирующее оценивание 3.)
Являются ли следующие соотношения
пропорциональный?
Ответьте да или нет
Если ответ отрицательный, дайте соотношение,
пропорционально любому из заданных
отношения.
Применить основной закон
пропорция, найдя недостающее
переменная.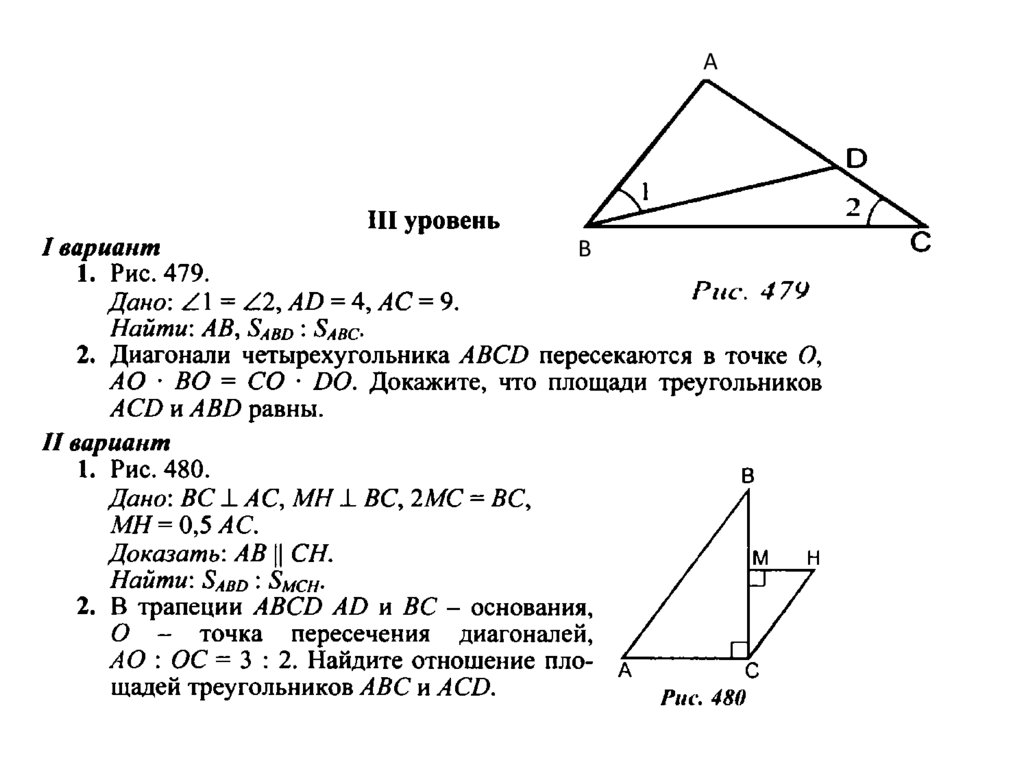 Теорема подобия AA
Два треугольника подобны, если два
углы одного треугольника равны
равны двум углам
другой треугольник.
Теорема подобия SSS
Два треугольника подобны, если
соответствующие стороны
два треугольника
пропорциональный
х 10
14
Икс
Z
Д
21 год
12
2
М
Н
О
Н
Теорема подобия AA
Два треугольника подобны, если два
углы одного треугольника равны
равны двум углам
другой треугольник.
Теорема подобия SSS
Два треугольника подобны, если
соответствующие стороны
два треугольника
пропорциональный
х 10
14
Икс
Z
Д
21 год
12
2
М
Н
О
Н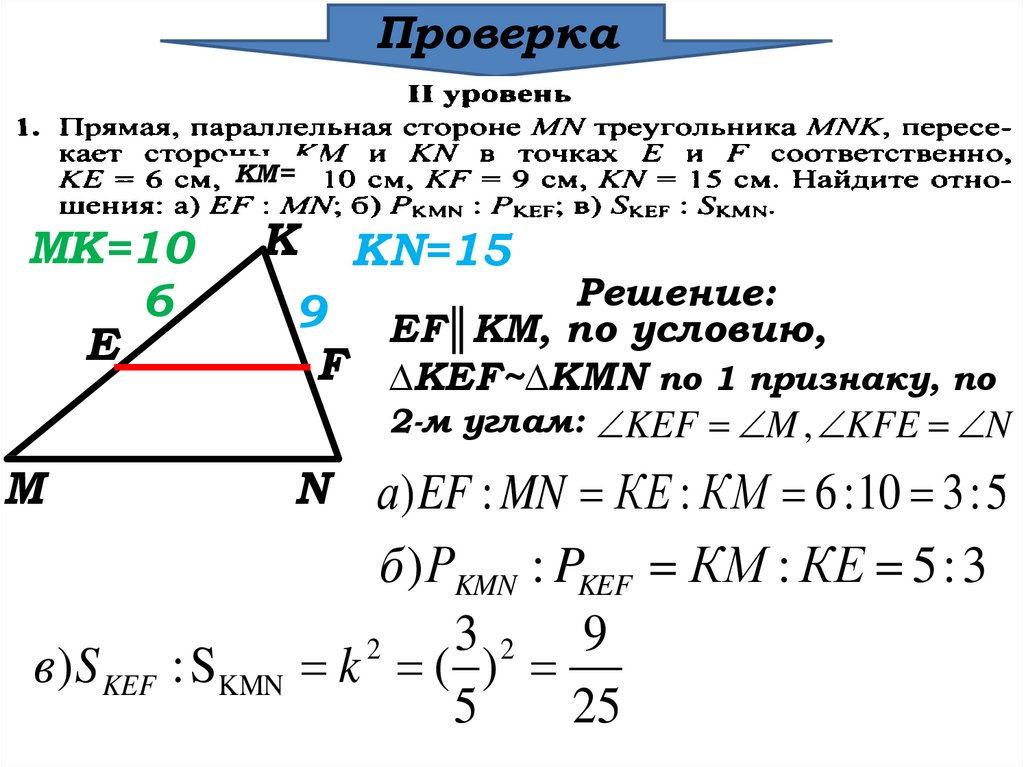
 2
2 3
3 14159..
14159..

 com , http://visualfractions.com/calculator/long-division/what-is-14-divided-by-2-using-long-division/. По состоянию на 21 апреля 2023 г.
com , http://visualfractions.com/calculator/long-division/what-is-14-divided-by-2-using-long-division/. По состоянию на 21 апреля 2023 г.