Урок по теме «Пересечение и объединение множеств». 6-й класс
Тип урока: изучение нового материала.
Цели:
- формирование знаний о пересечении и объединении множеств;
- развитие умений и нахождение числа элементов пересечения и объединения множеств, выявлять закономерность, обобщать и делать выводы, воспитание ответственного отношения к учебе.
Ход урока
1. Организационный момент.
2. Повторение изученного по теме «Множества».
Вопросы для учащихся:
- Что такое множество?
- Что такое элементы множества?
- Какое множество конечно и бесконечно?
- Какое множество называется пустым?
3. Изучение нового материала «Пересечение множеств».
Учитель. Рассмотрим следующие два множества: М – множество всех точек круга, N – множество точек прямой, пересекающей круг. Каждый видит, что пересечение круга с прямой – это отрезок; обозначим его концы буквами А и В. Задумаемся: каким свойством обладают точки этого отрезка по отношению к множествам М и N? Ответ ясен: точки отрезка АВ – это в точности те точки, которые принадлежат и множеству М, и множеству N. Так что множество всех точек отрезка АВ естественно назвать пересечением множеств М и N.
Каждый видит, что пересечение круга с прямой – это отрезок; обозначим его концы буквами А и В. Задумаемся: каким свойством обладают точки этого отрезка по отношению к множествам М и N? Ответ ясен: точки отрезка АВ – это в точности те точки, которые принадлежат и множеству М, и множеству N. Так что множество всех точек отрезка АВ естественно назвать пересечением множеств М и N.
Точно так же можно определить пересечение любых двух множеств М и N. Пересечением множеств М и N называется множество, состоящее из всех элементов, принадлежащих каждому из множеств М и N. Пересечение множеств М и N обозначают М ∩ N. Читают: «пересечение М и N» или «М пересечение N». Знак ∩ называется знаком пересечения.
Обсудим несколько примеров.
Пример 1. М – множество всех учениц какой-то школы, N – множество всех учащихся данного класса этой школы. Тогда М ∩ N – это множество всех девочек из данного класса.
Пример 2. М – множество всех квартир на 1-м этаже в каком-то доме, N – множество всех квартир в данном подъезде этого дома. Тогда М ∩ N – это множество всех квартир на 1-м этаже в данном подъезде.
Пересечение множеств точек двух фигур на плоскости легче представить, если нарисовать эти фигуры. Сделаем это, например, для двух кругов. Множество всех точек первого круга обозначим М, второго – N. Для пересечения М ∩ Nмогут быть три варианта; они изображены на рисунке.
Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то легко записать их пересечение.
Примеры:
Пересечение можно образовывать не только для двух множеств, но и для любого их числа.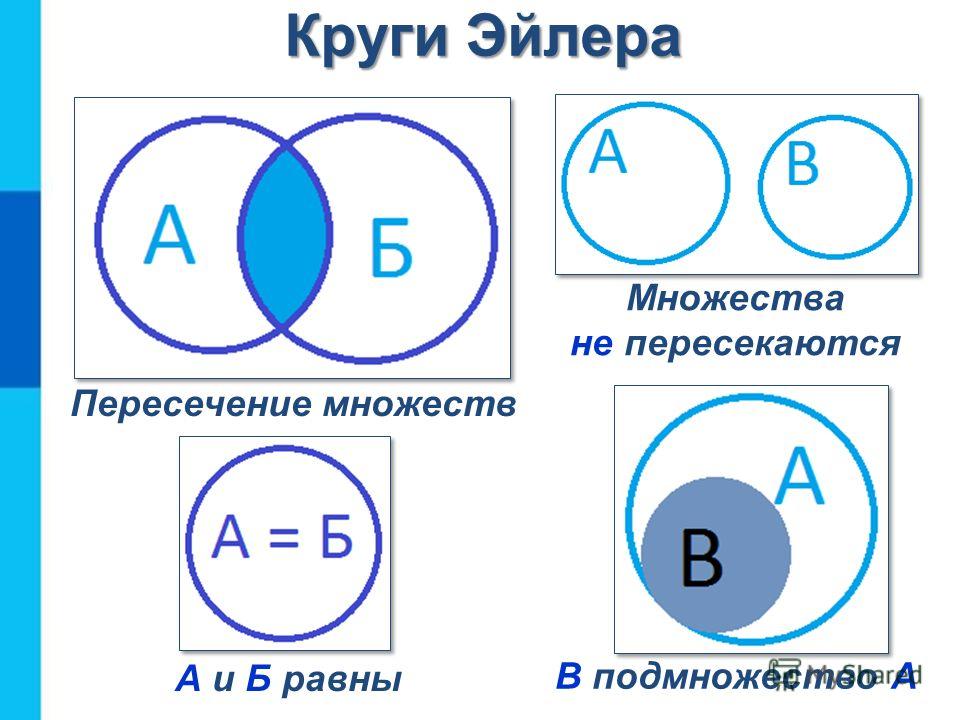 Определяется это точно так же, как и для двух множеств: пересечением данных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из этих множеств. Пересечение множеств М, N и Р обозначается М ∩N ∩ Р.
Определяется это точно так же, как и для двух множеств: пересечением данных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из этих множеств. Пересечение множеств М, N и Р обозначается М ∩N ∩ Р.
Вопрос для учащихся:
Что обозначает запись Р ∩ Q ∩ R ∩ S? Какому множеству равно это пересечение, если
4. Первичное закрепление понятия пересечения множеств.
Вопросы:
- Что такое пересечение двух множеств; нескольких множеств?
- Что значит, что два множества не пересекаются? Приведите 2-3 примера непересекающихся множеств.
- Какое множество обозначается знаком ?
Практические задания:
1. Для каждой пары множеств М и Nзапишите их пересечение:
N – множество всех неправильных дробей.
2. Для каждой пары множеств М и N укажите их пересечение:
- М – множество всех нечетных чисел, N – множество всех натуральных чисел, делящихся на 4;
- М – множество всех правильных дробей, N – множество всех десятичных дробей;
- М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 5.
3. Дан многоугольник. Каждую его сторону будем рассматривать как множество всех точек, принадлежащих этой стороне. Для каждой пары сторон многоугольника укажите множество, равное пересечению этих двух сторон, если многоугольник – это:
а) треугольник АВС;
б) прямоугольник KLMN.
4. Рассмотрите три множества {1, 2}, {2, 3}, и {3, 1}. Убедитесь, что их пересечение пусто, а пересечение любых двух из этих множеств не пусто.
5. Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.
Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.
- Запишите всевозможные попарные пересечения этих множеств. Имеются ли среди них равные?
- Запишите всевозможные пересечения троек этих множеств. Имеются ли среди них равные?
- Запишите пересечение всех этих множеств. Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?
5. Изучение нового материала «Объединение множеств».
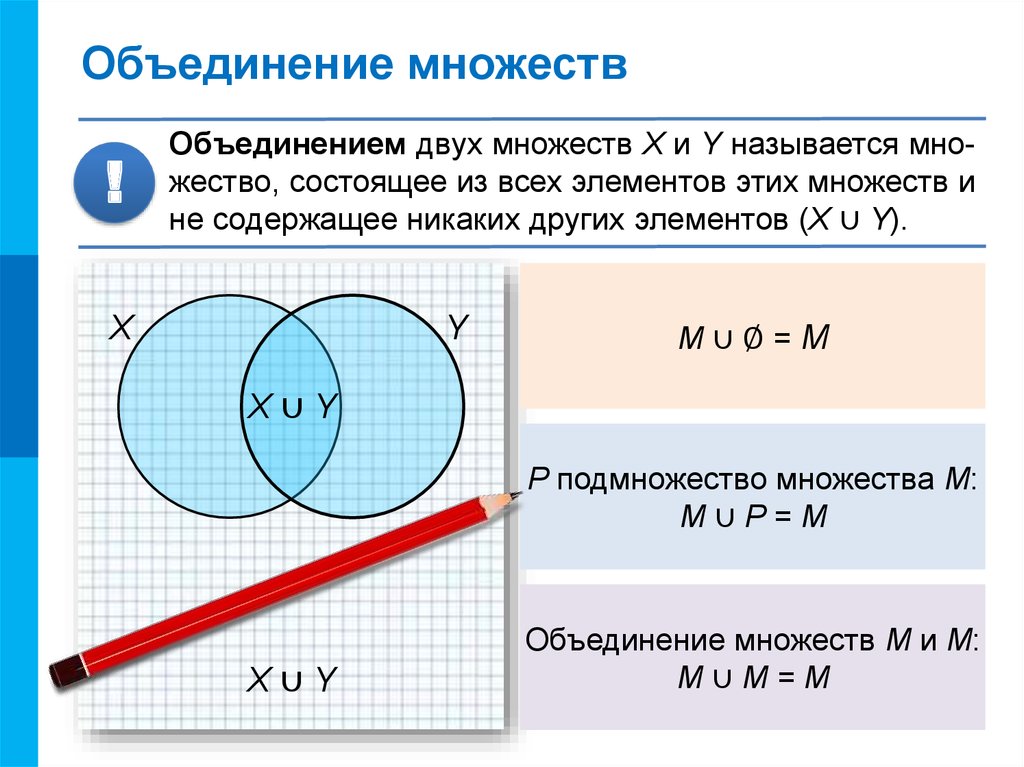
Учитель. Объединением множеств М и N называется множество всех элементов, принадлежащих хотя бы одному из множеств М и N.
Объединение множеств М и N обозначают М N. Читают: «объединение М и N» или «М объединение N». Знак называется знаком объединения.
Разберем несколько примеров. Обдумайте каждый из них.
Пример 1. М – множество всех учеников данного класса, получивших на сегодняшний день пятерку по какому-нибудь предмету, N – множество всех учеников того же класса, получивших в этот день четверку по какому-нибудь предмету. Тогда М N – это множество всех учеников данного класса, получивших за сегодняшний день повышенные отметки.
Пример 2. М – множество всех правильных дробей, N – множество всех неправильных дробей. Тогда М N – это множество всех обыкновенных дробей.
Пример 3. М – множество всех букв слова КОШКА, N – множество всех букв слова МЫШКА. Тогда М N = {А, К, М, О, Ш, Ы}.
Задание для учащихся: Приведите сами какой-нибудь пример объединения двух множеств.
Учитель. Как и пересечение, объединение можно образовать не только для двух множеств, но и для любого их числа: объединением данных множеств называется множество, состоящее…
Закончите определение. Догадайтесь, как записать объединение трех множеств М, N и Р.
Догадайтесь, как записать объединение трех множеств М, N и Р.
Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то, как и для пересечения, легко записать их объединения.
Для любых множеств М и N можно образовать их пересечение М ∩ N и объединение М N. Это похоже на то, что происходит при действиях над числами: для любых двух чисел m и n можно образовать их произведение m n и сумму m+n. Так получаются действия, которые назвали умножением и сложением. Поэтому образование пересечения и образование объединения можно назвать действиями над множествами.
Выполняются ли те же законы для пересечения и объединения множеств? Давайте рассуждать. Начнем с переместительного закона.
Повторим, что такое пересечение двух множеств: множество М ∩ N состоит из всех элементов, принадлежащих каждому из множеств М и N, а множество N ∩М состоит из всех элементов, принадлежащих каждому из множеств Nи М. Но сказать «каждому из множеств М и N» или «каждому из множеств N и М» — значит сказать одно и то же: ведь ясно, что неважно, в каком порядке перечислять здесь множества. Значит, множества М ∩N и N ∩М состоят из одних и тех же элементов, т.е.
Но сказать «каждому из множеств М и N» или «каждому из множеств N и М» — значит сказать одно и то же: ведь ясно, что неважно, в каком порядке перечислять здесь множества. Значит, множества М ∩N и N ∩М состоят из одних и тех же элементов, т.е.
М ∩ N = N ∩М.
Данное равенство и означает, что переместительный закон для пересечения верен.
Чтобы проверить сочетательный закон, надо убедиться, что для любых трех множеств М, N и Р выполняется равенство
М ∩(N ∩Р)= (М ∩N) ∩Р
Легко понять, что в левой и правой частях этого равенства записаны множества, состоящие из всех элементов, принадлежащих каждому из множеств М, N и Р, т.е. состоящие из одних и тех же элементов. Это и означает, что требуемое равенство выполняется.
6. Первичное закрепление изученного понятия объединения множеств.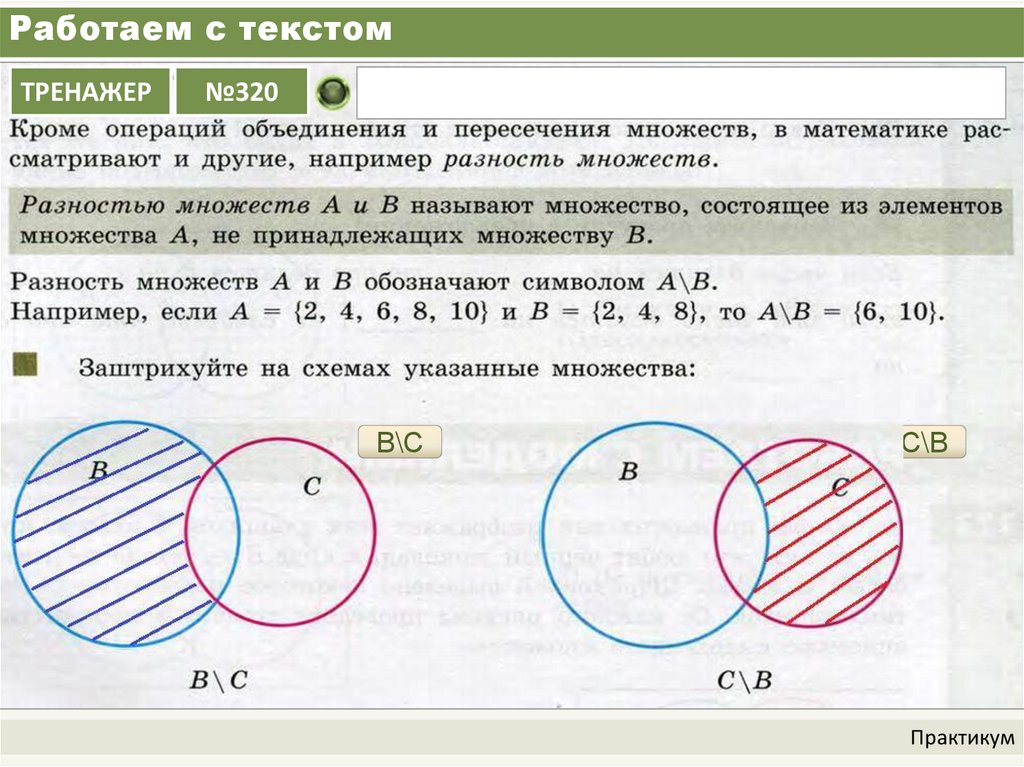
Вопросы:
- Что такое объединение двух множеств; нескольких множеств?
- О выполнении каких законов для действий пересечения и объединения множеств идет речь в объяснительном тексте этого параграфа?
- Каким множеством – конечным или бесконечным – будет объединение: а) двух конечных множеств; б) двух бесконечных множеств; в) конечного и бесконечного множеств?
Практические задания:
1. Для каждой пары множеств М и N запишите их объединение:
2. Для каждой пары множеств М и N укажите их объединение:
- М – множество всех нечетных чисел, N – множество всех четных чисел;
- М – множество всех квадратов на плоскости, N – множество всех прямоугольников на той же плоскости, четырехугольников;
- М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 15.

3. Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.
- Запишите всевозможные попарные объединения этих множеств. Имеются ли среди них равные?
- Запишите всевозможные объединения троек этих множеств. Имеются ли среди них равные?
- Запишите объединение всех этих множеств. Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?
7. Изучение нового – вывод правила подсчета числа элементов объединения и пересечения множеств.
Учитель. Чтобы вывести правило давайте разберем конкретный пример. Пусть М = {Вася, Валя, Вера, Игорь}, т.е. m=4;
N = {Валя, Гриша, Игорь}, т.е. n=3.
Запишем объединение этих множеств:
М N = {Вася, Валя, Вера, Гриша, Игорь}.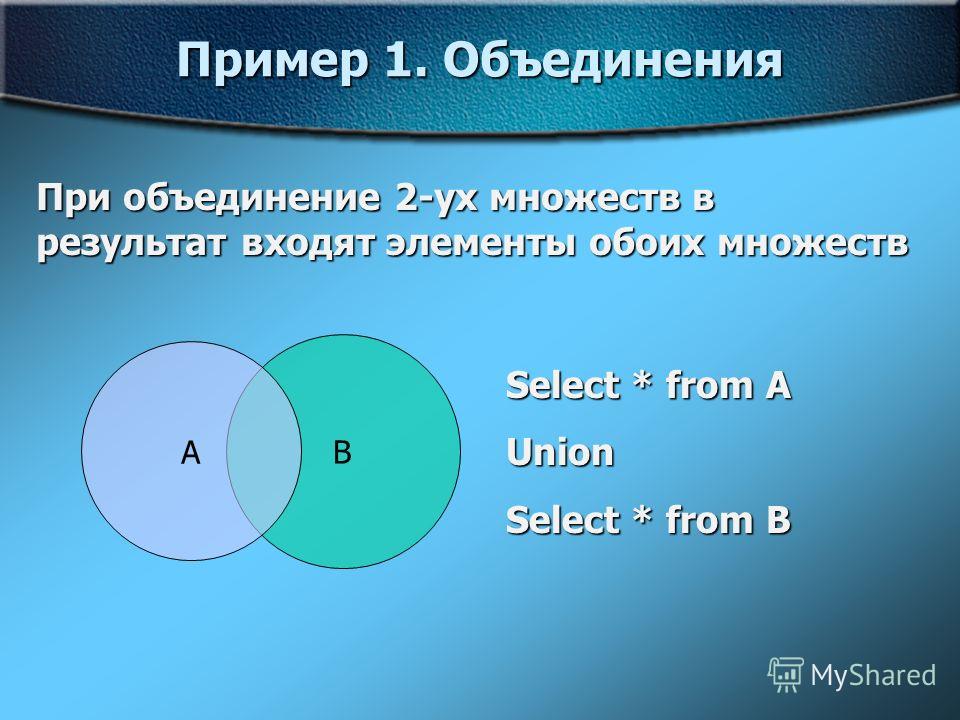
В множестве МN пять элементов, а m+n=4+3=7. Вот мы и видим, что в МN элементов меньше чем 7.
Почему так получилось? Да потому, что в данном примере можно указать учеников, которые в этот день получили и пятерку, и четверку. Другими словами здесь пересечение М ∩N не пусто: М ∩ N = {Валя, Игорь}. Но в объединении-то МN каждый элемент пересечения М ∩N присутствует (и подсчитывается) только один раз, а не два раза.
Давайте-ка изобразим ситуацию нашего примера на рисунке.
Если бы подсчитали здесь сумму m+n (т.е. 4+3), то каждый элемент пересечения (в данном примере Валя и Игорь, т.е. 2 элемента) оказался бы подсчитанным дважды. Значит, чтобы узнать число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов пересечения. В данном примере получаем 4+3-2=5.
Данная задача была решена с помощью рисунка, этот способ называется «Круги Эйлера».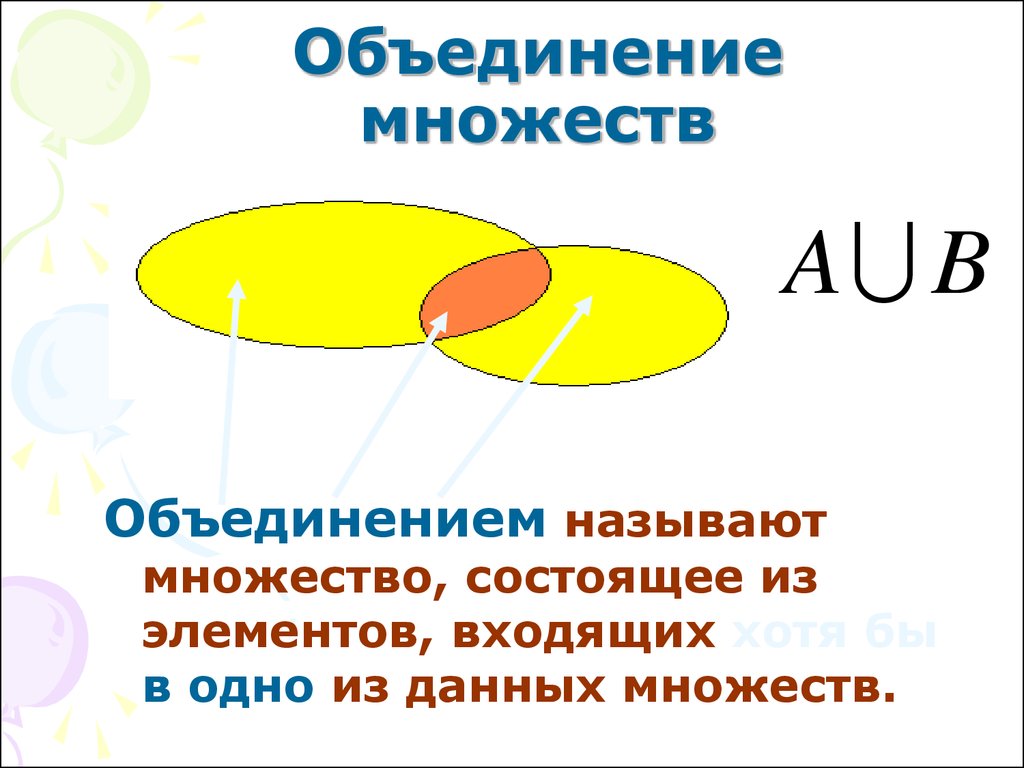 Леонард Эйлер – швейцарский математик, который в 18 веке работал в Российской академии наук и сделал много открытий для нашей науки.
Леонард Эйлер – швейцарский математик, который в 18 веке работал в Российской академии наук и сделал много открытий для нашей науки.
Итак, если мы возьмем сумму m+n, то в ней элементы пересечения М ∩N будут сосчитаны дважды. Значит, чтобы определить число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов из М ∩N, т.е. число р. Получим такую формулу: q=m+n-p.
Сформулируем правило для нахождения числа элементов объединения множеств:
Чтобы найти число элементов объединения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их пересечения.
Сформулируем правило для нахождения числа элементов пересечения множеств:
Чтобы найти число элементов пересечения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их объединения.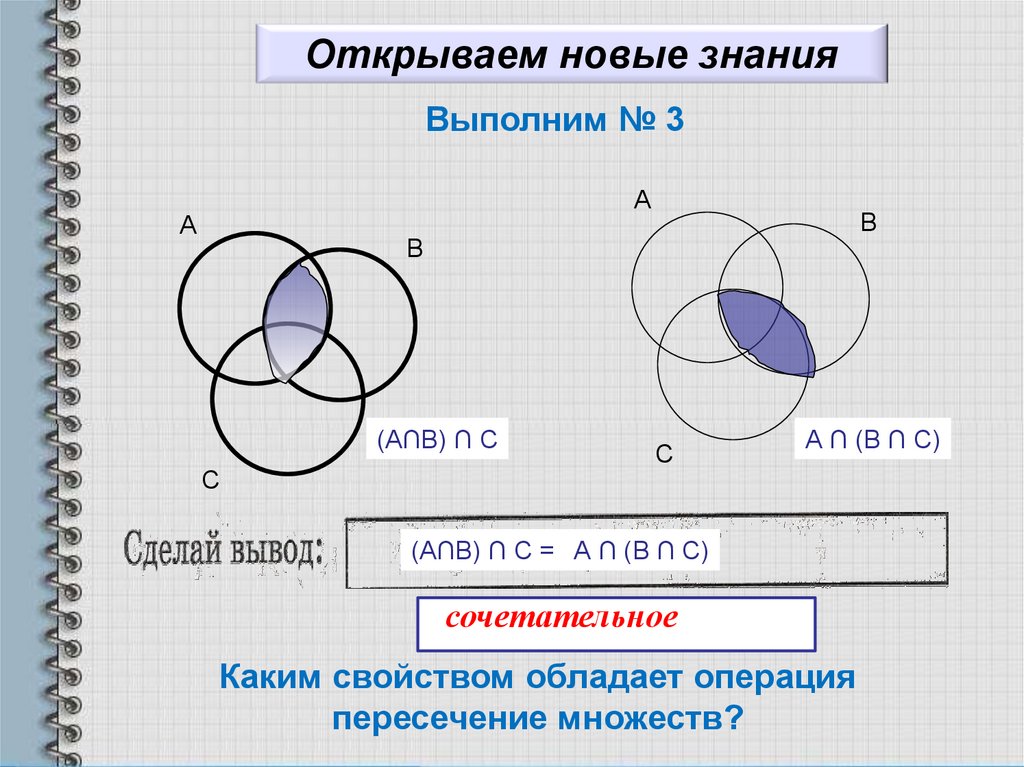
8. Первичное закрепление изученного.
Практические задания (устно):
1. Вычислите число элементов в объединении множеств М и N, если:
- М содержит 10 элементов, N – 15 элементов, а М ∩N – 7 элементов;
- М содержит 27 элементов, N – 18 элементов, а М ∩N – 13 элементов;
- М содержит 45 элементов, N – 57 элементов, а М ∩N – 1 элемент.
2. Вычислите число элементов в пересечении множеств М и N, если:
- М содержит 10 элементов, N – 15 элементов, а М ∩N – 17 элементов;
- М содержит 27 элементов, N – 18 элементов, а М ∩ N – 45 элементов;
- М содержит 45 элементов, N – 57 элементов, а М ∩N – 100 элементов.

Решение задач с помощью кругов Эйлера:
№1. В классе 28 учеников. Каждый из них начертил у себя в тетради один из двух четырехугольников – прямоугольник или ромб. При проверке прямоугольников оказалось 17, а ромбов – 15. Как такое могло случиться?
№2. В осенние каникулы 12 учеников класса участвовали в междугородных экскурсиях в Москву и Санкт-Петербург, при этом 8 из них посетили Санкт-Петербург, а 6 – Москву. Сколько из этих учеников побывало и в Москве, и в Санкт-Петербурге?
Задание на дом:
№1. Найдите пересечение множеств учителей, которые вели уроки в вашем классе: а) вчера и сегодня; б) вчера и позавчера. Оказалось ли какое-то из этих двух пересечений пустым?
№2. Вася, рассматривая свой дневник погоды, обнаружил, что в сентябре 17 раз отмечен дождь и 19 раз – сильный ветер. При этом дней, когда одновременно шел дождь и дул сильный ветер, оказалось 7. Был ли хоть один день, когда не было ни дождя, ни сильного ветра?
Был ли хоть один день, когда не было ни дождя, ни сильного ветра?
свойства, формулы включений и исключений, примеры
- Пересечение множеств
- Объединение множеств
- Универсум и отрицание
- Свойства операций пересечения и объединения
- Разность множеств
- Формулы включений и исключений
- Примеры
Пересечение множеств
Если множества не пересекаются, то $A \cap B = \varnothing $ — пустое множество в пересечении. Если $B \subseteq A$ — подмножество, то $A \cap B = B$ – пересечением будет меньшее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A \cap B$ = {3;5}.
Если A = {f|f-прямоугольник}, B = {f|f-ромб}, то $A \cap B$ = {f|f-квадрат}.
Если A = $\{n|n⋮3, n \in \Bbb N \}$ — натуральные числа, кратные 3, B = $\{n|n⋮5, n \in \Bbb N \}$ — натуральные числа, кратные 5, то $A \cap B = {n|n⋮15, n \in \Bbb N}$ — натуральные числа, кратные 15.
Если A = {a│a-слон}, B = {a|a-птица}, то $A \cap B = \varnothing$.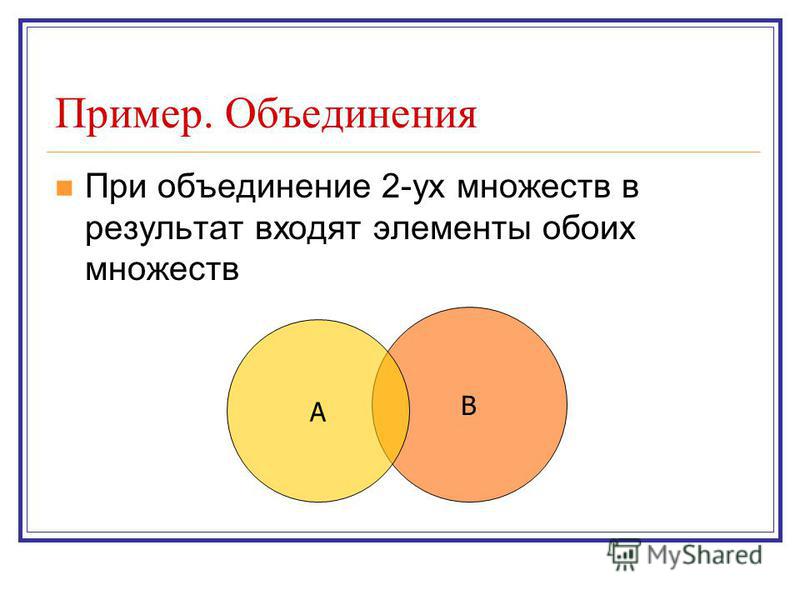 2-4 = 0, x \in \Bbb R\}, B = \{x|x+3 = 2, x \in \Bbb R \}, то A \cup$ B = {-2;-1;2}
2-4 = 0, x \in \Bbb R\}, B = \{x|x+3 = 2, x \in \Bbb R \}, то A \cup$ B = {-2;-1;2}
Если $A = \{n│n \in \Bbb Z \}$- все целые числа, $B = \{x|x = \frac{a}{b}, a \in \Bbb Z, b \in \Bbb N \}$ — все дроби, то $A \cup B = \{x│x \in \Bbb Q\}$ — множество рациональных чисел. Заметим, что в данном случае $A \subset B$.
Универсум и отрицание
Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.
В литературе универсум обозначают U.
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:
Примеры универсумов:
При рассмотрении целочисленных задач, универсум – это множество целых чисел.
При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.
Читается «не A».
У отрицания есть любопытное свойство: $\bar{\bar{Α}} = Α $(два раза «нет» — это «да»).
Например:
Если U = {1;2;3;4;5;6;7}, A = {3;4;5}, то $\bar{A} = \{1;2;6;7\}$
Если U = $\{x|x \in \Bbb R\}$ — все действительные числа, A = $\{x|x \gt 0, x \in \Bbb R \}$ — все положительные действительные числа, то $ \bar{A} = \{x|x \le 0, x \in \Bbb R\}$.
Свойства операций пересечения и объединения
Пересечение
Объединение
Коммутативность
$A \cap B = B \cap A$
$ A \cup B = B \cup A $
Ассоциативность
$(A \cap B) \cap C = A \cap (B \cap C)$
$ (A \cup B) \cup C = A \cup ( B \cup C) $
Дистрибутивность
$(A \cup B) \cap C = (A \cap C) \cup (B \cap C)$
$ (A \cap B) \cup C = (A \cup C) \cap (B \cup C) $
Идемпотентность
$A \cap A = A$
$ A \cup A = 0 $
Взаимодействие с отрицанием, пустым множеством и универсумом
$A \cap \bar{A} = \varnothing $
$A \cap U = A$
$A \cap \varnothing = \varnothing$
$A \cup \bar{A} = U $
$A \cup U = U$
$A \cup \varnothing = A$
Законы де Моргана
$ \overline{(A \cap B)} = \bar{A} \cup \bar{B} $
$ \overline{(A \cup B)} = \bar{A} \cap \bar{B} $
Закон поглощения
$ (A \cup B) \cap A = A $
$ (A \cap B) \cup A = A $
Разность множеств
Читается «A без B».
На диаграммах Эйлера разности для пересекающихся множеств выглядят так:
Получается, что отрицание – частный случай разности: $ \bar{A} = \{x|x \in \Bbb U, x \notin A \} $= U\A
«Не A» — это «универсум без A».
Формулы включений и исключений
Рассмотрим два конечных пересекающихся множества A и B.
Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A \cap B)$.
Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A \cup B)$?
Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:
$$n(A \cup B) = n(A)+ n(B)-n(A \cap B)$$
Выведем аналогичную формулу для трёх пересекающихся конечных множеств.
Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.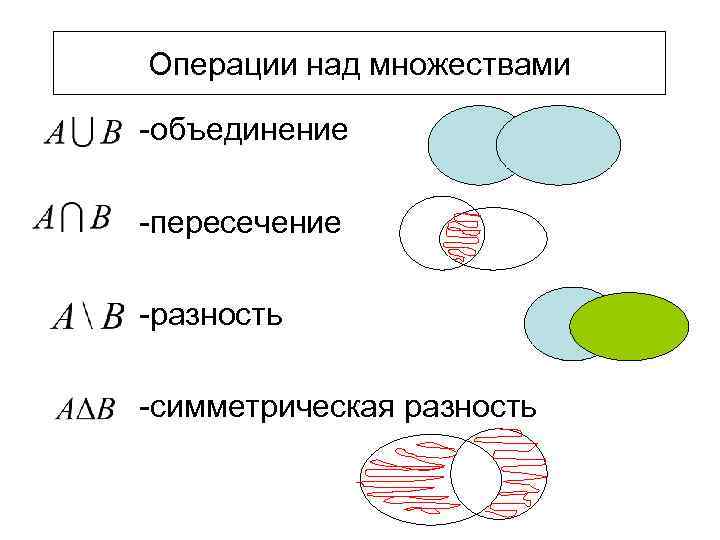 е. отнять сумму $(n(A \cap B)+n(A \cap C)+n(B \cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A \cap B \cap C)$; значит, его нужно «вернуть».
е. отнять сумму $(n(A \cap B)+n(A \cap C)+n(B \cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A \cap B \cap C)$; значит, его нужно «вернуть».
Получаем:
$$ n(A \cup B \cup C) = n(A)+ n(B)+n(C)- $$
$$ -(n(A \cap B)+n(A \cap C)+n(B \cap C) )+n(A \cap B \cap C) $$
Примеры
Пример 1. Найдите пересечение данных множеств:
а) A = {0;5;8;10},
B = {3;6;8;9}
$A \cap B$ = {8}
$б) A = \{x|x \lt 3, x \in \Bbb R\}, $
$ B = \{x|x \gt 1, x \in \Bbb R\} $
$A \cap B = \{x|1 \lt x \lt 3, x \in \Bbb R\}$ — отрезок
$в) A = \{x|x \lt 3, x \in \Bbb R\}, $
$ B = \{x|x \gt 1, x \in \Bbb N\} $
$A \cap B = \{x|1 \lt x \lt 3, x \in \Bbb N \} или A \cap B = \{2\}$ — одна точка
г) A = {f|f-правильный многоугольник},
B = {f|f-четырехугольник}
$A \cap B = \{f|f-квадрат\}$
Пример 2. Найдите объединение данных множеств:
а) A = {0;5;8;10}, B = {3;6;8;9}
$A \cup B$ = {0;3;5;6;8;9;10}
б) A = {1;2}, B = {1;2;3;4}
$A \subset B$ – строгое подмножество
$A \cup B $ = B = {1;2;3;4}
$в) A = \{x|x \lt 1, x \in \Bbb R\}, B = \{x|x \gt 1,x \in \Bbb R\} $
$A \cup B = \{x|x \neq 1, x \in \Bbb R \}$
$г) A = \{n│n⋮3, n \in \Bbb Z\}, B = \{n|n⋮9,n \in \Bbb N\} $
$B \subset A$ — строгое подмножество
$ A \cup B = A = \{n│n⋮3, n \in \Bbb Z\} $
Пример 3. Найдите отрицание данного множества на данном универсуме:
Найдите отрицание данного множества на данном универсуме:
а) U = {1;2;3;4;5}, A = {2;3}
$ \bar{A} = {1;4;5}$
б) U = $\{x│x \in \Bbb Q \}$, A = $\{ \frac{4}{5}, \frac{7}{8} \}$
$ \bar{A} = \{x|x \neq \frac{4}{5}, x \neq \frac{7}{8}, x \in \Bbb Q\} $
$в) U = \{x│x \in \Bbb R\}, A = \{x|x \ge 2, x \in \Bbb R\} $
$\bar{A} = \{x|x \lt 2, x \in \Bbb R\}$
г) U = { 0;1}, A = { 0}
$ \bar{A} = {1}$
Пример 4. Найдите обе разности данных множеств:
а) A = {0;1;2;3;4}, B = {2;4}
A\B = {0;1;3}, $B\A = \{∅\}$
б) A = {0;1;3}, B = {2;4;6}
A\B = {0;1;3}, B\A = {2;4;6}
$в) A = \{x|x \gt 1, x \in \Bbb R\}, $
$ B = \{x|x \lt 3, x \in \Bbb R\} $
A\B $ = \{x|x \ge 3, x \in \Bbb R\}$
B\A $ = \{x|x \le 1,x \in \Bbb R\} $
$ г*) A = \{(x,y)|x \gt 0, x \in \Bbb R, y \in \Bbb R\} $
$ B = \{(x,y)|x \le 5, x \in \Bbb R, y \in \Bbb R\} $
A\B $ = \{(x,y)|x \gt 5, x \in \Bbb R, y \in \Bbb R\} $
B\A $ = \{(x,y)|x \le 0, x \in \Bbb R, y \in \Bbb R\} $
Пример 5.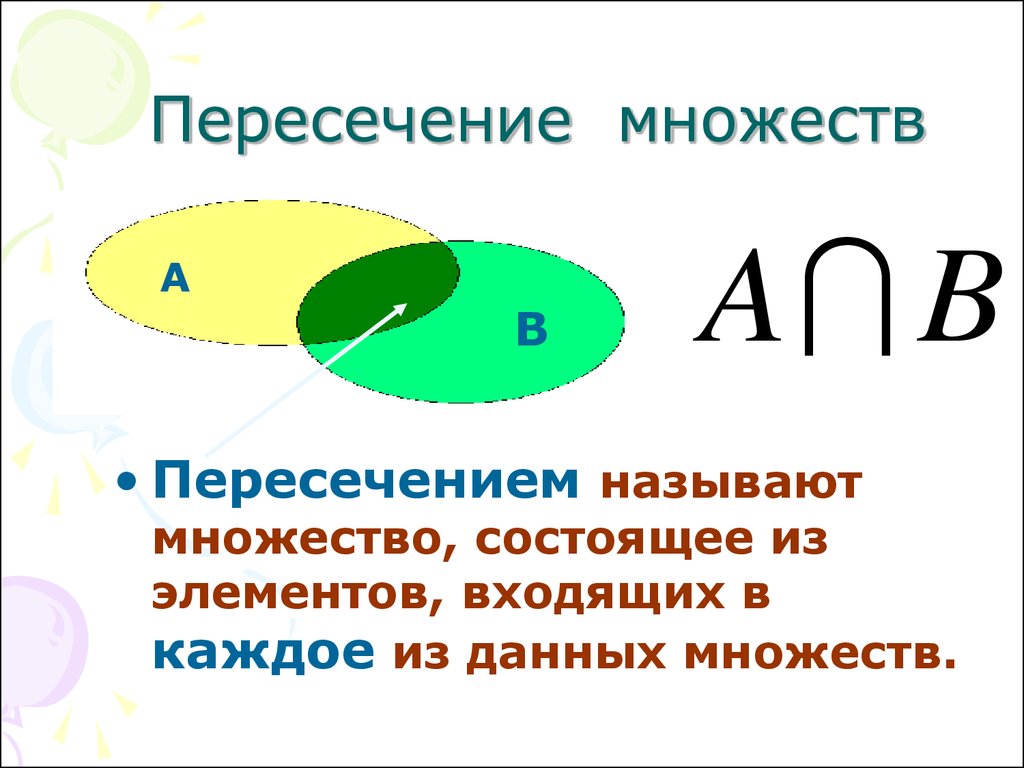 Из 100 студентов умеют программировать на Python 28 человек, на Java 30 человек, на C# 42 человека, на Python и Java 8 человек, на Python и C# 10 человек, на Java и C# 5 человек. Все три языка знают 3 студента. А сколько студентов не умеют программировать на этих языках?
Из 100 студентов умеют программировать на Python 28 человек, на Java 30 человек, на C# 42 человека, на Python и Java 8 человек, на Python и C# 10 человек, на Java и C# 5 человек. Все три языка знают 3 студента. А сколько студентов не умеют программировать на этих языках?
n(U) = 100
n(A) = 28, n(B) = 30, n(C) = 42
$ n(A \cap B) = 8, n(B \cap C) = 5, n(A \cap C) = 10 $
$n(A \cap B \cap C) = 3$
Всего программистов:
$ n(A \cup B \cup C) = n(A)+n(B)+n(C)- $
$ (n(A \cap B)+n(B \cap C)+n(A \cap C) )+n(A \cap B \cap C) $
$n(A \cup B \cup C) = 28+30+42-(8+5+10)+3 = 100-23+3 = 80$
Число не умеющих программировать:
$n(U)-n(A \cup B \cup C) = 100-80 = 20$
Ответ: 20 человек
Объединение, пересечение и дополнение | Математика для гуманитарных наук Необходимый предмет
Результаты обучения
- Выполнение операций объединения, пересечения, дополнения и разности над множествами, используя соответствующие обозначения.

- Уметь рисовать и интерпретировать диаграммы Венна отношений множеств и операций.
Обычно наборы взаимодействуют. Например, вы с новым соседом по комнате решаете устроить домашнюю вечеринку и приглашаете друзей. На этой вечеринке объединяются два набора, хотя может оказаться, что есть друзья, которые были в обоих наборах.
Математические слова и обозначения
Чтобы получить новые слова на новом для вас языке, требуется повторение и практика. Математика во многих отношениях ничем не отличается от изучения нового языка со всем его словарным запасом, синтаксисом и орфографическими соглашениями. Символы в этом разделе могут быть вам совершенно незнакомы. Если это так, вам нужно будет проводить с ними время, используя карточки и записывая их от руки в контексте.
Дайте себе время выучить и оценить язык математики!
Объединение, пересечение и дополнение
Объединение двух наборов содержит все элементы, содержащиеся в любом наборе (или в обоих наборах). Объединение обозначается как A ⋃ B. Более формально, x ∊ A ⋃ B , если x ∈ A или x (или оба)
Объединение обозначается как A ⋃ B. Более формально, x ∊ A ⋃ B , если x ∈ A или x (или оба)
пересечение двух наборов содержит только те элементы, которые есть в обоих наборах. Перекресток обозначен цифрой 9.0023 A ⋂ B. Более формально, x ∈ A ⋂ B , если x ∈ A и x 1 B 1, 0010 комплект комплекта А содержит все, что является , а не в наборе A . Дополнение обозначается как A’ , или A c , или иногда ~ A .
Универсальный набор — это набор, содержащий все интересующие нас элементы. Это должно определяться контекстом. 9{c}[/латекс]. Этот верхний индекс не является показателем степени. Это украшение, которое обозначает дополнение к набору .
Пример
- Если бы мы обсуждали поиск книг, универсальный набор мог бы включать все книги в библиотеке.

- Если бы мы группировали ваших друзей на Facebook, универсальный набор был бы всеми вашими друзьями на Facebook.
- Если вы работали с наборами чисел, универсальный набор мог бы состоять из всех целых чисел, всех целых чисел или всех действительных чисел
Пример
Предположим, что универсальный набор равен U = все целые числа от 1 до 9. Если A = {1, 2, 4}, то A c = {3, 5 6, 7, 8, 9}.
Попробуйте
символы пересечения и объединения
Символы пересечения [латекс]\чашка[/латекс] и объединения [латекс]\шапка[/латекс] немного напоминают буквы в алфавите. На самом деле, это уловка для их запоминания.
Символ объединения выглядит как заглавная буква U, что означает союз .
Символ пересечения немного похож на большую строчную букву n для на пересечении
Пример
Рассмотрим наборы:
A = {красный, зеленый, синий}
B = {красный, желтый, оранжевый}
C = {красный, оранжевый, желтый, зеленый, синий, фиолетовый}
Найдите следующее:
- Найдите A ⋃ B
- Найти А ⋂ В
- Найти A c ⋂ C
Показать решение
Попробуй
Обратите внимание, что в приведенном выше примере было бы сложно просто попросить A c , поскольку все, от цвета фуксии до щенков и арахисового масла, входит в комплект набора.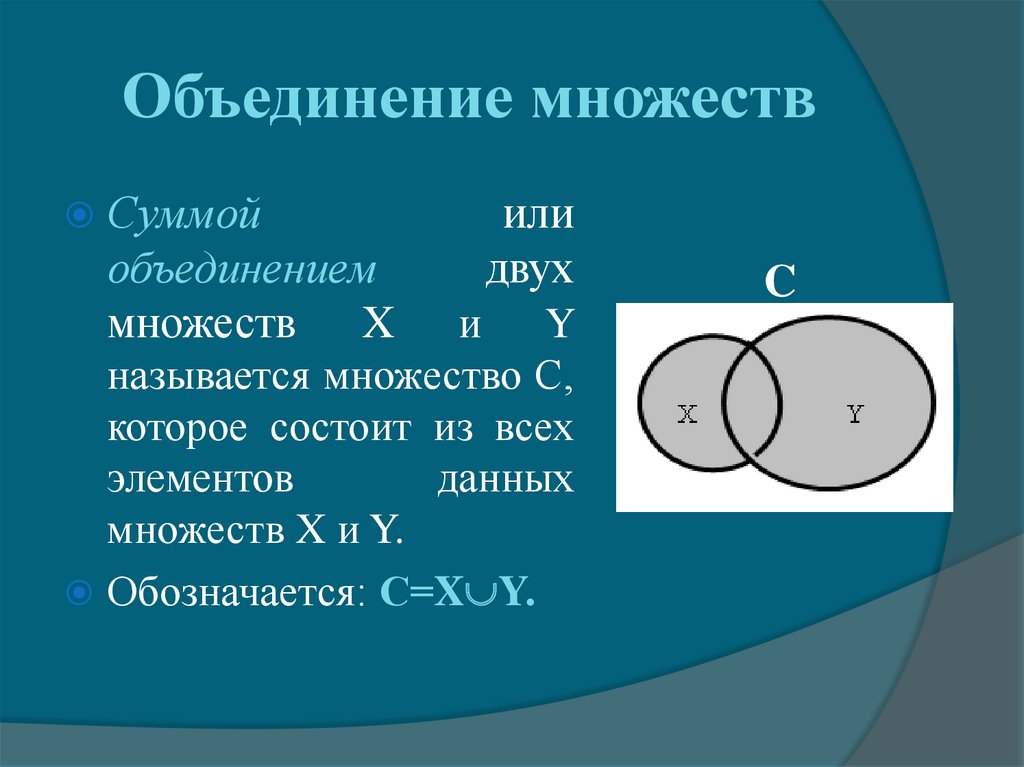 По этой причине дополнения обычно используются только с пересечениями или когда у нас есть универсальный набор.
По этой причине дополнения обычно используются только с пересечениями или когда у нас есть универсальный набор.
Как мы видели ранее с выражением A c ⋂ C , операции над множествами можно группировать вместе. Символы группировки можно использовать так же, как и с арифметикой — для принудительного порядка операций.
Пример
Предположим, H = {кошка, собака, кролик, мышь}, F = {собака, корова, утка, свинья, кролик}, и W = {утка, кролик, олень, лягушка, мышь}
- Найти ( H ⋂ F ) ⋃ W
- Найти В ⋂ ( Ж ⋃ В )
- Найти ( H ⋂ F ) c ⋂ W
Показать решение
Чтобы визуализировать взаимодействие множеств, Джон Венн в 1880 году решил использовать перекрывающиеся круги, опираясь на аналогичную идею, использованную Леонардом Эйлером в 18 веке. Эти иллюстрации теперь называются Диаграммы Венна .
Эти иллюстрации теперь называются Диаграммы Венна .
Диаграмма Венна
Диаграмма Венна представляет каждый набор в виде окружности, обычно нарисованной внутри прямоугольника, представляющего универсальный набор. Перекрывающиеся области обозначают элементы, общие для обоих наборов.
Основные диаграммы Венна могут иллюстрировать взаимодействие двух или трех множеств.
Пример
Создайте диаграммы Венна для иллюстрации A ⋃ B , A ⋂ B и Ac ⋂ B 3 A ⋃ B содержит все элементы либо набор.
Показать решение
Пример
Для иллюстрации используйте диаграмму Венна ( H ⋂ F ) c ⋂ W
Показать решение
Пример
Создайте выражение для представления выделенной части показанной диаграммы Венна.
Показать решение
Попробуйте
Создайте выражение, представляющее выделенную часть показанной диаграммы Венна.
Союз наборов | Математические вкусности
Форма поиска
Поиск
В предыдущих уроках мы использовали диаграммы Венна для представления отношений между множествами. Давайте посмотрим на пример 1 ниже.
Пример 1. В средней школе Гринвилля два класса будут объединены в один, чтобы сократить расходы. Если учащиеся оркестра и хора объединятся в один новый класс, то какие учащиеся будут в этом классе?
Дано: Дано = {Сэм, Киеша, Дерек, Лорри, Робин, Рауль, Ширли, Натан, Крис, Дана} , Группа = {Сэм, Лорри, Рауль, Дерек} и Хор = {Робин , Дерек, Киеша}, найдите Band Chorus.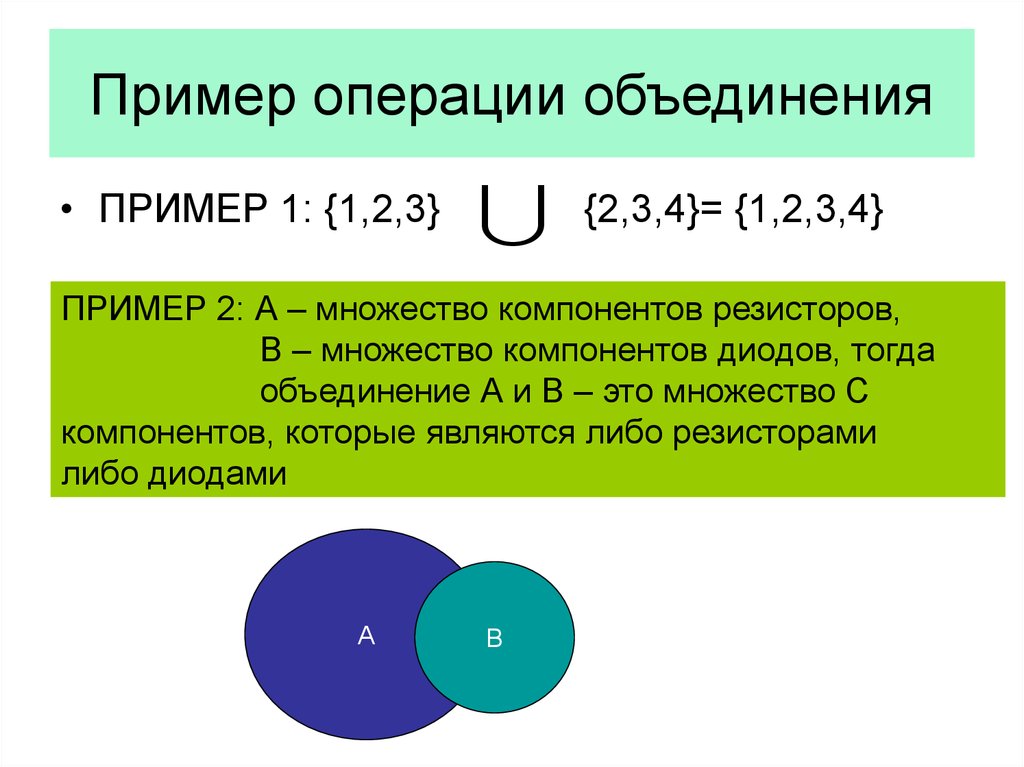
Анализ: эта задача требует от нас найти союз Band и Chorus. Чтобы решить эту проблему, мы должны перечислить всех учеников, которые находятся в группе, в хоре или в обеих группах.
Решение:
Объяснение:
Группа Хор = {Сэм, Лорри, Рауль, Дерек, Киеша, Робин}
Обратите внимание, что Дерек находится в их пересечении, поэтому Дерек находится в их пересечении. Однако Дерек прописывается в союзе только один раз.
Определение: Объединение двух множеств A и B, — это множество элементов, которые находятся в A или в B или в обоих Обозначается A B , и читается как « A соединение B ».
Сравним объединение и пересечение.
| Союз | Перекресток | |
| записывается как | А Б | А Б |
| читать как | A штуцер Б | A пересечение B |
| значение | A или B или оба | А и В |
| как найти | объединить все элементы | найти элементы, общие для обоих |
Союз часто считают браком.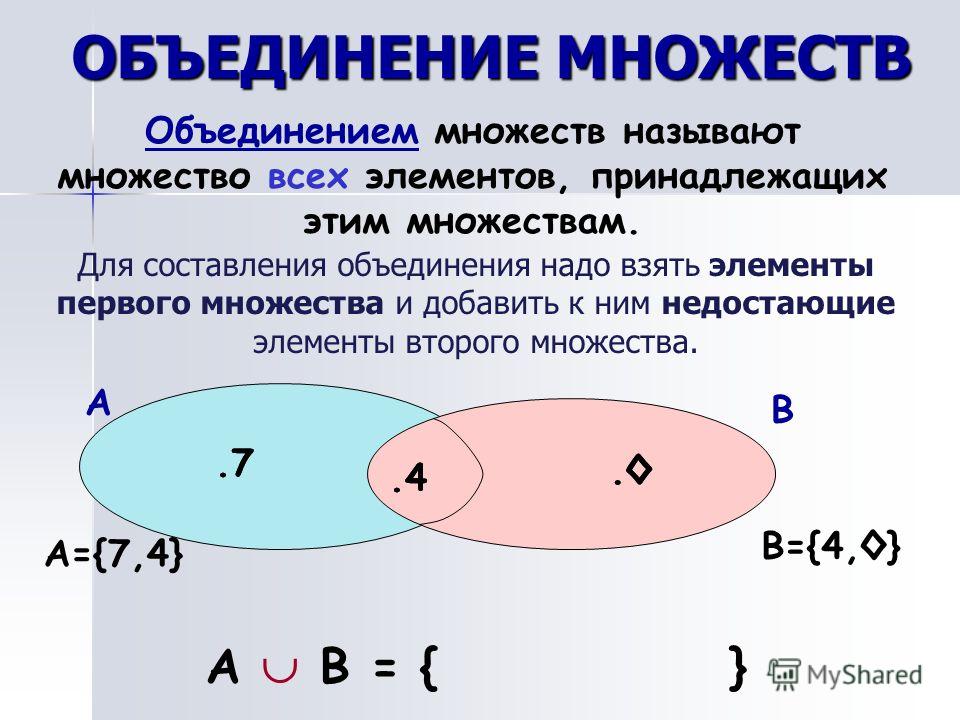 Мы используем «и» для пересечения» и » или» для объединения. Давайте рассмотрим еще несколько примеров объединения двух множеств.
Мы используем «и» для пересечения» и » или» для объединения. Давайте рассмотрим еще несколько примеров объединения двух множеств.
Пример 2: Let = {число чисел}, P = {кратное 3 меньше 20} и Q = {четные числа меньше 20}. Нарисуйте и подпишите диаграмму Венна, чтобы показать объединение P и Q .
Анализ: заштрихуйте элементы, которые находятся в P или в Q или в обоих . Заштрихованная область на диаграмме Венна ниже показывает P Q.
Решение:
9, 10, 12, 14, 15, 16 , 18}
Обратите внимание, что элементы 6, 12 и 18 находятся в обоих наборах (т. е. на пересечении P и Q ). Однако эти элементы пишутся в союзе только один раз.
Пример 3: Пусть = { k | 1 ≤ k ≤ 10}, X = {1, 6, 9} и Y = {1, 3, 5, 6, 8, 9}. Нарисуйте и подпишите диаграмму Венна, чтобы показать X Y.
Нарисуйте и подпишите диаграмму Венна, чтобы показать X Y.
Анализ: X является подмножеством Y . Таким образом, все элементы в X также содержатся в Y .
Объяснение: X Y = {1, 3, 5, 6, 8, 9}, что равно множеству Y.
Y , получаем, что X Y = 4 7 Это отношение определено ниже.
Другой способ определения объединения двух множеств заключается в следующем:
A B = {x | x A или x B }
Пример 4: 3 6 животных = 9 2 A = {10 собак} и B = {20 кошек }. Нарисуйте и подпишите диаграмму Венна, чтобы показать A B .
Нарисуйте и подпишите диаграмму Венна, чтобы показать A B .
Анализ: Эти множества не пересекаются и не имеют общих элементов. Таким образом, A B — это все элементы числа A и все элементы числа B.
10 собак, 20 кошек}
Пример 4 прямой союз двух наборов. Непересекающиеся множества не имеют общих элементов. Поэтому союз A и B не имеет общих элементов. Поскольку невозможно, чтобы собаки в A также были кошками в B , мы уверены, что количество элементов в объединении равно сумме всех собак в A и всех кошек в B . Таким образом, объединение получается в результате сложения всех элементов обоих наборов.
Объединение двух наборов А и В, представляет собой набор элементов, которые находятся в А или В 022 в обоих. Он обозначается A B , и читается как « A union B ». Формальное определение союза показано ниже:
Формальное определение союза показано ниже:
А В = {x | x A или x B }
Упражнение
0 0Указания: Нарисуйте и подпишите диаграмму Венна, чтобы помочь вам ответить на каждый вопрос ниже. Выберите свой ответ, нажав на соответствующую кнопку. Обратная связь по вашему ответу представлена в ОКНО РЕЗУЛЬТАТЫ. Если вы допустили ошибку, обдумайте свой ответ еще раз, а затем выберите другую кнопку.
| 1. | Дано = {яблоки, апельсины, бананы, груши} и 9 = {апельсины, 2 2, виноград 0, 2 2, груши} 0327 ? |
| P Q = Ø P , апельсины, яблоки, Q } P Q = {яблоки, апельсины , бананы, груши, виноград} Ничего из вышеперечисленного.  ЯЩИК РЕЗУЛЬТАТОВ: |
| 2. | Дано = {простые числа} и = {составные числа}, что такое 6 90? |
| A B = {целые числа} A B = {числа > 1} A B = {мнимые числа} Все вышеперечисленное. ЯЩИК РЕЗУЛЬТАТОВ: |
3. | Дано = {1, 4, 16} и = {1, 6 5, 1, 2, 9}0022 ? |
| X Y = {1, 4, 9, 16, 25, 36} X , 3 Х Y = Ø Ничего из вышеперечисленного. ОКНО РЕЗУЛЬТАТОВ: |
| 4. | Дано = {гласные} и = {согласные} 9 2, что такое 2 2 ? |
| P Q = Ø P , e , e о, и} Р Q = { согласные} P Q = {Английский алфавит} ЯЩИК РЕЗУЛЬТАТОВ: |
5. Верные цифры в широком смысле: 1.3. Запись приближенных значений величин. Верные знаки1.3. Запись приближенных значений величин. Верные знакиПриближенные значения величин обычно записывают в виде десятичных дробей с конечным числом цифр. Значащими цифрами в записи десятичной дроби называются все цифры, начиная с первой ненулевой слева. Например, в дроби 0,00102030004 значащими цифрами (подчеркнуты) являются все цифры, начиная с третьей после запятой. Цифра в записи приближенного значения числовой величиныx называется верной в широком (строгом) смысле слова, если абсолютная погрешность приближенного значения не превышает единицы (половины единицы) разряда, в котором стоит эта цифра. Все цифры верные в строгом смысле слова, очевидно, будут верными и в широком смысле. Рассмотрим несколько примеров. Пример 1 Пусть
,= 0,000007899.Требуется найти верные цифры в
записив широком и строгом смысле слова и
подчеркнуть их одинарной и двойной
линией соответственно. Отметим, что в разрядах, в которых в записи стоят незначащие нули, в записи стоят верные цифры в широком смысле слова. Пример 2 Пусть теперь ,=0,000007899. Требуется найти верные цифры в записив широком и строгом смысле слова. Абсолютная
погрешность нам неизвестна, а известна лишь ее оценка
.
Если оценка абсолютной погрешностиприближенного значения не превышает
единицы (половины единицы) разряда, в
котором стоит цифра (в записи ),
то эта цифра, очевидно, также будет
верной в широком (строгом) смысле слова
.
Проверяя для каждой цифры в записи это требование,
получим часть верных цифр:
. Отметим, что в тех разрядах, в которых в записи стоят незначащие нули, в записистоят верные цифры в широком смысле слова. Пример 3 Пусть, =0,123456789, =0,123457899. В записи точного и приближенного значений подчеркнуты совпадающие цифры. Непосредственная проверка для каждой цифры в записи требования, сформулированного в определении верных цифр, показывает, что все подчеркнутые (совпадающие) цифры являются верными в широком смысле слова, а неподчеркнутые – неверными. Но такое совпадение
верных цифр (в широком смысле слова) в
записи
с соответствующими цифрами в записииногда нарушается. Это связано с тем,
что некоторые вещественные числа могут
записываться в десятичной системе двумя
различными способами, например
1=1,0000. Пример 4 Пусть =1,0000…,=0,9999. В записи точного и приближенного значений нет ни одной совпадающей цифры. Непосредственная проверка для каждой цифры в записитребования, сформулированного в определении верных цифр, показывает, что цифры в записиявляются верными в широком смысле слова. В то же время если записатьдругим способом=0,9999…, то все верные цифры в записибудут совпадать с соответствующими цифрами в записи точного значения. Рассмотренные примеры позволяют сформулировать некоторые свойства верных цифр. Свойства верных цифр:
Установим теперь
связь между величинами абсолютной и
относительной погрешностей приближенного
значения и количеством верных цифр в
его записи. . Итак, если абсолютная погрешность приближенного значения равна , то после десятичной запятой в записи будетn верных знаков. Пусть теперь относительная погрешность приближенного значения равна. Установим общее количество верных знаков в записи. Для этого представимв показательной форме:. Здесь– вещественное число, называемое мантиссой, ар – целое число, называемое порядком . А для того, чтобы такое представление дроби было однозначным потребуем, чтобы . (1.3.1) Точное значение
величины
также запишем в показательной форме,
причем с тем же порядкомp:
. . Отсюда , и, согласно формуле (1.3.1), для абсолютной погрешности получается оценка (1.3.2) Запишем в общем виде . Из формулы (1.3.1)
следует, что первая цифра после десятичной
запятой в записи
должна быть отлична от нуля. Поэтому
все цифры в записипосле запятой являются значащими. Из
формулы (1.3.2) следует, что в записи
мантиссы должно быть не меньшеn и не больше (n+1)
верной цифры после десятичной запятой,
причем все они являются значащими. Таким образом, мы показали, что если относительная погрешность приближенного значения равна , то общее количество верных значащих цифр в записи равно либо n, либо (n+1). Лекции по математике для студентов 1 курса СПОЛекция 1.1 Дествительные числа.
I. Множество натуральных чисел – это множество чисел, которыми пользуются при счете предметов. . Всякому натуральному числу соответствует точка на числовой прямой.
Задание: Назовите самое маленькое натуральное число. Существует ли самое большое натуральное число?
II. Множество целых чисел – это множество, состоящее из натуральных чисел, им противоположных
чисел и нуля. . Всякому целому числу соответствует точка на числовой прямой.
Задания: 1. Существуют ли самое маленькое и самое большое целое число? 2. Верно ли утверждение: a. любое натуральное число является целым; b. любое целое число является натуральным?
III. Множество рациональных чисел – это множество несократимых дробей вида . Всякому рациональному числу соответствует точка на числовой прямой.
Свойство рациональных чисел: Всякое рациональное число можно представить в виде бесконечной периодической десятичной дроби. Обратно: всякая бесконечная периодическая десятичная дробь является рациональным числом.
Правило перевода периодических дробей в обыкновенные:
для чисто периодической дроби: в числителе пишется число, стоящее в периоде, а в знаменателе столько «9», сколько цифр в периоде, целая часть остается без изменения.
для смешанной периодической дроби: в числителе разность между числом, стоящим после запятой, и числом, стоящим после запятой до периода, а в знаменателе столько «9», сколько цифр в периоде, со столькими «0», сколько цифр после запятой до периода
Задания: 1.
Докажите, что числа являются
рациональными и отметьте эти числа на числовой прямой. 2. Верно ли утверждение: а) всякое натуральное число является рациональным; б) всякое целое число является рациональным; в) верно ли утверждение: Всякое рациональное число является целым? 3. Представьте рациональные числа в виде бесконечных периодических десятичных дробей. 4. Переведите периодические дроби в обыкновенные. Проверьте результат перевода. IV. Множество иррациональных чисел – это множество чисел, которые нельзя представить в виде несократимых дробей . Всякому иррациональному числу соответствует точка на числовой прямой.
Свойство иррациональных чисел: Всякое иррациональное число представимо в виде бесконечной десятичной непериодической дроби.
Пример: π ≈ 3,1415926535897932384626433832795…; …
Задание: Докажите,
что числа , , являются иррациональными.
V. Множество действительных (вещественных) чисел – это объединение множеств рациональных и иррациональных чисел. . Каждому действительному числу соответствует точка на числовой прямой.
Обратно: каждой точке на числовой прямой соответствует определенное действительное число.
Следовательно, между множеством действительных чисел и множеством точек на числовой прямой существует взаимно-однозначное соответствие.
Задания: 1. Верно ли утверждение: а) всякое целое число является действительным; б) всякое рациональное число является вещественным; в) всякое иррациональное число является вещественным; г) всякое действительное число является рациональным; д) всякое вещественное число является целым? 2.
Даны числа: .
Лекция 1.2 Абсолютная погрешность приближенного значения числа.
Модуль числа – это само число, если оно неотрицательно, и число, ему противоположное, если оно отрицательно.
Примеры: . С геометрической точки зрения модуль числа – это расстояние от этого числа до начала отсчета.
Вывод: модуль числа отрицательным быть не может!
Приближенные вычисления
Приближенное число есть такое число, которое отличается от точного на погрешность (ошибку), допущенную в соответствии с условиями данной задачи, и заменяет точное число в расчетной формуле.
Обозначим буквой a0 точное
число, а буквой a его приближенное
значение, тогда a0 ≈ a.
Абсолютная погрешность приближенного значения числа – это модуль разности между точным и приближенным значением этого числа, т.е. .
Так как точное число чаще всего неизвестно, то можно указать положительное число ∆а, удовлетворяющее неравенству . Число ∆а называется границей абсолютной погрешности.
1. Даны приближенные значения числа х = 2/3; а1= 0,6; а2 = 0,66; а3 = 0,67. Какое из этих трех приближений является лучшим?
;
а3 = 0,67 – лучшее приближение
2. Длина детали х (см) заключена в границах 33 ≤ х ≤ 34. Найти границу абсолютной погрешности измерения детали. ○ Примем за приближенное значение длины детали среднее арифметическое границ: а = (33 + 34)/2
= 33,5 (см). Тогда граница абсолютной
погрешности приближенного значения длины детали не превзойдет 0,5 (см). Величину Δа можно найти и как полуразность верхней и нижней границ, т. е. Δа = (34 — 33)/2 = 0,5 (см). Длина детали х, найденная с точностью до Δа = 0,5 см, заключена между приближенными значениями числа х: 33,5 — 0,5 ≤ x ≤ 33,5 + 0,5; x = 33,5 ± 0,5 (см). 3. Найдите абсолютную погрешность округления до единиц следующих чисел: 1) 0,8; 2) 7,6; 3) 19,3; 4) 563,58.
4. Граница абсолютной погрешности приближенного значения 386 числа х равна 0,5. Укажите границы, в которых заключено число х.
5. Найдите границу абсолютной погрешности измерений, полученных в виде неравенства 37 < x < 38.
5. Амперметр дает точность ±0,02 А. При измерении силы тока получили 10,63 А. Укажите границы этого числа.
6.
Атомная масса водорода — 1,0082 ± 0,0005, а меди — 63,44 ± 0,15. Укажите границы приближенных значений этих чисел.
8. Площадь квадрата равна 24,5 ± 0,3 (см2). Найдите границы измерения площади квадрата.
Задание: 1. Записать числа в виде двойного неравенства: а) а = 347,50; ∆а = 0,0047; б) а0 = 7,269 ± 0,0004. 2. Докажите, что число 1,7 является приближенным значением числа 1, 739 с точностью до 0,05. 3.
Точное значение числа х неизвестно, а
известно лишь, что 4. Вычислите приближенное значение величины х, равное среднему арифметическому границ, и укажите точность этого приближения, если: а) 3,6 ≤ х ≤ 4,2; б) 0,12 ≤ х ≤ 0,14. Лекция 1.3 Верные цифры числа. Запись приближенного значения числа.
Верные и значащие цифры числа. Цифра т приближенного числа а называется верной в широком смысле, если граница абсолютной погрешности числа а не превосходит единицы того разряда, в котором записывается цифра т. Цифра т приближенного числа а называется верной в строгом смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда, в котором записана цифра т. В числах, полученных в результате измерений или вычислений и используемых при расчетах в качестве исходных данных, а также в десятичной записи приближенного значения числа, все цифры должны быть верными. Наиболее употребительна такая запись приближенного числа (например, в математических таблицах), при которой цифры верны в строгом смысле. Граница абсолютной погрешности Δа находится непосредственно по записи
приближенного значения а числа х. Цифры в записи приближенного числа, о которых не известно, являются ли они верными, называются сомнительными. Значащими цифрами приближенного числа называются все его верные цифры, кроме нулей, стоящих перед первой цифрой (слева направо), отличной от нуля.
Округление чисел. При округлении числа а его заменяют числом a1 с меньшим количеством значащих цифр. Абсолютная величина разности |а – а1| называется погрешностью округления
При округлении числа до т значащих цифр отбрасывают все цифры, стоящие правее т-й значащей цифры, или при сохранении разрядов заменяют их нулями. При этом если первая слева из отброшенных цифр больше или равна 5, то последнюю оставшуюся цифру увеличивают на единицу. При применении
этого правила погрешность округления не превосходит половины единицы десятичного
разряда, определяемого последней оставленной значащей цифрой. Округление приближенных значений чисел с сохранением в записи только верных цифр производится до разряда, в котором записана первая справа верная цифра.
9. Найти границу абсолютной погрешности приближенного значения 0,1968 числа х, все цифры которого верны в строгом смысле.
○ Граница абсолютной погрешности этого числа равна 0,00005, т. е. половине единицы последнего разряда, сохраняемого в записи.●
10. Указать верные цифры (в широком смысле) следующих чисел: 1) 3,73 ± 0,056; 2) 3,627 ± 0,0008; 3) 4,732 ± 0,06; 4) 561 274 ± 500.
○ 1) Граница погрешности Δа = 0,056 не превосходит единицы разряда десятых (неравенство 0,056 < 0,1 верное). Следовательно, верными являются цифры 3 и 7. 2) Так как Δа = 0,0008 < 0,001, то все цифры приближенного числа 3,627 верны. 3) Поскольку Δа = 0,06 < 0,1, верными являются цифры 4 и 7. 4) Так как Δа =
500 < 1000, то верны цифры 5, 6 и 1. 11. За приближенное значение числа 26,7 взято число 27. Являются ли цифры числа 27 верными?
○ Так как |26,7 — 27| = 0,3 < 1, то цифры 2 и 7 — верные в строгом смысле.●
12. Приближенное значение числа 9,587 ± 0,03 округлить до первого справа верного разряда.
○ Первая справа верная цифра находится в разряде десятых, поэтому число 9,587 округляем до десятых: 9,587 ≈ 9,6. Новое значение границы погрешности Δа равно сумме границы погрешности 0,03 и погрешности округления 0,013, т. е. Δа = 0,03 + + 0,013 = 0,043 < 0,1. Число 9,6 является приближенным значением числа 9,587 с точ- ностью до 0,1. Цифры 9 и 6 верные.●
13. Укажите верные цифры (в широком смысле) следующих чисел: 1) 0,028 ± 0,004; 2) 0,463 ± 0,0008; 3) 0,078 ± 0,002; 4) 12,78 ± 0,0005; 5) 375 ± 20.
14. 15. За приближенное значение числа 999,82 взято число 1000. Укажите верные цифры числа 1000. 16. Сохраните только верные цифры в записи следующих приближенных значений чисел: 1) 280 ± 10; 2) 8900 ± 100; 3) 530 000 ± 100; 4) 5740 ± 10. 17. Округлите до первого справа верного разряда приближенные значения данных чисел: 1) 0,3281 ± 0,05; 2) 2,0637 ± 0,0025; 3) 14,0367 ± 0,8; 4) 24,734 ± 0,06.
18. Округлите приближенные значения данных чисел до первого справа верного разряда и запишите эти числа в стандартном виде: 1) 12 378 ± 25; 2) 15 763 ± 50; 3) 8724 ± 25; 4) 812 ± 6. 19. Укажите границу погрешности приближения, если в записи приближенных значений данных чисел все цифры верные (в широком смысле): 1) x ≈ 0,56; 2) х ≈ 84,3; 3) х ≈ 5,10; 4) х ≈ 4,100.
Лекция
1.
Относительная погрешность приближенного значения числа – это отношение абсолютной погрешности этого числа к самому числу, т.е. или в процентах .
Так как в большинстве случаев истинное значение величины a0 неизвестно, то на практике относительную погрешность оценивают некоторым числом , большим этой погрешности. В качестве можно взять отношение или любое число, большее этого отношения, но достаточно близкое к нему, т.е. . Число называется границей относительной погрешности. Качество измерений или вычислений тем лучше, чем меньше граница относительной погрешности.
Зависимость относительной погрешности от числа значащих цифр иллюстрируется табл. 1.1
Из табл.
Пример: Пусть а0 = 42,1 ± 0,2. Вычислить в процентах границу относительной погрешности приближенного значения величины а. Решение: Имеем а = 42,1; h = 0,2. Следовательно, . Задания: 1. Округлите число 123 до десятков и найдите абсолютную и относительную погрешность округления. 2. Округлите число 8, 2478 до сотых и найдите абсолютную и относительную погрешность округления. 3. Найдите относительную погрешность приближенных чисел: а) 35,148 ± 0,00074; б) 0,012 ± 0,001; в)
17,2 ± 0,25. 4. Установите, какое равенство точнее: . 5. Найдите верхнюю и нижнюю границы, если приближенное значение числа и относительная погрешность в процентах соответственно равны: а) 18 и 1%; б) 0,6 и 15%. Лекция 1.5 Действия над приближенными значениями числа
Сложение приближенных значений чисел Граница абсолютной погрешности суммы приближенных значений чисел равна сумме границ абсолютных погрешностей этих чисел: Δ(a + b) = Δa + Δb, (2.1) где а и b — приближенные значения чисел; Δa и Δb — границы абсо- лютных погрешностей соответствующих приближений. Граница относительной погрешности суммы вычисляется по фор- муле ( ) a b a b + a b _ = _ + + . (2. 1. Найти сумму S приближенных значений чисел 6,8 ± 0,05; 4,3 ± 0,05 и 3,575 ± 0,0005. ○ Имеем S = 6,8 + 4,3 + 3,575 = 14,675; ΔS = 0,05 + 0,05 + 0,0005 = 0,1005. Граница абсолютной погрешности заключена в пределах 0,05 < 0,1005 < 0,5. В приближенном значении суммы верными являются лишь две цифры (в разрядах десятков и единиц). Полученный результат округлим до единиц: S = 14,675 ≈ 15.● 2. Найдите сумму приближенных значений чисел 6,54 ± 0,005; 16,022 ± 0,0005 и 1,9646 ± 0,00005. 3. Вычислите сумму a = 5 + 11, взяв приближенные значения кор- ней с точностью до 0,001. Найдите а, Δа и εa. 4. Вычислите сумму a = 3 + 5 + 7 с четырьмя значащими циф- рами. Найдите а, Δa и εa. 5. Электрическая цепь состоит из трех последовательно соединен- ных проводников с сопротивлениями r1 = 4,8 ± 0,05 (Ом), r2 = 6,25 ± ± 0,005 (Ом) и r3 = 7,725 ± 0,0005 (Ом). цепи по формуле R = r1 + r2 + r3. Найдите R, ΔR и εR.
Вычитание приближенных значений чисел Граница абсолютной погрешности разности двух приближенных значений чисел равна сумме границ их абсолютных погрешностей: Δ(a — b) = Δa + Δb. (2.3) Граница относительной погрешности разности вычисляется по фор- муле a b a b − a b _ = _ + _ − . (2.4) 6. Вычислить разность двух приближенных значений чисел а = 5,863 ± ± 0,0005 и b = 2,746 ± 0,0005. Найти Δ(а — b) и εa–b. ○ По формуле (2.3) вычисляем границу абсолютной погрешности разности а — b: Δ(а — b) = 0,0005 + 0,0005 = 0,001. В приближенном значении разности цифра в разряде тысячных не может быть верной, так как Δ(а — b) > 0,0005. разности 0,001. В приближенном числе 3,12 все цифры верные. По формуле (2.4) находим относительную погрешность разности: εа–b = 0,001/3,12 = 0,00032 ≈ 0,03 %.● 7. Вычислите разность чисел 8,72 и 2,6532, границы абсолютной погрешности которых соответственно равны 0,005 и 0,00005. 8. Вычислите разность a = 13 − 5 с четырьмя значащимицифрами. Найдите Δa и εa.
Лекция 1.6. Комплексные числа
Определение 1. Число, квадрат которого равен -1, называется мнимой единицей и обозначается буквой i. i2 = -1. Следовательно, .
Определение 2. Числа
вида a + bi, где a
и b – действительные числа, i – мнимая единица, называются комплексными.
Данная форма записи комплексного числа называется алгебраической.
Число а является действительной частью комплексного числа, bi – его мнимой частью, число b называется коэффициентом при мнимой части.
Если b = 0, то комплексное число a + bi = a + 0i = a, то есть является действительным числом. Вывод: действительные числа являются частным случаем комплексных чисел.
Если а = 0, то комплексное число a + bi = bi и называется чисто мнимым.
Сложение, вычитание и умножение комплексных чисел выполняется по правилам соответствующих действий над многочленами.
Задания: 1. Выполните сложение, вычитание и умножение комплексных чисел: а) z1 = 3+5i и z2 = 7–2i; б) z1 = -2+3i и z2 = 7–4i; в) z1 = 3–2i и z2 = 7–i; г) z1 = 1–i и z2 = 1+i; д) z1 = 3–9i и z2 = 5+2i.
Определение 3. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью (a + bi и a – bi).
Произведение двух сопряженных комплексных чисел всегда равно действительному числу (проверьте!).
Для деления одного комплексного числа на другое необходимо умножить делимое и делитель на комплексное число, сопряженное делителю.
Примеры действий с комплексными числами
Даны два комплексных числа z1 = 3+5i и z2 = 7–2i. Выполнить их сложение, вычитание, умножение и деление.
I. Сложение Раскрываем скобки, применяем переместительный и сочетательный законы сложения и правило приведения подобных слагаемых.
II. Вычитание Применяем те же
правила, что и при сложении, но не забываем, что если перед раскрываемой
скобкой стоит знак «минус», то у всех слагаемых в скобке знак меняется на
противоположный. III. Умножение Используем правило умножения многочленов: каждое слагаемое в первой скобке умножаем на каждое слагаемое во второй скобке. Не забываем, что i2 = -1.
IV. Деление Число, сопряженное делителю , – это число 7+2i. Домножаем числитель и знаменатель дроби на число 7+2i и выполняем необходимые преобразования: в числителе перемножаем два комплексных числа по предыдущему правилу, а в знаменателе используем разность квадратов .
Задания:
Бесчисленное множество определений и значений — Merriam-Webster1 из 2мое объявление ˈmir-ē-əd 1 : десять тысяч 2 : большое число множество идей Является ли мириад существительным?: Руководство по использованию Недавняя критика использования мириад в качестве существительного, как во множественном числе мириады , так и во фразе мириады , по-видимому, отражает ошибочное мнение, что слово изначально было и до сих пор является лишь прилагательным. мириады 2 из 2 1 : бесчисленное множество эти мириады проблем также : многочисленные и разнообразные мириады тем 2 : имеющие бесчисленные аспекты или элементы ты знаешь? В английском языке значение «десять тысяч» мириад в основном появляется в ссылках на Древнюю Грецию, например, в следующем из Истории Греции английского историка Коннопа Тирволла: «4000 человек из Пелопоннеса сражались при Фермопилах с 300 мириадами . СинонимыСуществительное
Прилагательное
Просмотреть все синонимы и антонимы в тезаурусе Примеры предложенийСуществительное Г-н Маккалоу хвалит Адамса за его сверхъестественную прозорливость… предвидение множества событий, от сложности победы над британцами… до вызывающих разногласия последствий рабства. Сектантский протестантизм усилил как американский индивидуализм, так и тенденцию общества к самоорганизации в виде множества добровольных ассоциаций и сообществ. — Фрэнсис Фукуяма, Atlantic , май 1999 г. В баррио, под пальмами нипа, он слушал мириады гудящих цикад и крики гекконов. — Нина ФитцПатрик, 9 лет.0021 Басни ирландской интеллигенции , 1991 Чтобы читать Марию Корелли, вы должны были быть в состоянии следить за несколькими сотнями печатных слов за раз, и в Англии было множество людей, которые были на это способны. …сплел пальцы за головой и уставился на мириады крошечных цветных точек, из которых состоит тьма. — Джон Стейнбек, 9 лет.0021 К востоку от Эдема , 1952 г. Существует мириад из возможностей. автомобиль может быть оснащен мириадами опций Прилагательное … чем больше цитат можно было найти, тем легче можно было определить тонкие различия между (возможно) бесчисленным множеством вариантов использования и значениями любого отдельного слова. Эпоха белой вины с ее мириадами коррупции и ее почти расистской слепотой к индивидуальности меньшинства может когда-нибудь уйти, как ушел век расизма… — Шелби Стил, 9 лет.0021 Harper’s , ноябрь 2002 г. Вторая мировая война ускорила продвижение науки и техники в микромир. Ученые и технологи играли друг с другом в пятнашки в поисках микроскопического контроля. С помощью математики и множества теорий они определили новый микрокосм. — Джозеф А. Амато, Пыль , 2000 г. Проблем старой системы было мириадов . Последние примеры в Интернете Конечно, в каждом законе содержится мириадов деталей и условий, которые могут заставить скептиков жаловаться на то, что правила слишком сложны, чтобы знать, что делать, и ложатся чрезмерным бременем на работодателей.
— Меган М. Биро, 9 лет.0021 Forbes , 22 марта 2023 г.
Существует мириадов способов наблюдать за озером и окружающими старовозрастными лесами, включая тропы к живописным смотровым площадкам и геологическим чудесам, нежным водопадам и одним из самых кинематографичных прогулок на снегоступах в штате. Влияние Бекхэма в Балтиморе составляет мириадов . Эти примеры программно скомпилированы из различных онлайн-источников, чтобы проиллюстрировать текущее использование слова «бесчисленное множество». Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах. История словЭтимология Существительное и прилагательное Греческий myriad-, myrias , from myrioi бесчисленное количество, десять тысяч Первое известное употребление Существительное 1555, в значении, определенном в смысле 1 Прилагательное 1735, в значении, определенном в пункте 1 Путешественник во времени Первое известное использование мириад был в 1555 году Другие слова того же года ПодкастМузыкальная тема Джошуа Стэмпера ©2006 New Jerusalem Music/ASCAP Получайте «Слово дня» на свой почтовый ящик! Словарные статьи Околомириадымириакантус мириады бесчисленное множество Посмотреть другие записи поблизости Процитировать эту запись «Мириады». Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/myriad. По состоянию на 27 апреля 2023 года.
1 из 2
существительное Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/myriad. По состоянию на 27 апреля 2023 года.
1 из 2
существительноемое объявление ˈmir-ē-əd 1 : десять тысяч 2 : большое, но не указанное или не подсчитанное число мириады звезд мириады 2 из 2 прилагательное : чрезвычайно многочисленный мириады песчинок на пляже Еще от Merriam-Webster на темумириадыАнглийский: Перевод слова мириады для говорящих на испанском языке Britannica English: перевод мириад для говорящих на арабском языке Последнее обновление: — Обновлены примеры предложений Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы! Merriam-Webster без сокращений Можете ли вы решить 4 слова сразу?Можете ли вы решить 4 слова сразу?превратности См. Получайте ежедневно по электронной почте Слово дня! Поиск наборов номеров/проверка ℕ,ℤ,ℚ,ℝ,ℂ — N Z Q R CКалькулятор наборов номеровНомер для проверкиУстройство проверки наборов номеров
См. также: Решатель уравнений — Калькулятор Ответы на вопросы (FAQ)Что такое набор чисел? (Определение)Набор чисел — это математическое понятие, позволяющее помещать различные типы чисел в различные категории, иногда включаемые между ними. Классическим представлением обычных множеств является $$ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} $$ Что такое общие числовые наборы? В математике существует несколько наборов : натуральные числа N (или ℕ), набор целых чисел Z (или ℤ), все десятичные числа D или $\mathbb{D} $, набор рациональных чисел Q (или ℚ), набор действительных чисел R (или ℝ) и набор комплексных чисел С (или ℂ). Другие наборы, такие как набор десятичных чисел D или $ \mathbb{D} $, или набор чисто мнимых чисел I или $ \mathbb{I} $. Существуют также наборы трансцендентных чисел, кватернионов или гиперкомплексных чисел, но они зарезервированы для продвинутых математических теорий, NZQRC являются наиболее распространенными наборами. Что означает символ ∈?Знак ∈ (Unicode 2208) означает элемент или принадлежит . Пример: $ 2 \in \mathbb{N} $ читается 2 является элементом множества N Существует также знак ∊ (Unicode 220A), который такой же, но меньшего размера. Знак ∉ (Unicode 2209) означает, что не является элементом или не принадлежит . Пример: $ -2 \notin \mathbb{N} $ Знак ⊂ (Unicode 2282) означает 9{+} $ NB: В некоторых (старых) учебниках для этого набора указывается буква W вместо N , W означает Целые числа Набор N входит в наборы Z, D, Q, R и C. Какой номер Z установлен?Z — множество целых чисел, т.е. положительное, отрицательное или ноль. Пример: …, -100, …, -12, -11, -10, …, -5, -4, -3, -2, — 1, 0, 1, 2, 3, 4, 5 , … 10, 11, 12, …, 100, … $ \in \mathbb{Z} $ 9{p}} , a \in \mathbb{Z}, p \in \mathbb {N} \right\} $$Все десятичные дроби в D — это числа, которые можно записать конечным числом цифр (числа, содержащие точка и конечная десятичная часть). Пример: -123,45, -2,1, -1, 0, 5, 6,7, 8,987654 $ \in \mathbb{D} $ Таким образом, числа, использующие точки подвеса … для их десятичной записи, имеют бесконечное число десятичных знаков и поэтому не принадлежат множеству D. Множество D входит в состав множеств Q, R и C. Наборы N и Z включены в набор D (поскольку все целые числа являются десятичными числами без десятичных разрядов). Любое число в N или Z также находится в D. Что такое число Q? Q есть множество рациональных чисел , т. Пример: 1/3, -4/1, 17/34, 1/123456789 $ \in \mathbb{Q} $ Множество Q входит в множества R и C. Наборы N, Z и D входят в набор Q (поскольку все эти числа можно записать дробью). Любое число в N, Z или D также содержится в Q. Какой набор чисел R?R это набор действительных чисел , т.е. все числа, которые могут реально существовать, содержит кроме рациональных чисел, нерациональные или иррациональные числа в виде $\pi$ или $\sqrt{2}$. Иррациональные числа имеют бесконечную непериодическую десятичную часть. Пример: 9* $ (звездочка R минус) — набор ненулевых отрицательных действительных чисел, также обозначаемый как $ \mathbb{R}_{ Набор R входит в набор C. Наборы N, Z, D и Q входят в набор R. Любое число из N или Z или D или Q также входит в R. Что такое I номер установлен? I — набор (чистых) мнимых чисел, то есть комплексных чисел без действительных частей, квадратные корни отрицательных действительных чисел — чисто мнимые. Набор I входит в набор C. Что такое набор номеров C?C — это набор комплексных чисел , набор, созданный математиками как расширение набора действительных чисел , к которым добавляются числа, содержащие мнимую часть. Пример: $ a + i b \in \mathbb{C} $ Наборы N, Z, D, Q, R и I включены в набор C. Любое число из N или Z или D или Q или R или I тоже в C. Что такое пустой набор Ø?Пустой набор отмечен Ø , как видно из его названия, он пуст и не содержит ни одного номера. Что такое конструируемое число?Составные числа — это все числа, которые можно геометрически изобразить с помощью линейки и циркуля. Пример: $ \sqrt{2} $ — конструируемое число, а $ \pi $ — нет. Что такое алгебраическое число? Алгебраические числа — это набор чисел, которые можно вычислить как корень многочлена с рациональными коэффициентами. Что такое трансцендентное число?Трансцендентные числа — это набор чисел, которые нельзя вычислить как корень многочлена с рациональными коэффициентами (то есть не алгебраическими). Среди действительных или комплексных чисел большинство трансцендентных чисел. Что такое иррациональные числа?Иррациональные числа — это наборы чисел, которые не могут быть записаны в виде дроби (т. е. все числа, которые не находятся в $ \mathbb{Q} $) Что такое наборы чисел E и O?Некоторые книги определяют наборы E для четных номеров и O для нечетных номеров. Это не стандартное обозначение. Что входит в наборы?Связи между различными множествами представлены включениями: $$ N \подмножество Z \подмножество D \подмножество Q \подмножество R \подмножество C $$ Символ подмножества ⊆ является символом включения (в широком смысле), A ⊆ B, если каждый элемент A является элементом B. Онлайн задания по информатике: Тесты по информатике онлайн | Online Test PadОнлайн тесты по информатике и ИКТОнлайн тесты по информатике и ИКТДесятка лучших по информатике
ЕГЭ по информатике и ИКТ – экзамен по выбору. ЕГЭ по информатике и ИКТ не является профильным ни для одного направления подготовки высшего профессионального образования. Однако результаты ЕГЭ по информатике и ИКТ понадобятся при поступлении на технические специальности.
Экзаменационная работа состоит из двух частей.
Информатика Онлайн-репетитор и справка по заданиюИнформатика — это изучение компьютерных технологий, включая аппаратное и программное обеспечение. Поскольку компьютеры доминируют во многих аспектах современной жизни, информатика является популярной областью обучения для студентов колледжей. Когда вы изучаете информатику в колледже, вы будете тратить время на разработку, анализ и реализацию алгоритмов и компьютерного кода для решения проблем. Вы пройдете широкий спектр занятий, чтобы охватить широкий круг тем в этой области, с особым акцентом на математические навыки. Информатика — захватывающая, развивающаяся область с прекрасными карьерными перспективами. Фактически, рабочие места, связанные с информатикой, являются одними из самых востребованных должностей в США и во всем мире.
Если вы студент колледжа, изучающий сложный курс информатики, и вам нужна дополнительная помощь с домашними заданиями или заданиями или пониманием важных понятий, у 24HourAnswers есть команда онлайн-репетиторов по информатике, которые вам помогут. Независимо от того, начинаете ли вы изучать информатику или посещаете курсы повышения квалификации, мы подберем вам подходящего преподавателя, который поможет вам добиться успеха. Онлайн-репетиторы по информатике Когда вы обратитесь в 24HourAnswers за помощью в области информатики, вы получите квалифицированную помощь от наших онлайн-репетиторов. Сеансы репетиторства по информатикеЗапланируйте онлайн-виртуальный сеанс репетиторства с одним из наших репетиторов по информатике , чтобы получить все необходимые домашние задания или помощь в выполнении заданий. Мы используем современную технологию белой доски с видео, аудио, совместным использованием рабочего стола и возможностью загрузки файлов. Запланировав сеанс заранее, вы можете загружать такие материалы, как домашние задания, заметки и старые тесты, чтобы ваш репетитор по информатике мог их просмотреть заранее. Помощь с выполнением домашних заданий по информатике Если у вас возникли проблемы с алгоритмом или заданием по программированию, отправьте запрос на получение помощи по выполнению домашнего задания по информатике от наших опытных преподавателей. Они дадут вам подробные объяснения и примеры концепций, связанных с вашим заданием, которые вы сможете использовать для создания своего решения. Если вам нужна немедленная помощь, выполните поиск в нашей библиотеке домашних заданий, чтобы найти решенные задачи по информатике, связанные с вашим заданием. Темы информатикиНаши онлайн-репетиторы по информатике помогут вам с любой темой, от основ программирования до продвинутых алгоритмов. У нас есть преподаватели, которые специализируются в разных областях компьютерных наук и языков программирования. Вы можете получить задание или помочь с домашним заданием по широкому кругу тем по информатике в четырех основных категориях:
Почему стоит выбрать 24HourAnswers для помощи в области информатики? 24HourAnswers свяжет вас с высококвалифицированными преподавателями информатики. В отличие от других онлайн-репетиторов, в которых работают только студенты колледжей, у нас есть элитная команда опытных профессионалов. Многие из наших преподавателей имеют ученые степени в своей области, в том числе докторские степени или эквивалентные сертификаты. Мы тщательно проверяем всех наших кандидатов, тщательно проверяя их квалификацию, чтобы гарантировать, что мы нанимаем только лучших преподавателей информатики. Мы также предоставляем помощь 24/7, чтобы помочь вам, когда вам это нужно больше всего. Если у вас нехватка времени и вам как можно скорее нужна помощь с заданиями по информатике или домашним заданием, вы можете рассчитывать на нашу быструю и надежную академическую поддержку. Благодаря нашей простой процедуре вы можете быстро и легко получить помощь. Просто введите свой запрос или вопрос, загрузите любые соответствующие файлы, введите срок выполнения и укажите свой бюджет, чтобы начать. Вы получите ответ от репетитора по информатике в кратчайшие сроки — иногда в течение нескольких минут — с цитатой. Ваша указанная цена уникальна для вашего запроса, без скрытых затрат или обязательств. Вы также можете обсудить цитату со своим преподавателем. Запросите помощь по информатике уже сегодня!Создание учетной записи занимает менее 30 секунд. Отправьте запрос на онлайн-репетиторство или помощь в выполнении домашних заданий по информатике уже сегодня! Получите необходимую помощь в любое времяЧтобы выполнить нашу репетиторскую миссию онлайн-обучения, наши центры помощи с домашними заданиями в колледже и онлайн-репетиторские центры работают круглосуточно и без выходных, готовые помочь студентам колледжа, которым нужна помощь с домашними заданиями во всех аспектах информатики. Наши преподаватели информатики могут помочь со всеми вашими проектами, большими или маленькими, и мы призываем вас найти лучшие онлайн-репетиторы по информатике в любом месте. Наши преподаватели информатики могут помочь со всеми вашими проектами, большими или маленькими, и мы призываем вас найти лучшие онлайн-репетиторы по информатике в любом месте.Подробнее Справка по информатике для колледжаПоскольку у нас есть преподаватели по всем темам, связанным с информатикой, мы можем предоставить ряд различных услуг. Наши онлайн-репетиторы по информатике:
Благодаря этим возможностям наши преподаватели компьютерных наук в колледже предоставят вам инструменты, необходимые для получения всесторонних знаний в области компьютерных наук, которые вы сможете использовать в будущих курсах. 24HourAnswers Online Репетиторы по информатикеНаши репетиторы так же заинтересованы в ваших успехах в классе, как и вы, поэтому они доступны круглосуточно, чтобы помочь вам с вопросами, домашними заданиями, подготовкой к экзаменам и любыми дополнительными заданиями, связанными с информатикой. помогите доделать. Работая с нами, вы не только получите доступ к высококвалифицированным преподавателям, но и повысите уровень уверенности в себе в классе. Эта новообретенная уверенность позволит вам применить свои знания в области компьютерных наук на будущих курсах и обеспечить плавный прогресс в обучении. Поскольку преподаватели компьютерных наук в нашем колледже работают полностью удаленно, обратиться к ним за помощью несложно. Вместо того чтобы тратить драгоценное время на поиски местного репетитора по компьютерным наукам, которому вы можете доверять, просто обращайтесь к нашим репетиторам всякий раз, когда они вам нужны, без каких-либо конфликтующих графиков. Справка по информатике — CodersartsCodersarts — это веб-сайт с самым высоким рейтингом для студентов, которые ищут справку по информатике по программированию, помощь в выполнении домашних заданий, помощь в курсовых работах по языкам программирования, веб-разработке, базам данных, мобильной разработке, базам данных и машинному обучению СВЯЗАТЬСЯ С НАМИБудем рады получить от вас известияТемы программирования по запросуЛюбимые предметыЯзыки программирования: C, C++, Java, Python, C# Разработка веб-сайтов HTML, CSS, JavaScript, React.JS, Angular, Node.JS Разработка приложений Android, Sw ифт, iOS, React Native Data Science Machine Learning, Deep Learning, NLP, R Programming Database MySQL, Oracle, PostgreSQL, MongoDB Computer Science Assignment Help Coders arts — это веб-сайт с самым высоким рейтингом для студентов, который ищу справку по программированию в области компьютерных наук, помощь в выполнении домашних заданий, помощь в курсовых работах по языкам программирования (C, C++, Java, Python, C#, JavaScript, PHP, TypeScript), веб-программированию (HTML, CSS, JavaScript, React.
Мы предлагаем помощь по проекту по информатике, помощь в выполнении задания по информатике, руководство по проекту по информатике на выпускной год от эксперта по информатике.
Если вы только начинаете, то вам нужно проявить терпение во время изучения программирования и других предметов. сложны и не в состоянии понять эти темы, поэтому вы чувствуете себя немного подавленным и ищете кого-то, кто поможет вам и прояснит темы. Например, в задании по информатике или домашнем задании по информатике есть нечто большее. Но как вы можете доверять кому-то в сети, кто может выполнить вашу домашнюю работу до истечения срока. Служба CodersArts по оказанию помощи в выполнении заданий по информатике заслуживает доверия и стремится доставить ее раньше времени. Каждое задание по информатике написано экспертом исключительно для каждого учащегося. Мы здесь, чтобы решить вашу задачу по информатике.
Наши специалисты доступны 24/7, чтобы мгновенно помочь вам со всеми вашими вопросами и сомнениями. Помощь с домашним заданием по информатикеСуществуют следующие области услуг по информатике, как указано ниже: Программирование: Наиболее широко используемыми языками программирования являются Python, C, C++ и JAVA. Структуры данных: Это касается организации данных, присутствующих в основной памяти компьютера или даже в дисковом хранилище. Различные типы структур данных — это связанные списки, очереди, деревья, стеки и т. База данных: База данных представляет собой организованный набор данных. Реляционная база данных, в более узком смысле, представляет собой набор схем, таблиц, запросов, отчетов, представлений и других элементов. Разработчики баз данных обычно организуют данные для моделирования аспектов реальности таким образом, чтобы поддерживать процессы, требующие информации, такие как (например) моделирование доступности номеров в отелях таким образом, чтобы поддерживать поиск отеля со свободными местами. Примеры: Oracle, Mysql, SQL Server, MongoDb и т. д. Чего ожидает учащийся от изучения информатики Справка по заданию
Y f x построить график функции: Построение графика функции y = f(x + l) + m — урок. Алгебра, 8 класс.Как построить график функции y = f (x+l) и y = f (x)+m, если известен график функции y = f(x). 8-й класс
Разделы: Математика Класс: 8 Цели:
Оборудование: интерактивная доска,
проектор, презентация к уроку. ХОД УРОКА 1. Организационный момент 2. Устная работа (Приложение. Слайды 2-8.) Задание: Графики каких функций
изображены на рисунках? (у = x2, у = – x2,
, , ,
, у =| x |, у =
– | x |). 3. Изучение нового материала (Приложение) На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = x2 +1. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу вверх. (Слайд 10.) На координатной плоскости в тетрадях учащиеся
по точкам строят графики функций у = x2
и у = x2– 1. На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = (x – 1)2. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу вправо. (Слайд 12.) На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = (x + 1)2. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу влево. (Слайд 13.) С помощью учителя учащиеся формулируют правило
построения графика функции у = f (x + l) и
графика функции у = f (x) + m с помощью
сдвига графика функции у = f (x).
(Слайды 14-18. Анимация сдвигов графиков на
слайдах помогает лучшему восприятию правила. Затем рассматривается вариант построения графика функции у = f (x + l) и графика функции у = f (x) + m с помощью сдвига графика функции у = f (x), если известен график функции у = f (x) с помощью сдвига осей координат. (Слайды 19-23. Анимация сдвигов осей координат на слайдах помогает лучшему восприятию правила построения графиков.) Правила построения графиков функций у = f (x + l) и у = f (x) + m записываются в тетрадь. 4. Закрепление материала № 19.6, № 20.6, № 19.11(в), № 19.12(в), № 19.13(в), № 19.14(в), № 20.11(в), № 20.12(в), № 20.13(в), № 20.14(в). 5. Домашнее задание Параграф 19, 20 учебника, № 19.5, № 20.5, № 19.11–19.14(а), № 20.11–20.14(а). 6. Подведение итогов урока
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — ПланиметрияПоиск по сайту:
Элементарные преобразования графика функции y = f (x ) перечислены в следующей таблице.
Примеры элементарных преобразований графика функции y = x2 приведены в следующей таблице.
Примеры элементарных преобразований графика функции y = x2 – 6 x + 5 приведены в следующей таблице.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Поверхности как графики функций Если $f$ — скалярная функция одной переменной, $f:\R \to \R$ (перепутали?),
тогда графом $f$ называется множество точек $(x,f(x))$ для всех $x$ в области определения $f$. Функция f принимает два входа, $x$ и $y$, и возвращает одно число, которое мы называем $z$.
Если провести координатные оси $x$-$y$-$z$ стандартным образом,
ось $z$ представляет высоту, и это ключ к построению графика $f(x,y)$.
Если вы выберете точку $(x,y)$ на плоскости $xy$, то $z=f(x,y)$ представляет собой высоту графика в этой точке.
Например, вот график простой функции $g(x,y)=1$.
Независимо от того, какие значения вы выберете для $x$ и $y$,
функция $g$ всегда будет возвращать («высоту») единицу. Загрузка апплетаГоризонтальная плоскость. График функции $g(x,y)=1$ представляет собой горизонтальную плоскость высотой 1. Подробнее об апплете. График функции одной переменной $g(x)$ представляет собой линия с наклоном 1 через начало координат. Можете ли вы представить, что график ее обобщения на две переменные, функция $g(x,y)=x+y$, будет выглядеть? Это будет не линия, а плоскость. Этот график не будет иметь постоянную высоту, равную единице, но вы сможете сделать некоторые наблюдения:
Можете ли вы увидеть, правда ли это на графике? Загрузка апплета Наклонная плоскость. График функции $g(x,y)=x+y$ представляет собой наклонную плоскость. Вычислить площадь фигуры ограниченной параболами: Вычислить площадь фигуры, ограниченной линиями 2 Интегральные функции:
В выражениях можно применять следующие операции:
Другие функции:
Постоянные:
Вычислить площадь фигуры, ограниченную линиями.Пример 1:С помощью определённого интеграла вычислить площадь области D, ограниченной заданными линиями. Решение от преподавателя:Пример 2:Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж области. Решение от преподавателя:
Пример 3:Вычислить площадь фигуры, ограниченной линиями Решение от преподавателя:Пример 4:Решение от преподавателя:Пример 5:Найти площадь фигуры, ограниченной линиями построить схематический чертеж в декартовых координатах. Решение от преподавателя:Пример 6:Сделать чертеж области, ограниченной заданными линиями. Вычислить площадь полученной фигуры Решение от преподавателя:Построим область, площадь которой необходимо найти, заштрихуем искомую фигуру. Затем найдём ординаты точек пересечения кривой и прямой. Для этого приравняем правые части уравнений и прямой и решим полученное квадратное уравнение Корни этого уравнения Применим формулу: Вычислим искомую площадь: Ответ:
Пример 7:Вычислить площадь фигуры, ограниченной линиями: используя двойной интеграл. Решение от преподавателя:Пример 8:Найти площадь плоской фигуры с помощью двойного интеграла: Решение от преподавателя:Пример 9:Вычислить площадь фигуры, ограниченной осями координат играфиком функции Решение от преподавателя:Пример 10:Решение от преподавателя:Пример 11:Найти площадь фигуры, ограниченной графиком функции прямыми . Решение от преподавателя:Пример 12:Вычислить (с точностью до двух знаков после запятой) площадь фигуры, ограниченной указанными линиями. Решение от преподавателя:Пример 13:Вычислить площадь фигуры, ограниченной линиями. Решение от преподавателя:Пример 14:Вычислить площадь фигуры ограниченную линиями: y=sinx, y = cosx, x = 0. Решение от преподавателя:Расмотрим два случая: а) точка Согласно критерию Лебега, функция интегрируема, если существует конечное число точек разрыва (в данном случае 1) б) входит Пример 15:Вычислить площадь фигуры, ограниченной линиями. Решение от преподавателя:Пример 16:Вычислить площадь фигуры, ограниченной графиками функций: Решение от преподавателя:Пример 17:Вычислить площадь фигуры, ограниченной линиями: Решение от преподавателя:Пример 18:Найти площадь фигуры, ограниченной линиями построить схематический чертеж в декартовых координатах. Решение от преподавателя:Пример 19:Вычислить площади фигур, ограниченных графиками функций. Решение от преподавателя:Пример 20:Вычислить площадь фигуры, ограниченной осями координат и графиком функции: Решение от преподавателя:Пример 21:Вычислить площади фигур, ограниченных графиками функций. Решение от преподавателя:Пример 22:Вычислить площадь фигуры, ограниченной линиями используя двойной интеграл. Решение от преподавателя:
=0,5238 кв. ед. Пример 23:Вычислить площадь фигуры, ограниченной линиями x2 = y +2 и y =-x. Решение от преподавателя:y=x2 — 2 и y =-x Построим графики функций: Пример 24:Вычислите площадь фигуры, ограниченной линиями: y=4x-x2 ; y=0 Решение от преподавателя:Вначале построим фигуру, ограниченную данными линиями: Искомая площадь находится по формуле Ответ: Площадь искомой фигуры 32/3 (ед2). Пример 25:Найти площадь фигуры, ограниченной линиями: Решение от преподавателя:Построим фигуру: Находим точки пересечения: Искомая площадь состоит из двух одинаковых частей, поэтому достаточно найти площадь одной из них и умножить на 2: Ответ: Пример 26:Вычислить площадь фигуры, ограниченной линиями и расположенной в первой четверти координатной плоскости. Сделать чертеж. Решение от преподавателя:Сначала сделаем схематичный чертёж. Построим график функции Искомую площадь вычислим при помощи определённого интеграла. Ответ: Пример 27:Вычислить площадь фигуры, ограниченной линиями: Решение от преподавателя:
Пример 28:Вычислить площадь фигуры, ограниченной параболой , прямой . Решение от преподавателя:Пример 29:Найти площадь фигуры, ограниченной линиями: Решение от преподавателя:Пример 30:Вычислить площадь фигуры, ограниченной графиками функций Решение от преподавателя:Пример 31:Найти площадь фигуры, ограниченной линией: Решение от преподавателя:Пример 32:Найти площадь фигуры, ограниченной линиями: Решение от преподавателя:Пример 33:Найти площадь фигуры, ограниченной линиями: Решение от преподавателя:Работа вам нужна срочно.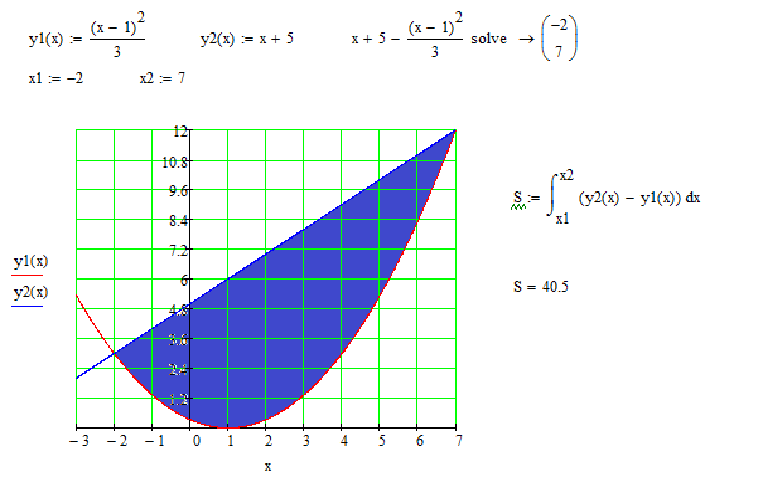 Не волнуйтесь, уложимся! Не волнуйтесь, уложимся!Заполните, пожалуйста, данные для автора:
вопросы: найдите площадь фигуры, ограниченной параболой, а парабола дана, наш X равен 2 y в квадрате, а X равен 1 минус 3 Y + 2 найдите площадь, которую они обе покрывают, чтобы они были окружены по этой параболе так что я сделал это нарисовал параболу вы сделали координатные оси и есть парабола и пометили несчастный теперь вы видите что это Х равно 1 минус 3 на 4 и Х равно равно минус 2 y в квадрате, чтобы найти площадь ограниченной фигуры, поэтому из диаграммы мы можем видеть, что все это представляет собой площадь, ограниченную параболой, поэтому в основном мы должны вычислить мы должны вычислить эту площадь, поэтому для этого что что вы собираетесь сделать, это мы собираемся вычислить площадь, ограниченную Воробьем, то есть X, равно 1 минус квадрат A, и вычесть площадь, ограниченную притчей 1 -2, как вызвать вы должны se как это это прямоугольная коробка и это маленькая прямоугольная коробка это но теперь мы должны рассчитать площадь дивана в этом месяце делая это либо мы находим размеры этого и вычисляем площадь либо иначе мы можем вычислить площадь весь прямоугольный блок и минус эта часть, так что в основном мы делаем C, используя ту же концепцию, что и вы, поэтому, когда мы вычисляем площадь, ограниченную параболой, она дает всю площадь, которая покрывается в нашем случае, например, это 1-3 вайшнавов, интегрируйте это когда мы интегрируем эту притчу из пределов 12, какой бы ограниченный вы ни хотели найти, область должна дать всю эту область, которая оказывается в левой части этого сайта сейчас, и аналогично для этого — белый для голосовых вызовов от 0 к нему будет включен вся часть слева, поэтому, когда область притяжения ограничена квадратом 1 минус 3 y, а мой пенис притягивает область, ограниченную США этим малым квадратом минус 2 y, мы получаем площадь, необходимую для этого, чтобы сначала найти это точки, где эти две, чтобы мы могли рассчитать, откуда и где найти угловой диван, делая то, что нам нужно, чтобы найти точку пересечения Итак, уравнения: X равно 1 минус 3 y квадрат и и X равно равно минус 2 y в квадрате sunao см. эта концепция X равна 1 минус 3 X получается -2, так что теперь мы идем отсюда, мы можем сказать, что две координаты, потому что тогда координаты станут -2 -1 и -2 Паван, так что это верхнее часть равна -2 кам — одна, а нижняя — -2 -1, поэтому мы получили наши значения, теперь мы должны вычислить это для этого, что мы собираемся сделать, это ограниченная область, так что теперь, если вы видите, что это площадь вдоль линии вдоль оси x, симметричная с обеих сторон, в основном область, расположенная ниже оси x, аналогична той, что находится над осью x, поэтому, что мы можем сделать, мы можем найти любой из них и просто удвоить x 2 получит всю область то же самое, чтобы сделать вашу поддержку, скажем, эту область, ограниченную областью, ограниченную парабола равна 2 x 2 X, поэтому мы должны интегрировать эту область от 0, потому что она не равна нулю, да, она равна нулю, потому что мы интегрируем ее по координатам y y, поэтому в основном от Y, если вы видите, что она идет от от нуля до единицы вычисляется значение Y, поэтому от 0 до 1 лакха для расчета, поэтому из пределов от нуля до единицы теперь то, что внешнее уравнение будет один минус 3 y в квадрате, так что это приведет к 1 минус 3 Y — из них уравнения шахтеров минус 2 y в квадрате, так что в DY, так что это вопрос, который мы должны решить только области гитары, супер делая 2 в 10 до 11 — 3 y в квадрате + 2 y в квадрате DY, так что получается Tu в 2021 году 1 минус y в квадрате на DY, так что теперь вы разделите студентов на 2021 Divine -2 в 2021 y в квадрате sunao aap для расчета решит эти Integra, поэтому, когда мы решим это kaun sa Ab To 12 vi от 0 до 1 минус 2 в кубе y на 3 от 0 до 1 12 футов значения нуля в одном, так что это выйдет 20 и 21 — 0 — 2 в это приведет к 1 на 3 минус ноль, поэтому, когда вы так на этом концерте к Bittu это будет становится слишком y3, поэтому, когда cal становится 6 — 2y 3, поэтому ответ считается равным 4 на 3 квадратных единицы MathScene — Интеграция — Урок 3MathScene — Интеграция — Урок 3
Урок 3 Области между графиками функции
Области, ограниченные графиками функций, можно найти интегрированием. Начнем с нахождение точек пересечения двух графиков, чтобы дать нам границы площади: х 2 + 5х 3 = х х 2 + 4х 3 = 0 Упрощать. (x 2 4x + 3) = 0 1 из-за скобки. (x 1)(x 3) = 0 Факторизация . (х 2 4x + 3) = 0 (x 1)(x 3) = 0 Точками пересечения являются x = 1 и x = 3. Они лежат на прямой y = x, поэтому координаты y совпадают с координатами x, то есть (1, 1) и (3, 3). Нам нужно только
используйте координаты x для вычисления площади между каждой кривой и осью x. Интеграл дает площадь между осью x и функцией е (х) = х 2 + 5x 3 на интервале от 1 до 3. Это заштрихованная область графика ниже
Таким же образом это площадь между y = x и x — на одном интервале. Снова на графике показана площадь найденный. Если мы соединим эти два графика, мы увидим, что область, которую мы хотим найти, является разница между двумя вышеперечисленными. Итак, мы просто нужно взять разницу между двумя интегралами, чтобы найти площадь, которую мы требовать.
Новое уравнение
параболы будет f(x) = x 2 + 5x 3 2
= x 2 + 5x 5 и линии y = x
2. Точки пересечения остаются прежними, так как мы добавили 2 к обеим сторонам уравнение. Ниже приведены расчеты, если вы не уверены! x 2 + 5x 5 = x 2 х 2 + 4х 3 = 0 Упростить . (x 2 4x + 3) = 0 (x 1)(x 3) = 0 Факторизация. И снова решения x = 1 и x = 3. Интегрируя таким же образом, вы можете видеть, что 2 снова упрощается, поэтому мы имеем тот же результат, что и раньше. Это означает что при вычислении площади между кривыми нам не нужно беспокоиться о независимо от того, находится ли область выше или ниже оси x, метод всегда один и тот же.
Пример 1 Найдите площадь между параболой f(x) = x 2 4 и линия у = х 2. Начнем с решение уравнения x 2 4 = x 2 найти площадь границы х 2 4 = х 2 x 2 4 х + 2 = 0 х 2 х 2 = 0 (х + 1)(х 2) = 0 Решения: х = 1 х = 2, Это хорошая идея, чтобы посмотреть на график и область, вовлеченную в калькулятор. Мы видим, что линия ограничивает область выше, поэтому мы вычитаем интеграл от парабола от линии. Пример 2 Найдите площадь, заключенную между графиками f(x) = sin x и g(x) = cos x.
на интервале 0 ≤ x < 2p
Мы снова должны начнем с поиска точек пересечения двух графиков. Решение уравнения
грех х = потому что х. sin x/cos x = 1 Разделить на cos х тангенс х = 1 х = коричневый 1 1 = /4 + номер Это означает что х = /4 и х = 5/4 на интервале 0 ≤ x < 2 График f(x) = sin x лежит над графиком g(x) = cos x на всех интервал между точками пересечения, поэтому расчеты площади выглядят как следует: Сейчас потому что /4 = грех / 4 «=» и cos 5/4 = грех 5/4 «=» Таким образом, точное значение площади равно .Пример 3 Найдите площадь, ограниченную графиками прямой y = 3x + 1 и многочлен f(x) = ⅓ x 3 2x 2 + 3x + 1. Сначала график рисуется с помощью калькулятора. Следующие значения окна должны работать Вот график: Теперь вычисляем точки пересечения. Найти наименьшее общее кратное чисел 14 и 28: НОД и НОК для 14 и 28 (с решением) 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Наименьшее общее кратное 14 и 28
Второй способ нахождения НОК для чисел 14 и 28 заключается в перечислении всех кратных для обоих чисел и выбор первого совпадающего:
Кратные числа 14: 14, 28, 42, 56
Кратные числа 28: 28, 56, 84, 112, 140, 168, 196, 224, 252, 280, 308, 336, 364, 392, 420, 448, 476, 504, 532, 560, 588, 616, 644, 672, 700, 728, 756, 784, 812, 840, 868, 896, 924, 952, 980, 1008, 1036, 1064, 1092, 1120, 1148, 1176, 1204, 1232, 1260, 1288, 1316, 1344, 1372, 1400, 1428, 1456, 1484, 1512, 1540, 1568, 1596, 1624, 1652, 1680, 1708, 1736, 1764, 1792, 1820, 1848, 1876, 1904, 1932, 1960, 1988, 2016, 2044, 2072, 2100, 2128, 2156, 2184, 2212, 2240, 2268, 2296, 2324, 2352, 2380, 2408, 2436, 2464, 2492, 2520, 2548, 2576, 2604, 2632, 2660, 2688, 2716, 2744, 2772, 2800, 2828, 2856, 2884, 2912, 2940, 2968, 2996, 3024, 3052, 3080, 3108, 3136, 3164, 3192, 3220, 3248, 3276, 3304, 3332, 3360, 3388, 3416, 3444, 3472, 3500, 3528, 3556, 3584, 3612, 3640, 3668, 3696, 3724, 3752, 3780, 3808, 3836, 3864, 3892, 3920, 3948, 3976, 4004, 4032, 4060, 4088, 4116, 4144, 4172, 4200, 4228, 4256, 4284, 4312, 4340, 4368, 4396, 4424, 4452, 4480, 4508, 4536, 4564, 4592, 4620, 4648, 4676, 4704, 4732, 4760, 4788, 4816, 4844, 4872, 4900, 4928, 4956, 4984, 5012, 5040, 5068, 5096, 5124, 5152, 5180, 5208, 5236, 5264, 5292, 5320, 5348, 5376, 5404, 5432, 5460, 5488, 5516, 5544, 5572, 5600, 5628, 5656, 5684, 5712, 5740, 5768, 5796, 5824, 5852, 5880, 5908, 5936, 5964, 5992, 6020, 6048, 6076, 6104, 6132, 6160, 6188, 6216, 6244, 6272, 6300, 6328, 6356, 6384, 6412, 6440, 6468, 6496, 6524, 6552, 6580, 6608, 6636, 6664, 6692, 6720, 6748, 6776, 6804, 6832, 6860, 6888, 6916, 6944, 6972, 7000, 7028, 7056, 7084, 7112, 7140, 7168, 7196, 7224, 7252, 7280, 7308, 7336, 7364, 7392, 7420, 7448, 7476, 7504, 7532, 7560, 7588, 7616, 7644, 7672, 7700, 7728, 7756, 7784, 7812, 7840, 7868, 7896, 7924, 7952, 7980, 8008, 8036, 8064, 8092, 8120, 8148, 8176, 8204, 8232, 8260, 8288, 8316, 8344, 8372, 8400, 8428, 8456, 8484, 8512, 8540, 8568, 8596, 8624, 8652, 8680, 8708, 8736, 8764, 8792, 8820, 8848, 8876, 8904, 8932, 8960, 8988, 9016, 9044, 9072, 9100, 9128, 9156, 9184, 9212, 9240, 9268, 9296, 9324, 9352, 9380, 9408, 9436, 9464, 9492, 9520, 9548, 9576, 9604, 9632, 9660, 9688, 9716, 9744, 9772, 9800, 9828, 9856, 9884, 9912, 9940, 9968, 9996, 10024, 10052, 10080, 10108, 10136, 10164, 10192, 10220, 10248, 10276, 10304, 10332, 10360, 10388, 10416, 10444, 10472, 10500, 10528, 10556, 10584, 10612, 10640, 10668, 10696, 10724, 10752, 10780, 10808, 10836, 10864, 10892, 10920, 10948, 10976, 11004, 11032, 11060, 11088, 11116, 11144, 11172, 11200, 11228, 11256, 11284, 11312, 11340, 11368, 11396, 11424, 11452, 11480, 11508, 11536, 11564, 11592, 11620, 11648, 11676, 11704, 11732, 11760, 11788, 11816, 11844, 11872, 11900, 11928, 11956, 11984, 12012, 12040, 12068, 12096, 12124, 12152, 12180, 12208, 12236, 12264, 12292, 12320, 12348, 12376, 12404, 12432, 12460, 12488, 12516, 12544, 12572, 12600, 12628, 12656, 12684, 12712, 12740, 12768, 12796, 12824, 12852, 12880, 12908, 12936, 12964, 12992, 13020, 13048, 13076, 13104, 13132, 13160, 13188, 13216, 13244, 13272, 13300, 13328, 13356, 13384, 13412, 13440, 13468, 13496, 13524, 13552, 13580, 13608, 13636, 13664, 13692, 13720, 13748, 13776, 13804, 13832, 13860, 13888, 13916, 13944, 13972, 14000, 14028, 14056, 14084, 14112, 14140, 14168, 14196, 14224, 14252, 14280, 14308, 14336, 14364, 14392, 14420, 14448, 14476, 14504, 14532, 14560, 14588, 14616, 14644, 14672, 14700, 14728, 14756, 14784, 14812, 14840, 14868, 14896, 14924, 14952, 14980, 15008, 15036, 15064, 15092, 15120, 15148, 15176, 15204, 15232, 15260, 15288, 15316, 15344, 15372, 15400, 15428, 15456, 15484, 15512, 15540, 15568, 15596, 15624, 15652, 15680, 15708, 15736, 15764, 15792, 15820, 15848, 15876, 15904, 15932, 15960, 15988, 16016, 16044, 16072, 16100, 16128, 16156, 16184, 16212, 16240, 16268, 16296, 16324, 16352, 16380, 16408, 16436, 16464, 16492, 16520, 16548, 16576, 16604, 16632, 16660, 16688, 16716, 16744, 16772, 16800, 16828, 16856, 16884, 16912, 16940, 16968, 16996, 17024, 17052, 17080, 17108, 17136, 17164, 17192, 17220, 17248, 17276, 17304, 17332, 17360, 17388, 17416, 17444, 17472, 17500, 17528, 17556, 17584, 17612, 17640, 17668, 17696, 17724, 17752, 17780, 17808, 17836, 17864, 17892, 17920, 17948, 17976, 18004, 18032, 18060, 18088, 18116, 18144, 18172, 18200, 18228, 18256, 18284, 18312, 18340, 18368, 18396, 18424, 18452, 18480, 18508, 18536, 18564, 18592, 18620, 18648, 18676, 18704, 18732, 18760, 18788, 18816, 18844, 18872, 18900, 18928, 18956, 18984, 19012, 19040, 19068, 19096, 19124, 19152, 19180, 19208, 19236, 19264, 19292, 19320, 19348, 19376, 19404, 19432, 19460, 19488, 19516, 19544, 19572, 19600, 19628, 19656, 19684, 19712, 19740, 19768, 19796, 19824, 19852, 19880, 19908, 19936, 19964, 19992, 20020, 20048, 20076, 20104, 20132, 20160, 20188, 20216, 20244, 20272, 20300, 20328, 20356, 20384, 20412, 20440, 20468, 20496, 20524, 20552, 20580, 20608, 20636, 20664, 20692, 20720, 20748, 20776, 20804, 20832, 20860, 20888, 20916, 20944, 20972, 21000, 21028, 21056, 21084, 21112, 21140, 21168, 21196, 21224, 21252, 21280, 21308, 21336, 21364, 21392, 21420, 21448, 21476, 21504, 21532, 21560, 21588, 21616, 21644, 21672, 21700, 21728, 21756, 21784, 21812, 21840, 21868, 21896, 21924, 21952, 21980, 22008, 22036, 22064, 22092, 22120, 22148, 22176, 22204, 22232, 22260, 22288, 22316, 22344, 22372, 22400, 22428, 22456, 22484, 22512, 22540, 22568, 22596, 22624, 22652, 22680, 22708, 22736, 22764, 22792, 22820, 22848, 22876, 22904, 22932, 22960, 22988, 23016, 23044, 23072, 23100, 23128, 23156, 23184, 23212, 23240, 23268, 23296, 23324, 23352, 23380, 23408, 23436, 23464, 23492, 23520, 23548, 23576, 23604, 23632, 23660, 23688, 23716, 23744, 23772, 23800, 23828, 23856, 23884, 23912, 23940, 23968, 23996, 24024, 24052, 24080, 24108, 24136, 24164, 24192, 24220, 24248, 24276, 24304, 24332, 24360, 24388, 24416, 24444, 24472, 24500, 24528, 24556, 24584, 24612, 24640, 24668, 24696, 24724, 24752, 24780, 24808, 24836, 24864, 24892, 24920, 24948, 24976, 25004, 25032, 25060, 25088, 25116, 25144, 25172, 25200, 25228, 25256, 25284, 25312, 25340, 25368, 25396, 25424, 25452, 25480, 25508, 25536, 25564, 25592, 25620, 25648, 25676, 25704, 25732, 25760, 25788, 25816, 25844, 25872, 25900, 25928, 25956, 25984, 26012, 26040, 26068, 26096, 26124, 26152, 26180, 26208, 26236, 26264, 26292, 26320, 26348, 26376, 26404, 26432, 26460, 26488, 26516, 26544, 26572, 26600, 26628, 26656, 26684, 26712, 26740, 26768, 26796, 26824, 26852, 26880, 26908, 26936, 26964, 26992, 27020, 27048, 27076, 27104, 27132, 27160, 27188, 27216, 27244, 27272, 27300, 27328, 27356, 27384, 27412, 27440, 27468, 27496, 27524, 27552, 27580, 27608, 27636, 27664, 27692, 27720, 27748, 27776, 27804, 27832, 27860, 27888, 27916, 27944, 27972, 28000, [. ..], 28
..], 28
Следовательно, НОК для 14 и 28 равняется 28
Вычисление наименьшего общего кратного
Введите цифры
- Три автобуса
Три автобуса общественного транспорта отправляются вместе с автовокзала утром. Первый автобус возвращается на станцию через 18 минут, второй – через 12 минут, а третий – через 24 минуты. Как долго снова будем вместе на вокзале? Пожалуйста, экспресс - Портниха
Портниха оставила кусок холста короче 5 метров. Она решает, сшить ли ей юбку или платье. Холста было ровно столько, сколько они израсходовали, разрезав юбку до 120 см, или 180 сантиметров. Какой кусок холста оставил ей? - LCM двух чисел
Найдите наименьшее кратное 63 и 147 - Различные 6975
Три разных автобусных маршрута, 80, 81 и 82, отправляются с конечной станции в 5 ч 20 мин. Маршрут 80 отправляется каждые 30 минут, маршрут 81 — каждые 20 минут, а маршрут 82 — каждые 40 минут. Во сколько они снова уйдут?
Во сколько они снова уйдут? - Напоминание и частное
Даны числа A = 135, B = 315. Найдите наименьшее натуральное число R, большее единицы, чтобы отношения R:A, R:B были с остатком 1. - Бакалейная лавка
Сьюзен решила сделать продуктовые наборы для своего магазина. Оптовый торговец, у которого она покупает, продает сахар в упаковках по 20 штук в коробке, муку в упаковках по 12 штук в коробке и 15 мешков риса в коробке. Сколько штук каждого предмета она должна купить, чтобы их было одинаковое количество - Вокруг клумбы
Вокруг прямоугольной клумбы размерами 5,25 м и 3,5 м нужно посадить розы через равные промежутки так, чтобы розы находились в каждом углу клумбы и потреблять как можно меньше. а) На каком расстоянии посажены розы? б) Сколько роз - Автобусы
На остановке в 10 часов встретились автобусы №2 и №9. Автобус №2 ходит с интервалом 4 минуты, а автобус №9 с интервалом 9 минут. Сколько раз автобус встречается в 18:00 по местному времени? - Зубчатая передача
Зубчатая передача состоит из двух колес. У одного 88, а у второго 56 зубов. Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо?
У одного 88, а у второго 56 зубов. Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо? - Автобусы 4
Интервалы: 1-й автобус 40 мин. 2-й автобус 2 часа 3-й бутон 20 минут Через какое время они встретятся — как можно скорее? - Четыре класса
Учащиеся всех 7, 8 и 9 классов одной школы могут занимать 4, 5, 6 и 7 ряд подряд, и никого не останется. Сколько в среднем учеников в одном классе, если в каждом классе всегда четыре класса? - Gcd и lcm
Вычислить наибольший общий делитель и наименьшее общее кратное чисел. a) 16 и 18 b) 24 и 22 c) 45 и 60 d) 36 и 30 - Вычислить 2976
Вычислить наименьшее общее кратное чисел 120, 660 и 210. - Уточните: 4001
Укажите: a = D (240,320) b = n (40,64) - Pardubická 4651
Йирка решил разделить выигрыш от пари в Velká Pardubická между собой и тремя своими младшими братьями по возрасту в соотношении 2:3:5:7.


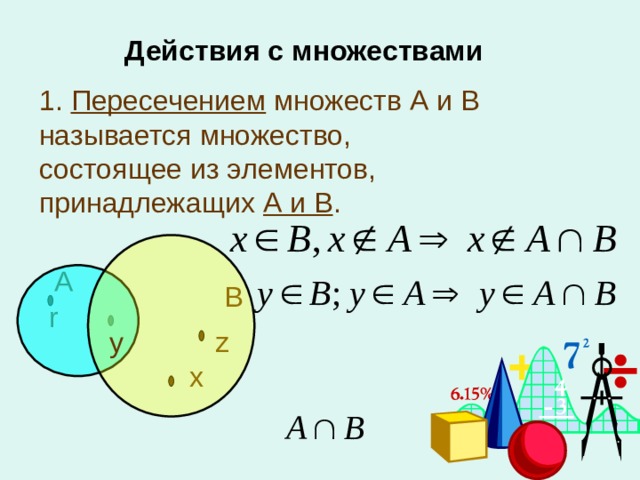


 Но, поскольку мы проверяем заведомо
более жесткое требование, чемэто,
среди неподчеркнутых цифр также могут
оказаться верные, если погрешность
окажется намного меньше своей оценки.
Но, поскольку мы проверяем заведомо
более жесткое требование, чемэто,
среди неподчеркнутых цифр также могут
оказаться верные, если погрешность
окажется намного меньше своей оценки. ..=0,9999… .
..=0,9999… .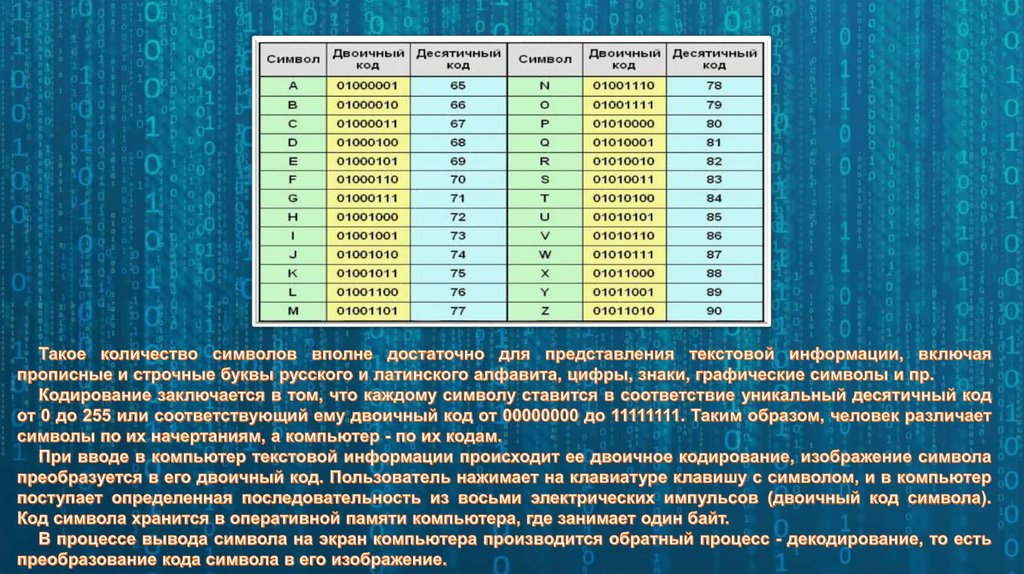 Пусть абсолютная погрешность
приближенного значения
равна.
Определим количество верных цифр в
широком смысле слова в записипосле запятой. Запишемв общем виде, указывая только разряды
и не указывая конкретных цифр, и подчеркнем
разряды, в которых будут располагаться
верные цифры в широком смысле слова:
Пусть абсолютная погрешность
приближенного значения
равна.
Определим количество верных цифр в
широком смысле слова в записипосле запятой. Запишемв общем виде, указывая только разряды
и не указывая конкретных цифр, и подчеркнем
разряды, в которых будут располагаться
верные цифры в широком смысле слова: Для мантиссы точного значенияне будет выполняться условие (1.3.1).
Значенияиестественно считать точным и приближенным
значениями мантиссы величиныx.
Тогда
ипредставляют собой абсолютную и
относительную погрешности приближенного
значения мантиссы.
Соответствующие цифры в записиидолжны совпадать попарно.Поэтому
и количество верных цифр в записи
ибудет одинаковым. Далее определяем
количество верных цифр в записи.
Запишем относительную погрешность
Для мантиссы точного значенияне будет выполняться условие (1.3.1).
Значенияиестественно считать точным и приближенным
значениями мантиссы величиныx.
Тогда
ипредставляют собой абсолютную и
относительную погрешности приближенного
значения мантиссы.
Соответствующие цифры в записиидолжны совпадать попарно.Поэтому
и количество верных цифр в записи
ибудет одинаковым. Далее определяем
количество верных цифр в записи.
Запишем относительную погрешность Итак,
в мантиссе имеется или n или (n+1)
верная значащая цифра. Поэтому общее
количество верных значащих цифр в записи
также будет равно либоn, либо (n+1).
Итак,
в мантиссе имеется или n или (n+1)
верная значащая цифра. Поэтому общее
количество верных значащих цифр в записи
также будет равно либоn, либо (n+1).










 ●
● Назовите верные цифры числа π ≈ 3,14, считая π ≈ 3,1416.
Назовите верные цифры числа π ≈ 3,14, считая π ≈ 3,1416. 4 Относительная
погрешность приближенного значения числа
4 Относительная
погрешность приближенного значения числа 1.1 ясно,
что три верные значащие цифры обеспечивают точность результата (относительную
погрешность) от 0,05 до 0,5 %. В технических и других расчетах, не требующих
особо высокой точности, достаточно бывает обеспечить точность результата
порядка десятых долей процента. Поэтому в технических расчетах принято
выполнять вычисления с тремя значащими цифрами.
1.1 ясно,
что три верные значащие цифры обеспечивают точность результата (относительную
погрешность) от 0,05 до 0,5 %. В технических и других расчетах, не требующих
особо высокой точности, достаточно бывает обеспечить точность результата
порядка десятых долей процента. Поэтому в технических расчетах принято
выполнять вычисления с тремя значащими цифрами.
 2)
2)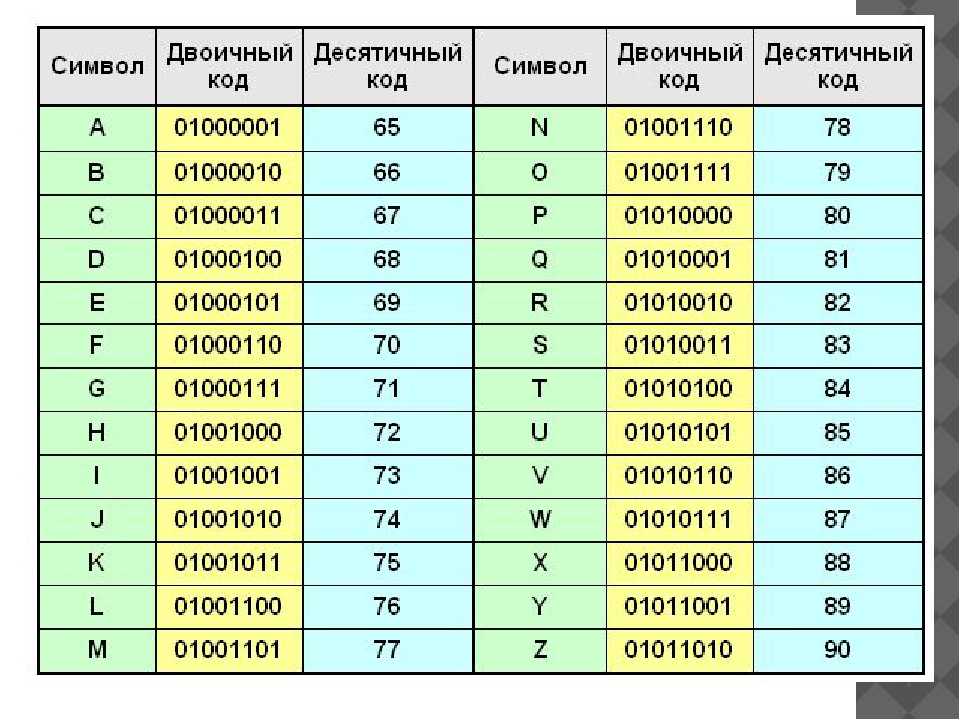 Вычислите общее сопротивление
Вычислите общее сопротивление Итак, а — b = 3,117 ≈ 3,12.
Абсолютная погрешность
Итак, а — b = 3,117 ≈ 3,12.
Абсолютная погрешность



 Однако, как показывают записи здесь, это существительное на самом деле является более старой формой, датируемой 16 веком. Существительное мириады появлялись в произведениях таких писателей, как Мильтон (множественное число мириады ) и Торо ( мириады ), и оно продолжает часто встречаться в уважаемом английском языке. Нет причин избегать этого.
Однако, как показывают записи здесь, это существительное на самом деле является более старой формой, датируемой 16 веком. Существительное мириады появлялись в произведениях таких писателей, как Мильтон (множественное число мириады ) и Торо ( мириады ), и оно продолжает часто встречаться в уважаемом английском языке. Нет причин избегать этого. » Чаще англоговорящие используют мириады в широком смысле — как существительное в единственном числе («мириады крошечных частиц»), так и существительное во множественном числе («мириады крошечных частиц»). Мириады также могут служить прилагательным, означающим «бесчисленное множество» («мириады частиц»). В то время как некоторые комментаторы употребления критикуют использование существительного, оно прочно вошло в английский язык с 16 века и фактически примерно на 200 лет старше прилагательного. Мириад происходит от греческого мириас , которое, в свою очередь, происходит от мириады , что означает «бесчисленное количество» или «десять тысяч».
» Чаще англоговорящие используют мириады в широком смысле — как существительное в единственном числе («мириады крошечных частиц»), так и существительное во множественном числе («мириады крошечных частиц»). Мириады также могут служить прилагательным, означающим «бесчисленное множество» («мириады частиц»). В то время как некоторые комментаторы употребления критикуют использование существительного, оно прочно вошло в английский язык с 16 века и фактически примерно на 200 лет старше прилагательного. Мириад происходит от греческого мириас , которое, в свою очередь, происходит от мириады , что означает «бесчисленное количество» или «десять тысяч». — Митико Какутани, 9 лет.0021 Нью-Йорк Таймс , 22 мая 2001 г.
— Митико Какутани, 9 лет.0021 Нью-Йорк Таймс , 22 мая 2001 г.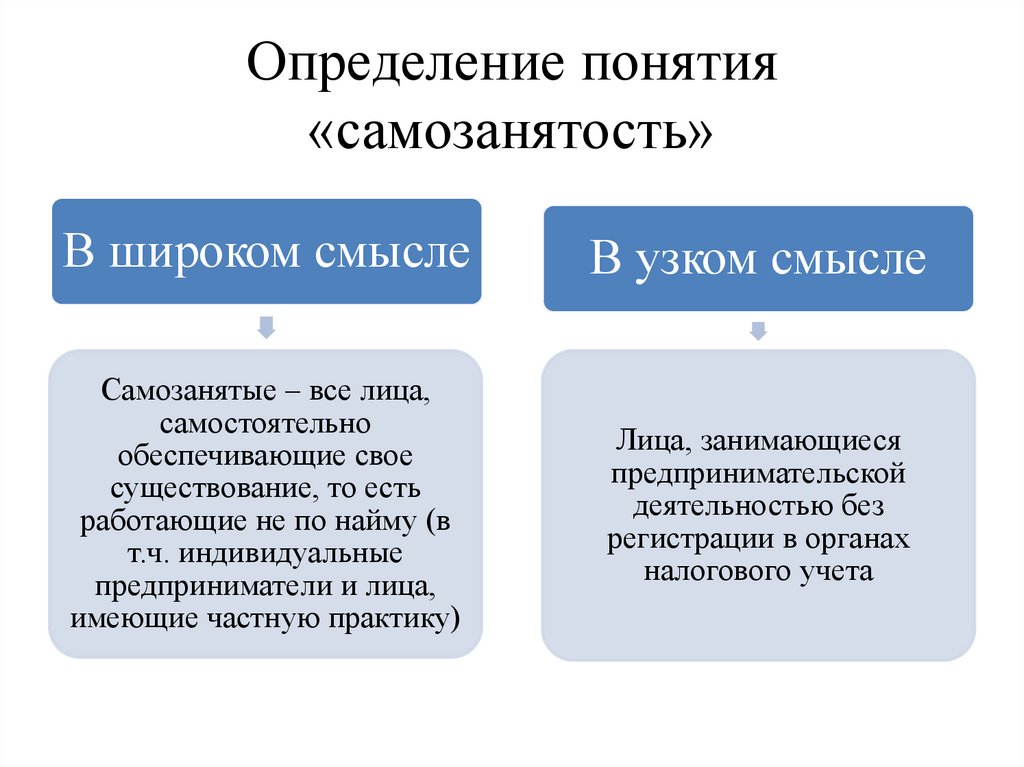 — Хью Кеннер, Тонущий остров , 1987 г.
— Хью Кеннер, Тонущий остров , 1987 г. Так создаются исторические словари…
— Саймон Винчестер, Значение всего , 2003 г.
Так создаются исторические словари…
— Саймон Винчестер, Значение всего , 2003 г. мириады проблем, с которыми сталкиваются сегодняшние города
Узнать больше
мириады проблем, с которыми сталкиваются сегодняшние города
Узнать больше — Jd Shadel, Condé Nast Traveler , 21 марта 2023 г.
Что нужно знать о полках для обуви перед покупкой0021 мириады стилей обувных стеллажей, но основными являются напольные стеллажи и наддверные стеллажи.
— Таня Эдвардс, Better Homes & Gardens , 17 марта 2023 г.
С ноября по апрель в Montage Big Sky предлагается бесчисленное множество зимних развлечений.
— Ванесса Уилкинс, Travel + Leisure , 17 марта 2023 г.
Напротив, вторая статья, опубликованная в декабре, была посвящена жителям сельских городов, многие из которых живут за чертой бедности, которым грозит множество проблем, потому что их водная инфраструктура остро нуждается в ремонте.
—Майкл Брага, , Республика Аризона, , 9 марта 2023 г.
Не в последнюю очередь Скотт — вместе с промоутерами Live Nation, Scoremore, XX Global и другими — столкнулся с мириадами судебных исков на общую сумму к северу от 2 миллиардов долларов потенциального ущерба.
— Jd Shadel, Condé Nast Traveler , 21 марта 2023 г.
Что нужно знать о полках для обуви перед покупкой0021 мириады стилей обувных стеллажей, но основными являются напольные стеллажи и наддверные стеллажи.
— Таня Эдвардс, Better Homes & Gardens , 17 марта 2023 г.
С ноября по апрель в Montage Big Sky предлагается бесчисленное множество зимних развлечений.
— Ванесса Уилкинс, Travel + Leisure , 17 марта 2023 г.
Напротив, вторая статья, опубликованная в декабре, была посвящена жителям сельских городов, многие из которых живут за чертой бедности, которым грозит множество проблем, потому что их водная инфраструктура остро нуждается в ремонте.
—Майкл Брага, , Республика Аризона, , 9 марта 2023 г.
Не в последнюю очередь Скотт — вместе с промоутерами Live Nation, Scoremore, XX Global и другими — столкнулся с мириадами судебных исков на общую сумму к северу от 2 миллиардов долларов потенциального ущерба.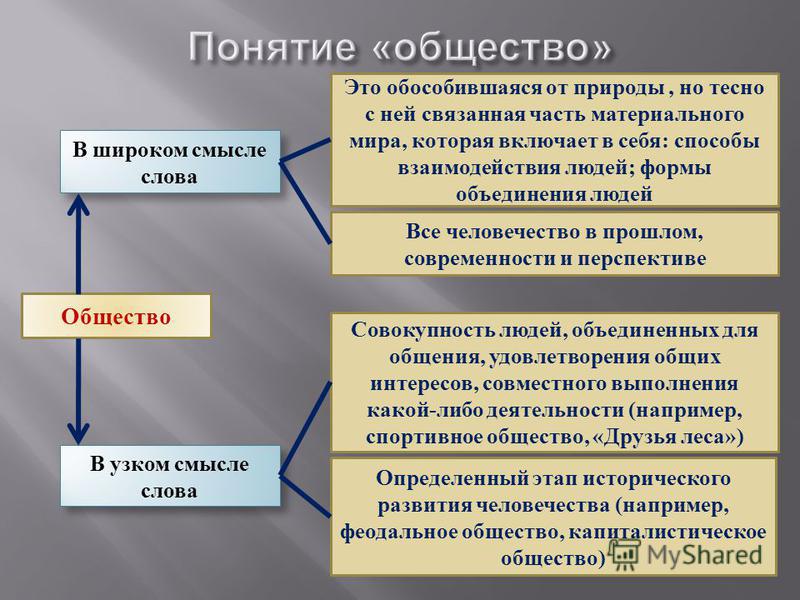 — Итан Шанфельд, Variety , 3 марта 2023 г.
Есть Мириады способов, которыми, как известно ученым, выбросы парниковых газов, связанные с деятельностью человека, вызывают повышение глобальной температуры, сообщил ранее USA TODAY климатолог НАСА Джош Уиллис.
— Изабелла Фертель, USA TODAY , 10 февраля 2023 г.
Есть мириады разных причин, но они делят друг с другом одежду.
— Ланэ Броуди, Peoplemag , 8 февраля 2023 г.
— Итан Шанфельд, Variety , 3 марта 2023 г.
Есть Мириады способов, которыми, как известно ученым, выбросы парниковых газов, связанные с деятельностью человека, вызывают повышение глобальной температуры, сообщил ранее USA TODAY климатолог НАСА Джош Уиллис.
— Изабелла Фертель, USA TODAY , 10 февраля 2023 г.
Есть мириады разных причин, но они делят друг с другом одежду.
— Ланэ Броуди, Peoplemag , 8 февраля 2023 г. — Брайан Вакер, Baltimore Sun , 10 апреля 2023 г.
Обзор показал, что методология многих предыдущих исследований была ошибочной и что риск бесчисленного множества проблем со здоровьем значительно увеличился после менее чем двух порций алкоголя в день для женщин и после трех для мужчин.
— Рони Кэрин Рабин, New York Times , 4 апр. 2023 г.
Теперь расцвели мириады других методов лечения.
— Ангус Маккиннон, CNN , 3 апреля 2023 г.
Увеличить / Портрет Бетховена работы Йозефа Карла Штилера, 1820 г. Beethoven-Haus Bonn Людвиг ван Бетховен — один из величайших композиторов всех времен, но на протяжении всей своей жизни он страдал от мириадов проблем со здоровьем, в частности, к 1818 году он почти полностью оглох.
— Дженнифер Уэллетт, 9 лет.
— Брайан Вакер, Baltimore Sun , 10 апреля 2023 г.
Обзор показал, что методология многих предыдущих исследований была ошибочной и что риск бесчисленного множества проблем со здоровьем значительно увеличился после менее чем двух порций алкоголя в день для женщин и после трех для мужчин.
— Рони Кэрин Рабин, New York Times , 4 апр. 2023 г.
Теперь расцвели мириады других методов лечения.
— Ангус Маккиннон, CNN , 3 апреля 2023 г.
Увеличить / Портрет Бетховена работы Йозефа Карла Штилера, 1820 г. Beethoven-Haus Bonn Людвиг ван Бетховен — один из величайших композиторов всех времен, но на протяжении всей своей жизни он страдал от мириадов проблем со здоровьем, в частности, к 1818 году он почти полностью оглох.
— Дженнифер Уэллетт, 9 лет. 0021 Ars Technica , 22 марта 2023 г.
Отчеты, которые повторяли тезисы Кремля по мириадам тем, бездоказательно утверждали, что власти Огайо лгали об истинных последствиях разлива химикатов.
— Дэвид Клеппер, The Enquirer , 20 марта 2023 г.
Может быть, еще один абзац: отчеты, которые повторяли тезисы Кремля по мириадам тем, утверждали без каких-либо доказательств, что власти Огайо лгали об истинных последствиях разлива химикатов.
— Джей Нордлингер, 9 лет.0021 National Review , 20 марта 2023 г.
Отчеты, которые повторяли тезисы Кремля по мириадам тем, бездоказательно утверждали, что власти Огайо лгали об истинных последствиях разлива химикатов.
— Кевин Фрекинг, Fortune , 18 марта 2023 г.
На самом деле, вы можете быть удивлены мириадами методов, позволяющих даже самой маленькой кухонной зоне выглядеть великолепно.
0021 Ars Technica , 22 марта 2023 г.
Отчеты, которые повторяли тезисы Кремля по мириадам тем, бездоказательно утверждали, что власти Огайо лгали об истинных последствиях разлива химикатов.
— Дэвид Клеппер, The Enquirer , 20 марта 2023 г.
Может быть, еще один абзац: отчеты, которые повторяли тезисы Кремля по мириадам тем, утверждали без каких-либо доказательств, что власти Огайо лгали об истинных последствиях разлива химикатов.
— Джей Нордлингер, 9 лет.0021 National Review , 20 марта 2023 г.
Отчеты, которые повторяли тезисы Кремля по мириадам тем, бездоказательно утверждали, что власти Огайо лгали об истинных последствиях разлива химикатов.
— Кевин Фрекинг, Fortune , 18 марта 2023 г.
На самом деле, вы можете быть удивлены мириадами методов, позволяющих даже самой маленькой кухонной зоне выглядеть великолепно. — Анна Фикссен, 9 лет.0021 ELLE Decor , 7 марта 2023 г.
Узнать больше
— Анна Фикссен, 9 лет.0021 ELLE Decor , 7 марта 2023 г.
Узнать больше Определения и примеры »
Определения и примеры » Эти 5 наборов иногда обозначаются аббревиатурой NZQRC .
Эти 5 наборов иногда обозначаются аббревиатурой NZQRC .
 е. представлена дробью a/b, где a принадлежит Z, а b принадлежит Z * (исключая деление на 0).
е. представлена дробью a/b, где a принадлежит Z, а b принадлежит Z * (исключая деление на 0). 2=-1 $
2=-1 $

 А вы уверены, что знаете всё? Тогда эта викторина для вас!
А вы уверены, что знаете всё? Тогда эта викторина для вас! Тест-викторина «Следствие ведут Знатоки»
Тест-викторина «Следствие ведут Знатоки»
 Умеете ли вы с ними обращаться? Проверьте в этом тесте!
Умеете ли вы с ними обращаться? Проверьте в этом тесте! В этом тесте вы сможете проверить свои знания о компьютерных вирусах.
В этом тесте вы сможете проверить свои знания о компьютерных вирусах.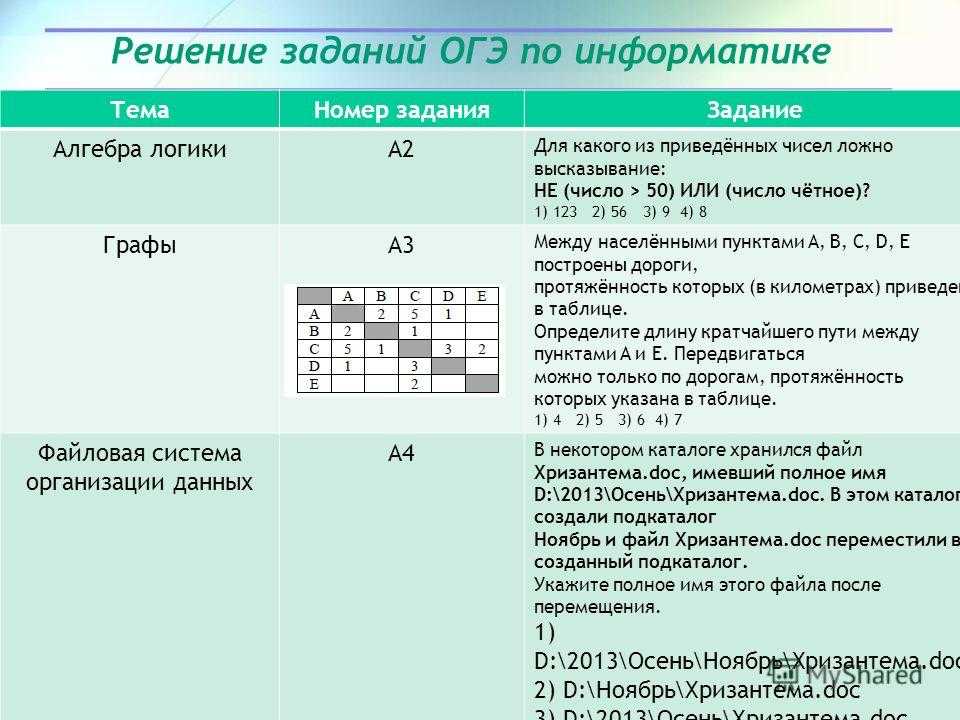 А вы уверены, что знаете всё? Тогда эта викторина для вас!
А вы уверены, что знаете всё? Тогда эта викторина для вас! За это время сменилось несколько поколений вычислительных машин, а самые первые компьютеры уже стали музейными экспонатами.
За это время сменилось несколько поколений вычислительных машин, а самые первые компьютеры уже стали музейными экспонатами. Тест-викторина «Следствие ведут Знатоки»
Тест-викторина «Следствие ведут Знатоки»
 А вы уверены, что знаете всё? Тогда эта викторина для вас!
А вы уверены, что знаете всё? Тогда эта викторина для вас! Пожалуй, сегодня уже трудно представить более удобное и универсальное устройство для работы с информацией, чем компьютер.
Пожалуй, сегодня уже трудно представить более удобное и универсальное устройство для работы с информацией, чем компьютер.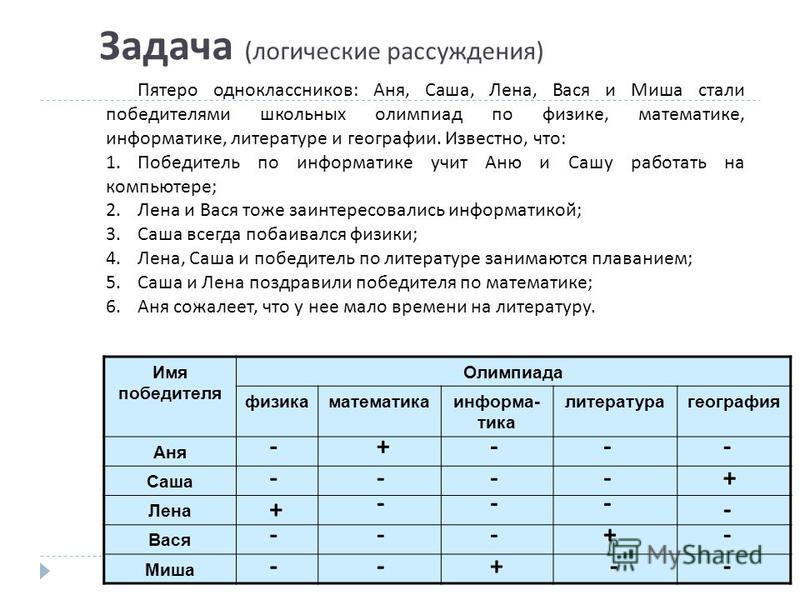 Узнайте об особенностях разных систем счисления в этом тесте!
Узнайте об особенностях разных систем счисления в этом тесте! Знаете ли вы ученых, подаривших миру эти изобретения?
Знаете ли вы ученых, подаривших миру эти изобретения?

 .. Как хорошо знакомы вам эти понятия? Проверьте в данном тесте!
.. Как хорошо знакомы вам эти понятия? Проверьте в данном тесте! В этом тесте вы узнаете, как работал и какого размера был первый компьютер.
В этом тесте вы узнаете, как работал и какого размера был первый компьютер.
 Какие-то из них дополняют и улучшают функции компьютера или просто предназначены для поднятия настроения и развлечения.
Какие-то из них дополняют и улучшают функции компьютера или просто предназначены для поднятия настроения и развлечения. Алгоритмы проникли в нашу жизнь. Проверьте свои знания о алгоритмах и исполнителях в этом тесте по информатике.
Алгоритмы проникли в нашу жизнь. Проверьте свои знания о алгоритмах и исполнителях в этом тесте по информатике. Проверьте что же вы знаете об информации, которая нас окружает.
Проверьте что же вы знаете об информации, которая нас окружает. К., зав. каф. начального образования НИРО
К., зав. каф. начального образования НИРО Информация и информационные процессы
Информация и информационные процессы 2. Информационные процессы
2. Информационные процессы 3. Всемирная паутина
3. Всемирная паутина Пиктограммы» (N 135159)
Пиктограммы» (N 135159)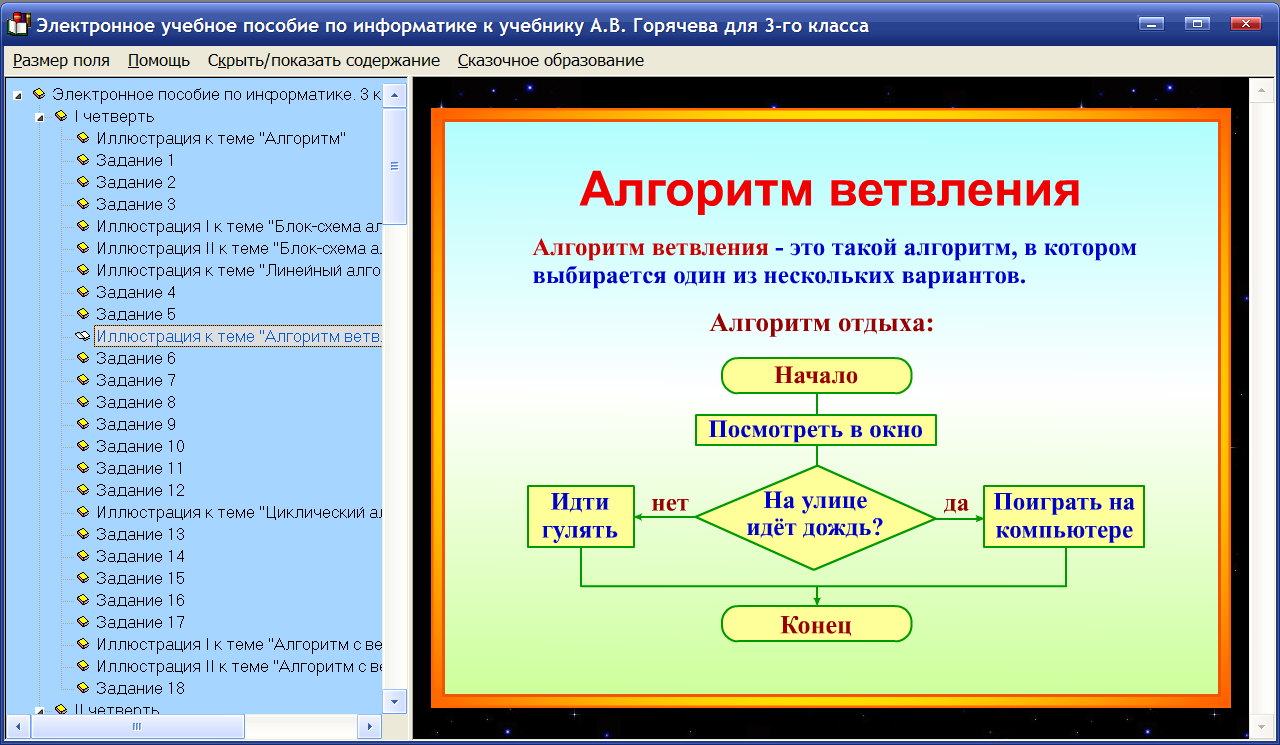 6. Измерение информации
6. Измерение информации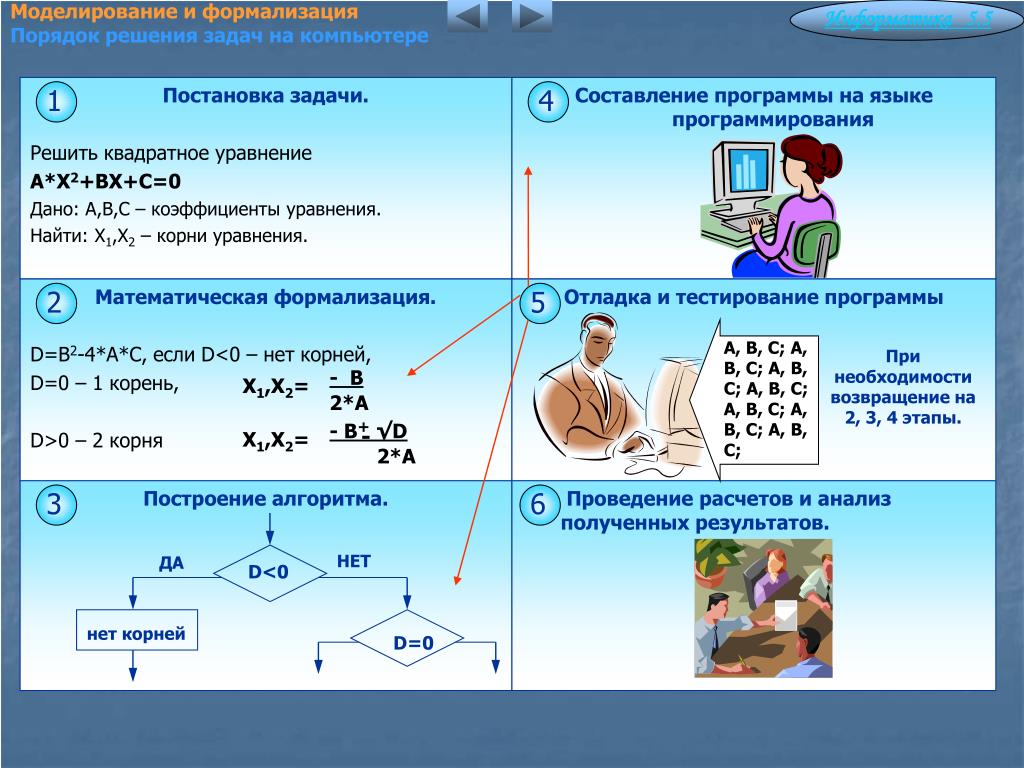 Вариант 1
Вариант 1 Вариант 1
Вариант 1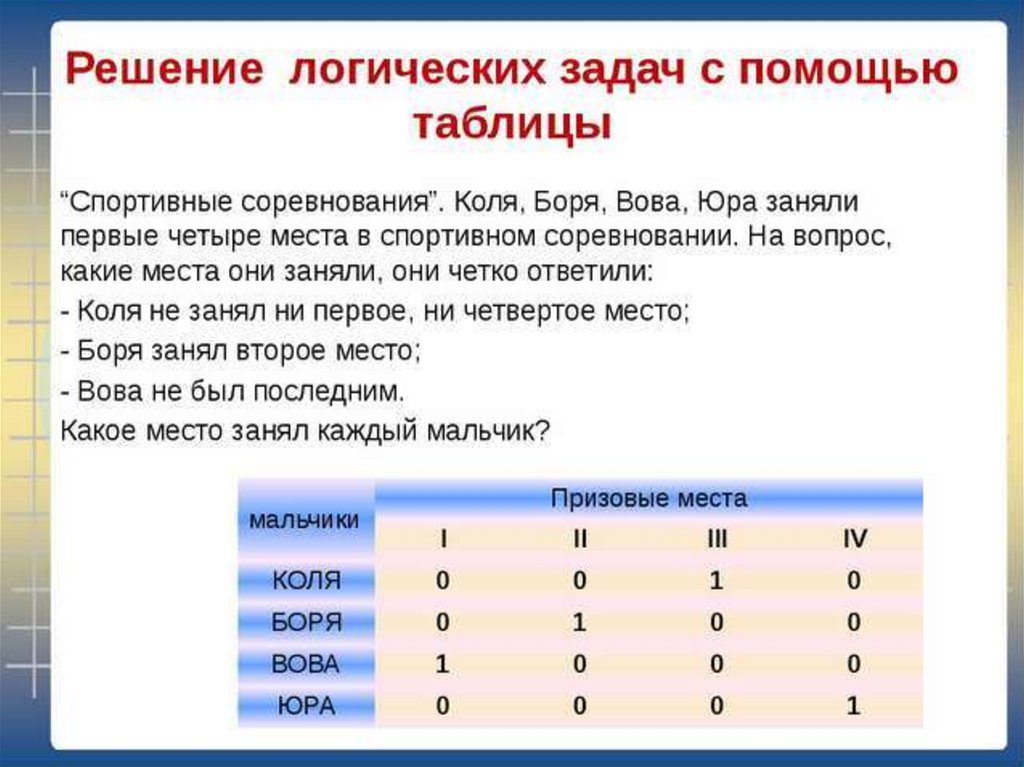 Выбор конфигурации в зависимости от решаемых задач»
Выбор конфигурации в зависимости от решаемых задач» 4. Файлы и файловые структуры
4. Файлы и файловые структуры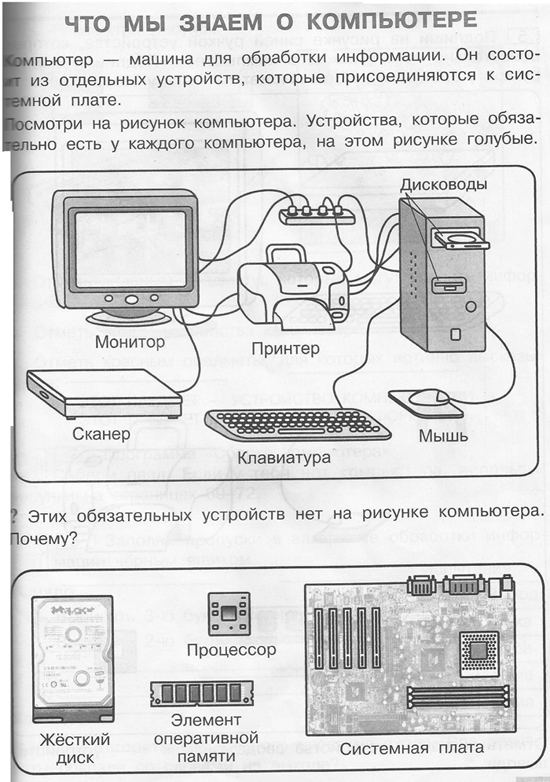 Обработка графической информации
Обработка графической информации Вариант 2
Вариант 2 2.
2. 2. Создание текстовых документов на компьютере
2. Создание текстовых документов на компьютере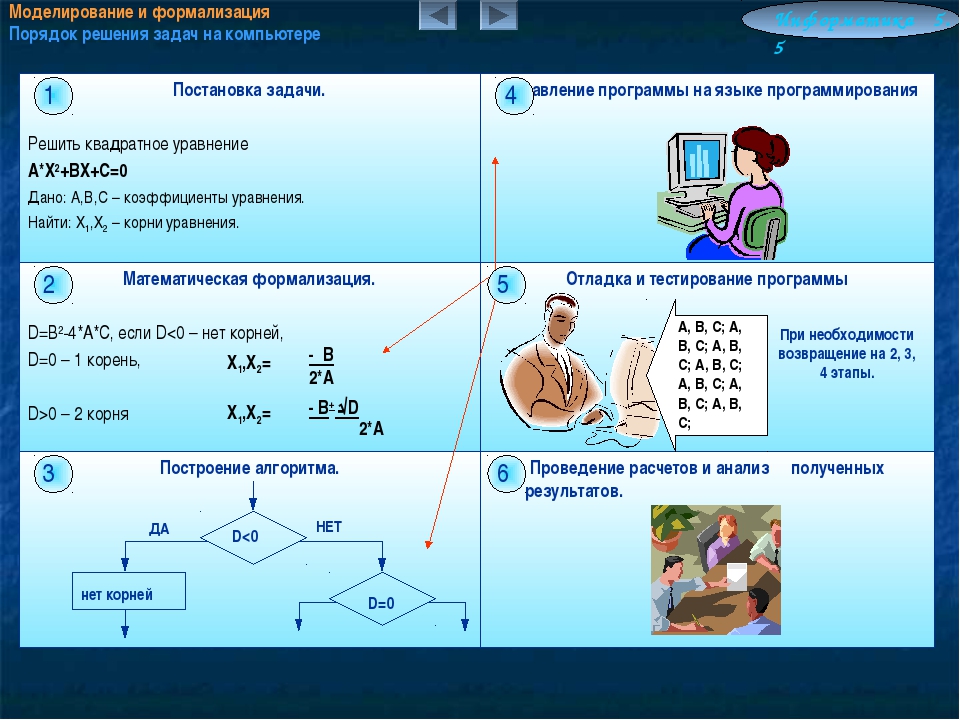 Вариант 1
Вариант 1 Вариант 1
Вариант 1 rtf
rtf 2. Компьютерные презентации
2. Компьютерные презентации Некоторые популярные карьерные пути для специалистов по компьютерным наукам включают:
Некоторые популярные карьерные пути для специалистов по компьютерным наукам включают: Вы можете запланировать сеанс репетиторства или получить помощь с домашним заданием практически по любой теме компьютерных наук.
Вы можете запланировать сеанс репетиторства или получить помощь с домашним заданием практически по любой теме компьютерных наук.
 Темы включают искусственный интеллект, научные вычисления и компьютерную визуализацию.
Темы включают искусственный интеллект, научные вычисления и компьютерную визуализацию.

 js, Angular, Node .js, Next.js, MERN Stack, Django, Flask, микросервисы Spring Boot), базы данных (Oracle, MySQL, PostGreSQL, SQLite, MongoDB), машинное обучение, структура данных и алгоритмы, выпускной проект, Android и т. д. для студентов на всех уровнях, будь то школа, колледж и университетский уровень Помощь в курсовой работе или проект в реальном времени.
js, Angular, Node .js, Next.js, MERN Stack, Django, Flask, микросервисы Spring Boot), базы данных (Oracle, MySQL, PostGreSQL, SQLite, MongoDB), машинное обучение, структура данных и алгоритмы, выпускной проект, Android и т. д. для студентов на всех уровнях, будь то школа, колледж и университетский уровень Помощь в курсовой работе или проект в реальном времени. Эта задача немного трудоемкая и скучная. Каждый раз вам нужно искать и назначать кого-то, кто сделает вашу домашнюю работу.
Эта задача немного трудоемкая и скучная. Каждый раз вам нужно искать и назначать кого-то, кто сделает вашу домашнюю работу. д. Благодаря реализации структуры данных операции с данными могут выполняться эффективно, экономя много памяти и времени. В каждом типе структуры данных доступ к данным осуществляется уникальным способом.
д. Благодаря реализации структуры данных операции с данными могут выполняться эффективно, экономя много памяти и времени. В каждом типе структуры данных доступ к данным осуществляется уникальным способом.
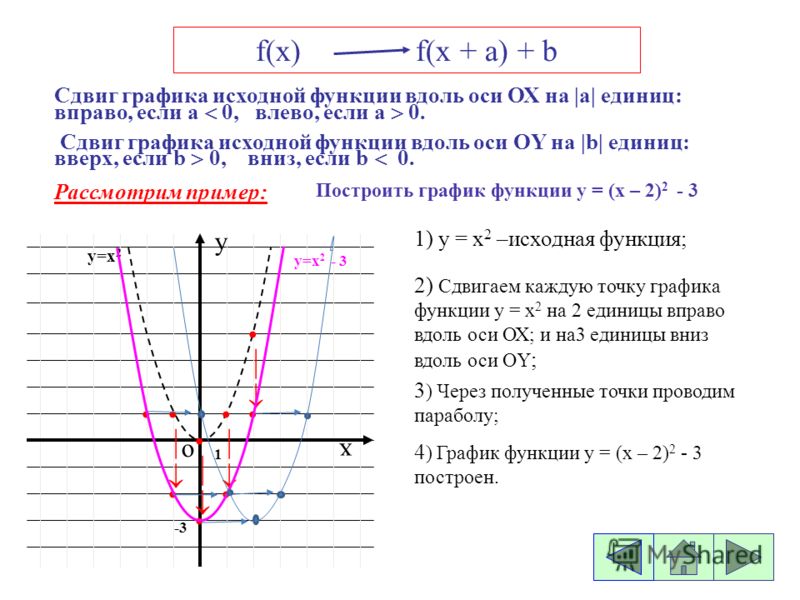 Учащиеся
самостоятельно приходят к выводу о сдвиге
параболы (параллельном переносе) на 1 единицу
вниз. (Слайд 11.)
Учащиеся
самостоятельно приходят к выводу о сдвиге
параболы (параллельном переносе) на 1 единицу
вниз. (Слайд 11.)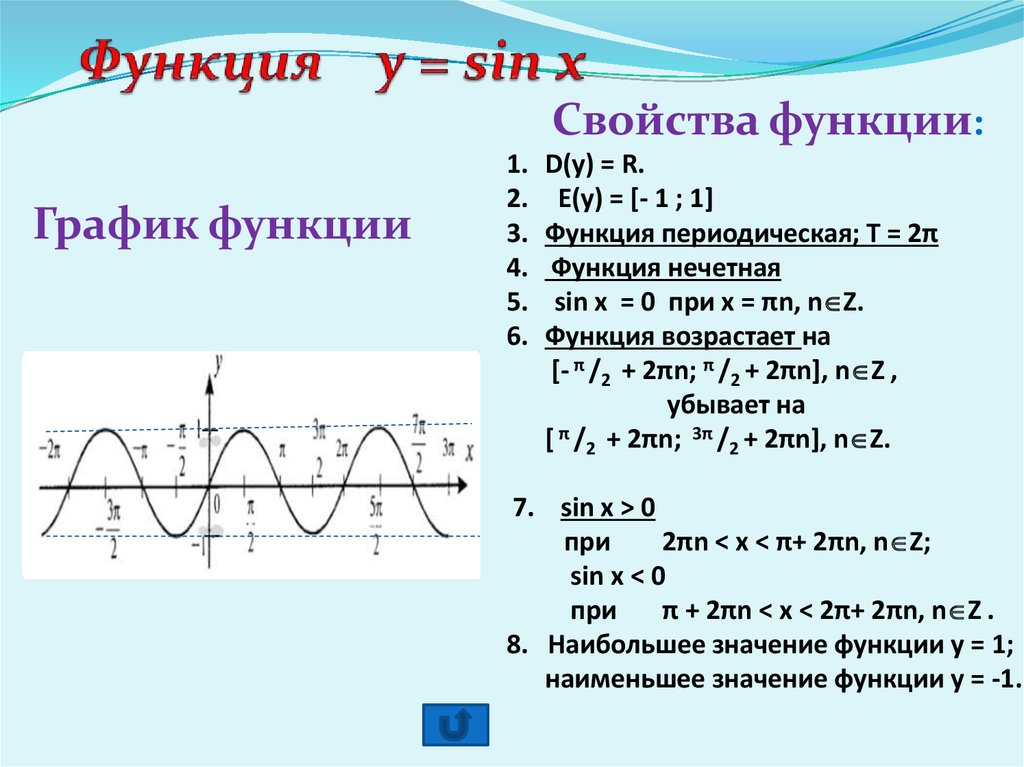 )
)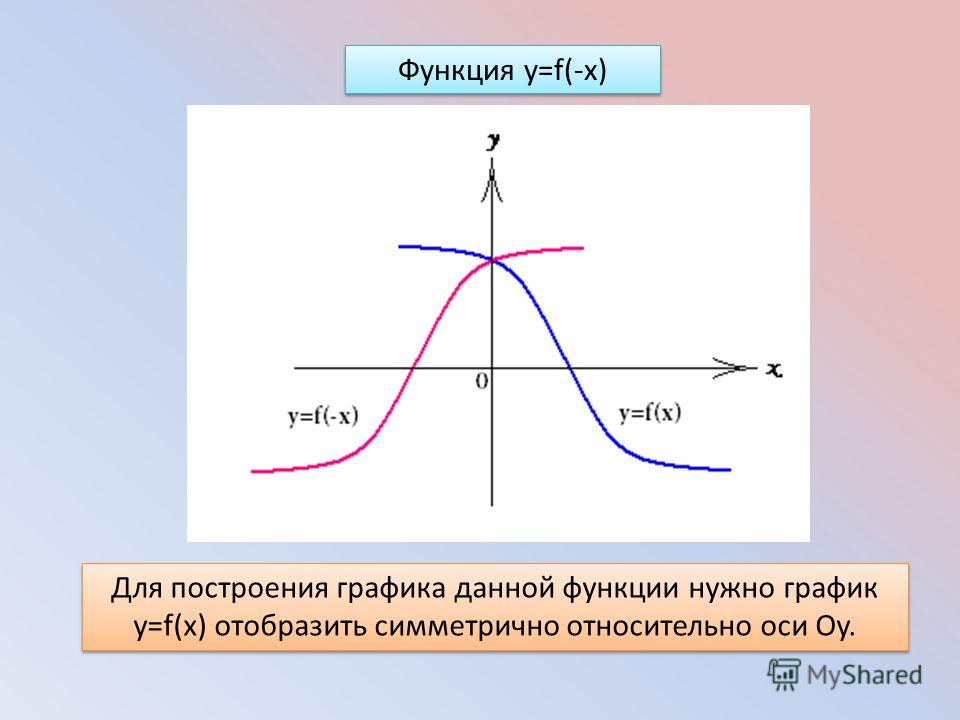
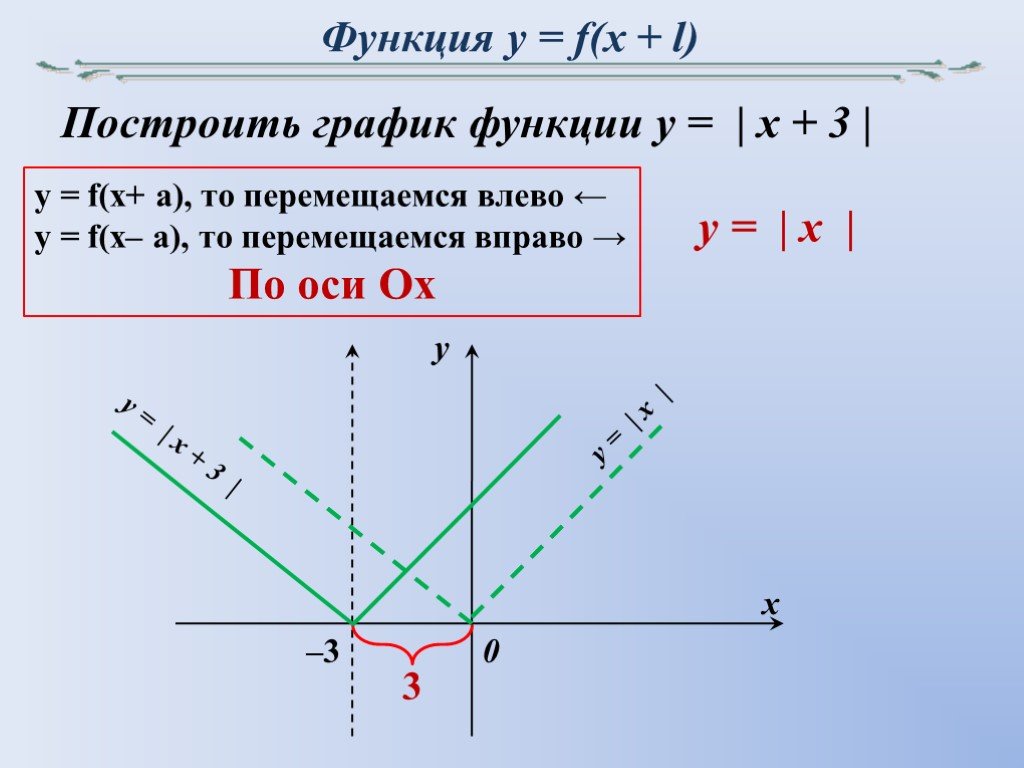

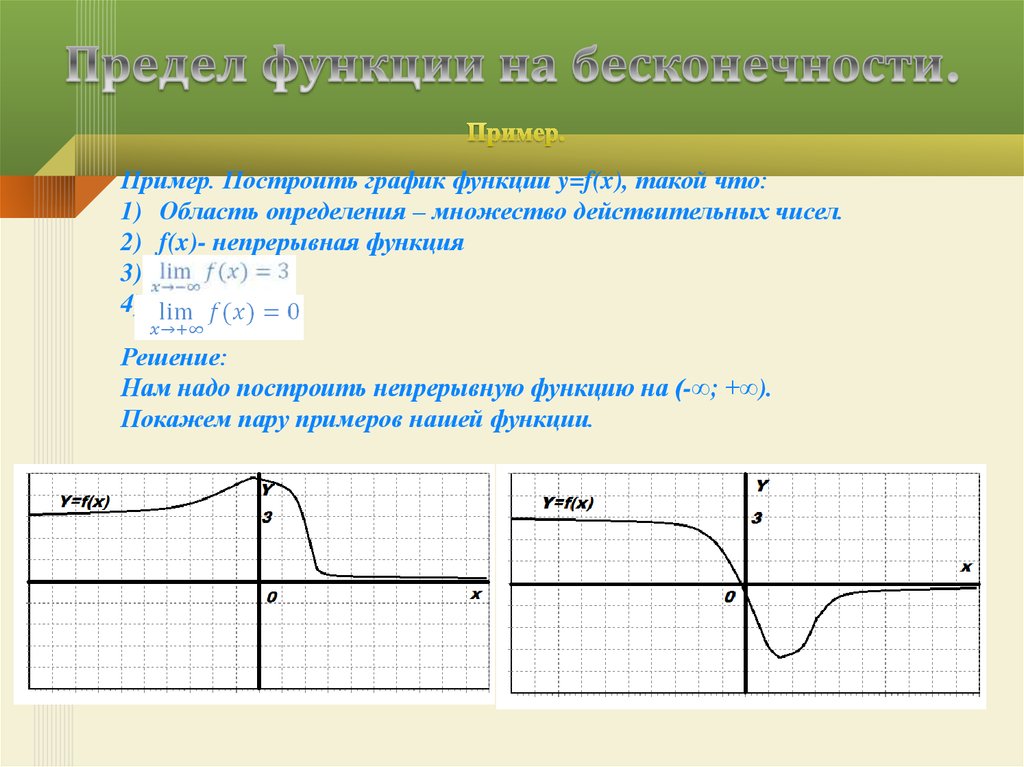

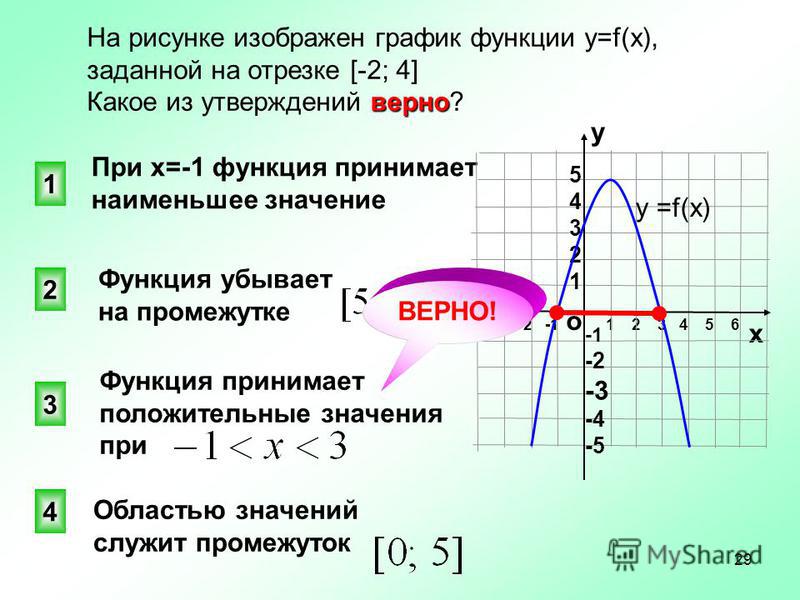 Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.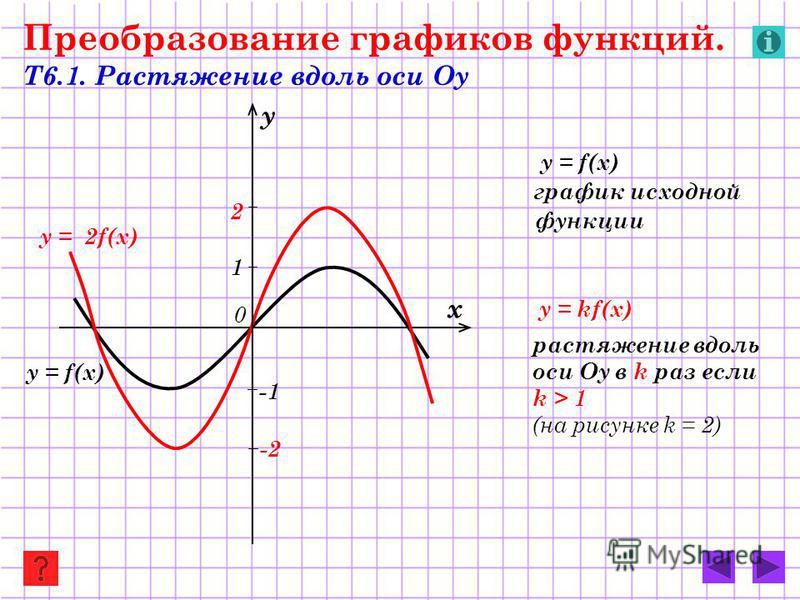

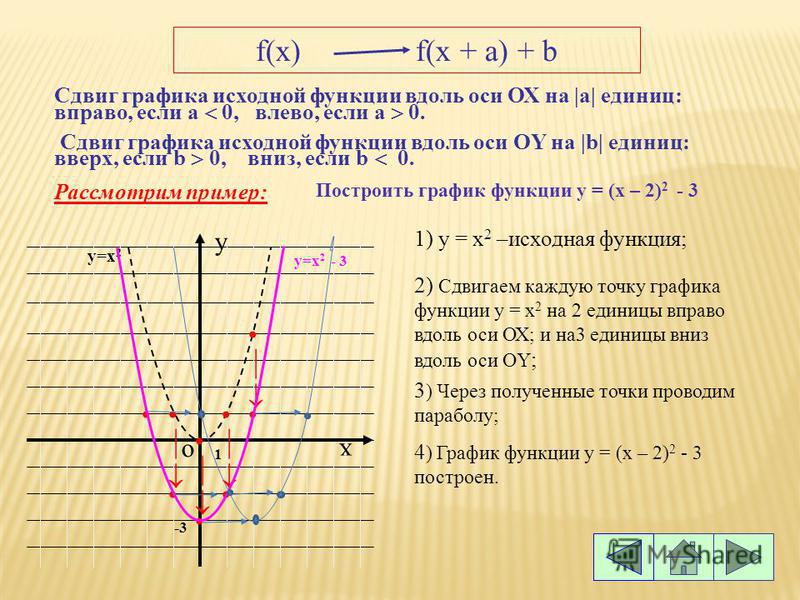 Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.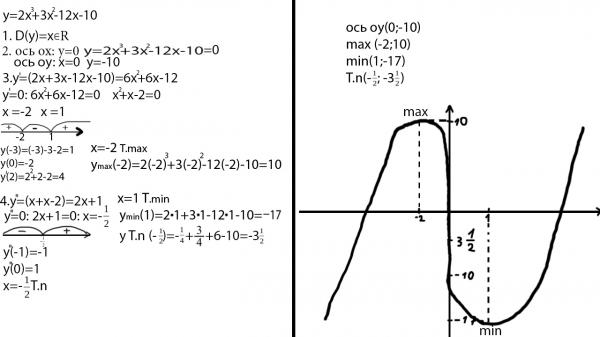

 Когда часто называют это
график $y=f(x)$, поскольку мы считаем, что точки лежат в $xy$-плоскости. При нанесении точек на $xy$-плоскость они обычно образуют кривую a точек, например график
$f(x)=\sin x$ показано ниже. 92 \to \R$ таким же образом. График представляет собой набор точек
$(x,y,f(x,y))$ для всех $(x,y)$ в области определения $f$.
Когда часто называют это
график $z=f(x,y)$, так как мы считаем, что точки лежат в
$xyz$-пространство. Вы можете не найти это формальное определение особенно информативным,
но мы можем показать, что график $f(x,y)$ является поверхностью.
Когда часто называют это
график $y=f(x)$, поскольку мы считаем, что точки лежат в $xy$-плоскости. При нанесении точек на $xy$-плоскость они обычно образуют кривую a точек, например график
$f(x)=\sin x$ показано ниже. 92 \to \R$ таким же образом. График представляет собой набор точек
$(x,y,f(x,y))$ для всех $(x,y)$ в области определения $f$.
Когда часто называют это
график $z=f(x,y)$, так как мы считаем, что точки лежат в
$xyz$-пространство. Вы можете не найти это формальное определение особенно информативным,
но мы можем показать, что график $f(x,y)$ является поверхностью.
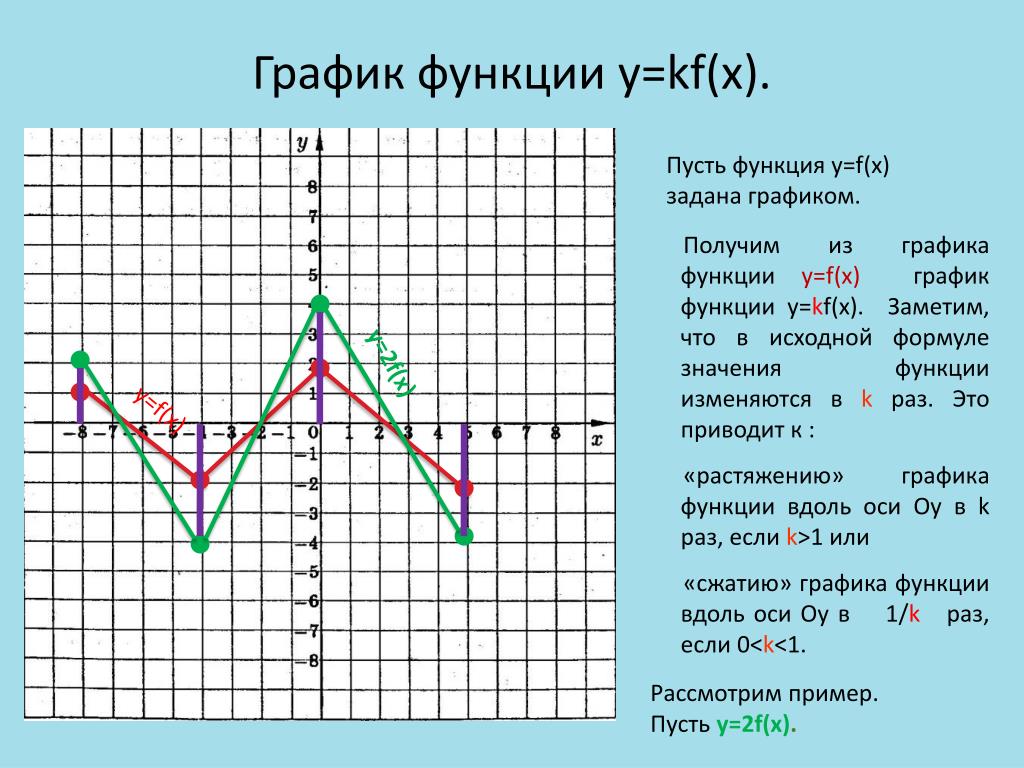
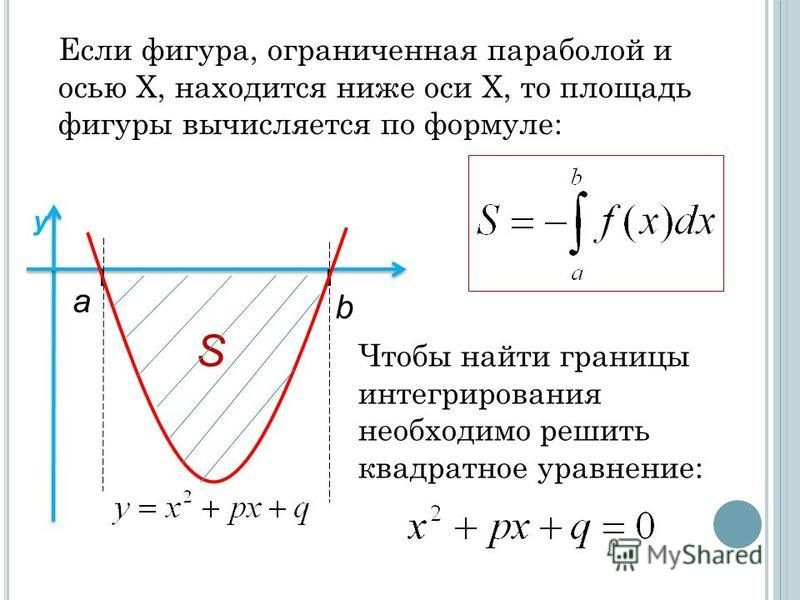 14159..
14159..

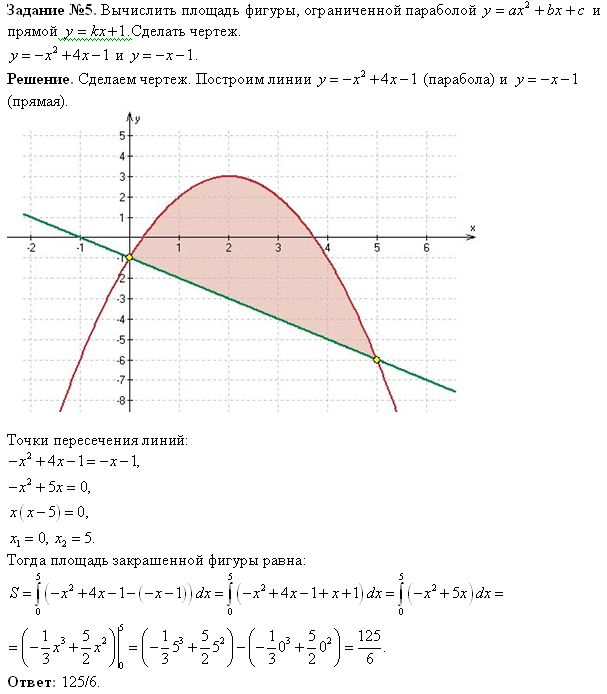

 оба уравнения с обоими уравнениями 1 минус 3 y в квадрате равно минус 2 y в квадрате, поэтому, когда мы возьмем это слева, это станет одним минус y в квадрате равно нулю, поэтому почему появляется сперма чтобы быть одним, поэтому отсюда, почему из вас выходит -1, и это два значения того, почему теперь Forex Forex поместит значение Y, так что это от x дано нам 1 минус 3 y квадратный закон в обоих вопрос Вы можете видеть, что это было именно так, в основном, когда у вас есть -11, значение x будет выглядеть так, как будто вы будете использовать один год, поэтому X равно 1 минус 3 в одном квадрате
оба уравнения с обоими уравнениями 1 минус 3 y в квадрате равно минус 2 y в квадрате, поэтому, когда мы возьмем это слева, это станет одним минус y в квадрате равно нулю, поэтому почему появляется сперма чтобы быть одним, поэтому отсюда, почему из вас выходит -1, и это два значения того, почему теперь Forex Forex поместит значение Y, так что это от x дано нам 1 минус 3 y квадратный закон в обоих вопрос Вы можете видеть, что это было именно так, в основном, когда у вас есть -11, значение x будет выглядеть так, как будто вы будете использовать один год, поэтому X равно 1 минус 3 в одном квадрате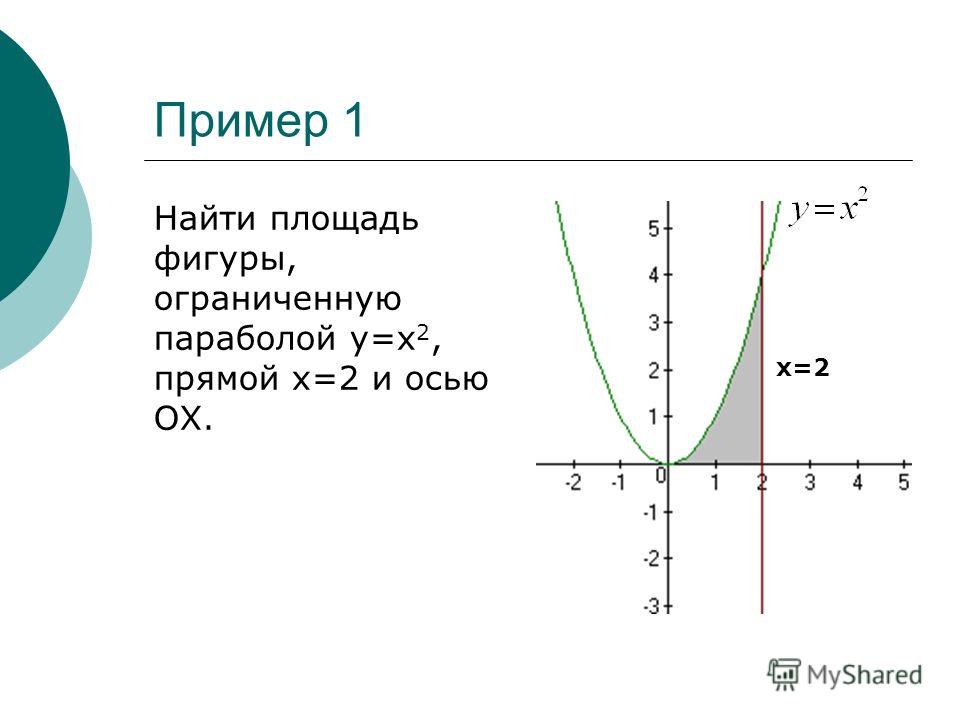 Для
Например, мы найдем площадь, ограниченную двумя графиками f(x) = x 2 + 5x 3
и у = х.
Для
Например, мы найдем площадь, ограниченную двумя графиками f(x) = x 2 + 5x 3
и у = х. 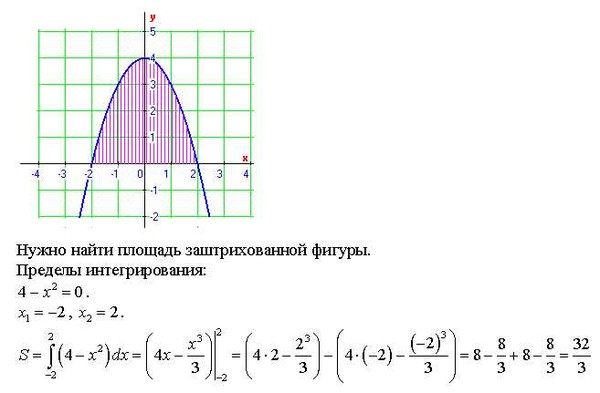
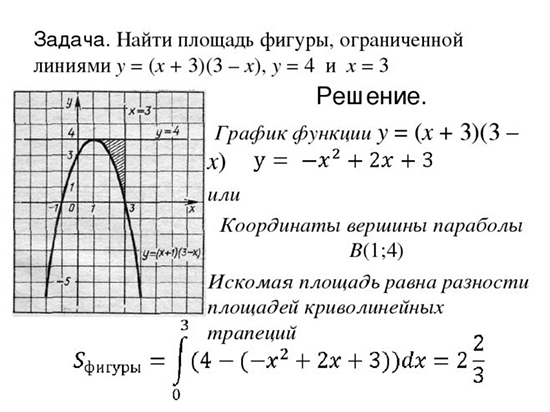 На диаграмме показана новая ситуация.
На диаграмме показана новая ситуация.
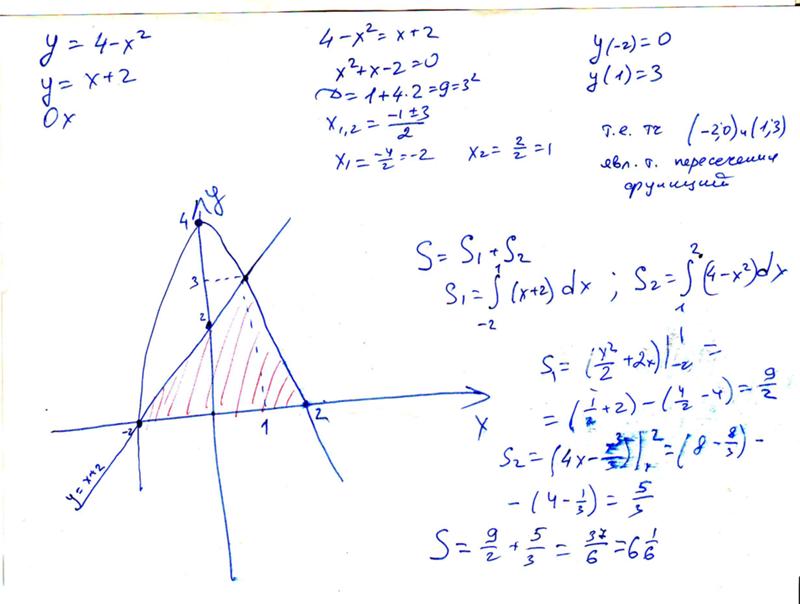

 Во сколько они снова уйдут?
Во сколько они снова уйдут? У одного 88, а у второго 56 зубов. Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо?
У одного 88, а у второго 56 зубов. Сколько раз поверните меньшее колесо, чтобы попасть в те же зубья, что и в начале? Сколько раз мы повернём самое большое колесо?

 Введем это понятие, чтобы отличать объектные высказывания от субъектных.
Введем это понятие, чтобы отличать объектные высказывания от субъектных. Проще говоря, высказывание — это серия OR, соединенных AND, как в примере ниже:
Проще говоря, высказывание — это серия OR, соединенных AND, как в примере ниже:
 СДНФ : для каждого набора переменных на которых функция=1, записывают минтерм ранга n , в которых с отрицанием берутся переменные = 0 на данном наборе. Все минтермы объединены дизъюнктивно.
СДНФ : для каждого набора переменных на которых функция=1, записывают минтерм ранга n , в которых с отрицанием берутся переменные = 0 на данном наборе. Все минтермы объединены дизъюнктивно.
 1 Привести к ДНФ формулу
1 Привести к ДНФ формулу
 Запишем СКНФ функции по данным задачи
Запишем СКНФ функции по данным задачи Любая помощь будет здорово.
Любая помощь будет здорово.
 Просто введите его ниже и нажмите
кнопка «Конвертировать»:
Просто введите его ниже и нажмите
кнопка «Конвертировать»: Некоторые действительные атомы: "
Некоторые действительные атомы: " 
 13].
13]. Анализируя последовательно результаты таких простейших явлений, как подбрасывание монеты, игральной кости, выброс карты из колоды и т.п., мы замечаем две особенности, присущие такого рода экспериментам. Во-первых, не представляется возможным предсказать исход последующего эксперимента по результатам предыдущих, как бы ни было велико число проведённых испытаний. Во-вторых, относительная частота определённых исходов по мере роста числа испытаний стабилизируется, приближаясь к определённому пределу [6, с.8].
Анализируя последовательно результаты таких простейших явлений, как подбрасывание монеты, игральной кости, выброс карты из колоды и т.п., мы замечаем две особенности, присущие такого рода экспериментам. Во-первых, не представляется возможным предсказать исход последующего эксперимента по результатам предыдущих, как бы ни было велико число проведённых испытаний. Во-вторых, относительная частота определённых исходов по мере роста числа испытаний стабилизируется, приближаясь к определённому пределу [6, с.8]. При 10 миллионах шарах вытянуть самое большое число (10000000) практически невозможно [7].
При 10 миллионах шарах вытянуть самое большое число (10000000) практически невозможно [7]. Таким образом, понятие вероятности использовалось на интуитивном уровне, но оно не было выделено в новую категорию. Тем не менее, античные ученые заложили прекрасный фундамент для возникновения этого научного понятия. В средние века, можно сказать, и зародилась теория вероятности, когда были приняты первые попытки математического анализа, таких азартных игр как кости, орлянка, рулетка [8].
Таким образом, понятие вероятности использовалось на интуитивном уровне, но оно не было выделено в новую категорию. Тем не менее, античные ученые заложили прекрасный фундамент для возникновения этого научного понятия. В средние века, можно сказать, и зародилась теория вероятности, когда были приняты первые попытки математического анализа, таких азартных игр как кости, орлянка, рулетка [8]. Тогда же теория вероятностей стала находить сферы своего применения – демографию, страховое дело, оценку ошибок наблюдений [8].
Тогда же теория вероятностей стала находить сферы своего применения – демографию, страховое дело, оценку ошибок наблюдений [8]. Эта тенденция в значительной степени объясняется тем, что большинство возникших в последние десятилетия новых математических дисциплин, которое ныне обозначается собирательным термином «кибернетика», оказалось тесно связанным с теорией вероятностей. Тем самым теория вероятностей стала чуть ли не самой первой по прикладному значению из всех математических дисциплин. При этом возникновение новых, в большинстве своем «порожденных» теорией вероятностей наук, скажем «теория игр», «теория информации», «страховая математика» или «стохастическая финансовая математика» привело к положению, при котором теорию вероятностей также приходится рассматривать как объединение большого числа разнородных и достаточно глубоко развитых математических дисциплин [10, с.4].
Эта тенденция в значительной степени объясняется тем, что большинство возникших в последние десятилетия новых математических дисциплин, которое ныне обозначается собирательным термином «кибернетика», оказалось тесно связанным с теорией вероятностей. Тем самым теория вероятностей стала чуть ли не самой первой по прикладному значению из всех математических дисциплин. При этом возникновение новых, в большинстве своем «порожденных» теорией вероятностей наук, скажем «теория игр», «теория информации», «страховая математика» или «стохастическая финансовая математика» привело к положению, при котором теорию вероятностей также приходится рассматривать как объединение большого числа разнородных и достаточно глубоко развитых математических дисциплин [10, с.4]. Случайным ли образом возникают мутации, насколько зависит историческое развитие от отдельной личности, можно ли считать Вселенную случайным отклонением от законов сохранения? [8]
Случайным ли образом возникают мутации, насколько зависит историческое развитие от отдельной личности, можно ли считать Вселенную случайным отклонением от законов сохранения? [8] Возможности теракта в метрополитене, экономического кризиса или ядерной войны – все это можно выразить в процентах. А главное, предпринимать соответствующие контрдействия исходя из полученных данных. [9]
Возможности теракта в метрополитене, экономического кризиса или ядерной войны – все это можно выразить в процентах. А главное, предпринимать соответствующие контрдействия исходя из полученных данных. [9] Опасней переходить дорогу по зебре, чем лететь на самолете.
Опасней переходить дорогу по зебре, чем лететь на самолете. Теория вероятностей – это одна из составляющих частей успеха. Если стремиться учитывать законы вероятностей и, в том случае, если вероятность неблагоприятная, предпринимать соответствующие контрдействия, то можно упростить себе жизнь в разы и сэкономить своё время, которое так ценно для каждого из нас.
Теория вероятностей – это одна из составляющих частей успеха. Если стремиться учитывать законы вероятностей и, в том случае, если вероятность неблагоприятная, предпринимать соответствующие контрдействия, то можно упростить себе жизнь в разы и сэкономить своё время, которое так ценно для каждого из нас. В. Теория вероятностей и математическая статистика [Текст]: учебное пособие/Т. В. Крупкина, С. В. Бабенышев, Е. С. Кирик. – Красноярск: Сибирский федеральный университет, 2007. – 199 с.
В. Теория вероятностей и математическая статистика [Текст]: учебное пособие/Т. В. Крупкина, С. В. Бабенышев, Е. С. Кирик. – Красноярск: Сибирский федеральный университет, 2007. – 199 с. Теория вероятности в жизни [Электронный ресурс]. – Режим доступа: https://allowwonder.com/teoriya-veroyatnosti-v-zhizni/ (дата обращения – 6.02.2018)
Теория вероятности в жизни [Электронный ресурс]. – Режим доступа: https://allowwonder.com/teoriya-veroyatnosti-v-zhizni/ (дата обращения – 6.02.2018) Возможность и действительность) в ситуациях неопределённости.
Возможность и действительность) в ситуациях неопределённости.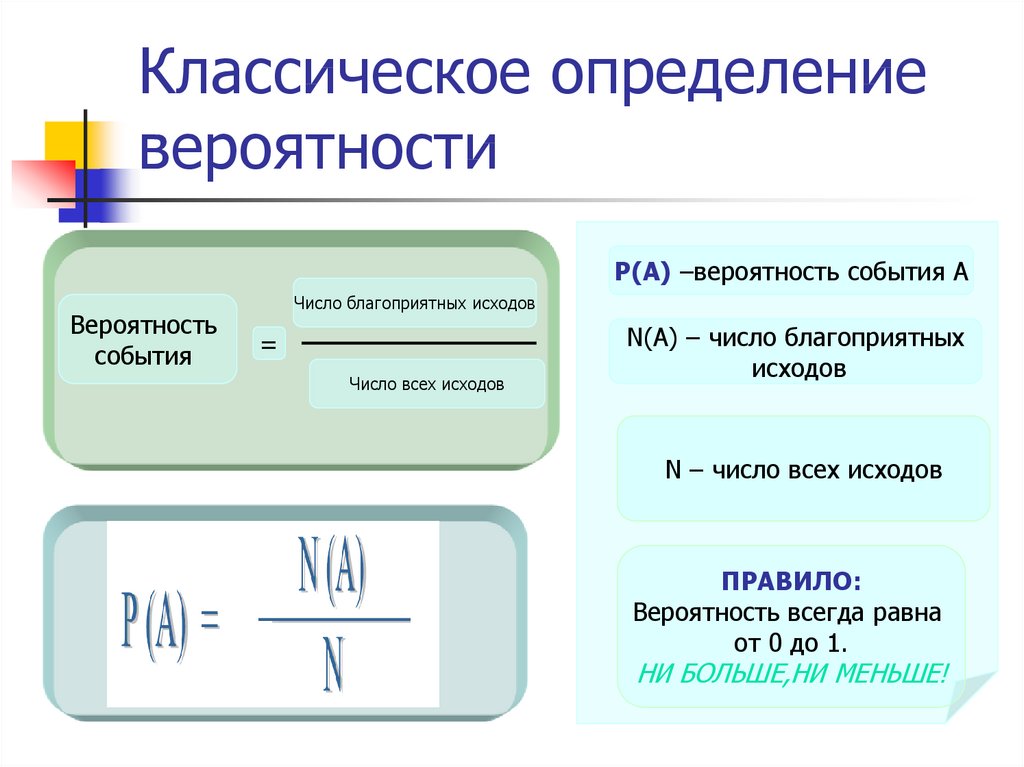 Воздействие идеи вероятности на научное мышление, на развитие познания прямо связано с разработкой теории вероятностей как математической дисциплины. Зарождение математического учения о вероятности относится к XVII веку, когда было положено начало разработке ядра понятий, допускающих количественную (числовую) характеристику и выражающих вероятностную идею. Интенсивные приложения вероятности к развитию научного познания приходятся на вторую половину XIX — первую половину XX века. Вероятность вошла в структуры таких наук, как физика, генетика, кибернетика, квантовая теория, теория информации и другие. Соответственно вероятность олицетворяет тот этап в развитии науки, который ныне определяется как неклассическая наука. Анализ природы вероятности в этих науках опирается на частотную, статистическую её трактовку, которая доминирует в научном познании, поскольку она наиболее достоверно отражает специфический характер закономерностей, присущих массовым явлениям случайного характера. Во многих физических, биологических, экономических, социальных процессах приходится учитывать действие множества случайных факторов, которые характеризуются устойчивой частотой.
Воздействие идеи вероятности на научное мышление, на развитие познания прямо связано с разработкой теории вероятностей как математической дисциплины. Зарождение математического учения о вероятности относится к XVII веку, когда было положено начало разработке ядра понятий, допускающих количественную (числовую) характеристику и выражающих вероятностную идею. Интенсивные приложения вероятности к развитию научного познания приходятся на вторую половину XIX — первую половину XX века. Вероятность вошла в структуры таких наук, как физика, генетика, кибернетика, квантовая теория, теория информации и другие. Соответственно вероятность олицетворяет тот этап в развитии науки, который ныне определяется как неклассическая наука. Анализ природы вероятности в этих науках опирается на частотную, статистическую её трактовку, которая доминирует в научном познании, поскольку она наиболее достоверно отражает специфический характер закономерностей, присущих массовым явлениям случайного характера. Во многих физических, биологических, экономических, социальных процессах приходится учитывать действие множества случайных факторов, которые характеризуются устойчивой частотой. Выявление этой устойчивой частоты и количественная её оценка с помощью вероятности даёт возможность раскрыть необходимость, которая прокладывает себе путь через совокупное действие множества случайностей.
Выявление этой устойчивой частоты и количественная её оценка с помощью вероятности даёт возможность раскрыть необходимость, которая прокладывает себе путь через совокупное действие множества случайностей. Случайность означает, что в рамках массовости бытие каждого элементарного явления не зависит и не определяется бытием других явлений. В то же время сама массовость явлений обладает устойчивой структурой, содержит определённые регулярности. Массовое явление вполне строго делится на подсистемы, и относительное число элементарных явлений в каждой из подсистем (относительная частота) весьма устойчиво. Эта устойчивость сопоставляется с вероятностью. Массовое явление в целом характеризуется распределением вероятностей, то есть заданием подсистем и соответствующих им вероятностей. Язык теории вероятностей есть язык вероятностных распределений. Соответственно теорию вероятностей и определяют как абстрактную науку об оперировании распределениями.
Случайность означает, что в рамках массовости бытие каждого элементарного явления не зависит и не определяется бытием других явлений. В то же время сама массовость явлений обладает устойчивой структурой, содержит определённые регулярности. Массовое явление вполне строго делится на подсистемы, и относительное число элементарных явлений в каждой из подсистем (относительная частота) весьма устойчиво. Эта устойчивость сопоставляется с вероятностью. Массовое явление в целом характеризуется распределением вероятностей, то есть заданием подсистем и соответствующих им вероятностей. Язык теории вероятностей есть язык вероятностных распределений. Соответственно теорию вероятностей и определяют как абстрактную науку об оперировании распределениями. Однако равновозможные случаи редко встречаются в действительности, и поэтому эта интерпретация уступила место частотной, или статистической, где вероятность рассматривается как относительная частота массовых случайных событий при достаточно длительных наблюдениях, число которых определяется характером событий. На практике было замечено, что такие события обладают устойчивой относительной частотой, и поэтому она практически принимается за вероятность, значение которой определяется статистическими исследованиями. Однако это эмпирическое определение вероятности не совпадает с теоретическим, и поэтому, например, Р. Мизес и его сторонники определяют вероятность как предел относительной частоты массовых событий, или статистических коллективов, при неограниченном числе наблюдений.
Однако равновозможные случаи редко встречаются в действительности, и поэтому эта интерпретация уступила место частотной, или статистической, где вероятность рассматривается как относительная частота массовых случайных событий при достаточно длительных наблюдениях, число которых определяется характером событий. На практике было замечено, что такие события обладают устойчивой относительной частотой, и поэтому она практически принимается за вероятность, значение которой определяется статистическими исследованиями. Однако это эмпирическое определение вероятности не совпадает с теоретическим, и поэтому, например, Р. Мизес и его сторонники определяют вероятность как предел относительной частоты массовых событий, или статистических коллективов, при неограниченном числе наблюдений. Поэтому для их интерпретации сначала стали обращаться к фактической вере субъекта, но так как она разная у различных людей, то в дальнейшем стали тем или иным способом модифицировать такой подход. В персоналистской интерпретации вероятности постулируется, что степени веры субъекта должны удовлетворять аксиомам теории вероятности, в других интерпретациях речь идёт о рациональной вере разумно действующего субъекта. Поэтому решения, принимаемые на основе такой вероятности, являются разумными и не зависят от индивидуальных особенностей и склонностей субъекта. Субъективный характер очень затрудняет количественную оценку величины вероятности в этих случаях и делает невозможным построение на базе такого понятия вероятности строгой науч. теории, помогающей понять объективно существующие закономерности (подробнее об имеющихся в этом направлений попытках см. Логика вероятностная).
Поэтому для их интерпретации сначала стали обращаться к фактической вере субъекта, но так как она разная у различных людей, то в дальнейшем стали тем или иным способом модифицировать такой подход. В персоналистской интерпретации вероятности постулируется, что степени веры субъекта должны удовлетворять аксиомам теории вероятности, в других интерпретациях речь идёт о рациональной вере разумно действующего субъекта. Поэтому решения, принимаемые на основе такой вероятности, являются разумными и не зависят от индивидуальных особенностей и склонностей субъекта. Субъективный характер очень затрудняет количественную оценку величины вероятности в этих случаях и делает невозможным построение на базе такого понятия вероятности строгой науч. теории, помогающей понять объективно существующие закономерности (подробнее об имеющихся в этом направлений попытках см. Логика вероятностная). Эти степени подтверждения заключены в интервале между 0 и 1, поэтому индуктивная логика оказывается разновидностью многозначной логики. В эмпирических науках типичным примером логической вероятности служит отношение между гипотезой и её свидетельствами, степенью подтверждения которых оценивается правдоподобие гипотезы. Относительно количественной оценки логической вероятности мнения разных авторов расходятся: одни считают, что она может быть выражена лишь в сравнительных терминах (больше, меньше и равно), другие — в метрических (численно).
Эти степени подтверждения заключены в интервале между 0 и 1, поэтому индуктивная логика оказывается разновидностью многозначной логики. В эмпирических науках типичным примером логической вероятности служит отношение между гипотезой и её свидетельствами, степенью подтверждения которых оценивается правдоподобие гипотезы. Относительно количественной оценки логической вероятности мнения разных авторов расходятся: одни считают, что она может быть выражена лишь в сравнительных терминах (больше, меньше и равно), другие — в метрических (численно). Проблема применимости вероятностных методов решается в рамках развития математической теории, углубления знания в соответствующих прикладных областях и осмысления накапливаемого опыта. Формализация понятия вероятности и терминов, связанных с ним, а также развитие соответствующего аналитического аппарата и методики решения прикладных задач при помощи вероятностных методов составляют содержание раздела математики — теории вероятности и родственных ей дисциплин: математической статистики, метода случайных испытаний, теории стохастического управления, теории принятия решений и ряда других.
Проблема применимости вероятностных методов решается в рамках развития математической теории, углубления знания в соответствующих прикладных областях и осмысления накапливаемого опыта. Формализация понятия вероятности и терминов, связанных с ним, а также развитие соответствующего аналитического аппарата и методики решения прикладных задач при помощи вероятностных методов составляют содержание раздела математики — теории вероятности и родственных ей дисциплин: математической статистики, метода случайных испытаний, теории стохастического управления, теории принятия решений и ряда других. — ГТТИ, 1935.
— ГТТИ, 1935. Вероятность и статистика. — М., Л., 1930.
Вероятность и статистика. — М., Л., 1930. — L.-NY, 1921.
— L.-NY, 1921. Два из них особенно важны для развития и приложений математической теории вероятностей. Одним из них является интерпретация вероятностей как относительных частот, примером чего могут служить простые игры с монетами, картами, костями и колесами рулетки. Отличительной особенностью азартных игр является то, что исход данного испытания нельзя предсказать с уверенностью, хотя совокупные результаты большого числа испытаний обнаруживают некоторую закономерность. Например, утверждение о том, что вероятность выпадения «орла» при подбрасывании монеты равна половине, согласно интерпретации относительной частоты, подразумевает, что при большом количестве подбрасываний относительная частота, с которой действительно выпадает «орел», будет приблизительно равна одной. -половина, хотя это не подразумевает исход любого данного броска. Есть много подобных примеров, связанных с группами людей, молекулами газа, генами и так далее. Актуарные заявления об ожидаемой продолжительности жизни для лиц определенного возраста описывают коллективный опыт большого числа людей, но не претендуют на то, чтобы сказать, что произойдет с каждым конкретным человеком.
Два из них особенно важны для развития и приложений математической теории вероятностей. Одним из них является интерпретация вероятностей как относительных частот, примером чего могут служить простые игры с монетами, картами, костями и колесами рулетки. Отличительной особенностью азартных игр является то, что исход данного испытания нельзя предсказать с уверенностью, хотя совокупные результаты большого числа испытаний обнаруживают некоторую закономерность. Например, утверждение о том, что вероятность выпадения «орла» при подбрасывании монеты равна половине, согласно интерпретации относительной частоты, подразумевает, что при большом количестве подбрасываний относительная частота, с которой действительно выпадает «орел», будет приблизительно равна одной. -половина, хотя это не подразумевает исход любого данного броска. Есть много подобных примеров, связанных с группами людей, молекулами газа, генами и так далее. Актуарные заявления об ожидаемой продолжительности жизни для лиц определенного возраста описывают коллективный опыт большого числа людей, но не претендуют на то, чтобы сказать, что произойдет с каждым конкретным человеком. Точно так же прогнозы о вероятности возникновения генетического заболевания у ребенка родителей с известным генетическим составом являются утверждениями об относительной частоте встречаемости в большом количестве случаев, но не являются прогнозами относительно данного человека.
Точно так же прогнозы о вероятности возникновения генетического заболевания у ребенка родителей с известным генетическим составом являются утверждениями об относительной частоте встречаемости в большом количестве случаев, но не являются прогнозами относительно данного человека. Набор всех возможных результатов эксперимента называется «выборочным пространством». Эксперимент с однократным подбрасыванием монеты приводит к выборке пространства с двумя возможными исходами: «орел» и «решка». Бросание двух игральных костей имеет выборочное пространство с 36 возможными исходами, каждый из которых может быть отождествлен с упорядоченной парой ( i , j ), где i и j принимают одно из значений 1, 2, 3, 4, 5, 6 и обозначают грани, показанные на отдельных костях. Важно думать о костях как об идентифицируемых (например, по разнице в цвете), чтобы результат (1, 2) отличался от (2, 1). «Событие» — это четко определенное подмножество выборочного пространства. Например, событие «сумма граней, выпавших на двух костях, равна шести» состоит из пяти исходов (1, 5), (2, 4), (3, 3), (4, 2) и ( 5, 1).
Набор всех возможных результатов эксперимента называется «выборочным пространством». Эксперимент с однократным подбрасыванием монеты приводит к выборке пространства с двумя возможными исходами: «орел» и «решка». Бросание двух игральных костей имеет выборочное пространство с 36 возможными исходами, каждый из которых может быть отождествлен с упорядоченной парой ( i , j ), где i и j принимают одно из значений 1, 2, 3, 4, 5, 6 и обозначают грани, показанные на отдельных костях. Важно думать о костях как об идентифицируемых (например, по разнице в цвете), чтобы результат (1, 2) отличался от (2, 1). «Событие» — это четко определенное подмножество выборочного пространства. Например, событие «сумма граней, выпавших на двух костях, равна шести» состоит из пяти исходов (1, 5), (2, 4), (3, 3), (4, 2) и ( 5, 1). . Несмотря на простоту этого эксперимента, его глубокое понимание дает теоретическую основу для проведения опросов общественного мнения и выборочных опросов. Например, лица в популяции, поддерживающие определенного кандидата на выборах, могут быть идентифицированы шарами определенного цвета, те, кто поддерживает другого кандидата, могут быть идентифицированы другим цветом и так далее. Теория вероятностей обеспечивает основу для изучения содержимого урны по выборке шаров, извлеченных из урны; приложение должно узнать об электоральных предпочтениях населения на основе выборки, взятой из этого населения.
. Несмотря на простоту этого эксперимента, его глубокое понимание дает теоретическую основу для проведения опросов общественного мнения и выборочных опросов. Например, лица в популяции, поддерживающие определенного кандидата на выборах, могут быть идентифицированы шарами определенного цвета, те, кто поддерживает другого кандидата, могут быть идентифицированы другим цветом и так далее. Теория вероятностей обеспечивает основу для изучения содержимого урны по выборке шаров, извлеченных из урны; приложение должно узнать об электоральных предпочтениях населения на основе выборки, взятой из этого населения. В простом случае, когда лечение можно рассматривать как успех или неудачу, цель клинического испытания состоит в том, чтобы выяснить, приводит ли новое лечение к успеху чаще, чем стандартное лечение. Больных этим заболеванием можно определить по шарикам в урне. Красные шарики — это те пациенты, которые вылечились новым лечением, а черные шарики — те, кто не вылечился. Обычно есть контрольная группа, которая получает стандартное лечение. Они представлены второй урной с, возможно, другой долей красных шаров. Цель опыта по извлечению из каждой урны некоторого количества шаров состоит в том, чтобы на основе выборки выяснить, в какой урне больше красных шаров. Вариант этой идеи можно использовать для проверки эффективности новой вакцины. Возможно, самым крупным и известным примером было испытание вакцины Солка от полиомиелита, проведенное в 1954. Она была организована Службой общественного здравоохранения США и охватила почти два миллиона детей. Его успех привел к почти полной ликвидации полиомиелита как проблемы здравоохранения в промышленно развитых частях мира.
В простом случае, когда лечение можно рассматривать как успех или неудачу, цель клинического испытания состоит в том, чтобы выяснить, приводит ли новое лечение к успеху чаще, чем стандартное лечение. Больных этим заболеванием можно определить по шарикам в урне. Красные шарики — это те пациенты, которые вылечились новым лечением, а черные шарики — те, кто не вылечился. Обычно есть контрольная группа, которая получает стандартное лечение. Они представлены второй урной с, возможно, другой долей красных шаров. Цель опыта по извлечению из каждой урны некоторого количества шаров состоит в том, чтобы на основе выборки выяснить, в какой урне больше красных шаров. Вариант этой идеи можно использовать для проверки эффективности новой вакцины. Возможно, самым крупным и известным примером было испытание вакцины Солка от полиомиелита, проведенное в 1954. Она была организована Службой общественного здравоохранения США и охватила почти два миллиона детей. Его успех привел к почти полной ликвидации полиомиелита как проблемы здравоохранения в промышленно развитых частях мира. Строго говоря, эти приложения представляют собой задачи статистики, основу для которых дает теория вероятностей.
Строго говоря, эти приложения представляют собой задачи статистики, основу для которых дает теория вероятностей.
 Поскольку есть два возможных исхода для каждого броска, количество элементов в пространстве выборки равно 2 n . Из них только один исход соответствует отсутствию орла, поэтому требуемая вероятность равна 1/2 n .
Поскольку есть два возможных исхода для каждого броска, количество элементов в пространстве выборки равно 2 n . Из них только один исход соответствует отсутствию орла, поэтому требуемая вероятность равна 1/2 n . Исход случайного события не может быть определен до того, как оно произойдет, но может быть любым из нескольких возможных исходов. Считается, что фактический результат определяется случайностью.
Исход случайного события не может быть определен до того, как оно произойдет, но может быть любым из нескольких возможных исходов. Считается, что фактический результат определяется случайностью. -половина, хотя это не подразумевает исход любого данного броска. Есть много подобных примеров, связанных с группами людей, молекулами газа, генами и так далее. Актуарные заявления об ожидаемой продолжительности жизни для лиц определенного возраста описывают коллективный опыт большого числа людей, но не претендуют на то, чтобы сказать, что произойдет с каждым конкретным человеком. Точно так же прогнозы о вероятности возникновения генетического заболевания у ребенка родителей с известным генетическим составом являются утверждениями об относительной частоте встречаемости в большом количестве случаев, но не являются прогнозами относительно данного человека.
-половина, хотя это не подразумевает исход любого данного броска. Есть много подобных примеров, связанных с группами людей, молекулами газа, генами и так далее. Актуарные заявления об ожидаемой продолжительности жизни для лиц определенного возраста описывают коллективный опыт большого числа людей, но не претендуют на то, чтобы сказать, что произойдет с каждым конкретным человеком. Точно так же прогнозы о вероятности возникновения генетического заболевания у ребенка родителей с известным генетическим составом являются утверждениями об относительной частоте встречаемости в большом количестве случаев, но не являются прогнозами относительно данного человека. к важным научным вопросам.
к важным научным вопросам. Важно думать о костях как об идентифицируемых (например, по разнице в цвете), чтобы результат (1, 2) отличался от (2, 1). «Событие» — это четко определенное подмножество выборочного пространства. Например, событие «сумма граней, выпавших на двух костях, равна шести» состоит из пяти исходов (1, 5), (2, 4), (3, 3), (4, 2) и ( 5, 1).
Важно думать о костях как об идентифицируемых (например, по разнице в цвете), чтобы результат (1, 2) отличался от (2, 1). «Событие» — это четко определенное подмножество выборочного пространства. Например, событие «сумма граней, выпавших на двух костях, равна шести» состоит из пяти исходов (1, 5), (2, 4), (3, 3), (4, 2) и ( 5, 1). Теория вероятностей обеспечивает основу для изучения содержимого урны по выборке шаров, извлеченных из урны; приложение должно узнать об электоральных предпочтениях населения на основе выборки, взятой из этого населения.
Теория вероятностей обеспечивает основу для изучения содержимого урны по выборке шаров, извлеченных из урны; приложение должно узнать об электоральных предпочтениях населения на основе выборки, взятой из этого населения. Они представлены второй урной с, возможно, другой долей красных шаров. Цель опыта по извлечению из каждой урны некоторого количества шаров состоит в том, чтобы на основе выборки выяснить, в какой урне больше красных шаров. Вариант этой идеи можно использовать для проверки эффективности новой вакцины. Возможно, самым крупным и известным примером было испытание вакцины Солка от полиомиелита, проведенное в 1954. Она была организована Службой общественного здравоохранения США и охватила почти два миллиона детей. Его успех привел к почти полной ликвидации полиомиелита как проблемы здравоохранения в промышленно развитых частях мира. Строго говоря, эти приложения представляют собой задачи статистики, основу для которых дает теория вероятностей.
Они представлены второй урной с, возможно, другой долей красных шаров. Цель опыта по извлечению из каждой урны некоторого количества шаров состоит в том, чтобы на основе выборки выяснить, в какой урне больше красных шаров. Вариант этой идеи можно использовать для проверки эффективности новой вакцины. Возможно, самым крупным и известным примером было испытание вакцины Солка от полиомиелита, проведенное в 1954. Она была организована Службой общественного здравоохранения США и охватила почти два миллиона детей. Его успех привел к почти полной ликвидации полиомиелита как проблемы здравоохранения в промышленно развитых частях мира. Строго говоря, эти приложения представляют собой задачи статистики, основу для которых дает теория вероятностей. Другой пример — крутить спиннер. Для идеализированного счетчика, состоящего из отрезка прямой линии, не имеющего ширины и повернутого в его центре, набор возможных исходов представляет собой набор всех углов, которые конечная позиция счетчика образует с некоторым фиксированным направлением, что эквивалентно всем действительным числам в [0 , 2π). Многие измерения в естественных и социальных науках, такие как объем, напряжение, температура, время реакции, предельный доход и т. д., производятся на непрерывных шкалах и, по крайней мере, теоретически включают бесконечное множество возможных значений. Если повторные измерения на разных субъектах или в разное время на одном и том же субъекте могут привести к разным результатам, теория вероятностей является возможным инструментом для изучения этой изменчивости.
Другой пример — крутить спиннер. Для идеализированного счетчика, состоящего из отрезка прямой линии, не имеющего ширины и повернутого в его центре, набор возможных исходов представляет собой набор всех углов, которые конечная позиция счетчика образует с некоторым фиксированным направлением, что эквивалентно всем действительным числам в [0 , 2π). Многие измерения в естественных и социальных науках, такие как объем, напряжение, температура, время реакции, предельный доход и т. д., производятся на непрерывных шкалах и, по крайней мере, теоретически включают бесконечное множество возможных значений. Если повторные измерения на разных субъектах или в разное время на одном и том же субъекте могут привести к разным результатам, теория вероятностей является возможным инструментом для изучения этой изменчивости.
 )
) )
) )
) )
) )
)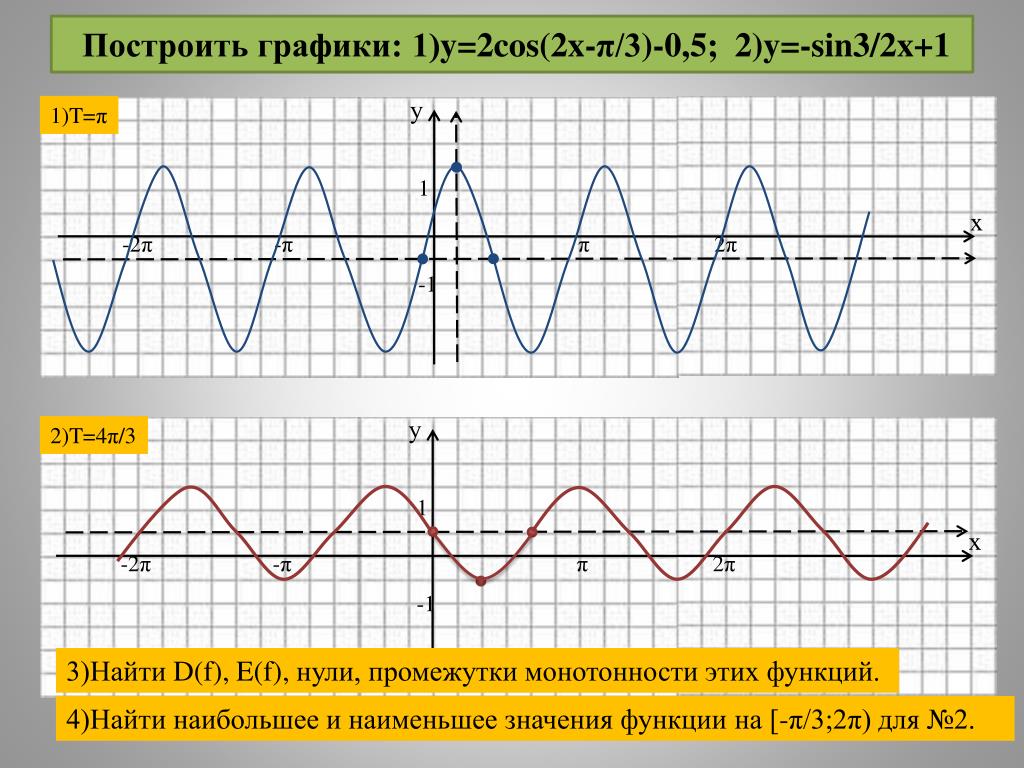 )
) )
) )
) 10.21
10.21
 )/3
)/3
 Разложим левую часть уравнения (2) на множители:
Разложим левую часть уравнения (2) на множители:




 2 + b*x + c = 0,где x- переменная, a,b,c – константы; a<>0. Задача состоит в отыскании корней уравнения.
2 + b*x + c = 0,где x- переменная, a,b,c – константы; a<>0. Задача состоит в отыскании корней уравнения. 2 и осуществим преобразование
2 и осуществим преобразование 2+x-6=0.
2+x-6=0.
 2+(2а+6)х-3а-9=0 имеет более одного корня?
2+(2а+6)х-3а-9=0 имеет более одного корня?
 Мы также рассмотрим несколько примеров и объясним, почему в этих случаях существует бесконечное число решений.
Мы также рассмотрим несколько примеров и объясним, почему в этих случаях существует бесконечное число решений. Например, sin(x) = 0 имеет бесконечно много решений, поскольку каждое целое число, кратное π радианам, является решением (таким образом, π, 2π, 3π, 4π,… все являются решениями).
Например, sin(x) = 0 имеет бесконечно много решений, поскольку каждое целое число, кратное π радианам, является решением (таким образом, π, 2π, 3π, 4π,… все являются решениями). Итак, исходное уравнение имеет бесконечное число решений — подойдет любое реальное значение x!
Итак, исходное уравнение имеет бесконечное число решений — подойдет любое реальное значение x!
 Ниже вы можете увидеть график, показывающий некоторые точки пересечения y = 2sin(x) и y = 1.
Ниже вы можете увидеть график, показывающий некоторые точки пересечения y = 2sin(x) и y = 1. Существует бесконечное количество решений уравнения уравнение cos(x) = 1.
Существует бесконечное количество решений уравнения уравнение cos(x) = 1. У уравнения sin(x) = cos(x) есть бесконечные решения.
У уравнения sin(x) = cos(x) есть бесконечные решения.






