Бизнес — планирование. СПО. Итог [Архив]
Какие категории работников составляютвнутренний торговый персонал?
Выберите один ответ:
1. Коммерческие представители
2. Продавцы в торговых залах
3. Брокеры
4. Агенты
Какой показатель располагают в знаменателе
при расчете рентабельности инвестиций по
прибыли, остающейся в распоряжении
организации в десятичном виде?
выберите один ответ:
1. Дополнительная прибыль, остающаяся в распоряжении организации от данной операции
2. Себестоимость, обеспечивающая реализацию проектируемого технического изделия
3. инвестиции, обеспечивающие реализацию проектируем°ro технического изделия
4. Дополнительный доход, остающийся в распоряжении организации от данной операции
С чем связаны преимущества высшего уровня?
Выберите один ответ:
1. с использованием дорогих ресурсов
2. С оригинальностью конструкции, уникальностью технологии, высокой квалификацией специалистов и репутацией организации
3. монопольное положение компании на рынке
4. СС использованием недорогих ресурсов
Какие действия осуществляются при
конкуренции качества?
Выберите один ответ:
1. Продажа по той же цене, что и у конкурентов, более качественного или универсального товара
2. Предложение аналогичного товара по более низкой цене
3. Обеспечение своих изделий более надежным послепродажным обслуживанием товара по более высокой цене
Что представляет собой изделие аналогичного
назначения?
Выберите один ответ:
1. Изделие, на основе которого создается новое изделие
2. изделие, которое не имеет аналогов
3. изделие, у которого есть аналоги
4. изделие, которое заменяется в эксплуатации новым изделием
Какое средство маркетинга включает в себя
каталоги?
выберите один ответ:
(прямая почтовая рассылка
1. Печатные медиа
2. Буклеты
3. Рекламные подарки
Какие элементы включает в себя расчет
себестоимости выполняемых работ (услуг)?
Выберите один ответ:
1. Затраты на амортизацию
2. Стоимость сооружений и оборудования ремонтных организаций
3. Стоимость сооружений и оборудования организации, эксплуатирующих изделие
4. сопутствуюшие капиталовложения
Какой элемент относится к сегментам рынка?
выберите один ответ:
1. Доходы
2. Цена
3. удобство
Что означают мощности как аспект бизнес-
деятельности?
Выберите один ответ:
1. количество требующихся работников
2. Количество времени и человеческих ресурсов, необходимое для производства товаров или услуг
3. Мера количества продукции, которую может выпустить раоочая сила, применяя имеющиеся здания, сооружения и орудование
4. Мероприятия, осуществляемые с целью поддержания стандартов для каждого товара или услуги
mti.prioz.ru
Бизнес-планирование одо 4 курс, 8 сем. зачет с ответами
1. (40c.) Как называется человек занимающийся бизнесом?
(один ответ)
1) бизнесмен;
2) комермант;
3) предприниматель;
4) все ответы верны;
Правильные ответы
4.
2. (40c.) Предпринимательская деятельность, предпринимательство представляет собой?
(один ответ)
1) барыга;
2) лица, осуществляющие инициативную деятельность на свой риск;
3) инициативную самостоятельную деятельность граждан и их объединений направленную на получение прибыли;
Правильные ответы
3.
3. (60c.) Бизнес — это;
(один ответ)
1) любое занятие, дело, приносящее доход;
2) совокупность отношений между всеми его участниками, образующими команду единомышленников с целью
Получения дохода, прибыли, развития фирмы, предприятия, организации;
3) приносящая доход деятельность граждан, имеющих собственность
4) верно 1 и 2;
5) верно 2 и 3;
6) верны все варианты ответа;
Правильные ответы
6.
4. (60c.) Кто выступает в виде участников бизнеса;(несколько вариантов ответа)
(несколько ответов)
1) работники, осуществляющие трудовую деятельность;
2) предприятия;
3) предпринематели;
4) обычные люди;
Правильные ответы
1.3.
5. (40c.) Бизнес как система представляет собой явление, наделенное четырьмя свойствами, какими;
(один ответ)
1) целесообразностью, целостностью, противоречивостью и активностью;
2) целесообразностью, объективностью, противоречивостью и активностью;
3) целесообразностью, правдивостью, противоречивостью и активностью;
4) целесообразностью, решительностью, противоречивостью и активностью;
Правильные ответы
1.
6. (60c.) В 1980-е гг. наблюдался бум предпринимательства, в основе которого лежали многие причины, в том числе;
(несколько вариантов ответа)
(несколько ответов)
1) вступление мировой экономики в очередной этап НТР;
2) высокая степень ориентации на нововведения;
3) обострение конкурентной борьбы;
4) повышение уровня образования кадров;
Правильные ответы
1.3.4.
7. (40c.) Интрапренеры — это;
(один ответ)
1) это предприниматели, добившиеся успеха;
2) это новаторы, добившиеся реализации своих новаторских идей;
3) бизнесмены потерпевшие неудачу;
Правильные ответы
2.
8. (40c.) Основной чертой интрапренерства являются;
(один ответ)
1) высокая степень ориентации на нововведения;
2) высокие показатели;
3) низкая рентабельность;
4) стабильность государственной и социальной политики;
Правильные ответы
1.
9. (40c.) Считается, что отрицательное воздействие на развитие предпринимательской деятельности оказывают
Следующие факторы:
(один ответ)
1) высокие налоговые ставки;
2) психология исключительности;
3) низкая норма накопления;
4) все варианты верны;
Правильные ответы
4.
10. (40c.) Как по другому называют бизнес-планирование;
(один ответ)
1) предпрининимательское планирование;
2) комерческое планирование;
3) деловое планирование;
4) индивидуальное планирование;
Правильные ответы
3.
11. (40c.) Бизнес-планирование — это;
(один ответ)
1) самостоятельный вид плановой деятельности, которая непосредственно связана с предпринимательством;
2) самостоятельный вид деятельности, которая непосредственно связана с предпринимательством;
3) самораскрытие для себя чего-то нового, которое непосредственно связано с предпринимательством;
Правильные ответы
1.
12. (40c.) Какое формальное планирование, безусловно, требует усилий;
likedoc.top
Тест Бизнес-планирование
1) Входит ли в структуру биснес-плана организационный и финансовый планы :
1. Да;
2. Нет;
3. Только организационный;
4. Только финансовый;
5. Только маркетинговый и план производства;
2) Проектирование организационной структуры управления предпологает планирование:
1. Управленческих групп;
2. Управленческих команд;
3. Связей между управленческими группами и командами;
4. Верно 1 и 2;
5. Все ответы верны
3)Выбрать верное утверждение.
А. Для реализации бизнес-рлана важно, чтобы оргструктура управления соответствовала принятой стратегии и кадровой политики предприятия;
Б. Организационная структура управления не является основанием для разработки штатного расписания;
В. Организационная структура управления служит основанием для разработки штатного расписания;
1. Верно только А
2. Верно только Б
3. Верно только В
4. Верно А и Б
5. Верно А и В
4) Ключевые менеджеры это —
А. Менеджеры, занимающие основные руководящие посты;
Б. Менеджеры отвечающие за разработку концепции и стратегии компании;
В. Все менеджеры являются ключевыми;
1. Верно только А
2. Верно только Б
3. Верно только В
4. Верно А и Б
5. Все варианты верны
5) Информация по ключевым менеджерам должна включать в себя :
А. ФИО, год рождения;
Б. Номер и серия паспорта;
В. Стаж работы;
Г. Занимаемая должность;
Д. Уровень и условия вознаграждения;
1. А, В, Д;
2. Б, Г, Д;
3. А, Б, В, Г, Д;
4. А, Г, Д;
5.А, Б, Г;
6) В случае предпологаемого расширения существующей команды менеджеров необходимо указать потребности в руководящих работниках, а именно:
1. Должности;
2. Основные обязанности и полномочия
3. Требуемая квалификация и опыт
4. Процесс найма персонала
5. Сроки занятости
6. Ожидаемый вклад в успех компании
7. Уровень и условия вознаграждения
А. 1,3,5,7
Б. 2,4,6,8
В. 1,2,5,7
Г. 1,2,3,4,5,6,7,8
Д. 3,4,7,8
7) Кадровая политика —
А. Система правил и норм работы с персоналом;
Б. Обеспечивает процессы воспроизводства, управления и развития персонала;
В. Осуществляется в соответствии с выбранной стратегией организации;
1. Верно только А
2. Верно только Б
3. Верно только В
4. Нет правильного ответа
5. Все ответы верны
8) При разработке календарного плана учитываются:
1. Затраты времени на выполнение работ;
2. Сроки выполнения;
3. Последовательность проведения работ;
4. Учитываются только 1 и 2
5. Учитывается все 1,2,3
9) Затраты времени на выполнение работ это затраты на :
А. Государственную регистрацию;
Б. Оформление лицензий;
В. Заключение договоров аренды помещений;
Г. Разработка рабочего проекта;
1. А,В,Г
2. А,Б,Г
3. Б,В,Г
4. А,Б,В, Г
5. А,Г
10) В финансовом плане необходимо отразить следующие разделы:
А. Прибыль;
Б. Цены на продукцию;
В. Денежный поток;
1. Верно только А
2. Верно только Б
3. Верно только В
4. Верно А и Б
5. Верно А и В
6. Верно Б и В
11) Предпринимателям и менеджерам финансовый план показывает:
1. Какое соотношение запланированных доходов от продаж и ожидаемых расходов;
2. На какую прибыль можно расчитывать в результате осуществления проекта и реализации выбранной стратегии;
3. Когда и откуда ожидается поступление денежных средств;
4. Каким будет финансовое положение предприятия к концу года;
5 Все ответы верны;
12) Потенциальным инвесторам(кредиторам) финансовый план позволяет получить ответы на вопросы:
А. Сколько реально потребуется денежных средств;
Б. На получение какой прибыли можно расчитывать;
В. Какова экономическая эффективность проекта;
1. Верно А и Б;
2.Верно А и В;
3. Верно Б и В
4. Верно А
5. Верно А, Б, В;
13) Финансовый раздел бизнес-плана включает в себя разработку трех основных документов:
А. План прибылей и убытков;
Б. Реестр цен;
В. План денежных потоков;
Г. Баланс;
1. А,Б, В;
2. А,В,Г;
3. Б,В,Г;
4. Нет правильного ответа;
5. Все ответы верны;
14) Активы складываются из:
А. Текущие активы;
Б. Побочные активы;
В. Основные активы;
Г. Прочие активы;
1. А,Б,В;
2. Б,В,Г;
3. А,В,Г;
4. А,Б;
5. А,Б,В,Г;
15) Чистая прибыль равна:
1. Выручка + Затраты;
2. Выручка — Затраты;
3. Выручка × Затраты;
4. Выруча / Затраты;
5. Выручка = Чистая прибыль;
16) План денежных потоков включает :
А. Инвестиционная деятельность;
Б. Операционная деятельность;
В. Хозяйственная деятельность;
Г. Финансовая деятельность;
1. А,В,Г;
2. Б,В,Г;
3. В,Г;
4. А,Б,В,Г;
5. А,Б,Г;
17) Финансовый документ, который отражает доходы, расходы и финансовые результаты деятельности предприятия за определенный период :
1.План денежных потоков;
2. План прибылей и убытков;
3. Реестр цен;
4. Баланс;
5. Нет правильного ответа;
18) Показывает потоки денежных средств предприятия от операционной, инвестиционной и финансовой деятельности предприятия за период:
1.План денежных потоков;
2. План прибылей и убытков;
3. Реестр цен;
4. Баланс;
5. Нет правильного ответа;
19) Характеризует финансовое положение предприятия на определенную дату:
1.План денежных потоков;
2. План прибылей и убытков;
3. Реестр цен;
4. Баланс;
5. Нет правильного ответа;
20) Все виды издержек делят на две основные категории :
А. Относящиеся к переменным затратам;
Б. Относящиеся к постоянным затратам;
В. Относящиеся к переменным расходам;
Г. Относящиеся к постоянным расходам;
1. А,Б;
2. Б,В;
3. А,Г;
4. Б,Г;
5. А,Б,В,Г;
21) Включает в себя поступления денежных средств от покупателей, прочие поступления от текущей деятельности, а также выплаты поставщикам, работникам, уплату налогов и прочих платежей, возникающих непосредственно в результате текущей операционной деятельности предприятия:
1. Операционный денежный поток;
2. Финансовый денежный поток;
3. Хозяйственный денежный поток;
4. Инвестиционный денежный поток;
5. Нет правильного ответа;
22) Отражает платежи за приобретенное оборудование и прочие расходы, а также поступления от реализации активов, которые не используются в производстве:
1. Операционный денежный поток;
2. Финансовый денежный поток;
3. Хозяйственный денежный поток;
4. Инвестиционный денежный поток;
5. Нет правильного ответа;
23) Отражает поступление денежных средств от выпуска акций, в виде долгосрочных и краткосрочных кредитов, вкладов владельцев предприятия, а также платежи в виде выплаты дивидентов, процентов по кредитам, финансовые вложения свободных денежных средств:
1. Операционный денежный поток;
2. Финансовый денежный поток;
3. Хозяйственный денежный поток;
4. Инвестиционный денежный поток;
5. Нет правильного ответа;
24) Построение денежного потока проекта может быть осуществленно:
1. Прямым и обратным методами;
2. Прямым и косвенным методами;
3. Обратным и косвенным методами;
4. Все ответы верны;
5. Нет правильного ответа;
25) Баланс в финансовом плане составляется на конец первого года и характеризует:
А. Активы и пассивы фирмы;
Б. Средства, вложенные в развитие производства самим предпринимателем и его партнерами;
В. Нераспределенную прибыль;
1. Только А;
2.Только Б;
3. Только В;
4. А и В;
5. А,Б,В;
26) Выделяют три основных варианта финансирования:
А. Финансирование из собственных средств;
Б. Финансирование из заемных средств;
В. Частное финансирование;
Г. Государственное финансирование;
Д. Смешанное финансирование;
1. А,Б,В;
2. А,Б,Г;
3. А,Б,Д;
4. В,Г,Д;
5. Б,В,Г;
27) Риск — это:
1. «Вероятность того, что произойдет какое-нибудь неблагоприятное событие»;
2. Опасность, незащищенность от потерь или ущерба;
3. Вероятность (угроза) потери предприятием части своих ресурсов, недополучения доходов или появления дополнительных расходов в результате осуществления проекта;
4. Верно 2 и 3;
5. Все варианты ответа верны;
28) Виды рисков:
А. Производственный риск;
Б. Коммерческий риск;
В. Рыночный риск;
Г. Инфляционный риск;
Д. Финансовый риск;
Е. Научно-технический риск;
Ж. Политический риск;
З. Внешнеэкономический риск;
И. Чистый риск;
1. А,В,Д,Ж,И;
2. Б,Г,Е,З;
3. А,Б,В,Ж,Е,З;
4. А,Б,В,Г,Д,Е,Ж,З,И;
5. Б,В,Д,Е,З;
29) Риск связанный с падением спроса на продукт, колебаниями курса валют, неопределенностью действий конкурентов и т.д.:
1. Производственный риск;
2. Комерческий риск;
3. Рыночный риск;
4. Инфляционный риск;
5. Финансовый риск;
30) Риск, связанный с убытками от пожаров, несчастных случаев, катастроф и других стихийных бедствий:
1. Финансовый риск;
2. Научно-технический риск;
3. Политический риск;
4. Внешнеэкономический риск;
5. Чистый риск;
studfiles.net
Моделирование бизнес процессов 09.06.13 [Архив]
Что из себя представляет вход бизнес-системы?совокупность объектов, необходимых для выполнения процессов системы
Бизнес-процесс подразделения:
Выполняется в рамках отдельного подразделения
Имеет длину, меньшую нежели межфункциональный процесс
Чем определяется масштаб процесса?
Его сложностью
Его важностью для бизнес-системы в целом
Как следует использовать функциональный и процессный подход к управлению?
Они должны дополнять друг друга
В пользу какого термина Дж.Мартин отказался от использования термина «бизнес-процесс»?
Поток ценностей
Какой процесс реализуется в рамках границы структурного подразделения?
Бизнес-процесс подразделения
В связи с какими управленческими понятиями концепция получило в последнее время популярность понятие «бизнес-процесса»?
Реинжиниринг бизнес-процессов
Всеобщее управление качеством
Постоянное улучшение процессов
В связи с какими управленческими понятиями концепция получило в последнее время популярность понятие «бизнес-процесса»?
Реинжиниринг бизнес-процессов
Всеобщее управление качеством
Постоянное улучшение процессов
Можно ли отнести к ресурсам бизнес-процесса технологию его выполнения?
Да
Чем определяется уровень бизнес-процесса?
Степенью детальности его рассмотрения
Что в себя включает универсальная структурная схема бизнес-процесса?
Входы
Ресурсы
Деятельность по управлению бизнес-процессом
Выходы
Насколько обоснованным представляется противопоставление процессного и функционального подхода?
У данного противопоставления есть основания, но в целом оно непродуктивно
Межфункциональный процесс проходит сквозь:
Несколько подразделений
Результаты как базовые элементы процессов представляют собой:
Выберите один ответ:
Активные субъекты деятельности, объединенные в системы, взаимодействующие друг с другом и другими ресурсами
??Продукт процесса, воплощающий в себе ранее поставленные цели
Пассивные средства и предметы деятельности, используемые для выполнения процессов
Совокупность материальных, энергетических и информационных объектов, необходимых для выполнения процесса
Кто является клиентом основных процессов?
Внутренние клиенты
Другие процессы организации
Внешние клиенты
Конечные потребители
Организационно-обеспечивающие процессы – это:
Процессы жизнеобеспечения и поддержания заданных режимов функционирования бизнес-системы
Какими могут быть результаты процессов?:
Косвенные
Нематериальные
Прямые
Промежуточные
Материальные
Управляющая подсистема бизнес-системы является:
Субъектом прямой связи
Что такое обратная связь в рамках бизнес-процесса?:
Анализ и сопоставление результатов процесса с ранее поставленными целями
Человеческие ресурсы как базовые элементы процессов представляют собой:
Активные субъекты деятельности, объединенные в системы, взаимодействующие друг с другом и другими ресурсами
Цепочка создания ценность состоит из:
Совокупности взаимодействующих бизнес-процессов
Что можно отнести к преимуществам процессного подхода?
Возможность полноценного делегирования полномочий и ответственности за конечный результат
Обогащение труда сотрудников за счет интеграции их деятельности с деятельностью смежных подразделений, за счет освоения смежных операций процесса
Сокращение зависимости результатов деятельности от функциональной иерархии
Производственно-технологические процессы – это:
Процессы системы, связанные целью создания продукции, в дальнейшем передаваемой заказчику/потребителю
Что представляет собой процесс бизнес-системы?
Совокупность операций по обработке входа
Что не следует рассматривать в качестве отличительного признака бизнес-процесса?
Наращивание стоимости
Согласно ISO 9000: 2000 процесс – это:
Совокупность взаимосвязанных или взаимодействующих видов деятельности, преобразующая «входы» в «выходы»
Что можно отнести к числу недостатков функционального управления?
Большая часть реальных рабочих процессов в организациях и предприятиях включает множество функций, т. е. выходит за рамки отдельных подразделений
Функциональный подход стимулирует бюрократизацию деятельности организации
Функционально-ориентированная организация не стимулирует заинтересованность работников в конечном результате
Какой из представленных бизнес-процессов можно назвать самым длинным?
Межорганизационный
Можно ли говорить о процессном подходе как об особом направлении в современном менеджменте?
Выберите один ответ:
Скорее нет, чем да
Скорее да, чем нет
?? Как о самостоятельном направлении нет, но как о части другого направления — да
mti.prioz.ru
Тест по дисциплине экономика на тему Бизнес
Тест по теме «Бизнес — план»
1) Входит ли в структуру биснес-плана организационный и финансовый планы :
1. Да;
2. Нет;
3. Только организационный;
4. Только финансовый;
5. Только маркетинговый и план производства;
2) Проектирование организационной структуры управления предпологает планирование:
1. Управленческих групп;
2. Управленческих команд;
3. Связей между управленческими группами и командами;
4. Верно 1 и 2;
5. Все ответы верны
3)Выбрать верное утверждение.
А. Для реализации бизнес-рлана важно, чтобы оргструктура управления соответствовала принятой стратегии и кадровой политики предприятия;
Б. Организационная структура управления не является основанием для разработки штатного расписания;
В. Организационная структура управления служит основанием для разработки штатного расписания;
1. Верно только А
2. Верно только Б
3. Верно только В
4. Верно А и Б
5. Верно А и В
4) Ключевые менеджеры это —
А. Менеджеры, занимающие основные руководящие посты;
Б. Менеджеры отвечающие за разработку концепции и стратегии компании;
В. Все менеджеры являются ключевыми;
1. Верно только А
2. Верно только Б
3. Верно только В
4. Верно А и Б
5. Все варианты верны
5) Информация по ключевым менеджерам должна включать в себя :
А. ФИО, год рождения;
Б. Номер и серия паспорта;
В. Стаж работы;
Г. Занимаемая должность;
Д. Уровень и условия вознаграждения;
1. А, В, Д;
2. Б, Г, Д;
3. А, Б, В, Г, Д;
4. А, Г, Д;
5.А, Б, Г;
6) В случае предпологаемого расширения существующей команды менеджеров необходимо указать потребности в руководящих работниках, а именно:
1. Должности;
2. Основные обязанности и полномочия
3. Требуемая квалификация и опыт
4. Процесс найма персонала
5. Сроки занятости
6. Ожидаемый вклад в успех компании
7. Уровень и условия вознаграждения
А. 1,3,5,7
Б. 2,4,6,8
В. 1,2,5,7
Г. 1,2,3,4,5,6,7,8
Д. 3,4,7,8
7) Кадровая политика —
А. Система правил и норм работы с персоналом;
Б. Обеспечивает процессы воспроизводства, управления и развития персонала;
В. Осуществляется в соответствии с выбранной стратегией организации;
1. Верно только А
2. Верно только Б
3. Верно только В
4. Нет правильного ответа
5. Все ответы верны
8) При разработке календарного плана учитываются:
1. Затраты времени на выполнение работ;
2. Сроки выполнения;
3. Последовательность проведения работ;
4. Учитываются только 1 и 2
5. Учитывается все 1,2,3
9) Затраты времени на выполнение работ это затраты на :
А. Государственную регистрацию;
Б. Оформление лицензий;
В. Заключение договоров аренды помещений;
Г. Разработка рабочего проекта;
1. А,В,Г
2. А,Б,Г
3. Б,В,Г
4. А,Б,В, Г
5. А,Г
10) В финансовом плане необходимо отразить следующие разделы:
А. Прибыль;
Б. Цены на продукцию;
В. Денежный поток;
1. Верно только А
2. Верно только Б
3. Верно только В
4. Верно А и Б
5. Верно А и В
6. Верно Б и В
11) Предпринимателям и менеджерам финансовый план показывает:
1. Какое соотношение запланированных доходов от продаж и ожидаемых расходов;
2. На какую прибыль можно расчитывать в результате осуществления проекта и реализации выбранной стратегии;
3. Когда и откуда ожидается поступление денежных средств;
4. Каким будет финансовое положение предприятия к концу года;
5 Все ответы верны;
12) Потенциальным инвесторам(кредиторам) финансовый план позволяет получить ответы на вопросы:
А. Сколько реально потребуется денежных средств;
Б. На получение какой прибыли можно расчитывать;
В. Какова экономическая эффективность проекта;
1. Верно А и Б;
2.Верно А и В;
3. Верно Б и В
4. Верно А
5. Верно А, Б, В;
13) Финансовый раздел бизнес-плана включает в себя разработку трех основных документов:
А. План прибылей и убытков;
Б. Реестр цен;
В. План денежных потоков;
Г. Баланс;
1. А,Б, В;
2. А,В,Г;
3. Б,В,Г;
4. Нет правильного ответа;
5. Все ответы верны;
14) Активы складываются из:
А. Текущие активы;
Б. Побочные активы;
В. Основные активы;
Г. Прочие активы;
1. А,Б,В;
2. Б,В,Г;
3. А,В,Г;
4. А,Б;
5. А,Б,В,Г;
15) Чистая прибыль равна:
1. Выручка + Затраты;
2. Выручка — Затраты;
3. Выручка × Затраты;
4. Выруча / Затраты;
5. Выручка = Чистая прибыль;
16) План денежных потоков включает :
А. Инвестиционная деятельность;
Б. Операционная деятельность;
В. Хозяйственная деятельность;
Г. Финансовая деятельность;
1. А,В,Г;
2. Б,В,Г;
3. В,Г;
4. А,Б,В,Г;
5. А,Б,Г;
17) Финансовый документ, который отражает доходы, расходы и финансовые результаты деятельности предприятия за определенный период :
1.План денежных потоков;
2. План прибылей и убытков;
3. Реестр цен;
4. Баланс;
5. Нет правильного ответа;
18) Показывает потоки денежных средств предприятия от операционной, инвестиционной и финансовой деятельности предприятия за период:
1.План денежных потоков;
2. План прибылей и убытков;
3. Реестр цен;
4. Баланс;
5. Нет правильного ответа;
19) Характеризует финансовое положение предприятия на определенную дату:
1.План денежных потоков;
2. План прибылей и убытков;
3. Реестр цен;
4. Баланс;
5. Нет правильного ответа;
20) Все виды издержек делят на две основные категории :
А. Относящиеся к переменным затратам;
Б. Относящиеся к постоянным затратам;
В. Относящиеся к переменным расходам;
Г. Относящиеся к постоянным расходам;
1. А,Б;
2. Б,В;
3. А,Г;
4. Б,Г;
5. А,Б,В,Г;
21) Включает в себя поступления денежных средств от покупателей, прочие поступления от текущей деятельности, а также выплаты поставщикам, работникам, уплату налогов и прочих платежей, возникающих непосредственно в результате текущей операционной деятельности предприятия:
1. Операционный денежный поток;
2. Финансовый денежный поток;
3. Хозяйственный денежный поток;
4. Инвестиционный денежный поток;
5. Нет правильного ответа;
22) Отражает платежи за приобретенное оборудование и прочие расходы, а также поступления от реализации активов, которые не используются в производстве:
1. Операционный денежный поток;
2. Финансовый денежный поток;
3. Хозяйственный денежный поток;
4. Инвестиционный денежный поток;
5. Нет правильного ответа;
23) Отражает поступление денежных средств от выпуска акций, в виде долгосрочных и краткосрочных кредитов, вкладов владельцев предприятия, а также платежи в виде выплаты дивидентов, процентов по кредитам, финансовые вложения свободных денежных средств:
1. Операционный денежный поток;
2. Финансовый денежный поток;
3. Хозяйственный денежный поток;
4. Инвестиционный денежный поток;
5. Нет правильного ответа;
24) Построение денежного потока проекта может быть осуществленно:
1. Прямым и обратным методами;
2. Прямым и косвенным методами;
3. Обратным и косвенным методами;
4. Все ответы верны;
5. Нет правильного ответа;
25) Баланс в финансовом плане составляется на конец первого года и характеризует:
А. Активы и пассивы фирмы;
Б. Средства, вложенные в развитие производства самим предпринимателем и его партнерами;
В. Нераспределенную прибыль;
1. Только А;
2.Только Б;
3. Только В;
4. А и В;
5. А,Б,В;
26) Выделяют три основных варианта финансирования:
А. Финансирование из собственных средств;
Б. Финансирование из заемных средств;
В. Частное финансирование;
Г. Государственное финансирование;
Д. Смешанное финансирование;
1. А,Б,В;
2. А,Б,Г;
3. А,Б,Д;
4. В,Г,Д;
5. Б,В,Г;
27) Риск — это:
1. «Вероятность того, что произойдет какое-нибудь неблагоприятное событие»;
2. Опасность, незащищенность от потерь или ущерба;
3. Вероятность (угроза) потери предприятием части своих ресурсов, недополучения доходов или появления дополнительных расходов в результате осуществления проекта;
4. Верно 2 и 3;
5. Все варианты ответа верны;
28) Виды рисков:
А. Производственный риск;
Б. Коммерческий риск;
В. Рыночный риск;
Г. Инфляционный риск;
Д. Финансовый риск;
Е. Научно-технический риск;
Ж. Политический риск;
З. Внешнеэкономический риск;
И. Чистый риск;
1. А,В,Д,Ж,И;
2. Б,Г,Е,З;
3. А,Б,В,Ж,Е,З;
4. А,Б,В,Г,Д,Е,Ж,З,И;
5. Б,В,Д,Е,З;
29) Риск связанный с падением спроса на продукт, колебаниями курса валют, неопределенностью действий конкурентов и т.д.:
1. Производственный риск;
2. Комерческий риск;
3. Рыночный риск;
4. Инфляционный риск;
5. Финансовый риск;
30) Риск, связанный с убытками от пожаров, несчастных случаев, катастроф и других стихийных бедствий:
1. Финансовый риск;
2. Научно-технический риск;
3. Политический риск;
4. Внешнеэкономический риск;
5. Чистый риск;
infourok.ru

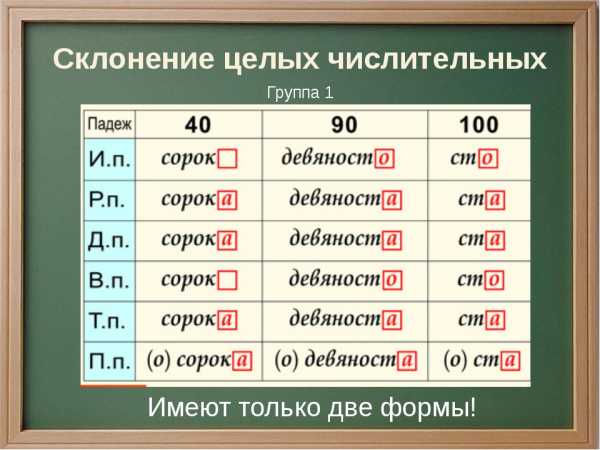
 Но я думаю вопрос был не в падежах. ДЕВЯНОСТО. так как это сложное слово и образовано оно от двух слов девять и сто. Такие имена числительные. В сочетании с предлогом по по девяноста и допустимо по девяносто числ. Таким образом. Существует много способов сделать так. чтобы окружающие не захотели иметь с вами ничего общего. Чтобы подтвердить эти слова. приведем несколько наглядных примеров Как видите.
Но я думаю вопрос был не в падежах. ДЕВЯНОСТО. так как это сложное слово и образовано оно от двух слов девять и сто. Такие имена числительные. В сочетании с предлогом по по девяноста и допустимо по девяносто числ. Таким образом. Существует много способов сделать так. чтобы окружающие не захотели иметь с вами ничего общего. Чтобы подтвердить эти слова. приведем несколько наглядных примеров Как видите.