Рубрика: Школьная жизнь

Бесекерский В.А. Сборник задач по теории автоматического регулирования и управления. Решебник по ТАУ.

Сборник задач по теории автоматического регулирования и управления, под редакцией В. А. Бесекерского

Сборник рассчитан на студентов, специализирующихся в области теории автоматического регулирования и следящих систем, а также студентов других специальностей, изучающих теорию автоматического регулирования и управления. Сборник, ориентируется на ряд используемых в вузах книг. В качестве основной принята книга В.А. Бесекерского и Е.П. Попова “Теория систем автоматического регулирования”. Построение сборника, содержание, терминология и методика изложения в основном соответствует этой книге.

Список решенных задач из данного задачника вы можете посмотреть ниже:

Если нужных вам задач нет в списке решенных напишите нам и мы в кратчайшие сроки выложим их на сайт.

РАЗДЕЛ I.
ЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

ГЛАВА 1.
Дифференциальные уравнения и передаточные функции звеньев и автоматических систем

§ 1.1. Дифференциальные уравнения и передаточные функции звеньев

§ 1.2. Типовые динамические звенья

§ 1.3. Дифференциальные уравнения и передаточные функции автоматических систем

§ 1.4. Структурные схемы и их преобразование

ГЛАВА 2.
Частотные характеристики динамических звеньев и систем автоматического регулирования

§ 2.1. Характеристики динамических звеньев

§ 2.2. Амплитудно-фазовые характеристики разомкнутых систем автоматического регулирования

§ 2.3. Вещественные частотные характеристики замкнутых систем автоматического регулирования

§ 2.4. Логарифмические характеристики систем автоматического регулирования

ГЛАВА 3.
Устойчивость линейных систем

§ 3.1. Алгебраические критерии устойчивости

§ 3.2. Критерий устойчивости Михайлова

§ 3.3. Критерий устойчивости Найквиста

§ 3.4. Определение устойчивости по логарифмическим частотным характеристикам разомкнутой системы

§ 3.5. Построение областей устойчивости

ГЛАВА 4.
Построение переходных процессов в системах автоматического регулирования

§ 4.1. Классический метод решения дифференциальных уравнений

§ 4.2. Применение изображений Лапласа и Карсона – Хевисайда

§ 4.3. Приближенные методы расчета переходных процессов

ГЛАВА 5.
Оценка качества регулирования

§ 5.1. Определение точности при наличии задающего воздействия

§ 5.2. Определение точности при наличии возмущающего воздействия

§ 5.3. Корневые методы оценки динамических свойств

§ 5.4. Оценка по кривой переходного процесса

§ 5.5. Интегральные оценки

§ 5.6. Частотные оценки динамических свойств

ГЛАВА 6.
Синтез линейных систем

§ 6.1. Выбор параметров САР по требуемой точности

§ 6.2. Алгебраические методы выбора параметров САР

§ 6.3. Частотные методы выбора параметров САР. Расчёт последовательных корректирующих устройств

§ 6.4. Расчёт дополнительных обратных связей и прямых параллельных корректирующих связей

§ 6.5. Расчёт систем комбинированного управления

§ 6.6. Расчёт последовательных корректирующих контуров, работающих на несущей частоте

Если нужных вам задач нет в списке решенных напишите нам и мы в кратчайшие сроки выложим их на сайт.

Сергей Пост Июль 27th, 2015

Posted In: Платные работы, Сборник задач по теории автоматического регулирования и управления под редакцией В.А.Бесекерского, ТАУ

www.zachet.ru

Решения задач зкз ТАУ

14

Задача 1.Линеаризовать уравнение характеристики элемента умножения y=x₁x₂в точке y₀=x₀₁x₀₂.Р е ш е н и е. В соответствии с малыми приращениями y₀+ Δy=(x₀₁+x₁)(x₀₂+x₂)= x₀₁x₀₂+x₀₁Δx₂+x₀₂Δx₁+Δx₁Δx₂= =y₀+x₀₁Δx₂+x₀₂Δx₁+ Δx₁Δx₂=y₀+x₀₁Δx₂+x₀₂Δx₁, пренебрегая малыми высшего порядка. Тогда вычитая значение y₀из левой и правой частей, получим y= x₀₁Δx₂+x₀₂Δx₁= k₁Δx₁+k₂Δx₂, где k₁= x₀₂; k₂=x₀₁, т.е. элемент умножения может быть приближенно представлен в виде сумматора и двух усилителей (линейных звеньев).Задача 2. Написать уравнения состояния и построить электронную модель системы, имеющей матрицы состояния:;C=.

Р е ш е н и е. В соответствии с матрицами А,В и С уравнения состояния запишем в виде:Тогда электронная модель с использованием идеальных интеграторов и усилителей будет иметь вид:

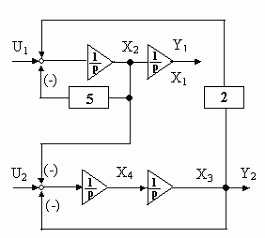
Задача 3. Начертить блок-схему и написать уравнения состояния системы, описываемой дифференциальным уравнением, где g — входная величина; y — выходная величина.Р е ш е н и е. Разрешим уравнение относительно старшей производнойи составим блок- схему ее получения рис.1

Рис.1 Блок-схема системы

В соответствии с выбранными переменными состояния на рис.2.8 запишем уравнения в нормальной форме

или в матричной форме где:

Задача 4. построить л.а.х. и л.ф.х. системы, описываемой передаточной функцией W(p)=100/(0.1p+1)(0.01p+1).Р е ш е н и е. Представим передаточную функцию в виде произведения элементарных звеньевНизкочастотный участок л.а.х. пойдет с наклоном 0 дБ/дек на уровне 20 lg 100= 40 дБ. Частоты сопряжения для апериодических составляющих будут соответственно ω₁=1/0.1=10 и ω₂=1/0.01=100. Фазочастотная характеристика строится в соответствии с уравнением Φ(ω)= arctg (0.1ω) + arctg (0.01ω). Ниже представлены графики л.а.х. и л.ф.х., соответствующие заданной передаточной функции.

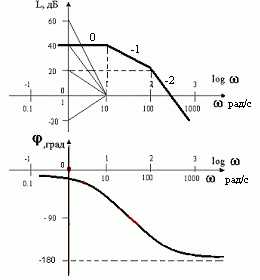
Задача 5. Определить передаточную функцию минимально-фазового устройства, л.а.х. которого представлена ниже

Рис. 1. Логарифмическая амплитудночастотная характеристика устройства

Р е ш е н и е. Двигаясь по л.а.х. в направлении возрастания частоты определяем, что звено принадлежит к дифференцирующему типу, т.к. наклон низкочастотного участка равен +20дБ/дек (+1). Передаточная функция равна W(p)=0.2p. При частоте излома л.а.х. ω=50 наклон меняется на -20дБ/дек (-1). Очевидно добавлены два звена с передаточной функциейТогда суммарная передаточная функция, соответствующая заданной л.а.х. будет иметь вид

Задача 6. Пользуясь правилами структурных преобразований привести представленную на рис.3.4. структурную схему замкнутой многоконтурной системы к одноконтурной и найти передаточные функции:

Рис.2. Структурная схема многоконтурной САУ

Р е ш е н и е:перед тем, как находить передаточные функции необходимо освободиться от перекрестных связей 1 и 2 на рис.3.4, для чего необходимо перенести или узел, или сумматор с добавлением соответствующих звеньев. Кроме того, целесообразно привести возмущающее воздействие f(t) ко входу САУ. Тогда получим схему на рис.3.5.

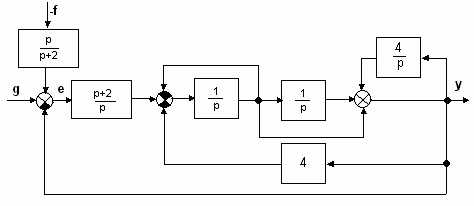Рис.3.5. Преобразованная структурная схема без перекрестных связей

Пользуясь правилами структурных преобразований свернем внутренние контура и получим одноконтурную замкнутую САУ на рис.3.

Рис.3. Одноконтурная структурная схема САУ

Тогда требуемые передаточные функции замкнутой САУ запишем в виде:

Найденные с помощью правил структурных преобразований передаточные функции позволяют достаточно просто определить временные и частотные характеристики, а так же получить качественные и количественные оценки динамики и статики САУ.

Задача 7. Определить критический коэффициент усиления Ккр системы, разомкнутая передаточная функция которой .Р е ш е н и е. Найдем характеристическое уравнение замкнутой системы D(p) = p*(p²+ p + 2) + k = p³+ p²+ 2p + k = 0. Для системы третьего порядка граница устойчивости из определителя (минора) определятся правилом: произведение средних членов характеристического уравнения равно произведению крайних при положительном первом члене, т.е. 2*1=1*К_кр. Откуда К_кр=2.

Задача 8.Определить количество правых корней m системы третьего порядка, годограф Михайлова которой имеет вид

Р е ш е н и е. Из рисунка видно, что при изменении частоты от 0 до +ω суммарный угол поворота годографа Михайлова равен -. Тогда в соответствии с формулой (4.3). Откуда число положительных корней m = 2.

Задача 9. Определить порядки астатизма по управляющему g(t) и возмущающему f(t) воздействиям САУ, структурная схема которой приведена на рис.5.11.

Рис.5.11. Структурная схема САУ

Р е ш е н и е. Сначала необходимо привести исходную структурную схеме к одноконтурной, как показано на рис.5.12.

Рис.5.12. Приведенная структурная схема

Из рис. 5.12 видно, что при охвате идеального интегратора отрицательной обратной связью получается апериодическое звено 1-го порядка. Поэтому пользуясь правилом определения порядка астатизма, приведенным выше, можно заключить, и по управляющему, и по возмущающему воздействию астатизм равен 1.

Задача 10. Определить предельное значение коэффициента передачи k нелинейного элемента из условия обеспечения абсолютной устойчивости нелинейной системы, передаточная функция линейной части которой

Р е ш е н и е.Амплитудно-фазовая характеристика линейной части

Тогда видоизмененная частотная характеристика

Изменяя частоту от 0 до построим видоизмененную частотную характеристику (рис.7.4).

Рис. 7.4. Видоизмененная частотная характеристика.

Вся характеристика W_лч*(jω) располагается во втором квадранте, поэтому линию (прямую) Попова предельную (наиболее близко подходящую к началу координат) можно провести через начало координат. В этом случае будет выполнятся условие, что вся видоизмененная а.ф.х. W*(jω) будет находится справа от прямой Попова. И предельный коэффициент нелинейного элемента К=находится из условия (1/К)=0, т.е. нелинейность для обеспечения абсолютной устойчивости может располагаться в угле arctg K=90°.

Задача 11.Определить возможную частоту автоколебаний при введении в САУ, имеющей ЛЧХ вида (рис.1), однозначной нелинейности в виде двухпозиционного реле.

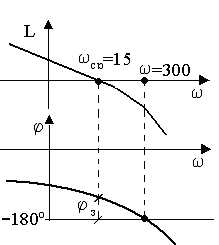Рис.1. ЛЧХ линейной части

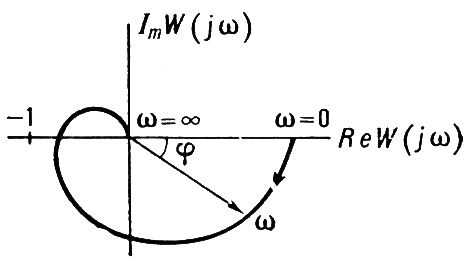
Р е ш е н и е. Известно, что характеристика — 1/W_нэ(jω,А) однозначного нелинейного элемента (двухпозиционного реле) полностью располагается на отрицательной действительной полуоси, поэтому а.ф.х. линейной части W_лч(jω) может ее пересечь только при угле -180°. Частота возможных автоколебаний определяется по W_лч(jω), а л.ф.х. (рис.7.8) показывает, что фазовый угол сдвига -180° происходит на частоте ω = 300 рад/с. Это и есть возможная частота автоколебаний при введении в САУ однозначной нелинейности.

Задача 12. Изобразить фазовые траектории для нелинейной системы с тремя различными нелинейностями — двухпозиционное реле, трехпозиционное реле с зоной нечувствительности (±0,2) и двухпозиционное реле с гистерезисом (±0,1), если линейная часть имеет передаточную функцию . Примем для всех нелинейностей величину сигнала на выходе реле ±2.Р е ш е н и е. В соответствии с заданием модель нелинейной системы можно представить в виде рис.7.10.

Рис.7.10. Модель нелинейной САУ

Тогда уравнения состояния (7.9) запишутся в виде

Разделив второе из уравнений на первое, получим уравнение фазовой траектории

В зависимости от того, с какой стороны от линии переключения реле находится изображающая точка, решения дифференциального уравнения будут следующие [2]: справа от линии переключения при x₁> 0 x₁= 4 ln |x₂+ 10| — 0,4x₂+ c₁; cлева от линии переключения при x₁< 0 x₁= 4 ln |x₂— 10| — 0,4x₂+ c₂; для трехпозиционного реле движение изображающей точки в пределах зоны нечувствительности -0,2<x₁<+0,2 соответствует уравнению x₁= — 0,4x₂+c₃, где с₁, с₂и с₃— постоянные интегрирования, зависящие от начальных условий. На рис. 7.11 изображены фазовые траектории нелинейной САУ с различными нелинейными элементами. Припасовывание или сшивание участков фазовых траекторий происходит по линиям переключений.

Задача 13. На рис.7.13 представлены АФХ -1/W_нэ(A) и W_лч(jω). Кроме того в нее вводится звено чистого запаздывания. Определить критическое время чистого запаздывания, при котором в нелинейной системе возникают автоколебания.

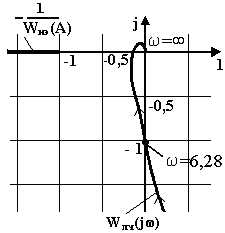Рис.7.13. АФХ нелинейности -1/W_нэ(A) и линейной части W_лч(jω)

Р е ш е н и е. Известно, что звено чистого запаздывания меняет только фазовый сдвиг и не меняет амплитуду сигнала. Ближайшее расстояние АФХ обратной передаточной функции нелинейного элемента от начала координат равно (-1). Модуль АФХ линейной части, равный единице, приобретает свое значение на частоте ω_ср= ω_кр= 6,28. Запас по фазе равен φ_кр= φ_зап= -90°=-π/2. Тогда τ_кр= φ_кр/ω_кр= 0,25 c.

Рис. 7.11. Фазовые траектории релейных систем

Анализируя фазовые траектории, можно сделать следующие выводы: 1. при взятых начальных условиях все системы устойчивы. Причем системы с двухпозиционными реле устойчивы «в большом»; 2. у систем с двухпозиционными реле наблюдаются устойчивые колебания. Абсцисса предельного цикла определяет амплитуду колебаний А_о, а частота может быть определена из ординаты предельного цикла А_оω_о; 3. система с трехпозиционным реле с зоной нечувствительности имеет «особый отрезок». Система может после прохождения переходного процесса занять любое значение внутри зоны нечувствительности, как показано на рис.7.11.

Задача 14. Определить дискретную передаточную функцию системы, непрерывная часть которой состоит из ПИ — регулятора и нейтрального объекта, а в качестве импульсного элемента используется экстраполятор нулевого порядка и экстраполятор с АИМ 1-го рода. Принять период дискретности Т₀=2с, общий коэффициент усиления К=20 с^-2, посто-янную времени τ=5 с, импульсы длительности γ=0,2 с.Р е ш е н и е. В соответствии с формулой (8.7) передаточная функция цифровой системы (экстраполятор нулевого порядка)

В соответствии с таблицами z — преобразований [2,6] находим

В соответствии с формулой (8.10) передаточная функция импульсной системы (экстраполятор с АИМ 1-го рода)

В соответствии с таблицами z — преобразований находим

Как видим, передаточные функции импульсной системы в значительной степени зависят от вида и параметров экстраполяторов, что необходимо

Задача 15.Построить логарифмические частотные характеристики импульсной системы с экстраполятором нулевого порядка, период дискретности которой T_o=2с, а передаточная функция непрерывной части

.

Р е ш е н и е. Выбираем частоту среза ω_cр<2/T_o<1 c^-1. В соответствии с заданными постоянными времени для непрерывной части определяем сопрягающую частоту ω_cопр1=1/5=0.2^c-1— низкочастотный диапазон. В соответствии с уравнением (8.18) передаточная функция от псевдочастоты будет иметь вид:

, где = 0.

В соответствии с уравнением (8.19) фазочастотная характеристика будет иметь вид:

На рис.8.9 представлены асимптотические ЛЧХ, соответствующие λ_ср=ω_ср=0,5; λ_сопр1=ω_сопр1=1/5=0,2; λ_сопр2=1/1=1. Коэффициент усиления К может быть выбран из условия прохождения среднечастотного участка через λ_срс наклоном -20 дБ/дек.

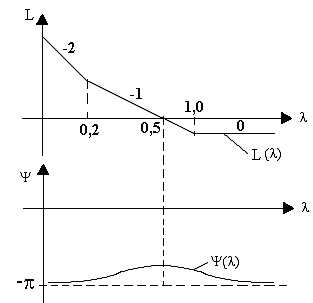Рис. 8.9. ЛЧХ импульсной системы

Задача 16. Дать заключение об устойчивости импульсной системы, характеристическое уравнение которой D(z)=10z³+4z²+6z+2+0.Р е ш е н и е. Для ответа на поставленный вопрос воспользуемся билинейным преобразованием, т.е. сделаем подстановку в характеристическое уравнение (8.11)

Тогда получим характеристическое уравнение от wD(w)=5w³+ 13w²+ 11w+ 11=0. Используя критерий Гурвица на основании линейной ТАУ для системы третьего порядка необходимым и достаточным условием устойчивости является произведение средних членов характеристического уравнения должно быть больше произведения крайних, т.е. 11*13 — 5*11 = 88>0. Таким образом импульсная система устойчива.

Задача 17.Написать разностное уравнение, связывающее выходную координату y[nT] и входное воздействие x[nT] импульсной системы, передаточная функция которой

Р е ш е н и е. В соответствии с дискретной передаточной функцией первоначально надо составить структурную схему в виде одной из форм рис.1. Представим заданную W(z) в форме 1

Домножим числитель и знаменатель W(z) на z^-2. В результате получим

Разностное уравнение имеет вид: y[n] -2y[n-1] +y[n-2] = 240 x[n-1] -160 x[n-2]. Тогда выходная переменная может быть получена, как (при нулевых начальных условиях) y[n] = 2y[n-1] -y[n-2] + 240 x[n-1] -160 x[n-2]. В соответствии с последним уравнением расчетная структурная схема представлена на рис.8.14

Рис.1. Расчетная структурная схема импульсной системы

Задача 18. Определить скоростную ошибку регулирования импульсной системы при подаче на вход управляющего воздействия g(t)=g₁t, если ее разомкнутая передаточная функция

Период квантования Т_о=2 с.Р е ш е н и е. В соответствии с формулой (8.22) и таблицей z — преобразований для линейно нарастающего сигнала, получим

Этот результат вполне закономерен, так как система обладает астатизмом второго порядка.

Задача 19. Пусть передаточная функция разомкнутой системы W(p)=k/(p(Tp+1)). На САУ подается полезный сигнал g(t)=g₁t и помеха «белый шум» со спектральной плотностью S_f(ω)=N. Определить систематическую ошибку m_εи среднеквадратическую ошибку σ. Структурная схема представлена на рис.1.

Рис.1. САУ со случайным сигналом

Р е ш е н и е. Систематическая ошибка определяется с применением коэффициентов ошибок

Тогда m_ε=0*g₁t + g₁(1/k)=g₁/k.Дисперсия ошибки по формуле (9.20)

Для системы второго порядка величина интеграла J2 вычисляется по формуле [2,19]

где т.е. b_o=0; a₂=k; b₁=k; a₀=T; a₁=1. Очевидно D_ε=Nk/2 или.

Из полученных результатов следует, что увеличение общего коэффициента передачи разомкнутой цепи системы k с одной стороны ведет к уменьшению установившегося значения систематической ошибки системы m_ε. В тоже время, для уменьшения дисперсии ошибки, вызванной помехой на входе, необходимо, чтобы значение общего коэффициента передачи разомкнутой цепи системы k было минимально.

Задача 20. Оценить свойства управляемости и наблюдаемости САУ, заданной уравнениями состояния

где:

Р е ш е н и е. Находим матрицу управляемости N_У=[B | AB]

Так как ранг r=2=n , то система полностью управляема. Находим матрицу наблюдаемости N_Н=[C^T| (CA)^T]

Так как ранг r=2=n, то САУ полностью наблюдаема.

Задача 21 . Определить управляемость САУ третьего порядка n=3 с одним управляющим воздействием m=1, представленных уравнениями состояния x=Ax + Bu с матрицами системы А и В вида

Р е ш е н и е. Тогда матрица управляемостиdet(N_y)=-27, rang(N_y)=n=3, т.е. система управляема.

studfiles.net

Решение задач по ТАУ

Решение задач по ТАУ
(смотрите также решение задач по материаловедению)

Как и многие другие специальные дисциплины, теория автоматического управления способна вызвать проблемы у студентов, которые сталкиваются с ней впервые. Теория вызывает чувство недоумения, а решение задач по ТАУ кажется чем-то не для земного ума. На самом деле, конечно, там нет ничего запредельно сложного (по крайней мере, в учебном курсе). Однако как переубедить эмоции, которые криком кричат – «Это какой-то кошмар!»?

ТАУ – это не только специальная, но и специфическая дисциплина. Понимание теории в ней само по себе требует достаточно специфического склада ума (впрочем, на профильных факультетах это нормально), но и затрат времени, не говоря уже о решении задач по ней. Увы, не все студенты могут затратить достаточно времени и сил на все предметы своего расписания. Некоторые работают и вынуждены тратить время на зарабатывание денег, другие предпочитают уделить внимание более важным для своего будущего предметам. Тем более далеко не во всех случаях ТАУ оказывается предметом, важным в реальной практической работе.

Но попробуйте объяснить это преподавателю, который ждёт от студентов полного погружения в свой предмет, и для него неважно, сколько ещё экзаменов в вашей сессии! Он потребует от вас понимания предмета, на которое надо тратить много времени. К тому же специфика здесь такова, что примеры задач по ТАУ не получится механически приложить к другим исходным условиям – нужно действительно понимать суть дисциплины.

Пример оформления задач по ТАУ нашими специалистами:

Есть ли универсальные методы решения задач по ТАУ? Как ни парадоксально, есть. Один из таких методов – решение задач по ТАУ на заказ. Мы предлагаем вам решения от самых лучших специалистов, преподавателей, знакомых не только с теорией автоматического управления как таковой, но и с учебными курсами по этому предмету. Предлагаем решение задач по различным системам автоматического управления (дискретным, линейным, нелинейным).

Мы поможем вам разобраться с самыми разными заданиями по ТАУ, с контрольными работами по этому предмету, с подготовкой к лабораторным работам, с решением задач для курсовых и дипломных работ и с подготовкой к защите учёных степеней. Мы также можем помочь вам с решением исследовательских задач в рамках исследовательских действий.

Выполненные нашими специалистами решения задач по ТАУ будут не только верными, но и подробными, с пояснениями по каждому шагу. Более того, такие задачи можно не только показать преподавателю и рассчитывать на хорошую оценку. Они станут для вас подспорьем в реальном освоении ТАУ, когда вы возьмётесь за это дело. А вы ведь возьмётесь, правда? Нам бы хотелось, чтобы наши услуги стали для вас не поводом отказываться от самостоятельной работы, а помощью в ней.

Вникнув в ход решения задачи, вы сможете не только вручить преподавателю распечатку, но и аргументированно пояснить своему преподавателю все шаги решения задачи. Кроме ответа, вы получаете набор практических знаний и рекомендаций по дальнейшему решению задач. Благодаря прямому сотрудничеству с автором вы получаете постоянные консультации в реальном времени, возможность уточнять и корректировать задание, и всё это за более чем разумную плату. В случае каких-либо изменений в содержании задания или сроках его сдачи вы можете сразу сообщить об этом нам, чтобы мы откорректировали план действий. Мы предлагаем также большой выбор вариантов оплаты (электронные деньги, банковские переводы и т.д.)

Примеры решений задач по ТАУ вы можете увидеть на нашем сайте (однако помните, что предмет достаточно нетривиален, и механическая подстановка данных одних задач в условия других может и не дать верного ответа!)

Заказать нам работу!

dx-dy.ru

Задачи теории автоматического управления

Теория автоматического управления изучает общие принципы построения автоматических систем и методы их исследования, независимо от физических процессов, протекающих в этих системах. Основными задачами теории управления являются исследования статических (или установившихся) и динамических свойств автоматических систем и разработка систем, свойства которых удовлетворяют заданным требованиям. При создании системы автоматического управления необходимо оценить её ожидаемое поведение при эксплуатации и предусмотреть такие технические решения устройства управления, которые обеспечили бы достижение требуемого результата управления во всех предусмотренных случаях функционирования объекта управления.

Управление представляет собой процесс, протекающий в реальном времени функционирования объекта управления. Этот процесс характеризуется изменением состояния объекта управления, изменением управляющих воздействий, изменением возмущений и т.д. Характер таких изменений может быть различным, в том числе и недопустимым с точки зрения цели функционирования объекта. Все эти особенности необходимо выявить ещё до реализации системы автоматического управления.

На рис. 8 показаны процессы, возможные в системе автоматического регулирования скорости вращения вала двигателя при разных характеристиках регулятора. Характеристики регулятора могут меняться в процессе его изготовления и настройки. Управляемой величиной в рассматриваемом примере является угловая скорость вращения вала двигателя. За единицу принята номинальная скорость вращения вала.

График 1 относится к случаю, когда двигатель медленно и плавно набирает обороты выходного вала до установления заданной скорости вращения. На внешние возмущения регулятор в этом случае будет реагировать медленно и переходные процессы в системе растягиваются во времени.

В случае 2 переходный процесс в системе также плавный, но протекает существенно быстрее, чем в первом случае. Следовательно, регулятор будет быстро реагировать на возникающие возмущения, плавно и быстро устраняя их последствия. Быстродействие системы высокое.

В случае, иллюстрируемом графиком 3, переходный процесс носит колебательный характер. Заданная скорость вращения устанавливается медленно, и процесс сопровождается периодическими колебаниями скорости вращения, которые постепенно затухают. При этом на начальном отрезке процесса наблюдается существенное превышение заданной скорости вращения вала, или перерегулирование. Перерегулирование, как правило, – нежелательное свойство системы автоматического управления. Колебательный процесс приводит к возникновению в системе знакопеременных динамических нагрузок, что является нежелательным свойством системы с колебательным переходным процессом.

В случае 4 процесс в системе также носит колебательный характер, однако с течением времени процесса колебания не только не затухают, но, наоборот, их амплитуда возрастает. Вал двигателя в этом случае будет вращаться в неустойчивом режиме: то останавливаясь, то набирая предельную скорость вращения. Использовать двигатель в таком режиме нельзя, и система автоматического управления становится неработоспособной. Системы с подобными свойствами называют неустойчивыми.

При проектировании системы автоматического управления необходимо стремиться получить наилучший процесс в системе, так чтобы нужный режим устанавливался плавно и за минимальное время. Проектируемая система должна иметь достаточно высокое быстродействие. Кроме того, отклонения управляемой величины от заданного значения (ошибка системы) не должны превышать допустимых значений. Система автоматического управления должна обеспечивать требуемую точность управления.

Во всех случаях система автоматического управления должна быть устойчивой и адекватно реагировать на задающие воздействия, переходя при изменении уставок в требуемый установившийся режим работы. При выводе системы из состояния установившегося равновесия внешними возмущениями система автоматически должна возвращаться в это состояние.

Предметом изучения теории автоматического управления являются методы, позволяющие описывать свойства системы автоматического управления математическими методами, исследовать поведение автоматической системы с использованием её математической модели и создавать системы автоматического управления с заданными свойствами.

Методы теории автоматического управления позволяют решать следующие задачи для систем автоматического управления:

• создание системы автоматического управления с заданными свойствами, определяющими быстродействие системы и точность управления (задача синтеза системы).

studfiles.net

Бороденко В.А. Сборник задач по ТАУ

1 Одномерные линейные непрерывные системы

1.1 Передаточная функция

1.1.1 Структурные преобразования Как правило, по структурной схеме при известных функциях

передачи отдельных звеньев требуется найти эквивалентную передаточную функцию (ПФ) некоторого объединения звеньев (объекта, регулятора), либо всей системы в целом. Для этого используют правила преобразования последовательного, параллельного и встречно-парал-лельного (с обратной связью) соединений.

Эквивалентная передаточная функция последовательно соединенных звеньев равна произведению передаточных функций этих звеньев. Считают, что перестановка последовательно включенных по пути сигнала звеньев не влияет на результат, т. е. W1W2 =W2W1.

Эквивалентная передаточная функция параллельно соединенных звеньев равна сумме передаточных функций этих звеньев (с учетом знака входа сумматора на пути сигнала).

Путь от входа к выходу системы называется прямой связью, от выхода ко входу – обратной связью. Если сигнал на пути меняет знак (обычно на инвертирующем входе сумматора), обратная связь называется отрицательной (ООС), если не меняет знак – положительной (ПОС). Замкнутый путь называется контуром, например, замкнутый контур обратной связи (ЗКОС). Эквивалентная передаточная функция соединения с обратной связью равна дроби, в числителе которой записана ПФ звена на прямом пути, а в знаменателе – единица минус произведение ПФ звеньев по замкнутому контуру обратной связи. Ве-

n

личина 1n 1 Wi называется определителем ЗКОС.

i 1

Особенности этого вида соединения звеньев:

-если в системе есть хоть одна обратная связь, передаточная функция системы будет всегда представлять собой дробь;

-знак перед произведением ПФ звеньев в знаменателе (в определителе ЗКОС) обычно противоположен знаку обратной связи.

Для систем с перекрещивающимися (мостиковыми) связями применяют правило переноса: в переносимую ветвь вводят фиктивное звено с передаточной функцией, равной ПФ потерянного, либо обратной ПФ появившегося при переносе элемента.

По Мейсону структурная схема может быть описана целиком, без деления на звенья. Передаточная функция многоконтурной системы образует дробь, числитель которой равен сумме произведений передаточных функций прямых путей на совокупные определители

studfiles.net

решение задач по ТАУ — FREEWRITERS

Вы изучаете теорию автоматического управления? Тогда вам будет полезна предлагаемая нашей группой авторов услуга «решение задач по ТАУ».

Пример оформления раздела РГР по ТАУ нашими специалистами:

Теория автоматического управления – дисциплина специфическая. И в большинстве случаев, чтобы справиться с задачами по ней, необходимо глубокое понимание темы и знание теории. Далеко не все студенты могут себе позволить тратить большое количество времени, чтобы разобраться во всех вопросах. Тем более что некоторые их них не так уж и важны, но задачи, связанные с ними все равно задаются преподавателями. Просто перечитать примеры задач по ТАУ, и решить поставленные перед вами по шаблону не получиться. Здесь нужно действительно разбираться в теме. Так что, если вы не уверены в своих силах, и просто не обладаете временем, необходимым для выполнения задания, обратитесь к специалистам в этой области. 

Что мы предлагаем в рамках предоставления услуги В состав нашей группы свободных авторов «Freewriters» входят специалисты, имеющие большой опыт работы с данной дисциплиной. Мы учитываем требования вашего вуза по оформлению задач. Обратившись к нам, клиент, которому необходимо решение задач по данному предмету, получает не просто готовый ответ. Мы предоставляем все необходимые пояснения по ходу решения задач, за счет чего вы можете защитить решение, и показать преподавателю свою компетентность. 

Решение ТАУ на заказ: какие задания мы выполняем Обращайтесь к нам, если вам необходимо выполнить домашнее задание по теории автоматического управления: 

— в рамках контрольных работ поданной дисциплине; 

— в ходе проведения лабораторных работ; 

— при выполнении курсовых и дипломных работ; 

— в рамках исследовательских действ мероприятий; 

— при подготовке к защите различных ученых степеней. 

Если вам нужно решение задач по дискретным, линейным или нелинейным системам автоматического управления, или любым другим разделам данной дисциплины, мы выполним их. 

Решение ТАУ: сотрудничество с автором напрямую Обратившись к нам, вы сотрудничаете с тем, кто занимается решением задач по ТАУ для вас, напрямую. А это значит, что при возникновении вопросов по порядку решения задач и их оформления вы всегда сможете оперативно получить ответ на них. 

Сотрудничество с исполнителем напрямую — это еще и приемлемая стоимость услуг. Ведь в этом случае отсутствуют какие-либо посредники, которым необходимо платить деньги. Возможность заказа онлайн и удобные для студентов варианты оплаты При обращении к нам вы можете оформить заявку на решение задач в режиме онлайн. Вам просто нужно будет отправить нам условие задачи при помощи специальной формы, указать особенности (если они есть) и ждать решения. Мы предлагаем различные варианты оплаты услуг. Вы можете заплатить при помощи банковской карточки, электронными деньгами и т.д. Специалисты, решающие для вас задачи на заказ, знакомы с общими требованиями для всех ВУЗов, а также со специфическими особенностями каждого учебного заведения. Так что, обращайтесь к нам смело, и мы без проблем решим любые задачи.

freewriters.narod.ru

задачи по практике ТАУ

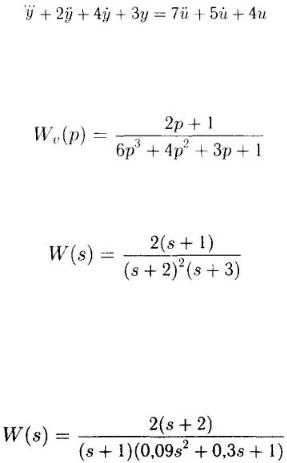
1.ЗАДАЧИ ПО ТАУ ДЛЯ МАГИСТРАНТОВ

1)Определить передаточную функцию в операторной форме системы управления, которая описываются следующим уравнением:

2)Записать дифференциальное уравнение системы управления передаточные функция которой имеет следующий вид:

3)Определить весовую и переходную функции для звена со следующей передаточной функцией:

4)Определить частотную передаточную функцию, вещественную, мнимую, амплитудную, фазовую, логарифмическую амплитудную частотные функции, переходную и весовую функции апериодического звена.

5)На вход системы подается сигналu = 2sin 0,5t. Определить в установившемся режиме реакцию системы со следующей передаточной функцией:

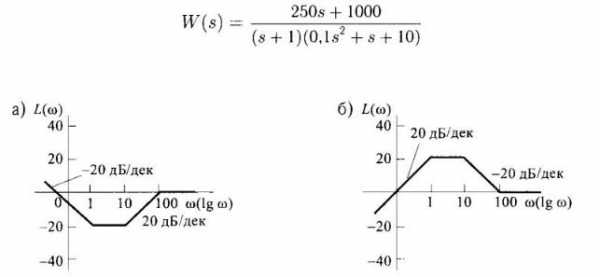
6)Построить асимптотическую ЛАЧХ звена со следующей передаточной функцией:

7)Записать передаточные функции звеньев, если их асимптотические ЛАЧХ имеют следующий вид:

8) Для системы на рисунке определить следующие передаточные функции (ПФ):

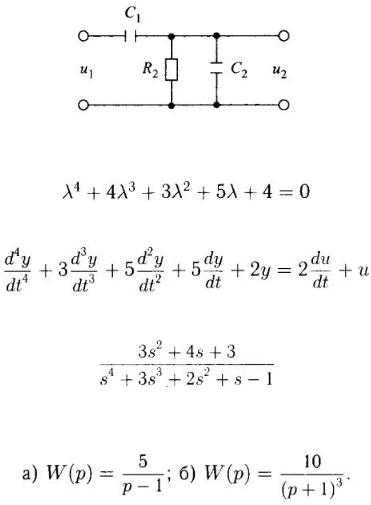
9) Составить передаточную функцию для пассивного четырехполюсника, показанного на рисунке: C1 = 4 мкФ, R2 = 200 кОм, С2 = 1 мкФ.

10)Исследовать устойчивость системы управления, у которой характеристическое уравнение имеет следующий

вид:

11)Исследовать устойчивость системы управления, которая описывается следующим уравнением:

12)Исследовать устойчивость замкнутой системы при следующей передаточной функции разомкнутой систе-

мы:

13)Пользуясь критерием Найквиста исследовать устойчивость замкнутой системы, если передаточная функция разомкнутой системы имеет вид:

14)Передаточная функция разомкнутой системы W(p) = k/(Тр+ 1)3. Определить область устойчивости замкнутой системы на плоскости параметров (к,Т).

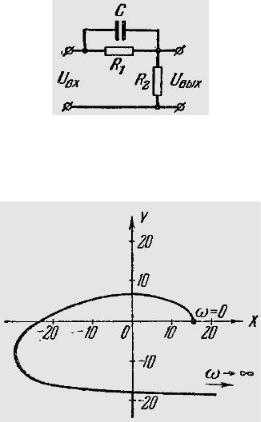
15) Найти уравнение кривой, представляющей собой амплитудно-фазовуюхарактеристику дифференцирующего звена, изображенного на рисунке. Построитьамплитудно-фазовуюхарактеристику звена для случаяR1 = 40

кОм, R2 = 10 кОм, С = 2,5 мкф.

16) Система автоматического управления имеет характеристическое уравнение четвертого порядка. Кривая Михайлова системы приведена на рисунке. Определить устойчивость автоматической системы.

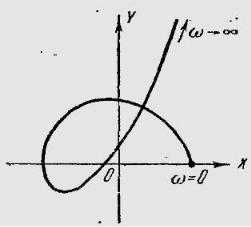
17) Система автоматического управления имеет характеристическое уравнение пятого порядка. На рисунке приведена кривая Михайлова системы. Определить число корней характеристического уравнения с отрицательной вещественной частью и число корней характеристического уравнения с положительной вещественной частью.

2.ТЕМЫ ДЛЯ РЕФЕРАТОВ

1)Качество систем автоматического управления;

2)Основы синтеза линейных систем автоматического управления;

3)Математическое описание дискретных систем;

4)Улучшение качества процессов управления при помощи корректирующих звеньев;

5)Адаптивные системы автоматического регулирования;

6)Чувствительность автоматических систем;

7)Оптимальные процессы в САУ.

8)Частотные методы исследования устойчивости САУ.

9)Использование метода переменных состояния в ТАУ.

Объем реферата не менее10 страниц. В случае, если исследуемая тема имеет значительный объем, выделить основные ее моменты или рассмотреть1-2основных метода анализа/синтеза в заданной области ТАУ. По итогам реферата подготовить доклад на5-10минут, раскрывающий основные положения выбранной темы.

3.ЛИТЕРАТУРА

1)Попов Е.П. Теория линейных систем автоматического управления и регулирования.

2)Филипс Ч., Харбор Р. Системы управления с обратной связью.

3)Бесекерский В.А., Попов Е.П. Теория систем автоматического управления.

4)Ким Д.П. Теория автоматического управления. т1. Линейные системы.

5)Ким Д.П. Теория автоматического управления. т2. Многомерные, нелинейные, оптимальные и адаптивные системы.

6)Лурье Б.Я., Энрайт П. Дж. Классические методы автоматического управления.

7)Лукас. Теория управления техническими средствами.

8)Цыпкин Я.З. Основы теории автоматических систем.

9)Мирошник И.В. Теория автоматического управления: Линейные системы.

10)Мирошник И.В. Теория автоматического управления: Нелинейные и оптимальные системы.

11)Дорф Р., Бишоп Р. Современные системы управления.

12)Бесекерский В.А, Цифровые автоматические системы.

studfiles.net

Mathway | Популярные задачи

www.mathway.com

Обратные тригонометрические функции, их свойства и графики.

Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки «арк» обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.

Функция арксинус y = arcsin(x).

Изобразим график функции арксинус:

Свойства функции арксинус y = arcsin(x).

• Областью определения функции арксинус является интервал от минус единицы до единицы включительно: .

• Область значений функции y = arcsin(x): .

• Функция арксинус — нечетная, так как .

• Функция y = arcsin(x) возрастает на всей области определения, то есть, при .

• Функция вогнутая при , выпуклая при .

• Точка перегиба (0; 0), она же ноль функции.

• Асимптот нет.

Функция арккосинус y = arccos(x).

График функции арккосинус имеет вид:

Свойства функции арккосинус y = arccos(x).

• Область определения функции арккосинус: .

• Область значений функции y = arccos(x): .

• Функция не является ни четной ни нечетной, то есть, она общего вида.

• Функция арккосинус убывает на всей области определения, то есть, при .

• Функция вогнутая при , выпуклая при .

• Точка перегиба .

• Асимптот нет.

Функция арктангенс y = arctg(x).

График функции арктангенс имеет вид:

Свойства функции арктангенс y = arctg(x).

Функция арккотангенс y = arcctg(x).

Изобразим график функции арккотангенс:

Свойства функции арккотангенс y = arcctg(x).

studfiles.net

Обратные тригонометрические функции

Определение обратных тригонометрических функций

Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение   y = sin x,   при заданном   ,   имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x   такой корень, то и   x + 2πn   (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны. Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус:   y = sin x.   Если ограничить аргумент x интервалом , то на нем функция   y = sin x   монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом:   x = arcsin y.

Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.

Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ), имеющая область определения и множество значений .

Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ), имеющая область определения и множество значений .

Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ), имеющая область определения и множество значений .

Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ), имеющая область определения и множество значений .

Графики обратных тригонометрических функций

Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой   y = x. См. разделы Синус, косинус, Тангенс, котангенс.

y = arcsin x

Основные формулы

Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.

arcsin(sin x) = x     при
sin(arcsin x) = x
arccos(cos x) = x     при
cos(arccos x) = x

arctg(tg x) = x     при
tg(arctg x) = x
arcctg(ctg x) = x     при
ctg(arcctg x) = x

Формулы, связывающие обратные тригонометрические функции

Формулы суммы и разности

     при или

     при и

     при и

     при или

     при и

     при и

     при

     при

     при

     при

     при

     при

     при

     при

     при

     при

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов.     Опубликовано: 04-07-2014

1cov-edu.ru

Методические разработки по теме: «Обратные тригонометрические функции»

Разделы: Математика

Тема: Обратные тригонометрические функции.

Для тригонометрической функции Y = sin x, рассматриваемой в интервале , переход к однозначной обратной функции невозможен, так как одному значению у соответствует множество значений аргумента х. Поэтому обратная функция у = arcsin x при каждом значении х, лежащем на отрезке , имеет бесчисленное множество значений. При изучении функции, обратной синусу, выбирают отрезок , на котором функция Y= sin x возрастает, и рассматривают соответствующую этому отрезку обратную функцию у = аrcsin x, которую называют главным значением у = Arcsin x.

Определение 1. Обратной тригонометрической функцией у=arcsin x. называют дугу (угол) у, взятую на отрезке , синус которой равен х. ( Равенства у=Arcsin x и Х= sin у - эквивалентны).

Основные свойства функции у = аrcsin x.

1. Функция у = аrcsin x определена на отрезке, D(у).

2. На отрезке функция у = аrcsin x возрастает, E(у).

3. Функция у = аrcsin x нечетная, аrcsin (-x) = -аrcsin (x).

4. Функция у= аrcsin x называется главным значением у = arcsin x. Все значения дуг (углов) синус которых равен х, определяются формулой

Аrcsin x =(-1), где n . (1.1)

1.2. Функция у= arccos x.

Определение 2. Обратной тригонометрической функцией у=arccos x называют дугу (угол) у, взятую на отрезке , косинус которой равен х. (Равенство у=arccos x и cos y=x эквивалентны).

Основные свойства функции у=аrccos x.

1. Функция у=аrccos x определена на отрезке, D(у).

2. На отрезке функция у=аrccos x возрастает, E(у).

3. Функция у=аrccos x свойством нечетности и четности не обладает, справедливо равентсво arccos (-x) =

4. Функция у= аrccos x называется главным значением у= Аrccos x. Все значения дуг(углов)косинус которых равен х, определяются формулой

Аrcсos x =, где n . (1.2)

1.3 Функция у= arctg x

Определение 3. Обратной тригонометрической функцией у=arctg x. называют дугу (угол) у, взятую на отрезке , тангенс которой равен х. ( Равенства у=arctg x и Х= tg у - эквивалентны).

Основные свойства функции у = аrctg x.

1. Функция у=аrctg x определена на отрезке , D(у)= .

2. На отрезке функция у=аrctg x возрастает, E(у).

3. Функция у = аrctg x нечетная, аrctg (-x) = -аrctg (x).

4.Функция у = аrctg x называется главным значением функции у = Аrctg x. Все значения дуг (углов) синус которых равен х, определяются формулой x

Аrctg x =, где n . (1.3)

1.4 Функция у= arcctg x

Определение 4. Обратной тригонометрической функцией у=arcctg x называют дугу (угол) у, взятую на отрезке x, котангенс которой равен х. (Равенства у=arcсtg x и Х= сtg у – эквивалентны).

Основные свойства функции у=аrcсtg x.

1. Функция у = аrcctg x определена на отрезке , D(у)= .

2. На отрезке функция у = аrcсtg x убывает, E(у)=

3. Функция у = аrсctg x не обладает ни свойством четности, ни свойством нечетности, но для нее справедливо arcctg (-x)=

4.Функция у = аrcctg x называется главным значением у = Аrcctg x. Все значения дуг (углов) котангенс которых равен х, определяются формулой x

Аrcсtg x =, где n . (1.4)

2. Основные соотношения для обратных тригонометрических функций:

sin(arcsinx)=x, если (2.1)

cos(arccosx)=x, если (2.2)

tg(arctgx)=x, если (2.3)

ctg(arcctgx)=x, если (2.4)

arcsin(sinx)=x, если (2.5)

arcos(cosx)=x, если (2.6)

arctg(tgx)=x, если (2.7)

arcctg(ctgx)=x, если (2.8)

3. Применение свойств обратных тригонометрических функций.

Решая различные вычислительные задачи с обратными тригонометрическими функциями, я подразделила их на следующие:

1) Вычисление значений обратных тригонометрических функций разными способами: применяя свойства функций, тригонометрические формулы и графический способ. (Эти вопросы я рассматриваю в данной статье).

2) Решение уравнений, неравенств и систем, содержащих обратные тригонометрические функции.

3) Построение графиков, содержащих обратные тригонометрические функции.

4) Решение уравнений, систем, неравенств с параметром.

3.1 Вычислите:

1).

Дополнительно:

6).

7).

9)

3.1. Учитывая область значений аркфункций и формулы 2.5-2.8 , вычислите:

График фигуры Y=Arccos(cosx) .

главный- arccos(cosx)=x, если

y(10)= 4?-10 12,56-10=2,56, 2,56.(При условии, что )

12) arcsin(sin6)=

График фигуры Y=Arcsin(sin(x)) в приложении №1.

Учитывая, что главный арксинус имеет область значений тогда

arcsin(sinx)=x, если

Ответ: arcsin(sin6)=.

13) arctg(tg. Учитывая, что y=tgx имеет период , то

Ответ:.

Дополнительно:

14) ,

15) arcos(cos8)=3-8

16) arctg(tg4)=4-.

Для вычисления значений некоторых обратных тригонометрических функций удобно пользоваться следующими формулами

Докажем, данные формулы.

1) , .

2) arcsin z=, arccos z=.

4) Учитывая пункт 2), получим :

.

Аналогично доказывается и второе равенство.

3.2 Вычислить:

17)

Решение: ,

?-3 + arcos(sin3) = ,

Ответ: arcos(sin3) =3- .

18) Решение: arctg(tg)+arcctg(ctg)=,

arctg(tg)+ =,

Ответ: arctg(tg)= — .

Дополнительно:

19);

20);

21);

22) .

3.3. Вычислить, используя формулы двойного, тройного и половинного аргумента.

Дополнительно:

28) sin(2arctg3)=

29)

13.03.2006

xn--i1abbnckbmcl9fb.xn--p1ai

Функция arccos График функции y = arccosx

Функция arccos

График функции y = arccosx.

Арккосинусом числа m называется такой угол x, для которого

Функция y = cosx непрерывна и ограничена на всей своей числовой прямой. Функция y = arccosx является строго убывающей.

• 
  cos(arccosx) = x при
  
• 
  arccos(cosy) = y при
  
• 
  D(arccosx) = [ − 1;1], (область определения),
  
• 
  E(arccosx) = [0;π]. (область значений).
  

Свойства функции arccos

• 
  arccos( − x) = π − arccosx (функция центрально-симметрична относительно точки
  
• 
  arccosx > 0 при
  
• 
  arccosx = 0 при x = 1.
  
• 
  
  
• 
  
  

Получение функции arccos

Функция arctg

График функции .

Арктангенсом числа m называется такой угол α, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

Получение функции arctg

Функция arcctg

График функции y=arcctg x

Арккотангенсом числа m называется такой угол x, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.

Свойства функции arcctg

• 
  (график функции центрально-симметричен относительно точки
  
• 
  при любых x.
  
• 
  
  

Получение функции arcctg

Функция arcsec

Функция arccosec

Производные от обратных тригонометрических функций

Интегралы от обратных тригонометрических функций

Неопределённые интегралы

Для действительных x≥1:

Разложение в бесконечные ряды

Для арктангенса используется также более быстро сходящийся ряд, открытый Леонардом Эйлером:

(член в сумме при n= 0 принимается равным 1).

Использование в геометрии

Прямоугольный треугольник ABC

Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например с помощью теоремы косинусов.

В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:

α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)

МОУ Балабановская школа № 4

Т Р И Г О Н О М Е Т Р И Я

Выполнила: Баширова Вероника

Преподаватель: Заречкова Л.И.

2009 г.

Список литературы:

1. 
   Большая советская энциклопедия
   
2. 
   Энциклопедия Брокгауз и Ефрон
   
3. 
   www.wikipedia.ru
   

bigpo.ru

Функция arccos График функции y = arccosx

Функция arccos

График функции y = arccosx.

Арккосинусом числа m называется такой угол x, для которого

Функция y = cosx непрерывна и ограничена на всей своей числовой прямой. Функция y = arccosx является строго убывающей.

• 
  cos(arccosx) = x при
  
• 
  arccos(cosy) = y при
  
• 
  D(arccosx) = [ − 1;1], (область определения),
  
• 
  E(arccosx) = [0;π]. (область значений).
  

Свойства функции arccos

• 
  arccos( − x) = π − arccosx (функция центрально-симметрична относительно точки
  
• 
  arccosx > 0 при
  
• 
  arccosx = 0 при x = 1.
  
• 
  
  
• 
  
  

Получение функции arccos

Функция arctg

График функции .

Арктангенсом числа m называется такой угол α, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

Получение функции arctg

Функция arcctg

График функции y=arcctg x

Арккотангенсом числа m называется такой угол x, для которого

Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.

Свойства функции arcctg

• 
  (график функции центрально-симметричен относительно точки
  
• 
  при любых x.
  

Получение функции arcctg

Функция arcsec

Функция arccosec

Производные от обратных тригонометрических функций

Интегралы от обратных тригонометрических функций

Неопределённые интегралы

Для действительных x≥1:

Разложение в бесконечные ряды

Для арктангенса используется также более быстро сходящийся ряд, открытый Леонардом Эйлером:

(член в сумме при n= 0 принимается равным 1).

Использование в геометрии

Прямоугольный треугольник ABC

В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:

α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)

МОУ Балабановская школа № 4

Т Р И Г О Н О М Е Т Р И Я

Выполнила: Баширова Вероника
Преподаватель: Заречкова Л.И.

2009 г.

Список литературы:

1. 
   Большая советская энциклопедия
   
2. 
   Энциклопедия Брокгауз и Ефрон
   
3. 
   www.wikipedia.ru
   

www.birmaga.ru

Функции и Графики — сайт по математике и не только!!! Всё о Математических функциях и их графиках…

fgraphiks.narod.ru

Модули

Модуль — больная тема для многих учеников. И дело вовсе не в каких-то особо сложных теоремах и выкладках. Просто учителя зачастую сами не умеют работать с этой функцией.

Добавьте к этому крайне непродуманную школьную программу, когда в 8—9 классах учителя говорят: «Модули — это для старших классов. Еще успеете изучить», а в 10—11 классах — «Чем вы занимались раньше? Вы должны уже все это знать!». Ну и как в таких условиях учиться?

Так вот, знайте: модули — один из самых простых и понятных разделов математики. Посмотрите видеоуроки — и убедитесь в этом сами. Решайте задачи, практикуйтесь — и не верьте школьным сказкам про «должны знать».

Глава 1.

Модуль числа

§ 4.

Графики функций, содержащих модуль, и их свойства

Глава 2.

Уравнения с модулем

§ 1.

Как решать уравнения с модулем

§ 2.

Простейшие уравнения с модулем

§ 3.

Уравнение с двумя модулями

§ 4.

Дробно-рациональные уравнения с модулем

§ 5.

Уравнения с модулем: учет области значений

§ 6.

Нестандартные уравнения с модулем

§ 12.

Уравнения с модулем в модуле — как их решать с помощью разных приёмов

Глава 3.

Неравенства с модулем

§ 1.

Неравенства с модулем: графическое решение

§ 2.

Решение неравенств с модулем: 4 способа

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

76

77

78

79

80

81

www.berdov.com

Модули — Математика — Теория, тесты, формулы и задачи

Оглавление:

Основные теоретические сведения

Базовые сведения о модуле

К оглавлению…

Определение модуля может быть дано следующим образом: Абсолютной величиной числа a (модулем) называется расстояние от точки, изображающей данное число a на координатной прямой, до начала координат. Из определения следует, что:

Таким образом, для того чтобы раскрыть модуль необходимо определить знак подмодульного выражения. Если оно положительно, то можно просто убирать знак модуля. Если же подмодульное выражение отрицательно, то его нужно умножить на «минус», и знак модуля, опять-таки, больше не писать.

Основные свойства модуля:

Некоторые методы решения уравнений с модулями

К оглавлению…

Существует несколько типов уравнений с модулем, для которых имеется предпочтительный способ решения. При этом данный способ не является единственным. Например, для уравнения вида:

Предпочтительным способом решения будет переход к совокупности:

А для уравнений вида:

Также можно переходить к почти аналогичной совокупности, но так как модуль принимает только положительные значения, то и правая часть уравнения должна быть положительной. Это условие нужно дописать в качестве общего ограничения для всего примера. Тогда получим систему:

Оба этих типа уравнений можно решать и другим способом: раскрывая соответствующим образом модуль на промежутках где подмодульное выражение имеет определённый знак. В этом случае будем получать совокупность двух систем. Приведем общий вид решений получающихся для обоих типов уравнений приведённых выше:

Для решения уравнений в которых содержится более чем один модуль применяется метод интервалов, который состоит в следующем:

• Сначала находим точки на числовой оси, в которых обращается в ноль каждое из выражений, стоящих под модулем.
• Далее делим всю числовую ось на интервалы между полученными точками и исследуем знак каждого из подмодульных выражений на каждом интервале. Заметьте, что для определения знака выражения надо подставить в него любое значение x из интервала, кроме граничных точек. Выбирайте те значения x, которые легко подставлять.
• Далее на каждом полученном интервале раскрываем все модули в исходном уравнении в соответствии с их знаками на данном интервале и решаем полученное обычное уравнение. В итоговый ответ выписываем только те корни этого уравнения, которые попадают в исследуемый промежуток. Еще раз: такую процедуру проводим для каждого из полученных интервалов.

educon.by

Тема урока: «Модуль числа» (6 класс)

1. Модуль числа. Иллюстрирующий пример. Определение. Примеры

Рассмотрим чертеж. Координата точки М – . Знак минус указывает, что точка М лежит левее начала отсчета. Число шесть говорит о том, что расстояние от точки О до точки М равно шесть единичных отрезков.

Число 6 называют модулем числа . Записывают это так: 

Определение.

Модулем числа a называют расстояние от начала координат до точки с координатой a.

Мы помним, что расстояние на координатной прямой измеряется в единичных отрезках.

Примеры.

Модуль числа 5 равен 5, так как точка с координатой пять удалена от точки начала отсчета на пять единичных отрезков.

Модуль 0 равен 0, так как точка с координатой ноль – это и есть начало отсчета.

2. Модуль противоположных чисел

Модуль числа – это расстояние. Поэтому он не может быть отрицательным. Для положительного числа его модуль равен самому числу, а для отрицательного – противоположному.

Примеры:

Заметим, что противоположные числа имеют равные модули. В общем виде это можно записать так:

3. Задание 1

Найдите значение выражения    , если   .

Решение.

Сначала подставим значения переменных.

  – число отрицательное. Его модуль равен противоположному числу   .

Модуль числа  равен 3,6.

Выполним вычитание. Получим: 10,9.

4. Задание 2

Отметьте на координатной прямой числа, модуль которых равен 2.

Решение.

Начертим координатную прямую. Для этого на прямой выберем начало отсчета, единичный отрезок и направление.

Поставим точки на расстоянии 2 единичных отрезка от начала отсчета.

Таких точки две. Одной соответствует число  , а другой число 2.

5. Задание 3

Найдите значение выражений:

        ;            4 

Решение.

1)      

Модуль числа  равен 8. Модуль числа 5 равен 5.

2)          

Модуль числа 10 равен 10. Модуль числа  равен 15.

3)      .

  Раскрыв модули, получим сумму чисел 2,3 и 3,7

4)      

Модули данных чисел равны соответственно 24 и 80.

6.

infourok.ru

Технология модульного обучения

Модульное обучение – обучение, при котором учебный материал разбит на информационные блоки-модули. Технология построена на самостоятельной деятельности обучающихся, которые осваивают модули в соответствии с поставленной целью обучения.

Особенности модульного обучения

Ключевой элемент структуры в данной технологии – информационный модуль.

Модуль – это отдельный блок, включающий теоретический материал, тренировочные задания, методические рекомендации для учащихся. Составной элемент модуля – контрольные вопросы и тесты, а также ключи для самопроверки или взаимопроверки. Благодаря изучению модуля учащиеся достигают определенной дидактической или педагогической цели.

Содержание учебного занятия конструируется из нескольких логически связанных между собой модулей, каждый из которых решает конкретную учебную задачу. На выполнение модуля дается фиксированное время. Вместе все модульные блоки направлены на достижение предметных и личностных результатов.

Технология основана на деятельностном подходе, ориентирована на личность каждого ученика. Предполагается самостоятельная деятельность обучающихся в освоении материала. Минимальная продолжительность занятия – 2 академических часа. Учащиеся должны быть психологически готовы к самостоятельной деятельности с высокой степенью интенсивности. Поэтому возраст школьников, которые эффективно смогут работать в технологии модульного обучения, – 13-14 лет.

Виды модульного обучения

• Модульная программа. Планирование курса модульных уроков, которые связаны между собой целью, обеспечивающей достижение предметных, личностных и регулятивных результатов. Это программа деятельности учащихся.

• Модульный урок. Это элемент модульной программы.

• Планирование в формате модуля. Использование технологических карт – особой формы структурирования учебного материала.

Цели использования модульного обучения в средней школе

• Освоение учебного материала в процессе активной деятельности учеников.

• Развитие навыков самостоятельности и самоконтроля.

• Повышения познавательного интереса обучающихся.

• Развитие у обучающихся умения планировать свою деятельность.

Принципы

• Модульность. Учебный материал разбивается на отдельные законченные блоки, логически связанные между собой и объединенные одной дидактической целью.

• Динамичность. Модули можно свободно дополнять, заменять в зависимости от изменений в программах, по которым строится обучение.

• Гибкость. Адаптация содержания модуля к индивидуальным запросам обучающихся.

• Осознанная перспектива. Перед учащимся ставятся ближние и дальние цели. Обучение строится на осознанном отношении к процессу освоения знаний.

• Индивидуальные консультации и инструкции для каждого обучающегося.

Роль преподавателя

Учитель разбивает учебный материал на блоки, составляет модульную программу, разрабатывает модульные уроки.

Главная цель – организация самостоятельной деятельности учащихся при работе с модулем. Для этого в продолжение занятия преподаватель контролирует учебный процесс, оказывает консультационную помощь. Следит за временем выполнения каждого учебного элемента и сообщает обучающимся о лимите времени.

Преимущество для учащихся

• Самостоятельное освоение учебного материала.

• Психологическая комфортность на занятиях.

• Работа с модулями осуществляется в индивидуальном темпе.

• Индивидуальная траектория работы на каждом модульном уроке.

Преимущество для учителя

• На уроке освобождается время для индивидуального консультирования учащихся.

Основные трудности для учащихся

• Временной дефицит при выполнении заданий.

• Высокий темп выполнения заданий.

• Не все учащиеся умеют работать самостоятельно. Низкое и фрагментарное качество освоения учебных тем.

Основные трудности для учителя

• Разработка материалов для модуля (комплект заданий, тестов, инструкций) требует больших затрат времени и сил.

• Необходим высокий уровень профессиональной компетенции.

• Материальные затраты на копирование комплектов заданий для каждого учащегося.

Структура модульного урока

1. Мотивационный этап. Беседа, настраивающая на самостоятельную деятельность на уроке. Инструкции к последующей работе.

2. Работа с модульными блоками – учебными элементами (УЭ), которые структурируются в определенном порядке, нумеруются и предлагаются учащимся в индивидуальных комплектах. Ограничения: количество УЭ на уроке должно быть не более семи.

3. Рефлексия. Самооценка уровня продуктивности работы на уроке. Дифференцированное задание для работы дома, выбор которого зависит от результата работы с модулем.

Содержание учебных элементов в модуле:

• УЭ 0 – для учащегося определяется цель, которая будет достигнута в результате освоения модуля по теме урока.

• УЭ 1 – входная диагностика, проверяющая сформированность необходимых умений для освоения модуля. Дается ключ для самопроверки или взаимопроверки, если предполагается парная или групповая работа.

• УЭ 2 – УЭ 6 – обучающие модули, которые включают теоретические и практические задания.

• УЭ 7 – выходная диагностика, оценивающая степень усвоения темы. Ключ к заданию может быть у учителя или также проводится самопроверка.

В печатных комплектах для учащихся обязательно размещается технологическая карта, которая включает следующие элементы:

• Номер УЭ. Время на выполнение каждого учебного блока.

• Учебный материал.

• Инструкции для выполнения каждого учебного элемента.

• Ключи (если предусмотрена самопроверка).

Перспективы развития

Для активного внедрения технологии модульного обучения необходимо повышение мотивации ученика. У школьников должно быть хорошо развито умение самостоятельной познавательной деятельности. Важно, чтобы материальная база учебного заведения позволяла обеспечить учащихся индивидуальными комплектами для работы на модульных уроках.

aujc.ru

Модуль числа. Видеоурок. Математика 6 Класс

Положительные числа, натуральные, а затем и дробные мы ввели для указания количества:  дерева,  литра молока (рис. 1).

Рис. 1. Пример использования положительных чисел

Затем мы ввели отрицательные числа: например, . Теперь число, кроме количества, содержит еще и знак, который указывает, что нужно делать с этим количеством – добавить или отнять. То есть после того, как были введены отрицательные числа, мы можем сказать, что любое число состоит из количества (реально существующего) и знака (придуманного нами для упрощения записи арифметических действий).

Но иногда бывает важна только одна характеристика – количество, а знак нас не интересует.

Рассмотрим такой пример. Для таксиста важно, какой длины путь он преодолевает с пассажиром (рис. 2).

Рис. 2. Километраж

Ведь, если в конце поездки пассажира привозят обратно домой, это не означает, что он ничего таксисту не должен, так как он проехал какое-то расстояние с начала поездки (рис. 3).

Рис 3. Путь, проделанный такси

Пусть теперь такси может ездить только вдоль прямой (вправо или влево). У нас уже есть подходящая модель – координатная прямая (рис. 4).

Рис. 4. Аналогия с координатной прямой

Предположим, клиенты проехали  км влево, затем  км вправо, затем ещё  км вправо, затем ещё  км влево. В результате автомобиль отъехал на  км влево от исходной точки:  (рис. 5).

Рис. 5. Сколько проехала машина (считаем с помощью числовой прямой)

Но ведь путь, который проделало такси, значительно больше:  км.

Для подсчёта пути мы складывали только количества, без учёта знака.

Ту часть числа, которая указывает на количество, называют абсолютным значением (или модулем числа). То есть можно сказать и так: любое число состоит из знака и абсолютного значения (модуля). Если знак плюс, то для краткости его обычно не пишут.

Например, у числа  знак минус и модуль , у числа , знак плюс и модуль  (рис. 6).

Рис. 6. Из чего состоят противоположные числа

Пример: машина проехала  км по дороге. Используем для этой ситуации математическую модель – числовую прямую. Машина из точки  могла двигаться вправо или влево. Можно так и говорить: перемещение на  км вправо, перемещение на  км влево. Но у нас есть удобный инструмент, отрицательные числа. Поэтому короче мы можем говорить так: перемещение  или перемещение  (рис. 7).

Рис. 7. Возможные движения машины

Перемещение было разное, но удалился автомобиль от начальной точки (от ) на одно и то же расстояние – на  км. Но  – это и есть модуль (как для числа , так и для ).

То есть про модуль числа можно сказать и так: модуль – это расстояние от числа до нуля (на самом деле это определение более универсальное, но об этом вы узнаете в старших классах).

В физике два этих понятия так и называют:

• перемещение: для него важен результат – где были и где оказались в итоге;
• путь: здесь важно расстояние, которое мы прошли, и не важно, где мы оказались в итоге.

Так, если машина, двигалась из точки  вправо  км, а потом влево  км, то она вернется в начальную точку. Перемещение равно , но путь равен  км (рис. 8).

Рис. 8. Перемещение и путь

Перемещение от одной точки до другой изображают отрезком со стрелкой. Называют его вектором (рис. 1).

Рис. 9. Вектор

Здесь ситуация как с числами: есть количественная часть (длина) и есть направление (у числа их было всего два ( и ), а здесь направлений может быть бесконечно много).

Сам вектор обозначают со стрелкой сверху. Длину вектора называют модулем (помните, как и у числа: модуль – это количественная часть) и обозначают с прямыми скобками или просто как отрезок (рис. 2).

Рис. 10. Обозначение вектора и его длины

Если нам нужно попасть из одной точки в другую, мы не всегда можем пройти по прямой. Например, из точки  мы движемся в точку , обходя газон, по которому ходить запрещено. То есть мы переместились два раза и. Итоговое перемещение  (рис. 3).

Рис. 11. Перемещение

Перемещение  – это сумма двух перемещений : . Для путей это не верно. Длина отрезка  меньше суммы длин отрезков  и : . Путь по прямой короче, чем в обход.

Все это можно записать одним неравенством: . Оно означает вот что: сумма двух перемещений – это итоговое перемещение. Его длина меньше, чем сумма длин каждого перемещения по отдельности: .

Подумайте, может ли здесь быть равенство, если по-другому будут расположены векторы перемещения? А противоположный знак, то есть знак ?

Рассмотрим такой пример. Человек гуляет с собакой, он движется из точки  в точку  по прямой, при этом собака движется еще из стороны в сторону, насколько позволяет поводок (рис. 4).

Рис. 12. Иллюстрация к примеру

Перемещение человека  (рис. 5).

Рис. 13. Перемещение человека

Перемещение собаки складывается из кусочков и тоже в итоге равно  (рис. 6).

Рис. 14. Перемещение собаки

Но если складывать не перемещения, а пути, т.е. не векторы, а их модули, то окажется, что собака пробежала путь, в два или три раза больший. Собака, совершая одинаковое перемещение с хозяином, могла пробежать и в , и в  раз больший путь, все ограничивается ее активностью.

Есть такая задача: измерение длины береговой линии. С перемещением от точки  до точки  вдоль берега все понятно. Это вектор  (рис. 7).

Рис. 15. Перемещение

А вот путь складывается из кусочков (рис. 8). Тут вроде бы как с собакой: нужно сложить модули таких перемещений, векторов.

Рис. 16. Кусочки пути

Но если смотреть более точно, каждое такое перемещение складывается из еще более мелких перемещений. Путь сильно возрастает (рис. 9).

Рис. 17. Возрастание пути

Но это еще не все: если смотреть еще более точно, то и они делятся на маленькие перемещения. Береговая линия все более и более изрезана (рис. 10). И это никогда не заканчивается.

Рис. 18. Изрезанная береговая линия

То есть длину береговой линии не получается точно измерить таким образом.

Вот так получается, что, не отходя далеко от общего вектора перемещения, можно получить очень большой (как путь собаки) или даже бесконечный путь (как береговая линия).

Модуль числа договорились обозначать вертикальными скобками. Итак, модуль положительного числа  равен самому числу , модуль отрицательного числа  тоже равен , то есть противоположному числу: , .

Остался вопрос: чему равен модуль нуля? Расстояние от нуля до нуля равно нулю. Поэтому модуль нуля считать равным нулю: .

Итак, мы уже все знаем, чтобы дать более точное определение, что такое модуль числа.

Модуль числа – это число, равное ему самому, если число положительное, противоположному числу, если оно отрицательное, и все равно какому (самому или противоположному), если число равно нулю. Пусть будет самому: .

Чтобы запись была короче, объединим первую и третью строчки. И определение теперь звучит так: модуль числа равен самому числу, если оно неотрицательное (положительное или ноль), и противоположному числу, если оно отрицательное: .

Это определение не объясняет суть, что такое модуль. Но мы про суть уже поговорили раньше. Оно является удобным инструментом для выполнения арифметических действий. Особенно пригодится это определение, когда мы будем решать уравнения с модулем.

Если отвлечься от задач про путь и перемещение, то нахождения модуля интересно еще вот чем. Раньше мы выполняли операции с двумя или несколькими числами. Например, брали два числа, складывали их, получали новое число, сумму: . Или сравнивали два числа: .

Модуль же – это операция с одним числом. Берем одно число и находим для него другое число – модуль: . Сходная ситуация была при округлении чисел, хотя сам смысл процедуры там был совсем другой: .

Итак, мы обсудили, что такое модуль, для чего он нужен, дали ему точное определение. Теперь перейдем к технике вычислений. Потренируемся этот модуль находить.

Для того чтобы найти модуль числа, необязательно изображать число на координатной прямой и измерять расстояние до нуля. Чтобы найти модуль числа, нужно просто не обращать внимания на знак числа: . То есть даже определение модуля нам пока не очень понадобится. Нужно просто записывать число без знака. Таким образом, у противоположных чисел модули равны: .

Решим несколько примеров на нахождение модуля.

Как быть с модулем переменной величины? Про нее мы можем не знать, отрицательная она или положительная. Она может быть равна и нулю. Что нам известно про её модуль в такой ситуации? Мы не можем утверждать, что модуль  равен самому числу . Ведь может оказаться, что  отрицательно, но модуль не может быть отрицательным.

Рассмотрим противоположное число . Знак минус перед  не означает, что оно отрицательно. Поэтому с модулем этого числа тоже нет определенности.

Что мы знаем наверняка, так это, что модули этих двух чисел равны друг другу. И этот модуль равен одному из этих чисел, тому, которое неотрицательно: или .

Итак, подведем итог.

• Модуль числа – это расстояние от числа до нуля (рис. 9).

Рис. 19. Модуль числа

• Чтобы найти модуль числа, нужно записать это число без учета знака (рис. 10).

Рис. 20. Как найти модули

• Модули противоположных чисел равны (рис. 11).

Рис. 21. Модули противоположных чисел

• Точное определение модуля выглядит так:модуль числа равен самому числу, если оно неотрицательное (положительное или ноль), и противоположному числу, если оно отрицательное (рис. 12).

Рис. 22. Определение модуля

Список рекомендованной литературы

1. Зубарева И.И., Мордкович А.Г. Математика. 6 класс. М.: ИОЦ «Мнемозина», 2014.
2. Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Учебник в 3 частях. Ч. 2. М.: «Просвещение».
3. Виленкин Н.Я. и др. Математика. Учебник для 6 класса. М.: ИОЦ «Мнемозина», 2013.

Рекомендованные ссылки на ресурсы сети Интернет

1. Yaklass.ru (Источник). 
2. Math-prosto.ru (Источник).
3. Cleverstudents.ru (Источник).

Домашнее задание

1. Точка  лежит на  единицы от начала отсчета влево, а точка  – вправо на  единицы. Найдите координаты точек и модули этих координат.
2. Найдите значение выражения: .
3. Какое из предложенных чисел имеет наибольший модуль: ?

interneturok.ru

Тема «Модули»

Во вводной части лекции следует объяснить учащимся, что только с появлением модулей Паскаль стал средством разработки больших профессиональных программных комплексов. Модуль, как и процедуры, служит реализации идеи модульности — выделения подзадач внутри большой задачи. Отличие модуля от набора «внутренних» процедур — возможность отдельной трансляции и отдельного от программы хранения; к модулю может обращаться не °Дна программа, а много разных программ. Благодаря модулям в Паскале возможно организовывать внешние библиотеки программ По различным проблемам.

Целью школьного спецкурса не может быть самостоятельная Разработка учащимися модулей. Такое задание возможно в качестве проекта для некоторых учащихся, а для большинства эта тема является ознакомительной. Вполне достаточно привести примеры двух-трех несложных модулей и разобрать как их внутреннее устройство, так и механизм взаимодействия с обращающимися к ним программами.

Описав общую структуру модуля и объяснив назначение основных его разделов (заголовок, интерфейсная часть, раздел реализации, раздел инициализации), приведите пример модуля. Допустим, мы хотим дополнить’Паскаль средствами работы с комплексными числами (хотя бы на уровне четырех арифметических действий). В школе, в которой углубленно изучается программирование, учащиеся скорее всего с комплексными числами знакомы. Возможны два подхода к реализации этой задачи.

1. Комплексное число представляется парой действительных (а, Ь). Конструируют четыре процедуры — действия над комплексными числами; у каждой из них по 4 параметра-значения и по 2 параметра-переменных. Сводят их в модуль, в интерфейсной части которого находятся заголовки этих процедур. Показывают, как обращается к нему внешняя программа, объясняют смысл наличия в ней инструкции uses <список модулей.

2. Комплексное число представляется одним идентификатором, т.е. мы хотим иметь возможность записывать присваивания вида А := В + ЕС, где А, В и С — комплексные числа. Эта задача потруднее. Путь к ее решению — создать тип (назвав его Complex), элементы которого — двухполевые записи; первое поле — действительная часть числа, второе — коэффициент при мнимой части.

Всякий раз, разбирая примеры модулей, подчеркните, что разработчику внешней программы, использующему модули, нет никакой необходимости знать устройство процедур, составляющих раздел реализации. Вполне достаточно иметь детальное описание интерфейсной части и назначения модуля.

Более детально учащиеся знакомятся с модулями и приходят, в частности, к пониманию сформулированного выше утверждения на примерах стандартных модулей, входящих обычно в комплект программ Турбо Паскаля. Наиболее доступны из них два модуля — Crt (доступ к экрану дисплея в текстовом режиме, работа с клавиатурой, звуком) и Graph (управление графическим режимом работы дисплея).

Тема «Графические возможности Турбо Паскаля»

Изучение изобразительных (графических) возможностей — традиционно популярная тема при изучении языков программирования. Приходится удивляться, с каким старанием учащиеся программируют построение изображений, хотя прекрасно знают, что большинство из этих изображений можно гораздо проще реализовать с помощью специализированных программ.

Во вводной беседе уместно напомнить учащимся об основных способах формирования изображений — растровом и векторном, напомнить, что такое пиксел, как пикселы отражаются в видеопамяти.

Рассказ о процедурах модуля Graph начните с процедуры перехода в графический режим InitGraph. Надо заметить, что поскольку в модуле Graph более 50 графических процедур и функций, то целесообразно подготовить к занятиям короткий, на одной странице, справочник по основным из них. Поскольку уроки по этой теме ограничатся скорее всего построением простых геометрических примитивов, то именно с этой точки зрения и надо отобрать те процедуры, с которыми следует в первую очередь познакомить учащихся. Все остальные можно всему классу не приводить, а тем учащимся, которые получат задания на разработку соответствующих проектов, предоставить возможность самостоятельного изучения необходимых изобразительных средств.

Приведем список этих основных процедур (их назначение, списки параметров и др. — в любом учебнике по Паскалю, в котором разобран состав модуля Graph):

Arc Bar	CloseGraph Circle
Ellipse FillEllipse	FloodFill InitGraph
Rectangle OutTextXY	OutText PiesLice
PutPixel SetFillStyle	Sector SetLine
StileLine SetTextStyle

Для описания действия этих процедур желателен лекционный режим. Он может при наличии соответствующего оборудования сопровождаться экранными проекциями — демонстрациями действия процедур.

Традиционно первые практические занятия по этой теме проводят в «свободном полете»: рисование несложных изображений, закрашивание их частей, эксперименты с цветами и т.д. Нарисовать домик, снежную бабу и т.д. — вполне подходящие задания.

Освоив простейшие приемы графики Паскаля, целесообразно научиться строить графики функций. Это реализует связь с математикой, позволяет освоить масштабирование, формирует навыки пользования «экранной» системой координат. Поскольку эта система направлена нетрадиционно (начало координат — верхний левый угол экрана, ось ординат направлена вниз, а не вверх), то встает задача научиться простым аффинным преобразованиям Координат. Поставленная задача будет полностью выполнена, если Написанная учащимися программа может выполнить следующую Работу: построить на экране график произвольной функции (задаваемой внутри программы в строке function) на произвольном отрезке, координаты которого вводятся в диалоге. График должен включать оси координат, ориентированные традиционным образом, их разметку, кривую, изображающую функцию. Такая программа достаточно сложна; промежуточным этапом может быть построение графика одной хорошо знакомой учащимся функции на фиксированном отрезке (например: построить график функции у = sin(x) на отрезке от 0 до 2).

Разумеется, с наиболее подготовленными учащимися можно идти дальше и осваивать такие приемы графики, как управление видеостраницами и покадровая мультипликация, но в целом это следует признать для данного этапа обучения чрезмерным.

studfiles.net

Тема «Модули»

Во вводной части лекции следует объяснить учащимся, что только с появлением модулей Паскаль стал средством разработки больших профессиональных программных комплексов. Модуль, как и процедуры, служит реализации идеи модульности — выделения подзадач внутри большой задачи. Отличие модуля от набора «внутренних» процедур — возможность отдельной трансляции и отдельного от программы хранения; к модулю может обращаться не °Дна программа, а много разных программ. Благодаря модулям в Паскале возможно организовывать внешние библиотеки программ По различным проблемам.

Целью школьного спецкурса не может быть самостоятельная Разработка учащимися модулей. Такое задание возможно в качестве проекта для некоторых учащихся, а для большинства эта тема является ознакомительной. Вполне достаточно привести примеры двух-трех несложных модулей и разобрать как их внутреннее устройство, так и механизм взаимодействия с обращающимися к ним программами.

Описав общую структуру модуля и объяснив назначение основных его разделов (заголовок, интерфейсная часть, раздел реализации, раздел инициализации), приведите пример модуля. Допустим, мы хотим дополнить’Паскаль средствами работы с комплексными числами (хотя бы на уровне четырех арифметических действий). В школе, в которой углубленно изучается программирование, учащиеся скорее всего с комплексными числами знакомы. Возможны два подхода к реализации этой задачи.

1. Комплексное число представляется парой действительных (а, Ь). Конструируют четыре процедуры — действия над комплексными числами; у каждой из них по 4 параметра-значения и по 2 параметра-переменных. Сводят их в модуль, в интерфейсной части которого находятся заголовки этих процедур. Показывают, как обращается к нему внешняя программа, объясняют смысл наличия в ней инструкции uses <список модулей.

2. Комплексное число представляется одним идентификатором, т.е. мы хотим иметь возможность записывать присваивания вида А := В + ЕС, где А, В и С — комплексные числа. Эта задача потруднее. Путь к ее решению — создать тип (назвав его Complex), элементы которого — двухполевые записи; первое поле — действительная часть числа, второе — коэффициент при мнимой части.

Всякий раз, разбирая примеры модулей, подчеркните, что разработчику внешней программы, использующему модули, нет никакой необходимости знать устройство процедур, составляющих раздел реализации. Вполне достаточно иметь детальное описание интерфейсной части и назначения модуля.

Более детально учащиеся знакомятся с модулями и приходят, в частности, к пониманию сформулированного выше утверждения на примерах стандартных модулей, входящих обычно в комплект программ Турбо Паскаля. Наиболее доступны из них два модуля — Crt (доступ к экрану дисплея в текстовом режиме, работа с клавиатурой, звуком) и Graph (управление графическим режимом работы дисплея).

Тема «Графические возможности Турбо Паскаля»

Изучение изобразительных (графических) возможностей — традиционно популярная тема при изучении языков программирования. Приходится удивляться, с каким старанием учащиеся программируют построение изображений, хотя прекрасно знают, что большинство из этих изображений можно гораздо проще реализовать с помощью специализированных программ.

Во вводной беседе уместно напомнить учащимся об основных способах формирования изображений — растровом и векторном, напомнить, что такое пиксел, как пикселы отражаются в видеопамяти.

Рассказ о процедурах модуля Graph начните с процедуры перехода в графический режим InitGraph. Надо заметить, что поскольку в модуле Graph более 50 графических процедур и функций, то целесообразно подготовить к занятиям короткий, на одной странице, справочник по основным из них. Поскольку уроки по этой теме ограничатся скорее всего построением простых геометрических примитивов, то именно с этой точки зрения и надо отобрать те процедуры, с которыми следует в первую очередь познакомить учащихся. Все остальные можно всему классу не приводить, а тем учащимся, которые получат задания на разработку соответствующих проектов, предоставить возможность самостоятельного изучения необходимых изобразительных средств.

Приведем список этих основных процедур (их назначение, списки параметров и др. — в любом учебнике по Паскалю, в котором разобран состав модуля Graph):

Arc Bar	CloseGraph Circle
Ellipse FillEllipse	FloodFill InitGraph
Rectangle OutTextXY	OutText PiesLice
PutPixel SetFillStyle	Sector SetLine
StileLine SetTextStyle

Для описания действия этих процедур желателен лекционный режим. Он может при наличии соответствующего оборудования сопровождаться экранными проекциями — демонстрациями действия процедур.

Традиционно первые практические занятия по этой теме проводят в «свободном полете»: рисование несложных изображений, закрашивание их частей, эксперименты с цветами и т.д. Нарисовать домик, снежную бабу и т.д. — вполне подходящие задания.

Освоив простейшие приемы графики Паскаля, целесообразно научиться строить графики функций. Это реализует связь с математикой, позволяет освоить масштабирование, формирует навыки пользования «экранной» системой координат. Поскольку эта система направлена нетрадиционно (начало координат — верхний левый угол экрана, ось ординат направлена вниз, а не вверх), то встает задача научиться простым аффинным преобразованиям Координат. Поставленная задача будет полностью выполнена, если Написанная учащимися программа может выполнить следующую Работу: построить на экране график произвольной функции (задаваемой внутри программы в строке function) на произвольном отрезке, координаты которого вводятся в диалоге. График должен включать оси координат, ориентированные традиционным образом, их разметку, кривую, изображающую функцию. Такая программа достаточно сложна; промежуточным этапом может быть построение графика одной хорошо знакомой учащимся функции на фиксированном отрезке (например: построить график функции у = sin(x) на отрезке от 0 до 2).

Разумеется, с наиболее подготовленными учащимися можно идти дальше и осваивать такие приемы графики, как управление видеостраницами и покадровая мультипликация, но в целом это следует признать для данного этапа обучения чрезмерным.

studfiles.net

Площадь — линия — Большая Энциклопедия Нефти и Газа, статья, страница 1

Площадь — линия

Cтраница 1

Площадь линии может быть существенно уменьшена при разветвлении потока на участках охлаждения, что также легко осуществить на роликовом конвейере. Для той же цели используют транспортные тележки, не связанные между собой цепью и перемещающиеся по рельсовому пути. Достоинством роликового конвейера и транспортных тележек является также то, что отдельные их секции приводятся в действие не строго одновременно. В результате резко уменьшаются динамические нагрузки, пере-даваемыена строительные конструкции.  [1]

Площадь линии фотоэлектронного спектра данного соединения, ионизованного фотонами, должна быть пропорциональна концентрации этого соединения, так как эффективность ионизации зависит от потока фотонов, сечения ионизации орбитали и количества молекул образца, взаимодействующих с фотонами. Для УФЭС это предположение еще недостаточно проверено. Результаты двух выполненных к настоящему моменту работ [21] вызывают сомнения из-за наличия в них серьезных экспериментальных трудностей.  [2]

СБИС, площадь линий связи на кристалле начинает превышать площадь, занимаемую логическими элементами в схеме. В [9, 10] показано, что чем больше степень интеграции СБИС, тем больше часть площади кристалла, приходящаяся на линии связи. В указанных работах делается вывод о том, что без осуществления оптимизации межэлементных связей на кристалле процесс повышения степени интеграции практически будет приостановлен, вследствие достижения физических пределов при распределении площади кристалла.  [3]

Таким образом, площадь лоренцевой линии, обрезанной достаточно далеко от точки половинной мощности, очень близка к площади обычной лоренцевой линии.  [4]

На участке ABCDEF требуется выделить площадь S линий MN, параллельной АВ.  [6]

При частичном загружении q множится на площадь линии влияния, находящейся под нагрузкой.  [8]

Равномерно распределенная нагрузка располагается над всей площадью линии влияния одного знака. В к А, соединяются Л и С и проводится DE AC; точка Е располагается на критическом грузе.  [9]

Площадь между линией влияния и осью абсцисс дает площадь линии влияния. Отыскание по линии влияния наибольшей величины соответствующего усилия ведется без особого затруднения.  [10]

Так как нагр зка расположена па всем пролете, то площади линий влияния надо вычислять на протяжении всего пролета.  [11]

Наиболее точный метод определения величин / и / заключается в измерении площади линии резонансного поглощения, наблюдаемой в скоростном спектре.  [12]

А если хоть для одного положительного е такой области не удастся найти, тогда площадь линии не равна нулю.  [13]

При равномерно распределенной нагрузке для определения изгибающего момента величину погонной нагрузки q множат на площадь линии влияния. При частичном загружении балки величину q множат на ту часть площади линии влияния, которая расположена под нагрузкой.  [15]

Страницы:      1    2    3    4

www.ngpedia.ru

Площадь — линия — Большая Энциклопедия Нефти и Газа, статья, страница 3

Площадь — линия

Cтраница 3

При разбавлении диметилформамидом растворов хлорида железа ( Ш), содержащих полиядерные частицы Fe ( III), в мессбауэровском спектре начинают проявляться особенности, характерные для мономерной структуры. Предполагая, что факторы Дебая — Уэллера индивидуальных сольватов одинаковы, из значений площадей линий в спектрах можно рассчитать отношение концентраций различных мономерных и полиядерных комплексов железа.  [31]

Если щель уже нормальной, освещенность линии пропорциональна ширине щели, так как при уменьшении ширины щели световой по-ток уменьшается, как это следует из (III.15), а площадь линии остается постоянной. Если щель шире нормальной, освещенность линии от ширины не зависит, так как с увеличением ширины щели пропорционально увеличиваются и площадь линии и световой поток.  [33]

Диапазон изменения значений коэффициента Q достаточно широкий. Они могут быть очень малы, например, в случае расчета процесса торможения, при котором эффективная площадь входной линии значительно больше площади выхлопной линии. Здесь приведены графики для диапазона изменения Q от 0 25 до 10, что достаточно для обычных процессов.  [34]

С помощью метода ЯМР можно легко изучать кинетику медленно протекающих реакций, применяя обычную аналитическую методику для измерения концентраций реагентов и продуктов реакции по площади линии поглощения.  [35]

В нашей работе [65] была измерена не только величина ( х) — — ( х), но и абсолютные значения ( х — 0 48 10 — 18 см. и ( х) 1 76 10 — 18 см3 для ядер олова в молекулах SnO, химически сорбированных на поверхности силикагеля при температуре 213 К. В обеих работах наблюдался рост асимметрии компонент квадрупольного расщепления с увеличением температуры, что является одной из характерных особенностей асимметрии, связанной с анизотропией фактора Дебая — Валлера, отличающей ее ( наряду с различием площадей линий, соответствующих разным переходам) от релаксационной асимметрии по Блюму [123], которая ослабевает с ростом температуры.  [36]

Рисунок 3.55 показывает изменения интенсивности для компонентов линии НЗОо за три года. Площадь линии отнесена к излучению в континууме калибровочного источника DR21, имеющего большую интенсивность и стабильность. Кажется есть небольшое уменьшение относительной интенсивности широкополосного компонента линии ( пьедестала), но отношение сигнал / шум недостаточное. Временные изменения красного компонента отчетливо видны относительно ошибок измерений. Интенсивность меняется в пределах трех раз с нерегулярным характером. Аналогичная картина наблюдается у голубого компонента.  [37]

В квантометрах и спектроскопах, как правило, щели и осветительные устройства постоянны и не подлежат перестройке. При фотографической регистрации спектра желательно увеличение площади линий. Фотоэмульсия неоднородна, между светочувствительными зернами имеются участки, нечувствительные к свету. При узкой щели линия может попасть на пустой участок пластинки или на участок с большой концентрацией светочувствительных зерен.  [38]

Ферма жесткости мостового крана имеет, как правило, ту же схему, что и главная. Это позволяет проектанту использовать построенные ранее линии влияния для определения усилий в элементах — фермы жесткости. Они могут быть найдены путем умножения площадей линий влияния, построенных для стержней, на величину погонной нагрузки от собственного веса фермы жесткости. Учет сосредоточенных сил производится умножением ординат линий влияния на величины сосредоточенных сил, приложенных к ферме.  [39]

Невыгоднейшее положение системы грузов ( линия влияния — треугольник): 1) По крайней мере один из грузов ( называемый критическим) находится над вершиной линии влияния. Критический груз выбирается по следующему признаку: если он расположен слева от вершины, то средняя погонная нагрузка левого участка превышает правую, а при расположении его справа от вершины — наоборот. Равномерно распределенная нагрузка располагается над всей площадью линии влияния одного знака. Графический прием определения критического груза для треугольной линии влияния показан на фиг.  [40]

Невыгоднейшее положение системы грузов ( линия влияния — треугольник): 1) По крайней мере один из грузов ( называемый критическим) находится над вершиной линии влияния. Критический груз выбирается по следующему признаку: если он расположен слева от вершины, то средняя погонная нагрузка левого участка превышает правую, а при расположении его справа от вершины — наоборот. Равномерно распределенная нагрузка располагается над всей площадью линии влияния одного знака. Графический прием определения критического груза для треугольной линии влияния показан па фиг.  [41]

Вышеприведенное рассмотрение предполагало, что линии имеют естественные ширины. Однако легко видеть, что оно остается в силе также и в том случае, когда Гизл Г, Гпогл Г, но Гизл — ГПОГл; в выражение (1.31) не входит экспериментальная ширина линии. ГПОГл, но уширение обусловлено причинами, не изменяющими площадь линии поглощения, например паразитными вибрациями установки.  [42]

Если размер плоской линии менее 1 / 8 длины волны, ее емкость с достаточной точностью описывается формулой плоского конденсатора C 0 9S / a, здесь С — емкость в пикофарадах; 5 — площадь линии в квадратных сантиметрах; d — зазор между линией и землей в миллиметрах.  [44]

На линии Л-450 ( КВ-301) ком с отливкой выдавливается без разрушения вверх, затем толкателем по столу перемещается на пластинчатый конвейер для дальнейшего охлаждения. На конвейере вплотную друг к другу устанавливаются три кома. Шаг кома примерно в 2 раза меньше шага тележек литейного конвейера, поэтому скорость охлаждающего конвейера в 6 — 7 раз меньше скорости литейного конвейера. Такое решение позволяет значительно сократить площадь линии, существенно уменьшает парк опок, однако оно возможно только при использовании высокопрочных смесей. Мелкие и средние отливки отделяются от смеси на вибрационных выбивных решетках или в решетчатых барабанах.  [45]

Страницы:      1    2    3    4

www.ngpedia.ru

Вычисление площадей фигур, ограниченных заданными линиями

Вычисление площади фигуры – это, пожалуй, одна из наиболее сложных задач теории площадей. В школьной геометрии учат находить площади основных геометрических фигур таких как, например, треугольник, ромб, прямоугольник, трапеция, круг и т.п. Однако зачастую приходится сталкиваться с вычислением площадей более сложных фигур. Именно при решении таких задач очень удобно использовать интегральное исчисление.

Определение.

Криволинейной трапецией называют некоторую фигуру G, ограниченную линиями y = f(x), у = 0, х = а и х = b, причем функция f(x) непрерывна на отрезке [а; b] и не меняет на нем свой знак (рис. 1). Площадь криволинейной трапеции можно обозначить S(G).

Определенный интеграл ʃ_а^b f(x)dx для функции f(x), являющийся непрерывной и неотрицательной на отрезке [а; b], и есть площадь соответствующей криволинейной трапеции.

То есть, чтобы найти площадь фигуры G, ограниченной линиями y = f(x), у = 0, х = а и х = b, необходимо вычислить определенный интеграл  ʃ_а^b f(x)dx.

Таким образом, S(G) = ʃ_а^b f(x)dx.

В случае, если функция y = f(x) не положительна на [а; b], то площадь криволинейной трапеции может быть найдена по формуле S(G) = -ʃ_а^b f(x)dx.

Пример 1.

Вычислить площадь фигуры, ограниченной линиями у = х³; у = 1; х = 2.

Решение.

Заданные линии образуют фигуру АВС, которая показана штриховкой на рис. 2.

Искомая площадь равна разности между площадями криволинейной трапеции DACE и квадрата DABE.

Используя формулу S = ʃ_а^b f(x)dx = S(b) – S(a), найдем пределы интегрирования. Для этого решим систему двух уравнений:

{у = х³,
{у = 1.

Таким образом, имеем х₁ = 1 – нижний предел и х = 2 – верхний предел.

Итак, S = S_DACE – S_DABE = ʃ₁² x³ dx – 1 = x⁴/4|₁² – 1 = (16 – 1)/4 – 1 = 11/4 (кв. ед.).

Ответ: 11/4 кв. ед.

Пример 2.

Вычислить площадь фигуры, ограниченной линиями у = √х; у = 2; х = 9.

Решение.

Заданные линии образуют фигуру АВС, которая ограничена сверху графиком функции

у = √х, а снизу графиком функции у = 2. Полученная фигура показана штриховкой на рис. 3.

Искомая площадь равна S = ʃ_а^b(√x – 2). Найдем пределы интегрирования: b = 9, для нахождения а, решим систему двух уравнений:

{у = √х,
{у = 2.

Таким образом, имеем, что х = 4 = а – это нижний предел.

Итак, S = ∫₄⁹ (√x – 2)dx = ∫₄⁹ √x dx –∫₄⁹ 2dx = 2/3 x√х|₄⁹ – 2х|₄⁹ = (18 – 16/3) – (18 – 8) = 2 2/3 (кв. ед.).

Ответ: S = 2 2/3 кв. ед.

Пример 3.

Вычислить площадь фигуры, ограниченной линиями у = х³ – 4х; у = 0; х ≥ 0.

Решение.

Построим график функции у = х³ – 4х при х ≥ 0. Для этого найдем производную у’:

y’ = 3x² – 4, y’ = 0 при х = ±2/√3 ≈ 1,1 – критические точки.

Если изобразить критические точки на числовой оси и расставить знаки производной, то получим, что функция убывает от нуля до 2/√3 и возрастает от 2/√3 до плюс бесконечности. Тогда х = 2/√3 – точка минимума, минимальное значение функции у_min = -16/(3√3) ≈ -3.

Определим точки пересечения графика с осями координат:

если х = 0, то у = 0, а значит, А(0; 0) – точка пересечения с осью Оу;

если у = 0, то х³ – 4х = 0 или х(х² – 4) = 0, или х(х – 2)(х + 2) = 0, откуда х₁ = 0, х₂ = 2, х₃ = -2 (не подходит, т.к. х ≥ 0).

Точки А(0; 0) и В(2; 0) – точки пересечения графика с осью Ох.

Заданные линии образуют фигуру ОАВ, которая показана штриховкой на рис. 4.

Так как функция у = х³ – 4х принимает на (0; 2) отрицательное значение, то

S = |ʃ₀² (x³ – 4x)dx|.

Имеем: ʃ₀² (x³ – 4х)dx =(x⁴/4 – 4х²/2)|₀²= -4, откуда S = 4 кв. ед.

Ответ: S = 4 кв. ед.

Пример 4.

Найти площадь фигуры, ограниченной параболой у = 2х² – 2х + 1, прямыми  х = 0, у = 0 и касательной к данной параболе в точке с абсциссой х₀ = 2.

Решение.

Сначала составим уравнение касательной к параболе у = 2х² – 2х + 1 в точке с абсциссой х₀ = 2.

Так как производная y’ = 4x – 2, то при х₀ = 2 получим k = y’(2) = 6.

Найдем ординату точки касания: у₀ = 2 · 2² – 2 · 2 + 1 = 5.

Следовательно, уравнение касательной имеет вид: у – 5 = 6(х – 2) или у = 6х – 7.

Построим фигуру, ограниченную линиями:

у = 2х² – 2х + 1, у = 0, х = 0, у = 6х – 7.

Г_у =  2х² – 2х + 1 – парабола. Точки пересечения с осями координат: А(0; 1) – с осью Оу; с осью Ох – нет точек пересечения, т.к. уравнение  2х² – 2х + 1 = 0 не имеет решений (D < 0). Найдем вершину параболы:

x_b = -b/2a;

x_b = 2/4 = 1/2;

y_b = 1/2, то есть вершина параболы точка В имеет координаты В(1/2; 1/2).

Итак, фигура, площадь которой требуется определить, показана штриховкой на рис. 5.

Имеем: S_ОAВD = S_OABC – S_ADBC.

Найдем координаты точки D из условия:

6х – 7 = 0, т.е. х = 7/6, значит DC = 2 – 7/6 = 5/6.

Площадь треугольника DBC найдем по формуле S_ADBC = 1/2 · DC · BC. Таким образом,

S_ADBC = 1/2 · 5/6 · 5 = 25/12 кв. ед.

Далее:

S_OABC = ʃ₀²(2x² – 2х + 1)dx = (2x³/3 – 2х²/2 + х)|₀² = 10/3 (кв. ед.).

Окончательно получим: S_ОAВD = S_OABC – S_ADBC = 10/3 – 25/12 = 5/4 = 1 1/4 (кв. ед).

Ответ: S = 1 1/4 кв. ед.

Мы разобрали примеры нахождения площадей фигур, ограниченных заданными линиями. Для успешного решения подобных задач нужно уметь строить на плоскости линии и графики функций, находить точки пересечения линий, применять формулу для нахождения площади, что подразумевает наличие умений и навыков вычисления определенных интегралов.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Площадь — линия — Большая Энциклопедия Нефти и Газа, статья, страница 2

Площадь — линия

Cтраница 2

При равномерно распределенной нагрузке для определения изгибающего момента величину погонной нагрузки q множат на площадь линии влияния. При частичном загружении балки вели-чину q множат на ту часть площади линии влияния, которая расположена под нагрузкой.  [16]

При равномерно распределенной нагрузке, расположенной на части фермы, погонную нагрузку q множат на площадь линии влияния, расположенную под нагрузкой. При определении усилия в раскосе от равномерно распределенной нагрузки принимают алгебраическую сумму площадей участков линии влияния, расположенных под нагрузкой.  [17]

Таким образом, площадь лоренцевой линии, обрезанной достаточно далеко от точки половинной мощности, очень близка к площади обычной лоренцевой линии.  [18]

С помощью метода ЯМР можно легко изучать кинетику медленно протекающих реакций, применяя обычную аналитическую методику для измерения концентрации реагентов и продуктов реакции по площади линии поглощения.  [19]

Если щель уже нормальной, освещенность линии пропорциональна ширине щели, так как при уменьшении ширины щели световой по-ток уменьшается, как это следует из (III.15), а площадь линии остается постоянной. Если щель шире нормальной, освещенность линии от ширины не зависит, так как с увеличением ширины щели пропорционально увеличиваются и площадь линии и световой поток.  [21]

Садижан [11] указывает, что при квадратичном эффекте Штарка электроны ( ударная теория) ведут к симметричному, а ионы ( статистическая теория) — к асимметричному уширению. Разделяя всю площадь линии по вертикали пополам, он определял величину смещения, отсюда — плотность ионов и наконец температуру. При исследовании профиля линии сравниваемые результаты измерений и расчетов должны всегда относиться к одинаковой полной площади.  [22]

Конденсаторы представляют собой короткие и широкие отрезки линии, близко расположенные друг от друга. Чем больше площадь линий и чем ближе они расположены к подложке платы, тем больше емкость конденсатора.  [23]

Для определения общего поглощения в спектре ЭПР использовались элементы аналоговых ЭВМ, схематически представленные на фиг. Прямое определение площади линии по описанному в данной работе методу иллюстрируется на фиг. На форму же кривой первой производной перемодуляция влияет гораздо сильнее. Это очень важное замечание, поскольку при регистрации слабых сигналов неизбежно используется большая глубина модуляции. ЭПР структура спектров разрешается лучше. С целью получения еще лучшего разрешения Джонсон и Чанг [80] записывали даже третью производную сигнала поглощения.  [24]

Это равносильно измерению площади линии. Оуэне и Джиардино ( 1963) указывали, что в идеальном случае интенсивность ионов следует измерять, предварительно превращая каждую точку профиля почернения линии в интенсивность с помощью характеристической кривой и затем интегрируя полученный профиль интенсивности. Для строго линейной характеристической кривой в результате интегрирования профиля почернения получается величина, пропорциональная интегралу интенсивности. На практике интегрирование профиля почернения предпочитают другим методам оценки интенсивности линий, поскольку этот способ учитывает все изменения формы линии.  [25]

Однако эти случаи следует рассматривать скорее как исключения. Большей частью приходится принимать в расчет всю площадь линии и, следовательно, интегральное поглощение А. При определении температуры по интенсивности одной линии измерения должны производиться в абсолютных единицах. Кроме того, должна быть хотя бы приблизительно известна оптическая толщина слоя; впрочем, часто бывает достаточно знать, лежит ли она в пределах оптически тонких или оптически толстых слоев. Этим, конечно, данный метод сильно усложняется, поэтому он и применяется для определения температуры сравнительно редко. Эленбаас [13], измеряя температуру плазмы ртутного разряда при высоком давлении, полагал, что работает с оптически тонким слоем. По интенсивности излучения дублета 5570 / 90 А с помощью формулы ( 20) он установил, что температура на оси равна 5900 К — При этом, конечно, необходимо было учитывать ее спад у стенок и интегрировать излучение по всем слоям.  [26]

При равномерно распределенной нагрузке для определения изгибающего момента величину погонной нагрузки q множат на площадь линии влияния. При частичном загружении балки величину q множат на ту часть площади линии влияния, которая расположена под нагрузкой.  [27]

При равномерно распределенной нагрузке для определения изгибающего момента величину погонной нагрузки q множат на площадь линии влияния. При частичном загружении балки вели-чину q множат на ту часть площади линии влияния, которая расположена под нагрузкой.  [28]

Основу такой классификации составляет атомарная единица ( пространства), содержащая представления площадей линий и точек.  [29]

Страницы:      1    2    3    4

www.ngpedia.ru

Как вычислить площадь фигуры, ограниченной графиками функций 🚩 вычислите площадь фигуры ограниченной графиком функции 🚩 Математика

Инструкция

Тогда площадь фигуры можно выразить формулой, интегрирующей разность функций на интервале [a, b]. Вычисление интеграла производится по закону Ньютона-Лейбница, согласно которому результат равен разности первообразной функции от граничных значений интервала.

Пример1.
Найти площадь фигуры, ограниченной прямыми линиями y = -1/3·x – ½, x = 1, x = 4 и параболой y = -x² + 6·x – 5.

Решение.
Постройте графики всех линий. Вы можете увидеть, что линия параболы находится выше прямой y = -1/3·x – ½. Следовательно, под знаком интеграла в данном случае должна стоять разность между уравнением параболы и заданной прямой. Интервал интегрирования, соответственно, находится между точками x = 1 и x = 4:
S = ∫(-x² + 6·x – 5 – (-1/3·x – 1/2))dx = (-x² +19/3·x – 9/2)dx на отрезке [1, 4].

Найдите первообразную для полученного подынтегрального выражения:
F(-x² + 19/3x – 9/2) = -1/3x³ + 19/6x² – 9/2x.

Подставьте значения концов отрезка:
S = (-1/3·4³ + 19/6·4² – 9/2·4) – (-1/3·1³ + 19/6·1² – 9/2·1) = 13.

Пример2.
Вычислите площадь фигуры, ограниченной линиями y = √(x + 2), y = x и прямой x = 7.

Решение.
Эта задача является более сложной по сравнению с предыдущей, поскольку в ней нет второй прямой, параллельной оси абсцисс. Это значит, что второе граничное значение интеграла неопределенно. Следовательно, его нужно найти из графика. Постройте заданные линии.

Вы увидите, то прямая линия y = x проходит диагонально относительно координатных осей. А график функции корня – это положительная половина параболы. Очевидно, что линии на графике пересекаются, поэтому точка пересечения и будет нижним пределом интегрирования.

Найдите точку пересечения, решив уравнение:
x = √(x + 2) → x² = x + 2 [x ≥ -2] → x² – x – 2 = 0.

Определите корни квадратного уравнения с помощью дискриминанта:
D = 9 → x1 = 2; x2 = -1.

Очевидно, что значение -1 не подходит, поскольку абсцисса токи пересечения – положительная величина. Следовательно, второй предел интегрирования x = 2. Функция y = x на графике выше функции y = √(x + 2), поэтому в интеграле она будет первой.
Проинтегрируйте получившееся выражение на интервале [2, 7] и найдите площадь фигуры:
S = ∫(x — √(x + 2))dx = (x²/2 – 2/3·(x + 2)^(3/2)).

Подставьте интервальные значения:
S = (7²/2 – 2/3·9^(3/2)) – (2²/2 – 2/3·4^(3/2)) = 59/6.

www.kakprosto.ru

ЦЕНТР ТЯЖЕСТИ ОБЪЁМА, ПЛОЩАДИ, ЛИНИИ

Сила, с которой тело притягивается к Земле, называется силой тяжести. Точка приложения этой силы — центром тяжести. Поскольку силы тяжести действуют на каждую частицу тела, то её надо считать распределённой. При небольших (по сравнению с Землей) размерах тела силы тяжести с большой степенью точности можно считать параллельными. Для определения равнодействующей и точки приложения силы тяжести разобьём тело на » » достаточно малых элементов. Предельным переходом, устремляя , получим точные формулы.

Вес элементарного объема можно выразить через удельный вес формулой . При вычислении центра тяжести пластинки постоянной толщины его элементарный объём можно представить в виде . При вычислении элементарного объёма стержня можно воспользоваться соотношением , где — площадь поперечного сечения стержня.

Тогда формулы для определения центра тяжести плоской фигуры

криволинейного стержня (линии)

Динамика

Динамика — раздел механики, в котором изучается движение материальных объектов в зависимости от действующих на них сил. Простейшим материальным объектом является материальная точка. Это модель материального тела любой формы, размерами которого в рассматриваемых задачах можно пренебречь и принять за геометрическую точку, имеющую определенную массу. Более сложные материальные объекты — механические системы и сплошные тела — считают состоящими из материальных точек.

Сила считается в механике основным, первичным понятием. Свойства сил, приложенных к твердому телу и точке, рассматривались в статике. В динамике силы оцениваются по их динамическому действию, т.е. по изменению ими характеристик движения материальных объектов.

Движение материальных объектов следует рассматривать относительно определенной системы отсчета. Оно совершается в пространстве с течением времени. В классической механике пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от движущихся в нем материальных объектов. Время в классической механике инвариантно по отношению к выбору системы координат.

В основу классической механики положены законы или аксиомы Ньютона, которые были получены им путём обобщений целого ряда опытных данных и теоретических исследований.

ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

Задачи динамики материальной точки можно разделить на три раздела:

· Динамика свободной материальной точки;

· Динамика несвободной материальной точки;

· Динамика относительного движения материальной точки.

Динамика свободной материальной точки

Основные законы классической механики были сформулированы как законы движения по отношению к некоторой абсолютно неподвижной системе — «абсолютному пространству». Ньютон принимал «абсолютное время», не зависящее от движения тел и систем отсчёта.

Законы механики Галилея-Ньютона

Закон инерции

«Изолированная материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока действие других тел не изменит это состояние».

Материальная точка, на которую не действуют силы или действует уравновешенная система сил, называется изолированной (свободной) материальной точкой.

Смысл закона инерции заключается в постулировании существования так называемых инерциальных систем отсчёта, которые движутся по отношению к “абсолютному пространству” поступательно, равномерно и прямолинейно. В этих системах отсчета выполняются законы классической механики.

Закон инерции характеризует основное свойство материи постоянно находиться в состоянии равномерного прямолинейного движения (движения по инерции).

Свойство материальной точки сохранять при движении свою скорость называется инертностью. Количественная мера инертности материальной точки, пропорциональная количеству вещества, заключенного в ней, называется массой материальной точки.

Масса представляет собой основную динамическую характеристику точки, она является скалярной положительной величиной.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Найти площадь фигуры, ограниченной линиями

Из данной статьи вы узнаете, как найти площадь фигуры, ограниченной линиями, используя вычисления с помощью интегралов. Впервые с постановкой такой задачи мы сталкиваемся в старших классах, когда только-только пройдено изучение определенных интегралов и пора приступить к геометрической интерпретации полученных знаний на практике.

Итак, что потребуется для успешного решения задачи по поиску площади фигуры с помощью интегралов:

• Умение грамотно строить чертежи;
• Умение решать определенный интеграл с помощью известной формулы Ньютона-Лейбница;
• Умение «увидеть» более выгодный вариант решения — т.е. понять, как в том или ином случае будет удобнее проводить интегрирование? Вдоль оси икс (OX) или оси игрек (OY)?
• Ну и куда без корректных вычислений? ) Сюда входит понимание как решать тот иной тип интегралов и правильные численные вычисления.

Алгоритм решения задачи по вычислению площади фигуры, ограниченной линиями:

1. Строим чертеж. Желательно это делать на листке в клетку, с большим масштабом. Подписываем карандашом над каждым графиком название этой функции. Подпись графиков делается исключительно ради удобства дальнейших вычислений. Получив график искомой фигуры, в большинстве случаев будет видно сразу, какие пределы интегрирования будут использованы. Таким образом мы решаем задачу графическим методом. Однако бывает так, что значения пределов дробные или иррациональные. Поэтому, можно сделать дополнительные расчеты, переходим в шагу два.

2. Если явно не заданы пределы интегрирования, то находим точки пересечения графиков друг с другом, и смотрим, совпадает ли наше графическое решение с аналитическим.

3. Далее, необходимо проанализировать чертеж. В зависимости от того, как располагаются графики функций, существуют разные подходы к нахождению площади фигуры. Рассмотрим разные примеры на нахождение площади фигуры при помощи интегралов.

3.1. Самый классический и простой вариант задачи, это когда нужно найти площадь криволинейной трапеции. Что такое криволинейная трапеция? Это плоская фигура, ограниченная осью икс ( у = 0 ), прямыми х = а, х = b и любой кривой, непрерывной на промежутке от a до b. При этом, данная фигура неотрицательна и располагается не ниже оси абсцисс. В этом случае, площадь криволинейной трапеции численно равна определенному интегралу, вычисляемого по формуле Ньютона-Лейбница:

Пример 1. Вычислить площадь фигуры, ограниченной линиями y = x2 — 3x + 3, x = 1, x = 3, y = 0.

Решение:

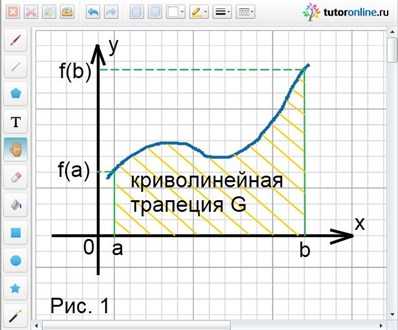
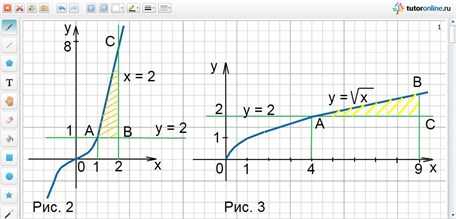
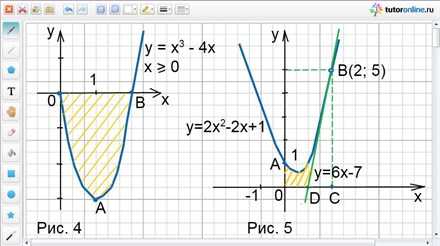
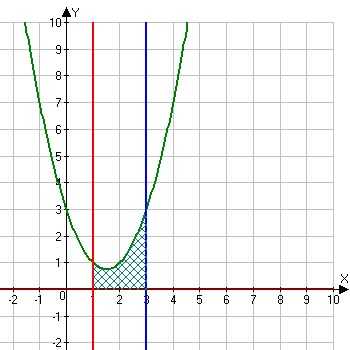Какими линиями ограничена фигура? Имеем параболу y = x2 — 3x + 3, которая располагается над осью ОХ, она неотрицательна, т.к. все точки этой параболы имеют положительные значения. Далее, заданы прямые х = 1 и х = 3, которые пролегают параллельно оси ОУ, являются ограничительными линиями фигуры слева и справа. Ну и у = 0, она же ось икс, которая ограничивает фигуру снизу. Полученная фигура заштрихована, как видно из рисунка слева. В данном случае, можно сразу приступать к решению задачи. Перед нами простой пример криволинейной трапеции, которую далее решаем с помощью формулы Ньютона-Лейбница.

3.2. В предыдущем пункте 3.1 разобран случай, когда криволинейная трапеция расположена над осью икс. Теперь рассмотрим случай, когда условия задачи такие же, за исключением того, что функция пролегает под осью икс. К стандартной формуле Ньютона-Лейбница добавляется минус. Как решать подобную задачу рассмотрим далее.

Пример 2. Вычислить площадь фигуры, ограниченной линиями y = x2 + 6x + 2, x = -4, x = -1, y = 0.

Решение:

В данном примере имеем параболу y = x2 + 6x + 2, которая берет свое начало из-под оси ОХ, прямые х = -4, х = -1, у = 0. Здесь у = 0 ограничивает искомую фигуру сверху. Прямые х = -4 и х = -1 это границы, в пределах которых будет вычисляться определенный интеграл. Принцип решения задачи на поиск площади фигуры практически полностью совпадает с примером номер 1. Единственное различие в том, что заданная функция не положительная, и все также непрерывная на промежутке [-4; -1]. Что значит не положительная? Как видно из рисунка, фигура, которая заключается в рамках заданных иксов имеет исключительно «отрицательные» координаты, что нам и требуется увидеть и помнить при решении задачи. Площадь фигуры ищем по формуле Ньютона-Лейбница, только со знаком минус в начале.

Статья не завершена.

matematyka.ru

экстремум функции двух переменных — 22 Июля 2014 — Примеры решений задач

Ключевые слова: калькулятор экстремумов, найти экстремум функции двух переменных, частные производные первого и второго порядков, стационарные точки, калькулятор частных производных.

Пример 1. Исследовать на экстремум функцию:

Алгоритм решения следующий:

1) находим частные производные первого порядка:

Примечание: найти частные производные онлайн  (первого и второго порядка) можно с помощью калькулятора.

2). Решаем систему уравнений:

и таким образом находим стационарные точки функции.

Точки, в которых значение производной функции равно нулю, называются стационарными точками.

Для данного примера  получаем систему уравнений:

стационарная точка: (-1;1)

3) Находим вторые частные производные

Вычисляем значения этих частных производных второго порядка в каждой из найденных в п.2 стационарных точках M(x₀;y₀).

Для данного примера, получаем

4) Делаем вывод о наличии экстремумов:
а) если AC – B² > 0 и A < 0 , то в точке M имеется максимум;
б) если AC – B² > 0 и A > 0 , то в точке M имеется минимум;
в) если AC – B² < 0, то экстремума нет;
г) если AC – B² = 0, то вопрос о наличии экстремума остается открытым;

Тогда в точке    x=-1, y=1

Следовательно в точке x=-1, y=1 функция имеет локальный минимум

Ответ: min{z}=0

Проверить правильность решения можно с помощью калькулятора «экстремум функции».

www.reshim.su

Экстремумы функции двух переменных

Определение. Точками экстремума функции двух переменных называются точки минимума и максимума этой функции. Значения самой функции в точках экстремума называются экстремумами функции двух переменных.

Определение. Точка P(x0, y0) называется точкой максимума функции двух переменных z = z(x, y), если значение функции в этой точке больше, чем в точках её окрестности. Значение функции в точке максимума называется максимумом функции двух переменных.

Определение. Точка P(x0, y0) называется точкой максимума функции двух переменных z = z(x, y), если значение функции в этой точке больше, чем в точках её окрестности. Значение функции в точке максимума называется максимумом функции двух переменных.

Теорема (необходимый признак экстремума функции двух переменных). Если точка P(x0, y0) — точка экстремума функции двух переменных z = z(x, y), то первые частные производные функции (по «иксу» и по «игреку») в этой точке равны нулю или не существуют:

и

.

Определение. Точки, в которой первые частные производные функции двух переменных равны нулю, называются стационарными точками.

Определение. Точки, в которой первые частные производные функции двух переменных равны нулю или не существуют, называются критическими точками.

Как и в случае с функцией одной переменной, необходимое условие существования экстремума функции двух переменных не является достаточным. Встречаются немало функций, в случаях которых первая частная производная функции равна нулю или не существует, но экстремумов в соответствующих точках нет. Каждая точка экстремума является критической точкой, но не каждая критическая точка является экстремумом.

Достаточный признак существования экстремума функции двух переменных. В точке P существует экстремум функции двух переменных, если в окрестности этой точки полное приращение функции не меняет знак. Так как в критической точке первый полный дифференциал равен нулю, то приращение функции определяет второй полный дифференциал

.

Наилучшее понимание применения полного дифференциала придёт при изучении и практическом применении шагов 3 и 4 алгоритма нахождения экстремумов функции двух переменных, который следует вторым пунктом этого урока.

Локальный характер экстремумов функции двух переменных. Максимум функции двух переменных на каком-либо участке области определения функции не обязательно является максимумом во всей области определения, так же как и минимум на каком-либо участке не является минимумом во всей области определения. Пусть мы рассматриваем высоту волн на участке прибрежной области моря (участок меньше области). Тогда на этом участке мы можем зафиксировать (по-крайней мере, зрительно) наибольшую высоту волны. Но на другом участке, на котором ветер вызывает бОльшую высоту волн, мы фиксируем минимальную высоту волны. Это к тому, что максимум высоты волны на первом участке может оказаться меньше, чем минимум высоты волны на втором участке. Поэтому, как и в случае экстремума функции одной переменной, необходимо уточнить это понятие и говорить об экстремумах как о локальных экстремумах функции двух переменных.

Наибольший интерес представляет алгоритм нахождения экстремумов функции двух переменных, так как он, во-первых, отличается от алгоритма нахождения экстремумов функции одной переменных, а во-вторых, по аналогии с ним можно составить алгоритм нахождения функции трёх переменных. В частности, потребуется вычислять определители.

Итак, алгоритм нахождения экстремумов функции двух переменных.

Дана функция двух переменных .

Шаг 2. Составляем систему уравнений из равенств этих производных нулю (их равенство нулю и есть необходимый признак существования экстремума):

Решения этой системы уравнений являются точками возможного экстремума — критическими точками.

Шаг 3. Пусть является критической точкой, найденной на шаге 2. Чтобы убедиться, что в ней существует экстремум функции двух переменных, находим частные производные второго порядка

как частные производные от частных производных первого порядка, найденных на шаге 1.

Шаг 4. Присваиваем частным производным второго порядка, найденным на шаге 3, буквенные обозначения:

Находим определитель и проверяем достаточный признак существования экстремума.

Если , то экстремума в найденной критической точке нет,

если , то экстремум в найденной критической точке есть,

если , то требуются дополнительные исследования.

Если экстремум в найденной точке есть и если , то в этой точке существует минимум функции двух переменных, если , то максимум.

Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значение экстремума функции двух переменных (минимума или максимума).

Примеры начнём с более сложного, в котором составленная система уравнений имеет несколько решений, а, значит, найдено несколько критических точек.

Пример 1. Найти экстремумы функции двух переменных .

Решение. Следуем изложенному выше алгоритму.

Шаг 1. Находим частные производные:

.

Шаг 2. Составляем систему уравнений из равенств этих производных нулю:

Делим первое уравнение системы на 3, а второе на 6 и получаем

Из второго уравнения выражаем , подставляем в первое уравнение и получаем

Умножаем это уравнение на и получаем

.

Производим замену переменной: и получаем

.

Решаем полученное квадратное уравнение: .

Так как и , то

Таким образом, получили четыре критических точки — точки возможного экстремума.

Шаг 3. Находим частные производные второго порядка

Шаг 4. Находим определитель :

, т. е. экстремума в найденной критической точке нет,

, т. е. экстремума в найденной критической точке нет,

и , т. е. в найденной критической точке есть минимум функции двух переменных,

и , т. е. в найденной критической точке есть максимум функции двух переменных.

Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значения экстремума функции двух переменных:

,

Найти экстремумы функции двух переменных самостоятельно, а затем посмотреть решение

Третий пример — на десерт, так как в нём только одна критическая точка.

Пример 3. Найти экстремумы функции двух переменных .

Шаг 1. Находим частные производные:

.

Шаг 2. Составляем систему уравнений из равенств этих производных нулю:

Решаем систему уравнений:

Таким образом, получили критическую точку — точку возможного экстремума.

Шаг 3. Находим частные производные второго порядка

Шаг 4. Находим определитель , т. е. в найденной критической точке есть экстремум, причём так как , то это минимум.

Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значение экстремума функции двух переменных:

.

Найти экстремумы ещё одной функции двух переменных самостоятельно, а затем посмотреть решение

Функции нескольких переменных

function-x.ru

Как найти условные экстремумы функции двух и более переменных

В задачах оптимизации возникает необходимость найти экстремумы функции двух и более переменных при условии, что существует связь между переменными этой связи, заданная уравнением . В этом случае говорят, что требуется найти условный экстремум.

Для того чтобы найти условный экстремум требуется находить частные производные и решать системы уравнений Существует алгоритм нахождения условного экстремума из трёх шагов, который сейчас и разберём на примере, и геометрический смысл условного экстремума, который должен дойти до каждого при разборе этого самого примера.

Итак, алгоритм, который разберём на примере самой распространённой задачи — нахождение условного экстремума функции двух переменных..

Шаг 1. Вводится функция Лагранжа

,

где первое слагаемое — сама исходная функция, а второе слагаемое со знаком минус — левая часть уравнения условия связи, умноженная на (лямбда) — множитель Лагранжа.

Пример 1. Найти условные экстремумы функции двух переменных , выражающей площадь прямоугольника через его стороны x и y при условии , означающем, что существует верёвка, которой можно ограничить этот прямоугольник, и длина этой верёвки равна 100.

Шаг 1. Решение. Приведём уравнение условия связи к требуемому виду с нулём в правой части:

.

Составим функцию Лагранжа:

.

Шаг 2. Составляем систему уравнений из равенств частных производных нулю и уравения условия связи (необходимый признак существования условного экстремума):

Решения этой системы уравнений являются точками возможного условного экстремума — стационарными точками или, как ещё говорят, критическими точками.

Пример 1. Шаг 2.

Решение. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:

Из первого и второго уравнений выразим соответственно x и y:

Подставим эти выражения в третье уравнение и найдём значение множителя Лагранжа:

Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции:

Получили и . Эти значения являются также координатами стационарной точки. Таким образом, получили стационарную точку .

Шаг 3. Пусть является стационарной точкой, найденной на шаге 2. Чтобы определить, является ли условный экстремум минимумом или максимумом, нужно найти второй дифференциал функции Лагранжа

и в полученном выражении подставить вместо «лямбды» её значения (значения множителя Лагранжа), найденные на шаге 2.

Если значение второго дифференциала функции Лагранжа меньше нуля (), то стационарная точка является точкой максимума, если больше нуля (), то стационарная точка является точкой минимума. Если значение второго дифференциала функции Лагранжа равно нулю, то требуются дополнительные исследования, но такие случаи практически не попадаются в задачах, задаваемых студентам.

Координаты стационарных точек подставляются в исходную точку и, таким образом, мы окончательно находим условные экстремумы (или минимум и максимум или что-то одно из этих экстремумом).

Пример 1. Шаг 3.

Решение. Найдём второй дифференциал функции Лагранжа:

В нашем случае, так как первое и третье составляющие равны нулю, нам не придётся подставлять в них значения множителя Лагранжа. Зато нужно найти отношения между дифференциалами dx и dy:

Так как полученные значения — противоположные по знаку, то получаем, что в любом случае .

Теперь можем найти значение условного экстремума исходной функции, являющееся максимумом:

.

Это заданная исходной функцией максимальная площадь прямоугольника, который можно ограничить верёвкой, длина которой равна 100.

Пример 2. Найти условные экстремумы функции двух переменных при условии .

Решение.

Шаг 1. Составим функцию Лагранжа:

.

Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:

Из первого и второго уравнений выразим соответственно x и y:

Подставим эти выражения в третье уравнение и найдём значения множителя Лагранжа:

Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции при двух значениях множителя Лагранжа:

Эти значения икса и игрека являются координатами двух стационарных точек. Таким образом, получили стационарные точки .

Шаг 3. Найдём частные производные второго порядка функции Лагранжа:

:

Найдём второй дифференциал функции Лагранжа по формуле

:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, меньшее нуля, следовательно, точка — точка условного максимума:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, большее нуля, следовательно, точка — точка условного минимума:

.

Таким образом, условные экстремумы заданной функции найдены.

Пример 3. Найти условные экстремумы функции двух переменных при условии .

Решение.

Шаг 1. Составим функцию Лагранжа:

.

Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:

Из первого и второго уравнений выразим соответственно x и y:

Получаем, что , однако подстановка этих значений переменных в третье уравнение системы не даёт верного равенства. Поэтому считаем, что на самом деле второй сомножитель равенства равен нулю: . Отсюда получаем

Ищем координаты стационарных точек при значении множителя Лагранжа . Тогда из выражений для икса и игрека из системы уравнений следует, что . Из третьего уравнения системы получаем:

Получили две стационарные точки:

Ищем координаты стационарных точек при значении множителя Лагранжа . Тогда из выражений для икса и игрека из системы уравнений следует, что .

На основании вычислений двух первых стационарных точек получилаем ещё две стационарные точки:

Шаг 3. Найдём частные производные второго порядка функции Лагранжа:

:

Найдём второй дифференциал функции Лагранжа по формуле

:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, меньшее нуля, следовательно, точки — точки условного максимума:

.

Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа :

Получили значение, большее нуля, следовательно, точки — точки условного минимума:

.

Таким образом, условные экстремумы заданной функции найдены.

Аналогичным образом можно находить условные экстремумы функций трёх и более переменных.

Функции нескольких переменных

function-x.ru

Найти экстремум функции — 31 Июля 2013 — Примеры решений задач

www.reshim.su

Нахождение точек локального экстремума функции онлайн

Локальный экстремум

Определение 1. Пусть существует число такое, что функция определена в -окрестности точки то есть на множестве и пусть для всех выполняется неравенство

Тогда говорят, что функция имеет в точке локальный минимум.

Аналогично, если существует число такое, что для всех выполняется неравенство

то говорят, что функция имеет в точке локальный максимум.

Определение 2. Если точка  является точкой локального минимума или локального максимума функции то говорят, что — точка локального экстремума функции

Теорема Ферма

Теорема (Ферма). Если функция имеет локальный экстремум в точке и дифференцируема в этой точке, то

Этой теоремой пользуются для нахождения точек локального экстремума.

umath.ru

Экстремум функции 3 переменных. Контрольные онлайн

Экстремум функции трех переменных

Решение
Найдем стационарные точки заданной функции, то есть точки, в которых выполняется необходимое условие существования экстремума. Для функции трех переменных  стационарные точки (координаты точек) находятся из системы
Для заданной функции , ,  

и система примет вид
Решениями системы являются  и
Получили две стационарные точки  и .
Для проверки достаточных условий экстремума в стационарной точке необходимо определить знаки определителей ,
 и  в этой точке.
Найдем , , , , , .
Для точки  ,

,
.

Так как , , , то в точке  функция имеет максимум, при этом
.
Для точки  ,

,

.

Так как , , , то в точке  функция не имеет экстремума.

www.matem96.ru

Экстремум функции двух переменных

Экстремум функции двух переменных

Говорят, что функция имеет максимум в точке , т.е. при , если для всех точек , достаточно близких к точке и отличных от неё.

Говорят, что функция имеет минимум в точке , т.е. при , если для всех точек , достаточно близких к точке и отличных от неё.

Максимум и минимум функции называются экстремумами функции.

Теорема (необходимое условие экстремума функции двух переменных). Если функция достигает экстремума при , то каждая частная производная первого порядка от или обращается в нуль при этих значениях аргументов, или не существует.

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку функция имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка является критической точкой функции , т.е.
,
тогда при :
1) имеет максимум, если дискриминант и , где ;
2) имеет минимум, если дискриминант и ;
3) не имеет ни минимума, ни максимума, если дискриминант ;
4) если , то экстремум может быть, а может и не быть (требуется дополнительное исследование).

Примеры решения задач

Пример 1. Исследовать на экстремум функцию .

Решение.

На первом шаге, в соответствие с достаточным условием экстремума функции двух переменных, найдем точки, удовлетворяющие условию:

Частные производные первого порядка от функции равны:

Приравняем их к нулю и решим систему уравнений:

Выпишем отдельно первое уравнение системы и найдем его корни:

Подставим найденные значения переменной во второе уравнение системы:

и

Таким образом, получили две точки и , в которых будет продолжено исследование функции на экстремум.

На втором шаге найдем все вторые частные производные от функции :

На третьем шаге для каждой из точек и установим наличие экстремума функции (для этого вычислим значения вторых производных и найдем знак дискриминанта в указанных точках).

1) Для точки :

Так как дискриминант больше нуля и , то функция имеет минимум в точке :
.

2) Для точки :

Так как дискриминант меньше нуля, то функция не имеет в точке ни минимума, ни максимума.

Ответ: в точке функция имеет минимум.

pgsksaa07.narod.ru

Переведите 5 часов 48 минут это сколько минут? срооочно

348 минут конечноже

5 на 60 не умножить? 48 не прибавить? Совсем обленилась школота….

348 минут (1 час=60мин, т. е. 5чх60=300мин; 300+48мин=348мин

Для этого нужно 60 минут (1 час) умножить на 5, количество часов. И прибавить оставшиеся 48 минут. Получается: 60х5=300, 300+48= 348. Ответ: 348 минут.

в 1 часе-60 минут 60х5=300 300+48=348

touch.otvet.mail.ru

сколько секунд. в 5 минутах четверти часа в одном часе в четверти минуты в трети минуты в половине минуты

запятые расставь, ничего же не понятно

ты думаешь мы тут все будем считать?

Это так 5 мин=60*5=300сек 1/4 часа= 15 мин=60*15=900сек 1 час=60 мин=60*60=3600 сек 1/4 мин=60*1/4=15 сек 1/3 мин=60*1/3=20сек 1/2 мин=60*1/2=30 сек

5 минут=300 секунд четверть часа=15 минут=900 секунд 1 час=60 минут=3600 секунд четверть минуты=15 секунд треть минуты=20 секунд половина минуты=30 секунд

5 мин=300сек 15мин=900сек 1час=3600сек 1/4 мин=15сек 1/3мин=20сек 1/2мин=30сек

touch.otvet.mail.ru

0,5 часа сколько это в минутах?

Так как в одном часе 60 минут, то 0,5 часа это 30 минут.

Ахахахахах))) ) 150 минут

touch.otvet.mail.ru

сколько минут в 1,5 часа

90 мля, если считать не умеешь!!!

126599 минут 34 секунды.

1.5 часа-1час30мин. -90минут-5400 секунд) пожалуйста

90 минут, тупица.

90 минут, ты чё в каменном веке живёшь.

Чё вы человека оскорбляете? Не видите она пишет я такая какая есть кому не нравится — идите к черту!

90 мин пока что»!!

ЛЮДИ НЕ 90! ТАКОГО ОТВЕТА НЕТ! ОТВЕТ БУДЕТ 12 МИНУТ

touch.otvet.mail.ru

Тесты с ответами по предмету управление качеством – пройти тест онлайн бесплатно

71 вопрос

Вопрос:

Какое понятие отражено определением: «Предельно общее фундаментальное понятие, отражающее наиболее существенные, закономерные связи и отношения реальной действительности и познания»?

Варианты ответа:

1. свойство;
2. категория;
3. мера.

Вопрос:

Какой закон диалектики определен следующим образом: «Изменение качества объекта происходит тогда, когда накопление количественных изменений достигает определенного предела»?

Варианты ответа:

1. закон отрицания;
2. закон перехода количественных изменений в качественные;
3. закон взаимной связи и взаимообусловленности.

Вопрос:

Какая философская категория выражает внешнюю определенность объекта?

Варианты ответа:

1. мера;
2. количество;
3. качество.

Вопрос:

Какая философская категория выражает диалектическое единство качественных и количественных характеристик объекта?

Варианты ответа:

1. мера;
2. количество;
3. качество.

Вопрос:

Какое понятие отражено определением: «Способ проявления определенной стороны качества объекта по отношению к другому объекту, с которым он вступает во взаимодействие»?

Варианты ответа:

1. категория;
2. мера;

zaochnik.com

Управление качеством МФПА Тест с ответами

Правильных ответов не менее 95%

Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)

Качество товара (услуги) – это …

совокупность характеристик, которые позволяют ей выполнять

способность полностью удовлетворить ожидания потребителя

+способность удовлетворять установленным и предполагаемым потребностям 

функции (соответствовать описанию)

Цикл Шухарта-Деминга включает …

этапы: планирование, организация, мотивация и контроль 

11 этапов, в том числе: 1-маркетинг, 11- утилизация 

+этапы: Plan (Планируй) – Do (Внедряй) – Check (Проверь) – Act (Действуй с учетом внедрения) 

Неверно, что в 8 принципов управления качеством входит принцип …

постоянного улучшения процессов

принятия решений на основе фактов 

+комплексного подхода к решению проблем

Принцип … относится к 8 принципам управления качеством

комплексного подхода к решению проблем

сохранения конкурентных преимуществ

+взаимовыгодных отношений с поставщиками

минимальных издержек 

Друзья, более 600 собак Воронежского приюта Дора https://vk.com/priyt_dora очень нуждаются в поддержке! Приют бедствует, не хватает средств на корм и лечение.  Не откладывайте добрые дела, перечислите прямо сейчас любую сумму на «Голодный телефон» +7 960 111 77 23 или карту сбербанка 4276 8130 1703 0573. По всем вопросам обращаться +7 903 857 05 77 (Шамарин Юрий Иванович) 

Неверно, что подсистема … входит в число 5 основных подсистем СМК

обучения

мотивации 

+контроля 

… — это стадия жизненного цикла продукта, которую принято считать последней

Описание продукта после его снятия с производства

Реализация и распределение продукции

+Утилизация после использования

Профиль желаемого качества включает характеристики, которые …

потребитель желает видеть в продукте

+являются неожиданными для потребителя, т.е. идут сверх запрашиваемых им характеристик

желательно добавить к новому продукту 

… профиль качества, — это профиль качества, включающий характеристики, которые потребитель считает само собой разумеющимися

Требуемый

Желаемый

+Базовый 

… метод определения показателей качества основан на использовании информации, получаемой путем подсчета числа определенных событий и/или предметов

Расчетным

Органолептическим

+Регистрационным 

… метод определения показателей качества основан на использовании информации, получаемой с помощью теоретических или эмпирических зависимостей

Органолептическим 

Регистрационным

+Расчетным 

… метод оценки уровня качества продукции основан на сравнении показателя качества оцениваемого вида продукции с соответствующим базовым показателем

Расчетный 

Относительный

+Дифференцированный 

Значение индекса воспроизводимости технологического процесса Cр при повышении управляемости процесса …

зависит от других факторов

уменьшается

+увеличивается 

Увеличение дисперсии выборки результатов технологического процесса свидетельствует о том, что управляемость процесса …

возрастает

не меняется

+уменьшается 

Ошибкой первого рода является …

ошибочное признание бракованной продукции годной

любое ошибочное составление плана статистического контроля

+ошибочное признание годной продукции бракованной 

Ошибкой второго рода является …

любое ошибочное решение по итогам статистического контроля

ошибочное признание годной продукции бракованной 

+ошибочное признание бракованной продукции годной 

изображает такой инструмент качества, как …

гистограмма

диаграмма рассеивания

+контрольная карта

… — это данные, достаточные для построения гистограммы при известной выборке

Максимальное и минимальное значение и их разница (размах)

Парные сочетания «значение – количество значений в выборке»

Ширина столбца, суммарная высота столбцов

+Ширина столбца, количество вхождений в каждый 

Контрольным листком называют …

любой документ, содержащий результаты контроля;

регистр, предназначенный для регистрации данных, выходящих за контрольные нормативы

+регистр, подготовленный для сбора данных определенного вида 

В соответствии с контрольной картой технологический процесс удовлетворителен, если результаты контроля …

не приближаются к границам допустимых значений

остаются вне пределов допустимых значений

+не выходят за границы допустимых значений 

Стандарт …

устанавливает требования, обязательные для исполнения, а технический регламент — характеристики, использование которых является добровольным

и технический регламент — это взаимозаменяемые понятия

+устанавливает характеристики, использование которых является добровольным, а технический регламент – требования, обязательные для исполнения

Существуют …

государственные стандарты и стандарты предприятий

государственные и международные стандарты 

+стандарты предприятий и организаций, национальные и международные стандарты 

Принцип … является теоретической базой стандартизации

взаимозаменяемости

системности

+предпочтительности

Неверно, что существует такой научно-технический принцип стандартизации, как …

обеспечение функциональной взаимозаменяемости

взаимоувязка стандартов 

+дополнительная функциональная надежность

Основное преимущество процессного подхода состоит в том, что он позволяет …

повысить управляемость предприятия в целом

построить оптимальную организационную структуру

+преодолеть функциональные барьеры и ориентировать организацию на потребителя 

«…» — это характерный признак, который может отсутствовать у процесса

Стоимость (или ценность) «выхода» у процесса выше стоимости «входа»

У процесса всегда есть владелец

+у процесса всегда есть внешний потребитель 

Сеть процессов на предприятии должна содержать …

в общей сложности не более 12 процессов 

основные процессы, количество которых на предприятии <= 5+-2, и вспомогательные процессы, количество которых на предприятии <= 7±2 

+основные процессы, количество которых на предприятии <= 7+-2, и вспомогательные процессы, количество которых на предприятии <= 5±2 

… — это таблица, в которой отмечается участие сотрудников в выполнении работ по процессу 

Матрица участия 

Схема процесса 

+Матрица ответственности

Стандарт ИСО 9004:2000 …

содержит основные положения и словарь, а ИСО 9001:2000 — нет

содержит рекомендации по внедрению процессного подхода, а ИСО 9001:2000

+нацеливает организацию на эффективность, а ИСО 9001:2000 — на результативность

Число обязательных документированных процедур, проведения которых требует стандарт ИСО 9001:2000, равно …

3

+6

0

1

Система «кайдзен» …

свойственна только японскому стилю управления и никак не связана с инновациями

это то же самое, что и инновация

+означает постепенное совершенствование, а инновация – значительное преобразование

test-for-you.ru

Тесты по управлению качеством

Лекция 1.

1) Что является первым звеном в петле качества?

а) Производство

б) Проектирование и разработка

в) Маркетинг

г) Упаковка и хранение

2. Степень соответствия характеристик продукции установленным требованиям – это:

а) Качество

б) Управление качеством

в) Надежность

г) Эргономичность

2. Что не входит в петлю качества?

а) Утилизация

б) Эксплуатация

в) Маркетинг

г) Прогнозирование

2. Совокупность объектов управления качеством продукции образует:

а) Петлю качества

б) Качество продукта

в) Жизненный цикл продукта

г) Стандарт ISO

Лекция 2.

1. На каком этапе производится оценка технического уровня продукции?

а) На этапе проектирования

б) На этапе производства

в) На этапе контроля

г) На этапе эксплуатации

2. Образец продукции, представляющий передовые научно-технические достижения – это:

а) Базовый образец

б) Технический уровень

в) Полезная модель

г) Опытный образец

3. Какое количество этапов оценки технического уровня выделяют?

а) 4

б) 5

в) 6

г) 3

4. При сравнении дифференциальным методом значение означает, что:

а) Оцениваемый продукт соответствует образцу

б) Оцениваемый продукт уступает базе

в) Оцениваемый продукт необходимо сравнивать другим методом

г) оцениваемый продукт превосходит базу

Лекция 3

1. Какой метод не относится к методам определения весомости:

а) Метод предпочтения

б) Метод попарного сопоставления

в) Метод последовательного сопоставления

г) Метод Дельфи

2. Формула надежности:

а)

б)

в)

г)

3. Предикаторность – это:

а) Способность предсказывать будущее объекта

б) Способность видеть неочевидное

в) Способность видеть проблемы с разных точек зрения

г) Способность вырабатывать новые идеи

4. Трансформация шкал применяется для:

а) Перехода от абсолютных значений свойств к одной размерности

б) Перехода от абсолютных значений свойств к относительным

в) Перехода от относительных значений свойств к абсолютным

г) Определения относительного значения свойства

5. В формуле надежности — это:

а) Число случаев, в которых эксперт выдвинул гипотезу, подтвердившуюся впоследствии

б) Относительный показатель надежности экспертов

в) Общее число случаев

г) Весомость фактора

Лекция 5

1. Затраты на контроль входят в:

а) Затраты на соответствие

б) Предупредительные затраты

в) Внутренние потери

г) Затраты на несоответствие

2. Общие затраты на качество делятся на:

а) Предупредительные затраты и затраты на контроль

б) Внутренние и внешние потери

в) Затраты на соответствие и несоответствие

г) Прямые и косвенные

3. На этапе подготовки и организации производства после отгрузки следует:

а) Обслуживание

б) Хранение

в) Производство

г) Снабжение

4. Затраты на несоответствие делятся на:

а) Предупредительные затраты и затраты на контроль

б) Общие затраты на качество и затраты на соответствие

в) Внутренние и внешние потери

г) Затраты на контроль и внешние потери

5. Проектирование осуществляется на стадии:

а) Планирования мощностей

б) Организации и подготовки производства

в) Технологического планирования

г) Производственного планирования

studfiles.net

Тесты по дисциплине «Управление качеством»

1. Назовите современное определение качества ( по ИСО 9000-2000)?

А. Качество продукции – это соответствие требованиям  стандартов или других нормативно- технических документов

Б. Под качеством продукции понимается совокупность характеристик объекта, относящихся к его способности удовлетворять обусловленные или предполагаемые потребности

В. Качество- степень соответствия присущих характеристик требованиям

1. Что такое  «характеристика» качества ?

А. присущая характеристика продукции, процесса  или системы , вытекающая из требования

Б.свойство продукции

В.свойство продукции или услуги, удовлетворяющее требованиям заинтересованных сторон

1.  Управление, обеспечение и улучшение качества осуществляется  с использованием всем известного  «цикла Деминга». Назовите основные этапы данного цикла.

А. Планирование, реализация ( выполнение), контроль (проверка), исправление

Б. Планирование, обеспечение, управление, улучшение

      В. Обеспечение, управление, улучшение, мониторинг

1. Современные представления о качестве основаны на :

А) требованиях и пожеланиях потребителей

Б) принципах деятельности и производственных возможностях производителей

В) законодательных требованиях государства и международных стандартов

1. Ценность продукции для производителя- это :

А) максимально возможная  цена продукции

Б) отсутствие препятствий для продажи продукции

В) высокое качество продукции

1. Управление качеством  согласно современным определениям  включает в себя :

А) менеджмент качества

Б) то же, что и менеджмент качества

В) Является частью менеджмента качества

1. Планирование качества – это :

А). Определение производственных процессов и ресурсов для достижения качества продукции

Б) определение характеристик качества нового изделия и процессов

В) планирование производства бездефектной продукции  для  удовлетворения потребителей

1. Эволюция систем качества насчитывает :

А) шесть фаз

Б) пять фаз

В) четыре фазы

1. «Звезды качества» не включают :

А) систему мотивации

Б) систему взаимоотношений с поставщиками

В) систему взаимоотношений с инвесторами

10.Из российских систем управления качеством наибольшую известность получила система КС УКП .Расшифруйте данную аббревиатуру –это :

А) Качественная система управлением и контролем продукции

Б) Комплексная система управления качеством продукции

В) Комплексная стандартизация уровня качества продукции

11.До какого времени управление качеством сводилось к контролю качества и относилось к инженерно- техническим  задачам ?

А. До 80-х годов

Б. До 50-х годов

В. До 30- х годов

12.Методология всеобщего управления качеством  «TQM» —  это :

А) система обеспечения качества продукции, основанная на спирали качества

Б) подход к руководству организацией,   основанный на всеобщем документировании функций и процессов управления  предприятия

В) подход к руководству организацией,  нацеленный на качество, основанный на участии всех его членов и направленный на достижение долговременного успеха путем удовлетворения потребителя и  выгоды для всех  членов организации и общества

13.Будущее TQM в  « концепциях совершенства бизнеса». Данные концепции включают  :

А. самооценку; измерение характеристик бизнеса ; сбалансированную  систему показателей; баланс интересов различных групп, заинтересованных в результатах деятельности; человеческий фактор; удовлетворенность персонала , ориентацию на общество

Б. ориентацию на общество ;человеческий фактор; удовлетворенность персонала; требования потребителей;  моральную  ответственность; ориентацию на инвесторов

В. возможности организации;  конкурентоспособность организации; ориентация на общество; социальная ответственность;  вовлеченность персонала

14. Кто из гуру качества является автором концепции «тотального управления качеством» ( TQC )?

А. Ф. Кросби

Б. Дж Джуран

В. А. Фейгенбаум

15..Большинство  национальных премий качества, являющихся моделью конкурентоспособного предприятия , использует две группы критериев. Первая группа критериев включает результаты деятельности компании  . Вторая группа критериев включает :

А) возможности компании

Б) управление финансами

В)  рентабельность инвестиций

Г) стратегии

16.Система менеджмента качества по ИСО 9001-2000  опирается на 8 основных принципов . Назовите эти принципы .

А.  Фокус  на потребителей, лидерство руководителей, процессный подход,  проверочный аудит;  вовлеченность персонала;  статистические методы; взаимовыгодные отношения с поставщиками, непрерывное улучшение

Б. Фокус на потребителя, интергративность, взаимосвязь и взаимодействие элементов управления, наличие  политики и цели в области качества  ; человеческие ресурсы; процессный подход; взаимоотношения с поставщиками; предоставление объективных свидетельств качества

В. Ориентация на потребителей, лидерство руководителей, процессный подход, системный подход;  вовлеченность персонала; принятие решений, основанных на фактах; взаимовыгодные отношения с поставщиками, непрерывное улучшение

17. 17. Одним из международных стандартов, интегрированных в современные системы управления, являются требования стандартов OHSASЧто даст организации применение данного стандарта ?

А. даст возможность контролировать риски  в отношении социальной ответственности перед обществом

Б. даст возможность контролировать риски   в отношении промышленной безопасности  и охраны труда

В.даст возможность контролировать риски в отношении профессионального здоровья и безопасности и улучшения своих характеристик

18.Что такое аудит ( проверка) системы менеджмента качества?

А. Систематическая оценка качества продукции компании третьей стороной

Б. Деятельность, предпринимаемая для установления пригодности, результативности рассматриваемого объекта для достижения установленных требований

В. Систематический , независимый и документированный процесс получения свидетельств аудита и объективного  их оценивания с целью установления степени выполнения согласованных критериев проверки

19. Важное значение для управления качеством имеет система измерений. Система управления измерениями – это :

А) организационная структура, несущая ответственность за определение и внедрение системы управления измерениями

Б) совокупность операций, необходимая для обеспечения соответствия измерительного оборудования требованиям отвечающим его назначению

В) совокупность взаимосвязанных или взаимодействующих элементов, необходимых для достижения метрологического подтверждения пригодности и постоянного управления измерениями

20.По закону РФ «О техническом регулировании»( от 27.12.2002)  предусмотрена 2-х уровневая структура нормативно- правовых документов. Нижняя ступень – гармонизированные добровольные стандарты- национальные стандарты. . А верхняя ступень- это :

А) государственные стандарты — ГОСТЫ

Б) международные стандарты

В) технические регламенты

21. По закону « О техническом регулировании « оценка соответствия — это прямое или косвенное определение соблюдения требований, предъявляемых к объекту;. Оценка соответствия может проводиться в следующих  формах

А) государственного контроля (надзора), аккредитации, испытаний, регистрации, подтверждения соответствия, приемки и ввода в эксплуатацию законченного строительством объекта и в иных формах;

Б) госконтроля, аккредитации, подтверждения соответствия

В) надзора, подтверждение соответствия, аккредитация

22. По закону « О техническом регулировании « Знак соответствия – это :

А).  Документ, которым изготовитель подтверждает , что продукция соответствует нормативно- технической документации

Б) документ, которым изготовитель на основе имеющихся у него собственных доказательств и (или) доказательств, полученных с участием третьей стороны, подтверждает наличие у него сертификата соответствия

В) обозначение, служащее для информирования приобретателей о соответствии объекта сертификации требованиям системы добровольной сертификации или национальному стандарту;

23.Одним из  признанных в мире авторитетов в области качества является Ф. Кросби. Ему принадлежит знаменитый афоризм:  «Качество – бесплатно». В чем его смысл?

       А.  Был предложен новый способ учета затрат на качество, включающий предупреждение  появления несоответствий, а не выявление брака и устранение дефектов

        Б. Повышение качества  не требует больших затрат, так как повышение качества одновременно ведет к повышению производительности, снижению затрат

       В. За  повышенные требования к качеству продукции  платит не производитель, а потребитель

24. В соответствии с требованиями стандарта ИСО – 9001-2000 предприятию необходимо разработать политику предприятия в области качества . Политика предприятия в области качества  – это :

А) общие намерения и направления деятельности организации в области качества, официально сформулированные высшим руководством

Б) часть менеджмента качества, направленная на установление целей в области качества и определяющая необходимые р процессы и соответствующие ресурсы

В) часть стратегии предприятия в области качества

25. План качества согласно словарю ИСО –это :

А) документ, определяющий какие процедуры и соответствующие ресурсы, кем, когда должны применяться к конкретному проекту, продукции, процессу или контракту

Б) документ, устанавливающий требования к продукции

В) деятельность, предпринимаемая для установления пригодности, адекватности, результативности рассматриваемого объекта для достижения установленных целей

26.Что такое  «процесс»  в системе менеджмента качества ?

А. Установленный способ осуществления деятельности

Б. Совокупность взаимосвязанных и взаимодействующих видов деятельности, преобразующих входы в выходы

В. Совокупность взаимосвязанных и взаимодействующих видов деятельности по управлению качеством продукции

27.Важнейшими характеристиками процессов является результативность. Результативность – это :

А. Повторяющаяся деятельность по увеличению способности выполнять требования

Б. Связь между достигнутым результатом и использованными ресурсами

В. Степень реализации запланированной деятельности и достижения запланированных результатов

28.Что такое « удовлетворенность потребителей» в определениях ИСО 9000 ?

А. Восприятие потребителями степени выполнения их требований

Б. Степень соответствия характеристик продукции ожидаемым потребностям

В. Степень соответствия присущих характеристик требованиям

29.Важное место в управлении качеством занимают статистические методы. Назовите 7 простых методов статистического контроля качества.

А. Диаграммы Исикавы, график Парето,  матричные диаграммы, причинно- следственные диаграммы, контрольные карты, матриц а приоритетов

Б График Парето, выборочные контроль, сплошной контроль качества, операционный контроль , диаграмма Исикавы

В. Контрольные листки, гистограммы, диаграмма Исикавы, анализ Парето, диаграмма разброса, стратификация данных, карты Шухарта

30. Промышленная логика TQM включает «систему MRP» . Данная система 

А. это система  автоматизированного гибкого производства

Б.это система, опирающаяся на логистику, рассчитывает потребность в материалах

В. это система , рассчитывающая потребность в человеческих ресурсах и оборудовании

31. Качество продукции является одним из важнейших факторов реализации национальных интересов России в различных сферах. В частности, цель в экономической сфере звучит следующим образом : Подъем качества отечественной продукции для достижения ее конкурентоспособности как на внутреннем, так и на внешнем рынках и … ( продолжить)

А… обеспечение задач, связанных с развитием платежеспособного спроса, структурной деформации экономики

Б  … обеспечение на этой основе устойчивого развития экономики страны и интеграции ее в мировую экономику.

В… наращивания производственного потенциала предприятий, внедрения систем менеджмента качества,  увеличения экспортного потенциала

32.Качество- степень соответствия присущих характеристик требованиям. Что такое «требование» ?

А. Потребность или ожидание, которое установлено, обычно предполагается или является обязательным

Б. Потребность потребителя или других заинтересованных сторон, соответствие законодательным характеристикам

В. Соответствие законодательным нормам, потребностям потребителей

33.Управление качеством тесно связано с концепциями общего менеджмента. С какой общей концепции начинался и общий  менеджмент, и системы качества?

А. С концепции Э. Деминга

Б. С концепции  Ф.У. Тейлора.

В. С концепции В. Шухарта

34.Все системы качества имели в своей основе пять основных аспектов:

А. Систему обеспечения качества, систему планирования качества, систему мониторинга качества, систему инженерного обеспечения качества, систему технологического обеспечения качества

Б. Анализ требований потребителей, лидерство руководителей, разработка стандартов, контроль качества, приемочный контроль

В. Документированную систему качества, систему взаимоотношений с поставщиками, систему взаимоотношений с потребителями, система мотивации, система обучения персонала

35.Ценность продукции для потребителя- это :

А) низкая цена без учета качества продукции

Б) высокое качество без учета цены продукции

В) разумное сочетание цены и качества продукции

36.Менеджмент качества сегодня – TQM. TQM – это .. ?

А. Всеобщий (тотальный ) менеджмент качества

Б. Всеобщий контроль качества

В.  Всеобщий производственный менеджмент

37.В нашей стране  в 80-е годы  распространенной системой качества была система  «БИП» .  Расшифруйте название этой системы .

      А.   безпроектное изменение процессов

      Б. бездефектное изготовление продукции

       В. бездефектное   измерение продукции

38.До какого времени управление качеством сводилось к контролю качества и относилось к инженерно- техническим  задачам ?

А. До 80-х годов

Б. До 50-х годов

В. До 30- х годов

39.Одним из  признанных в мире авторитетов в области качества является Ф. Кросби. Ему принадлежит знаменитый афоризм:  «Качество – бесплатно». В чем его смысл?

       А.  Был предложен новый способ учета затрат на качество, включающий предупреждение  появления несоответствий, а не выявление брака и устранение дефектов

        Б. Повышение качество не требует больших затрат, так как повышение качества одновременно ведет к повышению производительности, снижению затрат

       В. За  повышенные требования к качеству продукции  платит не производитель, а потребитель

40. Что такое «ИСО» ?

      А. Международный стандарт качества

Б. Международная организация по стандартизации

В.  Международная система качества

41.Что такое « удовлетворенность потребителей» в определениях ИСО 9000 ?

А. Восприятие потребителями степени выполнения их требований

Б. Степень соответствия характеристик продукции ожидаемым потребностям

В. Степень соответствия присущих характеристик требованиям

42.Что означает правило « 10-кратных затрат на качество» ?

      А. Затраты на качество могут возрастать на порядок при росте требований потребителей к качеству продукции

      Б. Затраты на качество продукции при испытаниях на порядок выше затрат на входной контроль сырья и материалов

     В. Затраты на  исправление брака при переходе от одного этапа жизненного цикла продукции к последующему изменяются на порядок

43.Основным принципом  современного менеджмента является «  процессный подход».   По классификации процессы делятся на :

А. Основные, обеспечивающие, процессы менеджмента, процессы развития

Б.  Макропроцессы, Бизнес- процессы, микропроцессы

В. Основные, управления ресурсами, процессы жизненного цикла

44.Кто из гуру качества является  идеологом системы «Z – дефектов» ?

А. Ф. Кросби

Б. Э.Деминг

В. К. Исикава

45. Дайте правильное определение «системы менеджмента качества» ( по ИСО 9000-2000):

А. Система менеджмента  для руководства и управления организацией применительно к качеству

Б. Часть менеджмента качества, направленная  на увеличение способности выполнить требования к качеству

В. Совокупность взаимосвязанных и взаимодействующих элементов по  обеспечению и улучшению качества

46.В системе менеджмента качества важнейшими  характеристиками процессов является эффективность .  Эффективность– это :

А. Повторяющаяся деятельность по увеличению способности выполнять требования

Б. Связь между достигнутым результатом и использованными ресурсами

В. Степень реализации запланированной деятельности и достижения запланированных результатов

47.Назовите основные группы показателей качества продукции  ?

А. Показатели назначения, надежности, регламентируемые, стандартизируемые, патентной чистоты и защиты, нормируемые

Б. Показатели назначения, надежности, технологичности, эргономические, эстетические, унификации и  стандартизации, патентно-правовые, экономические

В. Показатели классификационные, регламентируемые, интегральные эксплуатационные, назначения, стандартизации

48.Назовите основные  составляющие  затрат на качество, принятые в  системе управления затратами на качество.

А. Затраты на превентивные действия, затраты на инспекцию, затраты  на внутренний брак, затраты на внешний брак

Б. Постоянные и переменные затраты, затраты на входной контроль материалов, затраты на приемочный контроль готовой продукции, затраты на операционный контроль

В. Затраты на брак, затраты на исправление брака, общие и административные затраты

49. Стандарт ИСО 9001-2000 состоит из следующих основных  разделов ( макропроцессов)..

А.  Требования потребителей; , требования к системе менеджмента; ответственность руководства, непрерывное улучшения

Б. Ориентация на потребителя; изготовление продукции; управление ресурсами; улучшение

В. Ответственность руководства ,требования к системе менеджмента ; менеджмент ресурсов, процессы жизненного цикла; измерения, анализ, улучшения.

50.В 1996 году была учреждена Российская премия качества. Модель оценки характеризуется 9.ю критериями. Назовите  три наиболее значимых критерия.

А. Удовлетворенность потребителей, результаты работы организации, управление технологическими процессами и процессами выполнения работ

Б. Удовлетворенность потребителей, результаты работы организации,, рациональное использование ресурсов

В. Удовлетворенность потребителей,  рациональное использование ресурсов, использование потенциала работников

51.По закону « О техническом регулировании»  декларация о соответствии –  это :

А) документ, которым изготовитель (продавец) на основе имеющихся у него собственных доказательств и (или) доказательств, полученных с участием третьей стороны, удостоверяющий соответствие выпускаемой им в обращение продукции требованиям технических регламентов;

Б) документ, которым изготовитель на основе имеющихся у него собственных доказательств и (или) доказательств, полученных с участием третьей стороны, удостоверяющий соответствие выпускаемой им в обращение продукции требованиям нормативно- технической документации

В) документ, которым изготовитель подтверждает соответствие требованиям потребителя

52.По закону  ФЗ « О техническом регулировании «  подтверждение соответствия – документальное удостоверение соответствия (в виде декларации о соответствии или сертификата соответствия)продукции или иных объектов, процессов производства, эксплуатации, хранения, перевозки, реализации и утилизации, выполнения работ или оказания услуг

А) требованиям ГОСТОВ, ТУ

Б) требованиям технических регламентов, положениям стандартов, или условиям гражданско-правовых договоров;

В)требованиям технических регламентов, ГОСТОВ, добровольных стандартов

53.В настоящее время  ряд предприятий и организаций внедрили интегрированные системы  менеджмента  ( ИСМ). Дайте определение ИСМ :

А.это системы , включающие систему управления персоналом, окружающей средой, стратегией организации, политикой и целями в области качества

Б.  это система менеджмента, отвечающая требованиям международных и российских стандартов качества

В.часть системы общего менеджмента организации, отвечающая требованиям двух и более международных стандартов на основе систем менеджмента качества и функционирующая как единое целое.

54. Важным объектом стандартизации становится социальная ответственность. Под «социальной ответственностью» понимается :

А. определение положительного имиджа организации как  ориентированной на цели общества

Б.определение и реализация социального поведения с целью укрепления законности деятельности внутри предприятия и вне его

В. определение и реализация  социального поведения с целью положительного имиджа как организации , заботящейся об окружающей среде

55.Одним из международных стандартов, интегрированных в современные системы управления, являются требования стандартов OHSAS 18001. Какие требования устанавливает данный стандарт ? 

А. требования к системе менеджмента профессионального здоровья  и безопасности

Б. требования к системе контроля окружающей среды и рабочего места

В. требования к системе менеджмента промышленной безопасности и окружающей среды

56.Одним из международных стандартов, интегрированных в современные системы управления, являются требования стандартов ИСО 14001.Какие критерии установлены в данном стандарте?

А.  не навредить окружающей среде,  соответствовать предельно-допустимым концентрациям  вредных веществ

Б. не навредить окружающей среде, уменьшить отрицательное воздействие на настоящее и будущее поколение  людей, обеспечить рациональное использование природных ресурсов

В.учет требований регламентирующих  национальных и международных органов

57.Согласно современным определениям менеджмент качества состоит из .. ( продолжите )  :

А. планирования качества, управления качеством , обеспечения качества, улучшения качества

Б. планирования качества, организации работ, мотивации , обучения

В. планирование,  организация работ, мотивация персонала , контроль

58. В современных системах качества большая роль отводится персоналу, его компетентности. «Компетентность»– это -……

А. выраженная способность применять свои знания и умения.

Б профессиональная пригодность и стаж работы по специальности

В. совокупность знаний, умений  и навыков

59. Промышленная логика TQM включает систему « JIT «   (« джаст инд тайм») . Эта система относится к :

А. вытягивающей системе  ( pull system )

Б. выталкивающей системе ( push system )

В. Системе автоматической остановки  ( jidohka )

60.Система менеджмента качества  является документированной системой. Назовите основные документы СМК.

А. Миссия организации;  Стратегия и цели организации; Руководство  по качеству, Бизнес- процессы; Положения о подразделениях, должностные инструкции

Б Стратегия и цели организации; Руководство  по качеству; Положения о подразделениях; должностные инструкции

В. Политика и цели в области качества; Руководство по качеству; документированные процедуры; документы, необходимые для планирования и управления организацией; записи.

ara5.ru

Тест по «Управлению качеством» — тест

2. аналитические; 

 логические;

3. планирования;

 4. инженерно-математические.

 Правильный ответ: 4. Инженерно-математические

Вопрос 5. К каким методам  относятся методы оценки качества продукции?

1. стимулирования;

 2. контроля;

3. мотивации; 

4. самоконтроля;

5. статистическим.

 Правильный ответ: 2. контроля

Задание 10.

 Отметить правильный  вариант ответа в карточке  ответов. 

 Вопрос 1. В каком году  в Японии на предприятиях образовались  «кружки качества?

1. 1958;

2. 1959;

3. 1960;

4. 1961;

 5. 1962.

 Правильный ответ: 5. 1962

Вопрос 2. Какая система  организации взаимоотношений способствует улучшению работы предприятия за счет грамотного руководства и сознательного  поведения каждого работника  фирмы?

1. контролирующая;

2. демократическая; 

 3. корпоративная культура;

4. научная; 

5. технологическая. 

 Правильный ответ: 3. Корпоративная культура

Вопрос З. Что является необходимым условием перехода на предприятии к самоконтролю продукции?

 1. переподготовка персонала;

2. изменение технологического  режима;

3. повышение качества  технической документации;

4. стимулирование руководства  предприятия; 

5. разработка системы  поощрения рабочих. 

 Правильный ответ: 1. Переподготовка персонала

Вопрос 4. Какие методы управления качеством продукции признаны важным условием повышения рентабельности продукции?

1. самоконтроля;

2. статистические;

3. экономико-математические;

4. социальные;

5. технические. 

 Правильный ответ: 2. статистические

Вопрос 5. Сколько используется известных методов (инструментов) качества на предприятии?

1. 5;

2. 6;

 3. 7;

4. 8;

5. 9.

 Правильный ответ: 3. 7

Задание 11.

 Отметить правильный  вариант ответа в карточке  ответов. 

 Вопрос 1. Какие данные  используются при построении  гистограммы? 

1. бухгалтерского учета; 

2. аналитические; 

3. обобщенные;

 4. измеряемые;

5. совокупные.

 Правильный ответ: 4. измеряемые

Вопрос 2. Какой метод оценки качества продукции применяется, когда  требуется установить, сколько колебаний  в процессе вызывается случайными изменениями?

1. контрольная  карта;

2. временные ряды;

3. диаграмма Парето;

4. гистограмма; 

5. диаграмма рассеяния. 

 Правильный ответ: 1. Контрольная карта

Вопрос 3. Какой анализ позволяют  проводить контрольные карты?

1. экономической эффективности; 

2. технической целесообразности;

3. спроса на производимую  продукцию; 

 4. возможностей процесса;

5. причин брака. 

 Правильный ответ: 4. Возможностей процесса

Вопрос 4. Сколько видов  контрольных карт применяется для  характеристики качественных признаков  продукции?

1. два; 

2. три; 

 3. четыре;

4. пять;

5. шесть. 

 Правильный ответ: 3. четыре

Вопрос 5. Какой метод оценки качества продукции применяется, когда  требуется определить, что происходит с одной из переменных величин, если другая переменная изменяется?

1. контрольная карта; 

2. временные ряды;

3. диаграмма Парето;

4. гистограмма; 

 5. диаграмма рассеяния.

 Правильный ответ: 5. Диаграмма рассеяния

Задание 12.

 Отметить правильный  вариант ответа в карточке  ответов. 

 Вопрос 1. Какой термин  обозначает проверку соответствия  объекта контроля установленным  техническим требованиям? 

1. организация контроля; технический контроль; контроль  на соответствие ГОСТу; 

2. оценка качества продукции; 

3. документальный контроль.

 Правильный ответ: технический контроль

Вопрос 2. На что направлены, в первую очередь, усилия ведущих  фирм мира в области контроля качества продукции?

1. совершенствование методов  контроля;

2. разработку эффективной  системы поощрения работников  за снижение брака; 

 3. предупреждение брака;

4. изменения методов наказания  за допущенный брак;

5. совершенствование технологического  режима.

 Правильный ответ: 3. Предупреждение брака

Вопрос 3. Целью какого метода контроля является исключение случайных изменений качества продукции?

1. гносеологического; 

2. аналитического;

 3. статистического;

4. математического анализа; 

5. социального. 

 Правильный ответ: 3. Статистического

Вопрос 4. В каком виде планов статистического контроля партии продукции количество шагов контроля заранее задается?

1. одноступенчатом; 

2. двухступенчатом; 

3. многоступенчатом;

4. последовательном;

5. дискретном.

 Правильный ответ: 3. многоступенчатом

Вопрос 5. Что является вероятностным  показателем плана статистического  контроля?

 1. оперативная характеристика;

2. уровень качества продукции; 

3. объем производства;

4. коэффициент использования  производственных мощностей; 

5. производительность труда. 

 Правильный ответ: 1. Оперативная характеристика

Задание 13.

 Отметить правильный  вариант ответа в карточке  ответов. 

 Вопрос 1. Какой вид  имеет оперативная характеристика  для планов выборочного контроля?

1. ломаной линии; 

2. прямой линии; 

3. столбика;

 4. плавной кривой;

5. прерывистой линии. 

 Правильный ответ: 4. Плавной криво й 

Вопрос 2. Какая процедура  контроля продолжается до тех пор, пока в выборке не появится дефектный  экземпляр?

1. сплошная;

2. дискретная;

3. технологически необходимая; 

4. опытно-статистическая;

5. с ослабленным  режимом.

 Правильный ответ: 5. С ослабленным режимом

Вопрос 3. Как называются контрольные карты, которые используются при принятии решений о режиме контроля качества продукции?

1. регистрационные; 

 2. кумулятивные;

3. дубль-карты;

4. простые, 

5. сложные. 

 Правильный ответ: 2. кумулятивные

Вопрос 4. С какого документа  о проверке качества продукции начинается превращение мнений и предположений  в факты?

1. гистограмма; 

2. диаграмма рассеяния; 

3. контрольная карта; 

 4. контрольный листок;

5. диаграмма Парето.

 Правильный ответ: 4. Контрольный листок

Вопрос 5. Какой метод контроля качества используется, когда требуется  предсгавить относительную важность всех проблем с целью выявления отправной точки для решения проблем?

1. гистограмма; 

2. диаграмма рассеяния; 

3. контрольная карта; 

4. контрольный листок;

 5. диаграмма Парето.

 Правильный ответ: 5. Диаграмма Парето

Задание 14.

 Отметить правильный  вариант ответа в карточке  ответов. 

 Вопрос 1. Как называется  нормативно-технический документ, устанавливающий  основные требования к качеству  продукции? 

1. технические условия; 

 2. стандарт;

3. регламент; 

4. норматив;

5. эталон.

 Правильный ответ: 2. стандарт

Вопрос 2. Как называется состояние изделия, при котором  оно в данный момент времени соответствует  всем требованиям, установленным в  отношении основных параметров, характеризующих  нормальное выполнение заданных функций?

1. исправность; 

2. отказ; 

3. безотказность; 

 4. работоспособность;

5. ремонтопригодность.

 Правильный ответ: 4. работоспособность

Вопрос 3. Какой исполнительный орган формирует и реализует  государственную политику в области  стандартизации, осуществляет государственный  контроль и надзор за соблюдением  требований государственных стандартов?

1. Министерство экономики  РФ;

2. Министерство труда  и социальных вопросов;

 3. Госстандарт РФ;

4. Правительство РФ;

5. Госстрой РФ.

 Правильный ответ: 3. Госстандарт РФ

Вопрос 4. К какому виду документов относятся стандарты отраслей:

1. рекомендательным;

2. действующим на уровне предприятий;

3. обязательным;

4. международным 

 5. нормативным.

 Правильный ответ: 5. нормативным

Вопрос 5. Сколько вариантов  применения международных стандартов установил Госстандарт РФ в ГОСТ Р 1.5-92?

 1. два;

2. три; 

3. четыре;

4. пять;

5. шесть. 

 Правильный ответ: 1. два

Задание 15.

 Отметить правильный  вариант ответа в карточке  ответов. 

 Вопрос 1. Какими объектами  являются стандарты предприятий  и стандарты научно-технических  обществ? 

1. государственными;

2. отраслевыми; 

3. региональными; 

4. авторского  права;

5. предприятий. 

 Правильный ответ: 4. Авторского права

Вопрос 2. С какого времени  вводятся в действие государственные  стандарты, принятые Госстроем РФ?

1. после их опубликования; 

2. после их  государственной регистрации в  Госстандарте РФ;

3. после их принятия  Госдумой;

4. после утверждения Советом  Федерации; 

5. через месяц после  принятия Госдумой.

 Правильный ответ: 2. После их государственной регистрации в Госстандарте РФ

Вопрос 3. За соблюдением каких требований государственных стандартов осуществляется государственный контроль?

1. всех;

2. имеющихся в ГОСТе;

 3. обеспечивающих безопасность продукции, работ и услуг;

4. по усмотрению контролирующего  органа;

5. международных стандартов.

 Правильный ответ: 3. Обеспечивающих безопасность продукции, работ и услуг

Вопрос 4. На какой орган  исполнительной власти возложен контроль за соблюдением требований по безопасности товаров в розничной сети?

 1. Госторгинспекция;

2. Территориальный орган  Госстандарта РФ;

3. Министерство сельского  хозяйства РФ;

4. Министерство труда  и социальных вопросов;

5. Министерство обороны. 

 Правильный ответ: 1. Госторгинспеция

Вопрос 5. Из какого источника  осуществляется финансирование работ  по государственной стандартизации?

1. местного бюджета; 

 2. федерального бюджета;

3. регионального бюджета; 

4. отчислений предприятий; 

5. международных финансовых  фондов.

 Правильный ответ: 2. Федерального бюджета

Задание 16.

 Отметить правильный  вариант ответа в карточке  ответов. 

 Вопрос 1. Какой процесс  был значительно ускорен в  результате стандартизации телефонных, факсовых и компьютерных сетей: 

1. создание единых тарифов; 

2. разработаны Технические  условия на использование средств связи в разных странах мира;

 3. международный обмен информацией;

4. поставка комплектующих  изделий; 

5. сокращены расходы на  техническое обслуживание.

 Правильный ответ: 3. Международный обмен информацией

Вопрос 2. Сколько международных  организаций занимаются вопросами  стандартизации?

1. 200;

2. 250;

3. 300;

4. 350;

5. свыше 400.;

 Правильный ответ: 5. Свыше 400

Вопрос 3. Кто является высшим органом ИСО?

1. Совет учредителей; 

 2. Генеральная Ассамблея;

 3. Центральный секретариат;

 4. Генеральный директор;

 5. Президент.

 Правильный ответ: 2. Генеральная Ассамблея

Вопрос 4. Что является первым и последним этапом системы качества?

 1. маркетинг;

2. контроль;

3. проектирование;

4. квалификация персонала; 

5. организация работы  служб технического контроля.

 Правильный ответ: 1. маркетинг

Вопрос 5. Сколько стандартов МС ИСО серии 9000 были разработаны  ИСО/ТК 176 в 1987 г.?

1. два; 

2. три; 

3. четыре;

4. пять;

5. шесть. 

 Правильный ответ: 4. пять

Задание 17.

 Отметить правильный  вариант ответа в карточке  ответов. 

 Вопрос 1. Что является  необходимым инструментом, гарантирующим  соответствие качества продукции  требованиям нормативно-технической  документации?

1. стандартизация;

 2. сертификация;

3. метрология;

4. идентификация; 

5. менеджмент.

 Правильный ответ: 2. сертификация

Вопрос 2. Какой документ подтверждает соответствие продукции  всем минимальным требованиям, установленным  национальным законодательством?

1. паспорт продукции; 

2. гарантийный талон; 

 3. сертификат соответствия;

4. проект;

5. аттестат качества.

 Правильный ответ: 3. Сертификат соответствия

Вопрос 3. Сколько схем сертификации третьей стороной определены Международной  организацией сертификации?

1. 5;

2. 6:

3. 7;

 4. 8;.

5. 9.

 Правильный ответ: 4. 8

Вопрос 4. Кто осуществляет испытания образцов продукции?

1. предприятие-изготовитель;

2. покупатель;

3. третья сторона; 

4. Госстандарт РФ;

 5. испытательные лаборатории.

 Правильный ответ: 5. Испытательные лаборатории

Вопрос 5. Как называется процесс официального признания  того, что органы по сертификации продукции  и испытательные лаборатории  имеют право проводить работы по сертификации?

1. аттестация;

 2. аккредитация;

3. приватизация;

4. стандартизация;

5. нормализация.

 Правильный ответ: 2. аккредитация

Задание 18.

 Отметить правильный  вариант ответа в карточке  ответов. 

 Вопрос 1. Кто определен  в качестве национального органа  по сертификации в Российской  Федерации? 

1. Министерство экономики  РФ;

2. Госстрой РФ;

3. Министерство высшего  и специального образования; 

 4. Госстандарт РФ;

5. Министерство труда  и социальных вопросов.

 Правильный ответ: 4. Госстандарт РФ

Вопрос 2. По чьей инициативе проводится добровольная система сертификации?

 1. производителя;

2. покупателя;

3. третьей стороны; 

4. Госстандарта РФ;

5. министерства или объединения. 

 Правильный ответ: 1. производителя

Вопрос 3. Какой закон РФ был первым законодательным актом, вводящим в стране обязательную сертификацию?

1. О сертификации биржевых  товаров; 

myunivercity.ru

Тест: Правильные ответы на тест по управлению качеством

Тема: Правильные ответы на тест по управлению качеством

Раздел: Бесплатные рефераты по управлению качеством

Тип: Тест | Размер: 41.61K | Скачано: 534 | Добавлен 29.10.10 в 11:22 | Рейтинг: +42 | Еще Тесты

Остальные вопросы и ключ ответов смотрите в файле!

Задание 1

Выбрать к вопросу правильный вариант ответа.

Вопрос 1. Каким термином определено долговременное управление качеством и организацией работ по контролю на предприятии соответствие государственным стандартам выпускаемой продукции?

1. управление качеством

2. всеобщее управление качеством

3. сертификация

4. стандартизация

5. метрология

Вопрос 2. Каким термином обозначают взаимосвязь между зависимыми и независимыми переменными, выраженными в виде таблицы, текста, графика?

1. свойство

2. принцип

3. закон

4. характеристика

5. потребность

Вопрос 3. Каким термином принято обозначать результат деятельности или процессов внутренней деятельности предприятий?

1. услуга

2. объект

3. продукция

4. деньги

5. система

Вопрос 4. Что означает совокупность организационной структуры, методик, процессов и ресурсов, необходимых для осуществления общего руководства качеством?

1. система качества

2. уровень качества

3. относительное качество

4. характеристика

5. процесс

Вопрос 5. Какое место в мире занимала Россия по уровню качества жизни населения в 1994г.?

01.янв

02.июн

мар.27

апр.37

5. 112

Задание 2

Выбрать к вопросу правильный вариант ответа.

Вопрос 1. На какой стадии формируется качество продукции?

1. заключения контракта на поставку

2. изготовления

3. сборки

4. контроля качества

5. проектирования

Вопрос 2. С чьих позиций рассматривалось качество продукции в условиях командно-административной экономики?

1. потребителя

2. руководства предприятия

3. вышестоящего органа управления

4. министерства

5. Госстандарта РФ

Вопрос 3. Как называется наука о способах измерения и количественной оценке качества продукции и услуг?

1. механика

2. логика

3. квалиметрия

4. маркетинг

5. электроника

Вопрос 4. Чему способствует повышение качества производимой отечественными товаропроизводителями продукции?

1. росту импорта товаров

2. снижению конкурентоспособности

3. увеличению золотого запаса

4. росту экспортных возможностей

5. эффективному использованию природных ресурсов

Вопрос 5. С чем сравниваются в процессе проверки качества производимой продукции изделия?

1. аналогичной продукцией других предприятий

2. проектными данными

3. стандартами предприятия

4. контрольным образцом

5. эталоном(стандартом)

Задание 3.

Отметить правильный вариант ответа в карточке ответов.

Вопрос 1. Сколько международных стандартов серии 9000 X по системам качества были разработаны и утверждены в 1987 г. Техническим комитетом Международной организации по стандартизации?

1. два;

2. три;

3. четыре;

4. пять;

5. шесть.

Вопрос 2. Сколько этапов жизненного цикла продукции предусматривает стандарт ИСО?

1. 10;

2. 12;

3. 13;

4. 14.

Вопрос 3. Принятие решений в управлении качеством продукции на предприятии базируется на контроле, учете и:

1. анализе;

2. планировании;

3. прогнозировании;

4. маркетинге;

5. проектировании.

Вопрос 4. Сколько основополагающих условий сформулированы в современном менеджменте качества?

1. пять

2. семь

3. десять

4. двенадцать

.

Вопрос 5. С производства какого вида товара следует начинать освоение производства?

1. технологичного;

2. дорогого;

3. менее трудоемкого;

4. пользующегося спросом;

5. на который разработана техническая документация.

Задание 4.

Отметить правильный вариант ответа в карточке ответов.

Вопрос 1. На основании какого документа осуществлялось в начале века получение потребителем информации о качестве товара?

1. паспорта;

2. рекламации

3. спецификации;

4. чертежа;

5. гарантии изготовителя.

Вопрос 2. Как называется фигура в международном бизнесе, но форме похожая на бывший «Знак качества»?

1. Мавзолей;

2. Акрополь;

3. Эйфелева башня;

4. Пентагон;

5. Слоновий бивень.

Вопрос 3. Назовите пример встречного (снизу вверх) вертикального управления качеством продукции:

1. система бездефектного труда;

2. научная организация работ по повышению моторесурса двигателей;

3. кружки качества;

4. комплексная система управления качеством;

5. бездефектное изготовление продукции.

Вопрос 4. Сколько этапов развития систем качества можно выделить в истории XX века?

1. пять;

2. шесть;

3. семь;

4. восемь;

5. девять.

Вопрос 5. На каких циклах основана система всестороннего управления качеством?

1. Фейгенбаума;

2. Прудона;

3. Исикава;

4. Деминга;

5. Боголюбова.

Задание 5.

Отметить правильный вариант ответа в карточке ответов.

Вопрос 1. Кто является координирующим федеральным органом исполнительной власти в таких сферах деятельности, как стандартизация, сертификация, метрология?

1. Госкомитет по науке и технике;

2. Минэкономики РФ;

3. Министерство труда и социальных вопросов РФ;

4. Госстрой РФ;

5. Госстандарт РФ.

Вопрос 2. Какие методы управления являются научной основой современного технического контроля?

1. Дельфи;

2. балансовый:

3. математико-статистические;

4. комплексного анализа;

5. прогнозирования.

Вопрос 3. Какой подход к оптимизации процессов обеспечивает статистическое регулирование процессов?

1. случайный

2. индивидуальный;

3. комплексный;

4. систематический:

5. постоянный.

Вопрос 4. Сколько этапов исторически возникало при оценке качества продукции?

1. два;

2. три;

3. четыре:

4. пять;

5. шесть.

Вопрос 5. Что является первым этапом оценки качества продукции?

1. определение номенклатуры аттестуемой продукции;

2. приобретение необходимой для контроля качества аппаратуры;

3. выбор номенклатуры показателей качества;

4. обучение персонала отдела технического контроля;

5. составление плана проверок.

Задание 6.

Отметить правильный вариант ответа в карточке ответов.

Вопрос 1. Какая система организации бездефектного изготовления продукции (БИП) получила распространение в нашей стране в 1950-е годы?

1. ленинградская;

2. волгоградская;

3. саратовская;

4. минская;

5. калининградская.

Вопрос 2. Какой метод контроля качества продукции на предприятиях являлся основным при использовании саратовской системы БИП?

1. сплошной;

2. выборочный;

3. отсутствие контроля;

4. самоконтроль;

5. бригадный.

Вопрос 3. Что являлось основным критерием применения комплексной системы управления качеством продукции:

1. соответствие качества продукции высшим достижениям науки и техники;

2. соответствие качества результата труда установленным требованиям;

3. соответствие достигнутого уровня моторесурса запланированному значению;

4. соответствие качества первых промышленных изделий установленным требованиям;

5. соответствие мировым стандартам качества.

Вопрос 4. Целью какой системы управления качеством продукции являлось обеспечение выпуска продукции отличного качества, высокой надежности и долговечности?

1. КАНАРСПИ;

2. НОРМ;

3. БИЛ;

4. КСУКП;

5. СБТ.

Вопрос 5. Какая система управления качеством продукции охватывала многие виды работ на стадии исследования и проектирования и на стадии эксплуатации?

1. КАНАРСПИ;

2. НОРМ;

3. БИЛ;

4. КСУКП;

5. СБТ.

Задание 7.

Отметить правильный вариант ответа в карточке ответов.

Вопрос 1. На сколько процентов был увеличен гарантийный срок работы двигателя в результате использования системы управления качеством НОРМ?

1. 50

2. 60

3. 70

4. 80

5. 90

Вопрос 2. В каком году были разработаны и утверждены Госстандартом Основные принципы Единой системы государственного управления качеством продукции?

1. 1960

2. 1970

3. 1974

4. 1978

Вопрос 3. Какое подразделение на предприятии координирует планирование мероприятий в области качества?

1. плановый отдел;

2. технический отдел;

3. технологический отдел;

4. конструкторский отдел;

5. отдел обеспечения качества.

Вопрос 4. Кто на предприятии отвечает за практическое использование системы управления качеством продукции?

1. главный инженер;

2. директор;

3. зам. директора по качеству;

4. начальник отдела технического контроля;

5. начальник технического отдела.

Вопрос 5. В каком плане принципиально важным для системы ИСО 9000-1у94 является вновь введенное положение о том, что вся работа, выполняемая организацией, рассматривается как совокупность взаимосвязанных процессов?

1. методологическом

2. техническом

3. идеологическом

4. технологическом

5. экономическом.

Задание 8.

Отметить правильный вариант ответа в карточке ответов.

Вопрос 1. Кредо процветающих фирм во всем мире — завоевание покупателя производится через:

1. низкие цены;

2. качество;

3. дизайн;

4. низкую трудоемкость;

5. экономичность продукции.

Вопрос 2. Какое количество компаний в мире имеет сертифицированные системы качества?

1. 20 000

2. 30 000

3. 40 000

4. 50 000

5. 70 000

Вопрос 3. На повышение каких результатов деятельности предприятий направлено улучшение качества производимой продукции?

1. технических

2. технологических

3. экономических

4. общих

5. конструкторских

Вопрос 4. Сколько процентов контрактов на поставку продукции в России предусматривают подтверждения о наличии системы обеспечения качества, соответствующей ИСО серии 9000?

1. 60

2. 70

3. 80

4. 90

5. 100

Вопрос 5. Сколько предприятий в России прошли сертификацию систем качества?

1. 100;

2. 200;

3. 300;

4. 400;

5. 500.

Задание 9.

Отметить правильный вариант ответа в карточке ответов.

Вопрос 1. В каком городе состоялся первый Всеобщий форум управления качеством в 1994 г.?

1. Лондоне;

2. Париже;

3. Москве;

4. Милане;

5. Хартуме.

Вопрос 2. Как называются договоры, заключаемые Российской Федерацией на правительственном уровне?

1. государственные;

2. международные;

3. министерские;

4. межрегионалъные ;

5. отраслевые.

Вопрос 3. Что влияет, в первую очередь, на процесс внедрения всеобщего управления качеством?

1. общественное мнение;

2. состояние экономики;

3. рыночные отношения;

4. законодательство страны;

5. желание руководителей предприятий.

Вопрос 4. Какие методы используются для анализа и регулирования процессов на всех стадиях жизненного цикла продукции?

1. Статистические;

2. аналитические;

логические;

3. планирования;

4. инженерно-математические.

Вопрос 5. К каким методам относятся методы оценки качества продукции?

1. стимулирования;

2. контроля;

3. мотивации;

4. самоконтроля;

5. статистическим.

Задание 10.

Отметить правильный вариант ответа в карточке ответов.

Вопрос 1. В каком году в Японии на предприятиях образовались «кружки качества?

1. 1958;

2. 1959;

3. 1960;

4. 1961;

5. 1962.

Вопрос 2. Какая система организации взаимоотношений способствует улучшению работы предприятия за счет грамотного руководства и сознательного поведения каждого работника фирмы?

1. контролирующая;

2. демократическая;

3. корпоративная культура;

4. научная;

5. технологическая.

Вопрос З. Что является необходимым условием перехода на предприятии к самоконтролю продукции?

1. переподготовка персонала;

2. изменение технологического режима;

3. повышение качества технической документации;

4. стимулирование руководства предприятия;

5. разработка системы поощрения рабочих.

Вопрос 4. Какие методы управления качеством продукции признаны важным условием повышения рентабельности продукции?

1. самоконтроля;

2. статистические;

3. экономико-математические;

4. социальные;

5. технические.

Задание 11.

Отметить правильный вариант ответа в карточке ответов.

Вопрос 1. Какие данные используются при построении гистограммы?

1. бухгалтерского учета;

2. аналитические;

3. обобщенные;

4. измеряемые;

5. совокупные.

Вопрос 2. Какой метод оценки качества продукции применяется, когда требуется установить, сколько колебаний в процессе вызывается случайными изменениями?

1. контрольная карта;

2. временные ряды;

3. диаграмма Парето;

4. гистограмма;

5. диаграмма рассеяния.

Вопрос 3. Какой анализ позволяют проводить контрольные карты?

1. экономической эффективности;

2. технической целесообразности;

3. спроса на производимую продукцию;

4. возможностей процесса;

5. причин брака.

Вопрос 4. Сколько видов контрольных карт применяется для характеристики качественных признаков продукции?

1. два;

2. три;

3. четыре;

4. пять;

5. шесть.

Вопрос 5. Какой метод оценки качества продукции применяется, когда требуется определить, что происходит с одной из переменных величин, если другая переменная изменяется?

1. контрольная карта;

2. временные ряды;

3. диаграмма Парето;

4. гистограмма;

5. диаграмма рассеяния.

Задание 12.

Отметить правильный вариант ответа в карточке ответов.

Вопрос 1. Какой термин обозначает проверку соответствия объекта контроля установленным техническим требованиям?

1. организация контроля; технический контроль; контроль на соответствие ГОСТу;

2. оценка качества продукции;

3. документальный контроль.

Вопрос 2. На что направлены, в первую очередь, усилия ведущих фирм мира в области контроля качества продукции?

1. совершенствование методов контроля;

2. разработку эффективной системы поощрения работников за снижение брака;

3. предупреждение брака;

4. изменения методов наказания за допущенный брак;

5. совершенствование технологического режима.

Вопрос 3. Целью какого метода контроля является исключение случайных изменений качества продукции?

1. гносеологического;

2. аналитического;

3. статистического;

4. математического анализа;

5. социального.

Вопрос 4. В каком виде планов статистического контроля партии продукции количество шагов контроля заранее задается?

1. одноступенчатом;

2. двухступенчатом;

3. многоступенчатом;

4. последовательном;

5. дискретном.

Вопрос 5. Что является вероятностным показателем плана статистического контроля?

1. оперативная характеристика;

2. уровень качества продукции;

3. объем производства;

4. коэффициент использования производственных мощностей;

5. производительность труда.

Задание 13.

Отметить правильный вариант ответа в карточке ответов.

Вопрос 1. Какой вид имеет оперативная характеристика для планов выборочного контроля?

1. ломаной линии;

2. прямой линии;

3. столбика;

4. плавной кривой;

5. прерывистой линии.

Вопрос 2. Какая процедура контроля продолжается до тех пор, пока в выборке не появится дефектный экземпляр?

1. сплошная;

2. дискретная;

3. технологически необходимая;

4. опытно-статистическая;

5. с ослабленным режимом.

Вопрос 3. Как называются контрольные карты, которые используются при принятии решений о режиме контроля качества продукции?

1. регистрационные;

2. кумулятивные;

3. дубль-карты;

4. простые,

5. сложные.

Вопрос 4. С какого документа о проверке качества продукции начинается превращение мнений и предположений в факты?

1. гистограмма;

2. диаграмма рассеяния;

3. контрольная карта;

4. контрольный листок;

5. диаграмма Парето.

Вопрос 5. Какой метод контроля качества используется, когда требуется предсгавить относительную важность всех проблем с целью выявления отправной точки для решения проблем?

1. гистограмма;

2. диаграмма рассеяния;

3. контрольная карта;

4. контрольный листок;

5. диаграмма Парето.

Понравилось? Нажмите на кнопочку ниже. Вам не сложно, а нам приятно).

Чтобы скачать бесплатно Тесты на максимальной скорости, зарегистрируйтесь или авторизуйтесь на сайте.

Важно! Все представленные Тесты для бесплатного скачивания предназначены для составления плана или основы собственных научных трудов.

Друзья! У вас есть уникальная возможность помочь таким же студентам как и вы! Если наш сайт помог вам найти нужную работу, то вы, безусловно, понимаете как добавленная вами работа может облегчить труд другим.

Если Тест, по Вашему мнению, плохого качества, или эту работу Вы уже встречали, сообщите об этом нам.

Добавить отзыв могут только зарегистрированные пользователи.

studrb.ru

Тест по дисциплине «Управление качеством продукции»

Фонд оценочных средств

Промежуточный материал для текущего контроля

по учебной дисциплине

управление качеством продукции

оп.17 основной профессиональной образовательной программы

специальности СПО

140448 Техническая эксплуатация и обслуживание электрического и электромеханического оборудования (по отраслям)

базовый уровень

Разработала: Вологжанина Т. И.

Тольятти 2014г.

Тестовое задание по теме: Стандарты ISO 9000

Вариант-1

№

п/п

Задание(вопрос)

Варианты ответа

Эталон ответа

Инструкция по выполнению заданий 1-24:

Выберите букву, соответствующую правильному варианту ответа

1.

На скольких принципах основана идеология всеобщего управления?

1. 6

2. 7

3. 8

4. 9

2

2.

Сколько основных составляющих всеобщего управления качеством(TQM)…

1. 3

2. 4

3. 5

4. 6

3

3.

Метод и виды деятельности оперативного характера, используемые для выполнения требований к качеству…

1.Контроль качества

2.Политика в области качества

3.Планировние качества

4.Улучшение качества

1

4.

Основные направления и цели организации в области качества, официально сформулированные высшим руководством…

1.Контроль качества

2. Политика в области качества

3.Планирвоание качества

4.Улучшение качества

2

5.

Деятельность, устанавливающая цели и требования к качеству и применению элементов системы качества

1.Контроль качества

2. Политика в области качества

3.Планирвоание качества

4.Улучшение качества

3

6.

Мероприятия внутри организации с целью повышения эффективности или результативности деятельности и процессов для получения выгоды как для организации, так и для ее потребителей

1.Контроль качества

2. Политика в области качества

3.Планирование качества

4.Улучшение качества

4

7.

Количество принципов качества управления доктора Деминга

1.12

2.14

3.16

4.18

2

8

Характеристика системы качества БИП…

1.Научная организация труда по увеличению моторесурсов

2.Качество, надежность, ресурс с первых изделий

3.Система бездефектного труда

4. Бездефектное изготовление продукции

4

9.

Характеристика системы качества СБТ…

1.Научная организация труда по увеличению моторесурсов

2.Качество, надежность, ресурс с первых изделий

3.Система бездефектного труда

4. Бездефектное изготовление продукции

3

10.

Характеристика системы качества КАНАРСПИ…

1.Научная организация труда по увеличению моторесурсов

2.Качество, надежность, ресурс с первых изделий

3.Система бездефектного труда

4. Бездефектное изготовление продукции

2

11.

Характеристика системы качества НОРМ…

1.Научная организация труда по увеличению моторесурсов

2.Качество, надежность, ресурс с первых изделий

3.Система бездефектного труда

4. Бездефектное изготовление продукции

1

12.

Количество этапов внедрения статических методов…

1.7

2.3

3.9

4.10

2

13

Сертификация продукции…

1. Действие третьей стороны (органа по сертификации), идентифицированная продукция соответствует конкретно стандарту или другому нормативному документу.

2. Сертификация, вводимая в качестве необходимого условия реализации продукции на территории какой-либо страны для использования по прямому назначению.

3.Сертификация продукции влияющей на безопасность и охрану окружающей среды, обязательное требование Закона «О защите прав потребителей».

1

14

Обязательная сертификация..

1. Действие третьей стороны (органа по сертификации), идентифицированная продукция соответствует конкретно стандарту или другому нормативному документу.

2. Сертификация, вводимая в качестве необходимого условия реализации продукции на территории какой-либо страны для использования по прямому назначению.

3.Сертификация продукции влияющей на безопасность и охрану окружающей среды, обязательное требование Закона «О защите прав потребителей».

2

15.

Аудит проводится самой организацией

1. Аудит третьей стороны

2. Аудит второй стороны

3. Аудит первой стороны

3

16.

Аудит проводится организацией для своих собственных целей, но в другой организации..

1. Аудит третьей стороны

2. Аудит второй стороны

3. Аудит первой стороны

2

17.

Аудит проводится независимой организацией (третьей стороной)…

1. Аудит третьей стороны

2. Аудит второй стороны

3. Аудит первой стороны

1

18.

Функции: качество новых разработок, сроки их освоения и конкурентоспособность автомобилей…

1.Департамента развития.

2.Департамента работы с персоналом.

3.Департамента экономики и финансов.

4. Дирекция по производству.

1

19.

Функции: снижение затрат из-за низкого качества изготовления, стабильный выпуск продукции, соответствующей установленным требованиям…

1.Коммерческая дирекция.

2. Департамента работы с персоналом.

3.Департамента экономики и финансов.

4. Дирекция по производству.

4

20.

Функции: создание систем мотивации труда, качество обслуживания при продаже и после продаж…

1.Коммерческая дирекция.

2. Департамента работы с персоналом.

3.Департамента экономики и финансов.

4. Дирекция по производству.

3

21.

Функции: постоянное повышение квалификации персонала и области управления качеством, создание системы социально-психологической и моральной мотивации персонала к качественному труду…

1. Коммерческая дирекция.

2. Департамента работы с персоналом.

3.Департамента экономики и финансов.

4. Дирекция по производству.

2

22.

Функции: обеспечение качества поставок, устанавливает предприятия, способные обеспечить необходимый уровень качества поставок…

1. Коммерческая дирекция.

2. Департамента работы с персоналом.

3.Департамента экономики и финансов.

4. Дирекция по производству.

1

23.

Функции: сертификация продукции, аудит внутренний и внешний, корректирующие воздействия…

1.Дирекция по качеству.

2. Дирекция по информационным системам.

3. Дирекция по производству.

4. Коммерческая дирекция.

1

24.

Функции: достоверность информации, обеспечение системы качества информационными технологиями…

1.Дирекция по качеству.

2. Дирекция по информационным системам.

3. Дирекция по производству.

4. Коммерческая дирекция.

2

Вариант-2

№

п/п

Задание(вопрос)

Варианты ответа

Эталон ответа

Инструкция по выполнению заданий 1-24:

Выберите букву, соответствующую правильному варианту ответа.

1.

Кто обеспечивает благоприятную инвестиционно-финансовую политику в вопросах качества автомобилей, менеджмента…

1.Генеральный директор департамента экономики и финансов.

2. Генеральный директор департамента работы с персоналом.

3. Директор по информационным системам

4. Директор по производству.

1

2.

Маркетинг- это …

1. Совокупность финансовых, организационно-технических и коммерческих функций управления предприятия.

2. Систематическое сопоставление элементов деятельности предприятия.

3. Стратегический план обновления модельного ряда.

4. Процесс разработки и постановки на производство новых и модернизированных моделей.

1

3.

Кто обеспечивает полноту и достоверность информации, используемой в системе качества …

1.Генеральный директор департамента экономики и финансов.

2. Генеральный директор департамента работы с персоналом.

3. Директор по информационным системам.

4. Директор по производству.

3

4.

Кто определяет ответственность и полномочия подразделений в должностных лиц по вопросам обеспечения качества в процессе производства …

1.Генеральный директор департамента экономики и финансов.

2. Генеральный директор департамента работы с персоналом.

3. Директор по информационным системам.

4. Директор по производству.

4

5.

Кто организует работу по обеспечению стабильного качества продукции и несет ответственность за соответствие выпускаемой продукции установленным требованиям…

1.Генеральный директор департамента экономики и финансов.

2. Генеральный директор департамента работы с персоналом.

3. Директор по информационным системам

4. Директор по производству.

1

6.

Исследовательские испытания, проводимые при разработке продукции с целью оценки влияния вносимых в нее изменений для достижения заданных значений показателей ее качества называется…

1. доводочные испытания

2. приемочные испытания

3. квалификационные испытания

4. сертификационные испытания

1

7.

Контрольные испытания опытных образцов, проводимые с целью решения вопроса о целесообразности постановки этой продукции на производство называется…

1. доводочные испытания

2. приемочные испытания

3. квалификационные испытания

4. сертификационные испытания

2

8.

Контрольные испытания первой промышленной партии, проводимые с целью оценки о готовности предприятия к выпуску продукции данного типа в заданном объеме называются…

1. доводочные испытания

2. приемочные испытания

3. квалификационные испытания

4. сертификационные испытания

3

9.

Контрольные испытания продукции, проводимые с целью установления соответствия характеристик ее свойств национальным и (или) нормативным документов называется …

1. доводочные испытания

2. приемочные испытания

3. квалификационные испытания

4. сертификационные испытания

4

10.

В скольких уровнях можно представить документацию по качеству…

1.2

2.3

3.4

4.5

2

11.

Уровень документации по качеству относится описание системы качества в соответствии с политикой в области качества и стандартами ИСО 9000 …

1.1

2.2

3.3

1

12.

Уровень документации по качеству относится описание работ, необходимых дл реализации элементов системы качеств …

1.1

2.2

3.3

2

13.

Уровень документации по качеству относится подробные рабочие инструкции …

1.1

2.2

3.3

3

14.

Уровень дефектности является средним уровень дефектности партий, который для целей приемки продукции является удовлетворительным(приемлемым).

1. Приемочным

2. Постоянным

3. Критическим

4. Малозначительным

1

15.

Дефект. при наличии которого использование продукции по назначению практически невозможно или недопустимо по правилам безопасности называется…

1. Критический

2. Значительный

3. Малозначительный

4. Приемочный

1

16.

Дефект, который существенно влияет на использование продукции по назначению и (или) на долговечность, но не является критическим, называется…

1. Критический

2. Значительный

3. Малозначительный

4. Приемочный

2

17.

Дефект, который существенно влияет на использование продукции по назначению и (или) на долговечность называется…

1. Критический

2. Значительный

3. Малозначительный

4. Приемочный

3

18.

Сколько уровней идентификации…

1.2

2.3

3.4

4.5

1

19.

Организующая основа для проведения корректирующий действий…

1. Задание по улучшению качеств автомобилей

2. Задание готовой дирекции по качеству

3. Работа по определению причин неисправности

4. Координацию работ по выполнению заданий

1

20.

Антикоррозийная защита и упаковка должна предохранять изделия от коррозии в течении … со дня их отправки с завода.

1. двух

2. трех

3. четырех

4. одного

2

21.

Установление статическими методами значений показателей точности и стабильности технологического процесса и определение закономерностей его протекании во времени -это…

1. Статический анализ точности и стабильности технологического процесса

2. Статическое регулирование технологического процесса

3. Статический приемочный контроль качества продукции

4. Статический уровень качества

1

22.

Корректирование значений параметров технологического процесса по результатам выборочного контроля контролируемых параметров, осуществляемое для технологического обеспечения требуемого уровня качества продукции — это …

1. Статический анализ точности и стабильности технологического процесса

2. Статическое регулирование технологического процесса

3. Статический приемочный контроль качества продукции

4. Статический уровень качества

2

23

Выборочный контроль качества продукции, основанный на применение методов математической статистики для проверки соответствия качества продукции установленным требованиям и принятия решения -это…

1. Статический анализ точности и стабильности технологического процесса

2. Статическое регулирование технологического процесса

3. Статический приемочный контроль качества продукции

4. Статический уровень качества

3

24.

Сколько принципов системы мотивации…

1. 6

2.7

3.8

4.9

3

infourok.ru

Исследование функции онлайн с подробным решением

«ИССЛЕДОВАНИЕ ФУНКЦИЙ»

Министерство образования Российской Федерации Российский государственный университет нефти и газа имени И.М. Губкина В.И. Иванов С.И. Васин Методические указания к изучению темы «ИССЛЕДОВАНИЕ ФУНКЦИЙ»

Множества чисел (натуральные, целые, рациональные, действительные). Комплексные числа, их свойства и действия над ними. Множество натуральных чисел

N = {1, 2, 3, ……} – множество натуральных чисел.

Обозначим буквой N₀множество, состоящее из всех натуральных чисел и нуля. Так как через N мы обозначили множество всех натуральных чисел, то можно записать: N₀=N0, NN₀.

Рассмотрим уравнение х+а=b,a,bN₀.

Если аb, то существует единственное число c=baN₀, являющееся решением этого уравнения. Если жеa>b, то во множестве N₀уравнение не имеет решений. Чтобы для любыхa,bN₀существовало решение уравнения, надо расширить множество N₀. Такое расширение осуществляется добавлением к каждому числуанового элемента, обозначаемого а, так чтобы в сумме саполучался нуль:

( а)+а=0, а+( а)=0.

Этот новый элемент называется отрицательным числом, противоположным натуральному числу а (или обратным для aпо сложению). Наоборот, положительное числоаназывается противоположным отрицательному числу-а.

Условимся числа изображать точками на прямой. Нулю соответствует фиксированная точка, называемая начальной или началом. Справа от начала с одинаковыми интервалами между двумя соседними числами, равными единице масштаба, располагаются натуральные числа, а слева от начала — отрицательные числа.

Множество целых чисел

Множество, состоящее из всех натуральных чисел, нуля и всех отрицательных чисел, называется множеством целых чисел и обозначается буквой Z (от немецкого слова «die Zahl» — число). Имеем: NN₀ Z.

Так как на числовой оси меньшее число располагается левее большего, то всякое отрицательное число меньше любого положительного числа и нуля. Запись m<0 означает, чтоm— отрицательное число.

Во множестве Z уравнение x+a=bвсегда имеет единственное решение:х=b а.

Так как знак минус означает симметрию относительно начала, то

 ( а)=а, а b=а+( b), а (b с)=а b+с.

При умножении справедливы следующие правила знаков:

( а) b=а ( b)=(  а )b, ( а) ( b)=а b.

Правила арифметических действий над отрицательными числами легко выводятся из общих законов арифметических операций: переместительности (коммутативности) и сочетательности (ассоциативности) сложения и умножения, а также распределительности (дистрибутивности) умножения относительно сложения:

а+b=b+а, аb=bа, а+(b+с)=(а+b)+с, а(bс)=(аb)с, а(b+с)=аb+ас.

Отрицательные числа впервые появились в Древнем Китае. Уже в VI-XI веках они систематически употреблялись в Индии при решении задач. Однако, в европейской науке отрицательные числа получили окончательное признание лишь в XVII веке во времена Рене Декарта (1596-1650), давшего геометрическое истолкование чисел как направленных отрезков.

Рациональные числа

Рассмотрим уравнение ах=b, гдеа,b— целые числа, причема 0. Еслиbделится наабез остатка, т.е.b=am,mZ, то во множестве целых чисел исходное уравнение имеет единственное решениех=m. В противном случае это уравнение не имеет решений во множестве Z. Чтобы уравнение имело решение при любых целыхаиbприа 0, надо расширить множество Z, добавляя новые элементы,a,bZ,а 0.

Число называется рациональным числом или дробью с числителемbи знаменателема. Если в рассматриваемое уравнение вместохподставить, то получится тождество. Два рациональных числасчитаются равными, если.

Введение положительных рациональных чисел (дробей) явилось исторически первым расширением понятия натурального числа. Оно было вызвано тем, что не всегда единица измерения укладывается на измеряемой величине целое число раз. Дробные числа были уже известны в Древнем Египте и Вавилоне. Китайцы и индусы в начале новой эры уже производили над дробями все арифметические действия. Сначала пользовались единичными дробями, т. е. дробями с числителем единица. Дробьопределялась как суммаmодинаковых единичных дробей со знаменателемn. Лишь с развитием арифметики как науки о числе стали представлять дроби как отношение двух целых чисел, т.е.. Отсюда и возникло название «рациональное число» от латинского «ratio» — отношение.

Положительная дробь называется правильной, если 0<m<n, т.е. если числитель меньше знаменателя, и неправильной, еслиm≥n>0. Применяя алгоритм деления, всякую неправильную дробь можно представить в виде суммы натурального числа и правильной дроби:

, 0r<n.

Сумму символически записывают в видеи называют смешанной дробью с целой частьюq. Дробь со знаменателем единица отождествляется с целым числом, равным числителю, т.е.. Если НОД(m,n)=1, то дробьназывается несократимой.

Дробь называется десятичной, если ее знаменательnявляется натуральной степенью числа 10. Для десятичной дроби употребляется особый вид записи. Например, вместо, пишут: 0,0213. Дробь же, записанную в виде, гдеmиn— целые числа,n0, называют обыкновенной.

Десятичные дроби ввел в начале XVв. самаркандский математик аль-Каши, умерший около 1436 г., а в Европе они стали распространяться после выхода книги Симона Стевина (1548-1620) «Десятая» в 1585 г. В этой книге десятичные дроби стали составной частью унификации всей системы мер на десятичной основе.

Десятичные дроби, имеющие после запятой конечное число ненулевых цифр, называются конечными. Для их превращения в обыкновенные или смешанные дроби достаточно записать соответствующий знаменатель 10n, взяв числителем число из цифр после запятой и сохранив целую часть числа, если она есть. Например, число 2,023=2.

Десятичная дробь, имеющая сколь угодно много ненулевых цифр после запятой, называется бесконечной. Бесконечные десятичные дроби разбиваются на два класса — периодические, когда, начиная с некоторого момента, одна и та же группа цифр неограниченно повторяется, а других цифр, кроме этой группы, нет, и непериодические, если не существует такой бесконечно повторяющейся группы цифр после запятой. Повторяющуюся группу цифр в периодической десятичной дроби заключают в круглые скобки. Например, вместо 0,2353535… пишут 0,2(35).

Применяя алгоритм деления числителя на знаменатель, можно представить всякую обыкновенную дробь либо в виде конечной десятичной дроби (если простыми множителями знаменателя являются только двойки или пятерки), либо в виде бесконечной периодической (в остальных случаях). Например, .

Для того, чтобы периодическую десятичную дробь превратить в обыкновенную (или смешанную, если дробь больше единицы), надо в знаменателе дробной части записать слева направо столько девяток, сколько цифр в периоде, и столько нулей, сколько цифр до периода, а в числителе — разность между натуральным числом из цифр после запятой до второго периода и натуральным числом из цифр после запятой до первого периода.

Для доказательства этого утверждения умножим дробную часть хдесятичной периодической дроби сначала на 10^k, гдеk— число цифр после запятой до второго периода, затем — на 10^h, гдеh— число цифр до первого периода. Вычитая из первого результата второй, получают справа натуральное число, равное числителю искомой обыкновенной дроби, а слева — указанный в теореме знаменатель, умноженный на данную дробную частьх. Целая же часть числа остается неизменной.

Рассмотрим, например, периодическую десятичную дробь 3,2(15). Здесь дробная часть х=0,2(15),k=3,h=1.

Имеем: 10³х 10х = 215  2. Следовательно,, а значит,.

Множество всех рациональных чисел обозначается буквой Q от латинского слова «quotient» — «частное».

Имеем: NN₀ Z Q.

Арифметические операции — сложение и умножение рациональных чисел удовлетворяют тем же законам ассоциативности, коммутативности и дистрибутивности, что и натуральных и целых чисел.

Заметим, что на числовой оси рациональные числа располагаются «всюду плотно», т.е. между любыми точками числовой прямой существует точка, изображающая рациональное число.

Рассмотрим на числовой прямой точку, являющуюся концом отрезка, равного диагонали квадрата, который построен на единичном отрезке этой прямой. Эту точку нельзя задать никаким рациональным числом. Действительно, предположим противное, т.е. что ей соответствует несократимая дробь , гдеm,n— ненулевые целые числа.

По теореме Пифагора получаем 1²+1²=2=, и далееm²=2n². Следовательно,m², а значит иm— числа четные, т.е.m=2k,kZ. Получаем: (2k)²=2n²Отсюда 2k²=n². Значит,n— тоже число четное, т.е. дробьоказалась сократимой. Пришли к противоречию.

Так как квадрат этого нового числа равен двум, то оно обозначается символом .

Рассмотрим множество всех рациональных чисел, добавив к ним новые элементы, соответствующие тем точкам числовой оси, которые не изображают никакие рациональные числа. Каждый такой элемент называется иррациональным числом (от лат. «irrational» — безрассудный, не определяемый отношением).

Множество всех рациональных и иррациональных чисел образует новое множество, называемое множеством действительных чисел. Оно обозначается буквой R ( от фр. «r ee l» — действительный, реальный).

Всякому действительному числу соответствует единственная точка на числовой прямой. Наоборот, всякой точке на числовой прямой соответствует единственное действительное число.

Имеем: NN₀ Z Q R.

Пусть х— произвольное действительное число. Откладывая от начала координат единичный отрезок в положительном (прих≥0) или отрицательном (прих<0) направлении, убеждаемся, что существует единственное целое числоnтакое, что

Если x=n, то процесс закончен. Если жех>n, то, разбивая единичный отрезок на 10 частей и откладывая от точкиnв положительном направлении десятые доли, получим:

n,n₁ x< n,(n₁+1).

Продолжая, в случае неравенства, процесс откладывания сотых, тысячных и т.д. частей, убеждаемся, что всякое действительное число либо совпадает с конечной десятичной дробью, либо выражается бесконечной десятичной дробью, лежащей с любой степенью точности между двумя конечными десятичными дробями. При этом конечная и бесконечная периодическая десятичная дробь является рациональным числом, а бесконечная непериодическая десятичная дробь — иррациональным числом.

Операции сложения и умножения иррациональных чисел осуществляются путем предельного перехода результатов соответствующих операций над конечными десятичными дробями, являющимися приближениями исходных чисел. Например, для нахождения суммы составляют монотонно возрастающую ограниченную сверху последовательность десятичных дробей:

1,4+1,7=3,1;

1,41 + 1,73=3,14;

1,414+1,732=3,146;

1,4142+1,7320=3,1462;

1,41421+1,73205=3,14626;

1,414213+1,732050=3,146263,

1,4142135+1,7320508=3,1462643; и т.д. В пределе эта последовательность и дает число .

Арифметические операции над действительными числами удовлетворяют тем же законам ассоциативности, коммутативности, дистрибутивности, что и над рациональными числами.

Знак минус перед действительным числом означает переход к противоположному числу, изображаемому симметричной относительно начала числовой прямой точкой. Следовательно,

-(-х)=хдля любогоxR.

Модулем действительного числа хназывается число, равноех, еслиx≥0, и равное-х, еслих<0. Обозначается |х|. Например, |5|=5, |-7|=7, |0|=0. Геометрически модульхесть расстояние от точкихдо начала числовой прямой. Очевидно, |x|>0, |х+y|  |х|+|y|.

Кроме того, (-х)у=х(-у)=-ху,(-х)(-у)=ху.

Научная теория действительных чисел исчерпывающе была разработана немецкими математиками Вейерштрассом(1815-1897) и Дедекиндом(1831-1916).

studfiles.net

Множество натуральных чисел — N, множество целых чисел Z, множество рациональных чисел Q, множество иррациональные чисел, множество действительных = вещественных чисел R. Понятия и обозначения, русский и английский = международный подходы. Обозначения

Техническая информация тут Перевод единиц измерения величин Таблицы числовых значений Алфавиты, номиналы, единицы Математический справочник тут Физический справочник Химический справочник Материалы Рабочие среды Оборудование Инженерное ремесло Инженерные системы Технологии и чертежи Личная жизнь инженеров Калькуляторы Поиск на сайте DPVAПоставщики оборудованияПолезные ссылкиО проектеОбратная связьОтветы на вопросы.Оглавление

Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа.  / / Множество натуральных чисел — N, множество целых чисел Z, множество рациональных чисел Q, множество иррациональные чисел, множество действительных = вещественных чисел R. Понятия и обозначения, русский и английский = международный подходы. Обозначения Действительные (= вещественные) числа R: натуральные числа — множество N, целые числа — множество Z, рациональные числа — множество Q, иррациональные числа — множество R. Понятия и обозначения. Поиск в инженерном справочнике DPVA. Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: Шпаргалки по математике, алгебре и геометрии Правила сложения и вычитания. Таблица сложения от 1 до 10. Таблица сложения до 20. Таблица сложения в пределах 10. Таблица вычитания от 1 до 10. Таблица вычитания до 20. Таблица вычитания через десяток. Таблица умножения для 2 класса — традиционная 10×10, 12х12 и 20х20 Таблицы деления — традиционная 10×10 и 12х12

dpva.ru

Натуральные N, целые Z, рациональные Q, действительные R, иррациональные I. Арифметические действия с дробями (сложение, сокращение, вычитание, умножение). Модуль числа. Свойства модуля.

dpva.ru

Смотреть фильмы онлайн в хорошем качестве HD 720 и 1080 бесплатно

Мы очень рады приветствовать всех кинолюбителей на Kino-FS –масштабном портале с огромнейшей базой материала, предлагаемого для хорошего отдыха дома и без труда смотреть фильмы онлайн. Многие имеющиеся на этом сайте фильмы, мультфильмы, развлекательные или документальные передачи, аниме и другие интересные программы предлагаются вам к обзору исключительно в высоком разрешении, без раздражительных искажений, шумов и потери цветов.

На портале Вы можете смотреть онлайн фильмы разных жанровых направлений. Вы сможете отыскать самые горячие новинки или с ностальгией пересмотреть какой-нибудь легендарный фильм 90/80-х годов прошлого века. В любом случае у нас вы гарантировано сможете найти по вкусу и максимально быстро перейти к отдыху. Это возможно благодаря наличию поисковой системы, которая будет понимать вашу цель поиска с полуслова.

Кроме этого мы предоставляем вам оценить самые популярные, захватывающие, интригующие или даже классические сериалы, которые сегодня начали пользоваться большим интересом у зрителя и по своей мере затягивать на долгие часы просмотра превзошли даже самые ажиотажные голливудские фильмы hd 720. Практически каждый сегодня знает о «Игра престолов», «Во все тяжкие», «Физрук», «LOST» и другие горячие хиты. Но самое главное, что большая часть зрительской аудитории предпочитает смотреть сериалы онлайн, и лишь немногие скачивают их на свой ПК. Что, кстати говоря, мы так же предлагаем к услугам.

Большой ассортимент кинолент уже говорит о том, что у нас вы не соскучитесь. Но еще мы рады вам предложить различные мультипликационные работы в виде художественных фильмов или сериалов. Даже не менее популярные аниме со своими невероятными приключениями и эмоциональными сценариями нашли здесь место быть, и не в малом количестве. Мы настоятельно рекомендуем смотреть мультфильмы онлайн на нашем сайте в кругу семьи, с детьми или просто для собственного развития, ведь нередко даже в таких картинах можно найти хорошую коллекцию полезных советов или поучительных жизненных ситуаций.

Вместе с вышеперечисленным Кино-ФС сможет вас порадовать наличием самых разнообразных шоу, как отечественного, так и зарубежного производства. У нас представлены кулинарные шоу, интересные документальные сюжеты, зрелищные шоу, мюзиклы, семейные или судебные разбирательства, путешествия, кулинария и много чего другого, что можно увидеть в программе телевизионных студий или еще даже в анонсах.

Мы активно работаем только для вас и стараемся предоставить максимально удобный в использовании интерфейс, обеспечить наилучшим качеством видео, подарить лучшие эмоции от просмотров онлайн и все это абсолютно бесплатно. FS.to

kino-fs.me

Сериалы ТУТ! — смотреть онлайн сериалы на сезонвар бесплатно HD 720

Среди огромного многообразия, которое способна предложить современная киноиндустрия наиболее высоким спросом сегодня пользуются многосерийные фильмы, успевшее превратиться в настоящие произведения искусства. Еще недавно немногие отдавали предпочтение теленовелла, превознося полнометражные картины, но в последние несколько лет ситуация изменилась с точностью до наоборот.

Удобно ли смотреть бесплатно сериалы онлайн?

Миллионы киноманов по всей планете более охотно начинают смотреть многосерийные фильмы, позабыв о посещение кинотеатров. Но телевидение не отвечает поклонникам взаимностью, принуждая зрительскую аудиторию терпеть продолжительные рекламные ролики, ставшие преградой на пути к организации комфортного времяпровождения у экранов телевизоров. Подобная тенденция сошла на нет, ведь эпоха технического прогресса принесла сериаломанам повсеместное распространение всемирной паутины.

Больше нет необходимость спешить к трансляции в строго назначенное время, ведь гораздо удобнее получать доступ к актуальным обновлениям полюбившегося телешоу, когда появляется для этого свободная минутка. Команда данного ресурса трудится в круглосуточном режиме, чтобы предоставить посетителям выбор, который будет единственно правильный. Лучшего варианта провести незабываемый вечер в уютной домашней обстановке, чем открыть сайт в поисковой строке браузера и насладиться очередным эпизодом любимой истории не отыскать.

Сериалы онлайн в хорошем качестве всегда на нашем сайте!

На страницах нашего интерактивного кинопортала каждый пользователь виртуальной сети сможет воспользоваться замечательной возможностью смотреть сериалы, своевременно вкушая все приготовленные телевизионщиками сюрпризы. Ознакомление со всеми шедеврами режиссеров, творящих на телевизионном поприще, пройдет без каких-либо ограничений, вроде внесения платы или обязательного прохождения процедуры регистрации, что позволит сделать досуг красочным и разнообразным.

serialytut.info

3 Система массового обслуживания. Элементы системы. Классификация.

Предмет ТМО-построение мат.моделей,связывающих заданюусловия работы СМО (число каналов, их произв-ть, правила работы, х-р потока заявок) с показателямиэф-ти системы. В кач-ве к-рых м.б. среднее число заявок обслуживаемых системами в ср.вр., средн.число заявок в очереди,сред.вр. ожидания обслуживания.

Задача ТМО сост в выработке рекомендаций по рац построению СМО, рац организации их работы и регулир потока заявок с целью обеспеч высокую эф-ть обслуж-ия и функционир-ия системы.

Заявки или требования – объекты, нуждающиеся в услугах или в выполнении работ.

СМО – совокуп однор-ых устройств, наз-х каналами и заявок, нуждающихся в обслуживании.

Элементы СМО:

1.Входящие заявки

2.Обслуживающие устр-ва, т.е каналы

3.обслуживание, т.е процесс удовлетвор заявок

4.выходящие заявки как обслужен так и необслужен

5.очередь, т.е заявки поступившие в систему при занятых каналах и ожидающие начала обслуживания.

Классификация СМО:

1.одноканальные,к-рые содерж 1 канал

2.многоканальные, больше 1 канала

сущ 2 основ типа СМО:

с отказами или выбыванием

с ожиданием

Для систем с отказами х-ми явл, то, что заявки поступившие в систему при занятых каналах получают отказ, т.е выбывают необслужен., и в дальнейшем ф-нии системы не учавствуют.

При использ систем с ожиданием заявка, поступившая в систему, когда канал занят, становится в очередь и обслуживается при освобождении канала.

По хар-ру ожидания СМО:

1.с неогран временем ожидания

2.с огран

в (1) заявка пребывает в очереди до тех пор, пока не будет обслужена как бы долго не продолжалось ожидание.

Во (2) заявка после определ-го срока пребывания в очереди выбывает из сист необслуженной.

По хар-ру обслуж-ия СМО:

случайные

упорядоченные

с приоритетным обслуживанием

4 Сущность имитационного моделирования. Область применения.

ИМ – процесс изучения объектов путем проведения экспериментов на их мат. моделях, реализуемых на ЭВМ. Сущность метода: описывая вз-вие составных частей исследуемой системы с помощью мат. соотношений, м. получить небх. о ней инфо, не обращаясь к натуральным экспериментам.При разработке имитационных маделей рекомендуется следовать трем правилам: 1). участие в создании модели специалистов, которые впоследствии должны ее использовать; 2). поэтапность внедрения, т.к. в практической деятельности могут найти применение отдельные блоки имитационной модели для исследования вопросов, связанных с изучаемой проблемой; 3). доступность, пользователь должен получать результаты вычислительного эксперимента в привычной для него форме: в виде таблиц, графиков, гистограмм.

Области применения ИМ. ИМ используется при решении следующих задач:

1. теоретических (математика, физика, химия).Напр., вычисление площадей фигур, ограниченных кривыми;

2.практических задач организованного управления:

-задачи производственно-технологических процессов (в сфере управления запасами, при создании СМО). Известны имитацион. модели таких устройств как прокатный стан, химический реактор, а также модели форм и отраслей промышленности.

-задачи систем экономического характера (процессы планирования, экономич. прогнозирования, инвестицион. процессы).

ИМ целесообразно применять там, где недопустимо участие людей (исслед-ие воз-вия лекарств на организм чел-а, ход боевых действий). Осн. этапы построения ИМ-ей объекта:

1. Постановка задачи и определение целей эксперимента.Рассм-ся вар-ты тех. схем, типы взаимозаменяемого оборуд-ния, виды сырья и способы его подготовки, кот. б. приняты для сопоставительного анализа. Устан-ся инфо, необх. для проведения исследований. Опр-ся параметры, кот. должны войти в ИМ-ль в кач-ве вход. и выход. переменных. Дается качествен. описание их взаимосвязи и др.

2. Изучение исследуемого явления. Концептуальная модель – модель абстрактного, описательного типа, отраж. представление (концепцию) исследователя о сущ-ти процесса ф-ния исслед-го объекта при рассм-нии этого процесса в границах, определяемых целями исследования. Изучение процесса ф-ния объекта в установлен. границах – наблюдение за объектом, если объект реально существует в теч. достаточ. длитель. времени. Ознакомление с документацией по объекту. Консультации со специалистами, проектировщиками и др. В результате уточняются вход. и выход. данные и ограничения., устанавл-ся критерии , с помощью кот. б. оценив-ся эф-ть ф-ния системы. Результаты проверенного изучения объекта систематизир-ся и излагаются и в словесной форме и в графическом виде.

3. Планирование эксперимента (ПЭ). Предшествует проведению эксперимента. Стратегическое П – ПЭ, кот. должно дать необх. инфо. Тактичес. П – опр-ие способа проведения каждой серии испытаний, предусмотрен. планом эксперимента. Экспериментирование – с целью получения желаемых данных.

4. Формализация (ф-я) мат. модели (выделение главных факторов и исключение второстепенных). Система разбивается на блоки. Ф-ся з-ны моделирования и правдоподоб. гипотезы относ-но поведения как системы вцелом, так и отдель. ее блоков. При это м в каждом блоке для их описании м. исп-ся свой мат. аппарат (графики, схемы и др.). В 1 блок объед-ся родствен., т.е. преобр-ся по близким правилам компоненты. Ф-ую мат. модель графически представляют в виде блрок-схемы, наз. алгоритмом процесса.

5. Составление машинной программы. Выбор языка программирования + генерирование послед-ти случ. чисел, имеющих задан. распределение.

6. Проверка мат. модели на адекватность. Провер-ся наличие принципиаль. (ПО) и технич. ошибок (ТО). ПО – неправиль. выбор списка переменных, невер. гипотеза, связывающ, переменные. ТО – обр-ся при составлении программы (их находят локальной проверкой по этапам блоком программы).

7. Проведение эксперимента и обработка результатов. Эксперимент вып-ся в диалоговом режиме. Обработка результатв проводится методами мат. статистики, н-р с исп-ем регрессион., кореляцион., дисперсион. анализа.

5 Расчёт и оптимизация сетевых моделей Задачей расчета сетевой модели явл опр-е критического пути, его продолжительности, всех ост-ых параметров, хар-щих модель. Сущ табличный и граф методы расчета. Рассм графич он более точный.

Порядок выполнения расчета:

1вычерчивают сетевую модель комплекса работ

2нумеруют события и работы

3рассчит ран сроки наступления событиядля исходного события он = 0для каждого из событий ранга 1 он = продолжит-сти выполнения работы, ведущей к этому событию. Построение работ и событий их завершения проводят в порядке возрастания ранга работ.

1. Если к событию ведет несколько работ от разных событий, то рассчит все суммы и наибол из них опр-ет ран срок наступ события

1Расчет продолжают до завершающего события.

2рассчит поздние сроки наступления события

4.1расчет выполняется в обратном порядке от завершающего события к начальному

4.2для завершающего события поздний срок = раннему. Для остальных он определяется вычитанием из наибольш по продолжит-ти пути следующего за данным событием.

5.Опр-ют резервы всех событий. Все результаты впис в кружки, отражающие события.

6.опр-ют крит путь. Он проходит через события не имеющие резервов.

7.по формулам рассчит ран и позд сроки начала и окончания работ и резервы работ.

8.на основании величин резервов и выбранного предела различие м-ду критич и подкритич путями устанавливают подкритич работы и пути.

Когда расчет сетевой модели выполнен величина сравнивается с, т.е дириктивно установленной на более высок уровне управления продолжительностью выполнения всего комплекса работ.

Если , то счит-ся, что задан сроки выдерживаются и выполнение всех работ надо организовать в соответ-ии с построен моделью. В противном случае сетевую модель необх-мо модернизировать.

Выполняется за счет внеш. вложений доп. ресурсов. Задача сводится к задаче лин. прогр.

Матем. модель:

Критерий –доп.затраты ресурсов на выполнение ij-работ.

Ограничения:

1доп.затраты на кажд.из работ не д.превосходить выделенного лимита ресурсов. Вкладываемые в критич.работы ресурсы однородны по своей природе либо фнансов.либо трудовые.

1сокращен. критич. Путь д.б.небольше директивного.Сам критич.путь своего положения на сетевом графике не изменяет в рез.сокращения длительности критич.работ.

технолог.коэ-т.(из справочника)

studfiles.net

СМО — это… Что такое СМО?

СМО

страховая медицинская организация

мед., организация

СМО

собственная мышечная оболочка

мед.

СМО

система материального обеспечения

Словарь: Словарь сокращений и аббревиатур армии и спецслужб. Сост. А. А. Щелоков. — М.: ООО «Издательство АСТ», ЗАО «Издательский дом Гелеос», 2003. — 318 с.

СМО

специальное математическое обеспечение

матем.

Словарь: С. Фадеев. Словарь сокращений современного русского языка. — С.-Пб.: Политехника, 1997. — 527 с.

СМО

Сибирское межрегиональное отделение

Источник: http://www.vedomosti.ru/newspaper/article.shtml?2004/08/10/79409

Пример использования

СМО РФФИ

СМО

Севастопольская морская обсерватория

Крым, морск.

СМО

специальные монтажные операции

Словарь: С. Фадеев. Словарь сокращений современного русского языка. — С.-Пб.: Политехника, 1997. — 527 с.

СМО

студенческий механизированный отряд

образование и наука

СМО

Совет министров обороны

государств-участников СНГ

воен., гос.

СМО

система математического обеспечения

матем.

Словарь: С. Фадеев. Словарь сокращений современного русского языка. — С.-Пб.: Политехника, 1997. — 527 с.

СМО

система массового обслуживания

Словарь: С. Фадеев. Словарь сокращений современного русского языка. — С.-Пб.: Политехника, 1997. — 527 с.

СМО

средства медицинского обеспечения

мед.

Словарь: С. Фадеев. Словарь сокращений современного русского языка. — С.-Пб.: Политехника, 1997. — 527 с.

СМО

специальная монтажная операция

СМО

сельское муниципальное образование

РФ

Источник: http://www.su-rk.ru/index.php?option=com_content&task=view&id=265

СМО

совет муниципальных образований

образование и наука

Примеры использования

СМО Санкт-Петербурга

СМО Волгоградской области

СМО

строительно-монтажная организация

организация

СМО

субфедеральные и муниципальные облигации

РФ

Источник: http://www.cfin.ru/finmarket/municipal_bonds.shtml

Словарь сокращений и аббревиатур. Академик. 2015.

sokrasheniya.academic.ru

смо

 Главная Поиск: ТЭГИ приколы видео орел и решка черногория русские молодые политика спорт музыка события факты звёзды Дота 2 женщины альтернатива КВН драки война мультики актёры кино онлайн масяня приколы наруто видеоклипы видеобитва машины видеореклама вконтакте однокласники видеоролик дня видеоролики 2018 видеоролики без смс казино АТО ДНР ополчение смешное видео youtube приколы дом2 драки стоп хам драки я приколы видео дом2 серии дорогой ты где был русские детективные сериалы бэк ту скул пранки над друзьями новые видеоклипы, Поздравления РЕКЛАМА Денди Купить| Dendy Купить игровую приставку ПАРТНЁРЫ Сообщество

смо . Лунтик — 6 сезон Нажми для просмотра Новая серия «Страшно добрая фея» Yandex-market Лунтик: …       Тэги:   Лекция 18: Теория массового обслуживания. Системы массового обслуживания Нажми для просмотра Классифика ция систем массового обслуживан ия. Рассматрив аются простейшие и более сложные системы масс…       Тэги:   Теория систем массового обслуживания Нажми для просмотра Легавый 2 сезон 1 серия. Сериал фильм криминал смотреть онлайн. Please Subscribe! Все серии сериала Легавый 2 …       Тэги:   Легавый 2 сезон 1 серия. Сериал фильм криминал смо� Нажми для просмотра Допуск персонала СМО в выгороженн ую зону, где проход на рабочее место проходит через действующе ю эл….       Тэги:   Допуск персонала СМО в электроустановку по наряду Нажми для просмотра Смотрите наши фильмы — на сайте http://кино-мо сфильм.рфП дпишитесь на наши страницы в социальных сетях!Facebook: …       Тэги:   Афоня (комедия, реж. Георгий Данелия, 1975 г.) Нажми для просмотра Использова ние метода Монте — Карло для моделирова ния сложных систем. Лекция и тесты в НОУ ИНТУИТ …       Тэги:   Лекция 19: Статистическое моделирование систем массового обслуживания Нажми для просмотра Оформи подписку на Яндекс.Плю всего за 169₽ в месяц: и слушай мой новый трек «Я люблю аниме» на…       Тэги:   DK — Я смотрю Аниме Нажми для просмотра Српска напредна странка на интернету:W ebsite:FacebookTwitt er …       Тэги:   Михајловић: На почетку смо великог инвестиционог циклуса Нажми для просмотра Добри смо ако се понашамо како би Европа желела, констатова о је данас председник Србије Александар …       Тэги:   Вучић: Добри смо ако се понашамо како би Европа желела Нажми для просмотра Одноканаль ные системы массового обслуживан ия с ожиданием и ограниченн ой очередью       Тэги:   Одноканальные СМО с ожиданием и ограниченной очередью Нажми для просмотра Новая серия «Страшно добрая фея» Yandex-market Лунтик: …       Тэги:   Лунтик — Самые лучшие серии (HD) Нажми для просмотра Вупсень и Пупсень не любят молоко – они его даже никогда не пробовали! Лунтик и Кузя решают открыть гусениц…       Тэги:   Лунтик — 378 — 389 серии Нажми для просмотра Новая серия «Страшно добрая фея» Yandex-market Лунтик: …       Тэги:   Лунтик и его друзья — 389 серия. Секрет победы Нажми для просмотра Всем привет, я Давидыч и это мой канал SmotraTV На данном канале вы не увидите банальные скучные авто обзоры,…       Тэги:   Лунтик — 439 серия. Страна игрушек Нажми для просмотра ● Фильмы и Сериалы ● Бесплатно и Онлайн ● Подписывай ся и Смотри! ● …       Тэги:   smotraTV Нажми для просмотра 30 година Делија.       Тэги:   Фильм 14+ «История первой любви» Смотреть в HD Нажми для просмотра ПОДПИСКА НА КАНАЛ ➜       Тэги:   Оздравили смо! Нажми для просмотра Емисија ,,Ослобађањ е историје’ ;’, гост Валерија Бркљач.Аут р: Весна Пешић       Тэги:   Девочка со Спичками мультфильм онлайн HD трейлер мултфильмов смо» rel=»spf-prefetch Нажми для просмотра Описание отсутсвует       Тэги:   Непобедиви смо!» rel=»spf-prefetch Нажми для просмотра Описание отсутсвует       Тэги:   Непобедиви смо!» rel=»spf-prefetch Нажми для просмотра Описание отсутсвует       Тэги:   Непобедиви смо!» rel=»spf-prefetch Нажми для просмотра Описание отсутсвует       Тэги:

funer.ru

Смотреть Онлайн ТВ в хорошем HD качестве бесплатно прямой эфир.

Онлайн ТВ бесплатно

Интернет занял важное место в жизни современного человека. Работа и развлечения тесно связаны с информационными технологиями. Прогресс не обошел стороной и телевидение. Теперь, для того чтобы смотреть ТВ, не обязательно находиться возле телевизора или быть привязанным к одному месту. Достаточно быть обладателем компьютера, ноутбука или планшета и быть подключенным к сети интернет. Таким образом, вы сможете просматривать интересные телепередачи, новости, любимые ток-шоу и реалити шоу в любое время, и в удобном для вас месте. Благодаря этому можно скоротать время в поездке и быть в курсе актуальных событий, где бы вы ни находились.

Преимущества онлайн ТВ

Наверное, одним из самых весомых преимуществ ТВ онлайн является то, что вам не нужно платить абонентскую плату. Нет необходимости выбирать определенные пакеты с ограниченным количеством каналов. Чтобы смотреть передачи и фильмы со всего мира больше не нужно приобретать дорогостоящее оборудование. Вам достаточно оплатить интернет трафик согласно тарифам своего оператора, таким образом, получив неограниченный доступ к трансляциям со всего мира.

Каналы на любой вкус

Здесь каждый пользователь обязательно для себя что-то интересное и познавательное, новостные каналы, исторические, культура и спорт, музыкальные и фильмовые. Вам доступны все категории без каких-либо дополнительных ограничений или дополнительных условий использования:

• Для детей представлено большое количество каналов с развлекательными и познавательными передачами, любимыми мультфильмами и героями.
• Деловые люди смогут следить за событиями мировой экономики и политическими изменениями.
• Домохозяйки смогут почерпнуть для себя множество интересных рецептов и всевозможных лайфхаков, способных упростить многие домашние дела.
• Для тех, кто увлекается спортом, приятным сюрпризом станет разнообразие спортивных каналов, транслирующих футбольные и хоккейные матчи, соревнования в бильярде, турниры по боксу и многим другим дисциплинам, проходящим в разных уголках планеты.
• Музыкальные каналы способны удовлетворить вкусы каждого поколения. Разные стили, яркие хит-парады и развлекательные передачи станут превосходным способом непринужденно провести время.

С помощью онлайн ТВ вы всегда сможете наслаждаться любимыми передачами, находясь в любой точке планеты.

lion-tv.org