Понятие о множествах — ПриМат
Понятие множества
Множество — это совокупность определенных объектов, которые могут иметь конкретные свойства.
Георг Кантор, который создал данную теорию давал следующее определение — «Под «множеством» мы понимаем соединение в некое целое $M$ определённых хорошо различимых предметов $m$ нашего созерцания или нашего мышления (которые будут называться «элементами» множества $M$).».
Множество состоит из отдельных объектов — элементов множества.
Множество обозначается большими буквами латинского алфавита, а его элементы — маленькими буквами латинского алфавита. Множества записываются в фигурных скобках $(X=\left\{a,b\right\})$.
Принято использовать следующие обозначения:
- $a\in\ X$ — символ принадлежности, читается как «элемент $a$ принадлежит множеству $X$»;
- $a\notin\ X$ — символ отрицания принадлежности, читается как«элемент $a$ не принадлежит множеству $X$»;
- $\forall$ — квантор произвольности, общности, читается как «любой» или «какой бы не был», или «для всех»;
- $\exists$ — квантор существования, например, $\exists\ y\in\ B$ — «существует (найдется) элемент $y$ из множества $B$»;
- $\exists!$ — квантор существования и единственности, например, $\exists!\ b\in\ C$ — «существует единственный элемент $b$ из множества $C$»;
- $:$ — символ пояснения, читается как «такой, что« или «обладающий свойством»;
- $\Rightarrow$ — символ следствия, читается как «отсюда следует« или «отсюда вытекает«;
- $\Leftrightarrow$ — квантор эквивалентности, равносильности, читается как «тогда и только тогда».
Существует два типа множеств — конечные и бесконечные.
Конечное множество — это множество, которое состоит из конечного числа элементов. Например, множество букв английского алфавита — представляет собой конечное множество.
Бесконечное множество — множество, которое состоит из бесконечного числа элементов. Например, множество рациональных чисел — представляет собой бесконечное множество.
Мощность множества — это число элементов, которое содержится в конечном множества $A$. Мощность обозначается как $\left|A\right|$.
Пустое множество — это множество, которое не содержит ни одного элемента — $\varnothing$.
Равные множества — это множества, которые включают в себя одни и те же элементы, то есть являются эквивалентными по отношению друг к другу.
Множества $X$ и $Y$ называются не равными ($X\ne\ Y$), если множество $X$ содержит в себе элементы, которые не содержит в себе множество $Y$. Другими словами — множество $X$ имеет элементы, которые не принадлежат множеству $Y$.
Символ равенства множеств имеет следующие свойства:
- $X=X$; — рефлексивность;
- если $X=Y$, $Y=X$ — симметричность;
- если $X=Y$, $Y=Z$, то $X=Z$ — транзитивность.
Согласно такому определению равенства множеств следует, что все пустые множества равны между собой или что существует только одно пустое множество.
Литература:
- Конспект лекций Г.С. Белозерова
- Линейная алгебра. Воеводин В.В. М.: Наука. Главная редакция физико-математической литературы, 1980, с.9-13
- Лекции по общей алгебре (издание второе). Курош А.Г. М.: Наука. Главная редакция физико-математической литературы, 1973, с.14-17
Поделиться ссылкой:
Похожее
ib.mazurok.com
что это такое, виды математических множеств
Что такое множество в математике? Математическое множество — это несколько отдельных элементов, рассматриваемых, как единое целое. Если обозначить такой элемент буквой a, а само множество — буквой А, то запись будет выглядеть следующим образом:
a ∈ A.
проговаривается эта запись так: a принадлежит А, или А содержит а, или а — элемент А.
Для перечисления элементов множества используются фигурные скобки — {}. То есть, например, множество, в котором а ∈ А, b ∈ A и c ∈ A, будет записываться в таком виде:
{a, b, c}.
Виды множеств.
Пустые множества.
Пустое множество – это то множество, которое вообще не содержит никаких элементов. Обозначается оно цифрой 0 или специальным значком ∅.
Примером пустого множества может служить любое нелогичное понятие, противоречащее самому себе — «множество птиц, живущих на дне океана», или «множество деревьев на Луне». Поскольку оба множества лишены смысла и не отвечают реальности, то, следовательно, они являются пустыми. Скажем, количество деревьев на Луне – 0, поэтому «множество деревьев на Луне» будет пустым (не будет содержать ни одного элемента).
Равные множества.
Равные множества – это два или более множеств, состоящих из равных наборов элементов. Приведём пример. Скажем, все члены Вашей семьи находятся на кухне. Таким образом, Множество «Члены семьи на кухне» будет равно множеству «Члены семьи в квартире».
Если два множества — А и B — состоят из одинакового набора элементов, то они будут равны, то есть А = B. Элементы множеств могут перечисляться в любой последовательности, на результат это никак не влияет. Множество {a, b, c} можно с тем же успехом записать, как {a, c, b}, или {с, b, a}, или {b, c, a}.
Подмножества и надмножества.
Если множества А и B состоят из одинаковых элементов {a, b, c}, то А будет считаться подмножеством B, а B — надмножеством А. Записывается это следующим образом:
A ⊆ B, B ⊇ A.
Бывает так, что множество В содержит в себе каждый из элементов множества А, но в то же время в нем присутствуют и другие элементы, множеству А не принадлежащие. В этом случае множество В становится собственным надмножеством А, в то время как множество А становится собственным подмножеством В.
Иначе говоря, если А ⊆ В, но при этом А ≠ В, то А ⊂ В, В ⊃ А.
Похожие статьи
infoogle.ru
Множества: понятие, определение, примеры
Людям постоянно приходится иметь дело с различными совокупностями предметов, что повлекло за собой возникновение понятия числа, а затем и понятия множества, которое является одним из основных простейших математических понятий и не поддается точному определению. Нижеследующие замечания имеют своей целью пояснить, что такое множество, но не претендуют на то, чтобы служить его определением.
Множеством называется собрание, совокупность, коллекция вещей, объединенных по какому-либо признаку или по какому-либо правилу. Понятие множества возникает путем абстракции. Рассматривая какую-либо совокупность предметов как множество, отвлекаются от всех связей и соотношений между различными предметами, составляющими множества, но сохраняют за предметами их индивидуальные черты. Таким образом, множество, состоящее из пяти монет, и множество, состоящее из пяти яблок, — это разные множества. С другой стороны, множество из пяти монет, расположенных по кругу, и множество из тех же монет, положенных одна на другую, — это одно и то же множество.
Приведем несколько примеров множеств. Можно говорить о множестве песчинок, составляющих кучу песка, о множестве всех планет нашей солнечной системы, о множестве всех людей, находящихся в данный момент в каком-либо доме, о множестве всех страниц этой книги. В математике тоже постоянно встречаются различные множества, например множество всех корней заданного уравнения, множество всех натуральных чисел, множество всех точек на прямой и т. д.
Математическая дисциплина, изучающая общие свойства множеств, т. е. свойства множеств, не зависящие от природы составляющих их предметов, называется теорией множеств. Эта дисциплина начала бурно развиваться в конце XIX и начале XX в. Основатель научной теории множеств — немецкий математик Г. Кантор.
Работы Кантора по теории множеств выросли из рассмотрения вопросов сходимости тригонометрических рядов. Это весьма обычное явление: очень часто рассмотрение конкретных математических задач ведет к построению весьма абстрактных и общих теорий. Значение таких абстрактных построений определяется тем, что они оказываются связанными не только с той конкретной задачей, из которой они выросли, но имеют приложения и в ряде других вопросов. В частности, именно так обстоит дело и с теорией множеств. Идеи и понятия теории множеств проникли буквально во все разделы математики и существенно изменили ее лицо. Поэтому нельзя получить правильного представления о современной математике, не познакомившись с элементами теории множеств. Особенно большое значение имеет теория множеств для теории функций действительного переменного.
Множество считается заданным, если относительно любого предмета можно сказать, принадлежит он множеству или не принадлежит. Иными словами, множество вполне определяется заданием всех принадлежащих ему предметов. Если множество \(M\) состоит из предметов \(a,\,b,\,c,\,\ldots\) и только из этих предметов, то пишут
\(M=\{a,\,b,\,c,\,\ldots\}\)
Предметы, составляющие какое-либо множество, принято называть его элементами. Тот факт, что предмет т является элементом множества \(M\) , записывается в виде
\(\Large{m\in M}\)
и читается: » \(m\) принадлежит \(M\) «, или » \(m\) есть элемент \(M\) «. Если же предмет \(m\) не принадлежит множеству \(M\) , то пишут: \(m\notin M\) . Каждый предмет может служить лишь одним элементом заданного множества; иными словами, все элементы (одного и того же множества отличны
друг от друга.
Элементы множества \(M\) могут сами быть множествами, однако, во избежание противоречий, приходится требовать, чтобы само множество \(M\) не было одним из своих собственных элементов: \(M\notin M\) .
Множество, не содержащее ни одного элемента, называется пустым множеством. Например, множество всех действительных корней уравнения
\(x^2+1=0\)
есть пустое множество. Пустое множество в дальнейшем будем обозначать через \(\varnothing\) .
Если для двух множеств \(M\) и \(N\) каждый элемент \(x\) множества \(M\) является также элементом множества \(N\) , то говорят, что \(M\) входит в \(\) , что \(M\) есть часть \(N\) , что \(M\) есть подмножество \(M\) или что \(M\) содержится в \(N\) ; это записывается в виде
\(M\subseteq N\) или \(N\supseteq M\)
Например, множество \(M=\{1,2\}\) есть часть множества \(N=\{1,2,3\}\) .
Ясно, что всегда \(M\subseteq M\) . Удобно считать, что пустое множество есть часть любого множества.
Два множества равны, если они состоят из одних и тех же элементов. Например, множество корней уравнения \(x^2-3x+2=0\) и множество \(M=\{1,2\}\) между собою равны.
Определим правила действий над множествами.
Объединение или сумма множеств
Пусть имеются множества \(M,N,P,\ldots\) . Объединением или суммой этих множеств называется множество \(X\) , состоящее из всех элементов, принадлежащих хотя бы одному из «слагаемых»
\(X=M+N+P+\ldots\) или \(X=M\cup N\cup P\cup\ldots\)
При этом, даже если элемент \(x\) принадлежит нескольким слагаемым, то он входит в сумму \(M\) лишь один раз. Ясно, что
\(M+M=M\cup M=M\)
и если \(M\subseteq N\) , то
\(M+N=M\cup N=N\)
Пересечение множеств
Пересечением или общей частью множеств \(M,N,P,\ldots\) . называется множество \(Y\) , состоящее из всех тех элементов, которые принадлежат одновременно всем множествам \(M,N,P,\ldots\) .
Ясно, что \(M\cdot M=M\) , и если \(M\subseteq N\) , то \(M\cdot N=M\) .
Если пересечение множеств \(M\) и \(N\) пусто: \(M\cdot N=\varnothing\) , то говорят, что эти множества не пересекаются.
Для обозначения операции суммы и пересечения множеств употребляют также знаки \(\textstyle{\sum}\) и \(\textstyle{\prod}\) . Таким образом,
\(E=\sum E_i\) есть сумма множеств \(E_i\) , a \(F=\prod E_i\) — их пересечение.
Читателю рекомендуется доказать, что сумма и пересечение множеств связаны обычным распределительным законом
\(M(N+P)=MN+MP,\)
а также законом
\(M+NP=(M+N)(M+P).\)
Разность множеств
Разностью двух множеств \(M\) и \(N\) называется множество \(Z\) всех тех элементов из \(Z\) , которые не принадлежат \(N\) :
\(Z=M-N\) или \(Z=M\setminus N\) .
Если \(N\subseteq M\) , то разность \(Z=M\setminus N=M-N\) называют также дополнением к множеству \(N\) относительно \(M\) .
Нетрудно показать, что всегда
\(M(N-P)=MN-MP\) и \((M-N)+MN=M.\)
Таким образом, правила действий над множествами значительно отличаются от обычных правил арифметики.
Конечные и бесконечные множества
Множества, состоящие из конечного числа элементов, называются конечными множествами. Если же число элементов множества неограниченно, то такое множество называется бесконечным. Например, множество всех натуральных чисел бесконечно.
Рассмотрим два каких-либо множества \(M\) и \(N\) и поставим вопрос о том, одинаково или нет количество элементов в этих множествах.
Если множество \(M\) конечно, то количество его элементов характеризуется некоторым натуральным числом — числом его элементов. В этом случае для сравнения количества элементов множеств \(M\) и \(N\) достаточно сосчитать число элементов в \(M\) , число элементов в \(N\) и сравнить полученные числа. Естественно также считать, что если одно из множеств \(M\) и \(N\) конечно, а другое бесконечно, то бесконечное множество содержит больше элементов, чем конечное.
Однако, если оба множества \(M\) и \(N\) бесконечны, то путь простого счета элементов ничего не дает. Поэтому сразу возникают такие вопросы: все ли бесконечные множества имеют одинаковое количество элементов, или же существуют бесконечные множества с большим и меньшим количеством элементов? Если верно второе, то каким способом можно сравнивать между собой количество элементов в бесконечных множествах? Этими вопросами мы теперь и займемся.
Взаимно однозначное соответствие множеств
Пусть снова \(M\) и \(N\) — два конечных множества. Как узнать, какое из этих множеств содержит больше элементов, не считая числа элементов в каждом множестве? Для этого будем составлять пары, объединяя в пару один элемент из \(M\) и один элемент из \(N\) . Тогда, если какому-нибудь элементу из \(M\) не найдется парного к нему элемента из \(N\) , то в \(M\) больше элементов, чем в \(N\) . Поясним это рассуждение примером.
Пусть в зале находится некоторое число людей и некоторое число стульев. Чтобы узнать, чего больше, достаточно попросить людей занять места. Если кто-нибудь остался без места, значит, людей больше, а если, скажем, все сидят и заняты все места, то людей столько же, сколько стульев. Описанный способ сравнения количества элементов во множествах имеет то преимущество перед непосредственным счетом элементов, что он без особых изменений применяется не только к конечным, но и к бесконечным множествам.
Рассмотрим множество всех натуральных чисел
\(M=\{1,\,2,\,3,\,4,\,\ldots\}\)
и множество всех четных чисел
\(N=\{2,\,4,\,6,\,8,\,\ldots\}\)
Какое множество содержит больше элементов? На первый взгляд кажется, что первое. Однако мы можем образовать из элементов этих множеств пары, как указано ниже.
Таблица 1
\({\color{blue}\begin{array}{c|c|c|c|c|c} {\color{black}M} &{\color{black}1} &{\color{black}2} &{\color{black}3} &{\color{black}4} &{\color{black}\cdots}\\\hline {\color{black}N} &{\color{black}2} &{\color{black}4} &{\color{black}6} &{\color{black}8} &{\color{black}\cdots} \end{array}}\)
Ни один элемент \(M\) и ни один элемент \(N\) не остается без пары. Правда, мы могли бы также образовать пары и так:
Таблица 2
\({\color{blue}\begin{array}{c|c|c|c|c|c|c} {\color{black}M}&{\color{black}1}&{\color{black}2}&{\color{black}3}&{\color{black}4}&{\color{black}5}&{\color{black}\cdots}\\\hline {\color{black}N}&{\color{black}-}&{\color{black}2}&{\color{black}-}&{\color{black}4}&{\color{black}-}&{\color{black}\cdots} \end{array}}\)
Тогда многие элементы из \(M\) остаются без пар. С другой стороны, мы могли бы составить пары и так:
Таблица 3
\({\color{blue}\begin{array}{c|c|c|c|c|c|c|c|c} {\color{black}M}&{\color{black}-}&{\color{black}1}&{\color{black}-}&{\color{black}2}&{\color{black}-}&{\color{black}3}&{\color{black}-}&{\color{black}\cdots}\\\hline {\color{black}N}&{\color{black}2}&{\color{black}4}&{\color{black}6}&{\color{black}8}&{\color{black}10}&{\color{black}12}&{\color{black}14}&{\color{black}\cdots} \end{array}}\)
Теперь многие элементы из \(M\) остаются без пар.
Таким образом, если множества \(A\) и \(B\) бесконечны, то различным способам образования пар соответствуют разные результаты. Если существует такой способ образования пар, при котором у каждого элемента \(A\) и каждого элемента \(B\) имеется парный к нему элемент, то говорят, что между множествами \(A\) и \(B\) можно установить взаимно однозначное соответствие. Например, между рассмотренными выше множествами \(M\) и \(N\) можно установить взаимно однозначное соответствие, как
это видно из табл. 1.
Если между множествами \(A\) и \(B\) можно установить взаимно однозначное соответствие, то говорят, что они имеют одинаковое количество элементов или равномощны. Если же при любом способе образования пар некоторые элементы из \(A\) всегда остаются без пар, то говорят, что множество \(A\) содержит больше элементов, чем \(B\) , или что множество \(A\) имеет большую мощность, чем \(B\) .
Таким образом, мы получили ответ на один из поставленных выше вопросов: как сравнивать между собой количество элементов в бесконечных множествах. Однако это нисколько не приблизило нас к ответу на другой вопрос: существуют ли вообще бесконечные множества. имеющие различные мощности? Чтобы получить ответ на этот вопрос, исследуем некоторые простейшие типы бесконечных множеств.
Счетные множества. Если можно установить взаимно однозначное соответствие между элементами множества \(A\) и элементами множества всех натуральных чисел
\(Z=\{1,\,2,\,3,\,\ldots\},\)
то говорят, что множество \(A\) счетно. Иными словами, множество \(A\) счетно, если все его элементы можно занумеровать посредством натуральных чисел, т. е. записать в виде последовательности
\(a_1,~a_2,~\ldots,~a_n,~\ldots\)
Таблица 1 показывает, что множество всех четных чисел счетно (верхнее число рассматривается теперь как номер соответствующего нижнего числа).
Счетные множества это, так сказать, самые маленькие из бесконечных множеств: во всяком бесконечном множестве содержится счетное подмножество.
Если два непустых конечных множества не пересекаются, то их сумма содержит больше элементов, чем каждое из слагаемых. Для бесконечных множеств это правило может и не выполняться. В самом деле, пусть \(G\) есть множество всех четных чисел, \(H\) — множество всех нечетных чисел и \(Z\) — множество всех натуральных чисел. Как показывает таблица 4, множества \(G\) и \(H\) счетны. Однако множество \(Z=G+H\) вновь счетно.
Таблица 4
\({\color{blue}\begin{array}{c|c|c|c|c|c} {\color{black}G}&{\color{black}2}&{\color{black}4}&{\color{black}6}&{\color{black}8}&{\color{black}\cdots}\\\hline {\color{black}H}&{\color{black}1}&{\color{black}3}&{\color{black}5}&{\color{black}7}&{\color{black}\cdots}\\\hline {\color{black}Z}&{\color{black}1}&{\color{black}2}&{\color{black}3}&{\color{black}4}&{\color{black}\cdots} \end{array}}\)
Нарушение правила «целое больше части» для бесконечных множеств показывает, что свойства бесконечных множеств качественно отличны от свойств конечных множеств. Переход от конечного к бесконечному сопровождается в полном согласии с известным положением диалектики — качественным изменением свойств.
Докажем, что множество всех рациональных чисел счетно. Для этого расположим все рациональные числа в такую таблицу:
Таблица 5
\(\)
Здесь в первой строке помещены все натуральные числа в порядке их возрастания, во второй строке 0 и целые отрицательные числа в порядке их убывания, в третьей строке — положительные несократимые дроби со знаменателем 2 в порядке их возрастания, в четвертой строке — отрицательные несократимые дроби со знаменателем 2 в порядке их убывания и т. д. Ясно, что каждое рациональное число один и только один раз находится в этой таблице. Перенумеруем теперь
все числа этой таблицы в том порядке, как это указано стрелками. Тогда все рациональные числа разместятся в порядке одной последовательности:
Номер места, занимаемого
рациональным числом 1 2 3 4 5 6 7 8 9 . . .
Рациональное число 1. 2, О, 3, — 1, 4 —2 _
Этим установлено взаимно однозначное соответствие между всеми рациональными числами и всеми натуральными числами. Поэтому множество всех рациональных чисел счетно.
Множества мощности континуума
Если можно установить взаимно однозначное соответствие между элементами множества \(M\) и точками отрезка \(0\leqslant x\leqslant1\) , то говорят, что множество \(M\) имеет мощность континуума. В частности, согласно этому определению, само множество точек отрезка \(0\leqslant x\leqslant1\) имеет мощность континуума.
Из рис. 1 видно, что множество точек любого отрезка \(AB\) имеет мощность континуума. Здесь взаимно однозначное соответствие устанавливается геометрически, посредством проектирования.
Нетрудно показать, что множества точек любого интервала \(x\in[a,b]\) и всей числовой прямой \(x\in[-\infty,+\infty]\) — имеют мощность континуума.
Значительно более интересен такой факт: множество точек квадрата \(0\leqslant x\leqslant1,\) \(0\leqslant y\leqslant1\) имеет мощность континуума. Таким образом, грубо говоря, в квадрате «столько же» точек, сколько и в отрезке.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
calcsbox.com
Математика. Множества. Равные множества. Подмножества. Объединение множеств.
Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями или сет-операциями. В результате операций из исходных множеств получаются новые. Множества обозначаются заглавными латинскими буквами, а их элементы – строчными. Запись aR означает, что элемент а принадлежит множеству R , то есть а является элементом множества R . В противном случае, когда а не принадлежит множеству R , пишут aR .
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества Аявляется элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
Сравнение множеств.
Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент В:
Говорят, что множество А содержится в множестве В или множество Аявляется подмножеством множества В ( в этом случае пишут А В ), если каждый элемент множества А одновременно является элементом множества В . Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: ØА и А А
В этом случае A называется подмножеством B, B — надмножеством A. Если , то A называется собственным подмножеством В. Заметим, что ,
По определению ,
Два множества называются равными, если они являются подмножествами друг друга
Операции над множествами
Пересечение.
Объединение.
Свойства.
1.Операция объединения множеств коммутативна
2.Операция объединения множеств транзитивна
3. Пустое множество X является нейтральным элементом операции объединения множеств
Примеры:
1. Пусть A = {1,2,3,4},B = {3,4,5,6,7}. Тогда
2. А={2,4,6,8,10}, В = {3,6,9,12}. Найдём объединение и пересечение этих множеств:
{2,4,6,8, 10,3,6,9,12}, = {6}.
3. Множество детей является подмножеством всего населения
4. Пересечением множества целых чисел с множеством положительных чисел является множество натуральных чисел.
5. Объединением множества рациональных чисел с множеством иррациональных чисел является множество положительных чисел.
6.Нуль является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.
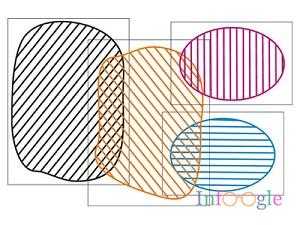
Диаграммы Венна (Venn diagrams) — общее название целого ряда методов визуализации и способов графической иллюстрации, широко используемых в различных областях науки и математики: теория множеств, собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства; разновидностями диаграмм Венна служат: диаграммы Эйлера,
Диаграмма Венна четырёх множеств.
Собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства. Обычная диаграмма Венна имеет три множества. Сам Венн пытался найти изящный способ с симметричными фигурами, представляющий на диаграмме большее число множеств, но он смог это сделать только для четырех множеств (см. рисунок справа), используя эллипсы.
Диаграммы Эйлера
Диаграммы Эйлера аналогичны диаграммам Венна.Диаграммы Эйлера можно использовать, для того, чтобы оценивать правдоподобность теоретико-множественных тождеств.
Задача 1. В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?
Решение: Сначала заметим, что из 30 человек не умеют петь 30 — 17 = 13 человек.
Все они умеют танцевать, т.к. по условию каждый ученик класса поёт или танцует. Всего умеют танцевать 19 человек, из них 13 не умеют петь, значит, танцевать и петь одновременно умеют 19-13 = 6 человек.
multiurok.ru
Равные множества. Видеоурок. Математика 1 Класс
Мы уже знаем, что такое множество и элементы множества. На этом уроке мы узнаем, какие множества называются равными.
Давайте рассмотрим первый пример (рис. 1).
Рис. 1. Иллюстрация к примеру
В одной руке – два карандаша, а в другой – три. Равны ли множества? Нет, не равны, потому что в них разное количество элементов (рис. 2).
Рис. 2. Иллюстрация к примеру
Другой пример: в одной руке – два карандаша, а в другой – карандаш и ручка (рис. 3).
Рис. 3. Иллюстрация к примеру
Равны ли множества теперь? В математике такие множества не равны, потому что предметы в множествах разные, одинаково только количество (рис. 4).
Рис. 4. Иллюстрация к примеру
Третий пример: в одной руке два карандаша, и в другой два карандаша (рис. 5).
Рис. 5. Иллюстрация к примеру
Равны ли множества теперь? Да, равны (рис. 6).
Рис. 6. Иллюстрация к примеру
Сделаем вывод: равными называются множества, состоящие из одинакового числа одинаковых элементов (рис. 7).
Рис. 7. Определение
Рассмотрим пример (рис. 8):
Рис. 8. Иллюстрация к примеру
Сравним элементы двух множеств. В первом множестве есть паровозик, во втором тоже есть. В первом множестве есть юла, во втором тоже есть. В первом множестве есть мишка, во втором тоже. В первом множестве – машинка, а во втором – лягушонок.
Делаем вывод: элементы множеств разные.
Из этого следует, что множества не равны (рис. 9).
Рис. 9. Иллюстрация к примеру
Рассмотрим второй пример (рис. 10).
Рис. 10. Иллюстрация к примеру
Сравним множества. В первом множестве – три вишни, во втором – тоже три вишни. В первом множестве – две ягоды малины, во втором множестве – тоже две ягоды. В первом множестве – одна клубника, во втором – тоже одна.
Делаем вывод: элементы множеств одинаковые. Количество элементов в множествах одинаковое. Значит, множества равны (рис. 11).
Рис. 11. Иллюстрация к примеру
Рассмотрим третий пример (рис. 12).
Рис. 12. Иллюстрация к примеру
В двух множествах одинаковые желтые цветы. В первом множестве – 6 цветков, во втором – пять.
Вывод: элементы множеств одинаковые. Количество элементов в множествах разное. Значит, множества не равны (рис. 13).
Рис. 13. Иллюстрация к примеру
Подведем итог: множества будут равными, если они состоят из одинакового количества одинаковых элементов (рис. 14).
Рис. 14. Определение
Закрепим на практике полученные знания.
Задача 1: найдем равное данному множество.
Первое множество отличается цветом. Второе – количеством. Третье множество равно исходному (рис. 15).
Рис. 15. Иллюстрация к задаче
Задача 2: уравняем множества, убрав лишний элемент (рис. 16).
Рис. 16. Иллюстрация к задаче
Сравним множества. Лишний элемент в первом множестве – тарелка. Уберем её и получим равные множества (рис. 17).
Рис. 17. Иллюстрация к задаче
Задача 3: уравняем множества, добавив элемент (рис. 18).
Рис. 18. Иллюстрация к задаче
В первое множество следует добавить кленовый лист. Теперь множества равны (рис. 19).
Рис. 19. Иллюстрация к задаче
Сделаем вывод: чтобы уравнять множества, добавьте недостающий элемент или уберите лишний (рис. 20).
Рис. 20. Правило
Задача 4: найдем равные множества (рис. 21).
Рис. 21. Иллюстрация к задаче
Сравним множества и выясним, что равны множества 1 и 4, 3 и 6.
Подведем итог урока: множества считаются равными, если они состоят из одинакового числа одинаковых элементов.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика. 1 класс. – М: Мнемозина, 2012.
- Башмаков М.И., Нефёдова М.Г. Математика. 1 класс. – М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. – М.: Русское слово, 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Открытый класс (Источник).
- Myshared.ru (Источник).
- School.xvatit.com (Источник).
Домашнее задание
- Какие множества называются равными?
- Какими способами можно уравнять множества?
- Нарисуйте картинку-задачу на поиск равных множеств.
interneturok.ru
[Билет 1] Множества. Способы задания множеств. Характеристическое свойство множеств. Равные множества, подмножества. Универсальное множество. Конечные и бесконечные множества. Пустое множество. Основные числовые и геометрические множества.
Множества.Множество — совокупность различных элементов, мыслимая как единое целое
Элемент множества — объект А называется элементом множества, если он обладает характеристическим свойствами этого множества.
Способы задания множеств.
1) Перечислением — и перечислении множества его элементы принято заключать в фигурные скобки:
{2,4,6,…} — множество четных чисел,
{3,6,9,…}— множество чисел кратных трем.
Под многоточием в данных случаях подразумеваются все последующие числа: в первом случае — четные, а во втором — кратные трем.
2) Описание свойств — для задания (описания) некоторого множества
X, состоящего из элементов, обладающих свойством α, используют запись X={x |α(x)}. Читается как: «X — множество элементов x таких, что α(x)». Например, Y={y | y∈N и y<7} — множество натуральных чисел, меньших 7.
Характеристическое свойство множеств.
Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, не принадлежащий ему.
Равные множества, подмножества.
Два множества A и B называются равными, если они состоят из одних и тех же элементов, т. е. если каждый элемент множества A принадлежит B и, обратно, каждый элемент B принадлежит A. Тогда пишут A = B. Таким образом, множество однозначно определяется его элементами и не зависит от порядка записи этих элементов. Например, множество из трех элементов a, b, c допускает шесть видов записи:
{a, b, c} = {a, c, b} = {b, a, c} = {b, c, a} = {c, a, b} = {c, b, a}.
Множество является подмножеством множества , если любой элемент, принадлежащий , также принадлежит . Формальное определение:Универсальное множество.
Определение: Универсальное множество — это такое множество, которое состоит из всех элементов, а так же подмножеств множества объектов исследуемой области
Конечные и бесконечные множества.
Множества, состоящие из бесконечного числа элементов называются бесконечными, из конечного — конечными
Пустое множество.
Множество, не содержащее ни одного элемента, называется пустым. ∅
Основные числовые и геометрические множества.
Z− множество целых чисел;
Q− множество рациональных чисел;
I− множество иррациональных чисел;
R− множество действительных чисел;
C− множество комплексных чисел.
fizmatinf.blogspot.com
множества
§ 1. Понятие множества. Элемент множества. Пустое множество
Множество – основное понятие математики и поэтому не определяется через другие.
Обычно под множеством понимают совокупность предметов, объединенных по общему признаку. Так, можно говорить о множестве студентов в группе, множестве букв русского алфавита и т.д. В повседневной жизни вместо слова «множество» употребляют слова «набор», «коллекция», «группа» и т.д. Множества принято обозначать прописными буквами латинского алфавита: А, В, С, …, Z.
Для числовых множеств в математике приняты специальные обозначения:
N – множество натуральных чисел;
N0 – множество целых неотрицательных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
R – множество действительных чисел.
Объекты, из которых образовано множество, называют его элементами. Например, сентябрь является элементом множества месяцев в году, число 5 – элемент множества натуральных чисел. Элементы множества принято обозначать строчными буквами латинского алфавита. Элементами множества могут быть множества. Так можно говорить о множестве групп института. Элементы этого множества – группы, являющиеся в свою очередь множествами студентов.
Связь между множеством и его элементом выражают при помощи слова «принадлежит». Высказывание «Элемент а принадлежит множеству А» записывают так: а А, причем эта запись может быть прочитана иначе: «а – элемент множества А», «множество А содержит элемент а». Высказывание «Элемент а не принадлежит множеству А» записывают так: а А (иначе: «а не является элементом множества А», «множество А не содержит элемент а»).
Если в обыденной речи слово «множество» связывают с большим числом предметов, то в математике этого не требуется. Множество может содержать один элемент, не содержать ни одного элемента.
Множество, не содержащее ни одного элемента, называют пустым и обозначают символом . Существует лишь одно пустое множество. Примерами пустого множества могут служить множество людей на Солнце, множество натуральных корней уравнения х + 8 = 0.
Множества могут быть конечными и бесконечными.
Множество называется конечным, если существует натуральное число п, такое, что все элементы множества можно перенумеровать числами от 1 до п. в противном случае множество называют бесконечным. Примером конечного множества является множество цифр, бесконечного – множество натуральных чисел.
§ 2. Способы задания множеств
Множество считают заданным, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.
Множество можно задать, перечислив все его элементы. Запись С = {а, б, в, г} обозначает, что множество С содержит элементы а, б, в, г.
Каждый элемент входит в множество только один раз. Например, множество различных букв в слове «математика» запишется так: {м, а, т, е, и, к}.
Данный способ применим для конечных множеств, которые содержат небольшое число элементов.
Иногда, используя данный способ, можно задать и бесконечное множество. Например, множество натуральных чисел может быть представлено в виде: N = {1, 2, 3, 4, …}. Такой способ записи возможен лишь тогда, когда из записанной части множества видно, что скрывается под многоточием.
Другой способ задания множеств состоит в следующем: указывают характеристическое свойство его элементов. Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
Случается, что одно и то же множество можно задать, указав различные характеристические свойства его элементов. Например, множество двузначных чисел, делящихся на 11 и множество натуральных чисел первой сотни, записанных двумя одинаковыми цифрами, содержат одни и те же элементы.
При данном способе задания множество может быть записано так: в фигурных скобках пишут сначала обозначение элемента, затем проводят вертикальную черту, после которой записывают свойство, которым обладают элементы данного множества. Например, множество А натуральных чисел, меньших 5, запишется так: А = {ххN, х < 5}.
§ 3. Отношения между множествами. Графическая иллюстрация множеств
Определение. Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно множествам А и В, то говорят, что эти множества пересекаются.
Например, множества А = {1, 2, 3, 4} и В = {0, 3, 5} пересекаются, т.к. имеют общий элемент 3.
На диаграмме пересекающиеся множества изображают следующим образом:
А В
Определение. Множества А и В не пересекаются, если не имеют общих элементов.
Множества А = {1, 2, 3, 4} и В = {0, 8, 5} не пересекаются.
Если множества не пересекаются, то их изображают следующим образом:
А В
Определение. Множества А и В называются равными, если они состоят из одних и тех же элементов. Обозначают: А = В.
Например, множества А = {1, 2, 3} и В = {2, 3, 1} равны, т.к. состоят из одинаковых элементов. Таким образом, множество не изменится, если переставить его элементы. С понятием равных множеств связано следующее положение: одно и то же множество может быть задано с помощью различных характеристических свойств.
Определение. Множество В называется подмножеством множества А, если каждый элемент множества В принадлежит множеству А (обозначают В А).
Согласно данному определению, каждое множество является подмножеством самого себя. Кроме этого считают, что пустое множество есть подмножество любого множества. Само множество и пустое множество называют несобственными подмножествами; все остальные подмножества множества А, если они существуют, – собственные подмножества.
Например, множество А = {1, 2, 3} имеет шесть собственных подмножеств А1 = {1}, А2 = {2}, А3 = {3}, А4 = {1, 2}, А5 = {1, 3}, А6 = {2, 3} и два несобственных подмножества А7 = {1, 2, 3} и А8 = .
Доказано, что если множество состоит из п элементов, то у него 2п различных подмножеств.
Если В А и А В, то А = В. Отсюда вытекает один из способов доказательства равенства множеств: если доказано, что любой элемент из множества А является элементом множества В и, в свою очередь, любой элемент из множества В является элементом множества А, то делают вывод, что А = В.
Часто случается, что все множества, рассматриваемые в задаче, являются подмножествами одного и того же множества. Такое множество называют универсальным (обозначают I).
Условимся изображать универсальное множество прямоугольником, а его подмножества – кругами в этом прямоугольнике.
Описанный способ изображения множеств носит названия кругов Эйлера или диаграмм Венна. Мы будем подобные изображения называть диаграммами Эйлера-Венна.
§ 4. Операции над множествами
Из элементов двух и более множеств можно образовывать новые множества.
1. Пересечение множеств.
Определение. Пересечением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множествам А и В одновременно (обозначают А В).
Данное определение можно записать в таком виде:
А В = {хх А х В}.
На диаграмме пересечение множеств А и В изображено заштрихованной областью.
А В
Если множества А и В не имеют общих элементов, то говорят, что множества не пересекаются, и пишут А В = .
Если элементы множеств А и В перечислены, то чтобы найти их пересечение, достаточно перечислить элементы, которые одновременно принадлежат множеству А и множеству В, т.е. их общие элементы.
Пусть А = {1, 2, 3, 4, 5}, В = {4, 5, 6, 7}, тогда А В = {4, 5}.
Если множества А и В заданы указанием их характеристических свойств, то в их пересечение войдут только те элементы, которые обладают одним и другим свойством одновременно.
Например, если множество А – множество однозначных чисел, В – множество натуральных чисел, делящихся на 5, то множеству А В принадлежат натуральные числа, делящиеся на 5.
2. Объединение множеств.
Определение. Объединением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат хотя бы одному из данных множеств (обозначают А В).
Данное определение можно записать в таком виде:
А В = {хх А х В}.
На диаграмме пересечение множеств А и В изображено заштрихованной областью.
А В
Пусть А = {1, 2, 3, 4, 5}, В = {4, 5, 6, 7}, тогда А В = {1, 2, 3, 4, 5, 6, 7}.
Рассмотрим случай, когда множества заданы указанием характеристического свойства. Пусть А – множество чисел, кратных 2; В – множество чисел, кратных 3. Тогда объединению этих множеств будут принадлежать числа, кратные 2 или 3.
Понятие пересечения и объединения множеств можно обобщить на любое конечное число множеств.
3. Разность множеств.
Определение. Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В (обозначают А \ В).
Данное определение можно записать так:
А \ В = {хх А х В}.
На диаграмме пересечение множеств А и В изображено заштрихованной областью.
А В
Если А = {1, 2, 3, 4, 5}, В = {4, 5, 6, 7}, тогда А \ В = {1, 2, 3}.
Часто приходится выполнять вычитание множеств в случае, когда одно из множеств является подмножеством другого. Если В А, то разность А \ В называют дополнением множества В до множества А (обозначают ).
Множество на рисунке показано штриховкой.
А
В
Определение. Дополнением множества А до универсального называется множество, состоящее из тех и только тех элементов, которые принадлежат универсальному, но не принадлежат множеству А (обозначают ).
Например, если I – множество цифр, а множество А = {1, 2, 3, 4, 5}, то = {6, 7, 8, 9, 0}.
Если множества заданы указанием характеристического свойства и В А, то множество с помощью характеристического свойства, общий вид которого «х А х В». Так, если А множество натуральных чисел, кратных 3, а В – множество натуральных чисел, кратных 9, то – это множество, содержащее натуральные числа, кратные 3, но не кратные 9.
Мы рассмотрели различные операции над множествами. Часто для доказательства равенства множеств бывает необходимо знать, в каком случае элемент принадлежит тому или иному множеству. Для удобства составим таблицу.
х Î А Ç В х Î А Ù х Î В х А Ç В х А х В |
х Î А В х Î А х Î В х А В х А Ù х В |
х Î А \ В х Î А Ù х В х А \ В х А х Î В |
х Î х А х х ÎА |
Выясним, каков порядок выполнения действий над множествами.
Пересечение множеств – более «сильная» операция, чем объединение, поэтому в выражении А В С вначале нужно найти пересечение множеств В и С, а затем найти объединение множества А с полученным множеством.
Условились считать, что пересечение – более «сильная» операция, чем вычитание, поэтому в выражении А \ В С сначала находят пересечение множеств В и С, а затем полученное множество вычитают из множества А.
Объединение и вычитание множеств считают равноправными, поэтому их выполняют в том порядке, в каком они записаны в выражении.
studfiles.net


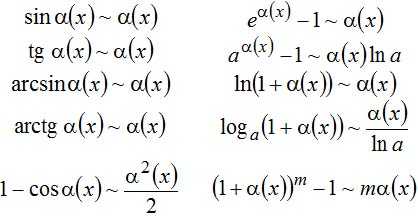

 называется бесконечно
малой при
называется бесконечно
малой при 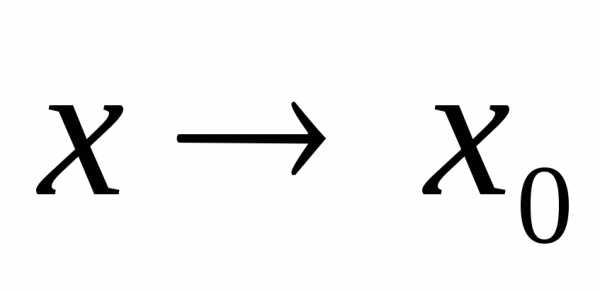 ,
если
,
если 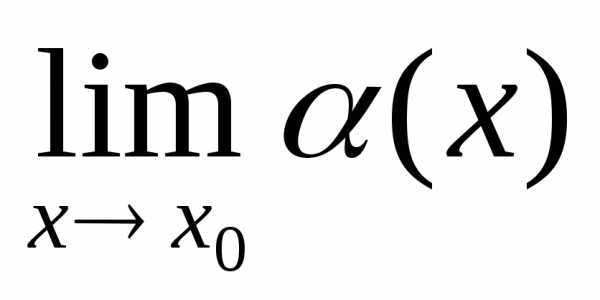 =0. Теорема
(критерий эквивалентности):
=0. Теорема
(критерий эквивалентности):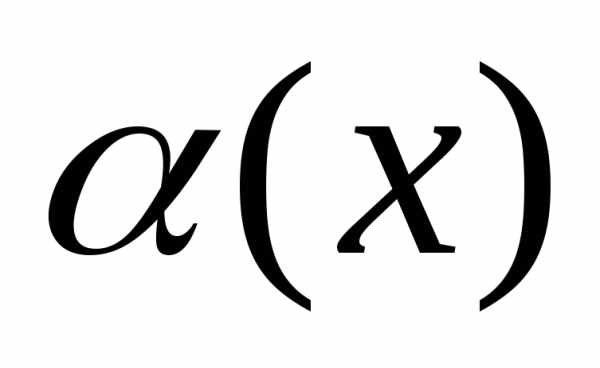 ,
, -бесконечно
малые функции при
-бесконечно
малые функции при 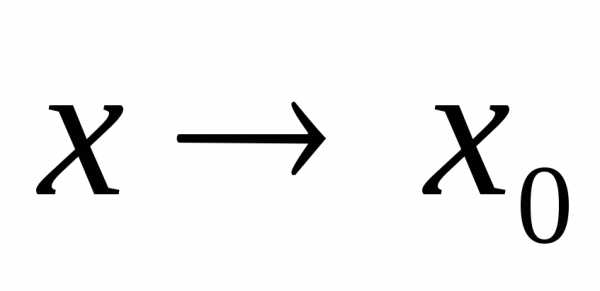 .
.
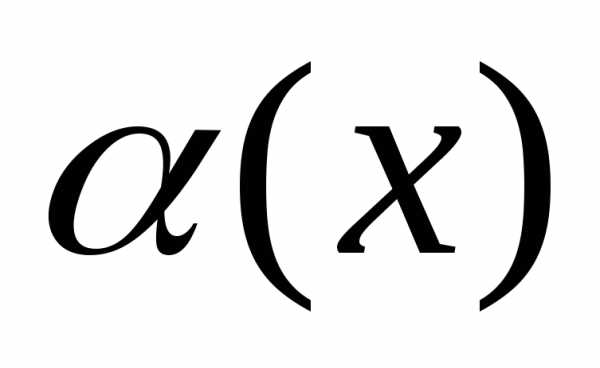 —
— .
Тогда
.
Тогда 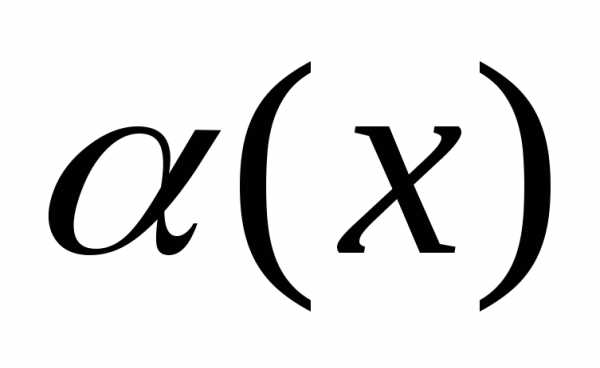 ~
~ при
при 
 .
. ). Пусть
). Пусть 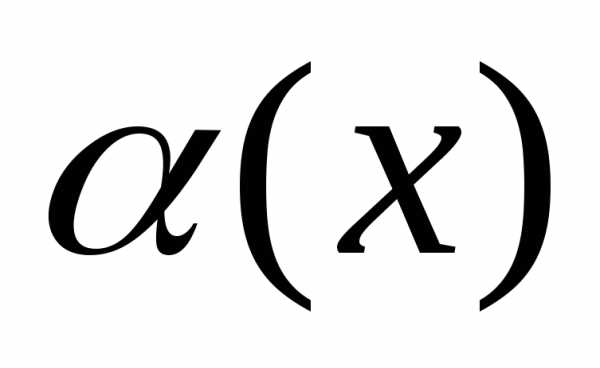 ~
~ ,
, 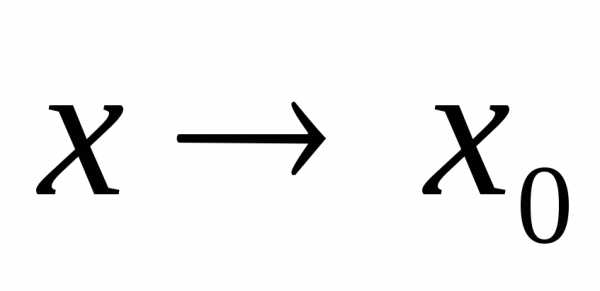 ,
то есть
,
то есть 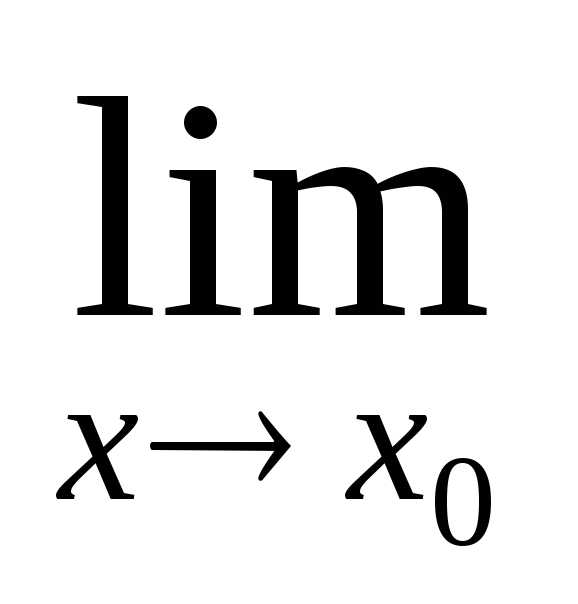
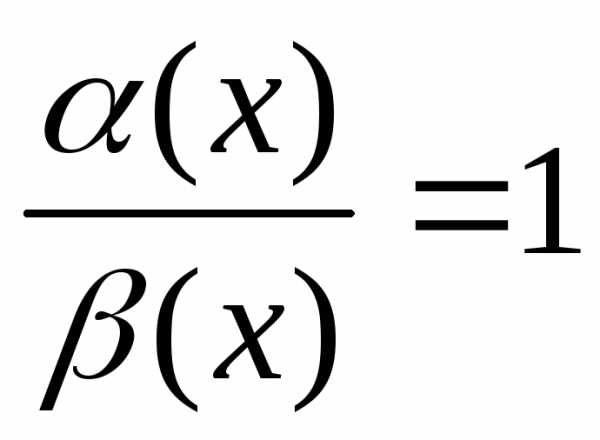 .
.
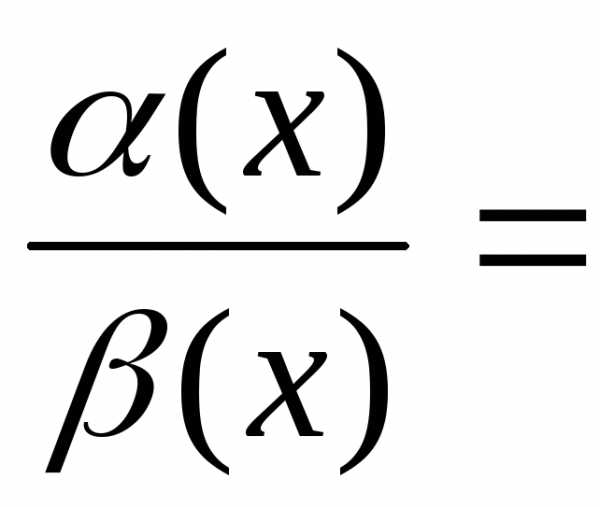
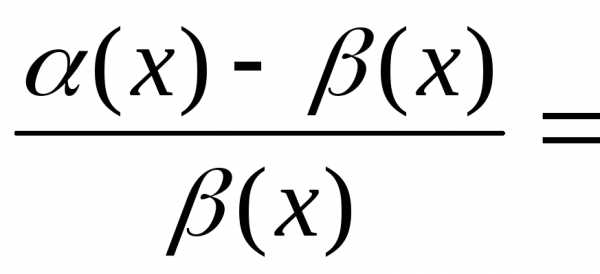

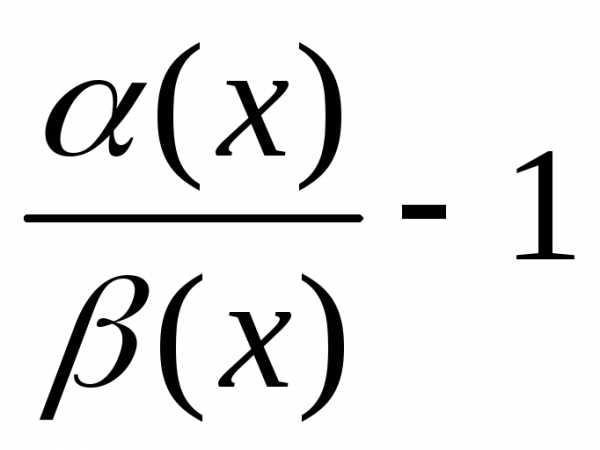 =0,
=0, .
. ).
). .,
.,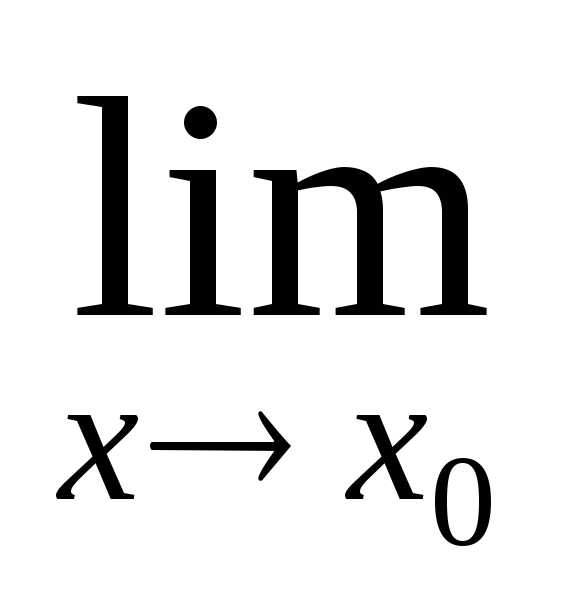
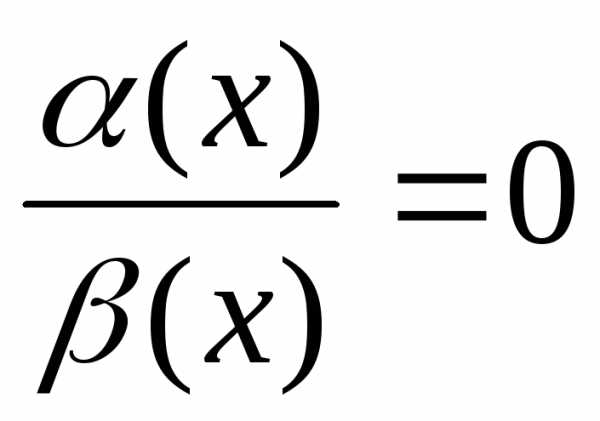 .
.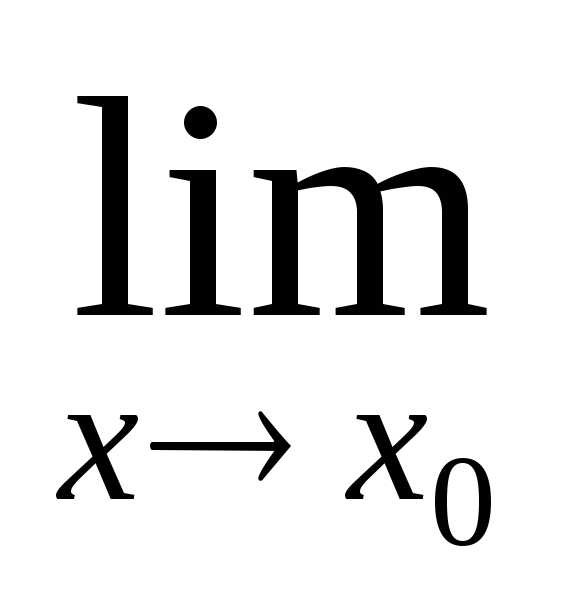

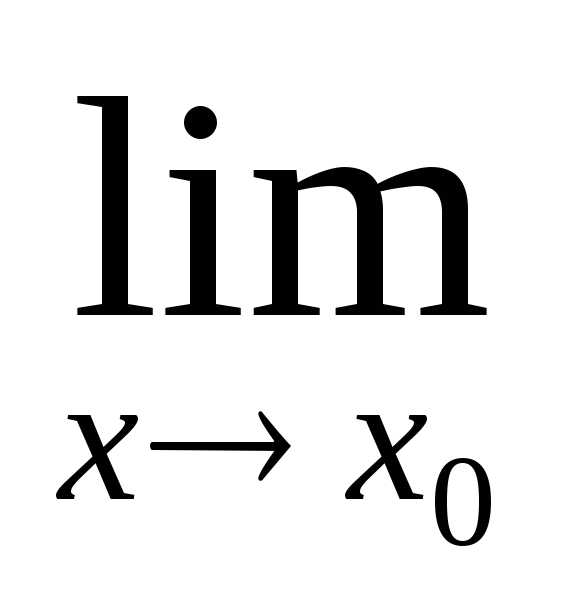
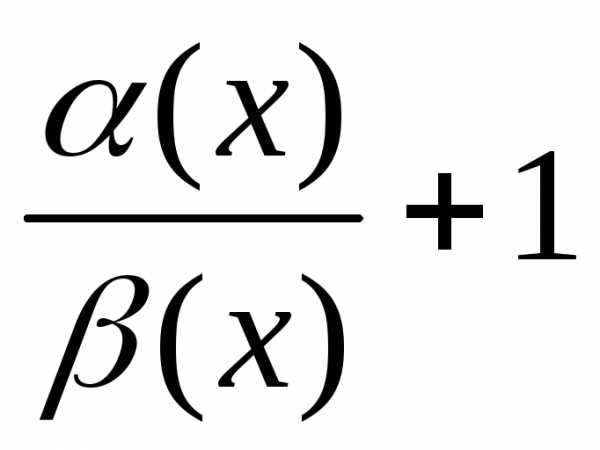 =1.
=1.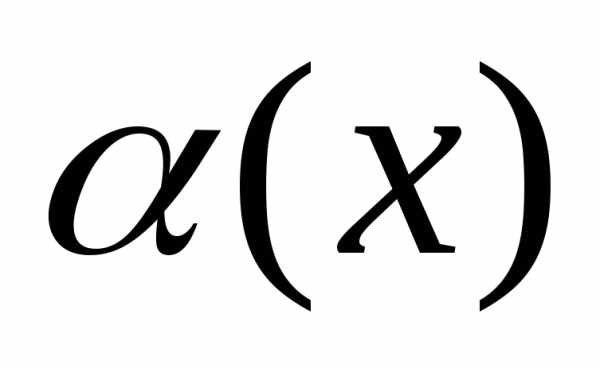 называется бесконечно
малой при
называется бесконечно
малой при  ,
если
,
если  =0.
=0.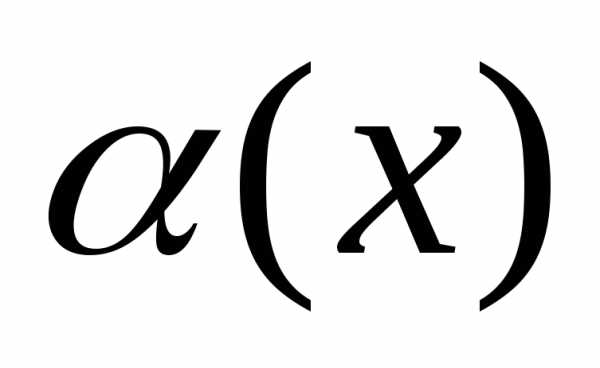 ~
~ ,
,  ~
~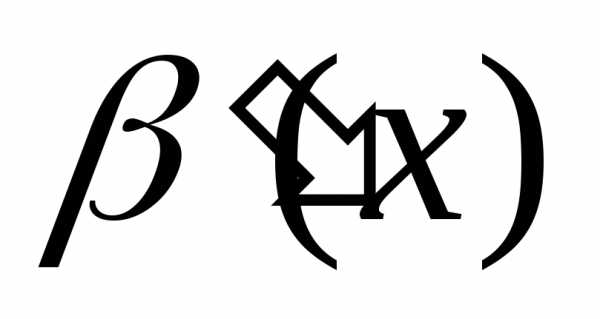 при
при 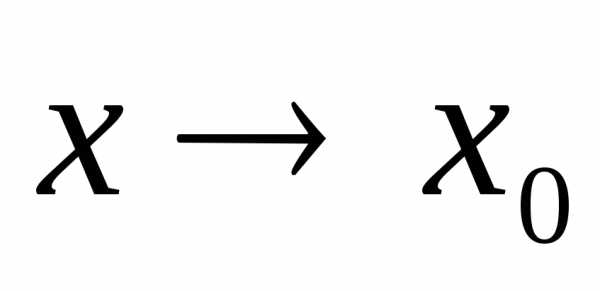 и существует
и существует 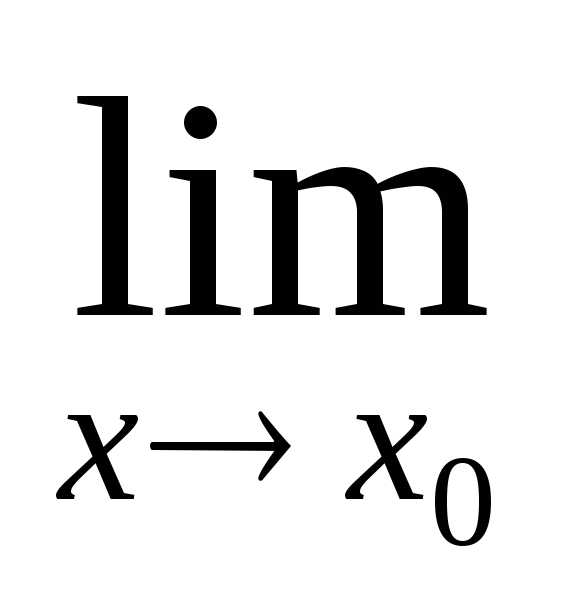
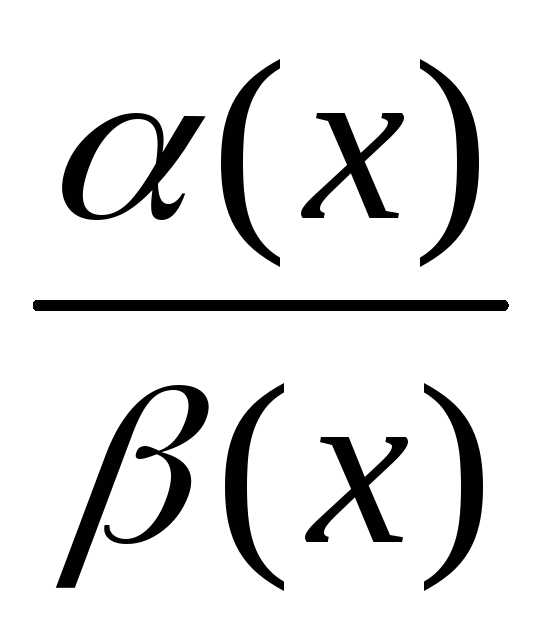 ,
тогда существует и
,
тогда существует и 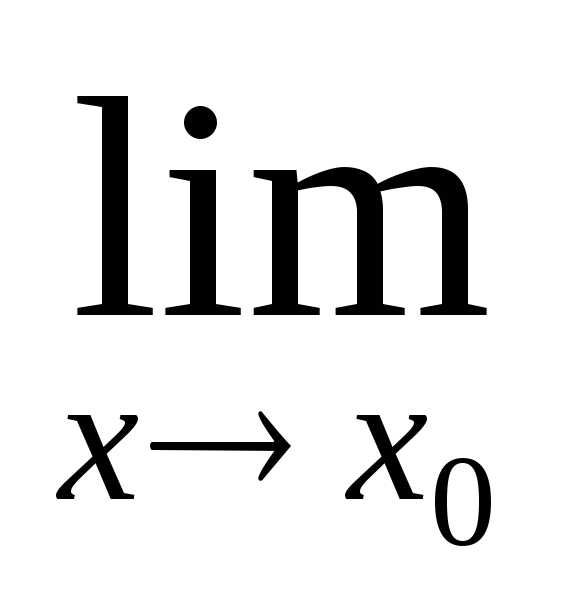
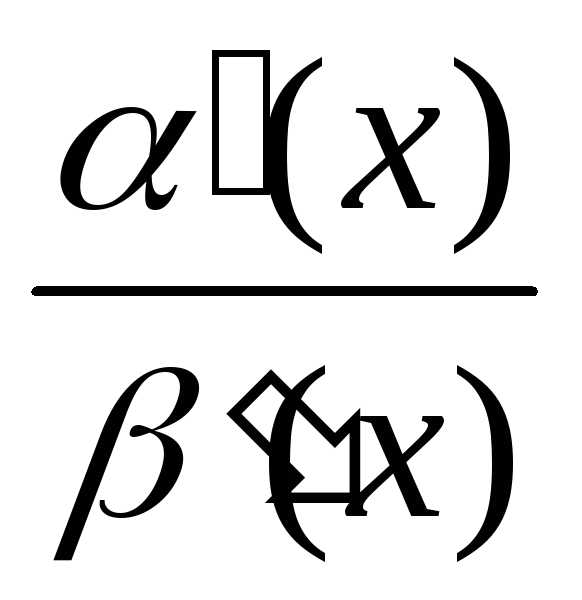 =
=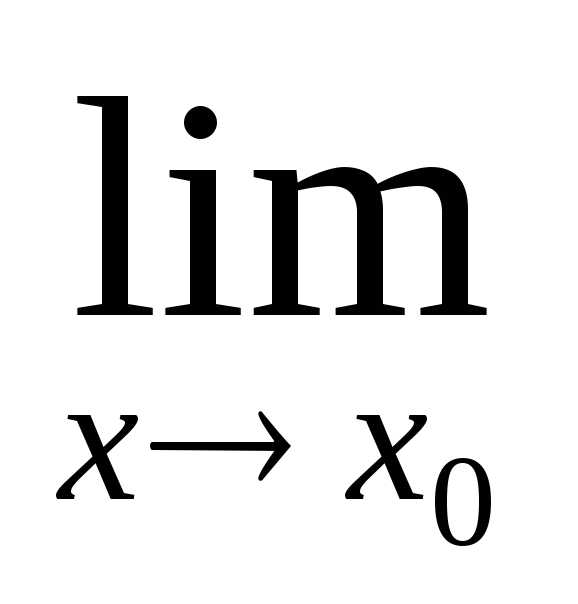
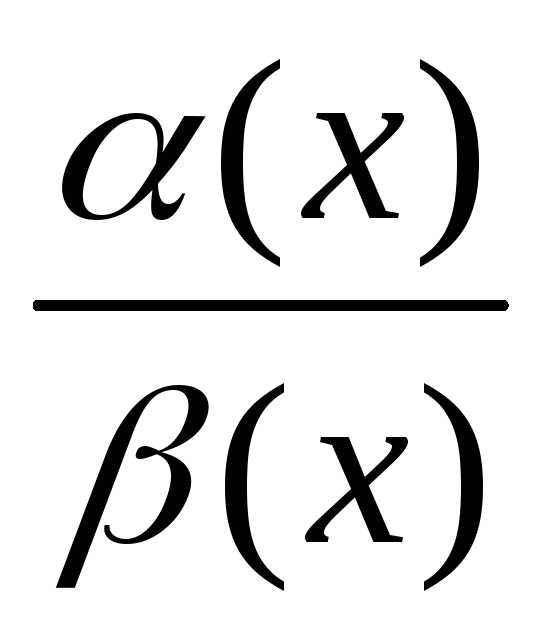 .
То есть выражение или функцию можно
заменять на эквивалентное.
.
То есть выражение или функцию можно
заменять на эквивалентное.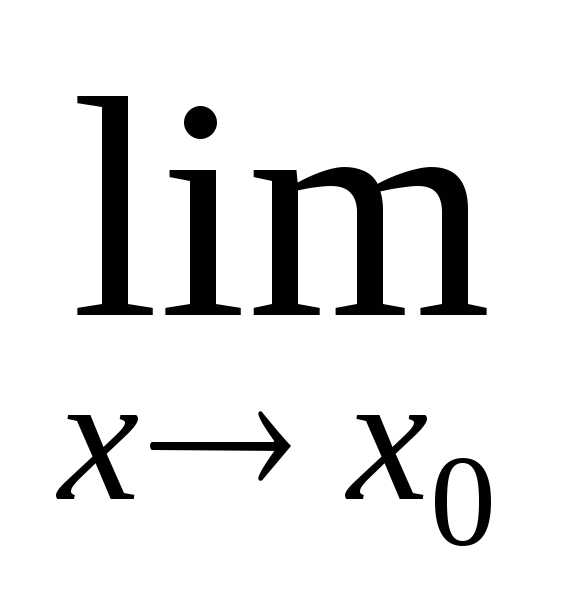
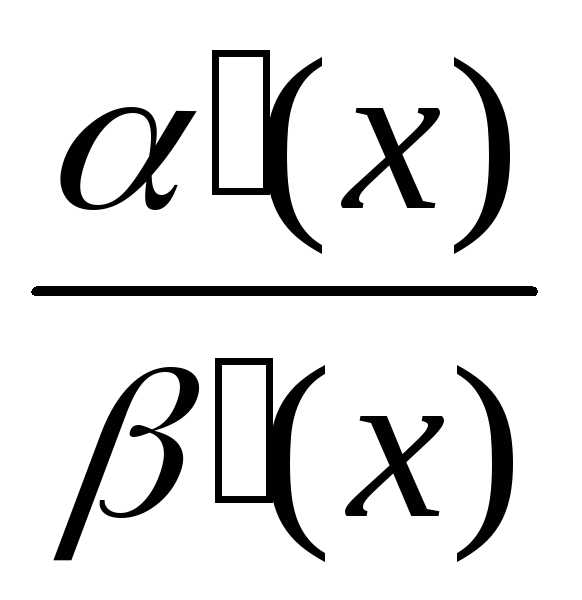 =
=
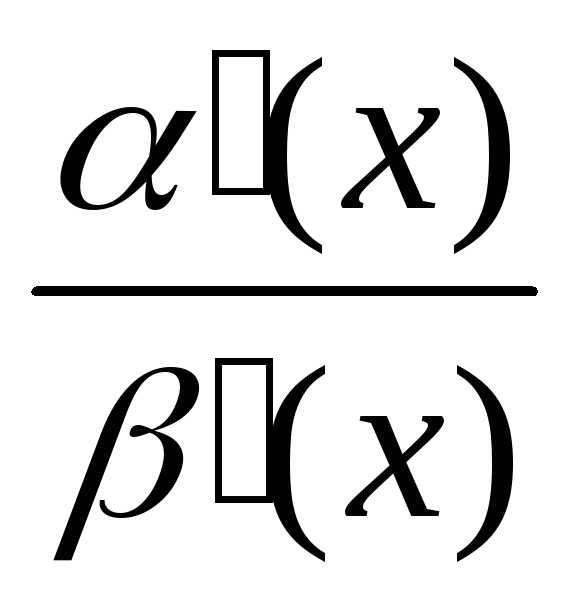 *
* *
* =
=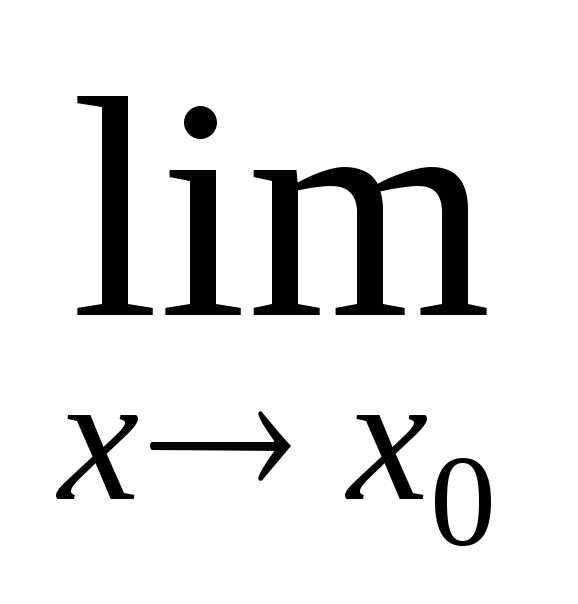
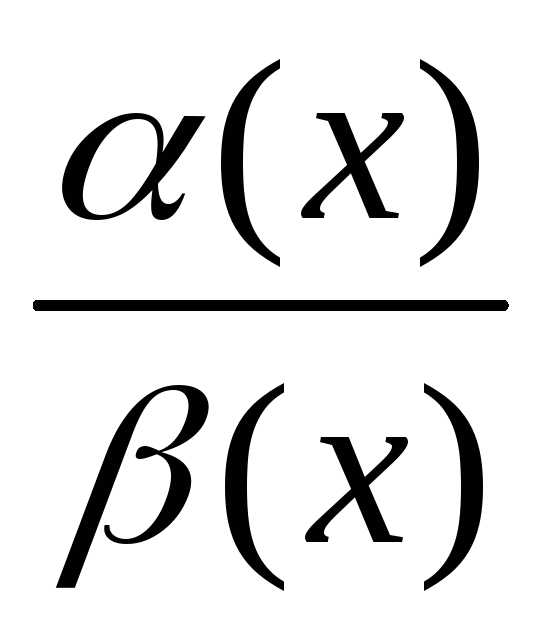 .
.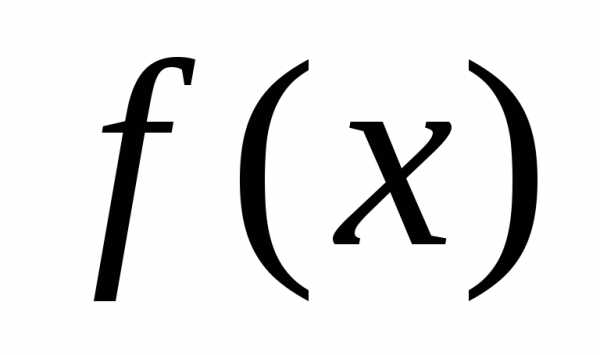 непрерывна
в точке
непрерывна
в точке 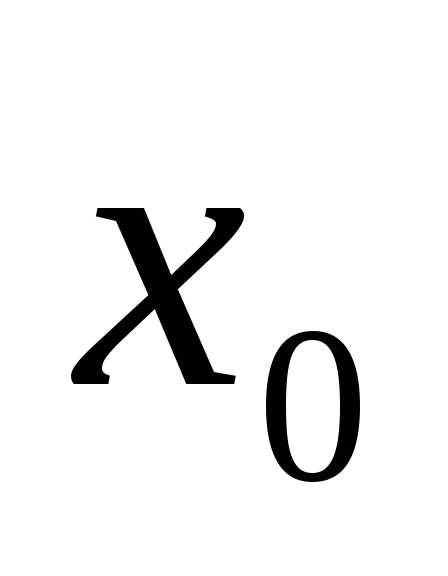 ,
если
.
,
если
. непрерывна
в точке
непрерывна
в точке  ,
если
,
если 
 , .
, . непрерывна
в точке
непрерывна
в точке  ,
если
,
если 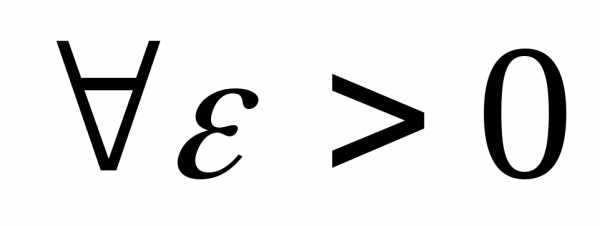


 непрерывна
в точке
непрерывна
в точке  ,
тогда
,
тогда 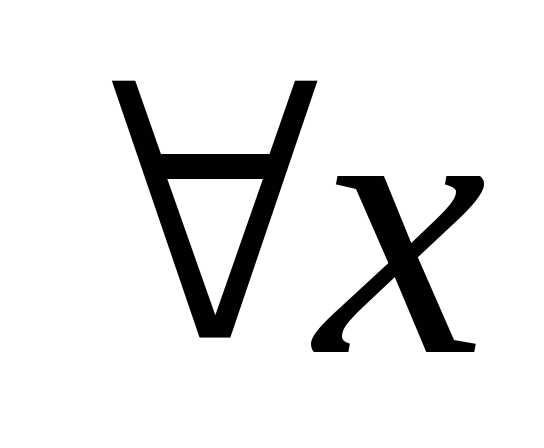
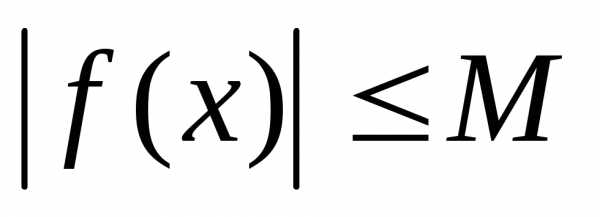 .
. непрерывна
в точке
непрерывна
в точке 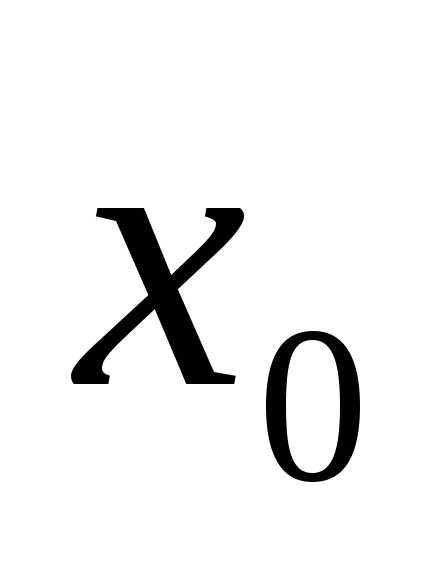 и
и 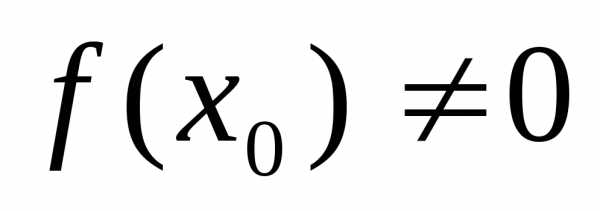 ,
тогда
,
тогда
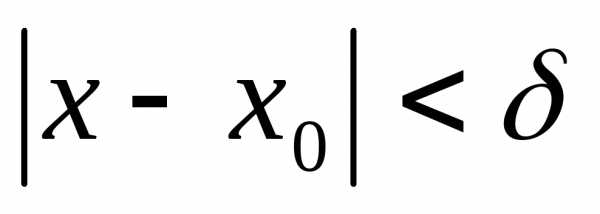
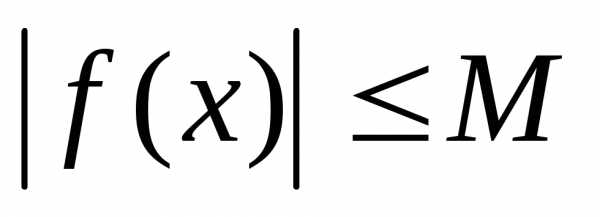 . .
. . ,
,  непрерывны
в точке
непрерывны
в точке  ,
тогда:
,
тогда: .
. .
.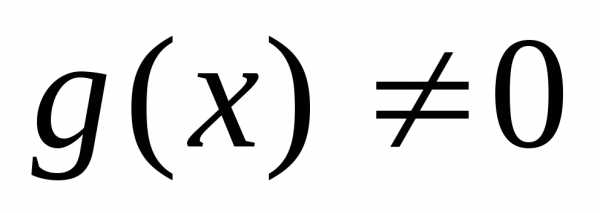 ,
то
,
то  непрерывно
в точке
непрерывно
в точке  .
.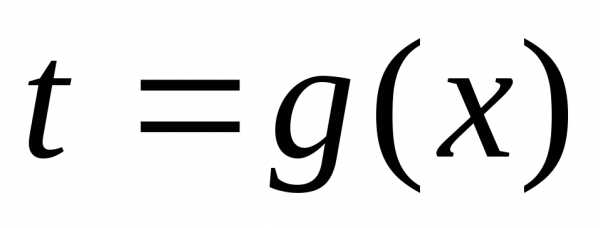 непрерывна
в точке
непрерывна
в точке 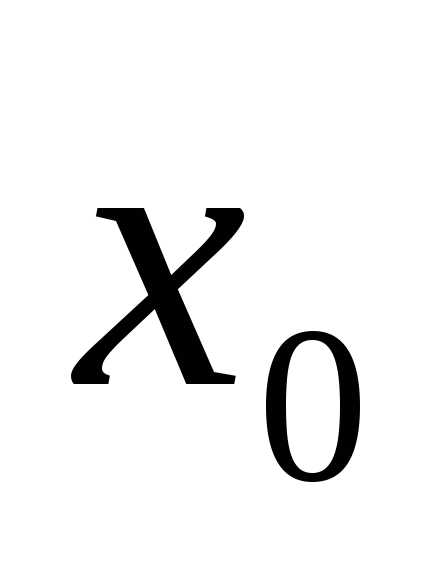 ,
а функция
,
а функция 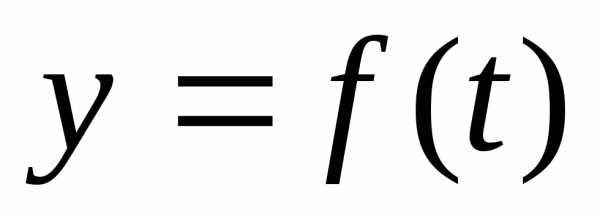 непрерывна
в точке то сложная функция
непрерывна
в точке то сложная функция 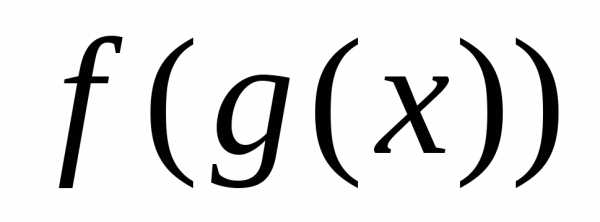 непрерывна в точке
непрерывна в точке 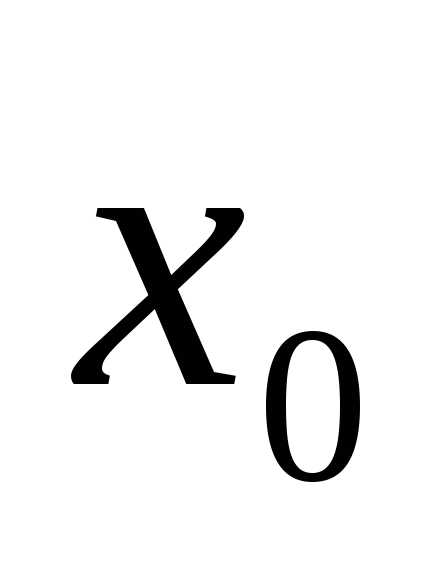 .
. >0.
Так как функция
>0.
Так как функция 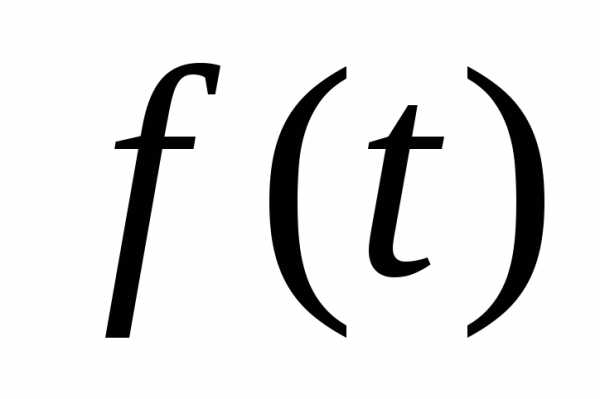 непрерывна
в точке
то
можно подобрать такое число
непрерывна
в точке
то
можно подобрать такое число 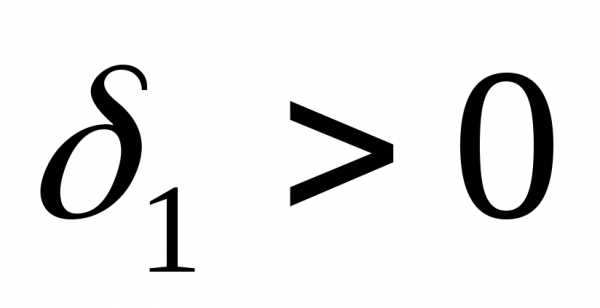 ,
что
,
что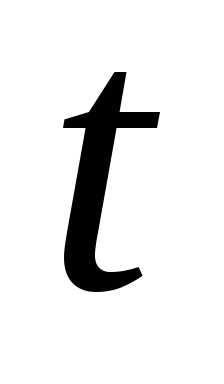 ,
такого, что
,
такого, что 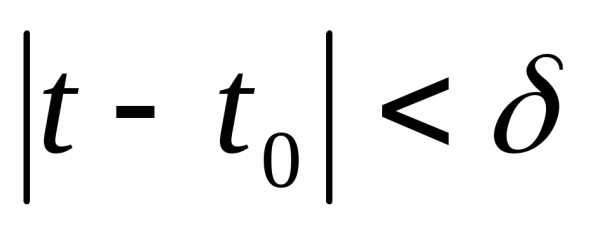 . (1)
. (1) непрерывна в точке
непрерывна в точке  ,
то для положительного числа
,
то для положительного числа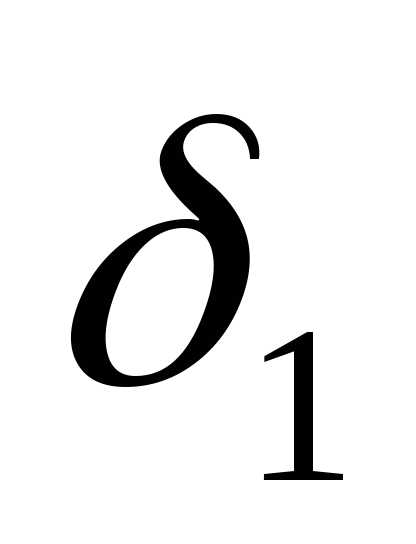 можно подобрать такое число
можно подобрать такое число 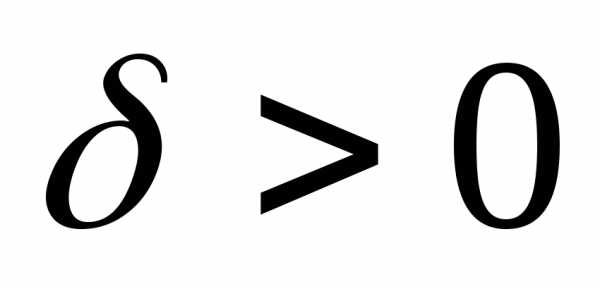 ,
что
,
что ,
такого, что
,
такого, что 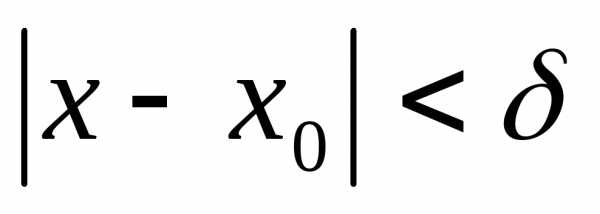 . (2)
. (2)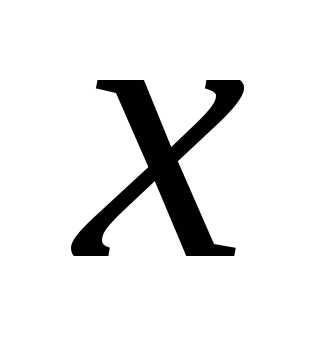 такое, что
такое, что 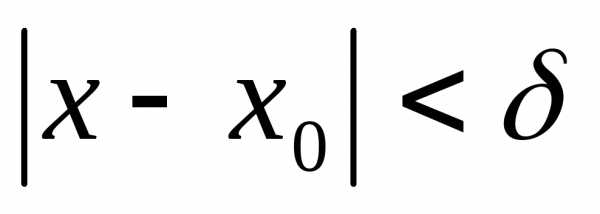 .
Тогда в силу (2) число
.
Тогда в силу (2) число 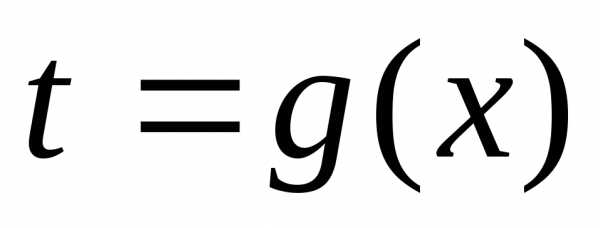 удовлетворяет неравенству
,
и поэтому в силу (1) .
Так как все эти вычисления проведены
для любого
удовлетворяет неравенству
,
и поэтому в силу (1) .
Так как все эти вычисления проведены
для любого  >0,
то непрерывность функции
>0,
то непрерывность функции 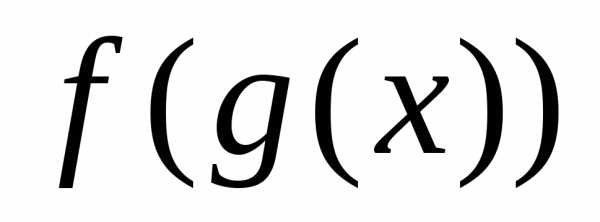 в точке
в точке 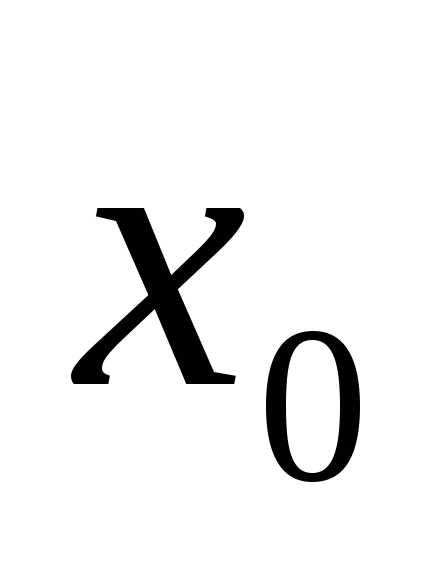 доказана
доказана -точка
разрыва функции
-точка
разрыва функции  ,
если в точке
,
если в точке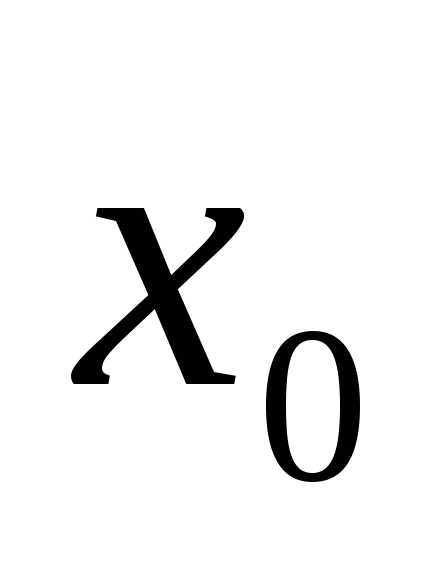 функция
функция не
является непрерывной.
не
является непрерывной. -точка
устранимого разрыва функции
-точка
устранимого разрыва функции 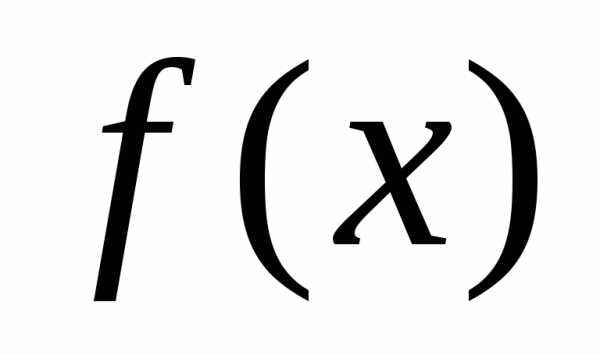 ,
если существует
,
если существует  ,
но
,
но 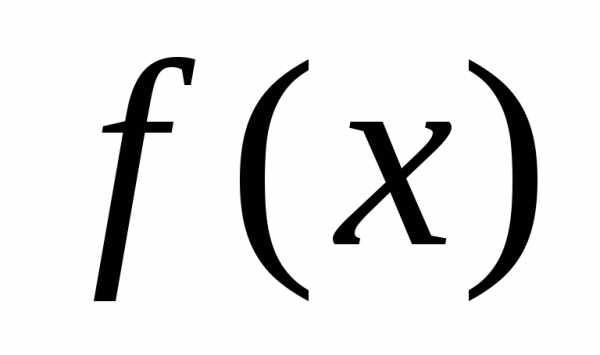 неопределена
в точке
неопределена
в точке 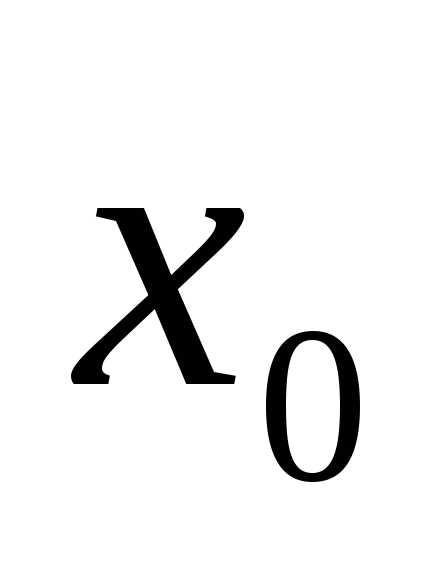 ,
либо
.
,
либо
.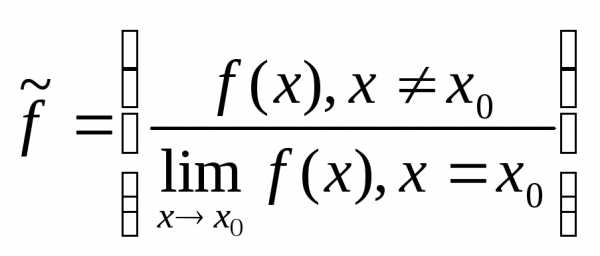 —
непрерывна в точке
—
непрерывна в точке  .
. .
.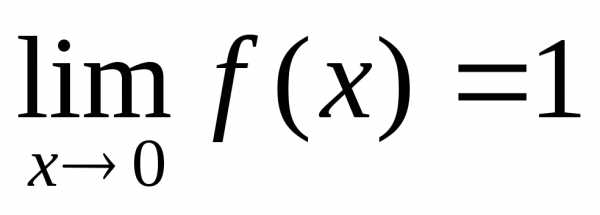 ,
, 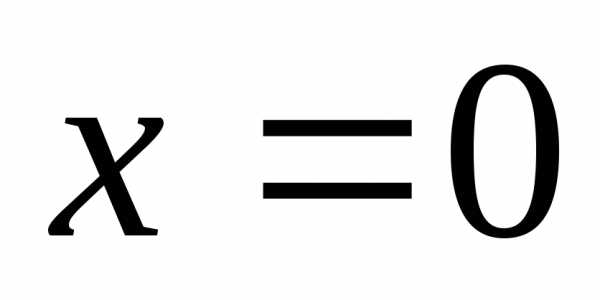 —
точка устранимого разрыва
—
точка устранимого разрыва  .
.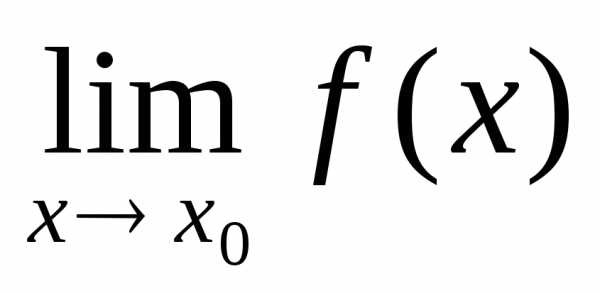 не
существует, то
не
существует, то  -точка
неустранимого
-точка
неустранимого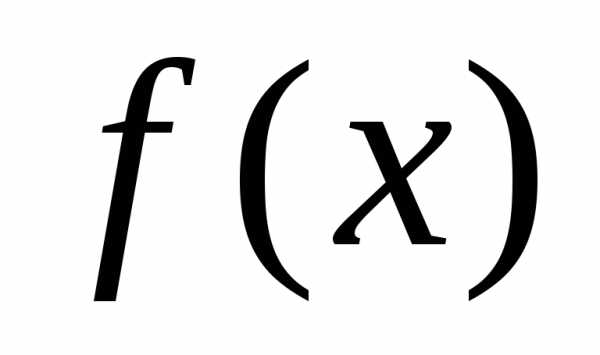 .
. -точка
неустранимого разрыва функции
-точка
неустранимого разрыва функции  ,
тогда:
,
тогда: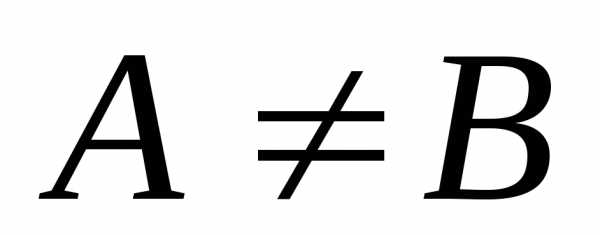 ,
то
,
то  -точка
разрыва функции
-точка
разрыва функции  1-го рода.
1-го рода.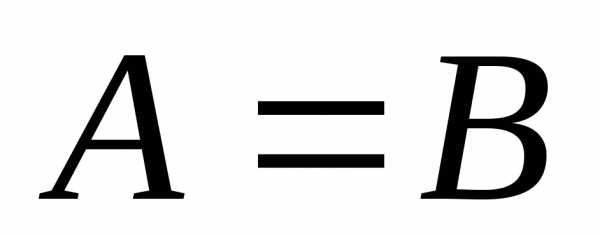 ,
то
,
то 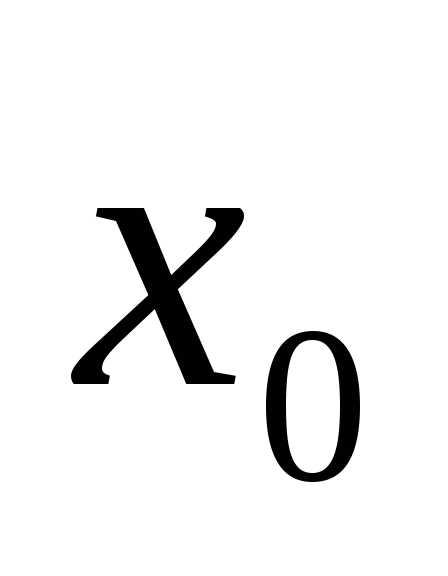 -точка
разрыва функции
-точка
разрыва функции 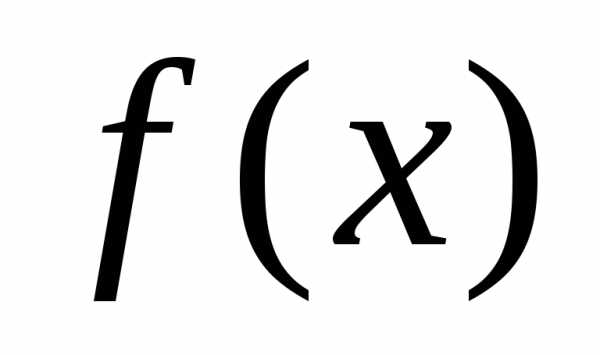 2-го рода.
2-го рода.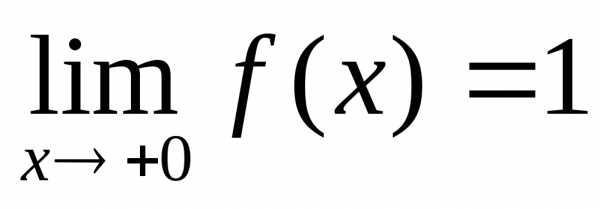 ,
,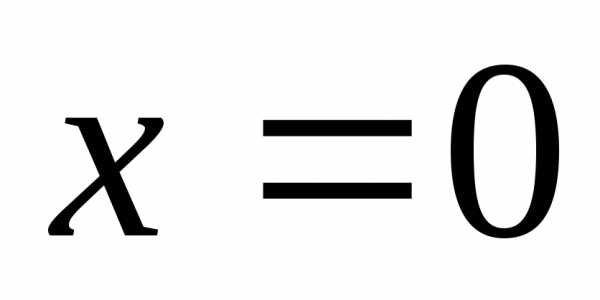 —
точка разрыва
—
точка разрыва 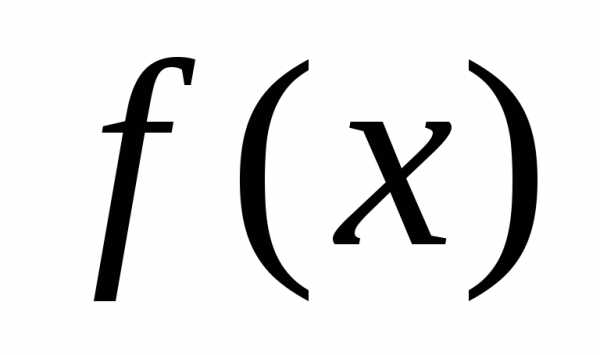 1-го рода.
1-го рода. .
. —
точка разрыва
—
точка разрыва  2-го рода.
2-го рода.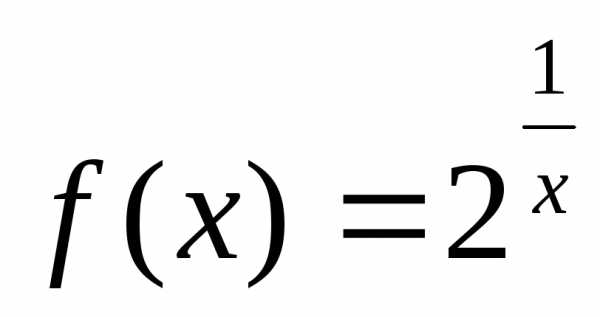
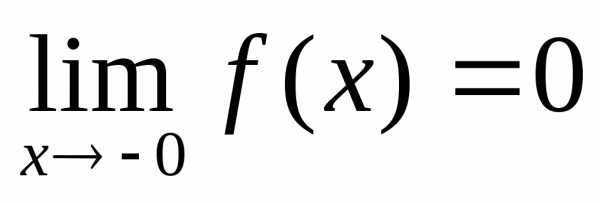
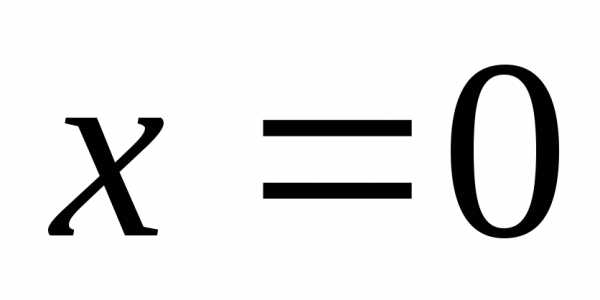 —
точка разрыва
—
точка разрыва 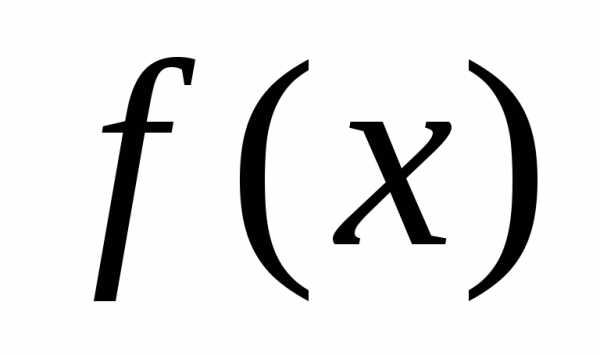 2-го рода.
2-го рода.

 не существует
не существует  точка
точка  —
точка разрыва
—
точка разрыва 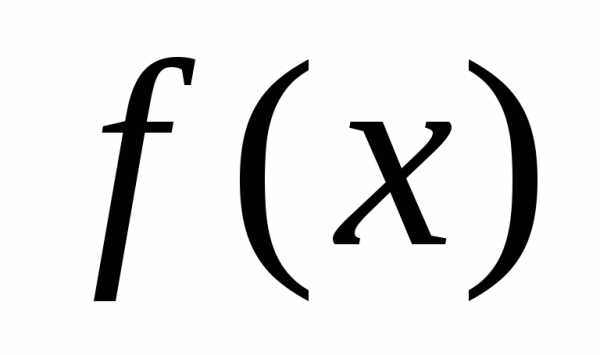 2-го рода.
2-го рода. —
точка разрыва
—
точка разрыва 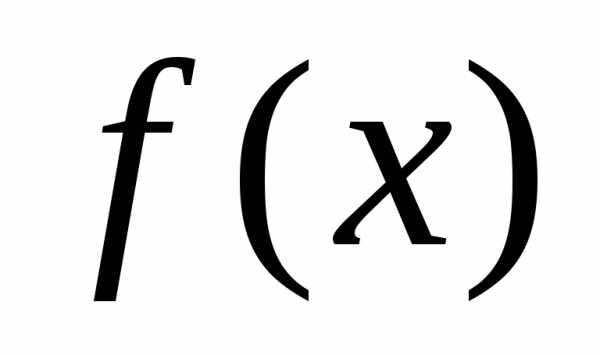 2-го рода
2-го рода ограничена
на
ограничена
на .
.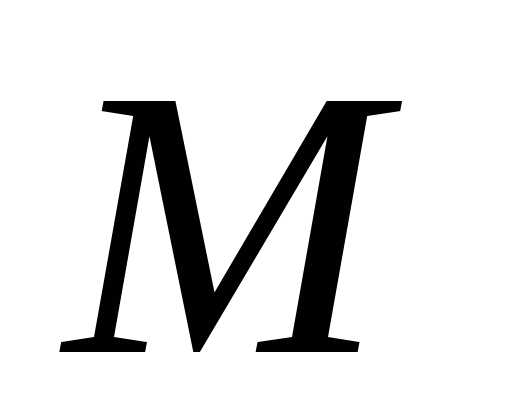 =1,2,3…
=1,2,3…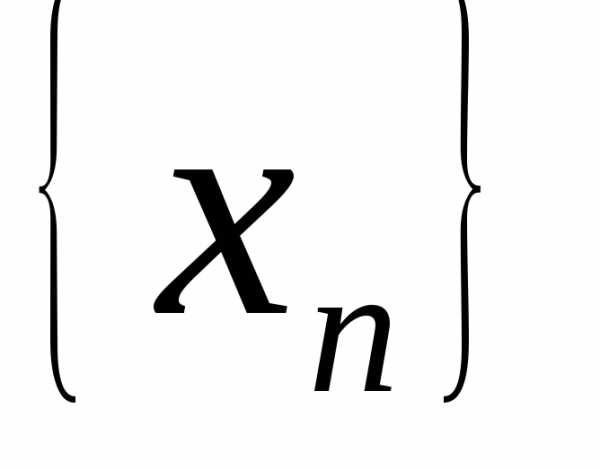 :
: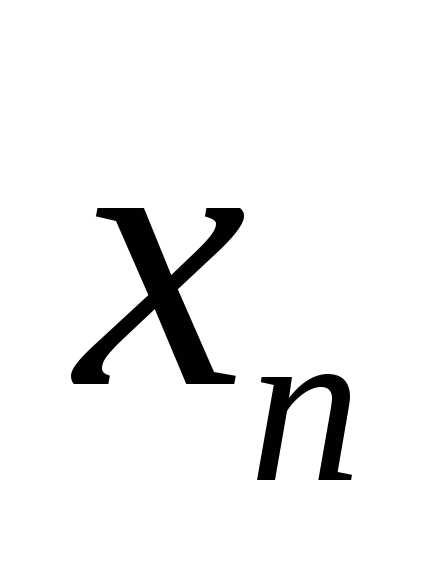

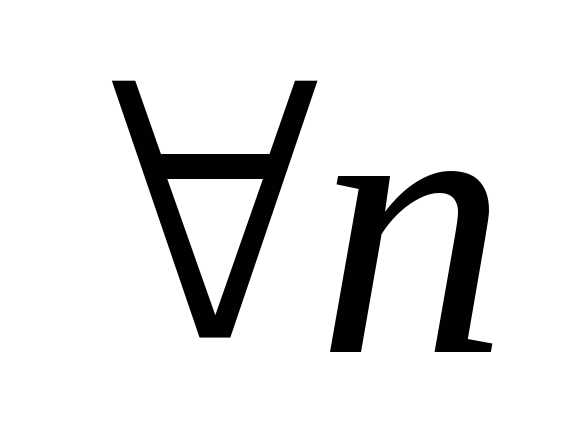

 .
.
 =>
=> 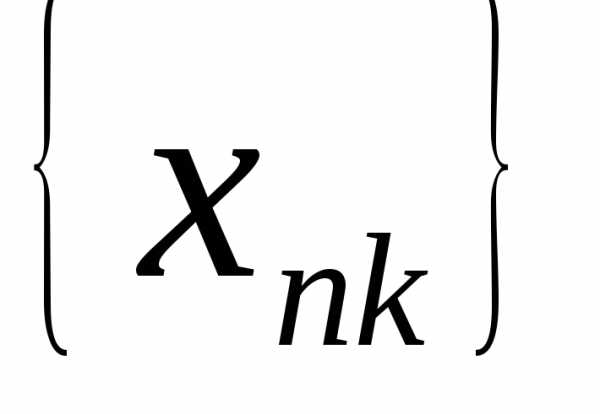 -подпоследовательность
последовательности
-подпоследовательность
последовательности  :
: .
. => .
=> .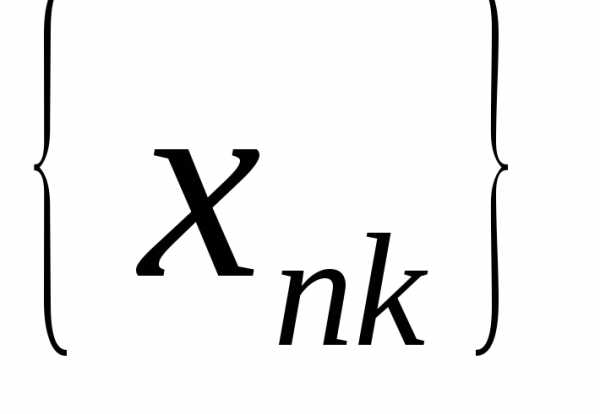 -подпоследовательность
последовательности
-подпоследовательность
последовательности 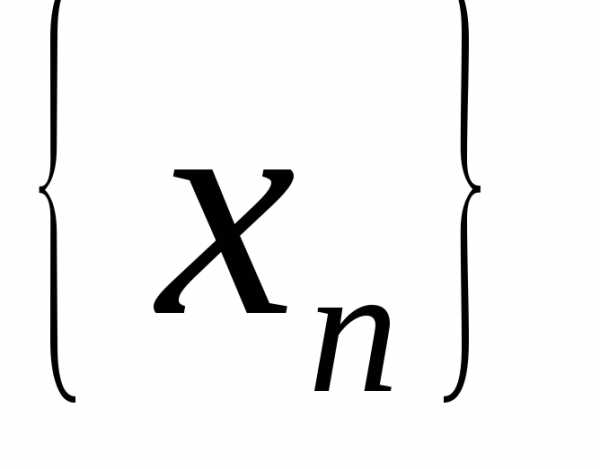 : => .
Противоречие.
: => .
Противоречие. по
существу.
по
существу. 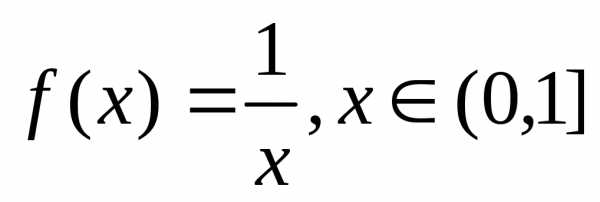 , ,
но
, ,
но 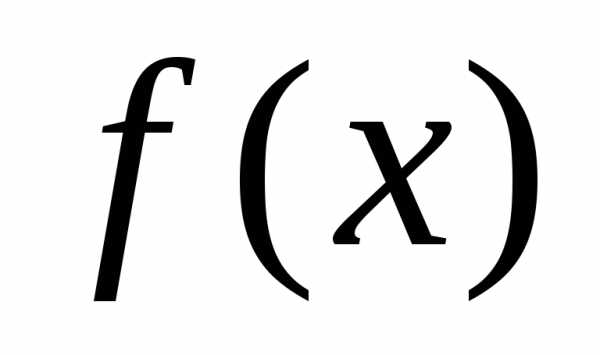
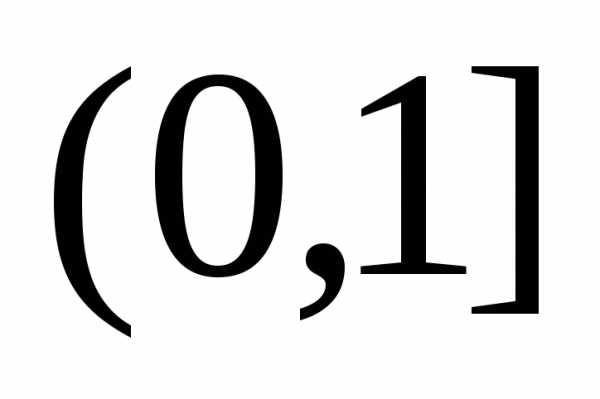 .
. функция на этом отрезке достигает своего
наибольшего и наименьшего значения,
причем в условиях теоремы отрезок по
существу.
функция на этом отрезке достигает своего
наибольшего и наименьшего значения,
причем в условиях теоремы отрезок по
существу.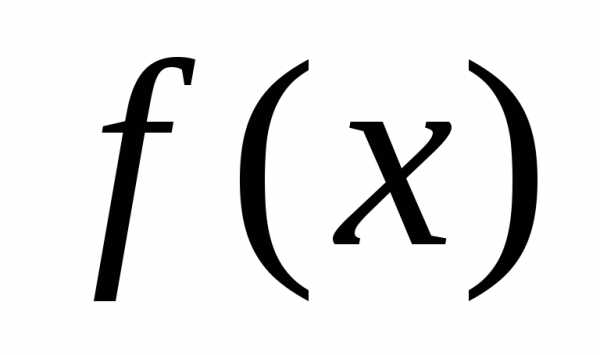 ограничена
на
ограничена
на 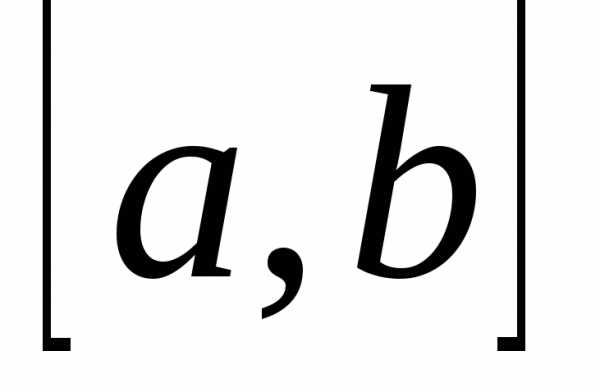 => Докажем, что
.
Предположим противное, то есть
=> Докажем, что
.
Предположим противное, то есть 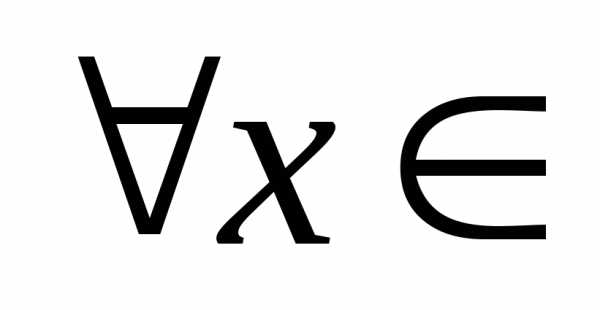
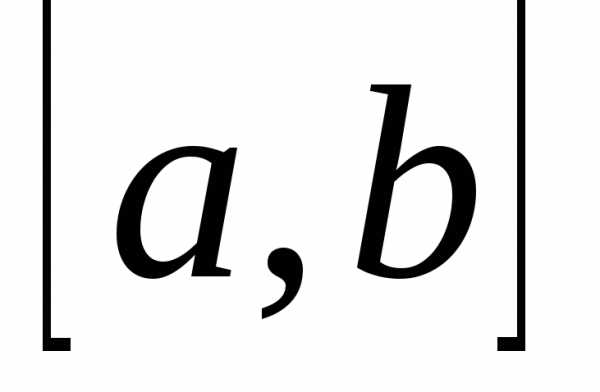 .
Рассмотрим вспомогательную функцию на
.
Рассмотрим вспомогательную функцию на 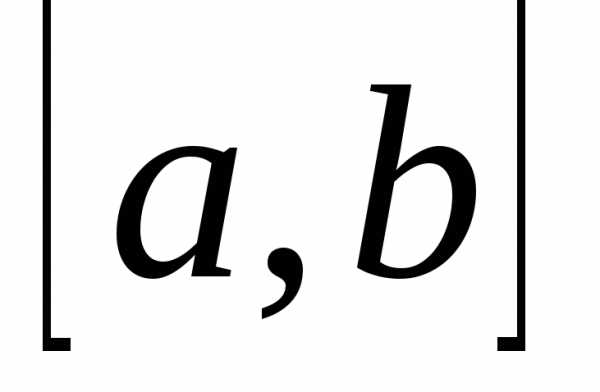 .
По 1 теореме Вейерштрасса
ограничена
на
.
По 1 теореме Вейерштрасса
ограничена
на  ,
то есть
,
то есть 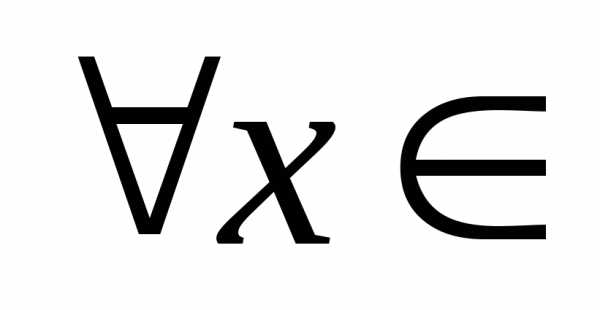
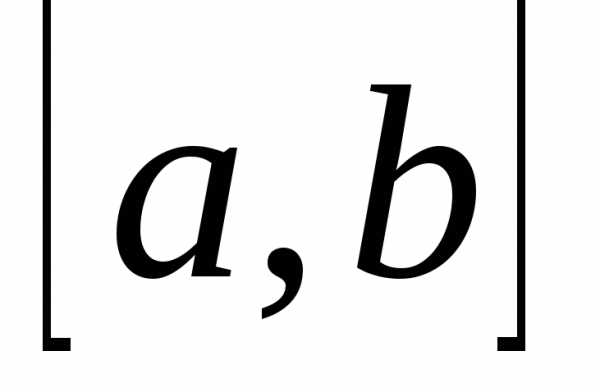 .
.

 (<
(<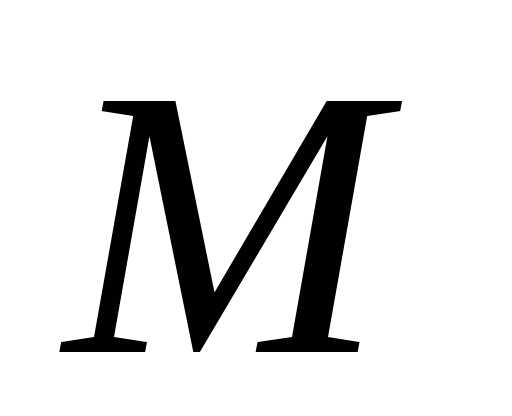 )-
верхняя граница.
)-
верхняя граница.  ,
то есть
,
то есть 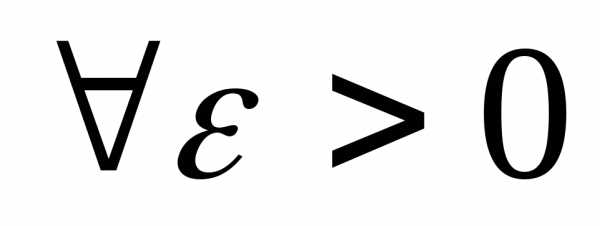 .
.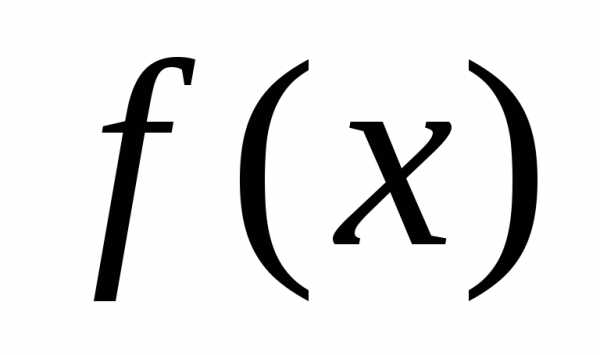 непрерывна на
непрерывна на 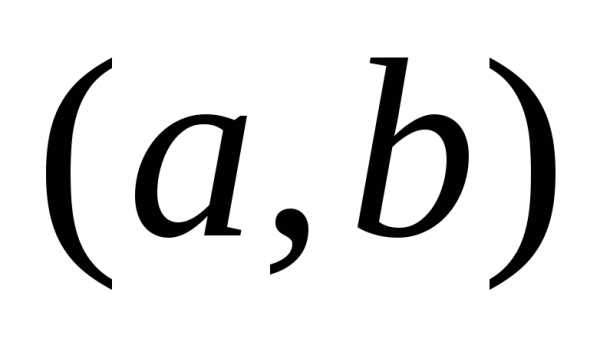 ,
если
,
если 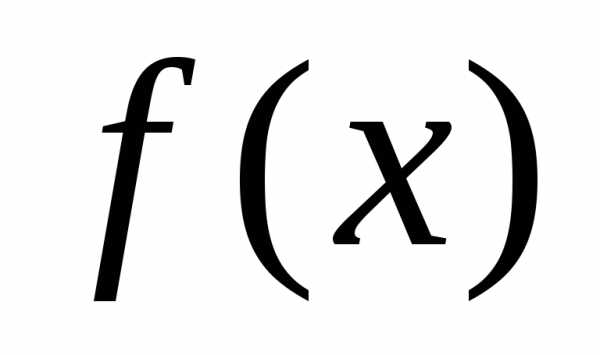 непрерывна в точке
непрерывна в точке  ,
, непрерывна на
непрерывна на 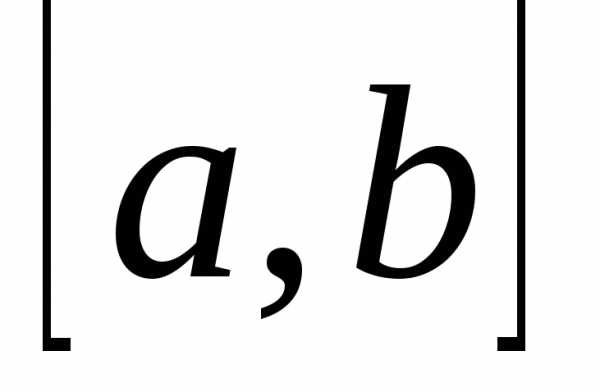 ,
если
,
если  непрерывна в точке
непрерывна в точке 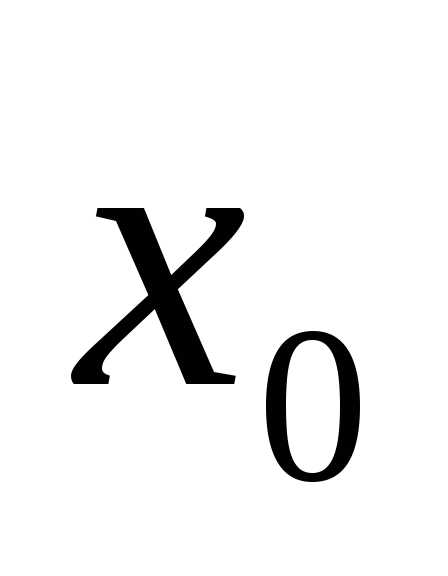 , и
, и определена на
определена на 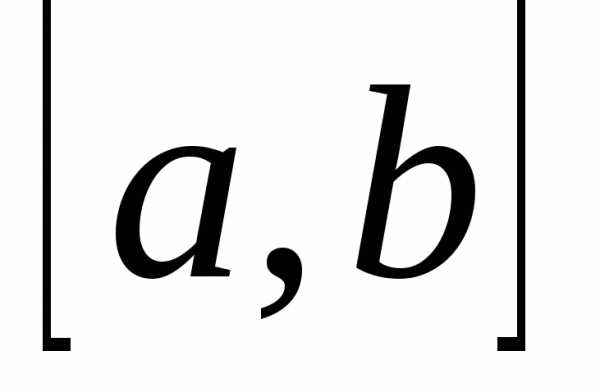 и
,
причем
.
Тогда
и
,
причем
.
Тогда ,
, 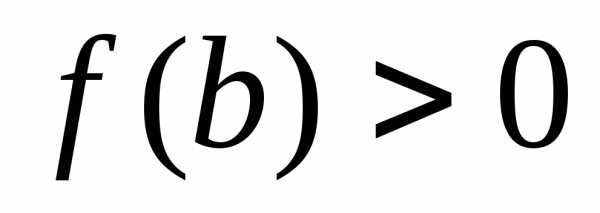 .
Используем метод деления отрезка
пополам.
.
Используем метод деления отрезка
пополам.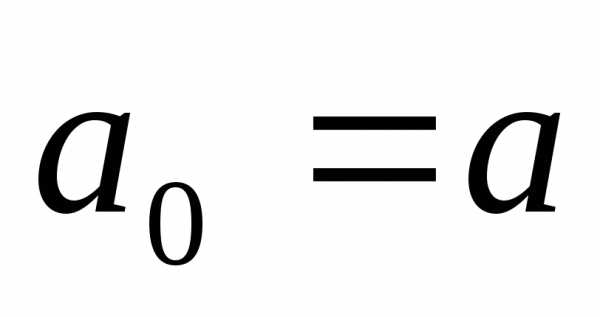 ,
, 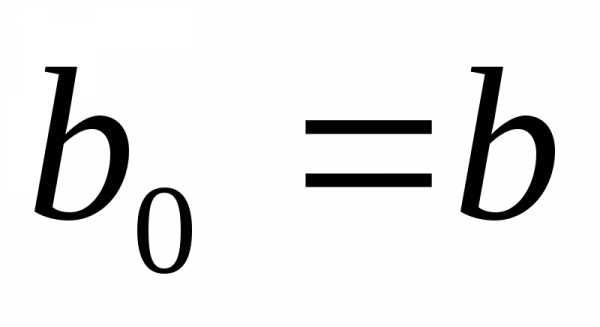 .
.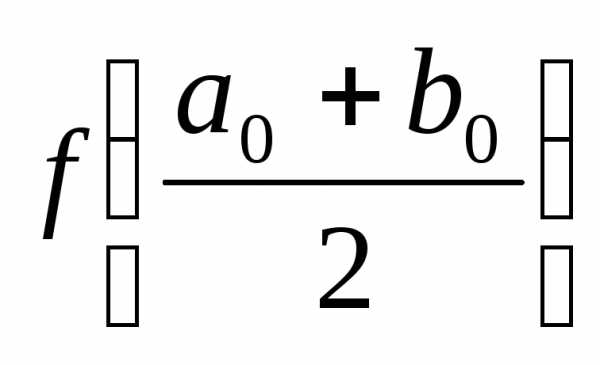
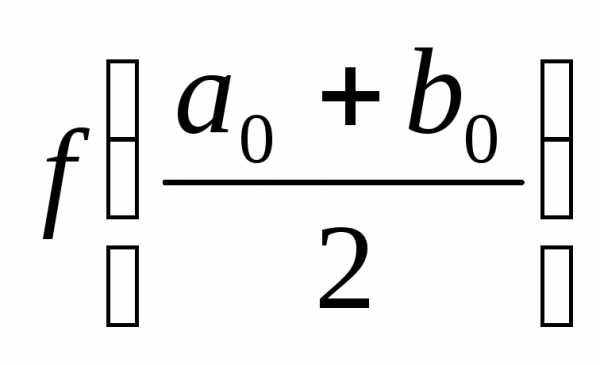 =0
=0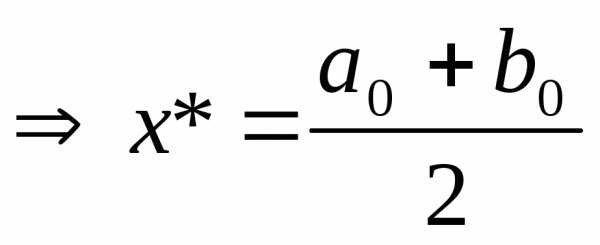 .
.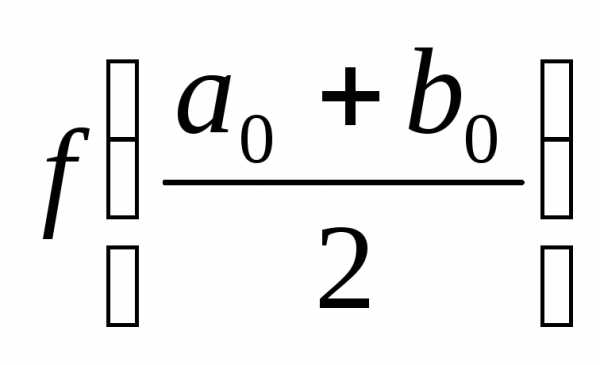 <
0
<
0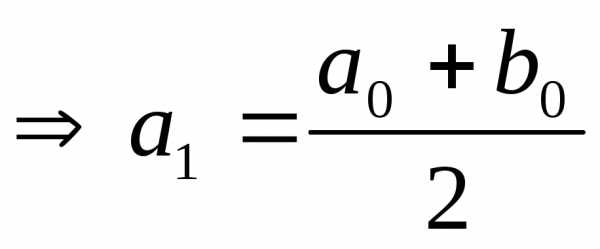 ,
, 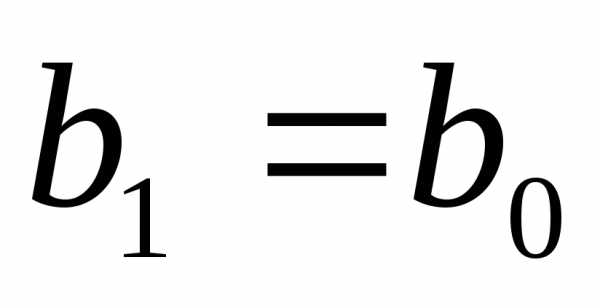 .
.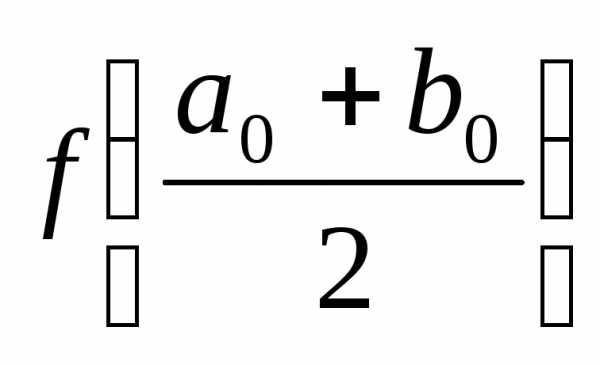 >
0
>
0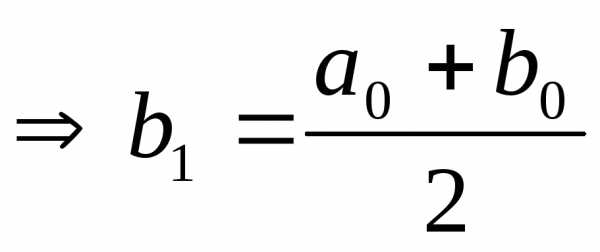 ,
, 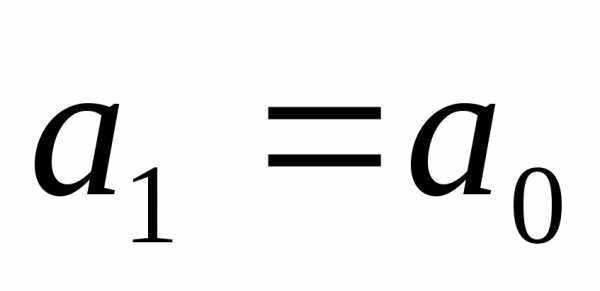 и так далее.
и так далее.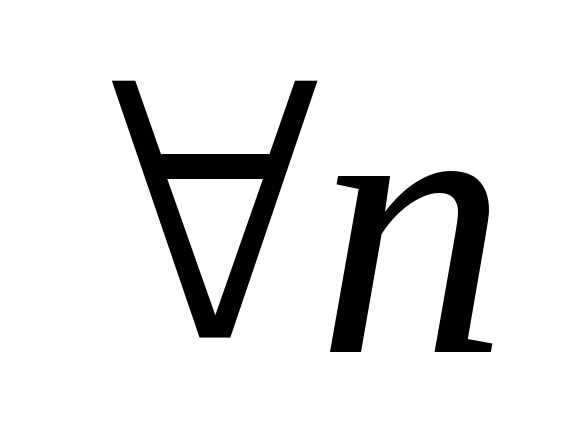 .
.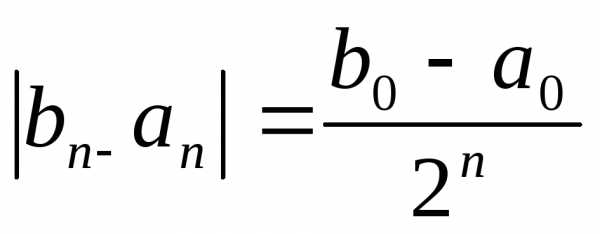 .
.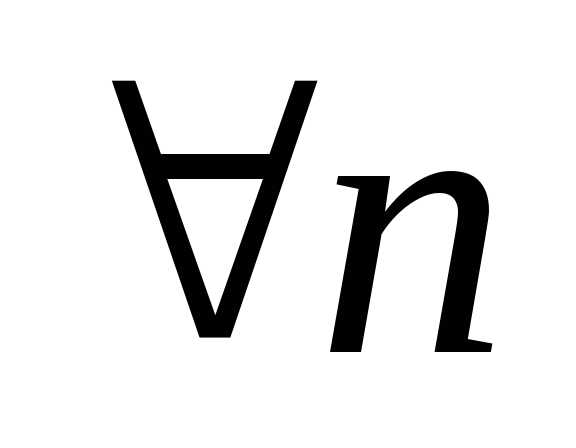 ,
то есть
,
то есть  .
. :
: .
. определена на
определена на 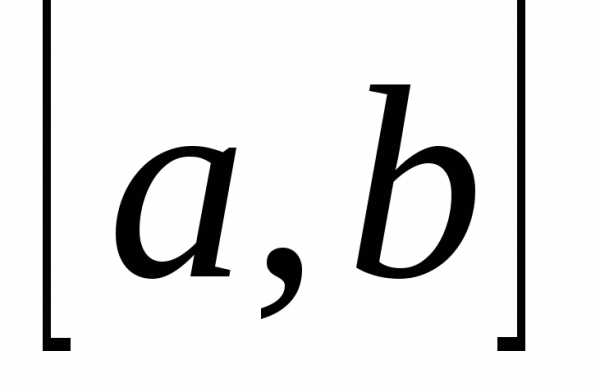 и
, ,
и
, ,  ,
, 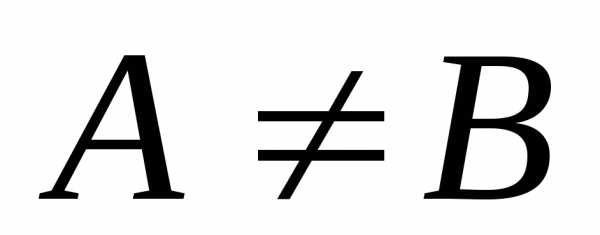
 : .
: . .
.