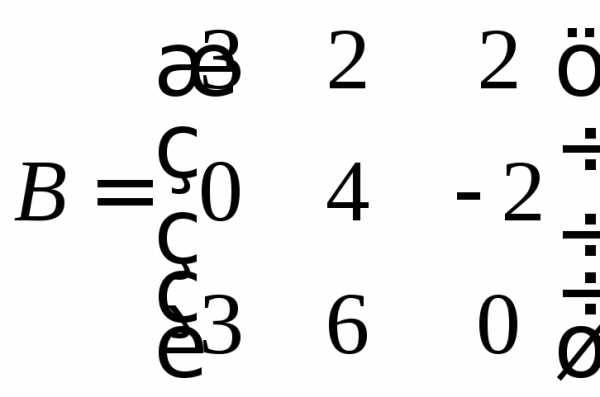Определенный интеграл, примеры решений
Определенный интеграл от функции на промежутке обозначается и равен разности двух значений первообразной функции, вычисленных при и (формула Ньютона-Лейбница):
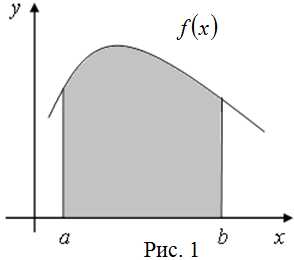
Геометрический смысл определенного интеграла. Определенный интеграл есть площадь криволинейной трапеции ограниченной графиком функции , осью и прямыми и (рис. 1), то есть
Для вычисления определенных интегралов подходят все методы, которые используются для нахождения неопределенных интегралов.
Примеры
ПРИМЕР 1| Задание | Вычислить интеграл
|
| Решение | Преобразуем подынтегральное выражение
Разобьем интеграл от суммы на сумму интегралов и вынесем за знак интеграла константы:
Полученные интегралы являются табличными, вычислим их:
|
| Ответ |
| Задание | Вычислить интеграл
|
| Решение | Вынесем константу за знак интеграла и вычислим полученный табличный интеграл:
|
| Ответ |
| Задание | Вычислить интеграл
|
| Решение | Сделаем замену , при этом пределы интегрирования изменятся: и . Подставляя все это в исходный интеграл, получим:
|
| Ответ |
| Задание | Вычислить интеграл
|
| Решение | Внесем под знак дифференциала, тогда
Подставляя все в исходный интеграл, получим:
|
| Ответ |
| Задание | Вычислить площадь криволинейной трапеции ограниченной функцией , осью и прямыми и . |
| Решение | Сделаем рисунок (рис. 2).
По геометрическому смыслу определенного интеграла нахождение площади заданной криволинейной трапеции сводится к вычислению интеграла
Вычислим этот интеграл: (кв. ед.) |
| Ответ |
ru.solverbook.com
Вычисление определенного интеграла
Здравствуйте. Меня зовут Андрей Зварыч. Я онлайн-репетитор сайта Tutoronline по высшей математике. Очень часто ко мне обращаются студенты с просьбой помочь разобраться с вычислением определенных интегралов. Сегодня я покажу несколько примеров решения. Надеюсь, моя статья будет полезной.
Итак, если F(x) – одна из первообразных непрерывной функции f(x) на [a,b], то справедлива формула Ньютона-Лейбница
Если функция f(x) непрерывна на отрезке [a,b], а функция x = φ(t) непрерывно дифференцирована на отрезке [t1,t2], причем a = φ(t1), b = φ(t2), то имеет место формула
Если функции u(x), v(x) и их производные u'(x), v'(x) непрерывны на отрезке [a,b], то справедлива формула интегрирования по частям
Пример 1. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
Пример 2. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
Пример 3. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
Пример 4 Вычислить интеграл
Решение.
На основании формулы произведения синусов, таблицы основных интегралов и формулы (1) имеем:
Пример 5. Вычислить интеграл
Решение.
Разложим подынтегральную функцию на сумму простых дробей,
Решив систему
Получим
Тогда на основании таблицы основных интегралов и формулы (1) имеем
Пример 6. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Сделаем замену ex + 4 = t2, тогда ex= t2– 4, ex dx = 2t dt,
Если x= ln5, то t = 3; если x= ln12, то t = 4. Тогда
Пример 7. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Пример 8. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Сделаем подстановку t = cosx
Если x = 0, то t = cos 0 = 1, если
Следовательно
Пример 9. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Найдем пределы по t:
Находим
Следовательно,
Пример 10. Вычислить интеграл
Решение.
Хороший метод решения интегралов, это метод занесения под дифференциал, его плюс состоит в том, что не требуется менять пределы интегрирования
Пример 11. Вычислить интеграл
Решение. На основании таблицы основных интегралов и формулы (3) имеем (интегрируем по частям)
Если у Вас остались вопросы или Вам нужна помощь в решении «ваших интегралов», записывайтесь на мои занятия. Буду рад Вам помочь!
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Определенный интеграл. Примеры решений — Мегаобучалка
Для того, чтобы научиться решать определенные интегралы необходимо:
1) Уметь находить соответствующие неопределенные интегралы.
2) Уметь вычислить определенный интеграл.
Как видите, для того, чтобы освоить определенный интеграл, нужно достаточно хорошо ориентироваться в «обыкновенных» неопределенных интегралах. Поэтому, если вы только-только начинаете погружаться в интегральное исчисление, и чайник еще не совсем закипел, то лучше начать с урока Неопределенный интеграл. Примеры решений.
В общем виде определенный интеграл записывается так:
Что прибавилось по сравнению с неопределенным интегралом?
Прибавились пределы интегрирования.
Нижний предел интегрирования стандартно обозначается буквой a.
Верхний предел интегрирования стандартно обозначается буквой b.
Отрезок [a; b] включает граничные точки и называется отрезком интегрирования.
Что такое определенный интеграл? Можно посмотреть в учебниках про диаметр разбиения отрезка, предел интегральных сумм и т. д., но урок носит практический характер. Поэтому скажем, что определенный интеграл – это, прежде всего, самое что ни на есть обычное ЧИСЛО.
Есть ли у определенного интеграла геометрический смысл?Есть. И очень хороший. Самая популярная задача вычисления определённого интеграла – вычисление площади с помощью определенного интеграла.
Что значит решить определенный интеграл?Решить определенный интеграл – это значит, найти число, равное приращению первообразной функции на отрезке [a; b].
Как решить определенный интеграл?С помощью знакомой со школы формулы Ньютона-Лейбница:
.
Формулу лучше переписать на отдельный листочек, она должна быть перед глазами на протяжении всего урока.
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию F(X) (неопределенный интеграл). Обратите внимание, что константа C в определенном интеграле никогда не добавляется.
Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла, по сути – это просто отчёркивание. Зачем нужна сама запись
?
Это подготовка для применения формулы Ньютона-Лейбница.
2) Подставляем значение верхнего предела в первообразную функцию: F(b).
3) Подставляем значение нижнего предела в первообразную функцию: F(a).
4) Рассчитываем (без ошибок!) разность F(b)-F(a), то есть, находим число, равное приращению первообразной (от подынтегральной) функции на отрезке [a; b].
Готово.
Всегда ли существует определенный интеграл? Нет, не всегда существует всё, что мы напишем в виде определённого интеграла. Например, интеграла
не существует, поскольку отрезок интегрирования не входит в область определения подынтегральной функции и значения под квадратным корнем не могут быть отрицательными. А вот менее очевидный пример:
.
Такого интеграла тоже не существует на всём отрезке [-2; 3], так как в точках
,
этого отрезка подынтегральная функция f(x) = tg(x) не существует.
Для того, чтобы определенный интеграл существовал на данном отрезке, необходимо, чтобы подынтегральная функция была непрерывной на отрезке интегрирования.
Из вышесказанного следует первая важная рекомендация: перед тем, как приступить к решению ЛЮБОГО определенного интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования. Бывает так, что подолгу мучаешься с нахождением трудной первообразной, а когда наконец-то ее находишь, то ещё и ломаешь голову над вопросом: «что за ерунда получилась?». Например, если получилось примерно так:
???!!!
то нельзя подставлять отрицательные числа под корень! Если для решения в контрольной работе, на зачете или экзамене Вам предложен несуществующий интеграл вроде
,
то нужно дать ответ, что интеграла не существует и обосновать – почему.
Может ли определенный интеграл быть равен отрицательному числу?Может. И отрицательному числу. И нулю. Может даже получиться бесконечность, но это уже будет несобственный интеграл, коим отведена отдельная лекция.
Может ли нижний предел интегрирования быть больше верхнего предела интегрирования?Может, и такая ситуация реально встречается на практике. Интеграл
преспокойно вычисляется по формуле Ньютона-Лейбница.
Без чего не обходится высшая математика? Конечно же, без всевозможных свойств. Поэтому рассмотрим некоторые свойства определенного интеграла.
В определенном интеграле можно переставить верхний и нижний предел, сменив при этом знак:
Например, в определенном интеграле перед интегрированием
целесообразно поменять пределы интегрирования на «привычный» порядок:
.
В таком виде интегрировать значительно удобнее.
Как и для неопределенного интеграла, для определенного интеграла справедливы свойства линейности:
Это справедливо не только для двух, но и для любого количества функций.
В определенном интеграле можно проводить замену переменной интегрирования, правда, по сравнению с неопределенным интегралом тут есть своя специфика, о которой мы еще поговорим.
Для определенного интеграла справедлива формула интегрирования по частям: .
Пример 1
Вычислить определенный интеграл
.
Решение:
(1) Выносим константу за знак интеграла.
(2) Интегрируем по таблице с помощью самой популярной формулы
.
(3) Используем формулу Ньютона-Лейбница
.
Сначала подставляем в x3 верхний предел, затем – нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.
Пример 2
Вычислить определенный интеграл
.
Это пример для самостоятельно решения, решение и ответ в конце урока.
Пример 3
Вычислить определенный интеграл
.
Решение:
.
(1) Используем свойства линейности определенного интеграла.
(2) Интегрируем по таблице, при этом все константы выносим – они не будут участвовать в подстановке верхнего и нижнего предела.
(3) Для каждого из трёх слагаемых применяем формулу Ньютона-Лейбница.
СЛАБОЕ ЗВЕНО в определенном интеграле – это ошибки вычислений и часто встречающаяся ПУТАНИЦА В ЗНАКАХ. Будьте внимательны! Особое внимание заостряем на третьем слагаемом:
,
т. к. очень часто машинально пишут
.
Следует заметить, что рассмотренный способ решения определенного интеграла – не единственный. При определенном опыте, решение можно значительно сократить. Например, так:
.
Здесь устно использованы правила линейности, устно проинтегрированы табличные интегралы. Получилась всего одна скобка с отчёркиванием пределов:
(в отличие от трёх скобок в первом способе). И в «целиковую» первообразную функцию мы сначала подставили 4, затем –2, опять же выполнив все действия в уме.
При втором способе существует повышенный риск допустить ошибку в вычислениях, поэтому студенту-чайнику лучше использовать первый способ, чтобы не терять знаки.
Несомненными преимуществами второго способа является быстрота решения, компактность записи и тот факт, что первообразная.
находится в одной скобке.
megaobuchalka.ru
Определенный интеграл, теория и примеры
Например.
Детальный разбор понятия «Определенный интеграл»
Рассмотрим функцию , определенную и непрерывную на некотором отрезке . Выполним разбиение заданного отрезка с помощью точек на частичных отрезков , ,…, . На каждом частичном отрезке выберем произвольную точку и вычислим значение заданной функции в ней. Умножим полученное значение на длину соответствующего частичного отрезка: . Составим сумму всех таких произведений:
Такая сумма называется интегральной суммой функции на отрезке .
Пусть – длина наибольшего частичного отрезка: . Если предел интегральной суммы , когда максимальный диаметр разбиения , не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то число называется определенным интегралом от заданной функции на отрезке и обозначается , то есть
Здесь числа и называются соответственно верхним и нижним пределами интегрирования; – подынтегральная функция; – подынтегральное выражение; – переменная интегрирования; – область или отрезок интегрирования.
Примеры решения задач
Функция называется интегрируемой на отрезке , если для нее на этом отрезке существует определенный интеграл .
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Примеры вычисления определенного интеграла
Пользуясь формулой Ньютона-Лейбница, вычислить определённый интеграл
а) 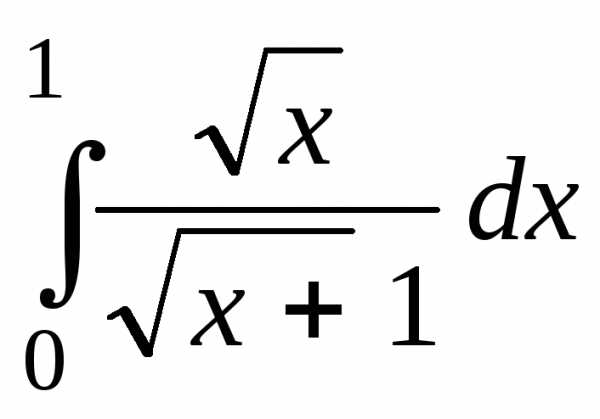

Решение
а) Для вычисления интеграла 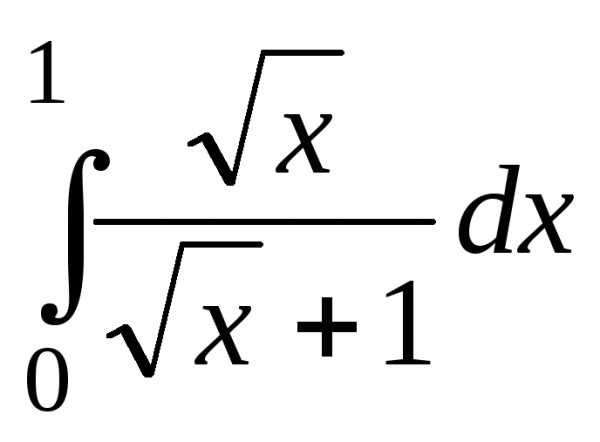 в подинтегральной функции проведём
замену переменной
в подинтегральной функции проведём
замену переменной
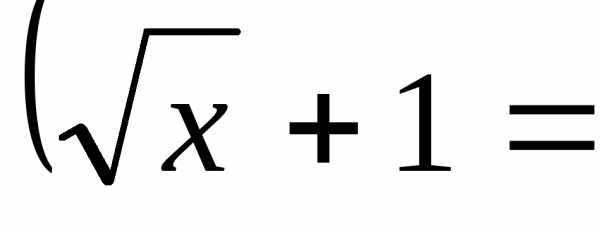 t
t  t-1
t-1
 =(t-1)2
=(t-1)2
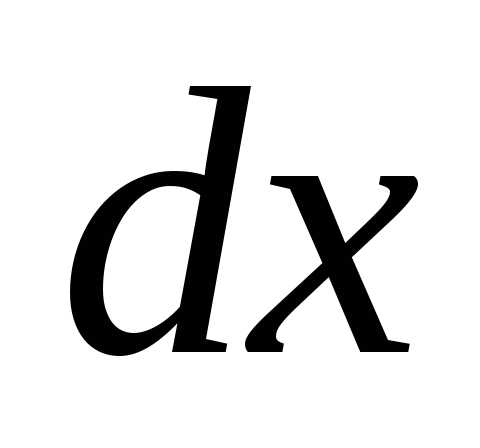 =d(t-1)2
=d(t-1)2
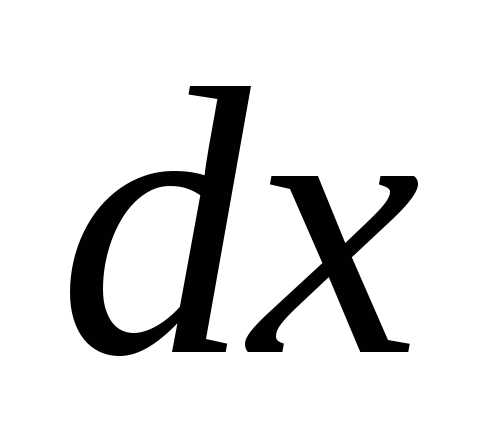 =2(t-1)dt).
=2(t-1)dt).
Найдём пределы интегрирования для новой переменной .
При x=0 имеемt = 1, приx= 1,t= 2.
Получим dt=
= dt.
dt.
Для вычисления полученного интеграла,
применим формулу Ньютона-Лейбница: 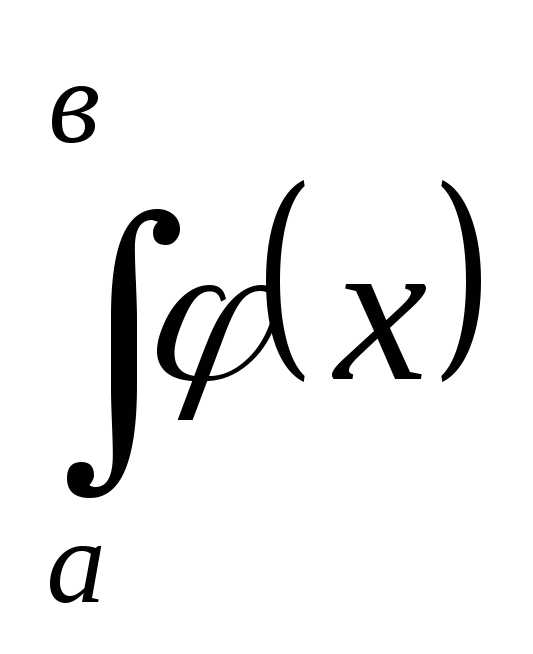
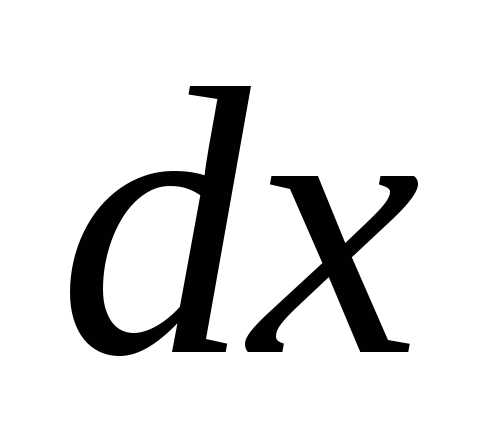
 =Окончательно будем иметь:
=Окончательно будем иметь:
=
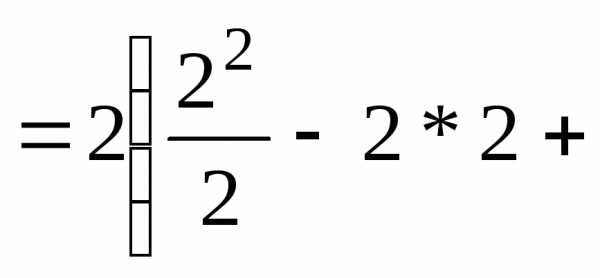 ln2)-2(
ln2)-2(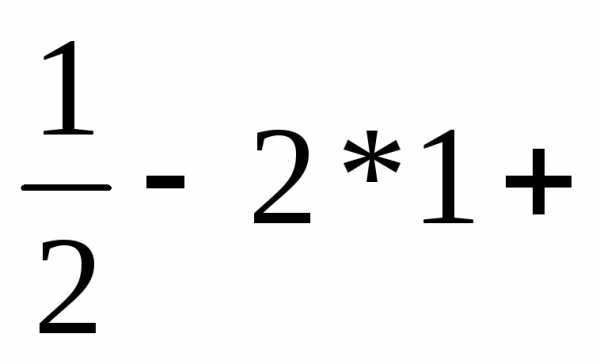 ln1)
=ln2-1.
ln1)
=ln2-1.
б) Вычислить определённый интеграл  cos3
cos3
Решение
Для нахождения определённого интеграла воспользуемся формулой и методом подведения под знак дифференциала:
 =
=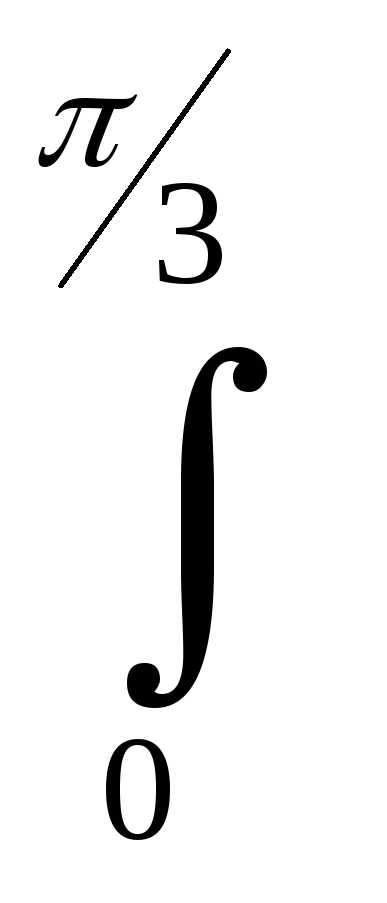
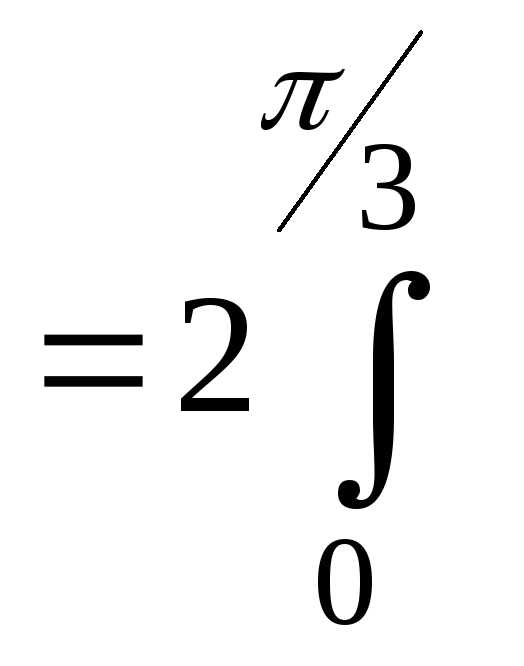
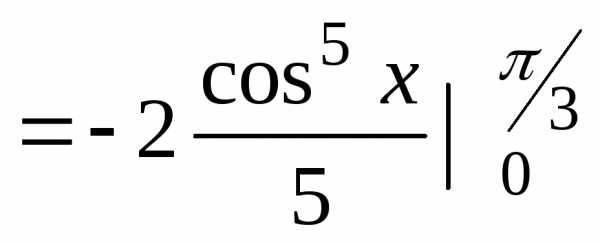 = —
= —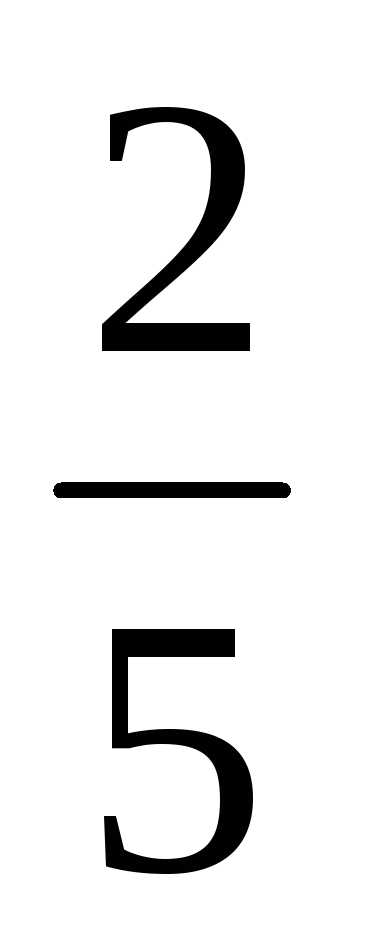 (
(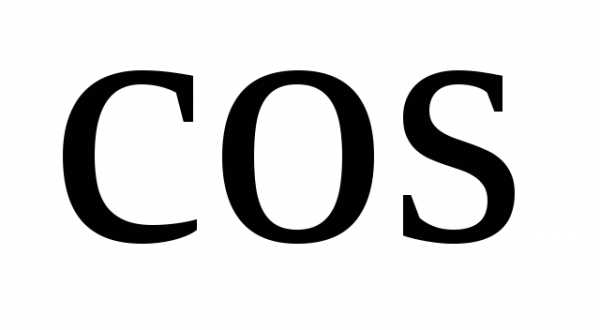 5
5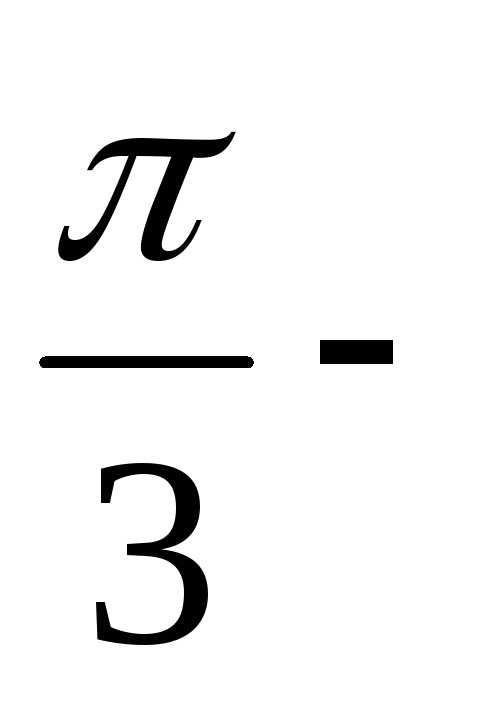
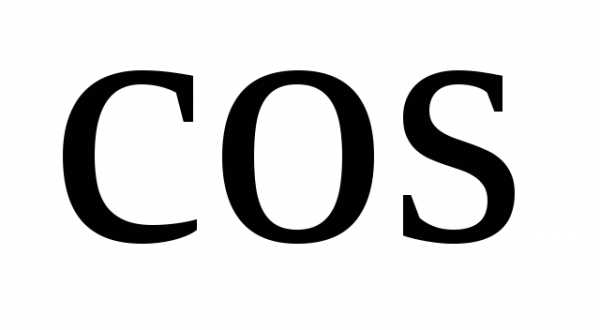 50)=
50)=
в) Вычислить определённый интеграл 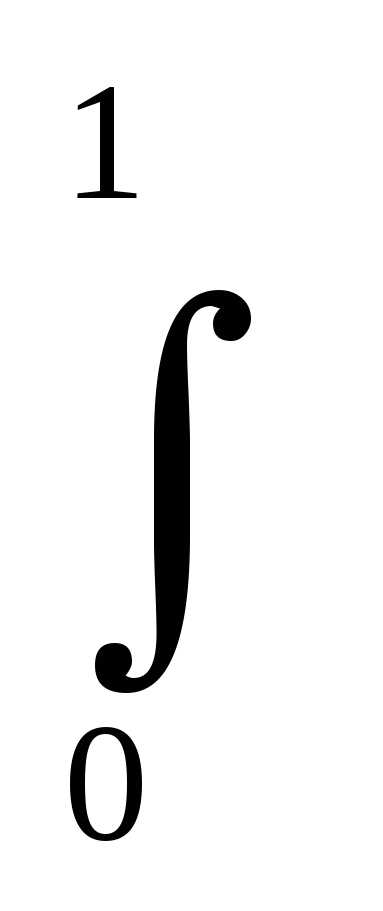 ln(
ln(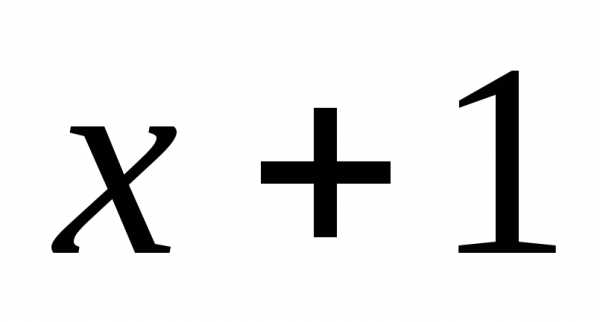 )
)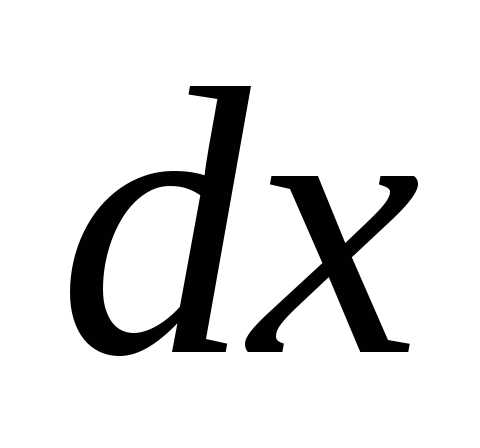
Решение
Воспользуемся способом интегрирования по частям в определённом интеграле
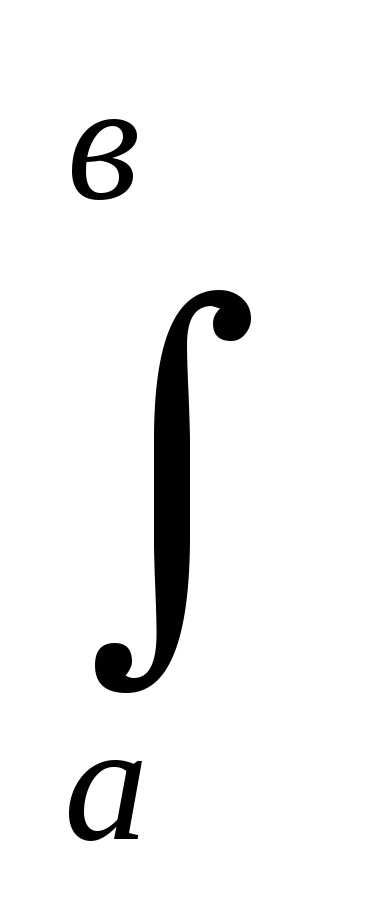 udv=uv
udv=uv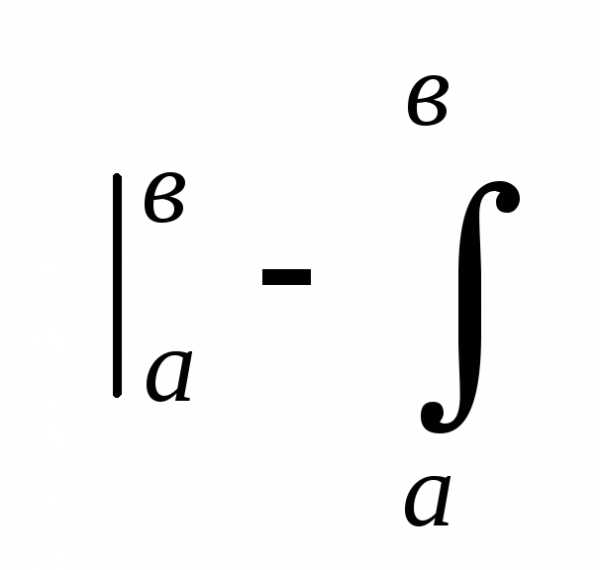 vdu
vdu
Положим ln(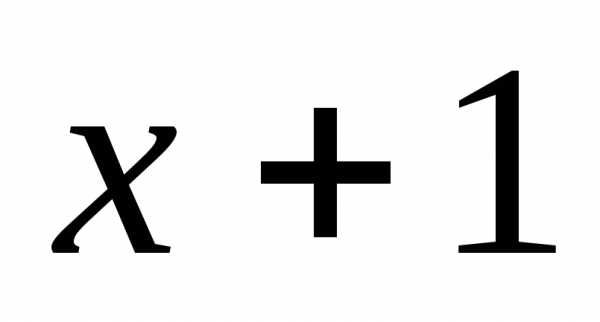 )=u,dv=
)=u,dv=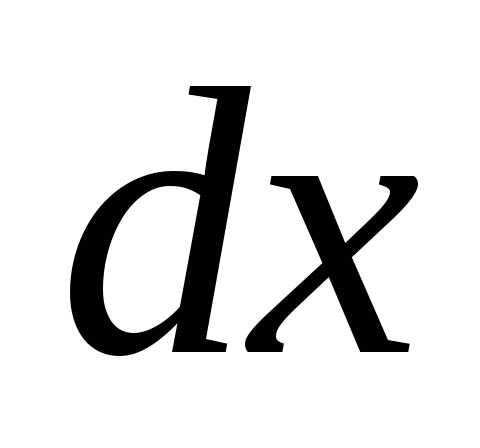 .
Найдёмd(ln(
.
Найдёмd(ln(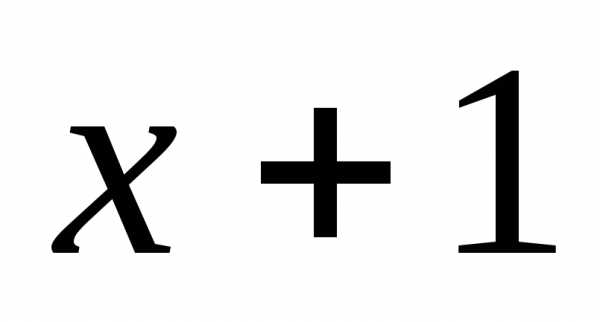 ))=du
))=du
du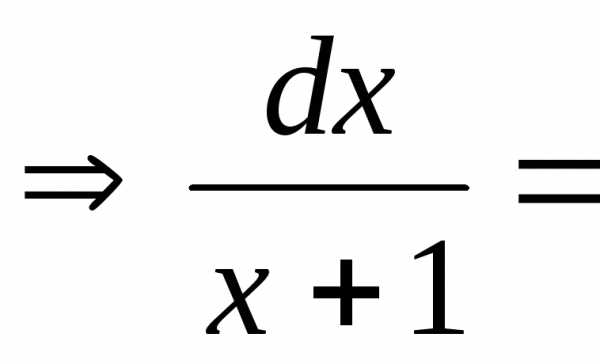 ,v=
,v=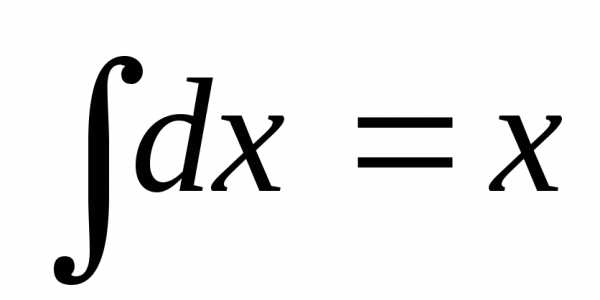
Вычислим интеграл
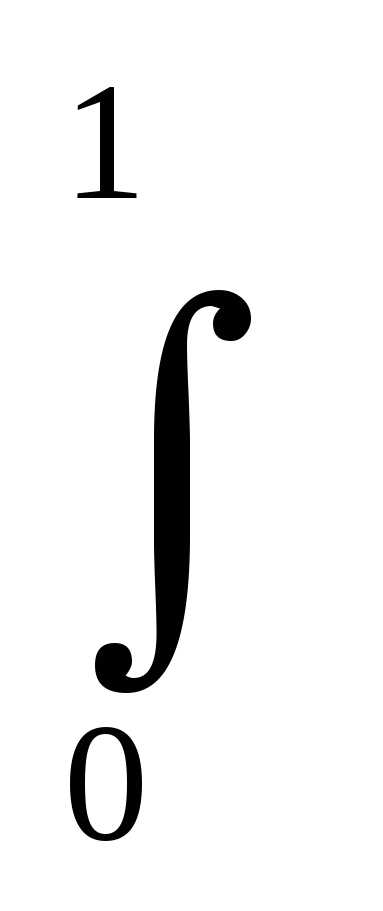 ln(
ln(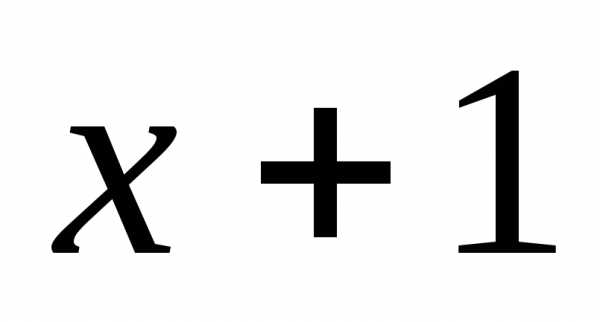 )
)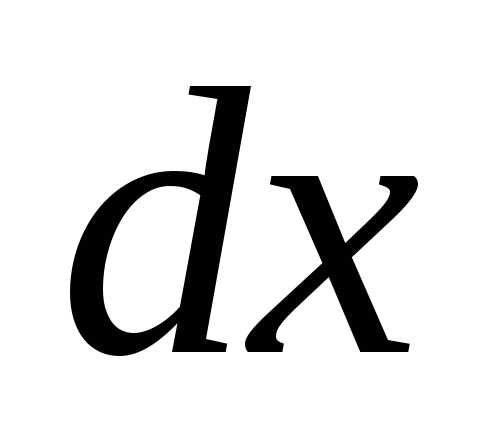 =ln(
=ln(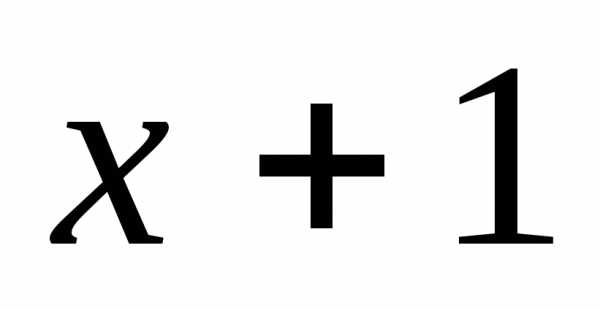 )
)
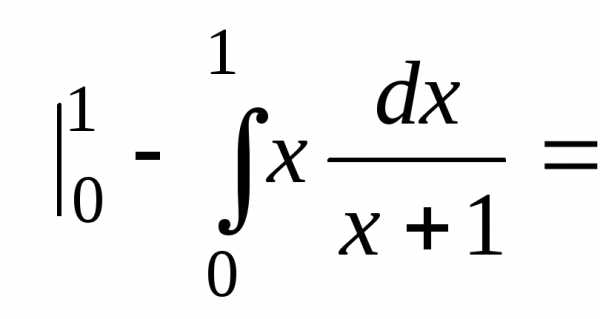 ln2-
ln2-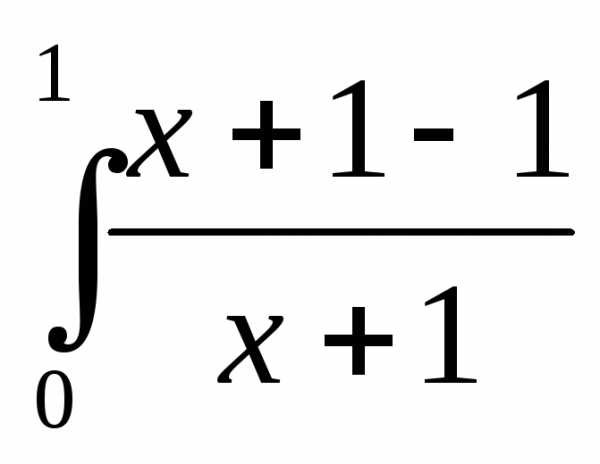
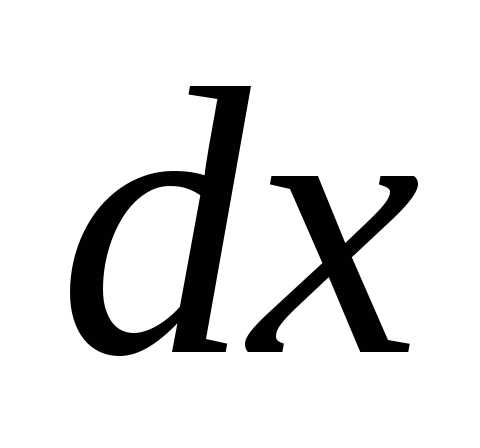 =
=
=ln2-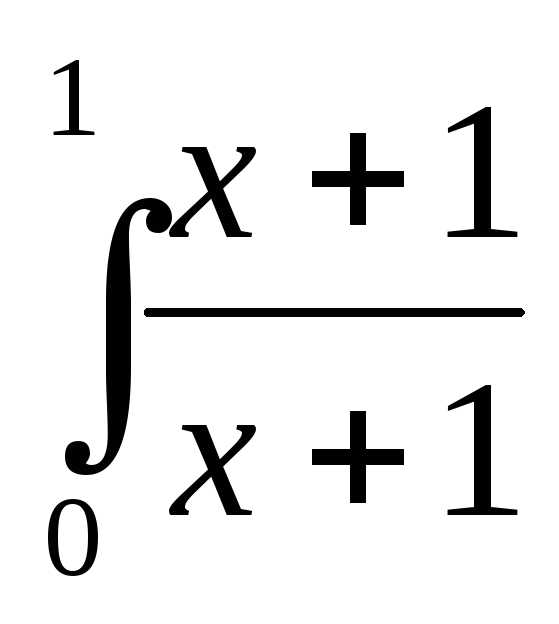
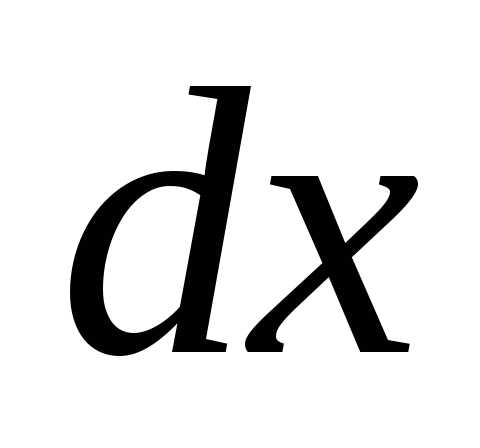 +
+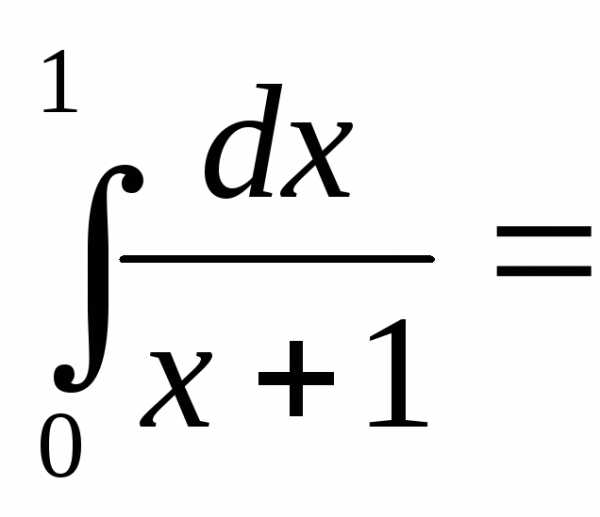 ln2-x
ln2-x ln(
ln(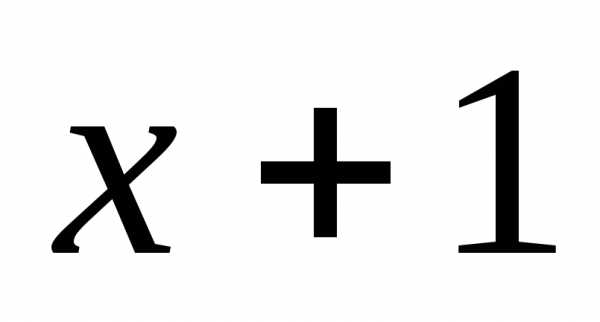 )
)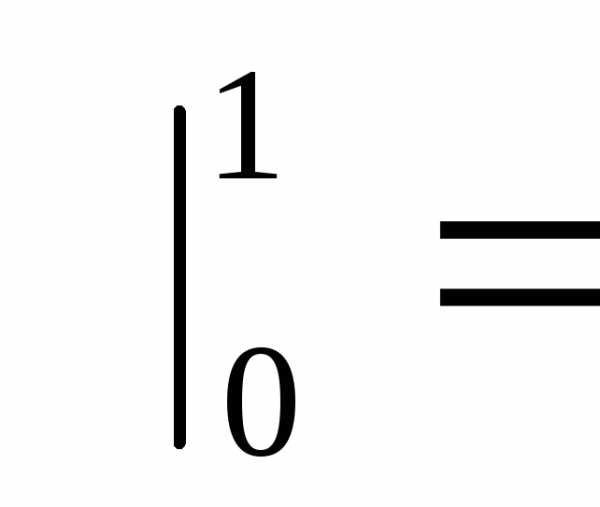
=ln2-(1-0)+ (ln2-ln1)=2ln2-1
Задания для самостоятельной работы
Вычислить значения определенных интегралов:
1)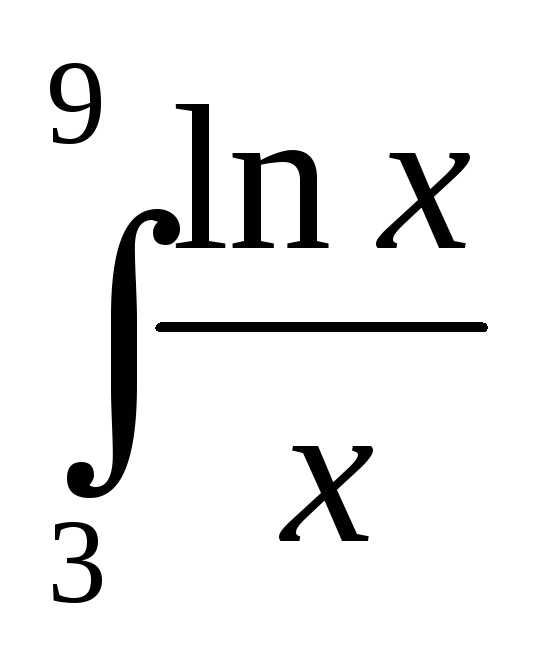 7
7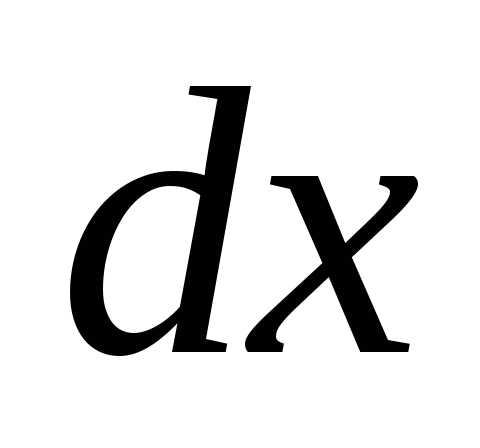 2)
2)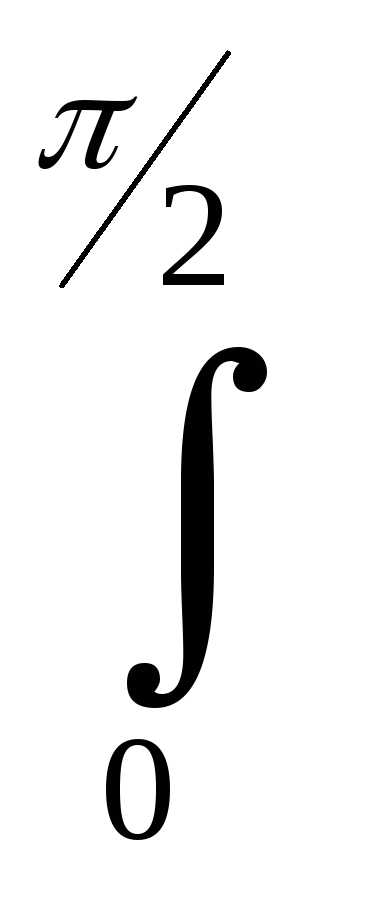
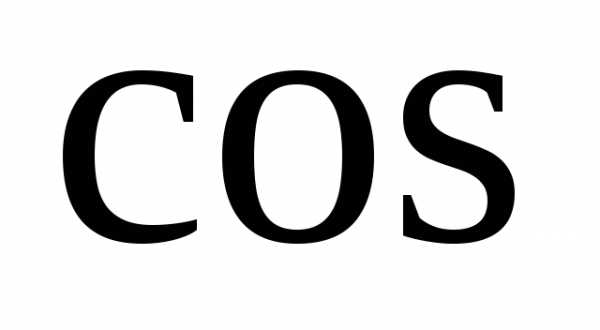 ²
²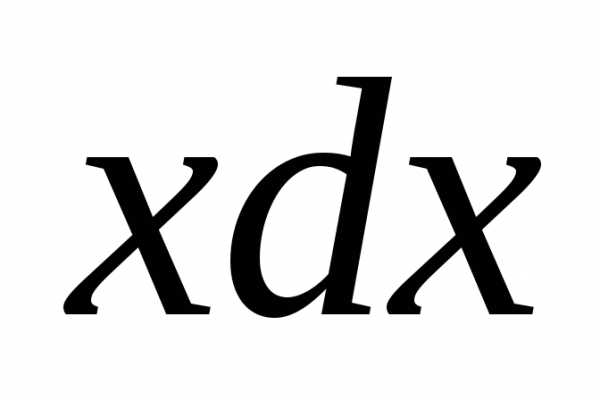 3)
3)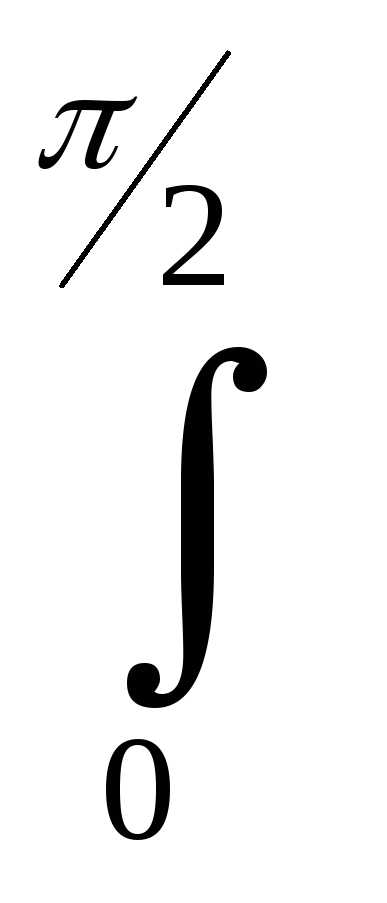
4) 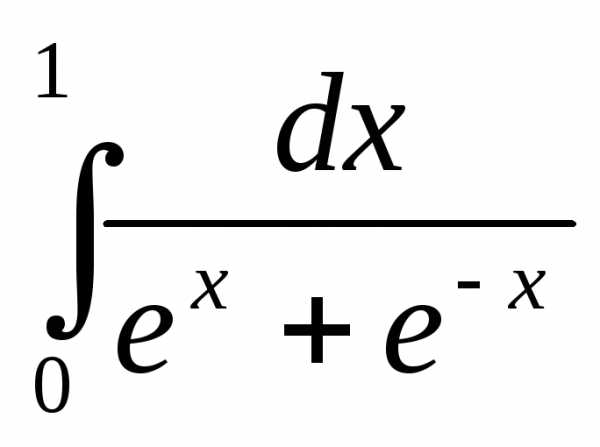 5)
5) 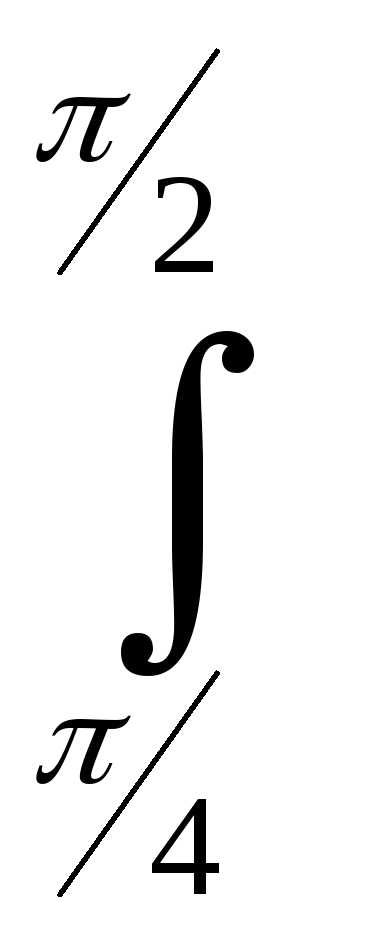
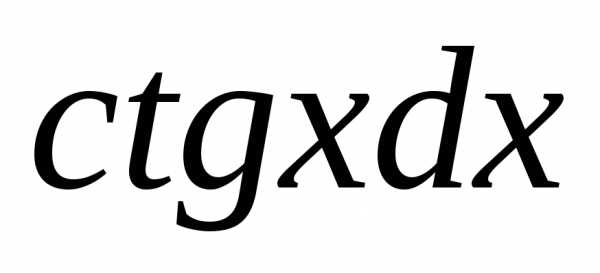 6)
6) 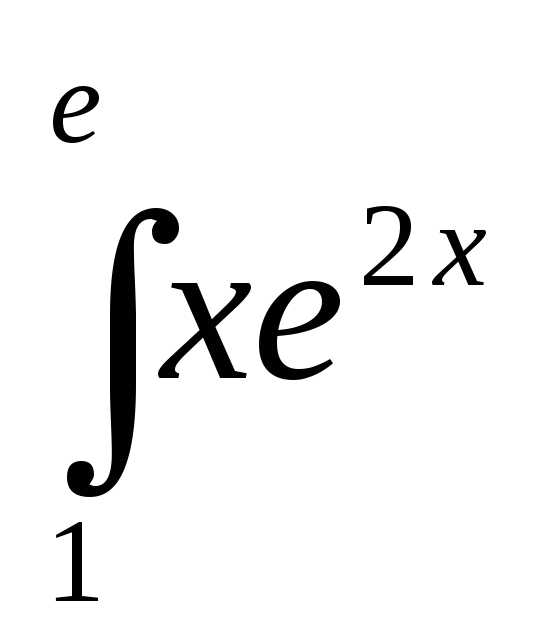
7) 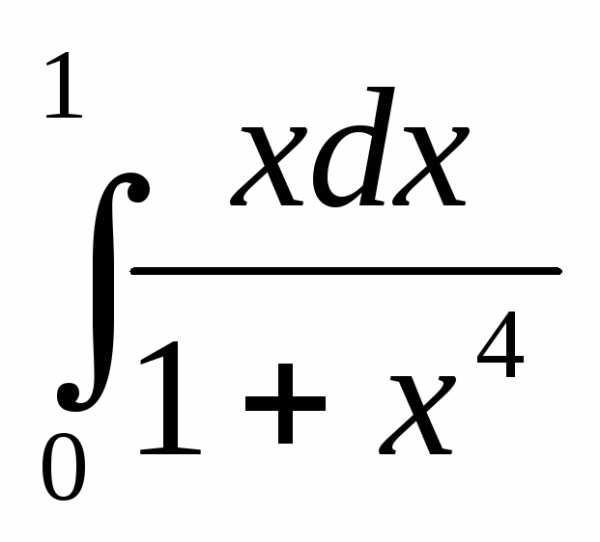 8)
8) 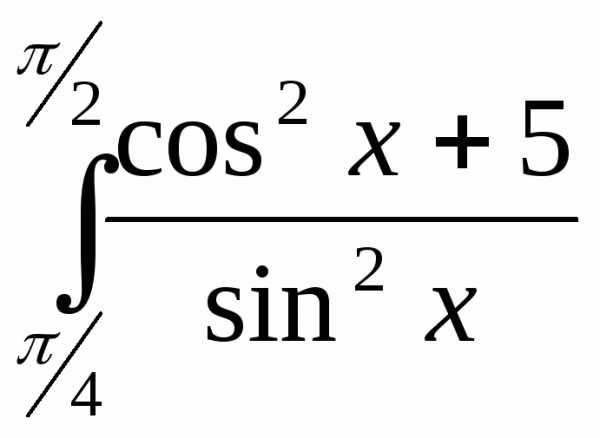
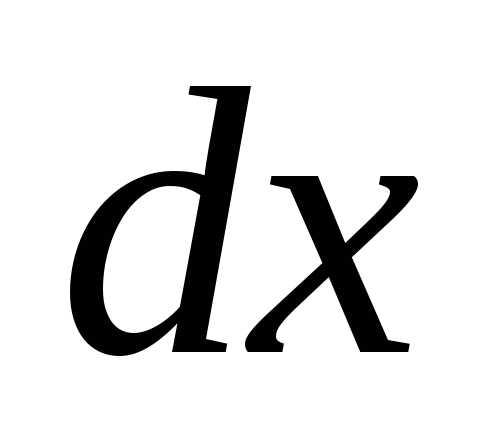 9)
9) 
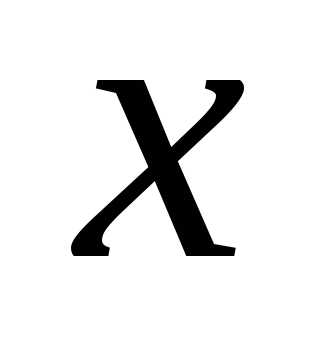 ln
ln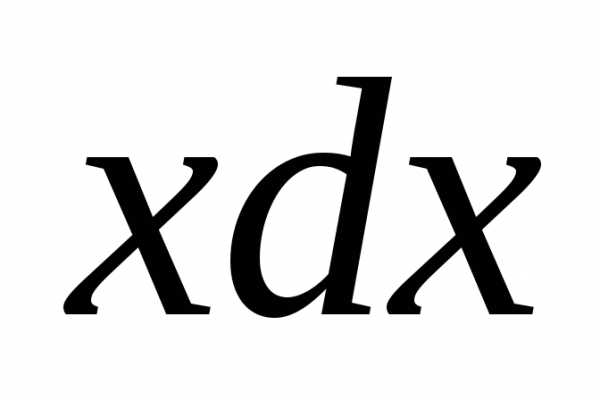
10) 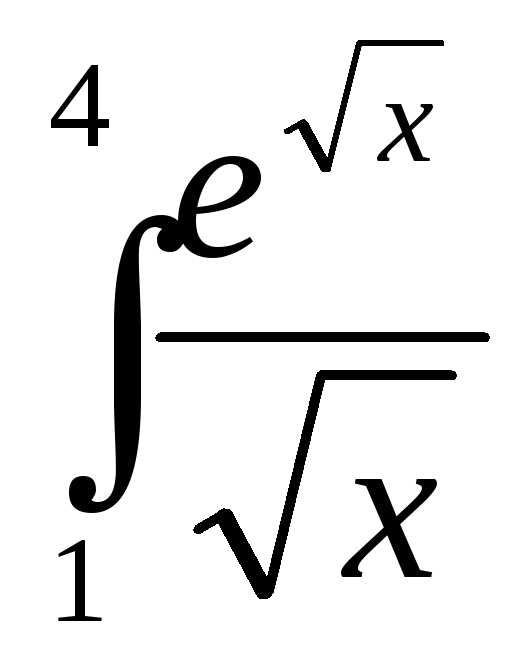 11)
11)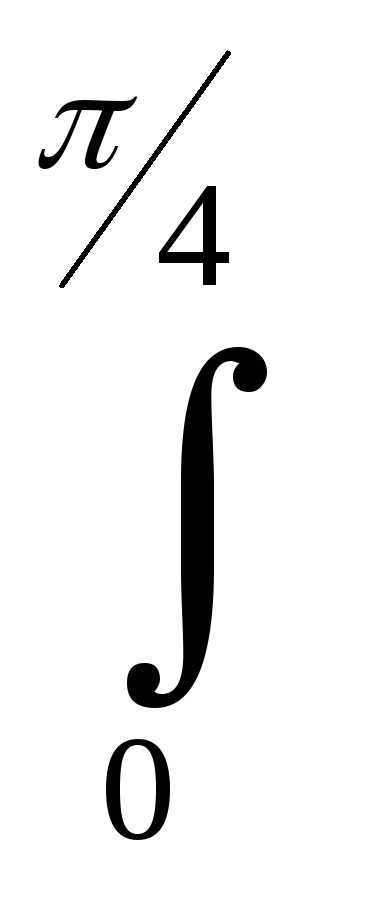
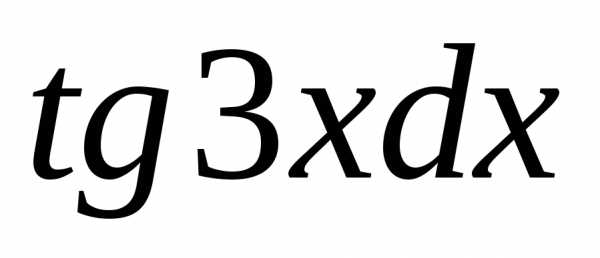 12)
12)
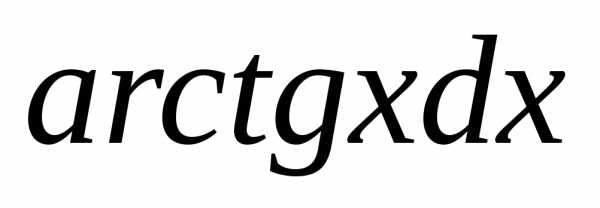
13) 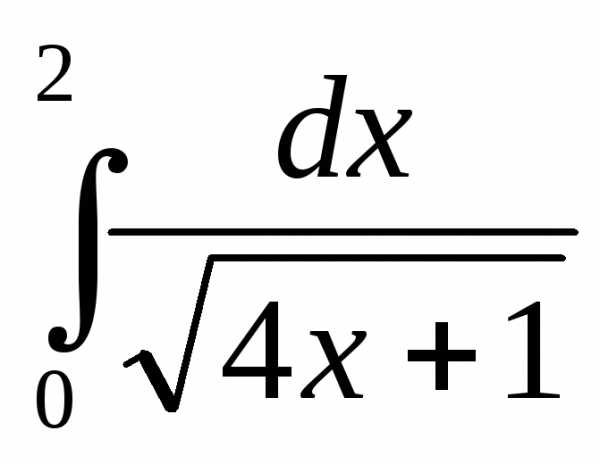 14)
14) 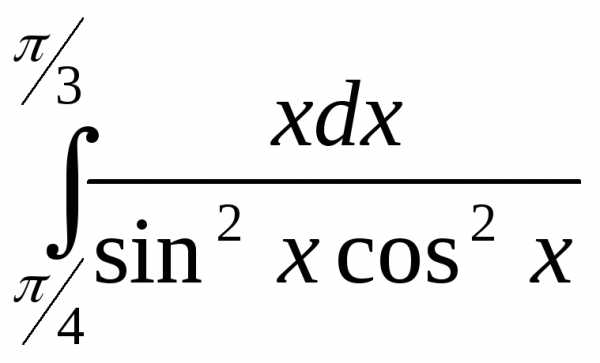 15)
15) 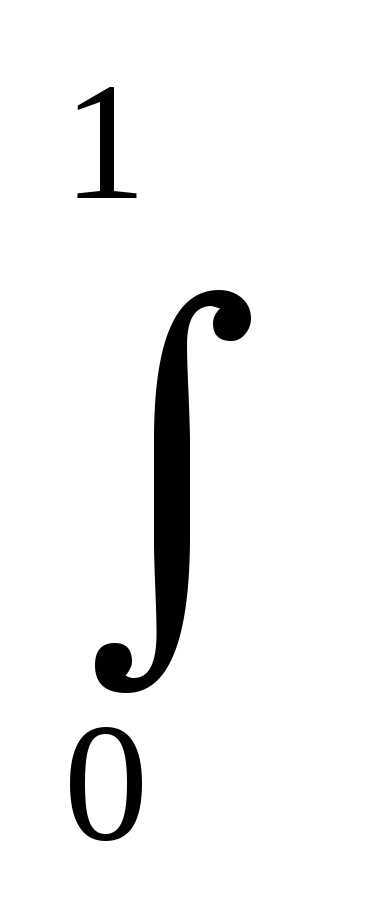 ln(
ln(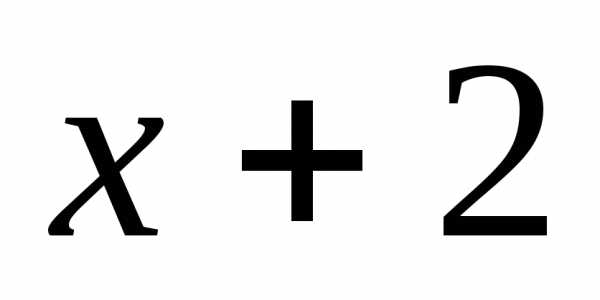 )
)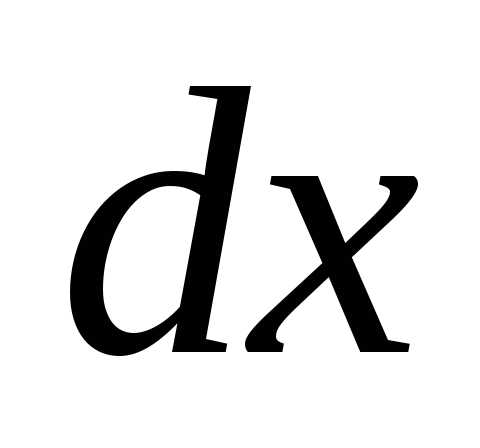
Геометрический смысл определенного интеграла.
Примеры на вычисление площадей.
Вычислить площадь фигуры, ограниченной
линиями:
и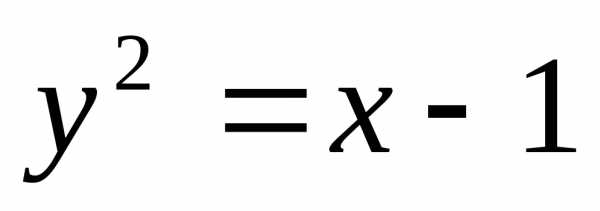 Сделать чертёж.
Сделать чертёж.
Решение:
Найдём абсциссы точек пересечения парабол из уравнения:
Изобразим на координатной плоскости ХОУ данную фигуру, ограниченную двумя параболами:
 и
и
Искомая площадь равна разности площадей двух криволинейных трапеций: S=

 =
=
 —
—
 =
=
Задания для самостоятельной работы
Вычислить площадь фигуры, ограниченной
линиями 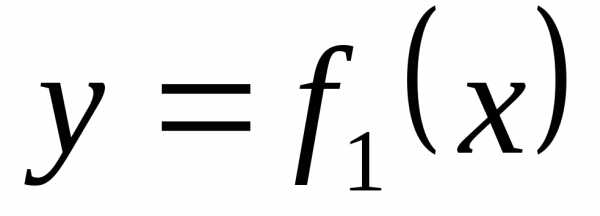 и
и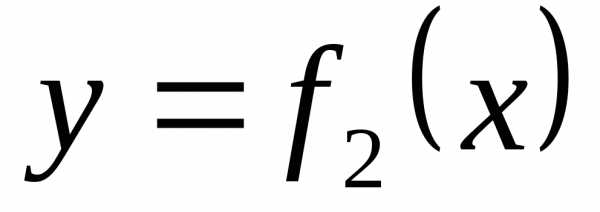 Сделать чертёж.
Сделать чертёж.
1)  =
=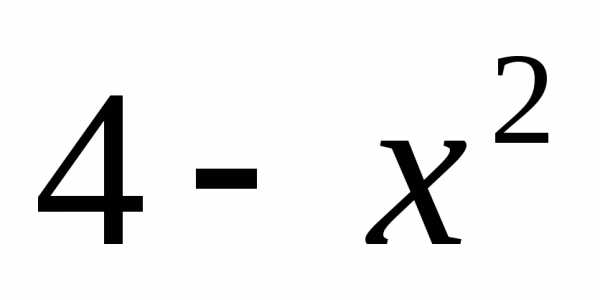 и
и =
=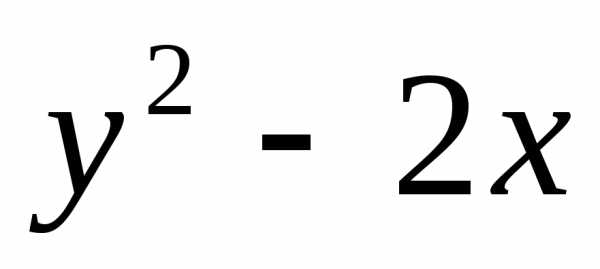
2)  =и
=и =
=
3)  =и
=и =
=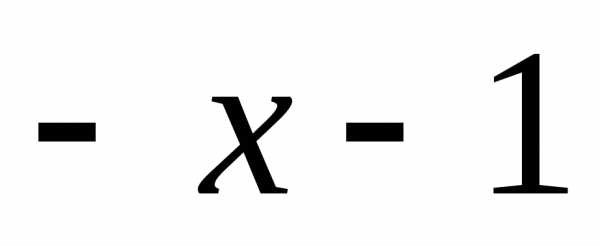
4)  =и
=и =
=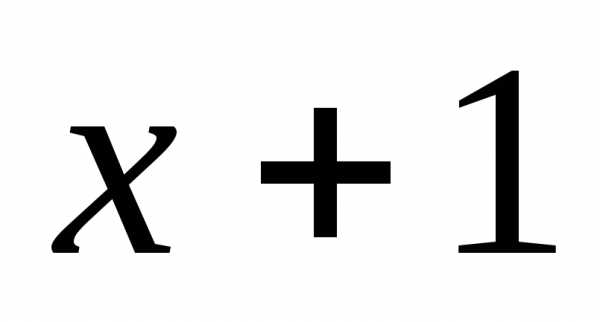
5)  =и
=и =
=
6)  =и
=и =
=
7)  =и
=и =
=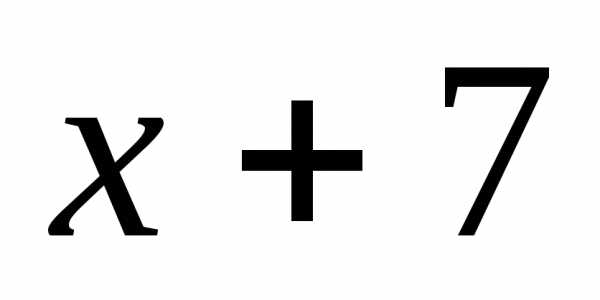
8) 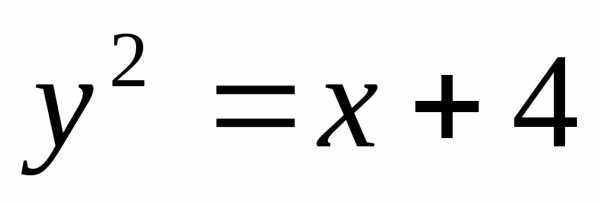 и
и =
=
9)  =и
=и =
=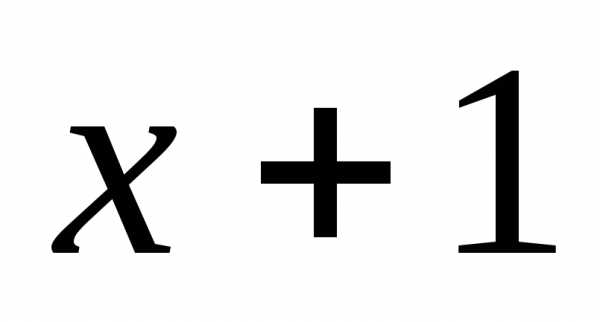
10) y=sinx,y=0,x=0,x=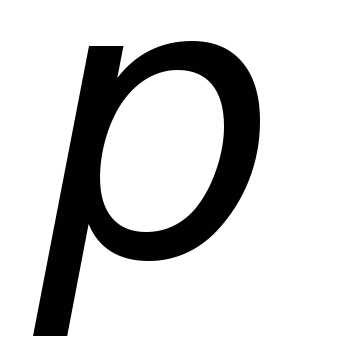
11) y=cosx,y=0,x=0,x=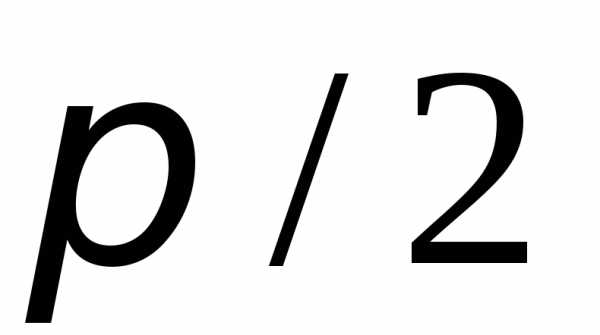 .
.
Форма контроля: Проверка решений задач и заданий
Функции двух переменных
Пример1. Построить область определения функцииz = arcsin(0,5 +x) + arcsin(0,7 +y).
Так как аргументarcsin(x) не может превышать по абсолютной величине единицу, то ограничения имеют вид:
-1 ≤ (0,5 + x) ≤ 1;
-1 ≤ (0,7 + y) ≤ 1, записав иначе, получим,
-1,5 ≤ x ≤ 0,5;
-1,7 ≤ y ≤ 0,3.
Соответствующая область определения приведена на рисунке 4.
Пример 2. Построить в плоскости0xy область определенияD функцииz=f(x,y), ограниченной прямойx=0, кривымиy=sinxи y=cosx.
Построив указанные прямую и кривые на плоскости 0xy, получим искомую область (рисунок 5). Точку пересечения кривых найдем из решения системы
y=sinx;
y=cosx;
Примеры для самостоятельного решения
Пример 3. Построить в плоскости0xy область определенияD функции
Пример 4. Построить в плоскости0xy область определенияD функции
Пример. Построить в плоскости0xy область определенияD функцииz=f(x,y),еслиD ограничена:
№5.Прямымиx = 0;y=1 и кривой y=tgx;
№6. Прямымиy = 0;y=x; y=1;y=3—x;
№7. Прямымиy = 0;y=1 и кривыми y=x2;y=(x-3)2;
№8. Прямымиx = 4;y=0 и кривой y=x1/2;
№9. Прямымиy=0 и кривой y=1 –x2.
Линии уровня.
Пример 10.В плоскости0xyопределено скалярное поле как расстояниеR(x,y) от заданной точкиM0(x0,y0). Построить линии уровней для заданного скалярного поля.
Зафиксировав конкретное расстояние R(x,y) =R0от заданной точки, найдем токи равноудаленные отM0(x0,y0). Эти точки образуют окружность с центромM0(x0,y0) и радиусомR0. ПридаваяRразличные значения, получим линии уровня — системуконцентрических окружностей с общим центром в точкеM0(x0,y0).
Если аналогичное скалярное поле задано в трехмерном пространстве, то поверхностями уровня будут вложенные друг в друга сферы.
Пример 11. Скалярное поле задано на плоскости0xyкак расстояние от заданной прямойAx+By+C=0. Построить линии уровня скалярного поля.
Все точки, равноудаленные от прямой на фиксированное расстояние, образуют две параллельные прямые по обе стороны от заданной. Задавая различные расстояния, получим систему параллельных прямых.
Пример 12.Пусть скалярное поле задано в виде функции двух переменныхz(x,y)=x2+y2— параболоид вращения. Построить линии уровня для заданного скалярного поля.
Будем придавать с равными шагами различные фиксированные значения функции z(x,y)=Ci. В результате получим уравнения окружностей с различными радиусамиx2+y2=Ci. В результате сечения трехмерного графика (рисунок 2) плоскостями параллельными плоскости0xyпо высоте получим окружности.
Их проекция на плоскость 0xyпредставляет собой так же систему концентрических окружностей.
В примере следует обратить внимание на то, что несмотря на равномерное разбиении по высоте, радиусы окружностей возрастают неравномерно (рисунок 7). Чем быстрее изменяется функция, чем круче ее график, тем плотнее располагаются линии уровня — окружности.
studfiles.net
Определённый интеграл, его свойства
Пусть на отрезке 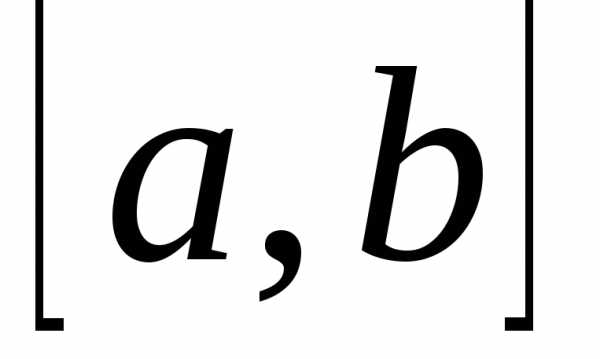 задана функция y=f(x).
Разобьем отрезок
задана функция y=f(x).
Разобьем отрезок 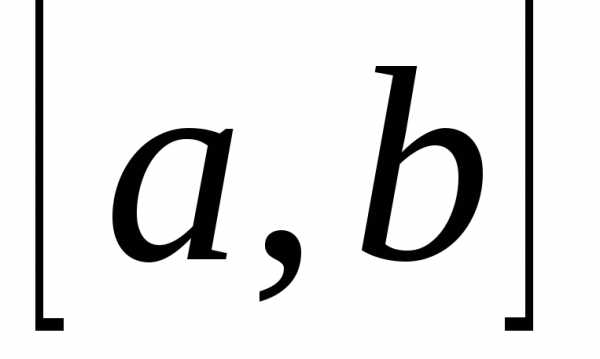 на n элементарных отрезков точками
.
На каждом отрезке
на n элементарных отрезков точками
.
На каждом отрезке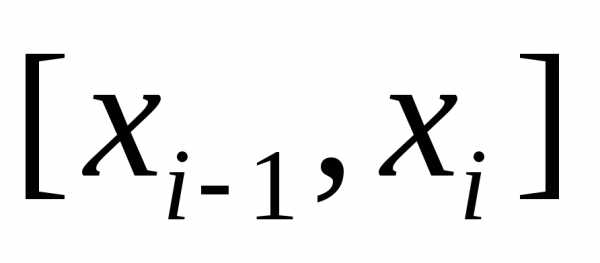 разбиения выберем некоторую точку
разбиения выберем некоторую точку и положим,
где.
Сумму вида
и положим,
где.
Сумму вида
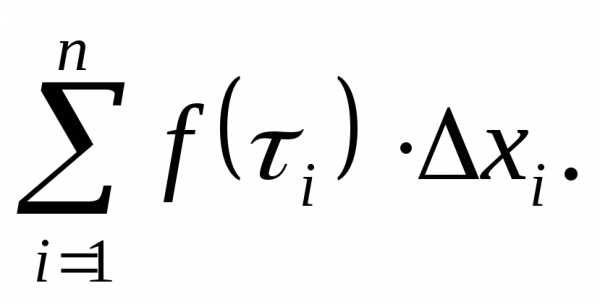
будем называть интегральной
суммой для функции y=f(x) на 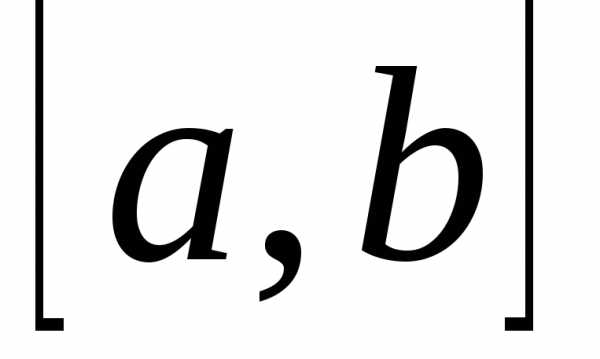 .
Очевидно, что интегральная сумма зависит
как от способа разбиения отрезка
.
Очевидно, что интегральная сумма зависит
как от способа разбиения отрезка 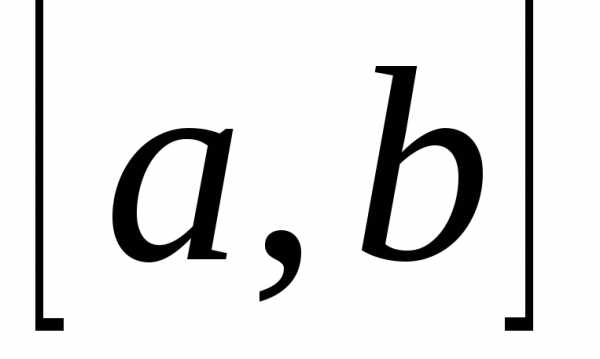 точками
,
так и от выбора точекна каждом из отрезков разбиения,.
точками
,
так и от выбора точекна каждом из отрезков разбиения,.
Если существует
предел 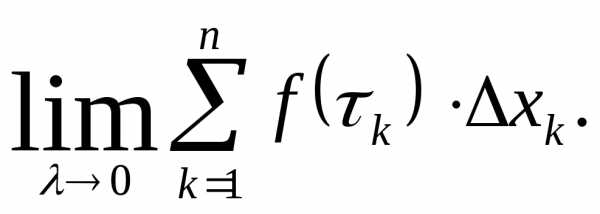 ,
не зависящий от способа разбиения
отрезка
,
не зависящий от способа разбиения
отрезка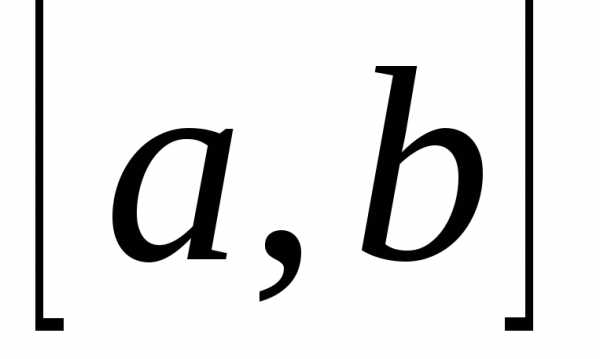 и выбора точек
и выбора точек ,
то этот предел будем называтьопределённым
интегралом функции f(x) на отрезке
,
то этот предел будем называтьопределённым
интегралом функции f(x) на отрезке 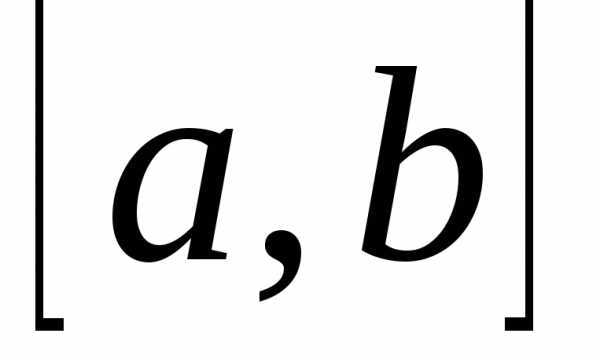 и обозначать
символом
и обозначать
символом 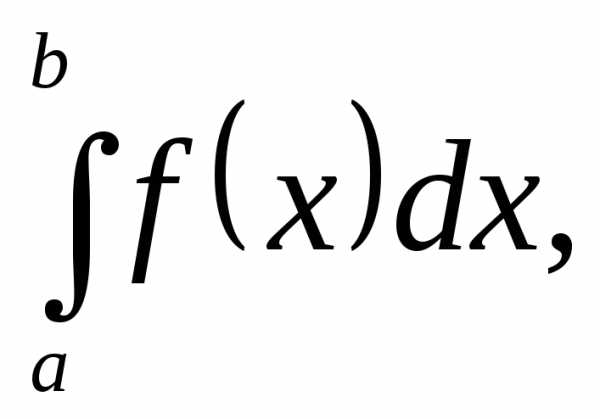 т.е.
т.е.
Функция f(x) в этом случае называется интегрируемой на отрезке 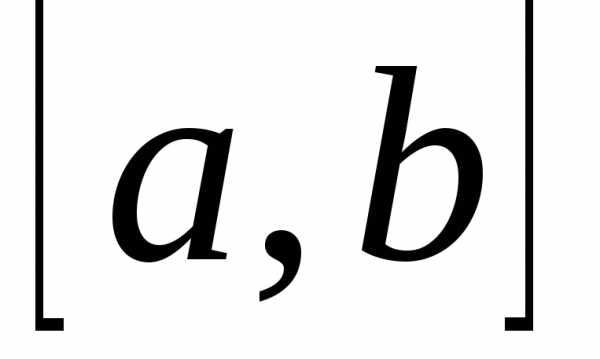 .
При этомf(x) называется подынтегральной
функцией, f(x)dx – подынтегральным
выражением, а
числа a и b – пределами
интегрирования (a – нижний предел, b – верхний предел), а сумма
.
При этомf(x) называется подынтегральной
функцией, f(x)dx – подынтегральным
выражением, а
числа a и b – пределами
интегрирования (a – нижний предел, b – верхний предел), а сумма 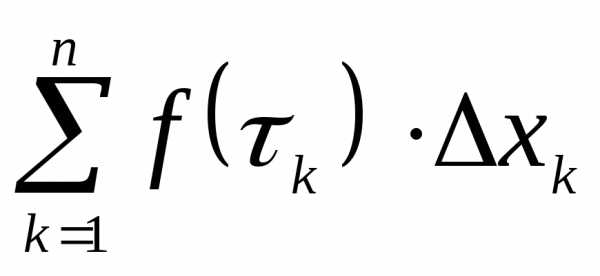 –интегральной
суммой.
–интегральной
суммой.
Теорема. Если
функция f(x) непрерывна на отрезке 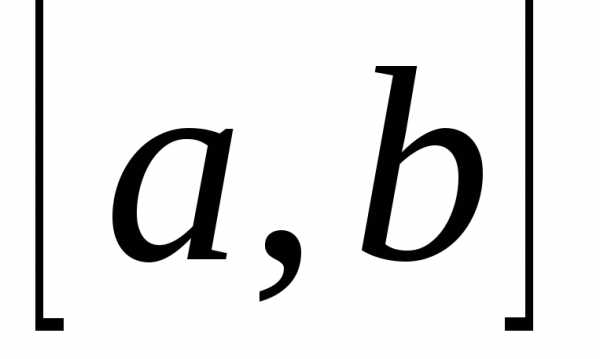 ,
то она интегрируема на этом отрезке.
,
то она интегрируема на этом отрезке.
Свойства определённого интеграла
1. 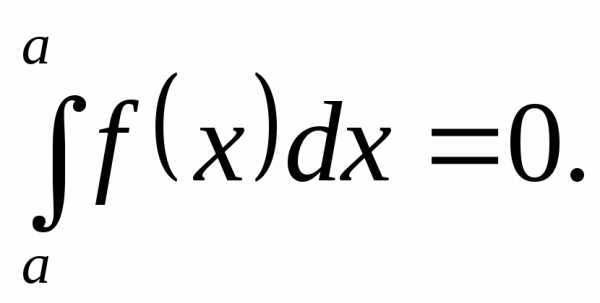
2. Постоянный множитель можно выносить за знак определённого интеграла:
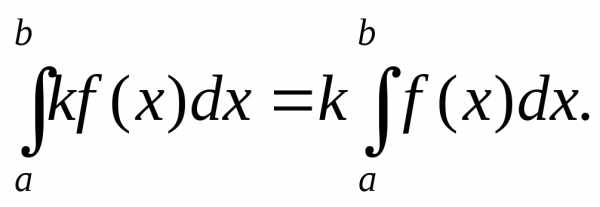
3. Определённый интеграл от суммы двух функций равен сумме определённых интегралов от этих функций:
4. При перестановке пределов интегрирования определённый интеграл меняет знак на противоположный:
5. Интеграл по отрезку равен сумме интегралов по его частям:
где a<c<b.
6. Теорема об оценке интеграла
Если для 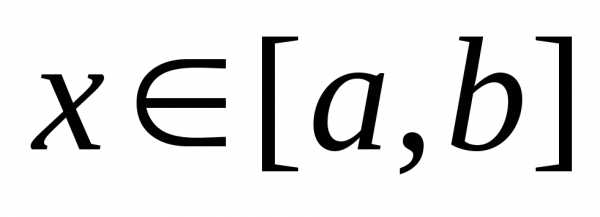 ,
тогда значения интеграла от этой функции
не менее произведения m на длину отрезка и не более произведения M на длину отрезка.
,
тогда значения интеграла от этой функции
не менее произведения m на длину отрезка и не более произведения M на длину отрезка.
7. Теорема о среднем значении
Если f(x)
непрерывна на отрезке  ,
то существует такое значение
,
то существует такое значение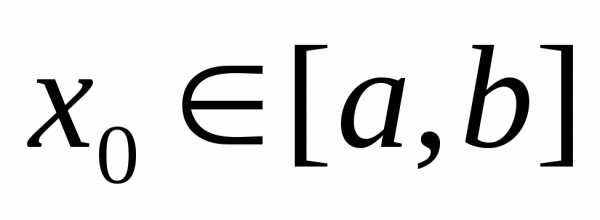 ,
что f(x0)=fср – среднее значение f на отрезке.
,
что f(x0)=fср – среднее значение f на отрезке.
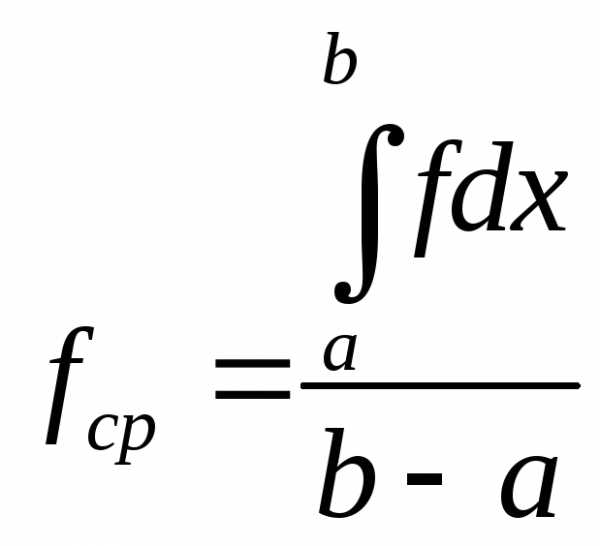
2.1.4 Теорема Ньютона-Лейбница
Если функция
f(x) непрерывна на отрезке 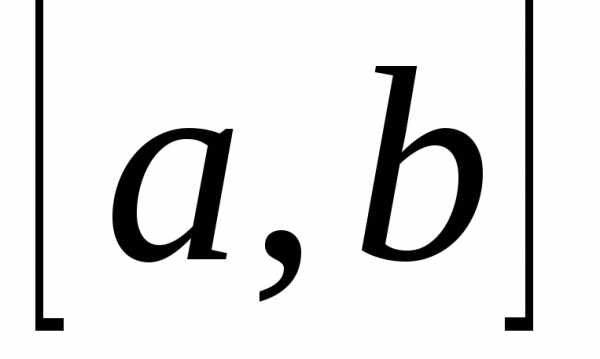 и F(x) – первообразная функции f(x) на этом
отрезке, то
и F(x) – первообразная функции f(x) на этом
отрезке, то
Эта формула называется формулой Ньютона-Лейбница.
При вычислении интегралов ее часто записывают в виде
Например, 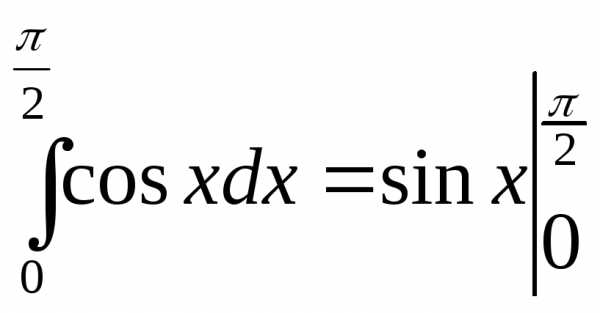 =
=
Замена переменной в определённом интеграле
Предположим, что
функция f(x) непрерывна на отрезке 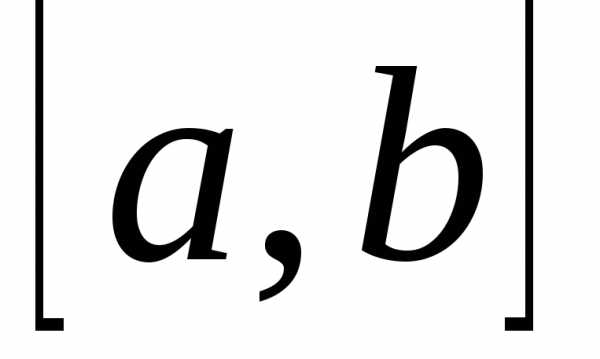 ,
функция
,
функция имеет на отрезке
имеет на отрезке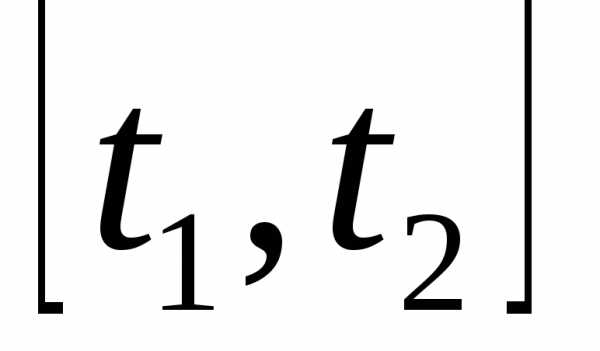 непрерывную производную, при этомиТогда
непрерывную производную, при этомиТогда
Пример 9. Найдём 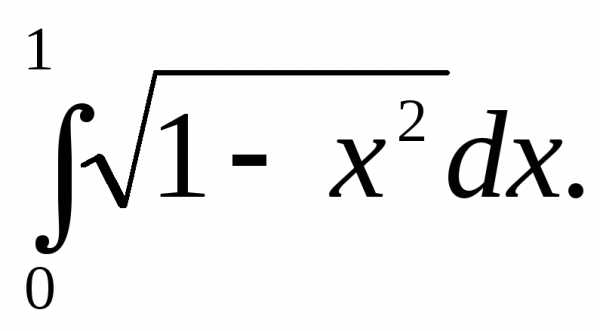
Решение:
Воспользуемся
подстановкой x=sint;
тогда
.
Найдём новые пределы интегрирования:
еслих=0,
то t=0,
если х=1,
то 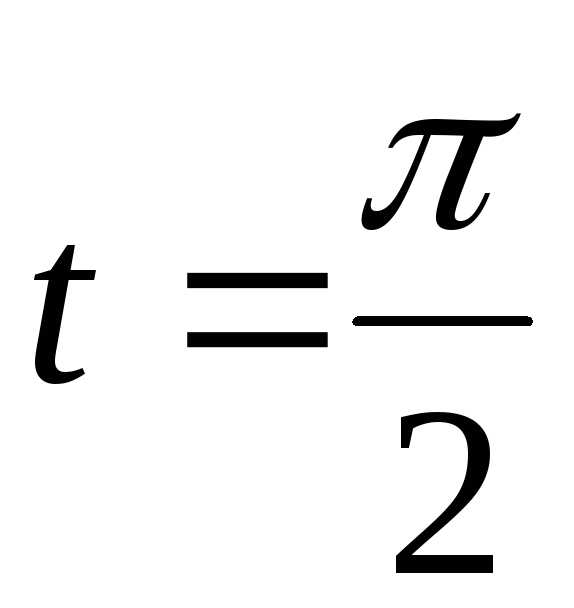 .
Получим
.
Получим
.
Интегрирование по частям
Пусть u=u(x),
v=v(x) –
непрерывно дифференцируемые на  функции. Тогда справедлива формула
функции. Тогда справедлива формула
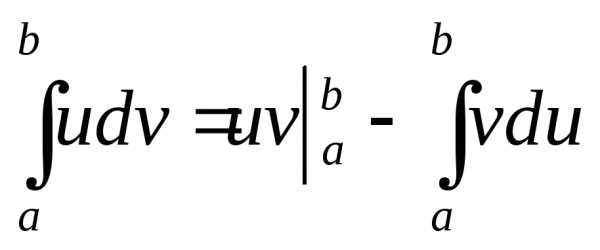
или
Пример 10. Найти 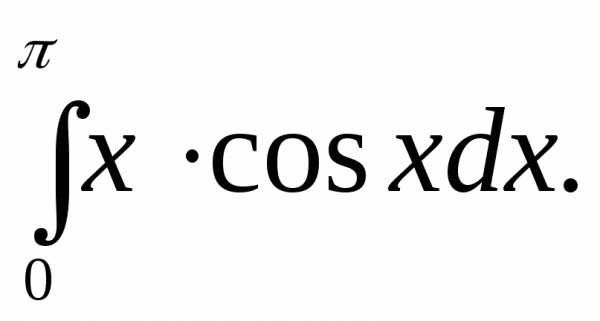
Решение: Положим u=x, откуда
Согласно формуле находим
2.1.5 Геометрические приложения определённого интеграла Вычисления площадей плоских фигур
Пусть функция f(x) непрерывна на отрезке 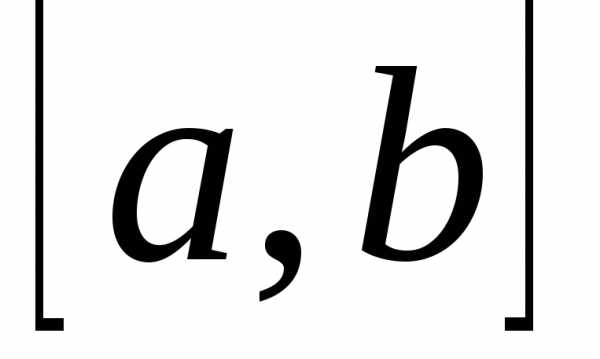 .
Если при этомf(x)
.
Если при этомf(x)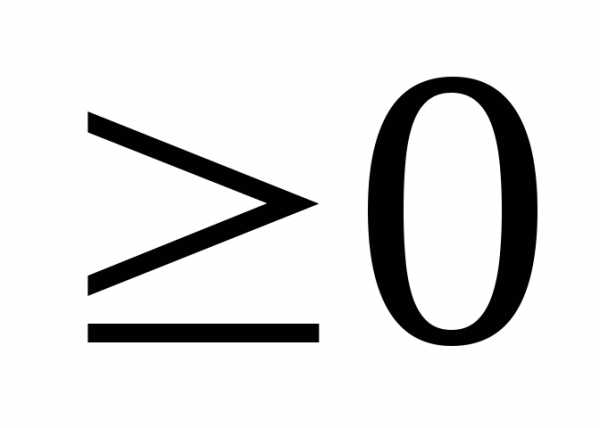 на этом отрезке, то площадьS криволинейной трапеции, ограниченной
линиями y=f(x),
y=0, x=a, x=b,
выразится с помощью интеграла:
на этом отрезке, то площадьS криволинейной трапеции, ограниченной
линиями y=f(x),
y=0, x=a, x=b,
выразится с помощью интеграла:
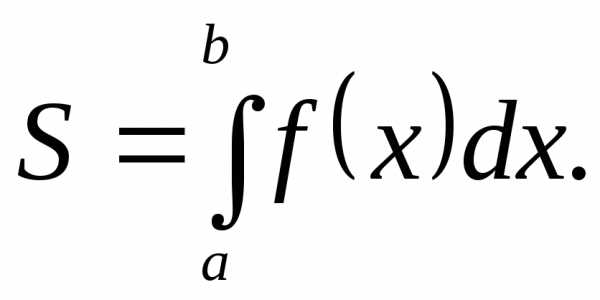
Замечания:
1. Если же 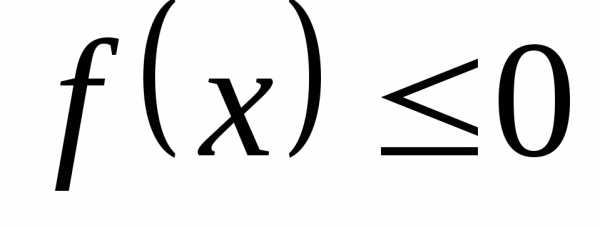 на
на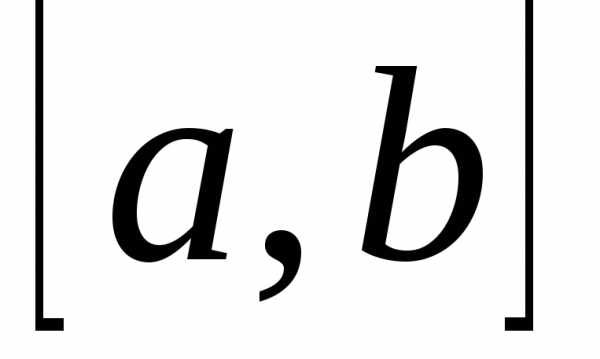 ,
то –f(х)
,
то –f(х) на этом отрезке. Поэтому площадьS соответствующей криволинейной трапеции
находится по формуле
на этом отрезке. Поэтому площадьS соответствующей криволинейной трапеции
находится по формуле
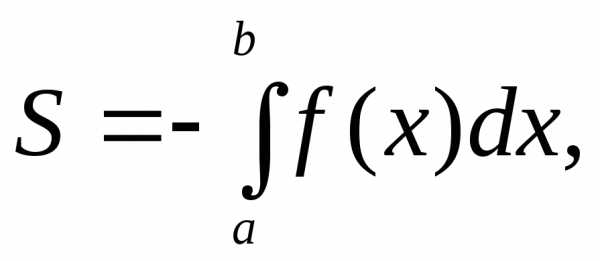
или
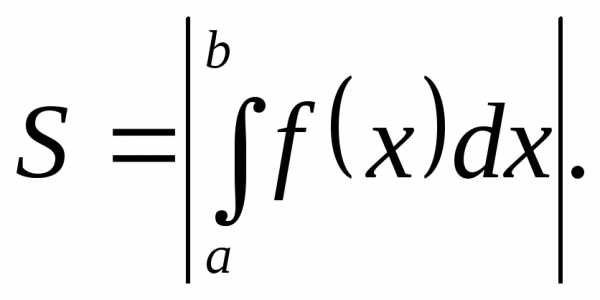
Наконец, если линия y=f(x) пересекает ось Ох,
то отрезок 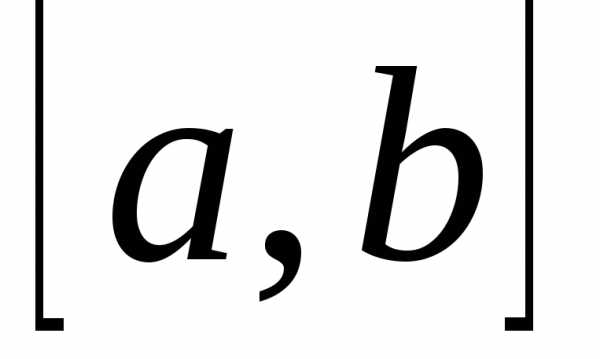 надо разбить на части, в пределах которыхf(x) не меняет знака, и к каждой части применить
ту из формул, которая ей соответствует.
надо разбить на части, в пределах которыхf(x) не меняет знака, и к каждой части применить
ту из формул, которая ей соответствует.
2. Площадь криволинейной фигуры, ограниченной сверху графиком функции y2=f2(x), снизу – графиком функции y1=f1(x), слева и справа прямыми x=a, x=b, вычисляется по формуле:

3. Площадь криволинейной фигуры, ограниченной справа графиком функции x2=2(y), слева – графиком функции x1=1(y), снизу и сверху прямыми y=c, y=d, вычисляется по формуле:
Пример 11. Найти площадь плоской фигуры, ограниченной графиком функции y = sinx и осью абсцисс при условии .
Решение:
Разобьём отрезок 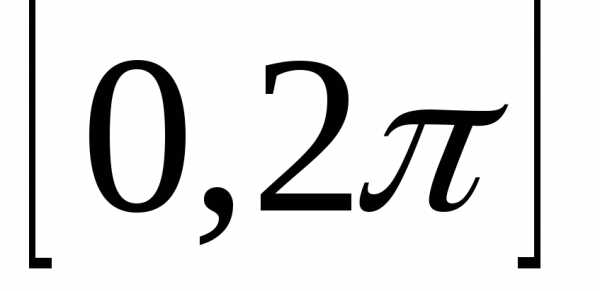 на два отрезка:
на два отрезка: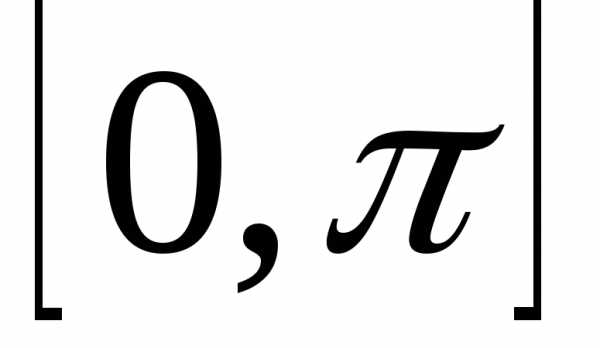 и
и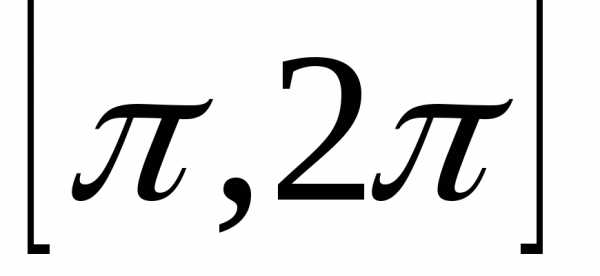 .
На первом из них sinx
.
На первом из них sinx ,
на второмsinx
,
на второмsinx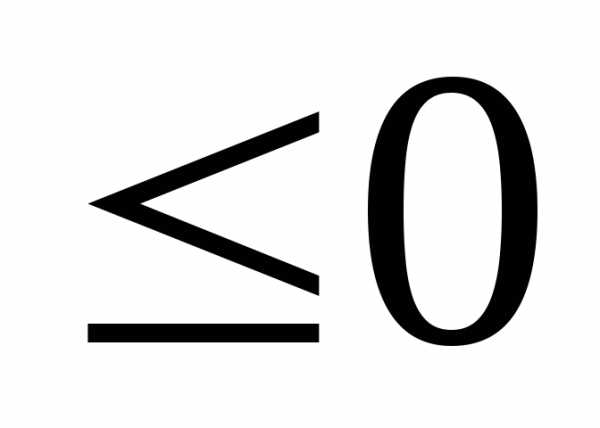 .
Тогда, используя формулы, находим искомую
площадь:
.
Тогда, используя формулы, находим искомую
площадь:
studfiles.net
Определенный интеграл.
Пора познакомиться с мощнейшим средством исследования в математике, физике, механике и других точных дисциплинах. Это средство — определенный интеграл. В средней школе определенный интеграл применяют при вычислениях площадей криволинейных трапеций, объемов тел вращения, нахождении моментов инерции и т.д.
Что такое определенный интеграл? Чем он отличается от неопределенного, с которым мы уже достаточно знакомы.
Сравните:
a и b — это границы, в которых изменяется переменная интегрирования х.
Сравниваем далее:
Неопределенный интеграл графически представляет собой семейство кривых, совмещаемых параллельным переносом (11.1.9).
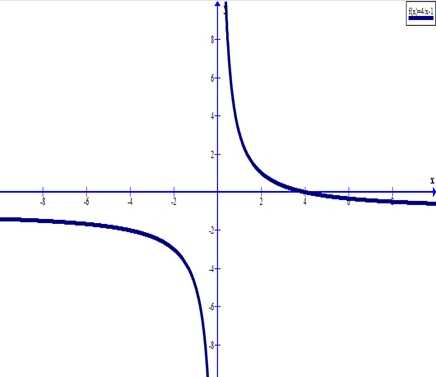
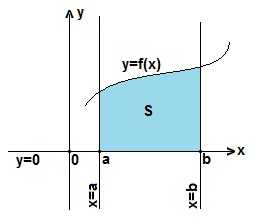 Определенный интеграл (см. рисунок слева) представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f (x), снизу — осью Ох, а слева и справа прямыми x=a и х=b.
Определенный интеграл (см. рисунок слева) представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f (x), снизу — осью Ох, а слева и справа прямыми x=a и х=b.
Значение определенного интеграла есть площадь S этой криволинейной трапеции:
Рассмотрим примеры на вычисление определенного интеграла.
Пример 1.
Найдем первообразную F (x) для подынтегральной функции f (x)=3x²-2x+1, а затем применим формулу Ньютона-Лейбница (ф. Н-Л).
Пример 2.
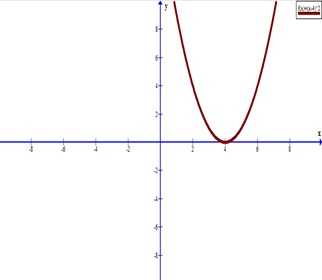
Возникает вопрос: раз определенный интеграл выражает собой площадь криволинейной трапеции, то нельзя ли увидеть эту криволинейную трапецию? А можно! Проиллюстрируем пример 2.
Полученный результат
выражает площадь криволинейной трапеции, ограниченной графиком функции y=(x+1)4, осью Ох и прямыми: х=0 (осью Оy) и х=1.
График функции y=(x+1)4 — парабола, ветви которой направлены вверх,
а вершина находится в точке О′(-1; 0).
Площадь этой криволинейной трапеции:
Запись имеет метки: определенный интеграл
www.mathematics-repetition.com

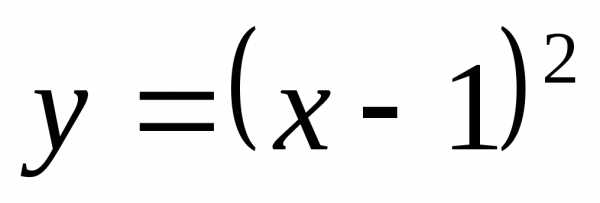 и
и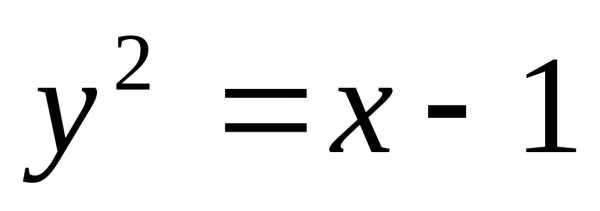

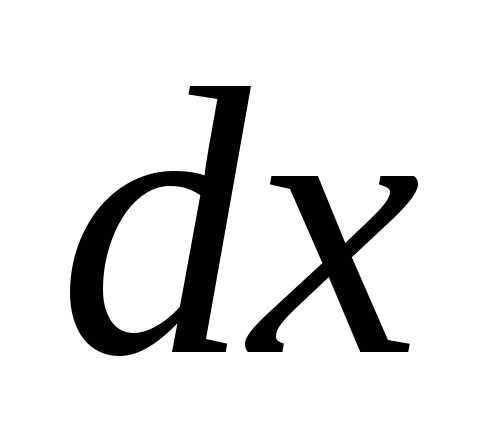 =
=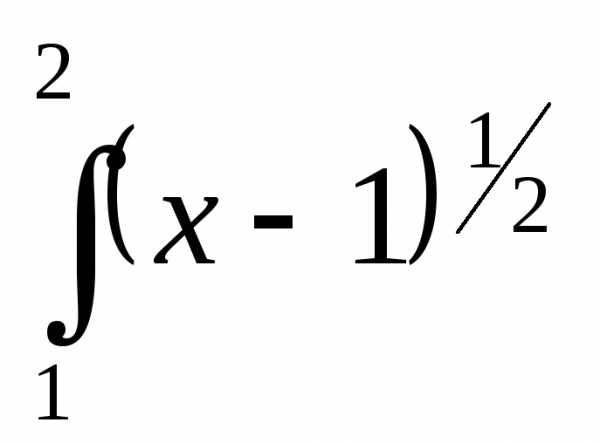
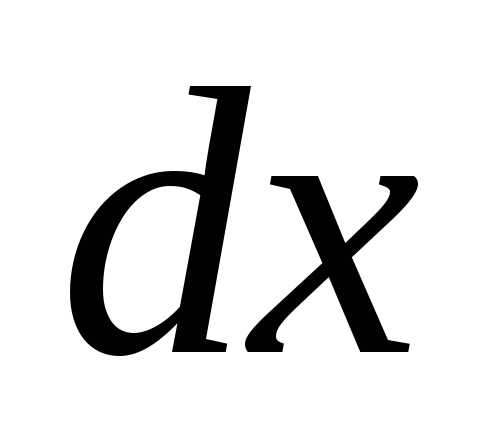 —
—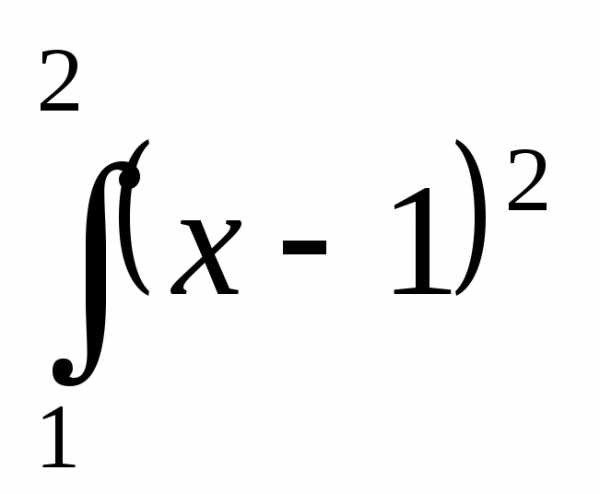
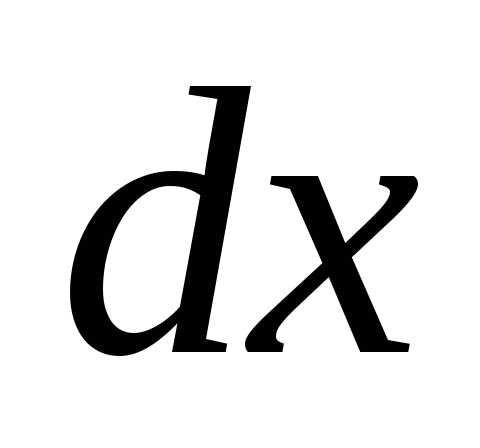 =
=
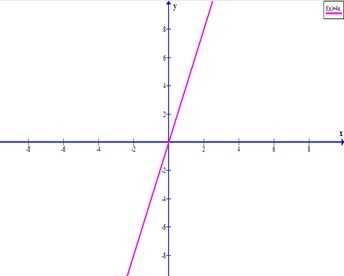
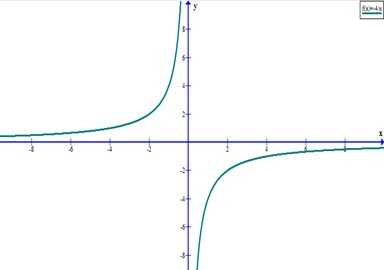









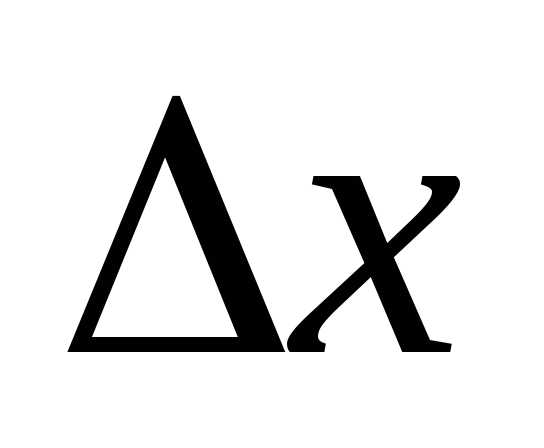 при
при 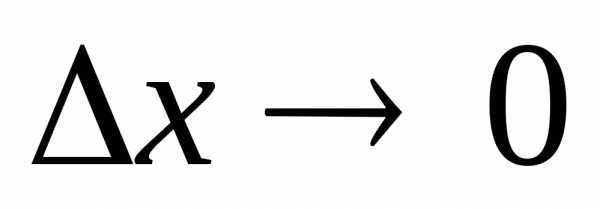 .
.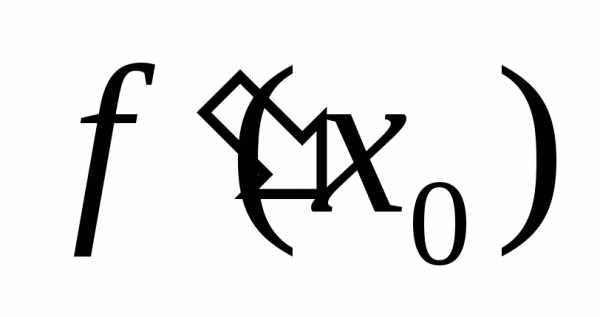 .
.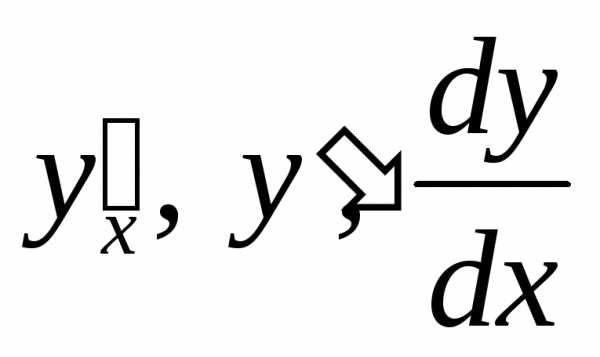 .
.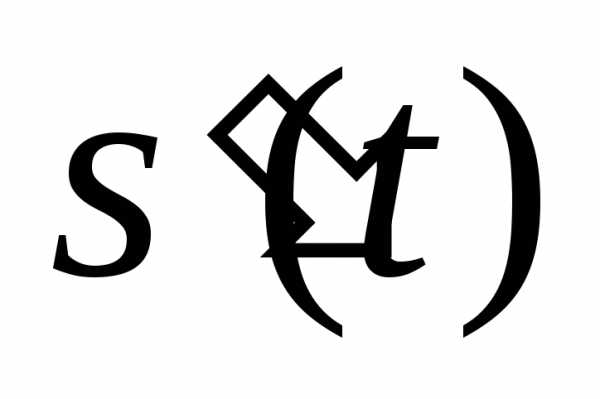 есть скорость этой точки в момент времениt.
есть скорость этой точки в момент времениt.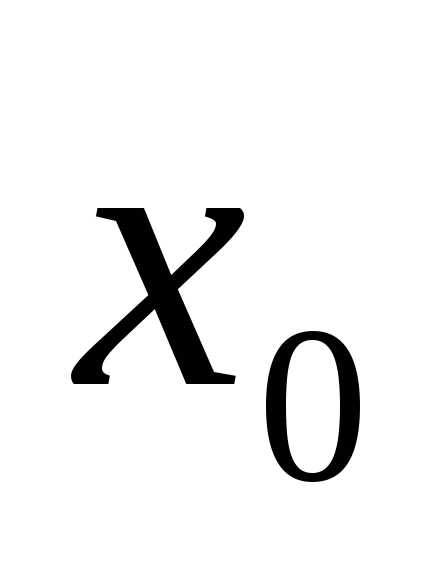 ,
то угловой коэффициент касательной к
графику функции в точкеравен
,
то угловой коэффициент касательной к
графику функции в точкеравен 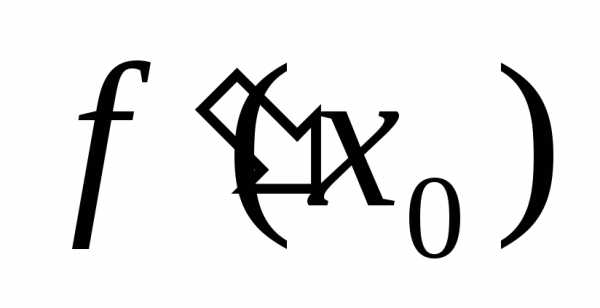 .
.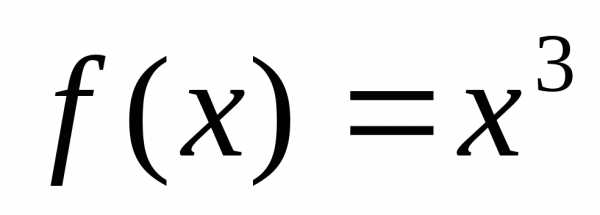 в точке
в точке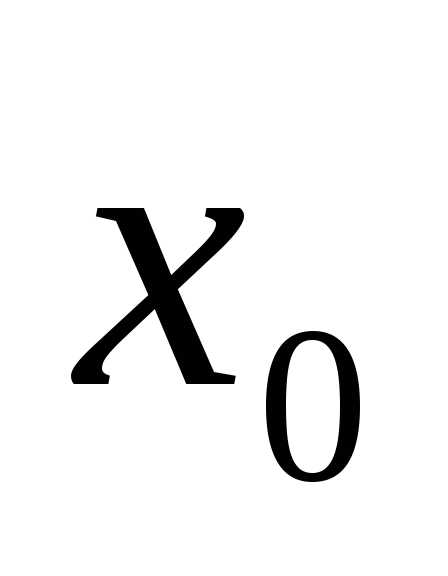 =2:
=2: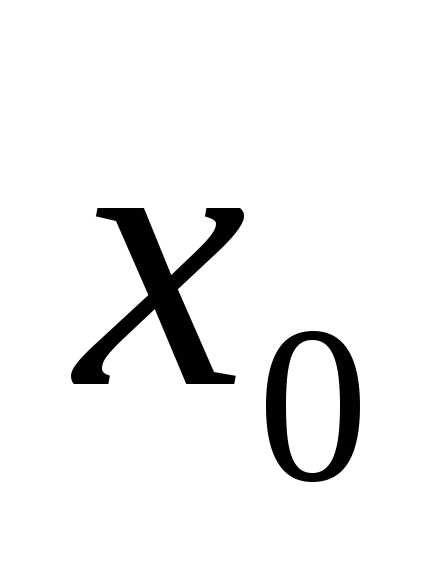 =2
приращение
=2
приращение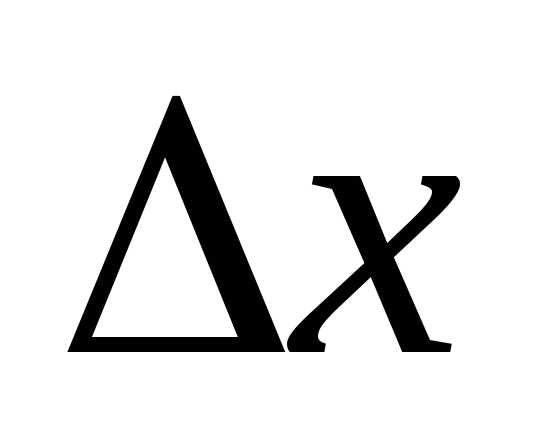 .
Заметим, что.
.
Заметим, что.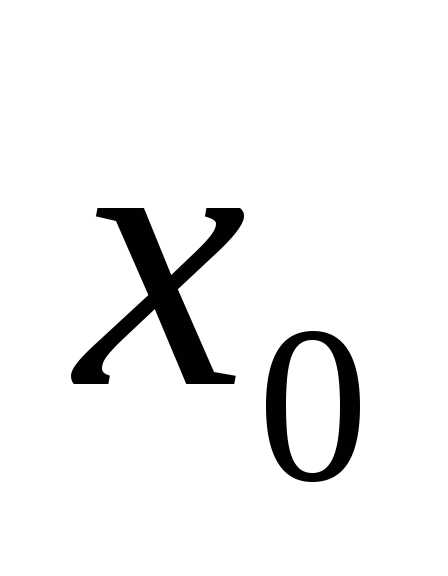 =2:
=2: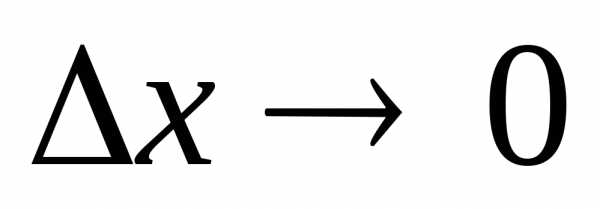 :
: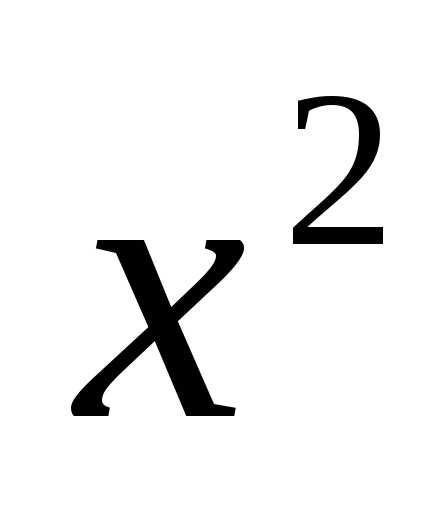 и вообщеy=
и вообщеy=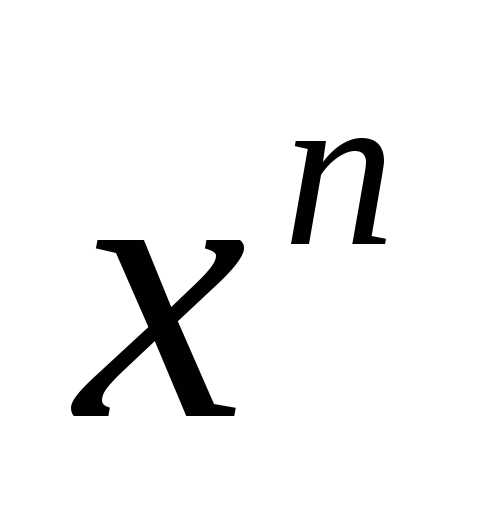 .
.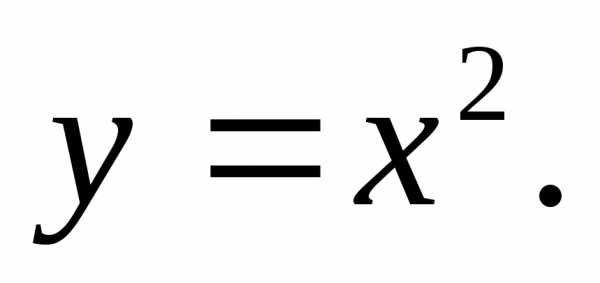
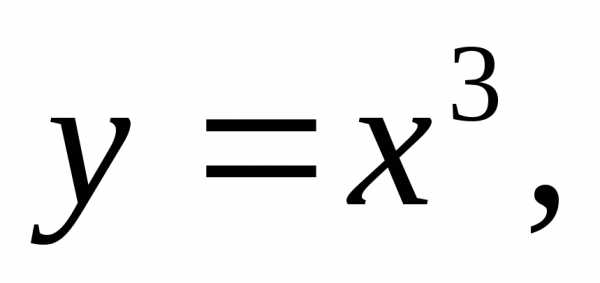 тогда
тогда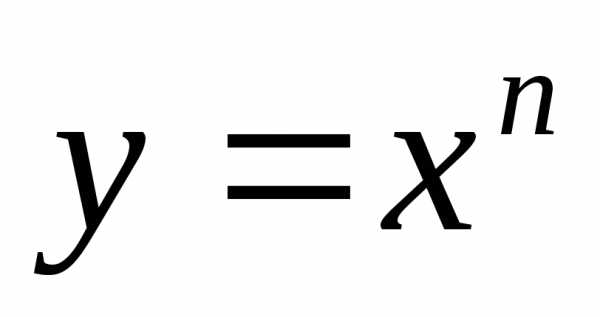 приn=1,2,3.
приn=1,2,3.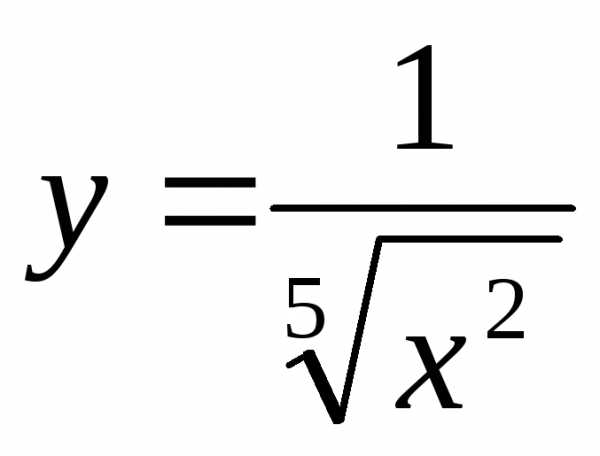 .
.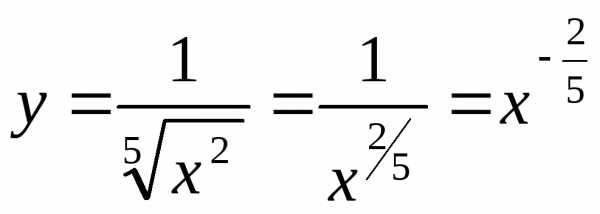 .
.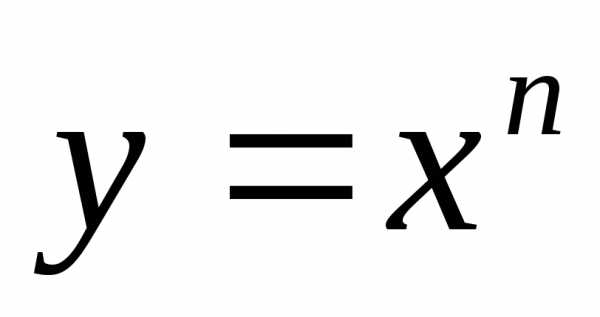 при
при 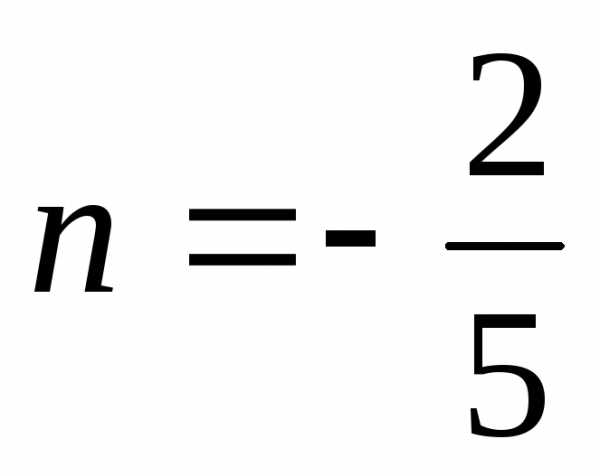 .
.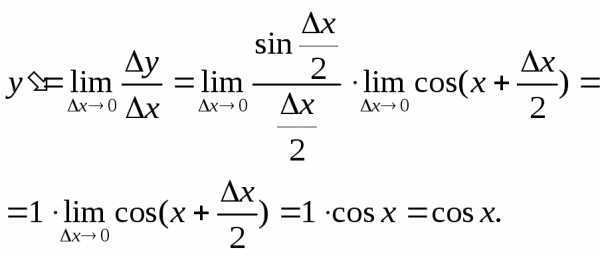
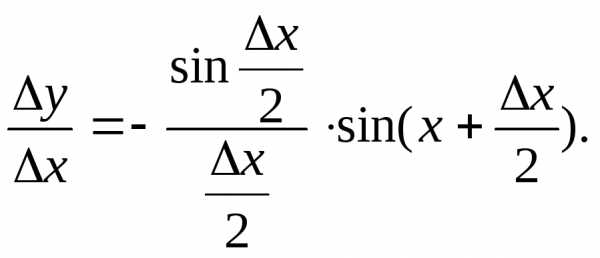

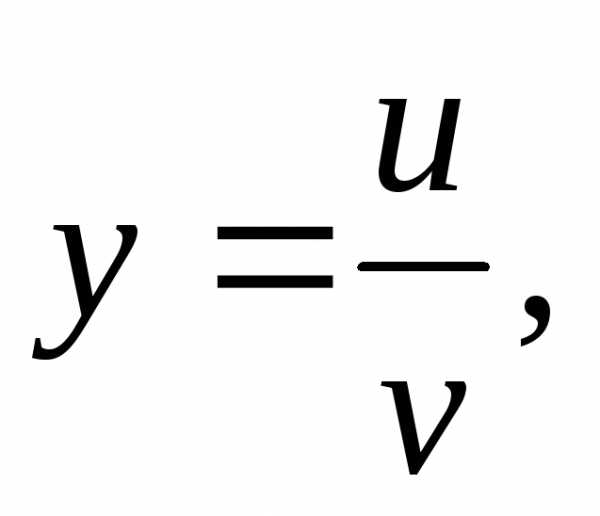 то
то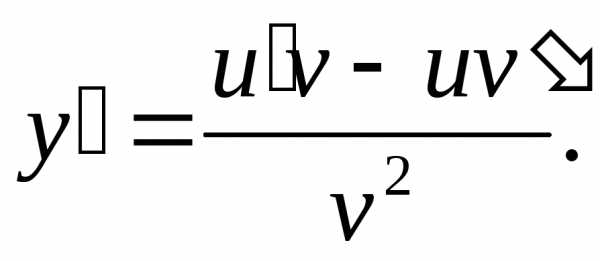 (5)
(5)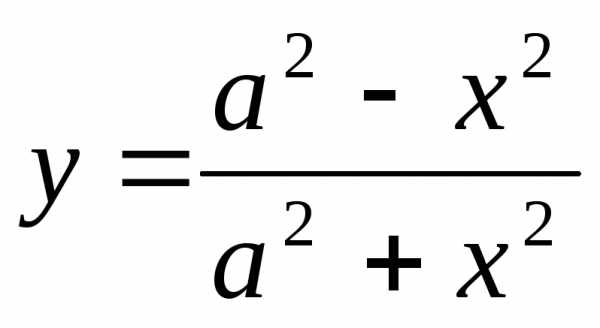 .
.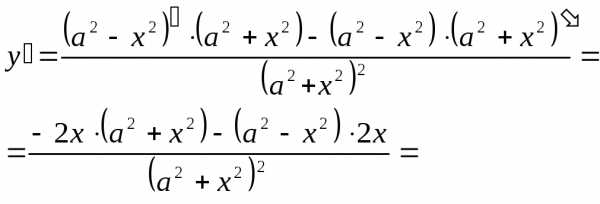
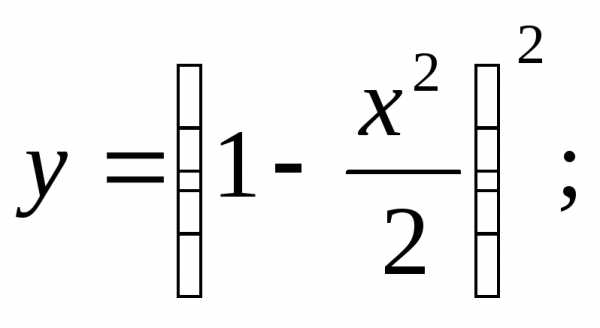
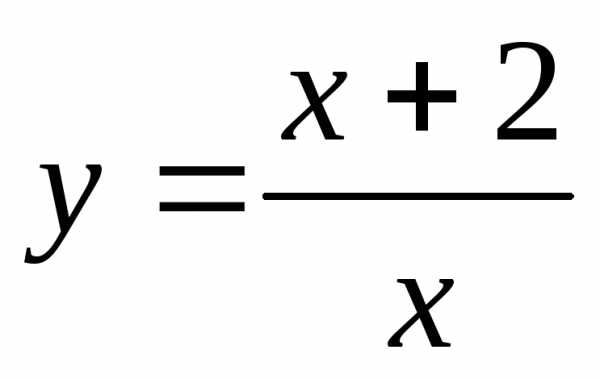 ;
12)
;
12)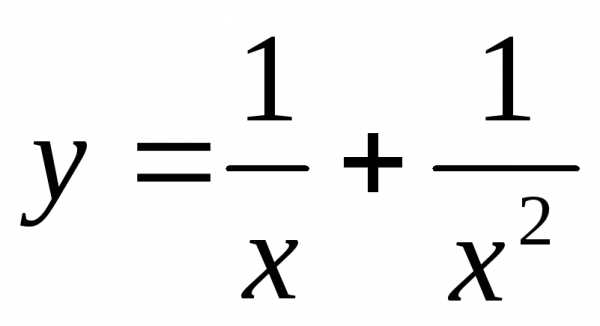 ;
;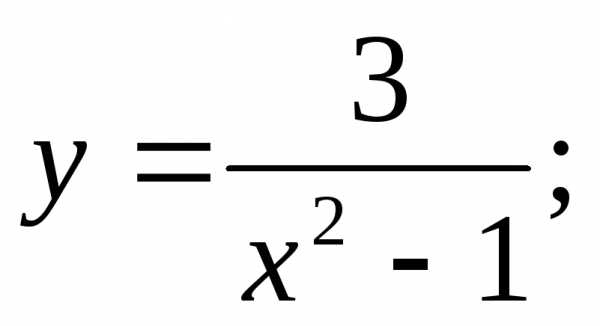 13)
13)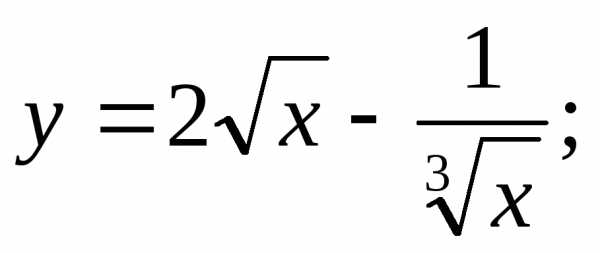 14)
14)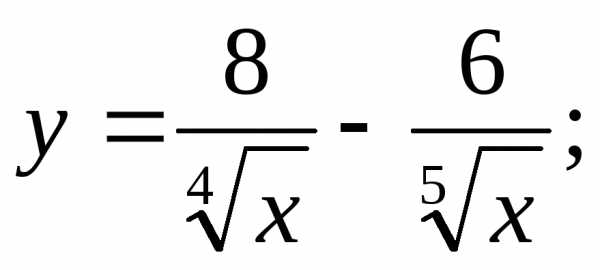
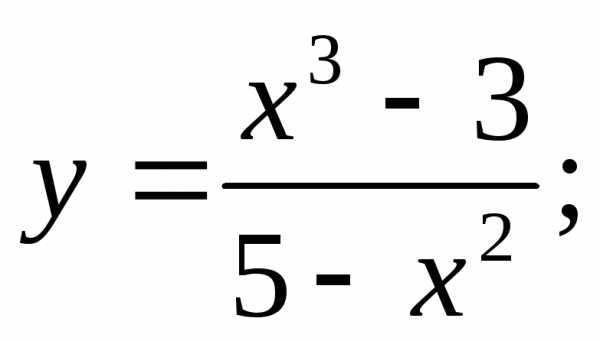 15)
15)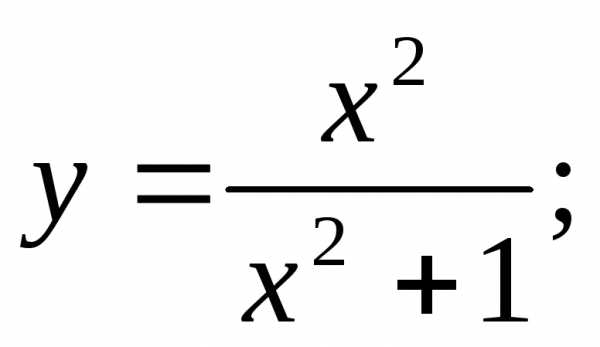
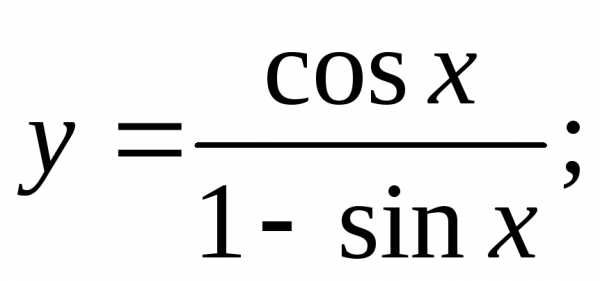
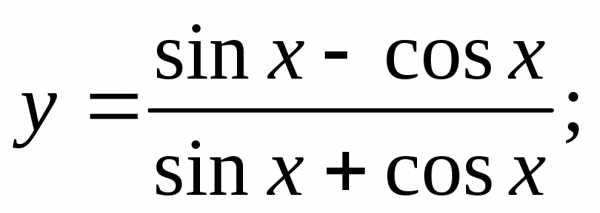 19)
19)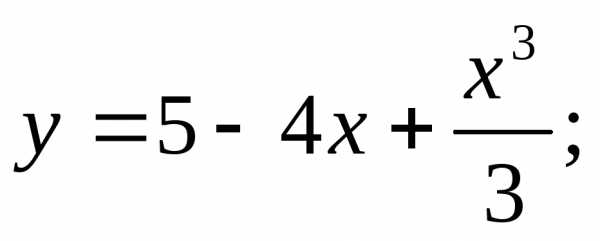 20)
20)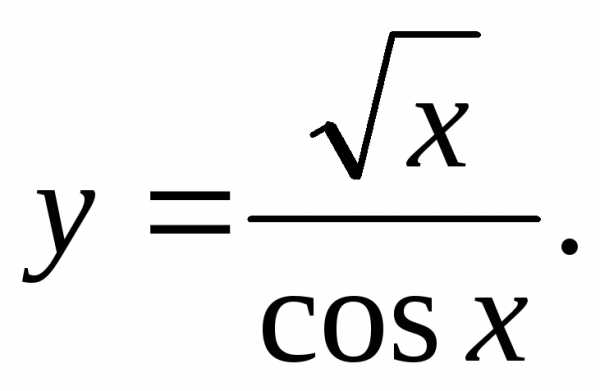
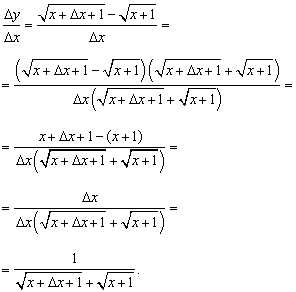
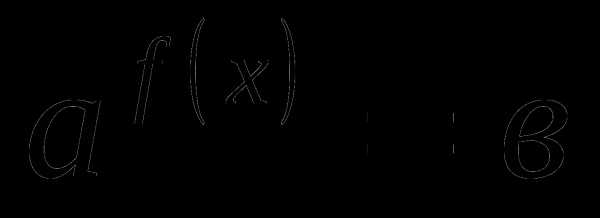




 Ответ: 5
Ответ: 5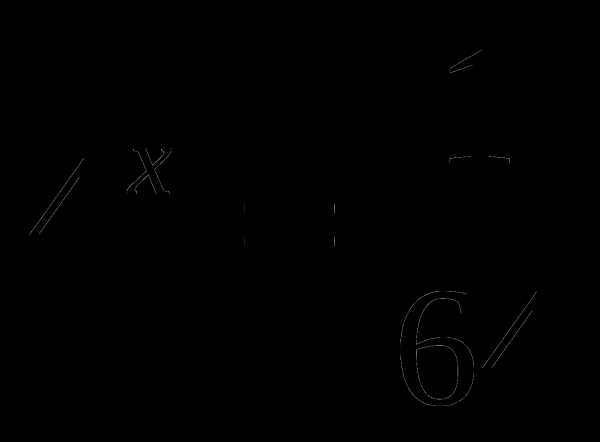


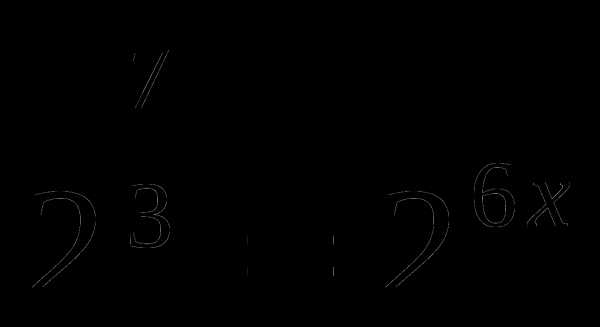
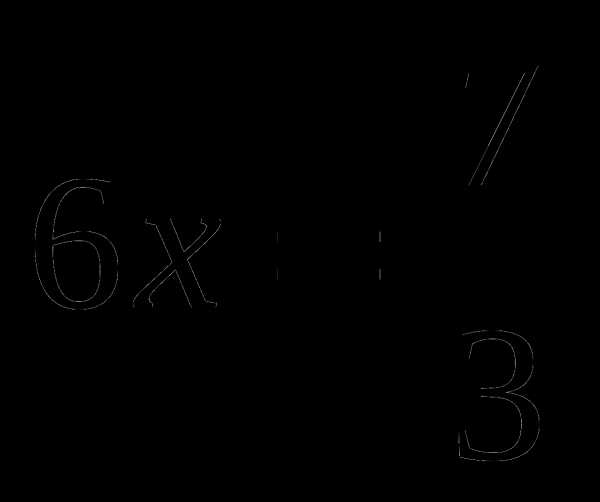
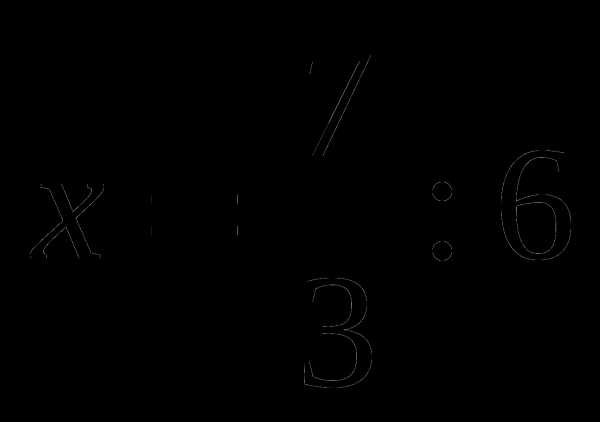
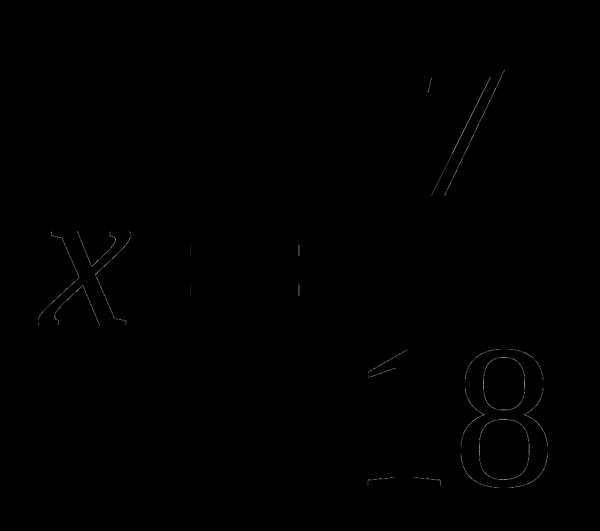
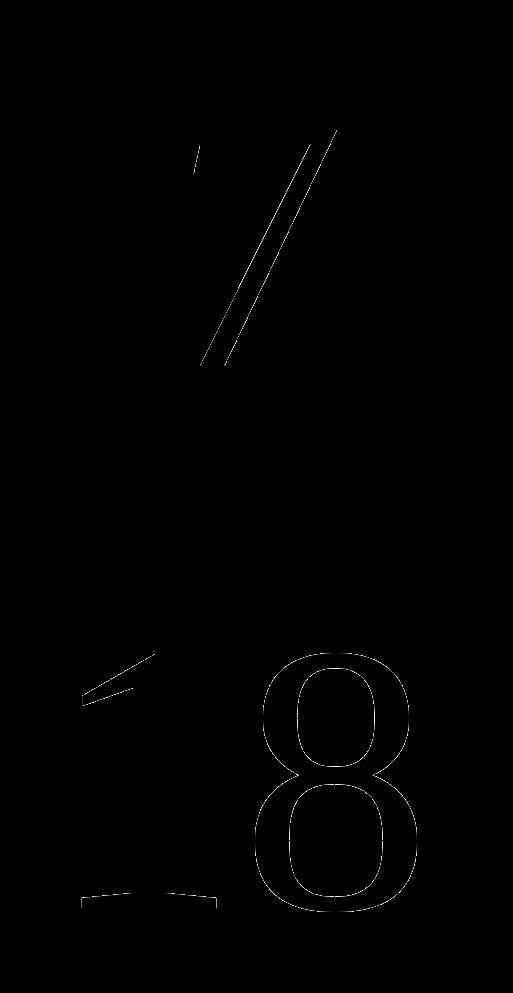 .
.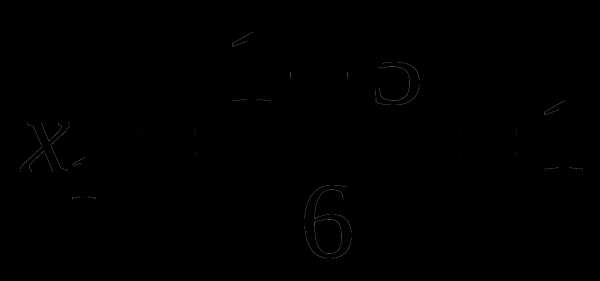
 .
.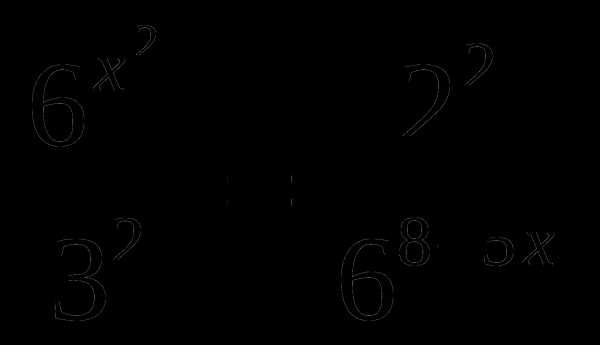


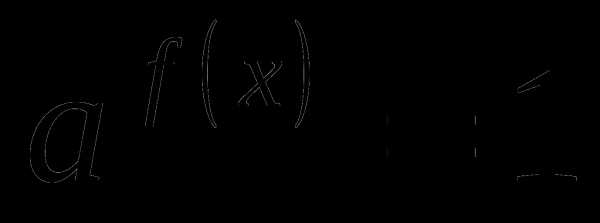
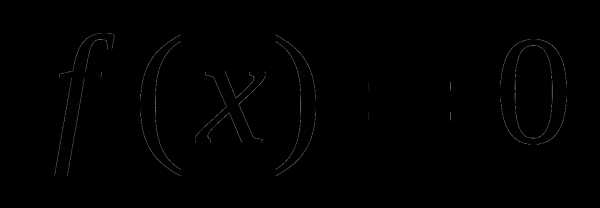
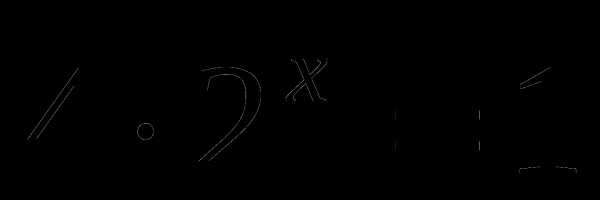

 или
или 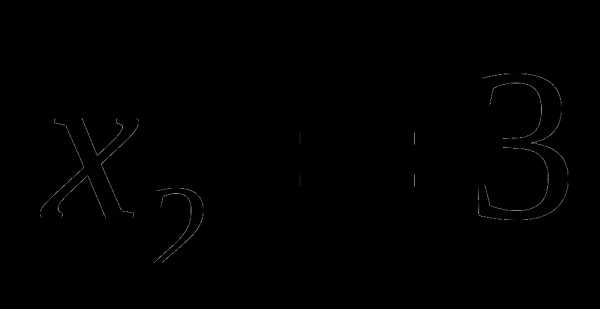
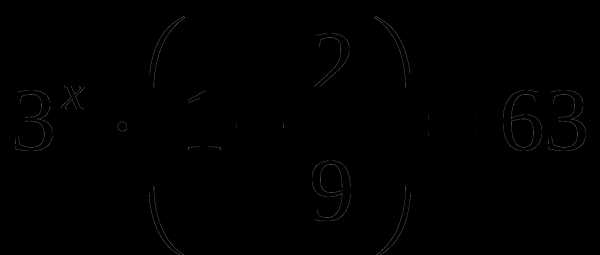
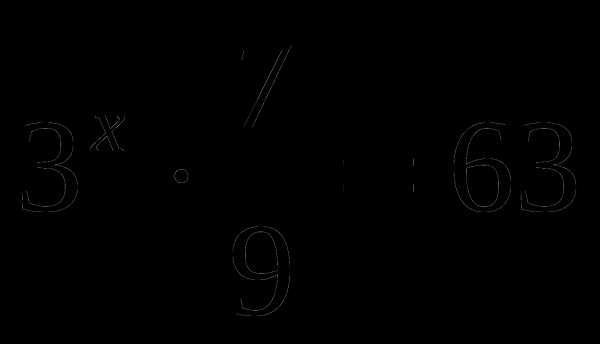
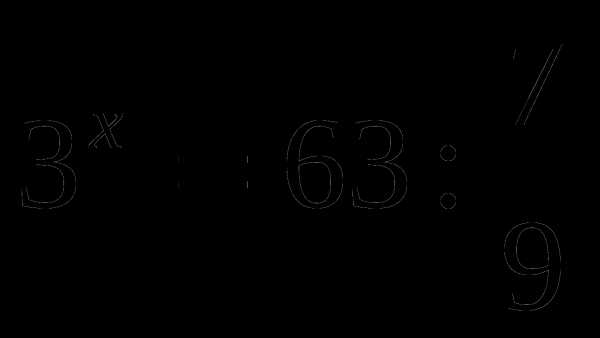
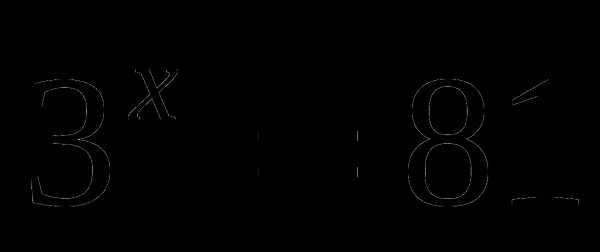


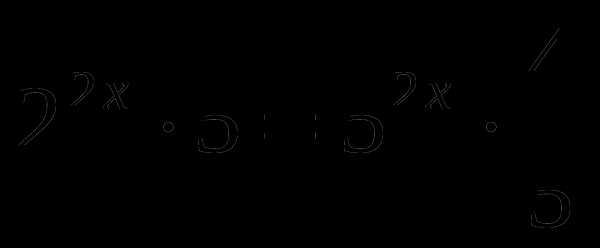
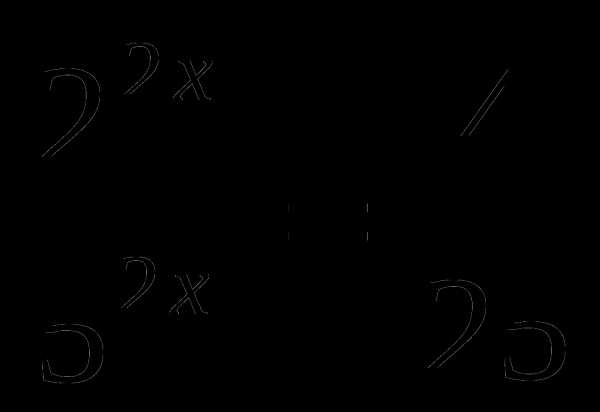
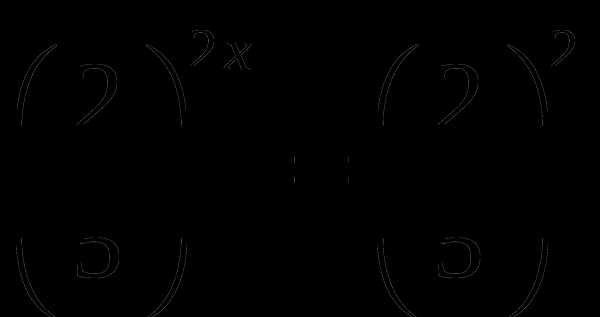

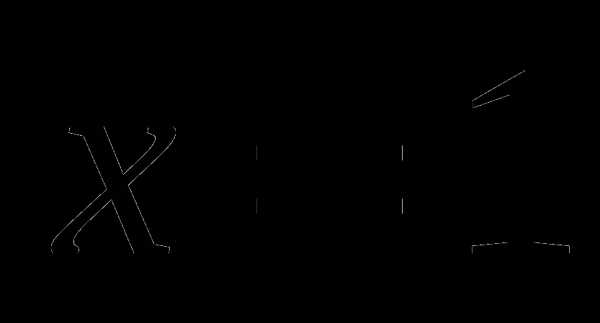



 ,
, 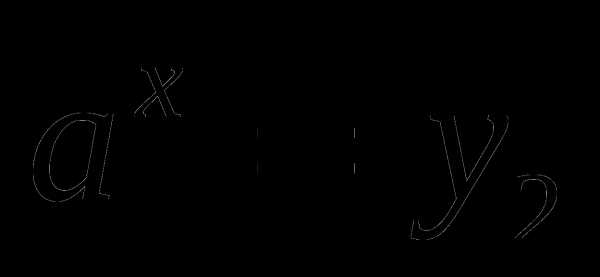 относительно х
относительно х
 или
или 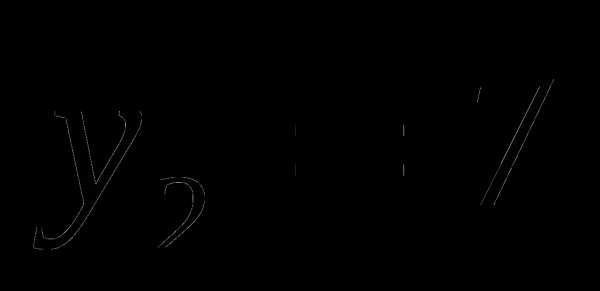

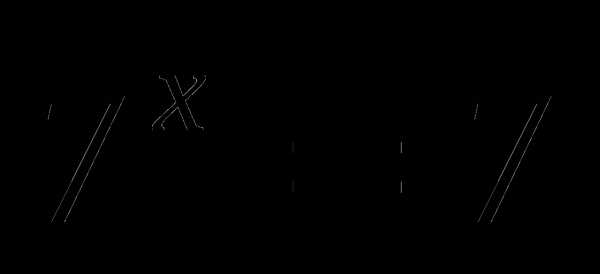



 или
или 




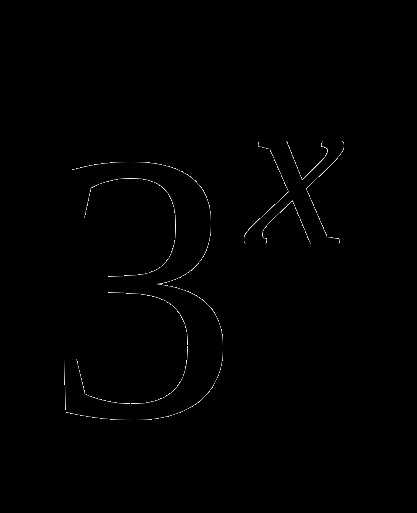 > 0 при любом
> 0 при любом 
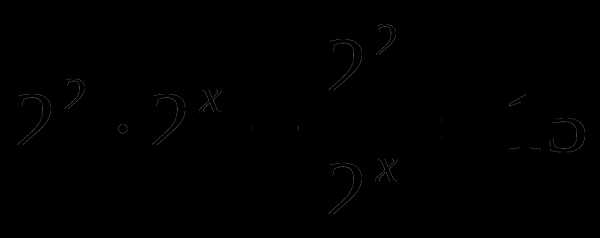
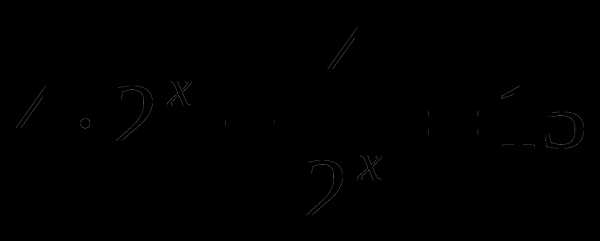


 , умножим всё уравнение на
, умножим всё уравнение на 
 или
или 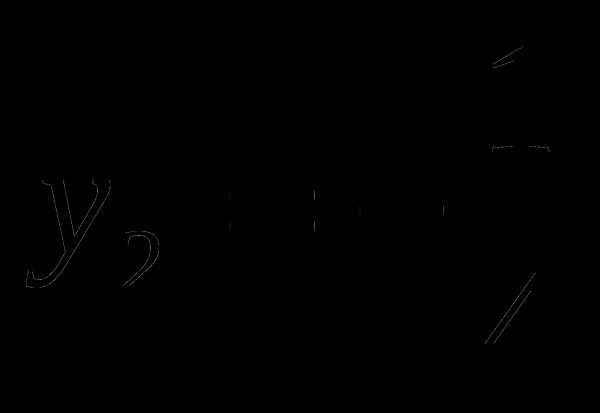

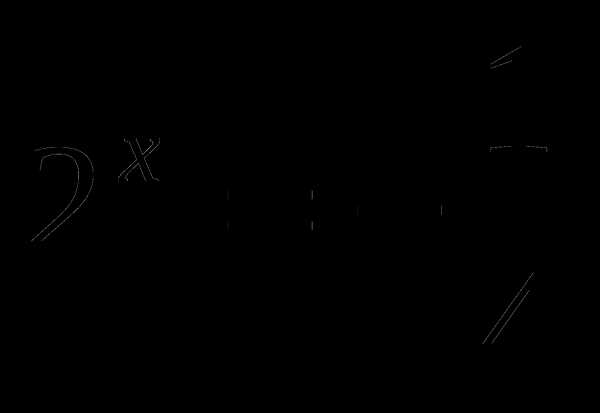
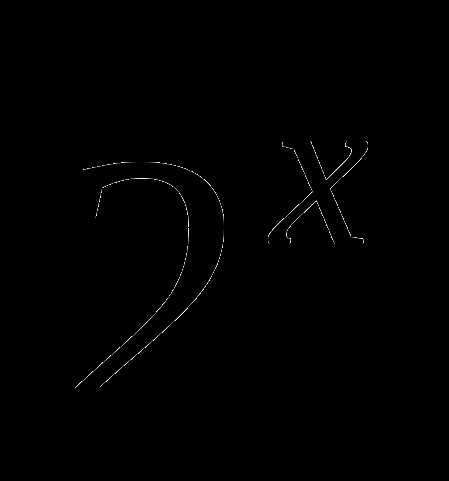 > 0 при любом
> 0 при любом 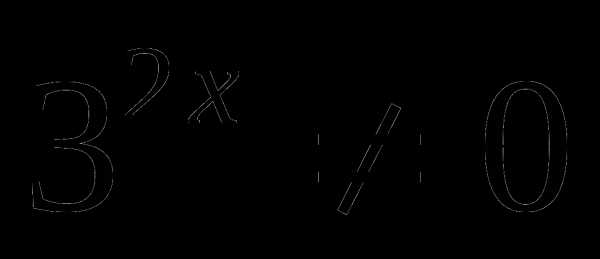
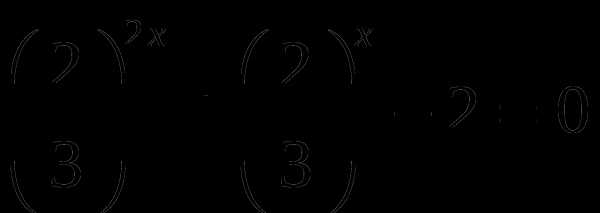
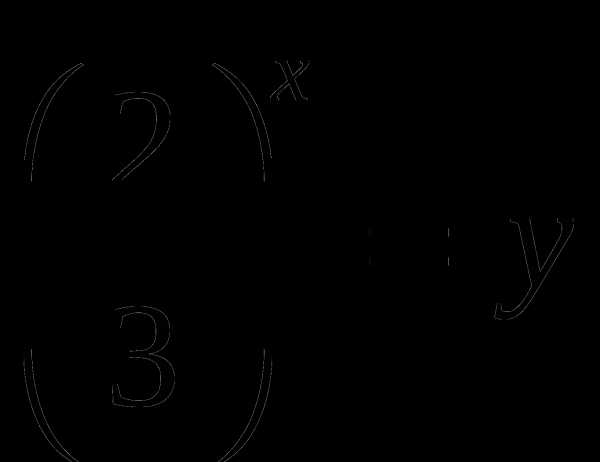
 или
или 
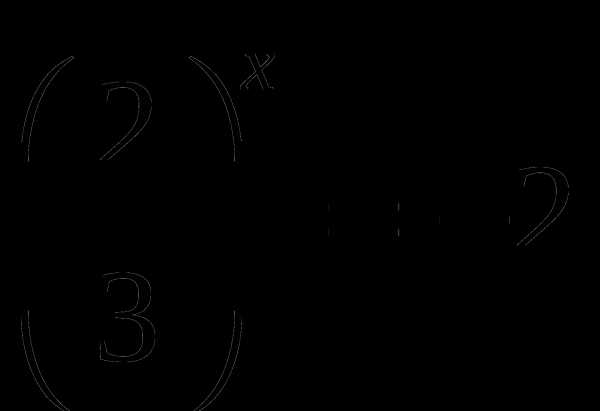
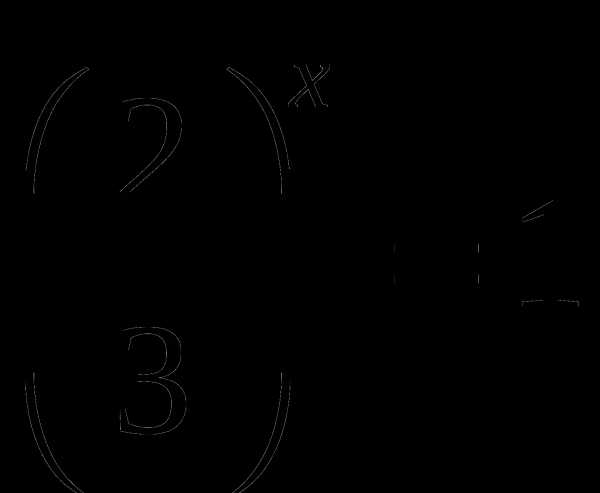

 называется обратной к квадратной матрице
называется обратной к квадратной матрице  ,
если
,
если — единичная матрица, имеющая тот же
порядок, что и матрица
— единичная матрица, имеющая тот же
порядок, что и матрица . Обратная
матрица существует только в том случае,
если,
и ее элементы находятся по формуле
. Обратная
матрица существует только в том случае,
если,
и ее элементы находятся по формуле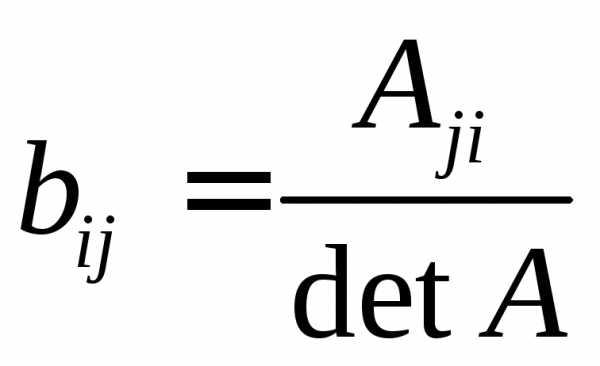 ,
, — алгебраическое дополнение к элементу
— алгебраическое дополнение к элементу .
. называетсявырожденной,
в противном случае невырожденной, т.е. обратная матрица существует только
для невырожденных матриц.
называетсявырожденной,
в противном случае невырожденной, т.е. обратная матрица существует только
для невырожденных матриц.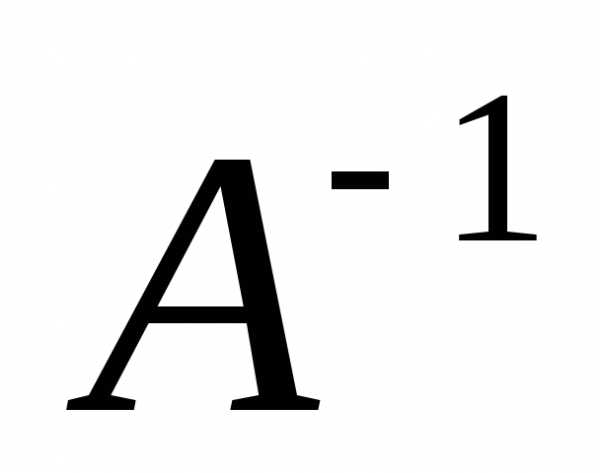 ,
т.е.
,
т.е.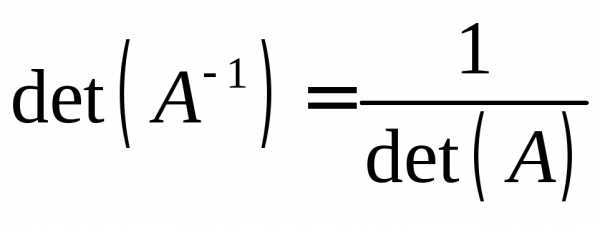 .
. и
и выполнены соотношения
выполнены соотношения — квадратная, невырожденная, то эти
уравнения имеют единственное решение,
которое можно получить с помощью обратной
матрицы. Так как при умножении матриц
коммутативный закон не выполняется,
указанные уравнения имеют различные
решения.
— квадратная, невырожденная, то эти
уравнения имеют единственное решение,
которое можно получить с помощью обратной
матрицы. Так как при умножении матриц
коммутативный закон не выполняется,
указанные уравнения имеют различные
решения.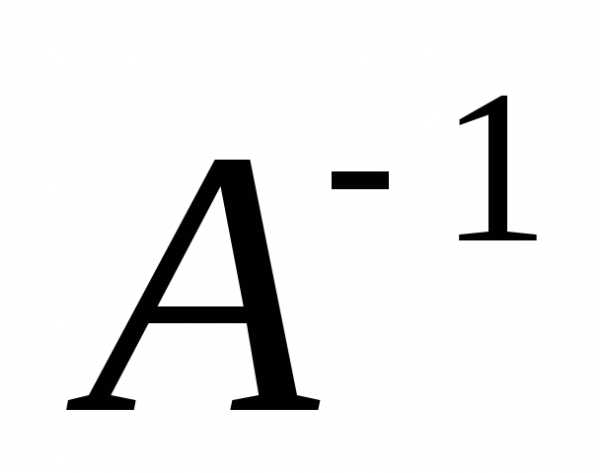 слева, а второе справа, т.е.
слева, а второе справа, т.е.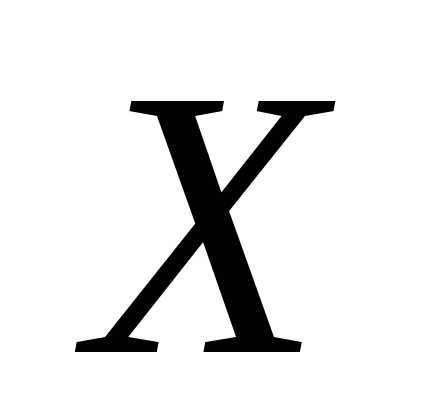 ,
если
,
если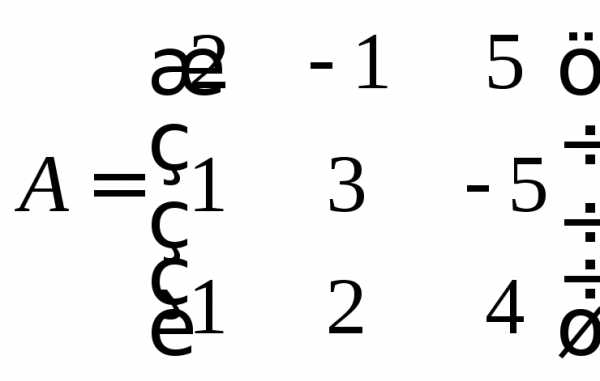 ;
;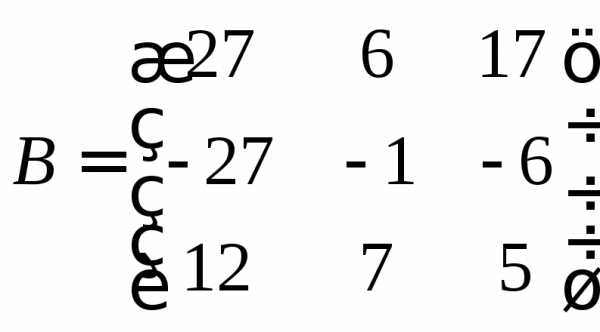 .
. невырожденная. Вычислим определитель
матрицы
невырожденная. Вычислим определитель
матрицы :
: невырожденная, и для нее существует
обратная матрица. Проведем вычисления,
необходимые для построения обратной
матрицы. Вычислим алгебраические
дополнения:
невырожденная, и для нее существует
обратная матрица. Проведем вычисления,
необходимые для построения обратной
матрицы. Вычислим алгебраические
дополнения:
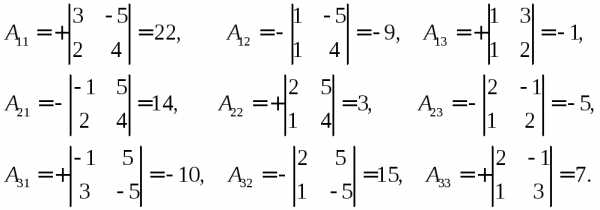
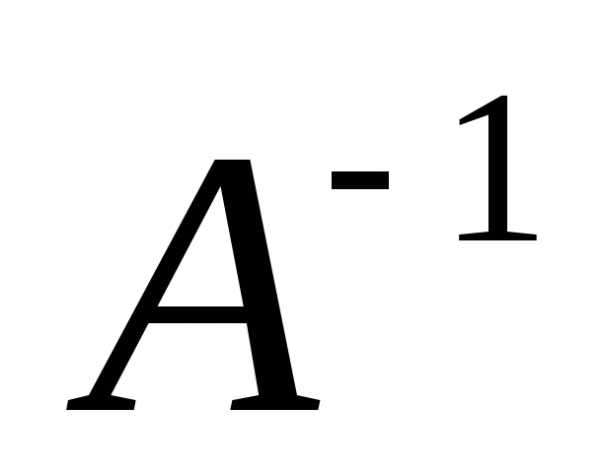 и
найдем неизвестную матрицу
и
найдем неизвестную матрицу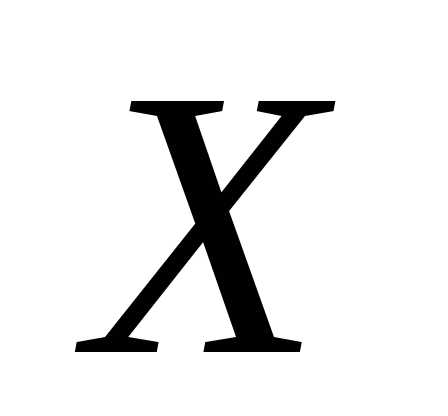 .
.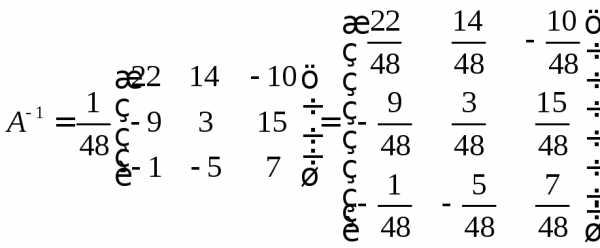 ,.
◄
,.
◄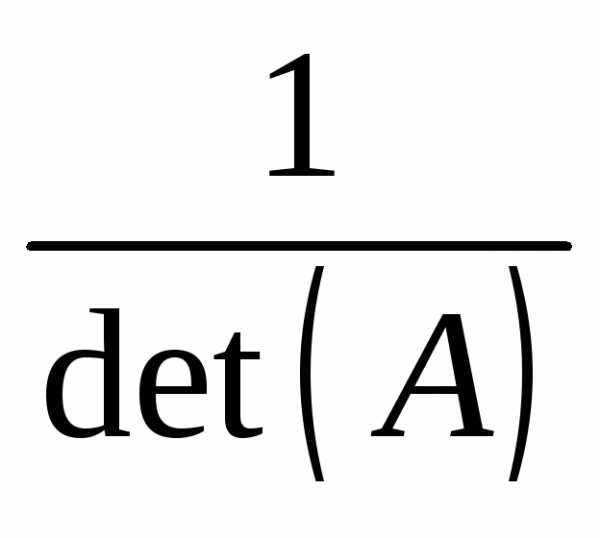 лучше оставлять перед матрицей и
проводить умножение полученной матрицы
на него на последнем этапе вычислений.
лучше оставлять перед матрицей и
проводить умножение полученной матрицы
на него на последнем этапе вычислений.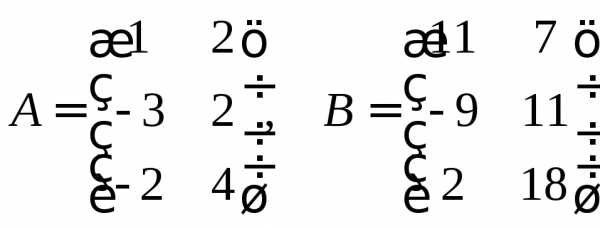 .
. не квадратная, следовательно, для нее
не существует обратной матрицы. Умножим
обе части уравнения на транспонированную
матрицу
не квадратная, следовательно, для нее
не существует обратной матрицы. Умножим
обе части уравнения на транспонированную
матрицу слева,
получаем
слева,
получаем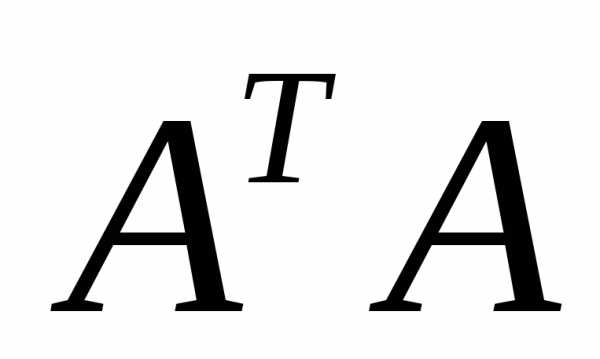 − квадратная и, если ее определитель
не равен нулю, то решение заданного
уравнения имеет вид
− квадратная и, если ее определитель
не равен нулю, то решение заданного
уравнения имеет вид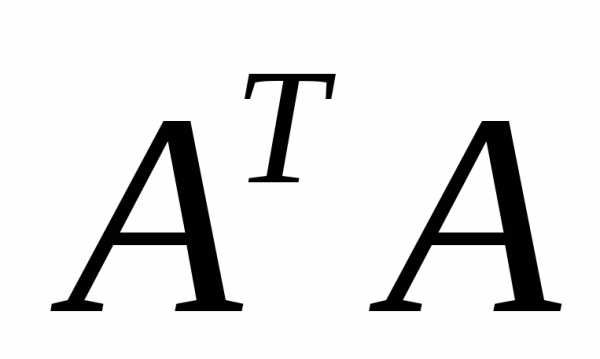 существует, и можно найти матрицу
существует, и можно найти матрицу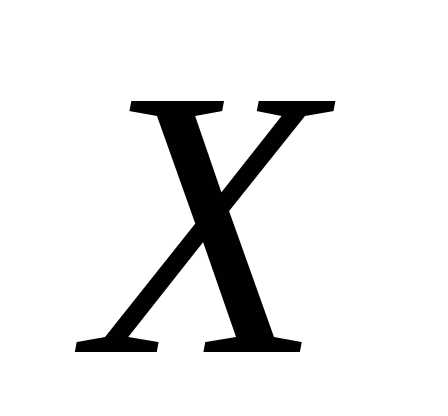 .
.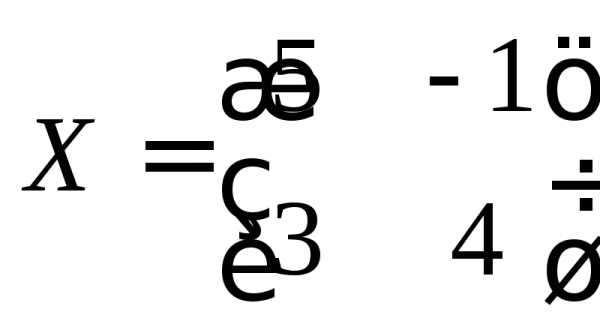 .
◄
.
◄ ;
б)
;
б)  ; в)
; в) 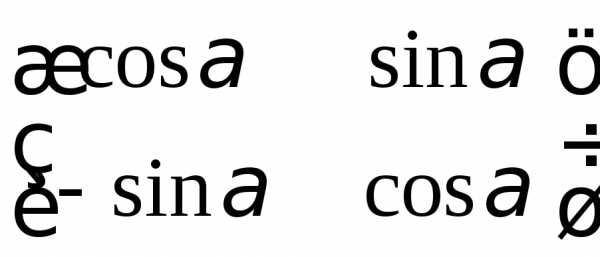 ; г)
; г) 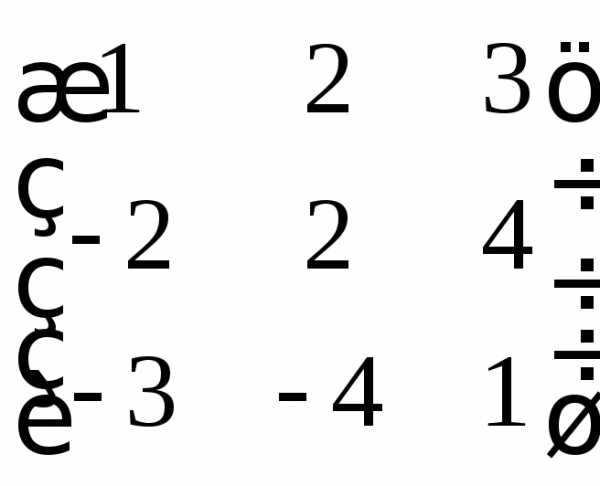 ; д)
; д)  .
.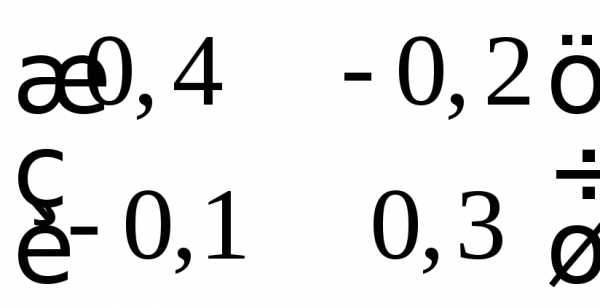 ;
б)
;
б) 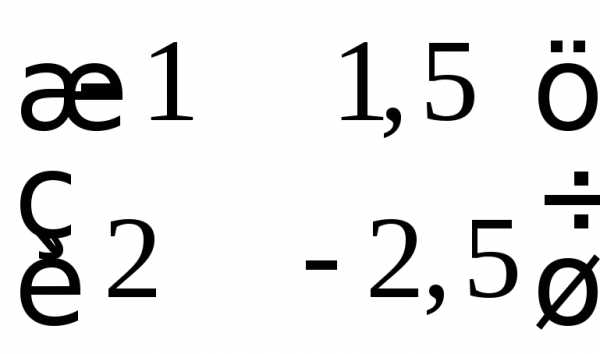 ; в)
; в) 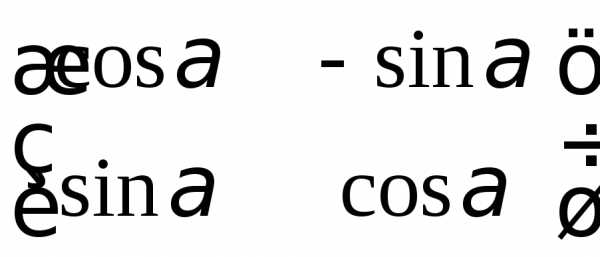 ;
г)
;
г) 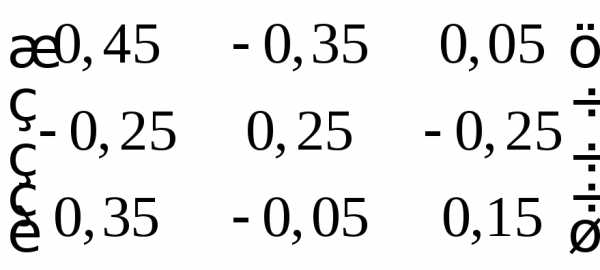 ;
;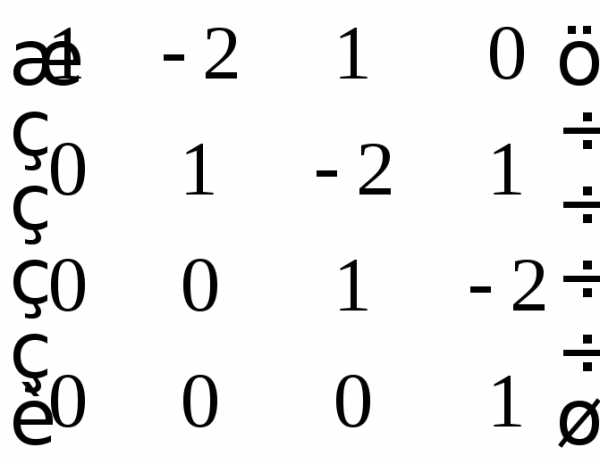 .
.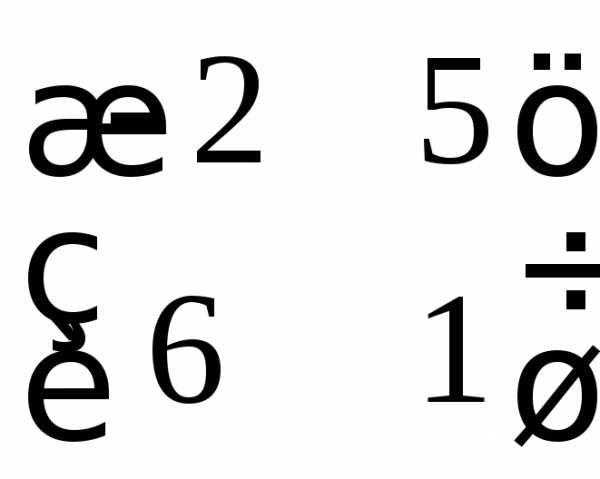 ;
б)
;
б)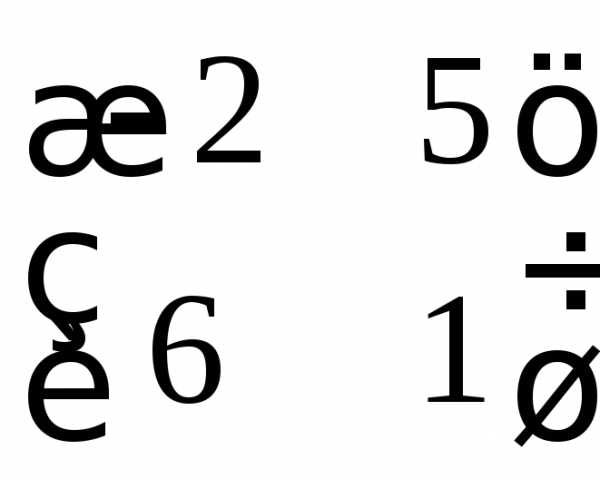 ;
в)
;
в)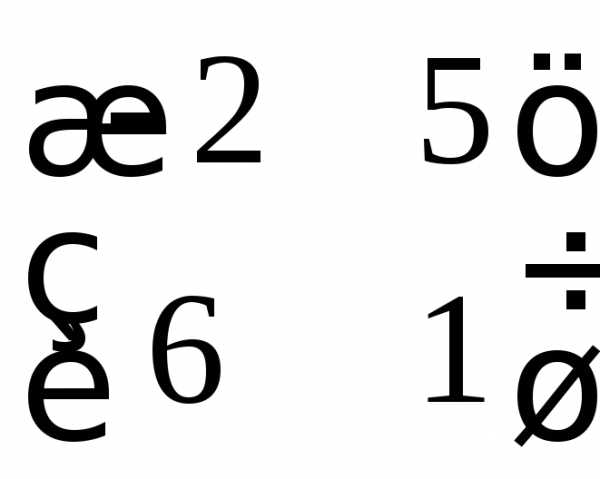 ;
г)
;
г) ;
д)
;
д) .
.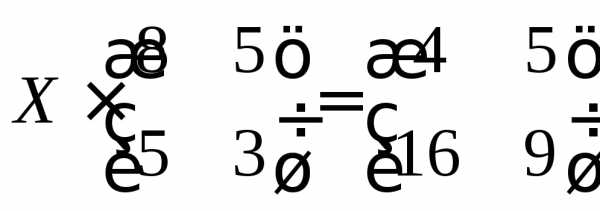
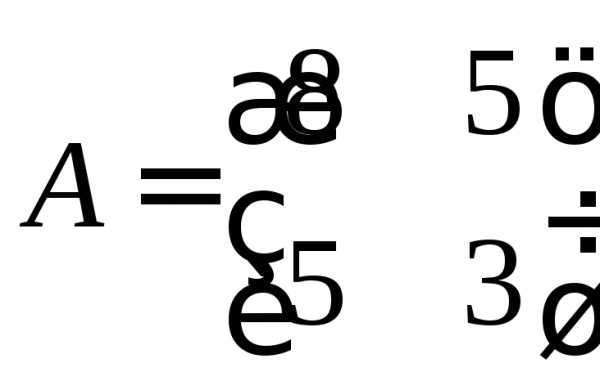 ,
,
,
,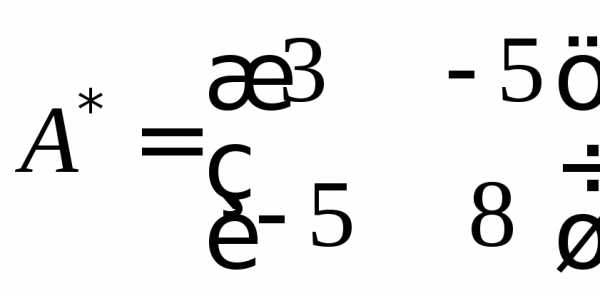
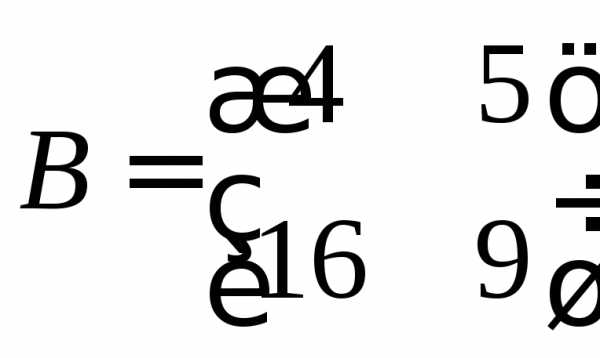
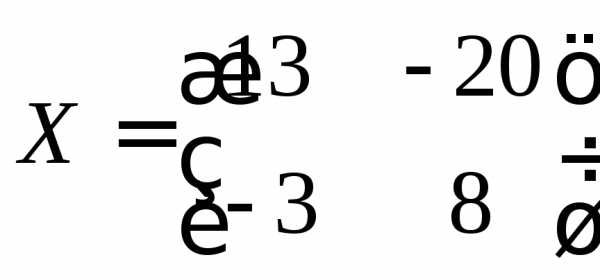 .
Чтоб убедиться в правильности, можно
выполнить проверку.
.
Чтоб убедиться в правильности, можно
выполнить проверку.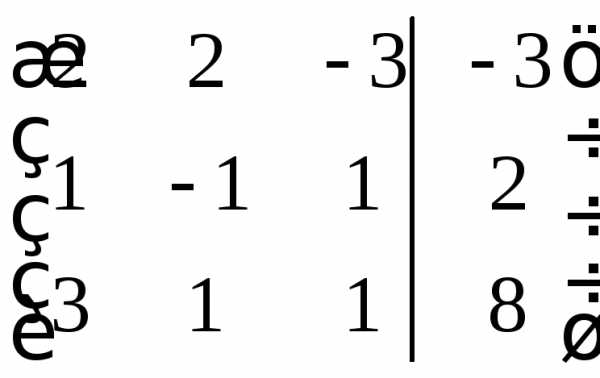
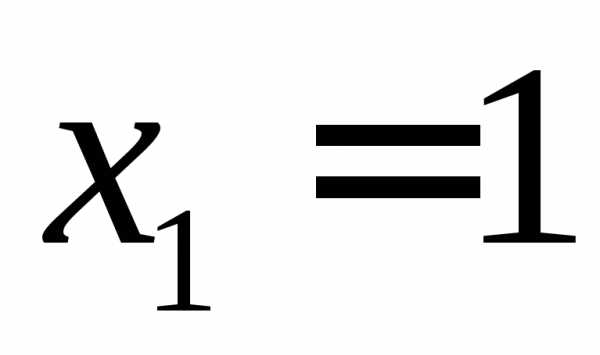 ,
,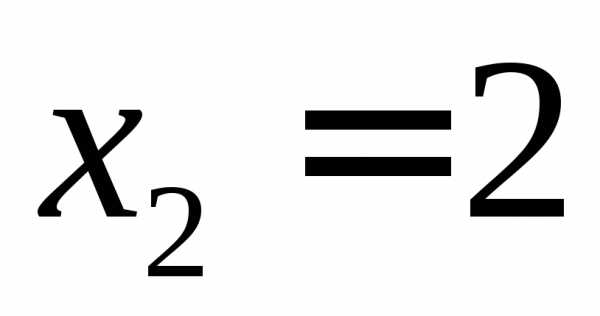 ,
,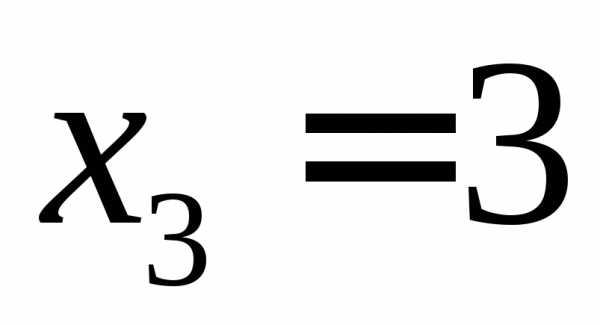 .
.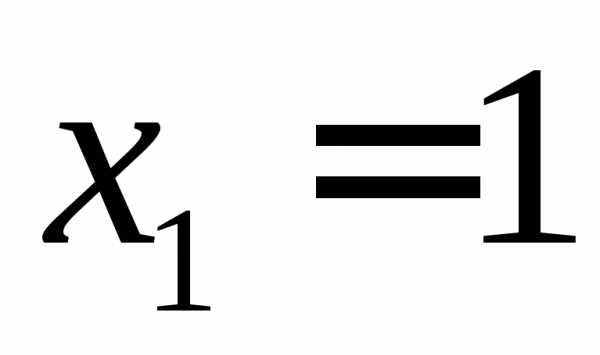 ,
,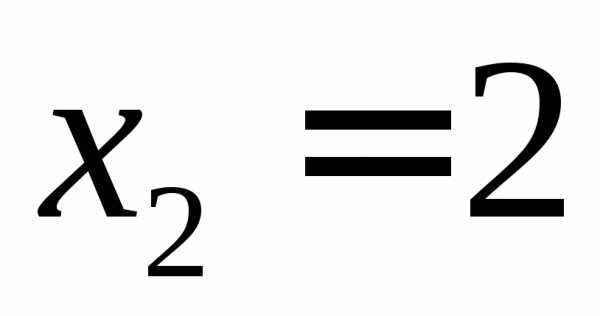 ,
,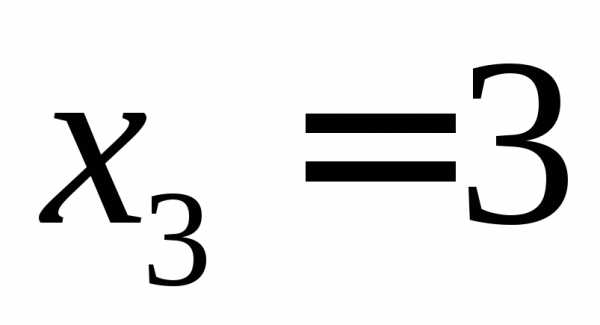 .
.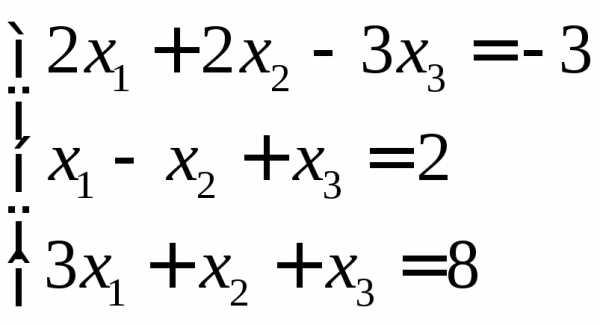
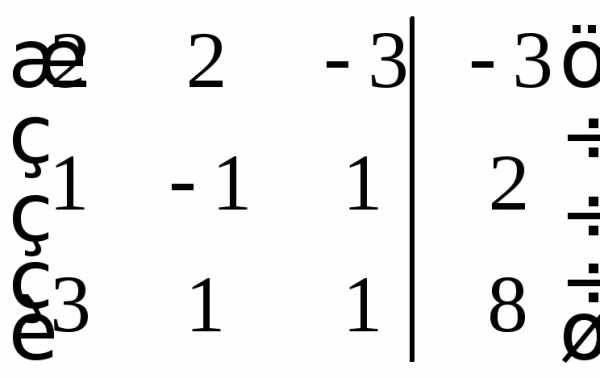
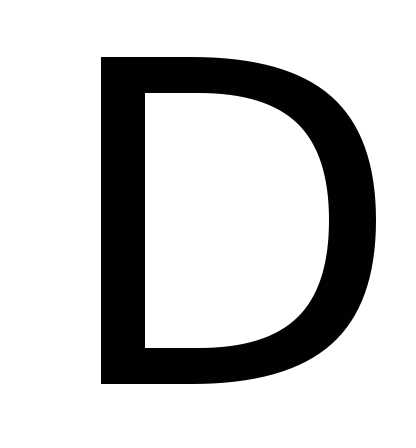 .
.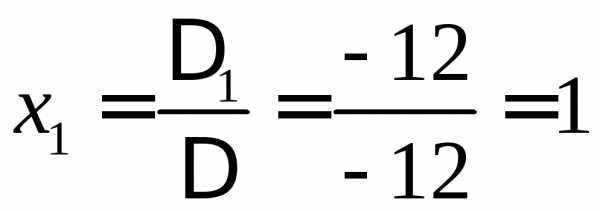 ,
, 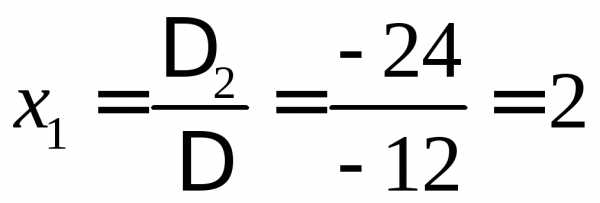 ,
,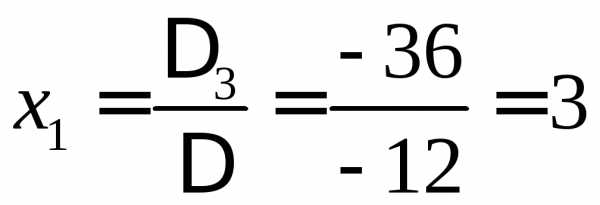
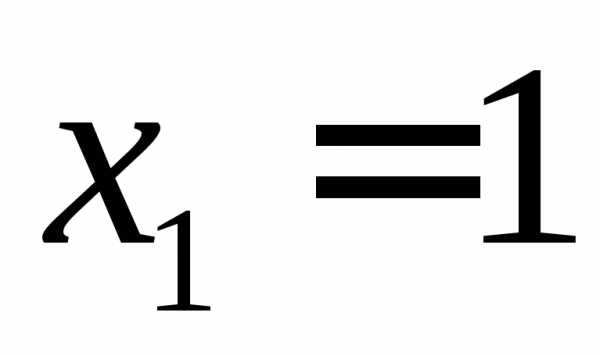 ,
,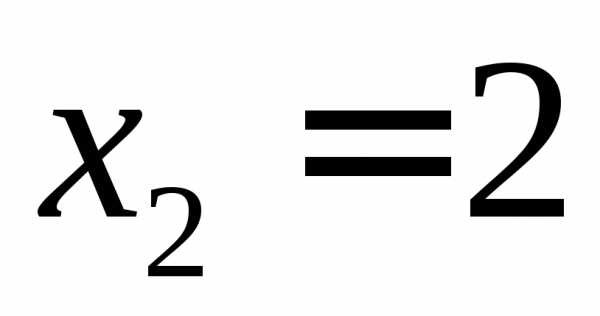 ,
,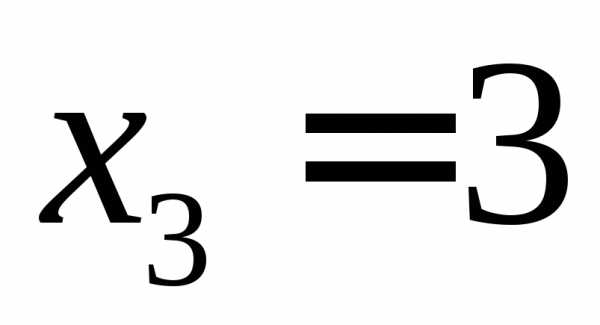 .
.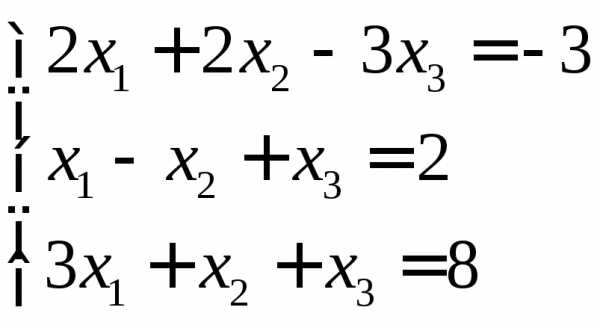
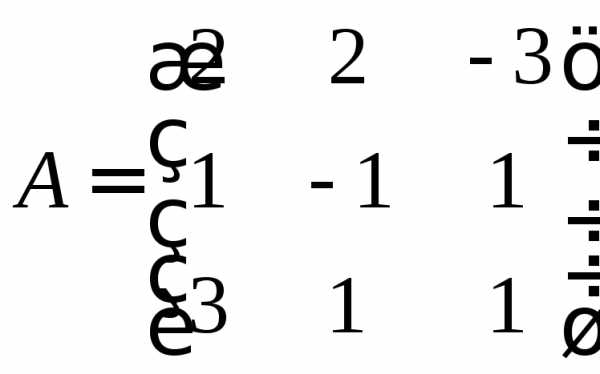 ,
, 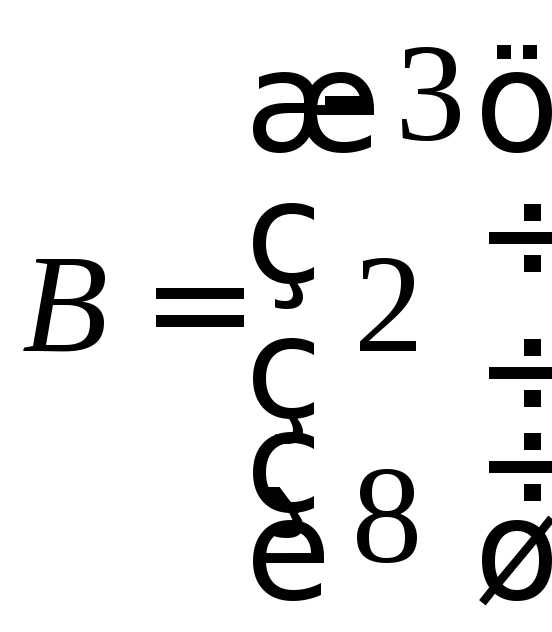
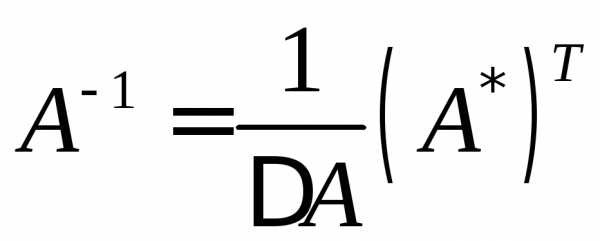
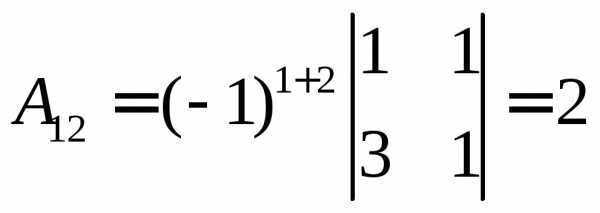 ,
,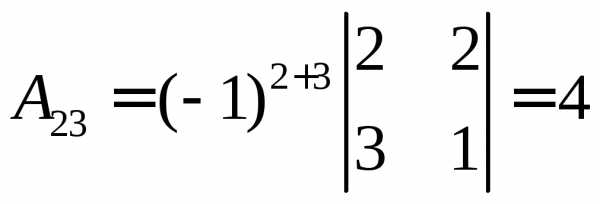
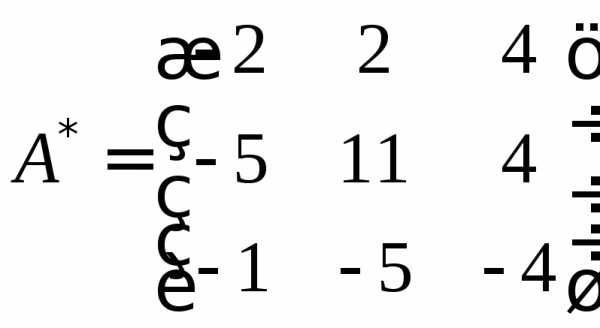
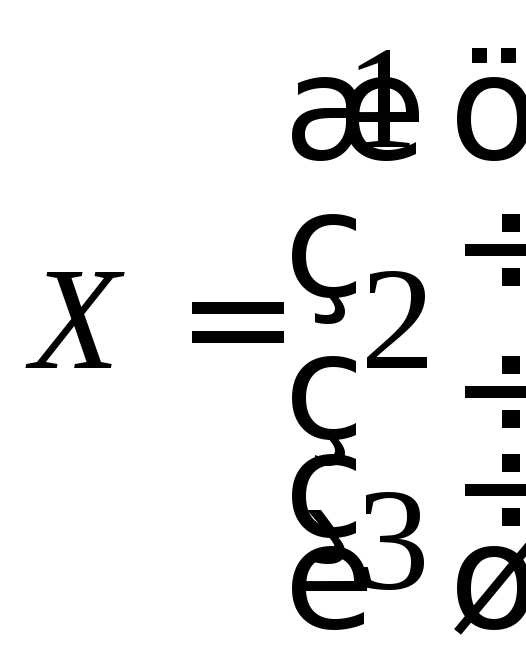
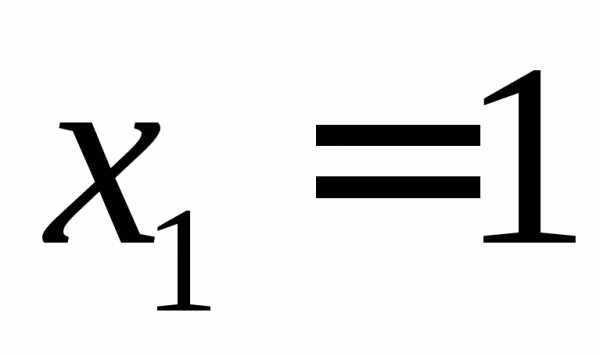 ,
,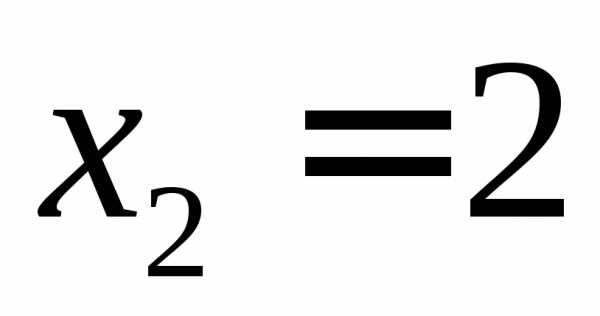 ,
,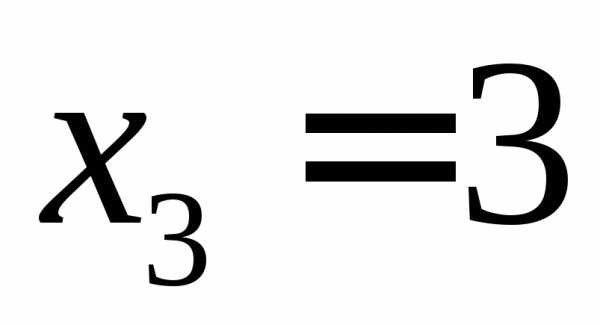 .
.