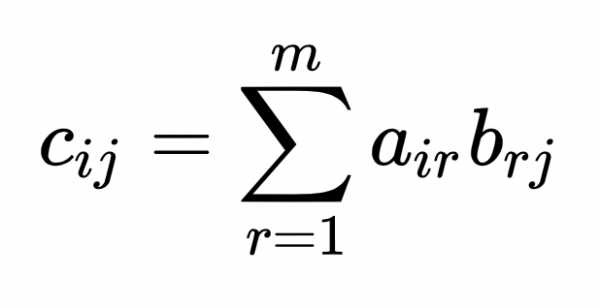Рубрика: Школьная жизнь

Методика «Числовые ряды» « Психологические тесты

Шкалы: уровень развития логического мышления

Темы: мышление

Тестируем: психические процессы · Возраст: взрослым, школьникам
Тип теста: вербальный · Вопросов: 20
Комментарии: 1 · написать

Назначение теста

Исследование логического аспекта математического мышления.

Инструкция к тесту

Детский вариант: «Внимательно прочитай каждый ряд чисел и в две свободных клеточки напиши такие два числа, которые продолжат данный числовой ряд».

Примеры:

Дописанные цифры выделены курсивом.

Тестовый материал

Инструкция к тесту

Взрослый вариант: «Вам предъявлены 7 числовых рядов. Вы должны найти закономерности построения каждого ряда и вписать вместо черточек «–» недостающие числа. Время выполнения работы – 5 минут».

 Тестовый материал

Ключ к тесту

Детский вариант

Взрослый вариант

Интерпретация результатов теста

Если испытуемый затрудняется при решении подобных задач, это может обозначать, что он плохо анализирует цифровой материал, не видит в нем скрытых закономерностей, поэтому не может ими воспользоваться, следовательно его логическое мышление в математике развито слабо.

Источники

• Методика “Числовые ряды” / Альманах психологических тестов. М., 1995, С.139-140.

vsetesti.ru

онлайн бесплатно, при приеме на работу, числовой тест shl

Предстоит пройти числовой тест при приеме на работу? На данной странице вы найдете всю необходимую информацию и сможете решить практические задания. Примеры числовых тестов максимально приближены к тем, что используют работодатели, а именно SHL, Kenexa, Talent Q и Ontarget. Наша платформа тестирования даст вам хорошее понимание того, с чем придется столкнуться, если работодатель просит пройти числовые тесты онлайн. Практика и ряд правильных советов – все, что нужно для того, чтобы успешно решать числовые тесты.

Числовой тест при приеме на работу

Получая тысячи откликов на вакансии, для работодателя обычная практика использовать тесты для оценки кандидатов. После отбора резюме, чаще всего при приеме назначают числовой тест онлайн. Если тест успешно пройден, то кандидата приглашают на собеседование. Зачастую работодатель попросит пройти тест повторно в офисе, чтобы удостоверится в том, что высокий результат, набранный в онлайн тесте, принадлежит именно вам. Поэтому просить друзей пройти тест за вас не лучшая идея. Лучший способ подготовится решить числовые тесты с ответами, представленные ниже.

Помимо прохождения теста онлайн, внимательно изучите советы, прочитайте ответы на часто задаваемые вопросы и ознакомьтесь с полезной информацией на данной странице.

Важным обстоятельством является то, что в отличие от математических тестов, числовые тесты на работу не требуют знания особых формул и долгих вычислений. Основные их характеристики следующие:

— Дается несколько вариантов ответов на выбор
— Не требуется специализированных знаний
— Ограниченное время решения
— Соответствуют предполагаемой должности
— Содержат всю необходимую информация для решения

Числовые тесты онлайн бесплатно

Числовой тест SHL содержит 20 вопросов. У вас будет 20 минут, чтобы правильно ответить на максимально возможное количество вопросов. Для решения теста рекомендуется иметь под рукой калькулятор и черновик.

Если вы не знаете ответ на вопрос, оставьте его и переходите к следующему. У вас будет возможность вернуться к вопросу при наличии оставшегося времени. В каждом вопросе четыре возможных варианта ответов, из которых только один правильный.

Числовой тест SHL

Числовые тесты бесплатно, выберете нужный вариант и нажмите на кнопку старт на следующей странице.

Числовые тесты Talent Q

Тест Talent Q содержит 10 вопросов. На решение одного вопроса отводится ровно 60 секунд. Старайтесь ответить на все вопросы. У вас не будет возможности вернуться и изменить ответ. В каждом вопросе десять возможных вариантов ответов, из которых только один правильный.

Примеры числового теста Talent Q

Пройти тесты Talent Q можно бесплатно. Для этого выберете вариант и нажмите на кнопку старт на следующей странице. Ответы будут доступны бесплатно после завершения теста.

Пример вопроса из числового теста

На графике представлены объемы продаж в квартальной динамике. Средний темп продаж накопителей HDD Q-to-Q в 2018 году в сравнении с 2017?

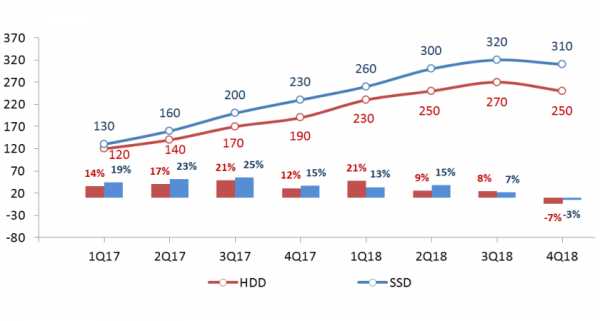
Шаг 1: Средний темп продаж HDD в 2017 году = (14% + 17% + 21% + 12%) / 4 = 16%.

Шаг 2: Средний темп продаж HDD в 2018 году = (21% + 9% + 8% — 7%) / 4 = 7,75%.

Шаг 3: Разница между средними темпами продаж Q-to-Q = 7,75% — 16% ≈ -8%.

Правильный ответ: Ниже на 8%.

Как успешно пройти числовые тесты?

1. Внимательно прочитайте или выслушайте инструкцию. Как правило, в начале числовых тестов при устройстве на работу следует инструкция и несколько примеров вопросов. Уделите достаточно времени, чтобы внимательно изучить их, это поможет в понимании предстоящего теста.

2. Игнорируйте чужие результаты. Не позволяйте себе думать о там, как быстро или медленно данные вопросы решали другие люди. Постарайтесь сконцентрироваться на том, что вы делаете.

3. Вопросы могут быть с подвохами. Иногда вопросы к числовым тестам составляются таким образом, чтобы увести вас в ложную сторону. Остерегайтесь таких вопросов, они сделаны специально, чтобы проверить вашу внимательность.

Какие знания по математике необходимы для того, чтобы пройти числовой тест онлайн?

Уровень знаний для решения числового теста сопоставим с уровнем, требуемым для решения базовой части ЕГЭ по математике. Ключевым моментом является поиск необходимой информации для решения в таблицах, графиках и диаграммах, в условиях ограниченного времени. Ниже приведен список наиболее часто используемых математических операций:

— Сложение
— Вычитание
— Умножение
— Деление
— Пропорция
— Проценты
— Коэффициенты

Если какое-либо из данных действий вызывает у вас затруднение, обратите внимание на этот тип вопросов. Постарайтесь проработать его как можно лучше, чтобы при решении подобных вопросов у вас не больше не возникало проблем.

Старайтесь решать тест не только быстро, но и точно. Большинство тестов не содержит системы анализа случайных ответов, но в некоторых она присутствуют. Если вы будете быстро ставить ответы наугад, то это может отразится в результатах теста, и работодатель поймет, что вы его не решали.

Числовые тесты для выпускников ВУЗов и профессиональных специалистов являются наиболее сложными. Для их решения по-прежнему требуется знание семи математических операций, описанных выше, однако, для анализа и интерпретации дается более сложная информация, и для решения схожего вопроса нужно выполнить больше действий.

Числовой тест онлайн, вопросы

Q: Разрешено ли пользоваться калькулятором?

Числовые тесты на работу для выпускников или менеджеров среднего звена можно проходить с использованием калькулятора. Но лучше уточнить у работодателя, разрешено ли использовать калькулятор, чтобы во время подготовки понимать нужно ли тренировать навыки счета в уме. Если вам предстоит пройти числовой тест в центре работодателя, то всем выдадут одинаковые калькуляторы для стандартизации, однако, взять с собой свой будет хорошей идеей, на случай если им разрешат пользоваться. Использование своего калькулятора позволит вам сэкономить несколько секунд на расчетах. Если тест проходит онлайн, то вы можете свободно пользоваться собственным калькулятором.

Q: Будет ли снижен мой рейтинг при попытке угадать ответы?

Кандидаты часто задают этот вопрос, чтобы понять, имеет ли смысл угадывать несколько последних ответов, когда заканчивается время тестирования. Ключевым моментом является то, что система вряд ли определит, что ответы были даны наугад, однако ваш процент точности существенно снизится. В некоторых тестах есть программное обеспечение, которое сможет определить, случайно выбранные ответы. Даже если оценщик не получит этих данных, вы все равно рискуете получить низкую оценку, которая в целом плохо отразится на вашей работе. Работодатель вряд ли сообщит, используют ли они подобные системы, и просто скажет: «Постарайтесь ответить правильно на столько вопросов сколько сможете». В результатах теста будет видно, на сколько заданных вопросов вы ответили правильно. Некоторые компании заинтересованы в точных и последовательных ответах, другие в количестве решенных заданий. Постарайтесь понять кого именно ищет работодатель.

Q: Можно ли попросить друзей помочь мне пройти онлайн тест, работодатель ведь не узнает?

В процессе приема на работу кандидаты сдают тест онлайн, затем отдел кадров попросит пройти проверочный тест в офисе работодателя. Повторный тест представляет собой выборочный набор вопросов из основного теста, который позволяет определить, что онлайн тестирование было выполнено тем же кандидатом. Поэтому просить друзей помочь вам решить тест может оказаться плохой идеей, поскольку это будет выявлено в результате проверочного тестирования.

Числовые тесты для отбора персонала на работу

Если работодатель просит вас пройти числовой тест при приеме, то постарайтесь уточнить кокой компанией разработан тест. Вы можете перейти на сайт этой компании, чтобы получить дополнительную информацию и, возможно, примеры тестовых вопросов. Сотрудники отдела кадров как правило идут на встречу. Если вы проходите числовой тест, то скорее всего он выпущен одной из следующих компаний:

Числовой тест SHL. Одним из наиболее часто используемых является тест SHL, вы скорее всего с ним столкнетесь во время поиска работы. На его прохождение отводится от 17 до 25 минут в зависимости от уровня сложности. Для хорошего результата нужно уметь анализировать информацию быстро и точно. Попробуйте пройти числовой тест SHL онлайн.

Тест числовых способностей Kenexa. Kenexa является дочерней компанией IBM, одним из крупнейших разработчиков тестов способностей. Их числовые тесты схожи с тестами SHL. Если вы будете практиковаться в подготовке к тесту числовых способностей Kenexa, вы также подготовитесь к тесту SHL, и наоборот. Для решения 24 вопросов кандидату обычно отводится 20 минут.

Динамические числовые тесты Talent Q. Главное отличие тестов Talent Q состоит в их адаптивности. Вопросы динамически изменяются в зависимости от ответов. Уровень сложности теста растет, если испытуемый дает правильные ответы, и снижается, если он допускает ошибки. Это позволяет произвести оценку навыков быстрее обычного теста. Время решение каждого вопроса ограничивается от 60 до 90 секунд, а количество вариантов ответов существенно больше чем в тестах SHL, что затрудняет процесс принятия решения. Проверьте свои навыки в числовом тесте Talent Q.

Тест числовой информации Ontarget. Тест состоит из двух частей, в первой проверяются умения производить точные расчеты, во-второй навыки оценки числовой информации. Обычно на тест из 20 вопросов отводится 20 минут.

Подготовка к числовому тесту

Важным элементом подготовки является практика, она помогает привыкнуть к неожиданным вопросам и таймеру. Кроме того, постарайтесь получить как можно больше информации о тесте, в том числе от работодателя. Возможно он предоставит учебные материалы.

На DigitalTests можно найти много полезной информации о тестах, а также пройти числовые тесты в режиме онлайн в удобное для вас время. Это будет хорошей практикой. Помните, что для подготовки вы можете использовать не только бесплатные числовые, но и вербальные тесты.

Если вы прошли все тесты, прочитали советы и ознакомились с полезной информацией, вам остается хорошенько выспаться, чтобы быть в тонусе.

И напоследок, удачи вам – мы в вас верим.

digitaltests.ru

Пройти тест. Тест на логику. Числовой ряд

С помощью данного теста  выполняется оценка логического аспекта математического мышления. Тест предназначен  для взрослых.
За 6 минут Вы должны найти закономерности построения каждого ряда чисел и вписать недостающие числа.
Перед вами классический тест на развитие логического математического мышления, где необходимо выбрать верное продолжение числового ряда.
Вам необходимо проанализировать каждый числовой ряд и установить закономерность его построения. Вы должны определить два числа, которые бы продолжили данный числовой ряд.
Время прохождение теста ограничено шестью минутами.

Тест на логику. Числовой ряд

Рекомендуем также обязательно ознакомиться с расчетами:

Расчет Числа Пути — Перейти на страницу расчета Числа Пути → → →

Расчет числа Судьбы — Перейти на страницу Расчет числа Судьбы → → →

Расчет Числа Сердца — Перейти на страницу расчета Числа Сердца → → →

Расчет Числа Индивидуальности — Перейти на страницу расчета Числа Индивидуальности → → →

Если у вас есть свой сайт или блог и вы бы хотели принести пользу посетителям вашего сайта, разнообразить информацию на сайте и привлечь дополнительное внимание к вашему сайту, есть хорошее решение.

Разместите на вашем сайте один или несколько наших информеров. Для их просмотра перейдите по ссылкам:
— Лунные информеры горизонтальные
— Информер расчета совместимости по биоритмам
— Информер расчёта индекса массы тела
— Информер расчёта восхода и захода солнца
— Информер-тест Расчёта суточных биоритмов человека

А может вас заинтересуют такие информеры?

Взято с сайта: Календарь лунных дней: фазы луны и биологические ритмы

Просмотров: 6867

lyna.info

Методика «Числовые ряды», или Оценка математического мышления — Мегаобучалка

megaobuchalka.ru

что это, как их решать -HRLider

Вам предстоит решать числовые тесты (математические, цифровые) при приеме на работу или на конкурсе Лидеры России? Возможно, у вас все отлично с вычислениями и вы легко решаете в уме даже сложные задачи. Но лично я начинаю потеть, и голова сразу пустеет при упоминании тестов на математику. К сожалению, этих тестов не избежать — практически 100% компаний при оценке соискателей требуют прохождения тестов на умение делать расчеты. Поэтому, если вы давно не решали числовые тесты, и вы такой же как я, то, скорее всего, вас тоже страшит перспектива проходить такое тестирование.

Но беспокоиться не о чем. В общем, математические тесты при приеме на работу разработаны таким образом, что каждому человеку предоставляется справедливая возможность получить высокий балл. Числовые тесты при приеме на работу (или для конкурса Лидеры России) не содержат задач, для решения которых требуется быть профессором высшей математики.

Некоторое предварительное знакомство может быть необходимо, чтобы правильно понимать суть задач, но, большей частью, числовые тесты просты и требуют только внимательности и минимального умения соотносить числовые данные. Просто постарайтесь предварительно ознакомиться с примерами числовых тестов с ответами и настройтесь на спокойную внимательную работу по их решению, и все будет в порядке.

Числовые тесты при приеме на работу — как к ним подготовиться?

Для успешного решения числовых тестов на собеседовании вы должны разбираться в основной арифметике и уметь быстро производить базовые операции сложения, вычитания, умножения и деления. Также надо уметь быстро определять десятичные числа, доли, отношения и проценты, вычислять периметры и области, решать простейшие уравнения и уметь интерпретировать данные, например, проводить анализ графиков, таблиц и диаграмм.  Числовые тесты почти всегда содержат графики, диаграммы и таблицы, которые перегружены информацией — вам надо уметь внимательно выбирать только нужные данные.

Вы также должны уметь решать логические задачи с численными рассуждениями.

Обычно такие числовые тесты представляют из себя числовые последовательности (числовые ряды). Вы должны уметь понять и высчитать, какое число продолжает последовательность. Шаблон может быть любым: например, все числа в последовательности являются квадратными корнями, или все простые числа, или все кратные 10 и т. д.

Предварительное ознакомление со всеми возможными шаблонами решений числовых тестов может дать вам огромное преимущество перед другими соискателями на вакансию.

Рассмотрим пример простой логической задачи — числовые ряды

Какое число будет следующим в этой последовательности:

5 25 625 X?

Если вы проанализируете данный числовой ряд, вы увидите, что правило последовательности состоит в том, что число справа всегда является результатом предыдущего числа, помноженного на себя. Это 5×5 = 25 и 25×25 = 625. По логической последовательности, следующее число должно быть результатом 625×625, что составляет 390625

Как можно гарантировать, что вы получите хороший результат на числовых тестах?

Мы рекомендуем следующее:

Повторите и запомните таблицу умножения и деления. Помните, что числовые тесты при приеме на работу — это тесты с жестким лимитом времени. Поэтому, если вы сможете быстро в уме производить операции умножения и деления, вы сэкономите значительное время. Калькулятором пользоваться обычно можно. Но однозначные числа вы должны уметь быстро считать в уме.

Четко следите за временем. Обычно на решение 1 задачи числового теста дается 60-90 секунд. Для неподготовленного человека это очень мало, но после подготовки это вполне реально — решать числовые тесты за минуту и менее.

Не задерживайтесь слишком долго на вопросе, который вам полностью непонятен и у вас нет идей его решения. Отметьте номер этого теста и вернитесь к нему позже, если у вас останется время. Обычно все вопросы равны в том смысле, что вы получаете одинаковый балл за каждый из них. Поэтому сначала решите более простые задания. Единственным исключением из этого правила будет, если правила теста подразумевают вычитание количества неверных ответов из количества верных.

Повторите основные математические правила. Вы должны знать основные формулы и концепции и быстро ориентироваться в них. Это особенно целесообразно, когда прошло длительное время с тех пор, как вы учились в школе и вы не занимались никакими математическими расчетами. Если вы занимаетесь поиском работы в середине карьеры и вам 30-50 лет, числовые тесты могут «подложить вам свинью». Потому что последний раз, когда вы слышали о дробях и пропорциях, было 10-20 лет назад!

Просто пересмотрите все основные правила по математике за среднюю школу — этого будет достаточно. Большая часть знаний у вас, вероятно, сохранилась. Но вам просто нужно обновить эти знания, чтобы уметь ими быстро пользоваться.

Если вы устраиваетесь на работу в банк или иную компанию финансового сектора, то вам, скорее всего, потребуется знание основных финансовых терминов и методов их расчета. Числовые тесты с финансовыми формулами более сложны и вы должны понимать, как рассчитать, например, коэффициент рентабельности инвестиций, ROI, показатели маржинальности и другие подобные показатели.

Узнайте, что вы можете принести на само тестирование. Вам разрешен калькулятор? Карандаш и бумага для записей? Выясните, что вам разрешено использовать во время сдачи числового теста. Будет глупо вручную вычислять все, что калькулятор мог бы рассчитать быстрее и точнее. Большинство работодателей и HR агентств разрешают пользоваться калькуляторами во время прохождения числовых тестов, потому что они понимают, что этот инструмент помогает только в вычислениях, но не в анализе задач.

Стоит ли заранее практиковаться в решении числовых тестов?

Да! Три раза да!!!!!

Приносим извинения за столько восклицательных знаков, но они здесь уместны. Предварительная подготовка в решении числовых тестов просто необходима для 99% всех соискателей. Впрочем, может быть, вы недавно проработали несколько лет финансовым аналитиком или доцентом математических наук и имели дело с расчетами и графиками каждый день. Тогда, видимо, вы входите в оставшийся 1% соискателей, для кого практика, наверное, уже будет лишней.

Если же нет, то подготовиться однозначно стоит. Только предварительная практика математических (числовых, цифровых) и других (вербальных, логических, психологических, на лидерство) тестов при приеме на работу может дать вам преимущество перед остальными соискателями. И это преимущество бесспорно стоит потраченного на него времени и денег.

Большинство числовых тестов следуют одному правилу — цифры и подача информации разные, но сам тип вопросов остается тем же самым. Поэтому отработайте основные типы математических (числовых) тестов крупнейших компаний-разработчиков, применяемых в России и мире — SHL, Kenexa и Talent Q. Подробнее о них читайте в статье Особенности тестов SHL, Talent Q, Saville, KENEXA

Ниже вы найдете 2 примера числовых тестов разных видов. В примерах на нашем сайте вы также можете пройти много числовых тестов бесплатно.

Пример числового теста 1:

Постарайтесь сначала решить этот числовой тест самостоятельно и только потом смотреть решение и ответ. Решение вы найдете в конце статьи.

Пример числового теста 2:

Постарайтесь сначала решить этот числовой тест самостоятельно и только потом смотреть решение и ответ. Решение вы найдете в конце статьи.

Мы также рекомендуем вам узнать больше о тестах компании SHL — основном разработчике числовых тестов при приеме на работу: Психометрические SHL тесты

Поймите, как тестовые вопросы могут выглядеть, как они обычно оформлены и какие подводные камни в них могут для вас приготовить разработчики. После такого ознакомления и практики вы сможете быстро узнавать тип вопроса, четко понимать задачу и быстро и безошибочно ее решать.

Поэтому, как говорил великий Ленин относительно математических тестов: «Учиться, учиться и еще раз учиться». Посмотрите примеры числовых тестов бесплатно, оцените свой уровень знаний и начните полноценную подготовку.

Внимание! Числовые тесты обычно это не единственные тесты, которые вам предстоит пройти при устройстве на работу или при прохождении конкурса Лидеры России. К ним обычно прибавляются вербальные тесты, тесты на логическое мышление и психологические (поведенческие) тесты. Читайте больше о вербальных, логических и психологических тестах при приеме на работу в наших специальных статьях:

Все о вербальных тестах

Логические тесты при приеме на работу — что это такое

Как пройти психологический тест при устройстве на работу

Мы призываем вас начать подготовку прямо сейчас, ведь лучше потратить 1-2 дня на решение примерных тестов сейчас, чем провалиться на реальном тестировании и жалеть об упущенном шансе потом.

Начать подготовку 

Пройти примеры тестов

Ответы и решение примеров тестов:

Числовой тест Пример 1:

Числовой тест Пример 2:

Начать подготовку 

hrlider.ru

Тест на мышление «Числовые ряды»

Для исследования логического аспекта математического мышления.

Материал

Лист бумаги с напечатанными на нем примерами.

Инструкция 

«Внимательно прочитай каждый ряд чисел и на два свободных места напиши такие два числа, которые продолжат данный числовой ряд».

Примеры:

2                                  4                6            8           

10                                9                3            7

      3                                  3                4            4

 Ключ к обработке

Интерпретация

Если испытуемый затрудняется при решении подобных задач, это может обозначать, что он плохо анализирует цифровой материал, не видит в нем скрытых закономерностей, поэтому не может ими воспользоваться, следовательно, его логическое мышление в математике развито слабо.

4. Когнитивные стили мышления

Методика на определение ведущей модальности

Модальность — форма отражения раздражителя в определенной сенсорной системе (зрительной, слуховой, тактильной). Пища для нашей нервной системы бывает разной, и разными бывают наши предпочтения. Кто-то предпочитает визуальную информацию, кто-то аудиальную (слуховую), кто-то — кинестетическую (прикосновения, внутренние ощущения и т.д.). Поэтому и сенсорный голод (недостаток впечатлений для зрения, слуха, осязания) следует утолять не чем попало, а информацией для ведущей модальности. Ведущая модальность — это наше предпочтение в сенсорной пище, с помощью которой мы лучше всего понимаем происходящее. В решении любой задачи один человек нарисует на бумажке разные варианты, другой проговорит их вслух, третий разложит перед собой предметы. Какая модальность для вас ведущая?  Инструкция: зачитайте предлагаемые утверждения. Поставьте знак «+», если вы согласны с  данным утверждением, и знак «-», если не согласны.

44. Я люблю фотографировать, выбирать удачные ракурсы для снимков.

45. Я долго помню то, что мне сказали.

46. После тяжелого дня самое большое желание – принять удобное положение и расслабиться.

47. Я узнаю по шагам, кто вошел в комнату.

48. Люблю наблюдать за облаками и звездами.

49. Я не стану носить очень модную вещь, если она неудобна.

50. Люблю петь, когда чем-нибудь занимаюсь.

51. Мне очень приятно, когда в лицо дует легкий теплый ветерок.

52. Для меня очень важны цвета, которые меня окружают.

53. Я иногда разговариваю сам с собой.

54. Стараюсь записать все важные дела, чтобы не забыть.

55. Вечером я обязательно должен принять душ или ванну.

56. Я люблю танцевать.

57. Не могу уснуть, когда рядом тикает будильник.

58. Не выношу беспорядка в комнате, где живу.

59. Я часто слушаю плеер.

60. Если мне приходится долго сидеть, я ужасно устаю.

61. Люблю рассматривать репродукции картин.

62. Мелодия прошлого лета переносит меня в него.

63. Я люблю читать во время еды.

64. Очень часто и помногу разговариваю по телефону.

65. Я не худой человек.

66. Люблю потягиваться, разминаться.

67. Я умею слушать собеседника.

68. Обожаю смотреть фильмы.

69. У меня хорошая память на лица.

70. Люблю слушать шум дождя.

71. Не люблю спать на слишком мягкой постели.

72. Меня развлекают пародии, умение подражать голосам.

73. Много времени уделяю своему внешнему виду.

74. Люблю массаж.

75. В общественном транспорте я рассматриваю людей.

76. Предпочитаю слушать чье-либо чтение вслух, чем читать самому.

77. Я согласен с японской мудростью, что один цветок больше передает красоту, чем огромный     букет.

78. Не могу долго ездить на машине.

79. Много информации о собеседнике содержится в интонациях его голоса.

80. Мне нравится, когда люди хорошо одеваются.

81. В шуме не могу сосредоточиться.

82. Когда слышу музыку, отбиваю такт ногой.

83. Не люблю синтетических тканей.

84. Найти удобную обувь для меня очень сложно.

85. От яркости освещения в комнате зависит мое настроение.

Обработка результатов методики на определение ведущей модальности : Визуал: 1, 5, 9, 11, 15, 18, 20, 22, 25, 26, 30, 32, 37, 42  Аудиал: 2, 4, 7, 10, 14, 16, 21, 24, 27, 29, 33, 36, 38 Кинестетик: 3, 6, 8, 12, 13, 17, 19, 23, 28, 31, 35, 39, 40, 41.

Интерпретация результатов:

5. Мотивация

studfiles.net

Ответы на тестовые задания

2.12. Ряды Числовые ряды

Основные понятия

Пусть дана числовая последовательность .

Выражение вида

(1)

называется числовым рядом, или просто рядом.

Числа называютсячленами ряда, член a_n с произвольным номером – общим членом ряда.

Суммы конечного числа членов ряда 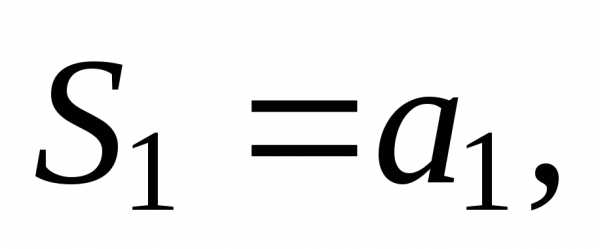…,… называютсячастичными суммами ряда (1). Так как число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм

(2)

Пример 1. Пусть дана числовая последовательность

. (3)

Тогда последовательность 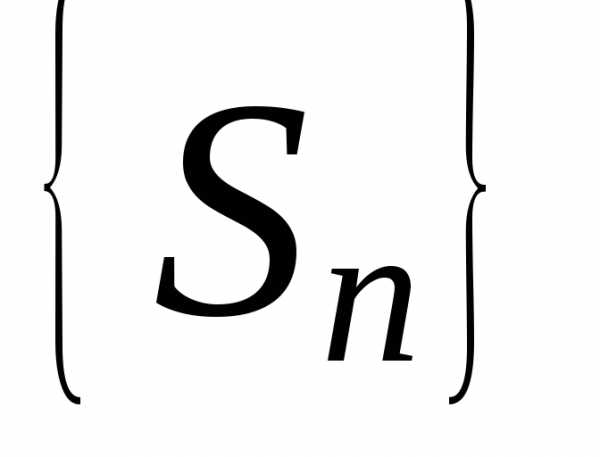будет иметь вид

…,

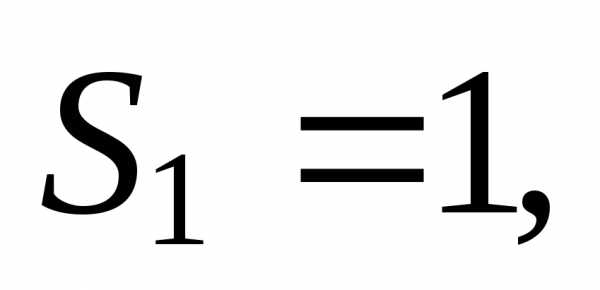
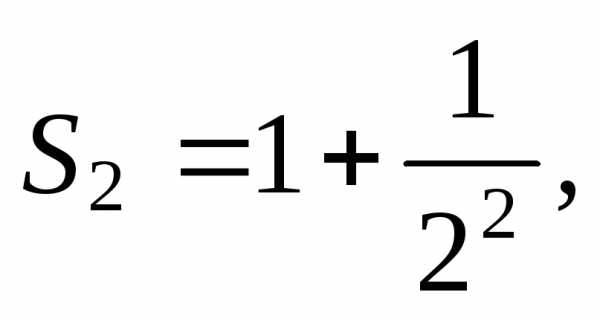
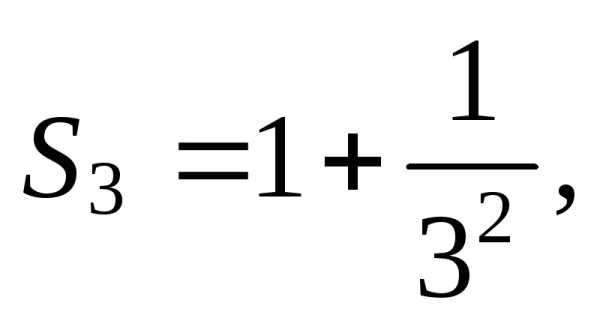Последовательности (3) соответствует ряд

(4)

Пример 2. Рассмотрим ряд

(5)

Найдем его частичную сумму S_n. Имеем

Его частичную сумму можно упростить, если заметить, что

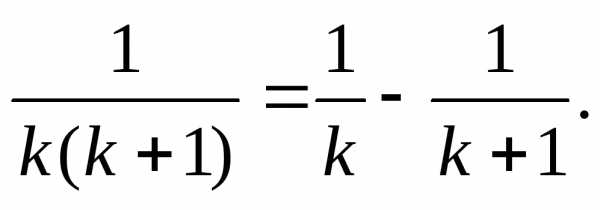
Получим

Тест 1. Определить второй член ряда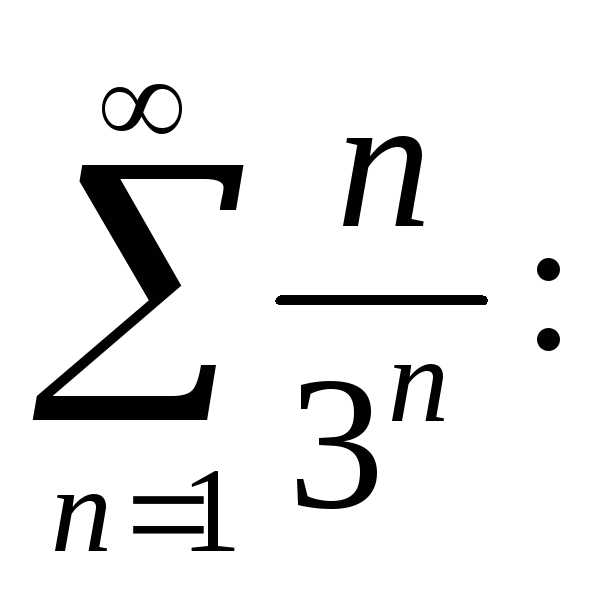

1)

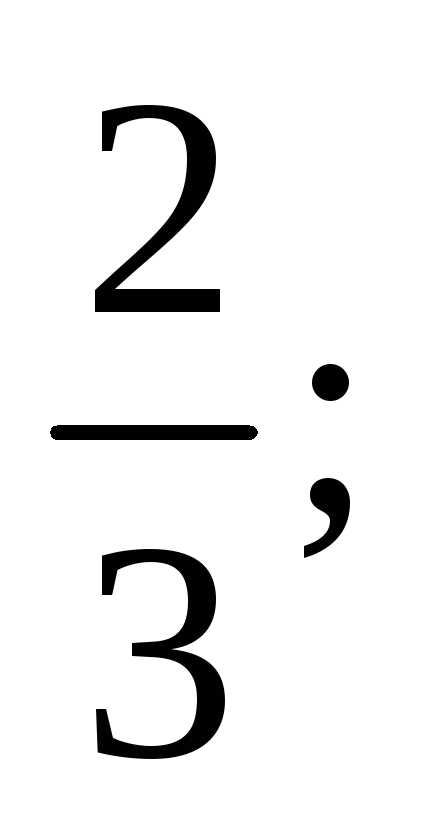
2)

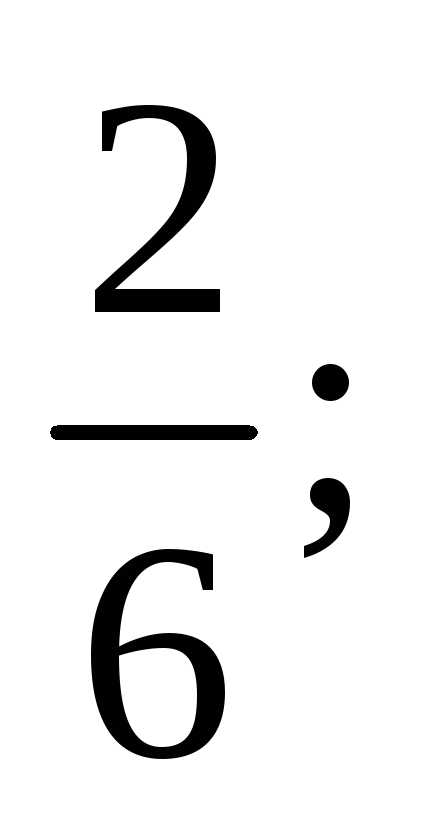
3)

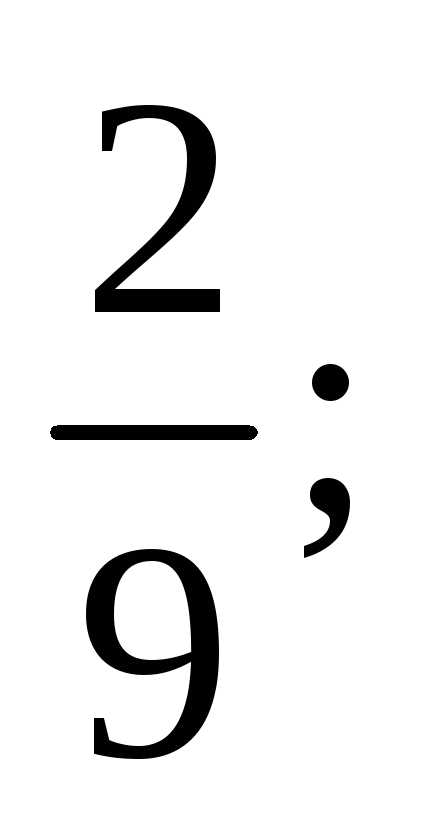
4)

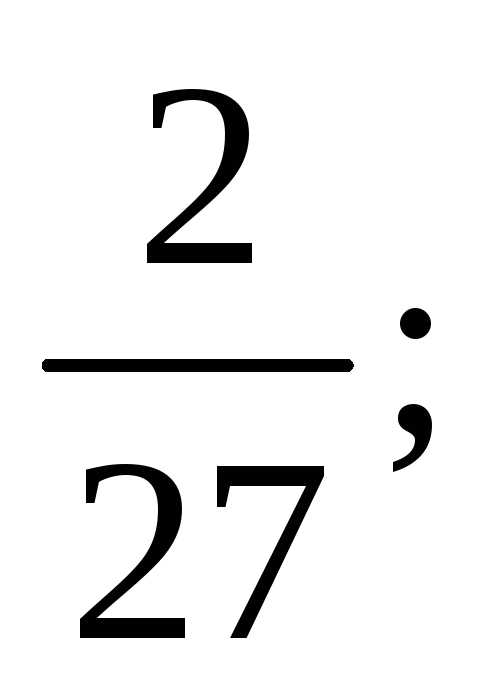
5)

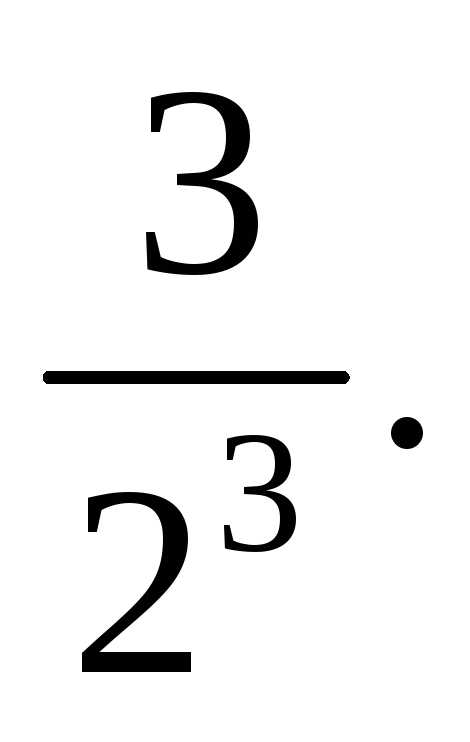
Ряд (1) называется сходящимся, если последовательность его частичных сумм (2) сходится к какому-нибудь числу S, которое называется суммой ряда (1). Символически

Если же последовательность частичных сумм (2) расходится, то ряд (1) называется расходящимся. Такой ряд суммы не имеет.

Тест 2. Определить частичную сумму S₃ ряда 1 ++++… :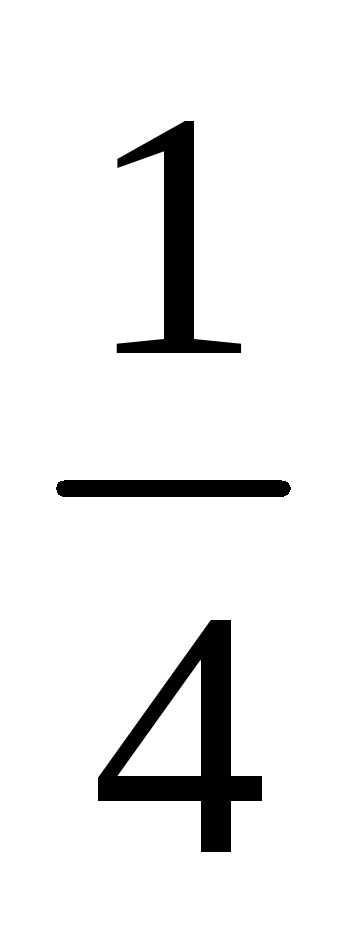

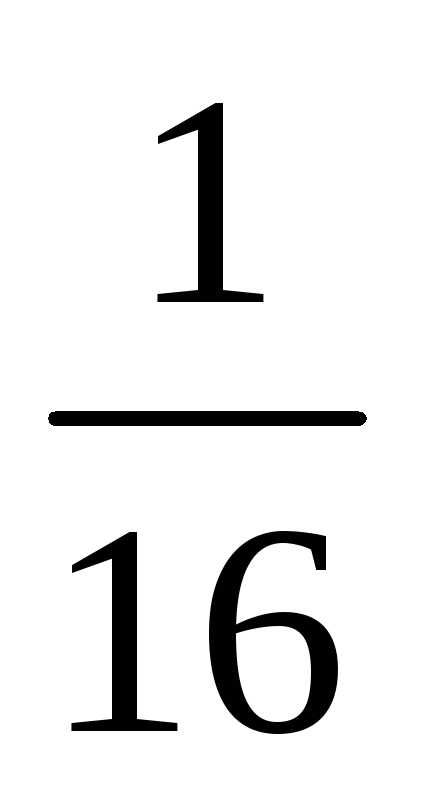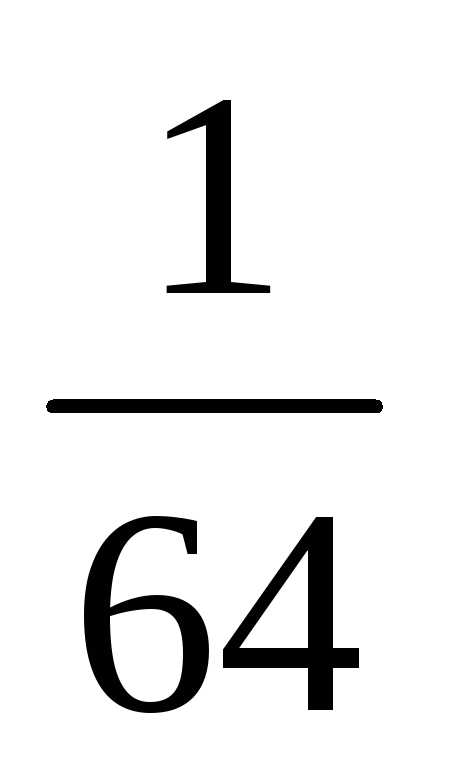1)

2)

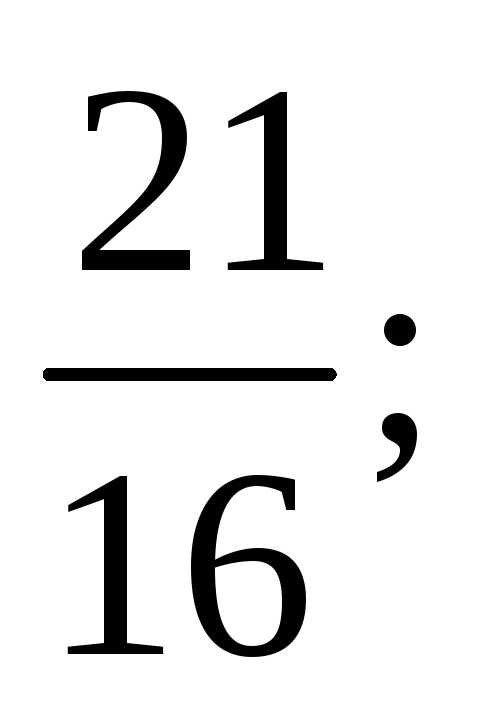
3)

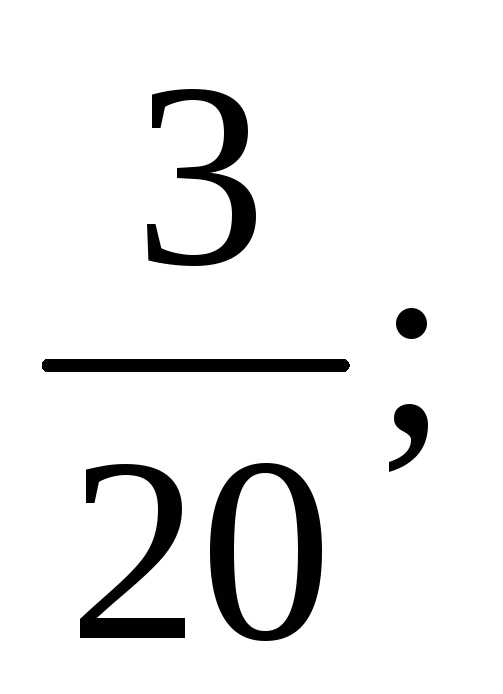
4)

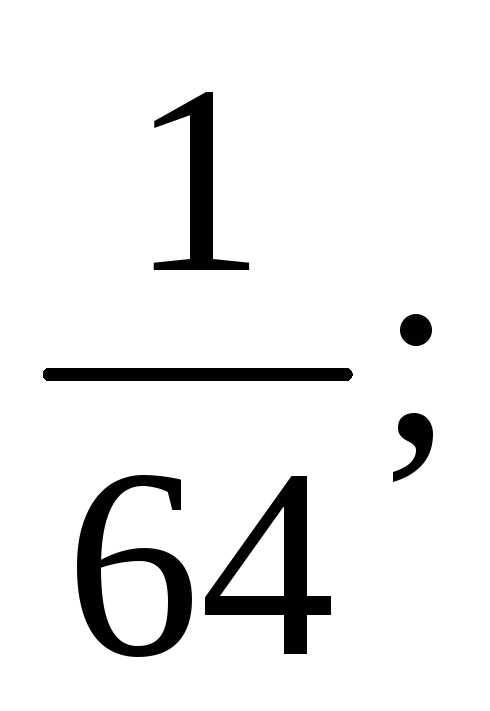
5) 3.

Простейшими примерами числовых рядов, вопрос о сходимости которых решен, являются следующие ряды:

1. 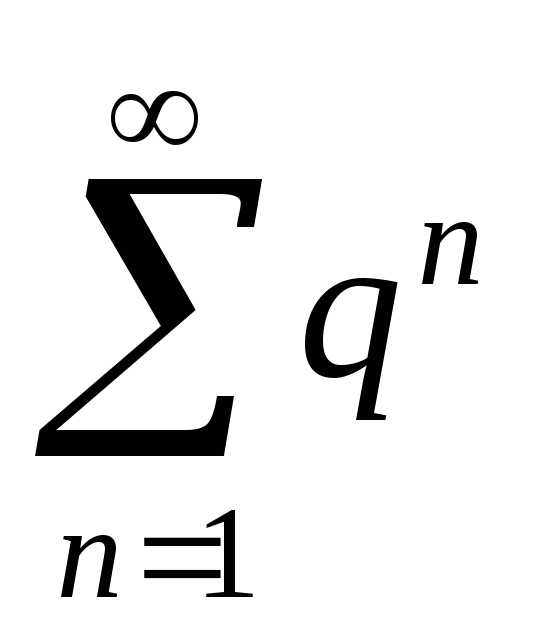–геометрический ряд, который при < 1 сходится, при 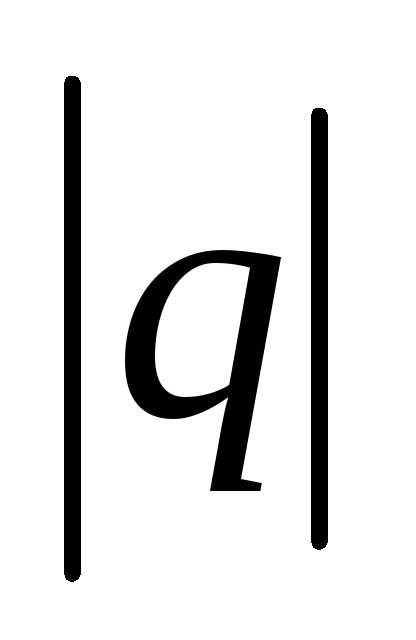≥ 1 расходится.

2. 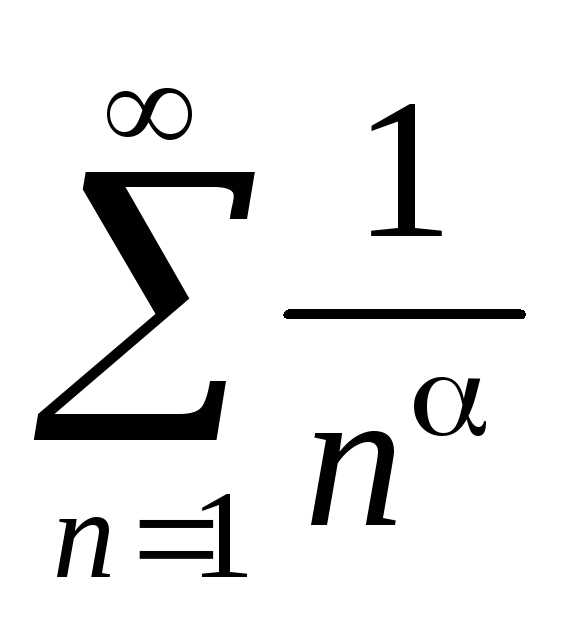–обобщенный гармоничный ряд, который при α > 1 сходится, при α ≤ 1 расходится.

Пример 3. Исследовать сходимость ряда +++…++… .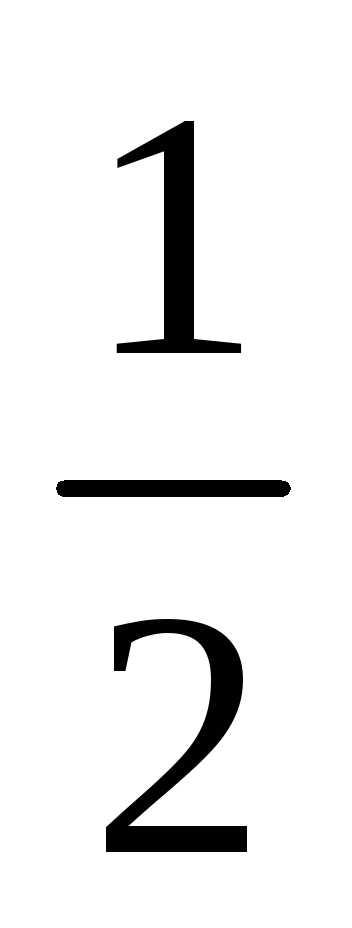

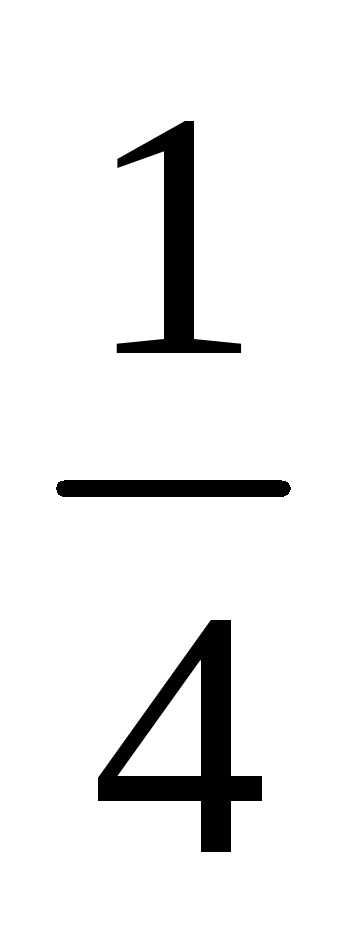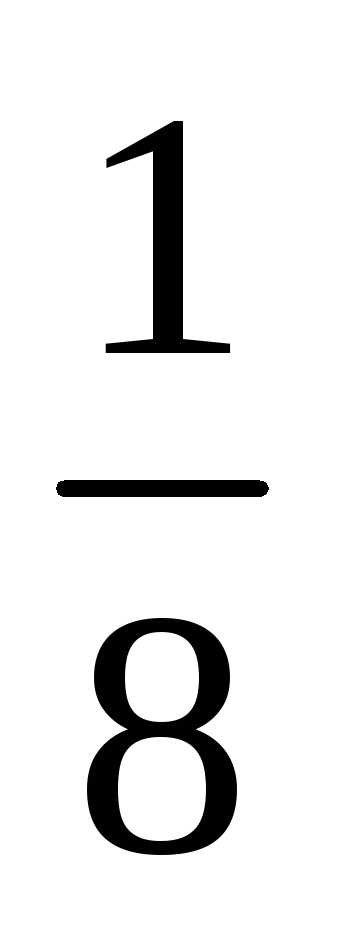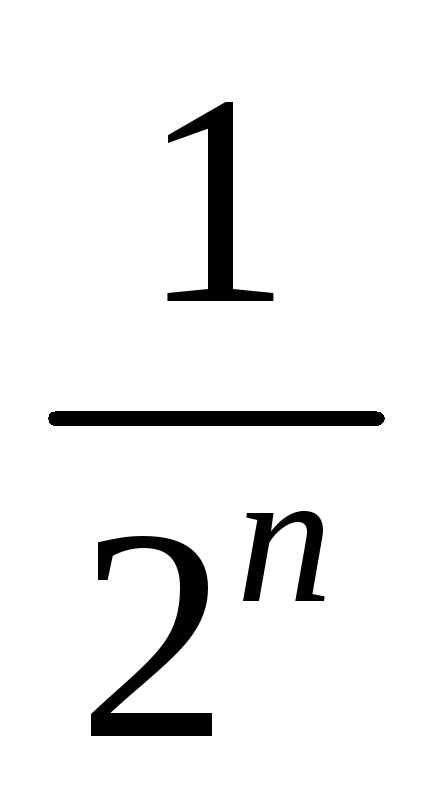Решение

Это геометрический ряд, так как q =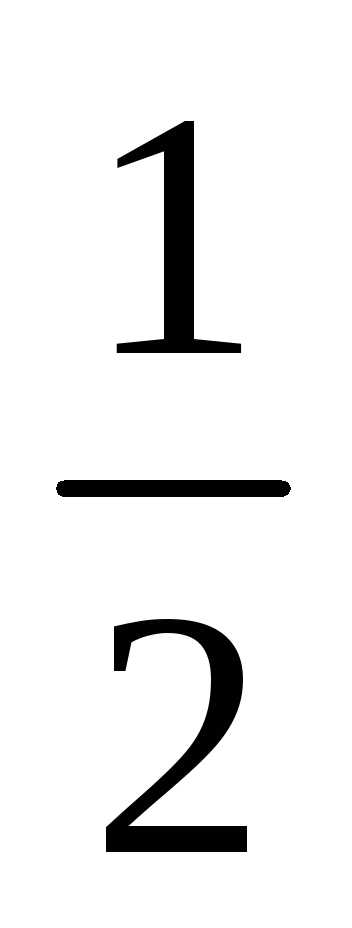< 1, то ряд является сходящимся.

Тест 3.Указать, при каких значенияхобобщенный гармонический ряд является сходящимся:

1) при любых ;

2) при 0 <  < 1;

3) при > 1;

4) при  ≤ 1;

5) при 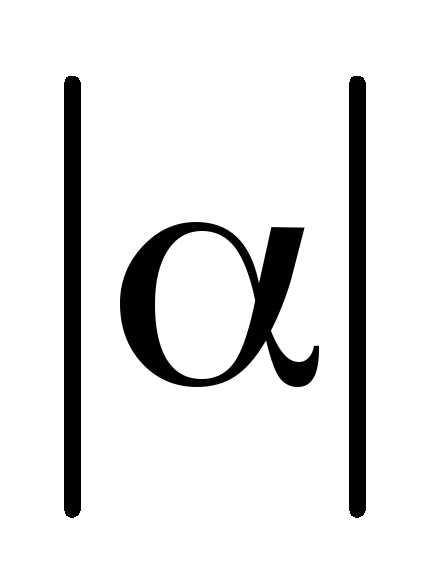< 1.

Тест 4.Для геометрического ряда 1+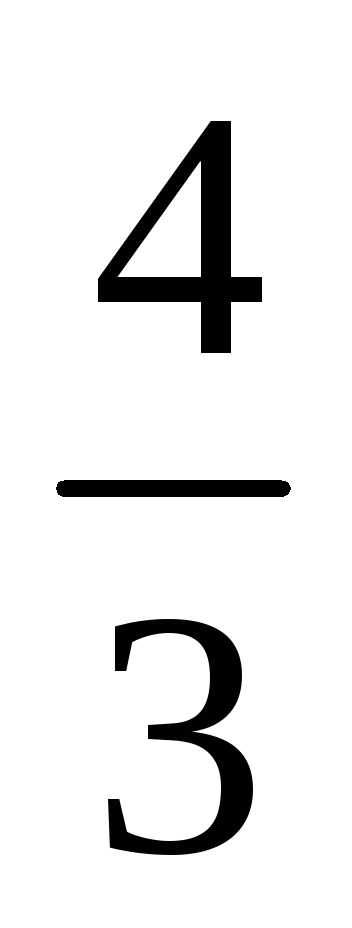++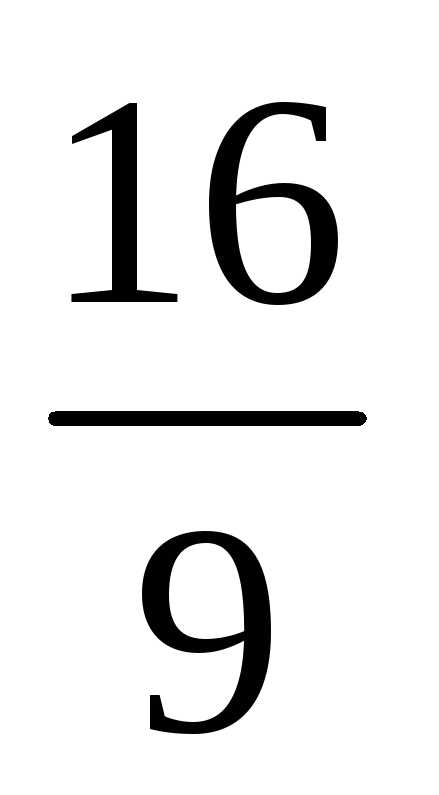+… определить знаменательq:

1)

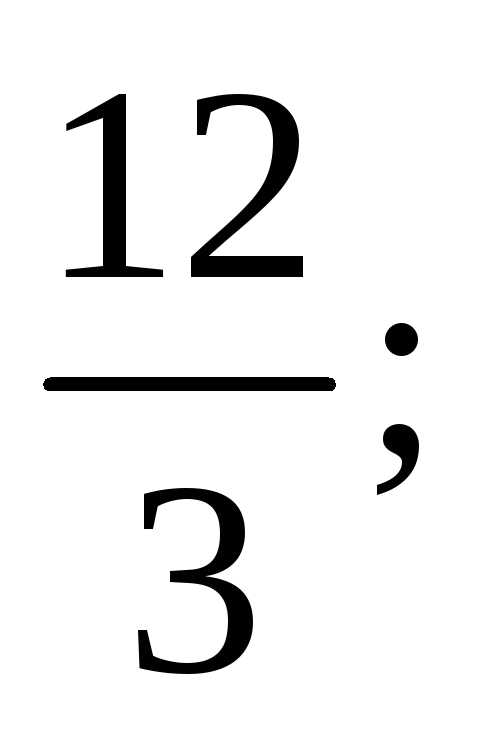
2)

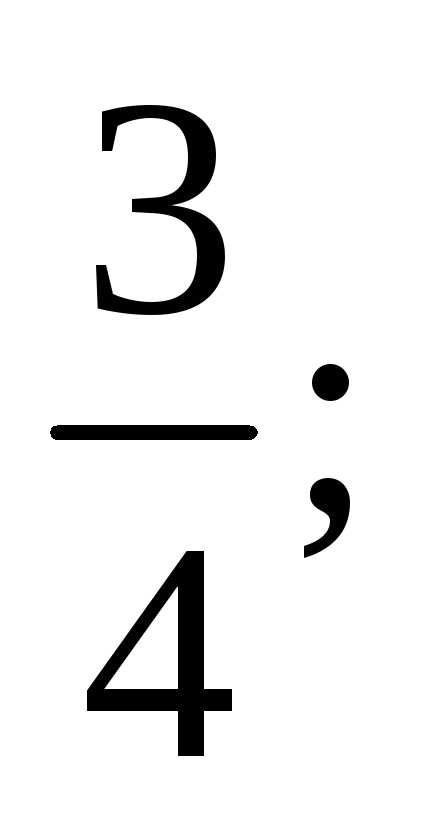
3)

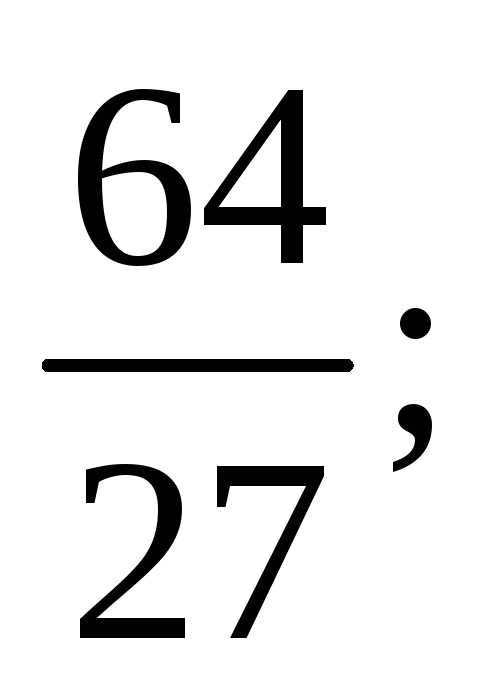
4)

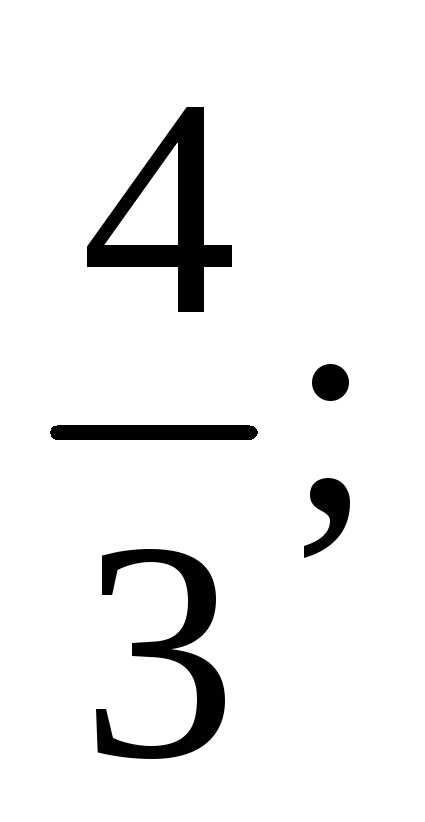
5)

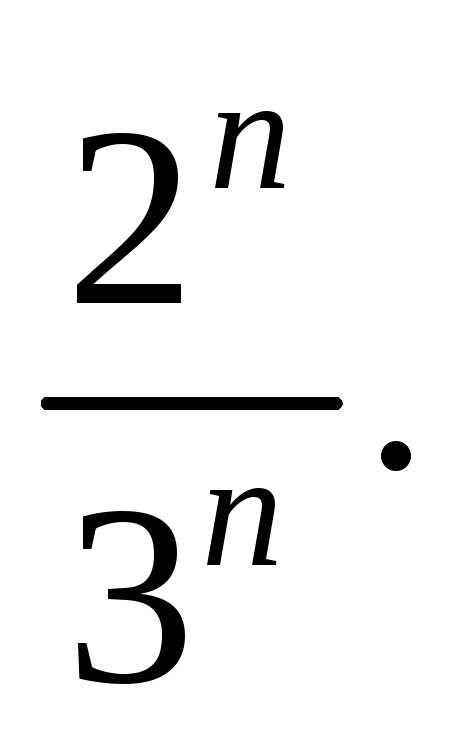
Факты сходимости и расходимости ряда устанавливаются с помощью признаков сходимости рядов, к рассмотрению которых и переходим.

Необходимый признак сходимости ряда

Необходимый признак сходимости ряда. Если ряд (1) сходится, то его общий член стремится к нулю, т. е.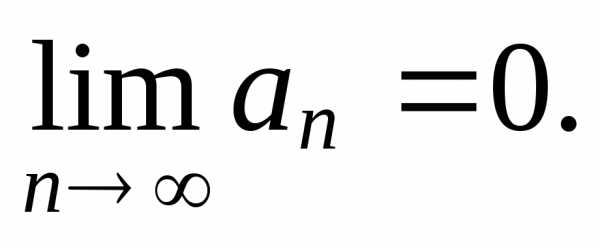

Следствие(достаточное условие расходимости ряда). Если общий член ряда не стремится к нулю, то ряд расходится.

Пример 4.В качестве примера можно привести гармонический ряд, т. е. ряд

,

в котором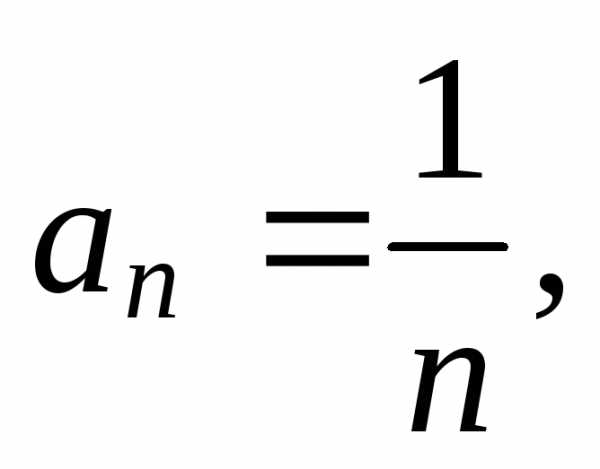

Но известно, что гармонический ряд расходится. Равенство нулю общего члена ряда является лишь необходимым, но недостаточным условием сходимости.

Пример 5. Исследовать сходимость ряда

.

Решение

Найдем предел общего члена ряда 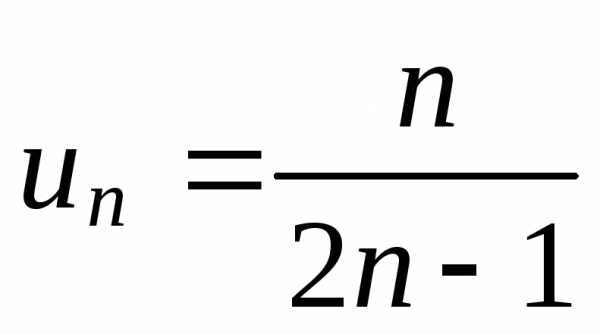приn

Значит, данный ряд расходится.

Тест 5.Рядрасходится, так как:

1) является гармоническим;

2)

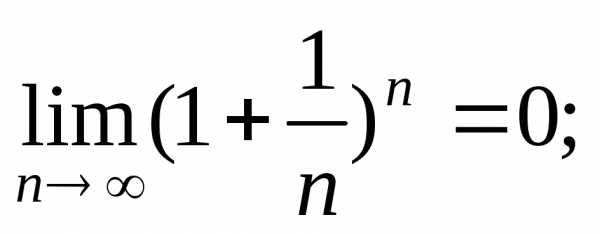
3)

4)

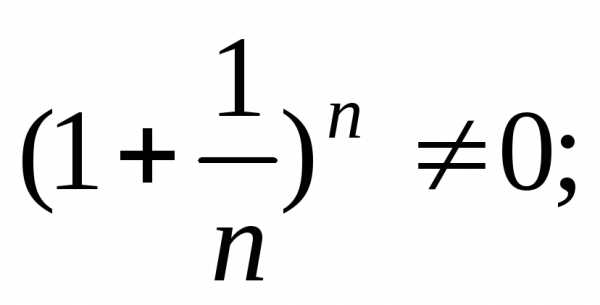
5) 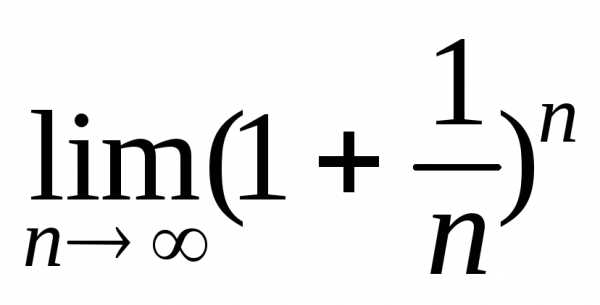не существует.

Достаточные признаки сходимости знакопостоянных рядов

Признак сравнения. Пусть даны два ряда с положительными членами

(6)

. (7)

Если для всех nвыполняется неравенство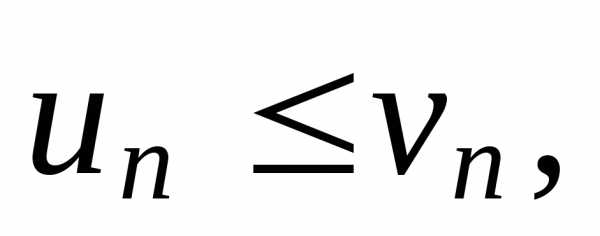то из сходимости ряда (7) следует сходимость ряда (6), а из расходимости ряда (6)следует расходимость ряда (7).

Замечание. При применении признака сравнения обычно в качестве эталонных рядов рассматриваются следующие ряды:

а) гармоничный ряд;

б) обобщенный гармонический ряд;

в) геометрический ряд.

Пример 6. Выяснить, сходится ли ряд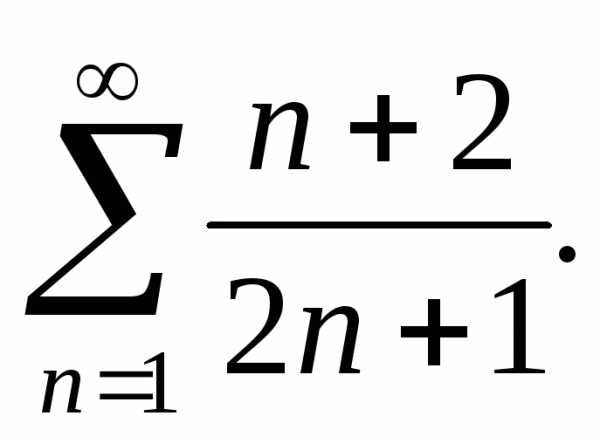

Решение

Так как , т. е.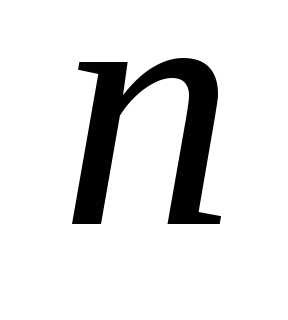-й член ряда не стремится к нулю прито ряд расходится.

Тест 6.Для исследования вопроса сходимости ряда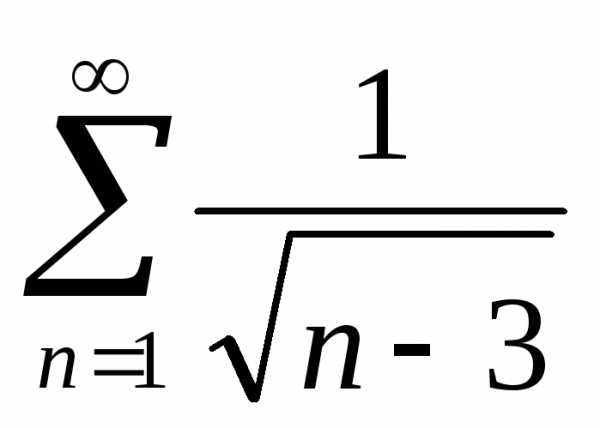сравниваем его с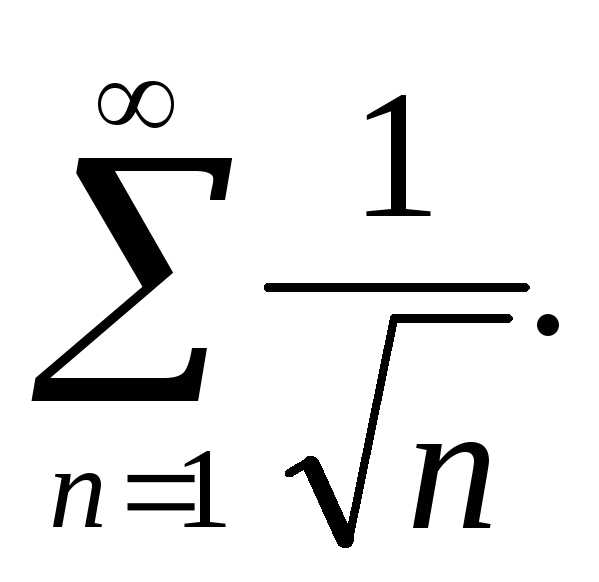Делаем вывод:

1) ряд расходится, так как >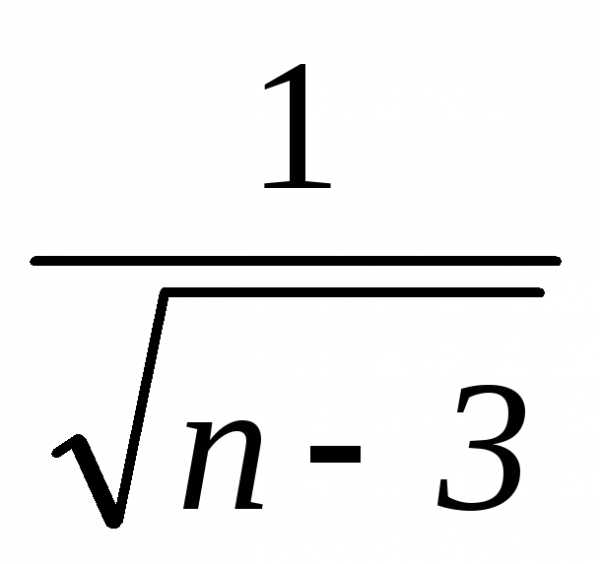

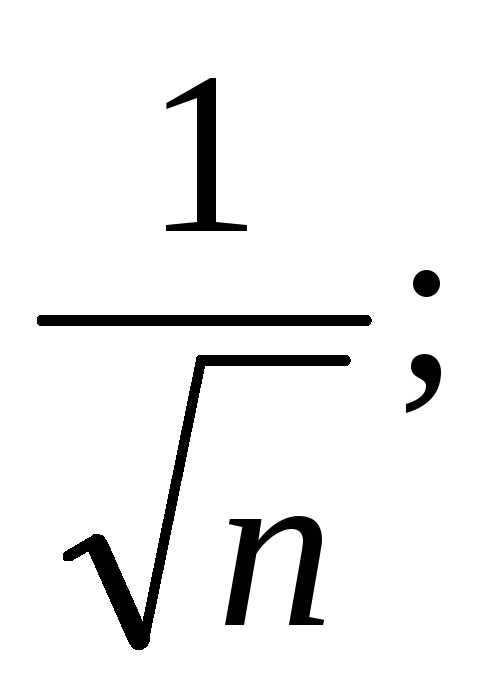
2) ряд сходится, так как <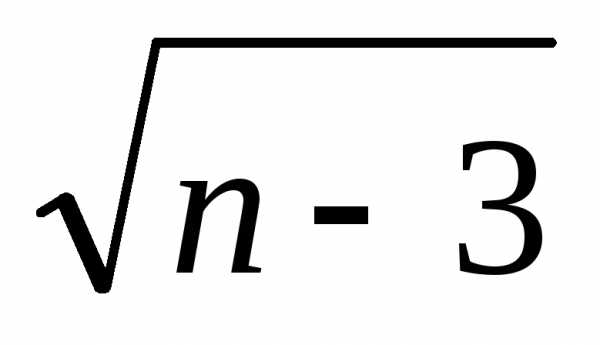 

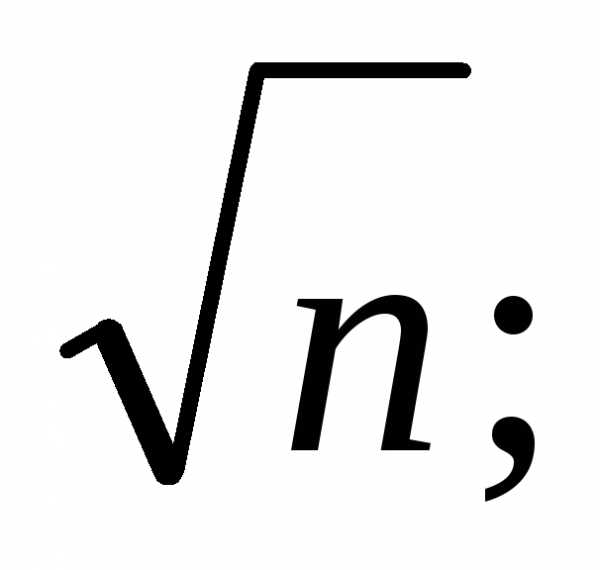
3) ряд сходится, так как>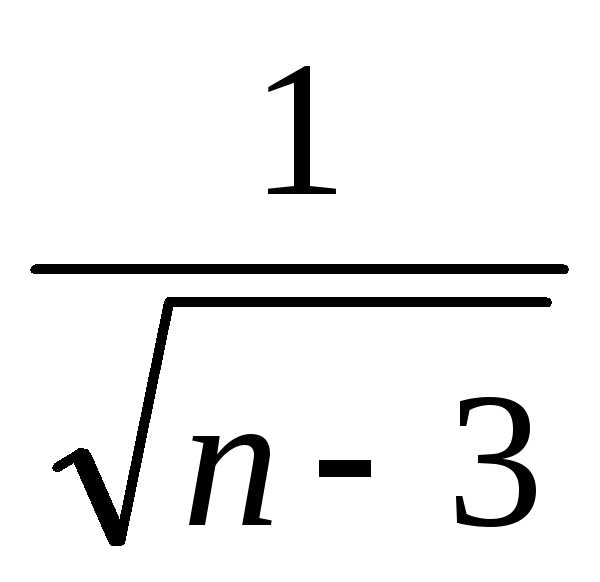

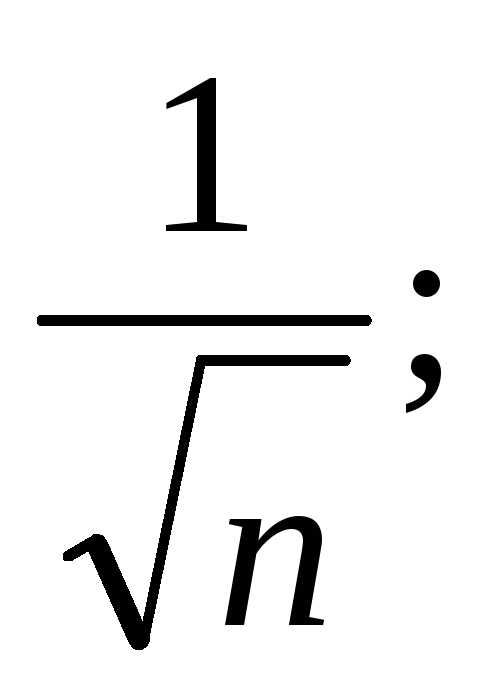
4) ряд расходится, так как>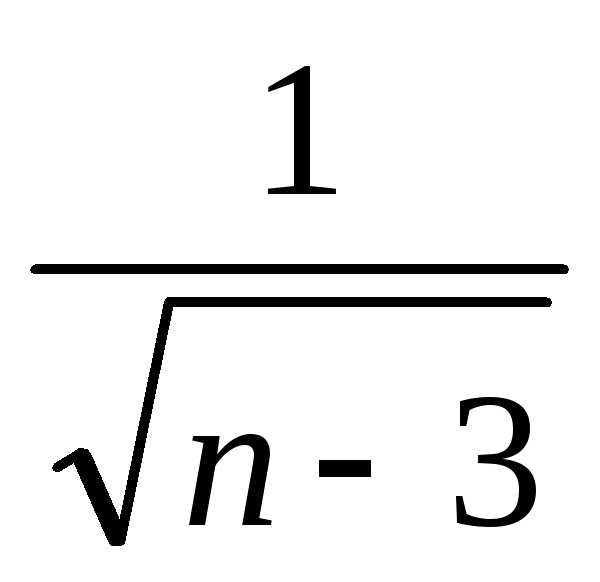

5) ряд расходится, так как >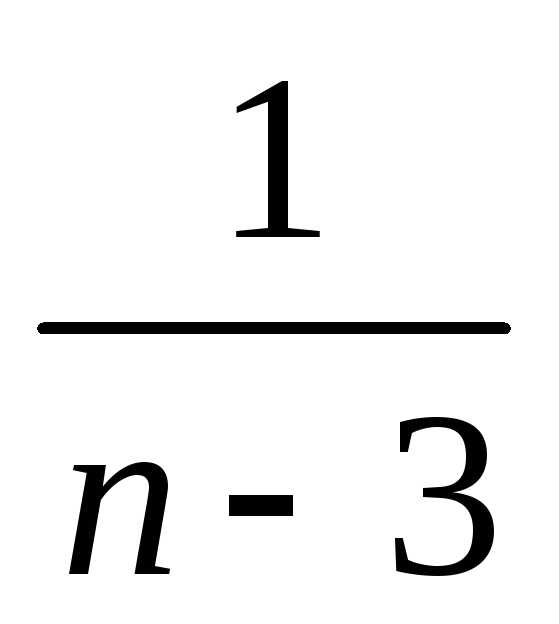

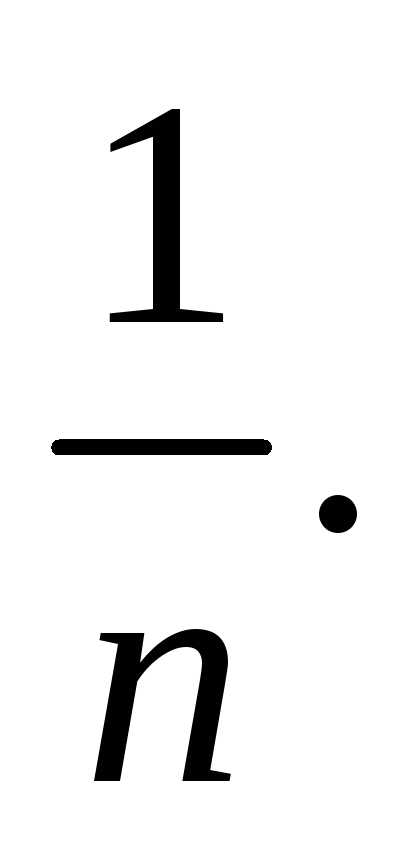
Предельный признак сравнения. Пусть даны два знакоположительных ряда

,

с неотрицательными членами,причем 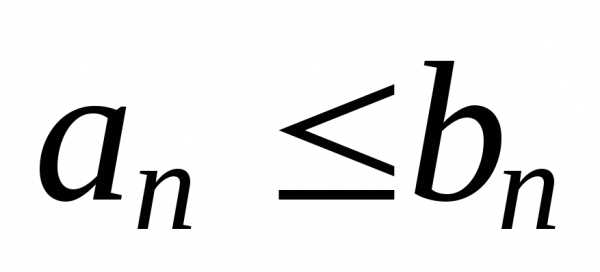для всехn,начиная с некоторого.

Тогда,если ряд сходится,сходится и ряд 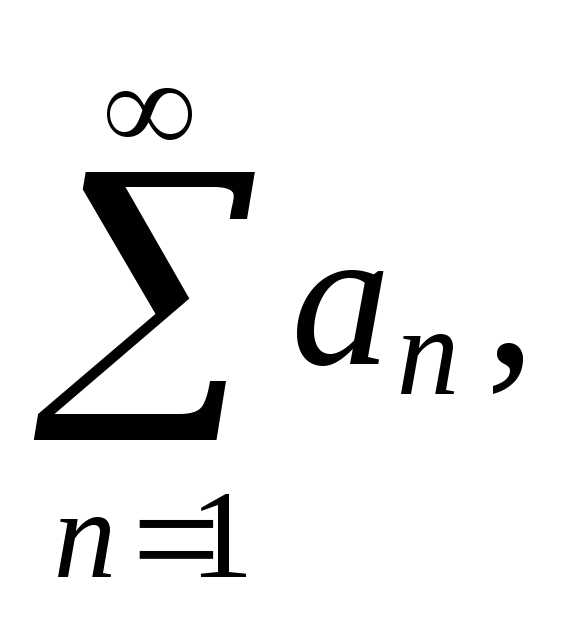если же ряд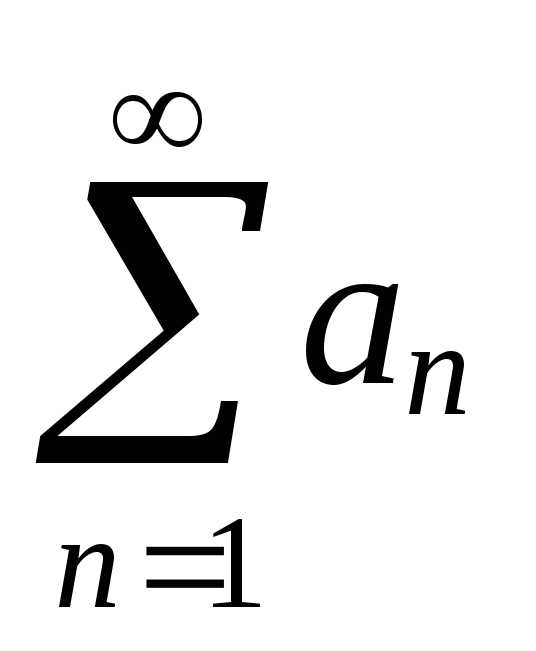расходится,то расходится и ряд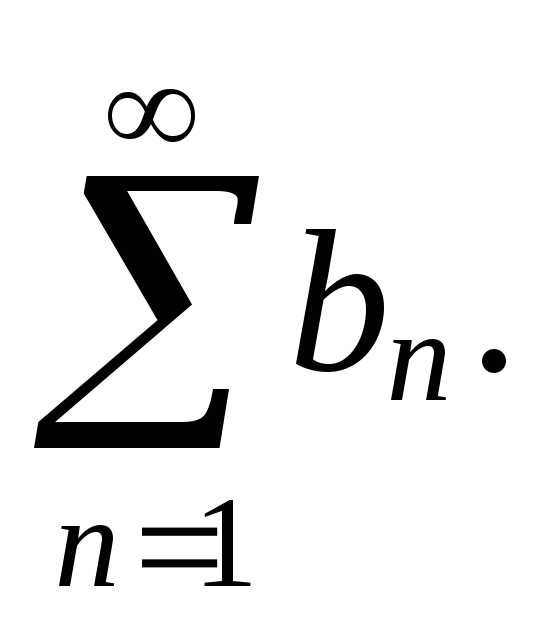

Пример 7. Исследовать сходимость ряда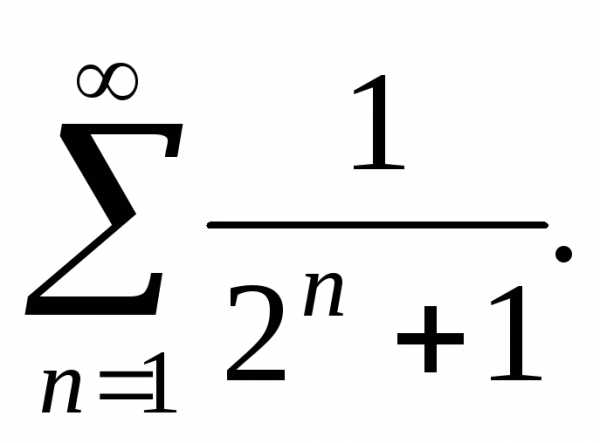

Решение

Члены ряда меньше соответствующих членов ряда, который, являясь рядом бесконечно убывающей геометрической прогрессии, сходится. Следовательно, сходится и данный ряд.

Тест 7.Чтобы исследовать ряд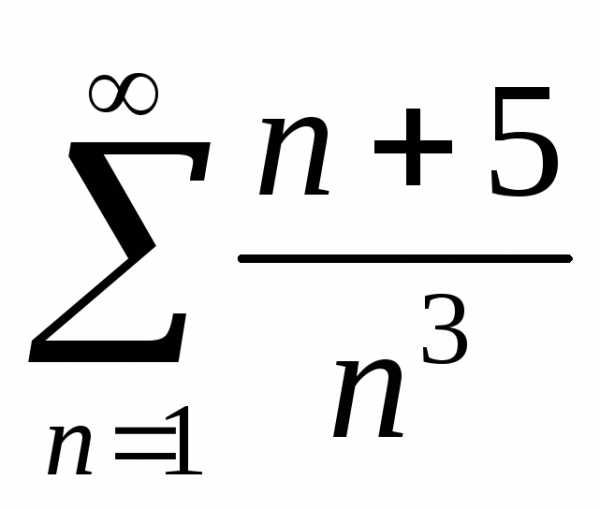с помощью предельного признака сравнения, используем ряд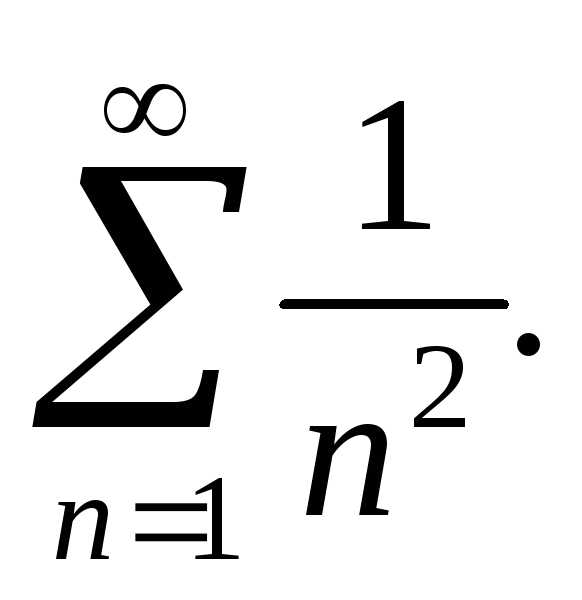Находим:

1)

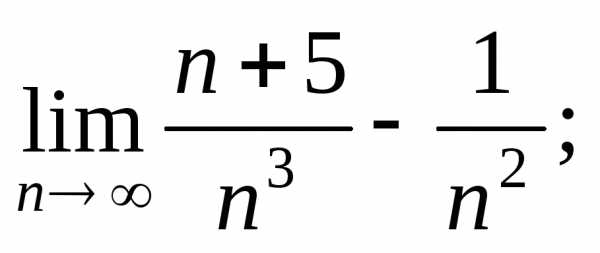
2)

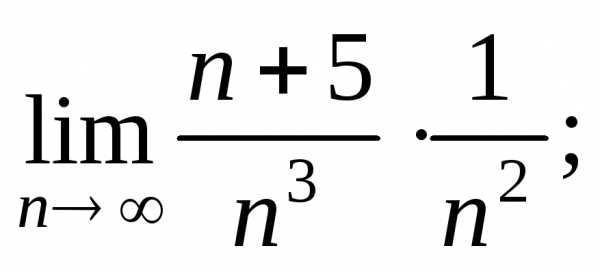
3)

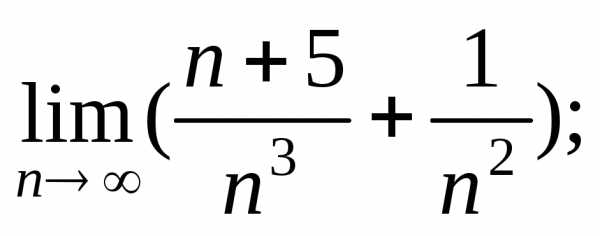
4) –

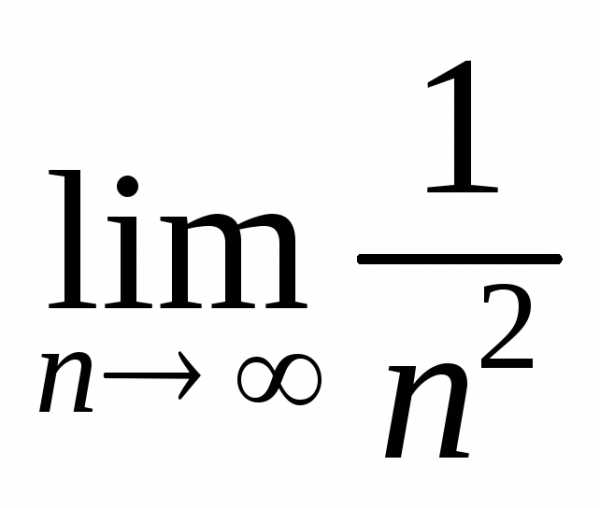5)

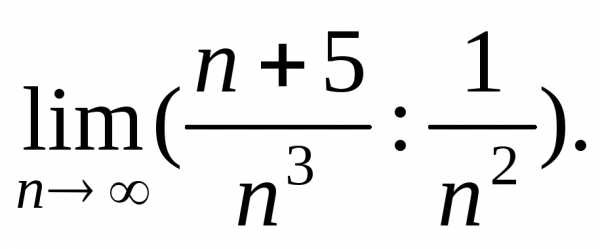
Признак Даламбера. Если существует предел 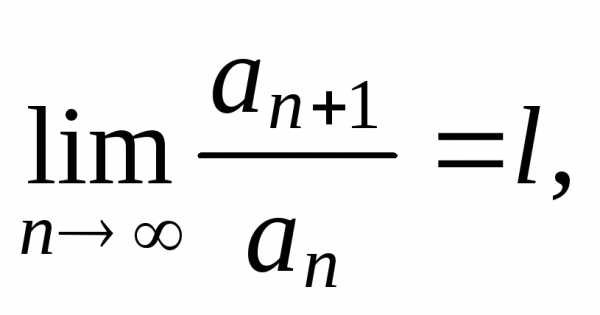то ряд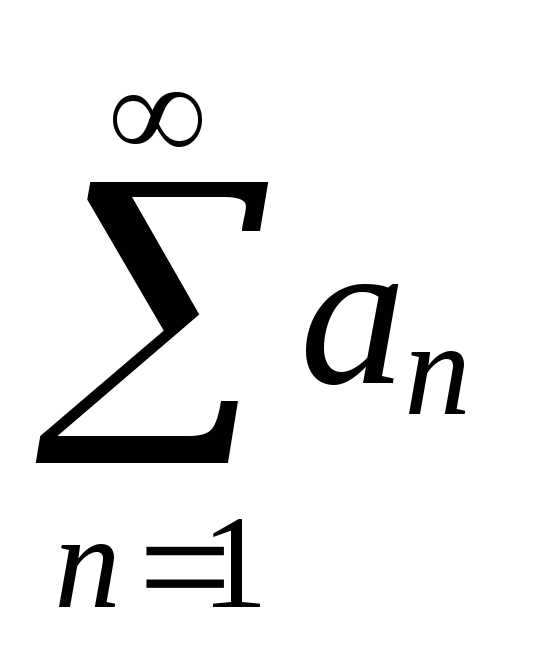сходится при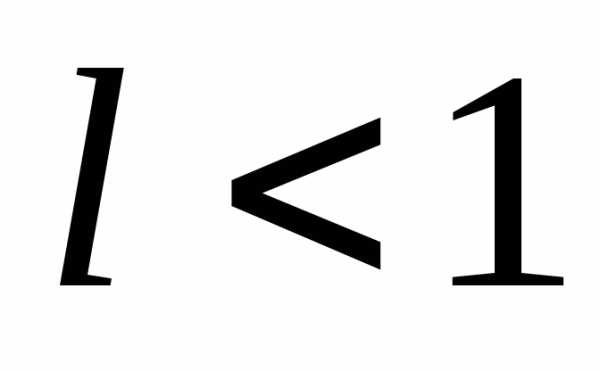и расходится при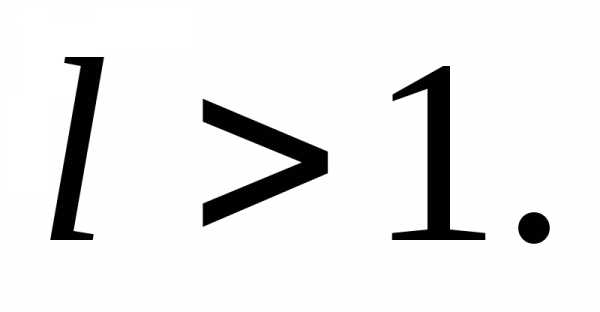

Замечание:

1. Если l= 1, то ряд может быть как сходящимся, так и расходящимся.

2. Признак Даламбера целесообразно применять, когда общий член ряда содержит выражение вида n! илиaⁿ.

Пример 8. Исследовать сходимость ряда

.

Решение

Воспользуемся признаком Даламбера. Общий член ряда ПоэтомуиРяд расходится. Заметим, что мы доказали также соотношение(общий член сходящегося ряда стремится к нулю).

Тест 8.С помощью признака Даламбера определяем сходимость ря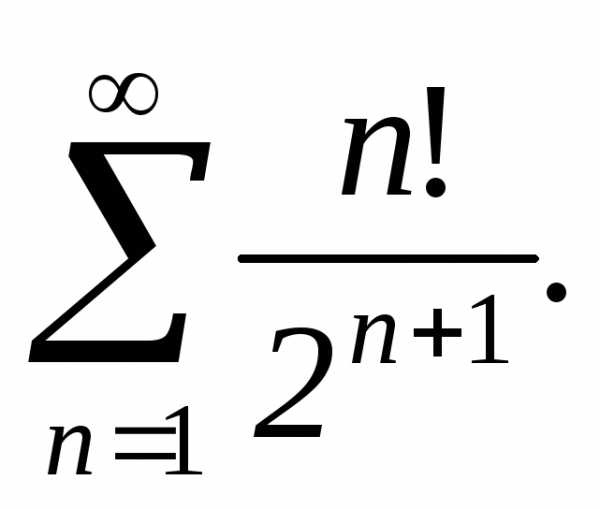даТогда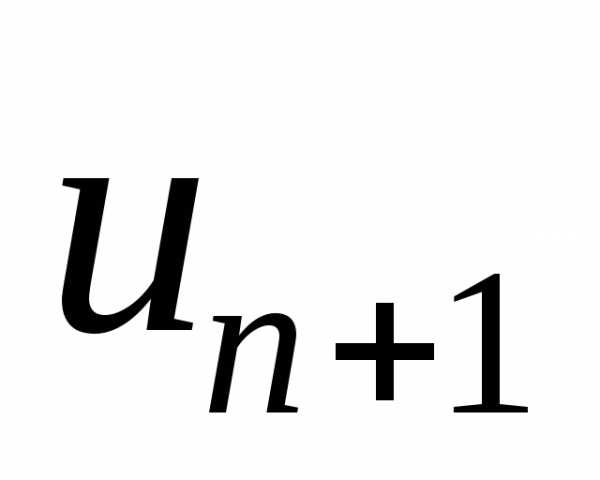равен:

1)

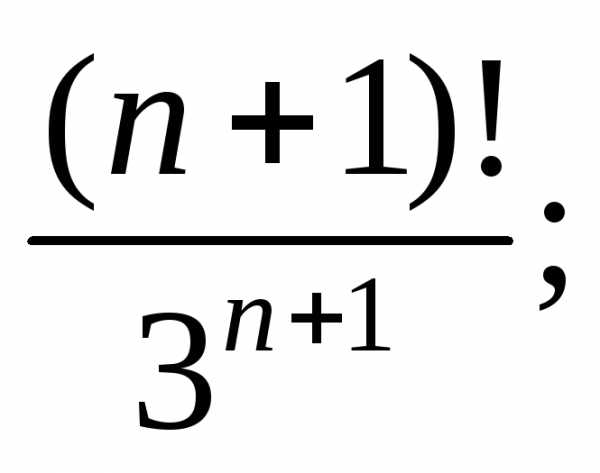
2)

3)

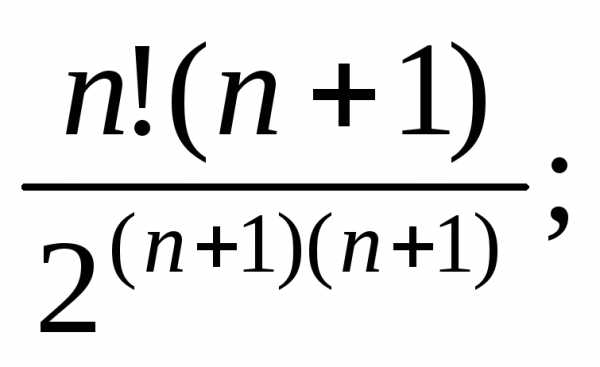
4)

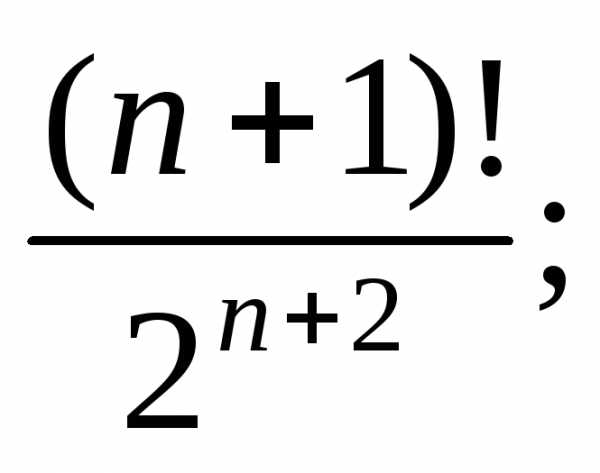
5)

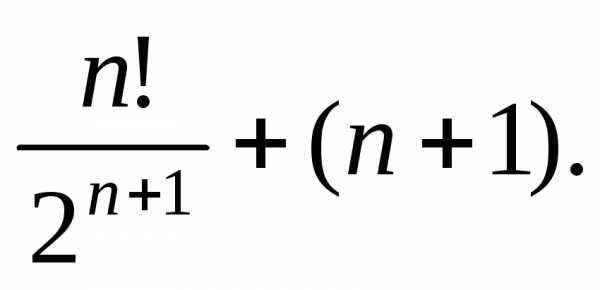
Признак Коши. Если существует предел

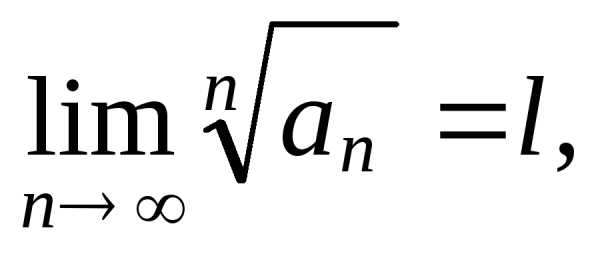(8)

то ряд 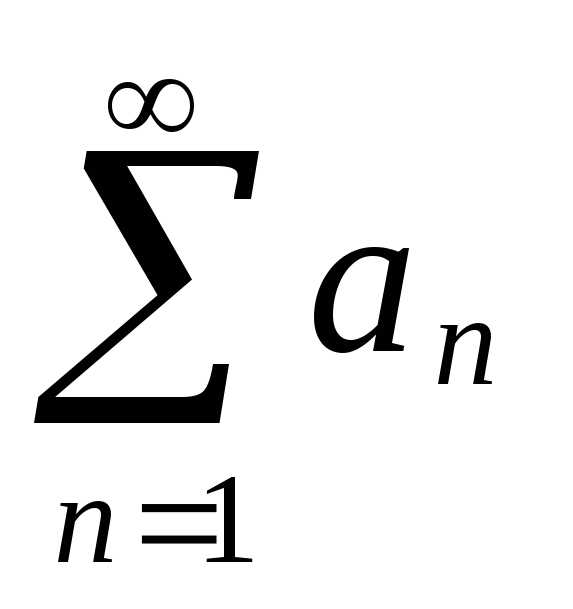сходится при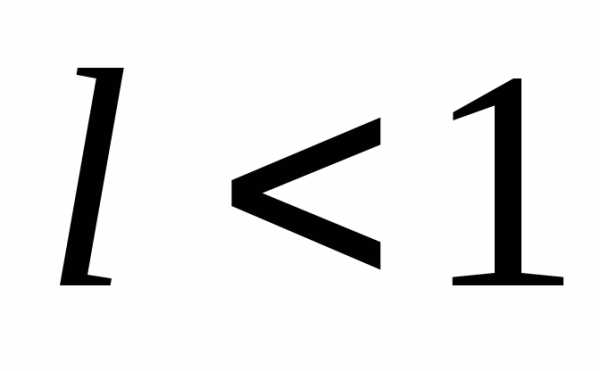и расходится при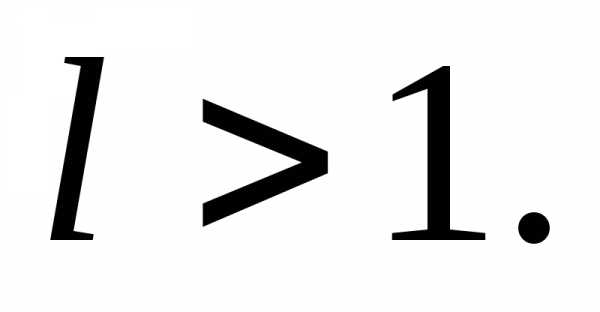

Замечание. Как и для признака Даламбера, в случае, когда l = 1, вопрос о сходимости ряда становится открытым.

Пример 9. Исследовать, сходится ли ряд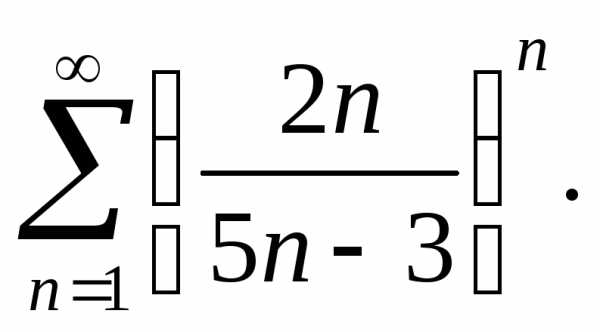

Решение

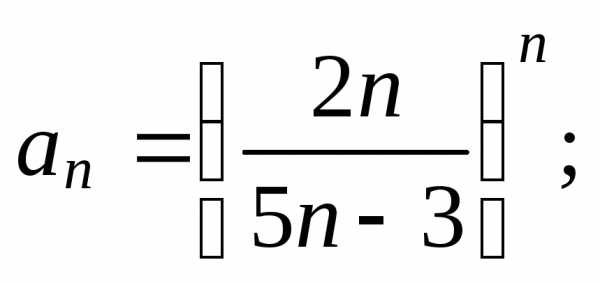Ряд сходится.

Тест 9. Чтобы исследовать ряд 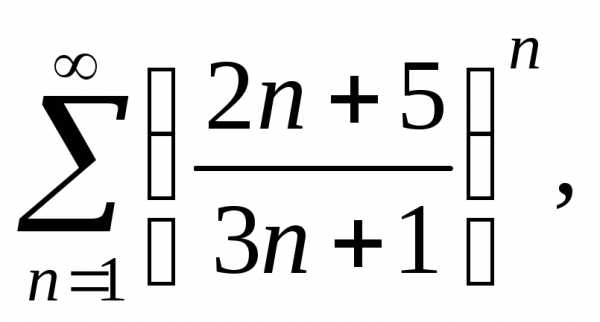применяя признак Коши, необходимо найти:

1)

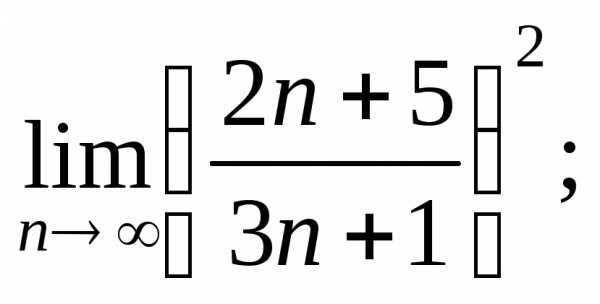
2)

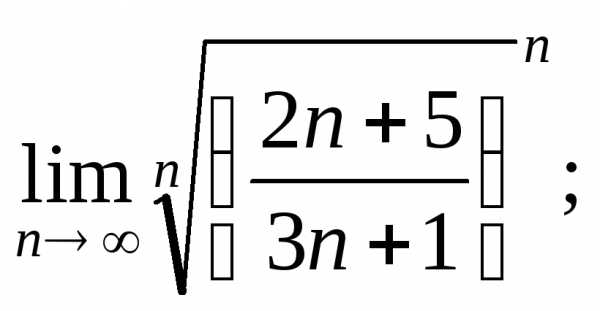
3)

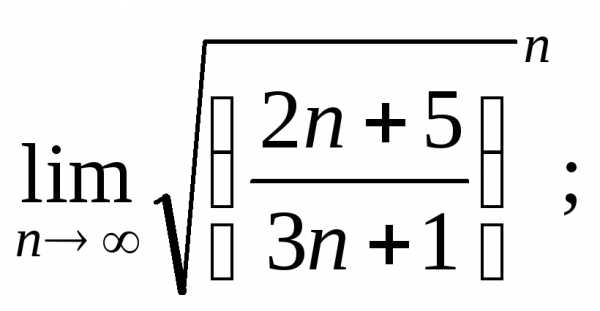
4)

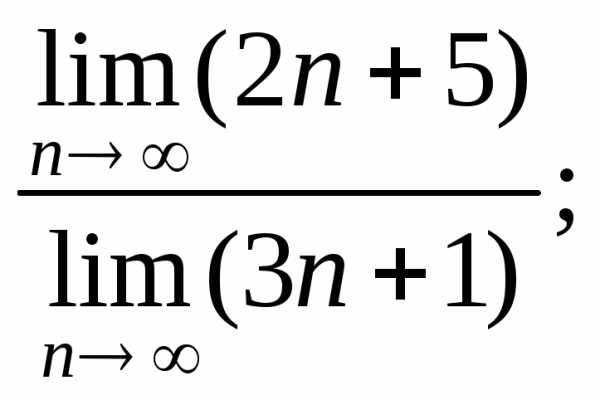
5)

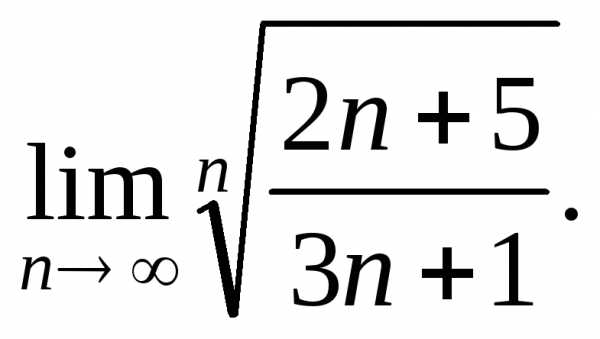
Пример 10. Исследовать сходимость ряда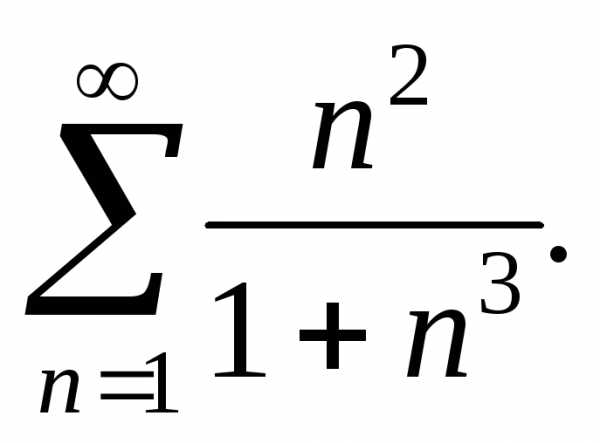

Решение

Применим интегральный признак Коши. По виду общего члена найдем функцию f(x)=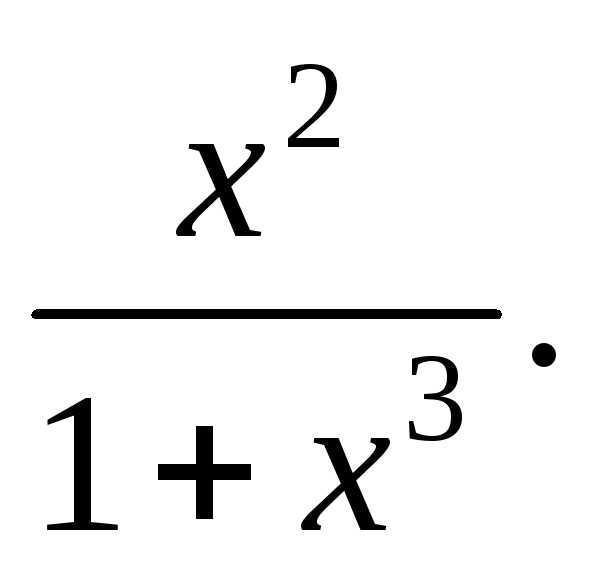

Вычислим несобственный интеграл

=

=

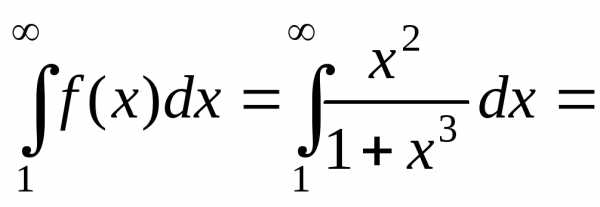
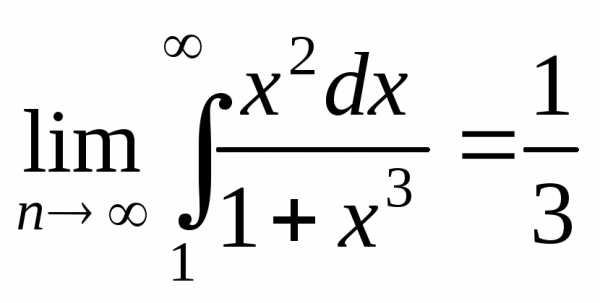
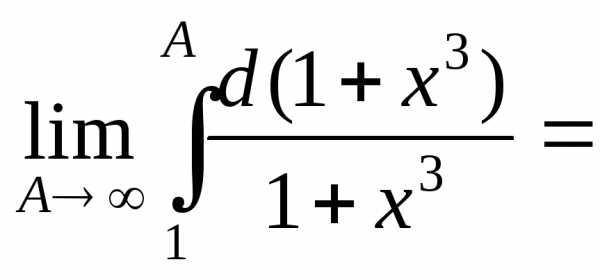
Интеграл расходится, следовательно, и ряд расходится.

Тест 10. Исследуем сходимость ряда 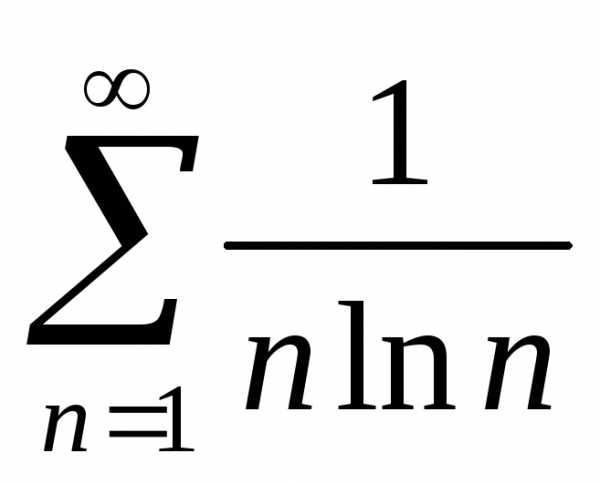с помощью интегрального признака Коши. Найдем:

1)

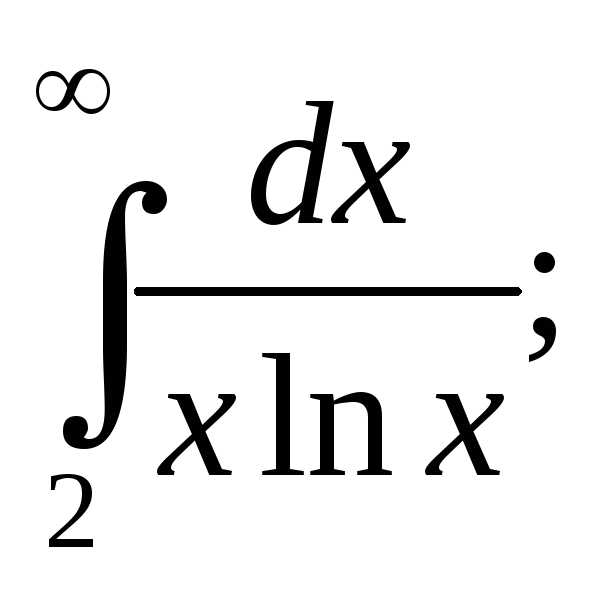
2)

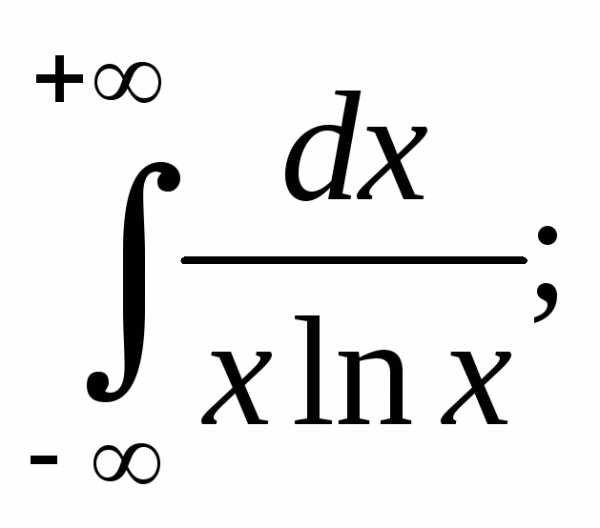
3)

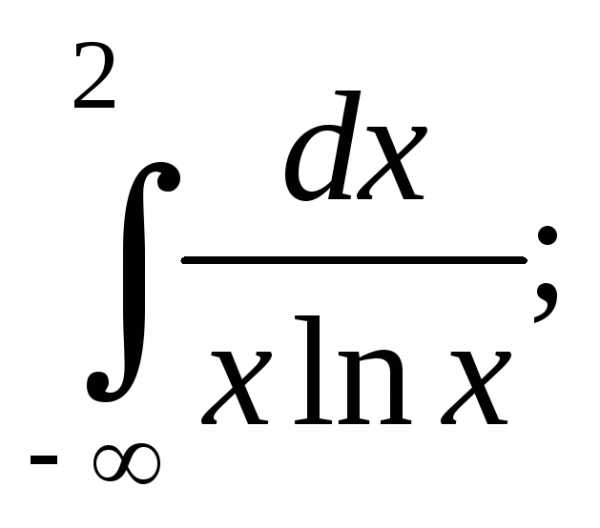
4)

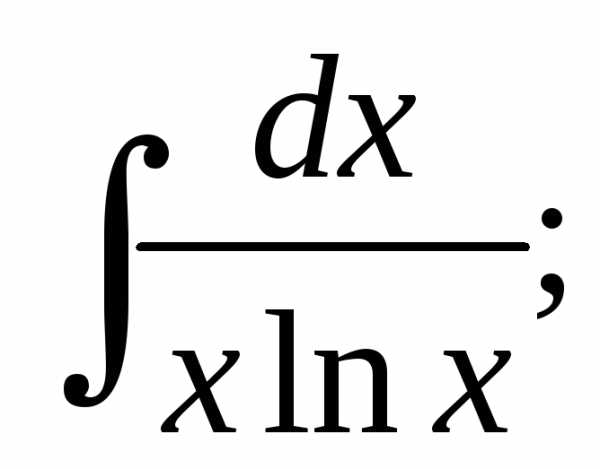
5)

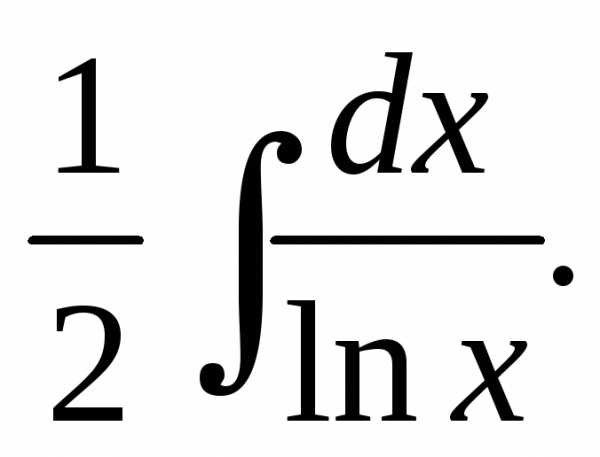
studfiles.net

Калькулятор дней

Калькулятор дат предназначен для вычисления количества дней между датами, а также для нахождения даты путем прибавления или вычитания определенного количества дней к известной дате.

Прибавить дни к дате

Для того, чтобы узнать какое число будет через определенное количество дней, воспользуйтесь этой опцией. Введите начальную дату и количество дней, которое нужно к ней прибавить. Для вычитания используйте значение с минусом. В калькуляторе также есть опция для прибавления только рабочих дней.

Вычисление количества дней между датами

Этот метод расчета ответит на вопрос «сколько дней прошло с даты». Введите начальную дату и конечную дату и нажмите кнопку «рассчитать». Калькулятор покажет, сколько дней между введенными датами. Отдельно калькулятор покажет количество рабочих дней.

С помощью этой опции можно вычислить сколько дней осталось до определенного события, например до дня рождения или праздника. Для этого в поле начальной даты укажите сегодняшнее число, а в поле конечной даты — дату события.

Праздничные дни

Калькулятор может вычислять, прибавлять и вычитать как календарные дни, так и рабочие. Официальными нерабочими праздничными днями являются:

• 1,2,3,4,5,6,8 января — новогодние каникулы
• 7 января — православное Рождество
• 23 февраля — День защитника Отечества
• 8 марта — Международный женский день
• 1 мая — Праздник Весны и Труда
• 9 мая — День Победы
• 12 июня — День России
• 4 ноября — День народного единства

Если праздничный день выпал на субботу или воскресенье, его переносят на ближайший рабочий день. Но иногда выходные переносят совсем в другое место календаря. Например, субботу и воскресенье, выпавшие на новогодние праздники, могут перенести на май, чтобы продлить майские праздники.

Так, в 2019 году ситуация следующая…

Перенос выходных в 2019 году

Помимо официальных праздничных дат, в 2019 году выходными также являются 2,3 и 10 мая за счет переносов выходных из новогодних каникул.

Наш калькулятор при расчете дней учитывает как официальные праздничные даты, так и все переносы.

calcus.ru

Онлайн-калькулятор рабочих и календарных дней между двумя датам — Контур.Экстерн

Калькулятор дней между двумя датами может пригодиться бухгалтеру или кадровику. Также данный инструмент расчета поможет юристу, когда для подачи судебного иска нужно узнать количество дней просрочки платежа.

Вы сможете посчитать:

• сколько календарных дней прошло между двумя заданными датами;
• сколько рабочих дней и часов в заданном вами периоде;
• сколько выходных дней было в заданном вами периоде.

Как работать с калькулятором дней между двумя датами

Вам понадобятся всего два значения. В соответствующих полях калькулятора нужно указать дату начала и конца периода — день, месяц и год. Просто кликните по нужной ячейке левой клавишей мыши и выберите из списка нужный вариант.

Также следует задать количество рабочих часов в день. Например, у офисных работников стандартный рабочий день составляет 8 часов, а на производстве рабочая смена может длиться 10 часов. По умолчанию в калькуляторе указано 8 рабочих часов в сутки.

После того как вы введете в поля калькулятора нужные значения, справа отразится полный расчет. В нем вы увидите количество календарных и рабочих дней, а также количество рабочих часов согласно заданным параметрам.

Пример. Директор ООО «Мечта» дал поручение главному бухгалтеру: рассчитать количество отработанных часов в IV квартале 2018 года. Все работники фирмы в этот период работали по графику, в отпуска не ходили. Главбух открыл онлайн-калькулятор и ввел следующие данные:

Начальная дата — 01.10.2018

Конечная дата — 31.12.2018

Поле «Количество рабочих часов» главбух оставил без изменений.

Калькулятор автоматически произвел расчет и выдал такие цифры:

• календарных дней — 92;
• рабочих дней — 65;
• рабочих часов — 520.

Калькулятор учитывает и сокращенные дни. Например, 02.11.2018 был сокращенный на один час день, и вместо 521 дней калькулятор выдал 520 дней (64 х 8 — 1). 

www.kontur-extern.ru

Скажите, что означает термин «календарный день»

Календарные -это те которые в календаре включая и выходные Календарные сутки исчисляются от 0:00 до 0:00 часов; просто сутки (не календарные) — это любые 24 часа (например, с 10 утра одного дня до 10 утра следующего дня) . Если, например, «отпуск 10 календарных дней» — то «вiдпустка 10 календарних днiв»; если же «оплата 10 гривен за календарные сутки» — то «оплата 10 гривень за календарну добу» (або просто «на добу», якщо йдеться про оплату за довiльнi 24 години) . Так что все зависит от конкретного контекста.

это означает что не рабочий день, а день по календарю

Это значит «день календаря». Один )) Любой ))

Есть рабочий день — это с понедельника по пятницу, а календарный день — это с понедельника по воскресенье.

пени придеться посчитать вместе с выходными :(, а вот пособия к начислению в рабочих, без выходных.

Есть рабочие дни, — 19,20,21, и редко 22 дня. А есть полные календарные дни 30-31 день. И вся разница, отличие.

1 день это сколько

touch.otvet.mail.ru

Календарные дни 2019 число календарных, количество, сколько дней

Кому важно знать о количестве календарных днях 2019 года, их число, сколько рабочих, выходных и праздников, предлагаем календарь с календарными другой важной информацией, о которой вы узнаете ниже и какая наверняка вам пригодится, так как она в полном объеме и необходимом не только для любителей, но и для работы профессионалов, а еще и утверждена нашим правительством, то есть она официальная.

К выходным и праздничным дням можно относиться по разному, как и проводить их, но вот не любить их нельзя, как и с нетерпением ждать их, будь вы трудящийся человек, школьник или студент, все мы ждем их и строим планы на эти дни недели. В выходные мы предоставлены сами себе и можем делать все чем нам интересно или важно заняться. Кто-то в свой выходной отсыпается, а кому-то нравится проводить время у телевизора или за компьютером, некоторые отправляются гулять с друзьями и подругами, ходят в гости к друг к другу, по магазинам, выезжают на природу или дачный участок, как говорится у кого какие интересы и предпочтения…

Любому школьнику, студенту и работающему человеку, время от времени нужно освежить в памяти и уточнить о будущих выходных днях своего отдыха от работы и учебы, того или иного месяца, как точно учебных, рабочих и праздничных днях, а  еще для трудящихся и о нормах рабочего времени, переносах и длинных выходных и не только ради интереса, а и для того, чтобы можно было строить планы на будущее, знать о нужной информации.

Нас интересует календарь выходных и рабочих дней работающим в пятидневную рабочую неделю на 2019 год, сколько календарных, число и количество, а также когда будем работать и праздновать, то есть по каким именно датам рабочие и официальные праздничные дни, что мы и найдем в этом календаре, на этой странице.

Выходные и рабочие дни в новом 2019 году, их количество по календарю дней, сколько их всего в месяце, квартале и полугодии, переносы, как и сокращенные, будут регулироваться трудовым законодательством и как обычно утверждаться правительством, только после чего этим календарем и можно безопасно для себя пользоваться, что и делают профессионалы, бухгалтера, кадровики и экономисты, другие специалисты и в самых направлениях своей деятельности.

Как бы мы ни упорствовали, а жизнь заставляет нас меняться, подстраиваться под новые условия, буквально на ходу перестраиваться, каждый день обновляться и так далее. Такой уж стремительный современный мир, что как говорится ты еще не успел привыкнуть к одним его требованиям и нововведениям, как уже нужно изучать и принимать другие, более усовершенствованные и если не хочешь отстать от жизни и всех остальных.

Человек всегда и во всем времена стремился к какому-то порядку, если не он сам, то тот от кого он зависит ставил его в определенные условия, которые и можно назвать порядком. Вот и современный человек старается жить по каким-то своим правилам и установленному графику, распорядку, для чего он  планирует свою жизнь, ставит какие-то перед собой цели и добивается их так и такими способами, как это у него получается.

Чтобы не запутаться в своих планах и графиках, распорядке и том, что и на какой день мы поставили перед собой какую-то цель, нам нужен обычный календарь с месяцами на весь будущий год, в котором мы можем отмечать даты о которых должны помнить, не забыть о них и в какой можно в любой момент заглянуть, чтобы вспомнить, освежить в памяти какую-то важную для нас информацию, о том или ином дне какого-то определенного месяца.

Для работающего человека, кто трудится на государственном предприятии или в каком-то учреждении, образовательном или медицинском заведении, работает в частном малом, среднем или крупном бизнесе и официально, важен производственный календарь или как еще его называют рабочий, в котором в отличии от простого календаря есть то, что его интересует лично и в связи с его трудовой деятельностью, а интересно ему знать о многом.

Календарь дней на 2019 год с их количеством календарных по месяцам, сколько их всего, когда мы будет работать, отдыхать в выходные дни и праздники — представляет собой официальный и утвержденный правительством сборник полезной информации для трудящегося населения нашей страны, а также для профессионалов, кому он нужно по долгу их службы, выполнения ими своих должностных обязанностей, то есть послужит им для их работы.

Что можно найти в официальном и утвержденном правительством календаре кроме рабочих, выходных и праздничных дней всех месяцев — много чего полезного, прежде всего, все переносы и сокращенные дни, в нем можно узнать когда длинные выходные и сколько всего будем работать и отдыхать.

Чем так важен и полезен календарь выходных дней на 2019 год, официальный и утвержденный со ввеми выходными и праздничными днями, как и рабочими для профессионалов, а это бухгалтера и работники отдела кадров, а также экономисты и другие специалисты из самых разных отраслей экономики, сферы услуг (например туризм, какие-то социальные службы) и так далее — по многим весьма веским причинам и в этом они не один раз убеждались на практике, в своей работе. 

Прежде всего польза его в том, что в нем есть вся необходимая им информация, а это — общее количество всех рабочих и выходных дней, нормы рабочего времени при работе в 24, 36 и 40 часовые рабочие недели, переносы праздников, сокращенные дни и длинные выходные. Одним словом в календаре выходных дней на будущий 2019 год и со всеми выходными днями, который утвержден есть вся та полнота информации, в которой нуждаются профессионалы и поэтому они им так важен и нужен.

Таблица умножения на 16

Автор: Bill4iam

kvn201.com.ua

Таблица умножения на 8

Автор: Bill4iam

kvn201.com.ua

Умножение на 16. Таблица умножения.

Задание

1	*	16	=	___
10	*	16	=	___
16	*	2	=	___
16	*	5	=	___
16	*	1	=	___
16	*	10	=	___
16	*	5	=	___
8	*	16	=	___
7	*	16	=	___
10	*	16	=	___
10	*	16	=	___
16	*	1	=	___
16	*	9	=	___
4	*	16	=	___
16	*	7	=	___
16	*	0	=	___
3	*	16	=	___
16	*	1	=	___
16	*	9	=	___
2	*	16	=	___
16	*	6	=	___
6	*	16	=	___
16	*	0	=	___
16	*	8	=	___
10	*	16	=	___
8	*	16	=	___
16	*	0	=	___
16	*	4	=	___
16	*	4	=	___
0	*	16	=	___
5	*	16	=	___
1	*	16	=	___
0	*	16	=	___
8	*	16	=	___
16	*	1	=	___
1	*	16	=	___
2	*	16	=	___
1	*	16	=	___
9	*	16	=	___
5	*	16	=	___
16	*	4	=	___
10	*	16	=	___
0	*	16	=	___
16	*	4	=	___
16	*	6	=	___
9	*	16	=	___
16	*	1	=	___
6	*	16	=	___
16	*	7	=	___
16	*	3	=	___
5	*	16	=	___
8	*	16	=	___
16	*	7	=	___
16	*	7	=	___
9	*	16	=	___
16	*	6	=	___
8	*	16	=	___
9	*	16	=	___
16	*	10	=	___
16	*	7	=	___
7	*	16	=	___
16	*	1	=	___
8	*	16	=	___
2	*	16	=	___
3	*	16	=	___
16	*	9	=	___
0	*	16	=	___
9	*	16	=	___
16	*	3	=	___
7	*	16	=	___

Ответы

1	*	16	=	16
10	*	16	=	160
16	*	2	=	32
16	*	5	=	80
16	*	1	=	16
16	*	10	=	160
16	*	5	=	80
8	*	16	=	128
7	*	16	=	112
10	*	16	=	160
10	*	16	=	160
16	*	1	=	16
16	*	9	=	144
4	*	16	=	64
16	*	7	=	112
16	*	0	=	0
3	*	16	=	48
16	*	1	=	16
16	*	9	=	144
2	*	16	=	32
16	*	6	=	96
6	*	16	=	96
16	*	0	=	0
16	*	8	=	128
10	*	16	=	160
8	*	16	=	128
16	*	0	=	0
16	*	4	=	64
16	*	4	=	64
0	*	16	=	0
5	*	16	=	80
1	*	16	=	16
0	*	16	=	0
8	*	16	=	128
16	*	1	=	16
1	*	16	=	16
2	*	16	=	32
1	*	16	=	16
9	*	16	=	144
5	*	16	=	80
16	*	4	=	64
10	*	16	=	160
0	*	16	=	0
16	*	4	=	64
16	*	6	=	96
9	*	16	=	144
16	*	1	=	16
6	*	16	=	96
16	*	7	=	112
16	*	3	=	48
5	*	16	=	80
8	*	16	=	128
16	*	7	=	112
16	*	7	=	112
9	*	16	=	144
16	*	6	=	96
8	*	16	=	128
9	*	16	=	144
16	*	10	=	160
16	*	7	=	112
7	*	16	=	112
16	*	1	=	16
8	*	16	=	128
2	*	16	=	32
3	*	16	=	48
16	*	9	=	144
0	*	16	=	0
9	*	16	=	144
16	*	3	=	48
7	*	16	=	112

uchik.ru

Калькулятор объёма шара

На сайте собраны калькуляторы, конвертеры, формулы, справочники, таблицы и много другой полезной и нужной информации для учёбы и работы.

Калькулятор объёма шара

Расчет объема шара онлайн

Входные данные

Радиус r:

Количество знаков после запятой в результате вычислений

1234567

Результат

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Читать по теме:

Интересные статьи:

О сайте

На нашем сайте вы найдете множество полезных калькуляторов и конвертеров.
На сайте используется технология LaTeX.

Самый простой способ сделать расчеты в сети

© 2019 Все калькуляторы online
Копирование материалов запрещено.

calcsbox.com

онлайн калькулятор, формулы, примеры решений

Шар — это геометрическое тело вращения, образованное путем вращения круга или полукруга вокруг его диаметра. Также шар — это пространство, ограниченное сферической поверхностью. Существует множество реальных сферических объектов и связанных с ними задач, для решения которых требуется определить объем шара.

Шар и сфера

Круг — самая древняя геометрическая фигура, и античные ученые придавали ей сакральное значение. Круг — это символ нескончаемого времени и пространства, символ Вселенной и бытия. По мнению Пифагора, круг — прекраснейшая из фигур. В трехмерном пространстве окружность превращается в сферу, такую же идеальную, космическую и прекрасную, как и круг.

Сфера по-древнегречески означает «мяч». Сфера представляет собой поверхность, образованную бесконечным множеством точек, равноудаленных от центра фигуры. Пространство, ограниченное сферой, и есть шар. Шар — идеальная геометрическая фигура, форму которой принимают многие реальные объекты. К примеру, в реальной жизни форму шара имеют пушечные ядра, подшипники или мячи, в природе — капли воды, кроны деревьев или ягоды, в космосе — звезды, метеоры или планеты.

Объем шара

Определение объема сферической фигуры — сложная задача, ведь такое геометрическое тело нельзя разбить на кубы или треугольные призмы, формулы объемов которых уже известны. Современная наука позволяет вычислить объем шара при помощи определенного интеграла, однако каким образом была выведена формула объема в Древней Греции, когда об интегралах еще никто не слышал? Архимед вычислил объем шара при помощи конуса и цилиндра, так как формулы объемов этих фигур были уже определены древнегреческим философом и математиком Демокритом.

Архимед представил половину шара при помощи одинаковых конуса и цилиндра, при этом радиус каждой фигуры был равен ее высоте R = h. Античный ученый представил конус и цилиндр разбитыми на бесконечное количество маленьких цилиндров. Архимед понял, что если из объема цилиндра Vc вычесть объем конуса Vk, он получит объем одной полусферы Vsh:

0,5 Vsh = Vc − Vk

Объем конуса вычисляется по простой формуле:

Vk = 1/3 × So × h,

но зная, что So в данном случае — это площадь круга, а h = R, то формула трансформируется в:

Vk = 1/3 × pi × R × R² = 1/3 pi × R³

Объем цилиндра вычисляется по формуле:

Vc = pi × R² × h,

но считая, что высота цилиндра равна его радиусу, мы получаем:

Vc = pi × R³.

Используя эти формулы, Архимед получил:

0,5 Vsh = pi × R³ — 1/3 pi × R³ или Vsh = 4/3 pi × R³

Современное определение формулы объема шара выводится из интеграла от площади сферической поверхности, однако результат остается все тем же

Vsh = 4/3 pi × R³

Расчет объема шара может понадобиться как в реальной жизни, так и при решении абстрактных задач. Для вычисления объема шара при помощи онлайн-калькулятора вам понадобится узнать всего один параметр на выбор: диаметр или радиус сферы. Рассмотрим пару примеров.

Примеры из жизни

Пушечные ядра

Допустим, вы хотите узнать, сколько чугуна необходимо для отливки пушечного ядра шестифутового калибра. Вы знаете, что диаметр такого ядра составляет 9,6 сантиметров. Введите это число в ячейку калькулятора «Диаметр», и вы получите ответ в виде

V = 463,24

Таким образом, для выплавки пушечного ядра заданного калибра вам понадобится 463 кубических сантиметров или 0,463 литра чугуна.

Воздушные шары

Пусть вам любопытно, сколько воздуха необходимо для накачки воздушного шара идеальной сферической формы. Вы знаете, что радиус выбранного шарика составляет 10 см. Вбейте это значение в ячейку калькулятора «Радиус» и вы получите результат

V = 4188,7

Это означает, что для накачки одного такого шара вам понадобится 4188 кубических сантиметров или 4,18 литров воздуха.

Заключение

Необходимость определения объема шара может возникнуть в самых разных ситуациях: от абстрактных школьных задач до научных изысканий и производственных вопросов. Для решения вопросов любой сложности используйте наш онлайн-калькулятор, который мгновенно представит вам точный результат и необходимые математические выкладки.

bbf.ru

Калькулятор онлайн — Вычисление объема шара

Этот математический калькулятор онлайн поможет вам вычислить объём шара. Программа для вычисления объёма шара не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: \( -\frac{2}{3} \)

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: \( -1\frac{5}{7} \)

www.math-solution.ru

FeO + CO2 = ? уравнение реакции

Оксид железа (II) (закись железа) – является сильным восстановителем. Это черное вещество, проявляющее пирофорные свойства, Обезвоживанием гидроксида железа (II) закись железа получить не удается. синтезируют, восстанавливая окись железа (III). Например:

Можно получить и разложением оксалата:

При нагревании оксида железа (II) в температурном диапазоне () происходит его диспропорционирование:

Теоретически возможна реакция взаимодействия между закисью железа, проявляющей амфотерные свойства с преобладанием основных и диоксида углерода (FeO + CO2 = ?) с образованием средней соли карбоната железа (II). Молекулярное уравнение реакции имеет вид:

Оксид железа (II) не реагирует с холодной водой. Вступает в реакции с кислотами:

гидроксидом натрия (при сплавлении):

Легко окисляется кислородом.

ru.solverbook.com

FeO + CO = ? уравнение реакции

В результате взаимодействия оксида железа (II) с монооксидом углерода (FeO + CO = ?) происходит образование железа и выделение диоксида углерода. Молекулярное уравнение реакции имеет вид:

Реакция носит обратимый характер и относится к окислительно-восстановительным, поскольку химические элементы железо и углерод изменяют свои степени окисления. Схемы электронного баланса выглядят следующим образом:

Диоксид углерода (углекислый газ) при обычных условиях представляет собой бесцветный газ, который в 1,5 раза тяжелее воздуха, что позволяет переливать его, как жидкость, из одного сосуда в другой. Растворимость диоксида углерода в воде невелика.
Под давлением диоксид углерода при комнатной температуре превращается в жидкость. А при быстром выливании его из баллона он превращается в твердую белую снегообразную массу.
Углекислый газ проявляет кислотные свойства: реагирует со щелочами, гидратом аммиака. Восстанавливается активными металлами, водородом, углеродом.

В промышленных условиях углекислый газ получают из дымовых газов или в качестве побочного продукта многих химических реакций, например при разложении природных карбонатов – известняка и доломита.

ru.solverbook.com

Mathway | Популярные задачи

www.mathway.com

Второй замечательный предел. Примеры решения.

Обычно второй замечательный предел записывают в такой форме:

Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $e\approx{2{,}718281828459045}$. Если сделать замену $t=\frac{1}{x}$, то формулу (1) можно переписать в следующем виде:

Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное – выполнение двух условий:

1. Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
2. Показатель степени (т.е. $x$ в формуле (1) или $\frac{1}{t}$ в формуле (2)) должен стремиться к бесконечности.

Говорят, что второй замечательный предел раскрывает неопределенность $1^\infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+\infty$ или $-\infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.

Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.

Пример №1

Вычислить предел $\lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right )^{4x+7}$.

Решение

Сразу отметим, что основание степени (т.е. $\frac{3x+1}{3x-5}$) стремится к единице:

При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $\lim_{x\to\infty}(4x+7)=\infty$.

Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^\infty$. Применим формулу (1) для раскрытия этой неопределённости. Для начала отметим, что в основании степени формулы (1) расположено выражение $1+\frac{1}{x}$, а в рассматриваемом нами примере основание степени таково: $\frac{3x+1}{3x-5}$. Посему первым действием станет формальная подгонка выражения $\frac{3x+1}{3x-5}$ под вид $1+\frac{1}{x}$. Для начала прибавим и вычтем единицу:

Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что

Так как $\frac{3x+1}{3x-5}-1=\frac{6}{3x-5}$, то:

Продолжим «подгонку». В выражении $1+\frac{1}{x}$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+\frac{6}{3x-5}$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:

Таким образом,

Итак, основание степени, т.е. $1+\frac{1}{\frac{3x-5}{6}}$, подогнано под вид $1+\frac{1}{x}$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:

Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $\frac{3x-5}{6}$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $\frac{6}{3x-5}$. Итак, имеем:

Выражение $\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right)^{\frac{3x-5}{6}}$ полностью соответствует записи второго замечательного предела согласно формуле (1). Следовательно, $\lim_{x\to\infty}\left(1+\frac{1}{\frac{3x-5}{6}}\right )^{\frac{3x-5}{6}}=e$. Учитывая это, получим:

Отдельно рассмотрим предел в степени:

Учитывая то, что степень стремится к 8, будем иметь:

Ответ получен, $\lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right)^{4x+7}=e^8$. Полное решение без пояснений и промежуточных выкладок выглядит так:

Ответ: $\lim_{x\to\infty}\left(\frac{3x+1}{3x-5}\right)^{4x+7}=e^8$.

Пример №2

Найти предел $\lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}}$.

Решение

Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $x\to{1}$, т.е. $\lim_{x\to{1}}(7-6x)=7-6\cdot1=1$. Для показателя степени, т.е. $\frac{x}{3x-3}$, получаем: $\lim_{x\to{1}}\frac{x}{3x-3}=\infty$. Итак, здесь мы имеем дело с неопределенностью вида $1^\infty$, которую раскроем с помощью второго замечательного предела.

Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $x\to{1}$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $x\to{1}$, то ${x-1}\to{0}$, т.е. $y\to{0}$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $y\to{0}$, получим:

Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $\frac{1}{t}$, т.е. в нашем случае в показателе степени следует получить $\frac{1}{-6y}$. Домножим показатель степени на выражение $\frac{1}{-6y}$. Для компенсации такого домножения нужно домножить показатель степени на обратную дробь, т.е. на выражение $\frac{-6y}{1}=-6y$:

Итак, $\lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}}=\frac{1}{e^2}$. Полное решение без пояснений таково:

Ответ: $\lim_{x\to{1}}\biggl(7-6x\biggr)^{\frac{x}{3x-3}}=\frac{1}{e^2}$.

Пример №3

Найти предел $\lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}}$.

Решение

Так как $\lim_{x\to{0}}(\cos{2x})=1$ и $\lim_{x\to{0}}\frac{1}{\sin^2{3x}}=\infty$ (напомню, что $\sin{u}\to{0}$ при $u\to{0}$), то мы имеем дело с неопределённостью вида $1^\infty$. Преобразования, аналогичные рассмотренным в примерах №1 и №2, укажем без подробных пояснений, ибо они были даны ранее:

Так как $\sin^2x=\frac{1-\cos{2x}}{2}$, то $\cos{2x}-1=-2\sin^2x$, поэтому:

Подробное описание того, как находить предел $\lim_{x\to{0}}\frac{\sin^2x}{\sin^2{3x}}$ дано в соответствующей теме.

Ответ: $\lim_{x\to{0}}\biggl(\cos{2x}\biggr)^{\frac{1}{\sin^2{3x}}}=e^{-\frac{2}{9}}$.

Пример №4

Найти предел $\lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right)$.

Решение

Так как при $x>0$ имеем $\ln(x+1)-\ln{x}=\ln\left(\frac{x+1}{x}\right)$, то:

Раскладывая дробь $\frac{x+1}{x}$ на сумму дробей $\frac{x+1}{x}=1+\frac{1}{x}$ получим:

Ответ: $\lim_{x\to+\infty}x\left(\ln(x+1)-\ln{x}\right)=1$.

Пример №5

Найти предел $\lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}}$.

Решение

Так как $\lim_{x\to{2}}(3x-5)=6-5=1$ и $\lim_{x\to{2}}\frac{2x}{x^2-4}=\infty$, то мы имеем дело с неопределенностью вида $1^\infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:

Можно решить данный пример и по-иному, используя замену: $t=\frac{1}{x-2}$. Разумеется, ответ будет тем же:

Ответ: $\lim_{x\to{2}}\biggl(3x-5\biggr)^{\frac{2x}{x^2-4}}=e^3$.

Пример №6

Найти предел $\lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x} $.

Решение

Выясним, к чему стремится выражение $\frac{2x^2+3}{2x^2-4}$ при условии $x\to\infty$:

Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^\infty$, которую раскроем с помощью второго замечательного предела:

Ответ: $\lim_{x\to\infty}\left(\frac{2x^2+3}{2x^2-4}\right)^{3x}=1$.

math1.ru

Второй замечательный предел

Вторым замечательным пределом называется предел

,

где

— иррациональное число.

Непосредственная подстановка бесконечности в выражение приводит к бесконечности вида .

Значит, если при непосредственном вычислении предела у вас получилась неопределённость такого вида, то решать задачу следует путём приведения ко второму замечательному пределу. Во всех этих задачах для получения второго замечательного предела требуется производить замену сложной функции более простой.

Второй замечательный предел может быть записан в другом виде, если положить тогда .

Из условия

получим

   (Alt)

Пример 1. Найти предел .

Решение. Подстановка вместо x бесконечности приводит к неопределённости:

.

Значит, нужно привести выражение ко второму замечательному пределу. Облегчим себе жизнь перед заменой сложной функции более простой, представив степень :

.

Заменяем функцию 6x переменной n, которая также стремится к бесконечности:

.

Это второй замечательный предел, индивидуальна только степень числа е:

.

Пример 2. Найти предел .

Решение. Непосредственная подстановка приводит к неопределённости «бесконечность делить на бесконечность в степени бесконечность»:

.

Бесконечность в показателе степени — признак того, что выражение можно привести к отношению двух вторых замечательных пределов. В самом деле, если числитель и знаменатель поделить почленно на x, то слева и в числителе и в знаменателе будет уже по единице:

.

Почти второй замечательный предел. А чтобы это было не почти, а вторым замечательным пределом, нужно, чтобы во вторых слагаемых и в числителе, и в знаменателе были единицы. Для этого произведём замены функций:

.

.

Подставляем и получаем:

.

Это уже отношение вторых замечательных пределов, а степени выражений в числителе и знаменателе — индивидуальны:

.

Пример 3. Найти предел

Решение. Применяем разновидность (Alt) второго замечательного предела:

Второй замечательный предел служит средством решения многих задач физики, биологии, социальных наук. Показательная функция с основанием e возникает при выводе количественного закона, которому подчиняются многие естественные процессы: рост народонаселения, рост количества древесины на лесных массивах, радиоактивный распад и т.д.

Для вывода этого закона используется формула сложных процентов

,

где — сумма, наращенная через t лет, — начальная сумма, p — процентная такса, t — время роста в годах.

При этом предполагается, что проценты присоединяются к начальной сумме в конце каждого года. Если же ввести условие присоединения процентов по отдельным частям года, равным 1/n доле его, а процентная такса p по-прежнему пусть относится к целому году, то по истечении каждой такой части года наращенные суммы соответственно составят

По прошествии одного года начальная сумма обратится в , по прошествии двух лет — в , по прошествии t лет — в .

Если же предположить, что прирост процентов происходит непрерывно, т. е. число промежутков, на которые делится год, неограниченно возрастает (), а каждый из них стремится к нулю, то величина наращенной суммы выразится следующей формулой:

,

очень напоминающей второй замечательный предел.

Используя формулу альтернативного представления второго замечательного предела (Alt), приведённую в начале статьи, получим показательный закон роста:

.

Заменив p на -p, получим показательный закон убывания:

.

Например, если население страны возрастает на 2% в год, то по формуле показательного закона роста можно с неплохим приближением рассчитать численность населения страны через t лет: , где — численность населения в начале отсчёта.

Начало темы «Предел»

Продолжение темы «Предел»

function-x.ru

Второй замечательный предел, следствия, примеры

Второй замечательный (особый) предел часто вызывает трудности у студентов, хотя сам предел довольно прост и понятен на практике. Он позволяет раскрывать неопределенности вида единица в степени бесконечность . Замечательный предел имеет следующий вид

где «е»-экспонента.

Следствия второго замечательного предела

1)
2)
3)
4)
5)
6)

На практике следствия второго предела реже встречаются на практике чем он сам, однако без них некоторые задачи в простой способ не решить.

Примеры на замечательный предел

Рассмотрим некоторые примеры из сборника А.В. Тевяшев, А.Г. Литвин, Г.М. Кривошеева и др.»Высшая математика в примерах и задачах. Ч.5 Тесты» (Харьков, 2007, ст. 99).

Пример 6.1. Найти предел функции
а)

Решение.
Преобразуем функцию к виду при котором возможно применить формулу замечательного предела

В результате можем применить правило замечательного предела

б)

Решение.
Подобно предыдущему примеру превращаем функцию в скобках чтобы применить замечательный предел

Нужно отметить, что в этом примере и во многих подобных константы в степенях, как правило вклада не несут. Функцию можно расписать следующим образом

Предел умышленно расписан в виде произведения двух множителей чтобы Вы убедились что константы в степенях вклада не несут. Их цель запутать Вас, если плохо знаете теоретический материал или сомневаетесь в правильности решения. Во всех последующих примерах мы не будем расписывать примеры на произведение двух границ, однако помните, что они не меняют конечного результата (вклад — множитель единица).

————————————

в)

Решение.
Выполняем преобразование заданной функции

Запись в таком виде сделана специально, потому что степень нужно свести к подобному виду

В такой простой способ получили искомый предел функции. В дальнейшем необходимые замены или подсказки будут выделены цветом из общего решения.

г)

Решение.
Выполним замену переменных в пределе

и определенные преобразования для нахождения предела

Бывают случаи, когда прямо применить правило второго замечательного предела довольно сложно, в таких ситуациях используйте простые замены которые Вам понятны и позволяют в быстрый способ найти предел.

Пример 6. 2 Вычислить предел функции

а)

Решение.
Сводим функцию к правилу замечательного предела

Подставляем и вычисляем, выполняя нужные манипуляции с показателями

в)

Решение.
За известным уже алгоритмом преобразуем функцию

Применяя определение второго важного предела находим

Пример 6. 3 Определить предел функции
б)

Решение.
Сведем функцию для применения замечательного предела

Подставляем в границу и упрощаем

г)

Решение.
«Как найти предел ? — скажете Вы, ведь переменная равна минус бесконечности.
В этом примере видим что аргумент стремится к минус бесконечности, кроме того функция в скобках следует не до единицы, а до 2 при больших аргументах.

Учитывая что степень отрицательный получим следующее значение предела

Во всех примерах второго замечательного предела следует сначала проверять условие что выражение в скобках стремится к единице. Если нет, то предел функции в зависимости от степени будет равен или нулю или бесконечности. Те из Вас кто часто решает примеры такие проверки осуществляет автоматически. Остальные сводят границу в экспоненте в определенном степени, но все равно вылезает множителем или ноль или бесконечность. В конечном варианте правы все, однако в первом случае тратится гораздо меньше времени, которое так необходима на контрольных работах, тестах, ВНО. Поэтому выбирайте для себя простой путь и делайте в обучении правильные выводы.

Пример 6. 5 Найти предел функции
а)

Решение.
Заданный пример на вид отличается от предыдущих, однако решение получаем по такой же схеме. Выполняем преобразования функции в скобках под правило замечательного предела

Осталось в степени выделить обратный множитель

и подставить в границу

По такой схеме вычисляйте все подобные пределы, она проста и не требует дополнительных пояснений.

————————————

в)

Решение.
К рассматриваемому примеру великих преобразований делать не нужно. Он имеет достаточно простую запись и решение осуществляем в одну строку

Практикуйте с подобными пределами, используйте удобные для себя схемы сведения задач под необходимое правило. Не бойтесь делать ошибки — без них обучение не обходится!

yukhym.com

Второй замечательный предел — примеры решений

Здесь мы рассмотрим примеры решений задач на вычисление пределов, в которых используется второй замечательный предел и его следствия.
Ниже перечислены формулы, свойства и теоремы, которые наиболее часто применяются в подобного рода вычислениях.

Здесь мы будем иметь дело со степенно-показательной функцией, у которой основание и показатель являются функциями от некоторой переменной: . Ее удобно представить как экспоненту: . В этой связи полезна следующая лемма.

Лемма о пределе степенно-показательной функции
Пусть – функции переменной x, имеющие конечные пределы:
. Здесь .
Тогда
.
Доказательство ⇓

В случае бесконечных пределов, или когда , мы проводим исследование произведения , применяя свойства пределов бесконечно больших и малых функций.

В случае и , мы имеем неопределенность вида единица в степени бесконечность. Для ее раскрытия используется второй замечательный предел.

Раскрытие неопределенности 1 в степени бесконечность

Пусть u и v есть функции от переменной x: . И пусть при . Тогда выражение является неопределенным при . Для раскрытия этой неопределенности, мы вводим переменную t из соотношения
.
Тогда . При .
;
.

Таким образом задача сводится к вычислению предела .

Доказательство леммы о пределе степенно-показательной функции

Примеры решений

Далее мы приводим подробные решения с объяснениями следующих пределов:
⇓,   ⇓,   ⇓,   ⇓,   ⇓.

Пример 1

Найти предел:
.

Решение

При ,   . Это неопределенность вида один в степени бесконечность.

Выполняем преобразования.
;
.

Сделаем замену переменной . При . Применим второй замечательный предел:
.

Находим предел дроби, разделив числитель и знаменатель на x:
.

Применяем лемму о пределе степенно-показательной функции ⇑
.

Ответ

.

Пример 2

Найдите предел:
.

Решение

При ,   .   при . Это неопределенность вида один в степени бесконечность. Раскрываем ее с помощью второго замечательного предела.

Введем переменную t из соотношения: . Тогда при ,
.
.

Применим второй замечательный предел к основанию степени:
.

Найдем предел показателя степени. Для этого применим тригонометрическую формулу

и первый замечательный предел:

.

Применяем лемму о пределе степенно-показательной функции ⇑ учитывая, что при :
.

Ответ

.

Пример 3

Найти предел последовательности:
.

Решение

При . Элементы последовательности равны единице. Поэтому . Рассмотрим случай .

При . Это неопределенность вида единица в степени бесконечность. Для ее раскрытия применим второй замечательный предел.

Введем переменную t из соотношения: . Тогда при ,
.
.

Применим второй замечательный предел к основанию степени:
.

Найдем предел показателя степени. Для этого применим тригонометрическую формулу

и первый замечательный предел:

.

Применяем лемму о пределе степенно-показательной функции ⇑ учитывая, что при :
.
Эта формула справедлива и при .

Ответ

.

Пример 4

Найти предел:
.

Решение

Пусть . Рассмотрим функцию в проколотой окрестности точки , на которой . Для определения предела, функция должна быть определена на любой проколотой окрестности этой точки. Считаем, что . Тогда . При . Поэтому .
Теперь рассмотрим предел при .

При . У нас неопределенность вида 0/0.

Для ее раскрытия приведем степенно-показательную функцию к основанию e учитывая, что :
.
Согласно следствию второго замечательного предела:
.
В последнем множителе сделаем замену переменной:
.
При . Кроме этого, при . Тогда
.

Применяем арифметические свойства предела функции:
.
Это же значение является правильным и при .

Ответ

.

Пример 5

Найдите предел функции:
.

Решение

При . Это неопределенность вида 0/0. Для ее раскрытия, применим следствия второго замечательного предела.

Преобразуем числитель дроби:

.
Преобразуем знаменатель:
.

Разделим числитель и знаменатель на x:
.
Чтобы не загромождать формулы, мы ввели обозначение .

Применяя первый замечательный предел и следствия второго, имеем:
;   ;   ;   ;   .
Применяем арифметические свойства предела функции:
.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 05-04-2019

1cov-edu.ru

Второй замечательный предел, примеры нахождения, задачи и подробные решения

Второй замечательный предел имеет вид:

или в другой записи

В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность .

Разберем несколько примеров нахождения предела по второму замечательному пределу сподробным оприсанием решения.

Пример.

Вычислить предел

Решение.

Подставляем бесконечность:

Пришли к неопределенности единица в степени бесконечность. Смотрим в таблицу неопределенностей для определения метода решения и останавливаемся на применении второго замечательного предела.

Сделаем замену переменных. Пусть

Если , то

Исходный предел после замены примет вид:

Ответ:

Пример.

Вычислить предел

Решение.

Подставляем бесконечность:

Пришли к неопределенности единица в степени бесконечность, которая указывает на применение второго замечательного предела. Выделим целую часть в основании показательно степенной функции:

Тогда предел запишется в виде:

Сделаем замену переменных. Пусть

Если , то

Исходный предел после замены примет вид:

В преобразованиях были использованы свойства степени и свойства пределов.

Ответ:

Пример.

Вычислить предел

Решение.

Преобразуем функцию, чтобы применить второй замечательный предел:

Сейчас домножим показатель на и разделим на это же выражение, затем используем свойства степени:

Так как показатели степени числителя и знаменателя дроби одинаковые (они равны 6), то предел этой дроби на бесконечности равен отношению коэффициентов при старших степенях (см. непосредственное вычисление пределов):

Если произвести замену , то получим второй замечательный предел в чистом виде, следовательно,

Ответ:

39.

40.

megaobuchalka.ru

Второй замечательный предел

Непрерывность показательной функции и логарифмической функции , а также теорема о непрерывности сложной функции позволяют утверждать, что степенно-показательная функция непрерывна всюду в области определения и

.

Пример 1. Найти а) ; б) ; в) .

Решение. а) При основание , показатель . Поэтому

= .

б) При основание , показатель :

.

в) При основание , показатель :

.▲

Особый интерес представляют случаи, когда при вычислении предела степенно-показательной функции получаем неопределённость вида , или . Неопределённость вида (т.е. основание , а показатель ) раскрывается с помощью второго замечательного предела.

Теорема.Предельное значение функции при существует и равно e (второй замечательный предел):

(1)

Следствие 1.Второй замечательный предел можно записать и в виде

(2)

Пример 2. Вычислить = .

Решение. Здесь при основание , показатель , поэтому воспользуемся вторым замечательным пределом в форме (1):

▲

Пример 3. Вычислить = .

Решение. Здесь при основание , показатель , поэтому воспользуемся вторым замечательным пределом в форме (2):

.▲

Формулам (1) и (2) можно придать другой вид. При стремлении аргумента к некоторому значению основание , значит, его можно представить в виде , где — бесконечно малая в точке функция. Чтобы воспользоваться вторым замечательным пределом в виде (1) или (2), надо в показателе иметь бесконечно большую в точке функцию :

(3)

Пример 4. Вычислить = .

Решение. Основание при , здесь — бесконечно малая функция при . Чтобы воспользоваться формулой (3), надо в показателе поставить бесконечно большую функцию = :

,

так как .▲

Пример 5. Вычислить = .

Решение. Функция при , поэтому её можно представить в виде = , при :

, .

Значит, в показателе надо поставить = :

Здесь учтено, что ▲

Следствие 2. Предельное значение функции при существует и равно :

. (4)

В частности,

. (5)

Действительно,

.

Пример 6. Вычислить .

Решение. Аргумент логарифма представлен в виде суммы , где — бесконечно малая при функция. Чтобы воспользоваться формулой (5), надо логарифм разделить на :

.

Здесь ▲

Следствие 3. Предельное значение функции при существует и равно :

. (6)

В частности,

. (7)

Действительно, введём новую переменную , при . В силу формулы (4) получаем:

.

Пример 7. Найти .

Решение. Чтобы воспользоваться формулой (7), надо в знаменателе записать бесконечно малую в точке функцию :

.▲

Пример 8. Найти .

Решение. Первый способ. Сначала представим числитель в виде , а затем воспользуемся теоремой о пределе произведения, формулой (7) и первым замечательным пределом:

.

Второй способ. В числителе вычтем и прибавим единицу, в результате приходим к разности пределов:

.

Найдем

и .

Теперь .

Пример 9.Найти .

Решение. Прежде всего преобразуем числитель к виду , прибавляя и вычитая единицу:

.

Остаётся вычислить

,

.

Значит, =1. ▲

Замечание. Неопределённости вида и научимся раскрывать позже с помощью правила Лопиталя.

studopedya.ru

Замечательные примеры. Определение и примеры.

В этой статье будут рассмотрены первый и второй замечательные пределы. Мы дадим их определение и разберем на примерах случаи практического применения. Перед прочтением рекомендую сначала ознакомиться с предыдущей статьей о пределах.

Итак, замечательными пределами будем называть тождества вида:

Первый замечательный предел

Как при решении конкретной задачи увидеть и использовать первый замечательный предел? Для этого нужно выяснить, стремится ли к нулю аргумент синуса. Понятно, что далеко не всегда синус будет зависеть именно от . Чаще всего это будут некоторые выражения, но главное, чтобы они обращались в при подстановке предельного значения .

Пример 1. Вычислить предел

Решение:   При подстановке предельного значения получаем неопределенность вида .  Очевидно, что аргумент синуса стремится к нулю при .

Таким образом, для использования первого замечательно предела нужно получить в знаменателе дроби в точности аргумент синуса . Умножим числитель и знаменатель дроби на :

Предел выражения    при равен единице, в соответствии с первым замечательным пределом.

Ответ:  

[свернуть]

Пример 2. Вычислить предел

Решение:   Подставляем предельное значение , получаем неопределенность вида .

В числителе имеем квадрат синуса, аргумент которого стремится к нулю. Следовательно, удобно будет воспользоваться первым замечательным пределом:

Ответ:  

Здесь был дважды применен первый замечательный предел. Мы воспользовались тем фактом, что предел выражения    равен при .

[свернуть]

Помимо стандартной формы записи первого замечательно предела, будет справедливо следующее равенство:

Рассмотрим пример с использованием данной  модификации.

Пример 3. Вычислить предел

Решение:   При подстановке предельного значения получаем неопределенность вида . Аргумент синуса стремится к нулю.

Для использования замечательного предела в числителе дроби должен иметь третью степень. Добьемся этого, умножив числитель и знаменатель дроби на :

Теперь, согласно первому замечательному пределу, вместо выражения    можно просто написать :

Ответ:  

[свернуть]

Разберем теперь пару примеров, в которых отсутствует синус, но его возможно получить, прибегнув к различным формулам тригонометрии.

Пример 4. Вычислить предел

Решение:   При подстановке предельного значения получаем неопределенность вида . Синуса не видно, однако, можно поступить следующим образом: запишем тангенс как отношение синуса к косинусу.

Синус появился и аргумент его стремится к нулю — всё хорошо, можно применять первый замечательный предел:

Ответ:  

[свернуть]

Пример 5. Вычислить предел

Решение:   При подстановке предельного значения получаем неопределенность вида . Синуса опять не видно. Как его получить, чтобы воспользоваться замечательным пределом? Предлагаю умножить и разделить дробь на :

В числителе появилась формула разности квадратов . У нас есть ее левая часть, то есть , а . Имеем:

Синуса мы не получили, однако в числителе хорошо просматривается основное тригонометрическое тождество . Таким образом, вместо можем смело написать :

Ответ:  

[свернуть]

И еще одна задача. Чтобы не было зацикливания на том, что обязательно 🙂

Пример 6. Вычислить предел

Решение:   При подстановке предельного значения получаем неопределенность вида .

Как видим, не стремится к нулю, а вот выражение стремится. Для решения такой задачи удобно ввести замену . При этом понятно, что . Получаем:

Синуса нет, но его легко получить, расписав котангенс как отношение косинуса к синусу:

Ответ:  

[свернуть]

Второй замечательный предел

Второй замечательный предел служит для избавления от неопределенности вида . Таким образом, если при подстановке предельного значения была получена неопределенность , то сразу понимаем, что предстоит работа именно со вторым замечательным пределом.

Пример 7. Вычислить предел

Решение: Самое первое действие — подставляем предельное выражение . При этом , а всё выражение представляет собой неопределенность .

Наша задача состоит в том, чтобы получить запись вида

Умножим и разделим показатель степени на .

Видим выражение — это второй замечательный предел, заменяем его на букву .

Ответ:  

[свернуть]

Замечание. — это иррациональное, равное , то есть приблизительно .

Пример 8. Вычислить предел

Решение: При подстановке предельного значения имеем неопределенность . Если с понимаем этого факта еще возникают сложности, читайте предыдущую статью о пределах.

В основании находится . Следовательно, в показателе степени должно оказаться выражение, обратное к , то есть . Чтобы ничего не изменилось, умножим и разделим показатель на .

Теперь выражение есть второй замечательный предел. Получаем:

Отдельно вычислим предел, обозначенный через :

Возвращаемся к решению исходного предела:

Ответ:  

[свернуть]

В обоих разобранных примерах основание степени изначально имело вид «единица плюс выражение от икс». Однако, чаще всего студенту нужно выделить эту единицу самостоятельно:

Пример 10. Вычислить предел

Решение:  При подстановке предельного значения получаем . Преобразуем основание степени, дробь, следующим образом:

Вновь мысленно подставляем предельное значение — получаем нашу неопределенность .

Ответ:  

[свернуть]

Рассмотрим самую популярную при решении практических задач модификацию второго замечательного предела:

Буквально пару дней назад встретил интересную задачу как раз для этой формулы:

Пример 11. Вычислить предел

Решение:  Икс не стремится ни к нулю, ни к бесконечности. Однако, при подстановке предельного значения мы вновь видим неопределенность . Прибавим и отнимем в основании степени единицу:

Теперь в основании появилась единица плюс выражение от икс, стремящееся к нулю. Используем модификацию второго замечательного предела:

В результате получили новый предел, с которым тоже нужно как-то разобраться. При подставке имеем неопределенность вида . Введем замену . При этом понятно, что .

Для тангенса применим формулу тангенса от суммы двух углов. Для косинуса применим формулу приведения.

Возвращаемся к исходному пределу:

Ответ:   

[свернуть]

На этом всё. Надеюсь, что статья была полезна.

Удачи в освоении пределов замечательных и не очень! 🙂

higher-math.ru

DOC в DOCX | Zamzar

www.zamzar.com

Как конвертировать doc в docx

Приветствую вас.

Сегодня я расскажу, как конвертировать doc в docx самыми простыми способами. Пока ещё не понимаете, что это и зачем нужно? Введу в курс дела.

Программа Word выпуска 97-2003 годов сохраняла документы в расширении .doc. Начиная с версии 2007 года, компания Microsoft внедрила новый формат — .docx. Не буду здесь останавливаться, потому что писал уже вот тута об этом: http://profi-user.ru/doc-i-docx.

Он имеет более широкий функционал и занимает гораздо меньше места, чем предшественник. В повседневном использовании вы можете и не заметить второе преимущество. Но когда дело касается объёмных файлов с большим количеством картинок, разница чувствуется.

Загвоздка в том, что если современной программой открыть документ со старым расширением, то мы увидим надпись ««Режим ограниченной функциональности». Это значит, что Ворд не сможет применить к этому файлу определённые функции. В ситуации наоборот, устаревший пакет Office может вовсе не распознать расширение .docx, и, следовательно, не открыть его.

Но после прочтения моей статьи вы будете знать, как быстро разрешить такие затруднения.

Используем средства Word

Чтобы перевести один формат в другой, можно обойтись без сторонних программ. Для этого вам нужно просто заново сохранить документ, но уже в необходимом расширении. Вот так:

• Открываете файл и нажимаете на логотип пакета Office или вкладку «Файл» в левом верхнем углу;
• В контекстном меню выбираете функцию «Сохранить как»;

• В появившемся окне указываете папку для размещения нового документа;
• Жмёте внизу на стрелочку в строке «Тип файла» и выбираете формат DOC или DOCX в зависимости от ситуации.

Разработчики спешат на помощь

Компания Microsoft выпустила специальный пакет совместимости офисных программ, чтобы у пользователей разных версий операционной системы не возникало проблем с открытием файлов. При автоматическом обновлении винды он скачивается и устанавливается самостоятельно. Если у вас такая функция отключена, загрузите сами пакет совместимости с официального сайта https://www.microsoft.com/ru-ru/download/details.aspx?id=3.

Преобразование форматов онлайн

Всегда имеете доступ к интернету и не хотите заморачиваться с описанными выше способами? Можно переформатировать документы из одного расширения в другое с помощью онлайн-сервисов. Их в сети полно, поэтому вам нужно лишь прописать соответствующий запрос в поисковике и воспользоваться понравившимся конвертером.

К примеру можно использовать такой https://document.online-convert.com/ru/convert-to-docx: загружаете документ при помощи кнопки «Выберите файл», затем нажимаете ниже «Преобразовать файл» и через несколько секунд он автоматически загрузится.

Вот и все дела. Не забудьте подписаться на обновления моего блога, если ещё этого не сделали. У меня для вас найдётся море интересной информации.

Удачи.

profi-user.ru

Онлайн-конвертеры DOCX в DOC

Несмотря на то, что Microsoft Office 2003 серьезно устарел и более не поддерживается компанией-разработчиком, многие продолжают использовать именно эту версию офисного пакета. И если вы до сих пор по каким-либо причинам работаете в «раритетном» текстовом процессоре Word 2003, файлы актуального на данный момент формата DOCX просто так у вас открыть не получится.

Впрочем, отсутствие обратной совместимости нельзя назвать серьезной проблемой, если необходимость просмотра и редактирования DOCX-документов не носит постоянный характер. Можно воспользоваться одним из онлайн-конвертеров DOCX в DOC и преобразовать файл из нового формата в устаревший.

Конвертируем DOCX в DOC онлайн

Для превращения документов с расширением DOCX в DOC существуют полноценные стационарные решения — компьютерные программы. Но если подобные операции вы проводите не особо часто и, что важно, имеется доступ в интернет, лучше использовать соответствующие браузерные инструменты.

Более того, онлайн-конвертеры обладают рядом преимуществ: они не занимают лишнее пространство в памяти компьютера и зачастую являются универсальными, т.е. поддерживают самые различные форматы файлов.

Способ 1: Convertio

Одно из самых популярных и удобных решений для конвертирования документов онлайн. Сервис Convertio предлагает пользователю стильный интерфейс и возможность работы с более чем 200 файловых форматов. Поддерживается преобразование документов Word, включая пару DOCX->DOC.

Онлайн-сервис Convertio

Начать конвертировать файл вы можете сразу при переходе на сайт.

1. Для загрузки документа на сервис воспользуйтесь большой красной кнопкой под надписью «Выберите файлы для преобразования».
   
   Можно импортировать файл с компьютера, загрузить по ссылке или при помощи одного из облачных сервисов.
2. Затем в выпадающем списке с доступными файловыми расширениями перейдите к пункту «Документ» и выберите «DOC».
   
   После нажмите на кнопку «Преобразовать».

   В зависимости от размера файла, скорости вашего соединения и загруженности серверов Convertio, процесс конвертирования документа займет некоторое время.

3. По завершении преобразования, все там же, справа от названия файла, вы увидите кнопку «Скачать». Нажмите на нее для загрузки итогового документа DOC.
   

Читайте также: Как выполнить вход в аккаунт Google

Способ 2: Standard Converter

Простой сервис, поддерживающий сравнительно небольшое количество файловых форматов для конвертирования, преимущественно офисные документы. Тем не менее, инструмент исправно выполняет свою работу.

Онлайн-сервис Standard Converter

1. Чтобы перейти непосредственно к конвертеру, нажмите на кнопку «DOCX TO DOC».
   
2. Перед вами появится форма для загрузки файла.
   
   Здесь для импорта документа нажмите «Выберите файл» и найдите DOCX в Проводнике. Затем кликните на большую кнопку с надписью «Convert».
3. После практически молниеносного процесса преобразования готовый DOC-файл будет автоматически скачан на ваш ПК.
   

И это вся процедура конвертирования. Сервис не поддерживает импорт файла по ссылке или с облачного хранилища, однако если вам нужно максимально быстро преобразовать DOCX в DOC, Standard Converter  — отличное решение.

Способ 3: Online-Convert

Этот инструмент можно назвать одним из самых мощных в своем роде. Сервис Online-Convert практически «всеядный» и если у вас высокоскоростной интернет, с его помощью можно быстро и бесплатно преобразовать любой файл, будь то изображение, документ, аудио или видео.

Онлайн-сервис Online-Convert

И конечно же, при необходимости конвертировать документ DOCX в DOC, данное решение без проблем справится с этой задачей.

1. Для начала работы с сервисом перейдите на его главную страницу и найдите блок «Конвертер документов».
   
   В нем откройте выпадающий список «Выберите формат конечного файла» и кликните на пункт «Конвертируйте в формат DOC». После этого ресурс вас автоматически перенаправит к странице с формой для подготовки документа к преобразованию.
2. Загрузить файл на сервис с компьютера можно при помощи кнопки «Выберите файл». Также есть опция загрузки документа с «облака».
   
   Определившись с файлом для загрузки, сразу жмите на кнопку «Преобразовать файл».
3. После конвертирования готовый файл будет автоматически скачан на ваш компьютер. Кроме того, сервис предоставит прямую ссылку для загрузки документа, действительную последующие 24 часа.
   

Способ 4: DocsPal

Еще один онлайн-инструмент, который, как и Convertio, отличается не только широкими возможностями по преобразованию файлов, но и максимальным удобством в использовании.

Онлайн-сервис DocsPal

Все нужные нам инструменты прямо на главной странице.

1. Итак, форма для подготовки документа к преобразованию находится во вкладке «Конвертировать файлы». Она открыта по умолчанию.
   
   Щелкните по ссылке «Загрузить файл» или нажмите на кнопку «Выберите файл», чтобы загрузить документ в DocsPal с компьютера. Также можно импортировать файл по ссылке.
2. Определив документ для загрузки, укажите его исходный и конечный формат.
   
   В выпадающем списке слева выберите «DOCX — Microsoft Word 2007 Document», а справа соответственно «DOC — Microsoft Word Document».
3. Если желаете, чтобы преобразованный файл был отправлен на ваш электронный ящик, отметьте чекбокс «Получить емейл с ссылкой на скачивание файла» и укажите email-адрес в поле ниже.
   
   Затем жмите на кнопку «Конвертировать файлы».
4. По окончании конвертирования готовый документ DOC можно скачать, кликнув по ссылке с его названием в панели внизу.
   

DocsPal позволяет одновременно конвертировать до 5 файлов. При этом размер каждого из документов не должен превышать 50 мегабайт.

Способ 5: Zamzar

Онлайн-инструмент, который может преобразовать практически любое видео, аудиофайл, электронную книгу, изображение или документ. Поддерживаются более 1200 файловых расширений, что является абсолютным рекордом среди решений подобного рода. И, конечно же, конвертировать DOCX в DOC этот сервис сможет без проблем.

Онлайн-сервис Zamzar

За преобразование файлов здесь отвечает панель под шапкой сайта с четырьмя вкладками.

1. Чтобы конвертировать документ, загруженный из памяти компьютера, воспользуйтесь разделом «Convert Files», а для импорта файла по ссылке используйте вкладку «URL Converter».
   
   Итак, щелкните «Choose Files» и выберите требуемый DOCX-файл в Проводнике.
2. В выпадающем списке «Convert files to» выберите конечный формат файла — «DOC».
   
3. Далее в текстовом поле справа укажите свой имейл. Именно на ваш почтовый ящик будет отправлен готовый файл DOC.
   
   Для запуска процесса конвертирования щелкните по кнопке «Convert».
4. Преобразование DOCX-файла в DOC занимает обычно не более 10-15 секунд.
   
   В результате вы получите сообщение об успешном конвертировании документа и его отправке на ваш электронный ящик.

При пользовании онлайн-конвертером Zamzar в бесплатном режиме вы можете преобразовывать не более 50 документов в сутки, а размер каждого не должен превышать 50 мегабайт.

Читайте также: Конвертируем DOCX в DOC

Как видите, преобразовать DOCX файл в устаревший ныне DOC можно очень легко и быстро. Для этого совсем не обязательно устанавливать специальное программное обеспечение. Все можно сделать, используя лишь браузер с доступом в интернет.

Помогла ли вам эта статья?

lumpics.ru

Как конвертировать docx в doc и открывать в Word документы любых поздних версий

Друзья, не знаю как Вы, а я до сих пор пользуюсь Word 2003, и в принципе всех его возможностей мне хватает. Однако часто приходится сталкиваться с документами в формате docx. Это формат, который присваивается по умолчанию текстовым документам в Word, начиная с 2007-го, и он не совместим с более ранними версиями программы. Такой ход делается производителями софта намеренно, чтобы люди постоянно обновляли свой софт, а следовательно их производителям капала денежка…

1. Онлайн конвертер

Бесплатный сервис, расположенный по адресу https://convertio.co/ru/docx-doc/, позволяет буквально за пару кликов мышью преобразовать DOCX в DOC. Выбираете откуда Вы хотите загрузить документ:

• С компьютера
• Из хранилища DropBox
• Из облака Google Drive
• Из интернета по ссылке

Документ можно просто перетянуть на открытую страничку конвертера в браузере, чтобы не кликать дополнительные кнопки.

Проследите, чтобы были выбраны правильный исходный и конечный форматы конвертации.

После загрузки файла, нажмите кнопку «Преобразовать»:

Буквально спустя пару секунд файл будет преобразован и его можно скачать в формате DOC либо отправить в DropBox или Google Drive:

Онлайн сервис Convertio абсолютно бесплатный, пользоваться им можно даже без регистрации. Единственное ограничение: размер вордовского файла, который Вы загружаете, не должен превышать 100 мегабайт, но таких «коней» еще надо поискать 🙂

2.Официальный способ от Microsoft

Существует патч под названием «Пакет обеспечения совместимости Microsoft Office для форматов файлов Word, Excel и PowerPoint», который можно скачать из Интернет. Ссылку на него найдите сами через поиск Google, потому что Microsoft регулярно удаляет этот патч со своего сайта либо меняет к нему путь.

Надеюсь, что отныне у Вас не будет проблем, и Вы сможете еще долго пользоваться той версией Microsoft Office, к которой привыкли!

P.S. Рекомендую прочитать про универсальный конвертер файлов, который выручит Вас в любой ситуации.

webtous.ru

Построение графика функции, заданной в полярной системе координат.

Создайте в новом проекте форму «График функции в полярной системе координат»

1.Условие:

Построить график функции, заданной в полярной системе координат.

R=10*(1+cos(t)), где t € [0; 2?] шаг изменения t h=0.01

2.Программа:

Результат;

Сохранитепроект в папкеЛабораторная работа 11/Задание 3.

Задание 4

Построение графиков функций

Создайте в новом проекте форму «Построение графиков функций»

Создаваемое приложение должно состоять из таблицы для задания списка точек графика функции и графического поля для рисования графика. При этом любое изменение данных в таблице должно вызывать обновление графика.

Описание работы

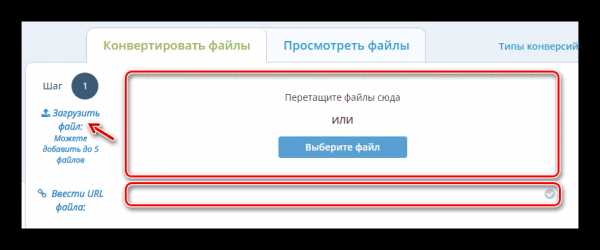
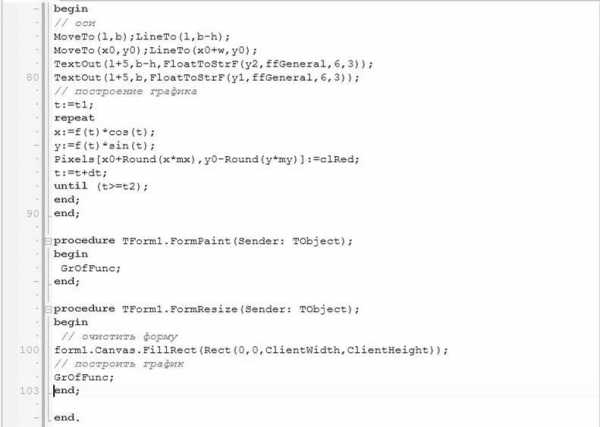
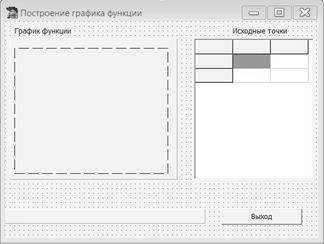Программа будет состоять из одной формы, на которой необходимо разместить: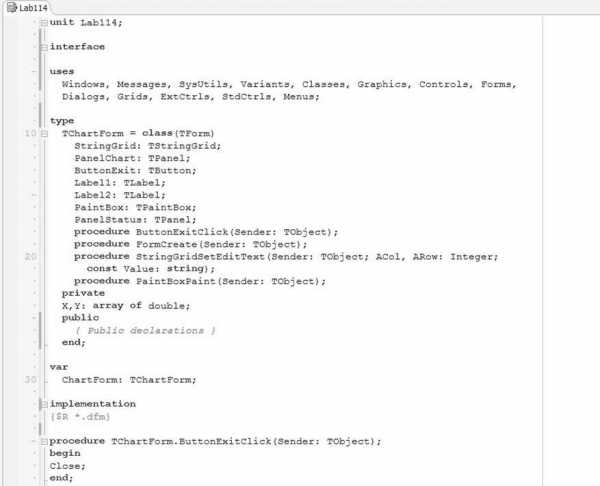

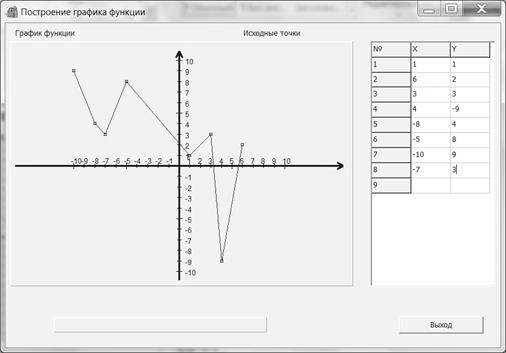
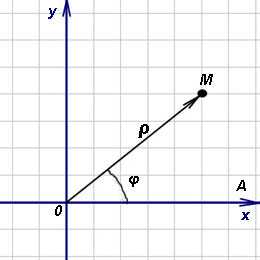
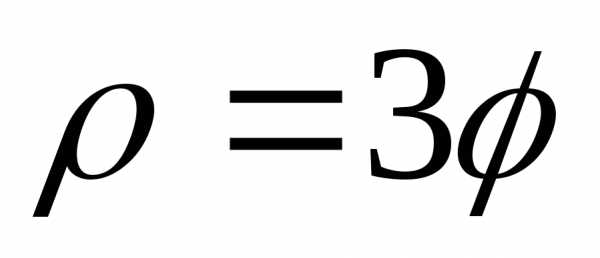Таблица для ввода координат точек должна автоматически изменять размер в соответствии с количеством уже введенных точек функции. Как это сделать, описано в предыдущих лабораторных работах.

После ввода данных необходимо сформировать два массива введенных координат X и Y, отсортировать их по оси X, после чего необходимо перерисовать окно с графиком.

Замечание

При необходимости перерисовки компонента в ответ на какое-то событие, например, нажатие кнопки, сразу не рисуйте, а вызовите метод Invalidate и создайте обработчик события OnPaint визуального компонента, например, формы или TPaintBox.

Рассмотрим, как Windows отображает все свои окна.

Окнами в общем случае являются кнопки, строки ввода, списки и т.д. Они могут находиться друг в друге, например, кнопки в диалоговом окне или окна внутри многодокументного интерфейса. Каждое окно при этом имеет специальную главную управляющую процедуру, которая обрабатывает поступающие от системы сообщения. Некоторые из этих сообщений Delphi преобразует в события, которые можно затем обрабатывать в программе.

Windows сама никогда не хранит изображения окон, поэтому одним из сообщений является команда о необходимости отображения содержимого окна на экране.

В нашей программе сразу же после ввода координат точек мы не должны вызывать процедуру рисования. При этом мы должны указать Windows, что как только появится свободное процессорное время, система должна послать сообщение о необходимости реального отображения окна. При таком подходе, если окно приложения будет временно закрыто другим окном и опять станет видимым, система автоматически пошлет сообщение о необходимости восстановления графического изображения в окне.

В Delphi для указания, что необходимо перерисовать любой элемент управления, нужно вызвать его метод Invalidate.

Для изображения произвольной графики в Delphi обычно используется компонент TPaintBox, находящийся на закладке System палитры компонентов. Этот компонент имеет событие OnPaint, для которого мы и должны создать обработчик для рисования графика.

Для прорисовки произвольных изображения используется класс TCanvas(холст), а также методы, позволяющие рисовать графические примитивы (краткое описание свойств и методов объектов для рисования графики приведено выше).

Для упрощения алгоритма рисования графика будем считать, что обе координаты всех точек попадают в интервал
[-10, 10]’. Процедура рисования графика при этом распадается на две части:

-рисование осей координат с засечками и подписями

-и собственно изображение графика.

Теперь рассмотрим вопрос автоматического изменения положения и размеров визуальных компонентов при изменении формы. Для этого у компонентов имеются такие свойства, как Align и Anchors. Собственно, свойство Align является подмножеством возможностей свойства Anchors. Свойство Anchors имеет 4 логических подсвойства:

-akLefn,

-akTop,

-akRight,

-akBotton

Например, если свойство akRight установлено в True, то правая сторона элемента будет находиться на одинаковом расстоянии от правой стороны содержащей его формы при изменении пользователем ее размера, иначе правая сторона элемента будет находиться на одинаковом расстоянии от левой стороны. При изменении свойства Align на самом деле изменяется свойство Anchors, которое впоследствии и учитывается при изменении размеров.

Замечание
По возможности делайте любое окно растягиваемым, но при этом не забывайте отслеживать, чтобы внутренности окна изменялись при изменении его размеров. Для этого используйте свойства Аlign и Anchors.

Поэкспериментируйте приведенными свойствами и добейтесь, чтобы в нашем приложении график растягивался в размерах при увеличении размеров формы, но в то же время таблица оставалась с правой стороны формы, a кнопка выхода в правом нижнем.Обратите внимание, что процедура рисования графика должна учитывать изменяющийся размер элемента TPaintBox.

Программа:

Результат

На рис. приведен внешний вид запущенного приложения после того, как окно растянуто.

Сохранитепроект в папкеЛабораторная работа 11/Задание 4.

Вопросы и задания для самостоятельной работы

1. Как Windows перерисовывает свои окна?

2. Как заставить Windows перерисовать какое-то окно?

3. Для чего используются свойства визуальных компонентов Align и Anchors?

4.Поместите на форму компоненты для выбора стиля изображения на графике введенных точек (кружочки, квадратики или «не изображать»), толщины и цвета линий. При этом график должен автоматически перерисовываться при изменении этих параметров.

5. Добавьте кнопку для генерации случайного набора точек.

Статьи к прочтению:

14 вопросов которые нужно задать до свадьбы? Сатья дас. Карпаты. 3.08.2017

Похожие статьи:

csaa.ru

Лепестковая диаграмма в Excel в полярной системе координат

Лепестковая диаграмма по внешнему виду напоминает паутину или звезду. Достаточно специфическое изображение, позволяющее отображать данные каждой категории вдоль отдельной оси. Каждая ось начинается в центре рисунка и заканчивается на внешнем круге.

Что показывает лепестковая диаграмма

Лепестковая диаграмма – разновидность круговой, которая отлично подходит для представления данных, сгруппированных по определенному признаку (по годам, месяцам, категории товаров и т.п.).

В каких ситуациях полезна именно лепестковая диаграмма:

• нужна максимальная наглядность;
• необходимо проиллюстрировать изменчивость показателей сразу по нескольким направлениям;
• важно показать на одном графике зависимость переменных величин от набора стабильных значений.

График паутинообразного типа напоминает по форме колесо. Каждый набор переменных отображается вдоль отдельной оси-спицы. Построение полярной кривой лепестковыми диаграммами выполняется очень просто. Вся графическая область этого типа диаграмм имеет полярную систему координат.

Как построить лепестковую диаграмму в Excel

1. На пустом листе создаем таблицу с данными. Или запускаем книгу, где хранится готовая информация для диаграммы лепесткового типа. Будьте внимательны: независимые переменные (причины) находятся в строках. Зависимые (воздействия) – в столбцах. Данные имеют одинаковый формат.
2. Выделяем данные, которые нужно отобразить на диаграмме. Переходим на вкладку «Вставка» в группу «Диаграммы». Лепестковые находятся в «Других диаграммах». Для примера выберем подтип «заполненной».
3. После нажатия ОК появится рисунок. Чтобы изменить цвет заливки, стиль, размер построенной диаграммы, используйте вкладки «Макет», «Формат», «Конструктор». В примере – объемная диаграмма лепесткового типа.

* При выделении ячеек с данными для включения в график названия тоже можно выделять. Excel распознает их и включает в подписи к секторам.

В примере получился такой рисунок, т.к. в таблице только один столбец с переменными значениями. Возьмем для построения диаграммы лепесткового типа данные из другого диапазона:

Добавились столбцы с переменными. Их нужно включить в диаграмму. Для этого щелкаем правой кнопкой мыши по области построения и нажимаем «Выбрать данные». В открывшемся диалоговом окне добавляем элементы легенды.

Получаем такой рисунок:

* Чтобы не перегружать рисунок, количество столбцов с данными не должно быть больше семи.

Построение графика в полярной системе координат с помощью Excel

В разных областях науки и техники существуют декартовые координаты и полярная система координат. Примеры знаменитых кривых в полярных координатах – уравнение кардиоиды, архимедова спираль, уравнение розы и др.

Инструмент «Лепестковая диаграмма» позволяет легко и быстро строить графики в полярной системе координат:

1. для каждой категории предусмотрена отдельная ось, а все оси выходят из одной точки – центра;
2. значение ряда данных – расстояние от центра до маркера – величина радиуса;
3. категория – угловая координата точки – наклон радиуса.

Известны следующие значения точек:

Уравнение функции:

r = 3 * sin (6 * ^φ)/

Заполним таблицу данных в Excel. Программа понимает число π и автоматически рассчитывает синусы.

Формулы для заполнения первого столбца берем из таблицы значений точек:

В соседнем столбце запишем формулу, по которой Excel будет считать значение функции r:

Выделим найденные значения функции. Перейдем на вкладку «Вставка». Подтип лепестковой диаграммы – «Лепестковая с маркерами». Получим в результате вот такой график в системе полярных координат:

На одной графической области в полярных координатах с помощью диаграммы лепесткового типа можно построить два и более графика.

exceltable.com

Полярная система координат: основные понятия и примеры

Полярная система координат определяется заданием некоторой точки O, называемой полюсом, исходящего из этой точки луча OA (обозначается также и как Ox), называемого полярной осью, и масштаба для изменения длин. Кроме того, при задании полярной системы координат должно быть определено, какие повороты вокруг точки O считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки).

Итак, выберем на плоскости (рисунок выше) некоторую точку O (полюс) и некоторый выходящий из неё луч Ox. Кроме того, укажем единицу масштаба. Полярными координатами точки M называются два числа ρ и φ, первое из которых (полярный радиус ρ) равно расстоянию точки M от полюса O, а второе (полярный угол φ, который называют также амплитудой) — угол, на который нужно повернуть против часовой стрелки луч Ox до совмещения с лучом OM.

Точку M с полярными координатами ρ и φ обозначают символом M(ρ, φ).

Установим связь между полярными координатами точки и её декартовыми координатами. Будем предполагать, что начало декартовой прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Пусть точка M имеет декартовы координаты x и y и полярные координаты ρ и φ.Тогда

x = ρ cos φ)

и

y = ρ sin φ).

Полярные координаты ρ и φ точки M определяются по её декартовым координатам следующим образом:

.

Для того, чтобы найти величину угла φ, нужно, используя знаки x и y, определить квадрант, в котором находится точка M, и, кроме того, воспользоваться тем, что тангенс угла φ равен .

Приведённые выше формулы называются формулами перехода от декартовых координат к полярным.

Пример 1. В полярной системе координат на плоскости даны точки

A(3; π/4);

B(2; —π/2);

C(3; —π/3).

Найти полярные координаты точек, симметричных этим точкам относительно полярной оси.

Решение. При симметрии длина луча не меняется. Следовательно, первая координата — длина луча — у симметричной относительно полярной оси точки будет как и у данной точки. Как видно из рисунка в начале урока, при построении симметричной относительно полярной оси точки данную точку нужно повернуть вокруг полярной оси на тот же угол φ. Следовательно, в полярной системе координат второй координатой симметричной точки будет угол для исходной точки, взятый с противоположным знаком, то есть -φ. Итак, полярные координаты точки, симметричной данной относительно полярной оси будут отличаться лишь второй координатой, и эта координата будет с противоположным знаком. Полярные координаты искомых симметричных точек будут следующими:

A’(3; —π/4);

B’(2; π/2);

C’(3; π/3).

Пример 2. В полярной системе координат на плоскости даны точки

A(1; π/4);

B(5; π/2);

C(2; —π/3).

Найти полярные координаты точек, симметричных этим точкам относительно полюса.

Решение. При симметрии длина луча не меняется. Следовательно, первая координата — длина луча — у симметричной относительно полюса точки будет как и у данной точки. Симметричная относительно полюса точка получается вращением исходной точки на 180 градусов против часовой стрелки, то есть на угол π. Следовательно, вторая координата точки, симметричной данной относительно полюса рассчитывается как φ + π (если в результате получится числитель больше знаменателя, то вычтем из полученного числа один полный оборот, то есть 2π). Получаем следующие координаты точек, симметричных данным относительно полюса:

A’(1; 3π/4);

B’(5; —π/2);

C’(2; 2π/3).

Пример 3. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В полярной системе координат даны точки

A(6; π/2);

B(5; 0);

C(2; π/4).

Найти декартовы координаты этих точек.

Решение. Используем формулы перехода от полярных координат к декартовым:

x = ρ cos φ)

и

y = ρ sin φ).

Получаем следующие декартовы координаты данных точек:

A(0; 6);

B(5; 0);

C’(√2; √2).

Пример 4. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В декартовой прямоугольной системе координат даны точки

A(0; 5);

B(-3; 0);

C(√3; 1).

Найти полярные координаты этих точек.

Решение. Определяем первую из полярных координат по формуле , а тангенс угла φ — второй из полярных координат как . Получаем следующие полярные координаты данных точек:

A(5; π/2);

B(3; π);

C(2; π/6).

Поделиться с друзьями

Весь блок «Аналитическая геометрия»

• Векторы
• Плоскость
• Прямая на плоскости

function-x.ru

Разработка урока «Красивые графики. Построение графиков функций в полярной системе координат в электронных таблицах Excel» — К уроку — Информатика

Практическая работа «Красивые графики функций»

1. Построить спираль Архимеда по следующим данным:
   — в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
   — в столбце В – значения r = 0,5*t
   — в столбце С – значения х = r*cos(t)
   — в столбце D – значения y = r*sin(t)
   — выделить значения в столбцах С и D и построить диаграмму
   (тип: точечная с гладкими кривыми)

2. Построить астроиду по следующим данным:
   — в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
   — в столбце В – значения х = 2*(cos (t))³
   — в столбце С – значения y = 2*(sin (t))³
   — выделить значения в столбцах B и С и построить диаграмму
   (тип: точечная с гладкими кривыми)

3. П остроить улитку Паскаля по следующим данным:
   — в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
   — в столбце В – значения t = a*π/180 (угол в радианах)
   — в столбце С – значения p = cos(t)–0,5
   — в столбце D – значения x = p*cos(t)
   — в столбце Е – значения у = p*sin(t)
   — выделить значения в столбцах D и E и построить диаграмму
   (тип: точечная с гладкими кривыми)
   
   

4. Построить лемнискату Бернулли по следующим данным:
   — в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
   — в столбце В – значения t = a*π/180 (угол в радианах)
   — в столбце С – значения r = 2*sin(2*t)²
   — в столбце D – значения x = r*cos(t)
   — в столбце E – значения y = r*sin(t)
   — выделить значения в столбцах D и E и построить диаграмму
   (тип: точечная с гладкими кривыми)

5. П остроить график в форме сердца по следующим данным:
   — в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
   — в столбце В – значения t = a*π/180 (угол в радианах)
   — в столбце С – значения x = 16*(sin(t))³
   — в столбце D – значения у =13*cos(t)–5*cos(2*t)–2*cos(3*t)–cos(4*t)
   — выделить значения в столбцах C и D и построить диаграмму
   (тип: точечная с гладкими кривыми)

pedsovet.su

5.2. Построение графиков в полярной системе координат при помощи MathCad

Для того чтобы построить график в полярной системе координат при помощи MathCAD, необходимо:

1. Определить  как дискретную переменную (в пределах области определения).

2. Задать функцию () .

3. Щелкнуть мышью в свободном месте. Выбрать из меню «Графика» PolarPlot (Полярный график).

4. В появившемся шаблоне напечатать  в нижнем поле, напечатать () в левом поле.

5. Щелкнуть мышью вне графика.

Пример 2. Построим график функции (спираль Архимеда) при помощиMathCAD.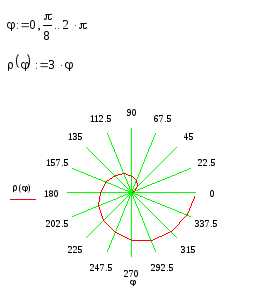

Решение.

График в полярных координатах можно форматировать.

Чтобы открыть окно форматирования графика поступают также как при форматировании декартово графика. Аналогично декартовому графику, для полярного графика можно задать стиль оформления осей (в частности, для наглядности удобно отразить вспомогательные угловые линии), изменить параметры кривой, создать надписи.

5.3. Задания для самостоятельного решения

1. Построить (в тетради) в полярной системе координат линию по точкам, придавая  значения от 0 до с шагом (для вычисления значений  можно использовать возможности MathCAD):

2. При помощи MathCAD построить кривые в полярной системе координат, придавая различные значения параметру а:

Лабораторная работа № 6 Тема: Символьные вычисления

Цель работы: Научиться производить символьные вычисления: преобразовывать выражения, вычислять пределы.

MathCAD позволяет получить значение некоторого выражения в численном виде (при помощи обычного знака равенства) или в символьном виде (при помощи знака символьного равенства, о котором будет рассказано ниже). В первом случае после знака равенства появляется одно или несколько чисел. Во втором случае результатом вычислений является некоторое выражение.

Прежде, чем производить символьные вычисления, необходимо убедиться, что символьный процессор включен в работу: в меню «Math» должны быть отмечены команды «Live Symbolics» («Использовать символику») и «Automatic Mode» («Автоматический режим»).

Знак символьного равенства представляет собой стрелку вправо () и набирается сочетанием клавиш [Ctrl] и [.], либо с палитры «Преобразования».

Чтобы произвести символьные вычисления, необходимо:

1. Ввести выражение, которое надо вычислить или преобразовать.

2. Выделить выражение синей выделительной рамкой и набрать знак символьного равенства.

3. Щелкнуть мышью вне выражения.

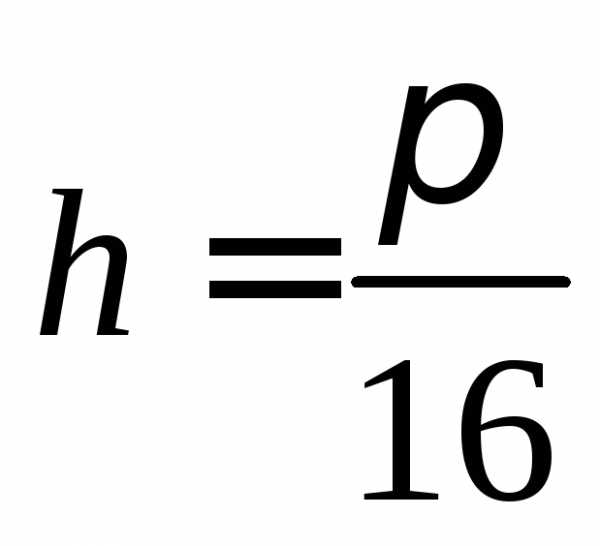
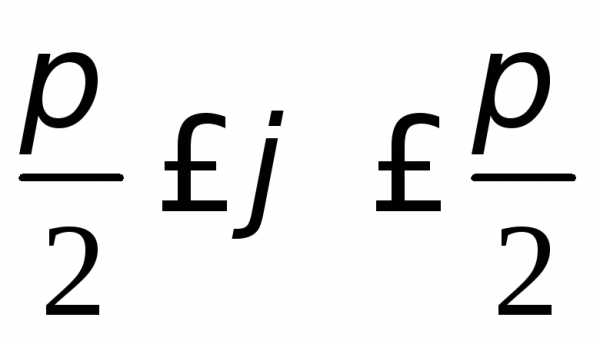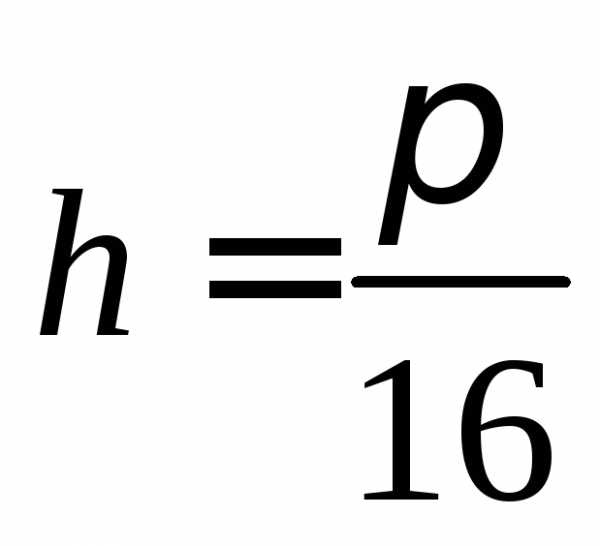
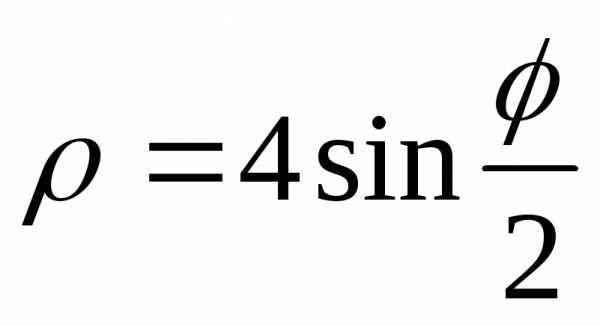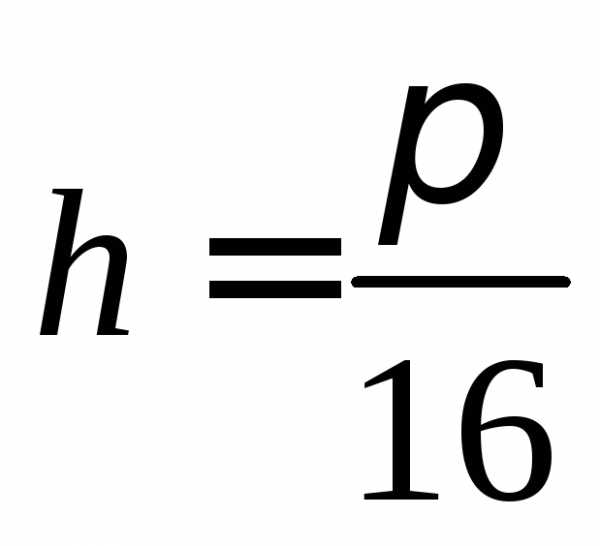
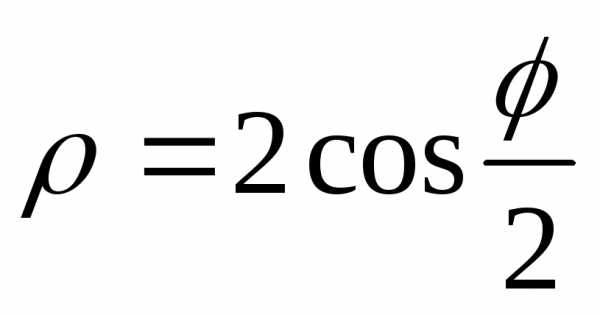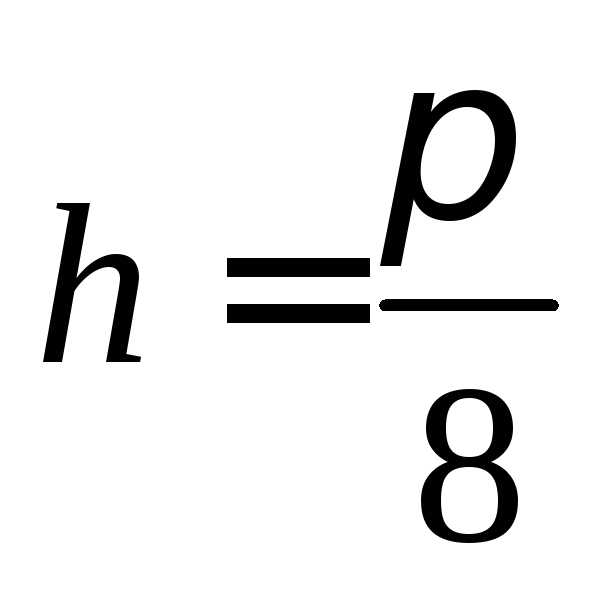
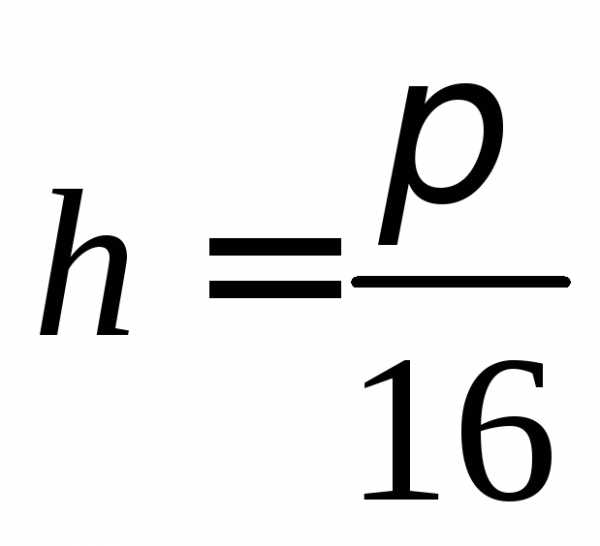
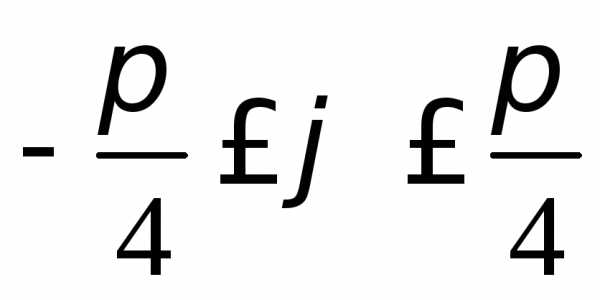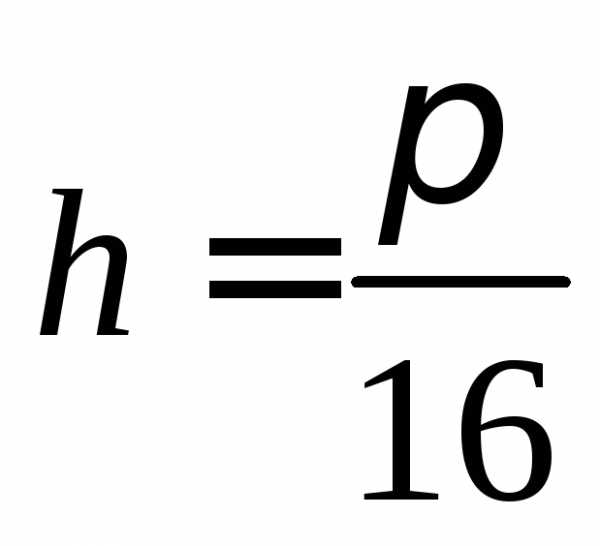
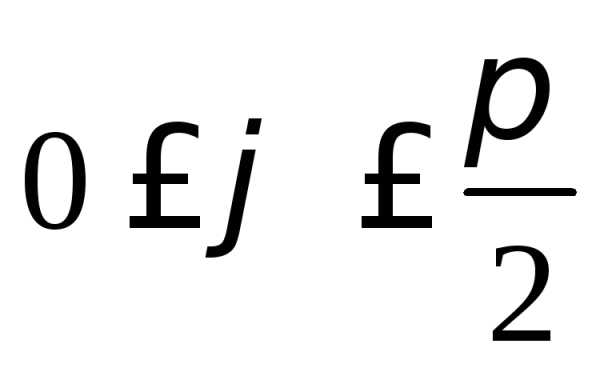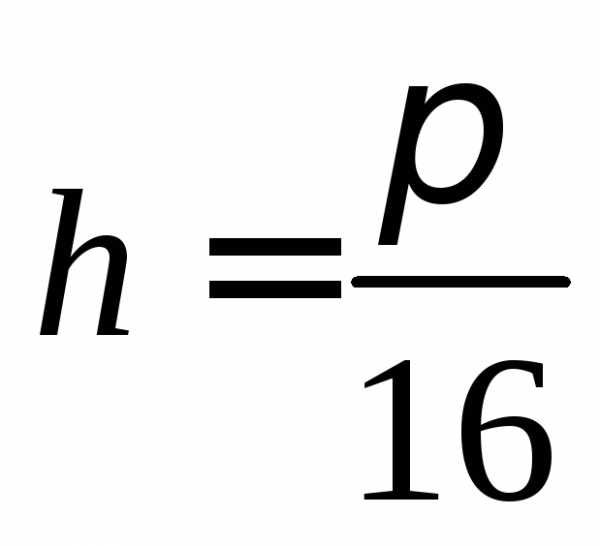
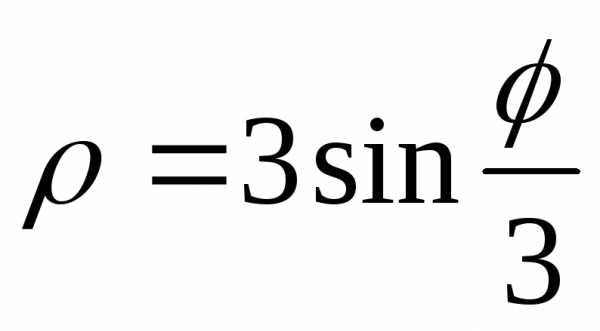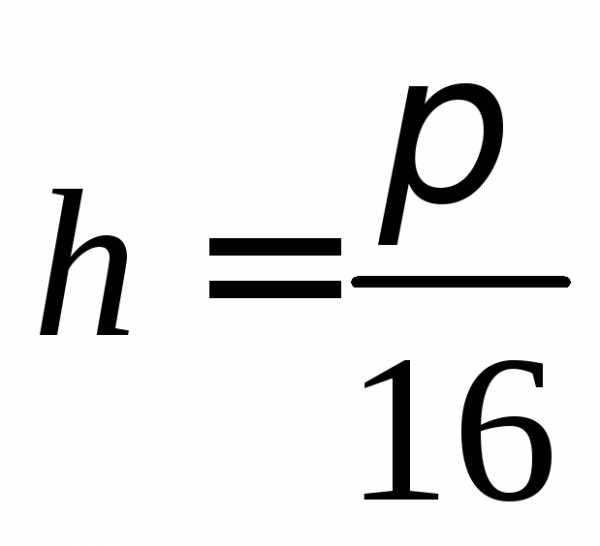
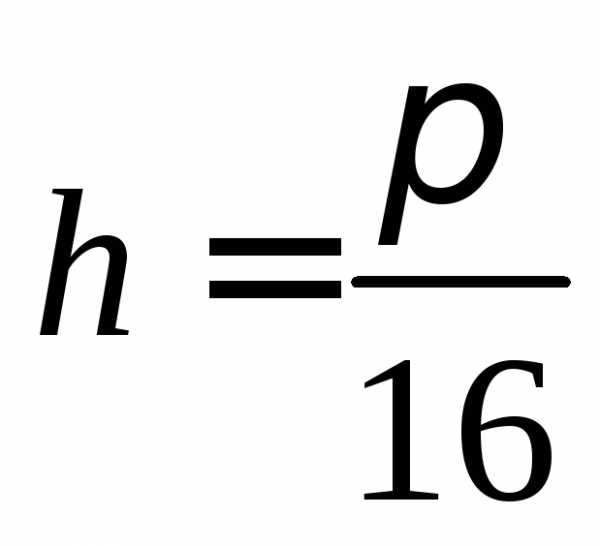
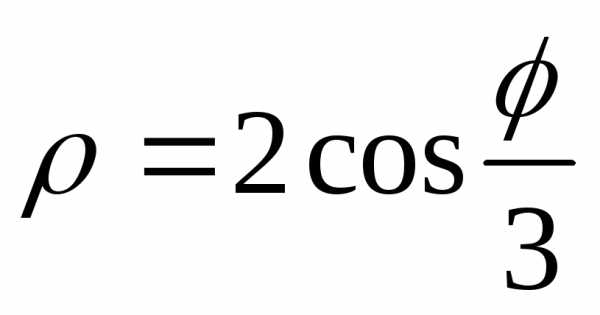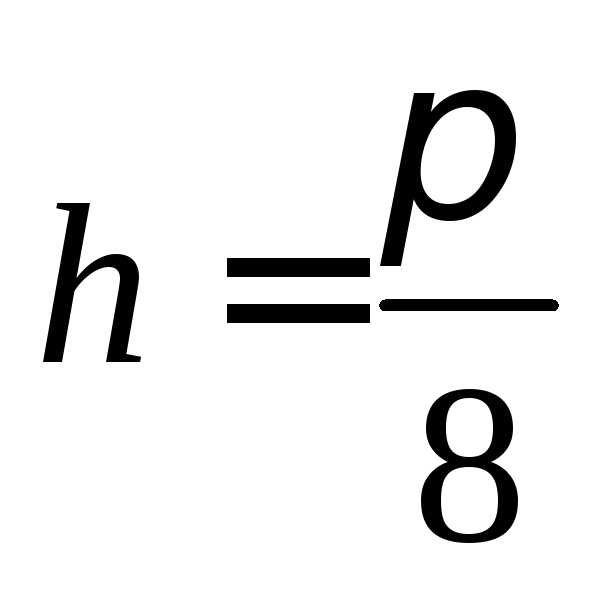
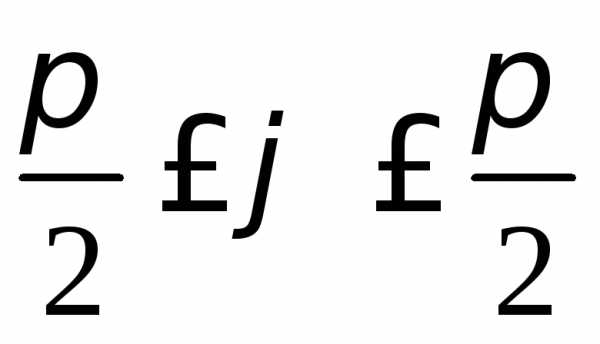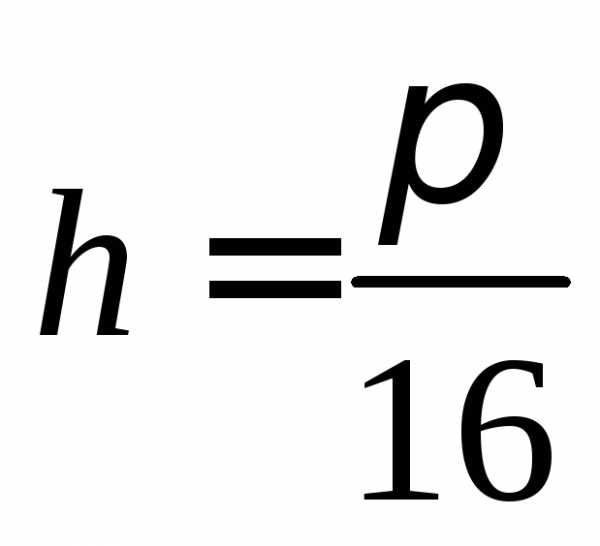
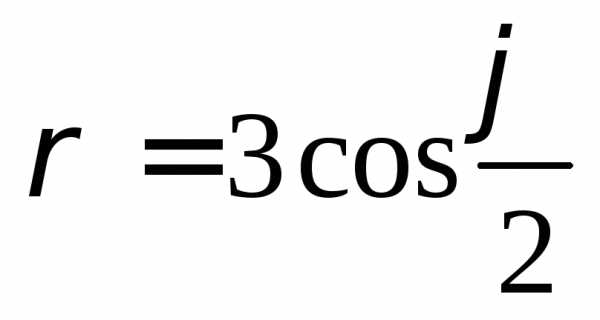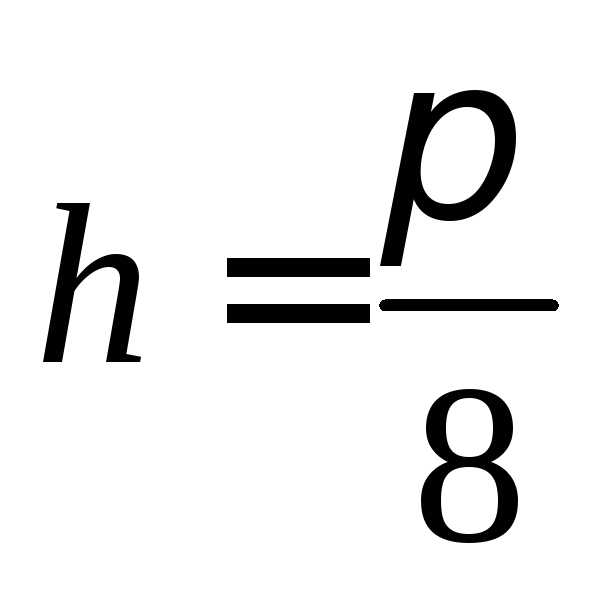
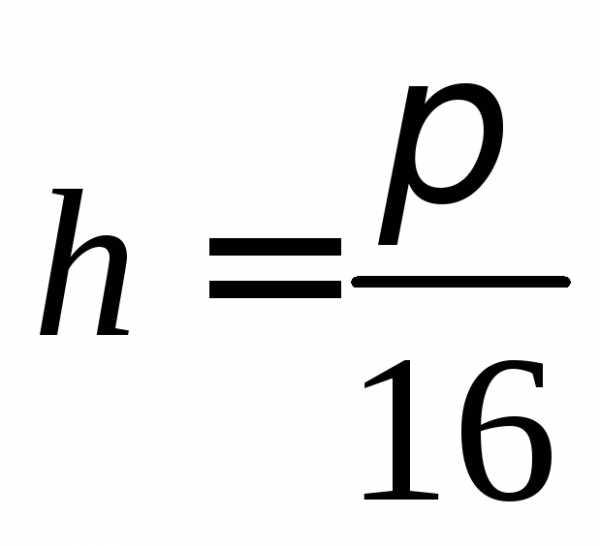
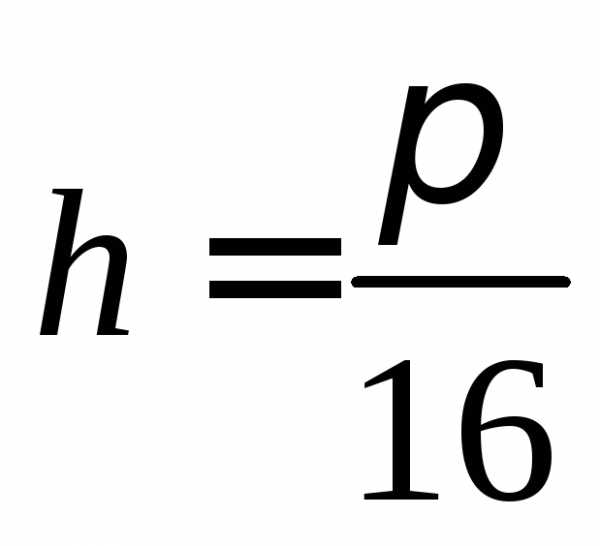
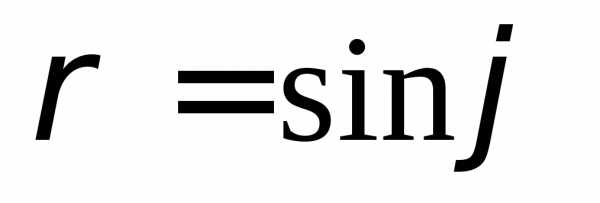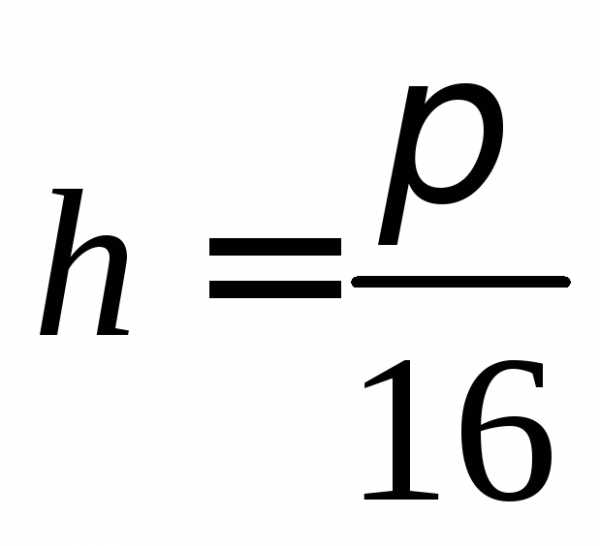
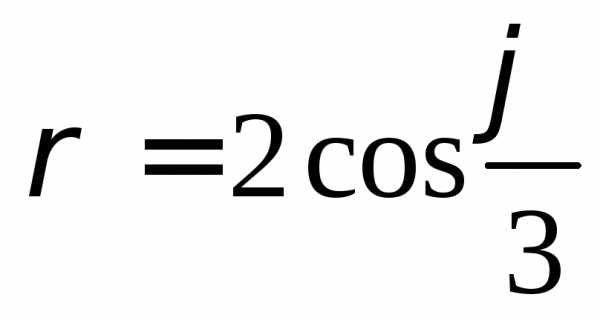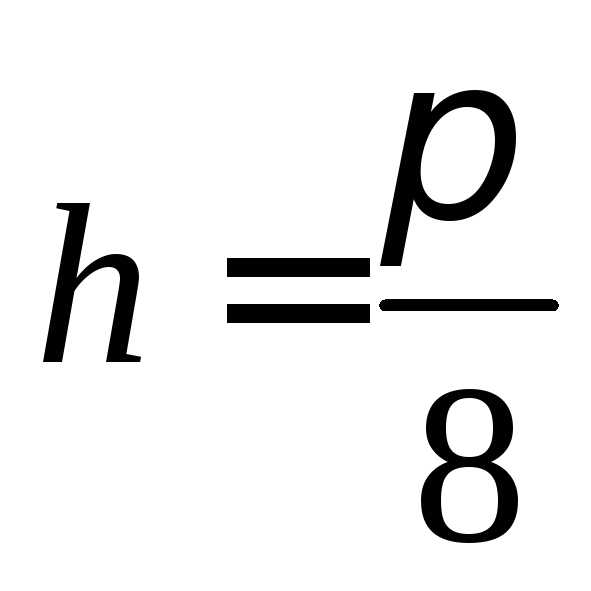
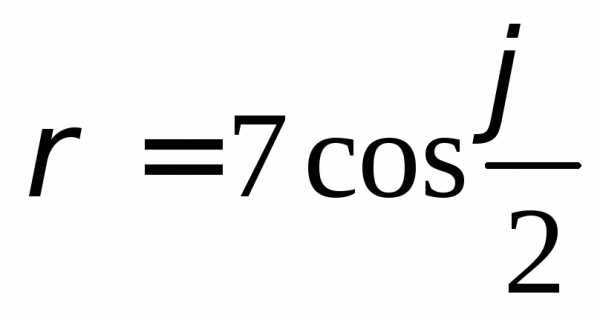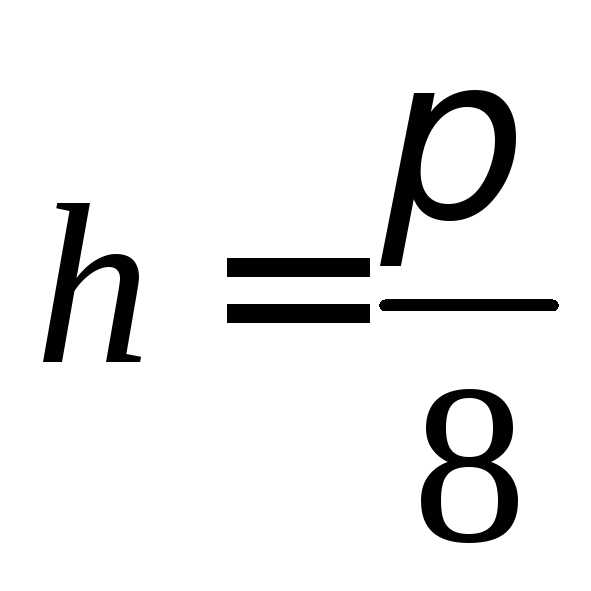
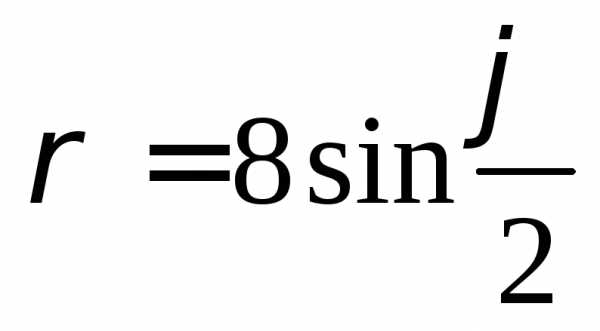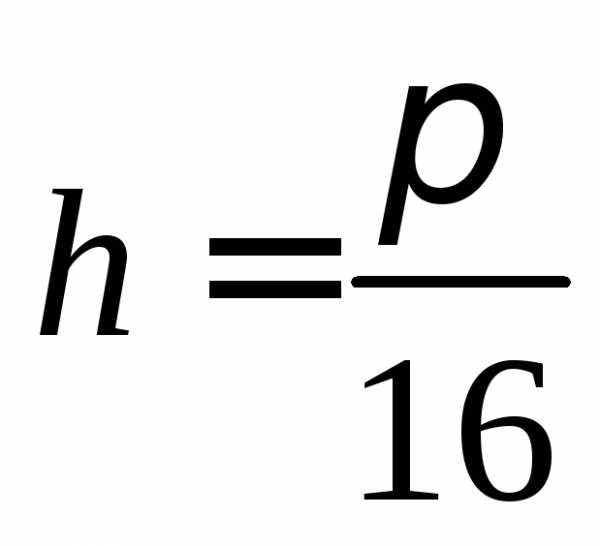
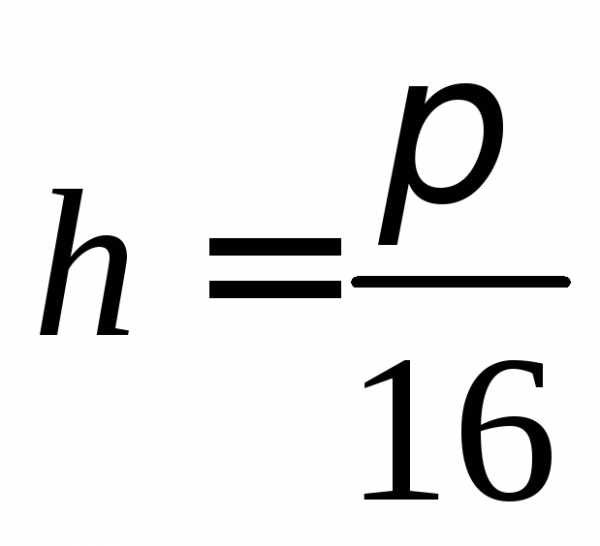
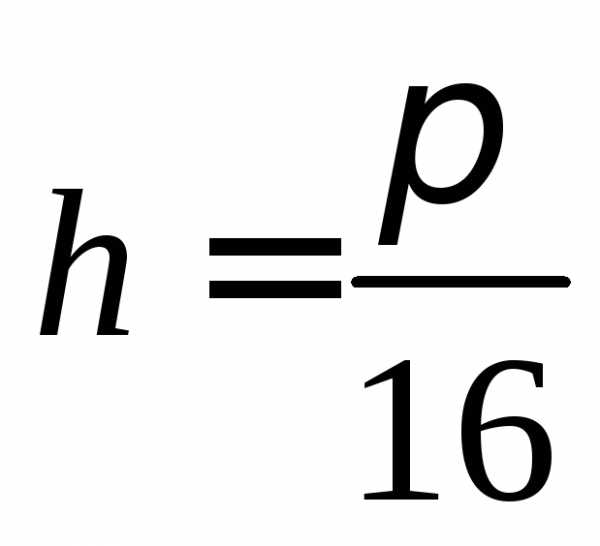
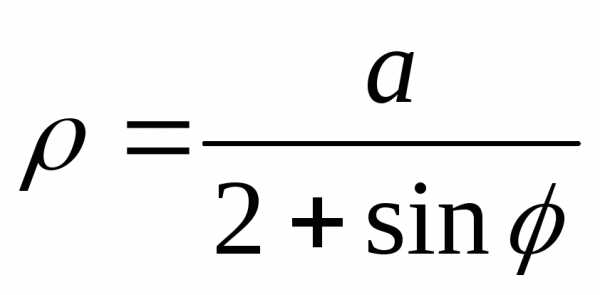
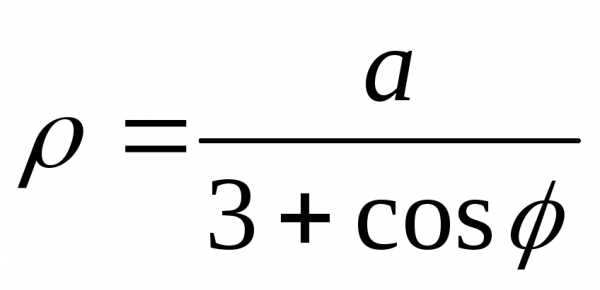
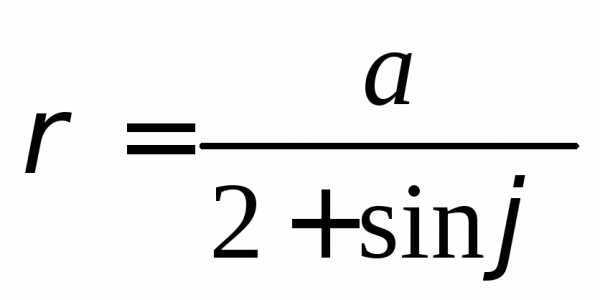
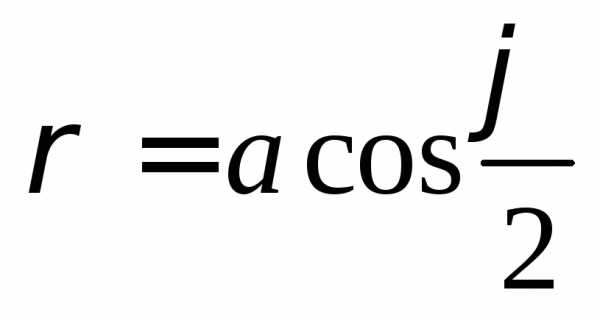
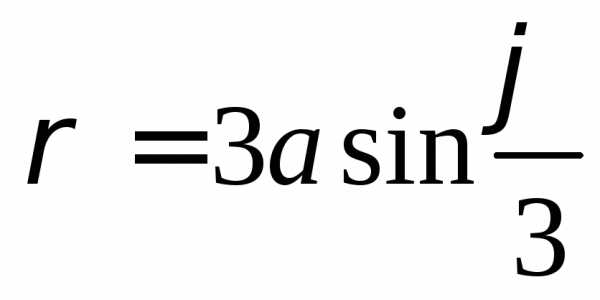
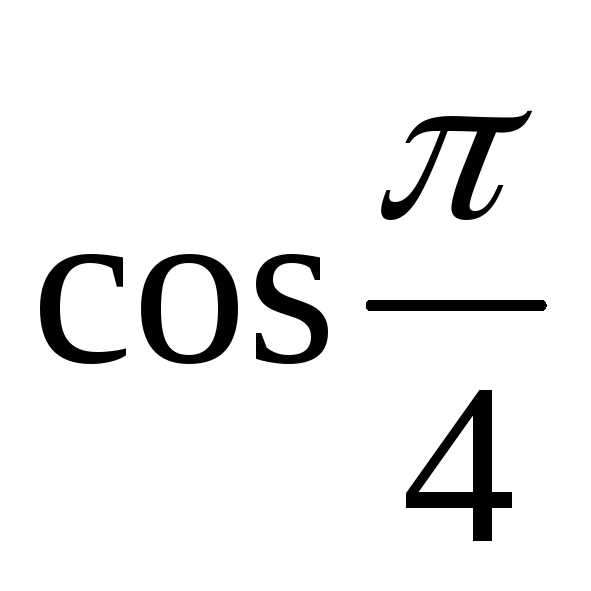Проиллюстрируем разницу между численным и символьным результатом на простом примере. Вычислим двумя способами:

Следует отметить, что для одних выражений можно произвести как численные, так и символьные вычисления, для других – только численные, для третьих – только символьные.

При помощи символьных вычислений можно вычислять пределы, решать неопределенные системы уравнений (т.е. системы, которые имеют множество решений), преобразовывать выражения, находить производные и т.д.

studfiles.net

Построение графиков функций в полярной системе координат — МегаЛекции

Онлайн калькулятор умножения матриц

Решение

Умножить две матрица можно только, если число столбцов матрицы А равно числу строк матрицы В

При умножении матрицы А размерности l × m на матрицу В размерности m × n получаем матрицу С размерности l × n

Элемент матрицы с индексом C_ij находится по формуле

c₁₁ = a₁₁ ⋅ b₁₁ + a₁₂ ⋅ b₂₁ = 4 ⋅ 0.45 + 1 ⋅ 3 = 4.8

c₁₂ = a₁₁ ⋅ b₁₂ + a₁₂ ⋅ b₂₂ = 4 ⋅ 12 + 1 ⋅ 1.4 = 49.4

c₁₃ = a₁₁ ⋅ b₁₃ + a₁₂ ⋅ b₂₃ = 4 ⋅ (-9) + 1 ⋅ 0 = -36

c₂₁ = a₂₁ ⋅ b₁₁ + a₂₂ ⋅ b₂₁ = 0 ⋅ 0.45 + 5 ⋅ 3 = 15

c₂₂ = a₂₁ ⋅ b₁₂ + a₂₂ ⋅ b₂₂ = 0 ⋅ 12 + 5 ⋅ 1.4 = 7

c₂₃ = a₂₁ ⋅ b₁₃ + a₂₂ ⋅ b₂₃ = 0 ⋅ (-9) + 5 ⋅ 0 = 0

c₃₁ = a₃₁ ⋅ b₁₁ + a₃₂ ⋅ b₂₁ = 2 ⋅ 0.45 + (-3) ⋅ 3 = -8.1

c₃₂ = a₃₁ ⋅ b₁₂ + a₃₂ ⋅ b₂₂ = 2 ⋅ 12 + (-3) ⋅ 1.4 = 19.8

c₃₃ = a₃₁ ⋅ b₁₃ + a₃₂ ⋅ b₂₃ = 2 ⋅ (-9) + (-3) ⋅ 0 = -18

matematika-club.ru

Онлайн калькулятор — умножение матриц

Следующий калькулятор служит для перемножения двух матриц. Таким образом дополняем нашу коллекцию калькуляторов о матрицах:

Ну а данный калькулятор может умножать две матрицы:

Основным, пожалуй, правилом при умножении двух матриц есть то, что количество строк первой матрицы должно быть равно количеству столбцов во второй матрице.

The field is not filled.

‘%1’ is not a valid e-mail address.

Please fill in this field.

The field must contain at least% 1 characters.

The value must not be longer than% 1 characters.

Field value does not coincide with the field ‘%1’

An invalid character. Valid characters:’%1′.

Expected number.

It is expected a positive number.

Expected integer.

It is expected a positive integer.

The value should be in the range of [%1 .. %2]

The ‘% 1’ is already present in the set of valid characters.

The field must be less than 1%.

The first character must be a letter of the Latin alphabet.

Su

Mo

Tu

We

Th

Fr

Sa

January

February

March

April

May

June

July

August

September

October

November

December

century

B.C.

%1 century

An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3

Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

s.sh.

u.sh.

v.d.

z.d.

yes

no

Wrong file format. Only the following formats: %1

Please leave your phone number and / or email.

hostciti.net

Умножение матрицы на число онлайн

Умножение матрицы на число

Операция умножения матрицы А на число k заключается в построении матрицы kA = [kaij]. Умножение матрицы на число допустимо для матриц любого размера, результатом умножения является матрица того же порядка, что и исходная матрица.

Таким образом, произведение матрицы А на число k – это результирующая матрица B = kA того же порядка, полученная умножением всех элементов aij исходной матрицы на заданное число.

Математически умножение матрицы на число можно представить следующими выражениями:
Аm×n × k = Вm×n
aij × k = bij,
где i принимает значение от 1 до m, j имеет значения от 1 до n

Пример умножения матрицы на число.

Даны матрица А и число k:

Найти произведение матрицы и числа.
Решение:

Свойства умножения матрицы на число:

1. Единица является нейтральным числом умножения любой матрицы, результатом умножения на нейтральное число является исходная матрица.
   1×А = А
2. Результатом умножения любой матрицы на ноль всегда является нулевая матрица, все элементы которой равняются нулю.
   0×А = О
3. Для матриц одного порядка и действительного числа выполняется свойство дистрибутивности умножения относительно сложения.
   k×(А+B) = k×A + k×B
4. Для любой матрицы и суммы действительных чисел выполняется свойство дистрибутивности. (k+n)×А = k×A + n×A
5. Для любой матрицы и произведения любых действительных чисел выполняется свойство ассоциативности умножения.
   (k×n)×А = k×(n×A)

Вы также можете

в качестве элементов матрицы вводить целые и дробные числа, а также выражения с переменной x (например, в ячейку матрицы можно ввести 2x, или sin(x), или даже ((x+2)^2)/lg(x)).
Полный список доступных функций можно найти в справке.

www.yotx.ru

sin (2 arcsin x)

Рассмотрим, как найти sin (2 arcsin x). Как и в случае с sin (2 arctg x), для начала воспользуемся формулой синуса двойного угла: sin 2α = 2sinαcosα.

Применяя эту формулу для нашего случая, получаем:

sin (2  arcsin x) = 2 ∙ sin ( arcsin x) ∙ cos ( arcsin x).

Поскольку

остается найти cos ( arcsin x).

Пример

Найти sin (2 arcsin 3/5).

Решение:

arcsin(3/5) — это угол альфа, синус которого равен 3/5. В прямоугольном треугольнике синус — это отношение противолежащего катета к гипотенузе. А нам нужно найти косинус этого же угла альфа. Косинус — это отношение прилежащего катета к гипотенузе. Прилежащий катет находим по теореме Пифагора:

Таким образом,

www.uznateshe.ru

Mathway | Популярные задачи