как стартовать и куда двигаться? / Habr
Бывает, что человек, совсем не связанный с IT, проникается интригующей красотой этой сферы и ставит себе задачу постепенно освоить программирование с нуля. И тут он зачастую просто теряется, не понимая, с чего начать, и нуждаясь в хорошем фундаменте и системном подходе.Я, будучи недавно в такой же ситуации, гуглила, искала мануалов на Хабре (кое-что нашла: Десять советов начинающим программистам, Начинающему программисту про стартапы и не только…), но в итоге всё же была вынуждена обратиться за советом к одному хорошему человеку, который составил для меня вот такой план. С разрешения этого человека размещаю данный план на Хабре – вдруг он пригодится и кому-то ещё. (Тем более, что перечисленные книги относятся к «золотому фонду» литературы в данной сфере и проверены временем.)
UPD: Новичкам советую обратить внимание на комментарии — там активно и аргументированно корректируется этот план.
Этап I. Основы
Нортон «Программно-аппаратная организация IBM PC»
Эта книга, несмотря на свою давность, относятся к тем, что пока отнюдь не устарели. Как новичок подтверждаю – повествование вполне понятно и для почти полного чайника в IT.
Гук «Аппаратные средства IBM PC»
А эту книгу стоит прочитать «поверх» – она расскажет о том, как дела в данной сфере обстоят сейчас.
Этап II. Hardware
Шаг 1
Морс, Алберт «Архитектура микропроцессора 80286»
Почему тут берётся за основу именно микропроцессор 80286 – станет понятно по изучении трудов первого этапа.
Шаг 2
Гук «Аппаратные интерфейсы ПК»
Гук «Интерфейсы устройств хранения»
Этап III. Операционные системы
Шаг 1
Таненбаум «Архитектура компьютера»
Шаг 2
Колисниченко, Аллен «Linux: полное руководство»
От общей теории переходим к изучению конкретной операционной системы – на примере Linux.
Немет, Снайдер, Хейн «Руководство администратора Linux»
Этап IV. Собственно программирование
Шаг 1
Керниган, Ричи «Язык программирования С»
Почему первым для освоения выбран именно язык Си? Как мне рассказали знающие товарищи, он поможет достичь правильного «программистского мышления», чего было бы сложно достичь, начиная изучение, скажем, с Паскаля. Кроме того, язык Си по-прежнему используется в наши дни и подходит как для прикладного, так и для системного программирования.
Шаг 2
Кнут «Искусство программирования»:
Том 1. Основные алгоритмы
Том 2. Получисленные алгоритмы
Том 3. Сортировка и поиск
Бентли «Жемчужины программирования»
Зачем осваивать эти труды? Как уже отмечали на Хабре – «наверное, нигде больше, чем в айти, не изобретается такое огромное количество велосипедов». Данные книги помогут этого избежать – и попутно будут прививать умение писать не просто код, а хороший код.
Ну а для затравки можно прочесть небольшой цикл лекций «Культура программирования» (автор – А. Бабий). Он помогает начинающим программистам понять, что их деятельность не будет проходить в вакууме, а неизбежно включит взаимодействие с другими программистами, с заказчиками и пользователями (а также включит необходимость копаться потом в своих собственных или в чужих программах).
Закономерный вопрос новичка: сколько времени займёт изучение всего этого? По прогнозам моего советчика, у человека, который может тратить на изучение программирования только вечера и выходные, на прочтение и осмысление литературы первых трёх этапов уйдёт полгода-год. На четвёртый этап тоже даётся год – чтение должно сопровождаться практикой по самостоятельному составлению программ. Как получится на самом деле – время покажет.
Буду крайне благодарна за ваши советы и уточнения.
habr.com
Обучение программированию с нуля: с чего начать изучение в домашних условиях
22.12.14 158.7KКаждый раз, с трудом преодолевая жизненные преграды, хочется взять и перекроить этот мир под себя. К сожалению, мы не рождены творцами этой вселенной. Тем, кто хочет удовлетворить свои амбиции создателя, остается лишь виртуальный мир.
Хотя для творения здесь понадобится не столько волшебство и знание рун, сколько знание основ программирования. Поэтому для всех начинающих творцов виртуальной реальности мы поведаем о том, как научиться программировать.
Как бы ни хотелось этого признавать, но в реальности программирование является не таким уж волшебным делом. Создание кода порой можно сравнить с хождением босыми ногами по морскому дну, устланному острыми каменными обломками.
Чтобы стать программистом, нужно быть не только умным, но еще терпеливым и настырным. Обучение программированию всегда сопровождается головой болью, красными от недосыпания глазами и отрешенным взглядом. Именно по нему можно легко узнать программиста.
Многие начинающие обучение считают написание кода чуть ли не самой романтической профессией. Особенно увеличилось количество желающих познать программирование после просмотра фильма «Матрица». Именно главный герой этой картины Нео подтолкнул многих к становлению на путь постижения программных наук:
Но большая часть начавших изучение бросают его уже через несколько недель. И основной причиной этого является неправильно выбранное направление обучения, методика или даже учебник по программированию.
После развала СССР все отечественные ВУЗы долгое время даже и не пытались перекроить свою систему обучения под потребности современного рынка. Не являлись исключением из этого правила и технические ВУЗы.
Программирования как отдельной отрасли и специализации не существовало как таковой. Его основы преподавались лишь как привязка к другим инженерным дисциплинам. И даже те крохи знаний, которые давались студентам в этой области, не соответствовали современным стандартам и утратили свою актуальность еще 20-30 лет назад.
В странах бывшего СССР основным языком программирования, преподаваемым в технических ВУЗах, был Бейсик.
Ситуация кардинально не изменилась и через 10 лет. Лишь некоторые учебные заведения, учуяв веяния нового времени, в начале двухтысячных года начали перекраивать свое обучение под мировые стандарты. И только с этого момента программирование стало восприниматься как отдельная профессия и специализация обучения:
В это же время стали появляться различные специализированные коммерческие курсы и учебные заведения. Но качество преподавания и даваемых в них знаний находились на крайне низком уровне. Не хватало грамотных профессионалов, способных обучить новичков не только теоретическим знаниям, но и практическим навыкам программирования.
А это в профессии программиста является наиболее важным аспектом. Поэтому большинство из сегодняшних гуру российской IT-индустрии начинали свое обучение программированию с нуля самостоятельно.
В некоторой мере такая тенденция сохраняется и по сей день. Хотя в наше время количество профессионалов, занимающихся преподаванием, заметно возросло.
Постижение программных наук характеризуется не только тяжелым обучением, но и его началом. Новичку порой трудно не только начать самостоятельное обучение, но и определиться с координатами отправной точки процесса. Поэтому мы постараемся помочь вам обойти все эти трудности:
Прежде чем ломать зубы об гранит науки, следует определиться, с чего начать изучение программирования. На первых этапах очень трудно определиться со специализацией. Поэтому начнем с подбора первого языка.
Чаще всего выбор падает на язык программирования C (си). Именно с него большинство новичков во всем мире начинают свое обучение. На основе C было создана основная часть программных языков, и во многом они наследуют его структуру и синтаксис.
Изучая C, вы постигаете основы не одного языка программирования, а сразу нескольких.
Рассмотрим особенности этого языка, делающего его оптимальным для изучения:
- Простая для понимания основа – часть встроенных возможностей языка для простоты вынесена в отдельно подключаемые библиотеки. К таким элементам относится большая часть математических функций и методов для работы с файловой системой;
- Оптимально подогнанная система типов – благодаря простому набору типов данных и строгой типизации уменьшается риск допущения ошибок в процессе написания программного кода;
- Направленность C на процедурный тип программирования, при котором соблюдается четкая иерархия всех элементов кода;
- Доступ к памяти машины с помощью указателей;
- Минимальное количество поддерживаемых ключевых слов;
- Поддержка области действия имен;
- Поддержка пользовательских типов данных (объединения и структуры).
Проще говоря, C – это то, с чего следует начинать новичку перед тем, как научиться программированию на других языках.
Для обучения программированию недостаточно одного лишь желания и наличия компьютера с выходом в интернет. Для написания программ на C вам потребуется специализированное программное обеспечение – компилятор.
Компилятор – специальная программа, переводящая программный код в форму, понятную для компьютера.
Вот несколько специализированных компиляторов с поддержкой языка C:
- Microsoft Visual Studio – профессиональный инструмент, поддерживающий множество языков, в том числе и несколько серверных. Подойдет для новичков, если брать его «на вырост»:
- Borland C++ — бесплатный компилятор, идеально подходящий для начинающего обучение. В отличие от предыдущего инструмента, отличается ясным и понятным интерфейсом. Поэтому его освоение не вызовет особых трудностей даже при самостоятельном освоении азов программирования:
- Code::Blocks – бесплатная среда разработки, поддерживающая написание кода на нескольких языках. Средний по сложности освоения вариант:
Что касается специализированной литературы, то советовать книги определенных авторов мы не будем. Тут, как говорится, выбирайте, что душе угодно. Потому что в большинстве случаев подбор самоучителя по программированию – это индивидуальный процесс. Используйте тот источник, который больше подходит именно для вас.
Да и в интернете можно найти очень много информации. Например, на нашем сайте специализированной литературе по IT тематике посвящен целый раздел.
После освоения основ программирования у многих сразу появится вопрос, куда двигаться дальше. Уже на этом этапе обучения следует задумываться о выборе основной специализации в области программирования. Вот те, которые больше всего востребованы на современном рынке:
- Веб-программирование – здесь понадобятся знания PHP, CSS и HTML;
- Разработка приложений под мобильную операционную систему Android – данная платформа построена на основе Java. Поэтому потребуется знание основ этого языка;
- C# (си sharp) – дальний потомок C. На основе C# построена веб-технология ASP.net от Microsoft.
И последний совет всем начинающим. Перед тем, как приступить к обучению программированию с нуля, следует запастить терпением. А также: таблетками от головной боли, кофе, чаем и побрить череп наголо. Потому что во время постижения программных наук, обучающиеся часто вырывают волосы со своей головы вместе с корнем. Удачного старта!
Еще не голосовали
рейтинг из
ХорошоПлохо
Ваш голос принят
www.internet-technologies.ru
Программирование с нуля: 4 лучших книги для детей и взрослых
Алена Лепилина
Не знать программирования через десять лет — это как не знать английского языка сейчас. Без знаний обойтись можно, но с ними открываются совсем другие перспективы. Выбрали книги по программированию с нуля для детей и взрослых.
Пусть вас не смущает, что книги детские — их заказывают себе многие взрослые, которым программирование в новинку, а освоить тот или иной язык хочется или требуется по работе (например, аналитикам). С профессиональных книг начинать сложновато, а вот самоучители — самое то.

Python — очень популярный язык программирования. На нем написаны многие мобильные банки, популярные приложения для браузера и программы, которыми вы пользуетесь каждый день. При этом язык очень прост в изучении и подходит для обучения программированию детей. И, конечно, взрослых. Вы создадите собственную игру, даже целых две!
Помимо простой структуры языка, в Python есть инструменты, заметно ускоряющие обучение и позволяющие создавать несложные анимации для своих видеоигр.

Эта книга позволит вам погрузиться в программирование и с легкостью освоить JavaScipt. Вы напишете несколько настоящих игр — поиск сокровищ на карте, «Виселицу» и «Змейку». На каждом шаге вы сможете оценить результаты своих трудов — в виде работающей программы, а с понятными инструкциями, примерами и забавными иллюстрациями обучение будет только приятным.
Эта книга — не только введение в JavaScript, но и вообще в программирование.

Scratch — простой, понятный и невероятно веселый язык программирования для детей. В нем нет кодов, которые нужно знать назубок и писать без ошибок. Все, что требуется, — это умение читать и считать. Как из конструктора, при помощи Scratch можно собирать программы из разноцветных «кирпичиков» — блоков. В программу можно вносить любые изменения в любой момент, и сразу видеть, как она работает.
Подробные объяснения, разобранные по шагам примеры и множество упражнений помогут освоить Scratch без труда.

Самоучитель, который почти два года не выходит из топа продаж. Мы живем в цифровую эпоху. И если вы хотите, чтобы ребенок был успешен и нашел себя в будущем, помогите ему ― учите программированию уже сейчас. И даже если он не выберет карьеру программиста, эти занятия помогут ему развить логику, научат мыслить аналитически и находить решения непростых задач.
Многие считают, что программирование — одно из наиболее важных в ХХI веке умений.
Читайте, учитесь и создавайте собственные программы. Это клево 😉
blog.mann-ivanov-ferber.ru
Программировать с нуля. «Сейчас» — самое подходящее время, чтобы начать

(Иллюстрации к статье А.П. Ершова «Программирование — вторая грамотность»)
Стив Джобс не написал ни строчки кода, Билл Гейтс — написал. Пол Грэм — первоклассный программист, Питер Тиль — юрист по образованию, сооснователь PayPal и владелец Palantir (написал ли он что-нибудь?), а Илон Маск в детстве написал свою игру и успешно её продал.
Никита truesnow из #tceh сказал мне, что на курсе «Врубаемся в Ruby» они научат программировать любого человека, даже с нуля. Я спросил его: «А с гуманитарием справитесь?» И мы задумались, были ли случаи, когда «гуманитарий» выучил язык программирования?
На ум сразу пришел бомж-программист, но после успеха с его приложением он предпочёл остаться «дзен-монахом». Есть ли еще примеры? Вдохновляющий пример, что научиться кодить может каждый — слепой программист. Когда я прочитал статью на Хабре «Смотря на код с закрытыми глазами», то понял, что нет преград, кроме собственных отмазок.
А у меня для вас есть три истории из моей жизни. Просто три истории.
История первая — ламер
Слово «ламер» я прочитал в «Компьютерре». Там давалось такое определение: «Ламер — отнюдь не безграмотный человек, не умеющий (как бы это помягче выразиться?) программировать». Окрылённый истиной я побежал и рассказал об этом друзьям-одноклассникам, но они предпочли поиграть в футбол, вместо того чтобы освоить суперспособности. Забавно, что потом все они зарабатывали программированием деньги, а я нет. Через неделю я записался в краевую станцию юных техников (КСЮТ), где был кружок по программированию. Там для новичков давали qbasic. А боги прогали на C.
Так вот как-то один из «богов» подозвал меня к монитору и спросил: «Так сможешь?». И показал прогу, которая ждала, когда пользователь введёт в командной строке любой символ, а потом поворачивала его на 90 градусов. Я был ошеломлен.
Наверное, меня это так зацепило, что я решил — во что бы то не стало, выучить все что можно, и стать самым крутым программистом. Заряда хватило на годы. Этот случай я позабыл, прошло несколько лет, и, вспомнив о нем, я написал не больше десятка строк на basic`e минут за 20. Программа работала идеально.
Вывод. Личные отношения с падаванами очень важны. Возможно, ваша простенькая программа определит судьбу человека и повлияет на выбор жизненного пути.
История вторая — первый шифр
Идея пришла внезапно. Пришла так, что не смог заснуть и сел кодить. Из шифров тогда я знал только про пляшущих человечков из Шерлока Холмса (а это класс 8 или 9, занимался программированием полгода-год). Мне захотелось написать шифр, чтобы нельзя было так просто его вскрыть простым анализом.
Задумка была следующая: каждой букве русского алфавита мы приписываем массив из 5 символов в виде букв русского и английского языка, спецсимволы. При шифровании мы рандомно выбираем один из них. Получалась «расширенная» простая замена. Это сейчас мне понятно как его ломать, но тогда для меня была запредельная высота. Через 3-4 года я поступлю на компьютерную безопасность.
Вывод. Решать интересные задачи — это круто. Но гораздо круче придумывать и находить задачи самому.
История третья — триумф BASIC`а
Я уже 2 года «занимался» программированием. И тут в школе появилась… информатика. Меня почему-то отправили в слабую группу. Как узнал позже, моё лицо не понравилось преподавательнице и она посчитала, что я тупой. Мои друзья ворвались в кабинет к директору и сказали, что я занял призовое место на краевой олимпиаде по программированию. Начались, разборки, но мне было так пофиг, что я остался в слабой группе, где учили вводить цифры в Exсel. За первую неделю я сдал всю программу и спокойно ходил играть в Diablo 2 в компьютерный клуб.
А на олимпиаде был забавный случай. Разрешённые языки — C, Pascal, а я то был прожжённым бейсичником. Выкрутился. Задачу принимали в виде exe’шника, а я подсуетился и нашёл бейсик, который кует exe’шники. Программы проходили тесты, а сами тесты принимались на серваке. Одна задача была сугубо вычислительная. Давались координаты центров и радиусы двух окружностей. Требовалось выдать взаимное расположение окружностей в текстовом виде: пересекаются, касаются, одна в другой, совпадают, и прочие.
С формулами было возиться лень, и недавно я как раз разбирался с графикой. Задачу решил графически, рисовал окружность одним цветом, а потом «сканировал» попиксельно по второй окружности, втыкаюсь ли я в уже окрашенный пиксель. Был большой страх, что прога не сможет работать на серваке без монитора, но все обошлось — 10 тестов из 10. На разборе задач был звездный час. Полсотни человек решили задачу один в один как автор, какого же было их удивление, когда я рассказал свой способ.
Вывод. Школа — зло. Результат — круто. Нестандартное мышление — прикольно. Обходной путь есть всегда.
Зачем взрослым учиться программировать
У меня есть три ответа на этот вопрос. Они зависят от горизонта планирования:
— Цель на 1 неделю или месяц — это вызов. Это как пробежать марафон или забраться на Эльбрус, проверить не засохли ли мозги, выйти из зоны комфорта.
— Цель на год-два — это бабло. За это время можно научиться создавать ценность и работать удаленно. Или учить других. Очень многие хотят научиться программировать.

сам поискал 8 сентября:
на русском в 1000 раз меньше:
— Цель на 5-10 лет — развитие в целом. Во-первых, вы улучшите своё мышление. Во-вторых, вы сделаете неоценимый подарок детям. Они получат несколько лет форы в изучении программирования и у вас появится много чудных моментов совместного написания программ. Для полного счастья останется научиться играть в компьютерные игры, но это вы скорее всего уже умеете.
Как научиться программировать
Есть заезженная картинка на этот счёт:

Почему-то все сразу начинают советовать Кнута, Кормена и прочее, но неподготовленный человек сможет осилить только предисловие. Если совсем проблемы с самооценкой возьмите детскую книгу и напишите игру.
Если готовы приступить по-взрослому, то есть множество ресурсов для самообучения. От Coursera (раз, два) до всяких %имя%academy (codeacademy, htmlacademy и пр)
Если намерения совсем серьёзные, могу посоветовать курс «Врубиться в Ruby».
Во-первых, есть живой преподаватель с хорошим бэкграундом в разработке. Виталий Куреннов, 6 лет пишет на Ruby и больше года обучает всех желающих этому навыку, работал над Ruby проектами для Nokia и Avaya.
Во-вторых, есть группа единомышленников, работая бок о бок с которыми, у вас многократно повысятся шансы дойти до победного конца и освоить программирование до того уровня, когда оно начнет приносить прибыль.

— Никита, почему именно Ruby?
— Все просто, мы нашли очень хорошего преподавателя.
Про Ruby
Попробовать сделать первые шаги можно прямо сейчас, займет всего 5-10 минут.

Нашел шикарный ресурс с геймификацией и сразу из браузера tryruby.org
За 5 минут выполняем несколько заданий, получаем ачивку и переходим на следующий уровень.

А зомбяк не хотите ли? railsforZOMBIES.org
Про Lisp
«Однако я не думаю, что смогу убедить кого-нибудь (старше 25) выучить Lisp.» Пол Грэм, «Побеждая посредственность»
Начитавшись Грэма, осваиваю Lisp.
;; Welcome to L(λ)THW!
(let ((llthw '(learn lisp the hard way)))
(format t "~{~@(~A~)~^ ~}, because ~{~A~^ ~} is easier!" llthw (cddr llthw)))
;; Common Lisp: Powerful, Expressive, Programmable, General Purpose, Multi-Paradigm.

Нашёл для себя удобную браузерную обучалку Learn Lisp The Hard Way
«За те годы, что я проработал в Viaweb, я прочитал множество объявлений о найме на работу. Примерно каждый месяц появлялся новый конкурент. Первое, что я делал после того, как проверял, доступна ли онлайновая демонстрация работы их программы, — смотрел список их вакансий. Через пару лет я научился отличать опасных конкурентов от неопасных. Чем больше отдавало IT-мэйнстримом от описания требуемых кандидатур, тем менее опасна была компания. Самыми безопасными были те, кому требовались специалисты по Oracle. О таких не стоило беспокоиться. Также мы были спокойны, если требовались разработчики на C++ или Java.Если требовались программисты на Perl или Python, это уже было слегка пугающе — это значило, что компанией или, по крайней мере, ее технической частью заправляли настоящие хакеры. Если бы я когда-нибудь увидел объявление о найме на работу Lisp-хакеров, я бы обеспокоился не на шутку.» Пол Грэм, «Побеждая посредственность»
Ещё пара советов
- Читайте Хабр. Например, вот это статья может очень помочь тем кто уже начал свой путь — «Почему научиться программировать так чертовски тяжело?» Или история успеха — «Как я сам научился программировать за 8 недель»
- Читайте Пола Грэма. Он вдохновит заняться программированием кого угодно. Даже меня. Даже на Lisp.
- Найдите единомышленников
- Найдите вдохновляющую задачу
напримерОбщие упражнения:
Project Euler содержит более 500 математических задач (на теорию чисел, числовых систем и пр.), которые нужно решить, используя программирование на любом языке.
Code Abbey хранит более 200 задач по программированию. За решения 125 из них выдают сертификат, чем мотивируют многих студентов.
Rosalind — это ещё один сайт наподобие Project Euler, который предоставляет на выбор более 200 задач по биоинформатике.
Codingbat.com дарит упражнения по Java и Python, как для новичков, так и для продвинутых программистов.
codegolf.stackexchange.com – сайт, на котором публикуют и обсуждают программистские головоломки.
Ruby Quiz — серия головоломок, в которых вас просят написать короткие программы различной сложности. Исходные решения описаны на Ruby, но их можно реализовать на любом языке.Задачи из олимпиад по программированию:
UVa Online Judge — коллекция из сотен задач с олимпиад по программированию, с онлайн-системой проверки решений.
TopCoder содержит сложные задачи на алгоритмы, собранные годами с разных соревнований. Также несколько раз в месяц проводит олимпиады по программированию.
CodeForces похож на TopCoder, но содержит больше задач на соревнованиях и несколько особых фишек, включая «виртуальные соревнования».
Timus — то же, что и UVA. Содержит задачи с последних соревнований (мирового и регионального уровня).
SPOJ — похож на UVA, с огромным числом языков программирования на выбор.
USACO содержит несколько задач на алгоритмы с руководством по их решению.Под определённые языки:
Для Prolog, Lisp и подобных языков посетите P-99 и L-99, наборы из 99 задач для повышения вашей эффективности в данных языках.
Python Challenge — объединяет загадки и головоломки, которые помогут вам серьёзно прокачаться в Python.
4Clojure — набор упражнений по программированию, специально разработанных под Clojure, Lisp-подобный язык. - Соревнуйтесь
- Играйте в Игры для программистов
- Пишите код каждый день
- Пишите о своих успехах и находках на Хабр
P.S.
Ещё интересные статьи с Хабра на тему быть/не быть программистом и как делать шаги на пути мастерства
P.P.S.
Алан Кэй делится яркой идеей об идеях. Архитектура, математика, обучение, программирование и много ещё интересного.
habr.com
Инструкция для тех, кто хочет стать программистом с нуля
Начать свой путь к карьере программиста стоит с ответа на вопрос, нужно ли вам программирование вообще? Этот вопрос не относится к тем, кто учится или учился по специальности, близкой к программированию. Если вам в школе математика давалась лучше, чем гуманитарные науки, если вам нравится проводить много времени за компьютером, если вам хочется изучать что-то новое, тогда программирование вам подойдёт.
С чего начать
Есть несколько вариантов развития событий, в результате которых человек становится программистом. Первый — родители-программисты, которые всему научили своих детей. Таким детям даже не нужно идти в университет. Второй вариант — модная профессия программиста. После школы нужно было выбрать, куда пойти учиться, и выбрали модное направление IT, вроде бы понравилось. И последний вариант — хобби, которое переросло в работу.
Если с вами ничего из вышеперечисленного не произошло, значит, у вас есть выбор из четырёх вариантов:
- Самообразование. Этот вариант можно использовать как самостоятельно, так и в паре с другими методами. В интернете полно сайтов, книг и приложений, которые помогают изучать различные языки программирования и технологии. Но это самый тяжёлый путь для начинающих.
- Университет. Если вы оканчиваете школу и хотите быть программистом, тогда идите в университет. Если не за знаниями, тогда за корочкой. Она может послужить бонусом при устройстве на работу. Хотя и какие-то знания вы тоже получите. Но не забывайте заниматься и самообучением. К выбору вуза стоит подойти очень ответственно. Внимательно изучите программы обучения и выбирайте лучшие технические вузы.
- Ментор. Будет очень неплохо, если вы найдёте человека, который согласится помочь вам и направит вас в правильную сторону. Он подскажет подходящие книги и ресурсы, проверит ваш код, даст полезные советы. Кстати, мы уже писали о полезном ресурсе, где вы сможете найти ментора. Наставника можно искать среди знакомых программистов, на IT-тусовках и конференциях, на онлайн-форумах и так далее.
- Специализированные практические курсы. Попробуйте поискать в своём городе курсы, где вас обучат какому-нибудь языку программирования или технологии. Я был приятно удивлён количеством таких курсов в Киеве, в том числе бесплатных и с последующим трудоустройством.
Какой язык, технологию и направление выбрать
Когда вы станете программистом, через годик-другой будете вольны выбирать любой язык, который вам нравится. Но при выборе первого языка программирования новичок должен учитывать следующие критерии:
- Наличие на рынке вакансий. Конечная цель этого пути — найти работу программистом. А это будет трудно сделать, если на рынке вакансий никто не будет искать разработчиков на вашем языке программирования. Проверьте сайты с вакансиями, посмотрите, кого больше ищут, выпишите десяток языков. И переходите к следующему критерию.
- Низкий уровень вхождения. Если вам придётся потратить длительное время на изучение языка, это может отбить у вас охоту к программированию вообще. Почитайте о тех языках, которые вы выбрали выше. Просмотрите литературу, которую нужно будет прочитать, чтобы изучить эти языки. И выберите те, о которых пишут, что они лёгкие, или которые вам показались лёгкими. Такими языками могут оказаться PHP, Ruby, Python.
- Кайф от процесса. Если вам не нравится писать код на выбранном языке, вы не будете получать удовольствия от этого процесса, от работы и от жизни. А оно вам надо? Делайте правильный выбор.
Также вам придётся определиться с направлением программирования. Мобильное, десктопное, игры, веб, низкоуровневое программирование и так далее. Самые популярные и относительно лёгкие отрасли — разработка под веб, мобильные и десктопные клиенты. Под каждое направление может подходить один язык и совсем не подходить другой. То есть при выборе языка программирования также стоит отталкиваться и от этого фактора.
В любом случае изучите веб-технологии. Это язык разметки HTML, стили CSS и JavaScript, который позволит сделать вашу страницу динамической. На следующем этапе изучите серверный язык (Python, PHP, Ruby и другие) и подходящие для него веб-фреймворки. Изучите базы данных: практически в каждой вакансии программиста это упоминается.
Как получить начальный опыт
Без опыта вы не получите работу. Без работы вы не получите опыт. Замкнутый круг реальной жизни. Но ничего страшного, мы из него выберемся.
Во-первых, не стоит ждать, пока вы прочитаете все книги по выбранному языку программирования. Начинайте писать свои первые строки кода уже после второй главы книги. Выполняйте все задания из книг, перепечатывайте примеры, разбирайтесь в них. Усложняйте примеры и задания из книг своими идеями. Создавайте свои задачи к пройденному материалу. Решайте эти задачи.
Во-вторых, вам нужно найти свои первые проекты. Это, наверное, самый сложный вариант, но рабочий. Вам придётся самому искать заказы, выполнять их, заморачиваться с оплатой. Для новичка это архисложно, но зато затем все остальные варианты покажутся плёвым делом. Выполненные проекты можно будет записать в опыт и показать вашему будущему работодателю. Реальные проекты являются большим плюсом в вашем резюме.
Если вы знаете английский язык, регистрируйтесь лучше на англоязычных биржах. Рынок там больше. Если не знаете английского, учите его. А пока что вам доступны русскоязычные биржи фриланса. Ищите небольшие проекты, которые соответствуют вашему уровню знаний или чуть выше него. Подайте заявку на пару десятков таких заданий. И приготовьтесь получить море отказов. Но если одна-две заявки выстрелят, у вас будет шанс получить реальный опыт.
Ещё одним неплохим вариантом для получения реального опыта является open source. Таким проектам всегда нужны новые люди, пусть даже и новички. Вы можете поискать в проекте баги или посмотреть в баг-трекере и предложить методы их решения. Найти такие проекты легко на GitHub или других сервисах для хостинга кода. Не стесняйтесь задавать там вопросы.
Четвёртый вариант получения опыта — помощь знакомым программистам. Попросите их передать вам маленькие и несложные задания. Если что-то не будет получаться, у вас всегда будет к кому обратиться. И при этом вы будете участвовать в реальном проекте.
Последний способ — собственные проекты, различные хакатоны или работа в коворкинге. Свои проекты сложно начинать самому, лучше поискать знакомых или друзей.
Почему стоит выбрать Python
Давайте немного подробнее поговорим о выборе первого языка программирования. Первый язык должен быть простым и популярным на рынке. Таким языком является Python. Я очень советую выбрать именно его в качестве первого языка программирования.
Код программы на Python читабелен. Вам даже не нужно быть программистом, чтобы в общих чертах понять, что происходит в программе. Из-за несложного синтаксиса Python вам понадобится меньше времени для написания программы, чем, например, на Java. Огромная база библиотек, которая сэкономит вам кучу сил, нервов и времени. Python является высокоуровневым языком. А значит, вам не нужно особо думать о ячейках памяти и о том, что там разместить. Python — язык широкого назначения. И он такой простой, что даже дети могут его выучить.
Справедливости ради стоит упомянуть и о других языках программирования. Java может стать неплохим выбором для новичка. Этот язык популярнее, чем Python, но и немного сложнее. Зато инструменты для разработки гораздо лучше проработаны. Стоит только сравнить Eclipse и IDLE. После Java вам будет проще перейти к работе с низкоуровневыми языками программирования.
PHP — ещё один очень популярный язык. И, мне кажется, он даже проще, чем Python. Очень легко найти себе ментора или решение какой-нибудь проблемы на форуме. Всё потому, что в мире существует огромное количество PHP-программистов разного уровня. В PHP нет нормального импорта, есть множество вариантов решения одной и той же задачи. А это усложняет обучение. И PHP заточен исключительно под веб.
Языки C и C# очень сложны для новичка. Ruby — хороший выбор в качестве второго языка, но не первого. JavaScript — очень простой язык, но ничему хорошему он вас не научит. А задача первого языка программирования всё-таки научить вас чему-то правильному, задать какую-то логику.
Важен ли английский язык
Важен! Не знаете? Учите. Знаете? Совершенствуйте. Учитесь читать, писать, слушать и говорить на английском. Делайте упор на техническую литературу. Слушайте англоязычные подкасты. Читайте англоязычные учебники по программированию.
Что нужно знать, кроме языка программирования
Конечно же, кроме языка программирования и английского, нужно знать что-то ещё. А вот что — зависит от направления, которое вы выберете. Веб-программист обязан знать HTML, CSS, JavaScript. Десктоп-программист учит API операционной системы и различные фреймворки. Разработчик мобильных приложений учит фреймворки Android, iOS или Windows Phone.
Всем нужно выучить алгоритмы. Попробуйте пройти курс на Coursera или найти подходящую для себя книгу по алгоритмам. Кроме этого, нужно знать одну из баз данных, паттерны программирования, структуры данных. Стоит также познакомиться с репозиториями кода. Хотя бы с одним. Обязательно знание систем версионного контроля. Выбирайте Git, он самый популярный. Вам нужно знать инструменты, с которыми вы работаете, операционную систему и среду разработки. И главный навык программиста — уметь гуглить. Без этого вы не проживёте.
Последние шаги
Вам нужно подготовить резюме. Не просто резюме, а хорошее резюме. Не стоит писать там лишней информации, но и умалчивать о своих умениях тоже не нужно. После того как вас пригласят на интервью, вы должны к нему подготовиться. Пройдитесь по материалу, который указан в вашем резюме. Вы должны быть уверены в своих знаниях. Просмотрите проекты, над которыми вы работали, вспомните технологии, которые вы применяли. И вперёд — к светлому будущему с новой профессией программиста.
lifehacker.ru
Современное программирование с нуля! — Программирование — Учебники
Современное программирование с нуля!
Автор — Виталий Потопахин
Книга Виталия Потопахина «Современное программирование с нуля!» предназначена для начинающих изучать программирование, или имеющих небольшой программисткий опыт. В общем это книга для неискушенных, но желающих научится многому. Конечно, для профессионального познания любой области, одной книги всегда мало, но если у вас хватит терпения и упорства в проработке практического материала, то можно быть уверенным, что ваш программисткий уровень станет достаточным для дальнейшего уже профессионального роста.
Книга состоит из трех глав и одного приложения. Первая глава «Неформальное введение», фактически самодостаточный логически завершенный самоучитель. Тщательное изучение неформального введения даст небольшой, но уверенный навык решения прикладных задач, и знание языка Компонентный Паскаль. Все неформальное введение от первой до последней страницы это решение задач. Каждая задача разбирается достаточно подробно, задачи используются и для рассказа о языке. Языковые конструкции вводятся по мере необходимости, тогда когда это нужно для решения очередной задачи. Это делает изучение языка хотя и несколько бессистемным (но в книге есть еще и систематическое введение), но прозрачным и понятным. Уровень сложности решаемых задач постепенное растет, но по настоящему сложных задач в неформальном введении все же нет, поэтому для его усвоения достаточно упорства и желания. Вторая глава — систематическое введение в язык Компонентный Паскаль. Здесь уже нет практики. Вся глава посвящена теории, а точнее изложению языка. Если в неформальном введении язык излагался «между делом», а главным было решение задач, то здесь главным становится язык, поэтому вторая глава отличается более строгой логикой и более трудна для понимания, но если неформальное введение вами пройдено успешно, то и вторая глава не должна создать серьезных затруднений. Еще одно важное отличие неформального введения от систематического. первой главе используется не весь язык Компонентный Паскаль. Вторая глава излагает язык в полном объеме. Третья глава — практикум, целиком посвящена задачам, но если в первом главе задачи использовались для объяснения, то в третьей главе задачи предлагаются для самостоятельного решения. Уровень сложности уже существенно выше. От вас не требуется решения с пустого места. Каждая предлагаемая в практикуме проблема снабжена пояснениями разного уровня.
Издательство – ДМК-Пресс
Год издания – 2010
Формат книги — DJVU
Размер — 44,2 Мб
СКАЧАТЬ с depositfiles.com
Любители печатных изданий могут заказать бумажный экземпляр этой же книги здесь.
it-ebooks.ru
10 способов научиться программировать самостоятельно | Статья
25 апреля 2015, 09:30
Программирование — один из ценнейших навыков для карьерного роста, саморазвития и создания чего-нибудь удивительного. Десять советов для тех, кто только начинает своё путешествие в мир программирования, от Lifehacker.
Читать далее

Выбранное направление в учёбе будет зависеть в большей степени от того, почему именно вы хотите научиться программировать и сколько времени вы готовы уделять этому процессу. Если вы хотите стать программистом, первое что следует сделать — это записаться на профессиональные курсы (Google скомпилировал список навыков и курсов для тех, кто хочет стать инженерами-программистами). Если вы хотите создавать игры и веб-сайты для развлечения в свободное время, лучшим выбором являются интерактивные курсы. Bloc создал сравнительную таблицу курсов в зависимости от загрузки, стоимости и причины изучения программирования.
Не существует лучшего языка программирования, и как только вы выучите один, вам будет нетрудно освоить и второй. Так что не стоит зацикливаться на выборе первого языка. Тем не менее, считается, что некоторые языки даются новичкам легче, чем другие.
Язык, с которого стоит начать, зависит от причины изучения. (К примеру, если вы хотите создать приложение под iOS, вам лучше начать с изучения Swift). Если вы со всей серьёзностью отнеслись к намерению программировать, можно начать с языка C. Хотя выбрав Python, вам будет проще влиться в струю программирования. Приводим инфографику для сравнения нескольких популярных языков программирования.
Независимо от выбора языка или метода обучения, вам следует начать с самого начала. Когда Дэвид Сински (David Sinsky) научился программировать за восемь недель, он, к примеру, потратил одни выходные на изучение основ Python, а другие — на Django. Взяв учебник, он удалял написанный код и снова проходил обучающий материал с нуля. Начните с основ и будьте терпеливы к себе. Взяв первый проект в программировании, разделите его на несколько этапов. И если один из способов обучения вам не подходит, не опускайте руки — попробуйте другой.
Сейчас даже малыши учатся программированию. Несмотря на то, что многие программы для детского обучения весьма просты, некоторые из них (например, Scratch) подходят для любого возраста. Не имеет значения, сколько вам лет, даже детские анимационные приложения могут научить основам программирования (у edX есть новый курс обучения по Scratch).
Бесплатные онлайн тренинги и проекты (Codecademy, Hour of Code и др.) могут помочь вам в написании первой программы. Учебные пособия от Khan Academy, Codecademy, Code.org и других познакомят с основами программирования и всем необходимым для создания игры, сайта или другого проекта. Найдите нужный источник в зависимости от языка программирования, воспользовавшись Bento. Это хорошая отправная точка, однако дальнейшее обучение вам нужно взять на себя.
Онлайн-курсы по программированию предполагают более обширную образовательную подготовку по сравнению с сайтами, предлагающами онлайн-тренинги по одному языку. Такие курсы предназначены для обучения основным навыкам в течение нескольких месяцев на занятиях университетского уровня. Я большой поклонник гарвардского онлайн-курса CS50 (его можно пройти бесплатно). Существуют также другие возможности. Вы даже можете получить образование университетского уровня, выбрав один из 15 онлайн-курсов.
Если вы застряли на какой-то проблеме или вам нужно найти ответ на свой вопрос, не стоит забывать о справочниках. На GitHub можно найти огромную коллекцию из более чем 500 бесплатных книг по программированию. Также доступна коллекция электронных книг, охватывающая 24 языка программирования.
Иногда лучшим способом обучения являются игры. В то время, как многие учебники по программированию обучают вас программировать простые либо сложные игры, некоторые обучающие сайты сами являются играми: Code Combat и CodinGame — инструменты, используя которые вы можете весело провести время.
Сообщество программистов полно людей, готовых помочь следующему поколению программистов. Hack.pledge() — сайт, который поможет вам найти наставника. Либо вы сами можете стать наставником для кого-то другого. Преподавание изученного поможет вам лучше запомнить информацию.
Переписывая чужой код, исследуя каждую строчку на предмет ошибок, вы сможете лучше понять общую картину. Благодаря открытым исходникам кода, вы имеете возможность узнать всё, что угодно — продолжайте учиться, используя инкрементально-хакерский подход. Только не забудьте поделиться своим кодом, если вам удастся улучшить часть ПО.
dev.by





 .
. .
. .
. .
. .
.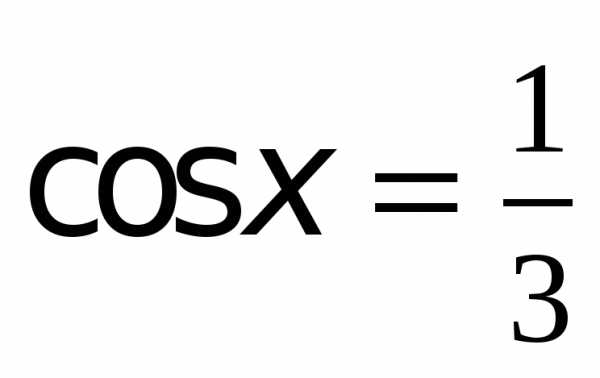 .
.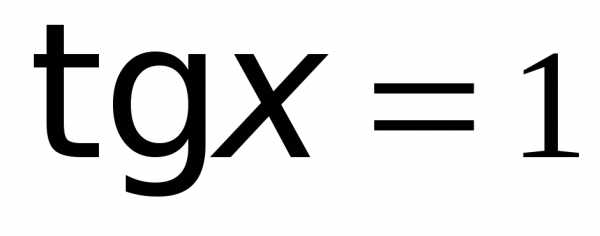 .
.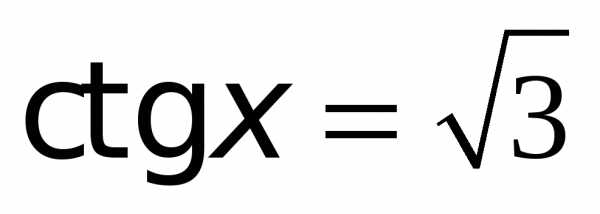 .
. ,
, 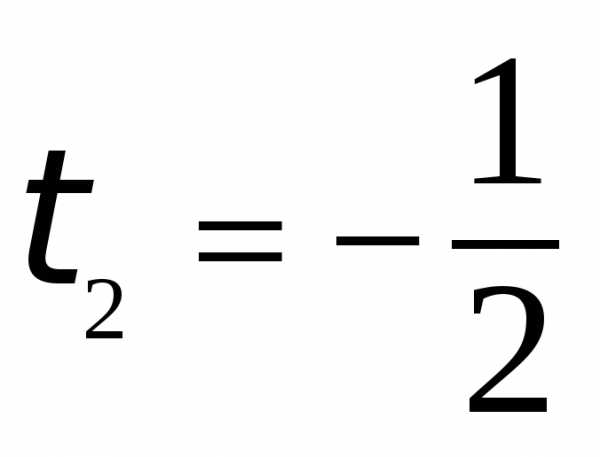
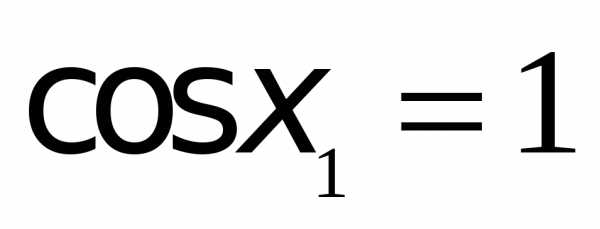 ,
,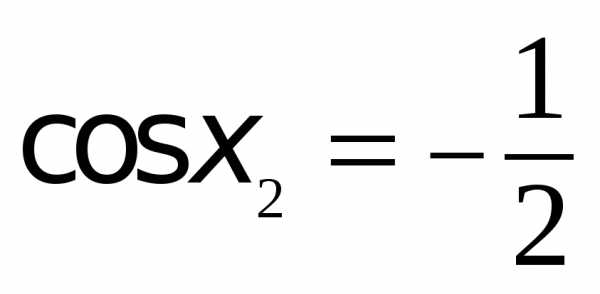 .
. .
.
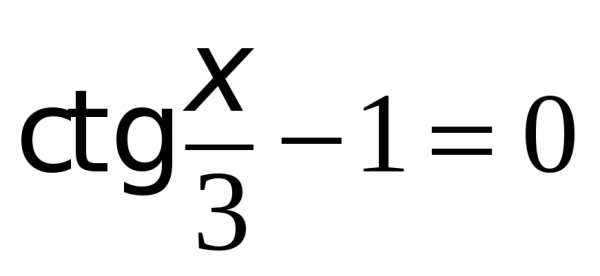
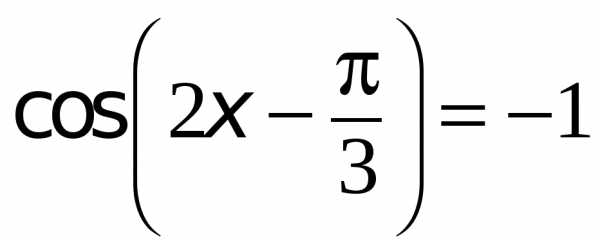
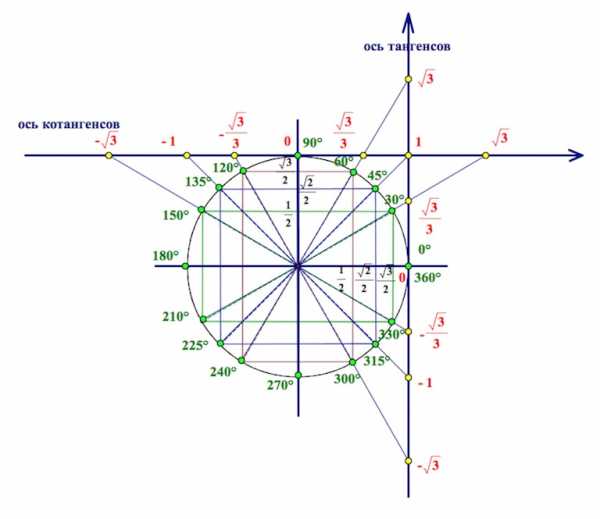
 есть ордината точки
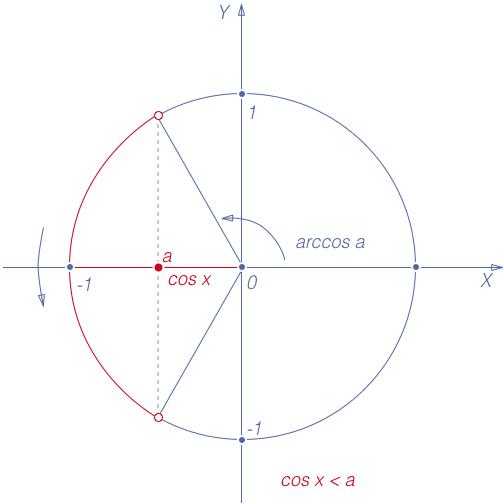
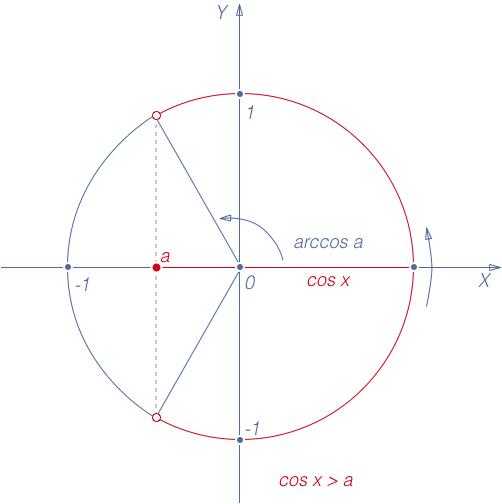
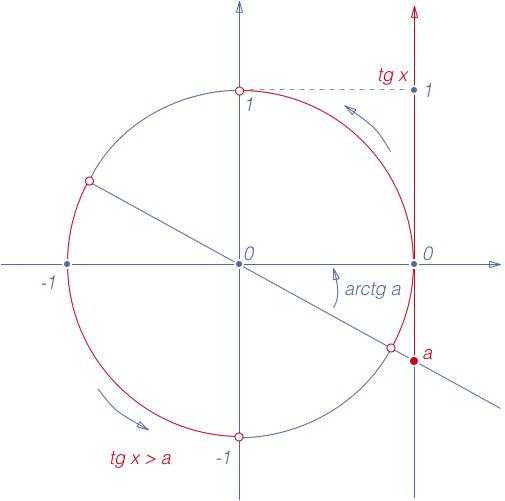
есть ордината точки  единичного круга (рис. 1), а косинусом – абсцисса этой точки. Этот факт используется при решении простейших тригонометрических неравенств с косинусом и синусом с помощью единичного круга.
единичного круга (рис. 1), а косинусом – абсцисса этой точки. Этот факт используется при решении простейших тригонометрических неравенств с косинусом и синусом с помощью единичного круга.



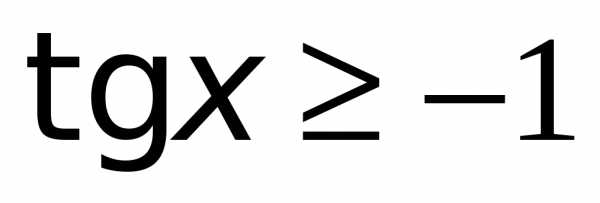




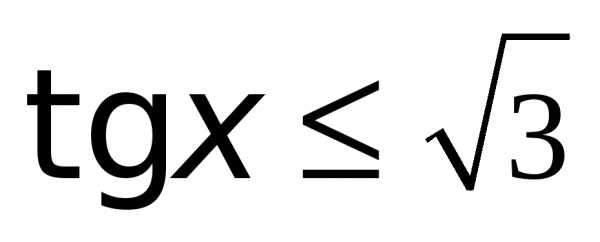
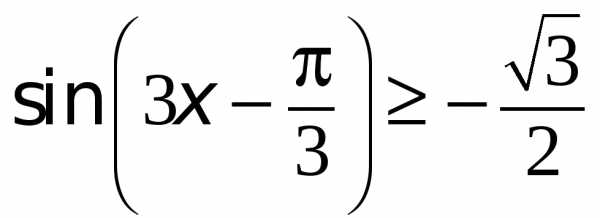

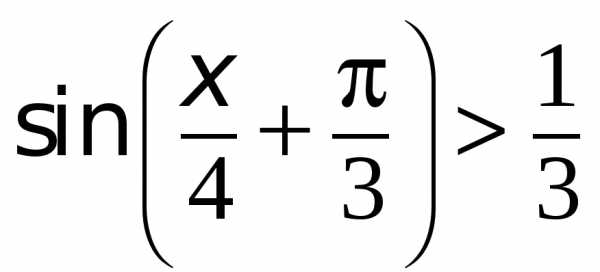







 Адрес для вставки QR-кода числа 384, размер 500×500:
Адрес для вставки QR-кода числа 384, размер 500×500:









 .
.














 \
\