Вычисление объемов тел вращения с помощью определенного интеграла
Разделы: Математика
Тип урока:
комбинированный.Цель урока: научиться вычислять объемы тел вращения с помощью интегралов.
Задачи:
- закрепить умение выделять криволинейные трапеции из ряда геометрических фигур и отработать навык вычислений площадей криволинейных трапеций;
- познакомиться с понятием объемной фигуры;
- научиться вычислять объемы тел вращения;
- способствовать развитию логического мышления, грамотной математической речи, аккуратности при построении чертежей;
- воспитывать интерес к предмету, к оперированию математическими понятиями и образами, воспитать волю, самостоятельность, настойчивость при достижении конечного результата.
Ход урока
I. Организационный момент.
Приветствие группы. Сообщение учащимся целей урока.
Рефлексия. Спокойная мелодия.
– Сегодняшний урок мне бы хотелось начать с притчи. “Жил мудрец, который знал все. Один человек захотел доказать, что мудрец знает не все. Зажав в ладонях бабочку, он спросил: “Скажи, мудрец, какая бабочка у меня в руках: мертвая или живая?” А сам думает: “Скажет живая – я ее умертвлю, скажет мертвая – выпущу”. Мудрец, подумав, ответил: “Все в твоих руках”. (Презентация. Слайд)
– Поэтому давайте сегодня плодотворно поработаем, приобретем новый багаж знаний, и полученные умения и навыки будем применять в дальнейшей жизни и в практической деятельности. “Все в Ваших руках”.
II. Повторение ранее изученного материала.
– Давайте вспомним основные моменты ранее изученного материала. Для этого выполним задание “Исключите лишнее слово”. (Слайд.)
(Учащийся выходит к И.Д.с помощью ластика убирает лишнее слово.)
– Правильно “Дифференциал”. Попробуйте оставшиеся слова назвать одним общим словом. (Интегральное исчисление.)
– Давайте вспомним основные этапы и понятия связанные с интегральным исчислением..
“Математическая гроздь”.
Задание. Восстановите пропуски. (Студент выходит и вписывает ручкой необходимые слова.)
– Реферат о применении интегралов мы заслушаем позже.
Работа в тетрадях.
– Формулу Ньютона-Лейбница вывели английский физик Исаака Ньютона (1643–1727) и немецкий философ Готфрида Лейбница (1646–1716). И это не удивительно, ведь математика – язык, на котором говорит сама природа.
– Рассмотрим, как при решении практических заданий используется эта формула.
Пример 1:
Вычислить площадь фигуры, ограниченной линиямиРешение:
Построим на координатной плоскости графики функций . Выделим площадь фигуры, которую надо найти.III. Изучение нового материала.
– Обратите внимание на экран. Что изображено на первом рисунке? (Слайд) (На рисунке представлена плоская фигура.)
– Что изображено на втором рисунке? Является ли эта фигура плоской? (Слайд) (На рисунке представлена объемная фигура.)
– В космосе, на земле и в повседневной жизни мы встречаемся не только с плоскими фигурами, но и объемными, а как же вычислить объем таких тел? Например объем планеты, каметы, метеорита, и т.д.
– Об объеме задумываются и строя дома, и переливая воду из одного сосуда в другой. Правила и приёмы вычисления объёмов должны были возникать, другое дело, насколько они были точны и обоснованны.
Сообщение студентки. (Тюрина Вера.)
1612 год был для жителей австрийского города Линц, где жил тогда известный астроном Иоганн Кеплер очень урожайным, особенно на виноград. Люди заготовляли винные бочки и хотели знать, как практически определить их объёмы. (Слайд 2)
– Таким образом, рассмотренные работы Кеплера положили начало целому потоку исследований, увенчавшихся в последней четверти XVII в. оформлением в трудах И. Ньютона и Г.В. Лейбница дифференциального и интегрального исчисления. Математика переменных величии заняла с этого времени ведущее место в системе математических знаний.
– Вот сегодня мы с вами и займемся такой практической деятельностью, следовательно,
Тема нашего урока: “Вычисление объемов тел вращения с помощью определенного интеграла”. (Слайд)
– Определение тела вращения вы узнаете, выполнив следующее задание.
“Лабиринт”.
Лабиринт (греческое слово) означает ход в подземелье. Лабиринт– запутанная сеть дорожек, ходов, сообщающихся друг с другом помещений.
Но определение “разбилось”, остались подсказки в виде стрелок.
Задание. Найдите выход из запутанного положения и запишите определение.
Слайд. “Карта инструктаж” Вычисление объемов.
При помощи определенного интеграла можно вычислить объем того или иного тела, в частности, тела вращения.
Телом вращения называется тело, полученное вращением криволинейной трапеции вокруг ее основания (рис. 1, 2)
Объем тела вращения вычисляется по одной из формул:
1., если вращение криволинейной трапеции вокруг оси ОХ.
2. , если вращение криволинейной трапеции вокруг оси ОУ.
Карту инструктаж получает каждый студент. Преподаватель подчеркивает основные моменты.
– Преподаватель объясняет решение примеров на доске.
Пример.
Рассмотрим отрывок из известной сказки А. С. Пушкина “Сказка о царе Салтане, о сыне его славном и могучем богатыре князе Гвидоне Салтановиче и о прекрасной царевне Лебеде” (Слайд 4):
…..
И привез гонец хмельной
В тот же день приказ такой:
“Царь велит своим боярам,
Времени не тратя даром,
И царицу и приплод
Тайно бросить в бездну вод”.
Делать нечего: бояре,
Потужив о государе
И царице молодой,
В спальню к ней пришли толпой.
Объявили царску волю –
Ей и сыну злую долю,
Прочитали вслух указ,
И царицу в тот же час
В бочку с сыном посадили,
Засмолили, покатили
И пустили в окиян –
Так велел-де царь Салтан.
(Слайд 5):
Какими же должен быть объем бочки, чтобы в ней поместились царица и её сын?
– Рассмотрим следующие задания
1. Найти объем тела, получаемого вращением вокруг оси ординат криволинейной трапеции, ограниченной линиями: x2 + y2 = 64, y = -5, y = 5, x = 0.
Решение.
Ответ : 1163 cm3.
Найти объем тела, получаемого вращением параболической трапеции, вокруг оси абсцисс y = , x = 4, y = 0.
Решение .
IV. Закрепление нового материала
Пример 2. Вычислить объем тела, образованного вращением лепестка, вокруг оси абсцисс y = x2, y2 = x.
Решение .
Построим графики функции. y = x2, y2 = x. График y2 = x преобразуем к виду y = .
Имеем V = V1 – V2 Вычислим объем каждой функции
– Теперь, давайте, рассмотрим башню для радиостанции в Москве на Шаболовке, построенной по проекту замечательного русского инженера, почётного академика В. Г. Шухова. Она состоит из частей – гиперболоидов вращения. Причём, каждый из них изготовлен из прямолинейных металлических стержней, соединяющих соседние окружности (рис.8, 9).
– Рассмотрим задачу.
Найти объем тела, получаемого вращением дуг гиперболы вокруг ее мнимой оси, как показано на рис. 8, где
Решение.
куб. ед.
Задания по группам. Учащиеся вытягивают жребий с задачами, рисунки выполняют на ватмане, один из представителей группы защищает работу.
1-я группа.
Удар! Удар! Ещё удар!
Летит в ворота мячик – ШАР!
А это– шар арбузный
Зелёный, круглый, вкусный.
Вглядитесь лучше – шар каков!
Он сделан из одних кругов.
Разрежьте на круги арбуз
И их попробуйте на вкус.
Найти объем тела, получаемого вращением вокруг оси ОХ функции, ограниченную
Решение.
Ошибка! Закладка не определена.
– Скажите, пожалуйста, где мы встречаемся с данной фигурой?
Дом. задание для 1 группы. ЦИЛИНДР (слайд) .
«Цилиндр – что такое?» – спросил я у папы.
Отец рассмеялся: Цилиндр – это шляпа.
Чтобы иметь представление верное,
Цилиндр, скажем так, это банка консервная.
Труба парохода – цилиндр,
Труба на нашей крыше – тоже,
Все трубы на цилиндр похожи.
А я привёл пример такой –
Калейдоскоп любимый мой,
Глаз от него не оторвёшь,
И тоже на цилиндр похож.
– Задание. Домашняя работа составить график функции и вычислить объем .
2-я группа. КОНУС (слайд).
Сказала мама: А сейчас
Про конус будет мой рассказ.
В высокой шапке звездочёт
Считает звёзды круглый год.
КОНУС – шляпа звездочёта.
Вот какой он. Понял? То-то.
Мама у стола стояла,
В бутылки масло разливала.
– Где воронка? Нет воронки.
Поищи. Не стой в сторонке.
– Мама, с места я не тронусь,
Расскажи ещё про конус.
– Воронка и есть в виде конуса лейка.
Ну-ка, найди мне её поскорей-ка.
Воронку я найти не смог,
Но мама сделала кулёк,
Картон вкруг пальца обкрутила
И ловко скрепкой закрепила.
Масло льётся, мама рада,
Конус вышел то, что надо.
Задание . Вычислить объем тела полученный вращением вокруг оси абсцисс
Дом. задание для 2-й группы. ПИРАМИДА (слайд).
Я видел картину. На этой картине
Стоит ПИРАМИДА в песчаной пустыне.
Всё в пирамиде необычайно,
Какая-то есть в ней загадка и тайна.
А Спасская башня на площади Красной
И детям, и взрослым знакома прекрасно.
Посмотришь на башню – обычная с виду,
А что на вершине у ней? Пирамида!
Задание. Домашняя работа составить график функции и вычислить объем пирамиды
Вывод.
– Объёмы различных тел мы вычисляли опираясь на основную формулу объёмов тел с помощью интеграла.
Это является ещё одним подтверждением того, что определённый интеграл есть некоторый фундамент для изучения математики.
– Ну а теперь давайте немного отдохнем.
Найди пару.
|
Математическое домино мелодия играет.
“Дорога та, что сам искал, вовек не позабудется…”
Исследовательская работа. Применение интеграла в экономике и технике.
Тесты для сильных учащихся и математический футбол.
Математический тренажер.
2. Совокупность всех первообразных от данной функции называется
А) неопределенным интегралом,
Б) функцией,
В) дифференциацией.
7. Найти объем тела, получаемого вращением вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
Д/З. Вычислить объемы тел вращения.
Рефлексия.
Приём рефлексии в форме синквейна (пятистишия).
1-я строка – название темы (одно существительное).
2-я строка – описание темы в двух словах, два прилагательных.
3-я строка – описание действия в рамках этой темы тремя словами.
4-я строка – фраза их четырёх слов, показывает отношение к теме (целое предложение).
5-я строка – синоним, который повторяет суть темы.
- Объем.
- Определенный интеграл, интегрируемая функция.
- Строим, вращаем, вычисляем.
- Тело, полученное вращением криволинейной трапеции (вокруг ее основания).
- Тело вращения (объемное геометрическое тело).
Вывод (слайд).
- Определенный интеграл – это некоторый фундамент для изучения математики, которая вносит незаменимый вклад в решение задач практического содержания.
- Тема “Интеграл” ярко демонстрирует связь математики с физикой, биологией, экономикой и техникой.
- Развитие современной науки немыслимо без использования интеграла. В связи с этим, начинать его изучение необходимо в рамках средне специального образования!
Выставление оценок . (С комментированием.)
Великий Омар Хайям – математик, поэт, философ. Он призывает быть хозяевами своей судьбы. Слушаем отрывок из его произведения:
Ты скажешь, эта жизнь – одно мгновенье.
Её цени, в ней черпай вдохновенье.
Как проведёшь её, так и пройдёт.
Не забывай: она – твоё творенье.
Приложение 2.
9.01.2014
xn--i1abbnckbmcl9fb.xn--p1ai
Объем тела вращения вокруг оси Ox, Oy
Объем тела V, образованного вращением вокруг оси Ox фигуры , , где y1(x) и y2(x) — непрерывные неотъемлемые функции, равняется определенному интегралу от разницы квадратов функций yi(x) по переменной x
Объем тела V, образованного вращением вокруг оси Oy фигуры , , где y(x) — однозначная непрерывная функция, равняется определенному интегралу, рассчитанному по формуле
Примеры выбраны из учебной программы для студентов механико-математического факультета Львовского национального университета имени Ивана Франко.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
Для изучения основных моментов схема интегрирования и формулы вычисления объема тела вращения будут повторяться из примера в пример.
ІV. Найти объемы тел, ограниченными поверхностями, полученными при вращении отрезков следующих линий
Пример 2.139 (2472) Найти объем тела, образованного вращением кривой (нейлоїд) xє[0;a] вокруг оси Ox.
Решение: Складываем подинтегральную функцию:
Пределы интегрирования известны за условием: [0;a].
Найдем объем тела интегрированием:
Всегда помните, что объем измеряется в кубических единицах.
Пример 2.140 (2473) Найти объем тела, образованного вращением кривой y=2x-x^2, y=0
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Запишем подинтегральные функции:
а)
б)
Из приведенных формул Вы можете видеть разницу, в каких случаях применять каждую из формул объема.
Найдем пределы интегрирования:
И заключительным шагом вычисляем объемы интегрированием.
а) Найдем объем тела вращения вокруг оси Ox:
б) Вычислим объем тела вращения вокруг оси Oy:
В этом примере интегралы легко берутся и нет потребности объяснять детали операций.
Пример 2.141 (2474) Вычислить объем тела, образованного вращением кривой y=sin(x)
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Выпишем подинтегральные функции:
а)
б)
Пределы интегрирования берем из начального условия:
Осталось вычислить определенные интегралы:
а) Найдем объем тела вращения вокруг оси Ox:
б) Выполняем вычисление объема тела при вращении вокруг оси Oy:
Замена переменных помогает найти последний интеграл.
Пример 2.142 (2475) Найти объем тела, образованного вращением кривой
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Чтобы записать подинтегральную функцию найдем разницу квадратов заданных функций:
а)
б) для тела, образованного вращением вокруг оси Oy подинтегральная функция имеет вид
Из условия равенства функций y1(x)=y2(x) определяем пределы интегрирования
x1=0, |x|=a поэтому
Пределы интегрирования :
а)
б)
При :
поэтому принимая во внимание симметрию имеем неравенство .
а) Вычисляем объем тела вращения вокруг оси Ox:
б) Через следующий интеграл определяем объем тела вращения вокруг оси Oy:
Здесь нет сложных моментов при вычислении интеграла.
Пример 2.143 (2476) Найти объем тела, образованного вращением кривой y=e— x, y=0,
а) вокруг оси Ox; б) вокруг оси Oy.
Решение: Уравнение подинтегральных функций :
а) y2=e-2x;
б) x*y (x) =xe-x.
Запишем пределы интегрирования (известно за условием):
а) Находим объем тела вращения вокруг оси Ox:
б) Найдем объем тела вращения вокруг оси Oy: 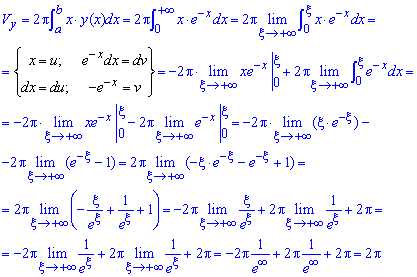
Здесь, чтобы вычислить интегралы придется находить границу при переменной направляющейся к безграничности.
Во втором интеграле выполняем интегрирование частями.
Пример 2.144 (2477) Вычислить объем тела, образованного вращением кривой x2+(y-b)2=a2, , вокруг оси Ox.
Решение: Фигурой вращения является круг с центром в точке (0;b) и радиусом a.
При выражении самой функции получим две ветки корневых функций:
При поднесении к квадрату разница слагаемых сложит такое выражение подинтегральной функции:
Запишем пределы интегрирования: для круга они равны xє[-a;a] или два полукруга из на промежутке xє[0;a].
Через интеграл находим объем тела вращения вокруг оси Ox:
Внимательно разберите приведенный пример.
Пример 2.145 (2478) Найти объем тела, образованного вращением кривой x2-xy+y2=a2, вокруг оси Ox.
Решение: Сведем кривую к каноническому виду (методами из аналитической геометрии) устанавливаем, что заданная линия является эллипсом
— уравнение в канонической системы координат.
В приведенной системе координат уравнения эллипса имеет вид:
Прямая y=x/2 является осью симметрии этой фигуры.
Запишем подинтегральную функцию:
Найдем пределы интегрирования из условия равности функций y2(x)=y1(x):
или двукратный объем на интервале
Но тогда еще нужно отнять объем тела в пределах
(которая не принадлежит эллипсу) и ограничена первой кривой
и результат умножить на 2 (симметрия).
Последним шагом вычисляем объем тела вращения вокруг оси Ox: 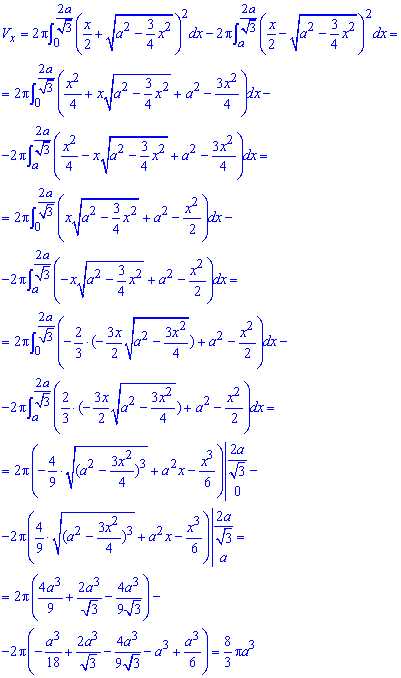
Формула интеграла вышла достаточно длинным, однако его удобно читать пользователям, которые заходят на сайт из мобильных устройств.
Пример 2.146 (2479) Найти объем тела, образованного вращением кривой вокруг оси Ox.
Решение: Запишем подинтегральную функцию:
y2(x)=e-2x*sin (x).
Установим пределы интегрирования: при , где k=0,1,2.
Таким образом имеем бесконечный ряд промежутков интегрирования.
При нахождении объема тела вращения вокруг оси Ox получим бесконечный ряд интегралов, который совпадает:
Здесь вычислили интеграл дважды выполнив замену переменных: 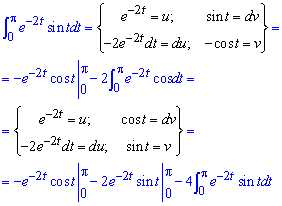
тому
— это числовой ряд.
В данном случае бесконечно нисходящая геометрическая прогрессия, у которой b1=1, b2=e-4Pi, поэтому q=e— 4Pi, а сумма прогрессии равна
Пример 2480 Найти объем тела, образованного вращением кривой x=a (t — sin (t)), y=a (1 — cos (t)), , y=0.
а) вокруг оси Ox; б) вокруг оси Oy;
в) вокруг прямой y=2a.
Решение: Вычислим подинтегральную функцию и дифференциал по аргументу:
y2=a2(1-cos (t))2, dx=a(1-cos(t)) dt.
Пределы интегрирования известны из начального условия: tє[0;2pi].
Переходим к применению формул объемов:
а) Первым вычислим объем тела вращения вокруг оси Ox: 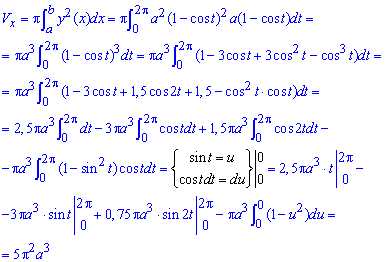
Здесь применили замену переменных и условие
б) Следующим найдем объем тела вращения вокруг оси Oy:
Его попробуйте расписать самостоятельно.
в) Последним вычислим объем тела вращения вокруг прямой y=2a:
Перейдем к новой системе координат по формулам y1=y-2a, x1=x.
Тогда искомый объем V=V1-V2, где V1 — объем колового цилиндра с высотой H=2pi*a и радиусом основы R=2a, поэтому объем цилиндра равен
куб. од.
Второй объем находим интегрированием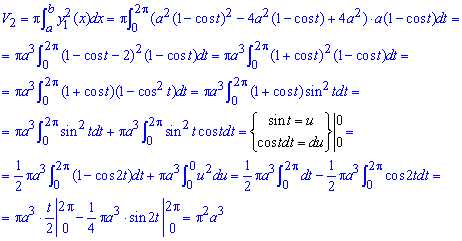
Как и в предыдущих задачах здесь использовали замену переменных под интегралом.
Напоследок находим разницу объемов
куб. од.
Объем тела, образованного вращением вокруг полярной оси плоской фигуры
Чтобы найти объем тела V, образованного в результате вращением вокруг полярной оси плоской фигуры r(phi)
необходимо вычислить определенный интеграл по формуле
Пример 2483 Найти объем тела, образованного вращением кривой r=a (1+cos (phi)), , y=0
а) вокруг полярной оси;
б) вокруг прямой
Решение: Чтобы достать подинтегральную функцию подносим к кубу заданную функцию:
Пределы интегрирования записываем из начального условия:
а) Сначала найдем объем тела вращения вокруг полярной оси:
Для упрощения вычислений переходим к новой переменной под интегралом.
б) Перейдем к новым координатам с помощью формул: x1=y, y1=-x-a/4.
Определяем пределы интегрирования:
при росте угла от 0 к Pi/2 координата x1 растет от 0 к , при росте от Pi/2 к Pi переменная x1 спадает от к 0, поэтому пределы ограничены интервалом
Запишем подинтегральную функцию:
Уравнения перехода между системами координат имеют вид
Подстановкой в уравнение получим:
,
Найдем объем тела вращения вокруг прямой :
откроем скобки, возведем подобные слагаемые и, приняв во внимание, что интеграл равен нулю получим
Здесь последние интегралы выражаются через факториалы
(смотри пример 2.59, часть І).
Парные факториалы вычисляем по правилу
Пример 2484.1 Найти объем тела, образованного вращением кривой r=a*phi (a>0)вокруг полярной оси.
Решение: Запишем подинтегральную функцию:
С пределами интегрирования проблем нет:
Чтобы найти объем тела вращения вокруг полярной оси выполняем ряд манипуляций с интегралами: 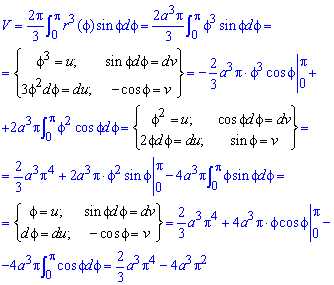
Внимательно проанализируйте, как находится этот «тригонометрический» интеграл.
Пример 2484.2 Найти объем тела, образованного вращением кривой phi=Pi*r3, phi=Pi, вокруг полярной оси.
Решение: Запишем подинтегральную функцию:
Пределы интегрирования:
Вычисляем объем тела вращения вокруг полярной оси:
Здесь синус вносим под дифференциал и выполняем интегрирование частями.
На данное время это все примеры, которые мы смогли подготовить для Вас по данной теме.
yukhym.com
Объем тела вращения и площадь поверхности тела вращения
Найти объем тела, образованного вращением (ОТВ) вокруг оси $Ox$ плоской фигуры, ограниченной сверху параболой $y_{1} =-2\cdot x^{2} +16\cdot x+18$, снизу — параболой $y_{2} =2\cdot x^{2} -8\cdot x+18$, а слева и справа прямыми $x=1$ и $x=5$ соответственно.
Выполняем графические построения:
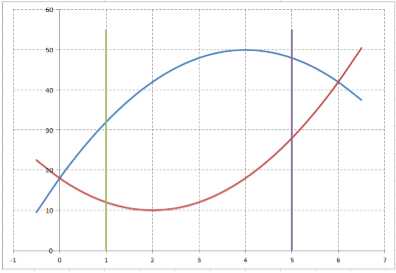
При вращении этой плоской фигуры вокруг оси $Ox$ верхняя парабола (обозначенная синим цветом) образует общий объем, а нижняя парабола (обозначенная оранжевым цветом) образует отверстие. Таким образом, ОТВ вычисляется как разность общего объема и объема отверстия.
Известно, что ОТВ (вокруг оси $Ox$) вычисляется по формуле $V=\pi \cdot \int \limits _{a}^{b}y^{2} \left(x\right)\cdot dx $, где $y=y\left(x\right)$ — неотрицательная непрерывная функция, образующая криволинейную трапецию на отрезке $\left[a,\; b\right]$.
Общий объем будем вычислять по формуле $V_{1} =\pi \cdot \int \limits _{1}^{5}y_{1}^{2} \cdot dx $.
Получаем:
\[V_{1} =\pi \cdot \int \limits _{1}^{5}\left(-2\cdot x^{2} +16\cdot x+18\right)^{2} \cdot dx =\] \[=\pi \cdot \int \limits _{1}^{5}\left(\left(-2\cdot x^{2} \right)^{2} +\left(16\cdot x\right)^{2} +\left(18\right)^{2} +2\cdot \left(-2\cdot x^{2} \right)\cdot \left(16\cdot x\right)+\right. \] \[\left. +2\cdot \left(-2\cdot x^{2} \right)\cdot 18+2\cdot \left(16\cdot x\right)\cdot 18\right)\cdot dx=\] \[=\pi \cdot \int \limits _{1}^{5}\left(4\cdot x^{4} -64\cdot x^{3} +184\cdot x^{2} +576\cdot x+324\right)\cdot dx =\] \[=\pi \cdot \left(4\cdot \int \limits _{1}^{5}x^{4} \cdot dx -64\cdot \int \limits _{1}^{5}x^{3} \cdot dx +184\cdot \int \limits _{1}^{5}x^{2} \cdot dx +576\cdot \int \limits _{1}^{5}x\cdot dx +324\cdot \int \limits _{1}^{5}dx \right)=\] \[=\pi \cdot \left(4\cdot \left[\frac{x^{5} }{5} \right]_{1}^{5} -64\cdot \left[\frac{x^{4} }{4} \right]_{1}^{5} +184\cdot \left[\frac{x^{3} }{3} \right]_{1}^{5} +576\cdot \left[\frac{x^{2} }{2} \right]_{1}^{5} +324\cdot \left[x\right]_{1}^{5} \right)=\] \[=\pi \cdot \left(4\cdot \frac{1}{5} \cdot \left(5^{5} -1^{5} \right)-64\cdot \frac{1}{4} \cdot \left(5^{4} -1^{4} \right)+184\cdot \frac{1}{3} \cdot \left(5^{3} -1^{3} \right)+\right. \] \[\left. +576\cdot \frac{1}{2} \cdot \left(5^{2} -1^{2} \right)+324\cdot \left(5-1\right)\right)=\] \[=\pi \cdot \left(4\cdot \frac{1}{5} \cdot 3124-64\cdot \frac{1}{4} \cdot 624+184\cdot \frac{1}{3} \cdot 124+576\cdot \frac{1}{2} \cdot 24+324\cdot 4\right)=\] \[=\pi \cdot \left(2499,2-9984+7605,3+6912+1296\right)=\pi \cdot 8328,5\approx 26151,5.\]Аналогичным образом находим объем отверстия:
\[V_{2} =\pi \cdot \int \limits _{1}^{5}y_{2} ^{2} \cdot dx =\pi \cdot \int \limits _{1}^{5}\left(2\cdot x^{2} -8\cdot x+18\right)^{2} \cdot dx .\]Теперь вычисляем объем тела: $V=V_{1} -V_{2} $.
Задача 2
Вычислить ОТВ, образованного вращением вокруг оси $Ox$ фигуры, ограниченной линиями $y=x^{4} $ и $y=x$.
Графическое изображение фигуры:
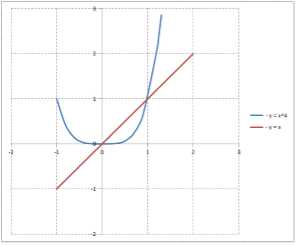
Решив совместно уравнения $y=x^{4} $ и $y=x$, получим $x_{1} =0$ и $x_{2} =1$ — этими прямыми фигура ограничена слева и справа.
Искомый объем определяется как разность объемов, полученных в результате вращения вокруг оси $Ox$ двух криволинейных трапеций: первая ограничена прямой $y_{1} =x$, вторая — параболой $y_{2} =x^{4} $.
ОТВ, образованного вращением вокруг оси $Ox$ криволинейной трапеции, ограниченной сверху кривой $y=y_{1} \left(x\right)$, снизу — кривой $y=y_{2} \left(x\right)$, а также двумя прямыми $x=a$ и $x=b$ слева и справа, будем вычислять по формуле $V=\pi \cdot \int \limits _{a}^{b}\left(y_{1}^{2} -y_{2}^{2} \right)\cdot dx $.
Имеем:
\[V=\pi \cdot \int \limits _{0}^{1}\left(\left(x\right)^{2} -\left(x^{4} \right)^{2} \right)\cdot dx =\pi \cdot \left[\frac{x^{3} }{3} -\frac{x^{9} }{9} \right]_{0}^{1} =\pi \cdot \left(\frac{1}{3} -\frac{1}{9} \right)=\pi \cdot \frac{2}{9} .\]Задача 3
Зайти площадь поверхности, образованной вращением вокруг оси $Ox$ кривої $y=\sqrt{80\cdot x+15} $ между точками з абсцисами $x=3$ и $x=13$.
Графическое изображение вращаемой кривой:
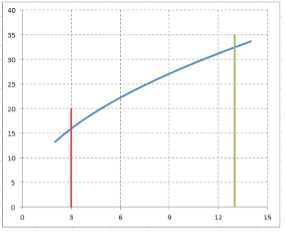
Площадь поверхности тела вращения выражается формулой $Q=2\cdot \pi \cdot \int \limits _{a}^{b}y\cdot \sqrt{1+y’^{2} } \cdot dx $, где $y=y\left(x\right)$ — неотрицательная функция, заданная на отрезке $\left[a,\; b\right]$.
Находим выражение $\sqrt{1+y’^{2} } $:
\[y’=\frac{80}{2\cdot \sqrt{80\cdot x+15} } ;\] \[\sqrt{1+y’^{2} } =\sqrt{1+\frac{80^{2} }{4\cdot \left(80\cdot x+15\right)} } =\frac{1}{2} \cdot \sqrt{\frac{320\cdot x+6460}{80\cdot x+15} } .\]Находим выражение для подынтегральной функции $y\cdot \sqrt{1+y’^{2} } $:
\[\sqrt{80\cdot x+15} \cdot \frac{1}{2} \cdot \sqrt{\frac{320\cdot x+6460}{80\cdot x+15} } =\frac{1}{2} \cdot \sqrt{320\cdot x+6460} .\]Записываем интеграл и вычисляем площадь поверхности:
\[Q=\pi \cdot \int \limits _{3}^{13}\sqrt{320\cdot x+6460} \cdot dx =\] \[=\pi \cdot \left[\frac{1}{320} \cdot \frac{\left(320\cdot x+6460\right)^{\frac{1}{2} +1} }{\frac{1}{2} +1} \right]_{3}^{13} =\pi \cdot \left[\frac{1}{480} \cdot \left(320\cdot x+6460\right)^{\frac{3}{2} } \right]_{3}^{13} =\] \[=\frac{\pi }{480} \cdot \left[\left(320\cdot x+6460\right)\cdot \sqrt{320\cdot x+6460} \right]_{3}^{13} =\] \[=\frac{\pi }{480} \cdot \left(\left(320\cdot 13+6460\right)\cdot \sqrt{320\cdot 13+6460} -\right. \] \[\left. -\left(320\cdot 3+6460\right)\cdot \sqrt{320\cdot 3+6460} \right)=\] \[=\frac{\pi }{480} \cdot \left(10620\cdot \sqrt{10620} -7420\cdot \sqrt{7420} \right)\approx \] \[\approx \frac{3,14}{480} \cdot \left(10620\cdot 103,053-7420\cdot 86,139\right)\approx \]$\approx \frac{3,14}{480} \cdot \left(1094423-639151\right)\approx \frac{3,14}{480} \cdot 455272\approx 2978$ кв.од.
spravochnick.ru
11 класс. Геометрия. Объемы тел. — Вычисление объемов тел с помощью определенного интеграла.
Комментарии преподавателя
Помимо нахождения площади плоской фигуры с помощью определенного интеграла важнейшим приложением темы является вычисление объема тела вращения. Материал простой, но читатель должен быть подготовленным: необходимо уметь решать неопределенные интегралы средней сложности и применять формулу Ньютона-Лейбница в определенном интеграле. Как и для задачи нахождения площади, нужны уверенные навыки построения чертежей – это чуть ли не самое важное (поскольку интегралы сами по себе чаще будут лёгкими). Освоить грамотную и быструю технику построения графиков можно с помощью методических материалов Графики и свойства Элементарных функций и Геометрические преобразования графиков. Но, собственно, о важности чертежей я уже неоднократно говорил на уроке Определенный интеграл. Как вычислить площадь фигуры.
Вообще в интегральном исчислении очень много интересных приложений, с помощью определенного интеграла можно вычислить площадь фигуры, объем тела вращения,длину дуги, площадь поверхности вращения и многое другое. Поэтому будет весело, пожалуйста, настройтесь на оптимистичный лад!
Представьте некоторую плоскую фигуру на координатной плоскости. Представили? … Интересно, кто что представил… =))) Её площадь мы уже находили. Но, кроме того, данную фигуру можно ещё и вращать, причем вращать двумя способами:
– вокруг оси абсцисс ;
– вокруг оси ординат .
В данной статье будут разобраны оба случая. Особенно интересен второй способ вращения, он вызывает наибольшие затруднения, но на самом деле решение практически такое же, как и в более распространенном вращении вокруг оси абсцисс. В качестве бонуса я вернусь к за
www.kursoteka.ru
III Вычисление объёмов тел вращения
Определение
3. Тело
вращения – это тело, полученное вращением
плоской фигуры  вокруг оси, не
пересекающей фигуру и лежащей с ней в
одной плоскости.
вокруг оси, не
пересекающей фигуру и лежащей с ней в
одной плоскости.
Ось вращения может и пересекать фигуру, если это ось симметрии фигуры.
Теорема
2. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции 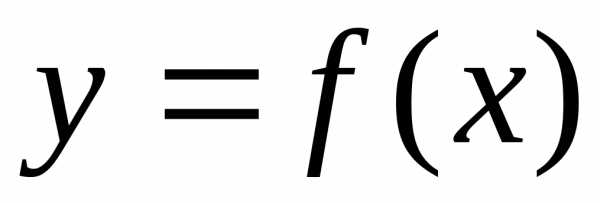 ,
осью
,
осью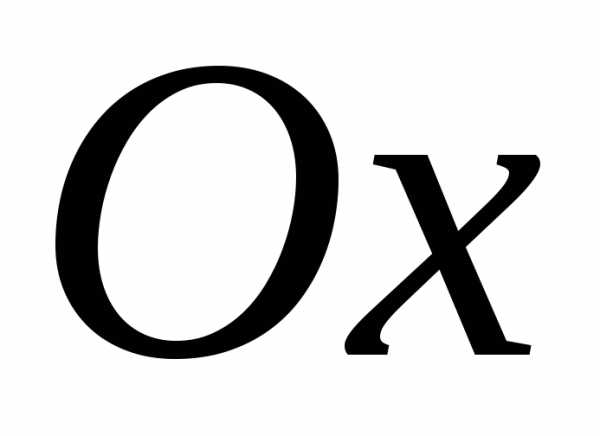 и отрезками прямых
и отрезками прямых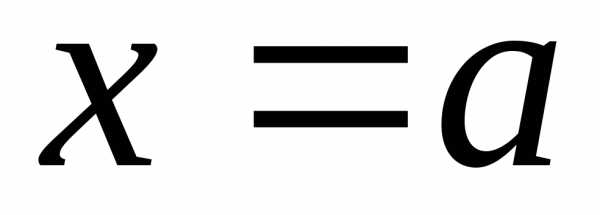 и
и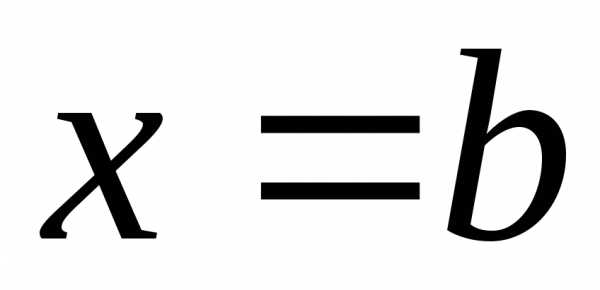
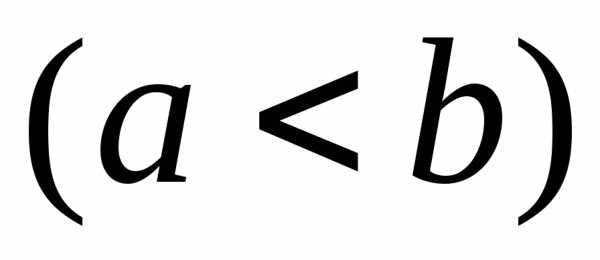 вращается вокруг оси
вращается вокруг оси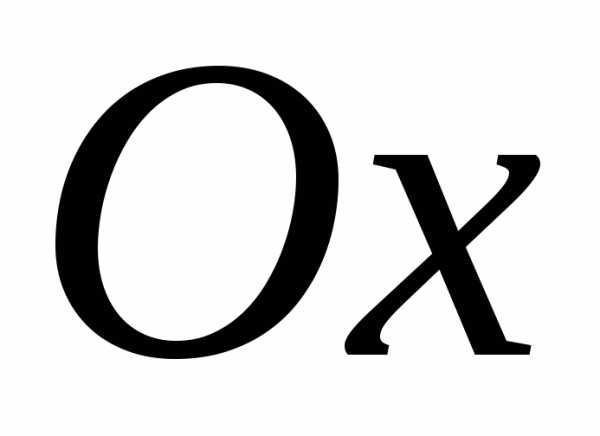 .
Тогда объём получающегося тела вращения
можно вычислить по формуле
.
Тогда объём получающегося тела вращения
можно вычислить по формуле
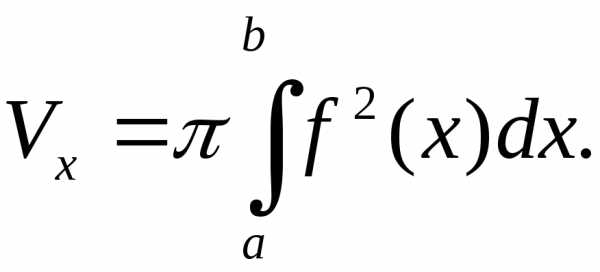 (2)
(2)
Доказательство. Для такого тела сечение с абсциссой 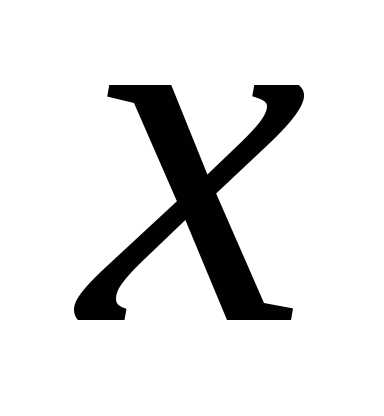 – это круг радиуса
– это круг радиуса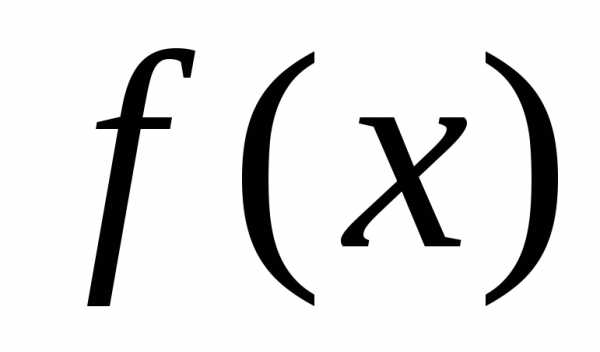 ,
значити формула (1) даёт требуемый результат.
,
значити формула (1) даёт требуемый результат.
Если фигура
ограничена графиками двух непрерывных
функций 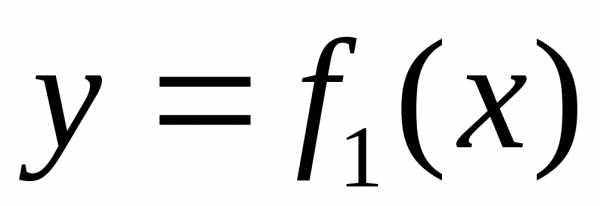 и,
и отрезками прямых
и,
и отрезками прямых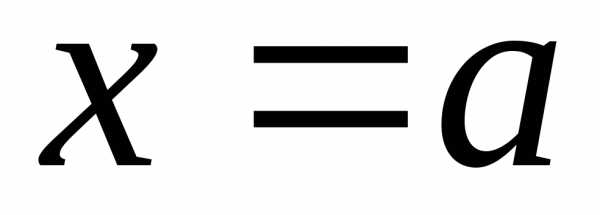 и
и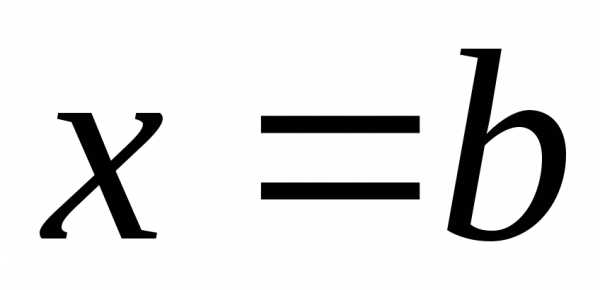 ,
причём
,
причём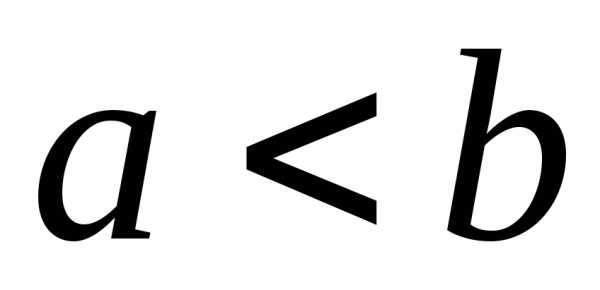 и,
то при вращении вокруг оси абсцисс
получим тело, объём которого
и,
то при вращении вокруг оси абсцисс
получим тело, объём которого
Пример 3. Вычислить объём тора, полученного вращением круга, ограниченного окружностью вокруг оси абсцисс.
Решение. Указанный круг снизу ограничен графиком функции , а сверху –. Разность квадратов этих функций:
Искомый объём
(графиком подынтегральной функции является верхняя полуокружность, поэтому написанный выше интеграл – это площадь полукруга).
Пример 4. Параболический сегмент с основанием 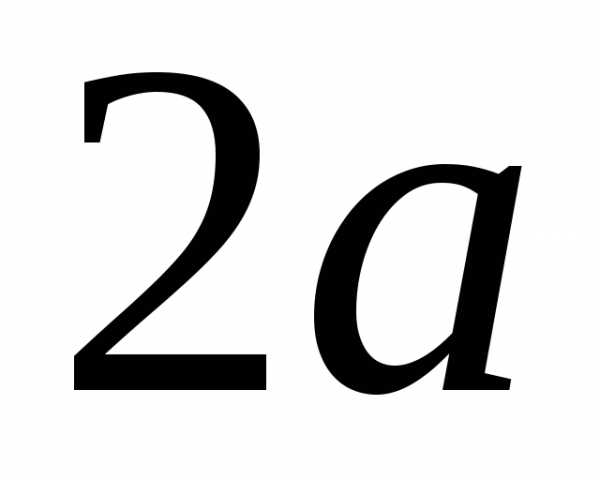 ,
и высотой
,
и высотой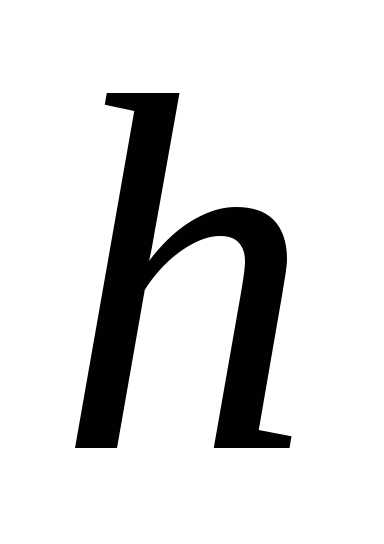 ,
вращается вокруг основания. Вычислить
объём получающегося тела («лимон»
Кавальери).
,
вращается вокруг основания. Вычислить
объём получающегося тела («лимон»
Кавальери).
Решение. Параболу расположим как показано на
рисунке. Тогда её уравнение
,
причем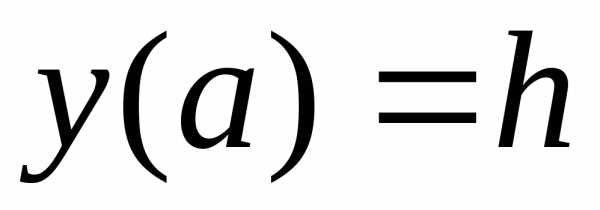 .
Найдём значение параметра
.
Найдём значение параметра :.
Итак, искомый объём:
:.
Итак, искомый объём:
Теорема
3. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции 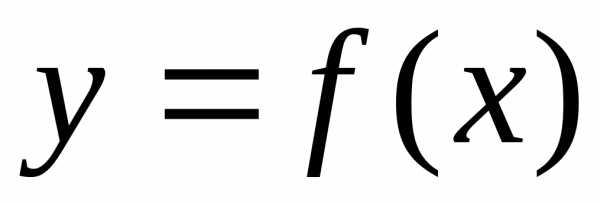 ,
осью
,
осью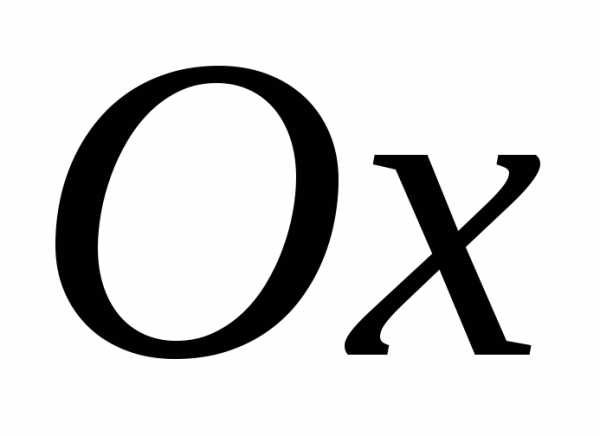 и отрезками прямых
и отрезками прямых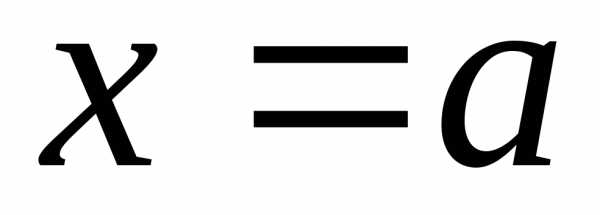 и
и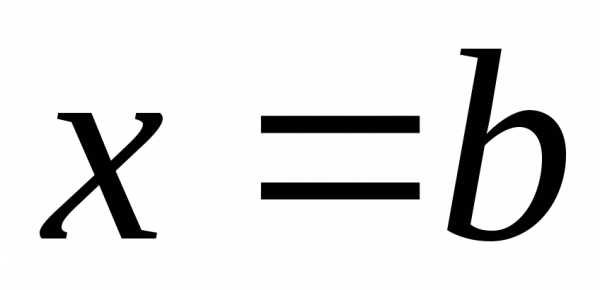 ,
причём,
вращается вокруг оси
,
причём,
вращается вокруг оси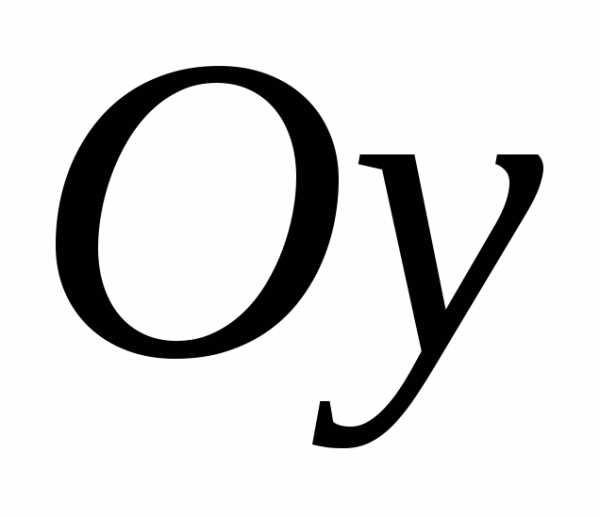 .
Тогда объём получающегося тела вращения
может быть найден по формуле
.
Тогда объём получающегося тела вращения
может быть найден по формуле
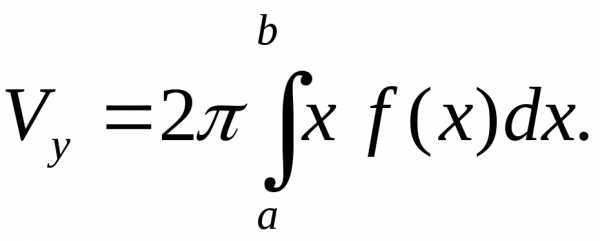 (3)
(3)
Идея
доказательства. Разбиваем отрезок 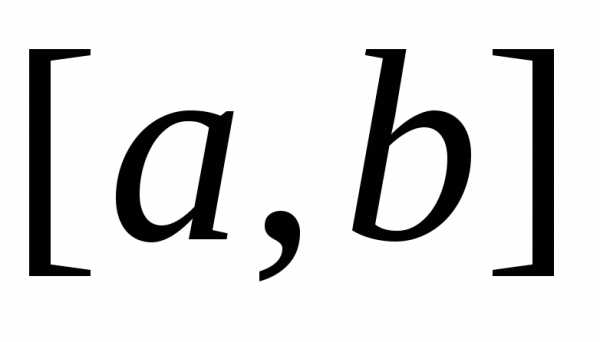 точками
точками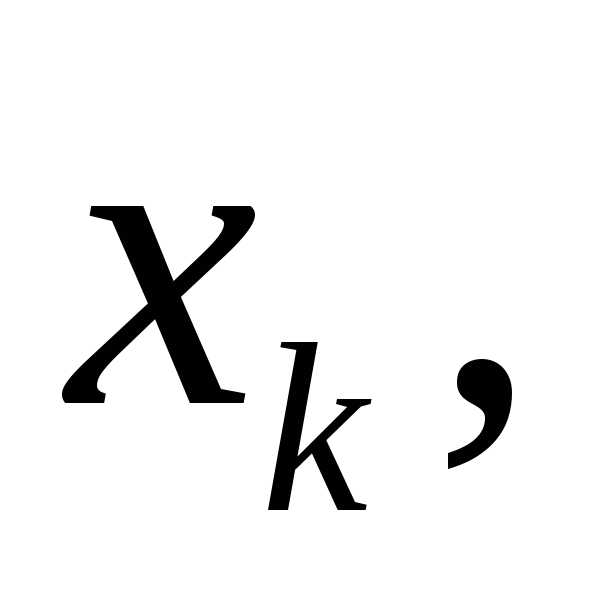 ,
на части и проводим прямые
,
на части и проводим прямые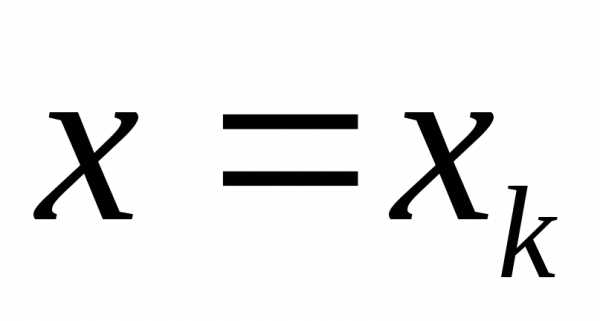 .
Вся трапеция разложится на полоски,
которые можно считать приближенно
прямоугольниками с основанием
.
Вся трапеция разложится на полоски,
которые можно считать приближенно
прямоугольниками с основанием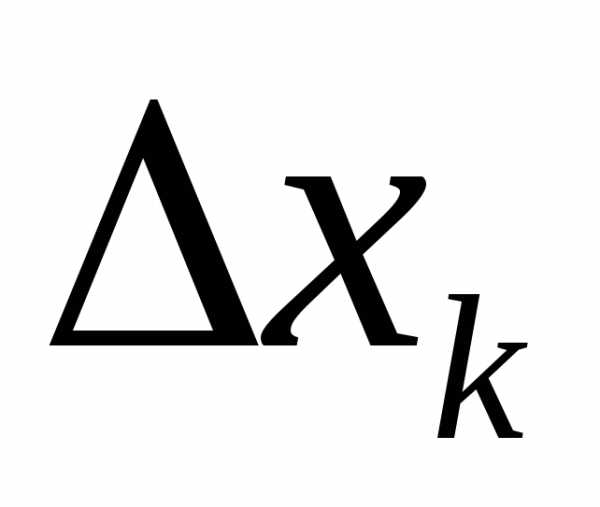 и высотой
и высотой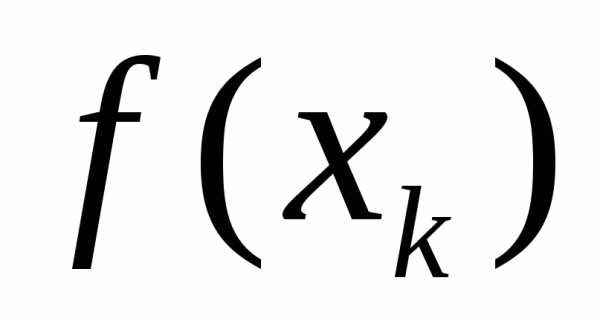 .
.
Получающийся при
вращении такого прямоугольника цилиндр
разрежем по образующей и развернём.
Получим «почти» параллелепипед с
размерами: 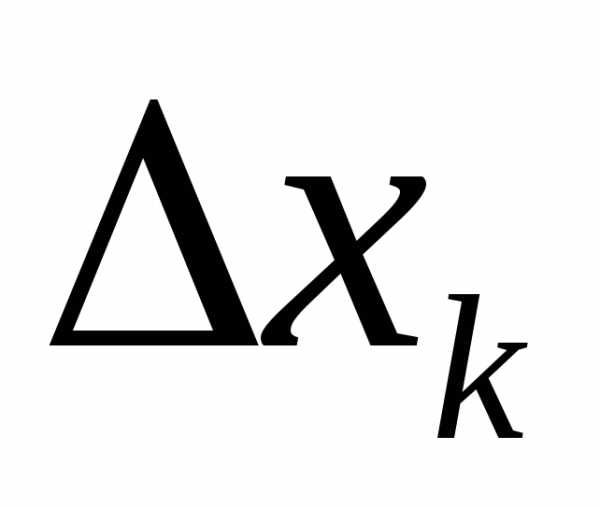 ,
,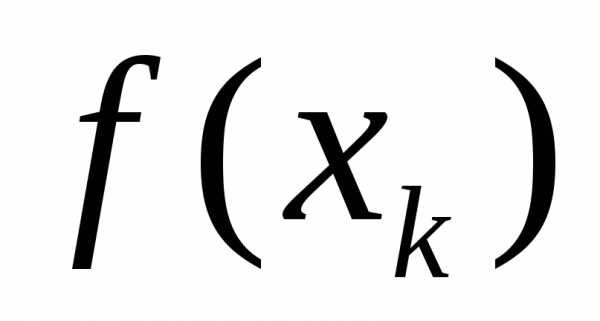 и
и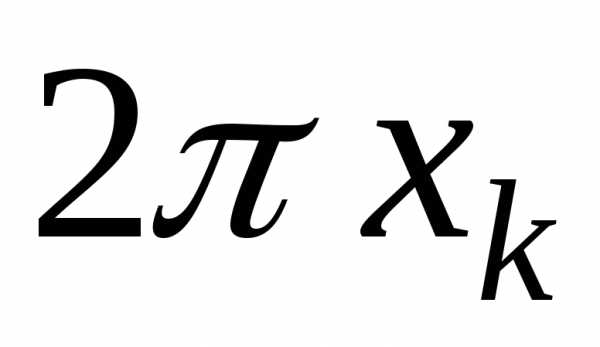 .
Его объём.
Итак, для объёма тела вращения будем
иметь приближенноё равенство
.
Его объём.
Итак, для объёма тела вращения будем
иметь приближенноё равенство
Для получения точного равенства надо перейти к пределу при . Написанная выше сумма есть интегральная сумма для функции , следовательно, в пределе получим интеграл из формулы (3). Теорема доказана.
Замечание
1. В теоремах
2 и 3 условие 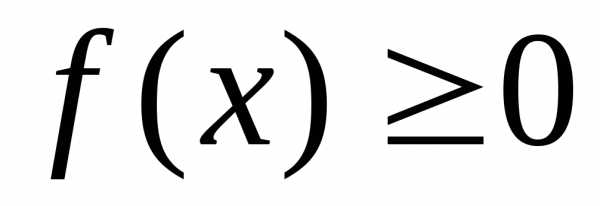 можно опустить: формула (2) вообще
нечувствительна к знаку
можно опустить: формула (2) вообще
нечувствительна к знаку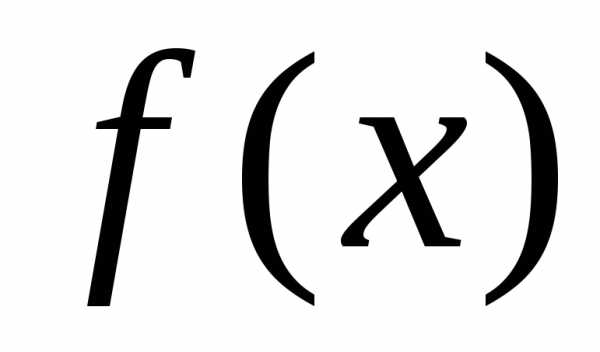 ,
а в формуле (3) достаточно
,
а в формуле (3) достаточно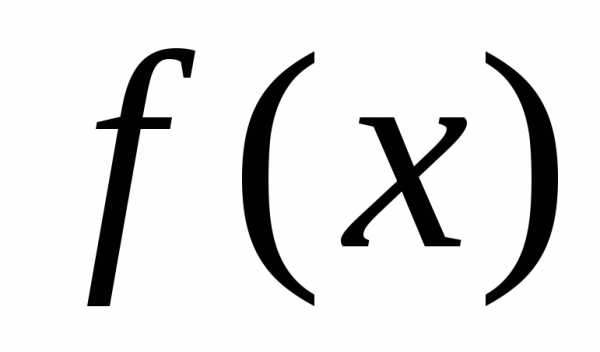 заменить на
заменить на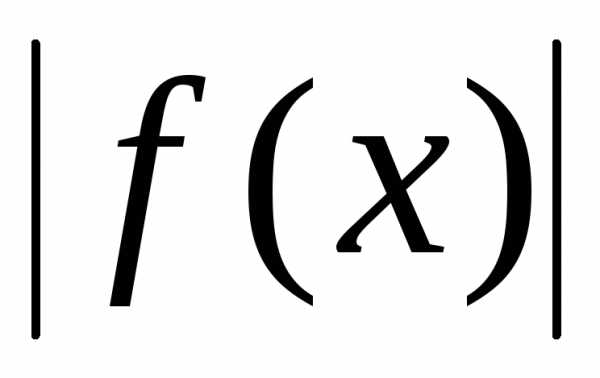 .
.
Пример
5. Параболический сегмент (основание 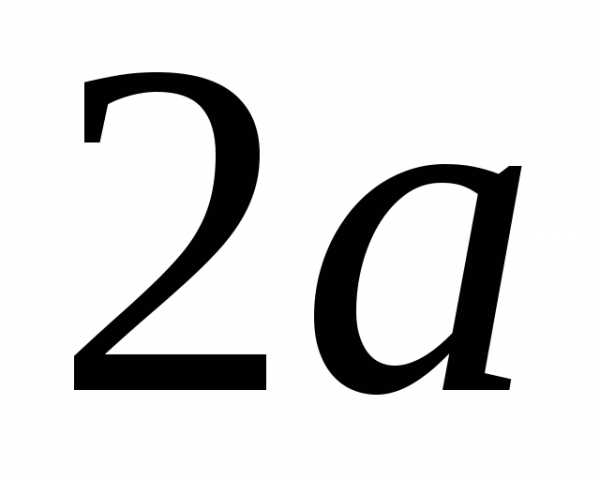 ,
высота
,
высота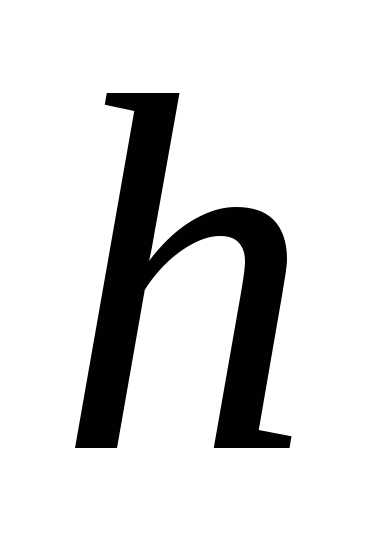 )
вращается вокруг высоты. Найти объём
получающегося тела.
)
вращается вокруг высоты. Найти объём
получающегося тела.
Решение. Расположим
параболу как показано на рисунке. И хотя
ось вращения пересекает фигуру, она –
ось – является осью симметрии. Поэтому
надо рассматривать лишь правую половину
сегмента. Уравнение параболы
,
причем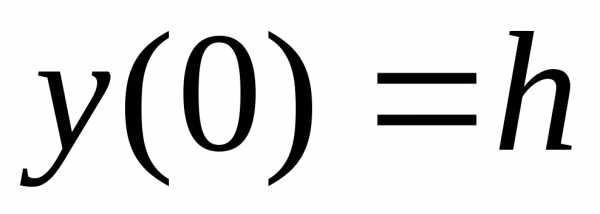 ,
значит
,
значит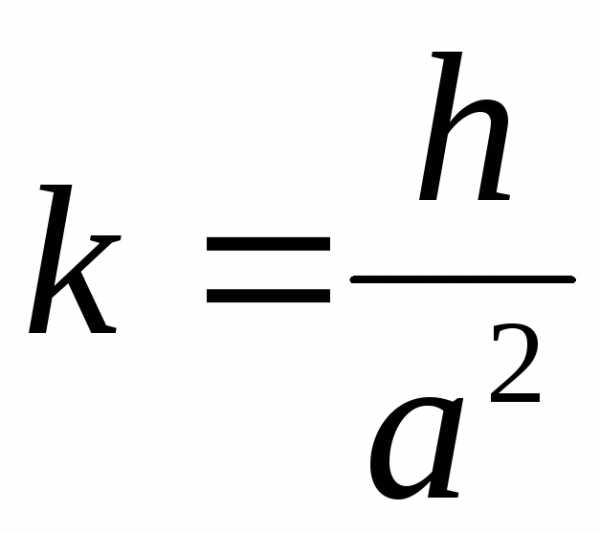 .
Имеем для объёма:
.
Имеем для объёма:
Замечание
2. Если
криволинейная граница криволинейной
трапеции задана параметрическими
уравнениями 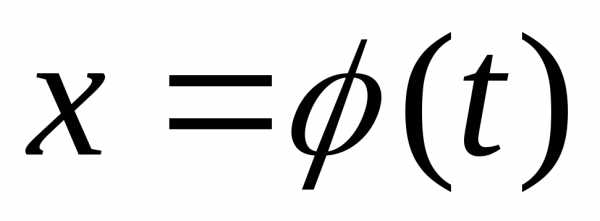 ,
,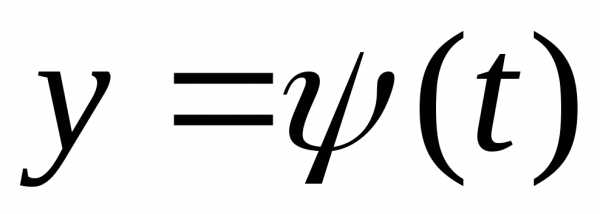 ,и,
,и,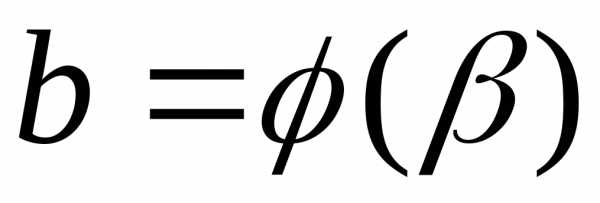 то можно использовать формулы (2) и (3) с
заменой
то можно использовать формулы (2) и (3) с
заменой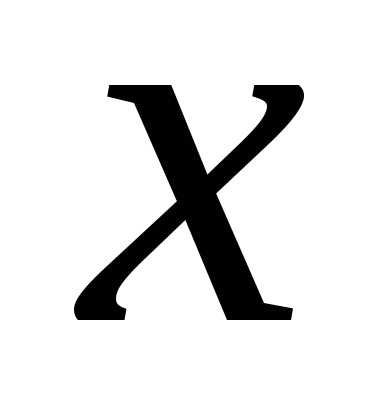 на
на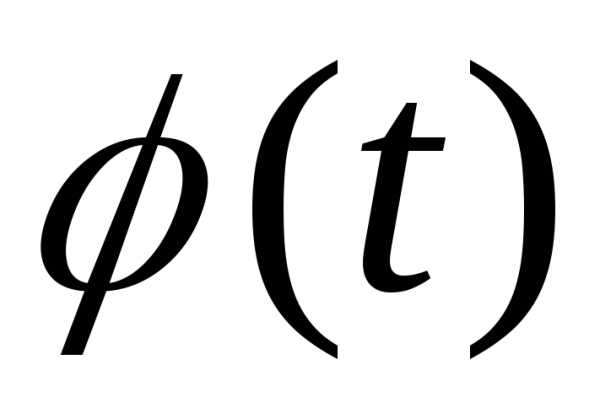 и
и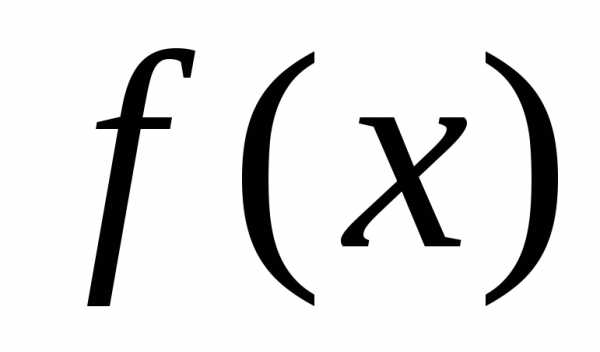 на
на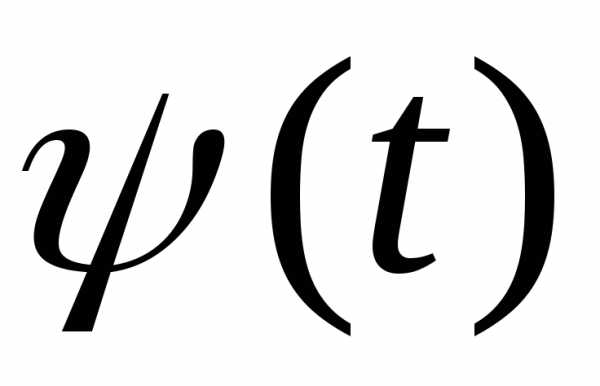 при измененииt от
при измененииt от  до
до .
.
Пример
6. Фигура
ограничена первой аркой циклоиды
,,,
и осью абсцисс. Найти объём тела,
полученного вращением этой фигуры
вокруг: 1) оси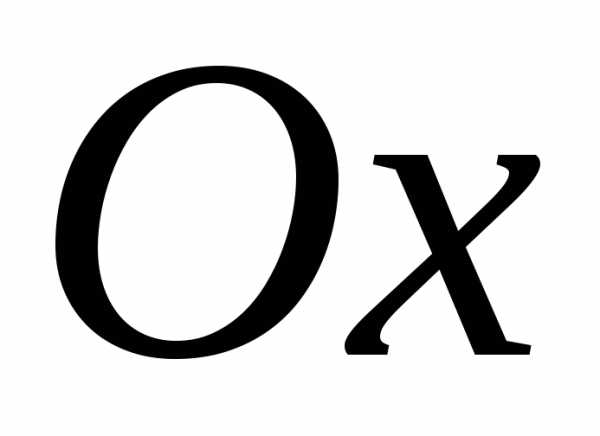 ;
2) оси
;
2) оси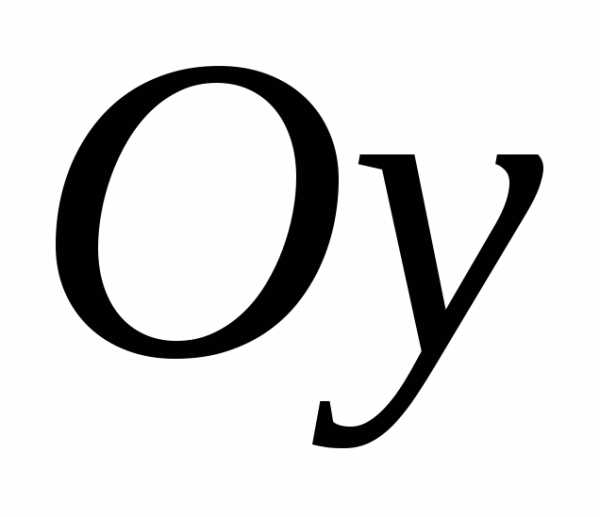 .
.
Решение. 1) Общая формула 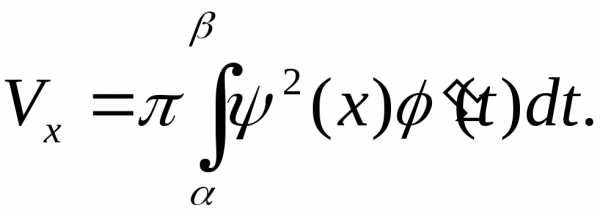 В нашем случае:
В нашем случае:
2) Общая формула Для нашей фигуры:
Предлагаем студентам самостоятельно провести все вычисления.
Замечание
3. Пусть
криволинейный сектор, ограниченный
непре-рывной линией
и лучами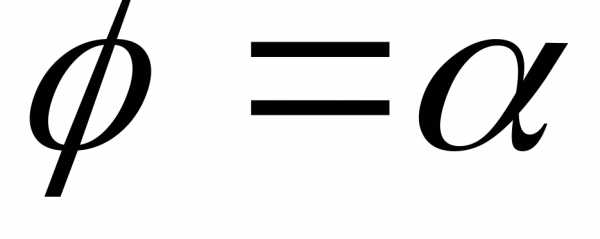 ,
,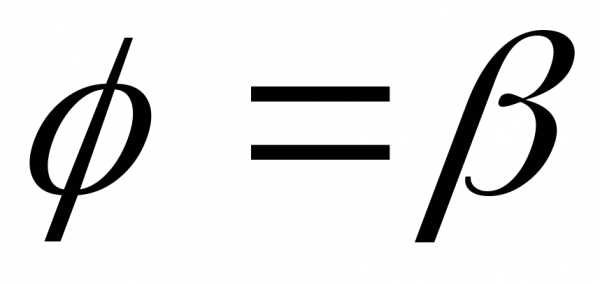 ,
вращается вокруг полярной оси. Объём
получающегося тела можно вычислить по
формуле.
,
вращается вокруг полярной оси. Объём
получающегося тела можно вычислить по
формуле.
Пример
7. Часть
фигуры, ограниченной кардиоидой
,
лежащая вне окружности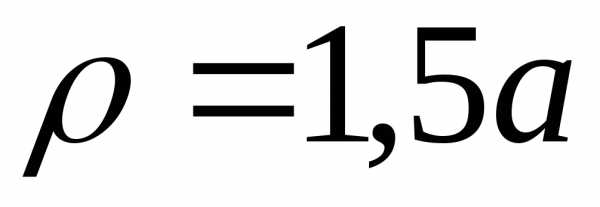 ,
вращается вокруг полярной оси. Найти
объём тела, которое при этом получается.
,
вращается вокруг полярной оси. Найти
объём тела, которое при этом получается.
Решение. Обе линии, а значит и фигура, которую
они ограничивают, симметричны относительно
полярной оси. Поэтому необходимо
рассматривать лишь ту часть, для которой .
Кривые пересекаются при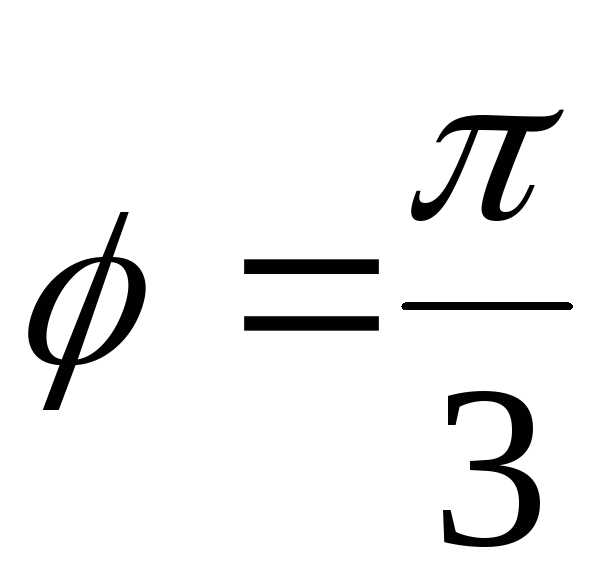 и
и
при 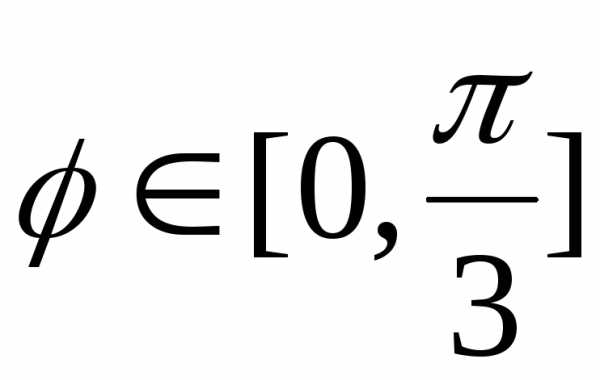 .
Далее, фигуру можно рассматривать как
разность двух секторов, а значит и объём
вычислять как разность двух интегралов.
Имеем:
.
Далее, фигуру можно рассматривать как
разность двух секторов, а значит и объём
вычислять как разность двух интегралов.
Имеем:
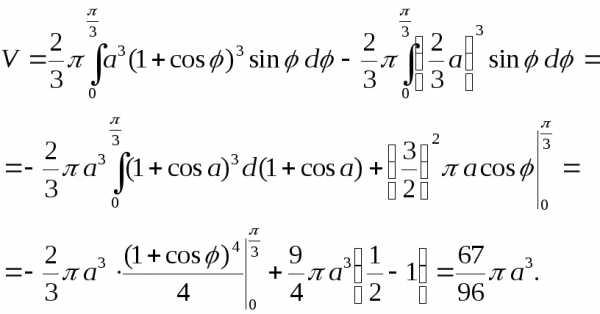
Задачи для самостоятельного решения.
1. Круговой сегмент,
основание которого 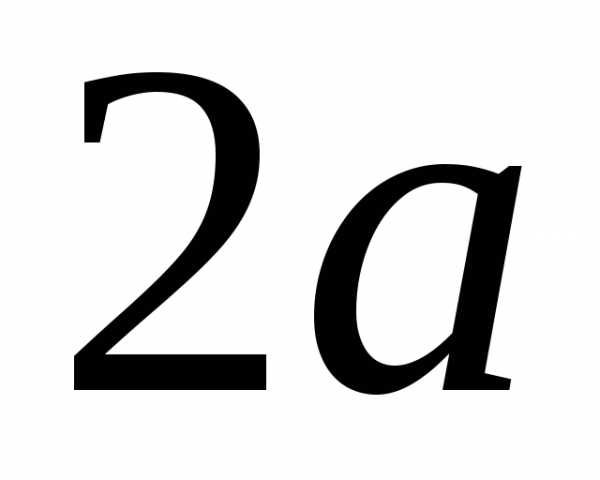 ,
высота
,
высота 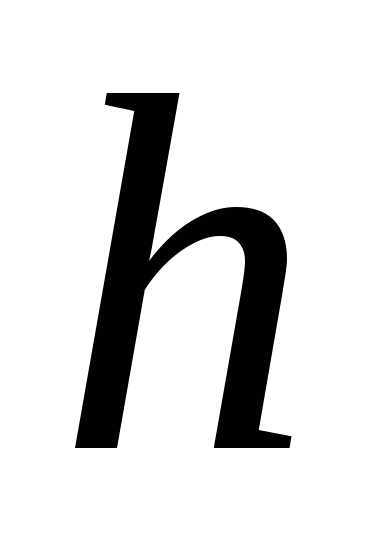 ,
вращается вокруг основания. Найти объём
тела вращения.
,
вращается вокруг основания. Найти объём
тела вращения.
2. Найти объём
параболоида вращения, основание которого  ,
а высота равна
,
а высота равна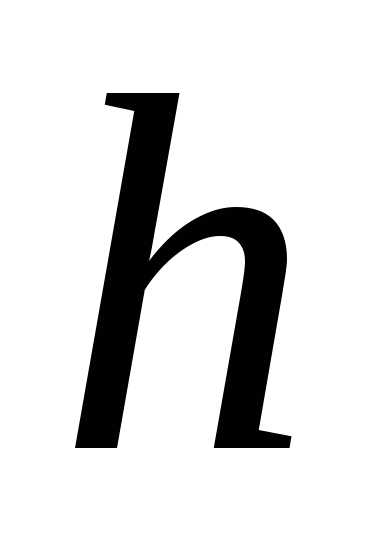 .
.
3. Фигура, ограниченная астроидой ,вращает-ся вокруг оси абсцисс. Найти объём тела, которое получается при этом.
4. Фигура, ограниченная
линиями 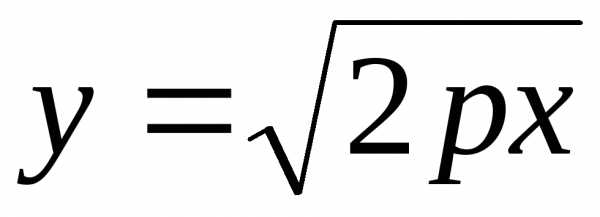 и
и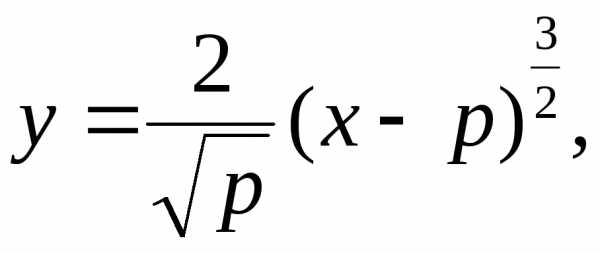 вращается вокруг оси абсцисс. Найти
объём тела вращения.
вращается вокруг оси абсцисс. Найти
объём тела вращения.
studfiles.net
Как вычислить объем тела вращения с помощью определенного интеграла?
Кроме нахождения площади плоской фигуры с помощью определенного интеграла (см. 7.2.3.)важнейшим приложением темы является вычисление объема тела вращения. Материал простой, но читатель должен быть подготовленным: необходимо уметь решать неопределенные интегралысредней сложности и применять формулу Ньютона-Лейбница в определенном интеграле, нужны также уверенные навыки построения чертежей. Вообще в интегральном исчислении много интересных приложений, с помощью определенного интеграла можно вычислить площадь фигуры, объем тела вращения, длину дуги, площадь поверхности тела и многое другое. Представьте некоторую плоскую фигуру на координатной плоскости. Представили? … Теперь данную фигуру можно ещё и вращать, причем вращать двумя способами:
– вокруг оси абсцисс;
– вокруг оси ординат.
Разберём оба случая. Особенно интересен второй способ вращения, он вызывает наибольшие затруднения, но на самом деле решение практически такое же, как и в более распространенном вращении вокруг оси абсцисс. Начнем с наиболее популярной разновидности вращения.
Вычисление объема тела, образованного вращением плоской фигуры вокруг оси OX
Пример 1
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями , вокруг оси .
Решение:Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости XOY необходимо построить фигуру, ограниченную линиями , , при этом не забываем, что уравнение задаёт ось . Чертёж здесь довольно прост:
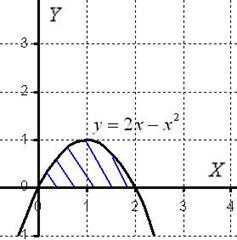
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси . В результате вращения получается такая немного яйцевидная летающая тарелка с двумя острыми вершинами на оси OX, симметричная относительно оси OX. На самом деле у тела есть математическое название, посмотрите в справочнике.
Как вычислить объем тела вращения? Если тело образовано в результате вращения вокруг осиOX, его мысленно разделяют на параллельные слои малой толщины dx, которые перпендикулярны оси OX. Объём всего тела равен, очевидно, сумме объёмов таких элементарных слоёв. Каждый слой, как круглая долька лимона, — низенький цилиндр высотой dx и с радиусом основания f(x). Тогда объём одного слоя есть произведение площади основания πf 2 на высоту цилиндра (dx), или π∙f 2(x)∙dx. А площадь всего тела вращения есть сумма элементарных объёмов, или соответствующий определённый интеграл. Объем тела вращения можно вычислить по формуле:
.
Как расставить пределы интегрирования «а» и «бэ», легко догадаться из выполненного чертежа. Функция … что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболы сверху. Это и есть та функция, которая подразумевается в формуле. В практических заданиях плоская фигура иногда может располагаться и ниже оси OX. Это ничего не меняет – функция в формуле возводится в квадрат: f 2(x), таким образом, объем тела вращения всегда неотрицателен, что весьма логично. Вычислим объем тела вращения, используя данную формулу:
.
Как мы уже отмечали, интеграл почти всегда получается простой, главное, быть внимательным.
Ответ:
В ответе нужно обязательно указать размерность – кубические единицы . То есть, в нашем теле вращения примерно 3,35 «кубиков». Почему именно кубические единицы? Потому что это наиболее универсальная формулировка. Могут быть кубические сантиметры, могут быть кубические метры, могут быть кубические километры и т.д., это уж, сколько зеленых человечков ваше воображение поместит в летающую тарелку.
Пример 2
Найти объем тела, образованного вращением вокруг оси OX фигуры, ограниченной линиями , , .
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Пример 3
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями , , и .
Решение:Изобразим на чертеже плоскую фигуру, ограниченную линиями , , , , не забывая при этом, что уравнение x = 0 задает ось OY:
Искомая фигура заштрихована синим цветом. При её вращении вокруг оси OX получается плоский угловатый бублик (шайба с двумя коническими поверхностями).
Объем тела вращения вычислим как разность объемов тел. Сначала рассмотрим фигуру, которая обведена красным цветом. При её вращении вокруг оси OX получается усеченный конус. Обозначим объем этого усеченного конуса через V1.
Рассмотрим фигуру, которая обведена зеленым цветом. Если вращать данную фигуру вокруг оси OX, то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через V2.
Очевидно, что разность объемов, V = V1 — V2, — это объем нашего «бублика».
Используем стандартную формулу для нахождения объема тела вращения:
1) Фигура, обведенная красным цветом ограничена сверху прямой , поэтому:
.
2) Фигура, обведенная зеленым цветом ограничена сверху прямой , поэтому:
.
3) Объем искомого тела вращения:
Ответ:
Любопытно, что в данном случае решение можно проверить, используя школьную формулу для вычисления объема усеченного конуса.
Само решение чаще оформляют короче, примерно в таком духе:
megaobuchalka.ru
Вычисление объемов тел вращения
Определение 1. Телом вращения называют пространствен-ную фигуру, которую можно получить вращением некоторой криволинейной трапеции вокруг оси .
Рассмотрим в плоскости кривую , ограниченную абсциссами и .
Разобьем тело вращения на п полос шириной .
Тогда полоса от вращения части тела шириной даст объем:
.
Объем тела вращения приближенно определяется суммой
.
Последняя сумма есть интегральная и потому
. (1)
Определение 2. Поверхностью вращенияназывают пространственную фигуру, которая образовывается вращением вокруг заданной прямой некоторой направленной простой дуги.
Площадь поверхности вращения можно найти по формуле
. (2)
Если криволинейная трапеция ограничена графиком непрерывной функции , прямыми , , , то объем тела вращения, образованного вращением этой трапеции вокруг оси 0у равняется
. (3)
Пример 1. Вычислить объем тела вращения, ограниченного линиями , , вокруг оси 0у.
Решение.
.
Формула объема тела вращения обобщается на случай тела, образованного вращением вокруг оси криволинейной трапеции , образованной графиками функций и , каждая из которых определена и непрерывна на отрезке , причем эти функции такие, что для всех . Объем такого тела вычисляется по формуле
. (4)
Пример 2.Найти объем тела, которое образовывается вращением вокруг оси фигуры, ограниченной линиями и .
Решение. Точками пересечения линий и (обе линии – параболы) есть точки с абсциссами 0 и 1. Поэтому, воспользовавшись формулой (11), будем иметь
.
Пример 3.Вычислить объем тела, образованного прямыми и при их вращении вокруг оси абсцисс.
Решение.
Имеем
куб. ед.
Если кривая линия задается в параметрической форме уравнениями
, причем ,
то объем тела вращения вычисляется по формуле:
, (5)
а площадь поверхности тела вращения:
. (6)
Пример 4. Вычислить объем и поверхность тела вращения, образованного одной аркой циклоиды
вокруг оси .
Решение.
.
.
Примеры использования интегрального исчисления в задачах экономического характера
Определенный интеграл применяют для вычисления суммарных экономических эффектов, общих, маргинальных взносов и т.д. Рассмотренные примеры не исчерпывают всех возможных применений определенного интеграла в экономике.
Затраты, доход и прибыль
Пусть будет функцией общих затрат на производство х единиц продукции, – функция маргинальных затрат. Тогда определенный интеграл
(1)
равняется изменению общих затрат при росте количества произведенной продукции от а до b единиц.
Отсюда вытекает важное следствие:
Изменение производственных затрат при росте произведенной продукции от а до b единиц равняется площади криволинейной трапеции, ограниченной графиком функции маргинальных затрат , отрезком и прямыми и .
Аналогично, если и – функции маргинального дохода и прибыли при росте реализации произведенной продукции от а до b единиц вычисляется по формулам:
; (2)
. (3)
Пример 1. Функция маргинальных затрат фирмы имеет вид .
Найти рост общих затрат, когда производство возрастет с 1000 до 2000 единиц.
Решение. По формуле
рост общих затрат будет:
= .
Итак, затраты возрастут на 200 гривен.
Максимизация прибыли во времени
Пусть , и – общие затраты, доход и прибыль, которые изменяются за время t. Тогда
, или .
Максимум общей прибыли будет тогда, когда
, или .
Другими словами, существует такое время , когда , т.е. скорости изменения дохода и затрат равны.
Общая прибыль за время можно найти по формуле
.
Пример 2. Скорости изменения затрат и дохода предприятия после начала его деятельности определялись формулами
и ,
где и измерялись миллионами гривен, а t – годами. Определить, как долго предприятие было прибыльным, и найти общую прибыль, которая было получено за это время.
Решение. Оптимальное для предприятия время получим из условия :
;
.
Итак, предприятие было прибыльным 4 года, за это время было получена прибыль
(млн. гр.).
Дисконтная прибыль
Пусть функция описывает изменение производительности работы некоторого предприятия за определенное время. Найдем объем продукции , которая выпущена за промежуток времени .
Известно, что если производительность работы за некоторое время постоянная, то объем продукции за промежуток времени задается формулой . В общем случае справедлива формула , где , которая тем точнее, чем меньше .
Разобьем отрезок на п частей, т.е.: .
Для величины объема продукции , который выпущен за время , имеем: ; . Тогда
.
Если , то
Поэтому по определению интеграла
,
если – производительность работы в момент времени t, тогда – объем продукции, которая выпущена за промежуток времени от 0 до T.
Определение начальной суммы по ее конечной величине, полученной за t лет при годовом проценте Р, называется дисконтированием.
Задачи этого класса встречаются при определении экономической эффективности капитальных вложений.
Пусть – конечная сумма, которая получена за t лет, которую в финансовом анализе называют современной суммой. Если проценты простые, то , где – процентная ставка.
Тогда .
Если проценты сложные, то , поэтому .
Пусть прибыль за год изменяется во времени и описывается функцией при удельной норме процента, равной i, процент начисляется непрерывно.
Дисконтная прибыль К за время Т вычисляется по формуле:
, где .
Пример 3. Определить дисконтную прибыль за 3 года при процентной ставке 8%, если базовые капиталовложения составили 10 млн. гривен, а ожидаемый прирост капитала 1 млн. гривен.
Решение.Очевидно, что капиталовложения задаются функцией
.
Получим дисконтную сумму капиталовложений по формуле:
, где .
млн. гривен.
Это означает, что получение одинаково нарощенной суммы через три года ежегодные вклады от 10 до 13 млн. гривен равновесны одновременному начальному вкладу 30,5 млн. гривен при той же непрерывной процентной ставке.
Пусть известна функция , которая задает изменение затрат t на изготовление продукции в зависимости от степени освоения производства, где х порядковый номер изделия в партии товара.
Тогда среднее время , затраченное на изготовление одного изделия в период освоения от а до b изделий, вычисляется по теореме о среднем значении определенного интеграл:
.
Что касается функции изменения затрат времени , то как правило, она такова: , где – затрата времени на одно изделие; – показатель производственного процесса.
Пример 4. Найти среднее время, которое затрачено на освоение выпуска одного изделия в период освоения от 10 до 20 изделий, если затрата времени на 1-но изделие = 200 мин., показатель производственного процесса .
Решение. По формуле
имеем:
мин.
infopedia.su

 Для любого программиста программа на языке Паскаль легкое и вполне обычное дело. Нельзя сказать, что этот язык программирования для современного мира слишком слаб. Паскаль считается базовым языком программирования. Его даже изучают в школе.
Для любого программиста программа на языке Паскаль легкое и вполне обычное дело. Нельзя сказать, что этот язык программирования для современного мира слишком слаб. Паскаль считается базовым языком программирования. Его даже изучают в школе.












 ;
; ;
; ;
4.
;
4. ;
;

















 xvatit.com
xvatit.com