Бесплатные ответы на тесты МФПУ «Синергия» по предмету «управление собственным бизнесом «
- 1.Профессиональный предпринимательский бизнес-это …
Отметьте правильный вариант ответа:
1)система ведения дел
2)особая деятельность
3)профессиональная деятельность
- 2. Компания со смешанным капиталом предполагает …
Отметьте правильный вариант ответа:
1)федеральную собственность на часть акций АО
2)собственность хозяйственных товариществ и муниципальных органов
3)собственность АО и хозяйственных товариществ
- 3. Предпринимательский статус-это …
Отметьте правильный вариант ответа:
1)образование предпринимателя
2)принадлежность к профессии
3)признаваемая обществом принадлежности к профессии
- 4. Объектами предпринимательского бизнеса являются …
Отметьте правильный вариант ответа:
1)ресурсы
2)услуги
3)работы по производству товаров
- 5. Государственное предпринимательство-это..
Отметьте правильный вариант ответа:
1)государственное участие в деятельности юридических лиц
2)деятельность госслужащих
3)предпринимательская деятельность федеральных органов
- 6. Уставный капитал ООО на момент регистрации должен быть оплачен …
Отметьте правильный вариант ответа:
1)не менее, чем на 25%
2)не менее, чем на 50%
3)полностью
- 7. Предпринимательские функции исполняются посредством …
Отметьте правильный вариант ответа:
1)предпринимательских действий
2)директивных распоряжений
3)определенных актов
- 8. «Ведение дел» не включает в себя …
Отметьте правильный вариант ответа:
1)поддержание бизнеса
2)развитие бизнеса
3)обучение бизнесу
- 9. Государственные унитарные предприятия учреждаются …
Отметьте правильный вариант ответа:
1)полными товарищами
2)уполномоченными государством органами
3)собственниками имущества
- 10. Одной из основных функций предпринимателя является ..
Отметьте правильный вариант ответа:
1)регистрация фирмы
2)принятие на себя обязательств
3)получение кредитов
- 11. Долевая собственность представляет собой …
Отметьте правильный вариант ответа:
1)неделимый фонд
2)союз
3)сумму долей
- 12. Каждый предприниматель вправе участвовать в деятельности …
Отметьте правильный вариант ответа:
1)нескольких фирм
2)одной фирмы
3)одного акционерного общества
- 13. Предпринимательское администрирование-это …
Отметьте правильный вариант ответа:
1)применение системы формализованных процедур
2)ведение дела
3)функционирование предпринимательской фирмы
- 14. Руководитель унитарного предприятия назначается …
Отметьте правильный вариант ответа:
1)собранием учредителей
2)собственником
3)органами опеки
- 15. Акционер-это …
Отметьте правильный вариант ответа:
1)учредитель АО
2)дольщик АО
3)участник АО
- 16. Предпринимательская власть-это …
Отметьте правильный вариант ответа:
1)полномочия
2)право и ответственность за включение объектов в бизнес
3)независимость в бизнесе
- 17. «Чистые» технологические схемы предполагают …
Отметьте правильный вариант ответа:
1)и следование, и нарушение
2)нарушение закона
3)следование закону
- 18. Предприниматель формирует ресурсы фирмы за счет …
Отметьте правильный вариант ответа:
1)кредитов
2)консолидации ресурсов
3)государственной поддержки
- 19. Предприниматель должен строить свою деятельность …
Отметьте правильный вариант ответа:
1)последовательно
2)в соответствии с особенностями ведения дел
3)исторически оправданно
- 20. Современная теория предпринимательства …
Отметьте правильный вариант ответа:
1)культурологическое, историческое направление науки
2)имеет разрозненный характер, включает элементы экономической теории, психологии, менеджмента
3)целостная теория
- 21. Участниками товарищества на вере являются …
Отметьте правильный вариант ответа:
1)полные товарищи
2)полные товарищи и коммандисты
3)коммандисты
- 22. Предпринимательской деятельностью не могут заниматься …
Отметьте правильный вариант ответа:
1)тинэйджеры в возрасте от 14 до 18 лет
2)пенсионеры
3)чиновники
- 23. Вхождение предпринимателей в состав участников фирмы сопровождается процедурой …
Отметьте правильный вариант ответа:
1)регистрации фирмы
2)реорганизации
3)создание фирмы
- 24. Величина уставного капитала ООО составляет …
Отметьте правильный вариант ответа:
1)10 МРОТ
2)100 МРОТ
3)1000 МРОТ
- 25. Бюджетные предприятия-это …
Отметьте правильный вариант ответа:
1)аналог унитарных предприятий
2)акционерные общества
3)коммандитные товарищества
- 26. Создание и организация рабочих мест является …
Отметьте правильный вариант ответа:
1)функцией предпринимателя
2)служебной обязанности менеджера
3)обязательством предпринимателя
- 27. Некоммерческие организации зарабатывать прибыль …
Отметьте правильный вариант ответа:
1)не имеют права
2)занимаются другой деятельностью
3)имеют право
- 28. «Серые» технологические схемы предполагают …
Отметьте правильный вариант ответа:
1)нарушение закона
2)и следование, и нарушение
3)следование закону
- 29. Под рациональностью в предпринимательском бизнесе понимают …
Отметьте правильный вариант ответа:
1)оптимальность
2)подчинение своего поведения целям
3)экономичность
xn—-etbfclc6azafijc8n.xn--p1ai
Ответы к тесту по предмету Оценка бизнеса
Стоимость открытых акционерных обществ по отношению к закрытым должна быть:- выше
- ниже
- равна
Расчетная величина, за которую предполагается переход имущества из рук в руки на дату оценки в результате сделки между продавцом и покупателем, называется:
- рыночная стоимость
- инвестиционная стоимость
- ликвидационная стоимость
- кадастровая стоимость
Рыночная стоимость может выражаться отрицательной величиной в случае оценки:
- нематериальных активов
- изношенного оборудования
- имущества, сданного в аренду
- устаревших объектов недвижимости, сумма затрат на снос которых превышает стоимость земельного участка
- экологически неблагополучных объектов
Какой документ является основанием для проведения оценки бизнеса?
- лицензия
- договор
- акт
- сертификат
- распоряжение
Потребителями результатов оценки могут являться:
- только заказчик оценки
- любой участник оценочной деятельности
- органы исполнительной власти
- собственник оцениваемого имущества
При балансовой или бухгалтерской оценке активы фирмы равны:
- сумме неосязаемых активов, обязательств и собственного капитала
- сумме обязательств и величины чистого собственного капитала
- чистому собственному капиталу
- сумме стоимости: гарантий, лицензии и страховки
Если расчет стоимости бизнеса производится с целью заключения сделки купли-продажи, то рассчитывается:
- инвестиционная стоимость
- стоимость замещения объекта оценки
- рыночная стоимость
- ликвидационная стоимость
К какому подходу относятся метод чистых активов и метод ликвидационной стоимости?
- затратному
- доходному
- сравнительному
Практика оценки бизнеса в России показывает, что наибольшее применение находит:
- доходный подход
- сравнительный подход
- затратный подход
К какому подходу относятся метод капитализации доходов и метод дисконтированных денежных потоков?
- затратному
- доходному
- сравнительному
Сумма затрат в рыночных ценах, существующих на дату оценки, необходимых для создания объекта идентичного объекту оценки, является:
- нормативной стоимостью
- рыночной стоимостью
- стоимостью воспроизводства
- инвестиционной стоимостью
В основу какого подхода к оценке бизнеса положен принцип замещения?
- затратного
- доходного
- сравнительного
В основу какого подхода к оценке бизнеса положен принцип ожидания?
- затратного
- доходного
- сравнительного
Какой метод оценки необходимо использовать в случае принятия собранием кредиторов решения о введении на предприятии конкурсного производства?
- дисконтированных денежных потоков
- капитализации доходов
- ликвидационной стоимости
- чистых активов
Как называется вероятность того, что доходы от инвестиций в оцениваемый бизнес окажутся больше или меньше прогнозируемых
- риск
- убыток
- прибыль
- дефицит
- избыток
«Чем больше предприятие способно удовлетворить потребность собственника, тем выше его стоимость» — это принцип:
- ожидания
- предвидения
- полезности
- вклада
- остаточной продуктивности
К какому подходу относятся метод рынка капитала, метод сделок и метод отраслевых коэффициентов?
- затратному
- доходному
- сравнительному
Максимальная стоимость предприятия определяется наименьшей ценой, по которой может быть приобретен другой объект с эквивалентной полезностью» — это принцип:
- предвидения
- полезности
- вклада
- замещения
В настоящее время в России для осуществления оценочной деятельности необходимо иметь:
- лицензию Министерства экономического развития
- свидетельство о членстве в СРОО оценщика
- лицензию Минимущества
- разрешение Министерства финансов
В договоре об оценке должны содержаться следующие условия:
- основания заключения договора
- вид объекта оценки
- вид определяемой стоимости (стоимостей) объекта оценки
- сведения о страховании гражданской ответственности оценщика
- все перечисленное
testyiotvety.blogspot.com
Оценка стоимости бизнеса.Тест Синергия — решенные тесты Синергия, тест Синергия,бизнес практикум Синергия
Сдано на 73баллов в 2017г. Скриншот с отметкой прилагается к работе. Ответы выделены цветом в Worde.
1. Оценщик указывает дату оценки объекта в отчете об оценке, руководствуясь принципом…
Изменения стоимости
Полезности
Соответствия
Предельной производительности
2. В случае выбора аналогов среди западных компаний необходимо провести с отчетностью оцениваемой компании процедуру …
Нормализации
Инфляционной корректировки
трансформации
3. Стоимость предприятия, определенная сравнительным подходом, составляет …, если известно, что мультипликатор «цена/прибыль» по компаниям-аналогам составил 6,3; «цена/денежный поток» – 10,5; «цена/выручка» – 4,3 (в расчетах значимость мультипликаторов принимается как равная), деятельность оцениваемой компании убыточна, ее выручка составила 1 200 000 ден.ед., а денежный поток – 200 000 ден.ед.
2100000 ден.ед.
3630000 ден.ед.
5160000 ден.ед.
4. Для определения величины ликвидационной стоимости используется формула «…»
5. Метод сделок основан…
На активах оцениваемой компании
На оценке минаритарных пакетов акций компаний-аналогов
На оценке контрольных пакетов акций компаний-аналогов
На будущих доходах оцениваемой компании
6. Модель Эдвардса-Бэлла-Ольсона устраняет недостаток…подхода в оценке бизнеса
Затратного
Сравнительного
Доходного
7. Основным недостатком затратного подхода в оценке бизнеса является
Его умозрительность
Отсутствие учета перспектив развития бизнеса
Отсутствие достоверной информации об объекте оценки
8. Для целей оценки дебиторской задолженности специалист должен изучить …
Справку бухгалтерии о составе и сроках возникновения и погашения дебиторской задолженности
Договоры с покупателями и заказчиками
Договоры с кредитными учреждениями
9. Чтобы принять результаты метода рынка капитала к согласованию с результатами доходного и затратного подходов, необходимо
Не применять никаких корректировок
Применить скидку за низкую ликвидность
Применить премию за контроль и при необходимости сделать скидку за низкую ликвидность
Применить скидку за неконтрольный характер
10. В соответствии с принципом … объект оценки, характеристики которого не соответствуют требованиям рынка, скорее всего, будет оценен ниже среднего уровня
Замещения
Соответствия
Вклада
Конкуренции
11. Чтобы определить стоимость неконтрольного пакета низколиквидных акций при известной стоимости 100% пакета на уровне контроля, необходимо…
Добавить премию за контрольный характер
Вычесть скидки за неконтрольный характер и низкую ликвидность хз
Вычесть скидку за неконтрольный характер
Вычесть скидку за низкую ликвидность
12.Если известно, что балансовая стоимость денежных средств организации составляет на дату оценки 50 000 ден.ед., дебиторской задолженности – 450 000 ден.ед. (12 % ее является безнадежной), рыночная стоимость недвижимости составляет на дату оценки 8 400 000 ден.ед, машин и оборудования – 13 520 000 ден.ед, запасов – 3 890 000 ден.ед., финансовых активов – 785 000 ден.ед., стоимость обязательств –22 760 000 ден.ед., то тогда стоимость предприятия, определенная затратным подходом, составляет …
4281000 ден ед
26310000ден ед
13. В отчете об оценке бизнеса принято приводить обзор макроэкономики …
Отрасли
Региона и отрасли
Страны, региона и отрасли
региона
14. Мультипликатор «…» является моментным
Цена/прибыль
Цена/денежный поток
Цены/чистые активы
15. В оценке стоимости предприятия выделяют … риски
16. Если известно, что среднее значение мультипликатора «цена/прибыль» у нескольких компаний-аналогов -6,5, прибыль оцениваемой компании – 80000ден.ед., а выручка – 1000000ден.ед., то стоимость оцениваемой компании составляет…
650000 ден.ед.
520000 ден.ед.
100000 ден.ед.
17. Нормализация отчетности проводится с целью
Определения доходов и расходов, характерных для нормально действующего бизнеса
Приведение ее к единым стандартам бухгалтерского учета
Упорядочения бухгалтерской отчетности
18. Ставка дисконтирования – это …
Ожидаемая ставка дохода по альтернативным вариантам инвестиций
Действующая ставка дохода по альтернативным вариантам инвестиций
Коэффициент, приводящий текущую стоимость денег к их будущей стоимости
19. Если известно, что доходы компании, ожидаемые к получению в прогнозном периоде составляют в 1-й год 750000ден.ед., во 2-й год 350000 ден.ед., в 3-й год – 500000ден.ед., в 4-тый год – 550000ден.ед., остаточная стоимость – 1200000ден.ед., а ставка дисконта – 8%, то текущая стоимость предприятия составляет…
2612570 ден.ед.
3101850 ден.ед.
2677720 ден.ед
20. Для бездолгового денежного потока ставка дисконтирования рассчитывается …
21. Стоимость предприятия, определенная рыночным подходом, составляет …, если известно, что мультипликатор «цена/прибыль» по компаниям-аналогам составил 6,3, «цена/выручка» – 4,3, деятельность оцениваемой компании убыточна, а ее выручка составила 1 200 000 ден.ед.
7560000 ден.ед.
279070 ден.ед.
5160000 ден.ед.
190476 ден.ед
22. В соответствии с … в отчете об оценке в обязательном порядке должно быть указано задание на оценку
Федеральным стандартом оценки №2
Федеральным стандартом оценки №3
ФЗ №135 «Об оценочной деятельности в РФ»
Федеральным стандартом оценки №1
23. Расположите в правильной последовательности этапы определения стоимости компании
A подписание договора на оценку
B определение стоимости компании
C сбор информации о компании
D формировании отчета об оценке
E вывод итоговой величины стоимости
24. Целью оценки объекта оценки может быть…
Принятие управленческих решений
Решение уполномоченного органа
Определение рыночной стоимости
Купля-продажа
25. Отчет об оценке в оценке бизнеса …
Может не составляться
Должен быть составлен в устной форме
Должен быть составлен в письменной форме
26. При оценке стоимости бизнеса акционерного общества объектом оценки будет выступать …
имущественный комплекс общества с ограниченной ответственностью;
право собственности на долю в уставном капитале общества с ограниченной ответственностью;
пакет акций акционерного общества.
27. Проведение финансового анализа в сравнительном подходе необходимо для определения
Степени риска, связанного с объектом оценки
Соотношения постоянных и переменных затрат в общей величине затрат
Рейтинга среди проданных аналогичных предприятий
Тенденции изменения доходов и расходов
28. Для случаев возрастающих во времени денежных потоков коэффициент капитализации…
Будет равен ставке дисконтирования
Будет всегда меньше ставки дисконтирования
Будет всегда больше ставки дисконтирования
Может быть как больше, так и меньше ставки дисконтирования
29. С помощью метода …можно определить стоимость миноритарного пакета акций
Сделок
Рынка капитала
Стоимости
30. Рыночная стоимость может быть выражена…
В денежных единицах
В денежном эквиваленте
В сочетании денежных средств и неликвидных ценных бумаг
xn--c1adalc1aweahc7n.xn--p1ai
Тест тема 1
ОЦЕНКА БИЗНЕСА
1. Стоимость открытых акционерных обществ по отношению к закрытым должна быть:
а) выше
б) ниже
в) равна
2. Расчетная величина, за которую предполагается переход имущества из рук в руки на дату оценки в результате сделки между продавцом и покупателем, называется:
а) рыночная стоимость
б) инвестиционная стоимость
в) ликвидационная стоимость
г) кадастровая стоимость
3. Рыночная стоимость может выражаться отрицательной величиной в случае оценки:
а) нематериальных активов
б) изношенного оборудования
в) имущества, сданного в аренду
г) устаревших объектов недвижимости, сумма затрат на снос которых превышает стоимость земельного участка
д) экологически неблагополучных объектов
4. Какой документ является основанием для проведения оценки бизнеса?
а) лицензия
б) договор
в) акт
г) сертификат
д) распоряжение
5. Потребителями результатов оценки могут являться:
а) только заказчик оценки
б) любой участник оценочной деятельности
в) органы исполнительной власти
г) собственник оцениваемого имущества
6. При балансовой или бухгалтерской оценке активы фирмы равны:
а) сумме неосязаемых активов, обязательств и собственного капитала
б) сумме обязательств и величины чистого собственного капитала
в) чистому собственному капиталу
г) сумме стоимости: гарантий, лицензии и страховки
7. Если расчет стоимости бизнеса производится с целью заключения сделки купли-продажи, то рассчитывается:
а) инвестиционная стоимость
б) стоимость замещения объекта оценки
в) рыночная стоимость
г) ликвидационная стоимость
8. К какому подходу относятся метод чистых активов и метод ликвидационной стоимости?
а) затратному
б) доходному
в) сравнительному
9. Практика оценки бизнеса в России показывает, что наибольшее применение находит:
а) доходный подход
б) сравнительный подход
в) затратный подход
10. К какому подходу относятся метод капитализации доходов и метод дисконтированных денежных потоков?
а) затратному
б) доходному
в) сравнительному
11. Сумма затрат в рыночных ценах, существующих на дату оценки, необходимых для создания объекта идентичного объекту оценки, является:
а) нормативной стоимостью
б) рыночной стоимостью
в) стоимостью воспроизводства
г) инвестиционной стоимостью
12. В основу какого подхода к оценке бизнеса положен принцип замещения?
а) затратного
б) доходного
в) сравнительного
13. В основу какого подхода к оценке бизнеса положен принцип ожидания?
а) затратного
б) доходного
в) сравнительного
14. Какой метод оценки необходимо использовать в случае принятия собранием кредиторов решения о введении на предприятии конкурсного производства?
а) дисконтированных денежных потоков
б) капитализации доходов
в) ликвидационной стоимости
г) чистых активов
15. Как называется вероятность того, что доходы от инвестиций в оцениваемый бизнес окажутся больше или меньше прогнозируемых
Ответ: Риск
16. «Чем больше предприятие способно удовлетворить потребность собственника, тем выше его стоимость» — это принцип:
а) ожидания
б) предвидения
в) полезности
г) вклада
д) остаточной продуктивности
17. К какому подходу относятся метод рынка капитала, метод сделок и метод отраслевых коэффициентов?
а) затратному
б) доходному
в) сравнительному
18. «Максимальная стоимость предприятия определяется наименьшей ценой, по которой может быть приобретен другой объект с эквивалентной полезностью» — это принцип:
а) предвидения
б) полезности
в) вклада
г) замещения
19. В настоящее время в России для осуществления оценочной деятельности необходимо иметь:
а) лицензию Министерства экономического развития
б) свидетельство о членстве в СРОО оценщика
в) лицензию Минимущества
г) разрешение Министерства финансов
20. В договоре об оценке должны содержаться следующие условия:
а) основания заключения договора
б) вид объекта оценки
в) вид определяемой стоимости (стоимостей) объекта оценки
г) сведения о страховании гражданской ответственности оценщика
д) все перечисленное
studfiles.net
Готовые тесты МФПУ( Синергия) и МИЭМП (им.Витте) |
В данной категории доступно часть тестов
с некоторыми ответами на каждый из тестов
таких институтов :
- МФПУ (Синергия)
- МИЭМП (им.Витте)
ДЛЯ быстрого ПОИСКА ТЕСТА воспользуйтесь формой «ПОИСК» — справа.
Если Вас интересует помощь в сдаче онлайн-тестов, то:
Быстро, недорого и на высокую оценку сдадим онлайн-тесты студентам дистанционной формы обучения:
 |
МЫ РАБОТАЕМ СЛЕДУЮЩИМ ОБРАЗОМ:
1) Вы передаете нам логин и пароль в Ваш личный кабинет;
2) Мы сдаем 1 тест для того, чтобы Вы убедились, что мы не обманем;
3) Вы оплачиваете тест, который мы сдали и оставшиеся тесты;
4) В течении 1-2 суток мы сдаем все оставшиеся тесты.
Мы гарантируем оценку не ниже «4» (70 баллов и выше).
70% наших оценок: 90-97 баллов
Примеры выполненных нами тестов



Свяжитесь с нами любым удобным для Вас способом
И получите бесплатную консультацию по любому вопросу!
xn--4-7sbqf2d.com
Ответы на тесты МФПУ Синергия
1. Как сдать тесты в Мегакампус Синергии
2. Примеры ответов на тесты Синергии
2.1. Физическая культура и спорт ответы
2.2. Информационные технологии в менеджменте — тесты с ответами
2.3. Тест по теории обучения и воспитания
2.4. Тест и экзамен по информатике
2.5. Концепции современного естествознания — тесты с ответами
2.6. Основы предпринимательства — тесты с ответами
2.7. Управление собственным бизнесом — тест с ответами
2.8. Тест Оценка стоимости бизнеса
2.9. Стратегический менеджмент — тесты с ответами
2.10. История — тест с ответами
2.11. Ответы на тест по микроэкономике
2.12. Бизнес практикум
2.13. Ответы на тест по экономике
2.14. Линейная алгебра — тест
2.15. Психология деловых отношений тест с ответами синергия
2.16. Оценочная деятельность тесты с ответами
2.17. Теория менеджмента Синергия ответы
2.18. Международные стандарты финансовой отчетности тест синергия
2.19. Ответы на тесты МФПУ Синергия Культурология
2.20. Юридическая логика тесты с ответами
2.21. Готовый тест по математике
2.22. Математика ответы
2.23. Тест Муниципальное право
2.24. Тест по английскому языку ответы
2.25. Тест Финансы Синергия
2.26. Теория и практика адвокатской деятельности тест
2.27. Международное частное право тесты с ответами
2.28. Экономическая теория тест вопросы
2.29. Тест правоохранительные органы МФПУ Синергия
2.30. Лидерство тесты с ответами
2.31. Ответы на тест Предпринимательское право
2.32. Психология тест
2.33. История и методология юридической науки тест
2.34. Ответы к тесту Основы оздоровительной гимнастики
2.35. Русский язык и культура речи тест
2.36. Управление человеческими ресурсами тесты с ответами синергия
2.37. Тест теория вероятности ответы
2.38. Конкуренция тесты с ответами МФПУ Синергия
2.39. Технологии обработки информации ответы на тесты
2.40. Тест в синергии 1 курс Педагогика
2.41. Тест Синергия онлайн Экономика и финансы организации
3. Где найти ответы на тесты бесплатно
4. Помощь в сдаче тестов, рефератов и курсовых работ
Возврат к списку
Выполнение контрольных, тестов, экзаменов точно в срок
Оправить заявку8 (800) 555-22-46, [email protected]
+7(930)-830-04-02Цены на стандартные типы работСтоимость выполнения задания зависит от сложности задания и временного интервала, поэтому рассчитывается индивидуально для каждого заказа. | |||
| Тип работы | Цена | ||
|---|---|---|---|
| Тесты, контрольные, задачи, рефераты, курсовые, чертежи | |||
| Тесты | от 800 руб | ||
| Контрольные, задачи | от 400 руб | ||
| Рефераты | от 900 руб | ||
| Курсовые | от 2000 руб | ||
| Чертежи | от 800 руб | ||
Порядок работы
| ❶ | Выяснение требований: вы можете прислать нам задания, или сообщить реквизиты личного кабинета |
| ❷ | Расчет стоимости: мы ознакомимся с заданием и сообщим вам цену в течение суток |
| ❸ | Оплата: вы можете оплатить каждое задание по отдельности, или весь семестр целиком |
| ❹ | Выполнение работ занимает до 14 рабочих дней, первые работы загружаются в личный кабинет на третий день |
| ❺ | Доработки до статуса «Зачтено»: мы доработаем и повторно загрузим все незачтенные задания, если это потребуется |
Наши преимущества
| ↯ | Быстрая оценка работ — вы узнаете стоимость в день обращения |
| ★ | Только профессионалы — задания выполняют наши образованные, ответственные специалисты: выпускники ВУЗов, преподаватели, кандидаты и доктора наук, которые проходят строгий отбор, поэтому задания сдаются с первого раза, это экономит ваше время |
| ₽ | Поэтапная оплата — вы можете разбить задания на группы и оплатить их постепенно, или оплатить весь семестр и получить скидку от большего количества заданий |
Ваши отзывы
Каждый положительный отзыв это результат кропотливого труда нашей команды. Спасибо Вам за добрые слова!
Здравствуйте! Вчера закрыл семестр! Все задания приняты с первого раза!Спасибо вам большое!!!
Не успевал сделать чертежи. Спасибо за оперативность, сдал вовремя на отл.
prorektor.ru
Бесплатные ответы на тесты МФПУ «Синергия» по предмету «история»
- 1.Председателем правительства РФ в 2004 г. стал …
Отметьте правильный вариант ответа:
1)М. Касьянов
2)В. Черномырдин
3)В. Путин
4)М. Фрадков
- 2.Расположите в хронологической последовательности
Варианты ответа:
А-Создание Организации Варшавского договора
В-Появление «доктрины Трумэна»
С-Создание военно-политического союза НАТО
D-Образование ФРГ
Ответ: BCDA
- 3.Среди командующих Красной Армии в годы гражданской войны были:
Отметьте правильный вариант ответа:1)Тухачевский, Миллер, Краснов
2)Троцкий, Каледин, Петлюра
3)Марков, Савинков, Алексеев
4)Вацетис, Егоров, Фрунзе
- 4.Расположите в хронологической последовательности
Варианты ответа:
А-Формирование Добровольческой армии
В-Мятеж чехословацкого корпуса
С-Заключение Брестского мираD-Появление интервентов во Владивостоке
Ответ:
ADCB
- 5.В 1990-ых годах произошло …
Отметьте правильный вариант ответа:
1)Первый Съезд народных депутатов
2)Принятие нового устава КПСС
3) «дело ЮКОСА»
4)создание СНГ
- 6. «Просвещенный абсолютизм» -это политика, характерная для правления …
Отметьте правильный вариант ответа:
1)Александра I
2)Екатерины II
3)Елизаветы Петровны
4)Петра Великого
- 7.Расположите события в правильной хронологической последовательности
Варианты ответа:
А-княжение Данила Александровича
В-княжение Ивана Калиты
C-нашествие монголо-татарских войск на Русь, приведшее к ее покорению
D-Куликовская битва
Ответ:
CABD
- 8.Автором работы «История государства Российского» является …
Отметьте правильный вариант ответа:
1)Н.М. Карамзин
2)В.Н. Татищев
3)С.Ф. Платонов
4)С.М. Соловьев
- 9.Иосифляне придерживались взглядов, в основе которых было мнение …
Отметьте правильный вариант ответа:
1)об отсутствии монастырского землевладения
2)о божественном характере великокняжеской власти
3)об отрешенности монахов от земных забот
- 10.Основопологающие вопросы общественной жизни России после Февральской революции предполагалось вынести на решение …
Отметьте правильный вариант ответа:
1)Учредительного собрания
2)Государственной группы
3)Временного правительства
4)Всероссийского съезда Совета
- 11.Расположите в хронологической последовательности Варианты ответа:
A-Второй кризис Временного правительства
В-Отречение Николая IIC-Корниловский мятеж
D-Складывание двоевластия
Ответ: DBAC
- 12.Советскими военноначальниками периода Великой Отечественной войны являлись:
Отметьте правильный вариант ответа:
1)Г.К. Жуков и А.И. Егоров
2)К.К. Рокоссовский и А.М. Василевский
3)П.К. Пономаренко и В.К. Блюхер
4)К.Е. Ворошилов и М.Н. Тухачевский
- 13.К параметрам Российского либерального проекта относится …
Отметьте правильный вариант ответа:
1)сохранение сословной иерархии
2)признание «борьбы классов» главным фактором исторического прогресса
3)критика капитализма
4)наличие параметра европейского типа
- 14.Новыми явлениями экономической жизни России XVII века стало …
Отметьте правильный вариант ответа:
1)появление мануфактур
2)введение подушной подати
3)отмена местничества
- 15.Расположите события 1905-1906 гг. в хронологической последовательностиВарианты ответа:
A-Всероссийская Октябрьская политическая стачка
B-1 съезд “Союза 17 октября»
C-Восстание на броненосце «Князь Потемкин-Таврический»
D-«Кровавое воскресенье»
Ответ: DCAB
- 16.Расположите в хронологической последовательности
Варианты ответа:
A-воцарение династии Романовых
B-правление «Семибоярщины»
C-возникновение раскола в Русской православной церкви
D-принятие Соборного уложения
Ответ: BADC
- 17.Автором работы «История России с древнейших времен» является …
Отметьте правильный вариант ответа:
1)С.М. Соловьев
2)В.Н. Татищев
3)Н.М. Карамзин
4)С.Ф. Платонов
- 18.Соотнесите исторические события и даты
A-Ввод советских войск в Афганистане
В-Карибский кризис
С-Совещание в Хельсинки
D-1979E-1975F-1962
Ответ: А-D, B-F, C-E19.
- 19 Хрущевская реформа управления народным хозяйством предусматривала …
Отметьте правильный вариант ответа:
1)понижение плановых показателей
2)развитие частного предпринимательства
3)конвертируемость советской валюты
4)ликвидацию отраслевых министерств
- 20.Характерной чертой политики «военного коммунизма» являлась …
Отметьте правильный вариант ответа:
1)продразверстка
2)функционирование акционерных обществ
3)национализация крупных предприятий
4)возможность хозяйственного самоуправления
- 21.Комплекс Контрреформ Александра III включал в себя …
Отметьте правильный вариант ответа:
1)отмену суда присяжных
2)циркуляр «О кухаркиных детях»
3)возврат системы крепостного права
4)военную контрреформу
- 22.Восточные славяне языческого периода поклонялись богам:
Отметьте правильный вариант ответа:
1)Даждьбогу и Хорсу
2)Перуну и Янусу
3)Макоши и Зевсу
4)Яриле и Марсу
- 23.Окончательное закрепощение крестьян было оформлено в …
Отметьте правильный вариант ответа:
1)Соборном уложении
2)Указе «О заповедных летах»
3)Судебнике Ивана IV
4)Судебник Ивана III
- 24.Расположите в хронологической последовательности Варианты ответа:
A-создание Центрального штаба партизанского движения
B-Убийство С.М. Кирова
C-провозглашение курса на индустриализацию
D-образование СССР
Ответ: D, C, B, A
- 25.Окончательный распад Древней Руси на отдельные самостоятельные территории произошел после смерти князя …Отметьте правильный вариант ответа:
1)Владимира Мономаха
2)Ярослава Мудрого
3)Мстислава Великого
4)Юрия Долгорукого
- 26.Приказ №1 Петроградского Совета рабочих и солдатских депутатов был посвящен …
Отметьте правильный вариант ответа:
1)продовольственному снабжению населения
2)взаимоотношениям между политическими партиями
3)заключению перемирия между воюющими сторонами
4)демократизации армии
- 27.Расположите события в правильной хронологической последовательности Варианты ответа:
A-появление в Киевской Руси первого письменного свода знаков
B-Монгольское нашествие на Русь
C-Появление «Повести временных лет»
D-Ледовое побоище
Ответ: A, C, B, D
- 28.Расположите в хронологической последовательности
Варианты ответа:
A-Подписание «Жалованной грамоты городам»
B-Указ «О вольных хлебопашцах»
C-Появление военных поселений
D-Появление категории «посессионных крестьян»
Ответ: D, A,B,C
- 30.Среди особенностей российского абсолютизма XVIII века можно назвать …
Отметьте правильный вариант ответа:
1)дворцовые перевороты
2)функционирование Земского собора
3)большую роль дворянского ополчения
4)существование института патриаршества в русской православной церкви
- 31.Среди реформ государственного управления, осуществленных в период правления Александра I, можно выделить …Отметьте правильный вариант ответа:
1)появление Государственного Совета, возникшего в соответствии с планом М.М. Сперанского
2)созыв Уложенной комиссии
3)возникновение Верховного Тайного Совета
4)возникновение коллегий
- 32.Для Владимиро-Суздальского княжества была характерна следующая политическая модель:Отметьте правильный вариант ответа:
1)развитие демократических вечевых порядков
2)сильная княжеская власть и тенденции к централизации
3)тесное сотрудничество княжеской власти, вече, и боярства
4)укрепление положения боярства
- 33.Расположите в хронологической последовательностиВарианты ответа:
A-Речь У. Черчилля в г. Фултон
B-Атомная бомбардировка японских городов Хиросимы и Нагасаки
C-Сражение под Сталинградом
D-Восстановление границы СССР
Ответ: C,D,B,A34.
Неверно, что к народническим организациям в России относился …
Отметьте правильный вариант ответа:
1)Кружок Н.В. Чайковского
2) «Народная воля»
3) «Земля и Воля»
4)Кружок Д. И. Благоева
- 35.Расположите в хронологической последовательности
Варианты ответа:
A-Принятие Декрета «О земле»
B-Осуществление политики «военного коммунизма»
C-Выборы в Учредительное собрание
D-Открытие II Всероссийского съезда Совета
Ответ: D, A, C, B
- 36.Комплекс «Великих реформ» Александра II включает в себя …
Отметьте правильный вариант ответа:
1)переход к федеративному государственному устройству
2)учреждение Государственной Думы
3)введение всеобщей воинской повинности
4)реформу ценообразования
- 37.Период царствования Николая I характеризуется …
Отметьте правильный вариант ответа:
1)усилением местного самоуправления
2)началом промышленного переворота
3)появлением «военных поселений»
4)либеральными реформами в области печати и образования
- 38. Расположите в хронологической последовательности
Варианты ответа:
A-Введение ограничения переходов крестьян, которые могли произойти только в период связанный с Юрьевым днем
B-Введение опричнины
C-Возникновение в России Земского собора
D-Образование Тушинского лагеря Лжедмитрия II
Ответ: C, B, D, A
- 39.Лидером партии социалистов-революционеров (эсеров) являлся …
Отметьте правильный вариант ответа:
1)П.Н. Милюков
2)П.А. Кропоткин
3)В.М. Чернов
4)Г.В. Плеханов
- 40.Среди предпосылок создания древнерусского государства необходимо назвать …
Отметьте правильный вариант ответа:
1)принятие христианства
2)социальное и имущественное расслоение
3)призвание варягов
- 41.Отличительными чертами НЭПа являлись: …
Отметьте правильный вариант ответа:
1)принудительный труд и внедрение элементов долгосрочного планирования
2)возрождение частного предпринимательства и денежная реформа
3)введение бесплатных коммунальных услуг и насаждение коммун в деревнях
- 42.Среди главных вопросов, обсуждаемых в тайных декабристских организациях, были вопросы …
Отметьте правильный вариант ответа:
1)введения в России Конституции и отмена крепостного права
2)о превращении России в республику и об осуществлении промышленного переворота
3)о превращении России в конституционную монархию и о расширении торговых связей
4)об укреплении в России самодержавия и о привлечении к трону образованных людей
- 43.События Крымской войны относятся к периоду …
Отметьте правильный вариант ответа:
1)1700-1721гг.
2)1812-1814 гг.
3)1877-1878 гг.
4)1853-1856 гг.
- 44. Расположите в хронологической последовательности
Варианты ответа:
A-стояние на реке Угре
B-обретение автокефальности Русской православной церковью
C-появление первого общерусского Судебника
D-начало династической войны в Московском княжестве
Ответ: D, B, A, C
- 45. Расположите в хронологической последовательностиВарианты ответа:
A-Полтавская битва
B-Заключение Ништадского мира
C-Заключение Тильзитского мира
D-Разделы Польши
Ответ: A, B, D, C
- 46.Экономическая политика индустриализации и коллективизации способствовала …
Отметьте правильный вариант ответа:
1)преодолению катастрофических последствий I Мировой войны и гражданской войны
2)созданию державы, полностью опирающейся на свои внутренние ресурсы
3)развитию в стране частных предприятий, опиравшихся на личную заинтересованность работника в результате труда
- 47.Центрами формирования белых сил периода Гражданской войны являлись:
Отметьте правильный вариант ответа:
1)Крым, часть Эстонии, южный Кавказ
2)Верхняя Волга, район Нарвы и Пскова, Тамбовская область
3)Донская область, Кубанская область, Южный Урал
4)район реки Терек, Архангельская область, Северный Урал
- 48.Среди основных причин распада Древней Руси можно назвать …
Отметьте правильный вариант ответа:
1)возросшее значение торгового пути «из варяг в греки»
2)возросшее значение крупнейших городов
3)усилившиеся враждебные соседи
- 49.К параметрам Российского консервативного проекта относится …
Отметьте правильный вариант ответа:
1)отмена исторических сословий
2)критика «деспотизма» русской монархии
3)вера в способность передовой русской интеллигенции возглавить политические-неграмотные массы в направлении справедливого переустройства общества
4)сохранение традиционного религиозного сознания-как высшей формы общественной морали
- 50. Расположите в хронологической последовательности
Варианты ответа:
A-Появление документа «Жалованная грамота дворянству»
B-Появление Сената
C-Подписание Указа «О престолонаследии»
D-Появление Манифеста «О вольности дворянской»
Ответ: C, D, A, B
- 51.Cреди причин, вызвавших кризис Российской государственности на рубеже XVI-XVII веке, можно назвать …
Отметьте правильный вариант ответа:
1)денежную реформу и реформу церкви
2)борьбу с Казанским и Астраханским ханством
3)последствия опричнины и Ливонской войны
- 52.Соотнесите представителей российской науки и культуры и сферу их деятельности
A-Историческая наука
B-География
C-Живопись
D-Н. М. Карамзин, Н. М. Погодин, Н. И. КостомаровE-П. П. Семенов-Тянь-Шанский, Н. М. Пржевальский, Н. Н. Мик-лухо-Маклай
F-А. Г. Венецианов, И. Н. Крамской, Н. Н. Ге
Ответ: A-D, B-E, C-F
- 53.В 1990-ых годах произошло …
Отметьте правильный вариант ответа:
1)Компания по борьбе с алкоголизмом
2)учреждение семи федеральных округов
3)ввод советских войск в Афганистане
4)танковый обстрел здания Верховного Совета
- 54. Соотнесите представителей российской науки и культуры и сферу их деятельности
A-Социология
B-Художественная литература
C-Музыкальное искусство
D-А. И. Гончаров, Н. А. Некрасов, М. Е. Салтыков-ЩедринE-П. Л. Лавров, Н. К. Михайловский, М. М. КовалевскийF-М. И. Глинка, М. П. Мусоргский, Н. А. Римский-Корсаков
Ответ: A-E, B-D, C-F
- 55.Борис Годунов стал правителем России …
Отметьте правильный вариант ответа:
1)по завещанию Ивана Грозного
2)по итогам избрания Боярской Думой
3)в результате захвата власти
4)в результате избрания сословно-представительным органом
- 56.Неверно, что к числу специальных (вспомогательных) исторических дисциплин относится …
Отметьте правильный вариант ответа:
1)генеалогия
2)орфография
3)источниковедение
4)палеография
- 57.Основополагающие вопросы общественной жизни России после Февральской революции предполагалось вынести на решение …
Отметьте правильный вариант ответа:
1)Всероссийского съезда Советов
2)Временного правительства
3)Учредительного собрания
4)Государственной Думы
- 58.Расположите в хронологической последовательности
Варианты ответа:
A-Оборона Севастополя
B-«битва народов»
C-Бородинская битва
D-Парижский мирный договор
Ответ: C, B, D, A
- 59.В первое столетие своего существования древнерусское государство представляло собой …
Отметьте правильный вариант ответа:
1)централизованное государство с развитым аппаратом, активно присоединяющее соседние территории
2)мощную республику с развитым государственным аппаратом
3)внутренне единое государственное образование, ведущее активную внешнюю политику
4)непрочную федерацию отдельных территорий, выплачивающих дань центру
- 60.Победа большевиков в России осенью 1917 года явилась следствием ряда факторов, среди которых …Отметьте правильный вариант ответа:
1)массовая поддержка населением первых решительных мер борьбы с контрреволюционерами
2)массовая поддержка населением первых общедемократических декретов советской власти
3)неспособность бывшего императора Николая II организовать сопротивление большевикам
- 61.К параметрам российского консервативного проекта относится…
Отметьте правильный вариант ответа:
1)вера в способность передовой русской интеллигенции возглавить политически-неграмотные массы в направлении справедливого переустройства общества
2)отмена исторических сословий
3)критика «деспотизма» русской монархии
4)сохранение традиционного религиозного сознания-как высшей формы общественной морали62.Конституция 1977 г. закрепляла положение …
Отметьте правильный вариант ответа:
1)о построении коммунизма к 1980 году
2)о ведущей роли КПСС в руководстве государством и обществом
3)об обострении классовой борьбы
4)о диктатуре пролетариата
- 63.Лидером старообрядцев был …
Отметьте правильный вариант ответа:
1)протопоп Аввакум
2)патриарх Филарет
3)патриарх Иосаф
4)патриарх Никон
- 64.Соотнесите исторические события и даты
A-Визит Н. Хрущева в СШАB-Создание Организации Варшавского Договора
C-Договора ОСВ-1
D-1959
E-1972
F-1955
Ответ: A-D, B-F, C-E
- 65.Важное значение для отражения набегов кочевников-половцев играла деятельность князя …Отметьте правильный вариант ответа:
1)Владимира I Святославовича
2)Владимира Мономаха
3)Ярослава Мудрого
4)Святослава
- 66.Автором работы «Лекции по русской истории» является …
Отметьте правильный вариант ответа:
1)С. М. Соловьев
2)Н. М. Карамзин
3)С. Ф. Платонов
4)В. Н. Татищев
- 67. Расположите в хронологической последовательности
Варианты ответа:
A-Открытие «второго фронта»
B-Битва на Курской дуге
C-Начало холодной войны
D-Капитуляция Японии
Ответ: B, A, D, C
68.Двенадцатое (12) декабря 1993 г. стал днем …
Отметьте правильный вариант ответа:
1)принятия Конституции РФ на референдуме
2)подписания Федеративного договора
3)начала войны в Чечне
4)выборов президента страны
- 69.Среди причин поражения России в I Мировой войне были …
Отметьте правильный вариант ответа:
1)неспособность к придуманным действиям и разложение правящей элиты страны
2)корыстные интересы союзников России
3)деятельность партии большевиков
4)дворцовые перевороты
- 70.Период правления Александра I характеризуется …
Отметьте правильный вариант ответа:
1)учреждением Сената
2)регулированием вопросов престолонаследия
3)укреплением режима самодержавия в начале царствования
4) «аракчеевщиной»
- 71. Расположите события в правильной хронологической последовательности
Варианты ответа:
A-Установление «уроков и погостов»
B-Принятие христианства на Руси
C-Призвание варягов во главе с Рюриком
D-Возникновение Древнерусского государства
Ответ: C, D, A, B72.
- После смерти В. И. Ленина соперниками И. В. Сталина во внутрипартийной борьбе, пользовавшиеся большим влиянием в ВКП(б), были: …
Отметьте правильный вариант ответа:
1)Н. И. Бухарин и Ф. Э. Дзержинский
2)А. И. Рыков и С. М. Киров
3)Л. Д. Троцкий и Г. Е. Зиновьев
4)В. М. Молотов и Л. Б. Каменев
- 73. Расположите в хронологической последовательностиВарианты ответа:
A-Разгром белых войск в Крыму
B-Начало советско-польской войны
C-Приход к власти адмирала Колчака
D-Поход войск Юденича на Петроград
Ответ: C, B, D. A
- 74.Первым правителем, официально принявшим титул «Государь всея Руси» был …
Отметьте правильный вариант ответа:
1)Ивана IV Грозный
2)Иван Калита
3)Дмитрий Донской
4)Иван III
- 75. Расположите в хронологической последовательности
Варианты ответа:
A-Образование Тушинского лагеря Лжедмитрия II
B-Введение опричнины
C-Введение ограничения переходов крестьян, которые могли произойти только в период, связанный с Юрьевым днем
D-Возникновение в России Земского собора
Ответ: C, D, B, A
xn—-etbfclc6azafijc8n.xn--p1ai


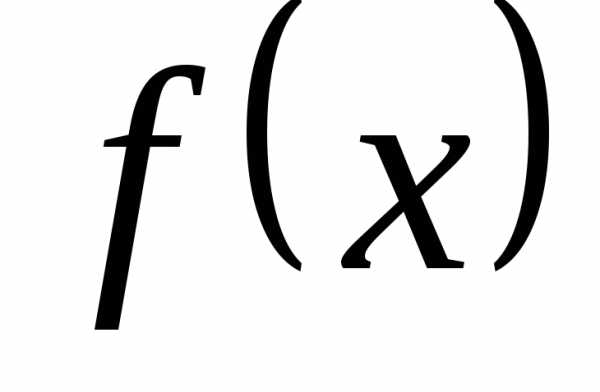 в точке
в точке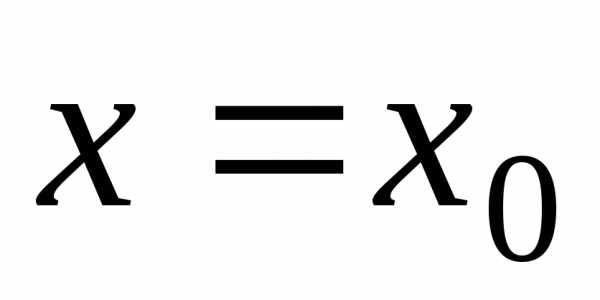 или принадо применить теоремы о пределах и
подставить предельное значение аргумента.
или принадо применить теоремы о пределах и
подставить предельное значение аргумента.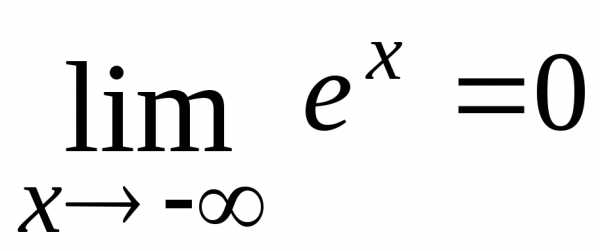 .
.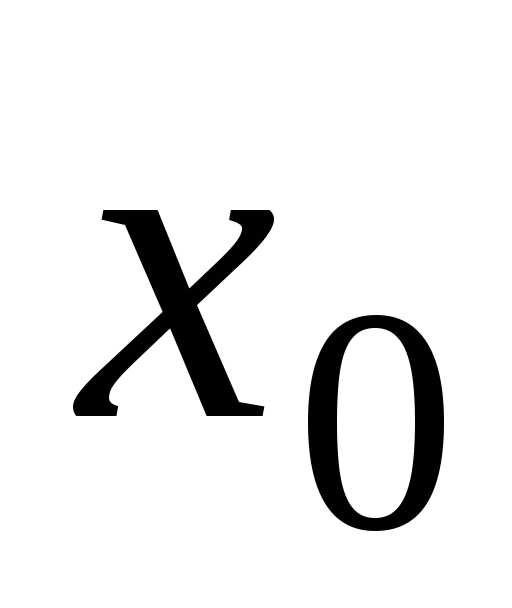 часто приводит к неопределенным
выражениям вида:
часто приводит к неопределенным
выражениям вида: ,
, ,
,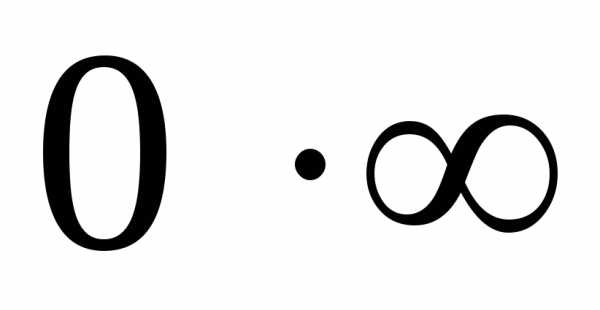 ,,
,,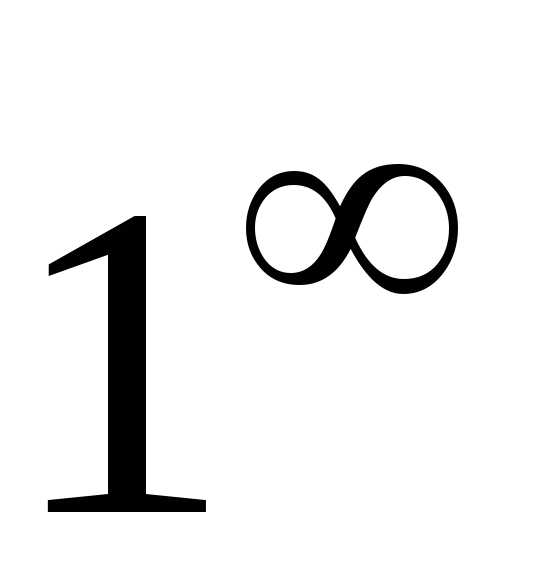 ,
,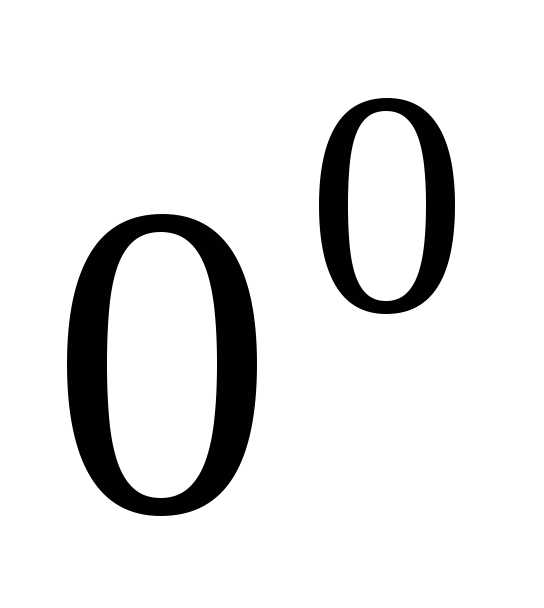 ,
,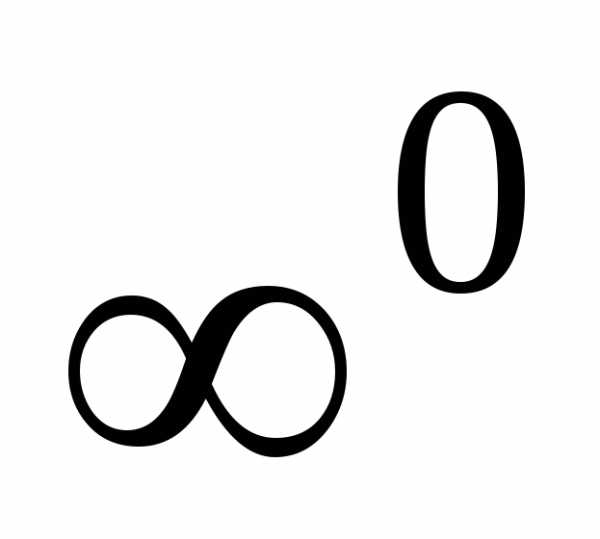 .
.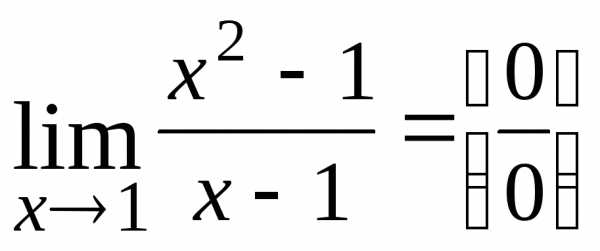 или
или .
. ,
, ,,
,,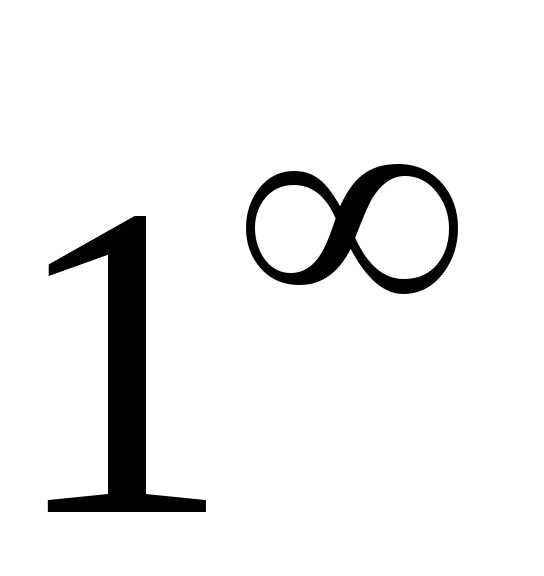 ,
,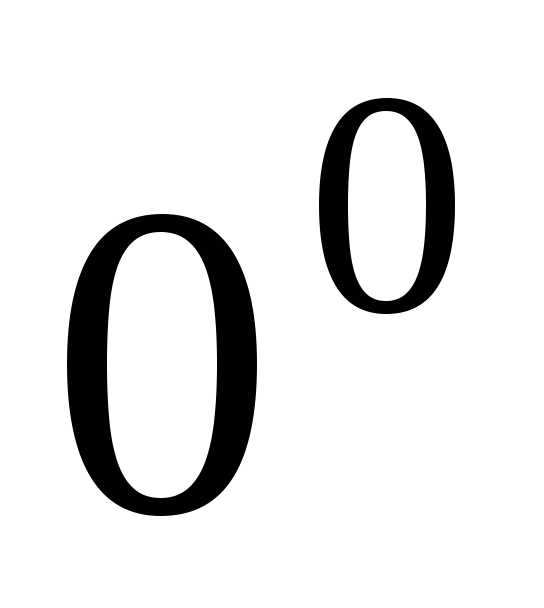 ,
,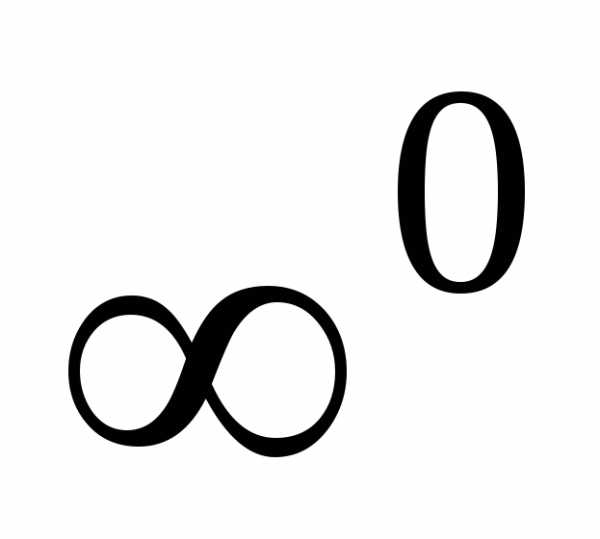 называютсянеопределенностями.
называютсянеопределенностями. (),
то говорят, что их частное
(),
то говорят, что их частное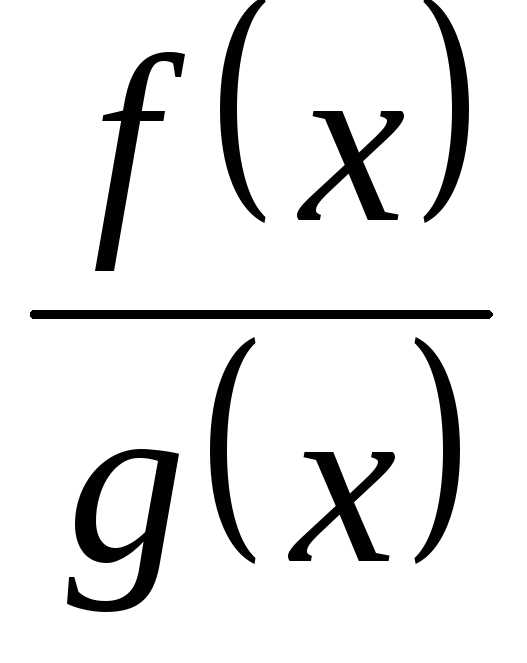 представляет собой неопределенность
вида
представляет собой неопределенность
вида .
. ,
заданную отношением двух многочленов,
надо и числитель и знаменатель разделить
на самую высокую входящую в них степеньх.
,
заданную отношением двух многочленов,
надо и числитель и знаменатель разделить
на самую высокую входящую в них степеньх.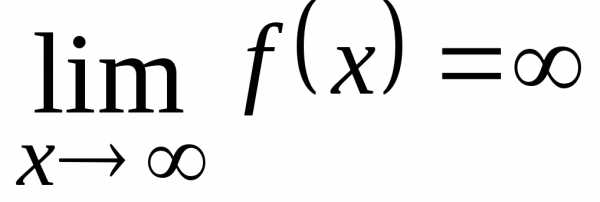 ,
если
,
если  ;
; ,
если
,
если  ;
;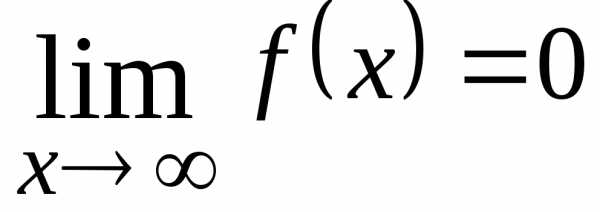 ,
если
,
если  .
.
 ,
где
,
где и
и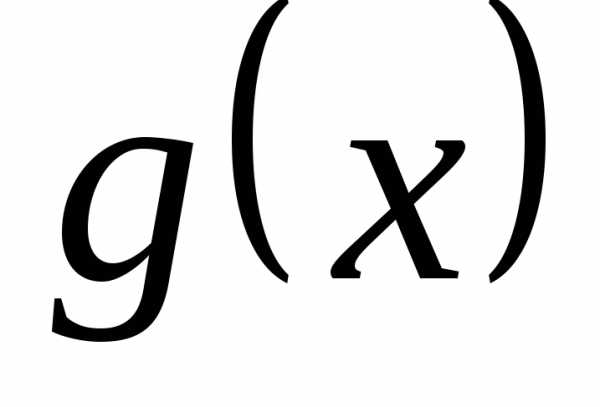 − бесконечно малые функции при
− бесконечно малые функции при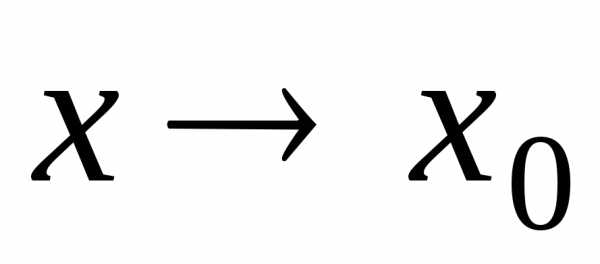 (),
т.е.,
то в этом случае вычисление предела
называют раскрытием неопределенности
вида
(),
т.е.,
то в этом случае вычисление предела
называют раскрытием неопределенности
вида  .
. ,
заданную отношением двух многочленов,
надо и в числителе и в знаменателе
выделить критический множитель и
сократить на него дробь.
,
заданную отношением двух многочленов,
надо и в числителе и в знаменателе
выделить критический множитель и
сократить на него дробь. ,
в которой числитель или знаменатель,
или тот и другой иррациональны, надо:
,
в которой числитель или знаменатель,
или тот и другой иррациональны, надо: ;
; ,
содержащей тригонометрические выражения,
используют первый замечательный предел:
,
содержащей тригонометрические выражения,
используют первый замечательный предел: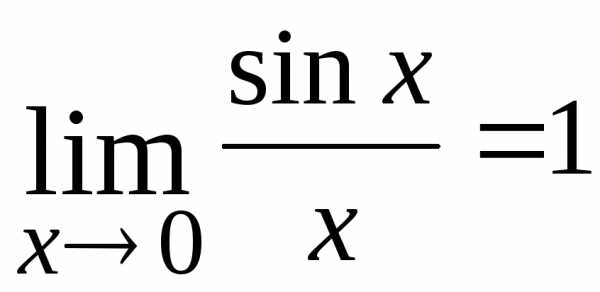 или
или 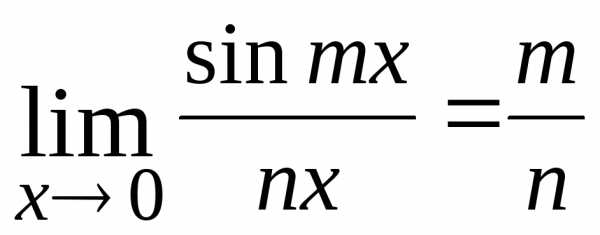 ,
, и
и .
. можно и числитель и знаменатель заменить
величинами им эквивалентными (п.2.12).
можно и числитель и знаменатель заменить
величинами им эквивалентными (п.2.12).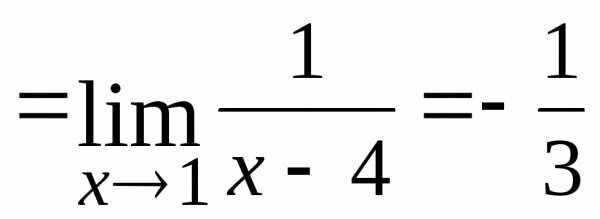 .
.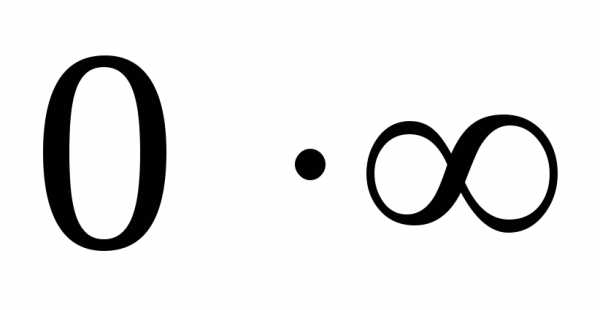
 ,
то их разностьпредставляет собой неопределенность
вида .
,
то их разностьпредставляет собой неопределенность
вида .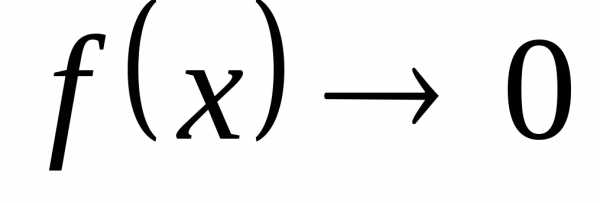 ипри
ипри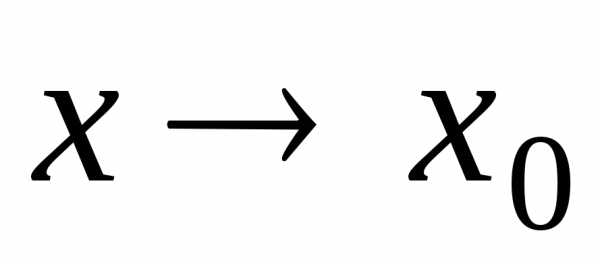
 ,
то их произведение− это неопределенность вида
,
то их произведение− это неопределенность вида 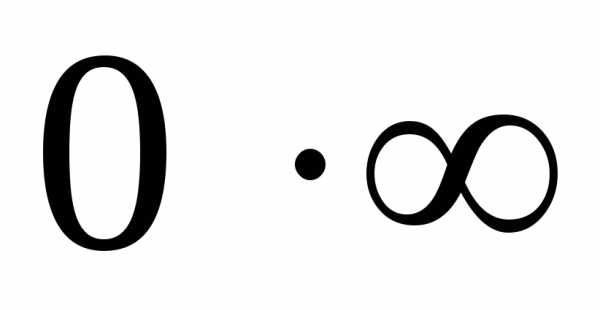 .
. раскрываются путем их преобразования
и сведения к неопределенностям вида
раскрываются путем их преобразования
и сведения к неопределенностям вида или
или .
.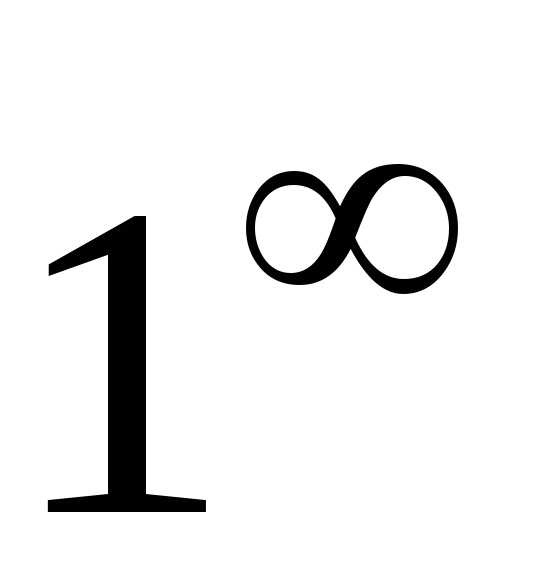 ,
,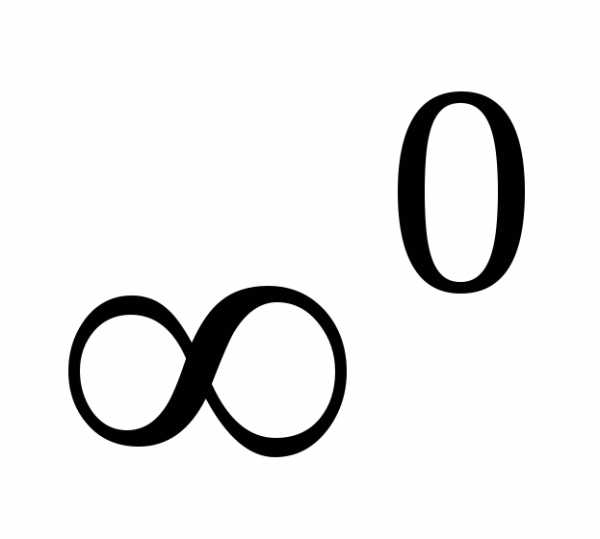 ,
,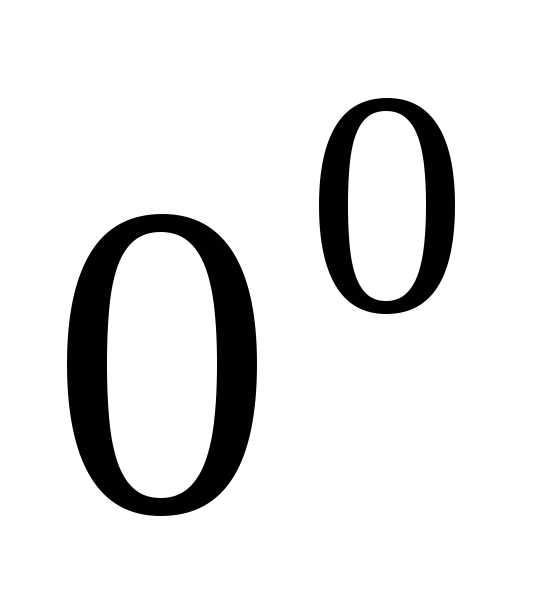
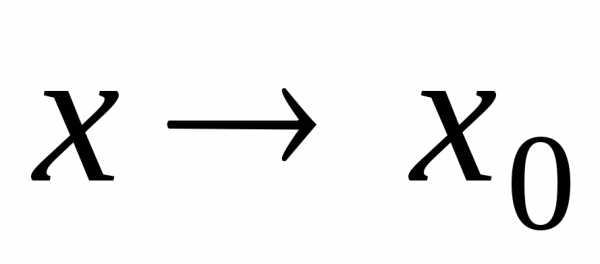
 ,
,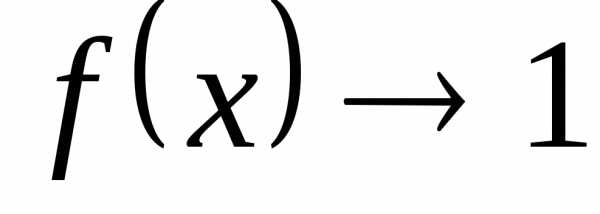 ,
а,
то имеем неопределенность вида
,
а,
то имеем неопределенность вида  .
Для раскрытия этой неопределенности
применяют второй замечательный предел:
.
Для раскрытия этой неопределенности
применяют второй замечательный предел: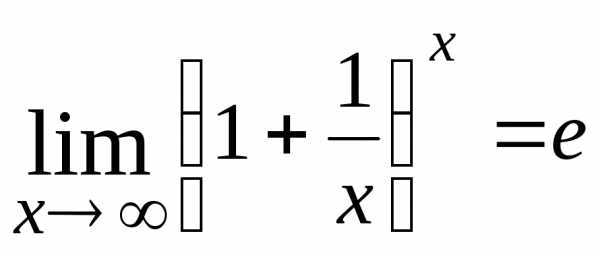 ;
; 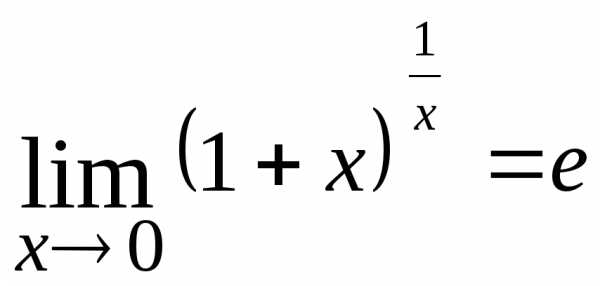 ;
;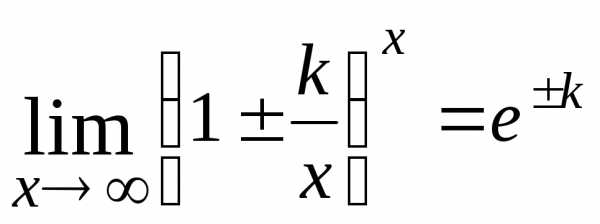 ;
; 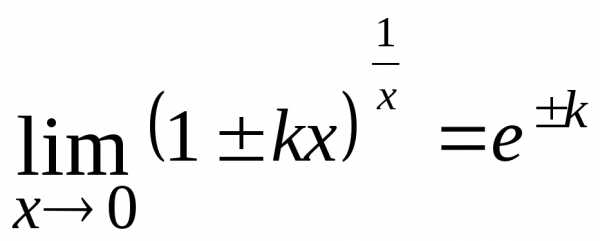 .
.
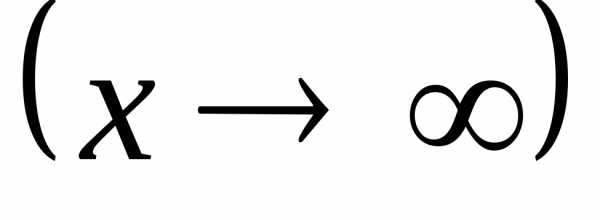 ,,
а
,,
а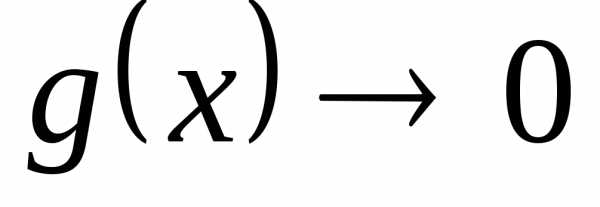 ,
то имеем неопределенность вида
,
то имеем неопределенность вида 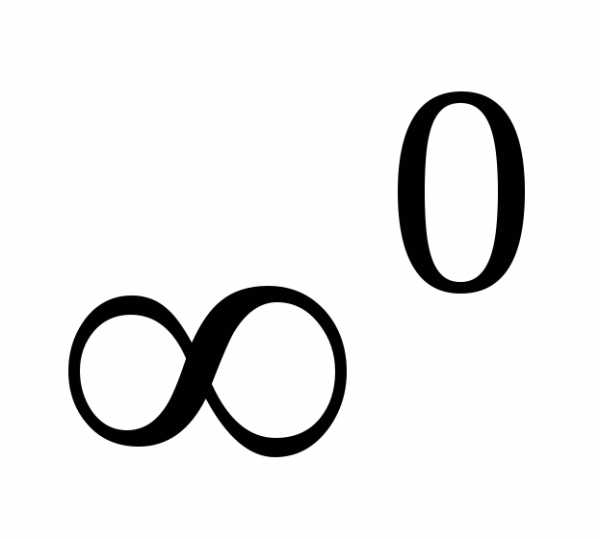 .
. и
и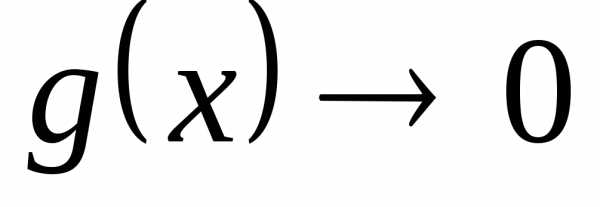 при
при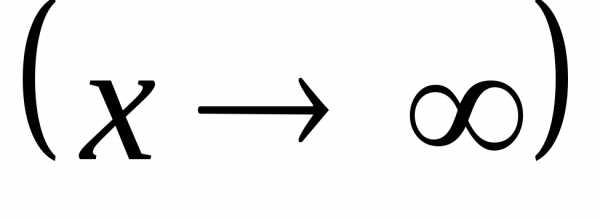 ,
то имеет место неопределенность
,
то имеет место неопределенность  .
.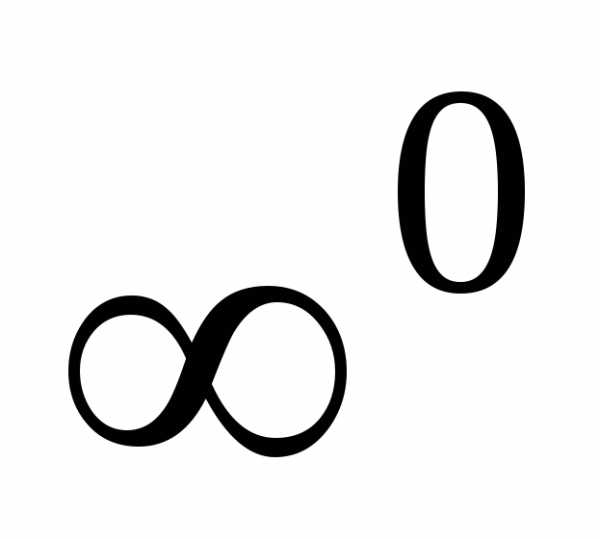 и
и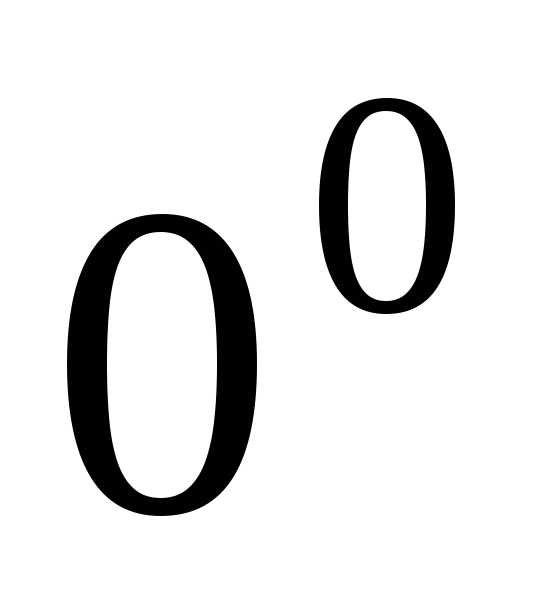 их преобразуют и сводят к неопределенности
вида
их преобразуют и сводят к неопределенности
вида следующим образом:
следующим образом: ; Ответ:
; Ответ: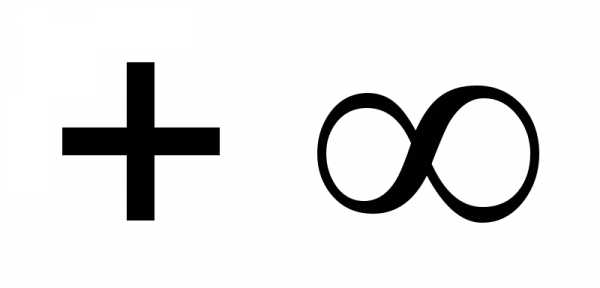 ;
;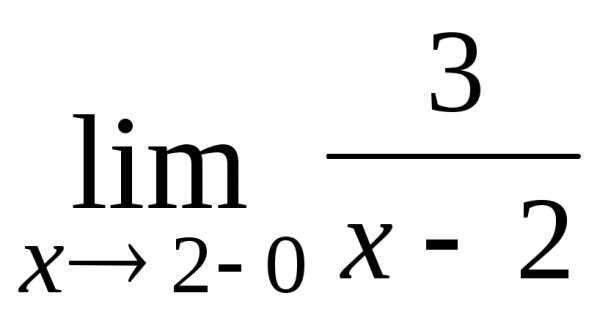 ; Ответ:
; Ответ:  ;
; ; Ответь:
; Ответь: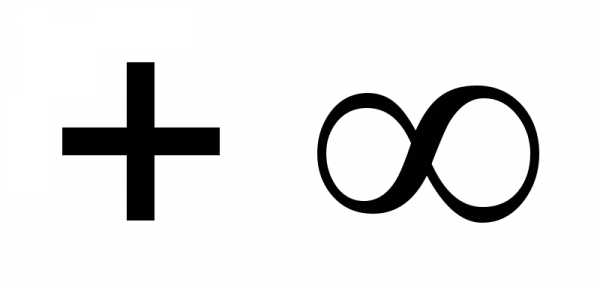 ;
;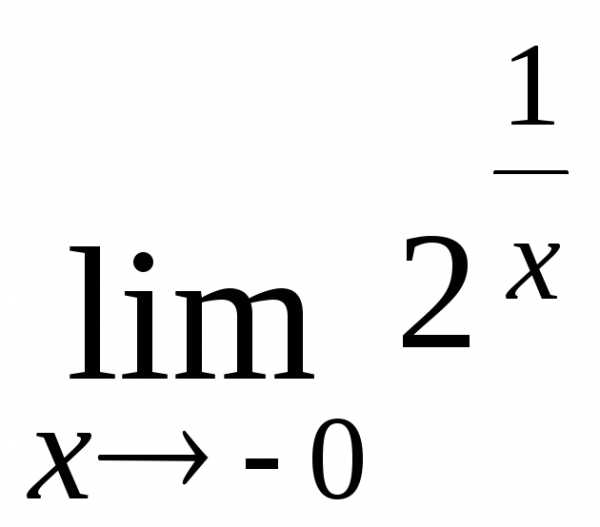 ; Ответ:
0.
; Ответ:
0.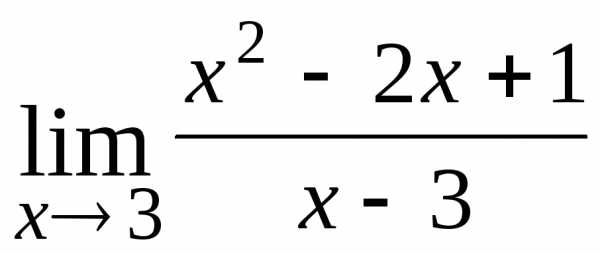 ; Ответ:
; Ответ: .
.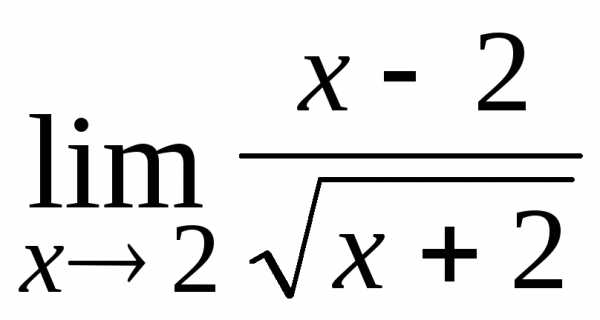 ; Ответ:
0.
; Ответ:
0. .
Найти пределы:
.
Найти пределы: ; Ответ:
0;
; Ответ:
0; ; Ответ:
-2;
; Ответ:
-2;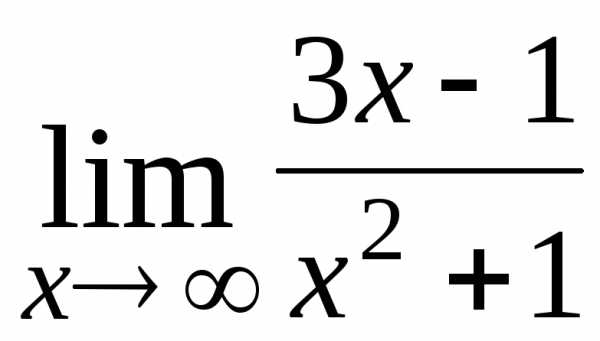 ; Ответ:
; Ответ: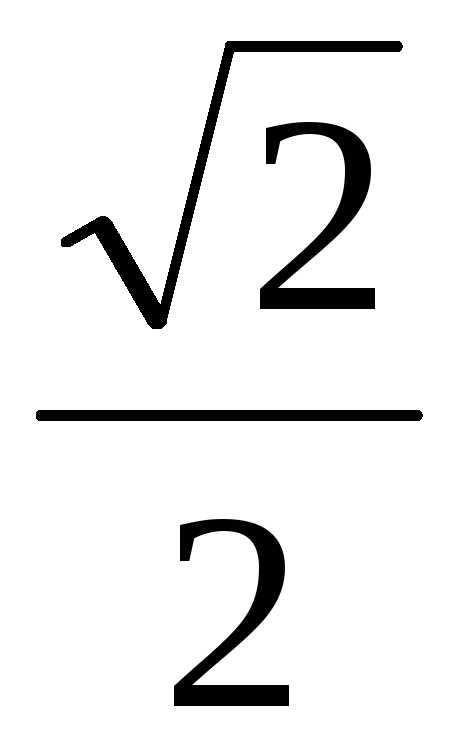 ;
; ; Ответ:
; Ответ: .
. .
Найти пределы:
.
Найти пределы: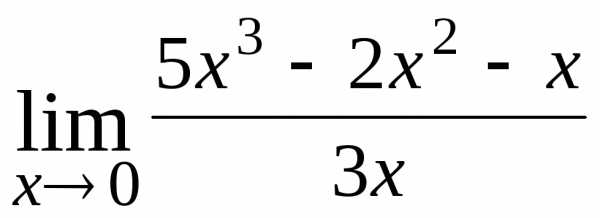 ; Ответ:
; Ответ: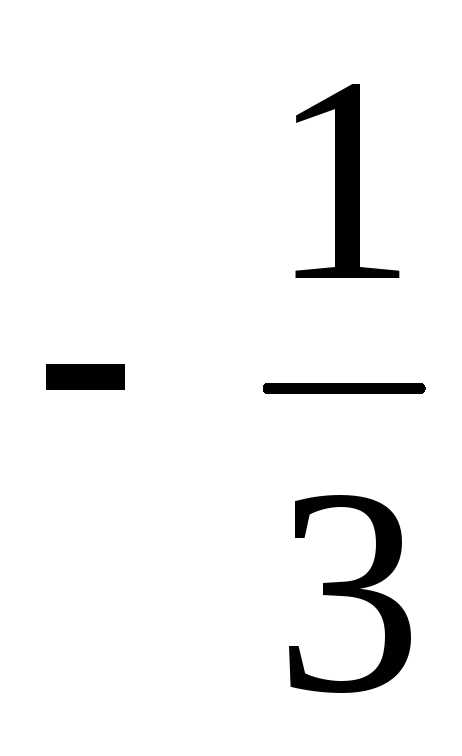 ;
; ; Ответ:
-2;
; Ответ:
-2; ; Ответ:
; Ответ: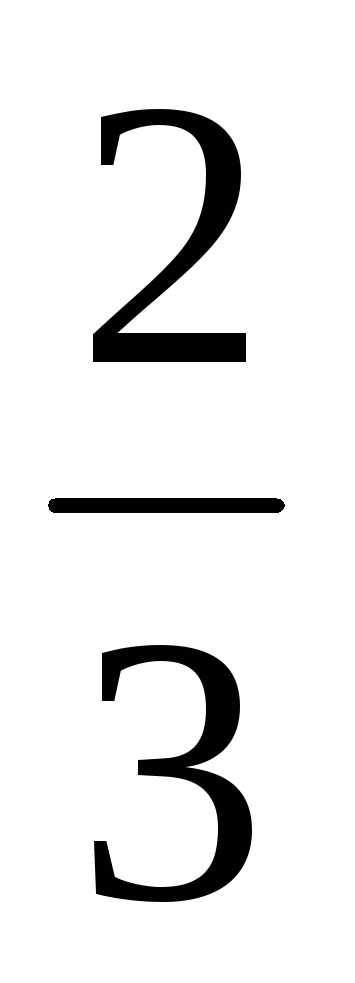 ;
;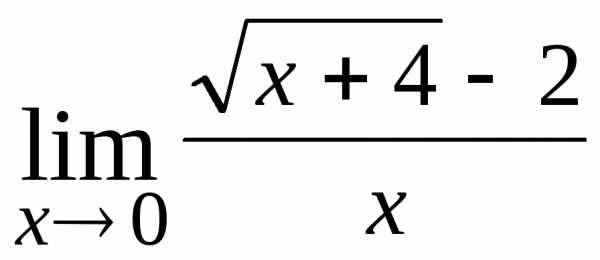 ; Ответ:
; Ответ: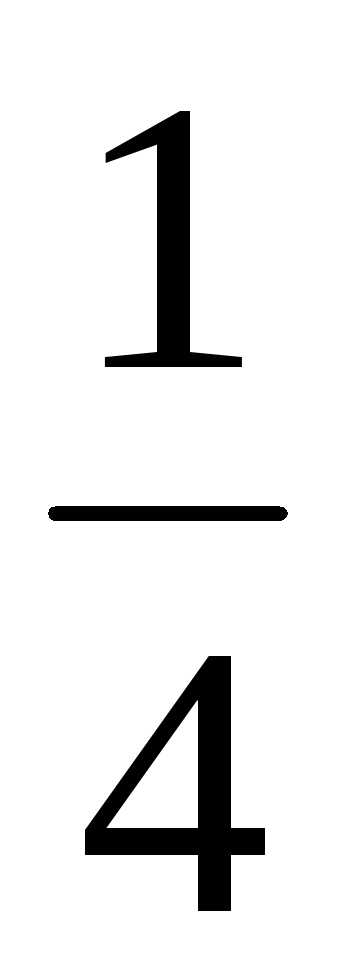 ;
; ; Ответ:
-12;
; Ответ:
-12;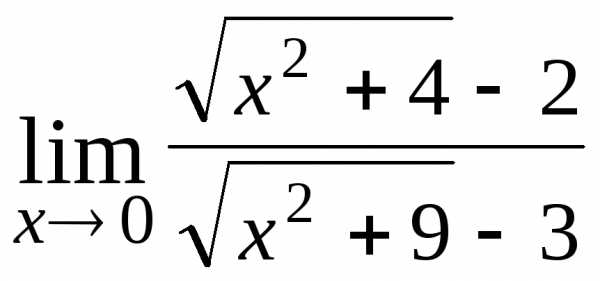 ; Ответ:
; Ответ: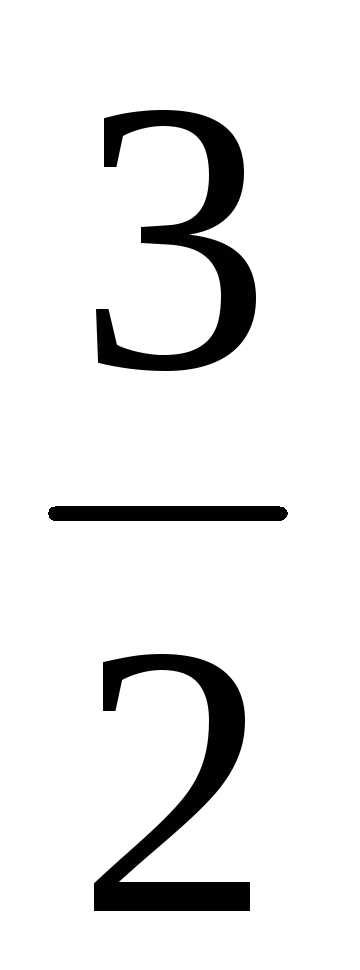 .
.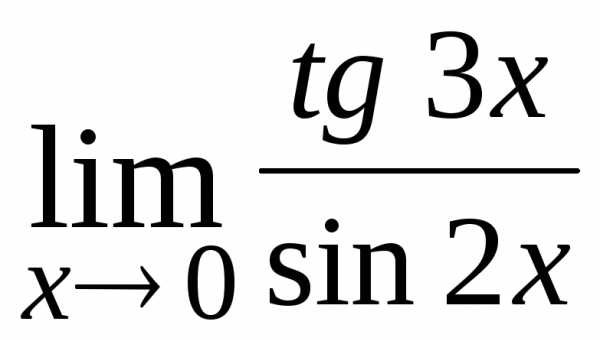 ; Ответ:
; Ответ: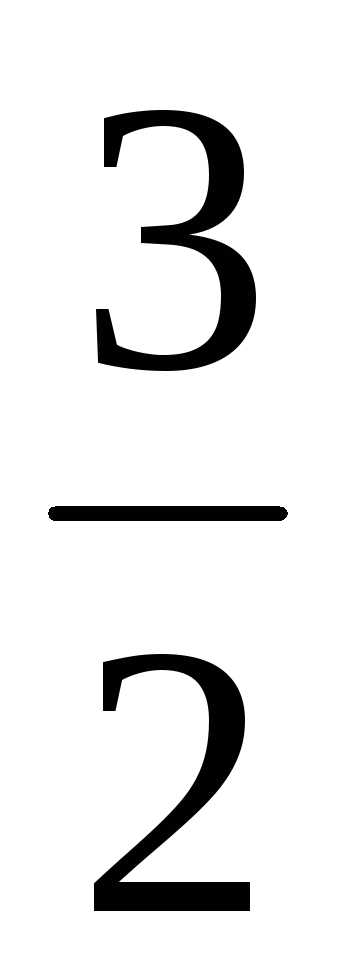 ;
; ; Ответ:
; Ответ: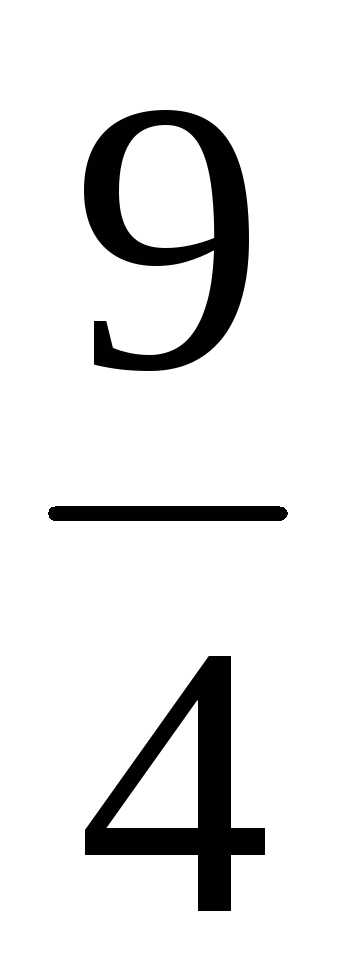 ;
; ; Ответ:
; Ответ: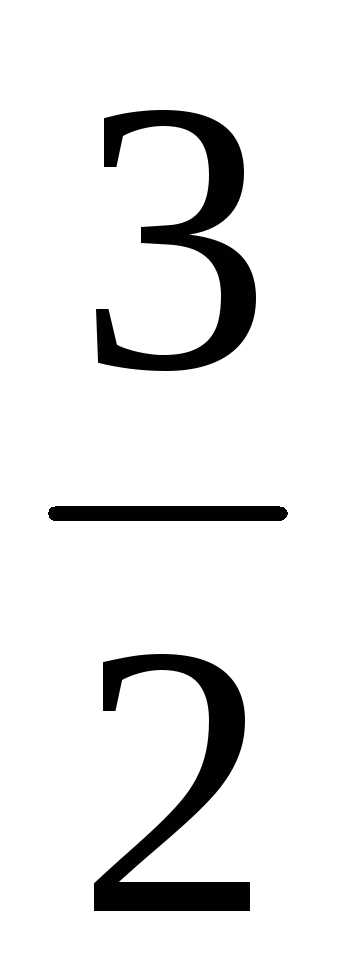 ;
; ; Ответ:
; Ответ: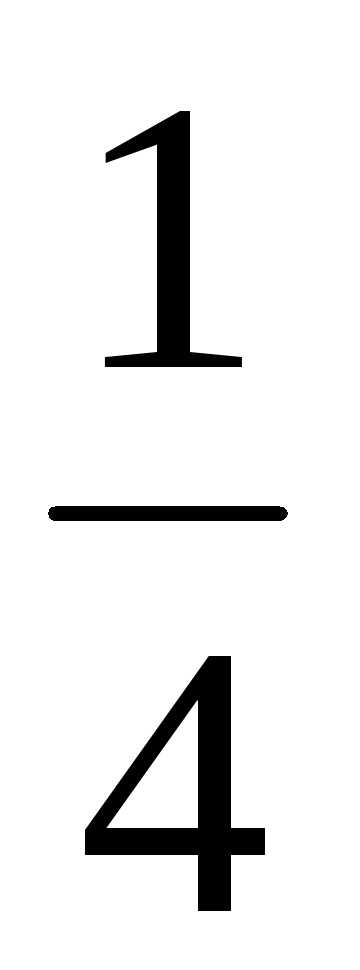 ;
;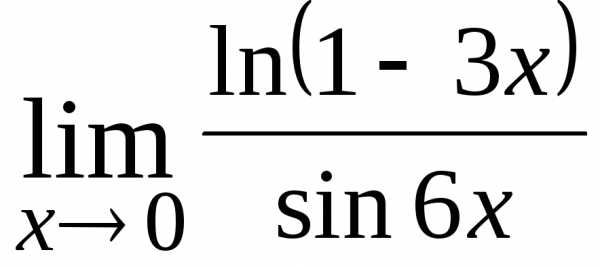 ; Ответ:
; Ответ: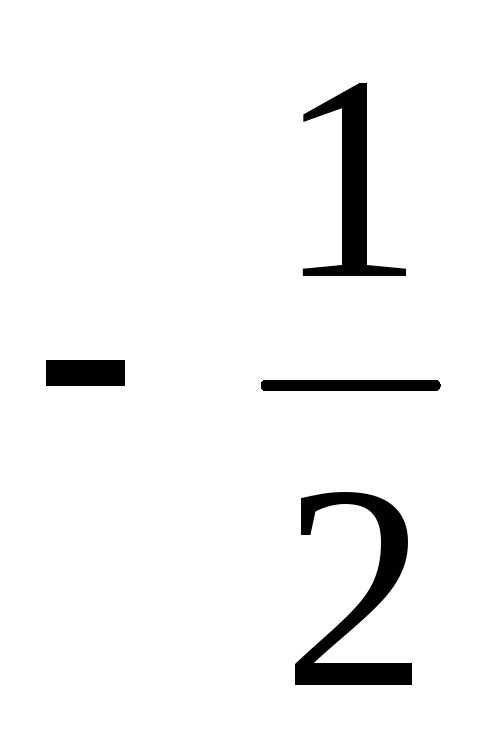 .
. ; Ответ:
; Ответ: ;
;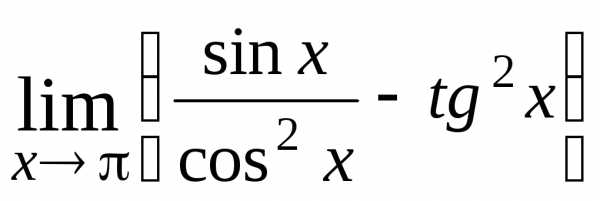 ; Ответ:
; Ответ: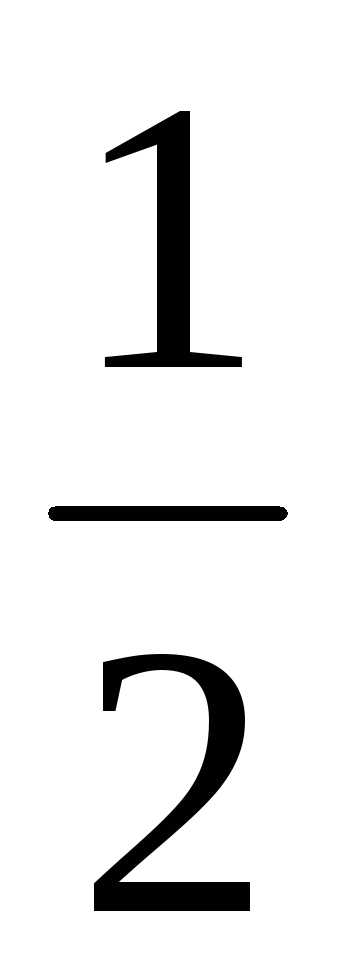 ;
;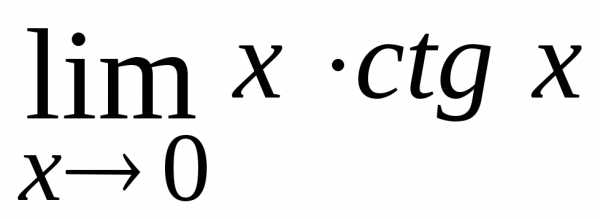 ; Ответ:
1.
; Ответ:
1.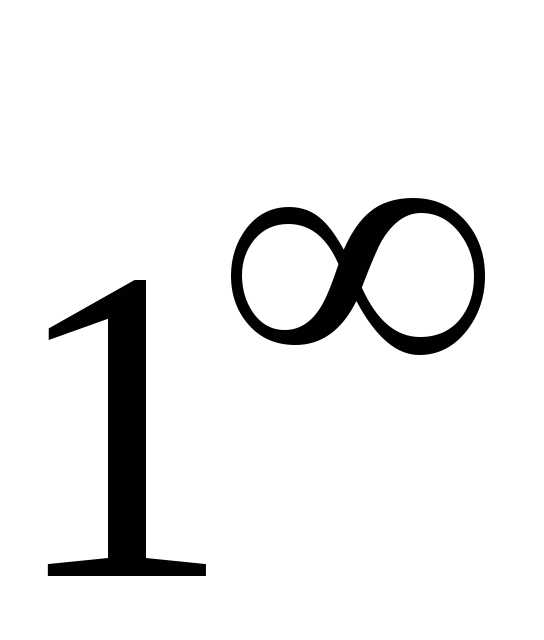 .
Найти пределы:
.
Найти пределы: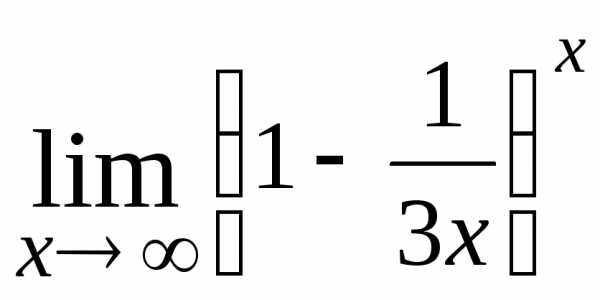 ; Ответ:
; Ответ: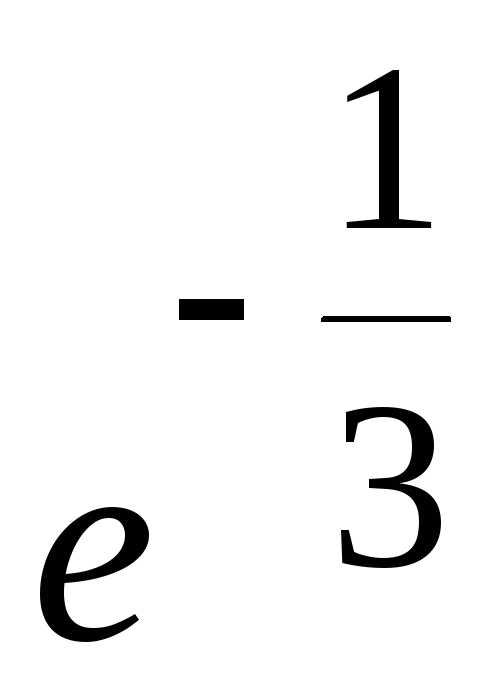 ;
;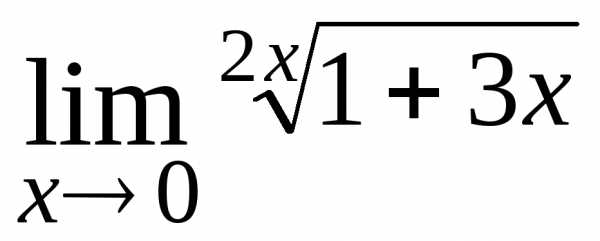 ; Ответ:
; Ответ: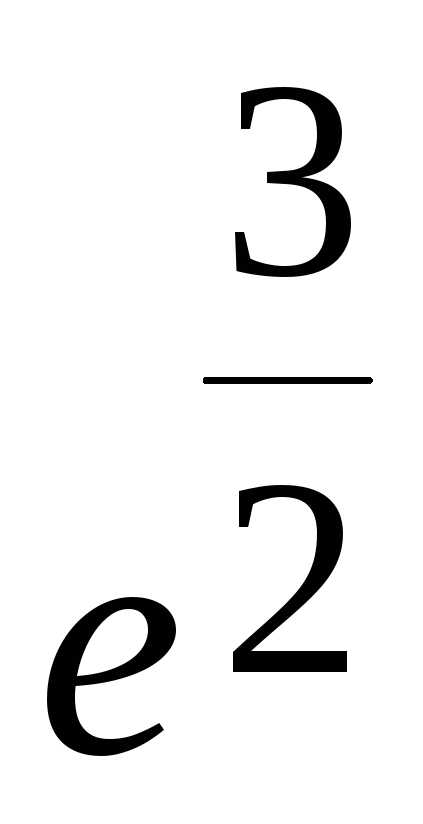 ;
;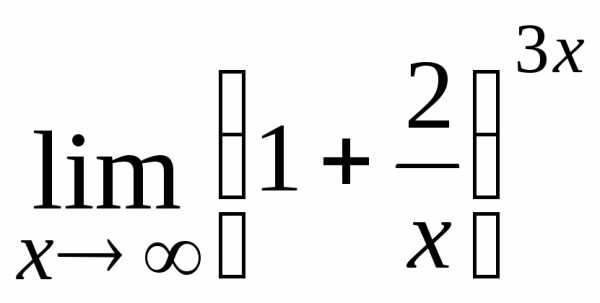 ; Ответ:
; Ответ: ;
; ; Ответ:
; Ответ: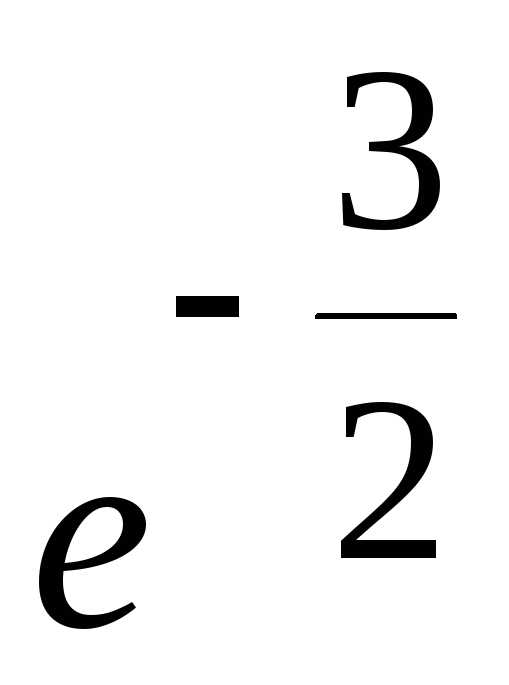 .
.
 Статья о методах решения уравнений. Задач, которые связаны с решением уравнений, довольно много в вариантах ЕГЭ и ГИА по математике. Поэтому как репетитор по математике рекомендую освежить с памяти связанный с этим вопросом материал. К каждому разобранному в статье примеру прилагается аналогичное задание для самопроверки. Все свои вопросы вы можете смело задавать в комментариях. Ни один вопрос без ответа не останется. В статье также имеется видеоразбор одного из заданий.
Статья о методах решения уравнений. Задач, которые связаны с решением уравнений, довольно много в вариантах ЕГЭ и ГИА по математике. Поэтому как репетитор по математике рекомендую освежить с памяти связанный с этим вопросом материал. К каждому разобранному в статье примеру прилагается аналогичное задание для самопроверки. Все свои вопросы вы можете смело задавать в комментариях. Ни один вопрос без ответа не останется. В статье также имеется видеоразбор одного из заданий.

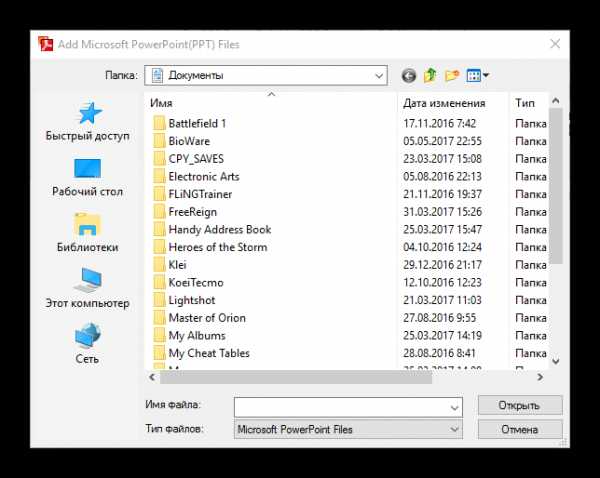


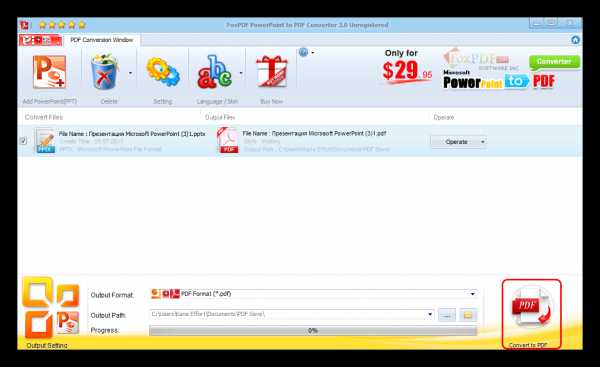
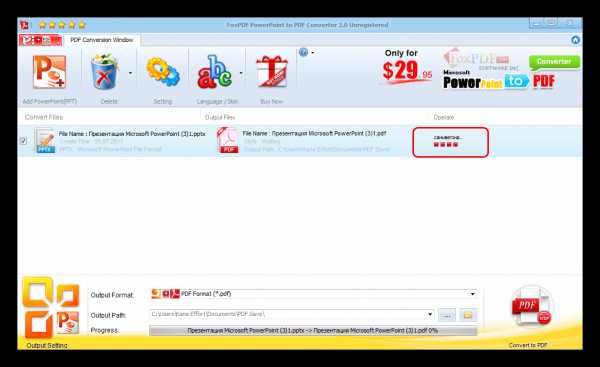


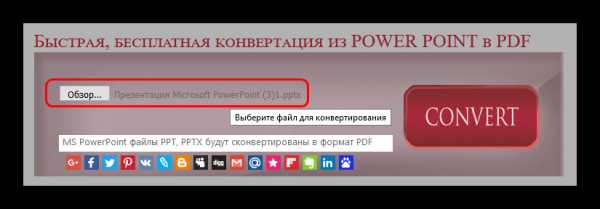
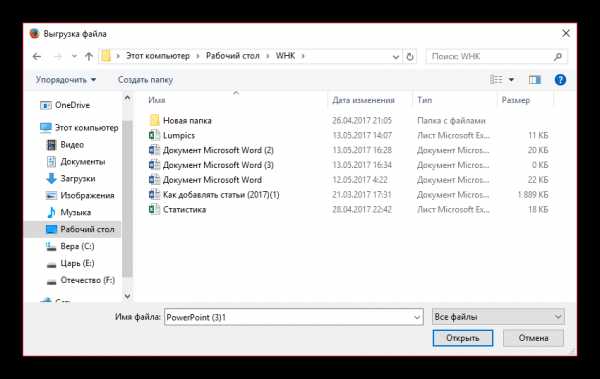
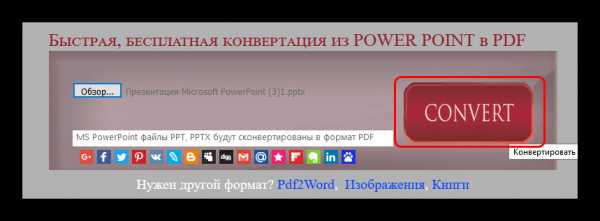




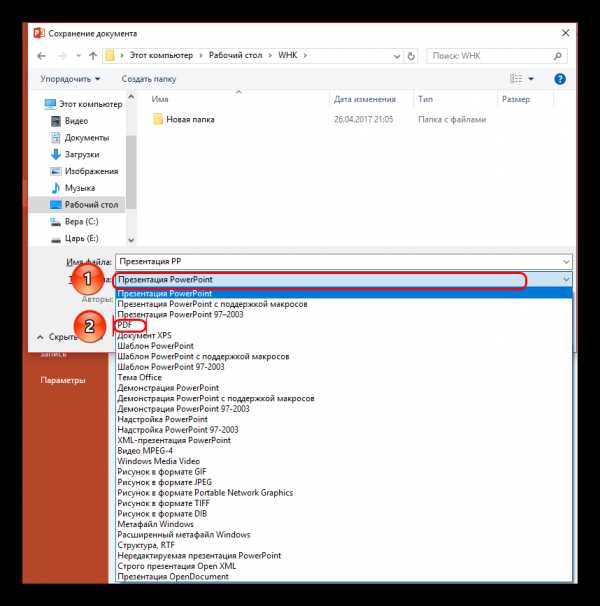
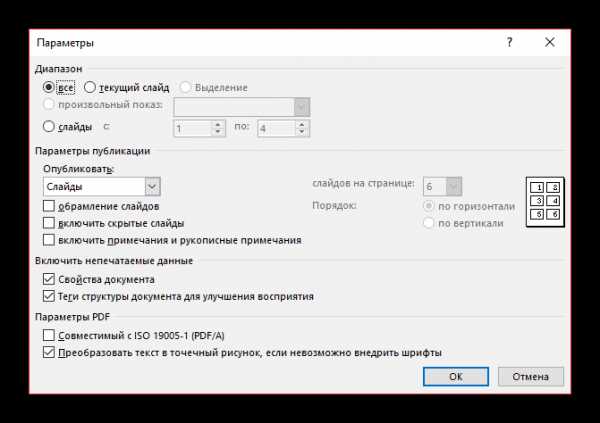
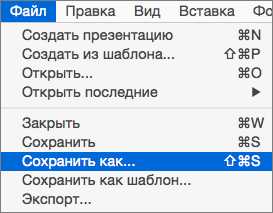
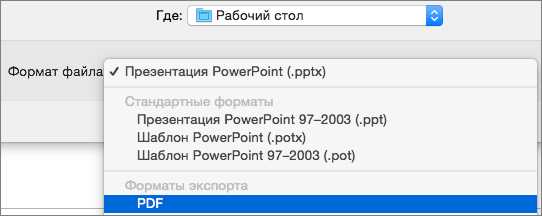



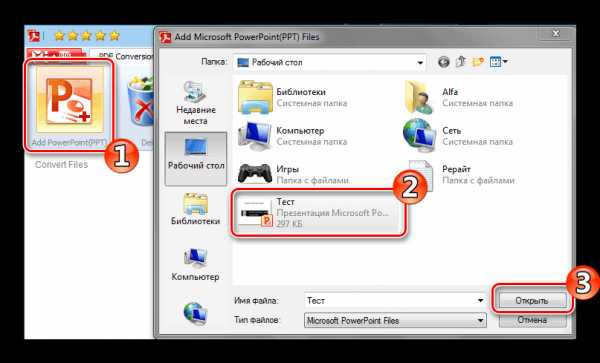

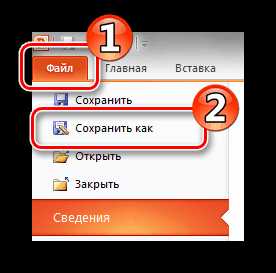
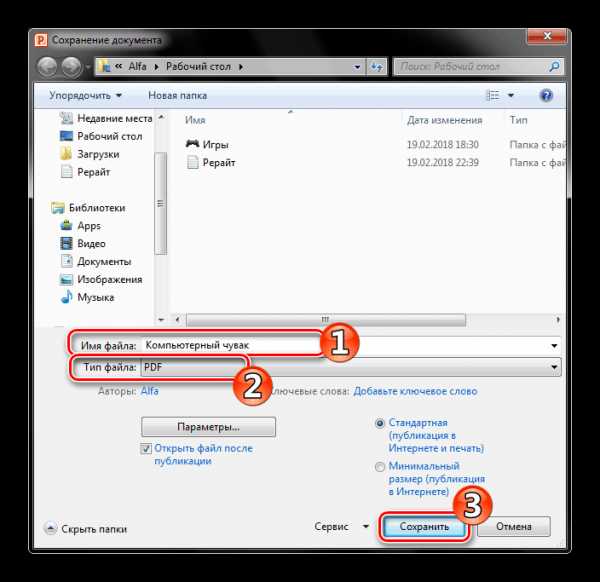
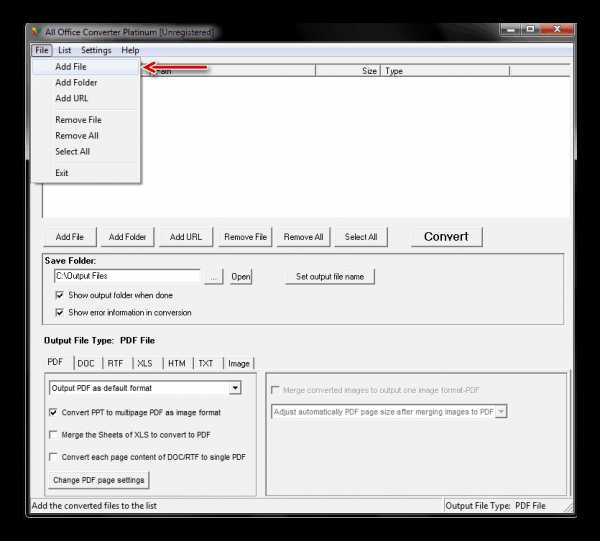
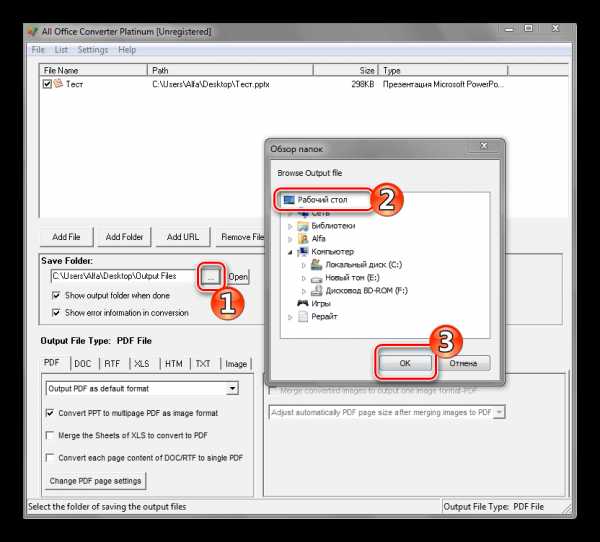
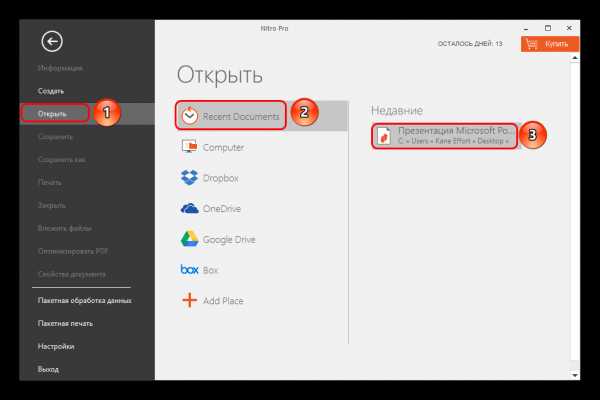
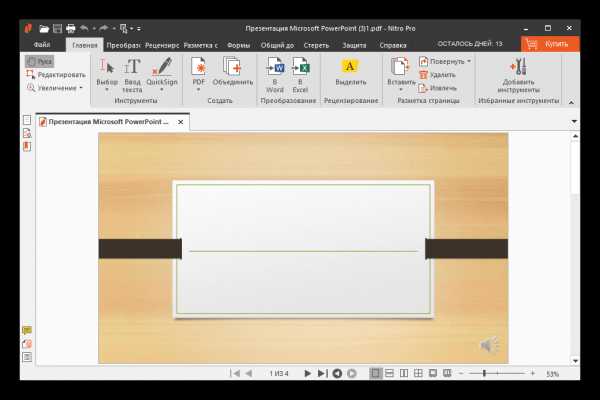
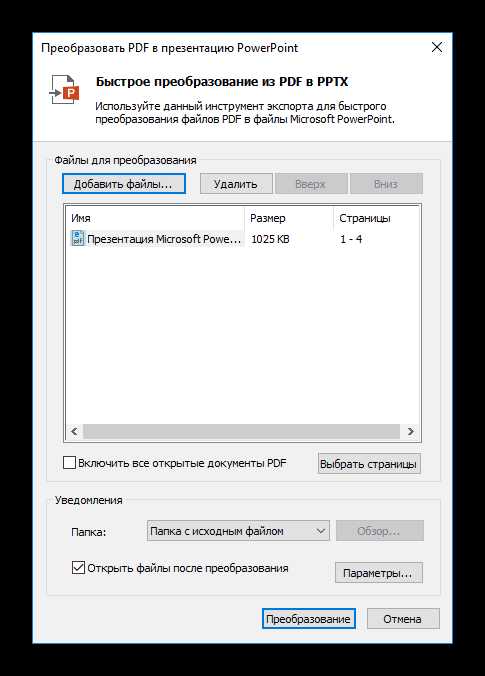
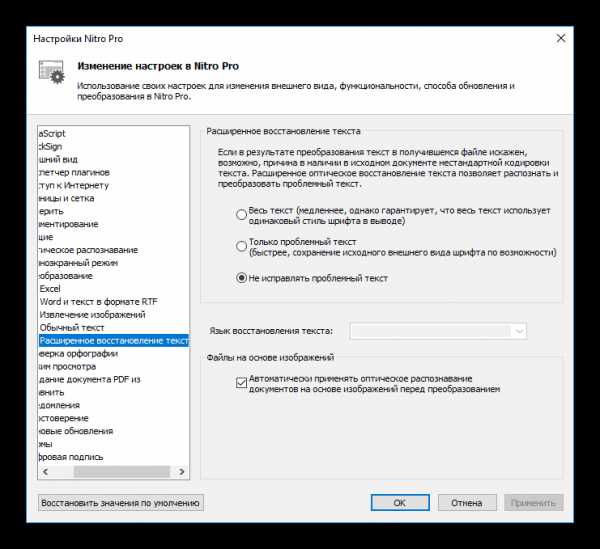
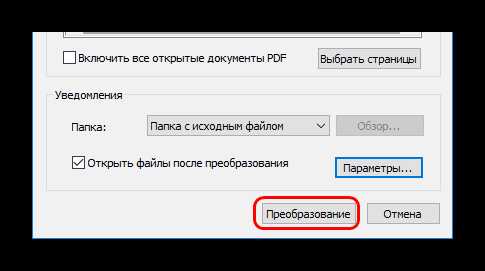
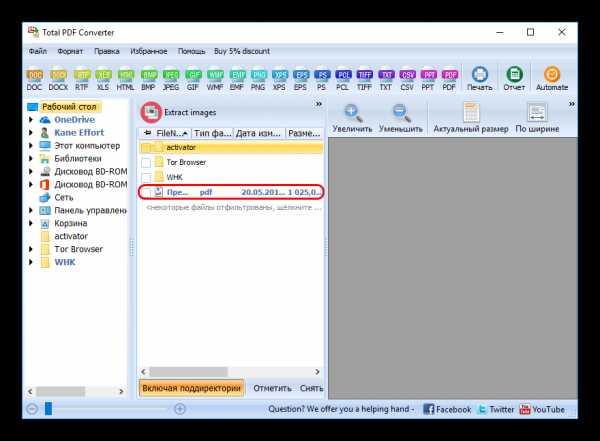
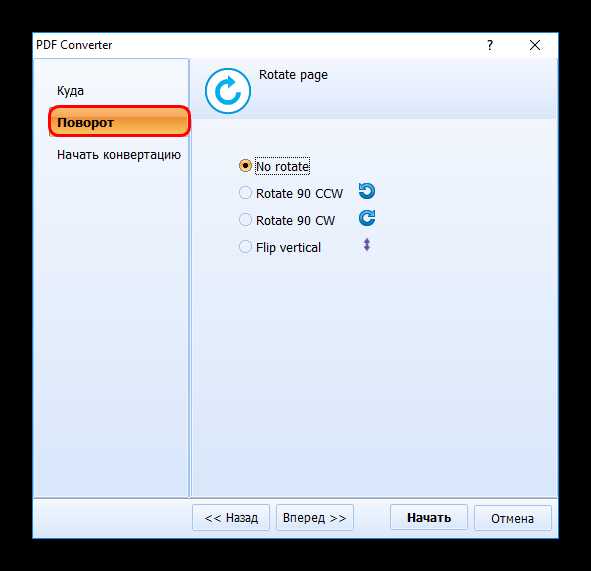
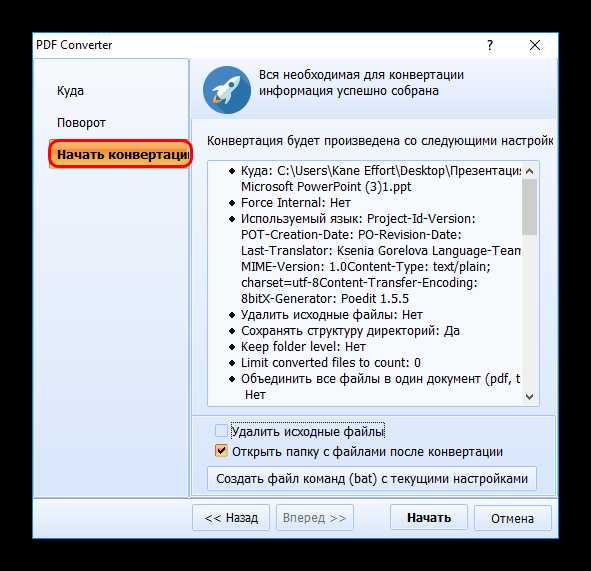
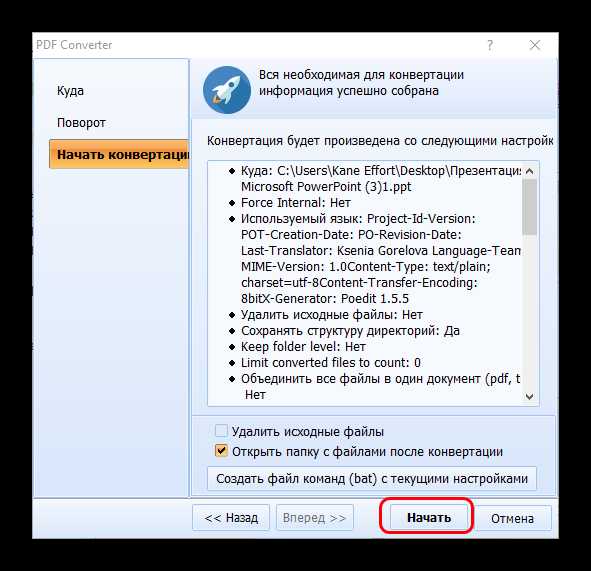
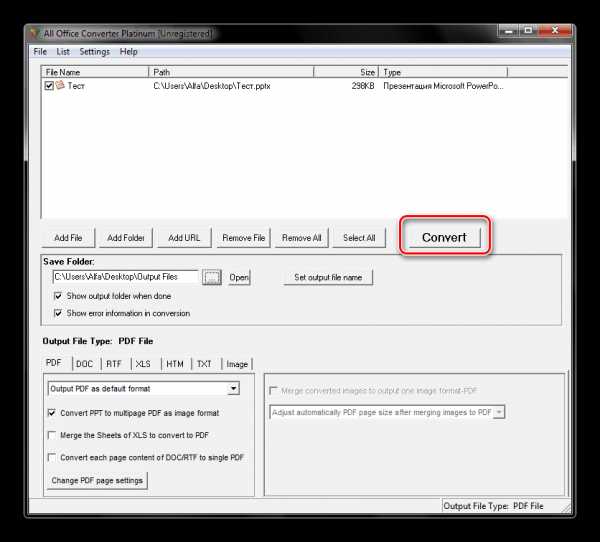 Файл будет находиться в той директории, которую вы указали в предыдущем шаге.
Файл будет находиться в той директории, которую вы указали в предыдущем шаге.