Как посчитать отрицательную степень 🚩 Отрицательная степень 🚩 Математика
Автор КакПросто!
Показатель у степенного выражения указывает, сколько раз число будет умножаться само на себя при возведении в данную степень. А как возвести число в отрицательную степень? Ведь «количество раз» не бывает отрицательным. Чтобы решить эту проблему, следует привести данное выражение в нормальный вид: придать степени положительное значение.
Инструкция
Для того чтобы вычислить значения числа, имеющего отрицательный показатель степени, приведите данное число в вид, в котором показатель степени приобретет положительное значение. Все числа с отрицательной степенью можно представить в виде обыкновенной дроби, в числителе которой стоит единица, а в знаменателе – первоначальное числовое выражение с той же степенью, только уже имеющей знак «плюс». (см рисунок).Если принять необходимые для примеров обозначения: 3^-5 – три в минус пятой степени, 3^5 – три в пятой степени, то решения подобных задач будут иметь вид, показанный в примерах.
Пример: 3^-5 = 1 /3^5. Три в минус пятой степени равно дроби: единица, деленная на три в пятой степени. Приведенное в дробный вид степенное выражение не усложняется, а просто преобразуется. Решить его далее несложно. Возведите в степень число, стоящее в знаменателе. Получится дробь, где в числителе, по-прежнему, стоит единица, а в знаменателе — уже возведенное в степень число.
Пример: 3^-5 = 1 /3^5 = 1 / 3 * 3 * 3 * 3 * 3 = 1 / 243. Единица, деленная на три в пятой степени, равна единице, деленной на двести сорок три. В знаменателе число три возведено в пятую степень, то есть умножено на себя пять раз. Получилась обыкновенная правильная дробь.
Далее, если вас устраивает данная дробь, примите ее за ответ, ежели нет, вычисляйте дальше. Для этого разделите числитель на знаменатель, то есть единицу на возведенное в степень число.
Пример: 3^-5 = 1 /3^5 = 1 / 3 * 3 * 3 * 3 * 3 = 1 / 243 = 0,0041. Обыкновенная дробь стала равна десятичной, округленной до десятитысячных долей.
При делении числителя на знаменатель (для перевода обыкновенной дроби в десятичную) зачастую ответ получается с большим остатком (длинным значением дробной части у ответа). В таких случаях принято просто округлять десятичную дробь до удобных долей.
Видео по теме
Источники:
- калькулятор отрицательную степень

Инструкция
Начнем с самых основ, с определения. Степень – это произведение равных множителей. Множитель называют основанием, а число множителей – показателем степени. Действие которое производят со степенью называется возведением в степень.Показатель степени может быть положительным и отрицательным, целым числом или дробью, правила действий со степенями остаются при этом прежними.
Если основание степени — отрицательное число, а показатель степени нечетный, то результат возведения в степень отрицателен, но если показатель степени четный, результат, в независимости от того, отрицательный или положительный знак перед основанием степени, всегда будет иметь знак плюс.
Все свойства, которые мы сейчас перечислим, действительны для степеней с одинаковым основанием. Если же основания у степеней разные, то сложить или вычесть можно только после возведения в степень. Так же как умножить и разделить. Потому что возведение в степень, согласно установленному порядку выполнения арифметических действий, имеет приоритет над умножением и делением, а также сложением и вычитанием, которые выполняются в последнюю очередь. А для изменения этой строгой последовательности действий, существуют скобки, в которые заключаются первоочередные действия.
Какие же особые правила арифметических действий существуют для степеней около одинаковых оснований? Запомните следующие свойства степеней. Если перед вами произведение из двух степенных выражений, к примеру a^n*a^m, то можно сложить степени, вот так a^(n+m). Аналогично действуют с частным, но степени уже вычитают одну из другой. a^n/a^m = a^(n-m).
В случае когда требуется возведение в степень другой степени (a^n)^m, то показатели степеней перемножаются и получаем а^(n*m).
Следующее важное правило, если основание степени можно представить в виде произведения, то мы можем преобразовать выражение из (a*b)^n в a^n*b^n. Аналогично можно преобразовать дробь. (а/b)^n = a^n/b^n.
Финальные наставления. В случае если показатель степени ноль, результатом возведения в степень всегда будет единица. Если показатель степени отрицательный, то это дробное выражение. То есть a^-n = 1/a^n. И самое последнее, если показатель степени дробный, то здесь актуально извлечение корня, так как a^(n/m) = m√a^n.
Видео по теме
Не все калькуляторы имеют функцию возведения числа в степень. Для того, чтобы определить возможности своего калькулятора, узнайте, является ли он инженерным. Если не знаете, то найдите кнопку вашего калькулятора, изображающую x в сепени y. Если она есть, значит, трюк удастся.

Вам понадобится
Инструкция
Определите, какой у вас калькулятор. Много ли на нем кнопок? Если видите только функции сложения, вычитания, умножения, деления и еще несколько кнопок, значит, на вашем калькуляторе такие действия, как возведение числа в степень, невозможны. Вы можете добиться нужной степени простым умножением числа на само себя нужное количество раз, а именно — равное вашей степени.Если у вас есть инженерный калькулятор, и вы видите на нем кнопку с изображением функции x, возведенной в степень y, то проделайте следующее действие. Введите значение числа, которое нужно возвести в степень, а затем нажмите кнопку, о которой шла речь выше. Теперь введите значение степени и получите результат, нажав на кнопку со знаком равно. Результат получен.
Полезный совет
Если вы пользуетесь калькулятором, который входит в стандартный набор программ Windows, то его вид можно изменить (расширить в инженерный и обратно).
Источники:
- значение кнопок на калькуляторе
Степень числа разбирают в школе на уроках алгебры. В жизни такая операция выполняется редко. Например, при расчете площади квадрата или объёма куба используются степени, потому что длина, ширина, а для куба и высота – равные величины. В остальном возведение в степень чаще всего носит прикладной производственный характер.

Вам понадобится
- Бумага, ручка, инженерный калькулятор, таблицы степеней, программные продукты (например, табличный редактор Excel).
Инструкция
Посчитать степень числа на математическом языке означает возвести любое число в какую-нибудь степень. Предположим, необходимо число Х возвести в степень n.Для этого число Х умножается само на себя n раз. Пусть Х = 125, а степень числа, т. е. n = 3. Это означает, что число 125 нужно умножить само на себя 3 раза.
125^3 = 125*125*125 = 1 953 125
Ещё пример.
3^4 = 3*3*3*3 = 81 При работе с отрицательным числом нужно быть аккуратным со знаками. Следует помнить, что четная степень (n) даст знак плюс, нечетная – знак минус.
Например
(-7)^2 = (-7)*(-7) = 49
(-7)^3 = (-7)*(-7)*(-7) = 343
Нулевая степень (n = 0) от любого числа всегда будет равна единице.
15^0 = 1
(-6)^0 = 1
(1/3)^0 = 1Если n = 1, число умножать само на себя не надо.
Будет
7^1 = 7
329^1 = 329
Операция, обратная возведению числа в степень, называется извлечение корня.
Если 5^2 = 25, то квадратный корень из 25 будет равен 5.
Если 5^3 = 125, то корень третей степени равен 5.
Если 8^4= 4 096, то корень четвертой степени из 4 096 будет равен 8.
Если n = 2, тогда степень называют квадратом, если n = 3, степень называют кубом. Вычисление квадрата и куба из чисел первого десятка производить достаточно легко. Но с увеличением числа, возводимого в степень, и с увеличением самой степени, вычисления становятся трудоемкими. Для таких вычислении были разработаны специальные таблицы. Также существуют специальные инженерные и online калькуляторы, программные продукты. В качестве простейшего программного продукта для операций со степенями можно использовать табличный редактор Excel.
Источники:
- http://www.bymath.net/studyguide/alg/sec/alg17.html
Для краткой записи произведения одного и того же числа самого на себя математики придумали понятие степени. Поэтому выражение 16*16*16*16*16 можно записать более коротким способом. Оно будет иметь вид 16^5. Выражение будет читаться как число 16 в пятой степени.

Вам понадобится
- Бумага, ручка.
Инструкция
В общем виде степень записывается как a^n. Эта запись означает, что число a умножается на себя n раз.Выражение a^n называется степенью,
a – это число, основание степени,
n – это число, показатель степени. Например, a = 4, n = 5,
Тогда запишем 4^5 = 4*4*4*4*4 = 1 024
Степень n может быть отрицательным числом
n = -1, -2, -3 и т.д.
Чтобы вычислить отрицательную степень числа, его необходимо опустить в знаменатель.
a^(-n) = (1/a)^n = 1/a*1/a*1/a* … *1/a = 1/(a^n)
Рассмотрим пример
2^(-3) = (1/2)^3 = 1/2*1/2*1/2 = 1/(2^3) = 1/8 = 0,125
Как видно из примера, -3 степень от числа 2 можно вычислить разными способами.
1) Сначала посчитать дробь 1/2 = 0,5; а затем возвести в степень 3,
т.е. 0,5^3 = 0,5*0,5*0,5 = 0,125
2) Сначала возвести знаменатель в степень 2^3 = 2*2*2 = 8, а затем вычислить дробь 1/8 = 0,125.
Теперь вычислим -1 степень для числа, т.е. n = -1. Правила, рассмотренные выше, подходят для этого случая.
a^(-1) = (1/a)^1 = 1/(a^1) = 1/a
Например, возведем число 5 в -1 степень
5^(-1) = (1/5)^1 = 1/(5^1) = 1/5 = 0,2.
Из примера наглядно видно, что число в -1 степени – это обратная дробь от числа.
Представим число 5 в виде дроби 5/1, тогда 5^(-1) можно арифметически не считать, а сразу написать дробь, обратную 5/1, это 1/5.Так, 15^(-1) = 1/15,
6^(-1) = 1/6,
25^(-1) = 1/25
Обратите внимание
При возведении числа в отрицательную степень следует помнить, что число не может быть равно нулю. Согласно правилу, мы должны число опустить в знаменатель. А ноль не может быть в знаменателе, потому что на ноль делить нельзя.
Полезный совет
Иногда при работе со степенями для упрощения расчета дробное число специально заменяют целым в -1 степени
1/6 = 6^(-1)
1/52 = 52^(-1).
Источники:
- http://www.coolmath.ru/lessons/7/360-chto-takoe-stepen-s-naturalnym-pokazatelem.html
- числа в 1 степени
Возведение числа в степень означает его многократное умножение на самого себя. Само число принято называть основанием, а количество раз, которое следует произвести операцию умножения — показателем степени. Если показатель степени равен трем, такая степенная операция имеет собственное название — «возведение в куб».

Инструкция
Умножайте число на само себя дважды, чтобы возвести его в куб. Для многих чисел (оснований степени) такую операцию нетрудно проделать в уме, а в других случаях можно, например, умножить в столбик или воспользоваться калькулятором. Раз у вас есть доступ к компьютеру, никакого дополнительного инструмента для вычислений не требуется. Если в вашем компьютере установлена операционная система Windows, калькулятор вы можете найти, раскрыв главное меню на кнопке «Пуск». В нем надо перейти в раздел «Все программы», в котором найти и открыть подраздел «Стандартные», а в нем — секцию «Служебные». В эту секцию и помещена строка «Калькулятор», щелчок по которой запускает нужное приложение.Введите число, которое является основанием степени — это можно сделать либо щелкая соответствующие кнопки в интерфейсе на экране, либо нажимая клавиши на клавиатуре. Затем нажмите клавишу (или щелкните кнопку) со звездочкой — это операция умножения. Вводить больше ничего не нужно, просто дважды нажмите клавишу со знаком равенства, и калькулятор дважды умножит число на само себя, то есть возведет его в куб. Все это будет происходить в стандартном интерфейсе калькулятора, который используется по умолчанию. Есть и другой способ возведения в куб с использованием другого интерфейса этого же программного калькулятора.
Раскройте в меню раздел «Вид» и выберите в нем пункт «Научный» либо «Инженерный» (в зависимости от используемой версии ОС). Интерфейс калькулятора изменится, и в новом варианте его оформления будет присутствовать отдельная кнопка для возведения введенного числа в куб — на ней написаны символы x^3. То есть в этом случае вам можно после введения основания просто щелкнуть эту кнопку.
Если пользоваться интернет-поисковиками вам удобнее, чем калькуляторами, можно использовать для возведения в куб поисковую систему Google. Этот вариант намного проще любого другого — просто введите соответствующий запрос в единственное поле на главной странице сайта. Например, для возведения в куб числа 3,14 поисковый запрос надо сформулировать так: «3.14 в кубе». Обратите внимание, что десятичным разделителем должна быть точка, как это принято в большинстве англоязычных стран, а не запятая.
Видео по теме
Возведением числа в степень называется математическая операция последовательного умножения этого числа на само себя столько раз, сколько это указывает его степень. Само число принято называть «основанием», а степень — «показателем». Как основание, так и показатель могут быть и положительными и отрицательными числами. Если с положительным показателем все достаточно понятно, то возведение числа в отрицательную степень немного сложнее при вычислении.

Инструкция
Преобразуйте исходную запись математического действия (возведение числа в отрицательную степень) к форме обыкновенной дроби. Если обозначить основание степени как X, а модуль показателя как a, то запись Xˉª можно представить в виде обыкновенной дроби Xˉª/1. Избавьтесь от минуса в показателе степени. Для этого надо поменять местами числитель и знаменатель в полученной на первом шаге обыкновенной дроби, оставив в показателе дроби (-a) модуль показателя (a): Xˉª = Xˉª/1 = 1/Xª.Найдите численное значение выражения, стоящего в знаменателе дроби (Xª). Например, если основанием дроби является число 12 (X=12), а модулем показателя — число 3 (a=3), то знаменателем дроби должно быть число 1728 (12³=1728). То есть обыкновенная дробь должна принять вид 1/1728.
Переведите дробь, полученную на предыдущем шаге, из обыкновенной формы записи в десятичную. Чаще всего в результате такого преобразования получается число с бесконечным количеством знаков после десятичной запятой (иррациональное число), поэтому десятичную дробь следует округлить до нужной вам степени точности. Например, при переводе обыкновенной дроби 1/1728 в десятичную с точностью до семи знаков после запятой получится число 0,0005787 (1/1728≈0,0005787).
Используйте, например, вычислительные возможности поисковых систем, если объяснять ход преобразований от вас никто не требует. Например, если нужно получить только численное значение использованного в предыдущих шагах примера, то нет необходимости последовательно производить все преобразования и промежуточные вычисления 12ˉ³ = 12ˉ³/1 = 1/12³ = 1/1728 ≈ 0,0005787. Достаточно перейти на главную страницу Google и ввести в поле поискового запроса 12^(-3). Встроенный в поисковик калькулятор произведет все необходимые преобразования и вычисления и покажет результат с точностью до 12 знаков после запятой: 12^(-3) ≈ 0.000578703704.
Источники:
- как избавиться от степени
Вам понадобится
- компьютер
- программа-калькулятор
Инструкция
Откройте программу-калькулятор на вашем компьютере. Введите число A, которое нужно возвести в большую степень N. Попробуйте произвести возведение в степень. В большинстве случаев программа-калькулятор успешно справится с заданием и выдаст результат на экран. Однако, прямой метод не всегда срабатывает. Программы-калькуляторы часто написаны не самым лучшим образом и могут не справляться с рядом простых с виду задач. Именно к таким задачам относится возведение в большую степень. Например, для значения N = 10000000000 калькулятор Windows отказывается считать результат, а калькулятор Ubuntu просто зависает.Разложите показатель степени N на несколько множителей, каждый из которых не превышает по значению 100000. С таким показателем большинство калькуляторов успешно справится. Если один из множителей окажется дробным числом, ничего страшного. Например, показатель степени 333333333 можно разложить на множители 100000 и 3333,33333.
Согласно формуле A^(N1*N2) = (A^N1)^N2 последовательно возведите основание А в степени, равные полученным на предыдущем шаге множителям. Например, сначала возведите число А в степень 100000, а затем получившийся результат возведите в степень 3333,33333. После этих расчетов вы получите необходимый вам результат.
Видео по теме
Обратите внимание
Если один из множителей получился дробным, а основание степени является отрицательным числом, программа-калькулятор не позволит вам произвести возведение отрицательного числа в дробную степень. В этом случае возводите модуль основания в нужную вам степень, а потом, если потребуется, измените знак результата. Результат должен быть отрицательным, если степень является нечетным числом.
Полезный совет
Если значение А близко к единице, а N очень велико, воспользуйтесь формулой (1 + 1/A)^N -> e. Например, 1,000005^200000 приблизительно равняется числу е.
Операции возведения числа в степень и извлечения из него корня — противоположные друг другу математические действия. Однако они могут быть совмещены в одной записи, если показатель степени числа представить в формате обыкновенной или десятичной дроби. При осуществлении записанной таким способом операции придется проделать последовательно оба этих математических действия.

Инструкция
Если в исходных условиях степень дана в формате обыкновенной дроби, то операцию нужно производить в два шага. Последовательность их на полученном результате никак не скажется — начните, например, с извлечения из числа корня той степени, которая указана в знаменателе дроби. К примеру, чтобы возвести в степень ⅔ число 64 на этом шаге из него надо извлечь кубический корень: 64^⅔ = (³√64)² = 4². Возведите полученное на первом шаге значение в степень, равную числу, стоящему в числителе дроби. Результат этой операции и будет результатом возведения числа в дробную степень. Для примера из предыдущего шага полностью описанный ход вычислений можно записать так: 64^⅔ = (³√64)² = 4² = 16.Исходите из простоты расчетов при определении последовательности описанных выше операций извлечения корня и возведения в степень. Например, если бы требовалось в ту же самую степень ⅔ возвести число 8, то начинать с извлечения кубического корня из восьмерки было бы нецелесообразно, так как результат был бы дробным числом. В этом случае лучше начать с возведения 8 в квадрат, а затем извлечь корень третьей степени из 64 и таким образом обойтись без дробных промежуточных значений: 8^⅔ = ³√(8²) = ³√64 = 4.
Если показатель степени в исходных данных приведен в формате десятичной дроби, то начните с преобразования его в обыкновенную дробь, а затем действуйте по описанному выше алгоритму. Например, для возведения числа в степень 0,75 трансформируйте этот показатель в обыкновенную дробь ¾, затем извлеките корень четвертой степени и возведите полученный результат в куб.
Используйте любой калькулятор, если ход вычислений значения не имеет, а важен лишь результат. Это может быть и скрипт, встроенный в поисковик Google — с его помощью найти нужное значение даже проще, чем с использованием стандартного калькулятора ОС Windows. Например, для возведения числа 15 в степень ⅗ перейдите на главную страницу сайта и введите в поле поискового запроса 15^(3/5). Результат вычислений с точностью до 8 знаков Google отобразит даже без нажатия кнопки отправки запроса: 15^(3 / 5) = 5,07755639.
Источники:
- как возводить в дробную степень
Операция возведения в степень является «бинарной», то есть имеет два обязательных входных параметра и один выходной. Один из исходных параметров называется показателем степени и определяет количество раз, которое операция умножения должна быть применена ко второму параметру — основанию. Основание может быть как положительным, так и отрицательным числом.

Инструкция
Используйте при возведении в степень отрицательного числа обычные для этой операции правила. Как и для положительных чисел, возведение в степень означает умножение исходной величины на саму себя количество раз, на единицу меньшее показателя степени. Например, чтобы возвести в четвертую степень число -2, его нужно трижды умножить на себя: -2⁴=-2*(-2)*(-2)*(-2)=16. Умножение двух отрицательных чисел всегда дает положительное значение, а результатом этой операции для величин с разными знаками будет число отрицательное. Из этого можно сделать вывод, что при возведении отрицательных значений в степень с четным показателем всегда должно получаться число положительное, а при нечетных показателях результат всегда будет меньше нуля. Используйте это свойство для проверки произведенных расчетов. Например, -2 в пятой степени должно быть числом отрицательным -2⁵=-2*(-2)*(-2)*(-2)*(-2)=-32, а -2 в шестой — положительным -2⁶=-2*(-2)*(-2)*(-2)*(-2)*(-2)=64.При возведении отрицательного числа в степень показатель может быть приведен в формате обыкновенной дроби — например, -64 в степени ⅔. Такой показатель означает, что исходную величину следует возвести в степень, равную числителю дроби, и извлечь из нее корень степени, равной знаменателю. Одна часть этой операции рассмотрена в предыдущих шагах, а здесь вам следует обратить внимание на другую.
Извлечение корня — нечетная функция, то есть для отрицательных вещественных чисел она может применяться только при нечетном показателе степени. При четном эта функция значения не имеет. Поэтому, если в условиях задачи требуется возвести отрицательное число в дробную степень с четным знаменателем, то задача решения не имеет. В остальных случая проделайте сначала операции из первых двух шагов, используя в качестве показателя степени числитель дроби, а затем извлеките корень со степенью знаменателя.
Для возведения числа в степень можно использовать как простейшие, так и научные калькуляторы. Во втором случае появляется возможность использовать в качестве показателя степени дробное или отрицательное число.

Инструкция
На простейшем калькуляторе можно возводить только в целые положительные степени. Для этого нажмите клавишу [C], введите число, а затем нажмите клавиши [X] и [=]. Число будет возведено в степень 2. Последующие нажатия клавиши [=] приведут к возведению введенного вами числа в степени 3, 4, 5, и так далее, до тех пор, пока не произойдет переполнение разрядной сетки. В последнем случае на индикаторе включится сегмент E или ERROR, а считать результат достоверным будет нельзя.Если показатель степени значителен, подсчитывать нажатия клавиши [=] можно при помощи второго калькулятора. Последовательно нажмите на нем клавиши [1], [+] и [=]. Последующие нажатия на клавишу [=] приведут к появлению на индикаторе чисел 2, 3, 4, 5, и так далее. Остается нажимать клавиши [=] на обоих калькуляторах синхронно с таким расчетом, чтобы показания индикатора второго прибора соответствовали степени, в которую возведено число на первом.
Для возведения в степень на научном калькуляторе с обратной польской записью вначале нажмите клавишу [C], затем число, подлежащее возведению, затем кнопку со стрелкой вверх (на аппаратах фирмы HP — с надписью Enter), затем показатель степени, а затем клавишу [xy]. Если эта надпись расположена не на самой клавише, а над ней, то перед ней нажмите клавишу [F]. Отличить такой калькулятор от научного с арифметической записью можно по отсутствию клавиши [=].При использовании научного калькулятора с алгебраической записью вначале нажмите клавишу [C], затем число, подлежащее возведению в степень, затем клавишу [xy] (при необходимости — совместно с клавишей [F], как указано выше), затем показатель степени, а затем — клавишу [=].
Наконец, при использовании двухстрочного калькулятора с формульной записью введите в верхнюю строку все выражение в том же виде, в каком оно записано на бумаге. Для ввода знака возведения в степень используйте клавишу [xy] или [^], в зависимости от типа аппарата. После нажатия клавиши [=] результат отобразится в нижней строке.
При отсутствии калькулятора для возведения в степень можно использовать компьютер. Для этого запустите на нем программу виртуального калькулятора: в Windows — Calc, в Linux — XCalc, KCalc, Galculator и др. Переключите программу в инженерный режим, если этого не было сделано ранее. Калькулятор XCalc можно перевести в режим обратной польской записи, запустив его командой xcalc -rpn. Компиляторы языка Паскаль использовать в качестве калькуляторов не рекомендуется — команды возведения в степень там нет, и реализовывать соответствующий алгоритм приходится вручную. В интерпретаторах языка Бейсик, например, UBasic, для осуществления этой операции служит знак ^.
www.kakprosto.ru
Как посчитать отрицательную степень
Показатель у степенного выражения указывает, сколько раз число будет умножаться само на себя при возведении в данную степень. А как возвести число в отрицательную степень? Ведь «количество раз» не бывает отрицательным. Чтобы решить эту проблему, следует привести данное выражение в нормальный вид: придать степени положительное значение.Инструкция
- Для того чтобы вычислить значения числа, имеющего отрицательный показатель степени, приведите данное число в вид, в котором показатель степени приобретет положительное значение. Все числа с отрицательной степенью можно представить в виде обыкновенной дроби, в числителе которой стоит единица, а в знаменателе – первоначальное числовое выражение с той же степенью, только уже имеющей знак «плюс». (см рисунок).
Если принять необходимые для примеров обозначения: 3^-5 – три в минус пятой степени, 3^5 – три в пятой степени, то решения подобных задач будут иметь вид, показанный в примерах.
Пример: 3^-5 = 1 /3^5. Три в минус пятой степени равно дроби: единица, деленная на три в пятой степени. - Приведенное в дробный вид степенное выражение не усложняется, а просто преобразуется. Решить его далее несложно. Возведите в степень число, стоящее в знаменателе. Получится дробь, где в числителе, по-прежнему, стоит единица, а в знаменателе — уже возведенное в степень число.
Пример: 3^-5 = 1 /3^5 = 1 / 3 * 3 * 3 * 3 * 3 = 1 / 243. Единица, деленная на три в пятой степени, равна единице, деленной на двести сорок три. В знаменателе число три возведено в пятую степень, то есть умножено на себя пять раз. Получилась обыкновенная правильная дробь. - Далее, если вас устраивает данная дробь, примите ее за ответ, ежели нет, вычисляйте дальше. Для этого разделите числитель на знаменатель, то есть единицу на возведенное в степень число.
Пример: 3^-5 = 1 /3^5 = 1 / 3 * 3 * 3 * 3 * 3 = 1 / 243 = 0,0041. Обыкновенная дробь стала равна десятичной, округленной до десятитысячных долей.
При делении числителя на знаменатель (для перевода обыкновенной дроби в десятичную) зачастую ответ получается с большим остатком (длинным значением дробной части у ответа). В таких случаях принято просто округлять десятичную дробь до удобных долей.
completerepair.ru
Как посчитать отрицательную степень | Сделай все сам
Показатель у степенного выражения указывает, сколько раз число будет умножаться само на себя при возведении в данную степень. А как построить число в негативную степень? Чай “число раз” не бывает негативным. Дабы решить эту загвоздку, следует привести данное выражение в типичный вид: придать степени позитивное значение.

Инструкция
1. Для того дабы вычислить значения числа, имеющего негативный показатель степени, приведите данное число в вид, в котором показатель степени приобретет позитивное значение. Все числа с негативной степенью дозволено представить в виде обычной дроби, в числителе которой стоит единица, а в знаменателе – изначальное числовое выражение с той же степенью, только теснее имеющей знак “плюс”. (см рисунок).Если принять нужные для примеров обозначения: 3^-5 – три в минус пятой степени, 3^5 – три в пятой степени, то решения сходственных задач будут иметь вид, показанный в примерах.Пример: 3^-5 = 1 /3^5. Три в минус пятой степени равно дроби: единица, деленная на три в пятой степени.
2. Приведенное в дробный вид степенное выражение не усложняется, а примитивно преобразуется. Решить его дальше нетрудно. Возведите в степень число, стоящее в знаменателе. Получится дробь, где в числителе, по-бывшему, стоит единица, а в знаменателе – теснее возведенное в степень число.Пример: 3^-5 = 1 /3^5 = 1 / 3 * 3 * 3 * 3 * 3 = 1 / 243. Единица, деленная на три в пятой степени, равна единице, деленной на двести сорок три. В знаменателе число три возведено в пятую степень, то есть умножено на себя пять раз. Получилась обычная положительная дробь.
3. Дальше, если вас устраивает данная дробь, примите ее за результат, если нет, вычисляйте дальше. Для этого поделите числитель на знаменатель, то есть единицу на возведенное в степень число. Пример: 3^-5 = 1 /3^5 = 1 / 3 * 3 * 3 * 3 * 3 = 1 / 243 = 0,0041. Обычная дробь стала равна десятичной, округленной до десятитысячных долей.При делении числителя на знаменатель (для перевода обычной дроби в десятичную) нередко результат получается с огромным остатком (длинным значением дробной части у результата). В таких случаях принято примитивно округлять десятичную дробь до комфортных долей.
Видео по теме
jprosto.ru
Возведение числа в отрицательную степень
Как известно, в математике существуют не только положительные числа, но и отрицательные. Если знакомство с положительными степенями начинается с определения площади квадрата, то с отрицательными всё несколько сложнее.
Основные понятия и положения
Это следует знать:
- Возведением числа в натуральную степень называется умножение числа (понятие число и цифра в статье будем считать эквивалентными) само на себя в таком количестве, каков показатель степени (в дальнейшем будем использовать параллельно и просто слово показатель). 6^3 = 6*6*6 = 36*6 =216. В общем виде это выглядит так: m^n = m*m*m*…*m (n раз).
- Нужно учитывать, что при возведении отрицательного числа в натуральную степень, оно станет положительным, если показатель чётный.
- Возведение числа в показатель 0 даёт единицу, при условии, что оно не равно нулю. Ноль в нулевой степени считается неопределённым. 17^0 = 1.
- Извлечением корня некой степени из числа называется нахождение такого числа, которое при возведении в соответствующий показатель даст искомое. Так, корень кубический из 125 равен 5, поскольку 5^3 = 125.
- Если требуется возвести число в дробную положительную степень, то необходимо возвести число в показатель знаменателя и извлечь из него корень показателя числителя. 6^5/7 = корень седьмой степени из произведения 6*6*6*6*6.
- Если требуется возвести число в отрицательный показатель, то необходимо найти цифру обратную данной. x^-3 = 1/x^3. 8^-4 = 1/8^4 = 1/8*8*8*8 = 1/4096.
Возведение в отрицательную степень числа по модулю от нуля до единицы
Сначала нам следует вспомнить, что такое модуль. Это расстояние на координатной прямой от выбранного нами значения до начала отсчёта (нуля координатной прямой). По определению он никогда не может быть отрицательным.
Значение больше нуля
При значении цифры в промежутке от нуля до единицы отрицательный показатель даёт увеличение самой цифры. Происходит это из-за уменьшения знаменателя, остающегося при этом положительным.
Рассмотрим на примерах:
- 1/7^-3 = 1/(1/7^3) = 1/(1/343) = 343;
- 0,2^-5 = 1/0,2^5 = 1/0,2*0,2*0,2*0,2*0,2 = 1/0,00032 = 3125.
Причём, чем больше модуль показателя, тем активнее растёт цифра. При стремлении знаменателя к нулю — сама дробь стремится к плюс бесконечности.
Значение меньше нуля
Сейчас рассмотрим как возводить в отрицательную степень, если цифра меньше нуля. Принцип тот же, что и в предыдущей части, но здесь имеет значение знак показателя.
Опять-таки обратимся к примерам:
- -19 / 21^-4 = 1/(-19/21)^4 = 1/(-19)^4/21^4 = 21^4/(-19)^4 = 21*21*21*21/(-19)*(-19)*(-19)*(-19) = 194481/130321 = 1,4923228;
- -29/40^-5 = 1/(-29/40)^5 = 1/(-29)^5/40^5 = 40^5/(-29)^5 = 40*40*40*40*40/(-29)*(-29)*(-29)*(-29)*(-29) = 102400000/(-20511149) = -4,9924.
В данном случае, мы видим, что модуль продолжает расти, а вот знак зависит от чётности или нечётности показателя.
Следует заметить, если мы возводим единицу, то она всегда останется сама собой. В случае, если нужно возвести число минус один, то при чётном показателе степени она превратится в единицу, при нечётном останется минус единицей.

Возведение в целую отрицательную степень если модуль больше единицы
Для цифр, чей модуль больше единицы, есть свои особенности действий. Прежде всего, нужно целую часть дроби перевести в числитель, то есть перевести в неправильную дробь. Если у нас имеется десятичная дробь, то её необходимо перевести в обычную. Делается это следующим образом:
- 6 целых 7/17 = 109/17;
- 2,54 = 254/100.
Теперь рассмотрим, как возвести число в отрицательную степень в данных условиях. Уже из вышеизложенного, мы можем предположить, чего нам ждать от результата вычислений. Так как двойная дробь при упрощениях переворачивается, то модуль цифры будет уменьшаться тем быстрее, чем больше модуль показателя.
Для начала рассмотрим ситуацию, когда данная в задании цифра положительная.
Прежде всего, становится понятно, что конечный результат будет больше нуля, ибо деление двух положительных всегда дает положительное. Снова рассмотрим на примерах как это делается:
- 6 целых 1/20 в минус пятой степени = 121/20^-5 = 1/(121/20)^5 = 1/121^5/20^5 = 20^5/121^5 = 3200000/25937424601 = 0,0001234;
- 2,25^-6 = (225/100)^-6 = 1/(225/100)^6 = 1/225^6/100^6 = 100^6/225^6 = 100*100*100*100*100*100/225*225*225*225*225*225 = 0,007413.
Как видим, особых сложностей действия не вызывают, и все наши первоначальные предположения оказались истинными.
Теперь обратимся к случаю отрицательной цифры.
Для начала можно предположить, что если показатель чётный, то итог будет положительным, если показатель нечётный, то и результат окажется отрицательным. Все предыдущие наши выкладки в данной части, будем считать действительными и сейчас. И снова разберём на примерах:
- -3 целых 1/2 в минус шестой степени = (-7/2)^-6 = 1/(-7/2)^6 = 1/(-7)^6/2^6 = 2*2*2*2*2*2/(-7)*(-7)*(-7)*(-7)*(-7)*(-7) = 64/117649 = 0,000544;
- -1,25^-5 = (-125/100)^-5 = 1/(-125/100)^5 = 1/(-125)^5/100^5 = 100^5/(-125)^5 = 100*100*100*100*100/(-125)*(-125)*(-125)*(-125)*(-125) = 10000000000/(-30517578125) = -0.32768.
Таким образом, все наши рассуждения оказались верными.

Возведение в случае отрицательного дробного показателя
Здесь нужно запомнить что подобное возведение есть извлечение корня степени знаменателя из числа в степени числителя. Все предыдущие наши рассуждения остаются верными и на сей раз. Поясним наши действия на примере:
- 4^-3/2 = 1/4^3/2 = 1/rad(4^3) = 1/rad64 = 1/8.
В этом случае, нужно иметь в виду, что извлечение корней высокого уровня возможно только в специально подобранном виде и, скорее всего, избавиться от знака радикала (корня квадратного, кубического и так далее) при точных вычислениях вам не удастся.
Все же, подробно изучив предыдущие главы, сложностей в школьных вычислениях ожидать не стоит.
Следует заметить, что под описание данной главы подходит и возведение с заведомо иррациональным показателем, например, если показатель равен минус ПИ. Действовать нужно по вышеописанным принципам. Однако, вычисления в подобных случаях становятся настолько сложными, что под силу только мощным электронно-вычислительным машинам.

Заключение
Действие, которое мы изучали, является одной из самых сложнейших задач в математике (особенно в случае дробно-рационального или иррационального его значения). Однако, подробно и пошагово изучив данную инструкцию, можно научиться без особых проблем проделывать это на полном автомате.
Видео
В видео подробно рассказывается о том, как производить вычисления, если степень с отрицательным показателем.
liveposts.ru
Как вычислить степень?
Как вычислить степень?

Возвести число а в степень n означает, что нужно число а умножить на а n раз. Это понятно, если а – целое число. Но бывают степени дробные или отрицательные. Сколько раз нужно перемножать число в этих случаях? О том, как вычислить дробную степень числа, написано в статье Как возводить в дробную степень? | Приведем примеры таких вычислений. Рассмотрим примеры для всех вариантов возведения в степень.
Как вычислить степень с целым показателем
Вычисление степени с положительным целочисленным показателем
При возведении любого числа в степень 0 всегда получается 1:
При возведении отрицательного числа в степень 0 будет -1:
- -3*0 = -1×3*0 = -1×1 = -1
При возведении числа в степень 1 число остаётся без изменений:
При возведении в чётную степень любого числа всегда получается положительное число:
При возведении в нечётную степень знак числа сохраняется без изменений:
Вычисление степени с отрицательным целочисленным показателем
Минус в показателе степени меняет местами числитель и знаменатель числа:
- 5*(-1) = 1/5 = 0,2
- -5*(-1) = -1/5 = -0,2
- (2/3)*(-1) = (3/2)*1 = 3/2
- 5*(-2) = (1/5²) = 1/25 = 0,04
При возведении в отрицательную степень отрицательного числа правило чётной степени сохраняется:
- -5*(-2) = (1/-5)² = 1/25 = 0,04
- -5*(-3) = (1/-5)³ = -1/125 = -0,016
Как вычислить степень числа с дробным показателем
Дробный показатель степени
elhow.ru
Как возводить число в отрицательную степень
Со школы всем нам известно правило о возведении в степень: любое число с показателем N равно результату перемножения данного числа на самого себя N-ное количество раз. Иными словами, 7 в степени 3 — это 7, умноженное на себя три раза, то есть 343. Еще одно правило – возведение любой величины в степень 0 дает единицу, а возведение отрицательной величины представляет собой результат обычного возведения в степень, если она четная, и такой же результат со знаком «минус», если она нечетная.

Правила же дают и ответ, как возводить число в отрицательную степень. Для этого нужно возвести обычным способом нужную величину на модуль показателя, а потом единицу поделить на результат.
Из этих правил становится понятно, что выполнение реальных задач с оперированием большими величинами потребует наличия технических средств. Вручную получится перемножить на самого себя максимум диапазон чисел до двадцати-тридцати, и то не более трех-четырех раз. Это не говоря уж о том, чтобы потом еще и единицу разделить на результат. Поэтому тем, у кого нет под рукой специального инженерного калькулятора, мы расскажем, как возвести число в отрицательную степень в Excel.
Решение задач в Excel
Для разрешения задач с возведением в степень Excel позволяет пользоваться одним из двух вариантов.
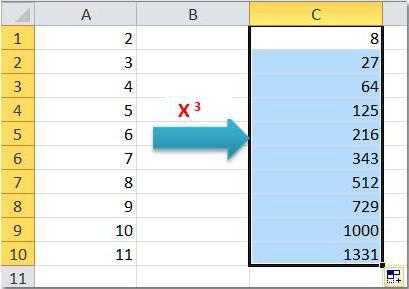
Первое – это использование формулы со стандартным знаком «крышечка». Введите в ячейки рабочего листа следующие данные:
B | C | Формула | Результат | |
2 | 7 | 3 | =B2^C2 | 343 |
Таким же образом можно возвести нужную величину в любую степень — отрицательную, дробную. Выполним следующие действия и ответим на вопрос о том, как возвести число в отрицательную степень. Пример:
B | C | Формула | Результат | |
2 | 7 | -3 | =B2^C2 | 0,002915 |
Можно прямо в формуле подправить =B2^-C2.
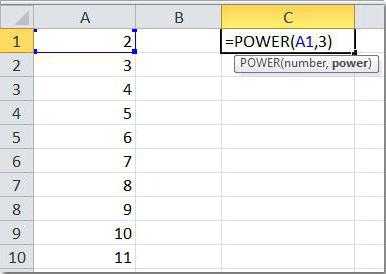
Второй вариант – использование готовой функции «Степень», принимающей два обязательных аргумента – число и показатель. Чтобы приступить к ее использованию, достаточно в любой свободной ячейке поставить знак «равно» (=), указывающий на начало формулы, и ввести вышеприведенные слова. Осталось выбрать две ячейки, которые будут участвовать в операции (или указать конкретные числа вручную), и нажать на клавишу Enter. Посмотрим на нескольких простых примерах.
B | C | Формула | Результат | |
2 | 7 | 3 | =СТЕПЕНЬ(B2;C2) | 343 |
3 | 7 | -3 | =СТЕПЕНЬ(B3;C3) |
Как видим, нет ничего сложного в том, как возводить число в отрицательную степень и в обычную с помощью Excel. Ведь для решения данной задачи можно пользоваться как привычным всем символом «крышечка», так и удобной для запоминания встроенной функцией программы. Это несомненный плюс!
Перейдем к более сложным примерам. Вспомним правило о том, как возводить число в отрицательную степень дробного характера, и увидим, что эта задача очень просто решается в Excel.
Дробные показатели
Если кратко, то алгоритм вычисления числа с дробным показателем следующий.
- Преобразовать дробный показатель в правильную или неправильную дробь.
- Возвести наше число в числитель полученной преобразованной дроби.
- Из полученного в предыдущем пункте числа вычислить корень, с условием, что показателем корня будет знаменатель дроби, полученной на первом этапе.
Согласитесь, что даже при оперировании малыми числами и правильными дробями подобные вычисления могут занять немало времени. Хорошо, что табличному процессору Excel без разницы, какое число и в какую степень возводить. Попробуйте решить на рабочем листе Excel следующий пример:
B (число) | C | Преобразование в дробь | Формула | Результат | |
2 | 7 | 0,4 | 2/5 | =СТЕПЕНЬ(B2;C2) | 2,177906424 |
Воспользовавшись вышеприведенными правилами, вы можете проверить и убедиться, что вычисление произведено правильно.
В конце нашей статьи приведем в форме таблицы с формулами и результатами несколько примеров, как возводить число в отрицательную степень, а также несколько примеров с оперированием дробными числами и степенями.
Таблица примеров
Проверьте на рабочем листе книги Excel следующие примеры. Чтобы все заработало корректно, вам необходимо использовать смешанную ссылку при копировании формулы. Закрепите номер столбца, содержащего возводимое число, и номер строки, содержащей показатель. Ваша формула должна иметь примерно следующий вид: «=$B4^C$3».
Число / Степень | 1 | 2 | 3 | 0,5 | -0,5 |
1 | 1 | 1 | 1 | 1 | 1 |
2 | 2 | 4 | 8 | 1,414214 | 0,707107 |
7 | 7 | 49 | 343 | 2,645751 | 0,377964 |
-7 | -7 | 49 | -343 | #ЧИСЛО! | #ЧИСЛО! |
0,2 | 0,2 | 0,04 | 0,008 | 0,447214 | 2,236068 |
0,4 | 0,4 | 0,16 | 0,064 | 0,632456 | 1,581139 |
-0,4 | -0,4 | 0,16 | -0,064 | #ЧИСЛО! | #ЧИСЛО! |
Обратите внимание, что положительные числа (даже нецелые) без проблем вычисляются при любых показателях. Не возникает проблем и с возведением любых чисел в целые показатели. А вот возведение отрицательного числа в дробную степень обернется для вас ошибкой, поскольку невозможно выполнить правило, указанное в начале нашей статьи про возведение отрицательных чисел, ведь четность – это характеристика исключительно ЦЕЛОГО числа.
fb.ru
Возведение в степень отрицательного числа
Как возвести в степень отрицательное число?
Возведение в степень отрицательного числа можно выполнить, основываясь на определении степени.
По определению степени, n-я степень отрицательного числа -a — это произведение n множителей, каждый из которых равен -a:
Например,
Произведение двух отрицательных чисел — положительное число. Произведение любого чётного количества отрицательных чисел — также положительное число. Таким образом, возведение в чётную степень отрицательного числа можно упростить.
Степень с отрицательным основанием и чётным показателем равна степени с основанием, противоположным данному и с тем же показателем:
(2n — чётное число).
Например,
Произведение трех отрицательных чисел — число отрицательное. Произведение любого нечётного количества отрицательных чисел — также отрицательное число. Следовательно, при возведении отрицательного числа в нечётную степень получим отрицательное число.
Чтобы возвести в нечётную степень отрицательное число, надо поставить знак «минус» и возвести в эту степень число, противоположное данному:
(2n+1 — нечётное число).
Например,
www.algebraclass.ru
























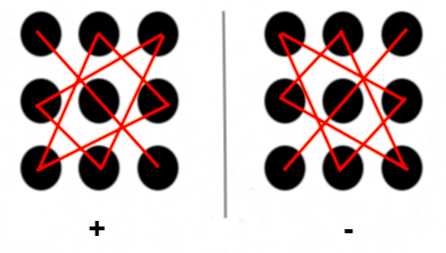
 Вычислите главный определитель матрицы. Для этого найдите произведения элементов, расположенных по диагоналям матрицы. Сначала умножьте все элементы первой диагонали, расположенной от левого верхнего до нижнего правого элемента матрицы. Потом вычислите так же вторую диагональ. От первого произведения отнимите второе. Результат вычитания и будет главным определителем системы. Если главный детерминант не равен нулю, значит система имеет решение.
Вычислите главный определитель матрицы. Для этого найдите произведения элементов, расположенных по диагоналям матрицы. Сначала умножьте все элементы первой диагонали, расположенной от левого верхнего до нижнего правого элемента матрицы. Потом вычислите так же вторую диагональ. От первого произведения отнимите второе. Результат вычитания и будет главным определителем системы. Если главный детерминант не равен нулю, значит система имеет решение.




 и
предыдущее равенство примет видоткуда
и
предыдущее равенство примет видоткуда
 то
получаемформулы
для нахождения неизвестных переменных
по методу Крамера .
то
получаемформулы
для нахождения неизвестных переменных
по методу Крамера .



 аналогично
вычисляются
аналогично
вычисляются




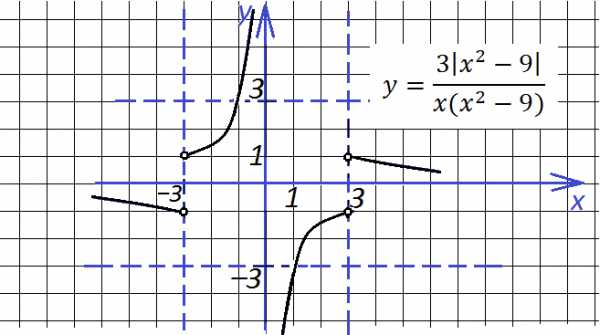

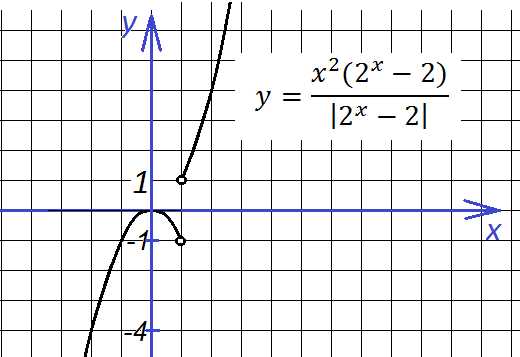

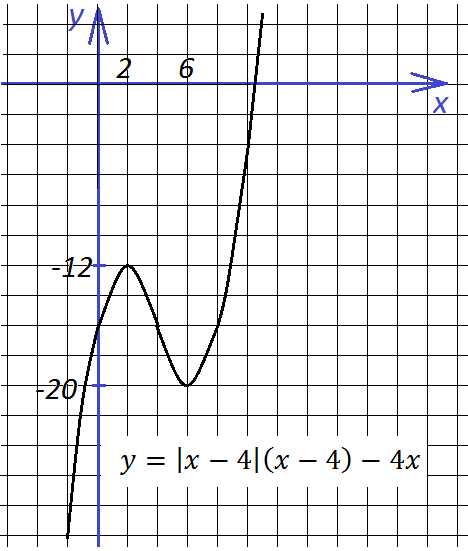
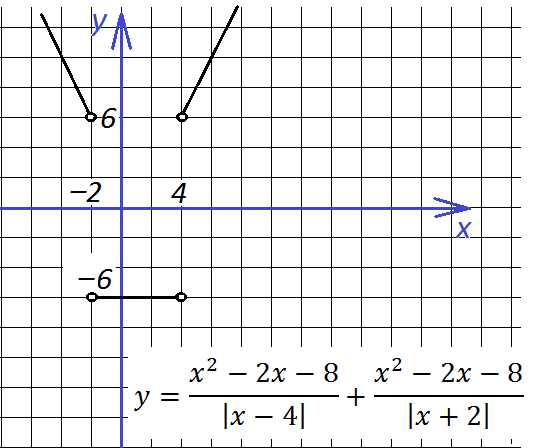



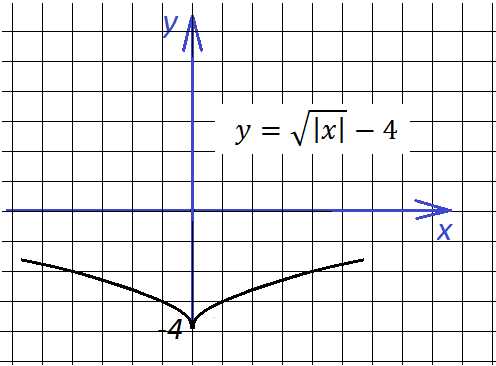
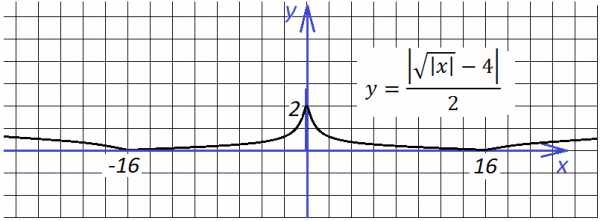
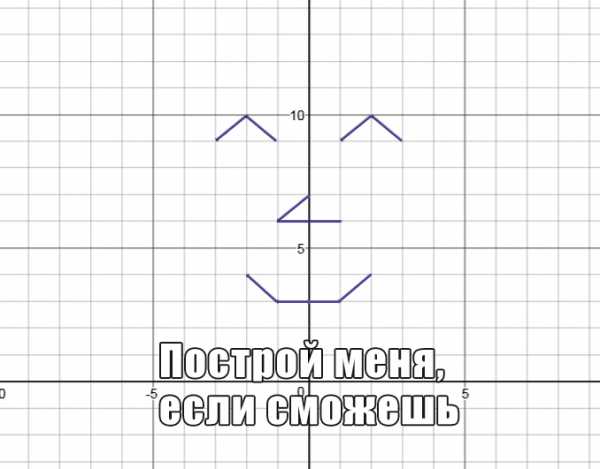


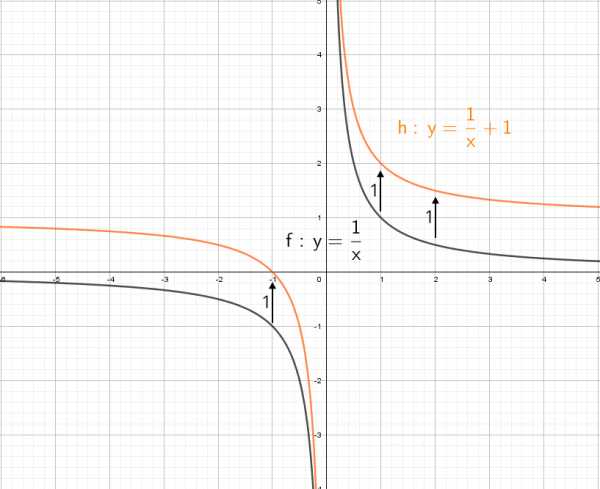 Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!
Глупый вопрос: а если добавить отдельно «−1» y = (1/x) − 1? Вниз на единицу!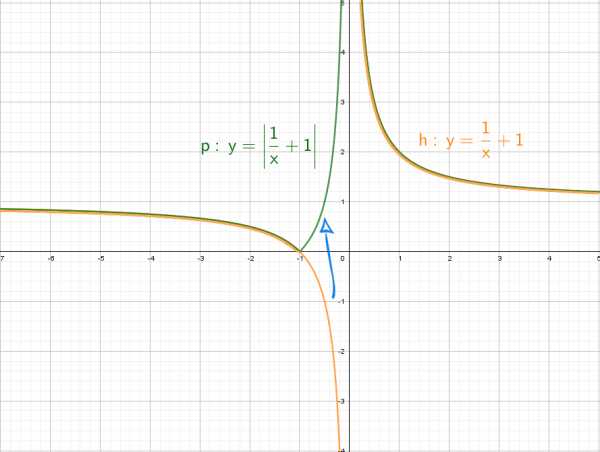

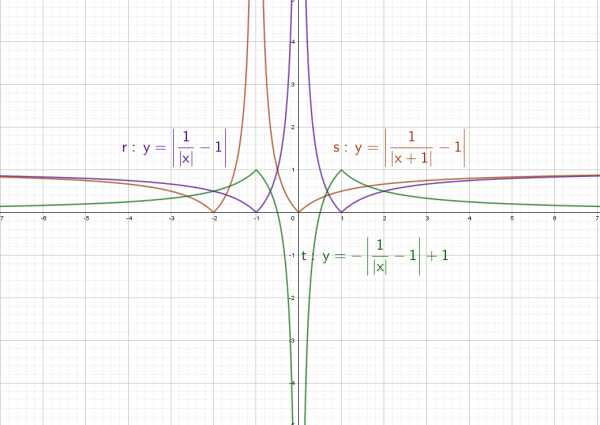

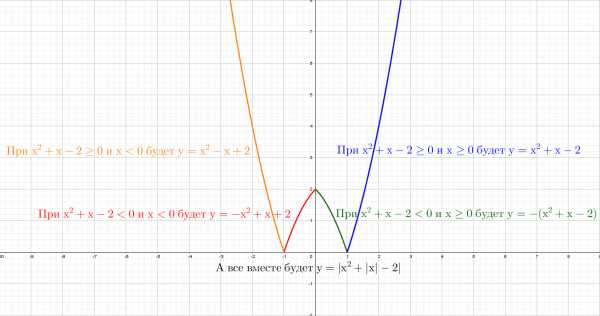 Таким способом, медленно и кропотливо можно построить любой график!
Таким способом, медленно и кропотливо можно построить любой график!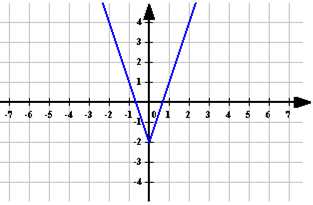
 остроение графика функции
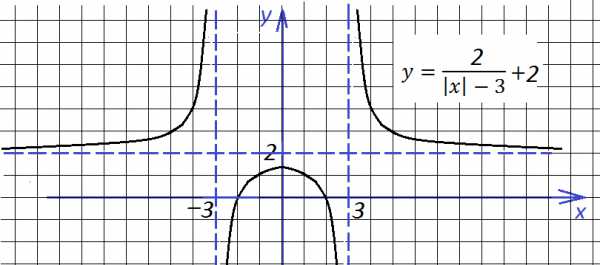
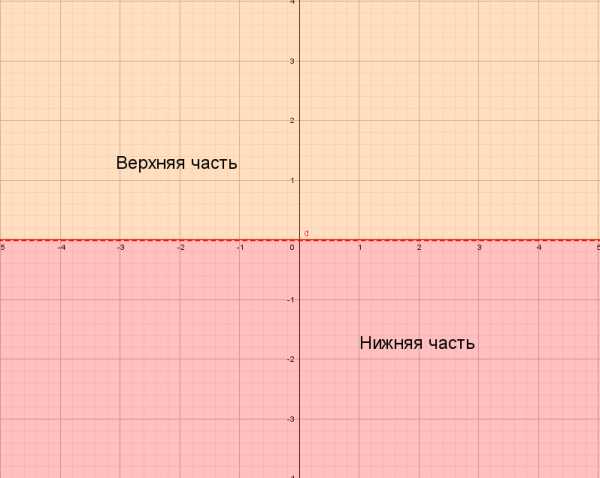
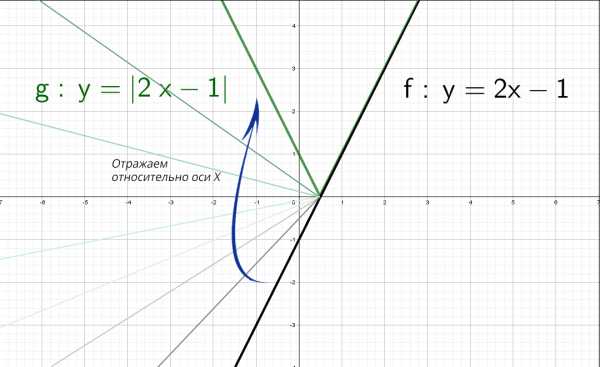
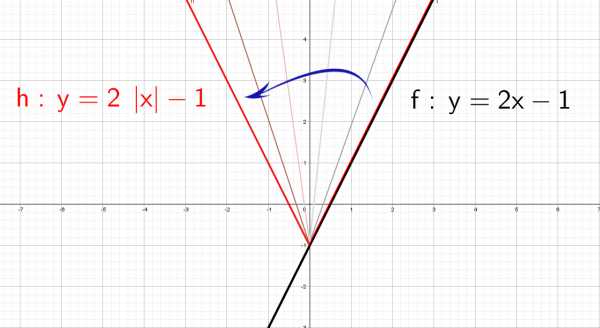
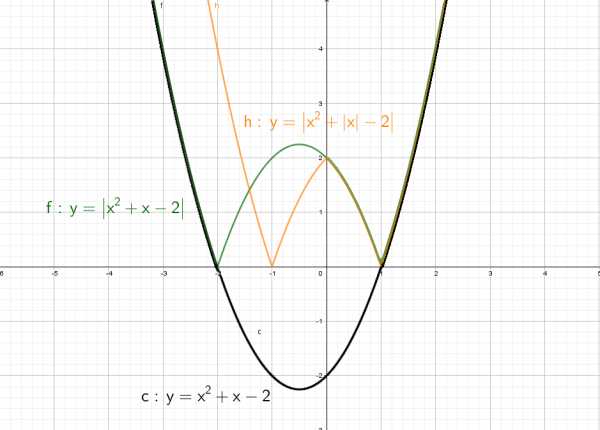
остроение графика функции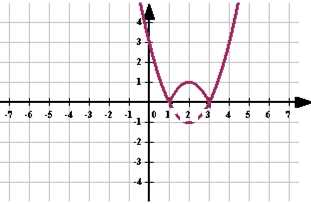 Чтобы построить график функции , если известен график функции , нужно оставить на месте ту его часть, где , и симметрично отобразить относительно оси Х другую его часть, где .
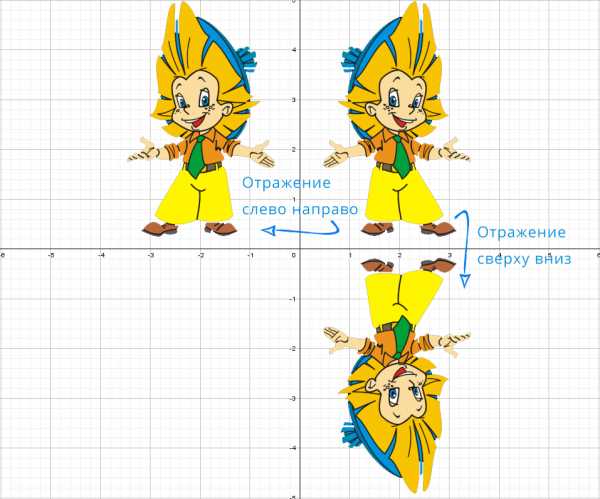
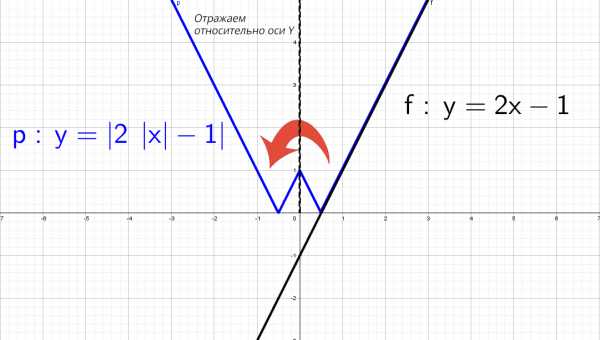
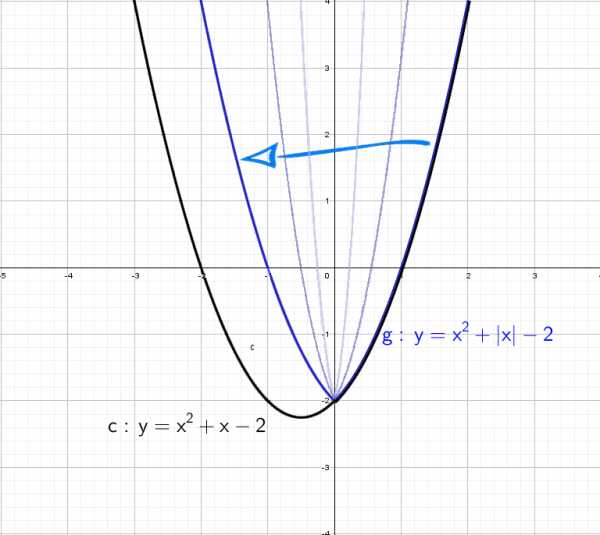
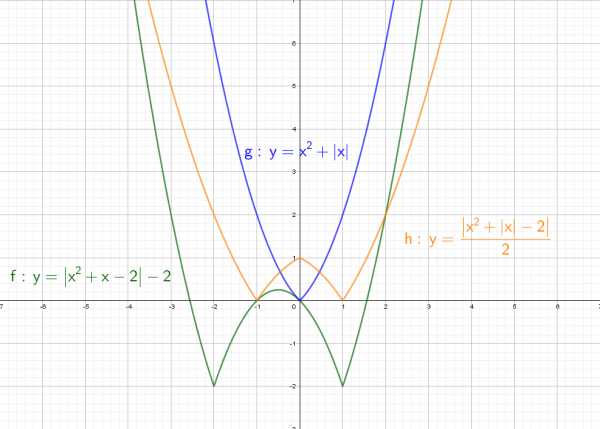
Чтобы построить график функции , если известен график функции , нужно оставить на месте ту его часть, где , и симметрично отобразить относительно оси Х другую его часть, где .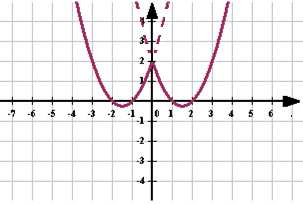 Чтобы построить график функции , если известен график функции , нужно оставить на месте ту его часть, где , а при отобразить построенную часть симметрично относительно оси ОУ.
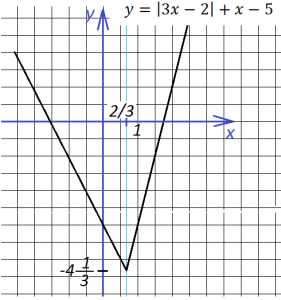
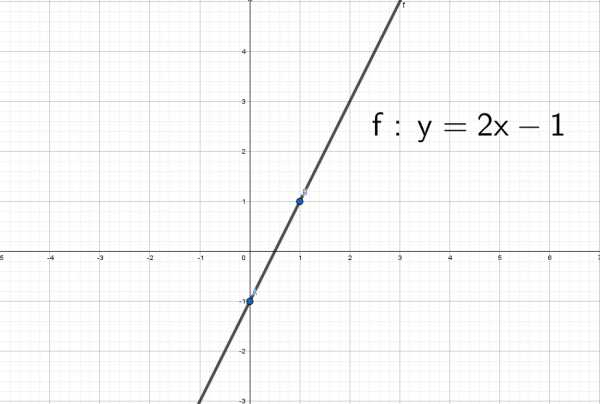
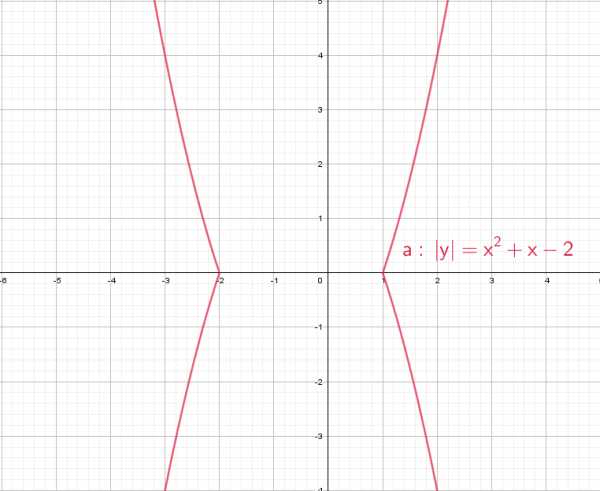
Чтобы построить график функции , если известен график функции , нужно оставить на месте ту его часть, где , а при отобразить построенную часть симметрично относительно оси ОУ. ыражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:
ыражение, стоящее под знаком модуля, меняет знак в точке х=2/3. При х<2/3 функция запишется так:





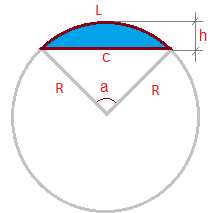 Сегмент круга
Сегмент круга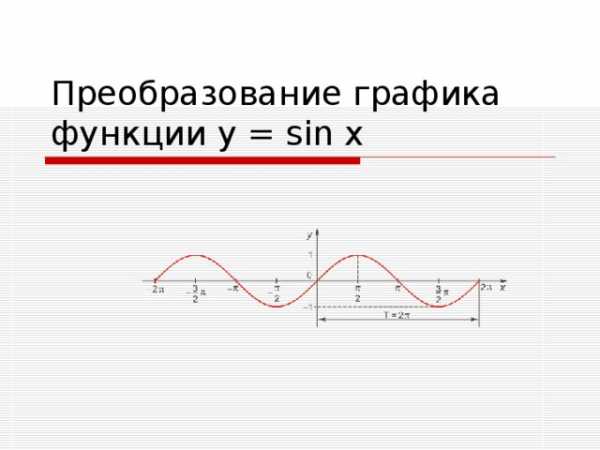
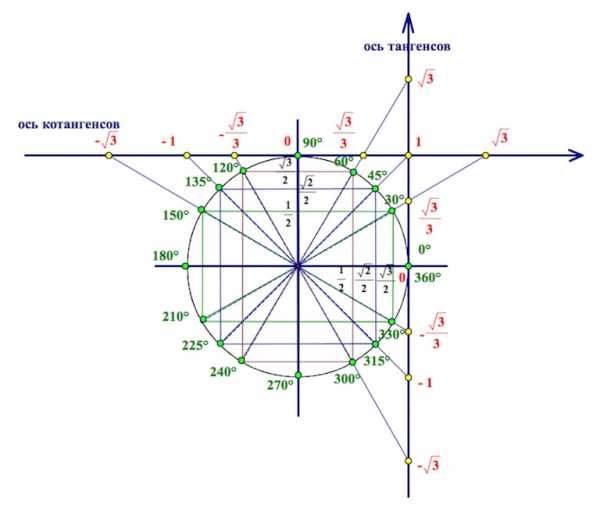
 0 (положительная) для всех x ∈ (2π·k, π+2π·k), sin x (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), Функция возрастает от −1 до 1 на промежутках: [- π /2+2 π k ; π /2+2 π k] Функция убывает от 1 до -1 на промежутках: [ π /2+2 π k ; 3 π /2+2 π k] Наибольшее значение функции sin x = 1 в точках: X= π /2 + 2 π k , Наименьшее значение функции sin x = −1 в точках: X= — π /2 + 2 π k , «
0 (положительная) для всех x ∈ (2π·k, π+2π·k), sin x (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), Функция возрастает от −1 до 1 на промежутках: [- π /2+2 π k ; π /2+2 π k] Функция убывает от 1 до -1 на промежутках: [ π /2+2 π k ; 3 π /2+2 π k] Наибольшее значение функции sin x = 1 в точках: X= π /2 + 2 π k , Наименьшее значение функции sin x = −1 в точках: X= — π /2 + 2 π k , «

 0 (положительная) для всех x ∈ (2π·k, π+2π·k), sin x Функция возрастает от −1 до 1 на промежутках: [- π /2+2 π k ; π /2+2 π k] , Функция убывает от 1 до -1 на промежутках: [ π /2+2 π k ; 3 π /2+2 π k] Наибольшее значение функции sin x = 1 в точках: X= π /2 + 2 π k , Наименьшее значение функции sin x = −1 в точках: X= — π /2 + 2 π k , «
0 (положительная) для всех x ∈ (2π·k, π+2π·k), sin x Функция возрастает от −1 до 1 на промежутках: [- π /2+2 π k ; π /2+2 π k] , Функция убывает от 1 до -1 на промежутках: [ π /2+2 π k ; 3 π /2+2 π k] Наибольшее значение функции sin x = 1 в точках: X= π /2 + 2 π k , Наименьшее значение функции sin x = −1 в точках: X= — π /2 + 2 π k , «
 1 – растяжение от оси X с коэффициентом m Если 0сжатие к оси X с коэффициентом 1/ m «
1 – растяжение от оси X с коэффициентом m Если 0сжатие к оси X с коэффициентом 1/ m «

 1, то сжатие к оси Y с коэффициентом к Если 0 «
1, то сжатие к оси Y с коэффициентом к Если 0 «





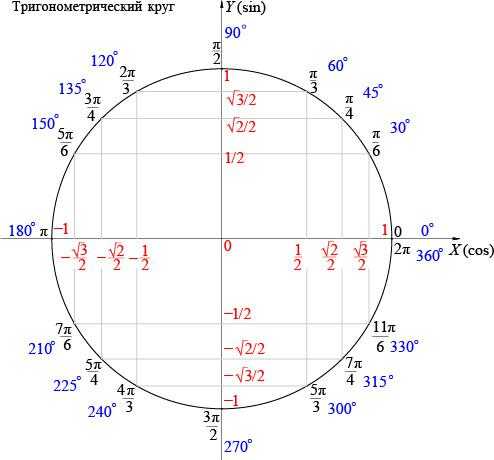
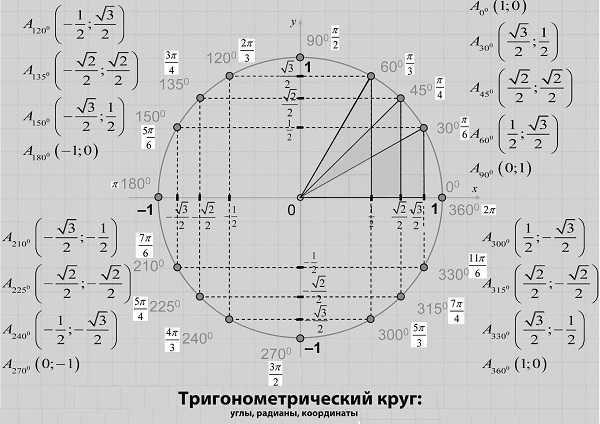


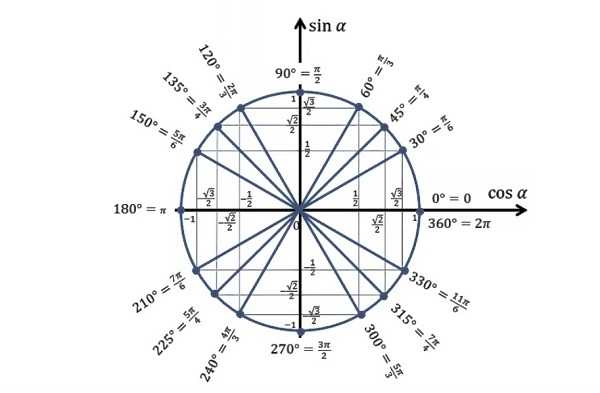






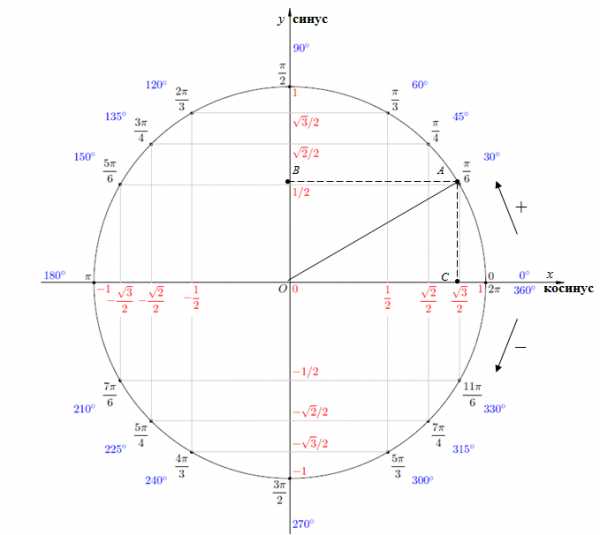
 Подробнее про радианы:+ показать
Подробнее про радианы:+ показать



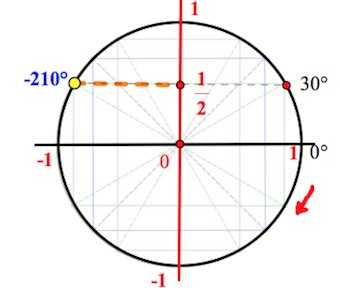 (позже, когда вы привыкнете к тригонометрическому кругу, вам не потребуется переводить радианы в градусы):
(позже, когда вы привыкнете к тригонометрическому кругу, вам не потребуется переводить радианы в градусы):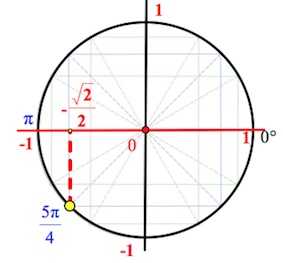 Все же, не будем переводить радианы в градусы, как в предыдущем примере.
Все же, не будем переводить радианы в градусы, как в предыдущем примере. Если мы пройдем или , да хоть , мы все равно окажемся в точке, которую мы обозначили как «старт». Поэтому, можно сразу пройти в точку на круге
Если мы пройдем или , да хоть , мы все равно окажемся в точке, которую мы обозначили как «старт». Поэтому, можно сразу пройти в точку на круге
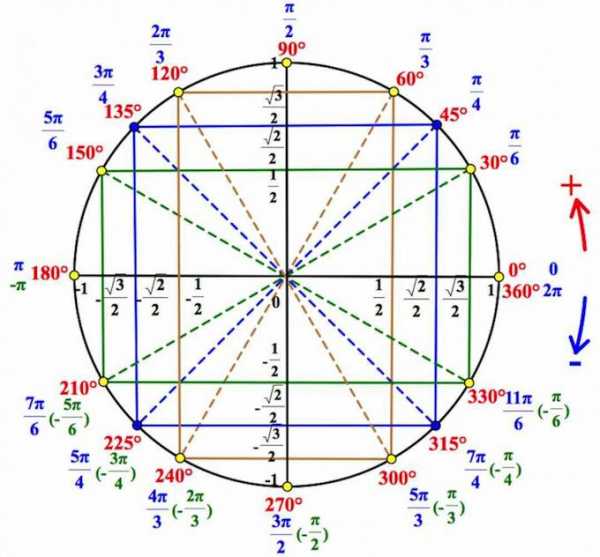
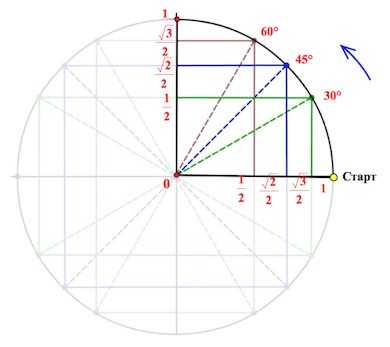 Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.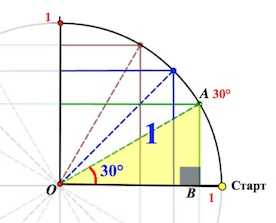

 Величина вписанного угла равна половине дуги, на которую он опирается.
Величина вписанного угла равна половине дуги, на которую он опирается.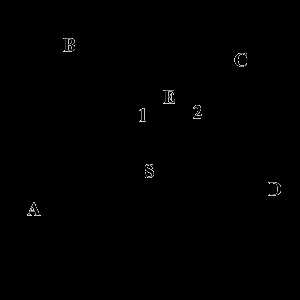
 ,
где
,
где – модуль вектора.
– модуль вектора. .
. .
Сравните с ответом в предыдущем пункте.
Сделайте выводы.
.
Сравните с ответом в предыдущем пункте.
Сделайте выводы.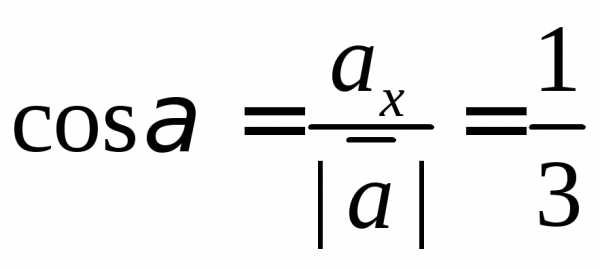
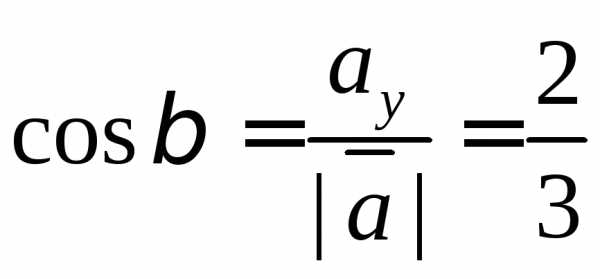

 ,
,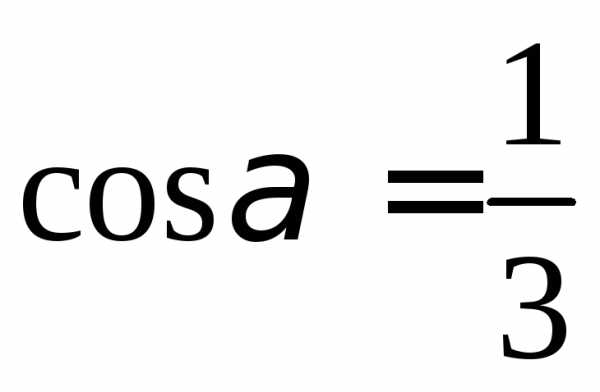 ,
,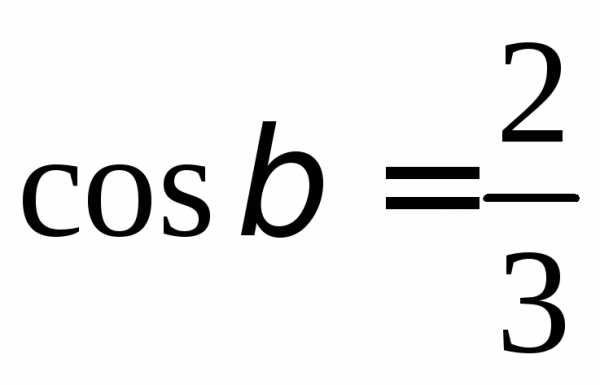 ,
,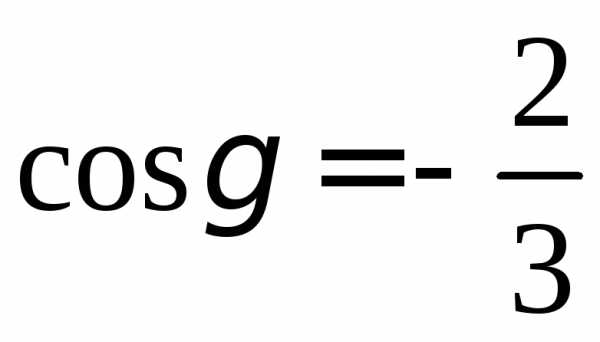 .
. ,
зная, что
,
зная, что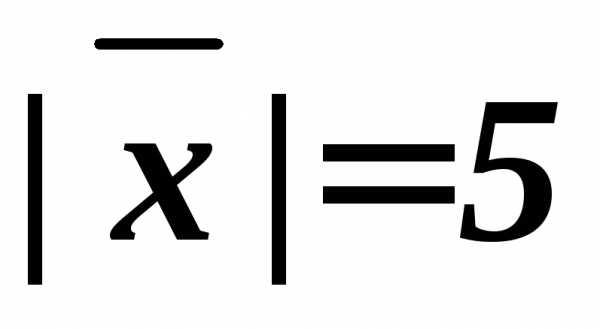 и он направлен в сторону, противоположную
вектору
и он направлен в сторону, противоположную
вектору .
.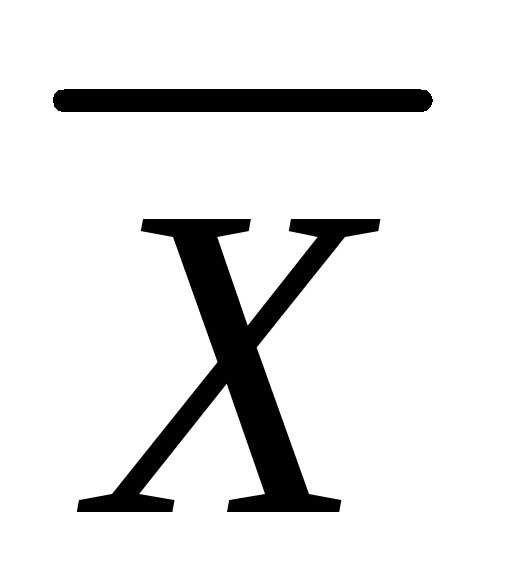 коллинеарен вектору
коллинеарен вектору ,
значит, его единичный вектор равен
единичному вектору
,
значит, его единичный вектор равен
единичному вектору только со знаком минус, т.к. направлен
в противоположную сторону.
только со знаком минус, т.к. направлен
в противоположную сторону.
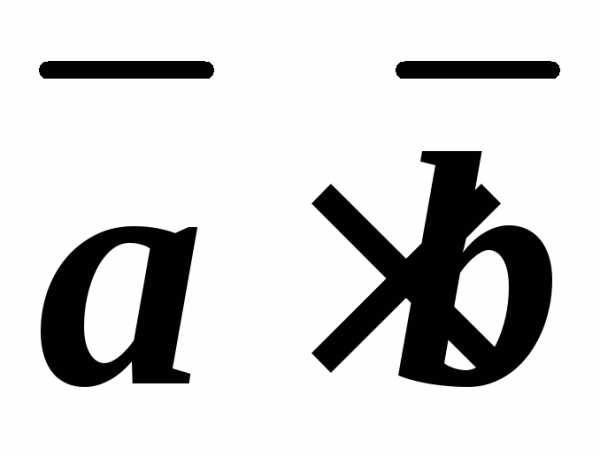 и
и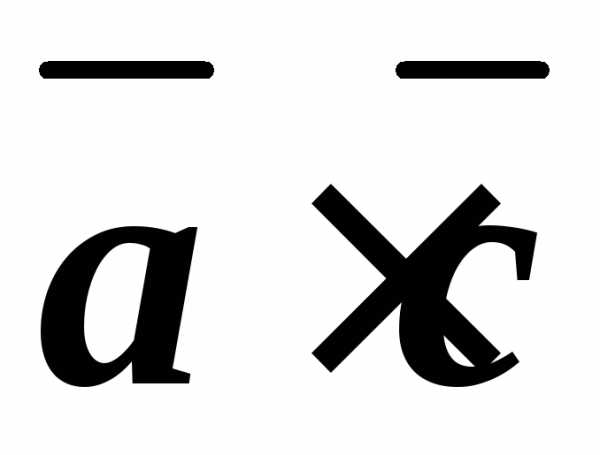 .
Перпендикулярны ли векторы
.
Перпендикулярны ли векторы и
и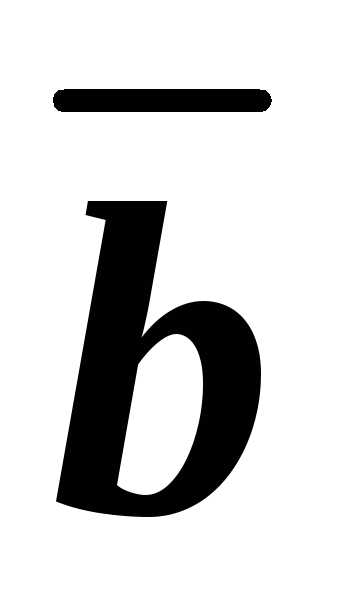 ,
, и
и между собой?
между собой? и
и перпендикулярны.
перпендикулярны. ,
,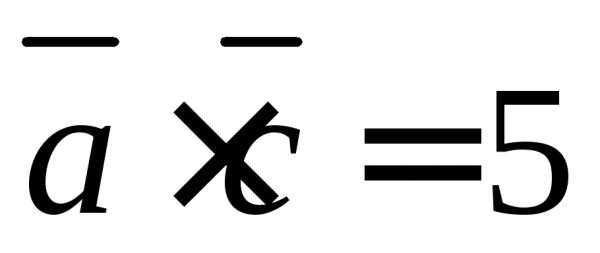 ,
векторы не перпендикулярны.
,
векторы не перпендикулярны. ,
вектор перемещения – это.
А произведение этих векторов и будет
искомой работой.
,
вектор перемещения – это.
А произведение этих векторов и будет
искомой работой.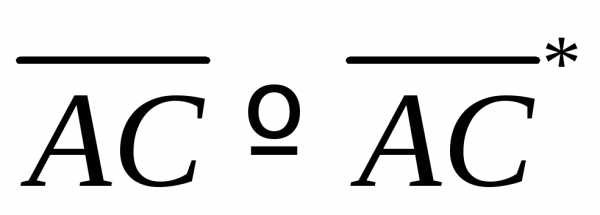 ,
только имеют разные начальные координаты.
,
только имеют разные начальные координаты.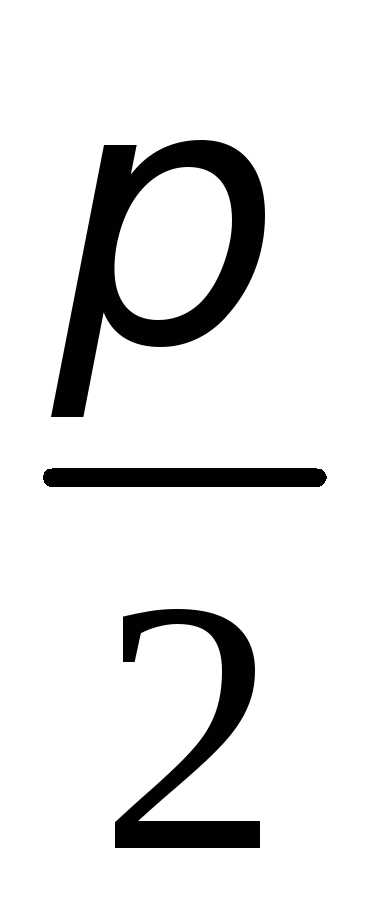 ,
внешний угол при вершине В =
,
внешний угол при вершине В =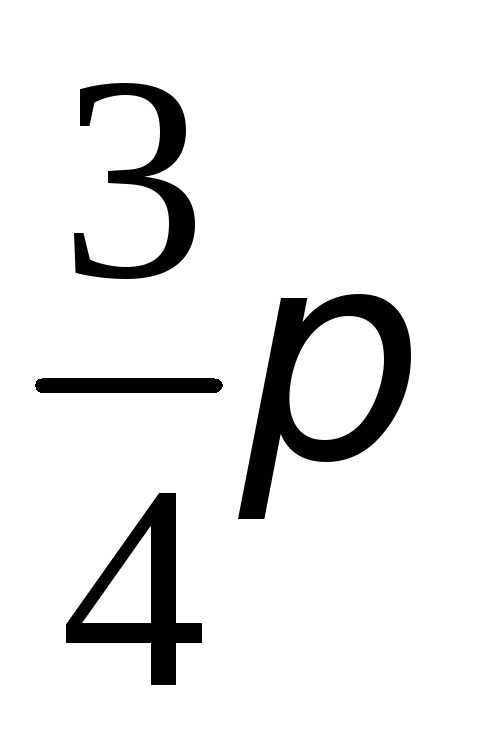 .
.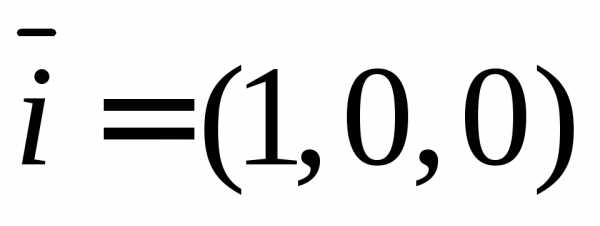 ,
,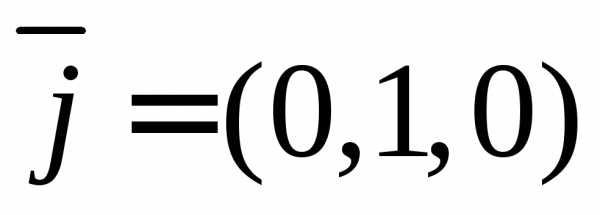 ,
,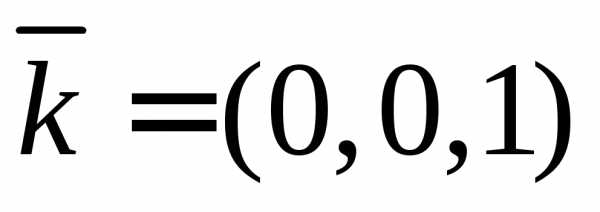 .
.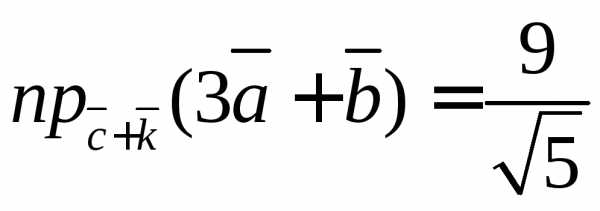 ,
, ,
, .
.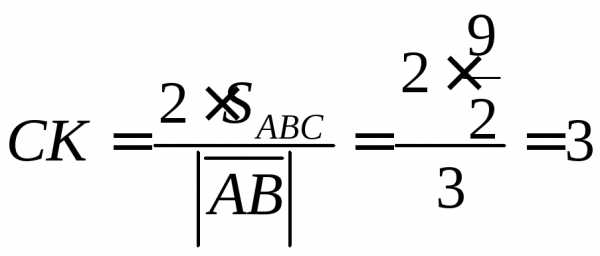
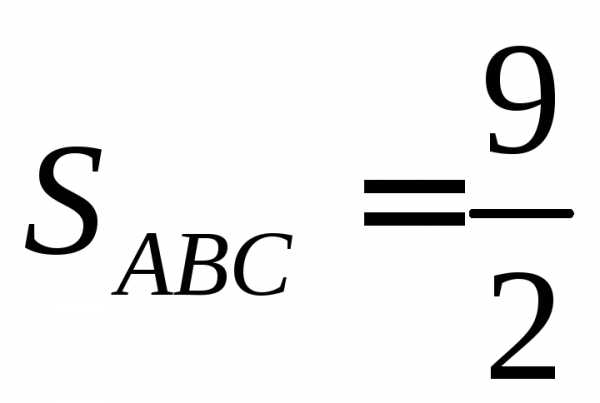 ,
,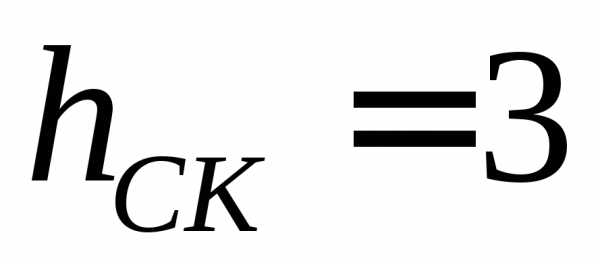 .
. и
и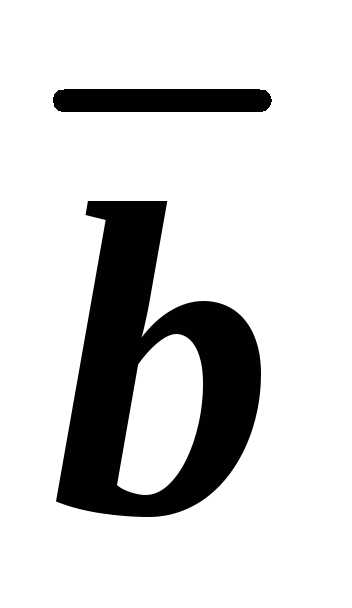 .
.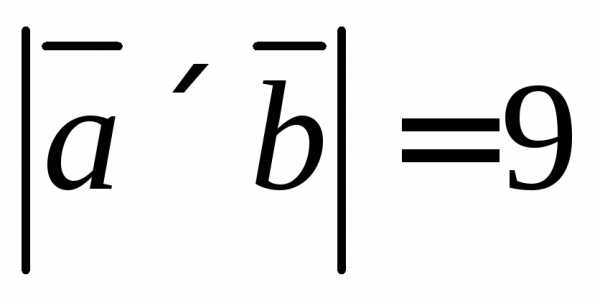
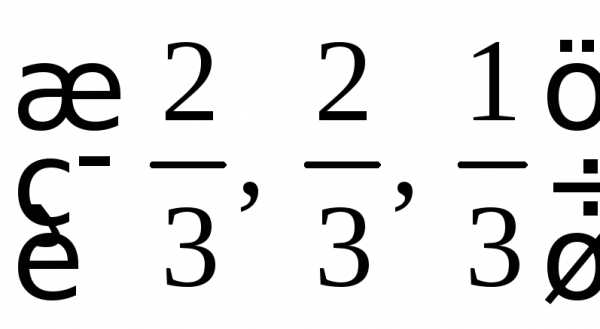 .
. ,
,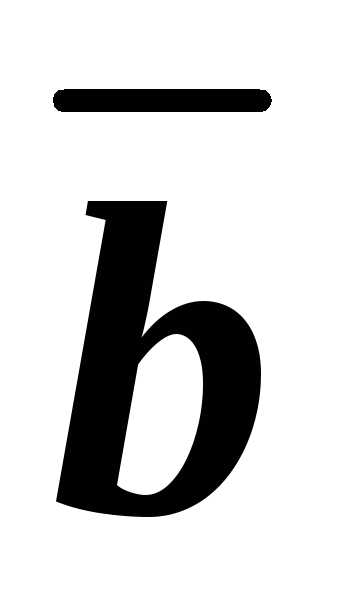 и
и в одной плоскости? Могут ли эти векторы
образовывать базис пространства? Почему?
Если могут, разложите по этому базису
вектор.
в одной плоскости? Могут ли эти векторы
образовывать базис пространства? Почему?
Если могут, разложите по этому базису
вектор. по этому базису.
по этому базису. ,
, и
и не лежат в одной плоскости.
не лежат в одной плоскости.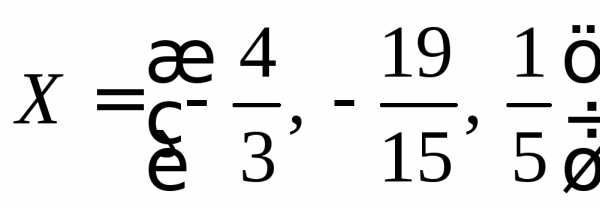 .
. .
Чему равен объём пирамиды с вершинами
A, B, C, D и её высота, опущенная из точки A
на основание BCD.
.
Чему равен объём пирамиды с вершинами
A, B, C, D и её высота, опущенная из точки A
на основание BCD.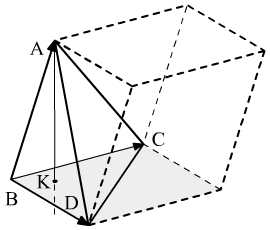 еометрический
смысл смешанного произведения в том,
что это объём параллелепипеда образованного
этими векторами.
еометрический
смысл смешанного произведения в том,
что это объём параллелепипеда образованного
этими векторами.

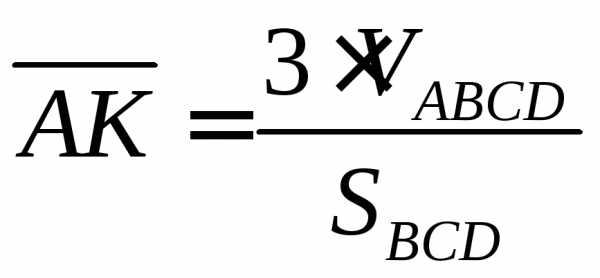
 .
. и
и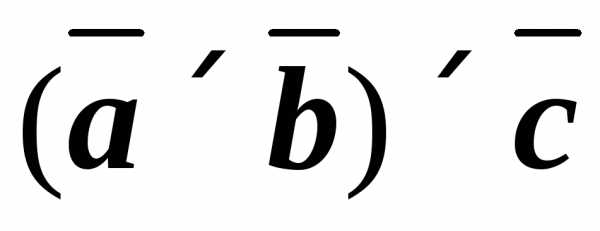 .
.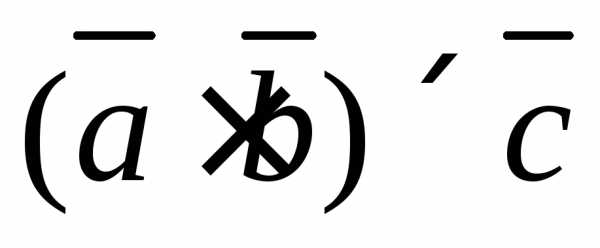 –над этим заданием
предлагаем вам подумать самим.
–над этим заданием
предлагаем вам подумать самим. –выполним
произведение.
–выполним
произведение. и
и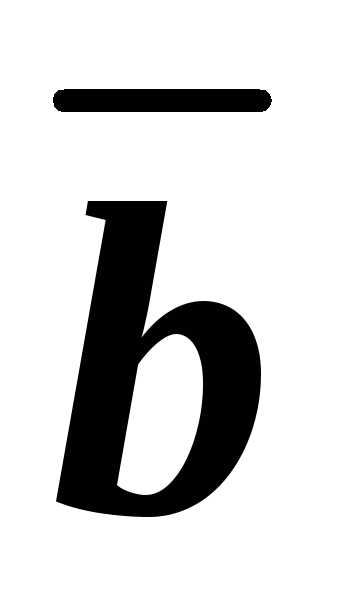 ,
а его проекция на вектор
,
а его проекция на вектор равна 5.
равна 5. и
и произвольной длинны.
произвольной длинны. через уравнение
через уравнение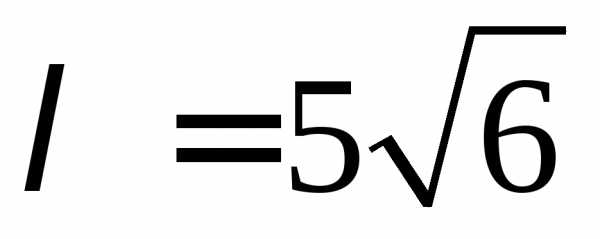
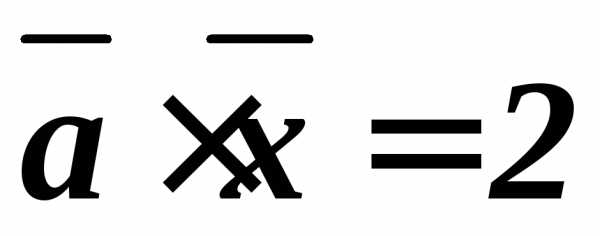 ,
, ,
,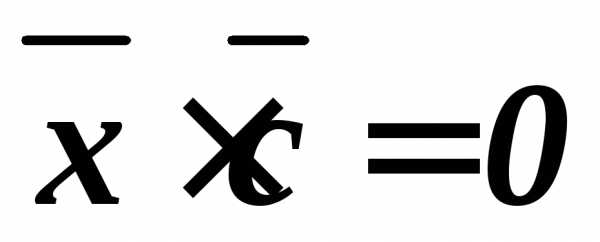 .
.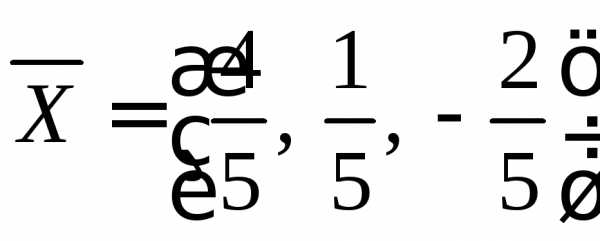
 и
и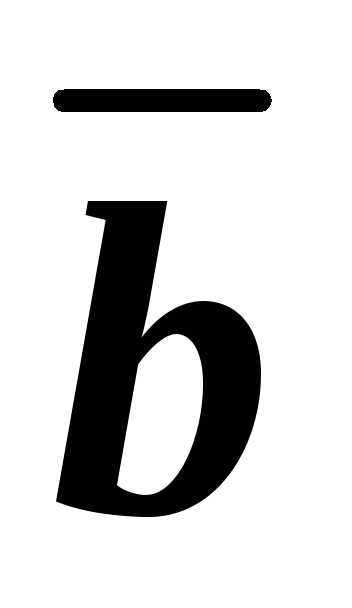 ,
и перпендикулярного вектору
,
и перпендикулярного вектору .
. .
.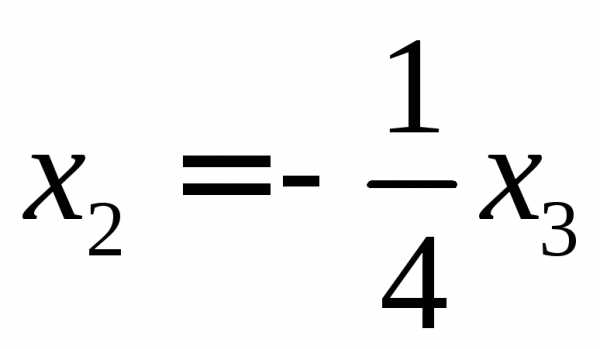
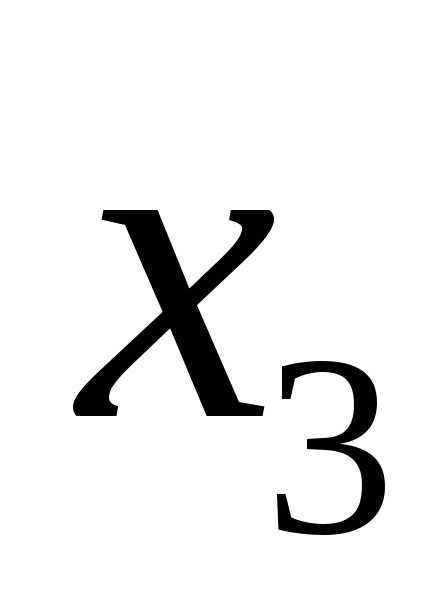 вектор будет удовлетворять условиям.
Подставим
вектор будет удовлетворять условиям.
Подставим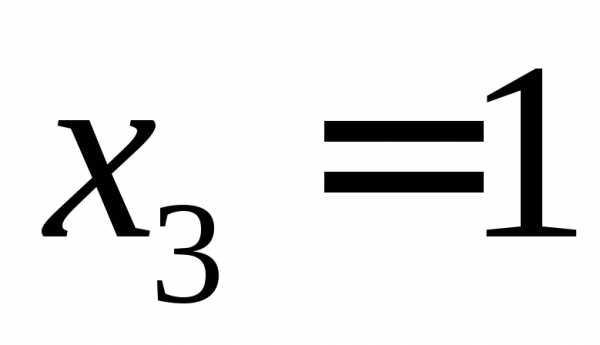 .
.