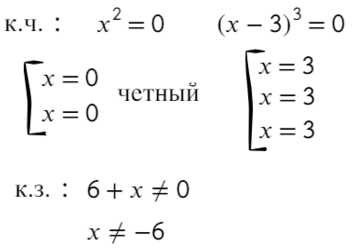Изопроцессы. Газовые законы — Класс!ная физика
Изопроцессы. Газовые законы
Газовые законы — это просто!
Давление (p), объем (V) и температура (T) являются основными параметрами состояния газа.
Всякое изменение состояния газа называется термодинамическим процессом.
Термодинамические процессы, протекающие в газе постоянной массы при неизменном значении одного из параметров состояния газа, называются изопроцессами.
Изопроцессы являются идеализированной моделью реального процесса в газе.
Изопроцессы подчиняются газовым законам.
Газовые законы определяют количественные зависимости между двумя параметрами газа при неизменном значении третьего.
Газовые законы справедливы для любых газов и газовых смесей.
Изотермический процесс (T = const)
Изотермическим процессом называются изменения состояния газа, протекающие при постоянной температуре.
Изотермический процесс в идеальном газе подчиняется закону Бойля-Мариотта:
Для газа данной массы произведение давления газа на его объем постоянно, если температура газа не меняется.
Формулу закона можно записать иначе
где
— параметры газа в разные моменты времени
Графическое представление изотермического процесса:
— изотерма — график, отражающий изотермический процесс.
(математически это гипербола)
На графиках представлены изотермы для разных температур газа, где Т12.
Изобарный процесс (p =const)
Изобарным процессом называются изменения состояния газа, протекающие при постоянном давлении.
Изобарный процесс в идеальном газе подчиняется закону Гей-Люсака:
Для газа данной массы отношение объема газа к его температуре постоянно, если давление газа не меняется.
Формулу закона можно записать иначе
где
— параметры газа в разные моменты времени
Графическое представление изобарного процесса:
— изобара — график, отражающий изобарный процесс.
(математически это линейная зависимость)
На графиках представлены изобары для разных давлений газа, где р12.
Изохорный процесс (V = const)
Изохорным процессом называются изменения состояния газа, протекающие при постоянном объеме.
Изохорный процесс в идеальном газе подчиняется закону Шарля:
Для газа данной массы отношение давления газа к его температуре постоянно, если объем газа не меняется.
Формулу закона можно записать иначе
где
— параметры газа в разные моменты времени
Графическое представление изохорного процесса:
— изохора — график, отражающий изохорный процесс.
(математически это линейная зависимость)
На графиках представлены изохоры для разных объемов газа, где V12.
Молекулярная физика. Термодинамика — Класс!ная физика
Основные положения МКТ. Масса и размер молекул. Количество вещества. — Взаимодействие молекул. Строение твердых тел, жидкостей и газов. — Идеальный газ. Основное уравнение МКТ. — Температура. Тепловое равновесие. Абсолютная шкала температур. — Уравнение состояния идеального газа. — Изопроцессы. Газовые законы. — Взаимные превращения жидкостей и газов. Влажность воздуха. — Твердые тела. Кристаллические тела. Аморфные тела.
class-fizika.ru
Газовые законы. Изопроцессы. Видеоурок. Физика 10 Класс
На прошлом уроке мы уже сформулировали так называемое уравнение состояния идеального газа – закон, связывающий между собой три макроскопических параметра газа: температуру, давление и объём.
или же
То есть, каким бы ни был переход от одного состояния к другому (что, собственно, и подразумевается под газовым процессом), соотношение между тремя параметрами не меняется (естественно, при неизменном количестве вещества рассматриваемой порции газа).
Теперь же рассмотрим не произвольные процессы, а более частные случаи, когда неизменной величиной является один из макроскопических параметров. Начнём с изотермического процесса.
Определение. Изотермический процесс – процесс перехода идеального газа из одного состояния в другое без изменения температуры. Закон, описывающий связь меду параметрами газа при таком процессе, называется закон Бойля-Мариотта в честь двух учёных, практически одновременно выведших его: англичанина Роберта Бойля и француза Эдма Мариотта (рис. 2). Запишем его:
Для начала запишем уравнения состояния идеального газа при постоянном количестве вещества:
А теперь учитывая: и
Получаем: для любых различных состояний газа, или же просто:
— закон Бойля-Мариотта
Из этого закона очевидно следует обратно пропорциональная связь давления и объёма: при увеличении объёма наблюдается уменьшение давления, и наоборот. График зависимости меняющихся величин в уравнении, то есть P и V, имеет следующий вид и называется изотермой (рис. 1):
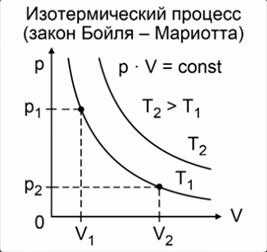
Рис. 1. Графики изотермических процессов в координатах P-V
Такая кривая в математике называется гиперболой. Также следствием закона Бойля-Мариотта является то, что площади показанных на графике прямоугольников равны между собой.
Рис. 2. Роберт Бойль и Эдм Мариотт соответственно (Источник), (Источник)
Рассмотрим следующий изопроцесс – изобарный процесс.
Определение. Изобарный (или изобарический) процесс – процесс перехода идеального газа из одного состояния в другое при постоянном значении давления. Впервые такой процесс рассмотрел французский учённый Жозеф-Луи Гей-Люссак (рис. 4), поэтому закон носит его имя. Запишем этот закон
Снова запишем обычное уравнение состояния:
А теперь учитывая: и
Получаем: для любых различных состояний газа, или же просто:
— закон Гей-Люссака
Из этого закона очевидно следует прямо пропорциональная связь между температурой и объёмом: при увеличении температуры наблюдается увеличение объёма, и наоборот. График зависимости меняющихся величин в уравнении, то есть T и V, имеет следующий вид и называется изобарой (рис. 3):
Рис. 3. Графики изобарных процессов в координатах V-T (Источник)
Следует обратить внимание на то, что, поскольку мы работаем в системе СИ, то есть с абсолютной шкалой температур, на графике присутствует область, близкая к абсолютному нулю температур, в которой данный закон не выполняется. Поэтому прямую в области, близкой к нулю, следует изображать пунктирной линией.
Рис. 4. Жозеф Луи Гей-Люссак (Источник)
Рассмотрим, наконец, третий изопроцесс.
Определение. Изохорный (или изохорический) процесс – процесс перехода идеального газа из одного состояния в другое при постоянном значении объёма. Процесс рассмотрен впервые французом Жаком Шарлем (рис. 6), поэтому закон носит его имя. Запишем закон Шарля:
Снова запишем обычное уравнение состояния:
А теперь учитывая: и
Получаем: для любых различных состояний газа, или же просто:
— закон Шарля
Из этого закона очевидно следует прямо пропорциональная связь между температурой и давлением: при увеличении температуры наблюдается увеличение давления, и наоборот. График зависимости меняющихся величин в уравнении, то есть T и P, имеет следующий вид и называется изохорой (рис. 5):
Рис. 5. Графики изохорных процессов в координатах V-T
В районе абсолютного нуля для графиков изохорного процесса также существует лишь условная зависимость, поэтому прямую также следует доводить до начала координат пунктиром.
Рис. 6. Жак Шарль (Источник)
Стоит обратить внимание, что именно такая зависимость температуры от давления и объёма при изохорных и изобарных процессах соответственно определяет эффективность и точность измерения температуры с помощью газовых термометров.
Интересен также тот факт, что исторически первыми были открыты именно рассматриваемые нами изопроцессы, которые, как мы показали, являются частными случаями уравнения состояния, а уже потом уравнения Клапейрона и Менделеева-Клапейрона. Хронологически сначала были исследованы процессы, протекающие при постоянной температуре, затем при постоянном объёме а последними – изобарические процессы.
Теперь для сравнения всех изопроцессов мы собрали их в одну таблицу (см рис. 7). Обратите внимание, что графики изопроцессов в координатах, содержащих неизменяющийся параметр, собственно говоря, и выглядят как зависимость константы от какой-либо переменной.
Рис. 7.
На следующем уроке мы рассмотрим свойства такого специфического газа, как насыщенный пар, подробно рассмотрим процесс кипения.
Список литературы
- Мякишев Г.Я., Синяков А.З. Молекулярная физика. Термодинамика. – М.: Дрофа, 2010.
- Генденштейн Л.Э., Дик Ю.И. Физика 10 класс. – М.: Илекса, 2005.
- Касьянов В.А. Физика 10 класс. – М.: Дрофа, 2010.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Slideshare.net (Источник).
- E-science.ru (Источник).
- Mathus.ru (Источник).
Домашнее задание
- Стр. 70: № 514–518. Физика. Задачник. 10-11 классы. Рымкевич А.П. – М.: Дрофа, 2013. (Источник)
- Какова зависимость между температурой и плотностью идеального газа при изобарном процессе?
- При надувании щёк и объём, и давление во рту возростают пр неизменной температуре. Противоречит ли это закону Бойля-Мариотта? Почему?
- *Как будет выглядеть график данного процесса в координатах P-V?
interneturok.ru
Изопроцессы. Газовые законы
Разделы: Физика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (1,3 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цель: сформировать и вывести законы для изопроцессов в газе.
Задачи:
- Образовательные:
- рассмотреть частные случаи закона Клапейрона
- получить газовые законы, доказать их справедливость экспериментально
- сформировать умения выделять и описывать изопроцессы
- продолжить формирования умения объяснять законы с молекулярной точки зрения
- Воспитательные:
- формирование коммуникативных качеств, культуры общения
- формирование интереса к изучаемому предмету
- стимулирование любознательности, активности на уроке
- развитие работоспособности
- Развивающие:
- развитие познавательного интереса
- развитие интеллектуальных способностей
- развитие умений выделять главное в изучаемом материале
- развитие умений обобщать изучаемые факты и понятия
Тип занятия: изучение нового материала
Методы: наглядный, словесный,самостоятельная работа,мультимедиа
Оборудование: компьютер, видеопроектор, демонстративный экран; приложение к уроку, телевизор, видеоролик, таблицы
Используемая литература:
1. Рябоволо Г.И., Самойленко П.И., Огородникова
Е.И. Планирование учебного процесса по физике.
Второе издание. – М. Высшая школа, 1998, с. 430.
2. Жданов Л.С., Жданов Г.Л. Физика. Учебник для
студентов средних специальных учебных
заведений. – М.: 2005, с 473.
3. Самойленко П.И., Сергеев А.В. Физика.Учебник
для студентов образовательных учреждений СПО. –
М.: Мастерство, 2002, с.395.
4. Самойленко П.И. Сборник задач по физике для
техникумов. – М.:Мир и образование, 2003, с.255.
План урока:
1) Организационный момент. Подготовка студентов
к работе на занятии. (Приветствие, организация
внимания, сообщения темы, цели, задачи урока,
мотивация учебной деятельности)
2) Проверка знаний, умений и навыков
3) Подготовка студентов к изучению нового
материала
4) Изучение нового материала
5) Формирование знаний и умений
6) Применение знаний
7) Домашнее задание
8) Подведение итогов
9) Рефлексия
ХОД УРОКА
1. Организационный момент
– Добрый день! Прошу садиться! Тема нашего
занятия «Изопроцессы. Законы идеальных газов»
В физике, как и других науках, происходит со
временем удивительный процесс. Многое из того,
что сейчас можно изложить кратко и ясно
несколько десятилетий (веков) назад появлялось
как новые истины, с большим трудом
воспринимаемые человеком.
Со временем опыт человека заставляет принять
новые идеи и привыкнуть к ним, а привыкнув,
начать использовать их в практической
деятельности, как вполне понятные и порой
тривиальные.
Примерно также и обстояло с изучением газа.
Древние ученые считали газ неуловимой формой
тела, представлявшего собой нечто среднее
между веществом и духом..Но такой взгляд
существовал до тех пор, пока в XVII веке
Торричелли и Паскаль показали, что воздух имеет
вес.
С тех пор физика начала изучать свойства газов.
2. Проверка знаний, умений и навыков
Организация самостоятельной работы.
Студенты пишут физический диктант на знание
основных формул молекулярной физики (Приложение
1)
Далее проводится взаимопроверка (работа в парах)
Ответы приводятся на доске (Приложение
10)
3. Подготовка студентов к изучению нового материала
Попробуем обобщить изученное по теме
«Основы молекулярно кинетической теории»
В основу нашего обобщения положим физическую
теорию. Этой теорией является МКТ
–молекулярно-кинетическая теория.
Большой вклад в развитие этой теории внесли
ученые разных стран (М.Ломоносов, Д.Джоуль,
Д.Бернаулли, Д.Менделеев)
Любая физическая теория включает в
себя основание, ядро, выводы.
Преподаватель ведет беседу по вопросам,
параллельно на доске составляется схема, на
которой изученный материал предстает в виде
физической теории (Приложение 2)
1) Назовите основные положения МКТ.
2) Какие явления говорят о том, что частицы
находятся в непрерывном движении?
3) Дайте определение диффузии, броуновского
движения.
4) Кем была определена скорость молекул?
5) Какие размеры имеют молекулы?
6) Какие значения имеют средние скорости молекул?
7) Какой массой обладают молекулы?
8) Что показывает число Авогадро? Назовите его
числовое значение.
9) Какой газ называют идеальным?
– Видим, что основание МКТ составляют идеализированный объект, эксперементальные факты и основные физические величины
Далее продолжается опрос студентов.
10) Назовите основное уравнение МКТ идеального
газа.
11) Что называют термодинамическими
параметрами газа?
12) Как связаны между собой абсолютная
температура и средняя кинетическая энергия
поступательного движения молекул?
13) Как связаны между собой абсолютная
температура и давление газа?
14) Запишите уравнение состояния идеального газа
(m<>const).
15) Запишите формулу объединенного газового
закона (m = const).
16) Что называют газовым законом?
– Сегодня мы рассмотрим частные случаи уравнения состояния идеального газа.
4. Изучение нового материала
Газы играют важную роль в природе и технике.
Земля окружена газовой оболочкой. Шины
автомобилей заполняются газом (воздухом)
Именно газы, расширяясь, выталкивают пулю из
ружья и снаряд из пушки. Газы вращают турбины,
толкают поршни в двигателях (студенты приводят
примеры).
Во всех случаях происходит изменение
состояния газа. Поэтому нужно знать к
чему приведет то или иное изменение состояния
газа. Уравнение состояния позволяет это сделать.
Изменение состояния газа
необязательно означает изменение всех трех
основных параметров. Любой из них можно
поддерживать постоянным. Прошу
изучить процессы, в которых масса и один из трех
параметров – p, V или T остаются неизменными.
Дать определение изопроцесса.
Изопроцессами называют процессы, при которых
масса газа и один из его параметров остаются
постоянными. Поскольку имеются три
параметра газа, существуют три
различных изопроцесса:
1) Изотермический (T = const)
2) Изохорный (V = const)
3) Изобарный (p = const)
При рассмотрении изопроцессов мы будем заполнять таблицу (каждому студенту выдается три шаблона таблиц).
Полное заполнения таблиц приводится в Приложении 3, Приложении
4, Приложении 5.
Изучение законов проходит с помощью просмотра
видеоролика и демонстрацией процесса на
проекционном экране (Диск «Физика в картинках НЦ
«Физикон»»)
Изотермический процесс (закон Бойля-Мариотта)
Демонстрация зависимости между объемом и давлением данной массы газа при постоянной температуре. По ходу рассмотрения процесса идет заполнение таблицы (Приложение 3)
Изохорный процесс (закон Шарля)
Демонстрация зависимости давления газа от температуры при постоянном объеме. При изучении процесса заполняется таблица (Приложение 4)
Изобарный процесс (закон Гей-Люссака)
Демонстрация зависимости объема газа от
температуры при постоянном давлении. После
рассмотрения данного процесса студенты
самостоятельно заполняют таблицу.
Проводится проверка заполненной таблицы (Приложении 5)
При изучении процессов один из студентов делает
сообщение. «История открытия газовых законов»
Историческая справка
1) Первый газовый закон был открыт английским
ученым Робертом Бойлем в 1661 году. Бойль изучал
изменение давления газа в зависимости от объема
при t = const. Данный процесс называют
изотермическим. Независимо от Бойля
несколько позднее французский ученый Эдм
Мариотт пришел к тем же выводам в 1676 году.
2) Шарль Жак Александр Сезар – французский физик,
исследовал расширение газов и установил в 1787
году закон изменения давления данной массы газа
с изменением температуры при V = const. Изобрел
ряд приборов, построил воздушный шар, осуществил
полет на этом шаре.
3) Гей-Люссак Жозеф Луи – французский физик и
химик в 1802 году открыл закон изменения объема
газа от температуры при p = const
5. Формирование знаний и умений
1. Разработать алгоритм решения задач по теме: «Уравнение состояния. Газовые законы» (Приложение 6)
2. Решить задачи (Приложение 7)
а) Решить задачу №1 (разбирается задача у доски)
б) Решить задачи самостоятельно:
Вариант
1
задача №2
Вариант
2
задача №3
Проверка задач (вызвать двух студентов к доске)
Задача №2 (ответ 1300см3)
Задача №3 (ответ 11.2*105 Па)
в) Дополнительно решить задачу №4 (если позволяет время)
г) Решить задачу № 5 (проанализировать графики изопроцессов газов)
6. Применение знаний (тестирование)
Ребята, мы с вами рассмотрели основные газовые законы, разобрали изопроцессы, графики изопроцессов. Теперь нам нужно обобщить наши знания, суммировать все понятия и определения. Для этого вы выполните тест. Время выполнения – 5 минут (Приложение 8)
7. Домашнее задание
1) Объяснить с точки зрения МКТ изохорный и
изобарный процессы (дополнить таблицу)
2) Подготовиться к зачету по теме: «Основы
молекулярно-кинетической теории» (по вопросам)
3) Решить задачи 3.3, 3.18, 3.34 [4]
8. Подведение итогов занятия
Ребята, сегодня мы с вами выяснили, что представляет собой изопроцесс :в зависимости от постоянства макроскопического параметра:
1) при T = const – изотермический
2) при p = const – изобарный
3) при V = const – изохорный
Вопросы для подведения итога:
1. Можно ли считать газовые законы следствием из
уравнения состояния идеального газа?
2. Применимы ли газовые законы для смеси газов?
3. Каковы условия применения газовых законов?
9. Рефлексия (анализ собственной деятельности студентов)
(Приложение 9)
11.03.2011
xn--i1abbnckbmcl9fb.xn--p1ai
Газовые законы, все формулы и примеры решений
Газовые законы были открыты экспериментально, но все они могут быть получены из уравнения Менделеева-Клапейрона.
Рассмотрим каждый из них.
Закон Бойля-Мариотта (изотермический процесс)
Изотермическим процессомназывают изменение состояния газа, при котором его температура остаётся постоянной.
Для неизменной массы газа при постоянной температуре произведение давления газа на объем есть величина постоянная:
Этот же закон можно переписать в другом виде (для двух состояний идеального газа):
Этот закон следует из уравнения Менделеева – Клапейрона:
Очевидно, что при неизменной массе газа и при постоянной температуре правая часть уравнения остается постоянной величиной.
Графики зависимости параметров газа при постоянной температуре называются изотермами.
Обозначив константу буквой , запишем функциональную зависимость давления от объема при изотермическом процессе:
Видно, что давление газа обратно пропорционально его объему. Графиком обратной пропорциональности, а, следовательно, и графиком изотермы в координатах является гипербола (рис.1, а). На рис.1 б) и в) представлены изотермы в координатах и соответственно.
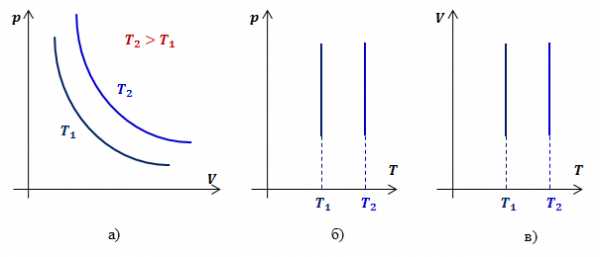
Рис.1. Графики изотермических процессов в различных координатах
Закон Гей-Люссака (изобарный процесс)
Изобарным процессомназывают изменение состояния газа, при котором его давление остаётся постоянным.
Для неизменной массы газа при постоянном давлении отношение объема газа к температуре есть величина постоянная:
Для двух состояний газа этот закон запишется в виде:
Этот закон также следует из уравнения Менделеева – Клапейрона:
Графики зависимости параметров газа при постоянном давлении называются изобарами.
Рассмотрим два изобарных процесса с давлениями и . В координатах и изобары будут иметь вид прямых линий, перпендикулярных оси (рис.2 а,б).
Определим вид графика в координатах .Обозначив константу буквой , запишем функциональную зависимость объема от температуры при изобарном процессе:
Видно, что при постоянном давлении объем газа прямо пропорционален его температуре. Графиком прямой пропорциональности, а, следовательно, и графиком изобары в координатах является прямая, проходящая через начало координат (рис.2, в). В реальности при достаточно низких температурах все газы превращаются в жидкости, к которым газовые законы уже неприменимы. Поэтому вблизи начала координат изобары на рис.2, в) показаны пунктиром.
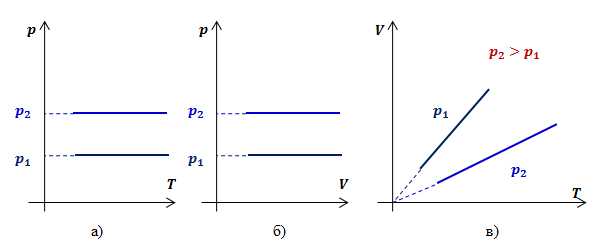
Рис.2. Графики изобарных процессов в различных координатах
Закон Шарля (изохорный процесс)
Изохорным процессомназывают изменение состояния газа, при котором его объем остаётся постоянным.
Для неизменной массы газа при постоянном объеме отношение давления газа к его температуре есть величина постоянная:
Для двух состояний газа этот закон запишется в виде:
Этот закон также можно получить из уравнения Менделеева – Клапейрона:
Графики зависимости параметров газа при постоянном давлении называются изохорами.
Рассмотрим два изохорных процесса с объемами и . В координатах и графиками изохор будут прямые, перпендикулярные оси (рис.3 а, б).
Для определения вида графика изохорного процесса в координатах обозначим константу в законе Шарля буквой , получим:
Таким образом, функциональная зависимость давления от температуры при постоянном объеме является прямой пропорциональностью, графиком такой зависимости является прямая, проходящая через начало координат (рис.3, в).
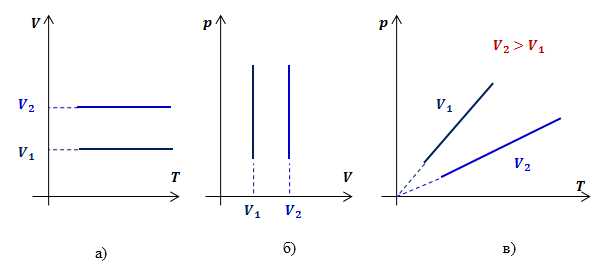
Рис.3. Графики изохорных процессов в различных координатах
Примеры решения задач
ru.solverbook.com
Изопроцессы. Газовые законы
Изопроцессами называют термодинамические процессы, протекающие в системе с неизменной массой при постоянном значении одного из параметров состояния системы.
1 ˚ Изотермический процесс.
Т = const, ΔT = 0
Р.Бойль (англ.), Э. Мариотт (фр.), ХХVII в.
Закон Бойля-Мариотта.
Произведение pV = const для данного количества газа при постоянной температуре.
Объяснение закона Бойля-Мариотта с точки зрения МКТ.
Давление — это обобщенная, усредненная действие молекул (атомов, частиц) на стены. При уменьшении объема в несколько раз во столько же раз увеличивается число молекул в единице объема (концентрация), а значит и число ударов молекул в стенки за единицу времени. Последнее ведет к росту давления.
Схема эксперимента
2 ˚ Изохорный процесс.
V = const, ΔV = 0
Ж. Шарль (фр.), 1787 год.
Закон Шарля.
Давление определенной массы газа при нагревании на 1 ˚ С при постоянном объеме увеличивается на 1/273 часть его давления при 0 ˚ С.
р = р0 (1 + αt)
где α = (p — p0) / p0t = 1/273 (K-1) — температурный коэффициент давления.
Tt = T — 273, р = р0 (1 + αt) = р0 + р0 α (T — 273) = p0αT.
Поэтому р = p0αT или р / Т = const при неизменной массе идеального газа.
Объяснение закона Шарля на основе МКТ.
Согласно основным положениям МКТ при росте температуры идеального газа растет средняя скорость движения молекул (атомов, частиц), а потому возрастает частота соприкосновения со стенками сосуда. Это вызывает рост давления молекул на стенки.
Схема эксперимента
3 ˚ Изобарный процесс.
р = const, ДР = 0
Ж. Гей-Люссак (фр.), 1802 год.
Закон Гей-Люссака.
Увеличение температуры газа на 1 ˚ С при постоянном давлении увеличивает его объем на 1/273 часть того объема, который занимает газ при 0 ˚ С.
V = V0 (1 + βt)
где β = (V — V0) / V0t — температурный коэффициент объемного расширения газа.
Учитывая, что t = T — 273, закон Гей-Люссака можно представить в следующем виде:
V = V0βt, V / T = const, при неизменной массе идеального газа.
Объяснение закона Гей-Люссака на основе МКТ.
Согласно основным положениям МКТ при росте температуры идеального газа растет средняя скорость движения молекул (атомов, частиц), а потому растет среднее расстояние между молекулами, и вызывает рост объема, который занимает идеальный газ.
Схема эксперимента
Объединенный газовый закон.
Законы Бойля-Мариотта, Шарля и Гей-Люссака, установленные экспериментально, объединяются в одну формулу, которую называют объединенным газовым законом.
Для данной массы идеального газа (m = const) в ходе произвольного равновесного термодинамического процесса величина pV / T остается постоянной:
pV / T = const
Если в ходе данного процесса масса газа меняется, то объединенный газовый закон приобретает следующий вид:
pV / (mT) = const
Уравнение состояния.
Уравнением состояния идеального газа называют соотношение, которое связывает между собой параметры идеального газа в равновесном состоянии: f (p, V, T, m) = 0.
Экспериментально установлено уравнение
pV = (m / μ) RT
называют уравнением состояния или уравнением Клапейрона-Менделеева.
В последнем уравнении R = 8,31 Дж / (моль • К) называют универсальной газовой постоянной, а число ν = m / μ указывает на количество молей вещества, для которых записано уравнение состояния и коре находятся в состоянии термодинамического равновесия.
worldofscience.ru
Законы идеальных газов
В XVII – XIX веках были сформулированы опытные законы идеальных газов. Кратко напомним их.Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.
1. Изохорический процесс. Закон Шарля. V = const.
Изохорическим процессом называется процесс, протекающий при постоянном объёме V. Поведение газа при этом изохорическом процессе подчиняется закону Шарля:
При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным: P/Т = const.
График изохорического процесса на РV-диаграмме называется изохорой. Полезно знать график изохорического процесса на РТ— и VT-диаграммах (рис. 1.6). Уравнение изохоры:
| (1.4.1) |
Рис. 1.6 Если температура газа выражена в градусах Цельсия, то уравнение изохорического процесса записывается в виде
| (1.4.2) |
Рис. 1.7 2. Изобарический процесс. Закон Гей-Люссака. Р = const.
Изобарическим процессом называется процесс, протекающий при постоянном давлении Р. Поведение газа при изобарическом процессе подчиняется закону Гей-Люссака:
При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.
График изобарического процесса на VT-диаграмме называется изобарой. Полезно знать графики изобарического процесса на РV— и РT-диаграммах (рис. 1.8).
Рис. 1.8 Уравнение изобары:
| . | (1.4.3) |
| (1.4.4) |
Рис. 1.9 3. Изотермический процесс. Закон Бойля – Мариотта. T = const.
Изотермическим процессом называется процесс, протекающий при постоянной температуре Т.
Поведение идеального газа при изотермическом процессе подчиняется закону Бойля – Мариотта:
При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.
График изотермического процесса на РV-диаграмме называется изотермой. Полезно знать графики изотермического процесса на VT— и РT-диаграммах (рис. 1.10).
Рис. 1.10 Уравнение изотермы:
| (1.4.5) |
Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой.
5. Политропический процесс. Процесс, при котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.
6. Закон Авогадро. При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных газов содержится одинаковое число молекул. В одном моле различных веществ содержится NA=6,02·1023молекул (число Авогадро).
7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов:
| (1.4.6) |
При , давление смеси газов:
| (1.4.7) |
В соответствии с законами Бойля – Мариотта (1.4.5) и Гей-Люссака (1.4.3) можно сделать заключение, что для данной массы газа
| (1.4.8) |
| Клапейрон Бенуа Поль Эмиль (1799–1864) – французский физик и инженер. Физические исследования посвящены теплоте, пластичности и равновесию твердых тел. Придал математическую форму идеям Н. Карно, первым оценил большое научное значение его труда. Вывел уравнения состояния идеального газа. Впервые ввел в термодинамику графический метод. |
ens.tpu.ru
Газовые законы — Класс!ная физика
Газовые законы
«Физика — 10 класс»
Состояние какого газа описывает уравнение Менделеева—Клапейрона.
Можно ли универсальную газовую постоянную считать фундаментальной постоянной?
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трёх параметров — давление, объём или температура — остаются неизменными.
Количественные зависимости между двумя параметрами газа при фиксированном значении третьего называют газовыми законами.
Процессы, протекающие при неизменном значении одного из параметров, называют изопроцессами.
Слово «изопроцесс» — сложное слово, первая часть которого происходит от греческого слова isos — равный, одинаковый.
Отметим, что в действительности ни один процесс не может протекать при строго фиксированном значении какого-либо параметра. Всегда имеются те или иные воздействия, нарушающие постоянство температуры, давления или объёма. Лишь в лабораторных условиях удаётся поддерживать постоянство того или иного параметра с высокой точностью, но в действующих технических устройствах и в природе это практически неосуществимо. Изопроцесс — это идеализированная модель реального процесса, которая только приближённо отражает действительность.
Изотермический процесс.
Процесс изменения состояния системы макроскопических тел (термодинамической системы) при постоянной температуре называют изотермическим.
Слово «изотермический» происходит от греческих слов isos — равный, одинаковый и therme — теплота.
Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплом с большой системой — термостатом. Иначе при сжатии или расширении температура газа будет меняться. Термостатом может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса. Согласно уравнению состояния идеального газа (10.4), если масса газа не изменяется, в любом состоянии с неизменной температурой произведение давления газа на его объём остаётся постоянным:
pV = const при Т = const. (10.6)
Этот вывод был сделан английским учёным Р. Бойлем (1627—1691) и несколько позже французским учёным Э. Мариоттом (1620—1684) на основе эксперимента. Поэтому он носит название закона Бойля—Mapuoттa.
Для газа данной массы произведение давления газа на его объём постоянно.
Закон Бойля—Мариотта справедлив обычно для любых газов, а также и для их смесей, например для воздуха. Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.
Кривую, изображающую зависимость давления газа от объёма при постоянной температуре, называют изотермой.
Изотерма газа изображает обратно пропорциональную зависимость между давлением и объёмом. Кривую такого рода в математике называют гиперболой (рис. 10.1).
Различным постоянным температурам соответствуют различные изотермы. При повышении температуры газа давление согласно уравнению состояния (10.4) увеличивается, если V = const. Поэтому изотерма, соответствующая более высокой температуре Т2, лежит выше изотермы, соответствующей более низкой температуре Т1 (см. рис. 10.1).
Для того чтобы процесс происходил при постоянной температуре, сжатие или расширение газа должно происходить очень медленно. Дело в том, что, например, при сжатии газ нагревается, так как при движении поршня в сосуде скорость и соответственно кинетическая энергия молекул после ударов о поршень увеличиваются, а следовательно, увеличивается и температура газа. Именно поэтому для реализации изотермического процесса надо после небольшого смещения поршня подождать, когда температура газа в сосуде опять станет равной температуре окружающего воздуха.
Кроме этого, отметим, что при быстром сжатии давление под поршнем сразу становится больше, чем во всём сосуде. Если значения давления и температуры в различных точках объёма разные, то в этом случае газ находится в неравновесном состоянии и мы не можем назвать значения температуры и давления, определяющие в данный момент состояние системы. Если систему предоставить самой себе, то температура и давление постепенно выравниваются, система приходит в равновесное состояние.
Равновесное состояние — это состояние, при котором температура и давление во всех точках объёма одинаковы.
Параметры состояния газа могут быть определены, если он находится в равновесном состоянии.
Процесс, при котором все промежуточные состояния газа являются равновесными, называют равновесным процессом.
Очевидно, что на графиках зависимости одного параметра от другого мы можем изображать только равновесные процессы.
Изобарный процесс
Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.
Слово «изобарный» происходит от греческих слов isos — равный, одинаковый и baros — вес, тяжесть.
Согласно уравнению (10.4) в любом состоянии газа с неизменным давлением отношение объёма газа к его температуре остаётся постоянным:
Этот закон был установлен экспериментально в 1802 г. французским учёным Ж. Гей-Люссаком (1778—1850) и носит название закона Гей-Люссака.
Закона Гей-Люссака:
Для газа данной массы при постоянном давлении отношение объёма к абсолютной температуре постоянно.
Согласно уравнению (10.7) объём газа при постоянном давлении пропорционален температуре:
V = const • Т. (10.8)
Прямую, изображающую зависимость объёма газа от температуры при постоянном давлении, называют изобарой.
Разным давлениям соответствуют разные изобары (рис. 10.2). Проведём на рисунке произвольную изотерму. С ростом давления объём газа при постоянной температуре согласно закону Бойля— Мариотта уменьшается. Поэтому изобара, соответствующая более высокому давлению р2, лежит ниже изобары, соответствующей более низкому давлению p1.
В области низких температур все изобары идеального газа сходятся в точке Т = 0. Но это не означает, что объём реального газа обращается в нуль. Все газы при сильном охлаждении превращаются в жидкости, а к жидкостям уравнение состояния (10.4) неприменимо. Именно поэтому, начиная с некоторого значения температуры, зависимость объёма от температуры проводится на графике штриховой линией. В действительности таких значений температуры и давления у вещества в газообразном состоянии быть не может.
Изобарным можно считать расширение газа при нагревании его в цилиндре с подвижным поршнем, если внешнее давление постоянно. Давление в цилиндре постоянно и равно сумме атмосферного давления и давления mпg/S поршня.
Изохорный процесс
Процесс изменения состояния термодинамической системы при постоянном объёме называют изохорным.
Слово «изохорный» происходит от греческих слов isos — равный, одинаковый и chora — место, пространство, занимаемое чем-нибудь.
Из уравнения состояния (10.4) вытекает, что в любом состоянии газа с неизменным объёмом отношение давления газа к его температуре остаётся постоянным:
Этот газовый закон был установлен в 1787 г. французским физиком Ж. Шарлем (1746—1823) и носит название закона Шарля.
Для газа данной массы отношение давления к абсолютной температуре постоянно, если объём не меняется.
Согласно уравнению (10.9) давление газа при постоянном объёме пропорционально температуре:
р = const • Т. (10.10)
Прямую, изображающую зависимость давления газа от температуры при постоянном объёме, называют изохорой.
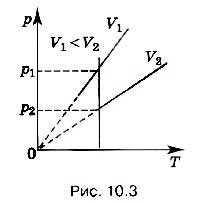
Разным объёмам соответствуют разные изохоры. Также проведём на рисунке произвольную изотерму (рис. 10.3). С ростом объёма газа при постоянной температуре давление его, согласно закону Бойля— Мариотта, падает. Поэтому изохора, соответствующая большему объёму V2, лежит ниже изохоры, соответствующей меньшему объёму V1.
В соответствии с уравнением (10.10) все изохоры идеального газа начинаются в точке Т = 0. Значит, давление идеального газа при абсолютном нуле равно нулю.
Увеличение давления газа в любом сосуде или в электрической лампочке при нагревании можно считать изохорным процессом. Изохорный процесс используется в газовых термометрах постоянного объёма.
В заключение составим опорную схему (рис. 10.4) и покажем логические переходы, связывающие различные законы и уравнения.
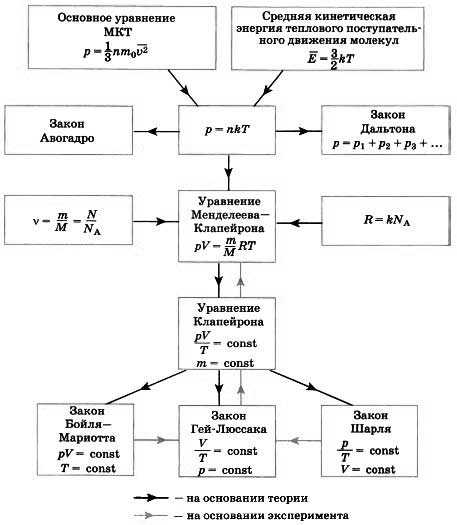
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Основные положения МКТ. Тепловые явления — Физика, учебник для 10 класса — Класс!ная физика
Почему тепловые явления изучаются в молекулярной физике — Основные положения молекулярно-кинетической теории. Размеры молекул — Примеры решения задач по теме «Основные положения МКТ» — Броуновское движение — Силы взаимодействия молекул. Строение газообразных, жидких и твёрдых тел — Идеальный газ в МКТ. Среднее значение квадрата скорости молекул — Основное уравнение молекулярно-кинетической теории газов — Примеры решения задач по теме «Основное уравнение молекулярно-кинетической теории» — Температура и тепловое равновесие — Определение температуры. Энергия теплового движения молекул — Абсолютная температура. Температура — мера средней кинетической энергии молекул — Измерение скоростей молекул газа — Примеры решения задач по теме «Энергия теплового движения молекул» — Уравнение состояния идеального газа — Примеры решения задач по теме «Уравнение состояния идеального газа» — Газовые законы — Примеры решения задач по теме «Газовые законы» — Примеры решения задач по теме «Определение параметров газа по графикам изопроцессов»
class-fizika.ru

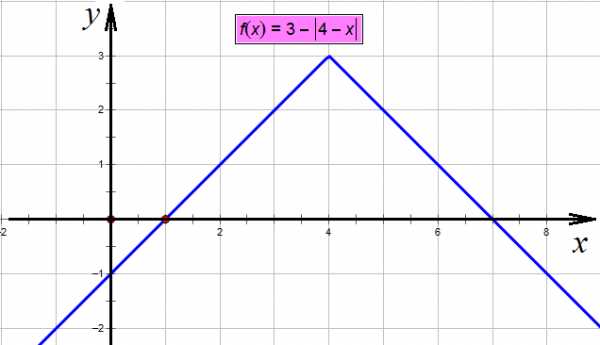
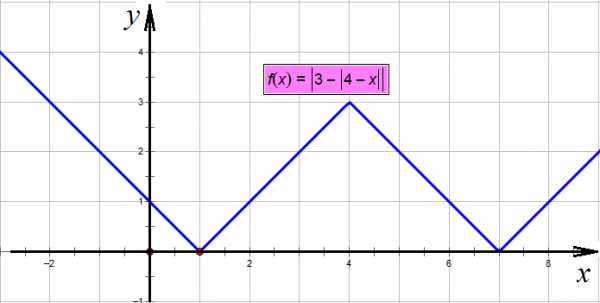
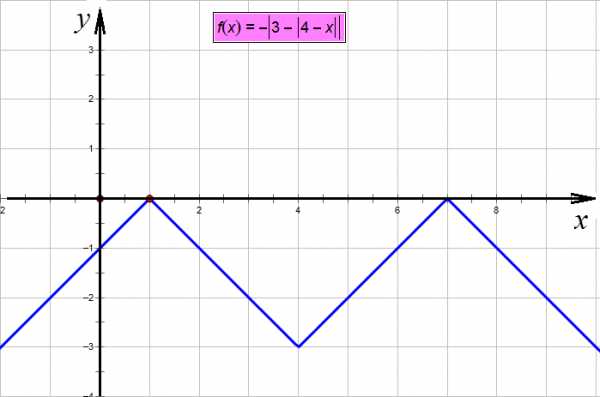
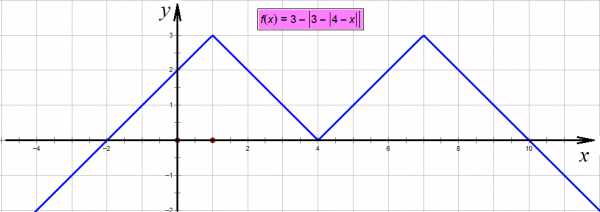

 ,
где
,
где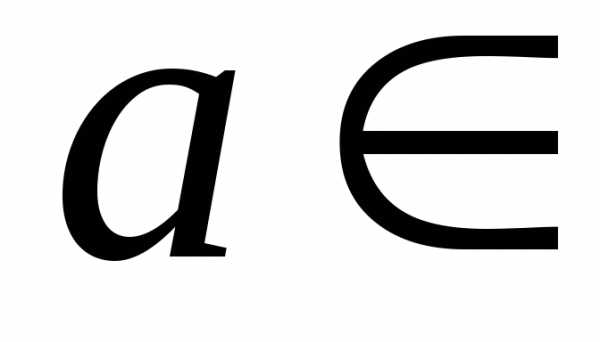
 ,
,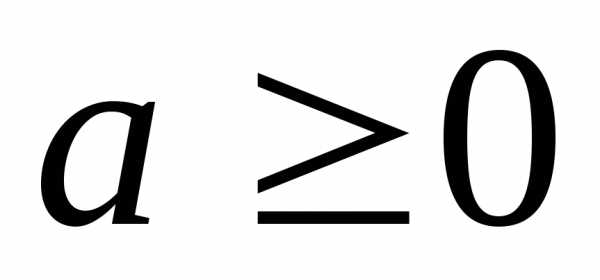 .
При
.
При неравенство решений не имеет.
неравенство решений не имеет.
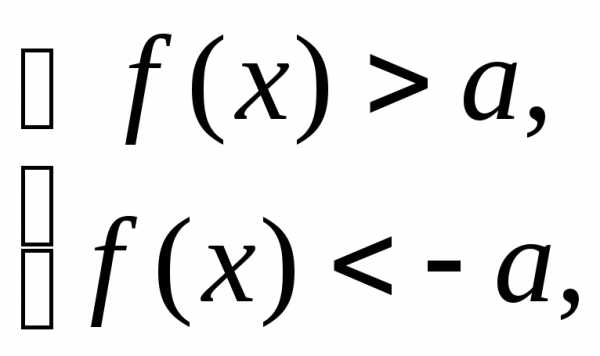
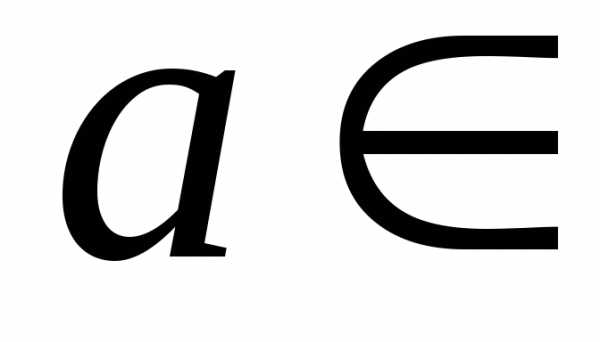
 ,
,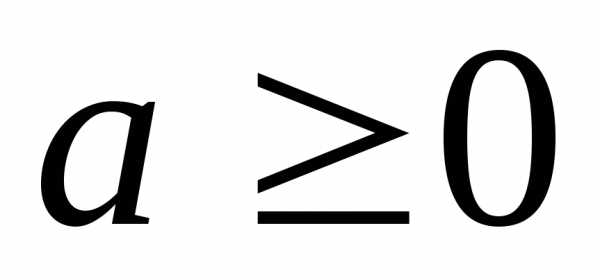 .
При
.
При неравенство выполняется для всех
неравенство выполняется для всех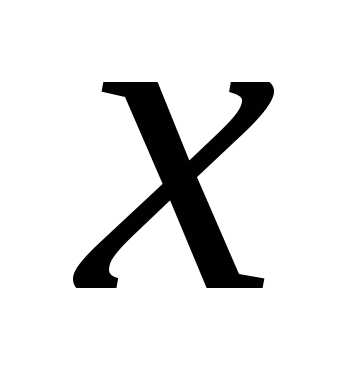 при которых функция
при которых функция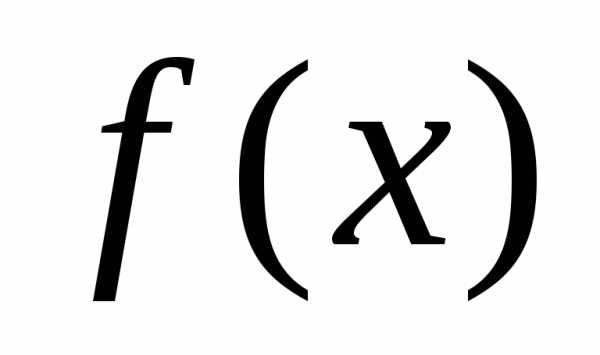 определена.
определена.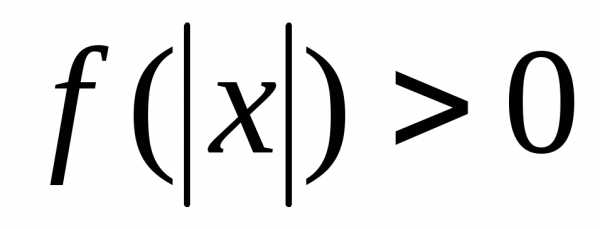 решают с помощью замены.
решают с помощью замены.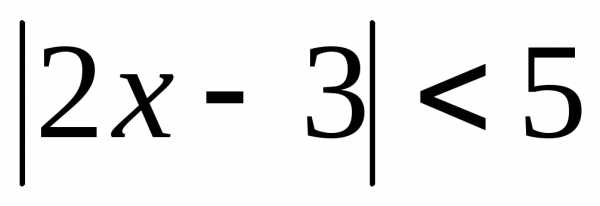 .
.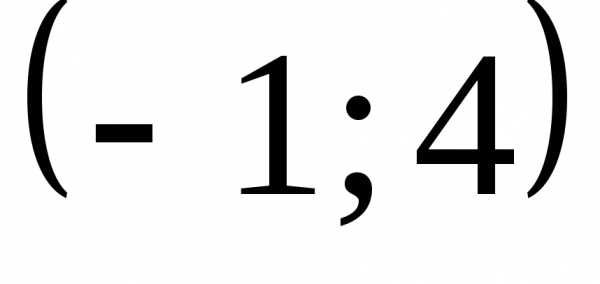 .
.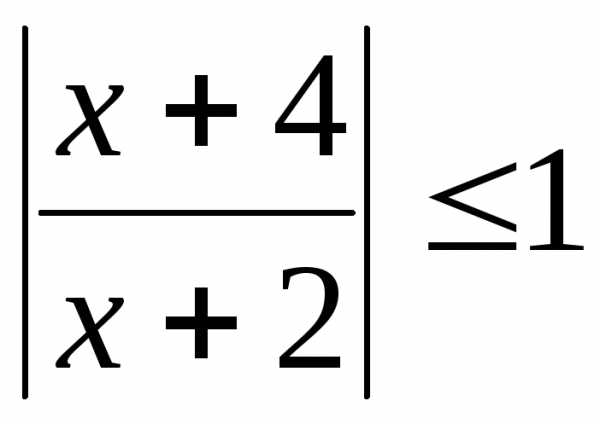 .
.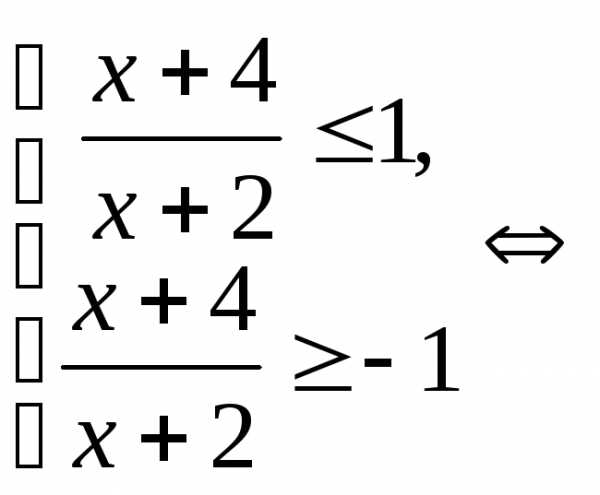
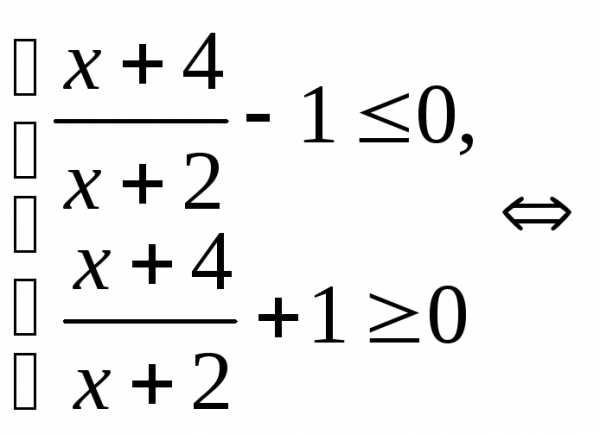
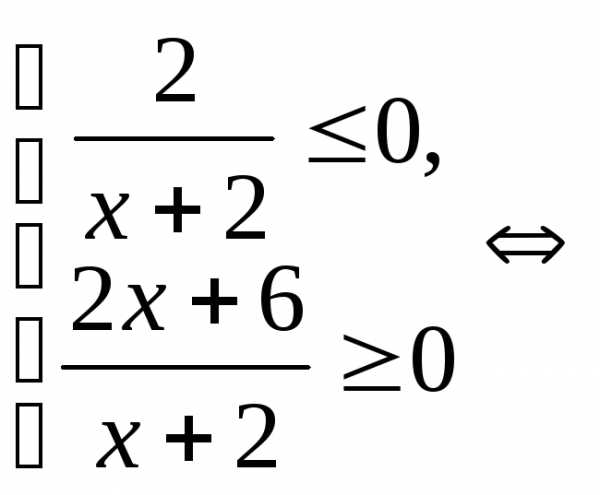
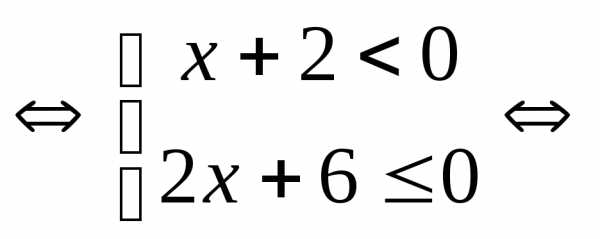
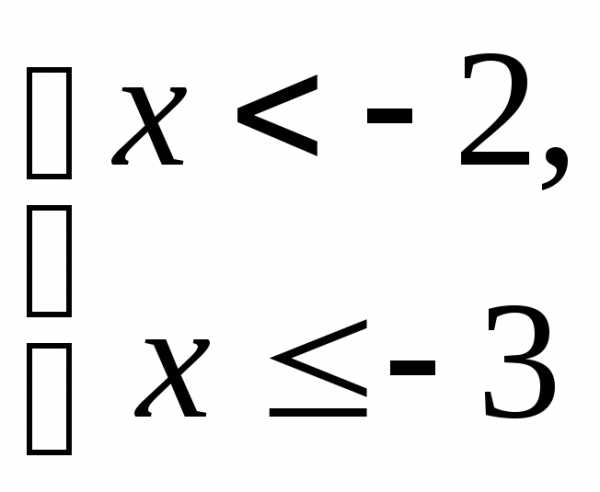 .
.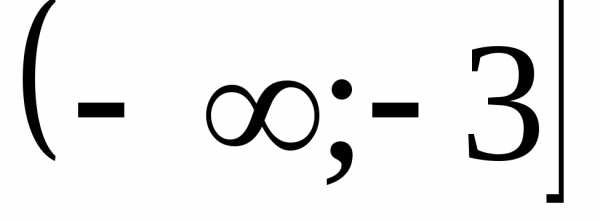 .
.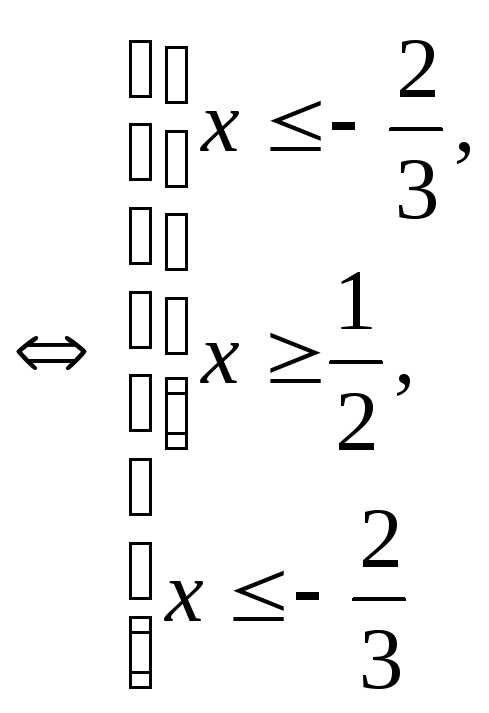 .
.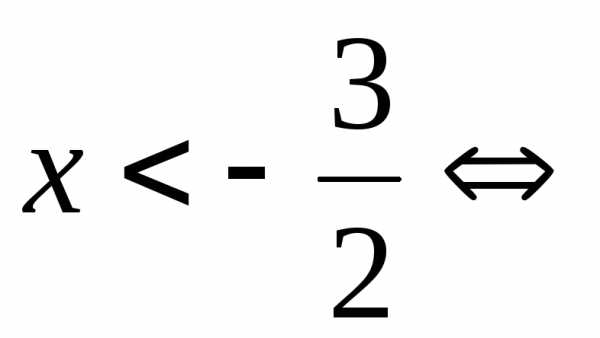
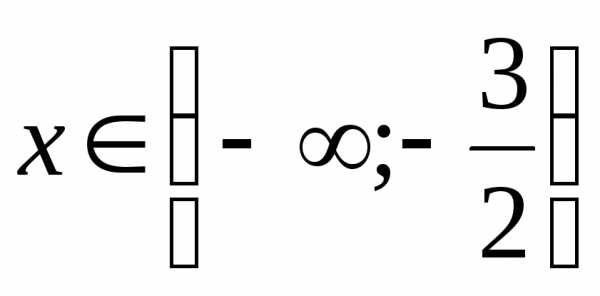 .
.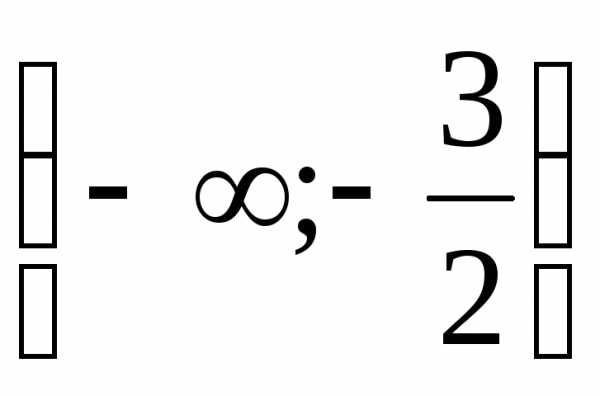 .
.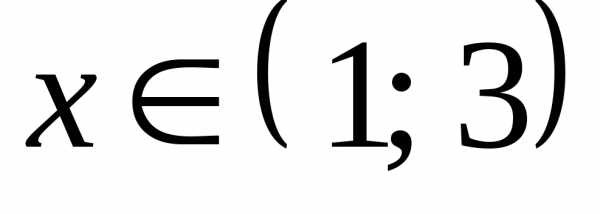
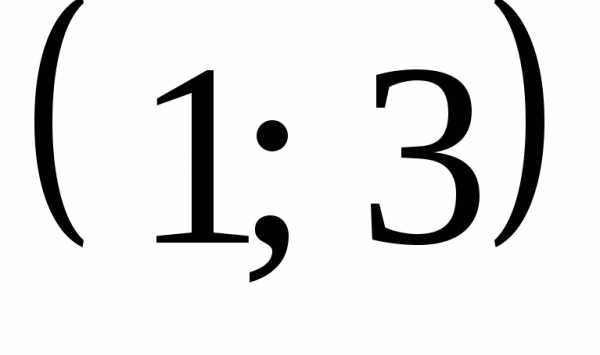 .
.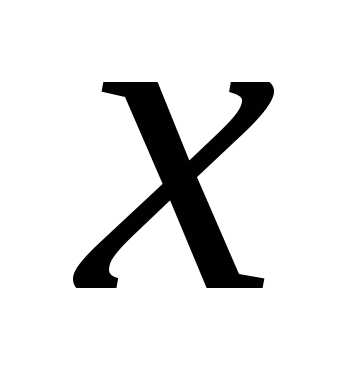 ,
получим:
,
получим: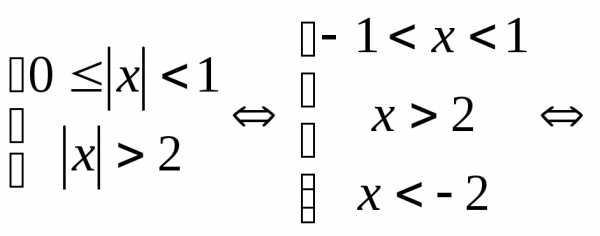 .
.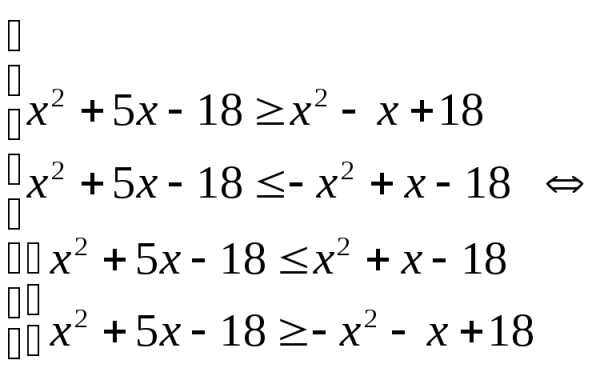
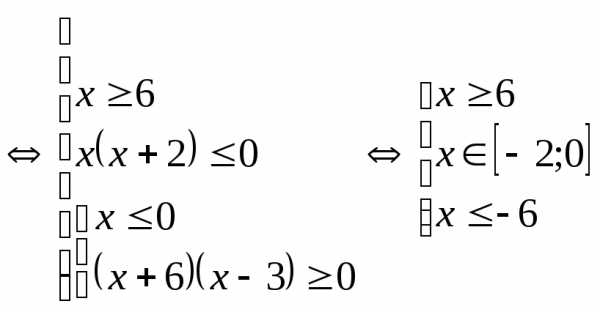 .
.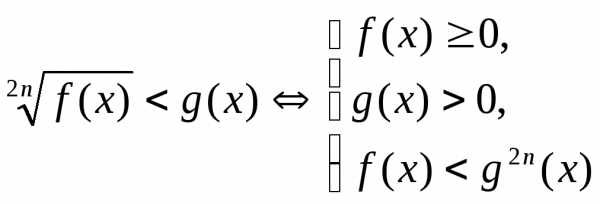 ,
,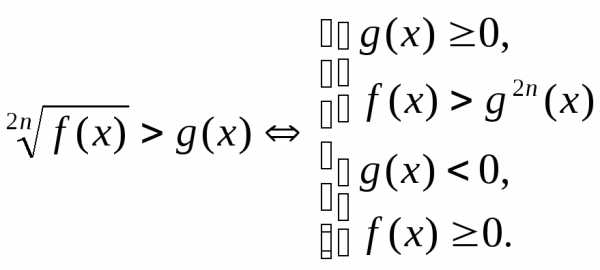
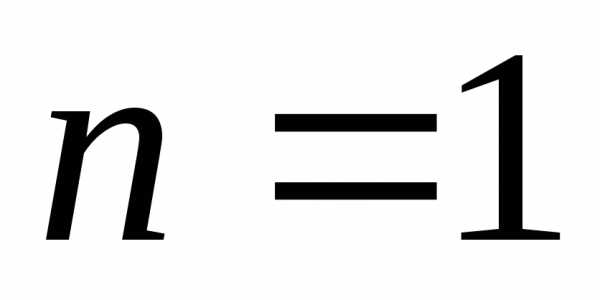
 ,
, 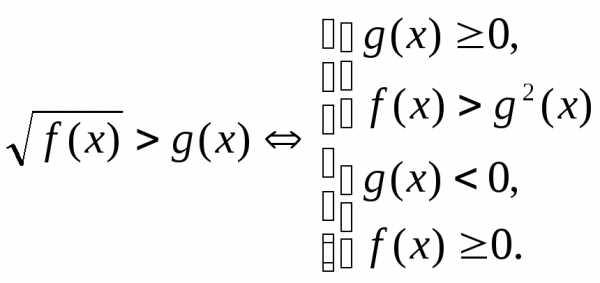

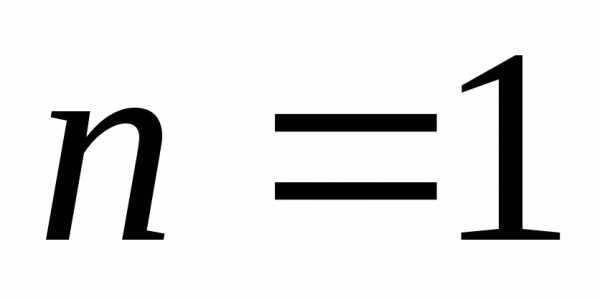
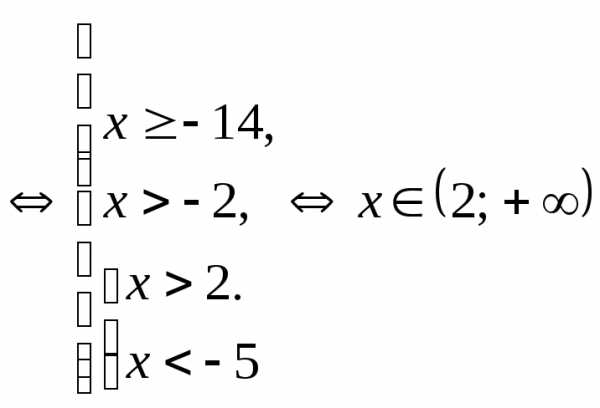 .
.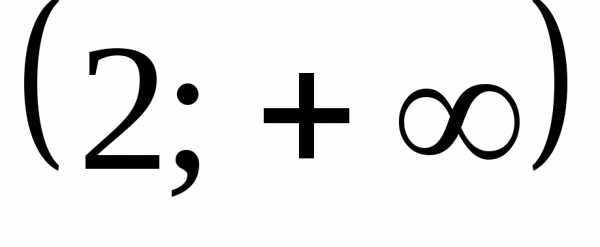 .
.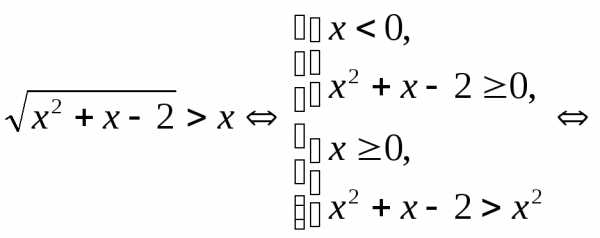
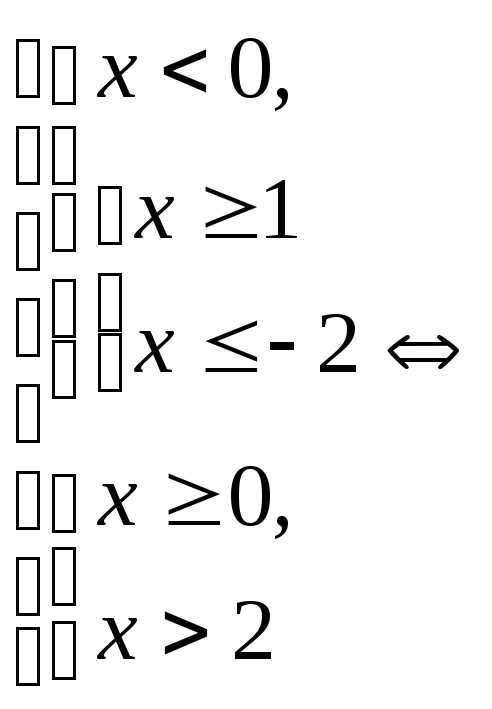
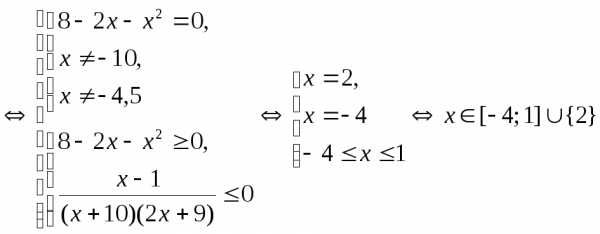 .
.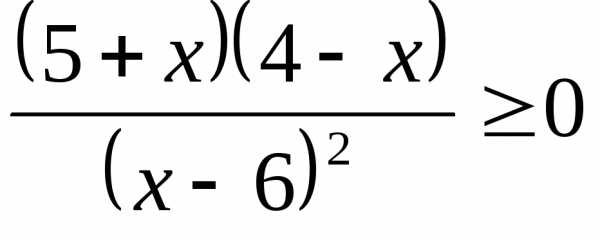 (Ответ:
(Ответ:  .)
.) .)
.)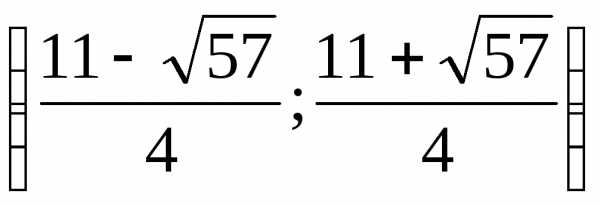 .)
.)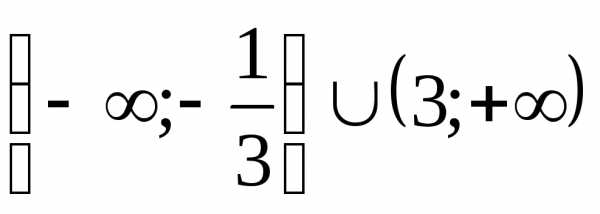 .)
.)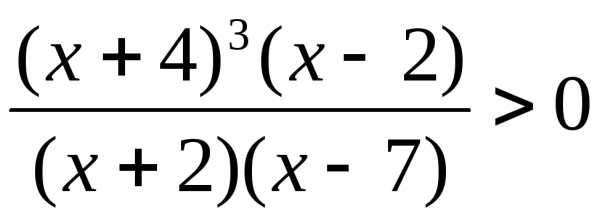 .
(Ответ: .)
.
(Ответ: .)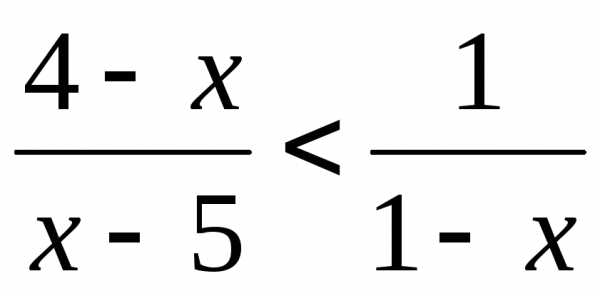 .
(Ответ: .)
.
(Ответ: .)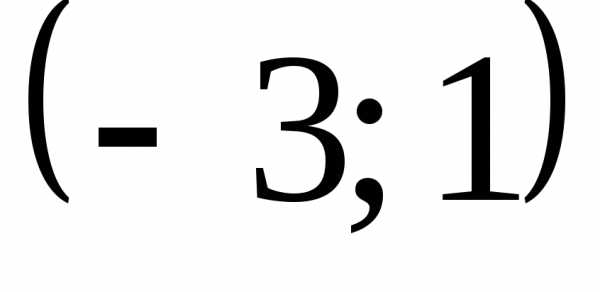 .)
.)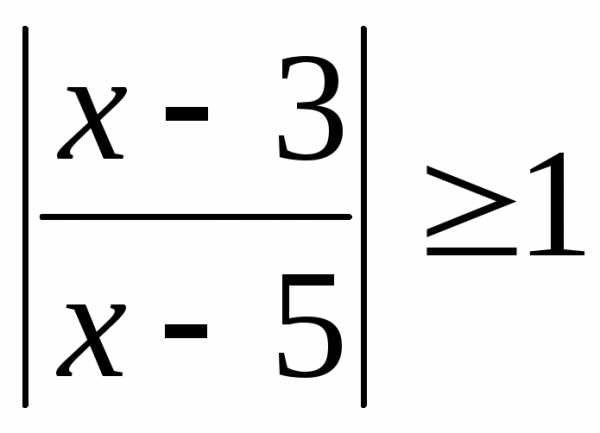 .
(Ответ: .)
.
(Ответ: .)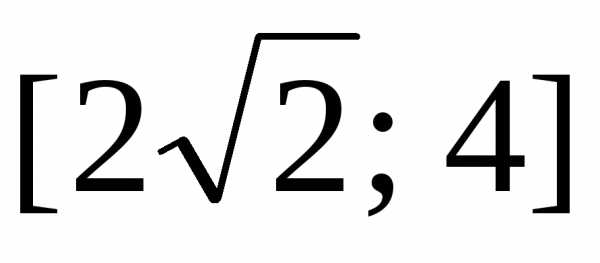 .)
.) .)
.)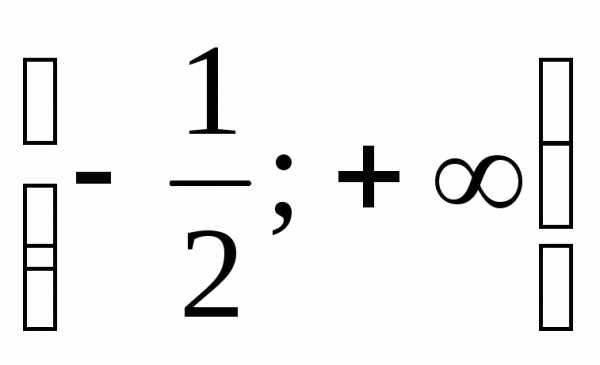 .)
.)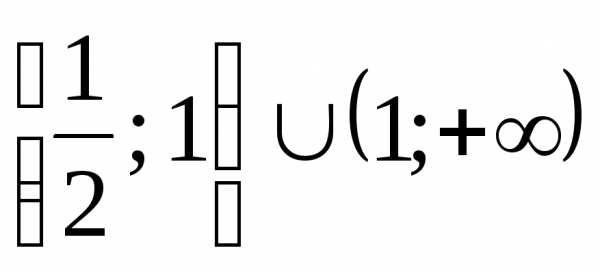 .)
.) .)
.)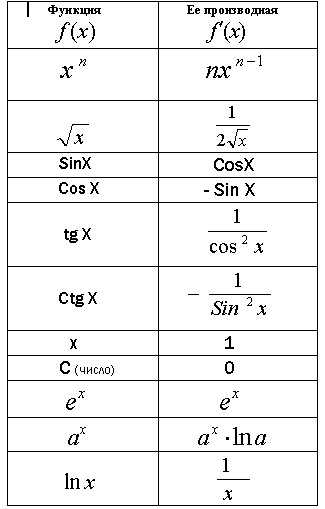
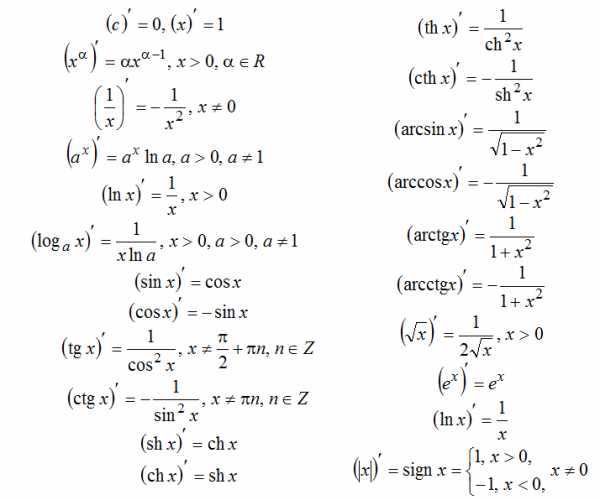
 мнаты и другое.
мнаты и другое. Рассмотрим на конкретном примере, как найти площадь прямоугольника. Длина b=10 ед. Ширина a=6 ед. Решение: S=a*b, S=10 ед.*6 ед., S=60 ед2. Задача. Как узнать площадь прямоугольника, если длина в 2 раза больше ширины и составляет 18 м? Решение: если b=18 м, тогда а=b/2, a=9 м. Как найти площадь прямоугольника, если известны обе стороны? Правильно, подставить в формулу. S=a*b, S=18*9, S=162 м2. Ответ: 162 м2. Задача. Сколько необходимо купить рулонов обоев для комнаты, если ее размеры составляют: длина 5,5 м ширина 3,5, а высота 3 м? Размеры рулона обоев: длина 10 м, ширина 50 см. Решение: сделаем рисунок комнаты.
Рассмотрим на конкретном примере, как найти площадь прямоугольника. Длина b=10 ед. Ширина a=6 ед. Решение: S=a*b, S=10 ед.*6 ед., S=60 ед2. Задача. Как узнать площадь прямоугольника, если длина в 2 раза больше ширины и составляет 18 м? Решение: если b=18 м, тогда а=b/2, a=9 м. Как найти площадь прямоугольника, если известны обе стороны? Правильно, подставить в формулу. S=a*b, S=18*9, S=162 м2. Ответ: 162 м2. Задача. Сколько необходимо купить рулонов обоев для комнаты, если ее размеры составляют: длина 5,5 м ширина 3,5, а высота 3 м? Размеры рулона обоев: длина 10 м, ширина 50 см. Решение: сделаем рисунок комнаты.  Площади противоположных сторон равны. Вычислим площадь стены с размерами 5,5 м и 3 м. Sстены 1=5,5*3,
Площади противоположных сторон равны. Вычислим площадь стены с размерами 5,5 м и 3 м. Sстены 1=5,5*3,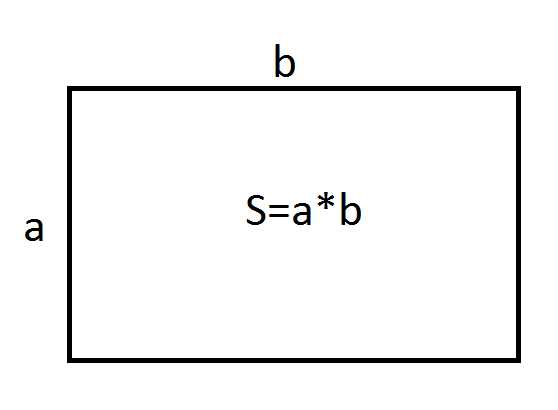
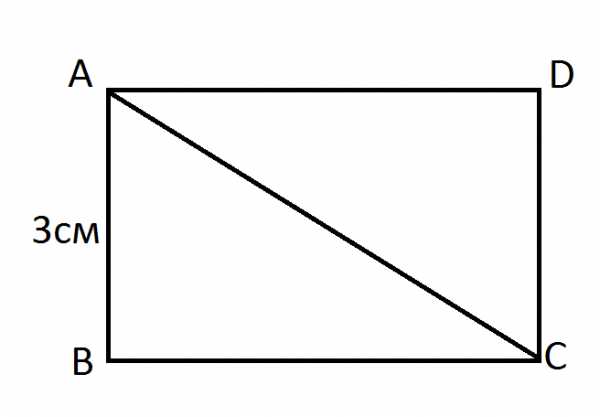 ВС2= АС2-АВ2 = (25-9) = 16 см.
ВС2= АС2-АВ2 = (25-9) = 16 см.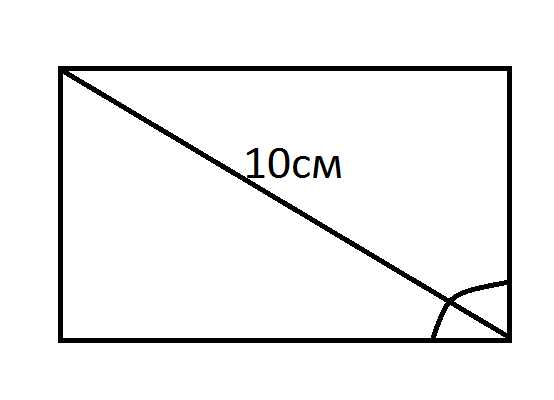 Так как угол между одной стороной и диагональю равен 60 градусам, то прямоугольник делится на два треугольника. Используя формулу S=1/2 d2*sin α, определяем:
Так как угол между одной стороной и диагональю равен 60 градусам, то прямоугольник делится на два треугольника. Используя формулу S=1/2 d2*sin α, определяем: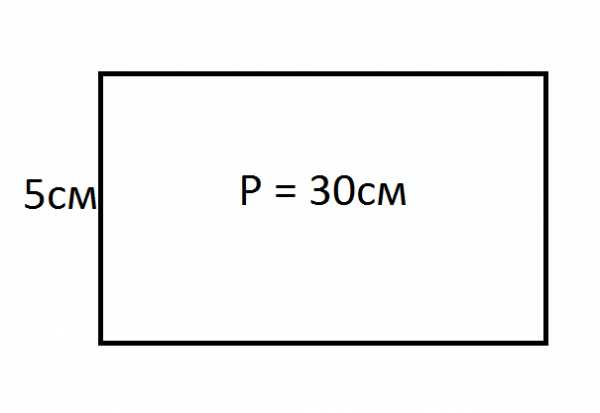 периметра: Р=2(а+b), можно вычислить, что вторая сторона прямоугольника будет равняться:
периметра: Р=2(а+b), можно вычислить, что вторая сторона прямоугольника будет равняться: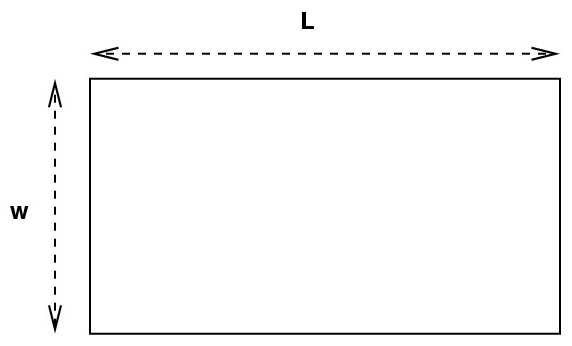
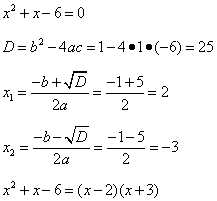


 Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая — из C и D.
Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая — из C и D.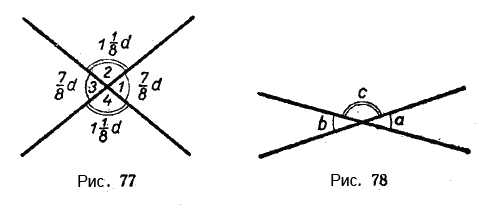
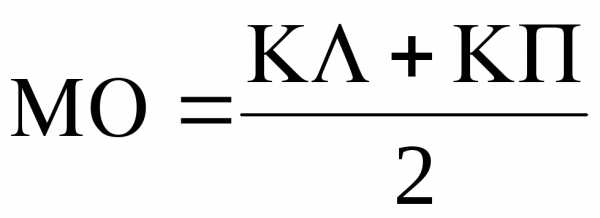 ;
; 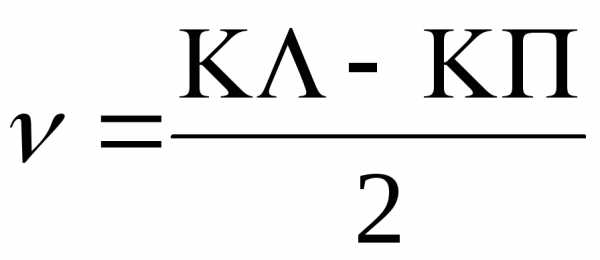 ; (4)
; (4)

 .
(6)
.
(6)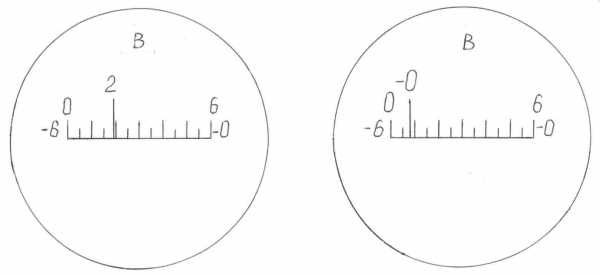
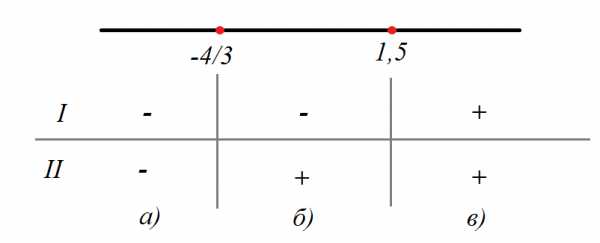
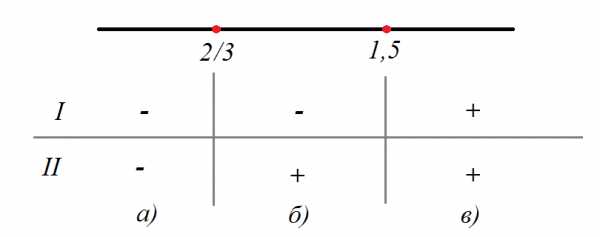
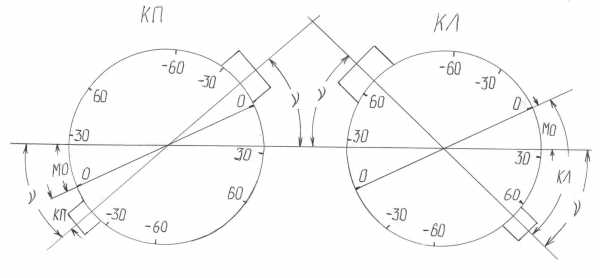
 и место нуля МО.
и место нуля МО.
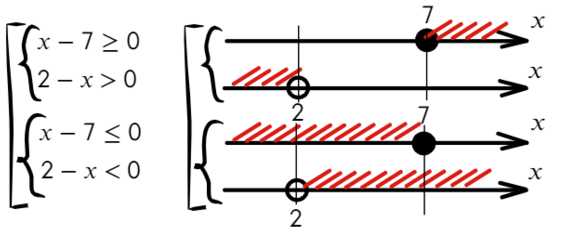
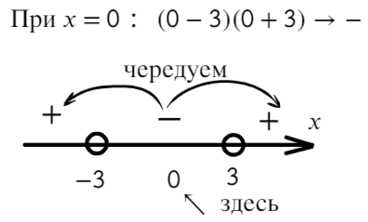
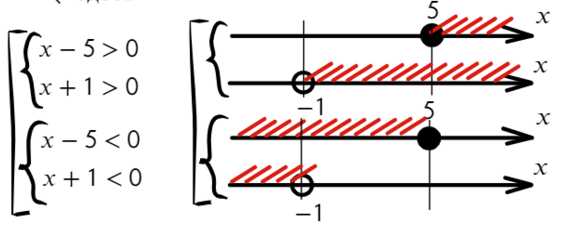
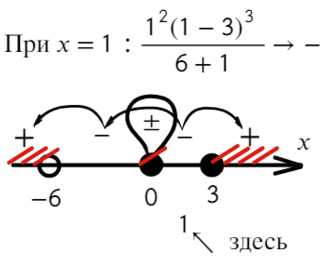
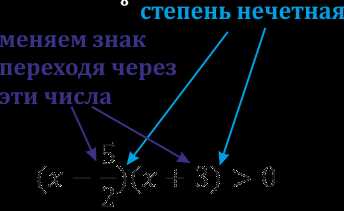
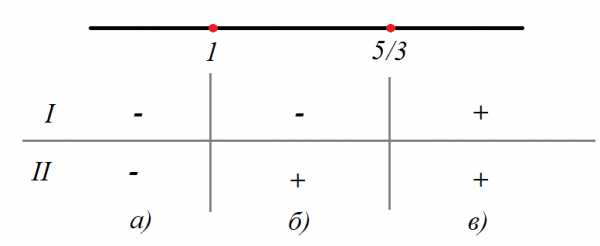
 Статья посвящена разбору примеров решения неравенств методом интервалов. При том, что этот метод решения неравенств достаточно универсален, важно помнить, что не всегда применение данного метода оправдано с точки зрения объема вычислений. Иногда бывает удобнее воспользоваться некоторыми другими методами решения неравенств. Все рассмотренные в статье неравенства взяты из реальных вариантов ЕГЭ по математике разных лет. Присутствует подробный видеоразбор одного из заданий.
Статья посвящена разбору примеров решения неравенств методом интервалов. При том, что этот метод решения неравенств достаточно универсален, важно помнить, что не всегда применение данного метода оправдано с точки зрения объема вычислений. Иногда бывает удобнее воспользоваться некоторыми другими методами решения неравенств. Все рассмотренные в статье неравенства взяты из реальных вариантов ЕГЭ по математике разных лет. Присутствует подробный видеоразбор одного из заданий. Решение неравенств
Решение неравенств