Таблица умножения до 1000 | Сайт о таблице умножения
Таблица умножения до 1000 представляет собой таблицу до 32. Таким образом получается весьма значительный материал, состоящий из 32 столбцов, по 32 примера в каждом. Максимальное значение таблицы 32 * 32 = 1024.
1 x 1 = 1
1 x 2 = 2
1 x 3 = 3
1 x 4 = 4
1 x 5 = 5
1 x 6 = 6
1 x 7 = 7
1 x 8 = 8
1 x 9 = 9
1 x 10 = 10
1 x 11 = 11
1 x 12 = 12
1 x 13 = 13
1 x 14 = 14
1 x 15 = 15
1 x 16 = 16
1 x 17 = 17
1 x 18 = 18
1 x 19 = 19
1 x 20 = 20
1 x 21 = 21
1 x 22 = 22
1 x 23 = 23
1 x 24 = 24
1 x 25 = 25
1 x 26 = 26
1 x 27 = 27
1 x 28 = 28
1 x 29 = 29
1 x 30 = 30
1 x 31 = 31
1 x 32 = 32
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
2 x 6 = 12
2 x 7 = 14
2 x 8 = 16
2 x 9 = 18
2 x 10 = 20
2 x 11 = 22
2 x 12 = 24
2 x 13 = 26
2 x 14 = 28
2 x 15 = 30
2 x 16 = 32
2 x 17 = 34
2 x 18 = 36
2 x 19 = 38
2 x 20 = 40
2 x 21 = 42
2 x 22 = 44
2 x 23 = 46
2 x 24 = 48
2 x 25 = 50
2 x 26 = 52
2 x 27 = 54
2 x 28 = 56
2 x 29 = 58
2 x 30 = 60
2 x 31 = 62
2 x 32 = 64
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
3 x 5 = 15
3 x 6 = 18
3 x 7 = 21
3 x 8 = 24
3 x 9 = 27
3 x 10 = 30
3 x 11 = 33
3 x 12 = 36
3 x 13 = 39
3 x 14 = 42
3 x 15 = 45
3 x 16 = 48
3 x 17 = 51
3 x 18 = 54
3 x 19 = 57
3 x 20 = 60
3 x 21 = 63
3 x 22 = 66
3 x 23 = 69
3 x 24 = 72
3 x 25 = 75
3 x 26 = 78
3 x 27 = 81
3 x 28 = 84
3 x 29 = 87
3 x 30 = 90
3 x 31 = 93
3 x 32 = 96
4 x 1 = 4
4 x 2 = 8
4 x 3 = 12
4 x 4 = 16
4 x 5 = 20
4 x 6 = 24
4 x 7 = 28
4 x 8 = 32
4 x 9 = 36
4 x 10 = 40
4 x 11 = 44
4 x 12 = 48
4 x 13 = 52
4 x 14 = 56
4 x 15 = 60
4 x 16 = 64
4 x 17 = 68
4 x 18 = 72
4 x 19 = 76
4 x 20 = 80
4 x 21 = 84
4 x 22 = 88
4 x 23 = 92
4 x 24 = 96
4 x 25 = 100
4 x 26 = 104
4 x 27 = 108
4 x 28 = 112
4 x 29 = 116
4 x 30 = 120
4 x 31 = 124
4 x 32 = 128
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
5 x 9 = 45
5 x 10 = 50
5 x 11 = 55
5 x 12 = 60
5 x 13 = 65
5 x 14 = 70
5 x 15 = 75
5 x 16 = 80
5 x 17 = 85
5 x 18 = 90
5 x 19 = 95
5 x 20 = 100
5 x 21 = 105
5 x 22 = 110
5 x 23 = 115
5 x 24 = 120
5 x 25 = 125
5 x 26 = 130
5 x 27 = 135
5 x 28 = 140
5 x 29 = 145
5 x 30 = 150
5 x 31 = 155
5 x 32 = 160
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
6 x 6 = 36
6 x 7 = 42
6 x 8 = 48
6 x 9 = 54
6 x 10 = 60
6 x 11 = 66
6 x 12 = 72
6 x 13 = 78
6 x 14 = 84
6 x 15 = 90
6 x 16 = 96
6 x 17 = 102
6 x 18 = 108
6 x 19 = 114
6 x 20 = 120
6 x 21 = 126
6 x 22 = 132
6 x 23 = 138
6 x 24 = 144
6 x 25 = 150
6 x 26 = 156
6 x 27 = 162
6 x 28 = 168
6 x 29 = 174
6 x 30 = 180
6 x 31 = 186
6 x 32 = 192
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 8 = 56
7 x 9 = 63
7 x 10 = 70
7 x 11 = 77
7 x 12 = 84
7 x 13 = 91
7 x 14 = 98
7 x 15 = 105
7 x 16 = 112
7 x 17 = 119
7 x 18 = 126
7 x 19 = 133
7 x 20 = 140
7 x 21 = 147
7 x 22 = 154
7 x 23 = 161
7 x 24 = 168
7 x 25 = 175
7 x 26 = 182
7 x 27 = 189
7 x 28 = 196
7 x 29 = 203
7 x 30 = 210
7 x 31 = 217
7 x 32 = 224
8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
8 x 5 = 40
8 x 6 = 48
8 x 7 = 56
8 x 8 = 64
8 x 9 = 72
8 x 10 = 80
8 x 11 = 88
8 x 12 = 96
8 x 13 = 104
8 x 14 = 112
8 x 15 = 120
8 x 16 = 128
8 x 17 = 136
8 x 18 = 144
8 x 19 = 152
8 x 20 = 160
8 x 21 = 168
8 x 22 = 176
8 x 23 = 184
8 x 24 = 192
8 x 25 = 200
8 x 26 = 208
8 x 27 = 216
8 x 28 = 224
8 x 29 = 232
8 x 30 = 240
8 x 31 = 248
8 x 32 = 256
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45
9 x 6 = 54
9 x 7 = 63
9 x 8 = 72
9 x 9 = 81
9 x 10 = 90
9 x 11 = 99
9 x 12 = 108
9 x 13 = 117
9 x 14 = 126
9 x 15 = 135
9 x 16 = 144
9 x 17 = 153
9 x 18 = 162
9 x 19 = 171
9 x 20 = 180
9 x 21 = 189
9 x 22 = 198
9 x 23 = 207
9 x 24 = 216
9 x 25 = 225
9 x 26 = 234
9 x 27 = 243
9 x 28 = 252
9 x 29 = 261
9 x 30 = 270
9 x 31 = 279
9 x 32 = 288
10 x 1 = 10
10 x 2 = 20
10 x 3 = 30
10 x 4 = 40
10 x 5 = 50
10 x 6 = 60
10 x 7 = 70
10 x 8 = 80
10 x 9 = 90
10 x 10 = 100
10 x 11 = 110
10 x 12 = 120
10 x 13 = 130
10 x 14 = 140
10 x 15 = 150
10 x 16 = 160
10 x 17 = 170
10 x 18 = 180
10 x 19 = 190
10 x 20 = 200
10 x 21 = 210
10 x 22 = 220
10 x 23 = 230
10 x 24 = 240
10 x 25 = 250
10 x 26 = 260
10 x 27 = 270
10 x 28 = 280
10 x 29 = 290
10 x 30 = 300
10 x 31 = 310
10 x 32 = 320
11 x 1 = 11
11 x 2 = 22
11 x 3 = 33
11 x 4 = 44
11 x 5 = 55
11 x 6 = 66
11 x 7 = 77
11 x 8 = 88
11 x 9 = 99
11 x 10 = 110
11 x 11 = 121
11 x 12 = 132
11 x 13 = 143
11 x 14 = 154
11 x 15 = 165
11 x 16 = 176
11 x 17 = 187
11 x 18 = 198
11 x 19 = 209
11 x 20 = 220
11 x 21 = 231
11 x 22 = 242
11 x 23 = 253
11 x 24 = 264
11 x 25 = 275
11 x 26 = 286
11 x 27 = 297
11 x 28 = 308
11 x 29 = 319
11 x 30 = 330
11 x 31 = 341
11 x 32 = 352
12 x 1 = 12
12 x 2 = 24
12 x 3 = 36
12 x 4 = 48
12 x 5 = 60
12 x 6 = 72
12 x 7 = 84
12 x 8 = 96
12 x 9 = 108
12 x 10 = 120
12 x 11 = 132
12 x 12 = 144
12 x 13 = 156
12 x 14 = 168
12 x 15 = 180
12 x 16 = 192
12 x 17 = 204
12 x 18 = 216
12 x 19 = 228
12 x 20 = 240
12 x 21 = 252
12 x 22 = 264
12 x 23 = 276
12 x 24 = 288
12 x 25 = 300
12 x 26 = 312
12 x 27 = 324
12 x 28 = 336
12 x 29 = 348
12 x 30 = 360
12 x 31 = 372
12 x 32 = 384
13 x 1 = 13
13 x 2 = 26
13 x 3 = 39
13 x 4 = 52
13 x 5 = 65
13 x 6 = 78
13 x 7 = 91
13 x 8 = 104
13 x 9 = 117
13 x 10 = 130
13 x 11 = 143
13 x 12 = 156
13 x 13 = 169
13 x 14 = 182
13 x 15 = 195
13 x 16 = 208
13 x 17 = 221
13 x 18 = 234
13 x 19 = 247
13 x 20 = 260
13 x 21 = 273
13 x 22 = 286
13 x 23 = 299
13 x 24 = 312
13 x 25 = 325
13 x 26 = 338
13 x 27 = 351
13 x 28 = 364
13 x 29 = 377
13 x 30 = 390
13 x 31 = 403
13 x 32 = 416
14 x 1 = 14
14 x 2 = 28
14 x 3 = 42
14 x 4 = 56
14 x 5 = 70
14 x 6 = 84
14 x 7 = 98
14 x 8 = 112
14 x 9 = 126
14 x 10 = 140
14 x 11 = 154
14 x 12 = 168
14 x 13 = 182
14 x 14 = 196
14 x 15 = 210
14 x 16 = 224
14 x 17 = 238
14 x 18 = 252
14 x 19 = 266
14 x 20 = 280
14 x 21 = 294
14 x 22 = 308
14 x 23 = 322
14 x 24 = 336
14 x 25 = 350
14 x 26 = 364
14 x 27 = 378
14 x 28 = 392
14 x 29 = 406
14 x 30 = 420
14 x 31 = 434
14 x 32 = 448
15 x 1 = 15
15 x 2 = 30
15 x 3 = 45
15 x 4 = 60
15 x 5 = 75
15 x 6 = 90
15 x 7 = 105
15 x 8 = 120
15 x 9 = 135
15 x 10 = 150
15 x 11 = 165
15 x 12 = 180
15 x 13 = 195
15 x 14 = 210
15 x 15 = 225
15 x 16 = 240
15 x 17 = 255
15 x 18 = 270
15 x 19 = 285
15 x 20 = 300
15 x 21 = 315
15 x 22 = 330
15 x 23 = 345
15 x 24 = 360
15 x 25 = 375
15 x 26 = 390
15 x 27 = 405
15 x 28 = 420
15 x 29 = 435
15 x 30 = 450
15 x 31 = 465
15 x 32 = 480
16 x 1 = 16
16 x 2 = 32
16 x 3 = 48
16 x 4 = 64
16 x 5 = 80
16 x 6 = 96
16 x 7 = 112
16 x 8 = 128
16 x 9 = 144
16 x 10 = 160
16 x 11 = 176
16 x 12 = 192
16 x 13 = 208
16 x 14 = 224
16 x 15 = 240
16 x 16 = 256
16 x 17 = 272
16 x 18 = 288
16 x 19 = 304
16 x 20 = 320
16 x 21 = 336
16 x 22 = 352
16 x 23 = 368
16 x 24 = 384
16 x 25 = 400
16 x 26 = 416
16 x 27 = 432
16 x 28 = 448
16 x 29 = 464
16 x 30 = 480
16 x 31 = 496
16 x 32 = 512
17 x 1 = 17
17 x 2 = 34
17 x 3 = 51
17 x 4 = 68
17 x 5 = 85
17 x 6 = 102
17 x 7 = 119
17 x 8 = 136
17 x 9 = 153
17 x 10 = 170
17 x 11 = 187
17 x 12 = 204
17 x 13 = 221
17 x 14 = 238
17 x 15 = 255
17 x 16 = 272
17 x 17 = 289
17 x 18 = 306
17 x 19 = 323
17 x 20 = 340
17 x 21 = 357
17 x 22 = 374
17 x 23 = 391
17 x 24 = 408
17 x 25 = 425
17 x 26 = 442
17 x 27 = 459
17 x 28 = 476
17 x 29 = 493
17 x 30 = 510
17 x 31 = 527
17 x 32 = 544
18 x 1 = 18
18 x 2 = 36
18 x 3 = 54
18 x 4 = 72
18 x 5 = 90
18 x 6 = 108
18 x 7 = 126
18 x 8 = 144
18 x 9 = 162
18 x 10 = 180
18 x 11 = 198
18 x 12 = 216
18 x 13 = 234
18 x 14 = 252
18 x 15 = 270
18 x 16 = 288
18 x 17 = 306
18 x 18 = 324
18 x 19 = 342
18 x 20 = 360
18 x 21 = 378
18 x 22 = 396
18 x 23 = 414
18 x 24 = 432
18 x 25 = 450
18 x 26 = 468
18 x 27 = 486
18 x 28 = 504
18 x 29 = 522
18 x 30 = 540
18 x 31 = 558
18 x 32 = 576
19 x 1 = 19
19 x 2 = 38
19 x 3 = 57
19 x 4 = 76
19 x 5 = 95
19 x 6 = 114
19 x 7 = 133
19 x 8 = 152
19 x 9 = 171
19 x 10 = 190
19 x 11 = 209
19 x 12 = 228
19 x 13 = 247
19 x 14 = 266
19 x 15 = 285
19 x 16 = 304
19 x 17 = 323
19 x 18 = 342
19 x 19 = 361
19 x 20 = 380
19 x 21 = 399
19 x 22 = 418
19 x 23 = 437
19 x 24 = 456
19 x 25 = 475
19 x 26 = 494
19 x 27 = 513
19 x 28 = 532
19 x 29 = 551
19 x 30 = 570
19 x 31 = 589
19 x 32 = 608
20 x 1 = 20
20 x 2 = 40
20 x 3 = 60
20 x 4 = 80
20 x 5 = 100
20 x 6 = 120
20 x 7 = 140
20 x 8 = 160
20 x 9 = 180
20 x 10 = 200
20 x 11 = 220
20 x 12 = 240
20 x 13 = 260
20 x 14 = 280
20 x 15 = 300
20 x 16 = 320
20 x 17 = 340
20 x 18 = 360
20 x 19 = 380
20 x 20 = 400
20 x 21 = 420
20 x 22 = 440
20 x 23 = 460
20 x 24 = 480
20 x 25 = 500
20 x 26 = 520
20 x 27 = 540
20 x 28 = 560
20 x 29 = 580
20 x 30 = 600
20 x 31 = 620
20 x 32 = 640
21 x 1 = 21
21 x 2 = 42
21 x 3 = 63
21 x 4 = 84
21 x 5 = 105
21 x 6 = 126
21 x 7 = 147
21 x 8 = 168
21 x 9 = 189
21 x 10 = 210
21 x 11 = 231
21 x 12 = 252
21 x 13 = 273
21 x 14 = 294
21 x 15 = 315
21 x 16 = 336
21 x 17 = 357
21 x 18 = 378
21 x 19 = 399
21 x 20 = 420
21 x 21 = 441
21 x 22 = 462
21 x 23 = 483
21 x 24 = 504
21 x 25 = 525
21 x 26 = 546
21 x 27 = 567
21 x 28 = 588
21 x 29 = 609
21 x 30 = 630
21 x 31 = 651
21 x 32 = 672
22 x 1 = 22
22 x 2 = 44
22 x 3 = 66
22 x 4 = 88
22 x 5 = 110
22 x 6 = 132
22 x 7 = 154
22 x 8 = 176
22 x 9 = 198
22 x 10 = 220
22 x 11 = 242
22 x 12 = 264
22 x 13 = 286
22 x 14 = 308
22 x 15 = 330
22 x 16 = 352
22 x 17 = 374
22 x 18 = 396
22 x 19 = 418
22 x 20 = 440
22 x 21 = 462
22 x 22 = 484
22 x 23 = 506
22 x 24 = 528
22 x 25 = 550
22 x 26 = 572
22 x 27 = 594
22 x 28 = 616
22 x 29 = 638
22 x 30 = 660
22 x 31 = 682
22 x 32 = 704
23 x 1 = 23
23 x 2 = 46
23 x 3 = 69
23 x 4 = 92
23 x 5 = 115
23 x 6 = 138
23 x 7 = 161
23 x 8 = 184
23 x 9 = 207
23 x 10 = 230
23 x 11 = 253
23 x 12 = 276
23 x 13 = 299
23 x 14 = 322
23 x 15 = 345
23 x 16 = 368
23 x 17 = 391
23 x 18 = 414
23 x 19 = 437
23 x 20 = 460
23 x 21 = 483
23 x 22 = 506
23 x 23 = 529
23 x 24 = 552
23 x 25 = 575
23 x 26 = 598
23 x 27 = 621
23 x 28 = 644
23 x 29 = 667
23 x 30 = 690
23 x 31 = 713
23 x 32 = 736
24 x 1 = 24
24 x 2 = 48
24 x 3 = 72
24 x 4 = 96
24 x 5 = 120
24 x 6 = 144
24 x 7 = 168
24 x 8 = 192
24 x 9 = 216
24 x 10 = 240
24 x 11 = 264
24 x 12 = 288
24 x 13 = 312
24 x 14 = 336
24 x 15 = 360
24 x 16 = 384
24 x 17 = 408
24 x 18 = 432
24 x 19 = 456
24 x 20 = 480
24 x 21 = 504
24 x 22 = 528
24 x 23 = 552
24 x 24 = 576
24 x 25 = 600
24 x 26 = 624
24 x 27 = 648
24 x 28 = 672
24 x 29 = 696
24 x 30 = 720
24 x 31 = 744
24 x 32 = 768
25 x 1 = 25
25 x 2 = 50
25 x 3 = 75
25 x 4 = 100
25 x 5 = 125
25 x 6 = 150
25 x 7 = 175
25 x 8 = 200
25 x 9 = 225
25 x 10 = 250
25 x 11 = 275
25 x 12 = 300
25 x 13 = 325
25 x 14 = 350
25 x 15 = 375
25 x 16 = 400
25 x 17 = 425
25 x 18 = 450
25 x 19 = 475
25 x 20 = 500
25 x 21 = 525
25 x 22 = 550
25 x 23 = 575
25 x 24 = 600
25 x 25 = 625
25 x 26 = 650
25 x 27 = 675
25 x 28 = 700
25 x 29 = 725
25 x 30 = 750
25 x 31 = 775
25 x 32 = 800
26 x 1 = 26
26 x 2 = 52
26 x 3 = 78
26 x 4 = 104
26 x 5 = 130
26 x 6 = 156
26 x 7 = 182
26 x 8 = 208
26 x 9 = 234
26 x 10 = 260
26 x 11 = 286
26 x 12 = 312
26 x 13 = 338
26 x 14 = 364
26 x 15 = 390
26 x 16 = 416
26 x 17 = 442
26 x 18 = 468
26 x 19 = 494
26 x 20 = 520
26 x 21 = 546
26 x 22 = 572
26 x 23 = 598
26 x 24 = 624
26 x 25 = 650
26 x 26 = 676
26 x 27 = 702
26 x 28 = 728
26 x 29 = 754
26 x 30 = 780
26 x 31 = 806
26 x 32 = 832
27 x 1 = 27
27 x 2 = 54
27 x 3 = 81
27 x 4 = 108
27 x 5 = 135
27 x 6 = 162
27 x 7 = 189
27 x 8 = 216
27 x 9 = 243
27 x 10 = 270
27 x 11 = 297
27 x 12 = 324
27 x 13 = 351
27 x 14 = 378
27 x 15 = 405
27 x 16 = 432
27 x 17 = 459
27 x 18 = 486
27 x 19 = 513
27 x 20 = 540
27 x 21 = 567
27 x 22 = 594
27 x 23 = 621
27 x 24 = 648
27 x 25 = 675
27 x 26 = 702
27 x 27 = 729
27 x 28 = 756
27 x 29 = 783
27 x 30 = 810
27 x 31 = 837
27 x 32 = 864
28 x 1 = 28
28 x 2 = 56
28 x 3 = 84
28 x 4 = 112
28 x 5 = 140
28 x 6 = 168
28 x 7 = 196
28 x 8 = 224
28 x 9 = 252
28 x 10 = 280
28 x 11 = 308
28 x 12 = 336
28 x 13 = 364
28 x 14 = 392
28 x 15 = 420
28 x 16 = 448
28 x 17 = 476
28 x 18 = 504
28 x 19 = 532
28 x 20 = 560
28 x 21 = 588
28 x 22 = 616
28 x 23 = 644
28 x 24 = 672
28 x 25 = 700
28 x 26 = 728
28 x 27 = 756
28 x 28 = 784
28 x 29 = 812
28 x 30 = 840
28 x 31 = 868
28 x 32 = 896
29 x 1 = 29
29 x 2 = 58
29 x 3 = 87
29 x 4 = 116
29 x 5 = 145
29 x 6 = 174
29 x 7 = 203
29 x 8 = 232
29 x 9 = 261
29 x 10 = 290
29 x 11 = 319
29 x 12 = 348
29 x 13 = 377
29 x 14 = 406
29 x 15 = 435
29 x 16 = 464
29 x 17 = 493
29 x 18 = 522
29 x 19 = 551
29 x 20 = 580
29 x 21 = 609
29 x 22 = 638
29 x 23 = 667
29 x 24 = 696
29 x 25 = 725
29 x 26 = 754
29 x 27 = 783
29 x 28 = 812
29 x 29 = 841
29 x 30 = 870
29 x 31 = 899
29 x 32 = 928
30 x 1 = 30
30 x 2 = 60
30 x 3 = 90
30 x 4 = 120
30 x 5 = 150
30 x 6 = 180
30 x 7 = 210
30 x 8 = 240
30 x 9 = 270
30 x 10 = 300
30 x 11 = 330
30 x 12 = 360
30 x 13 = 390
30 x 14 = 420
30 x 15 = 450
30 x 16 = 480
30 x 17 = 510
30 x 18 = 540
30 x 19 = 570
30 x 20 = 600
30 x 21 = 630
30 x 22 = 660
30 x 23 = 690
30 x 24 = 720
30 x 25 = 750
30 x 26 = 780
30 x 27 = 810
30 x 28 = 840
30 x 29 = 870
30 x 30 = 900
30 x 31 = 930
30 x 32 = 960
31 x 1 = 31
31 x 2 = 62
31 x 3 = 93
31 x 4 = 124
31 x 5 = 155
31 x 6 = 186
31 x 7 = 217
31 x 8 = 248
31 x 9 = 279
31 x 10 = 310
31 x 11 = 341
31 x 12 = 372
31 x 13 = 403
31 x 14 = 434
31 x 15 = 465
31 x 16 = 496
31 x 17 = 527
31 x 18 = 558
31 x 19 = 589
31 x 20 = 620
31 x 21 = 651
31 x 22 = 682
31 x 23 = 713
31 x 24 = 744
31 x 25 = 775
31 x 26 = 806
31 x 27 = 837
31 x 28 = 868
31 x 29 = 899
31 x 30 = 930
31 x 31 = 961
31 x 32 = 992
32 x 1 = 32
32 x 2 = 64
32 x 3 = 96
32 x 4 = 128
32 x 5 = 160
32 x 6 = 192
32 x 7 = 224
32 x 8 = 256
32 x 9 = 288
32 x 10 = 320
32 x 11 = 352
32 x 12 = 384
32 x 13 = 416
32 x 14 = 448
32 x 15 = 480
32 x 16 = 512
32 x 17 = 544
32 x 18 = 576
32 x 19 = 608
32 x 20 = 640
32 x 21 = 672
32 x 22 = 704
32 x 23 = 736
32 x 24 = 768
32 x 25 = 800
32 x 26 = 832
32 x 27 = 864
32 x 28 = 896
32 x 29 = 928
32 x 30 = 960
32 x 31 = 992
32 x 32 = 1024
Таблица умножения в таком виде пригодится исключительно как справочный материал. Изучить ее полностью задача слишком сложная.
tablica-umnozhenia.ru
Таблица умножения до 20 | Сайт о таблице умножения
1 x 1 = 1
1 x 2 = 2
1 x 3 = 3
1 x 4 = 4
1 x 5 = 5
1 x 6 = 6
1 x 7 = 7
1 x 8 = 8
1 x 9 = 9
1 x 10 = 10
1 x 11 = 11
1 x 12 = 12
1 x 13 = 13
1 x 14 = 14
1 x 15 = 15
1 x 16 = 16
1 x 17 = 17
1 x 18 = 18
1 x 19 = 19
1 x 20 = 20
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
2 x 6 = 12
2 x 7 = 14
2 x 8 = 16
2 x 9 = 18
2 x 10 = 20
2 x 11 = 22
2 x 12 = 24
2 x 13 = 26
2 x 14 = 28
2 x 15 = 30
2 x 16 = 32
2 x 17 = 34
2 x 18 = 36
2 x 19 = 38
2 x 20 = 40
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
3 x 5 = 15
3 x 6 = 18
3 x 7 = 21
3 x 8 = 24
3 x 9 = 27
3 x 10 = 30
3 x 11 = 33
3 x 12 = 36
3 x 13 = 39
3 x 14 = 42
3 x 15 = 45
3 x 16 = 48
3 x 17 = 51
3 x 18 = 54
3 x 19 = 57
3 x 20 = 60
4 x 1 = 4
4 x 2 = 8
4 x 3 = 12
4 x 4 = 16
4 x 5 = 20
4 x 6 = 24
4 x 7 = 28
4 x 8 = 32
4 x 9 = 36
4 x 10 = 40
4 x 11 = 44
4 x 12 = 48
4 x 13 = 52
4 x 14 = 56
4 x 15 = 60
4 x 16 = 64
4 x 17 = 68
4 x 18 = 72
4 x 19 = 76
4 x 20 = 80
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
5 x 9 = 45
5 x 10 = 50
5 x 11 = 55
5 x 12 = 60
5 x 13 = 65
5 x 14 = 70
5 x 15 = 75
5 x 16 = 80
5 x 17 = 85
5 x 18 = 90
5 x 19 = 95
5 x 20 = 100
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
6 x 6 = 36
6 x 7 = 42
6 x 8 = 48
6 x 9 = 54
6 x 10 = 60
6 x 11 = 66
6 x 12 = 72
6 x 13 = 78
6 x 14 = 84
6 x 15 = 90
6 x 16 = 96
6 x 17 = 102
6 x 18 = 108
6 x 19 = 114
6 x 20 = 120
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 8 = 56
7 x 9 = 63
7 x 10 = 70
7 x 11 = 77
7 x 12 = 84
7 x 13 = 91
7 x 14 = 98
7 x 15 = 105
7 x 16 = 112
7 x 17 = 119
7 x 18 = 126
7 x 19 = 133
7 x 20 = 140
8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
8 x 5 = 40
8 x 6 = 48
8 x 7 = 56
8 x 8 = 64
8 x 9 = 72
8 x 10 = 80
8 x 11 = 88
8 x 12 = 96
8 x 13 = 104
8 x 14 = 112
8 x 15 = 120
8 x 16 = 128
8 x 17 = 136
8 x 18 = 144
8 x 19 = 152
8 x 20 = 160
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45
9 x 6 = 54
9 x 7 = 63
9 x 8 = 72
9 x 9 = 81
9 x 10 = 90
9 x 11 = 99
9 x 12 = 108
9 x 13 = 117
9 x 14 = 126
9 x 15 = 135
9 x 16 = 144
9 x 17 = 153
9 x 18 = 162
9 x 19 = 171
9 x 20 = 180
10 x 1 = 10
10 x 2 = 20
10 x 3 = 30
10 x 4 = 40
10 x 5 = 50
10 x 6 = 60
10 x 7 = 70
10 x 8 = 80
10 x 9 = 90
10 x 10 = 100
10 x 11 = 110
10 x 12 = 120
10 x 13 = 130
10 x 14 = 140
10 x 15 = 150
10 x 16 = 160
10 x 17 = 170
10 x 18 = 180
10 x 19 = 190
10 x 20 = 200
11 x 1 = 11
11 x 2 = 22
11 x 3 = 33
11 x 4 = 44
11 x 5 = 55
11 x 6 = 66
11 x 7 = 77
11 x 8 = 88
11 x 9 = 99
11 x 10 = 110
11 x 11 = 121
11 x 12 = 132
11 x 13 = 143
11 x 14 = 154
11 x 15 = 165
11 x 16 = 176
11 x 17 = 187
11 x 18 = 198
11 x 19 = 209
11 x 20 = 220
12 x 1 = 12
12 x 2 = 24
12 x 3 = 36
12 x 4 = 48
12 x 5 = 60
12 x 6 = 72
12 x 7 = 84
12 x 8 = 96
12 x 9 = 108
12 x 10 = 120
12 x 11 = 132
12 x 12 = 144
12 x 13 = 156
12 x 14 = 168
12 x 15 = 180
12 x 16 = 192
12 x 17 = 204
12 x 18 = 216
12 x 19 = 228
12 x 20 = 240
13 x 1 = 13
13 x 2 = 26
13 x 3 = 39
13 x 4 = 52
13 x 5 = 65
13 x 6 = 78
13 x 7 = 91
13 x 8 = 104
13 x 9 = 117
13 x 10 = 130
13 x 11 = 143
13 x 12 = 156
13 x 13 = 169
13 x 14 = 182
13 x 15 = 195
13 x 16 = 208
13 x 17 = 221
13 x 18 = 234
13 x 19 = 247
13 x 20 = 260
14 x 1 = 14
14 x 2 = 28
14 x 3 = 42
14 x 4 = 56
14 x 5 = 70
14 x 6 = 84
14 x 7 = 98
14 x 8 = 112
14 x 9 = 126
14 x 10 = 140
14 x 11 = 154
14 x 12 = 168
14 x 13 = 182
14 x 14 = 196
14 x 15 = 210
14 x 16 = 224
14 x 17 = 238
14 x 18 = 252
14 x 19 = 266
14 x 20 = 280
15 x 1 = 15
15 x 2 = 30
15 x 3 = 45
15 x 4 = 60
15 x 5 = 75
15 x 6 = 90
15 x 7 = 105
15 x 8 = 120
15 x 9 = 135
15 x 10 = 150
15 x 11 = 165
15 x 12 = 180
15 x 13 = 195
15 x 14 = 210
15 x 15 = 225
15 x 16 = 240
15 x 17 = 255
15 x 18 = 270
15 x 19 = 285
15 x 20 = 300
16 x 1 = 16
16 x 2 = 32
16 x 3 = 48
16 x 4 = 64
16 x 5 = 80
16 x 6 = 96
16 x 7 = 112
16 x 8 = 128
16 x 9 = 144
16 x 10 = 160
16 x 11 = 176
16 x 12 = 192
16 x 13 = 208
16 x 14 = 224
16 x 15 = 240
16 x 16 = 256
16 x 17 = 272
16 x 18 = 288
16 x 19 = 304
16 x 20 = 320
17 x 1 = 17
17 x 2 = 34
17 x 3 = 51
17 x 4 = 68
17 x 5 = 85
17 x 6 = 102
17 x 7 = 119
17 x 8 = 136
17 x 9 = 153
17 x 10 = 170
17 x 11 = 187
17 x 12 = 204
17 x 13 = 221
17 x 14 = 238
17 x 15 = 255
17 x 16 = 272
17 x 17 = 289
17 x 18 = 306
17 x 19 = 323
17 x 20 = 340
18 x 1 = 18
18 x 2 = 36
18 x 3 = 54
18 x 4 = 72
18 x 5 = 90
18 x 6 = 108
18 x 7 = 126
18 x 8 = 144
18 x 9 = 162
18 x 10 = 180
18 x 11 = 198
18 x 12 = 216
18 x 13 = 234
18 x 14 = 252
18 x 15 = 270
18 x 16 = 288
18 x 17 = 306
18 x 18 = 324
18 x 19 = 342
18 x 20 = 360
19 x 1 = 19
19 x 2 = 38
19 x 3 = 57
19 x 4 = 76
19 x 5 = 95
19 x 6 = 114
19 x 7 = 133
19 x 8 = 152
19 x 9 = 171
19 x 10 = 190
19 x 11 = 209
19 x 12 = 228
19 x 13 = 247
19 x 14 = 266
19 x 15 = 285
19 x 16 = 304
19 x 17 = 323
19 x 18 = 342
19 x 19 = 361
19 x 20 = 380
20 x 1 = 20
20 x 2 = 40
20 x 3 = 60
20 x 4 = 80
20 x 5 = 100
20 x 6 = 120
20 x 7 = 140
20 x 8 = 160
20 x 9 = 180
20 x 10 = 200
20 x 11 = 220
20 x 12 = 240
20 x 13 = 260
20 x 14 = 280
20 x 15 = 300
20 x 16 = 320
20 x 17 = 340
20 x 18 = 360
20 x 19 = 380
20 x 20 = 400
По запросам в Интернете часто предлагают сокращенный вариант таблицы до 20, в котором отсутствует часть самых сложных примеров.
Сокращенная таблица умножения до 20
1 x 1 = 1
1 x 2 = 2
1 x 3 = 3
1 x 4 = 4
1 x 5 = 5
1 x 6 = 6
1 x 7 = 7
1 x 8 = 8
1 x 9 = 9
1 x 10 = 10
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
2 x 6 = 12
2 x 7 = 14
2 x 8 = 16
2 x 9 = 18
2 x 10 = 20
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
3 x 5 = 15
3 x 6 = 18
3 x 7 = 21
3 x 8 = 24
3 x 9 = 27
3 x 10 = 30
4 x 1 = 4
4 x 2 = 8
4 x 3 = 12
4 x 4 = 16
4 x 5 = 20
4 x 6 = 24
4 x 7 = 28
4 x 8 = 32
4 x 9 = 36
4 x 10 = 40
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
5 x 9 = 45
5 x 10 = 50
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
6 x 6 = 36
6 x 7 = 42
6 x 8 = 48
6 x 9 = 54
6 x 10 = 60
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 8 = 56
7 x 9 = 63
7 x 10 = 70
8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
8 x 5 = 40
8 x 6 = 48
8 x 7 = 56
8 x 8 = 64
8 x 9 = 72
8 x 10 = 80
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45
9 x 6 = 54
9 x 7 = 63
9 x 8 = 72
9 x 9 = 81
9 x 10 = 90
10 x 1 = 10
10 x 2 = 20
10 x 3 = 30
10 x 4 = 40
10 x 5 = 50
10 x 6 = 60
10 x 7 = 70
10 x 8 = 80
10 x 9 = 90
10 x 10 = 100
11 x 1 = 11
11 x 2 = 22
11 x 3 = 33
11 x 4 = 44
11 x 5 = 55
11 x 6 = 66
11 x 7 = 77
11 x 8 = 88
11 x 9 = 99
11 x 10 = 110
12 x 1 = 12
12 x 2 = 24
12 x 3 = 36
12 x 4 = 48
12 x 5 = 60
12 x 6 = 72
12 x 7 = 84
12 x 8 = 96
12 x 9 = 108
12 x 10 = 120
13 x 1 = 13
13 x 2 = 26
13 x 3 = 39
13 x 4 = 52
13 x 5 = 65
13 x 6 = 78
13 x 7 = 91
13 x 8 = 104
13 x 9 = 117
13 x 10 = 130
14 x 1 = 14
14 x 2 = 28
14 x 3 = 42
14 x 4 = 56
14 x 5 = 70
14 x 6 = 84
14 x 7 = 98
14 x 8 = 112
14 x 9 = 126
14 x 10 = 140
15 x 1 = 15
15 x 2 = 30
15 x 3 = 45
15 x 4 = 60
15 x 5 = 75
15 x 6 = 90
15 x 7 = 105
15 x 8 = 120
15 x 9 = 135
15 x 10 = 150
16 x 1 = 16
16 x 2 = 32
16 x 3 = 48
16 x 4 = 64
16 x 5 = 80
16 x 6 = 96
16 x 7 = 112
16 x 8 = 128
16 x 9 = 144
16 x 10 = 160
17 x 1 = 17
17 x 2 = 34
17 x 3 = 51
17 x 4 = 68
17 x 5 = 85
17 x 6 = 102
17 x 7 = 119
17 x 8 = 136
17 x 9 = 153
17 x 10 = 170
18 x 1 = 18
18 x 2 = 36
18 x 3 = 54
18 x 4 = 72
18 x 5 = 90
18 x 6 = 108
18 x 7 = 126
18 x 8 = 144
18 x 9 = 162
18 x 10 = 180
19 x 1 = 19
19 x 2 = 38
19 x 3 = 57
19 x 4 = 76
19 x 5 = 95
19 x 6 = 114
19 x 7 = 133
19 x 8 = 152
19 x 9 = 171
19 x 10 = 190
20 x 1 = 20
20 x 2 = 40
20 x 3 = 60
20 x 4 = 80
20 x 5 = 100
20 x 6 = 120
20 x 7 = 140
20 x 8 = 160
20 x 9 = 180
20 x 10 = 200
tablica-umnozhenia.ru
Как научить детей таблице умножения один раз и на всю жизнь

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
Таблица умножения — базовое понятие в математике, с которым мы знакомимся еще в начальной школе и которое потом используем всю жизнь вне зависимости от профессии. Вот только дети не спешат заучивать бесконечные столбики наизусть, особенно если задание пришлось на каникулы.
AdMe.ru даст советы, как легко выучить таблицу вместе с детьми и сделать этот процесс увлекательным.
Таблица Пифагора
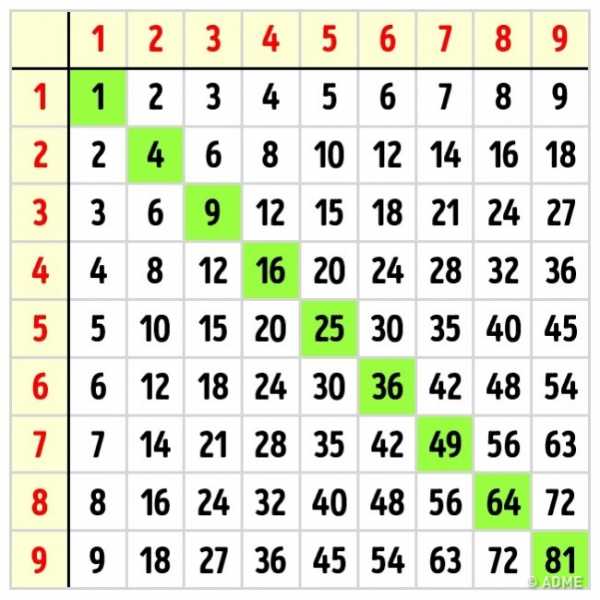
Несмотря на то что задача — выучить, то есть заучить, таблицу наизусть, прежде всего важно понять суть самого действия. Для этого можно заменить умножение сложением: одинаковые числа складываются столько раз, на сколько мы умножаем. Например, 6×8 — это сложить 8 раз по 6.
Выделяем цветом одинаковые значения
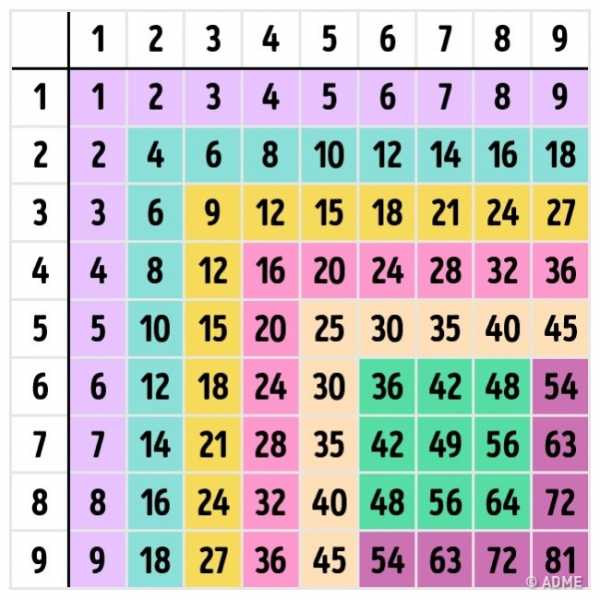
Отличным помощником для изучения умножения станет таблица Пифагора, которая также демонстрирует некоторые закономерности. Например то, что от перемены мест множителей произведение не меняется: 4×6 = 6×4. Отметьте такие «зеркальные» ответы определенным цветом — это поможет запомнить и не запутаться при повторении.
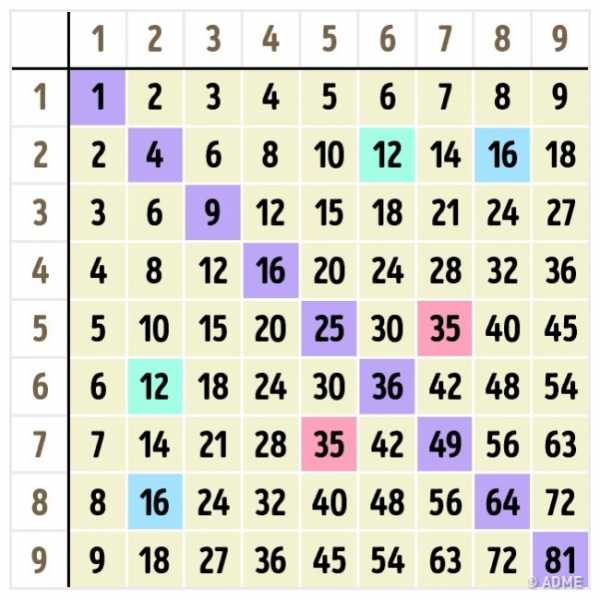
Начинать изучение таблицы Пифагора лучше с самых простых и понятных частей: умножения на 1, 2, 5 и 10. При умножении на единицу число остается неизменным, а умножение на 2 дает нам удвоенное значение. Все ответы умножения на 5 оканчиваются либо на 0, либо на 5. А вот умножив на 10, в ответе мы получим двузначное число из цифры, которую умножали, и нуля.
Таблица для закрепления результата
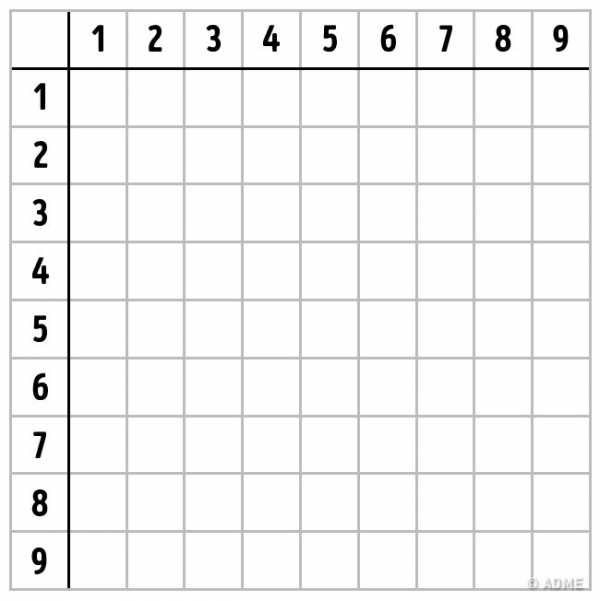
Для закрепления результатов нарисуйте с ребенком пустую таблицу Пифагора и предложите ему заполнить клеточки правильными ответами. Для этого вам понадобится всего лишь листок бумаги, карандаш и линейка. Нужно нарисовать квадрат и поделить его на 10 частей по вертикали и горизонтали. А затем заполнить верхнюю строчку и крайний левый столбик числами от 1 до 9, пропустив первую клетку.
Конечно, все дети индивидуальны и универсального рецепта не существует. Главная задача родителя — найти подход и поддержать свое чадо, ведь все мы когда-то начинали с таких одновременно простых и сложных шагов.
Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
www.adme.ru
Таблица умножения онлайн для детей. Как выучить таблицу умножения
История
Наиболее древние упоминания о таблицах были обнаружены при раскопках городов Месопотамии. Данные наносились на глиняные таблички клинописью. Таблицу умножения называют еще таблицей Пифагора, так как ее авторство приписывают ему. Но документальных подтверждений этому не существует или они просто не дошли до нас. Первое известное изображение, имевшее вид квадрата, было найдено в книге Никомаха Геразского. Он отмечал, что так таблицу изображал Пифагор. Запись древнегреческих чисел значительно отличается от современных чисел. Для записи не использовался нуль, не существовало знаков плюс и минус.
В Японии археологи нашли деревянную дощечку с фрагментом таблицы умножения, которую изготовили еще в 8 веке. Иероглифы, с помощью которых изображены были цифры, похожи на письмо, существовавшее во времена китайской династии Тан. Поэтому считается, что таблицу японцы заимствовали из Китая.
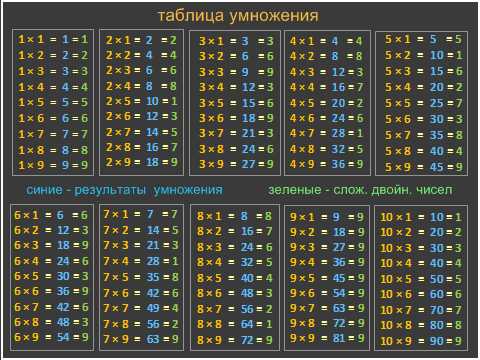
 Таблица умножение от 1 до 10
Таблица умножение от 1 до 10 








 Как изучают таблицу умножения в разных странах?
Как изучают таблицу умножения в разных странах?Благодаря введению заучивания таблицы умножения, считать стали быстрее, процесс стал легче. До этого людьми использовались различные способы вычисления, которые замедляли счет. Это часто служило причиной появления различных ошибок.
В Англии школьники стали учить таблицу до 12 в Средние века. Это связано с английской мерой длины 1 фут, который равен 12 дюймам. Изучить ее нужно до 11 лет. В Индии дети изучают вариант до 20. В России школьники постигают азы умножения в 8 лет и учат таблицу умножения до 10.
Секреты таблицы умножения
Современные научные исследования показывают, что таблицу умножения можно изобразить графически. Для построения образа необходимо провести нумерологическое сокращение, то есть сократить двузначные числа до однозначных чисел. Для этого нужно просто сложить цифры в двузначных числах. Можно увидеть в столбиках интересную закономерность. Результат показан на картинке зеленым цветом. Пифагорейцы использовали такое сокращение для исследования мироздания. Они считали, что нашим миром управляет Число.
 Матвеев А. А. изобрел специальный метод перевода цифр, который помогает графически изобразить таблицу. Полученный в результате вычислений цифровой ряд необходимо изобразить в обратной последовательности и перевести в структуру по принципу больше или меньше. Структура плюсов и минусов тогда даст нам графический образ. Для этого плюсы и минусы соединяются линиями. В результате чего можно увидеть эллипсы.
Матвеев А. А. изобрел специальный метод перевода цифр, который помогает графически изобразить таблицу. Полученный в результате вычислений цифровой ряд необходимо изобразить в обратной последовательности и перевести в структуру по принципу больше или меньше. Структура плюсов и минусов тогда даст нам графический образ. Для этого плюсы и минусы соединяются линиями. В результате чего можно увидеть эллипсы. 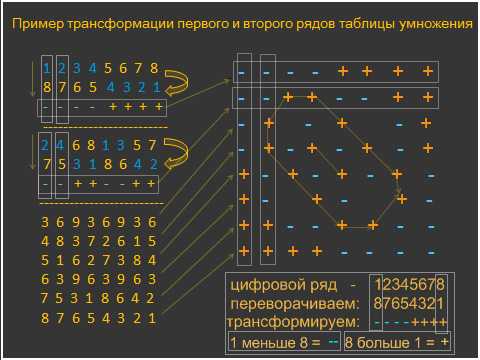 Как легко и быстро выучить таблицу умножения?
Как легко и быстро выучить таблицу умножения?Чтобы просто выучить необходимый материал достаточно внимательно посмотреть на примеры, которые представлены в таблице, а затем найти закономерности. Классический вариант состоит из 10 столбиков по 10 примеров.
- Необходимо запомнить 100 примеров. Это достаточно много, но присмотревшись внимательно, можно заметить, что некоторые примеры повторяются: 4*3=12 и 3*4=12 и др. Множители просто меняются местами. Поэтому необходимо запомнить всего 45 примеров.
- На 1 умножать легко, и запоминать не нужно. Чтобы умножить число на 10, необходимо просто добавить к нему нуль. Это тоже просто. Остается запомнить 36 примеров.
- Умножать на два легко. Для этого достаточно сложить число с самим собой. Для умножения на четыре необходимо прибавить к числу само число, а затем удвоить результат. Остается 21 пример.
- Умножать на 5 просто. Для этого можно умножить число на десять и поделить пополам. Можно воспользоваться и другим способом. Если число четное, то к его половине нужно дописать 0. Если нечетное, то к половине предыдущего числа приписываем 5. На тройку тоже умножать просто. Остается 10 самых трудных примеров.
- Решить оставшиеся примеры можно с помощью пальцев. Для этого руки необходимо повернуть ладошками к себе. Необходимо пронумеровать пальцы на обеих руках от 6 до 10, начиная с большого пальца и заканчивая мизинцем. Например, 7*8. Нижние пальцы включают отмеченные пальцы, и номера у которых меньше. Если их пересчитать, то получатся десятки. Верхние пальцы, находящиеся выше отмеченных пальцев, необходимы для получения единиц. Верхние пальцы левой руки умножаем на верхние пальцы правой руки и получаем единицы. При соединении десятков и единиц получаем ответ.
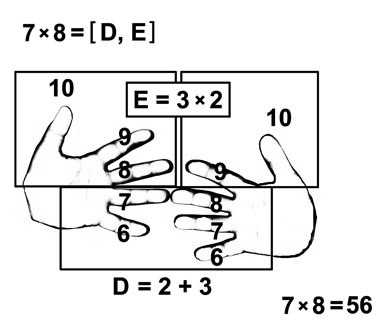 Чтобы умножить число на 9, необходимо умножить его на 10 и отнять само число.
Чтобы умножить число на 9, необходимо умножить его на 10 и отнять само число.Есть еще один метод запоминания таблицы умножения – благодаря поэзии! Предлагаем Вашему вниманию веселые и шуточные стишки. Читайте и запоминайте таблицу умножения с нами!










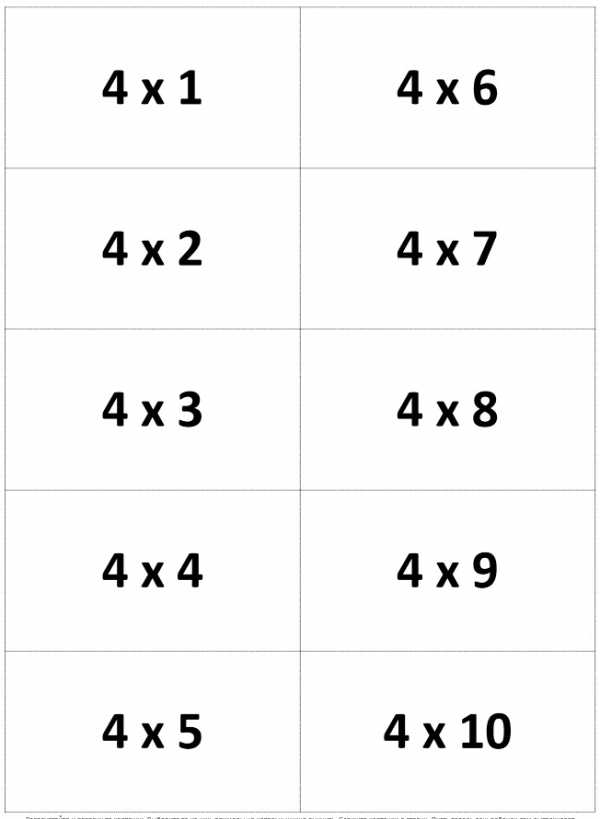
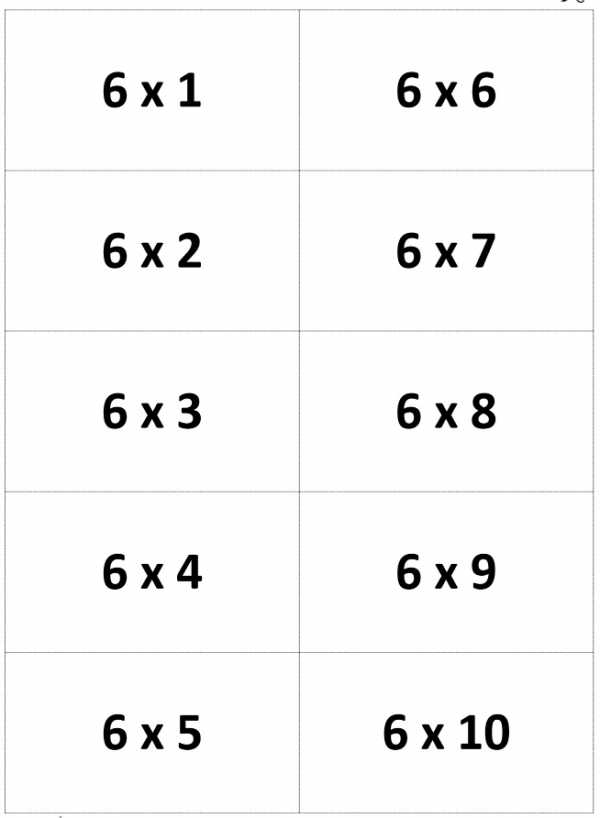
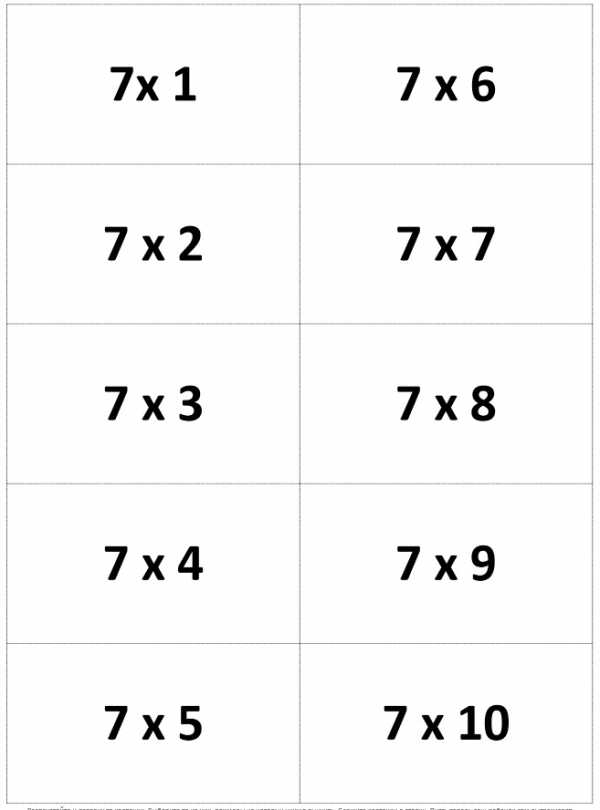
 А для того, чтобы проверить свои знания в таблице умножения, мы подготовили для вас карточки. Их можно распечатать и разрезать. Помните, таблица умножения прекрасно тренирует память, чтобы ее быстро выучить, необходимо систематически заниматься!
А для того, чтобы проверить свои знания в таблице умножения, мы подготовили для вас карточки. Их можно распечатать и разрезать. Помните, таблица умножения прекрасно тренирует память, чтобы ее быстро выучить, необходимо систематически заниматься! 




puzkarapuz.ru
Таблица умножения | Cubens
Таблица умножения чисел от 1 до 10
Таблица умножения на 2
(5 умножить на 2 будет 10)
Таблица умножения на 3
(2 умножить на 3 будет 6)
Таблица умножения на 4
(6 умножить на 4 будет 24)
Таблица умножения на 5
(6 умножить на 5 равно 30)
Таблица умножения на 6
(2 умножить на 6 будет равен 12)
Таблица умножения на 7
(3 умножить на 7 будет равняться 27)
Таблица умножения на 8
(5 умножить на 8 будет равен 40)
Таблица умножения на 9
(5 умножить на 9 равно 45)
Таблица Пифагора
Таблица умножения чисел от 1 до 20
Таблица умножения до 20 также называется таблица Пифагора
Для нахождения результатов умножения двух чисел, нужно одно число, взять в верхней строке таблицы умножения, второе число — по первом вертикальном столбце. На пересечении столбца и строки находится результат их умножения.
| х | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 54 | 57 | 60 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | 52 | 56 | 60 | 64 | 68 | 72 | 76 | 80 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 74 | 80 | 86 | 92 | 98 | 104 | 110 | 116 | 120 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | 91 | 98 | 105 | 112 | 119 | 126 | 133 | 140 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 | 128 | 136 | 144 | 152 | 160 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | 117 | 126 | 135 | 144 | 153 | 162 | 171 | 180 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | 190 | 200 |
| 11 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | 143 | 154 | 165 | 176 | 187 | 198 | 209 | 220 |
| 12 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 | 168 | 180 | 192 | 204 | 216 | 228 | 240 |
| 13 | 13 | 26 | 39 | 52 | 65 | 78 | 91 | 104 | 117 | 130 | 143 | 156 | 169 | 182 | 195 | 208 | 221 | 234 | 247 | 260 |
| 14 | 14 | 28 | 42 | 56 | 70 | 84 | 98 | 112 | 126 | 140 | 154 | 168 | 182 | 196 | 210 | 224 | 238 | 252 | 266 | 280 |
| 15 | 15 | 30 | 45 | 60 | 75 | 90 | 105 | 120 | 135 | 150 | 165 | 180 | 195 | 210 | 225 | 240 | 255 | 270 | 285 | 300 |
| 16 | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 | 272 | 288 | 304 | 320 |
| 17 | 17 | 34 | 51 | 68 | 85 | 102 | 119 | 136 | 153 | 170 | 187 | 204 | 221 | 238 | 255 | 272 | 289 | 306 | 323 | 340 |
| 18 | 18 | 36 | 54 | 72 | 90 | 108 | 126 | 144 | 162 | 180 | 198 | 210 | 234 | 252 | 270 | 288 | 306 | 324 | 342 | 360 |
| 19 | 19 | 38 | 57 | 76 | 95 | 114 | 133 | 152 | 171 | 190 | 209 | 228 | 247 | 266 | 285 | 304 | 323 | 342 | 361 | 380 |
| 20 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | 280 | 300 | 320 | 340 | 360 | 380 | 400 |
Примеры нахождения по таблице умножения:
Таблица умножения десятичных чисел изучается как составная часть элементарной арифметики по всему миру, поскольку она закладывает фундамент для арифметических операций с десятичными числами. Необходимо изучить таблицу 9 * 9 , или 12 * 12, чтобы быть искусным в традиционной математике.
cubens.com
|
|
|
|
dpva.ru
таблица умножения | интернет проект BeginnerSchool.ru
 Мы все знаем, что учить таблицу умножения необходимо. А необходимо потому, что зная назубок таблицу умножения/деления от 1 до 10, ребенок без труда освоит внетабличное умножение и деление. Но как же легче всего выучить таблицу умножения. Ответ неоднозначен, для каждого ребенка нужен индивидуальный подход. Но все же можно дать общие для всех советы.
Мы все знаем, что учить таблицу умножения необходимо. А необходимо потому, что зная назубок таблицу умножения/деления от 1 до 10, ребенок без труда освоит внетабличное умножение и деление. Но как же легче всего выучить таблицу умножения. Ответ неоднозначен, для каждого ребенка нужен индивидуальный подход. Но все же можно дать общие для всех советы.
Для начала надо объяснить ребенку, что такое умножение. Умножение связано с действием сложения. Объясните ребенку, что перемножаемые числа называются множителями, а полученное число называется произведением.
Итак, начинаем с умножения на 2:
Что такое 2 × 2, это 2 + 2 и равно 4. Положим две конфеты на одну тарелочку и еще две конфеты на другую. Если конфеты сосчитать все вместе получится четыре, то есть 2 конфеты умножить на 2 тарелочки, получится 4 конфеты: 2 × 2 = 4.
Теперь, чтобы проверить результат, разделите 4 конфеты обратно на две тарелки: 4 ÷ 2 = 2.
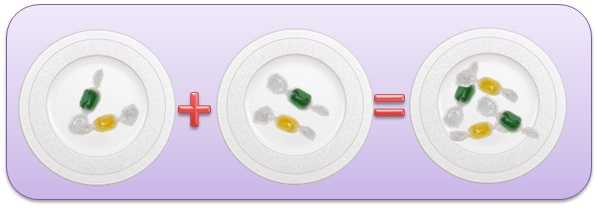
А как еще можно поровну разделить конфеты? Конечно же, по четырем тарелкам. Если на каждую тарелку положить по конфете:
4 ÷ 4 = 1
4 ÷ 1 = 4
проверим: 4 × 1 = 4.
Теперь добавим на каждую тарелочку еще по конфете. Считаем все конфеты, получаем 6, как получилось? Три конфеты умножили на две тарелочки: 3 × 2 = 3 + 3 = 2 + 2 + 2 = 6.
То есть три умножить на два это 2 раза по 3 или 3 раза по 2, и если взять три тарелочки по две конфеты, то все равно получится 6 конфет.
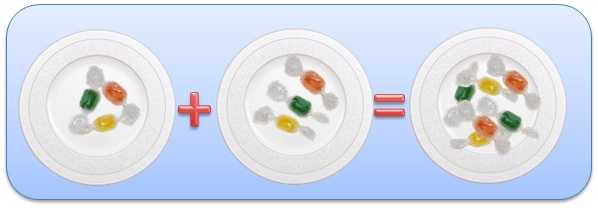
От перемены мест множителей произведение не меняется: 3 × 2 = 2 × 3 = 6.
Теперь деление: 6 ÷ 2 = 3, берем 6 конфет и раскладываем поровну на две тарелки, получаем на каждой по три конфеты. Также показываем деление шести конфет по трем тарелкам, получаем по две конфеты на каждой тарелке: 6 ÷ 3 = 2.
Таким образом, можно разобрать каждый пример умножения на 2, на 3 и так далее.
Когда ребенок уверенно будет решать такого рода примеры, приступайте к постепенному заучиванию таблицы умножения, сначала на 2, потом на 3 и так далее до 9.
Объясните особенности умножения на 1 и на 10:
При умножении любого числа на 1, в результате получите это же число:
1 × 1 = 1
1 × 2 = 2
1 × 3 = 3
1 × 99 = 99
и так далее.
При умножении любого числа на 10, в результате получим то же число, но с добавленным справа нулем: 10 × 3 = 30, один ноль, потому что в цифре 10 один ноль, а если умножать не на 10, а на 100, то получим справа два нуля: 100 × 3 = 300. И так далее с 1000, 10000…
То есть для того, чтобы умножить число на 10, 100, 1000 и так далее (например 4 × 10), сначала вспоминаем правило умножения на 1, то есть пишем то же число (4) и дописываем к нему справа столько нулей, сколько во втором множителе (10), (4 × 10 = 40).
Таблица умножения:
 Про особенности умножения на 9 мы писали в статье “Чудеса умножения“.
Про особенности умножения на 9 мы писали в статье “Чудеса умножения“.
О том как выучить таблицу умножения, читайте в статье “Как выучить таблицу умножения“.
После того (или вместе с тем), как ребенок освоит таблицу умножения, знакомим его с таблицей Пифагора:
В таблице Пифагора по вертикали (в первом столбце) и горизонтали (в первой строке) расположены числа от 1 до 10. На пересечении строк и столбцов располагаются произведения этих чисел:
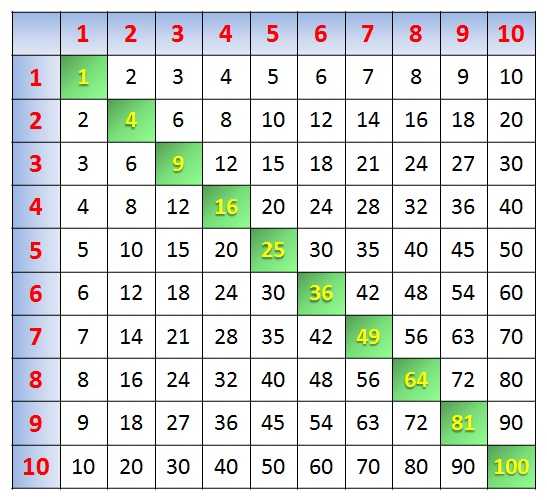
Проверить таблицу умножения можно следующим образом. Нарисуйте таблицу Пифагора, не заполняя произведения, заштрихуйте некоторые ячейки следующим образом:
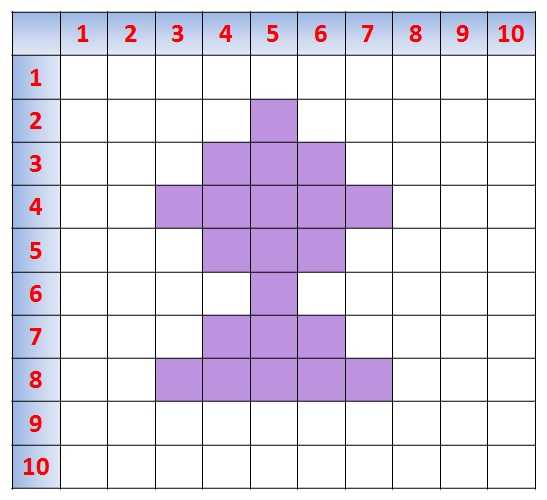
Теперь пусть ребенок самостоятельно заполнит заштрихованные клетки, должно получиться следующее:
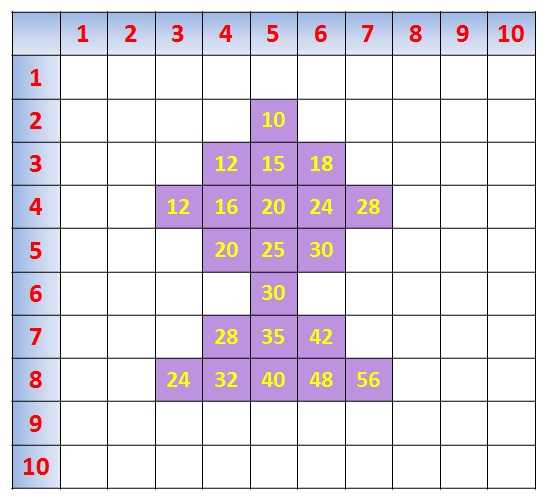
Теперь сами придумайте рисунок.
Если вы хотите получать анонсы наших статей, подпишитесь на рассылку “Новости сайта”.
Понравилась статья — поделитесь с друзьями:
Подпишитесь на новости сайта:
Оставляйте пожалуйста комментарии в форме ниже
beginnerschool.ru

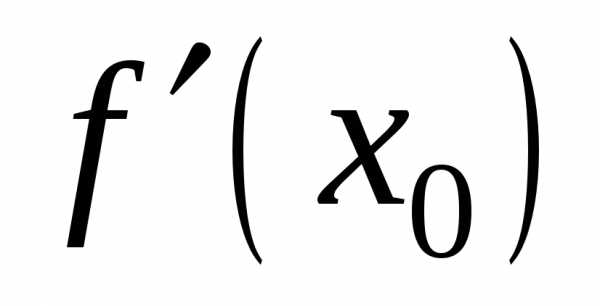 ,
то существует касательная и нормаль к
кривой (1).
,
то существует касательная и нормаль к
кривой (1). . (12)
. (12)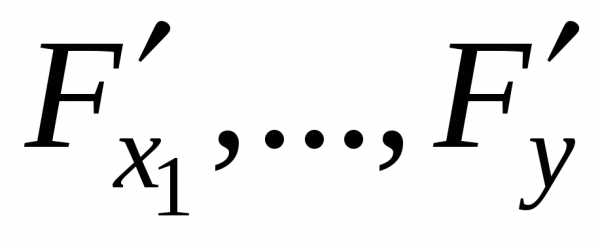 непрерывны в некоторой окрестности
точки,
и пусть,
а.
Тогда уравнение (13) определяет функциюопределенную, непрерывную и дифференцируемую
в некоторой окрестности точки
непрерывны в некоторой окрестности
точки,
и пусть,
а.
Тогда уравнение (13) определяет функциюопределенную, непрерывную и дифференцируемую
в некоторой окрестности точки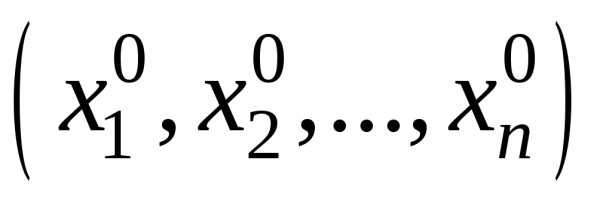 ,
причем,
а частные производные
,
причем,
а частные производные находятся по формулам:
находятся по формулам: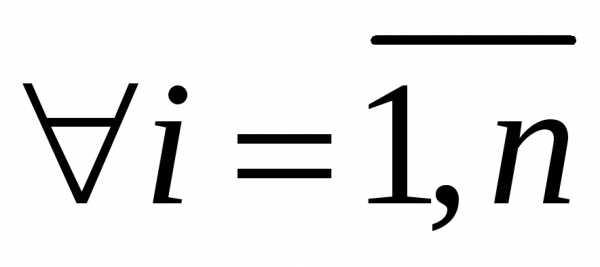 .
. дано уравнение
дано уравнение ,
т.е. справедливо тождество (16)F(x;y;f(x;y))
,
т.е. справедливо тождество (16)F(x;y;f(x;y)) 0.
Правая часть (16) – сложная функция отхиу.
В силу условий теоремы (2) (существуют
непрерывные
0.
Правая часть (16) – сложная функция отхиу.
В силу условий теоремы (2) (существуют
непрерывные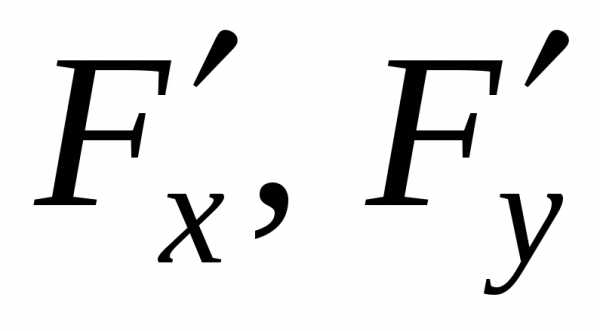 )
эта функция дифференцируема наD.
Дифференцируя (16) поx,
получим:
)
эта функция дифференцируема наD.
Дифференцируя (16) поx,
получим: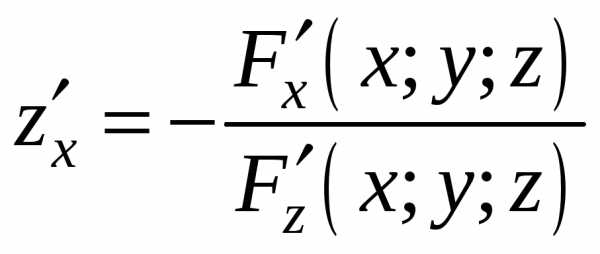 . (17)
. (17)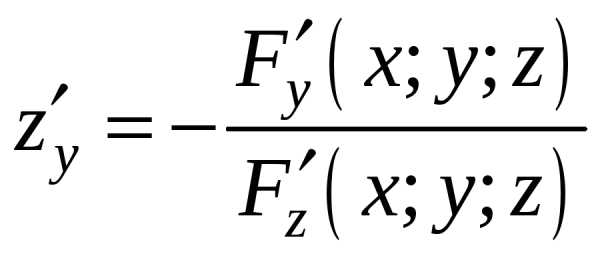 . (18)
. (18)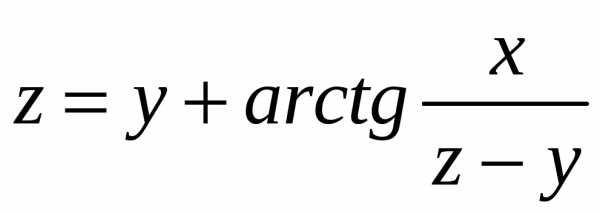 определяет функциюz=f(x;y).
Найти
определяет функциюz=f(x;y).
Найти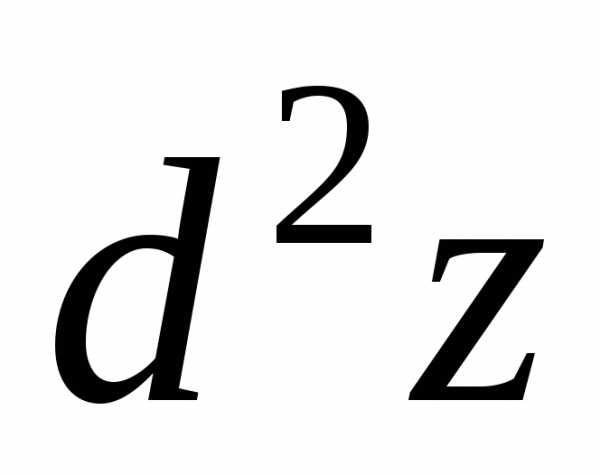
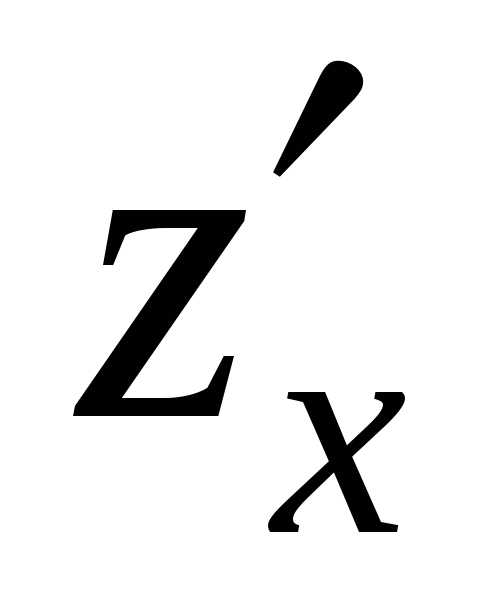 и
заменяяzнаf(x;y),
найдем
и
заменяяzнаf(x;y),
найдем .
. ,
такая, чтовыполнено неравенствоf(x;y)<f(х0;y0)
(f(x;y)>f(х0;y0)).
,
такая, чтовыполнено неравенствоf(x;y)<f(х0;y0)
(f(x;y)>f(х0;y0)).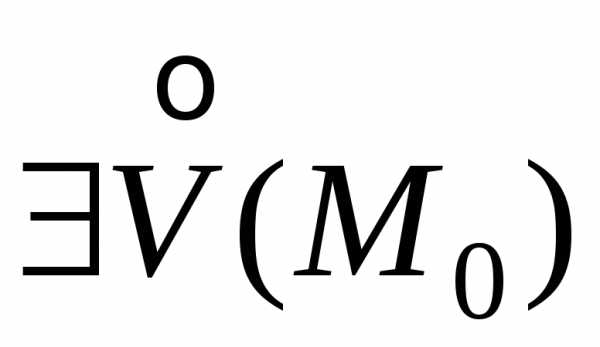 ,
такая, чтовыполнено неравенствоf(x;y)f(х0;y0)
(f(x;y)f(х0;y0)).
,
такая, чтовыполнено неравенствоf(x;y)f(х0;y0)
(f(x;y)f(х0;y0)).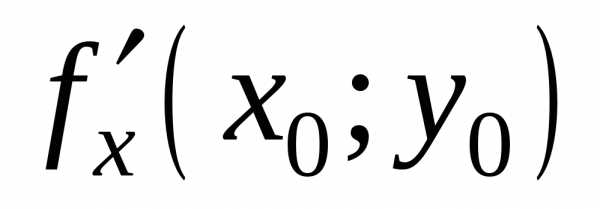 и
и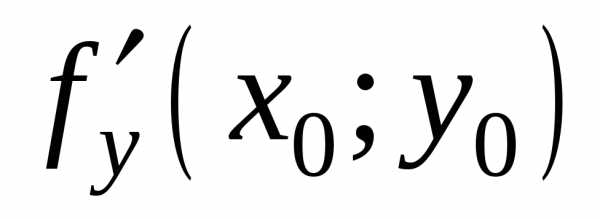 ,
то они в этой точке равны нулю, то есть
,
то они в этой точке равны нулю, то есть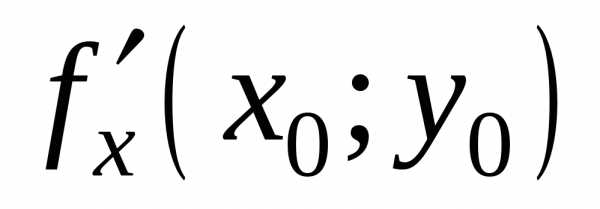 =0
и
=0
и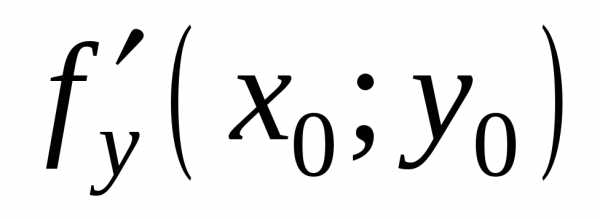 =0.
=0. Пустьz=f(x;y)
имеет в точкеM0(x0;y0)
максимум. Тогда
Пустьz=f(x;y)
имеет в точкеM0(x0;y0)
максимум. Тогда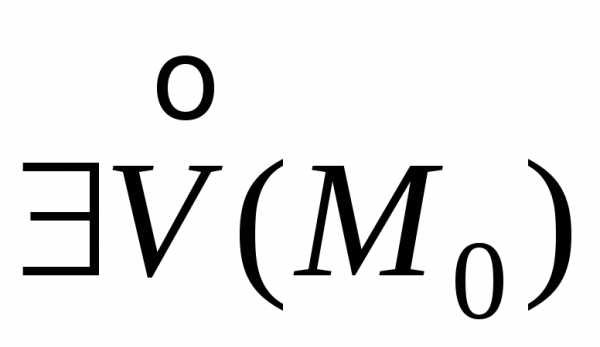 ,
такая, чтовыполнено
,
такая, чтовыполнено в точкех0,
т.е
в точкех0,
т.е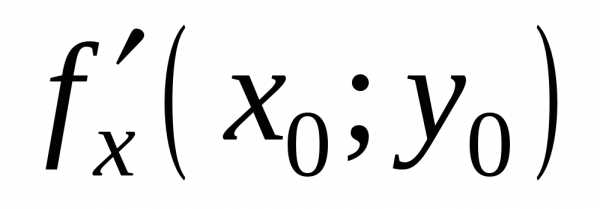 =
=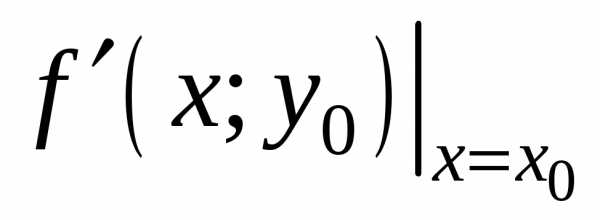 .
На основании необходимого условия
экстремума функции одной переменной
.
На основании необходимого условия
экстремума функции одной переменной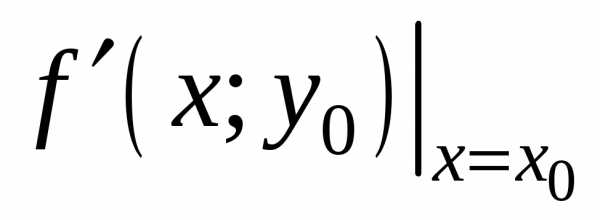 =0.
Следовательно,
=0.
Следовательно,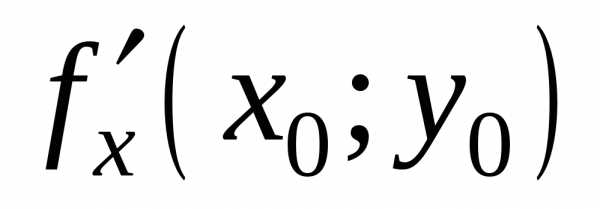 =0.
=0.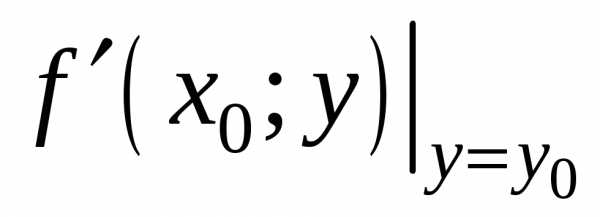 =0.
Следовательно,
=0.
Следовательно,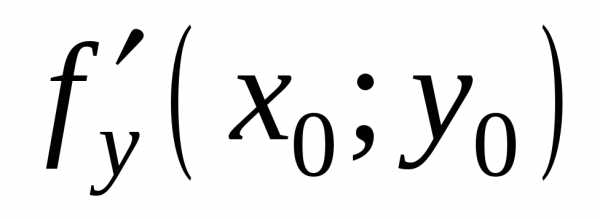 =0.
=0.
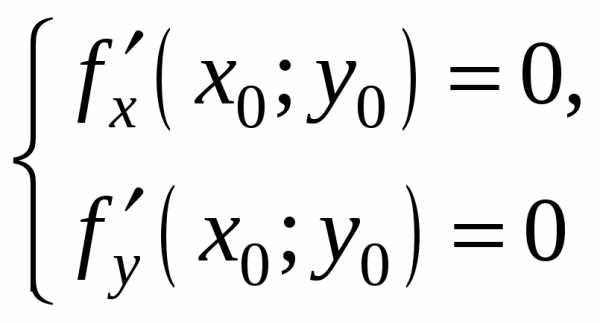 равносильно условиюdf(х0;y0)=0.
равносильно условиюdf(х0;y0)=0.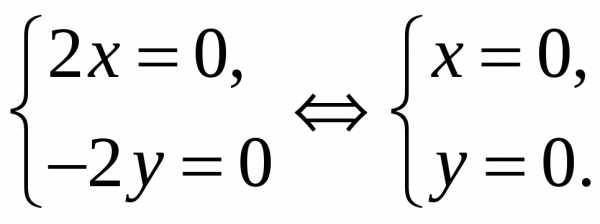
(0;0) – стационарная точка.
(0;0) – стационарная точка.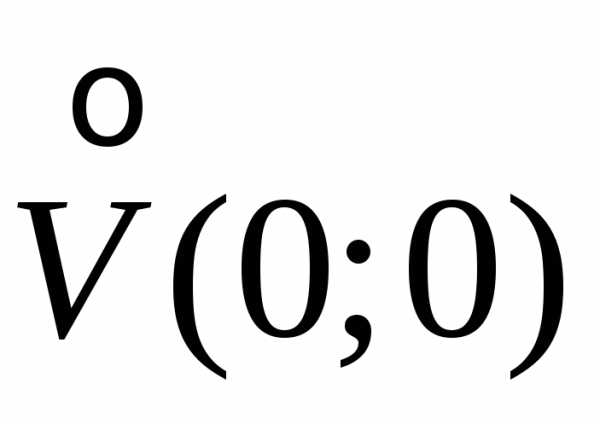 .
На оси Охf(x;0)=x2>0,
на оси Оуf(0;y)=—y2<0.
Следовательно, в любой окрестности
.
На оси Охf(x;0)=x2>0,
на оси Оуf(0;y)=—y2<0.
Следовательно, в любой окрестности есть значения функции, как большиеf(0;0)=0,
так и меньшиеf(0;0)=0.
Значит, точка (0;0) не может быть точкой
экстремума.
есть значения функции, как большиеf(0;0)=0,
так и меньшиеf(0;0)=0.
Значит, точка (0;0) не может быть точкой
экстремума.  Т.к.
по условию функция имеет непрерывные
частные производные второго порядка,
то можем записать для нее формулу Тейлора
с остаточным членом в форме Лагранжа,
ограничиваясь двумя членами:
Т.к.
по условию функция имеет непрерывные
частные производные второго порядка,
то можем записать для нее формулу Тейлора
с остаточным членом в форме Лагранжа,
ограничиваясь двумя членами:
 .
.
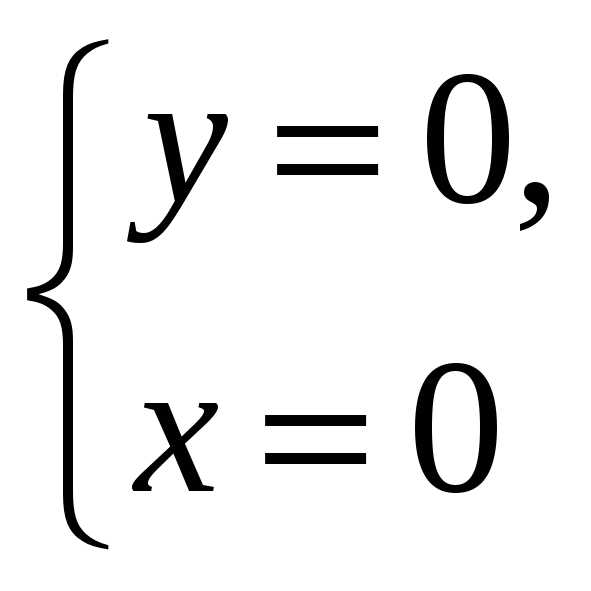
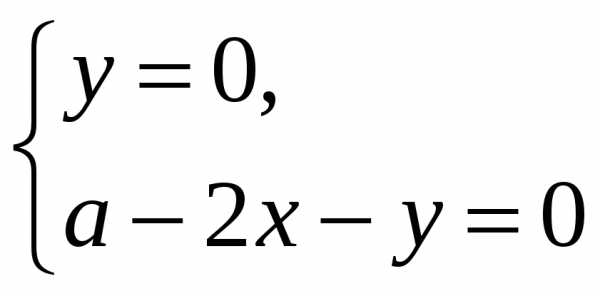
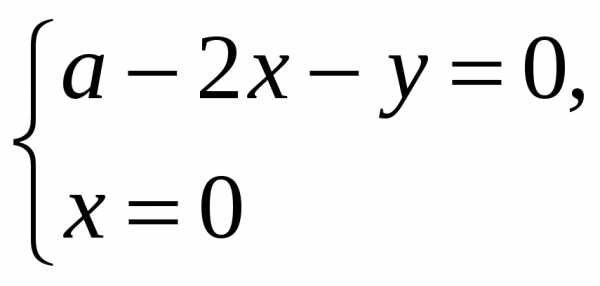
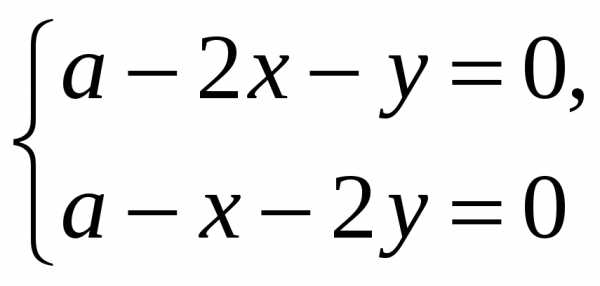
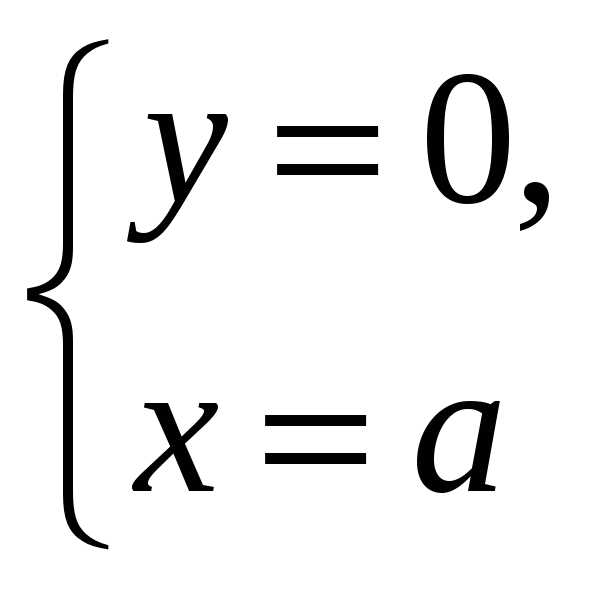
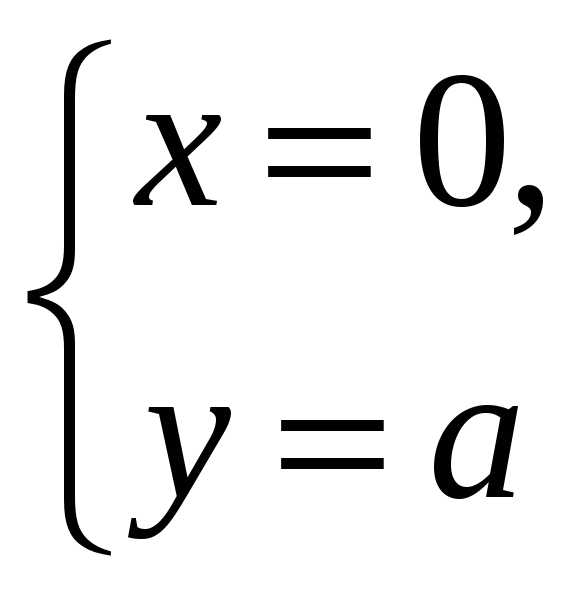
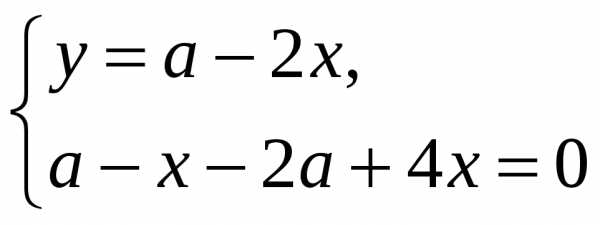
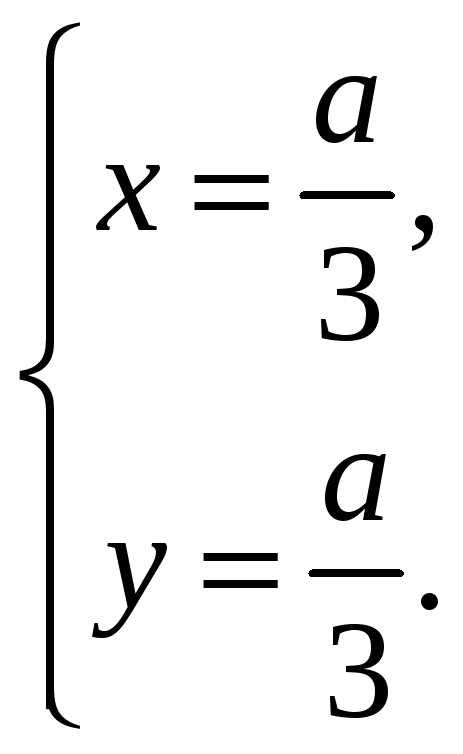
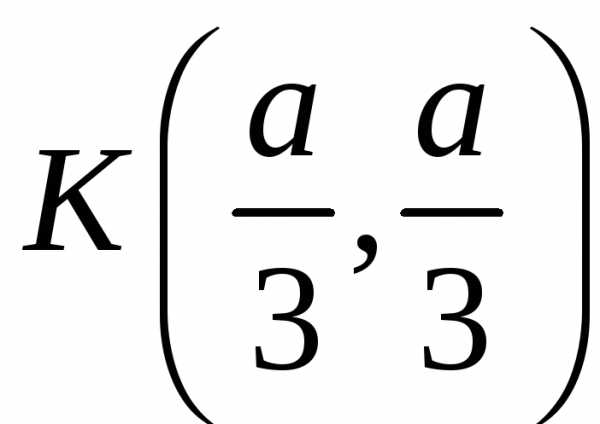 .
.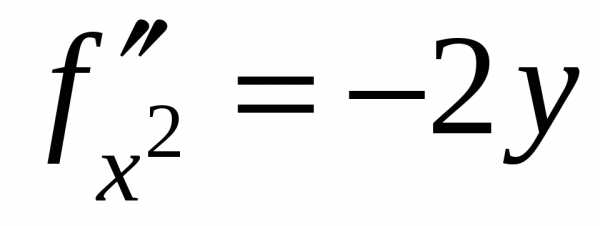 ,,
,,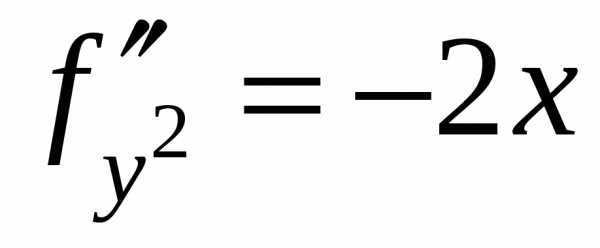 .
.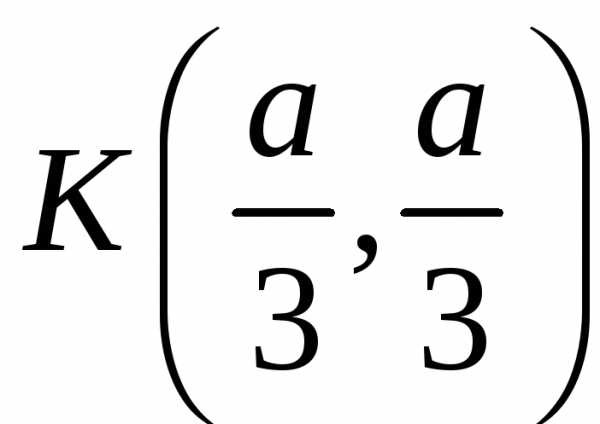 :
: ,,
,, ,
,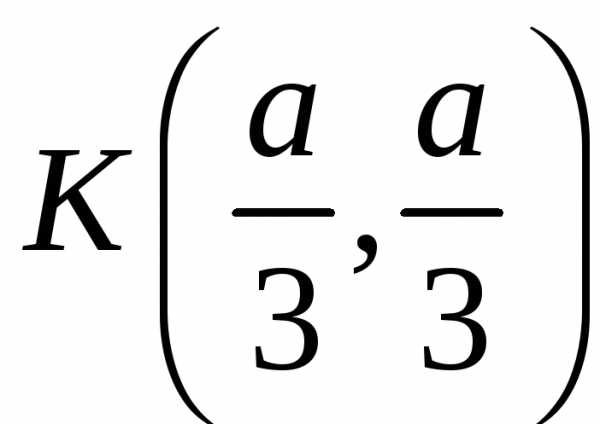 — точка максимума.
— точка максимума. 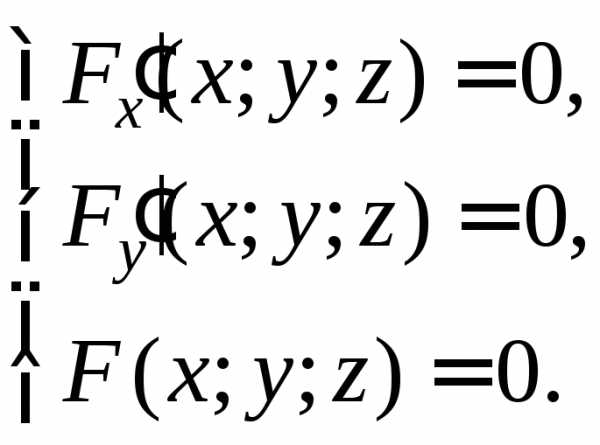

(0;0) – стационарная точка.
(0;0) – стационарная точка. -окрестность
этой точки, такая, что для всех точек
-окрестность
этой точки, такая, что для всех точек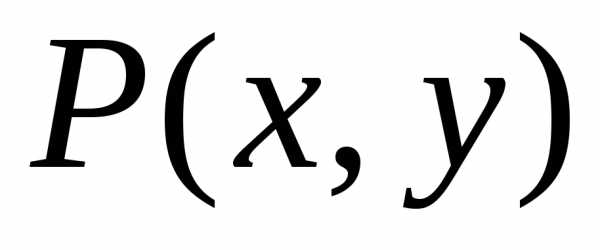 (принадлежащих
(принадлежащих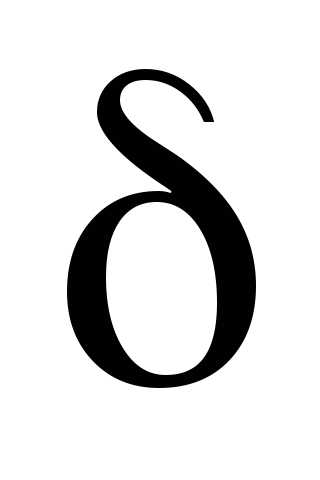 -окрестности
этой точки), отличных от точки,
выполняется неравенство().
-окрестности
этой точки), отличных от точки,
выполняется неравенство().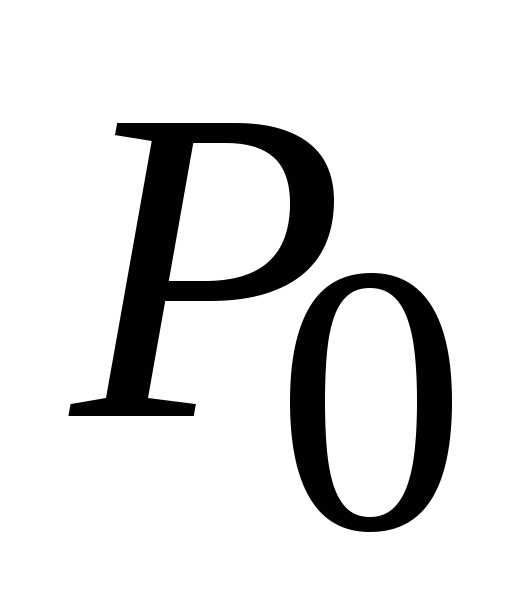 (1;
1):
(1;
1): (1,
1) = 1.
(1,
1) = 1.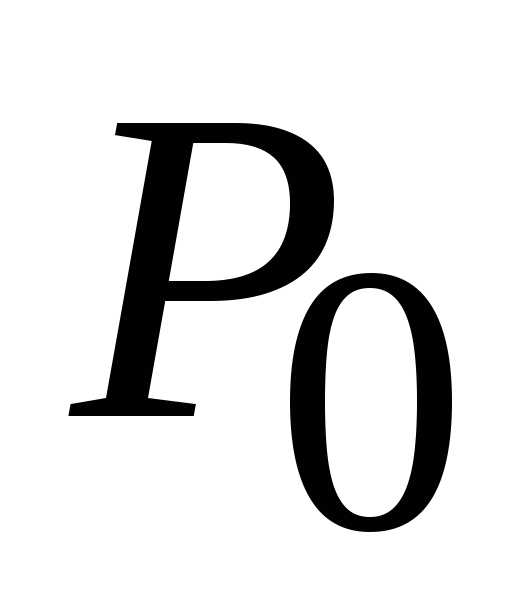 (1;
1), в которой выполняется условие
(1;
1), в которой выполняется условие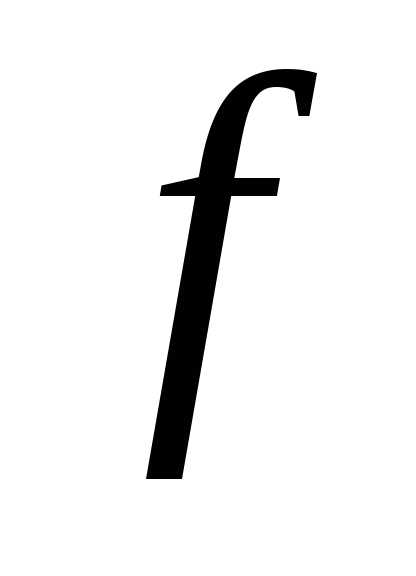 (1;
1) >
(1;
1) > для.
Графиком этой функции является поверхность
— параболоид вращения, представленный
на рисунке.
для.
Графиком этой функции является поверхность
— параболоид вращения, представленный
на рисунке. .
Однако для всех точек
.
Однако для всех точек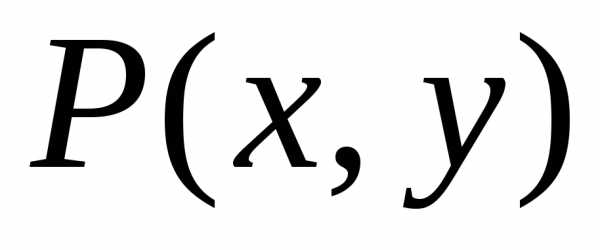
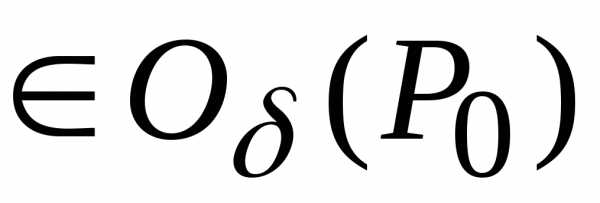 определить знак приращения
определить знак приращения практически невозможно, поэтому надо
искать другие условия, по которым можно
судить о наличии и характере экстремума
функции в данной точке.
практически невозможно, поэтому надо
искать другие условия, по которым можно
судить о наличии и характере экстремума
функции в данной точке. лишь те точки, для которых
лишь те точки, для которых .
Получим функциюодной переменной
.
Получим функциюодной переменной .
Эта функция имеет в точке
.
Эта функция имеет в точке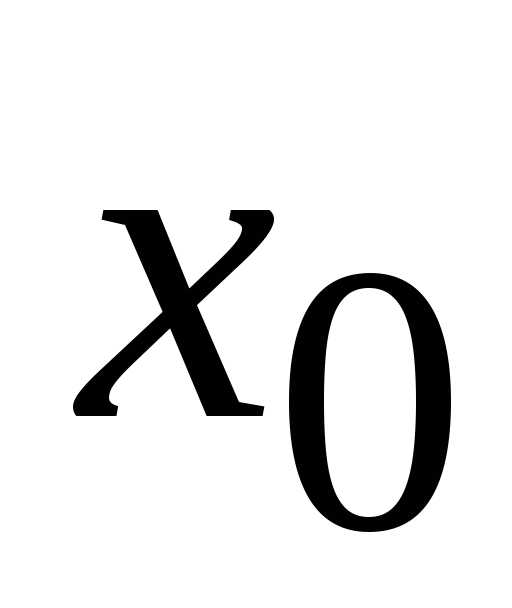 экстремум, следовательно,.
экстремум, следовательно,. (О)
выполняется условие
(О)
выполняется условие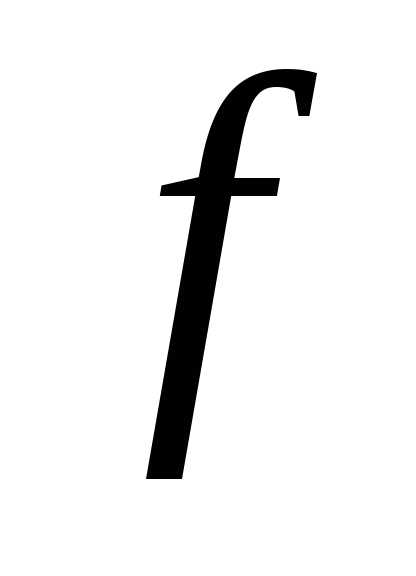 (0;
0) >
(0;
0) >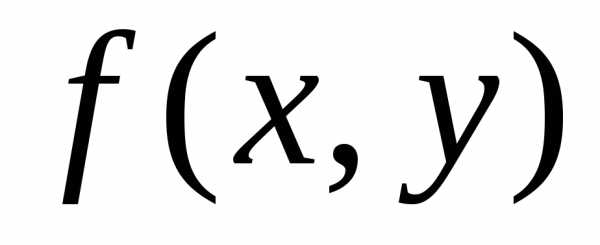 .
Частные производные
.
Частные производные ,
,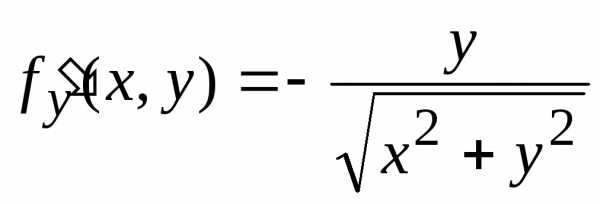
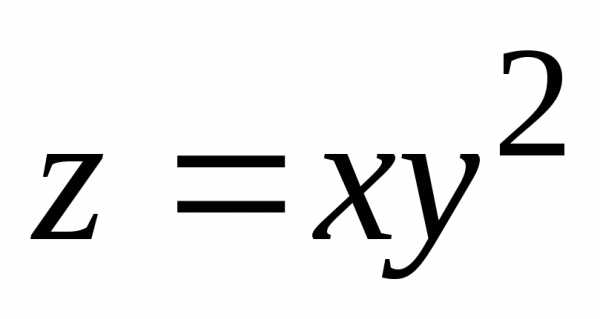 .
Она задана на всей числовой плоскостиR2. Точка О(0; 0) будет
критической, поскольку частные производные
в ней равны нулю. Так как функция равна
нулю в точке О, а в любой сколь угодно
малой окрестности
.
Она задана на всей числовой плоскостиR2. Точка О(0; 0) будет
критической, поскольку частные производные
в ней равны нулю. Так как функция равна
нулю в точке О, а в любой сколь угодно
малой окрестности (О)
она принимает как положительные, так и
отрицательные значения, то функция
(О)
она принимает как положительные, так и
отрицательные значения, то функция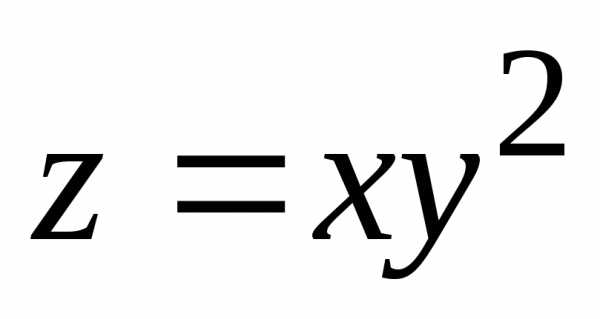 не имеет в точке О экстремума.
не имеет в точке О экстремума.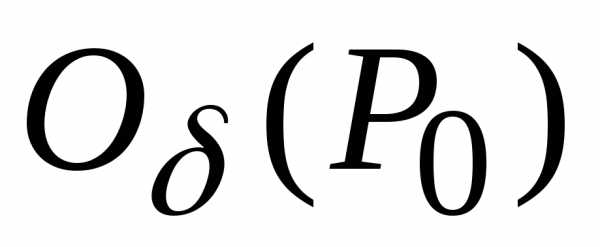 функциии пусть
функциии пусть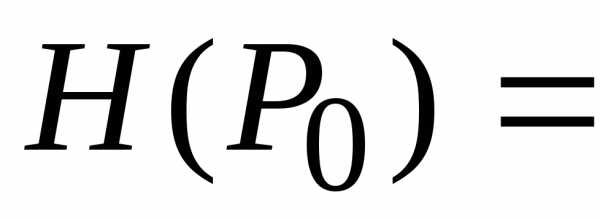 .
.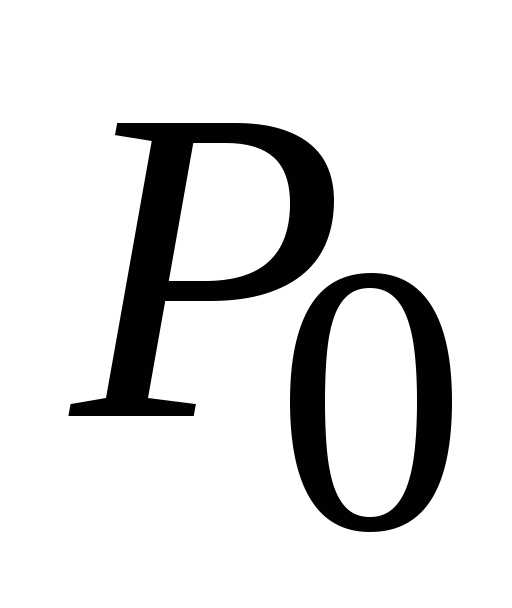 .
В этом случае необходимо произвести
дополнительные исследования знака
функциив
.
В этом случае необходимо произвести
дополнительные исследования знака
функциив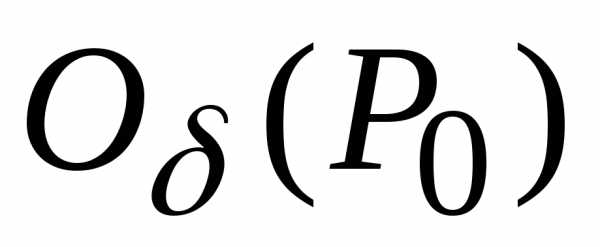 .
.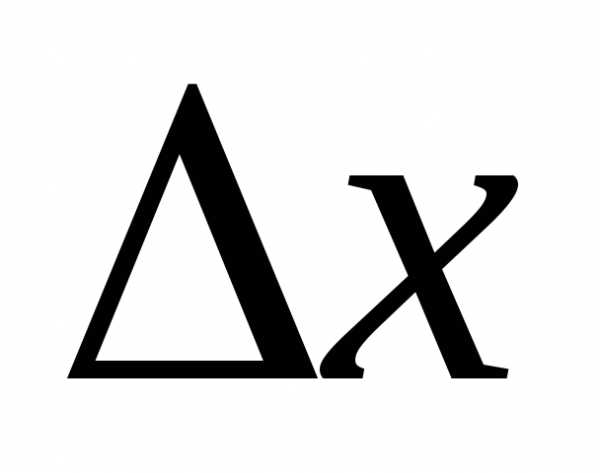 и
и не могут равняться нулю одновременно,
поскольку в подобном случае точкасовпала бы с точкойи функцияне получила бы никакого приращения.
не могут равняться нулю одновременно,
поскольку в подобном случае точкасовпала бы с точкойи функцияне получила бы никакого приращения.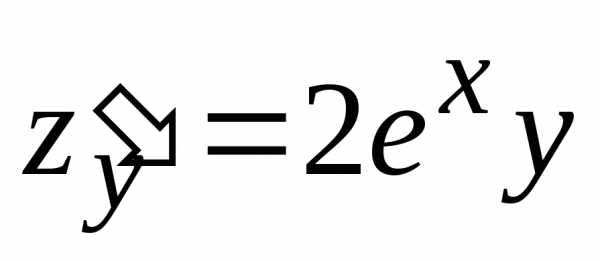 .
.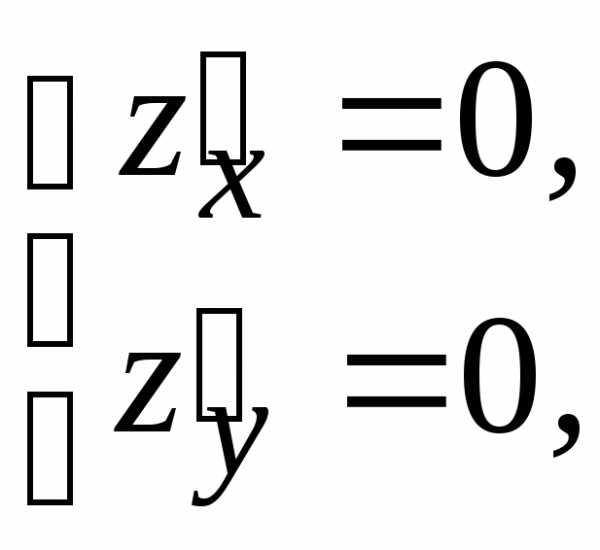

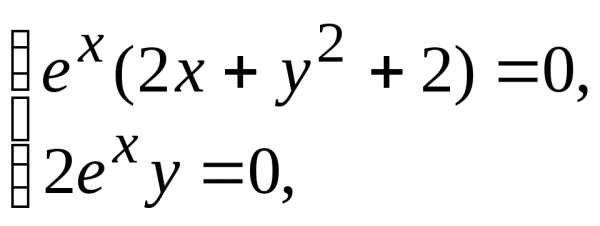
 (т. к.
(т. к.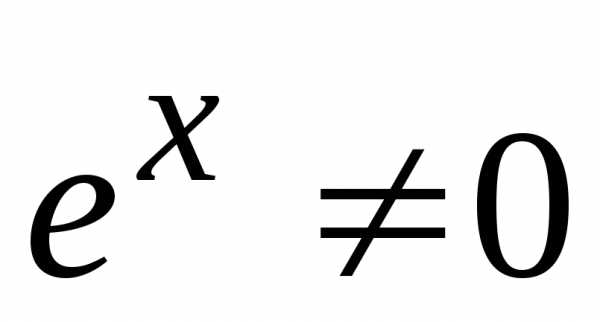 для
для R)
R) 
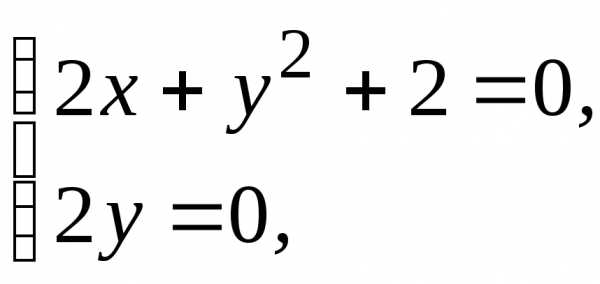


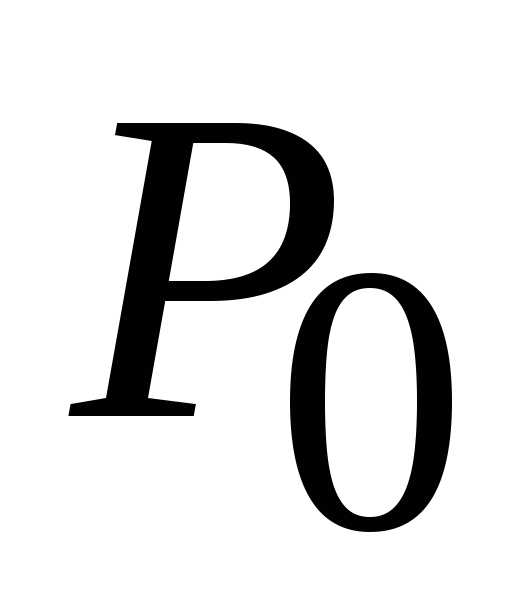 (1; 0), в которой
функция
(1; 0), в которой
функция может достигать экстремума.
может достигать экстремума.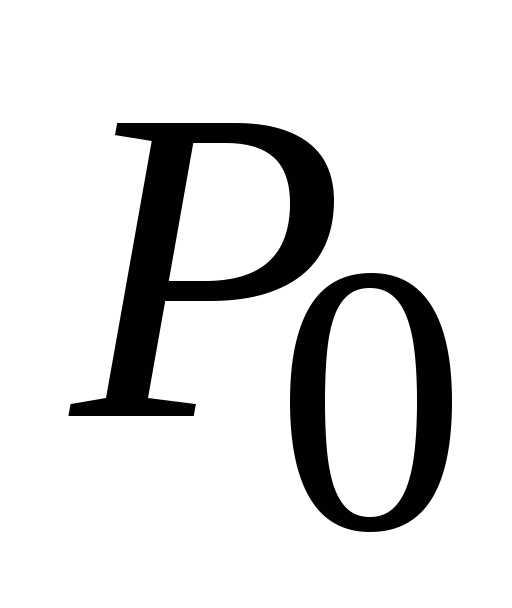 :
: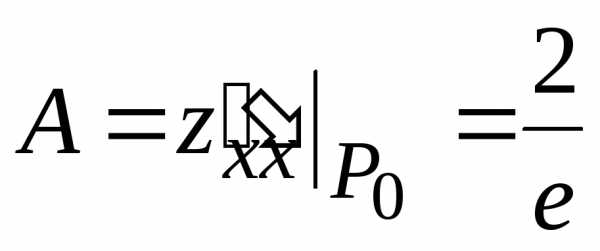 ,
,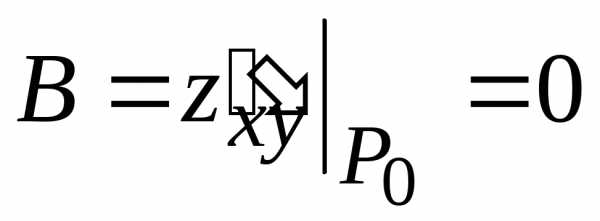 ,
,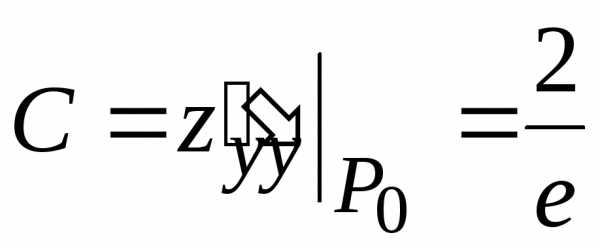 .
. (1;
0),
(1;
0),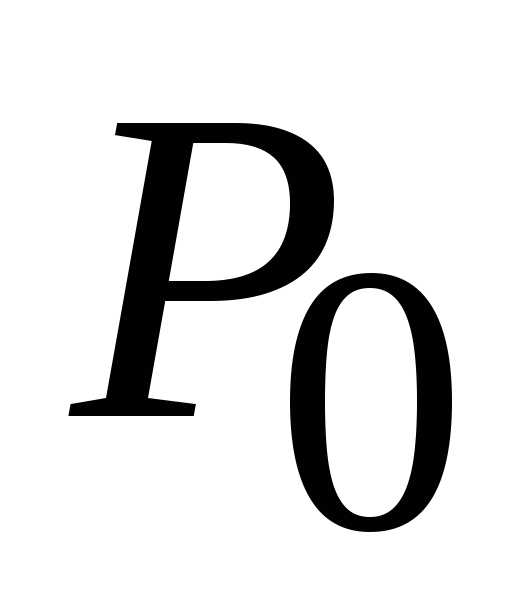 (1; 0) является
точкой локального экстремума, а т. к. А
> 0, то точка
(1; 0) является
точкой локального экстремума, а т. к. А
> 0, то точка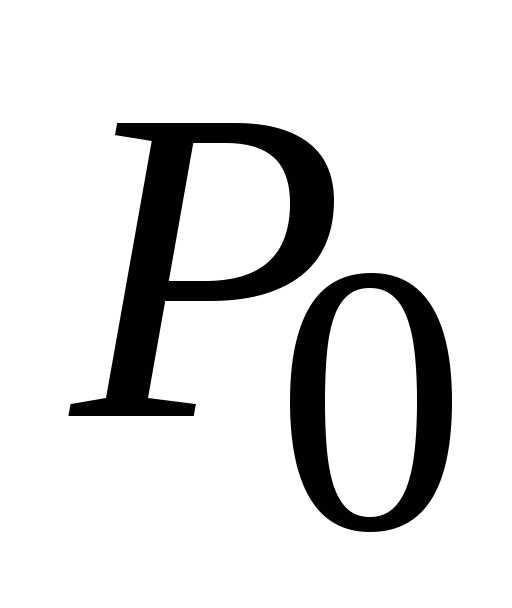 (1; 0) является
точкой локального минимума, при этом
(1; 0) является
точкой локального минимума, при этом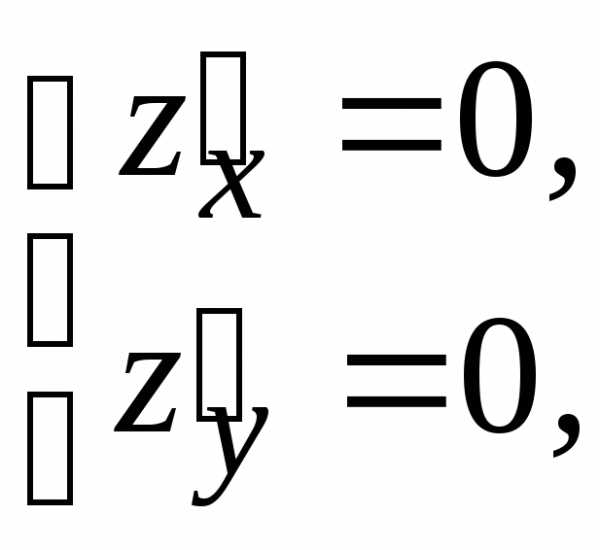

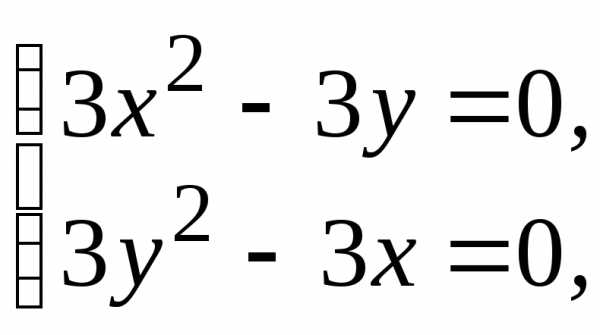


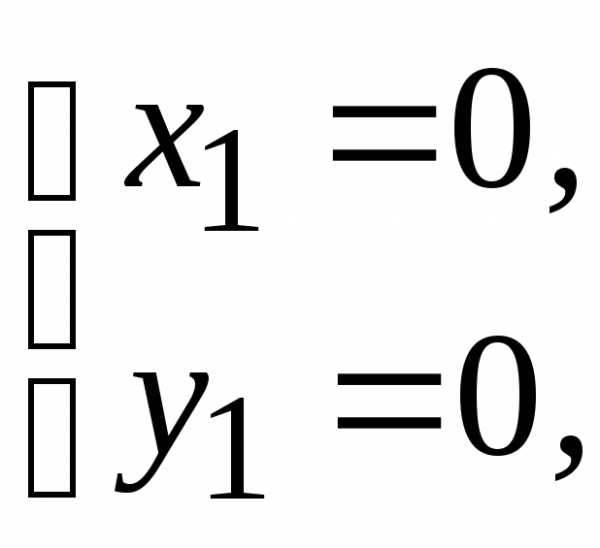 и
и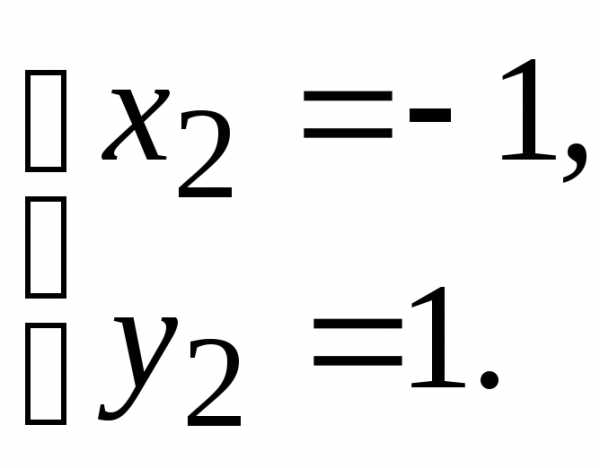
 (0;
0) и
(0;
0) и (1,
1). Вычислим частные производные второго
порядка функции
(1,
1). Вычислим частные производные второго
порядка функции :
: для точки
для точки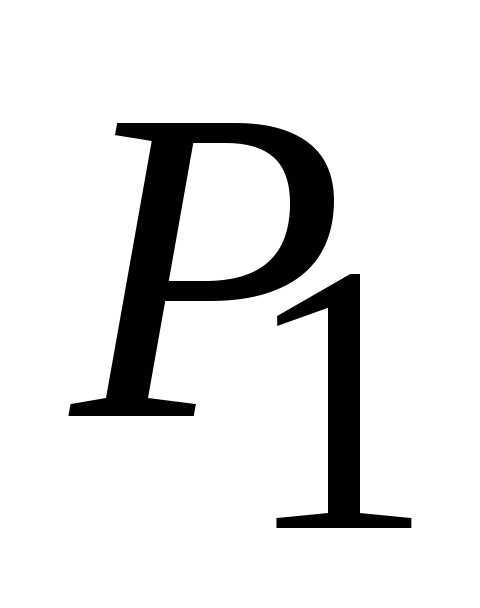 (0;
0). Так как
(0;
0). Так как (0;
0),
то в точке
(0;
0),
то в точке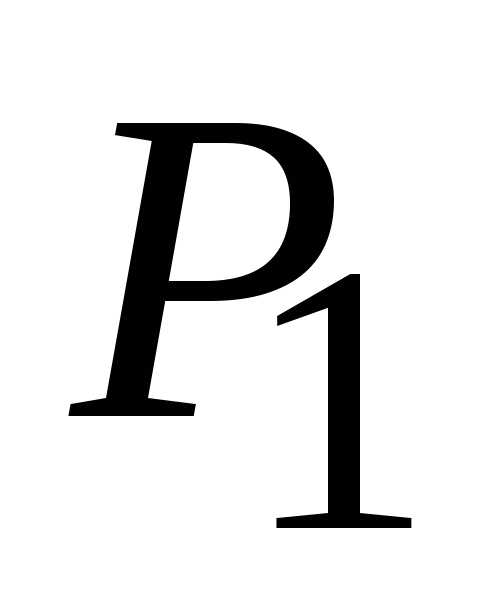 (0;
0) нет экстремума.
(0;
0) нет экстремума. для точки
для точки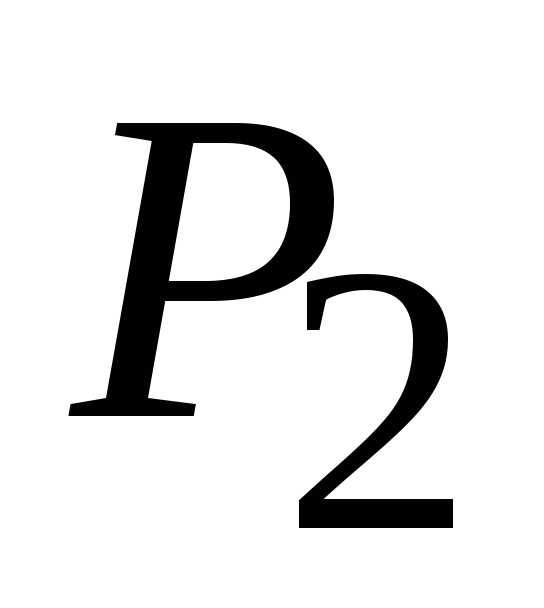 (1,
1). Т. к.
(1,
1). Т. к. (1;
1),
то точка
(1;
1),
то точка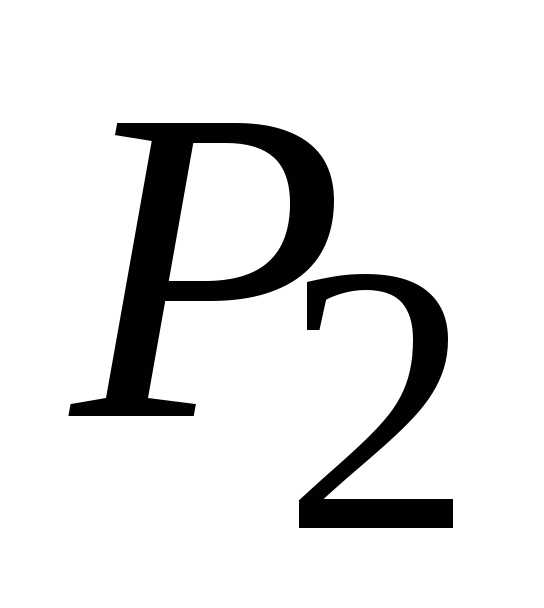 (1,
1) является точкой локального экстремума,
а т. к.
,
то точка
(1,
1) является точкой локального экстремума,
а т. к.
,
то точка (1,
1) является точкой локального максимума,
при этом
(1,
1) является точкой локального максимума,
при этом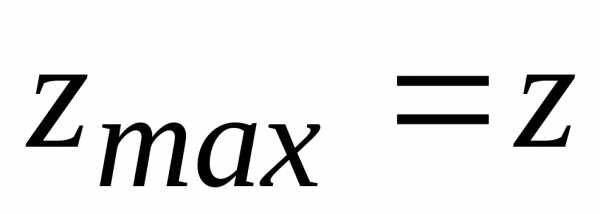 (1;
1)=9.
(1;
1)=9.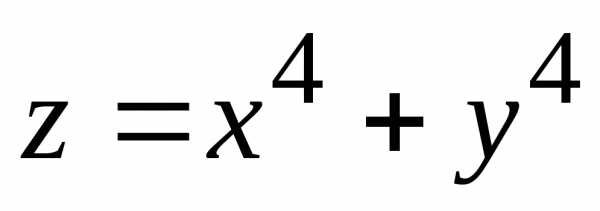 .
. :
:
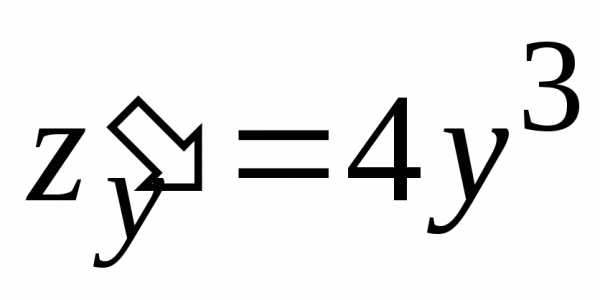 .
.

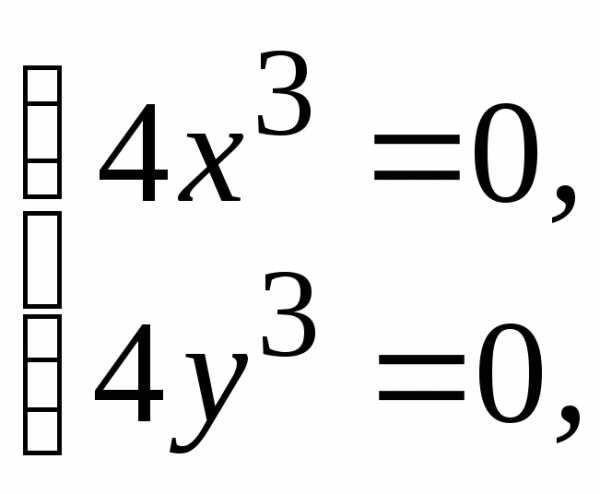

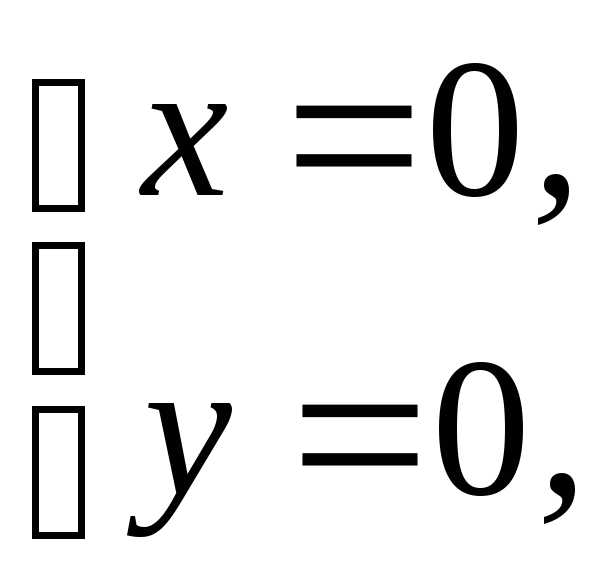
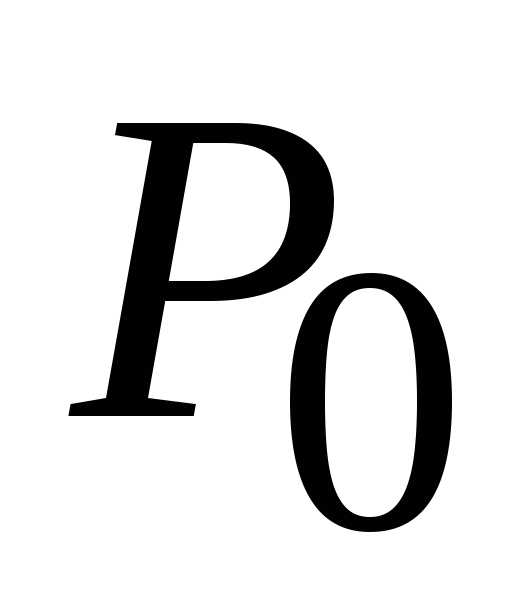 (0; 0) данной функции.
(0; 0) данной функции. :
:
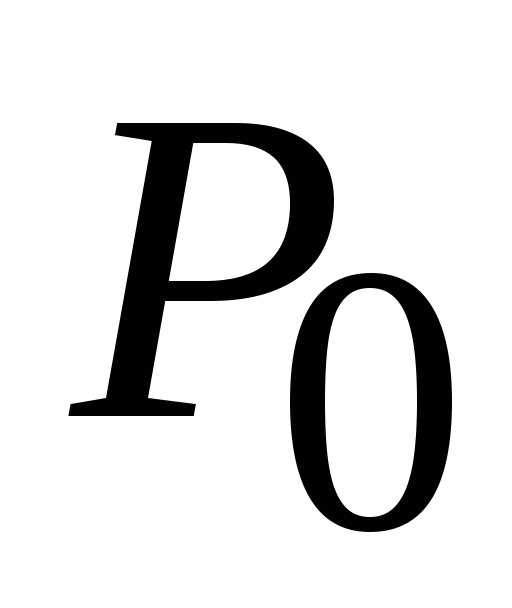 (0; 0)
(0; 0)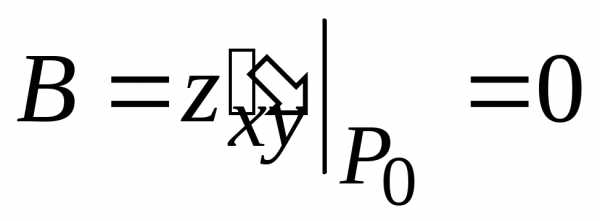 ,
,

 .
.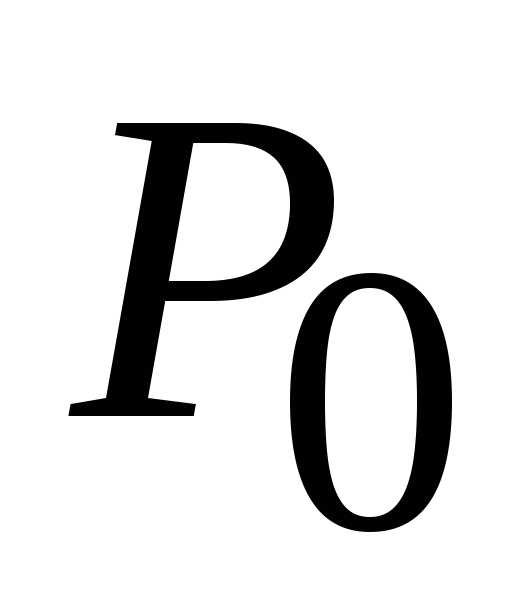 (0; 0). В данном случае стационарная
точка
(0; 0). В данном случае стационарная
точка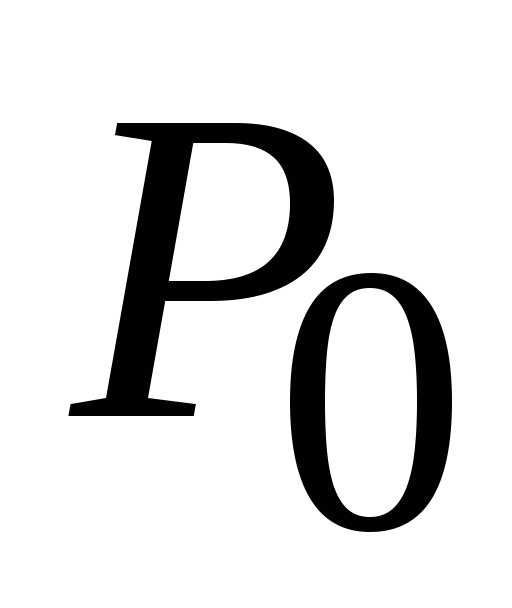 (0; 0) является точкой локального
минимума, поскольку,
(0; 0) является точкой локального
минимума, поскольку,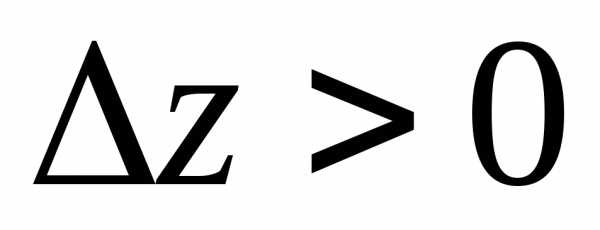 для
для
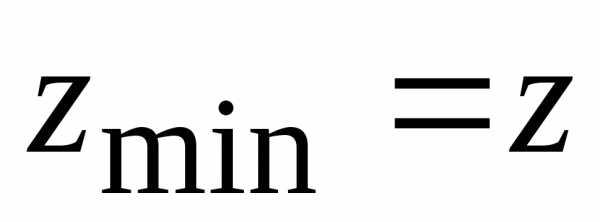 (0;
0)=0.
(0;
0)=0.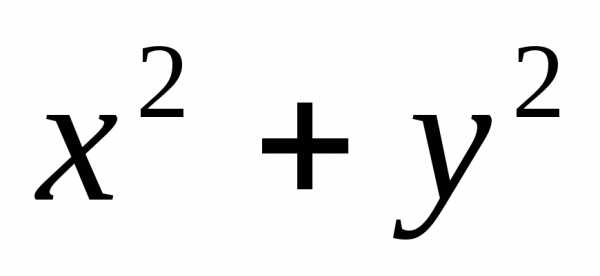 при
условии, что аргументы этой ф-ции
уовлетворяют условию связи х+у-1=0. Таким
образом, экстремумы ф-цииu=
при
условии, что аргументы этой ф-ции
уовлетворяют условию связи х+у-1=0. Таким
образом, экстремумы ф-цииu=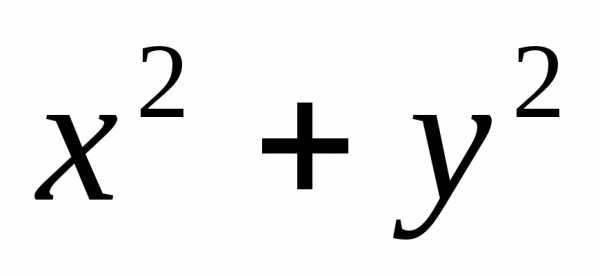 ищутся не на всей плоскости Оху, а лишь
на прямой х+у-1=0. Для решения подставим
в ур-ие ф-ции u=
ищутся не на всей плоскости Оху, а лишь
на прямой х+у-1=0. Для решения подставим
в ур-ие ф-ции u=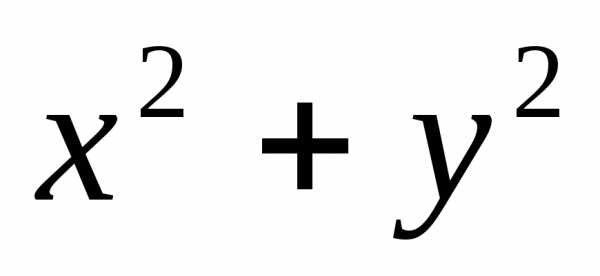 зн-ие у, определяемое из условия связи
х+у-1=0. Таким путём мы сведём поставленную
задачу к задаче об отыскании безусловного
экстремума ф-цииu=2
зн-ие у, определяемое из условия связи
х+у-1=0. Таким путём мы сведём поставленную
задачу к задаче об отыскании безусловного
экстремума ф-цииu=2 достигается в точке (0;0) и равенu=0.
(графиком явл парабалоид вращения) на
всей плоскости с ее минимумом на прямой
х+у-1=0.
достигается в точке (0;0) и равенu=0.
(графиком явл парабалоид вращения) на
всей плоскости с ее минимумом на прямой
х+у-1=0.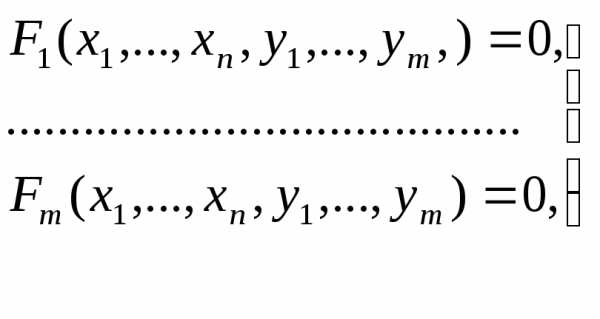 (41)
(41)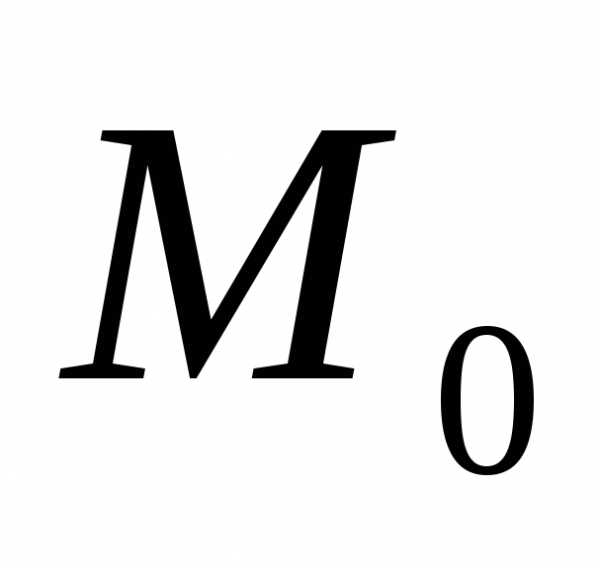 ,
в пределах которой зн-ие ф-ции (40) в точке
,
в пределах которой зн-ие ф-ции (40) в точке явл. наибольшим (наименьшим ) среди ее
зн-ий во всех точках, координаты которых
удовлетворяю условиям связи (41).
явл. наибольшим (наименьшим ) среди ее
зн-ий во всех точках, координаты которых
удовлетворяю условиям связи (41).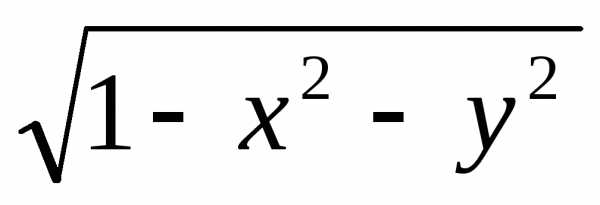 ,рассматривая
в круге
,
м/б неявно задана с пом. функцион-го Ур-я
,рассматривая
в круге
,
м/б неявно задана с пом. функцион-го Ур-я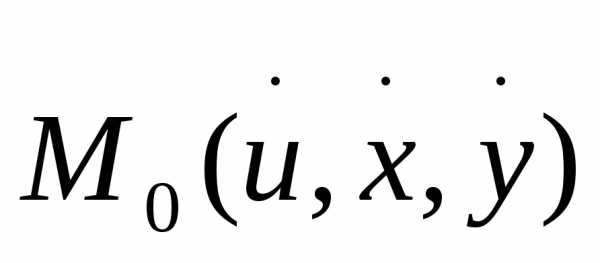 пр-ваR,
причём частная производная dF/du
непрерывна в точке
пр-ваR,
причём частная производная dF/du
непрерывна в точке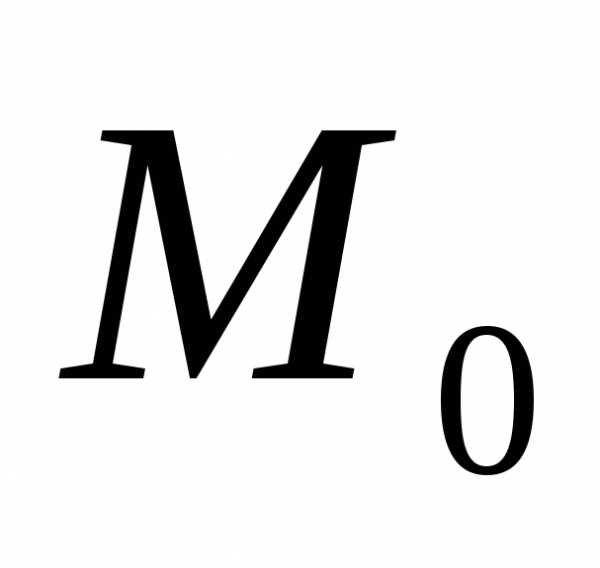 . Тогда если в точке
. Тогда если в точке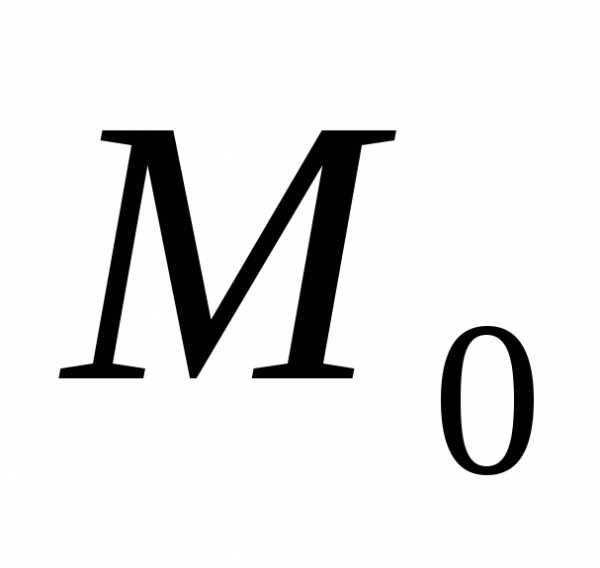 функцияFобращается
в нуль, а частная производная dF/du
не обращается в нуль, то для любого
достаточно малого положительного числа
функцияFобращается
в нуль, а частная производная dF/du
не обращается в нуль, то для любого
достаточно малого положительного числа  найдется такая окр-ть точки
найдется такая окр-ть точки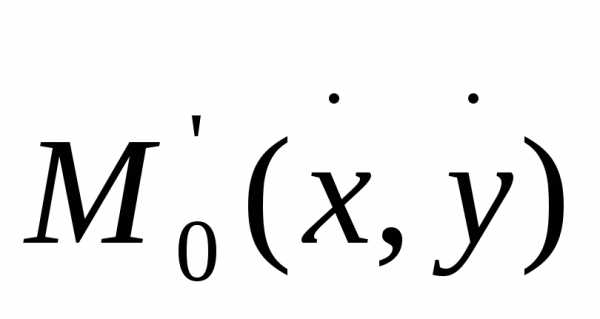 пр-ваR’
, что в пределах этой окр-ти сущ-ет
единственная ф-ия
которая
удовл-ет усл.
пр-ваR’
, что в пределах этой окр-ти сущ-ет
единственная ф-ия
которая
удовл-ет усл.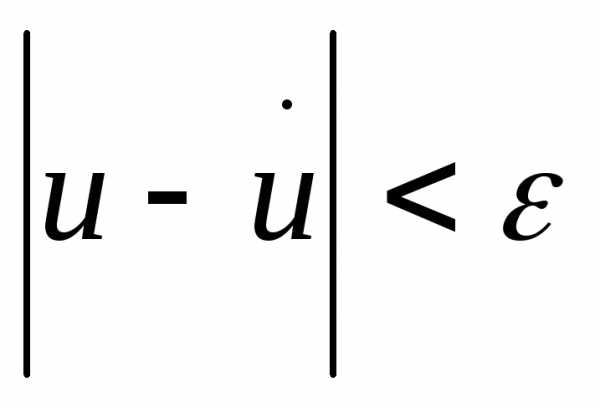 и явл. решением ур-я
и явл. решением ур-я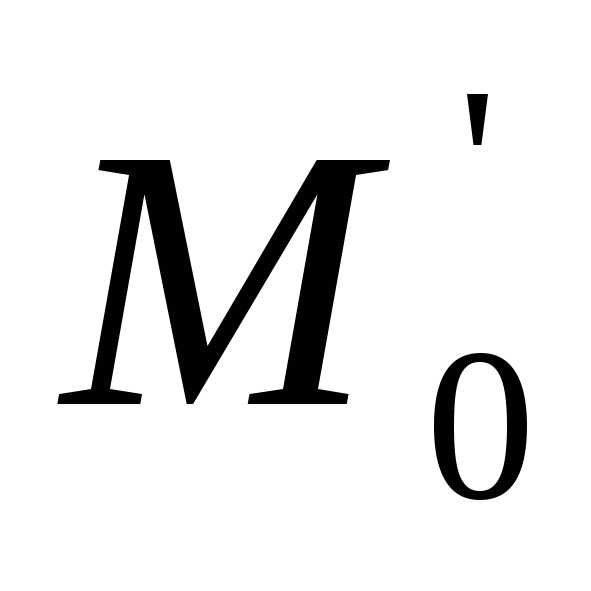 .
.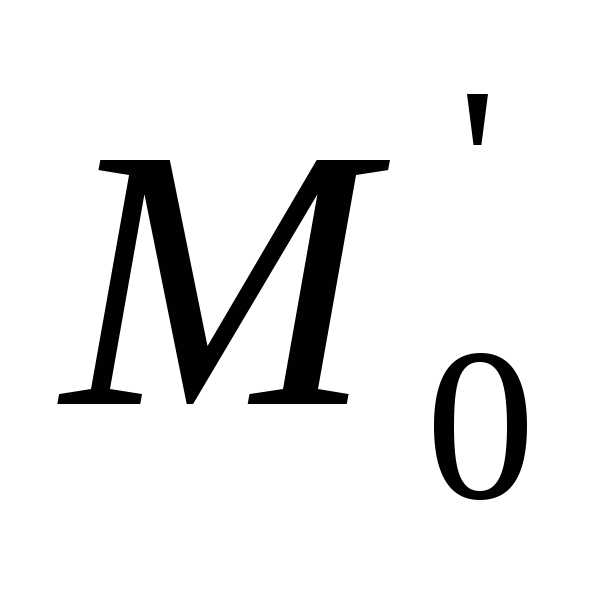 ,
но тогда придётся потребовать, чтобы
эта производная не обращалась к нулю
не только в самой точке
,
но тогда придётся потребовать, чтобы
эта производная не обращалась к нулю
не только в самой точке ,
но и в некоторой окр-ти этой самой точки
и сохраняла определенный знак в этой
окр-ти.
,
но и в некоторой окр-ти этой самой точки
и сохраняла определенный знак в этой
окр-ти. =
=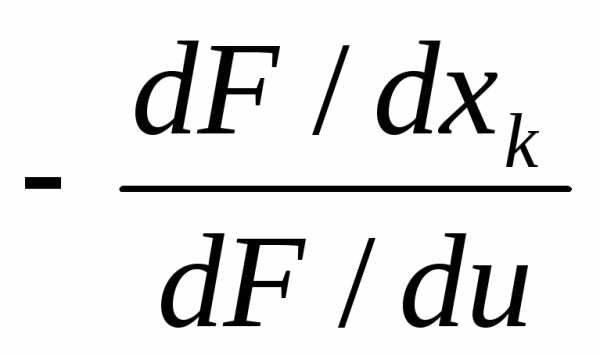 )
(k=1,2,…….м)
)
(k=1,2,…….м)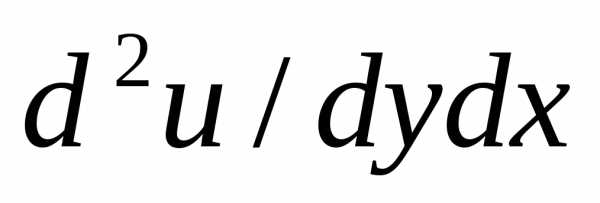 ф-ции ,заданной
использую ф-лу (15.11), получим du/dx=-(x/u),
du/dy=-(y/u).
ф-ции ,заданной
использую ф-лу (15.11), получим du/dx=-(x/u),
du/dy=-(y/u).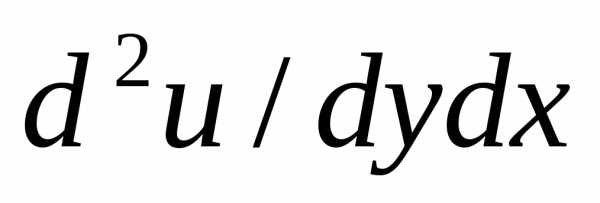 =D(du/dx)|Dy=D(-(x/u))/Dy=x
* du/dy|
=D(du/dx)|Dy=D(-(x/u))/Dy=x
* du/dy|  =-(xy)/
=-(xy)/ 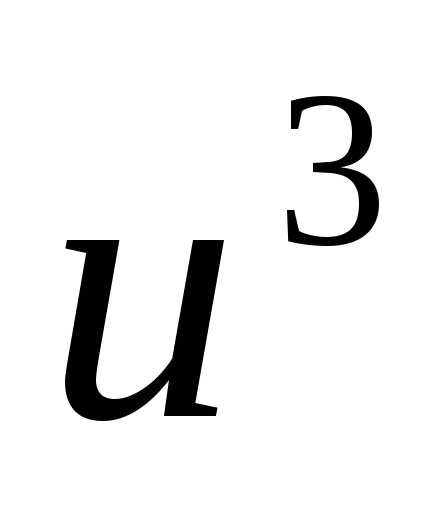
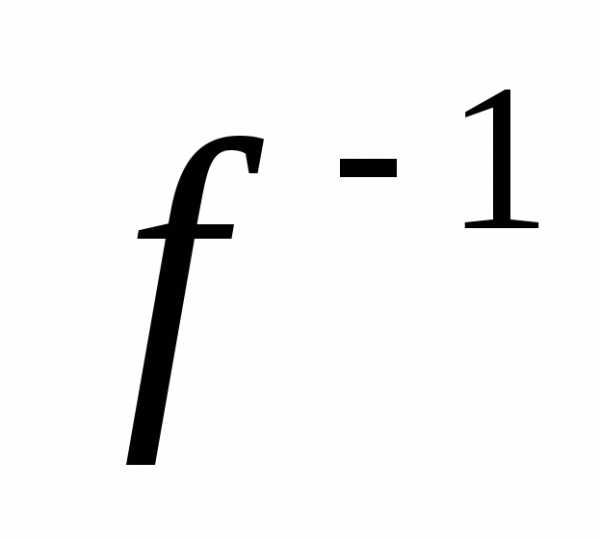 (y),
определенную в некоторойокр-ти точки
y0,
где y0=f(x0).
Будем рассматривать y=f(x)
как ф-ю, определяемую уравнением вида
F(x,y)=f(x)-y=0.
То вопрос о сущ-ии обр. ф-ии совпадает с
вопросом о разрешимости относительно
х указанного функционального уравнения. Если ф-ция y=f(x)
имеет отличную от нуля производную в
некоторой окр-ти точки х0, то для этой
ф-ции в окр-ти х0 существует обратная
ф-я x=
(y),
определенную в некоторойокр-ти точки
y0,
где y0=f(x0).
Будем рассматривать y=f(x)
как ф-ю, определяемую уравнением вида
F(x,y)=f(x)-y=0.
То вопрос о сущ-ии обр. ф-ии совпадает с
вопросом о разрешимости относительно
х указанного функционального уравнения. Если ф-ция y=f(x)
имеет отличную от нуля производную в
некоторой окр-ти точки х0, то для этой
ф-ции в окр-ти х0 существует обратная
ф-я x=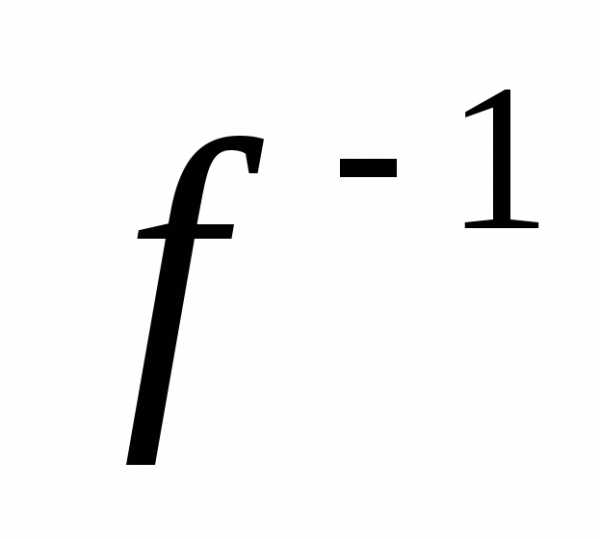 (y),
определенная и дифференцируемая в
некоторой окр-ти точки у0, где у0=f(x0).
Производная указанной обр. ф-ции в точке
у0 в силу второй из формул (15.11) равна
1/f’(x0).
(y),
определенная и дифференцируемая в
некоторой окр-ти точки у0, где у0=f(x0).
Производная указанной обр. ф-ции в точке
у0 в силу второй из формул (15.11) равна
1/f’(x0).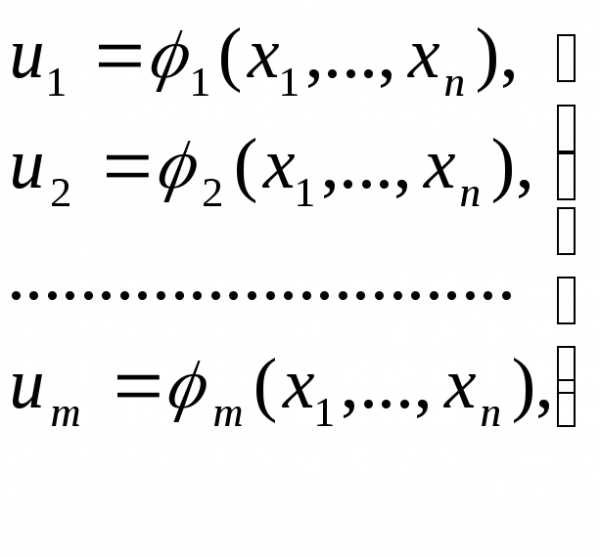 (13)
(13)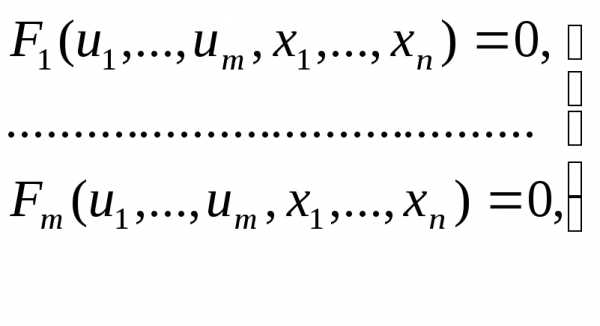 (14)
(14)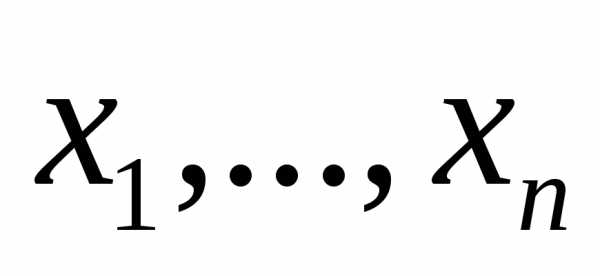 ,
если каждая из ф-ций (13) непрерывна и
диф-ма в областиD.
(символом R
будет пространство (m+n)
переменных
,
а сисмволомR’
пространство n
переменных
,
если каждая из ф-ций (13) непрерывна и
диф-ма в областиD.
(символом R
будет пространство (m+n)
переменных
,
а сисмволомR’
пространство n
переменных  )
)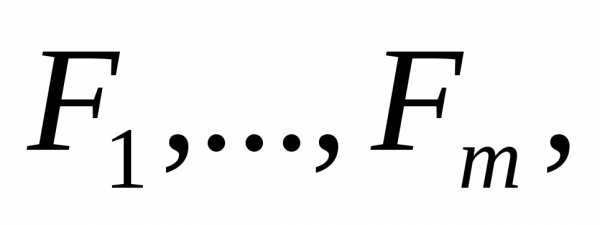 стоящих в левых частях системы (14), и
составим из частных производных этих
ф-ий следующий определитель:
стоящих в левых частях системы (14), и
составим из частных производных этих
ф-ий следующий определитель: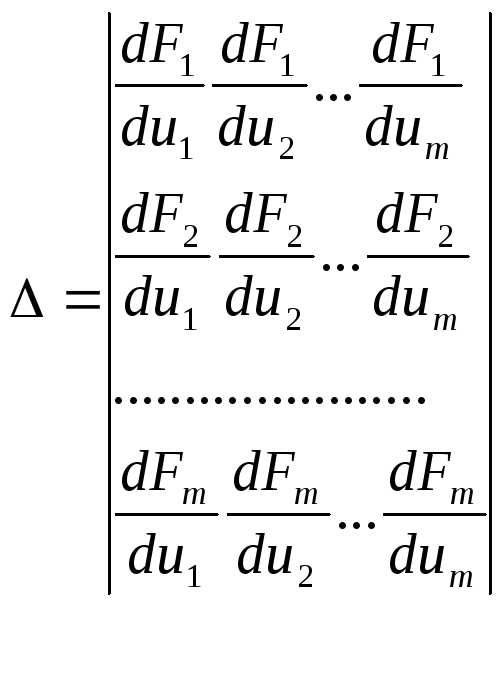 (15)(15)-
определитель Якоби. (или якобианом )
ф-ции
(15)(15)-
определитель Якоби. (или якобианом )
ф-ции 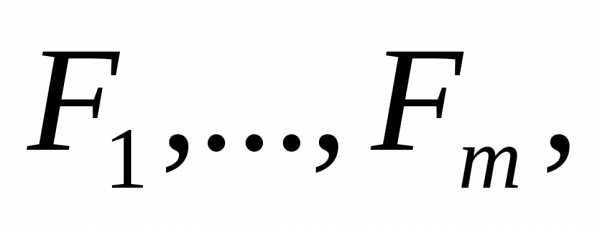 по переменным
по переменным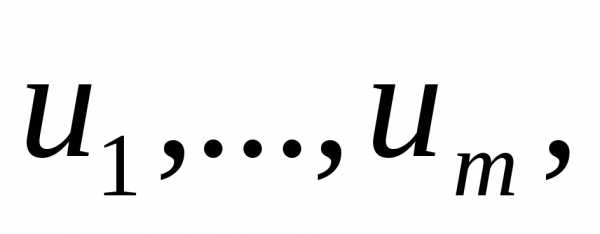 и кратко обозначать символом
и кратко обозначать символом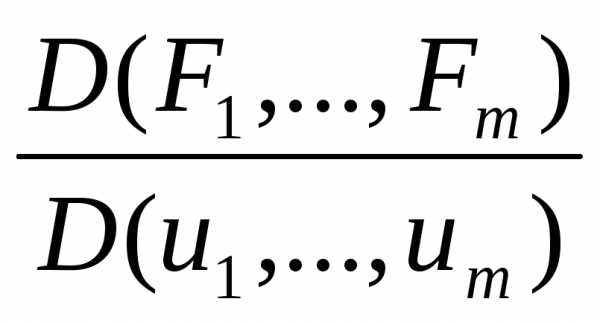 .
.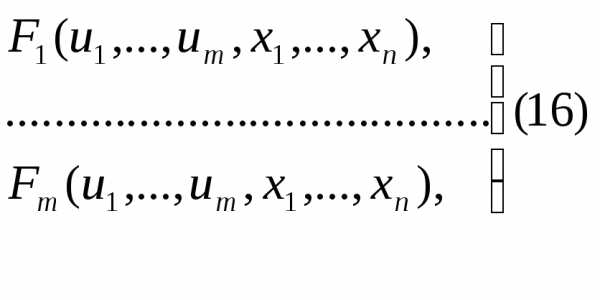 дифференцируемы в некоторой окр-ти
точки)
пространстваR,
причем частные производные этих ф-ий
по перевменным
дифференцируемы в некоторой окр-ти
точки)
пространстваR,
причем частные производные этих ф-ий
по перевменным 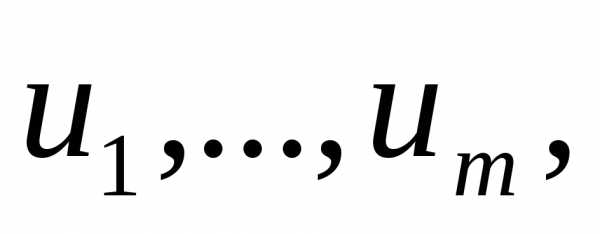 непрерывны в точке
непрерывны в точке 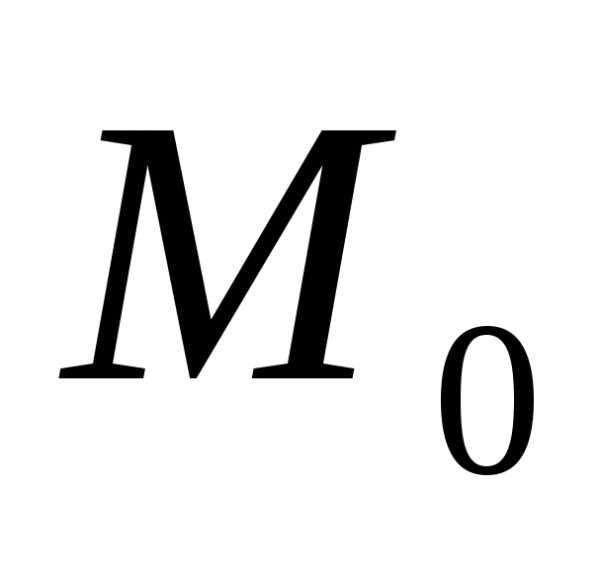 .
Тогда, если в точке
.
Тогда, если в точке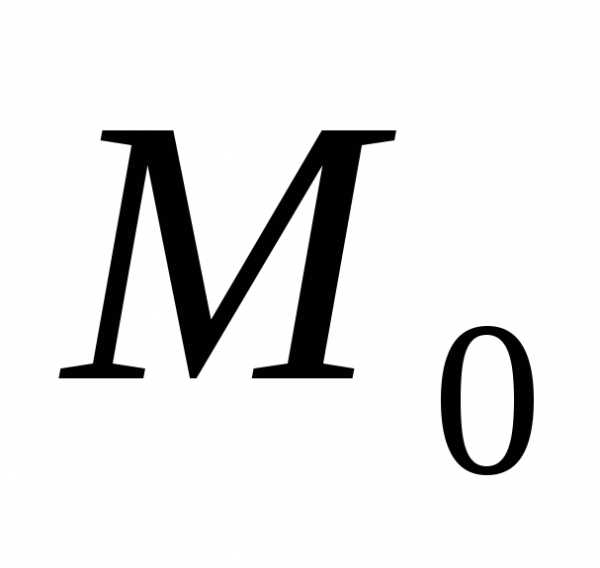 все ф-ции (16) обращаются в нуль, а якобиан
все ф-ции (16) обращаются в нуль, а якобиан 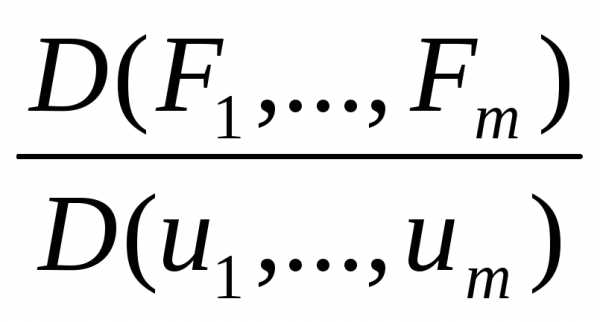 отличен от нуля, то для достаточно малых
положительных чисел
отличен от нуля, то для достаточно малых
положительных чисел найдется такая окр-ть точки
найдется такая окр-ть точки  пространстваR’,
что в пределах этой окр-ти сущ-ют
единственные m функций (13), которые удовлетворяют
условиям
и явл-ся решением системы Ур-ий (14), причём
это решение непрерывно и дифференцируемо
в указанной окр-ти точки
пространстваR’,
что в пределах этой окр-ти сущ-ют
единственные m функций (13), которые удовлетворяют
условиям
и явл-ся решением системы Ур-ий (14), причём
это решение непрерывно и дифференцируемо
в указанной окр-ти точки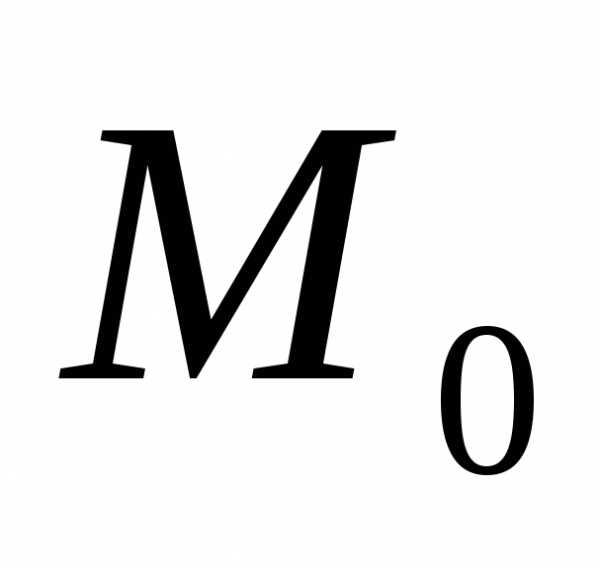 ’.
’. (28) Определены и
диф-мы в некоторой открытой n-мерной
области D.
(28) Определены и
диф-мы в некоторой открытой n-мерной
области D.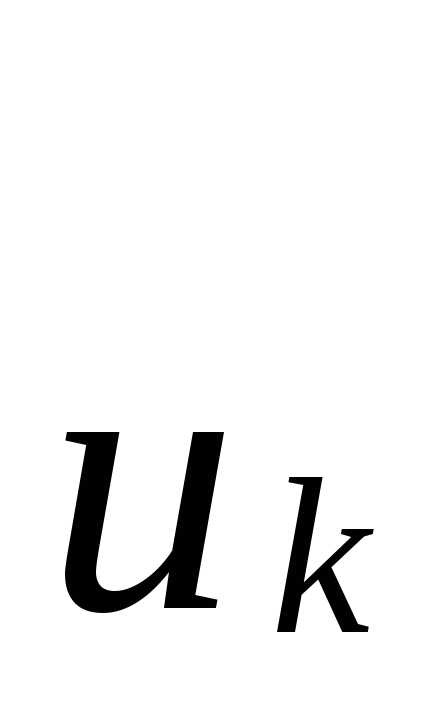 ,
зависит в областиD
от остальных ф-ций, если сразу для всех
точек
,
зависит в областиD
от остальных ф-ций, если сразу для всех
точек  в областиD (29), где Ф-некоторая ф-ия, определенная
и диф-ая в соответствующей области
изменения своих аргументов. Ф-ции
в областиD (29), где Ф-некоторая ф-ия, определенная
и диф-ая в соответствующей области
изменения своих аргументов. Ф-ции 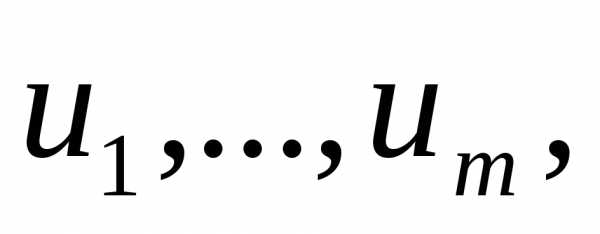 будем наз-ть зависимыми в областиD,
если одна из этих функций зависит в
области D
, еслиодна из этих ф-ций зависит в области
D
от остальных.
будем наз-ть зависимыми в областиD,
если одна из этих функций зависит в
области D
, еслиодна из этих ф-ций зависит в области
D
от остальных. )
этой области
)
этой области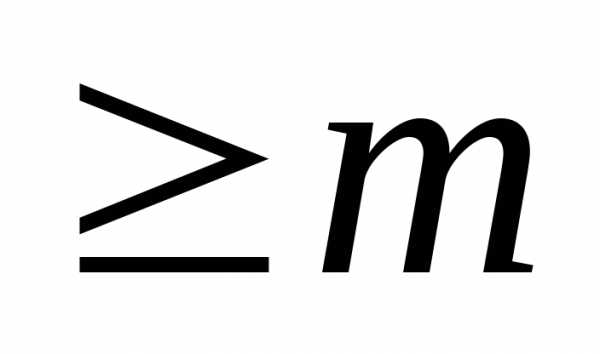 переменных
переменных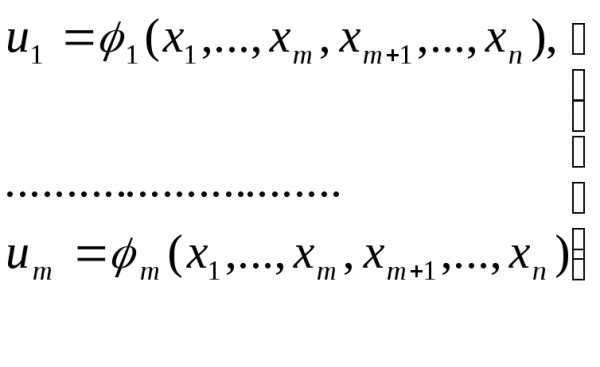
 ,
то эти ф-ции независимы в некоторой
окр-ти точки
,
то эти ф-ции независимы в некоторой
окр-ти точки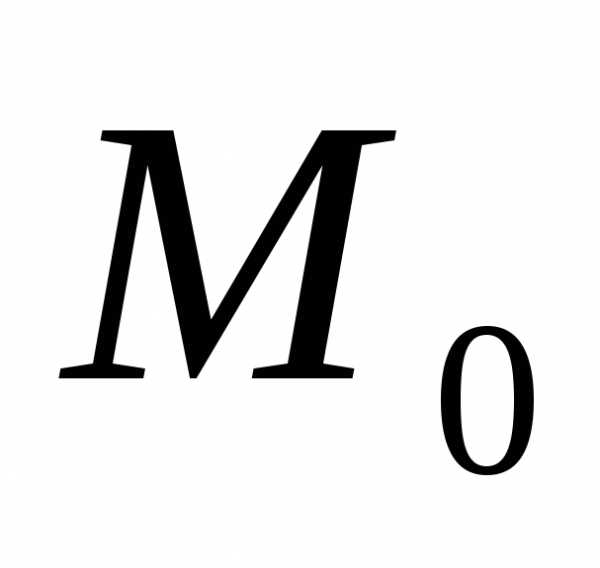 .
.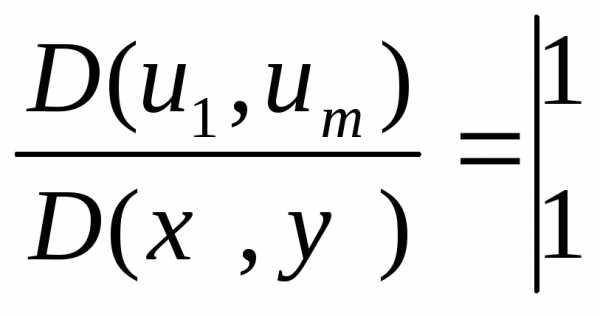
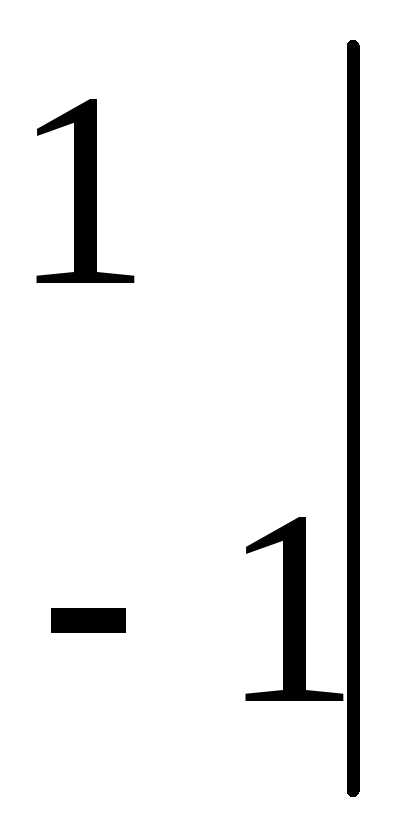 =-2не
равен нулю всюду.
=-2не
равен нулю всюду.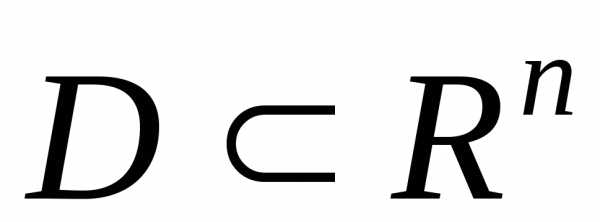 .
Таким образом, ведется поиск экстремума
не на всей области определения, а лишь
на множестве точек, удовлетворяющих
уравнениям связи. Такой экстремум
называетсяусловным.
.
Таким образом, ведется поиск экстремума
не на всей области определения, а лишь
на множестве точек, удовлетворяющих
уравнениям связи. Такой экстремум
называетсяусловным.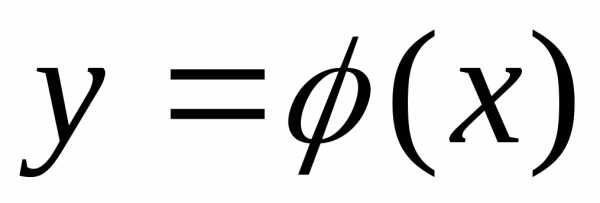 .
Подставив это выражение в,
получают– функцию одной переменной, которую
исследуют на обычный экстремум. Однако,
в большинстве более сложных случаев
решить этим способом задачу отыскания
экстремума не удается.
.
Подставив это выражение в,
получают– функцию одной переменной, которую
исследуют на обычный экстремум. Однако,
в большинстве более сложных случаев
решить этим способом задачу отыскания
экстремума не удается. является точкой условного экстремума
функциипри условиях,,…,,
то существует такое,
что точка
является точкой условного экстремума
функциипри условиях,,…,,
то существует такое,
что точка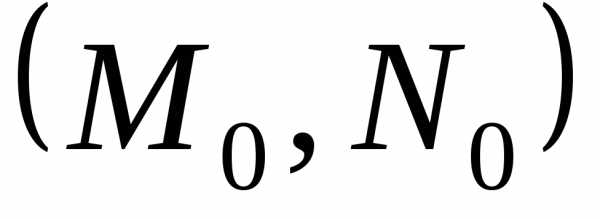 является точкой экстремума функции.
является точкой экстремума функции.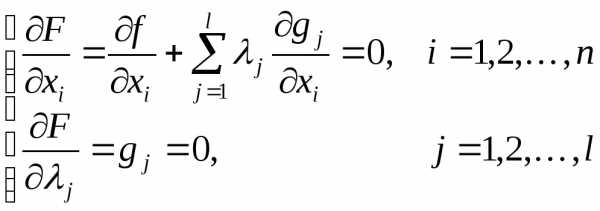
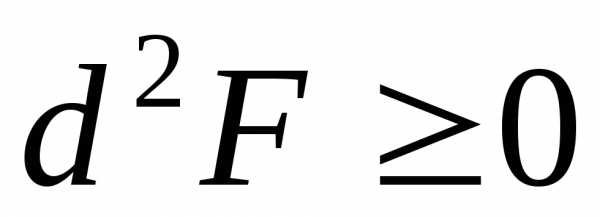 или
или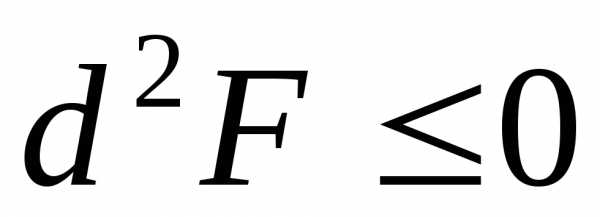 .
.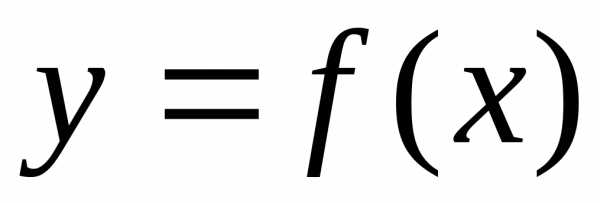 обычно предполагается, что это наиболее
гладкая кривая, согласованная с
экспериментальными данными. Кроме того,
для выбора этой функции привлекаются
дополнительные соображения, как правило,
не математического характера (теоретические
модели, опыт предшествующих исследований,
и т.п.).
обычно предполагается, что это наиболее
гладкая кривая, согласованная с
экспериментальными данными. Кроме того,
для выбора этой функции привлекаются
дополнительные соображения, как правило,
не математического характера (теоретические
модели, опыт предшествующих исследований,
и т.п.).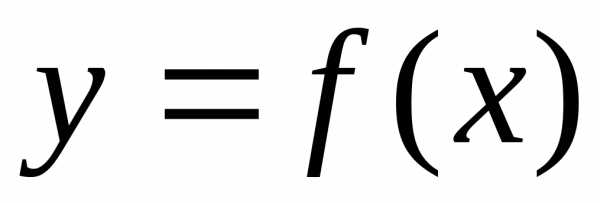 выбираются такие значения, которые
соответствуют минимальному значению
суммы квадратов отклонений эмпирических
значений
выбираются такие значения, которые
соответствуют минимальному значению
суммы квадратов отклонений эмпирических
значений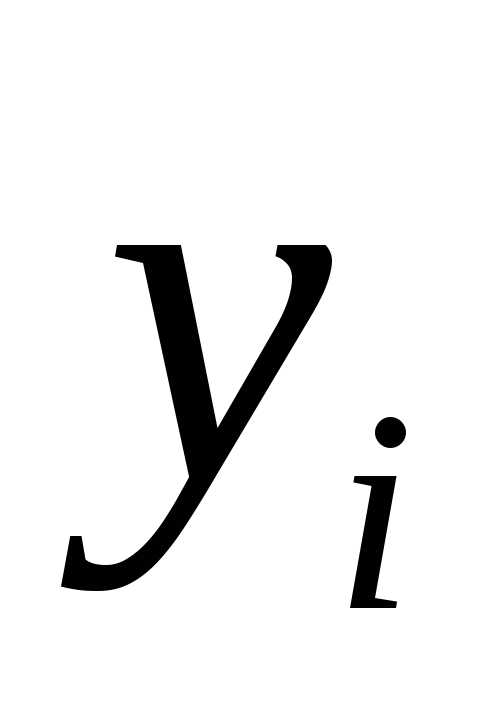 от значений функции
от значений функции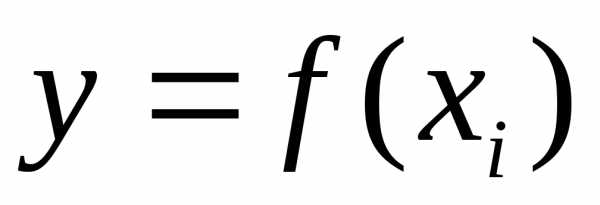 вычисленных по соответствующим им
значениям аргументов
вычисленных по соответствующим им
значениям аргументов ,
т.е.:
,
т.е.: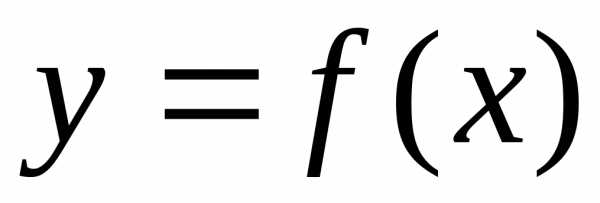 возникает необходимость поиска экстремума
функции нескольких переменных, поэтому
прежде чем решать эту задачу для
конкретных эмпирических функций,
необходимо рассмотреть свойства функций
нескольких переменных.
возникает необходимость поиска экстремума
функции нескольких переменных, поэтому
прежде чем решать эту задачу для
конкретных эмпирических функций,
необходимо рассмотреть свойства функций
нескольких переменных. – линейная, т.е..
Если это выражение приближенно описывает
зависимость между
– линейная, т.е..
Если это выражение приближенно описывает
зависимость между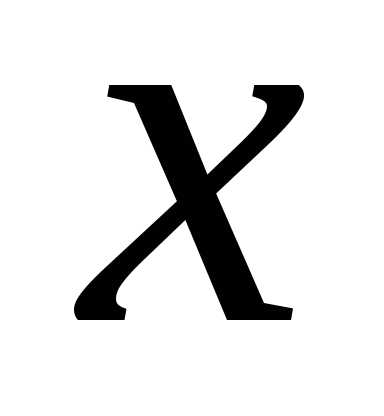 и
и ,
то сумма квадратов невязок должна быть
минимальной, т.е. значения параметров
,
то сумма квадратов невязок должна быть
минимальной, т.е. значения параметров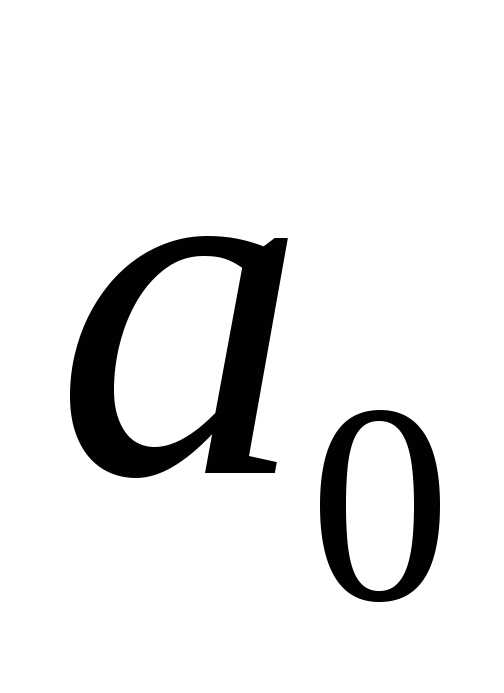 и
и должны соответствовать минимуму
величины:
должны соответствовать минимуму
величины: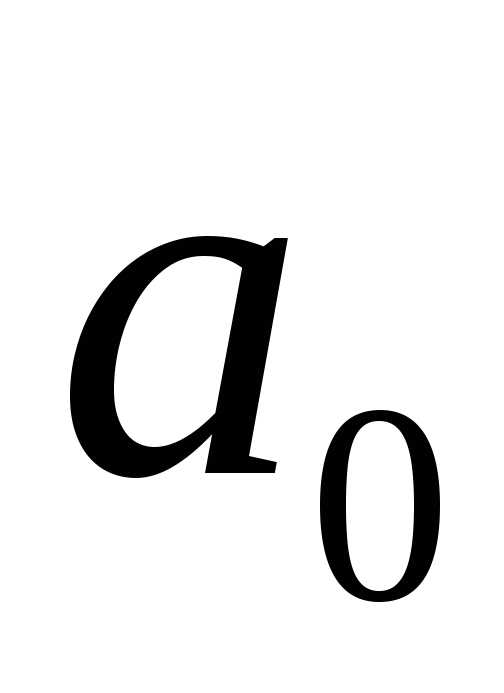 и
и ,
она непрерывна, дифференцируема,
неотрицательна и ограничена снизу. Для
того чтобы найти ее наименьшее значение,
необходимо ее частные производные
приравнять к нулю:
,
она непрерывна, дифференцируема,
неотрицательна и ограничена снизу. Для
того чтобы найти ее наименьшее значение,
необходимо ее частные производные
приравнять к нулю: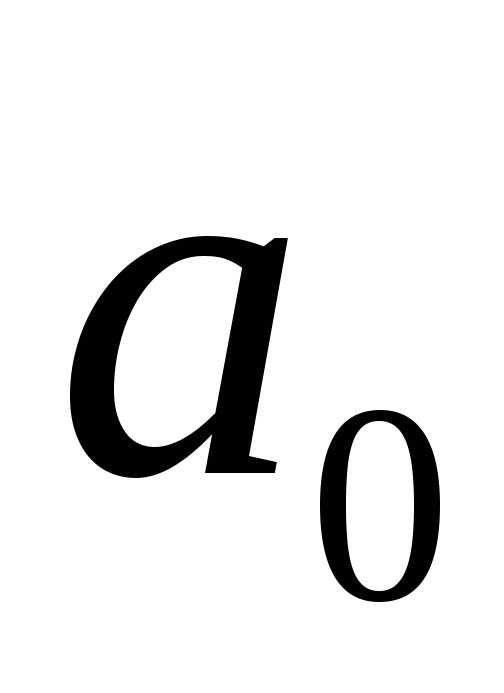 и
и необходимо решить систему уравнений:
необходимо решить систему уравнений: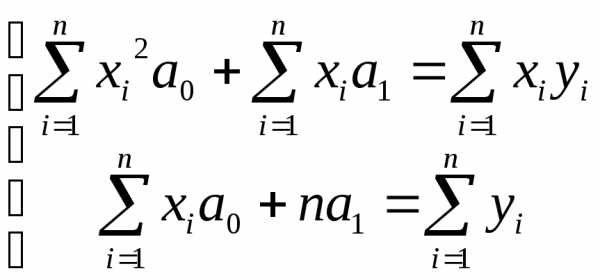
 равны:
равны: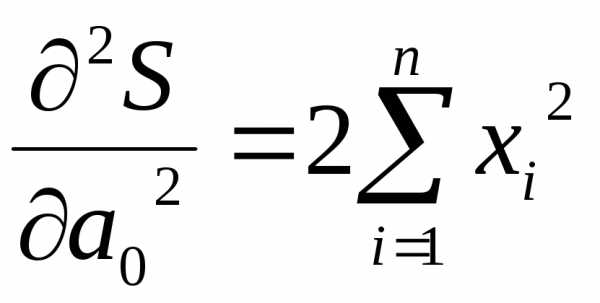 ;
; 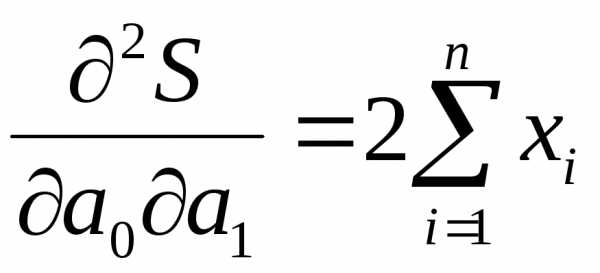 ;
;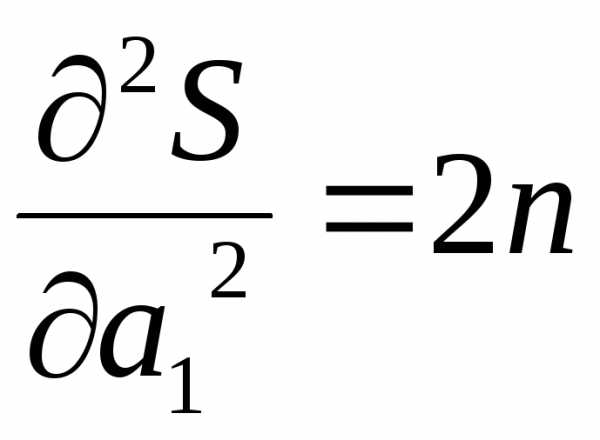 .
.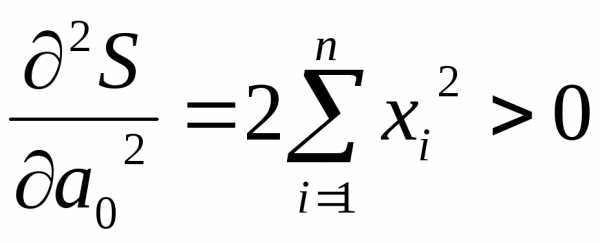 ;
;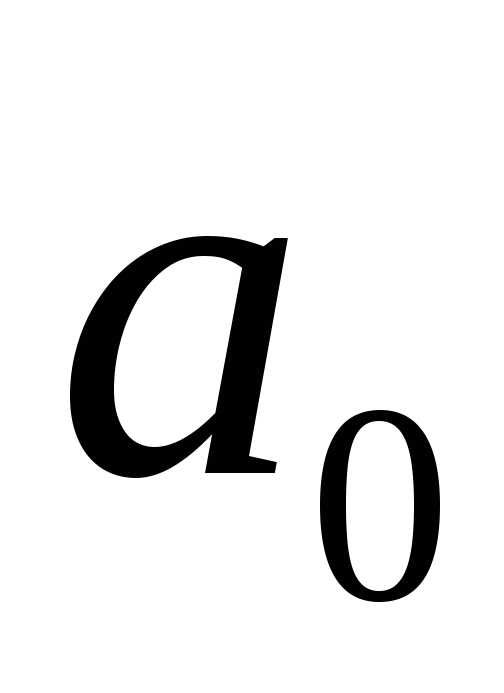 и
и ,
найденные при решении системы уравнений,
соответствуют минимуму функции
,
найденные при решении системы уравнений,
соответствуют минимуму функции .
.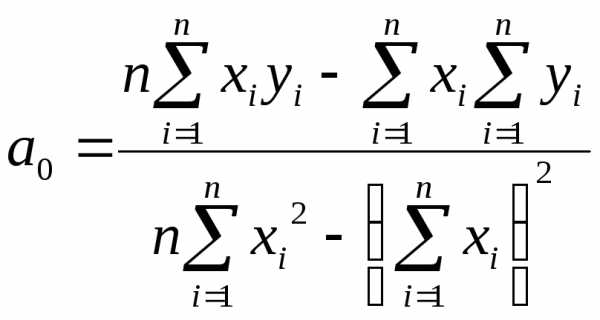 ,
,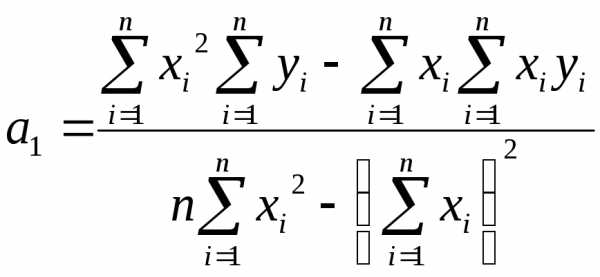 .
. -окрестность
этой точки, такая, что для всех точек
-окрестность
этой точки, такая, что для всех точек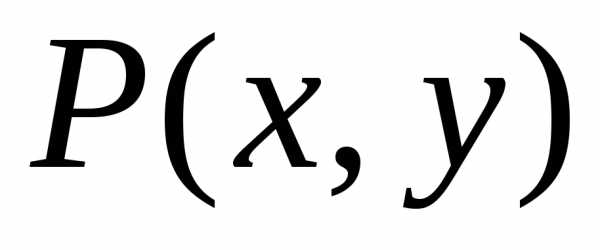
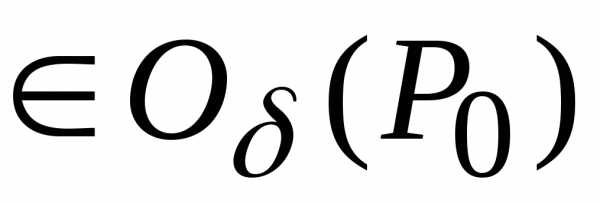 (принадлежащих
(принадлежащих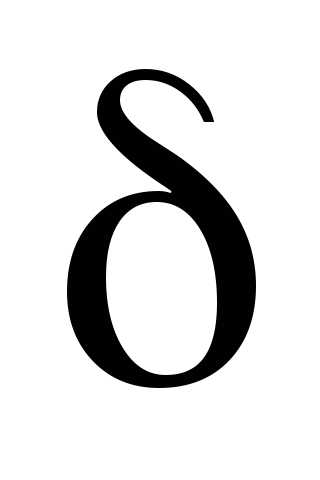 -окрестности
этой точки), отличных от точки,
выполняется неравенство().
-окрестности
этой точки), отличных от точки,
выполняется неравенство().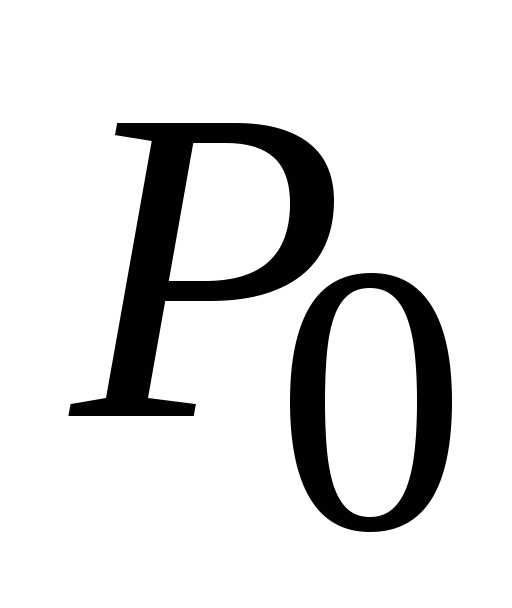 (1;
1):
(1;
1):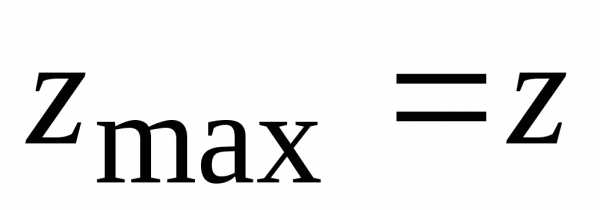 (1,
1) = 1.
(1,
1) = 1.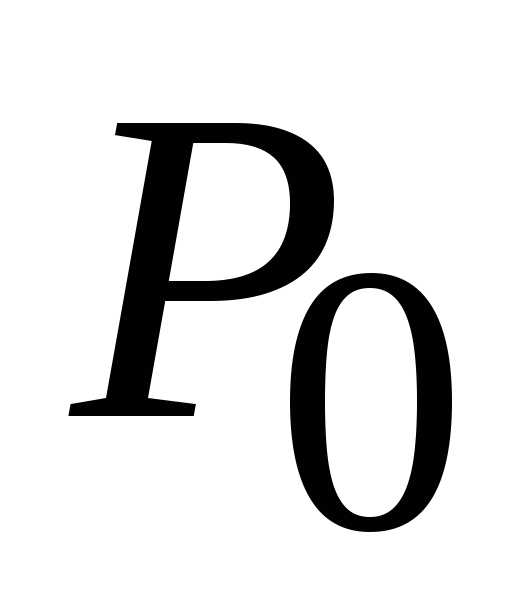 (1;
1), в которой выполняется условие
(1;
1), в которой выполняется условие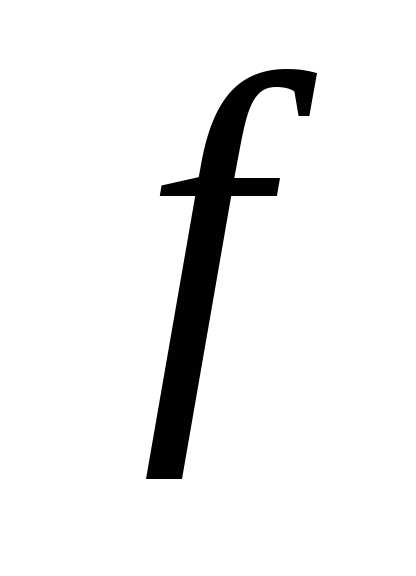 (1;
1) >
(1;
1) >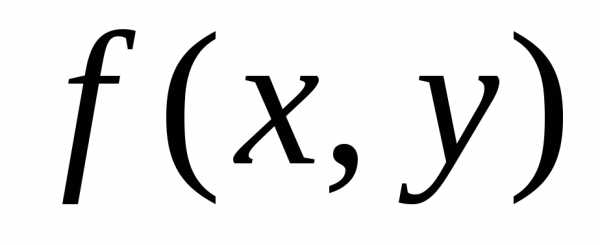 для.
Графиком этой функции является поверхность
— параболоид вращения, представленный
на рисунке.
для.
Графиком этой функции является поверхность
— параболоид вращения, представленный
на рисунке. .
Однако для всех точек
.
Однако для всех точек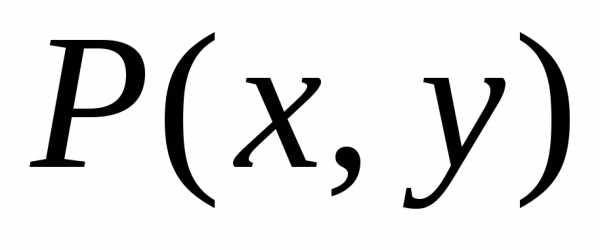
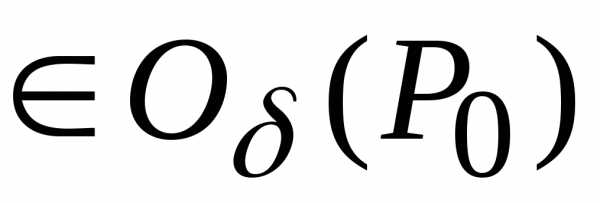 определить знак приращения
определить знак приращения практически невозможно, поэтому надо
искать другие условия, по которым можно
судить о наличии и характере экстремума
функции в данной точке.
практически невозможно, поэтому надо
искать другие условия, по которым можно
судить о наличии и характере экстремума
функции в данной точке.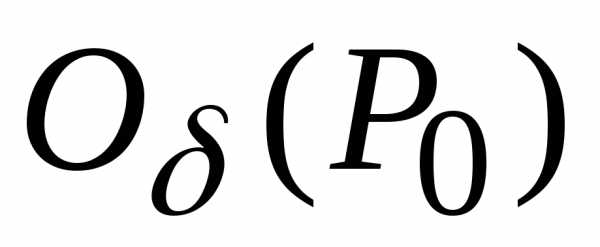 лишь те точки, для которых
лишь те точки, для которых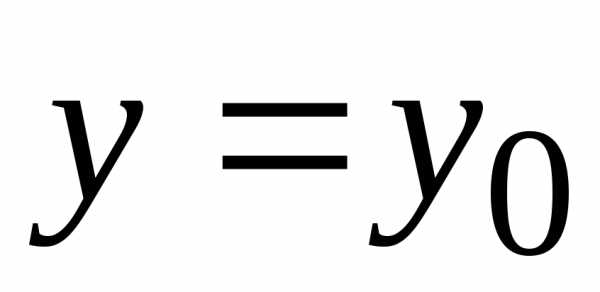 .
Получим функциюодной переменной
.
Получим функциюодной переменной .
Эта функция имеет в точке
.
Эта функция имеет в точке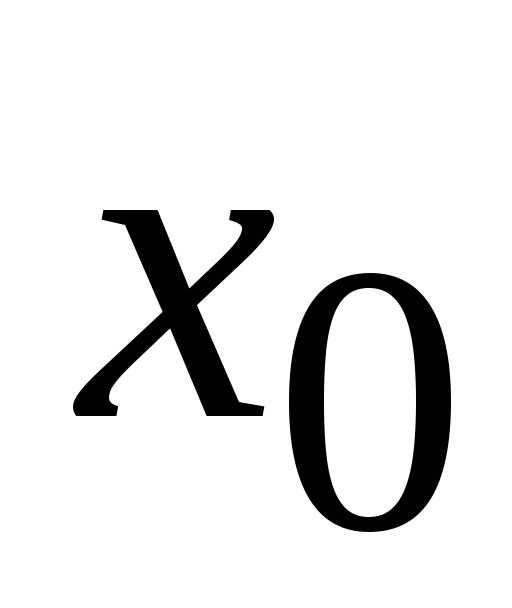 экстремум, следовательно,.
экстремум, следовательно,. (О)
выполняется условие
(О)
выполняется условие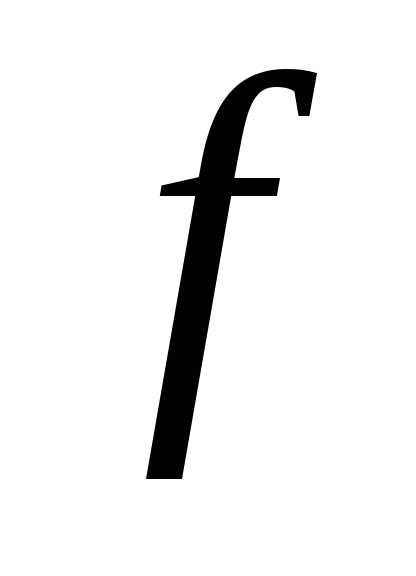 (0;
0) >
(0;
0) >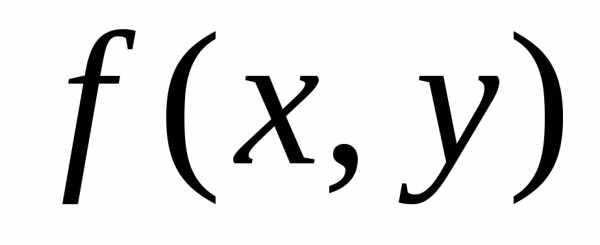 .
Частные производные
.
Частные производные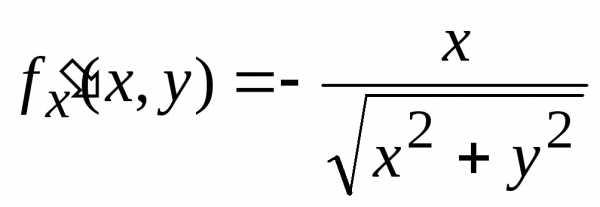 ,
,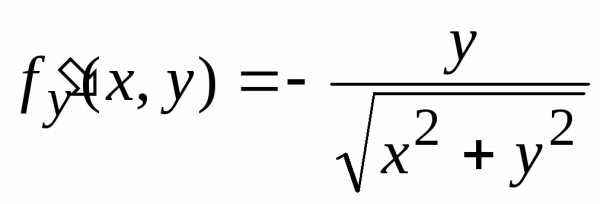
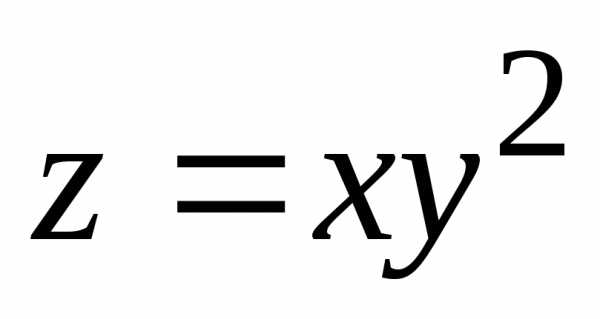 .
Она задана на всей числовой плоскостиR2. Точка О(0; 0) будет
критической, поскольку частные производные
в ней равны нулю. Так как функция равна
нулю в точке О, а в любой сколь угодно
малой окрестности
.
Она задана на всей числовой плоскостиR2. Точка О(0; 0) будет
критической, поскольку частные производные
в ней равны нулю. Так как функция равна
нулю в точке О, а в любой сколь угодно
малой окрестности (О)
она принимает как положительные, так и
отрицательные значения, то функция
(О)
она принимает как положительные, так и
отрицательные значения, то функция не имеет в точке О экстремума.
не имеет в точке О экстремума.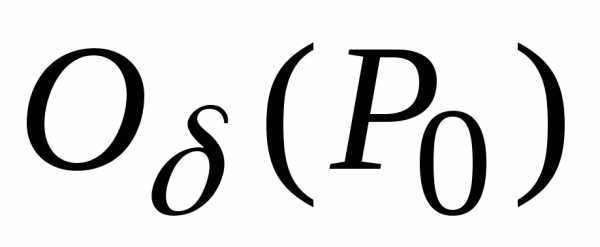 функциии пусть
функциии пусть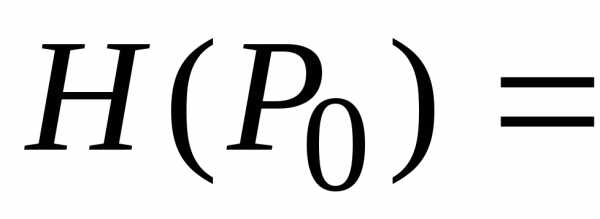 .
.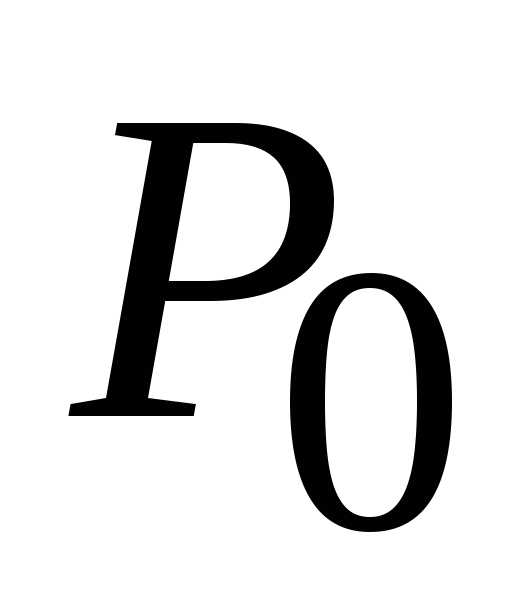 .
В этом случае необходимо произвести
дополнительные исследования знака
функциив
.
В этом случае необходимо произвести
дополнительные исследования знака
функциив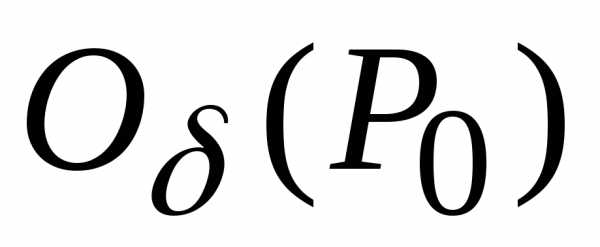 .
.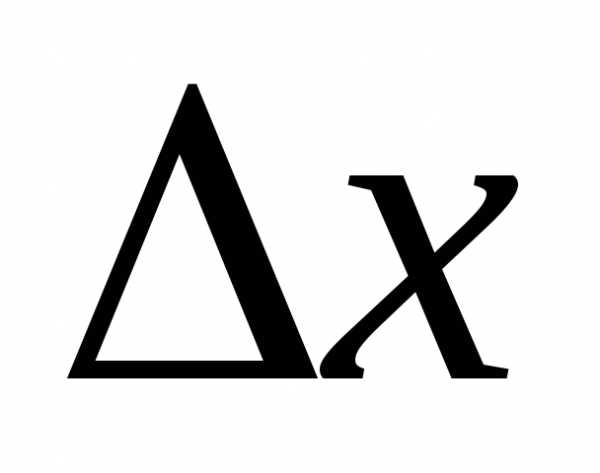 и
и не могут равняться нулю одновременно,
поскольку в подобном случае точкасовпала бы с точкойи функцияне получила бы никакого приращения.
не могут равняться нулю одновременно,
поскольку в подобном случае точкасовпала бы с точкойи функцияне получила бы никакого приращения.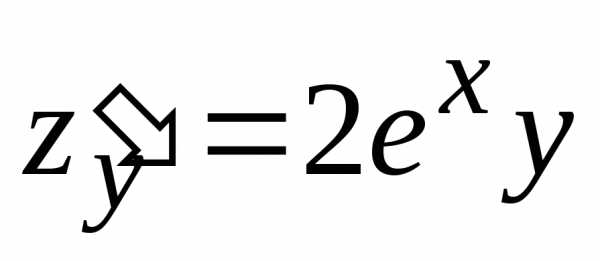 .
.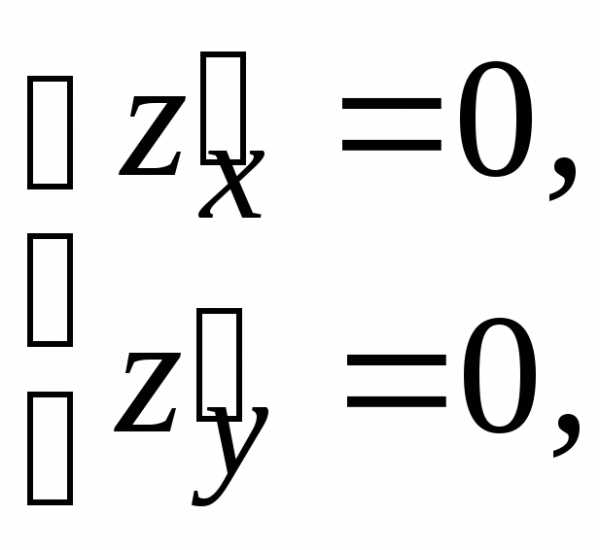

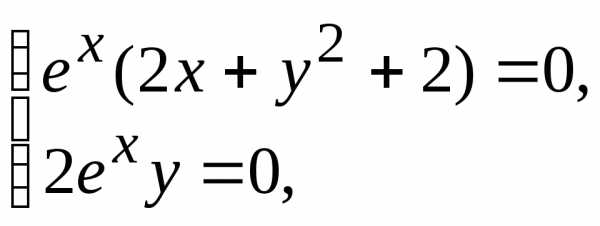
 (т. к.
(т. к.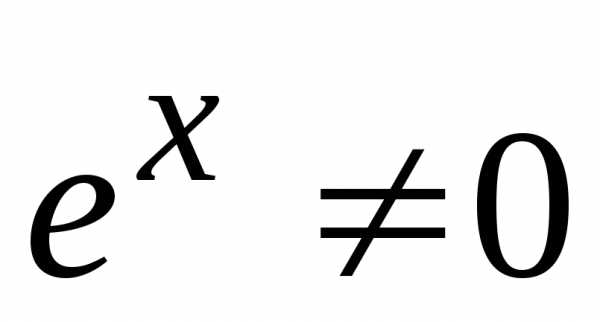 для
для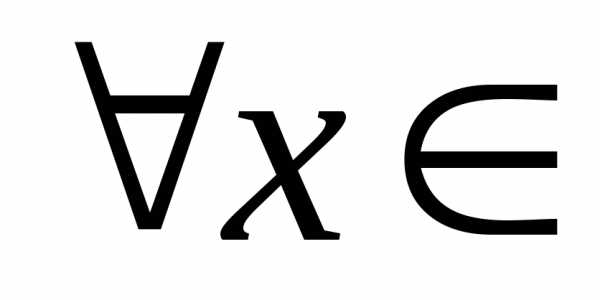 R)
R) 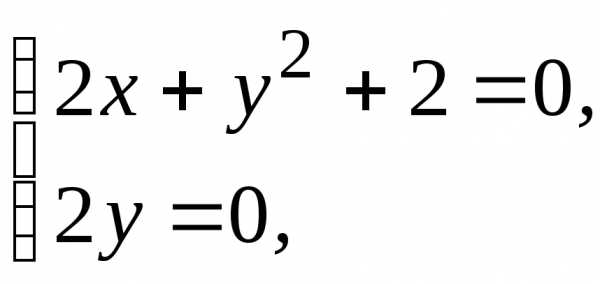

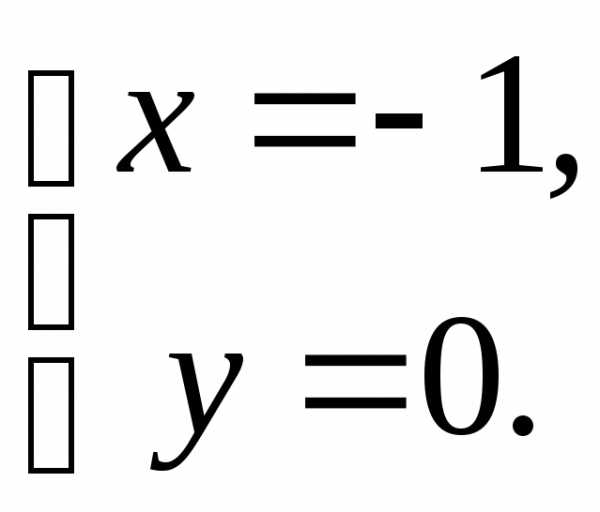
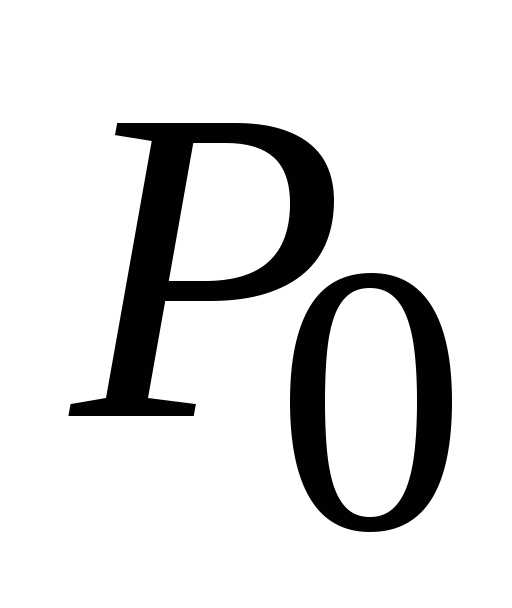 (1; 0), в которой
функция
(1; 0), в которой
функция может достигать экстремума.
может достигать экстремума.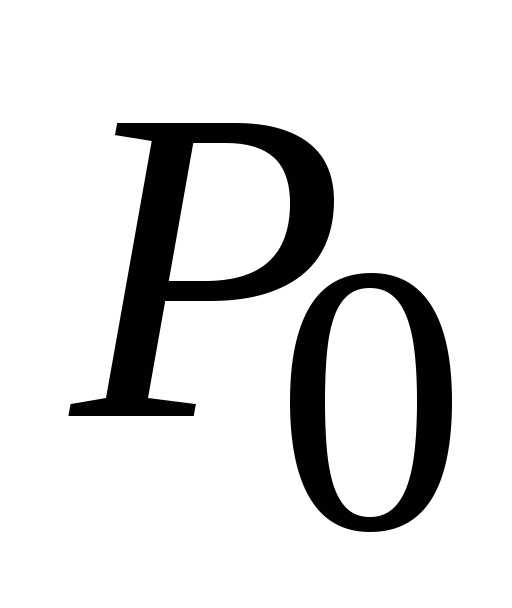 :
: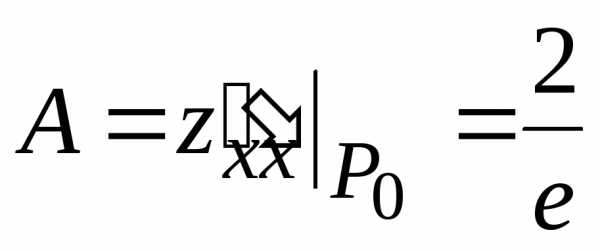 ,
,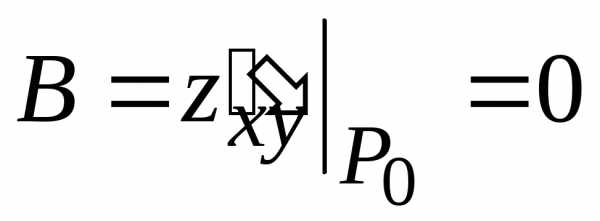 ,
,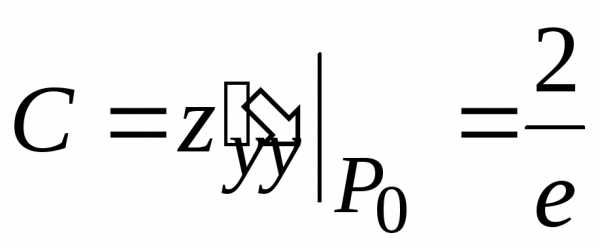 .
. (1;
0),
(1;
0),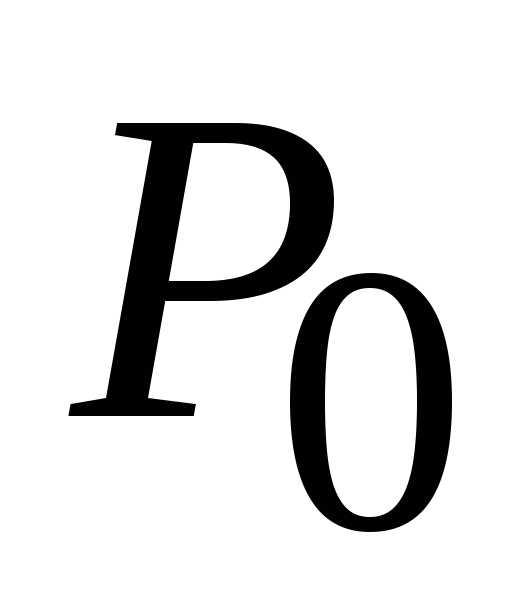 (1; 0) является
точкой локального экстремума, а т. к. А
> 0, то точка
(1; 0) является
точкой локального экстремума, а т. к. А
> 0, то точка (1; 0) является
точкой локального минимума, при этом
(1; 0) является
точкой локального минимума, при этом

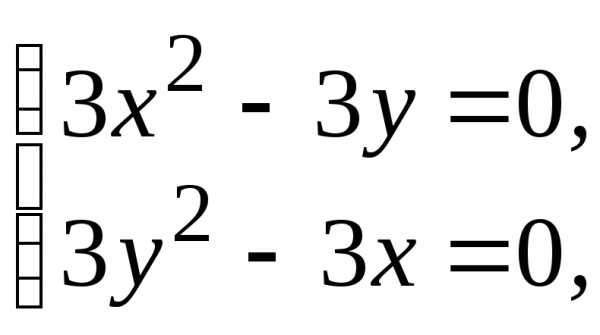

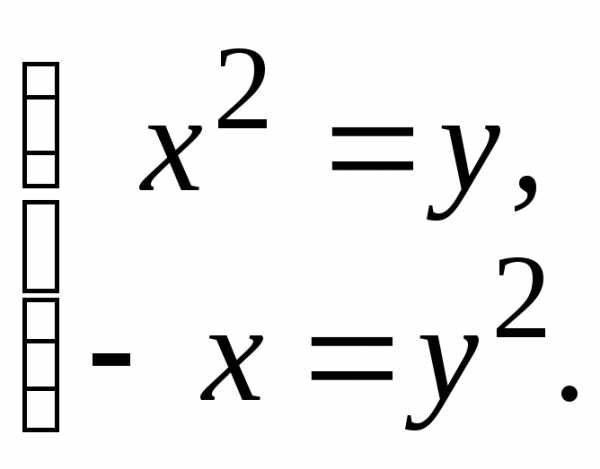
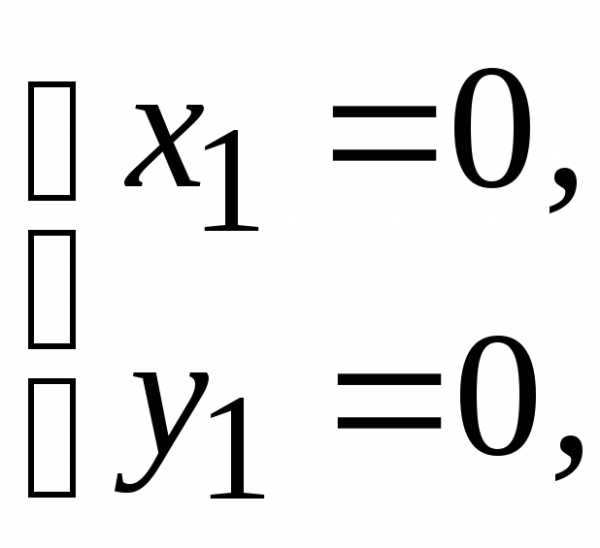 и
и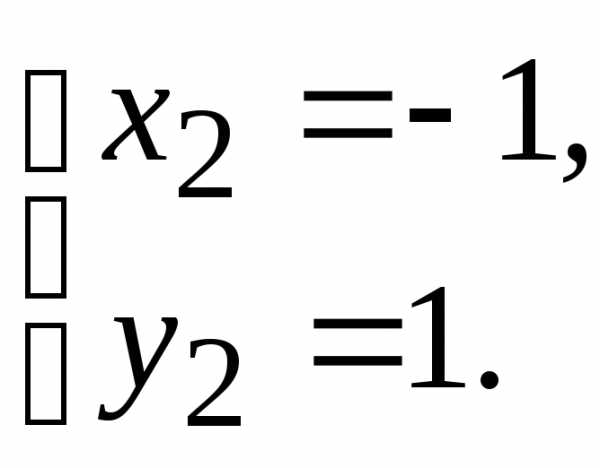
 (0;
0) и
(0;
0) и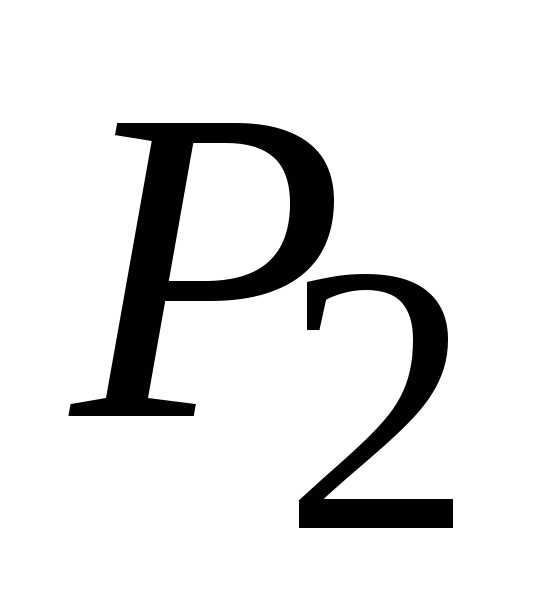 (1,
1). Вычислим частные производные второго
порядка функции
(1,
1). Вычислим частные производные второго
порядка функции :
: для точки
для точки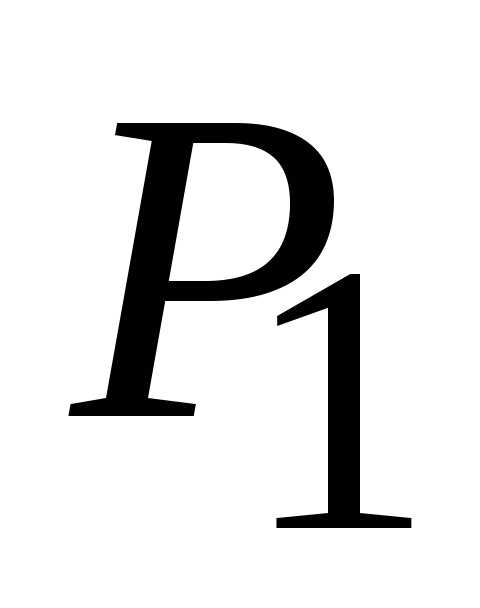 (0;
0). Так как
(0;
0). Так как (0;
0),
то в точке
(0;
0),
то в точке (0;
0) нет экстремума.
(0;
0) нет экстремума. для точки
для точки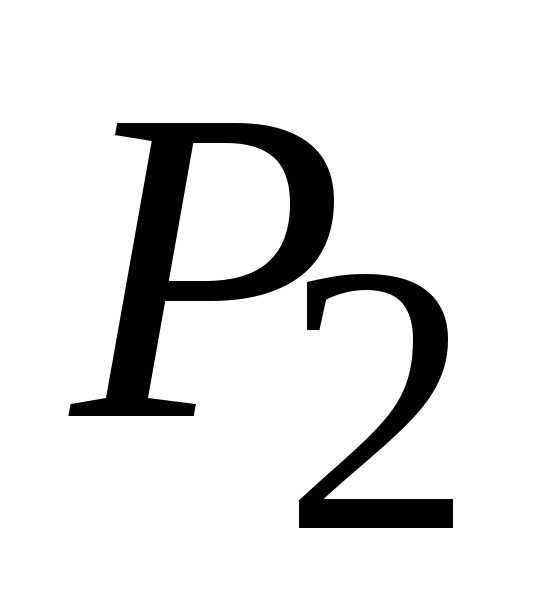 (1,
1). Т. к.
(1,
1). Т. к. (1;
1),
то точка
(1;
1),
то точка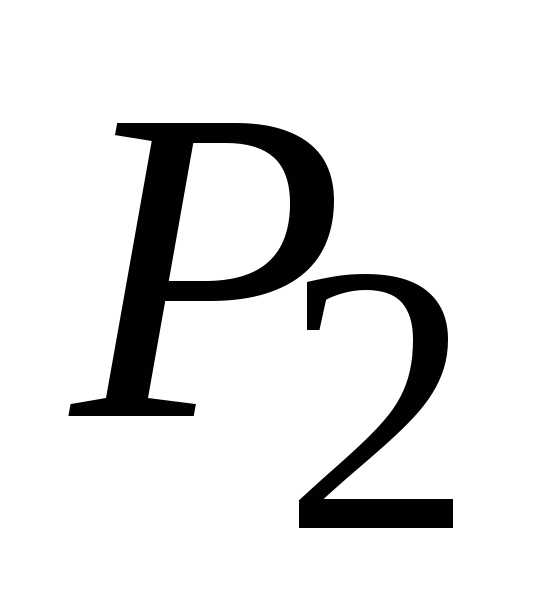 (1,
1) является точкой локального экстремума,
а т. к.
,
то точка
(1,
1) является точкой локального экстремума,
а т. к.
,
то точка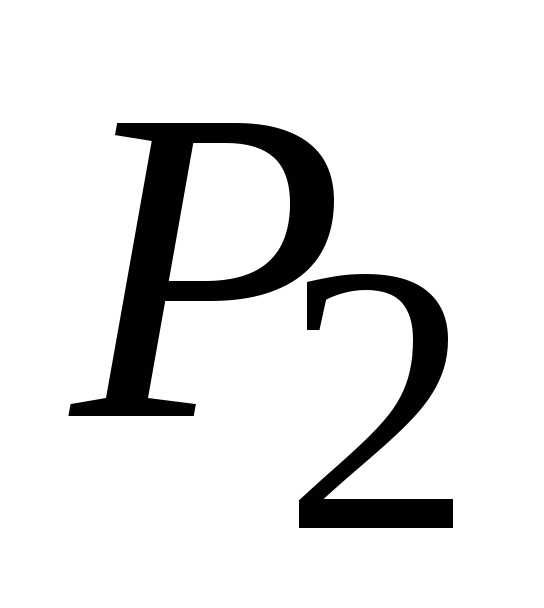 (1,
1) является точкой локального максимума,
при этом
(1,
1) является точкой локального максимума,
при этом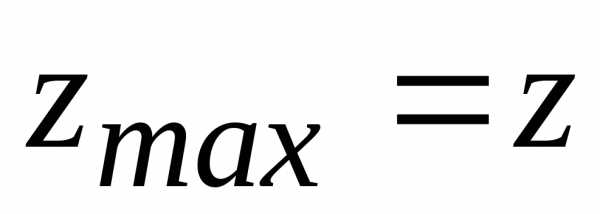 (1;
1)=9.
(1;
1)=9.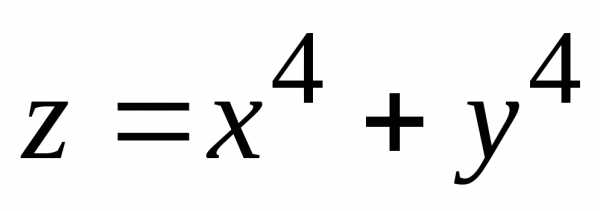 .
. :
:
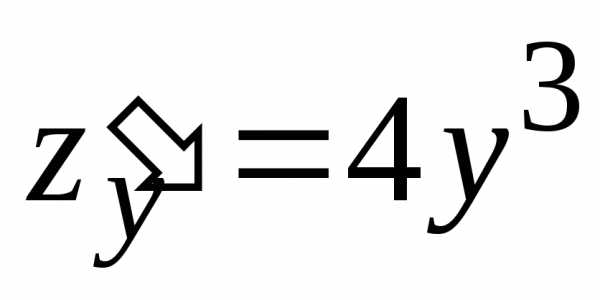 .
.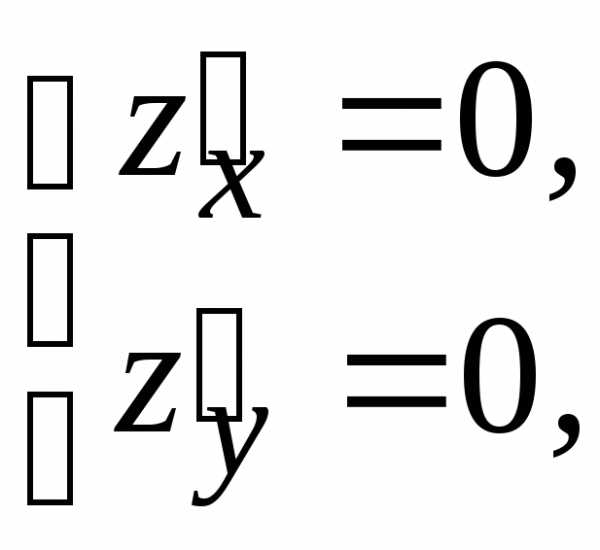

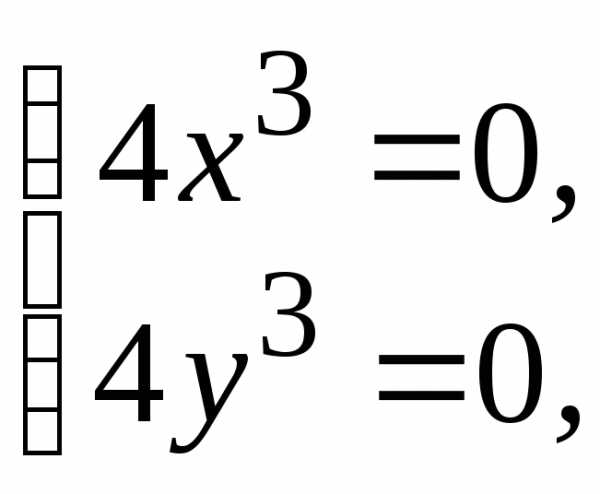

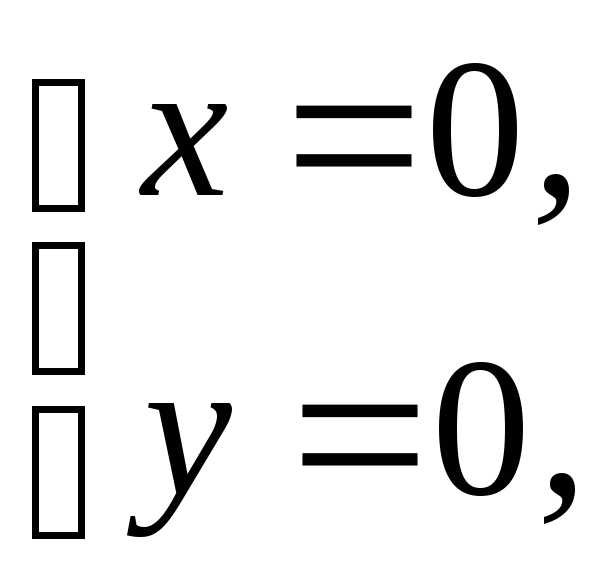
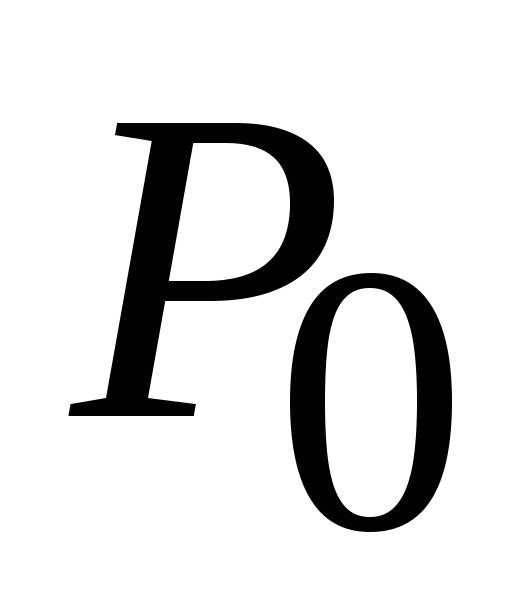 (0; 0) данной функции.
(0; 0) данной функции. :
:
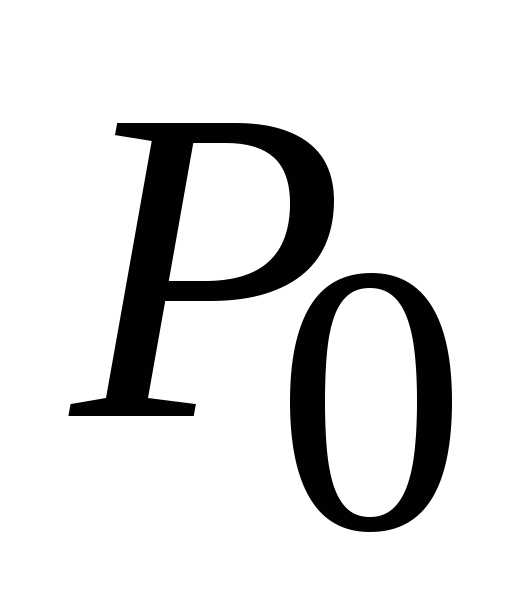 (0; 0)
(0; 0)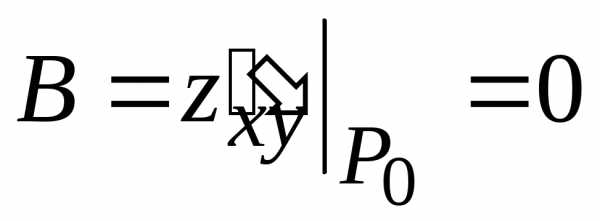 ,
,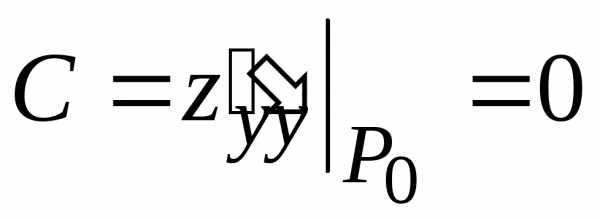

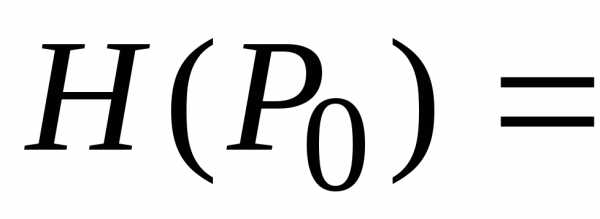 .
.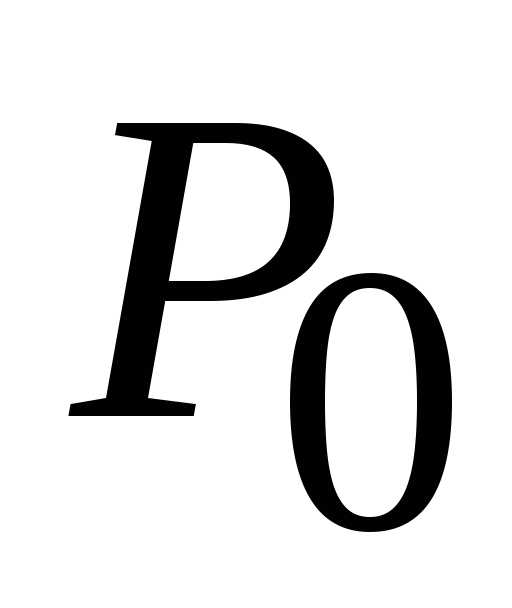 (0; 0). В данном случае стационарная
точка
(0; 0). В данном случае стационарная
точка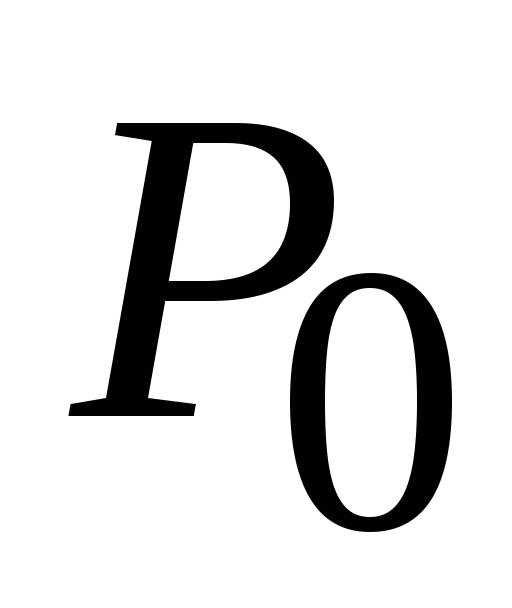 (0; 0) является точкой локального
минимума, поскольку,
(0; 0) является точкой локального
минимума, поскольку,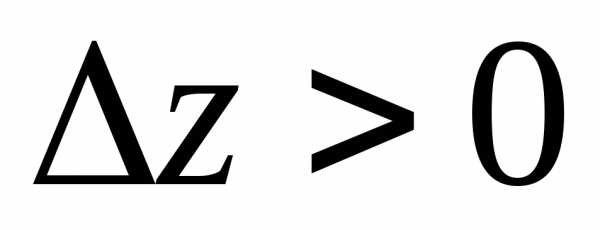 для
для
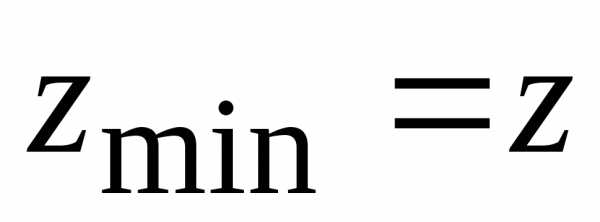 (0;
0)=0.
(0;
0)=0.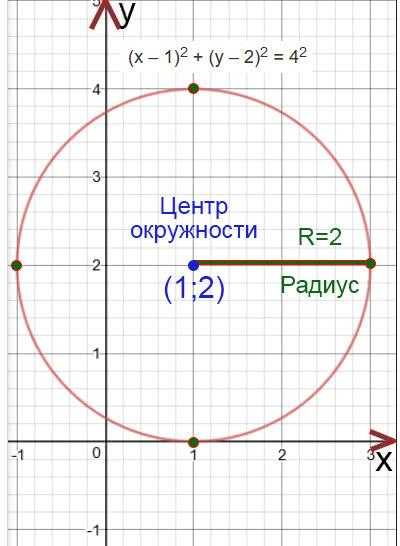
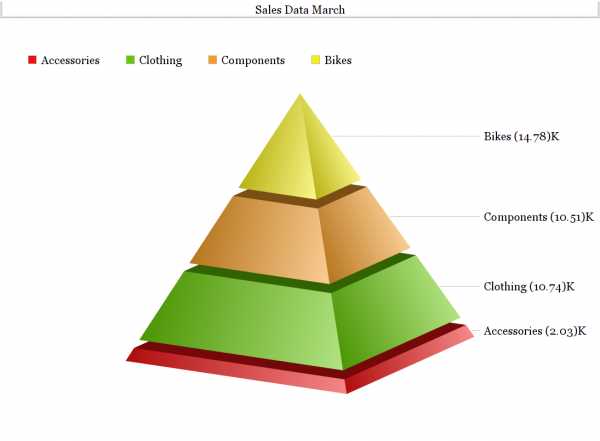
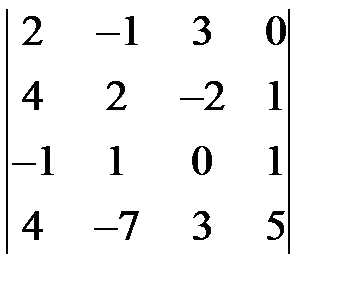 равен-…
равен-…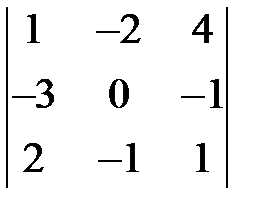 равен-…
равен-…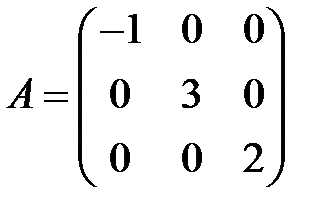 является
является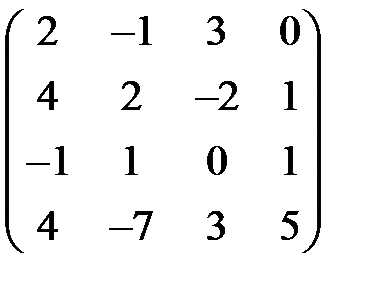 равен-…
равен-…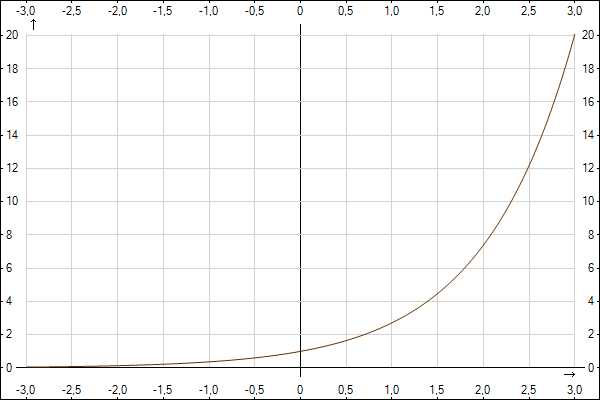







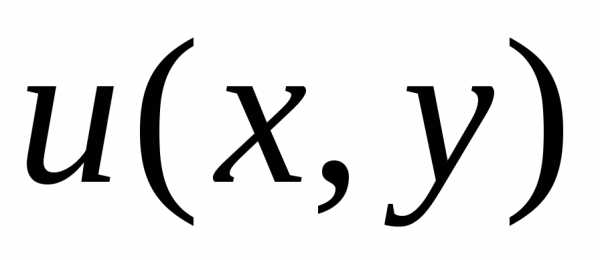 ,
удовлетворяющую неоднородному уравнению
Лапласа – уравнению Пуассона
,
удовлетворяющую неоднородному уравнению
Лапласа – уравнению Пуассона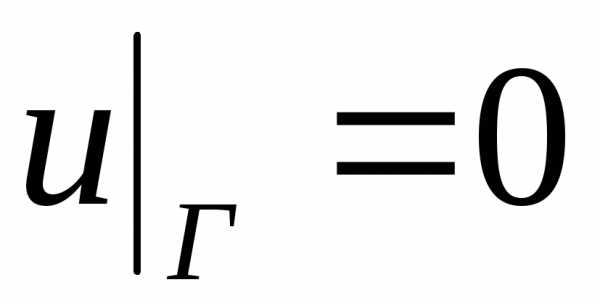 .
(2.108)
.
(2.108)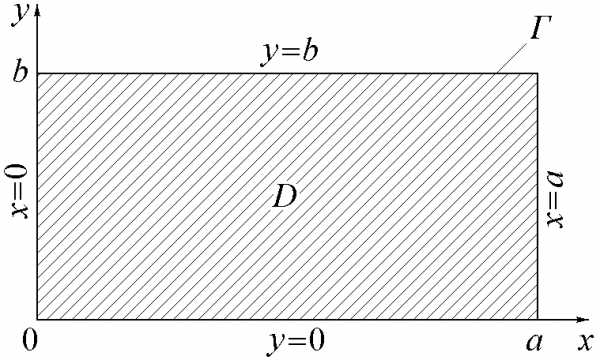
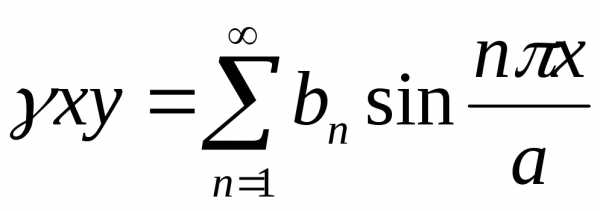 ,
(2.111)
,
(2.111)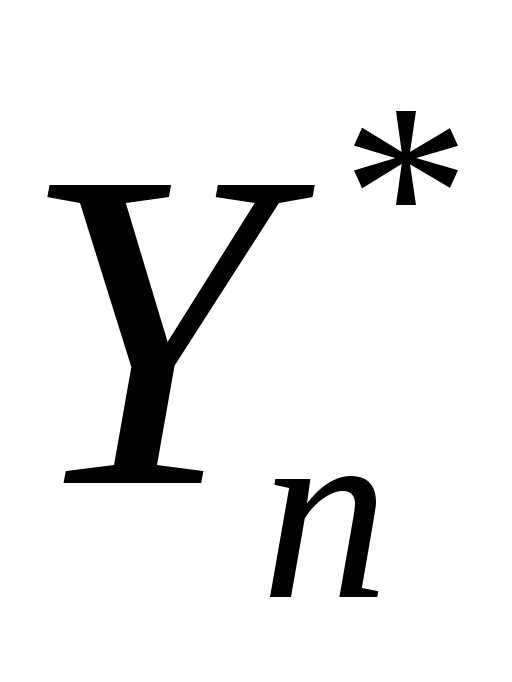 неоднородного уравнения (2.113) легко
находится методом подбора:
неоднородного уравнения (2.113) легко
находится методом подбора: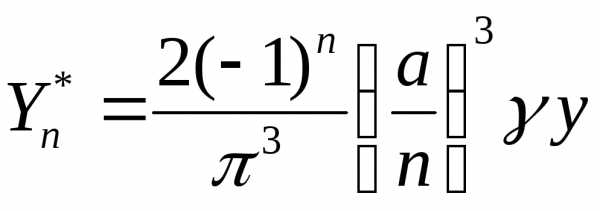 .
.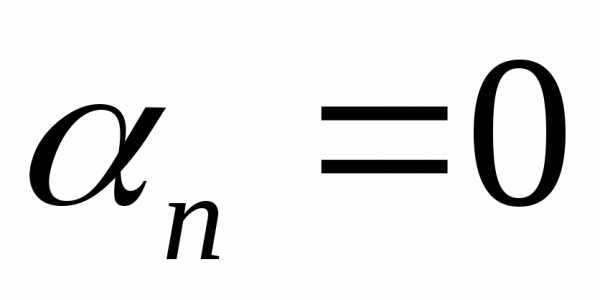 .
(2.116)
.
(2.116)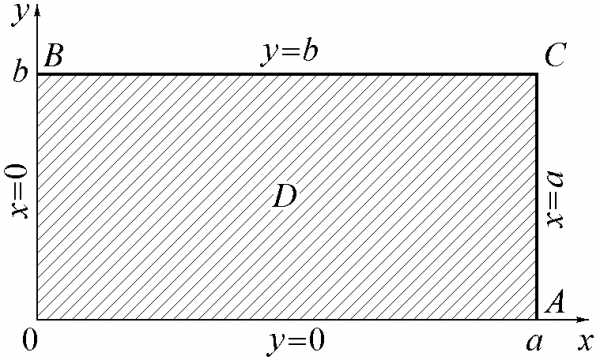
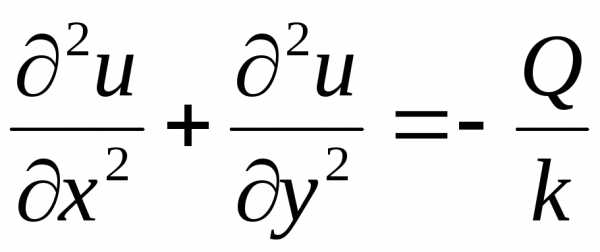 ,
(2.118)
,
(2.118)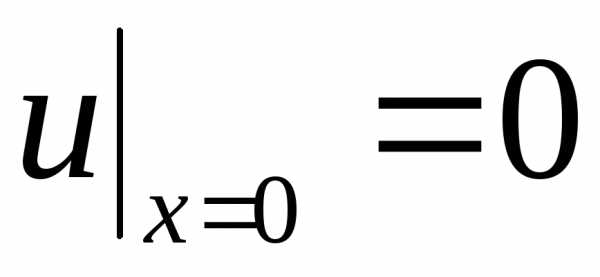 ,
, 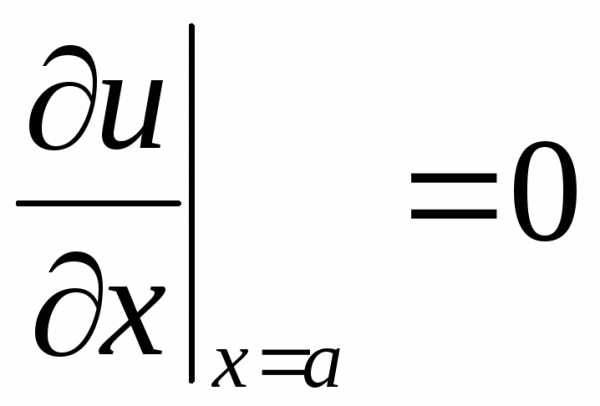 ,
(2.119)
,
(2.119)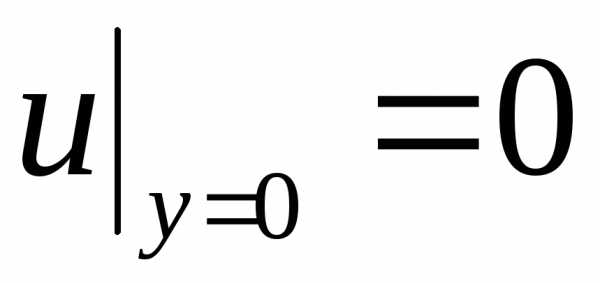 ,
, 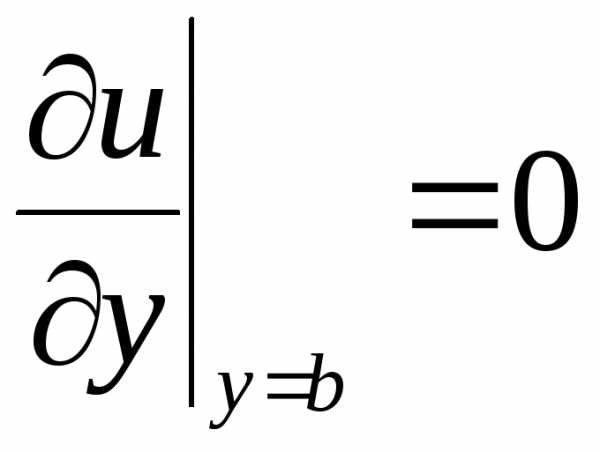 .
(2.120)
.
(2.120)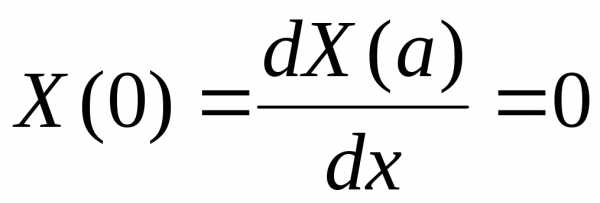 .
(2.121)
.
(2.121)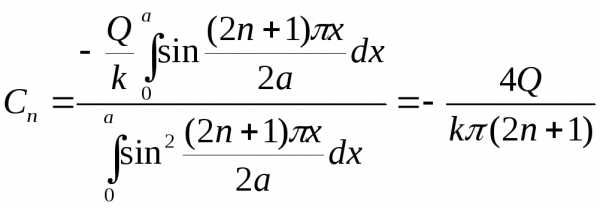 .
(2.126)
.
(2.126)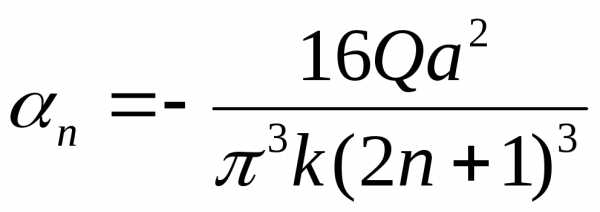 .
(2.130)
.
(2.130)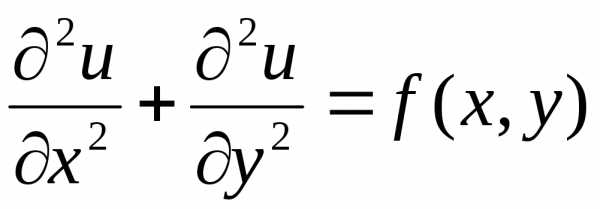 (2.132)
(2.132)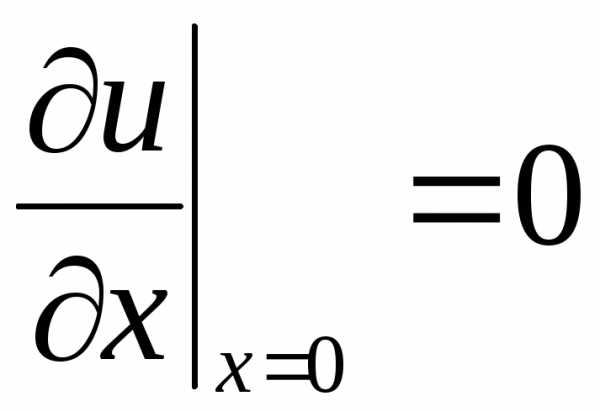 ,
, 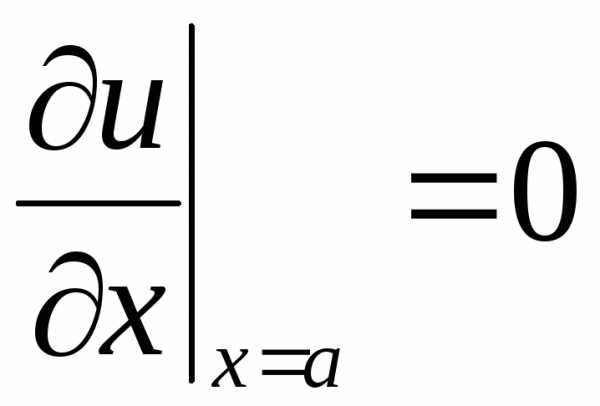 ,
(2.133)
,
(2.133)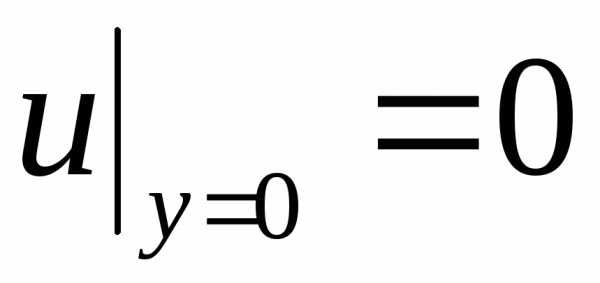 ,
, 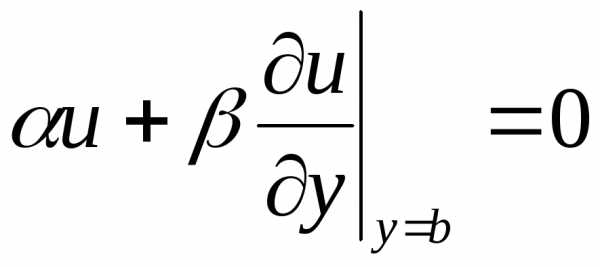 .
(2.134)
.
(2.134)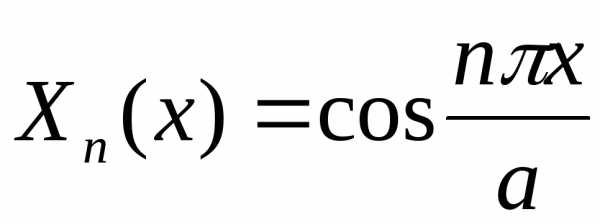 .
(2.137)
.
(2.137)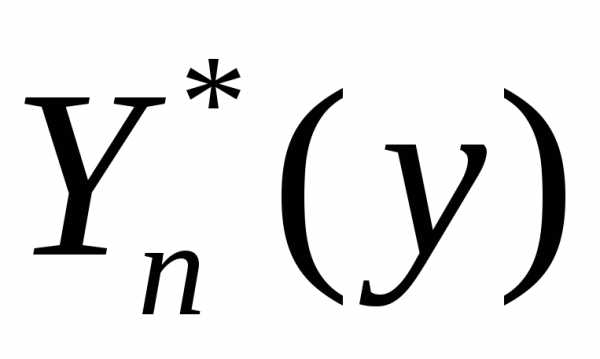 уравнений (2.141–2.142) находятся методом
подбора или методом вариации произвольных
постоянных. Далее должны быть определены
произвольные постоянные в общих решениях
уравнений (2.141–2.142)
уравнений (2.141–2.142) находятся методом
подбора или методом вариации произвольных
постоянных. Далее должны быть определены
произвольные постоянные в общих решениях
уравнений (2.141–2.142)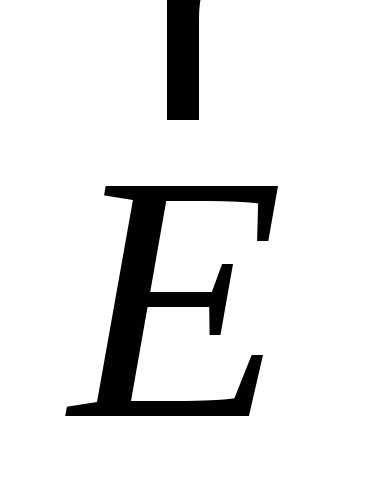 с волновым числомk;
уравнение Пуассона
с волновым числомk;
уравнение Пуассона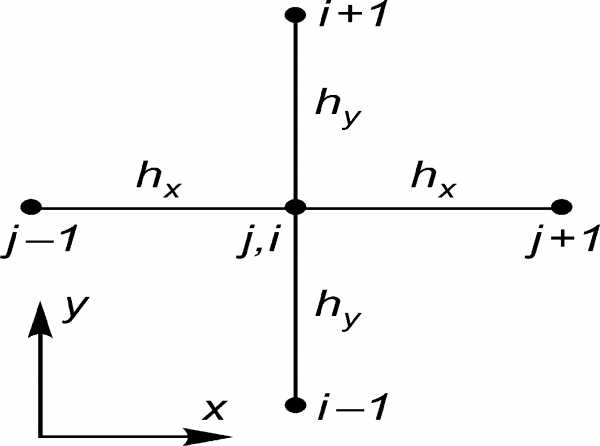
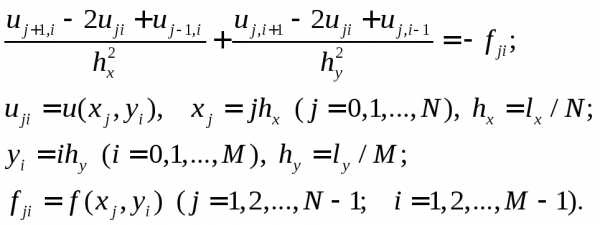
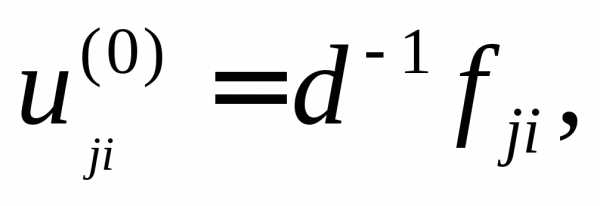
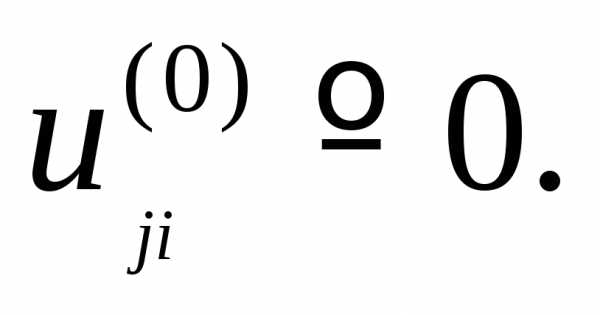
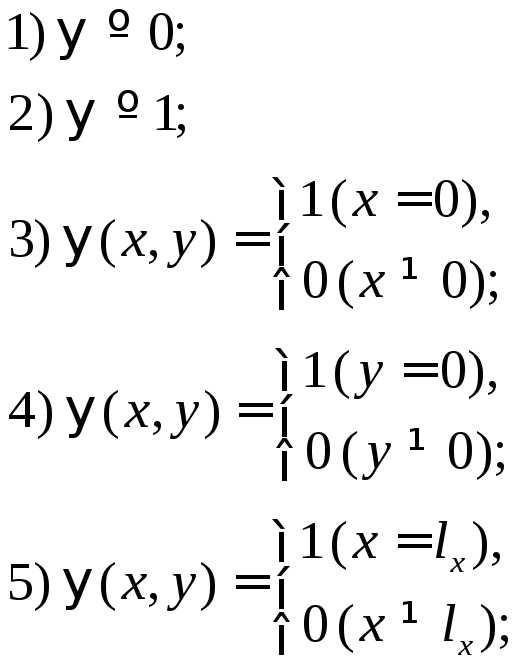

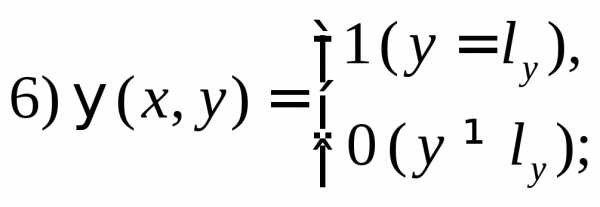
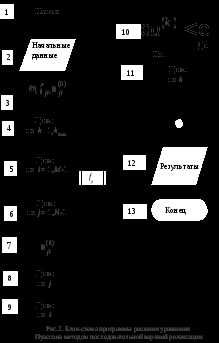
 следует
описать двумерные массивы. Правую часть
удобно оформить в виде подпрограммы-функции.
Норма (2) вычисляется на этапе релаксации
перед тем, как новое значение
следует
описать двумерные массивы. Правую часть
удобно оформить в виде подпрограммы-функции.
Норма (2) вычисляется на этапе релаксации
перед тем, как новое значение  посылается на место прежнего.
посылается на место прежнего.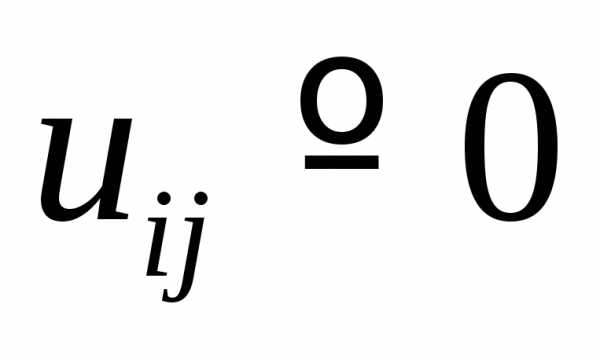
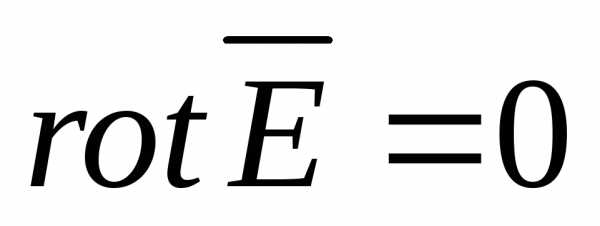 и
и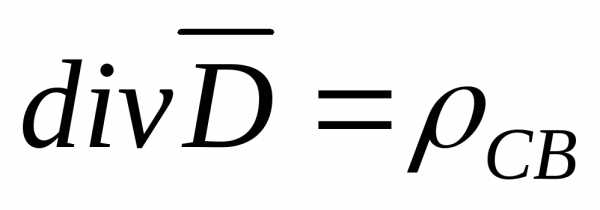 возможен только в простейших случаях.
Наиболее общим методом является расчет
электростатических полей на основе
решения уравнений Пуассона и Лапласа.
Выведем эти уравнения.
возможен только в простейших случаях.
Наиболее общим методом является расчет
электростатических полей на основе
решения уравнений Пуассона и Лапласа.
Выведем эти уравнения.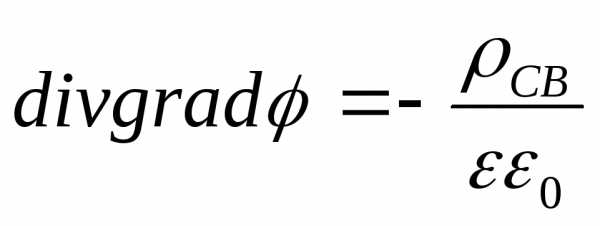 или
или 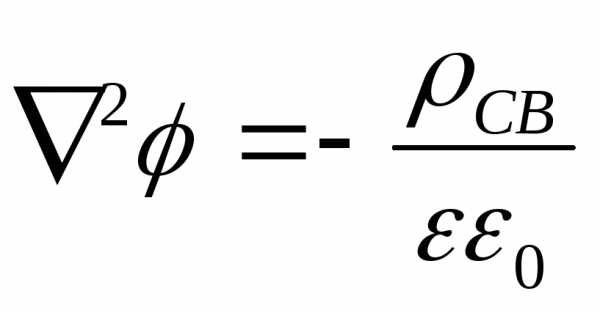 ― уравнение Пуассона.
― уравнение Пуассона.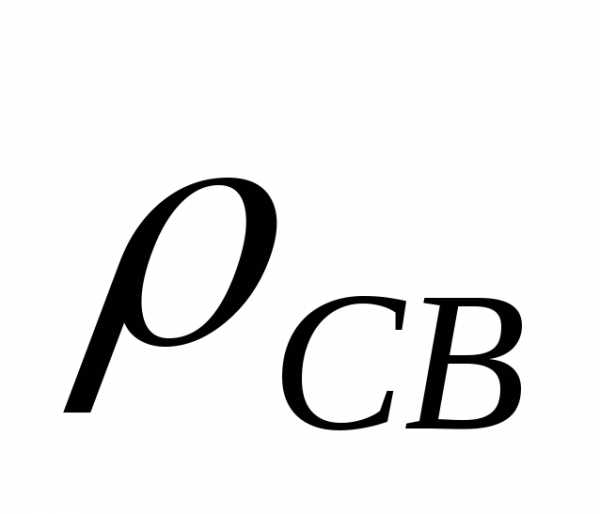 .
.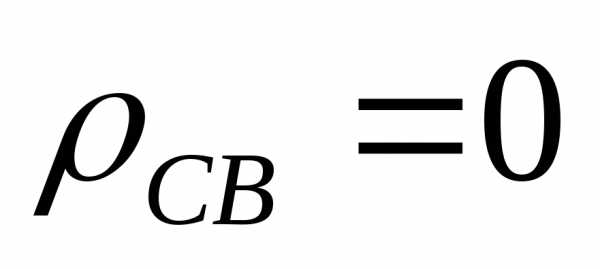 ),
уравнение Пуассона превращается в
уравнение Лапласа:
),
уравнение Пуассона превращается в
уравнение Лапласа: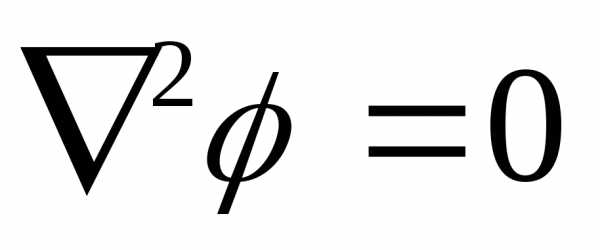 ― уравнение Лапласа.
― уравнение Лапласа.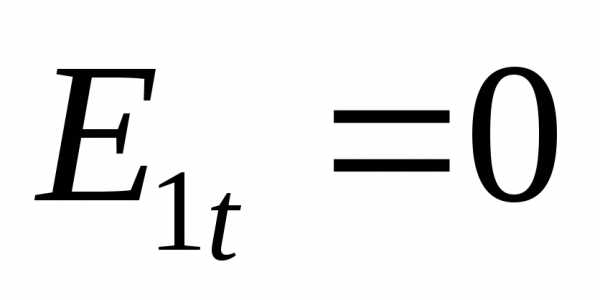 .
. записывают так:
записывают так: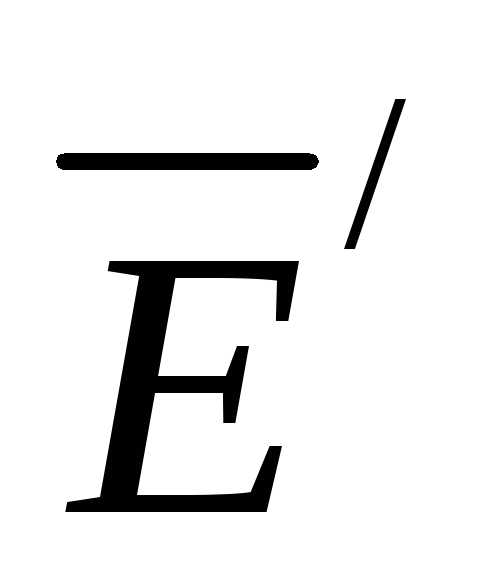 и
и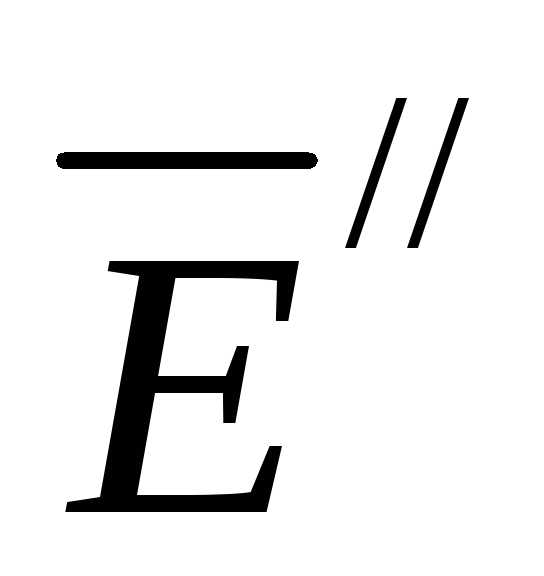 ,
оба удовлетворяющие граничным условиям
задачи. Тогда получим:
,
оба удовлетворяющие граничным условиям
задачи. Тогда получим: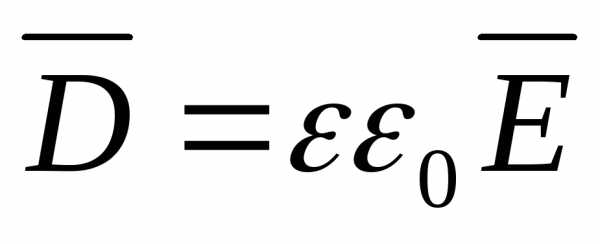 в силу симметрии во всех точках на
боковой поверхности цилиндра (r=const)
имеет одно и то же значение и направление
по радиусу, т.е. нормально к этой
поверхности.
в силу симметрии во всех точках на
боковой поверхности цилиндра (r=const)
имеет одно и то же значение и направление
по радиусу, т.е. нормально к этой
поверхности.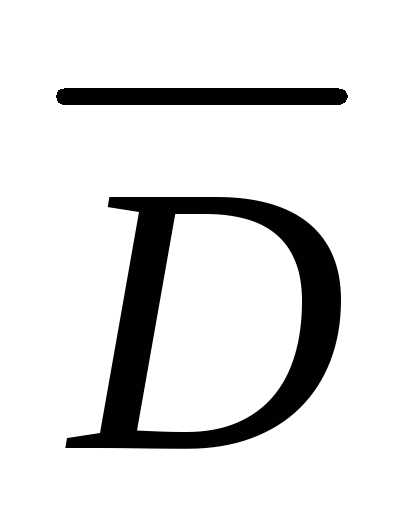 через торцевые поверхности цилиндра
равен нулю, так как линии вектора здесь
направлены по касательной к поверхности.
через торцевые поверхности цилиндра
равен нулю, так как линии вектора здесь
направлены по касательной к поверхности. будет зависеть только от радиусаr:
,
откуда
будет зависеть только от радиусаr:
,
откуда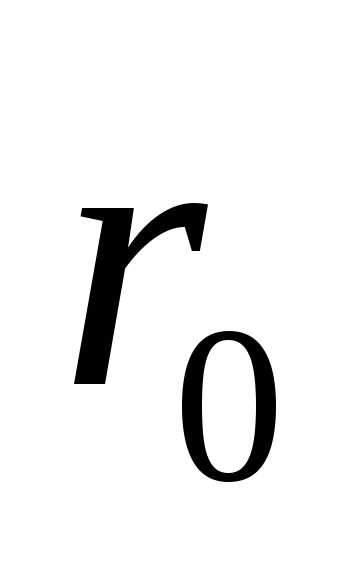 значение
потенциала равным нулю, то
значение
потенциала равным нулю, то 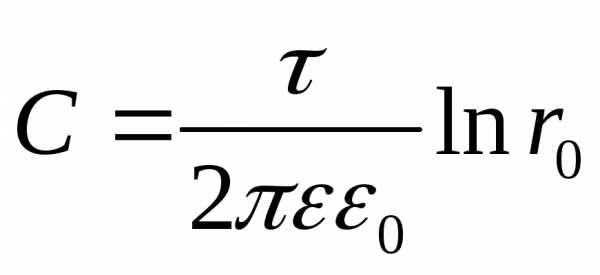 и значение потенциала на поверхности
произвольного радиуса будет равна:
и значение потенциала на поверхности
произвольного радиуса будет равна: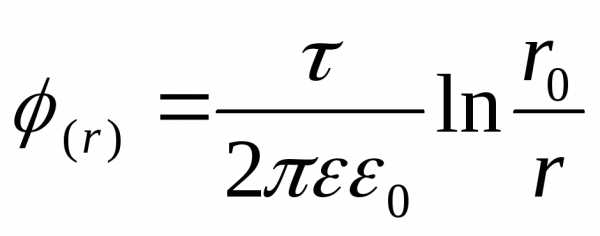 .
.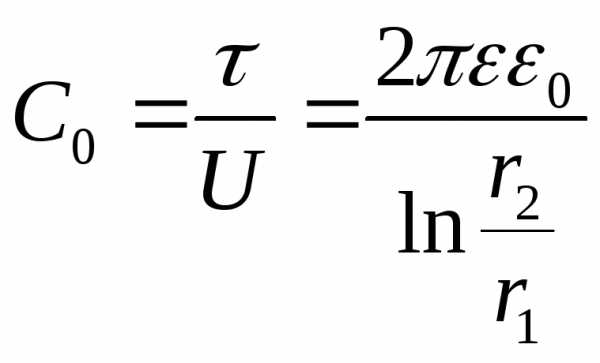 ,
откуда следует, что
,
откуда следует, что 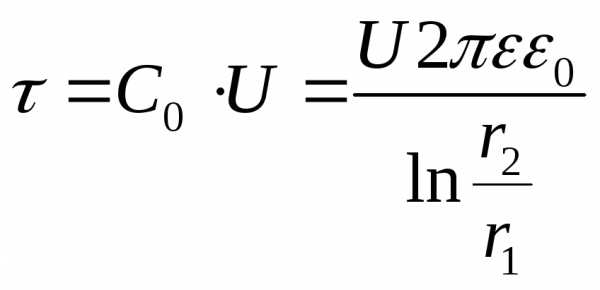 .
.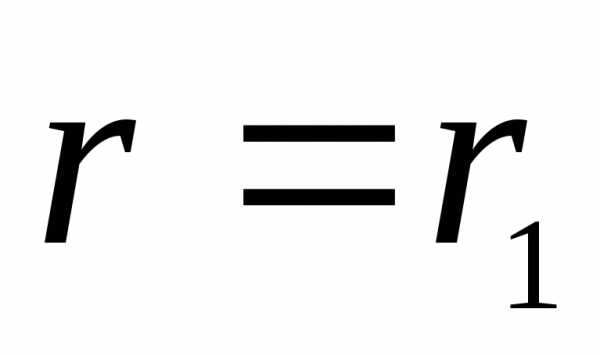 :
: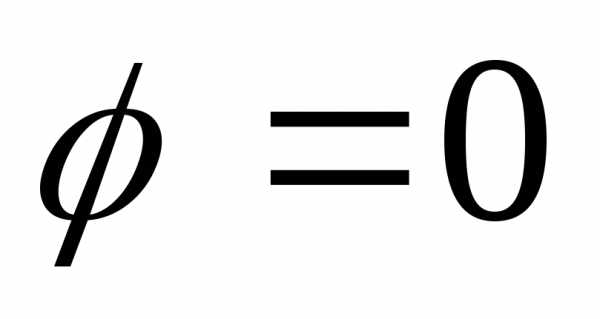 в точках равноудалённых от обеих осей
(
в точках равноудалённых от обеих осей
(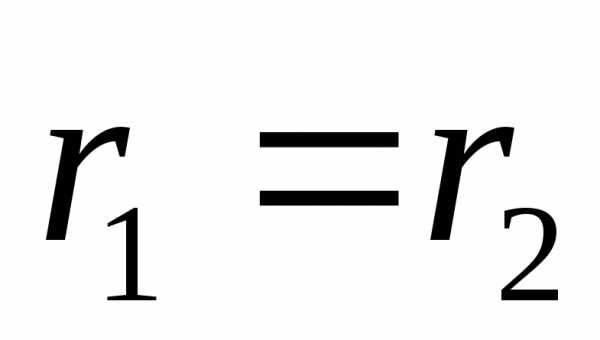 ),
то постоянная интегрирования будет
равна нулю (С=0),
тогда получим:
),
то постоянная интегрирования будет
равна нулю (С=0),
тогда получим: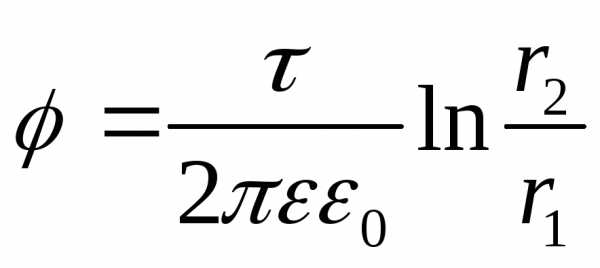 .
.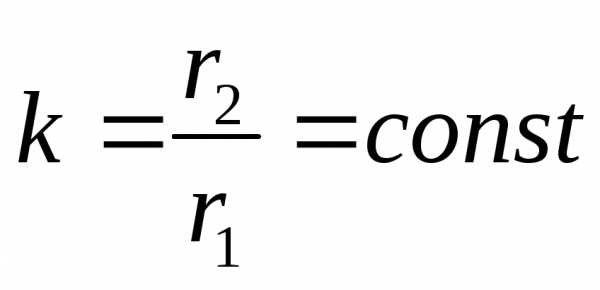 .
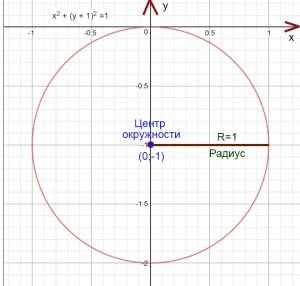
В геометрии есть малоизвестная теорема
Аполония, которая гласит, что геометрическим
местом точек, отношение расстояний от
которых до заданной пары точек постоянно,
является окружность, центр которой
лежит на линии, соединяющей заданную
пару точек. Эта окружность должна
удовлетворять следующему условию:
.
В геометрии есть малоизвестная теорема
Аполония, которая гласит, что геометрическим
местом точек, отношение расстояний от
которых до заданной пары точек постоянно,
является окружность, центр которой
лежит на линии, соединяющей заданную
пару точек. Эта окружность должна
удовлетворять следующему условию: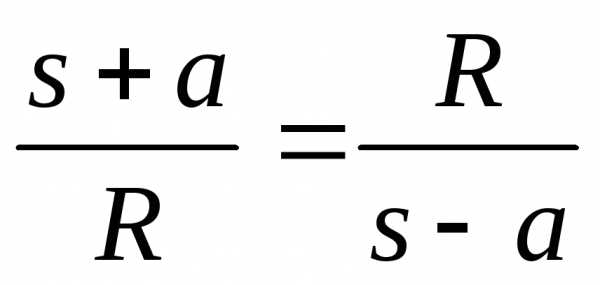 .
.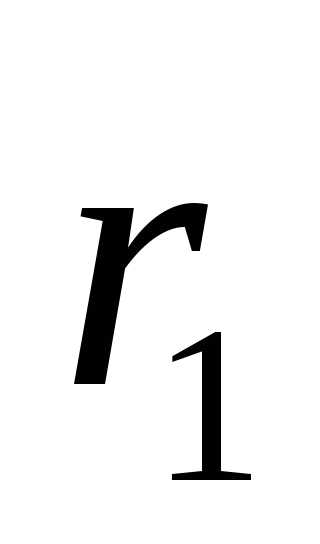 и
и 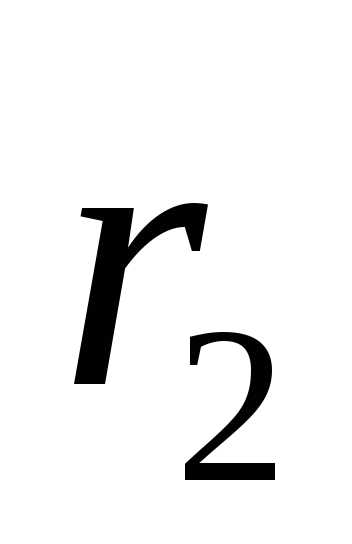 так, что их отношение остается постоянным
так, что их отношение остается постоянным 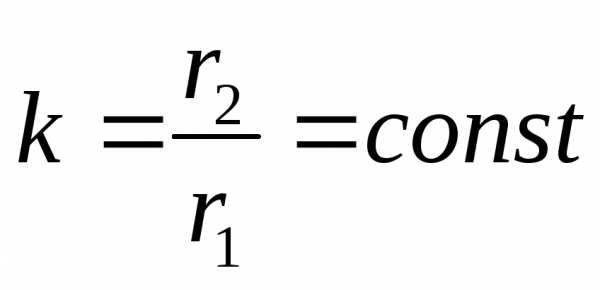 .
При изменении отношения
.
При изменении отношения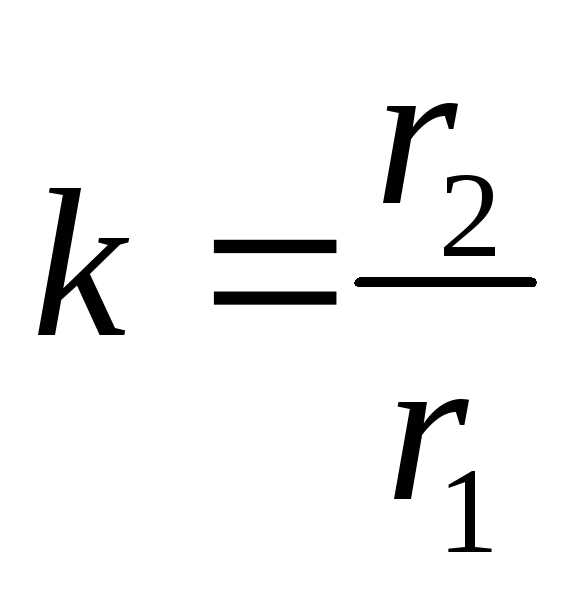 центр окружности перемещается вдоль
линии, соединяющую заданную пару
точек 1 и 2. Приk>1,
центр окружности перемещается вдоль
линии, соединяющую заданную пару
точек 1 и 2. Приk>1, 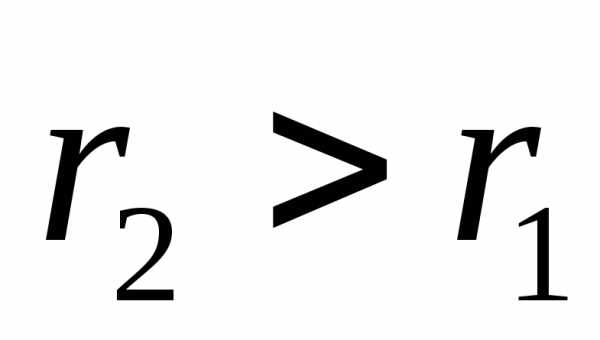 и центр окружности находиться в левой
полуобласти, приk<1,
и центр окружности находиться в левой
полуобласти, приk<1, 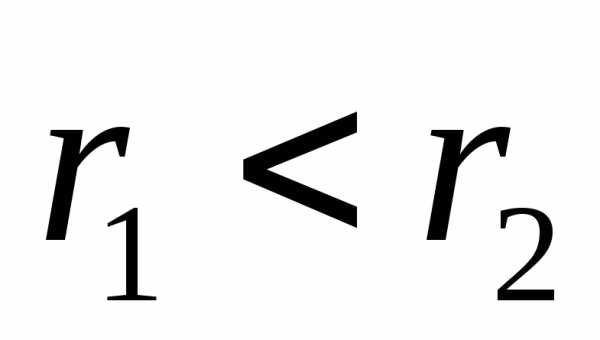 и центр окружности находится в
правой полуобласти, a приk=1,
и центр окружности находится в
правой полуобласти, a приk=1, 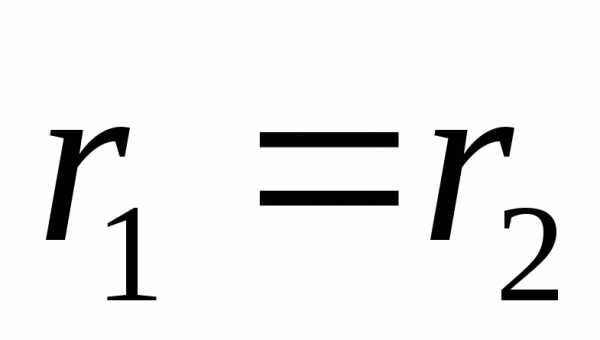 ,
центр окружности смещается в бесконечность,
а сама окружность превращается в прямую
линию, совпадающую с вертикальной
осью симметрии.
,
центр окружности смещается в бесконечность,
а сама окружность превращается в прямую
линию, совпадающую с вертикальной
осью симметрии. также является дугами окружности,
но с центрами, расположенными на
вертикальной оси симметрии.
также является дугами окружности,
но с центрами, расположенными на
вертикальной оси симметрии. .
Графическая диаграмма поля двух
разноименно заряженных осей имеет вид
рис. 259.
.
Графическая диаграмма поля двух
разноименно заряженных осей имеет вид
рис. 259. ,
, )
в любой точке.
)
в любой точке.
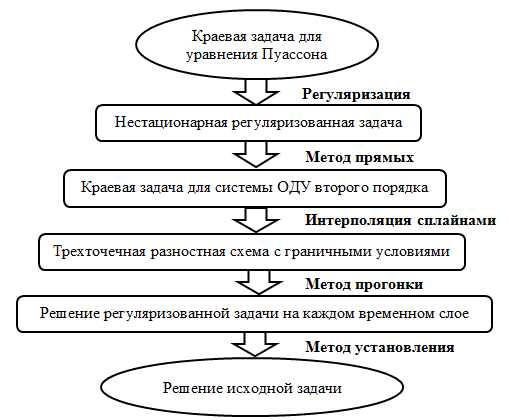
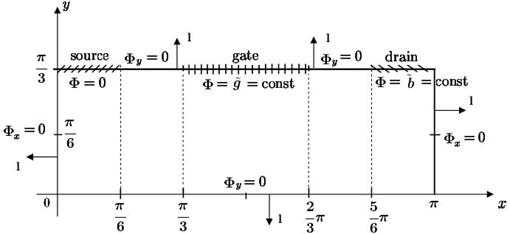
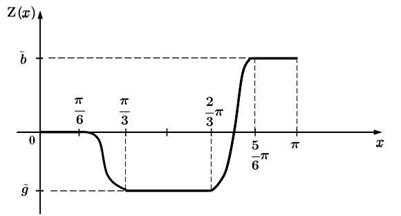
 Предлагается образец оформления титульного листа контрольной работы.
Предлагается образец оформления титульного листа контрольной работы.









 Работа должна включать следующие обязательные логические блоки:
Работа должна включать следующие обязательные логические блоки:

 и читают «хпринадлежитА». Чтобы
указать, чтохне является элементом
множестваА, записывают
и читают «хпринадлежитА». Чтобы
указать, чтохне является элементом
множестваА, записывают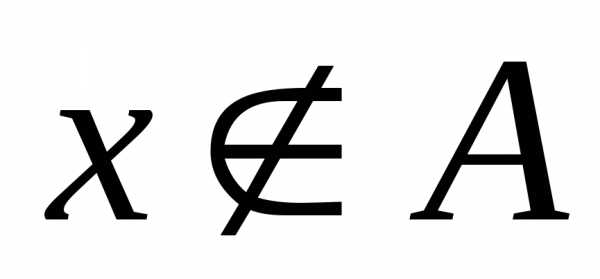 и читают «хне принадлежит множествуА».
и читают «хне принадлежит множествуА».
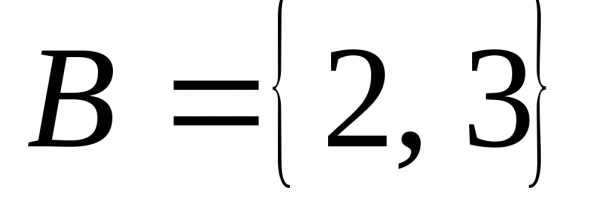 ,,
тогда,
т.е.
,,
тогда,
т.е. .
. и
и .
.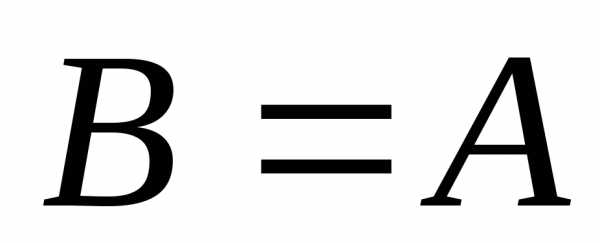
 .
. и
и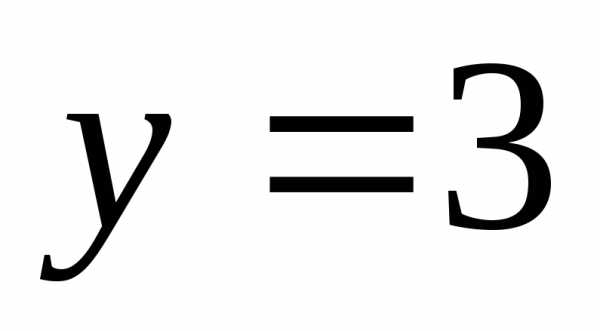 удовлетворяют
уравнению,
т.е.
удовлетворяют
уравнению,
т.е. ,
значит
,
значит .
.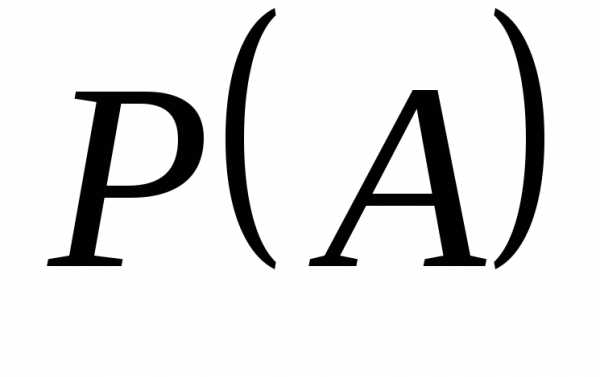
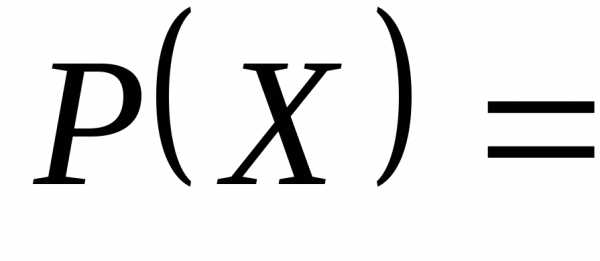 {Ø},
т.е. если множество состоит из двух
элементов, то множество-степень состоит
из четырех подмножеств.
{Ø},
т.е. если множество состоит из двух
элементов, то множество-степень состоит
из четырех подмножеств.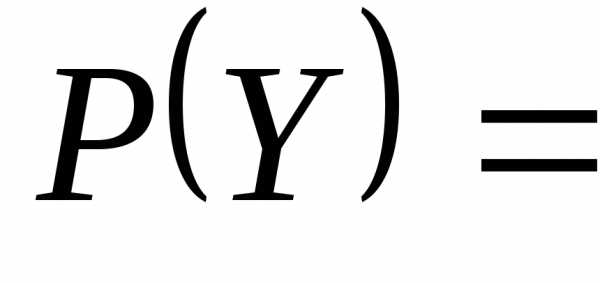 {{4},
{2,3}, {3,4}, {2,4}, Ø}, т.е. если множество состоит
из трех элементов, то множество-степень
состоит из восьми подмножеств.
{{4},
{2,3}, {3,4}, {2,4}, Ø}, т.е. если множество состоит
из трех элементов, то множество-степень
состоит из восьми подмножеств.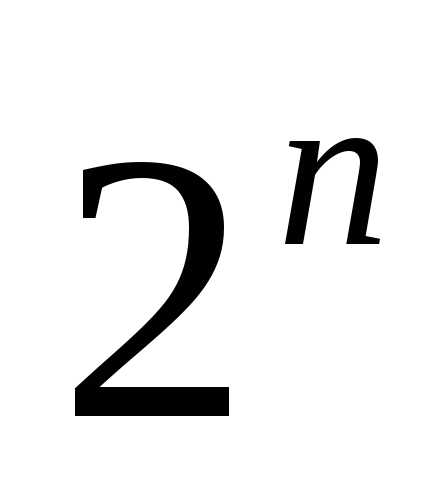 .
. ,
,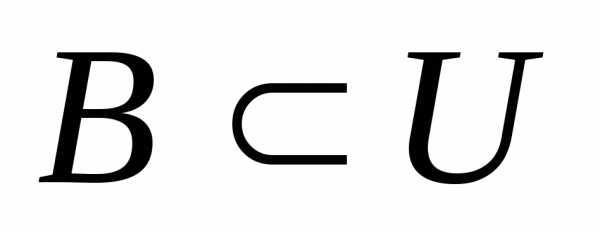 ,
, ,
…. .
,
…. .
 Х,
означает что объект х есть элемент
множества Х,
читается «х принадлежит
множеству Х»,
«х входит
в множество Х». Если х не принадлежит
множеству Х,
то пишут х
Х,
означает что объект х есть элемент
множества Х,
читается «х принадлежит
множеству Х»,
«х входит
в множество Х». Если х не принадлежит
множеству Х,
то пишут х  Х.
Х. N, 20
N, 20  N, 0
N, 0  N,
N,  N.
N. В (множество А содержится
во множестве В). Любое
множество является подмножеством самого
себя, т. е. справедливо утверждение А
В (множество А содержится
во множестве В). Любое
множество является подмножеством самого
себя, т. е. справедливо утверждение А  А.
А. Аи А
Аи А  В.
В.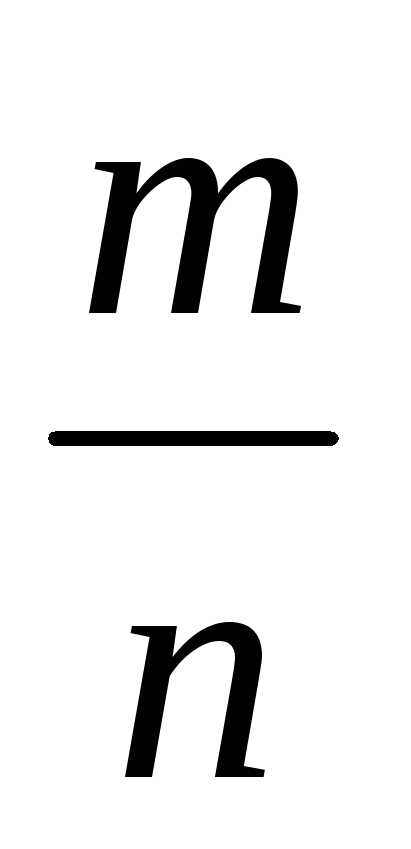 :m
:m  Z, n
Z, n  N}
– множество рациональных чисел –
множество чисел, которые можно представить
в виде обыкновенной дроби – множество
конечных и бесконечных периодических
десятичных дробей;
N}
– множество рациональных чисел –
множество чисел, которые можно представить
в виде обыкновенной дроби – множество
конечных и бесконечных периодических
десятичных дробей;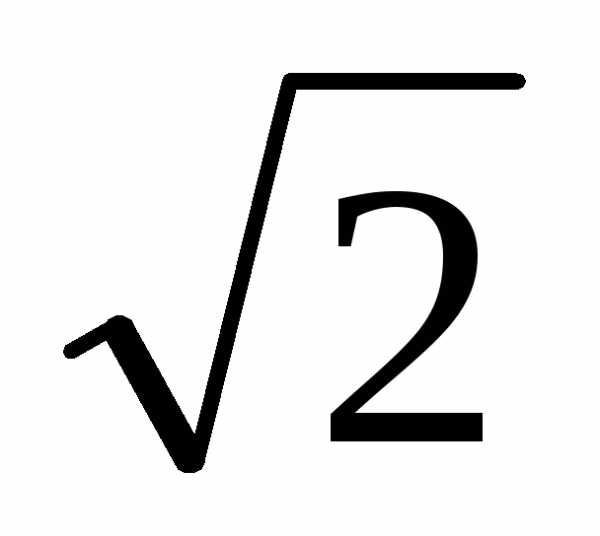 = 1,4142356…, π = 3,1415926… – иррациональные
числа.
= 1,4142356…, π = 3,1415926… – иррациональные
числа.