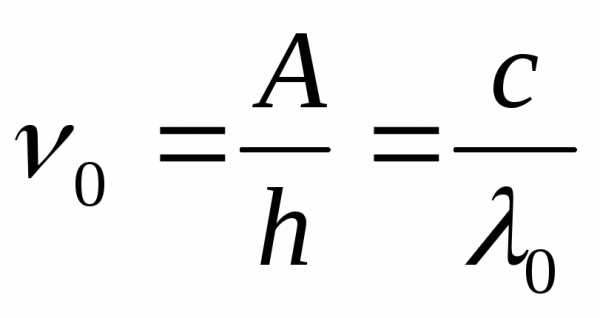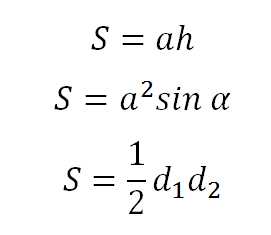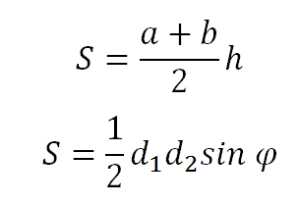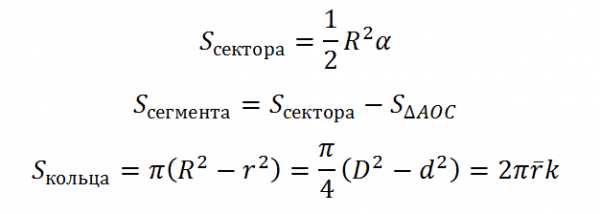Таблица умножения на 6
| Множители | Произведение (Результат) |
|---|---|
| 6 * 1 = | 6 |
| 6 * 2 = | 12 |
| 6 * 3 = | 18 |
| 6 * 4 = | 24 |
| 6 * 5 = | 30 |
| 6 * 6 = | 36 |
| 6 * 7 = | 42 |
| 6 * 8 = | 48 |
| 6 * 9 = | 54 |
| 6 * 10 = | 60 |
| 6 * 11 = | 66 |
| 6 * 12 = | 72 |
| 6 * 13 = | 78 |
| 6 * 14 = | 84 |
| 6 * 15 = | 90 |
| 6 * 16 = | 96 |
| 6 * 17 = | 102 |
| 6 * 18 = | 108 |
| 6 * 19 = | 114 |
| 6 * 20 = | 120 |
| 6 * 21 = | 126 |
| 6 * 22 = | 132 |
| 6 * 23 = | 138 |
| 6 * 24 = | 144 |
| 6 * 25 = | 150 |
| 6 * 26 = | 156 |
| 6 * 27 = | 162 |
| 6 * 28 = | 168 |
| 6 * 29 = | 174 |
| 6 * 30 = | 180 |
| 6 * 31 = | 186 |
| 6 * 32 = | 192 |
| 6 * 33 = | 198 |
| 6 * 34 = | 204 |
| 6 * 35 = | 210 |
| 6 * 36 = | 216 |
| 6 * 37 = | 222 |
| 6 * 38 = | 228 |
| 6 * 39 = | 234 |
| 6 * 40 = | 240 |
| 6 * 41 = | 246 |
| 6 * 42 = | 252 |
| 6 * 43 = | 258 |
| 6 * 44 = | 264 |
| 6 * 45 = | 270 |
| 6 * 46 = | 276 |
| 6 * 47 = | 282 |
| 6 * 48 = | 288 |
| 6 * 49 = | 294 |
| 6 * 50 = | 300 |
| 6 * 51 = | 306 |
| 6 * 52 = | 312 |
| 6 * 53 = | 318 |
| 6 * 54 = | 324 |
| 6 * 55 = | 330 |
| 6 * 56 = | 336 |
| 6 * 57 = | 342 |
| 6 * 58 = | 348 |
| 6 * 59 = | 354 |
| 6 * 60 = | 360 |
| 6 * 61 = | 366 |
| 6 * 62 = | 372 |
| 6 * 63 = | 378 |
| 6 * 64 = | 384 |
| 6 * 65 = | 390 |
| 6 * 66 = | 396 |
| 6 * 67 = | 402 |
| 6 * 68 = | 408 |
| 6 * 69 = | 414 |
| 6 * 70 = | 420 |
| 6 * 71 = | 426 |
| 6 * 72 = | 432 |
| 6 * 73 = | 438 |
| 6 * 74 = | 444 |
| 6 * 75 = | 450 |
| 6 * 76 = | 456 |
| 6 * 77 = | 462 |
| 6 * 78 = | 468 |
| 6 * 79 = | 474 |
| 6 * 80 = | 480 |
| 6 * 81 = | 486 |
| 6 * 82 = | 492 |
| 6 * 83 = | 498 |
| 6 * 84 = | 504 |
| 6 * 85 = | 510 |
| 6 * 86 = | 516 |
| 6 * 87 = | 522 |
| 6 * 88 = | 528 |
| 6 * 89 = | 534 |
| 6 * 90 = | 540 |
| 6 * 91 = | 546 |
| 6 * 92 = | 552 |
| 6 * 93 = | 558 |
| 6 * 94 = | 564 |
| 6 * 95 = | 570 |
| 6 * 96 = | 576 |
| 6 * 97 = | 582 |
| 6 * 98 = | 588 |
| 6 * 99 = | 594 |
| 6 * 100 = | 600 |
| … * 101 = | … |
Автор: Bill4iam
kvn201.com.ua
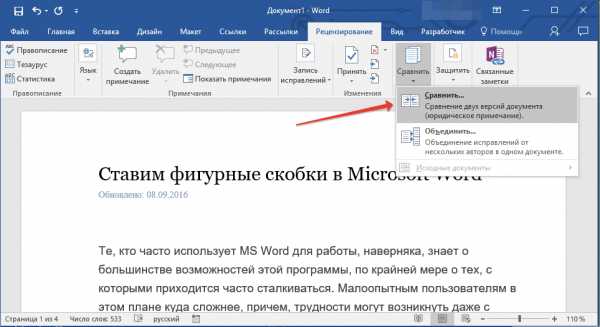
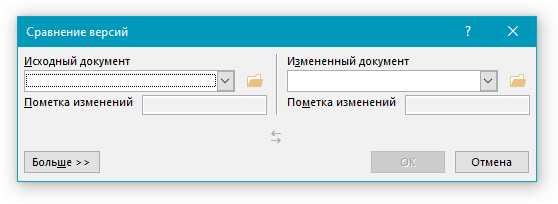
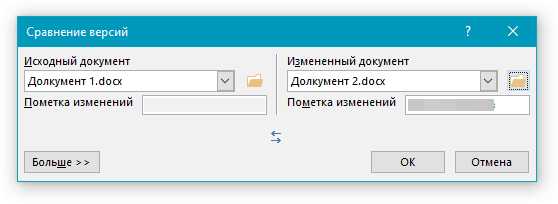
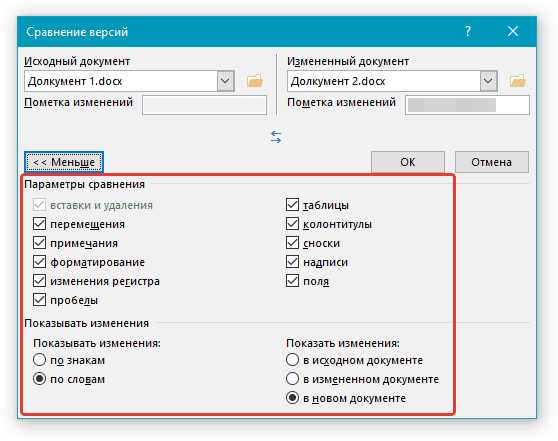
6 Таблицы
6.1 Параметры оформления таблиц и надписи к таблицам представлены в Таблице 6.1.
Таблица 6.1 — Параметры оформления таблиц и надписей к таблицам
Таблица | ||||
Надпись таблицы | ||||
Шрифт | Шрифт | Шрифт | Times New Roman | |
Начертание | Курсив | |||
Размер | 12 пт | |||
Цвет текста | Авто (черный) | |||
Подчеркивание | нет | |||
Видоизменение | нет | |||
Интервал | Масштаб | 100% | ||
Интервал | Обычный | |||
Смещение | Нет | |||
Анимация | Вид | Нет | ||
Абзац | Отступы и интервалы | Выравнивание | По левому краю | |
Отступ слева | 0 см | |||
Отступ справа | 0 см | |||
Первая строка | нет | |||
Интервал перед | 6 мм | |||
Интервал после | 0 мм | |||
Междустрочный | Одинарный | |||
Положение на странице | Разбивка на страницы | Не отрывать от следующего | ||
С новой страницы | ||||
Содержание таблицы | ||||
Шрифт | Шрифт | Шрифт | Times New Roman | |
Начертание | Обычный, полужирный, курсив | |||
Размер | 12 пт | |||
Цвет текста | Авто (черный) | |||
Подчеркивание | нет | |||
Видоизменение | нет | |||
Интервал | Масштаб | 100% | ||
Интервал | Обычный | |||
Смещение | Нет | |||
Анимация | Вид | Нет | ||
Абзац | Отступы и интервалы | Выравнивание | По левому краю, по центру | |
Отступ слева | 0 см | |||
Отступ справа | 0 см | |||
Первая строка | 0 см | |||
Интервал перед | 0 мм | |||
Интервал после | 0 мм | |||
Междустрочный | Одинарный | |||
6.2 Название таблицы пишется в одну строку с номером, через тире, с большой буквы, перед таблицей. Точка в конце не ставится. Пример, «Таблица 1.7 — Исходные данные».
6.3 При необходимости переноса части таблицы на другую страницу название помещается только над первой частью таблицы, нижнюю горизонтальную черту, ограничивающую таблицу, не проводят. Над другими частями пишется «Продолжение Таблицы 6.1», отформатированное стилем «Надпись. Таблица».
6.4 Автоподбор таблицы по содержимому.
6.5 Заголовки столбцов центрируются по ширине столбца, а заголовки строк выравниваются по левому краю. Заголовки граф и строк таблицы пишутся с прописной буквы в единственном числе, а подзаголовки граф — со строчной буквы, если они составляют одно предложение с заголовком, или с прописной буквы, если они имеют самостоятельное значение. В конце заголовков и подзаголовков таблиц знаки препинания не ставят. Диагональное деление ячеек таблицы не допускается.
6.6 Строка, следующая за таблицей, печатается с интервалом перед 6 мм.
6.7 Графу «№ п/п» в таблицу не включают. При необходимости нумерации показателей или других данных порядковые номера указывают в левом столбце таблицы перед их наименованием.
7 Иллюстрации
7.1 Иллюстрации (графики, схемы, фотографии и т.п.) располагаются так, чтобы их было удобно рассматривать без поворота текста или путем переворачивания по часовой стрелке на 90º. В таком случае ориентация в параметрах страницы изменяется с книжной на альбомную.
7.2 Название иллюстрации пишется после номера через тире и помещается после иллюстрации. Сокращение слова «Рисунок» не допускается. В конце названия иллюстрации точка не ставится. Пример: «Рисунок 1.4 — Детали прибора».
7.3 Параметры оформления надписи к иллюстрациям представлены в Таблице 7.1.
Таблица 7.1 — Параметры надписи к иллюстрации
Надпись к иллюстрациям
Шрифт
Шрифт
Шрифт
Times New Roman
Начертание
Полужирный
Размер
12 пт
Цвет текста
Авто (черный)
Подчеркивание
нет
Видоизменение
нет
Интервал
Масштаб
100%
Интервал
Обычный
Смещение
Нет
Анимация
Вид
Нет
Абзац
Отступы и интервалы
Выравнивание
По центру
Отступ слева
0 см
Отступ справа
0 см
Первая строка
нет
Интервал перед
0 мм
Интервал после
6 мм
Междустрочный
Одинарный
Положение на странице
Разбивка на страницы
Запрет висящих строк
studfiles.net
Таблица умножения на 6, 7, 8 и 9 на пальцах
Если моя память мне не изменяет, таблица умножения до 5 включительно далась достаточно легко. Но вот с умножением на 6, 7, 8 и 9 возникали определенные трудности. Если бы я знала такой трюк раньше, домашнее задание выполнялось бы минимум в два раза быстрее 😉

©photo
Умножение на 6, 7 и 8
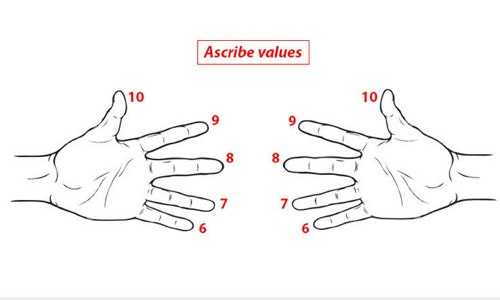 таблица умножения на пальцах
таблица умножения на пальцахПоверните кисти ладонями к себе и присвойте каждому пальцу цифры от 6 и до 10 начиная с мизинца.
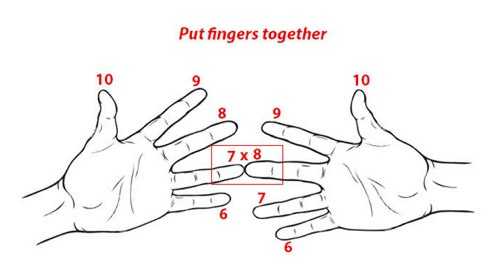
Теперь попробуем умножить, например, 7х8. Для этого соедините палец №7 на левой руке с пальцем №8 на правой.
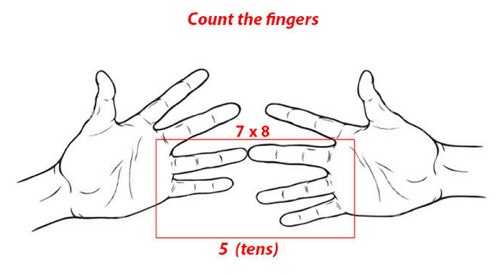 таблица умножения на пальцах
таблица умножения на пальцахА теперь считаем пальцы: количество пальцев под соединенными — это десятки.
таблица умножения на пальцах(картинка кликабельна)
А пальцы левой руки, оставшиеся сверху, умножаем на пальцы правой — это и будут наши единицы (3х2=6). Итоге равен 56.
Иногда бывает так, что при умножении «единиц» результат получается больше 9. В таких случаях нужно плюсовать оба результата в столбик.
Например, 7х6. В этом случае получается, что «единицы» равны 12 (3х4). В десятки равны 3.
3 (десятки)
+
12 (единицы)
________
42
Умножение на 9
Снова поверните кисти ладонями к себе, но теперь нумерация пальцев будет идти по порядку с лева на право, то есть от 1 до 10.
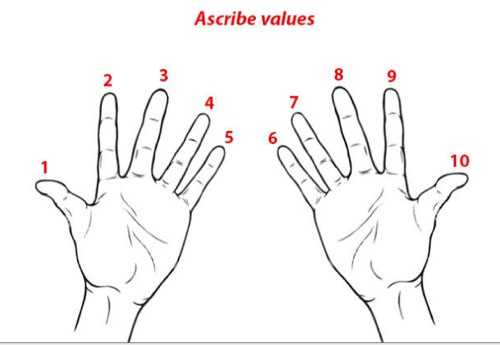
Теперь умножаем, например, 2х9. Все то, что идет до пальца №2 — это десятки (то есть 1 в этом случае). А все то, что остается после пальца №2 — единицы (то есть 8). В итоге получаем 18.
lifehacker.ru
4.6 Таблицы
Таблицы применяют для лучшей наглядности и удобства сравнения показателей. Наименование таблицы, при его наличии, должно отражать ее содержание быть точным, кратким. Наименование таблицы следует помещать над таблицей слева, без абзацного отступа в одну строку с ее номером через тире.
Таблицу следует располагать непосредственно после текста, в котором она упоминается впервые, или на следующей странице.
На все таблицы должны быть ссылки. При ссылке следует писать слово «таблица» с указанием ее номера.
Таблицу с большим количеством строк допускается переносить на другой лист (страницу). При переносе части таблицы на другой лист (страницу) слово «Таблица»,ее номер и наименование указывают один раз слева над первой частью таблицы, а над другими частями также слева пишут слова «Продолжение таблицы» и указывают номер таблицы.
Таблицу с большим количеством граф допускается делить на части и помещать одну часть под другой в пределах одной страницы. Если строки и графы таблицы выходят за формат страницы, то в первом случае в каждой части таблицы повторяется головка, во втором случае — боковик. При делении таблицы на части допускается ее головку или боковик заменять соответственно номером граф и строк. При этом нумеруются арабскими цифрами графы и (или) строки первой части таблицы.
Если повторяющийся в разных строках графы таблицы текст состоит из одного слова, то его после первого написания допускается заменять кавычками; если из двух и более слов, то при первом повторении его заменяют словами «То же», а далее — кавычками. Ставить кавычки вместо повторяющихся цифр, марок, знаков, математических и химических символов не допускается. Если цифровые или иные данные в какой-либо строке таблицы не приводят, то в ней ставят прочерк.
Цифровой материал, как правило, оформляют в виде таблиц. Пример оформления таблицы приведен на рисунке 1.
Таблица _______ _________________
номер название таблицы
Заголовки граф
Подзаголовки граф
Строки
(горизонтальные
ряды)
Боковик (графа для Графы (колонки)
заголовков)
Рисунок 1
Таблицы, за исключением таблиц приложений, следует нумеровать арабскими цифрами сквозной нумерацией.
Допускается нумеровать таблицы в пределах раздела. В этом случае номер таблицы состоит из номера раздела и порядкового номера таблицы, разделенных точкой (Приложение Л).
Таблицы каждого приложения обозначают отдельной нумерацией арабскими цифрами с добавлением перед цифрой обозначения приложения.
Если в записке одна таблица, то она должна быть обозначена «Таблица 1» или «Таблица В.1», если она приведена в приложении В.
Заголовки граф и строк таблицы следует писать с прописной буквы в единственном числе, а подзаголовки граф — со строчной буквы, если они составляют одно предложение с заголовком, или с прописной буквы, если они имеют самостоятельное значение. В конце заголовков и подзаголовков таблиц точки не ставят.
Таблицы слева, справа и снизу, как правило, ограничивают линиями. Допускается применять размер шрифта в таблице меньший, чем в тексте.
Разделять заголовки и подзаголовки боковика и граф диагональными линиями не допускается.
Горизонтальные и вертикальные линии, разграничивающие строки таблицы, допускается не проводить, если их отсутствие не затрудняет пользование таблицей.
Заголовки граф, как правило, записывают параллельно строкам таблицы. При необходимости допускается перпендикулярное расположение заголовков граф.
Головка таблицы должна быть отделена линией от остальной части таблицы.
Названия граф и строк в головке и боковике таблицы записываются в виде:
— слов и выражений, начинающихся с прописных букв;
— принятых буквенных условных обозначений величин, установленных ГОСТ 2.321-84;
— математических выражений;
— других обозначений, если они пояснены в тексте или приведены на иллюстрациях.
Названия последующих подграф и подстрок имеют аналогичное представление, но записываются со строчных букв, если их названия образуют одно предложение с заголовками граф (строк) предыдущего уровня, и с прописной буквы, если их названия представляют самостоятельные значения.
При написании заголовков к графам (строкам) допускаются сокращения слов. Запрещается деление элементов головки таблицы по диагонали. а также введение графы – «№ п/п».
Размерность физических величин указывается в таблице одним из следующих способов:
-если размерность одна на всю таблицу, то она указывается над таблицей справа;
— если размерность величина преимущественно одна и та же, то она указывается аналогично первому случаю. а в заголовках тех граф, которые имеют отличную размерность, указывается индивидуальная размерность величин после их названия через запятую;
— если размерность величин индивидуальна для каждой графы, то она указывается каждый раз после соответствующего заголовка через запятую;
— в боковике или головке таблицы может быть введена дополнительная графа (строка) или графа (колонка) с заголовком – «Единицы измерения», элементы которой заполняются названиями единиц измерений.
Заполне6ние таблицы ведется по всем назначенным в боковике и головке таблицы элементам разбиения. При отсутствии данных ставится прочерк.
Дробные числовые данные записываются только в десятичном виде. Исключение составляют размеры, выраженные в дюймах.
Для удобства чтения таблицы числовые данные в графах рекомендуется представлять с одинаковым число десятичных знаков и с выравниванием разрядов по вертикали.
При заполнении таблицы допускаются следующие упрощения:
— если имеется повторяющиеся данные в виде слова, то при повторах допускается заменять его значком » (кавычки). Указанное правило не распространяется на цифры, математические знаки, знаки процента и номера, обозначения марок материалов и типоразмеров изделий, обозначения нормативных документов;
— если имеется повторяющееся выражение (сочетание двух и более слов), то первый раз оно может быть заменено на сочетание «то же», а при последующих повторах – значком » (кавычки). Указанное правило также распространяется на повторяющиеся части фраз.
Ссылки на таблицу в тесте производятся по типу: первый раз – «(таблица 2.1)», при повторных ссылках – «(см. таблицу 2.1)».
studfiles.net
6.6 Таблицы
6.6.1 Таблицы применяют для лучшей наглядности и удобства сравнения показателей. Название таблицы должно отражать ее содержание, быть точным, кратким. Название таблицы следует помещать над таблицей слева в одну строку с ее номером через тире.
При переносе части таблицы название помещают только над первой частью таблицы, нижнюю горизонтальную черту, ограничивающую таблицу, не проводят.
Пример оформления таблиц приведен на рисунках 6.3, 6.4.
Таблица _____-________________________
номер название таблицы
Головка | }Заголовки граф }Подзаголовки граф Строки (горизонталь-ные ряды) | |||||
Боковик (графа Графа (колонки)
для заголовков)
Рисунок 6.3 – Структура таблицы.
Таблица 1.2 – ВАХ светоизлучающего диода VD1
Ток I, мА | 0 | 10 | 20 | 40 |
Напряжение U, В | 0 | 2.5 | 2.8 | 3 |
Рисунок 6.4 – Пример таблицы из двух строк.
6.6.2 Таблицу следует располагать в отчете непосредственно после текста, в котором она упоминается впервые, или на следующем листе.
6.6.3 На все таблицы должны быть ссылки в отчете. При ссылке следует писать слово «таблица» с указанием ее номера.
6.6.4 Таблицу с большим количеством строк допускается переносить на другой лист. При переносе части таблицы на другой лист над ней слева указывают «Продолжение таблицы» и номер этой таблицы.
Таблицу с большим количеством граф (колонок) допускается делить на части и помещать одну часть под другой в пределах одного листа. Если строки и графы таблицы выходят за формат листа, то в первом случае в каждой части таблицы повторяется головка, во втором случае — боковик.
Если в конце листа таблица прерывается и ее продолжение будет на следующем листе, в первой части таблицы нижнюю горизонтальную линию, ограничивающую таблицу, не проводят.
Таблицы с небольшим количеством граф допускается делить на части и помещать одну часть рядом с другой на одном листе, при этом повторяют головку таблицы.
Допускается помещать таблицу вдоль длинной стороны листа документа.
6.6.5 Если повторяющийся в разных строках графы таблицы текст состоит из одного слова, то его после первого написания допускается заменять кавычками; если из двух и более слов, то при первом повторении его заменяют словами «То же», а далее — кавычками. Ставить кавычки вместо повторяющихся цифр, марок, знаков, математических и химических символов не допускается. Если цифровые или иные данные в какой-либо строке таблицы не приводят, то в ней ставят прочерк.
Ограничительные слова «более», «не более», «менее», «не менее» и др. должны быть помещены в одной строке или графе таблицы с наименованием соответствующего показателя после обозначения его единицы физической величины, если они относятся ко всей строке или графе. При этом после наименования показателя перед ограничительными словами ставится запятая.
6.6.6 Таблицы следует нумеровать арабскими цифрами сквозной нумерацией.
Допускается нумеровать таблицы в пределах раздела. В этом случае номер таблицы состоит из номера раздела и порядкового номера таблицы, разделенных точкой.
Если в документе одна таблица, то она должна быть обозначена «Таблица 1».
6.6.7 Заголовки граф и строк таблицы следует писать с прописной буквы в единственном числе, а подзаголовки граф — со строчной буквы, если они составляют одно предложение с заголовком, или с прописной буквы, если они имеют самостоятельное значение. В конце заголовков и подзаголовков таблиц точки не ставят.
6.6.8 Допускается применять размер шрифта в таблице меньший, чем в тексте и одинарный межстрочный интервал.
Разделять заголовки и подзаголовки боковика и граф диагональными линиями не допускается.
Заголовки граф, как правило, записывают параллельно строкам таблицы. При необходимости допускается перпендикулярное расположение заголовков граф.
Головка таблицы должна быть отделена линией от остальной части таблицы.
Высота строк таблицы должна быть не менее 8 мм.
6.6.9 Оформление таблиц в отчете должно соответствовать ГОСТ 2.105.–95 “Единая система конструкторской документации. Общие требования к текстовым документам”.
studfiles.net
Делителемнатурального числаaназывают натуральное число, на котороеaделится без остатка. Число 12 имеет шесть делителей: 1, 2, 3, 4, 6 и 12. | |
Кратнымнатурального числаaназывают натуральное число, делится без остатка наa. Первые пять чисел, кратных 8: 8, 16,24, 32, 40. | |
Признаки делимости На 2 Если запись натурального числа оканчивается четной цифрой, то это число четно (делится без остатка на 2), а если запись числа оканчивается нечетной цифрой, то это число нечетно. На 3 Если сумма цифр числа делится на 3, то и число делится на 3. На 5 Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5. На 9 Если сумма цифр числа делится на 9, то и число делится на 9. На 10 Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10. | |
Число, делящееся только на 1 и само на себя – простое число. Число, имеющее более двух делителей – составное число. | |
Наибольшее натуральное число, на которое делятся без остатка числаaиb, называют наибольшим общим делителем этих чисел (НОД). Чтобы найти НОД нескольких натуральных чисел, надо: 1.)Разложить их на простые множители; 2.)Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел; 3.)Найти произведение оставшихся множителей. Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1. | |
Наименьшим общим кратным натуральных чиселaиbназывают наименьшее натуральное число, которое кратно иa, иb(НОК). Чтобы найти НОК нескольких натуральных чисел, надо: 1.)Разложить их на простые множители; 2.)Выписать множители, входящие в разложение одного из этих чисел; 3.)Добавить к ним недостающие множители из разложений остальных чисел; 4.)Найти произведение получившихся множителей. | |
| Основное свойство дроби Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. |
| Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби. |
60 = 2 · 2 · 3 · 5 168 = 2 · 2 · 2 · 3 · 7 Наименьший общий знаменатель: 2 · 2 · 2 · 3 · ·5 · 7 = 840 | Чтобы привести дроби к наименьшему общему знаменателю, надо: 1.)Найти НОК знаменателей этих дробей, оно и будет наименьшим общим знаменателем; 2.)Разделить наименьший общий знаменатель на знаменатели этих дробей, т. е. найти для каждой дроби дополнительный множитель; 3.)Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель. |
Чтобы сравнить (сложить, вычесть) дробис разными знаменателями, надо: 1.)Привести данные дроби к наименьшему общему знаменателю; 2.)Сравнить (сложить, вычесть) полученные дроби. | |
5 | Чтобы сложить смешанные числа, надо: 1.)Привести дробные части этих чисел к наименьшему общему знаменателю; 2.)Отдельно выполнить сложение целых частей и отдельно – дробных частей. Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить ее к полученной целой части. |
3 | Чтобы выполнить вычитание смешанных чисел, надо: 1.)Привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить ее в неправильную дробь, уменьшив на единицу целую часть; 2.)Отдельно выполнить вычитание целых частей и отдельно дробных частей. |
| Чтобы умножить дробь на натуральное число, надо ее числитель умножить это число, а знаменатель оставить без изменения. Чтобы умножить дробь на дробь, надо: 1.)Найти произведение числителей и произведение знаменателей этих дробей; 2.)Первое произведение записать числителем, а второе – знаменателем. Чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей. |
Чтобы найти дробь от числа, нужно умножить число на эту дробь. | |
| Два числа, произведение которых равно 1, называют взаимно обратными. |
| Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю. |
Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь. | |
| Частное двух чисел называют отношениемэтих чисел. Отношение показывает, во сколько раз первое число больше второго, или какую часть первое число составляет от второго. |
или a:b=c:d a·d=b·c | Равенство двух отношений называют пропорцией. Числа aиd–крайниечлены пропорции;bи с –средние В верной пропорции произведение крайних членов равно произведению средних. Если произведение крайних членов равно произведению средних членов пропорции, то пропорция верна. |
4 : 2 = 56 : 28 7 : 21 = 15 : 45 5 : 25 = 7 : 35 | Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз. Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны. |
Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз. Если две величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины. | |
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабомкарты. 1 : 100000 = | |
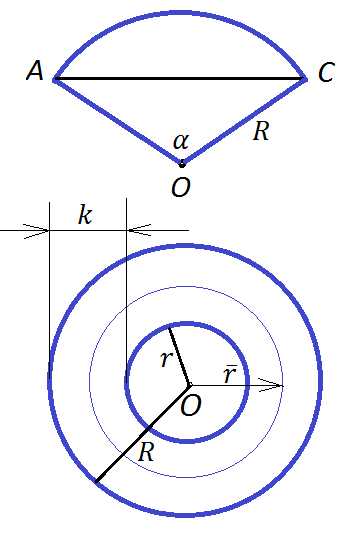
C = 2·π·r | Длина окружности r – радиус окружности π = 3,14 |
S = π·r2 | Площадь круга r – радиус окружности π = 3,14 |
Прямую, с выбранными на ней началом отсчета, единичным отрезком и направлением называют координатной прямой. Число, показывающее положение точки на прямой, называют координатойэтойточки. | |
2,6 и -2,6
| Два числа, отличающиеся друг от друга только знаками, называют противоположными числами. Натуральные числа, противоположные им числа и нуль называют целыми числами. |
Модулемчислаa(|a|) называют расстояние (в единичных отрезках) от начала координат до точки А (а). | |
– 8,7 + (– 3,5) = – (8,7 + 3,5) = – 12,2 | Чтобы сложить два отрицательных числа, надо: 1.)Сложить их модули; 2.)Поставить перед полученным числом знак –. |
6,1 + (– 4,2) = + (6,1 – 4,2) = 1,9 или 6,1 + (– 4,2) = 6,1 – 4,2 = 1,9 | Чтобы сложить два числа с разными знаками, надо: 1.)Из большего модуля слагаемых вычесть меньший; 2.)Поставить перед полученным числом знак того слагаемого, модуль которого больше. |
Если A(9) и В(– 5), то |AB|=9 – (– 5)= 14 | Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца. |
(–1,2)·0,3 = –(1,2·0,3) = –0,36 | Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным числом знак –. |
(–3,2)·( –9) = |–3,2|·|–9|=3,2·9=28,8 | Чтобы перемножить два отрицательных числа, надо перемножить их модули. |
(–12) : ( –4) = 12 : 4 = 3 | Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя. |
3,6 : (–3) = –(3,6:3) = –1,2 | При деление чисел с разными знаками, надо: 1.)Разделить модуль делимого на модуль делителя. 2.)Поставить перед полученным числом знак. |
x = | Число x, которое можно
записать в виде отношения |
16–(10–18+12) = 16+(–(10–18+12))=16+(–10+18–12) = 16–10+18–12=12 | Чтобы раскрыть скобки, перед которыми стоит знак –, надо заменить этот знак на +, поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки. |
0,3a·(–0,7b) = 0,3·a·(–0,7)·b = (0,3·(–0,7))·(a·b) = –0,21ab; –0,21 – коэффициент | Если выражение является произведением числа и одной или нескольких букв, то это число называют числовым коэффициентом(или просто коэффициентом). |
2m – 7m + 3m = m·(2–7+3) = –2m | Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми. Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть. |
Свойства уравнений 1.)Корни уравнения не изменяются, если обе части уравнения умножить или разделить на одно и то же число, не равное нулю. 2.)Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак. | |
Две прямые, образующие
при пересечении прямые углы, называют перпендикулярными ( | |
Две
непересекающиеся прямые на плоскости
называют параллельными ( Если две прямые в плоскости перпендикулярны третьей прямой, то они параллельны. Через каждую точку плоскости, не лежащую на данной прямой можно провести только одну прямую, параллельную данной прямой. | |
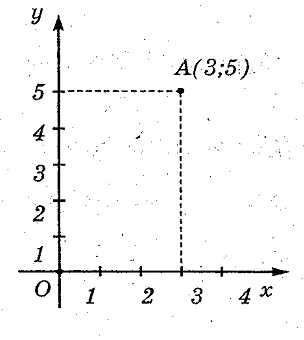
|
О – начало координат, x –ось абсцисс, y –ось ординат (3;5) – координаты точки А |
studfiles.net
06_ТАБЛИЦА_6 — это… Что такое 06_ТАБЛИЦА_6?
ДИНОЗАВРЫ — (Dinosauria), самая многочисл. группа вымерших пресмыкающихся подкласса архозавров. Дл. от 20 см до 30 м. Известны из триаса мела всех материков, кроме Антарктиды, в СССР осн. находки гл. обр. на терр. Казахстана и Ср. Азии. Доминировали в… … Биологический энциклопедический словарь
МЕЗОЗОЙ — мезозойская эра (от мезо… и греч. zoe жизнь), вторая эра фанерозоя. Следует за палеозоем, предшествует кайнозою. Начало по абс. исчислению 230±10 млн. лет, конец 66±3 млн. лет назад, длительность ок. 165 млн. лет. Включает триас, юру, мел.… … Биологический энциклопедический словарь
МЕЛОВОЙ ПЕРИОД — мел (назван по обилию писчего мела в отложениях этого возраста), третий период мезозоя. Следует за юрой, предшествует палеогену. Начало по абс. исчислению 136±5 млн. лет, конец 66±3 млн. лет назад, длительность ок. 70 млн. лет. В начале М. п.… … Биологический энциклопедический словарь
ОРНИТОМИМЫ — (Ornithomimus), род вымерших пресмыкающихся подотр.теропод. Известны из верхнего мела Сев. Америки. Дл. до 5 м. Беззубые животные с удлинённым черепом и роговым клювом. Шея и передние конечности удлинённые, кисть хватательного типа. 1 й палец… … Биологический энциклопедический словарь
ПАЛЕОГЕНОВЫЙ ПЕРИОД — палеоген (от палео… и греч. genos рождение, возраст), первый период кайнозоя. Следует за мелом, предшествует неогену. Включает палеоцен, эоцен, олигоцен. Начало по абс. исчислению 60±3 млн. лет, конец 25 ±2 млн. лет назад, длительность 41 ±2… … Биологический энциклопедический словарь
РОГАТЫЕ ДИНОЗАВРЫ — цератопсы (Ceratopsia), подотряд вымерших пресмыкающихся отр. птицетазовых динозавров. Известны из верхнего мела Сев. и Юж. Америки и Азии. Дл. до 6 м. Череп, как правило, с рогами непарным передним и 1 2 парами надглазничных. Задний край… … Биологический энциклопедический словарь
ФЕНАКОДУСЫ — (Phenacodus), род вымерших млекопитающих отр. кондилартр. Известны из нижнего эоцена Сев. Америки и Зап. Европы. Размеры средние с тапира; хвост длинный. По общему виду ф. были похожи скорее на хищных, чем на копытных. Передние конечности… … Биологический энциклопедический словарь
ЦЕЛУРОЗАВРЫ — (Coelurosauria), группа (инфраотряд) вымерших пресмыкающихся подотр. теропод. Известны из среднего триаса мела. Дл. от 25 см до 6 м. Череп небольшой, обычно низкий. Зубы у большинства мелкие, клыки слабо выражены или не дифференцированы; известны … Биологический энциклопедический словарь
dic.academic.ru

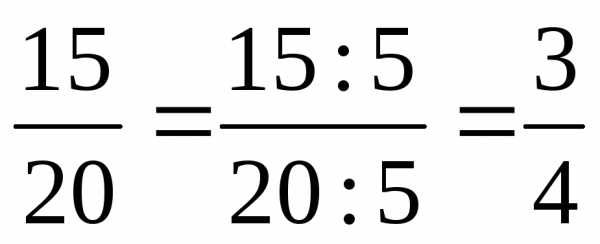
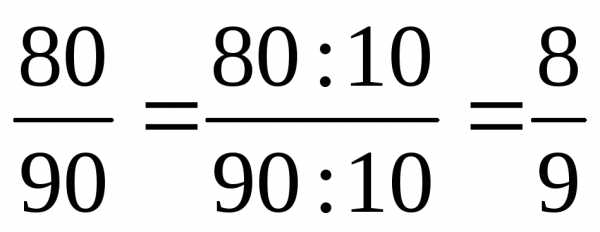
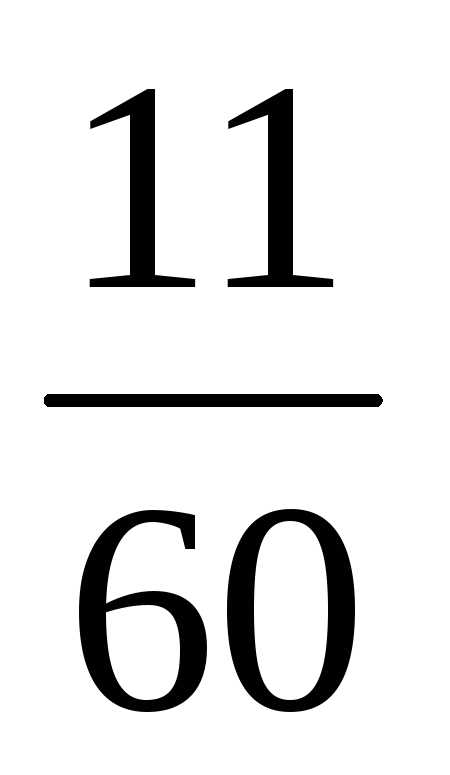 и
и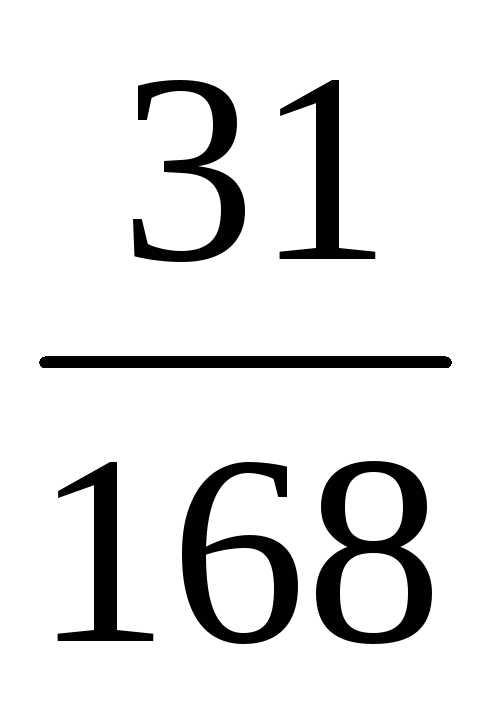
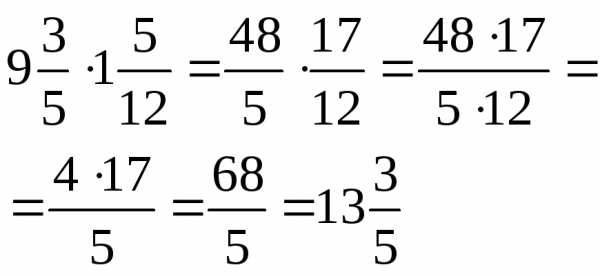
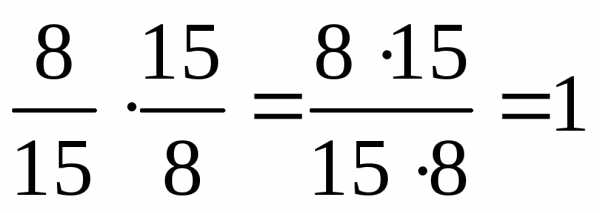
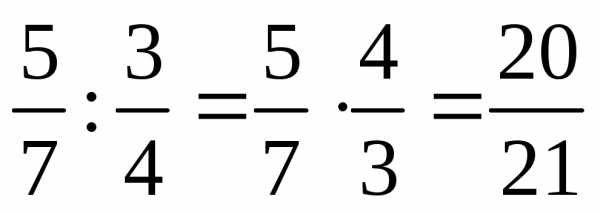
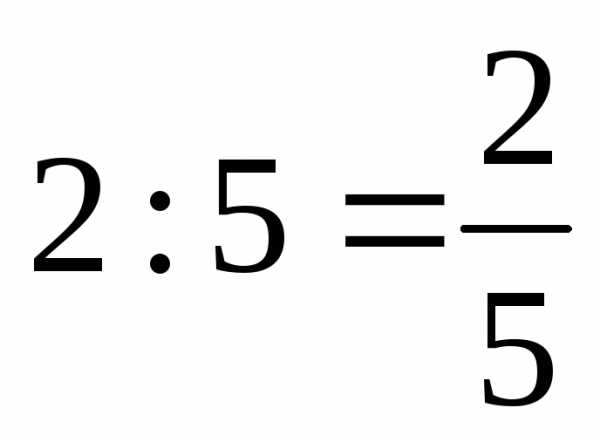
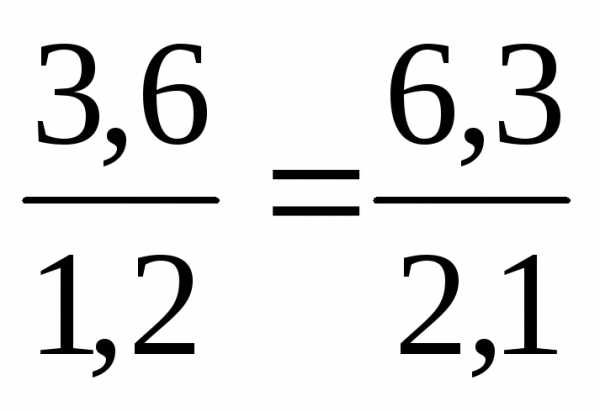
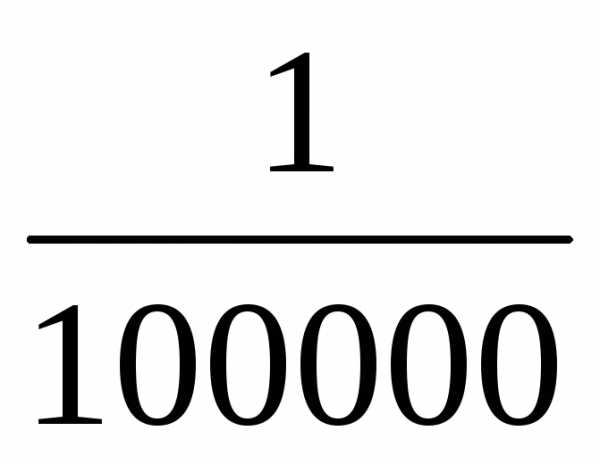 – карта выполнена в масштабе одна
стотысячная
– карта выполнена в масштабе одна
стотысячная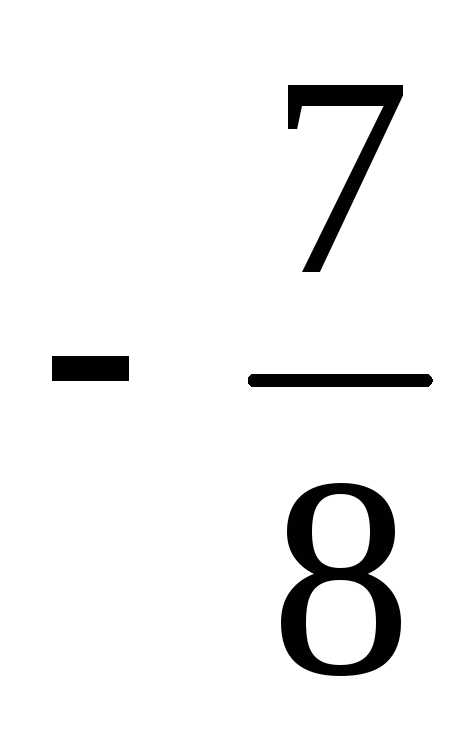 и
и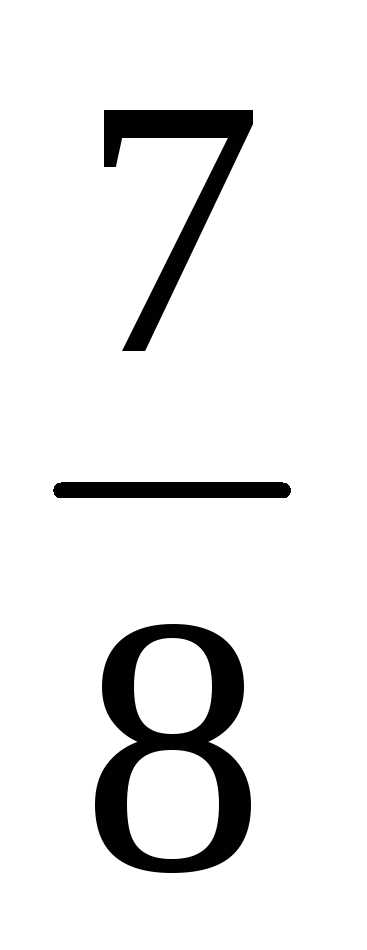
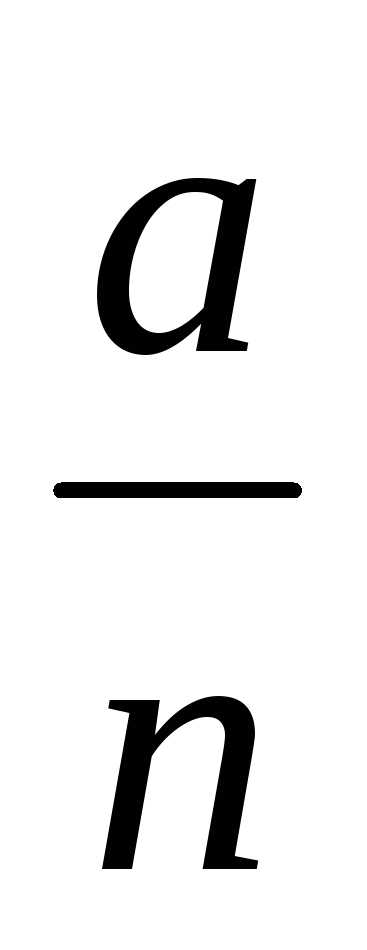
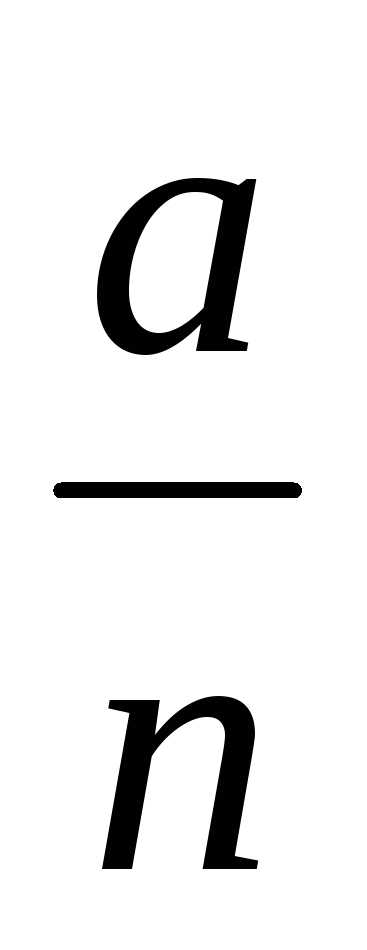 ,
гдеa– целое число, а n
– натуральное число, называютрациональным числом.
,
гдеa– целое число, а n
– натуральное число, называютрациональным числом.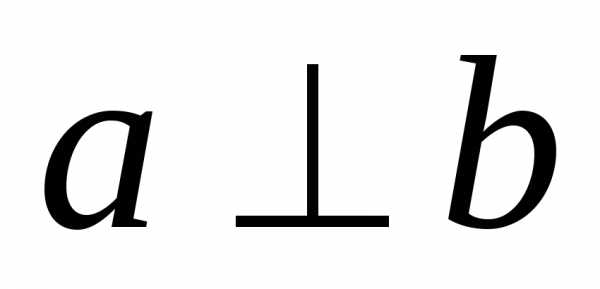 ).
).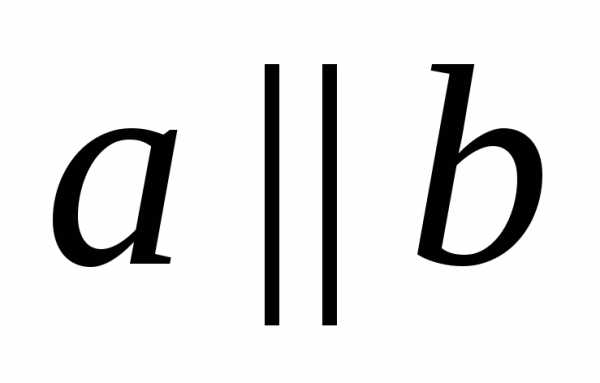 ).
).
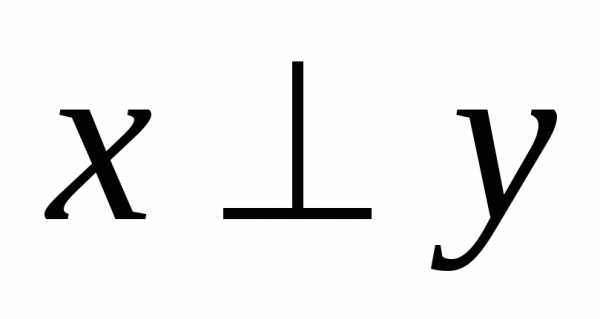 –система координат на плоскости
–система координат на плоскости



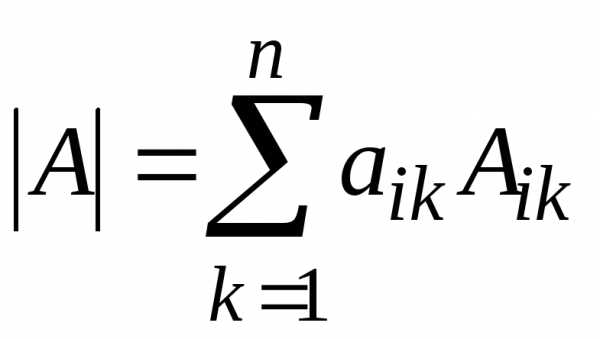 ,
где Аik алгебраические дополнения к
,
где Аik алгебраические дополнения к 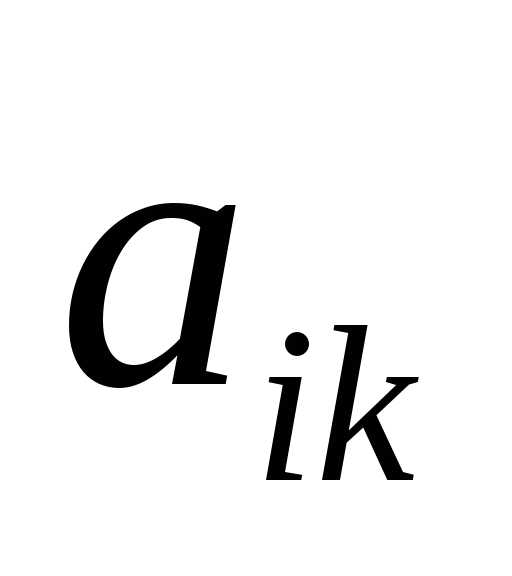 (разложение определителя поi-ой
строке). Либо
(разложение определителя поi-ой
строке). Либо 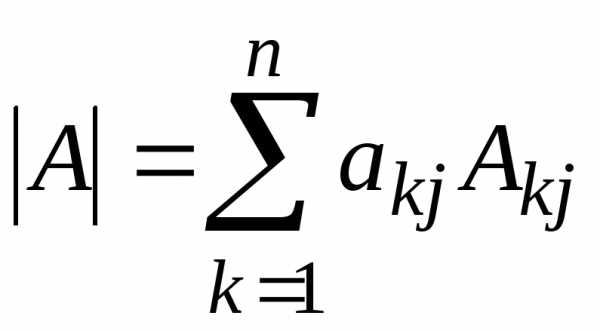 (разложение поj-тому
столбцу).
(разложение поj-тому
столбцу).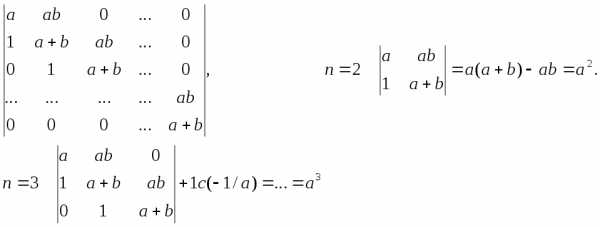 .
.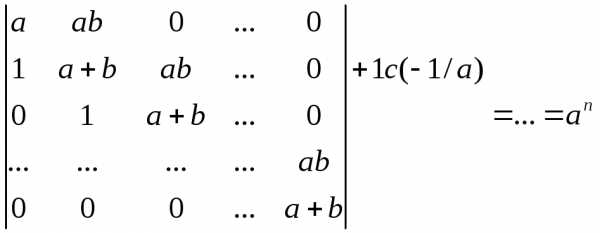 .
. называетсяприсоединенной, ее элементами являются алгебраические
дополнения
называетсяприсоединенной, ее элементами являются алгебраические
дополнения  транспонированной матрицы
транспонированной матрицы .
.
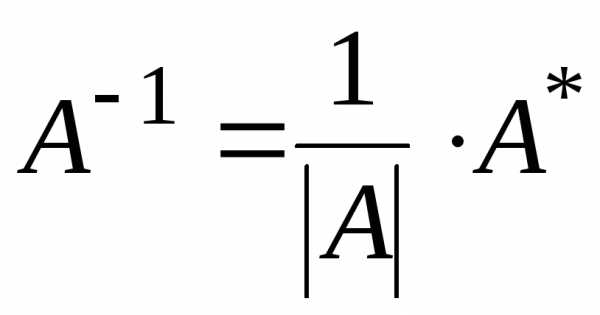 ,
где
,
где  .
.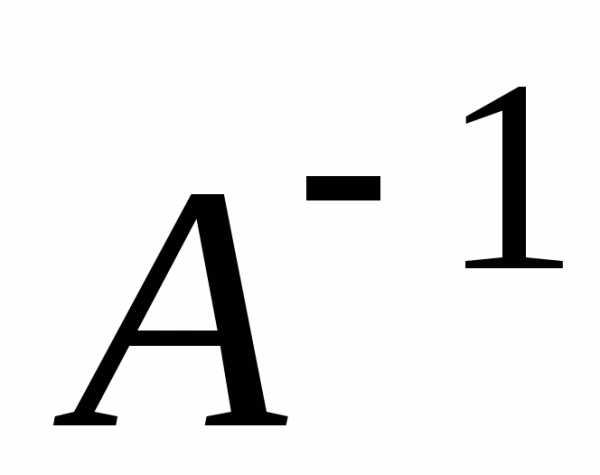 .
.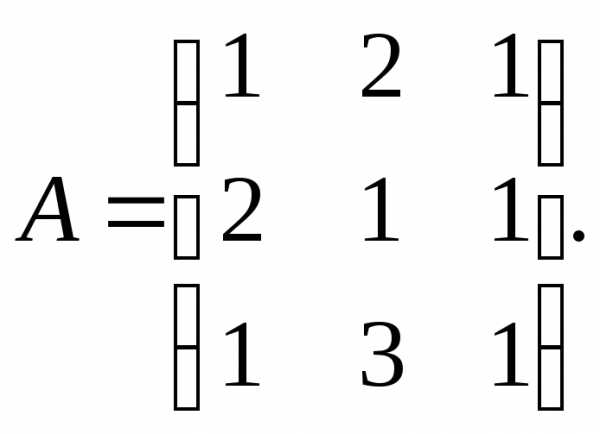

 .
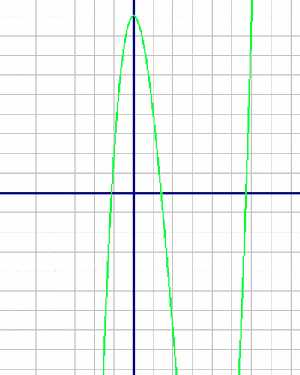
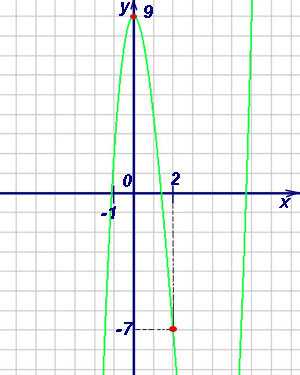
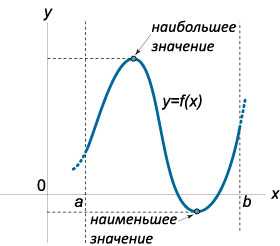
. В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.
В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.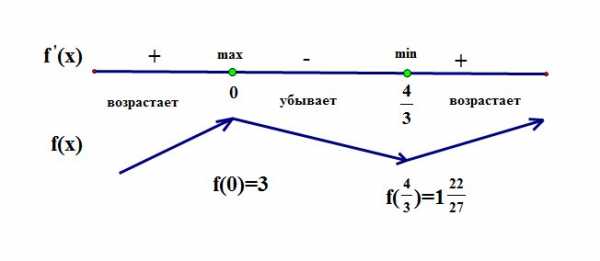

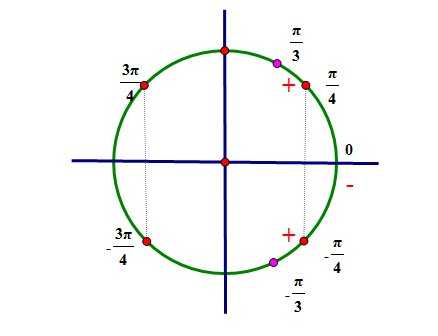
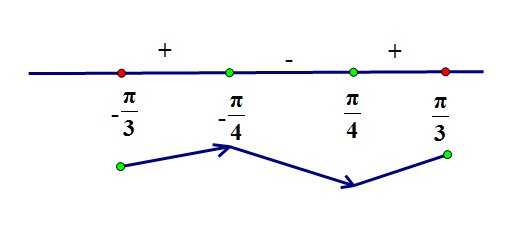

 Друзья, добрый день!
Друзья, добрый день!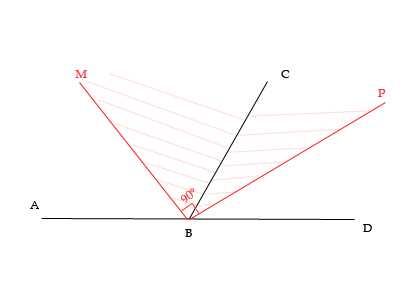 Приступая к изучению, первоначально определяют, что такое угол в планиметрии.
Приступая к изучению, первоначально определяют, что такое угол в планиметрии. Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.
Какой угол называется развернутым, было представлено выше. Определимся с понятием прямого.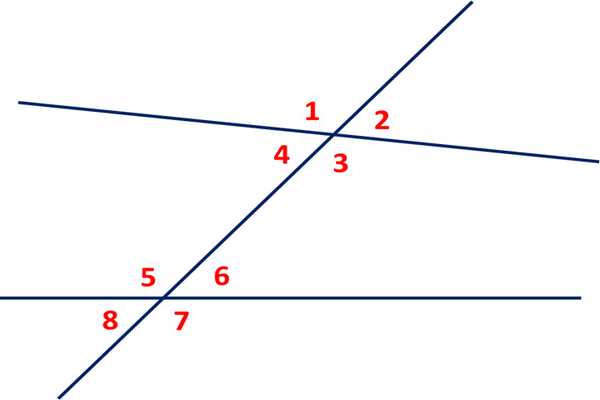




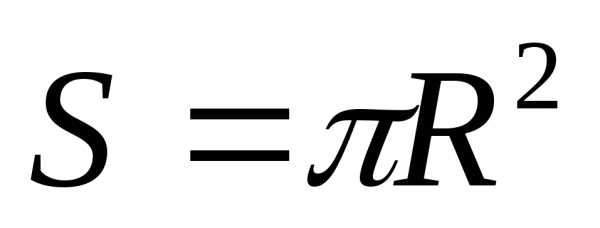


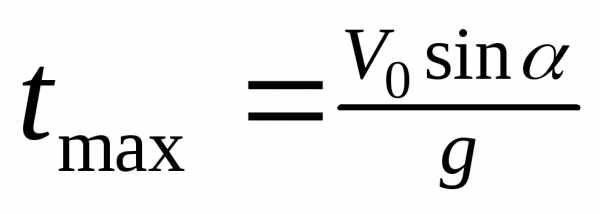
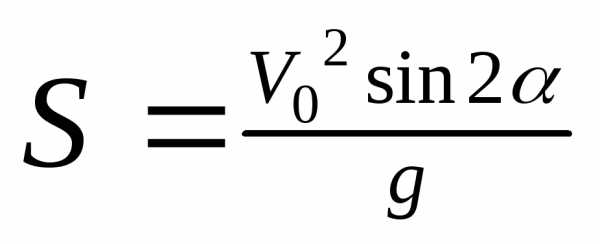
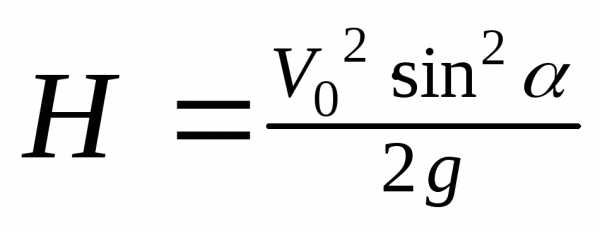

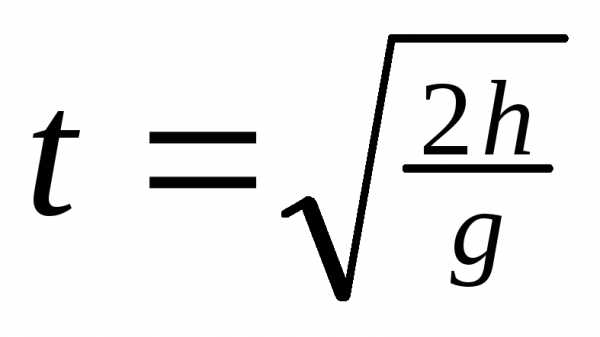 ;
; Динамика.
Динамика.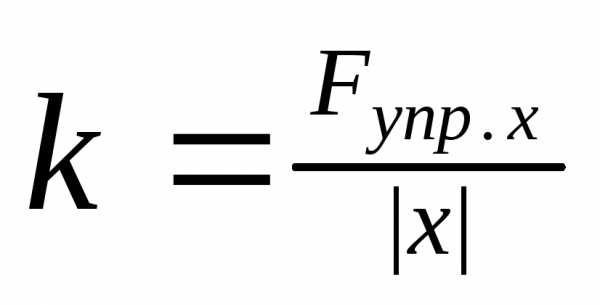
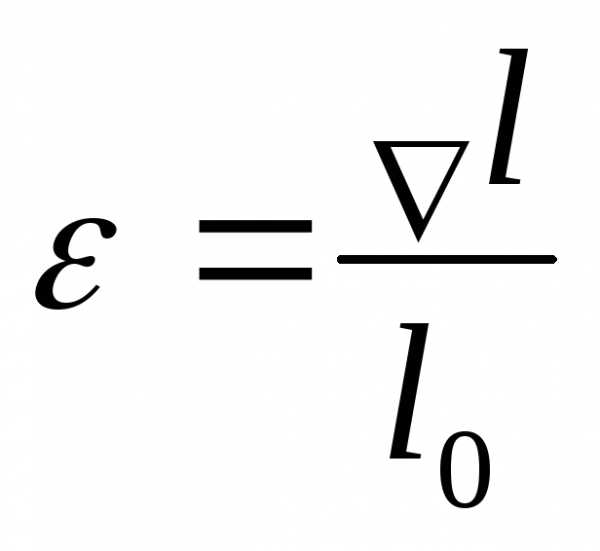

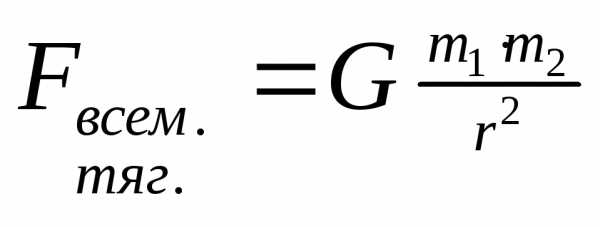
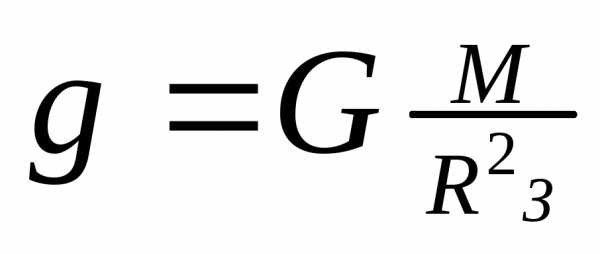
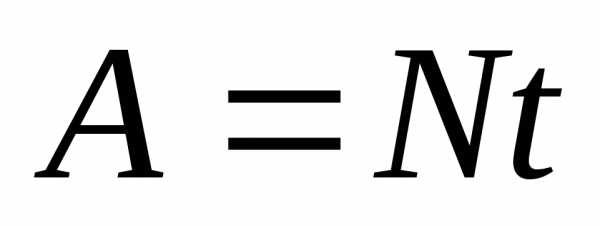
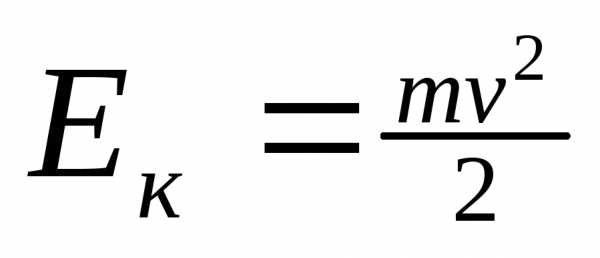 ;
;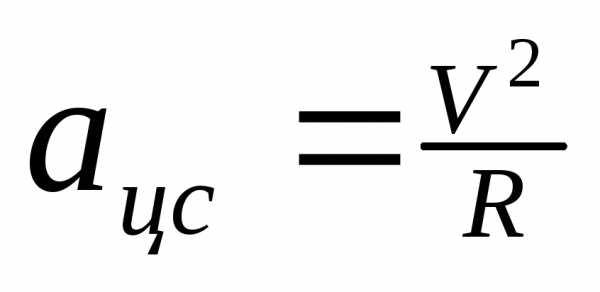 ;
; 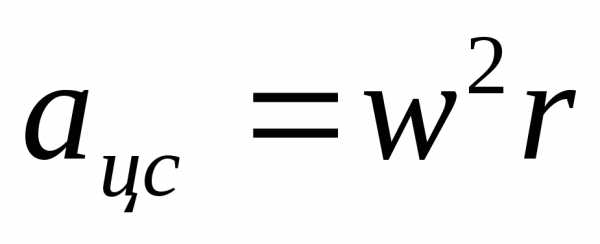

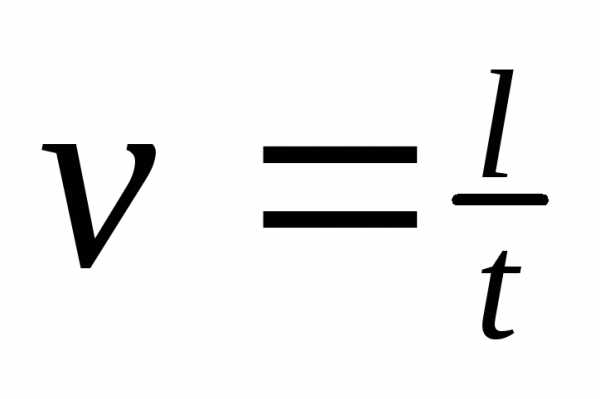 ;
; 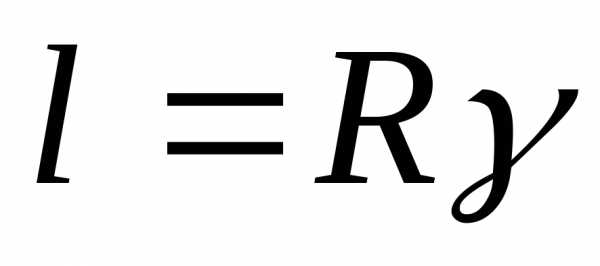 ;
;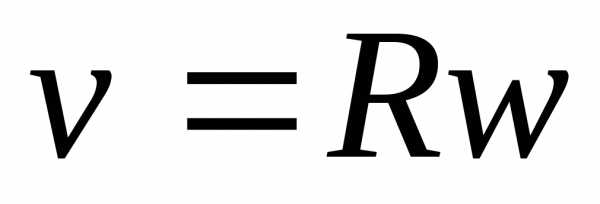
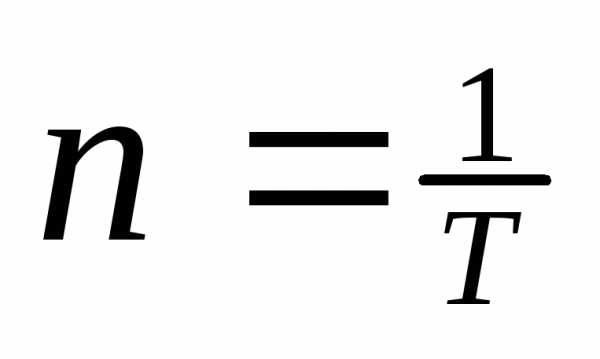 ;
; 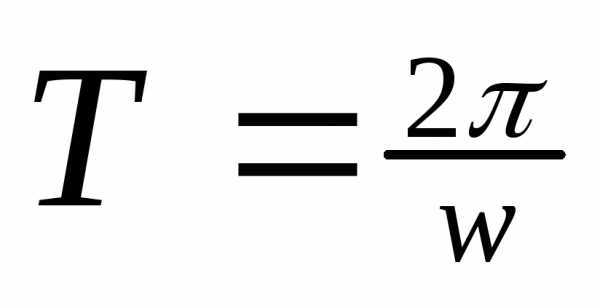 ;
;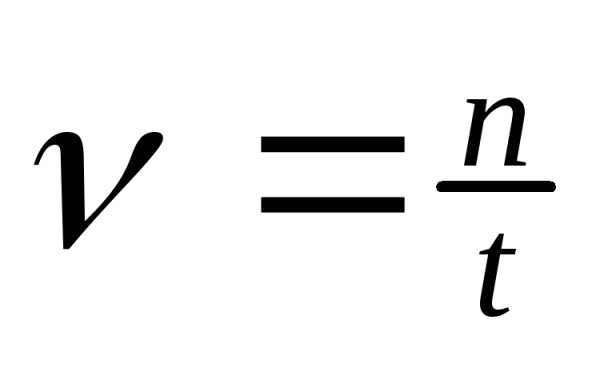 ;
; —
частота [1/с = 1 Гц]
—
частота [1/с = 1 Гц] —
угол.
—
угол.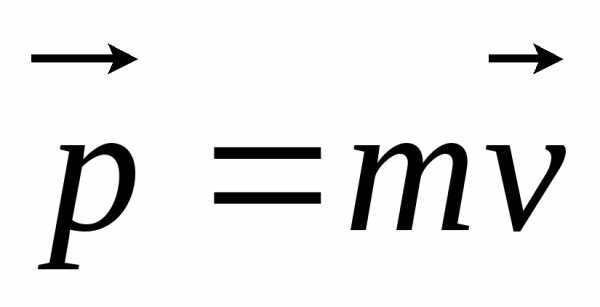 ;
;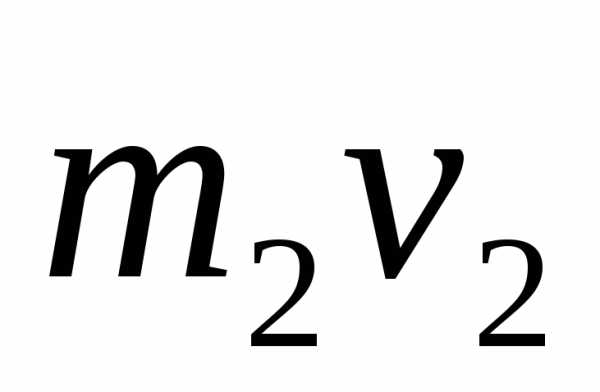 —
импульс газов
—
импульс газов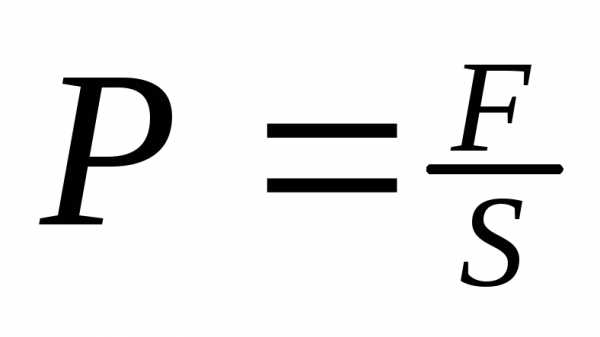 ;
F
– сила давления
;
F
– сила давления ]
] ;
; 
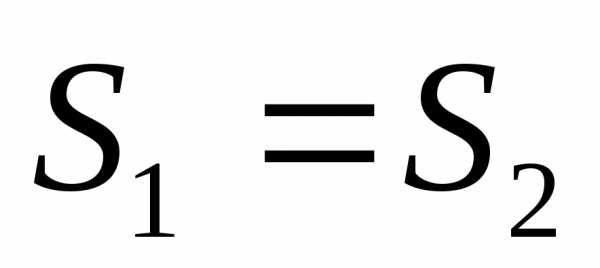 ;
; 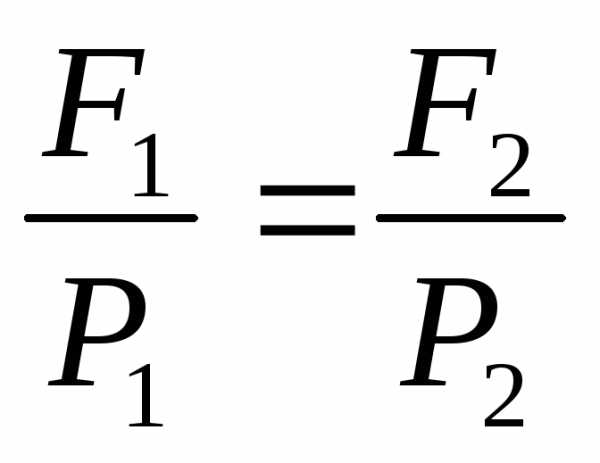
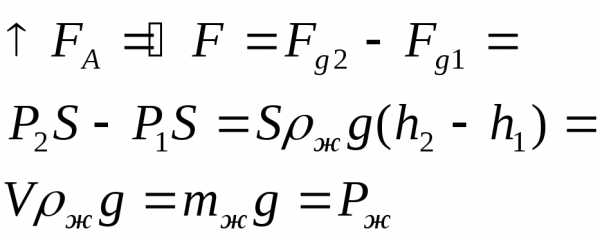 /
/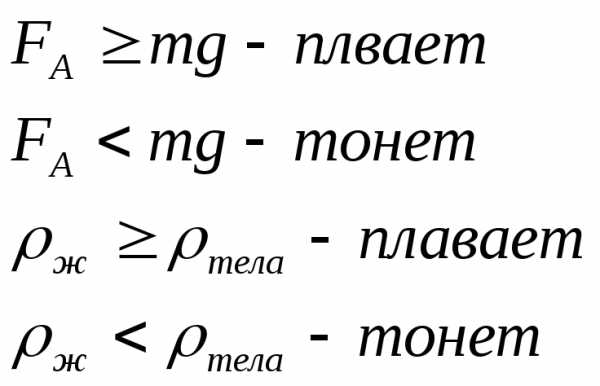

 — напряженность
— напряженность
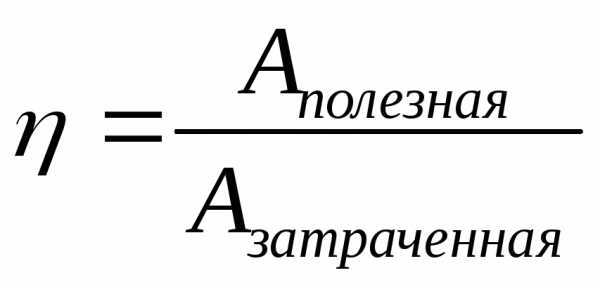
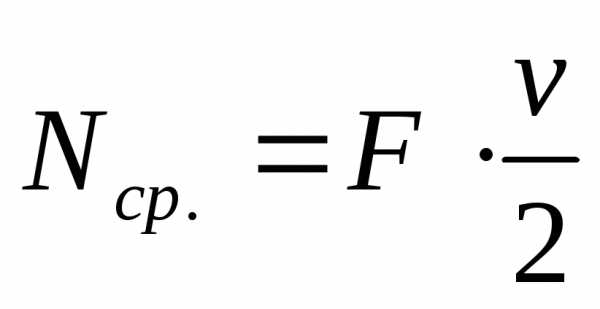 ;
[1дж/1с = 1 Вт]
;
[1дж/1с = 1 Вт] ;l
– длинна маятника
;l
– длинна маятника
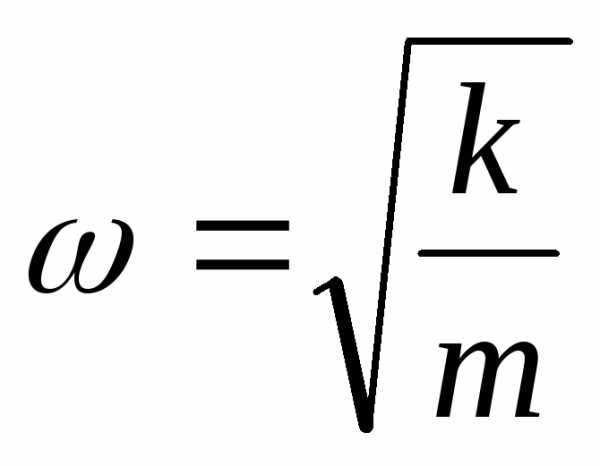 ;
; 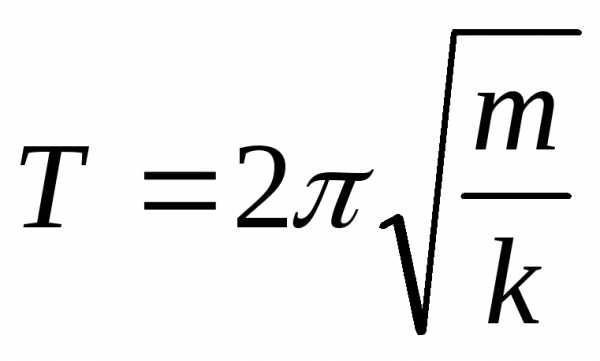
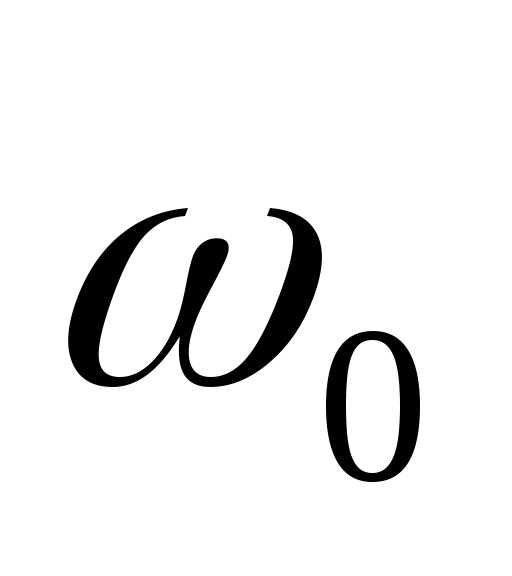 —
циклическая частота колебаний
—
циклическая частота колебаний —
угловая скорость
—
угловая скорость —
угол поворота
—
угол поворота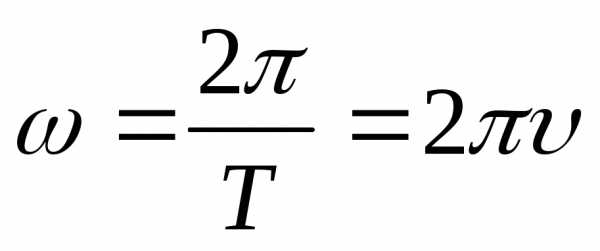
 ;
; 

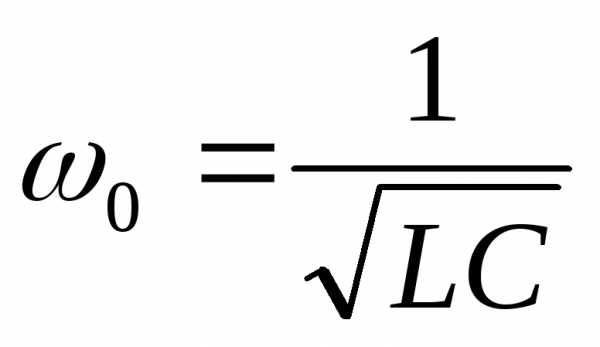 ;
;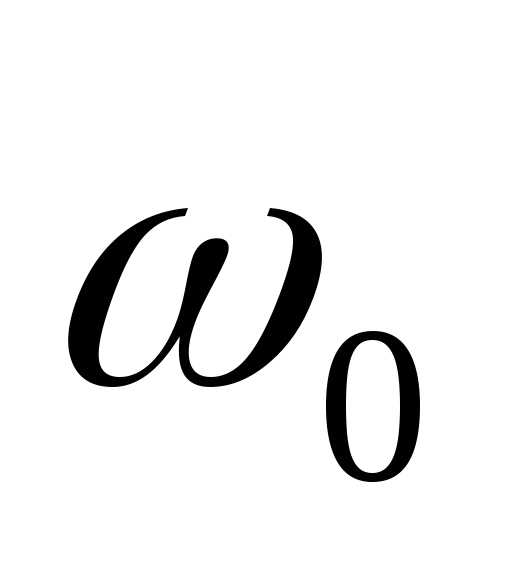 —
собственна частота колебаний в контуре
—
собственна частота колебаний в контуре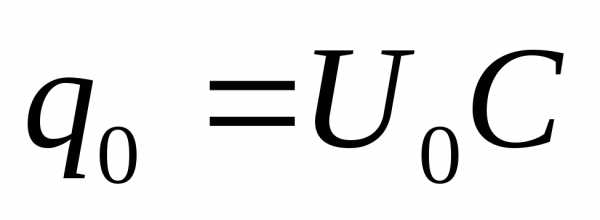 ;
; 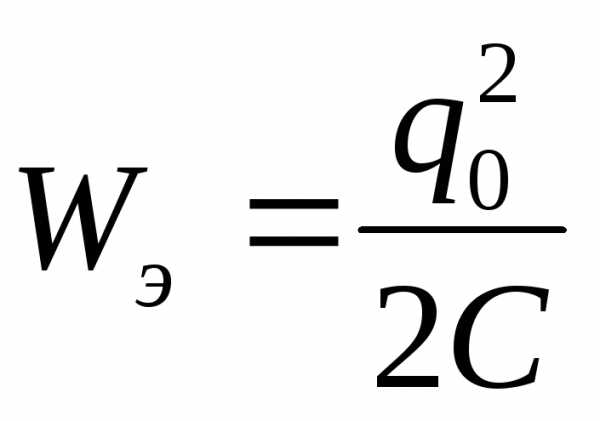
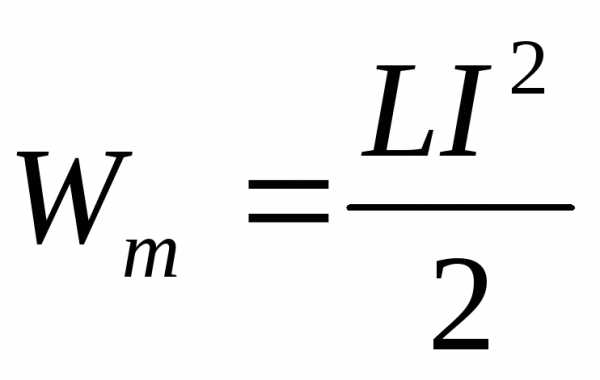 ;
;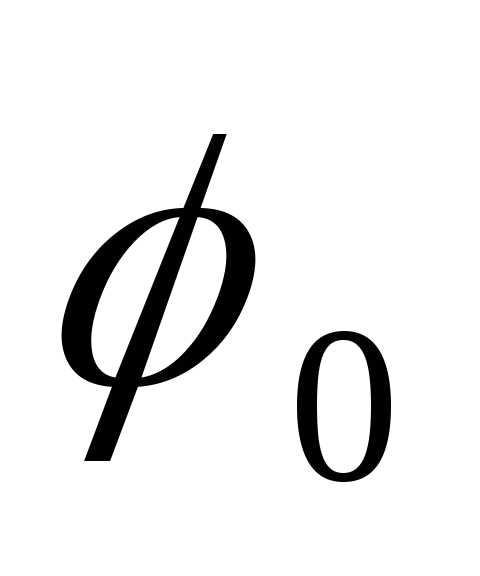 —
фаза
колебаний
—
фаза
колебаний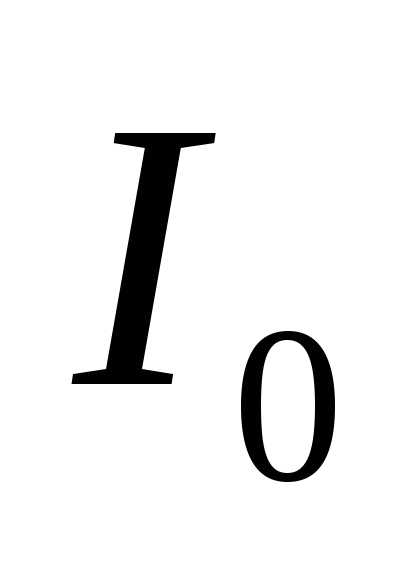 —
амплитуда тока
—
амплитуда тока
 ;
;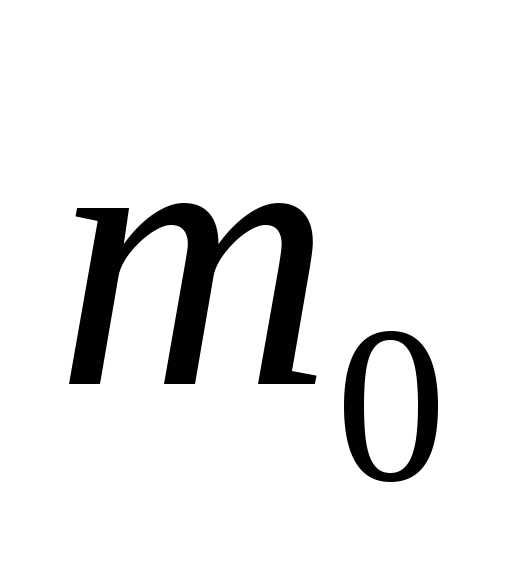 —
масса молекулы
—
масса молекулы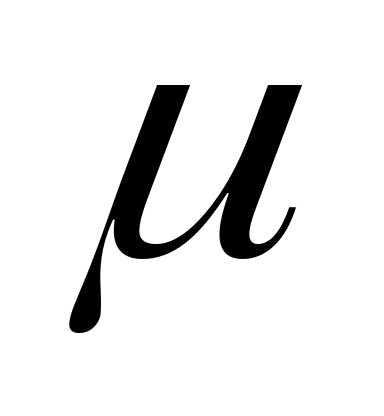 —
молярная масса
—
молярная масса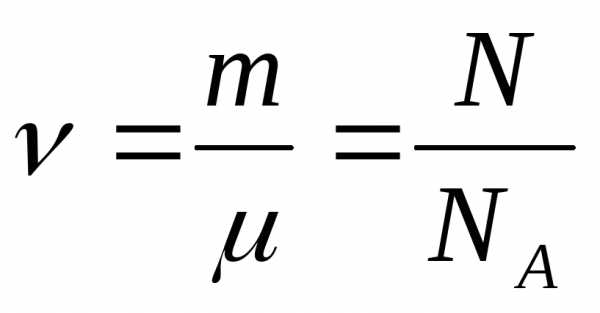 ; N –
число молекул.
; N –
число молекул.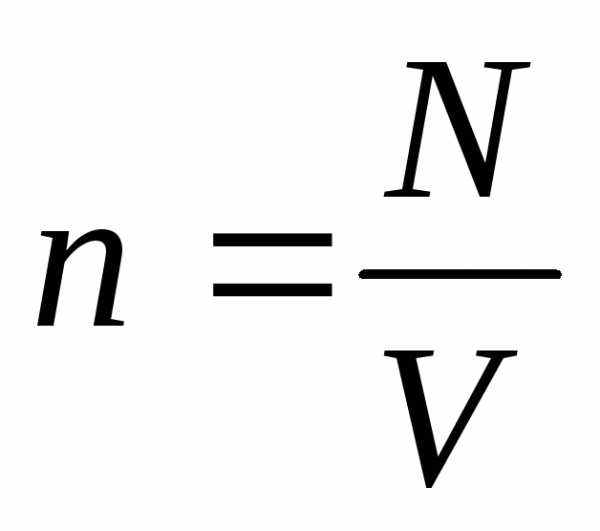
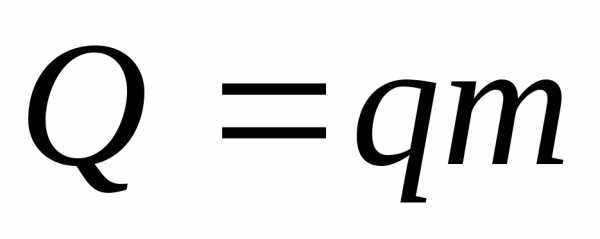
 —
кооф. линейного расширен.
—
кооф. линейного расширен.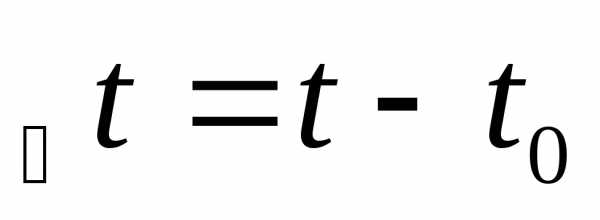 —
интервал температур.
—
интервал температур. —
кооф. объемного расш. тел.
—
кооф. объемного расш. тел.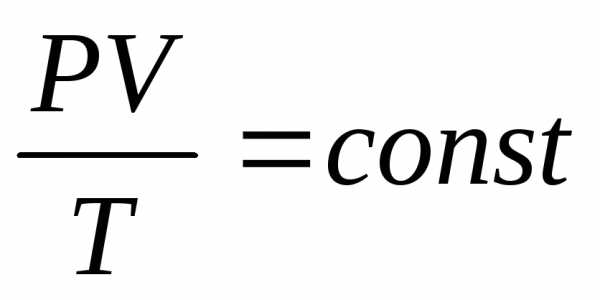
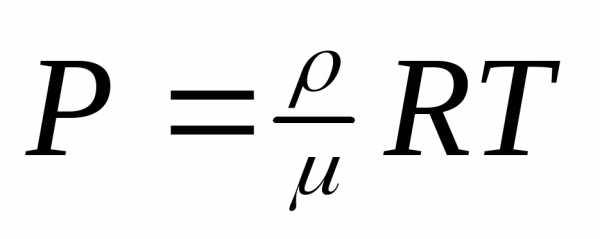
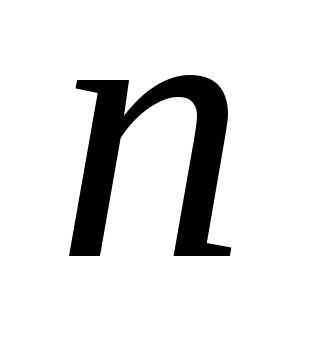 —
концентрация молекул
—
концентрация молекул =
8.31 Дж/моль*К
=
8.31 Дж/моль*К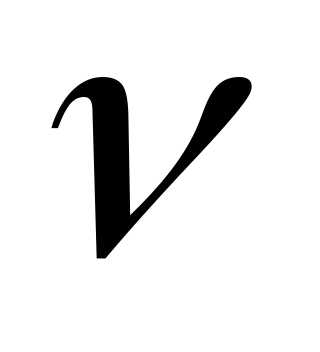 —
кол-во в-ва.
—
кол-во в-ва.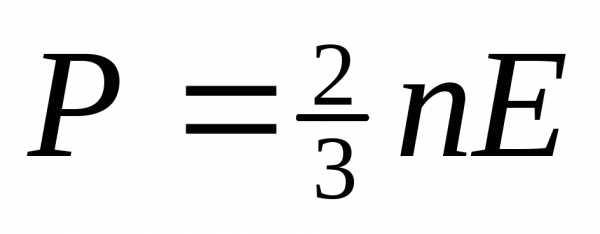 ;
; 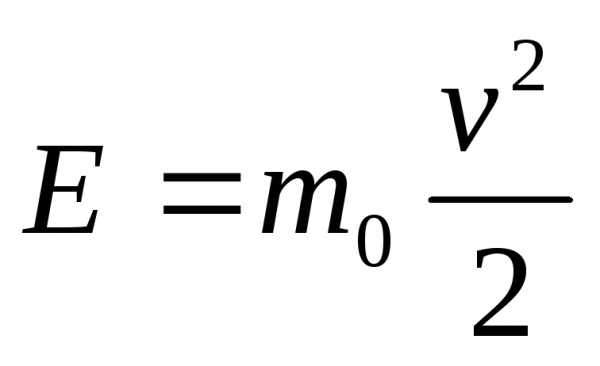
 ;
; 

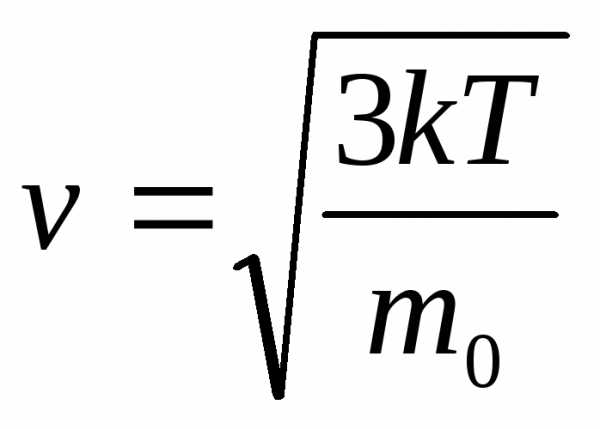
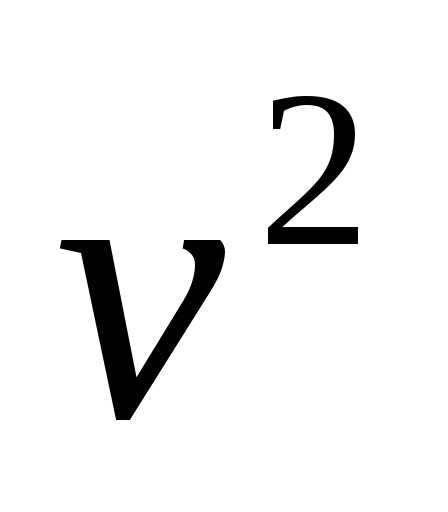 —
среднеквадратичная ск-ть
—
среднеквадратичная ск-ть —
средняя кинетич. энергия движ. мол-лы.
—
средняя кинетич. энергия движ. мол-лы. —
кол-во теплоты, получ. рабочим телом от
нагрев.
—
кол-во теплоты, получ. рабочим телом от
нагрев.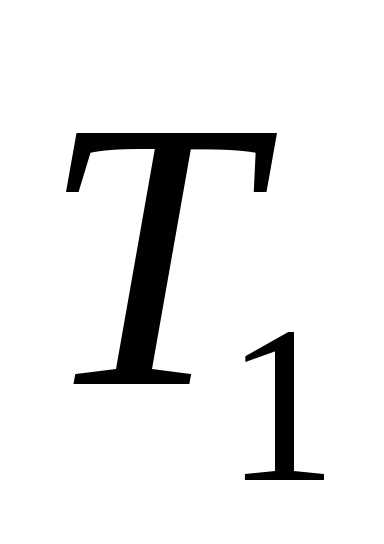 —
t
холод.
—
t
холод.
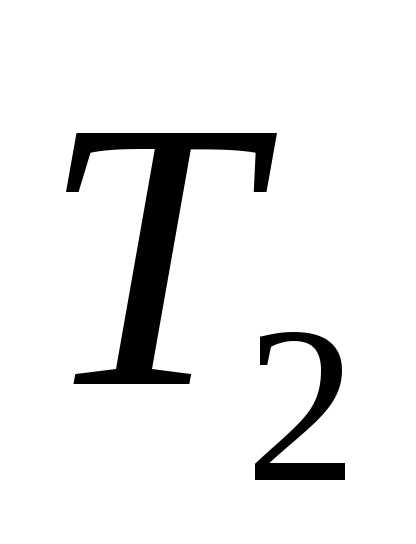 —
нагреват.
—
нагреват.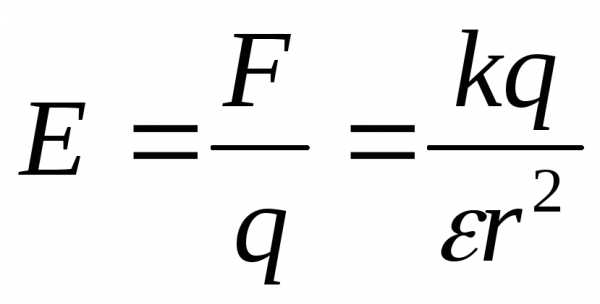 [В/м]
;
[В/м]
; 

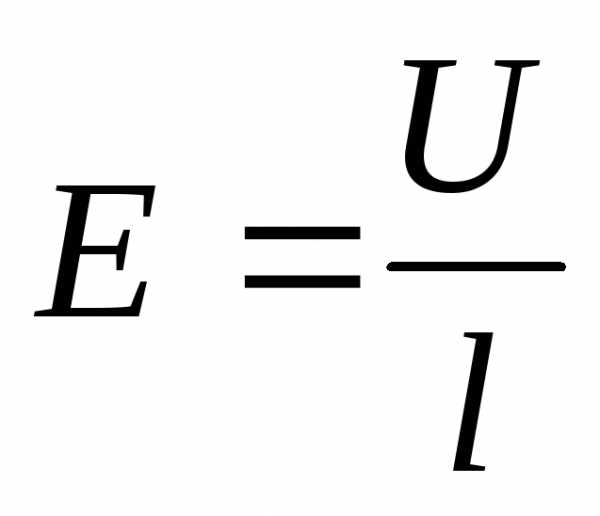 ;
; 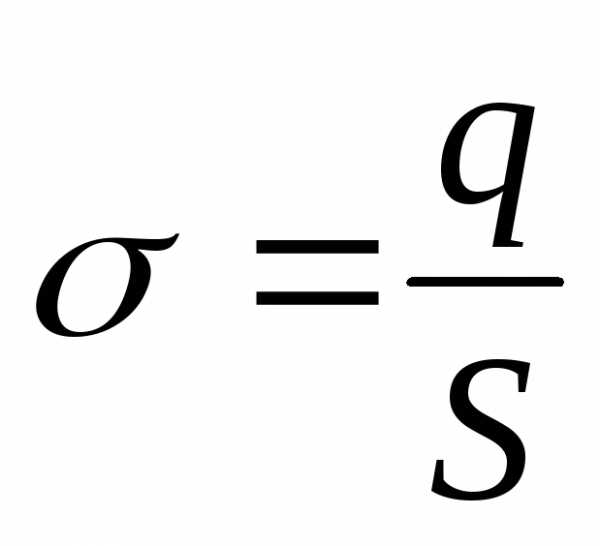
 —
поверхностная плотность заряда
—
поверхностная плотность заряда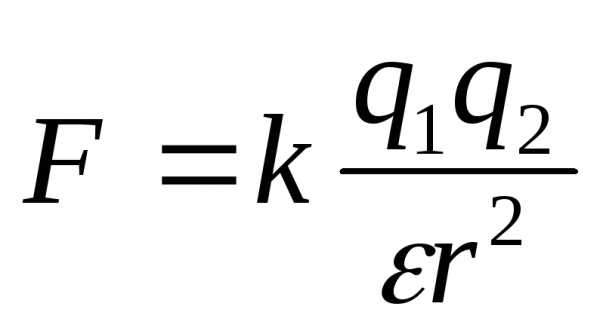 ;
[Н]
;
[Н]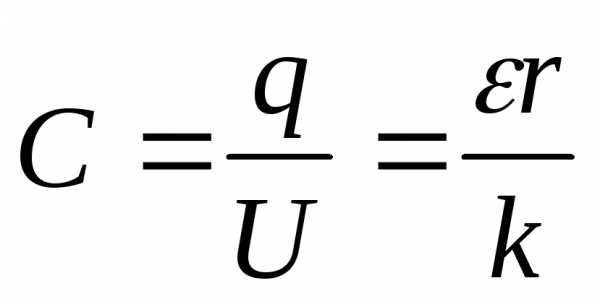
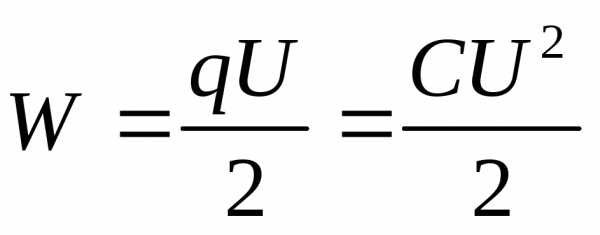 [Дж]
[Дж]
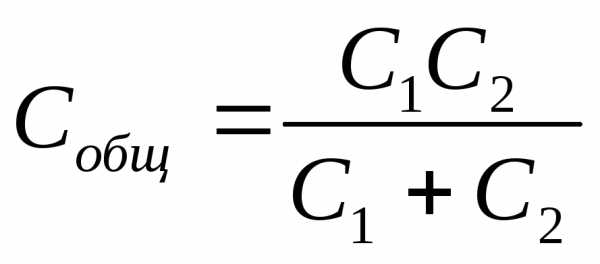
 ;
; 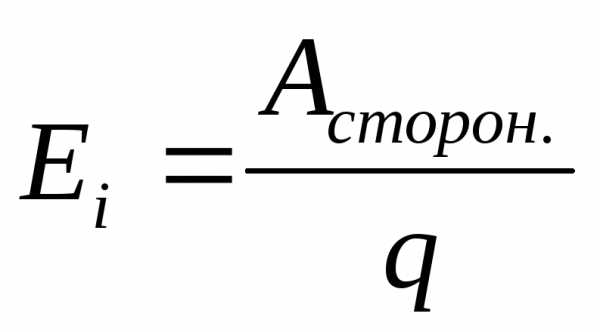
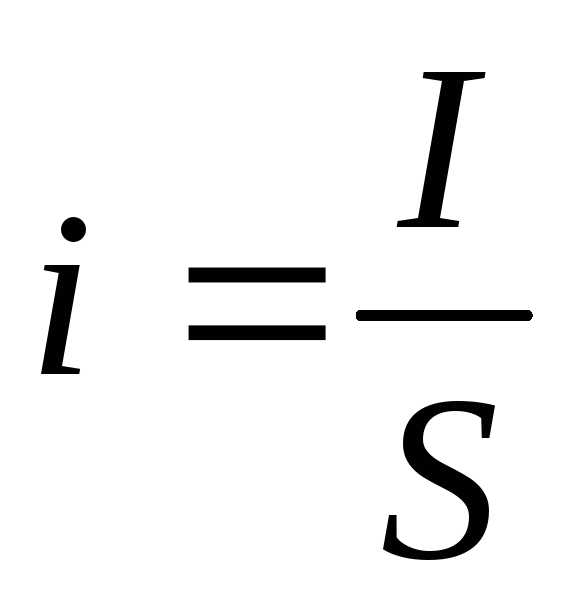 ;
i
– плотность тока
;
i
– плотность тока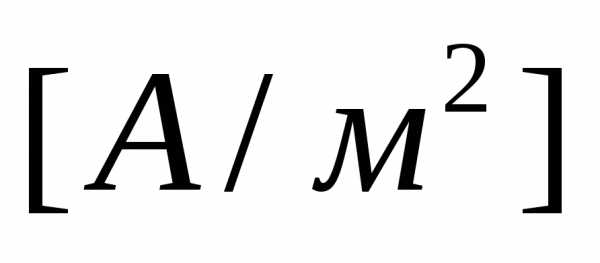
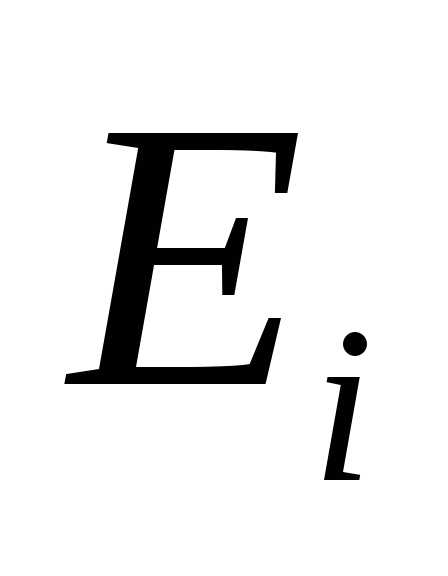 —
Электродвиж. сила
—
Электродвиж. сила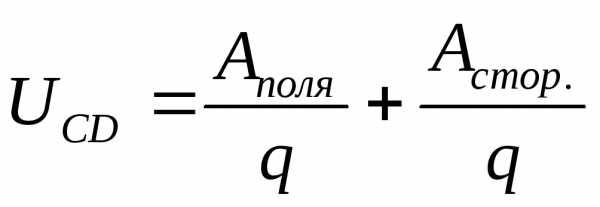 [В]
[В] —
работа, совершенная сторонними силами
—
работа, совершенная сторонними силами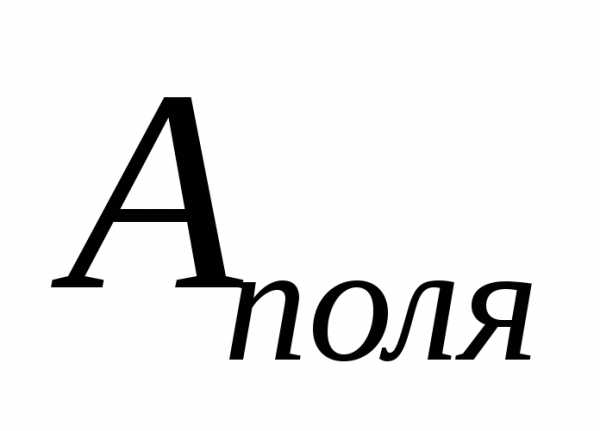 —
сила эл. поля
—
сила эл. поля
 ;
;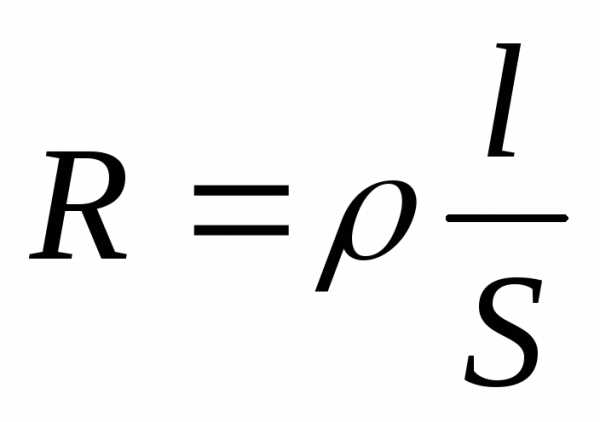
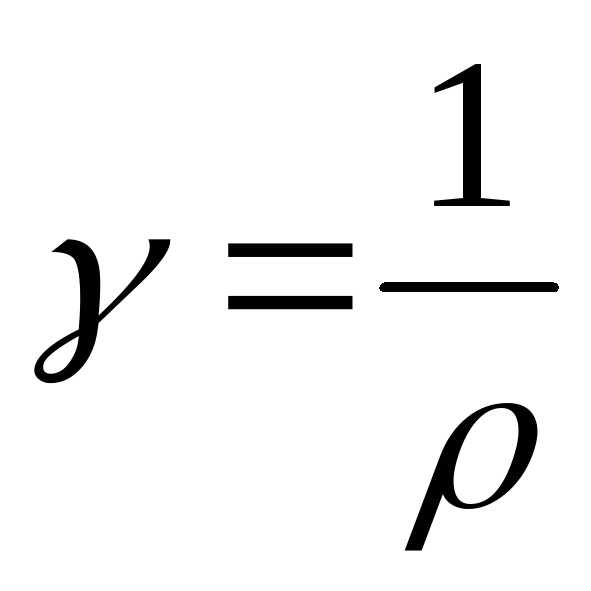 ;
; —
удельная проводимость.
—
удельная проводимость. —
температурный кооф. сопр.
—
температурный кооф. сопр. —
удельное сопротивление
—
удельное сопротивление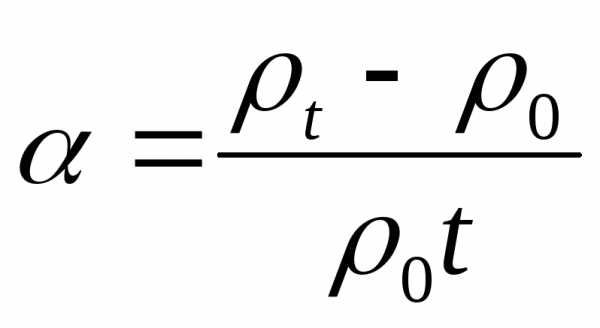 [1 град.
^ -1]
[1 град.
^ -1]
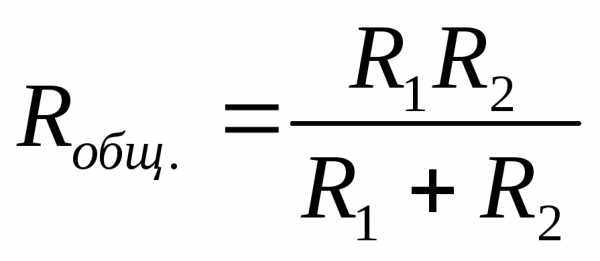
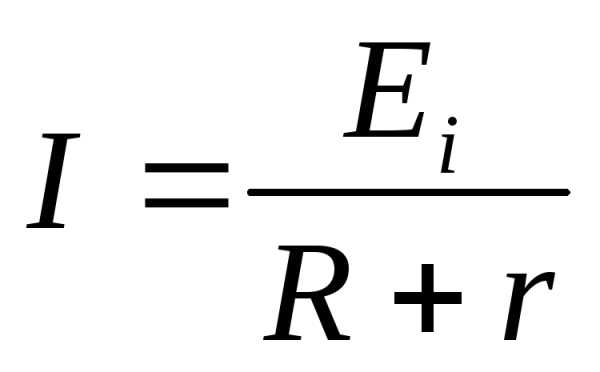
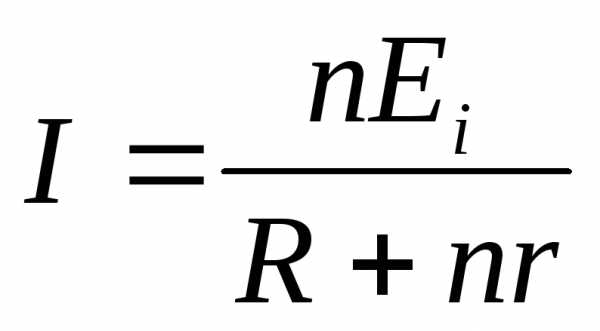 ;
; 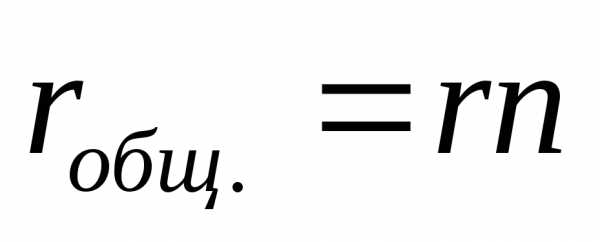
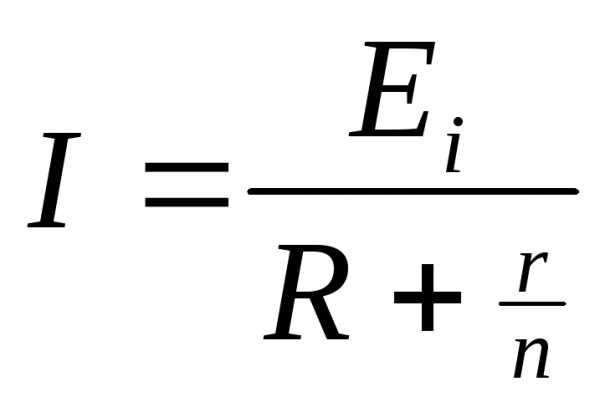 ;
; 
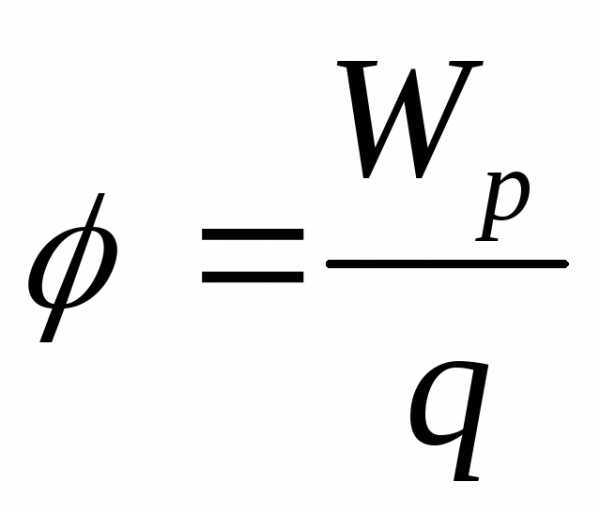 ;
; 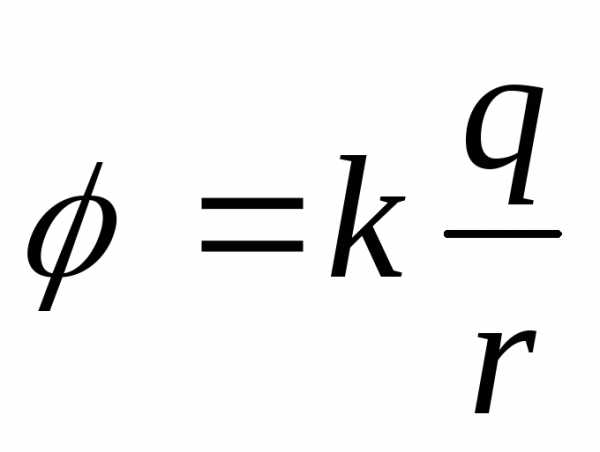
 — потенциал эл. поля
— потенциал эл. поля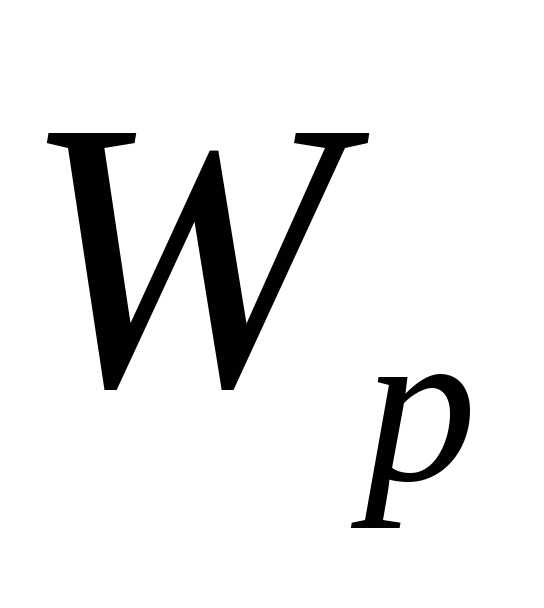 —
потенциальная энергия заряда в поле.
—
потенциальная энергия заряда в поле.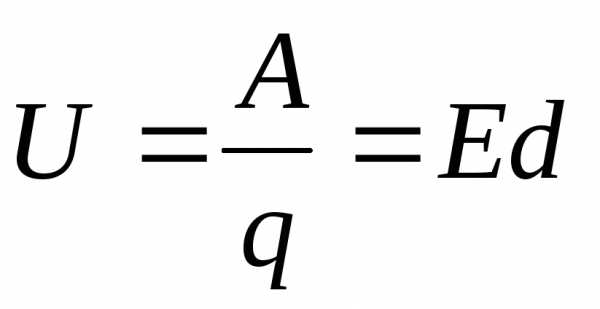
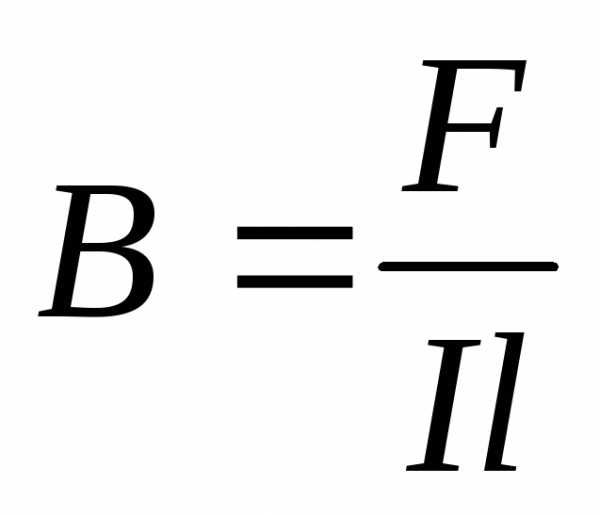 ;
; 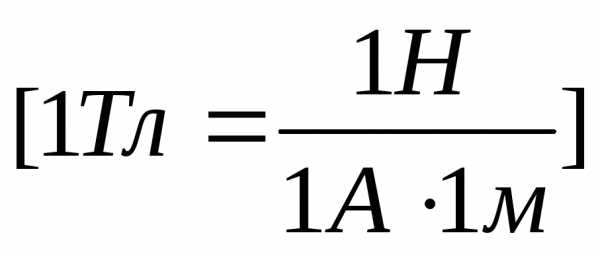


 ;
;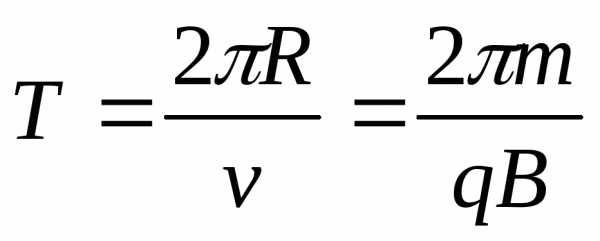
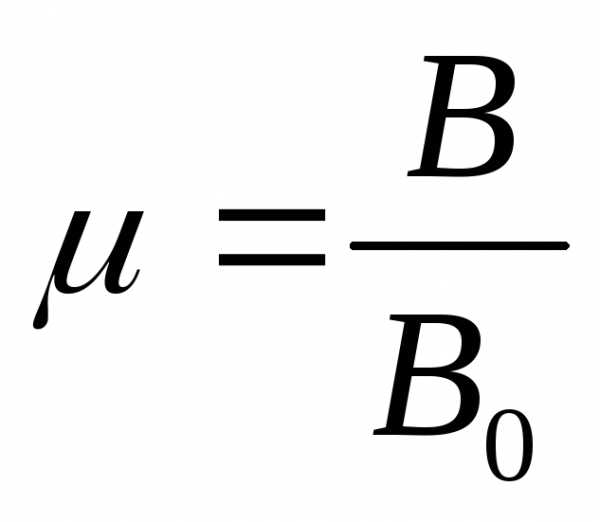 ;
;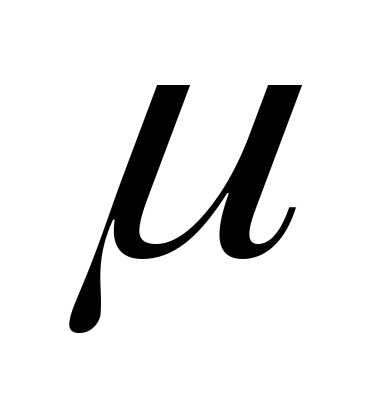 — магнитная
прониц. среды
— магнитная
прониц. среды ;
; 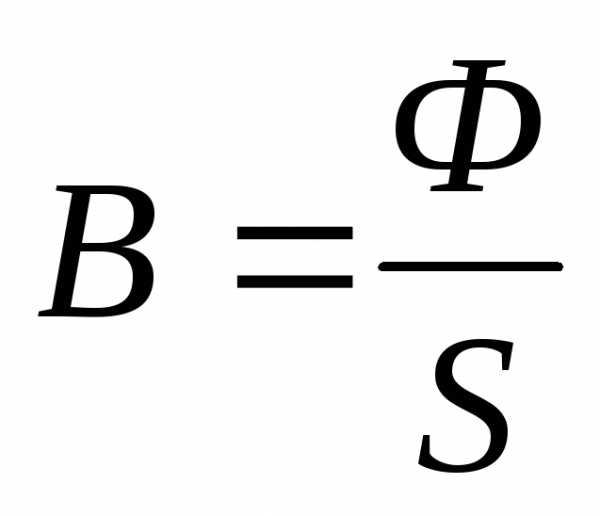
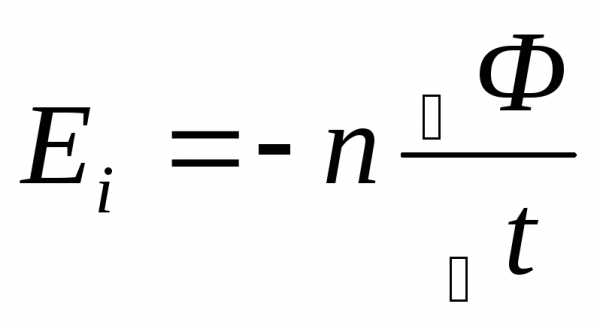 ;
; 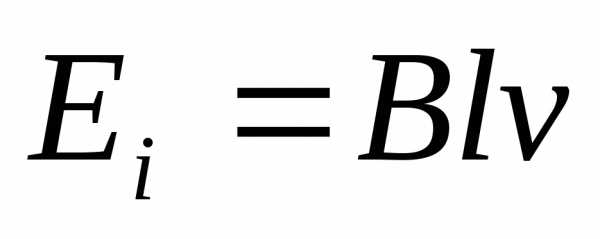
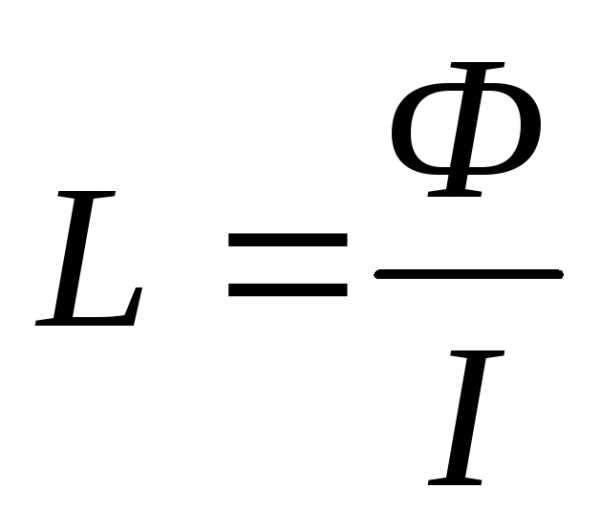 [Гн]
[Гн]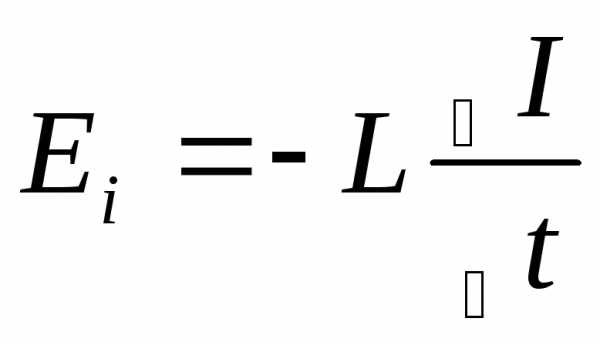 ;
; 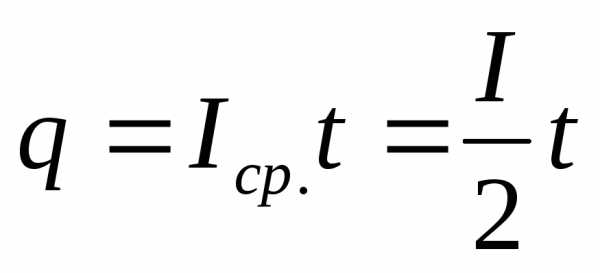
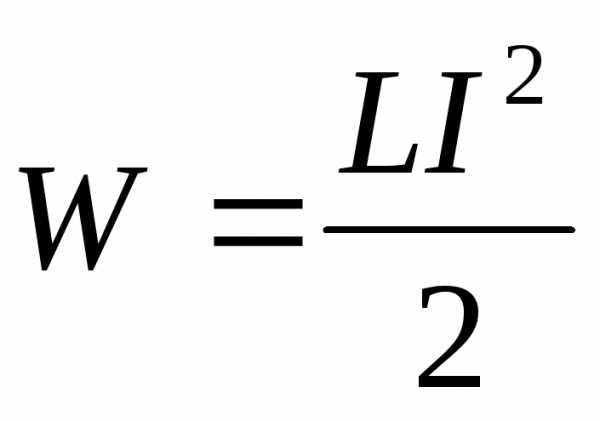 ;
W — энергия
;
W — энергия ;
; 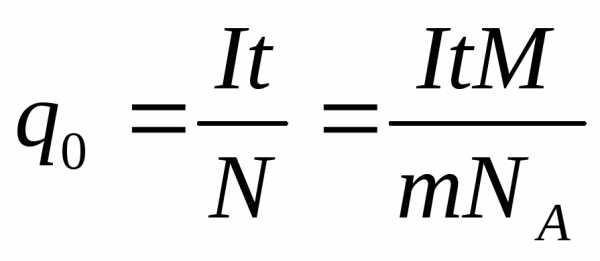
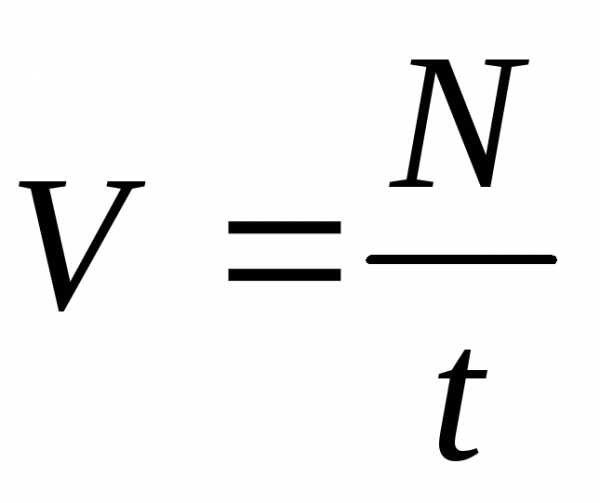
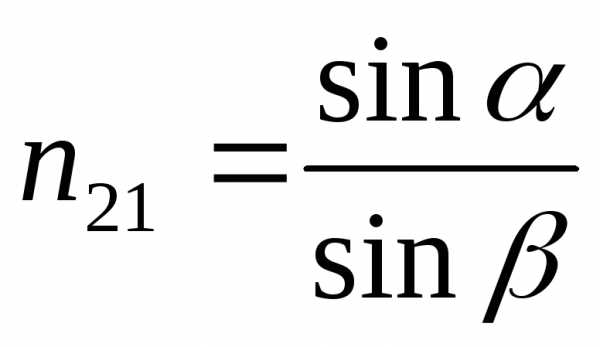 ;
; 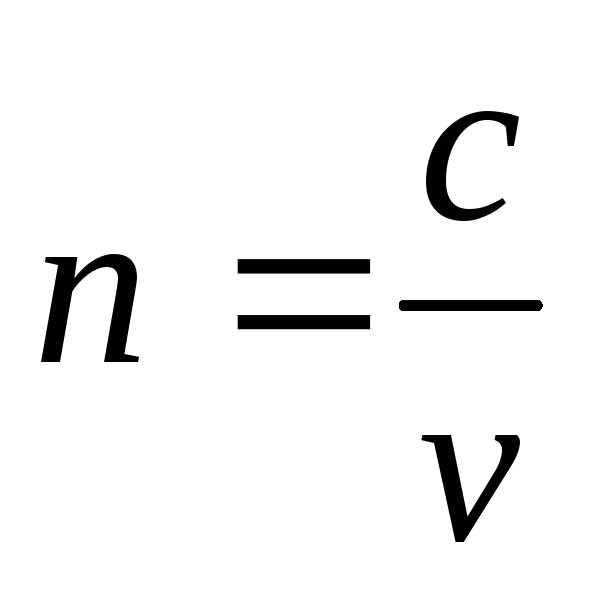 —
ваакум
—
ваакум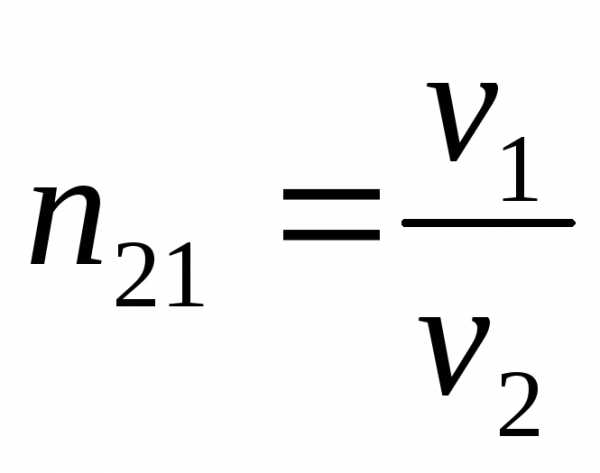 ;
; 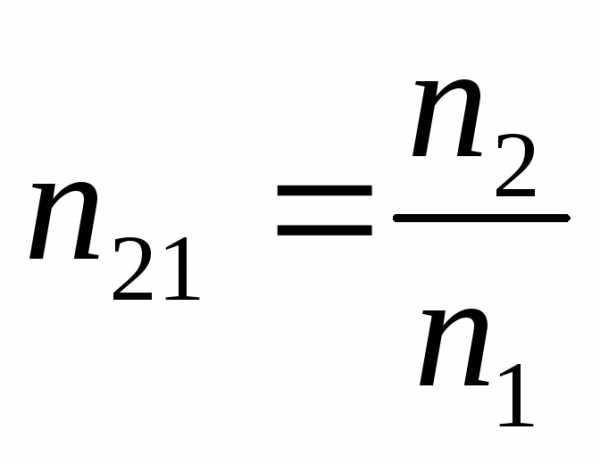 ;
;  ;
;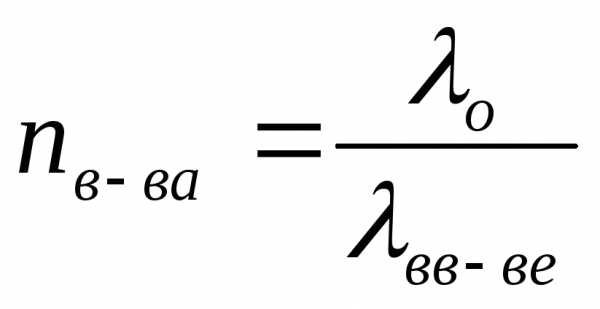
 —
относит. показатель преломления.
—
относит. показатель преломления. —
скорости света во 2-й и первой средах.
—
скорости света во 2-й и первой средах.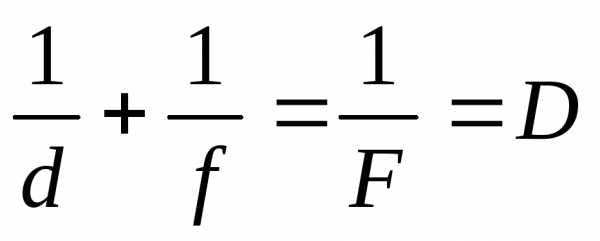
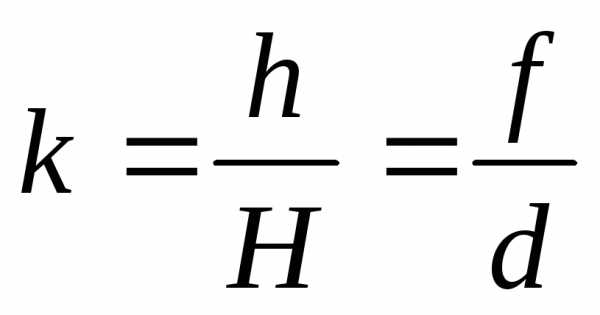
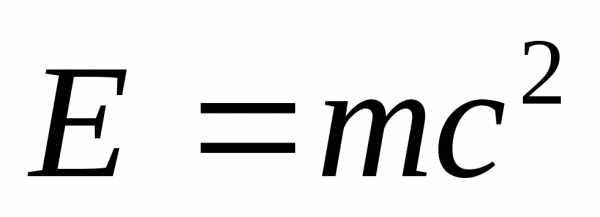 ;
; 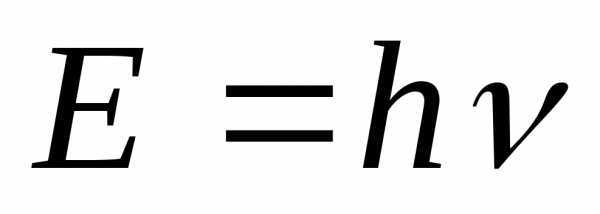 ;
; 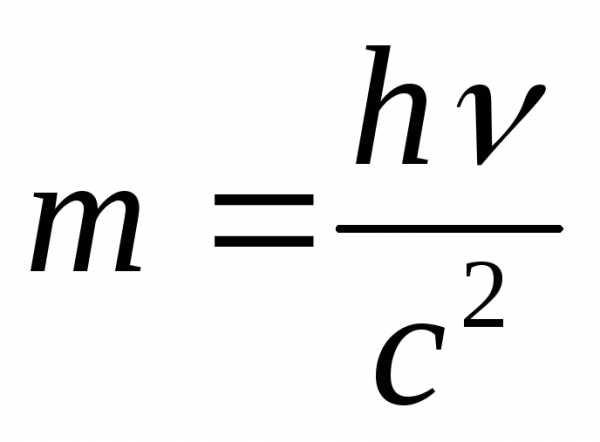
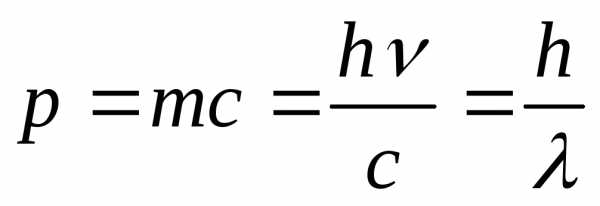 ;
; 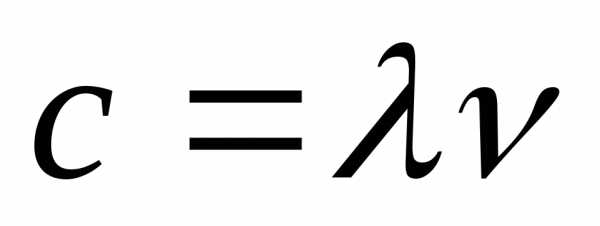
 —
длинна волны излучения
—
длинна волны излучения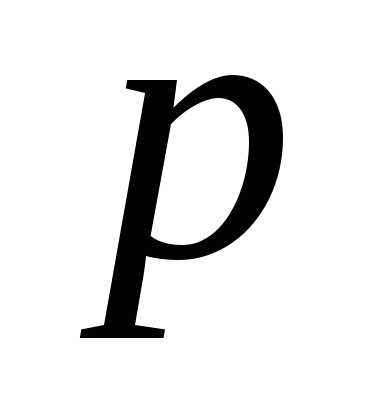 —
импульс фотона
—
импульс фотона —
частота излучения
—
частота излучения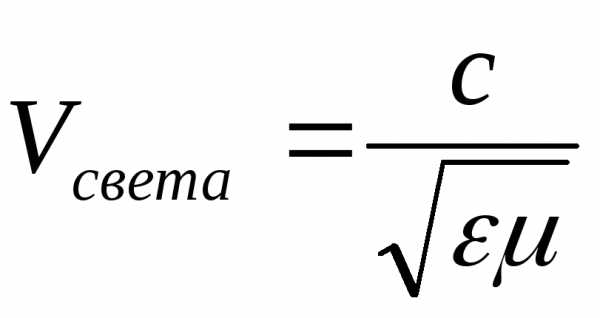
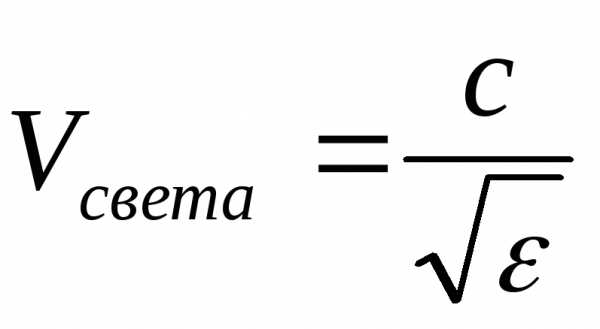
 —
относит. диэликтрич. проницаемость
среды
—
относит. диэликтрич. проницаемость
среды —
относит. магнитная проницаемость среды.
—
относит. магнитная проницаемость среды.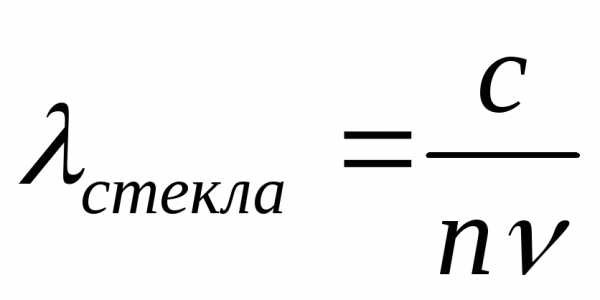
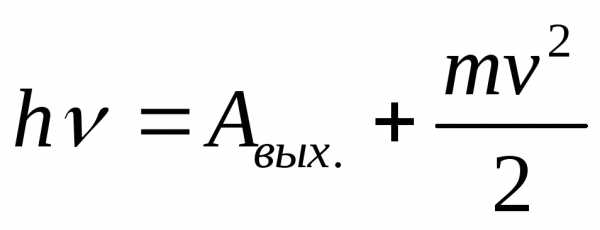 ;
;