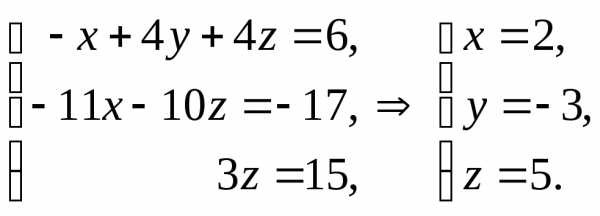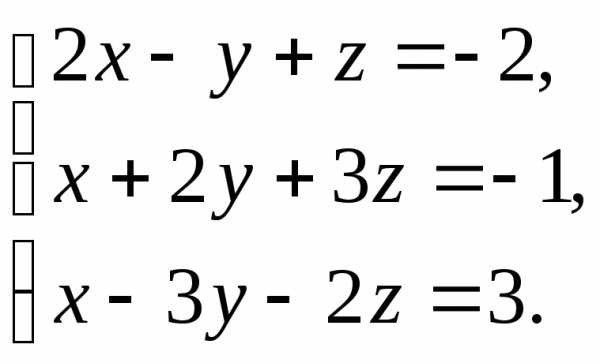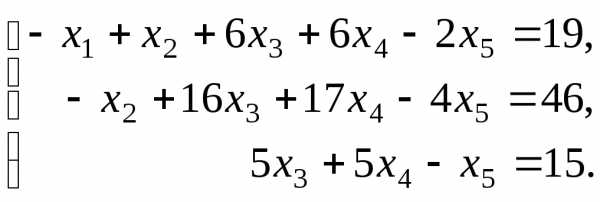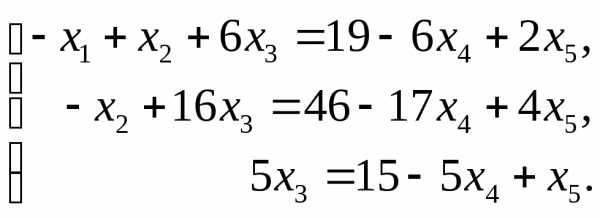Картотека (3 класс) по теме: Карточки с ваыражениями на порядок действий
52 – 24 : 6 • 8 =_______ 94 – 45 : 9 • 8 =_______ 58 + 56 : ( 14 – 7 ) =______ 94 – ( 12 – 3 ) • 6 =_______ 72 – ( 38 + 26 ) : 8 =_____ 45 : 5 + 4 • 9 =________ 7 • 7 + 6 • 6 =________ 28 : 7 + 18 : 2 =_______ 7 • 8 + 24 : 3 =________ 80 – 56 : 7 – 72 =______ 9 • 7 – 60 – 3 =________ 27 – 4 • 3 + 5 • 4 =_______ 8 • 2 + 35 : 5 – 4 • 5 =______ 6 • 3 : 2 + 7 • 7 – 36 =_____ 2 • ( 28 : 7 ) • 5 – 6 =_____ 99 –3• (18 – 12): 9–24 :4 =__ 63 : 9 + (54 – 47) • 6 =____ ( 14 + 3 • 7 ) : 7 + 37 =____ 48 : 8 + ( 65 – 56 ) • 5 =____ (36 : 9 +23)–3 • 6 +20 : 5=__ | 100 – 81 : 9 • 5 =_______ (64 : 8 + 24) : 4 =_______ ( 63 : 9 • 3 + 4 ) : 5 =______ (45 + 9 ) : 9 • 7 =_______ 90 – 36 + 42 : 6 =_______ ( 73 + 27 ) : 10 • 6 =______ 54 : 6 • 2 : 3 =_______ ( 7 + 5 • 7 ) : 7 + 43 =______ 6 • 6 + 6 • 8 – 42 =_______ (5 • 5 + 15 ) : 8 + 12 =_____ ( 70 – 9 + 2 ) : 9 • 8 =______ ( 15 + 15 ) : 5 • 9 =_______ ( 54 : 6 • 9 + 9 ) : 10 =_____ ( 72 : 8 ) • 4 + 44 =______ 6 • 2 : 3 • 9 + 71 =______ ( 57 + 18 : 6 ) : 10 =_____ ( 3 • 8 + 12 ) : 6 =____ 52 + 9 • 3 – 4 • 8 =_____ 5 • ( 71 – 68 ) + 6 • 9 =____ 8 • 5 + 3 • 6 =______ | 8 • 8 + 2 •7 =_______ 5 • 9 + 6 • 4 =_______ 7 • 8 – 4 • 7 =_______ 9 • 6 + 5 • 8 =_______ 7 • 7 + 6 • 8 =________ 6 • 7 – 81 : 9 =________ 54 : 9 + 7 • 7 =_______ 48 : 8 • 7 =________ 9 • 7 – 4 • 5 =_______ 8 • 9 – 4 • 7 =_______ 3 • 8 – 6• 3 =_______ 8 • 4 – 9 • 2 =_______ 9 • 9 – 6 • 7 =______ 4 • 5 – 54 : 9 =______ 63 : 9 + 6 • 8 =_______ 64 : 8 • 9 =______ 8 • 7 + 4 • 3 =_____ 3 • 9 + 7 • 7 =_____ 4 • 6 + 6 • 6 =______ 3 • 5 + 4 • 9 =______ |
nsportal.ru
Карточки по математике на порядок действия 3 класс
1. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
45 : 5 + 36 : 4 – 6=
27 + 7 · 8 – 35 : 35=
42 : 6 + 28 – 3 · 6=
9 · 7 – 3 · 7 + 29 – 24 : 4=
2. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
48 : 6 + 33 – 54 : 9 + 7 · 4=
15 + 21 : 21 · 5 – 27 : 9 · 2=
6 · 5 : 3 + 48 : 6 : 4 · 6 + 3 · 9=
100 – 6 · 4 : 3 · 9 – 19 + 7 · 5=
3. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
100 – 21 : 7 · 0 + 5 · 4=
2 · 5 + 24 : 6 + 18 : 3 · 9=
9 · 5 – 19 + 6 · 6 – 3 · 4=
7 · 6 + 35 : 7 · 5 – 16 : 2 : 4 · 5=
4. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
32 : 4 · 6 : 8 + 6 · 3 – 17=
5 · 8 + 4 · 6 + 15 – 14=
36 : 6 + 18 : 9 + 20 – 12 + 6 · 4=
27 : 3 – 35 : 7 + 8 · 0 + 5 · 5=
5. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
42 : 6 · 3 + 11 + 24 : 4 – 7 =
6 · 9 + 30 : 5 : 2 · 7 – 27=
90 — 7 · 5 – 24 : 8 · 5=
6 · 5 – 12 : 6 · 3 + 49=
6. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
32 : 8 · 5 + 48 : 6 : 2 · 5=
50 – 45 : 9 · 3 + 16 : 8 · 9=
1 · 8 + 25 – 24 : 4 · 2 + 14=
48 : 6 · 4 + 6 · 7 – 23 + 16=
7. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
42 : 7 + (19 + 11) : 5 – 2 · 6=
60 – (23 + 22) : 5 – 6 · 3 + 35=
(23 – 19) · 4 + 18 : 3 + (8 + 22) =
(82 – 82) : 2 · 7 + 7 · 7 — (63 – 27)=
8. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
= (50 – 23) : 3 + 8 · 5 – 6 · 5 =
3 · 4 + 9 · 6 – (27 + 9) : 4 · 5= (5 · 6 – 3 · 4 — 48 : 6) · 7 – 13=
9. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
9 · 4 – 6 · 4 : (33 – 25) · 5=
3 · (12 – 8) : 2 + 8 · 9 – 38=
(5 · 9 — 25) : 4 · 8 – 4 · 7 =
9 · (2 · 5) – 48 : 48 · 3 + 7 · 6 =
10. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(8 · 6 – 36 : 36) — 6 · 3 + 5 · 1=
7 · 4 + 9 · 4 – (2 · 7 + 54 : 6)=
(75 – 27 : 9 + 8) : 8 · 4=
(7 · 4 + 33) – 3 · 6 : 9=
11. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
( 7 · 4 – 16) : 6 + 7 · 5 – (85 – 85) : 2 · 5=
5 · 7 + (18 + 14) : 4 – 28 : 4 + 27 : 3 – (17 + 31) : 6=
12. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(58 – 31) : 3 – 2 + (58 – 16) : 6 + 8 · 5 – (60 – 42) : 3 =
(9 · 7 + 56 : 7) – (2 · 6 – 4) · 3 + 0 : 9=
13. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(8 · 5 + 28 : 7) + 12 : 2 – 6 · 5 + (13 – 5) · 4 + 5 · 4=
(7 · 8 – 14 : 14) + (7 · 4 + 12 : 6) – 10 : 5 + 63 : 9=
14. РЕШИ ВЫРАЖЕНИЯ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(7 · 4 + 28 : 7) + 14 : 2 – 6 · 6 + (18 – 9) · 3 + 2 · 6=
(3 · 8 – 24 : 6) + (5 · 3 + 12 : 12) – 15 : 5 + 54 : 6=
(5 ∙ 9 + 36 – 27) – (51 – 10 · 4) =
35 + (7 ∙ 4 + 47 – 25) : 10 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
70 : 7 + 6 · 8 – 42 : 7 =
24 : 6 · 3 : 2 · 5 : 3 · 7 =
92 – (40 – 21 + 37) + 46 =
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 =
35 : 5 · 4 : 7 · 9 : 6 =
9 · 4 : 6 · 7 : 42 · 64 : 8 =
(4 ∙ 9 + 28) – (27 : 3 + 15) =
82 – 44 · 0 – 82 =
(31 + 61 – 47) · 0 =
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 =
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
92 – (40 – 21 + 37) + 46 = |
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
35 : 5 · 4 : 7 · 9 : 6 = |
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
82 – 44 · 0 – 82 = |
(31 + 61 – 47) · 0 = |
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
92 – (40 – 21 + 37) + 46 = |
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
35 : 5 · 4 : 7 · 9 : 6 = |
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
82 – 44 · 0 – 82 = |
(31 + 61 – 47) · 0 = |
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
92 – (40 – 21 + 37) + 46 = |
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
35 : 5 · 4 : 7 · 9 : 6 = |
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
82 – 44 · 0 – 82 = |
(31 + 61 – 47) · 0 = |
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
92 – (40 – 21 + 37) + 46 = |
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
35 : 5 · 4 : 7 · 9 : 6 = |
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
82 – 44 · 0 – 82 = |
(31 + 61 – 47) · 0 = |
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
34 · 2 – 48 : 8 = |
56 : 7 + 42 : 6 = |
5 · (18 : 3) + 58 = |
8 ∙ 9 + (70 – 56) = |
48 : 6 + 24 : 6 = |
9 · (12 : 6) + 47 = |
6 · 2 + (90 – 73) = |
63 : 7 + 28 : 7 = |
48 : 8 · 2 : 3 · 0 : = |
56 : 8 + 7 · 7 = |
45 : (33 – 24) ∙ 6 =
63 + 27 : (30 : 10) =
60 – 54 : 6 =
60 – 18 : 2 ∙ 3 =
96 – (35 – 5) : 6 =
49 : 6 ∙ 3 : 0 =
72 : 8 + 63 : 7 + 81 : 9 =
60 : 2 + 60 : 3 + 100 : 2 =
27 : 3 ∙ 2 : 6 ∙ 3 ∙ 4 =
54 : 6 – 15 : 15 = |
0 : 12 + 13 ∙ 2 = |
18 : 1 ∙ 0 + 99 = |
56 : (24 : 4 · 3 : 9) + (40 – 25 : 25) = |
64 – (80 – 38 – 29) + (90 – 46 + 17) = |
4 · (71 – 58) – (60 – 40 : 4) = |
46 + (91 – 76) + 19 – (63 – 38) = |
35 + 57 – (62 – 29) – (71 – 48) = |
56 – 8 – 9 – ( 7 + 24) = |
56 : (15 – 7) + 4 =
9 ∙ (5 + 4) : 9 =
13 + (60 – 6) : 9 =
42 : 6 + 7 ∙ 4 =
72 + (40 – 4) : 9 =
63 : 7 + (20 – 5) – (9 + 6) =
18 + 36 : 9 + 6 ∙ 8 – 50 =
5 ∙ (4 + 3) + 19 – 10 =
(18 + 36) : 9 + 6 ∙ 8 – 40 =
7 · (18 : 3) – 32 : 4 =
67 – 9 : 3 · 9 + 28 =
45 : 5 + 12 : 4 ∙ 6 =
16 + 560 : 7 – 21 =
72 : (44 – 8) + 5 =
49 : 7 + 18 – 9 =
98 – 6 ∙ 4 + 17 =
630 : 7 + 40 : (4 ∙ 2) =
6 ∙ 4 : ( 560 : 70) ∙ 5 =
85 – 6 ∙ 8 : 4 =
(26 – 6) ∙ 5 : 4 =
7 ∙ 4 : 2 – 8 =
54 : 9 ∙ 7 – 20 =
420 : 7 · 8 – 24 : 6 =
47 – 30 : 5 + 7 · 7 =
20 : 4 ∙ 8 + 28 : 4 ∙ 7 =
14 + 12 : 6 · 8 – 45 : 5 =
6 · 2 : 3 · 7 – 81 : 9 =
18 + 27 : 3 · 8 – 8 · 8 =
4 ∙ (18 : 9) ·7 – 64 : 8 = |
7 · 3 + (28 + 8) : 6 · 5 = |
80 – (25 : 5 + 9) : 2 – 13 = |
2 · 9 – 36 : (3 · 8 : 6) = |
4 · 4 : 2 + (30 – 15) : 3 = |
(12 + 9 · 4) : 6 – 5 = |
20 – 3 · 3 · 2 + 48 : 8 · 5 = |
4 · 9 – 6 · 6 + 56 : 8 · 6 = |
12 + (9 · 4 : 6 – 5) = |
2 · 2 · 5 – 72 : 8 + 9 · 9 =
12 + 9 · 4 : (6 – 5) =
9 · 8 – (5 · 2 – 8) – 6 · 6 : 4 =
40 : 8 + 3 · 2 · 6 : 4 – 7 =
5 · (9 – 6) + 14 : 2 =
(5 · 5 – 7) : 9 + 7 · 8 – 81 : 9 =
3 · 3 · 7 – (7 · 2 – 1) + 28 : 7 =
5 · 9 – (6 + 14) : 2 =
5 · 3 + 5 · 6 + 5 · 7 =
(9 ∙ 6 – 5) : 7 + 3 ∙ 3 ∙ 9 – 12 = |
5 · 9 – (6 +14) : 2 = |
62 + (7 · 4 + 4) : 8 – 54 : 6 ∙ 3 = |
7 ∙ 4 + 28 – 17 + 32 : 8 + 7 = |
(72 : 8 + 3) · (15 – 6) = |
7 · 9 – 18 : 9 = |
81 : 9 – 21 : 7 + 40 : 5 = |
9 · 9 – 7 · 3 + 8 · 5 = |
7 · 4 + (28 -170 + 32 : 8 + 7 = |
5 · (27 : 9) · 10 – 640 : 80 =
5 · 50 : 10 + (45 – 15) : 3 =
9 · 4 – (35 + 14) : 7 · 3
6 · (36 : 40 ∙ 10 – 560 : 70 =
7 ∙ 4 – 32 : 4 + 10 =
6 ∙ 60 ∙ 10 + (65 – 5) : 6 ∙ 3 =
7 · 5 + 4 · 9 – 26 =
42 : 7 + 58 – 23 — 2 ∙ 7
32 + (74 – 20) : 9 ∙ 7 =
1 вариант
__________________________
37 – ( 24 – 20) х 2 = _____
( 50 : 5 – 5 ) х 3 = _______
27 : 3 + 4 х 2 = ________
100 – 8 х 4 = __________
78 – 3 х 8 = ________
1 вариант
__________________________
37 – ( 24 – 20) х 2 = _____
( 50 : 5 – 5 ) х 3 = _______
27 : 3 + 4 х 2 = ________
100 – 8 х 4 = __________
78 – 3 х 8 = ________
2 вариант
__________________________
24 : 3 + 5 х 3 _______
79 – 5 х 4 = _______
30 : (2 х 5 ) + 68 = ________
31 – 3 х 4 + 5 = __________
23 + 2 х 6 = ________
2 вариант
__________________________
24 : 3 + 5 х 3 _______
79 – 5 х 4 = _______
30 : (2 х 5 ) + 68 = ________
31 – 3 х 4 + 5 = __________
23 + 2 х 6 = ________
infourok.ru
Карточки «Порядок действий» — Математика
«Порядок действий»
Карточка 1
92 – (31 + 19) +58
73 + (61 – 45) – 26
(63 + 17) – (100 – 24)
(81 – 35) + (48 – 19)
Карточка 2
40 : 5 + 8 • 3
12 :3 – 28 :7
39 : 9 + 45 : 5
8 • 4 – 16 : 2
6 • 9 – 7 • 5
27 : 3 + 48 : 8
36 : 4 + 7 • 6
Карточка 3
(53 – 29) + (28 +48) – 55
72 – (100 – 47) + 81
(27 + 36) – (74 – 58) + 16
(57 + 34) – (25 +48)
(69 + 18) – (92 – 39) +66
(80 – 56) + (100 – 72)
Карточка 4
100 — (50 – 38) – (25 + 13)
(49 +11 – 16) – (92 – 76)
(51 – 17) + (85 – 46) + (43 – 24)
(29 + 64 – 72) – (35 + 35 – 49)
86 – 79 + 64 – (18 + 35)
Карточка 5
27 + (9 • 6 – 25) + 72 : 8
100 – (63 + 27 – 58) : 4
(31 – 30) • (63 : 7 + 64 : 8)
(6 • 4 + 3 • 8) : (70 – 69)
(42 – 18) : (60 – 36) + 99
Карточка 6
(63 – 23) • 2 – (45 + 45) : 30 – (72 + 28) : 10
(71 – 45) + (62 – 34) + (83 – 57)
(27 + 27) : 6 + (54 + 27) : 9 + (80 – 32) : 8
(56 : 8 + 81 : 9 + 4 • 1) • 4 : 40
(68 – 19) : 7 + (72 – 48) : 4
Карточка 7
24 : 2 + 30 : 2 + 50 : 2
72 : 18 + 95 : 19 + 80 : 16
100 – 55 : 11 – 85 : 17
45 : 15 + 51 : 17 + 66 : 11
76 : 19 + 40 : 2 – 57 : 19
Карточка 1.
42 : 6 + ( 19 + 6 ) : 5 – 6 • 2
( 27 – 19 ) • 4 + 18 : 3 + ( 8 + 27 ) : 5 – 17
60 – (13 + 22 ) : 5 – 6 • 4 + 25
Карточка 2.
( 82 – 74) : 2 • 7 + 7 • 4 – 19 + ( 63 – 27 ) : 4
( 91 – 83 ) • 3 : 4 + 12 : 6
32 : 8 + ( 27 + 15 ) : 6 + 8 • 5
Карточка 3.
9 • 5 – 36 : 6 : 2 – ( 38 – 23 ) : 5
90 – ( 40 – 24 : 3) : 4 • 6 + 3 • 5
3 • 4 + 9 • 6 – (27 + 9) : 4 • 5
Карточка 4.
(50 – 23 ) : 3 + 8 • 5 – 6 • 5 – (26 – 16 ) • 6
( 5 • 6 – 3 • 4 + 48 : 6) + ( 82 – 78 ) • 7 – 13
(69 – 45) : 3 • 2 + ( 43 – 34 ) • 2
Карточка 5.
9 • 6 – 6 • 4 : ( 33 – 25 ) • 7
( 5 • 9 – 25 ) : 4 • 8 – 4 • 7 – 13
3 • ( 12 – 8 ) : 2 + 6 • 9 — 33
Карточка 6.
( 76 – (27 + 9) + 8 ) : 6 • 4
9 • ( 2 • 3 ) – 48 : 8 • 3 + 7 • 6 – 34
( 7 • 4 + 33 ) – 3 • 6 : 2
Карточка 7.
( 9 • 4 – 6 • 5 ) • 4 – 42 : 7 + (60 – 11 )
7 • 6 + 9 • 4 – ( 2 • 7 + 54 : 6 • 5 )
(37 + 7 • 4 – 17 ) : 6 + 7 • 5
33 + 9 • 3 – ( 85 – 67 ) : 2 • 6
Карточка 8.
28 : 4 + 27 : 3 – (17 + 31 ) : 6
54 : 9 + ( 8 + 19 ) : 3 – 32 :4
( 8 • 6 – 36 : 6 ) : 6 • 3 + 5 • 9
21 : 7 + (42 – 14 ) : 4 – ( 44 – 14 ) : 5
Карточка 9.
8 • 5 – (60 – 42 ) : 3 + 9 • 2
5 • 7 + (18 +14) : 4 – (26 – 8 ) : 3 • 2
(58 – 31 ) : 3 – 2 + (58 – 16) : 6
( 9 • 7 + 56 : 7) – ( 2 • 6 – 4 ) • 3 + 54 : 9
1. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
45 : 5 + 36 : 4 – 6=
27 + 7 · 8 – 35 : 35=
42 : 6 + 28 – 3 · 6=
9 · 7 – 3 · 7 + 29 – 24 : 4=
2. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
48 : 6 + 33 – 54 : 9 + 7 · 4=
15 + 21 : 21 · 5 – 27 : 9 · 2=
6 · 5 : 3 + 48 : 6 : 4 · 6 + 3 · 9=
100 – 6 · 4 : 3 · 9 – 19 + 7 · 5=
3. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
100 – 21 : 7 · 0 + 5 · 4=
2 · 5 + 24 : 6 + 18 : 3 · 9=
9 · 5 – 19 + 6 · 6 – 3 · 4=
7 · 6 + 35 : 7 · 5 – 16 : 2 : 4 · 5=
4. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
32 : 4 · 6 : 8 + 6 · 3 – 17=
5 · 8 + 4 · 6 + 15 – 14=
36 : 6 + 18 : 9 + 20 – 12 + 6 · 4=
27 : 3 – 35 : 7 + 8 · 0 + 5 · 5=
5. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
42 : 6 · 3 + 11 + 24 : 4 – 7 =
6 · 9 + 30 : 5 : 2 · 7 – 27=
90 — 7 · 5 – 24 : 8 · 5=
6 · 5 – 12 : 6 · 3 + 49=
6. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
32 : 8 · 5 + 48 : 6 : 2 · 5=
50 – 45 : 9 · 3 + 16 : 8 · 9=
1 · 8 + 25 – 24 : 4 · 2 + 14=
48 : 6 · 4 + 6 · 7 – 23 + 16=
7. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
42 : 7 + (19 + 11) : 5 – 2 · 6=
60 – (23 + 22) : 5 – 6 · 3 + 35=
(23 – 19) · 4 + 18 : 3 + (8 + 22) =
(82 – 82) : 2 · 7 + 7 · 7 — (63 – 27)=
8. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(50 – 23) : 3 + 8 · 5 – 6 · 5 =
3 · 4 + 9 · 6 – (27 + 9) : 4 · 5= (5 · 6 – 3 · 4 — 48 : 6) · 7 – 13=
9. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
9 · 4 – 6 · 4 : (33 – 25) · 5=
3 · (12 – 8) : 2 + 8 · 9 – 38=
(5 · 9 — 25) : 4 · 8 – 4 · 7 =
9 · (2 · 5) – 48 : 48 · 3 + 7 · 6 =
10. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(8 · 6 – 36 : 36) — 6 · 3 + 5 · 1=
7 · 4 + 9 · 4 – (2 · 7 + 54 : 6)=
(75 – 27 : 9 + 8) : 8 · 4=
(7 · 4 + 33) – 3 · 6 : 9=
11. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
( 7 · 4 – 16) : 6 + 7 · 5 – (85 – 85) : 2 · 5=
5 · 7 + (18 + 14) : 4 – 28 : 4 + 27 : 3 – (17 + 31) : 6=
12. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(58 – 31) : 3 – 2 + (58 – 16) : 6 + 8 · 5 – (60 – 42) : 3 =
(9 · 7 + 56 : 7) – (2 · 6 – 4) · 3 + 0 : 9=
13. РЕШИ Я, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(8 · 5 + 28 : 7) + 12 : 2 – 6 · 5 + (13 – 5) · 4 + 5 · 4=
(7 · 8 – 14 : 14) + (7 · 4 + 12 : 6) – 10 : 5 + 63 : 9=
14. РЕШИ, РАССТАВИВ ПОРЯДОК ДЕЙСТВИЙ:
(7 · 4 + 28 : 7) + 14 : 2 – 6 · 6 + (18 – 9) · 3 + 2 · 6=
(3 · 8 – 24 : 6) + (5 · 3 + 12 : 12) – 15 : 5 + 54 : 6=
(5 ∙ 9 + 36 – 27) – (51 – 10 · 4) =
35 + (7 ∙ 4 + 47 – 25) : 10 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
18 : 2 ∙ 10 : 9 : 2 ∙ 7 : 35 ·1 =
80 : 10 · 3 : 6 ∙ 5 : 2 ∙ 7 : 10 ∙ 5 =
(64 – 26) + (35 : 7 + 45) : 10 =
70 – (32 + 19) + 24 – (60 : 10 + 28) =
24 : 6 + 42 : 7 =
56 : 8 – 35 : 5 =
40 – 24 : 8 =
21 : 3 + 28 :7 =
70 : 7 + 6 · 8 – 42 : 7 =
24 : 6 · 3 : 2 · 5 : 3 · 7 =
92 – (40 – 21 + 37) + 46 =
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 =
35 : 5 · 4 : 7 · 9 : 6 =
9 · 4 : 6 · 7 : 42 · 64 : 8 =
(4 ∙ 9 + 28) – (27 : 3 + 15) =
82 – 44 · 0 – 82 =
(31 + 61 – 47) · 0 =
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 =
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
92 – (40 – 21 + 37) + 46 = |
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
35 : 5 · 4 : 7 · 9 : 6 = |
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
82 – 44 · 0 – 82 = |
(31 + 61 – 47) · 0 = |
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
92 – (40 – 21 + 37) + 46 = |
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
35 : 5 · 4 : 7 · 9 : 6 = |
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
82 – 44 · 0 – 82 = |
(31 + 61 – 47) · 0 = |
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
92 – (40 – 21 + 37) + 46 = |
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
35 : 5 · 4 : 7 · 9 : 6 = |
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
82 – 44 · 0 – 82 = |
(31 + 61 – 47) · 0 = |
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
24 : 6 · 3 : 2 · 5 : 3 · 7 = |
92 – (40 – 21 + 37) + 46 = |
72 : 9 ∙ 3 : 6 ∙ 4 : 16 ∙ 8 = |
35 : 5 · 4 : 7 · 9 : 6 = |
9 · 4 : 6 · 7 : 42 · 64 : 8 = |
(4 ∙ 9 + 28) – (27 : 3 + 15) = |
82 – 44 · 0 – 82 = |
(31 + 61 – 47) · 0 = |
18 : 2 : 9 ∙ 27 : 3 ∙ 8 : 72 = |
34 · 2 – 48 : 8 = |
56 : 7 + 42 : 6 = |
5 · (18 : 3) + 58 = |
8 ∙ 9 + (70 – 56) = |
48 : 6 + 24 : 6 = |
9 · (12 : 6) + 47 = |
6 · 2 + (90 – 73) = |
63 : 7 + 28 : 7 = |
48 : 8 · 2 : 3 · 0 : = |
56 : 8 + 7 · 7 = |
45 : (33 – 24) ∙ 6 =
63 + 27 : (30 : 10) =
60 – 54 : 6 =
60 – 18 : 2 ∙ 3 =
96 – (35 – 5) : 6 =
49 : 6 ∙ 3 : 0 =
72 : 8 + 63 : 7 + 81 : 9 =
60 : 2 + 60 : 3 + 100 : 2 =
27 : 3 ∙ 2 : 6 ∙ 3 ∙ 4 =
54 : 6 – 15 : 15 = |
0 : 12 + 13 ∙ 2 = |
18 : 1 ∙ 0 + 99 = |
56 : (24 : 4 · 3 : 9) + (40 – 25 : 25) = |
64 – (80 – 38 – 29) + (90 – 46 + 17) = |
4 · (71 – 58) – (60 – 40 : 4) = |
46 + (91 – 76) + 19 – (63 – 38) = |
35 + 57 – (62 – 29) – (71 – 48) = |
56 – 8 – 9 – ( 7 + 24) = |
56 : (15 – 7) + 4 =
9 ∙ (5 + 4) : 9 =
13 + (60 – 6) : 9 =
42 : 6 + 7 ∙ 4 =
72 + (40 – 4) : 9 =
63 : 7 + (20 – 5) – (9 + 6) =
18 + 36 : 9 + 6 ∙ 8 – 50 =
5 ∙ (4 + 3) + 19 – 10 =
(18 + 36) : 9 + 6 ∙ 8 – 40 =
7 · (18 : 3) – 32 : 4 =
67 – 9 : 3 · 9 + 28 =
45 : 5 + 12 : 4 ∙ 6 =
16 + 560 : 7 – 21 =
72 : (44 – 8) + 5 =
49 : 7 + 18 – 9 =
98 – 6 ∙ 4 + 17 =
630 : 7 + 40 : (4 ∙ 2) =
6 ∙ 4 : ( 560 : 70) ∙ 5 =
85 – 6 ∙ 8 : 4 =
(26 – 6) ∙ 5 : 4 =
7 ∙ 4 : 2 – 8 =
54 : 9 ∙ 7 – 20 =
420 : 7 · 8 – 24 : 6 =
47 – 30 : 5 + 7 · 7 =
20 : 4 ∙ 8 + 28 : 4 ∙ 7 =
14 + 12 : 6 · 8 – 45 : 5 =
6 · 2 : 3 · 7 – 81 : 9 =
18 + 27 : 3 · 8 – 8 · 8 =
4 ∙ (18 : 9) ·7 – 64 : 8 = |
7 · 3 + (28 + 8) : 6 · 5 = |
80 – (25 : 5 + 9) : 2 – 13 = |
2 · 9 – 36 : (3 · 8 : 6) = |
4 · 4 : 2 + (30 – 15) : 3 = |
(12 + 9 · 4) : 6 – 5 = |
20 – 3 · 3 · 2 + 48 : 8 · 5 = |
4 · 9 – 6 · 6 + 56 : 8 · 6 = |
12 + (9 · 4 : 6 – 5) = |
2 · 2 · 5 – 72 : 8 + 9 · 9 =
12 + 9 · 4 : (6 – 5) =
9 · 8 – (5 · 2 – 8) – 6 · 6 : 4 =
40 : 8 + 3 · 2 · 6 : 4 – 7 =
5 · (9 – 6) + 14 : 2 =
(5 · 5 – 7) : 9 + 7 · 8 – 81 : 9 =
3 · 3 · 7 – (7 · 2 – 1) + 28 : 7 =
5 · 9 – (6 + 14) : 2 =
5 · 3 + 5 · 6 + 5 · 7 =
multiurok.ru
Карточки по математике «Числовые выражения (все действия)» для учащихся 3 класса — Карточки с примерами — Развивайка — Обучение и развитие — ПочемуЧка
Автор: Литвина Надежда Егоровна.
Место работы: МАОУ «СОШ № 71» г. Перми
Должность: учитель начальных классов
Возраст детей: 8-10 лет
Задания — карточки по математике. Материал можно использовать для проверки навыков счёта в пределах 100 (составление программы действий, табличное умножение и деление, сложение и вычитание в пределах 100 с переходом через десяток). Предлагается 13 вариантов. Можно использовать для групповой работы. Дети выполняют задания на карточке.
1. РЕШИ ВЫРАЖЕНИЯ:
35 : 5 + 36 : 4 — 3
26 + 6 х 8 – 45 : 5 24 : 6 + 18 – 2 х 6
9 х 6 – 3 х 6 + 19 – 27 :3
2. РЕШИ ВЫРАЖЕНИЯ:
48 : 8 + 32 – 54 : 6 + 7 х 4
17 + 24 : 3 х 4 – 27 : 3 х 2 6 х 4 : 3 + 54 : 6 : 3 х 6 + 2 х 9
100 – 6 х 2 : 3 х 9 – 39 + 7 х 4
3. РЕШИ ВЫРАЖЕНИЯ:
100 – 27 : 3 х 6 + 7 х 4
2 х 4 + 24 : 3 + 18 : 6 х 9 9 х 3 – 19 + 6 х 7 – 3 х 5
7 х 4 + 35 : 7 х 5 – 16 : 2 : 4 х 3
4. РЕШИ ВЫРАЖЕНИЯ:
32 : 8 х 6 : 3 + 6 х 8 – 17
5 х 8 – 4 х 7 + 13 — 11 24 : 6 + 18 : 2 + 20 – 12 + 6 х 7
21 : 3 – 35 : 7 + 9 х 3 + 9 х 5
5. РЕШИ ВЫРАЖЕНИЯ:
42 : 7 х 3 + 2 + 24 : 3 – 7 + 9 х 3
6 х 6 + 30 : 5 : 2 х 7 — 19 90 — 7 х 5 – 24 : 3 х 5
6 х 5 – 12 : 2 х 3 + 49
6. РЕШИ ВЫРАЖЕНИЯ:
32 : 8 х 7 + 54 : 6 : 3 х 5
50 – 45 : 5 х 3 + 16 : 2 х 5 8 х 6 + 23 – 24 : 4 х 3 + 17
48 : 6 х 4 + 6 х 9 – 26 + 13
7. РЕШИ ВЫРАЖЕНИЯ:
42 : 6 + (19 + 6) : 5 – 6 х 2
60 – (13 + 22) : 5 – 6 х 4 + 25 (27 – 19) х 4 + 18 : 3 + (8 + 27) :5 -17
(82 – 74) : 2 х 7 + 7 х 4 — (63 – 27): 4
8. РЕШИ ВЫРАЖЕНИЯ:
90 – ( 40 – 24 : 3) : 4 х 6 + 3 х 5
3 х 4 + 9 х 6 – ( 27 + 9 ) : 4 х 5
(50 – 23) : 3 + 8 х 5 – 6 х 5 + ( 26 + 16) : 6
(5 х 6 – 3 х 4 + 48 : 6) +(82 – 78) х 7 – 13
54 : 9 + ( 8 + 19) : 3 – 32 : 4 – 21 : 7 + (42 – 14) : 4 – (44 14) : 5
9. РЕШИ ВЫРАЖЕНИЯ:
9 х 6 – 6 х 4 : (33 – 25) х 7
3 х (12 – 8) : 2 + 6 х 9 — 33 (5 х 9 — 25) : 4 х 8 – 4 х 7 + 13
9 х (2 х 3) – 48 : 8 х 3 + 7 х 6 — 34
10. РЕШИ ВЫРАЖЕНИЯ:
(8 х 6 – 36 : 6) : 6 х 3 + 5 х 9
7 х 6 + 9 х 4 – (2 х 7 + 54 : 6 х 5) (76 – (27 + 9) + 8) : 6 х 4
(7 х 4 + 33) – 3 х 6 :2
11. РЕШИ ВЫРАЖЕНИЯ:
(37 + 7 х 4 – 17) : 6 + 7 х 5 + 33 + 9 х 3 – (85 – 67) : 2 х 5
5 х 7 + (18 + 14) : 4 – (26 – 8) : 3 х 2 – 28 : 4 + 27 : 3 – (17 + 31) : 6
12. РЕШИ ВЫРАЖЕНИЯ:
(58 – 31) : 3 – 2 + (58 – 16) : 6 + 8 х 5 – (60 – 42) : 3 + 9 х 2
(9 х 7 + 56 : 7) – (2 х 6 – 4) х 3 + 54 : 9
13. РЕШИ ВЫРАЖЕНИЯ:
(8 х 5 + 28 : 7) + 12 : 2 – 6 х 5 + (13 – 5) х 4 + 5 х 4
(7 х 8 – 14 : 7) + (7 х 4 + 12 : 6) – 10 : 5 + 63 : 9
pochemu4ka.ru
контрольная работа по математике 3 класс «Порядок действий
3 класс Конт.раб по мат-ке «Порядок действий» 1вариант 1. Реши задачу. В букете 30 красных роз, а белых в 6 раз меньше, чем красных. Сколько белых и красных роз? Составь выражение. 2. Укажите порядок выполнения действий и найдите значения выражений: 85 + 35 : 5 ( 92 – 87) · 9 96 – 72 : 12 + 15 8 · 8 – 9 · 4 7 · (63 : 9 — 7) 96 : 24 14 · 3 + 24 : 3 64 : 16 · 8 32+9 (19-16)-25 2 9-18:3 27:3 5+(35:5) 18:(11-5)+47 43-(20-7)+15 7 3-(16+4) 3. Вставьте в «окошки» числа так, чтобы равенства стали верными м 14 см = 714 см 250 см = м дм 400 см = дм | 3 класс Конт.раб по мат-ке «Порядок действий» 2 вариант 1 . Реши задачу. В пакет положили 6 репок, а в сумку – в 3 раза больше, чем в пакет. Сколько репок положили в сумку и в пакет? Составь выражение. 2. Укажите порядок выполнения действий и найдите значения выражений: 78 + 42 : 7 (65 – 58 ) · 8 78 – 19 · 2 + 34 9 · 8 – 6 · 7 5 · (81 : 9 – 8 ) 45 : 15 8 · 12 – 78 : 13 98 : 7 · 3 (63:9 3+4):5 30+6 (13-9) 90-(50-40:5) 2+30 37+9-6:2 3 44+8 (20-16) 12:(13-7)+89 3. Вставьте в «окошки» числа так, чтобы равенства стали верными м 16 см = 916 см 370 см = м дм 700 см = дм | 3 класс Конт.раб по мат-ке «Порядок действий» 1вариант 1. Реши задачу. В букете 30 красных роз, а белых в 6 раз меньше, чем красных. Сколько белых и красных роз? Составь выражение. 2. Укажите порядок выполнения действий и найдите значения выражений: 85 + 35 : 5 ( 92 – 87) · 9 96 – 72 : 12 + 15 8 · 8 – 9 · 4 7 · (63 : 9 — 7) 96 : 24 14 · 3 + 24 : 3 64 : 16 · 8 32+9 (19-16)-25 2 9-18:3 27:3 5+(35:5) 18:(11-5)+47 43-(20-7)+15 7 3-(16+4) 3. Вставьте в «окошки» числа так, чтобы равенства стали верными м 14 см = 714 см 250 см = м дм 400 см = дм | 3 класс Конт.раб по мат-ке «Порядок действий» 2 вариант 1 . Реши задачу. В пакет положили 6 репок, а в сумку – в 3 раза больше, чем в пакет. Сколько репок положили в сумку и в пакет? Составь выражение. 2. Укажите порядок выполнения действий и найдите значения выражений: 78 + 42 : 7 (65 – 58 ) · 8 78 – 19 · 2 + 34 9 · 8 – 6 · 7 5 · (81 : 9 – 8 ) 45 : 15 8 · 12 – 78 : 13 98 : 7 · 3 (63:9 3+4):5 30+6 (13-9) 90-(50-40:5) 2+30 37+9-6:2 3 44+8 (20-16) 12:(13-7)+89 3. Вставьте в «окошки» числа так, чтобы равенства стали верными м 16 см = 916 см 370 см = м дм 700 см = дм |
multiurok.ru
Карточки по математике для 3 класса
Карточка №1
1. Реши примеры:
123 + 305 =
89 + 702 =
416 + 305 =
18 + 605 =
350 + 19 =
534 + 67 =
789 + 123 =
239 + 301 =
403 + 555 =
4. Реши примеры:
605 — 399 =
894 — 698 =
416 — 105 =
345 — 205 =
350 — 419 =
784 — 675 =
777 — 389 =
695 — 496 =
897 — 555 =
5. Вставь вместо многоточия … множитель, чтобы выражение стало верным:
. * 9 = 63
5 *. = 45
. * 8 = 64
7 *. = 28
. * 6 = 42
4 *. = 32
8 *. = 64
9 *. = 54
3 *. = 12
6. Вставь вместо многоточия … делитель, делимое или частное, чтобы выражение стало верным:
. : 9 = 6
45 :. = 5
. : 8 = 8
27 : 3 =.
. : 3 = 6
14 :. = 2
16 :. = 4
. : 9 = 3
32 : 8 =.
7. Реши уравнение, соблюдая порядок арифметических действий:
16 : 4 + 8 — 5 * 2 =
45 : 9 — 4 + 3 * 5 =
72 : 8 — 18 : 3 + 10 =
90 : 9 — 5 * 2 + 23 =
54 — 32 : 8 — 14 : 7 =
72 : 9 + 24 : 8 * 3 =
46 : 2 — 20 : 5 — 3 + 14 =
64 : 8 — 15 — 2 * 4 + 20 =
32 : 8 — 56 : 8 + 12 =
8. Реши уравнение, соблюдая порядок арифметических действий:
36 : ( 4 + 2 ) + 5 * 7 =
81 : 9 — ( 4 + 3 ) * 7 =
12 : ( 8 — 5 ) + 3 * 10 =
92 + ( 9 — 4 ) * 2 — 24 =
( 64 — 32 ) : 8 — 21 : 7 =
56 : ( 9 — 2 ) + 8 * 3 =
46 : ( 20 — 18 ) + 5 * 3 + 22 =
( 64 — 8 ) : 7 + ( 15 — 2 ) * 4 =
32 : ( 8 — 6 ) : 8 + 12 =
9. Сравни длины, вставив вместо многоточия. знаки «<«, «>» или «=»:
10 мм. 1 см 1 мм
1 дм 1 см 1 мм. 111 мм
1 см 5 мм. 16 мм
1 дм 1 см. 11 см
15 мм. 2 см
20 мм. 2 см 2 мм
36 мм. 3 см 6 мм
4 дм 3 мм. 41 см
23 мм. 3 см
10. Начерти прямоугольник, стороны которого равны 3 см и 6 см. Найди периметр прямоугольника.
11. Реши задачу:
Вова и Вася собирают марки. У Вовы есть 134 марки, а у Васи — на 64 марки больше, чем у Вовы. Сколько всего марок у ребят?
Карточка №2
3. Реши примеры:
13 + 732 =
234 + 568 =
402 + 215 =
246 + 683 =
279 + 128=
269 + 567 =
358 + 84 =
289 + 367=
438 + 503 =
4. Реши примеры:
568 — 341 =
602 — 543 =
423 — 349 =
372 — 297 =
394 — 121 =
573 — 389 =
842 — 569 =
695 — 289 =
85 — 523 =
5. Вставь вместо многоточия … множитель, чтобы выражение стало верным:
. * 8 = 72
6 *. = 36
. * 7 = 35
9 *. = 81
. * 4 = 24
8 *. = 32
8 *. = 72
3 *. = 24
6 *. = 30
6. Вставь вместо многоточия … делитель, делимое или частное, чтобы выражение стало верным:
. : 7 = 8
50 : 10 =.
. : 9 = 9
49 :. = 7
. : 3 = 9
18 : 2 =.
14 :. = 2
. : 8 = 3
30 : 6 =.
7. Реши уравнение, соблюдая порядок арифметических действий:
18 : 9 + 81 — 4 * 3 =
45 : 5 — 8 + 5 * 6 =
64 : 8 — 24 : 3 + 21 =
80 : 8 — 6 * 2 + 28 =
58 — 40 : 8 — 21 : 7 =
63 : 9 + 32 : 4 * 5 =
48 : 6 — 20 : 10 — 3 + 29 =
64 : 8 — 36 — 7 * 4 + 67 =
56 : 8 — 40 : 8 + 32 =
8. Реши уравнение, соблюдая порядок арифметических действий:
42 : ( 2 + 4 ) + 8 * 9 =
81 : 9 + ( 8 — 5 ) * 7 =
16 : ( 8 — 4 ) + 7 * 9 =
19 + ( 9 — 4 ) * 5 — 14 =
( 80 — 32 ) : 8 — 18 : 6 =
50 : ( 9 — 4 ) + 7 * 8 =
32 : ( 21 — 17 ) + 9 * 4 + 26 =
( 64 — 28 ) : 2 + ( 18 — 9 ) * 3 =
36 : ( 8 — 2 ) + 8 * 6 =
9. Сравни длины, вставив вместо многоточия. знаки «<«, «>» или «=»:
12 мм. 1 см 1 мм
1 дм 1 см 8 мм. 118 мм
1 см 5 мм. 15 мм
2 дм 1 см. 21 см
19 мм. 2 см 1 мм
21 мм. 2 см 3 мм
1 дм 36 мм. 13 см 6 мм
3 дм 3 мм. 31 см
34 мм. 3 см
10. Начерти прямоугольник, стороны которого равны 8 см и 5 см. Найди периметр прямоугольника.
11. Реши задачу:
Нина и Валя собирали цветы на лугу. Нина собрала 203 цветка, а Валя — на 42 цветка меньше, чем собрала Нина. Сколько всего цветов собрала Валя?
Карточка №3
3. Реши примеры:
493 + 173 =
129 + 384 =
393 + 248 =
384 + 287 =
338 + 268 =
539 + 267 =
389 + 257 =
234 + 358 =
368 + 115 =
4. Реши прмеры:
545 — 356 =
843 — 653 =
544 — 235 =
334 — 267 =
313 — 215 =
462 — 457 =
777 — 125 =
695 — 655 =
897 — 345 =
5. Вставь вместо многоточия … множитель, чтобы выражение стало верным:
. * 5 = 35
8 *. = 48
. * 9 = 63
7 *. = 49
. * 6 = 36
8 *. = 72
9 *. = 18
. * 5 = 50
4 *. = 16
6. Вставь вместо многоточия … делитель, делимое или частное, чтобы выражение стало верным:
. : 3 = 8
81 : 9 =.
. : 7 = 8
25 :. = 5
28 : 3 =.
18 :. = 3
36 :. = 4
. : 8 = 3
42 :. = 6
7. Реши уравнение, соблюдая порядок арифметических действий:
24 : 4 + 39 — 6 * 2 =
49 : 7 — 7 + 42 : 6 =
64 : 8 — 24 : 3 + 32 =
72 : 8 — 5 * 6 + 44 =
154 — 35 : 7 — 24 : 6 =
70 : 7 + 27 : 9 * 5 =
78 : 2 — 20 : 4 — 13 + 38 =
72 : 8 + 59 — 2 * 8 — 32 =
40 : 5 — 64 : 8 + 18 =
8. Реши уравнение, соблюдая порядок арифметических действий:
36 : ( 5 + 4 ) + 8 * 3 =
90 : 9 — ( 3 + 7 ) * 9 =
12 : ( 6 — 3 ) + 4 * 9 =
45 + ( 18 — 9 ) * 3 — 14 =
( 60 — 30 ) : 5 — 24 : 8 =
18 : ( 9 — 7 ) + 8 * 8 =
44 : ( 20 — 16 ) + 7 * 6 + 23 =
( 64 — 8 ) : 7 + ( 26 — 24 ) * 8 =
30 : ( 8 — 6 ) : 5 + 32 =
9. Сравни длины, вставив вместо многоточия. знаки «<«, «>» или «=»:
122 мм. 12 см 2 мм
1 дм 1 см. 111 см
1 см 5 мм. 14 мм
3 дм 1 см. 31 см 1 мм
16 мм. 16 см
20 мм. 2 см 1 мм
46 мм. 4 см 6 мм
5 дм 8 мм. 58 см
22 мм. 3 см
10. Начерти прямоугольник, стороны которого равны 7 см и 1 см. Найди периметр прямоугольника.
11. Реши задачу:В первой группе детского сада есть 246 игрушек, а во второй группе на — 72 игрушки меньше, чем в первой. Сколько игрушек во второй группе детского сада?
Карточка №4
3. Реши примеры:
439 + 421 =
189 + 422 =
366 + 435 =
185 + 623 =
340 + 193 =
462 + 165 =
723 + 453 =
449 + 312 =
312 + 521 =
4. Реши примеры:
622 — 324 =
934 — 748 =
623 — 325 =
455 — 221 =
467 — 442 =
934 — 644 =
864 — 345 =
345 — 478 =
821 — 632 =
5. Вставь вместо многоточия … множитель, чтобы выражение стало верным:
. * 2 = 18
6 *. = 42
. * 8 = 72
6 *. = 24
. * 8 = 40
5 *. = 35
9 *. = 81
7 *. = 70
4 *. = 24
6. Вставь вместо многоточия … делитель, делимое или частное, чтобы выражение стало верным:
12 : 2 =.
18 :. = 3
. : 7 = 6
28 :.2 =.
. : 3 = 9
16 :. = 4
16 :. = 8
. : 9 = 8
40 : 10 =.
7. Реши уравнение, соблюдая порядок арифметических действий:
35 : 5 — 8 + 8 * 7 =
42 : 6 — 14 + 8 * 5 =
64 : 8 — 24 : 3 + 16 =
81 : 9 — 4 * 2 + 28 =
84 — 32 : 4 — 28 : 7 =
45 : 9 + 32 : 8 * 4 =
66 : 2 — 25 : 5 — 8 + 56 =
56 : 8 + 57 — 8 * 4 + 27 =
48 : 8 + 72 : 9 + 12 — 18 =
8. Реши уравнение, соблюдая порядок арифметических действий:
36 : ( 14 -11 ) + 6 * 8 =
90 : 9 + ( 5 + 3 ) * 8 =
18 : ( 9 — 6 ) + 8 * 9 =
94 + ( 9 — 7 ) * 6 — 28 =
( 60 — 32 ) : 7 + 21 : 3 =
56 : ( 9 — 1 ) + 9 * 4 =
56 : ( 20 — 12 ) + 5 * 7 + 45 =
( 90 — 1 ) : 9 + ( 17 — 14 ) * 8 =
30 : ( 8 — 3 ) : 6 + 34 =
9. Сравни длины, вставив вместо многоточия. знаки «<«, «>» или «=»:
11 мм. 1 см 1 мм
1 дм 1 см 0 мм. 111 мм
1 см 8 мм. 16 мм
1 дм 1 см. 110 см
18 мм. 2 см
21 мм. 2 см 3 мм
38 мм. 3 см 7 мм
4 дм 3 мм. 40 см
67 мм. 6 см 7 мм
12. Реши задачу:
В магазин привезли 489 коробки с печеньем и коробки с шоколадом, которых привезли на 124 штуки меньше, чем коробок с печеньем. Сколько коробок с шоколадом привезли в магазин?
13. Реши задачу:
Коля собрал в саду 9 яблок. Его старший брат Андрей собрал в 4 раза больше яблок, чем Коля. Сколько яблок собрал Андрей?
Просмотр содержимого документа
«Карточки по математике для 3 класса»
Карточка №1
1. Реши примеры:
123 + 305 = | 89 + 702 = | 416 + 305 = |
18 + 605 = | 350 + 19 = | 534 + 67 = |
789 + 123 = | 239 + 301 = | 403 + 555 = |
4. Реши примеры:
605 — 399 = | 894 — 698 = | 416 — 105 = |
345 — 205 = | 350 — 419 = | 784 — 675 = |
777 — 389 = | 695 — 496 = | 897 — 555 = |
5. Вставь вместо многоточия … множитель, чтобы выражение стало верным:
… * 9 = 63 | 5 * … = 45 | … * 8 = 64 |
7 * … = 28 | … * 6 = 42 | 4 * … = 32 |
8 * … = 64 | 9 * … = 54 | 3 * … = 12 |
6. Вставь вместо многоточия … делитель, делимое или частное, чтобы выражение стало верным:
… : 9 = 6 | 45 : … = 5 | … : 8 = 8 |
27 : 3 = … | … : 3 = 6 | 14 : … = 2 |
16 : … = 4 | … : 9 = 3 | 32 : 8 = … |
7. Реши уравнение, соблюдая порядок арифметических действий:
16 : 4 + 8 — 5 * 2 = | 45 : 9 — 4 + 3 * 5 = | 72 : 8 — 18 : 3 + 10 = |
90 : 9 — 5 * 2 + 23 = | 54 — 32 : 8 — 14 : 7 = | 72 : 9 + 24 : 8 * 3 = |
46 : 2 — 20 : 5 — 3 + 14 = | 64 : 8 — 15 — 2 * 4 + 20 = | 32 : 8 — 56 : 8 + 12 = |
8. Реши уравнение, соблюдая порядок арифметических действий:
36 : ( 4 + 2 ) + 5 * 7 = | 81 : 9 — ( 4 + 3 ) * 7 = | 12 : ( 8 — 5 ) + 3 * 10 = |
92 + ( 9 — 4 ) * 2 — 24 = | ( 64 — 32 ) : 8 — 21 : 7 = | 56 : ( 9 — 2 ) + 8 * 3 = |
46 : ( 20 — 18 ) + 5 * 3 + 22 = | ( 64 — 8 ) : 7 + ( 15 — 2 ) * 4 = | 32 : ( 8 — 6 ) : 8 + 12 = |
9. Сравни длины, вставив вместо многоточия … знаки «» или «=»:
10 мм … 1 см 1 мм | 1 дм 1 см 1 мм … 111 мм | 1 см 5 мм … 16 мм |
1 дм 1 см … 11 см | 15 мм … 2 см | 20 мм … 2 см 2 мм |
36 мм … 3 см 6 мм | 4 дм 3 мм … 41 см | 23 мм … 3 см |
10. Начерти прямоугольник, стороны которого равны 3 см и 6 см. Найди периметр прямоугольника.
11. Реши задачу:
Вова и Вася собирают марки. У Вовы есть 134 марки, а у Васи — на 64 марки больше, чем у Вовы. Сколько всего марок у ребят?
Карточка №2
3. Реши примеры:
13 + 732 = | 234 + 568 = | 402 + 215 = |
246 + 683 = | 279 + 128= | 269 + 567 = |
358 + 84 = | 289 + 367= | 438 + 503 = |
4. Реши примеры:
568 — 341 = | 602 — 543 = | 423 — 349 = |
372 — 297 = | 394 — 121 = | 573 — 389 = |
842 — 569 = | 695 — 289 = | 85 — 523 = |
5. Вставь вместо многоточия … множитель, чтобы выражение стало верным:
… * 8 = 72 | 6 * … = 36 | … * 7 = 35 |
9 * … = 81 | … * 4 = 24 | 8 * … = 32 |
8 * … = 72 | 3 * … = 24 | 6 * … = 30 |
6. Вставь вместо многоточия … делитель, делимое или частное, чтобы выражение стало верным:
… : 7 = 8 | 50 : 10 = … | … : 9 = 9 |
49 : … = 7 | … : 3 = 9 | 18 : 2 = … |
14 : … = 2 | … : 8 = 3 | 30 : 6 = … |
7. Реши уравнение, соблюдая порядок арифметических действий:
18 : 9 + 81 — 4 * 3 = | 45 : 5 — 8 + 5 * 6 = | 64 : 8 — 24 : 3 + 21 = |
80 : 8 — 6 * 2 + 28 = | 58 — 40 : 8 — 21 : 7 = | 63 : 9 + 32 : 4 * 5 = |
48 : 6 — 20 : 10 — 3 + 29 = | 64 : 8 — 36 — 7 * 4 + 67 = | 56 : 8 — 40 : 8 + 32 = |
8. Реши уравнение, соблюдая порядок арифметических действий:
42 : ( 2 + 4 ) + 8 * 9 = | 81 : 9 + ( 8 — 5 ) * 7 = | 16 : ( 8 — 4 ) + 7 * 9 = |
19 + ( 9 — 4 ) * 5 — 14 = | ( 80 — 32 ) : 8 — 18 : 6 = | 50 : ( 9 — 4 ) + 7 * 8 = |
32 : ( 21 — 17 ) + 9 * 4 + 26 = | ( 64 — 28 ) : 2 + ( 18 — 9 ) * 3 = | 36 : ( 8 — 2 ) + 8 * 6 = |
9. Сравни длины, вставив вместо многоточия … знаки «» или «=»:
12 мм … 1 см 1 мм | 1 дм 1 см 8 мм … 118 мм | 1 см 5 мм … 15 мм |
2 дм 1 см … 21 см | 19 мм … 2 см 1 мм | 21 мм … 2 см 3 мм |
1 дм 36 мм … 13 см 6 мм | 3 дм 3 мм … 31 см | 34 мм … 3 см |
10. Начерти прямоугольник, стороны которого равны 8 см и 5 см. Найди периметр прямоугольника.
11. Реши задачу:
Нина и Валя собирали цветы на лугу. Нина собрала 203 цветка, а Валя — на 42 цветка меньше, чем собрала Нина. Сколько всего цветов собрала Валя?
Карточка №3
3. Реши примеры:
493 + 173 = | 129 + 384 = | 393 + 248 = |
384 + 287 = | 338 + 268 = | 539 + 267 = |
389 + 257 = | 234 + 358 = | 368 + 115 = |
4. Реши прмеры:
545 — 356 = | 843 — 653 = | 544 — 235 = |
334 — 267 = | 313 — 215 = | 462 — 457 = |
777 — 125 = | 695 — 655 = | 897 — 345 = |
5. Вставь вместо многоточия … множитель, чтобы выражение стало верным:
… * 5 = 35 | 8 * … = 48 | … * 9 = 63 |
7 * … = 49 | … * 6 = 36 | 8 * … = 72 |
9 * … = 18 | … * 5 = 50 | 4 * … = 16 |
6. Вставь вместо многоточия … делитель, делимое или частное, чтобы выражение стало верным:
… : 3 = 8 | 81 : 9 = … | … : 7 = 8 |
25 : … = 5 | 28 : 3 = … | 18 : … = 3 |
36 : … = 4 | … : 8 = 3 | 42 : … = 6 |
7. Реши уравнение, соблюдая порядок арифметических действий:
24 : 4 + 39 — 6 * 2 = | 49 : 7 — 7 + 42 : 6 = | 64 : 8 — 24 : 3 + 32 = |
72 : 8 — 5 * 6 + 44 = | 154 — 35 : 7 — 24 : 6 = | 70 : 7 + 27 : 9 * 5 = |
78 : 2 — 20 : 4 — 13 + 38 = | 72 : 8 + 59 — 2 * 8 — 32 = | 40 : 5 — 64 : 8 + 18 = |
8. Реши уравнение, соблюдая порядок арифметических действий:
36 : ( 5 + 4 ) + 8 * 3 = | 90 : 9 — ( 3 + 7 ) * 9 = | 12 : ( 6 — 3 ) + 4 * 9 = |
45 + ( 18 — 9 ) * 3 — 14 = | ( 60 — 30 ) : 5 — 24 : 8 = | 18 : ( 9 — 7 ) + 8 * 8 = |
44 : ( 20 — 16 ) + 7 * 6 + 23 = | ( 64 — 8 ) : 7 + ( 26 — 24 ) * 8 = | 30 : ( 8 — 6 ) : 5 + 32 = |
9. Сравни длины, вставив вместо многоточия … знаки «» или «=»:
122 мм … 12 см 2 мм | 1 дм 1 см … 111 см | 1 см 5 мм … 14 мм |
3 дм 1 см … 31 см 1 мм | 16 мм … 16 см | 20 мм … 2 см 1 мм |
46 мм … 4 см 6 мм | 5 дм 8 мм … 58 см | 22 мм … 3 см |
10. Начерти прямоугольник, стороны которого равны 7 см и 1 см. Найди периметр прямоугольника.
11. Реши задачу:В первой группе детского сада есть 246 игрушек, а во второй группе на — 72 игрушки меньше, чем в первой. Сколько игрушек во второй группе детского сада?
Карточка №4
3. Реши примеры:
439 + 421 = | 189 + 422 = | 366 + 435 = |
185 + 623 = | 340 + 193 = | 462 + 165 = |
723 + 453 = | 449 + 312 = | 312 + 521 = |
4. Реши примеры:
622 — 324 = | 934 — 748 = | 623 — 325 = |
455 — 221 = | 467 — 442 = | 934 — 644 = |
864 — 345 = | 345 — 478 = | 821 — 632 = |
5. Вставь вместо многоточия … множитель, чтобы выражение стало верным:
… * 2 = 18 | 6 * … = 42 | … * 8 = 72 |
6 * … = 24 | … * 8 = 40 | 5 * … = 35 |
9 * … = 81 | 7 * … = 70 | 4 * … = 24 |
6. Вставь вместо многоточия … делитель, делимое или частное, чтобы выражение стало верным:
12 : 2 = … | 18 : … = 3 | … : 7 = 6 |
28 : .2 = … | … : 3 = 9 | 16 : … = 4 |
16 : … = 8 | … : 9 = 8 | 40 : 10 = … |
7. Реши уравнение, соблюдая порядок арифметических действий:
35 : 5 — 8 + 8 * 7 = | 42 : 6 — 14 + 8 * 5 = | 64 : 8 — 24 : 3 + 16 = |
81 : 9 — 4 * 2 + 28 = | 84 — 32 : 4 — 28 : 7 = | 45 : 9 + 32 : 8 * 4 = |
66 : 2 — 25 : 5 — 8 + 56 = | 56 : 8 + 57 — 8 * 4 + 27 = | 48 : 8 + 72 : 9 + 12 — 18 = |
8. Реши уравнение, соблюдая порядок арифметических действий:
36 : ( 14 -11 ) + 6 * 8 = | 90 : 9 + ( 5 + 3 ) * 8 = | 18 : ( 9 — 6 ) + 8 * 9 = |
94 + ( 9 — 7 ) * 6 — 28 = | ( 60 — 32 ) : 7 + 21 : 3 = | 56 : ( 9 — 1 ) + 9 * 4 = |
56 : ( 20 — 12 ) + 5 * 7 + 45 = | ( 90 — 1 ) : 9 + ( 17 — 14 ) * 8 = | 30 : ( 8 — 3 ) : 6 + 34 = |
9. Сравни длины, вставив вместо многоточия … знаки «» или «=»:
11 мм … 1 см 1 мм | 1 дм 1 см 0 мм … 111 мм | 1 см 8 мм … 16 мм |
1 дм 1 см … 110 см | 18 мм … 2 см | 21 мм … 2 см 3 мм |
38 мм … 3 см 7 мм | 4 дм 3 мм … 40 см | 67 мм … 6 см 7 мм |
12. Реши задачу:
В магазин привезли 489 коробки с печеньем и коробки с шоколадом, которых привезли на 124 штуки меньше, чем коробок с печеньем. Сколько коробок с шоколадом привезли в магазин?
13. Реши задачу:
Коля собрал в саду 9 яблок. Его старший брат Андрей собрал в 4 раза больше яблок, чем Коля. Сколько яблок собрал Андрей?
kopilkaurokov.ru
Учебно-методический материал по математике (3 класс) на тему: Примеры на порядок действий.
Составление выражения со скобками
1. Составь из следующих предложений выражения со скобками и реши их.
Из числа 16 вычти сумму чисел 8 и 6.
Из числа 34 вычти сумму чисел 5 и 8.
Сумму чисел 13 и 5 вычесть из числа 39.
Разность чисел 16 и 3 прибавь к числу 36
Разность чисел 48 и 28 прибавь к числу 16.
2. Реши задачи, сперва составив правильно выражения, а за тем последовательно их решив:
2.1. Папа принёс из леса мешок с орехами. Коля взял из мешка 25 орешков и съел. За тем Маша взяла из мешка 18 орешков. Мама то же взяла из мешка 15 орешков, но положила обратно 7 из них. Сколько осталось в итоге орешков в мешке, если в начале их было 78?
2.2. Мастер ремонтировал детали. В начале рабочего дня их было 38. В первой половине дня он смог отремонтировать 23 из них. После полудня ему принесли еще столько же, сколько было в самом начале дня. Во второй половине он отремонтировал еще 35 деталей. Сколько деталей ему осталось отремонтировать?
3. Реши примеры правильно выполняя последовательность действий:
45 : 5 + 12 * 2 -21 :3
56 — 72 : 9 + 48 : 6 * 3
7 + 5 * 4 — 12 : 4
18 : 3 — 5 + 6 * 8
Решение выражений со скобками
1. Реши примеры правильно раскрывая скобки:
1 + (4 + 8) = | 8 — (2 + 4) = | 3 + (6 — 5) = | 59 + 25 = |
82 + 14 = | 29 + 52 = | 18 + 47 = | 39 + 53 = |
37 + 53 = | 25 + 63 = | 87 + 17 = | 19 + 52 = |
2. Реши примеры правильно выполняя последовательность действий:
2.1. 36 : 3 + 12 * ( 2 — 1 ) : 3
2.2. 39 — ( 81 : 9 + 48 : 6) * 2
2.3. ( 7 + 5 ) * 2 — 48 : 4
2.4. 18 : 3 + ( 5 * 6 ) : 2 — 4
3. Реши задачи, сперва составив правильно выражения, а за тем последовательно их решив:
3.1. На складе было 25 упаковок стирального порошка. В один магазин увезли 12 упаковок. За тем во второй магазин увезли столько же. После этого на склад привезли в 3 раза больше упаковок, чем было раньше. Сколько упаковок порошка стало на складе?
3.2. В гостинице проживало 75 туристов. За первый день из гостиницы уехали 3 группы по 12 человек, а заехали 2 группы по 15 человек. На второй день уехали еще 34 человека. Сколько туристов осталось в гостинице к концу 2 дня?
3.3. В химчистку привезли 2 мешка одежды по 5 вещей в каждом мешке. За тем забрали 8 вещей. После полудня привезли ещё 18 вещей на стирку. А забрали только 5 выстиранных вещей. Сколько вещей в химчистке к концу дня, если в начале дня там было 14 вещей?
ФИ _________________________________
21 : 3 * 6 — (18 + 14) : 8 = | 63 : (81 : 9) + (8 * 7 — 2) : 6 = | 64 :2 : 4+ 9*7-9*1= |
37 *2 + 180 : 9 – 36 : 12 = | 52 * 10 – 60 : 15 * 1 = | 72 : 4 +58 :2= |
5 *0 : 25 + (72 : 1 – 0) : 9 = | 21 : (3 * 7) – (7* 0 + 1)*1 = | 6:6+0:8-8:8= |
91 : 7 + 80 : 5 – 5 : 5 = | 64:4 — 3*5 +80:2= | (19*5 – 5) : 30 = |
19 + 17 * 3 – 46 = | (39+29) : 4 + 8*0= | (60-5) : 5 +80: 5= |
54 – 26 + 38 : 2 = | 63: (7*3) *3= | (160-70) : 18 *1= |
200 – 80 : 5 + 3 * 4 = | (29+25): (72:8)= | 72:25 + 3* 17= |
80 : 16 + 660 : 6 = | 3 * 290 – 800= | 950:50*1-0= |
(48 : 3) : 16 * 0 = | 90-6*6+29= | 5* (48-43) +15 :5*7= |
54 : 9 *8 — 14 : 7 * 4 = | 63 : 7*4+70 :7 * 5= | 24 : 6*7 — 7*0= |
21 : 7 * 8 + 32 : 8 * 4 = | 27 : 3* 5 + 26-18 *4= | 54 : 6*7 — 0:1= |
45 : 9 * 6 + 7 * 5 – 26 = | 28 : 7 *9 + 6 * (54 – 47)= | 6*(9 : 3) — 40:5 = |
21 * 1 — 56 : 7 – 8 = | 9 * (64 : 8) — 18:18 | 3 *(14 : 2) — 63:9= |
4 * 8 + 42 : 6 *5 = | 0*4+0:5 +8* (48 : 8)= | 56:7 +7*6 — 5*1= |
31 * 3 — 17 – 80 : 16 * 1 = | 57:19 *32 — 11 *7= | 72-96:8 +60:15 *13= |
36 + 42 : 3 + 23 + 27 *0 = | 56:14 *19 — 72:18= | (86-78:13)* 4= |
650 – 50 * 4 + 900 : 100 = | 630 : 9 + 120 * 5 + 40= | 980 – (160 + 20) : 30= |
940 — (1680 – 1600) * 9 = | 29* 2+26 – 37:2= | 72:3 +280 : (14*5)= |
300 : (5 *60) * (78 : 13) = | 63+ 100: 4 – 8*0= | 84:7+70:14 – 6:6= |
45 : 15 – 180 : 90 + 84 : 7 = | 32+51 + 48:6 * 5= | 54:6 ?2 – 70:14= |
38 : 2 – 48 : 3 + 0 * 9 = | 30:6 * 8 – 6+3*2= | (95:19) *(68:2)= |
(300 — 8 * 7) * 10 = | 1:1 — 0*0 + 1*0 — 1*1= | (80: 4 – 60:30) *5 = |
2 * (120 : 6 – 80 : 20) = | 56:4+96:3- 0*7= | 20+ 20: 4 — 1*5= |
(18 + 14) : 8 – (7 *0 + 1) *1 = | (8*7-2):6 +63: (7*3)= | (50-5) : 5+21: (3*7)= |
19 + 17 * 3 – 60 : 15 * 1 = | 80: 5 +3*5 +80:2= | 54 : 9 *8-64:4 +16*0= |
72 * 10 — 64 : 2 : 4 = | 84 – 36 + 38:2 | 91:13+80:5 – 5:5 |
300 – 80 : 5 + 6 * 4 = | 950:190 *1+14 : 7*4= | (39+29) : 17 + 8*0= |
(120 — 30) : 18 * 1- 72 : 25 = | 210:30*60-0:1= | 90-6*7+3* 17= |
240 : 60 *7 – 7 * 0 = | 60:60+0:80-80:80= | 720 : 40 +580 :20= |
9 *7 – 9 *1 + 5 * 0 : 25 = | 21 : 7 * 6 +32 : 4 *5= | 80:16 +66:6 -63:(81:9)= |
(19 * 5 – 5) : 30 + 70 : 7 = | 15 :5*7 + 63 : 7 * 5= | 54 : 6 * 7 — (72:1-0):9= |
3 *290 – 600 – 5 * (48 – 43) = | (300-89*7)*10 — 3?2= | (80: 4) +30*2+ 180 : 9= |
30 : 6 * 8 – 6 + 48 : 3 + 0 *9 = | (95:19) *(68:34) — 60:30*5= | 27 : 3*5 — 48:3= |
3* 290 – 800 + 950 : 50 = | 80:16 +660:6*1-0= | 90-6*6+ 15 :5*7= |
5*(48 — 43) + (48 : 3) :16*0= | 280 : (14*5) +630 : 9*0= | 300: (50*6)* (78 : 6)= |
Если в примерах встретится вопросительный знак (?), следует его заменить на знак * — умножение.
1. РЕШИ ВЫРАЖЕНИЯ:
35 : 5 + 36 : 4 — 3
26 + 6 х 8 – 45 : 5 24 : 6 + 18 – 2 х 6
9 х 6 – 3 х 6 + 19 – 27 :3
2. РЕШИ ВЫРАЖЕНИЯ:
48 : 8 + 32 – 54 : 6 + 7 х 4
17 + 24 : 3 х 4 – 27 : 3 х 2 6 х 4 : 3 + 54 : 6 : 3 х 6 + 2 х 9
100 – 6 х 2 : 3 х 9 – 39 + 7 х 4
3. РЕШИ ВЫРАЖЕНИЯ:
100 – 27 : 3 х 6 + 7 х 4
2 х 4 + 24 : 3 + 18 : 6 х 9 9 х 3 – 19 + 6 х 7 – 3 х 5
7 х 4 + 35 : 7 х 5 – 16 : 2 : 4 х 3
4. РЕШИ ВЫРАЖЕНИЯ:
32 : 8 х 6 : 3 + 6 х 8 – 17
5 х 8 – 4 х 7 + 13 — 11 24 : 6 + 18 : 2 + 20 – 12 + 6 х 7
21 : 3 – 35 : 7 + 9 х 3 + 9 х 5
5. РЕШИ ВЫРАЖЕНИЯ:
42 : 7 х 3 + 2 + 24 : 3 – 7 + 9 х 3
6 х 6 + 30 : 5 : 2 х 7 — 19 90 — 7 х 5 – 24 : 3 х 5
6 х 5 – 12 : 2 х 3 + 49
6. РЕШИ ВЫРАЖЕНИЯ:
32 : 8 х 7 + 54 : 6 : 3 х 5
50 – 45 : 5 х 3 + 16 : 2 х 5 8 х 6 + 23 – 24 : 4 х 3 + 17
48 : 6 х 4 + 6 х 9 – 26 + 13
7. РЕШИ ВЫРАЖЕНИЯ:
42 : 6 + (19 + 6) : 5 – 6 х 2
60 – (13 + 22) : 5 – 6 х 4 + 25 (27 – 19) х 4 + 18 : 3 + (8 + 27) :5 -17
(82 – 74) : 2 х 7 + 7 х 4 — (63 – 27): 4
8. РЕШИ ВЫРАЖЕНИЯ:
90 – ( 40 – 24 : 3) : 4 х 6 + 3 х 5
3 х 4 + 9 х 6 – ( 27 + 9 ) : 4 х 5
(50 – 23) : 3 + 8 х 5 – 6 х 5 + ( 26 + 16) : 6
(5 х 6 – 3 х 4 + 48 : 6) +(82 – 78) х 7 – 13
54 : 9 + ( 8 + 19) : 3 – 32 : 4 – 21 : 7 + (42 – 14) : 4 – (44 14) : 5
9. РЕШИ ВЫРАЖЕНИЯ:
9 х 6 – 6 х 4 : (33 – 25) х 7
3 х (12 – 8) : 2 + 6 х 9 — 33 (5 х 9 — 25) : 4 х 8 – 4 х 7 + 13
9 х (2 х 3) – 48 : 8 х 3 + 7 х 6 — 34
10. РЕШИ ВЫРАЖЕНИЯ:
(8 х 6 – 36 : 6) : 6 х 3 + 5 х 9
7 х 6 + 9 х 4 – (2 х 7 + 54 : 6 х 5) (76 – (27 + 9) + 8) : 6 х 4
(7 х 4 + 33) – 3 х 6 :2
11. РЕШИ ВЫРАЖЕНИЯ:
(37 + 7 х 4 – 17) : 6 + 7 х 5 + 33 + 9 х 3 – (85 – 67) : 2 х 5
5 х 7 + (18 + 14) : 4 – (26 – 8) : 3 х 2 – 28 : 4 + 27 : 3 – (17 + 31) : 6
12. РЕШИ ВЫРАЖЕНИЯ:
(58 – 31) : 3 – 2 + (58 – 16) : 6 + 8 х 5 – (60 – 42) : 3 + 9 х 2
(9 х 7 + 56 : 7) – (2 х 6 – 4) х 3 + 54 : 9
13. РЕШИ ВЫРАЖЕНИЯ:
(8 х 5 + 28 : 7) + 12 : 2 – 6 х 5 + (13 – 5) х 4 + 5 х 4
(7 х 8 – 14 : 7) + (7 х 4 + 12 : 6) – 10 : 5 + 63 : 9
Тест «Порядок арифметических действий» (1 вариант)
1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)
1. Какое действие в выражении сделаешь первым?
110 – ( 60 +40) :10 х 8
а) сложение б) деление в) вычитание
2. Какое действие в этом же выражении сделаешь вторым?
а) вычитание б) деление в) умножение
3. Выбери правильный вариант ответа данного выражения:
а) 800 б) 8 в) 30
4. Выбери верный вариант расстановки действий:
а) 3 4 6 5 2 1 4 5 6 3 2 1
320 : 8 х 7 + 9 х ( 240 – 60:15) в) 320:8 х 7+9х(240 – 60 :15)
3 4 6 5 1 2
б) 320 : 8 х 7 + 9 х ( 240 – 60:15)
5. В каком из выражений последнее действие умножение?
а) 1001 :13 х (318 +466) :22
б) 391 х37 :17 х (2248:8 – 162)
в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие вычитание?
а) 2025 :5 – ( 524 – 24 :6) х45
б) 5870 + ( 90-50 +30) х8 -90
в) 5400 :60 х (3600:90 -90)х5
7. Выбери верное высказывание: «В выражении без скобок действия выполняются:»
а) по порядку б) х и : , затем + и — в) + и -, затем х и :
8. Выбери верное высказывание: «В выражении со скобками действия выполняются:»
а) сначала в скобках б)х и :, затем + и — в) по порядку записи
Выбери верный ответ:
9. 90 – ( 50- 40:5) х 2+ 30
а) 56 б) 92 в) 36
10. 100- (2х5+6 — 4х4) х2
а) 100 б) 200 в) 60
11. ( 10000+10000:100 +400) : 100 +100
а) 106 б) 205 в) 0
12. 150 : ( 80 – 60 :2) х 3
а) 9 б) 45 в) 1
Тест «Порядок арифметических действий»
1(1б)
2(1б)
3(1б)
4(3б)
5(2б)
6(2б)
7(1б)
8(1б)
9(3б)
10(3б)
11(3б)
12(3б)
1. Какое действие в выражении сделаешь первым?
560 – (80+20) :10 х7
а) сложение б) деление в) вычитание
2. Какое действие в этом же выражении сделаешь вторым?
а) вычитание б) деление в) умножение
3. Выбери правильный вариант ответа данного выражения:
а) 800 б) 490 в) 30
4. Выбери верный вариант расстановки действий:
а) 3 4 6 5 2 1 4 5 6 3 2 1
320 : 8 х 7 + 9 х ( 240 – 60:15) в) 320:8 х 7+9х(240 – 60 :15)
3 4 6 5 2 1
б) 320 : 8 х 7 + 9 х ( 240 – 60:15)
5. В каком из выражений последнее действие деление?
а) 1001 :13 х (318 +466) :22
б) 391 х37 :17 х (2248:8 – 162)
в) 10000 – (5 х 9+56 х 7) х2
6. В каком из выражений первое действие сложение?
а) 2025 :5 – ( 524 + 24 х6) х45
б) 5870 + ( 90-50 +30) х8 -90
в) 5400 :60 х (3600:90 -90)х5
7. Выбери верное высказывание: «В выражении без скобок действия выполняются:»
а) по порядку б) х и : , затем + и — в) + и -, затем х и :
8. Выбери верное высказывание: «В выражении со скобками действия выполняются:»
а) сначала в скобках б)х и :, затем + и — в) по порядку записи
Выбери верный ответ:
9. 120 – ( 50- 10:2) х 2+ 30
а) 56 б) 0 в) 60
10. 600- (2х5+8 — 4х4) х2
а) 596 б) 1192 в) 60
11. ( 20+20000:2000 +30) : 20 +200
а) 106 б) 203 в) 0
12. 160 : ( 80 – 80 :2) х 3
а) 120 б) 0 в) 1
nsportal.ru




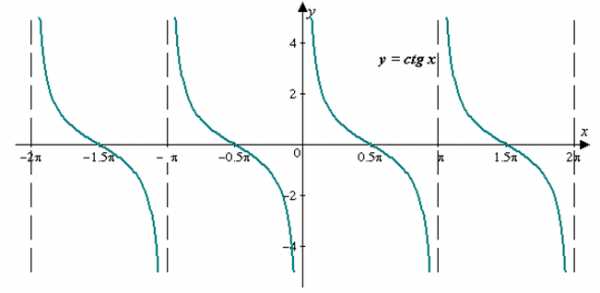


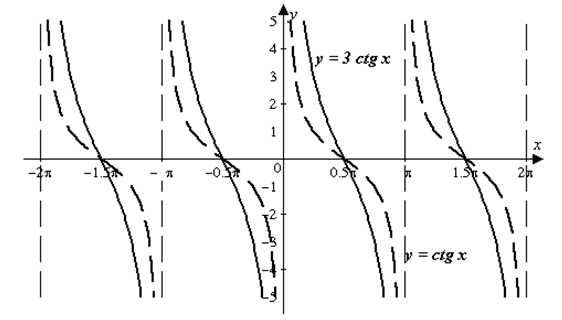

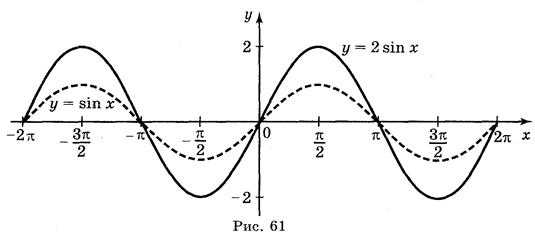
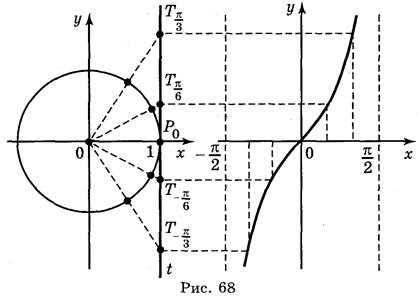


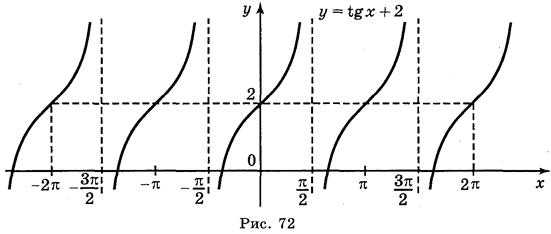
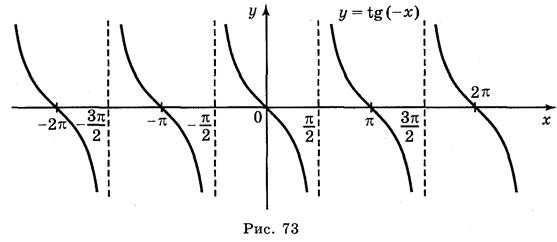

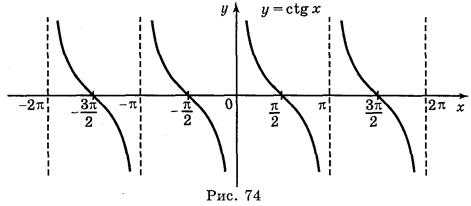

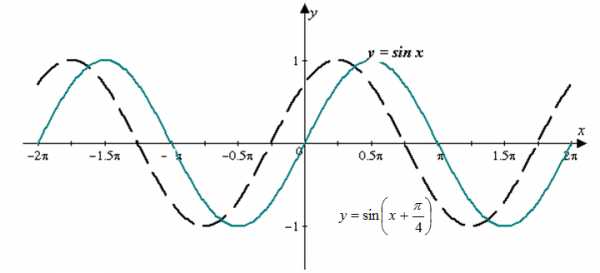
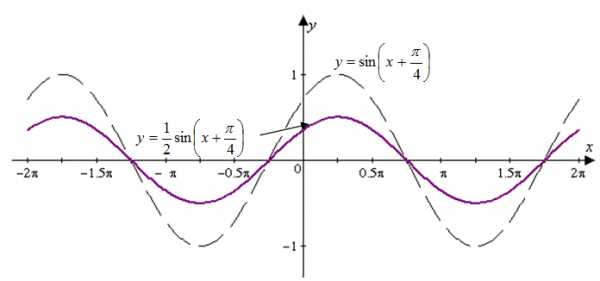
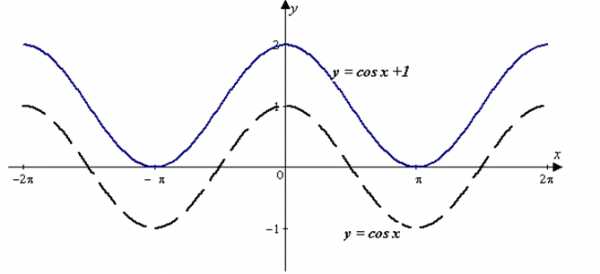
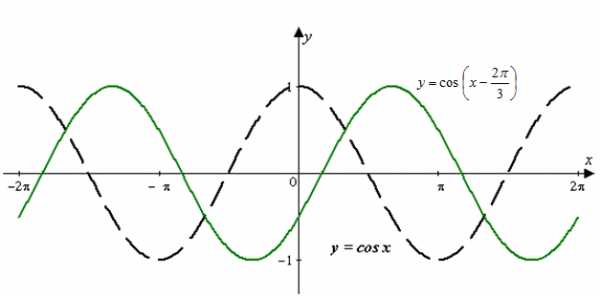
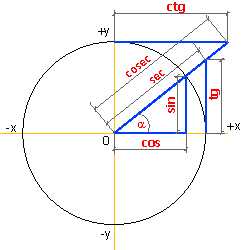 Простейшие тригонометрические функции
Простейшие тригонометрические функции





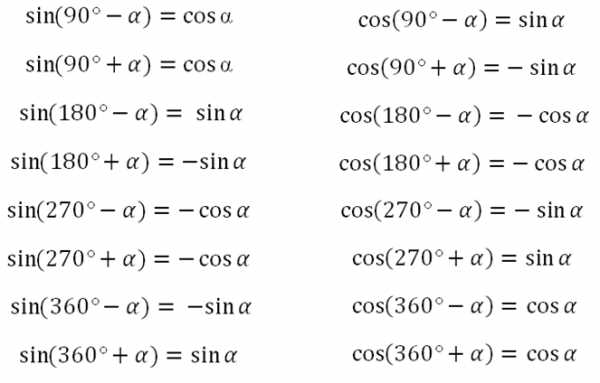
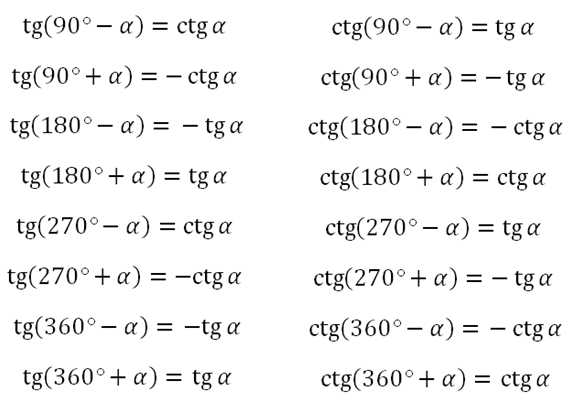
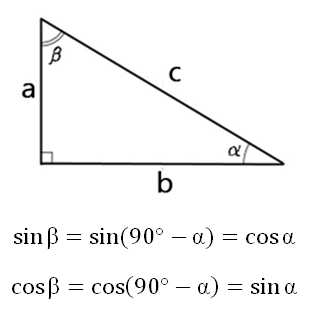
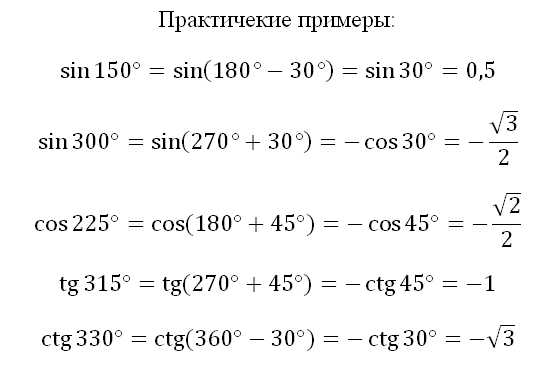

 Расшифровка «A C A B» весьма простая. Надпись обозначает начальные буквы слов из фразы: «All Cops Are Bastards», которую можно перевести как «Все копы — ублюдки». Сегодня она имеет практически мировую известность. В России даже существует аналог («менты – козлы»), который также часто встречается в виде граффити. Интересно то, что англоязычное сокращение в нашей стране живет намного дольше: его годами не стирают коммунальные службы. Русскоязычная же надпись исчезает за неделю–другую. Может, причина в банальном незнании значения этого слова, а может, в лояльности к иностранному языку.
Расшифровка «A C A B» весьма простая. Надпись обозначает начальные буквы слов из фразы: «All Cops Are Bastards», которую можно перевести как «Все копы — ублюдки». Сегодня она имеет практически мировую известность. В России даже существует аналог («менты – козлы»), который также часто встречается в виде граффити. Интересно то, что англоязычное сокращение в нашей стране живет намного дольше: его годами не стирают коммунальные службы. Русскоязычная же надпись исчезает за неделю–другую. Может, причина в банальном незнании значения этого слова, а может, в лояльности к иностранному языку.

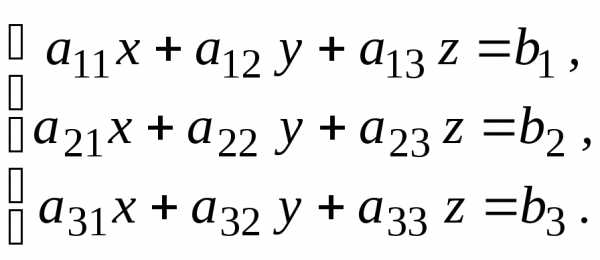 (1)
(1) .
. ,
,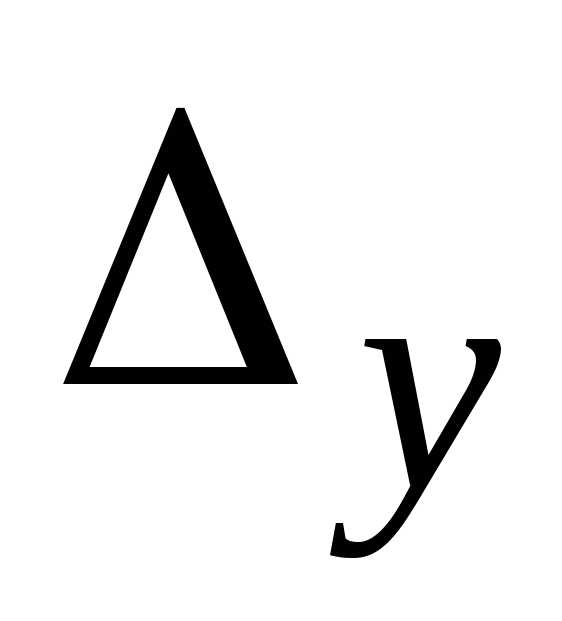 ,
, .
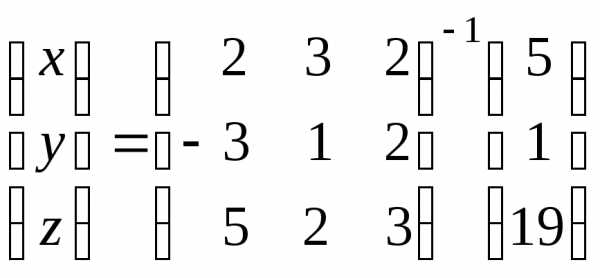
Для этого в главном определителе вместо
столбца коэффициентов при соответствующей
переменной записывается столбец
свободных членов, то есть
.
Для этого в главном определителе вместо
столбца коэффициентов при соответствующей
переменной записывается столбец
свободных членов, то есть ,
, 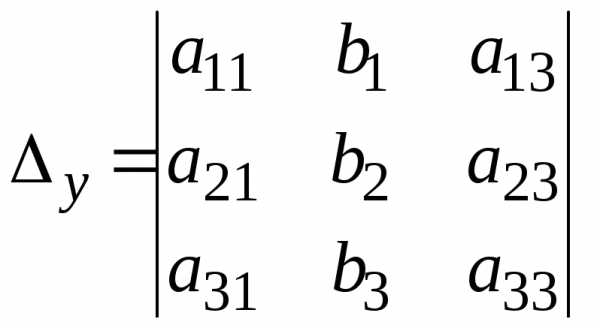 ,
,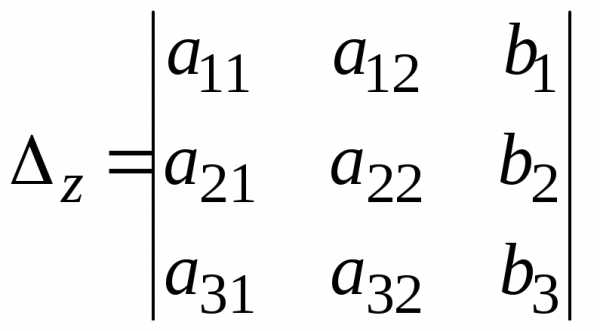 .
. ,
,  ,
, 
 .Если же
.Если же  и
и  =
0,
=
0,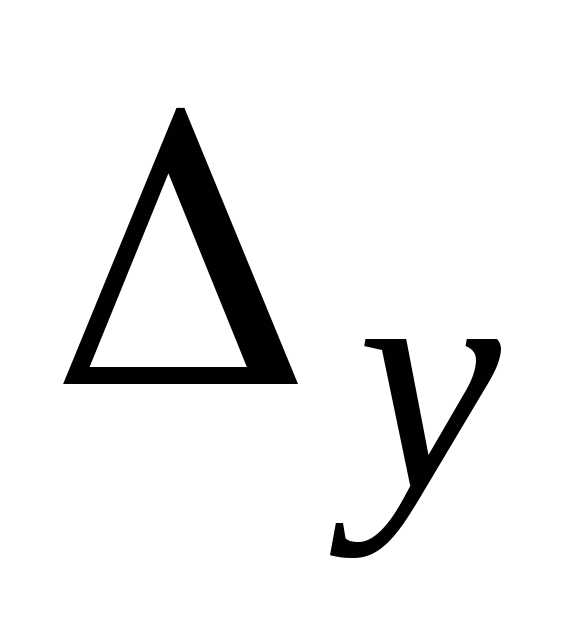 =
0,
=
0, =
0, то система имеет бесчисленное множество
решений, найти которые по формулам
Крамера нельзя. Если же
=
0, то система имеет бесчисленное множество
решений, найти которые по формулам
Крамера нельзя. Если же 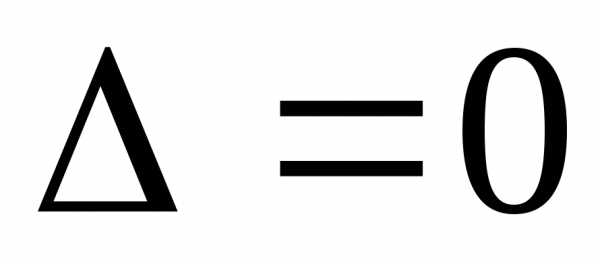 и
и 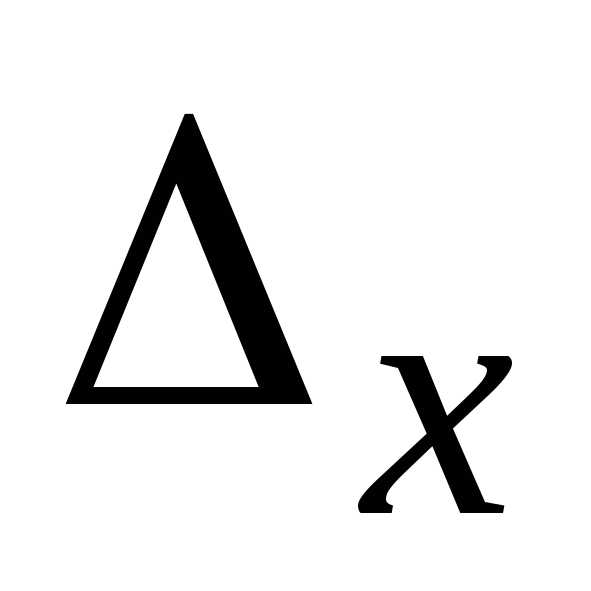
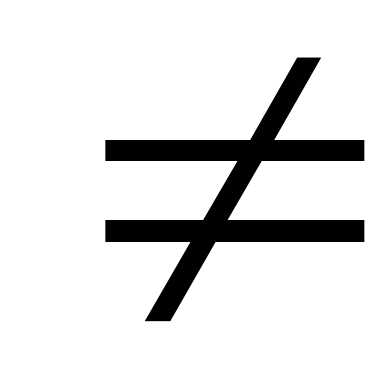 0,
или
0,
или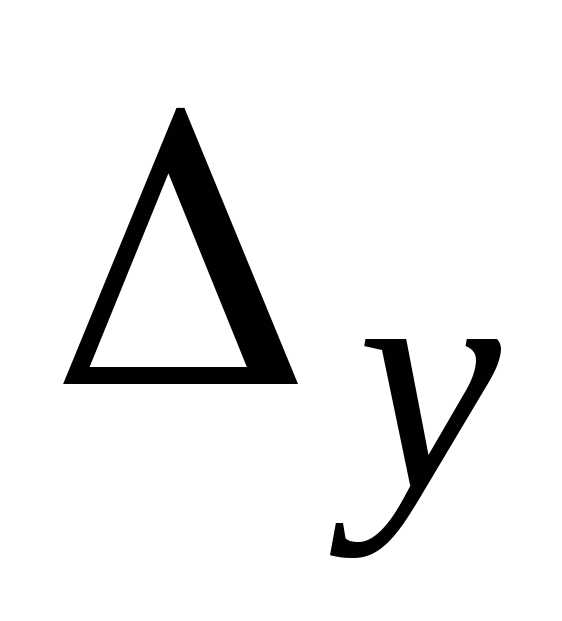
 0,или
0,или
 0,
то система уравнений несовместна, то
есть решений не имеет.
0,
то система уравнений несовместна, то
есть решений не имеет.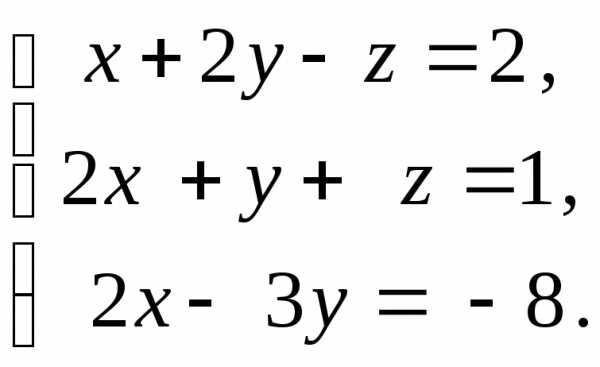
 ,
,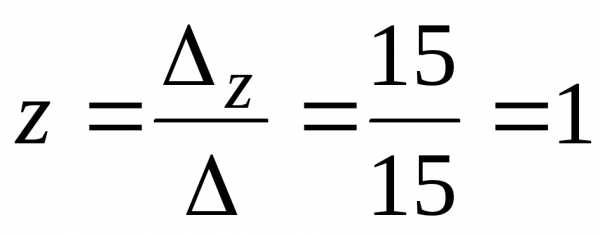 .
.
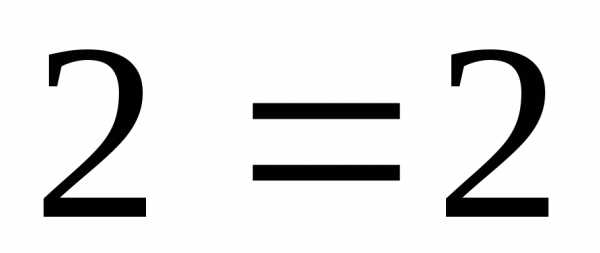 .
.


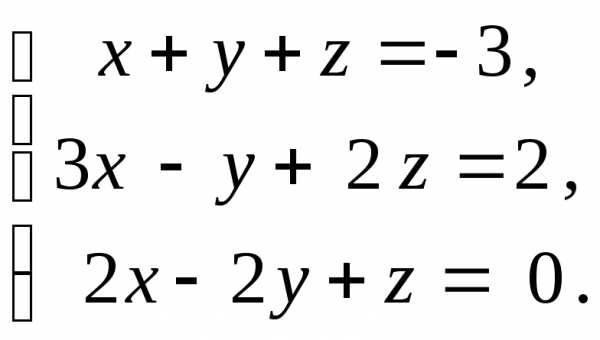
 ,
,  ,
следовательно, система несовместна.
,
следовательно, система несовместна.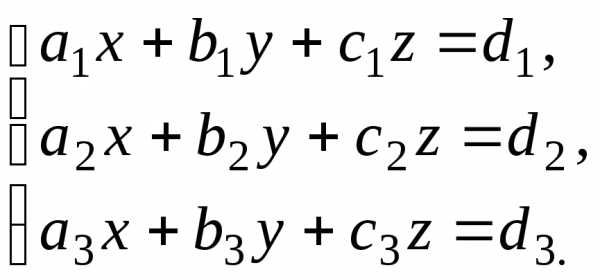 (1)
(1) .
Умножим первое уравнение на
.
Умножим первое уравнение на ,
а второе на (
,
а второе на ( )
и сложим полученные уравнения
)
и сложим полученные уравнения ,
, и
и соответственно,
получим новую пару уравнений
соответственно,
получим новую пару уравнений

 (2)
(2) .
Это означает, что решаемая система
несовместна.
.
Это означает, что решаемая система
несовместна.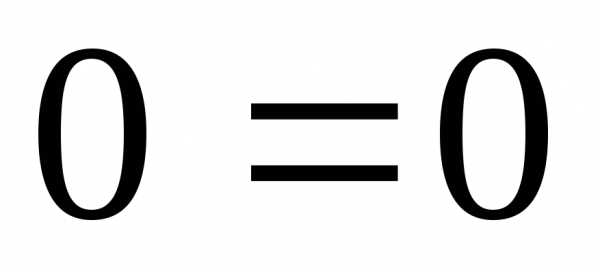 .
Такое уравнение исключается из системы,
в результате число уравнений в системе
становится меньше, чем число переменных,
и система имеет бесчисленное множество
решений, нахождение которых будет
показано на примере.
.
Такое уравнение исключается из системы,
в результате число уравнений в системе
становится меньше, чем число переменных,
и система имеет бесчисленное множество
решений, нахождение которых будет
показано на примере.
 равен нулю. Для этого все числа первой
строки умножим на (–2) и сложим с
соответствующими числами второй строки.
Полученные суммы запишем под горизонтальной
чертой (четвертая строка). Для того чтобы
вместо третьей строки (уравнения) также
получить строку (уравнение), в которой
коэффициент при
равен нулю. Для этого все числа первой
строки умножим на (–2) и сложим с
соответствующими числами второй строки.
Полученные суммы запишем под горизонтальной
чертой (четвертая строка). Для того чтобы
вместо третьей строки (уравнения) также
получить строку (уравнение), в которой
коэффициент при равен нулю, умножим все числа первой
строки на (–5) и сложим с соответствующими
числами третьей строки. Полученные
суммы запишем пятой строкой и проведем
под ней новую горизонтальную черту.
Четвертую строку (или пятую – по выбору)
обведем. Выбирается строка с меньшими
коэффициентами. В этой строке коэффициенты
останутся неизменными. Вместо пятой
строки надо получить строку, где уже
два коэффициента равны нулю. Умножим
четвертую строку на 3 и сложим с пятой.
Сумму запишем под горизонтальной чертой
(шестая строка) и обведем ее.
равен нулю, умножим все числа первой
строки на (–5) и сложим с соответствующими
числами третьей строки. Полученные
суммы запишем пятой строкой и проведем
под ней новую горизонтальную черту.
Четвертую строку (или пятую – по выбору)
обведем. Выбирается строка с меньшими
коэффициентами. В этой строке коэффициенты
останутся неизменными. Вместо пятой
строки надо получить строку, где уже
два коэффициента равны нулю. Умножим
четвертую строку на 3 и сложим с пятой.
Сумму запишем под горизонтальной чертой
(шестая строка) и обведем ее.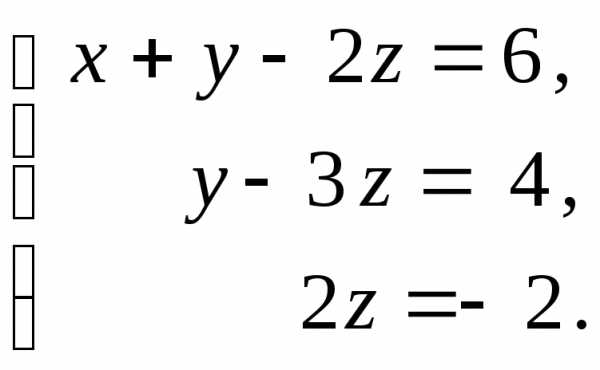 (3)
(3) ,
получимили
,
получимили .
. .
.
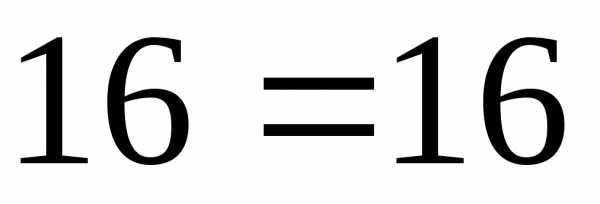
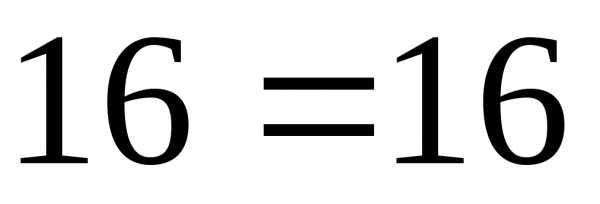
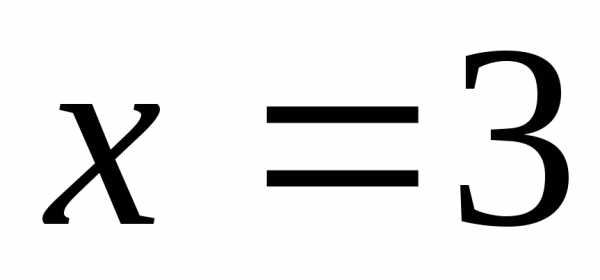 ,
,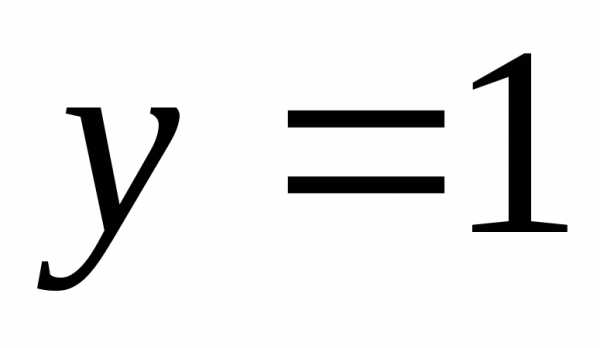 ,
,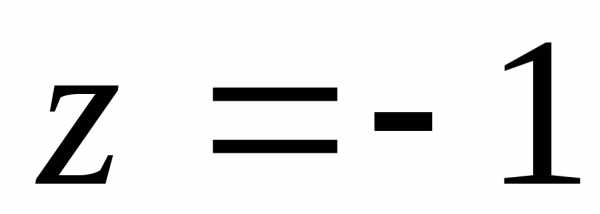 .
.


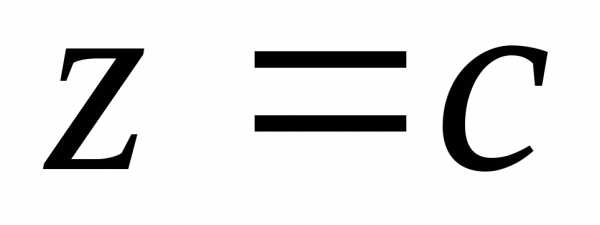 – свободная переменная.
– свободная переменная.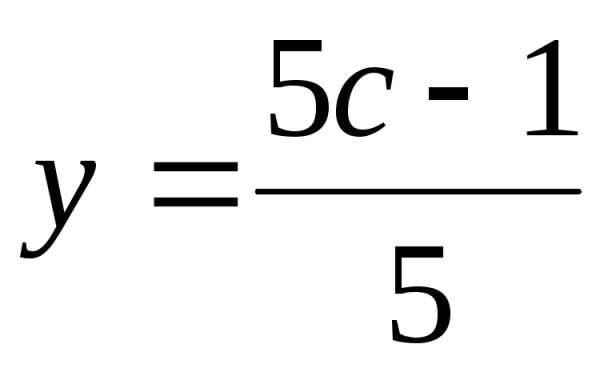 ,
а затем найдемx из первого уравнения
или.
,
а затем найдемx из первого уравнения
или.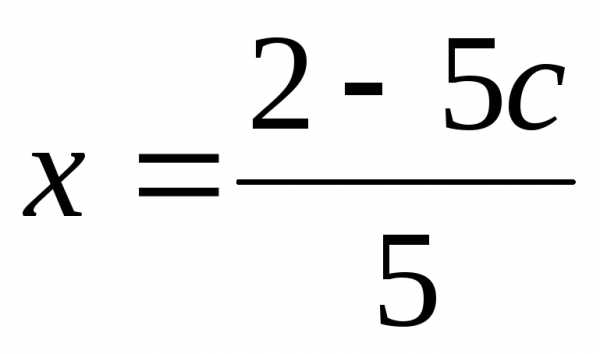 ;
; ;
;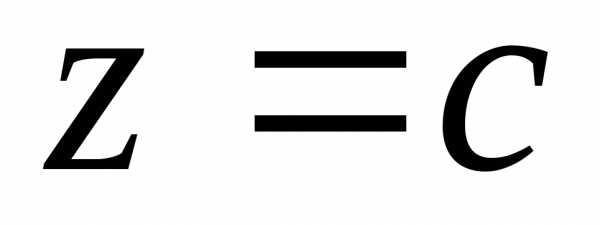 .
. и
и ,
то есть во втором и в третьем уравнениях
первоначальной системы.
,
то есть во втором и в третьем уравнениях
первоначальной системы. .
.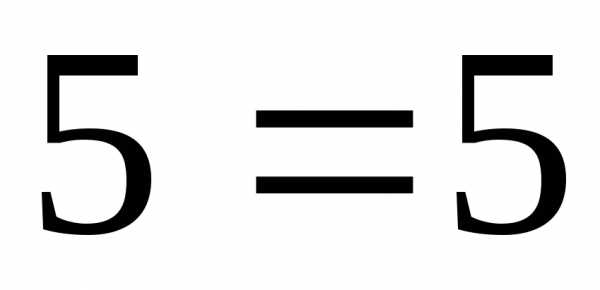 .
. различные значения, будем получать
различные значенияx, y и z.
различные значения, будем получать
различные значенияx, y и z.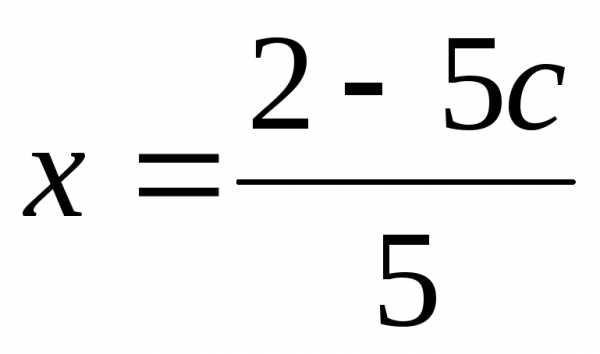 ;
; ;
;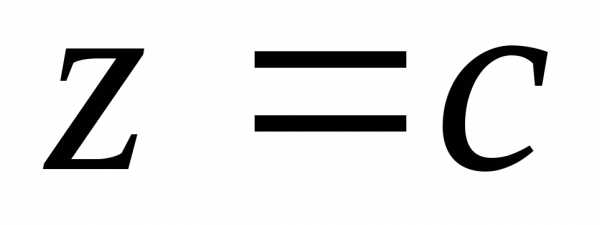 .
. линейных уравнений с
линейных уравнений с неизвестными называется совокупность уравнений, в
каждом из которых неизвестные присутствуют
в первой степени:
неизвестными называется совокупность уравнений, в
каждом из которых неизвестные присутствуют
в первой степени: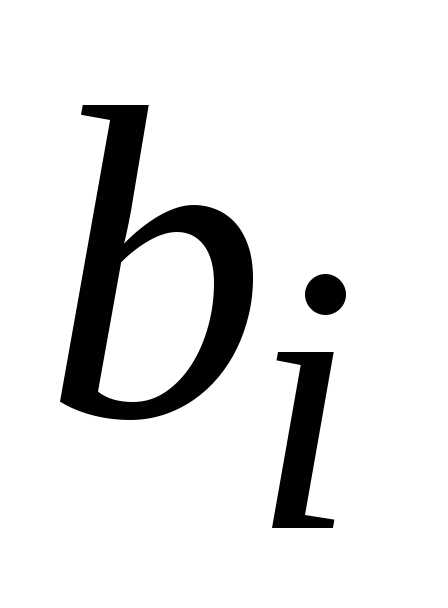 —
свободные члены.
—
свободные члены.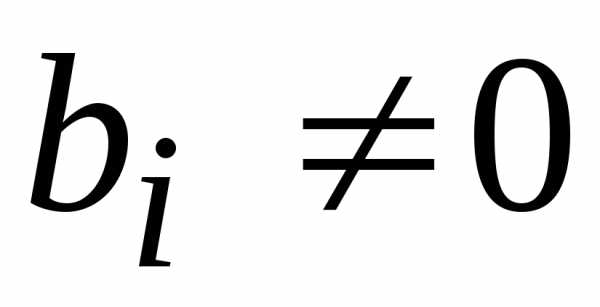 .
.
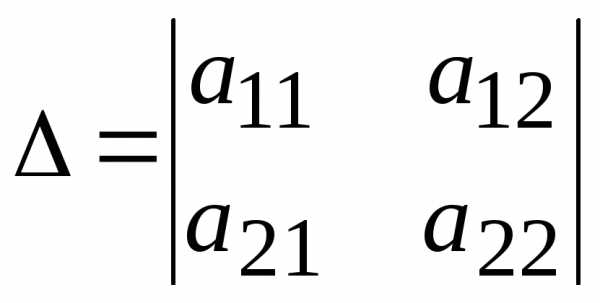 ,
, 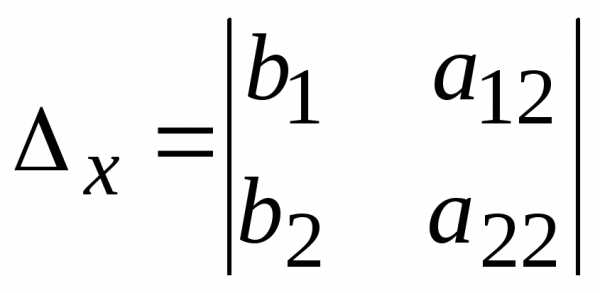 ,
,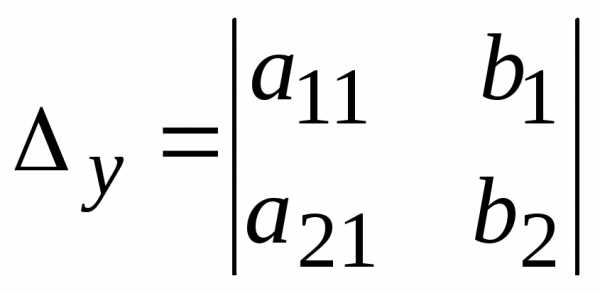 .
. —
определитель системы, составленный из
коэффициентов при неизвестных;
—
определитель системы, составленный из
коэффициентов при неизвестных;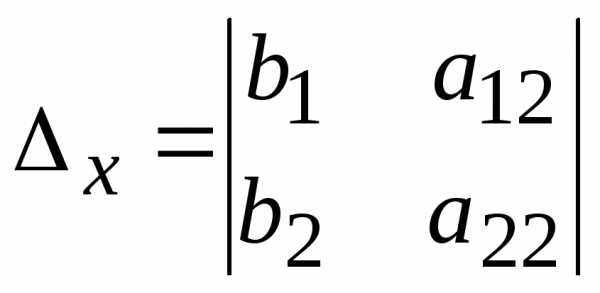 —
это определитель, полученный из
определителя
—
это определитель, полученный из
определителя  заменой столбца коэффициентов при
заменой столбца коэффициентов при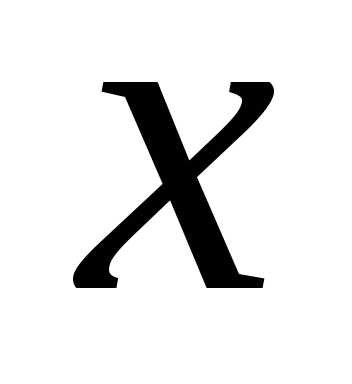 на столбец свободных членов;
на столбец свободных членов;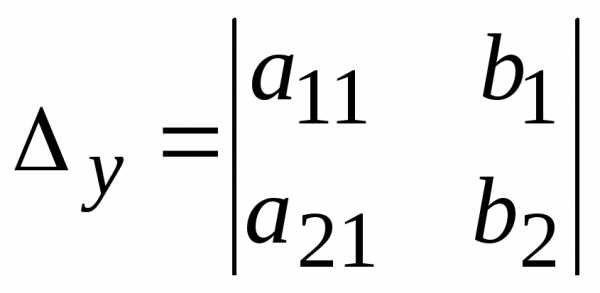 —
это определитель, полученный из
определителя
—
это определитель, полученный из
определителя  заменой столбца коэффициентов при
заменой столбца коэффициентов при на столбец свободных членов.
на столбец свободных членов. ,
тосистема совместная
и определенная,
то есть имеет единственное
решение, которое находится по формулам
Крамера:
,
тосистема совместная
и определенная,
то есть имеет единственное
решение, которое находится по формулам
Крамера: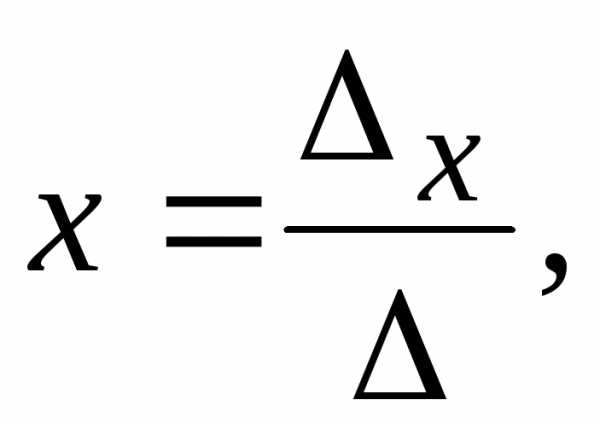
 .
.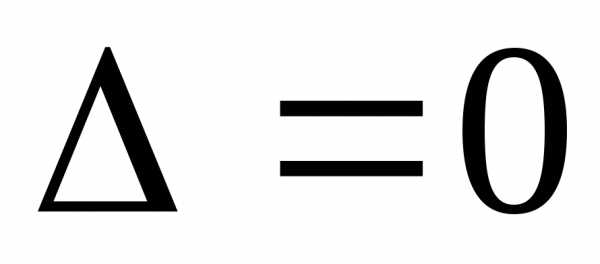 ,
а хотя бы один из определителей
,
а хотя бы один из определителей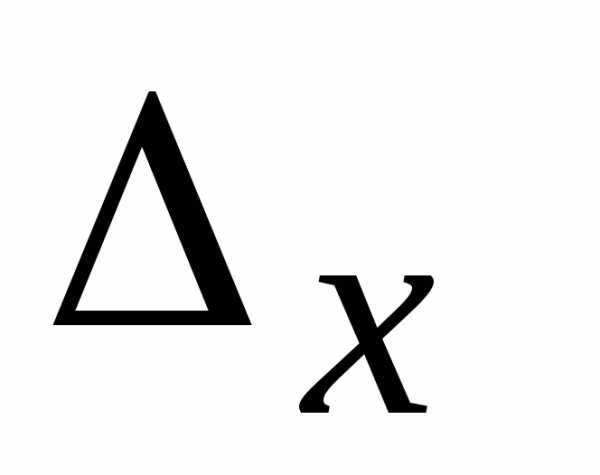 ,
, отличен от нуля, тосистема
не имеет решений (несовместная).
отличен от нуля, тосистема
не имеет решений (несовместная).
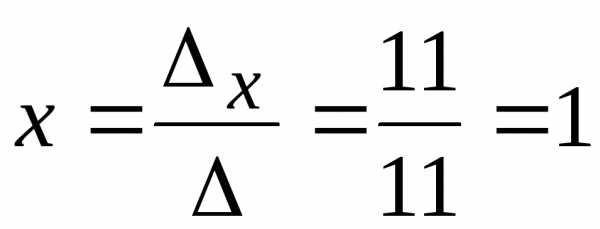 ;.
;.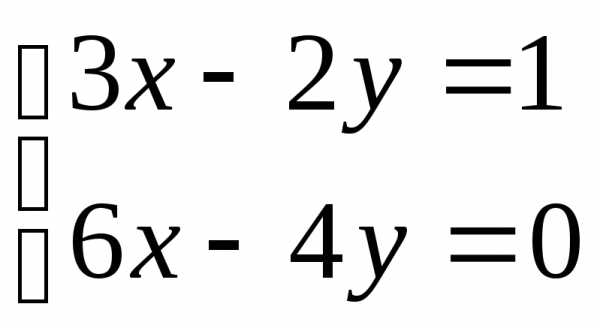 .
.
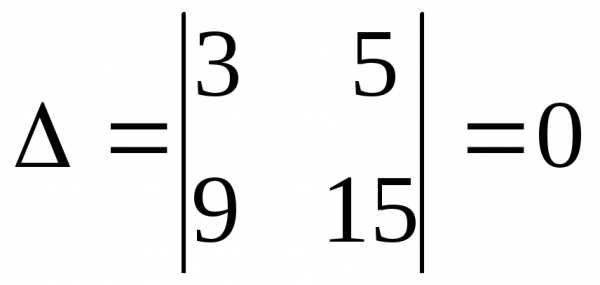 ,
, 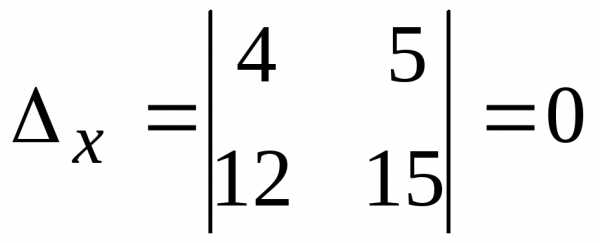 ,
, .
.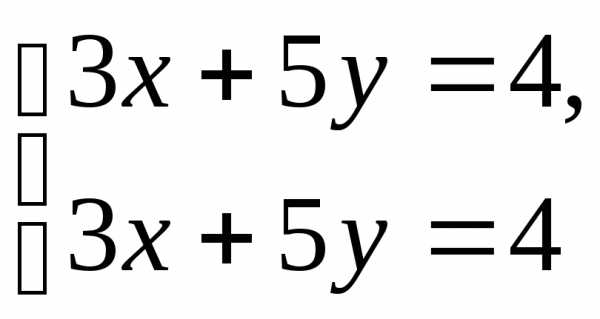 Оставим только одно из этих уравнений:.
Оставим только одно из этих уравнений:. через
через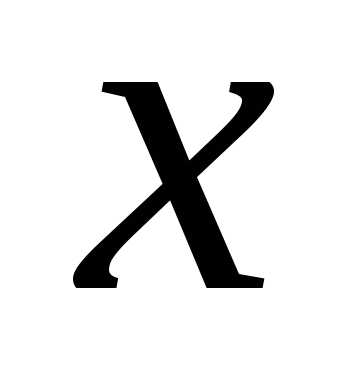 :
: ,
значение
,
значение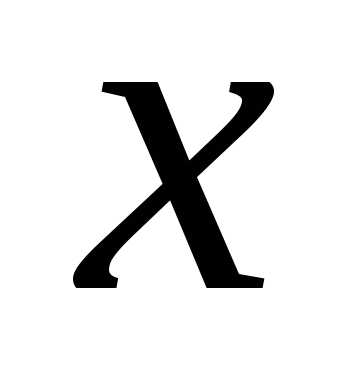 — любое действительное число. Это и есть
выражение дляобщего
решения СЛУ.
Ответ можно записать так:
— любое действительное число. Это и есть
выражение дляобщего
решения СЛУ.
Ответ можно записать так:  ,
где
,
где .
. различные значения, будем получать
бесконечное множествочастных
решений.
Например, при
различные значения, будем получать
бесконечное множествочастных
решений.
Например, при 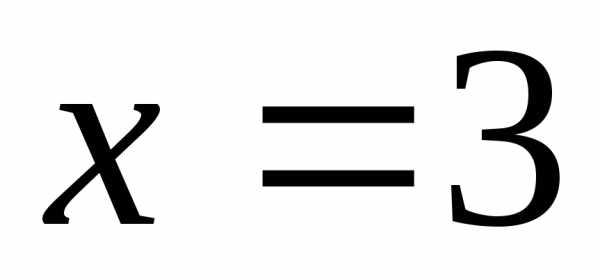 получим
получим и первое частное решение
и первое частное решение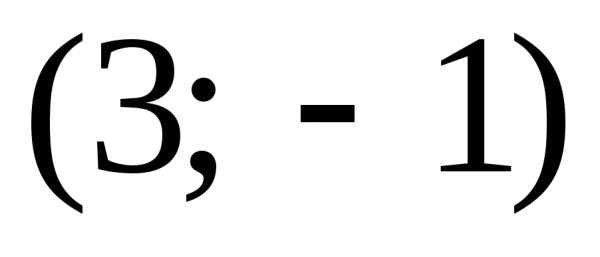 .
При
.
При получим
получим и второе частное решение
и второе частное решение ,
и так далее.
,
и так далее.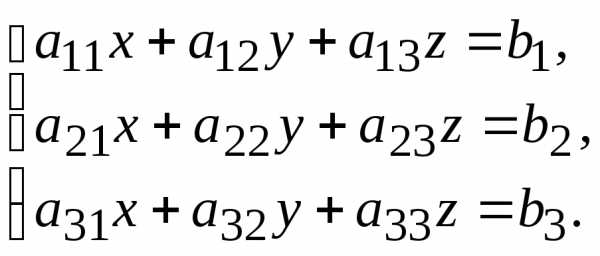
 ,
,  ,
,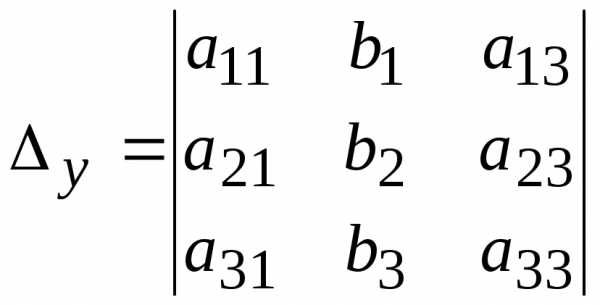 ,
.
,
. ,
то системаимеет единственное
решение, которое находится по формулам
Крамера:
,
то системаимеет единственное
решение, которое находится по формулам
Крамера: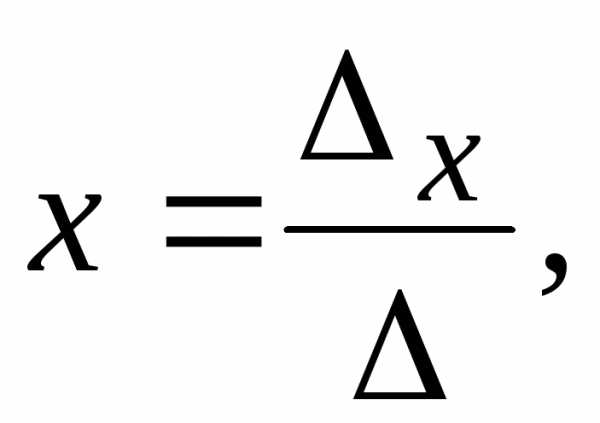
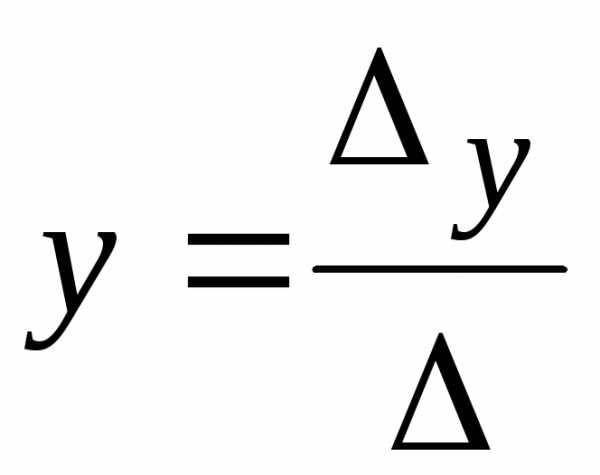 ,
,  .
.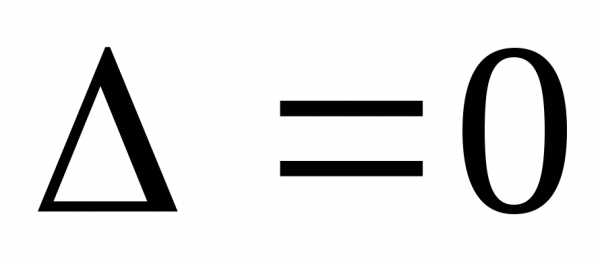 ,
а хотя бы один из определителей
,
а хотя бы один из определителей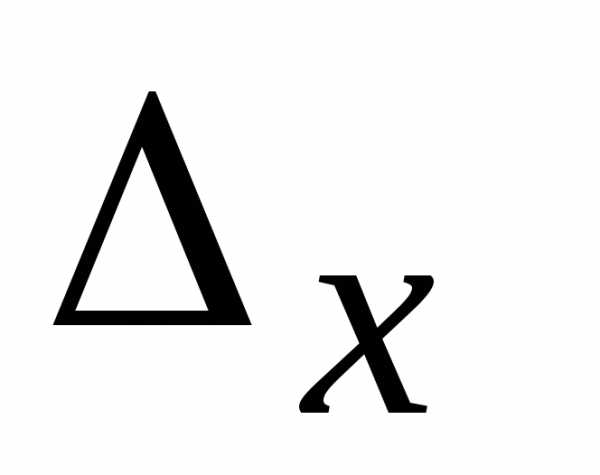 ,
, ,
,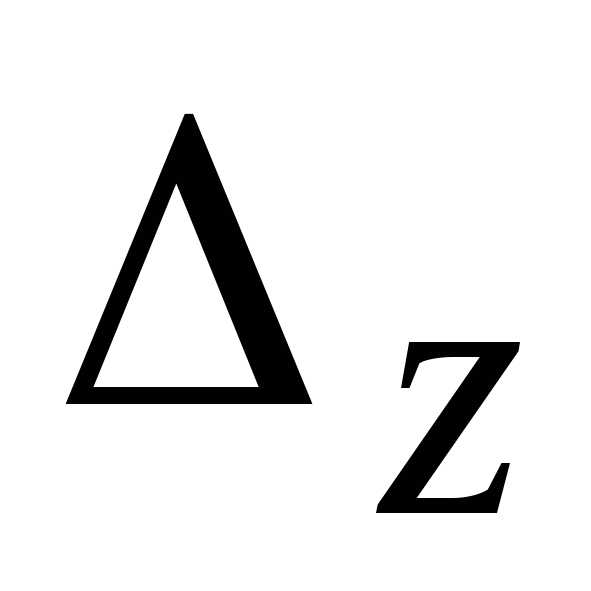 отличен от нуля, тосистема
не имеет решений.
отличен от нуля, тосистема
не имеет решений. .
.

 и
и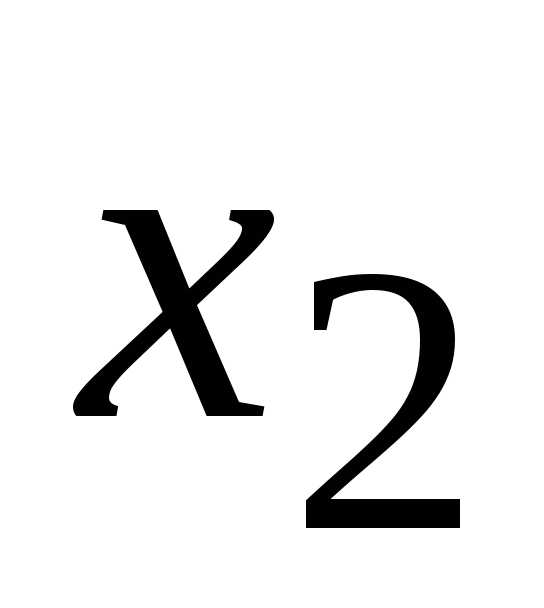 образуют определитель.
Поэтому оставим в левой части уравнений
слагаемые с
образуют определитель.
Поэтому оставим в левой части уравнений
слагаемые с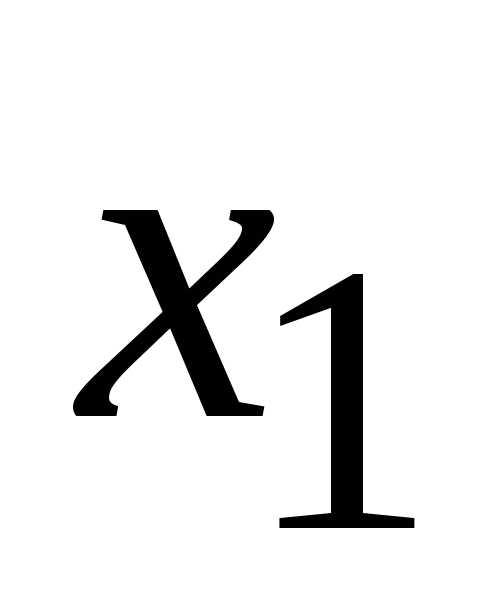 и
и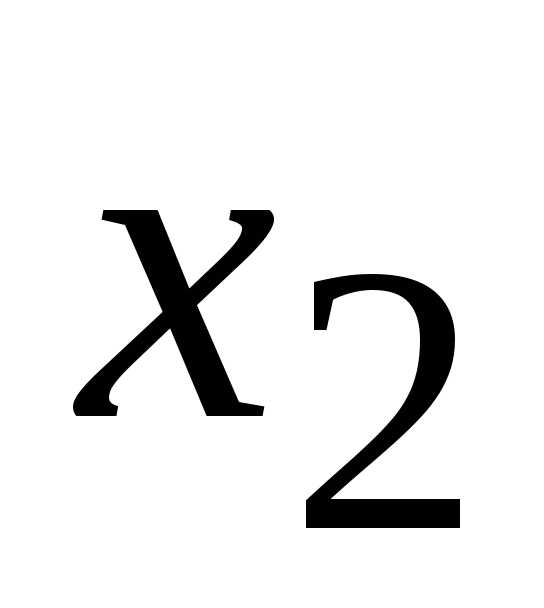 ,
а слагаемые с
,
а слагаемые с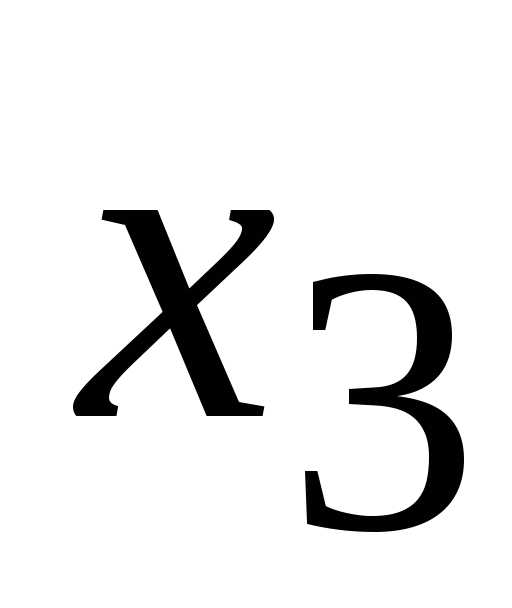 перенесем в правую часть с противоположным
знаком.
перенесем в правую часть с противоположным
знаком. и применим
к ней правило Крамера:
и применим
к ней правило Крамера: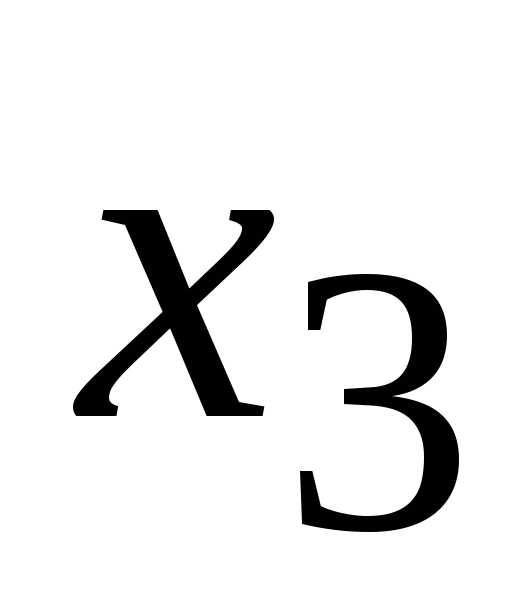 — любое действительное число.
— любое действительное число. (1.3)
(1.3) (1.5)
(1.5)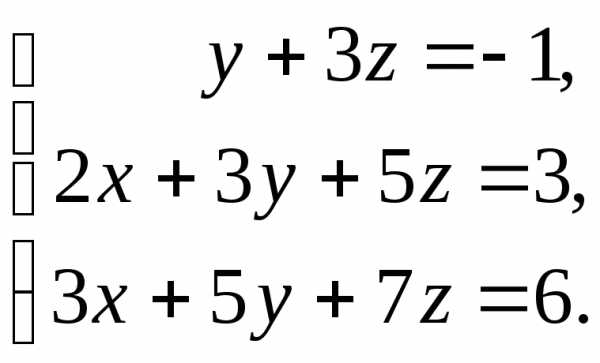


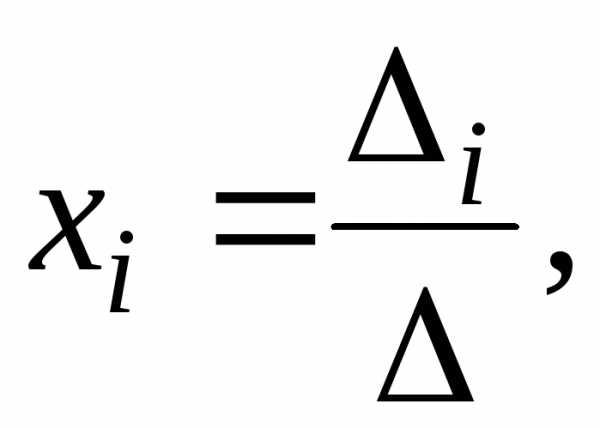

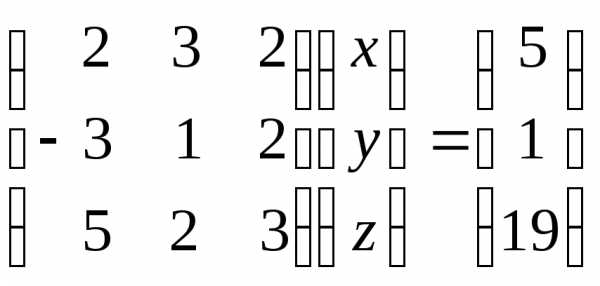 .
. .
. .
.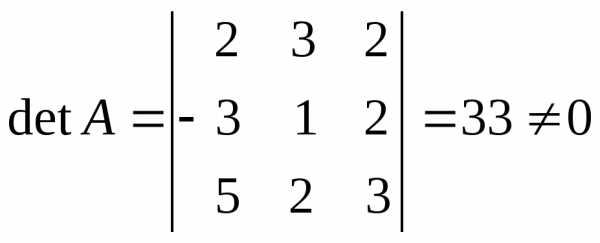 .
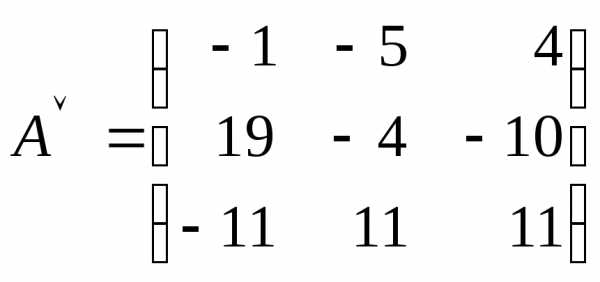
. .
.
 (1.5)
(1.5)
 .
.