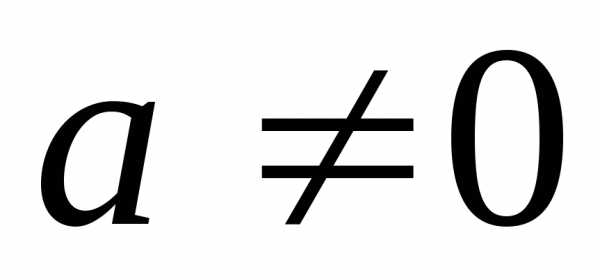Трехмерная графика
Этот вид компьютерной графики вобрал в себя очень много из векторной, а также из растровой компьютерной графики. Применяется она при разработке дизайн-проектов интерьера, архитектурных объектов, в рекламе, при создании обучающих компьютерных программ, видео-роликов, наглядных изображений деталей и изделий в машиностроении и др.Трёхмерная компьютерная графика позволяет создавать объёмные трёхмерные сцены с моделированием условий освещения и установкой точек зрения.

Трёхмерная компьютерная графика, как и векторная, является объектно-ориентированной, что позволяет изменять как все элементы трёхмерной сцены, так и каждый объект в отдельности. Этот вид компьютерной графики обладает большими возможностями для поддержки технического черчения. С помощью графических редакторов трёхмерной компьютерной графики, например Autodesk 3D Studio, можно выполнять наглядные изображения деталей и изделий машиностроения, а также выполнять макетирование зданий и архитектурных объектов, изучаемых в соответствующем разделе архитектурно-строительного черчения. Наряду с этим может быть осуществлена графическая поддержка таких разделов начертательной геометрии, как перспектива, аксонометрические и ортогональные проекции, т.к. принципы построения изображений в трёхмерной компьютерной графике частично заимствованы из них.
Для декоративно-прикладного искусства трёхмерная компьютерная графика предоставляет возможность макетирования будущих изделий с передачей фактуры и текстуры материалов, из которых эти изделия будут выполнены. Возможность увидеть с любых точек зрения макет изделия до его воплощения в материале позволяет внести изменения и исправления в его форму или пропорции, которые могут быть уже невозможны после начала работы (например, ювелирные изделия, декоративное литьё из металла и др.). В том же направлении трёхмерная компьютерная графика может быть использована для поддержки скульптуры, дизайна, художественной графики и др. Объёмная трёхмерная анимация и спецэффекты также создаются средствами трёхмерной графики. Создание учебных роликов для обучающих программ может стать основным применением этих возможностей трёхмерной компьютерной графики.
Уже тогда некоторые эксперты осторожно высказывали мнение, что МАХ может конкурировать с другими пакетами трехмерной графики. Осенью 2003 года discreet выпускает ЗD MAX 6. Новые инструменты анимации частиц в связке с модулями позволяют создавать фотореалистичные атмосферные эффекты. Появились встроенная поддержка капельно-сетчатых объектов, полноценная сетевая визуализация, импорт данных из САD-приложений, новые возможности для моделирования. Но кроме 3D Studio MAX есть и другие, не менее популярные программы трёхмерного моделирования, например Maya. Maya – это программа-аналог 3D Studio MAX, но она предназначена, в первую очередь, для анимации и для передачи мимики на лице трёхмерного актёра. Кроме того, в Maya удобнее рисовать. 3D Studio MAX направлен в первую очередь на качественную визуализацию предметов, ещё в нём можно выполнять примитивные чертежи.
 Вообще для черчения существуют свои программы трёхмерного моделирования, самые известные из них AutoCAD, ArhiCAD. AutoCAD предназначен, в первую очередь, для машиностроительного черчения, а ArhiCAD для архитектурного моделирования.
Вообще для черчения существуют свои программы трёхмерного моделирования, самые известные из них AutoCAD, ArhiCAD. AutoCAD предназначен, в первую очередь, для машиностроительного черчения, а ArhiCAD для архитектурного моделирования.
Что же требует трехмерная графика от человека?
Конечно же, умение моделировать различные формы и конструкции при помощи различных программных средств, а также знания ортогонального (прямоугольного) и центрального проецирования. Последняя — называется перспективой. Очень хорошее качество моделирования достигается при помощи тщательного подбора текстур и материалов в сочетании с правильным размещением в сцене источников освещения и камер. Основой для построения любой пространственной формы является плоскость и грань объекта. Плоскость в трехмерной графике задается с помощью трех точек, соединенных отрезками прямых линий.
Именно это условие дает возможность описать с помощью получаемых плоскостей «пространственную сетку», которая представляет собой модель объекта. Затем объекту дополнительно присваиваются характеристики поверхности объекта – материал. В свою очередь, материал характеризует качество поверхности, например, полированная, шероховатая, блестящая и др. Описывается и его текстура (камень, ткань, стекло и др.). Задаются и оптические свойства, например, прозрачность, отражение или преломление световых лучей и т.д.
Наряду с этим, трехмерному объекту можно задать условия освещения и выбрать точку обзора (камеру) для получения наиболее интересного наглядного изображения. Постановка, состоящая из трехмерного объекта, условий освещения и выбранной точки зрения, называется «трехмерной сценой». А вот для описания трехмерного пространства и объекта, находящегося внутри его, используется хорошо уже знакомый Вам координатный метод.
Существуют различные методы моделирования трехмерных объектов. Например, метод текстового описания модели с помощью специальных языков программирования «Скрипт».
esate.ru
Трехмерная графика.
Этот вид компьютерной графики вобрал в себя очень много из векторной, а так же и из растровой компьютерной графики. Применяется она при разработке дизайн-проектов интерьера, архитектурных объектов, в рекламе, при создании обучающих компьютерных программ, видео-роликов, наглядных изображений деталей и изделий в машиностроении и др. Трёхмерная компьютерная графика позволяет создавать объёмные трёхмерные сцены с моделированием условий освещения и установкой точек зрения.
Для изучения приёмов и средств композиции, таких как, передача пространства, среды, светотени, законов линейной, воздушной и цветовой перспективы здесь очевидны преимущества этого вида компьютерной графики над векторной и растровой графикой. В трехмерной графике изображения (или персонажи) моделируются и перемещаются в виртуальном пространстве, в природной среде или в интерьере, а их анимация позволяет увидеть объект с любой точки зрения, переместить в искусственно созданной среде и пространстве, разумеется, при сопровождении специальных эффектов.
Трёхмерная компьютерная графика, как и векторная, является объектно-ориентированной, что позволяет изменять как все элементы трёхмерной сцены, так и каждый объект в отдельности. Этот вид компьютерной графики обладает большими возможностями для поддержки технического черчения. С помощью графических редакторов трёхмерной компьютерной графики, например Autodesk 3D Studio, можно выполнять наглядные изображения деталей и изделий машиностроения, а также выполнять макетирование зданий и архитектурных объектов, изучаемых в соответствующем разделе архитектурно-строительного черчения. Наряду с этим может быть осуществлена графическая поддержка таких разделов начертательной геометрии как, перспектива, аксонометрические и ортогональные проекции, т.к. принципы построения изображений в трёхмерной компьютерной графике частично заимствованы из них.
Для декоративно-прикладного искусства трёхмерная компьютерная графика предоставляет возможность макетирования будущих изделий с передачей фактуры и текстуры материалов, из которых эти изделия будут выполнены. Возможность увидеть с любых точек зрения макет изделия до его воплощения в материале позволяет внести изменения и исправления в его форму или пропорции, которые могут быть уже невозможны после начала работы (например, ювелирные изделия, декоративное литьё из металла и др.). В том же направлении трёхмерная компьютерная графика может быть использована для поддержки скульптуры, дизайна, художественной графики и др. Объёмная трёхмерная анимация и спецэффекты также создаются средствами трёхмерной графики. Создание учебных роликов для обучающих программ может стать основным применением этих возможностей трёхмерной компьютерной графики.
К средствам работы с трёхмерной графикой, относят такой графический редактор как, 3D Studio MAX. Это один из самых известных трёхмерных редакторов, он часто используется при создании фильмов. Разработка программы 3D Studio МАХ была начата в 1993 году. Версия 3D Studio МАХ 1.0 вышла в 1995 году на платформе Windows NT.
Уже тогда некоторые эксперты осторожно высказывали мнение, что МАХ может конкурировать с другими пакетами трехмерной графики. Осенью 2003 года discreet выпускает Зd max 6. Новые инструменты анимации частиц в связке с модулями позволяют создавать фотореалистичные атмосферные эффекты. Появились встроенная поддержка капельно-сетчатых объектов, полноценная сетевая визуализация, импорт данных из САD-приложений, новые возможности для моделирования. Но кроме 3D Studio MAX есть и другие не менее популярные программы трёхмерного моделирования, например Maya. Maya – эта программа аналог 3D Studio MAX, но она предназначена в первую очередь для анимации и, например, для передачи мимики на лице трёхмерного актёра, так же в Maya удобнее рисовать. 3D Studio MAX направлен в первую очередь на качественную визуализацию предметов, ещё в нём можно выполнять примитивные чертежи.
Вообще для черчения существуют свои программы трёхмерного моделирования, самые известные из них AutoCAD, ArhiCAD. AutoCAD предназначен в первую очередь для машиностроительного черчения, а ArhiCAD для архитектурного моделирования.
Что же требует трехмерная графика от человека?
Конечно же, умение моделировать различные формы и конструкции при помощи различных программных средств, а также знания ортогонального (прямоугольного) и центрального проецирования. Последняя — называется перспективой. Очень хорошее качество моделирования достигается при помощи тщательного подбора текстур и материалов в сочетании с правильным размещением в сцене источников освещения и камер. Основой для построения любой пространственной формы является плоскость и грань объекта. Плоскость в трехмерной графике задается с помощью трех точек, соединенных отрезками прямых линий.
Именно это условие дает возможность описать с помощью получаемых плоскостей «пространственную сетку», которая представляет собой модель объекта. Затем объекту дополнительно присваиваются характеристики поверхности объекта – материал. В свою очередь, материал характеризует качество поверхности, например, полированная, шероховатая, блестящая и др. Описывается и его текстура (камень, ткань, стекло и др.). Задаются и оптические свойства, например, прозрачность, отражение или преломление световых лучей и т.д.
Наряду с этим, трехмерному объекту можно задать условия освещения и выбрать точку зрения (камеру) для получения наиболее интересного наглядного изображения. Постановка, состоящая из трехмерного объекта, условий освещения и выбранной точки зрения называется «трехмерной сценой». А вот для описания трехмерного пространства и объекта, находящегося внутри его, используется хорошо уже знакомый Вам координатный метод.
Существуют различные методы моделирования трехмерных объектов. Например, метод текстового описания модели с помощью специальных языков программирования «Скрипт».
studfiles.net
3D графика и ее применение
3D графика – это процесс создания объемной модели при помощи специальных компьютерных программ. Этот вид компьютерной графики вобрал в себя очень много из векторной, а так же и из растровой компьютерной графики. На основе чертежей, рисунков, подробных описаний или любой другой графический или текстовой информации, 3D дизайнер создает объемное изображение.В специальной программе модель можно посмотреть со всех сторон (сверху, снизу, сбоку), встроить на любую плоскость и в любое окружение. Трёхмерная компьютерная графика, как и векторная, является объектно-ориентированной, что позволяет изменять как все элементы трёхмерной сцены, так и каждый объект в отдельности. Этот вид компьютерной графики обладает большими возможностями для поддержки технического черчения. С помощью графических редакторов трёхмерной компьютерной графики, можно выполнять наглядные изображения деталей и изделий машиностроения, а также выполнять макетирование зданий и архитектурных объектов, изучаемых в соответствующем разделе архитектурно-строительного черчения. Наряду с этим может быть осуществлена графическая поддержка таких разделов начертательной геометрии как, перспектива, аксонометрические и ортогональные проекции, т.к. принципы построения изображений в трёхмерной компьютерной графике частично заимствованы из них.
Трехмерная графика может быть любой сложности. Вы можете создать простую трехмерную модель, с низкой детализацией и упрощенной формы. Или же это может быть более сложная модель, в которой присутствует проработка самых мелких деталей, фактуры, использованы профессиональные приемы (тени, отражения, преломление света и так далее). Конечно, это всерьез влияет на стоимость готовой трехмерной модели, однако позволяет расширить применение трехмерной модели.
Где применяется трехмерная графика
Трехмерное моделирование (3d графика) сегодня применяется в очень многих сферах. Конечно, в первую очередь, это строительство. Это может быть модель будущего дома, как частного, так и многоквартирного или же офисного здания, да и вообще любого промышленного объекта. Кроме того, визуализация активно применяется в дизайн-проектах интерьеров.3D модели очень популярны в сайтостроительстве. Для создания особенного эффекта некоторые создатели сайтов добавляют в дизайн не просто графические элементы, а трехмерные модели, иногда даже и анимированные. Программы и технологии трехмерного моделирования широко применяются и в производстве, например, в производстве корпусной мебели, и в строительстве, например, для создания фотореалистичного дизайн-проекта будущего помещения. Многие конструкторы уже давно перешли от использования линейки и карандаша к современным трехмерным компьютерным программам. Постепенно новые технологии осваивают и другие компании, прежде всего, производственные и торговые.
Конечно, в основном трехмерные модели используются в демонстрационных целях. Они незаменимы для презентаций, выставок, а также используются в работе с клиентами, когда необходимо наглядно показать, каким будет итоговый результат. Кроме того, методы трехмерного моделирования нужны там, где нужно показать в объеме уже готовые объекты или те объекты, которые существовали когда-то давно. Трехмерное моделирование это не только будущее, но и прошлое и настоящее.
Преимущества трехмерного моделирования
Преимуществ у трехмерного моделирования перед другими способами визуализации довольно много. Трехмерное моделирование дает очень точную модель, максимально приближенную к реальности. Современные программы помогают достичь высокой детализации. При этом значительно увеличивается наглядность проекта. Выразить трехмерный объект в двухмерной плоскости не просто, тогда как 3D визуализации дает возможность тщательно проработать и что самое главное, просмотреть все детали. Это более естественный способ визуализации.В трехмерную модель очень легко вносить практически любые изменения. Вы можете изменять проект, убирать одни детали и добавлять новые. Ваша фантазия практически ни чем не ограничена, и вы сможете быстро выбрать именно тот вариант, который подойдет вам наилучшим образом.
Однако трехмерное моделирование удобно не только для клиента. Профессиональные программы дают множество преимуществ и изготовителю. Из трехмерной модели легко можно выделить чертеж каких-либо компонентов или конструкции целиком. Несмотря на то, что создание трехмерной модели довольно трудозатратный процесс, работать с ним в дальнейшем гораздо проще и удобнее чем с традиционными чертежами. В результате значительно сокращаются временные затраты на проектирование, снижаются издержки.
Специальные программы дают возможность интеграции с любым другим профессиональным программным обеспечением, например, с приложениями для инженерных расчетов, программами для станков или бухгалтерскими программами. Внедрение подобных решений на производстве дает существенную экономию ресурсов, значительно расширяет возможности предприятия, упрощает работу и повышает ее качество.
Программы для трехмерного моделирования
Существует довольно большое количество самых разных программ для 3D моделирования. Так, одной из популярных программ, которые специально разработаны для создания трехмерной графики и дизайна интерьеров, является программа 3D Studio MAX. Она позволяет реалистично визуализировать объекты самой разной сложности. Кроме того, «3D Studio MAX» дает возможность компоновать их, задавать траектории перемещений и в конечном итоге даже создавать полноценное видео с участием трехмерных моделей. Хотя такая работа, конечно же, требует у специалиста серьезных навыков, а также больших компьютерных ресурсов, в первую очередь объемов памяти и быстродействие процессора.Редактор Maya назван в честь санскритского слова, которое означает иллюзия. Maya была разработана Alias Systems. В октябре 2005 года компания Alias влилась в Autodesk. Maya чаще используется для создания анимации и трехмерных эффектов в фильмах.
fevt.ru
Трехмерные графики функций в MathСad
Графики, которые включают две переменные, в Mathcad схожи с 2D-графиками, но есть отличия, которые необходимо знать. В Mathcad существует два вида таких графиков: контурный и 3D-график поверхности в трех осях.
Контурный график
Контурный график показывает изменения поверхности по высоте. Он являет собой линии равных высот. Для интеграции контурного графика нужно выбрать в Графики -> Кривые -> Вставить график -> Контурный график.
Давайте пропишем построение графика параболоида:
Такая функция имеет минимум в начале осей координат и возрастает при отходе от начала осей. Цвет нашего графика будет зависим от величины z.
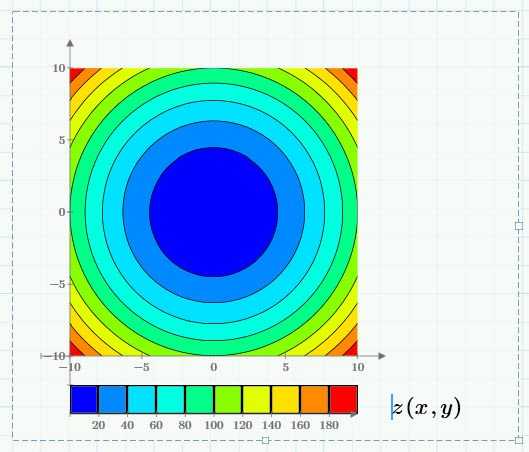
По стандарту в наших уроках используем диапазоны от -10 до 10 для x и у. Для оси z подбор диапазона будет автоматизирован. Изменение диапазонов возможно с изменением величины первой и последней меток, а изменение расстояния — изменением величины второй метки. Также можно выбирать одну из представленных в программе цветовых схем оформления или добавлять величины к контурным линиям.
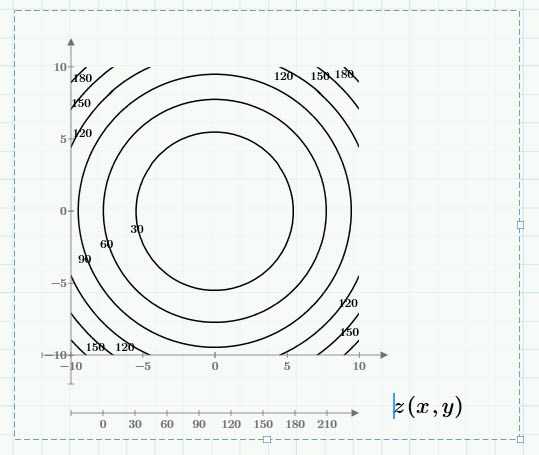
3D-график
Давайте вначале выясним, какие есть элементы у 3D-графика.
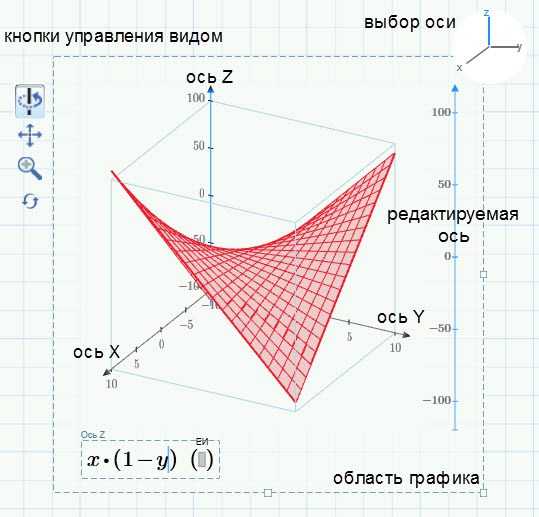
График имеет три оси: X, Y, Z. Обычно ось зет имеет вертикальное направление. Сам график, который изображен розовой сеткой на примере выше, ограничен прямоугольной областью, сторонами которой являются оси координат. Если в 2D-графиках были места для заполнения как для оси X, так и для оси Y, то здесь есть только одно место заполнения для оси Z.
Если вы посмотрите на правый верхний угол, то увидите кнопку выбора осей. При нажатии на нужную ось, она подсветится как на кнопке, так и на графике. Вы можете менять для каждой оси значение первой, второй и последней метки. Все это справедливо настолько же, насколько и для 2D-графика. Кроме того, можно изменять диапазоны как по осям, так и по числу меток.
Вам будет доступно расширение, перемещение и сжатие области, где размещен график. Для этого существуют специальные кнопки, которые размещены на границе области. Кнопки слева сверху предназначены для перемещения, вращения или масштабирования графика. А также есть кнопка «Сбросить график», которая оп своим функциям напоминает кнопку «Отменить».
Параболоид
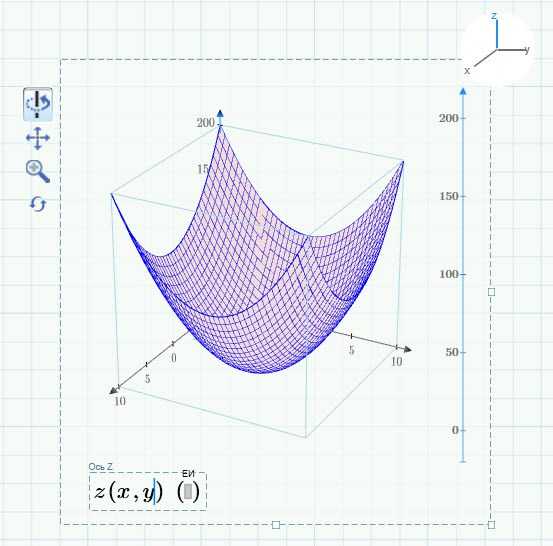
Попробуем построить график заданного параболоида. Разместите курсор на любое место рабочей области и нажмите Графики -> Кривые -> Вставить график -> 3D-график. В местозаполнитель введите [z(x,y] и нажмите на любое пустое место. Построится вот такой график:
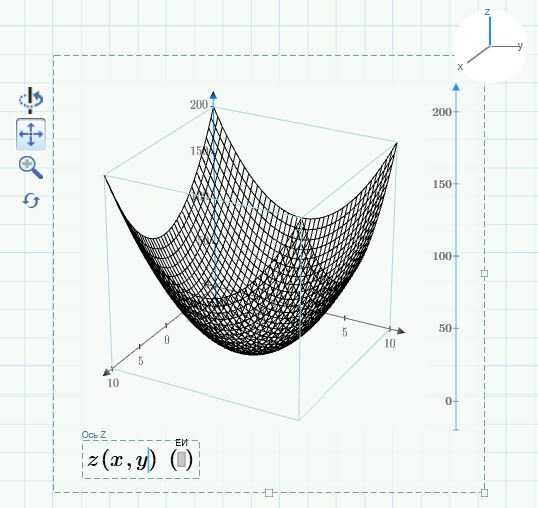
Поэкспериментируйте с кнопками управления видом графика, а когда получите достаточно опыта, нажмите на кнопку «Сброс вида».
Нажмите на ось Z справа сверху на кнопке выбора оси. Поменяйте обозначение последней метки с 200 на 400, а потом нажмите на любое пустое место вне графика, чтобы изменения применились. Если вам нужно будет вернуться в исходную позицию, то придется заново вручную поменять значение на 200, так как кнопка вида здесь работать не будет.
На следующей картинке вы видите тот же график, но с изменением цвета и заливки поверхности. Это можно сделать, воспользовавшись меню Графики -> Стили:
Две функции
Для добавления еще одной функции на график, нужно выбрать местозаполнитель с легендой и в меню перейти Графики -> Кривые -> Добавить кривую. На примере вы можете видеть функции параболоида и плоскости на одном координатной сетке.
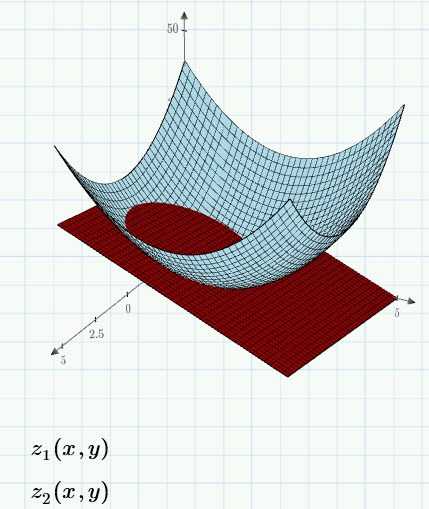
Для графиков лучше использовать отличные друг от друга цвета, чтобы их пересечение было более заметно. Вы можете повращать график, чтобы разобраться в форме этого пересечения.
Использование вектора
Мы производили построение 2D-графиков с использованием вектора. Что-то подобное можно использовать и для 3D-графиков, но нам потребуется вектор с осями X, Y, Z. Изобразим примером функцию, которая известна среди математиков под названием «мексиканская шляпа».
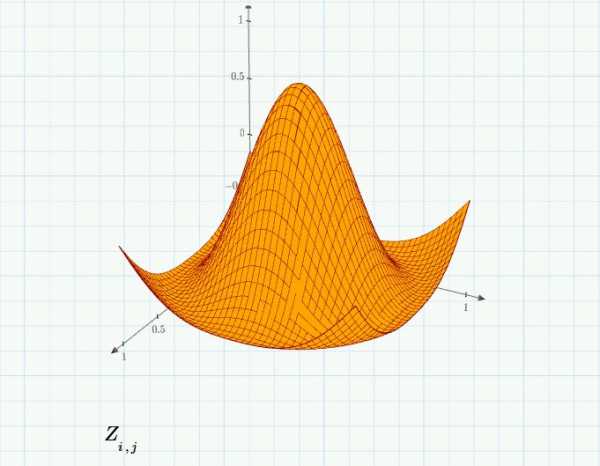
Сфера
Построение параметрической поверхности требует более серьезного подхода, чем 2D-графика. Все из-за того, что значение Z можно добавлять только непосредственно на графике. Расскажем, как это выполнить, используя пример построения графика сферы с помощью функции CreateMesh. Параметрические уравнения сферы выглядят так:
У параметра φ есть название — азимутальный угол. Параметр θ называется зенитным углом. Пропишем нужные нам диапазоны изменения параметров:
При использовании функции CreateMesh нам понадобится такая матрица:
Пропишите имя переменной матрицы в метозаполнитель 3D-графика и нажмите на любую пустую область вне его.
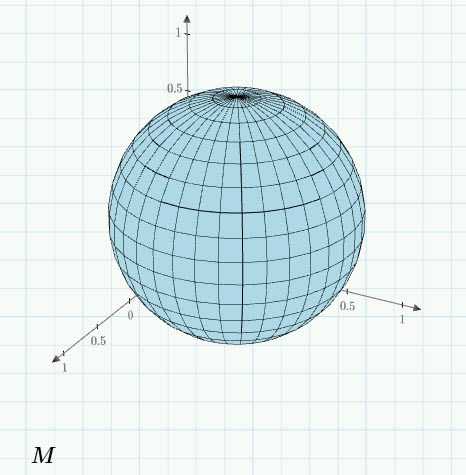
Резюме
3D-графики имеют некоторые отличия от двухмерных графиков, которые мы уже рассматривали:
- Существует 2 вида графика для построения функций с двумя переменными: контурные графики и 3D-графики. Их вставка производится из Графики -> Кривые -> Вставить график/
- Контурный график напоминает карту с линиями уровня.
- По принципам построения 3D-график отличается от плоского наличием третьей оси. Для выбора осей есть специальная кнопка, каждую ось можно редактировать отдельно. Так же как и для плоских графиков, значения первой, второй и последней метки можно редактировать.
- Управлять размерами и позицией графика на рабочей области можно с помощью перетягивания краев области графика.
- Вращение и перемещение самого графика доступно с помощью кнопок управления в левом верхнем углу.
- Для того, чтобы быстро построить функцию, задайте определения z(x,y), вставьте область с графиком и пропишите имя функции и место для заполнения.
- Также доступно создание вектора, который будет содержать определения значений для осей X, Y, Z и разместить имя вектора в местозаполнитель.
archicad-autocad.com
11. Трехмерная графика. Основные понятия Основные действия. Создание изображений средствами трехмерной графики.
3D-графика предназначена для имитации фотографирования или видеосъемки трехмерных образов объектов, которые должны быть предварительно подготовлены в памяти компьютера.
В большинстве подсистем трехмерной графики применяется графический конвейер.
Конвейер – это логическая группа вычислений, выполняемых последовательно, дающих на выходе синтезируемую сцену. Конвейер разделен на множество этапов, на каждом из которых аппаратно или программно выполняется некоторая функция. Наличием переходов между этапами конвейера обеспечивается возможность выбора между программной и аппаратной реализацией очередного этапа. Такой подход к настройке конвейера позволяет приложениям трехмерной графики получать преимущества аппаратной реализации. Таким образом, реализация конвейера может быть программной, полностью аппаратной или смешанной (программно- аппаратной).
Первоначально объект представляется в виде набора точек или координат в трехмерном пространстве. Трехмерная система координат определяется тремя осями: горизонтальной, вертикальной и глубины, т.е. осями x, y и z. Объектом может быть дом, человек, машина, самолет или целый 3D мир. Координаты определяют положение вершин (узловых точек) объекта в пространстве. При помощи соединения вершин объекта линиями можно получить каркасную модель трехмерного тела. Каркасная модель определяет области, составляющие поверхности объекта, которые могут быть заполнены цветом, текстурами и освещаться лучами света.
Основные понятия
Превращения. Операции изменения позиции, размера, или ориентации объекта в пространстве. В общем случае — перемещение, масштабирование и вращение.
Деформации. Операции подобные превращениям, однако, более сложные, так как их исполнение приводят к перемене внешнего вида объекта. К деформациям можно отнести искривление,поворот, рассогласование и т.п.
Распределение- процесс назначения объекту атрибутов придающих ему реалистичность. Важнейшая характеристика для оценки трехмерных сцен — реалистичность, однако, простое
моделирование трехмерных объектов не всегда позволяет добиться реалистичности. В этом
случае, на помощь приходит распределение текстур.
Мультитекстурирование позволяет конвейеризировать наложение текстур с использованием нескольких (обычно двух) блоков текстурирования.
Конвейер рендеринга выполняется по многоступенчатому механизму, называемому конвейером рендеринга. Конвейер рендеринга может быть разделен на три стадии: тесселяция, геометрическая обработка и растеризация. Если взять произвольный 3D- ускоритель, то он не будет ускорять все стадии конвейера, и даже более того, стадии могут лишь частично ускоряться им.
Тесселяция – процесс разбиения поверхности объектов на треугольники. Эта стадия проводится полностью программно вне зависимости от технического уровня и цены 3D- аппаратуры. Геометрическая обработка делится на несколько фаз и может частично ускоряться 3D-ускорителем.
Растеризация наиболее интенсивная операция, обычно реализуемая на аппаратном уровне. Растеризатор выполняет непосредственно рендеринг и является наиболее сложной ступенью конвейера. Если стадия геометрической обработки работает с вершинами, то растеризация включает операции над пикселями. Растеризация включает в себя затенение.
Трансформация – преобразование координат (вращение, перенос и масштабирование всех объектов).
Расчет освещенности – определение цвета каждой вершины с учетом всех световых источников.
Проецирование – преобразование координат в систему координат экрана.
Коррекция перспективы. Способность корректировать текстуры таким образом, чтобы у наблюдателя создавалось впечатление перспективы.
Антиалиасинг. Т.к. цифровые изображения, в основном, представляют собой матрицу из точек, строки этой матрицы, будучи проведенными не строго по горизонтали или вертикали прорисовывают объект неровными, зубчатыми линиями. Наиболее распространенный метод борьбы с этим эффектом состоит в том, что пиксели в зубчиках заполняются цветом
Наложение рельефа. Методика моделирования рельефных поверхностей. Для того чтобы подчеркнуть бугорки и впадины рельефа с помощью светотени, надо затемнить либо осветлить стенки этих бугорков и впадин. Другой метод состоит в симуляции рельефности глянцевой или зеркальной поверхности отражением окружающей среды. Это и делает техника наложения рельефа.
Затуманивание. Один из наиболее распространенных эффектов. Отдаленные объекты или их детали, как бы скрываются в тумане и проясняются по мере приближения зрителя к ним. Эффект используется не только для моделирования атмосферного явления – уменьшая число деталей разработчики делают сцену менее сложной.
studfiles.net

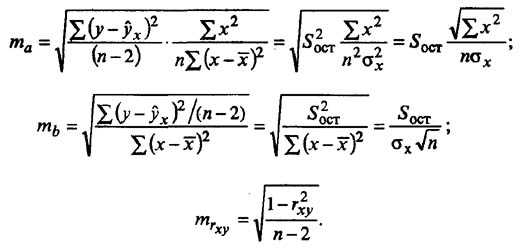
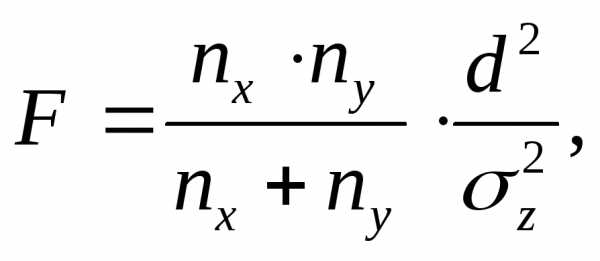 (7.4)
(7.4)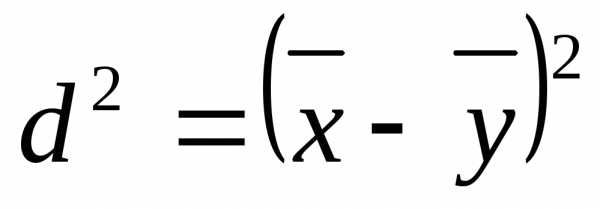 и(7.5, 7.6)
и(7.5, 7.6) и
и 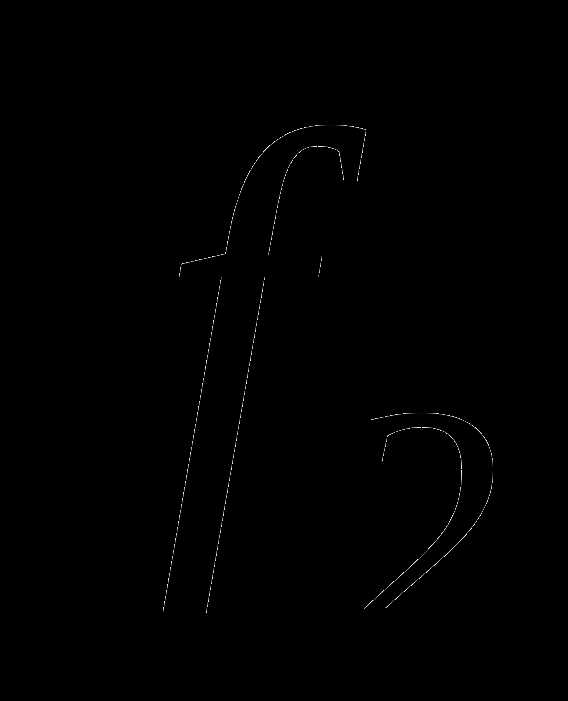 степеней
свободы. Будем считать, что первая
выборка взята из генеральной совокупности
с дисперсией
степеней
свободы. Будем считать, что первая
выборка взята из генеральной совокупности
с дисперсией 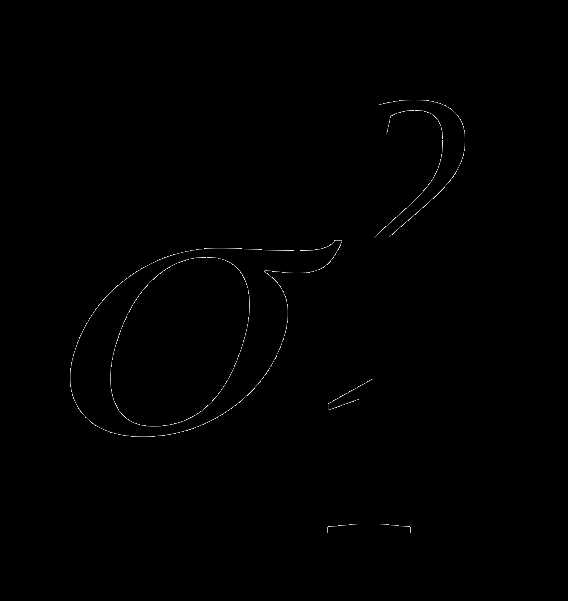 ,
а вторая – из генеральной совокупности
с дисперсией
,
а вторая – из генеральной совокупности
с дисперсией 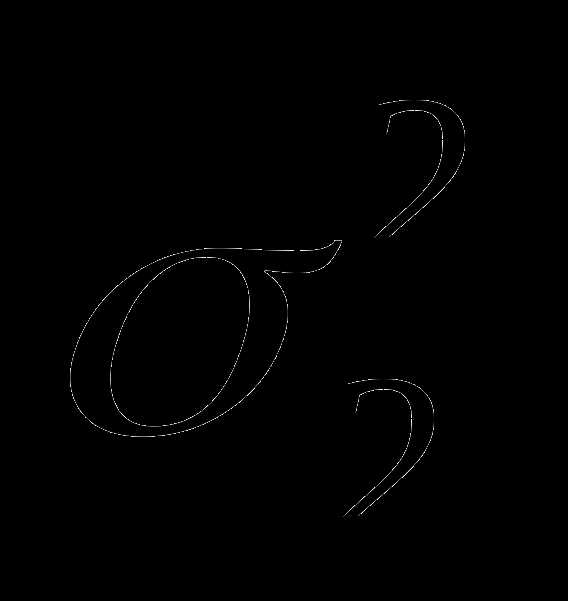 .
Выдвигается нулевая гипотеза о равенстве
двух дисперсий, т.е. H0:
.
Выдвигается нулевая гипотеза о равенстве
двух дисперсий, т.е. H0: 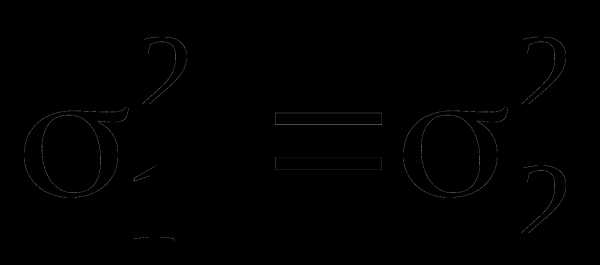 или
или 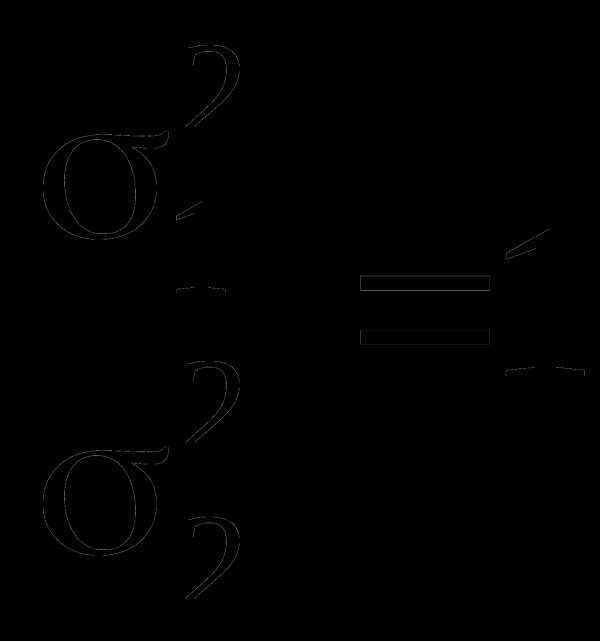 .
Для того, чтобы отвергнуть эту гипотезу
нужно доказать значимость различия при
заданном уровне значимости
.
Для того, чтобы отвергнуть эту гипотезу
нужно доказать значимость различия при
заданном уровне значимости 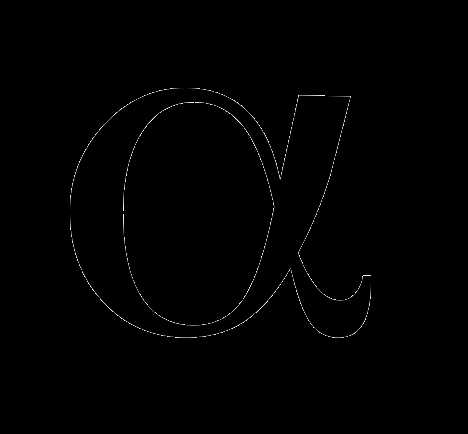 .
.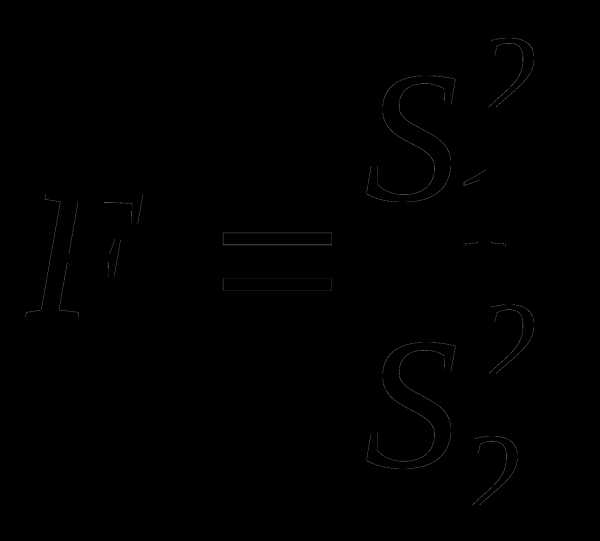 .
.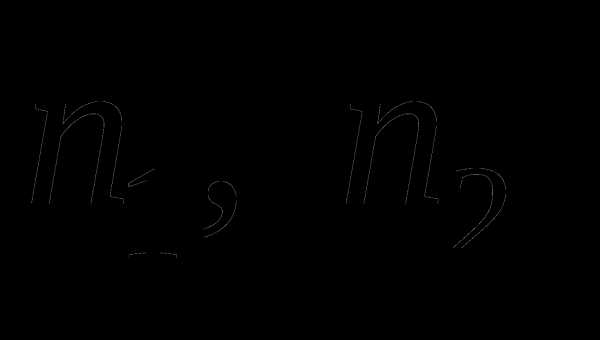 – объем первой и второй выборки
соответственно.
– объем первой и второй выборки
соответственно. и
и 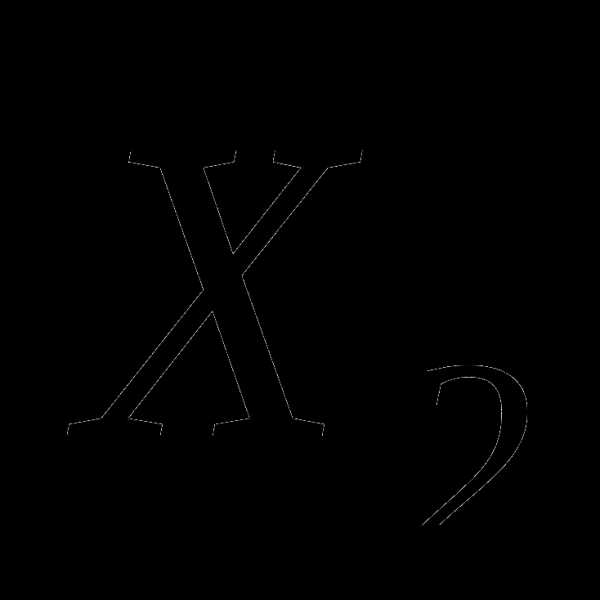 ,
а качество характеризуется соответствующими
выборочными дисперсиями оценок: и
.
При оценке уровня текущей успеваемости
оказалось, что он одинаков у обоих
учащихся:
,
а качество характеризуется соответствующими
выборочными дисперсиями оценок: и
.
При оценке уровня текущей успеваемости
оказалось, что он одинаков у обоих
учащихся:  =
= 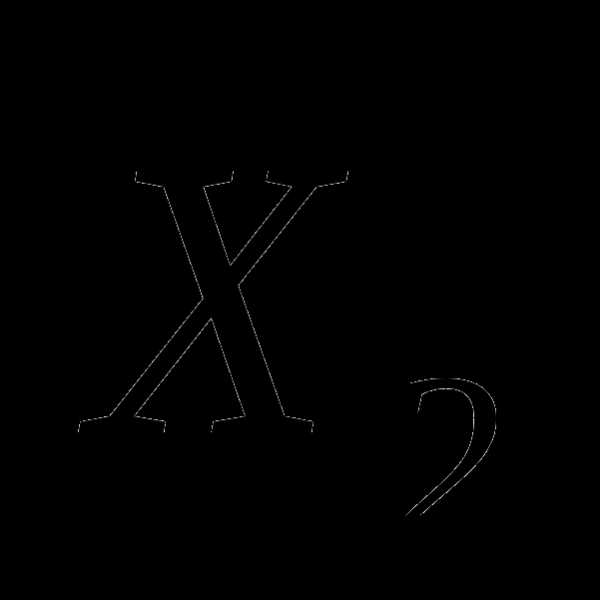 =
4,0. Выборочные дисперсии:
=
4,0. Выборочные дисперсии: 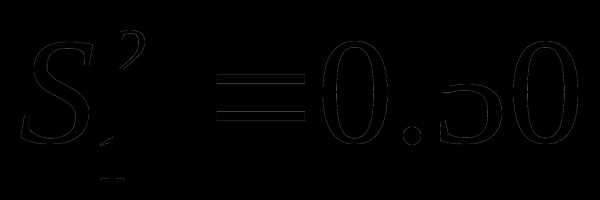 и
и 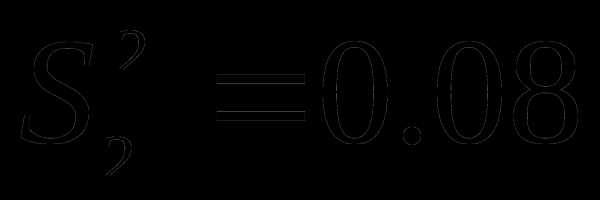 .
Числа степеней свободы, соответствующие
этим оценкам:
.
Числа степеней свободы, соответствующие
этим оценкам:  и
и 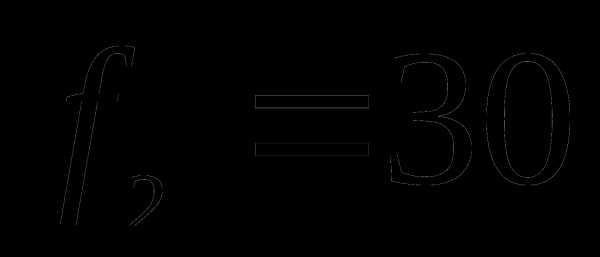 . Отсюда для установления различий в
эффективности обучения мы можем
воспользоваться стабильностью
успеваемости, т.е. проверим гипотезу
.
. Отсюда для установления различий в
эффективности обучения мы можем
воспользоваться стабильностью
успеваемости, т.е. проверим гипотезу
.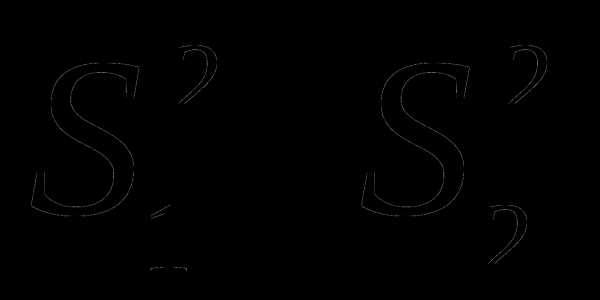 (у нас в числителе всегда большая
дисперсия). При проверке одностороннего
критерия получим
,
что меньше вычисленного выше значения.
Итак, нулевая гипотеза должна быть
отвергнута в пользу альтернативы
.
(у нас в числителе всегда большая
дисперсия). При проверке одностороннего
критерия получим
,
что меньше вычисленного выше значения.
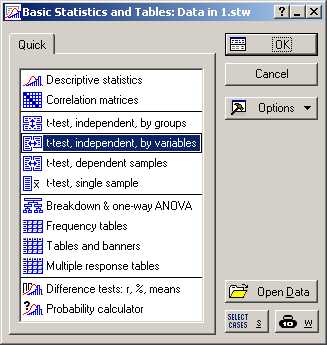
Итак, нулевая гипотеза должна быть
отвергнута в пользу альтернативы
.


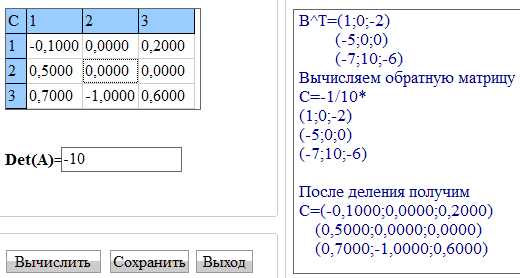
 Текст 1. Числовые множества
Текст 1. Числовые множества Задание 6. Рассмотрите схему и опишите её:
Задание 6. Рассмотрите схему и опишите её: