Уровни бюджетной системы в РФ
В соответствии с Бюджетным Кодексом РФ, структура бюджетной системы нашего государства состоит из трех уровней:
— 1 уровень составляют Федеральный Бюджет и государственные внебюджетные фонды РФ.
Федеральный бюджет и бюджеты государственных внебюджетных фондов Российской Федерации предназначены для исполнения расходных обязательств Российской Федерации.
Использование федеральными органами государственной власти иных форм образования и расходования денежных средств, предназначенных для исполнения расходных обязательств Российской Федерации, не допускается.
Федеральный бюджет и свод консолидированных бюджетов субъектов Российской Федерации (без учета межбюджетных трансфертов между этими бюджетами) образуют консолидированный бюджет Российской Федерации.
— 2 уровень составляют бюджеты Субъектов федерации и государственные территориальные внебюджетные фонды.
Каждый субъект Российской Федерации имеет собственный бюджет и бюджет территориального государственного внебюджетного фонда.
Бюджет субъекта Российской Федерации (региональный бюджет) и бюджет территориального государственного внебюджетного фонда предназначены для исполнения расходных обязательств субъекта Российской Федерации.
Использование органами государственной власти субъектов Российской Федерации иных форм образования и расходования денежных средств для исполнения расходных обязательств субъектов Российской Федерации не допускается.
В бюджетах субъектов Российской Федерации в соответствии с бюджетной классификацией Российской Федерации раздельно предусматриваются средства, направляемые на исполнение расходных обязательств субъектов Российской Федерации, возникающих в связи с осуществлением органами государственной власти субъектов Российской Федерации полномочий по предметам ведения субъектов Российской Федерации и полномочий по предметам совместного ведения, и расходных обязательств субъектов Российской Федерации, осуществляемых за счет субвенций из федерального бюджета.
Бюджет субъекта Российской Федерации и свод бюджетов муниципальных образований, входящих в состав субъекта Российской Федерации (без учета межбюджетных трансфертов между этими бюджетами), образуют консолидированный бюджет субъекта Российской Федерации.
— 3 уровень бюджетной системы РФ представляют местные бюджеты, в том числе бюджеты муниципальных районов, бюджеты городских округов, бюджеты внутригородских муниципальных образований городов федерального значения Москвы и Санкт-Петербурга, бюджеты городских и сельских поселений.
Каждое муниципальное образование имеет собственный бюджет.
Бюджет муниципального образования (местный бюджет) предназначен для исполнения расходных обязательств муниципального образования.
Использование органами местного самоуправления иных форм образования и расходования денежных средств для исполнения расходных обязательств муниципальных образований не допускается.
В местных бюджетах в соответствии с бюджетной классификацией Российской Федерации раздельно предусматриваются средства, направляемые на исполнение расходных обязательств муниципальных образований, возникающих в связи с осуществлением органами местного самоуправления полномочий по вопросам местного значения, и расходных обязательств муниципальных образований, исполняемых за счет субвенций из других бюджетов бюджетной системы Российской Федерации для осуществления отдельных государственных полномочий.
Бюджет муниципального района (районный бюджет) и свод бюджетов городских и сельских поселений, входящих в состав муниципального района (без учета межбюджетных трансфертов между этими бюджетами), образуют консолидированный бюджет муниципального района.
В качестве составной части бюджетов городских и сельских поселений могут быть предусмотрены сметы доходов и расходов отдельных населенных пунктов, других территорий, не являющихся муниципальными образованиями.
finekon.ru
11. Бюджетная система рф состоит из 3-х уровней:
1.Федеральный бюджет
и бюджеты государственных внебюджетных
фондов разрабатываются и утверждаются
в форме ФЗ.
2.Бюджеты субъектов
РФ и бюджеты территориальных внебюджетных
фондов – форма образования и расходования
денежных средств, предназначенных для
обеспечения задач и функций, отнесенных
к предметам ведения субъекта РФ,
разрабатываются и утверждаются в форме
законов субъектов РФ.
3.Местные бюджеты
разрабатываются и утверждаются в форме
правовых актов органов местного
самоуправления.
Все бюджеты
функционируют автономно. Местные бюджеты
своими доходами и расходами не входят
в бюджеты субъектов РФ, а последние не
включаются в федеральный бюджет.
Государственный
бюджет –
ведущее звено финансовой системы, это
основной финансовый план государства
на текущий год, имеющий силу закона.
Федеральный бюджет РФ – главное звено
бюджетной системы, через него мобилизуются
средства предприятий для финансирования
народного хозяйства, социально-культурных
мероприятий, обороны, содержания
управления, создания резервов и др.
Функции
государственного бюджета:
1.Перераспредлительная
2.Регулирующая 3.Социальная функция
4.Контролирующая – контроль за разработкой
и утверждением бюджетов.
Задачи
бюджетной политики: 1.финансовая
стабилизация 2.рост производства,
структурная перестройка 3.стимулирование
инвестиционной активности за счет
увеличения доли накопления в НД (национ.
Доход.) 4.укрепление доходности бюджета
за счет совершенствования налогообложения
5.усиление контроля за величиной
государственного долга 6.создание
системы действенного финансового
контроля за расходованием финансовых
средств.
Классификация
расходов:
1.По
роли в процессе воспроизводства: 1.1.расходы
на материальное производство 1.2.расходы
на непроизводственную сферу
2.Текущие
и капитального характера: 2.1.текущие
– зарплата, закупки товаров, долги
2.2.капитального характера – капитальные
вложения в основные фонды, капитальное
строительство и капитальный ремонт.
3.Функциональная
структура расходов: 3.1.расходы
на народное хозяйство 3.2.социально-культурные
мероприятия 3.3.оборона 3.4.наука 3.5.оплата
долгов – увеличивается ежегодно
3.6.дотации территориям – увеличиваются
Принципы
осуществления расходов: 1.целевой
характер использования 2.безвозмездность
ассигнований из бюджета, но есть бюджетные
ссуды по специальным распоряжениям
правительства
Основные
задачи в области государственных
расходов: 1.сокращение
числа федеральных целевых программ
2.обеспечение концентрации средств
бюджета на наиболее значимых направлениях
3.сокращение расходов на аппарат
управления 4.децентрализация инвестиционного
процесса 5.сокращение дотаций в угольную
промышленность и ЖКХ
Большая часть
доходов государственного бюджета –
налоговые (80%), из них косвенные налоги
(более 60% от налогов), НДС, акцизы, пошлины
и др. НДС был введен взамен налога с
оборота. Акцизы – вино, табак, автомобили,
нефть, газ. Таможенные пошлины –
импортные, экспортные и особые
(антидемпинговые), ставки по пошлинам
адвалорные – в % от стоимости
Прямые налоги –
на прибыль – не направлен на повышение
эффективности производства (объект
налогообложения – валовая прибыль).
Налог на доходы с физических лиц –
объект – совокупный доход физического
лица в году.
Бюджетный процесс
охватывает 4 стадии (этапа) бюджетной
деятельности:
1)Составление
проекта бюджета – осуществляется исполнительными
органами власти. Ему предшествует
разработка прогнозов развития территорий
и целевых программ, на основе которых
создается сводный финансовый Балан
государства (СФБ). 2)Рассмотрение
и утверждение бюджета – Федеральном собрании (Парламенте)
РФ, представительных органах субъектах
федерации, органах местного самоуправления.
Проект федерального бюджета направляется
для рассмотрения в комитеты Государственной
Думы. Результаты анализа и заключения
по каждому комитету направляются в
Комитет Государственной Думы по бюджету,
налогам, банкам и финансам, который
составляет сводное заключение. 3)Исполнение
бюджета — за
исполнение бюджетного процесса отвечает
Правительство РФ, Минфин, МНС,
государственный таможенный комитет,
федеральное казначейство.
4)Составление
отчета об исполнении бюджета и его
утверждение – вся работа по составлению
отчета возложена на Минфин и его
финансовые органы, Государственную
налоговую службу и ее органы, государственный
таможенный комитет и его органы. Эти
отчеты направляются соответствующим
органам государственной власти. Отчет
о федеральном бюджете предоставляется
Федеральному Собранию РФ, которое его
утверждает.
Для
контроля за исполнением федерального
бюджета Совет Федерации и Государственная
Дума образуют Счетную Палату. Все стадии
бюджетного процесса взаимообусловлены
и взаимосвязаны. Государственная
бюджетная система РФ включает
республиканский (федеральный) бюджет,
21 республиканский бюджет в составе РФ,
55 краевых и областных бюджетов, городские
бюджеты Москвы и Санкт-Петербурга, 10
окружных бюджетов автономных округов,
бюджет Еврейской автономной области и
около 29 тысяч местных бюджетов (городских,
районных, поселковых, сельских). Как
отмечалось, бюджеты нижестоящих органов
самоуправления не входят своими доходами
и расходами в бюджеты вышестоящих
уровней. Участниками бюджетного процесса
являются: (а) Президент РФ;
(б)
органы законодательной (представительной)
власти; (в) органы исполнительной власти
(высшие должностные лица субъектов РФ,
главы местного самоуправления, финансовые
органы, органы, осуществляющие сбор
доходов бюджетов, другие уполномоченные
органы; (г) органы денежно-кредитного
регулирования; (д) органы государственного
и муниципального финансового контроля;
(е) главные распорядители и распорядители
бюджетных средств; (ж) иные органы, на
которые законодательством Российской
Федерации и ее субъектов возложены
бюджетные, налоговые и иные полномочия.
Участниками бюджетного процесса также
являются бюджетные учреждения,
государственные и муниципальные
унитарные предприятия, другие получатели
бюджетных средств, а также кредитные
организации, осущ
12.Финансы
предприятий – основное звено финансовой
системы РФ.Финансы
предприятий явл. основным звеном фин
системы РФ, в котором формируются
фин.потоки, отражающие созданный ВВП,
подлежащий в дальнейшем перераспределению
через бюджетную систему в производственную
и социальную сфер. Особенности
финансов предприятий зависят от их
организационно-правовой формы и формы
собственности. По своему экон. содержанию
всю совокупность финансовых отношений
можно сгруппировать по следующим
направлениям:
1) между учредителями
в момент создания предприятия 2) между
предприятиями и организациями 3) между
предприятиями и его подразделениями
(филиалами, цехами отделами бригадами)
4) между предприятием и его работниками
5) между предприятием и вышестоящей
организацией, внутри финансово-промышленных
групп, внутри холдинга, с союзами и
ассоциациями, членом которых является
предприятие. 6) между коммерческими
организациями и предприятиями 7) между
предприятиями и финансовой системой
государства 8) между предприятиями
и банковской системой 9) между предприятиями
и страховыми компаниями и организациями
10) между предприятиями и инвестиционными
институтами.
Главная
цель финансов предприятий – достижение положительного финансового
результата, который свидетельствует
об эффективности управления финансовыми
ресурсами.
Принципы
организации финансов предприятий
следующие: 1.Принцип
хоз. самост-ти Хозяйствующие субъекты независимо
от формы собственности самостоятельно
определяют сферу экономической
деятельности, источники финансирования,
направления вложения денежных средств
с целью извлечения прибыли. Рынок
стимулирует коммерческие организации
и предприятия к поиску новых сфер
приложения капитала, созданию гибких
производств, соответствующих
потребительскому спросу. Однако о
полной хозяйственной самостоятельности
говорить нельзя, так как государство
регламентирует отдельные стороны их
деятельности.2.Принцип
самофинансирования Самофинансирование – фин. стратегия управления фондами
денежных средств предприятия в целях
накопления капитала, достаточного для
финансирования расширенного
воспроизводства. Самофинансирование
– необходимое условие развития
предприятия для расширения производства.
Предприятие, используя данную стратегию,
уплачивает налоги, платит ссудный
процент, финансирует инвестиции,
формирует оборотные средства, решает
социально-культурные вопросы своих
работников только за счет своих доходов 3.Принцип
материальной заинтересованности объективная необходимость этого принципа
обеспечивается основной целью
предпринимательской деятельности —
извлечением прибыли. Заинтересованность
в результатах предпринимательской
деятельности проявляется не только ее
участниками, но и государством в
целом. На уровне отдельных работников
предприятия реализация этого принципа
может быть обеспечена высоким уровнем
оплаты труда.
4.Принцип
материальной ответственности за
результаты хозяйственной деятельности. Предприятия,
нарушающие договорные обязательства,
расчетную дисциплину, сроки возврата
полученных кредитов, налоговое
законодательство и т.п., уплачивают
пени, штрафы, неустойки. К нерентабельным
предприятиям, не способным отвечать по
своим обязательствам, может быть
применена процедура банкротства.
5.Принцип
обеспечения финансовых резервов диктуется условиями предпринимательской
деятельности, сопряженной с определенными
рисками невозврата вложенных в бизнес
средств. В условиях рыночных отношений
последствия риска ложатся на
предпринимателя, который добровольно
и самостоятельно на свой страх и риск
реализует разработанную им программу.
На организацию
финансов предприятия оказывают влияние
2 фактора:
1)Организационно-правовая
форма хозяйствования,
которая определяется ГК РФ.. Юридические
лица – это коммерческие организации
(имеют в качестве цели деятельности
извлечение прибыли) и некоммерческие
организации. Коммерческие организации,
являющиеся юридическими лицами, могут
создаваться в форме хозяйственных
организаций и обществ, производственных
кооперативов, государственных и
муниципальных предприятий.
Финансовые
отношения возникают уже на стадии
формирования уставного капитала
хозяйствующего субъекта. Организационно-правовая
форма хозяйствования определяет
содержание финансовых отношений в
процессе создания уставного капитала:
-участники полного
товарищества должны внести не менее
50% своего вклада в складочный капитал
полного товарищества к моменту его
регистрации
-в учредительном
договоре товарищества на вере оговариваются
условия о величине и составе складочного
капитала, а также размер и порядок
изменения долей каждого из полных
товарищей в складочном капитале, состав,
сроки вкладов и ответственность за
нарушения.
-ОАО и ЗАО образуют
уставный капитал из номинальной стоимости
акций АО, приобретенных акционерами.
Его величина должна быть не менее
размера, предусмотренного Законом РФ
об АО.
-формирование
имущество коммерческих организаций
основано на принципах корпоративности.
Имущество муниципальных и государственных
предприятий формируется на базе
муниципального и государственного
имущества.
2)Отраслевые
технико-экономические особенности – выражаются в отраслевой специфике,
которая определяет структуру основных
фондов (фондоемкие, трудоемкие,
материалоемкие), длительность
производственного цикла, особенности
кругооборота средств, источники
финансирования, состав и структуру
финансовых ресурсов (собственные и
заемные), формирование финансовых
результатов.
13.Финансовый
рынок в РФ. Рынок
ценных бумаг (фондовый рынок) выступает
составной частью финансовой системы
государства.
Рынок
ценных бумаг — сфера, в которой формируются
финансовые источники экономического
роста, концентрируются и распределяются
инвестиционные ресурсы.Фондовый рынок
предназначен для аккумуляции временно
свободных денежных средств и эффективного
их использования. Функциональное
назначение РЦБ – способ движения
денежных средств от владельцев к
пользователям. Основные участники РЦБ
– эмитенты и инвесторы. Инвесторы –
юридические и физические лица, которые
накопили у себя временно свободные
денежные средства. Они предоставляют
эти деньги с целью получения дохода.
Эмитенты – субъекты хозяйствования и
органы государственной власти,
вкладывающие деньги в производство и
на ликвидацию и покрытие государственного
долга. Финансовые рынки включают:1.Денежный
рынок 2.Рынок капиталов 3.Рынок валют.
4.Рынок золота.Рынок ценных бумаг
охватывает часть денежного рынка и
рынка капиталов: векселя, долговые
обязательства (облигации), долевые
ценные бумаги (акции), сберегательные
сертификаты и др. Функции
рынка ценных бумаг.1.Общерыночные 1.1.Коммерческая
– получение прибыли от операции на
данном рынке. 1.2.Ценовая – рынок
обеспечивает процесс формирования цен
и их динамику. 1.3.Информационная — рынок
производит информацию об участниках
торговли и доводит до своих участников.
1.4.Регулирующая – рынок создает правила
торговли, устанавливает порядок
разрешения споров между
участниками.2.Специфические. 2.1.Страхование
финансовых и ценовых рисков.
2.2.Перераспределительная Задачи
рынка ценных бумаг: 1.Придает
массовый характер инвестиционному
процессу. 2.Посредством рынка ценных
бумаг осуществляется перелив капитала
в те отрасли, которые приносят наибольшую
доходность.3.Государство и корпорации
посредством фондовых операций осуществляют
структурную перестройку народного
хозяйства. 4.Через рынок ценных бумаг
реализуется государственная политика
(государственная приватизация).
Классификация
рынка ценных бумаг:
1.Первичный и
вторичный.
2.По видам ценных
бумаг 2.1.рынок акций («голубые фишки» —
акции высоколиквидных и высокодоходных
компаний, акции хороших компаний,
которые не дотягивают до «голубых фишек»
(Северсталь), неликвидные акции местных
АО) 2.2.рынок облигаций: государственных
и корпоративных. 3.рынок векселей 4.рынок
сертификатов – не развит.
Основными видами
ценных бумаг являются:
Акция, облигация,
вексель, чек, депозитный (сберегательный)
сертификат, опцион, фьючерс, коносамент
и др.
Акция – ценная бумага, выпускаемая АО
(корпорациями), удостоверяющая внесение
средств на цели развития предприятия
и дающая владельцам определенные права.
Облигация
– ценная
бумага, которая закрепляет право ее
держателя на получение от эмитента в
предусмотренный срок ее номинальной
стоимости и зафиксированного в ней
процента от этой стоимости, это долговое
обязательство.
Вексель
– ценная
бумага, определяющая отношения займа.
Сберегательный
сертификат — это письменное свидетельство кредитного
учреждения о депонировании на определенный
срок денежных средств вкладчика, а
именно физического лица, с безусловным
обязательством возврата вклада с
установленным процентом.
Депозитный
сертификат — также удостоверяет аналогичное право
вкладчика, в роли которого выступает
юридическая организация.
Ценной
бумагой является чек,
используемый как платежное средство.
Чек — это письменное распоряжение
чекодателя организации — плательщику
выплатить чекодержателю указанную
сумму денег.
К
ценным бумагам относится коносамент,
выражающий право собственности на
конкретный товар в процессе морской
перевозки. Коносамент выдается после
получения товара перевозчиком
грузоотправителю с указанием
грузополучателя.
Закладные
(ипотечные ценные бумаги) — ценные бумаги,
оформляющие отношения залога. Закладные
удостоверяют право на получение денежных
обязательств, обеспеченных ипотекой
имущества. В закладной обязательно
должен указываться кредитный или иной
договор, исполнение которого обеспечивается
ипотекой.Производные ценные бумаги —
ценные бумаги, удостоверяющие право
владельцев на приобретение (продажу)
ценных бумаг, эмитированных третьими
лицами (базовый актив) в сроки и на
условиях, указанных в сертификате и
решении о выпуске данных производных
ценных бумаг.Государственные
ценные бумаги – это бумаги, которые выпускаются и
обеспечиваются государством и используются
для покрытия бюджетных дефицитов,
регулирования денежного обращения и
ликвидности в банковской системе,
инвестиционных и иных целей. Профессиональные
посредники на рынке ценных бумаг.
Большинство сделок с ценными бумагами
заключается при участии профессиональных
участников рынка — брокеров и дилеров.
Брокеры совершают сделки в качестве
поверенного или комиссионера, действующего
на основании договора поручения или
комиссии. При совершении сделок брокер
действует от своего имени за счет и по
поручению клиента. В отличие от
брокеров дилеры совершают сделки от
своего имени и за свой счет. Профессиональные
участники рынка ценных бумаг — банки и
инвестиционные компании могут
совмещать брокерскую и дилерскую
деятельности.
14.Кредит:
сущность и необходимость. Формы и виды
кредита.Кредитная система.Кредит
как экономическая категория выражает
экономические отношения между
кредитором и заемщиком, возникающие в
процессе передачи денег или материальных
ценностей одними участниками договора
займа другим на условиях возврата.
Основными условиями
существования кредита можно назвать
следующие.
1. Несовпадение во
времени индивидуальных кругооборотов
и оборотов производственных фондов
отдельных товаропроизводителей.
2. Кредитор и заемщик
должны быть юридически самостоятельными
организациями, что обеспечивает
экономическую ответственность сторон
в процессе кредитных отношений.
3. Кредитор и заемщик
должны быть заинтересованы в кредитных
отношениях.
Кредит
выполняет следующие три
основные функции:
распределительную
заключается в распределении на возвратной
основе денежных средств.; эмиссионную
процессе кредитования создаются
платежные средства, т.е. в оборот наряду
с деньгами в наличной форме входят также
деньги в безналичной форме, действие
данной функции проявляется и тогда,
когда на основе замещения наличных
денег происходят безналичные расчеты.
; контрольную
состоит в осуществлении контроля за
эффективностью деятельности экономических
субъектов.
Принципами
кредитования являются: возвратность, срочность,
дифференцированность означает, что
коммерческие банки не должны одинаково
подходить к решению вопроса о выдаче
претендующим на получение кредита
клиентам. Банки стремятся предоставлять
кредит лишь тем клиентам, которые в
состоянии его своевременно вернуть.,
обеспеченность ссуд и платность. Коммерческий кредит предоставляется в товарной форме
продавцами товаров их покупателям в
виде рассрочки платежа за проданные
товары или предоставленные услуги.
Коммерческий кредит применяется с целью
ускорить реализацию товаров и оформляется
в виде долгового обязательства —
векселя, оплачиваемого через коммерческий
банк . Банковский
кредит предоставляется в виде денежных ссуд
коммерческими банками. Потребительский
кредит предоставляется, как правило, торговыми
компаниями, банками и специализированными
кредитно-финансовыми институтами для
приобретения населением товаров и услуг
с рассрочкой платежа Ипотечный кредит выдается на приобретение или строительство
жилья либо покупку земли. Межбанковский кредит предоставляется банками друг другу,
когда у одних банков возникают свободные
ресурсы, а у других их недостает.
Международный
кредит охватывает экономические отношения
между государством и международными
экономическими организациями.
В
процессе управления государственным
кредитом решаются следующие задачи: минимизация
стоимости долга для заемщика; недопущение
переполнения рынка заемными обязательствами
государства и резкого колебания их
курса; эффективное использование
мобилизованных средств и контроль за
их целевым использованием; обеспечение
своевременного возврата кредита;
максимальное решение задач, определенных
финансовой политикой
Специфика категории
государственного кредита определяет
и особенности оперативного управления
им. Обычно оно возлагается на Минфин и
ЦБ.
Классификация:
1. по основным группам заемщиков.
Кредит может быть выдан хозяйству,
населению, государственным органам
власти.
2. от срочности
кредитования.
При такой классификации выделяют
краткосрочные, среднесрочные и
долгосрочные ссуды.
3. По обеспечению — необеспеченные (бланковые) кредиты и
обеспеченные, которые, свою очередь, по
характеру обеспечения подразделяются
на залоговые, гарантированные и
застрахованные.
4. По способу выдачи банковские ссуды разграничиваются на
ссуды компенсационные и платежные.
5. По методам
погашения различают банковские ссуды, погашаемые
в рассрочку (частями, долями), и ссуды,
погашаемые единовременно, на определенную
дату.
. в зависимости
от платности его использования.
Здесь выделяют платный и бесплатный,
дорогой и дешевый кредиты. За основу
такого деления берется размер % ставки,
установленной за пользование ссудой.
Характеристика
кредитной системы Кр-е
подразумевают две ее стороны. Прежде
всего, этогда речь идет о кред системе,
то обычно о совокупность кред отношений,
форм и методов кредитования. Кроме того,
это совокупность банков, других
кредитно-фин институтов, аккумулирующих
свободные ден средства и предоставляющие
их в ссуду. Считают, что кред система —
понятие более широкое и емкое по сравнению
с банковской системой, поскольку
последняя включает лишь совокупность
действующих в стране банков. Кредитная
же система, помимо банков, являющихся,
естественно, ее ведущим звеном, включает
банковский, потребит, коммерч, гос,
международный кредиты со своими формами
отношений и методами кредитования.
Таким образом, кредитная система включает
Банк России, банки, филиалы и
представительства иностранных банков,
небанковские кредитные организации,
союзы и ассоциации кредитных организаций,
банковские группы и холдинги.
Новая структура
кредитной системы России стала в большей
степени отражать потребности рыночного
хозяйства, она строится на тех же
принципах, что и в странах с развитой
рыночной экономикой, все больше
приспосабливается к процессу проводимых
экономических реформ. В то же время
процесс становления новой кредитной
системы пока развивается сложно и
противоречиво, он выявил определенные
недостатку по всех ее звеньях.
Правовой статус
ЦБ РФ, его права и обязанности определены
ФЗ «О Центральном банке Российской
Федерации (Банке России)» в ре ФЗ от
26.04.95 г. № 65-ФЗ с последующими изменениями
и дополнениями. Банк России является
юр лицом, однако не регистрируется
в налоговых органах. Как юр лицо он
осуществляет свои расходы за счет
собственных доходов, но получение
прибыли не является целью его деятельности.
Банк России самостоятельно выполняет
свои функции и в текущей деятельности
независим от органов государственного
управления экономикой, однако подотчетен
законодательным и исполнительным
органам гос. власти.
ЦБ явл главным
банком гос-ва и признается единственным
на территории страны органом
денежно-кредитного и валютного
регулирования экономики. Основными
целями ЦБ РФ являются: защита и обеспечение
устойчивости рубля, в том числе его
покупательной способности и курса
по отношению к иностранным валютам;
развитие и укрепление банковской
системы России, обеспечение эффективного
и бесперебойного функционирования
системы расчетов.
Основные инструменты
реализации денежно-кредитной политики
ЦБ приведены ниже.
1. Процентные ставки
по операциям Банка России. Закон
предусматривает, что банк может
устанавливать одну или несколько %
ставок по различным видам операций или
проводить процентную политику без
фиксации процентных ставок. Причем
процентные ставки Банка России
представляют собой миним ставки, по
которым он осуществляет свои операции.
К таким операциям относятся выдаваемые
кредиты или депозитная политика.
2. Нормативы
обязательных резервов, депонируемых в
Банке России кредитными учреждениями
и коммерческими банками (резервные
требования). Посредством изменения
норматива резервных средств банк
регулирует объем выдаваемых коммерческими
банками кредитов и возможности
осуществления ими депозитной эмиссии.
3.Операции на
открытом рынке, под которыми понимается
купля-продажа ЦБ казначейских
векселей, государственных облигаций
и других государственных ценных бумаг.
Это наиболее гибкий метод регулирования
кредитных вложений и ликвидности
коммерческих банков, так как оказывает
прямое
воздействие на объем свободных
ресурсов, имеющихся у коммерческих
банков. 4.Рефинансирование банков, т. е.
кредитование Банком России других
банков, когда последние испытывают
финансовые трудности. Иными словами,
Банк России выступает кредитором
последней инстанции или банком
банков.
5. Валютное
регулирование, т. е. купля-продажа ЦБ
иностранной валюты на валютном рынке
для воздействия на курс рубля и на
суммарные спрос и предложение денег.
6.
Прямые количественные ограничения, под
которыми понимается установление
лимитов на рефинансирование банков,
проведение кредитными организациями
отдельных банковских позиций. Причем
ЦБ вправе применять прямые количественные
ограничения в исключительных случаях
с целью проведения единой государственной
денежно-кредитной политики только после
консультаций с Правительством РФ. Все
перечисленные выше инструменты и методы
денежно-кредитного регулирования
экономики должны служить базой основных
направлений денежно-кредитной политики
ЦБ, которые представляются ежегодно не
позднее 1 декабря в Государственную
Думу. Кредитование — одно из важнейших направлений
деятельности банка. На нем основываются
активные операции банка. Кредитование
заемщиков осуществляется в различных
формах; в зависимости от обеспечения
кредит предоставляется на различные
сроки; одинаковым для всех кредитных
операций остаются основные принципы
кредитования, как общие, так и
специфические, где первые учитывают
воздействие внешних факторов на
деятельность и поведение хозяйствующих
субъектов, а вторые — способность
заемщика в срок и с уплатой установленного
процента погасить свои обязательства.
Оформление кредитной
сделки сопровождается заключением
кредитного договора, условия которого
дифференцируются в каждом конкретном
случае, чаще от источников обеспечения
возврата ссуды. В договоре определяются
порядок погашения ссуды, сроки уплаты
процентов и возврата кредита, возможность
пролонгации и пр.
После достижения
согласованности по условиям заключения
кредитной сделки клиенту открывают
ссудный счет в банке, причем счет
может быть либо простым, либо специальным
или, если заемщик физическое лицо,
производится выдача наличных средств.
Далее, банковское
учреждение с момента выдачи или
перечисления финансовых ресурсов
до полного погашения кредита (имеются
в виду возврат основной суммы долга и
уплата причитающихся процентов)
находится в постоянном контакте с
клиентом: анализируются финансовые
и экономические условия деятельности,
осуществляется мониторинг по факту
использования средств на привлекаемые
нужды, формированию и использованию
прибыли, взаимоотношений с другими
кредиторами и дебиторами. Ежеквартально
(а иногда и ежемесячно) банк получает
от заемщика отчет о выполнении условий
кредитного договора.
Операции
ЦБ:1.Активные 1.1.Операции
с государственными ценными бумагами.
1.2.Вложения в золото-валютные ценности.
1.3.Операции с кассовой наличностью.
1.4.Ссудные операции – это операции по
предоставлению кредитов коммерческим
банкам. 1.5.Переучетные операции по ценным
бумагам коммерческих банков.
2.Пассивные 2.1.Эмиссия
денежных знаков 2.2.Формирование резервов
коммерческих банков 2.3.Операции по
корреспондентским счетам коммерческих
банков, по счетам правительственных
структур и организаций. 2.4.Операции с
фондами и резервами ЦБ.
Существует 3 вида
методов денежно-кредитного регулирования:
1)Административные – это прямые методы,: ограничения
количественных и качественных параметров
деятельности банков (лимиты):
2)Экономические
методы –. Инструментами
экономических методов являются: налоговые;
нормативные – главная Инструкция № 1
ЦБ от 1997 г.,
3)Корректирующие
методы –
связаны с поддержанием курса национальной
валюты, ликвидности коммерческих банков.
Эти инструменты осуществляются на
открытых рынках – рынке ценных бумаг
и рынке иностранной валюты.
studfiles.net
V2: Бюджетное устройство в рф
I:
S:
Принципом
построения бюджетной системы является:
-:
централизм;
-:
универсальность;
+: единство.
I:
S:
Сколько
уровней имеет бюджетная система России?
-:
два;
+: три;
-:
четыре.
I:
S:
Бюджет
следует рассматривать в качестве:
+: экономической категории;
-:
финансового инструмента рыночной
экономики;
-:
метода экономического хозяйствования.
I:
S:
Государственный
бюджет – это:
-:
финансовая программа государства;
+: основной
финансовый план государства;
-:
финансовая концепция экономической
политики государства.
I:
S:
Какой итог
бюджета представляется наиболее
благоприятным?
+: равенство
доходов и расходов;
-:
превышение доходами расходов;
-:
превышение расходами доходов.
I:
S:
Что лежит
в основе бюджетного устройства России?
-:
отраслевая структура экономики;
-:
формы собственности;
+: административно-территориальное
деление РФ.
I:
S:
Бюджетный
процесс – это процесс…
-:
рассмотрение и принятие бюджета;
-:
принятие и исполнение бюджета;
+: подготовки
проекта, рассмотрения, утверждения и
исполнения бюджета.
I:
S:
Какие
отношения выражает бюджет?
-:
отношения по поводу функционирования
ссудного капитала;
-:
отношения по поводу обращения денежных
ресурсов;
+: отношения
по поводу формирования и использования
фондов денежных средств.
I:
S:
Что не
относится к характерным свойствам
бюджета?
+: научность;
-:
стихийность;
-:
целенаправленность.
I:
S:
Бюджетная
система Российской Федерации включает
…. тысяч (тысячу) местных бюджетов:
-:
31;
+: 29;
-:
26.
I:
S:
Бюджетная
система Российской Федерации состоит
из ….уровней (уровня):
+: трех;
-:
двух;
-:
четырех.
I:
S:
Бюджетная
система унитарного государства:
-:
четырехзвенная;
+: двухзвенная;
-:
трехзвенная.
I:
S:
Бюджетная
система федеративных государств:
-:
четырехзвенная;
-:
двухзвенная;
+: трехзвенная.
I:
S:
Бюджетная
система является составной частью:
+: финансовой
системы;
-:
фискальной политики;
-:
экономической системы.
Тема 5. Внебюджетные фонды
I:
S:
Внебюджетные фонды – это:
-:
форма образования и расходования
денежных средств;
-:
форма перераспределения финансовых
ресурсов;
-:
форма образования и перераспределения
финансовых ресурсов;
+:
форма образования, перераспределения
и использования финансовых ресурсов.
I:
S:
В зависимости от целевого назначения
внебюджетные фонды делятся на:
-:
федеральные;
+:
социальные;
-:
региональные;
+:
экономические.
I:
S:
Внебюджетные фонды являются:
-:
акционерными обществами;
-:
государственными учреждениями;
-:
коммерческими банками;
+:
финансово-кредитными учреждениями.
I:
S:
Средства государственных внебюджетных
фондов находятся в собственности:
-:
самих фондов;
-:
соответствующего бюджета;
+:
государства.
I:
S:
Доходы внебюджетных фондов складываются
из:
+:
целевых налогов и сборов;
-:
отчислений от прибыли хозяйствующих
субъектов;
+:
бюджетных средств;
I:
S:
Выплата пособий по временной
нетрудоспособности, беременности и
родам при рождении ребенка выплачиваются
из:
+:
Фонда социального страхования;
-:
Фонда обязательного медицинского
страхования;
-:
Пенсионного фонда.
I:
S:
Пособия на детей до 1,5 лет, пособия на
погребение выплачиваются из:
-:
Фонда обязательного медицинского
страхования;
-:
Пенсионного фонда;
+:
Фонда социального
страхования.
I:
S:
Пособия по безработице выплачиваются
из:
-:
Фонда социального страхования;
-:
Пенсионного фонда;
+:
Государственного фонда занятости.
I:
S:
Пособия на детей в возрасте 1,5 – 6 лет
одиноким матерям, при
потере кормильца,
пострадавшим в результате аварии на
Чернобыльской АЭС выплачиваются из:
-:
Фонда обязательного медицинского
страхования;
-:
Фонда социального страхования;
+:
Пенсионного фонда.
I:
S:
ФОМС, ФСС, ПФ, ГФЗ относятся к:
-:
экономическим внебюджетным фондам;
+:
социальным внебюджетным
фондам.
I:
S:
Могут ли внебюджетные фонды использоваться
для покрытия
бюджетного дефицита?
-:
нет.
-:
по решению Правительства РФ;
+:
да, при наличии активного сальдо;
-:
да, через механизм кредита.
I:
S:
Внебюджетные
фонды – это денежные фонды обеспечивающие…
-:
расширение производства;
-:
непрерывность процесса общественного
воспроизводства;
+: удовлетворение
специфических потребностей экономических
субъектов общества.
I:
S:
Как
классифицируются внебюджетные фонды?
-:
отраслевые;
+: экономические;
-:
политические.
I:
S:
Взносы в
социальные внебюджетные фонды входя в
цену товара?
-:
«да»;
+: «нет».
I:
S:
В процентах
к какому показателю осуществляются
отчисления в Пенсионный фонд?
-:
выручке от реализации продукции;
-:
прибыли;
+: фонду
оплаты труда.
studfiles.net
Delo.ru — Уровни бюджетной системы РФ
Построение бюджетной системы Российской Федерации основано на Конституции РФ и конституциях республик в составе РФ. В соответствии с Конституцией РФ (ст. 71 и 132) и Бюджетным кодексом РФ (ст. 10) бюджетная система Российской Федерации состоит из трех уровней:
(1) федерального бюджета и бюджетов государственных внебюджетных фондов;
1 (2) бюджетов субъектов Федерации (региональных бюджетов) и бюджетов территориальных государственных внебюджетных фондов;
(3) местных бюджетов.
В настоящее время бюджетная система Российской Федерации включает: федеральный бюджет, 21 республиканский бюджет республик в составе РФ, 55 краевых и областных бюджетов и бюджетов городов Москвы и Санкт-Петербурга, один областной бюджет автономной области, десять окружных бюджетов, автономных округов и около 29 тысяч местных бюджетов (районные, городские, поселковые и сельские бюджеты).
Следует отметить, что в состав федерального и территориальных бюджетов (бюджетов субъектов РФ и местных бюджетов) входят целевые бюджетные фонды, формирующиеся за счет целевых источников и имеющие целевое расходование средств. В числе таких фондов — дорожный, экологический, воспроизводства минерально- сырьевой базы, восстановления и охраны водных ресурсов и др.
Бюджеты, входящие в бюджетную систему РФ, самостоятельны и не включаются друг в друга, т.е. бюджеты субъектов Федерации не включаются в федеральный бюджет, а местные бюджеты не включаются в региональные бюджеты.
Кроме федерального и территориальных бюджетов (бюджетов субъектов Федерации и местных бюджетов) в бюджетную систему входят государственные внебюджетные фонды (Пенсионный фонд РФ, Фонд социального страхования РФ, Федеральный внебюджетный фонд и внебюджетные фонды субъектов РФ обязательного медицинского страхования). Средства этих фондов по экономическому содержанию и направленности их использования мало чем отличаются от бюджетных средств. До 1991 г. они входили в состав государственного бюджета, в настоящее время имеется тенденция включения внебюджетных фондов в бюджет. Так, в 1999 г. в бюджет включены средства внебюджетного Федерального дорожного фонда РФ.
Принцип единства бюджетной системы — это единство правовой базы, денежной системы, форм бюджетной документации, принципов бюджетного процесса, санкций за нарушения бюджетного законодательства, а также единый порядок финансирования расходов бюджетов всех уровней бюджетной системы, ведения бухгалтерского учета средств федерального бюджета, региональных и местных бюджетов.
Принцип разграничения доходов и расходов между уровнями бюджетной системы Российской Федерации означает закрепление (полностью или частично) соответствующих видов доходов и полномочий по осуществлению расходов за органами власти Российской Федерации, органами государственной власти субъектов Федерации и органами местного самоуправления.
Важнейшим является принцип самостоятельности всех бюджетов, который означает:
- право законодательных (представительных) органов государственной власти и органов местного самоуправления на каждом уровне бюджетной системы самостоятельно осуществлять бюджетный процесс;
- наличие собственных источников доходов бюджетов каждого уровня бюджетной системы, определяемых в соответствии с законодательством РФ;
- законодательное закрепление регулирующих доходов бюджетов, полномочий по формированию доходов соответствующих бюджетов;
- право органов государственной власти и органов местного самоуправления самостоятельно определять направления расходования средств соответствующих бюджетов;
- право органов государственной власти и органов местного самоуправления самостоятельно определять источники финансирования дефицитов соответствующих бюджетов;
- недопустимость изъятия доходов, дополнительно полученных в ходе исполнения законов (решений) о бюджете, сумм превышения доходов над расходами бюджетов и сумм экономии по расходам бюджетов.
Принцип полноты отражения доходов и расходов бюджетов, бюджетов государственных внебюджетных фондов предполагает, что все доходы и расходы бюджетов, бюджетов государственных внебюджетных фондов и иные обязательные поступления подлежат отражению в бюджетах, бюджетах государственных внебюджетных фондов в обязательном порядке и полном объеме. Все государственные и муниципальные расходы подлежат финансированию за счет бюджетных средств, средств государственных внебюджетных фондов, аккумулированных в бюджетной системе РФ.
Принцип сбалансированности бюджета означает, что каждый бюджет должен быть сбалансирован, т.е. объем предусмотренных бюджетом расходов должен соответствовать суммарному объему доходов бюджета и поступлений из источников финансирования его дефицита.
Принцип эффективности и экономности использования бюджетных средств предполагает, что при составлении и исполнении бюджетов органы власти и получатели бюджетных средств должны исходить из необходимости достижения заданных результатов с использованием определенного бюджетом объема средств.
Принцип общего покрытия расходов означает, что все расходы бюджета должны покрываться общей суммой доходов из источников финансирования его дефицита.
Принцип гласности предполагает: (1) обязательное опубликование в открытой печати утвержденных бюджетов и отчетов об их исполнении, полноту представления информации о ходе исполнения бюджетов, а также доступность иных сведений по решению законодательных (представительных) органов государственной власти, органов местного самоуправления; (2) обязательную открытость для общества и средств массовой информации процедур рассмотрения и принятия решений по проектам бюджетов, в том числе по вопросам, вызывающим разногласия либо внутри законодательного (представительного) органа государственной власти, либо между законодательным (представительным) и исполнительным органами государственной власти.
Принцип достоверности бюджета — это надежность показателей прогноза социально-экономического развития соответствующей территории и реалистичность расчета доходов и расходов бюджета.
Принцип адресности и целевого характера бюджетных средств означает, что бюджетные средства выделяются в распоряжение конкретных получателей бюджетных средств с обозначением направления их на финансирование конкретных целей.
fin-delo.ru
Охарактеризуйте уровни бюджетной системы Российской Федерации.
Образование Охарактеризуйте уровни бюджетной системы Российской Федерации.
Количество просмотров публикации Охарактеризуйте уровни бюджетной системы Российской Федерации. — 690
| Наименование параметра | Значение |
| Тема статьи: | Охарактеризуйте уровни бюджетной системы Российской Федерации. |
| Рубрика (тематическая категория) | Образование |
Сегодня в России реальностью является трехуровневая бюджетная система (федеральный уровень, уровень субъектов Федерации, муниципальный уровень)
Первый уровень — федеральный. На этом уровне разрабатываются и исполняютсяфедеральный бюджет Российской Федерации и бюджеты государственных внебюджетных фондов (Пенсионный фонд. Фонд социального страхования, Федеральный фонд обязательного медицинского страхования). До 2000 ᴦ. в составе государственных внебюджетных фондов существовал Федеральный фонд занятости населения, соответственно утверждался его бюджет.
Второй уровень бюджетной системы образуютбюджеты субъектов РФ итерриториальные государственные внебюджетные фонды, к которым пока относятся территориальные фонды обязательного медицинского страхования. Другие территориальные государственные внебюджетные фонды действующим законодательством не предусмотрены. На этом уровне бюджеты являются формой централизации денежных средств для обеспечения задач и функций, отнесенных к предметам ведения субъекта Федерации. Из этих бюджетов в значительной мере финансируется развитие отраслей производственной сферы, в первую очередь местной, легкой и пищевой промышленности; коммунального хозяйства; развитие транспорта и связи. Важное значение имеют бюджеты субъектов Федерации в осуществлении общегосударственных и социальных задач, в первую очередь в распределении государственных средств на содержание и развитие социальной инфраструктуры общества.
Третий уровень бюджетной системы — бюджеты муниципальных образовании (муниципальных районов, поселений и городских округов). Иначе говоря, здесь имеются подуровни. На этом уровне государственные внебюджетные фонды не формируются. В связи с реформированием системы местного самоуправления в пределах нижнего уровня выделяются подуровни (бюджеты городских районов, муниципальных районов и поселений). Сегодня в России около 30 тыс. бюджетов муниципального уровня.
Бюджетный кодекс РФ определяет бюджет муниципального образования (местный бюджет) как форму образования и расходования денежных средств, предназначенных для обеспечения задач и функций, отнесенных к предметам ведения местного самоуправления.
Охарактеризуйте уровни бюджетной системы Российской Федерации. — понятие и виды. Классификация и особенности категории «Охарактеризуйте уровни бюджетной системы Российской Федерации.» 2017, 2018.
referatwork.ru
ЛЕКЦИЯ № 1. Бюджет, бюджетная система, бюджетное устройство РФ. Бюджетная система РФ: конспект лекций
ЛЕКЦИЯ № 1. Бюджет, бюджетная система, бюджетное устройство РФ
1. Экономическая сущность и содержание бюджета
Государственный бюджет является механизмом, который позволяет государству проводить социальную и экономическую политику в нашей стране.
Через государственный бюджет осуществляется влияние на образование и использование централизованных и децентрализованных фондов денежных средств.
Бюджет – это система образования и расходования денежных средств, которые предназначены для финансирования обеспечения задач и функций государства и местного самоуправления.
С помощью государственного бюджета государственные власти получают денежные ресурсы для содержания армии, государственного аппарата и т. д.
Государственный бюджет – это финансовый план государства, с помощью которого органы власти получают реальную экономическую возможность осуществлять властные полномочия.
В то же время бюджет является категорией, которая свойственна различным отношениям. С зарождением и формированием государства связано возникновение и развитие бюджета. Для государства бюджет – это инструмент обеспечения непосредственно своей деятельности, и в то же время он является важным элементом для проведения социальной и экономической политики.
Задачи бюджета:
1) перераспределение ВВП;
2) финансовое обеспечение бюджетной сферы и осуществление социальной политики государства;
3) государственное регулирование и стимулирование экономики;
4) контроль за образованием и использованием централизованных фондов денежных средств.
Через формирование и использование централизованных фондов денежных средств на уровнях государственной и территориальной власти проявляется распределительная функция бюджета.
Государство с помощью государственного бюджета регулирует хозяйственную жизнь страны, экономические отношения, направляя средства бюджета на развитие и восстановление отраслей, регионов. И в связи с этим государство может ускорять или сдерживать темпы производства, усиливать или ослаблять рост капиталов и сбережений, изменять структуру спроса и предложения.
Перераспределение ВВП через бюджет имеет две стадии.
1. Образование доходов бюджета.
В процессе образования доходов бюджета происходит изъятие части ВВП в пользу государства. В связи с этим возникают финансовые взаимоотношения государства с налогоплательщиками.
Доходы бюджета преследуют единственную цель, заключающуюся в формировании доходной части бюджетов разных уровней. Им свойственны обезличенность и денежная форма. Доходы бюджета могут носить налоговый и неналоговый характер. Источники налоговых доходов: прибыль, заработная плата, ссудный процент, рента, добавленная стоимость, накопления и др.
Неналоговые доходы бюджетов образуются в результате экономической деятельности государства или при перераспределении уже полученных государством доходов по уровням бюджетной системы.
2. Использование (расход) бюджетных средств.
Расходы бюджета – это денежные средства, которые направляются на финансовое обеспечение задач и функций государства и местного самоуправления.
Бюджетополучатели – это организации производственной и непроизводственной сферы, которые могут получать и распределять средства бюджета; они финансируются через бюджетные расходы.
В основном расходы бюджета носят безвозвратный характер.
За счет расходов бюджета происходит перераспределение средств бюджета по уровням бюджетной системы через дотации, бюджетные ссуды, субвенции и др.
Структура расходов бюджета устанавливается в бюджетном плане и зависит, как и доходы бюджета, от экономической и иной ситуации в стране.
Контрольная функция бюджета действует вместе с распределительной и дает возможность осуществления обязательного государственного контроля за поступлением и использованием бюджетных средств.
2. Бюджетная система РФ
Бюджетная система – это главное звено финансовой системы государства, является составляющей частью бюджетного устройства.
Бюджетная система – это совокупность бюджетов государств, административно-территориальных образований, государственных учреждений и фондов, которые самостоятельны в бюджетном отношении. Она основана на правовых нормах, экономических отношениях и государственном устройстве.
Построение бюджетной системы зависит от формы административного и государственного устройства страны. Все государства подразделяются, в зависимости от степени распределения власти между центром и административно-территориальными образованиями на: унитарные, федеративные и конфедеративные.
Унитарное государство – форма государственного устройства, при котором административно-территориальные образования не имеют собственной государственности и автономии.
Бюджетная система унитарного государства состоит из государственного и местных бюджетов.
Федеративное государство – это система государственного устройства, при которой государственные образования или административно-территориальные образования, входящие в государство, политически самостоятельны в рамках компетенций, распределенных между центром и ними, и имеют собственную государственность. Бюджетная система федеративного государства состоит из федеративного бюджета, бюджета членов федерации и местных бюджетов.
Конфедеративное государство – это постоянный союз суверенных государств, преследующий достижение политических или военных целей. Его бюджет формируется из взносов, входящих в конфедерацию. У государств-членов конфедерации существуют свои бюджетные и налоговые системы.
Бюджетная система состоит из бюджетов следующих уровней (ст. 10 БК РФ):
1) федеральный бюджет и бюджеты государственных внебюджетных фондов;
2) бюджеты субъектов РФ (РФ) и бюджеты территориальных государственных внебюджетных фондов;
3) местные бюджеты, в том числе:
а) бюджеты муниципальных районов, бюджеты городских округов, бюджеты внутригородских муниципальных образований городов федерального значения Москвы и Санкт-Петербурга;
б) бюджеты городских и сельских поселений. Согласно ст. 11 БК РФ, федеральный бюджет и бюджеты государственных внебюджетных фондов разрабатываются и утверждаются в форме федеральных законов, бюджеты субъектов РФ и бюджеты территориальных государственных внебюджетных фондов разрабатываются и утверждаются в форме законов субъектов РФ, местные бюджеты разрабатываются и утверждаются в форме правовых актов представительных органов местного самоуправления либо в порядке, установленном уставами муниципальных образований.
Годовой бюджет составляется на один финансовый год, который равен календарному году и длится с 1 января по 31 декабря.
Государственный внебюджетный фонд – фонд денежных средств, образуется вне федерального бюджета и бюджетов субъектов РФ, предназначен для реализации конституционных прав граждан на пенсионное обеспечение, социальное обеспечение в случае безработицы, социальное страхование, охрану здоровья и медицинскую помощь. Расходы и доходы государственного внебюджетного фонда формируются в определенном порядке, который устанавливается федеральным законом или предусматривается БК РФ.
Каждое муниципальное образование имеет собственный бюджет.
Бюджет муниципального образования, т. е. местный бюджет – форма образования и расходования денежных средств в расчете на финансовый год, предназначенных для исполнения расходных обязательств соответствующего муниципального образования.
В местных бюджетах, в соответствии с бюджетной классификацией РФ, раздельно предусматриваются средства, направляемые на исполнение расходных обязательств муниципальных образований в связи с осуществлением органами местного самоуправления полномочий по вопросам местного значения, и расходных обязательств муниципальных образований, исполняемых за счет субвенций из бюджетов других уровней для осуществления отдельных государственных полномочий (ст. 14 БК РФ).
Бюджет муниципального района, т. е. районный бюджет, и свод бюджетов городских и сельских поселений, входящих в состав муниципального района, образуют консолидированный бюджет муниципального района.
В качестве составной части бюджетов городских и сельских поселений могут быть предусмотрены сметы доходов и расходов отдельных населенных пунктов, других территорий, не являющихся муниципальными образованиями.
Каждый субъект РФ имеет собственный бюджет.
Бюджет субъекта РФ, т. е. региональный бюджет – форма образования и расходования денежных средств в расчете на финансовый год, предназначенных для исполнения расходных обязательств соответствующего субъекта РФ.
Использование органами государственной власти субъектов РФ иных форм образования и расходования денежных средств для исполнения расходных обязательств субъектов РФ не допускается.
В бюджетах субъектов РФ, в соответствии с бюджетной классификацией РФ, раздельно предусматриваются средства, направляемые на исполнение расходных обязательств субъектов РФ в связи с осуществлением органами государственной власти субъектов РФ полномочий по предметам ведения субъектов РФ и полномочий по предметам совместного ведения, указанных в п. 2 и 5 ст. 26.3 Федерального закона от 6 октября 1999 года № 184-ФЗ «Об общих принципах организации законодательных и исполнительных органов государственной власти субъектов РФ», и расходных обязательств субъектов РФ, осуществляемых за счет субвенций из федерального бюджета.
Бюджет субъекта РФ и свод бюджетов муниципальных образований, входящих в состав субъекта РФ, образуют консолидированный бюджет субъекта РФ.
В соответствии со ст. 16 БК РФ, федеральный бюджет – форма образования и расходования денежных средств в расчете на финансовый год, предназначенных для исполнения расходных обязательств РФ.
Использование федеральными органами государственной власти иных форм образования и расходования денежных средств, предназначенных для исполнения расходных обязательств РФ, не допускается, за исключением случаев, установленных БК РФ и иными федеральными законами.
Федеральный бюджет и свод бюджетов других уровней бюджетной системы РФ образуют консолидированный бюджет РФ.
Целевой бюджетный фонд – фонд денежных средств, образуемый в соответствии с законодательством РФ в составе бюджета за счет доходов целевого назначения или в порядке целевых отчислений от конкретных видов доходов или иных поступлений и используемый по отдельной смете. Средства целевого бюджетного фонда не могут быть использованы на цели, не соответствующие назначению целевого бюджетного фонда (ст.17 БК РФ).
3. Бюджетное устройство. Межбюджетные отношения
Бюджетное устройство – это организационные принципы построения бюджетной системы, ее структуры, взаимодействие входящих в нее бюджетов.
Бюджетная система – это совокупность всех бюджетов, существующих в стране.
Бюджетное устройство определяется государственным устройством. Бюджетная система в унитарных предприятиях включает два звена: государственный бюджет и местные бюджеты.
В соответствии с БК РФ, бюджетная система федеративных государств состоит из трех звеньев: государственный бюджет, бюджеты членов федерации (субъектов Федерации – в России), местные бюджеты.
Государственная бюджетная система состоит из трех звеньев и включает: республиканский (федеральный) бюджет; 21 республиканский бюджет в составе РФ, 55 краевых и областных бюджетов, городские бюджеты Москвы и Санкт-Петербурга, 10 окружных бюджетов автономных округов, бюджет Еврейской автономной области; около 29 тыс. местных бюджетов (городских, районных, поселковых, сельских).
Бюджетное устройство в РФ основывается на принципах единства, полноты, реальности, гласности и самостоятельности всех бюджетов, входящих в государственную бюджетную систему.
Сложной проблемой в бюджетном устройстве является бюджетный федерализм, т. е. бюджетные взаимоотношения центра и регионов.
В рамках межбюджетных отношений все бюджеты, которые входят в состав бюджетной системы РФ, взаимосвязаны.
Межбюджетные отношения – это отношения, которые возникают между органами государственной власти РФ, органами государственной власти субъектов РФ и органами местного самоуправления, которые связаны с формированием и исполнением соответствующих бюджетов (ст. 6 БК РФ).
Межбюджетные отношения основаны на следующих принципах:
1) распределение и закрепление расходов бюджетов по уровням бюджетной системы РФ;
2) разграничение регулирующих доходов по определенным уровням бюджетной системы РФ;
3) равенство бюджетных прав субъектов РФ, равенство бюджетных прав муниципальных образований;
4) равенство всех бюджетов во взаимоотношениях с федеральным бюджетом, равенство местных бюджетов во взаимоотношениях с бюджетами субъектов РФ;
5) выравнивание уровней минимальной бюджетной обеспеченности субъектов РФ, муниципальных образований.
Для совершенствования межбюджетных отношений необходимо:
1) оказывать поддержку субъектам Федерации таким образом, чтобы оставить им стимулы к развитию собственных источников дохода;
2) сделать схему группировки территорий по экономическим районам с учетом их экономического потенциала и природных условий более упорядоченной;
3) ввести эффективный механизм предоставления инвестиций для выравнивания уровней социально-экономического развития регионов.
Доходную часть территориальных бюджетов составляют закрепленные и регулирующие доходы, дотации и субвенции, а также кредитные ресурсы.
Закрепленными доходами считаются доходы, полностью поступающие в соответствующие бюджеты.
Регулирующими доходами являются средства, направляемые от вышестоящего звена бюджетной системы нижестоящему бюджету, превышающие закрепленные доходы, для покрытия его расходов. Они зачисляются в соответствующие бюджеты исходя из размеров процентных отчислений, устанавливаемых при утверждении вышестоящего бюджета.
Дотации – определенные суммы денежных средств, передаваемые из вышестоящего бюджета для сбалансирования нижестоящих бюджетов при их дефиците.
Субвенции – средства, передаваемые из вышестоящего бюджета нижестоящим бюджетам на финансирование строго целевого мероприятия.
Кредитные ресурсы – средства, передаваемые в качестве кредита, т. е. они должны быть возвращены с процентами или без них.
В 1994 г. введен новый механизм межбюджетных отношений, при котором основным регулятором выступал Целевой фонд финансовой поддержки регионов. Его средства распределяются для всех регионов по единому принципу.
Фонд финансовой поддержки субъектов Федерации оказывает помощь тем субъектам, у которых среднедушевой доход по бюджету за предыдущий год ниже, чем в среднем по РФ, а уровень собственных доходов и дополнительных средств, полученных из федерального бюджета, недостаточен для финансирования текущих расходов.
Регионы, получающие финансовую помощь из федерального бюджета, предоставляют в Министерство финансов РФ плановые и фактические данные о доходах и расходах бюджетов и внебюджетных фондов. Это производится для контроля.
Трансферты регионам перечисляются ежемесячно по мере фактического поступления налогов в федеральный бюджет с учетом удельного веса каждого региона в Фонде их финансовой поддержки. Тем не менее, сохранился порядок выделения регионам бюджетных ассигнований на капитальные вложения для осуществления федеральных целевых программ.
4. Бюджеты РФ
Федеральный бюджет является первым уровнем бюджетной системы РФ.
Федеральный бюджет – это основной финансовый план государства, который утверждается Федеральным Собранием в виде федерального закона. Федеральный бюджет – это основное средство перераспределения национального дохода и валового внутреннего продукта. Через Федеральный бюджет мобилизуются финансовые ресурсы, которые нужны для регулирования экономического и социального развития нашей страны и реализации ее политики. Его функцией является финансирование общегосударственных органов власти и управления, мероприятий, которые связаны с развитием научной деятельности в стране, обеспечением обороноспособности государства, подготовки высококвалифицированных специалистов для РФ.
Средства федерального бюджета – это основной источник для финансирования перестройки экономики, развития прибыльных и перспективных направлений в сфере производства, освоения новых комплексов для производства.
В развитии искусства, средств массовой информации, культуры и других сфер человеческой деятельности федеральный бюджет играет основную роль.
Федеральный бюджет наделен неналоговыми и налоговыми доходами, поступлениями от целевых бюджетных фондов.
Статьей доходов федерального бюджета являются налоговые доходы, к которым относятся:
1) федеральные налоги и сборы, перечень и ставки указаны в налоговом законодательстве РФ, а пропорции их перераспределения в различных уровнях бюджетной системы РФ утверждаются Федеральным законом о федеральном бюджете на определенный финансовый год;
2) государственная пошлина в соответствии с законодательством РФ;
3) таможенные пошлины, таможенные сборы и т. д.
К налоговым доходам также относятся:
1) доходы от пользования имуществом, которое находится в собственности у государства;
2) доходы от платных услуг, которые оказывают бюджетные учреждения;
3) доходы от реализации имущества, которое находится в собственности у государства;
4) доходы от внешнеэкономической деятельности;
5) доходы от реализации государственных запасов и резервов;
6) прибыль Банка России – по нормативам, установленным федеральными законами;
7) часть прибыли унитарных предприятий, которая остается после уплаты налогов и других обязательных платежей. Основным источником доходов федерального бюджета (около 76 %) являются налоговые доходы. В федеральный бюджет поступают такие виды налогов, как: налог на добавленную стоимость и акцизы, составляющие около 40 % от общего дохода бюджета, налог на прибыль (около 10 %), налоги на внешнюю торговлю и внешнеэкономические операции (около 8 %) (основное место в их числе занимают импортные пошлины). Остальную часть образуют подоходный налог с физических лиц, налог на имущество, платежи за пользование природными ресурсами.
Неналоговые доходы составляют около 12 %. Это доходы от государственной собственности, от внешнеэкономической деятельности, от продажи имущества, которое принадлежит государству, от продажи запасов государства.
Поступления от целевых бюджетных фондов – это около 11 % (Федеральный экологический фонд, Федеральный дорожный фонд и т. д.).
В соответствии с законодательством РФ, из федерального бюджета финансируются следующие расходы:
1) обеспечение деятельности Президента РФ, Центральной избирательной комиссии РФ, Федерального Собрания РФ, Счетной палаты РФ, федеральных органов исполнительной власти и их территориальных органов;
2) национальная оборона и обеспечение безопасности государства, осуществление конверсии оборонных отраслей промышленности;
3) функционирование федеральной судебной системы;
4) осуществление международной деятельности в общефедеральных интересах;
5) фундаментальные исследования и содействие научно-техническому прогрессу;
6) государственная поддержка транспорта: железнодорожного, воздушного и морского;
7) государственная поддержка атомной энергетики;
8) ликвидация последствий чрезвычайных ситуаций и стихийных бедствий федерального масштаба;
9) исследование и использование космического пространства;
10) содержание учреждений, находящихся в федеральной собственности или в ведении органов государственной власти РФ;
11) финансовая поддержка субъектов РФ;
12) статистический учет;
13) формирование федеральной собственности; обслуживание и погашение государственного долга РФ;
14) компенсация государственным внебюджетным фондам расходов на выплату государственных пенсий и других социальных выплат, подлежащих финансированию за счет средств федерального бюджета;
15) пополнение государственных запасов драгоценных металлов и драгоценных камней, государственного материального резерва;
16) проведение выборов и референдумов в РФ;
17) федеральная инвестиционная программа; обеспечение реализации решений федеральных органов государственной власти, приведших к увеличению бюджетных расходов или уменьшению бюджетных доходов бюджетов других уровней.
Средства федерального бюджета используются для финансирования мероприятий регионального и местного назначения.
Спецификой федерального бюджета является финансирование за счет себя общегосударственных расходов на оборону, международную деятельность, научные исследования. Федеральный бюджет финансирует 100 % общегосударственных расходов на оборону и международную деятельность, 93 % – на научные исследования, 76 % – на правоохранительную деятельность, 89 % – на предупреждение и ликвидацию чрезвычайных ситуаций и последствий стихийных бедствий.
Федеральный бюджет – это инструмент межрегионального перераспределения общегосударственных средств.
Региональные бюджеты – центральное звено территориальных бюджетов, которые служат для финансового обеспечения задач, лежащих на государственных органах управления субъекта РФ.
Целью региональных органов власти является обеспечение развития регионов, а также производственной и непроизводственной сфер на подведомственных территориях.
В последнее время наблюдается регионализация экономических и социальных процессов.
Роль региональных бюджетов усиливается.
С помощью региональных бюджетов государство проводит экономическую политику, выравнивая уровни экономического и социального развития территорий, которые в силу исторических, географических, военных и других условий отстали в своем экономическом и социальном развитии от других районов страны. Разрабатываются региональные программы, которые финансируются из региональных бюджетов.
В соответствии с БК РФ, доходы: региональных бюджетов формируются за счет собственных и регулирующих доходов.
Собственные доходы включают следующие региональные налоги и сборы:
1) налог на имущество предприятий;
2) налог на недвижимость;
3) дорожный налог;
4) транспортный налог;
5) налог с продаж;
6) налог на игорный бизнес;
7) региональные лицензионные сборы.
К собственным доходам относятся доходы от использования имущества, находящегося в собственности субъектов РФ, и доходы от платных услуг, оказываемых бюджетными учреждениями, находящимися в ведении органов государственной власти субъектов РФ.
Регулирующие доходы – это отчисления от федеральных налогов и сборов, распределенных к зачислению в бюджеты субъектов РФ по нормативам, определенным федеральным законом о федеральном бюджете на очередной финансовый год, а также дотаций, субвенций, субсидий и трансфертов, полученных за счет средств федерального бюджета.
Основные направления использования средств региональных бюджетов:
1) обеспечение функционирования органов законодательной и исполнительной власти субъектов РФ;
2) обслуживание и погашение государственного долга субъектов РФ;
3) проведение выборов и референдумов в субъектах РФ;
4) обеспечение реализации региональных целевых программ;
5) формирование государственной собственности субъектов РФ;
6) осуществление международных и внешнеэкономических связей субъектов РФ;
7) содержание и развитие предприятий, учреждений и организаций, находящихся в ведении органов государственной власти субъектов РФ;
8) обеспечение деятельности средств массовой информации субъектов РФ;
9) оказание финансовой помощи местным бюджетам;
10) обеспечение осуществления отдельных государственных полномочий, передаваемых на муниципальный уровень;
11) компенсация дополнительных расходов, возникших в результате решений, принятых органами государственной власти субъектов РФ, приводящих к увеличению бюджетных расходов или уменьшению бюджетных доходов местных бюджетов. Первое место в расходах занимают ассигнования на народное хозяйство (промышленность, строительство, сельское хозяйство, транспорт, дорожное хозяйство, связь, и др.).
Второе место – расходы на социально-культурные мероприятия (образование, культура и искусство, социальная политика) – свыше 25 %; расходы на управление и содержание правоохранительных органов составляют примерно 8 %.
Местные бюджеты – это третий уровень бюджетной системы РФ.
Согласно ст. 14 БК РФ, бюджет муниципального образования (местный бюджет) является формой образования и расходования денежных средств, предназначенных для обеспечения задач и функций, отнесенных к предметам ведения местного самоуправления.
Местное самоуправление осуществляется самим населением через свободно избранные им представительные органы. Для выполнения функций, возложенных на местные представительные и исполнительные органы, они наделяются определенными имущественными и финансово-бюджетными правами.
Местные бюджеты – один из главных каналов доведения до населения конечных результатов производства. Через них общественные фонды потребления распределяются между отдельными группами населения, из них финансируется развитие отраслей производственной сферы (местной и пищевой промышленности, коммунального хозяйства, объем продукции и услуги).
Местные бюджеты выполняют следующие функции:
1) формируют денежные фонды, которые являются финансовым обеспечением деятельности местных органов власти;
2) распределяют и используют эти фонды между отраслями хозяйства;
3) контролируют финансово-хозяйственную деятельность предприятий, учреждений, которые подведомственны этим органам власти.
Местные бюджеты в осуществлении общегосударственных экономических и социальных задач имеют большое значение, поскольку они распределяют государственные средства на содержание и развитие социальной инфраструктуры общества.
Собственные доходы не являются основным источником формирования местных бюджетов.
В состав собственных доходов местных бюджетов входят:
1) местные налоги и сборы:
а) земельный налог;
б) налог на имущество физических лиц;
в) налог на рекламу;
г) налог на наследство или дарение;
д) местные лицензионные сборы;
2) доходы от приватизации, в том числе:
а) доходы от приватизации объектов государственной и муниципальной собственности;
б) доходы от продажи земли;
в) доходы от продажи квартир гражданам;
3) средства обязательного медицинского страхования, средства внебюджетных и отраслевых фондов.
В главные регулирующие доходы местных бюджетов входят отчисления:
1) от налога на добавленную стоимость;
2) от акцизов;
3) от налога на прибыль предприятий;
4) от подоходного налога с физических лиц.
Из местных бюджетов финансируются функциональные расходы, которые включают в себя расходы на:
1) содержание органов местного самоуправления;
2) формирование муниципальной собственности и управление ею;
3) организация, содержание и развитие учреждений образования, здравоохранения, культуры;
4) средств массовой информации, других учреждений, находящихся в муниципальной собственности;
5) содержание муниципальных органов охраны общественного порядка;
6) организация, содержание и развитие муниципального жилищно-коммунального хозяйства;
7) содержание мест захоронения, находящихся в ведении муниципальных органов;
8) организация транспортного обслуживания населения и учреждений, находящихся в муниципальной собственности или в ведении органов местного самоуправления;
9) охрана окружающей природной среды на территориях муниципальных образований;
10) обслуживание и погашение муниципального долга;
11) целевое дотирование населения;
12) проведение муниципальных выборов и местных референдумов.
Основным направлением использования средств местных бюджетов является покрытие расходов, связанных с жизнеобеспечением человека (расходы на социально-культурные мероприятия и на жилищно-коммунальное хозяйство).
Структура расходов отдельных видов местных бюджетов не одинакова.
Одним из главных направлений использования финансовых ресурсов должно быть финансирование развития местной производственной базы как основы для получения в будущем собственных доходов.
В соответствии со статьей 6 БК РФ, консолидированный бюджет – это свод бюджетов всех уровней, который включает в себя федеральный бюджет и консолидированные бюджеты субъектов РФ. Консолидированный бюджет субъекта РФ включает региональный бюджет, т. е. бюджет субъекта РФ, и местные бюджеты.
Термин «консолидированный бюджет» был включен также в Закон РСФСР «Об основах бюджетного устройства и бюджетного процесса РСФСР» от 10 октября 1991 г. в связи с упразднением Государственного бюджета РФ, в который входили все звенья бюджетной системы России. Вышеуказанный закон в настоящее время не действует.
В бюджетном планировании используются показатели консолидированных бюджетов. Объемы консолидированных бюджетов административно-территориальных преобразований принимаются в расчет при определении размеров дотаций и величины нормативов отчислений от регулирующих налогов в бюджеты субъектов РФ.
Роль консолидированных показателей важна при проведении анализа формирования и использования централизованного финансового фонда страны.
Сводное финансовое планирование невозможно без расчета показателей консолидированных бюджетов. Из консолидированных бюджетов берутся показатели сводного финансового баланса государства и территориальных сводных финансовых балансов. В доходной части баланса используются данные: налог на добавленную стоимость и акцизы, налог на имущество, подоходный налог, налоги на внешнюю торговлю, средства бюджетных целевых фондов и т. д.
Расходная часть включает: расходы на социально-культурные мероприятия, которые финансируются за счет бюджета, затраты на государственные инвестиции, государственные дотации, расходы на науку из бюджета, на оборону, расходы на содержание правоохранительных органов, органов власти, судов прокуратуры и др.
Показатели консолидированного бюджета играют большую роль в перспективном планировании в целом и перспективном финансовом планировании в частности. Финансовые показатели, в основе которых лежат показатели консолидированных бюджетов, используются при разработке прогнозов экономического и социального развития государства и территорий.
Показатели консолидированных бюджетов используются при расчетах, которые характеризуют различные виды обеспеченности жителей страны и ее территорий.
5. Принципы бюджетной системы РФ
Бюджетная система РФ, согласно БК РФ, основана на принципах:
1) принцип единства бюджетной системы РФ – это единство бюджетного законодательства РФ, форм бюджетной документации и отчетности, принципов организации и функционирования бюджетной системы, бюджетной классификации бюджетной системы РФ, санкций за нарушение бюджетного законодательства, единый порядок установления и исполнения расходных обязательств, формирования доходов и осуществления расходов бюджетов бюджетной системы РФ, ведения бюджетного учета и отчетности бюджетов бюджетной системы РФ и бюджетных учреждений, единство порядка исполнения судебных актов по обращению взыскания на средства бюджетов бюджетной системы РФ;
2) принцип разграничения доходов и расходов между бюджетами разных уровней – это закрепление в соответствии с законодательством РФ доходов и расходов за бюджетами бюджетной системы РФ, определение полномочий органов государственной власти по формированию доходов, установлению и исполнению расходных обязательств;
3) принцип самостоятельности бюджетов означает:
а) право и обязанность органов государственной власти и органов местного самоуправления обеспечивать самостоятельно сбалансированность бюджетов и эффективность использования бюджетных средств;
б) право и обязанность органов государственной власти и органов местного самоуправления самостоятельно осуществлять бюджетный процесс;
в) право органов государственной власти и органов местного самоуправления устанавливать налоги и сборы, подлежащие зачислению в бюджеты соответствующего уровня бюджетной системы РФ;
г) право органов государственной власти и органов местного самоуправления самостоятельно определять формы и направления расходования средств бюджетов;
д) недопустимость установления расходных обязательств, подлежащих исполнению одновременно за счет средств бюджетов двух и более уровней бюджетной системы РФ, или за счет средств консолидированных бюджетов, или без определения бюджета, за счет средств которого должно осуществляться исполнение соответствующих расходных обязательств;
е) недопустимость непосредственного исполнения расходных обязательств органов государственной власти и органов местного самоуправления за счет средств бюджетовдругих уровней;
ж) недопустимость введения в действие в течение финансового года органами государственной власти решений и изменений бюджетного законодательства и законодательства о налогах и сборах, которые приведут к увеличению расходов и снижению доходов бюджетов других уровней без внесения изменений в законы о соответствующих бюджетах, предусматривающих компенсацию увеличения расходов, снижения доходов;
з) недопустимость изъятия дополнительных доходов в течение года, экономии по расходам бюджетов, полученных в результате эффективного исполнения бюджетов;
3) принцип равенства бюджетных прав субъектов РФ, муниципальных образований – это определение бюджетных полномочий органов государственной власти субъектов РФ и органов местного самоуправления, установление и исполнение расходных обязательств, формирование налоговых и неналоговых доходов бюджетов субъектов РФ и местных бюджетов, определение объема, форм и порядка предоставления межбюджетных трансфертов в соответствии с едиными принципами и требованиями, установленными БК РФ;
4) принцип полноты отражения доходов и расходов бюджетов, бюджетов государственных внебюджетных фондов означает, что все доходы и расходы бюджетов, бюджетов государственных внебюджетных фондов и иные обязательные поступления, определенные налоговым и бюджетным законодательством РФ, законами о государственных внебюджетных фондах, подлежат отражению в бюджетах, бюджетах государственных внебюджетных фондов в обязательном порядке и в полном объеме. Все государственные и муниципальные расходы подлежат финансированию за счет бюджетных средств, средств государственных внебюджетных фондов, аккумулированных в бюджетной системе РФ;
5) принцип сбалансированности бюджета означает, что объем предусмотренных бюджетом расходов должен соответствовать суммарному объему доходов бюджета и поступлений из источников финансирования его дефицита.
При составлении, утверждении и исполнении бюджета уполномоченные органы должны исходить из необходимости минимизации размера дефицита бюджета;
6) принцип эффективности и экономности использования бюджетных средств означает, что при составлении и исполнении бюджетов уполномоченные органы и получатели бюджетных средств должны исходить из необходимости достижения заданных результатов с использованием наименьшего объема средств или достижения наилучшего результата с использованием определенного бюджетом объема средств;
7) принцип общего покрытия расходов означает, что все расходы бюджета должны покрываться общей суммой доходов бюджета и поступлений из источников финансирования его дефицита.
Доходы бюджета и поступления из источников финансирования его дефицита не могут быть увязаны с определенными расходами бюджета, за исключением доходов целевых бюджетных фондов, средств целевых иностранных кредитов, а также в случае централизации средств из бюджетов других уровней бюджетной системы РФ;
8) принцип гласности означает:
а) обязательное опубликование в открытой печати утвержденных бюджетов и отчетов об их исполнении, полноту представления информации о ходе исполнения бюджетов, а также доступность иных сведений по решению законодательных органов государственной власти, органов местного самоуправления;
б) обязательную открытость для общества и средств массовой информации процедур рассмотрения и принятия решений по проектам бюджетов, в том числе по вопросам, вызывающим разногласия либо внутри законодательного органа государственной власти, либо между законодательным и исполнительным органами государственной власти;
9) принцип достоверности бюджета – это надежность показателей прогноза социально-экономического развития соответствующей территории и реалистичность расчета доходов и расходов бюджета;
10) принцип адресности и целевого характера бюджетных средств означает, что бюджетные средства выделяются в распоряжение конкретных получателей бюджетных средств с обозначением направления их на финансирование конкретных целей. Любые действия, приводящие к нарушению адресности, являются нарушением бюджетного законодательства РФ.
Поделитесь на страничке
Следующая глава >
econ.wikireading.ru
Бюджетная система — это… Что такое бюджетная система: виды и модели, структура, уровни
Добавлено в закладки: 0
Что такое бюджетная система? Описание и определение понятия.
Бюджетная система – главный элемент финансовой системы государства, в который включаются бюджеты муниципальных и государственных организаций, основанных на экономических отношениях и юридических нормах. Структура бюджетной системы страны связана с ее формой государственного устройства.
Унитарное государство имеет бюджетную систему, которая состоит из государственного и местных бюджетов. Федеративное государство имеет бюджетную систему, в которую входят местные бюджеты, бюджет членов федерации, федеративный бюджет.
Бюджетная система конфедерации государств образуется за счет взносов входящих в федерацию государств. Каждое государство, которое входит в конфедерацию, при этом имеет собственную бюджетную систему.
Рассмотрим, более детально, что значит бюджетная система.
Бюджетная система государства — комплекс всех бюджетов государства ( муниципальных, федеральных, региональных).
Все составляющие соответствующих бюджетных систем самостоятельны (это значит, что принимаются они соответствующими региональными и местными органами управления).
Бюджетная система определяется социально-экономическим и политическим строем страны, а её организационное построение зависит от формы государственного и административного устройства.
Различаются бюджетные системы в зависимости от политической структуры государства — с учетом того, является ли оно федеративным или унитарным. Бюджетная система унитарных государств более централизована. У государств с федеративным устройством наряду с федеральным и местными бюджетами выделяются бюджеты субъектов Федерации . Однако и в унитарных, и в федеративных государствах бюджеты нижестоящих уровней не входят в бюджеты вышестоящих уровней.
Структура бюджетной системы государства:
Унитарного (например, Швейцария, Япония, Франция)
- Госбюджет
- Местный бюджеты
Федерального (Россия, Канада, США)
- Госбюджет
- Федеральные бюджеты
- Местные бюджеты
В мировой практике в настоящее время функционируют бюджетные системы, которые различаются между собой по оновным трем критериям:
- Доля ВВП, централизуемая для финансирования государственных расходов .
- Реализация социальных функций за счет государственных расходов.
- Обратное воздействие бюджетной системы на сектор экономики.
В мире существуют различные бюджетные системы. К типичным относят американскую и европейскую, а также есть модель бюджетной системы, которая существенно отличается от всех остальных -это японская модель. Есть и другие модели, сочетающие в себе признаки названных (например, арабская, австралийская, китайская, и другие).
Характерные черты американской бюджетной системы
Для американской системы характерна обязательность жестко исполнять законы, которые регулируют государственные доходы и расходы. Разрабатывается бюджет правительством государства. Отдельные штаты имеют свои бюджеты и взаимодействуют с центральным бюджетом в более узких пределах, чем это принято в европейских странах. В американской бюджетной системе предполагается значительная самостоятельность отдельных штатов. Существенные особенности американской бюджетной системы: государство финансирует программы развития отдельных секторов экономики страны; стимулирует развитие предпринимательства путем предоставления различных налоговых льгот.
Для этой системы характерна довольно невысокая доля государственных расходов в объеме ВВП.
Характерные черты европейской бюджетной системы
Для европейского типа бюджетной системы характерно прежде всего то, что государство предоставляет гражданам социальные гарантии за счет бюджетных средств, вмешивается в решение финансовых проблем административно-территориальных структур, и, несмотря на относительную самостоятельность, обеспечивает определенное «выравнивание» экономических условий в регионах. Самой отличительной чертой всех бюджетных систем европейского типа является их гибкость. Также в бюджетном процессе четко учитываются финансовые обязательства государства, предусмотренные конституцией и действующими законами.
Характерные черты японской бюджетной системы
Отличительной чертой японской бюджетной системы является социализация бизнеса как основного фактора экономического роста и повышения благосостояния граждан.
Степень социальной ответственности бизнеса в Японии является наиболее высокой по сравнению с другими бюджетными системами мира. Именно с этим специалисты связывают высокий научно-технический прогресс в Японии.
По доле государственных расходов японская бюджетная система напоминает американскую и российскую — примерно около трети ВВП поступает в бюджетную систему, но растущую внушительную часть социальных расходов, связанных с оказанием социальных услуг работающим, берут на себя отдельные фирмы.Государственное вмешательство в экономику на основе финансирования приоритетных расходов делает се похожей на американскую модель. Японская модель не является статической, а постепенно трансформируется. Существенное значение фирмы придают развитию так называемых «социальных тылов» производства.
Различаются бюджетные системы и по степени их централизации. По этому признаку различают три типа моделей.
Децентрализованная модель бюджетной системы – активная роль принадлежит регионам в обеспечении финансирования развития их экономики за счет собственных доходов. При этом центральная власть берет на себя расходы, которые связаны с гарантиями, установленными законами государства. Самым ярким примером децентрализованной бюджетной системы является Канада.
Умеренно централизованная (или социально ориентированная модель) бюджетная система – расходы центра и регионов оптимально сбалансированы и закреплены за уровнями бюджетной системы.Каждый уровень несет ответственность за финансирование расходов, а значит, рост их доходов. Такая бюджетная модель характерна, например для Швейцарии.
Максимально централизованная бюджетная система (также социально ориентированная модель) характерна для государств, у которых практически нет проблемы реализации принципа бюджетного федерализма. Это характерно для шведской модели бюджетной системы.
Бюджетная система Российской Федерации
К сожалению, бюджетная система России сочетает в себе далеко не самые совершенные признаки американской, японской, европейской систем. Сходство с японской было в социальной ответственности бизнеса (то есть предприятия также имеют социальные фонды и обеспечивают социальную поддержку на достаточно высоком уровне). Пока что социальные функции бизнеса в России развиты слабо, и поэтому очень актуальной является проблема повышения социальной ответственности бизнеса.
Похожесть бюджетной системы России и бюджетной системы США заключена в том, что оплата большинства социальных услуг в России осуществляется за счет личного бюджета граждан, что на самом деле является нелогичным при низком уровне средней заработной платы. Также активно внедряется принцип платности всех услуг. Конечно, эта тенденция при низкой заработной плате делает бюджетную систему России, мягко говоря, неудачным копированием опыта США.
Подобие бюджетной системы России европейской системе заключается в том, что в ней еще присутствуют «остатки» прежней социальной защиты граждан за счет средств бюджетов всех уровней. Социальная направленность бюджетной политики России в последние годы проявляется все более отчетливо в связи с реализацией социально ориентированных национальных проектов, а также в связи с совершенствованием системы социального страхования в рамках политики радикальной реорганизации пенсионной системы.
Уровни бюджетной системы Российской Федерации
В России в настоящее время действует бюджетная система, которая состоит из трех уровней (включает муниципальный уровень, уровень субъектов Федерации и федеральный уровень).
Первый уровень – федеральный – разрабатывается федеральный бюджет Российской Федерации и рассматриваются бюджеты государственных внебюджетных фондов. Стоит заметить, что финансируются за счет средств федерального бюджета все расходы, которые связаны с централизованным управлением функций государства.
Второй уровень бюджетной системы включает бюджеты субъектов Российской Федерации и также территориальные государственные внебюджетные фонды (к которым пока относятся территориальные фонды обязательного медицинского страхования). Бюджеты на этом уровне бюджетной системы являются формой централизации денежных средств, и используются для решения задач и функций, которые отнесятся к предметам ведения субъекта Федерации. Стоит отметить, что из этих бюджетов в значительной степени финансируется развитие отраслей производственной сферы, в первую очередь местной, легкой и пищевой промышленности; коммунального хозяйства; развитие транспорта и связи. Бюджеты субъектов Федерации имеют важное значение в осуществлении общегосударственных и социальных задач, в первую очередь в распределении государственных средств на содержание и развитие социальной инфраструктуры общества.
Третий уровень бюджетной системы — это бюджеты муниципальных образовании (муниципальных районов, поселений и городских округов). Говоря проще, здесь имеются подуровни. На этом уровне государственные внебюджетные фонды не формируются. В пределах нижнего уровня выделяются подуровни (бюджеты городских районов, муниципальных районов и поселений).
Бюджетный кодекс Российской Федерации определяет местный бюджет (бюджет муниципального образования) как форму образования и расходования денежных средств, которые предназначены для эффективного обеспечения ведения местного самоуправления.
В настоящее время неотъемлемой составляющей социально-экономического развития страны является развитие именно муниципального сектора экономики.
Мы коротко рассмотрели бюджетная система.
Оставляйте свои комментарии или дополнения к материалу.
biznes-prost.ru





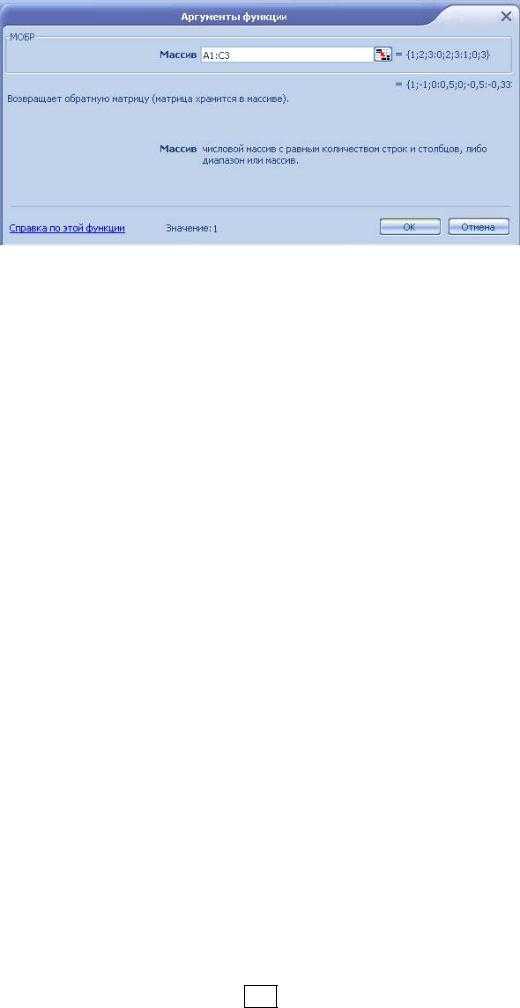
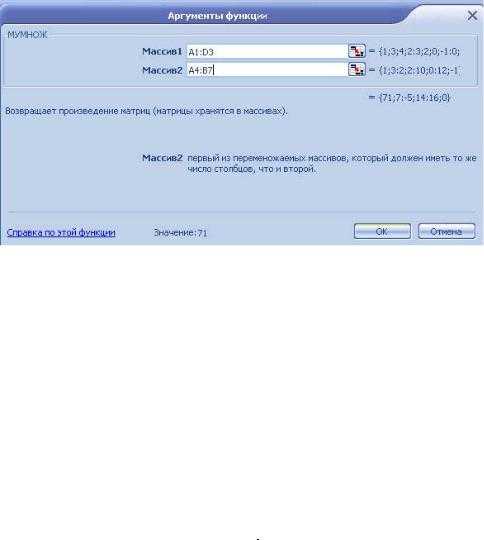

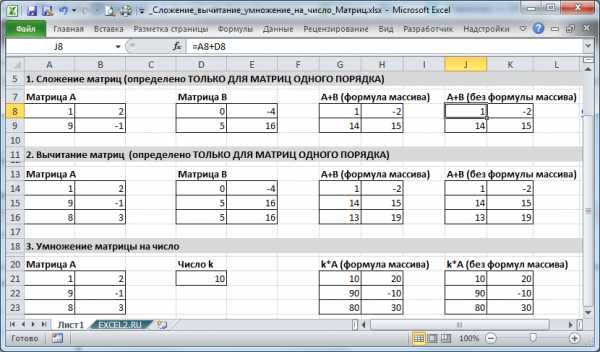

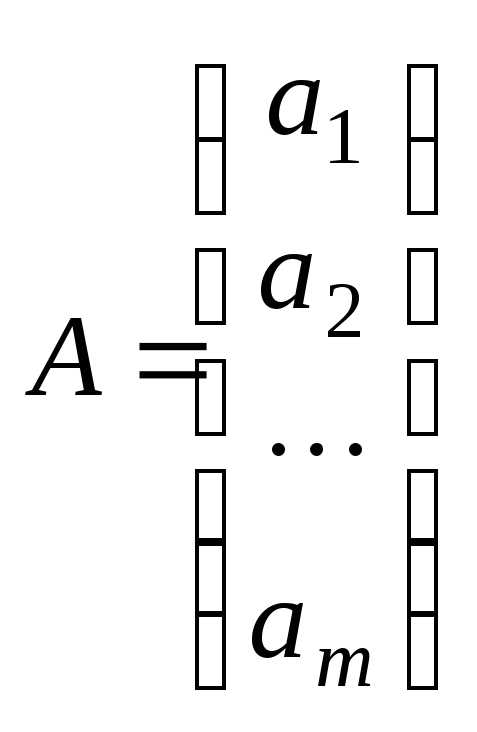

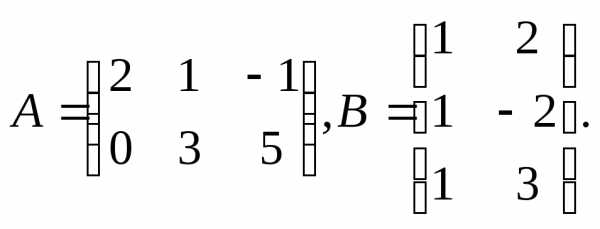

 .
.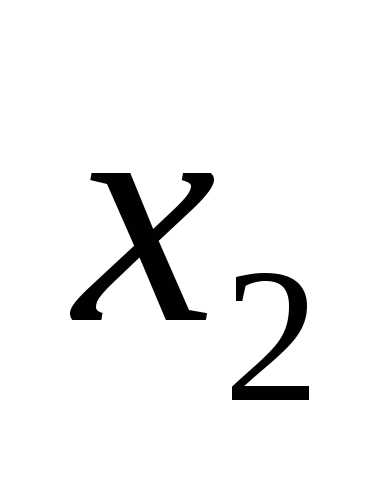 — в первом,
— в первом, — во втором,
— во втором, — в третьем.
— в третьем.
 ,
, ,
, — базисные переменные, то на пересечении
— базисные переменные, то на пересечении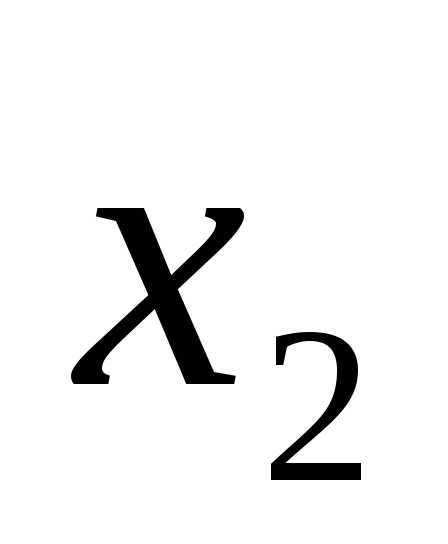 (5
строка)
с
(5
строка)
с  (столбецD)
должна
стоять 1
(ячейка
D5),
а в соответствующем столбце ниже –
нули, на пересечении
(столбецD)
должна
стоять 1
(ячейка
D5),
а в соответствующем столбце ниже –
нули, на пересечении  (6 строка)
с
(6 строка)
с  (столбецE)
должна
стоять 1 (ячейка
E6),
а в соответствующем столбце ниже –
нули,
(столбецE)
должна
стоять 1 (ячейка
E6),
а в соответствующем столбце ниже –
нули,  (7 строка)
с
(7 строка)
с  (столбецH)
должна
стоять 1 (ячейка
H7),
а в соответствующем столбце ниже –
нули.
(столбецH)
должна
стоять 1 (ячейка
H7),
а в соответствующем столбце ниже –
нули.

 )
к соответствующим элементам ведущего
столбца (
)
к соответствующим элементам ведущего
столбца ( ).
Например, в ячейку I5
введите
формулу =B5/C5.
Растяните формулы для ячеек I6,
I7,
исключая ячейку индексной строки (рис.
29).
).
Например, в ячейку I5
введите
формулу =B5/C5.
Растяните формулы для ячеек I6,
I7,
исключая ячейку индексной строки (рис.
29).

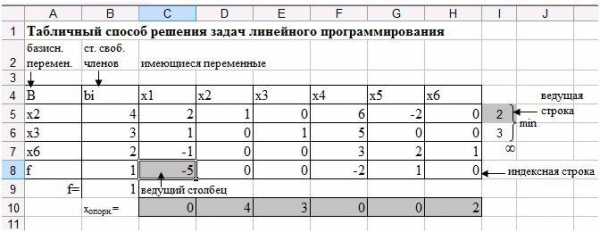
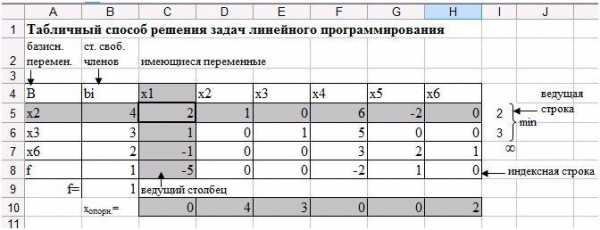
 из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец (рис. 33). В нашем
случае – это переменная
из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец (рис. 33). В нашем
случае – это переменная .
.
 — базисная переменная, то на пересечении
— базисная переменная, то на пересечении (13
строка)
с
(13
строка)
с  (столбецC)
должна
стоять 1
(ячейка
С13),
а в соответствующем столбце ниже –
нули. С помощью элементарных преобразований
сделайте ведущий столбец базисным.
(столбецC)
должна
стоять 1
(ячейка
С13),
а в соответствующем столбце ниже –
нули. С помощью элементарных преобразований
сделайте ведущий столбец базисным.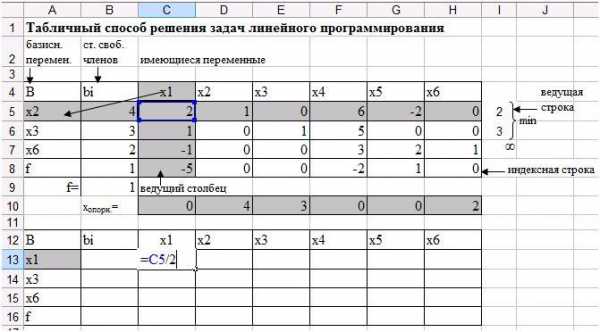

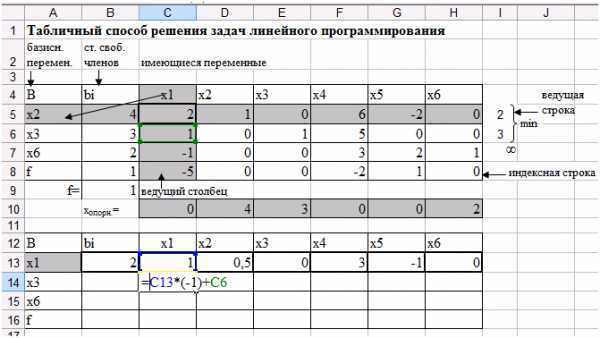



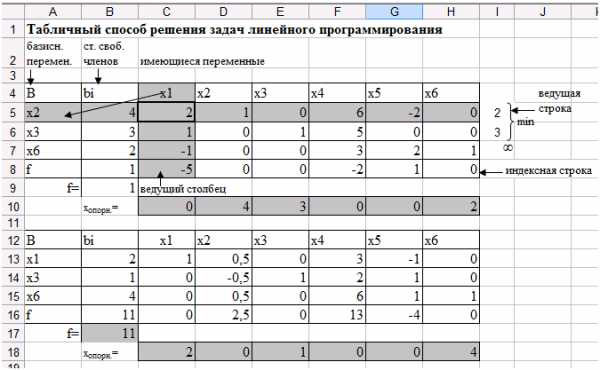

 .
.
 .
. — в первом,
— в первом, — во втором, в третьем ограничении нет
базисной переменной, следовательно,
необходимо применить М-метод.
— во втором, в третьем ограничении нет
базисной переменной, следовательно,
необходимо применить М-метод. и
и через небазисные. Подставьте выражения
в целевую функцию.
через небазисные. Подставьте выражения
в целевую функцию. и
и -строку
(рис. 42).
-строку
(рис. 42). ,
, ,
, — базисные переменные, то на пересечении
— базисные переменные, то на пересечении (5
строка)
с
(5
строка)
с  (столбецF)
должна
стоять 1
(ячейка
F5),
а в соответствующем столбце ниже –
нули, на пересечении
(столбецF)
должна
стоять 1
(ячейка
F5),
а в соответствующем столбце ниже –
нули, на пересечении  (6 строка)
с
(6 строка)
с 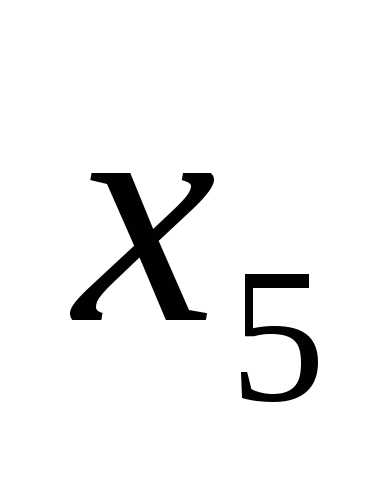 (столбецG)
должна
стоять 1 (ячейка
G6),
а в соответствующем столбце ниже –
нули,
(столбецG)
должна
стоять 1 (ячейка
G6),
а в соответствующем столбце ниже –
нули,  (7 строка)
с
(7 строка)
с 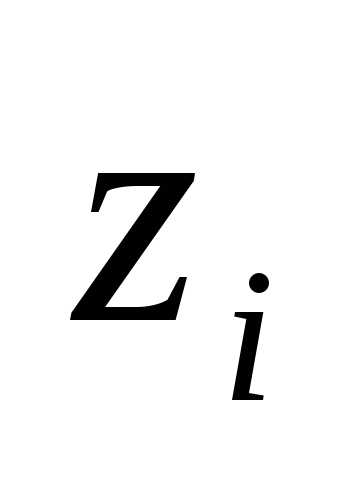 (столбецI)
должна
стоять 1 (ячейка
I7),
а в соответствующем столбце ниже –
нули.
(столбецI)
должна
стоять 1 (ячейка
I7),
а в соответствующем столбце ниже –
нули. -строку.
Получите.
-строку.
Получите. .
. )
к соответствующим элементам ведущего
столбца (
)
к соответствующим элементам ведущего
столбца ( ).
Найдите ведущую строку и ведущий элемент
(рис. 45).
).
Найдите ведущую строку и ведущий элемент
(рис. 45). из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец. Выполните симплексные
преобразования, таким же образом, как
и в лабораторной №4, получите базисный
столбец, который соответствует переменной
из базиса, на ее место запишите ту
переменную, которой соответствует
ведущий столбец. Выполните симплексные
преобразования, таким же образом, как
и в лабораторной №4, получите базисный
столбец, который соответствует переменной .
Значения столбца
.
Значения столбца можно удалить, так как переменная вышла
из базиса (рис. 46).
можно удалить, так как переменная вышла
из базиса (рис. 46).
 -строке
все нули, то ее можно удалить из таблицы
и получить таблицу, в которой будет
только функция
-строке
все нули, то ее можно удалить из таблицы
и получить таблицу, в которой будет
только функция (рис. 47).
(рис. 47).
 .
Так как в исходной задаче функция
стремится к минимуму, то
.
Так как в исходной задаче функция
стремится к минимуму, то