Решение тригонометрических уравнений | Математика, которая мне нравится
Простейшие тригонометрические уравнения
Уравнение при решений не имеет,
при имеет решения ,
при имеет решения ,
при имеет решения ,
при всех остальных имеет решения .
Уравнение при решений не имеет,
при имеет решения ,
при имеет решения >,
при имеет решения ,
при всех остальных имеет решения .
Уравнение имеет решения .
Уравнение имеет решения .
Приемы решения тригонометрических уравнений
1. Сведение к одной функции
1. заменяем на , — на .
Пример 1.
Пример 2.
2. заменяем на , — на , — на .
Пример 1.
1) 2) ,
В первом случае решений нет, во втором .
Пример 2.
Пример 3.
3. Однородные уравнения относительно .
Если , то деля обе части уравнения на или на , получаем равносильные уравнения. Действительно, пусть — корень уравнения и . Подставляя в уравнение, получаем, что и , а это невозможно.
Пример.
4. Уравнения, приводящиеся к однородным
а) Домножение на
Пример.
б) Переход к половинному аргументу
Пример.
5. Использование формулы
Пример.
6. Замена .
Пример.
Разложение на множители
1. Формулы преобразования суммы в произведение
2. Формулы
Пример 1.
Ответ. .
Пример 2.
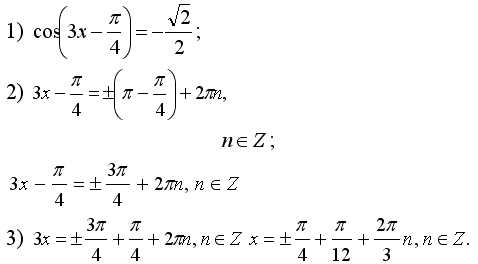
, решений нет,
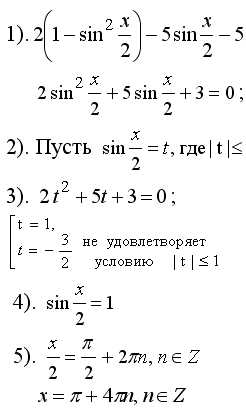
Ответ. , .
Понижение степени
Использование формул
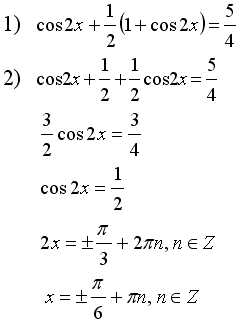
Сравнение левой и правой части
Пример 1.
что невозможно.
Ответ. .
Пример 2.
Ответ. .
Пример 3.
Пусть
Подставляем во второе уравнение:
Ответ. .
Пример 4.
или
Если , то . Если , то .
Ответ. .
hijos.ru
Решение тригонометрических уравнений
Автор Сергей Валерьевич
Пятница, Июнь 15, 2012
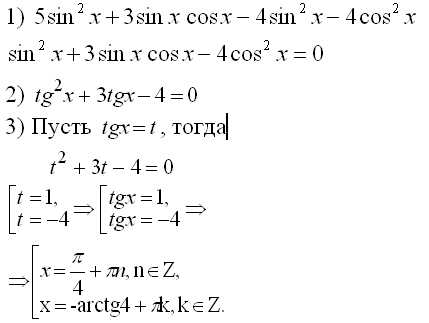
В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в заданиях C1 школьникам предлагаются для решения тригонометрические уравнения, поэтому в данной статье разобраны только они. Примеры структурированы по методам решения уравнений, от самых элементарных, до достаточно сложных.
Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.
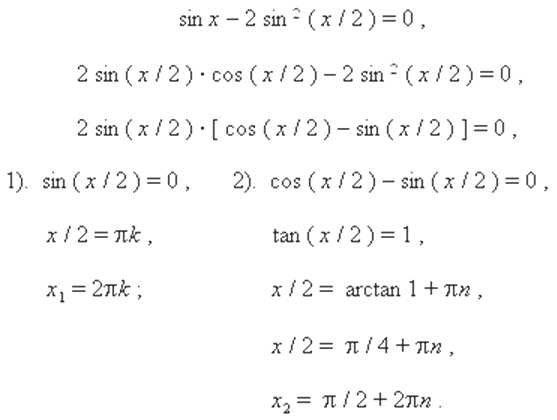
Основные тригонометрические формулы

Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений
Пример 1. Найдите корни уравнения
принадлежащие промежутку
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем (на всякий случай, эта запись означает, что числа и принадлежат множеству целых чисел):
Арккосинус есть число, заключенное в интервале от
yourtutor.info
Формулы для решения простейших тригонометрических уравнений
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Содержание статьи:
Простейшие тригонометрические уравнения
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| \leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`
Таблица арксинусов
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Таблица арккосинусов
Частные случаи для синуса и косинуса в графиках.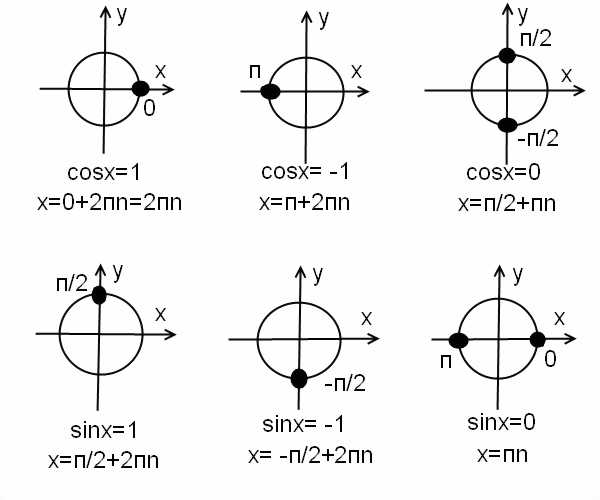
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
Таблица арктангенсов
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Таблица арккотангенсов
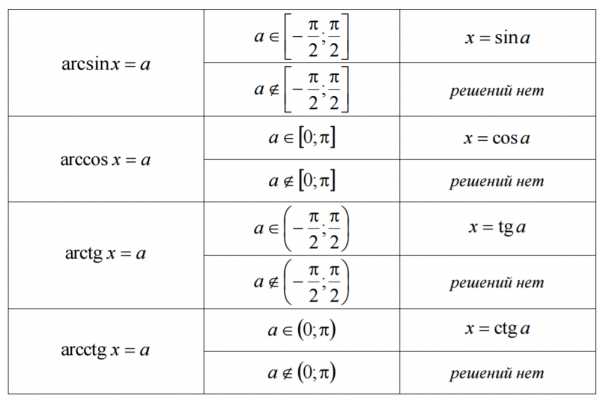
Формулы корней тригонометрических уравнений в таблице
Для синуса: Для косинуса:
Для косинуса: Для тангенса и котангенса:Формулы решения уравнений, содержащих обратные тригонометрические функции:
Для тангенса и котангенса:Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью тригонометрических формул преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 — x)+1=0`
Решение. Используя формулы приведения, имеем:
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
делаем замену: `cos(x+\frac \pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Ответ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n`, `x_2=\pi/2+ 2\pi n`.
Ответ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x \ne 0` — для первого случая, и на `cos^2 x \ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x \ne 0`, получим:
`\frac {sin^2 x}{cos^2 x}+\frac{sin x cos x}{cos^2 x} — \frac{2 cos^2 x}{cos^2 x}=0`
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Ответ. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Ответ. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt {a^2+b^2}`:
`\frac a{sqrt {a^2+b^2}} sin x +` `\frac b{sqrt {a^2+b^2}} cos x =` `\frac c{sqrt {a^2+b^2}}`.
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `\frac a{sqrt {a^2+b^2}}=cos \varphi`, ` \frac b{sqrt {a^2+b^2}} =sin \varphi`, `\frac c{sqrt {a^2+b^2}}=C`, тогда:
`cos \varphi sin x + sin \varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt {3^2+4^2}`, получим:
`\frac {3 sin x} {sqrt {3^2+4^2}}+` `\frac{4 cos x}{sqrt {3^2+4^2}}=` `\frac 2{sqrt {3^2+4^2}}`
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos \varphi` , `4/5=sin \varphi`. Так как `sin \varphi>0`, `cos \varphi>0`, то в качестве вспомогательного угла возьмем `\varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos \varphi sin x+sin \varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`sin (x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `\frac {sin x}{1+cos x}=1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
`\frac {sin x}{1+cos x}=` `\frac {(1-cos x)(1+cos x)}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {1-cos^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {sin^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}-` `\frac {sin^2 x}{1+cos x}=0`
`\frac {sin x-sin^2 x}{1+cos x}=0`
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Простейшие тригонометрические уравнения и их решение
К простейшим тригонометрическим уравнениям относятся уравнения вида
Решение простейших тригонометрических уравнений
Рассмотрим подробнее каждое из этих уравнений и их решение.
Уравнение вида . Так как для любого x, то при и уравнение не имеет корней. При , корни этого уравнения находятся по формуле
Особые случаи
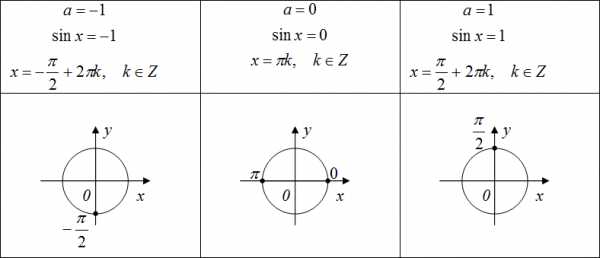
Примеры решения задач
Уравнение вида . Так как для любого x, то при и уравнение корней не имеет. При , корни этого уравнения находятся по формуле
Особые случаи:
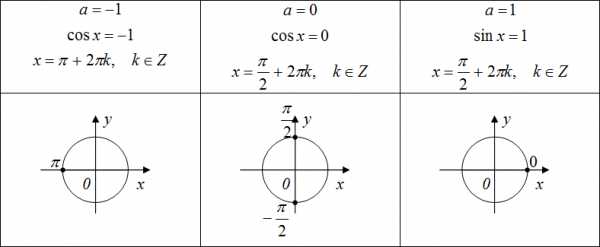 ПРИМЕР 4
ПРИМЕР 4| Задание | Решить уравнение — |
| Решение | Косинус – функция ограниченная и лежит в пределах , поэтому данное равенство не имеет смысла. |
| Ответ | Решений нет. |
Простейшие тригонометрические уравнения с тангенсами и котангенсами
Уравнение вида . Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
ПРИМЕР 5
| Задание | Решить уравнение |
| Решение | Выразим из этого равенства тангенс
В последнем равенстве положив , получим простейшее тригонометрическое уравнение , корни которого вычисляются по формуле
Тогда
Сделаем обратную замену
и выразим из полученного уравнения x:
поделим обе части последнего равенства на 2, тогда окончательно получим
|
| Ответ |
Уравнение вида . Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
ПРИМЕР 6
| Задание | Решить уравнение
|
| Решение | Ведем замену , тогда исходное уравнение преобразуется в простейшее тригонометрическое уравнение , корни которого вычисляются по формуле
Тогда
Сделаем обратную замену
и выразим из полученного уравнения x:
поделим обе части последнего равенства на 5, тогда окончательно получим
|
| Ответ |
Приведение тригонометрических уравнений к простейшим
Примеры тригонометрических уравнений, которые приводятся к простейшим тригонометрическим уравнениям с помощью элементарных преобразований или тригонометрических формул.
ПРИМЕР 8| Задание | Решить уравнение |
| Решение | Применим к правой части заданного уравнения формулу суммы синусов:
или
Последнее равенство равносильно совокупности простейших уравнений
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Тригонометрические уравнения и их решение
Простейшие тригонометрические уравнения
К простейшим тригонометрическим уравнениям относятся уравнения вида
Рассмотрим подробнее каждое из этих уравнений и их решение.
Уравнение вида . При и уравнение корней не имеет. При , корни этого уравнения находятся по формуле
Особые случаи:
Уравнение вида . При и уравнение корней не имеет. При , корни этого уравнения находятся по формуле
Особые случаи:
Замечание. .
Уравнение вида . Корни этого уравнения находятся по формуле
Уравнение вида . Корни этого уравнения находятся по формуле
Тригонометрические уравнения, приводящиеся к квадратным уравнениям
Это тригонометрические уравнения, которые после замены тригонометрической функции, которая входит в уравнение, становится квадратным.
Уравнение вида, где . Такие уравнения решают с помощью введения дополнительного угла. Считая, что , поделим обе части исходного уравнения на , получим
Для полученных коэффициентов при синусе и косинусе справедливы следующие соотношения
Тогда можно утверждать, что существует угол , такой что, например
Таким образом, последнее уравнение примет вид
По формуле суммы для тригонометрических функций, последнее уравнение сводится к простейшему тригонометрическому уравнению
откуда достаточно легко найти x.
Однородные тригонометрические уравнения
Однородные тригонометрические уравнения – это уравнения вида
где – действительные числа, . Такое уравнение легко приводится к уравнению относительно , если все его члены поделить на . При этом, если , то деление не приведет к потере корней. Действительно, если , то первоначальное уравнение примет вид , откуда , что не возможно, так как и одновременно не могут быть равны нулю.
Дробно-рациональные тригонометрические уравнения
Основной сложностью решения таких уравнений является отбор корней уравнения для формирования ответа.
ru.solverbook.com
Методы решения сложных тригонометрических уравнений
Методы решения сложных
тригонометрических уравнений
І тип. Двучленные уравнения. Уравнения, содержащие две тригонометрические функции с коэффициентами 1.
Пример 1.
Решение
или
Ответ: ;
Пример 2.
Решение
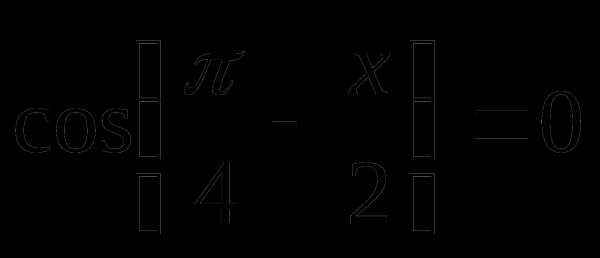
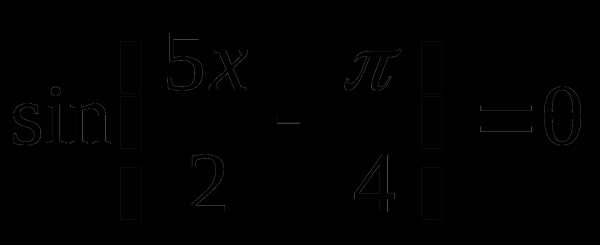
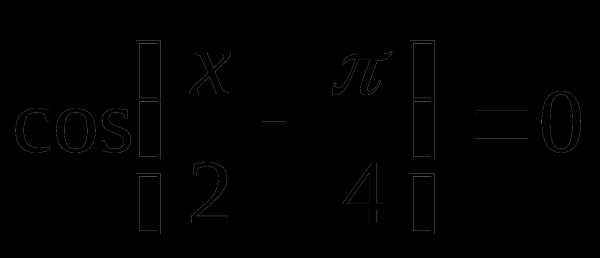
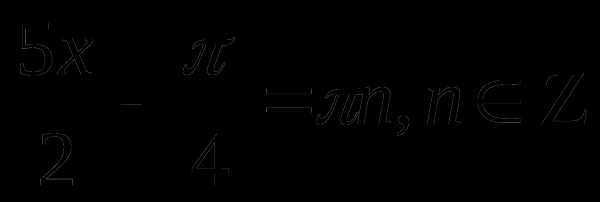
Ответ: 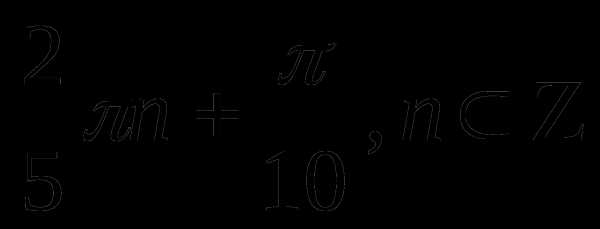 ;
; 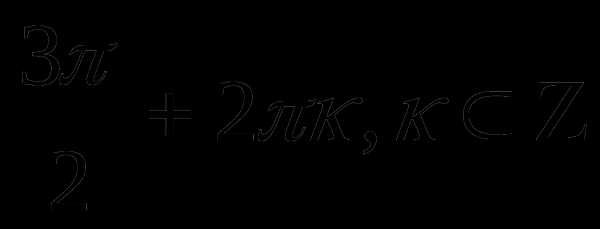 .
.
ІІ тип. Многочленные тригонометрические уравнения. Все функции содержащиеся в этом уравнении, переносят в левую часть и полученный тригонометрический многочлен раскладываю на множители.
Если многочлен уравнения содержит четную степень, то формулам понижают степень и превращают в произведение.
Если тригонометрический многочлен содержит функции таким образом, что этот многочлен будет стандартного вида, то применяют метод подстановки.
1)
2)
ІІІ тип. Однородные тригонометрические уравнения.
1) (уравнение І степени)
2) (уравнение ІІ степени)
3) ( уравнение ІІІ степени)
Эти уравнения решаются делением
этого уравнения на старшую степень 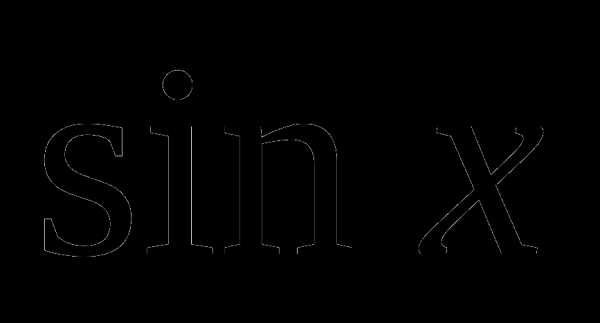
или .
1) /: ,
2)
3)
Пример 1.
Решение
Пусть 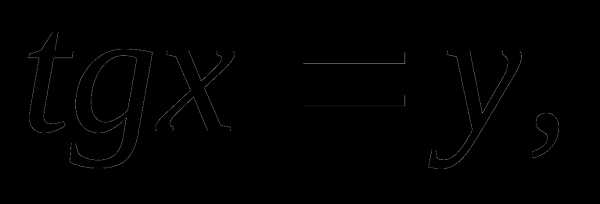 тогда
тогда
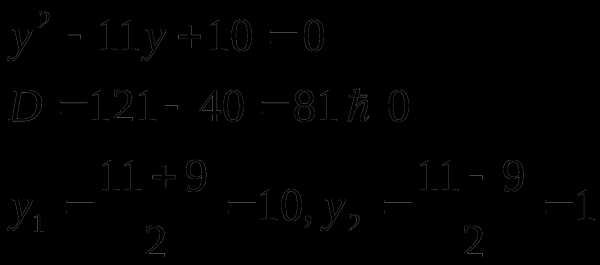
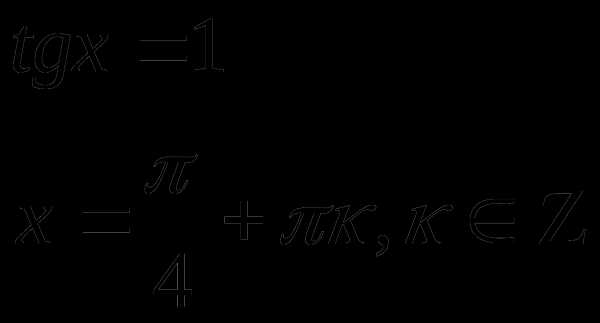
Ответ:
Пример 2.
Решение
Это уравнение можно свести к
однородному третьего порядка относительно
или 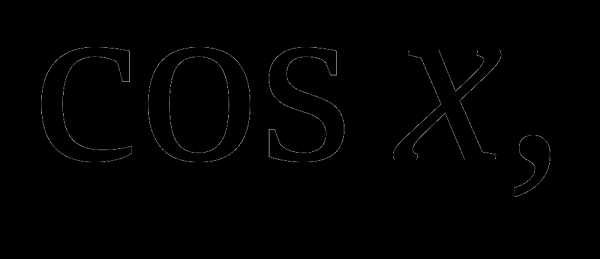 если заменить
если заменить
Получим
Разделили обе части уравнения на получим
Пусть 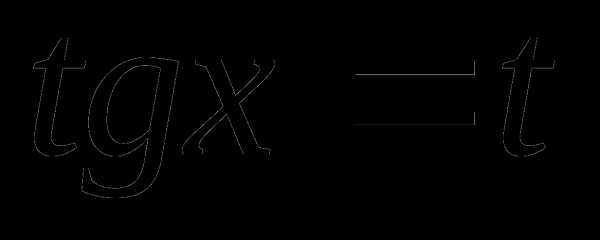
Легко
проверить, что 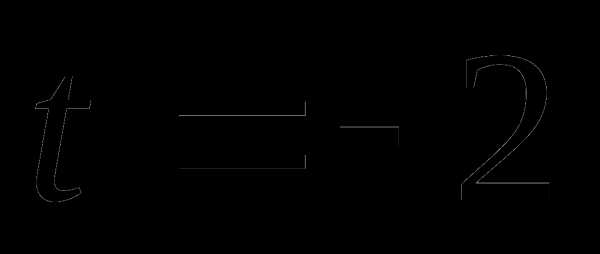 является
корнем этого уравнения.
является
корнем этого уравнения.
Поэтому
или
корней нет.
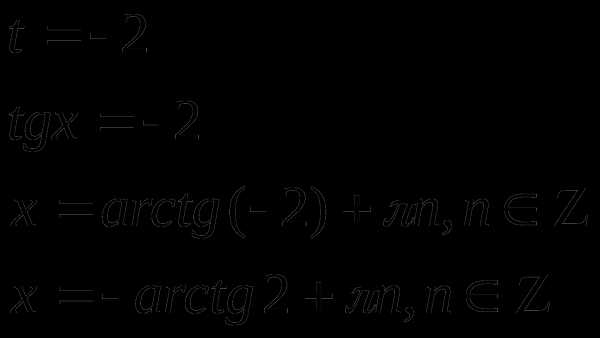
Ответ:
ІV тип. Линейные неоднородные тригонометрические уравнения.
1) если
то
делим на 
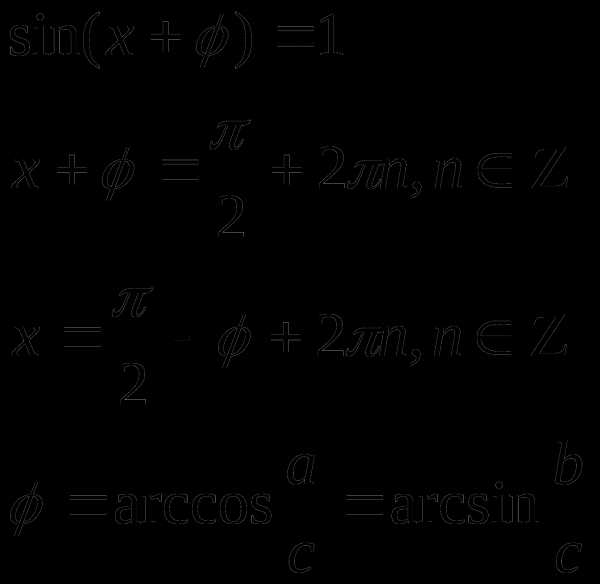
2) если тогда применяем метод универсальной подстановки
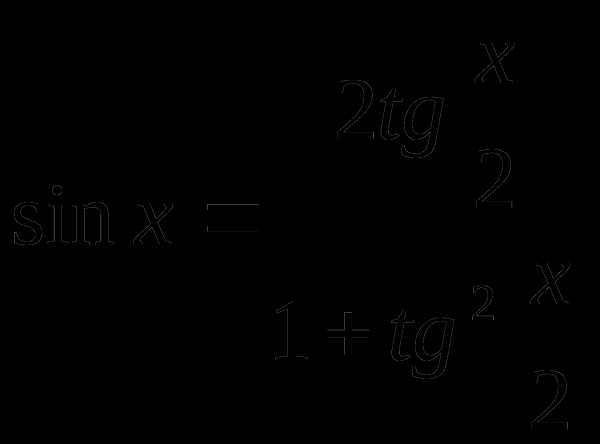
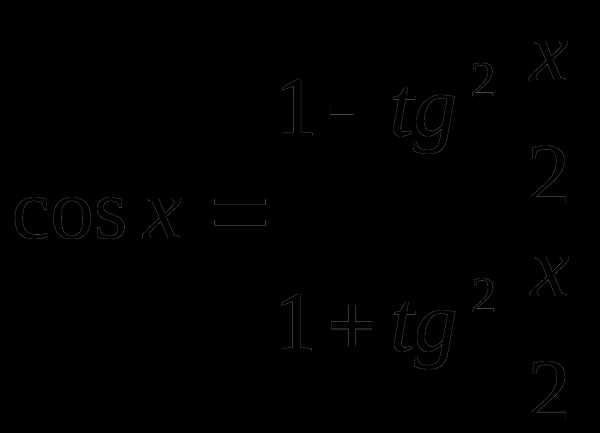
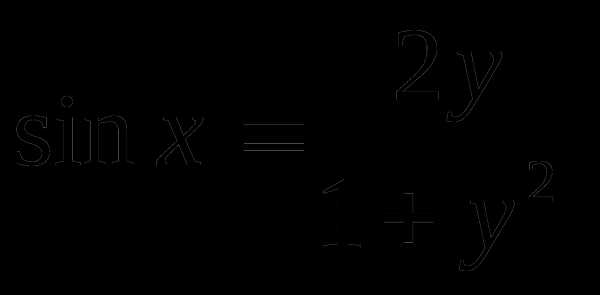
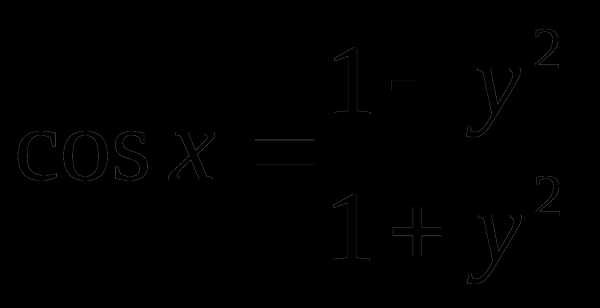
и так далее.
3) если то неоднородное уравнение приводим к однородному второй степени с помощью тригонометрической единицы.
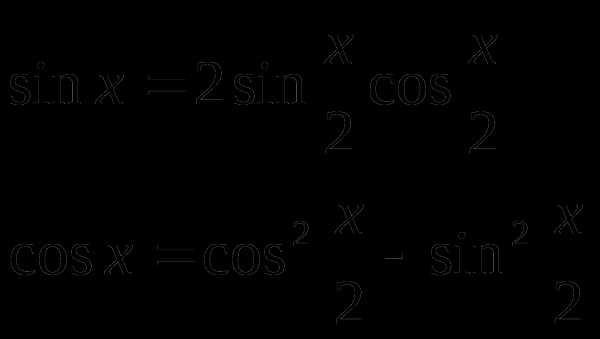
V тип. Уравнения, содержащие тригонометрические дроби.
Находим ОДЗ ( т.к. знаменатель  0).
Либо приводим к общему знаменателю,
либо применяем метод подстановки.
0).
Либо приводим к общему знаменателю,
либо применяем метод подстановки.
Пример 1.
Решение
ОДЗ:
Пусть 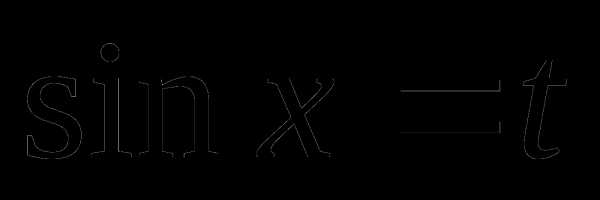 ,
тогда
,
тогда 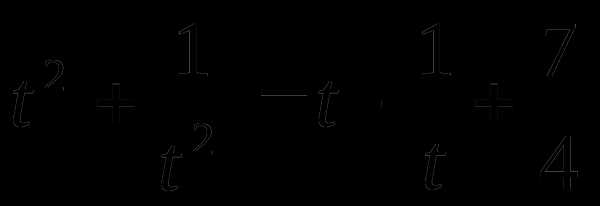
Это уравнение упростим, обозначив 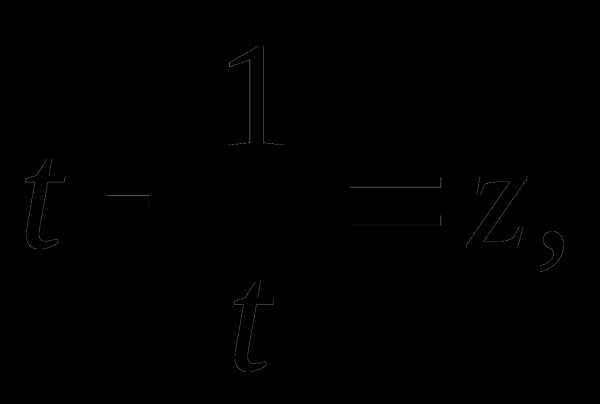 тогда
тогда 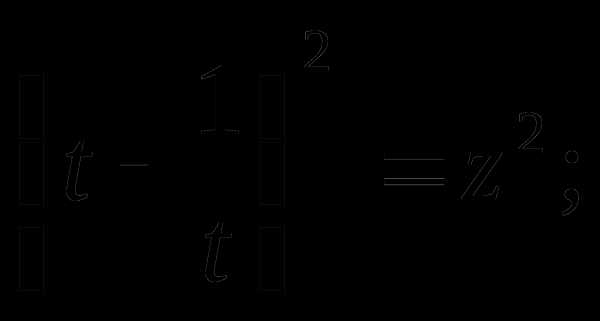
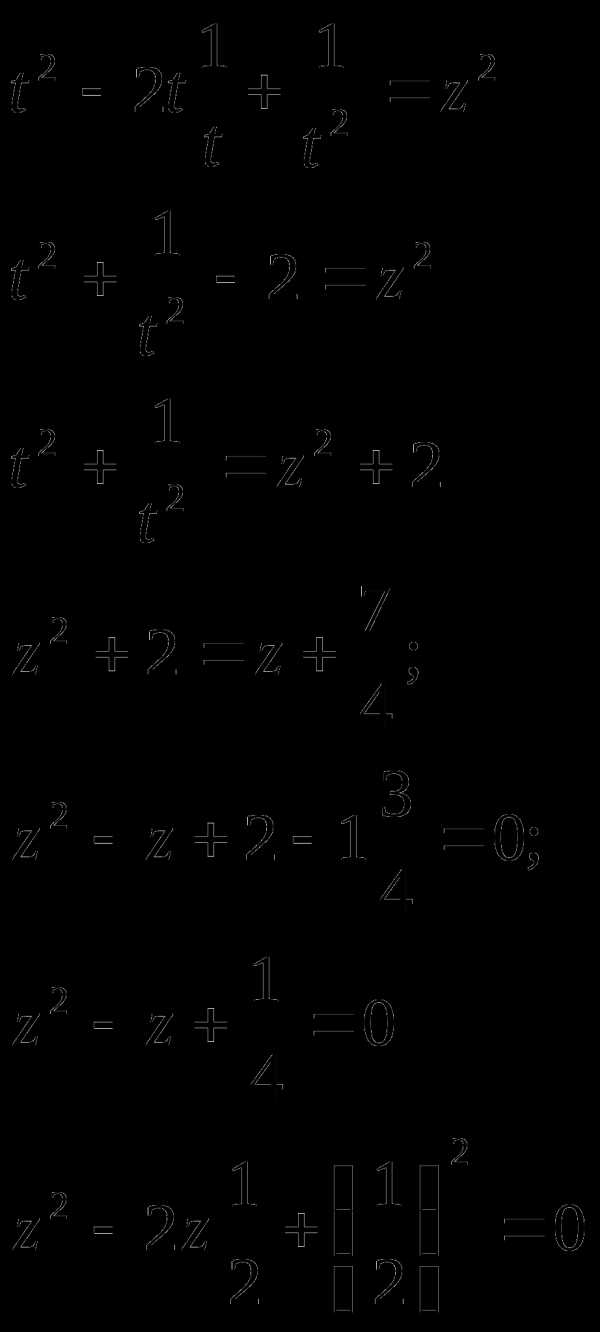
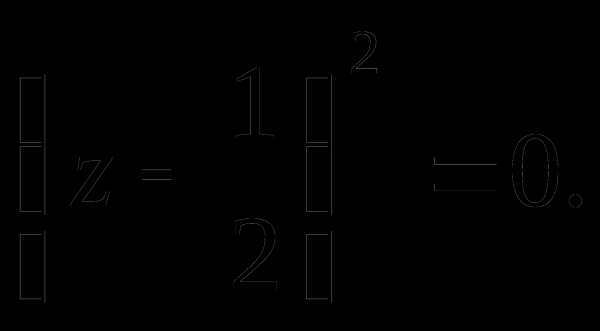 Тогда
Тогда 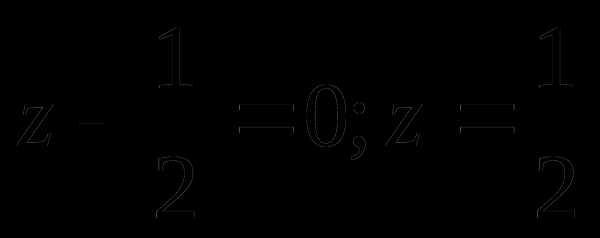
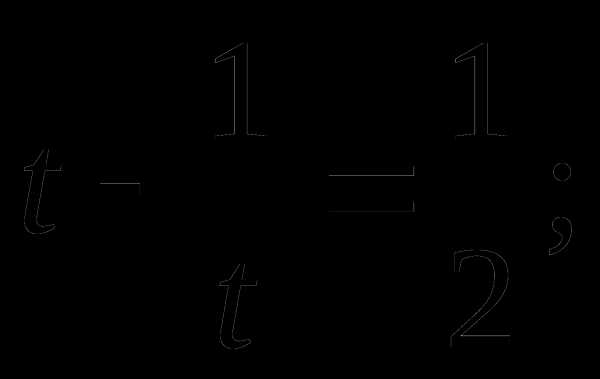
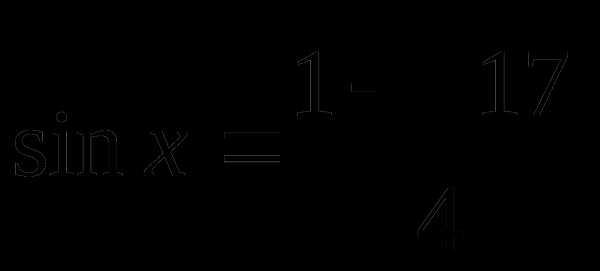
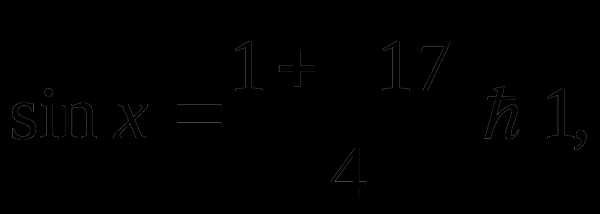 корней нет
корней нет
Ответ:
VІ тип. Иррациональные тригонометрические уравнения.
Содержание тригонометрические функции под знаком радикала.
Указать ОДЗ.
Пример 1. Решить уравнение
Решение
при любых 
Сделав замену 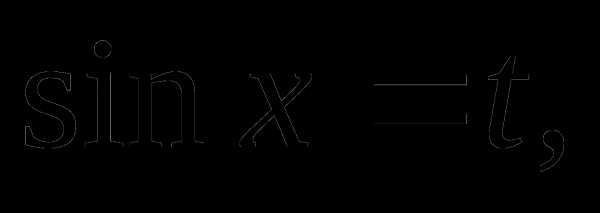 получим
иррациональное уравнение
получим
иррациональное уравнение
которое равносильно системе
Поэтому неравенству системы 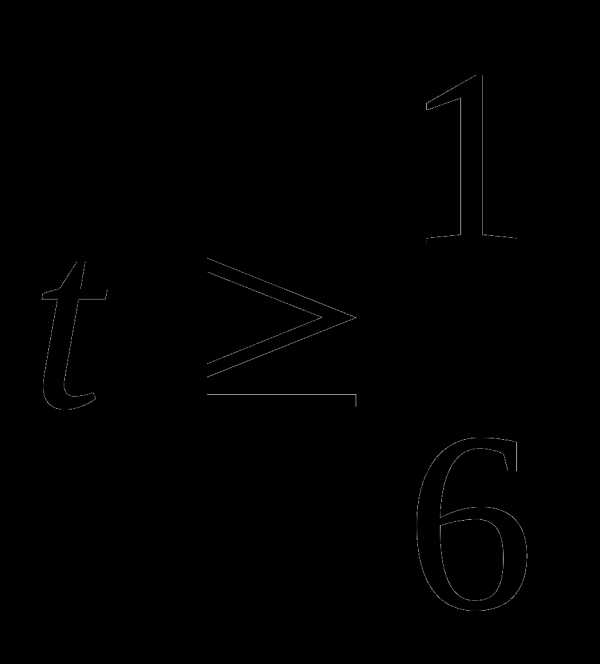 удовлетворяет только
удовлетворяет только 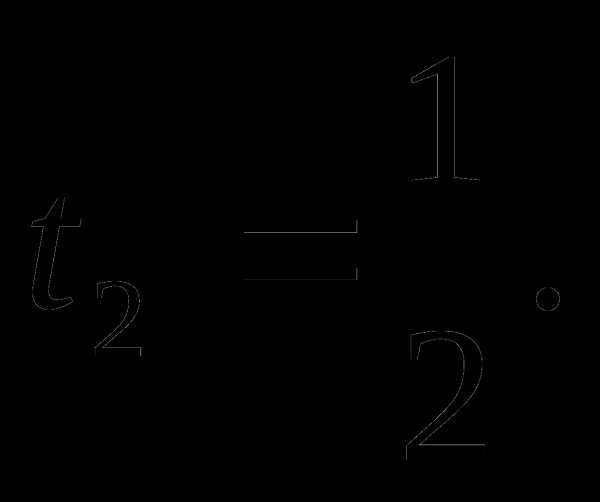
Значит 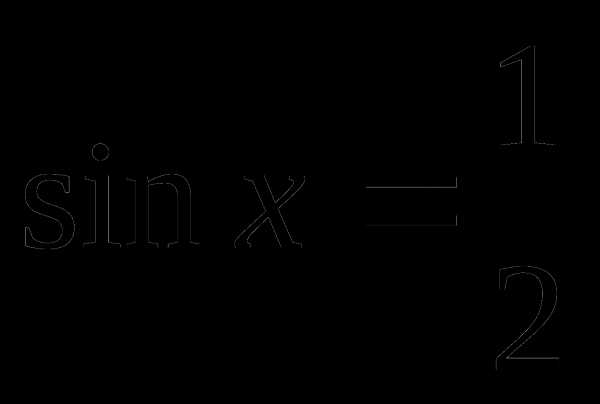 .
.
Ответ:
VІІ тип. Функциональные.
В качестве аргументов используются другие функции.
Пример 1.
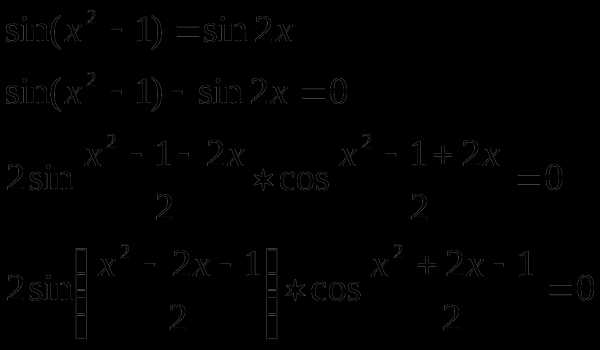
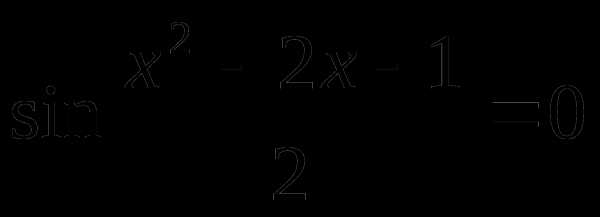 или
или 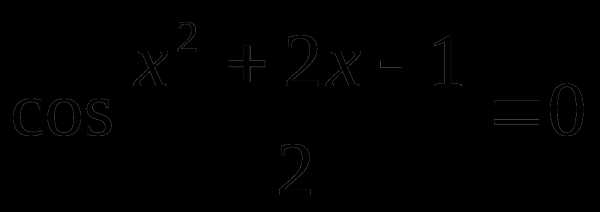
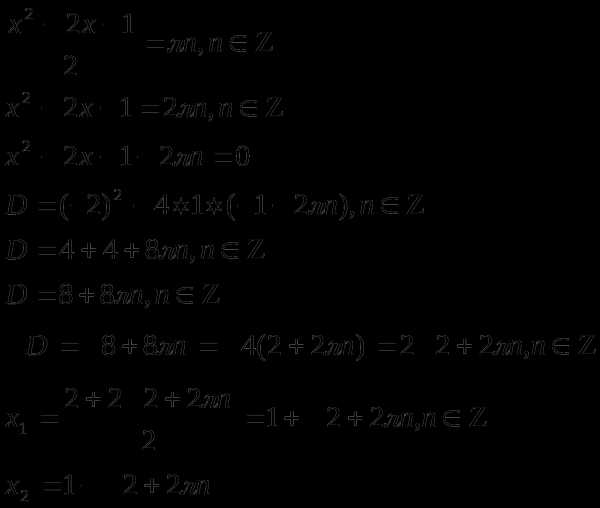
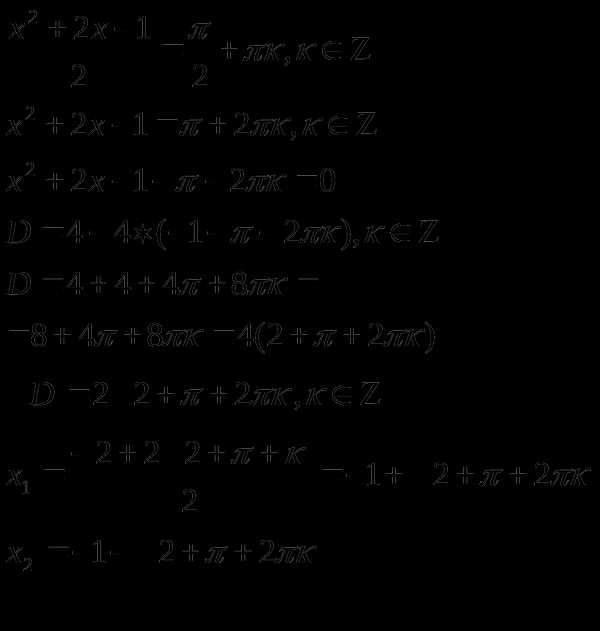
при при
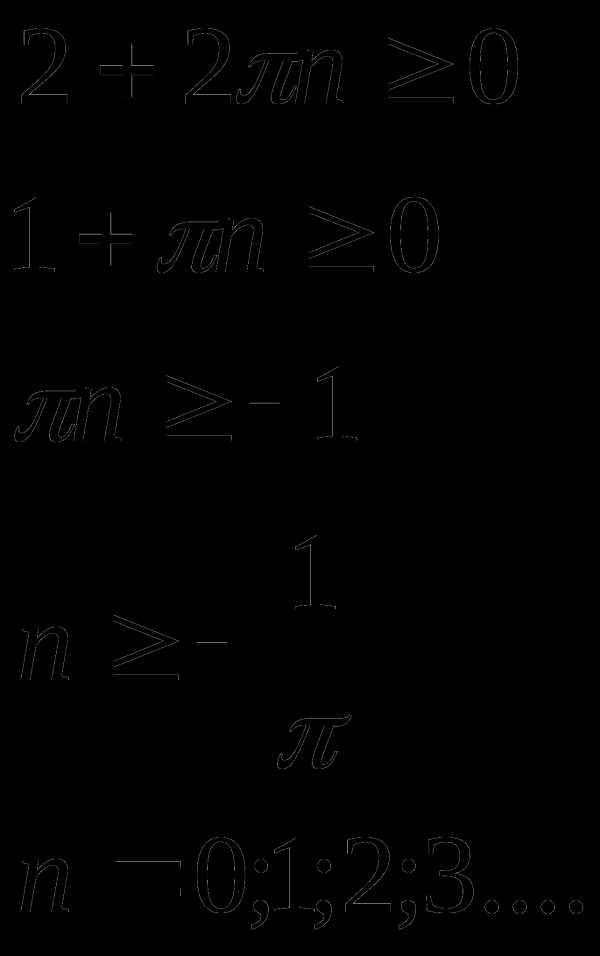
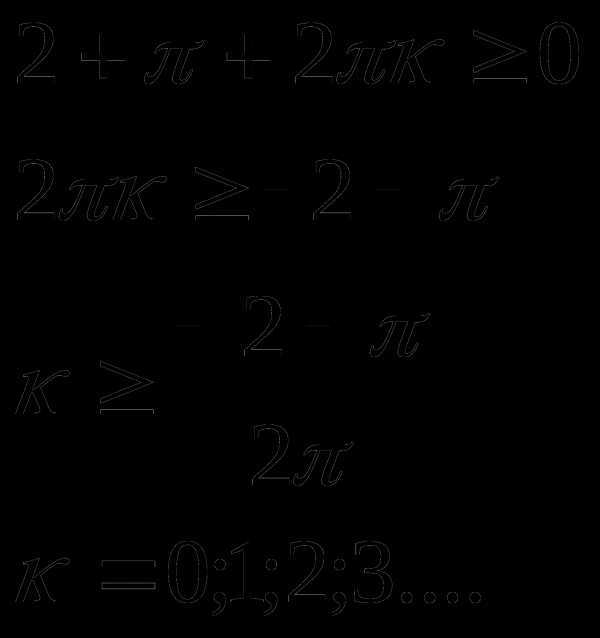
Ответ: где 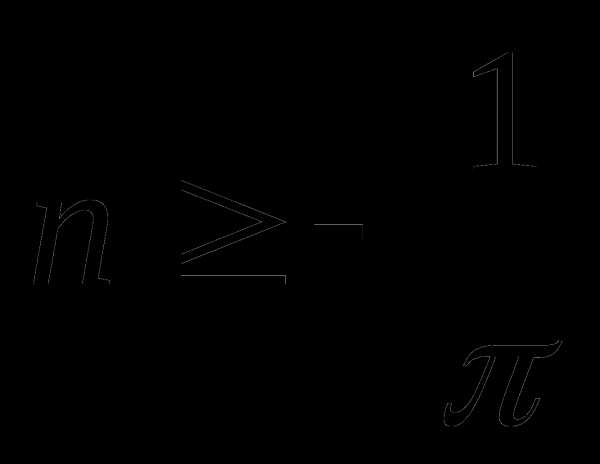 при
при
где 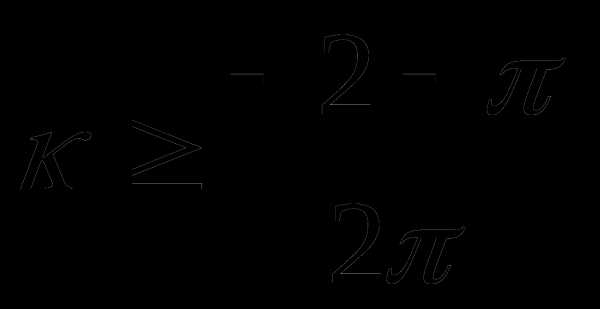 при
при
Пример 2.
Решение
Так как то
Пусть
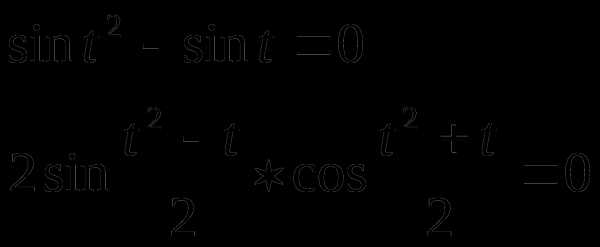
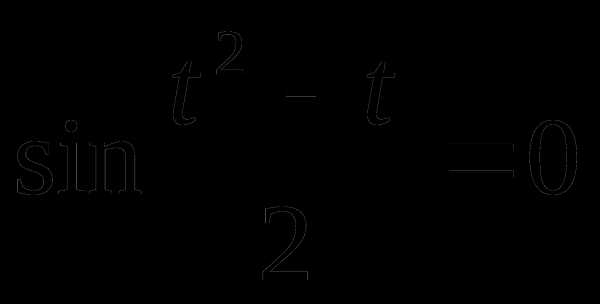 или
или 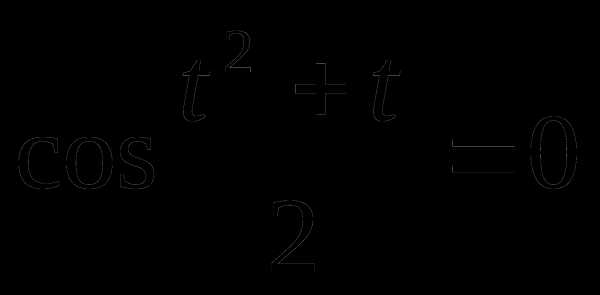
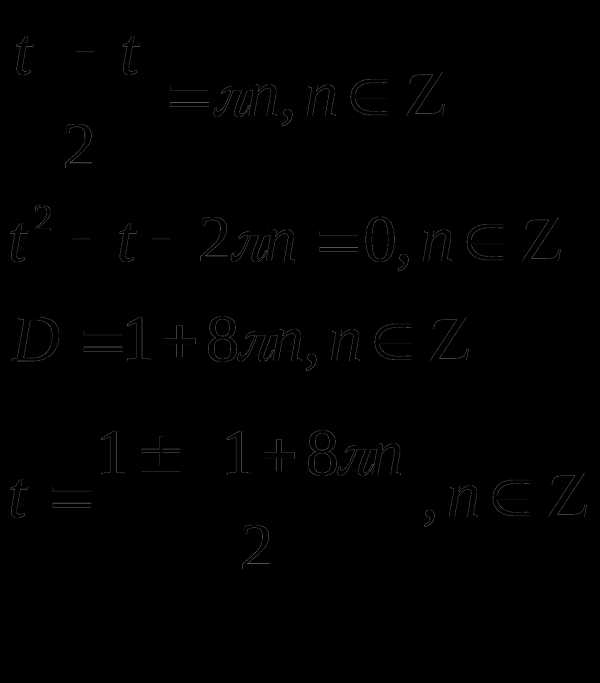
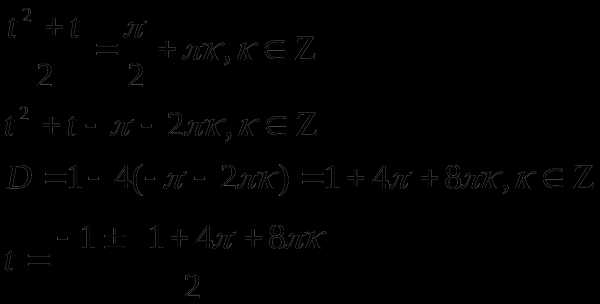
т.к. 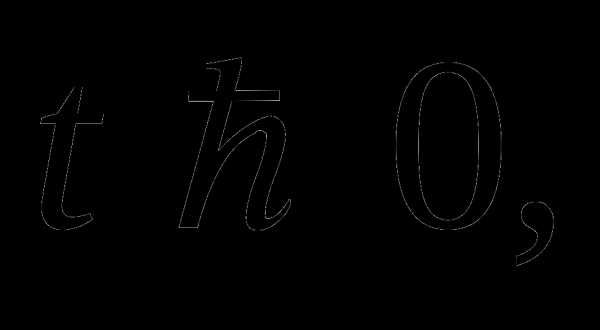 то
не
удовлетворяет
то
не
удовлетворяет
условию 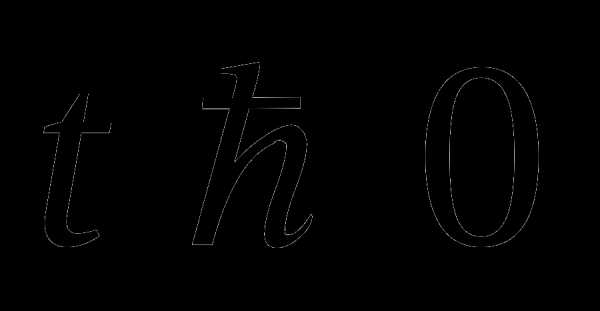
Подставив вместо t его значение
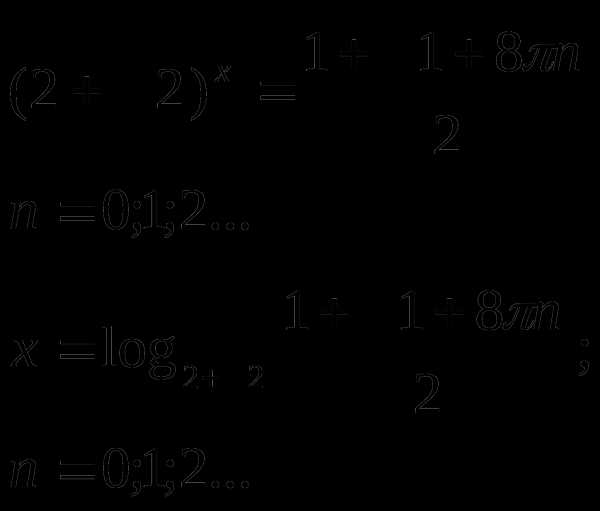
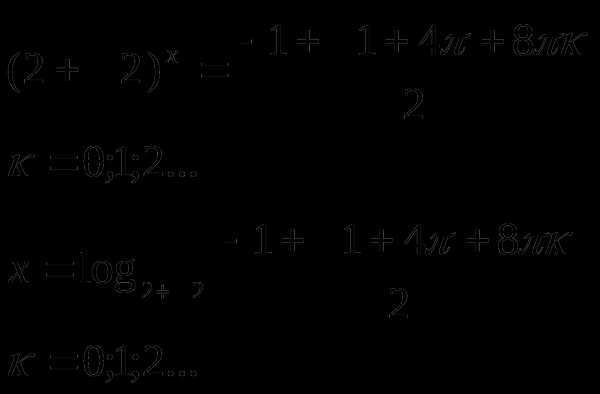
Ответ: 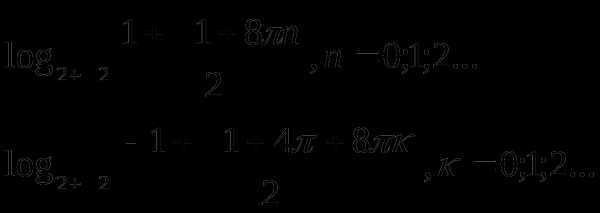
VІІІ тип. Уравнения, в
которых в качестве коэффициента число 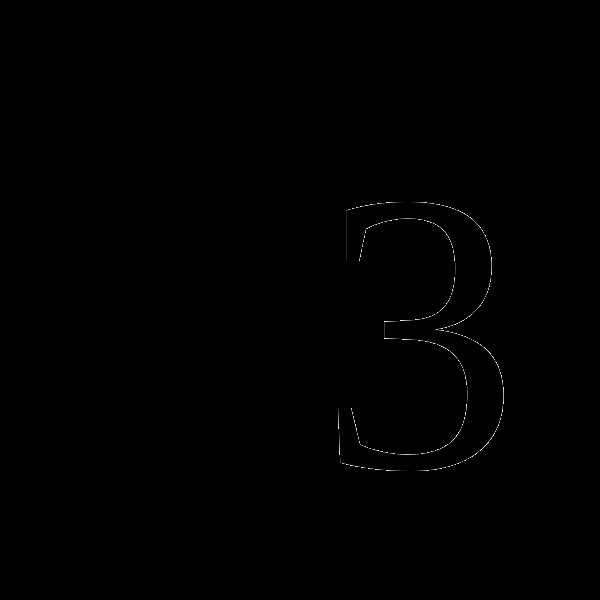 перед
или
перед
или ,
то делают числовую подстановку
,
то делают числовую подстановку  или
или  .
.
Пример.1 Решить уравнение
Решение
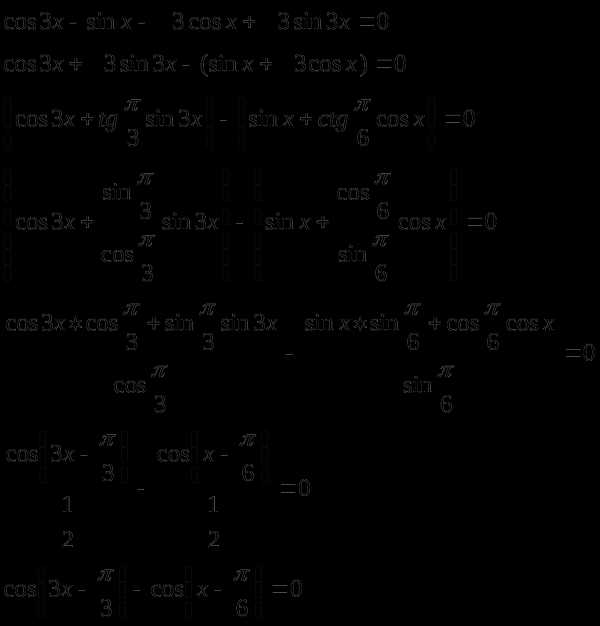

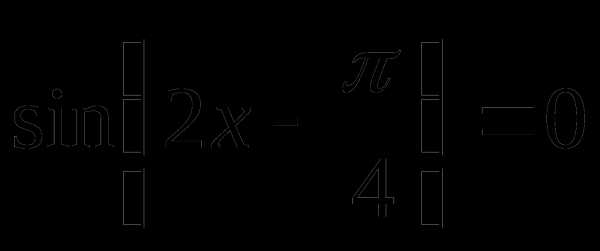 или
или 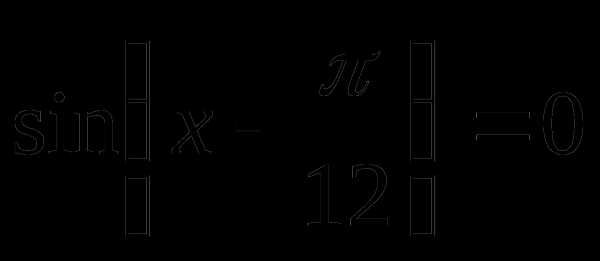
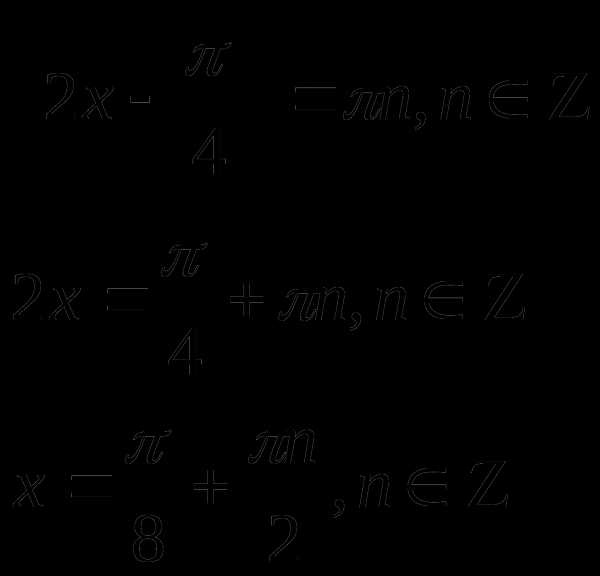
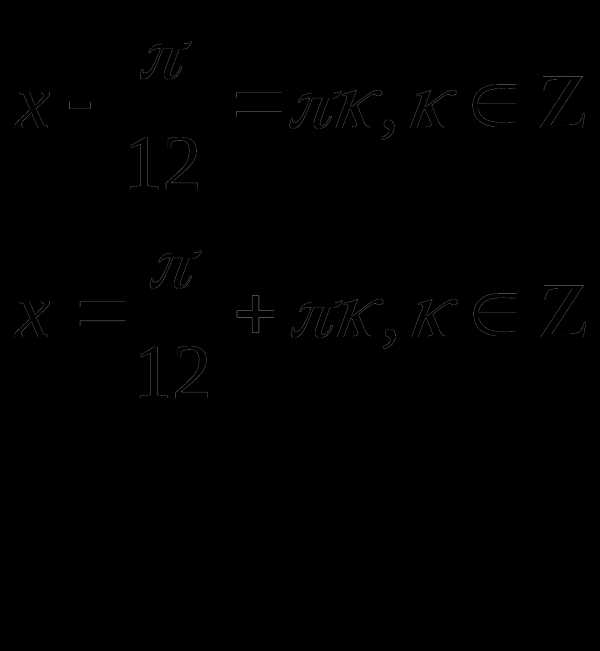
Ответ:
ІX тип. Уравнения вида
решаются с помощью замены или
1) 2)
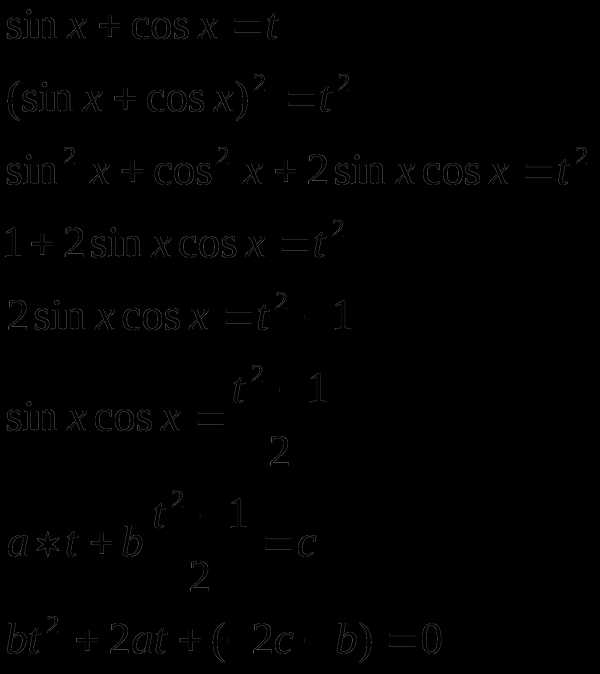
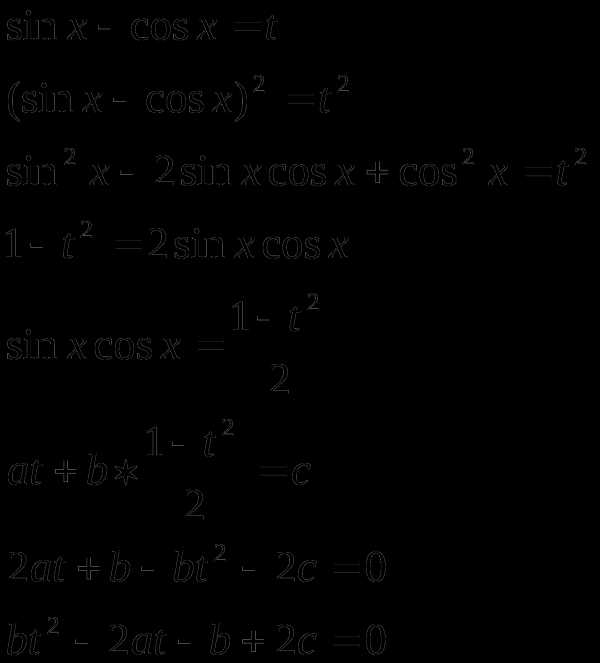
Пример 1. Решить уравнение
Решение
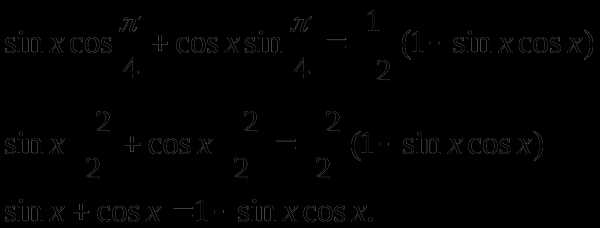
Пусть
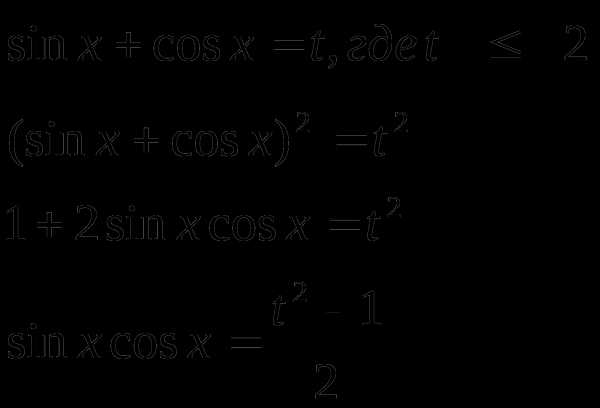
Тогда,
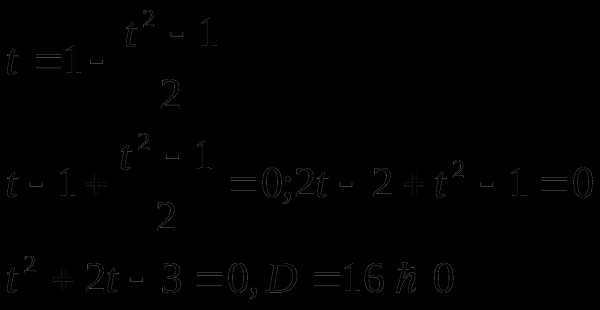
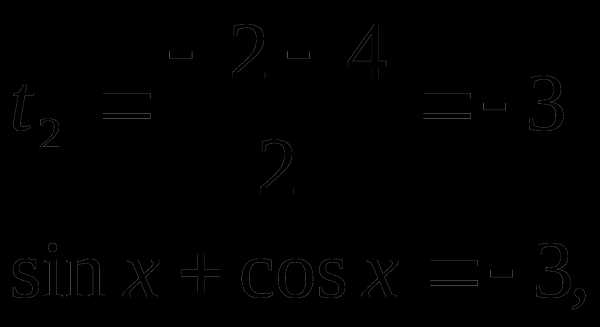
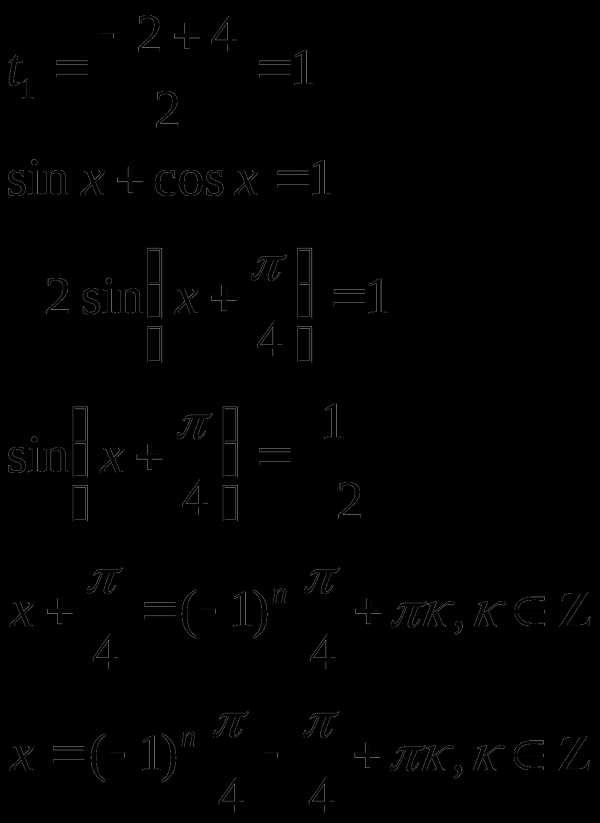
корней нет.
Ответ:
Метод оценок при решении тригонометрических уравнений
Некоторые тригонометрические
уравнения удается решить, используя
неравенства: верны для всех 
Пример 1. Решить уравнение
Решение
Поскольку и то причем
равенство здесь имеет место тогда и только тога, корда одновременно выполняются равенства и Значит исходное уравнение равносильно системе:
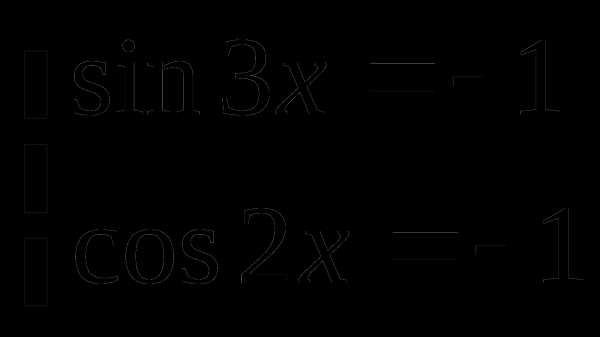
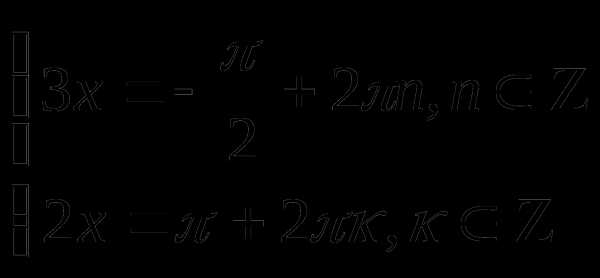
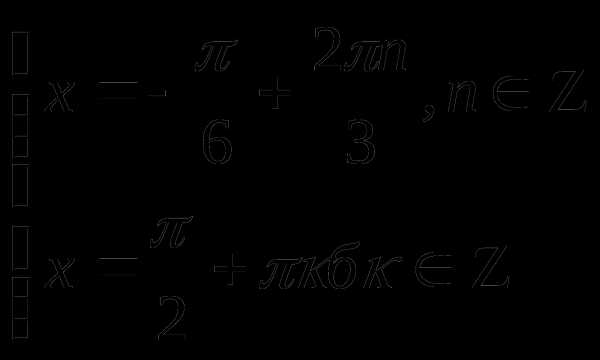
Изобразим эти решения соответствующими точками единичной окружности
( решения первого уравнения , решение второго уравнения – точки помеченные крестиком *).
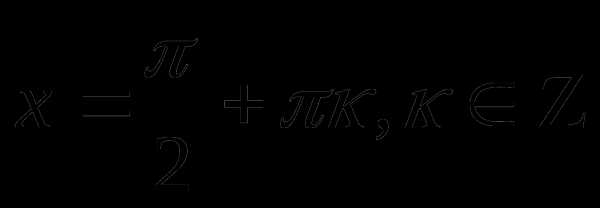 *
*
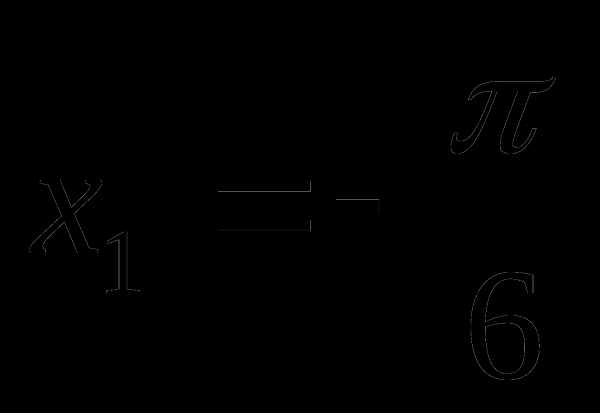
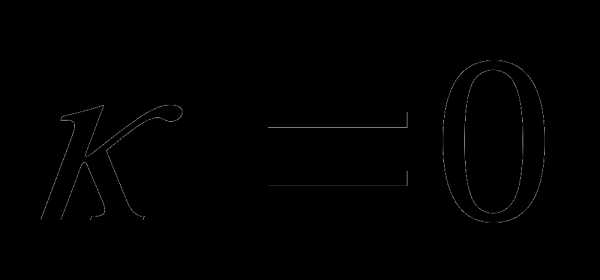
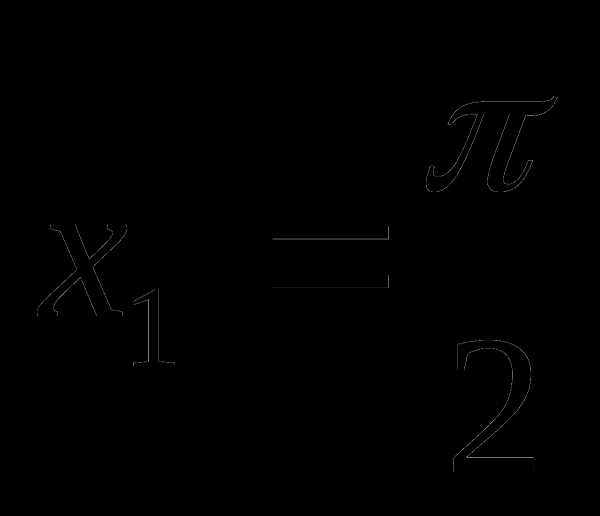
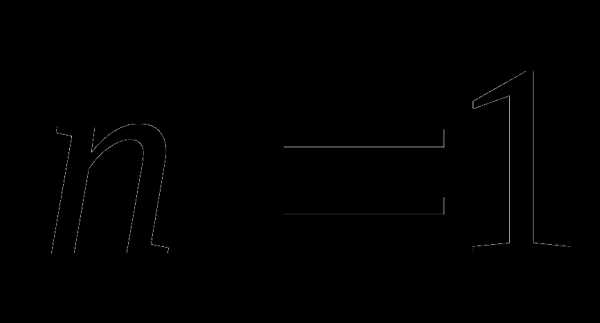
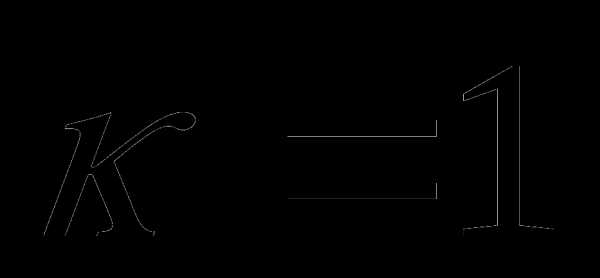
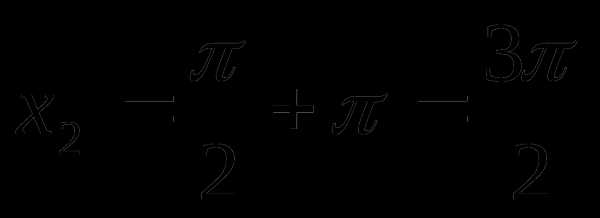

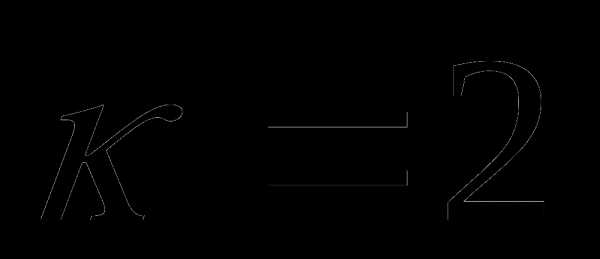

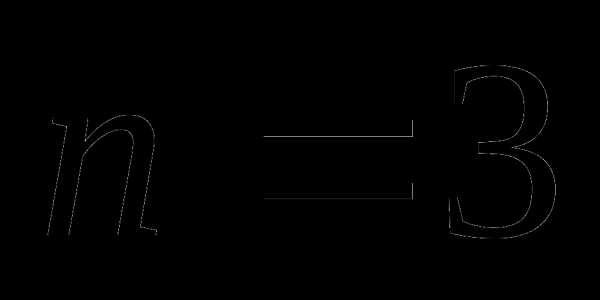
Число х будет решением системы тогда и только тогда, когда оно является решением обоих уравнений системы. Из рисунка видно, что такими числами являются числа
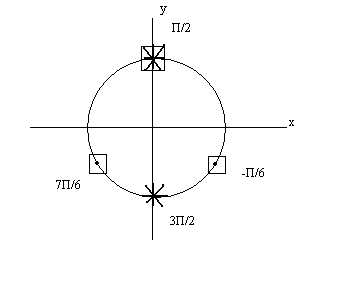
Ответ: 
Пример 2. Решить уравнение
Решение
Воспользуемся формулой
и , значит
Равенство возможно при и Значит данное неравенство равно системе:
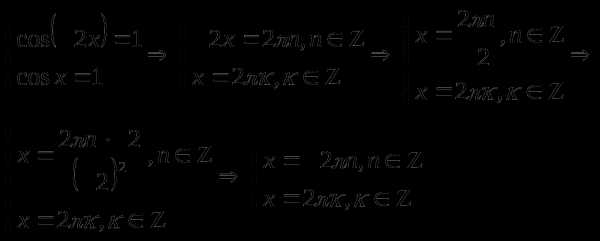
Решениями системы являются те
и только те значения 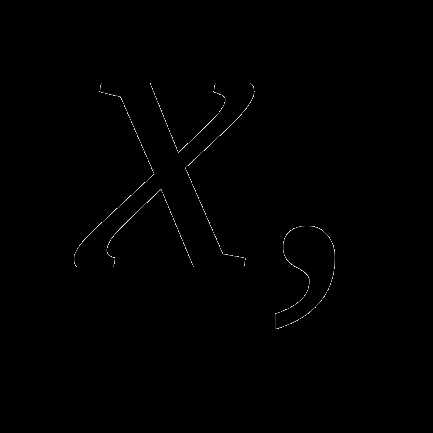 для которых при некоторых и
выполняются
равенства Найдем целые и
,
для которых
Сократив на
для которых при некоторых и
выполняются
равенства Найдем целые и
,
для которых
Сократив на  получим,
что
получим,
что 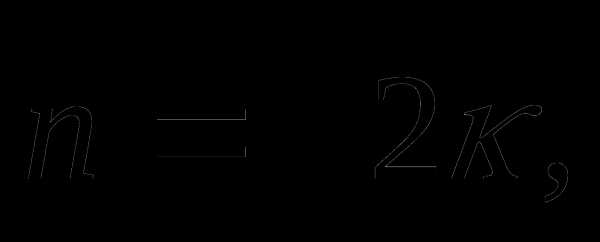 но это равенство возможно только при и
но это равенство возможно только при и 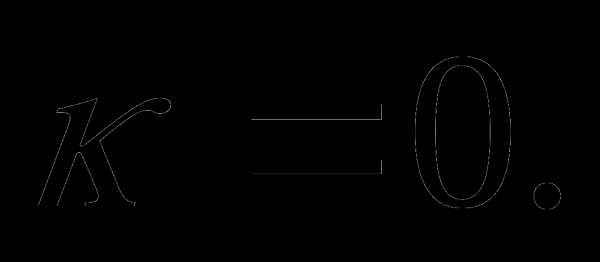 Таким образом система, а значит , и
исходное уравнение имеют единственное
решение
Таким образом система, а значит , и
исходное уравнение имеют единственное
решение
Ответ:
Пример 3. Решить уравнение
Решение

или
, данное уравнение равносильно
Решения первого уравнения , решение второго уравнения – точки помеченные крестиком *.
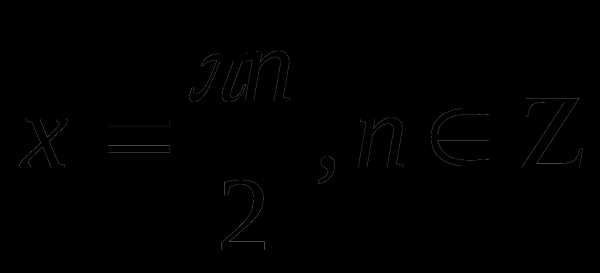
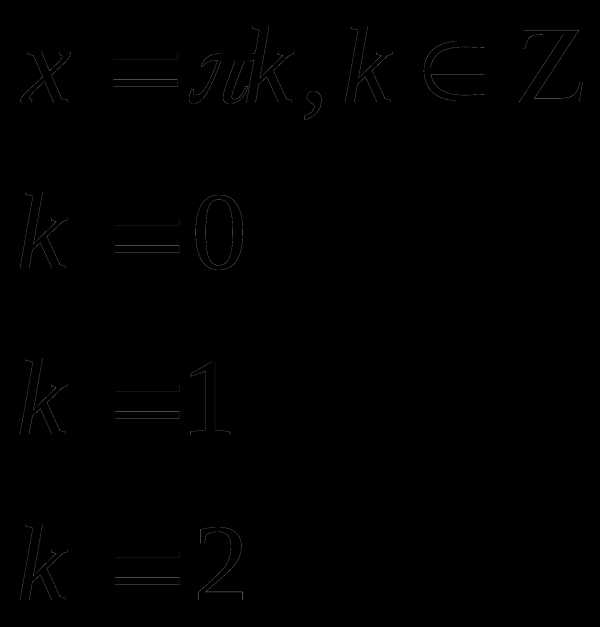
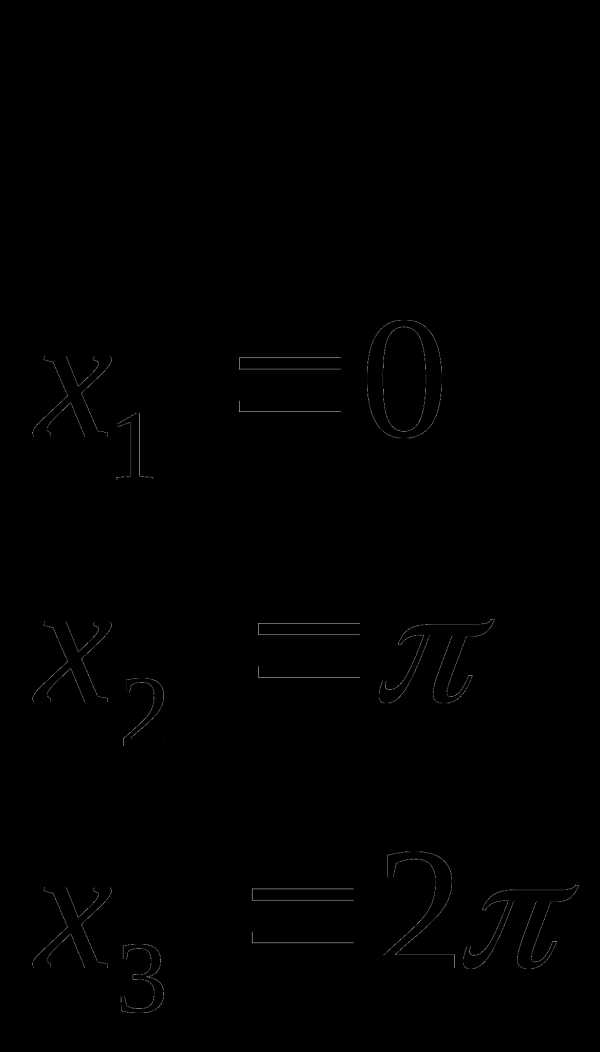
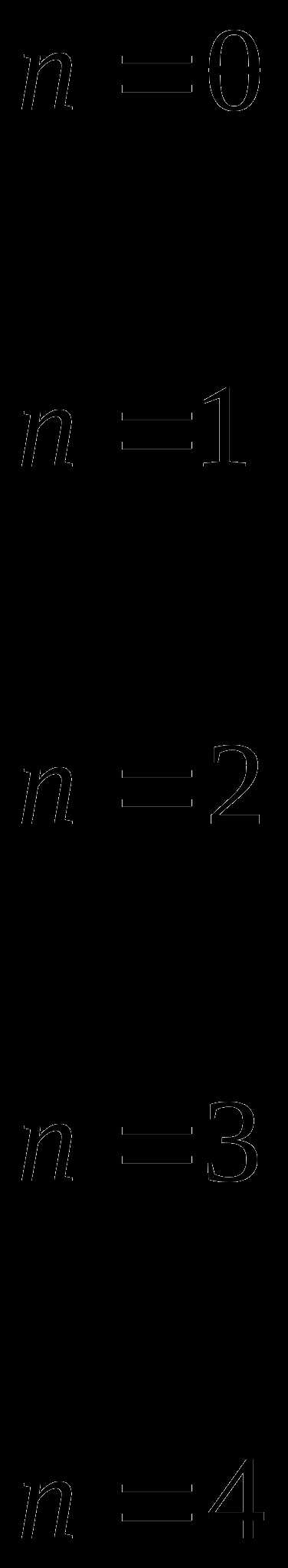
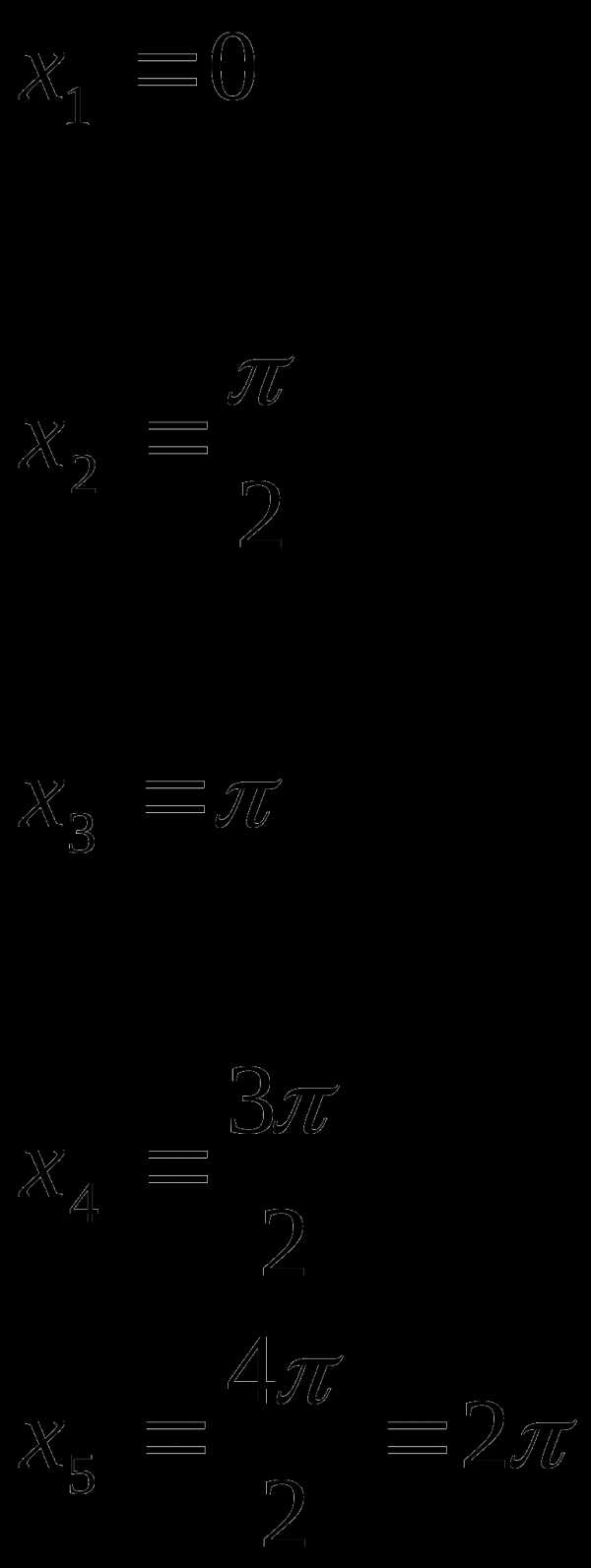
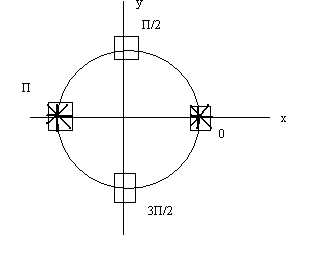
Ответ:
Использование области определения функции при решении уравнений.
К «функциональным» методам решения тригонометрических уравнений и неравенств относится применение основных свойств тригонометрических функций.
Иногда знание областей определения функций, входящих в уравнение или неравенство, дает возможность показать, что уравнение или неравенство не имеет решений. Иногда знание ОДЗ позволяет найти решения уравнения или неравенства непосредственной подстановкой чисел из ОДЗ.
Решить уравнение:
Решение
ОДЗ этого уравнения состоит из всех , удовлетворяющих условиям:
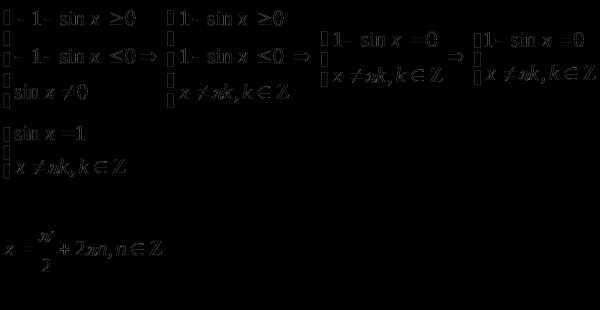 ОДЗ:
ОДЗ:
Подставляя эти значения в уравнение, получаем, что его правая и левая части равны нулю, а это означает, что все являются его решением.
Ответ:
Тригонометрические уравнение типа
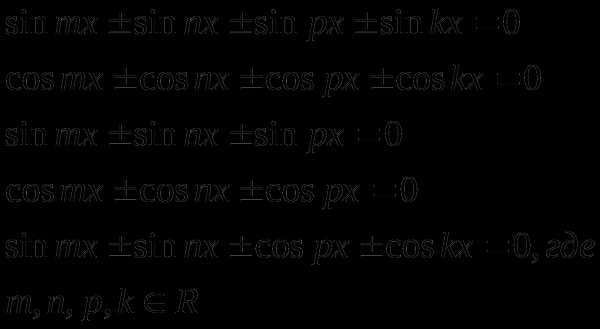
Решение таких уравнений сводится к группировке, последующему разложению правой части уравнения на множители и переходу к решению эквивалентной совокупности простейших уравнений.
Пример 1.
Решение
ОДЗ: 
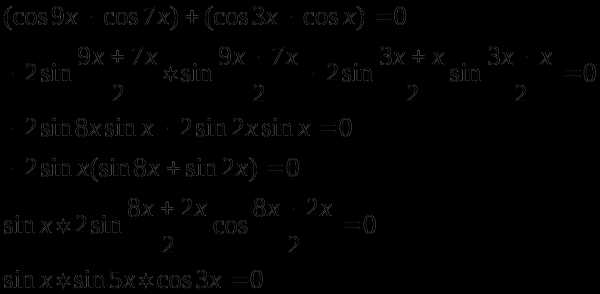
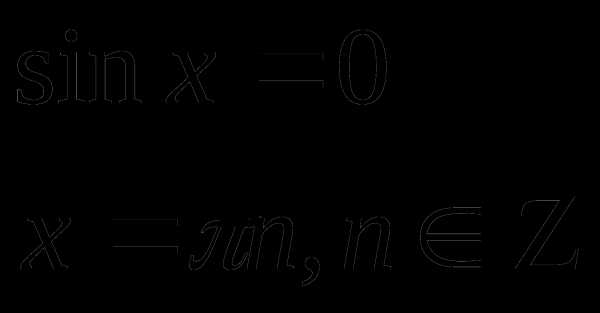 или
или 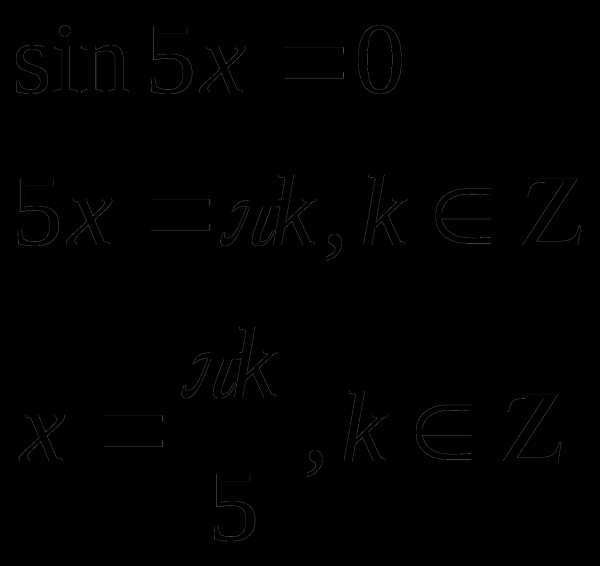 или
или 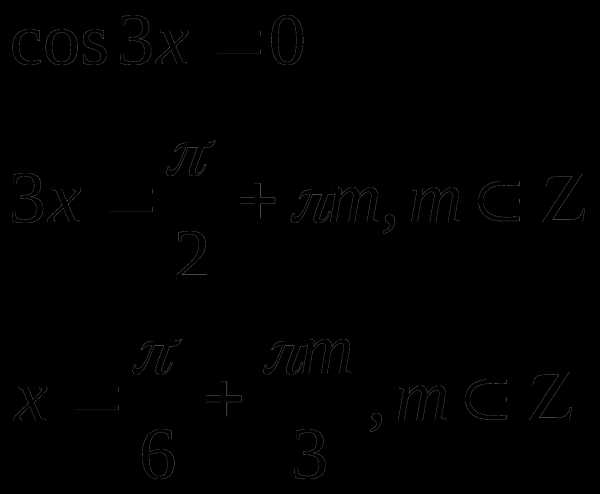
В общем случае предположим, что
серия решений содержит параметр 
а серия решений — параметр  Чтобы выяснить, содержится ли одна из
этих серий в другой, нужно приравнять
эти решения и найти зависимость
от
Чтобы выяснить, содержится ли одна из
этих серий в другой, нужно приравнять
эти решения и найти зависимость
от 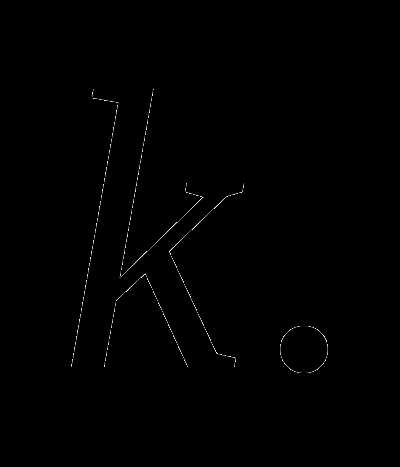
Если эта зависимость линейна и  то серия решений содержится в серии решения
то серия решений содержится в серии решения 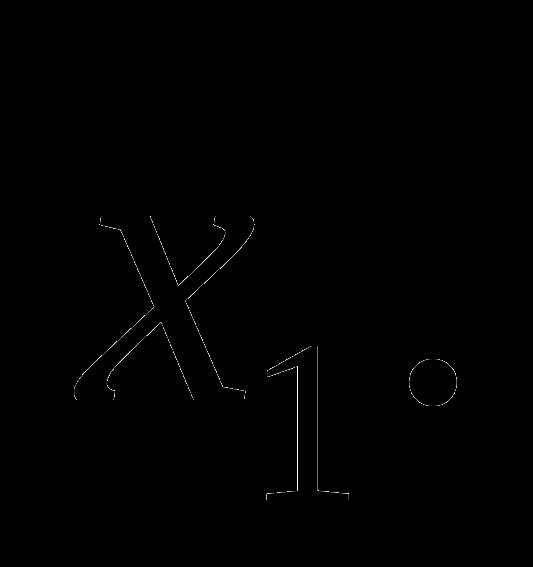 Если хотя бы один из коэффициентов (
Если хотя бы один из коэффициентов (  или
)
не целый, то нужно найти зависимость
или
)
не целый, то нужно найти зависимость  от
от  Если эта зависимость имеет вид где
Если эта зависимость имеет вид где  то серия решений содержится в серии решений
то серия решений содержится в серии решений 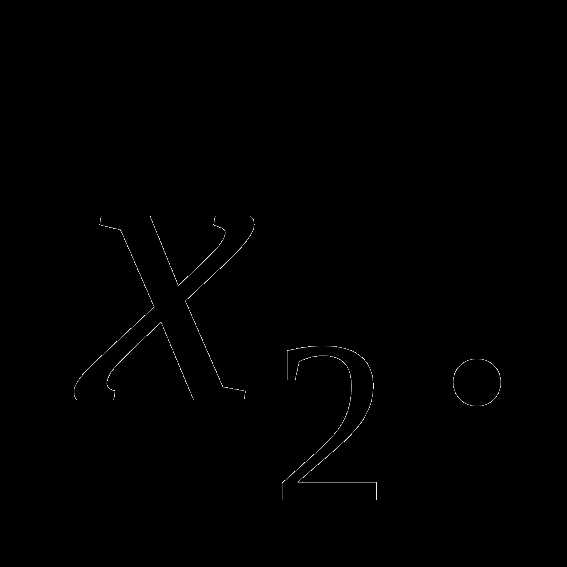 При
условии, что либо
При
условии, что либо 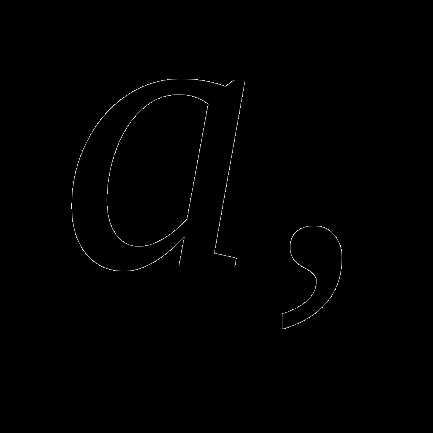 либо
не
целое, серии решений и не содержат одно другое.
либо
не
целое, серии решений и не содержат одно другое.
Выясним, не содержатся ли какие – либо из полученных серий решений в других:
1) 
 следовательно решение
следовательно решение  содержится в
содержится в
решении
поэтому 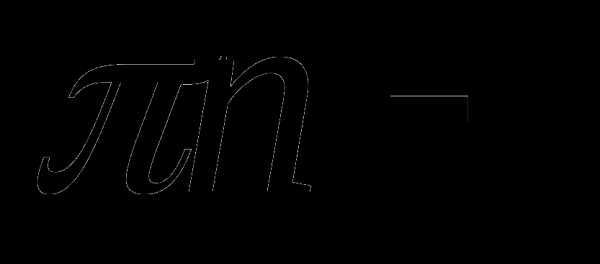 исключают
из решения.
исключают
из решения.
2) 
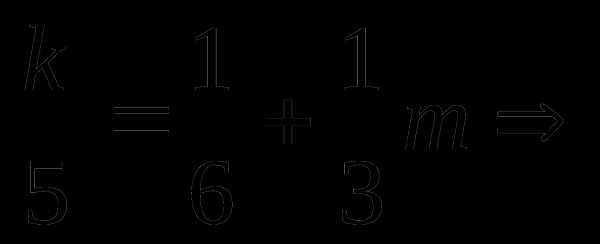
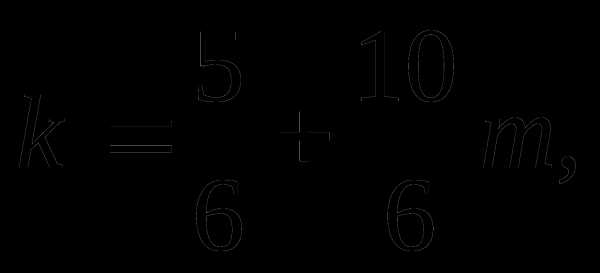 что невозможно
что невозможно
при 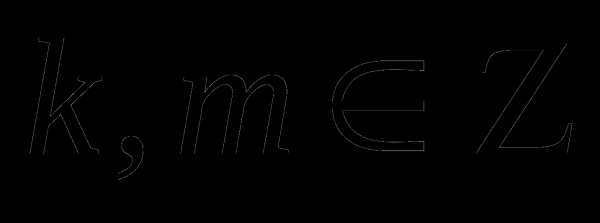
Ответ:
Пример 2.
Решение
или
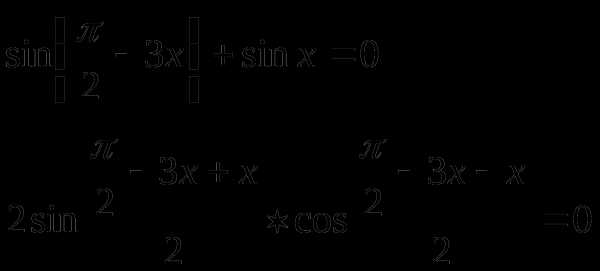

 или
или 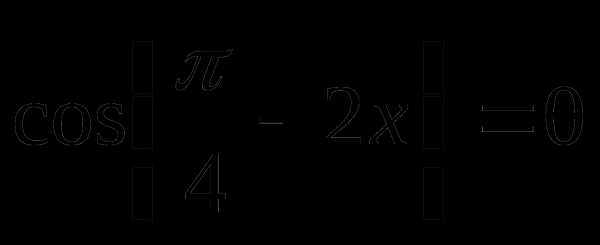
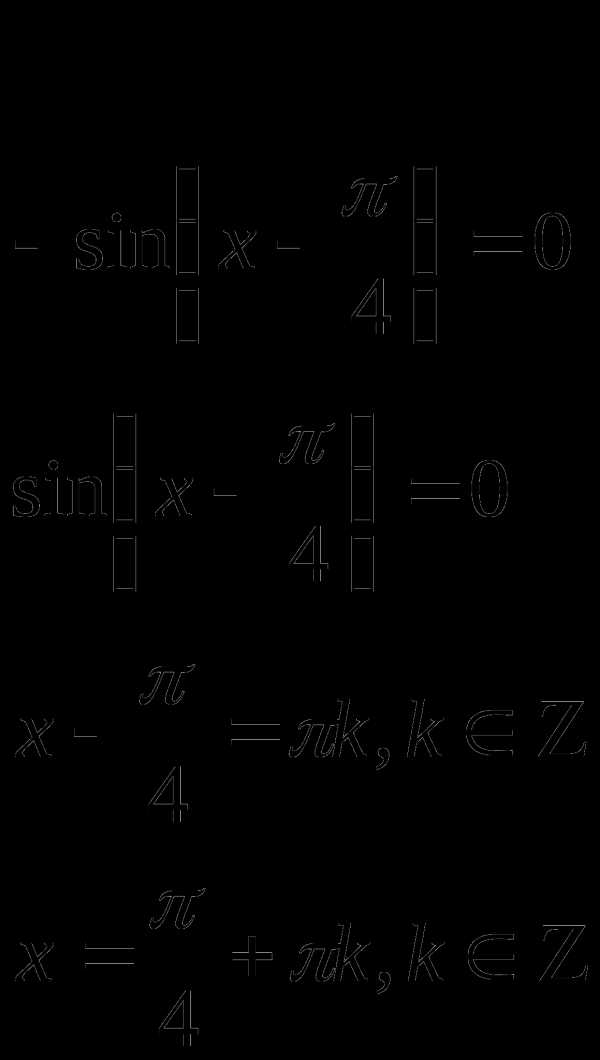
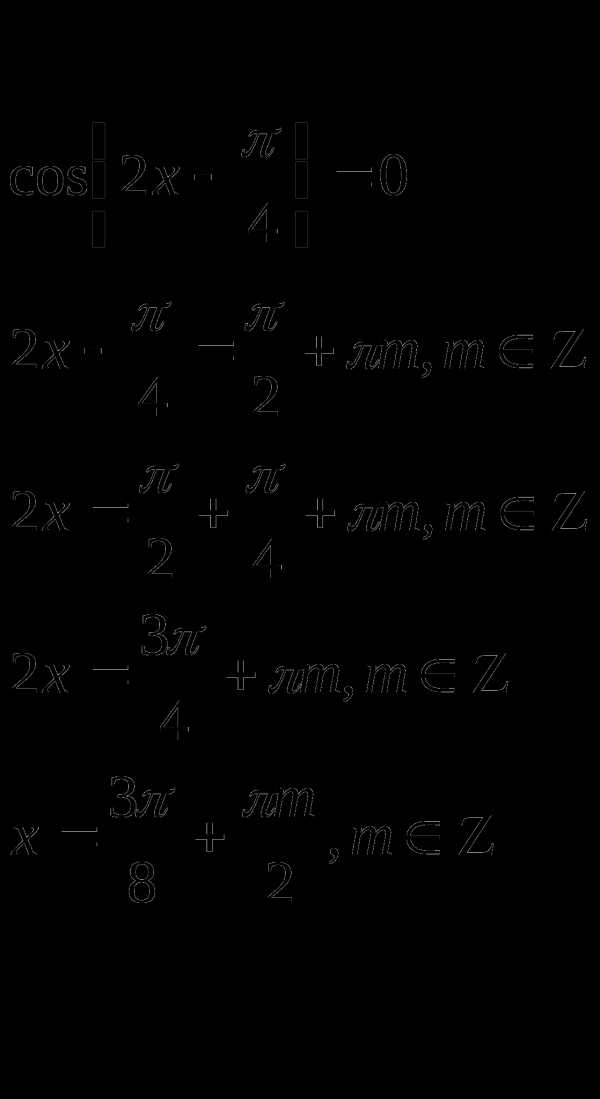
Сравним полученные решения
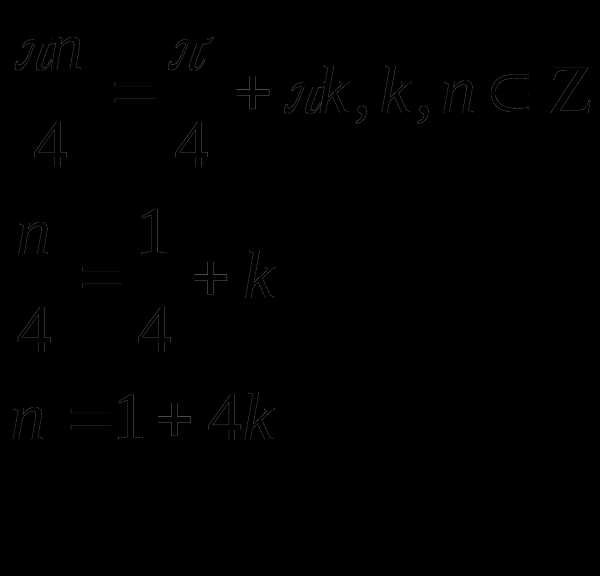
Следовательно серия решения  содержится в серии решений
содержится в серии решений

что
невозможно при 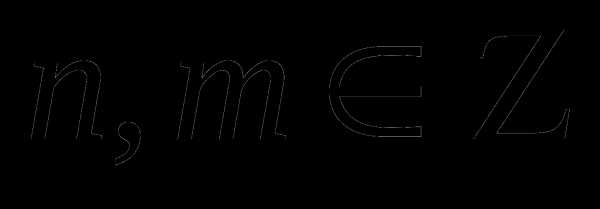
Ответ:
Пример 3.
Решение
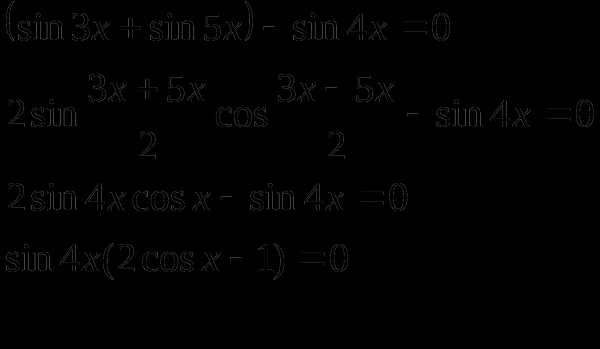
или
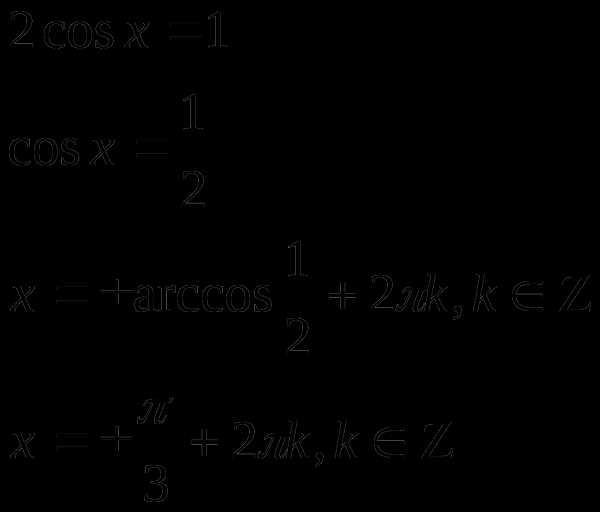
Сравним решения
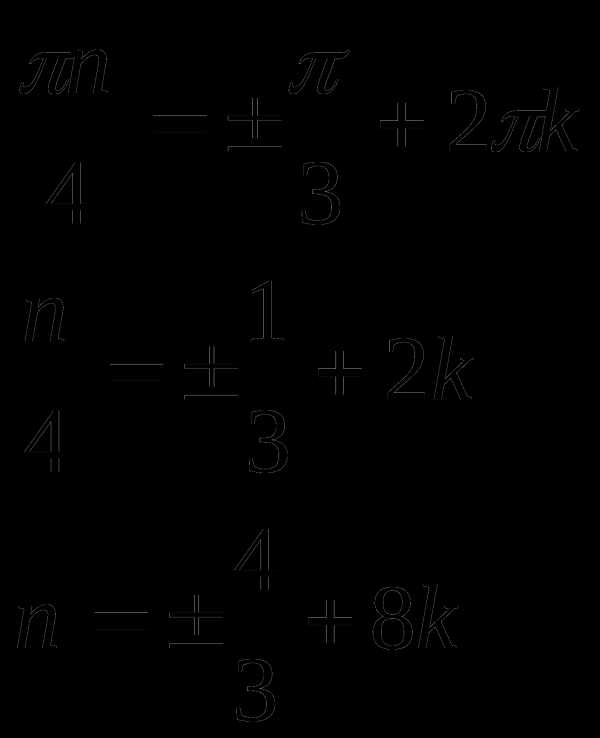
Серия 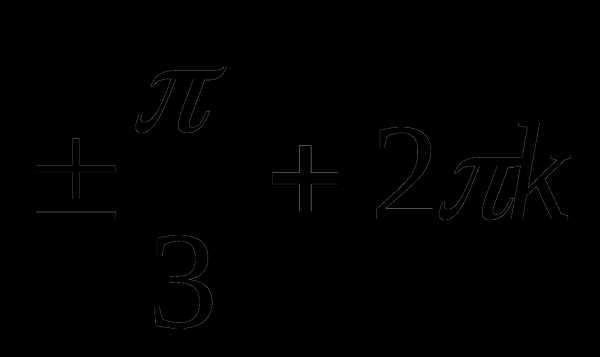 не содержится в серии
не содержится в серии
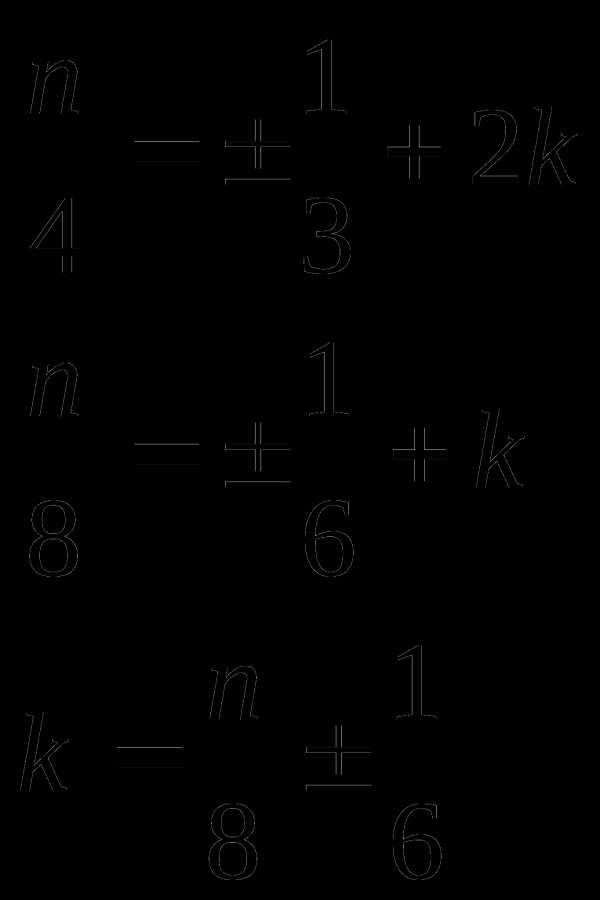
Значит и серия не содержится в серии
Ответ:
gigabaza.ru
Простейшие тригонометрические уравнения и неравенства
\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad
\mathrm{tg}\,x=b,\quad
\mathrm{ctg}\,x=b\), которые имеют смысл при \(-1\leq a\leq 1,\quad b\in \mathbb{R}\).
Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\)).
\[{\color{red}{\text{Решение простейших тригонометрических уравнений}}}\]
Рассмотрим несколько примеров:
Пример 1. Решить уравнение \(\sin x=\dfrac12\).
Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\), где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).
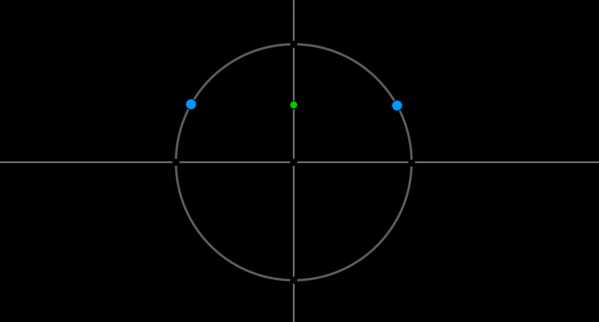
Таким образом, решением являются \(x_1=\dfrac{\pi}6+2\pi n,\
x_2=\dfrac{5\pi}6+2\pi n, \ n\in \mathbb{Z}\).
Пример 2. Решить уравнение \(\cos x=-\dfrac{\sqrt2}{2}\).
Найдем на оси косинусов точку \(-\dfrac{\sqrt2}{2}\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac{\sqrt2}{2}\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{3\pi}4\) и \(-\dfrac{3\pi}4\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число.
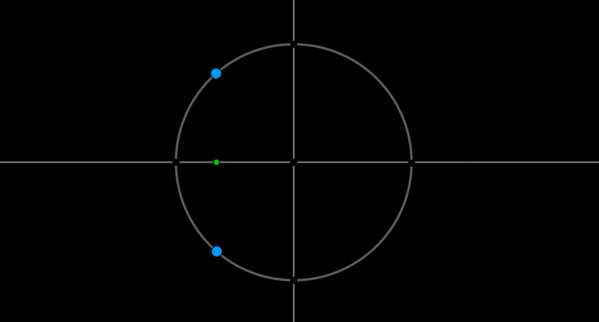
Таким образом, решением являются \(x_1=\dfrac{3\pi}4+2\pi n,\
x_2=-\dfrac{3\pi}4+2\pi n, \ n\in \mathbb{Z}\).
Пример 3. Решить уравнение \(\mathrm{tg}\,x=\dfrac{\sqrt3}3\).
Найдем на оси тангенсов точку \(\dfrac{\sqrt3}3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac{\sqrt3}3\).Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\).
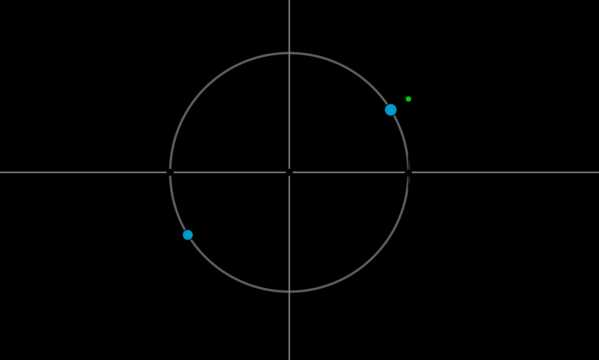
Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).
Пример 4. Решить уравнение \(\mathrm{ctg}\,x=\sqrt3\).
Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\).
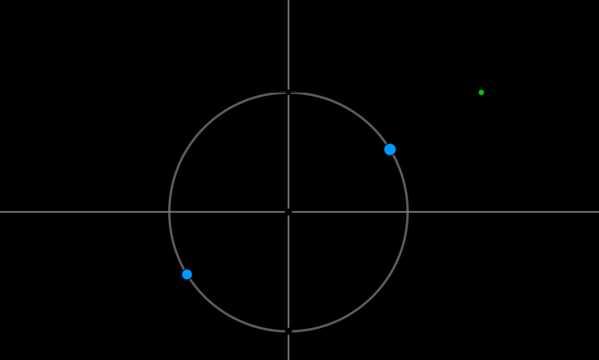
Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).
\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin{array}{l|c|c}
\hline \text{Уравнение} & \text{Ограничения} & \text{Решение}\\
\hline &&\\
\sin x=a & -1\leq a\leq 1 & \left[
\begin{gathered}
\begin{aligned}
&x=\arcsin a+2\pi n\\
&x=\pi -\arcsin a+2\pi n
\end{aligned}
\end{gathered}
\right. \ \ , \ n\in \mathbb{Z}\\&&\\
\hline &&\\
\cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in
\mathbb{Z}\\&&\\
\hline &&\\
\mathrm{tg}\, x=b & b\in \mathbb{R} & x=\mathrm{arctg}\, b+\pi n, \
n\in
\mathbb{Z}\\&&\\
\hline &&\\
\mathrm{ctg}\,x=b & b\in \mathbb{R} & x=\mathrm{arcctg}\, b+\pi n, \
n\in
\mathbb{Z}\\&&\\
\hline
\end{array}\] Иногда для более короткой записи решение для \(\sin x=a\) записывают как \(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb{Z}\).
\(\blacktriangleright\) Любые уравнения вида \(\mathrm{G}\,\big(f(x)\big)=a\), (где \(\mathrm{G}\) — одна из функций \(\sin, \ \cos, \ \mathrm{tg},\ \mathrm{ctg}\), а аргумент \(f(x)\) — некоторая функция) сводятся к стандартным уравнениям путем замены \(t=f(x)\).
Пример 5. Решить уравнение \(\sin{(\pi x+\dfrac{\pi}3)}=1\).
Сделав замену \(t=\pi x+\dfrac{\pi}3\), мы сведем уравнение к виду \(\sin t=1\). Решением данного уравнения являются \(t=\dfrac{\pi}2+2\pi n, n\in\mathbb{Z}\).
Теперь сделаем обратную замену и получим: \(\pi
x+\dfrac{\pi}3=\dfrac{\pi}2+2\pi n\), откуда \(x=\dfrac16+2n,\
n\in\mathbb{Z}\).
\[{\color{red}{\text{Объединение корней}}}\]
Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac{2\pi}n,\ n\in\mathbb{Z}\), где \(\alpha\) — один из этих углов.
Рассмотрим данную ситуацию на примере:
Пример 6. Допустим, решением системы являются \(x_1=\pm \dfrac{\pi}4+2\pi n, \ x_2=\pm \dfrac{3\pi}4+2\pi n, \ n\in\mathbb{Z}\). Отметим эти точки на окружности:
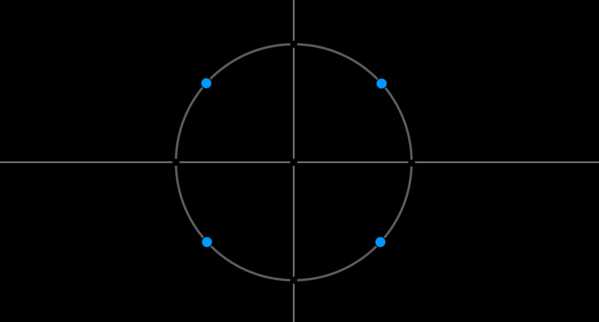
Заметим, что длины дуг \(\buildrel\smile\over{AB},
\buildrel\smile\over{BC}, \buildrel\smile\over{CD},
\buildrel\smile\over{DA}\) равны \(\dfrac{\pi}2\), то есть эти точки разбили окружность на \(4\) равных части. Таким образом, ответ можно записать в виде одной формулы: \(x=\dfrac{\pi}4+\dfrac{\pi}2n, \
n\in\mathbb{Z}\).
\[{\color{red}{\text{Геометрическая интерпретация решений неравенств вида }\mathrm{G}\,(x) \lor a,}}\]
где \(\lor\) — один из знаков \(\leq,\ <,\ >,\ \geq\).
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x >\dfrac12\).
Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, синус которых больше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).
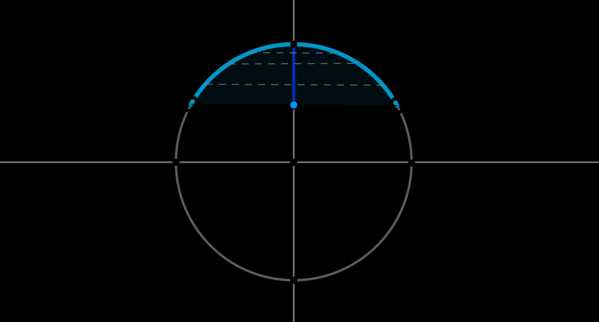
Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}6\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}6\), но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}6\). Тогда все числа из промежутка \(\left(\dfrac{\pi}6;\dfrac{5\pi}6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac{\pi}6+2\pi n;\dfrac{5\pi}6+2\pi
n\right), n\in\mathbb{Z}\), т.к. у синуса период \(2\pi\).
Пример 8. Изобразить на окружности множество решений неравенства \(\cos x <\dfrac12\).
Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, косинус которых меньше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).
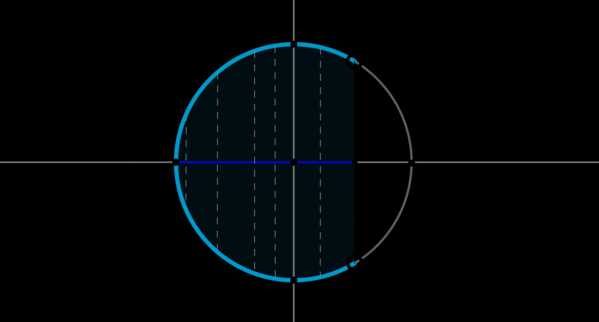
Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}3\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}3\), но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}3\). Тогда все числа из промежутка \(\left(\dfrac{\pi}3;\dfrac{5\pi}3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac{5\pi}3+2\pi n;-\dfrac{\pi}3+2\pi
n\right), n\in\mathbb{Z}\), т.к. у косинуса период \(2\pi\).
Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm{tg}\, x \geq \dfrac{\sqrt{3}}3\).
Для начала отметим на окружности корни уравнения \(\mathrm{tg}\, x = \dfrac{\sqrt{3}}3\). Это точки \(A\) и \(B\). Все точки, тангенс которых больше или равен \(\dfrac{\sqrt{3}}3\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них тангенс не определен.
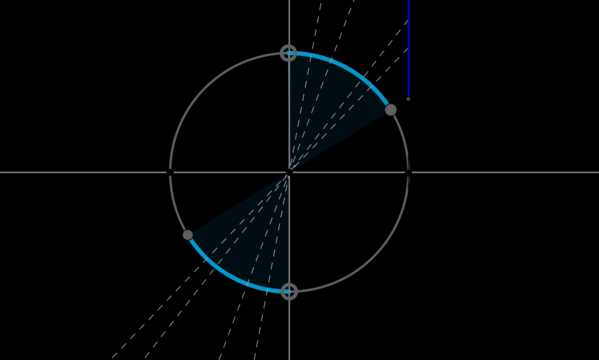
Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\dfrac{\pi}2\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\dfrac{\pi}2\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\dfrac{\pi}2\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\dfrac{\pi}2+\pi n\Big),
n\in\mathbb{Z}\), т.к. у тангенса период \(\pi\).
Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm{ctg}\, x \leq \sqrt{3}\).
Для начала отметим на окружности корни уравнения \(\mathrm{ctg}\, x = \sqrt{3}\). Это точки \(A\) и \(B\). Все точки, котангенс которых меньше или равен \(\sqrt{3}\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них котангенс не определен.
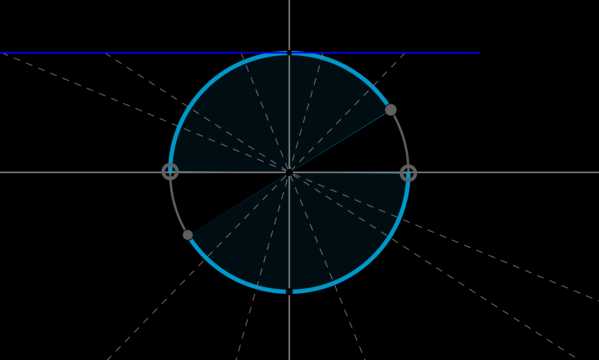
Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\pi\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\pi\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\pi\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\pi+\pi n\Big), n\in\mathbb{Z}\), т.к. период котангенса \(\pi\).
\[{\color{red}{\text{Отбор корней}}}\]
Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.
Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\), если \(\cos x\ne \dfrac{\sqrt3}2\).
В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.
Решением первого уравнения являются \(x_1=-\dfrac{\pi}6+2\pi n,\
x_2=-\dfrac{5\pi}6+2\pi n,\ n\in \mathbb{Z}\), решением второго являются \(x\ne \pm \dfrac{\pi}6+2\pi n,\ n\in\mathbb{Z}\). Отметим эти точки на окружности: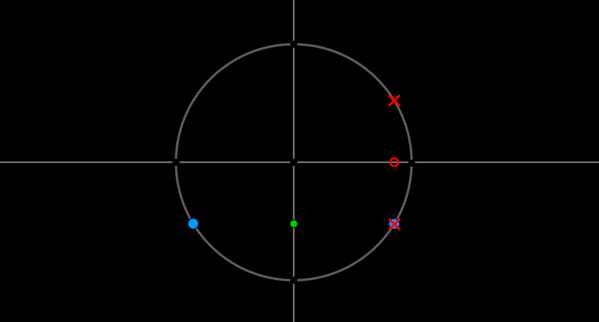
Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac{\pi}6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac{5\pi}6+2\pi n, n\in \mathbb{Z}\).
Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin{aligned}
&\sin{(\alpha+\pi n)}=\begin{cases} \sin \alpha, \text{при } n —
\text{ четном}\\ -\sin \alpha, \text{при } n — \text{ нечетном}
\end{cases}\\
&\cos{(\alpha+\pi n)}=\begin{cases} \cos \alpha, \text{при } n —
\text{ четном}\\ -\cos \alpha, \text{при } n — \text {нечетном}
\end{cases}\\
&\mathrm{tg}\,(\alpha+\pi n)=\mathrm{tg}\,\alpha\\
&\mathrm{ctg}\,(\alpha+\pi n)=\mathrm{ctg}\,\alpha\\
&\sin{\left(\alpha+\dfrac{\pi}2\right)}=\cos\alpha\\
&\cos{\left(\alpha+\dfrac{\pi}2\right)}=-\sin \alpha\\
&\,\mathrm{tg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{ctg}\,\alpha\\
&\,\mathrm{ctg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{tg}\,\alpha
\end{aligned}\]
Пример 12. Решить систему \(\begin{cases} \cos x=\dfrac12\\
\sin x+\cos x>0\end{cases}\)
Решением уравнения являются \(x_1=\dfrac{\pi}3+2\pi n,\ x_2=-\dfrac{\pi}3+2\pi n,\ n\in\mathbb{Z}\). Подставим в неравенство \(\sin x+\cos x>0\) по очереди оба корня:
\(\sin x_1+\cos x_1=\dfrac{\sqrt3}2+\dfrac12>0\), следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac{\sqrt3}2+\dfrac12<0\), следовательно, корень \(x_2\) нам не подходит.
Таким образом, решением системы являются только \(x=\dfrac{\pi}3+2\pi
n,\ n\in\mathbb{Z}\).
Алгебраический способ.
Пример 13. Найти корни уравнения \(\sin x=\dfrac{\sqrt2}2\), принадлежащие отрезку \([0;\pi]\).
Решением уравнения являются \(x_1=\dfrac{\pi}4+2\pi n, \
x_2=\dfrac{3\pi}4 +2\pi n, \ n\in\mathbb{Z}\). Для того, чтобы отобрать корни, решим два неравенства: \(0\leq x_1\leq\pi\) и \(0\leq
x_2\leq\pi\):
\(0\leq \dfrac{\pi}4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38\). Таким образом, единственное целое значение \(n\), удовлетворяющее этому неравенству, это \(n=0\). При \(n=0\) \(x_1=\dfrac{\pi}4\) — входит в отрезок \([0;\pi]\).
Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac{3\pi}4\).
Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:
\[ax+by=c, \quad a,b,c — \text{целые числа}\]
Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\).
Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\). Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\), то есть нечетное число.
Пример: Решить уравнение \(3x+5y=2\). Т.к. \(НОД(3,5)=1\), то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\):
\[x=\dfrac{2-5y}3=\dfrac{2-2y}3-y\]
Число \(\dfrac{2-2y}3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\): \(0\), \(1\) или \(2\).
Если \(y\) при делении на \(3\) имеет остаток \(0\), то оно записывается как \(y=3p+0\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2\cdot
3p}3=\dfrac23-2p\ne \text{целому числу}\]
Если \(y\) при делении на \(3\) имеет остаток \(1\), то оно записывается как \(y=3p+1\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2(3p+1)}3=-2p=\text{целому числу}\]
Значит, этот случай нам подходит. Тогда \(y=3p+1\), а \(x=\dfrac{2-2y}3-y=-5p-1\).
Ответ: \((-5p-1; 3p+1), p\in\mathbb{Z}\).
Перейдем к примеру:
Пример 14. Решить систему \[\begin{cases} \sin \dfrac x3=\dfrac{\sqrt3}2\\[3pt] \cos \dfrac x2=1 \end{cases}\]
Решим первое уравнение системы:
\[\left[ \begin{gathered} \begin{aligned} &\dfrac x3=\dfrac{\pi}3+2\pi n\\[3pt] &\dfrac x3=\dfrac{2\pi}3 +2\pi m \end{aligned} \end{gathered} \right.\quad n,m\in\mathbb{Z} \quad \Leftrightarrow \quad \left[ \begin{gathered} \begin{aligned} &x=\pi+6\pi n\\ &x=2\pi +6\pi m \end{aligned} \end{gathered} \right.\quad n,m\in\mathbb{Z}\]
Решим второе уравнение системы:
\[\dfrac x2=2\pi k, k\in\mathbb{Z} \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb{Z}\]
Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\), при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\):
\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]
Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\), то данное уравнение не имеет решений в целых числах.
Найдем целые \(m\) и \(k\), при которых совпадают решения в сериях \(2\pi +6\pi m\) и \(4\pi k\):
\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]
Данное уравнение имеет решение в целых числах. Выразим \(k=\frac{3m+1}2=m+\frac{m+1}2\).
Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\).
Если \(m=2p+0\), то \(\frac{m+1}2=\frac{2p+1}2=p+\frac12\ne \) целому числу.
Если \(m=2p+1\), то \(\frac{m+1}2=\frac{2p+1+1}2=p+1= \) целому числу.
Значит, \(m=2p+1\), тогда \(k=3p+2\), \(p\in\mathbb{Z}\).
Подставим либо \(m\), либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb{Z}\).
shkolkovo.net















 оставьте уравнение для решения задачи. Найти два натуральных числа, если:
оставьте уравнение для решения задачи. Найти два натуральных числа, если: 




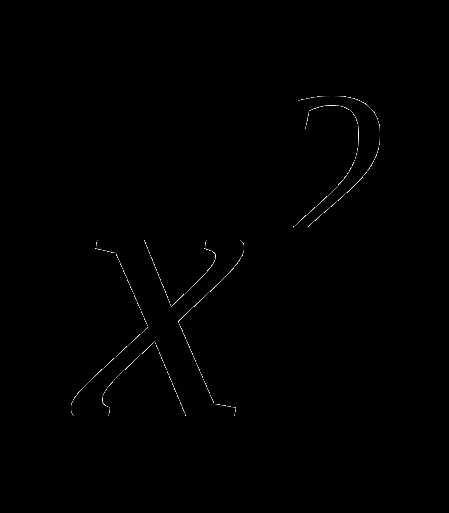 0, x — переменная, называется…
0, x — переменная, называется… …
…
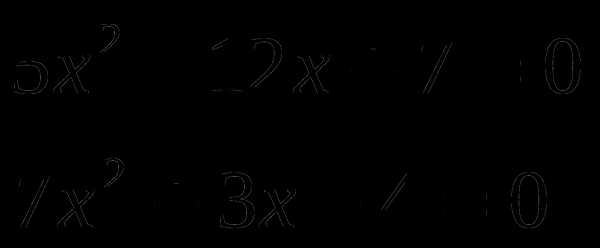 2 вариант:
2 вариант: 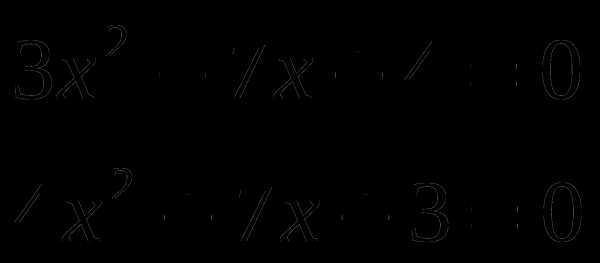


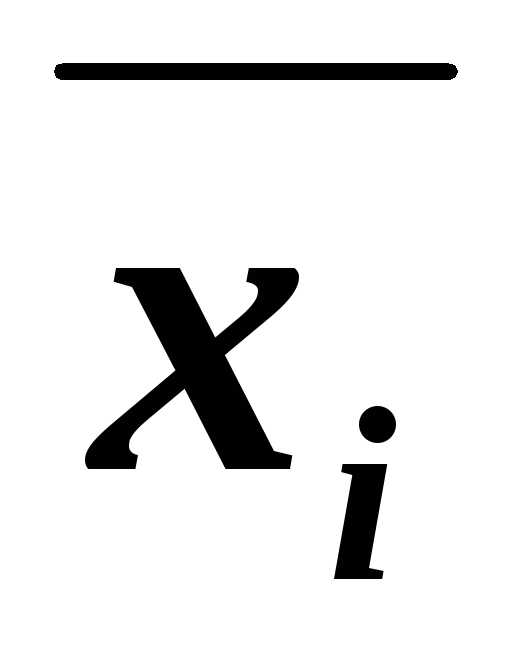
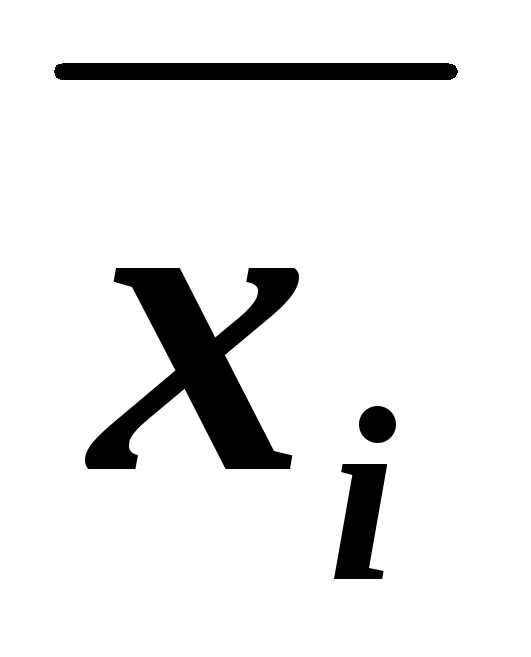 – для 2-й строки;
– для 2-й строки;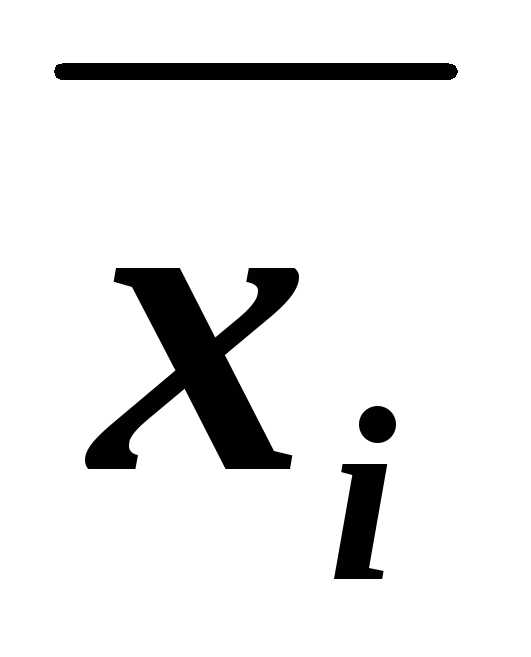 – для 3-й строки.
– для 3-й строки.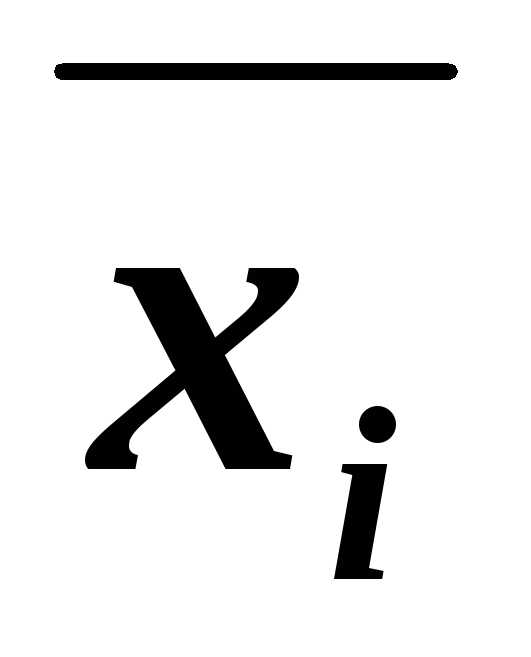 – для 1-й строки;
– для 1-й строки;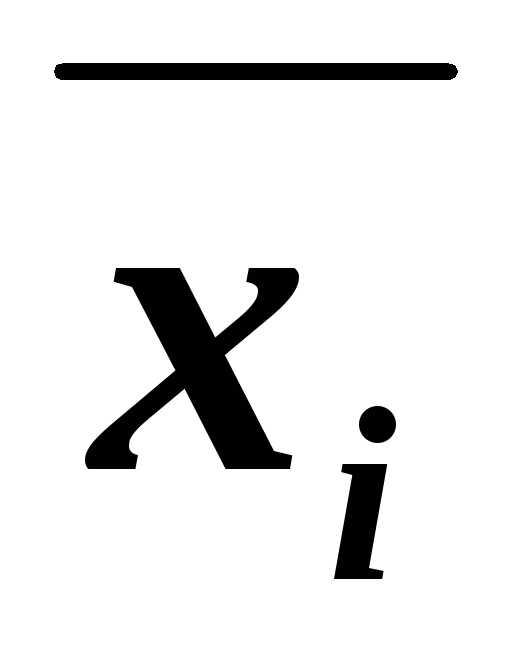 – для 4-й строки.
– для 4-й строки.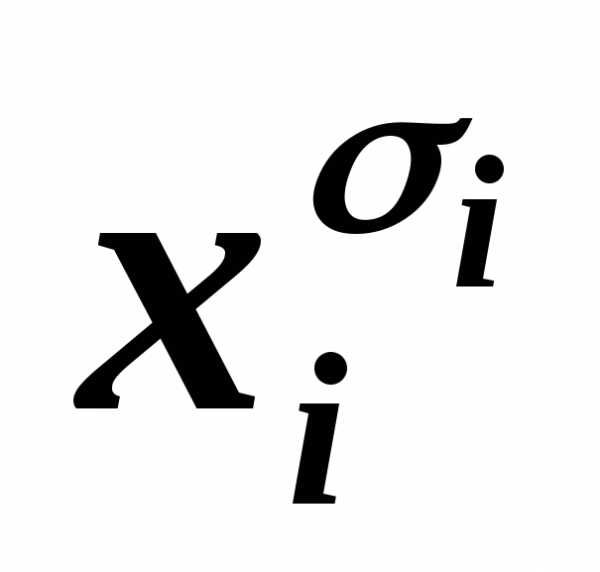 (
(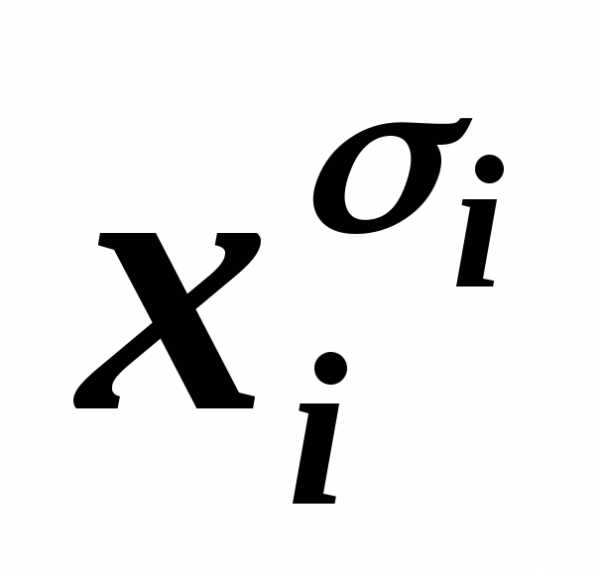 у)
имеем, например, КНФА~ху.
у)
имеем, например, КНФА~ху.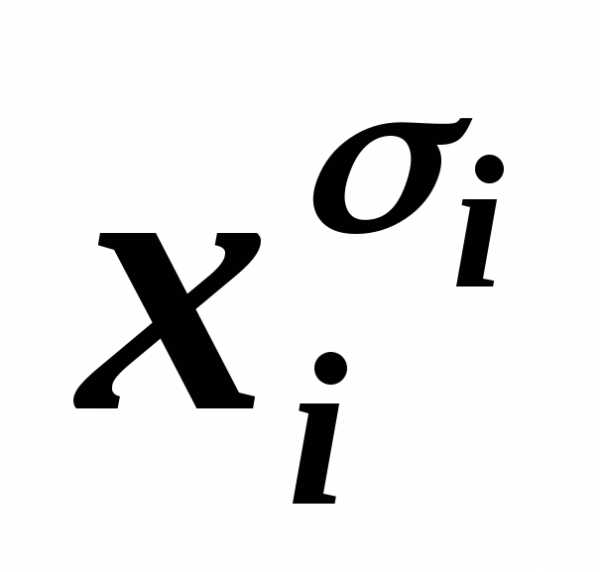 )~
~(Вхi)&(B
)~
~(Вхi)&(B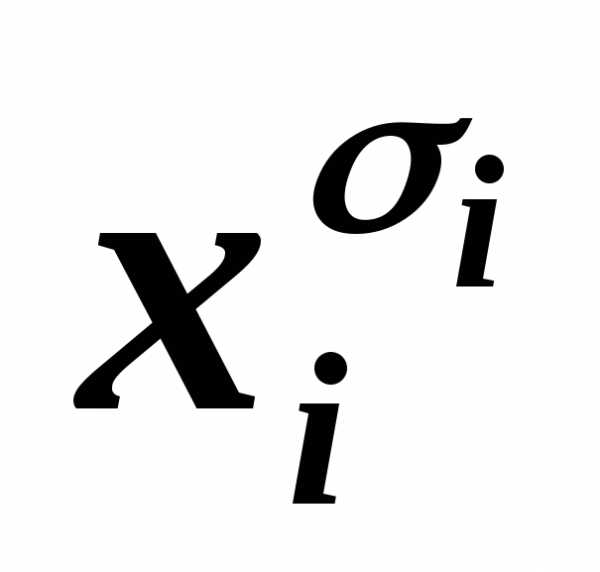 ),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B
),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B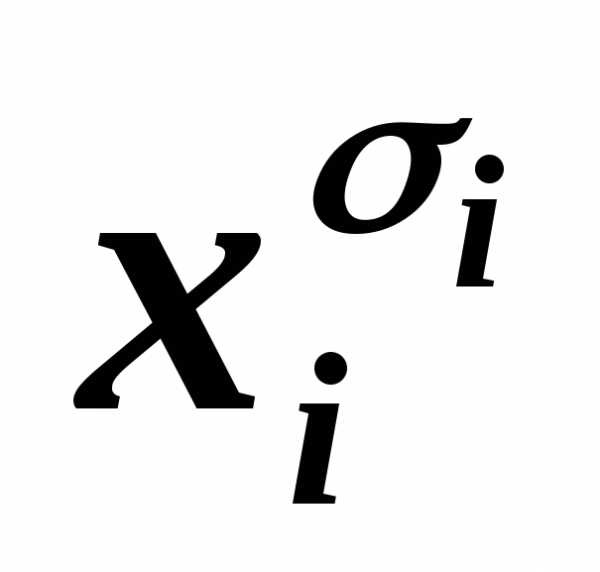 ),
каждая из которых содержитхi или её отрицание
),
каждая из которых содержитхi или её отрицание  .
.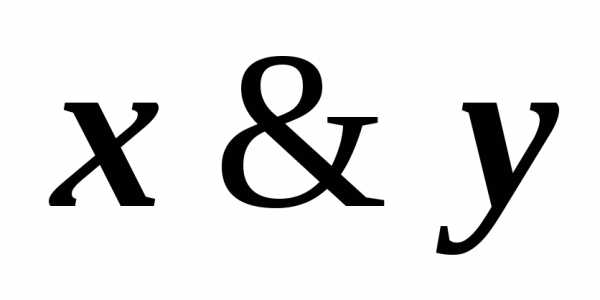 ,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.
,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА. дважды или более, то, пользуясь
равносильностью
дважды или более, то, пользуясь
равносильностью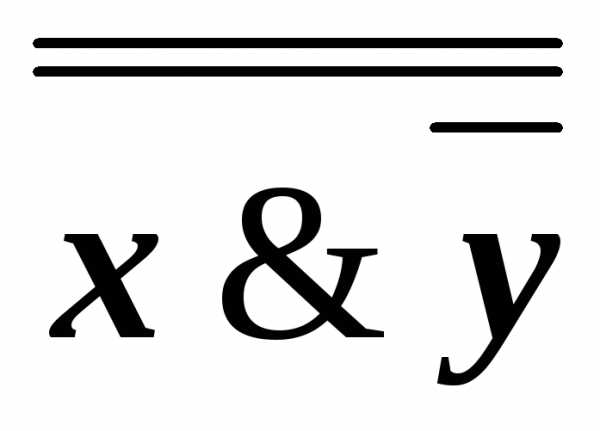
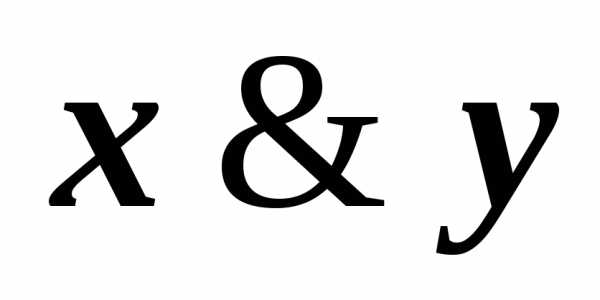 …
… ~
~ ,
лишние отбрасываем.
,
лишние отбрасываем. )(z
)(z )
) (
( )(z
)(z )
) (x&
(x& )
)
 (x&
(x& )
) (x&
(x&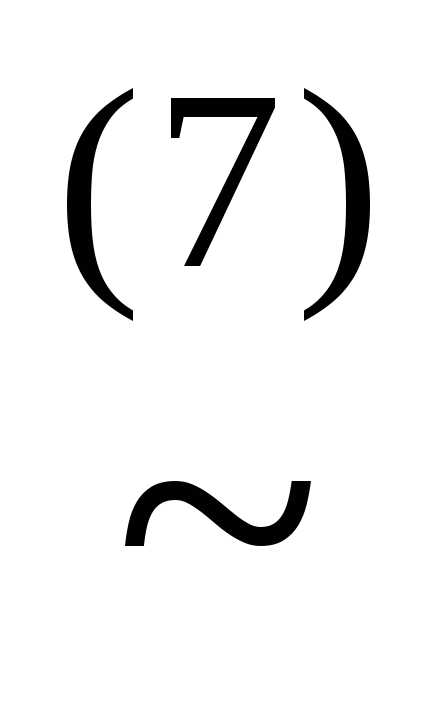 )
)
 (x&
(x& )
)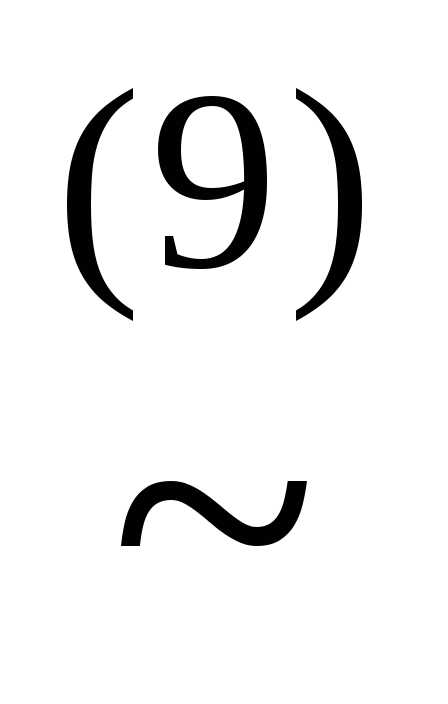 (x&
(x& )
)
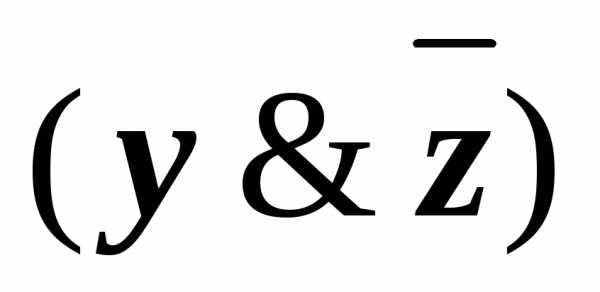 (x&
(x&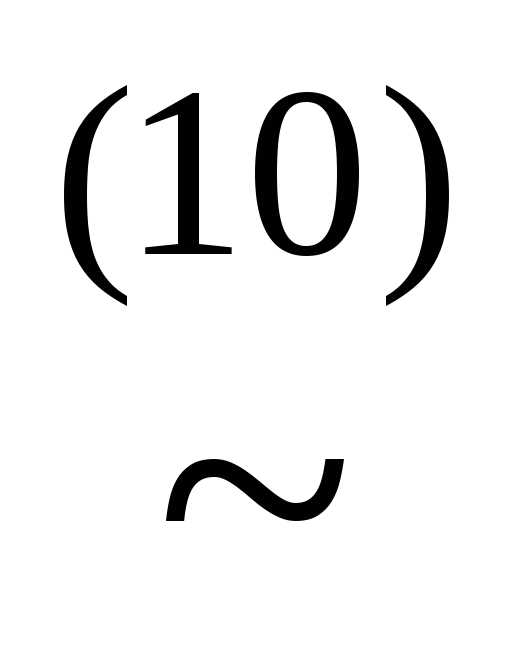 )(
)( (x&
(x&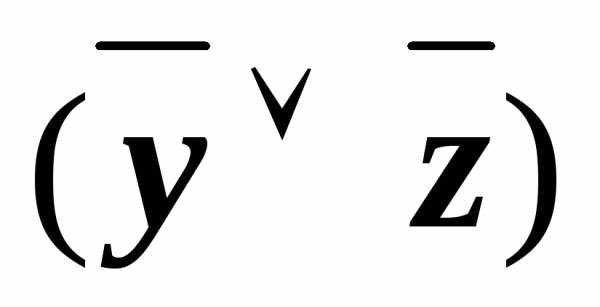 ))
))
 (x&(
(x&(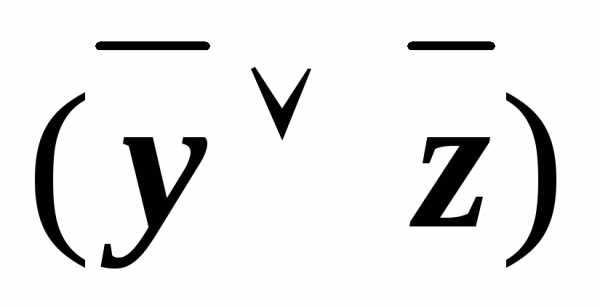
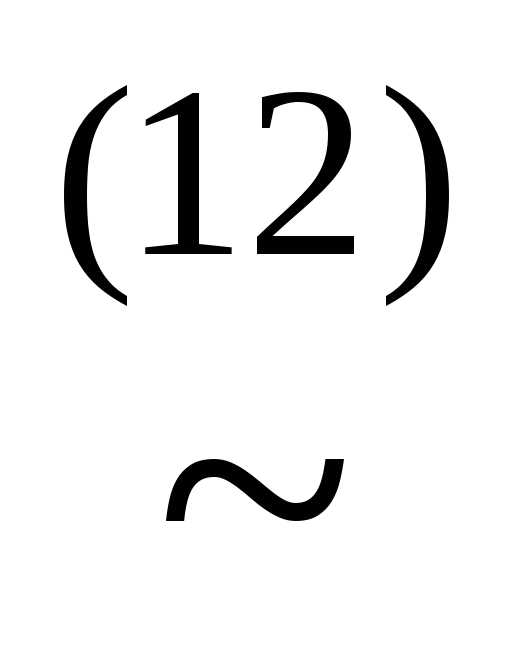 )))
))) (x&((
(x&(( у)&
у)&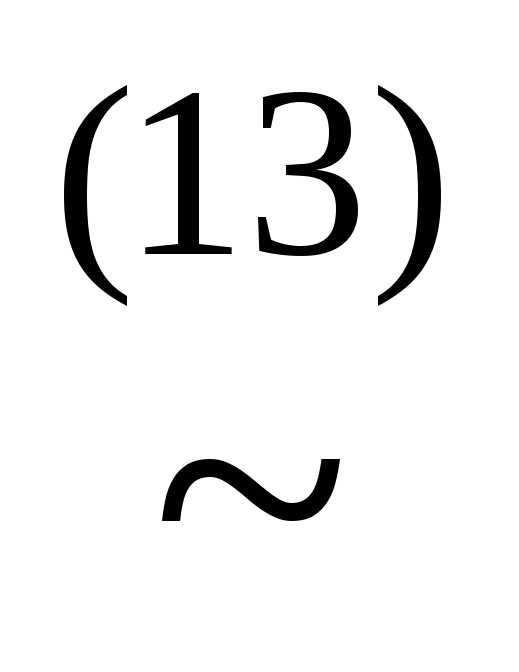 )))
)))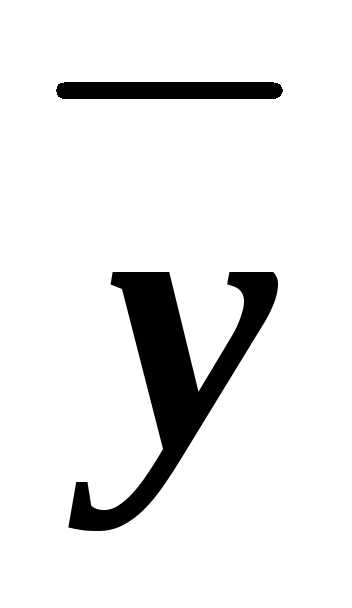
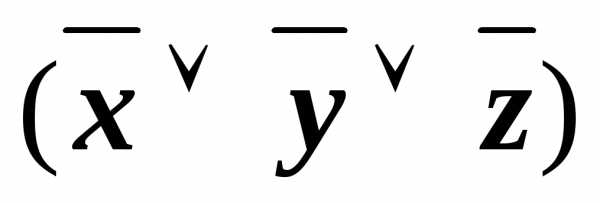 (x&
(x& ))
)) (xz)&
(xz)&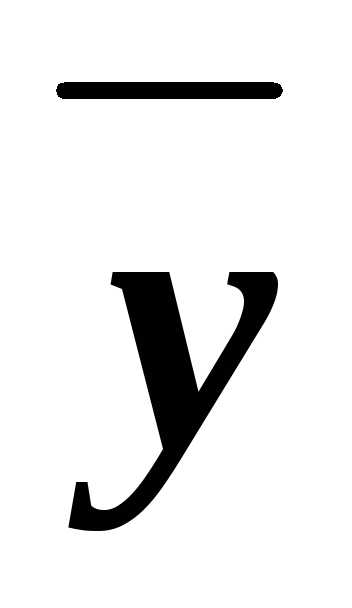 &&
&&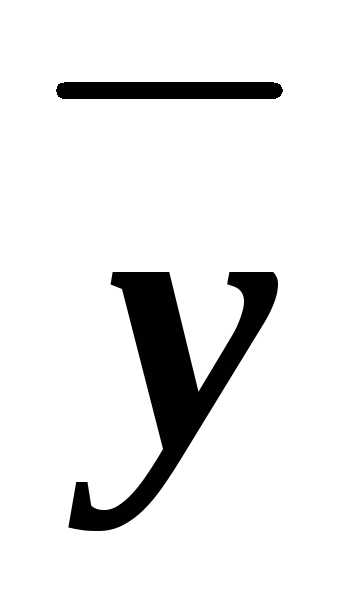
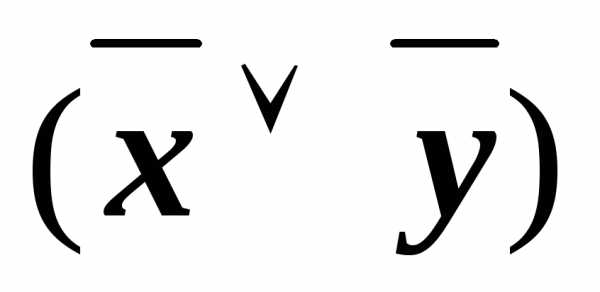 (xz)&
(xz)&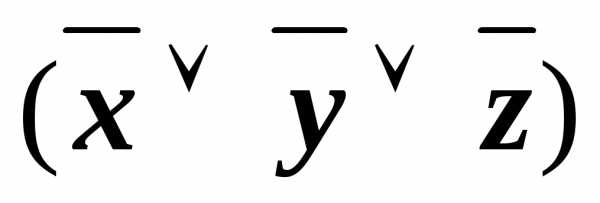 &
&

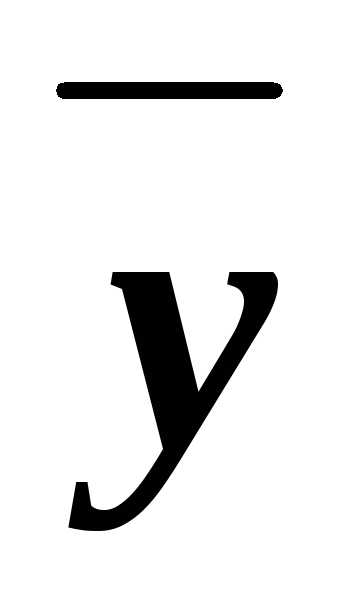 (xyz)&(x
(xyz)&(x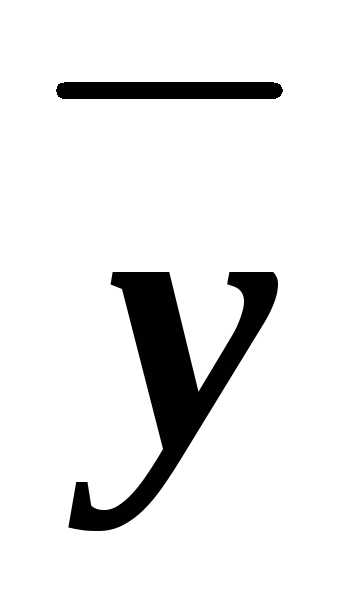 z)&(x
z)&(x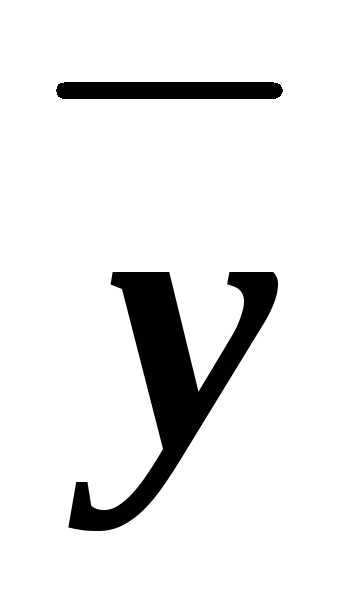 )&
)& &
&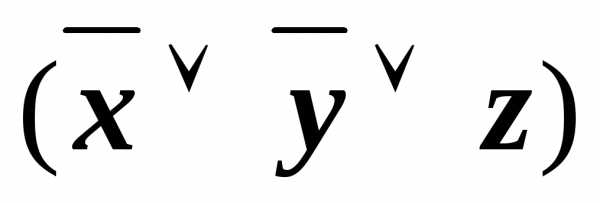
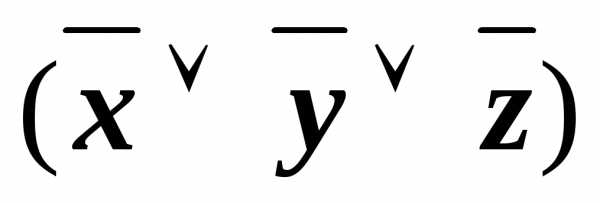
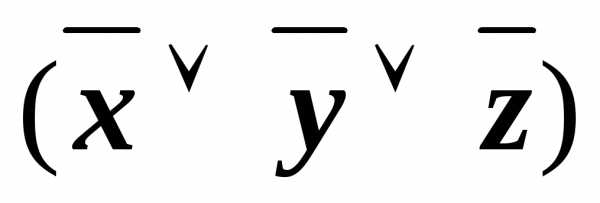 (xyz)&(x
(xyz)&(x z)&(x
z)&(x z)&(x
z)&(x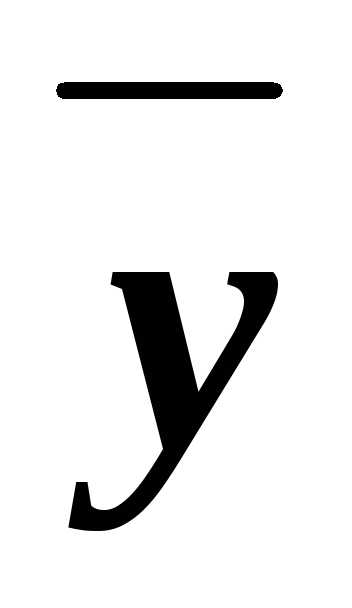
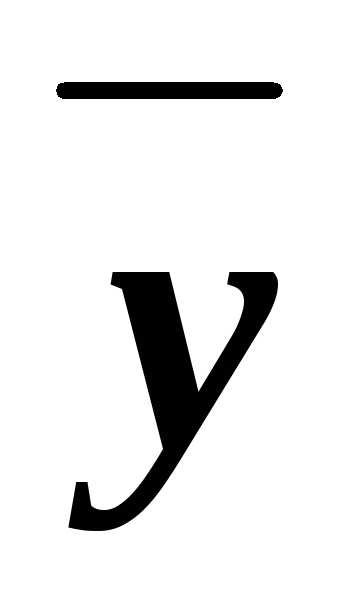 )&
)& &
&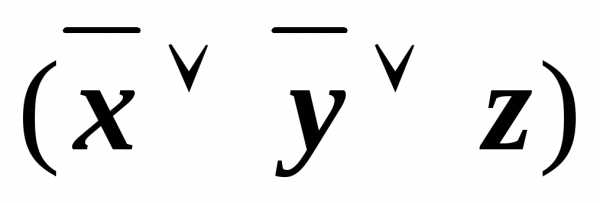 &
&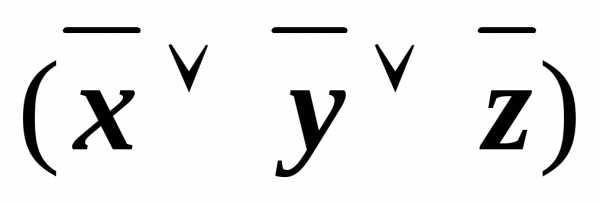

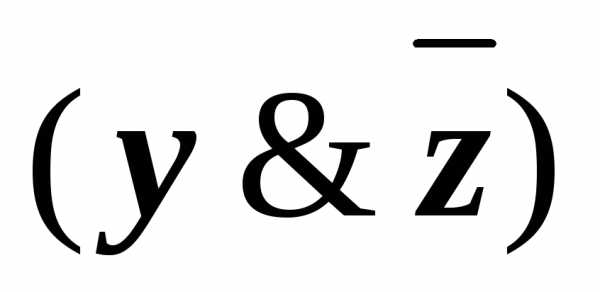 (xyz)&(x
(xyz)&(x z)&(x
z)&(x
 )&
)& &
&

 применили закон дистрибутивности.
применили закон дистрибутивности. у~1.
у~1. .
. (
(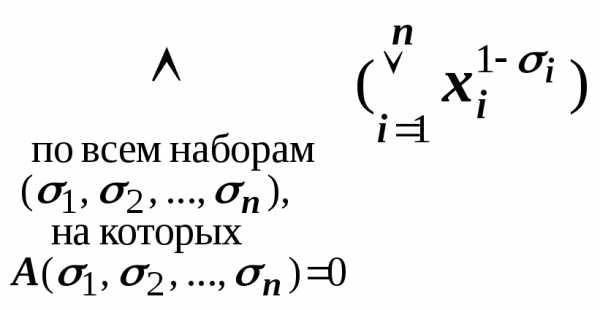 у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х
у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х ,
,  у и
у и 
 .
Из них значение 0 принимают только
.
Из них значение 0 принимают только 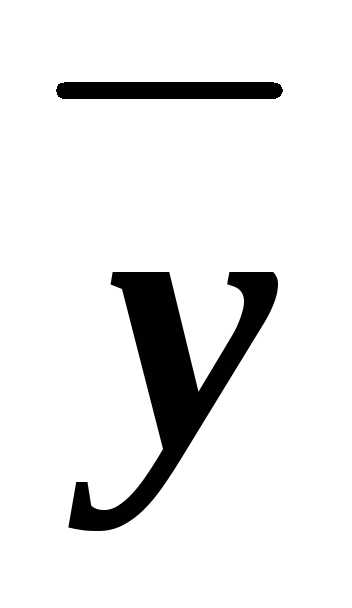
 при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.
при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху. .
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.
.
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.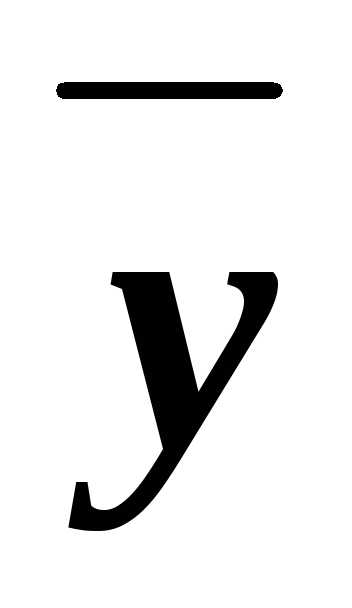 ,x
,x
 .
. )&(x
)&(x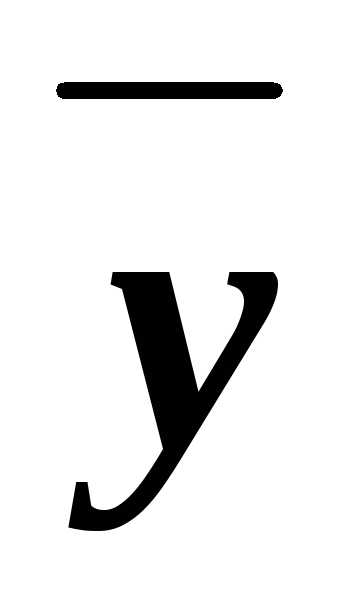
 ).
). )&(x
)&(x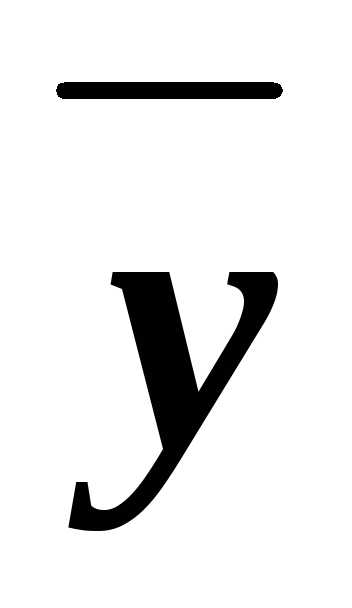
 ).
). (
( у)
имеем, например, КНФА~ху.
у)
имеем, например, КНФА~ху.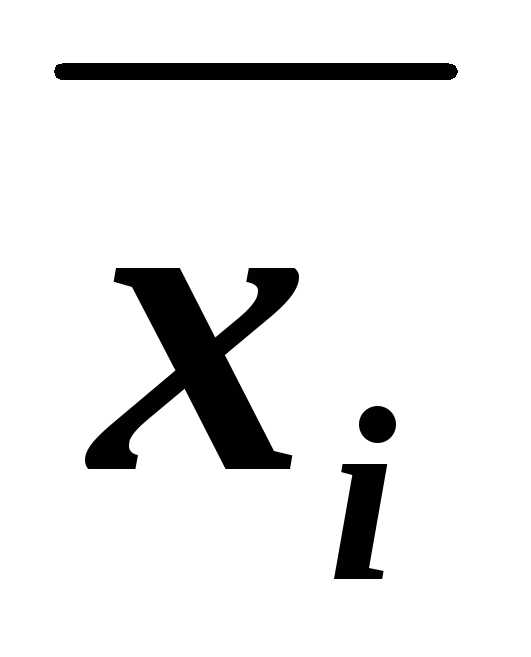 )~
~(Вхi)&(B
)~
~(Вхi)&(B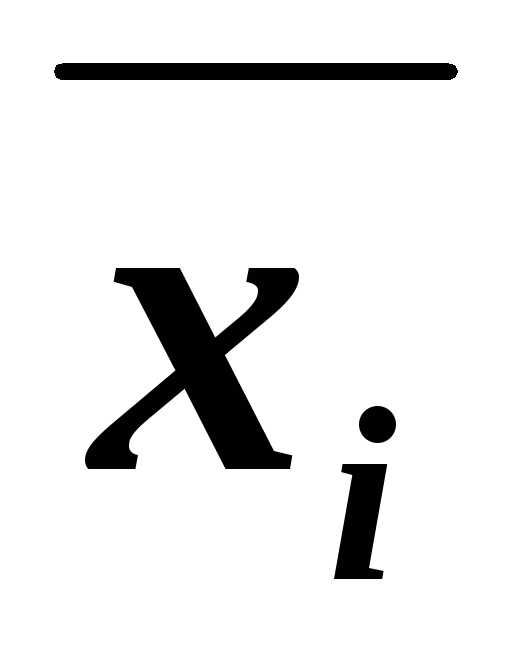 ),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B
),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B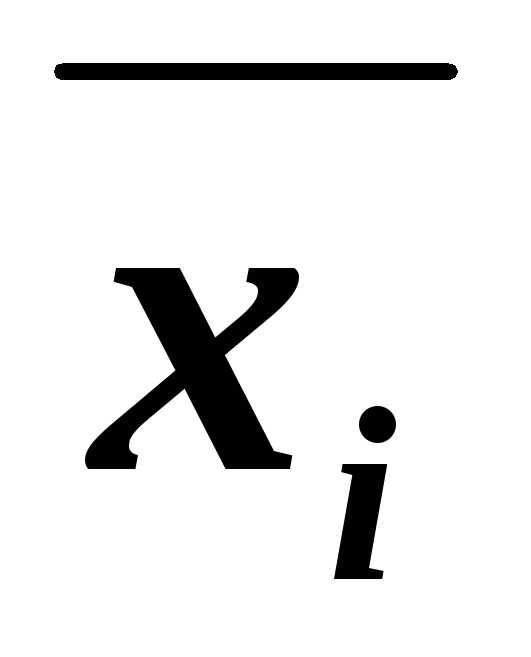 ),
каждая из которых содержитхi или её отрицание
),
каждая из которых содержитхi или её отрицание 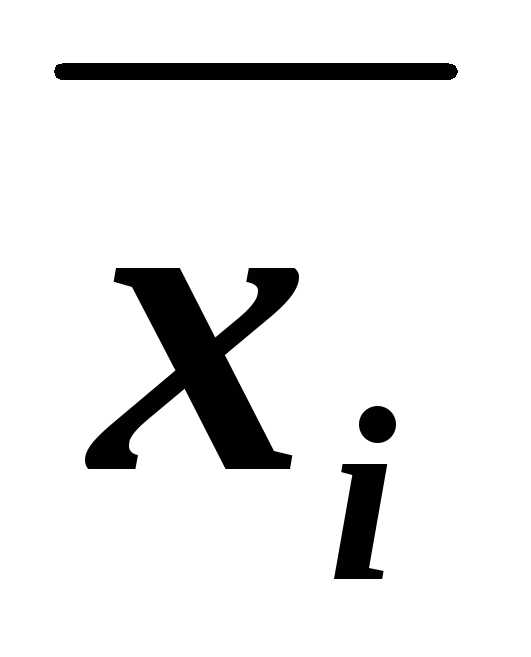 .
.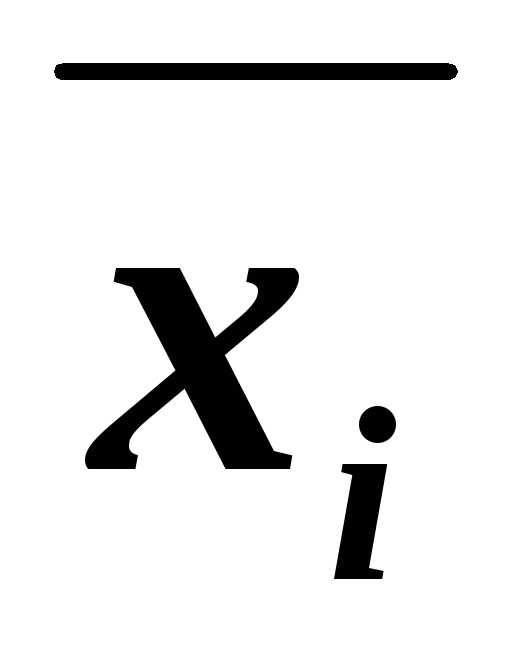 ,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.
,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.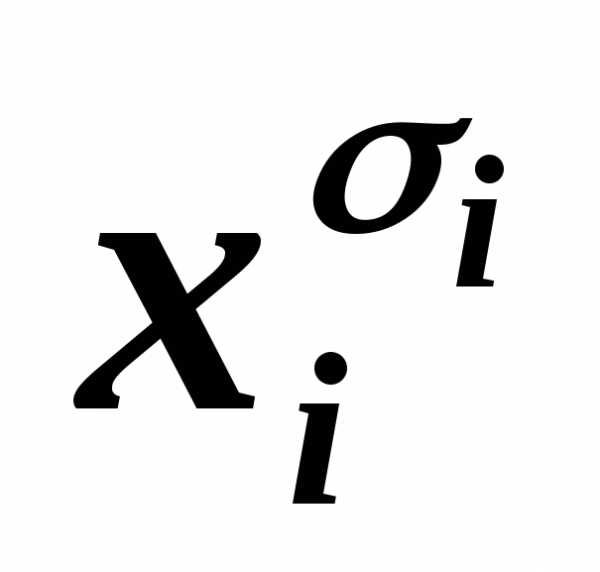 дважды или более, то, пользуясь
равносильностью
дважды или более, то, пользуясь
равносильностью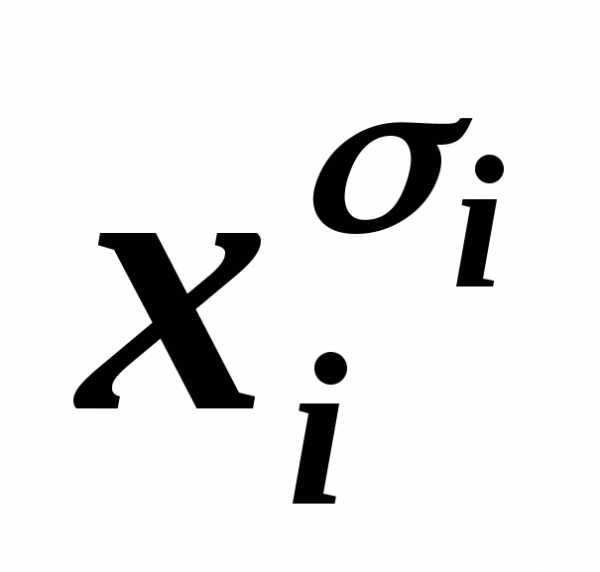
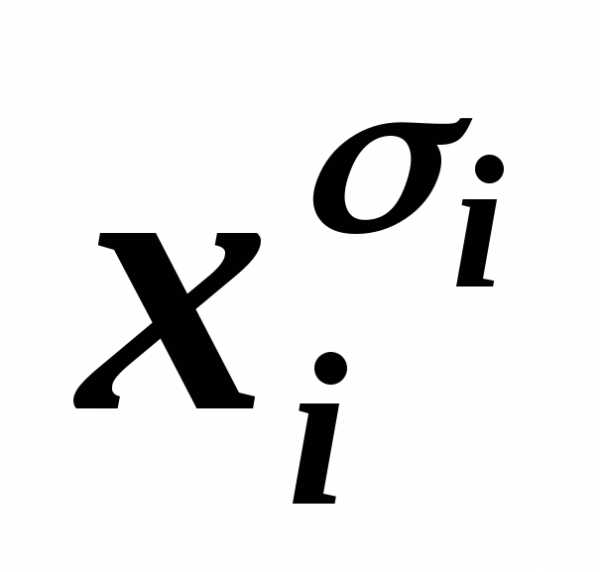 …
…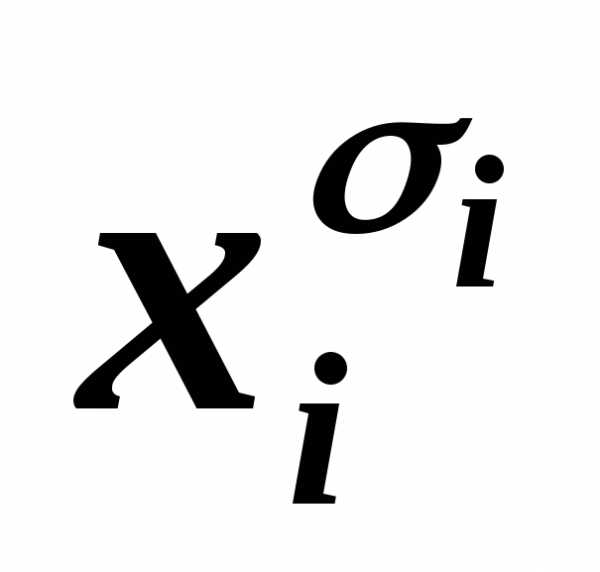 ~
~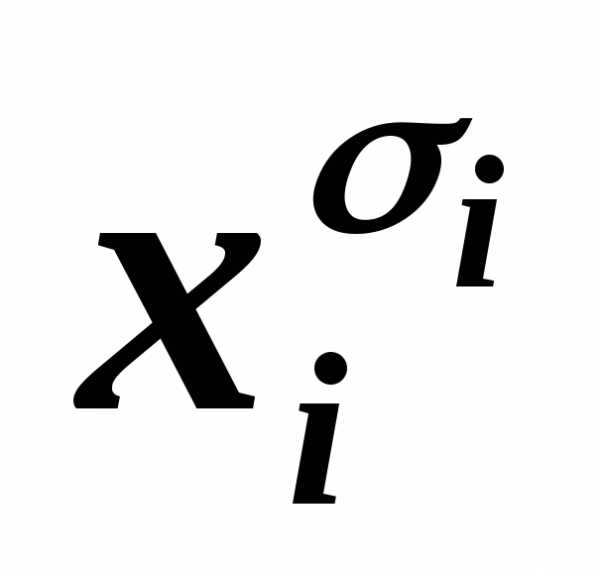 ,
лишние отбрасываем.
,
лишние отбрасываем. )(z
)(z )
)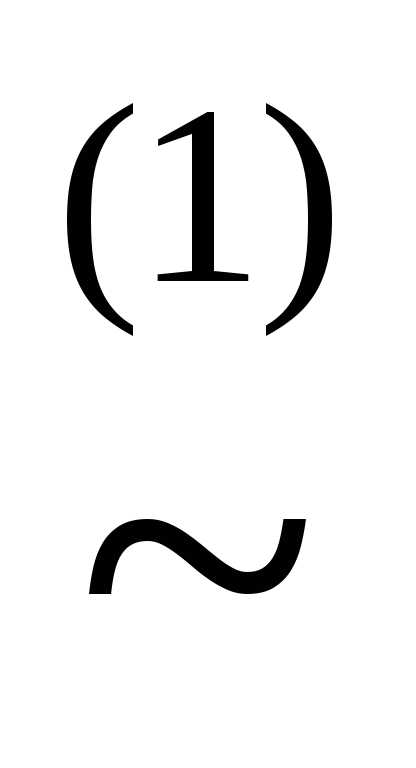 (
(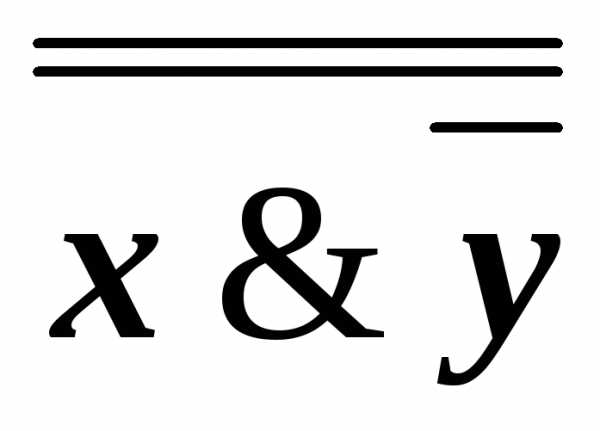 )(z
)(z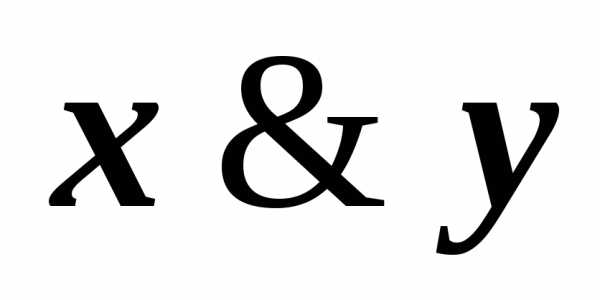 )
)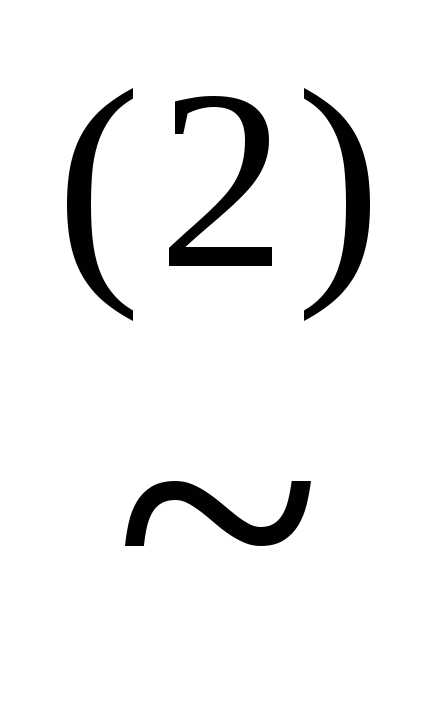 (x&
(x& )
)
 (x&
(x& )
) (x&
(x& )
)
 (x&
(x& )
) (x&
(x& )
)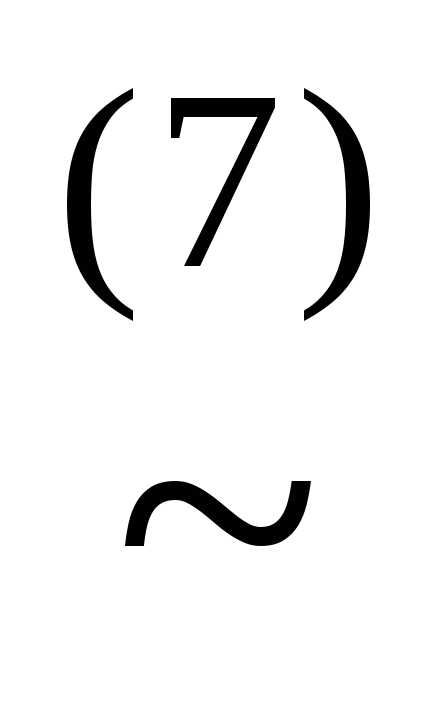
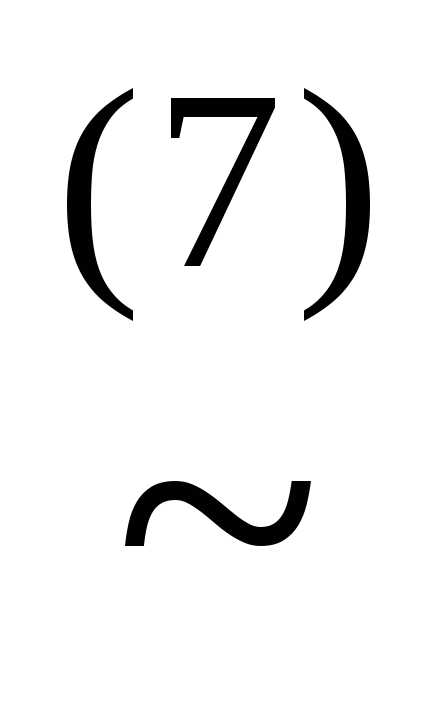 (x&
(x& )(
)( (x&
(x& ))
))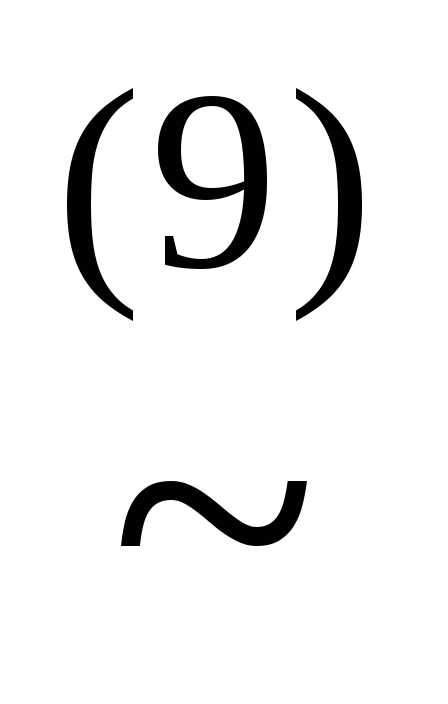
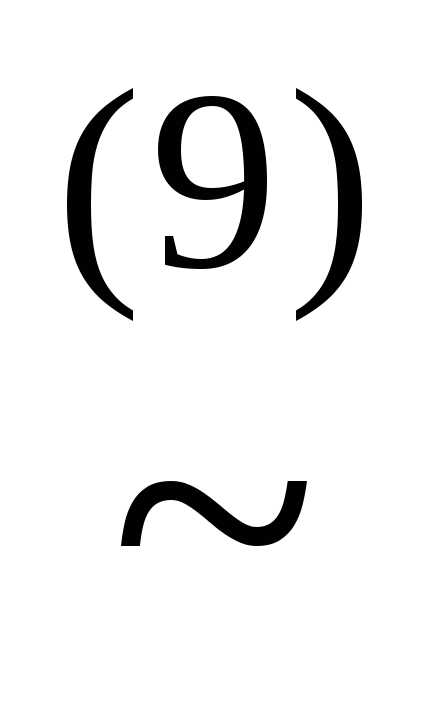 (x&(
(x&(
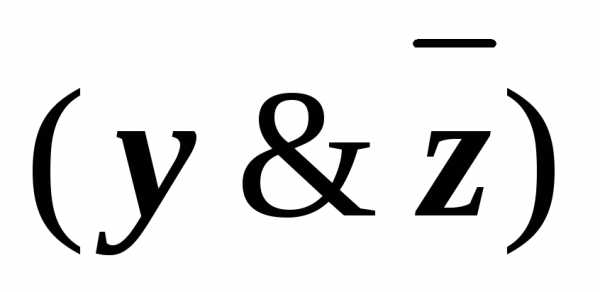 )))
)))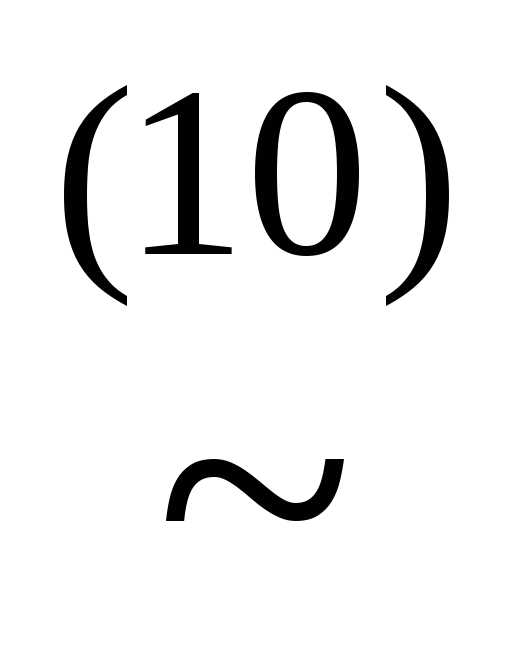 (x&((
(x&(( у)&
у)&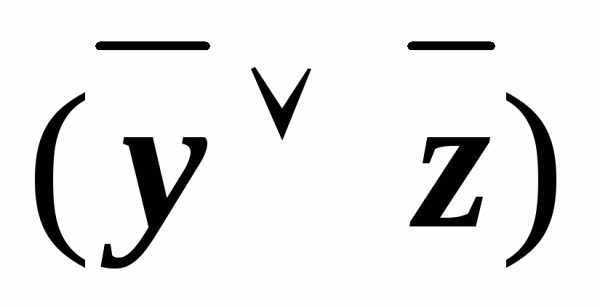 )))
)))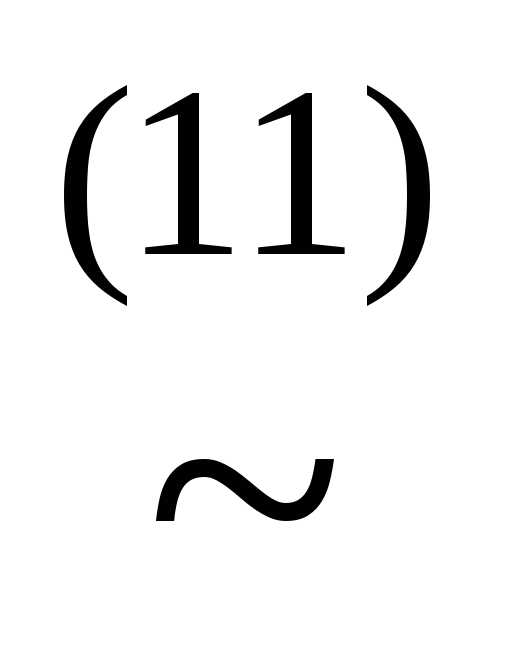
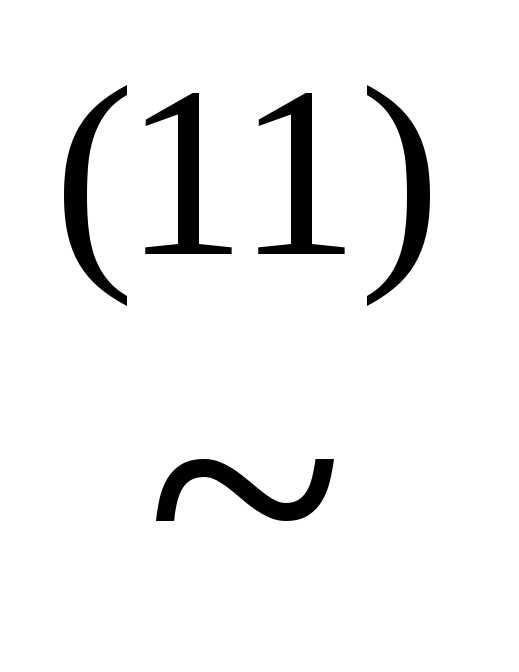 (x&
(x&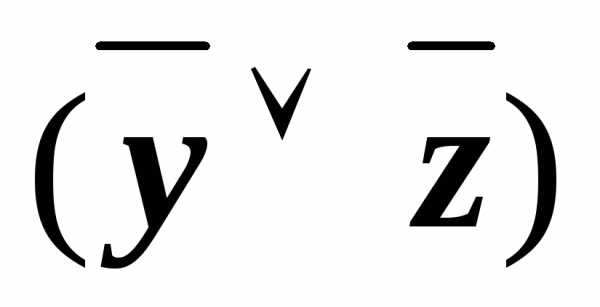 ))
))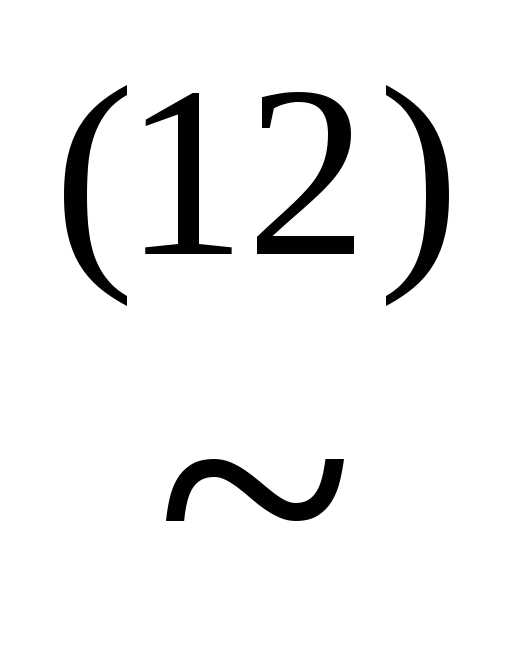 (xz)&
(xz)&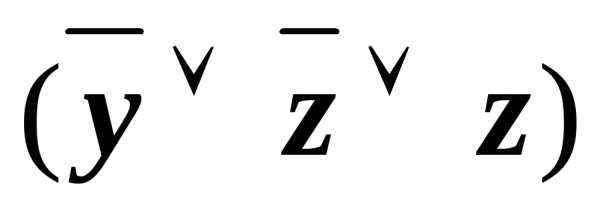 &&
&&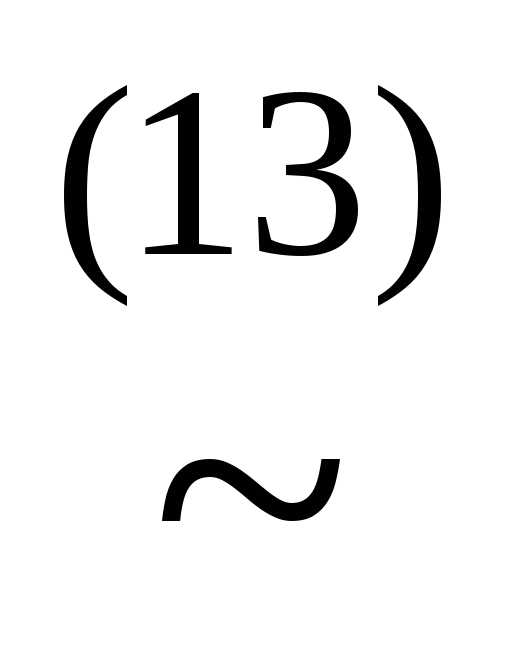
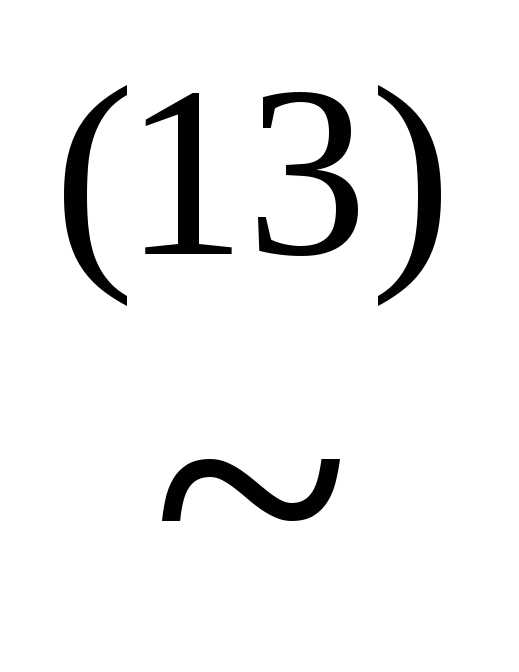 (xz)&
(xz)&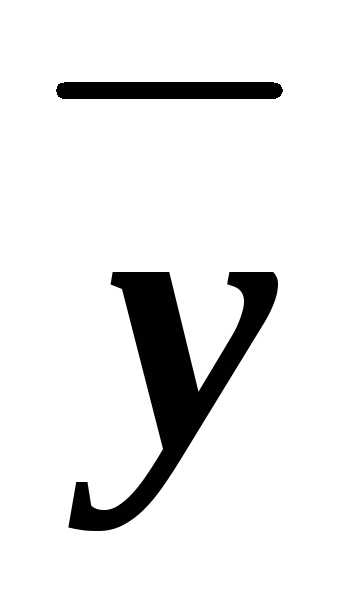 &
&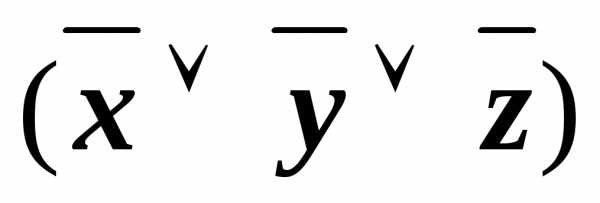
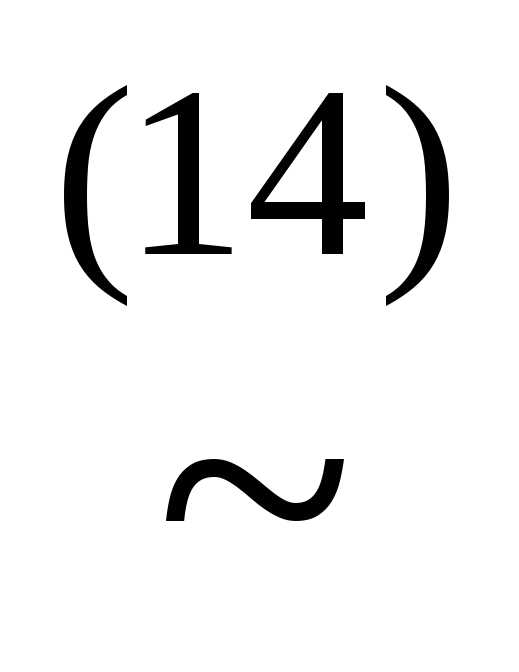
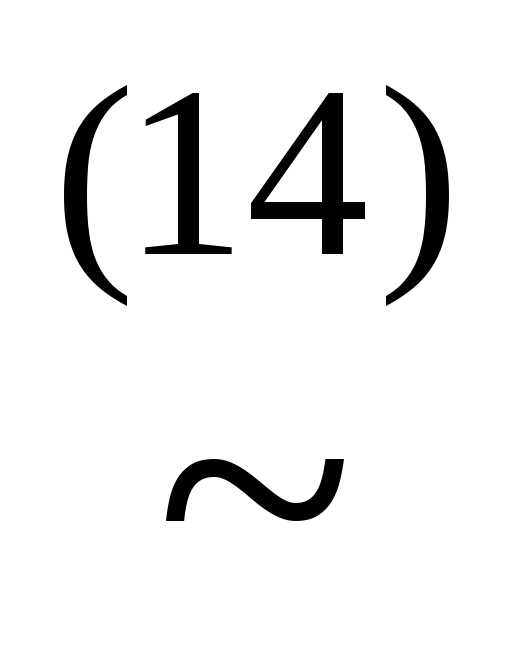 (xyz)&(x
(xyz)&(x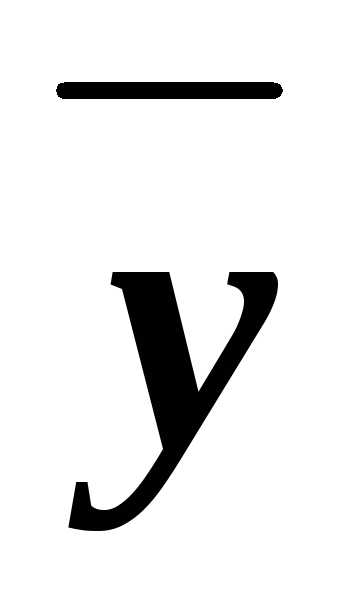 z)&(x
z)&(x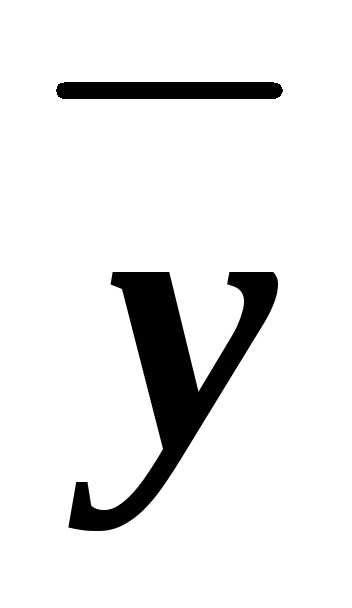 )&
)&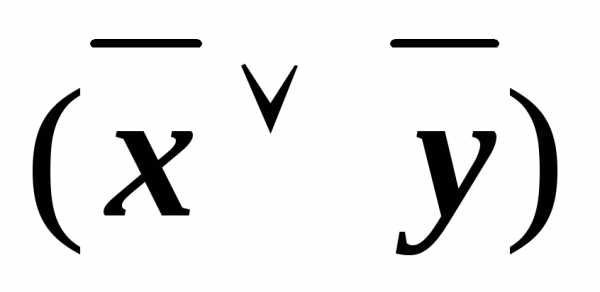 &
&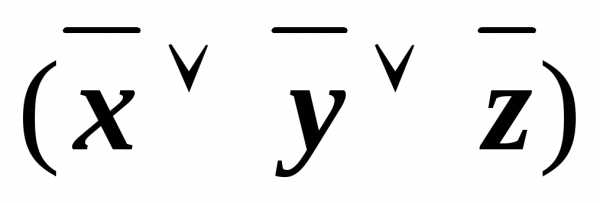

 (xyz)&(x
(xyz)&(x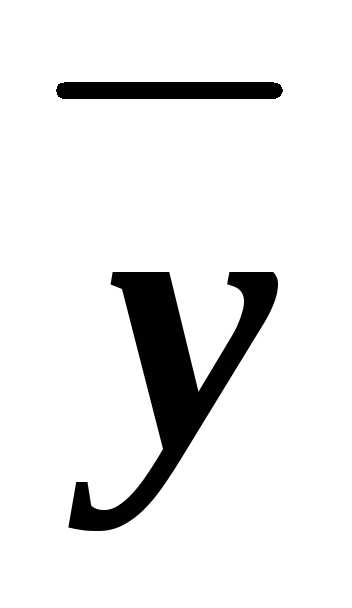 z)&(x
z)&(x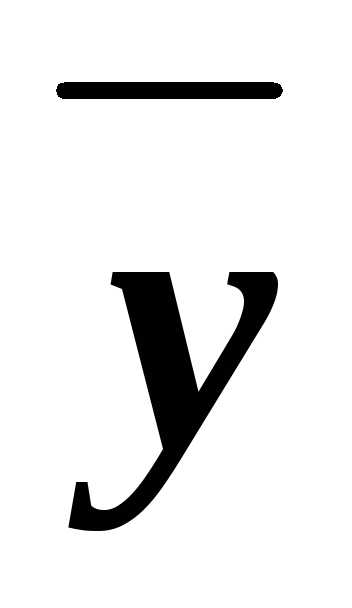 z)&(x
z)&(x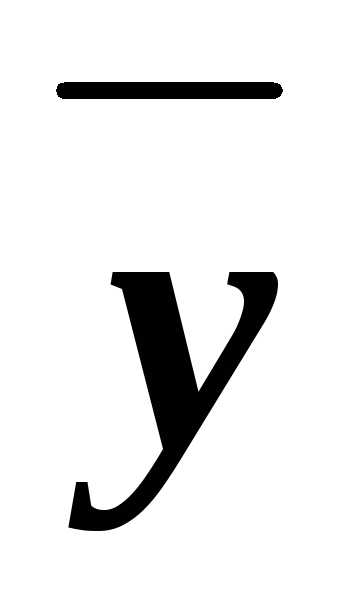
 )&
)&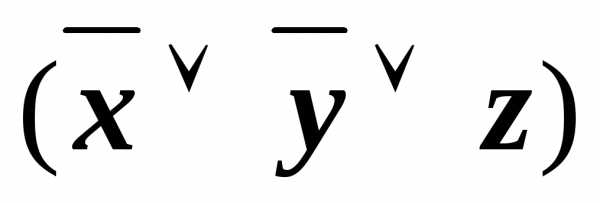 &
&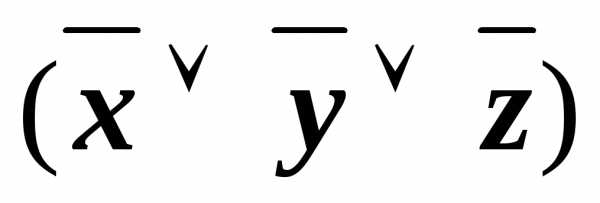 &
&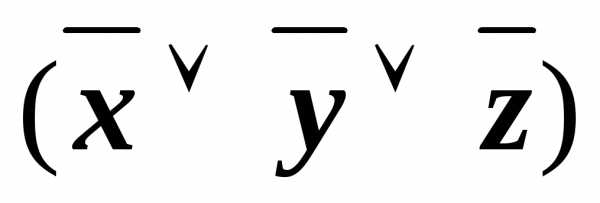
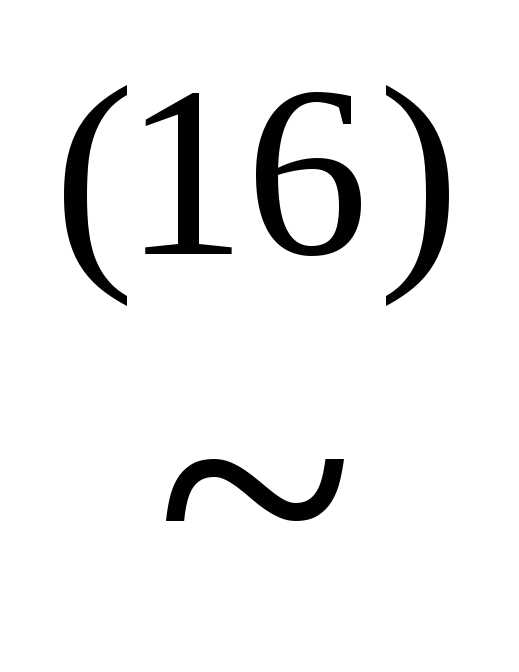
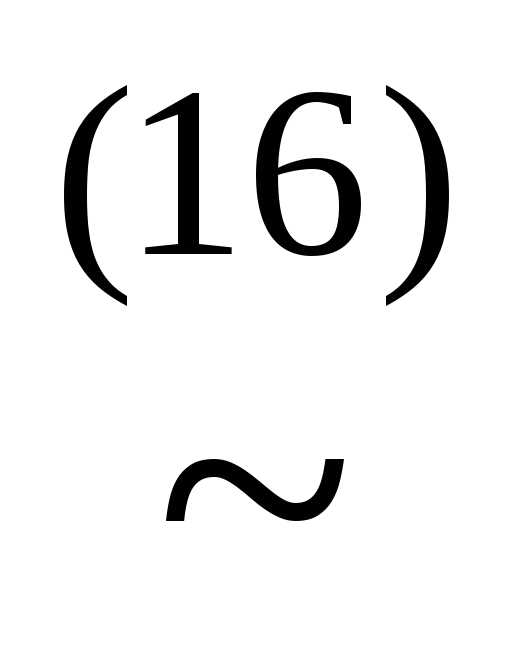 (xyz)&(x
(xyz)&(x z)&(x
z)&(x
 )&
)&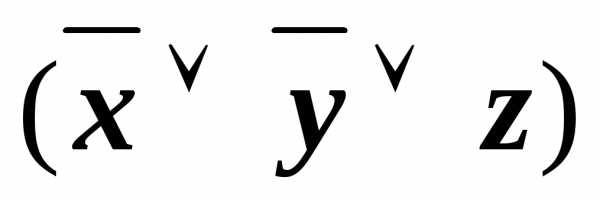 &
&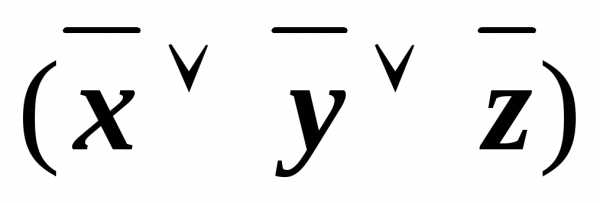

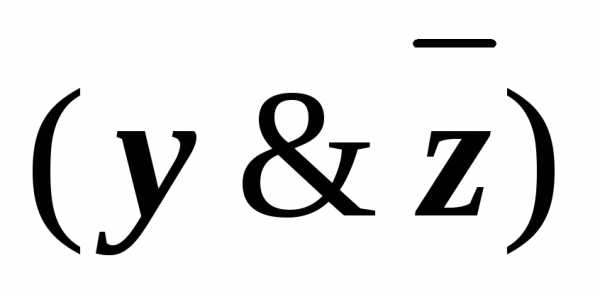 применили закон дистрибутивности.
применили закон дистрибутивности. у~1.
у~1.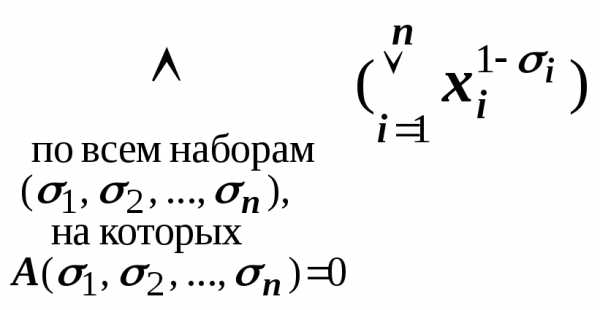 .
. (
( у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х
у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х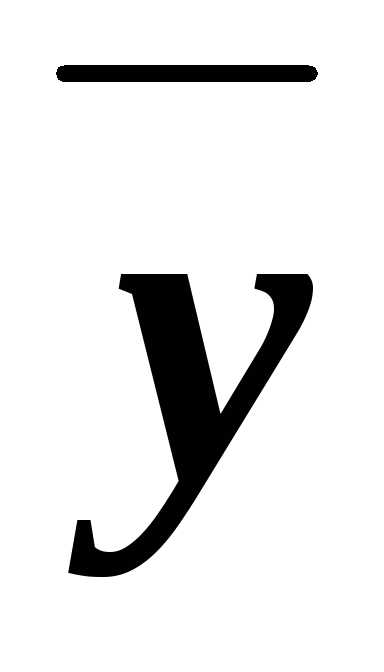 ,
,  у и
у и 
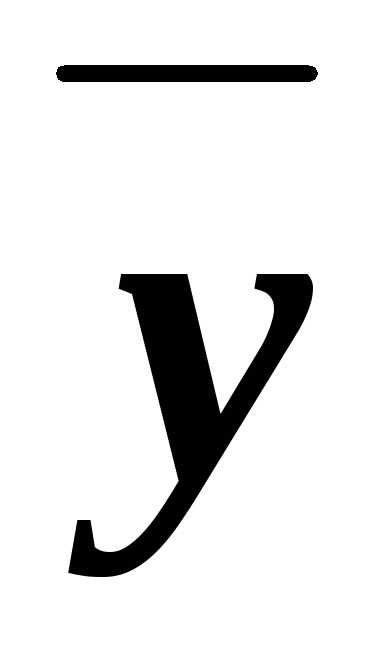 .
Из них значение 0 принимают только
.
Из них значение 0 принимают только 
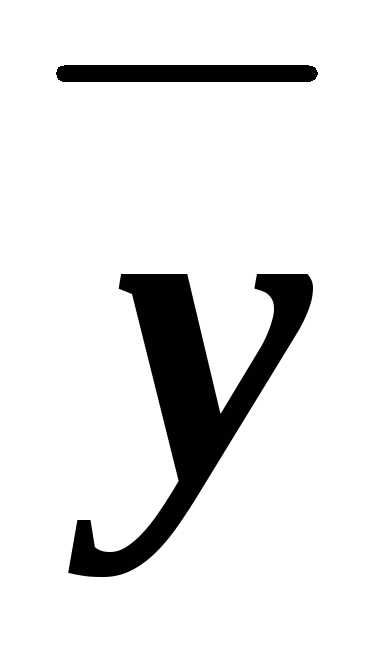 при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.
при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.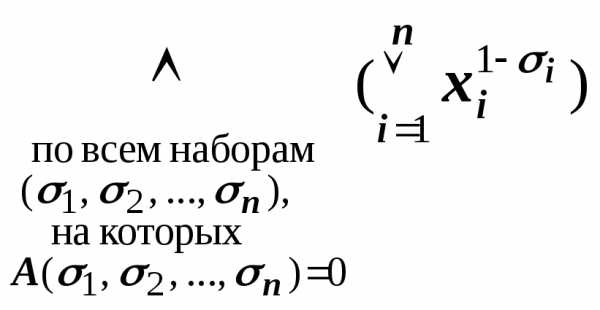 .
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.
.
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ. ,x
,x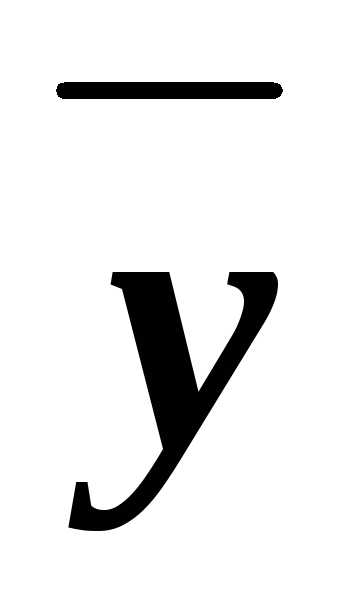
 .
. )&(x
)&(x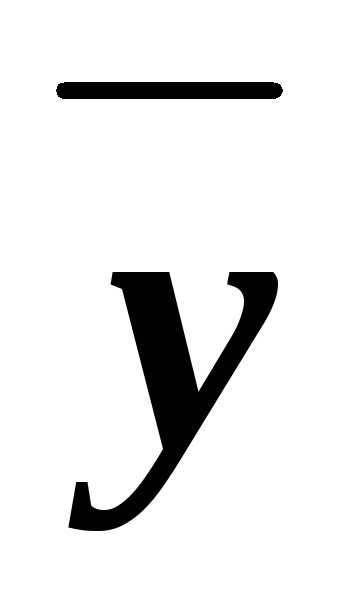
 ).
). )&(x
)&(x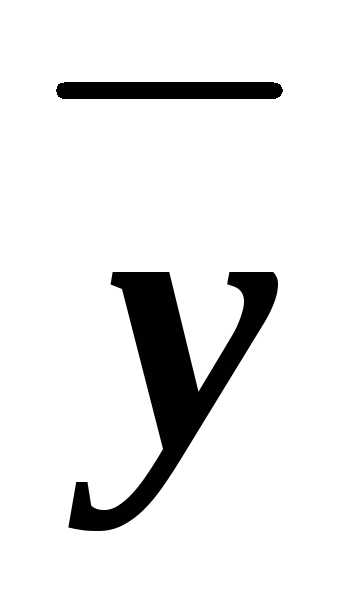
 ).
). (
( у)
имеем, например, КНФА~ху.
у)
имеем, например, КНФА~ху.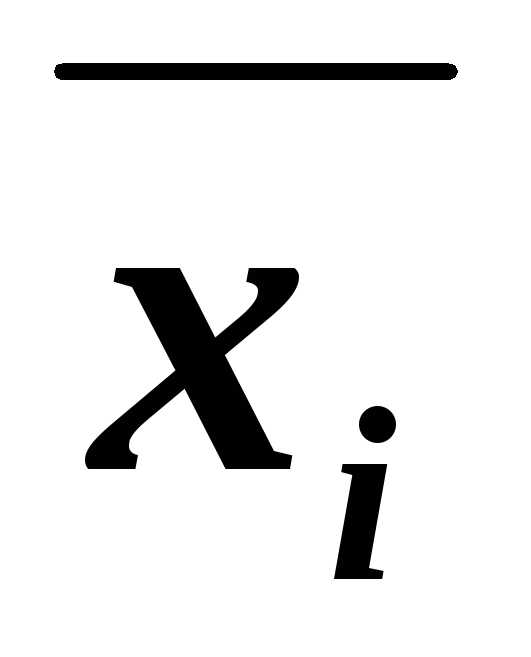 )~
~(Вхi)&(B
)~
~(Вхi)&(B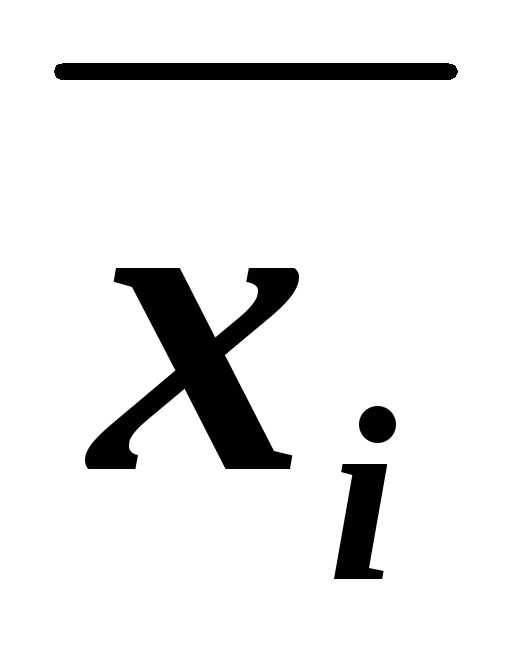 ),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B
),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B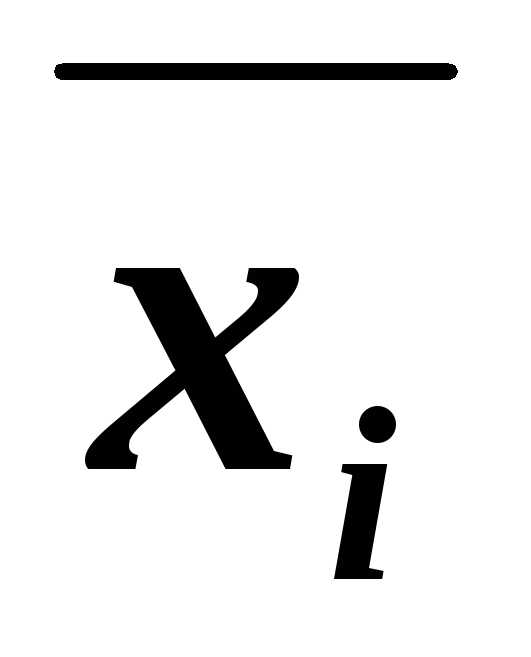 ),
каждая из которых содержитхi или её отрицание
),
каждая из которых содержитхi или её отрицание 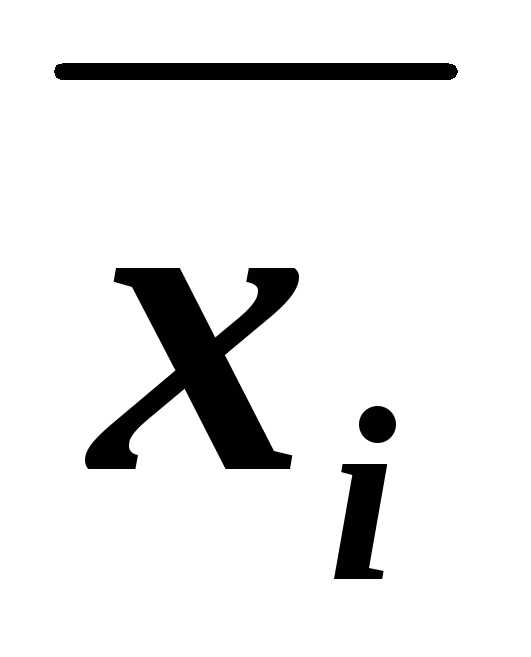 .
.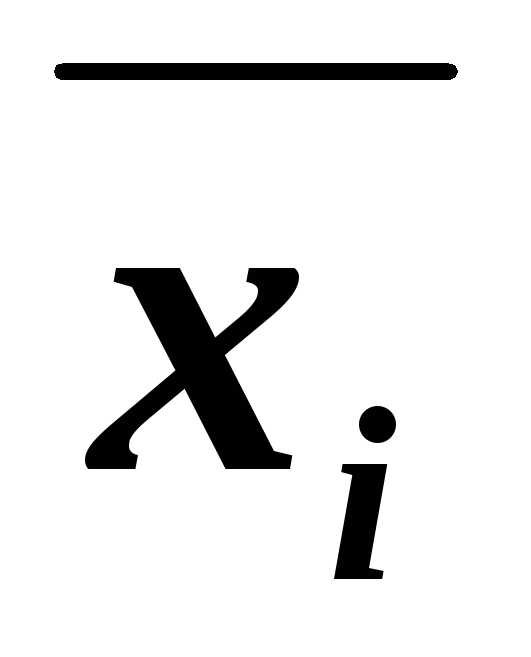 ,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.
,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.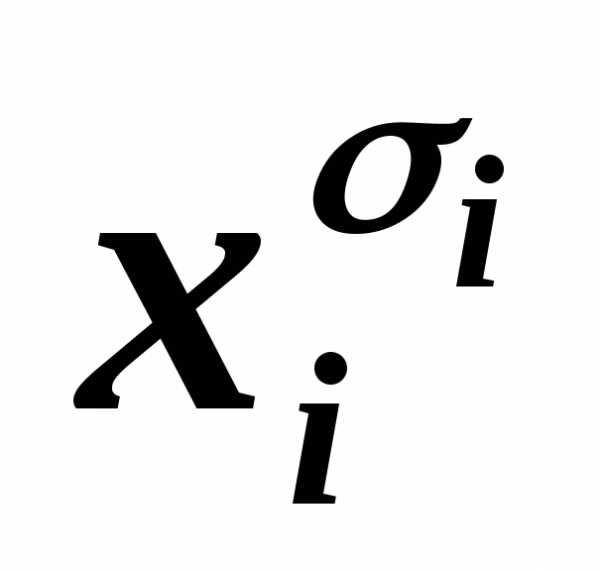 дважды или более, то, пользуясь
равносильностью
дважды или более, то, пользуясь
равносильностью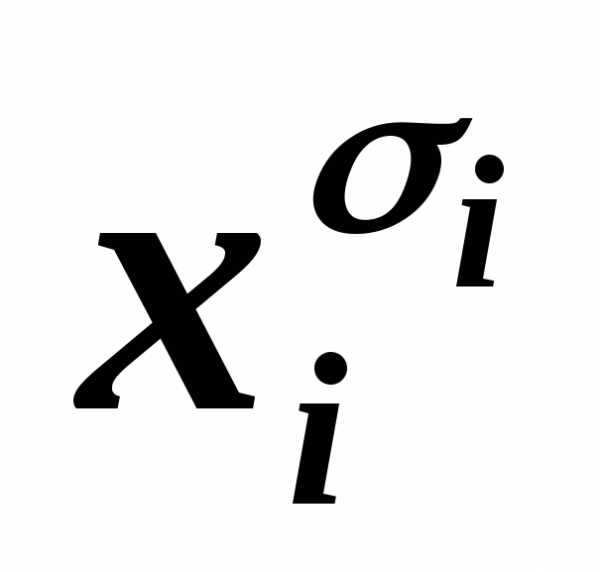
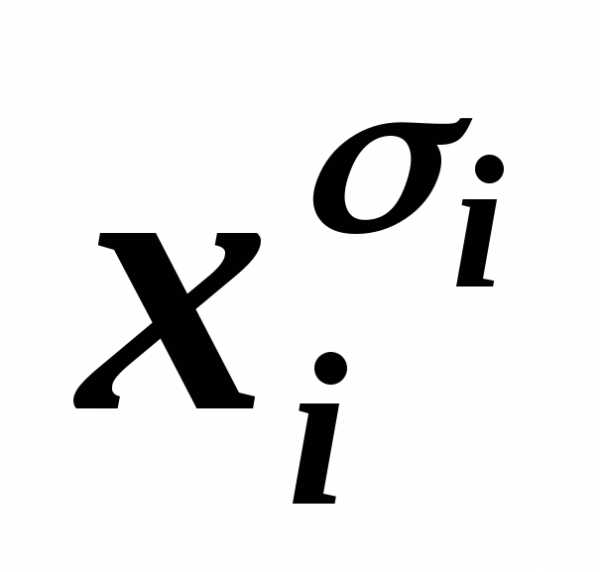 …
…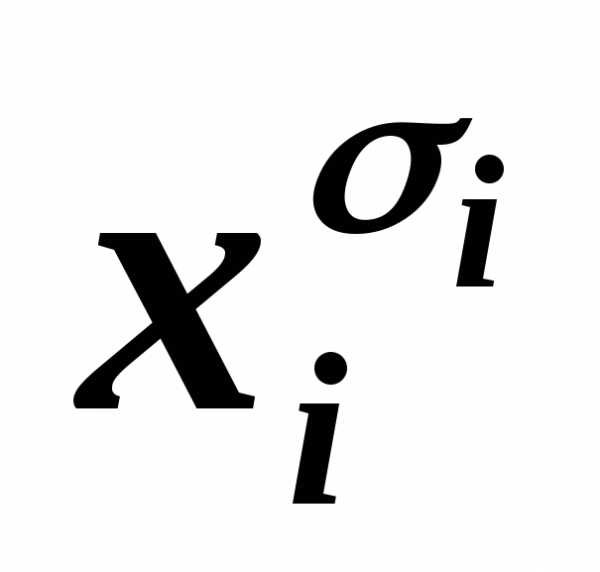 ~
~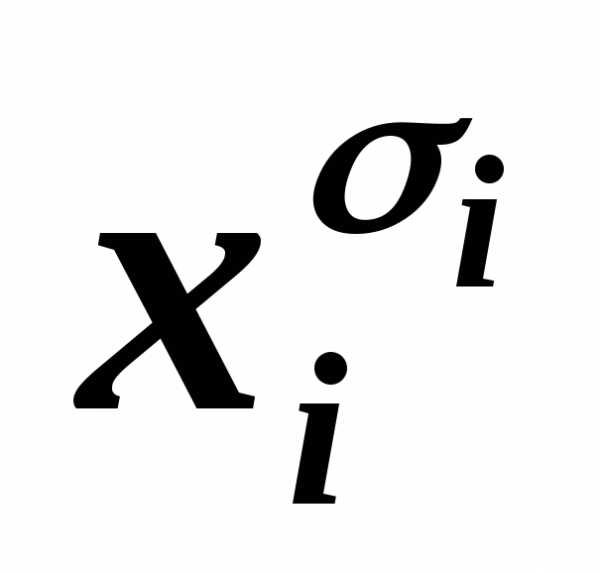 ,
лишние отбрасываем.
,
лишние отбрасываем. )(z
)(z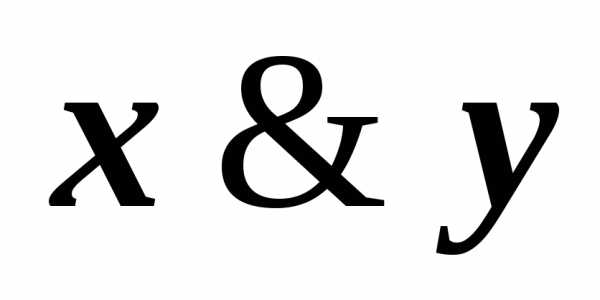 )
)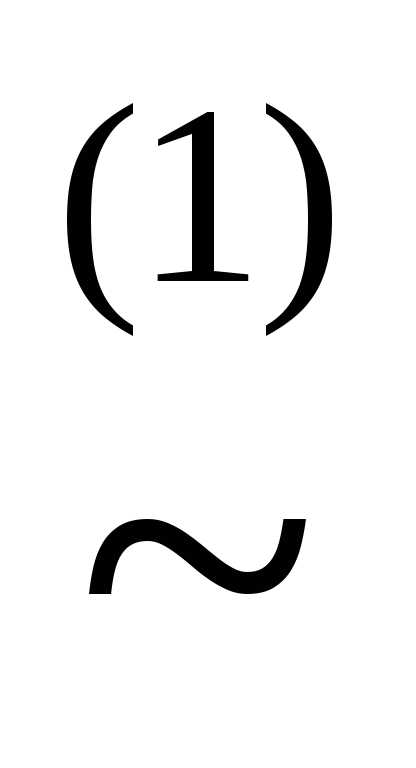 (
(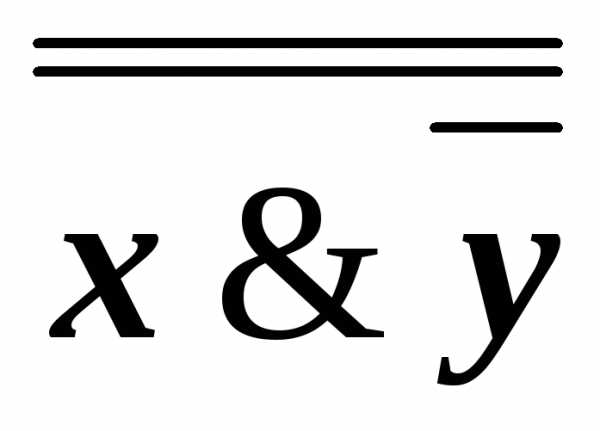 )(z
)(z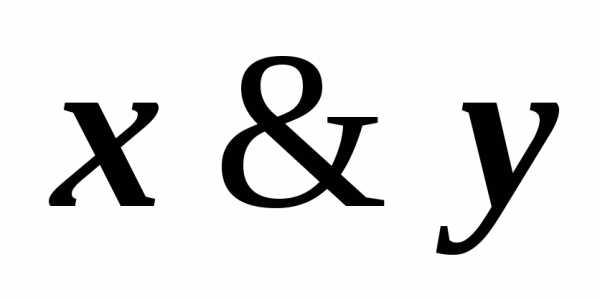 )
) (x&)
(x&)
 (x&
(x& )
) (x&
(x& )
)
 (x&
(x& )
) (x&
(x& )
)
 (x&
(x& )(
)( (x&
(x& ))
))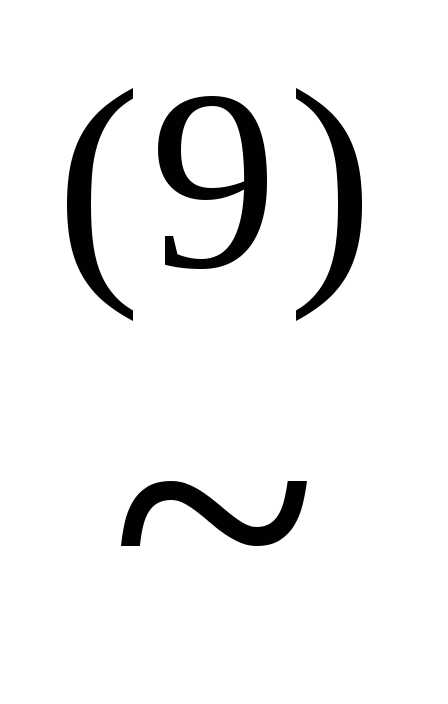
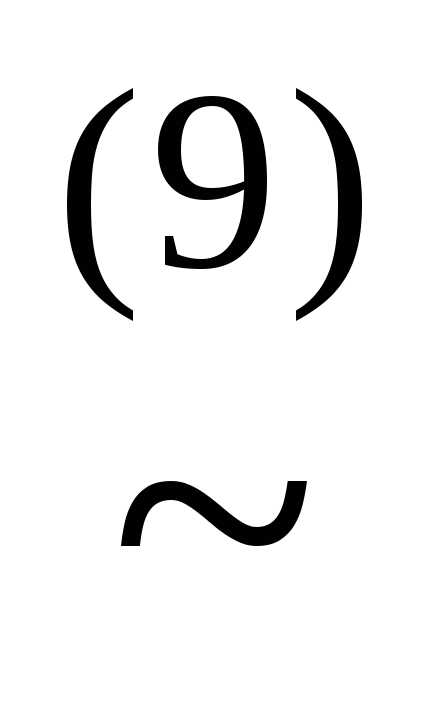 (x&(
(x&(
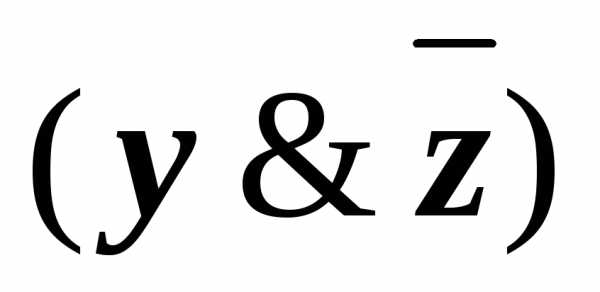 )))
))) (x&((
(x&(( у)&
у)&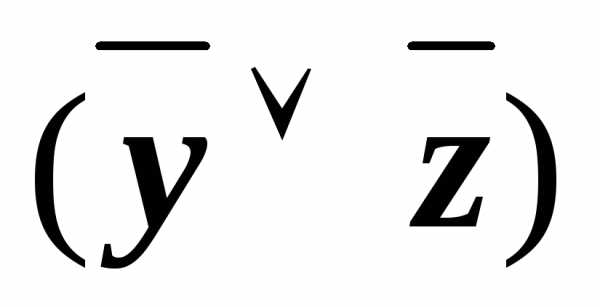 )))
)))
 (x&
(x&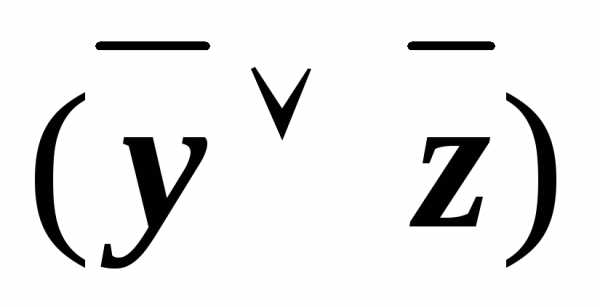 ))
))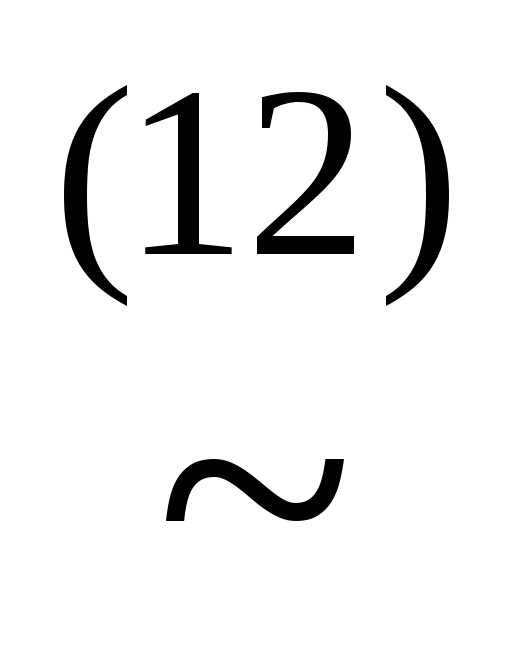 (xz)&
(xz)&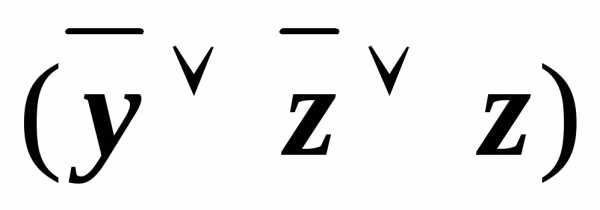 &&
&&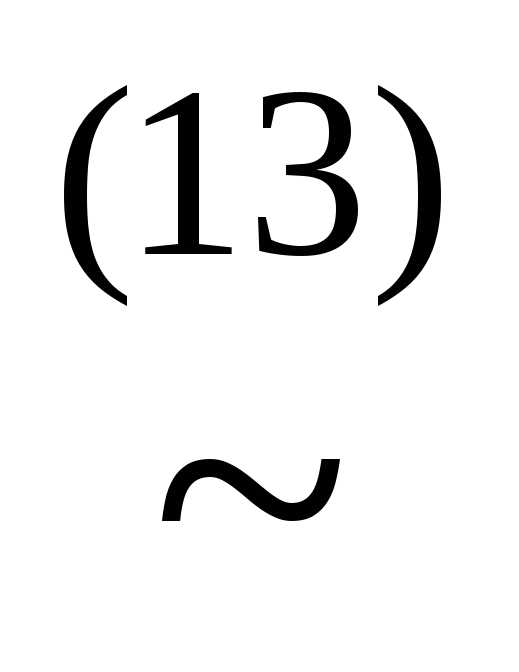
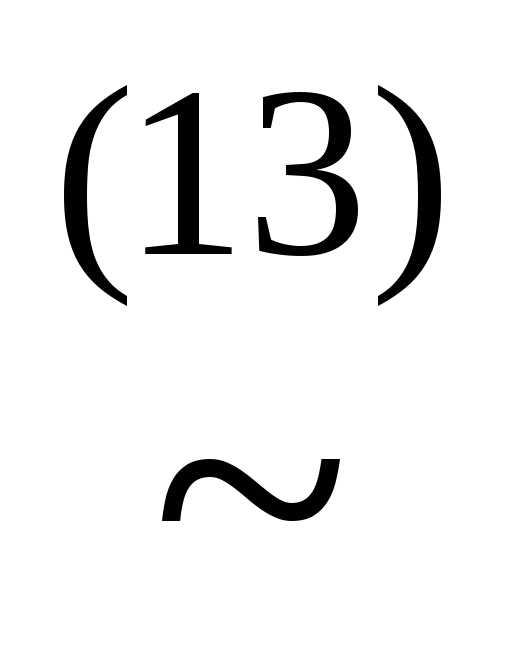 (xz)&
(xz)&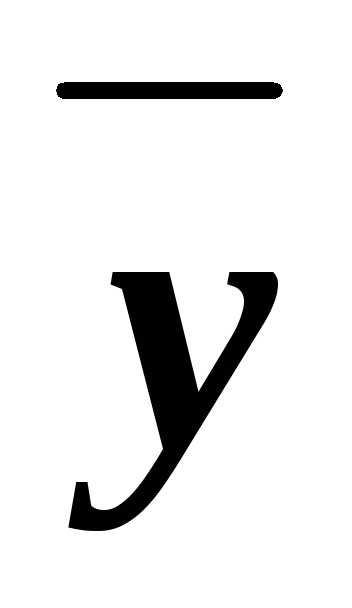 &
&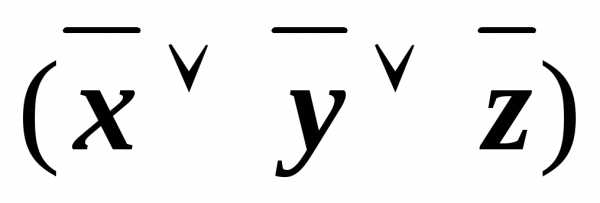
 (xyz)&(x
(xyz)&(x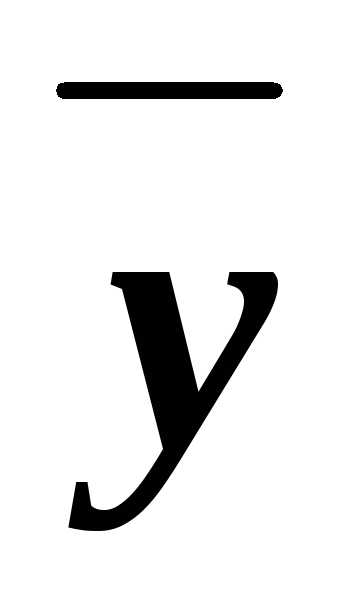 z)&(x
z)&(x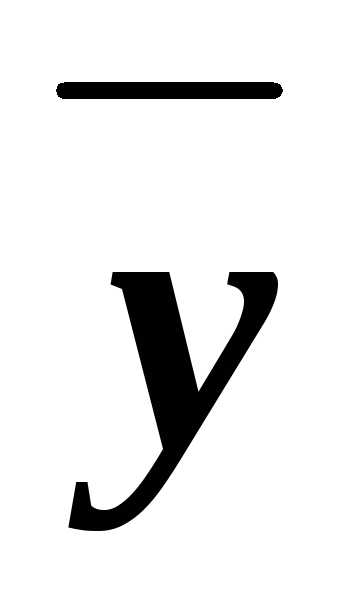 )&
)& &
&

 (xyz)&(x
(xyz)&(x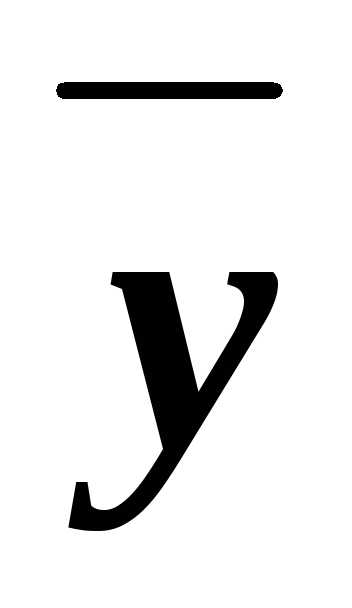 z)&(x
z)&(x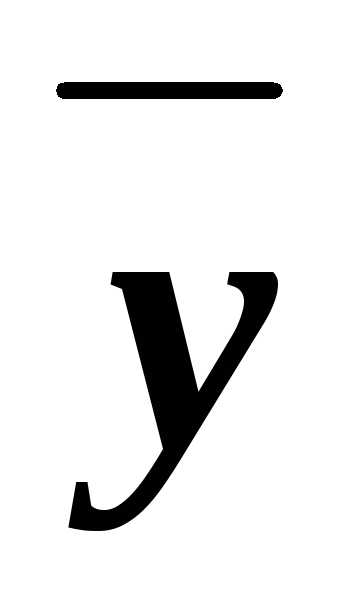 z)&(x
z)&(x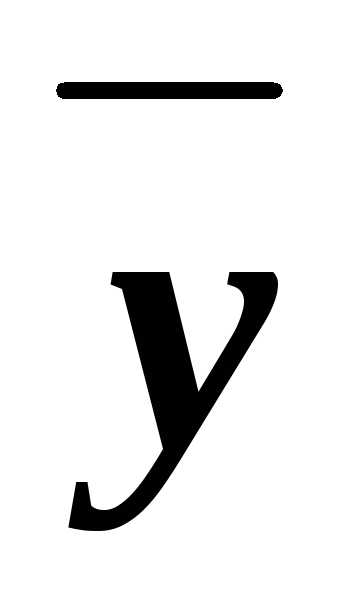
 )&
)&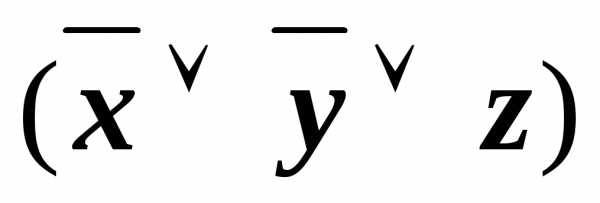 &
&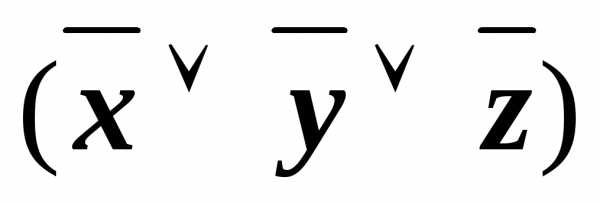 &
&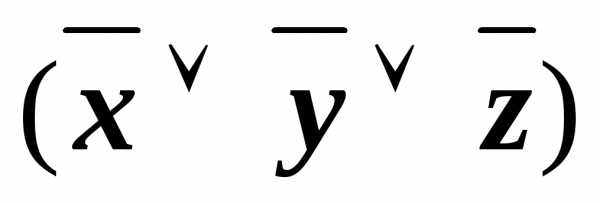
 (xyz)&(x
(xyz)&(x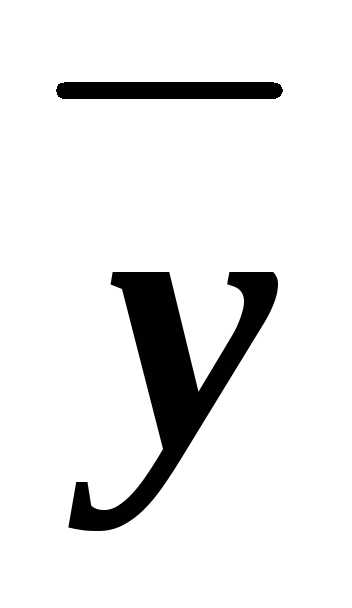 z)&(x
z)&(x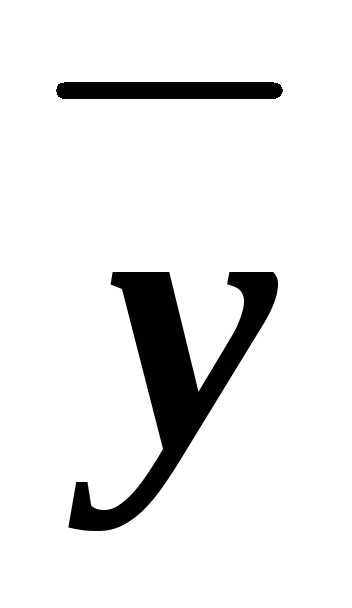
 )&
)&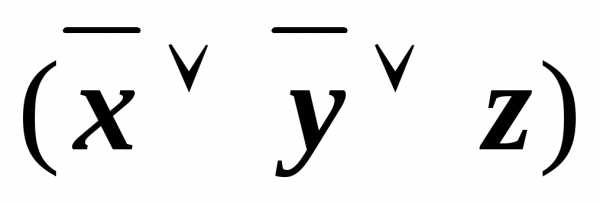 &
&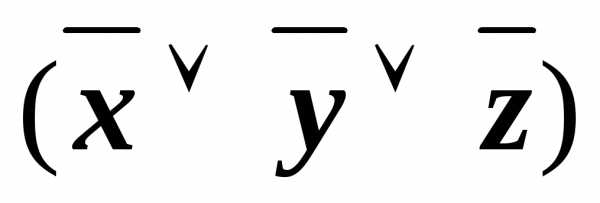

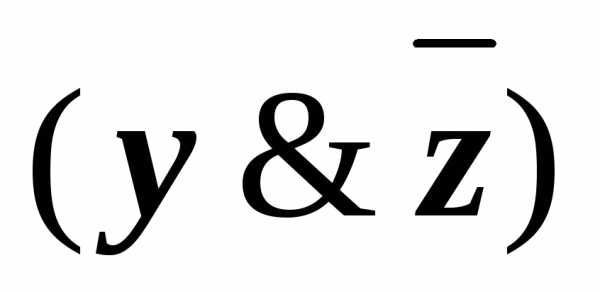 применили закон дистрибутивности.
применили закон дистрибутивности. у~1.
у~1.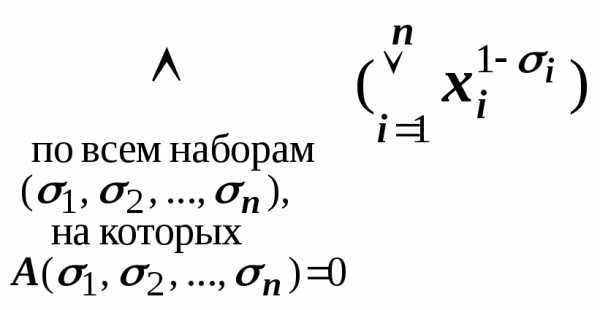 .
. (
( у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х
у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х ,
,  у и
у и 
 .
Из них значение 0 принимают только
.
Из них значение 0 принимают только 
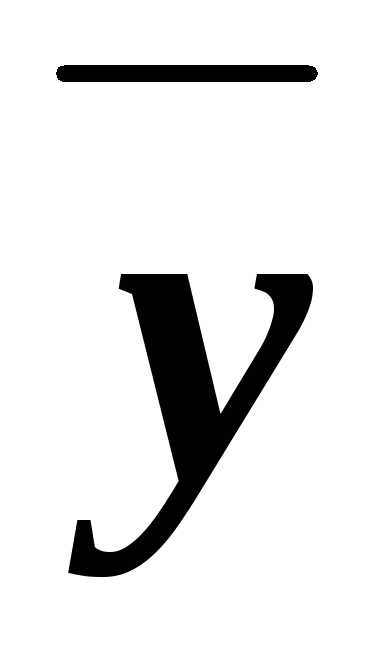 при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.
при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.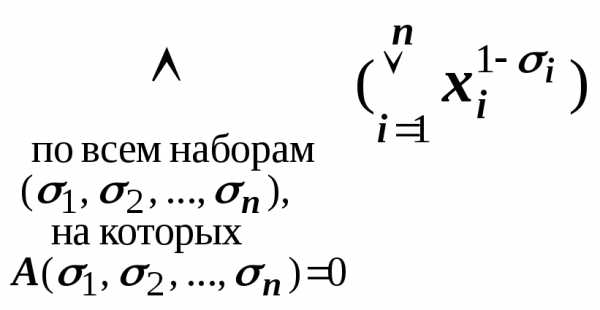 .
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.
.
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ. ,x
,x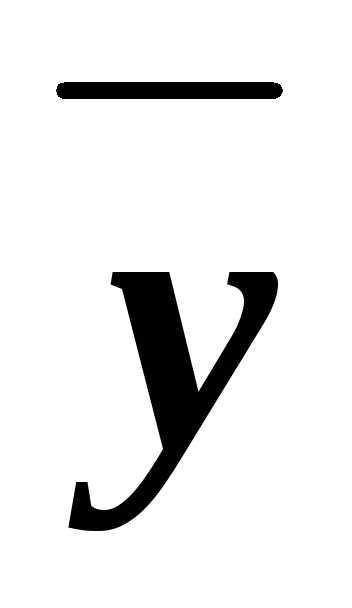
 .
. )&(x
)&(x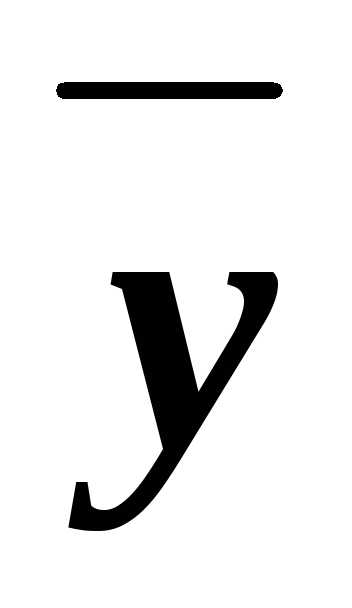
 ).
). )&(x
)&(x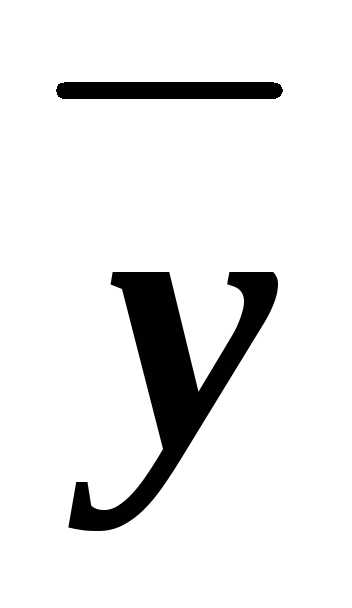
 ).
).