Школьная жизнь — Страница 333 — Таловская средняя школа

2 по римски – Римские цифры, арабско-римские цифры калькулятор

alexxlab / 20.12.201602.06.2019 / Школьная жизнь

Как можно написать римскую цифру 2 на клавиатуре компьютера латинскими символами

В век современных технологий римские цифры могут понадобиться любому пользователю, который постигает глубины интернета. Некоторым кажется, что это непостижимая задача. Но мы вас уверяем, что после прочтения данной статьи, вы с легкостью будете набирать римские цифры, даже не задумываясь о проделанном.

Самый простой вариант

Предварительная подготовка:

Переключите свою клавиатуру на английскую раскладку. (одновременное нажатие клавиш Shift + Alt)
Теперь включим Caps Lock, это облегчит вам жизнь, чтобы не пришлось нажимать Shift при каждом символе (но если хочется, то можно использовать Shift)

А теперь будем творить магию!

Единичка в римской нотации, как буква «I» в английском алфавите. Нажимаем на кнопочку, где находится эта буковка (русская буква «ш») и вуаля!
Как написать римское число 2 на клавиатуре? Аналогичным образом! Просто увеличьте количество палочек (их теперь будет две). Вот так: «II»
Римская цифра 3 на клавиатуре похожа на 2, только на 1 палочку больше. Вводить нужно так: «III»
С самым простым мы справились. Переходим на более сложный уровень. Начнем с 5. Она пишется галочкой, то есть буквой «V»
4 — это комбинация 5 и 1. Пишется так: «IV» (единица стоит слева, что означает на 1 меньше 5)
6 пишется зеркально 4. «VI» (на единицу больше 5)
7 и 8 пишется так: «VII» и «VIII» (на 2 и на 3 больше 5 соответственно)
10 набирается на компьютере немного иным способом — латинская буква «X».
9 и 11 очень похоже на образование 4 и 6. «IX» — 9, «XI» — 11.
12, 13 — добавлением 2 и 3 к 10: «XII» и «XIII»
Числа с 14 по 19 ввести будет очень просто: добавляете эти числа после 10 («X») в римской нотации
Дальше пойдем по десяткам: 20 и 30 легко записываются с помощью нужного количества десяток («XX», «XXX»)
Пойдем еще по новенькому: цифра 50 пишется латинской буквой «L»
Числа 40 и 60 образовываются схожим образом с 4 и 6: «XL», «LX»;
Ну и перейдем к трехзначным числам: 100 — это «C»
Следующая контрольная точка — 500. Это выглядит так: «D»
Ну и конечная наша точка — 1000. Обозначается буквой «M»
Все остальные варианты варьируются по вышеизложенным примерам. Например: 468 — это 4 по сто, 50 + 10 и 8. То есть пишется так: «CCCCLXVIII».

Коды ASCII

Вы также можете использовать альтернативный и более продвинутый способ перевода арабских цифр в римскую нотацию — это таблица ASCII. Это таблица кодирования, которая представляет из себя связь популярных символов с некоторым набором цифр. Следуя нижеприведенным инструкциям, вы сможете воспользоваться таблицей ASCII:

Потребуется включать режим Num Lock (достаточно нажать соответствующую клавишу).
Зажмите клавишу Alt и нажмите нужную вам комбинацию цифр на дополнительной клавиатуре справа.

Для римской нотации комбинации клавиш следующие:

Арабские цифры	Римские цифры	ASCII
1	«I»	73
5	«V»	86
10	«X»	88
50	«L»	76
100	«C»	67
500	«D»	68
1000	«M»	77

Word

Один из самых легких способов переводить арабские числа в римские — набрать их в Ворде или другом офисном приложении, которое вам по душе. Для этого вам придется следовать следующему алгоритму:

Используйте одновременное нажатие клавиш Ctrl + F9;
Появляются скобочки { };
Нужно набрать в скобках незамысловатое выражение: {=нужная цифра\*ROMAN};
Нажмите F9;
Поставленная цель достигнута!

На самом деле это очень хороший способ, когда у вас есть компьютер с офисным приложением, но ограничен доступ в интернет. Однако даже у такого хорошего и простого способа есть существенный недостаток: использовать его можно только в Ворде и подобных ему приложениях. Если вам понадобится ввести римскую цифру в каком-либо другом приложении, не относящимся к офисным (например, фотошоп), то придется выбирать альтернативу из двух вышеизложенных способов. Но есть и небольшой секрет: можно набрать нужное вам число в программе Ворд, а потом просто скопировать и вставить в нужное место. Все гениальное просто!

Сейчас мы с вами разобрали 3 способа, как можно набирать римские цифры на компьютере. Самый простой способ набрать римские цифры в нужном вам документе — просто напечатать их на клавиатуре через английскую раскладку. Самое большое преимущество данного метода — он универсален, и вы можете использовать его в любом приложении, на любой операционной системе. Единственный недостаток такого подхода — необходимость знания всех цифр данной системы счисления или того, как они образовываются. Но этот минус достаточно просто устранить.

Запомнить римскую нотацию не так уж сложно — если вы часто будете ей пользоваться, то скоро будете делать все на автомате, даже не задумываясь о нужных действиях. Если принять во внимание тот факт, что сегодня римские цифры не столь популярны, то всегда можно уделить немного времени для изучения данного вопроса. В конце концов, всегда можно сделать себе маленький черновик-подсказку и заглядывать туда время от времени. Таким образом осознание цифр придет быстрее и легче. Удачи вам в познаниях и изучении нового!

komp.guru

Малая таблица римских цифр от 1 до 20

Таблица римских цифр от 1 до 20
Арабские цифры	Римские цифры
1	I
2	II
3	III
4	IV
5	V
6	VI
7	VII
8	VIII
9	IX
10	X
11	XI
12	XII
13	XIII
14	XIV
15	XV
16	XVI
17	XVII
18	XVIII
19	XIX
20	XX

Римские цифры — 7 букв из латинского алфавита, предназначение для отображения и записи натуральных чисел. Все величины по установлением правилам возникают в результате перестановки и их повторении, но в совершено различных последовательностях и комбинациях друг с другом, каждый раз получаются совсем разные цифры.

Латинская буква	Число
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

Мнемоническое правило

Для простого запоминания буквенных обозначений цифр в порядке убывания и придумано это правило. Эту фразу на русском языке весьма легко запомнить:

Mы Даем Cоветы Лишь Хорошо Воспитанным Индивидуумам
Мир Даёт Силу Лишь Хорошим Воинам Империи
(М(М)-D(Д)-С(С)-L(Л)-X(Х)-V(В)-I(И))

В ней в заглавных буквах каждого из слов запечатлено в порядке убивания последовательность десятичного выражения римских цифр. Если Вы поняли суть, то я думаю Вам не составит труда и самому придумать ещо з десяток своих собственных мнемонических правил удобных для устного запоминания.

Автор: Bill4iam

kvn201.com.ua

Римские цифры от 1 до 100 « Абросайт — творит Абро!

Цифра 0 не представлена в римской системе счисления.

Цифра 1 в римских числах обозначается так: I
Цифра 2 в римских числах обозначается так: II
Цифра 3 в римских числах обозначается так: III
Цифра 4 в римских числах обозначается так: IV
Цифра 5 в римских числах обозначается так: V
Цифра 6 в римских числах обозначается так: VI
Цифра 7 в римских числах обозначается так: VII
Цифра 8 в римских числах обозначается так: VIII
Цифра 9 в римских числах обозначается так: IX
Число 10 в римских числах обозначается так: X

Подробнее о римских цифрах и о том, как переводить в эту систему счисления, вы можете прочитать здесь. Если вы хотите узнать другие числа римскими цифрами, кликните на соответствующую ссылку:

Число 11 в римских числах обозначается так
Число 12 в римских числах обозначается так
Число 13 в римских числах обозначается так
Число 14 в римских числах обозначается так
Число 15 в римских числах обозначается так
Число 16 в римских числах обозначается так
Число 17 в римских числах обозначается так
Число 18 в римских числах обозначается так
Число 19 в римских числах обозначается так
Число 20 в римских числах обозначается так

Число 21 в римских числах обозначается так
Число 22 в римских числах обозначается так
Число 23 в римских числах обозначается так
Число 24 в римских числах обозначается так
Число 25 в римских числах обозначается так
Число 26 в римских числах обозначается так
Число 27 в римских числах обозначается так
Число 28 в римских числах обозначается так
Число 29 в римских числах обозначается так

Число 30 в римских числах обозначается так
Число 31 в римских числах обозначается так
Число 32 в римских числах обозначается так
Число 33 в римских числах обозначается так
Число 34 в римских числах обозначается так
Число 35 в римских числах обозначается так
Число 36 в римских числах обозначается так
Число 37 в римских числах обозначается так
Число 38 в римских числах обозначается так
Число 39 в римских числах обозначается так

Число 40 в римских числах обозначается так
Число 41 в римских числах обозначается так
Число 42 в римских числах обозначается так
Число 43 в римских числах обозначается так
Число 44 в римских числах обозначается так
Число 45 в римских числах обозначается так
Число 46 в римских числах обозначается так
Число 47 в римских числах обозначается так
Число 48 в римских числах обозначается так
Число 49 в римских числах обозначается так

Число 50 в римских числах обозначается так
Число 51 в римских числах обозначается так
Число 52 в римских числах обозначается так
Число 53 в римских числах обозначается так
Число 54 в римских числах обозначается так
Число 55 в римских числах обозначается так
Число 56 в римских числах обозначается так
Число 57 в римских числах обозначается так
Число 58 в римских числах обозначается так
Число 59 в римских числах обозначается так

Число 60 в римских числах обозначается так
Число 61 в римских числах обозначается так
Число 62 в римских числах обозначается так
Число 63 в римских числах обозначается так
Число 64 в римских числах обозначается так
Число 65 в римских числах обозначается так
Число 66 в римских числах обозначается так
Число 67 в римских числах обозначается так
Число 68 в римских числах обозначается так
Число 69 в римских числах обозначается так

Число 70 в римских числах обозначается так
Число 71 в римских числах обозначается так
Число 72 в римских числах обозначается так
Число 73 в римских числах обозначается так
Число 74 в римских числах обозначается так
Число 75 в римских числах обозначается так
Число 76 в римских числах обозначается так
Число 77 в римских числах обозначается так
Число 78 в римских числах обозначается так
Число 79 в римских числах обозначается так

Число 80 в римских числах обозначается так
Число 81 в римских числах обозначается так
Число 82 в римских числах обозначается так
Число 83 в римских числах обозначается так
Число 84 в римских числах обозначается так
Число 85 в римских числах обозначается так
Число 86 в римских числах обозначается так
Число 87 в римских числах обозначается так
Число 88 в римских числах обозначается так
Число 89 в римских числах обозначается так

Число 90 в римских числах обозначается так
Число 91 в римских числах обозначается так
Число 92 в римских числах обозначается так
Число 93 в римских числах обозначается так
Число 94 в римских числах обозначается так
Число 95 в римских числах обозначается так
Число 96 в римских числах обозначается так
Число 97 в римских числах обозначается так
Число 98 в римских числах обозначается так
Число 99 в римских числах обозначается так
Число 100 в римских числах обозначается так

abrosait.ru

Римские цифры — Википедия РУ

Римские обозначения чисел известны ныне лучше, чем любая другая древняя система счисления. Объясняется это не столько какими-то особыми достоинствами римской системы, сколько тем огромным влиянием, которым пользовалась римская империя в сравнительно недавнем прошлом. Этруски, завоевавшие Рим в 7 в. до н. э., испытали на себе влияние восточно-средиземноморских культур. Этим отчасти объясняется сходство основных принципов Римской и аттической систем счисления. Обе системы были десятичными, хотя в обеих системах счисления особую роль играло число пять. Обе системы использовали при записи чисел повторяющиеся символы.

Старыми римскими символами для обозначения чисел 1, 5, 10, 100 и 1000 были, соответственно, символы I, V, X, Θ (или ⊕, или ⊗) и Φ (или ↀ , или CIƆ). Хотя о первоначальном значении этих символов было написано много, их удовлетворительного объяснения у нас нет до сих пор. Согласно одной из распространенных теорий, римская цифра V изображает раскрытую руку с четырьмя прижатыми друг к другу пальцами и отставленным большим пальцем; символ X, согласно той же теории, изображает две скрещенные руки или сдвоенную цифру V. Символы чисел 100 и 1000, возможно, берут начало от греческих букв Θ и φ. Неизвестно, произошли ли более поздние обозначения C и M от старых римских символов или они акрофонически связаны с начальными буквами латинских слов, означавших 100 (центум) и 1000 (милле). Полагают, что римский символ числа 500, буква D, возник из половинки старого символа, обозначавшего 1000. Если не считать, что большинство римских символов скорее всего не были акрофоническими и что промежуточные символы для обозначения чисел 50 и 500 не были комбинациями символов чисел 5 и 10 или 5 и 100, то в остальном римская система счисления напоминала аттическую. Разумеется, в деталях они отличались. Римляне часто использовали принцип вычитания, поэтому иногда вместо VIIII использовали IX ,а XC вместо LXXXX; сравнительно позднее символ IV вместо IIII.

В целом римляне не были склонны заниматься математикой, поэтому не испытывали особой потребности в больших числах. Тем не менее для обозначения 10000 они эпизодически использовали символ CCIƆƆ , а для числа 100000 — символ CCCIƆƆƆ. Половинки этих символов иногда использовались для обозначения чисел 5000 (IƆƆ) и 50000 (IƆƆƆ).

Дробей римляне избегали так же упорно, как и больших чисел. В практических задачах, связанных с измерениями, они не использовали дроби, подразделяя единицу измерения обычно на 12 частей, с тем чтобы результат измерения представить в виде составного числа, суммы кратных различных единиц, как это делается сегодня, когда длину выражают в ярдах, футах и дюймах. Английские слова «ounce» (унция) и «inch» (дюйм) происходят от латинского слова лат. uncia (унция), обозначавшего одну двенадцатую основной единицы длины.^[1]^[2]

Число	Обозначение
1	I
2	II
3	III
4	IV, до XIX века — IIII
5	V
6	VI
7	VII
8	VIII
9	IX
10	X
11	XI
20	XX
30	XXX
40	XL
50	L
60	LX
70	LXX
80	LXXX
90	XC
100	C
200	CC
300	CCC
400	CD
500	D; IƆ
600	DC; IƆC
700	DCC; IƆCC
800	DCCC; IƆCCC
900	CM; CCIƆ
1000	M; ↀ; CIƆ
2000	MM; CIƆCIƆ
3000	MMM; CIƆCIƆCIƆ
3999	MMMCMXCIX
4000	MV; ↀↁ; CIƆIƆƆ
5000	V; ↁ; IƆƆ
6000	VM; ↁↀ; IƆƆCIƆ
7000	VMM; ↁↀↀ; IƆƆCIƆCIƆ
8000	VMMM; ↁↀↀↀ; IƆƆCIƆCIƆCIƆ
9000	IX^[3]; ↀↂ; CIƆCCIƆƆ
10 000	X; ↂ; CCIƆƆ
20 000	XX; ↂↂ; CCIƆƆCCIƆƆ
30 000	XXX; ↂↂↂ; CCIƆƆCCIƆƆCCIƆƆ
40 000	XL; ↂↇ; CCIƆƆIƆƆƆ
50 000	L; ↇ; IƆƆƆ
60 000	LX; ↇↂ; IƆƆƆCCIƆƆ
70 000	LXX; ↇↂↂ; IƆƆƆCCIƆƆCCIƆƆ
80 000	LXXX; ↇↂↂↂ; IƆƆƆCCIƆƆCCIƆƆCCIƆƆ
90 000	XC; ↂↈ; CCIƆƆCCCIƆƆƆ
100 000	C; ↈ; CCCIƆƆƆ
200 000	CC; ↈↈ; CCCIƆƆƆCCCIƆƆƆ
300 000	CCC; ↈↈↈ; CCCIƆƆƆCCCIƆƆƆCCCIƆƆƆ
400 000	CD; CCCIƆƆƆIƆƆƆƆ
500 000	D; IƆƆƆƆ
600 000	DC; IƆƆƆƆCCCIƆƆƆ
700 000	DCC; IƆƆƆƆCCCIƆƆƆCCCIƆƆƆ
800 000	DCCC; IƆƆƆƆCCCIƆƆƆCCCIƆƆƆCCCIƆƆƆ
900 000	CM; CI; CCCIƆƆƆCCCCIƆƆƆƆ
1 000 000	M; I; CCCCIƆƆƆƆ

Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.

В системе римских цифр отсутствует ноль, но ранее использовалось обозначение нуля как nulla (нет), nihil (ничто) и N (первая буква этих слов).

При этом некоторые из цифр (I, X, C, M) могут повторяться, но не более трёх раз подряд; таким образом, с их помощью можно записать любое целое число не более 3999 (MMMCMXCIX). В ранние периоды существовали знаки для обозначения бо́льших цифр — 5000, 10 000, 50 000 и 100 000^{[источник не указан 2981 день]} (тогда максимальное число по упомянутому правилу равно 399 999). При записи чисел в римской системе счисления меньшая цифра может стоять справа от большей; в этом случае она прибавляется к ней. Например, число 283 по-римски записывается как CCLXXXIII, то есть 100+100+50+30+3=283. Здесь цифра, изображающая сотню, повторена два раза, а цифры, изображающие соответственно десяток и единицу, повторены по три раза.

Пример: число 1988. Одна тысяча M, девять сотен CM, восемь десятков LXXX, восемь единиц VIII. Запишем их вместе: MCMLXXXVIII.

Довольно часто, чтобы выделить числа в тексте, над ними рисовали черту: LXIV. Иногда черту рисовали и сверху, и снизу: XXXII — в частности, так принято выделять римские цифры в русском рукописном тексте (в типографском наборе это не используют из-за технической сложности). У других авторов черта сверху могла обозначать увеличение значения цифры в 1000 раз: V = 5000.

Часы марки Tissot с традиционным написанием «IIII»

Повсеместно записывать число «четыре» как «IV» стали только в XIX веке, до этого наиболее часто употреблялась запись «IIII». Однако запись «IV» можно встретить уже в документах манускрипта «Forme of Cury», датируемых 1390 годом. На циферблатах часов в большинстве случаев традиционно используется «IIII» вместо «IV», главным образом, по эстетическим соображениям: такое написание обеспечивает визуальную симметрию с цифрами «VIII» на противоположной стороне, а перевёрнутую «IV» прочесть труднее, чем «IIII». Существует и версия, что IV на циферблате не писалось потому, что IV — первые буквы имени бога Юпитера (IVPITER).

Меньшая цифра может быть записана и слева от большей, тогда её следует вычесть из большей. При этом вычитаться могут только цифры, обозначающие 1 или степени 10, а в качестве уменьшаемого выступать только ближайшие в числовом ряду к вычитаемой две цифры (то есть вычитаемое, умноженное на 5 или 10). Повторения меньшей цифры не допускаются. Таким образом, существует только шесть вариантов использования «правила вычитания»:

IV = 4
IX = 9
XL = 40
XC = 90
CD = 400
CM = 900

Например, число 94 будет XCIV = 100 − 10 + 5 − 1 = 94 — так называемое «правило вычитания» (появилось в эпоху поздней античности, а до этого римляне писали число 4 как IIII, а число 40 — как XXXX).

Необходимо отметить, что другие способы «вычитания» недопустимы; так, число 99 должно быть записано как XCIX, но не как IC. Однако, в наши дни в некоторых случаях используется и упрощенная запись римских чисел: например, в программе Microsoft Excel при преобразовании арабских цифр в римские при помощи функции «РИМСКОЕ()» можно использовать несколько видов представления чисел, от классического до сильно упрощенного (так, число 499 может быть записано как CDXCIX, LDVLIV, XDIX, VDIV или ID). Упрощение состоит в том, что для уменьшения какой-либо цифры слева от неё может писаться любая другая цифра:

999. Тысяча (M), вычтем 1 (I), получим 999 (IM) вместо CMXCIX. Следствие: 1999 — MIM вместо MCMXCIX
95. Сто (C), вычтем 5 (V), получим 95 (VC) вместо XCV
1950: Тысяча (M), вычтем 50 (L), получим 950 (LM). Следствие: 1950 — MLM вместо MCML

Случаи такой записи чисел (как правило, годов) часто встречаются в титрах телесериалов США. Например, для года 1998: IIMM вместо MCMXCVIII.

С помощью римских цифр можно записывать и большие числа. Для этого над теми цифрами, которые обозначают тысячи, ставится черта, а над цифрами, которые обозначают миллионы, — двойная черта. Например, число 123123 будет выглядеть так:

CXXIIICXXIII

А миллион как I, но только не с одной, а с двумя чертами во главе: I

Символы со сходным начертанием: L · Լ · ℒ Символы со сходным начертанием: D · Д Символы со сходным начертанием: M · Μ · М · м · Ϻ · ℳ · ᛖ Символы со сходным начертанием: ʕ · Ҁ · ҁ · Ϟ · Ϛ · Ⴚ

Стандарт Юникода рекомендует использовать для представления римских цифр обычные латинские буквы.^[4] Тем не менее стандарт включает также специальные символы для римских цифр как часть Числовых форм (англ. Number Forms)^[5] в области знаков с кодами с U+2160 по U+2188. Например, MCMLXXXVIII может быть представлено в форме ⅯⅭⅯⅬⅩⅩⅩⅧ. Этот диапазон включает как строчные, так и прописные цифры для записи чисел от 1 (Ⅰ или I) до 12 (Ⅻ или XII), в том числе и комбинированные глифы для составных чисел, таких как 8 (Ⅷ или VIII), главным образом для обеспечения совместимости с восточноазиатскими наборами символов в таких промышленных стандартах, как JIS X 0213, где эти символы определены. Комбинированные глифы используются для представления чисел, которые ранее составлялись из отдельных символов (например, Ⅻ вместо его представления как Ⅹ и Ⅱ). В дополнение к этому, глифы существуют для архаичных^[5] форм записи чисел 1000, 5000, 10 000, большой обратной C (Ɔ), поздней формы записи 6 (ↅ, похожей на греческую стигму: Ϛ), ранней формы записи числа 50 (ↆ, похожей на стрелку, указывающую вниз ↓⫝⊥^[6]), 50 000, и 100 000. Следует отметить, что маленькая обратная c, ↄ не включена в символы римских цифр, но включена в стандарт Юникод как прописная клавдиева буква Ↄ.

Римские цифры в Юникоде
Код	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
Значение^[7]	1	2	3	4	5	6	7	8	9	10	11	12	50	100	500	1 000
U+2160	Ⅰ 2160	Ⅱ 2161	Ⅲ 2162	Ⅳ 2163	Ⅴ 2164	Ⅵ 2165	Ⅶ 2166	Ⅷ 2167	Ⅸ 2168	Ⅹ 2169	Ⅺ 216A	Ⅻ 216B	Ⅼ 216C	Ⅽ 216D	Ⅾ 216E	Ⅿ 216F
U+2170	ⅰ 2170	ⅱ 2171	ⅲ 2172	ⅳ 2173	ⅴ 2174	ⅵ 2175	ⅶ 2176	ⅷ 2177	ⅸ 2178	ⅹ 2179	ⅺ 217A	ⅻ 217B	ⅼ 217C	ⅽ 217D	ⅾ 217E	ⅿ 217F
Значение	1 000		5 000		10 000		100		6		50		50 000		100 000
U+2180	ↀ 2180		ↁ 2181		ↂ 2182		Ↄ 2183		ↅ 2185		ↆ 2186		ↇ 2187		ↈ 2188

Отображение всех этих символов требует наличия программного обеспечения, поддерживающего стандарт Юникод, и шрифта, содержащего соответствующие этим символам глифы (например, шрифт Universalia).

www.http-wikipediya.ru

Онлайн калькулятор решения систем уравнений – Решение систем уравнений — Калькулятор Онлайн

alexxlab / 19.12.201602.06.2019 / Школьная жизнь

Решение уравнений бесплатно — Калькулятор Онлайн

С подробным решением:

С быстрым решением:

Вы учитесь? Тогда данные сервисы должны хоть как-то вам помочь. Решение уравнений онлайн позволяет быть уверенным в правильности решения уравнения.
В каждом из разделов приведены различные виды способов для помощи Вам. Правила ввода уравнений везде читайте и должно получиться.
Вообще этот сделан только для помощи Вам. Вы должны сами научиться решать уравнения — это пригодится в жизни (поможет по жизни мыслить логически в финансовых, экономических и инженерных вопросах)
Данный сервис позволяет проверить свои решения на правильность

Это он-лайн сервис в один шаг:

Ввести уравнение с неизвестным x

Перейти: «Решение обычных уравнений с ответом» →

Это он-лайн сервис в один шаг:

Ввести дифференциальное уравнение с неизвестной функцией y

Перейти: «Дифференциальные уравнения с ответом» →

Это он-лайн сервис в один шаг:

Введите выражение, которое надо упростить

Перейти: Онлайн сервис «Упрощение выражений» →

Это он-лайн сервис в три шага:

Ввести множитель a при неизвестной x в квадрате
Ввести множитель b при неизвестной x
Ввести свободное слагаемое с

Перейти: Решение квадратных уравнений →

www.kontrolnaya-rabota.ru

Системы линейных уравнений | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

Система линейных уравнений состоит из нескольких (от двух) уравнений с количеством переменных не менее количества уравнений в системе. Например, если в уравнениях, из которых состоит система, три неизвестных – x, y и z, то уравнений в системе должно быть не менее трех. Если уравнений больше, чем неизвестных, то добавочные уравнения служат для проверки совместности системы – то есть, если корни, найденные в первых уравнениях, удовлетворяют добавочным уравнениям.

Уравнения в системе могут быть первой и второй степени, реже встречаются кубические уравнения в системах, а если таковые и попадаются, то, скорее всего, третья степень нивелируется при решении остальных уравнений.

Рассмотрим решение системы линейных уравнений на примере системы из двух уравнений первой степени. Первое, что нужно сделать в любой системе, это выбрать наиболее простое уравнение и выразить в нем одну переменную через другие, то есть сделать так, чтобы справа от знака «равно» осталась только одна неизвестная с единичным коэффициентом. Затем, полученное для этой неизвестной выражение нужно подставить вместо нее во второе уравнение, и продолжить так, пока в последнем (или нет) уравнении не останется только одна неизвестная. Уравнение первой или второй степени с одной неизвестной решается согласно алгоритму, приведенному в соответствующем разделе. Найдя одну из переменных, возвращаемся в обратном порядке к первому уравнения, вычисляя все остальные.

Если есть добавочные уравнения, осуществляем проверку корней в них.

Существуют и другие способы решения систем линейных уравнений, более непостоянные и требующие внимательного подхода к заданным уравнениям, тем не менее, метод подстановки остается самым простым и действенным для любых систем уравнений.

Он-лайн калькулятор решения систем линейных уравнений вычисляет сразу готовый результат в виде корней уравнения, по введенным в него исходным коэффициентам и количеству переменных/уравнений.

geleot.ru

Решить систему уравнений онлайн

Системы уравнений с параметром решаются такими же стандартными методами, что и обычные. Хотя часто они вызывают сложности у учеников, разобравшись подробно в том, как это делать вы сможете решать системы уравнений легко и просто. Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Для их решения применяют метод подстановки, метод сложения уравнений, графический метод. Обладая знаниями графической интерпретации линейных систем, есть возможность быстро определить количество корней или их отсутствие.

Так же читайте нашу статью «Решить уравнения с синусом и косинусом онлайн»

Решим следующий пример:

\[\left\{\begin{matrix} x + (a^2 — 3)y = a\\ x + y = 2 \end{matrix}\right.\]

Данный пример можно решить двумя способами:

1. Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов \[ (а/a_1 = b/b_1 \ne c/c_1) \]. Тогда имеем:

\[\left\{\begin{matrix} а^2 — 3 = 1\\ а \ne 2\end{matrix}\right.\]

Из первого уравнения \[а^2 = 4\], поэтому с учетом условия, что \[а \ne 2,\] получаем ответ.

Ответ: \[а = -2.\]

2. Использование метода подстановки:

\[\left\{\begin{matrix}2 — у + (а^2 — 3)у = а\\ х = 2 — у \end{matrix}\right.\]

После вынесения в первом уравнении общего множителя у за скобки, получим:

\[\left\{\begin{matrix}(а^2 — 4)у = а — 2\\ х = 2 — у \end{matrix}\right.\]

Система не имеет решений, если первое уравнение не будет иметь решений, то есть

\[\left\{\begin{matrix} а^2 — 4 = 0\\ а — 2 \ne 0 \end{matrix}\right.\]

Очевидно, что \[а = \pm 2\], но с учетом второго условия в ответ идет только ответ с минусом.

Ответ: \[а = -2.\]

Как решать систему уравнений онлайн решателем?

Решить уравнение вы можете на нашем сайте pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто вdести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

Найти интервал сходимости степенного ряда онлайн – Радиус сходимости степенного ряда онлайн · Как пользоваться Контрольная Работа РУ

alexxlab / 18.12.201602.06.2019 / Школьная жизнь

Степенные ряды. Сходимость степенного ряда. Область сходимости ряда.

Степенные ряды на Math34.biz для практических занятий с целью закрепления пройденного материала. И оттачивания навыков студентов для того, чтобы научиться однозначно определять сходимость степенного ряда. Практические занятия в полной мере дают желаемый результат, если в курсе по изучению выделено достаточное количество занятий. Это в полной мере обеспечит высококлассную подготовку учащихся. Но что делать, когда их нет? В этом случае решить степенные ряды онлайн поможет как раз наш сайт, или аналогичный ресурс. Однако не всегда подобные калькуляторы смогут предоставить правильный ответ на поставленную задачу. Как раз для этого на примере одного условия нужно сравнить полученные ответы между решениями подобных сайтов. Можно заметить, что область сходимости ряда вычисляется порой по разным теоремам и ответ, хоть он и правильный, но может быть выражен отличными формами записи. Конечно, такое не будет считаться ошибкой, все дело в том, как именно вам будет удобнее его воспринимать. Короче говоря, найти сходимость степенного ряда с помощью того или иного сайта, решать вам, то есть как будет вам удобно для дальнейших применений ответа. Иногда само решение степенного ряда выражают через записи со знаками неравенств, а чаще всего через знак модуля. Это не случайно, поскольку на практике используют наиболее чаще приемы сравнений общих членов ряда с использованием модулей. Через ряд преобразований выделяют переменную, заключенную в модуль, и остается краткая запись, которая нормально воспринимается для понимания решения. Для наглядного представления радиус сходимости ряда можно представить на числовой оси с указанием граничных точек, это, кстати, тоже приветствуется в ряде случаев. Не нужно загонять себя в какие-то определенные рамки, которые сузят ваш кругозор. Вообще-то говоря, степенные ряды важная тема в математике, поскольку сложная и для того, чтобы её понять, вам придется изучить несколько курсов. Например, теорию предельного перехода и интегральное исчисление, поскольку для доказательства сходимости степенного ряда часто используют именно такие приемы, в которых присутствуют эти действия. Для вас мы предлагаем пройти практические занятия, и проверит свои знаний по изучению степенных рядов онлайн прямо на Math34.biz, поскольку мы даем гарантию, что все решаемые задачи выдаются с точным ответом, в считанные секунды и абсолютно бесплатно в режиме реального времени. Помимо области сходимости ряда, или как её еще называют радиус сходимости ряда, мы предлагаем вашему вниманию много других сопутствующих калькуляторов, которые вы, безусловно, оцените на высочайшем уровне. Если требуется найти сходимость степенного ряда, то предоставьте это сделать за вас именно нам, поскольку Math34.biz есть залог точности и гарантия безупречного качественного ответа. Многие студенты не редко задаются таким вопросом как быстрая подготовка в решении степенного ряда, но не просто решение, а качественное и правильное. Во все времена степенные ряды носили более обширный смысл, чем об этом сейчас рассказывают ученикам. Оно и понятно, потому что объясняется это тем, что нет времени в связи с необходимостью глубокого изучения более важные тем. С одной стороны — ДА, но тогда означает ли это, что можно пренебрегать сходимостью степенного ряда? Скорее всего, нет, так как, не изучив должным образом степенные ряды онлайн, вы попросту не сможете грамотно ответить на очевидные вопросы на защите курсовой или дипломной работы. Допустим, ваша предметная область включает такую дисциплину как механика сплошных сред или строительная механика. Очевидно, что устойчивость систем важна при проектировании стратегических объектов, тем более, если это напрямую касается охраны жизнедеятельности людей. Казалось бы, что можно вынести полезного, если научиться или хотя бы понять суть как находить область сходимости ряда? Трудно в одном предложении передать важность этого определения. Но поверьте на слово, найти сходимость степенного ряда такая же важная и необходимая процедура, как, к примеру, знать теорему Пифагора. Если решение степенного ряда будет выполнено с ошибкой, то в дальнейших расчетах обязательно это сыграет злую шутку со студентом. Бывает порой, что из-за досадной неточности в ошибке происходит крушение летательного аппарата уже на первых испытаниях. Согласитесь, это обидно после проделанных работ и колоссального вклада времени. Поэтому учитесь и еще раз учитесь находить радиус сходимости ряда, прививая тем самым с самого начала правильность т строгость в решении задач. Вернемся к теме степенные ряды и расскажем немного об этом разделе подробнее. В практике множество степенных рядов начинаются именно с первого члена, хотя встречаются такие ряды, в условии которых первый член может начаться и со второго, и с третьего члена. Во многом это связано с тем, что, например, начиная с первого члена, сразу обращается в бесконечность вся сумма ряда, что конечно тривиально, по сути. Сходимость степенного ряда как предмет изучения области его сходимости, на практике применяется не часто, особенно студентами, если они не проходят её на кафедре математического анализа. Суть ясна и задачи все расставлены. Наш калькулятор вычисляет степенные ряды онлайн, а также говорит о сходимости ряда, по какому признаку числовой ряд сходится, короче говоря, умеет определять сходимость степенных рядов. Попасть в область сходимости ряда переменная может, если удовлетворяет конкретному единственному условию, то есть чтобы соответствующий получившийся при этом числовой ряд сходился к конечному действительному числовому значению. Пожалуй, это не одно условие, нужно также, чтобы все члены ряда при любом порядковом натуральном значении параметра n существовал и однозначно определялся. Найти сходимость степенного ряда означает определить область его сходимости на числовой оси абсцисс, если речь идет о декартовой системе координат. Такое сделать представляется возможным по признаку Даламбера, однако, нужно понимать, что лишь по признаку, так как сам принцип устанавливает лишь интервал, в который попадет переменная. Помните, для функциональных рядов признак Даламбера не применим, он только для числовых рядов. Решение степенного ряда напрямую связано с нахождением радиуса сходимости этого ряда, но для краткости выражаются именно так. Мы тоже будем применять этот термин, дабы не отставать от тенденции в научном мире. Степенные ряды в граничных точках изучаются отдельно. Разумеется, это есть часть общей задачи по исследованию на сходимость степенного ряда. В этих граничных точках ряд исследуется как числовой — знакопостоянный или знакопеременный, в зависимости от вида общего члена ряда. Ряды, членами которых являются степенные функции, называются степенными рядами, а калькулятор может решать их онлайн. Когда так говорят, сразу приходит на ум следующее предположение, а если членами ряда будут являться периодические функции, то такой ряд наверно должен называться функциональным периодическим рядом! Забавное дело получается, но все очень серьезно. Когда мы определили область сходимости ряда, необходимо после этого проделать завершающие вычисления, а именно исследовать числовые ряды на сходимость, которые получаются путем подстановок границ определенного интервала вместо переменной x степенного ряда. Дальше сможете написать полноценный ответ с решением. Рассмотрим пример, как можно найти сходимость степенного ряда без применения основных теорем, а лишь сравнительным способом. При этом нужно грамотно составлять сравнения двух функциональных рядов до тех пор, пока не упростим исходный ряд до давно изученного элементарного. По этому принципу возьмем за ответ как раз результат давно известный всем наперед. По решению степенного ряда еще не однозначно можно предположить, какой же точно будет радиус сходимости ряда, поскольку перед этим еще надо произвести исследование как минимум двух числовых рядов на каждой из границ интервала. Однако это второстепенно и в этом вам сможет помочь калькулятор онлайн Math34.biz совершенно бесплатно. По виду все степенные ряды одинаковы тем, что их общий член представляет собой обычную функцию от аргумента. Суть изучения состоит как раз в том, чтобы определить допустимые значения этого аргумента для сходимости ряда (условной или безусловной), а также на каких интервалах соответствующий ему уже числовой ряд будет расходиться. Исследование степенного ряда на сходимость отнимает у вас уйму времени, и мы рекомендуем вам использовать готовый калькулятор Math34.biz. Нужно исследовать и границы интервала тоже, в противном случае задачу будет выполнена не полностью, а значит, гарантировано снимут два балла. На нашем сайте вы можете вычислить сумму степенных рядов онлайн. Всегда быстро, надежно, а главное бесплатно! Удобный интерфейс и понятный запрос данных. Разложение функций в степенные ряды очень просто только с нами на Math34.biz. По праву область сходимости ряда есть конкретное условие существования суммы ряда числового. Если значение на границе интервала дает расхождение полученного знакопеременного ряда. то говорят, что ряд сходится условно, то есть он конечно сходится в этой области, но при определенных условиях, что немаловажно в любом случае. Если абстрагироваться от понятия степенного ряда, и на миг просто представить себе сумму степенного ряда как некую функцию по переменной x, то речь уже пойдет не о том, чтобы найти сходимость степенного ряда, а об определении таких условий, при которых будет существовать значение функции при разных значениях её аргумента x. Короче говоря, задачу сведем к простейшему нахождению области определения функции. Правда ведь очень просто и понятно! Любое решение степенного ряда всегда говорит о радиусе сходимости такого степенного ряда и обычно определяется через признак Даламбера, но не напрямую, а лишь с условием. После этого раскрывают модуль полученного неравенства и исследуют числовые ряды на абсолютную или условную сходимость. Потом делают вывод. Очень интересно, когда степенные ряды в первоначальном виде интегрируются или дифференцируются, а потом уже вычисляется сумма ряда от нового степенного ряда. Отсюда следуют много вариантов как себя ведет ряд при тех или иных условиях. Найденная сумма степенного ряда от проинтегрированных членов исходного ряда, есть, по сути, проинтегрированная сумма исходного степенного ряда. Интересно и познавательно, не правда ли? Если грамотно сформулировать текст задачи, то он выглядит примерно так: найти интервал сходимости степенного ряда и исследовать его на границах найденного интервала. Отсюда ряд может сходиться или расходиться абсолютно, что не требует дополнительных исследований. Равномерная сходимость показывает степенные ряды в онлайн вычислении, складывая поочередно все члены исходного ряда, записанного в классическом виде, как в университете. Полагаясь только на свое чутье, студент рискует по неопытности попасть в ловушку своей самоуверенности, когда проще простого взять и воспользоваться калькулятором Math34.biz в самом начале учебы. Из области сходимости ряда делают выводы о сходимости функционального, а точнее степенного ряда, а именно устанавливают сходиться он либо условно, либо абсолютно. Все это необходимо для завершающей записи конечного ответа. Не усложняя ситуацию и не применяя названия сложных теорем, скажем, что найти сходимость степенного ряда будет проще для понимания, если представить в качестве суммы ряда некую функцию и уже исследовать именно ее. А это всем давно ясно и понятно как делать! Радиус сходимости ряда и решение степенного ряда понятия тождественные, так как означают одно и то же, точнее определяют однозначно ту область, значения переменной из которой дает сходимость соответственного числового ряда.

math24.biz

∑ Сумма ряда онлайн

Введите данные для подчета суммы ряда

Найдем сумму ряда чисел. Если не получается ее найти, то система вычисляет сумму ряда с определенной точностью.

Сходимость ряда

Данный калькулятор умеет определять — сходится ли ряд, также показывает — какие признаки сходимости срабатывают, а какие — нет.

Также умеет определять сходимость степенных рядов.

Также строится график ряда, где можно увидеть скорость сходимости ряда (или расходимости).

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x): Абсолютное значение x
(модуль x или |x|)
arccos(x): Функция — арккосинус от x
arccosh(x): Арккосинус гиперболический от x
arcsin(x): Арксинус от x
arcsinh(x): Арксинус гиперболический от x
arctg(x): Функция — арктангенс от x
arctgh(x): Арктангенс гиперболический от x
e: e число, которое примерно равно 2.7
exp(x): Функция — экспонента от x (что и e^x)
log(x) or ln(x): Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
pi: Число — «Пи», которое примерно равно 3.14
sin(x): Функция — Синус от x
cos(x): Функция — Косинус от x
sinh(x): Функция — Синус гиперболический от x
cosh(x): Функция — Косинус гиперболический от x
sqrt(x): Функция — квадратный корень из x
sqr(x) или x^2: Функция — Квадрат x
tg(x): Функция — Тангенс от x
tgh(x): Функция — Тангенс гиперболический от x
cbrt(x): Функция — кубический корень из x
floor(x): Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
sign(x): Функция — Знак x
erf(x): Функция ошибок (Лапласа или интеграл вероятности)

В выражениях можно применять следующие операции:

Действительные числа: вводить в виде 7.5, не 7,5
2*x: — умножение
3/x: — деление
x^3: — возведение в степень
x + 7: — сложение
x — 6: — вычитание

www.kontrolnaya-rabota.ru

Сходимость степенного ряда — радиус и область сходимости. Решение задач по высшей математике

Функциональным рядом называется ряд вида:

где – функции, определенные на некотором множестве .

Множество всех точек сходимости ряда (*) называется его областью сходимости.

В области сходимости определены функции:

( n-я частичная сумма ряда)

(сумма ряда)

(остаток ряда)

Ряд

называется абсолютно сходящимся, если сходится ряд

Из всех функциональных рядов наиболее часто применяют степенные ряды, которыми называют ряды вида

Действительные числа называют коэффициентами ряда.

Неотрицательное число , такое, что ряд (**) сходится в интервале и расходится вне этого интервала, называется радиусом сходимости этого ряда, а интервал – интервалом сходимости ряда.

Радиус сходимости степенного ряда можно найти по формулам:

или

Свойства степенных рядов

1. Сумма степенного ряда при всех значениях из интервала сходимости есть непрерывная функция.

2. Степенной ряд в его интервале сходимости можно почленно дифференцировать, то есть:

3. Степенной ряд можно интегрировать по любому отрезку, содержащемуся в интервале сходимости, причем:

100task.ru

Степенные ряды, их сходимость, разложение функций в степенные ряды

Среди функциональных рядов наиболее важное место занимают степенные ряды.

Степенным рядом называют ряд

члены которого – степенные функции, расположенные по возрастающим целым неотрицательным степеням x, а c0, c1, c2, cn — постоянные величины. Числа c1, c2, cn — коэффициенты членов ряда, c0 — свободный член. Члены степенного ряда определены на всей числовой прямой.

Ознакомимся с понятием области сходимости степенного ряда. Это множество значений переменной x, для которых ряд сходится. Степенные ряды имеют довольно простую область сходимости. Для действительных значений переменной x область сходимости состоит либо из одной точки, либо является некоторым интервалом (интервалом сходимости), либо совпадает со всей осью Ox.

При подстановке в степенной ряд значения x = 0 получится числовой ряд

c0+0+0+…+0+…,

который сходится.

Следовательно, при x = 0 сходится любой степенной ряд и, значит, область его сходимости не может быть пустым множеством. Структура области сходимости всех степенных рядов одинакова. Её можно установить с помощью следующей теоремы.

Теорема 1 (теорема Абеля). Если степенной ряд сходится при некотором значении x = x0, отличном от нуля, то он сходится, и притом абсолютно, при всех значениях |x| < |x0|. Обратите внимание: и отправное значение «икс нулевое» и любое значение «икса», которое сравнивается с отправным, взяты по модулю — без учёта знака.

Следствие. Если степенной ряд расходится при некотором значении x = x1, то он расходится и при всех значениях |x| > |x1|.

Как мы уже выяснили ранее, любой степенной ряд сходится при значении x = 0. Есть степенные ряды, которые сходятся только при x = 0 и расходятся при остальных значениях х. Исключая из рассмотрения этот случай, предположим, что степенной ряд сходится при некотором значении x = x0, отличном от нуля. Тогда, по теореме Абеля, он сходится во всех точках интервала ]-|x0|, |x0|[ (интервала, левой и правой границами которого являются значения икса, при котором степенной ряд сходится, взятые соответственно со знаком минус и со знаком плюс), симметричного относительно начала координат.

Если же степенной ряд расходится при некотором значении x = x1, то на основании следствия из теоремы Абеля он расходится и во всех точках вне отрезка [-|x1|, |x1|]. Отсюда следует, что для любого степенного ряда имеется интервал , симметричный относительно начала координат, называемый интервалом сходимости, в каждой точке которого ряд сходится, на границах может сходиться, а может и расходиться, при чем не обязательно одновременно, а вне отрезка ряд расходится. Число R называется радиусом сходимости степенного ряда.

В частных случаях интервал сходимости степенного ряда может вырождаться в точку (тогда ряд сходится только при x = 0 и считается, что R = 0) или представлять собой всю числовую прямую (тогда ряд сходится во всех точках числовой прямой и считается, что ).

Таким образом, определение области сходимости степенного ряда заключается в определении его радиуса сходимости R и исследовании сходимости ряда на границах интервала сходимости (при ).

Теорема 2. Если все коэффициенты степенного ряда, начиная с некоторого, отличны от нуля, то его радиус сходимости равен пределу при отношения абсолютных величин коэффициентов общего следующего за ним членов ряда, т.е..

(28)

Пример 1. Найти область сходимости степенного ряда

Решение. Здесь

т.е.

Используя формулу (28), найдём радиус сходимости данного ряда:

Исследуем сходимость ряда на концах интервала сходимости . В примере 13 показано, что данный ряд сходится при x = 1 и расходится при x = -1. Следовательно, областью сходимости служит полуинтервал .

Пример 2. Найти область сходимости степенного ряда

Решение. Коэффициенты ряда положительны, причём

Имеем

Найдём предел этого отношения, т.е. радиус сходимости степенного ряда:

Исследуем сходимость ряда на концах интервала . Подстановка значений x = -1/5 и x = 1/5 в данный ряд даёт:

Первый из этих рядов сходится (см. пример 5). Но тогда в силу теоремы параграфа «Абсолютная сходимость» сходится и второй ряд, а область его сходимости – отрезок

Пример 3. Найти область сходимости степенного ряда

Решение. Здесь

По формуле (28) находим радиус сходимости ряда:

Исследуем сходимость ряда при значениях . Подставив их в данный ряд, соответственно получим

Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при ). Итак, на обоих концах интервала сходимости данный ряд расходится, а область его сходимости – интервал .

Пример 4. Найти область сходимости степенного ряда

Решение. Здесь , а

Найдём отношение

Следовательно, радиус сходимости ряда

то есть ряд сходится при любом конечном значении x. Область его сходимости – бесконечный интервал .

Пример 5. Найти область сходимости степенного ряда

Решение. Находимо отношение , где , а :

Согласно формуле (28) радиус сходимости данного ряда

то есть ряд сходится только при x = 0 и расходится при остальных значениях х.

Примеры показывают, что на концах интервала сходимости ряды ведут себя различно. В примере 1 на одном конце интервала сходимости ряд сходится, а на другом – расходится, в примере 2 – на обоих концах сходится, в примере 3 – на обоих концах расходится.

Формула радиуса сходимости степенного ряда получена в предположении, что все коэффициенты членов ряда, начиная с некоторого, отличны от нуля. Поэтому применение формулы (28) допустимо только в этих случаях. Если это условие нарушается, то радиус сходимости степенного ряда следует искать с помощью признака Даламбера, или же, сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется.

Пусть для степенного ряда

(29)

радиус сходимости R > 0, т.е. этот ряд сходится на интервале .

Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f(x), можем записать равенство

(30)

понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции f(x) в этой точке. В этом же смысле будем говорить, что степенной ряд (29) сходится к функции f(x) на интервале сходимости.

Вне интервала сходимости равенство (30) не имеет смысла.

Можно доказать, что сумма степенного ряда f(x) непрерывна и дифференцируема на любом отрезке внутри интервала сходимости, в частности в любой точке интервала сходимости ряда.

Приведем теоремы о почленном дифференцировании и интегрировании степенных рядов.

Теорема 1. Степенной ряд (30) в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что исходный ряд, а суммы их соответственно равны .

Теорема 2. Степенной ряд (30) можно неограниченное число раз почленно интегрировать в пределах от 0 до х, если , причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны

Пусть дана функция f(x), которую требуется разложить в степенной ряд, т.е. представить в виде (30):

Задача состоит в определении коэффициентов ряда (30). Для этого, дифференцируя равенство (30) почленно, последовательно найдём:

……………………………………………….. (31)

Полагая в равенствах (30) и (31) х = 0, находим

Тогда

Подставляя найденные выражения в равенство (30), получим

(32)

Это разложение функции f(x) в ряд называется рядом Маклорена.

Найдём разложение в ряд Маклорена некоторых элементарных функций.

Пример 8. Разложить в ряд Маклорена функцию

Решение. Производные этой функции совпадают с самой функцией:

Поэтому при х = 0 имеем

Подставляя эти значения в формулу (32), получим искомое разложение:

(33)

Этот ряд сходится на всей числовой прямой (его радиус сходимости ).

Пример 9. Разложить в ряд Маклорена функции: 1) f(x) = sin x; 2) f(x) = cos x.

Решение.

1)Находим производные функции f(x) = sin x; имеем

Так как производная четвёртого порядка совпадает с функцией, то производные следующих порядков повторяются в той же последовательности. Найдём значения функции и её производных при х = 0:

Поэтому ряд Маклорена для f(x) = sin x имеет вид

(34)

2) Находим

производные следующих порядков повторяются в той же последовательности. Далее, имеем

В результате получаем следующее разложение функции f(x) = cos x в ряд Маклорена:

Разложить функцию в ряд Маклорена самостоятельно, а затем посмотреть решение

Пример 11. Разложить в ряд Маклорена функцию

Решение. Находим производные данной функции:

…………………………………….……..

(при n < m). Необходимо различать две возможности для показателя степени m. Если m – целое положительное число, то при n = m получим

т.е. постоянную величину, а потому производные следующих порядков равны нулю. Найдём значения функции и её производных при x = 0:

Подставляя эти значения в формулу (32), после упрощений получим

Это не ряд, а сумма, состоящая из конечного числа слагаемых и представляющая собой известное разложение бинома Ньютона.

Если же показатель m не является целым положительным числом, то производные в нуль не обратятся. Найденное выше выражение для производной n-го порядка справедливо для любого . При х = 0 получаем

Подстановка значений функции и её производных в равенство (32) в этом случае даёт

(35)

Полученный ряд называется биномиальным. Найдём его интервал сходимости. Так как коэффициенты этого ряда

то их отношение после упрощения принимает вид

Находим предел абсолютной величины этого отношения при :

Итак, радиус сходимости биномиального ряда R = 1, а — его интервал сходимости.

Всё по теме «Ряды»

function-x.ru

Радиус и область сходимости ряда

Степенные и функциональные ряды могут быть сходящимися на множестве действительных чисел, на определенном интервале, или быть расходящимися. Установка радиуса сходимости и области сходимости ряда является важным при исследовании рядов. Радиус сходимости равный половине ширины области сходимости. На практике обе характеристики найти не трудно и Вы в этом скоро убедитесь.

Пример: 3.6 Найти радиус сходимости и область сходимости степенных рядов:
а)
Вычисления: Для оценки сходимости ряда составим ряд с модулей членов заданного ряда, то есть ряд с последующим общим членом

Далее, исходя с того что полученный ряд имеет положительные члены — исследовать его на сходимость будем с помощью признака Даламбера:

Для этого выписываем следующий после общего член ряда

и подставляем в формулу предела. Вид членов ряда непрост, поэтому будьте внимательны при упрощении предела

Наконец приходим к экспоненте и функциональному множителю.
Если граница меньше единицы

то ряд сходится по теореме Даламбера, причем абсолютно.
Отсюда составляем ограничения на допустимые «иксы»

— область сходимости ряда.
Итак, ми нашли — радиус сходимости и
— область сходимости ряда в виде интервала.
Для себя запомните, что радиус сходимости функционального ряда равен половине расстояния между крайними точками области сходимости.
б)
Вычисления: Составим ряд из модулей членов заданного ряда, то есть с общим членом

Нетрудно видеть что такой прием позволяет получить ряд с положительными членами и при этом исследовать его на сходимость с помощью признака Даламбера.
Для предела нам еще нужен следующий член ряда

Подставляем члены ряда в предел и вычисляем

При пределе меньшей единицы — ряд убывает за Даламбером.
Из этого условия находим
— область сходимости в виде ограничений переменной.
В итоге мы нашли R=4 — радиус сходимости ряда и его область сходимости

Пример: 3.11 Найти радиус сходимости и область сходимости степенного ряда:
а)
Вычисления: Члены заданного функционального ряда

определены на всей действительной оси, то есть область определения следующая

Составляем ряд из модулей членов заданного ряда

Его общий член может бить выражен формулой

Поскольку новый ряд имеет положительные члены — исследуем на сходимость по Даламберу:

При — ряд совпадает по теореме Даламбера, то есть необходимо, чтобы выполнялись условия

Отсюда находим R = 2 — радиус сходимости ряда и (0; 4) — область сходимости.
б)

Вычисления: Члены заданного функционального ряда

определены для всех действительных переменных то есть область определения следующая

Составим ряд из модулей членов заданного ряда

Снова применяем признак Даламбера для исследования ряда на сходимость

За Даламбером при пределе меньше единицы — ряд убывает.
Отсюда находим область сходимости

и R=1/3 радиус сходимости. Из приведенных примеров
Вы могли увидеть такую закономерность что значение которое ограничивает модуль с переменной и является радиусом сходимости ряда.
Область сходимости имеет в два раза большую длину и определяется раскрытием модуля.

Пример: 3.17 Найти радиус сходимости и область сходимости степенных рядов:
а)
Вычисления: Члены функционального ряда

определены при то есть
Составим ряд из модулей членов заданного ряда

то есть

Исследуем его на сходимость по признаку Даламбера. Выписываем следующий после общего члена ряда

и подставляем в предел

При 3|x|<1 — ряд убывает,
отсюда находим
– область сходимости ряда.
Все что находится справа от модуля это R = 1/3 — радиус сходимости ряда, а ограничения на «икс»
– это область сходимости.
б)
Вычисления: Члены функционального ряда

определены на всей действительной прямой , их область определения имеет вид .
По схеме составляем ряд из модулей членов заданного ряда

и получаем ряд со следующим общим членом

Образованный ряд будем анализировать на сходимость по признаку Даламбера
Выписываем следующий член ряда

и подставляем в предел

При 2|x|<1- ряд будет сходящимся.
Раскрываем модуль и находим
— область сходимости и R=1/2 – радиус сходимости.
В виде интервала записываем область сходимости ряда

Пример: 3.27 Найти радиус сходимости и область сходимости степенного ряда
а)
Вычисления: Члены функционального ряда определены на действительной оси
Сначала составим ряд из модулей членов этого ряда

Общий член задается формулой

Исследуем ряд с модулей на сходимость по признаку Даламбера:
Находим предел отношения следующего члена ряда общему

Поскольку A=0<1 то ряд сходится при всех действительных переменных, то есть имеет неограниченную — область сходимости.
Ряд имеет бесконечный радиус сходимости.
б)
Вычисления: Члены ряда определены на множестве действительных чисел

Построим ряд с модулей членов ряда:

Далее записываем общий и следующий после него члены ряда

и подставляем в предел

По теореме Даламбера ряд сходится при
3|x|<1. Из этого условия определяем
— область сходимости ряда
и R=1/3 – радиус сходимости.
В виде интервала записываем в ответ область сходимости
Теперь Вы знаете как найти область сходимости и радиус сходимости ряда. Пользуйтесь приведенными формулами и успешной Вам сдачи сессии.

yukhym.com

Область сходимости степенного ряда. Примеры решения задач

Область сходимости степенного ряда

Задача Найти область сходимости степенного ряда Решение
   Заданный ряд является степенным рядом.
   Согласно признаку Даламбера, для абсолютной сходимости ряда достаточно, чтобы .
   Для решаемой задачи , .
   Так как , то ряд будет абсолютно сходиться при значениях , удовлетворяющих неравенству .
   Решением этого неравенства является интервал , следовательно, при исследуемый степенной ряд будет абсолютно сходиться.
   Исследуем поведение ряда на концах интервала, то есть при и .
   При получаем числовой ряд . Это знакочередующийся ряд, удовлетворяющий условиям теоремы Лейбница: , . Поэтому ряд сходится, и граница интервала принадлежит области сходимости. В область абсолютной сходимости ряда эта граница не входит, так как ряд расходится.
   При получаем числовой ряд . Это гармонический ряд, и он расходится. Следовательно, граница интервала не принадлежит области сходимости степенного ряда.

Итак, областью сходимости степенного ряда является полуинтервал

, а областью абсолютной сходимости степенного ряда является интервал

www.matem96.ru

Найти интервал сходимости степенного ряда — 6 Мая 2013 — Примеры решений задач

Пример на сходимость степенного ряда

Найти интервал сходимости степенного ряда

Решение. Применяя признак Даламбера

Согласно признака Даламбера, на данном интервале ряд сходится абсолютно.

При x=-√2/3,

Согласно принципа Лейбница, ряд сходится условно.

При x=√2/3

Ряд расходится.

И так, получаем, интервал сходимости

www.reshim.su

Матрицу как решать – Матрицы примеры решения задач, формулы и онлайн калькуляторы

alexxlab / 17.12.201602.06.2019 / Школьная жизнь

Матрицы примеры решения задач, формулы и онлайн калькуляторы

Задание. Вычислить $A B$ и $B A$, если $A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right), B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)$

Решение. Так как $A=A_{3 \times 2}$ , а $B=B_{2 \times 2}$ , то произведение возможно и результатом операции умножения будет матрица $C=C_{3 \times 2}$ , а это матрица вида $C=\left( \begin{array}{cc}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right)$ .

Вычисли элементы матрицы $C$ :

$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $

$ c_{12}=a_{11} \cdot b_{12}+a_{12} \cdot b_{22}=1 \cdot 1+(-1) \cdot 0=1 $

$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $

$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $

$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $

$ c_{31}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $

Итак, $C=A B=\left( \begin{array}{rl}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ .

Выполним произведения в более компактном виде:

$=\left( \begin{array}{rrr}{1 \cdot 1+(-1) \cdot 2} & {1 \cdot 1+(-1) \cdot 0} \\ {2 \cdot 1+0 \cdot 2} & {2 \cdot 1+0 \cdot 0} \\ {3 \cdot 1+0 \cdot 2} & {3 \cdot 1+0 \cdot 0}\end{array}\right)=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$

Найдем теперь произведение $D=B A=B_{2 \times 2} \cdot A_{3 \times 2}$. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.

Ответ. $A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы $B$ не совпадает с количеством строк матрицы $A$ .

www.webmath.ru

Решение уравнений методом обратной матрицы

Метод обратной матрицы используется при решении систем линейных алгебраических уравнений, если число неизвестных равно числу уравнений.

Суть метода

Пусть задана система линейных уравнений с неизвестными:

Эту систему можно записать в виде матричного уравнения ,

где – матрица системы,

– столбец неизвестных,

– столбец свободных коэффициентов.

Из полученного матричного уравнения необходимо выразить . Для этого умножим обе части матричного уравнения слева на , получим:

Так как , то или .

Далее находится обратная матрица и умножается на столбец свободных членов .

ЗАМЕЧАНИЕ Обратная матрица к матрице существует только при условии, что . Поэтому при решении системы линейных уравнений методом обратной матрицы в первую очередь вычисляется . Если , то система имеет единственное решение, которое можно найти методом обратной матрицы, если же , то методом обратной матрицы решить эту систему нельзя.

Пример решения методом обратной матрицы

ПРИМЕР 1

Задание

Решить систему линейных уравнений методом обратной матрицы

Решение

Данная система уравнений может быть записана матричным уравнением

где , , .

Выразив из этого уравнения , получим

Найдем определитель матрицы :

Так как , то система имеет единственное решение, которое можно найти методом обратной матрицы.

Найдем обратную матрицу с помощью союзной матрицы. Вычислим алгебраические дополнения к соответствующим элементам матрицы :

Запишем союзную матрицу , составленную из алгебраических дополнений элементов матрицы :

Далее запишем обратную матрицу согласно формуле . Будем иметь:

Умножая обратную матрицу на столбец свободных членов , получим искомое решение исходной системы:

Ответ

Решение матричных уравнений: теория и примеры

Матричным уравнением называется уравнение вида

A ⋅ X = B

или

X ⋅ A = B,

где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.

Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B, обе его части следует умножить на обратную к A матрицу слева:

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому

Так как E — единичная матрица, то E ⋅ X = X. В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A, слева, на матрицу B:

Как решить матричное уравнение во втором случае? Если дано уравнение

X ⋅ A = B,

то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A, и умножать матрицу B на неё справа:

Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X. То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A.

Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

A ⋅ X ⋅ B = C,

является

Пример 1. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

Найдём алгебраические дополнения матрицы A:

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A:

Наконец, находим неизвестную матрицу:

Решить матричное уравнение самостоятельно, а затем посмотреть решение

Пример 3. Решить матричное уравнение

Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

Найдём алгебраические дополнения матрицы A:

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

Находим матрицу, обратную матрице A:

Находим неизвестную матрицу:

До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.

Пример 4. Решить матричное уравнение

Решение. Это уравнение первого вида: A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

Найдём алгебраические дополнения матрицы A:

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

Находим матрицу, обратную матрице A, и делаем это легко, так как определитель матрицы A равен единице:

Находим неизвестную матрицу:

Пример 5. Решить матричное уравнение

Сначала найдём определитель матрицы A:

Найдём алгебраические дополнения матрицы A:

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

Находим матрицу, обратную матрице A:

Находим неизвестную матрицу:

Пример 6. Решить матричное уравнение

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C, то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

Найдём алгебраические дополнения матрицы A:

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

Находим матрицу, обратную матрице A:

Найдём матрицу, обратную матрице B.

Сначала найдём определитель матрицы B:

Найдём алгебраические дополнения матрицы B:

Составим матрицу алгебраических дополнений матрицы B:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B:

Находим матрицу, обратную матрице B:

Находим неизвестную матрицу:

Поделиться с друзьями

Начало темы «Матрицы»

Продолжение темы «Матрицы»

Другие темы линейной алгебры

function-x.ru

Как решать матрицы?

Математическая матрица – это таблица упорядоченных элементов. Размеры этой таблицы определяются по количеству строк и столбцов в ней. Что касается решения матриц, то им называют огромное количество операций, которые производятся над этими самыми матрицами. Математики различают несколько видов матриц. Для некоторых из них действуют общие правила по решению, а для других не действуют. Например, если матрицы имеют одинаковую размерность, то их можно сложить, а если они согласовываются между собой, то их можно перемножить. Обязательно для решения любой матрицы необходимо найти детерминант. Кроме того, матрицы подвергаются транспонированию и нахождению в них миноров. Итак, давайте рассмотрим, как решать матрицы.

Порядок решения матриц

Сначала записываем заданные матрицы. Считаем сколько в них строк и столбцов. Если количество строк и столбцов одинаковое, то такая матрица называется квадратной. Если каждый элемент матрицы оказался равен нулю, то такая матрица нулевая. Следующее, что мы делаем, это находим главную диагональ матрицы. Элементы такой матрицы находятся от правого нижнего угла до левого верхнего. Вторая же диагональ в матрице является побочной. Теперь необходимо произвести транспонирование матрицы. Чтобы это сделать, необходимо заменить в каждой из двух матриц элементы строк на соответствующие элементы столбцов. Например, элемент под а21 окажется элементом а12 или же наоборот. Таким образом, после этой процедуры должна появиться совершенно иная матрица.

Если матрицы имеют совершенно одинаковую размерность, то их можно запросто сложить. Чтобы это сделать, мы берем первый элемент первой матрицы а11 и складываем его с подобным элементом второй матрица b11. То, что получится в результате, записываем на ту же позицию, только уже в новую матрицу. Теперь аналогичным образом складываем все остальные элементы матрицы, пока не получится новая совершенно иная матрица. Посмотрим еще несколько способов, как решать матрицы.

Варианты действий с матрицами

elhow.ru

определение, теорема и примеры решения задач

Задание. Решить с помощью обратной матрицы систему

Решение. Запишем данную систему в матричной форме:

где — матрица системы, — столбец неизвестных, — столбец правых частей. Тогда

Найдем обратную матрицу к матрице с помощью союзной матрицы:

Здесь — определитель матрицы ; матрица — союзная матрица, она получена из исходной матрицы заменой ее элементов их алгебраическими дополнениями. Найдем , для этого вычислим алгебраические дополнения к элементам матрицы :

Таким образом,

Определитель матрицы

А тогда

Отсюда искомая матрица

Ответ.

www.webmath.ru

Расширенная матрица, формула и примеры

Пусть задана СЛАУ

Матрица , составленная из коэффициентов при неизвестных , называется основной матрицей системы или матрицей системы:

Матрица , полученная из основной матрицы, дописыванием справа столбца свободных членов, называется расширенной матрицей СЛАУ:

Примеры решения задач с расширенными матрицами

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Конвертировать пдф в изображения – PDF в JPG онлайн конвертер

alexxlab / 16.12.201602.06.2019 / Школьная жизнь

Конвертер PDF в JPG – конвертируйте свои PDF в изображения

Сохраняйте каждую страницу PDF как изображение JPG за считанные секунды.

Начать сначала

Only one file can be selected at a time. Multiple file conversion is supported only for members.

Выберите файл PDF

перетащите файлы сюда

Как конвертировать PDF в изображение JPG? Для отправки на конвертацию выберите файл PDF на компьютере или перетащите его. Дождитесь завершения отправки и конвертации изображения JPG в облаке.

Присоединяйтесь к 10+ миллионов наших пользователей

I can’t really find the words to thank you. You are amazing!

Наш пользователь Thomas Papoulakis, Greece

Оставайтесь на связи

Выбрать конвертер

Загрузить Сохранить на Диске Google

Сохранить в Dropbox

Удалить

Начать сначала

Документы неограниченного размера

Convert multiple documents at once

Неограниченный доступ ко всем инструментам

20 инструментов для извлечения, конвертирования, сжатия, слияния и разделения файлов PDF

Защита файлов при помощи 256-разрядного SSL-шифрования

Мгновенная конвертация

На любом компьютере

Приоритетная поддержка

www.freepdfconvert.com

Конвертер PDF в Изображение — конвертируйте PDF файлы в изображения с помощью бесплатного PDF24 Creator

Страницы PDF файлов могут быть конвертированы в изображения. Вы можете открыть PDF файл и сделать снимок экрана, но это не лучший способ, если Вы хотите создать изображение из страницы PDF файла. Бесплатный PDF24 Creator предлагает лучшее решение. Вы можете открыть PDF файл и экспортировать одну или больше страниц как изображение.

PDF24 Creator является бесплатным PDF конструктором и PDF принтером для создания PDF файлов, но программное обеспечение не ограничивается созданием только PDF файлов. Вы также можете экспортировать файлы как изображения, используя PDF24 Creator в качестве конвертера PDF в изображения.

Вот как это работает:

Загрузите и установите PDF24 Creator
Откройте PDF24 Creator
Загрузите PDF файл, перетащив в правую часть окна. Теперь Вы можете видеть файл в режиме предварительного просмотра. Вы можете поместить туда любой файл, не только PDF файлы.
Нажмите на иконку «Сохранить как» на панели инструментов
Затем Вы можете выбрать выходной фильтр для использования. Выберите тип нужный изображения и задайте необходимые параметры.
Нажмите «продолжить» и выберите файл, в котором Вы хотите сохранить изображение/-я.

Если файл содержит больше одной страницы, то каждая страница сохраняется в виде нового файла изображения. Номер страницы автоматически добавляется к выбранному имени файла изображения.

Подробнее о PDF24 Creator

Альтернатива: Преобразуйте картинки в PDF файлы онлайн

Если вы не хотите устанавливать какое-либо ПО или вам нужен онлайн инструмент для быстрого конвертирования страниц в картинки, тогда у нас есть подходящий онлайн инструмент из набора PDF24. PDF24 предлагает вам различные бесплатные PDF утилиты, с которыми вы сможете легко решать почти любые PDF проблемы и с одной из таких утилит вы можете превратить PDF файлы в изображения. Вот как это работает:

Преобразование PDF страниц в картинки онлайн

ru.pdf24.org

Конвертируем PDF в JPG

Опубликовано: 26.11.2013

Возможно, кому-то из моих читателей будет знакома данная ситуация. Жду я сегодня от одного человека на электронную почту комплект документов в отсканированном виде. Причем нужно, чтобы каждый документ был отдельным файлом. Но, как назло, мне присылают один PDF-файл, содержащий несколько отсканированных листов. Как же вытащить все изображения из этого PDF-документа? 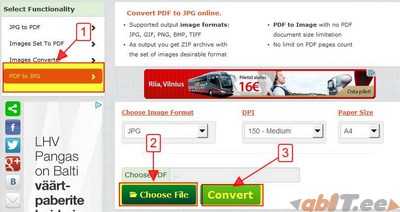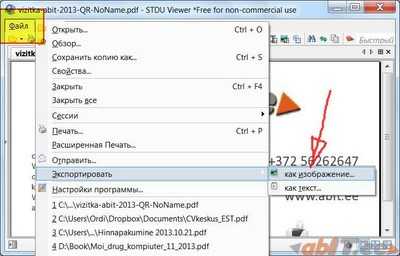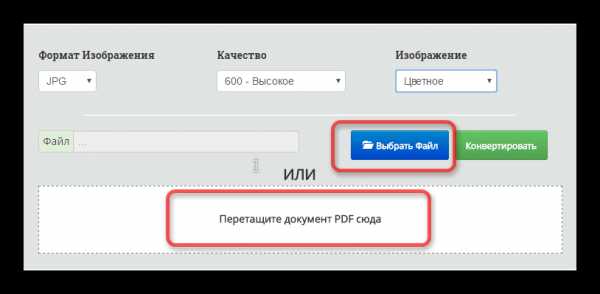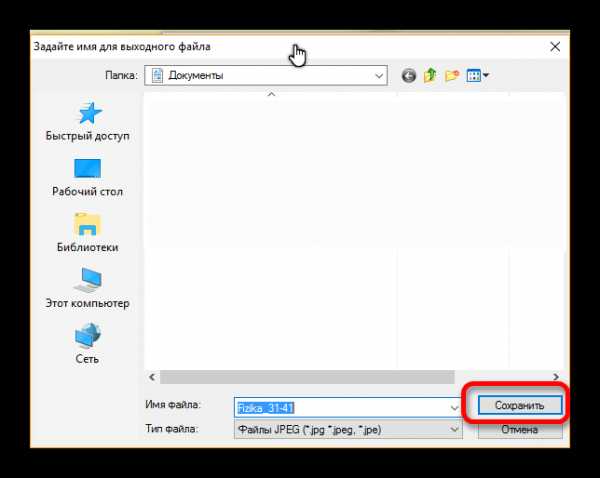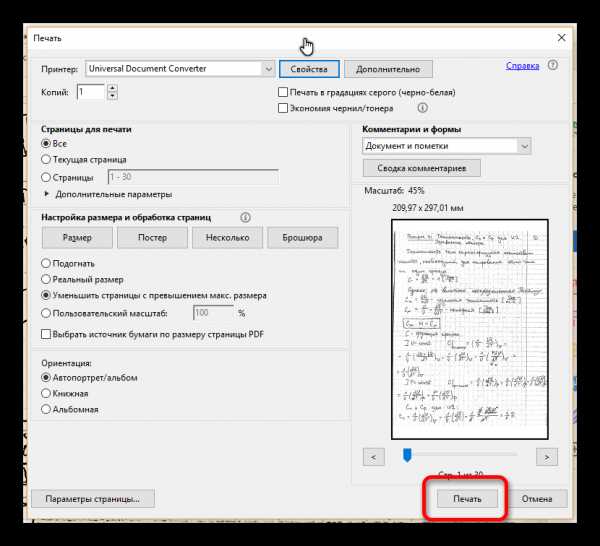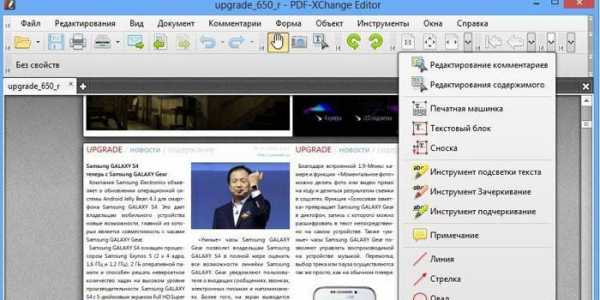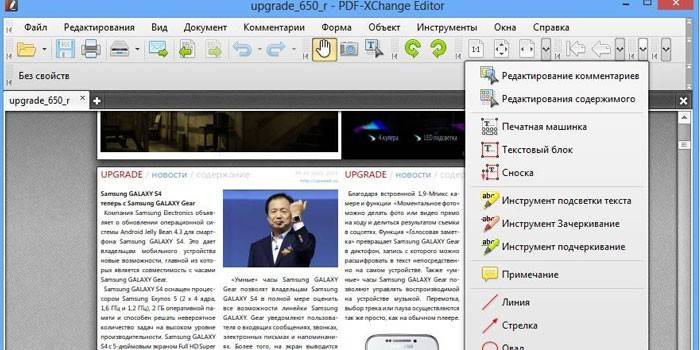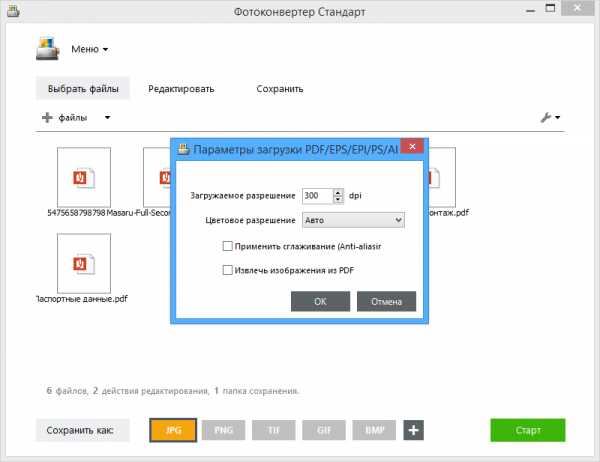Для этого сконвертируем PDF в JPG.Я испробовал множество офлайновых и онлайновых конвертеров, но большинство из них по разным причинам мне не подошли. В итоге я выбрал два оптимальных способа, как можно сконвертировать PDF в JPG.

1 способ: воспользоваться программой STDU Viewer

Этот просмотрщик PDF, DjVu и других форматов знаком очень многим. Программка имеет небольшой размер и к тому же бесплатна для некоммерческого использования. Скачать можно здесь.

Итак, открываем наш pdf-файл в STDU Viewer. В строке меню выбираем “Файл” – “Экспортировать” – “как изображение”:В следующем окне выбираем тип файла “JPEG-файл” (при желании можно выбрать и другой графический формат), затем указываем папку, куда будут сохранены извлеченные файлы. Жмем “ОК”.

На этом всё: в течении нескольких секунд из PDF файла будут извлечены все документы в JPG формате.

2 способ: воспользоваться онлайн-конвертером convert-my-image.com

Данный онлайн конвертер, пожалуй, самый лучший из всех, что мне удалось протестировать.

Зайдите на сайт – слева выберите раздел “PDF в JPG” – нажмите большую кнопку “Выбрать файл” для выбора нашего pdf-документа. Затем нажмите “Старт” для начала процесса загрузки и конвертации документа. При желании можно изменить формат выходных изображений и их качество.По окончании обработки мы получаем архив с набором изображений нужного формата.

Помимо конвертации PDF в JPG, на данном сайте можно выполнить множество других операций с изображениями. Можно сконвертировать изображения различных форматов в PDF, либо преобразовать набор из нескольких изображений в цельный PDF документ. Также здесь имеется конвертер изображений (можно преобразовать GIF в PNG, JPG в ICO и т.д.).

Просмотров: 52 925 &nbsp &nbsp &nbsp &nbsp &nbsp &nbsp

blogsisadmina.ru

Конвертируем документ PDF в файл формата JPG, или как сохранить файл PDF в виде изображения.

PDF – один из наиболее популярных форматов документов. Счета, инструкции, деловые письма, книги, журналы – все эти документы мы получаем и отправляем как файлы PDF. Для просмотра PDF-файлов существует множество программ, наиболее популярная из них – Adobe Reader. Создавать эти файлы в настоящее время можно не только в таких мощных и дорогих программах, как Adobe Acrobat или Adobe Photoshop, но и с помощью обычных офисных пакетов – Microsoft Office (платная) или OpenOffice.org (бесплатная программа, по своей функциональности способная поспорить со своим конкурентом от Microsoft).

Но иногда требуется преобразовать документ PDFв обычное изображение (файл формата JPG или PNG). Например, на многих порталах коммерческих объявлений разрешается использовать только фотографии или картинки для иллюстрации публикуемых рекламных текстов, публиковать документы или проекты на веб-сайтах удобнее в виде обычных графических файлов и так далее. В этой статье мы рассмотрим три способа преобразования документов PDF в графические файлы (JPG и др.) без использования дорогих коммерческих приложений – с помощью бесплатных программ Adobe Reader и STDU Viewer , а также посредством онлайн-сервиса convert-my-image.

Преобразование документов PDF в графические файлы с помощью бесплатной программы Adobe Reader.

Для того чтобы преобразовать документ PDF в графический файл (JPG или какой-нибудь другой), нам потребуется, кроме Adobe Reader, бесплатный графический редактор Paint, входящий в стандартный набор приложений Windows (конечно, можно прибегнуть к помощи любого другого приложения для редактирования изображений).

Итак, приступим. Для начала откроем PDF документ в программе Adobe Reader.

Выбираем в верхнем меню пункт «Редактирование» и ставим галочку напротив подпункта «Сделать снимок». Зажимаем левую кнопку мыши и обводим окно открытого документа. После этого мы увидим надпись: «Выбранная область скопирована». Можно закрывать AdobeReaderи переходить к работе с бесплатным графическим редактором Paint.

Запускаем Paint (проще всего найти это приложение через меню Старт – Все программы – Стандартные).

Щелкаем на иконке «Буфер обмена» и выбираем «Вставить».

Мы видим документ, помещенный в буфер обмена программой Adobe Reader и открытый в Paint. Теперь остается только сохранить его как изображение.

Щелкаем левой кнопкой мыши на иконку в левом верхнем углу интерфейса программы Paintи получаем доступ к меню. Здесь мы выбираем пункт Сохранить как – Изображение в формате JPEG (или BMP, PNG, GIF).

В открывшемся диалоговом окне мы озаглавить новый графический файл, а также выбрать папку, в которой он будет сохранен. Затем нажимаем кнопку Сохранить. Вот и все! Мы преобразовали документ PDF в графический файл формата JPEGс помощью программ Adobe Readerи Microsoft Paint.

Преобразование документов PDF в графические файлы с помощью онлайн-сервиса convert-my-image.com.

Следующий способ, который мы рассмотрим, предполагает наличие интернет-подключения – мы будем конвертировать PDF в графический файл с помощью онлайн-сервиса convert-my-image.com.

Для этого набираем в окне браузера вышеуказанный адрес (или просто переходим по ссылке) и видим простой и понятный интерфейс, который к тому же позволяет выбрать один из двух языков – английский и русский.

Предварительно необходимо убедиться, что выбрана функция PDF to JPG в левом верхнем углу веб-страницы.

Затем нажимаем кнопку Choose File (Выбрать файл), находим наш документ и нажимаем кнопку Convert (Старт), ждем немного, не перезагружая страницу, и видим диалоговое окно, позволяющее сохранить полученное изображение на жестком диске нашего компьютера. Просто и быстро!

Преобразование документов PDF в графические файлы с помощью бесплатной программы STDU Viewer.

Этот способ мне представляется наиболее удобным, простым и быстрым. Если Вы планируете в дальнейшем часто преобразовывать файлы PDF в изображения, то я рекомендую скачать и установить бесплатную программу STDU Viewer и уже с ее помощью выполнять данную работу.

Открываем наш документ PDF в программе STDU Viewer.

Выбираем пункт меню Файл – Экспортировать – Как графический файл.

В открывшемся диалоговом окне выбираем нужный нам тип файла, его название и папку, куда будет отправлен вновь создаваемое изображение и нажимаем ОК. Готово!

Как видите, в преобразовании документа PDF в обычное изображение нет ничего сложного, и сделать это можно различными способами. Если конвертировать нужно один-два документа, то можно воспользоваться онлайн-сервисом или прибегнуть к помощи программ Adobe Reader и Microsoft Paint. Но если данная операция будет выполняться неоднократно, то можно порекомендовать использование STDU Viewer.

www.abit.ee

Как конвертировать pdf в jpg

Не всегда пользователям удобно работать с файлами в формате pdf, так как для этого нужен современный браузер (хотя он есть почти у каждого) или программа, которая позволяет открывать документы подобного типа.

Но есть один вариант, который поможет удобно просматривать файлы pdf, передавать их любым другим пользователям и открывать без затрат времени. Ниже речь пойдет о преобразовании документов этого формата в графические файлы jpg.

Как конвертировать pdf в jpg

Есть много способов, чтобы переформатировать pdf в jpg, но не все из них выгодны и удобны. Некоторые и вовсе абсурдные, что о них даже слышать никому не стоит. Рассмотрим два самых популярных способа, которые помогут сделать из файла pdf набор изображений в формате jpg.

Способ 1: использование онлайн конвертера

Итак, первым делом надо зайти на сайт, где будет использоваться конвертер. Для удобства предлагается следующий вариант: Convert My Image. Он является одним из популярных для решения проблемы, плюс к этому довольно приятно оформлен и не зависает при работе с тяжелыми файлами.
После того, как сайт загрузился, можно добавлять в систему нужный нам файл. Сделать это можно двумя способами: нажать на кнопку «Выбрать файл» или перенести сам документ в окно браузера в соответствующую область.

Перед конвертацией можно изменить некоторые настройки, чтобы полученные в итоге документы jpg были качественными и читаемыми. Для этого пользователю представлена возможность изменить цвета графических документов, разрешение и формат изображений.

После загрузки документа pdf на сайт и настройки всех параметров можно нажимать на кнопку «Конвертировать». Процесс займет некоторое время, поэтому придется немного подождать.

Как только процесс конвертации завершится система сама откроет окно, в котором необходимо будет выбрать место для сохранения полученных файлов jpg (сохраняются они в одном архиве). Теперь осталось только нажать на кнопку «Сохранить» и пользоваться изображениями, полученными из документа pdf.

Способ 2: использование конвертера для документов на компьютере

Прежде, чем приступить к самой конвертации, необходимо скачать программное обеспечение, которое поможет выполнить все быстро и просто. Скачать программу можно тут.
Как только программа установлена на компьютер, можно приступать к конвертации. Для этого надо открыть документ, который необходимо преобразовать из формата pdf в jpg. Рекомендуется работать с документами pdf через программу Adobe Reader DC.
Теперь следует нажать на кнопку «Файл» и выбрать пункт «Печать…».

Следующим шагом надо выбрать виртуальный принтер, который будет использоваться для печати, так как нам не надо непосредственно распечатать сам файл, надо лишь получить его в другом формате. Виртуальный принтер должен называться «Universal Document Converter».

Выбрав принтер, необходимо нажать на пункт меню «Свойства» и убедиться, что сохраняться документ будет в формате jpg (jpeg). Кроме этого можно настроить много разных параметров, которые невозможно было изменить в онлайн-конвертере. После всех изменений можно нажимать на кнопку «Ок».

Нажатием на кнопку «Печать» пользователь начнет процесс преобразования документа pdf в изображения. После его завершения появится окно, в котором опять придется выбрать место сохранения, название полученного файла.

Вот такие два хороших способа являются наиболее удобными и надежными в работе с pdf файлами. Перевести данными вариантами документ из одного формата в другой довольно просто и быстро. Выбирать какой из них лучше следует только пользователю, ведь у кого-то могут возникнуть проблемы с подключением к сайту загрузки конвертера для компьютера, а у кого-то могут появиться и другие проблемы.

Если вы знаете какие-то еще способы конвертирования, которые будут простыми и не затратными по времени, то пишите их в комментарии, чтобы и мы узнали, о вашем интересном решении такой задачи как конвертирование документа pdf в jpg формат.

Мы рады, что смогли помочь Вам в решении проблемы.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.

Помогла ли вам эта статья?

ДА НЕТ

lumpics.ru

Как перевести pdf в jpeg формат с помощью программ конвертеров или онлайн бесплатно

Человек может столкнуться с проблемой, когда имеющийся файл находится в неудобном формате и его необходимо переконвертировать. Часто это происходит с документами в формате pdf, родной программой для них является Acrobat Reader. Причин для перевода изначального формата в картинку может быть несколько, способов конвертировать pdf в jpg тоже.

Как конвертировать pdf в jpeg

Статьи по теме

Для выполнения конвертации можно использовать несколько способов. Каждый из них по-своему удобен, конечный результат будет одинаков – вы получите графическое изображение вместо исходного формата. Конвертировать pdf в jpeg можно через специальные программы для преобразования, через бесплатные онлайн-сервисы или при помощи встроенных инструментов самой операционной системы. Последний вариант выполняется очень легко, если необходимо перевести пдф в jpg только для одной или пары страниц. Выполняется конвертирование следующим образом:

Откройте из папки-источника файл формата ПДФ.
Отрегулируйте масштаб так, чтобы на экране помещалась вся необходимая вам информация.
Далее на клавиатуре найдите кнопку PrtScr, нажмите ее. Система создаст снимок экрана, сохранит его в буфере обмена.
Вам понадобится любой графический редактор. Можно воспользоваться стандартным приложением Paint.
Откройте программу, создайте новый документ и выполните нажатие сочетания кнопок «Ctrl+V» или, через пункт «Правка» кликните по строчке «Вставить».
Появится изображение экрана со станицей из файла ПДФ. У вас будет возможность обрезать края снимка, чтобы на картинку не попали элементы интерфейса.
Далее необходимо кликнуть по кнопке «Сохранить». По умолчанию программа использует формат PNG, поэтому не забудь внизу окна выбрать вариант JPG.
Способ полностью бесплатный, можно повторить эту процедуру необходимое количество раз.

Перевод из pdf в jpeg онлайн

Если страниц в документе много и каждую скринить желания нет, то можно перевести из pdf в jpeg онлайн на специальных сайтах. Вариантов таких сервисов очень много, необходимо в поисковой системе вбить запрос вида «pdf2jpg» и перед вами будет широкий выбор вариантов для форматирования файла. Большинство их них работает по очень простому принципу:

Через специальное поле вам предложат загрузить источник.
Далее нужно будет указать почту, на которую придет конечный результат, либо сразу же нажать на кнопку «Convert».
Если файл не будет отправлен к вам на имейл, то появится ссылка для скачивания, и вы сможете сохранить документ в удобное для вас место.
Сервисы работают на бесплатной основе с неограниченным количеством страниц.

Программа для конвертации pdf в jpeg

Если у вас часто возникает необходимость перевести файлы из ПДФ, то можно установить специальный софт, который на это рассчитан. Программа перевода pdf в jpeg может быть бесплатной или с требованием приобрести лицензию. Такое ПО, как правило, не имеет сложного интерфейса, очень легкое в управлении. Чтобы перевести файл ПДФ можно использовать один из нижеописанных вариантов приложения.

STDU Viewer

Самый доступный и популярный конвертер pdf в jpg – STDU Viewer. Самый простой и надежный способ, если требуется изменить большое количество страниц. Установить приложение следует, если далее вы будете часто работать с данным форматом. Программа распространяется на бесплатной основе, способ поменять формат следующий:

Откройте через программу файл.
Выберите далее пункт «Файл» строчку «Экспортировать» и кликните по «Как графический файл».
В следующем окне просто установите нужный формат документа для сохранения, напишите название и укажите папку.
Жмите «Готово».

PDF-XChange Editor

Это еще одна бесплатная программа для Windows, которая предоставляет весь необходимый функционал тем, кто ищет, как перевести pdf в jpeg. PDF-XChange Editor работает только с рассматриваемым типом документов, но благодаря этому выдает прекрасную скорость конвертации. при необходимости вы можете не только перевести данные, но и обработать их. Если вам захочется использовать Pro версию программы, то за нее придется заплатить. Утилита предоставляет возможность:

настраивать масштаб;
подчеркивать карандашом интересные моменты в тексте, делать стрелки, рамки, кривые;
выделять маркером, зачеркивать важные места книги.

Total PDF Converter

Если предыдущие варианты программ вам не подошли, то можете попробовать перевести книгу при помощи Total PDF Converter. Интерфейс очень дружелюбен к пользователю, присутствует русская локализация, что значительно упрощает работу с приложением. Перевести книгу в картинку можно следующим образом:

Слева вы найдете проводник, через который можно выбрать книгу. Через него вы увидите все данные: дата изменения, размер, атрибуты, заголовок, тип, имя и т.д.
Затем необходимо кликнуть «Конвертировать в JPEG».
Программа может провести экспорт всех страниц на одном изображении, или каждой по отдельности.

Видео: как pdf перевести в jpeg

Нашли в тексте ошибку? Выделите её, нажмите Ctrl + Enter и мы всё исправим! Рассказать друзьям:

Статья обновлена: 13.05.2019

sovets.net

Конвертируем PDF в JPG | Фотоконвертер

Итак, у нас есть PDF файл и наш компьютер не может его открыть. У нас нет ни специализированных программ, ни времени возиться с этим форматом.

Существует один простой способ избежать все эти проблемы, нам просто нужно конвертировать PDF в JPG (JPEG). Это один из самых популярных форматов изображений и работать с ним намного проще.

Сделать это можно всего за несколько простых шагов с помощью программы Фотоконвертер.

Первый шаг:

Скачиваем и устанавливаем Фотоконвертер. У нас формат PDF, поэтому нам подходят 2 версии (Стандарт и Про). Загружаем одну из версий и двигаемся дальше.

Второй шаг:

Открываем Фотоконвертер и добавляем PDF файлы для конвертации. Мы так же можем загрузить несколько файлов сразу.

Важно учесть, что по умолчанию Фотоконвертер загружает файлы PDF с разрешением 300 dpi. Для того, чтобы уменьшить размер получаемых JPG файлов и ускорить процесс конвертации, можно изменить разрешение на 72 dpi. (Фотоконвертер → Меню → Параметры загрузки PDF файлов).

Переходим к следующему шагу.

Третий шаг:

Выбираем инструменты для редактирования.

Здесь мы можем поменять размер, повернуть, обрезать или применить еще множество разных эффектов, как к одному так и ко всем изображениям сразу.

Еще очень удобно, что готовый результат видно сразу. И мы можем отслеживать все наши действия на картинке справа. Если никакие изменения не нужны, этот шаг можно пропустить.

Четвертый шаг:

Выбираем формат вывода, в нашем случае это JPG(JPEG) и папку для сохранения файла. Так же можем поменять имя файла, если нам это нужно.

Пятый шаг:

Вот и все, нажимаем кнопку Старт, и через мгновенье получаем готовый результат.

Вот так, всего за 5 шагов можно перевести формат PDF в JPG.
Теперь наши файлы в более привычном нам формате. Смело открываем их в любой программе и на любом компьютере.

Установить Фотоконвертер

Онлайн конвертация

Некоторые возможности Фотоконвертера можно попробовать онлайн. Выберите файлы или ZIP архивы для конвертации:

Интерфейс командной строки

Профессиональные пользователи могут использовать командную строку для конвертации и редактирования в ручном или автоматическом режиме. За дополнительными консультациями по использованию cmd интерфейса обращайтесь в службу поддержки пользователей.

Рассказать друзьям

www.photoconverter.ru

Значений sin таблица – Таблица синусов.

alexxlab / 15.12.201602.06.2019 / Школьная жизнь

Таблица синусов | umath.ru

sin(1°) = 0,017452
sin(2°) = 0,034899
sin(3°) = 0,052336
sin(4°) = 0,069756
sin(5°) = 0,087156
sin(6°) = 0,104528
sin(7°) = 0,121869
sin(8°) = 0,139173
sin(9°) = 0,156434
sin(10°) = 0,173648
sin(11°) = 0,190809
sin(12°) = 0,207912
sin(13°) = 0,224951
sin(14°) = 0,241922
sin(15°) = 0,258819
sin(16°) = 0,275637
sin(17°) = 0,292372
sin(18°) = 0,309017
sin(19°) = 0,325568
sin(20°) = 0,342020
sin(21°) = 0,358368
sin(22°) = 0,374607
sin(23°) = 0,390731
sin(24°) = 0,406737
sin(25°) = 0,422618
sin(26°) = 0,438371
sin(27°) = 0,453990
sin(28°) = 0,469472
sin(29°) = 0,484810
sin(30°) = 0,5

sin(31°) = 0,515038
sin(32°) = 0,529919
sin(33°) = 0,544639
sin(34°) = 0,559193
sin(35°) = 0,573576
sin(36°) = 0,587785
sin(37°) = 0,601815
sin(38°) = 0,615661
sin(39°) = 0,629320
sin(40°) = 0,642788
sin(41°) = 0,656059
sin(42°) = 0,669131
sin(43°) = 0,681998
sin(44°) = 0,694658
sin(45°) = 0,707107
sin(46°) = 0,719340
sin(47°) = 0,731354
sin(48°) = 0,743145
sin(49°) = 0,754710
sin(50°) = 0,766044
sin(51°) = 0,777146
sin(52°) = 0,788011
sin(53°) = 0,798636
sin(54°) = 0,809017
sin(55°) = 0,819152
sin(56°) = 0,829038
sin(57°) = 0,838671
sin(58°) = 0,848048
sin(59°) = 0,857167
sin(60°) = 0,866025

sin(61°) = 0,874620
sin(62°) = 0,882948
sin(63°) = 0,891007
sin(64°) = 0,898794
sin(65°) = 0,906308
sin(66°) = 0,913545
sin(67°) = 0,920505
sin(68°) = 0,927184
sin(69°) = 0,933580
sin(70°) = 0,939693
sin(71°) = 0,945519
sin(72°) = 0,951057
sin(73°) = 0,956305
sin(74°) = 0,961262
sin(75°) = 0,965926
sin(76°) = 0,970296
sin(77°) = 0,974370
sin(78°) = 0,978148
sin(79°) = 0,981627
sin(80°) = 0,984808
sin(81°) = 0,987688
sin(82°) = 0,990268
sin(83°) = 0,992546
sin(84°) = 0,994522
sin(85°) = 0,996195
sin(86°) = 0,997564
sin(87°) = 0,998630
sin(88°) = 0,999391
sin(89°) = 0,999848
sin(90°) = 1

umath.ru

Таблица синусов, она-же косинусов (см.примечание внутри). Углы в угловых градусах. Таблица значений синусов.

0,0000

0,0175

0,0349

0,0523

0,0698

0,0872

0,1045

0,1219

0,1392

0,1564

0,1736

0,1908

0,2079

0,2250

0,2419

0,2588

0,2756

0,2924

0,3090

0,3256

0,3420

0,3584

0,3746

0,3907

0,4067

0,4226

0,4384

0,4540

0,4695

0,4848

0,5000

0,5150

0,5299

0,5446

0,5592

0,5736

0,5878

0,6018

0,6157

0,6293

0,6428

0,6561

0,6691

0,6820

0,6947

0,0058

0,0233

0,0407

0,0581

0,0756

0,0929

0,1103

0,1276

0,1449

0,1622

0,1794

0,1965

0,2136

0,2306

0,2476

0,2644

0,2812

0,2979

0,3145

0,3311

0,3475

0,3638

0,3800

0,3961

0,4120

0,4279

0,4436

0,4592

0,4746

0,4899

0,5050

0,5200

0,5348

0,5495

0,5640

0,5783

0,5925

0,6065

0,6202

0,6338

0,6472

0,6604

0,6734

0,6862

0,6988

0,0116

0,0291

0,0465

0,0640

0,0814

0,0987

0,1161

0,1334

0,1507

0,1679

0,1851

0,2022

0,2196

0,2363

0,2532

0,2700

0,2868

0,3035

0,3201

0,3365

0,3529

0,3692

0,3854

0,4014

0,4173

0,4331

0,4488

0,4643

0,4797

0,4950

0,5100

0,5250

0,5398

0,5544

0,5688

0,5831

0,5972

0,6111

0,6248

0,6383

0,6517

0,6648

0,6777

0,6905

0,7030

0,7071

0,7193

0,7314

0,7431

0,7547

0,7660

0,7771

0,7880

0,7986

0,8090

0,8192

0,8290

0,8387

0,8480

0,8572

0,8660

0,8746

0,8829

0,8910

0,8988

0,9063

0,9135

0,9205

0,9272

0,9336

0,9397

0,9455

0,9511

0,9563

0,9613

0,9659

0,9703

0,9744

0,9781

0,9816

0,9848

0,9877

0,9903

0,9925

0,9945

0,9962

0,9976

0,9986

0,9994

0,9998

0,7112

0,7234

0,7353

0,7470

0,7585

0,7698

0,7808

0,7916

0,8021

0,8124

0,8225

0,8323

0,8418

0,8511

0,8601

0,8689

0,8774

0,8857

0,8936

0,9013

0,9088

0,9159

0,9228

0,9293

0,9356

0,9417

0,9474

0,9528

0,9580

0,9628

0,9674

0,9717

0,9757

0,9793

0,9827

0,9858

0,9886

0,9911

0,9932

0,9951

0,9967

0,9980

0,9989

0,9996

0,9999

0,7153

0,7274

0,7393

0,7504

0,7622

0,7735

0,7844

0,7951

0,8056

0,8158

0,8258

0,8355

0,8450

0,8542

0,8631

0,8718

0,8802

0,8884

0,8962

0,9038

0,9112

0,9182

0,9250

0,9315

0,9377

0,9436

0,9492

0,9546

0,9596

0,9644

0,9689

0,9730

0,9769

0,9805

0,9838

0,9868

0,9894

0,9918

0,9939

0,9957

0,9971

0,9983

0,9992

0,9997

1,0000

tehtab.ru

Таблица синусов

Главная > с >

Таблица синусов для основных углов: 0°, 90°, 180°, 270°, 360°.

Угол х (в градусах)	0°	90°	180°	270°	360°
Угол х (в радианах)	0
sin x	0	1	0	-1	0

Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.

Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.

π = 3.141592653589793238462… (приблизительное значение числа Пи).

Таблица синусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°.

Угол х (в градусах)	0°	30°	45°	60°	90°	120°	135°	150°	180°
Угол х (в радианах)	0	π/6	π/4	π/3	π/2	2 x π/3	3 x π/4	5 x π/6	π
sin x	0	1/2 (0,5)	√2/2 (0,7071)	√3/2 (0,8660)	1	√3/2 (0,8660)	√2/2 (0,7071)	1/2 (0,5)	0

Таблица синусов углов от 0° — 360°. Углы с шагом в 1°.

Таблица синусов — это посчитанные значения синусов от 0° до 360°.

Если не под рукой калькулятора — таблица синусов очень пригодится.
Для того, чтобы узнать чему равен синус от нужного Вам угла достаточно найти его в таблице.

1°	sin= 0.0175	91°	sin= 0.9998	181°	sin= -0.0175	271°	sin= -0.9998
2°	sin= 0.0349	92°	sin= 0.9994	182°	sin= -0.0349	272°	sin= -0.9994
3°	sin= 0.0523	93°	sin= 0.9986	183°	sin= -0.0523	273°	sin= -0.9986
4°	sin= 0.0698	94°	sin= 0.9976	184°	sin= -0.0698	274°	sin= -0.9976
5°	sin= 0.0872	95°	sin= 0.9962	185°	sin= -0.0872	275°	sin= -0.9962
6°	sin= 0.1045	96°	sin= 0.9945	186°	sin= -0.1045	276°	sin= -0.9945
7°	sin= 0.1219	97°	sin= 0.9925	187°	sin= -0.1219	277°	sin= -0.9925
8°	sin= 0.1392	98°	sin= 0.9903	188°	sin= -0.1392	278°	sin= -0.9903
9°	sin= 0.1564	99°	sin= 0.9877	189°	sin= -0.1564	279°	sin= -0.9877
10°	sin= 0.1736	100°	sin= 0.9848	190°	sin= -0.1736	280°	sin= -0.9848
11°	sin= 0.1908	101°	sin= 0.9816	191°	sin= -0.1908	281°	sin= -0.9816
12°	sin= 0.2079	102°	sin= 0.9781	192°	sin= -0.2079	282°	sin= -0.9781
13°	sin= 0.2250	103°	sin= 0.9744	193°	sin= -0.2250	283°	sin= -0.9744
14°	sin= 0.2419	104°	sin= 0.9703	194°	sin= -0.2419	284°	sin= -0.9703
15°	sin= 0.2588	105°	sin= 0.9659	195°	sin= -0.2588	285°	sin= -0.9659
16°	sin= 0.2756	106°	sin= 0.9613	196°	sin= -0.2756	286°	sin= -0.9613
17°	sin= 0.2924	107°	sin= 0.9563	197°	sin= -0.2924	287°	sin= -0.9563
18°	sin= 0.3090	108°	sin= 0.9511	198°	sin= -0.3090	288°	sin= -0.9511
19°	sin= 0.3256	109°	sin= 0.9455	199°	sin= -0.3256	289°	sin= -0.9455
20°	sin= 0.3420	110°	sin= 0.9397	200°	sin= -0.3420	290°	sin= -0.9397
21°	sin= 0.3584	111°	sin= 0.9336	201°	sin= -0.3584	291°	sin= -0.9336
22°	sin= 0.3746	112°	sin= 0.9272	202°	sin= -0.3746	292°	sin= -0.9272
23°	sin= 0.3907	113°	sin= 0.9205	203°	sin= -0.3907	293°	sin= -0.9205
24°	sin= 0.4067	114°	sin= 0.9135	204°	sin= -0.4067	294°	sin= -0.9135
25°	sin= 0.4226	115°	sin= 0.9063	205°	sin= -0.4226	295°	sin= -0.9063
26°	sin= 0.4384	116°	sin= 0.8988	206°	sin= -0.4384	296°	sin= -0.8988
27°	sin= 0.4540	117°	sin= 0.8910	207°	sin= -0.4540	297°	sin= -0.8910
28°	sin= 0.4695	118°	sin= 0.8829	208°	sin= -0.4695	298°	sin= -0.8829
29°	sin= 0.4848	119°	sin= 0.8746	209°	sin= -0.4848	299°	sin= -0.8746
30°	sin= 0.5000	120°	sin= 0.8660	210°	sin= -0.5000	300°	sin= -0.8660
31°	sin= 0.5150	121°	sin= 0.8572	211°	sin= -0.5150	301°	sin= -0.8572
32°	sin= 0.5299	122°	sin= 0.8480	212°	sin= -0.5299	302°	sin= -0.8480
33°	sin= 0.5446	123°	sin= 0.8387	213°	sin= -0.5446	303°	sin= -0.8387
34°	sin= 0.5592	124°	sin= 0.8290	214°	sin= -0.5592	304°	sin= -0.8290
35°	sin= 0.5736	125°	sin= 0.8192	215°	sin= -0.5736	305°	sin= -0.8192
36°	sin= 0.5878	126°	sin= 0.8090	216°	sin= -0.5878	306°	sin= -0.8090
37°	sin= 0.6018	127°	sin= 0.7986	217°	sin= -0.6018	307°	sin= -0.7986
38°	sin= 0.6157	128°	sin= 0.7880	218°	sin= -0.6157	308°	sin= -0.7880
39°	sin= 0.6293	129°	sin= 0.7771	219°	sin= -0.6293	309°	sin= -0.7771
40°	sin= 0.6428	130°	sin= 0.7660	220°	sin= -0.6428	310°	sin= -0.7660
41°	sin= 0.6561	131°	sin= 0.7547	221°	sin= -0.6561	311°	sin= -0.7547
42°	sin= 0.6691	132°	sin= 0.7431	222°	sin= -0.6691	312°	sin= -0.7431
43°	sin= 0.6820	133°	sin= 0.7314	223°	sin= -0.6820	313°	sin= -0.7314
44°	sin= 0.6947	134°	sin= 0.7193	224°	sin= -0.6947	314°	sin= -0.7193
45°	sin= 0.7071	135°	sin= 0.7071	225°	sin= -0.7071	315°	sin= -0.7071
46°	sin= 0.7193	136°	sin= 0.6947	226°	sin= -0.7193	316°	sin= -0.6947
47°	sin= 0.7314	137°	sin= 0.6820	227°	sin= -0.7314	317°	sin= -0.6820
48°	sin= 0.7431	138°	sin= 0.6691	228°	sin= -0.7431	318°	sin= -0.6691
49°	sin= 0.7547	139°	sin= 0.6561	229°	sin= -0.7547	319°	sin= -0.6561
50°	sin= 0.7660	140°	sin= 0.6428	230°	sin= -0.7660	320°	sin= -0.6428
51°	sin= 0.7771	141°	sin= 0.6293	231°	sin= -0.7771	321°	sin= -0.6293
52°	sin= 0.7880	142°	sin= 0.6157	232°	sin= -0.7880	322°	sin= -0.6157
53°	sin= 0.7986	143°	sin= 0.6018	233°	sin= -0.7986	323°	sin= -0.6018
54°	sin= 0.8090	144°	sin= 0.5878	234°	sin= -0.8090	324°	sin= -0.5878
55°	sin= 0.8192	145°	sin= 0.5736	235°	sin= -0.8192	325°	sin= -0.5736
56°	sin= 0.8290	146°	sin= 0.5592	236°	sin= -0.8290	326°	sin= -0.5592
57°	sin= 0.8387	147°	sin= 0.5446	237°	sin= -0.8387	327°	sin= -0.5446
58°	sin= 0.8480	148°	sin= 0.5299	238°	sin= -0.8480	328°	sin= -0.5299
59°	sin= 0.8572	149°	sin= 0.5150	239°	sin= -0.8572	329°	sin= -0.5150
60°	sin= 0.8660	150°	sin= 0.5000	240°	sin= -0.8660	330°	sin= -0.5000
61°	sin= 0.8746	151°	sin= 0.4848	241°	sin= -0.8746	331°	sin= -0.4848
62°	sin= 0.8829	152°	sin= 0.4695	242°	sin= -0.8829	332°	sin= -0.4695
63°	sin= 0.8910	153°	sin= 0.4540	243°	sin= -0.8910	333°	sin= -0.4540
64°	sin= 0.8988	154°	sin= 0.4384	244°	sin= -0.8988	334°	sin= -0.4384
65°	sin= 0.9063	155°	sin= 0.4226	245°	sin= -0.9063	335°	sin= -0.4226
66°	sin= 0.9135	156°	sin= 0.4067	246°	sin= -0.9135	336°	sin= -0.4067
67°	sin= 0.9205	157°	sin= 0.3907	247°	sin= -0.9205	337°	sin= -0.3907
68°	sin= 0.9272	158°	sin= 0.3746	248°	sin= -0.9272	338°	sin= -0.3746
69°	sin= 0.9336	159°	sin= 0.3584	249°	sin= -0.9336	339°	sin= -0.3584
70°	sin= 0.9397	160°	sin= 0.3420	250°	sin= -0.9397	340°	sin= -0.3420
71°	sin= 0.9455	161°	sin= 0.3256	251°	sin= -0.9455	341°	sin= -0.3256
72°	sin= 0.9511	162°	sin= 0.3090	252°	sin= -0.9511	342°	sin= -0.3090
73°	sin= 0.9563	163°	sin= 0.2924	253°	sin= -0.9563	343°	sin= -0.2924
74°	sin= 0.9613	164°	sin= 0.2756	254°	sin= -0.9613	344°	sin= -0.2756
75°	sin= 0.9659	165°	sin= 0.2588	255°	sin= -0.9659	345°	sin= -0.2588
76°	sin= 0.9703	166°	sin= 0.2419	256°	sin= -0.9703	346°	sin= -0.2419
77°	sin= 0.9744	167°	sin= 0.2250	257°	sin= -0.9744	347°	sin= -0.2250
78°	sin= 0.9781	168°	sin= 0.2079	258°	sin= -0.9781	348°	sin= -0.2079
79°	sin= 0.9816	169°	sin= 0.1908	259°	sin= -0.9816	349°	sin= -0.1908
80°	sin= 0.9848	170°	sin= 0.1736	260°	sin= -0.9848	350°	sin= -0.1736
81°	sin= 0.9877	171°	sin= 0.1564	261°	sin= -0.9877	351°	sin= -0.1564
82°	sin= 0.9903	172°	sin= 0.1392	262°	sin= -0.9903	352°	sin= -0.1392
83°	sin= 0.9925	173°	sin= 0.1219	263°	sin= -0.9925	353°	sin= -0.1219
84°	sin= 0.9945	174°	sin= 0.1045	264°	sin= -0.9945	354°	sin= -0.1045
85°	sin= 0.9962	175°	sin= 0.0872	265°	sin= -0.9962	355°	sin= -0.0872
86°	sin= 0.9976	176°	sin= 0.0698	266°	sin= -0.9976	356°	sin= -0.0698
87°	sin= 0.9986	177°	sin= 0.0523	267°	sin= -0.9986	357°	sin= -0.0523
88°	sin= 0.9994	178°	sin= 0.0349	268°	sin= -0.9994	358°	sin= -0.0349
89°	sin= 0.9998	179°	sin= 0.0175	269°	sin= -0.9998	359°	sin= -0.0175
90°	sin= 1.0000	180°	sin= 0.0000	270°	sin= -1.0000	360°	sin= -0.0000

comments powered by HyperComments

tab.wikimassa.org

Таблица синусов — 2mb.ru

Таблица синусов позволяет получить значения синуса угла от 0 до 360 градусов без применения расчетов.
Эта таблица является одной из самых используемых в геометрии.
Таблица синусов 0° – 180°

sin(1°)	0.0175
sin(2°)	0.0349
sin(3°)	0.0523
sin(4°)	0.0698
sin(5°)	0.0872
sin(6°)	0.1045
sin(7°)	0.1219
sin(8°)	0.1392
sin(9°)	0.1564
sin(10°)	0.1736
sin(11°)	0.1908
sin(12°)	0.2079
sin(13°)	0.225
sin(14°)	0.2419
sin(15°)	0.2588
sin(16°)	0.2756
sin(17°)	0.2924
sin(18°)	0.309
sin(19°)	0.3256
sin(20°)	0.342
sin(21°)	0.3584
sin(22°)	0.3746
sin(23°)	0.3907
sin(24°)	0.4067
sin(25°)	0.4226
sin(26°)	0.4384
sin(27°)	0.454
sin(28°)	0.4695
sin(29°)	0.4848
sin(30°)	0.5
sin(31°)	0.515
sin(32°)	0.5299
sin(33°)	0.5446
sin(34°)	0.5592
sin(35°)	0.5736
sin(36°)	0.5878
sin(37°)	0.6018
sin(38°)	0.6157
sin(39°)	0.6293
sin(40°)	0.6428
sin(41°)	0.6561
sin(42°)	0.6691
sin(43°)	0.682
sin(44°)	0.6947
sin(45°)	0.7071

sin(46°)	0.7193
sin(47°)	0.7314
sin(48°)	0.7431
sin(49°)	0.7547
sin(50°)	0.766
sin(51°)	0.7771
sin(52°)	0.788
sin(53°)	0.7986
sin(54°)	0.809
sin(55°)	0.8192
sin(56°)	0.829
sin(57°)	0.8387
sin(58°)	0.848
sin(59°)	0.8572
sin(60°)	0.866
sin(61°)	0.8746
sin(62°)	0.8829
sin(63°)	0.891
sin(64°)	0.8988
sin(65°)	0.9063
sin(66°)	0.9135
sin(67°)	0.9205
sin(68°)	0.9272
sin(69°)	0.9336
sin(70°)	0.9397
sin(71°)	0.9455
sin(72°)	0.9511
sin(73°)	0.9563
sin(74°)	0.9613
sin(75°)	0.9659
sin(76°)	0.9703
sin(77°)	0.9744
sin(78°)	0.9781
sin(79°)	0.9816
sin(80°)	0.9848
sin(81°)	0.9877
sin(82°)	0.9903
sin(83°)	0.9925
sin(84°)	0.9945
sin(85°)	0.9962
sin(86°)	0.9976
sin(87°)	0.9986
sin(88°)	0.9994
sin(89°)	0.9998
sin(90°)	1

sin(91°)	0.9998
sin(92°)	0.9994
sin(93°)	0.9986
sin(94°)	0.9976
sin(95°)	0.9962
sin(96°)	0.9945
sin(97°)	0.9925
sin(98°)	0.9903
sin(99°)	0.9877
sin(100°)	0.9848
sin(101°)	0.9816
sin(102°)	0.9781
sin(103°)	0.9744
sin(104°)	0.9703
sin(105°)	0.9659
sin(106°)	0.9613
sin(107°)	0.9563
sin(108°)	0.9511
sin(109°)	0.9455
sin(110°)	0.9397
sin(111°)	0.9336
sin(112°)	0.9272
sin(113°)	0.9205
sin(114°)	0.9135
sin(115°)	0.9063
sin(116°)	0.8988
sin(117°)	0.891
sin(118°)	0.8829
sin(119°)	0.8746
sin(120°)	0.866
sin(121°)	0.8572
sin(122°)	0.848
sin(123°)	0.8387
sin(124°)	0.829
sin(125°)	0.8192
sin(126°)	0.809
sin(127°)	0.7986
sin(128°)	0.788
sin(129°)	0.7771
sin(130°)	0.766
sin(131°)	0.7547
sin(132°)	0.7431
sin(133°)	0.7314
sin(134°)	0.7193
sin(135°)	0.7071

sin(136°)	0.6947
sin(137°)	0.682
sin(138°)	0.6691
sin(139°)	0.6561
sin(140°)	0.6428
sin(141°)	0.6293
sin(142°)	0.6157
sin(143°)	0.6018
sin(144°)	0.5878
sin(145°)	0.5736
sin(146°)	0.5592
sin(147°)	0.5446
sin(148°)	0.5299
sin(149°)	0.515
sin(150°)	0.5
sin(151°)	0.4848
sin(152°)	0.4695
sin(153°)	0.454
sin(154°)	0.4384
sin(155°)	0.4226
sin(156°)	0.4067
sin(157°)	0.3907
sin(158°)	0.3746
sin(159°)	0.3584
sin(160°)	0.342
sin(161°)	0.3256
sin(162°)	0.309
sin(163°)	0.2924
sin(164°)	0.2756
sin(165°)	0.2588
sin(166°)	0.2419
sin(167°)	0.225
sin(168°)	0.2079
sin(169°)	0.1908
sin(170°)	0.1736
sin(171°)	0.1564
sin(172°)	0.1392
sin(173°)	0.1219
sin(174°)	0.1045
sin(175°)	0.0872
sin(176°)	0.0698
sin(177°)	0.0523
sin(178°)	0.0349
sin(179°)	0.0175
sin(180°)	0

Таблица синусов 180° – 360°.

sin(181°)	-0.0175
sin(182°)	-0.0349
sin(183°)	-0.0523
sin(184°)	-0.0698
sin(185°)	-0.0872
sin(186°)	-0.1045
sin(187°)	-0.1219
sin(188°)	-0.1392
sin(189°)	-0.1564
sin(190°)	-0.1736
sin(191°)	-0.1908
sin(192°)	-0.2079
sin(193°)	-0.225
sin(194°)	-0.2419
sin(195°)	-0.2588
sin(196°)	-0.2756
sin(197°)	-0.2924
sin(198°)	-0.309
sin(199°)	-0.3256
sin(200°)	-0.342
sin(201°)	-0.3584
sin(202°)	-0.3746
sin(203°)	-0.3907
sin(204°)	-0.4067
sin(205°)	-0.4226
sin(206°)	-0.4384
sin(207°)	-0.454
sin(208°)	-0.4695
sin(209°)	-0.4848
sin(210°)	-0.5
sin(211°)	-0.515
sin(212°)	-0.5299
sin(213°)	-0.5446
sin(214°)	-0.5592
sin(215°)	-0.5736
sin(216°)	-0.5878
sin(217°)	-0.6018
sin(218°)	-0.6157
sin(219°)	-0.6293
sin(220°)	-0.6428
sin(221°)	-0.6561
sin(222°)	-0.6691
sin(223°)	-0.682
sin(224°)	-0.6947
sin(225°)	-0.7071

sin(226°)	-0.7193
sin(227°)	-0.7314
sin(228°)	-0.7431
sin(229°)	-0.7547
sin(230°)	-0.766
sin(231°)	-0.7771
sin(232°)	-0.788
sin(233°)	-0.7986
sin(234°)	-0.809
sin(235°)	-0.8192
sin(236°)	-0.829
sin(237°)	-0.8387
sin(238°)	-0.848
sin(239°)	-0.8572
sin(240°)	-0.866
sin(241°)	-0.8746
sin(242°)	-0.8829
sin(243°)	-0.891
sin(244°)	-0.8988
sin(245°)	-0.9063
sin(246°)	-0.9135
sin(247°)	-0.9205
sin(248°)	-0.9272
sin(249°)	-0.9336
sin(250°)	-0.9397
sin(251°)	-0.9455
sin(252°)	-0.9511
sin(253°)	-0.9563
sin(254°)	-0.9613
sin(255°)	-0.9659
sin(256°)	-0.9703
sin(257°)	-0.9744
sin(258°)	-0.9781
sin(259°)	-0.9816
sin(260°)	-0.9848
sin(261°)	-0.9877
sin(262°)	-0.9903
sin(263°)	-0.9925
sin(264°)	-0.9945
sin(265°)	-0.9962
sin(266°)	-0.9976
sin(267°)	-0.9986
sin(268°)	-0.9994
sin(269°)	-0.9998
sin(270°)	-1

sin(271°)	-0.9998
sin(272°)	-0.9994
sin(273°)	-0.9986
sin(274°)	-0.9976
sin(275°)	-0.9962
sin(276°)	-0.9945
sin(277°)	-0.9925
sin(278°)	-0.9903
sin(279°)	-0.9877
sin(280°)	-0.9848
sin(281°)	-0.9816
sin(282°)	-0.9781
sin(283°)	-0.9744
sin(284°)	-0.9703
sin(285°)	-0.9659
sin(286°)	-0.9613
sin(287°)	-0.9563
sin(288°)	-0.9511
sin(289°)	-0.9455
sin(290°)	-0.9397
sin(291°)	-0.9336
sin(292°)	-0.9272
sin(293°)	-0.9205
sin(294°)	-0.9135
sin(295°)	-0.9063
sin(296°)	-0.8988
sin(297°)	-0.891
sin(298°)	-0.8829
sin(299°)	-0.8746
sin(300°)	-0.866
sin(301°)	-0.8572
sin(302°)	-0.848
sin(303°)	-0.8387
sin(304°)	-0.829
sin(305°)	-0.8192
sin(306°)	-0.809
sin(307°)	-0.7986
sin(308°)	-0.788
sin(309°)	-0.7771
sin(310°)	-0.766
sin(311°)	-0.7547
sin(312°)	-0.7431
sin(313°)	-0.7314
sin(314°)	-0.7193
sin(315°)	-0.7071

sin(316°)	-0.6947
sin(317°)	-0.682
sin(318°)	-0.6691
sin(319°)	-0.6561
sin(320°)	-0.6428
sin(321°)	-0.6293
sin(322°)	-0.6157
sin(323°)	-0.6018
sin(324°)	-0.5878
sin(325°)	-0.5736
sin(326°)	-0.5592
sin(327°)	-0.5446
sin(328°)	-0.5299
sin(329°)	-0.515
sin(330°)	-0.5
sin(331°)	-0.4848
sin(332°)	-0.4695
sin(333°)	-0.454
sin(334°)	-0.4384
sin(335°)	-0.4226
sin(336°)	-0.4067
sin(337°)	-0.3907
sin(338°)	-0.3746
sin(339°)	-0.3584
sin(340°)	-0.342
sin(341°)	-0.3256
sin(342°)	-0.309
sin(343°)	-0.2924
sin(344°)	-0.2756
sin(345°)	-0.2588
sin(346°)	-0.2419
sin(347°)	-0.225
sin(348°)	-0.2079
sin(349°)	-0.1908
sin(350°)	-0.1736
sin(351°)	-0.1564
sin(352°)	-0.1392
sin(353°)	-0.1219
sin(354°)	-0.1045
sin(355°)	-0.0872
sin(356°)	-0.0698
sin(357°)	-0.0523
sin(358°)	-0.0349
sin(359°)	-0.0175
sin(360°)	-0

Вы можете также ознакомиться с:

2mb.ru

Таблица значений тригонометрических функций

Примечание. В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/».

См. также полезные материалы:

Для определения значения тригонометрической функции, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2 ) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.

Синус пи, косинус пи, тангенс пи и других углов в радианах

Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах. Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.

Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам.

Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180.

Примеры:
1. Синус пи.
sin π = sin 180 = 0
таким образом, синус пи — это тоже самое, что синус 180 градусов и он равен нулю.

2. Косинус пи.
cos π = cos 180 = -1
таким образом, косинус пи — это тоже самое, что косинус 180 градусов и он равен минус единице.

3. Тангенс пи
tg π = tg 180 = 0
таким образом, тангенс пи — это тоже самое, что тангенс 180 градусов и он равен нулю.

Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)

Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.

Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов
0, 15, 30, 45, 60, 90 … 360 градусов
(цифровые значения «как по таблицам Брадиса»)

значение угла α (градусов)	значение угла α в радианах	sin (синус)	cos (косинус)	tg (тангенс)	ctg (котангенс)
0	0	0	1	0	-
15	π/12	0,2588	0,9659	0,2679	3,7321
30	π/6	0,5000	0,8660	0,5774	1,7321
45	π/4	0,7071	0,7071	1	1
50	5π/18	0,7660	0,6428	1.1918	0,8391
60	π/3	0,8660	0,5000	1,7321	0,5774
65	13π/36	0,9063	0,4226	2,1445	0,4663
70	7π/18	0,9397	0,3420	2,7475	0,3640
75	5π/12	0,9659	0,2588	3,7321	0,2679
90	π/2	1	0	-	0
105	5π/12	0,9659	-0,2588	-3,7321	-0,2679
120	2π/3	0,8660	-0,5000	-1,7321	-0,5774
135	3π/4	0,7071	-0,7071	-1	-1
140	7π/9	0,6428	-0,7660	-0,8391	-1,1918
150	5π/6	0,5000	-0,8660	-0,5774	-1,7321
180	π	0	-1	0	-
270	3π/2	-1	0	-	0
360	2π	0	1	0	-

Иногда для быстрых расчетов нужно не точное, а вычисляемое значение (число десятичной дробью), которое раньше искали в таблицах Брадиса. Поэтому, в дополнение к таблице точных значений тригонометрических функций приведены эти же самые значения, но в виде десятичной дроби, округленной до четвертого знака. Дополнительно в таблицу включены «нестандартные» значения тангенса, косинуса, синуса 140 градусов, синуса 105, 70, косинуса 105 и 50 градусов.

Начать курс обучения

profmeter.com.ua

Таблица синусов, она-же косинусов (см.примечание внутри). Углы в угловых градусах. Таблица значений синусов.

0,0000

0,0175

0,0349

0,0523

0,0698

0,0872

0,1045

0,1219

0,1392

0,1564

0,1736

0,1908

0,2079

0,2250

0,2419

0,2588

0,2756

0,2924

0,3090

0,3256

0,3420

0,3584

0,3746

0,3907

0,4067

0,4226

0,4384

0,4540

0,4695

0,4848

0,5000

0,5150

0,5299

0,5446

0,5592

0,5736

0,5878

0,6018

0,6157

0,6293

0,6428

0,6561

0,6691

0,6820

0,6947

0,0058

0,0233

0,0407

0,0581

0,0756

0,0929

0,1103

0,1276

0,1449

0,1622

0,1794

0,1965

0,2136

0,2306

0,2476

0,2644

0,2812

0,2979

0,3145

0,3311

0,3475

0,3638

0,3800

dpva.ru

СИНУСОВ И КОСИНУСОВ. ТАБЛИЦЫ БРАДИСА — ФОРМУЛЫ по МАТЕМАТИКЕ

Таблица квадратов 0 1 2 3 4 5 6 7 8 9 0 0 1 4 9 16 25 36 49 64 81 1 100 121 144 169 196 225 256 289 324 361 2 400 441 484 529 576 625 676 729 784 841 3 900 961 1024 1089 1156 1225 1296 1369 1444 1521 4 1600 1681 1764 1849 1936 2025 2116 2209 2304 2401 5 2500 2601 2704 2809 2916 3025 3136 3249 3364 3481 6 3600 3721 3844 3969 4096 4225 4356 4489 4624 4761 7 4900 5041 5184 5329 5476 5625 5776 5929 6084 6241 8 6400 6561 6724 6889 7056 7225 7396 7569 7744 7921 9 8100 8281 8464 8649 8836 9025 9216 9409 9604 9801 Если Вы только начинаете учить сложение, вычитание, умножение, деление, то есть считать, то можно перейти на ТРЕНАЖЕР и проверить свою технику счета.

СМОТРИТЕ ещё:

В степени: Число 2 3 4 5 6 7 8 9 10 2 4 8 16 32 64 128 256 512 1 024 3 9 27 81 243 729 2 187 6 561 19 683 59 049 4 16 64 256 1 024 4 096 16 384 65 536 262 144 1 048 576 5 25 125 625 3 125 15 625 78 125 390 625 1 953 125 9 765 625 6 36 216 1 296 7 776 46 656 279 936 1 679 616 10 077 696 60 …

СМОТРИТЕ ещё:

Для нахождения значений тригонометрических функций тангенса и котангенса мы используем таблицу Брадиса. В современных учебниках представлена эта таблица в упрощенном виде. tg 0’ 6’ 12’ 18’ 24’ 30’ 36’ 42’ 48’ 54’ 60’ ctg 1’ 2’ 3’ 0 90° 0° 0,000 0017 0035 0052 0070 0087 0105 0122 0140 0157 0175 89° 3 6 9 1° 0175 0192 0209 0227 0244 0262 0279 0297 0314 0332 0349 88° 3 6 9 2° 0349 0367 0384 0402 0419 0437 0454 0472 0489 0507 0524 87° 3 6 9 3° 0524 0542 0559 0577 0594 0612 0629 0647 0664 0682 0699 86° 3 6 9 4° 0699 0717 0734 0752 0769 0787 0805 0822 0840 0857 0,0875 85° 3 6 9 5° 0,0875 0892 0910 0928 0945 0963 0981 0998 1016 1033 1051 84° 3 6 9 6° 1051 1069 1086 1104 1122 1139 1157 1175 1192 1210 1228 83° 3 6 9 7° 1228 1246 1263 1281 1299 1317 1334 1352 1370 1388 1405 82° 3 6 9 8° 1405 1423 1441 1459 1477 1495 1512 1530 1548 1566 1584 81° 3 6 9 9° 1584 1602 1620 1638 1655 1673 1691 1709 1727 1745 0,1763 80° 3 6 9 10° 0,1763 1781 1799 1817 1835 1853 1871 1890 1908 1926 1944 79° 3 6 9 11° 1944 1962 1980 1998 2016 2035 2053 2071 2089 2107 2126 78° 3 6 9 12° 2126 2144 2162 2180 2199 2217 2235 2254 2272 2290 2309 77° 3 6 9 13° 2309 2327 2345 2364 2382 2401 2419 2438 2456 2475 2493 76° 3 6 9 14° 2493 2512 2530 2549 2568 2586 2605 2623 2642 2661 0,2679 75° 3 6 9 15° 0,2679 2698 2717 2736 2754 2773 2792 2811 2830 2849 2867 74° 3 6 9 16° 2867 2886 2905 2924 2943 2962 2981 3000 3019 3038 3057 73° 3 6 9 17° 3057 3076 3096 3115 3134 3153 3172 3191 3211 3230 3249 72° 3 6 10 18° 3249 3269 3288 3307 3327 3346 3365 3385 3404 3424 3443 71° 3 6 10 19° 3443 3463 3482 3502 3522 3541 3561 3581 3600 3620 0,3640 70° 3 7 10 20° 0,3640 3659 3679 3699 3719 3739 3759 3779 3799 3819 3839 69° 3 7 10 21° 3839 3859 3879 3899 3919 3939 3959 3979 4000 4020 4040 68° 3 7 10 22° 4040 4061 4081 4101 4122 4142 4163 4183 4204 4224 4245 67° 3 7 10 23° 4245 4265 4286 4307 4327 4348 4369 4390 4411 4431 4452 66° 3 7 10 24° 4452 4473 4494 4515 4536 4557 4578 4599 4621 4642 0,4663 65° 4 7 11 25° 0,4663 4684 4706 4727 4748 4770 4791 4813 4834 4856 4877 64° 4 7 11 26° 4877 4899 4921 4942 4964 4986 5008 5029 5051 5073 5095 63° 4 7 11 27° 5095 5117 5139 5161 5184 5206 5228 5250 5272 5295 5317 62° 4 7 11 28° 5317 5340 5362 5384 5407 5430 5452 5475 5498 5520 5543 61° 4 8 11 29° 5543 5566 5589 5612 5635 5658 5681 5704 5727 5750 0,5774 60° 4 8 12 30° 0,5774 5797 5820 5844 5867 5890 5914 5938 5961 5985 6009 59° 4 8 12 31° 6009 6032 6056 6080 6104 6128 6152 6176 6200 6224 6249 58° 4 8 12 32° 6249 6273 6297 6322 6346 6371 6395 6420 6445 6469 6494 57° 4 8 12 33° 6494 6519 6544 6569 6594 6619 6644 6669 6694 6720 6745 56° 4 8 13 34° 6745 6771 6796 6822 6847 6873 6899 6924 6950 6976 0,7002 55° 4 9 13 35° 0,7002 7028 7054 7080 7107 7133 7159 7186 7212 7239 7265 54° 4 8 13 36° 7265 7292 7319 7346 7373 7400 7427 7454 7481 7508 7536 53° 5 9 14 37° 7536 7563 7590 7618 7646 7673 7701 7729 7757 7785 7813 52° 5 9 14 38° 7813 7841 7869 7898 7926 7954 7983 8012 8040 8069 8098 51° 5 9 14 39° 8098 8127 8156 8185 8214 8243 8273 8302 8332 8361 0,8391 50° 5 10 15 40° 0,8391 8421 8451 8481 8511 8541 8571 8601 8632 8662 0,8693 49° 5 10 15 41° 8693 8724 8754 8785 8816 8847 8878 8910 8941 8972 9004 48° 5 10 16 42° 9004 9036 9067 9099 9131 9163 9195 9228 9260 9293 9325 47° 6 11 16 43° 9325 9358 9391 9424 9457 9490 9523 9556 9590 9623 0,9657 46° 6 11 17 44° 9657 9691 9725 9759 9793 9827 9861 9896 9930 9965 1,0000 45° 6 11 17 45° 1,0000 0035 0070 0105 0141 0176 0212 0247 0283 0319 0355 44° 6 12 18 46° 0355 0392 0428 0464 0501 0538 0575 0612 0649 0686 0724 43° 6 12 18 47° 0724 0761 0799 0837 0875 0913 0951 0990 1028 1067 1106 42° 6 13 19 48° 1106 1145 1184 1224 1263 1303 1343 1383 1423 1463 1504 41° 7 13 20 49° 1504 1544 1585 1626 1667 1708 1750 1792 1833 1875 1,1918 40° 7 14 21 50° 1,1918 1960 2002 2045 2088 2131 2174 2218 2261 2305 2349 39° 7 14 22 51° 2349 2393 2437 2482 2527 2572 2617 2662 2708 2753 2799 38° 8 15 23 52° 2799 2846 2892 2938 2985 3032 3079 3127 3175 3222 3270 37° 8 16 24 53° 3270 3319 3367 3416 3465 3514 3564 3613 3663 3713 3764 36° 8 16 25 54° 3764 3814 3865 3916 3968 4019 4071 4124 4176 4229 1,4281 35° 9 17 26 55° 1,4281 4335 4388 4442 4496 4550 4605 4659 4715 4770 4826 34° 9 18 27 56° 4826 4882 4938 4994 5051 5108 5166 5224 5282 5340 5399 33° 10 19 29 57° 5399 5458 5517 5577 5637 5697 5757 5818 5880 5941 6003 32° 10 20 30 58° 6003 6066 6128 6191 6255 6319 6383 6447 6512 6577 6643 31° 11 21 32 59° 6643 6709 6775 6842 6909 6977 7045 7113 7182 7251 1,7321 30° 11 23 34 60° 1,732 1,739 1,746 1,753 1,760 1,767 1,775 1,782 1,789 1,797 1,804 29° 1 2 4 61° 1,804 1,811 1,819 1,827 1,834 1,842 1,849 1,857 1,865 1,873 1,881 28° 1 3 4 62° 1,881 1,889 1,897 1,905 1,913 1,921 1,929 1,937 1,946 1,954 1,963 27° 1 3 4 63° 1,963 1,971 1,980 1,988 1,997 2,006 2,014 2,023 2,032 2,041 2,05 26° 1 3 4 64° 2,050 2,059 2,069 2,078 2,087 2,097 2,106 2,116 2,125 2,135 2,145 25° 2 3 5 65° 2,145 2,154 2,164 2,174 2,184 2,194 2,204 2,215 2,225 2,236 2,246 24° 2 3 5 66° 2,246 2,257 2,267 2,278 2,289 2,3 2,311 2,322 2,333 2,344 2,356 23° 2 4 5 67° 2,356 2,367 2,379 2,391 2,402 2,414 2,426 2,438 2,450 2,463 2,475 22° 2 4 6 68° 2,475 2,488 2,5 2,513 2,526 2,539 2,552 2,565 2,578 2,592 2,605 21° 2 4 6 69° 2,605 2,619 2,633 2,646 2,66 2,675 2,689 2,703 2,718 2,733 2,747 20° 2 5 7 70° 2,747 2,762 2,778 2,793 2,808 2,824 2,840 2,856 2,872 2,888 2,904 19° 3 5 8 71° 2,904 2,921 2,937 2,954 2,971 2,989 3,006 3,024 3,042 3,06 3,078 18° 3 6 9 72° 3,078 3,096 3,115 3,133 3,152 3,172 3,191 3,211 3,230 3,251 3,271 17° 3 6 10 73° 3,271 3,291 3,312 3,333 3,354 3,376 3 7 10 3,398 3,42 3,442 3,465 3,487 16° 4 7 11 74° 3,487 3,511 3,534 3,558 3,582 3,606 4 8 12 3,630 3,655 3,681 3,706 3,732 15° 4 8 13 75° 3,732 3,758 3,785 3,812 3,839 3,867 4 9 13 3,895 3,923 3,952 3,981 4,011 14° 5 10 14 tg 60’ 54’ 48’ 42’ 36’ 30’ 24’ 18’ 12’ 6’ 0’ ctg 1’ 2’ 3’ Как использовать таблицу? Смотрите пост «Как найти значения тангенса или …

СМОТРИТЕ ещё:

lyudmilanik.com.ua

Онлайн графики в полярных координатах – Построение графика функции в полярных координатах · Калькулятор Онлайн

alexxlab / 14.12.201602.06.2019 / Школьная жизнь

Построение графика функции в полярных координатах · Калькулятор Онлайн

Введите график функции

Важно phi должно лежать в правильном промежутке, иначе график не сможет построиться

Построим график функции в полярных координатах r=r(φ),
где 0 <= φ <= 2π,
но вы можете задать свои границы φ.
Задайте также полярную функцию r(φ).

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x): Абсолютное значение x
(модуль x или |x|)
arccos(x): Функция — арккосинус от x
arccosh(x): Арккосинус гиперболический от x
arcsin(x): Арксинус от x
arcsinh(x): Арксинус гиперболический от x
arctg(x): Функция — арктангенс от x
arctgh(x): Арктангенс гиперболический от x
e: e число, которое примерно равно 2.7
exp(x): Функция — экспонента от x (что и e^x)
log(x) or ln(x): Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
pi: Число — «Пи», которое примерно равно 3.14
sin(x): Функция — Синус от x
cos(x): Функция — Косинус от x
sinh(x): Функция — Синус гиперболический от x
cosh(x): Функция — Косинус гиперболический от x
sqrt(x): Функция — квадратный корень из x
sqr(x) или x^2: Функция — Квадрат x
tg(x): Функция — Тангенс от x
tgh(x): Функция — Тангенс гиперболический от x
cbrt(x): Функция — кубический корень из x
floor(x): Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
sign(x): Функция — Знак x
erf(x): Функция ошибок (Лапласа или интеграл вероятности)

В выражениях можно применять следующие операции:

Действительные числа: вводить в виде 7.5, не 7,5
2*x: — умножение
3/x: — деление
x^3: — возведение в степень
x + 7: — сложение
x — 6: — вычитание

www.kontrolnaya-rabota.ru

Примеры графиков функций в полярных координатах

Поделиться в соцсетях:

\[ r(t) = 1, \quad t \in [0; 2\pi] \\ r(t) = 2, \quad t \in [0; 2\pi] \]

\[ r(t) = 2t, \quad t \in [0; 8\pi] \]

\[ r(t) = 1 — \sin(t), \quad t \in [0; 2\pi] \]

\[ r(t) = 2 — 4\sin(t), \quad t \in [0; 2\pi] \]

\[ r(t) = \frac{1}{1 — \cos(t)}, \quad t \in [0; 2\pi] \]

\[ r(t) = \sin(6t), \quad t \in [0; 2\pi] \]

\[ r(t) = \sin\Big(\frac{7}{4}t\Big), \quad t \in [0; 8\pi] \]

\[ r(t) = \sin\Big(\frac{3}{4}t\Big), \quad t \in [0; 8\pi] \]

\[ r(t) = \mathrm{e}^{\sin(t)} — 2\cos(4t) + \sin^5\Big(\frac{2t — \pi}{24}\Big) \\ t \in [{-8\pi}; 8\pi] \]

\[ r(t) = 2 — 2\sin(t) + \sin(t)\frac{\sqrt{|\cos(t)|}}{\sin(t) + 1,4} \\ t \in [0; 2\pi] \]

grafikus.ru

Построить график функции онлайн

2D в декартовых координатах
2D график функции, которая задана параметрически
2D график функции, в полярных координатах
3D график поверхности, заданной уравнением
Построение графика по точкам
График неявно заданной функции

Это онлайн сервис в один шаг:

Ввести функцию, которую необходимо построить

Помимо построения графика функции, Вы получите результат исследования функции

Перейти: Онлайн сервис «Построение графика функции в декартовых координатах 2D» →

Это он-лайн сервис в три шага:

Ввести верхнюю и нижнюю границу для параметра
Ввести функцию x = x(t)
Ввести функцию y = y(t)

Перейти: Онлайн сервис «Построение графика функции параметрически» →

Это он-лайн сервис в два шага:

Указать границы полярного угла
Ввести функцию r=r(phi)

Перейти: Онлайн сервис «Построение графика функции в полярных координатах» →

Это онлайн сервис в два шага:

Ввести верхние и нижние границы для графика поверхности
Ввести уравнение, для которого необходимо построить поверхность

Перейти: Онлайн сервис «Построение поверхности в декартовых координатах 3D» →

Это он-лайн сервис в один шаг:

Введите точки

Перейти: Онлайн сервис «Построение графика по точкам» →

www.kontrolnaya-rabota.ru

Построение графика в полярных координатах. Контрольные онлайн

Построение графика в полярных координатах

Дано уравнение  кривой в полярной системе координат .
Требуется:
   а) построить кривую по точкам, придавая j  значения из промежутка  с шагом ; 
   б) записать уравнение этой кривой в  декартовой прямоугольной системе координат, согласованной с полярной, и определить  тип этой кривой.

Решение
а) Составим таблицу значений функции.

j	0	p/8	p/4	3p/8	p/2	5p/8	3p/4	7p/8	p	9p/8	5p/8	11p/8	3p/2	13p/8	7p/4	15p/8
r	3	2,8	2,32	1,72	1,5	1,26	1,11	1,02	1	1,02	1,11	1,26	1,5	1,72	2,32	2,8

По этим данным отметим точки на плоскости и, плавно соединяя соседние точки, построим линию.

б) Перейдём к декартовой прямоугольной системе координат, пользуясь формулами , .
Заданное уравнение примет вид .
Преобразуем это уравнение: ,

, , , .
Выделив полные квадраты переменных и , получим или .

Это уравнение эллипса с центром в точке и полуосями и .

www.matem96.ru

Построение графика функции, заданной параметрически

Введите график функции

Важно a должно быть меньше b, иначе график не сможет построиться

Видео пример:

Построим график параметрической функции x=x(t) и y=y(t),
где параметр t лежит в промежутке [a, b],
и вы можете задать свои границы.
Задайте также функции x и y, зависящих от параметра.

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x): Абсолютное значение x
(модуль x или |x|)
arccos(x): Функция — арккосинус от x
arccosh(x): Арккосинус гиперболический от x
arcsin(x): Арксинус от x
arcsinh(x): Арксинус гиперболический от x
arctg(x): Функция — арктангенс от x
arctgh(x): Арктангенс гиперболический от x
e: e число, которое примерно равно 2.7
exp(x): Функция — экспонента от x (что и e^x)
log(x) or ln(x): Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
pi: Число — «Пи», которое примерно равно 3.14
sin(x): Функция — Синус от x
cos(x): Функция — Косинус от x
sinh(x): Функция — Синус гиперболический от x
cosh(x): Функция — Косинус гиперболический от x
sqrt(x): Функция — квадратный корень из x
sqr(x) или x^2: Функция — Квадрат x
tg(x): Функция — Тангенс от x
tgh(x): Функция — Тангенс гиперболический от x
cbrt(x): Функция — кубический корень из x
floor(x): Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
sign(x): Функция — Знак x
erf(x): Функция ошибок (Лапласа или интеграл вероятности)

В выражениях можно применять следующие операции:

Действительные числа: вводить в виде 7.5, не 7,5
2*x: — умножение
3/x: — деление
x^3: — возведение в степень
x + 7: — сложение
x — 6: — вычитание

www.kontrolnaya-rabota.ru

Построение графиков функций | Cubens

Как пользоваться программой

С помощью данной программы на Cubens можно построить график функции онлайн.

Десятичные дроби нужно разделять точкой
В некоторых случаях можно не писать знаки умножения
Можно строить множество графиков функций одновременно
Можно настроить названия осей и их интервалы
График можно скачать как PNG изображение
График можно распечатать
Можно получить ссылку на график чтобы поделиться им с другими
При наведении курсора на график его можно двигать, а также увеличивать или уменьшать масштаб

Предложения и замечания по работе программы можно оставить в комментариях ниже.

Режимы

На текущий момент в программе доступны четыре режима:

Обычный — в этом режиме можно строить графики функций, заданных уравнением
Параметрический — позволяет строить графики кривых, заданных параметрически, то есть, в виде и
Полярные координаты — позволяет строить графики кривых, заданных в полярной системе координат, то есть уравнением , где — радиальная координата, а — полярная координата
По точкам — этот режим предназначен для построения графиков функций указывая координаты их точек

График функции

Зависимость переменной от переменной называется функцией, если каждому значению соответствует единственное значение .

Функция обозначается или одной буквой или или равенством .

Область определения функции — это все значения, которые может принимать аргумент (переменная ).

Область значений функции — это все значения, которые может принимать функция (переменная ) при всех из области определения функции.

Функцию можно задать с помощью таблицы, графика или формулы. Формула задает правило, по которому каждому значению аргумента ставится в соответствие значение функции .

Графиком функции называется множество всех точек координатной плоскости с координатами , где первая координата пробегает всю область определения функции , а вторая координата — это соответствующее значение функции в точке .

cubens.com

площадь фигуры в полярных координатах — 22 Марта 2015 — Примеры решений задач

Площадь фигуры, заданной в полярных координатах

Рассмотрим примеры вычисления площади фигуры, заданной в полярных координатах кривой ρ= ρ(φ), с помощью определенного интеграла по формуле

Пример 1. Вычислить площадь, ограниченную одним лепестком розы

Решение.

Шаг 1. Выполним рисунок графика функции с помощью калькулятора построения графиков функций в полярных координатах.

Шаг 2. Из рисунка видно, что угол φ в первой четверти изменяется от 0 до π/2, следовательно границы интегрирования φ₁=0, φ₂=π/2

Шаг 3. Уравнение кривой , и границы φ₁=0, φ₂=π/2, подставляем в формулу

получаем площадь фигуры:

Замечание. Вычислить площадь фигуры в полярных координатах можно с помощью калькулятора

www.reshim.su

Нахождение косинуса тангенса синуса – Cинус, косинус, тангенс и котангенс

alexxlab / 13.12.201602.06.2019 / Школьная жизнь

Нахождение значений синуса, косинуса, тангенса и котангенса

Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.

Yandex.RTB R-A-339285-1

В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.

Рассмотрим подробно каждый случай.

Определение 1

Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.

Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.

Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.

В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.

Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.

Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0°, 90°,

zaochnik.com

Замечательные отношения в прямоугольном треугольнике

Категория: ПланиметрияСправочные материалы

Елена Репина 2013-05-22 2013-08-04

На всякий случай, уточним, что гипотенузой называется та сторона треугольника, что лежит против угла в 90 градусов, две оставшиеся стороны называются катетами прямоугольного треугольника.

Подробнее про прямоугольный треугольник здесь.

Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.

Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.

Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.

Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.

Бывает (и на ЕГЭ, ГИА), что приходится иметь дело с косинусами, синусами и тангенсами внешних углов треугольника. Формулы приведения позволяют увидеть, что есть еще и вот такая связь между смежными углами (помимо того, что их сумма равна 180):

Смотрите подборку задач на применение указанных соотношений в статье «Прямоугольный треугольник. Вычисление длин и углов» часть I, часть II.

Автор: egeMax | комментариев 8 | Метки: шпаргалки-таблицы

egemaximum.ru

определения, формулы, примеры, угол поворота

Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Yandex.RTB R-A-339285-1

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.

Косинус угла (cosα) — отношение прилежащего катета к гипотенузе.

Тангенс угла (tg α) — отношение противолежащего катета к прилежащему.

Котангенс угла (ctg α) — отношение прилежащего катета к противолежащему.

Данные определения даны для острого угла прямоугольного треугольника!

Приведем иллюстрацию.

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Важно помнить!

Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Опре

zaochnik.com

Синус косинус

Синус косинус, определение. Друзья! В прошлой статье, где были рассмотрены задачи на решение прямоугольного треугольника, я пообещал изложить приём запоминания определений синуса и косинуса. Используя его, вы всегда быстро вспомните – какой катет относится к гипотенузе (прилежащий или противолежащий). Решил в «долгий ящик не откладывать», необходимый материал ниже, прошу ознакомиться 😉

Дело в том, что я не раз наблюдал, как учащиеся 10-11 классов с трудом вспоминают данные определения. Они прекрасно помнят, что катет относится к гипотенузе, а вот какой из них — забывают и путают. Цена ошибки, как вы знаете на экзамене – это потерянный бал.

Информация, которую я представлю непосредственно к математике не имеет никакого отношения. Она связана с образным мышлением, и с приёмами словесно-логической связи. Именно так, я сам, раз и на всегда запомнил данные определения. Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.

Напомню определения синуса и косинуса в прямоугольном треугольнике:

Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе:

Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:

Итак, какие ассоциации у вас вызывает слово косинус?

Наверное, у каждого свои 😉 Запоминайте связку:

Таким образом, у вас сразу в памяти возникнет выражение –

«… отношение ПРИЛЕЖАЩЕГО катета к гипотенузе».

Проблема с определением косинуса решена.

Если нужно вспомнить определение синуса в прямоугольном треугольнике, то вспомнив определение косинуса, вы без труда установите, что синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Ведь катетов всего два, если прилежащий катет «занят» косинусом, то синусу остаётся только противолежащий.

Как быть с тангенсом и котангенсом? Путаница та же. Учащиеся знают, что это отношение катетов, но проблема вспомнить какой к которому относится – то ли противолежащий к прилежащему, то ли наоборот.

Определения:

Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему:

Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему:

Как запомнить? Есть два способа. Один так же использует словесно-логическую связь, другой – математический.

СПОСОБ МАТЕМАТИЧЕСКИЙ

Есть такое определение – тангенсом острого угла называется отношение синуса угла к его косинусу:

*Запомнив формулу, вы всегда сможете определить, что тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему.

Аналогично. Котангенсом острого угла называется отношение косинуса угла к его синусу:

Итак! Запомнив указанные формулы вы всегда сможете определить, что:

— тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему

— котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему.

СПОСОБ СЛОВЕСНО-ЛОГИЧЕСКИЙ

О тангенсе. Запомните связку:

То есть если потребуется вспомнить определение тангенса, при помощи данной логической связи, вы без труда вспомните, что это

«… отношение противолежащего катета к прилежащему»

Если речь зайдёт о котангенсе, то вспомнив определение тангенса вы без труда озвучите определение котангенса –

«… отношение прилежащего катета к противолежащему»

Есть интересный приём по запоминанию тангенса и котангенса на сайте «Математический тандем», посмотрите.

СПОСОБ УНИВЕРСАЛЬНЫЙ

Можно просто зазубрить. Но как показывает практика, благодаря словесно-логическим связкам человек запоминает информацию надолго, и не только математическую.

Надеюсь, материал был вам полезен.

С уважением, Александр Крутицких

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Синус sin x косинус cos x

Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.

Геометрическое определение синуса и косинуса

|BD| — длина дуги окружности с центром в точке A.
α — угол, выраженный в радианах.

Определение
Синус (sin α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.

Косинус (cos α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.

Принятые обозначения

;
;
.

График функции синус, y = sin x

График функции косинус, y = cos x

Свойства синуса и косинуса

Периодичность

Функции y = sin x и y = cos x периодичны с периодом 2π.

Четность

Функция синус – нечетная. Функция косинус – четная.

Область определения и значений, экстремумы, возрастание, убывание

Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).

	y = sin x	y = cos x
Область определения и непрерывность	– ∞ < x < + ∞	– ∞ < x < + ∞
Область значений	–1 ≤ y ≤ 1	–1 ≤ y ≤ 1
Возрастание
Убывание
Максимумы, y = 1
Минимумы, y = –1
Нули, y = 0
Точки пересечения с осью ординат, x = 0	y = 0	y = 1

Основные формулы

Сумма квадратов синуса и косинуса

Формулы синуса и косинуса от суммы и разности

Формулы произведения синусов и косинусов

Формулы суммы и разности

Выражение синуса через косинус

Далее мы полагаем, что – целое число.

;
;
;
.

Выражение косинуса через синус

;
;
;
.

Выражение через тангенс

; .

При , имеем:
; .

При :
; .

Таблица синусов и косинусов, тангенсов и котангенсов

В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.

Выражения через комплексные переменные

;

Формула Эйлера

Выражения через гиперболические функции

;
;

Производные

; . Вывод формул > > >

Производные n-го порядка:
; .

Интегралы

;
См. также раздел Таблица неопределенных интегралов >>>

Разложения в ряды

{ –∞ < x < +∞ }
{ –∞ < x < +∞ }

Секанс, косеканс

Обратные функции

Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.

Арксинус, arcsin

Арккосинус, arccos

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов. Опубликовано: 15-02-2014 Изменено: 23-12-2018

1cov-edu.ru

что такое? Как найти синус, косинус и тангенс?

Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.

Истоки тригонометрии

Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.

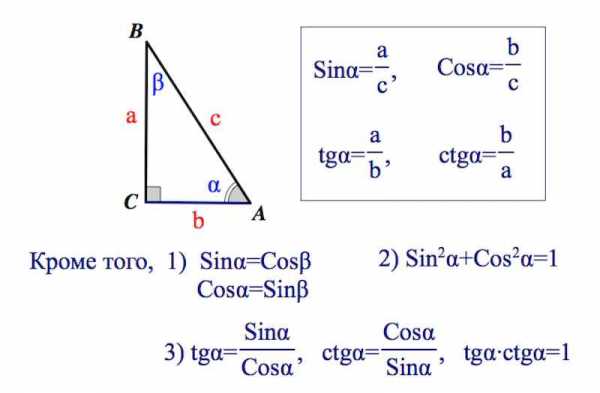
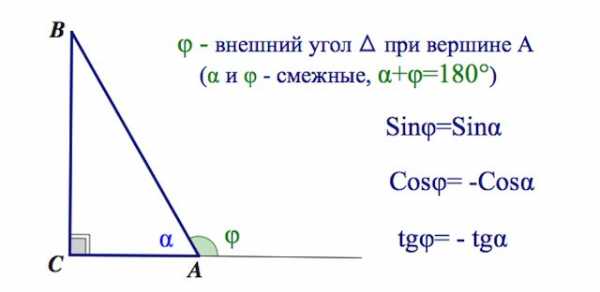
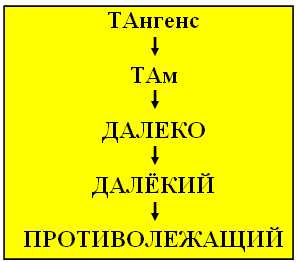
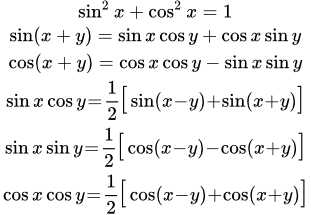
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.

Начальный этап

Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.

Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.

Сферическая тригонометрия

Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».

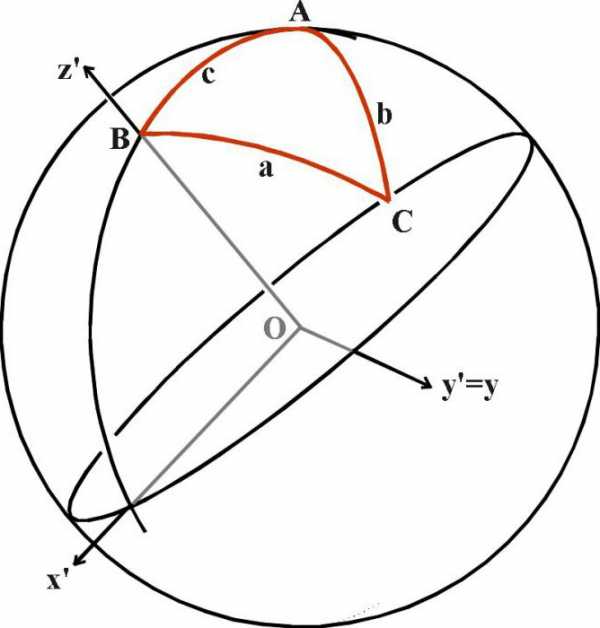Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание – она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.

Прямоугольный треугольник

Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.

Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза – это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.

Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.

Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.

Определение

Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.

Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.

Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза – это по умолчанию самая длинная сторона прямоугольного треугольника. Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.

Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.

Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.

Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.

Простейшие формулы

В тригонометрии не обойтись без формул – как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.

Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.

Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.

Формулы двойного угла и сложения аргументов

Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.

Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих – в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.

Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.

Теоремы

Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.

Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.

Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.

Ошибки по невнимательности

Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.

Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата – можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.

Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.

В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.

Применение

Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.

В заключение

Итак, вы знаете, что такое синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.

Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.

Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение – это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.

fb.ru

Основные тригонометрические тождества

Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.

Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.

\[ \sin^{2}\alpha + \cos^{2} \alpha = 1 \]

\[ tg \alpha = \dfrac{\sin \alpha}{\cos \alpha}, \enspace ctg \alpha = \dfrac{\cos \alpha}{\sin \alpha} \]

\[ tg \alpha \cdot ctg \alpha = 1 \]

Зависимость между синусом и косинусом

\[ \sin^{2} \alpha+\cos^{2} \alpha=1 \]

Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.

При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.

Нахождение тангенса и котангенса через синус и косинус

\[ tg \alpha = \dfrac{\sin \alpha}{\cos \alpha},\enspace ctg \alpha=\dfrac{\cos \alpha}{\sin \alpha} \]

Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой $ \dfrac{y}{x}=\dfrac{\sin \alpha}{\cos \alpha} $, а отношение $ \dfrac{x}{y}=\dfrac{\cos \alpha}{\sin \alpha} $ — будет являться котангенсом.

Добавим, что только для таких углов $ \alpha $, при которых входящие в них тригонометрические функции имеют смысл, будут иметь место тождества $ tg \alpha = \dfrac{\sin \alpha}{\cos \alpha} $, $ ctg \alpha=\dfrac{\cos \alpha}{\sin \alpha} $.

Например: $ tg \alpha = \dfrac{\sin \alpha}{\cos \alpha} $ является справедливой для углов $ \alpha $, которые отличны от $ \dfrac{\pi}{2}+\pi z $, а $ ctg \alpha=\dfrac{\cos \alpha}{\sin \alpha} $ — для угла $ \alpha $, отличного от $ \pi z $, $ z $ — является целым числом.

Зависимость между тангенсом и котангенсом

\[ tg \alpha \cdot ctg \alpha=1 \]

Данное тождество справедливо только для таких углов $ \alpha $, которые отличны от $ \dfrac{\pi}{2} z $. Иначе или котангенс или тангенс не будут определены.

Опираясь на вышеизложенные пункты, получаем, что $ tg \alpha = \dfrac{y}{x} $, а $ ctg \alpha=\dfrac{x}{y} $. Отсюда следует, что $ tg \alpha \cdot ctg \alpha = \dfrac{y}{x} \cdot \dfrac{x}{y}=1 $. Таким образом, тангенс и котангенс одного угла, при котором они имеют смысл, являются взаимно обратными числами.

Зависимости между тангенсом и косинусом, котангенсом и синусом

$ tg^{2} \alpha + 1=\dfrac{1}{\cos^{2} \alpha} $ — сумма квадрата тангенса угла $ \alpha $ и $ \alpha $, отличных от $ \dfrac{\pi}{2}+ \pi z $.

$ 1+ctg^{2} \alpha=\dfrac{1}{\sin^{2}\alpha} $ — сумма $ \alpha $, равняется обратному квадрату синуса данного угла. Данное тождество справедливо для любого $ \alpha $, отличного от $ \pi z $.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

calcsbox.com

Уравнение треугольника – Уравнение сторон треугольника | Треугольники

alexxlab / 12.12.201602.06.2019 / Школьная жизнь

Уравнение сторон треугольника | Треугольники

Как составить уравнение сторон треугольника по координатам его вершин?

Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.

Пример.

Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)

Составить уравнения сторон треугольника.

Решение:

1) Составим уравнение прямой AB, проходящей через 2 точки A и B.

Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:

Таким образом, уравнение стороны AB

2) Прямая BC проходит через точки B(7;-4) и C(3;7):

Отсюда уравнение стороны BC —

3) Прямая AC проходит через точки A(-5;1) и C(3;7):

Уравнение стороны AC —

Уравнение прямой

www.treugolniki.ru

Уравнение треугольника : Геометрия — Страница 2

Выглядит уравнение интуитивно понятно, но как это строго доказать?

Вообще говоря, это морока. Надо нарисовать три прямых, на каждой из которых один из модулей обращается в ноль и которые делят плоскость на семь частей, и раскрывать модули в каждой из этих частей отдельно.

Но если уж мы знаем, что ответом должен быть треугольник, притом сплошной треугольник, а не только его контур, то всё очень сильно упрощается. Функция линейна на любом из участков разбиения плоскости теми линиями. Поэтому чтобы доказать, что эта функция тождественно равна нулю внутри треугольника (и на его границе), достаточно проверить, что она равна нулю в вершинах треугольника, т.е. в точках , и . Ну это очевидно.

А снаружи эта функция положительна (т.е. там исходное равенство для и не выполняется), поскольку поверхность в пространстве, задаваемая уравнением , представляет собой выпуклый многогранник.

Или если не нравится выпуклость, то можно так. На любом из участков плоскости, смежным с одной из сторон треугольника, тождество нарушается просто потому, что при переходе через эту сторону один из модулей раскрывается по-другому, чем внутри треугольника, а два других — так же, как и раньше. При этом нарушается оно в положительную сторону — ведь на любом из шести лучей тех трёх прямых, уходящих из вершины треугольника в сторону бесконечности, функция может уходить только на плюс бесконечность, но никак не на минус (модули-то всё-таки неотрицательны). А тогда и внутри каждого из трёх углов, ограниченного одной из пар этих лучей, функция тоже положительна, раз она положительна на границе этого угла. Итого — она положительна всюду, кроме треугольника.

dxdy.ru

Уравнение высоты треугольника | Треугольники

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

Найти уравнение стороны треугольника.
Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Пример.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

Решение:

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

www.treugolniki.ru

Все формулы для треугольника

1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:

L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)

a, b — катеты прямоугольного треугольника

с — гипотенуза

α — угол прилежащий к гипотенузе

Формула длины биссектрисы через катеты, ( L):

Формула длины биссектрисы через гипотенузу и угол, ( L):

2. Найти по формулам длину биссектрисы из острого угла на катет:

L — биссектриса, отрезок ME , исходящий из острого угла

a, b — катеты прямоугольного треугольника

с — гипотенуза

α, β — углы прилежащие к гипотенузе

Формулы длины биссектрисы через катет и угол, (L):

Формула длины биссектрисы через катет и гипотенузу, (L):

www-formula.ru

Уравнение треугольника : Геометрия — Страница 2

Выглядит уравнение интуитивно понятно, но как это строго доказать?

dxdy.ru

Уравнение биссектрисы треугольника | Треугольники

Как составить уравнение биссектрисы треугольника по координатам его вершин?

1 способ

Используя уравнение биссектрисы угла:

Пример.

Даны вершины треугольника A(-5;4), B(7;-1) и C(3;10).

1) Составить уравнение биссектрисы треугольника ABC, выходящей из вершины A.

2) Найти длину этой биссектрисы.

Решение:

1) Угол A образован прямыми AB и AC. Составим уравнения этих прямых.

Уравнение прямой, проходящей через две точки, можно найти, например, по формуле

Уравнение прямой AB:

Уравнение прямой AC:

Подставляем уравнения прямых AB и AC в формулы уравнения биссектрис угла:

то есть

Из этих уравнений является уравнением биссектрисы внутреннего угла BAC треугольника, другое — биссектрисой внешнего угла при вершине A. Как отличить уравнение биссектрисы внутреннего угла?

Точки B и C лежат по одну сторону от биссектрисы внешнего угла, поэтому при подстановке координат B и C в уравнение мы получим числа одинакового знака. От биссектрисы внутреннего угла B и C лежат по разные стороны, поэтому подстановка их координат в уравнение биссектрисы внутреннего угла даёт нам числа разных знаков.

Подставляем в уравнение x-8y+37=0 координаты B и C.

B(7;-1): 7-8·(-1)+37>0

C(3;10): 3-8·10+37<0.

Таким образом, уравнение x-8y+37=0 является уравнением биссектрисы AF треугольника ABC.

2) Чтобы найти длину биссектрисы, найдём точку пересечения прямых AF и BF.

Уравнение прямой BC:

Координаты точки пересечения прямых AF и BC находим из системы уравнений

Решение системы —

Длину биссектрисы AF находим по формуле расстояния между точками A и F:

2 способ

Используя свойство биссектрисы треугольника:

По формулам деления отрезка в данном отношении

разделим отрезок BC в отношении 13 к 10, то есть

Составим уравнение биссектрисы AF треугольника ABC как уравнение прямой, проходящей через точки

www.treugolniki.ru

Уравнение медианы | Треугольники

Как составить уравнение медианы треугольника по координатам его вершин?

Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:

Найти координаты середины отрезка по координатам его концов.
Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.

Пример.

Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).

Найти уравнения медиан треугольника.

Решение:

Обозначим середины сторон BC, AC, AB через A₁, B₁, C₁.

1) По формулам координат середины отрезка

Уравнение медианы AA₁ будем искать в виде y=kx+b.

Найдём уравнение прямой, проходящей через точки A(3;1) и A₁(1,5;-5). Составляем и решаем систему уравнений:

Отсюда k= 4; b= -11.

Уравнение медианы AA₁: y=4x-11.

2) Аналогично, координаты точки B₁ — середины отрезка AC

Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B₁(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB₁ можно найти ещё быстрее: y= -3.

3) Координаты точки C₁ — середины отрезка BC:

C(-3;-7), C(4,5;-1), y=kx+b:

Отсюда уравнение медианы CC₁ : y=0,8x-4,6.

www.treugolniki.ru

Линейная интерполяция онлайн калькулятор – —

alexxlab / 11.12.201602.06.2019 / Школьная жизнь

Линейная интерполяция Онлайн

можно использовать:

дроби

1/2, -3/4, 5/7

дробные числа

1.52 или 0,19 можно иcпользовать как «.» так и «,»

квадратный корень

sqrt(4), sqrt(4/3)

тригонометрия

sin(1), cos(1), tan(1), atan(1)

возведение в степень

pow(3, 2) = 3*3 !при pow(3,2, 4,3) — система поймет что вы хотите 3.2 возвести в степень 4.3

арифметические операции

(3/4 + sqrt(5/7)) * pow(2, 4)

Сервис интерполяции и экстраполяции онлайн (линейная интерполяция/экстраполяция) поможет вам вычислить значение линейной функции, имея в распоряжении f(x) в двух различных точках, а также рассчитает уравнение прямой. Данный сервис автоматически определит нужный способ расчета — вам лишь надо ввести значения в двух произвольных точках, и указать необходимую точку, в которой нужно рассчитать значение. Если установить «галку» внутри кнопки «Рассчитать», калькулятор будет рассчитывать значение автоматически при любом изменении входных данных. Пример расчета интерполяции

Интерполяция — (от латинского interpolatio изменение, переделка), в математике и статике это способ вычислить промежуточное значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x), известны результаты значения f(x) в точке x₀ и точке x₂, интерполяця помогает найти значение f(x₁) при условии что x₁ принадлежит интервалу от x₀ до x₂. Если x₁ лежит вне интервала (x₀, x₂), интерполяция не поможет, для этого нужно использовать «экстраполяцию». Этот метод часто называют «линейная интерполяция«, он дает 100% верный результат для уравнения прямой. Для вычесления резултата функций с двумя переменными существует «Билинейная интерполяция (Двойная интерполяция)». Также для рассчета интерполяции можно воспользоваться сервисом Интерполяция — полином Ньютона и Интерполяция — полином Лагранжа

Экстраполяция — в математике и статике это способ вычислить значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x), известны результаты значения f(x) в точке x₁ и точке x₂, экстраполяция помогает найти значение f(x₀) либо f(x₃) при условии что x₀ либо x₃ меньше либо больше интервала x₁ до x₂. Если x_n лежит в интервале (x₁, x₂), экстраполяция не поможет, для того вам нужно использовать «интерполяцию» — для функций с одной переменной, и «двойная интерполяция» — для функций с двумя переменными.

Этот метод часто называют «линейная экстраполяция«, он дает 100% верный результат для уравнения прямой.

Как для интерполяции так и для экстраполяции в основе их рассчета лежит пропорция (y1 — y0)/(y2 — y0) = (x1 — x0)/(x2 — x0), прирощение значения в первой точке к прирощению значения во второй точке относится также как прирощение переменной в первой точке к прирощению переменной во второй точке (все относительно нулевой точки отсчета), из этой пропорции легко получить формулу рассчета любого значения

www.bl2.ru

Линейная интерполяция: онлайн калькулятор — формула и пример расчета

Интерполяция — метод нахождения промежуточных переменных функции по нескольким уже известным значениям. Впервые формулировка «интерполирование» была введена Джоном Валлисом в научном сочинении «Арифметика бесконечных».

Линейная интерполяция

Простейшим случаем интерполяции является «линейная», то есть нахождение величины по двум заданным точкам. Данный процесс вычисления можно рассмотреть как линейную функцию, тем самым делая расчёт более наглядным. Нанесение функции на систему координат называют аппроксимацией. Для этого на оси координат необходимо провести прямую через известные точки. Логично, что искомое значение, находящееся между первыми двумя точками, можно найти графически, зная абсциссу X. Если координата X искомой величины лежит за пределами известных значений (X₁, X₂), то процесс вычисления называется экстраполяция.

Калькулятор позволяет определить значение ординаты Y искомого значения, зная координаты X и Y двух других функций, а также её абсциссу. Для вычисления необходимо ввести значения заданных двух точек Х₁, Y₁ и X₂,Y₂, а также указать координату X искомой точки, а сервис автоматически определит метод расчёта и произведёт его.

Формула линейной интерполяции

Для вычисления используется следующая формула:

Пример расчёта

Дано: координаты двух точек А(3;1.5) и B(6;5).
Найти: ординату точки С с абсциссой 4.5.

Для удобства рекомендуется построить график: нанести точки на систему координат и провести прямую.

После этого подставляем значения в указанную формулу:

Y = 5 + (1.5 — 5) / (3 — 6) · (4.5 — 6) = 5 + (-3.5) / (-3) · (-1.5) = 3.25.

calcsoft.ru

Онлайн калькулятор: Аппроксимация функции одной переменной

Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.

83 71 64 69 69 64 68 59 81 91 57 65 58 62Значения x, через пробел183 168 171 178 176 172 165 158 183 182 163 175 164 175Значения y, через пробел Линейная аппроксимация Квадратичная аппроксимация Кубическая аппроксимация Аппроксимация степенной функцией Показательная аппроксимация Логарифмическая аппроксимация Гиперболическая аппроксимация Экспоненциальная аппроксимацияТочность вычисления

Знаков после запятой: 4

Линейная регрессия

Коэффициент линейной парной корреляции

Коэффициент детерминации